Foundations of nuclear and particle physics t w donnelly

Foundations of Nuclear and Particle Physics T. W. Donnelly

Visit to download the full and correct content document: https://textbookfull.com/product/foundations-of-nuclear-and-particle-physics-t-w-donn elly/

More products digital (pdf, epub, mobi) instant download maybe you interests ...

Particle Physics Brian R. Martin

https://textbookfull.com/product/particle-physics-brian-r-martin/

Concepts of elementary particle physics First Edition Peskin

https://textbookfull.com/product/concepts-of-elementary-particlephysics-first-edition-peskin/

Particle physics Fourth Edition. Edition Martin

https://textbookfull.com/product/particle-physics-fourth-editionedition-martin/

Scientific Foundations of Audiology Perspectives from Physics Biology Modeling and Medicine 1st Edition Anthony T. Cacace

https://textbookfull.com/product/scientific-foundations-ofaudiology-perspectives-from-physics-biology-modeling-andmedicine-1st-edition-anthony-t-cacace/

The ideas of particle physics 4th Edition James Dodd

https://textbookfull.com/product/the-ideas-of-particlephysics-4th-edition-james-dodd/

Solar Neutrino Physics The Interplay between Particle Physics and Astronomy Lothar Oberauer

https://textbookfull.com/product/solar-neutrino-physics-theinterplay-between-particle-physics-and-astronomy-lothar-oberauer/

Particle Accelerator Physics 4th Edition Helmut Wiedemann

https://textbookfull.com/product/particle-acceleratorphysics-4th-edition-helmut-wiedemann/

Particle Physics of Brane Worlds and Extra Dimensions 1st Edition Sreerup Raychaudhuri

https://textbookfull.com/product/particle-physics-of-braneworlds-and-extra-dimensions-1st-edition-sreerup-raychaudhuri/

Fundamentals of Nuclear Physics 1st Edition Noboru Takigawa

https://textbookfull.com/product/fundamentals-of-nuclearphysics-1st-edition-noboru-takigawa/

Foundations ofNuclearandParticlePhysics

This textbook brings together nuclear and particle physics, presenting a balanced overview of both fields as well as the interplay between the two. The theoretical as well as the experimental foundations are covered, providing students with a deep understanding of the subject In-chapter exercises ranging from basic experimental to sophisticated theoretical questions provide an important tool for students to solidify their knowledge Suitable for upper undergraduate courses in nuclear and particle physics as well as more advanced courses, the book includes road maps guiding instructors on tailoring the content to their course. Online resources including color figures, tables, and a solutions manual complete the teaching package. This textbook will be essential for students preparing for further study or a career in the field who requireasolidgraspofbothnuclear andparticlephysics.

Keyfeatures

Containsup-to-datecoverageofbothnuclear andparticlephysics,particularlythe areas where the two overlap, equipping students for the real-world occasions whereaspectsofbothfieldsarerequiredfor study

Covers the theoretical as well as the experimental foundations,providingstudents withadeepunderstandingofthefield

Exercises ranging frombasic experimental to sophisticated theoretical questions provideanimportanttool for readerstoconsolidatetheir knowledge

THOMAS WILLIAM DONNELLY is a Senior Research Scientist at MIT. He received his PhDinTheoretical Nuclear Physicsin1967fromtheUniversityofBritishColumbia.

JOSEPHANGELOFORMAGGIO is anAssociate Professor ofPhysics atMIT. He received his PhDinPhysics atColumbia Universityin2001. He has beena member ona number of experiments including the Sudbury Neutrino Observatory and the KATRIN neutrino experiment.

BARRYR HOLSTEIN is anEmeritus Professor Physics attheUniversityofMassachusetts. He received his PhDinPhysics fromCarnegie MellonUniversityin1969. He is Editor of Annual Reviews of Nuclear and Particle Physics, ConsultingEditor ofthe American Journal of Physics,andAssociateEditor ofthe Journal of Physics G.

RICHARD GERARD MILNER is a Professor ofPhysics atMIT. He received his PhDfrom the California Institute of Technologyin1985. He has proposed and led experiments at SLAC,DESY,MIT-Bates,andJeffersonLaboratory.

BERND SURROW is a Professor of Physics at Temple University. He gained his PhD in Physics at the University of Hamburg in 1998. He has been a member of a number of experiments includingthe STARexperimentatBNL, the CMS and OPALexperiments at

Foundationsof NuclearandParticle Physics

T. W. DONNELLY

Massachusetts Institute of Technology, Cambridge, MA

J. A. FORMAGGIO

Massachusetts Institute of Technology, Cambridge, MA

B. R. HOLSTEIN

University of Massachusetts, Amherst, MA

R. G. MILNER

Massachusetts Institute of Technology, Cambridge, MA

B. SURROW

Temple University, Philadelphia, PA

University PrintingHouse, Cambridge CB2 8BS, United Kingdom

Cambridge University Press is part of the University of Cambridge.

It furthers the University’s mission by disseminatingknowledge in the pursuit of education, learning, and research at the highest internationallevels of excellence www.cambridge.org

Information on this title:www.cambridge.org/9780521765114

© Cambridge University Press 2017

This publication is in copyright. Subject to statutory exception and to the provisions of relevant collective licensingagreements, no reproduction of any part may take place without the written permission of Cambridge University Press.

Printed in the United States of America by Sheridan Books

A catalogue record for this publication is available from the British Library.

Library of Congress Cataloguing in Publication Data

Names:Donnelly, T W (T William), 1943– author |Formaggio, Joseph A, 1974– author | Holstein, Barry R., 1943– author. |Milner, Richard Gerard, 1956– author. |Surrow, Bernd, 1998– author.

Title:Foundations of nuclear and particle physics / T. William Donnelly (Massachusetts Institute of Technology), Joseph A Formaggio (Massachusetts Institute of Technology), Barry R Holstein (University of Massachusetts, Amherst), Richard G. Milner (Massachusetts Institute of Technology), Bernd Surrow (Temple University, Philadelphia).

Description:Cambridge, United Kingdom ; New York, NY:Cambridge University Press, [2016] |Includes index.

Identifiers:LCCN 2016026959|ISBN 9780521765114 (hardback) | ISBN 0521765110 (hardback)

Subjects:LCSH:Nuclear physics–Textbooks. |Particles (Nuclear physics)–Textbooks.

Classification:LCC QC776 .D66 2016 |DDC 539.7–dc23 LC record available at https://lccn.loc.gov/2016026959

ISBN 978-0-521-76511-4 Hardback

Additionalresources for this publication at www.cambridge.org/9780521765114.

Cambridge University Press has no responsibility for the persistence or accuracy of URLs for externalor third-party Internet Web sites referred to in this publication, and does not guarantee that any content on such Web sites is, or willremain, accurate or appropriate.

Bill ⇔ toBarbara

Joe ⇔ to Mike, Hamish, Janet, and John, for their unwavering wisdom; to Jaymi, Coby,andJoshua,fortheirunquestioninglove

Barry ⇔ toJeremyandJesse

Richard ⇔ to LiamMilner for inspiration and to Eileen, Will, Sam, and David for love andsupport

Bernd ⇔ toSuzanne,Alec,Arianna,andCarlfortheirlove andsupport

1 Introduction

2 Symmetries

2.1 Introduction

2.2 Angular Momentumand SU(2)

2.3 SU(2) ofIsospin

2.4 ExtensionstoFlavor SU(3)

2.5 YoungTableaux

2.6 DiscreteSymmetries: P, C,and T

3 Building HadronsfromQuarks

3.1 LightMesonsBuiltfromu, d,and s Quarks

3.2 Baryons

3.3 BaryonGround-StateProperties

4 The Standard Model

4.1 ElectroweakInteraction: TheWeinberg–SalamModel

4.2 TheHiggsMechanism

4.3 TheHiggsBoson

4.4 QuarkMixing

4.5 MajoranaMass

4.6 LeptonMixing

5 QCD and Confinement

5.1 Introduction

5.2 Renormalization

5.3 FormulationoftheQCDLagrangian

5.4 LatticeQCD

5.5 NucleonModels

6 ChiralSymmetryand QCD

6.1 IntroductiontoChiral Symmetry

6.2 Renormalization

6.3 BaryonChiral PerturbationTheory

6.4 OntoHigher Energy: DispersionRelations

7 Introduction to Lepton Scattering

7.1 UnpolarizedElectronScattering

7.2 Spin-DependentLepton–NucleonScattering

7.3 Electron–NucleusScattering

7.4 ElectromagneticMultipoleOperators

7.5 Parity-ViolatingLeptonScattering

8 Elastic Electron Scattering fromthe Nucleon

8.1 TheElasticFormFactorsoftheNucleon

8.2 TheRoleofMesons

8.3 BeyondSingle-PhotonExchange

8.4 PVElectronScatteringandStrange-QuarkContentintheNucleon

8.5 TheShapeoftheProton

8.6 ElectromagneticFormFactorsinQCD

9 Hadron Structure via Lepton–Nucleon Scattering

9.1 DeepInelasticScattering

9.2 ThePartonModel

9.3 EvolutionEquations 94 Hadronization/Fragmentation

9.5 TheSpinStructureoftheNucleon: LeptonScattering

9.6 SpinStructureFunctionsinQCD

9.7 GeneralizedPartonDistributions

9.8 TheRoleofPartonsinNuclei

10 High-EnergyQCD

10.1 Introduction

10.2 BuildingtheTools

10.3 SpinStructureoftheNucleon: PolarizedProtonCollider

10.4 Flavor AsymmetryoftheSeaviatheDrell–YanProcess

10.5 Low-x Physics

10.6 Jets,Bosons,andTopQuarks

11 The Nucleon–Nucleon Interaction

11.1 Introduction

11.2 Nucleon–NucleonScattering

11.3 General FormofNucleon–NucleonInteraction

11.4 TheDeuteron

11.5 Low-EnergyScattering

11.6 ElectromagneticInteractions: np↔ dγ

11.7 EffectiveFieldTheory: the NN Interaction

11.8 Nucleon–NucleonInteractionfromQCD

12 The Structure and Propertiesof Few-BodyNuclei

12.1 Introduction

12.2 ElasticElectron–DeuteronScatteringandMeson-ExchangeCurrents

12.3 ThresholdDeuteronElectrodisintegration

12.4 Deuteron S- and D-StateProbedinSpin-dependent(e, e′p) Electron Scattering

12.5 TheThree-NucleonGroundState

126 Hypernuclear Physics

12.7 Fusion

13 Overview of Many-BodyNuclei

13.1 BasicPropertiesofFiniteNuclei

13.2 Nuclear andNeutronMatter

13.3 RelativisticModelingofNuclear Matter

14 Modelsof Many-BodyNuclei

14.1 Hartree–FockApproximationandtheNuclear MeanField

14.2 Rotational Model ofDeformedNuclei

14.3 Vibrational Model

14.4 Single-ParticleTransitionsandGiantResonances

15 Electron Scattering fromDiscrete States

15.1 Parity-ConservingElasticElectronScatteringfromSpin-0Nuclei

152 Parity-ViolatingElasticElectronScatteringfromSpin-0Nuclei

15.3 ElasticScatteringfromNon-Spin-0Nuclei: ElasticMagneticScattering

15.4 ElectroexcitationofLow-LyingExcitedStates

16 Electroexcitation of High-Lying Excitationsof the Nucleus

16.1 Introduction

16.2 QuasielasticElectronScatteringandtheFermi GasModel

16.3 InclusiveElectronScatteringandScaling

16.4 Δ-ExcitationinNuclei

16.5 Nuclear Spectral FunctionandtheNucleonMomentumDistribution

17 Beta Decay

17.1 Introduction

17.2 Nuclear BetaDecay

17.3 TheNucleusasaLaboratory

17.4 Experimental Constraints

17.5 Second-ClassCurrents

17.6 TimeReversal Tests

18 Neutrino Physics

18.1 Introduction

18.2 NeutrinoMass

18.3 NeutrinoOscillations

18.4 NeutrinoReactions

18.5 OutstandingQuestionsinNeutrinoPhysics

19 The Physicsof Relativistic HeavyIons

19.1 Introduction

19.2 Global EventCharacterization

193 CorrelationMeasurements

19.4 HardProcesses

19.5 SummaryandOutlook

20 Astrophysics

20.1 BigBangNucleosynthesis

20.2 Nuclear ReactionRates

20.3 Stellar Evolution

20.4 CosmicRays

21 Beyond the Standard ModelPhysics

21.1 Introduction

212 BSMPhysics: Phenomenological Approach

21.3 BSMPhysics: Theoretical Approaches

21.4 Summary

AppendixA UsefulInformation

A.1 NotationsandIdentities

A.2 DecayLifetimesandCrossSections

A.3 MathematicsindDimensions

AppendixB QuantumTheory

B.1 NonrelativisticQuantumMechanics

B.2 RelativisticQuantumMechanics

B.3 ElasticScatteringTheory

B.4 Fermi–WatsonTheorem

References Subject Index

Preface

The firstquestionone mightaskaboutthis bookis: Whydo we need another textonthe subjectofnuclear andparticlephysicswhenexcellenttextsalreadyexistinbothofthese areas? Indeed, it is true that eachsub-discipline has texts that range fromelementaryto veryadvancedandcover specifictopics invaryingdegrees ofdepththatcanbeusedfor the appropriate types of courses. For instance, there are fine books on quantum field theory[Bjo64, Pes95, Wei05, Sch14], onthe constituent quarkmodel [Clo79], onhighenergy physics [Gri08, Hal84], on hadron scattering [Col84], and on nuclear structure [Des74, Wal95, Won98, Pov08, Row10]. However, there are relatively few textbooks that cover several sub-disciplines in a coherent and balanced way, and those that do exist are either more elementary, e.g., Povhet al. [Pov08] thanthe present book, or are cast at a more theoretical level and are too advanced for the goals we as authors have set for ourselves. Having a book that stresses the interconnections between the two areas of subatomic physics is crucial, since increasingly one finds that the two fields overlap and that it is essential for a graduate student conducting frontier research and preparingfor a career inthe field to have anunderstandingof both. Anexample of this overlap occurs, for instance, in modern neutrino physics wherein experiments utilizing several-GeV neutrinos as probes almost always involve targets/detectors constructed from nuclei and specifics of nuclear structure are unavoidably required to properly interpretsuchdata.

One specific decision we have made in designing this book is to assume that the reader is familiar with the basics of quantum field theory. More elementary texts typically do not make this assumption and thus much of the discussion, for instance, of leptonscatteringfromhadrons and nuclei, or of the foundations of chiral symmetryand effective field theoryis limited and not at the frontier of the field. We realize that many students today do have at least an introductory course in quantum field theory, or are taking one simultaneously with a course that this book covers, and thus we have followed a somewhat more advanced approach than has been customary. We have included inAppendixB anoverview ofthe essential aspects ofquantummechanics and quantum field theory that are needed for the book. Furthermore, the subject of manybody theory underlies much of nuclear physics and the presentation of this subject can also be rather elementary, as is usuallythe case intexts thatcover the two fields, or too advanced for our purposes, focusingonGreen’s functions, diagrammatic techniques and nonperturbative approximations ata theoretical level We have chosena middle course: we have covered the basics of many-bodytheory, but also have introduced some of the important diagrammatic representations of the nonperturbative approximations employed very widely in quantum physics ranging from atomic and condensed matter

physicstothepresentcontextofnuclear andhadronicphysics.

The book’s central focus is to describe the current understanding of the sub-atomic world within the framework of the Standard Model. The layout of the book is summarized as follows: In the first quarter of the book, the Standard Model is developed Thestructureofthenucleonandfew-bodynuclei arediscussedinthesecond quarter. Inthe third quarter, the structure and properties of atomic nuclei are described. Lepton scattering is the principal tool used in the central narrative of the book to understand hadrons. Inthe final quarter ofthe bookwe present extensions ofthe earlier focus onEMleptonscatteringto include the weakinteractions ofleptons withnucleons and nuclei. This begins witha chapter onbeta-decayand progresses to intermediate-tohigh energy neutrino-induced reactions. These two chapters are followed by two more that build on what occurs earlier in the book, namely, on applications to nuclear and particle astrophysics and to studies of the hot, dense phase of matter formed in heavyioncollisions The bookcloses witha briefperspective onphysics beyond the Standard Model.

We should also emphasize that the use of word “foundations” inthe title of the book is intentional, indicating that this text is not an encyclopedia where one might find material on all of the major topics in the field, albeit at a superficial level. Rather, we have consciouslymade choices inwhat and what not to present. We have, for instance, not developed the topic of intermediate-energy hadron scattering, emphasizing lepton scatteringinstead and have notattempted to cover the lattice approachto the solutionof QCD. While the important areas of nuclear structure and the high-energy frontier are covered, we note thatexcellent, up-to-date, comprehensive textbooks onthese important areas are available. Our intent has beento provide the reader withbasic material upon whichto build bysubsequentlyemployingthe more advanced sources thatexistwhenit becomes necessary for a more in-depth understanding of specific subjects. In this regard, we have included references to review articles, so thatthe interested reader can pursue material to a more advanced level. Just what to emphasize and what merely to refer to in passing is, of course, subjective; however, having five co-authors has allowedustodebatethechoiceswehavemade

We view the approximately120 exercises provided throughout the bookand located at the end of each chapter as an important tool for the reader to consolidate their understanding of the material in the book. There exists significant variety in these exercises, rangingfrombasic experimental issues to sophisticated theoretical questions. Manyowe their origins to other sources, butwe have tried to tailor themto the material discussedhere.

The authors have all taught courses of the type described above at various levels. Specifically, at MIT the book covers the scopes set out for the introductory first-year graduate course in nuclear and particle physics (8.701), together with the second-year graduate courses in nuclear (8.711) and particle (8.811) physics. All graduate students inexperimental nuclear/particle physics atMIT are required to take the latter two, with theformer beingaprerequisite.Additionally,atMITthereisanadvancedundergraduate course innuclear/particle physics (8.276), as well as more advanced courses inmanybody theory (8.361), nuclear theory (8.712) and electroweak interactions (8.841) – all

taughtbyoneoftheauthors(TWD) –for whichatleastsomeofthistextisappropriate.

We acknowledge that the derivation of the QCD Lagrangian in Chapter 5 owes its origins to Professor FrankWilczek. We acknowledge thatChapter 19 was shaped bythe work of Professor Berndt Müller and his colleagues. We thank the Super-Kamiokande Collaborationfor permissiontousetheir imageonthecover

The book’s evolution profited from its use in draft form as a resource for the MIT course 8.711 taught by one of us (RGM) and Dr. Stephen Steadman in the spring semesters of2014,2015,and2016.We acknowledge the constructive feedbackfromthe MIT graduate students in those classes. Further, we acknowledge careful and critical readingofdrafts byDr.JanBernauer,Charles Epstein,Dr.Douglas Hasell,Dr.Rebecca Russell, Dr. Axel Schmidt, Dr. Stephen Steadman, Reynier Cruz Torres and Constantin Weisser at MIT, Professor James Napolitano, Dr. Matt Posik, Devika Gunarathne, Amani KraishanandDaniel OlvittatTemple University,Rosi ReedatLehighUniversity andRosi Esha atUCLA.We are grateful toDr.BrianHendersonfor a careful readingof all ofthe exercises. We thankConnor Dorothy-Pachuta for his considerable expertise in creatingmanyofthe figures inthe book. There are, ofcourse, manyothers to thankwho, over the years, have beenour collaborators – we cannotlistthemall, buttheywill find their efforts reflected inmanyofour choices for whatto present. We do, however, wish to acknowledge three who directly played roles in developing some of the figures in Chapters 16 and 18, namely, Professors Maria Barbaro and Juan Caballero, and GuillermoMegias.

Inadditionto beinganintegrated text, there are other aspects ofthis presentationthat we feel are important. Specifically, we have attempted to make strongconnections with contemporaryexperimentsandhavetried,whenever possible,tohelpthereader become aware ofthe relevantfrontier experimental facilities available and planned worldwide. Doingsois,ofcourse,timedependent;butwehavetriedtobeasuptodateaspossible. We have also made liberal use of the Particle Data Group website [PDG14] as a resource withwhichwe encourage all students tobecome familiar.Finally,inAppendix Awehavecollectedinformationthatwebelievewill beuseful toreaders.

1

Introduction

The past one hundred years has witnessed enormous advances in human understanding of the physical universe in which we have evolved. For the past fifty years or so, the Standard Model of the subatomic world has been systematically developed to provide the quantummechanical description of electricity and magnetism, the weak interaction, and the strong force. Symmetry principles, expressed mathematically via group theory, serve as the backbone of the Standard Model. At this time, the Standard Model has passed all tests in the laboratory. Notwithstanding this success, most of the matter available to experimental physicists is inthe formofatomic nuclei. The mostsuccessful descriptionofnuclei is interms ofthe observable protons, neutrons, and other hadronic constituents,andnotthe fundamental quarks andgluons ofthe StandardModel.Thus,the professional particle or nuclear physicist should be comfortable in applying the hadronic description of nuclei to understanding the structure and properties of nuclei. Experimentally, lepton scattering has proved to be the cleanest and most effective tool for unraveling the complicated structure of hadrons. Its application over different energies and kinematics to the nucleon, few-body nuclei, and medium- and heavy-mass nuclei has provided the solid bodyof precise experimental data onwhichthe Standard Model isbuilt.

In addition, the current understanding of the microcosm described in this book provides answers to manybasic questions: How does the Sunshine? Whatis the origin of the elements? How old is the Earth? Further, it underscores manyaspects of modern human civilization, e.g., MRI imaging uses the spin of the proton, nuclear isotopes are essential medical tools, nuclear reactions have powered the Voyager spacecraft since 1977intointerstellar space.

The purpose of the book is to allow the graduate student to understand the foundations and structure of the Standard Model, to apply the Standard Model to understanding the physical world with particular emphasis on nuclei, and to establish the frontiers ofcurrentresearch. There are manyoutstandingquestions thatthe Standard Model cannot answer. In particular, astrophysical observation strongly supports the existenceofdarkmatter,whosedirectdetectionhasthusfar remainedelusive.

Essential to making progress in understanding the subatomic world are the sophisticated accelerators that deliver beams of particles to experiments. Existing lepton scattering facilities include Jefferson Laboratory in the US, muon beams at CERN, and University of Mainz and University of Bonn in Germany. Intense photon beams areusedattheHIγ SfacilityatDuke Universityinthe U.S.,andinJapanatLEPS atSPring-8, and atElphs atTohokuUniversity. Hadrons beams are used atthe TRIUMF

laboratory in Vancouver, Canada, using the COSY accelerator in Juelich, Germany, at the Paul Scherrer Institute (PSI) in Switzerland, and at the Joint Institute for Nuclear Research (JINR), Dubna, Russia. Neutron beams are used for subatomic physics research at the Institut Laue-Langevin (ILL), Grenoble, France, at both the Los Alamos NeutronScience Center (LANSCE) and the SpallationNeutronSource (SNS) inthe US, and at the future European Spallation Source (ESS) in Sweden. The hot, dense matter presentinthe earlyuniverse is studied usingheavy-ionbeams atthe Relativistic Heavy Ion Collider (RHIC) in the US and at the Large Hadron Collider (LHC) at CERN. Of course, searches for new physics beyond the Standard Model are underwayat the highenergy frontier of 13 TeV at CERN. Understanding the structure of nuclei, with particular emphasis onthe limits ofstability, is a major worldwide endeavor. The most powerful facility at present is the Rare Isotope Beam Facility (RIBF) at RIKEN in Japan. In the US, the frontier experiments at present are carried out at the National Superconducting Cyclotron Laboratory at Michigan State University (MSU) and at the ATLAS facility at Argonne National Laboratory. A future Facility for Rare Isotope Beams (FRIB) is under construction at MSU and is expected to have world-leading capabilities by 2022, as is a facility in South Korea, the Rare Isotope Science Project (RAON). Hadron beams for research are available at Los Alamos and the Spallation Neutron Source in the US, GSI in Germany, J-PARC in Japan, and NICA at Dubna, Russia. Amajor new facility FAIR is planned at GSI. Neutrino beams are generated at Fermilab, CERN, and J-PARC and directed at detectors located both at the Earth’s surface and deep underground. A major new Deep Underground Neutrino Experiment (DUNE) is planned in the US using the Fermilab beam and the Sanford Underground ResearchLaboratoryinSouthDakota.BelleII,anexperimentatthehighluminosity e+e collider SuperKEKB in Japan, will come online within the next several years and provide new stringent tests of flavor physics. Annihilationof electrons and positrons is used to probe the Standard Model at both the Double Annular ϕ Factory for Nice Experiments (DAFNE) collider in Frascati, Italy as well as the Beijing Electron PositronCollider (BEPC) inChina. Finally, a highluminosityelectron–ioncollider has beenwidelyidentified byas the next machine to studythe fundamental quarkand gluon structure of nuclei and machine designs are under development in the US, Europe, and China.

To begin, let us remind the reader of the particles that comprise the Standard Model (see Fig. 1.1). As will be discussed in due course, the Standard Model starts with massless particles and then, through spontaneous symmetry breaking, these interacting particles acquire masses inalmostall cases. The measured spectrumofmasses is still a mystery; indeed, inthe case of the neutrinos, intense effort is goinginto determiningthe actual pattern of masses in Nature. Note that at this microscopic level, but also at the hadronic/nuclear level, when one says that particles interact with one another what is meantis thatsome particle is exchanged betweentwo other particles, therebymediating the interaction For instance, an electron can exchange a photon with a quark whereby the photon mediates the e q interaction. Or two nucleons (protons and neutrons) can exchangeapionandonehasthelong-rangepartofthe NN interaction.

Fig. 1.1 The particles of the Standard Model.

The organizational principle for this book centers on building from the underlying fundamental particles (leptons, quarks, and gauge bosons) to hadrons (mesons and baryons) built from q q and qqq, respectively, and on to many-body nuclei or hypernuclei built from these hadronic constituents. At very low energies and momenta the last are the relevant effective degrees of freedom, since, using the Heisenberg Uncertainty Principle, such kinematics translate into large distance scales where the microscopic ingredients are packaged into the macroscopic hadronic degrees of freedom. Then, as the energy/momentum is increased, more and more of the substructure becomes relevant, until atveryhighenergy/momentumscales the QCDdegrees offreedommustbeusedtorepresentwhatisobserved.

Naturally, there can be a blending between the different degrees of freedom and, where they overlap, it may be possible to use one language or the other. And in some cases it turns out to be important to address both the “fundamental” physics issues and the larger-scale nuclear structure issues at the same time. This bookattempts to present the foundations of the general field of nuclear/particle physics – sometimes called subatomic physics – in a single volume, trying to maintain a balance between the very microscopicQCDpictureandthehadronic/nuclear picture.

The outline ofthe bookis the following. After this introductorychapter, inChapter 2 the basic ideas ofsymmetries are introduced. Ingeneral discussions ofquantumphysics it is oftenadvantageous to exploit the exact (or at least approximate) symmetries inthe problem, for then selection rules emerge where, for instance, matrix elements between specific initial and final states of certain operators can only take on a limited set of

values. An example of what will be important in later discussions is the use of good angular momentum quantum numbers and the transformation properties of multipole operators (see Chapter 7) where conservationofangular momentumleads to a small set of allowed values for matrixelements of suchoperators takenbetweenstates that have known spins Another example of an important (approximate) symmetry is provided by invariance under spatial inversion, namely, parity: to the extent that parity is a good symmetry again only specific transitions can occur. Other symmetries discussed in Chapter 2 include charge conjugation and time reversal, as well as discrete unitary flavor symmetries, the latter being important for classifying the hadrons built from constituentquarks,namely,thesubjectofChapter 3.

After these introductorydiscussions the bookproceeds to build up fromparticles to hadrons to many-bodynuclei, startinginChapter 4 withthe Standard Model of particle physics. In this one begins with massless leptons, quarks, and gauge bosons together with the Higgs and then through spontaneous symmetry breaking generates the basic familiar buildingblocks withtheir measuredmasses.The recentsuccessful discoveryof theHiggsbosonattheLargeHadronCollider (LHC) issummarized.

The Standard Model has proven to be extremely successful and, at the time of writing, there is as yetno clear evidence thateffects beyond the Standard Model (BSM) are needed;inthe final chapter ofthe book, Chapter 21 we returnto summarize some of these BSM issues. For the present, following the path of increasing complexity, in Chapters 5 and 6 the ideas and models employed in descriptions of low-Q2 , strong couplingQCDare discussed insome detail, includingwhatis nottypicallycovered ina bookatthislevel,namely,chiral symmetry.

Chapters 7 through 10 form a distinct section where the aim is to visualize the structureofthe proton,neutron,andnuclei interms ofthefundamental quarks andgluons of QCD. At low and mediumenergies, this is carried out usingleptonscatteringwhere intense beams of high quality are available. Thus, snapshots of the nucleon charge and magnetism and quark momentum and spin distributions are directly obtainable in the form of structure functions and form factor distributions. Chapter 7 provides an introduction to lepton scattering, including both parity-conserving and parity-violating scattering. Since leptonscatteringis beingused as a commontheme inmuchof the rest ofthebook,Chapter 7 is the firststop alongthe waywhere the multipole decomposition of the electromagnetic current is developed insome detail. This is followed inChapter 8 bya discussionofelastic scatteringfromthe nucleon. Atthis time, a directconnection betweenelastic scatteringand QCDremains elusive and the mostsuccessful theoretical descriptionis interms of hadrons. Chapter 9 describes the current understandingof the structure of hadrons in terms of high-energy lepton scattering and this is directly interpretable in terms of perturbative QCD. Further, the gluon momentum and spin distributions are indirectly determined via the QCD evolution equations The parton distributions are snapshots of nucleon structure over different spatial resolutions and with different shutter speeds Lepton scattering constitutes a theme of the book at both high- andlow-energyscales andwiththe full electroweakinteraction.Duetothe lackof suitable lepton beams, QCD is at present probed at the highest energies using hadron beams. This is the focus of Chapter 10 and the measurements extend and complement

those with lepton beams in the previous chapters. For example, direct experimental informationonthe contributionof gluons to the spinof the protonhas become possible onlythroughpolarizedproton–protoncollisions.

The above constitutes the first part of the book after which the building-up process moves fromhadrons to nuclei The next step is to deal with the simplest systemthat is not a single baryon, namely, the system of two nucleons, discussing NN scattering and the properties ofthe onlybound state withbaryons number two, the deuteroninChapter 11. For the latter the EM form factors and electrodisintegration are treated in some detail. After this, inChapter 12 the so-called few-bodynuclei, those with A = 3 and 4, constitutethefocus.

For nuclei heavier than the A = 2, 3, and 4 cases, treating the many-body problem forms the basic issue, and accordinglyinChapter 13 anoverview ofthe general nuclear “landscape” is presented, showing the typical characteristics of nuclei, including the regions where nuclei are stable (the “valley of stability”) out to where they are just unstable (the “drip lines”), and their regions of especially tight binding (the “magic numbers”). Also inthis chapter the conceptofinfinite nuclear matter and neutronmatter is introduced and treated insome detail. This is followed inChapter 14 bya discussion ofa selectionoftypical nuclear models. As mentioned earlier, this bookis notintended to be a theoretical text on nuclear many-body theory. That said, this chapter has sufficient detail that the basic issues in this area can be appreciated. Importantly, the tools used in this part of the field must be capable of dealing with nonperturbative interacting systems and accordingly this provides a theme in this chapter where discussions of the so-called Hartree–Fock (HF) and Random Phase Approximations (RPA) are provided together withanintroductionto diagrammatic representations ofthe approximations. Also typical collective models are discussed as examples of how one may start with some classical oscillation or vibration of the nuclear fluid, make harmonic approximations to those movements, and then quantize the latter to arrive at semi-classical descriptions of nuclear excitations (“surfons,” “rotons,” etc.), as is done inmanyareasofphysicswheresimilar techniquesareemployed.

The above discussions are then followed by two chapters focused on electron scattering from nuclei, Chapter 15 where elastic scattering is treated in some detail, together with some applications of the models introduced in Chapter 14 for low-lying excited states. Chapter 16 continues this by treating higher-lying excitations where differentmodelingis required. Specifically, the Relativistic Fermi Gas (RFG) model is derivedandusedasaprototypefor moresophisticatedapproaches.Itisalsothestarting point for similar discussions ofneutrino scatteringfromnuclei to follow inChapter 18. Before those are presented, in Chapter 17 the weak interaction provides the focus and we see how precision beta-decay experiments can be used as a probe for beyond StandardModel physics. Chapter 18 deals withthe subjectofneutrinos and the factthat one flavor can oscillate into another, since neutrinos are known to have mass. At the time ofwriting, the detailed nature ofthe mass spectrum, whether or notCPviolationis presentinthe leptonic sector and whether neutrinos are Dirac or Majorana particles are still under investigation and intensive efforts are being undertaken worldwide to shed lightontheseinterestingquestions.

In Chapter 19 the high-energy regime (essentially quark–quark scattering) is revisited within the context of relativistic heavy-ion scattering. Here the nature of the modelingis somewhat different fromthat discussed inmost of the rest of the bookwith statistical mechanics being called into play together with fluid dynamics. An informed practitioner inthe general field of nuclear/particle physics should be familiar withthis subjectaswell.

ThebookconcludeswithChapter 20onnuclear andparticle astrophysics usingmany of the concepts treated in the rest of the book, and with Chapter 21 where the types of signatures of effects beyond the Standard Model are summarized, together with two appendiceswheresomeuseful material isgathered.

While we strongly advocate using the book to explore both nuclear and particle physics ina coherent, balanced way, nevertheless itmightbe thatitwill also be used in a course that emphasizes one subfield or the other. Accordingly, we suggest the following“roadmaps” tohelpthe reader negotiatethe textfor those purposes.Whenthe emphasis is placed on particle physics we suggest paying the closest attention to Chapters2 to 10 and 21, withsome parts ofChapters17,18, and perhaps 19, and when theemphasisisonnuclear physicsChapters2,7,11to18,20andperhaps19.

We strongly recommend the following online resources as important tools for enhancingthematerial presentedinthisbook.

1. TheReview ofParticlePhysics,ParticleDataGroup

http://pdg.lbl.gov includes a compilation and evaluation of measurements of the properties of the elementary particles. There is an extensive number of review articles onparticle physics, experimental methods, and material properties as well asasummaryofsearchesfor new particlesbeyondtheSM.

2. National Nuclear DataCenter

http://www.nndc.bnl.gov is a source of detailed information on the structure, properties,reactions,and decays ofknownnuclei.Itcontains aninteractive chartof the nuclides as well as a listingof the properties for ground and isomeric states of all knownnuclides.

We conclude this introductory chapter with some exercises designed to introduce some of the concepts which we hope our particle/nuclear students will be able to address.

Exercises

1.1 USEnergyProduction

In 2011, the United States of America required 3,856 billion kW-hours of electricity. About 20% of this power was generated by ∼100 nuclear fission reactors About67% was producedbythe burningoffossil fuels,whichaccounted for aboutone-third ofall greenhouse gas emissions inthe US. The remaining13% was generated using other renewable energy resources. Consider the scenario where all the fossil fuel power stations are replaced bynew 1-GWnuclear fission

1.2 GeothermalHeating

Itisestimatedthat20TWofheatingintheEarthisduetoradioactivedecay: 8TW from 238Udecay, 8 TWfrom 232Thdecay, and 4 TWfrom 40K decay. Estimate the total amount of 238U, 232Th, and 40K present in the Earth in order to produce such heating.

1.3 Radioactive ThermoelectricGenerators

A useful form of power for space missions which travel far from the Sun is a radioactive thermoelectric generator (RTG) Suchdevices were first suggested by the science fictionwriter Arthur C. Clarke in1945. AnRTG uses a thermocouple to convert the heat released bythe decayof a radioactive material into electricity bythe Seebeckeffect. The two Voyager spacecrafthave beenpowered since 1977 byRTGsusing238Pu.Assuminga mass of5kgof 238Pu,estimate the heatproduced and the electrical power delivered. (Do not forget to include the ∼ 5% thermocoupleefficiency.)

1.4 FissionversusFusion

Energycanbeproducedbyeither nuclear fissionor nuclear fusion.

a) Consider the fissionof 235Uinto 117Snand 118Sn, respectively. Using the mass information from a table of isotopes, calculate (i) the energy released per fissionand(ii) theenergyreleasedper atomicmassoffuel.

b) Consider thedeuteron–tritonfusionreaction

Using the mass information from the periodic table of the isotopes, calculate (i) the energyreleased per fusionand (ii) the energyreleased per atomic mass unitoffuel.

1.5 AbsorptionLengths

A flux of particles is incident upon a thick layer of absorbing material Find the absorption length, the distance after which the particle intensity is reduced by a factor of1/e ∼ 37% (theabsorptionlength) for eachofthefollowingcases:

a) When the particles are thermal neutrons (i e, neutrons having thermal energies),theabsorber iscadmium,andthecrosssectionis24,500barns.

b) When the particles are 2MeV photons, the absorber is lead, and the cross sectionis157barnsper atom

c) Whenthe particles are anti-neutrinos froma reactor, the absorber is the Earth, andthecrosssectionis10 19 barnsper atomicelectron.

Symmetries

2.1 Introduction

Whenstudyingquantumsystems, exploitingknowledge about the inherent symmetries is usually an important step to take before addressing issues of dynamics [Sch55, Sak94, Rom64, Gri08]. This motivates a discussion of group theory, and so we shall begin by summarizing some of the basic elements needed, particularly when discussing symmetries in particle and nuclear physics. More details can be found in specialized texts onthe subject[Ham62,Clo79]. Noether’s theoremstates thatifthe Hamiltonianis invariant under a continuous group of transformations, then there exist corresponding conserved quantities and accordingly one wants to discuss various natural symmetries and the conservation laws that accompany them (see [Rom64] Chapter IV for a clear discussionof Noether’s theorem, and also see Exercise 2.1). Specifically, in Table 2.1 are several important examples that are believed to be absolute symmetries and hence exact conservationlaws. Some of these specific examples are discussed inmore detail inwhatfollows.

Symmetry

Conservation law

translation in time energy

translation in space linear momentum rotation in space angular momentum

localgauge invariance charge

transformations in color space color

Furthermore, there are symmetries that are not completely respected in Nature, although characterizing the states used in terms of eigenstates of these approximate symmetries often proves fruitful; some examples are given in Table 2.2. We shall be usingall of these concepts throughout the book. Next let us turnto a brief discussionof someofthebasicsneededwhentreatingsymmetriesusinggrouptheory.

Approximate symmetry Conservation law

spatialinversion

particle–antiparticle interchange

Table 2.1 Exact conservation laws

Table 2.2 Approximate conservation laws

temporalinversion time-reversalinvariance, T transformations in isospace isospin, I (or T) transformations in flavor space flavor

Representations

Byan n-dimensional representationofagroup G onemeansamapping (2.1) (2.2) whichassigns toeveryelement g a linear operator A(g) insome n-dimensional complex vector space, the so-called carrier space of the representation GL(n), such that the imageoftheidentity e istheunitoperator I andthatgroupoperationsarepreserved (2.3)

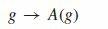
Throughout the book we shall frequently encounter infinite-dimensional continuous groups (Lie groups) whose elements are labeled uniquelybya set of parameters which can change continuously (see [Rom64] for an introductory discussion). An example is provided by the rotation group, that is, the group of continuous rotations. For the Lie groups that are encountered frequently in this book it is sufficient to study the mapping fromtheLiealgebrainto GL(n), (2.4)

where the {Tα} preserve the Lie-algebra commutation relations. If a subspace of the carrier spaceofsomerepresentationisleftunchangedbyall operators Tα,itis calledan invariantsubspace and the representationis reducible;otherwise itis irreducible. Ifthe correspondence (2.5) definesarepresentationofthegroup G,thenthecorrespondence (2.6) also defines a representationof the group, the so-called conjugate representation. For a Lie group we find that the representation matrices for the conjugate representation are givenby

(27)

When discussing the implications of symmetries in particle and nuclear physics one frequentlyencounters the special unitarygroups in N dimensions, SU(N), which can be representedusing N × N matrices U satisfying (2.8)

The importance of the continuous Lie group SU(N) lies in the fact that these matrices describe transformations between N basis states {|eα , α = 1, ..., N} preserving orthonormality (2.9)

We shall see several examples of physical states labeled using various symmetries, specifically by spin and by isospin (SU(2)), by flavor and by color (SU(3)), or by higher groups, e.g., SU(6) for spin-flavor. Withinthe context of SU(N), a representation is reducible if it is possible to choose a basis in which the matrices Tα take the block form (2.10)

where A, B, C, ... are lower-dimensional irreducible sub-matrices when the original matrix Tα is fully reduced. Given an irreducible representation {Tα}, the only linear operators O which commute with every Tα are multiples of the identity and also the converse: (2.11)

Anyunitarymatrixcanbewrittenas (2.12) where H is a traceless Hermitianmatrix. For a Lie group the elements of the group are characterized by a finite number of real parameters {aα} and for SU(N) one finds that thereare n = N2 1suchparameters.Accordingly,onecanwrite (2.13)

where the {Lα} forma basis for the N × N Hermitianmatrices knownas the generators of the group SU(N). To study the representations, it is sufficient to study the generators andtheir commutationrelations, (2.14) wherethelatter arecharacterizedbytheantisymmetricstructureconstants

2.2 AngularMomentumand SU(2)

Let us begin by discussing the representations of SU(2) in a systematic way. The basis space is three-dimensional and is spanned by S = (S1, S2, S3), that satisfy the commutationrelations[Edm74]

(2.15)

where ϵijk is the antisymmetric tensor, +1 if ijk is an evenpermutationof 123, 1 if an odd permutation and zero otherwise. In the carrier space a Hermitian scalar product exists: (2.16)

Next we need to label the states in the carrier space using the Cartan subalgebra, namely, the maximal setofmutuallycommutingoperators thatspanthe space. For SU(2) the subalgebra onlycontains a single operator, usuallychosento be Sz, where the z-axis is chosen by convention to point in some convenient direction; later in Section 2.4 we shall seethatfor SU(N) with N ≥3the situationis more complicated.The importance of devising such a mutually commuting set is well-known from quantum mechanics: it is thenpossible to diagonalize all ofthe matrices inthe setsimultaneouslyand to label the states withthe correspondingeigenvalues. Fromthis set of generators there are special operators that can be constructed which commute with all generators of the group, namely, the so-called Casimir operators. Again for SU(2) there is only one such operator (althoughmorefor SU(N) with N ≥3) namelythequadraticCasimir operator (2.17)

Asdiscussedabove,suchoperatorscommutewithall generatorsofthegroup, (218) and hence mustbe proportional to the unitmatrix, i.e., their eigenvalues maybe used to

label the representations. Letus now proceed to constructexplicitrepresentations using the commutation relations. One labels the basis states or representations with λ, the eigenvalues of the Casimir operator, and with quantum numbers m, the eigenvalues belongingtotheoperatorsintheCartansubalgebra,

Since S2 and Sz are Hermitian, λ and m are both real, and moreover, λ is positive and maybechosenbyconventiontobe

where j thenlabelstherepresentation.Correspondingly,wenow have

and,beingeigenstates ofHermitianmatrices,the states |j, m are orthogonal and canbe normalized Definingraisingandloweringoperators

itisstraightforwardtoshow that (2.25) (2.26)

Next using Eq. (2.25) one proves that, after operating on the states |j, m with the raising or lowering operators to form new states, S± |j, m, the latter are also eigenstatesof S2 and Sz, (2.27) (2.28)

thatis,witheigenvalues j(j +1) and m ±1.Writingthisresultintheform

andusingthefactthat

onethenhasthat (2.33)

Since ismadeupfromquadraticHermitianoperators,onehasthat (2.34)

and, since the allowed m-values change only in steps of 1 with the highest value mmax occurringwhen

one finds that mmax = j, justifying the choice made in the definition in Eq. (2.21). Collectingthese developments together, insummarywe have basis states characterizing the representation {|j, m} with non-negative Casimir quantum number j and quantum number m havingvalues runninginsteps ofunityfrom j to+j;thus the dimensionofthe representation is 2j + 1. The choice of phase usually made [Con35] is such that the raisingand loweringoperators actingonstates |j, m yield real c-numbers times states with m ±1: (2.36)

Next let us focus onspin SU(2), taking j → S with m → Sz and discuss the lowestdimensional representations in somewhat more detail. The simplest is the onedimensional,singletrepresentation(S =0) withbasisstate|0,0andhaving Sz |0,0 = S+ |0,0= S |0,0=0.Thefirstnontrivial representationistheso-calledfundamental one, which for SU(2) is two-dimensional (S = 1/2) with basis states |S = 1/2, Sz = ±1/2

Letting S± and Sz act on the basis states, it is straightforward to obtain explicit expressionsfor therepresentationmatrices: (2.38) or equivalently (2.39)

Conventionallyone writes Si ≡ σi/2,therebydefiningthe Pauli matrices σi, with i = 1, 2, 3,correspondingto x, y, z,respectively;weusethetwotypesofnotationinterchangably. Amorecomplicatedcaseistheonefor S =1(dimensionthree) withbasis states labeled |S, Sz: (2.40)

Asabove,letting S± and Sz actonthesestates,oneobtains (2.41) or equivalently (2.42)

This is the so-called adjoint or regular representation. This is anexample of an N2 1 dimensional representationof SU(N) givenbythe mappinginEqs. (2.1) and (2.2) with structureconstants(seeEq.(2.14)) (2.43)

Later when building hadrons in Chapter 3 we shall find it convenient to use weight diagrams. Since the generator in the Cartan subalgebra can be used to label states of a representation, the corresponding eigenvalues can be plotted in a diagramof this type, which here for SU(2) amounts to drawing a line with dots to indicate where the eigenvalues occur, as shown in Fig. 2.1. Below we shall see that in SU(N) with N ≥ 3

onehaspatternsin(N 1)-dimensional space.

Fig. 2.1 Weight diagrams for SU(2) for spins S =1/2, 1, and 3/2.

Coupling of AngularMomentum

Bytakingthe directproductoftwo representations, we find a new representationwhich in general is reducible. For instance, as an example in SU(2) let us consider the direct product of two S = 1/2 (two-dimensional) representations (see Eq. (2.37)), written in thefollowingway|S(1) =1/2, S3(1) =±1/2; S(2) =1/2, S3(2) = ±1/2, now for brevity simplyindicated|±±,yieldingfour states

with

Therepresentationmatricesinthedirectproductspaceare