Issuu

Seldom understood signals

Vinay B S

Introduction

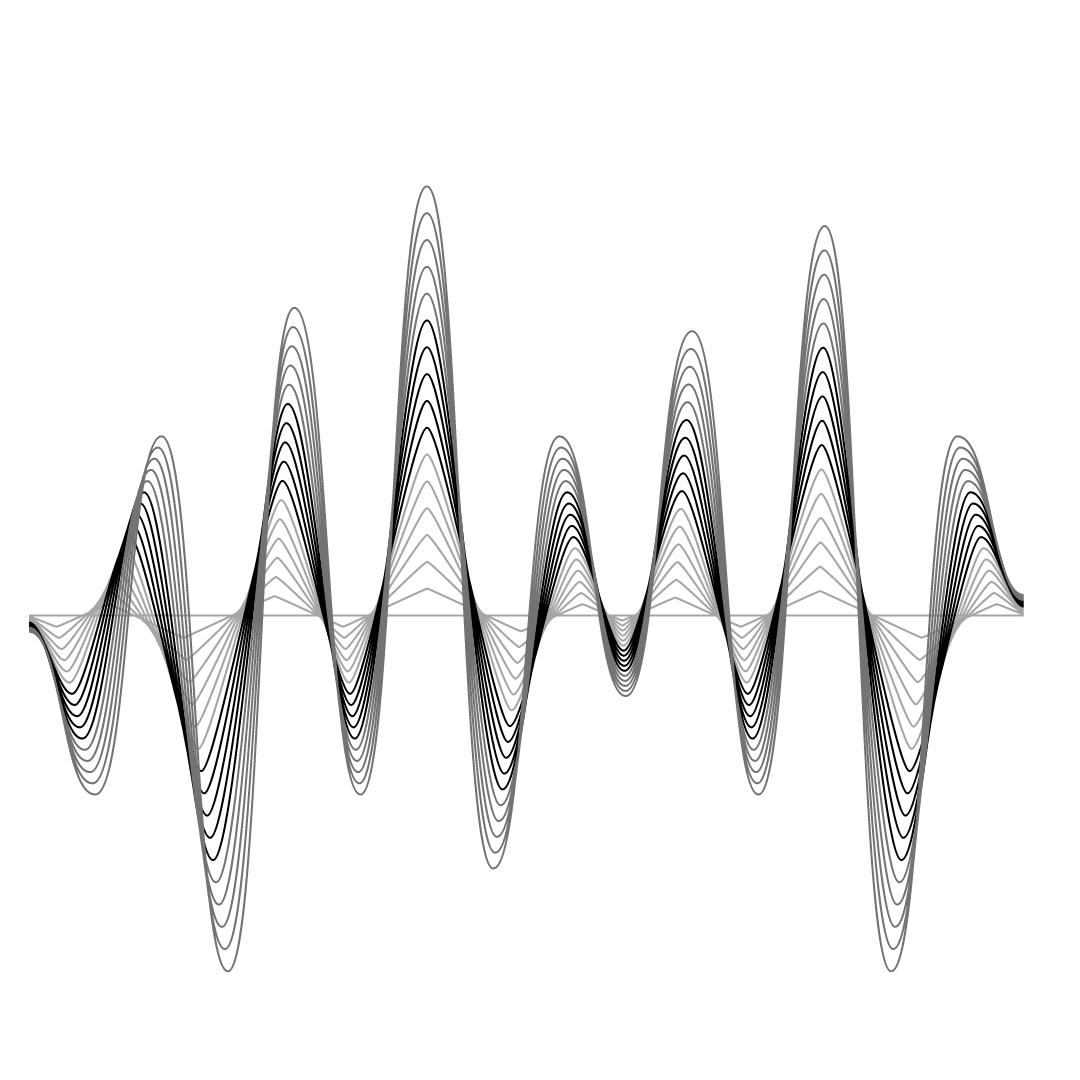
Signals carry data in some form. They are converted and processed from analog to digital in order to store, transmit and retrieve data. Verbal speech involves signals carrying some data humans understand, and it looks something like Fig. 1. A typical hum would look like a sine wave of sorts, as in Fig. 2. If the same is sampled, then the signal would look like Fig. 3a. Suppose a sine wave is quantized, it would look like Fig. 4. Signals change their behavior post processing and conversion.

In this context, the terms Analog, Digital, Continuous and Discrete are often used to differentiate signals. The reader can right away attempt to classify the kinds of signals the following six figures represent and re-assess one’s identification after going through this whitepaper.

Fig. 1 Fig

Fig. 3a

Fig. 3b

Fig. 4

Fig 5

Why This Whitepaper?

The invention of transistors in 1947 ushered the information age. The usage of the term ‘signal’ doubled and tripled since then and probably will never go out of relevance in engineering education. Yet, the said terms, Analog, Digital, Continuous and Discrete are seldom fully understood by a significant number of engineers, according to hiring entities.

This whitepaper is not going to discuss the technicalities of signal processing and conversion, but only attempts to give insights in order to classify signals in a manner they are supposed to. The paper will try to avoid textbook definitions and will include as many explanations as possible. However, the tone will be formal and conversational.

Conceptions

Spend some time with each of the following statements:

● Analog signals are always continuous.

● Analog signals cannot be discrete.

● Digital signals are always discrete.

● Digital signals cannot be continuous.

● Digital signals are always binary.

● Analog signals cannot look like digital signals.

● All natural signals are continuous.

The above statements are incorrect and are mis-conceptions, usually formed based on the ‘curviness’ and ‘looks’ of the signal at first glance. However, it is important to look at the definitions and meanings of the four terms in question in order to determine and classify signals.

What is a Signal?

A signal is defined as “a function that maps a domain, often time or space, into a range, often a physical measure such as air pressure or voltage.”

For simplicity, let us say, a signal consists of amplitude–on the y-axis that varies with time–on the x-axis. Amplitude can be any quantity related to the signal, as the definition says.

How to Classify?

Continuous and Discrete signals are classified with respect to time (x-axis) and are independent of the signal's amplitude characteristics. Analog and Digital signals are classified with respect to amplitude (y-axis) and this applies regardless of whether the signal is continuous or discrete in time.

Time Domain: Continuous and Discrete signals

Continuous signals are defined at every instant in time. This means, there are no gaps in time, one can infinitely divide the units in the time-axis and the signal can be measured at any point in time.

Discrete signals are defined only at specific, countable points in time. This means, there are gaps in time, one can only finitely divide the units in the time-axis and the signal can only be measured at specific intervals in time.

Usually, Sampling of a continuous signal (Fig. 2) at specific time intervals will result in a discrete signal (Fig. 3a).

Thus, Fig. 1, Fig. 2, Fig. 4 and Fig. 5 are continuous, while Fig. 3a and Fig. 3b are discrete.

Amplitude Domain: Analog and Digital signals.

Analog signals can take on any value within the range of amplitudes at a given time, even when the signal is Discrete. In other words, it can take infinitely many values on the y-axis.

Digital signals are limited to a finite set of amplitude values, irrespective of whether the signal is Discrete or Continuous. In other words, it can only take select values on the y-axis. If these values are 0 and 1, then they are Binary signals.

Usually, Quantization of an Analog signal to different levels will result in a digital signal. Fig. 3a is a Discrete-Analog signal. Quantization of the said signal will result in Fig. 3b, which is Discrete and Digital. Careful observation will tell that Fig. 3b is an approximation of Fif. 3a.

Thus, Fig. 1, Fig. 2 and Fig 3a are Analog, while Fig. 3b, Fig. 4 and Fig. 5 are Digital.

Note: Analog to Digital signal conversion is essential to store and transmit data. Therefore converting (sampling and quantization) a Continuous-Analog signal with infinite values will result in a Discrete-Digital signal with finite values so that they are stored in memory bits that are finite. Thus, Digital signals are approximations of analog ones.

Summary

Both Analog and Digital signals can either be Continuous or Discrete. In other words, we cannot have Analog-only or Digital-only signals. They exist in four combinations. That is, Continuous-Analog, Continuous-Digital, Discrete-Analog and Discrete-Digital.

Note: A Binary signal is a form of Digital signal (see Appendix).

Special Cases

1. An analog signal, by definition, can take on any value in a given range. This means it can, coincidentally, assume values that match those of a digital signal. As a result, it is possible for an analog signal to appear digital.

To illustrate, take a hypothetical situation in which a student’s marks are such that the score is always an even number Converting the mark-progression to a signal will result in a lookalike of a quantized Digital signal, as if the student was banned from scoring marks that are odd in number But the student is free to score any mark. Hence, the signal can be considered as Analog even though it looks Digital.

2. Natural signals need not always be Continuous. Quantum particles like electrons in atoms can only occupy discrete energy levels. They have discrete spin states that can be measured as either “up” or “down”, represented by +1/2 and -1/2 at a given time. This makes electrons naturally-discrete.

Further, natural light is made up of discrete energy packets called photons. DNA sequences consist of discrete nucleotide bases (A, T, C, G).

Answers

If the reader has attempted to reassess their classification of the six figures discussed earlier, these are the answers:

Fig. 1 - Continuous-Analog

Fig. 2 - Continuous-Analog

Fig. 3a - Discrete-Analog

Fig. 3b - Discrete-Digital

Fig. 4 - Continuous-Digital

Fig. 5 - Continuous-Binary

Glossary

Sampling: The process of converting a Continuous signal into a Discrete signal by measuring the amplitude of the signal at regular time intervals. Sampling is a key step in Analog-to-Digital conversion.

Quantization: The process of approximating a continuous range of amplitude values by a finite set of discrete levels. In Analog-to-Digital conversion, quantization follows sampling and involves rounding each sampled amplitude to the nearest predetermined discrete level. This process introduces a small error known as quantization noise. This is why the converted signal is an approximation of the original.

Appendix

Binary Signals

Binary signals are Digital signals that use only two distinct values to represent data. These values are typically represented by 0 and 1. They are further classified by the number of bits. A 2-bit Binary signal has four states 00, 01, 10, and 11. Similarly, a 4-bit binary signal has sixteen (24) possible states ranging from 0000 to 1111. Modern personal computers use up to 64-bits to process data.

Conversion

Digital data storage involves conversion of all other forms of signals to Binary signals. For this to be done, a signal must be converted to Discrete-Digital signals.

In other words, most signals in their natural state are Analog and Continuous, they must be sampled to make them Discrete in time and quantized to make them Digital in amplitude. Then, they are encoded.

Here is how a typical 2-bit encoding works: Assume a Discrete-Digital signal with four amplitude values, 0, 1, 2, 3 and the discrete time interval between two of these values is 1 second.

Then one can represent (encode) each of these 4 values using 2 bits: 0 = 00, 1 = 01, 2 = 10, 3 = 11. Now, the digitally encoded 2-bit binary signal will have values that are 00, 01, 10, 11, in place of 0, 1, 2, 3.

Further, all Binary signals are Digital and not all Digital signals are Binary.

References

1. Oppenheim, A.V., Willsky, A.S., and Nawab, S.H. (2013). Signals and Systems (2nd Edition). Pearson.

2. Proakis, J.G., and Manolakis, D.G. (2006). Digital Signal Processing (4th Edition). Pearson.

3. Lathi, B.P., and Green, R.A. (2017). Linear Systems and Signals (3rd Edition). Oxford University Press.

4. Haykin, S., and Van Veen, B. (2002). Signals and Systems (2nd Edition). John Wiley & Sons.

Seldom Understood Signals - A Whitepaper by Vinay B S