EngineeringQuarterly
Welcometothe secondissueofVolume2oftheEngineeringQuarterly,a newsletterpublished fourtimesayearby theUniversityofMary SchoolofEngineering,whichincludesarticlesfromeachofthefourengineeringmajors thatwecurrentlyofferoncampus:Electrical Engineering,MechanicalEngineering,Civil Engineering,andConstructionManagement.

Hands-ondesignconstitutesalargepartof ourengineeringdegreeprograminalldisciplinesandinallyearsfromfreshmanthrough senior.Inthefallsemesterofthesenioryear, ourstudentsdoaseniordesignprojectwithin theirengineeringdisciplineandinthespring semesteroftheirsenioryeartheydoacrossdisciplinarydesignproject.Thisfalltheseniordesignprojectswerepresentedtothe publicduringtheweekofDecember9to13. Wewilloutlinebelowsomeofthoseprojects aswellasotherdesignprojectsdonebyour sophomoreandjuniorlevelstudentsintheir courses.
InthisissueofEQ,wewilloutlinethe firstsemesterdesignprojectsaswellasother itemsandeventsofinteresttoengineeringstudents,engineeringcompanies,andalumniof ourengineeringprogramsuchasserviceand outreachactivitiesinthecommunity,scholarships,internships,guestspeakers,andeven assignmentandexamproblems.Enjoy!
TerryPillingOverthecourseofseveralmonths,I workedwithKileeHarmon,theDevelopment DirectorforCHISt.Alexius,todesignand plantheconstructionofthememorialspace. Theprojectbeganasadesigncompetitionthat theengineeringstudentsundertookduringthe springsemesterlastyear.Webrokeupinto groupsandeachgroupdesignedamemorial forthespaceatthehospital.
Theprojectwasbrokenintotwophases duetotiming.Phase1wastheconcretepad andmonument/benches,andphase2wasthe rampgoingfromthemonumenttothehospital.
Theconcretepadforthemonumentwas pouredonSeptember26,andthemonument alongwiththebencheswasshippedNovember1andinstalledshortlythereafter.WaldosConstructiondonatedtheconcretework atcostminus10%andColdspringdonated thebenchesandmonumentalsoatcostminus 10%.TheCHISt.AlexiusHealthAuxiliary ladiesfundedtherestoftheproject.

Wethenheldapostersessionwherethe stafffromCHISt.Alexiusstudiedeachof thestudentdesignsanddecidedonthewinningproject.Duringthesummer,professor WaldenmaierandImetwithrepresentatives fromSt.Alexiushospitalonseveraloccasions toworkoutfinaldesignplans.
WeareofferinganFEExamPreparation coursethissemesterwhichrunsonTuesday andThursdayeveningsfrom6pmto8pmat ourFrontAvenuelocationnorthoftheBismarckEventCenter.
OnNovember18,2018,aBismarckAir Medicalplanecrashed,killingmedicalstaff members.ToddLasky,a48-year-oldpilot,diedinthecrash,alongwithnurseBonnieCook,63,andMetroAreaAmbulance paramedicChrisIverson,47.Theywereen routefromBismarcktoWillistontopickup aneonatalpatientwhenthecrashoccurred. Shortlyafterthecrash,morethan1,400people,includinghundredsofemergencyrespondersfromthroughoutNorthDakota,attended acivicmemorialserviceforthethree.Dozens ofambulancesparticipatedinaprocession throughBismarck.Thisyear,onthefirstanniversaryofthecrash,BismarckAirMedical andCHISt.AlexiusHealtheachheldaprivatememorialservicesandthehospitalunveiledandblessedamemorialspaceoutside itsSouthBroadwayentrance.Thespaceisa sittingareadesignatedforreflectionandwas designedbyourUniversityofMarySchoolof Engineeringstudents.


Istartedtheconstructionofamodulefor thefinaldesignandpresentedittotheBenedictineSistersofAnnunciationMonastery. Followingthepresentation,Ibeganworkon thearchitecturalplansforbidding.St.Alexiuswantedasimplebutelegantdesign.The mainplatformwasmadeintheshapeofan arch.ThearchshapeisasymboloftheCHI hospital.Italsocreatesagreatdesignflow forthememorialasitestablishesaverywelcomingfeel,whichwillalsodrawpeopleinto lookatit.

Thenextmajorelementswerethebenches andthemaincenterpiece.Thecenterpieceis athree-sidedstoneslab,withthreebenches surroundingit.Eachofthethreevictimswill haveasideoftheslabdevotedtothem.Then threebencheswillthensitperpendicularto eachface.Thiswillallowpeopletocomein, paytheirrespectsandstayforalittlewhileif theysochoose.Therewillalsobeshort2’ bollardstolightupthememorialatnight.
Thecourseisopentoanyonewhowould liketotakeit.Soifyouareanengineerwhois currentlyworkinginindustryandwouldlike totaketheFEexamthisspring,orifyou plantotakeyourPEexamandwouldlike arefresheronthematerial,youcansignup forthepreparationcourseandthencometo whicheversessionscovertopicsthatareon yourspecificexam.
Thecoursecoversallofthetopicsonthe FundamentalsofEngineeringexamsforcivil, electrical,andmechanicalengineering.The formatoftheclassisquiteinformal.We simplymeetat6pmandgothroughproblemsfromoldFEexamsandfromthevarious studyguides,remindingstudentsofthekey elementstolookforandexplainingthefastest waystosolveeachtypeofproblem.
ThecoursebeganonJanuary9andwill continuethroughtoMarch17anditisour hopethatmost,ifnotall,thestudentswill thenimmediatelytaketheFEexam.
Weofferthiscourseeveryspringsemester anditwillremainopentoanyonewhowould
likearefresherontheFEexamsubjects. Formoreinformationandtoenrollinthis coursepleaseseetheUniversityofMary’s continuingeducationsitehere: https:// continuinged.umary.edu/
creativeyoungscientiststochooseacareerin engineering.Ofcourse,weattheUniversity ofMarySchoolofEngineeringjumpedatthe chancetoattendtheevent,totellourownindividualstories,andtoencouragethesestudentstochoosetheUniversityofMaryfor theirundergraduateengineeringdegree.
TheNDSPEChapter3helditsNovember meetingatourEngineeringSchool’stempo-


Itoldmystorytothestudentsanddiscussedourengineeringprogramandhowit differsfromotherschools.Ifollowedthisby handingoutissuesoftheEngineeringQuarterlyalongwithapplicationsmaterialsandinformationpacketsfortheUniversityofMary SchoolofEngineering.
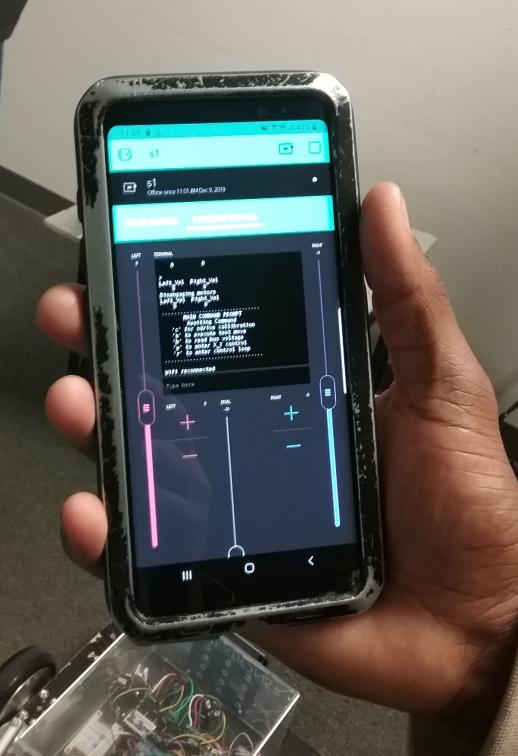
TheycallitaMobileAppControlledArticulatedVehicle(MACAV).Springsteendesignedthesystem,anddevelopedthecodefor themicrocontrollerboards,andthecellphone appsothatoperatorcancontrolthevehicle fromthesmartphone.

rarylocationonFrontAvenue.Theybrought pizzaforthestudentsandprofessorJames CarricogaveapresentationaboutourupcomingengineeringservicetriptoPeruthathe isorganizingforspring2020(seethearticle aboutthePerutripintheFall2019issueof EngineeringQuarterly).Thestudentsgotto seewhattheNDSPEhasbeendoinglately andthehopeisthattheywillbeencouraged tojointhisandotherengineeringserviceorganizationsandremainmembersthroughout theircareers.
Thefirstgroupofseniorelectricalengineeringstudentsbuiltanarticulatedelectric vehiclecontrolledbyasmartphone.The projectwassponsoredby GenesysGatesTechnology ofBismarck.
Basedonarticlesfromthemanufacturer onhowtorunthemotorsandhowtocontrolthemotorcontrollerboardsusingcommandlinefromacomputer,heputtogether astand-alonesystemcontrolledbymicrocontrollerdevelopmentboards,whichisableto handlealltheinformationtorunthemotors, calibrationofencoders,feedbackofthesystem,WiFiconnection,etc.andpairitwith anappthathasanoperator-friendlyuserinterface.
ScienceOlympiads,mathcompetitions, andsciencebowlsareveryimportantevents
forencouragingstudentstoexcelinSTEM fieldsandtochooseSTEMcareers.Welove toattendandhosttheseeventsandwealso lovetocongratulateandencouragethewinningteams.
IntheeveningofNov.20,2019,theNorth DakotaPetroleumCouncilhostedthewinning teamoftheLegacyScienceOlympiadtotheir locationtoeatpizzaandlistentoengineers fromvariousbranchesofengineeringtellhow theyendedupwithcareersasengineers,as wellasstoriesabouttheamazingprojectsthey haveworkedonuptonow.



Thesponsorgavethestudentsfour 3-phaseinductionmotors,twocontroller boards,twolinearactuators,andbatteries, withthegoalofmakingthemintoanelectric vehicle.

AaronBales(Bismarck,ND),Richard Bendish(Mandan,ND),andPhillipSpringsteen(Graham,WA)spentthesemesterworkingonthecodethatwouldrunthecontroller boardsandthemotors;reliabilitytestsforthe linearactuatorcontrol,anditspositioningand thecoolingsystemdesignofthecontroller boardscompartment.
Thegroupalsodevelopedthetesting equipmentusedtocontrolandcollectdata fromthecoolingsystemandtheactuatorcontroltestsinordertochoosethefinaldesign forthecoolingsystemandthepositionforthe linearactuator.
Microcontrollerswereprogrammedtorun apredeterminedsequenceandvariableswere
observed,suchascurrentandtemperature. Theresultofthesetestswereusedtochoose thefinaldesignforthis3-creditdesignclass.
“Icouldn’thavedonethisprojectwithouttherestofmyteammembers,”said Springsteen,whoisalsoanAcademicAllConferenceandAll-Americangrapplerfor theUniversityofMarywrestlingprogram. “Thiswasagroupprojectandweallcontributed.Everyone’spartinthisprojectwas necessary.”Springsteenaddsthatmechanically,thisprojectisnowherenearcomplete.
Theyhopetomakeadjustmentsandbe abledesignitsothattheMACAVisableto remotelycompletetasksaroundthehome–asiftheoperatorwasplayingavideogame ontheirphone.
thestudentshadalimitedbudgetandwerenot allowedtogooverit:$200includingeverything.
oftheproject.Thesestudentswereassigned thefollowingtasks:1)Theprojectionofthe requiredtexttotheLEDmatrix,2)Calibratingthetemperaturesensor,andgettingagood readingfromittobeprojectedtotheLEDmatrix,3)andfinallythestudentsaddedanintermissiondisplaybetweeneachphaseoftherequiredtextoneoftheseintermediatedisplays wasaclipofConways’GameofLife.
AfterassemblingtheLEDsinthebox,the powersupplyandtherestofthecomponents, thefrontsideoftheboxwascoveredwitha semi-transparentdisplayglasstodiffusethe highilluminationoftheLEDsandmakethe textbeingdisplayedcomfortablylegible.
Thefirstthingthatthestudentsthought of:AreahundredLEDsenoughtomakethe writinglegible?Toanswerthisquestion,they openedaspreadsheetandtriedtowritetheir namesbyfillingthecellsinthespreadsheet. TheyrealizedthattheyneededmoreLEDsto makethewritingonthesignreadablefrom adistance.Consequently,afterstudyingthe sizeoftheboxthathousedtheLEDs,and studyingtheproperminimumdistancebetweentwoadjacentLEDsforcorrectillumination,thestudentsdecidedthatthereshould be720LEDsinthatboxtoproperlydisplay thetext.Theyweretobeputinamatrixof 48 × 15 LEDs.
TheLEDsignwasagreatsuccess,and itwillbedisplayedinthenewEngineering buildingonceitisdone.Totakealookat atime-lapseshowingthestepsoftheproject usingthislink: https://tinyurl.com/ UmaryLED
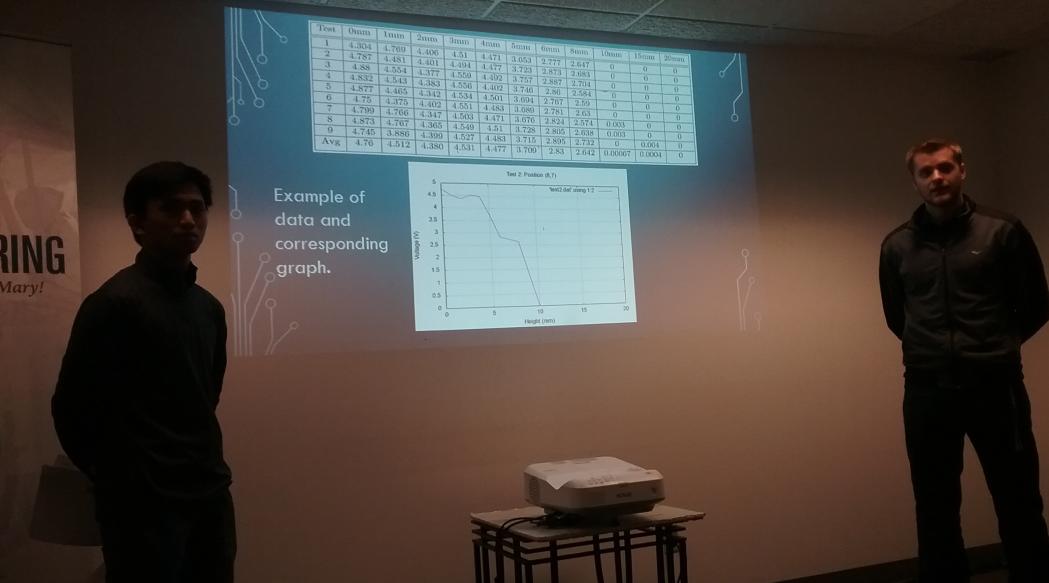
SeniorstudentsJosefSollmannandJohn Santiagostudiedanoff-the-shelfsmartphone chargingstationinordertodiscoverhowthe variouspropertiessuchasphonecasethicknessandphonepositionontopofthechargingpadaffectthestation’sabilitytocharge thephone.Thesevariableswerechosenbased theirperceptionasconsumersofissueswhen chargingtheirdevices.Theydidnumerous trialsandstatisticallyanalyzedthedatato comeupwithanoptimalconfigurationand testedthechargingcapacityofthewireless chargedandwirelesschargerreceiverusedin theproject.
DIGITAL LEDDISPLAY ByKHALIDOWEIS
Duringthefall2019semester,fourof theElectricalEngineeringjuniorstudentsin theElectronicsILab:GabrielZimmer,Josh Reiner,Snæd´ısDan´ıelsd´ottir,andJeffStrong, wereassignedaninterestingtermproject.The projectconsistedofa30by40inchelectronic signwithacoloredLEDmatrixthatincluded atleast100LEDs.Thesignshouldpresenta welcometothevisitorsoftheSchoolofEngineering.




ItshouldalsostatethesixBenedictinevaluesthattheUniversityofMaryholdsvery deeply(Community,Hospitality,Moderation, Prayer,RespectforPersons,Service)withoptionalexplanationforeachone.Thesevalues canbefoundhere: https://tinyurl. com/benvalues.Furthermore,thissign hastodisplaythecurrentindoortemperature.
Ontopofthat,theyhadtobuildeverythingfromscratch,includingtheboxthat housedtheLEDsandtheequipment.Finally,
Thenextstepwastobuildtheboxitself. Theygotthematerialsfromthelocalhardwarestore,andassembledtheboxofthedigitalsign.Theboxwasthenpaintedblack togiveitaprofessionalfeel.Theboxhad twomainlevelsandcompartments:Theback compartmenthousedtheDCpowersupply, theArduinomicrocontrollerthatcontrolled theLEDsandthewires.Thewireswent outfromthebackcompartmentveryneatly tothefrontcompartment.ThefrontcompartmenthadtheLEDsandtheplasticmeshgrid thatseparatedtheLEDsforclearillumination. TheygluedtheLEDswithevenspacingto thewallthatseparatedthecompartmentsin thebox.Thentheysolderedthewirestothe LEDs.
OurseniorMechanicalEngineeringstudentspresentedtheirprojectofdesigninga therapeuticvibrationplateforhorses,particularlythosethatcompeteinrodeocompetitions.ThisprojectwasrequestedbyProfessor AlannaDennisonintheAthleticTrainingand KinesiologyDepartment.Therequirements ofthedesignwerethatitneededtobelow cost,controlmultiplevibrationsettings,operateonuneventerrain,andportable.The studentsusedCAD,initialprototyping,and performedengineeringanalysisincomingup withafinaldesignforavibrationplatform. Furthermore,theyalsodevelopedadynamic simulationmodelonOctavetodeterminethe forcesandstressespotentiallyoccurringatthe jointswhenahorseexperiencesthevibrations generatedbytheplate.
Whilethehardwaredesignandbuilding wasbeingdonebytwostudents,theothertwo studentswereworkingonthesoftwareside
OursophomoreEngineeringstudentshad
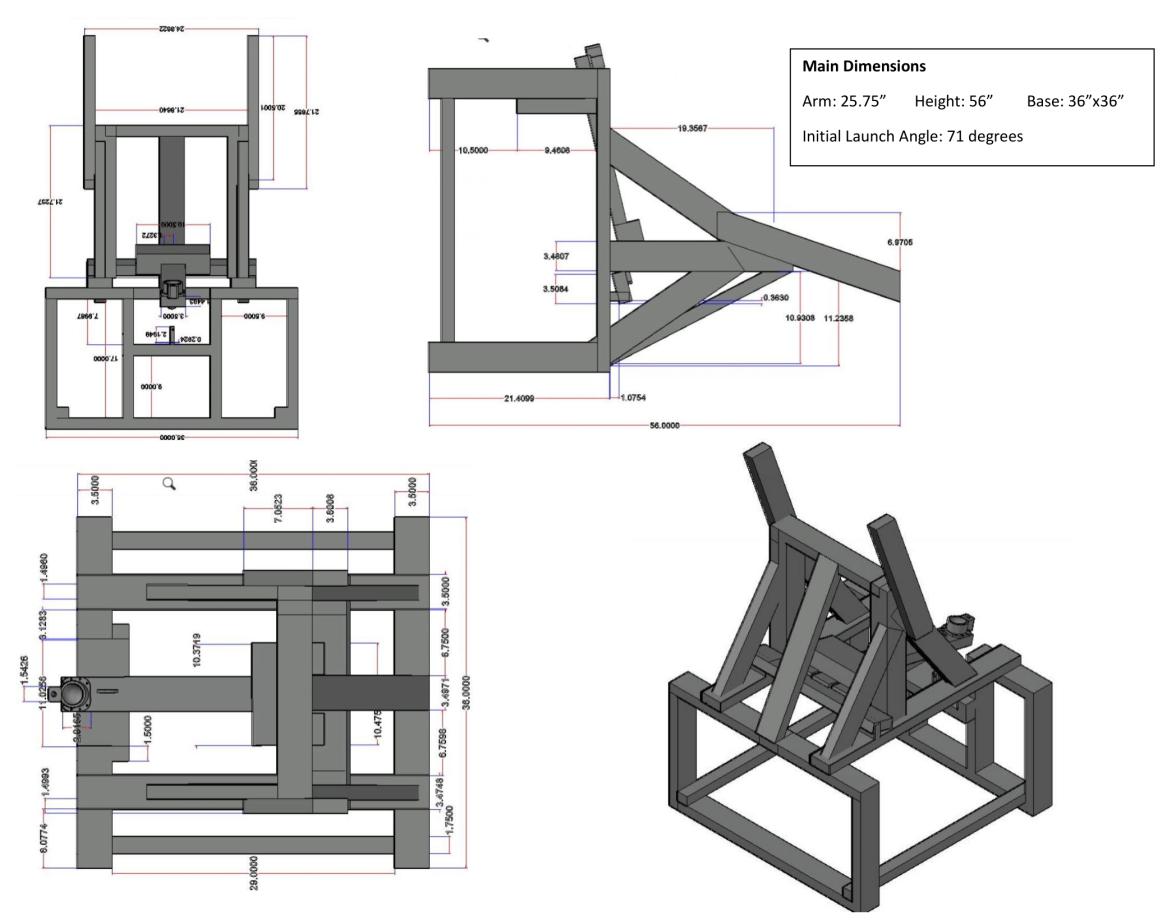
acatapultcompetitionintheirDynamicsclass inwhichtheyweretaskedtodesignandconstructacatapultwhichwouldlaunchaprojectiletohittheirinstructor,Dr.EricGarcia,in thefaceatadistanceatleast10metersaway. Thestudentswerelimitedtoonlytwoshots toensurethattheirdesignwasbasedontheir calculationsandnotjusttrialanderror.
Therewerefourteamsofthreestudents andeachteamwasonlyprovided$20worthof woodmaterialsandanyscrapwoodinthemachineshop.Eachteamcameupwithaunique designthatusedeitherropesorbungeecords. Oneteamevendesignedandbuilttheirown springusingourLatheinthemachineshop.
snowremoval,andtrafficflowissues,anddesignthecampusesstormwaterdistributionand drainagesystem.
OneteamsuccessfullyhitDr.Garciain thefaceandwasthefirstteamtodosoin thetwoyearsthisprojecthasbeenassigned. Theteam(pictured)thatsucceedinginhitting theirtargetwasKarsenMeyer,DanielMinor, andPeterSmith.Inadditiontoabuiltcatapult,studentsweretaskedtoputtogetherdesignreportsdocumentingtheirdesignprocess andcalculations.
Studentwerealsotaskedtoanalyzethe campus’infrastructure,identifyanyfunctionaland/oraestheticissueanddesignan engineeringsolutiontotheproblem.
kneejointisnotplanarbecausetheamountof rollingandslipisnotidenticalonthelateral andmedialsidesofthejoint.Tosimplifythe problem,studentsindesignofmachineryfocusedonthelateralside,whichexhibitsmore rollingthanslipandthuschosetomodelthe kneeaspurerollingcontact.Insodoing,the studentswereabletoapproximatetheinstantaneouscenterofrotation(ICR)betweenthe femurandtibiatobealwaysbeatthepoint ofcontactbetweenthetwoandthusfollow thecurveofthefemoralhead.Thissimplified thedesignofaknee-bracemechanismtobeingsimplythedesignofafour-barmechanism withanICRthatfollowedthetrajectorydescribedbythefemoralheadandtheappropriatejointangleforanygivenpointalongthat trajectory.
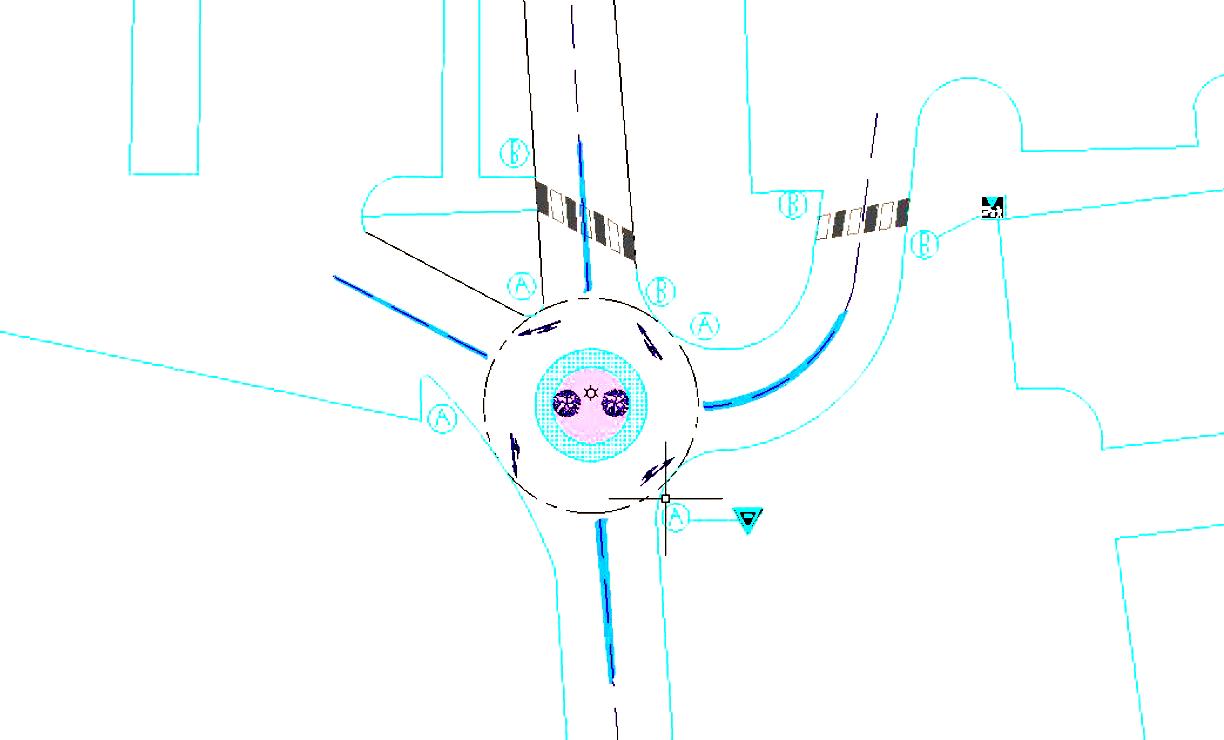
Bothteamscameupwithcreativeengineeringsolutionsanddesignstosolvevariousissuestheyidentifiedoncampussuchas indoorwalkwaysbetweencampusbuildings andbuildingexpansions.
GIVING TREE

CIVIL ENGINEERING SENIOR DESIGN ByERICGARCIA


TheseniorCivilEngineeringstudents wereseparatedintotwogroupsfortheirdesignprojects.Thefirstgroupconsistedof AustinKonschak,AlexDavis,ColinGudereit,andCalebWeisgarber,andthesecond groupconsistedofLeviClagett,JacksonPenner,andRobertSpady.

Eachteam’sdesignreportstotaledcloseto 100pagesofcalculations,technicaldrawings, costestimates,andotherdesigndetails!
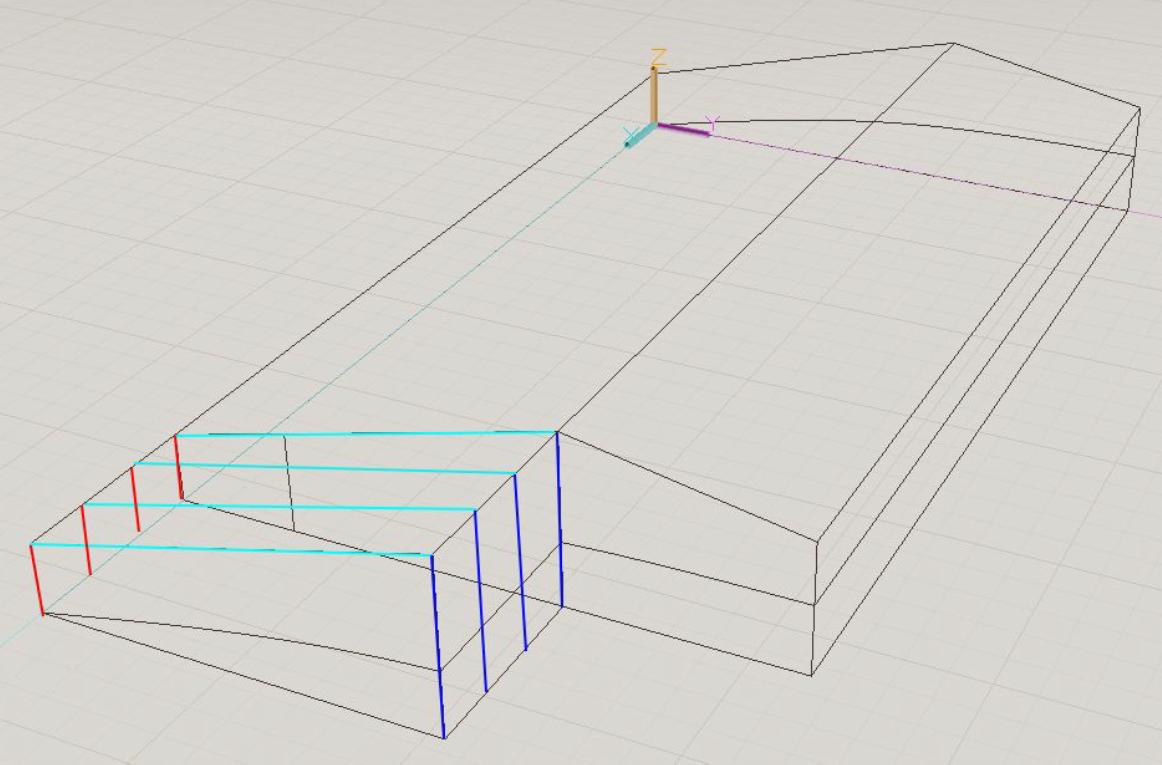
DESIGNOF MACHINERY ByJAMESCARRICO
TheschoolofEngineeringtookpartinthe university-widegivingtreecompetitionfor thefirsttimethisyear.
Thetreesarelocatedineachoftheschools andtheycontainornamentswhichlistitems
Theirprojectwastodeveloptheirown ‘landscapemasterplan’forPhaseIIofthe UniversityofMary’sVision2030plantoimprovethecampus’layout,functionality,and aesthetics.
Theoverarchinggoaloftheprojectwas toimprovetheinfrastructureoftheUniversity ofMarycampus.Thespecifictasksassigned weretodesignareinforcedconcreteparkingstructure,redesigntheroads/pavementsof campustoaddresscampusentrance,parking,
Indesignofmachinery,studentsare taskedwithsimulatingthemotionofphysical systemsandsynthesizingtheirownmechanismsideallywithsomepracticalend(togive authenticityandpurposefulnesstoprojects). Onelearningoutcomeofthesedesignprojects ishowfundamentallydifferentdevicescan exhibitidenticalmotiontoeachother.Thisis apowerfulinsightfordesignofmechanisms becauseitillustratesthewideisthesolution spacefordesignproblems.Ifdesiredoutcomescan’tbeachievedwithacammechanism,whataboutalinkage,ornon-circular gearing?Thisequivalencebetweendifferent mechanismssuggestsanapproachtodesign. Forinstance,onemethodtodesignofaknee bracemightbesummarilydescribedasidentifyingthetypeofjointakneeisandidentifyingmechanismsthatproduceanidentical motion.Intruth,akneejointisnotaplanar jointandexhibitsbothrollingandslip.The
thatareneededbyvariousnon-profitorganizationsintheBismarck-Mandancommunity. Theideaisthatthefacultyandstaffwillselect anornamentfromthetree,purchasetheitem, thenreturntheitemtothecollectionboxbesidethetree.
WegotourtreeontheDec.3andwe foundtoourdelightthatalloftheornaments
playedgames,ate,anddiscussedhowthe semesterwent.
Itwasasuccessfulsemestereventhough ithasbeenadifficultonegiventhatour
hadbeencompletedandtheitemsreturnedto thecollectionboxbyDecember4!
Asaresult,ourfacultyandstudentsenjoyedacelebrationofourgivingonDecem-
coursesweresplitbetweencampusanddowntownBismarck.Ourstudentsandourfaculty haven’tcomplained,andinfact,Ithinkwe allfeelwehaveplentytobethankfulforthis year.
andendwithablizzard.Winterstartedparticularlyearlyin2019,withourfirstsubstantial snowfalloccurringinearlyOctober.Thisleft inchesofsnowontheground.ECI313 GeneralSurveying isacoursecoveringthebasic elementsofalandsurvey;locatingandmeasuringpreciselocations,angles,elevations, anddistancesoflargelandareasandproperties.Thisbegsthequestion;howcanstudentslearntoconductanaccuratesurveyon icy,slippery,inaccessible,andsnow-covered landareas?
ber17thwhichconsistedofadonutandhot chocolatebuffet!Thebuffetlastedalldayand thestudentswereabletohaveacupofhot chocolateandadonutbetweentheirfinalexams.

ThankstoMelindaSeidlingforhelpingthe EngineeringSchoolgetinvolvedintheGivingTreethisyear.

Herearesomeproblemstakenfromour variousengineeringcoursesthatourstudents hadtosolve.Thesolutionscanbefoundat theendofthisnewsletter.
Duetotheinitialsnowfallandtheregularinclementweatherthatoccurredonsurvey labdays,thefall2019ECI313hadtoadapt. Surveyingwasbroughtindoorswithacombinationofinsideinstrumentuseandtheuse ofGoogleEarth.Theclasswasluckyenough toconductinitialleveling,profile,andbasic traversingsurveysusingtraditionalleveling instruments,staking,andtapingmethodsoutdoors.Asforadvancedsurveymethodsinvolvedintraversing,routeswereestablished withinconnectedbuildingsoncampus.The combinationofhands-onindoor/outdoorapplicationsallowedtheclasstounderstandthe basicprinciplesinvolvedinfieldtechniques.
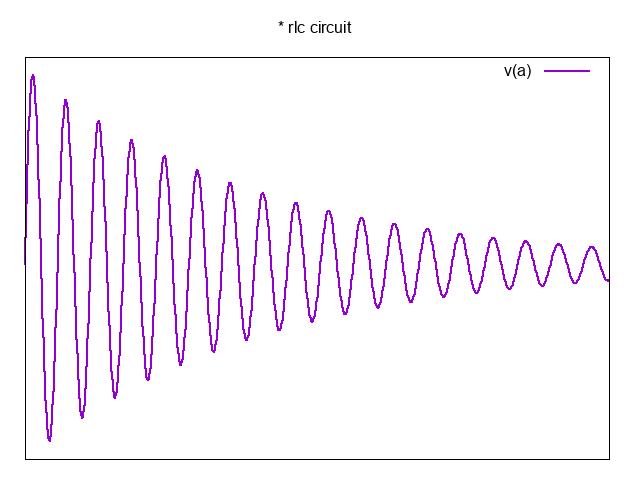
Writean NGSPICE netlistwhichwillplot thetransientresponseofandRLCcircuitbetween 0 5µs and 500µs foraninductorof L =100mH withaninitialcurrentof 1mA, acapacitorof C =200pF ,andaresistorof R =1kΩ.Showtheplotofthevoltageacross theresistorandthecurrentsthroughthecapacitorandtheinductor.
ThebasketballplayersnominatedprofessorAnthonyGarciaasoutstandingfacultythis semesterandonSaturday,December21,the men’sbasketballteamhostedahomegame weretheyannouncedprofessorGarcia’sname beforethelineup.
ProfessorGarciaevengotaT-shirtfrom theteam!Thankstoallourfacultyforhaving suchagreatimpactonourUniversityofMary studentathletes.
ThefacultyoftheUniversityofMary SchoolofEngineeringheldaChristmasparty


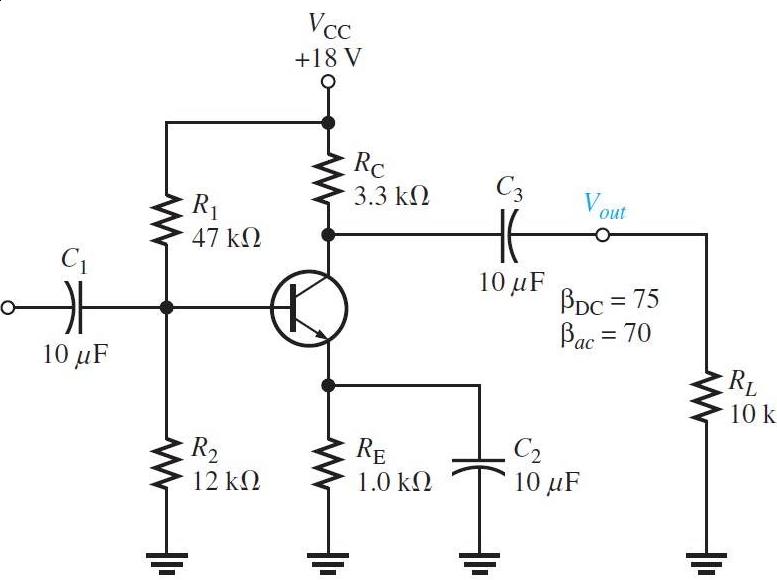
Problem: Fortheamplifierinthefigure, determine: (a) Rin(base), (b) Rin, (c) Av , (d) Ai,and (e) Ap S
atthetemporarybuildingonFrontAvenue justbeforefinalsweek,wherethefulltime professorsaswellastheadjunctprofessors
ForthereaderwholivesinNorthDakota, orreallyanywhereintheMidwest,wintercan makeanappearanceasearlyasSeptember.A weekmaystartwithtemperaturesinthe90s
Thefinallabprojectsforthecoursewere assignedusingstrictlycomputer-basedmethods.Studentsweretoconductaseriesofsurveysutilizingthemeasuringtoolsavailableon GoogleEarth;distance,elevation,andangles. Thefirstassignmentwasconductingalong open-linktraversespanningseveralmilesor aplotsurveyofaverylargestructure(such asasportsstadium).Studentsweretorecord measurementsconsistentwithfieldnotesfor allpointsobserved–treatingthesurveyas ifiswereon-site.Thefinalassignmentwas toconductathoroughsurveyofroughlyonethirdoftheUMarycampus.Thisincluded profilesofallroadsandwalkingpaths,grid surveysoffieldsandparkinglots,andperimetersofbuildingswithinthesection.Thegoal wastocombinetheeffortsofthethreegroups intoanall-inclusivecampussurvey.Students werealsodirectedtotieinknownelevations fromfieldsurveystocalibratetheelevation estimationfromGoogleEarth.
Conductingahands-onlabviacomputer wasnevertheplanforthecourse.However, itisarelieftoknowthattechnologycanhelp usadapttocopewithMotherNatureseverchangingplansforNorthDakota.
Problemtotryonyourown:
UsingGoogleEarth(https://earth. google.com/web/)conductaclosed-loop traverseofalocationofyourchoosing.Measuredistancesbetweenpointsandrecordelevations.Recommendationsforlocations: HighwaysectionsofBismarck,professional sportsstadiums,oracityblockfromyour hometown.
• Themeasuringtoolislocatedontheleft borderoftheapp(lowestoption)
• Selectanodeandnotetheelevation whichisfoundinthelowerrightcorner
• Selectthenextnodewiththemeasuring tool,recordthedistance,andnotethe elevationofthenode
• Proceedtothenextnodeandcontinue theprocessuntiltheendisreached(a
URVEYING INDOORS:USING MODERN TECHNOLOGYTO ACCOUNTFOR WINTER IN NORTH DAKOTA ByANTHONYWALDENMAIER
closedloopshouldendonthelocation oftheinitialnode)
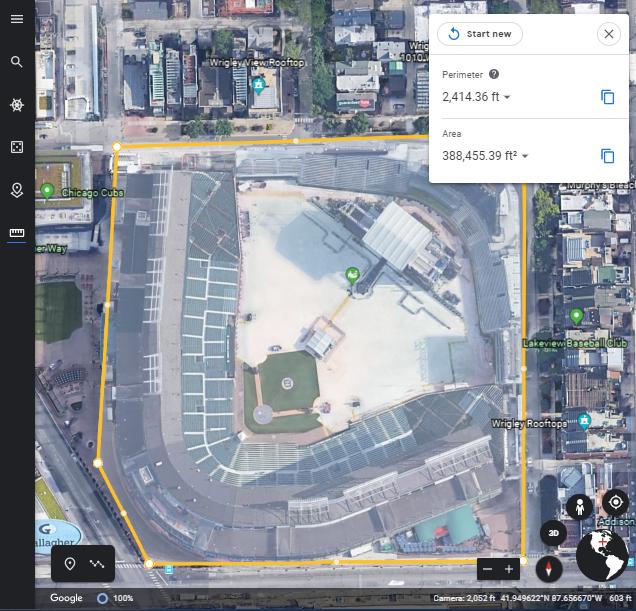
AsampleSurveyofWrigleyField(Chicago, IL)isprovidedbelow.
andthus
z = x + jy = r cos θ + jr sin θ
= r (cos θ + j sin θ)
= rejθ whereweusedEuler’sformulainthelaststep.
OnecoolthingthatyoucandowithEuler’sformulaisuseitasawayofderiving trigonometricidentitiesifyouhappentobe stuckonadesertedislandwithnointernetand ahostiletribeofcannibalsdemandstoknow thetrigidentitiesoryouwillbeeaten.Exponentshavethefollowingnicepropertyunder multiplication:
X aX b = X a+b
andso
ejθ ejφ = ej(θ+φ)
andifweinsertEuler’sformulainforthese exponentialswehave
cos(θ + φ)+ j sin(θ + φ)= [cos(θ)+ j sin(θ)]+[cos(φ)+ j sin(φ)]
systemwiththefunctionshowingupasasurfacegraph.
Nowwhataboutcomplexfunctions?
Acomplexnumber, z,isanumberwhich hasbotha real partandand imaginary part andcanbewrittenas z = x + jy where x and y arebothrealnumbersand j = √ 1.These numbersareveryfamiliartobothelectricalengineeringstudentsandmechanicalengineeringstudents,sincetheyappearanytime onedealswithoscillatingsystemssuchasAC circuitsorsprings,pendulums,orevensatellitesorbitingtheEarth.
Complexnumbersarecalled algebraically complete becausetherootsofanypolynomial equationwillbecomplexnumbers.Onthe otherhand,therealnumbersarenotalgebraicallycomplete.Forexample,theequation z2 +1=0 isapolynomialequationwhichhas nosolutionintherealnumbersbuthastwo solutionsinthecomplexnumbers: z = ±j arethesolutionsandbotharepureimaginary numbers.
Oneofthemostamazingpropertiesof complexnumberswasdiscoveredbythefamousmathematicianLeonhardEuler1 inthe mid1700’s.Thisisthefamous EulerFormula:
ejθ =cos θ + j sin θ
Thisisausefulformulainamultitudeofways
First,noticethatifyouput θ = π inEuler’s formulayougettheremarkableequation
ejπ = 1
whichrelates e =2 71828 , π = 3 141592 ,and j = √ 1
Complexnumberscanbewrittenasvectorsin2-dimensionalCartesiancoordinates byidentifyingtheverticalaxisasthe‘imaginaryaxis’andwriting
z = x + jy −→ (x,y)
andifyoutransformtopolarcoordinates wherethevectorshaveradius r2 = x2 + y2
andangle θ =tan 1(y/x) thenyouhave
x = r cos θ
y = r sin θ
whichwecanmultiplyout,usingthefactthat j 2 = 1,toget
cos(θ + φ)+ j sin(θ + φ)= [cos(θ)cos(φ) j sin(θ)sin(φ)] + j [cos(θ)sin(φ)+sin(θ)cos(φ)]
andequatingtherealpartsandtheimaginary partsgivesfinally:
cos(θ + φ)=cos(θ)cos(φ) sin(θ)sin(φ) sin(θ + φ)=cos(θ)sin(φ)+sin(θ)cos(φ)
Noticethat,if θ = φ thesebecome
cos(2θ)=cos2(θ) sin2(θ) sin(2θ)=2cos(θ)sin(θ)
andsoon.
Wehaveseenhowtovisualizecomplexnumbersasvectors,orpoints,ona 2-dimensionalplane.Whataboutcomplex functions?Recallthatweusuallyvisualizea functionusingagraph.
Forexampleifwehaveafunction f (x) ofasinglerealnumber x thenwecandraw ahorizontalaxistorepresentthevaluesof x andthendrawaverticalaxistorepresentthe valuesof f (x) andthefunctionwillthenbea curvedrawnonthisgraph.
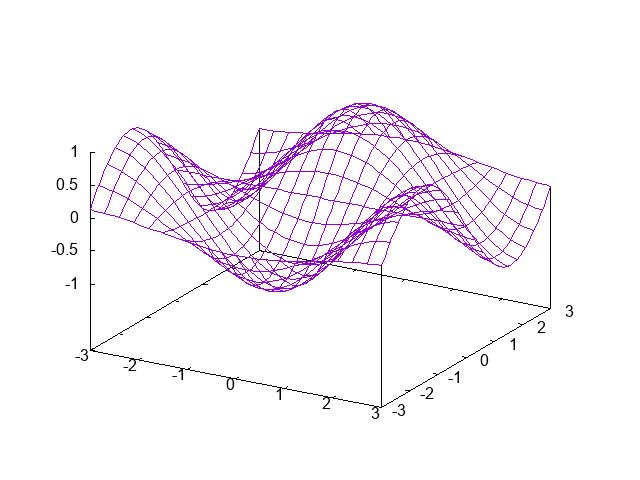
Whataboutafunctionoftwovariables x and y?Wellinthatcasethefunctionis f (x,y) andsoweusetwoaxesforthe x andthe y variablesandweuseathirdonefor f (x,y) whichwillgiveusa3-dimensionalcoordinate
Whatifwewanttographafunction f (z) from thecomplexnumberstothecomplexnumbers?Inotherwordsboth z isacomplexnumberand f (z) isalsoacomplexnumber.This isabitproblematicsincethecomplexnumbersareequivalentto2-dimensionalvectors. Sowewouldneed2dimensionsforthedomain–justlikeour f (x,y) plotabove,butwe wouldalsoneed2dimensionsfortherange since f (z) isalsotwodimensional.Thusthe actualgraphwouldbea3-dimensional“surface”ina4-dimensionalspace!Itisimpossibletographthisinour3-dimensionaluniverse.Henceweneedadifferentwaytovisualizewhatisgoingonhere.
Hereisamethodthatwecanuse:We pickarandompointandplotitinacertain colorandthenweplotthevaluethatthepoint mapstounderthefunction.Soifthecomplexfunctionwas f (z)= z2 forexample, wewouldchoosearandompoint,say z = 0 54+0 32j =(0 54, 0 32) andweplotit, thenwealsoplot
f (z)= z 2 =(0 54+0 32j) ∗ (0 54+0 32j) =0 1892+0 3456j =(0 1892, 0 3456)

inadifferentcolor.Nowifwechooseawhole bunchofrandomnumbersfromaregionofthe xy-planesuchasasquarebetween x = ±1 and y = ±1 andmapeachofthepointswe shouldgetafeelforwhatthecomplexmapis doingtothepoints.HereisaGNUPLOT script thatchooses5000randomnumbersbetween zeroandone,thenshiftsthemsotheyarebetween 1 and +1 andplotsboththeoriginal squareregionandtheregionthatitmapsto underthecomplexfunction f (z)= z2
Thegraphshowsthattheoriginalsquare regiongetswarpedintoasortofovalregion wherethedensityofpointsincreasestoward thecenter.
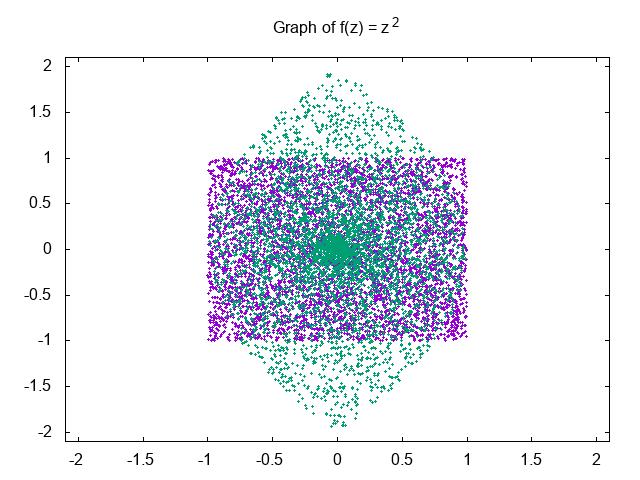
complex-map.gnuplot
settitle ”f(z)=zˆ2”
setxrange [ 2:2]
setyrange [ 2:2]
unset key
set offset0.1,0.1,0.1,0.1
setsamples 5000
fx(x,y)=x ∗x y ∗ y
fy(x,y)=2∗ x ∗ y
plot ’+’ using (x=rand (0),y= rand (0),2∗ x 1):(2 ∗ y 1)pt 7ps0.2, \
’+’ using (x=rand (0),y=rand (0) ,fx(2 ∗ x 1,2∗ y 1)):(fy(2 ∗ x 1,2∗ y 1))pt7ps0.3
Sothemap f (z)= z2 ispushingpointstowardthecenteranditisalsostretchingthem outvertically.Thiscanbeseenmoreeasilyby recallingEuler’sformula:
f (z)= z 2
⇒ f (rejθ )= r 2 ej2θ
weseebytheformulathattheanglesareall doubledandtheradiusesaresquared.Hence radiiwhicharelessthan1willbecompressed (ifyousquareanumberthatislessthan1it getsevensmaller)andradiiwhicharegreater than1arestretched.Thisiswhyweseethe accumulationattheorigin.Alsothedoubling oftheanglesiswhytheovalshapeappears.
Let’stakealookatanothercomplexfunctionforfun.Thistimewewilllookat f (z)= 1/(z +1).Westartbyjustlookingatrandompointsinsideasquarebetween0and1 onboththe x andthe y coordinates.Hereis theGNUPLOT codethatgeneratesit
complex-map2.gnuplot
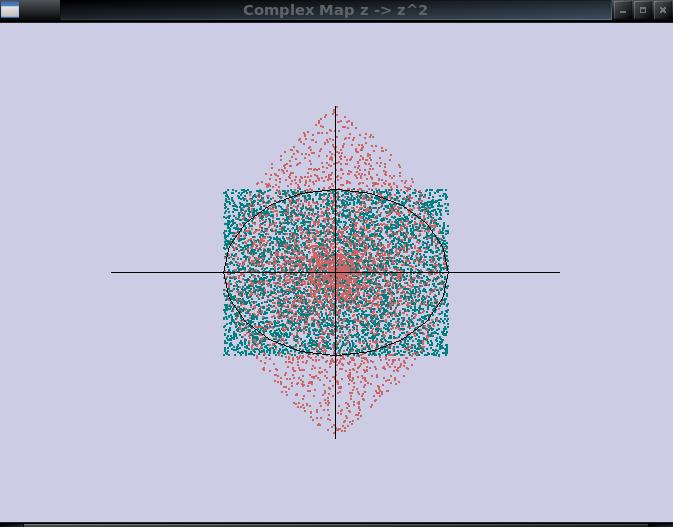
settitle ”f(z)=1/(z+1)”
setxrange [ 1:1]
setyrange [ 1:1]
set offset0.1,0.1,0.1,0.1
unset key
setsamples 2000
fx(x,y)=(x+1)/(x ∗ x+2∗ x+1+y ∗ y)
fy(x,y)= y/(x ∗ x+2∗ x+1+y ∗ y)
plot ’+’ using (x=rand (0),y= rand (0),x):(y)pt7ps

0.2, \
’+’ using (x=rand (0),y=rand (0) ,fx(x,y)):(fy(x,y))pt7ps
0.3
Interestingly,weseethattheoriginal squaregetsshrunkendown,rotatedandhas somecusps.Itactuallystillhasfourcorners whichleadsustobelievethatcornersmapto cornersandedgestoedges.Isthereaway
2
mightliketotry.
Assignment: Modularforms arefunctionsofcomplexnumbersthatobeythefollowingsymmetryrelation:
f az + b cz + d =(cz + d)k f (z)
toprovethisusingEuler’sformulaorsome othermethod?
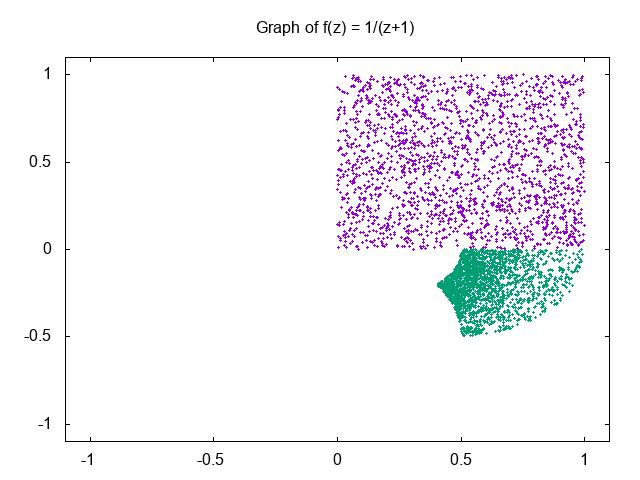
Let’sshiftthesquareregionsothatitsurroundstheoriginlikewedidinourfirstplot. Hereisthecodethatdoesit:
complex-map3.gnuplot
settitle ”f(z)=1/(z+1)”
setxrange [ 1:1.5]
setyrange [ 1.5:1.5]
unset key set offset0.1,0.1,0.1,0.1
setsamples 10000
fx(x,y)=(x+1)/(x ∗ x+2∗ x+1+y ∗ y)
fy(x,y)= y/(x ∗ x+2∗ x+1+y ∗ y)
plot ’+’ using (x=rand (0),y= rand (0),2∗ x 1):(2 ∗ y 1)pt 7ps0.2, \
’+’ using (x=rand (0),y=rand (0) ,fx(2 ∗ x 1,2∗ y 1)):(fy(2 ∗ x 1,2∗ y 1))pt7ps0.3
Nowweseethatcornersdon’tseemto maptocornersafteralldothey?Thereseems tobemorethanfourcornersontheimageand morethanfouredgesalso.Itisacoolmap though.
isamatrixinthegroup SL(2,Z).I.e.it isa 2 × 2 matrixwithintegerentrieswhich hasdeterminantequalto1.Therearemany unsolvedproblemsandopenresearchquestionsdealingwithmodularforms.Theyare usedinCryptography,NumberTheory,and inQuantumPhysics,HighEnergyQuantum FieldTheory,QuantumGravity,Superstring Theory,andtheywerefamouslyusedbyProfessorAndrewWilesinhisproofofthe400 yearoldproblemcalled Fermat’sLastTheorem2
Wewouldliketotrytoplaywithmodular formsusingourplottingmethodtotryandget amoreintuitivefeelforthem,however,usinggnuplotisabittootediouswhenrapidly changingparametersandtryingnewthingson thefly.Betteristowriteaprogramthatacceptsparametersfromthecommandlineor fromamenusoyoucanuseittoplayand exploreideasquickly.Tothisend,writea programinC++usingtheOpenGLgraphics librarywhichtakesintegers a,b,c,d asinput parametersandoutputsthetransformationof asquareregionofthecomplexplaneunder thelinearfractionaltransformation:
z −→ az + b cz + d inawaysimilartothemethodweusedwith GNUPLOT.
Complexmapsarethefirststeptoward generatingfractalsasyoumayhaveguesses bytheimagesthatweareseeing.Thesecond ingredientthatyouneedtogeneratefractals isrepeatediterationsofacomplexmap.One thingyoumightwanttotryforfunisthefollowingtechnique:
z
andsooniterativelycoloringeachiteration byadifferentcolor.Iwonderwhatcool imagesyouwouldfind?IfyouareinterestedbythisstuffyoumightenjoythearticlefromourSpring2019issueofthe EngineeringQuarterly entitled EtherealDelights whichexploresrepeatedexponentialcomplex mapsandshowsthecoolpicturesthatappear. HereisanassignmentproblemfromourEEL 461AdvancedProgrammingcoursethatyou
Aboveisascreenshotoftheoutputofthe desiredC++programunderthe z → z2 transformationwestudiedbeforeusingGNUPLOT Theproblemistomodifyittooutputtheresultofalinearfractionaltransformationinsteadof z2
Onepossiblesolutiontothisproblem,usingOpenGLalongwiththe(nowmostlydeprecated) GLUT windowinglibraryisgivenat theendofthisnewsletter.
Notethatiftheentriesofthelinear fractionaltransformationmatrixarecomplex numbers,ratherthanintegers,thetransformationiscalledaMobiustransformation.These areusedinmodernimageprocessingtocreate 360◦ sphericaleffects.ForexampleGoogle StreetViewandvirtualtoursofbuildingsare
createdbytakingpicturesfromvariouspositionsandthenpatchingthemtogetherusingtransformationslikethese.Forsome coolvideosandpicturesofMobiustransformationsappliedtoimagestakealookhere: ima.umn.edu/ arnold/moebius/
SOLUTIONSTO PROBLEMS
ElectronicsIIproblem:
Firstwefind
VTH = R2 R1 + R2 Vcc =3 66V
RTH = R1R2 R1 + R2 =9 56kΩ
IE = VTH VBE RE RTH /βDC =2 63mA
andusingthese,thesolutionsare
(a) Rin(base) = βac(25mV/IE )=665Ω
(b) Rin = R1||R2||Rin(base) =622Ω
(c) Av = RC ||RL re =261
(d) Ai = βac =70
(e) Ap = AµAi =(261)(70)=18270
CircuitsIIProblem:
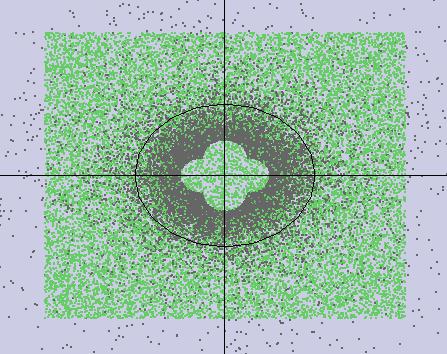
ComplexNumbersProblem: Thesolutionis aprogramproducingaMobiustransformation forusersuppliedintegersa,b,c,anddsothat theoutputfromthecommand ./moebius 0110 isthefollowingpicture
} void draw axes( void ) { glColor3f(0.0,0.0,0.0);
glEnable(GL LINE SMOOTH); glLineWidth(1.0);
glBegin(GL LINES); glVertex2f( Lx+1,0); glVertex2f(Lx 1,0); glVertex2f(0, Ly+1); glVertex2f(0,Ly 1);
glEnd();
glBegin(GL LINES); for ( int k=0;k <20;k++) { glVertex2f(cos(2 ∗ M PI ∗ k /20),sin(2 ∗ M PI ∗ k/20) ); glVertex2f(cos(2 ∗ M PI ∗ (k +1)/20),sin(2 ∗ M PI ∗ (k +1)/20));
}
glEnd(); } void draw points( void ) { glPointSize(2.0);
ThefollowingisaprogramwritteninCusing OpenGLandglutwhichproducestheplot
moebius.c
//gcc omoebiusmoebius.c lm
// lGL lGLU lglut
#include <time.h>
#include <math.h>
#include < stdio.h>
#include <GL/gl.h>
#include <GL/glu.h>
#include <GL/glut.h>
#define Lx5
#define Ly5
#define lx1
#define ly1
RLCdampedoscillatorinNGSpice
∗ RLCcircuit
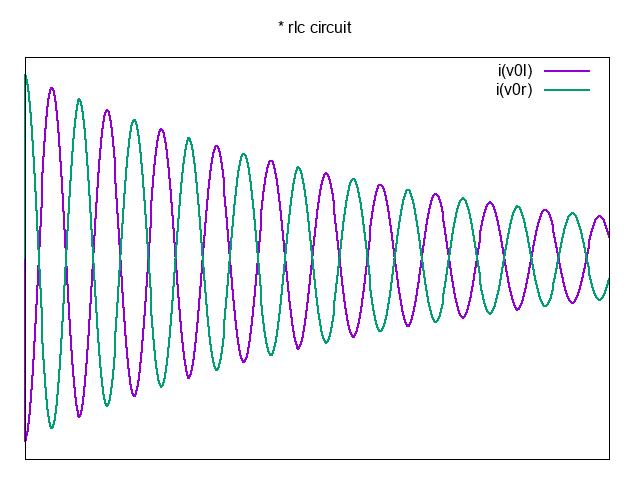
L1ba100mHIC=1mA
R1ad1000
C1dc200p
V0Lb00V
V0Rc00V
.control
tran0.5u500uuic
gnuplotvoltageV(a)
gnuplotcurrentsi(V0L)i(V0R)
.endc
.end
}
#define N20000 int a,b,c,d; void Initialize( void ); void display( void ); void draw axes( void ); void draw points( void ); void key( unsignedchar , int , int ) ; float U( float , float ); float V( float , float ); void Timer( int );
float U( float x, float y) { float numerator=(a ∗ x+b) ∗ (c ∗ x+d)+a ∗ c ∗ y ∗ y; float denominator=(c ∗ x+d) ∗ ( c ∗ x+d)+c ∗ c ∗ y ∗ y; float transformed=numerator /denominator; return (transformed);
}
float V( float x, float y) { float numerator=a ∗ y ∗ (c ∗ x+d) c ∗ y ∗ (a ∗ x+b); float denominator=(c ∗ x+d) ∗ ( c ∗ x+d)+c ∗ c ∗ y ∗ y; float transformed=numerator /denominator; return (transformed);
} void Initialize( void ) { glClearColor(0.8,0.8,0.9, 1.0); gluOrtho2D( Lx,Lx, Ly,Ly);
} void display( void ) { glClear(GL COLOR BUFFER BIT); draw points(); draw axes(); glutSwapBuffers();
}
glBegin(GL POINTS); for ( int i=0;i <N;i++) { int sign1=rand()%2; if (!sign1)sign1= 1; int sign2=rand()%2; if (!sign2)sign2= 1; float x=sign1 ∗ (( float )( rand()%10000))/5000; float y=sign2 ∗ (( float )( rand()%10000))/5000; float u=U(x,y); float v=V(x,y); glColor3f(0.4,0.8,0.4); glVertex2f(x,y); glColor3f(0.4,0.4,0.4); glVertex2f(u,v);
glEnd();
void key( unsignedchar key, int x, int y) { switch (key) { case ’q’: exit(0); default : break ; }
} int main( int argc, char ∗ argv []) {
if (argc!=5) { fprintf(stderr,”Usage:%sa bcd \ n”,argv[0]); fprintf(stderr,”whereabc dareintegers \ n”); return 1;
}
a=atoi(argv[1]);
b=atoi(argv[2]);
c=atoi(argv[3]); d=atoi(argv[4]); srand(time(NULL)); glutInit(&argc,argv);
glutInitDisplayMode( GLUT DOUBLE | GLUT RGB); glutInitWindowPosition(200, 100);
glutInitWindowSize(1000,800)
; glutCreateWindow(”ComplexMap z > zˆ2”);
glutDisplayFunc(display); glutKeyboardFunc(key);
Initialize();
glutMainLoop();
return 0; }
