WELCOME!
Welcometothelast issueofVolume1of theEngineeringQuarterly,anewsletterpublishedfourtimesayear bytheUniversityof MarySchoolofEngineering.Initweincludearticlesfromeachof thefourengineeringmajorsthatwecurrently offeroncampus:ElectricalEngineering,MechanicalEngineering,CivilEngineering,and ConstructionManagement.
Wereportonitemsandeventsofinteresttoengineeringstudentsandcompanies suchasserviceandoutreachactivitiesinthe community,scholarships,internships,guest speakers,andweevenincludeassignment problemsandprojectsthatourstudentshave completedaspartoftheircoursework.The EQ’sintendedaudienceareengineers,engineeringstudents,engineeringalumni,future engineeringstudents,andpeopleworkingin fieldscloselyrelatedtoengineeringsuchas science,computing,andmathematics.
AsthisistheSummerissueofEQthere arefewstudentactivitiestoreport.Thestudentsareeitherawayoninternshipsorhome withtheirfamiliesacrossthenationandthe world.Therefore,inthisissue,ourarticles mainlydealwithprogramdevelopments.We havestartedconstructionofournewengineeringbuildingandhavemovedintoatemporary spaceinBismarckwherewewillbeforthe nextyearuntilthenewbuildingiscompleted. Weoutlineourengineeringcurriculumfor eachofourmajorsandwelistthecourserequirementsforeachdegree.Weincludeafew articlesthatyoumayfindinterestingsuchas articlesaboutChaosTheory,aprisonteaching programattheNorthDakotaStatePenitentiary,concreteinancientRome,aswellas problemsyoucantryandaword-searchpuzzletocelebratethe50thanniversaryofthe Apollo11moonlanding.Enjoy!
TerryPilling
WashingtonUniversityin2011withafocus inBiomedicalEngineering.Hisdissertation wastitled DevelopmentalAnalysisofActivationPatternsinLanguageRegionofInterests intheHumanBrainforHealthySubjectsand PatientsofEpilepsy:AnfMRIstudy.Since 2012,Dr.Oweishasbeenafacultymember (andChair)oftheDepartmentofElectrical EngineeringattheAmericanUniversityof MadabainJordan.Weareveryhappyto welcomeDr.Oweistoourschool.Thisfall semesterhewillbeteachingEEL321 ElectronicsI,EEL321L ElectronicsILab,and EEL409 PowerSystemsI
ADJUNCT PROFESSORS
TheUniversityofMarySchoolofEngineeringconsidersitveryimportantthatour studentsgetplentyofrealworldexperience duringtheireducation.Thiscomesfroma numberofsourcesincludinginternships,Coops,designprojectsrequestedbycompanies, andalsoinstructionbyprofessionalsfromindustry.Thereforeweeagerlyinvitepracticing engineerstocomeinandteachcoursesforus intheirareasofexpertise.Webelievethisis avaluableexperienceforthestudentsandensuresthattheyarelearningthecuttingedge toolsandtechniquesthatarebeingusedintoday’sworkplace.Below,weintroduceyouto thefourAdjunctProfessorswhoarejoining usandteachingcoursesthisfall.

thisfall,acoursewhichhedesignedand builtusingagenerousequipmentdonation fromBobcat/DoosaninBismarck.Dwight isalsotheauthorofanewbookcalled Puppies,Lambs,Bunnies&Motorcycles whichis availableonAmazon.
NancyBarth
NancyBarthearned herAssociatedegree inArtsatSacramento CityCollegein1996,a BachelorofArtsdegreeinGeophysics fromtheUniversityof CaliforniaatBerkeley

in2001,aMasterofScienceinGeologyat CaliforniaStateUniversity,Sacramento,in 2010,andaPhDinCivilandEnvironmental EngineeringfromtheUniversityofIowain 2018.NancycurrentlyworksasaHydrologistfortheU.S.G.SinBismarckandwillbe teachingourECI421 Hydrology coursethis fall.
TomVolkman
TomVolkmanearned hisBachelorofScience degreeinElectronicEngineeringTechnologyfrom DeVryInstituteofTechnologyinKansasCityin 1986,hisMasterofSciencedegreeinElectricalEngineeringfrom theUniversityofCalifornia,SanDiegoin 1999,andhisEPSEdiplomafromtheUniversityofCalifornia,SanDiegoin2007.Since 2000TomhasbeentheSeniorPrincipalEngineerforHughesNetworkSystems,andsince 2018heworksatNationalInformationSolutionsCooperative(NISC)inMandan.Tom willbeteachingourEEL452andEEL452L EmbeddedSystems courseandlab.
WesDickhutearned hisBachelorofSciencedegreeinGeologicalEngineeringfrom theColoradoSchoolof Minesin1993andhis MasterofSciencein GeologicalEngineeringfromtheUniversityofIdahoin1999.
WesisaprofessionalengineerinNorth Dakota,SouthDakota,Montana,and Wyoming(formerlyalsolicensedinNew York,Ohio,Indiana,andKentucky)and iscurrentlyAssociatePrincipalEngineerat BraunIntertecCorporationinBismarck.Wes hastaughtour SoilScienceLab courseas wellasour EarthDynamicsandGeophysics coursehereatMaryEngineeringsincethe Fallof2017andthisfallhewillbeteaching ECI444 ContractsandSpecifications

 NEW PROFESSOROF PHYSICS
NEW PROFESSOROF PHYSICS
ProfessorKhalid Oweishasjoinedour teamstartingthisFall andwillbeteaching ElectricalEngineering courses.Dr.Oweis earnedhisBachelor ofSciencedegreein ElectricalEngineering fromtheUniversityofJordanin2002,his Master’sinComputerEngineeringfromthe UniversityofMassachusettsin2004,andhis PhDinElectricalEngineeringfromGeorge

KhalidOweis
DwightHinkel
DwightHinkel earnedhisAssociate ofArtsdegreeinBusinessfromBismarck JuniorCollegein1970 alongwithcertificationsinDataProcessing,SystemsAnalysis,andMetalFabrication.Hefollowedthis withaBachelorofScienceinMechanical EngineeringfromNDSUin1982.Dwight hasbeenaProfessionalengineersince1984 inNorthDakotaandsince1999inTexas. DwightfoundedAppliedEngineeringin1985 andAppliedSolutions,Inc.in1990.Dwight willbeteachingEME425 FluidsPowerLab
ProfessorTony Musumbahasjoined ourPhysicsdepartmentstartinginthe Fall.Dr.Musumba earnedhisBachelorofSciencedegree inPhysicsfromMoi University,Kenya,in 1995,hisMasterof PhilosophyinPhysicsfromMoiUniversityin 2001,andhisPhDinPhysicsfromtheUniversityofTexasatDallasin2008wherehe specializedinSpaceSciencewithdissertation entitled Mid-LatitudeF-Regionstudiesusing ISS-BandDE-2satelliteobservations.Tony taughtatBismarckStateCollegefrom2008 untilhejoinedourphysicsdepartmentthis year.Physicsisanimportantpartoftheedu-

cationofallofourengineeringstudentsand weareexcitedtoworkwithTonyonstudent coursedesignandresearchprojects.
THE ENGINEERING CURRICULUM
Overthepastfouryears,aswehave beendevelopingourengineeringprogram,we haveinterviewednumerouscompaniesand organizationswhohaveaninterestinhiring ourgraduates,wehavecloselyexaminedthe coursesandoutcomesofothertopengineeringschoolsacrossthenation,andwehave discussedanddebatedthecoursesanddegreepathsamongourselvesinordertodesign thebestpossiblecollectionofcourseswhich wouldsatisfytherequirementsofABETas wellasprepareourgraduatesforthegreatest chanceofsuccess.Ourcourseshavetherefore evolvedsignificantlysincewebegantheEngineeringprogramandwenowhaveafairlystablecollectionofcoursesineachofourmajors whichhavebeenvettedbyprofessors,students,andengineersfromindustry.Starting inFallof2020,ourdegreerequirementswill beasgivenbelow.
Webeginbylistingthecommoncorerequirementsintheartsandhumanitieswhich aretakenbyallstudentsregardlessoftheir major.Wefollowthiswiththerequirements foreachofthespecificmajors:CivilEngineering,MechanicalEngineering,andElectricalEngineering.PleasenotethatourConstructionManagementprogramisstillbeing developedandhasthefirst5semesterscompletedthusfar.Wewilloutlinethedegreerequirementsforthatdegreeinafutureissueof the EngineeringQuarterly
CommonCoreRequirements (takenbyallmajors)
HUM122/ELA110FirstYearExperienceSeminar (withPresidentsSeminar)
ENG121CompositionII
COM110OralCommunication
ART:SELECTONEOFTHEFOLLOWING
ART108IntroductiontoPhotography
ART116IntroductiontoFilm
ART121ArtofRomeandParis(Romecampus)
ART127IntroductiontoDrawing
ART210TopicsinTextileArts
COM200VisualCommunication
ENG140IntroductiontoNarrative
THR105ActingTechniqueI
MUS196IntroductiontoMusic
MUS211ConcertBand(3semesters)
MUS212ConcertChoir(3semesters)
GLOBALSTEWARDSHIP:
POL101ResponsibleCitizenship
andoneofthefollowing:
ANT171CulturalAnthropology
SOC107GeneralSociology
HIS103/104WesternCivilizationand
WorldHistoryIorII
ECN101EconomicsofSocialIssues
CTH/HIS330Catholicism&TheModernWorld
CLA/HIS311GrandeurofRome(Romecampus)
Language(any300levelorabove)
THEOLOGY:
THE120SearchforGod
THE/CTH234Benedict-yesterday&today
PHILOSOPHY:
PHI108SearchforTruth
andoneofthefollowing:
PHI208/308PhilosophicalEthics
PHI/CTH210SearchforHappiness:
FaithandReasoninLife.
SENIORASSESSMENT:
HUM499seniorassessment
CivilEngineering DegreeRequirements
MAT209CalculusI
CHE111GeneralInorganicChemistryI
ENR101IntroductiontoEngineering
ENR200ComputerApplicationsinEngineering
MAT210CalculusII
ENR210ComputerAidedMeasurements
PHY251EngineeringPhysicsI
PHY251LEngineeringPhysicsILab
MAT211CalculusIII
PHY252EngineeringPhysicsII
PHY252LEngineeringPhysicsIILab
ENR201EngineeringMechanicsI
ECI313GeneralSurveyingwithLab
ENR280EngineeringDesignLabI
ECI202CivilEngineeringandSustainability
ENR203EngineeringMechanicsII
ENR203LEngineeringMechanicsIILab
GEOL203EarthDynamics&Geophysics
ENR281EngineeringDesignLabII
MAT334DifferentialEquations
ENR338AdvancedEngineeringMathematics
ECI301CivilEngineeringMaterialsLab
ENR306FluidMechanics
ECI351StructuralMechanicswithLab
ECI412SoilMechanicswithLab
ECI416TransportationEngineering
ECI431WaterResourceswithLab
ECI432EnvironmentalEngineeringwLab
ECI451SteelDesign
ENR419EngineeringDataAnalysis
ECI453ReinforcedConcreteDesign
ECI482CivilEngineeringDesignProject
ECI4xxTechnicalElective1
ENR498FEExamPreparation
ECI4xxTechnicalElective2
ECI444ContractsandSpecifications
ENR460EngineeringEconomy
ENR470EngineeringEthics
ENR488SeniorDesign
TECHNICALELECTIVES
ECI404CivilEngineeringInternship
ECI414FoundationEngineering
ECI421Hydrology
ECI4xxPavementDesignandMgtwLab
MechanicalEngineering
DegreeRequirements
MAT209CalculusI
CHE111GeneralInorganicChemistryI
ENR101IntroductiontoEngineering
ENR200ComputerApplicationsinEngineering
MAT210CalculusII
ENR210ComputerAidedMeasurement
PHY251EngineeringPhysicsI
PHY251LEngineeringPhysicsILab
MAT211CalculusIII
PHY252EngineeringPhysicsII
PHY252LEngineeringPhysicsIILab
EME298ManufacturingTechnologiesLab
ENR201EngineeringMechanicsI
ENR280EngineeringDesignLabI
ENR304ComputerAidedAnalysis
ENR203EngineeringMechanicsII
ENR203LEngineeringMechanicsIILab
ENR206FundamentalsofElectricalEngineering
ENR281EngineeringDesignLabII
PHY253EngineeringPhysicsIII
MAT334DifferentialEquations
ENR306FluidMechanics
EME322DesignofMachinery
EME305SystemDynamics
ENR338AdvancedEngineeringMathematics
EME301MaterialsScience
ENR405ControlSystems
ENR405LControlSystemsLab
EME418ManufacturingProcesses
EME341ThermodynamicsI
EME483MechanicalMeasurementsLab
EME487MechanicalEngineeringDesignProject
EME4xxTechnicalElective1
ENR419EngineeringDataAnalysis
EME323MachineComponentDesign
EME323LMachineComponentDesignLab
EME441ThermodynamicsII
ENR498FEExamPreparation
ENR460EngineeringEconomy
ENR488SeniorDesign
ENR470EngineeringEthics
EME474FundamentalsofHeatandMassTransfer
TECHNICALELECTIVES:
EME404MechanicalEngineeringInternship
EME455FluidPowerLab
EME461Vibrations
EME462FiniteElementMethod
EME406AdvancedSystemsModeling
ENR450Robotics
ElectricalEngineering DegreeRequirements
MAT209CalculusI
CHE111GeneralInorganicChemistryI
ENR101IntroductiontoEngineering
ENR200ComputerApplicationsinEngineering
ENR210ComputerAidedMeasurements
PHY251EngineeringPhysicsI
PHY251LEngineeringPhysicsILab
MAT210CalculusII
MAT211CalculusIII
PHY252EngineeringPhysicsII
PHY252LEngineeringPhysicsIILab
ENR304ComputerAidedAnalysis
EEL206CircuitsI
EEL206LCircuitsILab
ENR280EngineeringDesignLabI
PHY253EngineeringPhysicsIII
ENR281EngineeringDesignLabII
EEL313CircuitsII
EEL313LCircuitsIILab
MAT334DifferentialEquations
ENR338AdvancedEngineeringMathematics
EEL321ElectronicsI
EEL321LElectronicsLaboratoryI
EEL314SignalsandSystems
EEL314LSignalsandSystemsLab
EEL316Electric&MagneticFields
EEL421ElectronicsII
EEL421LElectronicsLaboratoryII
ENR405ControlSystems
ENR405LControlSystemsLab
EEL462DigitalSystemswithLab
EEL409PowerSystemsI
EEL452EmbeddedSystems
EEL452LEmbeddedSystemsLab
EEL480ElectricalEngineeringDesignProject
ENR419EngineeringDataAnalysis
EEL4xxTechnicalElective1
EEL461AdvancedProgramming
ENR498FEExamPreparation
EEL4xxTechnicalElective2
ENR488SeniorDesign
ENR460EngineeringEconomy
ENR470EngineeringEthics
EEL4xxTechnicalElective3
TECHNICALELECTIVES:
EEL401ElectricDrivesLab
EEL404ElectricalEngineeringInternship
EEL410PowerSystemsII
ENR450Robotics
NEW ENGINEERING BUILDING
ThedemolitionofourengineeringfacilitiesoncampusbeganinMayassoonasthe

studentshadleftforthesummer.
Thenewbuildingconstructionwilltake placeoverthecourseofayearwithcompletioninJuneofnextyear.Wemoved theentireengineeringschool,includingoffices,labequipment,andclassrooms,toour newtemporarylocationattheBismarckBurleighPublicHealthBuildinginBismarck.
Wewillbeusingthelowerlevelofthatbuildingtoholdourclassesandlabsforthenext twosemestersuntilFall,2020,whenourpermanentfacilityoncampusiscompleted.We haveretainedalaboratoryfacility,classroom,

andmachineshoponcampuswherewewill continuetoholdsomeofourcoursesandstore ourlargeequipmentsuchasUniversalTestingMachines,Mills,Lathes,CNCRouters, aswellasourwoodshopandmetalsshop.

Theelectronicslaboratories,computerprogramminglab,aswellasconstructionmanagementlabswithlargescaleblueprints printerandscannerswillbelocatedinthe temporaryfacilityandallofourJuniorand Seniorlevelcourseswillbeheldthere.The FreshmancourseswillcontinuetobeheldentirelyoncampuswhiletheSophomorelevel coursesaresplitbetweencampusandthe Bismarckfacility.Theengineeringpartof thetemporarybuildingisentirelycontained onthelowerlevelandtheupperfloorswill continuetobeoccupiedbycompaniesand variousotherorganizations.Abusservice hasbeenarrangedtotransportthestudents toandfromthemaincampus.Wealsohave akitchenanddiningroomavailableinthe spaceforstudentstohangoutandeatbetween classes.Ofcourse,beingrightindowntown Bismarck,thereareplentyofrestaurantsnear byforstudentstowalktoaswell.
Thekidsenjoyedplayingwiththescienceandengineeringfocusedhands-ondisplaysforacoupleofhoursbeforegoingtothe game.Onethingthatwediscoveredduring thiseventaswellasotherswehaveattended, suchas DiscoverEngineering,isthatyoung childrenrespondbesttohands-onitemsand italsohelpsiftheactivitiesinvolveseveral kidsatthesametime.Forexample,oneof theitemsthatwasverypopularatourtable wasplasticwaterbottlesthatwefilledwith waterandironfilings.Wehadseveralpowerfulneodymiummagnetsthatthekidscould thenusetomold,move,andshapethefilings throughthesideofthebottle.Thisallowed themtoseethemagneticfieldfromthemagnetsandlearnhowtomanipulatethingswith it.WealsohadanelectricgeneratorbutI thinkweneedtoputabitmoreworkintothat onetomakeitmoreinterestingtokids.One ofourgoalsforthecommingschoolyearis toputsometimeintodesigningbetterdisplay activitiesandgive-awayswhichwillhelpthe youngergenerationsbecomemoreinterested inscienceandengineering.

IDENTIFYTHIS PHOTOGRAPH ByMATTHEWSCERBAK
AnyonewhoisinterestedintheFibonacci SequenceorFractalswillfindthisphotograph absolutelyfascinating.Whatisit?

Bysymmetry,the CofM mustlieon theangularbisectoroftheslice.
TheeventwasheldattheBismarckLarks baseballgamewhereanumberofdifferent companiesandorganizationsweretheretoexplainthescienceandtechnologyofenergyto elementaryschoolstudentswhowerebusedin toseethebaseballgame.

The ONE-HANDEDPIZZAGRAB isacommonforagingtechnique,performedbyundergraduatestudentsaroundtheworld,inwhich onegraspsapizzaslicedirectlybeneathits centreofmass[CofM]soastoreducethelikelihoodofthetoppingsslidingoff.Ourgoalis toascertainthelocationofthe CofM ofapizza slice,employingthefollowingmodel.
Theentirepizzahastotalmass MT , radius R,area A = πR2,andaneffectivelyconstantarealmassdensity, σ0
Thesliceisacircularwedgewithangularwidth Θ0 =2 × θ0 andradius R
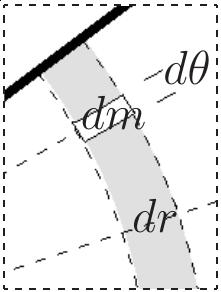
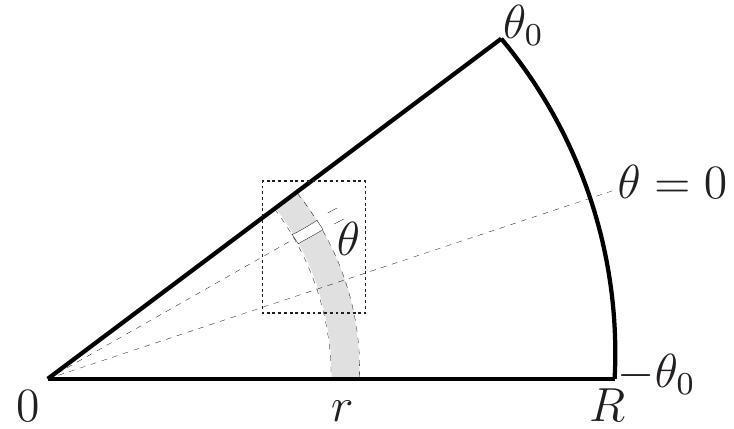
(a) Computethemassofthesliceofthe pizza.[HINT: dm = σ0 dA = σ0 rdrdθ]
(b) Re-expressthemassofthesliceinterms of MT
(c) Computethemass-weighteddistanceof thepizzaelementsprojectedontothe angularbisectoroftheslice.[HINT: Masselementswiththesame r,butdifferent θ,do NOT contributeequallytothe mass-weightedsum.]
(d) Determinethemass-weightedaverage positionofthepizzaelementsbydividingtheresultin(c)bythemassofthe slice,determinedin(a).
(e) Confirmyourresultbytakingthelimits:
(i) Θ0 → 0,(ii) Θ0 → π,(iii)
Θ0 → 2π
FPGAVERILOGPROBLEM ByTERRYPILLING
BuildacombinationalcircuitforanFPGA writteninVerilog.Thecircuitshouldhave fourinputs, in[3:0],andthreeoutputs: out and:outputofa4-inputANDgate, out or:outputofa4-inputORgate,and out xor:outputofa4-inputXORgate.
Hereisthestartofthesolution,trytocompleteit:
moduletop_module( input[3:0]in, outputout_and, outputout_or, outputout_xor );
Atitsworststate,theangleofinclinationoftheleaningtowerofPisareachedof 5.5degreesfromtheglobalvertical(y-axis) andstayedinequilibriumwithoutcollapsing.
Inthisproblemassumethat:
-thetowerreaches60mhigh.
-thetowerisahollowcylinderforthefirst7 floorswiththecross-sectionshown.
-thetopfloorishalftheweightoftheother floors(i.e.heightoftheflooristhesameas therest,butitsvolumeishalfoftheothers.)
-thetoweriscompletelymadeofTuscanmarblethathasadensityof 2600kg/m3
-theweightofthetoweractsatthecenter ofgravitywiththecoordinates x =12mand y =30m.
-alateralwindforceof1620kNactsatthe mid-height(y=30m)ofthetower,fromleftto right.
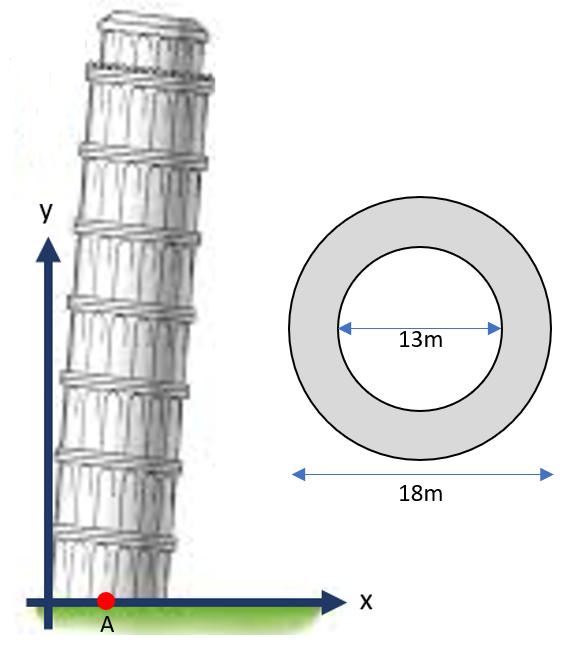
-allreactionsatthebaseareactingafixed supportatpointA(x=9m,y=0).
Determine:
(a) Volumeofthetower’smarbleshellusing thecross-sectiongiven.
(b) Massofthetower’smarbleshell
(c) Totalweightofthetower’smarbleshell
(d) Alloftheunknownreactionsatthebase thatwouldkeepthistowerinequilibrium.
trytopredicttoofarahead.ThethingIfind mostinterestingaboutthesesystemsisthat theyarebasedon deterministicequations.In otherwords,ifweknewthecurrentstateof thesystem exactly wecouldusetheequations topredictthefuturestateexactlyaswell.With chaoticsystems,thesensitivitytosmallvariationsintheinitialconditionsiswhytheybecomeupredictable.Ourtechnologycannever measurethecurrentstateofanysystemexactlydowntoinfinitelymanydecimalplaces. Inthecaseofthedoublependulumwecan’t gettheexactinitialangleandevenbeingoff byateenytinyamountinmeasuringtheinitialanglewillresultinahugedifferencein thefinalpositionafteronlyashorttime.With theweather,thesituationisevenworseinthat therearejusttoomanyparticlesmakingup theatmosphereforustohaveanyhopeof measuringtheirinitialstates.
Commercialaircraftareaerodynamically stable,sothatasmallturbulentnudgewont pushtheplaneoutofalevelflightpath.On theotherhand,thisstabilityissomewhatof aninconveniencetofighterpilotswhoprefertheiraircrafttomakerapidchangeswith minimaleffort.Modernfighterjetsachieve greatmaneuverabilitybyvirtueofbeingaerodynamically unstable theslightestnudgeis enoughtodrasticallyaltertheirflightpath. Theyareequippedwithon-boardcomputers whichconstantlyadjusttheflightsurfacesto cancelouttheunwantedchaoticeffects,leavingthepilotfreetoexploitthesensitivityand makerapidmovesinshorttimeperiods.
SowhatisthevalueofstudyingChaos Theoryifwecannevergetexactpredictions? Well,itturnsoutthattherearepatternswhich emergeandallowustoextractvaluableinformationaboutthesystemwithoutneeding toknowexactinitialnumbers.IntheLorenz modelofatmosphericconvectionwefindregionsofthesolutionspacedubbed StrangeAttractors.Theseareregionswherethesystem willhaveahigherprobabilityoffindingitself evenwithintheoverallchaos.
atjusttherighttimetoproduceahealthy heartbeat.Fortunately,thisintricatestateof synchronizationisanattractorofthesystem –butitisnottheonlyone.Ifthesystemis joltedsomehow,itmayfinditselfonanaltogetherdifferentattractorcalledfibrillation, inwhichthecellsconstantlycontractandrelaxinthewrongsequence.Thepurposeof adefibrillator,thedevicethatappliesalarge voltageofelectricityacrosstheheart,isnot to“restart”theheartcellsassuch,butrather togivethechaoticsystemenoughofakickto moveitoffthefibrillatingattractorandback tothehealthyheartbeatattractor.
Whatwewouldliketodointhisarticleisexploretheattractorofachaoticsystem.Wewillstartbysimulatingsuchasystemonacomputerandthenwewillbuild anelectriccircuitthatmodelsthesamesystem.Theattractorthatwearegoingtoexplorehereisafamousonecalledthe“Lorenz Attractor”namedaftermeteorologistEdward Lorenzwhofounditwhilestudyingweather patterns.TheLorentzAttractorisdescribed bythefollowingsystemofdifferentialequations:
dx
dt = s(y x)
dy
dt = rx y xz
dz
dt = xy bz
where s, r,and b areconstantparameters. Asusual,thewaywewillsimulatedifferentialequationsistofirstdiscretizethetime intostepsofsize ∆t andwriteourdifferential equationsas
∆x
∆t = s(y x)
∆y
∆t = rx y xz
∆z
∆t = xy bz
Chaostheoryisabranchofmathematicswhichexploresthebehaviorofdynamical systemsthatarehighlysensitivetoinitialconditions.Thissensitivityresultsinunpredictivebehavioreventhoughtheequationsthemselvesarecompletelydeterministic.ThesubjectofChaoshasbeenmadepopularamong thegeneralpublicinHollywoodmoviessuch as TheButterflyEffect, SlidingDoors, About Time, JurasicPark,andothers.
Intheconventionalequationsofphysics, ifwetakemeasurementsofthestateofasystem–forexample,thepositionandvelocity ofaprojectile–wecanverypreciselydeterminewhereitwillbeinthefuture.Thisis behaviorthatwehavecometoexpectfrom largeclassesofsystemsinnatureandis,in fact,thereasonwhyscienceworks!Ifknowingthecurrentstateofasystemdid not allow predictionoffuturestateswewouldnothave discoveredthelawsofnatureinthefirstplace.
Ontheotherhand,wealsoseechaotic systemsinnature.Examplesarethedouble pendulum,thelogisticmodelofpopulation growth(forcertainparametervalues),andthe LorenzAttractormodeloftheweather.Even thesolarsystemisachaoticsystemifyou
Sothekeytounlockingthehiddenstructureofachaoticsystemistodetermineitspreferredsetofbehaviors–itsattractors.The mathematicianIanStewartusedthefollowingexampletoillustrateanattractor.Imagine takingaping-pongballfaroutintotheocean andlettingitgo.Ifreleasedabovethewateritwillfall,andifreleasedunderwaterit willfloat.Nomatterwhereitstarts,theball willimmediatelymoveinaverypredictable waytowardsitsattractor,theoceansurface. Oncethereitclingstoitsattractorasitisbuffetedtoandfroinaliteralseaofchaos,and quicklymovesbacktothesurfaceiftemporarilythrownaboveordumpedbelowthewaves. Thoughwemaynotbeabletopredictexactly howachaoticsystemwillbehavemomentto moment,knowingtheattractorallowsusto narrowdownthepossibilitiesanditalsoallowsustoaccuratelypredicthowthesystem willrespondifitisjoltedoffitsattractor.
Oneimportantapplicationofthisliesin understandingyourheartbeat.Themillionsof cellsthatmakeupyourheartareconstantly contractingandrelaxingseparatelyaspartof anintricatechaoticsystemwithcomplicated attractors.Thesemillionsofcellsmustwork insync,contractinginjusttherightsequence
where ∆x = xn+1 xn isthechangein x duringthe nthtimeinterval ∆t andsimilarlyfor ∆y and ∆z.Oursystemofequationsthenbecomesasystemwecaniterateonacomputer:
xn+1 = xn + s(yn xn)∆t
yn+1 = yn +(rxn yn xnzn)∆t
zn+1 = zn +(xnyn bzn)∆t HereisacomputerprogramwritteninC whichsimulatestheseequations:
lorenz-attractor.c
//simulatingtheLorenz attractordifferential equations:
//dx/dt=s(y x)
//dy/dt=rx y xz
//dz/dt=xy bz
#include < stdio.h>
#include < stdlib.h>
#define dt0.001
#define TIME100.0
#define X01
#define Y01
#define Z01
int main( int argc, char ∗∗ argv ) { if (argc!=4) { fprintf(stderr,”USAGE:%ss
rb \ n”,argv[0]); return 1; }
float s=atof(argv[1]); float r=atof(argv[2]); float b=atof(argv[3]); float t,x=X0,y=Y0,z=Z0; for (t=0.0;t <TIME;t+=dt) {
x=x+s ∗ (y x) ∗ dt;
y=y+(r ∗x y x ∗ z) ∗ dt; z=z+(x ∗y b ∗ z) ∗ dt;
fprintf(stdout,”%f \ t%f \ t%f \ t %f \ n”,t,x,y,z);
} return 0; }
Ifyouruntheprogramwithparameters s =10, r =28 and b = 2 66 andplottheresultingoutputas z versus x youfindthefollowingpicturewhichshowstheLorenzAttractor.

screen.Asstudentsinourelectricalengineeringprogramdiscoverintheirelectronics courses,differentialequationscanbesolved byoperationalamplifiers.Thisisoneofthe mainusesofopampsandcomesfromthefact thattheycanbesetupasdifferentiators,integrators,andsummers.Weusethesewhenwe designcontrolsystemscircuitsandallowus tocontroleverythingfromchemicalrefineries andthermostatstocarsandfighterjetsusing them.Itallcomesdowntodifferentialequations.
SohowdowerecreateoursystemofdifferentialequationsfortheLorenzAttractor usingoperationalamplifiers?Let’sreview someelectronicstheory.Hereisanoperationalamplifierwiredasanintegrator.
Ifwenowwiretwosourcestotheintegrator inthefollowingway x
y x wegetaasummerintegratorcircuitwhich solvesthefollowingdifferentialequation
dx dt = s(y x)
Youseethattherearetworegionsaround which x(t) and z(t) cyclebutthattheactual values,atanygiventimestep,areunpredictablychaotic.
Fortheremainderofthisarticle,wewant togetoutourcircuitboardsandseeifwecan getthispicturetoshowuponanoscilloscope
Thetheoryofidealopampstellsusthatno currentflowsintotheopampthrougheither the + orthe terminals.Hencethenodevoltagemethod(i.e.currentconservation)atthe negativeinputgivesthecurrentthroughthe capacitoras iC = a/R.Theelementlaw forthecapacitorgives
iC = C dx dt (1) andso,withtheopampwiredlikethis,the outputvoltage x satisfiestheequation:
WORD PUZZLECOMMEMORATINGTHE 50TH ANNIVERSARYOF THE 1969APOLLO 11MOON LANDING
YTNECSERCBCYTMGRWDGENB
SGMVDZGNOLARBNBHOISOAI
VAKYETIMEUPIAWOUBPIRVW
RETROREFLECTORGBITTLER
JCIUDTTZIWORNLOLASUSOW
YFOLRQTZLAMEAUCIIATCON
FTAMDNTUAXTSSEVBPIKOIM ONIDMRVBGIRMNARBNEDWIJ
ROLLQUARANTINEDGTSDCQJ TIVIITNSQGDALJHDTEHYAW
YTLNTULIEXCTROYOSATCOM
SCDIITQQOINTUNCGEWYQGJ EAJYELLNRNSSEKRLRWVWGR
VRLAONPEAWEMDERDNUHROU
EFORMLMPWRIXORCEENMCMH NEOMAAFVEETLDMAOOEOMGF
WRPSHELKIZSXCGEXLLRIAT SZLTEFYDNEDTLDITULEHIN IZRRSSIDRITEGNOMELIDTL XOIONGAFOIPNLWBVYRENBE
NVHNAMSHTONBAIPAESYDSY RMWGAMKUPHGYAMRLDRRMQW
1. firstastronautfirstname(4letters)
2. secondastronautfirstname(5letters)
3. thirdastronautfirstname(7letters)
4. secondastronautnickname(4letters)
5. secondastronautlastname(6letters)
6. thirdastronautlastname(7letters)
7. landingsitename(11letters)
where s =1/RC.Whichisexactlythefirst ofthedifferentialequationswewanttosolve fortheLorenzAttractor.Iwillleaveitasan exerciseforthereadertofigureouthowto gettheothertwodifferentialequations.The onlyaddedcomplicationisthattheyinvolve theproductsofvoltages xz and xy.Toget theseweuseanintegratedcircuitcalledan analogmultiplier.TheonethatIusediscalled anMPY634producedbyTexasInstruments andyousimplyinputthetwovoltagesthat youwanttomultiplyandtheoutputwillbethe productofthevoltagesdividedbyascalefactorof10.Youcantheninputthisintoopamp integratorssimilartotheonesaboveandfix theresistorandcapacitorvaluestogiveyou theparameters s =10, r =28,and b =2 66 Finally,youtaketheoutputs x and z andfeed themintoanoscilloscopesetto x y mode andyouwillseetheLorenzAttractorappear onthescreen.
8. commandmodulename(8letters)
9. mainrocketengine(7letters)
10. astronautwasalsoanengineer(6letters)
11. abbreviationforcapsulecommunicationspersonnel(6letters)
12. lunarmodulename(5letters)
13. presidentmadephonecallfromovalofficetolunarsurface(5letters)
14. warprotestsatHarvard3monthsbeforemoonlanding(7letters)
15. releasedtheirfirstalbumtheyearofthemoonlanding(2words,10letters)
16. giantoutdoorconcert1monthaftermoonlanding(9letters)
17. numberofdaysjourneytothemoon(5letters)
18. shipthatpickedupthecrewaftersplashdown(6letters)
19. numberofpoundsofmoonrocksbroughthome(2words,11letters)
20. deviceleftonthemoontotakeseismicmeasurements(11letters)
21. deviceleftonmoontopreciselymeasureEarth-Moondistance(*****reflector)
22. engineeringcompanydesignedandbuiltthelunarlander(7letters)
23. engineeringcompanydesignedandconstructedtheCommandServiceModule(3letteracronym)
24. engineeringcompanydesignedandconstructedthesecondstageoftheSaturnVrocket(21letters,samecompanyasabove)
25. engineeringcompanydesignedandbuiltthelargeengineontheSaturnV (10letters)
26. engineeringcompanybuilttherealtimecomputersforMissionControl(3 letteracronym,computers)
27. engineeringcompanydesignedandbuildthethirdstageoftheSaturnV(7 letters,nowcalledMcDonnell-Douglas)
28. engineeringcompanydesignedandbuildtheastronautspacesuits(ILC D***r)
29. engineeringcompanydesignedandbuilttheguidancesystemsforthelunar module(2letters,GeneralMotors)
30. engineeringcompanydesignedandbuilttheEngineCompartmentConditioningSystemfortheSaturnVsecondstage(8letters,blimp)
31. engineeringcompanydesignedandbuiltthespacekitchenandfreezedried food(9letters)
32. engineeringcompanydesignedandbuiltthelunarcamera(12letters,electric corporation)
33. engineersandgeologistsfromthisorganizationmadethefirstdetailedmaps ofthelunarsurface(4letteracronym)
34. four*******thousandengineersworkedonthemoonlandingproject
35. earthgravityisthismanytimeshigherthanmoongravity
36. howdidthethreeastronautsoftheApolloOnemissiondiein1967?(4 letters)

37. orangedrinkastronautsdrankwhileinspacefortheApollomissions(4letters)
38. nameofthecraternearthelunarlandingsiteforApollo11(l*******st)
39. whodidBuzzAldrinpunchinthefacein2002?(2words,justGoogleit)
40. ThisastronautwasanEagleScout?(9letters)
41. BuzzAldrinperformedthisreligiousritualonthemoon(9letters)
42. theastronautswere***********fortwoweeksafterarrivingbackonEarth (11letters)
43. popewhoblessedthecrewmenofApollo11(****VI)
44. differentshapesofthemoonarecalled(6letters)
45. onceina****moon(4letters)
46. atypeofmoonshape(8letters,thin)
47. moonphasemeaning“gettingbigger”(6letters)
48. moonphasejustafterfirstquarter(7letters)
49. discoveredcratersonthemoon(7letters,b.1564)
50. mooncoverssun(7letters)
51. scatteringofsunlightintheEarth’satmosphere(namedafterLord R******h)
52. bendinglightthroughmaterial(10letters)
Haveyoueverwondered,whiledriving underbridgesoroverpasses,whyyousee spalledconcreteandexposedrebar?Inother words,whymodernconcreteseemstobreak downafteronlyfiftyyearswhileRomanconcretestructuresarestillstandingafter2,000? Engineersandscientistshavepuzzledover thisquestionforalongtime.WhydoesRomanconcretegetstrongerwithtimeunlike modernconcrete?Progressanyone?
ThepreciseformulationofRomancement,thecriticalelementinconcrete(aggregateandwaterbeingtheothertwoingredients)hasactuallybeenapuzzleformuch longerthanyoumightthink.FewpeoplerealizethatafterthefallofRomein476AD, knowledgeoftheingredientsofRomancementwerelosttotime,andwesterncivilizationwaswithoutconcreteasabuildingmaterialforover1,000years.ThegreatcathedralofFlorence,SantaMariadelFiore,which soughttobestoneofthemostbrilliantconcretestructuresofalltime-theRomanPantheon-bybuildingitsdomejustafewfeet indiameterlargerthanthedomeofthePantheon,wasdoneentirelyinbrickmasonry. Thatwasin1420,andserioustinkeringwith cementmixturesdidnotbeginuntilthe16th Century.ModernPortlandcementcameinto useinthe1850’s,nottoolongbeforethe AmericanCivilWar,butthesedevelopments wereindependentofanyknowledgeofwhat theRomansusedtomaketheirconcrete.
ScientistsdidknowonethingaboutRomanconcrete:itcontainedaveryrarehydrothermalmineralcalledaluminumtobermorite(Al-tobermorite).Graduallydevelopingoverdecadesandthencenturies,itwas thismineralstructurethatgaveRomanconcreteitsstrength.Al-tobermoritecouldbereproducedinalaboratory,butthequestionwas
53. oceaneffectcausedbymoon(5letters)
54. darksideofthemoonalbum(2words,9letters)
55. themoonisthe*****largestsatelliteinthesolarsystem(5letters)
56. satellitecommunications(6letterabbreviation)
3DFOOTPRINTSONTHE MOON
Eachofthepicturesabovewastakenfromaslightlydifferentpositiontocreateastereo-graphicimage.Squintyoureyesandtryto focusthetwopicturessimultaneouslyuntiltheymergeintoasingle3Dimageoftheastronaut’sfootprint.Itisverycoolwhenyoumanage todoit.
howwasitincorporatedintoconcrete,accomplishedinthefield,andonaRomanjobsite?
Theanswer,discoveredbyscientistsin 2017,turnedouttobesurprisingly-ifnot stunninglysimple,thekindofthingthatis missedalthoughitwasthereinfullviewall along.TheRomansusedseawaterinstead ofregularwaterintheirconcretemix.The seawaterpercolatedthroughthecementmatrixandreactedwithvolcanicashandcrystalstoformAl-tobermoriteandaporousmineralcalledphillipsite.Sincethesetwomineralstakecenturiestoform,scientistsandengineersaretryingtodevelopformulationsthat takemuchlesstime.SaltwaterpresentsproblemswiththeironreinforcinginmodernconcretewhichissomethingtheRomansdidnot use(thismakestheirachievementsevenmore remarkable).ThePantheonwascompletedin 126AD,butperhapsbefore2,000yearshave elapsed,we’llseeamodernversionofRoman concrete,aconcretethatnotonlylastsbutgets strongerwithtime.
moduletop_module( input[3:0]in, outputout_and, outputout_or, outputout_xor ); assignout_and= in[0]&in[1]&in[2]&in[3]; assignout_or= in[0]|in[1]|in[2]|in[3]; assignout_xor= in[0]ˆin[1]ˆin[2]ˆin[3]; endmodule
SOLUTIONTO STATICS PROBLEM
ThephotographisaplantcalledaRomanescoCauliflower.Isawitatafarmers marketinFairbanks,Alaska.Iaskedtheproduceriftheycouldbringbacksomelargepristineonesthefollowingweek,whichtheydid, andsoIboughtonetookithometophotograph.Theyalsoinvitedmetocomeoutto theirfarmandphotographanythingIliked, andsoIdidthatonseveraloccasions.They hadalargevarietyofbeautifulandunusual vegetables,plants,andflowers.Wikipedia saystheRomanescoCauliflowerhasbeencultivatedinItalysincethethe16thCentury.I wasstunnedbythecrossbetweenmathematicsandvegetableinthisplant,which,bythe way,tastesexactlylikecaulifloweralthoughit istechnicallyinacategoryallit’sown.Itis alsoreferredtoasRomanescoBroccoli.
(a) Vfloor =(π92 π6 52)(60m/8)=913m3
ΣVTotal =(Vfloor × 7)+(Vfloor /2)=6848m3
(b) mtotal = Vtotal × ρ =6848m3 × 2600kg/m3 =17, 804, 800kg
(c) W = mg =1 75 × 105kN
(d) ΣFx =0=(1620kN )(30m)+ Ax
⇒ Ax =1620kN ←
ΣFy =0= Ay 1 75 × 105kN
⇒ Ay =1 75 × 105kN ↑
ΣM =0=(1620kN )(30m)+(1 75 × 105kN )(3m)+ MA
⇒ MA =573, 600KNm



