1. What is the domain of ?
ANSWER: a
2. What is the domain of ?
ANSWER: d
3. What is the domain of ?
ANSWER: c
4. What is the domain of ?
a. all real numbers except
b. all real numbers except
c. all real numbers except
Copyright Macmillan Learning. Powered by Cognero. Page
Name: Class:
Chapter 1
d. all real numbers
ANSWER: b
5. If , compute
a. –15
b. –3
c. 0
d. 3
ANSWER: a
6. If , compute . a.
ANSWER: b
7. If , compute .
a. 0 b.
c. 6
d. undefined
ANSWER: b
8. If , compute . a.
Date:
ANSWER: d
Copyright Macmillan Learning. Powered by Cognero. Page 2
9. If , compute
b
10. If , compute , where . a. 1 b. 5
d. 5h ANSWER: b
11. If , then , where .
c
12. What is the range of ? a.
c
Copyright Macmillan Learning. Powered by Cognero. Page
13. What is the range of ? a. b. c.
d.
ANSWER: d
14. Define h(x) by =
ANSWER: 2
15. Does this equation determine y as a function of x? Explain.
ANSWER: No. Observe that , so . So, for instance, the input x = 0 has two outputs, namely, y = 3 and y = –3. So, this equation cannot determine y as a function of x.
16. Does this equation determine y as a function of x? Explain.
ANSWER: Yes. Solve for y as follows:
Note that for any , there is exactly one output y. So, the equation determines y as a function of x.
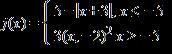
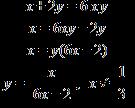
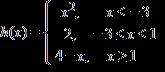
17. Define j(x) by
ANSWER: 3
Copyright Macmillan Learning. Powered by Cognero. Page 4
18. If , then the average rate of change of f(x) over the interval [–2, 5] is
a. positive.
b. negative.
c. zero.
d. unable to be determined from this information.
ANSWER: b
19. Calculate the average rate of change for on the interval [–5, 20].
ANSWER: 5
20. Calculate the average rate of change for on the interval [0, 6].
ANSWER: 0
21. Calculate the average rate of change for on the interval [–8, 8].
ANSWER:
22. What are the units associated with the average rate of change for the function described in this scenario: H(z) is the length (in inches) of a corn stalk z days after it sprouts.
ANSWER: inches per day
23. What are the units associated with the average rate of change for the function described in this scenario: S(r) is the volume of a sphere (measured in cubic meters) whose radius r is measured in meters.
ANSWER: cubic meters per meter, or square meters
24. Compute the average rate of change of on the interval
ANSWER: c
25. Compute the average rate of change of on the interval [1, 1 + h]. a.
Copyright Macmillan Learning. Powered by Cognero. Page 5
ANSWER: b
26. Compute the average rate of change of on the interval [2, 2 + h].
ANSWER: d
27. If f(3) = f(4), what must be the average rate of change of f(x) on the interval [3, 4]?
ANSWER: 0
28. Refer to the graph here. On what interval(s) is this function increasing?
Copyright Macmillan Learning. Powered by Cognero. Page 6
Copyright Macmillan Learning. Powered by Cognero. Page
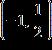
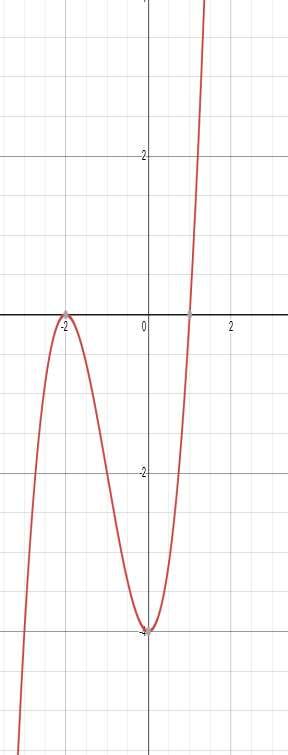
ANSWER: b
29. Refer to the graph here. On what interval is this function concave down?

Copyright Macmillan Learning. Powered by Cognero. Page
ANSWER: a
30. Which of these statements about the graph is true?
Copyright Macmillan Learning. Powered by Cognero. Page 9
a. The function is decreasing on
b. The function has a local maximum at x = –2.

c. The local minimum of this function is 0.
d. The function is always concave up.
Copyright Macmillan Learning. Powered by Cognero. Page
ANSWER: b
31. Refer to the graph here. On which of these intervals is the average rate of change of this function positive?
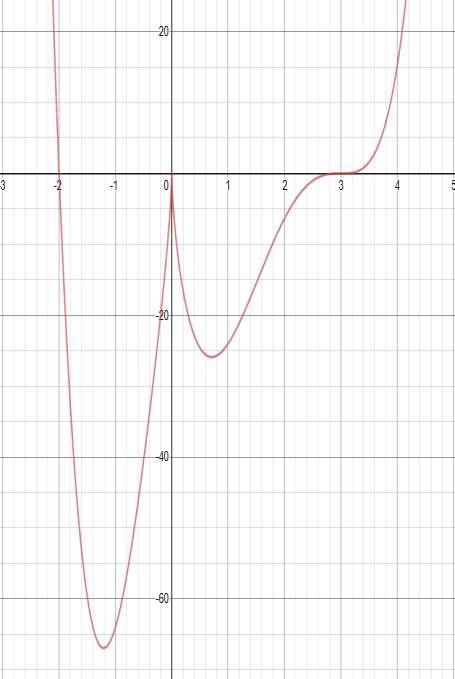
ANSWER: d
Copyright Macmillan Learning. Powered by Cognero. Page 11
32. Refer to the graph here. At which value of x does this function have a local minimum?
a. –0.8
b. –2
c. 0
d. 3
ANSWER: a
33. Refer to the graph here. On which interval(s) is the function decreasing?
Copyright Macmillan Learning. Powered by Cognero. Page 12

ANSWER:
34. Refer to the graph here. At what x-value(s) approximately does this function have a local minimum?
Copyright Macmillan Learning. Powered by Cognero. Page

ANSWER: –1.2, 0.7
35. Refer to the graph here. What is the approximate absolute minimum of this function on the interval shown?
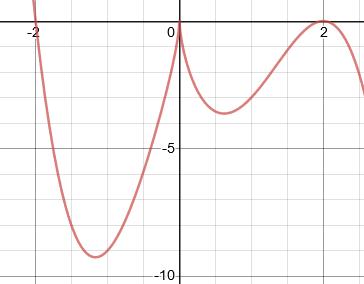

ANSWER: –9.2
36. Refer to the graph here. At what x-value(s) approximately does this function have a local maximum on the interval [–10, 5]?
Copyright Macmillan Learning. Powered by Cognero. Page
ANSWER: –9, –3, 4
37. Refer to the graph here. What is the approximate absolute maximum of this function on the interval [
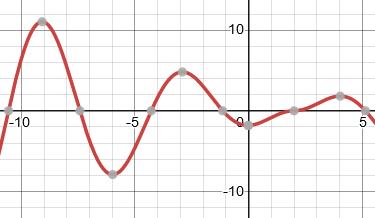

10, 5]?
ANSWER: 10.5
38. Compute the limit: as a. 0 b. 1
d. ANSWER: a
39. Compute the limit: as
0 b. 1
ANSWER:
Copyright Macmillan Learning. Powered by Cognero. Page 15
40. Compute the limit: as
a. 1
b. 0
c.
d.
ANSWER: d
41. Compute the limit: as
ANSWER:
42. Compute the limit: as
ANSWER: 0
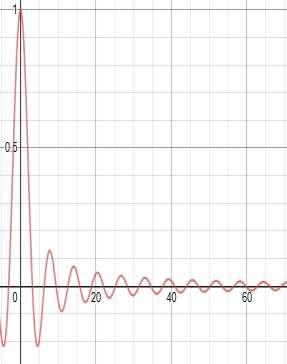
43. Estimate the limit of f(x) as from the graph: a. 0

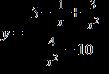
Copyright Macmillan Learning. Powered by Cognero. Page 16
Chapter 1
b. 1
c. 60
d.
ANSWER: a
44. Use the fact that the limit of f(x) as is –3 to compute the limit as of .
a. 0
b.
c.
d.
ANSWER: c
45. Use the fact that the limit of f(x) as is 5 to compute the limit as of
ANSWER: –2
46. Use the fact that the limit of f(x) as is 8 to compute the limit as of
a.
b. 1
c. 0
d.
ANSWER: a
47. Compute the limit: as
c.
d.
ANSWER: d
Copyright Macmillan Learning. Powered by Cognero. Page 17
48. Compute the limit: as
ANSWER: c
49. Compute the limit: as
ANSWER: d
50. Compute the limit: as
ANSWER: c
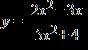
Copyright Macmillan Learning. Powered by Cognero. Page 18
