Theory
2.1PROBLEMS
2.1 From(A.7),theHamiltonianforafreecomplexscalarfieldis
Showthat
Assumethat H isnormalordered.
Solution:From(2.93)andusing
wefind
2.2 TheCMdifferentialandtotalcrosssectionsfortheelasticscatteringofaHermitian scalarofmass m withpotential(2.22)isgivenin(2.59)and(2.61).Choose m =0 5GeV, λ =0 3,and κ =1 2GeV.PlottheCMdifferentialcrosssection dσ/d cos θ inunitsof fm2 =10 26 cm2 asafunctionofcos θ for s =5m2,6m2,and7m2,andplotthetotalcross sectionasafunctionof √s for2m< √s< 3m.Useanyconvenientplottingprogram.
Solution:Wehave t = 2p 2(1 cos θ),u = 2p 2(1+cos θ) with p = s 4m2/2
Also,
TheStandardModelandBeyond
Thesemustbemultipliedby ( c)2 =(0 197 GeV-fm)2,toconvertfromGeV 2 tofm2
Left: dσ/d cos θ inunitsoffm2 asafunctionof cos θ for s =5m2 , 6m2,and 7m2 (from uppertolower).Right: σ(s) inunitsoffm2 asafunctionof √s
2.3 Derive(2.64)forthespecialcase m1 = m3 =0and m2 = m4 byLorentztransforming (2.57).Hint:usethefactthat σ, s,and t areinvariant.
Solution:Inthelab,using(2.42)and(2.46),
and
whileintheCM
But σ isinvariant,so
fromwhichtheresultfollowseasily.
2.4 Considertheprocess π+(p1)π (p2) → π+(p3)π (p4),with p1 = p3 and p2 = p4,in thetheoryofacomplexscalarfieldwithLagrangiandensitygivenin(2.88)with VI = λ 4 (φ†φ)2 .
AsshowninAppendixB,thetree-levelamplitude Mfi isgivenby
Calculatethisexplicitlyusingthefree-fieldexpressionfor φ0,andshowthat Mfi = iλ.
Solution:ThisissimilartothecalculationfortheHermitianscalarfieldinAppendixB. Here,therelevantmatrixelementis
wherethefree-fieldexpressionsfor φ0 and φ† 0 aregivenin(2.93).Similarto(B.7)onecan movethe a’sand b’sfromthefieldstotheright,andthe a†’sand b†’stotheleft.Theonly survivingtermsinvolvethecommutatorswiththe a3,b4,a† 1,and b† 2.The δ3(p ) functions eliminatethemomentumintegrals,andthe (2π)32Ep factorsfromthecommutatorscancel thedenominatorsinthefields.Therearetwowaystoassociatethe a’sfromthe φ0’swith a† 1,andtwowaystoassociatethe a†’sfromthe φ† 0’swith a3,sooneobtains
2.5 ConsidertheLagrangiandensityin(2.84)for3non-identicalHermitianfields.Calculatethelowestorderdifferentialcrosssectioninthecenterofmassfor φ1(p1 )φ2(p2 ) → φ1(p3 )φ2(p4 )asafunctionof s andtheCMscatteringangle θ forthespecialcase m1 = m2 = m3.
Solution:Therearetwodiagrams,involving φ3 exchangeinthe s and u channels.The scatteringamplitudeis
fi =( iκ)2
and
where(forequalexternalmasses)
and
= 2p2(1+cos
2.6 Supposethattheinteractionpotentialforacomplexscalarfieldwere
(ratherthan λ(φ†φ)2/4),whichis not U (1)invariant.Showthatchargeisnotconserved andcalculatethelowestorderamplitudefor
Solution:Bothoperatorsin φ0 lowerchargebyoneunit,whilethosein φ† 0 raiseitbyone. Thus,thefirsttermlowersthechargeby4.Therelevantmatrixelementis
Thereare 4! waystoassociatethefour φ0 fieldswiththeexternalstates,so Mfi = 24iσ4.
TheStandardModelandBeyond
2.7 ConsiderchargedpionQEDwitha massive photon,i.e.,addtheterm 1 2 M 2 AAµAµ to theLagrangiandensityin(2.133)(with(VI =0).Assume MA > 2m.(Thephotonmass termisnotgaugeinvariant,butthemodelstillmakessenseattreelevel.)
(a)Calculatethedecayratefor γ → π+π inthephotonrestframeattreelevelforan unpolarizedmassivephoton.
(b)Calculatethe π+ angulardistribution dΓ/d cos θ forapolarizedphoton,where θ isthe anglebetweenthephotonpolarizationdirectionintherestframeandthe π+ direction.
(c)Showthatonerecoverstheresultin(a)when dΓ/d cos θ isintegratedovercos θ.
Solution:(a)Definemomentaby γ(k ) → π+(p1) π (p2).Intherestframe, k = p1 + p2 =(MA, 0),p1 =(Ef , pf ),and p2 =(
),where Ef = MA/2 and pf ≡|pf | = M 2 A 4m2/2.Justasforamasslessphoton,thetree-levelamplitudeis Mfi = ie(p1 p2) · (k,λ).Thus,thespin-averagedsquaredamplitudeis
Foramassivevector,
But k · (p1 p2)=0,and (p1 p
Chooseaxessothat =(0, 0, 0, 1),p1
Then,
(c)Integrating +1 1
from(a),i.e.,thedecayrateisindependentof thespindirection.
2.8 Consider π+(p1)π (p2) → π+(p3)π (p4)in massivescalarelectrodynamics,i.e.,with
where A,theanalogoftheelectromagneticfield,isaHermitianspin-0fieldwithmass µ =0. Theanalogofthechargeis g,whichnowhasdimensionsofmass. (a)FindexpressionsforthedifferentialandtotalcrosssectionsintheCMtolowestnontrivialorder,intermsof s, m, µ, g,andcos θ. (b)Definethedimensionlessvariable x = s/m2 ≥ 4,andspecializetothevalues m = g =1
GeV, µ =0 5GeV.Plot dσ/d cos θ vscos θ inunitsof1fm2 =10 26 cm2 for x =4, 4 2, and4.4.Useanyotherplottingprogram.
(c)Plot σ inunitsof1fm2 vs x forthesameparametervaluesandtherange4 ≤ x ≤ 5.
Solution:(a)The ππA vertexis ig ∝−iVI .Thescalarphotoncanbeexchangedin the s or t channels,so Mfi =( ig)2 i s µ2 + i t µ2 , where t = 2p 2(1
4
2 2 ,E = √s 2 , and θ istheCMscatteringangle.Then
(b,c)Plugginginthenumericalvalues,andmultiplyingby ( c)2 =(0 197 GeV-fm)2 to converttheunitsfromGeV 2 tofm2 onecanevaluateandplotthesefunctionsnumerically.
Left: dσ/d cos θ inunitsoffm2 for
and4.4.Right: σ inunitsoffm2 vs x
2.9 Provedirectlyfromthedefiningrelationsthat
Solution:Using(2.155),
γ5 mustbeoftheform C
from example,e.g.,
2.10 Provethe Gordondecomposition formulas
TheStandardModelandBeyond
where u1,2 aretwoDirac u spinorsforaparticleofmass m
Solution:Using(2.161)and(2.170),
andsimilarlyforotheridentities.
2.11 Provetheidentity
Solution:Any 4 × 4 matrixcanbeexpandedintermsof I,γ
,γ
,γ
and
.Inthis case,only γσ and γ
5 willcontribute,sincewehaveanoddnumberof γ matrices.Thus
where A and B dependon µ,ν, and ρ.Clearly,
Theresultfollowsusing(2.172).
2.12 ShowbyexplicitconstructionthatthePauli-Diracandchiralrepresentationsare relatedbyaunitarytransformation,i.e.,thatthereexistsaunitarymatrix U suchthat
(Theextrasigninthe v-spinortransformationisduetoasignconvention.)
Solution: U mustcommutewith γi butnot γ0,soitshouldbeofform
, wheretheexplicitformisobainedbythetransformationof γ0.Thecorrecttransformation ofthespinorsfollowsbyinspection.
2.13 TheangularmomentumoperatorforaDiracfieldcanbewrittenas
(x)+orbital, wherenormalorderingisimplied.Show,inthefreefieldlimit,that J 3 hastheexpected behavior J 3|ψ (p,s1,2) = ± 1 2 |ψ (p,s1,2) ,J 3|ψc (p,s1,2) = ± 1 2 |ψc (p,s1,2) , where ψ and ψc representparticleandantiparticlestates, p isintheˆ z direction(sothat
theorbitaltermsdonotenter),and s = s1 or s2 representspinsinthe ±ˆ z direction.
Solution:Onehas
Usingtheexpression(2.159)forthefreefermionfield
sothat
.Thecalculationissimilarfor ψc exceptfortwocompensatingsigns:
wherethe signisbecause b and b† hadtobeanticommuted.Butthisis
2.14 Derivetheresultsin(2.181)forthehelicityprojectionsinthemasslesslimit.
Solution:Write
Similarly, (
2.15 Weakchargedcurrenttransitionsinvolvethechiralspinors uL(p,s)and vL(p,s)definedin(2.203).Showthatintherelativisticlimitsuchtransitionsmainlyinvolvenegative helicityparticlesorpositivehelicityantiparticles,andestimatethesuppressionfactorfor transitionsinvolvingthe“wrong”helicity.
Solution:Expressionsforthehelicityspinorsinthechiralrepresentationaregivenin (2.193).For E m, λ+ → m/E and λ → 2.Then,applying PL = I 0 00 ,
sotheratesforthewronghelicityaresuppressedby m2/4E2 .
2.16 Showintwowaysthat |u(p2, +)u(
,where u(p, ±)arethehelicity spinorsforamasslessfermion:(a)directlyfromtheformofthespinorsinthechiralrepresentation,(b)usingtracetechniques.
Solution:(a)From(2.195)andTable2.1,
sothat
(b)From(2.181)
2.17 ProvetheFierzidentityin(2.216).
Solution:Expand
Onlythe cν surviveswheninsertedbackinthel.h.s.of(2.216),yielding
But
(Thelaststepwouldyieldanextraminussignforanticommutingfields.)
2.18 Supposeafermion ψ ofmass m interactswithaHermitianscalar φ ofmass µ with LI = hψψφ, where h issmall.
(a)Calculatethespin-averageddifferentialcrosssectionfor ψ(p1)ψ(p2) → ψ(p
)ψ(p4)in theCMintermsoftheinvariants s, t,and u.
(b)Specializeto m = µ =0.Showthatthescatteringisisotropicinthatlimitandcalculate thetotalcrosssection.
Solution:(a)
sothat
(b)
Therefore,
2.19 Consider e (k1) π+(p1) → e (k2) π+(p2)elasticscattering.Showthatthespinaverageddifferentialcrosssectioninthepionrestframeis
where θL istheelectronscatteringangleandwehaveneglectedtheelectronmass.Hint:use (2.224).
Solution:From(2.65)and(2.46),
Butfrom(2.224)andusing
But
sothat
2.20 CalculatetheCMdifferentialcrosssectionfortheprocess e (p1)µ+(k1) → e (p2)µ+(k2)intermsof s = E2 CM ,theCMscatteringangle θ,andthemuonmass mµ. Neglecttheelectronmass.
Solution:Similarto(2.225),
wherethe u spinorsreferto
. Then,
IntheCM,thefour-momentaare
Therefore,
sothat
2.21 VerifytheexpressionsforBhabhascatteringin(2.234)and(2.235).Rewritethefinal resultintermsof s andcos θ
Solution:From(2.233)and(2.208),
whichyields(2.234).Thefirsttermis
andsimilarlyforthesecond.Using(2.174),thethirdtermis
andthesameforthelastterm.Formasslessparticles,
leadingto
whichdisplaysthesingularityfromthe t-channelpoleintheforwarddirection.
TheStandardModelandBeyond
2.22 CalculatethedifferentialcrosssectionforunpolarizedMøllerscattering, e e → e e ,bothintermsoftheinvariantsand θ
Solution:Fromthe t and u-channeldiagramsinFigure2.14
ByacalculationessentiallyidenticaltotheoneforBhabhascattering,
showingthesingularitiesfor θ =0 and π
2.23 Calculatethespin-averagedifferentialcrosssection dσ/d cos θ inthecenterofmass for e (p1)e+(p2) → π (
)π+(p4),andthetotalcrosssection¯ σ.Neglecttheelectronmass butnotthepionmass.Ignorestronginteractioneffects.Theangulardistributionshouldbe proportionaltosin2 θ.Interpretthisresult.
Solution:Thecalculationissimilarto e π+ scatteringand e e+ → ff inSection2.8. Thedifferentialcrosssectionisthesameasin(2.226),withthekinematicvariablesgiven in(2.229)(with mf = mπ).Theamplitudeduetothe s channelphotondiagramis
sothat
wherewehaveused(2.229)and(2.230).Then,
Becauseoftheirvectorcouplings,theinitial e and e+ haveoppositehelicitiesintherelativisticlimit.Thus,the z componentofangularmomentumis ±1.Thepionshavenospin andthereisnoorbitalangularmomentuminthedirectionofmotion,sotheycannotmove inthe ±z direction.Equivalently,theirangulardistributionshouldbe ∝ (|Y 1 1 |2 + |Y 1 1 |2) ∼ sin2 θ,where Y m l isasphericalharmonic.
2.24 (a)ConsidertheMottscatteringprocessinwhichanelectronofmomentum p = βE scattersfromastaticCoulombpotentialofcharge Ze,
Showthattheunpolarized(Mott)crosssectionforscatteringangle θ is
ThelastformulaisthetheRutherfordcrosssection.
(b)SupposetheCoulombpotentialforanelectroninanuclearfieldtransformedasascalar ratherthanasthetimecomponentofafour-vector,i.e.,
Calculatetheunpolarizeddifferentialcrosssection,andcompareitwiththeMottformula.
Solution:(a)Thisisanexampleofscatteringfromastaticsource,with LI (x) in(2.66) givenby
Therefore,from(2.74)
fromwhichtheresultfollows.
(b)CalculationisidenticaltoMottscattering,except
isreplacedby
2.25 Theinteractionofthe Z (amassiveneutralvectorbosonintheelectroweaktheory) withafermion f is
where G,gV , and gA arerealconstants.Calculatethewidthfor Z → ff .Let MZ and m bethe Z and f masses,andset G =1.
Solution:Theamplitudefor Z(p1) → f (p2)f (p3) is
From(2.82)thedifferentialdecayrateis
with 1 3
2.26 TheΛisaheavyspin- 1 2 hyperonthatdecaysinto pπ viathenon-leptonicweak interactions.Thedecayinteractioncanbemodeledby
where gS and gP arecomplexconstantsthatleadrespectivelyto S and P -wavefinalstates.
(a)CalculatethewidthΓandthedifferentialwidth dΓ/d cos θ intheΛrestframefora polarizedΛ,where θ istheanglebetweenˆ sΛ andtheprotonmomentum pp.Usetrace techniques.
(b)Showthat dΓ/d cos θ isnotreflectioninvariantfor e (gP g∗ S ) =0,i.e.,thatitisnot invariantunder pp →−pp, ˆ sΛ → ˆ sΛ
(c)Repeat(a),butuseexplicitexpressionsfortheΛand p spinorsinthePauli-Diracrepresentation.Justifytheclaimthat gS and gP generate S and P -waveamplitudes.
Solution:(a,b)Thedecayamplitudeanddifferentialwidthare
where pf isthefinalstatemomentuminthe Λ restframe,givenbyaformsimilarto(2.83). Summingovertheprotonspin,
ReviewofPerturbativeFieldTheory
whereweused pΛ · sΛ =0.But pp · pΛ = EpmΛ and pp · sΛ = pf cos θ,where θ istheangle between pp and ˆ sΛ.Therefore,
Thisisclearly not invariantunder cos θ →− cos θ (c)TheDiracspinorsinthePauli-Diracrepresentationare
Usingtheexpressionsin(2.164)for
and
whichareobviously S and P wave.Therefore,
wherewehaveused
= I.Taking
wehave
whichreproducestheresultobtainedfromthetracecalculation.
2.27 Avectorresonance Vµ ofmass MV andwidthΓV couplestomasslessfermions a and b withtheinteractionin(F.12)ofAppendixF.Calculatethetotalspin-averagedcross sectionfor aa → bb.Assumethatthepropagatorin(2.129)ismodifiedtotheBreit-Wigner form
andexpresstheresultinaformsimilarto(F.11).
TheStandardModelandBeyond
Solution:The kµkν /M 2 V terminthepropagatorvanisheswhencontractedwiththemassless fermionbilinears.Thetotalcrosssectioncalculationisthenalmostidenticaltotheonefor e+e → ff .Applyingtheobviousmodificationsto(2.232)onefinds
Toputthisintotheform(F.11)wecalculatethespin-averagetotalwidthfor V
withasimilarformfor Γaa.Therefore
wherethebranchingratiointo
2.28 Considertheinteraction
betweendistinctfermions ψa and ψb,where φ isacomplexscalarand g isreal.Showthat theLagrangianviolates P and C,butis CP invariant.
Solution:Underspacereflection
I (t, x )
†
where ηP isaparityphasefromthe3fields,the (t, x ) → (t, x ) dependenceisimplicit,and wehaveusedTable2.2.Thisis = LI (t, x ) forany ηP .Similarly,underchargeconjugation
However,under CP = PC,
, whichisequalto LI (t, x ) forthephasechoice ηC ηP =1.
2.29 Consider e (k1) π+(p1) → e (k2) π+(p2)scattering,asinFigure2.15.UsethetwocomponentformalismofSection2.11tocalculatetheamplitudes M ( , )and M (+, +)for me =0and mπ =0.Expressyourresultsintermsof α, βπ,andtheCMscatteringangle θ (Thetwoamplitudesshouldbeequaluptoapossiblesignby(2.278).)
Solution:From(2.342),(2.207),andFigure2.10,
( , )= ie
M (+, +) isthesameexcept φ (ki) →
+(
i) and σ
→ σµ,where σµ and σµ aredefined in(2.167).But,
ThespinorsaregiveninTable2.1,i.e.,
2.30 Considerthenon-relativisticlimitofthematrixelement(2.356)foran e inastatic externalfield.
(a)Computethelimittolinearorderinthemomenta.Hint:usetheexplicitformsforthe spinorsinthePauli-Diracrepresentation.Itsimplifiesthecalculationtorewrite¯
usingtheGordondecomposition.
(b)SupposethatΓµ(p2,p1)in(2.352)containedaterm iσ
G2(q2).Thisviolates P and T butinprinciplecouldbegeneratedbyanewinteraction.Showhow G2(0)isrelated totheelectricdipolemoment de oftheelectron,whichisdefinedbythenon-relativistic interaction HEDM = de E(x ),where E isanexternalelectricfield.NotethattheHermiticitycondition(2.354)requiresthat G2 ispureimaginary.
Solution:(a)UsingthefirstGordonidentityinProblem2.10,ther.hs.of(2.356)is
Fromtheexplicitformsforthe γ matricesin(2.164)andforthespinorsin(2.184),only theuppertwocomponentscontributetolinearorder,yielding
forthefirstterm.Onlythespacecomponentscontributeat O(q ) inthesecondterm,giving
since ijkqj Ai(q )= iBk(q ) (b)The σi0q0 and σij qj termsaresecondorderinthemomenta,whilethe σ0iqi termreduces to
TheStandardModelandBeyond
where E(q )= iqA0(q ) istheFouriertransformoftheelectricfield E(x )= ∇A0(x ). Thiscorrespondstothecovariantlynormalizedmomentumspacematrixelementof HEDM for de = ieG2(0) 2m σ.
2.31 Supposethereisasmallelectriccharge-violatingcouplingbetweentheelectronand amasslessleft-chiralneutrino νL,with
Calculatethelifetimefor e → νLγ,andfindthevalueof δ correspondingtothelimitin Table2.3.
Solution:Thedecayamplitudeis
From(2.178)and(2.181),
inthemasslesslimit,with PL ≡ (1 γ5)/2 Therefore,
with pe pν = m2 e/2.Therefore,
Using =6 6 × 10 22 MeV-sand me ∼ 0 51 MeVfromTable1.1,thelimit τ> 6 6 × 1022 yr =2.1 × 1036 scorrespondsto δ< 5.8 × 10 28 .
2.32 Considertheprotonmatrixelement¯ u(p2)Γµ Q(q)u(p1)oftheelectromagneticcurrent in(2.393),withΓµ Q givenby(2.397).CalculatethisexplicitlyintheBreitframe,inwhich q0 =0,i.e., q =(0, 0, 0, Q2),p1 =(E, 0, 0, Q2/2),p2 =(
Expressthetimeandspacecomponentsintermsoftheelectricandmagneticformfactors definedin(2.398)andinterprettheresults.
Solution:UsingtheGordonidentity,
But (p1 + p
i =0.Writingoutthespinorsand γ matricesinthePauli-Diracrepresentation,
where φ1,2 arethePaulispinorsandweused p2 = p1 = q/2.Then,similarto(2.356)(but fortheprotonwithcharge +e),
sothat GE,M canbeinterpretedastheFouriertransformsoftheelectricandmagnetic distributionsoftheproton.
2.33 Let V (x1 x2)bethepotentialbetweentwonon-identicalspin- 1 2 particlesinnonrelativisticquantummechanics(NRQM).(V mayalsodependontheirspinandmomentum operators).Oneshowsintime-dependentperturbationtheorythatthetransitionamplitude Ufi from |
where φi isatwo-componentPaulispinor,and V containsappropriatespinmatrices.Note thatthesestatesareinourcovariantnormalizationconvention,whichhasanextrafactor 2π)32Ei ∼ 2π)32mi forthe ith externalparticlecomparedtotheusualconventionsof NRQM.Thecorrespondingformulainfieldtheoryis
where M isthescatteringamplitudewiththephaseconventionofAppendixB.Comparing theseresults,wecanreadofftheequivalentnon-relativisticpotentialcorrespondingtoa givenscatteringamplitude.Specifically,for
Non-leadingtermsin p canbeinterpretedasthenon-relativisticmomentumoperator. (a)Calculatethepotentialcorrespondingtotheeffectivefour-fermiHamiltoniandensity HI = λψ1ψ1 ψ2ψ2 (b)Considertheinteraction
betweentwofermionsandaHermitianscalarofmass mφ.Calculatethepotentialbetween ψ1 and ψ2 generatedby t-channel φ exchange,andshowthatitisattractivefor g1g2 > 0. (c)Calculatethepotentialgeneratedby
where Vµ isaspin-1particleofmass MV .Showthatitisrepulsivefor g1g2 > 0. (d)Repeatparts(b)and(c)forthecase g1g2 > 0,butforthepotentialbetweenantiparticle 1andparticle2andinterprettheresults.Hint:itisslightlyeasiertousethecharge
TheStandardModelandBeyond
conjugationformalismofSection2.10.
(e)Considertheinteractionin(2.269)ofa π0 withprotonsandneutrons.Calculatethe tree-levelamplitudefor p(p1) n(p2) → p(p3) n(p4)by t-channel π0 exchange,andshowthat itleadstothenon-relativisticpotential
where mp ∼ mn, σp(σn)arethePaulimatricesactingonthe p (n)spin, x = mπr,and S is thetensoroperator
Solution:(a)Wehave
wherewehaveusedtheexplicitexpressionsforthe u spinorsinthePauli-Diracrepresentation.Theabsolutesignfollowsfromexplicitlywritingoutthefieldsandusing
Thus, V (q )= λ and V (r )= λδ3(r ). (b)
wherethesecondformisthenon-relativisticlimitintheCM.Thus
theYukawapotential.Itisattractivefor g1g2 > 0 andrepulsivefor g1g2 < 0 (c)Thecalculationissimilartopart(b),exceptthepropagatorhas igµν inthenumerator. Onlythe µ = ν =0 termssurviveintheNRlimit,yielding
whichisrepulsiveforsamesignchargesandattractiveforoppositesignsasexpected.For MV → 0 and gi = eQi,werecovertheCoulombpotential V (r)= αQ1Q2/r,with α = e2/4π (d)From(2.296)andTable2.2,wehavethat
Thus,thescalarexchangepotentialisunchangedfor 1 → 1 (i.e.,itremainsattractive), whilethevectorexchangechangessignandbecomesattractive.Onecanalsowriteoutthe matrixelementsusingtheoriginal ψ1 field.Inbothcasesthereisanextraminussignfrom anticommutingthe b and b† operators,andanotherminussignforthescalarcasebecause ofthe γ0 in ψ,e.g.,
ReviewofPerturbativeFieldTheory
(e)The p and n verticesarerespectively iL = ∓gπγ5,so
But γ0γ5 = 0 I I 0 ,so
Therefore,
wherewehavetaken mp ∼ mn.Notethat σp and σn actontheirownspinors.Usingcontour integration,theintegralisjusttheYukawaform
Also, ∇ = mπ∇x where ∇x = d d
But
Therefore,
Thesecondtermreducesto
yieldingtheresultafteraslightrearrangement.
2.34 Supposethatanewlepton-flavorviolatinginteractionleadstotheeffectiveinteraction
TheStandardModelandBeyond
where A and B arerespectivelymagneticandelectricdipoletransitionmoments.Calculate thedecayratefor µ → eγ,neglecting me
Solution: Leff leadstothematrixelement
where q = pµ pe isthephotonmomentum, isthepolarizationvector,andwehaveused q ∗ =0.But pµ ∗ =0 also,andonecanchoosealinearpolarizationbasissothat is real.Then
and

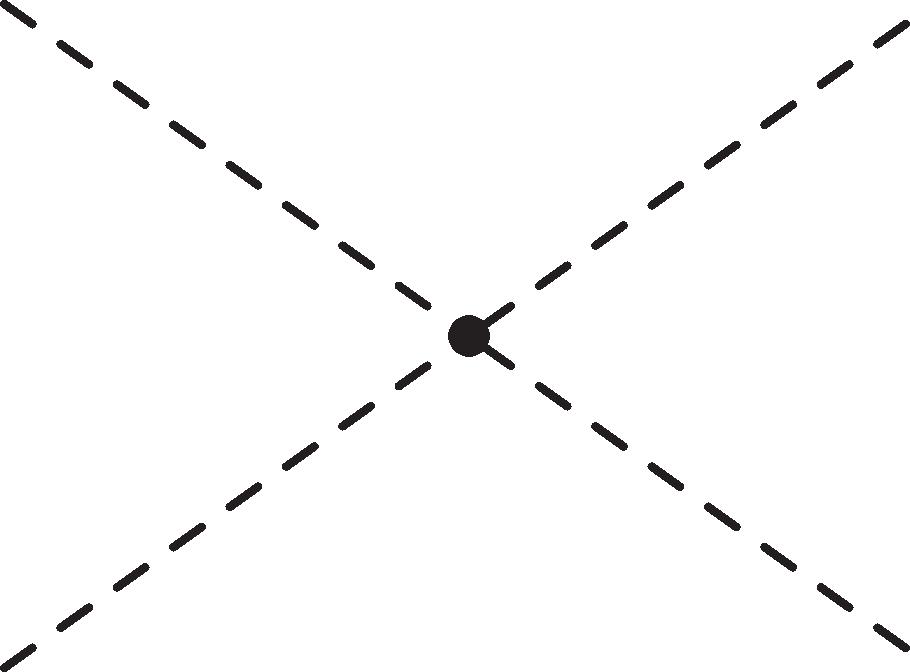
Figure 2.1 Three- and four-point interactions of a Hermitian scalar field ϕ. The factor is the coefficient of ϕ n/n! in iL , as described in Appendix B. 002x001.eps


Figure 2.2 Diagrams with additional factors of 1/2! (left) and 1/3! (right), required because not all of the (4!)2 ways of associating the four fields at each vertex with four lines lead to distinct diagrams.
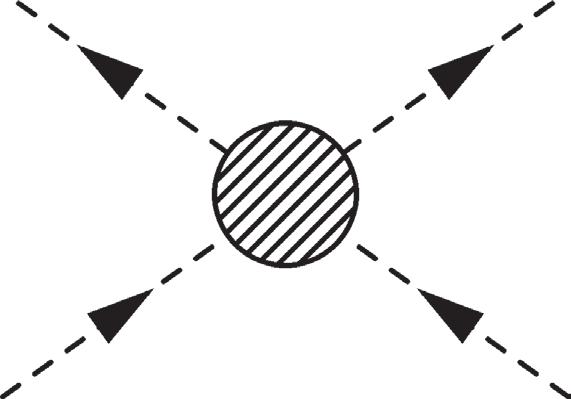
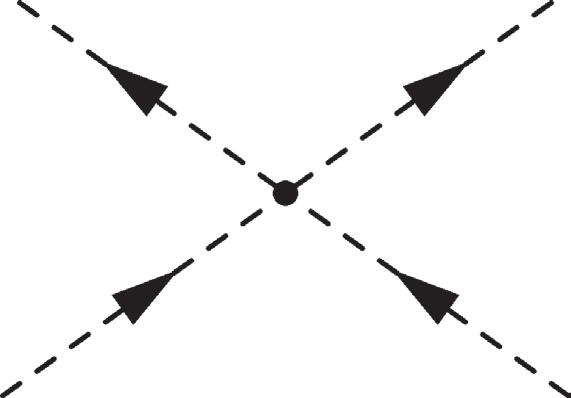



Figure 2.3 Tree level diagrams for =〉MppMpp fi
|| 34 12 for a Hermitian scalar field. The arrows label the directions of momentum flow, and pij ≡ pi–pj . The arrangement of lines in the last diagram is modied to allow the diagram to be drawn without crossing lines.
Figure 2.4 Scattering kinematics in (i) the center of mass, (ii) the lab, and (iii) the Breit frames.
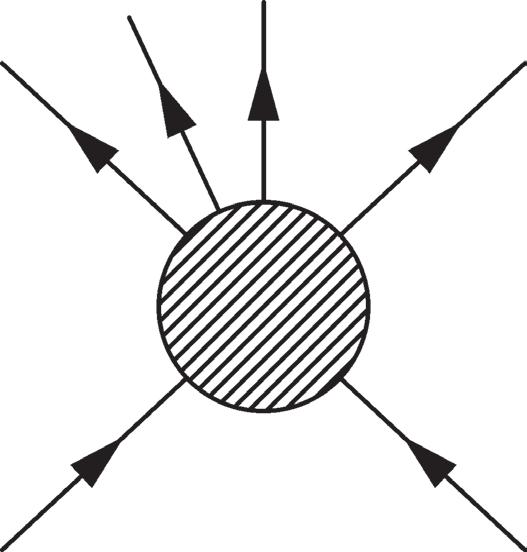


Figure 2.5 The 2 → n scattering process p1 p 2 → pf1 … pf n (left); 1 → n scattering p1 → pf1 … pf n from a potential, represented by a cross (middle); and the 1 → n decay process p1 → pf1 … pf n (right).
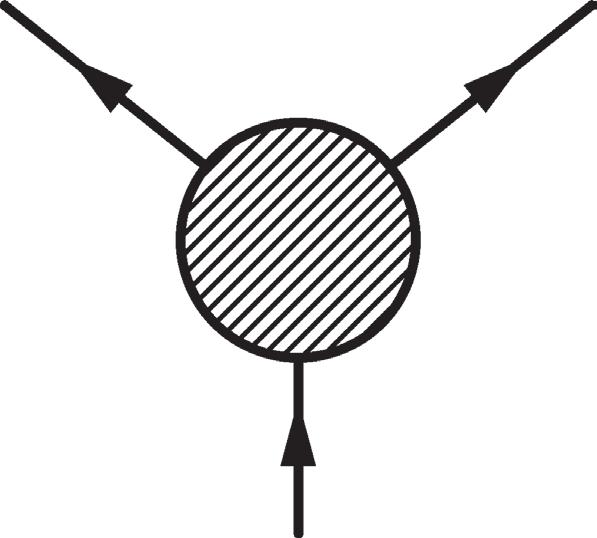
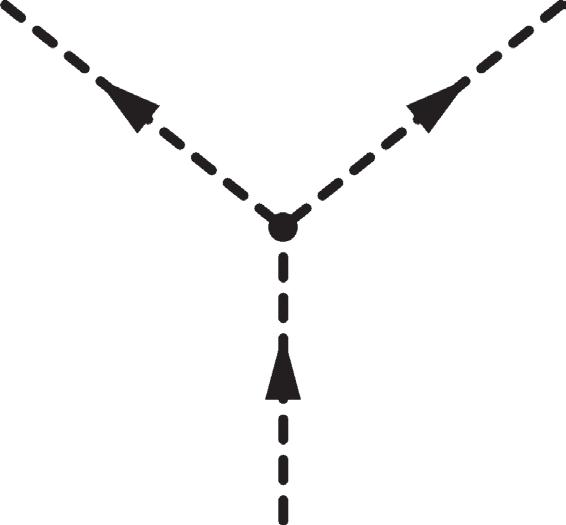
Figure 2.6 The two-body decay of the spin-0 scalar 1 into 2 + 3, and the associated Feynman diagram corresponding to (2.84).

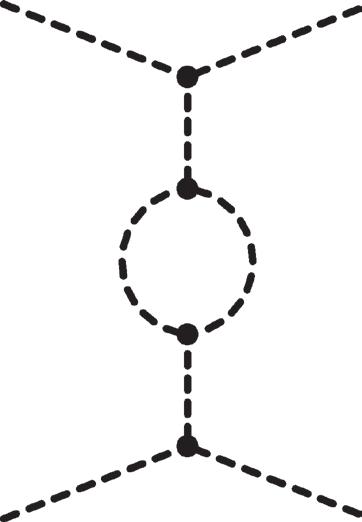


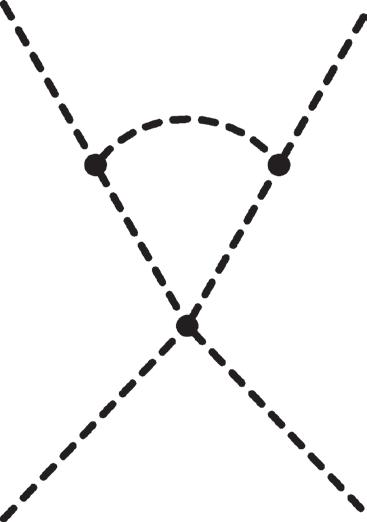
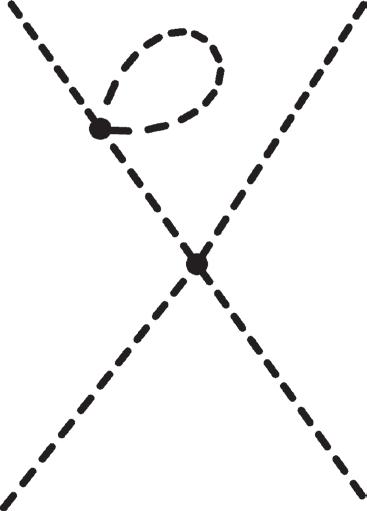
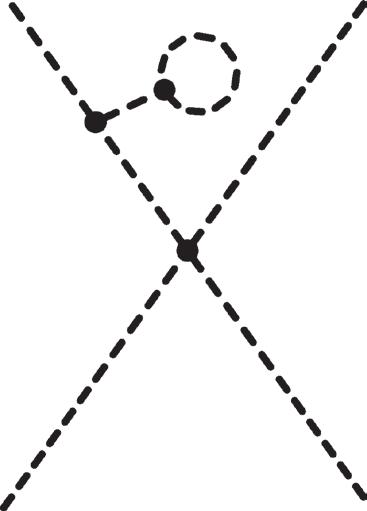
Figure 2.7 Examples of one-loop diagrams contributing to the process p1p 2 → p 3 p 4.



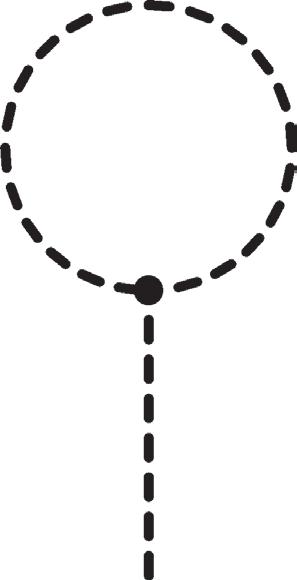
Figure 2.8 Left: A typical one-loop diagram, with the momenta flowing through each line labeled. Right: Divergent (sub)diagrams in the super-renormalizable ϕ 3 theory. The second (tadpole) diagram contributes to the d1 term in (2.21) and must be included in the field redenition that eliminates it.
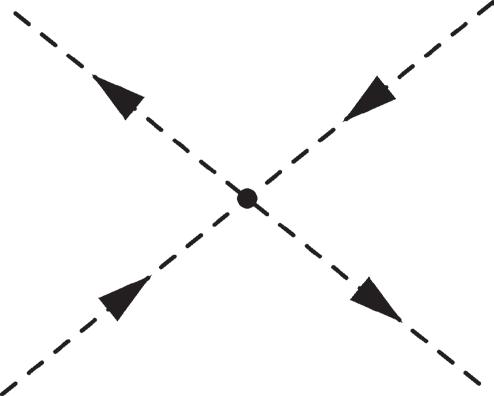
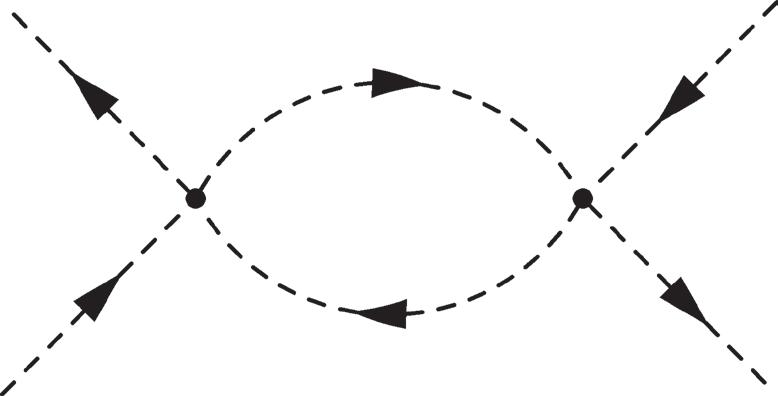
Figure 2.9 Left: Tree-level diagram for ππ
pppp
() () () (), 1 –23 –4 where p 1, 2 p () 3, 4 are the physical initial (final) momenta. Right: An example of a one-loop diagram. ΔF (k) is dened in (2.29).




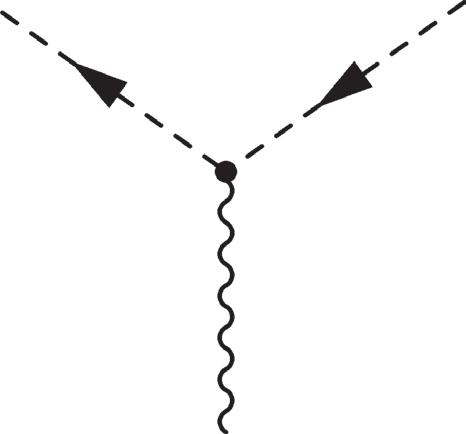
Figure 2.10 Vertices involving charged pions and one or two photons. In the onephoton diagrams the initial pions enter from the bottom and the final leave from the top. Antiparticle (p –) vertices are obtained from particle ones by twisting the lines and replacing p by ≡ pp–, where p is the physical four-momentum and p follows the direction of the arrow. The wavy lines represent photons.
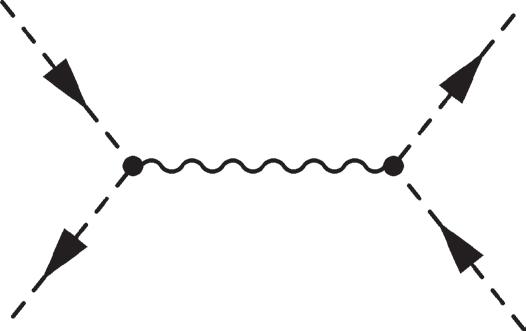
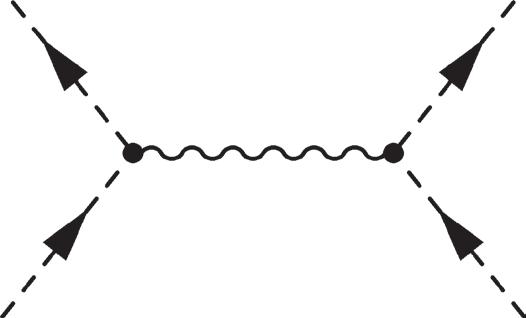
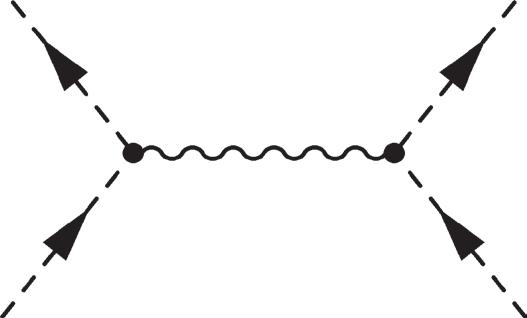
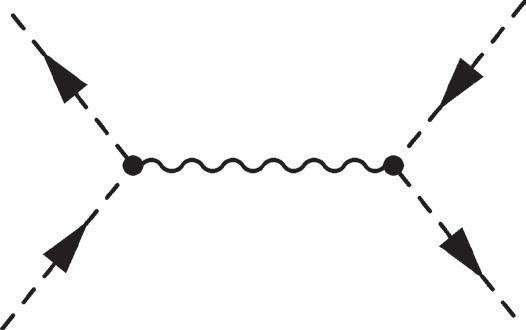
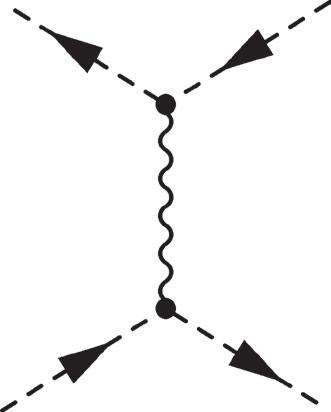
2.11 Feynman diagrams for ππ ππ ππ ++→→ ++ ++ KK (top), (middle), and ππ ππ → +− +− (bottom).
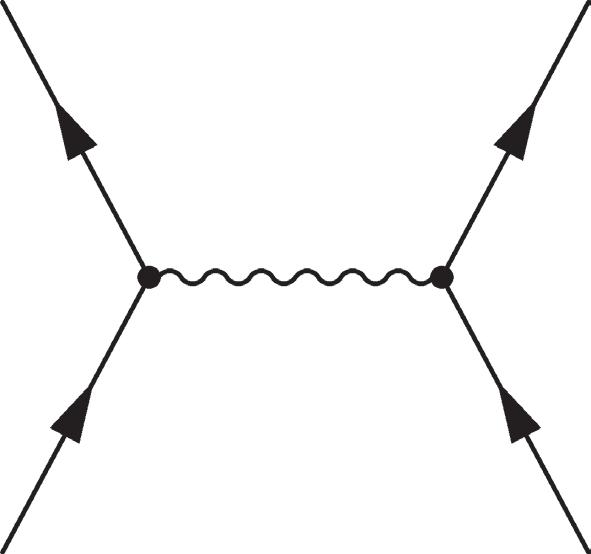

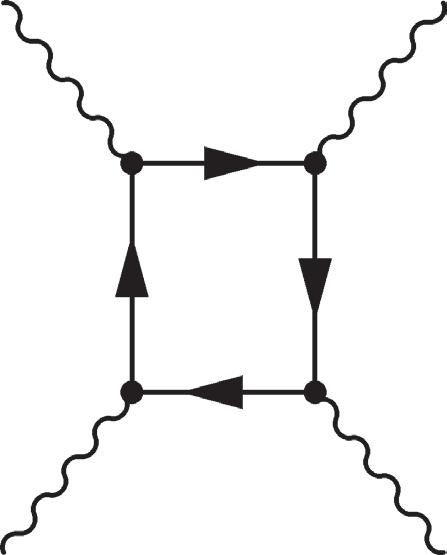
Figure 2.14 Left and center: relative minus signs between diagrams involving exchanged fermion lines, with ≡ uups iii
(, ). Right: a closed loop diagram, with an extra factor of −1.
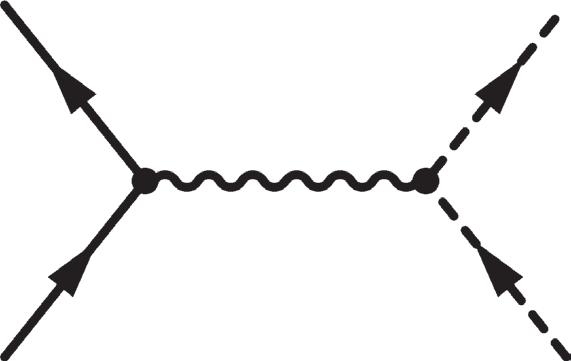

Figure 2.15 Left: lowest order diagram for
22 Right: diagram for
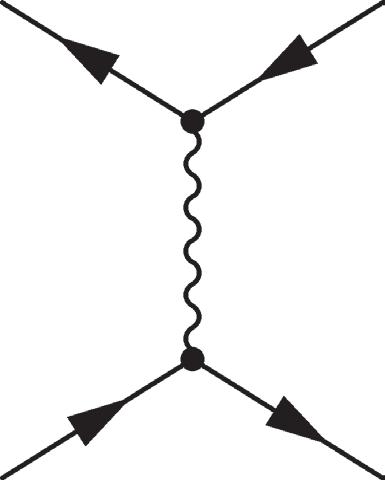
Figure 2.16 Feynman diagrams for

The relative minus sign between the two diagrams is independent of state conventions.



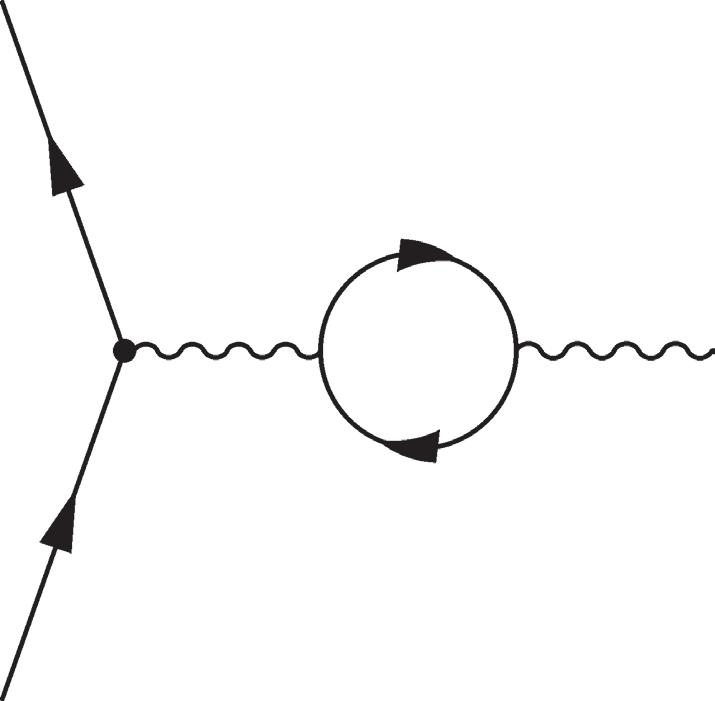
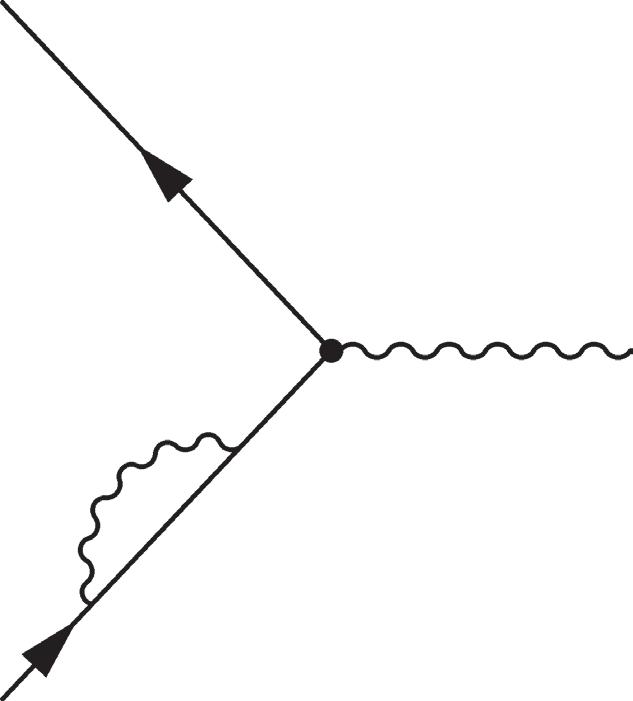
Figure 2.17 Electron-photon vertex (top left), and one-loop corrections, corresponding to the vertex correction(top middle), the vacuum polarization (or photon self-energy) correction (top right), and electron self-energy corrections (bottom).

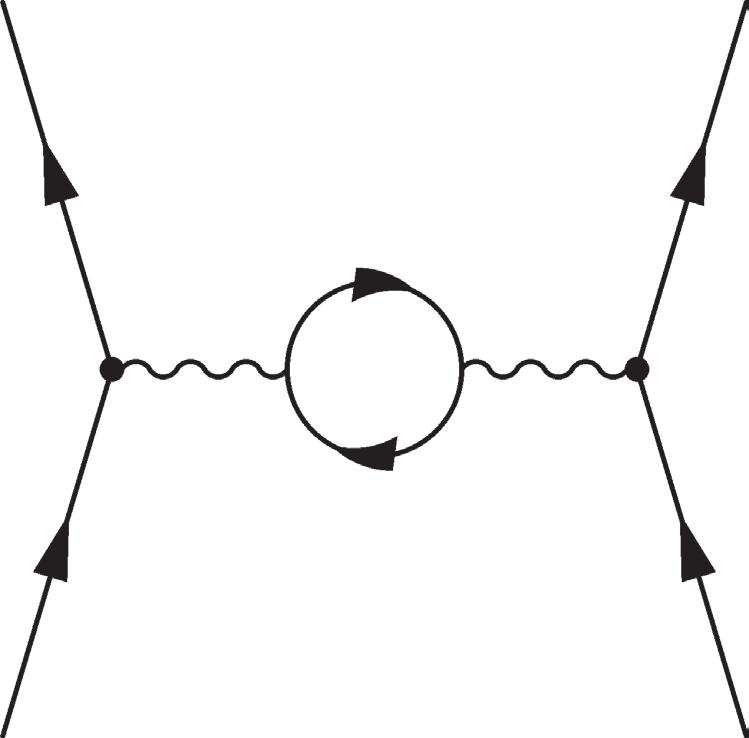
2.18 One photon exchange and one-loop vacuum polarization “bubble.”

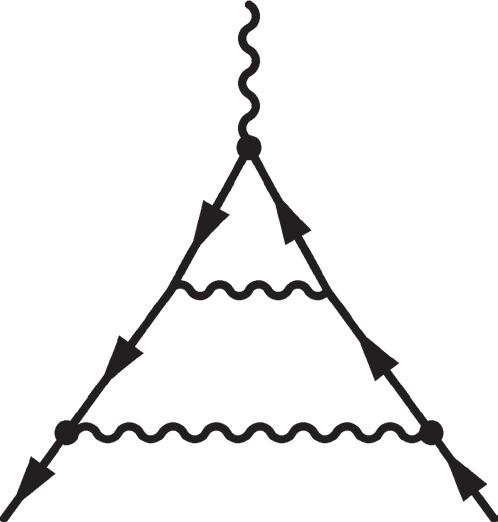
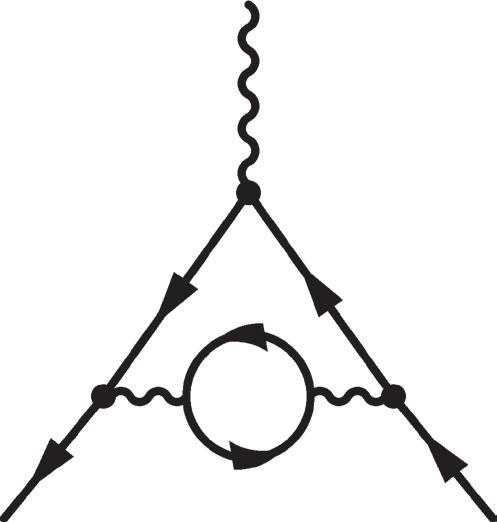
Figure 2.19 One-loop and typical two-loop diagrams contributing to the anomalous magnetic moment of the electron.
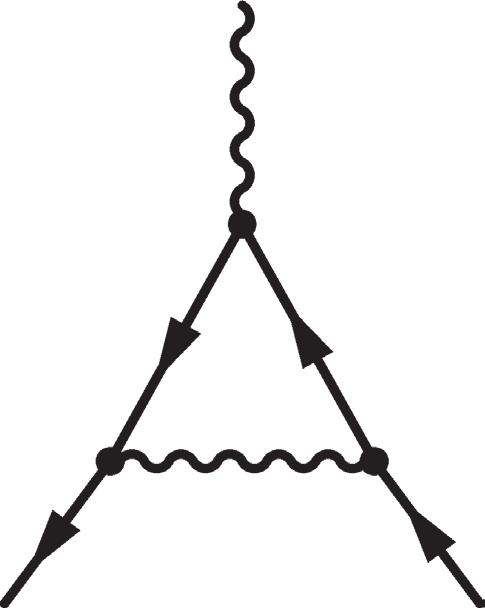

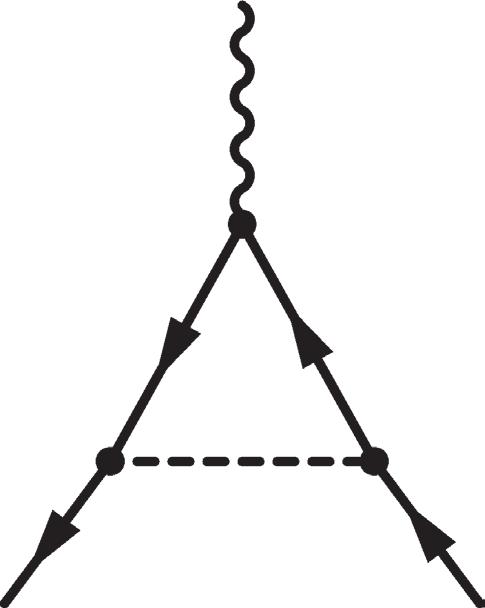
2.20 One-loop electroweak contributions to =− µµag(2)/ 2.

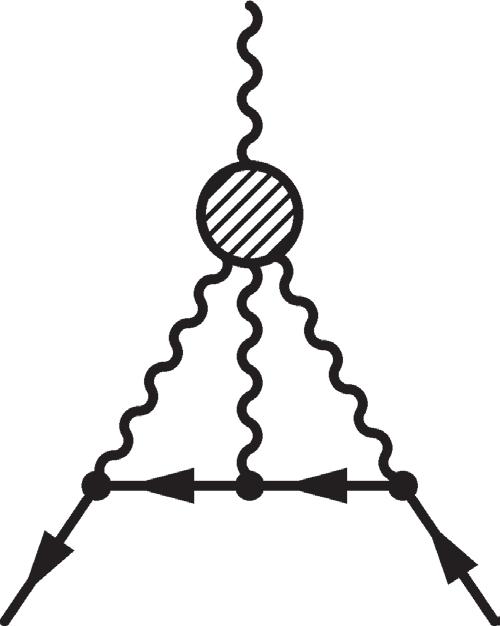
Figure 2.21 Two-loop hadronic vacuum polarization (left) and hadronic light by light (right) diagrams.The shaded blobs represent hadronic states.
Figure 2.22 New contributions to αμ in the supersymmetric extension of the SM . µ
and v are the spin-0 superpartners of the μ and ν, while χ ± ,0 are spin –1 2 superpartners of the electroweak gauge bosons and Higgs fields.




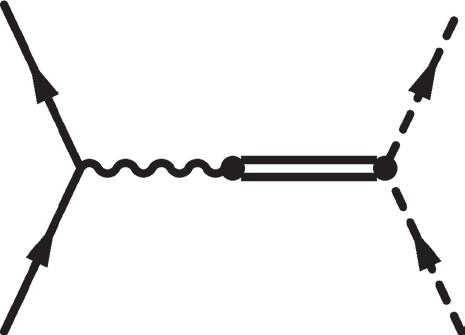
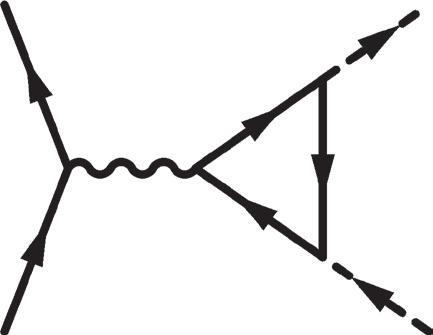



Figure 2.23 Top: interaction vertices described by (2.381). Middle: representative strong interaction diagrams contributing to ππ 〈〉 µ ++ J Q || involving nucleons, pions, and the ρ 0 resonance. Bottom left: diagrams in the quark model description in which the π+ is a ud bound state. Bottom right: parametrization of the strong interaction effects by a form factor, represented by a shaded circle.
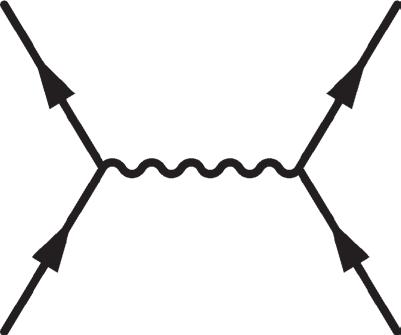
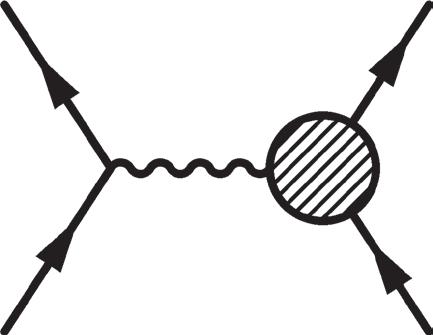




Figure 2.24 Top: tree-level amplitude for for a point proton and with proton form factors (shaded circle). Bottom: representative strong interaction corrections in terms of virtual hadrons (three left diagrams) or in terms of quark constituents (right).
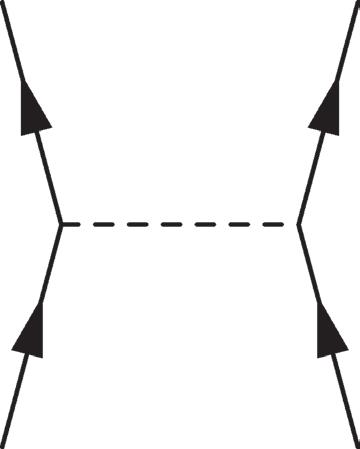

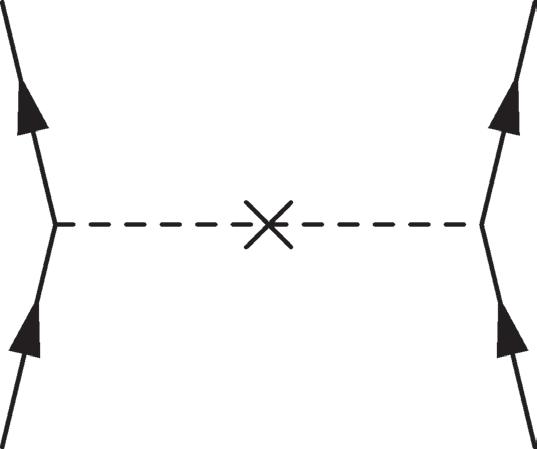

Figure 2.25 t-channel diagrams for ψψ ψψ → , 12 34 treating the m12 2 term in (2.410) as a perturbative mass insertion.
There are additional u channel diagrams with (3 ↔ 4).
