2
Maxwell’sequationand Electromagnetic Waves
2.1 Consideravectorfield V(r) = 4xx0 + 5yy0 + 6zz0 andaclosed,cubical S surface withsidelength L andonecornerattheorigin,lyinginthefirstoctant.Evaluatethe integral S V · dA byfirstcarryingoutthedotproductandintegraloneachofthesix facesofthecube,andaddingthemup.Checkyouranswerbyusingthedivergence theorem,whichyouarelikelyabletodoinyourhead.
Solution
Makeatabletoexplicitlyevaluatethesurfaceintegral:
2.2 ShowthattheintegralformofCoulomb’slawcanbederivedfromGauss’s law.First,arguewhyrotationalsymmetryimpliesthattheelectricfieldfromapoint charge q hastobeisotropicinalldirections,andcanonlydependonthedistance
QuantumMechanicsSixthEditionSolutionsManual
r fromthecharge.Next,usethistochooseanappropriate“Gaussiansurface” S so thattheintegralinEquation(2.4a)issimpletoevaluate.Finally,useEquation(2.5) toshowthattheforce F onanothercharge q is
Solution
Itisobviousthatthefieldcanonlydependon r becausethereisnopreferred direction.Similarly,itcanonlyberadiallyoutward(orinward),sochooseaGaussian surfacethatisasphereofradius r centeredattheorigin.Themagnitude E ofthe electricfieldisgivenby(2.4a)as
andtheforceonacharge q isjust q E
2.3 A“parallelplatecapacitor”ismadefromtwoplaneconductingsheets,each witharea A,separatedbyadistance d.Theplatescarryequalbutoppositecharges ±Q,uniformlydistributedovertheirsurface,andthiscreatesapotentialdifference V betweenthem.Inferthe(constant)electricfieldbetweentheplates,anduseGauss’s lawtoshowthat Q = CV,where C dependsonly A and d (and 0).
Solution
Thesurfacechargedensityis σ = Q/A,soa“pillbox”Gaussiansurfacewithoneflat surfaceinsidethemetalplate(wherethefieldiszero)andtheotherflatsurfaceinthe gap,gives E = σ/ 0.Thepotentialdifferenceforthis(constant)electricfieldisjust V = Ed =
2.4 Usetheconceptofaparallelplatecapacitortofindtheenergydensityinan electricfield.Chargeisaddedinsmallincrements dQ toaninitiallyuncharged capacitorgivingapotentialdifference V .Eachincrementchangesthestoredenergy by V dQ = (Q /C)dQ where C isthecapacitance.(SeeProblem2.3.)Integrateto findthetotalenergywhencharge Q isstoredinthecapacitor.Dividebythevolume ofthecapacitortofindtheelectricfieldenergydensity uE = 1 2 0 E2 where E istheelectricfieldinsidethecapacitor.
Solution
Justdoastheproblemstatementtellsyoutodo:
Maxwell’sequationandElectromagneticWaves 17
2.5 Calculatethemagneticfieldatadistance r fromaninfinitelylongstraightwire whichcarriesacurrent I.First,usingGauss’slawformagnetism,explainwhythe fieldmustbetangentialtoacircleofradius r,centeredonthewireandlyingina planperpendiculartothewire.ThenuseAmp´ere’slawtoshowthatthemagnitude ofthemagneticfieldis
Solution
Theproblemhascylindricalsymmetry,butthereisahandednesssetbythedirection ofthecurrent.ByGauss’Lawformagnetism,therecanbenoradialcomponent,asa cylindricalGaussiansurfacecanpassnonoflux.Withacircularloopatradius r,the lineintegralofAmpere’sLaw(2.4d)isjust B · 2πr foranazimuthalfield B,hence B = µ0 I/2πr
2.6 Alongcylindricalcoilofwireiscalleda solenoid andcanbeusedtostorea magneticfield.Ifthecoilisinfinitelylong,thereisauniformmagneticfieldinthe axialdirectioninsidethecoil,andnofieldoutsidethecoil.Usean“AmperianLoop” thatisarectangleenclosingsomelengthofthecoil,withoneleginsideandoneleg outside,toshowthatthemagneticfieldis
B = µ0 In
where I isthecurrentinthewireandthereare n turnsperunitlengthinthecoil.
Solution
Thecurrentenclosedintherectangularloopis nI where isthelengthoftheloop. Thereisnofieldoutsidethesolenoid,andthefieldinsideisparalleltotheaxis,so thelineintegraljustgives B ,hence B = µ0nI.
2.7 Findthevectorpotential A(r) whichgivesthemagneticfieldforthelong straightwireinProblem2.5.Itiseasiesttoletthewireliealongthe z-axisand expressyourresultintermsof r = (x2 + y2)1/2,andtocarryoutthecalculationin cylindricalpolarcoordinates (r,θ, z).
Solution
2.8 Followthisguidetoconvinceyourselfthatthesecondtermontherightin(2.4d) isneededforthewholeequationtomakesense.First,imaginealongstraightcurrentcarryingwire,withassociatedmagneticfieldgiveninProblem2.5.Now“cut”the wire,andinsertaverythincapacitor,withplatesperpendiculartothedirectionof thewire.Currentcontinuestoflowthroughthewirewhilethecapacitorchargesup, butnocurrentflowsbetweenthecapacitorplates,soitwouldseemthereshouldbe nomagneticfieldthere.Butthatdoesn’tmakesense:howcouldthemagneticfield juststopatthecapacitor?Intuitively,youexpectittobecontinuousrightthroughit.
18
QuantumMechanicsSixthEditionSolutionsManual
Finally,showthatthesecondterm,calleda displacementcurrent,infactgivesyou thesame B insidethecapacitor.
Solution Thecapacitorplatesarecircularwitharea A = πr2.Theelectricfieldflux throughthisareais Aσ/ 0 = Q/ 0,since σ = Q/A.Theleftsideof(2.4d)mustequal µ0 I,where I = dQ/dt,so
= K I
whichimpliesthat K = 0µ0,establishing(2.4d).
2.9 A“ 1/r2”vectorfield,suchastheelectricfieldfromapointchargeorthe gravitationalfieldfromapointmass,takestheform
ShowbyanexplicitcalculationinCartesiancoordinatecoordinates,that ∇· V = 0 everywhere,exceptattheorigin.Then,usingasphericalsurfaceabouttheorigin, showthat V dA = 4πk.Hencearguethatthechargedensityforapointcharge q locatedattheoriginis qδ3(
) = q
(
)δ(
)δ(z),where δ(x) isaDirac δ(x) functionas definedinChapter1.
Solution
Thecalculationisstraightforward,althoughabittedious:
for r 0.Forasphereofradius r abouttheorigin, V ·
= 4πk. So,byGauss’Theoremforthissphericalvolume, ∇ V = 4πk,butsince ∇ V = 0 everywhereexcepttheorigin,considerasmallcubearoundtheorigin,anditisclear that ∇ V satisfiesthepropertiesofthe3D δ-function,i.e. ∇ V = 4πkδ(x)δ(y)δ(z) = 4πkδ(3)(r).ForCoulomb’sLaw, V = E and k = q/4π 0,soGauss’Lawtakestheform ∇ E = qδ(3)(r)/ 0.Comparingto(2.19a),thisimplies ρ(r) = qδ(3)(r) forapoint charge q
2.10 A“ 1/r”vectorfield,suchasthemagneticfieldfromaninfinitelylongcurrent carryingwire,takestheform
V(r) = k r φ0 = k rz yx0 + xy0
ShowbyanexplicitcalculationinCartesiancoordinatecoordinates,that ∇× V = 0 everywhere,exceptattheorigin.Then,usingacircularcurveaboutthez-axis,show that V dl = 2πk.Hencearguethatthecurrentdensityforaninfinitelylongcurrent carryingwireofzerothicknesslocatedalongthe z-axisis Iδ(x)δ(y).
Solution
Thecalculationisstraightforward,buttedious.Also,noteherethat r2 = x2 + y2
exceptfor r 0.Forthecircularloop, V dl = (k/r)(2πr) = 2πk.Therefore,usingthe magneticfield B fromalinecurrent,weget k = µ0 I/2π.ApplyingStokes’Theorem alongwith(2.19d)impliesthat j = Iδ(2)(r)z0.
2.11 Derivethewaveequationforthemagneticfield B fromMaxwell’sequations.
Solution
StartwithEquations(2.19),andtakethecurlof(2.19b)with j = 0:
since µ0 0 = 1/c2,andusing(2.32)with(2.19c)and(2.19b).Thisgives
2.12 Showthat(2.39)isasolutiontothewaveEquation(2.34).Itiseasiertodo ifyouexpresstheLaplacianinsphericalcoordinates,butyoumayfinditmore satisfyingtoworkitthroughinCartesiancoordinatecoordinates,rememberingthat r = (x2 + y2 + z2)1/2 .
Solution
Thereisatypointheproblem.Itshouldasktoshowthat(2.41)isasolution,not (2.39).Thatis,takingtimederivativesandwith ω = kc,weneedtoshowthat
TheLaplacianinsphericalcoordinatesiseasyenoughtofind,forexample(6.19).
So,
Nowworkonthefirsttermonthelefthandsideoftheaboveequation:
20
QuantumMechanicsSixthEditionSolutionsManual Thatis,thiscancelswiththerightsideofthewaveequation,leaving
whichisadifferentialequationthatcanbesolvedfor g(θ,φ)
2.13 Findtheelectrostaticpotential V(r) atadistance r fromapointcharge q,with theintegrationconstantdefinedsothat V(r) → 0 as r →∞.Youcandothiseitherby directlyintegrating C E · dl alongsomepath C,orbysimplyguessingthefunction V(r) whichsatisfies(2.20).
Solution
Letthecurve C bethestraightlinestartingat r andextendingradiallyto ∞.Thatis, dl = dr andwith E = (1/4π
/r3,wehave
Goingtheotherway,andusingCartesiancoordinates,weneedtocalculate
2.14 An“electricdipole”isformedbytwopointcharges ±q separatedbyadistance d.Formsuchasystembyputtingthetwochargesonthe z-axisat z = ±d/2 and calculatetheelectricfield E(r).Showthatfordistances r d,theelectricfieldcan bewrittenintermsofthe electricdipolemoment vector p = qdz0 insteadofexplicitly oneither q or d
Solution
Justgoaheadandaddtheelectricfieldsofthetwocharges:
For r d,thedenominatorscanbeexpandedusing
Therefore
2.15 Findtheelectrostaticpotential V(r) atadistance r fromthecenterofthe electricdipoleinProblem2.14.Expressyouranswerintermsoftheelectricdipole moment p
Solution
Weneedtofindthe V(r) thatsatisfies E = ∇V.Workinginsphericalpolar coordinateswith
and
Thecorrectformfor V(r) isnowapparent,namely
,thisbecomes
Ofcourse,onecanalsojustaddtheelectricpotentialofthetwocharges:
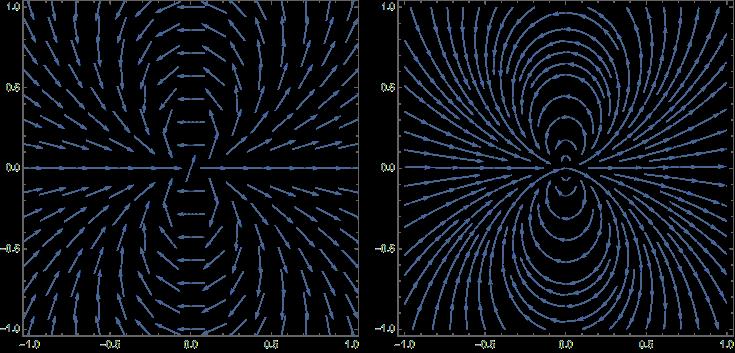
2.16 Drawtheelectricfieldlinesforandelectricdipolewithdipolemoment p = pz0.
Superimposecontourlinesofelectricpotentialontopofthefieldlines.Thisisbest donebychoosingsomespecificvaluesandusingaprogramsuchasMATHEMATICA.
Solution
MakingdipolefieldplotsinMATHEMATICA isrelativelystraightforward,infact, amoduleintheirdocumentationshowshowtodothisinthreedimensions.The plotsbelowweremadebywritingthepotentialinpolarcoordinates,calculatingthe fieldfromthegradient,andusingthe TransformedField functiontotransformto Cartesiancoordinatesbeforegeneratingtheplot.(Thedipoleliesinthe x-direction.)
Inbothcases, ContourPlot isusedtoplotthepotential,specifyingthecontourline values.Theleftuses VectorPlot forthefield.Therightuses StreamPlot,which
22 QuantumMechanicsSixthEditionSolutionsManual requireslessadjustmentofoptions,butwhichplotsonlyenougharrowssothatthe densityacrosstheplotismoreorlessconstant.
2.17 Anelectricdipole p = qdz0 sitsinauniform,externalelectricfield E.By consideringthetorqueonthedipole,fromtheinteractionofthecharges ±q with E,calculatetheworkneededtorotatethedipolethroughanangle θ,aboutanaxis perpendiculartotheplaneformedby p and E.Therebyshowthattheelectrostatic potentialenergyofthedipoleintheexternalfieldis UE = p E.
Solution
Seethefigure.Thetorqueonthedipoleis τ = 2F(d/2)sin θ = qdE sin θ,sothework neededtorotateittothispositionis

2.18 A“magneticdipole”isformedbyaplanarloopofwirewitharea A and carryingcurrent I.UsinganapproachsimilartothatinProblem2.17,showthat themagneticpotentialenergyofamagneticdipoleinanexternalmagneticfield B is UB = µ B.Here,themagneticmoment µ hasmagnitude IA anddirection perpendiculartotheplaneoftheloop.Youcandothisrathereasilyifyoumodelthe loopasasquareofsidelength L,inwhichcase A = L2,thenuseanargumentsimilar tothatusedtoproveStokes’theoremtoexplainwhyderivingthisforasquareis equivalenttosolvingitforanyplanarloop.
Solution
Maxwell’sequationandElectromagneticWaves 23
ThisisessentiallythesameasProblem17.Orientthesquareloopsothatthenormal totheplaneandthemagneticfieldformaplanethatisparalleltotwosidesofthe square.Thentheforceonthosetwosidesjustpointinto,oroutof,theloop,withno torqueornetforce.Theforceontheothertwosides,however,areeach ILB witha leverarm L/2,sothetorqueontheloopis 2 × (ILB)(L/2)sin θ = (IL2)B sin θ,where θ istheanglebetweentheloopnormalandthemagneticfield.Integratingtofindthe workgives UB = µ · B
The“Stokes’Theorem”argumentjustsaysthatwecanbuildupanyloopoutofa largenumberoftinysquareloops,andthetorquesaddup,asdoestheareaofthebig loop.
2.19 Givenascalarfunction χ(r, t),showexplicitlythatthetransformation A → A + ∇χ hasnoeffectonthemagneticfield.Thenfindtheconditionthatneedstobe satisfiedby χ sothattheadditionaltransformation V → V + χ hasnoeffectonthe electricfield.
Solution For A → A = A + ∇χ,wehave,using(2.24),
sincethecurlofanygradientiszero.Nowfollowing(2.25)wewrite
Therefore,theexpressioninparenthesismustbezerofortheelectricfieldtoremain unchanged.Intermsofspecialrelativity,thismeansthatthe“fourgradient”of χ mustbezero.
2.20 ThePoyntingVector S = (1/µ0)E × B foranelectromagneticwave.Whatis thedirectionofthisvector?ShowthatthePoyntingVectorhasthedimensionsof “energyflux,”thatis,energyperunitareaperunittime.
Solution
From(2.39),weseethat
since k0 isperpendicularto E0.Thus,thedirectionofthePoyntingvectorisin factthedirectionofthewavepropagation.(ThePoyntingvector“points.”)Now since
weseethatthePoyntingvectorhasdimensions velocity × energydensity = energy/ (area × time) (SeeProblem2.4.Also, k0 isadimensionlessunitvector.)

FIGURE 2.1. The resistor as used in electrical circuits. The upper symbol was completely standard,but has more recently been replaced by the lower one. They are used in circuit diagrams regardless of the specific type of resistor used. We can model a resistor as a long cylinder, made of some uniform, isotropic material, with wires attached to the flat faces. The model quite resembles a standard carbon resistor. The colored bands on the resistor are a code for its resistance value and precision standards.
FIGURE 2.2. Geometric explanation of the derivation of the divergence theorem. (a) The volume integral over a region is the sum of small rectangles (or rectangular blocks in three dimensions). (b) Any quantity proportional to the area of a volume element cancels on adjacent cells, leaving only the edges on the boundary. (c) Coordinate system for analyzing the integral over one small cell.
FIGURE 2.3. Geometric explanation of the derivation of Stokes' theorem. (a) The surface integral over a regionis the sum of small rectangles. (b) Any quantity proportional to a loop over the area element cancels on adjacent cells, leaving only the edges on the boundary. (c) Coordinate system for analyzing the integral over one small cell.

FIGURE 2.4. A Betatron accelerates particles using the electric field from magnetic induction. The diagram shows the principle, and defines quantities that allow us to derive the so-called Betatron Condition. The photograph (Courtesy Department of Physics, University of Illinois at Urbana-Champaign) shows early Betatrons with inventor, Donald Kerst.
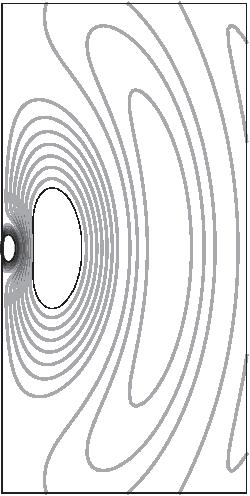
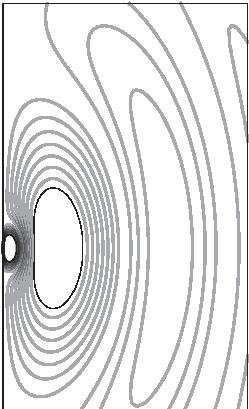
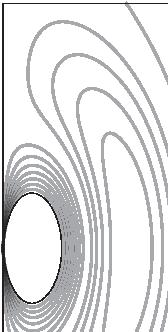

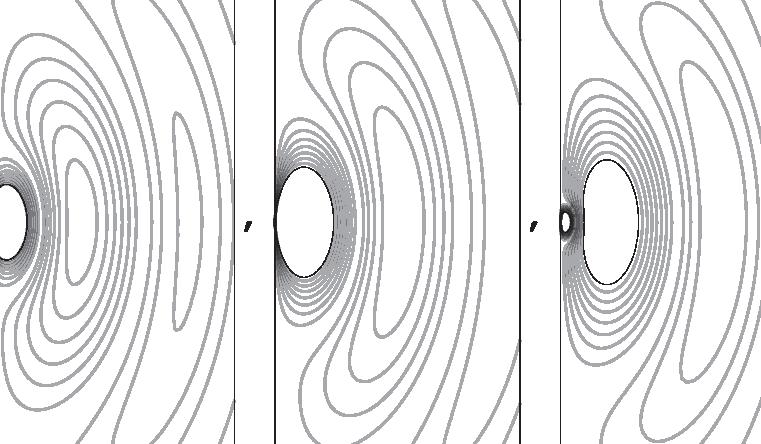
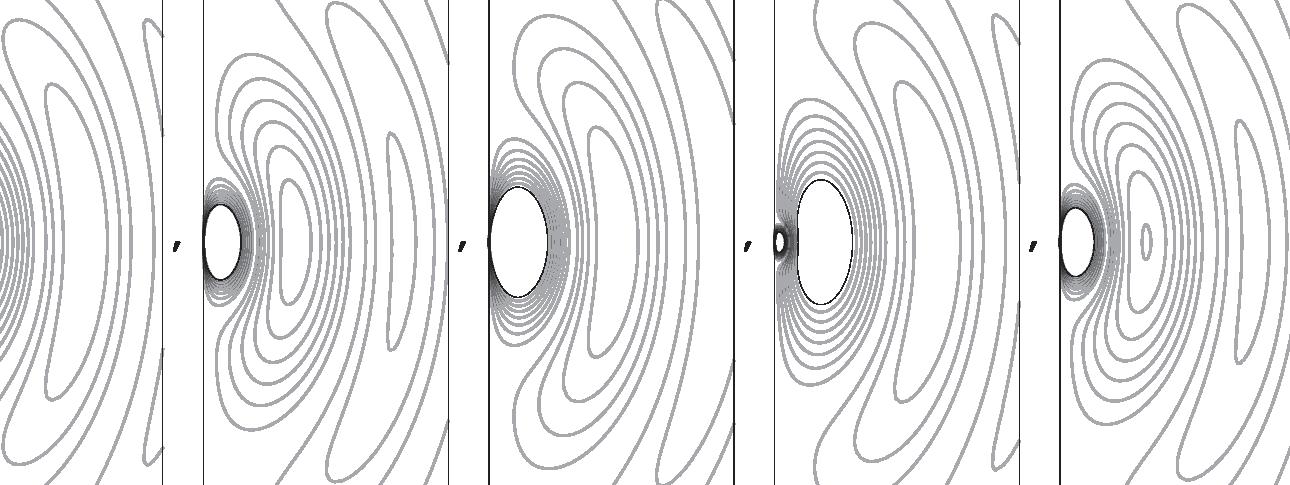

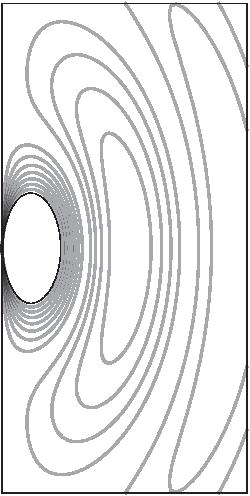
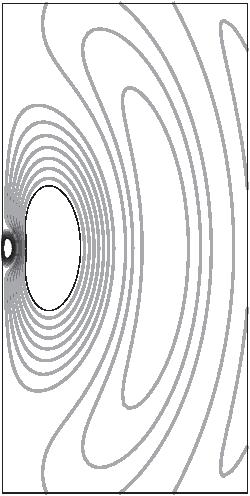

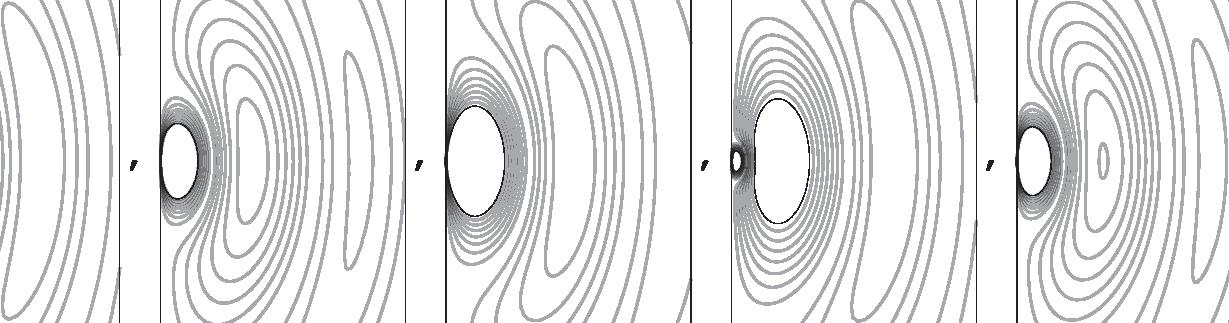
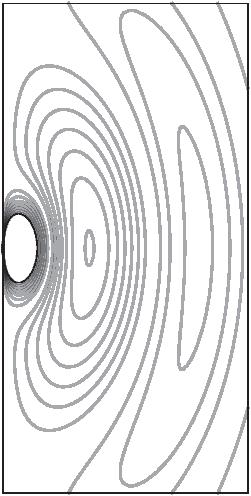
FIGURE 2.5. A schematic representation of electric dipole radiation. The frames from left to right represent increasing time, while each frame represents the same portion of space. The lines are contours of constant electric field strength. The source is an infinitesimally small oscillating electric dipole at the origin, oriented in the vertical direction. The field strength is inversely proportional to distance from the origin, with the field lines forming closed loops that move away from the dipole.
