LimitsandTheirProperties
Section2.1APreviewofCalculus
1. Calculus is the mathematics of change. Precalculus is more static. Answers will vary. Sampleanswer:
Precalculus: Area of a rectangle
Calculus: Area under a curve
Precalculus: Work done by a constant force
Calculus: Work done by a variable force
Precalculus: Center of a rectangle
Calculus: Centroid of a region
2. A secant line through a point P is a line joining P and another point Q on the graph.
The slope of the tangent line P is the limit of the slopes of the secant lines joining P and Q, as Q approaches P
3. Precalculus: ()() 20ft/sec15sec300ft =
4. Calculus required: Velocity is not constant. ()() Distance20ft/sec15sec300ft ≈=
5. Calculus required: Slope of the tangent line at 2 x = is the rate of change, and equals about 0.16.
6. Precalculus: rate of changeslope0.08 ==
(c) At () 4,2 P the slope is 11 0.25. 4 42 == + You can improve your approximation of the slope at 4 x = by considering x-values very close to 4.
8. 2 ()6 f xxx =− (a) (b) () ()() () 2 68 24 slope4,2 22 xx xx mxx xx
For 3,431xm==−= For 3 2.5,42.51.5 2 xm==−== For 5 1.5,41.52.5 2 xm==−==
(c) At ()2,8, P the slope is 2. You can improve your approximation by considering values of x close to 2.
9. (a)
(b) You could improve the approximation by using more rectangles.
10. Answers will vary. Sampleanswer: The instantaneous rate of change of an automobile’s position is the velocity of the automobile, and can be determined by the speedometer.
11. (a) ()() 22 1 511516165.66 D
(b)
(c) Increase the number of line segments.
Section2.2FindingLimitsGraphicallyandNumerically
1. As the graph of the function approaches 8 on the horizontal axis, the graph approaches 25 on the vertical axis.
2. (i) The values of f approach different (ii) The values of f increase without (iii) The values of f oscillate between numbers as x approaches c from bound as x approaches c: two fixed numbers as x approaches c: different sides of c:
No. For example, consider Example 2 from this section.
x
f
f (
f (x) 3.99982 4 4 0 0
)
23. () 3 lim41 x x → −=
24. 0 limsec1 x x → =
25. ()()22 limlim42 xx fxx →→ =−=
26. () () 2 11 limlim34 xx fxx →→ =+=
27. 2 2 lim 2 x x x → does not exist.
For values of x to the left of 2, () 2 1, 2 x x =− whereas for values of x to the right of 2, () 2 1. 2 x x =
28. 1 0 4 limdoes not exist. 2 x x e → + The function approaches 2 from the left side of 0 and it approaches 0 from the right side of 0.
29. () 0 limcos1 x x → does not exist because the function oscillates between –1 and 1 as x approaches 0.
30. 2 limtan x x π → does not exist because the function increases without bound as x approaches 2 π from the left and decreases without bound as x approaches 2 π from the right.
31. (a) () 1 f exists. The black dot at (1, 2) indicates that ()12. f =
(b) () 1 lim x f x → does not exist. As x approaches 1 from the left, f (x) approaches 3.5, whereas as x approaches 1 from the right, f (x) approaches 1.
(c) () 4 f does not exist. The hollow circle at () 4,2 indicates that f is not defined at 4.
(d) () 4 lim x f x → exists. As x approaches 4, () f x approaches 2: () 4 lim2. x fx → =
32. (a) () 2 f does not exist. The vertical dotted line indicates that f is not defined at –2.
(b) () 2 lim x f x →− does not exist. As x approaches –2, the values of () f x do not approach a specific number.
(c) () 0 f exists. The black dot at () 0,4 indicates that ()04. f =
(d) () 0 lim x f x → does not exist. As x approaches 0 from the left, () f x approaches 1 2,whereas as x approaches 0 from the right, () f x approaches 4.
(e) () 2 f does not exist. The hollow circle at () 1 2 2, indicates that () 2 f is not defined.
(f ) () 2 lim x f x → exists. As x approaches 2, () f x approaches () 2 11 22 :lim. x fx → =
(g) () 4 f exists. The black dot at ()4,2indicates that ()42. f =
(h) () 4 lim x f x → does not exist. As x approaches 4, the values of () f x do not approach a specific number.
33.
34.
35. One possible answer is 1 212345 1 2 1 2 3 4 5 6 y x f
() lim xc f x → exists for all values of 4. c ≠
() lim xc f x → exists for all values of c π ≠
36. One possible answer is
37. You need () () 31320.4.fxxx−=+−=−< So, take 0.4. δ = If 020.4, x <−< then () () 21330.4,xxfx −=+−=−< as desired.
38. You need () 12 110.01. 11 x fx xx −=−=< Let 1 . 101 δ = If 1 02, 101 x <−< then 1111 2111 101101101101 100102 1 101101 100 1 101 xx x x −<−< −<−<+
<−< −> and you have () 1211011 110.01. 11100101100 x fx xx −=−=<==
39. You need to find δ such that 01 x δ <−< implies () 1 110.1. fx x −=−< That is, 1 0.110.1 1 10.110.1 9111 1010 1010 911 1010 111 911 11 1. 911 x x x x x x −<−< −<<+ << >> −>−>− >−>−
So take 1 11 δ = Then 01 x δ <−< implies 11 1 1111 11 1. 119 x x −<−< −<−<
Using the first series of equivalent inequalities, you obtain () 1 110.1. fx x −=−<
40. You need to find δ such that 01 x δ <−< implies () 11 1211. fx xx ε −=−−=−< 1 1 1 1 1 11 11
1 11 εε εε εε εε εε εε −<−< −<<+ >> −+ −>−>− −+ >−> −+ x x x x x
For 0.05 0.05, take 0.05. 10.05 εδ==≈
For 0.01 0.01, take 0.01. 10.01 εδ==≈ For 0.005 0.005, take 0.005. 10.005 εδ==≈
As ε decreases, so does δ
41. () 2 lim323(2)28 x x L → +=+==
(a) () 0.01 3 3280.01 360.01 320.01 020.0033 x x x x δ +−< −< −< <−<≈=
So, if 0.01 3 02, x δ <−<= you have
320.01 360.01 3280.01 0.01. x x x fxL −< −< +−<
(b) () 3280.005 360.005 320.005 0.005 020.00167 3 x x x x δ +−< −< −< <−<≈=
Finally, as in part (a), if 0.005 02, 3 x <−< you have () 3280.005. x +−<
42. 6 6 lim664 33 x x L →
−< −−< −< <−<=
As in part (a), if 060.015, x <−< you have 640.005. 3 −−< x 43. ()22 2 lim3231 x x L → −=−== (a) () ()() 2 2 310.01 40.01 220.01 220.01 0.01 2 2 x x xx xx x x −−< −< +−< +−< −< +
If you assume 13, x << then 0.0150.002. δ ≈=
(a) 1 3 640.01 3 20.01 3 (6)0.01 60.03 060.03 x x x x x δ
−−< −< −−< −< <−<=
So, if 060.03, x δ <−<= you have () 1 3 (6)0.01 20.01 3 640.01 3 0.01. x x x fxL −−< −<
−< (b) () 640.005 3 20.005 3 1 60.005 3 60.015 060.015 x x x x x δ
So, if 020.002, x δ <−<≈ you have () () () () 2 2 11 20.0020.010.01 52 220.01 40.01 310.01 0.01. x x xx x x fxL −<=< + +−< −< −−< −< (b) () ()() 2 2 310.005 40.005 220.005 220.005 0.005 2 2 x x xx xx x x −−< −< +−< +−< −< +
If you assume 13, x << then 0.005 0.001. 5 δ ==
Finally, as in part (a), if 020.001, x <−< you have () 2 310.005. x −−<
44. ()22 4 lim64622 x x L → +=+== (a) () ()() 2 2 6220.01 160.01 440.01 440.01 0.01 4 4 x x xx xx x x +−< −< +−< +−< −< +
If you assume 35, x << then 0.01 0.00111. 9 δ =≈
So, if 0.01 04, 9 x δ <−<≈ you have () () 2 2 0.010.01 4 94 (4)(4)0.01 160.01 6220.01 0.01. x x xx x x fxL −<< + +−< −< +−< −< (b) () ()() 2 2 6220.005 160.005 440.005 440.005 0.05 4 4 x x xx xx x x +−< −< −+< −+< −< +
If you assume 35, x << then 0.005 0.00056. 9 δ =≈
Finally, as in part (a), if 0.005 04, 9 x <−< you have () 2 6220.005. x +−<
45. () 2 4 lim16412 x x xL → −=−== (a) () ()() 2 120.01 430.01 430.01 0.01 4 3 xx xx xx x x −−< −+< −+< −< +
If you assume 35, x << then 0.01 0.00125. 8 δ ==
So, if 0.01 04, 8 x <−< you have () () 2 2 0.01 4 3 430.01 120.01 120.01 0.01 x x xx xx xx fxL −< + −+< −−< −−< −< (b) () ()() 2 120.005 430.005 430.005 0.005 4 3 xx xx xx x x −−< −+< −+< −< +
If you assume 35, x << then 0.005 0.000625. 8 δ ==
Finally, as in part (a), if 0.005 04, 8 x <−< you have () 2 120.005. xx−−<
46. 22 3 lim39 x x L → ===
(a) ()() 2 90.01 330.01 330.01 0.01 3 3 x xx xx x x −< −+< −+< −< +
If you assume 24, x << then 0.01 0.0014. 7 δ =≈
So, if 0.01 03, 7 x <−< you have () 2 0.01 3 3 330.01 90.01 0.01 x x xx x fxL −< + −+< −< −< (b) ()() 2 90.005 330.005 330.005 0.005 3 3 x xx xx x x −< −+< −+< −< +
If you assume 24, x << then 0.005 0.00071. 7 δ =≈
Finally, as in part (a), if 0.005 03, 7 x <−< you have 2 90.005. x −<
47. () 4 lim2426 x x → +=+=
Given 0: ε > ()26 4 x x ε εδ +−< −<=
So, let δε = So, if 04, x <−<=δε you have () () 4 26 x x fxL ε ε ε −< +−< −<
48. () 2 lim454(2)53 x x →− +=−+=−
Given 0: ε > ()45(3) 48 42 2 4 x x x x ε ε ε ε δ +−−< +< +< +<=
So, let . 4 ε δ =
So, if 02, 4 x ε δ <+<= you have () 2 4 48 (45)(3) . x x x fxL ε ε ε ε +< +< +−−< −<
49. () () 4 11 22 lim1413 x x →− −=−−=−
Given 0: ε > () () () () 1 2 1 2 1 2 13 2 4 42 x x x x ε ε ε ε −−−< +< −−< −−<
So, let 2. δε =
So, if () 042, x <−−<=δε you have () () () 1 2 1 2 42 2 13 x x x fxL ε ε ε ε −−< +< −+< −<
50. () () 3 3313 lim131444 x x → +=+=
Given 0: ε > ()313 44 39 44 3 4 4 3 1 3 3 x x x x ε
So, let 4 3 δε =
So, if 4 3 03, x <−<=δε you have
51. 6 lim33 x → =
Given 0: ε > 33 0 ε ε −< <
So, any 0 δ > will work.
So, for any 0, δ > you have
fxL
52. () 2 lim11 x → −=−
Given ()0:11 0 εε ε >−−−< <
So, any 0 δ > will work.
So, for any 0, δ > you have ()() () 11 fxL ε ε −−−< −<
53. 3 0 lim0 x x → =
Given 0: ε > 3 3 3 0 x x x ε ε εδ −< < <=
So, let 3δε = So, for 3 00, x −=δε you have () 3 3 3 0 . x x x fxL ε ε ε ε < < −< −< 54. 4 lim42 x x → ==
Given 0: ε > 2 222 42 x xxx xx ε ε ε −< −+<+ −<+
Assuming 19, x << you can choose 3. δε = Then, 04342 2. xxx x δεε ε <−<= −<+ −<
55. () 5 lim5551010 x x →− −=−−=−=
Given 0: ε > () () () 510 51050 5 5 x xx x x ε ε ε ε −−< −−−<−< −−< −−<
So, let δε = So for ()5, x −−<=δε you have () () () () 5 510 510because 50 x x xx fxL ε ε ε ε −+< −−−< −−<−< −<
56. 3 lim3330 x x → −=−=
Given 0: ε > 30 3 x x ε ε −−< −<
So, let δε = So, for 03, x <−<=δε you have () 3 30 . x x fxL ε ε ε −< −−< −<
57. ()22 1 lim1112 x x → +=+=
Given 0: ε > () ()() 2 2 12 1 11 1 1 x x xx x x ε ε ε ε +−< −< +−< −< +
If you assume 02, x << then 3. δε =
So for 01, 3 x ε δ <−<= you have () () 2 2 11 1 31 1 12 2. x x x x fx εε ε ε ε −<< + −< +−< −<
58. ()22 4 lim4(4)4(4)0 x xx →− +=−+−=
Given 0: ε > () 2 40 (4) 4 xx xx x x ε ε ε +−< +< +<
If you assume 53, x −<<− then 5 ε δ =
So for 0(4), 5 x ε δ <−−<= you have () () 2 1 4 5 (4) 40 . x x xx xx fxL ε ε ε ε ε +<< +< +−< −<
59. () limlim44 xx fx ππ →→ ==
60. () limlim xx fxx ππ π →→ ==
61. () () 4 53 4 1 lim 6 x x fx x fx → +− = =
0.5
The domain is [ )() 5,44,. −∪∞ The graphing utility does not show the hole at 1 4,. 6
62. () () 2 0 1 1 lim 2 x x e fx x fx → = =
The domain is all 0. x ≠ The graphing utility does not show the hole at 1 0, . 2
63. () 9.990.791, 0 Cttt=−−>
(a) () () 10.759.990.79110.75 9.990.7910 $17.89 C =−− =−− = () 10.75 C represents the cost of a 10-minute, 45-second call.
(b)
8 6 16 2 1 2 2
(c) The limit does not exist because the limits from the left and right are not equal.
64. () 5.790.991, 0 Cttt=−−>
(a) () () 10.755.790.99110.75 5.790.9910
$15.69 C =−− =−− = () 10.75 C represents the cost of a 10-minute, 45-second call.
(b)
(c) The limit does not exist because the limits from the left and right are not equal.
65. Choosing a smaller positive value of δ will still satisfy the inequality () . fxL ε −<
66. In the definition of () lim, xc f x → f must be defined on both sides of c, but does not have to be defined at c itself. The value of f at c has no bearing on the limit as x approaches c
67. No. The fact that ()24 f = has no bearing on the existence of the limit of () f x as x approaches 2.
68. No. The fact that () 2 lim4 x fx → = has no bearing on the value of f at 2.
69. (a) 2 63 0.9549cm 22 Cr C r π πππ = ===≈
(b) When 5.5 5.5:0.87535cm 2 Cr π ==≈ When 6.5 6.5:1.03451cm 2 Cr π ==≈ So 0.875351.03451. r << (c) () 3 lim26;0.5;0.0796 x r π πεδ → ==≈
06 4 x 2345 2 3 7 3211 1 1 (0,2.7183) y x f (x) –0.1 2.867972 –0.01 2.731999 –0.001 2.719642 –0.0001 2.718418
70. 3 4 ,2.48 3 VrV π == (a) 3 3 4 2.48 3 1.86 0.8397in. r r r π π = = ≈ (b) 3 3 2.452.51 4 2.452.51 3 0.58490.5992 0.83630.8431 V r r r π ≤≤ ≤≤ ≤≤ ≤≤ (c) For 2.512.480.03,0.003εδ =−=≈
71. ()() () 1 1 0 1 lim12.71828 x x x fxx xe → =+ +=≈
)
72. () 11xx fx x +−− = () 0 lim2 x fx → =
Note that for () ()() 11 11,0,2. xx xxfx x ++− −<<≠==
0.002
1.9982.002 0 (1.999,0.001) (2.001,0.001)
Using the zoom and trace feature, 0.001. δ = So ()() 2,21.999,2.001. δδ −+=
Note: 2 4 2 2 x x x =+ for 2. x ≠
74. (a) () lim xc f x → exists for all 3. c ≠− (b) () lim xc f x → exists for all 2,0. c ≠−
75. False. The existence or nonexistence of () f x at x c = has no bearing on the existence of the limit of () f x as x c →
76. True
77. False. Let () 4,2 0,2 xx fx x −≠ = =
()20 f = ()()22 lim lim420 xx fxx →→ =−=≠
78. False. Let () 4,2 0,2 xx fx x −≠ = = ()()22 lim lim42 xx fxx →→ =−= and ()202 f =≠
79. () f xx = 0.25 lim0.5 x x → = is true. As x approaches 1 4 0.25 = from either side, () f xx = approaches 1 2 0.5. =
80. () f xx = 0 lim0 x x → = is false. () f xx = is not defined on an open interval containing 0 because the domain of f is 0. x ≥
81. Using a graphing utility, you see that 0 0 sin lim1 sin2 lim2,etc. x x x x x x → → = = So, 0 sin lim. x nx n x → =
82. Using a graphing utility, you see that 0 0 tan lim1 tan2 lim2,etc. x x x x x x → → = = So, () 0 tan lim. x nx n x → =
83. If () 1 lim xc f xL → = and () 2 lim, xc f xL → = then for every 0, ε > there exists 1 0 δ > and 2 0 δ > such that () 11 xcfxLδε −< −< and () 22 xcfxLδε −< −< Let δ equal the smaller of 1 δ and 2.δ Then for , xc δ −< you have ()() () () 121212 LLLfxfxLLfxfxL −=−+−≤−+−<+εε Therefore, 12 2. LL ε −< Since 0 ε > is arbitrary, it follows that 12L L =
84. () ,0.fxmxbm=+≠ Let 0 ε > be given.
Take . m ε δ =
If 0, xc m ε δ <−<= then ()() mxc mxmc mxbmcb ε ε ε −< −< +−+< which shows that () lim. xc mxbmcb → +=+
85. () lim0 xc fxL → = means that for every 0 ε > there exists 0 δ > such that if 0, xc δ <−< then () () 0. fxL ε −−<
This means the same as () fxL ε −< when 0. xc δ <−<
So, () lim. xc f xL → =
So, ()() 2 31310.010 xxx+−+> if
2 1010 x −< and 2 9010. x −<
Let () 11 ,,. 9090 ab =−
For all 0 x ≠ in (),,ab the graph is positive. You can verify this with a graphing utility.
(b) You are given () lim0. xc gxL → => Let 1 2 L ε =
There exists 0 δ > such that 0 xc δ <−< implies that () . 2 L gxL ε −<= That is,
For x in the interval (),,, ccxc δδ −+≠ you have () 0, 2 L gx >> as desired.
Section2.3EvaluatingLimitsAnalytically
1. For polynomial functions (), px substitute c for x, and simplify.
2. An indeterminant form is obtained when evaluating a limit using direct substitution produces a meaningless fractional expression such as 00. That is, () () lim xc f x g x → for which ()() limlim0 xcxc fxgx →→ ==
3. If a function f is squeezed between two functions h and g, ()()(), hxfxgx ≤≤ and h and g have the same limit L as , x c → then () lim xc f x → exists and equals L
87. The radius OP has a length equal to the altitude z of the triangle plus 2 h So, 1. 2 h z =− 1 Area triangle122 Area rectangle h b bh
=−
= Because these are equal, 1 1 22 12 2 5
88. Consider a cross section of the cone, where EF is a diagonal of the inscribed cube. 3,2.ADBC== Let x be the length of a side of the cube. Then 2. EFx = By similar triangles, 23 23 EFAG BCAD x x = = Solving for x, () 3262 3226 6926 0.96. 7 322 xx x x =− += ==≈ +
4. () 0 0 1 0 sin lim1 1cos lim0 lim1 x x x x x x x x x e → → → = = +=
5. ()() 3 lim252351 x x →− +=−+=−
6. ()() 9 lim4149136135 x x → −=−=−=
7. () ()() 2 2 3 lim3333990 x xx →− +=−+−=−=
8. () ()() 3 3 1 lim26521615 2651 x xx → −+=−+ =−+=
9. 3 lim83811 x x → +=+=
10. 3 3 2 33 lim12312(2)3 243273 x x → +=+ =+==
11. ()() 3 3 3 4 lim1145125 x x →− −= ==
12. ()() 44 4 0 lim323(0)2(2)16 x x → −=−=−=
13. () 2 333 lim 212215 x x → == ++
14. 5 555 lim 3532 x x →− ==− +−+
15. 22 1 11 lim 4145 x x x → == ++
16. 1 353(1)5358 lim4 11122 x x x → +++ ==== ++
17. () 7 37 321 lim7 3 272 x x x → === ++
18. 3 63693 lim 23255 x x x → ++ === ++
19. (a) () 1 lim514 x fx → =−=
(b) () 3 4 lim464 x gx → ==
(c) () () () () () 1 lim1464 x gfxgfg → ===
20. (a) ()() 3 lim374 x fx →− =−+=
(b) () 2 4 lim416 x gx → ==
(c) () () () 3 lim416 x gfxg →− ==
21. (a) () 1 lim413 x fx → =−=
(b) () 3 lim312 x gx → =+=
(c) () () () 1 lim32 x gfxg → ==
22. (a) () () () 2 4 lim2434121 x fx → =−+=
(b) () 3 21 lim2163 x gx → =+=
(c) () () () 4 lim213 x gfxg → ==
23. 2 limsinsin1 2 x x π π → ==
24. limtantan0 x x π π → ==
25. 1 1 limcoscos 332 x x ππ → ==
26. () 2 2 1 limsin sin sin 121262 x x π ππ → ===
27. 0 limsec2sec01 x x → ==
28. limcos3cos31 x x π π → ==−
29. 56 51 limsinsin 62 x x π π → ==
30. 53 51 limcoscos 32 x x π π → ==
31. 3 3 limtantan1 44 x x ππ → ==−
32. 7 723 limsecsec 663 x x ππ → ==
33. 0 0 limcos2cos01 x x exe → ==
34. 0 0 limsinsin00 x x exe π → ==
35. () 1 limln3ln3 x x x ee → +=+
36. 1 1 1 limlnlnln1 x x x e ee → ===−
37. () () 2 lim, lim2 5 xcxc fxgx →→ ==
(a) ()()()lim55 lim5210 xcxc gxgx →→ ===
(b) ()()()()limlimlim 2 2 5 12 5 xcxcxc f xgxfxgx →→→ +=+ =+ =
=
(c) ()()()() () limlimlim 2 2 5 4 5 xcxcxc f xgxfxgx →→→
= =
(d) () () () () lim 251 lim lim25 xc xc xc fx fx gxgx → → → ===
38. ()() 3 lim2, lim 4 xcxc fxgx →→ ==
===
(a) ()() lim44lim4(2)8 xcxc fxfx →→
(b) ()()()() 311 limlimlim2 44 xcxcxc fxgxfxgx →→→
(c) ()()()() 33 limlimlim2 42 xcxcxc fxgxfxgx →→→
(d) () () () () () lim 28 lim lim343 xc xc xc fx fx gxgx → → → ===
39. () lim16 xc fx → =
(a) ()()() 2 2 2 limlim16256 xcxc fxfx →→
=
(b) () () limlim164 xcxc fxfx →→ ===
==
=
(c) ()()() lim33lim31648 xcxc fxfx →→
==
(d) () () ()32 3232 limlim1664 xcxc fxfx →→
=
40. () lim27 xc fx → =
(a) () () 3 3 3 limlim273 xcxc fxfx →→ ===
(b) () () lim 273 lim 18lim18182 xc xc xc fx fx → → → ===
===
(c) ()()() 2 2 2 limlim27729 xcxc fxfx →→
===
(d) () () () 23 23 23 limlim279 xcxc fxfx →→
41. () 2 1(1)(1) 11 xxx fx xx −+− == ++ and () 1 gxx=− agree except at 1. x =− ()()()111 limlimlim1112 xxx fxgxx →−→−→− ==−=−−=−
42. () 2 352(2)(31) 22 xxxx fx xx +−+− == ++ and () 31gxx=− agree except at 2. x =−
()()()222 limlimlim31 3(2)17 xxx fxgxx →−→−→− ==− =−−=−
43. () 3 8 2 x fx x = and () 2 24gxxx=++ agree except at 2. x =
()() () 2 222 2 limlimlim24 22(2)412 xxx fxgxxx →→→ ==++ =++=
44. () 3 1 1 x fx x + = + and () 2 1 gxxx=−+ agree except at 1. x =− ()() () 2 111 2 limlimlim1 (1)(1)13 xxx fxgxxx →−→−→− ==−+
45. () ()() () () ()() 2 44 4 ln6ln6 and 164 agree except at 4. ln2 limlim0.0866 8 xx xxx fxgx xx x fxgx →−→− +++ == =− ==≈−
46. () () 2 1 and 1 1 x x x e fxgxe e ==+ agree except at 0. x = ()() 0 00 limlim12 xx fxgxe →→ ==+=
47. () 2 000 11 limlimlim1 1101xxx xx xxxxx →→→ ====−
48. () 32 2 00 7 limlim7000 xx xx xx x →→ =−=−=
49. ()() 2 44 4 44 limlim 1644 111 lim 4448 xx x xx xxx x →→ → = −+− === ++
50. () ()() 2 55 5 5 5 limlim 2555 111 lim 55510 xx x x x xxx x →→ → = −−+ ===− ++
51. ()() ()() 2 2 33 3 32 6 limlim 933 23255 lim 33366 xx x xx xx xxx x x →−→− →− +− +− = −+− ====
52. ()() ()() 2 2 22 2 24 28 limlim 221 4246 lim2 1213 xx x xx xx xxxx x x →→ → −+ +− = −−−+ ++ ==== ++
53. () () () 44 4 4 limlim535353 44 53 59 lim 453 111 lim 6 5393 xx x x xxx xx x x xx x →→ → → +−+−++ =⋅ ++ +− = −++ === +++
54. () 33 3 3 121212 limlim 33 12 3 lim 312 111 lim 4 1242 xx x x xxx xx x x xx x →→ → → +−+−++ =⋅ ++ = −++ === +++
55. () () 00 00 555555 limlim 55 55 1115 limlim 10 555525 55 xx xx xxx xx x x x xx →→ →→ +−+−++ =⋅ ++ +− ===== +++ ++
56. () 00 00 222222 limlim 22 221112 limlim 4 222222 22 xx xx xxx xx x x x xx →→ →→ +−+−++ =⋅ ++ +− ===== +++ ++
57. () ()() ()()() () 0000 11 33 111 33 limlimlimlim 333333(3)39xxxx x x x xxxxxx→→→→ −+ + =====− +++
58. () () () 000 44 11 44 111 44 limlimlim 444(4)16 xxx x x x xxx→→→ −+ + + ====− +
59. () 0000 22 2222 limlimlimlim22 xxxx xxx xxxx xxx Δ→Δ→Δ→Δ→ +Δ− +Δ−Δ ==== ΔΔΔ
60. () () () () 22222 0000 22 limlimlimlim22 xxxx xxxxxxxxxxx x xx xxx Δ→Δ→Δ→Δ→ +Δ−+Δ+Δ−Δ+Δ ===+Δ= ΔΔΔ
61. ()() () () () 2 2 2 22 0 0 0 2121 222121 limlim lim2222 x x x xxxxxx xxxxxxxx xx xxx Δ→Δ→ Δ→ +Δ−+Δ+−−+ +Δ+Δ−−Δ+−+− = ΔΔ =+Δ−=−
62. () ()() () ( ) () ( ) 2 2 3233323 000 2 22 0 33 33 limlimlim lim333 xxx x x xxxx xxxxxxxxxx
63. () 00 limlim1sinsin111 5555xx xx xx→→
64. () () ()() 00 31cos1cos limlim3300 →→
67. () 2 00 sinsin limlimsin1sin00 xx xx x xx→→
68. ()() 22 00022 limlimlimtansinsinsin coscos 100 xxx x xxx x xxxx→→→
==
== xx xx x x xxx
65. ()() ()() 2 00 sin1cos sin1cos limlim 100 →→ =⋅
66. 00 costansin limlim1 θθ θθθ →→θθ ==
69. () () ()() 2 00 1cos 1cos limlim1cos 000 hh h h h hh→→ =− ==
70. ()limsec1 φπ φφ ππ → =−=−
71. 0 66 cos 66 cos 066 lim0 333 x x → ===
72. () () 000 00 cos sin 1sin cos 1 limlimlim 222 1sin 11cos lim lim 22 111 10 222 xxx xx xxxx xxx x x xx →→→ →→ =+ =−− =−−=−
73. () 000 0 1 11 limlimlim 111 lim1 x x xxx xxxxxxx x x ee eee eeee e →→→ → =⋅= ==
74. () ()() () () 2 00 0 41411 limlim 11 lim41428 xxx xxxx x x eee ee e →→ → −−+ =
75. () 00 limlim1sin3sin3333 23222tt tt tt→→
76. () () 00 sin2sin213 limlim2 sin323sin3 12 211 33 xx xxx x xx →→
80. () 5 32 2 x fx x = It appears that the limit is 80.
The
(Hint: Use long division to factor 5
81. () sin3t ft t = It appears that the limit is 3.
The graph has a hole at 0. t = Analytically,
82.
83. () 2 sin x fx x = It appears that the limit is 0.
The graph has a hole at 0. x = Analytically, () 22 2 00 sinsin limlim010. →→
84. () 3 sin x fx x = It appears that the limit is 0.
The graph has a hole at 0. x =
85. () ln 1 x fx x = It appears that the limit is 1. Analytically,
Let 1, then 1 and 0 as 1. yxxyyx =−=+→→
So, () ()1 11 10 limlnlimln1ln 1. y x xy xye →→ =+==
87. () 32fxx=−
88. ()
89. () 2 4 f xxx =−
90. () 2 31fxx=+ ()() () () ( ) () () 2 2 2 22 000 2 00 3131 363131 limlimlim
91. () 2 f xx =
92. () 5 fxx=−
93. () 1 3 fx
94. () 2 1 fx x =
95. () () () () 22 000 0 lim4limlim3 4lim4 xxx x x fxx fx →→→ → −≤≤+
Therefore,
Therefore, () lim. xa f xb → =
97. () sin f xxx = 0 limsin0 x xx → =
98. () cos f xxx = 0 limcos0 x xx → =
99. () 1 sin fxx x = 0 1 limsin0 x x x →
=
100. () 1 cos = fxx x 0 1 limcos0 x x x →
=
101. (a) Two functions f and g agree at all but one point (on an open interval) if ()() f xgx = for all x in the interval except for , x c = where c is in the interval.
(b) () 2 1(1)(1) 11 xxx fx xx −+− == and () 1 gxx=+ agree at all points except 1. x =
(Other answers possible.)
102. Answers will vary. Sampleanswers:
(a) linear: () () 8 111 ; lim84 222 x fxxx → ===
(b) polynomial of degree 2: () 2 60; fxx=− ()22 8 lim608604 → −=−= x x
(c) rational: () () 8 88 ; lim4 21421428142 x xx fx xx → ====
(d) radical: () 8 8; lim888164 x fxxx → =++=+==
(e) cosine: ()()()() 8 4 cos; lim4 cos 4 cos 8414 x fxxxπππ → ====
====
(f) sine: () () 8 4 sin; lim4 sin4 sin 414 16162 x fxxx
→
(g) () 880 8 4; lim444xx x fxeee → ===
(h) ()()() 8 4 ln7; lim4 ln74 ln 4 x fxexexe →
103. ()()() sin ,sin, x fxxgxxhx x ===
When the x-values are “close to” 0 the magnitude of f is approximately equal to the magnitude of g. So, 1 gf ≈ when x is “close to” 0.
104. (a) Use the dividing out technique because the numerator and denominator have a common factor.
(b) Use the rationalizing technique because the numerator involves a radical expression.
106. () 2 165000stt=−+= when 50055 sec. 162 t == The velocity
The paint can is falling at about 64 feet/second.
108.
The velocity of the object when it hits the ground is about 62.6 m/sec.
109. Let () 1 f xx = and ()() 0 1/.lim x g xxfx → =− and () 0 lim x g x → do not exist. However,
and therefore does not exist.
110. Suppose, on the contrary, that () lim xc g x → exists. Then, because () lim xc f x → exists, so would ()() lim, xc f xgx → + which is a contradiction. So, () lim xc g x → does not exist.
111. Given () , f xb = show that for every 0 ε > there exists a 0 δ > such that () fxb ε −< whenever xc δ −< Because () 0 fxbbb ε −=−=< for every 0, ε > any value of 0 δ > will work.
112. Given () , n f xxn = is a positive integer, then
=
== ==
113. If 0, b = the property is true because both sides are equal to 0. If 0, b ≠ let 0 ε > be given. Because () lim, xc f xL → = there exists 0 δ > such that () f xLb ε −< whenever 0. xc δ <−< So, whenever 0, xc δ <−< we have () () or bfxLbfxbLεε −<−< which implies that () lim. xc bfxbL → =
114. Given () lim0: xc fx → = () () () () () For every0,there exists0such that 0whenever 0.
Now 00for .Therefore, lim0. xc fxxc fxfxfx xcfx εδ
115. () ()()() () () ()()()() ()()()() ()() limlimlim 0lim0 0lim0 →→→ → → −≤≤ −≤ ≤ −≤ ≤ ≤ ≤ xcxcxc xc xc MfxfxgxMfx M fxfxgxMfx MfxgxM fxgx
Therefore, ()() lim0. → = xc fxgx
116. (a) () () () ()() () ()() () If lim0,thenlim0. limlimlim 0lim0 xcxc xcxc xc xc fxfx fxfxfx fxfxfx fx →→ →→ → → =−= −≤≤ −≤≤ ≤≤
Therefore, () lim0. xc fx → = (b) Given () lim: xc f xL → =
For every 0, ε > there exists 0 δ > such that () fxL ε −< whenever 0. xc δ <−< Since () () fxLfxL ε −≤−< for , xc δ −< then () lim. xc f xL → =
117. Let () () 00 4,if0 4,if0 limlim44. xx x fx x fx →→ ≥ = −< == ()
0 lim x f x → does not exist because for () 0,4xfx<=− and for () 0,4.xfx≥=
118. The graphing utility was set in degree mode, instead of radian mode.
119. The limit does not exist because the function approaches 1 from the right side of 0 and approaches 1 from the left side of 0.
125. () () ()() 00 22 00 0 00 1cos1cos1cos limlim 1cos 1cossin limlim 1cos1cos sinsin lim 1cos sinsin limlim 1cos 100 xx xx x xx xxx xxx xx x xxx xx xx xx xx →→ →→ → →→ −−+ =⋅ + == ++ =⋅ + = + ==
120. False. sin0 lim0 x x x π π → ==
121. True.
122. False. Let () 1 ,1. 31 xx fxc x ≠ == = Then () 1 lim1 x fx → = but ()11. f ≠
123. False. The limit does not exist because () f x approaches 3 from the left side of 2 and approaches 0 from the right side of 2.
124. False. Let () 2 1 2 f xx = and () 2 g xx = Then ()() f xgx < for all 0. x ≠ But ()()00 limlim0. xx fxgx →→ ==
126. () () 0,if is rational 1,if is irrational
0,if is rational ,if is irrational x fx x x gx xx = =
() 0 lim x f x → does not exist.
No matter how “close to” 0 x is, there are still an infinite number of rational and irrational numbers so that () 0 lim x f x → does not exist. () 0 lim0 x gx → = when x is “close to” 0, both parts of the function are “close to” 0.
127. () 2 sec1 x fx x =
(a) The domain of f is all 0,/2. x n ≠+ππ
(b)
The domain is not obvious. The hole at 0 x = is not apparent.
(c) () 0 1 lim 2 x fx → = (d) () () 22 22 22 2 22 sec1sec1sec1 sec1 sec1tan sec1sec1 1sin1 cossec1 xxx xxx xx xxxx x xxx −−+ =⋅ + == ++ = + So, () 2 00222 sec11sin1 limlim cossec1 11 11. 22 xx xx xxxx→→ = +
==
128. (a)
Section2.4ContinuityandOne-SidedLimits
1. A function f is continuous at a point c if there is no interruption of the graph at c.
2. 1 1 because lim212110 x cx + →− =−+=−+=
3. The limit exists because the limit from the left and the limit from the right and equivalent.
4. If f is continuous on a close interval [ ] , ab and ()(), f afb ≠ then f takes on all values between ()() and . f afb
5. (a) () 4 lim3 x fx + → =
(b) () 4 lim3 x fx → =
(c) () 4 lim3 x fx → =
The function is continuous at 4 x = and is continuous on (),. −∞∞
6. (a) () 2 lim2 x fx + →− =− (b) () 2 lim2 x fx →− =−
(c) () 2 lim2 x fx →− =−
The function is continuous at 2. x =−
7. (a) () 3 lim0 x fx + → =
(b) () 3 lim0 x fx → =
(c) () 3 lim0 x fx → =
The function is NOT continuous at 3. x =
(b) From part (a), 2 2 2 1cos1 1cos 2 1 cos 2 1 1for 2 0. x x x x x x x ≈ ≈ ≈− ≈
(c) () () 2 1 cos0.110.10.995 2 ≈−= (d) () cos0.10.9950,which agrees with part (c). ≈
8. (a) () 3 lim3 x fx + →− = (b) () 3 lim3 x fx →− = (c) () 3 lim3 x fx →− =
The function is NOT continuous at 3 x =− because ()() 3 34lim. x f fx →− −=≠
9. (a) () 2 lim3 x fx + → =−
(b) () 2 lim3 x fx → =
(c) () 2 lim x f x → does not exist
The function is NOT continuous at 2. x =
10. (a) () 1 lim0 x fx + →− = (b) () 1 lim2 x fx →− = (c) () 1 lim x f x →− does not exist.
The function is NOT continuous at 1. x =− 11. 8 111 lim 88816 + → == ++ x x 12. 3 221 lim 3333 + → == ++ x x 13. 2 55 5 55 limlim 25(5)(5) 11 lim 510 xx x xx xxx x ++ →→ + → = −+− == + 14. 2 444 limlimlim4(4)1 16(4)(4)4 11 448 xxx xx xxxx +++ →→→ == −+−+ ==− +
21. () 33 25 limlim 22 xx x fx →→ + ==
22. () () () () 2 33 2 33 limlim4691263 limlim4291221 xx xx fxxx fxxx →→ →→++ =−+=−+=
Since these one-sided limits disagree, () 3 lim x f x → does not exist.
23. limcot x x π → does not exist because limcot x x π+ → and limcot x x π → do not exist.
24. 2 limsec x x π → does not exist because () 2 limsec x x π + → and () 2 limsec x x π → do not exist.
25. () () () 4 lim575378 3for34 x x xx → −=−= =≤<
26. () () 2 lim22222 x xx + → −=−=
27. 1 1 lim33132 33 x x →−
+=−+=−+=
28. () 1 lim1112 2 x x →
−−=−−=
29. () 3 limln3ln0 does not exist. x x + → −=
30. () 6 limln6ln0 does not exist. x x → −=
−=
31. ()() 2 2 limln3ln41ln4 x xx →
32. 5 5 limlnlnln5 1 4 x x x + → ==
33. () 2 1 4 fx x = has discontinuities at 2 x =− and 2 x = because () 2 f and () 2 f are not defined.
34. () 2 1 1 x fx x = + has a discontinuity at 1 x =− because () 1 f is not defined.
35. () 2 x f xx =+ has discontinuities at each integer k because ()() limlim. xkxk f xfx →→−+ ≠
36. () ,1 2,1 21,1 xx fxx xx < == −> has a discontinuity at 1 x = because ()() 1 12lim1. x ffx → =≠=
37. () 2 49 g xx =− is continuous on [ ] 7,7.
38. () 2 39 f tt =−− is continuous on [ ] 3,3.
39. ()() 00 lim3lim. xx f xfx −+ →→ == f is continuous on [ ] 1,4.
40. () 2 g is not defined. g is continuous on [ ) 1,2.
41. () 4 6 fx x = has a nonremovable discontinuity at 6 x = because () 6 lim x f x → does not exist.
42. () 2 1 1 fx x = + is continuous for all real x.
43. () 3cos f xxx =− is continuous for all real x.
44. () sin 8 f xxx =− is continuous for all real x
45. () 2 x fx x x = is not continuous at 0,1. x =
Because 2 1 1 x xxx = for 0,0xx≠= is a removable discontinuity, whereas 1 x = is a nonremovable discontinuity.
51. () 1,2 2 3,2 x x fx xx +≤ =
−>
has a possible discontinuity at 2. x =
1. () 2 212 2 f =+=
=+=
=−=
2. () ()() () 22 2 22 limlim12 2 limdoes not exist. limlim31 xx x xx x fx fx fxx →→ → →→++
Therefore, f has a nonremovable discontinuity at 2. x =
46. () 2 4 x fx x = has nonremovable discontinuities at 2 x = and 2 x =− because () 2 lim x f x → and () 2 lim x f x →− do not exist.
47. () ()() 2 22 31025 xx fx xxxx ++ == −−+−
has a nonremovable discontinuity at 5 x = because () 5 lim x f x → does not exist, and has a removable discontinuity at 2 x =− because () 22 11 limlim. 57 xx fx x →−→− ==−
48. () 2 22 6(3)(2) xx fx xxxx ++ == −−−+ has a nonremovable discontinuity at 3 x = because () 3 lim x f x → does not exist, and has a removable discontinuity at 2 x =− because () 22 11 limlim. 35 xx fx x →−→− ==−
49. () 7 7 x fx x + = + has a nonremovable discontinuity at 7 x =− because () 7 lim x f x →− does not exist.
50. () 23 3 x fx x = has a nonremovable discontinuity at 3 x = because () 3 lim x f x → does not exist.
52. () 2 2,2 41,2 xx fx xxx −≤
has a possible discontinuity at 2. x =
1. ()() 2224 f =−=−
2. ()() () () () 22 2 2 22 limlim24 limdoes not exist. limlim413 xx x xx fxx fx fxxx →→ → →→++
Therefore, f has a nonremovable discontinuity at 2. x =
53. () tan ,1 4 ,1 tan ,11 4 ,1or1 x x fx xx x x xxx π
has possible discontinuities at 1,1.xx=−=
1. ()() 1111ff −=−=
2. ()()11 lim1lim1 xx fxfx →−→ =−=
3. ()()()() 11 1lim1lim xx f fxffx →−→ −==
f is continuous at 1,=± x therefore, f is continuous for all real x
54. () csc ,32 6 2,32 csc ,15 6 2,1or5 x x fx x x x xx
has possible discontinuities at 1,5.==xx
1. () () 5 1csc 25csc 2 66ffππ ====
2. ()()15 lim2lim2 xx fxfx →→ ==
3. ()()()() 15 1lim5lim xx f fxffx →→ == f is continuous at 1 = x and 5, = x therefore, f is continuous for all real x
55. () () 2 ln1,0 1,0 xx fx xx +≥
= −<
has a possible discontinuity at 0. x =
1. ()() 0ln01ln10 f =+==
2. () () () 0 0 0 lim101 limdoes not exist. lim0 x x x fx fx fx → → + → =−= =
So, f has a nonremovable discontinuity at 0. x =
56. () 5 3 5 103,5 10,5 x ex fx xx −> = −≤
has a possible discontinuity at 5. x = 1. ()57 f = 2. () () () () 55 5 5 5 3 5 lim1037 lim7 lim1057 x x x fxe fx fx
3. ()() 5 5lim x f fx → = f is continuous at 5, x = so, f is continuous for all real x
57. () csc2 = f xx has nonremovable discontinuities at integer multiples of 2. π
58. () tan 2 x fx π = has nonremovable discontinuities at each 21, + kk is an integer.
59. () 8 fxx=− has nonremovable discontinuities at each integer k.
60. () 5 f xx =− has nonremovable discontinuities at each integer k
61. ()28 f = Find a so that 2 2 2 8 2 lim82. x axa + → = ==
62. ()13 f = () () 1 Find so thatlim43 143 7. x aax a a → −= −= =
63. () () 22 limlim lim2 xaxa xa xa gx xa x aa →→ → = =+=
Find a such 284. = = aa
64. () ()() 00 00 4sin limlim4 limlim2 xx xx x gx x g xaxa →→ →→++ == =−=
Let 4. = a
65. ()() 1arctan1122 f =−+=
Find a such that () 1 1 lim32 x x ae → += 11 32 32 1. ae a a += += =−
66. () 4 422 a fe=−
Find a such that () 24 4 limln322 a x xxe + → −+=− () 24 4 4 2 ln43422 1622 9 ln94 ln9ln3ln3 442 a a a e e e a a −+=− =− = = ===
67. () () () 2 2 11 1 56 == +− fgx x x
Nonremovable discontinuities at 1=± x
68. () () 1 1 = fgx x
Nonremovable discontinuity at 1; x = continuous for all 1 x >
69. () () tan 2 x fgx =
Not continuous at ,3,5, ... x =±±±πππ Continuous on the open intervals ..., (3, ), (, ), (, 3),...ππππππ
70. () () 2 sin = f gxx
Continuous for all real x
71. yxx =−
Nonremovable discontinuity at each integer
72. () 2 11 215(5)(3) hx xxxx == +−+−
Nonremovable discontinuities at 5 x =− and 3 x =
73. () 2 3,4 25,4 xxx gx xx −> =
Nonremovable discontinuity at 4 x =
74. () cos1 ,0 5,0 x x fx x xx < =
≥ ()() 0500 f == () () 00 cos1 limlim0 xx x fx x →→ == ()() 00 limlim50 xx fxx →→++ ==
Therefore, ()() 0 lim00 x fxf → == and f is continuous on the entire real line. () 0 was the only possible discontinuity. = x
75. () 2 2 = ++ x fx xx
Continuous on () , −∞∞
76. () 1 + = x fx x Continuous on () 0, ∞
77. () 3 f xx =− Continuous on [ ) 0, ∞ 7 3 2 3
78. () 3 =+fxxx
Continuous on [ ) 3, −∞
79. () sec 4 π = x fx
Continuous on: ()()()() ,6,2,2,2,2,6,6,10,
80. () 1 cos fx x =
Continuous on (, 0) and (0, ) −∞∞
81. () 2 1 ,1 1 2,1 x x fx x x ≠
=
=
Since () 2 111 1 1(1)(1) limlim lim 11 lim (1)2, xxx x xxx fx xx x →→→ → −−+ == =+= f is continuous on (, ).−∞∞
82. () 24,3 1,3 xx fx x −≠ = =
Since ()()33 limlim2421, xx fxx →→ =−=≠ f is continuous on (, 3) and (3, ). −∞∞
87. () 2 2cos 2 x hxex =− is continuous on the interval 0,. 2
83. () 43 1 12 4 =−+fxxx is continuous on the interval [ ] 1,2. () 37 12 1 f = and () 8 3 2. f =− By the Intermediate Value Theorem, there exists a number c in [ ]1,2 such that () 0. = fc
84. is continuous on the interval [ ] 0,1. and ()13. = f By the Intermediate Value Theorem, there exists a number c in [ ]0,1 such that () 0. = fc
85. () 2 2cos f xxx =−− is continuous on [ ] 0,. π ()03 =− f and () 2 18.870. f ππ=−≈> By the Intermediate Value Theorem,for at least one value of c between 0 and π
86. () 5 tan 10 x fx x π =−+
=−+≈−
is continuous on the interval [ ] 1,4. ()15tan4.7 10 f π
and () 52 4tan1.8. 45 f π
=−+≈
By the Intermediate Value Theorem, there exists a number c in [ ]1,4 such that () 0. = fc
()020 and 0.910. 2 hh π =−<≈>
By the Intermediate Value Theorem, there exists a number c in 0, 2
such that () 0. hc =
88. () ()() 32 22 ln4gtttt=+−+ is continuous on the interval [ ] 0,1. ()() 02.770 and 11.610. gg≈−<≈>
By the Intermediate Value Theorem, there exists a number c in [ ]0,1 such that () 0. gc =
89. Consider the intervals [ ] [ ] 1, 3 and 3, 5 for ()() 2 32. fxx=−= ()() 120 and 320, ff=>=−< so f has at least one zero in [ ] 1, 3. ()() 320 and 520, ff=−<=> so f has at least one zero in [ ] 3, 5.
So, f has at least two zeros in [ ] 1, 5.
90. Consider the intervals [ ] [ ] 1, 3 and 3, 5 for () 2 cos . f xx = ()12 cos 11.080 f =≈> and ()32 cos 31.980, f =≈−< so f has at least one zero in [ ] 1, 3. ()32 cos 31.980 f =≈−< and ()52 cos 50.570, f =≈> so f has at least one zero in [ ] 3, 5.
So, f has at least two zeros in [ ] 1, 5. () 3 53=+−fxxx ()03 =− f () 0 = fc
91. () 3 1 fxxx=+−
() f x is continuous on [ ] 0,1. ()01 =− f and ()11 = f
By the Intermediate Value Theorem, () 0 fc = for at least one value of c between 0 and 1. Using a graphing utility to zoom in on the graph of (), f x you find that 0.68. x ≈ Using the root feature, you find that 0.6823. x ≈
92. () [] 42 31 () is continuous on 0, 1. fxxxx fx =−+−
(0)1 f =− and (1)2 f =
By the Intermediate Value Theorem, () 0 fc = for at least one value of c between 0 and 1. Using a graphing utility to zoom in on the graph of (), f x you find that
0.37. x ≈ Using the root feature, you find that 0.3733. x ≈
93. () 2 17196fxxx=++−
[ ] is continuous on 0, 1. f
()01961.640 f =−≈−<
()13760.080 f =−≈>
By the Intermediate Value Theorem, () 0 fc = for at least one value of c between 0 and 1. Using a graphing utility to zoom in on the graph of (), f x you find that 0.95. x ≈ Using the root feature, you find that 0.9472. x ≈
94. () 4 39134fxxx=++−
[ ] is continuous on 0, 1. f ()01340.390 f =−≈−< ()15343.280 f =−≈>
By the Intermediate Value Theorem, () 0 fc = for at least one value of c between 0 and 1. Using a graphing utility to zoom in on the graph of (), f x you find that 0.08. x ≈ Using the root feature, you find that 0.0769. ≈ x
95. () 2cos3=− g ttt
g is continuous on [ ] 0,1. ()020 => g and ()11.90. ≈−< g
By the Intermediate Value Theorem, () 0 gc = for at least one value of c between 0 and 1. Using a graphing utility to zoom in on the graph of (), g t you find that 0.56. t ≈ Using the root feature, you find that 0.5636. ≈ t
96. () tan34 h θθθ=+− is continuous on [ ] 0,1. ()04 h =− and ()1tan(1)10.557. h =−≈
By the Intermediate Value Theorem, () 0 hc = for at least one value of c between 0 and 1. Using a graphing utility to zoom in on the graph of (), h θ you find that 0.91. θ ≈ Using the root feature, you obtain 0.9071. θ ≈
97. () 3 fxxex=+−
f is continuous on [ ] 0,1.
() 0 0320fe=−=−< and ()11320. fee=+−=−>
By the Intermediate Value Theorem, () 0 fc = for at least one value of c between 0 and 1. Using a graphing utility to zoom in on the graph of (), f x you find that 0.79. x ≈ Using the root feature, you find that 0.7921. x ≈
98. ()()5ln12gxx=+−
g is continuous on [ ] 0,1.
()() 05ln0122 g =+−=− and ()() 15ln220. g =−>
By the Intermediate Value Theorem, () 0 gc = for at least one value of c between 0 and 1. Using a graphing utility to zoom in on the graph of (), g x you find that 0.49. x ≈ Using the root feature, you find that 0.4918. x ≈
99. () 2 1 =+−fxxx
f is continuous on [ ] 0,5.
()() 01and529 11129 ff=−= −<<
The Intermediate Value Theorem applies. ()() () 2 2 111 120 430 4or3 34 is not in the interval. xx xx xx xx cx +−= +−= +−= =−= ==−
So, ()311. = f
100. () 2 68=−+fxxx
f is continuous on [ ] 0,3. ()() 08and31 108 ff==− −<<
The Intermediate Value Theorem applies.
103. () 3 4 x x fx x = [ ] is continuous on 1, 3. f The nonremovable discontinuity, 4, x = lies outside the interval.
() 11 103 14 f ==<
() 2 680 240 2or4
2 4 is not in the interval. xx xx xx cx −+= −−= == ==
So, ()20. = f
101. () 72 fxx=+−
[ ] is continuous on 0, 5. f
()0720.64581 f =−≈< ()51221.46411 f =−≈>
The Intermediate Value Theorem applies. 721 73 79 2 2 +−= += += = = x x x x c
So, ()21. f =
102. () 3 8 fxx=+ [ ] is continuous on 9,6. f
()()13 9985.91996 f −=−+≈<
()()13 6686.18296 f −=−+≈>
The Intermediate Value Theorem applies. () 3 3 3 86 2 28 8 x x x c += =− =−=− =−
So, ()86. f −=
()3243 f =>
The Intermediate Value Theorem applies. () () 3 3 3 2 3 4 312 2120 2260 2 xx x xxx xx xxx x = −=− +−= −++= = () 2 26 has no real solution. xx++ 2 c =
So, ()23. f =
104. () 2 1 + = x x fx x f is continuous on 5 ,4. 2 The nonremovable discontinuity, 1, = x lies outside the interval.
() 53520 and4 263 3520 6 63 ff
The Intermediate Value Theorem applies. ()() () 2 2 2 6 1 66 560 230 2or3 3 2 is not in the interval. xx x xxx xx xx xx cx + = +=− −+= −−= == == So, ()36. = f
105. Answers will vary. Sampleanswer: () ()() 1 fx x axb =
106. Answers will vary. Sampleanswer:
The function is not continuous at 3 = x because ()() 33 lim10lim. +− →→ =≠= xx f xfx
107. If f and g are continuous for all real x, then so is + f g (Theorem 1.11, part 2). However, f g might not be continuous if () 0. = gx For example, let () = f xx and () 2 1. =−gxx Then f and g are continuous for all real x, but f g is not continuous at 1.=± x
108. A discontinuity at c is removable if the function f can be made continuous at c by appropriately defining (or redefining) () f c Otherwise, the discontinuity is nonremovable.
(a) () 4 4 = x fx x (b) () ()sin4 4 x fx x + = + (c) () 1,4 0,44 1,4 0,4 x x fx
4 = x is nonremovable, 4=− x is removable
110. True. If ()(),, f xgxxc =≠ then ()()limlim xcxc f xgx →→ = (if they exist) and at least one of these limits then does not equal the corresponding function value at . = x c
111. False. () cos f xx = has two zeros in [ ] 0, 2. π
However, ()() 0 and 2 ff π have the same sign.
112. True. For () 1, 0, 1,∈−=−xx which implies that 0 lim1. x x → =−
113. False. A rational function can be written as ()() PxQx where P and Q are polynomials of degree m and n, respectively. It can have, at most, n discontinuities.
114. False. () 1 f is not defined and () 1 lim x f x → does not exist.
115. The functions agree for integer values of x: ()
109. True
1. () = f cL is defined.
2. () lim xc f xL → = exists.
3. ()() lim xc f cfx → =
All of the conditions for continuity are met.
() ()
333 for an integer 33 gxxxx x fxxx
However, for non-integer values of x, the functions differ by 1. ()
For example, () () () 11 22303,314. =+==−−=fg 116.
At the end of day 3, the amount of chlorine in the pool has decreased to about 28 ounces. At the beginning of day 4, more chlorine was added, and the amount is now about 56 ounces.
117. () 107.51, 0 Cttt=−−>
There is a nonremovable discontinuity at every integer value of t, or gigabyte.
+ =−
118. () 2 252 2 t N tt
t 0 1 1.8 2 3 3.8 ()Nt 50 25 5 50 25 5
There is a nonremovable discontinuity at every positive even integer. The company replenishes its inventory every two months.
122. Let c be any real number. Then () lim xc f x → does not exist because there are both rational and irrational numbers arbitrarily close to c. Therefore, f is not continuous at c.
123. If 0, = x then ()00 = f and () 0 lim0. x fx → = So, f is continuous at 0. = x
y t 24681012 10 20 30 40 50 N Time(inmonths) Number of units
119. Let () s t be the position function for the run up to the campsite. ()( 00 0 st== corresponds to 8:00 A.M., () 20 = s k (distance to campsite)). Let ()rt be the position function for the run back down the mountain: ()() 0,100. ==rkr Let ()()() =− f tstrt
When 0 = t (8:00 A M.), ()()() 00000. =−=−<fsrk
When 10 = t (8:00 A M.), ()()() 1010100. =−>fsr
Because ()00 < f and ()100, > f then there must be a value t in the interval [ ]0,10 such that () 0. = ft If () 0, = ft then ()() 0, −=strt which gives us ()() = s trt Therefore, at some time t, where 010, ≤≤ t the position functions for the run up and the run down are equal.
120. Let 3 4 3 π = Vr be the volume of a sphere with radius r V is continuous on [ ] 5,8. () 500 5523.6 3 π =≈ V and () 2048 82144.7. 3 π =≈ V Because 523.615002144.7, << the Intermediate Value Theorem guarantees that there is at least one value r between 5 and 8 such that () 1500. = Vr (In fact, 7.1012.) ≈ r
121. Suppose there exists 1x in [ ] , ab such that () 1 0 > fx and there exists 2x in [ ] , ab such that () 2 0. < fx Then by the Intermediate Value Theorem, () f x must equal zero for some value of x in [ ] [ ] () 122121 ,or,if. < x xxxxx So, f would have a zero in [ ] ,,ab which is a contradiction. Therefore, () 0 > fx for all x in [ ] , ab or () 0 < fx for all x in [ ] ,.ab
If 0, ≠ x then () lim0 tx ft → = for x rational, whereas () limlim0 txtx ftktkx →→ ==≠ for x irrational. So, f is not continuous for all 0. ≠ x
124. () 1,if0 sgn0,if0 1,if0 x xx x −< ==
>
(a) () 0 limsgn1 x x → =− (b) () 0 limsgn1 x x + → = (c) () 0 limsgn x x → does not exist.
125. (a)
(b) No. The frequency is oscillating.
126. (a) () 0,0 ,2 x b fx bbxb ≤< = <≤ NOT continuous at . = x b (b) () ,0 2 ,2 2 x x b gx x bbxb
≤≤
−<≤
Continuous on [ ] 0,2. b
127. () 2 1, , −≤ = > x xc fx x xc
f is continuous for < x c and for > x c At , = x c you need 2 1. −=cc Solving 2 1, +−cc you obtain 11415 22 −±+−± == c
129. () 2 ,0 xcc fxc x +− =>
Domain: 22 0 +≥ ≥− x cxc and ) () 2 0,,00, ≠−∪∞ xc
128. Let y be a real number. If 0, = y then 0. = x If 0, > y then let 0 02 π << x such that 0 tan => M xy ( this is possible since the tangent function increases without bound on [ )) 0, 2. π By the Intermediate Value Theorem, () tan = f xx is continuous on [ ] 0 0, x and 0, <<yM which implies that there exists x between 0 and 0x such that tan. = x y The argument is similar if 0. < y
Define ()() 012 f c = to make f continuous at 0. x =
130.1. () f c is defined.
2. ()()() 0 limlim xcx f xfcxfc →Δ→ =+Δ= exists.
[Let x cx=+Δ As ,0]→Δ→xcx
3. ()() lim. xc f xfc → =
Therefore, f is continuous at = x c
131. () = hxxx
h has nonremovable discontinuities at 1,2,3,. x =±±±
132. (a) Define ()()() 21=− f xfxfx Because 1f and 2 f are continuous on [ ] , , ab so is f ()()() 21 0 =−>fafafa and ()()() 21 0 =−<fbfbfb
By the Intermediate Value Theorem, there exists c in [ ] , ab such that () 0. = fc ()()()()() 2112 0 =−= = f cfcfcfcfc
(b) Let () 1 = f xx and () 2 cos, = f xx continuous on [ ] ()() 12 0,2,00 π < ff and () () 1222. ππ > ff
So by part (a), there exists c in [ ]0,2 π such that () cos. = cc
Using a graphing utility, 0.739. ≈ c
133. The statement is true.
If 0 ≥ y and 1, ≤ y then () 2 10,−≤≤ yyx as desired. So assume 1. > y There are now two cases.
Case l: Case 2: 1 2 If , then 212 and xyxy ≤−+≤ If 1 2 ≥−xy
yyyyy
In both cases, () 2 1.yyx −≤ 3 3 3 15
Continuing this pattern, you see that () = Pxx for infinitely many values of x So, the finite degree polynomial must be constant: () = Pxx for all x
Section2.5InfiniteLimits
1. A limit in which () f x increases or decreases without bound as x approaches c is called an infinite limit. ∞ is not a number. Rather, the symbol () lim xc fx → =∞ Says how the limit fails to exist.
2. The line x c = is a vertical asymptote if the graph of f approaches ±∞ as x approaches c.
3. 2 2 2 2
6. 2 2 limsec 4 limsec 4 x x x x π π +
11. () 2 1 9 = fx x () () 3 3 lim lim x x fx fx →− +
() f x
7. () 1 4 = fx x
As x approaches 4 from the left, 4 x is a small negative number. So, () 4 lim x fx → =−∞
As x approaches 4 from the right, 4 x is a small positive number. So, () 4 lim x fx + → =∞
8. () 1 4 = fx x
As x approaches 4 from the left, 4 x is a small negative number. So, () 4 lim. x fx → =∞
As x approaches 4 from the right, 4 x is a small positive number. So, () 4 lim. x fx + → =−∞
9. () () 2 1 4 = fx x
As x approaches 4 from the left or right, () 2 4 x is a small positive number. So, ()() 44 limlim. xx fxfx →→+− ==∞
10. () () 2 1 4 = fx x
As x approaches 4 from the left or right, () 2 4 x is a small positive number. So, ()() 44 limlim. xx fxfx →→−+ ==−∞
16. () tan 6 x fx π = () () 3 3 lim lim x x fx fx →− + →− =∞ =−∞
x –3.5
–2.5 () f x 3.73
17. 22 2 22 22 22 () 4(2)(2) limandlim 44xx xx fx xxx xx xx −+ →−→− == −+− =∞=−∞
Therefore, 2=− x is a vertical asymptote.
22 22 22 limandlim 44xx xx xx −+ →→ =−∞=∞
Therefore, 2 = x is a vertical asymptote.
18. 2 1 () 1 t gt t = +
No vertical asymptotes because the denominator is never zero.
19. 2 33 () 2(2)(1) fx xxxx == +−+−
22 22 33 lim and lim 22xxxxxx −+ →−→− =∞=−∞ +−+−
Therefore, 2 x =− is a vertical asymptote.
22 11 33 lim and lim 22xxxxxx −+ →→ =−∞=∞ +−+−
Therefore, 1 x = is a vertical asymptote.
20. () ()() 2 3 2 2 525 125 525 5525 1 5 xx gx x xx xxx x −+ = + −+ = +−+ = + 55 11 lim and lim 55xxxx −+ →−→− =−∞=∞ ++
Therefore, 5 x =− is a vertical asymptote.
21. () () () ()() ()() () 2 32 2 46 2918 432 29 4 ,3,2 3 xx fx xxxx xx xxx x xx +− = −−+ +− = =≠− 00 lim() and lim() xx fxfx −+ →→ =∞=−∞
Therefore, 0 x = is a vertical asymptote. 33 lim() and lim() xx fxfx −+ →→ =−∞=∞
Therefore, 3 x = is a vertical asymptote.
2 4 lim()2 2(23) x fx → ==− and 3 42 lim() 3(33)9 →− == x fx
Therefore, the graph has holes at 2 x = and 3. x =−
22. () ()() ()()() 2 32 9 33 33 113 3 , 3 (1)(1) x hx xxx xx xxx x x xx = +−− −+ = −++ =≠− +− 11 lim() and lim() xx hxhx −+ →−→− =−∞=∞
Therefore, 1 x =− is a vertical asymptote. 11 lim() and lim() xx hxhx −+ →→ =∞=−∞
Therefore, 1 x = is a vertical asymptote.
3 333 lim() (31)(31)4 x hx →− ==− −+−−
Therefore, the graph has a hole at 3. x =−
23. () 2 1 x e fx x = () 11 lim and lim xx fx −+ →→ =−∞=∞
Therefore, 1 x = is a vertical asymptote.
24. () 2 x g xxe =
The function is continuous for all x. Therefore, there are no vertical asymptotes.
25. () () 2 ln1 2 t ht t + = + () 22 lim and lim tt ht −+ →−→− =−∞=∞
Therefore, 2 t =− is a vertical asymptote.
26. () () ()() ()() 2 ln4ln22 ln2ln2 fzzzz zz =−= +− =++−
The function is undefined for 22. z −<< ()() 22 lim and lim zz fzfz −+ →−→− =−∞=−∞
Therefore, the graph vertical asymptotes at 2. z =±
27. () 1 1 x fx e = ()() 00 lim and lim xx fxfx −+ →→ =−∞=∞
Therefore, 0 x = is a vertical asymptote.
28. ()() ln3fxx=+ () 3 lim x fx →− =−∞
Therefore, 3 x =− is a vertical asymptote.
29. () 1 csc sin fxx x π π ==
Let n be any integer. lim() or xn fx → =−∞∞
Therefore, the graph has vertical asymptotes at x n =
30. () sin tan cos 21 cos0 for , where is an integer. 2 x fxx x n xxn π π π π == + == 21 2 lim() or n x fx + → =∞−∞
Therefore, the graph has vertical asymptotes at 21 . 2 n x + =
31. () sin
sin 0 for , where is an integer. t st t ttnn π = == lim() or (for 0) tn stn π → =∞−∞≠
Therefore, the graph has vertical asymptotes at , for 0. tnn π =≠ () 0 lim1 t st → =
Therefore, the graph has a hole at 0. t =
32. () tan sin cos cos 0 for , where is an integer. 2 g nn θθ θ
π θθπ == ==+ 2 lim () or n g π θπ θ →+ =∞−∞
Therefore, the graph has vertical asymptotes at 2 n π θπ =+ 0 lim ()1 g θ θ → =
Therefore, the graph has a hole at 0. θ =
33. () 2 11 1 limlim12 1 xx x x x →−→− =−=− + Removable discontinuity at 1 x =−
35. () () 2 1 2 1 cos1 lim 1 cos1 lim 1 x x x x x x →− + →− =−∞ + =∞ + Vertical asymptote at 1 = x 3 3
34. 2 1 2 1 28 lim 1 28 lim 1 x x xx x xx x →− + →− =∞ + =−∞ + Vertical asymptote at 1 x =−
44. 0 1 lim3 x x x + → −+=−∞
45. 0 1 limsin x x x + → +=∞
46. () 2 2 lim cos x x π + → =∞
47. ()3 8 lim 8 x x e x → =−∞
48. () 2 4 limln16 x x + → −=−∞
49. () 2 limlncoslncosln0 2 x x π π → ===−∞
50. () 0.5 0 limsin100 x x ex + → ==
51. () ()1212 lim sec lim cos xx x xx x π π →→ ==∞
52. () 2 12 limtan x xx π + → =−∞
53. () ()() () 22 3 2 11 11 1 11 1 limlim 1 xx xxxx fx x xxx fx x →→++ ++++ == −++ ==∞
54. () ()() ()() 2 3 22 11 11 1 11 limlim10 xx xxx x fx xxxx fxx →→ −++ == ++++ =−=
55. ()() lim and lim2 xcxc fxgx →→ =∞=−
(a) ()() lim2 xc fxgx → + =∞−=∞
(b) ()()() lim2 xc fxgx → =∞−=−∞
(c) () () 2 lim0 xc gx fx → == ∞
56. ()() lim and lim3 xcxc fxgx →→ =−∞=
(a) ()() lim3 xc fxgx → + =−∞+=−∞
(b) ()()()() lim3 xc fxgx → =−∞=−∞
(c) () () 3 lim0 xc gx fx → == −∞
57. One answer is () ()() 2 33 62412 xx fx xxxx == −+−−
58. No. For example, () 2 1 1 fx x = + has no vertical asymptote. 5 3 4 3 88 4 4
Total distance
64. (a) () () ()
(b)
Average speed Total time 2 50 2 50 50502 50250 50225 25 25 d dxdy xy yx yxxy xxyy xyx x y x = = + = + += =− =− =
Domain: 25 x >
(c) 25 25 lim 25 x x x + → =∞
As x gets close to 25 miles per hour, y becomes larger and larger.
65. (a) ()() () 2 2 11 22 11 1010tan10 22 50tan50 Abhr θ θθ θθ =− =− =−
Domain: 0, 2 π
(b)
(c) 2 lim A θπ → =∞
66. (a) Because the circumference of the motor is half that of the saw arbor, the saw makes 17002850 = revolutions per minute.
(b) The direction of rotation is reversed.
(c) ()() 220cot210cot: φφ + straight sections. The angle subtended in each circle is 22 2. 2 π π φ π φ −−=+ So, the length of the belt around the pulleys is ()()() 202102302. π φ π φ π φ +++=+ ()
Total length60cot302 φ π φ =++
Domain: 0, 2 π
(d) (e)
(f) () 2 lim60188.5 L φπ π → =≈
(All the belts are around pulleys.)
(g) When the angle θ approaches , 2 π the total length of the belt approaches the sum of the circumferences of the two pulleys, which is 204060 cm. πππ +=
(h) 0 lim L φ + → =∞
67. True. The function is undefined at a vertical asymptote.
68. True
69. False. The graphs of tan,cot,sec yxyxyx === and csc yx = have vertical asymptotes.
70. False. Let () 1 ,0 3,0. x fx x x
The graph of f has a vertical asymptote at 0, x = but ()03. f =
72. Given () lim xc fx → =∞ and () lim: xc g xL → =
(1) Difference: Let ()(). hxgx =− Then () lim, xc hxL → =− and ()()()() limlim, by the Sum Property. xcxc fxgxfxhx →→
= + =∞
(2) Product:
If 0, L > then for 20 L ε => there exists 1 0 δ > such that () 2 g xLL −< whenever 1 0. xc δ <−< So, () 232. L gxL<< Because () lim xc fx → =∞ then for 0, M > there exists 2 0 δ > such that () () 2 f xML > whenever 2 xc δ −< Let δ be the smaller of 1 δ and 2δ Then for 0, xc δ <−< you have ()() ()() 22. f xgxMLLM >= Therefore ()() lim. xc fxgx → =∞ The proof is similar for 0. L <
(3) Quotient: Let 0 ε > be given.
There exists 1 0 δ > such that () 32fxL ε > whenever 1 0 xc δ <−< and there exists 2 0 δ > such that () 2 g xLL −< whenever 2 0. xc δ <−< This inequality gives us () 232. L gxL<< Let δ be the smaller of 1 δ and 2δ Then for 0, xc δ <−< you have () () 32 . 32 gx L fxL ε ε <= Therefore, () () lim0. xc gx fx → =
73. Given () lim, xc fx → =∞ let () 1. gx = Then () () lim0 xc gx fx → = by Theorem 1.15.
74. Given () 1 lim0. xc fx → = Suppose () lim xc f x → exists and equals L
Then, () () lim1 11 lim0. lim xc xc xc fxfxL → → → ===
This is not possible. So, () lim xc f x → does not exist.
75. () 1 3 fx x = is defined for all 3. x > Let 0 M > be given. You need 0 δ > such that () 1 3 f xM x => whenever
33. x δ <<+ Equivalently, 1 3 x M −< whenever 3,3.xx δ −<> So take 1 M δ = Then for 3 x > and 11 3, 38 x M x δ −<>= and so () f xM > Thus, 3 1 lim. 3 x x + → =∞
76. () 1 5 fx x = is defined for all 5. x < Let 0 N < be given. You need 0 δ > such that () 1 5 f xN x =< whenever
55. x δ −<< Equivalently, 1 5 x N −> whenever 5,5.xx δ −<< Equivalently, 11 5 x N <− whenever 5,5.xx δ −<< So take 1 . N δ =− Note that 0 δ > because 0. N < For 5 x δ −< and 11 5,, 5 x N x δ <>=− and 11 . 55 N xx =−< Thus, 5 1 lim. 5 x x → =−∞
77. () 3 8 fx x = is defined for all 8. x > Let 0 N < be given. You need 0 δ > such that () 3 8 f xN x =< whenever
88. x δ <<+ Equivalently, 81 3 x N > whenever 8, 8. xx δ −<> Equivalently, 3 8 x N −< whenever 8, 8. xx δ −<> So, let 3 . N δ = Note that 0 δ > because 0. N < Finally, for 8 and 8, xx δ −<> 1133 , , and . 8388 N NN xxx δ >=<< Thus, () 8 lim. x fx + → =−∞
78. () 6 9 fx x = is defined for all 9. x < Let 0 M > be given. You need 0 δ > such that () 6 9 f xM x => whenever
99. δ −<< x Equivalently, 6 9 −< x M whenever 9, 9. xx δ −<< So, let 6 M δ = Finally, for 9 and 9, xx δ −<< 6 9, x M −< 16 , and . 969 M M xx >> Thus, () 9 lim. x fx δ → =
ReviewExercisesforChapter2
1. Calculus required. Using a graphing utility, you can estimate the length to be 8.3. Or, the length is slightly longer than the distance between the two points, approximately 8.25.
2. Precalculus. ()() 22 91318.25 L =−+−≈
3. () 2 3 712 x fx xx = −+ () 3 lim1.0000 x fx →
5. () 2 2 x hxx =−+
(a) The limit does not exist at 2. x = The function approaches 3 from the left side of 2, but it approaches 2 from the right side of 2. (b)
or
or
6. () ()ln2 t ft t + =
(a)
7. () 1 lim4145 x x → +=+=
Let 0 ε > be given. Choose .δε = Then for 01, x <−<=δε you have
8. 9 lim93 x x → ==
Let 0 ε > be given. You need 333393.
Assuming 416, x << you can choose 5. δε =
So, for 095, x <−<=δε you have
9. ()22 2 lim1123 x x → −=−=−
Let 0 ε > be given. You need () 22
Assuming 13, x << you can choose 5 ε δ =
So, for 02, 5 x
10. 5 lim99. x → = Let 0 ε > be given. δ can be any positive number. So, for 05, x δ <−< you have () 99 fxL ε
11. 22 6 lim(6)36 x x →− =−=
12. ()() 0 lim535033 x x → −=−=−
13. () () () 44 4 33 4 27 lim127131216 x x → −=−=−==
14. 33 2 lim1218193 x x → +=+=+==
15. 4 444 lim 1413 x x → ==
16. 22 2 222 lim 121415 x x x → === +++
21. () () () 000 111 11 1 limlimlim1 11xxx x x xxxx
() () () 00 0 0 0 limlim939393 93 99 lim 93 lim 93 1 lim 93
30.
34.
The
The object will hit the ground after about 7.1 seconds. When 50 , 7 a = the velocity is ()() () ()() ()
43. () 2 lim0 x fx → =
44. () 1 lim112 x gx + → =+=
45. () 1 lim t ht → does not exist because () 1 lim112 t ht → =+= and () () 1 1 2 lim111. t ht + → =+=
46. () 2 lim2 s fs →− =
47. () () 2 lim212113 x x → +=+=
48. 4 lim1 x x → does not exist. There is a break in the graph at 4. x =
49. ()() ()() 2 22 2 22 4 limlim 22 lim2224 xx x xx x xx x →→ → −+ = =−+=−+=−
50. () () 1 lim11110 x xx + → −=−=
51. The function () 3 8 g xx =− is continuous on [ ] 2, 2 because [ ] 3 80 on 2, 2. −≥− x
52. The function () 3 5 hx x = is not continuous on [ ] 0, 5 because () 5 h is not defined.
53. () 4 81 =− f xxx is continuous for all real x
54. 2 ()20 fxxx=−+ is continuous for all real x
55. 4 () 5 fx x = has a nonremovable discontinuity at 5 x = because () 5 lim does not exist. x fx →
56. 2 11 () 9(3)(3) fx xxx == −−+ has nonremovable discontinuities at 3 x =± because 33 lim() and lim() xx f xfx →→− do not exist.
57. 32 1 (),0 (1)(1)(1) xx fxx xxxxxx ===≠ −−−+ has nonremovable discontinuities at 1 x =± because 11 lim() and lim() do not exist, xx fxfx →−→ and has a removable discontinuity at 0 x = because 00 1 lim()lim1. (1)(1) xx fx xx →→ ==− −+
58. 2 331 (), 318(3)(6)6 3 xx fx xxxxx x ++ === −−+−− ≠−
has a nonremovable discontinuity at 6 x = because 6 lim() x f x → does not exist, and has a removable discontinuity at 3 x =− because 33 11 lim()lim. 69 xx fx x →−→− ==−
59. ()25 f =
Find c so that () 2 lim65. x cx + → += ()265 21 1 2 c c c += =− =−
60. () 11 13134fe −+ −=+=+=
So, find c such that () 2 1 lim24. x cxx →− −= ()() 2 1214 24 2 c c c −−−= += =
61. () 2 37fxx=−+ Continuous on () , −∞∞
62. ()() 2 412 472 () 22 xx xx fx xx −+ +− == ++
Continuous on (,2)(2,). −∞−∪−∞ There is a removable discontinuity at 2. x =−
63. () cos f xxx =+ is continuous on [ ) 0, . ∞
64. () 3 fxx=+
lim33 xk xk + → +=+ where k is an integer.
lim32 xk xk → +=+ where k is an integer.
Nonremovable discontinuity at each integer k Continuous on () ,1kk + for all integers k
65. () 4 2 x gxe = is continuous on all intervals () , 1, nn + where n is an integer. g has nonremovable discontinuities at each n
66. () 2 ln5 hxx =−−
Because 50 x −> except for 5, x = h is continuous on ()() , 55, . −∞∪∞
67. () ()() ()() 2 11 321 32 11 limlim325 xx xx xx fx xx fxx →→ +− == =+=
Removable discontinuity at 1 x = Continuous on ()() ,11, −∞∪∞
68. () () () 2 2 5,2 23,2 lim53 lim231 x x xx fx xx x x → + → −≤ = −> −= −=
Nonremovable discontinuity at 2 x = Continuous on ()() ,22, −∞∪∞
69. () 3 23fxx=−
f is continuous on [ ] () 1,2.110 f =−< and ()2130. f => Therefore by the Intermediate Value
Theorem, there is at least one value c in () 1,2 such that 3 230. c −=
70. () 2 2 fxxx=+−
Consider the intervals [ ] [ ] 3, 0 and 0, 3.
()() 2 333240 f −=−−−=>
()020 =−< f
By the Intermediate Value Theorem, there is at least one zero in [ ] 3, 0.
()020 f =−<
()() 2 3332100 f =+−=>
Again, there is at least one zero in [ ] 0, 3.
So, there are at least two zeros in [ ] 3, 3.
71. () 2 54fxxx=+−
[ ] is continuous on 1, 2. f
()()() 2 1151482 f −=−+−−=−< ()() 2 22524102 f =+−=>
The Intermediate Value Theorem applies. ()() () 2 2 542 560 610 1 6 lies outside the interval. 1 xx xx xx xx c +−= +−= +−= ==− =
So, ()12. f =
72. ()()3 64 fxx=−+ [ ] is continuous on 4, 7. f
()()3 44648443 f =−+=−+=−<
()()3 77641453 f =−+=+=>
The Intermediate Value Theorem applies. () () 3 3 643 61 61 5 5 x x x x c −+= −=− −=− = = So, ()53. f = 73. 6 6 1 lim 6 1 lim 6 → + → =−∞
75. () 0 0 3 3 lim 3 lim x x fx x x x → + → = =−∞ =∞
Therefore, 0 x = is a vertical asymptote.
76. () 4 44 22 5 (2) 55 limlim (2)(2)xx fx x xx−+ →→ = =∞=
Therefore, 2 x = is a vertical asymptote.
77. () 33 2 33 22 33 9(3)(3) lim andlim 99xx xx fx xxx xx xx −+ →−→− == −+− =−∞=∞
Therefore, 3 x =− is a vertical asymptote. 33 22 33 lim andlim 99xx xx xx −+ →→ =−∞=∞
Therefore, 3 x = is a vertical asymptote.
78. () 2 22 66 66 36(6)(6) 66 lim andlim 3636xx xx fx xxx xx xx−+ →−→− ==− −+− =∞=−∞
Therefore, 6 x =− is a vertical asymptote.
22 66 66 lim andlim 3636xx xx xx−+ →→ =∞=−∞
Therefore, 6 x = is a vertical asymptote.
79. () 1 sec 2 cos 2 x fx x π π ==
cos 0 when 1,3, 2 x x π ==±±
Therefore, the graph has vertical asymptotes at 21,xn=+ where n is an integer.
80. () () 1 csc sin sin 0 for , where is an integer. lim or xn fxx x xxnn fx π π π → == == =∞−∞
Therefore, the graph has vertical asymptotes at x n =
85. 32 11 111 limlim 113xx x xxx++ →−→− + == +−+
86. ()() 4 2 11 111 limlim 14 11 xx x x xx →−→− + ==− +−
87. 3 0 1 lim x x x + → −=−∞
88. 3 2 2 1 lim 4 x x → =−∞
89. 00 limlimsin44sin44 5545xx xx xx→→++
==
90. 3 0 sec lim 2 x x x → =−∞ () 3 sec 1 for near 0. xx ≈ Note:
91. 00 limlimcsc21 sin2 xx x xxx→→++ ==∞
92. 2 0 cos lim x x x → =−∞
+−
81. () () ()() () () 2 2 5 2 5 ln25ln55 limln250 limln250 x x g xxxx x x → →− =−=
Therefore, the graph has holes at 5. x =± The graph does not have any vertical asymptotes.
82. () 3 3 0 7 lim7 x x x fxe e → = =∞
Therefore, 0 x = is a vertical asymptote.
83. 2 1 21 lim 1 x xx x → ++ =−∞
84. () 12 lim 21 x x x + → =∞
ProblemSolvingforChapter2
93. () 0 limlnsin x x + → =−∞
94. 2 0 lim12 x x e → =∞
95. 80,000 , 00 100 p Cp p =≤<
(a) () ()80,00050 50$80,000 10050 C ==
(b) () ()80,00090 90$720,000 10090 C ==
(c) () 100 lim p Cp → =∞ It would be financially impossible to remove 100% of the pollutants.
(b) () () () 2 2224 2 424 11 11 xxxx rx xxxx +−+++ = −++++
(c) () 0 1012 lim1 1012 x rx + → ++ === ++
2. (a) ()() ()() 2 11 Area1 222 11 Area1 2222 x PAObhx yx PBObhy Δ=== Δ====
(b) () 2 Area2 Area2 PBOx axx PAOx Δ === Δ
(c) () 00 limlim0 xx axx →→++ ==
3. (a) There are 6 triangles, each with a central angle of 603. π °= So,
(b) There are n triangles, each with central angle of 2. n θπ = So, ()
4. (a) 404 Slope 303 ==
(b) 3 Slope 4 =− Tangent line: () 3 43 4 325 44 yx yx −=−−
(c) Let () (
Qxyxx ==−
5. (a) 12 Slope 5 =−
(b) Slope of tangent line is 5 12 () 5 125 12 5169 Tangent line 1212 yx yx +=− =− (c) () ( ) 2 ,,169 Qxyxx ==−−
(d)
This is the slope of the tangent line at P.
Letting 3 a = simplifies the numerator.
Setting 3, 33 b = + you obtain 6. b = So, 3 a = and 6. b =
(a) 13
This is the same slope as part (b).
(d) ()
8. () () () 22 00 0 00 limlim22 tan limlimbecauselim1 tan xx x xx fxaa fxaaxx xx →→ ++ → →→ =−=−
Thus, ()() 2 2 2 20 210 1,2 aa aa aa a −= −−=
9. (a) () 14 2 lim3:, x f xgg → =
(b) f continuous at 2: 1g (c) () 134 2 lim3:,, x f xggg → = 10.
(a) () () () 1 4 1 3 44 30 111 f f f
(b) () () () () 1 1 0 0 lim1 lim0 lim lim x x x x fx fx fx fx → + → → + → = = =−∞ =∞
(c) f is continuous for all real numbers except 11 23 0,1,,, x =±±± 11.
y
(a) () () () () () () 1 2 111110 00 011 2.7321 f f f f =+−=+−= = =+−=− −=−+=−
(b) () () () 1 1 12 lim1 lim1 lim1 x x x fx fx fx → + → → =− =− =−
(c) f is continuous for all real numbers except 0,1,2,3, x =±±±
12. (a) 22 0 22 0 22 0 2 0 0 192,000 48 192,000 48 192,000 48 192,000 lim 48 v vv r vv r r vv r v → =+− =−+ = −+ = Let 0 4843misec. v ==
(b) 22 0 22 0 22 0 2 0 0 1920 2.17 1920 2.17 1920 2.17 1920 lim 2.17 v vv r vv r r vv r v → =+− =−+ = −+ = Let () 0 2.17misec1.47mi/sec. v =≈ (c) 22 0 2 0 0 10,600 6.99 10,600 lim 6.99 v r vv r v → = −+ = Let 0 6.992.64misec. v =≈
Because this is smaller than the escape velocity for Earth, the mass is less. 1 1 1 2 3 2 1 y x
(b) (i) () , lim1 ab xa Px + → =
(ii) () , lim0 ab xa Px → =
(iii) () , lim0 ab xb Px + → =
(iv) () , lim1 ab xb Px → =
(c) , Pab is continuous for all positive real numbers except ,. x ab =
(d) The area under the graph of U, and above the x-axis, is 1.
14. Let 0 a ≠ and let 0 ε > be given. There exists 1 0 δ > such that if 1 00 x δ <−< then () fxL ε −< Let 1 . a δδ = Then for 1 00, x a <−<=δδ you have () 1 1 x a ax faxL
< < −<
As a counterexample, let 0 a = and () 1,0 . 2,0 x fx x ≠ = =
Then () 0 lim1, x f xL → == but ()() 000 limlim0lim22. xxx faxf →→→ === x b 2 a 1 y
Chapter 2 Limits and Their Properties
Chapter Comments
Section 2.1 gives a preview of calculus. On pages 67 and 68 of the textbook are examples of some of the concepts from precalculus extended to ideas that require the use of calculus. Review these ideas with your students to give them a feel for where the course is heading.
The idea of a limit is central to calculus. So, you should take the time to discuss the tangent line problem and or the area problem in this section. Exercise 11 of Section 2.1 is yet another example of how limits will be used in calculus. A review of the formula for the distance between two points can be found in Appendix C.
The discussion of limits is difficult for most students the first time that they see it. For this reason, you should carefully go over the examples and the informal definition of a limit presented in Section 2.2. Stress to your students that a limit exists only if f (x) moves arbitrarily close to a single real number as x approaches c from either side (the function does not have to exist at x = c). Otherwise, the limit fails to exist, as shown in Examples 3, 4, and 5 of this section. You might want to work Exercise 71 of Section 2.2 with your students in preparation for the definition of the number e coming up in Section 2.3. You may choose to omit the formal definition of a limit.
Carefully go over the properties of limits found in Section 2.3 to ensure that your students are comfortable with the idea of a limit and also with the notation used for limits. Suggest that students write these properties of limits on a sheet of paper for reference. By the time you get to Theorem 2.6, it should be obvious to your students that all of these properties amount to direct substitution.
When direct substitution for the limit of a quotient yields the indeterminate form 0 0 , remind your students that they must rewrite the fraction using legitimate algebra. Then do at least one problem using dividing out techniques and another using rationalizing techniques. Exercises 58 and 60 of Section 2.3 are examples of other algebraic techniques needed for the limit problems. It is important to go over the Squeeze Theorem, Theorem 2.8, with your students so that you can use it to prove lim x → 0 sin x x = 1 The proof of Theorem 2.8 and many other theorems can be found in Appendix A. Your students need to memorize all three of the special limits in Theorem 2.9 as they will need these facts to do problems throughout the textbook. Most of your students will need help with Exercises 63–85 in this section.
Continuity, which is discussed in Section 2.4, is another idea that often puzzles students. However, if you describe a continuous function as one in which you can draw the entire graph without lifting your pencil, the idea seems to stay with them. Distinguishing between removable and nonremovable discontinuities will help students determine vertical asymptotes.
To discuss infinite limits, Section 2.5, remind your students of the graph of the function f (x) = 1 x studied in Section 1.3. Be sure to make your students write a vertical asymptote as an equation, not just a number. For example, for the function y = 1 x, the vertical asymptote is x = 0
Section 2.1 A Preview of Calculus
Section Comments
2.1 A Preview of Calculus—Understand what calculus is and how it compares with precalculus. Understand that the tangent line problem is basic to calculus. Understand that the area problem is also basic to calculus.
Teaching Tips
In this first section, students see how limits arise when attempting to find a tangent line to a curve. Be sure to say to students that they can think about the word tangent as meaning “touching” a curve at one particular point. Drawing a circle with a line that touches the circle at a specific point can illustrate tangency. Drawing a curve where a line intersects a curve twice illustrates a line that is not tangent to a curve as it crosses the curve more than once.
How Do You See It? Exercise
Page 71, Exercise 10 How would you describe the instantaneous rate of change of an automobile’s position on a highway?
Solution
Answers will vary. Sample answer: The instantaneous rate of change of an automobile’s position is the velocity of the automobile, and can be determined by the speedometer.
Suggested Homework Assignment
Page 71: 1–9 odd.
Section 2.2 Finding Limits Graphically and Numerically
Section Comments
2.2 Finding Limits Graphically and Numerically—Estimate a limit using a numerical or graphical approach. Learn different ways that a limit can fail to exist. Study and use a formal definition of limit.
Teaching Tips
In this section, we turn our focus to limits in general, and numerical and graphical ways we can find them. Ask students to consider f (x) = x 2 4 x 2 and what is happening to f (x) as x approaches 2. This will lead into the definition of a limit.
Make sure that students find limits analytically instead of using their graping utilities, as they can be misleading. For example, present to the class, lim x → 0 sin π x Constructing a table of values of x = 1, 1 3 , 0.1, 1 2 , 1 4 , and 0.01 leads to the assumption that lim x → 0 sin π x = 0 However, this limit does not exist.
When introducing the definition of a limit, using graphs will help students understand the meaning of the definition. Suggested graphs are below:
How Do You See It? Exercise
Page 82, Exercise 74 Use the graph of f to identify the values of c for which lim x → c f (x) exists.
(a) y x
Solution
(a) lim x
c f (x) exists for all c ≠ 3.
(b) lim x
f (x) exists for all c ≠ 2, 0
(b) y x
Suggested Homework Assignment
Pages 79–82: 1, 5, 7, 9, 15, and 19–35 odd.
Section 2.3 Evaluating Limits Analytically
Section Comments
2.3 Evaluating Limits Analytically—Evaluate a limit using properties of limits. Develop and use a strategy for finding limits. Evaluate a limit using the dividing out technique. Evaluate a limit using the rationalizing technique. Evaluate a limit using the Squeeze Theorem.
Teaching Tips
When starting this section, review how to factor using differences of two squares and two cubes, sum of two cubes, and rationalizing numerators. If you do not have time to review these concepts, encourage students to study the following material in Precalculus, 10th edition, by Larson.
• Factoring the difference of two squares: Precalculus Appendix A.3
• Factoring the difference of two cubes: Precalculus Appendix A.3
• Factoring the sum of two cubes: Precalculus Appendix A.3
• Rationalizing numerators: Precalculus Appendix A.2
State all limit properties as presented in this section and discuss the proper ways to write solutions when finding limits analytically. Give examples of direct substitution; some suggested examples include lim x → 2 x2 3x + 4 x + 2 and lim x → 3 4x3 5x + 1
When rationalizing the numerator, start with an example without limits. A suggestion is √x + 2 √2 x . After rationalizing the numerator, find the limit as x approaches 0.
When evaluating trigonometric limits, show students examples directly related to Theorem 2.9 in the text. Some examples are lim x → 0 sin 7x 4x and lim θ → 0 cos θ 1 sin θ .
How Do You See It? Exercise
Page 92, Exercise 104 Would you use the dividing out technique or the rationalizing technique to find the limit of the function? Explain your reasoning.
(a)
Solution
(a) Use the dividing out technique because the numerator and denominator have a common factor.
(b) Use the rationalizing technique because the numerator involves a radical expression.
Suggested Homework Assignment
Pages 91–93: 1–75 odd, 89, 99, 105, 107, and 119–123 odd.
Section 2.4 Continuity and One-Sided Limits
Section Comments
2.4 Continuity and One-Sided Limits—Determine continuity at a point and continuity on an open interval. Determine one-sided limits and continuity on a closed interval. Use properties of continuity. Understand and use the Intermediate Value Theorem.
Teaching Tips
Students have trouble with limits involving trigonometric functions and rationalizing denominators and numerators. Students also have trouble with limits involving rational functions. Encourage students to sharpen their algebra skills by studying the following material in the text or in Precalculus, 10th edition, by Larson.
• Trigonometric functions: Section 1.4
• Rationalizing numerators: Precalculus Appendix A.2
• Simplifying rational expressions: Precalculus Appendix A.4
Address the following for this section:
• Describe the difference between a removable discontinuity and a nonremovable discontinuity.
• Write a function that has a removable discontinuity.
• Write a function that has a nonremovable discontinuity.
• Write a function that has a removable discontinuity and a nonremovable discontinuity. Students will need to know these concepts when they study vertical asymptotes (Section 2.5), improper integrals (Section 8.8), and functions of several variables (Section 13.2).
Discuss the difference between a removable discontinuity and a nonremovable discontinuity.
Use the function f (x) = ∣x 4∣ x 4 to illustrate a function with a nonremovable discontinuity.
Note that it is not possible to remove the discontinuity by redefining the function. When you illustrate a removable discontinuity, as in the function f (x) = sin(x + 4) x + 4 , note that the function can be redefined to remove the discontinuity. Ask students how they would do this. (Let f ( 4) = 1 ) Finally, illustrate the example below. Show students the function and the graph, and then ask them if there are any removable or nonremovable discontinuities. Once they have properly identified x = 4 as removable and x = 4 as nonremovable, ask them to redefine f to remove the discontinuity at x = 4 (Let f ( 4) = 0 )
Ask students to consider the following function with its graph below: f (x) = { 0, 1, 0, 1, x < 4 x = 4 4 < x < 4 x ≥ 4
x = 4 is nonremovable. x = 4 is removable.
Use this example to show which are removable and nonremovable discontinuities. In addition, use a rational function with both a vertical asymptote and a hole to show the differences between removable and nonremovable discontinuities. A suggested example is f (x) = 8x 2 + 26x + 15 2x2 x 15
How Do You See It? Exercise
Page 105, Exercise 116 Every day you dissolve 28 ounces of chlorine in a swimming pool. The graph shows the amount of chlorine f (t) in the pool after t days. Estimate and interpret lim
4 f (t) and lim
At the end of day 3, the amount of chlorine in the pool has decreased to about 28 ounces. At the beginning of day 4, more chlorine was added, and the amount is now about 56 ounces.
Suggested Homework Assignment
Pages 103–105: 1, 3, 7–19 odd, 21, 23, 25, 29, 31, 33, 37, 39, 47, 49, 51, 55, 59, 61, 65, 67, 75–81 odd, 83, 99, 101, 105, and 109–113 odd.
Section 2.5 Infinite Limits
Section Comments
2.5 Infinite Limits—Determine infinite limits from the left and from the right. Find and sketch the vertical asymptotes of the graph of a function.
Teaching Tips
It is vital for students to know asymptotes of a rational function for this section. Encourage students to review material on asymptotes by studying Section 2.6 in Precalculus, 10th edition, by Larson.
Students need to be able to decipher when vertical asymptotes versus holes will occur in a rational function. A suggested problem for students to consider is to determine if x = 1 is a vertical asymptote of f (x) = p(x) x 1 .
In class, you can ask students who believe the graph of f has a vertical asymptote at x = 1 to prove it. For those who think this is not always true, ask them to provide a counterexample. A sample answer is given in the solution. If desired, you could also ask students the following:
(a) At which x-values (if any) is f not continuous?
(b) Which of the discontinuities are removable?
Solution
No, it is not always true. Consider p(x) = x 2 1 The function
f (x) = x2 1 x 1 = p(x) x 1 has a hole at (1, 2), not a vertical asymptote.
How Do You See It? Exercise
Page 113, Exercise 62 For a quantity of gas at a constant temperature, the pressure P is inversely proportional to the volume V What is the limit of P as V approaches 0 from the right? Explain what this means in the context of the problem.
As the volume of the gas decreases, the pressure increases.
Suggested Homework Assignment
Pages 112–114: 1, 3, 7, 13, 17–31 odd, 37–51 odd, 55, 57, and 67–71 odd.
Chapter 2 Project
Medicine in the Bloodstream
A patient’s kidneys purify 25% of the blood in her body in 4 hours.
Exercises
In Exercises 1–3, a patient takes one 16-milliliter dose of a medication.
1. Determine the amount of medication left in the patient’s body after 4, 8, 12, and 16 hours.
2. Notice that after the first 4-hour period, 3 4 of the 16 milliliters of medication is left in the body, after the second 4-hour period, 9 16 of the 16 milliliters of medication is left in the body, and so on. Use this information to write an equation that represents the amount a of medication left in the patient’s body after n 4-hour periods.
3. Can you find a value of n for which a equals 0? Explain.
In Exercises 4–9, the patient takes an additional 16-milliliter dose every 4 hours.
4. Determine the amount of medication in the patient’s body immediately after taking the second dose.
5. Determine the amount of medication in the patient’s body immediately after taking the third and fourth doses. What is happening to the amount of medication in the patient’s body over time?
6. The medication is eliminated from the patient’s body at a constant rate. Sketch a graph that shows the amount of medication in the patient’s body during the first 16 hours. Let x represent the number of hours and y represent the amount of medication in the patient’s body in milliliters.
7. Use the graph in Exercise 6 to find each limit.
8. Discuss the continuity of the function represented by the graph in Exercise 6. Interpret any discontinuities in the context of the problem.
9. The amount of medication in the patient’s body remains constant when the amount eliminated in 4 hours is equal to the additional dose taken at the end of the 4-hour period. Write and solve an equation to find this amount.
Chapter 3 Differentiation
Chapter Comments
The material presented in Chapter 3 forms the basis for the remainder of calculus. Much of it needs to be memorized, beginning with the definition of a derivative of a function found on page 123. Students need to have a thorough understanding of the tangent line problem and they need to be able to find an equation of a tangent line. Frequently, students will use the function f ′(x) as the slope of the tangent line. They need to understand that f ′(x) is the formula for the slope and the actual value of the slope can be found by substituting into f ′(x) the appropriate value for x On pages 125–126 of Section 3.1, you will find a discussion of situations where the derivative fails to exist. These examples (or similar ones) should be discussed in class.
As you teach this chapter, vary your notations for the derivative. One time write y ′; another time write dy dx or f ′(x). Terminology is also important. Instead of saying “find the derivative,” sometimes say, “differentiate.” This would be an appropriate time, also, to talk a little about Leibnitz and Newton and the discovery of calculus.
Sections 3.2, 3.3, and 3.4 present a number of rules for differentiation. Spending time on the notation of the higher derivatives can be beneficial. Have your students memorize the Product Rule and the Quotient Rule (Theorems 3.8 and 3.9) in words rather than symbols. Students tend to be lazy when it comes to trigonometry and therefore, you need to impress upon them that the formulas for the derivatives of the six trigonometric functions need to be memorized also. You will probably not have enough time in class to prove every one of these differentiation rules, so choose several to do in class and perhaps assign a few of the other proofs as homework.
The Chain Rule, in Section 3.4, will require two days of your class time. Students need a lot of practice with this and the algebra involved in these problems. Many students can find the derivative of f (x) = x2√1 x2 without much trouble, but simplifying the answer is often difficult for them. Insist that they learn to factor and write the answer without negative exponents. Strive to get the answer in the form given in the back of the book. This will help them later on when the derivative is set equal to zero.
Implicit differentiation is often difficult for students. Have students think of y as a function of x and therefore y 3 is [ f (x)] 3 This way they can relate implicit differentiation to the Chain Rule studied in the previous section.
Try to get your students to see that related rates, discussed in Section 3.7, are another use of the Chain Rule.
Section 3.1 The Derivative and the Tangent Line Problem
Section Comments
3.1 The Derivative and the Tangent Line Problem—Find the slope of the tangent line to a curve at a point. Use the limit definition to find the derivative of a function. Understand the relationship between differentiability and continuity.
Teaching Tips
Ask students what they think “the line tangent to a curve” means. Draw a curve with tangent lines to show a visual picture of tangent lines. For example:
CHAPTER12
Vector-ValuedFunctions
Section12.1Vector-ValuedFunctions
1. You can use a vector-valued function to trace the graph of a curve. Recall that the terminal point of the position vector () t r coincides with a point on the curve.
2. A vector-valued function r is continuous at the point ta = if ()() lim. ta ta → = rr
3. () 1 3 12 rijk t tt t =+− +
Component functions: () () () 1 1 2 3 ft t t gt htt = + = =−
Domain: ()() ,11, −∞−∪−∞
4. () 22 46 tttt rijk =−+−
Component functions: () () () 2 2 4 6 f tt gtt htt =− = =−
Domain: [ ]2,2
5. () ln t ttet rijk =−−
Component functions: () () () ln t f tt g te htt = =− =−
Domain: () 0, ∞
6. () sin4cos rijk tttt =++
Component functions: () () () sin 4cos f tt g tt htt = = =
Domain: () , −∞∞
7. ()()() () () cossincossin2cos tttttttttt rFGijkijik =+=−+++=+
Domain: [ ) 0, ∞
8. () t r = ()() ()() ()() () () 22 22 ln5343 ln15433ln1 Fijkijk ijkij tGtttttt ttttttt −=+−−+− =−+−+−+=−+
Domain: () 0, ∞
9. ()()() 22 sincos0cossincossin 0sincos ttttttttt tt ijk rFGijk =×==−+
Domain: () , −∞∞
10. ()()() () () () 3 3 333 3 22 11 1 2 1 tt ttt ttttttttttt tt tt t ijk rFGijk
=×==−+−−+−++
++
+ +
Domain: ()() ,1,1, −∞−−∞
11. () () 2 1 2 1 ttt rij =−−
(a) () 1 2 1 ri = (b) () 0 rj =
(c) () ()() () 1122 22 11111 s ssss rijij +=+−+−=+−
(d) ()() ()()() () () () () () () () 22 2 11 22 11 22 2222122212 24 rrijijijij ijij tttttt tttttt +Δ−=+Δ−+Δ−−−=+Δ+Δ−+Δ−+ =Δ+Δ−Δ=ΔΔ+−Δ
12. () cos2sin ttt rij =+
(a) () 0 ri =
(b) 2 2 42 rij π
=+
(c) ()()()cos2sincos2sin rijij θπθπθπθθ −=−+−=−−
(d) cos2sincos2sin 666666 ttt rrijij
13. ()() 0,0,0,5,2,2PQ
5,2,2 PQ == v () 522,01ttttt =++≤≤rijk 5,2,2,01,xtytztt ===≤≤ Parametric equation (Answers may vary.)
15. ()() 3,6,1,1,9,8PQ
13,96,812,3,7 PQ ==−+−+−+=−− v
14. ()() 0,2,1,4,7,2PQ 4,5,3 v PQ ==
()()()42513,01rijk ttttt =+++−+≤≤ 4,25,13, x tytzt==+=−+
01,Parametric equation t ≤≤ () Answers may vary.
()()()()326317,01ttttt =−++−−+−−≤≤rijk 32,63,17,01,xtytztt =−+=−−=−−≤≤ Parametric equation (Answers may vary.)
16. ()() 1,6,8,3,2,5PQ
4,4,3 v PQ ==−−
()()()()146483,01ttttt rijk=−+−++−≤≤
14, x t =− 64,yt =−+ 83,zt =− 01, Parametric equation t ≤≤ (Answers may vary.)
17. ()()()() ()() ()233 323332 1 4 3184 3245,a scalar. tttttt tttttt ru⋅=−+−+ =−−+=−
No, the dot product is a scalar-valued function.
18. ()()()()()()()()232 3cos4sin2sin6cos22, ttttttttttru⋅=+−+−=− a scalar.
No, the dot product is a scalar-valued function.
19. () 2 2,22ttttt rijk=++−≤≤ 2 ,2, x tytzt===
So, 2 zx = Matches (b)
20. ()()() ()() 2 2 cossin,11 cos,sin, rijk ttttt xtytzt ππ ππ =++−≤≤ ===
So, 22 1. xy+= Matches (c)
21. () 20.75 20.75 ,22 ,, t t tttet xtytze rijk=++−≤≤ ===
So, 2 yx = Matches (d)
22. () 2 ln,0.15 3 2 ,ln, 3 t tttt t xtytz rijk=++≤≤ ===
So, 2 3 zx = and ln.yx = Matches (a)
23.
32 23 , x tyt yx == =
22 , x ttytt =+=−
2 2 cos,3sin 1,Ellipse 9 xy y x ==θθ += 28. 22 2cos 2sin 4, circle x t yt xy = = +=
24. 55 5 x ttx yt yx =− =− = =− Domain: 0 t ≥
22 3sec,2tan 1,Hyperbola 94 xy xy ==θθ =+
30. 33 2cos,2sin x tyt== 2323 22 232323 cossin 22 1 2 xy tt xy
= +=
31. 1 42 23 xt yt zt =−+ =+ =+
Line passing through the points: ()() 0,6,5,1,2,3
32. 25 3 x t yt yt = =− =
Line passing through the points: () () 515 0,5,0,,0,22
33. 2cos,2sin, x tytzt === 22 1 44 xy zt += =
Circular helix
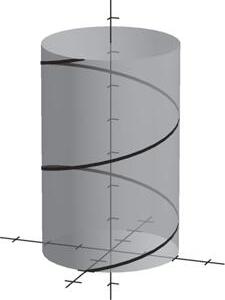
34. ,3cos,3sin x tytzt=== ()() 33 22 3cos3sin9yztt+=+=
Circular helix along cylinder 22
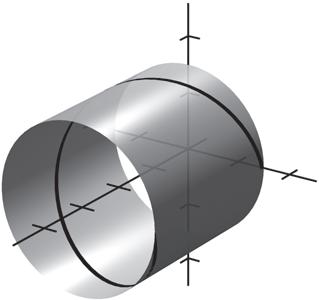
2sin,2cos, t x tytze=== 22 4 t xy ze += =

2 2 3 ,2, 2 3 , 44 x tytzt y xzy === ==
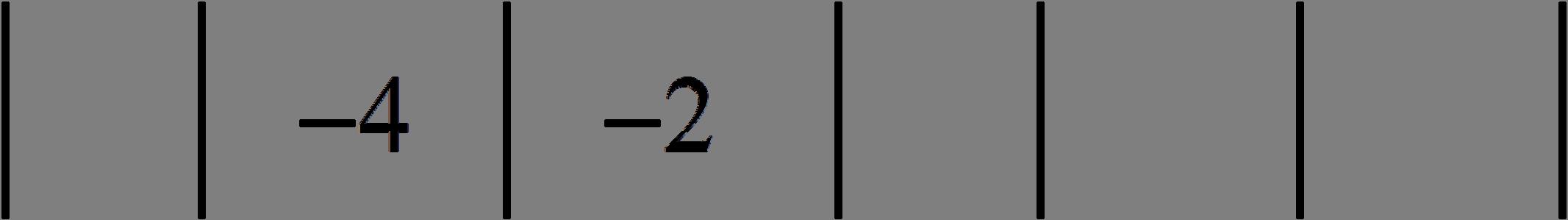
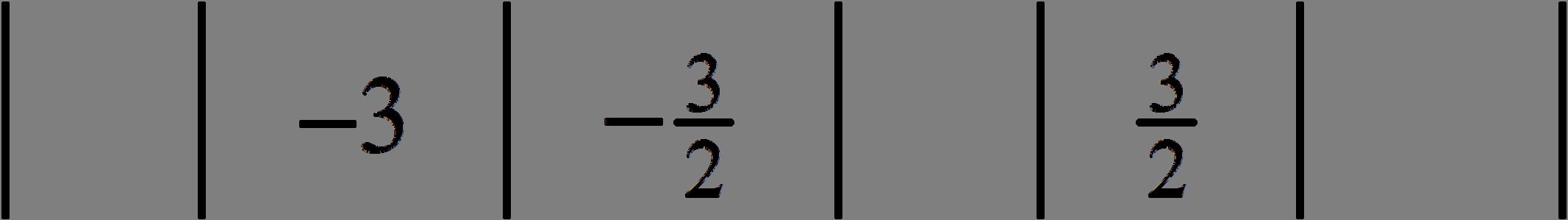
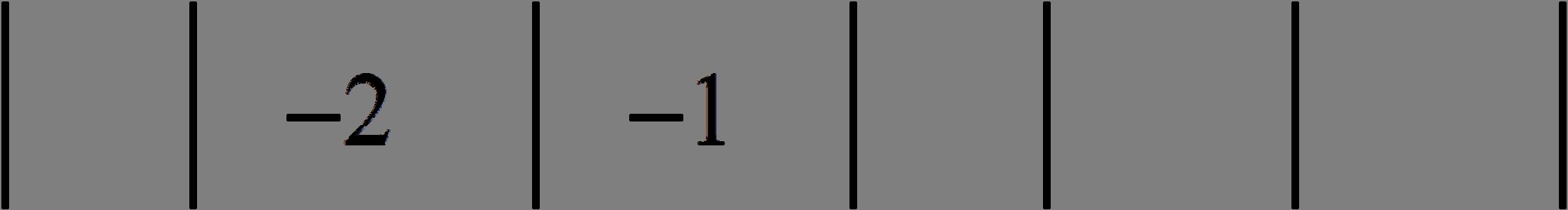
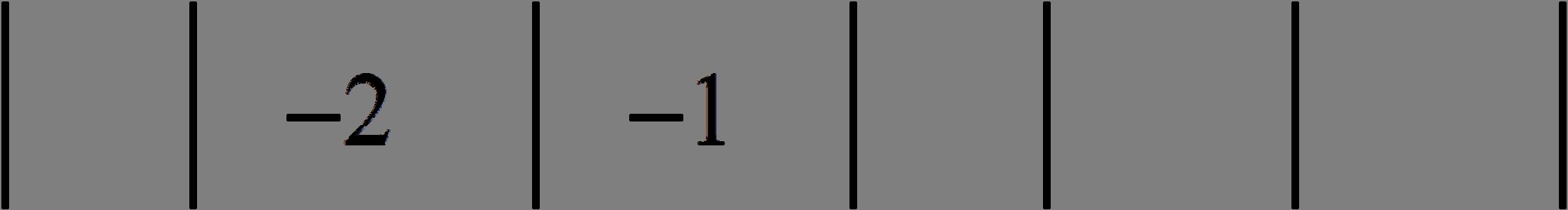
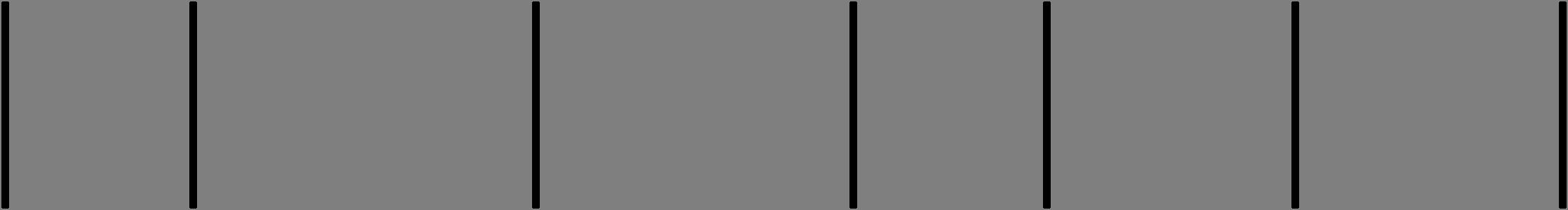
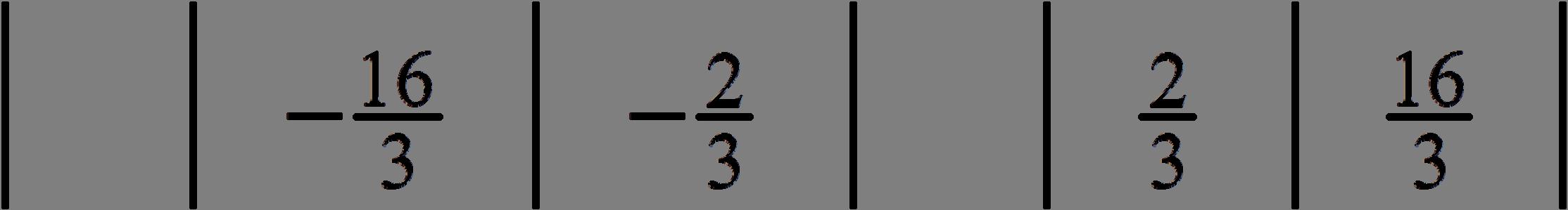
38. cossin sincos x ttt yttt
zt =+ =− = 2222 11 x ytz +=+=+ or 222 1 xyz+−=
zt =
32234
Helix along a hyperboloid of one sheet
39. () 1322 22 tttt rijk =−+−
40. () 2sin2cos2sin tttt rijk =−++
The helix is translated
The height of the helix 2 units back on the x-axis. increases at a faster rate. (c) (d)
The orientation of the The radius of the helix is helix is reversed. increased from 2 to 6.
42. () 23 1 2 rijh tttt =++
(a) () 23 1 2 tttt uijk =++ has the roles of x and y interchanged. The graph is a reflection in the plane x y =
(b) ()() 4 tt urk =+ is an upward shift 4 units.
(c) () 23 1 8 tttt uijk =++ shrinks the z-value by a factor of 4. The curve rises more slowly.
(d) ()() ttur=− reverses the orientation.
43. ()()()() 2 2312ttttt =+=+−++ urkijk
44. ()() () () 2 311 ttttt =+=++−+ uriijk
45. ()() 2 321 tttt =+−+ uijk
46. ()() 2 313 tttt =+−+ uijk
47. 5 yx=+
Let , x t = then 5 yt=+
()() 5 ttt rij =++
48. 2350 xy−+=
Let , x t = then () 1 3 25.yt=+ () () 1 3 25 tt ritj =++
49. () 2 2 yx=−
Let , x t = then () 2 2. yt=−
()() 2 2 ttt rij =+−
50. 2 4 yx =−
Let , x t = then 2 4.yt =−
() () 2 4 ttt rij =+−
51. 22 25 xy+=
Let 5cos, x t = then 5sin.yt = () 5cos5sin ttt rij =+
52. () 2 2 24xy−+=
Let 22cos,2sin. x tyt−==
()()22cos2sin ttt rij =++
53. 22 1 164 xy −=
Let 4sec,2tan. x tyt== () 4sec2tan ttt rij =+
54. 22 1 916 xy+=
Let 3cos x t = and 4sin yt =
Then 22 22 cossin1 916 xy tt +=+= () 3cos4sin rij ttt =+
55. 22 ,0zxyxy=++=
Let , x t = then yxt =−=− and 2222.zxyt =+=
So, 2 ,,2. x tytzt==−= () 2 2 tttt rijk =−+
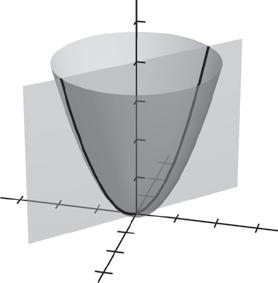
56. 22 ,4zxyz=+=
So, 22 4 xy+= or 2cos, x t = 2sin,4.ytz== () 2cos2sin4ttt rijk =++
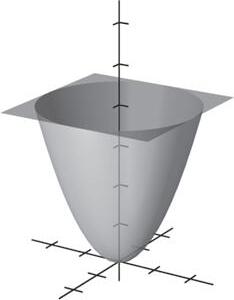
22
57. 222 22 4, 2sin,2cos 4sin x yzx x tyt zxt +== == == () 2sin2cos4sin2 tttt rijk =++
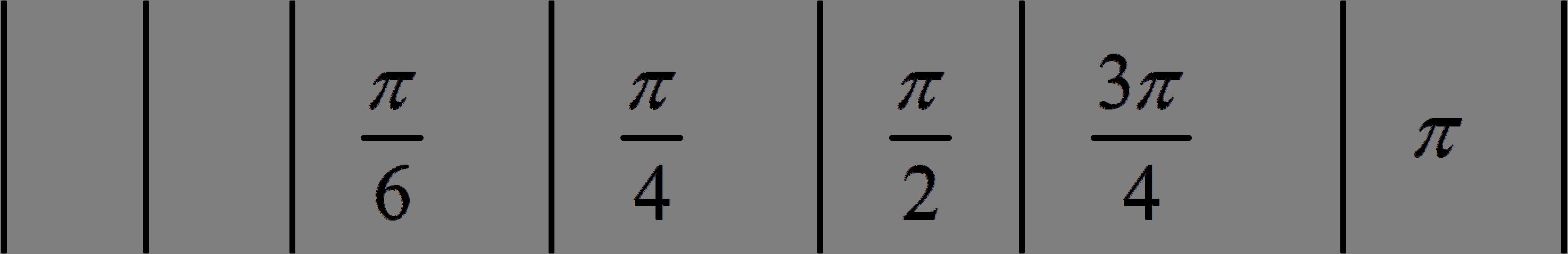
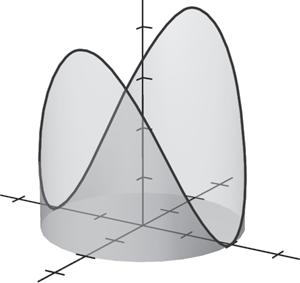
58. 4416,2222 x yzxz++==
If , zt = then 2 x t = and 42 1 2 164. y tt=−− () 242 1 2 164 ttttt rijk =+−−+
59. 222 4,2xyzxz++=+=
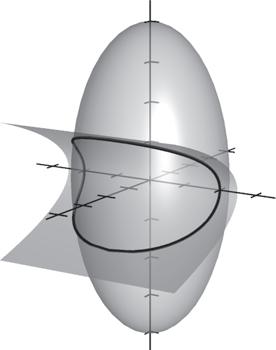
Let 1sin, x t =+ then 21sin zxt =−=− and 222 4. xyz++= ()()22222 1sin1sin22sin4 tytty +++−=++= 222cos,2cos 1sin,2cos 1sin ytyt x tyt zt ==± =+=±
()() () ()() () 1sin2cos1sinand 1sin2cos1sin tttt tttt rijk rijk =++−−
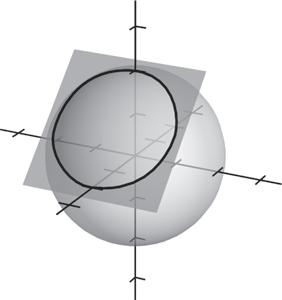
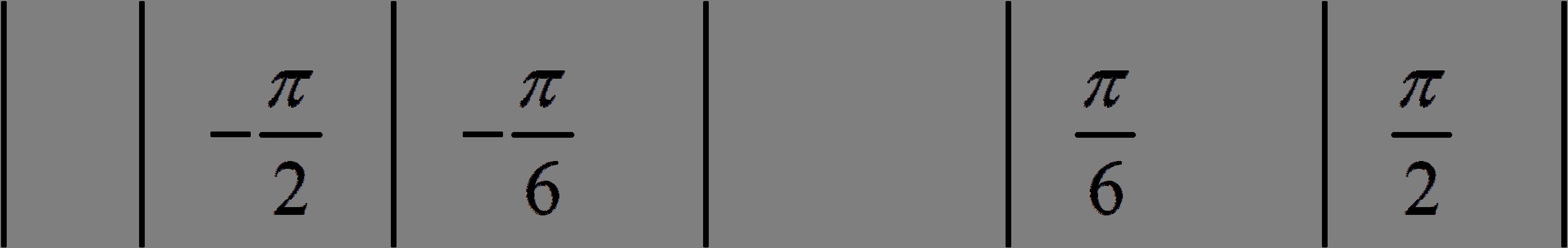
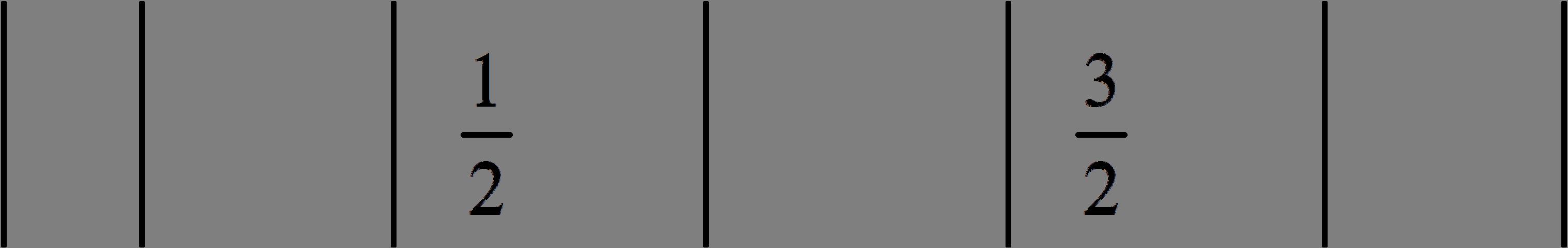
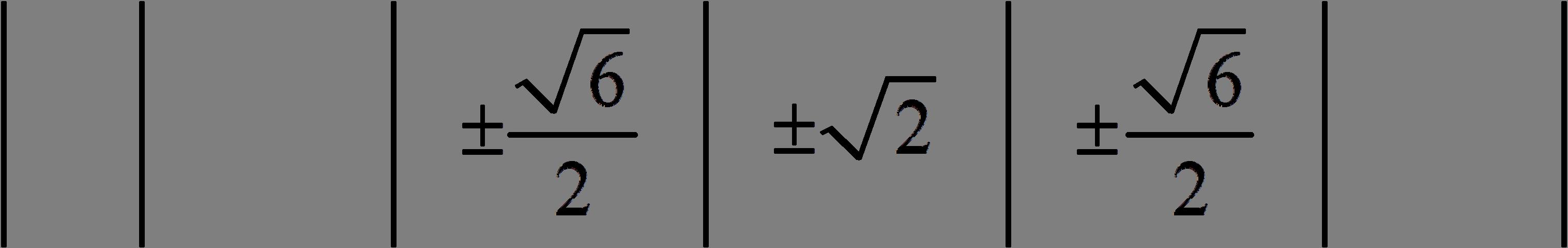
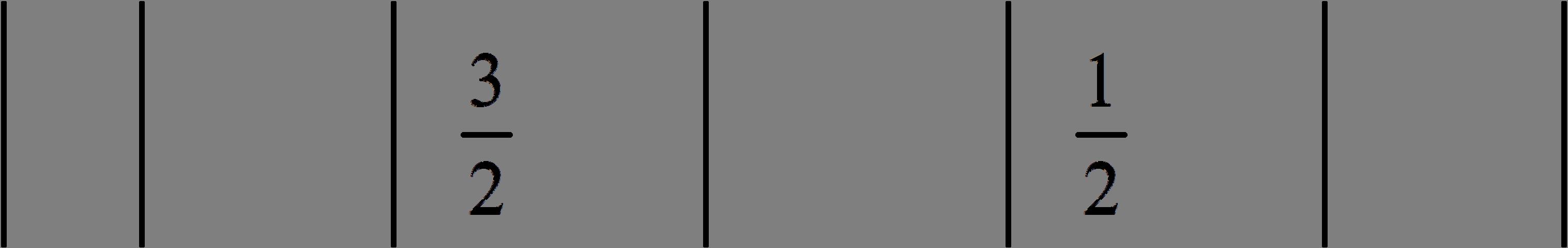
60. 222 10,4xyzxy++=+=
Let 2sin, x t =+ then 2sin yt =− and
()() 222 22 22 2 10 102sin 2 sin 1044 sin sin 44 sin sin 22 sin zxy tt tttt t =−− =−+−− =−++−−+ =−
Taking square roots, () 2 21sin2cos. ztt =−=
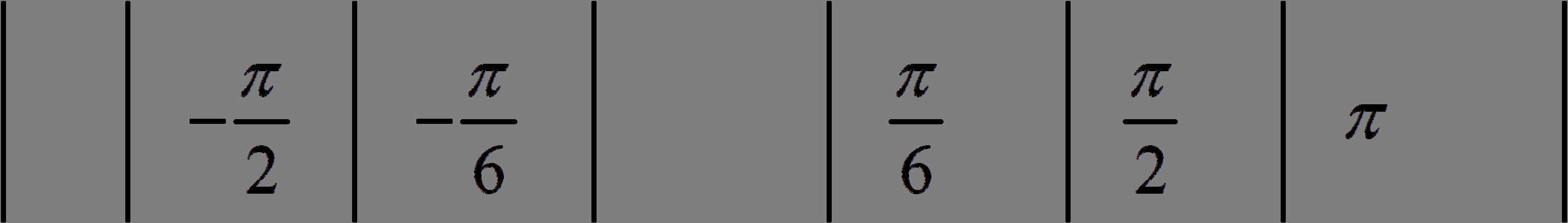
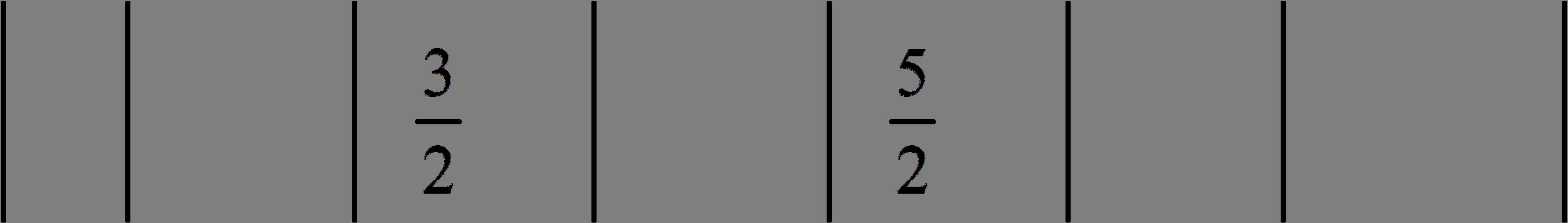
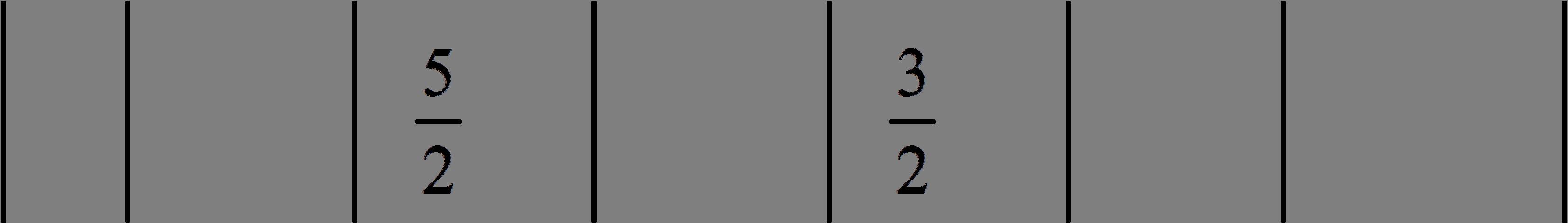
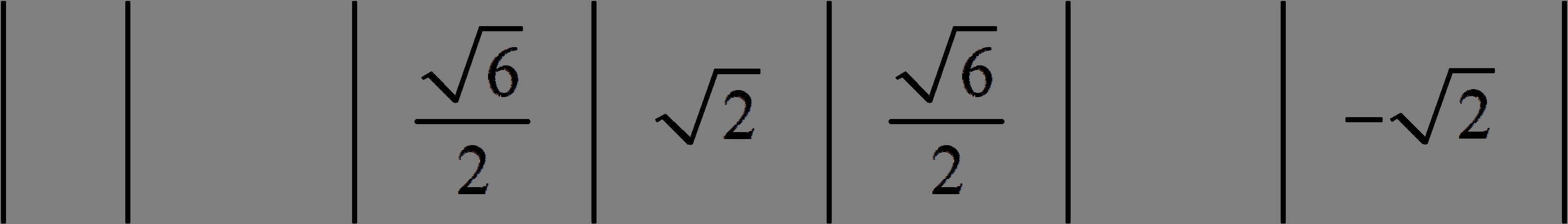
()()()2sin2sin2cos tttt rijk =++−+
61. 22224,4 xzyz+=+=
Subtracting, you have 22 0 xy−= or yx =±

So, in the first octant, if you let , x t = then , x t = , yt = 2 4.zt =− () 2 4 tttt rijk =++−
62. () 222 16,4first octant xyzxy++==
Let , x t = then 4 y t = and 22222 2 16 16. xyztz t ++=++= 42 1 1616ztt t =−+− ( ) 843843 t −≤≤+ () 42 41 1616tttt tt rijk =++−+− t 0 x 1 2 3 2 y 3 2 1 2 z 0 0


63. ()() 22 2222 2cos2sin44 y ztttttx +=+==
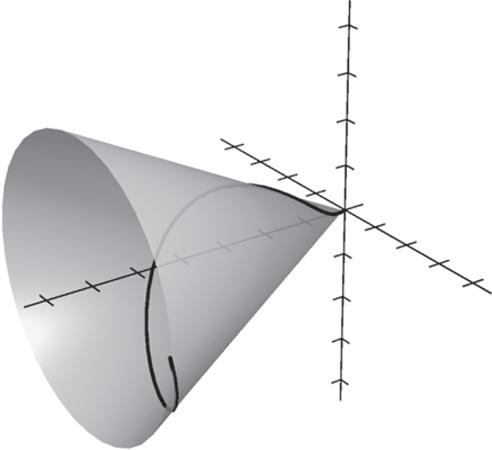
64. ()() 22 2222 cossin ttt x yetetez +=+==
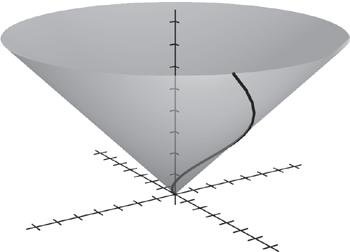
65. ()limcossinijkij t ttt π π → ++=−
66. 2 2 2121 lim36 132 t t tt ijkijk → ++=++
67. 2 0 1cos lim30 t t tt t ijk → ++= because 00 1cossin limlim0. 1 tt tt t →→ == () L'Hôpital's Rule
68. 2 1 ln1 lim 11 t t t tt ijk → ++ does not exist because 1 1 lim 1 t t → does not exist.
69. 0 sin lim tt t t ee t ijkijk → ++=++ because () 00 sincos limlim1L'Hôpital's Rule 1 tt tt t →→ ==
70. 1 1 lim tt t et t →∞ ++ ijk
Note that 1 lim1 t t t →∞ = because if 1 , t yt = then 1 lnln0 yt t =→ as t →∞
Hence, 1. y → So, the limit is 00. ++= ijkk
71. () 11 21 t tt =+ + rij
The function is not continuous at 1 2 t =− and 0. t = So,
() t r is continuous on the intervals 11 ,,,0, 22 −∞−−
and () 0,. ∞
72. () 1 ttt rij =+−
Continuous on [ ) 1, ∞
73. ()() arcsin1tttt rijk =++−
Continuous on [ ]1,1
74. ()() 2,,ln1 tt teet r =−
Continuous on 10 t −> or () 1:1,. t >∞
75. () 2 ,,tan t tett r =
Discontinuous at 2 tn π π =+
Continuous on , 22 nn ππ ππ
76. () 3 8,, ttt r =
Continuous on [ ) 0, ∞
77. Yes. () t r represents a line. Answers will vary.
78. Not necessarily. For example, the function () 333 tttt =++ rijk represents a line.
79. Answers will vary. Sampleanswer: () ,3 ,3 t t t +≥ = −+< ij r ij
80. (a) 3cos1,xt=−+ 5sin2,yt=+ 4 z = () () 1222 1,4 925 xy z +==
(b) 4, x = 3cos1,yt=−+ 5sin2zt=+ () () 1222 1,4 925 yz x +==
(c) 3cos1,xt=− 5sin2,yt=−− 4 z = () () 1222 1,4 925 xy z ++ +==
(d) 3cos21,xt=−+ 5sin22,yt=+ 4 z = () () 1222 1,4 925 xy z +==
(a) and (d) represent the same graph
82. (a) View from the negative x-axis: () 20,0,0
(b) View from above the first octant: () 10,20,10
(c) View from the z-axis: () 0,0,20
(d) View from the positive x-axis: () 20,0,0
×
81. () 1 cossin,04ttttt π π =++≤≤rijk
83. Let ()()()() 111 txtytzt rijk =++ and ()()()() 222 txtytzt uijk =++ Then: ()()()()()()()()()()()()()() { } ()()()()()()()() ()()() 122112211221 12211221 122 limlim limlimlimlimlimlimlimlim limlimlimlim ruijk ij tctc tctctctctctctctc tctctc ttytztytztxtztxtztxtytxtyt ytztytztxtztxtzt xtytxt →→ →→→→→→→→ →→→
=++×++ =×
=−−− +− () ()()()()()() ()() 1 111222 limlimlimlimlimlim limlim k ijkijk ru tc tctctctctctc tctc yt xtytztxtytzt tt → →→→→→→ →→
84. Let ()()()() 111 txtytzt rijk =++ and ()()()() 222 txtytzt uijk =++ Then: ()()()()()()()() ()()()()()() ()()()()()() ()() 121212 121212 111222 limlim limlimlimlimlimlim limlimlimlimlimlim limlim tctc tctctctctctc tctctctctctc tctc ttxtxtytytztzt xtxtytytztzt x tytztxtytzt tt ru ijkijk ru →→ →→→→→→ →→→→→→ →→
= ++ =++
=++⋅++ =⋅
85. Let ()()()() . txtytzt rijk =++ Because r is continuous at ,tc = then ()() lim. tc tcrr → = ()()()()()()() ,, cxcyczcxcyczc rijk =++ are defined at c. () () () () () () () () () () () () () 222 222 lim r rr tc xtytzt x cyczcc → =++ =++= So, r is continuous at c.
86. Let () 1,if 0 1,if 0 t ft t ≥ = −< and ()() tft ri = Then r is not continuous at 0, c = whereas, 1 r = is continuous for all t
87. No, not necessarily. See Exercise 90.
88. Yes. See Exercise 89.
89. ()() ()()() 22 2 920 3454. rijk uijk tttt ssss =+−+ =+++−
Equating components: 2 2 2 34 920 54 ts ts ts =+ −= =− So, 2 34544 920164. sss tst +=− = −== =
The paths intersect at the same time 4 t = at the point () 16,16,16.The particles collide.
90. () ()()() 23 238122 tttt ssss rijk uijk =++ =−++++
Equating components
2 3 23 8 122 ts ts ts =−+ = =+ () ()() 2 2 2 238 41298 42090 29210 s s s ss ss ss −+= −+= −+= −−=
For 1 2 , s = () 1 2 232. t =−+=
For 9 2 , s = () 9 2 236 t =−+=− and () 2 9 2 836 t == and () 3 9 2 1254. t == Impossible.
The paths intersect at ()2,4,8,but at different times () 1 2 2and.ts== No collision.
Section12.2DifferentiationandIn tegrationofVector -ValuedFunctions
1. () 0 t ′ r represents the vector that is tangent to the curve represented by () t r at the point 0 t
2. You have ()() tdtt=+ rRC because () () () d tt dt += RCr
3. () () 2 0 1,3tttt=−+=rij ()() 2 1, x ttytt =−= 2 1 x y =−
() () () 383 2 36 tt =−+ ′ =−+ ′ =−+ rij rij rij
() 0 t ′ r is tangent to the curve at 0 3. t = y x 161284 2 4 2 4 r ′ r (8,3)
4. ()() 3 0 1,1tttt rij=++=
() () () 3 3 1 1 x tt ytt yx =+ = =−
() () () 2 12 3 13 tt rij rij rij =+ ′ =+ ′ =+
() 0 t r ′ is tangent to the curve at 0 t
5. ()
()() 0 22 cossin, 2 cos,sin 1 tttt xttytt xy rij π =+= == += () 2 sincos 2 ttt rj rij ri π π
=
′ =−+
′ =−
() 0 t r ′ is tangent to the curve at 0 t
6. () ()() 0 22 3sin4cos, 2 3sin,4cos 1,ellipse 34 tttt xttytt xy rij π =+= ==
+=
=
′ =−
() 3 2 3cos4sin 4 2 i ttt r rij rj π π
′ =−
() 0 t r ′ is tangent to the curve at 0 t
7. () 2 0 ,,0tt teet r ==
()() () () () () 2 2 2 2 , ,0 01,1 ,2 01,2 r r r ttt tt x teytee yxx tee === => = ′ = ′ = () 0 r t ′ is tangent to the curve at 0 t
8. () () () 0 ,,0 1 , 1 ,0 tt tt t teet x teyte e yx x r == === => () () () 01,1 , 01,1 r r r teett = ′ =− ′ =−
() 0 r t ′ is tangent to the curve at 0 t
9. () 0 3 2cos2sin, 2 ttttt rijk π =++=
22 4, x yzt+==
() 2sin2cos 33 2 22 3 2 2 ttt rijk rjk rik ππ π ′ =−++
=−+
′ =+
10. () 2 0 3 2 ,2tttt rijk=++= 2 3 2 , yxz== () () () 3 2 2 224 24 tt rij rijk rij
′ =+ =++
′ =+
11. () () 4 3 5 45 ttt tt =− ′ =− rij rij
12. () () () 3 2 1 1 3 2 ttt tt t rij rij =+−
′ =−
13. () 33 3cos2sin ttt=++ rijk
()()() 22 22 9cossin6sincos 9sincos6sincos ttttt tttt ′ =−+ =−+ rij ij
14. () 4ln22 ttttt rijk =++ () 2 32 22 2 2 252 2 t ttt t tt t t t rijk ijk
′ =+++
15. () () () 45 55 tt ttt tete teete rijk rik =++ ′ =−++
19. () 32 1 2 ttt rij =+
(a) () 2 3 ttt rij ′ =+
r r = ′ =−
16. () () 3 2 ,cos3,sin3 3,3sin3,3cos3 tttt tttt
(b) () 6 rij tt ′′ =+
(c) ()()()23 3618 tttttttrr ′′′ ⋅=+=+
r r = ′ =+−
17. () () sin,cos, sincos,cossin,1 tttttt ttttttt
18. () () 22 arcsin,arccos,0 11 ,,0 11 r r ttt t tt = ′ =−
21. () 4cos4sin ttt rij =+
(a) () 4sin4cos ttt rij ′ =−+
(b) () 4cos4sin ttt rij ′′ =−−
(c) ()()()()()4sin4cos4cos4sin0ttttttrr ′′′ ⋅=−−+−=
22. () 8cos3sin ttt rij =+
(a) () 8sin3cos ttt rij ′ =−+
(b) () 8cos3sin rij ttt ′′ =−−
20. () ()() 22 ttttt rij =++−
(a) ()()() 2121 tt rtij ′ =++−
(b) () 22 rij t ′′ =+
(c) ()()()()()()2122128 rrttttt′′′ ⋅=++−=
(c) ()()()()()8sin8cos3cos3sin55sincos ttttttttrr ′′′ ⋅=−−+−=
23. () 1123 26 tttt =−+ rijk
(a) () 2 1 2 ttt ′ =−+ rijk
(b) ()tt ′′ =+ rik
(c) ()()()()() () 1123 110 22 ttttttt′′′ ⋅=+−+=+rr
=−−+ ijk rr ijk ijk
′′′ ×=
(d) ()() () 2 22 2 1 1 2 10 1 2 1 2 tt tt t ttt tt
24. () () () 322335tttt =+++− rijk
(a) () 2 343ttt ′ =++ rijk
(b) () 64tt ′′ =+ rij
(c) ()()()()() 2 3 364430 1816 ttttt tt ′′′ ⋅=++ =+ rr
′′′ ×=
(d) ()() ()() () 2 22 2 343 640 0120181224 121812 tt tt t ttt tt
=−−−+− =−+− ijk rr ijk ijk
25. () cossin,sincos, tttttttt =+− r
(a) () sinsincos,coscossin,1 cos,sin,1 ttttttttt tttt ′ =−++−+ = r
(b) () cossin,sincos,0 ttttttt ′′ =−+ r
(c) ()()()()()() () 2222 22 coscossinsinsincos10 coscossinsinsincos cossin tttttttttttt tttttttttt tttt ′′′⋅=−+++ =−++ =+= rr
(d) ()() ()() () ()() 2222 2 2 cossin1 cossinsincos0 sincoscossincossincossincossin sincoscossin sincos,cossin, tttttt tttttt tttttttttttttttt ttttttt ttttttt
′′′ ×= −+ =−−+−++−+ =−−+−+ =−−− ijk rr ijk ijk
26. () 2 ,,tan t tett = r
(a) () ,2,sec2 t tett ′ =− r
(b) () 2 ,2,2sectan t tett ′′ = r
(c) ()() 2442sectan t ttettt′′′ ⋅=−++rr
(d) ()() () 2 2 2222 2222 2sec 22sectan 22sectan2sec2sectansec22 4sectan2sec2sectansec22 t t tttt tttt ttett ett ttttettetete ttttettetete
27. ()
() () 23 2 23 0 ttt ttt rij rij r0 =+ ′ =+ ′ =
Smooth on ()() ,0,0, −∞∞
(Note: 0 t = corresponds to a cusp at ()() ,0,0.xy = )
28. () 24 5 ttt =− rij
() 25443 ttt ′ =− rij
() 0 ′ = r0
Smooth on ()() ,0,0, −∞∞
29. () () 33 22 2cos3sin 6cossin9sincos 2 rij rij r0 n θθθ
Smooth on () 1 22,, n n n π π +
any integer.
30. ()()() ()() () () sin1cos 1cossin 21,any integer rij rij r0nn θθθθ θθθ π =++− ′ =++ ′ −=
Smooth on ()() () 21,21 nn−+ππ
35. ()() ()() 223 2 3,4 32,423 tttttttt ttttt =++=++ ′′ =++=++ rijkuijk rijkuijk
(a) () 32 tt ′ =++ rijk
31. () () () () 2 33 34 3322 22 88 164322 88 tt t tt ttt t tt rij rij =+ ++ ′ =+ ++
() t r0 ′ ≠ for any value of t
r is not continuous when 2. t =−
Smooth on ()() ,2,2, −∞−−∞
32. () () 3 3 tt tt teet tee rijk rijk0 =−+ ′ =++≠
r is smooth for all t: () , −∞∞
33. () () 2 3tan 3sec tttt tt rijk rijk0 =−+ ′ =−+≠
r is smooth for all 21 22 n tn π ππ + ≠+=
Smooth on intervals of form 22,, nn ππ ππ
n is an integer.
34. () () () 2 1 1 4 11 2 4 2 tttt tt t rijk rijk0 =+−+ ′ =++≠
r is smooth for all ()0:0, t >∞
(b) ()()()() () () ()() () () () 2 2 2 33 332423 349263 9263 d tttt dt ttt ttt ttt
=−+−+− ruru ijkijk ijk ijk
(c)
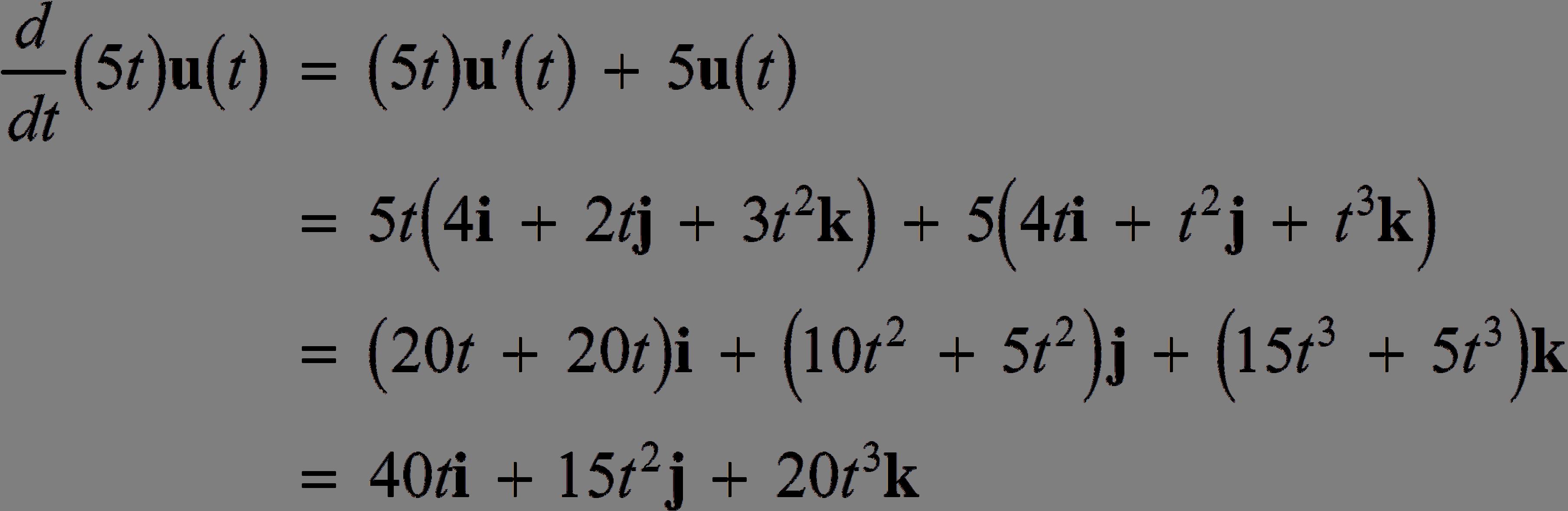
(d) ()()()()()() ()()()() ()() ()()()() ()() ()() 2223 2424 24 43231432 463432 895 d tttttt dt ttttttttt tttttt ttt ′′
=++ rururu
(e) ()()()()()() ()()()() ()() 32323232 3232 743212812 8124324 d tttttt dt tttttttttt ttttt
=+−+−++−+− =+−+− rururu ijkijk ijk
(f) ()() () 222 2322 268 d tt dt t t ′ = =
36. ()() ()() 2 1 2sin2cos,2sin2cos 1 2cos2sin,2cos2sin rijkuijk rijkuijk ttttttt t tttttt t =++=++ ′′=+−=−+−
(a) () 2cos2sin ttt ′ =+− rijk
=−
(b) ()()()() () ()() 2 2 2 33 1 32cos2sin2cos2sin 1 36cos2cos6sin2sin 1 34cos4sin ruru ijkijk ijk ijk d tttt dt tttt t tttt t tt t ′′
=++−+−+
(c) ()()()()() ()() 2 555 11 52cos2sin52sin2cos 55 10cos10sin10sin10cos 10cossin10cossin uuu ijkijk ijkijk jk d ttttt dt ttttt tt tttttt tt tttttt
(d) ()()()()()() () ()()()()() ()()()() () 2 11 2sin2cos2cos2sin12cos2sin2sin2cos 11 4sincos4sincos4sincos4sincos
37. ()()2,234 tttttt rijkuk =++=
(a) ()() 7 tttru⋅=
(i) ()() 6 7 Dt tttru =
(ii) Alternate Solution: ()()()()()() ()()()()23324666 2443437 Dt tttttttttttttttt rururuijkkijkk ′′
=⋅+⋅=++⋅+++⋅=+=
(b) ()() 2365 4 22 00 ttttttt t ijk ruij ×==−
(i) ()() 12554 Dt tttt ruij × =−
(ii) Alternate Solution: ()()()()()() 23254 34 2143125 00400 ijkijk rururuij t Dttttttttttttt tt ′′
× =×××=+=−
38. () cossin,tttt rijk =++ ()tt ujk =+
(a) ()() 2 sin ttttru⋅=+
(i) ()() cos2 Dt ttttru =+
(ii) Alternate Solution: ()()()()()() ()()() cossinsincoscos2cos t Dtttttt ttttttttttt rururu ijkkijkjk
(b) ()() ()() cossinsincoscos 01 ttttttttttt t ijk ruijk ×==−−+
× =+−−−−
(i) ()()()()cossin1cossinsin Dt ttttttttt ruijk
(ii) Alternate Solution: ()()()()()() ()() cossinsincos1sincos1sincossin 00101 t Dtttttt tttttttttttt t rururu ijkijk ijk
× =×+× =+−=+−+−−
39. () 2 299 ijkijkC tdtttt ++=+++
40. ()34232 8 3 4643 ijkijkC tttdtttt +−=+−+
41. 123252 ln 5 tdtttt t +−=+−+ ijkijkC
45. () ()coscossintt ettdtetttt ++=++++ ijkijkC
(Note: Integration by parts needed for cos. ttdt )
42. () 1 lnlnln tdtttttt t ++=−+++ ijkijkC (Integration by parts)
43. ()34 5 45 ln5 t t tdttt ++=+++ ijkijkC
44. 2 2 1 sectanarctan 1 ijijC tdttt t +=++ +
46.
(Note: Integration by parts needed for the first integral. Also, you could combine the constants + kC )
47.
52. 2242 1 tttttt ij+=+=+ for
53. () () () () () 22 2 4323 02323 231 rijijC rijCiCj rij tttt tt teedtee tee =+=++ =++= =− =+−
54. () () () () () 2332 332 364 02 24 rjkjkC rij rijk tttdttt C ttt =+=++ ==+ =+++
55. () () () () () () () () () () 1 1 2 2 3232 06003600
600360016 0 600360016 tdtt tt ttdt ttt tttt rjjC rCij rij rij ijC rC0 rij ′ =−=−+ ′ ==+ ′ =+− =+− =+−+ ==
600360032
600360032
56. () () () () () () 1 11 2 22 4cos3sin 4sin3cos 033 4cos3sin 0440 4cos3sin ttt ttt ttt j ttt rjk rjkC rkkCC0 rjkC rCjC rjk ′′ =−− ′ =−++ ′ ==+ = =++ =+= = =+
57. () ( ) () 22 1 2 11 02 22 tttt tteedteet =−+=−+++ =−++=−+ =−+ rijkijkC rijCijkCijk () () () () () 2 2 1 121 2 2 21 2 tt t t teet e et rijk ijk =−+−++
=+−++
58.
59. At 0 , tt = the graph of () t u is increasing in the x, y, and z directions simultaneously.
60. Sampleanswer: ()()3,4 ttttt =+=− fijgij
()() 2 43 tttt ⋅=−fg
61. Let ()()()() txtytzt rijk =++ Then ()()()() ctcxtcytczt rijk =++ and ()()()() ()()()() d ctcxtcytczt
() () ()11 00 3 21 4 tdttdt⋅=−≠fg
62. Let ()()()() 111 txtytzt rijk =++ and ()()()() 222 txtytzt uijk =++ ()()()()()()()() ()()()()()()()() ()()()()()()()() 121212 121212 111222 ttxtxtytytztzt d ttxtxtytytztzt dt x tytztxtytzttt
63. Let ()()()() , txtytzt rijk =++ then ()()()()()()()() rijk wttwtxtwtytwtzt =++ ()()()()()()()()()()()()()() ()()()()()()()()()()()() d wttwtxtwtxtwtytwtytwtztwtzt dt wtxtytztwtxtytztwttwtt
=+ rijk ijkijkrr
64. Let ()()()() 111 txtytzt rijk =++ and ()()()() 222 . txtytzt uijk =++ ()()()()()()()()()()()()()() ()()()()()()()()()()()()()()()()()() ()()()()()()()() ()()() 121212121212 1212121212121212 12121212 1212 ruijk ruij k ttytztztytxtztztxtxtytytxt d ttytztytztztytztytxtztxtztztxtztxt dt xtytxtytytxtytxt ytztzty ×=
65. Let ()()()() rijk txtytzt =++ Then () () () () () () () ()wtxwtywtzwt rijk =++ and () () () () ()()() ()()() ()() ()()() () () () () ()()() Chain Rule
d wtxwtwtywtwtzwtwt dt wtxwtywtzwtwtwt
rijk ijkr
66. Let ()()()() txtytzt rijk =++ Then ()()()() txtytzt rijk ′′′′ =++ ()()()()()()()()()()()()()() ()()()()()()()()()()()()()()()()()() ()()()()()()()() ()()()()()()() ttytztztytxtztztxtxtytytxt d ttytztytztztytztytxtztxtztztxtztxt dt xtytxtytytxtytxt ytztztytxtztzt
67. Let ()()()() 111 , txtytzt rijk =++ ()()()() 222 , txtytzt uijk =++ and ()()()() 333 . txtytzt vijk =++ Then: ()()()()()()()()()()()()()()()()()() ()()() () ()()()()()()()()()()()() ()()()()()()()()()()()()()()() ()()() 123231232312323 123123123132 132132123123123 123 tttxtytztztytytxtztztxtztxtytytxt d tttxtytztxtytztxtytztxtytzt dt xtytztxtytztytxtztytxtztytxtzt ytztxt
()()()()()()()()()()()() ()()()()()()()()()()()() ()()()()()()()()()()()()()()() { } ()()()()()()()()()() 123123123123 123123123123 123321232312323 1233212323 ytztxtytztxtztxtytztxtyt ztxtytztytxtztytxtztytxt xtytztytztytxtztztxtztxtytytxt xtytztytztytxtztztxt
()()()()() { } ()()()()()()()()()()()()()()() { } ()()()()()()()()() 12323 123321232312323 ztxtytytxt x tytztytztytxtztztxtztxtytytxt ttttttttt
68. Let ()()()() txtytzt rijk =++ If ()() ttrr ⋅ is constant, then: ()()() ()()() [] ()()()()()() ()()()()()() ()() 222 222 2220 20 20. t xtytztC d x tytztDC dt xtxtytytztzt xtxtytytztzt tt ++= ++= ′′′ ++= ′′′ ++ = ′
= rr So, ()() 0. ttrr ′ ⋅=
69. ()()() sin1cos tttt rij =−+− (a)
The curve is a cycloid. (b) ()() () 1cossin sincos rij rij ttt ttt ′ =−+ ′′ =+ () 12coscossin22 22cos r tttt t ′ =−++ =−
Minimum of () t r ′ is 0, ()0. t =
Maximum of () t r ′ is 2, (). t π = () 22 sincos1ttt r ′′ =+=
Minimum and maximum of () r t ′′ is 1. 40 0 0 5
70. () 2cos3sin rttt ij=+
(a) Ellipse
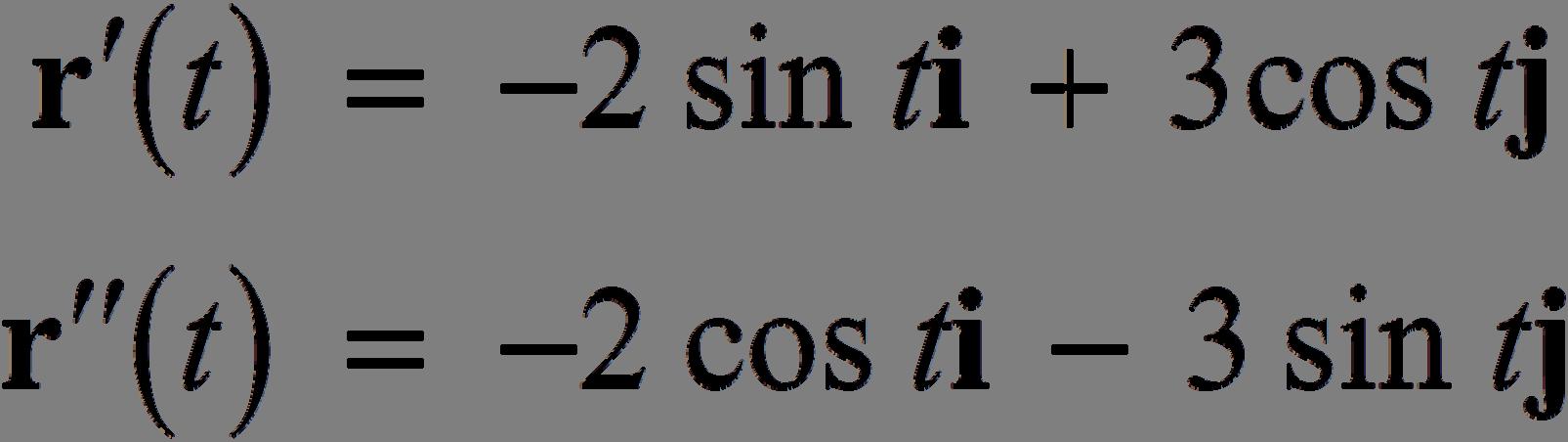
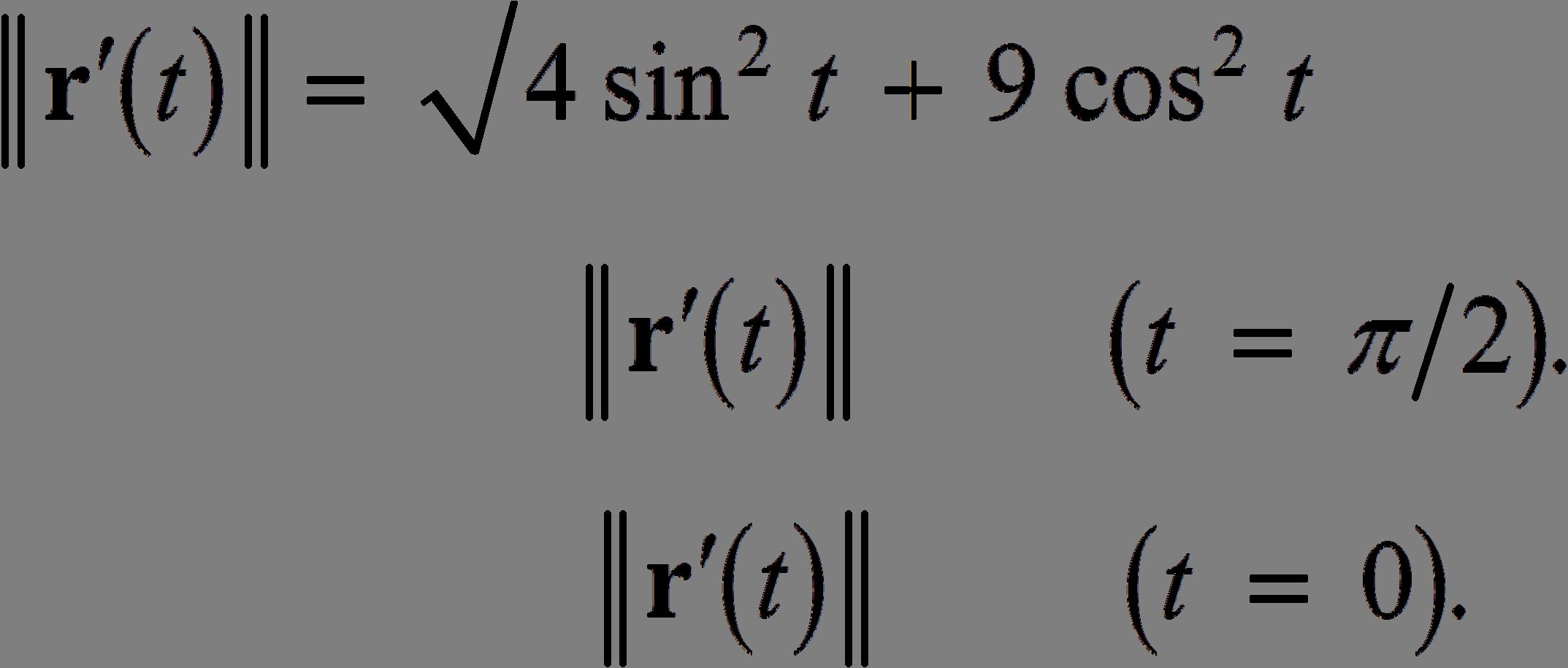
Minimum of is 2, Maximum of is 3,
Minimum of Maximum of
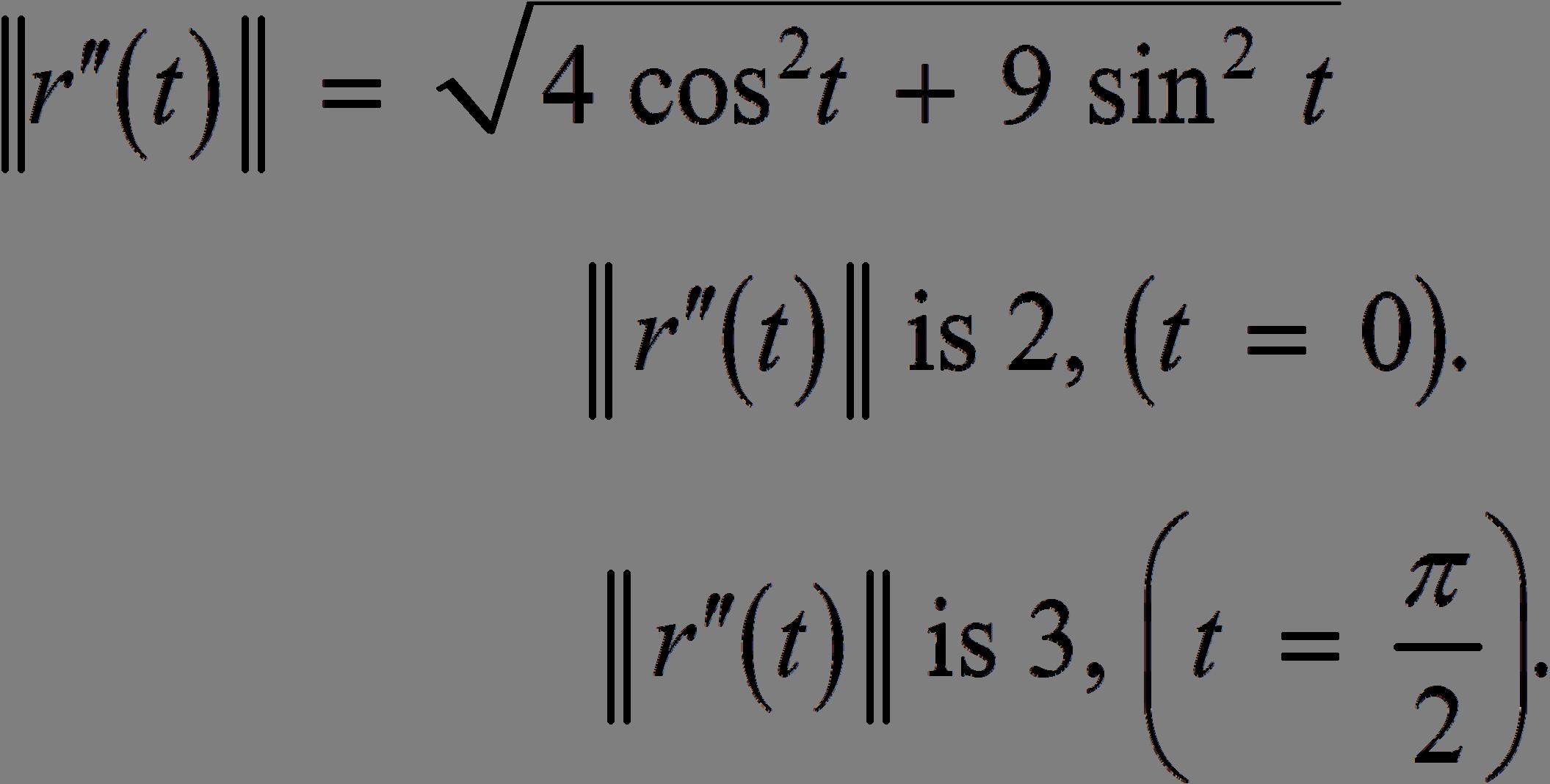
71. () () ()() () ()() ()() 22 sincos cossincossin sincossincoscossinsincos2cos2sin 2sincos2sincos0
So, () t r is always perpendicular to (). t r ′′
72. (a) : both components positive 4 5 : -component negative, -component positive 6 5 : -component positive, -component negative 4 t txy txy
(b) No. There is a cusp when 0, t = at ()1,0.
73. True
74. False. The definite integral is a vector, not a real number.
75. False. Let () cos sin . rijk ttt=++
76. False. ()()()()()() d tttttt
(See Theorem 2.2, part 4)
Section12.3VelocityandAcceleration
1. The direction of the velocity vector provides the direction of motion at time t. The magnitude of the velocity vector provides the speed of the object.
(b) The acceleration vector points downward due to gravity. y x 1 313 1 2 1 2 (b)
2. (a) The acceleration vector points toward the sun. The comet’s speed increases as it gets closer to the vertex of the parabola and decreases as it moves farther from the vertex.
3. ()()() 31,3,0ttt=+− rij
(a) ()() () ()() 22 3 Speed3110 tt t tt ′ ==+ ==+= ′′ == vrij v ar0
(b) At ()3,0,1. t = ()() 13,1 vija0 =+=
(c) 3, x t = 1 yt=− 1,line 3 x y =−
4. () () () 2 4,1,3ttt =+− rij
(a) ()() () () ()() 2 2 2 Speed1214 2 ttt ttt tt ′ ==− ==+−=+ ′′ ==− vrij v arj
(b) At ()1,3,1. t = ()() 12,12 =−=− vijaj
(c) , x t = 2 4 yt =− 2 4,parabolayx =−
5. ()() 2 ,4,2 ttt =+ rij
(a) ()() () ()() 2 2 Speed41 2 ttt tt tt ′ ==+ ==+ ′′ == vrij v ari
(b) At ()4,2,2. t = ()() 24,22 vijai =+=
(c) 2 , x t = yt = 2 ,parabola xy =
6. () () 3 1 1,3,2 4 ttt =++ rij
(a) ()() () () 2 4 3 4 9 Speed1 16 3 2 ttt tt tt ′ ==+ ==+ = vrij v ai
(b) At ()3,2,2. t = ()() 23,23 =+= vijai
(c) 3 1 1, 4 xt=+ yt = () 3 3 1 141 4 xyyx =+ =−
4 6 2 4 6
v a 42
7. () () 2cos2sin,2,2ttt =+ rij
(a) ()() () () 22 2sin2cos Speed4sin4cos2 2cos2sin tttt ttt ttt ′ ==−+ ==+= =−− vrij v aij
(b) At ()2,2,. 4 t π = 22 4 22 4 π π
=−+
vij aij
=−−
(c) 2cos,2sin x tyt== 22 4,circle xy+=
8. ()() 3cos2sin,3,0ttt =+ rij
(a) ()() () () 22 3sin2cos Speed9sin4cos 3cos2sin tttt ttt ttt ′ ==−+ ==+ =−− vrij v aij
(b) At ()3,0,0. t = ()() 02,03 ==− vjai
(c) 3cos,2sin x tyt== 22 22 cossin1,ellipse 32 xy tt +=+=
(2,2) 3 3 3 3 x v a y v a (3,0) y x 1 1 2112 3 3
9. () ()sin,1cos,,2tttt π =−− r
(a) ()() () () () 2 2 1cos,sin Speed1cossin22cos sin,cos tttt tttt ttt ′ ==− ==−+=− = vv v a
(b) At (),2,. t ππ = () () 2,0,0,1 ππ==−va
10. () (),,1,1teett = r
(a) ()() () ()() ()() 22 22 , Speed , tt tttt tt ttee teeee ttee ′ ==− ==−+=+ ′′ == vr v ar
(b) At ()1,1,0. t = () () 01,1,01,1 =−=va
11. () 53,1ttttt=++=rijk
(a) ()() () ()() 222 53 Speed15335 vrijk v ar0 tt t tt ′ ==++ ==++= ′′ ==
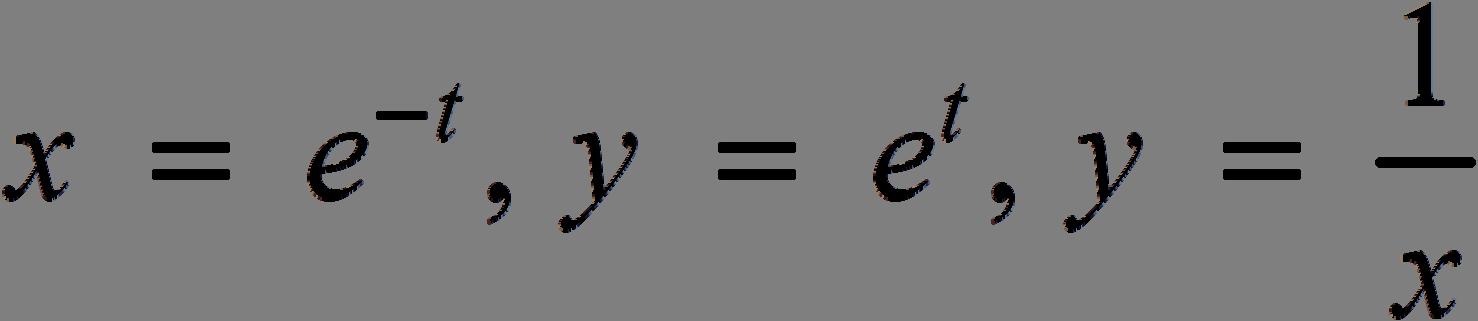
(,2) v x 2 a 4 2 π π π y (c) 1 1 2 2 x (1,1) va y (c)
(b) () () 153 1 =++ = vijk a0
12. () 442,3rijk ttttt=+−=
(a) ()() () () ()() 2 22 442 Speed442366 vrijk v ar0 tt t tt ′ ==+− ==++−== ′′ ==
(b) () () 3442 3 =+− = vijk a0
13. () 22 1 ,4 2 ttttt=++=rijk
(a) ()() () ()() 222 2 Speed1415 2 tttt tttt tt ′ ==++ ==++=+ ′′ ==+ vrijk v arjk
(b) () () 484 42 =++ =+ vijk ajk
14. () 2 1 3,2 4 ttttt=++=rijk
(a) ()() () () 22 1 3 2 11 Speed911044 1 2 vrijk v ak ttt ttt t ′ ==++ ==++=+ =
(b) () () 23 1 2 2 =++ = vijk ak
17. () 4,3cos,3sin, ttttt π == r
15. () 2 9,0ttttt=−+−=rijk
(a) ()() () ()() () 2 22 22 32 2 9 18 Speed11 99 9 9 vrijk v ark t tt t tt t tt tt t ′ ==−− ==++= ′′ ==−
(b) () () 32 0 91 0 93 =− =−=− vij akk
16. () 2322,4ttttt=++=rijk
(a) ()() () () 2 23 Speed419 3 2 2 tttt ttt t t ′ ==++ ==++ =+ vrijk v aik
(b) () () 486 3 42 4 =++ =+ vijk aik
(a) ()() () ()() ()() 22 2 4,3sin,3cos Speed43sin3cos1695 0,3cos,3sin vr v ar tttt ttt tttt
18. () 2 2cos,sin3,, 4 r ttttt π ==
(b) () () 4,0,3 0,3,0 π π =− = v a
(a) ()() () ()() () 22 2222 2sin,3cos3,2 Speed2sin3cos344 sin 9 cos 34 2cos,9sin3,2 vr v a ttttt ttttttt ttt ′ ==− ==−++=++ =−−
(b) 22 2,3,2 4224 3 2,2, 22 22 2,9,2 422 9 2,2,2 2 v a
19. () cos,sin,,0 ttt tetetet == r
(a) ()() cossin,sincos, ttttt ttetetetete ′ ==−+vr () ()() 22 Speedcossincossin222 3 ttt t tettette e ==−+++ = v ()() cossinsincos,sincoscossin, 2sin,2cos, ttttttttt ttt tt etetetetetetetete etete ′′ = =−−−++− =− ar (b) () () 01,1,1 00,2,1 = = v a
20. () 4 2 1 ln,,,3 r tttt t ==
(a) ()() () ()() 3 3 6 26 2 24 12 ,,4 14 speed16 16 ,,12 vr v ar ttt tt tt tt ttt tt ′ ==− ==++ ′′ ==−
(b) () () 12 3,,123 333 12 3,,36 33 v a =− =−
21. ()()() ()() ()()()() ()() () ()() () ()() 2 2 ,0,0 0,, 2 0,, 2 22222 t tdtttt tttttt t ttttdt t t aijkv0r0 vijkijkC vC0vijkvijk rijkijkC rC0rijk rijkijk
22. ()()() ()() ()() ()() ()() () 22 22 3 2 3 2 23,04,0 2323 04243 2434 004 2486 t tdttt ttt tttdtttt tttt aikvjr0 vikikC vCjvijk rijkijkC rCrijk rijk =+==
24. ()()() () ()()() ()() () ()()() () () 2 2 32032,052 3232 03232132 321323216 052352216 2660 t
ak,vijkrjk vkkC vCijkvijk rijkijkC rCjkrijk rijk
25. ()()() ()() () () ()() () () ()()() cossin,0,0 cossinsincos
0 sincos sincoscossin 0 cossin 2cos2sin22 ttt tttdttt ttt tttdtttt tttt aijvjkri vijijC vjCjkCk vijk rijkijkC riCiC0 rijk rijk =−−=+= =−−=−++ =+=+
26. ()()() () () () () () () () () () ()() () () ()() 2 2 8,023,0 88 0233 1318 1318 34 0 134 t tt t t t t te tedtet tet tetdt etttt tetttt =−=++= =−=−+ =+=++
aikvijkr0 vikikC viCijkCijk vijk rijk ijkC riC0Ci rijk
27. ()()()() ()()()()() 2 140cos222.5140sin2216 140cos22140sin2232 tttt ttt =°++°− ′ ==°+°− rij vrij
The maximum height occurs when ()() 140sin2235 140sin22320sin221.639. 328 yttt ° ′ =°−=
The maximum height is () 2 3535 2.5140sin22sin2216sin2245.5 feet. 88 y =+°°−°≈
When 375 375,2.889. 140cos22 xt==≈ °
For this value of ,20.47 feet. ty ≈
So the ball clears the 10-foot fence.
28. ()()() () 22 900cos453900sin451645023450216 rijij ttttttt =°++°−=++−
The maximum height occurs when () 4502320,ytt ′ =−= which implies that () 225216. t =
The maximum height reached by the projectile is 2 2252225250,649 34502166331.125 16168 y
The range is determined by setting ()
which implies that 4502405,192 39.779 32 t =≈ seconds
The ball is 90 feet from where it is thrown when
seconds. The height of the ball at this time is
(a)
Graphing
(c)
From
(a) 0 cos3590vt°= when () 2 0 7sin35164 vtt
(b) The maximum height occurs when () 0 sin35320.ytvt ′ =°−=
At this time, the height is ()0.96922.0ft. y
(c) ()() 0 90cos3590
(a) You want to find the minimum initial speed v as a function of the angle θ Because the bale must be thrown to the position ()16,8,you have
()16costv θ = from the first equation. Substituting into the second equation and solving for , v you obtain:
Substituting into the equation for ,28.78ftsec.
36. Place the origin directly below the plane. Then 0, θ =
00 cos30,000sin1679230,00016 79232. rijij vij tvtvtttt tt
and ()()()()() ()
39. (a) 10, θ =° 0 66ftsec v =
Maximum height: 2.052 feet
Range: 46.557 feet
(b) 10, θ =° 0 146ftsec v =
Maximum height: 10.043 feet
Range: 227.828 feet
(c) 0 45,66ftsec v θ =°=
() 2 2 66cos45066sin4516 46.6746.6716 tttt tttt rij rij =°++°−
Maximum height: 34.031 feet
Range: 136.125 feet
(d) 45, θ =° 0 146ftsec v =
146cos450146sin4516 103.24103.2416 tttt tttt rij rij
Maximum height: 166.531 feet
Range: 666.125 feet
(e) 0 60,66ftsec v θ =°=
2 66cos60066sin6016 3357.1616 tttt tttt rij rij
()
Maximum height: 51.047 feet
Range: 117.888 feet
(f) 0 60,146ftsec v θ =°=
=°++°−
2 146cos600146sin6016 73126.4416 rij rij tttt tttt
()
Maximum height: 249.797 feet
Range: 576.881 feet
Exercise
40. (a) ()() () 2 00cossin16 ttvtvt rij θθ =+−
() 0 sin160tvt θ −= when 0 sin 16 v t θ =
Range: 2 00 0 sin cossin2 3232 vv xv θ θθ
The range will be maximum when 2 0 2cos20 32 dxv dt θ
or 2,rad. 24 θθππ == (b) () 2 0 sin16 y ttvt θ =− 0 sin320 dy vt dt θ =−= when 0 sin 32 v t θ =
Maximum height: 222222 0000 2 sinsinsinsin 16 32323264 vvvv y θθθθ
Maximum height when sin1, θ = or . 2 π θ =
50
when
43.
the
41. ()()() ()() 2 00 2 cossin4.9 100cos301.5100sin304.9 tvthvtt ttt rij ij θθ=++−
The projectile hits the ground when () 2 1 2 4.91001.5010.234 ttt−++= ≈ seconds.
So the range is ()() 100cos3010.234886.3 °≈ meters.
The maximum height occurs when 0. dydt = 100sin309.85.102sec tt = ≈
The maximum height is ()()() 2 1.5100sin305.1024.95.102 129.1meters. y =+°− ≈
44. 0 5.75,41,42.5,32hvg θ ===°=
Exercise
The
45. ()()() ()()() () ()() ()() () () () 222 2 sin1cos cossin1cossin sincossincos 21cos rij vijij aijij v a tbttbt tbtbtbtbt
(a) () 0 t v = when 0,2,4,. t ωππ = (b) () t v is maximum when ,3,, t ωππ = then () 2. v tbω =
46. ()()() ()()() sin1cos 1cossin rij vij tbttbt tbtt ωωω ωωω =−+− =
Speed () 22 12coscossin21cos. v tbtttbt ==−++=−ωωωωωω
The speed has a maximum value of 2bω when ,3, t ωππ = () 60mih88ftsec88radsecsince1. b ===
So, the maximum speed of a point on the tire is twice the speed of the car: () 288ftsec120mih =
47. ()()() ()()()()()() 22 sincos sincossincos0 vij rv tbtbt ttbttbvtt ωωωω ωωωωω =−+ ⋅=−+=
So, () t r and () t v are orthogonal.
48. (a) Speed v = ()() ()()2222222222 sincossincos btbtbttb ωωωωωωωω =+=+= (b)
The graphing utility draws the circle faster for greater values of ω
49. ()()()()()() 2222 cossincossin aijijr tbtbtbttt =−−=−ωωωωωωωω + =− () t a is a negative multiple of a unit vector from ()0,0to () cos,sintt ωω and so () t a is directed toward the origin.
50. () ()() 22 cossin aij tbtvtb =+=ωωω
51. () 2 1 , 2 tbb ω == a () () () () () () 222 11 32 4432 11 2512162 4322 1 16282 ft/sec 2 Fa v mmm mb tb
52. () 30mih44ftsec t v == () 44 radsec 300 v t b ω == () () () 2 2 2 3400442057300lb 323003 F atb mb ω ω =
Let n be normal to the road. cos3400 2057 sin 3 n n θ θ = =
Dividing, 121 tan 600 11.4 θ θ =
53. The particle could be changing direction. For example, let () cossin. ttt =+ rij Then the speed is () 1, t = r but () t a is not constant.
54. Let ()() 214. tt = rr Then ()()21 4 tt′′ = rr and () () () () 221144. tttt ′′ === vrrv
55. No. This is true for uniform circular motion only.
56. () cossin rij tatbt =+ωω
(a) ()() sincos rvij ttatbt ωωωω ′ ==−+ Speed () 222222 sincos v tatbt ==+ωωωω
(b) ()() ttav ′ = () () 22 2 2 cossin cossin ij ij r atbt atbt t ωωωω ωωω ω =−− =−− =−
57. () ()() () () ()() () () 1 11 2 22 sincos cossin 0 cossin sincos 0 sincos aij vaijC viiCC0 vij rvijC rjjCC0 rij ttt ttdttt ttt ttdttt ttt =− ==−−+ =−=−+ = =−− ==−++ ==+ = =−+
The path is a circle.
58. The angle at time 1t is obtuse.
The angle at time 2 t is acute.
The speed is decreasing at time 1t because the projectile is reaching its maximum height.
The speed is increasing at time 2 t because the object is accelerating due to gravity.
59. ()()()() txtytzt rijk =++ Position vector ()()()() txtytzt vijk ′′′ =++ Velocity vector ()()()() txtytzt aijk ′′′′′′ =++ Acceleration vector
Speed () ()()() 222 ,is a constant. txtytzt CC v ′′′ ==++ = ()()() ()()()()()() ()()()()()() ()() 222 0 2220 20 0 d xtytzt dt xtxtytytztzt xtxtytytztzt ttva ′′′ ++= ′′ ′′′′′′′ ++= ′′′′′′′′′ ++ = ⋅=
Orthogonal
60. ()()() ()()() ()()()() ()()() ()()()22 ,and are constants. ,is a constant. txtyt ytmxtbmb txtmxtb txtmxt txtmxtCC rij rij vij s =+ =+
= +
=
So, () () ()()() 2 1 0 C xt m xt txtmxt aij0 ′ = + ′′ = ′′′′ =+=
61. True
62. False. For example, () 3 ri tt = Then () 2 3 vi tt = and () 6.ai tt = () v t is not orthogonal to (). a t
63. False. Consider () 22 ,.ttt =− r Then () 2,2 ttt =− v and () 2 8.tt = v
Section12.4TangentV ectorsandNormalVectors
1. The unit tangent vector points in the direction of motion.
2. The principal unit normal vector points in the direction in which the curve is turning.
3. () 2 2,1ttttrij=+= () 22,tt rij ′ =+ () 22 4421ttt r
4. () () () () () () () 32 2 42 2,1 34 916 1 134 134 55 1 916 rij rij r r Tijij r tttt
5. () () () 22 5cos5sin, 3 5sin5cos 25sin25cos5 31 3 sincos 33322 3 rij rij r r Tijij r tttt
6. () () 6sin2cos, 6 6cos2sin tttt ttt π =−= ′ =+ rij rij () 31 6233 622 27128 6 1 33 6 28 rijij r Tij
8. () () () () () () () cos,0 cossin 0 0 22 0 22 0 2 rij rij rij rij Tij r tt ttt tetet tetete =+= ′ =−+ ′ =+ ′ + ===+
9. ()() () 2 ,0,0,0 2 ttttP tt rijk rijk =++ ′ =++ When 0, t = ()0, rik ′ =+ () 0at0,0,0. t = () () () () 0 2 0 2 0 r Tik r ′ ==+ ′
Direction numbers: 1, a = 0, b = 1 c =
Parametric equations: , x t = 0, y = zt =
10. () 2 4 , 3 ttt rijk =++ 4 1,1, 3 P
() 2 tt rij ′ =+
When 1, t = ()() 4 1211,1,. 3 ttatrrij
′′ ==+=
() () () () 1 25 12 5 1 5 rij Tij r ′ + ===+ ′
Direction numbers: 2, a = 1, b = 0 c =
Parametric equations: 21,xt=+ 1, yt=+ 4 3 z =
11. ()()() cos3sin34,1,0,4ttttP =++−−rijk
() sin3cos3ttt ′ =−++ rijk
0 t = at () 1,0,4 P
()033 ′ =+ rjk
()09932 ′ =+= r
() () () 12 033 2 32 =+=+ Tjkjk
Direction numbers: 0,1,1abc===
Parametric equations: 1,3,43 x ytzt===−+ or 1,,4 x ytzt ===−+
12. () () 2 ,,4,1,1,3ttttP r =−
() 2 1,1, 4 t t t r ′ =−
When 1, t = () 1 11,1,, 3 r ′ =− 1 t = at () 1,1,3.
() () () 1 211 11,1, 7 1 3 r T r ′ ==− ′
Direction numbers: 1 1,1, 3 abc===−
Parametric equations: 1, xt=+ 1, yt=+ 1 3 3 zt=−+
13. () () () 2cos,2sin,4,2,2,4 2sin,2cos,0 r r tttP ttt = ′ =−
When , 4 t π = 2,2,0, 4 r π ′ =−
() at2,2,4. 4 t π
==−
() () 1 2,2,0 42 4 r4 T r π π π ′
Direction numbers: 2,2,0abc=−==
Parametric equations: 22,xt=−+ 22,yt=+ 4 z =
14. () () () 2 2sin,2cos,4sin,1,3,1 2cos,2sin,8sincos r r ttttP ttttt = ′ =−
When , 6 t π = 3,1,23, 6 r π ′ =− () at1,3,1. 6 t π
==−
() () 6 1 3,1,23 64 6 r T r π π π
Direction numbers: 3, a = 1, b =− 23 c =
Parametric equations: 31,xt=+ 3, yt=−+ 231zt=+
15. () 2 1 ,2 2 ttttrij=+=
()tt rij ′ =+
() () () 2 1 t t t t t Trij r ′ + == ′ +
() () () 223232 1 11 t t tt Tij ′ =+ ++
() 3232 21 2 55 Tij ′ =+
() () () () 2 1255 22 55 2 5 T Nijij T ′ ==−+=+ ′
16. () 6 ,3ttt t rij=+=
() 2 6 t t rij ′ =−
==−
() () () () 2 4 2 2 4 16 136 6 36 t ti t t t t
t r Tj r ij ′
() () () 3 443232 7212 3636 tt t tt Tij ′ =+ ++
() 3232 14496 2 5252 Tij ′ =+
() () () () 2 1 232 2 13 T Nij T ′ =++ ′
17. () 2 ln,1ttttt rijk=++=
() 1 2 tt t rijk ′ =++ () () ()
Trijkijk
() () () () 433 424242323232 14248 414141 ttttt t tttttt Tijk −+−− ′ =++ ++++++
() [] 32323232 3693 123 6666 Tijkijk ′ =++=−+−
() 2314214314 1 141414 14 ijk Nijk −+−− ==+−
18. () 2,0rijk tt tteet=++=
() 2 teett rijk ′ =+−
() () 2 22 2 tttttt teeeeee r ′ =++=+=+
() () () 2 tt tt t ee t ee t Trijk r ′ +− == ′ +
() () () () () 222 2 22 tt tttttt ee t eeeeee Tijk ′ =++ +++
() 11 0 22 Tjk ′ =+
() 22 0 22 Njk =+
19. () 3 6cos6sin, 4 tttt rijk π =++=
() 6sin6cos ttt rij ′ =−+
() () () sincos t ttt t r Tij r ′ ==−+ ′
()()cossin,1tttt TijT ′′ =−−=
() () 34 322 422 34 T Nij T π π π ′
==−
′
20. () cos32sin3, tttt rijk π =++=
() 3sin36cos3 ttt rij ′ =−+
() () () 22 3sin36cos3 9sin336cos3 Trij r t tt t t tt ′ −+ == ′ +
The normal vector is perpendicular to () t T and points toward the z-axis:
() 22 6cos33sin3 9sin336cos3 tt t tt Nij = +
() 6 36 i Ni π ==
21. () 0 1 ,2ttt t rij=+= 1 ,1xtyxy t == =
() 2 1 t t rij ′ =−
() 2 4 1 t t t Tij = + () 2 4 1 t t t Nij + = + () 1 22 2 rij =+
() () 17 24 17 Tij =−
() () 17 24 17 Nij =+
22. () 3 ,1tttt=−=rij 33 , x tytyx==− =−
() () () () () () () () 2 1 3 13 11910 10 13 10 10 13 10 tt =− ′ =− ′ =− ′ =+= =− =−+ rij rij rij r Tij Nij
23. ()() 2 0 21,2tttt rij=+−= 21,xt=+ 2 2 1 2 x yt =−=−
()254 rij =−
() 22 tt rij ′ =−
() 22 22 441 tt t tt Tijij == ++
() 2 2 5 Tij = () 2 2, 5 Nij = perpendicular to () 2 T
24. () 2222 7 2cos2sin, 6 4cos4sin4,circle tttt xytt π =+= +=+= rij
() () () 7 3 6 2sin2cos 2 sincos 713 622 731 622 rij rij r Tij Tij Nij ttt t ttt π π π =−−
′ =−+ ′ = =−+
=−
=+
25. () 1 ,1ttt t =+=rij () 2 1 , t t vij =− ()1, vij =−
() () 3 2 ,12 t t ajaj ==
() () () () 2 2 2 44 11 11 t t tt t t tt v Tijij v ==−=− ++
() () () 12 1 2 2 Tijij =−=−
() () () () () () () 3 443232 4 2 4 22 11 2 1 1 1 tt tt t t t t t t t ij T N T ij + ++ ′ == ′ + =+ +
() () () 12 1 2 2 2 2 T N Nijij aT aN a a =+=+ =⋅=− =⋅=
26. () 2 2,1ttttrij=+=
()()22,122tt vijvij =+=+
()()2,12 t aiai ==
() () () () () 22 11 22 441 v Tijij v t ttt t tt ==+=+ ++
() () 122 1 22 2 Tijij =+=+
() () () () () () 223232 2 2 1 11 1 1 1 1 t tt t t t t t t ij T N T ij + ++ ′ == ′ + =+ + () 22 1 22 Nij =− 2 aTaT=⋅= 2 aNaN=⋅=
27. () 2 ,0 tt teet rij=+=
()() 2 2,02teett vijvij =−=−
()() 2 4,04teett aijaij =+=+
() () () 2 42 2 4 tt tt t ee t t ee Tvij v == +
() 2 0 5 Tij =
() 2 0 5 Nij + = () 175 18 5 5 aTaT=⋅=−= () 165 24 5 5 aNaN=⋅=+=
28. () ()() ()() ,0 ,0 ,0 tt tt tt teet tee tee =+= =−=− =+=+ rij vijvij aijaij
() () () () () 02 2 0 2 2 0 2 = =− =+ v Tij Nij () () () () 2 0 2 2 2 2 a a =⋅=+⋅−= =⋅=+⋅+= T N aTijij aNijij
29. () ()() cossin, 2 tt tetett π =+=rij
()()() cossincossin tt tettett vij =−++
()()() 2sin2costt tetet aij =−+
At , 2 t π = () () 12 2 2 v Tijij v ==−+=−+
Motion along r is counterclockwise. So, () () 12 2 2 Nijij =−−=−+ 2 2 2 2 ae ae T N aT aN π π =⋅= =⋅=
30. () 4cos34sin3, tttt π =+=rij
() 12sin312cos3 ttt =−+ vij
() () 36cos336sin3 36 ttt π =−− = aij ai
At () ,12and t πππ ==−=− vjTj
Movement is counterclockwise around a circle. So, () . π = Ni 0 36 a a =⋅= =⋅= T N aT aN
31. () cossin rij tatat =+ωω () sincos vij tatat =−+ωωωω
() 22cossin aij tatat =−−ωωωω
() () () sincos v Tij v t ttt t ==−+ωω
() () () cossin T Nij T t ttt t ωω ′ ==−− ′ 0 aTaT=⋅= 2 NaN aaω =⋅=
32. () t T points in the direction that r is moving. () t N points in the direction that r is turning, toward the concave side of the curve. x a a N T y
33. Speed: ()v taω =
The speed is constant because 0. aT =
34. If the angular velocity ω is halved, 2 2 24 N a aa ωω
aN is changed by a factor of 1 . 4
35. () 23,1ttttt rijk=+−=
() 23 t vijk =+−
() t a0 = () () ()() 1 23 14 14 231 14 t v T v ijk ijkT = =+− =+−=
() t T N T ′ = ′ is undefined. , aaTN are not defined.
36. () cossin2, 3 ttttt rijk π =++=
() sincos2ttt vijk =−++
() cossin,1ttt aija=−−=
() 22 sincos45ttt v =++=
() () () () 1 sincos2 5 t ttt t v Tijk v ==−++
()() 0 att TaT=⋅=
37. () 2 2 ,1 2 t tttt rijk=++=
() () () () ()
() () 30 152 30 Nijk =−++
6 aTaT=⋅= 30 6 aNaN=⋅= 38. ()() 2 214,2ttttt rijk=−+−=
()
() 22 224, 20425 tt ttt vijk v =+− =+=+
() 2,2 t aja==
() () 22 2241 2 255 t tt tt ijk Tijk +− ==+− ++
()() () 1 22,222 3 ajTijk ==+−
()() 4 22 3 aTaT=⋅= 22 162 45 93 aa NT a =−=−=
() 42 2225 93 aTNjTNijkN aa ==+=+−+
=−+−
() 34 222 9 25 25545 15315 Njijk ijk
=++
39. () sincos,0 ttt tetetet =++=rijk
() ()() cossinsincos ttttt tetetetete vijk =++−++
() 0 vijk =++
() 2cos2sinttt tetete aijk =−+
()02 aik =+
()
()() 1 cossinsincos 3 t tttt v T v ijk = = ++−++
() [] 1 0 3 Tijk =++
() ()() 1 sincoscossin 2 ttttt Nij = −++−−
() 22 0 22 Nij =− 3 aTaT=⋅= 2 aNaN=⋅=
40. () 2,0tt tetet rijk=++=
()()2,422 tttt teetee vijkv=+−=++
()() 22 , tttt teetee aika=+=+
()() 02,0 vijkaik =+−=+
() 2 0 6 Tijk +− = 0 aTaT=⋅= 22 2 NT a aa=−= () 2 1 2 aaTN aikTNN Nik =+=+= =+
41. If 0, aN = then the motion is in a straight line.
42. If 0, aT = then the speed is constant.
43. () 34 ttt rij =+ ()()()34,9165ttt vrijv ′ ==+=+=
()() tt av0 ′ ==
() () () 34 55 t t t v Tij v ==+
()() 0 ttTN ′ = does not exist.
The path is a line. The speed is constant (5).
44. (a)(i) The vector s represents the unit tangent vector because it points in the direction of motion.
(ii) The vector t represents the unit tangent vector because it points in the direction of motion.
(b)(i) The vector z represents the unit normal vector because it points in the direction that the curve is bending.
(ii) The vector z represents the unit normal vector because it points in the direction that the curve is bending.
45. () sin,1cos r tttt =−−πππ
The graph is a cycloid.
(a) () sin,1cos r tttt =−−πππ () cos,sin v ttt =−πππππ
() 22sin,cos a ttt ππππ = () () () () 1 1cos,sin 21cos v T v t ttt t t ππ π ==− () () () () 1 sin,1cos 21cos T N T t ttt t t ππ π ′ ==−+ ′
2 22 1sin sin1coscossin 21cos21cos TaT t atttt tt ππ ππππππ ππ =⋅=−+=
When 222 122 :, 222 2 taa TN πππ ====
When 2 1:0, taaTN π ===
When 3 : 2 t = 2222 , 22 aa TN ππ =−=
(b) Speed: () () () 2 21cos sin 21cos T v s tt dst a dt t ππ ππ π ==− ==
When 2 12 :0 22 taT π ==> the speed in increasing.
When 1:0taT == the height is maximum.
When 2 32 :0 22 taT π ==−< the speed is decreasing.
46. (a) () cossin,sincos r ttttttt =+−ππππππ () 2222 sinsincos,coscossincos,sin v ttttttttttttt ππππππππππππππππ =−++−+= () 2323 cossin,sincos a ttttttt ππππππππ =−+ () () () cos,sin v T v t ttt t ππ == ()() coscossinsinsincos23232 TaT atttttttt πππππππππππ =⋅=−++= () 2242243 1 aatt NT a =−=+−=ππππ
When 1, t = 2 , aT π = 3 . aN π = When 2, t = 2 , aT π = 3 2. aN π = (b) Because 2 0 aT π => for all values of t, the speed is increasing when 1 t = and 2. t = x t =1 t = 2 1 t = 2 3 y
47. () 0 2cos2sin, 22 t tttt rijk π =++= () 1 2sin2cos 2 ttt rijk ′ =−++ () 2171 2sin2cos 172 ttt Tijk
48. () 3 2 0 ,1 3 t tttt rijk=++= () 2 2 ttt rijk ′ =++ () () 2 24 1 2 14 ttt tt Tijk =++ ++ () ()()() 343 2424 1 212 141 tttttt tttt Nijk
() 1 1 3 rijk =++
() () 1 12 6 Tijk =++ () () () 12 133 2 63 Nikik =−+=−+
49. () 0 sincos, 4 tttt rijk π =++=
() cossin,ttt rjk ′ =−
() 1 t
′ = 22 4422 rTjk
() sincos,ttt Tjk ′ =−− 22 422 Njk
=−−
22 0 44422 22 0 22 ijk
50. () 0 2cossin,0 ttt teetett rijk=++=
() ()() 2cossinsincos ttttt teetetetet rijk ′ =+−++
()() () 1 0202 6 rijkTijk ′ =++ =++
() () 222222222222 22222 4cossin2cossinsincos2sincos 42cossin6 ttttttt ttt teetetettetetett eette r ′ =++−+++ =++=
() 6 tet r ′ =
() () () ()() 1 2cossinsincos 6 t ttttt t r Tijk r ′ == +−++ ′
() ()() 1 sincoscossin 6 ttttt Tjk ′ = −−+−
() [] () 122 00 22 6 TjkNjk ′ =−+ =+
()()() 211 333 000 666 333 22 0 22 ijk BTNijk =×==−−
51. () 0 4sin4cos2, 3 ttttt rijk π =++= () 4cos4sin2,ttt rijk ′ =−+ () 22 16cos16sin42025ttt r
151555 22323 35555 25 Tijkijkijk
() () 1 4sin4cos 25 ttt Tij ′ =−− 31 322 Nij
52. () 3cos23sin2, 4 ttttt rijk π =++=
() 6sin26cos2 ttt rijk ′ =−++
() 37 t r ′ = 6 4 rik
() () () () 1 6sin26cos2 37 rt ttt rt Tijk
() () 1 12cos212sin2 37 ttt Tij
=−+
53. () () () 2 2 32 34 4 916 16 ttt tt t t t =+ =+ = ⋅=+ ⋅= rij vij aj vv va ()() () ()() 2 91641634 4836 ttt t ⋅−⋅=+−+ =−+ vvavavjij ij
()() ()() () 2 1 43 916 t t ==−+ + vvavav Nij vvavav
54. () () () 22 3cos23sin2 6sin26cos2 12cos212sin2 36sin236cos236 0 rij vij aij vv va ttt ttt ttt tt =+ =−+ =−− ⋅=+= ⋅= ()() ()() () () 3612cos212sin2 3612cos212sin2 cos2sin2 tt tt tt == ⋅−⋅−− =−− Nvvavavij vvavavij ij
55. () () () 2 22 24 242 2 4164204 4 rijk vijk ak vv va tttt tt t tt t =++ =++ = ⋅=++=+
⋅=
()() () () 2 20424242 81640 ttt tt ⋅−⋅=+−++ =−−+ vvavavkijk ijk ()() ()() () 2 1 25 525 tt t ==−−+ ⋅−⋅ + vvavav Nijk vvavav
56. () () () 5cos5sin3 5sin5cos3 5cos5sin 25934 0 rijk vijk aij vv va tttt ttt ttt =++ =−++ =−−
⋅=+=
⋅=
()()() 345cos5sintt⋅−⋅=−− vvavavij
()() ()() () () 345cos5sin cossin 345cos5sin tt tt tt ===−− vvavavij Nij vvavavij
57. From Theorem 12.3 you have:
()() () 2 00cossin16 tvthvtt rij θθ =++−
()() 00cossin32 tvvt vij θθ =+−
() 32 t aj =−
() ()() () 00 2 22 00 cossin32 cossin32 Tij vvt t vvt θθ θθ +− = +−
() () () () 00 2 22 00 Motion is clockwise. sin32cos cossin32 Nij vtv t vvt θθ θθ = +−
() () 0 2 22 00 32sin32 cossin32 TaT vt a vvt θ θθ =⋅= +−
() 0 2 22 00 32cos cossin32 NaN v a vvt θ θθ =⋅= +−
Maximum height when 0 sin320;vt θ −= () vertical component of velocity
At maximum height, 0 aT = and 32. aN =
58. 0 45,150 v θ =°=
(e) From Exercise 61, using 0 120 v = and 30, θ =°
2 2 2 2 326032 6036032 32603 6036032
60. (a) ()()() ()() 2 00 2 2 1 2 cossin 220cos454220sin4516 11024110216 tvthvtgt ttt ttt rij ij ij
(b)
Maximum height 382.125 ≈ at 4.86 t ≈ Range 1516.4 ≈
(c) () () () () () 22 1102110232 1102110232 32 tt tt t vij v aj
(d)
61. () 1 20 10cos10,10sin10,44,0 r ttttt ππ =+≤≤
(a) ()()() () ()()()() () 2222 2 2 100sin10,100cos10,4 100sin10100cos1016 1001646251314mih r r ttt ttt ππππ
(b) 0 aT = and 2 1000 aN π = 0 aT = because the speed is constant
62. 600mih880ftsec =
() () 2 8801636,000ttt rij =+−+ () 88032 tt vij =−
() 32 t aj =− () 22 88032552 164t30254t3025 Tijij tt t == ++
Motion along r is clockwise, therefore () 2 255 43025 Nij t t t = + 2 64 43025 t a t TaT=⋅= + 2 1760 43025 NaNa t =⋅= +
(b) Let 0 2. aa = Then 222 0 1 22 aN a aa ωωω ⋅=== or the centripetal acceleration is halved when the radius is halved. t 0.5 1.0 1.5 2.0 2.5 3.0
63. ()()() cossin rij tatat =+ωω
From Exercise 31, you know 0 aT⋅= and 2 aN aω ⋅=
(a) Let 0 2. ωω = Then () 2 22 0 24 aN aaa ⋅===ωωω or the centripetal acceleration is increased by a factor of 4 when the velocity is doubled.
64. ()()() cossin rij trtrt =+ωω
()()() sincos vij trtrt =−+ωωωω
() 1 v trrv ωω ===
() () () 2 coscos aij trtrt =−+ωωωω
() 2 a trω =
(a)
(b) By Newton’s Law: 2 2 2 ,, mvGMmGMGM vv rrrr === 65. 9.56104 4.74misec 4000255 GM r × ==≈ + v 66. 9.56104 4.69misec 40003460 v GM r × ==≈ + 67. 9.56104 4.67misec 4000385 v × =≈ +
68. Let
243600
69. False. These vectors are perpendicular for an object traveling at a constant speed but not for an object traveling at a variable speed.
70. True.
71. (a) ()()() ()() ()()2222 coshsinh,0 cosh,sinh coshsinh1,hyperbola tbtbtb xbtybt xybtbt rij=+> == −=−=
(b) ()()() sinhcosh tbbtbbt vij =+ ()()()() 222 coshsinh tbbtbbtbt aijr =+=
72. Let () cossin t Tij φ φ =+ be the unit tangent vector. Then () () dt sincos. T T T ijM d t dddd ddtdtdt φφφ φφ φ ′ = ==−−= () () sincos cos2sin2 Mij ij φ φ φπφπ =−+ = + + + and is rotated counterclockwise through an angle of 2 π from T
If 0, ddt φ > then the curve bends to the left and M has the same direction as T′ So, M has the same direction as , T N T ′ = ′ which is toward the concave side of the curve.
If 0, ddt φ < then the curve bends to the right and M has the opposite direction as T′ Thus, T N T ′ = ′ again points to the concave side of the curve.
73. ()()() txtyt rij =+
()()() , y tmxtb =+ m and b are constants.
()()()() txtmxtb rij =++
()()() txtmxt vij ′′ =+
() ()() () 22 2 1 txtmxtxtm v ′′′ = + =+
() () () () 2 ,constant 1 tm t t m Tvij v ±+ == +
So, () t T0 ′ =
Section12.5ArcLengthandCurvature
74. Using , aaTN aTN =+ ,TT0 ×= and 1, TN×= you have: () () () () aa aa a aa TN TN N NN vavTTN vTTvTN vTN vavTNv ×=×+ =×+× =× ×=×=
So, aN va v × =
75. ()() 2 2222 22 222 2 aaaa aaaa aa aa TNTN TTNN TN NT aaa TNTN TTNN a =⋅ =+⋅+ =+⋅+ =+ =−
Because 0, aN > we have 22aa NT a =−
76. () 1 dvdv Fma dtdt === Force
23 x atbtct=++ 2 23 dx vabtct dt ==++
26 dv bct dt =+ () () 2222 22 2 42436 41223 412 Fbbctct bcbtct bcva =++ =+++ =++− () 2 41212 Ffvbaccv ==±−+
The sign of the radical is the sign of 26, bct + which cannot change.
1. The curve bends more sharply at Q than at P 2. t is the arc length parameter if () 1. t ′ = r
3. () [ ]3,0,3ttt rij =−
3,1,0dxdydz dtdtdt ==−= () 3 3 2 2 0 0 3110310sdtt
4. () [ ] 2 ,0,4 ttt =+ rij
1, dx dt = 2, dy t dt = 0 dz dt =
5. () [ ] 32 ,0,1 ttt rij =+ 2 3,2,0dxdydz tt dtdtdt === () () ()
6. () [ ] 2 4,0,5ttt =− rij 2,4,0dxdydz t dtdtdt ==−= ( ) () () ()
7. () [ ] 33 cossin,0,2tatat π =+ rij
22 3cossin,3sincos dxdyattatt dtdt =−=
2 2222 0 22
00 43cossin3sincos 12sincos32sin23cos26 sattattdt attdtatdtata
8. () [ ] cossin,0,2tatat π =+ rij sin,cos dxdyatat dtdt =−=
9. () 2 502350216 rij tttt
() ()50250232 tt vij =+− 2 35021604.4614 ttt+−= ≈ () () 22 4.4614 0 50250232362.9ftstdt =+−≈
10. (a) () 2 40344016 rij tttt=++−
() ()4034032 tt =+− vij
(b) () ()
11. () [ ]43,0,1tttt rijk =−++ 1,4,3dxdydz dtdtdt =−== 1 1 0 0 11692626sdtt
12. () [ ] 23 ,0,2 ttt rijk =++
13. ()
tttt r
4,sin,cos dxdydztt dtdtdt ===
14. () [ ] 2sin,5,2cos,0,tttt r π = 2cos,5,2sin dxdydztt dtdtdt ===− 22 00 4cos254sin2929sttdtdt
15. () [ ] cossin,0,2tatatbt π =++ rijk sin,cos, dxdydzatatb dtdtdt =−==
17. () () [ ] 23 4,0,2tttt =+−+ rijk
(a) () () 00,4,0,22,0,8rr== distance 222 24884 2219.165 =++=
(b) ()00,4,0 r = ()0.50.5,3.75,0.125 r = ()11,3,1 r = ()1.51.5,1.75,3.375 r = ()22,0,8 r =
(c) Increase the number of line segments.
(d) Using a graphing utility, you obtain 9.57057.
18. () 2cos,2sin, tttt r =
(a)
19. () 22 11 22 s ss rij
20. ()() 3 ss
21. () () () 3 cossin 222 131 sincos,1 22222
rijk rijkr
() () () () 131 sincos 22222 11 cossin 4242 s
s s ss s
r Tijk r Tik () 22 111 cossin 1621624 ss Ks
22. () cossin5sss=++ rijk
()()sincos,1ssss ′′=−+= rijr
() sincos s ss=−+ Tij
() cossin s ss ′ =−− Tij
() 22 cossin1Ksss ′ ==+= T
23. () 42,1tttt=−=rij
() 42 t vij =−
() () 1 2 5 t Tij =−
() () () 0 t t K t T0 T r ′ = ′ == ′
(The curve is a line.)
24. () 2 ,2ttt=+=rij
() 2 tt vi =
() t Ti =
() t T0 ′ = () () 0 t K t T r ′ == ′
25. () 1 ,1ttt t =+=rij
() 2 1 t t vij =−
() 1 vij =−
() 3 2 t t aj =
()12 aj =
() 2 1 t t t 4 Tij = +
() () () 2 12 4 1 1 tt t Nij =+ +
() () 1 1 2 Nij =+ 2 2 2 K aN v ⋅ ==
26. () 3 1 ,2 9 tttt=+=rij
() 2 1 3 tt vij =+
() 4 2, 2 vij =+ () 165 21 93 v =+=
() 2 3 tt aj =
() 4 2 3 aj =
() 2 2 44 1 3 3 9 1 9 t t t tt Tijij + + == + +
() 34 2 5 Tij + =
() 43 2 Nij 5 −+ = 2 4536 259125 aN v K ⋅ ===
27. () ,sin, 2 tttt π == r
() () 1,cos,1cos2 ttttrr ′′ ==+ 1,0,1 22 rr ππ
′′ ==
() 0,sin,0,1 2 tt aa π
=−=−
() 2 1 1,cos 1cos tt t T = +
=
1,0 2 T π
=−
0,1 2 N
2 1 1 1 K aN v ===
28. () 5cos,4sin, 3 tttt r π ==
()()5cos,4sin x ttytt == ()() ()()()() 32 22 32 22 32 22 5sin4sin4cos5cos 25sin16cos 20 25sin16cos xyyx K xy tttt tt tt = ′′′′′′ ′′ + = + = +
() ()32 2016091 38281 25341614 K π
==
+
29. () 4cos24sin2 ttt rij =+ππ
() 8sin28cos2 ttt rij ππππ ′ =−+
() sin2cos2 ttt Tij π =−+
() 2cos22sin2 ttt Tij ππππ ′ =−−
() () 21 84 T r t K t π π ′ === ′
30. () 2cossin ttt rij =+ππ
() 2sincos ttt rij ππππ ′ =−+
() 22 4sincos ttt r πππ ′ =+
() 22 2sincos 4sincos tt t tt Tij ππ ππ −+ = +
() ()32 22 2cos4sin 4sincos tt t tt Tij ππππ ππ ′ = + () () () 22 22 32 22 2 4sincos 4sincos 2 4sincos T r t tt K t tt tt π ππ πππ ππ ′ + == ′ + = +
31. () cossin rij tatat =+ωω
() sincos rij tatat ωωωω ′ =−+
() sincos Tij ttt =−+ωω
() () () cossin 1 Tij T r ttt t K aa t ωωωω ω ω ′ =−− ′ === ′
32. ()()() cossin rij tatbt =+ωω
()()() sincos rij tatbt ωωωω ′ =−+
() ()() ()()2222 sincos sincos Tij atbt t atbt ωω ωω −+ = +
() ()() ()() 22 32 2222 cossin sincos Tij abtabt t atbt ωωωω ωω ′ = +
() () ()() ()() ()() 2222 2222 32 2222 sincos sincos sincos T r ab t atbt K t atbt ab atbt ω ωω ωωω ωω ′ + == ′ + = +
33. () 2 2 2 t ttt rijk =++
() 2 ttt rijk ′ =++
() 2 2 15 tt t t Tijk ++ = + () ()32 2 52 15 t t t Tijk −++ ′ = + () () () () 2 32 2 2 5 15 5 15 15 t t K t
T r + ′ === ′ + +
36. () 222cossin ttt teetet rijk =++
34. () 22 1 2 2 tttt rijk =++
() 4 ttt rijk ′ =++
() 2 4 117 tt t t Tijk ++ = + () ()32 2 417 117 t t t Tijk −+ ′ = + () () () () () 2 12 2 32 2 32 2 28917 117 117 17 117 T r t t Kt t t t ′ + ==+ ′ + = +
35. () 43cos3sin tttt rijk =++
() 43sin3cos ttt rijk ′ =−+
() [] 1 43sin3cos 5 ttt Tijk =−+
() [] 1 3cos3sin 5 ttt Tjk ′ =−− () () 353 525 t K t T r ′ === ′
() ()() ()() 222222 22cossin2sincos22cossin2sincos rijkijk tttttt teetetetetetttt ′ =+−++=
() ()() [] 12 12 2222222 44cos4cossinsin4sin4sincoscos93 t tetttttttteett r ′ =+−++++==
() () () 22121 cossinsincos 33333 t ttttt t r Tijk r ′ ==+−++ ′
() 2121 sincoscossin 3333 ttttt Tjk ′ =−−+−
() 12 2222 4144145 sincossincoscossincossin 9999993 ttttttttt T ′ =++++−= () () 22 5 5 3 39tt t K ee t T r ′ === ′
37. ()() 2 32,3,21tttPtrij=+− =−
3, x t = 3, x ′ = 0 x ′′ = 2 2,yt = 4,yt ′ = 4 y ′′ =
()() () () 2223232 340 94 xyyx K xyt ′′′′′′ ==
At 1, t =− ()32 1212 125 916 K == +
39. () () 3 2 ,2,4,22 4 t tttPt rijk =++ =
() 2 3 2 4 ttt rijk ′ =++
()() 243,226rijkr ′′ =++=
() 3 2 2 tt rjk ′′ =+
()223 rjk ′′ =+
()() 22143632 023 ijk rrijk ′′×==−+
()() 22497rr ′′′ ×== 332 7726 26676 K rr r ′′′ × === ′
40. ()()cossin,1,0,10 ttt tetetePt rijk =++ =
() ()() cossinsincos ttttt tetetetete rijk ′ =−+++
38. ()()4,1,00 t tetPtrij =+ = , t x e = , t x e ′ = t x e ′′ = 4,yt = 4, y ′ = 0 y ′′ =
()() () 3232 32 22 04 4 17 116 xyyx K xy ′′′′′′ === + ′′ +
() ()() 2222 cos2cossinsinsin2sincoscos13 t tettttttttet r ′ =−+++++=
() ()() 1 cossinsincos 3 ttttt Tijk = −+++
() ()() 1 sincoscossin 3 ttttt Tij ′ = −−+−
()() 003rijkr ′′ =++ =
() ()() 12 00 33 TijT ′′ =−+ = () () 0 232 3 0 3 K T r ′ === ′
41. 6,3yxx==
This is a line, so the curvature is 0. 1 0, K K = is undefined.
42.
,8 x yex
yxx
49. () 2 13, yx=−+ () 21,yx ′ =− 2 y ′′ = () ( ) () 3232 2 2 22 141 121 K x x == +− +
() 52 2 241 141 x dK dx x = +−
(a) K is maximum when 1 x = or at the vertex ()1,3. (b) lim0 x K →∞ =
50. 3 , yx = 2 3,yx ′ = 6 yx ′′ = ()32 4 6 19 x K x = + () () 4 52 4 6451 19 x dK dx x = +
(a) K is maximum at 444433 1111 ,,,. 45454545
(b) lim0 x K →∞ =
51. 23 , yx = 13 2 , 3 yx ′ = 43 2 9 yx ′′ =−
() () 43 3232 23 1323 29 6 149 94 x K x xx ==
+ + () () 23 52 4323 891 94 x dK dx xx −+ = +
(a) K →∞ as 0. x → No maximum (b) lim0 x K →∞ =
52. 1 , y x = 2 1 , y x ′ =− 3 2 . y x ′′ = Assume 0.
() () 24 52 4 61 1 x x dK dx x = +
(a) K has a maximum at 1 x = () and 1by symmetry. x =−
(b) lim0 x K →∞ =
53. ln,yx = 1 , y x ′ = 2 1 y x ′′ =− () () 2 3232 2 2 1 1 11 xx K x x ==
+ +
2 52 2 21 1 dKx dx x −+ = +
(a) K has a maximum when 1 . 2 x = (b) lim0 x K →∞ =
54. , yex = yyex ′′′ == () () 3232 2 2 1 1 x x y e K e y ′′ == + ′ + () () 2 52 2 12 1 x x x ee dK dx e = +
(a) 22 1111 120lnln2 2222 xx eex
−= = ==−
K has maximum curvature at 1 ln2. 2 x =−
(b) lim0 x K →∞ =
55. 432 1,4,12 yxyxyx ′′′ =−=−=− () 2 32 2 3 12 00 14 x Kx x == = +−
Curvature is 0 at ()0,1.
56. () 6 23 y xx=−+ () () 5 4 623 302 yx yx ′ =−+ ′′ =− () () 4 32 2 302 0 1 x K y == ′ + at 2 x =
Curvature is 0 at ()2,6.
57. 11 cos,sin,cos 22242 x xx yyy ′′′ ==−=−
So, 2 22 x nxn π πππ =+ =+
Curvature is 0 at () 2,0. n ππ +
58. sin,yx = cos,yx ′ = sin yx ′′ =−
32 2 sin 0 1cos x K x == + for x nπ =
Curvature is 0 for () :,0xnnππ = 59. 2 ,, cxcxcx yeyceyce ′′′ ===
61. () 42 f xxx =−
(a) 2 64232 261 161641 x K xxx = −++
c = + K is a maximum at 2. c =±
At the smooth relative extremum 0, y ′ = so K y ′′ = Yes, for example, 4 yx = has a curvature of 0 at its relative minimum ()0,0.The curvature is positive at any other point on the curve.
(b) For 0, x = 2. K = ()00. f = At ()0,0,the circle of curvature has radius 1 2 Using the symmetry of the graph of , f you obtain 2 2 11 24 xy ++=
For () 1,255.xK== ()10. f = At ()1,0,the circle of curvature has radius 51 2 K =
Using the graph of f, you see that the center of curvature is
+−=
To graph these circles, use 2 11 24 yx =−±− and 2 15 24 yx =±−
(c) The curvature tends to be greatest near the extrema of f, and K decreases as x →±∞ f and K, however, do not have the same critical numbers.
Critical numbers of f : 0, x = 2 0.7071 2 ±≈±
62. () 2 rij ttt =+ (a) 1,2dxdy t dtdt ==
(b) Let 2 , yx = 2,yx ′ = 2 y ′′ =
At 0, t = 0, x = 0, y = 0, y ′ = 2 y ′′ = []32 2 2 10 K == +
At
At 2, t = 2, x = 4, y = 4 y ′ = 2 y ′′ = []32 32 22 0.0285 17 116 K ==≈ +
(c) As t changes from 0 to 2, the curvature decreases. 63. () 12 , 2 x yaxbxy x =−= +
You observe that ()0,0is a solution point to both equations. So, the point P is origin. () 1 , yaxbx =− () 1 2, y abx ′ =− 1 2 ya ′′ =−
2 , 2 x y x = + () 2 2 2 , 2 y x ′ = + () 2 3 4 2 y x ′′ = +
At P, () 1 0 y ab ′ = and () () 2 2 21 0. 2 02 y ′ == +
Because the curves have a common tangent at ,P ()() 1200 yy ′′ = or 1 2 ab = So, () 1 1 0. 2 y ′ =
Because the curves have the same curvature at P, ()() 1200.KK = () () () () () 1 1 223232 1 0 2 0 112 10 y a K y ′′ ==
+ + () () () () () 2 2 223232 2 0 12 0 112 10 y K y ′′ == + +
So, 1 2 2 a =± or 1 4 a =± In order that the curves intersect at only one point, the parabola must be concave downward. So, 1 4 a = and 1 2. 2 b a ==
() 1 1 2 4 yxx =− and 2 2 x y x = + 2 4 4 2 424 x y1= x (2 x 1) 4 P y y2= x x +2
64. From the shape of the ellipse, you see that the curvature is greatest at the endpoints of the major axis, ()2,0, ± and least at the endpoints of the minor axis, () 0,1. ±
65. (a) Imagine dropping the circle () 2 2 16 xyk+−= into the parabola 2 yx = The circle will drop to the point where the tangents to the circle and parabola are equal.
2 yx = and () () 2 2 2221616 xykxxk +−= +−=
Taking derivatives, () 220 xyky′ +−= and 2.yx ′ = So, () x ykyxy yk ′′ −=− = So, () ()22
Finally, 2 1 16.25, 2 kx=+= and the center of the circle is 16.25 units from the vertex of the parabola. Because the radius of the circle is 4, the circle is 12.25 units from the vertex. (b) In 2-space, the parabola 2 zy = () 2 or zx = has a curvature of 2 K = at ()0,0.The radius of the largest sphere that will touch the vertex has radius 1 1. 2 K ==
66. c s K =
67. () 00 , Pxy point on curve (). yfx = Let () , αβ be the center of curvature. The radius of curvature is 1 . K ()yfx ′′ = Slope of normal line at ()
Equation of normal line:
() , αβ is on the normal line: ()()000 f
00 , x y lies on the circle:
Substituting Equation 1 into Equation 2:
Similarly, ()00x fxz α ′
68. (a) () , x y fxe== ()()() ,0,1 fxfxex ′′′
,02,122,3αβ =−+=− (b) 2 1 ,,1,1, 22 x yyxy
() () 2 11 2 1 f z f ′ + == ′′ () 15 ,12,21, 22 αβ
(c) () 2 ,2,2,0,0yxyxy ′′′ === () () 2 10 1 02 f z f ′ + == ′′ () 11 ,0,00, 22 αβ =+=
Equation 1
Equation 2
69. ()()() cossincossinrrrffijij θθθθθθθ =+=+
()() cos xfθθθ = ()() sin yfθθθ =
()()()sincosxff θθθθθ ′′ =−+
()()()cossinyff θθθθθ ′′ =+
()()()()()()()() cossinsincoscos2sincos xfffffff θθθθθθθθθθθθθθθ ′′′′′′′′′ =−−−+=−−+
()()()()()()()() sincoscossinsin2cossin yfffffff θθθθθθθθθθθθθθθ ′′′′′′′′′ =−+++=−++
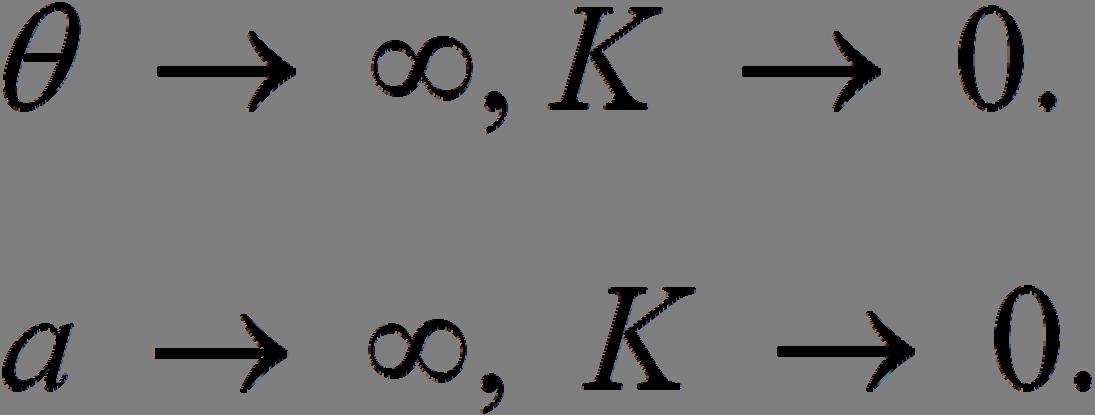
72.
75.
K → as t →±∞
77. ()() ()() () sin 1cos sin xa xa xa θθθ θθ θθ =− ′ =− ′′ = ()() () () 1cos sin cos ya ya ya θθ
1coscossin 1cossin cos1 1 22cos 11cos 1cos0 221cos 11 csc 42 222cos xyyx K xy aa aa a a a a θθθθ θθ θθθ θθ θ θ θ θ θ θ ′′′′′′ = ′′ + = −+ = =−≥ ==
222
78. (a) () () () () 23 2 33 633 tttt ttt rij vij =+− =+− () () 2 2 2 31,6 dsds ttt dtdt v ==+= () 2 2 2 31 K t = + 2 2 6 ds at dt T == () () 2 2 2 2 2 2 916 31 ds aKt dt t N ==⋅+= + 4 4 0 5
Minimum: 1 4 a () θπ =
Maximum: none () as0 K θ →∞→
(b) () 22 1 2 tttt rijk =++
() 2 ttt vijk =++ () 2 51 ds tt dt v ==+
2 2 2 5 51 dst dt t = + () 2 t ajk =+
()()()() 122 021 rrva ijk jk tttt tt ′′′ ×=× ==−+ ()() () ()32 3 2 5 51 rr r tt K t t ′′′ × == ′ + 2 2 2 5 51 dst a dt t T == + () () 2 2 32 2 2 5 51 51 5 51 N ds aKt dt t t
==+
+ = +
82. (a) () () () () () ,by the Chain Rule dddt Ks dsdtds tt ddt dsdt tt
(b) () () () ()tt t dsdt t rr T r ′′ == ′ () () ds tt dt rT ′ = () () () 2 2 dsds ttt dtdt rTT
′′′ =+
()() ()() ()() 2 2 2 dsdsds tttttt dtdtdt
Because ()() tt TT0 ×= and () , ds t dt r ′ = you have: ()()() ()() ()() () ()() () () () () ()() 2 222 1from () rrrTT rrrTTrTTrr ttttt
So, ()() () 3 . tt K t rr r ′′′ × = ′
83. False. See Exploration on page 855.
91. From Exercise 88, you have concluded that planetary motion is planar. Assume that the planet moves in the xy-plane with the sum at the origin. From Exercise 90, you have . GM r r rLe ′ ×=+
Because rL ′ × and r are both perpendicular to ,L so is e So, e lies in the xy-plane. Situate the coordinate system so that e lies along the positive x-axis and θ is the angle between e and r Let e e = Then coscos. re rere⋅==θθ Also,
2 cos. LLL rrL rrL r re rr re GM r GM r GMrer θ =⋅ ′
So, 2 1cos GM r e L θ = + and the planetary motion is a conic section. Because the planet returns to its initial position periodically, the conic is an ellipse.
92.Lrr′ =×
rij
Let: () () cossin sincos r
Then: 22 cossin0 and. sincos0 ijk rrkLrr dd rr rr dtdt dd rr dtdt θθ
93. 2 1 2 A rdβ α θ =
So, 2 11 22 dAdAdd r dtddtdt L θθ θ === and r sweeps out area at a constant rate.
94. Let P denote the period. Then 0 1 2 L PdA A dtP dt
Also, the area of an ellipse is abπ where 2 a and 2b are the lengths of the major and minor axes. 1 2 2 L L abP ab P π π = =
ReviewExercisesforChapter12
1. ()tan rijk ttt =++
(a) Domain: , 2 tn π π ≠+ n an integer
(b) Continuous for all , 2 tn π π ≠+ n an integer
2. 1 () 4 rijk tt t =++
(a) Domain: () [0,4) and 4, ∞
(b) Continuous except at 4 t =
5. ()() 2 212 rijk tttt =++−+
(a) ()02 rik =−
(b) ()234 rij −=−+
(c) ()()() 2 12111 rijk cccc −=−+−−+
3. () () 2 9ln1ttt =−−+− rijk
(a) 229093,3 101 tttt tt −≥ ≥ ≤−≥ −> >
Domain: [ ) 3, ∞
(b) Continuous for all 3 t ≥
4. ()() 2 21 rijk tttt =+++
(a) Domain: () , −∞∞
(b) Continuous for all t
(d) ()()()() () ()
2 2 112111333 2233 rrijkijk ijk tttt tttt +Δ−= +Δ+ ++Δ−+Δ−+−
6. (a) ()03 rij =+
(b) 22 rk ππ =−
(c) ()()() () () 3cos1sin rijk ssss ππππ −=−+−−−−
(d) ()()()() () ()() () 3cos(1sin)3 3cos3sin tttt ttt ππππππ +Δ−=+Δ+−+Δ−+Δ−−+− =−Δ++Δ−Δ rrijkijk ik
7. ()() 3,0,5,2,2,3PQ
()()() 1,2,2 3252,01 3,2,52,01 PQ ttttt xtytztt ==−−− =−−+−≤≤ =−=−=−≤≤ v rijk (Answers may vary)
8. ()() 2,3,8,5,1,2PQ
()()()() 7,4,10 2734810,01 27,34,810,01 PQ ttttt xtytztt ==− =−++−++−≤≤ =−+=−+=−≤≤ v rijk
(Answers may vary)
9. () cos,sin r ttt ππ = cos,sin x tyt==ππ 222 , xy π += circle y x
10. () 2 2,1 r ttt=+−
22xttx =+ =− () 2 2 121, parabola ytx=−=−−
11. ()()()1312 tttt =++−+ rijk 1,31,2 x tytzt=+=−=
This is a line passing through the points () 1,1,0 and () 2,2,2.
(0,4,2) (1,1,0) 34
12. () 2cos2sin tttt =++ rijk 2cos,,2sin x tytzt===
22 4, Circular helix xz+=
x
20. () 5cos2sin ttt =+ rij
(a) () 5sin2cos ttt ′ =−+ rij
(b) () 5cos2sin ttt ′′ =−− rij
(c) ()()()()()() 5sin5cos2cos2sin 21sincos tttttt tt ′′′ ⋅=−−+− = rr x y 11235 4 2 1 1 2 4 3 x y (2,2,2)
13. 34120 xy+−=
Let 123 ,then . 4 t xty== () 123 4 t rtt=+ij
Alternate solution: 4,33 x tyt==−
()() 433 rttt =+−ij
14. 2 9 yx =−
Let 2 ,then 9. x tyt ==−
() () 2 9 rttt =+−ij
15. 22 ,2zxyy=+= 2 4 zx=+ 2 ,2,4xtyzt===+
16. 22 2 4,0, ,,4 x zxytx xtytzt +=−== ===±−
() () 2 2 4 4 rijk rijk tttt tttt =++− =+−−
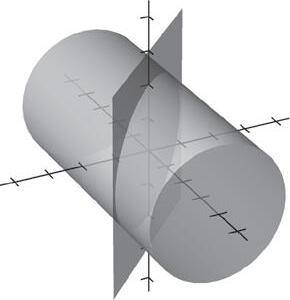
17. 3 11 lim3lnln3 3 t tt t → −+−=− ijkjk
18. 0 sin2 lim424 t t t e t → ++=++ ijkijk 00 sin22cos2 limlim2 1 tt tt t →→ ==
Note:
19. () ()22 43 tttt =+− rij
(a) ()()246 ttt ′ =+− rij
(b) () 26 t ′′ =− rij
(c) ()()()()()() 24266 408 tttt t ′′′⋅=++−− =+ rr
21. () 2432 tttt =+− rijk
(a) () 2 642 ttt ′ =+− rijk
(b) () 122tt ′′ =− rik
(c) ()()()()() 2 3 61222 724 ttttt tt ′′′ ⋅=+−− =+ rr
′′′ ×=−
(d) ()() () () 2 22 2 642 1202 8122448 81248 tttt t ttt tt
=−−−++− =−−− ijk rr ijk ijk
22. ()() ()22 4324tttt=++++ rijk
(a) () 424 ttt ′ =++ rijk
(b) () 24 t ′′ =+ rjk
(c) ()()()()()() 2244 41620 tttt ttt ′′′⋅=+ =+= rr
(d) ()() ()()() 424 024 8816080 168 tttt tt
=−−−+− =−+ ijk rr ijk jk
25. ()()() ()() 23 2 2 3 31, 3,22 ttttttt tttt =+−=++ ′′ =+=++ rijuijk rijuijk
(a) () 3 t ′ =+ rij
23. ()()() 1134ttt=−+− rij
()()() 314123ttt ′ =−+− rij
Not smooth at 1. t =
Smooth on () ,1−∞ and () 1, ∞
24. () 1,1,2 2 t ttttt t =+++≥−≠rijk () () 2 21 21 2 t t t ′ =++ + rijk
Smooth on () 1,2 and () 2, ∞
(b) ()()()() () () ()() () 2 2 2 22 2223 16222 5222 d tttt dt tt tt tt ′′
=− =++−+ =−+−+ =−+−+ urur ijkij ijk ijk
(c) ()()()()() ()()() () () 333 33331 93933 1863 d ttttt dt ttt tttt tt ′ =+ =++ +− =+++− =+− rrr ijij ijij ij
(d) ()()()()()() ()()()()()() ()()()() ()() ()() 223 22 2 2 3 311202310 3223 43 d tttttt dt ttttttt ttttt tt ′′
=⋅+⋅
=+−++ =+ rururu
=+−++++
(e) ()()()()()()
(f) ()() ()() 2 2 222 22222 2816 d tt dt tt tt
(a) () cossin ttt ′ =−+ rijk
(b) ()()()() () 2 2 22 1 cossin2cossin 1 cossin2 d tttt dt tttt t tt t
=+
d ttttt dt tttttt ttttttt
=−++++ =++−+ rrr ijkijk ijk
(c) ()()()()() ()()() ()() 333 3cossin3sincos 3cos3sin3cos3sin6
(d) ()()()()()() ()()()()() ()()()()() 2 11 sincoscossincossinsincos1 11 sincossincossincossincos 0 d tttttt dt ttttttttt tt tttttttt tt ′′
=⋅+⋅
=−−+−+ = rururu
=+−+−++−+
(e) ()()()()()() ()
28. ()() 2 62ln6ln ijkijkC ttdrttttt −+=−+−+
33. ()
35. () () () () ()()() 2 2 2 03524 124 rijkijkC rjkCijkCijk ri+jk tttt tt tteedttee ttee =++=+−+
36. () () () ()
ttttdt
37. () 3 4,1ttttt=+−=rijk
(a) ()() () ()() 2 44 43 Speed1691179 6 ttt ttt ttt
(b) () () 143 16 =+− = vijk aj 38. () 2 52,4ttttt=++=rijk (a) ()() () ()() 2 32 1 54 2 1 Speed2516 4 1 4 4 ttt t tt t tt t ′ ==++ ==++
==−+ vrijk v arik (b) () () 1 4516 4 1 44 32 =++ =−+ vijk aik
39. () 33 cos,sin,3, ttttt π == r
(a) ()() 22 3cossin,3sincos,3 tttttt ′ ==−vr () () 4242 2222 22 Speed9cossin9sincos9 3cossincossin1 3cossin1 v ttttt tttt tt ==++ =++ =+ () ()() () ()() 2222 2222 6cossin3coscos,6sincos3sinsin,0 3cos2sincos,3sin2cossin,0 a ttttttttt tttttt =−−+−+− =−−
40. () ,tan,,0 t tttet=−= r
(a) ()() () () 2 42 2 1,sec, Speed1sec 0,2sectan, vr v a t t t ttte tte ttte ′
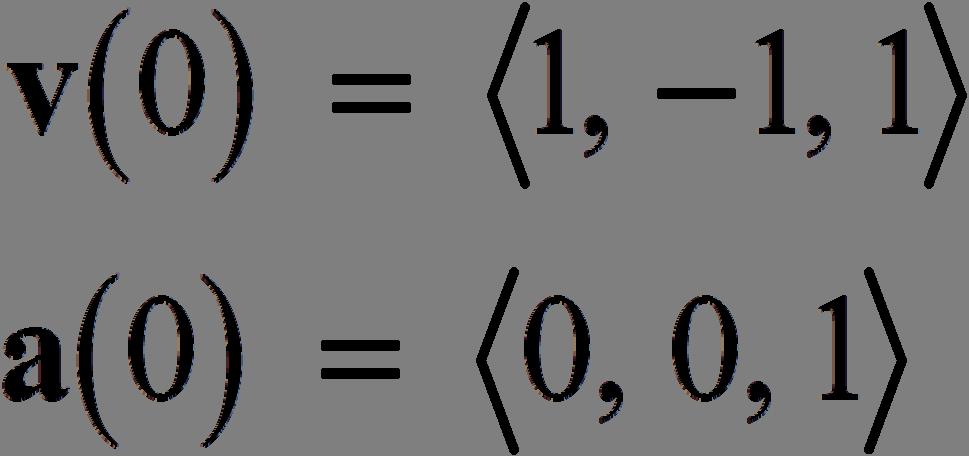
41. ()()() ()()() () 2 00 2 2 cossin16 120cos303.5120sin3016 6033.56016 tvthvtt ttt ttt θθ
=++− rij ij ij ()() ()6036032 ttt ′ ==+− rvij
Find the maximum height () 6015 603201.875 328 ttt ′ =−= === y 2 151515 3.5601659.75 ft, 888 y =+−=
37525253 3756033.608 12 60343 tt = ===≈ 253 11.67 ft 12 y
The baseball clears the 8-foot fence.
42. ()()() ()() 2 00 2 1 cossin 2 400cos606400sin6016 rvivj ij tthtgt ttt
() 200200332 tt
Maximum height: () 2 2003 200332010.825 sec 32 20032003 6400sin60161881 ft 3232 tt−= =≈
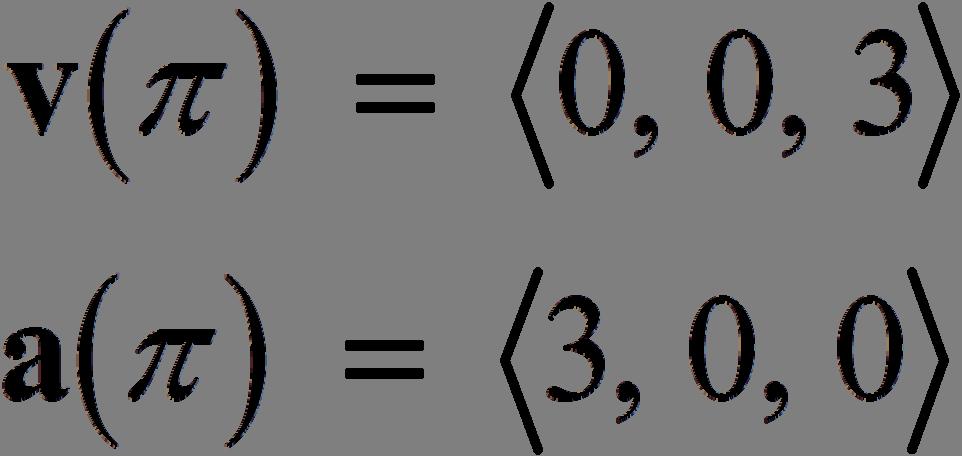
43. () 2 6,2tttt=−=rij
() () 62 264, tt ′ =− ′ =− rij rij ()23616213 ′ =+= r
() () 1 232 13 =− Tij
44. () ()
2sin4cos, 6 2cos4sin
45. ()() 2 cossin3,1,1,0 t tettP =+− rijk
() 2 2sin3cos3 t tett ′ =−− rijk
At () 1,1,0,0.Pt =
() () () 0 023 04913 =+ ′ =− ′ =+= rij rik r () () 1 023 13 =− Tik
Direction numbers: 2,0,3abc===−
Parametric equations: 12,1,3 x tyzt=+==−
=++
=++
=
46. () () () () () () 23 2 2 3 16 ,2,4, 3 22 16 2 at 2,4, 3 248 2 48148 2 9999 2 rijk rijk rijk rijk Tijk r ttttP ttt tP
Direction numbers: 1,4,8abc===
Parametric equations: 16 3 2,44,8 xtytzt =+=+=+
47. () ()() () () () () () () 2 2 23,1 26,126 436,140210 1 261 13 1 21010 tttt tt tt =+= ′′ =+=+ ′′ =+== ′ + ===+ ′ rij rijrij rr rij Tij r
() 1 N is orthogonal to () 1 T and points towards the concave side. Hence, () () 1 13. 10 =−+ Nij
48. () () () () () () () () 2 2 ln,2 11 ,2 2 111 11,25 2 2 2121 2 2 2 555 rij rijrij rr r Tijij r tttt t t tt tt =+= ′′ =+=+ ′′ =+=+=
==+=+
() 2 N is orthogonal to () 2 T and points towards the concave side. Hence, () 12525 55 55 t =−=− Nijij
49. () ()() () () ()() () () 3cos23sin23, 4 6sin26cos2,6 sin2cos2,4 2cos22sin2,2 cos2sin2 4 tttt tttt ttt tttt ttt π π π =++= ′′ =−+= =−+=− ′′ =−−= =−− =− rijk rijr TijTi TijT Nij Nj
50. () ()() () ()() () 2 4cos4sin, 3 4sin4cos,4 231 sincos, 322 cossin,1 213 cossin, 322 tttt tttt ttt tttt ttt π π π =++= ′′ =−+=
rijk rijr TijTij TijT NijNij
=−+=−−
′′ =−−=
=−−=−
51. () () () () () () () () () 2 3 2 2 4 4 3 6,3 31 6,36 3 62 ,3 9 3 6 36 9 314 36 35418131813 3 6565 31324325 rij vijvij aiai
ijij Tij
() 3 N is orthogonal to ()3, T and points in the direction the curve is bending. Hence, () 18181313 3. 6565 325 ==− ij Nij 2213 585 9325 4413 65 325 a a =⋅=−=− =⋅== T N aT aN
52. () () () () () () () () () 22 3cos23sin2, 6 6sin26cos2,333 6 12cos212sin2,663 6 36sin236cos26 1 6sin26cos2 6 sin2cos2 31 622 2cos22sin2 tttt ttt ttt ttt t ttt t tt ttt
rij vijvij aijaij v v Tij v ij Tij Tij () ,2 t ′ = T () () () cos2sin2 13 622 T Nij T Nij t ttt
=− rij rij
56. () [ ] () 2 2,0,3 22 ttt tt =+ ′ =+ rik rik
r b a s tdttdt tttt ′ ==+
() () 3 2 0 3 22 0 44 ln11 ln10331011.3053
z y (9,0,6) (0,0,0) x
57. () () () 2 2sin,, 2 2cos 4cos2cos tt tt ttt π π =+ ′ = ′ == rij ri r [] () 2 2 2cos 2sin 022 s tdt t π
59. () [ ] () 324,0,3 324 tttt t =−++ ′ =−++ rijk rijk () 3 0 3 0 9416 29329 r b a s tdtdt dt ′ ==++ ==
58. () [ ] () () 10cos10sin,0,2 10sin10cos 10 ttt ttt t π =+ ′ =−+ ′ = rij rij r 2 0 1020sdt π π ==
60. () [ ] ()() 2 2 2,0,2 22, 54 tttt tttt =++ ′′ =++=+ rijk rijkr () () 2 2 0 55 44 54 21ln5ln105456.2638 r b a stdttdt ′ ==+ =+−−≈
2 1 1 3 1 2 24 z y x (2,4,4) x y z π 4 864 6 (8,8 0,0) 0,8,2 π 2) )
61. () () () 8cos,8sin,,0, 2 8sin,8cos,1, 65 tttt tttt π = ′′ =−= r rr () 2 0 65 65 2 r b a stdtdt π π ′ ===
62. ()()() () () 2 2sincos,2cossin,,0, 2 2sin,2cos,1, 41 tttttttt ttttttt
r rr () ( ) 2 2 0 22 41 1 ln113.055 44 r b a stdttdt π π πππ ′ ==+ =++++≈
63. () 32 rij ttt =+ Line 0 K =
64. () () () () 32 23 1119 3, 9 1 2 rij rijr ri ttt t tt
65. () () () 22 2 1 2 2 22,54 2 rijk rijkr rjk tttt tttt t
66. () ()() () 25cos5sin 25sin5cos,29 5cos5sin rijk rijkr rjk tttt tttt ttt =++ ′′ =−+=
′′ =− 25sin5cos 05cos5sin 2510sin10cos ijk rr ijk tt tt tt
′′′ ×=− =+− ()32 3 725 72525295 29 2929 29 rr rr r K
′′′ ×= ′′′ × ==== ′
67. () ()() ()() 23 2 1111 ,,1,1 2323 ,1 2,12 rijk rijkrijk rikrik ttttPt ttt tt =++ =
′′ =++=++ ′′′′=+=+ ()3 3 1112 102 41162 3 33 3 ijk rrijk rr r K
′′′ ×==−− ′′′ × ++ ==== ′
68. ()() ()() ()() 4cos3sin,4,0, 4sin3cos,3 4cos3sin,4 rijk rijkrjk rijri ttttPt ttt ttt ππ π π =++− = ′′ =−++=−+ ′′′′ =−−= ()32 3 031412 400 161442 5 91 ijk rrjk rr r K ′′′ ×=−=+
′′′ × + === ′ +
69. 2 1 ,4 2 1 1 yxxx yx y =+= ′ =+ ′′ = () () 3232 2 2 32 32 1 1 1 1 At 4,and262626. 26 y K x y xKr ′′ == + ′ + ====
70. () 2 22 2 3232 2 ,0 11 , 24 1 4 1 1 1 4 x xx x x yex yeye e y K y e == ′′′ =−= ′′ == ′ + +
At ()32 32 142225 0,, 525 55 54 xK===== 55 2 r =
ProblemSolvingforChapter12
(b)
(c) Ka==ππ (length) 2. 232323 x ya+= () 1313 13 13 22 0 33 Slope at ,. xyy y yPxy x ′ += ′ = () () () () () () () 33 22 cossin 3cossin3sincos 3cossin cossin sincos ttt ttttt ttt t ttt t ttt rij rij ri r Tij r Tij =+
() 0,0,0 Q origin () 33 cos,sin,0 P tt = on curve.
()3333 cossin0cossinsincos cossin0 PQtttttt tt ×==− ijk Tk () () cossin 1 3cossin T T T r PQ Dtt t K tt t × == ′ ==
So, the radius of curvature, 1 , K is three times the distance from the origin to the tangent line.
3. Bomb: () 2 1 5000400,320016 r ttt =−−
Projectile: ()()() 2 200cos,sin16r tvtvtt θθ =−
At 1600 ft: Bomb:
2 320016160010 tt−= = seconds.
Projectile will travel 5 seconds:
()() 0 0 5sin16251600 sin400. v v θ θ −= =
Horizontal position:
At () 10,bomb is at 5000400101000. t =−=
At 0 5,projectile is at 5cos.tv θ = So, 0 cos200. v θ =
Combining,
0 0 sin400 tan263.43. cos200 v v θ θθ θ = = ≈°
0 200 447.2 cos v θ =≈ ft/sec
4. Bomb: () 2 1 5000400,320016 r ttt =+−
Projectile: ()() () 2 200cos,sin16r tvtvtt θθ =−
At 1600 ft: Bomb:
2 320016160010 tt−= =
Projectile will travel 5 seconds:
()() 0 0 5sin16251600 sin400. v v θ θ −= =
Horizontal position:
At () 10,bomb is at 5000400109000. t =+=
At () 0 5,projectile is at cos5. tv θ =
So,
0 0 5cos9000 cos1800. v v θ θ = =
Combining,
0 0 sin4002 tan12.5. cos18009 v v θ θθ θ = = ≈°
0 1800 1843.9 cos v θ =≈ ft/sec
5. ()()1cos,sin,0xyθθθθθπ ′′=−=≤≤2 ()() () 222 2 2 1cossin 22cos4sin 2 xyθθθθ θ θ ′′ =−+ =−=
() ()() 2sin4cos4cos 222 sin,cos t t t std xy π π θθ θ θθθθ
() 3 3 1cos cos sin sin 2 sin 2 cos 1 8 sin 2 1 4 sin 2 K
= = So, 1 4sin 2 t K ρ == and 222216cos16sin16. 22 tt s ρ
=−
1cos sin r r θ
= ()() 2 2 1cossin22cos 2sin4cos4cos 222 tt t t s tdd t d ππ π π θθθθθ
θ =−+=−
==−=−
() () ()()() 2 2 32 2 2 2 2 3 2 33 2 2sin1coscos1cos 8sin 2 sin 33cos 33 2 4 8sinsin4sin 222 4sin 1 2 3 rrrr K rr K
22 s θθ ρ +=+=
(b) 2 2 42,000cos42,000sin 1212 42,000,0,0 rij
2 2 ,0 12 dd dtdt θπθ == So, 2 2 875 42,000. 123 auu rr π π
=−=−
Radial component: 2 875 3 π Angular component: 0 9. () ()() () 4cos4sin3, 2 4sin4cos3,5 4cos4sin ttttt tttt ttt rijk rijkr rij π =++= ′′ =−++= ′′ =−− 443 sincos 555 44 cossin 55 cossin 334 sincos 555 tt tt tt tt =−++
=−+
=−− =−− =×=−+ Tijk Tij Nij BTNijk At , 2 t π = 43 255 2 34 255 Tik Nj Bik π π π
=−
10. () () () cossin, 4 sincos, 1 sincos cossin cossin rijk rijr Tij Tij Nij
11. (a) 1constant length B BTNB d ds =×= ⊥
()()() ()() () 0 B TNTNTN B TTTNTTN T TTNTT T dd dsds d ds ′′ =×=×+× ′′ ⋅=⋅×+⋅×
So, and BBB BTN ddd dsdsds τ ⊥⊥ = for some scalar τ
(b) .BTN =× Using Section 11.4, exercise 58, ()() ()() BNTNNNTN NNTNTN T ×=××=−×× =− =− ()() ()() BTTNTTTN TNTTTN N ×=××=−××
= Now, () () () T TT NT T s dd Ks dsds s ′ ′ === ′ Finally, () ()()() ()() NBTBTBT BNNT TB d s ds K K τ τ ′′ ′ =×=×+× =×+−× =−+ 12. 52 32 12 1 32 5 64 15 128 yx yx yx = ′ = ′′
cos,sin,02 r tttttt ππ =≤
(d)
(e) lim0 t K →∞ = (f) As , t →∞ the graph spirals outward and the curvature decreases.
14.
(a) Eliminate the parameter to see that the Ferris wheel has a radius of 15 meters and is centered at 16. j At 0, t = the friend is located at () 1 0, rj = which is the low point on the Ferris wheel.
(b) If a revolution takes t Δ seconds, then () 2 1010 tt t π π π +Δ =+ and so 20 t Δ= seconds. The Ferris wheel makes three revolutions per minute.
(c) The initial velocity is ()20 8.0311.47. ij rt ′ =−+ The speed is 22 8.0311.4714meters per second. +≈ The angle of inclination is 11.47 arctan0.96 8.03 ≈
radians or 55. °
(d) Although you may start with other values, 0 0 t = is a fine choice. The graph at the right shows two points of intersection. At 3.15 t = sec the friend is near the vertex of the parabola, which the object reaches when () 0 11.47 1.17 24.9 tt−=−≈ seconds.
So, after the friend reaches the low point on the Ferris wheel, wait 0 2 t = seconds before throwing the object in order to allow it to be within reach.
(e) The approximate time is 3.15 seconds after starting to rise from the low point on the Ferris wheel. The friend has a constant speed of () 1 15meters per second. r t ′ = The speed of the object at that time is () () 2 2 2 3.158.0311.479.83.1528.03meters per second. r ′ =+
Chapter 2, Section 1, page 69
() 1,1 P and () () 1 2.2511.25 1.5,1.5:2.5 1.510.5 Qfm ===
() 1,1 P and () () 2
() 1,1 P and () () 3
() 1,1 P and () () 4 1.0020010.002001 1.001,1.001:2.001 1.00110.001 Qfm ===
() 1,1 P and () () 5
2 m =
Chapter 2, Section 1, page 70
The width of each rectangle is 1 . 5
The area of the inscribed set of rectangles is: () 111121314 0 555555555 114916 0 525252525 130 525 6 0.24. 25
Chapter 2, Section 2, page 72
The graph of () 2 32 2 xx fx x −+ = agrees with the graph of () 1 gxx=− at all points but one, where 2. x = If you trace along f getting closer and closer to 2, x = the value of y will get closer and closer to 1.
Chapter 2, Section 4, page 94
x y x = looks continuous on (),.
You cannot trust the results you obtain graphically. In these examples, only part a. is continuous. Part b. is discontinuous at 2; x = part c. is discontinuous at 0; x = part d. is discontinuous at 2. x =−
Chapter 2, Section 5, page 108
SECTION PROJECTS
Chapter 2, Section 5, page 114 Graphs and Limits of Trigonometric Functions
(a) On the graph of f, it appears that the y-coordinates of points lie as close to 1 as desired as long as you consider only those points with an x-coordinate near to but not equal to 0.
(b) Use a table of values of x and () f x that includes several values of x near 0. Check to see if the corresponding values of () f x are close to 1. In this case, because f is an even function, only positive values of x are needed.
x 0.5 0.1 0.01 0.001 f (x) 0.9589 0.9983 1.0000 1.0000
(c) The slope of the sine function at the origin appears to be 1. (It is necessary to use radian measure and have the same unit of length on both axes.)
(d) In the notation of Section 2.1, 0 c = and cxx +Δ= Thus, sec sin0 0 x m x =
This formula has a value of 0.998334 if 0.1; x = sec 0.999983 m = if 0.01. x =
The exact slope of the tangent line to g at () 0,0 is sec 00 sin limlim1. xx x m x →→ ==
(e) The slope of the tangent line to the cosine function at the point () 0,1 is 0. The analytical proof is as follows: () () sec 000 cos011cos limlimlim0. Δ→Δ→Δ→ +Δ−−Δ ==−= ΔΔxxx xx m xx
(f) The slope of the tangent line to the graph of the tangent function at () 0,0 is: () () sec 00 tan00sin 11 limlimlim11. cos1 xxx xx m xxxΔ→∞Δ→Δ→ +Δ−Δ ==⋅=⋅= ΔΔΔ
Chapter 3, Section 5, page 177 Optical Illusions
(a) 222 220 x yC xyy x y y += ′ += ′ =− at the point () 3 3,4, 4 y ′ =−
(b) 0 xyC xyy y y x = ′ += ′ =− at the point ()1,4,4 y ′ =−
