CHAPTER11
VectorsandtheGeometryofSpace
Section11.1V ectorsinthePlane
1. Answers will vary. Sample answer: A scalar is a real number such as 2. A vector is represented by a directed line segment. A vector has both magnitude and direction. For example 3,1 has direction 6 π and a magnitude of 2.
2. Notice that () 6,724,16. QP =−=−−−−=
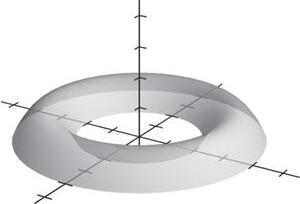
Hence, Q is the initial point and P is the terminal point.
3. (a) 51,424,2 v =−−= (b)
4. (a) () 42,336,0 v =−−−−−=− (b)
5. 53,622,4 31,842,4 u v uv
6. () () 14,805,8 72,715,8 u v
9. (b) 52,503,5 v =−−=
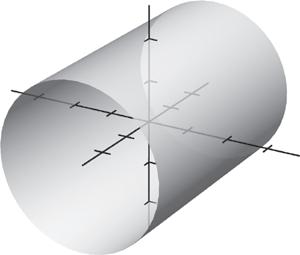
(c) 35 vij =+ (a), (d)
x 112345
(c) 53 vij =−+ (a) and (d). 2345 1 1 3 2 4 5 x v (4,2) y
7. 60,236,5 93,5106,5 u v uv
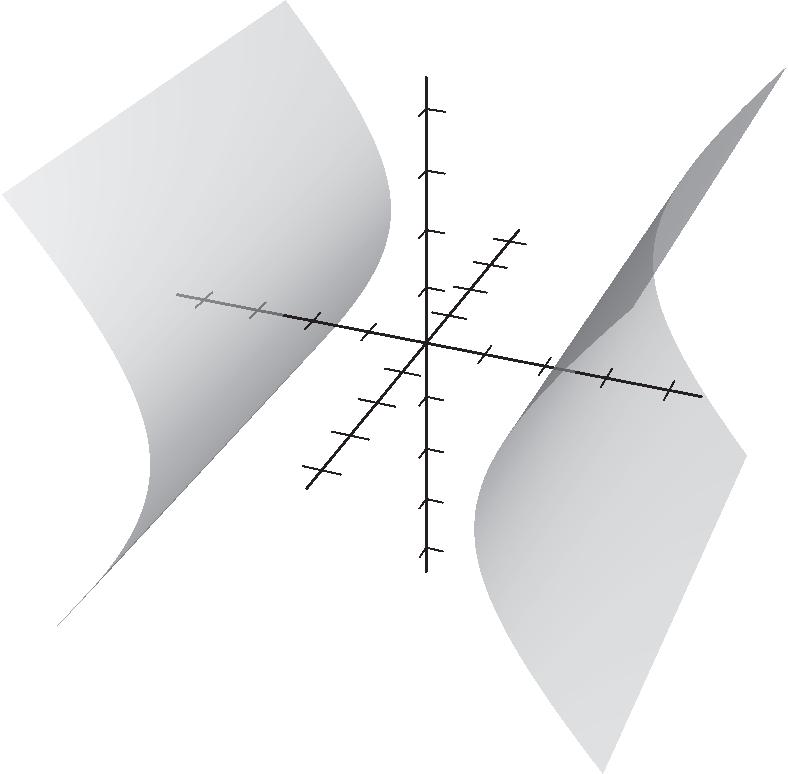
8. ()() 114,4115,3 250,101315,3 u v uv =−−−−−=−
10. (b) () 34,661,12 v =−−−=− (c) 12 vij =−+ (a), (d)
11. (b) 68,132,4 v =−−−=−−
(c) 24 vij =−− (a), (d)
2 3 4 5(3,5) (2,0) (5,5) v y 642 826810 4 6 2 4 6 8 x v y (4,6) (3,6) (1,12) x (8,3) (6,1) (2,4) v 2 4248 6 2 4 6 y x v 6422 4 2 2 (5,3) (0,4) (5,1) y
12. (b) () 50,145,3 v =−−−−−=−
13. (b) 66,620,4 v =−−=
(c) 4 vj = (a) and (d).
14. (b) () 37,1110,0 v =−−−−−=−
(c) 10 vi =− (a) and (d).
15. (b) 1435 2233 ,31, v =−−=−
(c) 5 3 vij =−+ (a) and (d)
16. (b) 0.840.12,1.250.600.72,0.65 v =−−=
(c) 0.720.65 vij =+ (a) and (d).
17. () 1 2 41 23 3,5 u u Q
22 8,15 81517 = =+= v v 22. () 2 2 24,7 24725 =− =−+= v v 23. ()() 22 5 1526 =−− =−+−= vij v 24. 22 33 331832 =+ =+== vij v 25. (a) 223,56,10 v == (b) 39,15 v −=−− (c) 735 21 222 , v = 46 6 4 2 2 x v (6,6) (0,4) (6,2) y x v 86422468 3 2 1 2 3 (10,0) ((7,1) 3,1) y 12 3 2 21 x v 1 (2,3( 3 2 4 (,3 ( 5 (1,3 ( y x v 0.751.00 0.251.25 0.50 1.25 1.00 0.75 0.50 0.25 (0.72,0.65) (0.84,1.25) (0.12,0.60) y x (6,10) (3,5) v 2v y 2246810 2 2 4 6 8 10 x (9,15) (3,5) v 3v y 12963 1536 6 9 12 15 3 6 x (3,5) v v y 35 2 21 2 7 2 (,( 3369121518 3 3 6 9 12 15 18
(d) 10 2 33 2, v =
26. (a) 442,38,12 v =−=−
(b) 3 1 22 1, v −=−
Section 11.1 Vectors in the Plane 1093
27. 4,9,2,5uv==−
(a) 8 22 3334,9,6 u ==
(b) 332,56,15 =−=− v (c) 2,54,92,14 vu−=−−=−−
(d) 2524,952,5 8,1810,25 18,7 uv+=+− =+− =−
28. 3,8,8,7=−−=uv
(a) 16 22 333 3,82, =−−=−− u
(b) 338,724,21 == v (c) 8,73,811,15 u −=−−−= v
(d) 2523,858,7 6,1640,35 34,19 uv+=−−+ =−−+ = 29.
(c) 00,0 v = (d) 612,18 u −=−
Twice as long as given vector u.
35. 3,12 v = 22 312153 v =+= v u v == 3,12 312 , 153153153 17417,unit vector 1717 = =
36. 5,15 25225250510 5,15 10310 ,unit vector 1010 510 v v v u v =− =+== ===−
37. 35 , 22 v = 22 3534 222 v
35 , 22 35 , 343434 2 334534,unit vector 3434 v u v
38. ()() 22 6.2,3.4 6.23.45052 6.2,3.4 312172 ,unit vector 5050 52 v v v u v =− =−+== ===−
39. 1,1,1,2uv=−=−
(a) 112 u =+=
(b) 145 v =+=
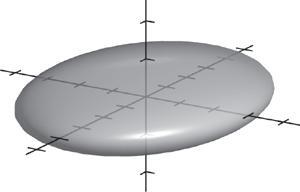
(c) 0,1 011 uv uv += +=+= (d) 1 1,1 2 1 u u u u =− = (e) 1 1,2 5 1 v v v v =− = (f ) 0,1 1 uv uv uv uv + = + + = +
40. 0,1,3,3uv==−
(a) 011 u =+= (b) 9932 v =+= (c) 3,2 9413 uv uv +=− +=+= (d) (e) 1 3,3 32 1 v v v v =− = (f ) 1 3,2 13 1 uv uv uv uv + =− + + = + 0,1 1 u u u u =
41. 1 1,,2,3 2 uv==
(a) 15 1 42 u =+= (b) 4913 v =+= (c) 7 3, 2 4985
2,4,5,5uv=−=
41625
252552
=≈ += +=≈ +≤+ ≤+ 44. 3,2 133.606 1,2 52.236 2,0 2 2135 u u v v uv uv u+vuv =− =≈ =− =≈ +=− += ≤+ ≤+ 45. 1 0,30,1 3 660,10,6 0,6 u u u u v ==
= 46. 1 1,1 2 4221,1 22,22 u u u u v =
=
= 47. 112 1,2, 555 12 55,5,25 55 5,25 u u u u v =−=−
=−
=−=−
1 3,3 23 1 23,3 3 1,3 u u u u v =
50. ()() 5cos120sin120 553553 , 2222 vij ij = °+° =−+=−
51. ()() 2cos150sin150 33,1 vij ij = °+°
52. ()() 4cos3.5sin3.5 3.99250.2442 3.9925,0.2442 vij ij = °+° ≈+ =
53. ()() ()() cos0sin0 3232 3cos453sin45 22 2323223232 , 2222 uiji vijij uvij =°+°= =°+°=+
54. ()() ()() 4cos04sin04 2cos302sin303 535,3 uiji vijij uvij =°+°= =°+°=+ +=+=
55. ()() ()() ()() 2cos42sin4 cos2sin2 2cos4cos22sin4sin2 2cos4cos2,2sin4sin2 uij vij uvij =+ =+ +=+++
56. ()() ()() ()() () 5cos0.55sin0.5
5cos0.55sin0.5
5cos0.55sin0.5 10cos0.510cos0.5,0 uij ij vij uvi
57. The forces act along the same direction. θ =0°
58. The forces cancel out each other. 180. θ =° 59. 0. XYYZZX++= Vectors that start and end at the same point have a magnitude of 0.
60. (a) True. d has the same magnitude as a but is in the opposite direction.
(b) True. c and s have the same length and direction.
(c) True. a and u are the adjacent sides of a parallelogram. So, the resultant vector, , + au is the diagonal of the parallelogram, c
(d) False. The negative of a vector has the opposite direction of the original vector.
(e) True. () 0 +=+−=adaa
(f) False. () ()()()() 2 2222224 uvuuu btbbbuu −=−−= −+=−+=−=−
61. 4,51,21,1 ab ==+− v 4 52 ab ab =+ =−
Adding the equations, 933. aa = =
Then you have 4431.ba=−=−= 3,1ab==
62. 7,21,21,1 ab =−−=+− v
7 22 ab ab −=+ −=−
Adding the equations, 933. aa −= =−
Then you have () 7734.ba=−−=−−−=− 3,4ab=−=−
63. 6,01,261,1 a =−=+− v
6 02 ab ab −=+ =−
Adding the equations, 632. aa −= =−
Then you have () 6624.ba=−−=−−−=− 2,4ab=−=−
64. 0,61,21,1 v ab ==+−
0 62 ab ab =+ =−
Adding the equations, 632. aa = =
Then you have 2. ba=−=− 2,2ab==− X Y Z
65. 1,31,21,1 ab =−=+− v 1 32 ab ab =+ −=−
Adding the equations, 2 23. 3 aa −= =−
Then you have 25 11. 33 ba =−=−−= 25 , 33 ab=−=
67. ()()() 2 ,2,36fxxfxxf ′′ ===
Section 11.1 Vectors in the Plane 1097
66. 1,81,21,1 ab =−=+− v 1 82 ab ab −=+ =−
Adding the equations, 7 73. 3 aa = =
Then you have 710 11. 33 ba=−−=−−=− 710 , 33 ab==−
(a) 6. m = Let 1,6,37,ww== then 1 1,6. 37 w w ±=±
(b) 1 6 m =− Let 6,1,37,ww=−= then 1 6,1. 37 w w ±=±−
68. (a) 2. m =− Let 1,2, w =− 5, w = then 1 1,2. 5 w w ±=±−
(b) 1 2 m = Let 2,1,5,ww== then 1 2,1. 5 w w ±=±
69. ()()32 ,33fxxfxx ′ === at 1. x =
(a) 3. m = Let 1,3, w = 10, w = then 1 1,3. 10 w w =±
(b) 1 3 m =− Let 3,1,10,ww=−= then 1 3,1. 10 w w =±−
70. ()()32 ,312fxxfxx ′ === at 2. x =−
(a) 12. m = Let 1,12, w = 145, w = then 1 1,12. 145 w w =±
(b) 1 12 m =− Let 12,1,145,ww=−= then 1 12,1. 145 w w =±−
71. () 2 25 f xx =− () 2 3 4 25 x fx x ′ == at 3. x =
(a) 3 4 m =− Let 4,3, w =− 5, w = then 1 4,3. 5 w w =±−
(b) 4 3 m = Let 3,4,5,ww== then 1 3,4. 5 w w =±
()()() 2 5,2,12fxxfxxf ′′ =−+=−=− x y 2246810 2 4 6 8 10 (3,9) (a) (b) 1 3123 1 1 2 3 4 x y (1,4) (a) (b) x y 12 1 2 (a) (1,(b) 1) 42 624 4 6 10 x y (a) (b) x y 112345 1 2 3 4 (3,4) (a)(b)

Magnitude: 22 430.8890440.18 +≈ newtons (c) (d)
M decreases because the forces change from acting in the same direction to acting in the opposite direction as increases from to
77. ()()() () () 123 123 123 7512575125 2222 75cos3075sin30100cos45100sin45125cos120125sin120
79. () () cos30sin30 cos130sin130 CB CA uuij vvij ==°+° ==°+°
Vertical components:
Horizontal components:
sin30sin1303000uv°+°= cos30cos1300uv°+°=
Solving this system, you obtain 1958.1 u ≈ pounds, 2638.2 v ≈ pounds.
80. 1 24 arctan0.8761or50.2 20 θ =≈°
2 24 arctan1.9656or112.6 10 θπ =+≈°
11 22 cossin cossin uuij vvij θθ θθ =+ =+
Vertical components: 12 sinsin5000uvθθ+=
Horizontal components: 12 coscos0uvθθ+=
Solving this system, you obtain 2169.4 u ≈ and 3611.2. v ≈
81. Horizontal component cos 1200cos61193.43ftsec v θ = =°≈
Vertical component sin 1200sin6125.43ftsec v θ = =°≈
82. To lift the weight vertically, the sum of the vertical components of u and v must be 100 and the sum of the horizontal components must be 0. () () cos60sin60 cos110sin110 uuij vvij =°+° =°+°
So, sin60sin110100,uv°+°= or 3 sin110100. 2 uv
+°=
And cos60cos1100uv°+°= or 1 cos1100. 2 uv
+°=
Multiplying the last equation by () 3 and adding to the first equation gives () sin1103cos11010065.27pounds uv °−°= ≈
+°=
Then, 1 65.27cos1100 2 u
gives 44.65pounds u ≈
(a) The tension in each rope: 44.65lb, 65.27lb u v = =
(b) Vertical components: sin6038.67lb, sin11061.33lb u v °≈ °≈
83. () () 900cos148sin148 100cos45sin45 uij vij =°+° =°+° ()() ()() 22 900cos148100cos45900sin148100sin45
692.53547.64 547.64 arctan38.34;38.34North of West 692.53 692.53547.64882.9kmh
Direction North of East: N84.46E≈° Speed: 336.35mih ≈
85. False. Weight has direction.
86. True
87. True
88. True
89. True 90. True
91. True
92. False 0 ab==
93. False 2 aba ij+= 94. True
95. 22 22 cossin1, sincos1 u v θθ θθ =+= =+=
96. Let the triangle have vertices at ()() 0,0,,0, a and (),.bc
Let u be the vector joining () 0,0 and (),,bc as indicated in the figure. Then v, the vector joining the midpoints, is () 222 22 11 22 abac bc bc vij i+j iju. +
= =+=
So, 1 xy+= and 0. xy−= Solving you have 1 2 xy== x a + bc a 22 2 (,( (( ,0 (b, c) (a (0,,0) 0) u v y u s r v
97. Let u and v be the vectors that determine the parallelogram, as indicated in the figure. The two diagonals are uv + and vu So, ()() ,4. x ruvsvu =+=− But, ()()()()x yxyxy urs uvvuuv =− =+−−=++−
(x, y) x y α
If 22 0 2 0 , 22 vgx y g v ≤− then α can be chosen to hit the point (),.x y To hit ()0,: y Let 90. α =° Then 2 22 00 2 0 0 1 1, 222 vvg yvtgtt ggv =−=−−
and you need
The set H is given by 0, x ≤ 0 y < and 22 0 2 0 22 vgx y g v ≤−
Note: The parabola 22 0 2 0 22 vgx y g v =− is called the “parabola of safety.”
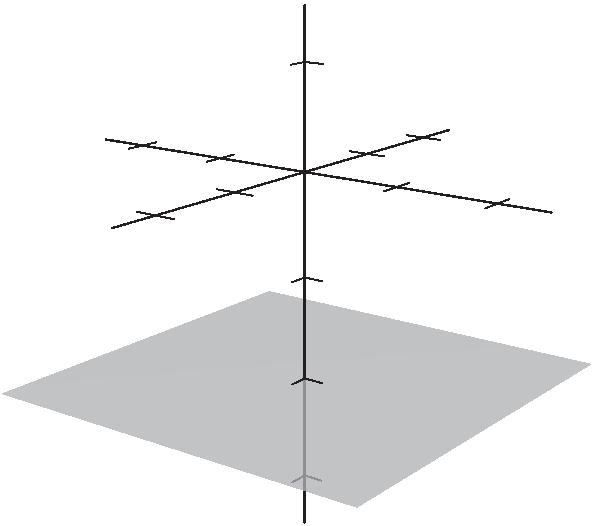
Section11.2SpaceCoor dinatesandVectorsinSpace
1. 0x is directed distance to yz-plane.
0y is directed distance to xz-plane.
0z is directed distance to xy-plane.
2. The y-coordinate of any point in the xz-plane is 0.
4. The nonzero vectors u and v are parallel if there exists a scalar such that c = uv sincos 22 tantan 2 coscos 22
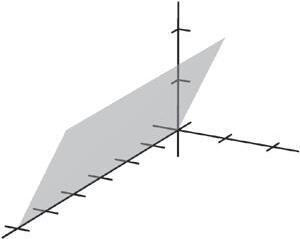
3. (a) 4 x = is a point on the number line. (b) 4 x = is a vertical line in the plane. (c) 4 x = is a plane in space.
2 2 4 6 6 6 xy (4,0,5) (0,4,5) 8 z 6 2 2 4 6 6 6
9. 3, x =− 4, y = 5: z = () 3,4,5
10. 7, x = 2, y =− 1: z =− () 7,2,1
11. () 0,12:12,0,0yzx===
12. ()0,3,2:0,3,2xyz===
13. The point is 1 unit above the xy-plane.
14. The point is 6 units in front of the xz-plane.
15. The point is on the plane parallel to the -plane yz that passes through 3. x =−
16. The point is 5 units below the xy-plane.
17. The point is to the left of the xz-plane.
18. The point more than 4 units away from the yz-plane.
19. The point is on or between the planes 3 y = and 3. y =−
20. The point is in front of the plane 4. x =
21. The point () ,,x yz is 3 units below the xy-plane, and below either quadrant I or III.
22. The point () ,,x yz is 4 units above the xy-plane, and above either quadrant II or IV.
23. The point could be above the xy-plane and so above quadrants II or IV, or below the xy-plane, and so below quadrants I or III.
24. The point could be above the xy-plane, and so above quadrants I and III, or below the xy-plane, and so below quadrants II or IV.
25. ()()() 222 842165 1611 1832 d =−+−+− =++ ==
26. () () ()() 2 31513122 41616 366 d =−−−+−+−− =++ ==
27. ()()() 222 302284 9016 255 d =−+−+− =++ ==
28. () () ()() 2 53874122 4125 30 d =−−−+−+−− =++ =
29. ()()() 0,0,4,2,6,7,6,4,8ABC () ()() 222 2 22 22 2 222 263497 641219614 421524575 24549196 AB AC BC BCABAC =++== =++−== =+−+−== ==+=+ Right triangle
30. ()()() 3,4,1,0,6,2,3,5,6 94114 012526 911626 ABC AB AC BC =++= =++= =++= Because , ACBC = the triangle is isosceles.
31. ()()() 1,0,2,1,5,2,3,1,1ABC 0251641 AB =++= 41914 AC =++= 436141 BC =++=
Because , ABBC = the triangle is isosceles.
32. ()()() 4,1,1,2,0,4,3,5,1 41914 136037 125935 ABC AB AC BC =++= =++= =++=
Neither
33. () 4808620 ,,6,4,7 222 ++−+ =
39. Center is midpoint of diameter: 2113313 ,,,2,1 2222 ++− =
Radius is distance from center to endpoint: ()() 2 22 3121 1231114 242 d =−+−++=++=
−+−+−=
()() 2 22 321 21 24xyz
40. Center is midpoint of diameter: () 244053 ,,3,2,1 222 −−+−+ =−−
34. 7522231 ,,1,0, 2222 =−
35. () 314860 ,,2,6,3 222 +++ =
36. ()52 93733 ,,,3,5 2222 +−
−++ =−
37. Center: () 7,1,2
Radius: 1 ()()() 222 7121xyz −+−++=
38. Center: () 1,5,8
Radius: 5 ()()() 222 15825xyz ++++−=
Radius is distance from center to endpoint: () () ()() () 22 2 430231141621 d =−−−+−+−−=++= ()()() 222 32121xyz ++−++=
41. Center: () 7,7,6
Tangent to xy-plane
Radius is z-coordinate, 6.
()()() 222 77636xyz ++−+−=
42. Center: () 4,0,0
Tangent to yz-plane
Radius is distance to yz-plane, 4.
() 2 22 416xyz+++=
43. ()()() ()()() 222 222 222 26810 216981611916 13425 xyzxyz xxyyzz xyz ++−+++= −+++++++=−+++ −++++=
Center: () 1,3,4
Radius: 5
45.
Center: 9 ,1,5 2
Radius: 109 2
46.
Center: () 1 3 ,1,0
Radius: 1
Center: () 1 2 3,,1
Radius: 4
47. (a) 24,42,312,2,2 v =−−−=− (b) 222 vijk =−++ (c)
48. (a) 40,05,314,5,2 v =−−−=− (b) 452 vijh =−+ (c)
49. (b) () 31,32,434,1,1 v =−−−−= (c) 4 vijk =++ (a), (d)
(1,2,3) (3,3,4) (0,0,0) (4,1,1) v xy 12 (4,3,7) (6,4,9) (2,1,2) z 9 6 3 9 9
50. (b) ()() 42,31,726,4,9 v =−−−−−−=− (c) 649 vijk =++ (a), (d) x
51. 43,12,601,1,6 113638 v v =−−−=− =++=
Unit vector: 1,1,6 116 ,, 38383838 =
52. () 21,42,241,6,6 v =−−−−−=− 1363673 v =++=
Unit vector: 1,6,6 166 ,, 73737373 =
53. 04,52,204,3,2=−−−=− v () 2 22 432169429=−++=++= v
Unit vector: 1432 4,3,2,, 29292929 −=−
54. () () 2 22 11,22,300,0,3 0033 =−−−−−−=− =++−= v v
Unit vector: 1 0,0,30,0,1 3 −=−
55. ()()() 123,,0,6,23,5,6qqq −=− () 3,1,8 Q =
56. () () () () 123 5 21 232 4 3 ,,0,2,1,, 1,,3 qqq Q −=− =−
57. (a) 22,4,4 v = (b) 1,2,2 v −=−−− (c) 33 22 ,3,3 v = (d) 00,0,0 v =
58. (a) 2,2,1 v −=−− (b) 24,4,2 v =− (c) 11 22 1,1, v =− (d) 55 22 5,5, v =− x
59. 1,2,32,2,14,0,4 3,0,0 z =−+ =−−+− = uvw
60. 1 2 53 5,10,156,6,32,0,2 3,4,20 zuvw =−− =−−−− =−
61. 1 3 3 1 3 3 93 91,2,334,0,4 9,18,2712,0,12 21,18,15 −= =+ =+ =+− =+− = zuw zuw zuw
62. 123 123 11 22 33 2321,2,32,2,14,0,43,,0,0,0 0,6,93,3,30,0,0 0300 6302 9303 0,2,3 zzz zzz zz zz zz uvwz z +−+=+−−−+=
63. (a) and (b) are parallel because 6,4,1023,2,5 −−=−− and 10 42 333 2,,3,2,5. −=−
64. (b) and (d) are parallel because ()41233 32234 2 ijkijk −+−=−−+ and ()3933 12 482234 ijkijk −+=−+
65. 342 zijk =−++
(a) is parallel because 6842. ijkz−++=
66. 7,8,3 z =−−
(b) is parallel because () 14,16,6. z z −=−
67. ()()() 0,2,5,3,4,4,2,2,1 PQR 3 2 3,6,9 2,4,6 3,6,92,4,6 PQ PR = = =
So, PQ and PR are parallel, the points are collinear.
68. ()()() 1 2 4,2,7,2,0,3,7,3,9 6,2,4 3,1,2 3,1,26,2,4 PQR PQ PR =−− =− −=−−−
So, PQ and PR are parallel. The points are collinear.
69. () 1,2,4, P ()() 2,5,0,0,1,5QR 1,3,4 1,1,1 PQ PR =− =−−
Because PQ and PR are not parallel, the points are not collinear.
70. ()()() 0,0,0,1,3,2,2,6,4 1,3,2 2,6,4 PQR PQ PR =− =−
Because PQ and PR are not parallel, the points are not collinear.
71. ()()()() () 2,9,1,3,11,4,0,10,2,1,12,5 1,2,3 1,2,3 2,1,1 2,1,1 ABCD
AB CD AC BD = = =− =−
Because ABCD = and ,ACBD = the given points form the vertices of a parallelogram.
72. ()()()() 1,1,39,1,2,11,2,9,3,4,4 8,2,5 8,2,5 2,3,7 2,3,7 ABCD
AB DC AD BC =−− =−− =− =−
Because ABDC = and , ADBC = the given points form the vertices of a parallelogram.
73. () 2 22 1,0,1 101 112 =− =−++ =+= v 74. ()()() 222 5,3,4 534 25916 50 52 =−−− =−+−+− =++ = = v
75. 350,3,5 092534 vjk v =−=− =++=
76. 252,5,1 425130 vijk v =+−=− =++=
Section 11.2 Space Coordinates and Vectors in Space 1107
77. 231,2,3 14914 vijk v =−−=−− =++=
78. 4374,3,7vijk=−++=− 1694974 v =++=
79. 2,1,2 4143 v v =− =++=
(a) 1 2,1,2 3 v v =− (b) 1 2,1,2 3 v v −=−−
80. 6,0,8 3606410 v v = =++= (a) 1 6,0,8 10 v v = (b) 1 6,0,8 10 v v −=−
81. 453 162595052 =−+ =++== vijk v
(a) () 122232 453 5210 52 =−+=−+ vijkijk v
(b) () 122232 453 5210 52 −=−−+=−+− vijkijk v
82. 53 259135 =+− =++= vijk v
(a) () 13533535 53 73535 35 =+−=+− vijkijk v (b) () 13533535 53 73535 35 −=−+−=−−+ vijkijk v
83. 0,3,3 1010 32 111010 100,,0,, 2222 u v u == ==
84. 1,1,1 33 3 111333 3,,,, 333333 u v u == ==
85. () 2,2,1 3332211 ,,1,1, 22323332 u v u ====−
86. 4,6,2 14217 77,, 14 2141414 u v u ===
2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.
87. ()() 2cos30sin30 30,3,1 vjk jk = ±°+±° =±=±
88. () () () () 52 5cos45sin45or 2 52 5cos135sin135 2 vikik vikik =°+°=+ =°+°=−+
89. ()()() 2 3 3,6,3 2,4,2 4,3,02,4,22,1,2 v v =−− =−− +−−=−
90. () () () 10 2 33 1013 33 5,6,3 ,4,2 1,2,5,4,2,6,3 v v =− =− +−=
91. A sphere of radius 4 centered at () 111,,.x yz ()()() 211 222 111 ,, 4 v xxyyzz xxyyzz =−−− =−+−+−= ()()() 222 111 16 xxyyzz −+−+−=
92. ()()() ()()() 222 0 222 1112 1114 rr xyz xyz −=−+−+−= −+−+−=
This is a sphere of radius 2 and center () 1,1,1.
93. The set of all points () ,,x yz such that 1 > r represent outside the sphere of radius 1 centered at the origin.
94. (a) ()() ,,3,3,3xyz = 3,3,33,0,0 33,30,300,3,3 =− =−−−= v
(b) ()() ,,4,4,8xyz = 4,4,84,0,0 44,40,800,4,8 =− =−−−= v
95. The terminal points of the vectors , tt uuv + and s t uv + are collinear.
96. (a)
(b) () 0 abaabb wuvijk =+=+++= 0,0,0aabb=+==
So, a and b are both zero.
(c) () 2 1,2,1 aabb aabb ijkijk wuv +++=++ =+== =+
(d) () 23 1,2,3 aabb aabb ijkijk +++=++ =+== Not possible
97. Let α be the angle between v and the coordinate axes. ()()() () coscoscos 3cos1 13 cos 3 3 33 1,1,1 33 vijk v vijk ααα α α =++ == == =++=
98. () () 2 2 5507550100
99. (a) The height of the right triangle is 2218.hL=− The vector PQ is given by 0,18,.PQh =−
The tension vector T in each wire is 0,18, ch T =− where 24 8. 3 ch == So, 8 0,18, h h T =− and
(b) (d)
(e) From the table, 10 T = implies 30 L = inches.
100. As in Exercise 99(c), x a = will be a vertical asymptote. So, 0
and is a horizontal asymptote.
102. Let A lie on the y-axis and the wall on the x-axis. Then ()() 0,10,0,8,0,6,AB== () 10,0,6 C =− and 8,10,6,10,10,6.ABAC=−=−−
102,259ABAC==
Thus, 12420,650 ABAC ABAC FF== 12
103. ()() 2 dAPdBP =
Sphere; center: 41 ,3,, 33
radius: 211 3
Section11.3TheDotProductofTwoVectors
1. The vectors are orthogonal (perpendicular) if the dot product of the vectors is zero.
2. If 2 arccos30, v =° v then 2 cos30. v °= v
So, the angle between v and j is 30°.
3. 3,4,1,5uv==−
(a) ()() 314517 uv⋅=−+=
(b) ()() 334425 uu⋅=+=
(c) () 2 2 2 1526 v =−+=
(d) () 171,517,85 uvv⋅=−=−
(e) ()()() 3331751uvuv⋅=⋅==
4. 4,10,2,3uv==−
(a) ()() 4210322 uv⋅=−+=
(b) ()() 441010116 uu⋅=+=
(c) () 2 222313 v =−+=
(d) () 222,344,66 uvv⋅=−=−
(e) ()()() 3332266uvuv⋅=⋅==
5. 6,4,3,2u=v−=−
(a) ()()() 634226 uv⋅=−+−=−
(b) ()()() 664452 uu⋅=+−−=
(c) () 2 223213 v =−+=
(d) () 263,278,52 uvv⋅=−−=−
(e) ()()() 3332678uvuv⋅=⋅=−=−
6. 7,1,4,1 =−−=−−uv
(a) ()() 741129⋅=−−+−−=uv
(b) ()() 771150⋅=−−+−−=uu
(c) ()() 2224117 =−+−= v
(d) () 294,1116,29⋅=−−=−−uvv
(e) ()()() 3332987 ⋅=⋅==uuuv
7. 2,3,4,0,6,5uv=−=
(a) ()()()()() 2036452 uv⋅=+−+=
(b) ()()()() 22334429 uu⋅=+−−+=
(c) 222206561 v =++=
(d) () 20,6,50,12,10 uvv⋅==
(e) ()()() 33326uvuv⋅=⋅==
8. 5,0,5,1,2,1=−=−uv
(a) ()()() 51025110⋅=−−++=uv
(b) ()()()()() 55005550⋅=−−++=uu
(c) () 22 22 1216=−++= v
(d) () 101,2,110,20,10⋅=−=−uvv
(e) ()()() 3331030 ⋅=⋅==uvuv
9. 2 , uijkvik =−+=−
(a) ()()()() 2110111 uv⋅=+−+−=
(b) ()()()()() 2211116 uu⋅=+−−+=
(c) () 2 22112 v =+−=
(d) ()uvvvik ⋅==−
(e) ()()() 33313uvuv⋅=⋅==
10. 22,32 uijkvijk =+−=−+
(a) ()()()() 2113225 uv⋅=+−+−=−
(b) ()()()() 2211229 uu⋅=++−−=
(c) () 2 22213214 v =+−+=
(d) ()()53251510 uvvijkijk ⋅=−−+=−+−
(e) ()()() 333515uvuv⋅=⋅=−=−
11. 1,1,2,2uv==− 0 cos0 28 θ === uv uv
(a) 2 π θ = (b) 90 θ =°
12. 3,1,2,1uv==− 51 cos 1052 θ === uv uv
(a) 4 π θ = (b) 45 θ =°
13. 3,24 uijvij =+=−+ 21 cos 102052 θ === uv uv
(a) 1 arccos1.713 52 θ =−≈
(b) 98.1 θ ≈°
ππ ππ θ =+=+ =+=−+
uijij vijij uv uv
=−+=−
14. () 31 cossin 6622 3322 cossin 4422 cos 32122 13 22224
(a) () 27 arccos13 42 π θ
=−=
(b) 105 θ =°
15. 1,1,1,2,1,1uv==− 22 cos 3 36 θ === uv uv
(a) 2 arccos1.080 3 θ =≈
(b) 61.9 θ ≈°
16. 32,23 uijkvij =++=− ()() 32230 cos0 θ +−+ === uv uvuv
(a) = 2 π θ (b) 90 θ =°
17. 34,=23=+−+ uijvjk 8813 cos 65 513 θ ⋅−− === uv uv
(a) 813 arccos2.031 65 θ =−≈
(b) 116.3 θ ≈°
18. 23,2 uijkvijk =−+=−+ 99321 cos 14 146221 θ ==== uv uv
(a) 321 arccos0.190 14 θ =≈
(b) 10.9 θ ≈°
19. cos uv uv θ ⋅ = ()()85cos20 3 uv π ⋅==
20. ()() cos 5 4025cos5003 6 uv uv uv θ π = ⋅==−
21. 12 4,3,,23 not parallel 0orthogonal uv uv uv c ==− ≠ ⋅=
22. () 1 3 1 6 2,24 parallel uijvij uv =−−=− =−
28. Consider the vector 3,0,0 joining () 0,0,0 and () 3,0,0, and the vector 1,2,3 joining () 0,0,0 and () 1,2,3: 3,0,01,2,330 −⋅=−<
The triangle has an obtuse angle, so it is an obtuse triangle.
29. ()() () 3 1 22 2,0,1,0,1,2,,,0ABC 53 22 11 22 2,1,1 ,,1 ,,2 AB AC BC =− =−− =−− 53 22 11 22 2,1,1 ,,1 ,,2 BA CA CB =−− =− =− 3 2 1 2 53 44 510 120 20
ABAC BABC CACB ⋅=+−> ⋅=−−+> ⋅=++>
The triangle has three acute angles, so it is an acute triangle.
23. 6,2 not parallel 80not orthogonal
Neither ujkvijk uv uv c =+=−− ≠ ⋅=−≠
24. 23,2 uijkvijk =−+−=+− not parallel c uv ≠ 0orthogonal uv⋅=
25. 2,3,1,1,1,1 not parallel 0orthogonal uv uv uv c =−=−−− ≠ ⋅=
26. cos,sin,1, sin,cos,0 not parallel 0orthogonal u v uv uv c θθ θθ =− =− ≠
⋅=
27. The vector 1,2,0 joining () 1,2,0 and () 0,0,0 is perpendicular to the vector 2,1,0 joining () 2,1,0 and () 0,0,0: 1,2,02,1,00 ⋅−=
The triangle has a right angle, so it is a right triangle.
30. ()()() 2,7,3,1,5,8,4,6,1 ABC 3,12,5 2,13,4 5,1,9 AB AC BC =− =− =− 3,12,5 2,13,4 5,1,9 BA CA CB =−− =−− =−− 6156200 1512450 1013360
ABAC BABC CACB ⋅=−+−> ⋅=−+> ⋅=++>
The triangle has three acute angles, so it is an acute triangle.
31. 22,1443 =++=++=uijku 222 1 3 2 3 2 3 144 999 cos1.2310 or 70.5 cos0.8411 or 48.2
cos0.8411 or 48.2 coscoscos1 αα ββ γγ αβγ = ≈° = ≈° = ≈° ++=++= 32. 222 53,259135 5 cos0.5639 or 32.3 35 3 cos1.0390 or 59.5 35 1 cos1.7406 or 99.7 35 2591 coscoscos1 353535 uijku αα ββ γγ αβγ =+−=++= = ≈° = ≈° = ≈° ++=++=
33. 7,491151 =+−=++=uijku
7 cos11.4 51 αα = ≈° 1 cos82.0 51 ββ = ≈° 1 cos98.0 51 γγ =− ≈°
34. 435,169255052uijku=−++=++== 222 4 cos2.1721or124.4 52 3 cos1.1326or64.9 52 51 cosor45 4 522 16925 coscoscos1 505050
35. 222 0,6,4,0361652213 cos0 or 90 2 3 cos0.5880 or 33.7 13 2 cos2.1588 or 123.7 13 94 coscoscos01 1313
36. 1,5,2,125430uu=−=++=
1 cos1.7544or100.5 30
5 cos0.4205or24.1 30 2 cos 1.1970or68.6 30 1254 coscoscos 1 303030
37. ) 6,7,1,4uv==
(a) 1w = ()() 2 22 proj 6174 1,4 14 34 1,42,8 17 v uv uv v ⋅ = + = + == (b) ) 21 6,72,84,1 wuw=−=−=−
38. 9,7,1,3uv==
(a) 1w = ()() 2 2 proj 9173 1,3 13 30 1,33,9 10 v uv uv v ⋅ = + = + ==
(b) 21 9,73,96,2 wuw=−===−
39. 232,3,55,1uijvij =+==+=
(a) 1w = ()() 2 2 proj 2531 5,1 51 1351 5,1, 2622 v uv uv v = + = + == (b) 21 5115 2,3,, 2222 wuw=−=−=−
40. 232,3,323,2uijvij =−=−=+=
(a) 1w = ()()() 2 22 proj 2332 3,2 32 03,20,0 v uv uv v = +− = + == (b) 21 2,3 wuw=−=−
41. 0,3,3,1,1,1uv==−
(a)
(b) 21 0,3,32,2,22,1,1 wuw=−=−−=
42. () 8,2,0,2,1,1uv==−
(a) 1
43. 924,44 =−−−=+ uijkvjk
(b) 21 9,2,40,3,3 9,1,1 =− =−−−−−−
(b) 21 8,2,06,3,32,1,3 wuw=−=−−=−
44. 5,58 =−−=−++ uijkvijk
5 18 ,1, 55 v uv wuv v
45.u is a vector and vw is a scalar. You cannot add a vector and a scalar.
46. 2 c uv vuuvu v ⋅ = =
47. Yes, 22 22 11 uvvu vu vu
and v are parallel.

This represents the total revenue the restaurant earned on its three products. (b)
48. (a) Orthogonal, 2 π θ = (b) Acute, 0 2 π θ << (c) Obtuse, 2 π <<θπ
49. 3240,1450,2235 2.25,2.95,2.65 = = u v ()()() 32402.2514502.9522352.65 $17,490.25 ⋅=++ = uv
50. 3240,1450,2235 2.25,2.95,2.65 = = u v Decrease prices by 2%: 0.98v New total revenue:
51. Answers will vary. Sample answer: 13 42 uij =−+ Want 0. uv⋅= 122 vij =+ and 122 vij−=−− are orthogonal to u.
52. Answers will vary. Sample answer: 94. uij =− Want 0. uv⋅= 49 vij =+ and 49 vij−=−− are orthogonal to u
53. Answers will vary. Sample answer: 3,1,2. u =− Want 0. uv⋅= 0,2,1 v = and 0,2,1 v −=−− are orthogonal to u
54. Answers will vary. Sample answer: 4,3,6. u =− Want 0 uv⋅=
0,6,3 v = and 0,6,3 v −=−− are orthogonal to u
55. Let s = length of a side. ,, 3 s ss s v v = =
56. 1 1 2 2 ,, 3 ,,0 2 226 cos 3 23 6 arcos35.26 3 sss s ss s v v v v θ θ = = = = == =≈°
57. (a) Gravitational Force 48,000 Fj =− () ()() () 1 2 1 cos10sin10 48,000sin10 8335.1cos10sin10 8335.1lb vij Fv wvFvv v v ij w =°+° ==⋅ =−° ≈−°+° ≈ (b) () 21 48,0008335.1cos10sin10 8208.546,552.6 wFw jij ij =− =−+°+° =− 2 47,270.8lb w ≈
58. (a) Gravitational Force 5400 =− Fj () ()() () 1 2 1 cos18sin18 5400sin18 1668.7cos18sin18 1668.7lb =°+° ==⋅ =−° ≈−°+° = vij Fv wvFvv v v ij w (b) () 21 54001668.7cos18sin18 1587.04884.3 =− =−+°+° ≈− wFw jij ij 2 5135.7lb ≈ w y x v s s s z y x v1 v2 (s, s,0) (s,s,s) z
=+
59. 13 85 22 10 425ft-lb W Fij vi Fv
= =⋅=
60. ()()() proj cos20 cos206550 3054.0 ft-lb PQ WPQ PQ = =° =° ≈ F F
61. ()1600cos25sin25 2000 Fij vi =°+° = () 16002000cos25
2900.2km-N Fv W =⋅=° ≈ ≈
2,900,184.9Newton meters (Joules)
62. () ()() proj cos60 1 40040 2 8000 Joules PQ WPQ PQ = =° = = F F
63. False.
For example, let 1,1,2,3uv== and 1,4. w = Then 235 uv⋅=+= and 145. uw⋅=+=
64. True () 000 wuvwuwv ⋅+=⋅+⋅=+= so, w and uv + are orthogonal.
65. (a) The graphs 2 1 yx = and 13 2 yx = intersect at () 0,0 and ()1,1.
(b) 1 2 y x ′ = and 2 23 1 3 y x ′ =
At ()0,0,1,0 ± is tangent to 1y and 0,1 ± is tangent to 2y
At () 1 1,1,2 y ′ = and 2 1 . 3 y ′ = 1 1,2 5 ± is tangent to 1 1 ,3,1 10 y ± is tangent to 2y
(c) At ()0,0, the vectors are perpendicular ()90. °
At ()1,1, ()() 11 1,23,1 51 510 cos 11 502
45 θ θ === =°
66. (a) The graphs 3 1 yx = and 13 2 yx = intersect at ()1,1, () 0,0 and ()1,1.
(b) 2 1 3 yx ′ = and 2 23 1 3 y x ′ =
At ()0,0, 1,0 ± is tangent to 1y and 0,1 ± is tangent to 2y
At ()1,1, 1 3 y ′ = and 2 1 3 y ′ = 1 1,3 10 ± is tangent to 1 1 ,3,1 10 y ± is tangent to 2y
(0,0) y = x 1/3 y x 2112 1 2 1 2 (1,1) (0,0) (1,1) y = x 3 y = x 1/3
(c) At ()0,0, the vectors are perpendicular ()90. °
At ()1,1, ()() 11 1,33,1 63 1010 cos. 11105
0.9273or53.13 θ θ === ≈°
By symmetry, the angle is the same at () 1,1. y x 112 1 1 2 y = x 2 (1,1)
At () 1 1,1,3 y ′ −−= and 2 1 3 y ′ = 1 1,3 10 ± is tangent to 1 1 ,3,1 10 y ± is tangent to 2y
67. (a) The graphs of 2 1 1 yx =− and 22 1 yx=− intersect at () 1,0 and ()1,0.
(b) 1 2 y x ′ =− and 2 2. y x ′ =
At () 1 1,0,2 y ′ =− and 2 2. y ′ = 1 1,2 5 ±− is tangent to 1 1 ,1,2 5 y ± is tangent to 2y
At () 1 1,0,2 y ′ −= and 2 2. y ′ =− 1 1,2 5 ± is tangent to 1 1 ,1,2 5 y ±− is tangent to 2.y
(c) At ()1,0, 113 cos1,21,2. 5 55 θ =−⋅−=
0.9273or53.13 θ ≈°
By symmetry, the angle is the same at ()1,0.
68. (a) To find the intersection points, rewrite the second equation as 3 1.yx += Substituting into the first equation () 2 6 10, 1. yxxxx += = =
There are two points of intersection, () 0,1 and ()1,0,as indicated in the figure.
(b) First equation: ()() () 2 1 1211 21 yxyyy y ′′ += += = +
At () 1 1,0,. 2 y ′ =
Second equation: 32 13.yxyx ′ =− = At ()1,0, 3. y ′ = 1 2,1 5 ± unit tangent vectors to first curve, 1 1,3 10 ± unit tangent vectors to second curve
69. In a rhombus, uv = The diagonals are uv + and .uv
()()()() 22 0 uvuvuvuuvv uuvuuvvv uv +⋅−=+⋅−+⋅ =⋅+⋅−⋅−⋅ =−=
So, the diagonals are orthogonal.
⇔+⋅+=−⋅− ⇔+=− ⇔ y x 112 2 1 (1,0) (0,1) y = x 31 x =( y +1) 2 u v u + v u v u v u + v u − v
At ()0,1, the unit tangent vectors to the first curve are 0,1, ± and the unit tangent vectors to the second curve are 1,0. ±
(c) At ()1,0, 1151 cos2,11,3. 510502 θ =⋅== 4 π θ ≈ or 45°
At () 0,1 the vectors are perpendicular, 90. θ =°
or
70. If u and v are the sides of the parallelogram, then the diagonals are uv + and , uv as indicated in the figure.
the parallelogram is a rectangle.
⇔⋅= ⇔⋅=−⋅
()()()() 22 0 22
The diagonals are equal in length. uv uvuv uvuvuvuv uvuv
or
71. (a)
(b) Length of each edge: 22202 kkk ++=
(c) ()() 2 1 cos 2 22 1 arccos60 2 k kk θ
(d) 1 2 ,,0,,,, 222222 0,0,0,,,, 222222
72. cos,sin,0,cos,sin,0uv==ααββ
The angle between u and v is α β ( Assuming that αβ) > Also, () ()() cos coscossinsin 11 coscossinsin. uv uv αβ α
α β α β −= + = =+
1. × uv is a vector that is perpendicular (orthogonal) to both u and v
2. If u and v are the adjacent sides of a parallelogram, then A =×uv
73. ()() ()() () 2 22 2 22 2 2 uvuvuv uvuuvv =uuvuuvvv uuvv uuvvuv +=+⋅+ =+⋅++⋅ ⋅+⋅+⋅+⋅ =+⋅+ ≤++≤+
So, uvuv +≤+
74. Let 1 proj, v wu = as indicated in the figure. Because 1w is a scalar multiple of ,v you can write 122 c uwwvw =+=+
Taking the dot product of both sides with v produces ()22cc uvvwvvvwv ⋅=+⋅=⋅+⋅
2 , c v = because 2 w and v are orthogonol.
So, 2 2 cc uv uvv v ⋅= = and 1 2 proj. c v uv wuvv v ===
75. cos cos cos becausecos1. uvuv uvuv uv uv θ θ θ θ ⋅= ⋅= = ≤≤
Section11.4TheCrossProd uctofTwoVectorsinSpace
4. 010 001 ijk jki ×== x y (k,0, k) (kk,0) (0, kk) k k k z θ w1 w2 u v
3. 010 100 ijk jik ×==−
5. 100 001 ijk ikj ×==−
6. 001 100 ijk kij ×==
7. (a) 240201016 325 ijk uvijk ×=−=+−
11. 4,1,0,6,3,0=−=−uv
41060,0,6 630 ×=−== ijk uvk
()()()()()4010060 ⋅×=+−+= ⊥× uuvuuv
()()()()6030060⋅×=−++= ⊥× vuvvuv
12. 5,2,2,0,1,8=−=uv
5221440514,40,5 018 ×=−=+−=− ijk uvijk
()()()()()514240250 ⋅×=−++−= ⊥× uuvuuv
()()()()()014140850 vuvvuv ⋅×=++−= ⊥× xy 1 i k j z 1 1 1
(b) () 201016 vuuvijk ×=−×=−−+ (c) vv0 ×=
8. (a) 30515169 232 ijk uvijk ×==−++
(b) () 15169 vuuvijk ×=−×=−−
(c) vv0 ×=
9. (a) 732173310 115 ijk uvijk ×==−−
(b) () 173310 vuuvijk ×=−×=−++
(c) vv0 ×=
10. (a) 219 621 19562 ×=− =−++ ijk uv ijk
(b) () 19562×=−×=−− vuuvijk
(c) 0 vv×=
13. ,2 uijkvijk =++=+− 111232,3,1 211 ijk uvijk ×==−+−=−−
()()()() 121311 0 uuv uuv ⋅×=−++− = ⊥×
()()()()() 221311 0 vuv vuv ⋅×=−++−− = ⊥×
14. 6,2 uijvijk =+=−++ 160613 211 ijk uvijk ×==−+
()()()() 16610 uuvuuv ⋅×=+−= ⊥×
()()()()() 26111130 vuvvuv ⋅×=−+−+= ⊥×
15. 4,3,1 2,5,3 431141026 253 1 14,10,26 972 1 14,10,26 183 7513 ,, 939393 =− = ×=−=−−+ × =−− × =−− =−− u v ijk uvijk uv uv
16. 8,6,4 10,12,2 8646024156 10122 1 60,24,156 3622 5213 ,, 322322322 =−− =−− ×=−−=++ × = × = u v ijk uvijk uv uv
17. 325 4 32537 114 1 3,7,1 59 371 ,, 595959 =−+− =−+ ×=−−=++ × = × = uijk vijk ijk uvijk uv uv
18. () 2 46 0028 406 1 80,1,0 8 = =+ ×== × === × uk vik ijk uvj uvjj uv
19. 010 011 uj vjk ijk uvi = =+ ×== 1 uvi A =×== 20. 111 011 uijk vjk ijk uvjk =++ =+ ×==−+ 2 uvjk A =×=−+=
21. 3,2,1 1,2,3 3218,10,4 123 u v ijk uv =− = ×=−=− 8,10,418065 A uv =×=−==
22. 2,1,0 1,2,0 u v =− =−
2100,0,3 120 0,0,33 A ijk uv uv ×=−= =×==
23. ()()()() 0,3,2,1,5,5,6,9,5,5,7,2 ABCD
AB DC BC AD = = = =
1,2,3 1,2,3
5,4,0 5,4,0
Because ABDC = and ,BCAD = the figure ABCD is a parallelogram.
AB and AD are adjacent sides 12312,15,6 540 ABAD ijk ×==−− 1442253695 AABAD=×=++=
24. ()()()() 2,3,1,6,5,1,7,2,2,3,6,4 ABCD
4,8,2 4,8,2 1,3,3 1,3,3 AB DC BC AD =− =− =− =−
Because ABDC = and ,BCAD = the figure ABCD is a parallelogram.
AB and AD are adjacent sides 48218,14,20 133 3241964002230 ABAD AABAD ijk ×=−=−− =×=++=
25. ()()() 0,0,0,1,0,3,3,2,0ABC 1111 222 1,0,3,3,2,0 1036,9,2 320 36814 ABAC
ABAC AABAC ijk ==− ×==−− =×=++=
26. ()()() 2,3,4,0,1,2,1,2,0ABC 11 22 2,4,2,3,5,4 242622 354 4411 ABAC ABAC AABAC ijk ijk =−−=−− ×=−−=−−+ =×==
27. 20 Fk =− () 1 2 cos40sin40 0cos402sin40210cos40 0020 10cos407.66ft-lb PQ PQ PQ jk ijk Fi F =°+° ×=°°=−° ×=°≈
28. () 2000cos30sin30100031000 0.16 000.16 0100031000 1603 1603ft-lb PQ PQ PQ Fjkjk k ijk F i F =−°+°=−− = ×= = ×=
29. (a) () 5 15inchesfeet 4 12inches1foot 5 4 180cossin AC BC AB jk Fjk θθ == == =−+ =−+
(c) When 13 30,225180268.38 22
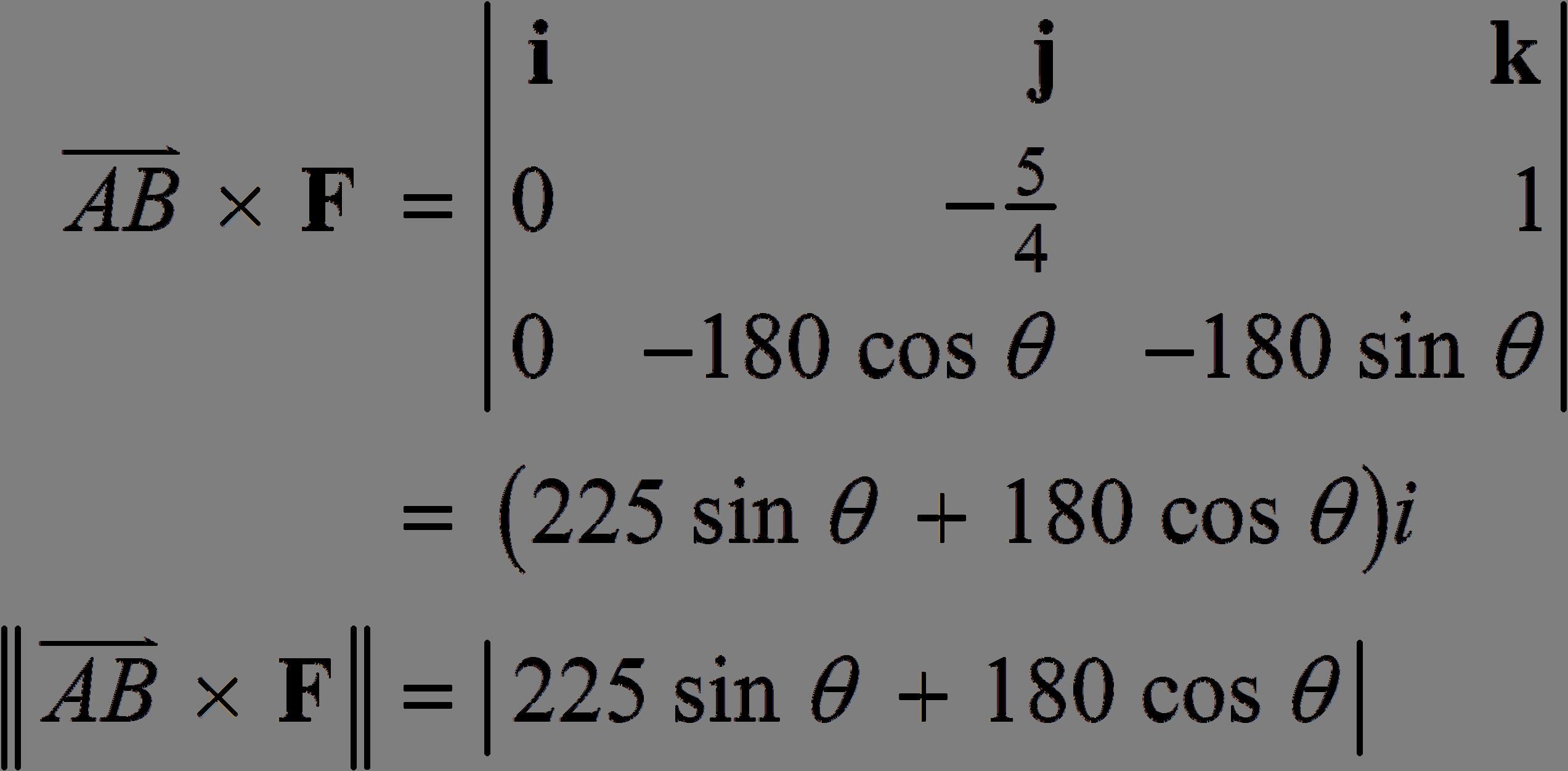
(d) If 225sin180cos, T =+θθ 0 T = for 4 225sin180costan141.34. 5 θθθθ =−
0141.34,
and F are perpendicular. (e)
From part (d), the zero is 141.34, θ ≈° when the vectors are parallel.
30. (a) Place the wrench in the xy-plane, as indicated in the figure. The angle from AB to F is 30180210°+°+=°+θθ
423sin210coscos210sin42cos210cossin210sin 1331 423cossin42cossin84sin 2222 k k kk
(b) When 2 45,8442259.40 2 F OA θ =°×==≈
(c) Let 84sin 84cos0when90. T dT d θ θθ θ = ===°
This is reasonable. When 90, θ =° the force is perpendicular to the wrench.
31. () 100 0101 001 uvw×==
32. () 111 2101 001 uvw⋅×==−
33. () 201 0306 001 uvw⋅×==
34. () 200 1110 022 uvw⋅×==
35. () () 110 0112 101 2 V uvw uvw ⋅×== =⋅×=
36. () () 131 06672 404 72 uvw uvw V ⋅×==− =⋅×=
37. () () 3,0,0 0,5,1 2,0,5 300 05175 205 75 V u v w uvw uvw = = = ⋅×== =⋅×=
38. () () () 0,4,0 3,0,0 1,1,5 040 30041560 115 60 u v w uvw uvw V = =− =− ⋅×=−=−−= =⋅×=
39. (a) ()()() ()()() ()()() ()()() b c d h x uvwvwu wuvuvw vwuuwv vwuwuv ⋅×=×⋅ =⋅×=×⋅ =⋅×=−⋅ =⋅×=×⋅ (e) ()()() ()()() f g uwvwvu wvuuvw ⋅×=⋅× =⋅×=−×⋅
So, abcdh ==== and efg ==
40.uv0u ×= and v are parallel. uv0u ⋅= and v are orthogonal.
So, u or v (or both) is the zero vector.
41. The cross product is orthogonal to the two vectors, so it is orthogonal to the yz-plane. It lies on the x-axis, since it is of the form ,0,0. k
42. Form the vectors for two sides of the triangle, and compute their cross product.
212121313131 ,,,, x xyyzzxxyyzz −−−×−−−
43. False. If the vectors are ordered pairs, then the cross product does not exist.
44. False. The cross product is zero if the given vectors are parallel.
45. False. Let ,0 1,0,0,1,0,1,0,0.uvw ===−
Then, ,but. uvuw0vw ×=×=≠
46. True
48. 123123 ,,,,,,is a scalar: uuuvvvcuv==
49.
50.
51.
233213311221 233213113212213 233213113212213 uvijk uvu0 uvv0 uvuvuvuvuvuv uvuvuuvuvuuvuvu uvuvvuvuvvuvuvv ×=−−−+− ×⋅=−+−+−= ×⋅=−+−+−= So, uvu ×⊥ and uvv ×⊥
52. If u and v are scalar multiples of each other, c uv = for some scalar c ()()() uvvvvv00 ccc ×=×=×==
If ,uv0 ×= then sin0. uv θ = () Assume,. u0v0 ≠≠ So, sin0,0, θθ== and u and v are parallel. So, c uv = for some scalar c
53. sin uvuv θ ×=
If u and v are orthogonal, 2 θπ = and sin1. θ = So, uvuv ×=
54. 111222333 , ,,,,,,, c ababcabcuvw ===
Section11.5LinesandPlanesinSpace
1. The parametric equations of a line L parallel to ,,,abc v = and passing through the point () 111 ,, Pxyz are 1 , x xat=+ 1 , y ybt=+ 1 zzct =+ The symmetric equations are 111 x xyyzz abc ==
2. In the equation of the plane ()()() 214350, xyz −+−−+= 2,4,ab== and 1. c =− Therefore, the normal vector is 2,4,1.
3. Answers will vary. Any plane that has a missing xvariable in its equation is parallel to the x-axis.
Sample answer: 35 yz−=
4. First choose a point Q in one plane. Then use Theorem 11.13: PQn D
where P is a point in the other plane and n is normal to that plane.
5. 2,3,4 x tytzt =−+==+
(a) () 0,6,6: For 02, x t ==−+ you have 2. t =
Then () 326 y == and 426. z =+= Yes, ()0,6,6lies on the line.
(b) () 2,3,5: For 22, x t ==−+ you have 4. t =
Then () 34123. y ==≠ No, () 2,3,5 does not lie on the line.
(c) () 4,6,2: For 42, x t =−=−+ you have 2. t =−
Then () 326 y =−=− and 422. z =−= Yes, () 4,6,2 lies on the line.
6. 37 2 28 xy z ==+
(a) () 7,23,0: Substituting, you have 73237 02 28 222 ==+ == Yes, () 7,23,0 lies on the line.
(b) () 1,1,3: Substituting, you have 1317 32 28 111 ==−+
−=−=− Yes, () 1,1,3 lies on the line.
(c) () 7,47,7: Substituting, you have 73477 72 28 555 ==−+ −≠≠−
No, () 7,47,7 does not lie on the line.
7. Point: () 0,0,0
Direction vector: 3,1,5
Direction numbers: 3, 1, 5
(a) Parametric: 3,,5 x tytzt===
(b) Symmetric: 35 x z y ==
8. Point: () 0,0,0
Direction vector: 5 2,,1 2 v =−
Direction numbers: 4,5,2
(a) Parametric: 4,5,2 x tytzt=−==
(b) Symmetric: 452 x yz ==
9. Point: () 2,0,3
Direction vector: 2,4,2 v =−
Direction numbers: 2,4,2
(a) Parametric: 22,4,32 x tytzt=−+==−
(b) Symmetric: 23 242 xyz+− ==
10. Point: () 3,0,2
Direction vector: 0,6,3 v =
Direction numbers: 0, 2, 1
(a) Parametric: 3,2,2 x ytzt =−==+
(b) Symmetric: 2,3 2 y zx =−=−
11. Point: () 1,0,1
Direction vector: 32 vijk =−+
Direction numbers: 3,2,1
(a) Parametric: 13,2,1 x tytzt =+=−=+
(b) Symmetric: 11 321 xyz ==
12. Point: () 3,5,4
Directions numbers: 3,2,1
(a) Parametric: 33,52,4 x tytzt =−+=−=+
(b) Symmetric: 35 4 32 xy z +− ==−
13. Points: () 22 5,3,2,,,1 33
Direction vector: 1711 3 33 vijk =−−
Direction numbers: 17,11,9
(a) Parametric: 517,311,29 x tytzt =+=−−=−−
(b) Symmetric: 532 17119 xyz−++ ==
14. Points: ()() 0,4,3,1,2,5
Direction vector: 1,2,2
Direction numbers: 1,2,2
(a) Parametric: ,42,32 x tytzt ==+=−
(b) Symmetric: 43 22 yz x ==
15. Points: ()() 7,2,6,3,0,6
Direction vector: 10,2,0
Direction numbers: 10,2,0
(a) Parametric: 710,22,6xtytz =−=−+=
(b) Symmetric: Not possible because the direction number for z is 0. But, you could describe the line as 72 , 6. 102 xy z −+ ==
16. Points: ()() 0,0,25,10,10,0
Direction vector: 10,10,25
Direction numbers: 2,2,5
(a) Parametric: 2,2,255 x tytzt===−
(b) Symmetric: 25 225 xyz ==
17. Point: () 2,3,4
Direction vector: vk =
Direction numbers: 0, 0, 1
Parametric: 2,3,4 x yzt ===+
18. Point: () 4,5,2
Direction vector: vj =
Direction numbers: 0,1,0
Parametric: 4,5,2xytz=−=+=
19. Point: () 2,3,4
Direction vector: 32 vijk =+−
Direction numbers: 3,2,1
Parametric: 23,32,4 x tytzt =+=+=−
20. Point () 4,5,2
Direction vector: 2 vijk =−++
Direction numbers: 1,2,1
Parametric: 4,52,2 x tytzt =−−=+=+
21. Point: () 5,3,4
Direction vector: 2,1,3 v =−
Direction numbers: 2,1,3
Parametric: 52,3,43 x tytzt=+=−−=−+
22. Point: () 1,4,3
Direction vector: 5 vij =−
Direction numbers: 5,1,0
Parametric: 15,4,3xtytz =−+=−=−
23. Point: () 2,1,2
Direction vector: 1,1,1
Direction numbers: 1,1,1
Parametric: 2,1,2 x tytzt =−=+=+
24. Point: () 6,0,8
Direction vector: 2,2,0
Direction numbers: 2,2,0
Parametric: 62,2,8xtytz=−−==
25. Let () 0:3,1,2tP==−− () other answers possible 1,2,0 v =− () any nonzero multiple of is correct v
26. Let ()0:0,5,4tP== () other answers possible 4,1,3 v =− () any nonzero multiple of is correct v
27. Let each quantity equal 0: () 7,6,2 P =−− () other answers possible 4,2,1 v = () any nonzero multiple of is correct v
28. Let each quantity equal 0: () 3,0,3 P =− () other answers possible
5,8,6 v = () any nonzero multiple of is correct v
29. 11:3,2,4L =− v and () 6,2,5 P =− on 1L
22:6,4,8L =−− v and () 6,2,5 P =− on 2L
The lines are identical.
30. 11:2,1,3L =− v and () 1,1,0 P =− on 1L
22:2,1,3L =− v and P not on 1L
The lines are parallel.
31. 11:4,2,3L =− v and () 8,5,9 P =−− on 1L
22:8,4,6L =−− v and () 8,5,9 P =−− on 2L
The lines are identical.
32. 11:4,2,4L = v and () 1,1,3 P =− on 1L
22:1,0.5,1L = v and P not on 2L
The lines are parallel.
33. At the point of intersection, the coordinates for one line equal the corresponding coordinates for the other line. So, (i) 4222, ts+=+ (ii) 323, s =+ and (iii) 11.ts −+=+
From (ii), you find that 0 s = and consequently, from (iii), 0. t = Letting 0, st== you see that equation (i) is satisfied and so the two lines intersect. Substituting zero for s or for t, you obtain the point () 2,3,1.
4First line 22Second line 817717 cos 51 179317
55.5 uik vijk uv uv
34. By equating like variables, you have (i) 3131, ts −+=+ (ii) 4124, ts+=+ and (iii) 241. ts+=−+
From (i) you have , s t=− and consequently from (ii), 1 2 t = and from (iii), 3. t =− The lines do not intersect.
35. Writing the equations of the lines in parametric form you have
3 14 xt x s = =+ 2 2 yt ys =− =−+ 1 33. zt zs =−+ =−−
For the coordinates to be equal, 314 ts =+ and 22. ts−=−+ Solving this system yields 17 7 t = and 11 7 . s = When using these values for s and t, the z coordinates are not equal. The lines do not intersect.
36. Writing the equations of the lines in parametric form you have
23 32 x t x s =− =+ 26 5 yt ys =+ =−+ 3 24. zt zs =+ =−+
By equating like variables, you have 2332, ts−=+ 265, ts+=−+ 324. ts+=−+ So, 1,1ts=−= and the point of intersection is () 5,4,2.
41. Point: () 3,2,2
Normal vector: 23 nijk =+−
()()() 2332120 23100 xyz xyz −+−−−= +−−=
42. Point: () 0,0,0
Normal vector: 32 nik =−+
() () 3,6,1First line 2,1,4Second line 442966 cos 483 4621966
82.6 u v uv uv θ θ =− = ==== ≈°
37. 2410xyz+−−=
(a) ()()()() 7,2,1:7224110 −−−+−−−=
Point is in plane.
(b) ()()() 5,2,2:5224210 +−−=
Point is in plane.
(c) ()()() 6,1,1:62141110 −−−+−−−=−≠
Point is not in plane.
38. 2360 xyz++−=
(a) ()()() 3,6,2:2363260 −++−−=
Point is in plane.
(b) ()()() 1,5,1:21531660 −−−++−−=−≠
Point is not in plane.
(c) ()()() 2,1,0:22130610 ++−=−≠
Point is not in plane.
39. Point: () 1,3,7
Normal vector: 0,1,0 nj==
()()() () 0113070 30 xyz y −+−+−−= −=
40. Point: () 0,1,4
Normal vector: 0,0,1 nk==
()()() 0001140 40 xyz z −+++−= −=
()()() 3000200 320 xyz xz −−+−+−= −+=
43. Point: () 1,4,0
Normal vector: 2,1,2 v =−−
()()() 2114200 2260 xyz xyz +−−−−= −−+=
44. Point: () 3,2,2
Normal vector: 43 vijk =+− ()()() 432320 4380 xyz xyz −+−−−= +−−=
45. Let u be the vector from () 0,0,0 to ()2,0,3:2,0,3 u =
Let u be the vector from () 0,0,0 to ()3,1,5:3,1,5 v −−=−−
Normal vectors: 2033,19,2 315 ijk uv×==−−
()()() 30190200 31920 xyz xyz −−−−−= −−=
46. Let u be the vector from () 3,1,2 to () 2,1,5: 1,2,3 u =−
Let u be the vector from () 3,1,2 to () 1,2,2: 2,1,4 v =−−−
Normal vector: 1235,10,551,2,1 214 ijk uv×=−=−−=−−
()()() 132120 210 xyz xyz −++−−= +−+=
47. Let u be the vector from () 1,2,3 to ()3,2,1:22uik =−
Let v be the vector from () 1,2,3to ()1,2,2:24vijk−−=−−−
Normal vector:
() () 1 2 101434 241 ijk uvijk ×−=−=−+
()()() 4132430 434100 xyz xyz −−−+−= −+−=
48. () 1,2,3,Normal vector: () ,110,10vi xx =−=−=
49. () 1,2,3,Normal vector: () ,130,30 vk zz =−=−=
50. The plane passes through the three points ()() () 0,0,0,0,1,0,3,0,1.
The vector from ()0,0,0to () 0,1,0: uj =
The vector from ()0,0,0to ()3,0,1:3vik =+
Normal vector: 0103 301 ijk uvik ×==−
30xz−=
51. The direction vectors for the lines are 2, uijk =−++ 34. vijk =−+−
Normal vector: ()2115 341 ijk uvijk ×=−=−++
Point of intersection of the lines: () 1,5,1
()()()1510 50 xyz xyz ++−+−= ++−=
52. The direction of the line is 2. uijk =−+ Choose any point on the line, ()0,4,0,for example, and let v be the vector from ()0,4,0to the given point () 2,2,1: 22 vijk =−+
Normal vector: 2112 221 ijk uvik ×=−=−
()()2210 20 xz xz −−−= −=
53. Let v be the vector from () 1,1,1 to () 2,2,1: 32 vijk =++
Let n be a vector normal to the plane 233:23 xyz nijk−+==−+
Because v and n both lie in the plane P, the normal vector to P is 312711 231 ijk vnijk ×==−−
()()() 72121110 71150 xyz xyz −+−−−= +−−=
54. Let v be the vector from ()3,2,1to () 3,1,5: 6 vjk =−−
Let n be the normal to the given plane: 672 nijk =++
Because v and n both lie in the plane P, the normal vector to P is: () 01640366 672 220183 ijk vnijk ijk ×=−−=−+ =−+ ()()() 203182310 20183270 xyz xyz −−−+−= −+−=
55. Let ui = and let v be the vector from () 1,2,1 to () 2,5,6: 77 vijk =++
Because u and v both lie in the plane P, the normal vector to P is: ()100777 177 ijk uvjkjk ×==−+=−−
()()210 10 yz yz
−+=
56. Let uk = and let v be the vector from ()4,2,1to () 3,5,7: 736 vijk =−++ Because u and v both lie in the plane P, the normal vector to P is:
()0013737 736 ijk uvijij ×==−−=−+
()() 34720 37260 xy xy −+−= +−=
57. Let () ,,x yz be equidistant from ()2,2,0and () 0,2,2. ()()() ()()() 222222 222222 220022 44444444 4848 0Plane xyzxyz xxyyzxyyzz xz xz −+−+−=−+−+− −++−++=+−++−+ −+=−+ −=
58. Let () ,,x yz be equidistant from () 1,0,2and () 2,0,1. ()()() ()()() 222222 222222 102201 21444421 245425 220 0Plane xyzxyz xxyzzxxyzz xzxz xz
59. Let () ,,x yz be equidistant from () 3,1,2 and () 6,2,4. ()()() ()()() 222222 222222 312624 692144123644816 62414124856 1864420 932210Plane xyzxyz xxyyzzxxyyzz xyzxyz xyz xyz ++−+−=−+++−
60. Let () ,,x yz be equidistant from () 5,1,3 and () 2,1,6 ()()() ()()() 222222 222222 513216 1025216944211236 102635421241 1441860 72930Plane xyzxyz xxyyzzxxyyzz xyzxyz xyz
61. First plane: 1 5,2,8=−− n and () 0,3,0 P = on plane
Second plane: 21 15,6,243 =−=− nn and P not on plane
Parallel planes
(Note: The equations are not equivalent.)
62. First plane: 1 2,1,3=− n and () 4,0,0 P = on plane
Second plane: 21 8,4,124=−= nn and P not on plane.
Parallel planes (Note: The equations are not equivalent.)
63. First plane: 1 3,2,5=− n and () 0,0,2 P = on plane
Second plane: 21 75,50,12525=−= nn and P on plane
Planes are identical.
(Note: The equations are equivalent.)
64. First plane: 1 1,4,1=−− n and () 6,0,0 P =− on plane
Second plane: 21 555 222 ,10, =−−= nn and P on plane
Planes are identical.
(Note: The equations are equivalent.)
65. (a) 1 32 nijk =+− and 2 42 nijk =−+ 12 12 7 6 cos 6 1421 nn nn θ === 65.91 θ ≈°
(b) The direction vector for the line is () 2 14272. 321 1 ijk nnjk ×=−=+
Find a point of intersection of the planes. 64214 420 714 2 xyz xyz x x +−= −+= = =
Substituting 2 for x in the second equation, you have 422 yz −+=− or 21.zy=− Letting 1, y = a point of intersection is () 2,1,1.
2,1,12 x ytzt==+=+
66. (a) 1 2,1,1 =− n and 2 6,3,2=− n
12 12 13 136 cos 42 649 40.70 θ θ === ≈° nn nn
(b) The direction vector for the line is () 12 21152. 632 ijk nnij ×=−=+
Find a point of intersection of the planes. 6336 6324 510 2 xyz xyz z z −++= −+= = =
Substituting 2 for z in the first equation, you have 20 xy −+= or 2.yx = Letting 0, x = a point of intersection is () 0,0,2. 5,10,2xtytz=== or ,2,2xtytz===
67. (a) 1 3,1,1=− n and 2 4,6,3 = n
12 12 9 9671 cos 671 1161 69.67 θ θ === ≈° nn nn
(b) The direction vector for the line is 12 3119522. 463 ×=−=−−+ ijk nnijk
Find a point of intersection of the planes. 186642 4632 22944 xyz xyz xz −+= ++= +=
Let 0,22442zxx == = and () 32071. yy−+= =−
A point of intersection is () 2,1,0. 29,15,22 x tytzt=−=−−=
68. (a) 1 63, nijk =−+ 2 5 nijk =−++
12 12 4 2138 cos 207 4627 1.684596.52 nn nn θ θ === ≈≈°
(b) The direction vector for the line is 12 63116,31,3. 115 ijk nn×=−=−−
Find a point of intersection of the planes. 635 55 xyz xyz −+= −++= 635 663030 33135 xyz xyz yz −+= −++= +=
Let () 9,244,9,2. 416,931,23 yzx x tytzt =−= =− =−−=−−=+
69. The normal vectors to the planes are 1 5,3,1, n =− 2 1,4,7, n = 12 12 cos0. nn nn θ ==
So, 2 θπ = and the planes are orthogonal.
70. The normal vectors to the planes are 1 3,1,4, n =− 2 9,3,12. n =−−
Because 213,nn =− the planes are parallel, but not equal.
71. The normal vectors to the planes are 1 36, nijk =−+ 2 5, nijk =+−
12 12 536 41382138 cos. 414207 4627 nn nn θ ⋅−− ====

=š
So, 2138 arccos83.5. 207 θ
72. The normal vectors to the planes are 1 32, nijk =+− 2 42, nijk =−+
12 12 382 766 cos. 426 1421 nn nn θ ====
So, 6 arccos65.9. 6 θ =≈°
73. The normal vectors to the planes are 1 1,5,1 n =−− and 2 5,25,5. n =−− Because 215,nn = the planes are parallel, but not equal.
74. The normal vectors to the planes are 122,0,1,4,1,8, nn=−= 1 12 cos0 2 nn nn θ ==
So, 2 π θ = and the planes are orthogonal.
75. 2 y ≤−

42612 xyz++=

3626 xyz++=
234 xyz−+=

82. 24 xyz−+=
83. Writing the equation of the line in parametric form and substituting into the equation of the plane you have: 72,4,15 x tytzt=−+=+=−+
()()() 7234156 66 ttt −+++−−+= =
The equation is valid for all t
The line lies in the plane.
84. Writing the equation of the line in parametric form and substituting into the equation of the plane you have: ()() 14,2,36 1 214325, 2 x tytzt ttt =+==+ ++=−=
Substituting 1 2 t =− into the parametric equations for the line you have the point of intersection () 1,1,0.
The line does not lie in the plane.
85. Writing the equation of the line in parametric form and substituting into the equation of the plane you have: 13,12,3 x tytzt =+=−−=+ ()() 21331210,110, tt ++−−=−= contradiction
So, the line does not intersect the plane.
86. Writing the equation of the line in parametric form and substituting into the equation of the plane you have: ()() 42,13,25 54231317,0 x tytzt ttt =+=−−=−+ ++−−==
Substituting 0 t = into the parametric equations for the line you have the point of intersection () 4,1,2.
The line does not lie in the plane.
87. Point: () 0,0,0 Q
Plane: 23120 xyz++−=
Normal to plane: 2,3,1 n =
Point in plane: () 6,0,0 P
Vector 6,0,0 PQ =−
88. Point: () 0,0,0 Q
1 1 426 9 54 PQ D === n n x y 1 4 3 4 1 2 z
Plane: 590 xyz+−−=
Normal to plane: 5,1,1 n =−
Point in plane: () 0,9,0 P
Vector 0,9,0 PQ =− 9 3 27 PQ D n n ===
89. Point: () 2,8,4 Q
Plane: 25 xyz++=
Normal to plane: 2,1,1 n =
Point in plane: 0,0,5 P
Vector: 2,8,1 PQ =− 11116 6 6 PQ D n n ===
90. Point: () 1,3,1 Q
Plane: 34560 xyz−+−=
Normal to plane: 3,4,5 n =−
Point in plane: () 2,0,0 P
Vector :1,3,1PQ 20 22 50 PQ D n n ===
91. The normal vectors to the planes are 1 1,3,4 n =− and 2 1,3,4. n =− Because 12 , nn = the planes are parallel. Choose a point in each plane.
() 10,0,0 P is a point in 3410.xyz−+=
() 6,0,0 Q is a point in 346.xyz−+=
4,0,0, PQ =− 1 1 4226 13 26 PQ D n n ===
92. The normal vectors to the planes are 1 2,7,1 = n and 2 2,7,1. = n Because 12 , = nn the planes are parallel. Choose a point in each plane.
() 0,0,13 P is a point in 2713. xyz++=
() 0,0,9 Q is a point in 279. xyz++=
0,0,4 PQ =
93. The normal vectors to the planes are 1 3,6,7 n =− and 2 6,12,14. n =−− Because 212,nn =− the planes are parallel. Choose a point in each plane.
() 0,1,1 P is a point in 3671. xyz −++=
25 ,0,0 6 Q is a point in 6121425. xyz−−= 1 1 25 ,1,1 6 272 272794 188 94294 PQ PQ D n n =− ⋅ ====
94. The normal vectors to the planes are 1 1,6,2=− n and 2 1 2 ,3,1. =− n Because 122, = nn the planes are parallel. Choose a point in each plane.
() 3,0,0 P is a point in 623.xyz −++=
() 0,0,4 Q is a point in 1 2 34.xyz −++=
3,0,4 PQ = 1 1 5541 41 41 PQ D === n n
95. 4,0,1 u =− is the direction vector for the line.
() 1,5,2 Q is the given point, and () 2,3,1 P is on the line.
3,2,3 PQ =−
3232,9,8 401 PQ ijk u ×=−=−−−
1492533 17 17 PQ D u u × ===
96. 2,1,2 u = is the direction vector for the line.
() 1,2,4 Q is the given point, and () 0,3,2 P is a point on the line () let 0. t = 1,1,2 PQ = 1120,2,1 212 ijk u PQ ×==− 55 3 9 u u PQ D × ===
97. 1,1,2 u =−− is the direction vector for the line.
() 2,1,3 Q is the given point, and () 1,2,0 P is on the line () let 0in the parametric equations for theline. t =
3,1,3 PQ =−−
3131,9,4 112 PQ ijk u ×=−−=−−−
1811698773 3 11463 u u PQ D × ++ ===== ++
98. 0,3,1 u = is the direction vector for the line.
() 4,1,5 Q is the given point, and () 3,1,1 P is on the line.
1,2,4 PQ =−
12414,1,3 031 PQ ijk u ×=−=−− 2 1419206103515 1055 91 PQ D u u × = ++ ==== +
99. The direction vector for 1L is 1 1,2,1. v =−
The direction vector for 2L is 2 3,6,3. v =−−
Because 213,vv =− the lines are parallel.
Let () 2,3,4 Q to be a point on 1L and () 0,1,4 P a point on 2L 2,2,0. PQ =
2 uv = is the direction vector for 2L 2 2206,6,18 363 PQ ijk v ×==−− 2 2 36363243962266 5433 9369 PQ D v v × = ++ ==== ++
100. The direction vector for 1L is 1 6,9,12. v =−
The direction vector for 2L is 2 4,6,8. v =−
Because 12 3 2 , vv = the lines are parallel.
Let () 3,2,1 Q to be a point on 1L and () 1,3,0 P a point on 2.4,5,1.LPQ =−
2 uv = is the direction vector for 2L 2 45134,36,44 468 PQ ijk v ×=−= 2 2 222 343644 163664 4388109731813 2929 116 PQ D v v × = ++ = ++ ===
105. 0.230.146.85zxy=++
(a) The approximations are close to the actual values.
(b) If x and y both increase, then so does z
106. On one side you have the points ()() 0,0,0,6,0,0,and () 1,1,8.
1 600486 118 ijk njk ==−−
101. Exactly one plane contains the point and line. Select two points on the line and observe that three noncolinear points determine a unique plane.
102. There are an infinite number of planes orthogonal to a given plane in space.
103. Yes, Consider two points on one line, and a third distinct point on another line. Three distinct points determine a unique plane.
104. (a) 0 axbyd++= matches (iv). The plane is parallel to the z-axis.
(b) 0 axd+= matches (i). The plane is parallel to the yz-plane.
(c) 0 czd+= matches (ii). The plane is parallel to the xy-plane.
(d) 0 axczd++= matches (iii). The plane is parallel to the y-axis.
On the adjacent side you have the points ()() 0,0,0,0,6,0,and () 1,1,8.
2 060486 118 ijk nik ==+
107. 11:6;L xt =+ 1 8,yt =− 1 3 zt =+
22:1,L xt =+ 2 2,yt =+ 2 2 zt =
(a) At 0, t = the first insect is at () 1 6,8,3 P and the second insect is at () 2 1,2,0. P
Distance ()()() 222 618230708.37=−+−+−=≈ inches
(b) Distance ()()() ()() 2222222 121212 562353070,010 xxyyzzttttt =−+−+−=+−+−=−+≤≤
(c) The distance is never zero.
(d) Using a graphing utility, the minimum distance is 5 inches when 3 t = minutes.
108. First find the distance D from the point () 3,2,4 Q to the plane. Let () 4,0,0 P be on the plane. 2,4,3 n =− is the normal to the plane.
7,2,42,4,3 14812 181829 29 41692929 n n PQ D −+−
The equation of the sphere with center () 3,2,4 and radius 182929 is ()()() 222 324 324. 29 xyz ++−+−=
109. The direction vector v of the line is the normal to the plane, 3,1,4. v =−
The parametric equations of the line are 53, x t =+ 4,yt =− 34. zt =−+
To find the point of intersection, solve for t in the following equation: ()()() 4 13 35344347 268 ttt t t +−−+−+= = =
Point of intersection: () () () () 774823 444 53,4,34,,131313131313 +−−+=−
110. The normal to the plane, 2,1,3 n =−− is perpendicular to the direction vector () 2,4,0 v = of the line because 2,1,32,4,00. −−⋅=
So, the plane is parallel to the line. To find the distance between them, let () 2,1,4 Q be on the line and () 2,0,0 P on the plane. 4,1,4. PQ =−− 4,1,42,1,3 191914 14 41914 PQ D n n = === ++
111. 251211113 314 ijk uvijk ×=−=−−−
Direction numbers: 21,11,13 21,111,413 x tytzt==+=+
112. The unknown line L is perpendicular to the normal vector 1,1,1 n = of the plane, and perpendicular to the direction vector 1,1,1. u =− So, the direction vector of L is 1112,2,0. 111 ijk v ==−
The parametric equations for L are 12, x t =− 2,yt = 2. z =
113. True
114. False. They may be skew lines. () See Section Project.
115. True
116. False. For example, the lines , x t = 0, y = 1 z = and 0, x = , yt = 1 z = are both parallel to the plane 0, z = but the lines are not parallel.
117. False. For example, planes 7115 xyz+−= and 5241 xyz+−= are both perpendicular to plane 233, xyz−+= but are not parallel.
118. True
Section11.6SurfacesinSpace
1. Quadric surfaces are the three-dimensional analogs of conic sections.
2. In the xz-plane, 2 zx = is a parabola. In three-space, 2 zx = is a cylinder.
3. The trace of a surface is the intersection of the surface with a plane. You find a trace by setting one variable equal to a constant, such as 0 x = or 2. z =
4. No. For example, 222 0 xyz++= is a single point and 22 1 xy+= is a right circular cylinder.
5. Ellipsoid Matches graph (c)
6. Hyperboloid of two sheets Matches graph (e)
7. Hyperboloid of one sheet Matches graph (f )
8. Elliptic cone Matches graph (b)
9. Elliptic paraboloid Matches graph (d)
10. Hyperbolic paraboloid Matches graph (a)
11. 22 9 yz+=
The x-coordinate is missing so you have a right circular cylinder with rulings parallel to the x-axis. The generating curve is a circle.

Section 11.6 Surfaces in Space 1137
12. 2 6 yz+=
The x-coordinate is missing so you have a parabolic cylinder with the rulings parallel to the x-axis. The generating curve is a parabola.

The z-coordinate is missing so you have an elliptic cylinder with rulings parallel to the z-axis. The generating curve is an ellipse.

The x-coordinate is missing so you have a hyperbolic cylinder with rulings parallel to the x-axis. The generating curve is a hyperbola.
15. 222 41 xyz−−=
Hyperboloid of two sheets
xy-trace: 22 41 xy−= hyperbola
yz-trace: none
xz-trace: 22 41 xz−= hyperbola

16. 222 1 162525 xyz++=
Ellipsoid
xy-trace: 22 1 1625 xy+= ellipse
xz-trace: 22 1 1625 xz += ellipse
yz-trace: 22 25 yz+= circle
17. 222 2 22 16164 441 4 xyz y xz −+= −+=
Hyperboloid of one sheet

xy-trace: 2 2 41 4 y x −= hyperbola
xz-trace: () 22 41 xz+= circle
yz-trace: 2 2 41 4 y z += hyperbola

18. 22 4 zxy =+
Elliptic paraboloid
xy-trace: point () 0,0,0
xz-trace: 2 zx = parabola
yz-trace: 2 4 zy = parabola

19. 222 1 141 xyz++=
Ellipsoid
xy-trace: 22 1 14 xy+= ellipse
xz-trace: 22 1 xz+= circle
yz-trace: 22 1 41 yz+= ellipse
20. 2 22 1 4 y zx−−=
Hyperboloid of two sheets
xy-trace: none
xz-trace: 22 1 zx−= hyperbola
yz-trace: 2 2 1 4 y z −= hyperbola
10: z =± 22 1 936 xy+= ellipse

21. 2 22 9 y zx=+
Elliptic cone
xy-trace: point () 0,0,0
xz-trace: zx =±
yz-trace: 3 y z =±

When 1, z =± 2 2 1 9 y x += ellipse
22. 22 3 zyx =−+
Hyperbolic paraboloid
xy-trace: yx =±
xz-trace: 2 1 3 zx =
yz-trace: 2 1 3 zy =−

23. 22 0 xyz−+=
Hyperbolic paraboloid
xy-trace: yx =±
xz-trace: 2 zx =−
yz-trace: 2 zy = 1: y =± 2 1 zx =−
24. 222 22 x yz=+
Elliptic Cone
xy-trace: 2 x y =±
xz-trace: 2 x z =±
yz-trace: point: () 0,0,0
25. 22 0 xyz−+=
Elliptic paraboloid
xy-trace: 2 yx =
xz-trace: () 22 0, point 0,0,0 xz+=
yz-trace: 2 yz = 1: y = 22 1 xz+=
26. 222 222 818182 9941 xyz yzx −++= +−=
Hyperboloid of one sheet



xy-trace: 22 941 yx−= hyperbola
yz-trace: 22 991 yz+= circle
xz-trace: 22 941 zx−= hyperbola

27. These have to be two minus signs in order to have a hyperboloid of two sheets. The number of sheets is the same as the number of minus signs.
28. Yes. Every trace is an ellipse (or circle or point).
29. No. See the table on pages 800 and 801.
30. 22 zxy =+
(a) You are viewing the paraboloid from the x-axis: () 20,0,0
(b) You are viewing the paraboloid from above, but not on the z-axis: () 10,10,20
(c) You are viewing the paraboloid from the z-axis: () 0,0,20
(d) You are viewing the paraboloid from the y-axis: () 0,20,0
31. () 2 22 x zry+= and () 5,zryy == so
22225. x zy+=
32. () 2 22 x zry+= and () 3,zryy =± so
22 9. x zy+=
33. () 2 22 x yrz+= and () 13 2, y rzz== so
22234. x yz+=
34. () 2 22 x yrz+= and () , z x rze== so
222 z x ye+=
35. () 2 22 yzrx += and () 2 , yrx x == so 2 2222 2 24 yzyz x x += +=
36. () 2 22 yzrx += and () 2 1 2 4,zrxx ==− so ()222 1 4 4 yzx +=− 222444. xyz++=
37. () 22 2 22 20 2 xyz x yz +−= +=
Equation of generating curve: 2 yz = or 2 x z =
38. 222 cos x zy+=
Equation of generating curve: cosorcos x yzy==
39. ( ) 2 2222 5858 yzxx +=−=−
Equation of generating curve: 2 58 yx =− or 2 58 zx =−
43. 22 24 x y z =+
(a) When 2 z = we have 22 2, 24 x y =+ or 22 1 48 x y =+
Major axis: 2842 =
Minor axis: 244 = 2222,4,2 cabcc=−==
Foci: () 0,2,2 ±
(b) When 8 z = we have 22 8, 24 x y =+ or 22 1. 1632 x y =+
Major axis: 23282 =
Minor axis: 2168 = 2 321616,4cc=−==
Foci: () 0,4,8 ± 44. 22 24 x y z =+
47. 222 222 1 396339633950 xyz++= x 1234 4 3 2
(a) When 4 y = you have 2 4, 2 x z =+ () 2 1 44. 2 zx −=
Focus: 9 0,4, 2
(b) When 2 x = you have () 2 2 2,42. 4 y zzy =+−=
Focus: () 2,0,3
45. If () ,,x yz is on the surface, then ()()2222 2222 22 22 4444 8 yxyz yyxyyz xzy +=+−+ ++=+−++ +=
Elliptic paraboloid
Traces parallel to xz-plane are circles.
46. If () ,,x yz is on the surface, then () 2 222 2222 22 22 4 816 8162 88 zxyz zxyzz xy zxyz =++− =++−+ =++ =++
Elliptic paraboloid shifted up 2 units. Traces parallel to xy-plane are circles.


Letting , x at = you obtain the two intersecting lines , x at = , ybt =− 0 z = and , x at = 222 ,2. ybtabzabtab =+=+
50. Equating twice the first equation with the second equation: 222222 2644826432 4832 346,a plane xyzyxyzx yx xy +−+−=+−−−
51. The Klein bottle does not have both an “inside” and an “outside.” It is formed by inserting the small open end through the side of the bottle and making it contiguous with the top of the bottle.
Section11.7CylindricalandSphericalCoordinates
1. The cylindrical coordinate system is an extension of the polar coordinate system. In this system, a point P in space is represented by an ordered triple () ,,.rz θ () , r θ is a polar representation of the projection of P in the xy-plane, and z is the directed distance from () , r θ to P.
2. The point is 2 units from the origin, in the xz-plane, and makes an angle of 30° with the z-axis.
3. () 7,0,5, cylindrical cos7cos07 sin7sin00 5 xr yr z θ θ ==−=− ==−= = () 7,0,5, rectangular
4. () 2,,4, π cylindrical
() 2,0,4, rectangular
5. 3,,1, 4
9. ()0,5,1,rectangular
cylindrical
10. () 6,23,1,rectangular
6. 3 6,,2,cylindrical 2
()0,6,2,rectangular
7. 7 4,,3,cylindrical
11. () 2,2,4, rectangular () 2 2 2222 r =+−= () 2 tan arctan1 24 π θθ = =−=− 4 z =− 22,,4, 4 π
cylindrical
12. () 3,3,7, rectangular () () 2 2 331832 3 tan arctan1 34 7 r z π θθ =+−== = =−=−
32,,7, 4 π
cylindrical
13. () 1,3,4, rectangular () 2 2 132 3 tan arctan3 13 4 r z π θθ =+= = ==
2,,4, 3 π
cylindrical
14. () 23,2,6, rectangular 1244 15 arctan 6 3 6 r z π θ =+=
6 π
cylindrical
15. 4 z = is the equation in cylindrical coordinates. (plane)
16. 9,rectangular equation cos9 9sec,cylindrical equation x r r θ θ = = =
17. 22225, xyz+−= rectangular equation 2225,rz−= cylindrical equation
18. 22 2 11,rectangular equation 11,cylindrical equation zxy zr =+− =−
19. 2 , yx = rectangular equation () 2 2 sincos sincos sectan,cylindrical equation
20. 22 2 8,rectangular equation 8cos 8cos,cylindrical equation xyx rr r
21. () 22 2 2 222 10,rectangular equation sin10 sin10,cylindrical equation yz rz rz θ θ =− =−
22. 222 22 30,rectangular equation 30,cylindrical equation xyzz rzz ++−= +−=
23. 22 22 3, cylindrical equation 3 9, rectangular equation r xy xy = += +=
2, z =− cylindrical equation 2, z =− rectangular equation
, cylindrical equation

22 222 5, cylindrical equation 5, rectangular equation rz xyz +=
28. 22 2 cos, cylindrical equation , rectangular equation zr zx θ = =

29. () 2 22 22 2 2 4sin,cylindrical equation 4sin 4 444 24,rectangular equation r rr xyy xyy xy θ θ = = += +−+= +−=
30. () 2 22 22 2 2 2cos, cylindrical equation 2cos 2 20 11, rectangular equation r rr xyx xyx xy θ θ = = += +−= −+=
31. ()4,0,0,rectangular 222 4004 ρ =++= tan00 y x θθ == = arccos0 2 π φ == 4,0,,spherical 2 π
spherical x y z 321 9 123456
32. () 4,0,0, rectangular () 2 22 4004 tan00 arccosarccos0 2 4,0,,spherical 2 y x z ρ θθ π φ ρ π =−++= == = ===
33. () 2,23,4, rectangular () () 2 2 2 223442 ρ =−++= 23 tan3 2 2 3 y x θ π θ ===− = 1 arccos arccos 4 2 2 42,,,spherical 34 z π φ ρ ππ ===
34. ()5,5,2,rectangular ()() () 2 22 55252213 ρ =−+−+== 5 tan1 54 y x π θθ === = 226 arccosarccosarccos 26 213 z φ ρ === 26 213,,arccos,spherical 426 π
35. () 3,1,23, rectangular 31124 ρ =++= 1 tan 3 6 y x θ π θ == = 3 arccos arccos 26 z π φ ρ === 4,,, 66 ππ
36. () 1,2,1, rectangular
() () 2 22 1216
tan2arctan2 1 arccos arccos 6 y x z
37. 4,,, 64 ππ
41. 5,,,spherical 412 ππ
sincos5sincos0.915 124 x ππ ρφθ ==≈
sinsin5sinsin0.915 124 y ππ
cos5cos4.830 12 z π ρθ ==≈
() 0.915,0.915,4.830,rectangular
42. 3 7,,,spherical 49 ππ
cos 4cos22 4 6,2,22,rectangular x
spherical ()
sin cos 4sincos6 46
sin sin 4sinsin2 46
38. () 6,,,spherical 2
sin cos 6sincos6 2
sin sin 6sinsin0 2
cos 6cos0 2 6,0,0,rectangular
3 sincos7sincos1.693 94 x ππ ρφθ ==≈− 3 sinsin7sinsin1.693 94 y ππ ρφθ ==≈
cos7cos6.578 9 z π ρφ ==≈
()1.693,1.693,6.578,rectangular
43. 2, y = rectangular equation sinsin2 2csccsc,spherical equation ρφ θ ρφθ = =
44. 6,rectangular equation z = cos6 6sec,spherical equation ρφ ρφ = =
45. 222 2 49, 49 7, xyz ρ ρ ++= = = rectangular equation spherical equation
0,0,12,rectangular x
39. () 12,,0,spherical 4
sin cos 12sin0cos0 4
sin sin 12sin0sin0 4
cos 12cos012
40. () 9,,,spherical 4
0,0,9,rectangular x y
sin cos 9sincos0 4
sin sin 9sinsin0 4
cos 9cos9
46. () 222 2222 222 2 30,rectangular equation 4 4cos 14cos 1 cos 2 ,conespherical equation 3 xyz xyzz ρρφ φ φ π φ +−= ++= = = = =
47. 22 16, xy+= rectangular equation
4csc,spherical equation
48. 13, x = rectangular equation sincos13 13cscsec,spherical equation
49.
50.
equation
51. 1,spherical equation ρ = 221 1,rectangular equation xyz


54. , spherical equation

55. 4cos, spherical equation ρφ =
57.
58. 4cscsec, spherical equation 4 sincos sincos4

56. 2sec, spherical equation cos2 ρφ ρφ = = 2, rectangular equation z

61. 6,,6,cylindrical 2
62.
63.
64. 22 22 4,,3,cylindrical 2 435 2 3 arccos arccos 5 3 5,,arccos,spherical 25
65. 10,,,spherical 62 10sin10 2 6 10cos0 2 10,,0,cylindrical 6 r z
66. 4,,,spherical 182 4sin4 2 18 4cos0 2 4,,0,cylindrical 18
67. 6,,,spherical 63 6sin33 3 6 6cos3 3 33,,3,cylindrical 6
68. 5 5,,,spherical 6 5sin0 5 6 5cos5 5 0,,5,cylindrical 6 r
69. 7 8,,,spherical 66 8sin4 6 7 6 83 8cos 62 7 4,,43,cylindrical 6
70. 3 7,,,spherical 44 372 7sin 42 4 372 7cos 42 7272,,,cylindrical 242
71. 5 r =
Cylinder
Matches graph (d)
72. 4 π θ =
Plane
Matches graph (e)
73. 5 ρ = Sphere
Matches graph (c)
74. 4 π φ =
Cone
Matches graph (a)
75. 222 , rzxyz =+=
Paraboloid
Matches graph (f )
76. 4sec,cos4 z ρφρφ ===
Plane
Matches graph (b)
77. c θ = is a half-plane because of the restriction 0. r ≥
78. (a) The surface is a cone. The equation is (i)
222 4 9 x yz+=
In cylindrical coordinates, the equation is 222 22 4 9 4 9 2 3 x yz rz rz += = =
(b) The surface is a hyperboloid of one sheet. The equation is (ii) 222 2. xyz+−=
In cylindrical coordinates, the equation is 222 22 22 2 2 2. xyz rz rz +−= −= =+
79. 222 27 xyz++=
(a) 22 27 rz+= (b) 2 2733ρρ = =
80. ()222 4 x yz+= (a) 22 42 rzrz = = (b) () 22222222 4sincossinsincos ρφ θ ρφ θ ρφ += 22 2 4sincos, 1 tan, 4 11 tanarctan 22 φφ φ φφ = = = =
81. 222 20xyzz++−= (a) () 2 2222011 rzzrz +−= +−= (b) () 2 2cos0 2cos0 2cos ρρφ ρρφ ρ φ −= −= =
82. 22 x yz+=
(a) 2 rz = (b) 22 2 2 sincos sincos cos sin csccot ρφρφ ρφφ φ ρ φ ρφφ = = = =
83. 22 4 x yy+= (a) 2 4sin,4sinrrr==θθ (b) () 22sin4sinsin sinsin4sin0 4sin sin 4sincsc ρφρφ θ ρφρφθ θ ρ φ ρ θ φ = −= = =
84. 22 45 xy+=
(a) 2 45 r = or 35 r = (b) 222222 22 sincossinsin45 sin45 35csc
85. 22 9 xy−=





95. Rectangular

96. Cylindrical:

97. Spherical

98. Cylindrical

99. Cylindrical coordinates:

100. Spherical coordinates:

101. False. ()() ,,0,0,1rz θ = and ()() ,,0,,1rzθπ = represent the same point ()() ,,0,0,1.xyz =
102. True () except for the origin.
103. sin,1 sin 1 zr yy zy r θ θ == ====
The curve of intersection is the ellipse formed by the intersection of the plane zy = and the cylinder 1. r =
104. 2seccos22plane 4sphere z ρφρφ ρ = = = =
The intersection of the plane and the sphere is a circle.
ReviewExercisesforChapter11
1. ()()() 1,2,4,1,5,4PQR===
(a) 41,123,1 51,424,2 PQ PR u v ==−−=− ==−−=
(b) 3,42=−=+ uijvij
(c) () 2 222 3110 422025=+−==+==uv
(d) 333,14,25,5 uv −+=−−+=−
2. ()()() 2,1,5,1,2,4PQR =−−=−=
(a) ()() ()() 52,117,0 22,414,5 PQ PR ==−−−−−= ==−−−−= u v
(b) 7,45==+ uivij
(c) 2222 70497 4541=+===+= uv
(d) 337,04,517,5 uv −+=−+=−
3. () () cossin 8cos60sin60 13 84434,43 22 vvij ij ijij =+θθ =°+° =+=+=
4. cossin 11 cos225sin225 22 2222 , 4444 vvi+vj ij ij = θθ =°+° =−−=−−
5. () 0,4,5: 5,4,0 zyx===−−
6. 3 y = describes a plane parallel to the xz-plane and passing through () 0,3,0.
7. ()()() 222 213653 99422 d =−−+−+− =++=
8. () () ()() () 22 2 421115 3641656214 d =−−+−−+−−− =++==
9. ()()() ()()() 222 2 222 3264 32616 xyz xyz −+++−= −+++−=
10. Center: () 040640 222,,2,3,2 +++ =
Radius: ()()() ()()() 222 222 20302449417 23217xyz −+−+−=++= −+−+−=
11. ()() ()() 222 23 2 4469449 239 xxyyz xyz −++−++=−++ −+−+=
Center: () 2,3,0
Radius: 3
12. ()() () ()()() 22 2 222 102569 44342594 5324 xxyy zz xyz −++++ +−+=−+++ −+++−=
Center: () 5,3,2
Radius: 2
13. (a), (d)

15. 1 3 2 1 5,2,330,2,16,6,2 2 5,2,30,6,33,3,1 8,5,1 z =−++ =−−++−− =−−++−− =− uvw
16. () () 20 1 2 1 5,2,30,2,16,6,2 2 1 1,10,4 2 1 ,5,2 2 uvwz uvw z −+−= =−+ =−−+−− =−− =−−
17. 13,64,914,2,10 v =−−−+=− 53,34,612,1,5 =−−−+=−− w
Because 2,−=wv the points lie in a straight line.
18. 85,54,573,1,2 =−−+−=−− v 115,64,376,10,4 =−+−=− w
Because v and w are not parallel, the points do not lie in a straight line.
19. Unit vector: 2,3,5235 ,, 38383838 == u u
20. 6,3,2 8482416 86,3,2,, 7777 49 =−=−
21. 5,0,0,4,4,0,2,0,6PQR ===
(b) () 42,41,732,5,10 v =−−−−−=− (c) 2510=+− vijk
14. (a), (d)
x y 123 45 5 3 1 2 3 2 9 10 8 z (2,1,3) (4,4,7) (2,5,10) x y 1 3 4 2 1 5 6 1 6 5 7 8 z (3,3,8) (3,5,8) (6,2,0) v
(b) 36,32,803,5,8 v =−−−−=−−
(c) 358 vijk =−−+
(a) 1,4,0 PQ ==− u 3,0,6 PR =− v=
(b) ()()()() 1340063 ⋅=−−++=uv
(c) 93645⋅=+=vv
22. 2,1,3,0,5,1,5,5,0PQR =−==
(a) 2,6,2 PQ ==−− u 3,6,3 PR ==− v
(b) ()()()()()() 23662336⋅=−++−−=uv
(c) 936954⋅=++=vv
2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.
23. [] 5cossin3352 442 ππ =+=−+
=+=−+
22 2cossin3 33 ππ
vijij () 52 13 2 ⋅=+uv 2525 5132 22 =+==+= uv ()() () 52213 26 cos 524 θ + + === uv uv
(a) 26 arcos0.262 412 π θ + ==≈
(b) 15 θ ≈°
24. () 1,0,3 2,2,1 1 1910 4413 1 cos 310 θ =−
(a) 1 arccos1.465 310 θ
(b) 83.9 θ =°
25. 7,2,3,1,4,5uv=−=−
Because 0, ⋅=uv the vectors are orthogonal.
26. 3,0,931,0,33 =−=−−=− uv
The vectors are parallel.
27. 4,2,3,4==uv
== v uv wuv v
=
(a) 1 2 proj 20 3,4 25 41216 3,4, 555
(b) 21 121686 4,2,, 5555 wuw=−=−=−
28. 1,1,1,2,0,2=−=uv
(a) 1 2 proj 4 2,0,21,0,1 8
==
== v uv wuv v (b) 21 1,1,11,0,10,1,0 wuw=−=−−=−
29. There are many correct answers. For example: 6,5,0. v =±−
30. ()() cos758cos30 3003ft-lb WPQPQ θ =⋅==° = FF
ijk uvijk
×==−+−
31. (a) 4369267 521
(b) () 9267×=−×=−+ vuuvijk
(c) ×= vv0
ijk uvijk
×==+−
32. (a) 021112 134
(b) () 112×=−×=−−+ vuuvijk
(c) ×= vv0
33. 2108324852 468
×=−=++ ijk uvijk
60324377×==uv
Unit vector: 1 8,12,13 377
34. 3,1,5,2,4,1=−=−uv
31519710 241 ×=−=+− ijk uvijk () 2 22 19710 510 A =×=++− = uv
35. 40 =− Fk () 3 4 9 in.ft = () 3333 cos60sin60 488 PQ =°+°=+jkjk
The moment of F about P is 333 015 88 0040 MPQ=×==− ijk Fi
Torque15 ft-lb =
=⋅⋅===
uvw
36. () () 210 0212510 012 V
37. 93,110,626,11,4 v =−−−=
(a) Parametric equations: 36,11,24 x tytzt=+==+
(b) Symmetric equations: 32 6114 xyz ==
38. 81,104,539,6,2 v =+−−=
(a) Parametric equations: 19,46,32 x tytzt=−+=+=+
(b) Symmetric equations: 143 962 xyz+−− ==
39. () 6,8,2 P =−−
0,1,0 ==vj
6,8,2xytz=−=−+=
40. Direction numbers: () 1,1,1,1,1,1 1,2,3 P = v 1,2,3 x tytzt =+=+=+
41. ()()() [] 3,4,2,3,4,1,1,1,2 0,8,1,4,5,4 08127432 454 ijk nijk PQR PQPR PQPR =−−=−=− =−=− =×=−=−−−
()()() 273443220 2743233 xyz xyz −+−+−−= ++=−
42. 3 nijk =−+ ()()() 3213110 380 xyz xyz +−−+−= −++=
43. The two lines are parallel as they have the same direction numbers, 2,1,1. Therefore, a vector parallel to the plane is 2. vi+jk =−+ A point on the first line is () 1,0,1 and a point on the second line is () 1,1,2. The vector 23 uijk =−− connecting these two points is also parallel to the plane. Therefore, a normal to the plane is () 211 213 2422. ijk vu ijij ×=− =−−=−+
Equation of the plane: ()120 21 xy xy −+= +=
44. Let 52,12,313,3,2 v =−+−= be the direction vector for the line through the two points. Let 2,1,1 n =− be the normal vector to the plane. Then
3325,7,3 211 ijk vn×==−−
is the normal to the unknown plane. ()()() 5571330 573270 xyz xyz −−+−−−= −+−+=
45. () 1,0,2 Q point 2366 xyz−+= A point P on the plane is () 3,0,0.
2,0,2 PQ =−
2,3,6 n =− normal to plane 8 7 n n PQ D ==
46. () 3,2,4 Q point
2510 xyz−+=
A point P on the plane is () 5,0,0.
2,2,4 PQ =−−
2,5,1 n =− normal to plane 1030 3 30 n n PQ D ===
47. The normal vectors to the planes are the same, () 5,3,1. n =−
Choose a point in the first plane () 0,0,2. P Choose a point in the second plane, () 0,0,3. Q
0,0,5 5 535 7 3535 n n PQ PQ D =− ====
48. () 5,1,3 Q point
1,2,1 u =−− direction vector () 1,3,5 P point on line
6,2,2 PQ =−−− 6222,8,14 121 ijk u PQ ×=−−−=−− 264 211 6 PQ D u u × ===
49. 236xyz++= Plane
Intercepts: ()()() 6,0,0,0,3,0,0,0,2,

50. 2 yz =
Because the x-coordinate is missing, you have a cylindrical surface with rulings parallel to the x-axis. The generating curve is a parabola in the yz-coordinate plane.

51. 1 2 yz = Plane with rulings parallel to the x-axis.
52. cos y z =
Because the x-coordinate is missing, you have a cylindrical surface with rulings parallel to the x-axis. The generating curve is cos. y z =

53. 22 2 1 169 xy z ++= Ellipsoid xy-trace: 22 1 169 xy+= xz-trace: 2 2 1 16 x z += yz-trace: 2 2 1 9 y z += x y 6 3 3 (0,0,2) (6,0,0)
54. 222 161690 xyz+−= Cone
xy-trace: point () 0,0,0
xz-trace: 4 3 x z =±
yz-trace: 4 3 y z =±
22 4,9zxy=+=

55. 22 2 22 2 1 169 1 916 xy z yx z −+=− −−=
Hyperboloid of two sheets
xy-trace: 22 1 916 yx −=
xz-trace: None
yz-trace: 2 2 1 9 y z −=

56. 222 1 254100 xyz+−=
Hyperboloid of one sheet
xy-trace: 22 1 254 xy+=
xz-trace: 22 1 25100 xz −=
yz-trace: 22 1 4100 yz −=

57. 22 4. xz+= Cylinder of radius 2 about y-axis

58. 22 16. yz+= Cylinder of radius 4 about x-axis
59. 2 2 zy = revolved about y-axis () 2 22 22 2 2 2 zy x zryy xzy =± += = +=
60. 231 xz+= revolved about the x-axis 12 3 x z = () 2 2 22 12 , 3 x yzrx += =
Cone
61. ()3,3,5,rectangular (a) () 2 2 331223 r =−+== 3 tan 3 3 π θθ = =− 5 z =−
2
62. ()8,8,1,rectangular
(a) 22 8882 r =+= 8 tan1 84 π θθ == = 1 z = 82,,1, cylindrical 4 π
(b) 222 881129 ρ =++= 8 tan1 84 π θθ == = 1 arccosarccos 129 z φ ρ == 129 129,,arccos,spherical 4129 π
63. ()5,,1,cylindrical π cos5cos5 sin5sin0 1 xr yr z θπ θπ ===− === =
()5,0,1,rectangular
66. 8,,,spherical 63 ππ
64. 2,,3,cylindrical 3 π
cos2cos1 3 sin2sin3 3 3 xr yr z π θ π θ
1,3,3,rectangular
65. 4,,,spherical 4 π π
sinsin4sinsin0 4 cos4cos22 4 x y z π
sincos4sincos22 4
()22,0,22,rectangular
() 6,23,4,rectangular
67. 22 2 x yz
(a) Cylindrical:
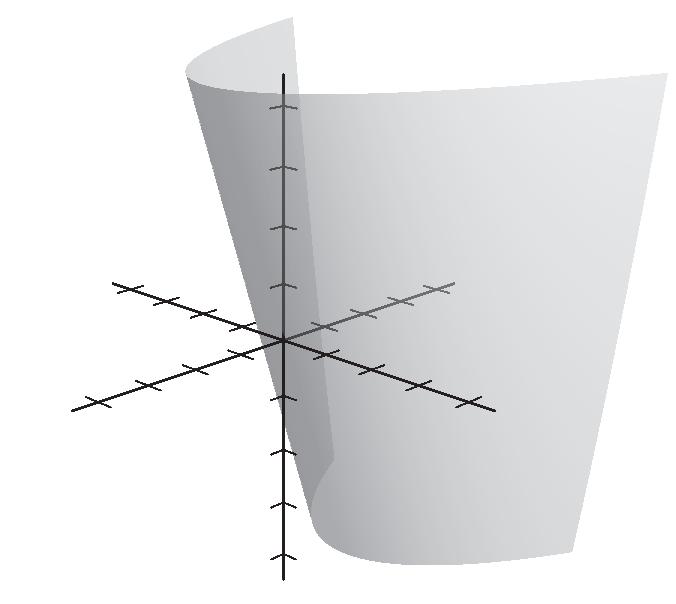
68. 222 16 xyz++=
(a) Cylindrical: 22 16 rz
Spherical:
70. 5,cylindrical equation rz =− 22 222

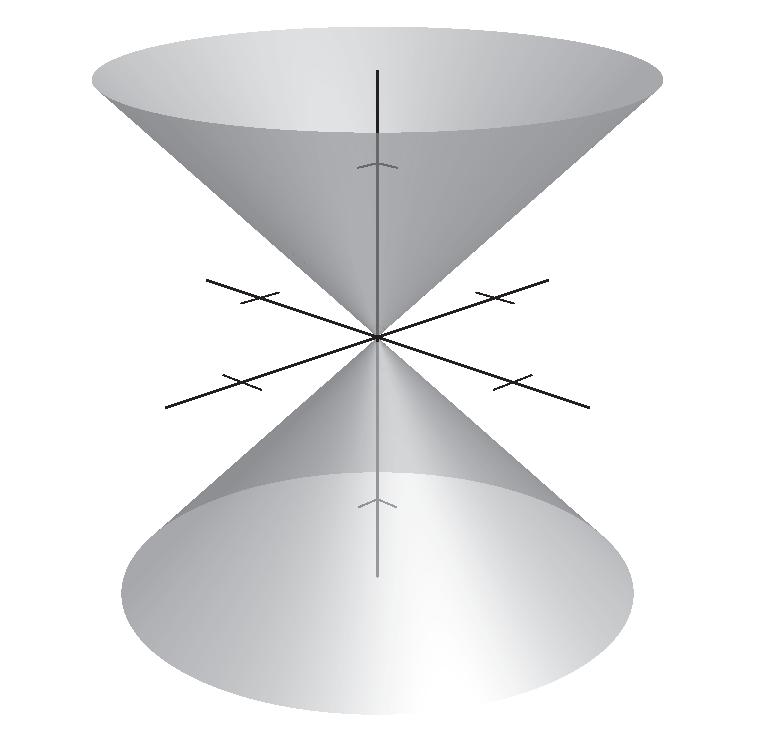
72. 9sec,spherical equation ρθ = cos9 9,rectangular equation z ρ θ = =
ProblemSolvingforChapter11
1. () ()() abc0
3. Label the figure as indicated. From the figure, you see that 1111 and . 2222 SPRQSRPQ abab =−==+=
Because and ,SPRQSRPQ == PSRQ is a parallelogram.
4. Label the figure as indicated. ()() 22 0, because ab ba abbaba PR SQ =+ =− +⋅−=−= ab = in a rhombus.
5. (a) 0,1,1 u = is the direction vector of the line determined by 1P and 2P 1 2,0,10,1,1 2 1,2,2 332 2 22 u u PQ D × = −× = ===
(b) The shortest distance to the line segment is 1 2,0,15. PQ =−=
6. ()() 00nnPPPP+⊥−
Figure is a square. So, 0 PP n = and the points P form a circle of radius n in the plane with center at 0 . P
7. (a) () 1 2 2 1 0 0 1 22 z Vzdzπππ ===
Note: 1 2 (base)(altitude) () 11 1 22 ==ππ
(b) () () () 22 22 22 22 : slice at 1 xy zzc ab xy cacb +== += At ,zc = figure is ellipse of area ()()cacbabcππ = 22 0 0 22 k k abcabk Vabcdc ππ π =⋅==
(c) () 11 22 Vabkk π == (area of base)(height)
8. (a) () 3 2223 0 0 4 22 33 r r x Vrxdxrxr πππ =−=−=
(b) At height 0, zd=> 222 222 22222 2222 1 1 xyd abc x ydcd abcc ++= +=−= () () 22 222222 22 1. xy acdbcd cc += Area () () () 222222 22 222 acdbcd ab cd ccc π π
() 22 2 0 3 2 2 0 2 24 33 c c ab Vcddd c abdcdabc c π π π =− =−=
9. From Exercise 54, Section 11.4, ()()()() .uvwzuvzwuvwz ×××= ×⋅
10. () 1 3,1,21;4,3, 2 x tytztQs =−+=+=−=
(a) 2,1,4 u =− direction vector for line
() 3,1,1 P =− point on line 1,2,1PQs=+ ()() 121 214 7625 PQs ss ijk u ijk ×=+ =−+−−+ ()() 22 76225 21 u u PQ ss D × −+−−+
(b)
The minimum is 2.2361 at 1. Ds≈=−
(c) Yes, there are slant asymptotes. Using , s x = you have () () 2 22 1555 ()5101102221211 21 212121 Dsxxxxxx =++=++=++→±+ () 105 1 21 ys=±+ slant asymptotes.
11. (a) 2sin ρφ = Torus (b) 2cos Sphere ρ φ =

12. (a) 2cos r θ = Cylinder

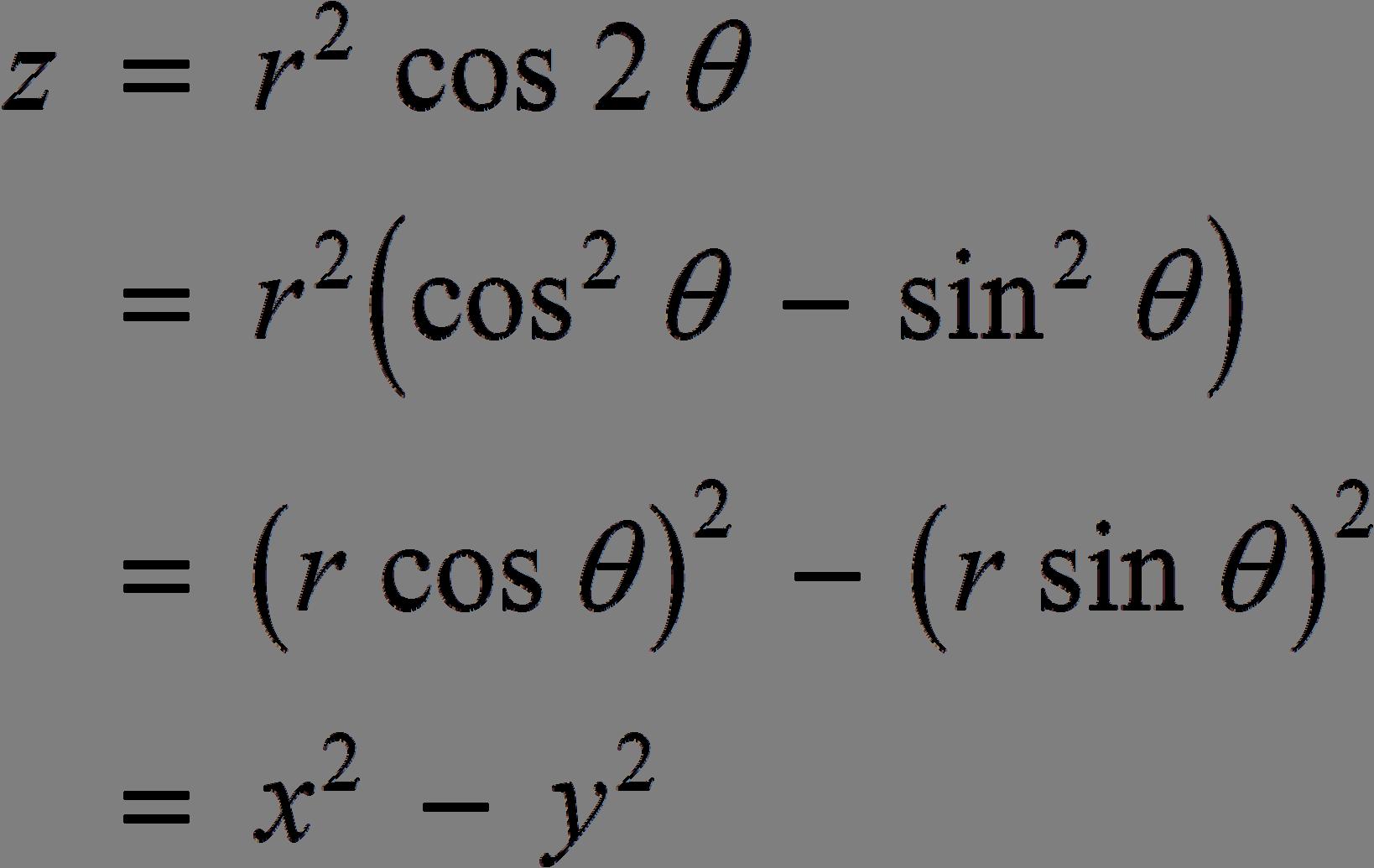
Hyperbolic paraboloid
13. (a) () cos0sin0 uuijui =+=
Downward force wj =− ()()
sin 1cos uT T
= = If () () 212 30,12and 1321.1547 lb and 0.5774 lb 2 33 θ
(b) From part (a), tanand sec. ==θθuT Domain: 090 θ ≤≤° (c) (d)
(e) Both are increasing functions. (f) 22 lim and lim. Yes. As increases, both and increase.
14. (a) The tension T is the same in each tow line. () () () ()6000cos20cos20sin20sin20 2cos20 6000 3192.5 lb 2cos20 iij i TT T T =°+−+°+−° =° =≈ °
(b) As in part (a), 60002cos i T θ = 3000 cos T θ = Domain: 090 θ <<° (c) (d)
(e) As θ increases, there is less force applied in the direction of motion.
15. Let , θα β =− the angle between u and v. Then () sin. uvvu uvuv αβ ×× −==
For cos,sin,0 u αα = and cos,sin,0,1vuv ββ === and ()cossin0sincoscossin cossin0 ijk vuk. ββαβαβ αα ×==−
So, () sinsincoscossin. vu αβαβαβ −=×=−
16. (a) Los Angeles: () 4000,118.24,55.95 −°°
4000sin55.95cos118.24
4000sin55.95sin118.24 4000cos55.95
Rio de Janeiro: () 4000,43.23,112.90 −°°
(b) Los Angeles: ()() ()() () ()()
(d) () 40001.596360 srθ ==≈ miles 090 0 10,000
,,1568.2,2919.7,2239.7 x y z xyz =°−° =°−° =° ≈−−
4000sin112.90cos43.23
Rio de Janeiro: ()() ()() () ()()
4000sin112.90sin43.23 4000cos112.90 ,,2684.7,2523.8,1556.5 x y z xyz =°−° =°−° =° ≈−−
(c) ()()()()()() ()() 1568.22684.72919.72523.82239.71556.5 cos 0.02047 40004000
91.17 or 1.59 radians uv uv θ θ −+−−+− ==≈− ≈°
(e) For Boston and Honolulu:
a. Boston: () 4000,71.06,47.64 −°°
4000sin47.64sin71.06
4000cos47.64
Honolulu: () 4000,157.86,68.69 −°°
b. Boston: () () () 4000sin47.64cos71.06
959.4,2795.7,2695.1 x y z =°−° =°−° =°
4000sin68.69sin157.86
4000cos68.69
Honolulu: () () () 4000sin68.69cos157.86
3451.7,1404.4,1453.7 x y z =°−° =°−° =°
c. ()()()()()() ()() 959.43451.72795.71404.42695.11453.7 cos 0.28329 40004000
73.54 or 1.28 radians uv uv θ θ
≈° d. () 5120 miles srθ ==40001.28≈
17. From Theorem 11.13 and Theorem 11.7 (6) you have () ()
18. Assume one of ,,,abc is not zero, say a Choose a point in the first plane such as () 1 ,0,0. da The distance between this point and the second plane is ()()()
19. 22 1 xy+= cylinder 2 zy = plane
Introduce a coordinate system in the plane 2.zy =
The new u-axis is the original x-axis. The new v-axis is the line 2,0.zyx==
Then the intersection of the cylinder and plane satisfies the equation of an ellipse:

Chapter 2 Differentiation
Chapter Comments
The material presented in Chapter 2 forms the basis for the remainder of calculus. Much of it needs to be memorized, beginning with the definition of a derivative of a function found on page 103. Students need to have a thorough understanding of the tangent line problem and they need to be able to find an equation of a tangent line. Frequently, students will use the function f ′(x) as the slope of the tangent line. They need to understand that f ′(x) is the formula for the slope and the actual value of the slope can be found by substituting into f ′(x) the appropriate value for x On pages 105–106 of Section 2.1, you will find a discussion of situations where the derivative fails to exist. These examples (or similar ones) should be discussed in class.
As you teach this chapter, vary your notations for the derivative. One time write y ′; another time write dy dx or f ′(x). Terminology is also important. Instead of saying “find the derivative,” sometimes say, “differentiate.” This would be an appropriate time, also, to talk a little about Leibnitz and Newton and the discovery of calculus.
Sections 2.2, 2.3, and 2.4 present a number of rules for differentiation. Have your students memorize the Product Rule and the Quotient Rule (Theorems 2.7 and 2.8) in words rather than symbols. Students tend to be lazy when it comes to trigonometry and therefore, you need to impress upon them that the formulas for the derivatives of the six trigonometric functions need to be memorized also. You will probably not have enough time in class to prove every one of these differentiation rules, so choose several to do in class and perhaps assign a few of the other proofs as homework.
The Chain Rule, in Section 2.4, will require two days of your class time. Students need a lot of practice with this and the algebra involved in these problems. Many students can find the derivative of f (x) = x2√1 x2 without much trouble, but simplifying the answer is often difficult for them. Insist that they learn to factor and write the answer without negative exponents. Strive to get the answer in the form given in the back of the book. This will help them later on when the derivative is set equal to zero.
Implicit differentiation is often difficult for students. Have students think of y as a function of x and therefore y 3 is [ f (x)] 3 This way they can relate implicit differentiation to the Chain Rule studied in the previous section.
Try to get your students to see that related rates, discussed in Section 2.6, are another use of the Chain Rule.
Section 2.1 The Derivative and the Tangent Line Problem
Section Comments
2.1 The Derivative and the Tangent Line Problem—Find the slope of the tangent line to a curve at a point. Use the limit definition to find the derivative of a function. Understand the relationship between differentiability and continuity.
Teaching Tips
Ask students what they think “the line tangent to a curve” means. Draw a curve with tangent lines to show a visual picture of tangent lines. For example:
= f (x)
(x)
When talking about the tangent line problem, use the suggested example of finding the equation of the tangent line to the parabola y = x2 at the point (1, 1)
Compute an approximation of the slope m by choosing a nearby point Q(x, x2) on the parabola and computing the slope mPQ of the secant line PQ.
After going over Examples 1–3, return to Example 2 where f (x) = x2 + 1 and note that f ′(x) = 2x. How can we find the equation of the line tangent to f and parallel to 4x y = 0?
Because the slope of the line is 4,
2x = 4
x = 2
So, at the point (2, 5), the tangent line is parallel to 4x y = 0 The equation of the tangent line is y 5 = 4(x 2) or y = 4x 3
Be sure to find the derivatives of various types of functions to show students the different types of techniques for finding derivatives. Some suggested problems are f (x) = 4x3 3x2 , g(x) = 2 (x 1), and h(x) = √2x + 5.
How Do You See It? Exercise
Page 108, Exercise 64 The figure shows the graph of g ′
(a) g′(0) =
(b) g′(3) =
(c) What can you conclude about the graph of g knowing that g′(1) = 8 3 ?
(d) What can you conclude about the graph of g knowing that g′( 4) = 7 3 ?
(e) Is g(6) g(4) positive or negative? Explain.
(f) Is it possible to find g(2) from the graph? Explain.
Solution
(a) g′(0) = 3
(b) g′(3) = 0
(c) Because g′(1) = 8 3 , g is decreasing (falling) at x = 1
(d) Because g′( 4) = 7 3 , g is increasing (rising) at x = 4
(e) Because g′(4) and g′(6) are both positive, g(6) is greater than g(4) and g(6) g(4) > 0
(f) No, it is not possible. All you can say is that g is decreasing (falling) at x = 2
Suggested Homework Assignment
Pages 107–109: 1, 3, 7, 11, 21–27 odd, 37, 43–47 odd, 53, 57, 61, 77, 87, 93, and 95.
Section 2.2 Basic Differentiation Rules and Rates of Change
Section Comments
2.2 Basic Differentiation Rules and Rates of Change—Find the derivative of a function using the Constant Rule. Find the derivative of a function using the Power Rule. Find the derivative of a function using the Constant Multiple Rule. Find the derivative of a function using the Sum and Difference Rules. Find the derivatives of the sine function and of the cosine function. Use derivatives to find rates of change.
Teaching Tips
Start by showing proofs of the Constant Rule and the Power Rule. Students who are mathematics majors need to start seeing proofs early on in their college careers as they will be taking Functions of a Real Variable at some point.
Go over an example in class like f (x) = 5x2 + x x . Show students that before differentiating they can rewrite the function as f (x) = 5x + 1 Then they can differentiate to obtain f ′(x) = 5
Use this example to emphasize the prudence of examining the function first before differentiating. Rewriting the function in a simpler, equivalent form can expedite the differentiating process.
Give mixed examples of finding derivatives. Some suggested examples are:
This will test students’ understanding of the various differentiation rules of this section.
How Do You See It? Exercise
Page 119, Exercise 76 Use the graph of f to answer each question. To print an enlarged copy of the graph, go to MathGraphs.com.
(a) Between which two consecutive points is the average rate of change of the function greatest?
(b) Is the average rate of change of the function between A and B greater than or less than the instantaneous rate of change at B?
(c) Sketch a tangent line to the graph between C and D such that the slope of the tangent line is the same as the average rate of change of the function between C and D.
Solution
(a) The slope appears to be steepest between A and B
(b) The average rate of change between A and B is greater than the instantaneous rate of change at B.
(c)
Suggested Homework Assignment
Pages 118–120: 1, 3, 5, 7–29 odd, 35, 39–53 odd, 55, 59, 65, 75, 85–89 odd, 91, 95, and 97.
Section 2.3
Product and Quotient Rules and Higher-Order Derivatives
Section Comments
2.3 Product and Quotient Rules and Higher-Order Derivatives—Find the derivative of a function using the Product Rule. Find the derivative of a function using the Quotient Rule. Find the derivative of a trigonometric function. Find a higher-order derivative of a function.
Teaching Tips
Some students have difficulty simplifying polynomial and rational expressions. Students should review these concepts by studying Appendices A.2–A.4 and A.7 in Precalculus, 10th edition, by Larson.
When teaching the Product and Quotient Rules, give proofs of each rule so that students can see where the rules come from. This will provide mathematics majors a tool for writing proofs, as each proof requires subtracting and adding the same quantity to achieve the desired results. For the Project Rule, emphasize that there are many ways to write the solution. Remind students that there must be one derivative in each term of the solution. Also, the Product Rule can be extended to more that just the product of two functions. Simplification is up to the discretion of the instructor. Examples such as f (x) = (2x2 3x)(5x3 + 6) can be done with or without the Product Rule. Show the class both ways.
After the Quotient Rule has been proved to the class, give students the memorization tool of LO d HI – HI d LO. This will give students a way to memorize what goes in the numerator of the Quotient Rule.
Some examples to use are f (x) = 2x
+
x and g(
) = 4 (
x) 3 x
Save f (x) for the next section as this will be a good example for the Chain Rule. g(x) is a good example for first finding the least common denominator.
How Do You See It? Exercise
Page 132, Exercise 120 The figure shows the graphs of the position, velocity, and acceleration functions of a particle.
(a) Copy the graphs of the functions shown. Identify each graph. Explain your reasoning. To print an enlarged copy of the graph, go to MathGraphs.com
(b) On your sketch, identify when the particle speeds up and when it slows down. Explain your reasoning.
s position
v velocity function a acceleration function
(b) The speed of the particle is the absolute value of its velocity. So, the particle’s speed is slowing down on the intervals (0, 4 3), and (8 3, 4) and it speeds up on the intervals (4 3, 8 3) and (4, 6)
Suggested Homework Assignment
Pages 129–132: 1, 3, 9, 13, 19, 23, 29–55 odd, 59, 61, 63, 75, 77, 91–107 odd, 111, 113, 117, and 131–135 odd.
Section 2.4 The Chain Rule
Section Comments
2.4 The Chain Rule—Find the derivative of a composite function using the Chain Rule. Find the derivative of a function using the General Power Rule. Simplify the derivative of a function using algebra. Find the derivative of a trigonometric function using the Chain Rule.
Teaching Tips
Begin this section by asking students to consider finding the derivative of F(x) = √x2 + 1 F is a composite function. Letting y = f (u) = √u and u = g(x) = x2 + 1, then y = F(x) = f (g(x)) or F = f ∘ g When stating the Chain Rule, be sure to state it using function notation and using Leibniz notation as students will see both forms when studying other courses with other texts. Following the definition, be sure to prove the Chain Rule as done on page 134.
Be sure to give examples that involve all rules discussed so far. Some examples include:
f (x) = (sin(6x))4 , g(x) = ( 3 + sin(2x) 3 √x + 3 )2 , and h(x) = (√x 2 x ) ∙ [8x + cos(x2 + 1)]3
You can use Exercise 98 on page 141 to review the following concepts:
• Product Rule
• Chain Rule
• Quotient Rule
• General Power Rule
Students need to understand these rules because they are the foundation of the study of differentiation.
Use the solution to show students how to solve each problem. As you apply each rule, give the definition of the rule verbally. Note that part (b) is not possible because we are not given g′(3)
Solution
(a)
f (x) = g(x)h(x)
f ′(x) = g(x)h′(x) + g′(x)h(x)
f ′(5) = ( 3)( 2) + (6)(3) = 24
(b) f (x) = g(h(x))
f ′(x) = g′(h(x))h′(x)
f ′(5) = g′(3)( 2) = 2g′(3)
Not possible. You need g′(3) to find f ′(5).
(c) f (x) = g(x) h(x)
f ′(x) = h(x)g′(x) g(x)h′(x) [h(x)]2
f ′(x) = (3)(6) ( 3)( 2) (3)2 = 12 9 = 4 3
(d) f (x) = [g(x)]3
f ′(x) = 3[g(x)]2g′(x)
f ′(5) = 3( 3)2(6) = 162
How Do You See It? Exercise
Page 142, Exercise 106 The cost C (in dollars) of producing x units of a product is C = 60x + 1350 For one week, management determined that the number of units produced x at the end of t hours can be modeled by x = 1 6t3 + 19t2 0 5t 1 The graph shows the cost C in terms of the time t 1 2345 Time (in hours)
of Producing a Product
C t
(a) Using the graph, which is greater, the rate of change of the cost after 1 hour or the rate of change of the cost after 4 hours?
(b) Explain why the cost function is not increasing at a constant rate during the eight-hour shift.
Solution
(a) According to the graph, C ′(4) > C ′(1).
(b) Answers will vary.
Suggested Homework Assignment
Pages 140–143: 1–53 odd, 63, 67, 75, 81, 83, 91, 97, 121, and 123.
Section 2.5 Implicit Differentiation
Section Comments
2.5 Implicit Differentiation—Distinguish between functions written in implicit form and explicit form. Use implicit differentiation to find the derivative of a function.
Teaching Tips
Material learned in this section will be vital for students to have for related rates. Be sure to ask students to find dy dx when x = c.
You can use the exercise below to review the following concepts:
• Finding derivatives when the variables agree and when they disagree
• Using implicit differentiation to find the derivative of a function
© 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.
Determine if the statement is true. If it is false, explain why and correct it. For each statement, assume y is a function of x
(a) d dx cos(x 2) = 2x sin(x 2)
(b) d dy cos( y2) = 2y sin( y2)
(c) d dx cos( y2) = 2y sin( y2)
Implicit differentiation is often difficult for students, so as you review this concept remind students to think of y as a function of x Part (a) is true, and part (b) can be corrected as shown below. Part (c) requires implicit differentiation. Note that the result can also be written as 2y sin( y2) dy dx .
Solution
(a) True
(b) False. d dy cos( y2) = 2y sin( y2).
(c) False. d dx cos( y2) = 2yy ′ sin( y2)
A good way to teach students how to understand the differentiation of a mix of variables in part (c) is to let g = y Then g ′ = y ′ So, d dx cos( y2) = d dx cos( g2) = sin ( g2) ∙ 2gg ′ = sin( y2) ∙ 2y y ′
How Do You See It? Exercise
Page 151, Exercise 70 Use the graph to answer the questions.
(a) Which is greater, the slope of the tangent line at x = 3 or the slope of the tangent line at x = 1?
(b) Estimate the point(s) where the graph has a vertical tangent line.
(c) Estimate the point(s) where the graph has a horizontal tangent line.
Solution
(a) The slope is greater at x = 3.
(b) The graph has vertical tangent lines at about ( 2, 3) and (2, 3)
(c) The graph has a horizontal tangent line at about (0, 6)
Suggested Homework Assignment
Pages 149–150: 1–17 odd, 25–35 odd, 53, and 61.
Section 2.6 Related Rates
Section Comments
2.6 Related Rates—Find a related rate. Use related rates to solve real-life problems.
Teaching Tips
Begin this lesson with a quick review of implicit differentiation with an implicit function in terms of x and y differentiated with respect to time. Follow this with an example similar to Example 1 on page 152, outlining the step-by-step procedure at the top of page 153 along with the guidelines at the bottom of page 153. Be sure to tell students, that for every related rate problem, to write down the given information, the equation needed, and the unknown quantity. A suggested problem to work out with the students is as follows:
A ladder 10 feet long rests against a vertical wall. If the bottom of the ladder slides away from the wall at a rate of 1 foot per second, how fast is the top of the ladder sliding down the wall when the bottom of the ladder is 6 feet from the wall?
Be sure to go over a related rate problem similar to Example 5 on page 155 so that students are exposed to working with related rate problems involving trigonometric functions.
How Do You See It? Exercise
Page 159, Exercise 34 Using the graph of f, (a) determine whether dy dt is positive or negative given that dx dt is negative, and (b) determine whether dx dt is positive or negative given that dy dt is positive. Explain.
(i) (a) dx dt negative ⇒ dy dt positive
(b) dy dt positive ⇒ dx dt negative
(ii) (a) dx dt negative ⇒ dy dt negative
(b) dy dt positive ⇒ dx dt positive
Suggested Homework Assignment
Pages 157–160: 1, 7, 11, 13, 15, 17, 21, 25, 29, and 41.
Chapter 2 Project
Timing a Handoff
You are a competitive bicyclist. During a race, you bike at a constant velocity of k meters per second. A chase car waits for you at the ten-mile mark of a course. When you cross the ten-mile mark, the car immediately accelerates to catch you. The position function of the chase car is given by the equation s(t) = 15 4 t 2 5 12 t 3 , for 0 ≤ t ≤ 6, where t is the time in seconds and s is the distance traveled in meters. When the car catches you, you and the car are traveling at the same velocity, and the driver hands you a cup of water while you continue to bike at k meters per second.
Exercises
1. Write an equation that represents your position s (in meters) at time t (in seconds).
2. Use your answer to Exercise 1 and the given information to write an equation that represents the velocity k at which the chase car catches you in terms of t.
3. Find the velocity function of the car.
4. Use your answers to Exercises 2 and 3 to find how many seconds it takes the chase car to catch you.
5. What is your velocity when the car catches you?
6. Use a graphing utility to graph the chase car’s position function and your position function in the same viewing window.
7. Find the point of intersection of the two graphs in Exercise 6. What does this point represent in the context of the problem?
8. Describe the graphs in Exercise 6 at the point of intersection. Why is this important for a successful handoff?
9. Suppose you bike at a constant velocity of 9 meters per second and the chase car’s position function is unchanged.
(a) Use a graphing utility to graph the chase car’s position function and your position function in the same viewing window.
(b) In this scenario, how many times will the chase car be in the same position as you after the 10-mile mark?
(c) In this scenario, would the driver of the car be able to successfully handoff a cup of water to you? Explain.
10. Suppose you bike at a constant velocity of 8 meters per second and the chase car’s position function is unchanged.
(a) Use a graphing utility to graph the chase car’s position function and your position function in the same viewing window.
(b) In this scenario, how many times will the chase car be in the same position as you after the ten-mile mark?
(c) In this scenario, why might it be difficult for the driver of the chase car to successfully handoff a cup of water to you? Explain.

Preparation for Calculus



P.2 Linear Models and Rates of Change
Copyright © Cengage Learning.All rights reserved.
Objectives
Find the slope of a line passing through two points.
Write the equation of a line with a given point and slope.
Interpret slope as a ratio or as a rate in a real-life application.
Sketch the graph of a linear equation in slopeintercept form.
Write equations of lines that are parallel or perpendicular to a given line.
The
Slope of a Line
The Slope of a Line
The slope of a nonvertical line is a measure of the number of units the line rises (or falls) vertically for each unit of horizontal change from left to right.
Consider the two points (x1, y1) and (x2, y2) on the line in Figure P.12.
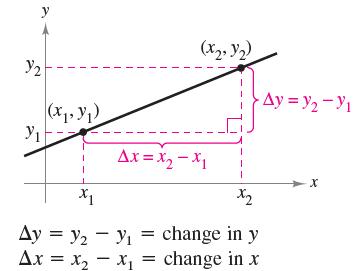
P.12
The Slope of a Line
As you move from left to right along this line, a vertical change of units corresponds to a horizontal change of units. (The symbol ∆ is the uppercase Greek letter delta, and the symbols ∆y and ∆x are read “delta y” and “delta x.”)
The Slope of a Line

The Slope of a Line
When using the formula for slope, note that
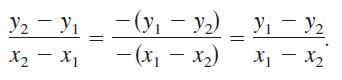
So, it does not matter in which order you subtract as long as you are consistent and both “subtracted coordinates” come from the same point.
The Slope of a Line
Figure P.13 shows four lines: one has a positive slope, one has a slope of zero, one has a negative slope, and one has an “undefined” slope. In general, the greater the absolute value of the slope of a line, the steeper the line.
Equations of Lines
Equations of Lines
Any two points on a nonverticalline can be used to calculate its slope.
This can be verified from the similar triangles shown in Figure P.14.
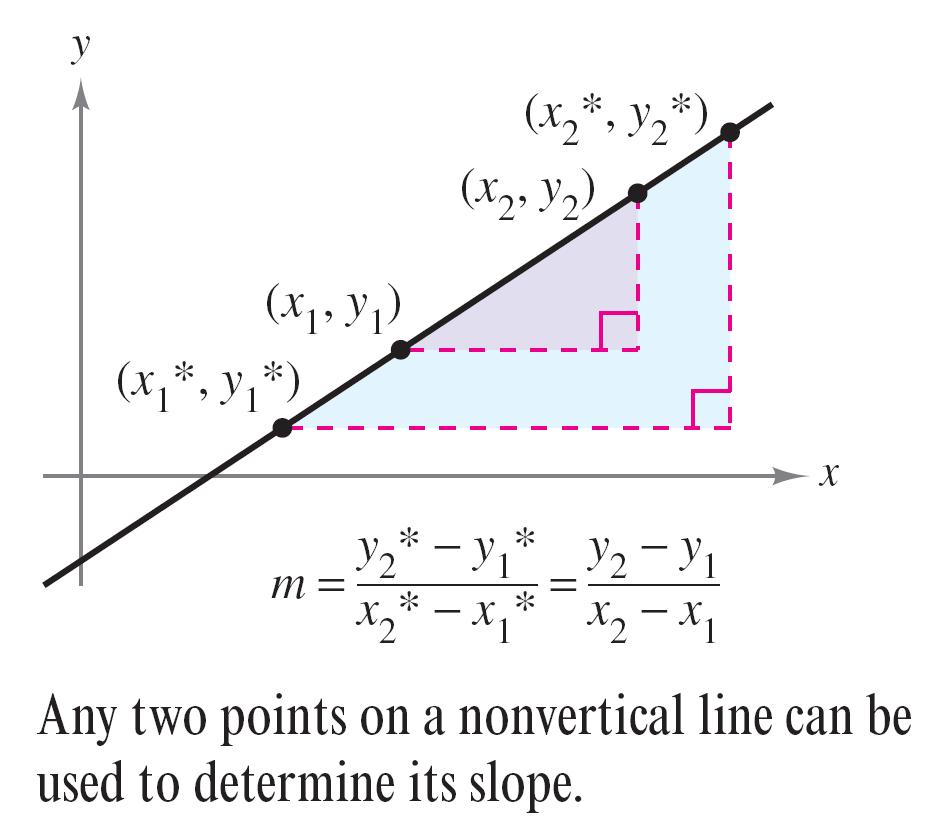
P.14
Equations of Lines
If (x1, y1) is a point on a nonvertical line that has a slope of m and (x, y) is any other point on the line, then

This equation in the variables x and y can be rewritten in the form
y – y1 = m(x – x1) which is called the point-slope form of the equation of a line.
Equations of Lines

Example 1 – Finding an Equation of a Line
Find an equation of the line that has a slope of 3 and passes through the point (1, –2). Then sketch the line.
Solution:
Example 1 – Solution
To sketch the line, first plot the point (1, –2). Then, because the slope is m = 3, you can locate a second point on the line by moving one unit to the right and three units upward, as shown in Figure P.15.
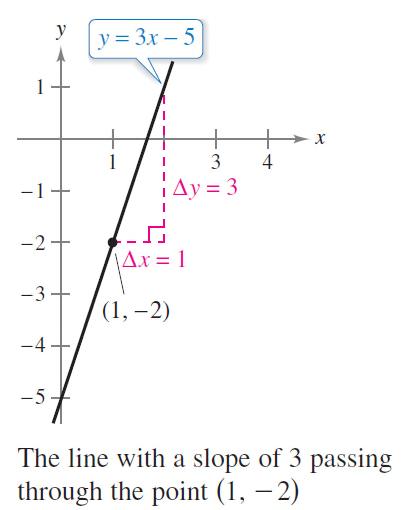
Figure P.15
Ratios and Rates of Change
Ratios and Rates of Change
The slope of a line can be interpreted as either a ratio or a rate.
If the x-and y-axes have the same unit of measure, then the slope has no units and is a ratio.
If the x-and y-axes have different units of measure, then the slope is a rate or rate of change.
Example 2 – Using Slope as a Ratio
The maximum recommended slope of a wheelchair ramp is 1/12. A business installs a wheelchair ramp that rises to a height of 22 inches over a length of 24 feet, as shown in Figure P.16. Is the ramp steeper than recommended?

Example 2 – Solution
The length of the ramp is 24 feet or 12 (24) = 288 inches. The slope of the ramp is the ratio of its height (the rise) to its length (the run).


Because the slope of the ramp is less than ½ ≈ 0.083, the ramp is not steeper than recommended. Note that the slope is a ratio and has no units.
Example 3 – Using Slope as a Rate of Change
The population of Oregonwas about 3,831,000 in 2010 and about 3,970,000 in 2014. Find the average rate of change of the population over this four-year period. What will the population of Oregonbe in 2024?
Solution:
Over this four-year period, the average rate of change of the population of Oregon was

Example 3 – Solution

Assuming that Oregon’s population continues to increase at this same rate for the next 10 years, it will have a 2024 population of about 4,318,000.
(See Figure P.17.)
Population of Oregon
P.17
Ratios and Rates of Change
The rate of change found in Example 3 is an average rate of change. An average rate of change is always calculated over an interval.
Graphing Linear Models
Graphing Linear Models
Many problems in analytic geometry can be classified in two basic categories:
1. Given a graph (or parts of it), find its equation.
2. Given an equation, sketch its graph.
For lines, problems in the first category can be solved by using the point-slope form. The point-slope form, however, is not especially useful for solving problems in the second category.
Graphing Linear Models
The form that is better suited to sketching the graph of a line is the slope-intercept form of the equation of a line.

Example 4 – Sketching Lines in the Plane
Sketch the graph of each equation.
a. y = 2x + 1
b. y = 2
c. 3y + x –6 = 0
Example 4(a) – Solution
Because b = 1, the y-intercept is (0, 1).
Because the slope is m = 2, you know that the line rises two units for each unit it moves to the right, as shown in Figure P.18(a).
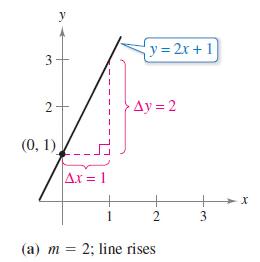
Example 4(b) – Solution cont’d
By writing the equation y = 2 in slope-intercept form
y = (0)x + 2
you can see that the slope is m = 0 and the y-intercept is (0,2).
Because the slope is zero, you know that the line is horizontal, as shown in Figure P.18(b).

Example 4(c) – Solution
Begin by writing the equation in slope-intercept form.
In this form, you can see that the y-intercept is (0, 2) and the slope is m = This This means that the line falls one unit for every three units it moves to the right.

Example 4(c) – Solution
This is shown in Figure P.18(c).

Graphing Linear Models
Because the slope of a vertical line is not defined, its equation cannot be written in the slope-intercept form. However, the equation of any line can be written in the general form where A and B are not both zero. For instance, the vertical line can be represented by the general form
Graphing Linear Models

Parallel and Perpendicular Lines
Parallel and Perpendicular Lines
The slope of a line is a convenient tool for determining whether two lines are parallel or perpendicular, as shown in Figure P.19.

P.19
Parallel and Perpendicular Lines

Example 5 – Finding Parallel and Perpendicular Lines
Find the general forms of the equations of the lines that pass through the point (2, –1) and are
(a) parallel to the line 2x –3y = 5
(b) perpendicular to the line 2x –3y = 5.
Example 5 – Solution
Begin by writing the linear equation 2x –3y = 5 in slope-intercept form.

So, the given line has a slope of (See Figure P.20.)


Example 5 – Solution
a. The line through (2, –1) that is parallel to the given line also has a slope of 2/3.
Note the similarity to the equation of the given line, 2x –3y = 5.
Example 5 – Solution
b. Using the negative reciprocal of the slope of the given line, you can determine that the slope of a line perpendicular to the given line is –3/2.
