Chapter2
15.(a) Theisoclineshavetheform y = x + c,whicharestraight lineswithslope 1.
(b) Theisoclineshavetheform x2 + y2 = c,whicharecircles centeredattheorigin.
16.(a) When x =0or y =4, dy/dx = 2sothelinealelementshaveslope 2.When y =3or y =5, dy/dx = x 2,sothelinealelementsat(x, 3)and(x, 5)haveslopes x 2.
(b) At(0,y0)thesolutioncurveisheadeddown.If y →∞ as x increases,thegraphmust eventuallyturnaroundandheadup,butwhileheadingupitcannevercross y =4 whereatangentlinetoasolutioncurvemusthaveslope 2.Thus, y cannotapproach ∞ as x approaches ∞.
17. When y< 1 2 x2 , y′ = x2 2y ispositiveandtheportionsof solutioncurves“outside”thenullclineparabolaareincreasing. When y> 1 2 x2 , y′ = x2 2y isnegativeandtheportionsofthe solutioncurves“inside”thenullclineparabolaaredecreasing.
18.(a) Anyhorizontallinealelementshouldbeatapointonanullcline.InProblem1the nullclinesare x2 y2 =0or y = ±x.InProblem3thenullclinesare1 xy =0or y =1/x.InProblem4thenullclinesare(sin x)cos y =0or x = nπ and y = π/2+ nπ, where n isaninteger.Thegraphsonthenextpageshowthenullclines fortheequations inProblems1,3,and4superimposedonthecorrespondingdirectionfield.
(b) Anautonomousfirst-orderdifferentialequationhastheform y′ = f (y).Nullclineshave theform y = c where f (c)=0.Thesearethegraphsoftheequilibriumsolutionsofthe differentialequation.
19. Writingthedifferentialequationintheform dy/dx = y(1 y)(1+ y)weseethat criticalpointsare y = 1, y =0,and y =1.Thephaseportraitisshownatthe right.
20. Writingthedifferentialequationintheform dy/dx = y2(1 y)(1+ y)weseethat criticalpointsare y = 1, y =0,and y =1.Thephaseportraitisshownatthe right.
21. Solving y 2 3y = y(y 3)=0weobtainthecriticalpoints0and3.Fromthe phaseportraitweseethat0isasymptoticallystable(attractor)and3isunstable (repeller).

22. Solving y 2 y 3 = y 2(1 y)=0weobtainthecriticalpoints0and1.Fromthephase portraitweseethat1isasymptoticallystable(attractor) and0issemi-stable.

23. Solving(y 2)4 =0weobtainthecriticalpoint2.Fromthephaseportraitwesee that2issemi-stable.

24. Solving10+3y y2 =(5 y)(2+ y)=0weobtainthecriticalpoints 2and5. Fromthephaseportraitweseethat5isasymptoticallystable(attractor)and 2is unstable(repeller).

25. Solving y 2(4 y 2)= y 2(2 y)(2+ y)=0weobtainthecriticalpoints 2,0,and 2.Fromthephaseportraitweseethat2isasymptoticallystable(attractor),0is semi-stable,and 2isunstable(repeller).

26. Solving y(2 y)(4 y)=0weobtainthecriticalpoints0,2,and4.Fromthephase portraitweseethat2isasymptoticallystable(attractor) and0and4areunstable (repellers).

27. Solving y ln(y+2)=0weobtainthecriticalpoints 1and0.Fromthephaseportrait weseethat 1isasymptoticallystable(attractor)and0isunstable(repeller).

28. Solving yey 9y = y(ey 9)=0(since ey isalwayspositive)weobtainthe criticalpoints0andln9.Fromthephaseportraitweseethat 0isasymptotically stable(attractor)andln9isunstable(repeller).
29. Thecriticalpointsare0and c becausethegraphof f (y)is0atthesepoints.Since f (y) > 0 for y< 0and y>c,thegraphofthesolutionisincreasingonthe y-intervals(−∞, 0)and (c, ∞).Since f (y) < 0for0 <y<c,thegraphofthesolutionisdecreasingonthe y-interval (0,c).
30. Thecriticalpointsareapproximatelyat 2, 2,0.5,and1.7.Since f (y) > 0for y< 2.2 and0 5 <y< 1 7,thegraphofthesolutionisincreasingonthe y-intervals(−∞, 2 2)and (0 5, 1 7).Since f (y) < 0for
5and y> 1 7,thegraphisdecreasingonthe y-interval( 2 2, 0 5)and(1 7, ∞).
31. Fromthegraphsof z = π/2and z =sin y weseethat (2/π)y sin y =0hasonlythreesolutions.Byinspection weseethatthecriticalpointsare π/2,0,and π/
Fromthegraphattherightweseethat
Thisenablesustoconstructthephaseportraitshownattheright.Fromthisportraitwesee that π/2and π/2areunstable(repellers),and0isasymptoticallystable(attractor).
32. For dy/dx =0everyrealnumberisacriticalpoint,andhenceallcriticalpointsarenonisolated.
33. Recallthatfor dy/dx = f (y)weareassumingthat f and f ′ arecontinuousfunctionsof y onsomeinterval I.Nowsupposethatthegraphofanonconstantsolutionofthedifferential equationcrossestheline y = c.Ifthepointofintersectionistakenasaninitialcondition wehavetwodistinctsolutionsoftheinitial-valueproblem.Thisviolatesuniqueness,sothe
graphofanynonconstantsolutionmustlieentirelyononesideofanyequilibriumsolution. Since f iscontinuousitcanonlychangesignsatapointwhereitis0. Butthisisacritical point.Thus, f (y)iscompletelypositiveorcompletelynegativeineachregion Ri.If y(x)is oscillatoryorhasarelativeextremum,thenitmusthaveahorizontaltangentlineatsome point(x0,y0).Inthiscase y0 wouldbeacriticalpointofthedifferentialequation,butwesaw abovethatthegraphofanonconstantsolutioncannotintersectthegraphoftheequilibrium solution y = y0.
34. ByProblem33,asolution y(x)of dy/dx = f (y)cannothaverelativeextremaandhencemust bemonotone.Since y′(x)= f (y) > 0, y(x)ismonotoneincreasing,andsince y(x)isbounded aboveby c2,limx→∞ y(x)= L,where L ≤ c2.Wewanttoshowthat L = c2.Since L isa horizontalasymptoteof y(x),limx→∞ y′(x)=0.Usingthefactthat f (y)iscontinuouswe have
f (L)= f lim x→∞ y(x) =lim x→∞ f (y(x))=lim x→∞ y ′(x)=0
Butthen L isacriticalpointof f .Since c1 <L ≤ c2,and f hasnocriticalpointsbetween c1 and c2, L = c2
35. Assumingtheexistenceofthesecondderivative,pointsofinflectionof y(x)occurwhere y′′(x)=0.From dy/dx = f (y)wehave d2y/dx2 = f ′(y) dy/dx.Thus,the y-coordinateofa pointofinflectioncanbelocatedbysolving f ′(y)=0.(Pointswhere dy/dx =0correspond toconstantsolutionsofthedifferentialequation.)
36. Solving y2 y 6=(y 3)(y +2)=0weseethat3and 2 arecriticalpoints.Now d2y/dx2 =(2y 1) dy/dx =(2y 1)(y 3)(y +2),sotheonlypossiblepointofinflectionisat y = 1 2 , althoughtheconcavityofsolutionscanbedifferentoneither side of y = 2and y =3.Since y′′(x) < 0for y< 2and 1 2 <y< 3, and y′′(x) > 0for 2 <y< 1 2 and y> 3,weseethatsolution curvesareconcavedownfor y< 2and 1 2 <y< 3andconcave upfor 2 <y< 1 2 and y> 3.Pointsofinflectionofsolutionsof autonomousdifferentialequationswillhavethesame y-coordinates becausebetweencriticalpointstheyarehorizontaltranslationsof eachother. x y 5 –5 –5 5
37. If(1)inthetexthasnocriticalpointsithasnoconstantsolutions.Thesolutionshave neitheranuppernorlowerbound.Sincesolutionsaremonotonic,everysolutionassumesall realvalues.
38. Thecriticalpointsare0and b/a.Fromthephaseportraitweseethat0isan attractorand b/a isarepeller.Thus,ifaninitialpopulationsatisfies P0 >b/a, thepopulationbecomesunboundedas t increases,mostprobablyinfinitetime, i.e. P (t) →∞ as t → T .If0 <P0 <b/a,thenthepopulationeventuallydiesout, thatis, P (t) → 0as t →∞.Sincepopulation P> 0wedonotconsiderthecase P0 < 0. 0 b a
39. Fromtheequation dP/dt = k (P h/k)weseethattheonlycriticalpointoftheautonomous differentialequationisthepositivenumber h/k.Aphaseportraitshowsthatthispointis unstable,thatis, h/k isarepeller.Foranyinitialcondition P (0)= P0 forwhich0 <P0 <h/k, dP/dt< 0whichmeans P (t)ismonotonicdecreasingandsothegraphof P (t)mustcrossthe t-axisortheline P 0atsometime t1 > 0.But P (t1)=0meansthepopulationisextinct attime t1.
40. Writingthedifferentialequationintheform
dt = k m mg k v
weseethatacriticalpointis mg/k.
Fromthephaseportraitweseethat mg/k isanasymptoticallystablecriticalpoint. Thus,lim t→∞ v = mg/k
41. Writingthedifferentialequationintheform
dv dt = k m mg k v 2 = k m mg k v mg k + v
weseethattheonlyphysicallymeaningfulcriticalpointis mg/k. Fromthephaseportraitweseethat mg/k isanasymptoticallystablecritical point.Thus,lim t→∞ v = mg/k.
42.(a) Fromthephaseportraitweseethatcriticalpointsare α and β.Let X(0)= X0. If X0 <α,weseethat X → α as t →∞.If α<X0 <β,weseethat X → α as t →∞.If X0 >β,weseethat X(t)increasesinanunboundedmanner, butmorespecificbehaviorof X(t)as t →∞ isnotknown.
(b) When α = β thephaseportraitisasshown.If X0 <α,then X(t) → α as t →∞.If X0 >α,then X(t)increasesinanunboundedmanner.This couldhappeninafiniteamountoftime.Thatis,thephaseportraitdoesnot indicatethat X becomesunboundedas t →∞. α
(c) When k =1and α = β thedifferentialequationis dX/dt =(α X)2.For X(t)= α 1/(t + c)wehave dX/dt =1/(t + c)2 and
dX dt
For X(0)= α/2weobtain
For X(0)=2α weobtain
For X0 >α, X(t)increaseswithoutboundupto t =1/α.For t> 1/α, X(t)increases but X → α as t →∞.
2.2 SeparableVariables
Inmanyofthefollowingproblemswewillencounteranexpressionoftheform ln |g(y)| = f (x)+c Tosolvefor g(y) weexponentiatebothsidesoftheequation.Thisyields |
whichimplies g(y)= ±ecef (x) .Letting c1 = ±ec weobtain g(y)= c1ef (x)
1. From dy =sin5xdx weobtain y = 1 5 cos5x + c
2. From dy =(x +1)2 dx weobtain y = 1 3 (x +1)3 + c
)|
3. From dy = e 3x dx weobtain y = 1 3 e 3x + c.
4. From 1 (y 1)2 dy = dx weobtain 1 y 1 = x + c or y =1 1 x + c
5. From 1 y dy = 4 x dx weobtainln |y| =4ln |x| + c or y = c
6. From
7. From e 2y dy = e3xdx weobtain3e 2y +2e 3x = c
8. From yey dy = e x + e 3x dx weobtain yey ey + e x + 1 3 e 3x = c
9. From y +2+ 1 y dy = x 2 ln xdx weobtain y2 2 +2
10. From
11. From 1 csc y dy = 1 sec2 x dx orsin ydy = cos2 xdx = 1 2 (1+cos2x) dx weobtain cos y = 1 2 x 1 4 sin2x + c or4cos y =2x +sin2x + c1.
12. From2ydy = sin3x cos3 3x dx or2ydy = tan3x sec2 3xdx weobtain y2 =
13. From ey (ey +1)2 dy = ex (ex +1)3 dx weobtain (ey +1) 1 = 1 2 (ex +1) 2 + c
14. From y (1+ y2)1/2 dy = x (1+ x2)1/2 dx weobtain 1+ y 2 1/2 = 1+ x 2 1/2 + c. 15. From 1 S dS = kdr weobtain S = cekr
16. From 1 Q 70 dQ = kdt weobtainln |Q 70| = kt + c or Q 70= c1ekt 17. From 1 P P 2 dP = 1 P + 1 1 P dP = dt weobtainln |P |− ln |1 P | = t + c sothat ln P 1 P = t + c or P 1 P = c1e t.Solvingfor P wehave P =
From 1
19. From y 2 y +3 dy = x 1 x +4 dx or 1 5 y +3 dy = 1 5 x +4 dx weobtain y 5ln |y +3| = x 5ln |x +4| + c or x +4 y +3 5 = c1ex y
20. From y +1 y 1 dy = x +2 x 3 dx or 1+ 2 y 1 dy = 1+ 5 x 3 dx weobtain y +2ln |y 1| = x +5ln |x 3| + c or (y 1)2 (x 3)5 = c1e x y
21. From xdx =
22. From 1 y2 dy = 1 ex + e x dx = ex (ex)2 +1 dx weobtain 1 y =tan 1 e x + c or y = 1 tan 1 ex + c
23. From 1 x2 +1 dx =4 dt weobtaintan 1 x =4t + c.Using x(π/4)=1wefind c = 3π/4.The solutionoftheinitial-valueproblemistan
24. From
|y 1|−
c =1.Asolutionoftheinitial-valueproblemis
(2)=2we
25. From 1 y dy = 1 x x2 dx = 1 x2 1 x dx weobtainln |y| = 1 x ln |x| = c or xy = c
Using y( 1)= 1wefind c1 = e 1.Thesolutionoftheinitial-valueproblemis
or y = e (1+1/x)/x
26. From 1 1 2y dy = dt weobtain
|
find c1 = 4.Thesolutionoftheinitial-valueproblemis1
27. Separatingvariablesandintegratingweobtain
Setting x =0and y = √3/2weobtain c = π/3.Thus,animplicitsolutionoftheinitialvalueproblemissin 1 x sin 1 y = π/3.Solvingfor y andusinganadditionformulafrom trigonometry,weget
28. From 1 1+(2y)2 dy = x 1+(x2)2 dx weobtain
Using y(1)=0wefind c1 = π/4.Thus,animplicitsolutionoftheinitial-valueproblemis tan 1 2y +tan 1 x 2 = π/4.Solvingfor y andusingatrigonometricidentityweget
29. SeparatingvariablesandthenproceedingasinExample5weget
30. SeparatingvariablesandthenproceedingasinExample5weget
31. Separatingvariablesweget

Thecondition y( 2)= 1implies c = 1.Thus y2 = x2 + x 1and y = √x2 + x 1in orderfor y tobenegative.Moreoverforanintervalcontaining 2forvaluesof x suchthat x2 + x 1 > 0weget −∞, 1 2 √5 2 .
32. Separatingvariablesweget
(2y 2) dy dx =3x 2 +4x +2 (2y 2) dy = 3x 2 +4x +2 dx
(2y 2) dy = ˆ 3x 2 +4x +2 dx
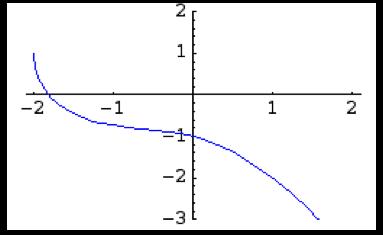
Thecondition y(1)= 2implies c =4.Thus y =1 √x3 +2x2 +2x +4wheretheminus signisindicatedbytheinitialcondition.Now x3 +2x2 +2x+4=(x +2) x2 +1 > 0implies x> 2,sotheintervalofdefinitionis( 2, ∞).
33. Separatingvariablesweget

Thecondition y(0)=0implies c =2.Thus e y =2 ex.Therefore y = ln(2 ex).Now wemusthave2 ex > 0or ex < 2.Since ex isanincreasingfunctionthisimples x< ln2 andsotheintervalofdefinitionis(−∞, ln2).
34. Separatingvariablesweget sin xdx + ydy =0 ˆ sin xdx + ˆ ydy = ˆ 0 dx cos x + 1 2 y 2 = c

Thecondition y(0)=1implies c = 1 2 .Thus cos x + 1 2 y2 = 1 2 or y2 =2cos x 1. Therefore y = √2cos x 1wherethepositiverootisindicatedbytheinitialcondition.Now wemusthave2cos x 1 > 0orcos x> 1 2 .Thismeans π/3 <x<π/3,sothetheinterval ofdefinitionis( π/3,π/3).
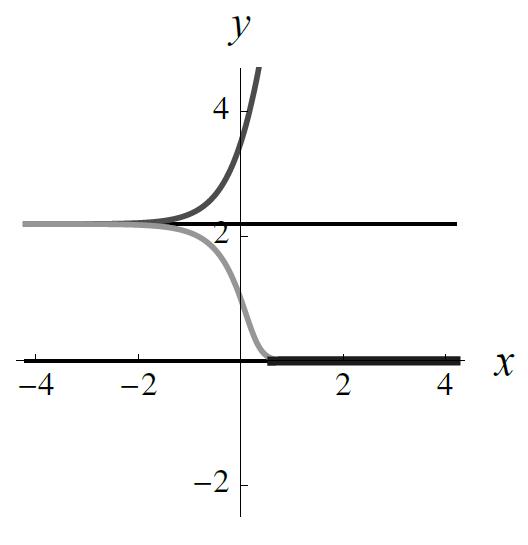
35.(a) Theequilibriumsolutions y(x)=2and y(x)= 2satisfytheinitialconditions y(0)=2
and y(0)= 2,respectively.Setting x = 1 4 and y =1in y =2(1+ ce4x)/(1 ce4x)we obtain 1=2 1+
Thesolutionofthecorrespondinginitial-valueproblemis
(b) Separatingvariablesandintegratingyields
Solvingfor y weget y =2(c + e4x)/(c e4x).Theinitialcondition y(0)= 2implies 2(c +1)/(c 1)= 2whichyields c =0and y(x)= 2.Theinitialcondition y(0)=2 doesnotcorrespondtoavalueof c,anditmustsimplyberecognizedthat y(x)=2isa solutionoftheinitial-valueproblem.Setting x = 1 4 and y =1in y =2(c + e4x)/(c e4x ) leadsto c = 3e.Thus,asolutionoftheinitial-valueproblemis
36. Separatingvariables,wehave
Usingpartialfractions,weobtain
Solvingfor y weget y =1/(1 c1x).Wenotebyinspectionthat y =0isasingularsolution ofthedifferentialequation.
(a) Setting x =0and y =1wehave1=1/(1 0),whichistrueforallvaluesof c1.Thus, solutionspassingthrough(0, 1)are y =1/(1 c1x).
(b) Setting x =0and y =0in y =1/(1 c1 x)weget0=1.Thus,theonlysolutionpassing through(0, 0)is y =0.
(c) Setting x = 1 2 and y = 1 2 wehave 1 2 =1/(1 1 2 c1),so c1 = 2and y =1/(1+2x).
(d) Setting x =2and y = 1 4 wehave 1 4 =1/(1 2c1),so c1 = 3 2 and y =1/(1+ 3 2 x)=2/(2+3x).
37. Singularsolutionsof dy/dx = x 1 y2 are y = 1and y =1.Asingularsolutionof (ex + e x)dy/dx = y2 is y =0.
38. Differentiatingln(x2 +10)+csc y = c weget 2x x2 +10 csc y cot y dy dx =0, 2x x2 +10 1 sin y · cos y sin y dy dx =0, or 2x sin2 ydx (x 2 +10)cos ydy =0.
Writingthedifferentialequationintheform dy dx = 2x sin2 y (x2 +10)cos y weseethatsingularsolutionsoccurwhensin2 y =0,or y = kπ,where k isaninteger.
39. Thesingularsolution y =1satisfiestheinitial-valueproblem. x y
0.98 1 1.01 –0.004–0.0020.0020.004
40. Separatingvariablesweobtain dy (y 1)2 = dx.Then 1 y 1 = x + c and y = x + c 1 x + c .
y
Setting x =0and y =1 01weobtain c = 100.Thesolution is y = x 101 x 100 . –0.004–0.0020.0020.004 x
41. Separatingvariablesweobtain dy (y 1)2 +0 01 = dx.Then
10tan 1 10(y 1)= x + c and y =1+ 1 10 tan x + c 10 .
Setting x =0and y =1weobtain c =0.Thesolutionis y =1+ 1 10 tan x 10 .
42. Separatingvariablesweobtain dy (y 1)2 0.01 = dx.Then, with u = y 1and a = 1 10 ,weget
5ln 10y 11 10y 9 = x + c.
Setting x =0and y =1weobtain c =5ln1=0.The solutionis
y
y
x
5ln 10y 11 10y 9 = x. –0.004–0.0020.0020.004 x 0.9996
Solvingfor y weobtain y = 11+9ex/5 10+10ex/5 . Alternatively,wecanusethefactthat ˆ dy (y 1)2 0 01 = 1 0 1 tanh 1 y 1 0 1 = 10tanh 1 10(y 1).
(Weusetheinversehyperbolictangentbecause |y 1| < 0.1or0.9 <y< 1.1.This followsfromtheinitialcondition y(0)=1.)Solvingtheaboveequationfor y weget y = 1+0 1tanh(x/10).
43. Separatingvariables,wehave
Integrating,weget
When y> 1,thisbecomes
Letting x =0and y =2wefind c =ln(2/√3).Solvingfor y weget y1(x)=2ex/√4e2x 3, where x> ln(√3/2).
When0 <y< 1wehave
Letting x =0and y = 1 2 wefind c =ln(1/√3).Solvingfor y weget y2(x)= ex/√e2x +3, where −∞ <x< ∞. When 1 <y< 0wehave
y) 1 2 ln(1 y) 1 2 ln(1+ y)=ln y 1 y2 = x + c.
Letting x =0and y = 1 2 wefind c =ln(1/√3).Solvingfor y weget y3(x)= ex/√e2x +3, where −∞ <x< ∞ When y< 1wehave ln( y) 1 2 ln(1 y) 1 2 ln( 1 y)=ln y y2 1 = x + c.
Letting x =0and y = 2wefind c =ln(2/√3).Solvingfor y weget y4(x)= 2ex/√4e2x 3,where x> ln(√3/2).
44.(a) Thesecondderivativeof y is d2y dx2 = dy/dx (y 1)2 = 1/(y 3) (y 3)2 = 1 (y 3)3
Thesolutioncurveisconcavedownwhen d2y/dx2 < 0 or y> 3,andconcaveupwhen d2y/dx2 > 0or y< 3. Fromthephaseportraitweseethatthesolutioncurve isdecreasingwhen y< 3andincreasingwhen y> 3.
(b) Separatingvariablesandintegratingweobtain (y 3) dy = dx 1 2 y 2 3y = x + c
Theinitialconditiondictateswhethertousetheplusorminussign.
When y1(0)=4wehave c1 =1and y1(x)=3+ √2x +1where( 1/2, ∞).
When y2(0)=2wehave c
When y3(1)=2wehave c1 = 1and y3(x)=3
When y4( 1)=4wehave c1 =3and y4(x)=3+ √2x +3where( 3/2, ∞).
45. Weseparatevariablesandrationalizethedenominator.Then
Integrating,wehave y =tan x sec x + C
46. Separatingvariableswehave √ydy =sin √xdx.Then
Tointegratesin √x wefirstmakethesubstitution u = √x.Then du = 1 2√x dx = 1 2u du and
Usingintegrationbypartswefind
47. Separatingvariableswehave
wesubstitute
Integratingtheseparateddifferentialequationwehave
48. Separatingvariablesandintegratingwehave
49. Separatingvariableswehave ydy = e√x dx.If u = √x ,then u2 = x and2udu = dx.Thus,
e√x dx = ˆ 2ueu du and,usingintegrationbyparts,wefind
and
Tofind C wesolve y(1)=4.
(1)=2
andthesolutionoftheintial-valueproblemis y
50. Seperatingvariableswehave ydy = x tan 1 xdx.Integratingbothsidesandusingintegration bypartswith u =tan 1 x and dv = xdx wehave
= x tan 1 xdx
Tofind C1 wesolve y(0)=3.
andthesolutionoftheinitial-valueproblemis y = √x2 tan 1 x x +tan 1 x +9.
51.(a) While y2(x)= √25 x2 isdefinedat x = 5and x =5, y′ 2(x)isnotdefinedatthese values,andsotheintervalofdefinitionistheopeninterval ( 5, 5).
(b) Atanypointonthe x-axisthederivativeof y(x)isundefined,sonosolutioncurvecan crossthe x-axis.Since x/y isnotdefinedwhen y =0,theinitial-valueproblemhasno solution.
52. Thederivativeof y = 1 4 x2 1 2 is dy/dx = x 1 4 x2 1 .Wenotethat xy1/2 = x 1 4 x2 1 . Weseefromthegraphsof y (black), dy/dx (red),and xy1/2 (blue),belowthat dy/dx = xy1/2 on(−∞, 2]and[2, ∞).


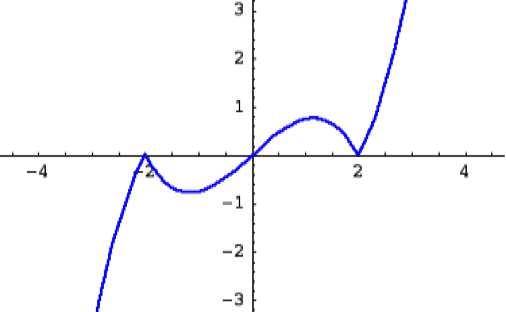
Alternatively,because √X 2 = |X| wecanwrite xy 1/2 = x√y = x 1 4 x2 1 2 = x 1 4 x 2 1
Fromthisweseethat dy/dx = xy1/2 on(−∞, 2]andon[2, ∞).
53. Separatingvariableswehave dy/ 1+ y2 sin2 y = dx whichisnotreadilyintegrated(evenbyaCAS).We notethat dy/dx ≥ 0forallvaluesof x and y andthat dy/dx =0when y =0and y = π,whichareequilibrium solutions. –6–4–22468 x
54.(a) Thesolutionof y′ = y, y(0)=1,is y = ex.Usingseparationofvariableswefindthatthe solutionof y′ = y [1+1/ (x ln x)], y(e)=1,is y = ex e ln x.Solvingthetwosolutions simultaneouslyweobtain ex = ex e ln x, so ee =ln x and x = eee
(b) Since y = e(ee e ) ≈ 2.33 × 101,656,520 ,the y-coordinateofthepointofintersectionofthe twosolutioncurveshasover1.65milliondigits.
55. Wearelookingforafunction y(x)suchthat y 2 + dy dx 2 =1
Usingthepositivesquarerootgives dy dx = 1 y2 dy 1 y2 = dx sin 1 y = x + c.
Thusasolutionis y =sin(x + c).Ifweusethenegativesquarerootweobtain y =sin(c x)= sin(x c)= sin(x + c1)
Notethatwhen c = c1 =0andwhen c = c1 = π/2weobtainthewellknownparticular solutions y =sin x, y = sin x, y =cos x,and y = cos x.Notealsothat y =1and y = 1 aresingularsolutions.
56.(a) x x y –33 –3 3
(b) For |x| > 1and |y| > 1thedifferentialequationis dy/dx = y2 1 /√x2 1.Separatingvariablesandintegrating,weobtain dy y2 1 = dx √x2 1 andcosh 1 y =cosh 1 x + c.
Setting x =2and y =2wefind c =cosh 1 2 cosh 1 2=0andcosh 1 y =cosh 1 x.
Anexplicitsolutionis y = x.
57. Sincethetension T1 (ormagnitude T1)actsatthelowestpointofthecable,weusesymmetry tosolvetheproblemontheinterval[0,L/2].Theassumptionthattheroadbedisuniform (thatis,weighsaconstant ρ poundsperhorizontalfoot)implies W = ρx,where x ismeasured infeetand0 ≤ x ≤ L/2.Therefore(10)becomes dy/dx =(ρ/T1)x.Thislastequationisa separableequationoftheformgivenin(1)ofSection2.2inthetext.Integratingandusingthe initialcondition y(0)= a showsthattheshapeofthecableisaparabola: y(x)=(ρ/2T1 )x2 +a Intermsofthesag h ofthecableandthespan L,weseefromFigure2.2.5inthetextthat y(L/2)= h + a.Byapplyingthislastconditionto y(x)=(ρ/2T1)x2 + a enablesustoexpress ρ/2T1 intermsof h and L: y(x)=(4h/L2 )x2 + a.Since y(x)isanevenfunctionof x,the solutionisvalidon L/2 ≤ x ≤ L/2.
58.(a) Separatingvariablesandintegrating,wehave (3y2 +1) dy = (8x +5) dx and y3 + y = 4x2 5x + c UsingaCASweshowvariouscontoursof f (x,y)= y3 + y +4x2 +5x.Theplotsshownon [ 5, 5]×[ 5, 5]correspondto c-valuesof0, ±5, ±20, ±40, ±80,and ±125.
y
(b) Thevalueof c correspondingto y(0)= 1is f (0, 1)= 2; to y(0)=2is f (0, 2)=10;to y( 1)=4is f ( 1, 4)=67; andto y( 1)= 3is 31.
59.(a) Animplicitsolutionofthedifferentialequation(2y +2)dy (4x3 +6x) dx =0is y 2 +2y x 4 3x 2 + c =0.
Thecondition y(0)= 3impliesthat c = 3.Therefore y2 +2y x4 3x2 3=0.
(b) Usingthequadraticformulawecansolvefor y intermsof x:
Theexplicitsolutionthatsatisfiestheinitialconditionisthen
(c) Fromthegraphofthefunction f (x)= x4 +3x3 +4belowweseethat f (x) ≤ 0onthe approximateinterval 2 8 ≤ x ≤−1 3.Thustheapproximatedomainofthefunction y = 1 x4 +3x3 +4= 1 f (x) is x ≤−2.8or x ≥−1.3.Thegraphofthisfunctionisshownbelow.
(d) UsingtherootfindingcapabilitiesofaCAS,thezerosof f arefound tobe 2.82202and 1.3409.Thedomainofdefinitionofthesolution y(x)isthen x> 1.3409.Theequalityhasbeenremovedsincethe derivative dy/dx doesnotexistatthepointswhere f (x)=0.The graphofthesolution y = φ(x)isgivenontheright.
60.(a) Separatingvariablesandintegrating,wehave ( 2y + y 2) dy =(x x 2) dx and y 2 + 1 3 y 3 = 1 2 x 2 1 3 x3 + c
UsingaCASweshowsomecontoursof
)=2y
Theplotsshownon[ 7, 7] × [ 5, 5]correspondto c-valuesof 450, 300, 200, 120, 60, 20, 10, 8.1, 5, 0.8,20,60,and120.
(b) Thevalueof c correspondingto y(0)= 3 2 is f 0, 3 2 = 27 4 .Theportionofthegraphbetweenthedotscorrespondstothesolutioncurve satisfyingtheintialcondition.Todeterminethe intervalofdefinitionwefind dy/dx for
Usingimplicitdifferentiationweget y′ =(x x2)/(y2 2y),whichisinfinitewhen y =0 and y =2.Letting y =0in2y3 6y2 +2x3 3x2 = 27 4 andusingaCAStosolvefor x weget x = 1 13232.Similarly,letting y =2,wefind x =1 71299.Thelargestinterval ofdefinitionisapproximately( 1 13232, 1 71299).
(c) Thevalueof c correspondingto y(0)= 2is f (0, 2)= 40.Theportionofthegraphtothe rightofthedotcorrespondstothesolutioncurve satisfyingtheinitialcondition.Todeterminethe intervalofdefinitionwefind dy/dx for 2
–4–20246810
Usingimplicitdifferentiationweget y′ =(x x2)/(y2 2y),whichisinfinitewhen y =0 and y =2.Letting y =0in2y3 6y2 +2x3 3x2 = 40andusingaCAStosolvefor x weget x = 2 29551.Thelargestintervalofdefinitionisapproximately( 2 29551, ∞).
2.3 LinearEquations
1. For y′ 5y =0anintegratingfactoris
for −∞ <x< ∞
5
2. For y′ +2y =0anintegratingfactoris e´ 2 dx = e2x sothat d dx e 2x y =0and y = ce 2x for
<x< ∞.Thetransienttermis ce 2x
3. For y′ + y = e3x anintegratingfactoris e´ dx = ex sothat d dx [exy]= e 4x and y = 1 4 e3x + ce x for −∞ <x< ∞.Thetransienttermis ce x .
4. For y′+4y = 4 3 anintegratingfactoris e´ 4 dx = e4x sothat d
for −∞ <x< ∞.Thetransienttermis ce 4x .
4
5. For y′ +3x2y = x2 anintegratingfactoris e´ 3x2 dx = ex3 sothat d dx e x3 y = x 2 e x3 and y = 1 3 + ce x3 for −∞ <x< ∞.Thetransienttermis ce x3 .
6. For y′ +2xy = x3 anintegratingfactoris e´ 2xdx = ex2 sothat d dx e x
and y = 1 2 x2 1 2 + ce x2 for −∞ <x< ∞.Thetransienttermis ce x2
7. For y′+ 1 x y = 1 x2 anintegratingfactoris e´ (1/x) dx = x sothat d dx [xy]= 1 x and y = 1 x ln
+ c x for0 <x< ∞.Theentiresolutionistransient.
8. For y′ 2y = x2+5anintegratingfactoris e ´ 2 dx = e 2x sothat d dx e 2x y = x 2 e 2x+5e 2x and y = 1 2 x2 1 2 x 11 4 + ce2x for −∞ <x< ∞.Thereisnotransientterm.
9. For y ′ 1 x y = x sin x anintegratingfactoris e ´ (1/x) dx = 1 x sothat d dx 1 x y =sin x and y = cx x cos x for0 <x< ∞.Thereisnotransientterm.
10. For y ′ + 2 x y = 3 x anintegratingfactoris e´ (2/x)dx = x2 sothat d dx x 2 y =3x and y = 3 2 +cx 2 for0 <x< ∞.Thetrancienttermis cx 2
11. For y′ + 4 x y = x 2 1anintegratingfactoris e´ (4/x)dx = x4 sothat d dx x 4 y = x6 x 4 and y = 1 7 x3 1 5 x + cx 4 for0 <x< ∞.Thetransienttermis cx 4
12. For y′ x (1+ x) y = x anintegratingfactoris e ´ [x/(1+x)]dx =(x +1)e x sothat d dx (x +1)e x y = x(x +1)e x and y = x 2x +3 x +1 + cex x +1 for 1 <x< ∞.There isnotransientterm.
13. For y ′ + 1+ 2 x y = ex x2 anintegratingfactoris e´ [1+(2/x)]dx = x2ex sothat d dx [x 2 e x y]= e 2x and y = 1 2 ex x2 + ce x x2 for0 <x< ∞.Thetransienttermis ce x x2 .
14. For y ′ + 1+ 1 x y = 1 x e x sin2x anintegratingfactoris e´ [1+(1/x)]dx = xex sothat d dx [xexy]=sin2x and y = 1 2x e x cos2x + ce x x for0 <x< ∞.Theentiresolution istransient.
15. For dx dy 4 y x =4y 5 anintegratingfactoris e ´ (4/y) dy = eln y 4 = y 4 sothat d dy y 4 x =4y and x =2y6 + cy4 for0 <y< ∞.Thereisnotransientterm.
16. For dx dy + 2 y x = ey anintegratingfactoris e´ (2/y) dy = y2 sothat d dy y 2 x = y 2 ey and
x = ey 2 y ey + 2 y2 ey + c y2 for0 <y< ∞.Thetransienttermis c y2
17. For y′ +(tan x)y =sec x anintegratingfactoris e´ tan xdx =sec x sothat d dx [(sec x)y]=sec2 x and y =sin x + c cos x for π/2 <x<π/2.Thereisnotransientterm.
18. For y′ +(cot x)y =sec2 x csc x anintegratingfactoris e´ cot xdx = eln | sin x| =sin x sothat d dx [(sin x) y]=sec2 x and y =sec x + c csc x for0 <x<π/2.Thereisnotransientterm.
19. For y′ + x +2 x +1 y = 2xe x x +1 anintegratingfactoris e´ [(x+2)/(x+1)]dx =(x +1)ex,so d dx [(x +1)exy]=2x and y = x2 x +1 e x + c x +1 e x for 1 <x< ∞.Theentire solutionistransient.
20. For y′ + 4 x +2 y = 5 (x +2)2 anintegratingfactoris e´ [4/(x+2)] dx =(x +2)4 sothat
d dx (x +2)4 y =5(x +2)2 and y = 5 3 (x +2) 1 + c(x +2) 4 for 2 <x< ∞.The entiresolutionistransient.
21. For dr dθ + r sec θ =cos θ anintegratingfactoris e´ sec θdθ = eln | sec x+tan x| =sec θ +tan θ so that d dθ [(sec θ +tan θ)r]=1+sin θ and(sec θ +tan θ)r = θ cos θ + c for π/2 <θ<π/2. Thereisnotransientterm.
22. For dP dt +(2t 1)P =4t 2anintegratingfactoris e´ (2t 1) dt = et2 t sothat d dt e t2 tP = (4t 2)e t2 t and P =2+ cet t2 for −∞ <t< ∞.Thetransienttermis cet t2 .
23. For y′ + 3+ 1 x y = e 3x x anintegratingfactoris e´ [3+(1/x)]dx = xe3x sothat d dx xe3xy =1 and y = e 3x + ce 3x x for0 <x< ∞.Thetransienttermis ce 3x/x
24. For y′ + 2 x2 1 y = x +1 x 1 anintegratingfactoris e´ [2/(x2 1)]dx = x 1 x +1 sothat d dx x 1 x +1 y =1and(x 1)y = x(x +1)+ c(x +1)for 1 <x< 1.Thereisno transientterm.
25. For y′ 5y = x anintegratingfactoris e´ 5 dx = e 5x sothat d dx e 5x y = xe 5x and y = e5x ˆ xe
If y(0)=3then c = 1 25 and y = 1 5 x 1 25 + 76 25 e5x.Thesolutionisdefinedon I =(−∞, ∞).
26. For y′ +3y =2x andintegratingfactoris e´ 3 dx = e 3x sothat d dx e 3x y =2xe 3x and
(0)= 1
then
e 3x.THesolutionisdefinedon I =(−∞, ∞).
27. For y′ + 1 x y = 1 x e x anintegratingfactoris e´ (1/x)dx = x sothat d dx [xy]= e x and y = 1 x e x + c x for0 <x< ∞.If y(1)=2then c =2 e and y = 1 x ex + 2 e x .Thesolutionisdefinedon I =(0, ∞).
28. For dx dy 1 y x =2y anintegratingfactoris e ´ (1/y)dy = 1 y sothat d dy 1 y x =2and x =2y2 + cy for0 <y< ∞.If y(1)=5then c = 49/5and x =2y 2 49 5 y.Thesolutionis
definedon I =(0, ∞).
29. For di dt + R L i = E L anintegratingfactoris e´ (R/L) dt = eRt/L sothat d dt eRt/L i = E L eRt/L and i = E R + ce Rt/L for −∞ <t< ∞.If i(0)= i0 then c = i0 E/R and i = E R + i0 E R e Rt/L.Thesolutionisdefinedon I =(−∞, ∞)
30. For dT dt kT = Tmk anintegratingfactoris e´ ( k) dt = e kt sothat d dt [e ktT ]= Tmke kt and T = Tm +cekt for −∞ <t< ∞.If T (0)= T0 then c = T0 Tm and T = Tm +(T0 Tm)ekt
Thesolutionisdefinedon I =(−∞, ∞)
31. For y ′ + 1 x y =4+ 1 x anintegratingfactoris e´ (1/x) dx = x sothat d dx [xy]=4x +1and y = 1 x ˆ (4x +1) dx = 1 x 2x 2 + x + c =2x +1+ c x
If y(1)=8then c =5and y =2x +1+ 5 x .Thesolutionisdefinedon I =(0, ∞).
32. For y ′ +4xy = x 3 e x2 anintegratingfactoris e´ 4xdx = e 2x2 sothat d dx [e 2x2 y]= x 3 e 3x2 and
If y(0)= 1then c = 17 18 and y = 1 6 x2ex2 1 18 ex2 17 18 e 2x2 .Thesolutionisdefinedon
I =(−∞, ∞).
33. For y ′+ 1 x +1 y = ln x x +1 anintegratingfactoris e´ [1/(x+1)] dx = x+1sothat d dx [(x+1)y]=ln x and y = x x +1 ln x x x +1 + c x +1 for0 <x< ∞.
If y(1)=10then c =21and y = x x +1 ln x x x +1 + 21 x +1 .Thesolutionisdefinedon
I =(0, ∞).
34. For y′ + 1 x +1 y = 1 x (x +1) anintegratingfactoris e´ [1/(x+1)] dx = x +1sothat d dx [(x +1) y]= 1 x and y = 1 x +1 ˆ 1 x dx = 1 x +1 (ln x + c)= ln x x +1 + c x +1 . If y(e)=1then c = e and y = ln x x +1 + e x +1 .Thesolutionisdefinedon I =(0, ∞).
35. For y′ (sin x) y =2sin x anintegratingfactoris e´ ( sin x) dx = e cos x sothat d dx [e cos x y]= 2(sin x) ecos x and y = e cos x ˆ 2(sin x) ecos x dx = e cos x ( 2ecos x + c)= 2+ ce cos x
If y(π/2)=1then c =3and y = 2+3e cos x.Thesolutionisdefinedon I =(−∞, ∞).
36. For y′ +(tan x)y =cos2 x anintegratingfactoris e´ tan xdx = eln | sec x| =sec x sothat d dx [(sec x) y]=cos x and y =sin x cos x + c cos x for π/2 <x<π/2.If y(0)= 1
then c = 1and y =sin x cos x cos x.Thesolutionisdefinedon I =( π/2,π/2).
37. For y′ +2y = f (x)anintegratingfactoris e2x sothat
2x =
If y(0)=0then c1 = 1/2andforcontinuitywemust have c2 = 1 2 e6 1 2 sothat
38. For y′ + y = f (x)anintegratingfactoris
x y 5 1
If y(0)=1then c1 =0andforcontinuitywemusthave
c2 =2e sothat
If y(0)=2then c1 =3/2andforcontinuitywemusthave
c2 = 1 2 e + 3 2 sothat
40. For y ′ + 2x 1+ x2 y =
anintegratingfactoris1+ x2 sothat
y(0)=0then c1 =0andforcontinuitywemusthave c2 =1sothat
41. Wefirstsolvetheinitial-valueproblem y′ +2y =4x, y(0)=3ontheinterval[0, 1].Theintegratingfactoris
e´ 2 dx = e2x,so d dx
Usingtheinitialcondition,wefind y(0)= 1+ c1 =3,so c1 =4and y =2x 1+4e 2x , 0 ≤ x ≤ 1.Now,since y(1)=2 1+4e 2 =1+4e 2 ,wesolvetheinitial-valueproblem
y′ (2/x)y =4x, y(1)=1+4e 2 ontheinterval(1, ∞).Theintegratingfactoris e´ ( 2/x) dx = e 2ln x = x 2,so
2
=4ln x + c2 y =4x 2 ln x + c2x 2
(Weuseln x insteadofln |x| because x> 1.)Usingtheinitialconditionwefind
y (1)= c2 =1+4e 2 ,so y =4x2 ln x +(1+4e 2 )x2 , x> 1.Thus,
42. Wefirstsolvetheinitial-valueproblem y ′ + y =0, y (0)=4ontheinterval[0, 2].Theintegratingfactor is e´ 1 dx = ex ,so d dx [ex y ]=0 e x y = ˆ 0 dx = c1 y = c1 e x x y 5 1 –1
Usingtheinitialcondition,wefind y (0)= c1 =4,so c1 =4and y =4e x ,0 ≤ x ≤ 2.Now, since y (2)=4e 2 ,wesolvetheinitial-valueproblem y ′ +5y =0, y (1)=4e 2 ontheinterval (2, ∞).Theintegratingfactoris e´ 5 dx = e5x ,so d dx e5x y =0 e5x y = ˆ 0 dx = c2 y = c2 e 5x
Usingtheinitialconditionwefind
(2)=
4e8 5x , x> 2.Thus,thesolutionoftheoriginalinitial-valueproblem is y =
4e x , 0 ≤ x ≤ 2 4x 8 5x ,x> 2
43. Anintegratingfactorfor y′ 2xy =1is e x2 .Thus
From y(1)=(√π/2)e erf(1)+ ce =1weget c
initial-valueproblemis
44. Anintegratingfactorfor y′ 2
From y(0)= √π/2,andnotingthaterf(0)=0,weget c = √π/2.Thus
45. For y′ + exy =1anintegratingfactoris eex .Thus
From y(0)=1weget c
46. Dividingby x2 wehave
y(1)=0weget
47. Anintegratingfactorfor y ′ + 2 x y = 10sin x x3 is x2.Thus
From y(1)=0weget c = 10Si(1).Thus
48. Theintegratingfactorfor
Letting t = π/2 u wehave dt = π/2 du and
.Then
49. Wewant4tobeacriticalpoint,soweuse y′ =4 y
50.(a) Allsolutionsoftheform y = x5ex x4ex + cx4 satisfytheinitialcondition.Inthiscase, since4/x isdiscontinuousat x =0,thehypothesesofTheorem1.2.1arenotsatisfied andtheinitial-valueproblemdoesnothaveauniquesolution.
(b) Thedifferentialequationhasnosolutionsatisfying y(0)= y0, y0 > 0.
(c) Inthiscase,since x0 > 0,Theorem1.2.1appliesandtheinitial-valueproblemhasa uniquesolutiongivenby y =
51. Ontheinterval( 3, 3)theintegratingfactoris
andso
52. Wewantthegeneralsolutiontobe y =3x 5+ ce x.(Ratherthan e x,anyfunctionthat approaches0as x →∞ couldbeused.)Differentiatingweget
sothedifferentialequation y′ + y =3x 2hassolutionsasymptotictotheline y =3x 5.
53. Theleft-handderivativeofthefunctionat x =1is1/e andtheright-handderivativeat x =1 is1 1/e.Thus, y isnotdifferentiableat x =1.
54.(a) Differentiating yc = c/x3 weget
soadifferentialequationwithgeneralsolution yc = c/x3 is xy′ +3y =0.Nowusing yp = x3 xy ′ p +3yp = x(3x 2)+3(x 3)=6x 3
soadifferentialequationwithgeneralsolution y = c/x3 + x3 is xy′ +3y =6x3.This willbeageneralsolutionon(0, ∞).
(b) Since y(1)=13 1/13 =0,aninitialconditionis y(1)=0. Since y(1)=13 +2/13 =3,aninitialconditionis y(1)=3. Ineachcasetheintervalofdefinitionis(0, ∞).Theinitialvalueproblem xy′ +3y =6x3 , y(0)=0hassolution y = x3 for −∞ <x< ∞.Inthefigurethelowercurveisthe graphof y(x)= x3 1/x3,whiletheuppercurveisthe graphof y = x3 2/x3 . x y 5 –3 3
(c) Thefirsttwoinitial-valueproblemsinpart(b)arenotunique.Forexample,setting y(2)=23 1/23 =63/8,weseethat y(2)=63/8isalsoaninitialconditionleadingto thesolution y = x3 1/x3
55. Since e´ P (x) dx+c = ece´ P (x) dx = c1e´ P (x)
whichisthesameas(4)inthetext.
56. Weseebyinspectionthat y =0isasolution.
57. Thesolutionofthefirstequationis x = c1e λ1 t.From x(0)= x0 weobtain c1 = x0 andso x = x0e λ1 t.Thesecondequationthenbecomes
whichislinear.Anintegratingfactoris
.Thus
From y(0)= y0 weobtain c2 =(y0λ2 y0λ1 x0λ1) / (λ2 λ1).Thesolutionis
58. Writingthedifferentialequationas dE dt + 1 RC E =0weseethatanintegratingfactoris
et/RC .Then
From E(4)= ce 4/RC = E0 wefind c = E0e4/RC .Thus,thesolutionoftheinitial-value problemis
59.(a) x x y 5 5 (b) UsingaCASwefind y(2) ≈ 0.226339. 60.(a) x x y
(b) Fromthegraphinpart(b)weseethattheabsolutemaximumoccursaround x =1.7.
Usingtheroot-findingcapabilityofaCASandsolving y′(x)=0for x weseethatthe absolutemaximumis(1 688, 1 742).
61.(a) x
y
2.4
(b) Fromthegraphweseethatas x →∞, y(x)oscillateswithdecreasingamplitudesapproaching9 35672.Sincelim x→∞ S(x)= 1 2 ,wehavelim x→∞ y(x)=5e√π/8 ≈ 9 357,and sincelim x→−∞ S(x)= 1 2 ,wehavelim x→−∞ y(x)=5e √π/8 ≈ 2 672.
(c) Fromthegraphinpart(b)weseethattheabsolutemaximumoccursaround x =1 7 andtheabsoluteminimumoccursaround x = 1 8.Usingtheroot-findingcapabilityof aCASandsolving y′(x)=0for x,weseethattheabsolutemaximumis(1.772, 12.235) andtheabsoluteminimumis( 1.772, 2.044).
ExactEquations
1. Let M =2x 1and N =3y +7sothat My =0= Nx.From fx =2x 1weobtain f = x2 x + h(y), h′(y)=3y +7,and h(y)= 3 2 y2 +7y.Asolutionis x2 x + 3 2 y2 +7y = c.
2. Let M =2x + y and N = x 6y.Then My =1and Nx = 1,sotheequationisnotexact.
3. Let M =5x +4y and N =4x 8y3 sothat My =4= Nx.From fx =5x +4y weobtain f = 5 2 x2 +4xy + h(y), h′(y)= 8y3,and h(y)= 2y4.Asolutionis 5 2 x2 +4xy 2y4 = c.
4. Let M =sin y y sin x and N =cos x + x cos y y sothat My =cos y sin x = Nx.From fx =sin y y sin x weobtain f = x sin y + y cos x + h(y), h′(y)= y,and h(y)= 1 2 y2.A solutionis x sin y + y cos x 1 2 y2 = c
5. Let M =2y2x 3and N =2yx2 +4sothat My =4xy = Nx.From fx =2y2x 3weobtain f = x2y2 3x + h(y), h′(y)=4,and h(y)=4y.Asolutionis x2y2 3x +4y = c
6. Let M =4x3 3y sin3x y/x2 and N =2y 1/x +cos3x sothat My = 3sin3x 1/x2 and Nx =1/x2 3sin3x.Theequationisnotexact.
7. Let M = x2 y2 and N = x2 2xy sothat My = 2y and Nx =2x 2y.Theequationis notexact.
8. Let M =1+ln x + y/x and N = 1+ln x sothat My =1/x = Nx.From fy = 1+ln x we obtain f = y + y ln x + h(x), h′(x)=1+ln x,and h(x)= x ln x.Asolutionis y + y ln x + x ln x = c
9. Let M = y3 y2 sin x x and N =3xy2 +2y cos x sothat My =3y2 2y sin x = Nx.From fx = y3 y2 sin x x weobtain f = xy3 + y2 cos x 1 2 x2 + h(y), h′(y)=0,and h(y)=0.A solutionis xy3 + y2 cos x 1 2 x2 = c
10. Let M = x3 + y3 and N =3xy2 sothat My =3y2 = Nx.From fx = x3 + y3 weobtain f = 1 4 x4 + xy3 + h(y), h′(y)=0,and h(y)=0.Asolutionis 1 4 x4 + xy3 = c.
11. Let M = y ln y e xy and N =1/y + x ln y sothat My =1+ln y + xe xy and Nx =ln y Theequationisnotexact.
12. Let M =3x2y + ey and N = x3 + xey 2y sothat My =3x2 + ey = Nx.From fx =3x2y + ey weobtain f = x3y+xey +h(y), h′(y)= 2y,and h(y)= y2.Asolutionis x3y+xey y2 = c
13. Let M = y 6x2 2xex and N = x sothat My =1= Nx.From fx = y 6x2 2xex weobtain f = xy 2x3 2xex +2ex + h(y), h′(y)=0,and h(y)=0.Asolutionis
xy 2x3 2xex +2ex = c
14. Let M =1 3/x + y and N =1 3/y + x sothat My =1= Nx.From fx =1 3/x + y weobtain f = x 3ln |x| + xy + h(y), h′(y)=1 3 y ,and h(y)= y 3ln |y|.Asolutionis x + y + xy 3ln |xy| = c.
15. Let M = x2y3 1/ 1+9x2 and N = x3y2 sothat My =3x2y2 = Nx.From fx = x2y3 1/ 1+9x2 weobtain f = 1 3 x3y3 1 3 arctan(3x)+ h(y), h′(y)=0,and h(y)=0.Asolutionis x3y3 arctan(3x)= c.
16. Let M = 2y and N =5y 2x sothat My = 2= Nx.From fx = 2y weobtain f = 2xy + h(y), h′(y)=5y,and h(y)= 5 2 y2.Asolutionis 2xy + 5 2 y2 = c
17. Let M =tan x sin x sin y and N =cos x cos y sothat My = sin x cos y = Nx.From fx =tan x sin x sin y weobtain f =ln | sec x| +cos x sin y + h(y), h′(y)=0,and h(y)=0.
Asolutionisln | sec x| +cos x sin y = c
18. Let M =2y sin x cos x y +2y2exy2 and N = x +sin2 x +4xyexy2 sothat My =2sin x cos x 1+4xy 3 exy2 +4yexy2 = Nx.
From fx =2y sin x cos x y +2y2exy2 weobtain f = y sin2 x xy +2exy2 + h(y), h′(y)=0, and h(y)=0.Asolutionis y sin2 x xy +2exy2 = c.
19. Let M =4t3y 15t2 y and N = t4 +3y2 t sothat My =4t3 1= Nt.From ft =4t3y 15t2 y weobtain f = t4y 5t3 ty + h(y), h′(y)=3y2,and h(y)= y3
Asolutionis t4y 5t3 ty + y3 = c
20. Let M =1/t +1/t2 y/ t2 + y2 and N = yey + t/ t2 + y2 sothat My = y2 t2 / t2 + y2 2 = Nt.From ft =1/t +1/t2 y/ t2 + y2 weobtain f =ln |t|− 1 t arctan t y + h(y), h′(y)= yey ,and h(y)= yey ey .Asolutionis ln |t|− 1 t arctan t y + yey ey = c.
21. Let M = x2 +2xy + y2 and N =2xy + x2 1sothat My =2(x + y)= Nx.From fx = x2 +2xy + y2 weobtain f = 1 3 x3 + x2y + xy2 + h(y), h′(y)= 1,and h(y)= y.The solutionis 1 3 x3 +x2y +xy2 y = c.If y(1)=1then c =4/3andasolutionoftheinitial-value problemis 1 3 x3 + x2y + xy2 y = 4 3 .
22. Let M = ex + y and N =2+ x + yey sothat My =1= Nx.From fx = ex + y we obtain f = ex + xy + h(y), h′(y)=2+ yey ,and h(y)=2y + yey ey .Thesolutionis ex + xy +2y + yey ey = c.If y(0)=1then c =3andasolutionoftheinitial-valueproblem is ex + xy +2y + yey ey =3.
23. Let M =4y +2t 5and N =6y +4t 1sothat My =4= Nt.From ft =4y +2t 5
weobtain f =4ty + t2 5t + h(y), h′(y)=6y 1,and h(y)=3y2 y.Thesolutionis 4ty + t2 5t +3y2 y = c.If y( 1)=2then c =8andasolutionoftheinitial-valueproblem is4ty + t2 5t +3y2 y =8.
24. Let M = t/2y4 and N = 3y2 t2 /y5 sothat My = 2t/y5 = Nt.From ft = t/2y4 we obtain f = t2 4y4 + h(y), h′(y)= 3 y3 ,and h(y)= 3 2y2 .Thesolutionis t2 4y4 3 2y2 = c.If y(1)=1then c = 5/4andasolutionoftheinitial-valueproblemis t2 4y4 3 2y2 = 5 4 .
25. Let M = y2 cos x 3x2y 2x and N =2y sin x x3 +ln y sothat My =2y cos x 3x2 = Nx. From fx = y2 cos x 3x2y 2x weobtain f = y2 sin x x3y x2 + h(y), h′(y)=ln y,and h(y)= y ln y y.Thesolutionis y2 sin x x3y x2 + y ln y y = c.If y(0)= e then c =0 andasolutionoftheinitial-valueproblemis y2 sin x x3y x2 + y ln y y =0.
26. Let M = y2 + y sin x and N =2xy cos x 1/ 1+ y2 sothat My =2y +sin x = Nx.From fx = y2 + y sin x weobtain f = xy2 y cos x + h(y), h′(y)= 1 1+ y2 ,and h(y)= tan 1 y
Thesolutionis xy2 y cos x tan 1 y = c.If y(0)=1then c = 1 π/4andasolutionof theinitial-valueproblemis xy 2 y cos x tan 1 y = 1 π 4
27. Equating My =3y2 +4kxy3 and Nx =3y2 +40xy3 weobtain k =10.
28. Equating My =18xy2 sin y and Nx =4kxy2 sin y weobtain k =9/2.
29. Let M = x2y2 sin x +2xy2 cos x and N =2x2y cos x sothat My = 2x2y sin x +4xy cos x = Nx.From fy =2x2y cos x weobtain f = x2y2 cos x + h(y), h′(y)=0,and h(y)=0.Asolutionofthedifferentialequationis x2y2 cos x = c.
30. Let M =(x2 +2xy y2)/(x2 +2xy + y2)and N =(y2 +2xy x2)/(y2 +2xy + x2)so that My = 4xy/(x + y)3 = Nx.From fx = x2 +2xy + y2 2y2 /(x + y)2 weobtain f = x + 2y2 x + y + h(y), h′(y)= 1,and h(y)= y.Asolutionofthedifferentialequationis x2 + y2 = c(x + y).
31. Wenotethat(My Nx)/N =1/x,soanintegratingfactoris e´ dx/x = x.Let M =2xy2 +3x2 and N =2x2y sothat My =4xy = Nx.From fx =2xy2 +3x2 weobtain f = x2y2 +x3 +h(y), h′(y)=0,and h(y)=0.Asolutionofthedifferentialequationis x2y2 + x3 = c.
32. Wenotethat(My Nx)/N =1,soanintegratingfactoris e´ dx = ex.Let M = xyex + y2ex + yex and N = xex +2yex sothat My = xex +2yex + ex = Nx.From fy = xex +2yex weobtain f = xyex + y2ex + h(x), h′(x)=0,and h(x)=0.Asolutionof thedifferentialequationis xyex + y2ex = c.
33. Wenotethat(Nx My )/M =2/y,soanintegratingfactoris e´ 2 dy/y = y2.Let M =6xy3 and N =4y3 +9x2y2 sothat My =18xy2 = Nx.From fx =6xy3 weobtain f =3x2y3 + h(y), h′(y)=4y3,and h(y)= y4.Asolutionofthedifferentialequationis3x2y3 + y4 = c.
34. Wenotethat(My Nx)/N = cot x,soanintegratingfactoris e ´ cot xdx =csc x.Let
M =cos x csc x =cot x and N =(1+2/y)sin x csc x =1+2/y,sothat My =0= Nx.From fx =cot x weobtain f =ln(sin x)+ h(y), h′(y)=1+2/y,and h(y)= y +ln y2.Asolution ofthedifferentialequationisln(sin x)+ y +ln y2 = c.
35. Wenotethat(My Nx)/N =3,soanintegratingfactoris e´ 3 dx = e3x.Let
M =(10 6y + e 3x)e3x =10e3x 6ye3x +1and N = 2e3x,sothat My = 6e3x = Nx.
From fx =10e3x 6ye3x +1weobtain f = 10 3 e3x 2ye3x + x + h(y), h′(y)=0,and h(y)=0. Asolutionofthedifferentialequationis 10 3 e3x 2ye3x + x = c
36. Wenotethat(Nx My)/M = 3/y,soanintegratingfactoris e 3 ´ dy/y =1/y3 .Let
M =(y2 + xy3)/y3 =1/y + x and N =(5y2 xy + y3 sin y)/y3 =5/y x/y2 +sin y,sothat
My = 1/y2 = Nx.From fx =1/y+x weobtain f = x/y+ 1 2 x2 +h(y), h′(y)=5/y+sin y,and h(y)=5ln |y|− cos y.Asolutionofthedifferentialequationis x/y + 1 2 x2 +5ln |y|− cos y = c
37. Wenotethat(My Nx)/N =2x/(4+ x2),soanintegratingfactoris
e 2 ´ xdx/(4+x2 ) =1/(4+ x2).Let M = x/(4+ x2)and N =(x2y +4y)/(4+ x2)= y,so that My =0= Nx.From fx = x(4+ x2)weobtain f = 1 2 ln(4+ x2)+ h(y), h′(y)= y,and h(y)= 1 2 y2.Asolutionofthedifferentialequationis 1 2 ln(4+ x2)+ 1 2 y2 = c.Multiplyingboth sidesby2thelastequationcanbewrittenas ey2 x 2 +4 = c1.Usingtheinitialcondition y(4)=0weseethat c1 =20.Asolutionoftheinitial-valueproblemis ey2 x 2 +4 =20.
38. Wenotethat(My Nx)/N = 3/(1+x),soanintegratingfactoris e 3 ´ dx/(1+x) =1/(1+x)3
Let M =(x2 + y2 5)/(1+ x)3 and N = (y + xy)/(1+ x)3 = y/(1+ x)2,sothat My =2y/(1+ x)3 = Nx.From fy = y/(1+ x)2 weobtain f = 1 2 y2/(1+ x)2 + h(x), h′(x)=(x2 5)/(1+ x)3,and h(x)=2/(1+ x)2 +2/(1+ x)+ln |1+ x|.Asolutionofthe differentialequationis y2 2(1+ x)2 + 2 (1+ x)2 + 2 (1+ x) +ln |
Usingtheinitialcondition y(0)=1weseethat c =7/2.Asolutionoftheinitial-value problemis y2 2(1+ x)2 + 2 (1+
39.(a) Implicitlydifferentiating x3 +2x2y + y2 = c andsolvingfor dy/dx weobtain 3x 2 +2x 2
Bywritingthelastequationindifferentialformweget(4xy +3x2)dx+(2y +2x2 )dy =0.
(b) Setting x =0and y = 2in x3 +2x2y + y2 = c wefind c =4,andsetting x = y =1we alsofind c =4.Thus,bothinitialconditionsdeterminethesameimplicitsolution.
(c) Solving x3 +2x2y + y2 =4for y weget y
and
Observeinthefigurethat y1(0)= 2and y2(1)=1.
40. Toseethattheequationsarenotequivalentconsider dx = (x/y) dy.Anintegratingfactor is µ(x,y)= y resultingin ydx + xdy =0.Asolutionofthelatterequationis y =0,butthis isnotasolutionoftheoriginalequation.
41. Theexplicitsolutionis y = (3+cos2 x)/(1 x2).Since3+cos2 x> 0forall x wemust have1 x2 > 0or 1 <x< 1.Thus,theintervalofdefinitionis( 1, 1).
42.(a) Since fy = N (x,y)= xe
)sothat
x
. (b) Since fx = M (x,y)= y1/2x 1/2 + x x2 + y 1 weobtain
43. Firstnotethat
Then xdx + ydy = x2 + y2 dx becomes x x2 + y2 dx + y x2 + y2 dy = d x2 + y2 = dx.
Theleftsideisthetotaldifferentialof x2 + y2 andtherightsideisthetotaldifferentialof x + c.Thus x2 + y2 = x + c isasolutionofthedifferentialequation.
44. Toseethatthestatementistrue,writetheseparableequationas g(x) dx + dy/h(y)=0. Identifying M = g(x)and N =1/h(y),weseethat My =0= Nx,sothedifferential equationisexact.
45.(a) Indifferentialform v 2 32x dx + xvdv =0
Thisisnotanexactequation,but µ(x)= x isanintegratingfactor.Thenewequation xv2 32x2 dx + x2vdv =0isexactandsolvingyields 1 2 x2v2 32 3 x3 = c.When x =3, v =0andso c = 288.Solving 1 2 x2v2 32 3 x3 = 288for v yieldstheexplicitsolution v(x)=8 x 3 9 x2 .
(b) Thechainleavestheplatformwhen x =8,andso v(8)=8 8 3 9 64 ≈ 12 7ft/s
46.(a) Letting M (x,y)= 2xy (x2 + y2)2 and N (x,y)=1+ y2 x2 (x2 + y2)2 wecompute My = 2x3 8xy2 (x2 + y2)3 = Nx,
sothedifferentialequationisexact.Thenwehave
Thus, g′(y)=1and g(y)= y.Thesolutionis y y x2 + y2 = c.When c =0thesolution is x2 + y2 =1.
(b) Thefirstgraphbelowisobtainedin Mathematica using f (x,y)= y y/(x2 + y2)and
ContourPlot[f[x,y], {x,-3,3}, {y,-3,3}, Axes >True,AxesOrigin >{0,0},AxesLabel >{x,y}, Frame >False,PlotPoints >100,ContourShading >False, Contours >{0,-0.2,0.2,-0.4,0.4,-0.6,0.6,-0.8,0.8}]
Thesecondgraphuses x = y3 cy2 y c y and x = y3 cy2 y c y
Inthiscasethe x-axisisverticalandthe y-axisishorizontal.Toobtainthethirdgraph, wesolve y y/(x2 +y2)= c for y inaCAS.Thisappearstogiveonerealandtwocomplex solutions.Whengraphedin Mathematica however,allthreesolutionscontributetothe graph.Thisisbecausethesolutionsinvolvethesquareroot ofexpressionscontaining c. Forsomevaluesof c theexpressionisnegative,causinganapparentcomplexsolutionto actuallybereal.
2.5 SolutionsbySubstitutions
1. Letting y = ux wehave (x ux) dx + x(udx + xdu)=0 dx + xdu =0 dx x + du =0
2. Letting y = ux wehave
3. Letting x = vy wehave
4. Letting x = vy wehave y(vdy + ydv) 2(vy + y) dy =0 ydv (v +2) dy =0 dv v +2 dy y =0
5. Letting y = ux wehave
2 dx xdu =0
x du u2 =0 ln |x| + 1 u = c ln |x| + x y = c y ln |x| + x = cy.
6. Letting y = ux andusingpartialfractions,wehave
7. Letting y = ux wehave (ux x) dx (ux + x)(udx + xdu)=0 u 2 +1 dx + x(u +1) du =0
x + u +1 u2 +1 du =0
8. Letting y = ux wehave (x +3ux) dx (3x + ux)(udx + xdu)=0 u 2 1 dx + x(u +3) du =0 dx x + u +3 (u 1)(u +1) du =0
9. Letting y = ux wehave
10. Letting y = ux wehave x2 u2x2 dx x 2 du =0 x 1 u2 dx x 2 du =0, (x> 0)
dx x du √1 u2 =0
ln x sin 1 u = c sin 1 u =ln x + c1 sin 1 y x =ln x + c2 y x =sin(ln x + c2) y = x sin(ln x + c2)
SeeProblem33inthissectionforananalysisofthesolution
11. Letting y = ux wehave x 3 u 3 x 3 dx + u 2 x 3(udx + xdu)=0 dx + u 2xdu =0 dx x + u 2 du =0 ln |x| + 1 3 u3 = c 3x 3 ln |x| + y 3 = c1x 3
Using y(1)=2wefind c1 =8.Thesolutionoftheinitial-valueproblemis3x3 ln |x|+y3 =8x3
12. Letting y = ux wehave (x 2 +2u 2 x 2)dx ux 2(udx + xdu)=0 x 2(1+ u 2)dx ux 3 du =0 dx x udu 1+ u2 =0 ln |x|− 1 2 ln(1+ u 2)= c x2 1+ u2 = c1 x 4 = c1(x 2 + y 2).
Using y( 1)=1wefind c1 =1/2.Thesolutionoftheinitial-valueproblemis2x4 = y2 + x2
13. Letting y = ux wehave
(x + uxe u) dx xe u(udx + xdu)=0
dx xeu du =0
dx x e u du =0
ln |x|− eu = c ln |x|− ey/x = c.
Using y(1)=0wefind c = 1.Thesolutionoftheinitial-valueproblemisln |x| = ey/x 1.
14. Letting x = vy wehave
y(vdy + ydv)+ vy(ln vy ln y 1) dy =0 ydv + v ln vdy =0 dv v ln v + dy y =0 ln |ln |v|| +ln |y| = c y ln x y = c1
Using y(1)= e wefind c1 = e.Thesolutionoftheinitial-valueproblemis y ln x y = e
15. From y ′ + 1 x y = 1 x y 2 and w = y3 weobtain dw dx + 3 x w = 3 x .Anintegratingfactoris x3 so that x3w = x3 + c or y3 =1+ cx 3 .
16. From y′ y = exy2 and w = y 1 weobtain dw dx + w = e x.Anintegratingfactoris ex so that exw = 1 2 e2x + c or y 1 = 1 2 ex + ce x .
17. From y′ + y = xy4 and w = y 3 weobtain dw dx 3w = 3x.Anintegratingfactoris e 3x so that e 3xw = xe 3x + 1 3 e 3x + c or y 3 = x + 1 3 + ce3x .
18. From y ′ 1+ 1 x y = y 2 and w = y 1 weobtain dw dx + 1+ 1 x w = 1.Anintegrating factoris xex sothat xexw = xex + ex + c or y 1 = 1+ 1 x + c x e x
19. From y ′ 1 t y = 1 t2 y 2 and w = y 1 weobtain dw dt + 1 t w = 1 t2 .Anintegratingfactoris t so that tw =ln t + c or y 1 = 1 t ln t + c t .Writingthisintheform t y =ln t + c,weseethatthe solutioncanalsobeexpressedintheform et/y = c1t
20. From y ′ + 2 3(1+ t2) y = 2t 3(1+ t2) y 4 and w = y 3 weobtain dw dt 2t 1+ t2 w = 2t 1+ t2 .An integratingfactoris 1 1+ t2 sothat w 1+ t2 = 1 1+ t2 + c or y 3 =1+ c 1+ t2
21. From y ′ 2 x y = 3 x2 y 4 and w = y 3 weobtain dw dx + 6 x w = 9 x2 .Anintegratingfactor is x6 sothat x6w = 9 5 x5 + c or y 3 = 9 5 x 1 + cx 6.If y(1)= 1 2 then c = 49 5 and y 3 = 9 5 x 1 + 49 5 x 6
22. From y′ + y = y 1/2 and w = y3/2 weobtain dw dx + 3 2 w = 3 2 .Anintegratingfactoris e3x/2 so that e3x/2w =
2.If y(0)=4then c =7and y3/2 =1+7
23. Let u = x + y +1sothat du/dx =1+ dy/dx.Then du dx 1= u 2 or 1 1+ u2 du = dx.Thus tan 1 u = x + c or u =tan(x + c),and x + y +1=tan(x + c)or y =tan(x + c) x 1.
24. Let u = x + y sothat du/dx =1+ dy/dx.Then du dx 1= 1 u u or udu = dx.Thus 1 2 u2 = x + c or u2 =2x + c1,and(x + y)2 =2x + c1
25. Let u = x + y sothat du/dx =1+ dy/dx.Then du dx 1=tan2 u orcos2 udu = dx.Thus
1 2 u + 1 4 sin2u = x + c or2u +sin2u =4x + c1,and2(x + y)+sin2(x + y)=4x + c1 or 2y +sin2(x + y)=2x + c1
26. Let u = x + y sothat du/dx =1+ dy/dx.Then du dx 1=sin u or 1 1+sin u du = dx.
Multiplyingby(1 sin u)/(1 sin u)wehave 1 sin u cos2 u du = dx or(sec2 u sec u tan u)du = dx.
Thustan u sec u = x + c ortan(x + y) sec(x + y)= x + c
27. Let u = y 2x +3sothat du/dx = dy/dx 2.Then du dx +2=2+ √u or 1 √u du = dx.Thus 2√u = x + c and2√y 2x +3= x + c
28. Let u = y x +5sothat du/dx = dy/dx 1.Then du dx +1=1+ e u or e udu = dx.Thus e u = x + c and e y+x 5 = x + c.
29. Let u = x + y sothat du/dx =1+ dy/dx.Then du dx 1=cos u and 1 1+cos u du = dx.Now 1 1+cos u = 1 cos u 1 cos2 u = 1 cos u sin2 u =csc 2 u csc u cot u
sowehave ´ (csc2 u csc u cot u) du = ´ dx and cot u +csc u = x + c.Thus cot(x + y)+ csc(x + y)= x + c.Setting x =0and y = π/4weobtain c = √2 1.Thesolutionis
csc(x + y) cot(x + y)= x + √2 1
30. Let u =3x +2y sothat du/dx =3+2 dy/dx.Then du dx =3+ 2u u +2 = 5u +6 u +2 and u +2 5u +6 du = dx.Nowbylongdivision
+2 5u
=
+ 4
u
sowehave
1 5 + 4 25u +30 du = dx and 1 5 u + 4 25 ln |25u +30| = x + c.Thus
5 (3x +2y)+ 4 25 ln |75x +50y +30| = x + c.
Setting x = 1and y = 1weobtain c = 4 25 ln95.Thesolutionis
31. Wewritethedifferentialequation M (x,y)dx + N (x,y)dy =0as dy/dx = f (x,y)where f (x,y)= M (x,y) N (x,y)
Thefunction f (x,y)mustnecessarilybehomogeneousofdegree0when M and N arehomogeneousofdegree α.Since M ishomogeneousofdegree α, M (tx,ty)= tαM (x,y),and letting t =1/x wehave M (1,y/x)= 1 xα M (x,y)or M (x,y)= x αM (1,y/x)
Thus dy dx = f (x,y)= xαM (1,y/x) xαN (1,y/x) = M (1,y/x) N (1,y/x) = F y x .
32. Rewrite(5x2 2y2)dx xydy =0as xy dy dx =5x 2 2y 2 anddivideby xy,sothat dy dx =5 x y 2 y x .
Wethenidentify F y x =5 y x 1 2 y x .
33.(a) Byinspection y = x and y = x aresolutionsofthedifferentialequationandnot membersofthefamily y = x sin(ln x + c2).
(b) Letting x =5and y =0insin 1 (y/x)=ln x + c2 weget sin 1 0=ln5+ c2 or c2 = ln5.Then sin 1 (y/x)=ln x ln5=ln(x/5).Becausetherangeof thearcsinefunctionis[ π/2,π/2]wemusthave
Theintervalofdefinitionofthesolutionisapproximately[1 04, 24 05].
34. As x →−∞, e6x → 0and y → 2x+3.Nowwrite(1+ce6x )/(1 ce6x )as(e 6x +c)/(e 6x c).
Then,as x →∞, e 6x → 0and y → 2x 3.
35.(a) Thesubstitutions y = y1 + u and dy dx = dy1 dx + du dx leadto dy1 dx + du dx = P + Q(y1 + u)+ R(y1 + u)2
ThisisaBernoulliequationwith n =2whichcanbereducedtothelinearequation dw dx +(Q +2y1R)w = R bythesubstitution w = u 1 .
(b) Identify
36. Writethedifferentialequationintheform x(y′/y)=ln x +ln y andlet u =ln y.Then du/dx = y′/y andthedifferentialequationbecomes x(du/dx)=ln x + u or du/dx u/x =
(ln x)/x,whichisfirst-orderandlinear.Anintegratingfactoris e ´ dx/x =1/x,sothat (usingintegrationbyparts)
Thesolutionis
37. Writethedifferentialequationas
andlet u = v2 or v = u1/2.Then
andsubstitutingintothedifferentialequation,wehave
Thelatterdifferentialequationislinearwithintegratingfactor
and
38. Writethedifferentialequationas dP/dt aP = bP 2 andlet u = P 1 or P = u 1.Then dp dt = u 2 du dt , andsubstitutingintothedifferentialequation,wehave u 2
Thelatterdifferentialequationislinearwithintegratingfactor
and
2.6 ANumericalMethod
1. Weidentify f (x,y)=2x 3y +1.Then,for h =0 1,
and
For h =0.05,
and
2. Weidentify f (x,y)= x + y2.Then,for h =0 1, yn+1 = yn +0 1(xn + y 2 n)=0 1
and y(0 1) ≈ y1 =0 1(0)+0+0 1(0)2 =0 y(0 2) ≈ y2 =0 1(0 1)+0+0 1(0)
For h =0 05,
, and y(0 05) ≈ y1 =0 05(0)+0+0 05(0)2 =0 y(0 1) ≈ y2 =0 05(0 05)+0+0 05(0)2 =0 0025 y(0 15) ≈ y3 =0 05(0 1)+0 0025+0 05(0 0025)2 =0 0075 y(0.2) ≈ y4 =0.05(0.15)+0.0075+0.05(0.0075)2 =0.0150
3. Separatingvariablesandintegrating,wehave dy y = dx andln |y| = x + c.
Thus y = c1ex and,using y(0)=1,wefind c =1,so y = ex isthesolutionoftheinitial-value problem.
4. Separatingvariablesandintegrating,wehave
Thus y = c1ex2 and,using y(1)=1,wefind
h = 0.1 h = 0.05
11. TablesofvalueswerecomputedusingtheEulerandRK4methods.Theresultingpointswere plottedandjoinedusing ListPlot in Mathematica
12. SeethecommentsinProblem11above.
13. Usingseparationofvariableswefindthatthesolutionofthe differentialequationis y = 1/(1 x2),whichisundefinedat x =1,wherethegraphhasaverticalasymptote.Because theactualsolutionofthedifferentialequationbecomesunboundedat x approaches1,very smallchangesintheinputs x willresultinlargechangesinthecorrespondingoutputs y.This canbeexpectedtohaveaseriouseffectonnumericalprocedures.Thegraphsbelowwere obtainedasdescribedinProblem11.
14.(a) ThegraphtotherightwasobtainedusingRK4 and ListPlot in Mathematicawith h =0 1.

(b) Writingthedifferentialequationintheform y′ +2xy =1weseethatanintegrating factoris e´ 2xdx = ex2 ,so
and
Thissolutioncanalsobeexpressedintermsoftheinverseerrorfunctionas
Letting x =0and y(0)=0wefind c =0,sothesolutionoftheinitial-valueproblemis
(c) Using FindRoot in Mathematica weseethat y′(x)=0when x =0.924139.Since y(0 924139)=0 541044,weseefromthegraphinpart(a)that(0 924139, 0 541044)is arelativemaximum.Now,usingthesubstitution u = t intheintegralbelow,wehave
Thus, y(x)isanoddfunctionand( 0 924139, 0 541044)isarelativeminimum.
Chapter2inReview
1. Writingthedifferentialequationintheform y′ = k(y + A/k)weseethatthecriticalpoint A/k isarepellerfor k> 0andanattractorfor k< 0.
2. Separatingvariablesandintegratingwehave
Weseethatwhen x =0, y =0,sotheinitial-valueproblemhasaninfinitenumberofsolutions for k =0andnosolutionsfor k =0.
3. True; y = k2/k1 isalwaysasolutionfor k1 =0.
4. True;writingthedifferentialequationas a1(x) dy + a2(x)ydx =0andseparatingvariables yields
y = a2(x) a1(x) dx.
5. d3y dx3 = x sin y (Therearemanyanswers.)
6. False: dr dθ = rθ + r + θ +1=(r +1)(θ +1).
7. True
8. Sincethedifferentialequationintheform y′ =2 −|y| isseentobeautonomous,2 −|y| =0 hascriticalpoints2and 2so y1 =2and y2 = 2areconstant(equilibrium)solutions.
9. dy y = e x dx
ln y = e x + c y = e ex +c = e c e ex or y = c1e ex
10. y ′ = |x| ,y( 1)=2
dy dx = x,x< 0 x,x ≥ 0 y =
Theinitialcondition y( 1)=2implies2= 1 2 + c1 andthus c1 = 5 2 .Now y(x)issupposed tobedifferentiableandsocontinuous.At x =0thetwopartsofthefunctionsmustagree andso c2 = c1 = 5 2 .So, y =
11. y = e cos x ˆ x 0 te cos
dy dx = ecos xxe cos x +( sin x) ecos x ˆ x 0 te cos t dt
dy dx = x (sin x) y or dy dx +(sin x) y = x.
12. dy dx = y +3, dy dx =(y +3)2
13. dy dx =(y 1)2(y 3)2
14. dy dx = y(y 2)2(y 4)
15. When n isodd, xn < 0for x< 0and xn > 0for x> 0.Inthiscase0isunstable.When n is even, xn > 0for x< 0andfor x> 0.Inthiscase0issemi-stable.
When n isodd, xn > 0for x< 0and xn < 0for x> 0.Inthiscase0isasymptotically stable.When n iseven, xn < 0for x< 0andfor x> 0.Inthiscase0issemi-stable.
16. UsingaCASwefindthatthezeroof f occursatapproximately P =1.3214.Fromthegraph weobservethat dP/dt> 0for P< 1 3214and dP/dt< 0for P> 1 3214,so P =1 3214is anasymptoticallystablecriticalpoint.Thus,lim t→∞ P (t)=1 3214.
17. x x y
18.
(a) linearin y,homogeneous,exact
(b) linearin x
(c) separable,exact,linearin x and y (d) Bernoulliin x
(e) separable
(g) linearin x
(i) Bernoulli
(k) linearin x and y,exact,separable, homogeneous
(m) homogeneous
(f) separable,linearin x,Bernoulli
(h) homogeneous
(j) homogeneous,exact,Bernoulli
(l) exact,linearin y
(n) separable
19. Separatingvariablesandusingtheidentitycos2 x = 1 2 (1+cos2x),wehave cos 2 xdx = y y2 +1 dy,
and
20. Writethedifferentialequationintheform y ln x y dx = x ln x y y dy.
Thisisahomogeneousequation,solet x = uy.Then dx = udy + ydu andthedifferential equationbecomes
Separatingvariables,weobtain
21. Thedifferentialequation
isBernoulli.Using w = y3,weobtainthelinearequation
Anintegratingfactoris6x +1,so
and
(Note:Thedifferentialequationisalsoexact.)
22. Writethedifferentialequationintheform(3y2 +2x)dx +(4y2 +6xy)dy =0.Letting M =3y2 +2x and N =4y2 +6xy weseethat My =6y = Nx,sothedifferentialequationis exact.From fx =3y2 +2x weobtain f =3xy2 +x2 +h(y).Then fy =6xy +h′(y)=4y2 +6xy and h′(y)=4y2 so h(y)= 4 3 y3.Aone-parameterfamilyofsolutionsis 3xy 2 + x 2 + 4 3 y 3 = c.
23. Writetheequationintheform
Anintegratingfactoris eln t = t,so
24. Letting u =2x + y +1wehave
andsothegivendifferentialequationistransformedinto
Separatingvariablesandintegratingweget
Resubstitutingfor u givesthesolution
25. Writetheequationintheform
Anintegratingfactoris
26. Letting M =2r2 cos θ sin θ + r cos θ and N =4r +sin θ 2r cos2 θ weseethat Mr =4r cos θ sin θ +cos θ = Nθ,sothedifferentialequationisexact.From fθ =2r2 cos θ sin θ + r cos θ
+ h(r).Then fr = 2r cos2 θ +sin θ + h′(r)=4r +sin θ 2r cos2 θ and h′(r)=4r so h(r)=2r2.The solutionis
27. Weputtheequation dy dx +4(cos x) y = x inthestandardform dy dx +2(cos x) y = 1 2 x then theintegratingfactoris e´
28. Theequation dy dx
29. Weputtheequation x dy dx +2y = xex2 intostandardform dy dx + 2 x y = ex2 .Thentheintegrating
factoris e´ 2 x dx = eln x2 = x2.Therefore
30.
Theintegratingfactoris
33. Thedifferentialequationhastheform(d/dx)[(sin x)y]=0.Integrating,wehave(sin x)y = c or y = c/ sin x.Theinitialconditionimplies c = 2sin(7π/6)=1.Thus, y =1/ sin x,where theinterval(π, 2π)ischosentoinclude x =7π/6.
34. Separatingvariablesandintegratingwehave
(t +1)2 + c
= 1 (t +1)2 + c1 , where c = c1
Theinitialcondition y(0)= 1 8 implies c1 = 9,soasolutionoftheinitial-valueproblemis y = 1 (t +1)2 9 or y = 1 t2 +2t 8 , where 4 <t< 2.
35.(a) For y< 0, √y isnotarealnumber.
(b) Separatingvariablesandintegratingwehave
√y = dx and2√y = x + c.
Letting y(x0)= y0 weget c =2√y0 x0,sothat 2√y = x +2√y0 x0 and y = 1 4 (x +2√y0 x0)2
Since √y> 0for y =0,weseethat dy/dx = 1 2 (x +2√y0 x0)mustbepositive.Thus, theintervalonwhichthesolutionisdefinedis(x0 2√y0, ∞).
36.(a) Thedifferentialequationishomogeneousandwelet y = ux.Then (x 2 y 2) dx + xydy =0 (x 2 u 2 x 2) dx + ux 2(udx + xdu)=0 dx + uxdu =0 udu = dx x 1 2 u 2 = ln |x| + c y2 x2 = 2ln |x| + c1
Theinitialconditiongives c1 =2,soanimplicitsolutionis y2 = x2(2 2ln |x|).
(b) Solvingfor y inpart(a)andbeingsurethattheinitialconditionisstillsatisfied,wehave y = √2 |x|(1 ln |x|)1/2 , where e ≤ x ≤ e sothat1 ln |x|≥ 0.Thegraphof thisfunctionindicatesthatthederivativeisnotdefinedat x =0and x = e.Thus,thesolutionoftheinitial-value problemis y = √2 x(1 ln x)1/2 ,for0 <x<e
37. Thegraphof y1(x)istheportionoftheclosedbluecurvelyinginthefourthquadrant.Its intervalofdefinitionisapproximately(0.7, 4.3).Thegraphof y2(x)istheportionofthe left-handbluecurvelyinginthethirdquadrant.Itsintervalofdefinitionis(−∞, 0).
38. ThefirststepofEuler’smethodgives y(1 1) ≈ 9+0 1(1+3)=9 4.ApplyingEuler’smethod onemoretimegives y(1.2) ≈ 9.4+0.1(1+1.1√9.4) ≈ 9.8373.
39. Sincethedifferentialequationisautonomous,alllineal elementsonagivenhorizontallinehavethesameslope. Thedirectionfieldisthenasshowninthefigureatthe right.Itappearsfromthefigurethatthedifferential equationhascriticalpointsat 2(anattractor)and at2(arepeller).Thus, 2isanaymptoticallystable criticalpointand2isanunstablecriticalpoint.
40. Sincethedifferentialequationisautonomous,alllineal elementsonagivenhorizontallinehavethesameslope. Thedirectionfieldisthenasshowninthefigureatthe right.Itappearsfromthefigurethatthedifferential equationhasnocriticalpoints.