CHAPTER 2 LIMITS AND CONTINUITY
2.1 RATES OF CHANGE AND TANGENTS TO CURVES
1. (a)
2. (a)
(3)(2) 289 321 19 fff x Δ− Δ− ===
(3)(1)() 3 1 312 2 gg g x Δ Δ− ===
(b)
(1)(1) 20 1(1)2 1 fff x Δ−− Δ−− ===
(b) (4)(2) 88 4(2)6 0 gg g x Δ Δ−− ===
3. (a) () () 3 44 3 442 114 hh h t ππ πππ π Δ Δ ===− (b) () ()26 263 0333 hh h t ππ πππ π Δ Δ ===
4. (a)
()(0)(21)(21) 2 00 ggg t π πππ Δ−−−+ Δ−− ===−
5. (2)(0) 811 31 2022 1 RR R θ +− Δ Δ− ====
6. (2)(1)(81610)(145) 211 22 0 PP P θ −−+−−+ Δ Δ− ===−=
(b) ()()(21)(21) ()2 0 ggg t ππ πππ Δ−−−−− Δ−− ===
7. (a) 22 2 ((2)5)(25) 4451 yh hh xhh Δ+−−− ++−+ Δ === 2 4 4 hh h h + =+ As 0,44hh→+→ at (2,1) P the slope is 4. (b) (1)4(2)148yxyx −−=− +=− y = 49 x
8. (a) 22 2 (7(2))(72) 7443 yh
→−−→ 4 at (2,3) P the slope is 4. (b) 3(4)(2)3yxy −=−− −= 48 x −+ 411yx=−+
9. (a) 22 ((2)2(2)3)(22(2)3)yhh xh Δ+−+−−−−
at (2,3) P the slope is 2. (b) (3)2(2)3yxy −−=− +=
10. (a) 22 ((1)4(1))(14(1))yhh xh Δ+−+−− Δ
P the slope is 2. (b) (3)(2)(1)322 yxyx −−=−−
13. (a) 33 (1)12(1)(112(1))yhh xh Δ+−+−− Δ == 23 23 1331212(11) 93 hhhh hhh hh +++−−−− −++ == 2 93hh++
As 0, h → 2 93hh ++→ 9 at (1,11) P the slope is 9 (b) (11)(9)(1)119 yxyx −−=−− +=−+ 9 92.yx =−−
14. (a) 3232 (2)3(2)4(23(2)4)yhh xh Δ+−++−−+ Δ == 81261212340323223 hhhhhhh hh +++−−−+−+ = = 2 3 . hh + As 2 0,30hhh→+→ at (2,0) P the slope is 0. (b) 00(2)0.yxy −=− =
15. (a) Q Slope of p t PQ Δ Δ =
1(10,225)Q 650225 2010 42.5m/sec =
2 (14,375) Q 650375 2014 45.83m/sec =
3 (16.5,475) Q 650475 2016.5 50.00m/sec =
4 (18,550) Q 650550 2018 50.00m/sec =
(b) At 20, t = the sportscar was traveling approximately 50 m/sec or 180 km/h.
16. (a) Q Slope of p t PQ Δ Δ =
1(5,20)Q 8020 105 12m/sec =
2 (7,39) Q 8039 107 13.7m/sec =
3 (8.5,58) Q 8058 108.5 14.7m/sec =
4 (9.5,72) Q 8072 109.5 16m/sec =
(b) Approximately 16 m/sec
17. (a)
(b) 17462 112 201420122 56 p t Δ Δ− === thousand dollars per year
(c) The average rate of change from 2011 to 2012 is 6227 20122011 35 p
== thousand dollars per year.
thousand dollars per year. The average rate of change from 2012 to 2013 is 11162 20132012 49
So, the rate at which profits were changing in 2012 is approximately 1 2 (3549)42 += thousand dollars per year.
18. (a) ()(2)/(2)Fxxx=+− x
(b) The rate of change of ()Fx at 1 x = is 4
19. (a) (2)(1) 21 2121 0.414213 ggg x Δ− Δ−− ==≈
ggg x Δ− Δ− ==≈ (1)(1) 11 (1)1 gghg h xhh Δ+− +− Δ+− ==
(b) () gxx =
+
+
() 11/hh+−
(c) The rate of change of ()gx at 1 x = is 0.5.
(d) The calculator gives 11 1 2 0 lim. h h h +− → =
20. (a) i) 111 326 (3)(2) 1 32116 ff ===− ii) 112 222 ()(2) 2 2222(2) T TTT
(c) The table indicates the rate of change is 0.25 at 2 t = (d) ()11 24 2 lim T T → =−
NOTE: Answers will vary in Exercises 21 and 22.
21. (a) 150 10 [0,1]:15mph; s t Δ− Δ− == [1,2.5]: s t Δ Δ = 201510 2.513 mph; = 3020 3.52.5 [2.5,3.5]: s t Δ− Δ− == 10mph (b) At () 1 2 ,7.5: P Since the portion of the graph from 0 t = to 1 t = is nearly linear, the instantaneous rate of change will be almost the same as the average rate of change, thus the instantaneous speed at 1 2 t = is 157.5 10.5 = 15mi/hr. At (2,20): P Since the portion of the graph from 2 t = to 2.5 t = is nearly linear, the instantaneous rate of change will be nearly the same as the average rate of change, thus 2020 2.52 0mi/hr. v == For values of t less than 2, we have
Q Slope of s t PQ Δ Δ =
1(1,15)Q 1520 12 5mi/hr =
2 (1.5,19) Q 1920 1.52 2mi/hr =
3 (1.9,19.9) Q 19.920 1.92 1mi/hr =
Thus, it appears that the instantaneous speed at 2 t = is 0 mi/hr. At (3,22) : P
Q Slope of s t PQ Δ Δ =
1(4,35)Q 3522 43 13mi/hr =
2 (3.5,30) Q 3022 3.53 16mi/hr =
3 (3.1,23) Q 2322 3.13 10mi/hr =
Q Slope of s t PQ Δ Δ =
1(2,20)Q 2022 23 2mi/hr = 2 (2.5,20) Q 2022 2.53 4mi/hr = 3 (2.9,21.6) Q 21.622 2.93 4mi/hr =
Thus, it appears that the instantaneous speed at 3 t = is about 7 mi/hr.
(c) It appears that the curve is increasing the fastest at 3.5. t = Thus for (3.5,30) P
Q Slope of s t PQ Δ Δ =
1(4,35)Q 3530 43.5 10mi/hr =
2 (3.75,34) Q 3430 3.753.5 16mi/hr =
3 (3.6,32) Q 3230 3.63.5 20mi/hr =
Q Slope of s t PQ Δ Δ =
1(3,22)Q 2230 33.5 16mi/hr =
2 (3.25,25) Q 2530 3.253.5 20mi/hr =
3 (3.4,28) Q 2830 3.43.5 20mi/hr =
Thus, it appears that the instantaneous speed at 3.5 t = is about 20 mi/hr.
22. (a) gal 1015 30day [0,3]:1.67; A t Δ Δ− =≈− [0,5]: A t Δ Δ gal 3.91550day2.2;=≈− 01.4 107 [7,10]: A t Δ Δ− = gal day 0.5≈−
(b) At (1,14): P
Q Slope of A t PQ Δ Δ =
1(2,12.2)Q
2 (1.5,13.2) Q
3 (1.1,13.85) Q
Q Slope of A t PQ Δ Δ =
1(0,15)Q 1514 01 1gal/day=−
2 (0.5,14.6) Q 14.614 0.51 1.2gal/day=−
3 (0.9,14.86) Q 14.8614 0.91 1.4gal/day=−
Thus, it appears that the instantaneous rate of consumption at 1 t = is about 1.45gal/day.
At (4,6): P Q Slope of A t PQ Δ Δ =
1(5,3.9)Q
2 (4.5,4.8) Q
=−
=−
3 (4.1,5.7) Q 5.76 4.14 3gal/day=−
Q Slope of A t PQ Δ Δ =
1(3,10)Q 106 34 4gal/day=−
2 (3.5,7.8) Q 7.86 3.54 3.6gal/day=−
3 (3.9,6.3) Q 6.36 3.94 3gal/day=−
Thus, it appears that the instantaneous rate of consumption at 1 t = is 3gal/day.
At (8,1) : P
Q Slope of A t PQ Δ Δ =
1(9,0.5)Q 0.51 98 0.5gal/day=−
2 (8.5,0.7) Q 0.71 8.58 0.6gal/day=−
3 (8.1,0.95) Q 0.951 8.18 0.5gal/day=−
Q Slope of A t PQ Δ Δ =
1(7,1.4)Q 1.41 78 0.6gal/day=−
2 (7.5,1.3) Q 1.31 7.58 0.6gal/day=−
3 (7.9,1.04) Q 1.041 7.98 0.6gal/day=−
Thus, it appears that the instantaneous rate of consumption at 1 t = is 0.55gal/day. (c) It appears that the curve (the consumption) is decreasing the fastest at 3.5. t = Thus for (3.5,7.8) P
Q Slope of A t PQ Δ Δ =
1(4.5,4.8)Q
2 (4,6) Q
=−
3.6gal/day=−
3 (3.6,7.4) Q 7.47.8 3.63.5 4gal/day=−
Q Slope of s t PQ Δ Δ =
1(2.5,11.2)Q 11.27.8 2.53.5 3.4gal/day =−
2 (3,10) Q 107.8 33.5 4.4gal/day=−
3 (3.4,8.2) Q 8.27.8 3.43.5 4gal/day=−
Thus, it appears that the rate of consumption at 3.5 t = is about 4gal/day.
2.2 LIMIT OF A FUNCTION AND LIMIT LAWS
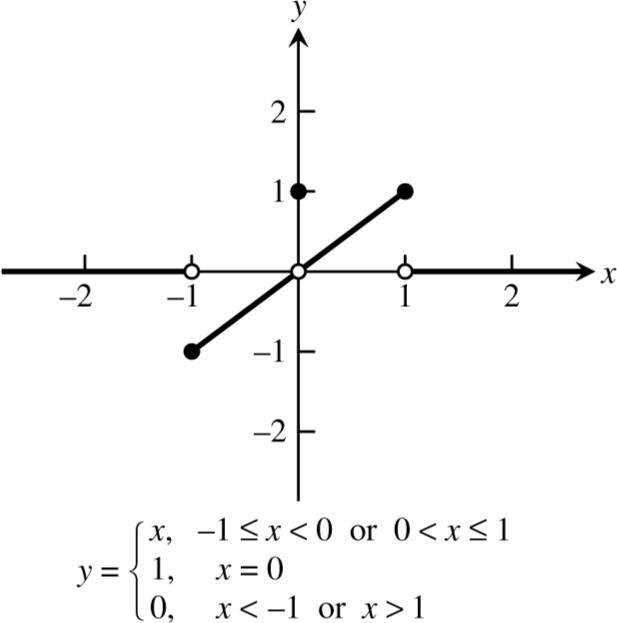
1. (a) Does not exist. As x approaches 1 from the right, ()gx approaches 0. As x approaches 1 from the left, ()gx approaches 1. There is no single number L that all the values ()gx get arbitrarily close to as 1 x → (b) 1 (c) 0 (d) 0.5
2. (a) 0 (b) 1
Copyright 2016 Pearson Education, Inc.
(c) Does not exist. As t approaches 0 from the left, ()ft approaches 1 As t approaches 0 from the right, ()ft approaches 1. There is no single number L that ()ft gets arbitrarily close to as 0. t → (d) 1
3. (a) True (b) True (c) False (d) False (e) False (f) True (g) True
4. (a) False (b) False (c) True (d) True (e) True
5. || 0 lim x x x → does not exist because || 1 xx xx == if 0 x > and || 1 xx xx ==− if 0. x < As x approaches 0 from the left, || x x approaches 1 As x approaches 0 from the right, || x x approaches 1. There is no single number L that all the function values get arbitrarily close to as 0 x →
6. As x approaches 1 from the left, the values of 1 1 x become increasingly large and negative. As x approaches 1 from the right, the values become increasingly large and positive. There is no number L that all the function values get arbitrarily close to as 1, x → so 1 1 1 lim x x → does not exist.
7. Nothing can be said about ()fx because the existence of a limit as 0xx → does not depend on how the function is defined at 0x In order for a limit to exist, ()fx must be arbitrarily close to a single real number L when x is close enough to 0x That is, the existence of a limit depends on the values of ()fx for x near 0 , x not on the definition of ()fx at 0x itself.
8. Nothing can be said. In order for 0 lim() x fx → to exist, ()fx must close to a single value for x near 0 regardless of the value (0) f itself.
9. No, the definition does not require that f be defined at 1 x = in order for a limiting value to exist there. If (1) f is defined, it can be any real number, so we can conclude nothing about (1) f from 1 lim()5. x fx → =
10. No, because the existence of a limit depends on the values of ()fx when x is near 1, not on (1) f itself. If 1 lim() x fx → exists, its value may be some number other than (1)5. f = We can conclude nothing about 1 lim(), x fx → whether it exists or what its value is if it does exist, from knowing the value of (1) f alone.
11. 22 3 lim(13)(3)139134 x x →− −=−−=−=−
12. 22 2 lim(52)(2)5(2)2 x xx → −+−=−+− 41024 = −+−=
13. 6 lim8(5)(7)8(65)(67)8 t tt → −−=−−=−
14. 3232 2 lim(248)(2)2(2) x xxx →− −++=−−− 4(2)8888816 + −+=−−−+=−
15. 33 2(2)5 25 1111(2) 2 lim x x x + + → = 9 3 3 ==
16. () () () () () () ()2241 3333 2/3 lim(83)(21)8521(82)1(6)2 t ss → −−=−−=−−==
17. () () () () () 2 22 2 3525 11 22222 1/2 lim4(34)434(2)4(2) x xx →− +=−−+=−−+=−=−
18. 22 2 22441 4106205 56(2)5(2)6 2 lim y yy y + + ++ ++++ → ====
19. () 4 4/34/34/31/3 3 lim(5)[5(3)](8)(8) y y →− −=−−== 4 216==
20. 22 4 lim1041016106 z z → −=−=−=
21. 3333 2 3113(0)1111 0 lim h h +++++ → ===
22. 542542542 542 00 limlimhhh hh h hh +−+−++ ++ →→ =⋅ = () () (54)4 5 00542542 limlim h h hhhhhh +− →→++++ = 0 lim h → = 555 4 54242 h +++ ==
23. 2 55 1 (5)(5)5 25 555 limlimlim xx xxx x xxx →→→+−+ == 11 5510 + = =
24. 2 33 1 (3)(1)1 43 333 limlimlim xx xxx xx xxx ++ +++ ++ →−→−→− == 11 312−+ = =−
25. 2 (5)(2) 310 55 555 limlimlim xx xx xx xxx +− +− ++ →−→−→− == (2)527 x −=−−=−
26. 2 (5)(2) 710 22 222 limlimlim(5) xx xx xx xxx x →→→ ==− 253 = −=−
27. 2 2 (2)(1) 223 12 (1)(1)1112 1 111 limlimlim tt ttt ttt t t tt +− +−+ + →→→−+++ ====
28. 2 2 (2)(1) 322 (2)(1)2 2 111 limlimlim tt ttt ttt tt t tt ++ +++ →−→−→−−+− == 121 123 −+ = =−
29. 3222 2(2) 24 2 2(2) 222 limlimlim x x xxxxxxxx −+ ++ →−→−→− == 21 42 = =−
30. 322 42222 58(58)58 316(316)316 000 limlimlimyyyyy yyyyyyyy +++ →→→ == 8 1 162 = =−
31. () 1 1 11 1 111 1111 limlimlimlim x x xx xxxx xxxx →→→→ ==⋅= 1 1 x =−
32. ( ) (1)(1) 11 (1)(1) 11 2 122 0000(1)(1)(1)(1)1 limlimlimlim2 xx xx xx x xxxxxxxxxxx ++− −+ −+ + →→→→−+−+− ==⋅===−
Copyright 2016 Pearson Education, Inc.
33. 2 4 32 (1)(1)(1) 1 1(1)(1) 111 limlimlim uuu u uuuu u uu ++− −++− →→→ == 2 2 (1)(1)(11)(11) 4 1113 1 uu uu ++++ ++
34. 2 3 42 (2)(24) 8 16(2)(2)(4) 222 limlimlim vvv v vvvv v vv −++ −−++
35. 33 111 96 999(3)(3)393 limlimlim xx x xxxxxx →→→−+++ ====
36. 2 (4)(2)(2) 4 222 444 limlimlimxxxxx xx xxxxxx −+− →→→ ==
37. () ()() (1)32 1 32 3232 111 limlimlim xx x x xx xxx −++ +−
38.
39. ()() () 22 2 2 124124 124 2 22 (2)124 limlim xx x x xx xx +−++ +− →→
40. () ()()
2 22 (2)53 2 22 53 5353 limlim xx x xx x xx +++ + →−→− +− +−++ ==
2 (2)53 (5)9 2 lim xx x x +++ +− →− () 2 (2)53 (2)(2) 2 lim xx xx x +++ +− →− = 2 5393 3 242 2 lim x x x +++ →− = ==−
41. ()() () 22 2 2 2525 25 3 33 (3)25 limlim xx x x xx xx −−+− + →−→− ++− = () 2 2 4(5) 3 (3)25 lim x x xx →− ++− = () 2 2 9 3 (3)25 lim x x xx →− ++− = () 2 2 (3)(3) 363 2 24 33 25 (3)25 limlim xx x xx x xx −+ + →−→− +− ++− = ===
42. () ()() 2 2 22 (4)59 4 444 59 5959 limlimlim xx x xxx x xx −++ →→→ −+ −+++ == () 2 2 (4)59 25(9) xx x −++ −+ () 2 2 (4)59 16 4 lim xx x x −++ → = 4 lim x → = () 2 2 (4)59 59525 5 (4)(4)484 4 lim xx x xxx x −++ +++ −++ → ===
43. 0 lim(2sin1)2sin01011 x x → −=−=−=− 44. 2 222 00 limsinlimsin(sin0)00 xx xx →→ ====
45. 111 coscos01 00 limseclim1 x xx x →→ ==== 46. sinsin00 coscos01 00 limtanlim0 x x xx x →→ ====
47. 1sin10sin0100 1 3cos3cos033 0 lim xx x x ++++++ → ===
48. 22 0 lim(1)(2cos)(01)(2cos0) x xx → −−=−− (1)(21)(1)(1)1 = −−=−=−
49. lim4cos()lim4lim xxx xxx ππ π π →−→−→− ++=+⋅ cos()4cos0 x ππ +=−+⋅ 414ππ = −⋅=−
50. 22 00 lim7seclim(7sec) xx xx →→ +=+ 222 0 7limsec7sec07(1) x x → = +=+=+ 22 =
51. (a) quotient rule
(b) difference and power rules (c) sum and constant multiple rules
52. (a) quotient rule (b) power and product rules (c) difference and constant multiple rules
53. (a) lim()()lim()lim() xcxcxc fxgxfxgx →→→
(5) = (2)10 −=−
(b) lim2()()2lim()lim() xcxcxc fxgxfxgx →→→
2(5)(2)20 = −=−
(c) lim[()3()]lim()3lim() xcxcxc fxgxfxgx →→→ +=+ 53(2) 1 = +−=−
(d) lim() () 55 ()()lim()lim()5(2)7 lim xc x cxc fx fx fxgxfxgx xc → →→ → ===
54. (a) 444 lim[()3]lim()lim3330 xxx gxgx →→→ +=+=−+=
(b) 444 lim()limlim()(4)(0)0 xxx xfxxfx →→→ =⋅==
(c) 2 22 44 lim[()]lim()[3]9 xx gxgx →→
==−=
(d) 4 44 lim() () 3 ()1lim()lim101 4 lim3 x x x gx gx fxfx x → →→ → ===
55. (a) lim[()()]lim()lim() xbxbxb fxgxfxgx →→→ +=+ 7(3) 4 = +−=
(b) lim()()lim()lim() xbxbxb fxgxfxgx →→→
(7)(3)21 = −=−
(c) lim4()lim4lim()(4)(3) xbxbxb gxgx →→→
12 = (d) 77 33 lim()/()lim()/lim() xbxbxb fxgxfxgx →→→ ===−
56. (a) 22 lim[()()()]lim() xx pxrxsxpx →−→− ++= 22 lim()lim()40(3)1 xx rxsx →−→− + +=++−=
(b) 222 lim()()()lim()lim() xxx pxrxsxpxrx →−→−→−
(c) 2 lim[4()5()]/() x pxrxsx →− −+ 2 4lim() x px →−
57. 22 2 (1)1 121 00 limlim h hh hhhh +− ++− →→ = (2) 0 lim hh h h + → = 0 lim(2)2 h h → = +=
58. 22 2 (2)(2) 444 000 limlimlim h hh hh hhh −+−− −+− →→→ == (4) 0 lim(4)4 hh h h h → =−=−
59. [3(2)4][3(2)4] 3 00 limlim3 h h hhhh +−−− →→ ==
60. () ()11 2 22 2 1 2(2) 00022(2) limlimlim h h h hhhhhhh −+− −+ −−−+ →→→−−−+ == 1 (42)4 0 lim h hh h → = =−
61. ()() () 7777 77 77 00 limlim hh h h hh hh +−++ +− ++ →→ = () () (7)7 007777 limlim h h hhhhhh +− →→++++ = = 0 lim h → = 11 7727 h ++ =
62. ()() () 311311 3(0)13(0)1 311 00 limlim hh h h hh hh +−++ ++−+ ++ →→ = () () (31)1 3 00311311 limlim h h hhhhhh +− →→++++ = = 0 lim h → = 33 2 311 h ++ =
63. 22 0 lim5252(0)5 x x → −=−= and 0 lim x → 22 55(0)5; x −=−= by the sandwich theorem, 0 lim()5 x fx → =
64. 2 0 lim(2)20 2 x x → −=−= and 0 lim2cos x x → = 2(1)2; = by the sandwich theorem, 0 lim() 2 x gx → =
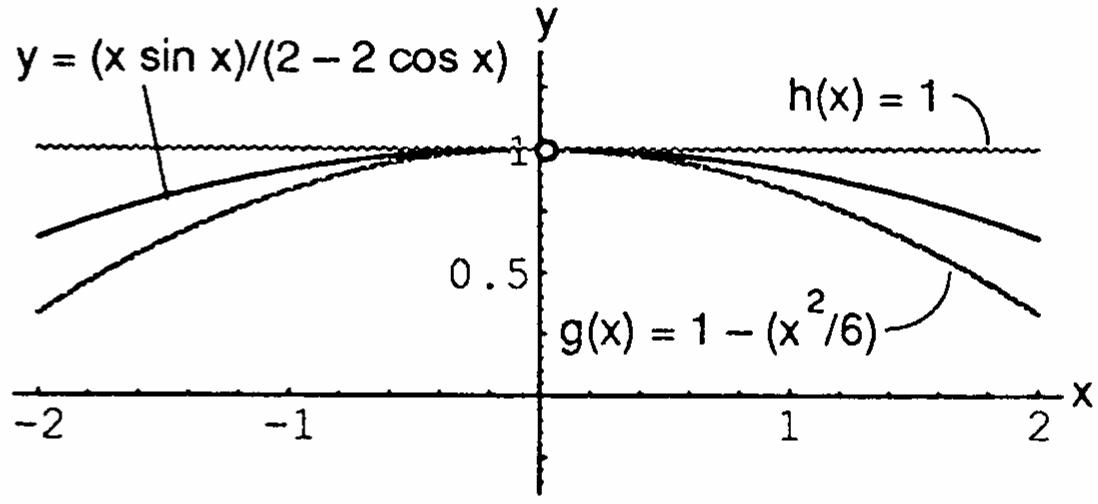
65. (a) ( ) 2 0 66 0 lim11 1 x x → −=−= and 0 lim11; x → = by the sandwich theorem, sin 22cos 0 lim1 xx x x → = (b) For 0,(sin)/(22cos) xyxxx ==− / lies between the other two graphs in the figure, and the graphs converge as 0. x →
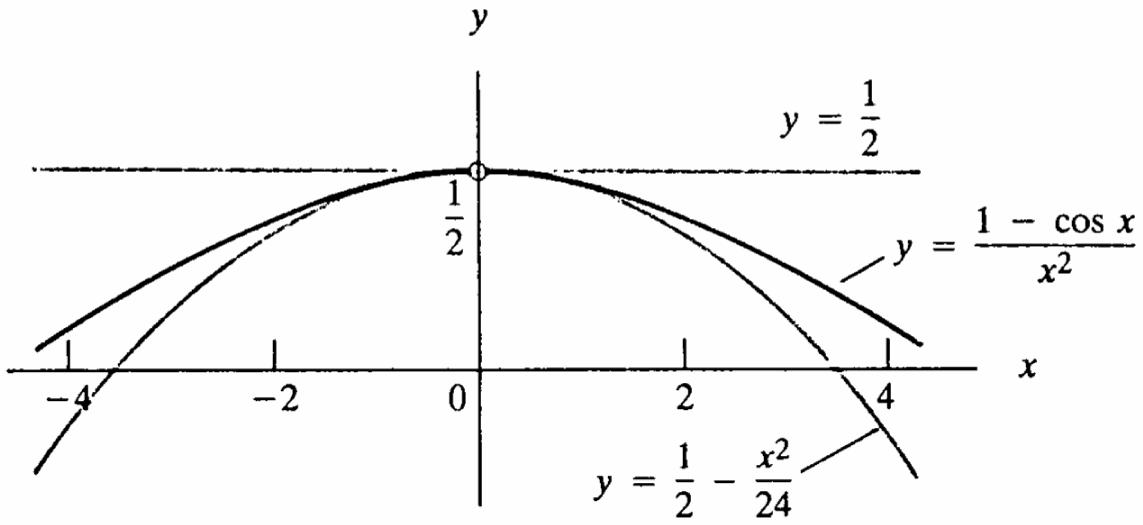
66. (a) ( ) 22 1111 00022422422 limlimlim0 xx xxx →→→ −=−=−= and 11 22 0 lim; x → = by the sandwich theorem, 2 1cos 1 2 0 lim x x x → = (b) For all 0, x = / the graph of 2 ()(1cos)/ fxxx =− lies between the line 1 2 y = and the parabola 2 1 2 / 24, yx =− and the graphs converge as 0 x →
67. (a) 2 ()(9)/(3) fxxx=−+ x
fx
The estimate is 3 lim()6. x fx →− =−
(b)

(c) 2 (3)(3) 9 33 ()3 xx x xx fxx +− ++ ===− if 3, x =− / and 3 lim(3)336. x x →− −=−−=−
68. (a) () 2 ()(2)/2 gxxx=−− x
()gx

(c) ()() () 2 22 2 2 2 ()2 xx x x x gxx +− ===+ if 2, x = / and () 2 lim222 x x → +=+= 22.
69. (a) 2 ()(6)/(412) Gxxxx =++− x 5.9 5.99
()Gx .126582 .1251564 .1250156 .1250015 .1250001 .1250000 x 6.1 6.01
6.000001 ()Gx .123456 .124843 .124984 .124998 .124999 .124999 (b)
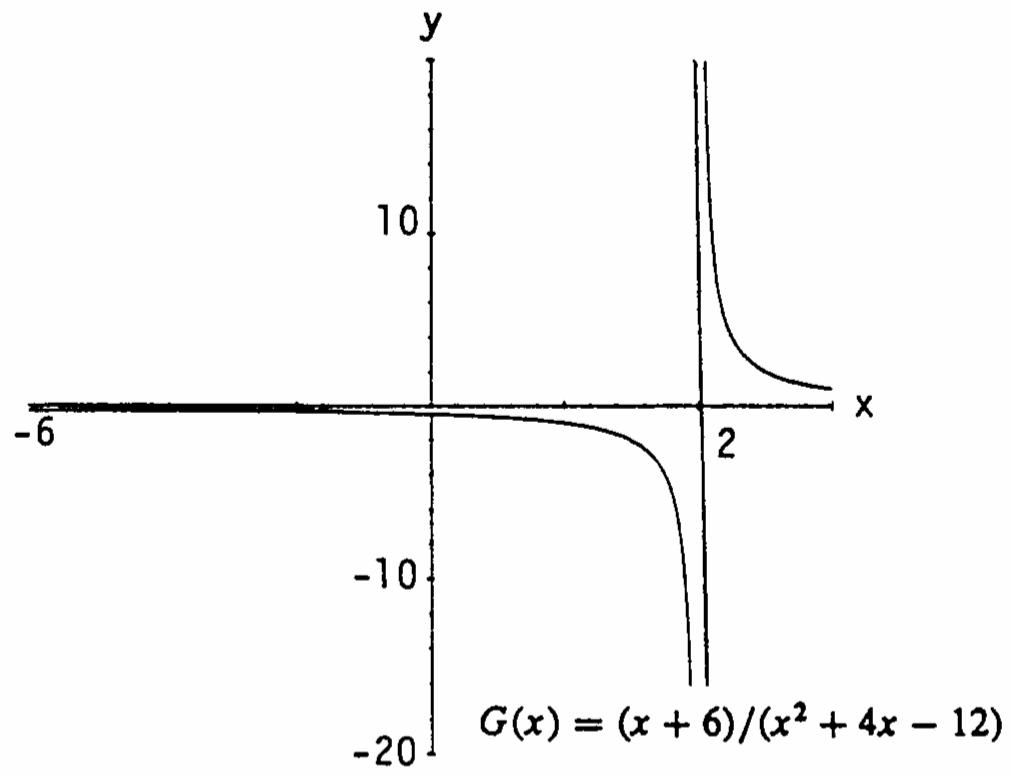
(c) 2 66 1 (6)(2)2 (412) () xx xxx xx Gx ++ +−− +− === if 6, x =− / and 111 2628 6 lim x x →− ==−= 0.125.
Copyright 2016 Pearson Education, Inc.
70. (a) 22 ()(23)/(43) hxxxxx =−−−+
(b)

71. (a) 2 ()(1)/(||1) fxxx=−−

(b) (c) 2 (1)(1) 1 1 (1)(1) 1 (1) 1,0and1 (), 1,0and1 xx x x xx x x xxx fx xxx
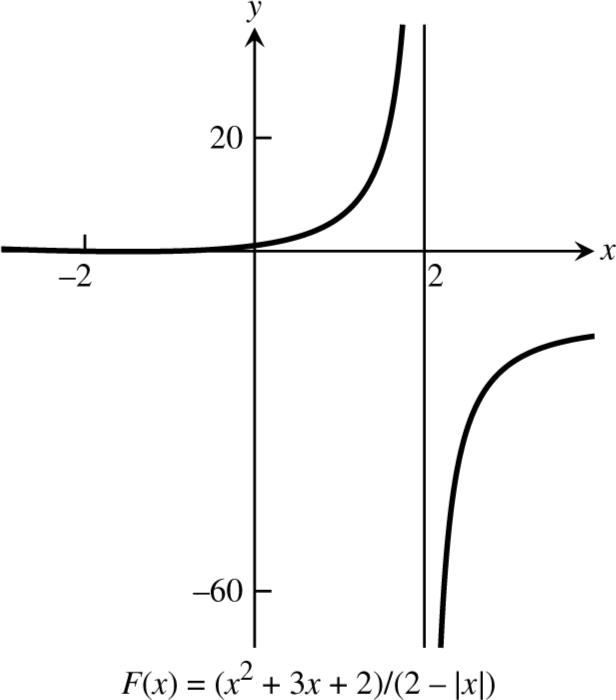
(a) 2 ()(32)/(2||) Fxxxx
73. (a) ()(sin)/ g θθ θ =
θ
(b)
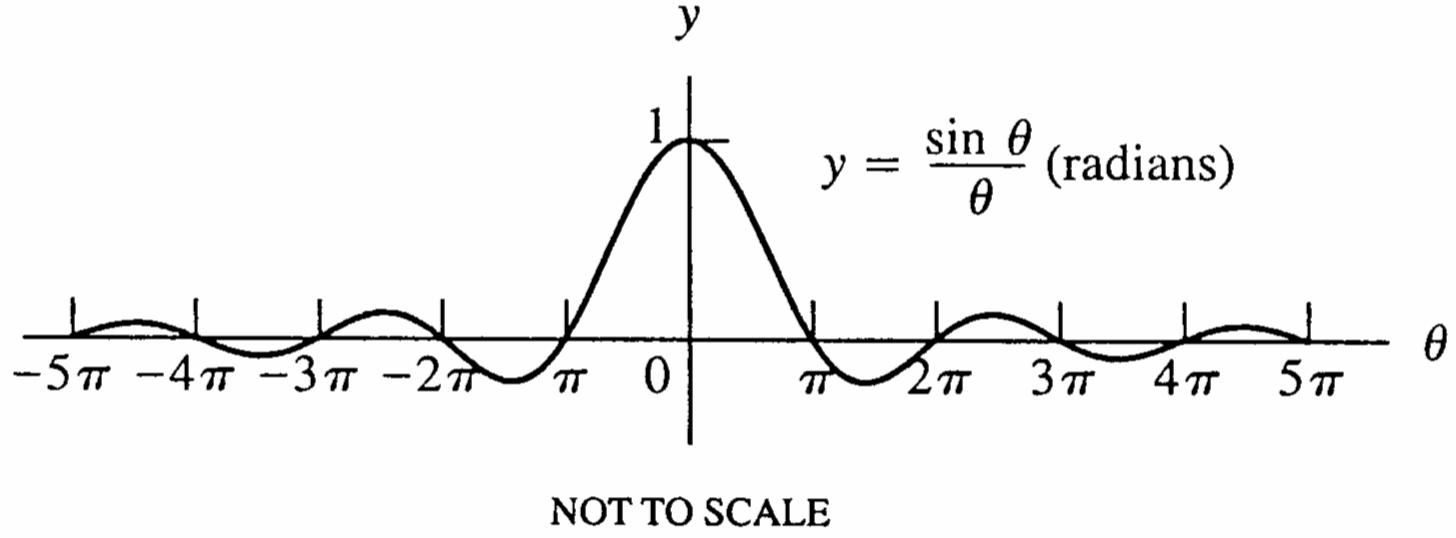
74. (a) 2 ()(1cos)/ Gttt =− t
(b)
0 lim()0.5 t Gt → =

75. (a) 1/(1) () x fxx =
x .9 .99 .999 .9999 .99999 .999999 f(x) .348678 .366032 .367695 .367861 .367877 .367879 x
) .385543 .369711 .368063 .367897 .367881 .367878
1 lim()0.36788 x fx → ≈
(b)

Graph is NOT TO SCALE. Also, the intersection of the axes is not the origin: the axes intersect at the point (1, 2.71820).
76. (a) ()(31)/ x fxx =−
x .1 .01 .001 .0001 .00001 .000001
f(x) 1.161231
1 lim()1.0986 x fx → ≈
(b)

77. lim() xc fx → exists at those points c where 4 lim xc x → = 2 lim xc x → Thus, 4222(1)00,1, c cccc = −= = or 1
Moreover, 2 00 lim()lim0 xx fxx →→ == and 11 lim()lim()1. xx fxfx →−→ ==
78. Nothing can be concluded about the values of ,,fg and h at 2 x = Yes, (2) f could be 0. Since the conditions of the sandwich theorem are satisfied, 2 lim()50. x fx → =−= /
79. 444 44 lim()lim5lim()5 ()5 2limlim242 4 1 lim xxx x x fxfx fx xx x →→→ →→ → === 44 lim()52(1)lim()257. xx fxfx →→ −= =+=
80. (a) 22 22 2 lim()lim() () 4 lim 2 1 lim xx x fxfx fx xx x →−→− →− →− === 2 lim()4. x fx →− =
(b) 2 ()() 1 222 1 limlimlim fxfx xx x xxx →−→−→−
81. (a) ()5 2 22 0 30limlim(2) fx x xx x →→
(b) ()5 2 22 0 40limlim(2) fx x xx x

(b)
(a)
85-90. Example CAS commands: Maple: f :x-(x^416)/(x2); =>− x0:2; = plot(f(x),xx0-1..x01,colorblack, =+=
title"Section 2.2,85(a); #" ) = limit(f(x),xx; 0 ) =
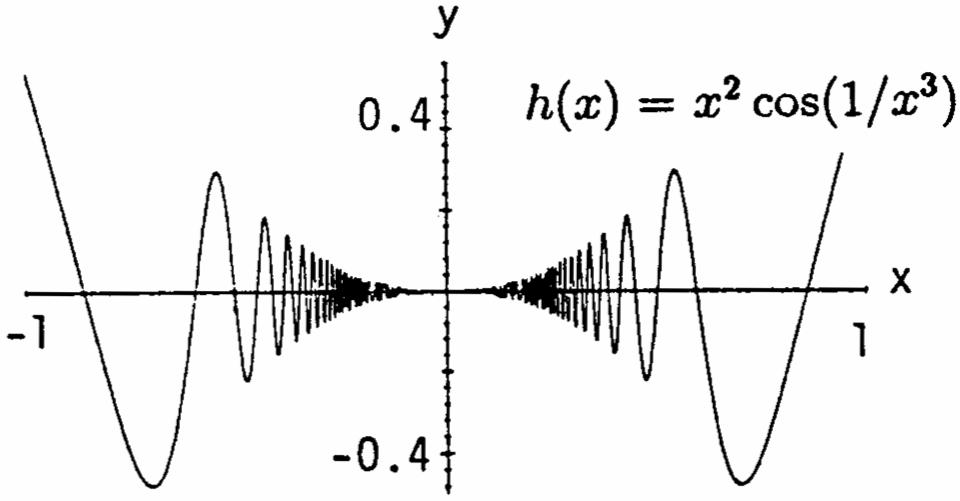
In Exercise 87, note that the standard cube root, x^(1/3), is not defined for x<0 in many CASs. This can be overcome in Maple by entering the function as f :x-(surd(x1,3)1)/x. =>+−
Mathematica: (assigned function and values for x0 and h may vary)
Clear[f,x]
322 f [x_]:(xx5x3)/(x1) =−−−+
x01;h0.1; =−=
Plot[f[x],{x,x0h,x0h}] −+
Limit[f[x],xx0] →
2.3 THE PRECISE DEFINITION OF A LIMIT
1.

Step 1: 55xxδδδ −< −<−< 55 x δδ+<<+
Step 2: 572,δδ += = or 514.δδ += =
The value of δ which assures 51 x δ −< < 7 x < is the smaller value, 2 δ =
2.

Step 1: 22xx δδ δ −< −<−< 22 x δδ −+<<+
Step 2: 211,δδ += = or 275.δδ += =
The value of δ which assures 2 x δ −< 1 7 x << is the smaller value, 1. δ =
3.

Step 1: (3)3xxδδδ −−< −<+< 33 x δδ−<<−
Step 2: 7 1 22 3,δδ
The value of δ which assures (3) x δ −−< 7 1 22 x <<− is the smaller value, 1 2 δ =
4.
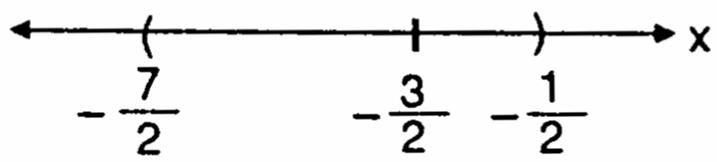
Step 1: ()33 22xxδδδ −−< −<+< 33 22 x δδ−<<−
Step 2: 37
5.
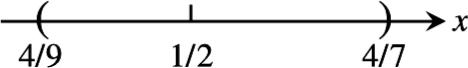
Step 1: 11 22xx δδ δ −< −<−< 11 22 x δδ+<<+
Step 2: 141 2918 , δδ += = or 14 27 δ += 1 14 δ =
The value of δ which assures 1 2 x δ −< 44 97 x << is the smaller value, 1 18 δ =
Copyright 2016 Pearson Education, Inc.
6.
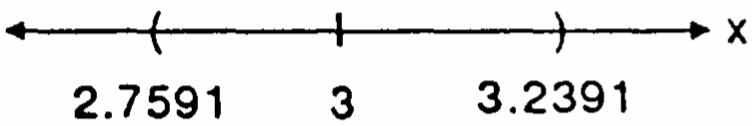
Step 1: 33xxδδδ −< −<−< 33 x δδ+<<+
Step 2: 32.75910.2409,δδ += = or 33.23910.2391.δδ += =
The value of δ which assures 3 x δ −< 2.75913.2391 x << is the smaller value, 0.2391. δ =
7. Step 1: 55xxδδδ −< −<−< 55 x δδ+<<+
Step 2: From the graph, 54.90.1,δδ += = or 55.10.1;δδ += = thus 0.1 δ = in either case.
8. Step 1: (3)3xxδδδ −−< −<+< 33 x δδ−<<−
Step 2: From the graph, 33.10.1,δδ −=− = or 32.90.1;δδ −=− = thus 0.1. δ =
9. Step 1: 11xxδδδ −< −<−< 1 1 x δδ+<<+
Step 2: From the graph, 97 1616 1,δδ += = or 259 1616 1; δ δ += = thus 7 16 . δ =
10. Step 1: 33xxδδδ −< −<−< 33 x δδ+<<+
Step 2: From the graph, 32.610.39,δδ += = or 33.410.41;δδ += = thus 0.39. δ =
11. Step 1: 22xxδδδ −< −<−< 22 x δδ+<<+
Step 2: From the graph, 23 δδ += = 230.2679, −≈ or 25 δ δ += = 52−≈ 0.2361; thus 52. δ =−
12. Step 1: (1)1xxδδδ −−< −<+< 11 x δδ−<<−
Step 2: From the graph, 5 2 1 δδ −=− = 52 2 0.118 ≈ or 323 22 1 δ δ −=− =≈ 0.1340; thus 52 2 . δ =
13. Step 1: (1)1xxδδδ −−< −<+< 11 x δδ−<<−
Step 2: From the graph, 167 99 1 δδ −=− =≈ 0.77, or 169 2525 1 δ −=− = 0.36; thus 9 25 δ == 0.36.
14. Step 1: 11 22xxδδδ −< −<−< 11 22 x δδ+<<+
Step 2: From the graph, 111 22.012δδ += = 1 2.01 0.00248, ≈ or 11 21.99 δ δ += = 11 1.992 0.00251; −≈ thus 0.00248. δ =
15. Step 1: (1)50.0140.01 xx +−< −< 0.0140.013.994.01 xx<−< <<
Step 2: 44xxδδδ −< −<−< 440.01. x δδδ +<<+ =
16. Step 1: (22)(6)0.02240.02 xx −−−< +< 0.02240.02 x −<+< 4.0223.982.011.99 xx −<<− −<<−
Step 2: (2)2xxδδδ −−< −<+< 220.01. x δδδ −<<− =
17. Step 1: 110.10.1110.1xx +−< −<+−< 0.911.1 x <+< 0.8111.21 x <+< 0.190.21 x −<<
Step 2: 0.xxδδδ −< −<< Then, 0.19 δ =− 0.19 δ = or 0.21; δ = thus, 0.19. δ =
18. Step 1: 11 220.10.10.1xx −< −<−< 0.40.60.160.36 xx<< <<
Step 2: 11 44xxδδδ −< −<−< 11 44 . x δδ+<<+
Then 1 4 0.160.09δδ += = or 1 4 or0.360.11;thus0.09 δδδ += ==
19. Step 1: 193111931 xx−−< −<−−< 219441916 xx <−< <−< 41916153 xx −>−>− >> or 3 15 x <<
Step 2: 1010xx δδ δ −< −<−< 1010. x δδ+<<+
Then 1037,δδ += = or 1015 δ += 5; δ = thus 5. δ =
20. Step 1: 7411741xx −−< −<−−< 3759725 xx <−< <−< 16x32 <<
Step 2: 2323xx δδ δ −< −<−< 23x23δδ −+<<+
Then 23167,δδ += = or 23 δ += 329; δ = thus 7. δ =
21. Step 1: 1111440.050.050.05xx −< −<−< 1010 1 23 0.20.3 x x << >> or 10 3 5. x <<
Step 2: 44xxδδδ −< −<−< 44 x δδ+<<+
Then 10 3 4 δ += or 2 3 , δ = or 45 δ += or 1; δ = thus 2 3 . δ =
22. Step 1: 2230.10.130.1 xx −< −<−< 2 2.93.12.93.1 xx<< <<
Step 2: 33xxδδδ −< −<−< 33. x δδ+<<+
Then 32.932.90.0291,or33.13.130.0286; δδδδ += =−≈+= =−≈ thus 0.0286 δ =
23. Step 1: 2240.50.540.5 xx −< −<−< 2 3.54.53.54.5 xx<< << 4.53.5, x −<<− for x near 2.
Step 2: (2)2xxδδδ −−< −<+< 22. x δδ−<<−
Then 24.54.52δδ −=− =−≈ 0.1213, or 23.523.5 δ δ −=− =−≈ 0.1292; thus 4.520.12. δ =−≈
24. Step 1: 11(1)0.10.110.1 xx −−< −<+< 91010 111 1010119 x x <<− −>>− or 1010 911 x <<−
Step 2: (1)1xxδδδ −−< −<+< 11. x δδ−<<−
Then 10 1 99 1,δδ −=− = or 1 δ −= 10 1 1111 ; δ = thus 1 11 δ =
25. Step 1: 22 (5)111161 xx −−< −< 22 11611517 xx<−< << 1517. x <<
Step 2: 44xxδδδ −< −<−< 44. x δδ+<<+
Then 415415δδ += =−≈ 0.1270, or 417174 δ δ += =−≈ 0.1231; thus 1740.12. δ =−≈
26. Step 1: 120120120 511514 xxx −< −<−< < 11 41206 63020 x x < >> >> or 20 30. x < <
Step 2: 2424xxδδδ −< −<−< 2424. x δδ+<<+
Then 24204,δδ += = or 24 δ += 306; δ = thus 4 δ =
27. Step 1: 20.030.0320.03mxmmxm −< −<−< 0.0320.032 mmxm −+<<+ 0.03 22 m x −<<+ 0.03 . m
Step 2: 22xxδδδ −< −<−< 22. x δδ+<<+
Then 0.030.03 22, mm δδ +=− = or 0.030.03 22 mm δ δ +=+ = In either case, 0.03 m δ =
Copyright 2016 Pearson Education, Inc.
28. Step 1: 33 mxmccmxmc −< −<−< 33 cmmxcm +<<+ 33cc mm x −<<+
Step 2: 33xxδδδ −< −<−< 33 x δδ+<<+
Then 33, cc mm δδ +=− = or 3 δ += 3 . cc mm δ + = In either case, . c m δ =
29. Step 1: ()22 ()mxbbccmxmm +−+< −<− 22 ccmxcmm < −+<<+ 11 22 cc mm x −<<+
Step 2: 11 22xxδδδ −< −<−< 11 22 . x δδ+<<+
Then 11 22 , cc mm δδ +=− = or 1 2 δ += 1 2 cc mm δ + = In either case, c m δ =
30. Step 1: 0.050.05 ()()0.050.050.050.050.05 11. mm mxbmbmxmmmxm x +−+< −<−< −+<<+ −<<+
Step 2: 11xxδδδ −< −<−< 11. x δδ+<<+
Then 0.050.05 11, mm δδ +=− = or 0.050.05 11. mm δ δ +=+ = In either case, 0.05 m δ =
31. 3 lim(32)32(3)3 x x → −=−=−
Step 1: (32)(3)0.020.0262 xx−−−< −<−< 0.026.0225.98 x −<−<− 3.01 x > 2.99 > or 2.993.01. x <<
Step 2: 0 33xxδδδ <−< −<−< 33 x δδ+<<+
Then 32.990.01,δδ += = or 33.010.01;δδ += = thus 0.01. δ =
32. 1 lim(32)(3)(1)21 x x →− −−=−−−=
Step 1: (32)10.030.0333 xx−−−< −<−− 0.030.0110.01 x < >+>− 1.01 0.99. x < <−
Step 2: (1)1xxδδδ −−< −<+< 11. x δδ−<<−
Then 11.010.01,δδ −=− = or 10.990.01;δδ −=− = thus 0.01. δ =
33. 2 (2)(2) 4 222(2) limlim xx x xxxx +− →→ = = 2 lim(2)224, x x → +=+= 2 x = /
Step 1: ( ) 2 (2)(2) 4 2(2) 40.050.05 xx x xx +− −< −< 4 0.053.9524.05,2 xx < <+<= / 1.952.05,2. xx <<= /
Step 2: 22xxδδδ −< −<−< 22 x δδ+<<+
Then 21.950.05,δδ += = or 2 δ + = 2.050.05; δ = thus 0.05. δ =
34. 2 (x5)(x1) x6x5 x5x5x5(x5) limlim ++ ++ →−→−++ == 5 lim(1)4,5. x xx →− +=−=− /
Step 1: ( ) 2 65 5 (4)0.05 xx x ++ + −−< (5)(1) (5) 0.0540.05 xx x ++ + −<+< 4.0513.95, x −<+<− 5 x =− / 5.054.95, x −<<− 5. x =− /
Step 2: (5)5xxδδδ −−< −<+< 55. x δδ−<<−
Then 55.050.05,δδ −=− = or 5 δ −= 4.950.05; δ = thus 0.05. δ =
35. 3 lim1515(3)164 x x →− −=−−==
Step 1: 1540.50.515 xx−−< −<− 40.53.5154.5 x < <−< 12.251520.25 x <−< 11.25519.253.852.25. xx <−< −<<
Step 2: (3)3xxδδδ −−< −<+< 33. x δδ−<<−
Then 33.850.85,δδ −=− = or 32.250.75; δ −=− thus 0.75. δ =
Copyright 2016 Pearson Education, Inc.
36. 44 2 2 lim2 x x → ==
Step 1:
Step
Then
37. Step 1: (9)54xx−−< −<−<
Step 2:
Then
38. Step 1: (37)239 xx
Step 2: 33xxδδδ −< −<−< 33. x δδ+<<+
Then 33 33,δδ +=− = or 3 δ += 33 3 δ + = Thus choose 3 δ =
39. Step 1: 525xx −−< −<− 2 < 252 x −<−<+
22 (2)5(2) x −<−<+ 22 (2)5(2)5. x −+<<++
Step 2: 99xxδδδ −< −<−< 99. x δδ+<<+
Then 22 9494,δδ +=−+ =− or 22 9494. δ δ +=++ =+ Thus choose the smaller distance, 2 4 δ =−
40. Step 1: 4242 xx−−< −<−− < 242 x −<−<+ 22 (2)4(2) x −<−<+ 2222 (2)4(2)(2)4(2)4. xx −+<−<−− −++<<−−+
Step 2: 0.xxδδδ −< −<<
Then 22 (2)44 δ =−++=−− 2 4, δ =+ or 22 (2)44. δ =−−+=− Thus choose the smaller distance, 2 4. δ =−
41. Step 1: For 22 1,11xxx =−< −<−< / 2 1 1 x −<<+ 11 x −<<+ 11near1. xx −<<+=
Step 2: 111xxδδδδ −< −<−< −+ 1. x δ < <+
Then 1111,δδ +=− =−− or 1111. δ δ +=+ =+− Choose { } min11,11, δ =−−+− that is, the smaller of the two distances.
42. Step 1: For 22 2,44xxx =−−< −<−< / 2 444xx
4near2. x < −−=−
Step 2: (2)2xxδδδ −−< −<+< 22. x δδ−<<−
Then 2442,δδ −=−+ =+− or 2424 δ δ −=−− =−−
Choose { min42,
43. Step 1: 1111 xx
Step 2: 11
44. Step 1: 22 11111
Step
45.
Step 2: (3)3
Then
46. Step 1: ( ) 2
Step 2: 11xx
Then 1 1,
47. Step 1: 1:(42)2022
1:(64)206xx x
Step 2: 11xx
Then
48. Step 1: 0:2020xxx <−< −<< 2 0; x < < 2 0:002. x xx ≥−< ≤< Step 2: 0.xxδδδ −< −<< Then 22 , δδ =− = or 2 δ = 2. δ = Choose 2 . δ =
49. By the figure, 1 sin x xxx ≤≤ for all 0 x > and 1 sinfor0. x xxxx ≥≥< Since 0 lim() x x → = 0 lim0, x x → = then by the sandwich theorem, in either case, 1 0 limsin0 x x x → =
50. By the figure, 222 1 sin x xxx ≤≤ for all x except possibly at 0 x = Since 2 0 lim() x x → −= 2 0 lim0, x x → = then by the sandwich theorem, 2 1 0 limsin0. x x x → =
51. As x approaches the value 0, the values of ()gx approach k. Thus for every number 0, > there exists a 0 δ > such that 0 0 x δ <−< ().gxk−<
52. Write xhc =+ Then 0 xc δ <−<⇔ , xc δδ <−< ()xchc δ =⇔−<+ / , c δ < , hcch +=⇔−<<δδ / 0 h =⇔ / 0 0. h δ <−< Thus, lim() xc fxL → =⇔ for any 0, > there exists 0 δ > such that () fxL−< whenever 0 xc δ <−<⇔ () fhcL+−< whenever 0 00lim(). h hfhcL δ → <−<⇔+=
53. Let 2 ().fxx = The function values do get closer to 1 as x approaches 0, but 0 lim()0, x fx → = not 1 The function 2 () fxx = never gets arbitrarily close to 1 for x near 0.
54. Let 1 0 2 ()sin,,and0 fxxLx=== There exists a value of x 6 (namely) x π = for which 1 2 sin x −< for any given 0. > However, 0 limsin0, x x → = 1 2 not. The wrong statement does not require x to be arbitrarily close to 0 . x As another example, let 11 2 ()sin,, x gxL== and 0 0. x = We can choose infinitely many values of x near 0 such that 11 2 sin x = as you can see from the accompanying figure. However, 1 0 limsin x x → fails to exist. The wrong statement does not require all values of x arbitrarily close to 0 0 x = to lie within 0of L >= 1 2 Again you can see from the figure that there are also infinitely many values of x near 0 such that 1 sin0. x = If we choose 1 4 < we cannot satisfy the inequality 11 2 sin x −< for all values of x sufficiently near 0 0. x =
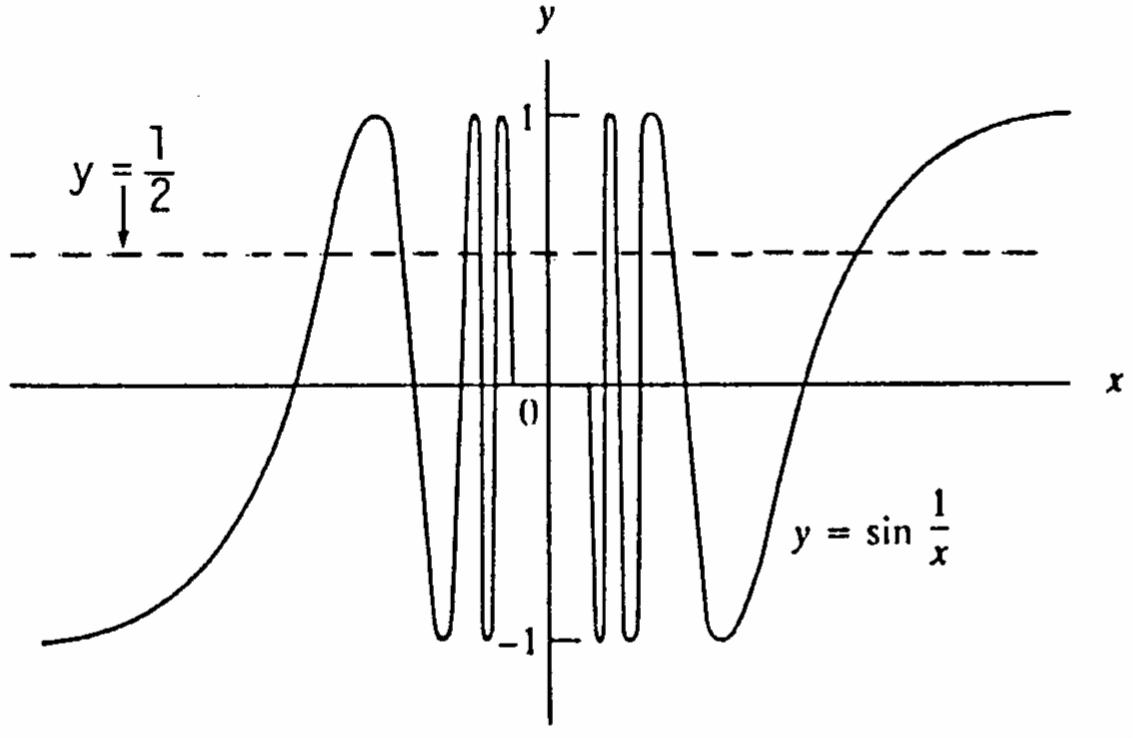
228.999.01 x ππ ≤≤ or3.3843.387. x ≤≤ To be safe, the left endpoint was rounded up and the right endpoint was rounded down. 56. 50.1 VV RR V
To be safe, the left endpoint was rounded up and the right endpoint was rounded down.
57. (a) 1011xxδδ <−< −<< (). fxx = Then ()222211 fxxx−=−=−>−= That is, 1 2 ()21fx −≥≥ no matter how small δ is taken when 1 1 1lim x x δ → −<< ()2.fx = / (b) 0 111() xxfx δδ <−< <<+ = 1. x + Then ()1(1)1 fxxx−=+−== 1. x > That is, ()11fx −≥ no matter how small δ is taken when 1 1 1lim x x δ → <<+ ()1.fx = / (c) 1011(). xxfxxδδ <−< −<< = Then ()1.51.51.5 fxxx −=−=−> 1.510.5. −= Also, 0 11 xx δ <−< < 1()1. fxx δ < + =+ Then ()1.5fx −= (1)1.50.5 xx+−=− 0.510.50.5 x = −>−= Thus, no matter how small δ is taken, there exists a value of x such that 1 x δδ <−< but 1 2 ()1.5fx −≥ 1 lim()1.5. x fx → = /
58. (a) For 22()2()42. xhxhx δ <<+ = −= Thus for 2,()4 hx <−≥ whenever 22 x δ <<+ no matter how small we choose 2 0lim()4. x hx δ → > = /
(b) For 22()2()31 xhxhx δ <<+ = −= Thus for 1,()3 hx <−≥ whenever 22 x δ <<+ no matter how small we choose 2 0lim()3. x hx δ → > = /
(c) For 2 22()xhxx δ −<< = so 2 ()22.hxx−=− No matter how small 0 δ > is chosen, 2 x is close to 4 when x is near 2 and to the left on the real line 2 2 x will be close to 2. Thus if 1,()2 hx <−≥ whenever 22 x δ −<< no matter how small we choose 2 0lim()2. x hx δ → > = /
59. (a) For 3 3()4.8()40.8.xfxfx δ −<< > −≥ Thus for 0.8,()4 fx <−≥ whenever 3 3 x δ −<< no matter how small we choose 3 0lim()4 x fx δ → > = /
(b) For 3 3()3()4.81.8xfxfx δ <<+ < −≥ Thus for 1.8,()4.8 fx <−≥ whenever 3 3 x δ <<+ no matter how small we choose 3 0lim()4.8. x fx δ → > = /
(c) For 3 3()4.8()31.8xfxfx δ −<< > −≥ Again, for 1.8,()3 fx <−≥ whenever 3 3 x δ −<< no matter how small we choose 3 0lim()3. x fx δ → > = /
60. (a) No matter how small we choose 0, δ > for x near 1 satisfying 11, x −<<−+δδ the values of ()gx are near 1 ()2gx is near 1. Then, for 1 2 = we have 1 2 ()2gx −≥ for some x satisfying 11, x −<<−+δδ or 1 0 1lim()2. x xgx δ →− <+< = /
(b) Yes, 1 lim() 1 x gx →− = because from the graph we can find a 0 δ > such that ()1gx −< if 0 (1). x δ <−−<
61-66. Example CAS commands (values of del may vary for a specified eps): Maple:
f :x-(x^4-81)/(x-3);x0:3; =>=
plot(f(x),xx0-1..x01,colorblack, =+=
title"Section 2.3,#61(a)"); =
# (a)
L:limit(f(x),xx0); == # (b) epsilon:0.2; = # (c) plot([f(x),L-epsilon,Lepsilon],xx0-0.01..x00.01, +=+ colorblack, linestyle[1,3,3],title"Section 2.3, #61(c)"); ===
q :fsolve(abs(f(x)-L )epsilon, xx0-1..x01);===+ # (d) delta:abs(x0-q); = plot([f(x),L-epsilon,Lepsilon],xx0-delta..x0delta,colorblack,title"Section 2.3,#61(d)"); +=+== for eps in [0.1,0.005,0.001]do # (e)
q :fsolve(abs(f(x)-L)eps,xx0-1..x01); ===+ delta:abs(x0-q); = head:sprintf("Section 2.3,#61(e)\n epsilon%5f,delta%5f\n",eps,delta);=== print(plot([f(x),L-eps,Leps],xx0-delta..x0delta, +=+ colorblack,linestyle[1,3,3],titlehead)); === end do:
Mathematica (assigned function and values for x0, eps and del may vary):
Clear[f,x]
y1:Leps;y2:Leps;x01; =−=+= 2 f [x_]:(3x(7x1)Sqrt[x]5)/(x1) =−++−
Plot[f[x],{x,x00.2,x00.2}] −+
L:Limit[f[x],xx0] =→ eps0.1;del0.2; ==
Plot[{f[x],y1,y2},{x,x0del,x0del}, PlotRange{L2eps, L2eps}]−+→−+
Copyright 2016 Pearson Education, Inc.
2.4 ONE-SIDED LIMITS
1. (a) True
(b) True (c) False (d) True
(e) True (f) True (g) False (h) False (i) False (j) False (k) True (l) False
2. (a) True (b) False (c) False (d) True
(e) True (f) True (g) True (h) True (i) True (j) False (k) True
3. (a) 2 2 2 lim()12, x fx + → =+= 2 lim()32 1 x fx → =−=
(b) No, 2 lim() x fx → does not exist because 22 lim()lim() xx fxfx →→+− = /
(c) 4 2 4 lim()13, x fx → =+= 4 2 4 lim()1 3 x fx + → =+=
(d) Yes, 4 lim()3 x fx → = because 44 3 lim()lim() xx fxfx →→−+ ==
4. (a) 2 2 2 lim()1, x fx + → == 2 lim()321,(2)2 x fxf → =−==
(b) Yes, 2 lim() 1 x fx → = because 22 1 lim()lim() xx fxfx →→+− ==
(c) 1 lim()3(1)4, x fx →− =−−= 1 lim()3(1)4 x fx + →− =−−=
(d) Yes, 1 lim()4 x fx →− = because 11 4lim()lim() xx fxfx →−→−−+ ==
5. (a) No, 0 lim() x fx + → does not exist since () 1 sin x does not approach any single value as x approaches 0
(b) 00 lim()lim00 xx fx →→ ==
(c) 0 lim() x fx → does not exist because 0 lim() x fx + → does not exist
6. (a) Yes, 0 lim()0 x gx + → = by the sandwich theorem since () xgxx ≤≤ when 0 x >
(b) No, 0 lim() x gx → does not exist since x is not defined for 0 x <
(c) No, 0 lim() x gx → does not exist since 0 lim() x gx → does not exist
7. (a)
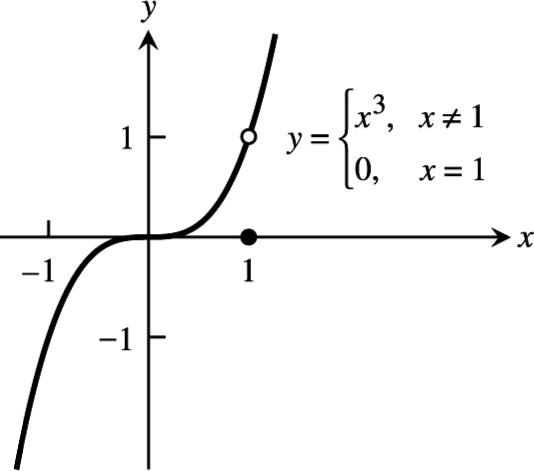
(b) 11 lim()1lim() xx fxfx −+ →→ ==
(c) Yes, 1 lim()1 x fx → = since the right-hand and left-hand limits exist and equal 1
8. (a)

9. (a) domain: 02 x ≤≤ range: 0 1 y <≤ and 2 y =
(b) lim() xc fx → exists for c belonging to (0,1)(1,2) ∪
(c) 2 x =
(d) 0 x =
10. (a) domain: x ∞ << ∞ range: 11 y ≤≤
(b) lim() xc fx → exists for c belonging to (,1)(1,1)(1,) −∞−∪−∪∞
(c) none
(d) none
(b) 11 lim()0lim() xx fxfx +− →→ ==
(c) Yes, 1 lim()0 x fx → = since the right-hand and left-hand limits exist and equal 0
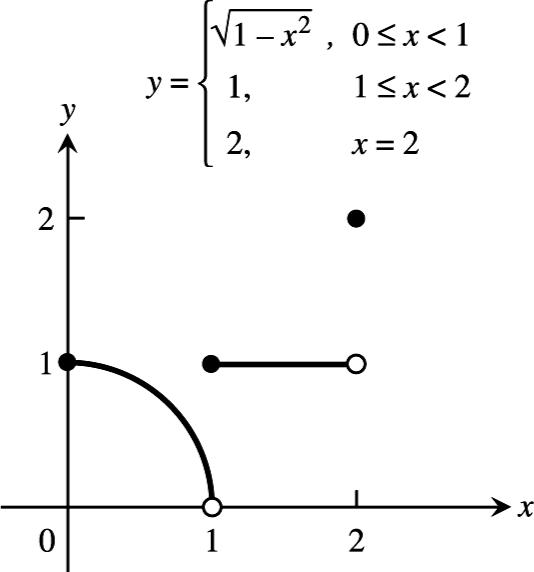
17. (a) 2 (2) 222(2) lim(3)lim(3) x x xx xx xx ++ + + ++ →−→− +=+ (|2|(2)for2) xxx +=+>− 2 lim(3)((2)3) 1 x x + →− = +=−+= (b) 2 (2) 222(2) lim(3)lim(3) x x xx xx xx + −+ ++ →−→−
(|2|(2)for2) xxx +=−+<− 2 lim(3)(1)(23) 1 x x →− = +−=−−+=−
limlim
18. (a) 2(1)2(1) (1)
(1)
19.
21. sin2 sin 2 00 limlim1 x x x θ θ θ→→
22. sinsinsinsin 0000 limlimlimlim1 ktkktk tkt t t kkkθθ →→→→θθθθ ====⋅= (where) kt θ =
23. sin33sin3sin333sin3 1 4434344 0000 limlimlimlim yyy yyyyyy θ θ θ →→→→ ==== (where3) y θ =
24. () () sin sin3 3
3 1111111 sin33sin33333 lim 000 limlimlim1 h h hh hh hhh
→→→
====⋅=
(where3) h θ =
25. () sin2 cos2 tan2sin22sin2 1 00000cos2cos22 limlimlimlimlim12 2 x x xxx xxxxxxxxxxx →→→→→
26. () sin sin cos 0 2cos 1 tansin lim 0000 lim2lim2lim2limcos2112 t t t t t tttt tt t ttt t → →→→→
27. () () csc2211111 cos5sin2cos52sin2cos522 0000 limlimlimlim1(1) xxxx xxxxxxxxx →→→→
28. () 2 2 6cos2 000sinsin2sinsin2 lim6(cot)(csc2)limlim3cos3113 xxxx xxxxxxx xxxx →→→ ==⋅⋅=⋅⋅=
29. () () coscos 1 sincossincossincossincossin 0000 limlimlimlim xxxxxxxx xxxxxxxxxxxxx + →→→→ =+=⋅+ () sinsin 111 cos 000 limlimlim(1)(1)12 xx x x x xxx →→→
30. () () 2 sinsin1111 00222222 limlim0(1) 0 xxxxx xxxx −+ →→ =−+=−+=
31. 22 (1cos)(1cos) 1cos1cossin sin2(2sincos)(1cos)(2sincos)(1cos)(2sincos)(1cos) 0000 limlimlimlim θθ θθθ θθθθθθθθθθ θ θθθ −+ →→→→+++ === sin0 (2cos)(1cos)(2)(2) 0 lim0 θ θθ θ + → = ==
32. () () () (1cos) 1cos 1 1cos 1 2 9 9909 222222 sin3 sin3sin3 2 33 9 0 lim (0) (1cos) cos sin3sin31 0000 lim limlimlimlim 0 x x x x x xxx x xx xx x x xx xxx xx xxxx → → →→→→ ======
33. sin(1cos) sin 1cos 00 limlim1since1cos0as 0 t t t tt θ θ θ θ →→ ===−→→
34. sin(sin) sin sin 00 limlim1sincesin0as 0 h h h hh θ θ θ θ →→ ===→→
35. () () sinsin2sin2111 sin2sin222sin222 000 limlimlim11 θθθθθ θθθθθ θ θθ →→→ =⋅=⋅=⋅⋅=
36. () () sin5sin5455sin5455 sin4sin45445sin444 000 limlimlim11 xxxxx xxxxxxxx →→→ =⋅⋅=⋅=⋅⋅=
37. 0 limcos010 θ θθ → =⋅=
38. cos2cos2cos2 1 0000sin22sincos2cos2 limsincot2limsinlimsinlimθθθ θθθθ θ θθθ θθθθ →→→→ ====
39. () () tan3sin3sin383 11 sin8cos3sin8cos3sin838 000 limlimlimxxxx xxxxxxxxx →→→ =⋅=⋅⋅⋅ () () () 3sin3833 1 8cos33sin888 0 lim111 xx xxx x → = =⋅⋅⋅=
40. ( ) ( ) ( ) ( ) sin3cot5sin3sin4cos5sin3sin4cos5345 000cot4cos4sin5cos4sin5345 limlimlimyyyyyyyyy yyyyyyyyyyyy →→→ ==
( ) ( ) ( ) ( ) () sin3sin45cos5 34 1212 34sin5cos4555 0 lim1111 yyyy yyyy y → = =⋅⋅⋅⋅=
41. sin cos 222 cos3 sin3 tansinsin3 000cot3coscos3 limlimlim θ θ θ θ θθθ θθθθθθ θ θθ →→→ == () () () ()sinsin333 3coscos311 0 lim(1)(1)3 θθ θθθθ θ→ = ==
42. cos4 2 2 sin4 2222222 2 cos2 2 sin2 cos4(2sincos) cot4cos4sin2 sincot2sincos2sin4sincos2sin4 0000 sin limlimlimlim
θθθ θ→ = () () ( ) 222 2 22sin422 4 4cos4coscos4coscos4cos 4 1111 sin41 cos2sin4cos2cos21 000 limlimlim1 θ
22 22 cos4(4sincos) sincos2sin4 0 lim
43. Yes. If lim()lim(), xaxa fxLfx →→+− == then lim() xa fxL → = If lim()lim(), xaxa fxfx →→+− = / then lim() xa fx → does not exist.
Copyright 2016 Pearson Education, Inc.
44. Since lim() xc fxL → = if and only if lim() xc fxL + → = and lim(), xc fxL → = then lim() xc fx → can be found by calculating lim(). xc fx + →
45. If f is an odd function of x, then ()(). fxfx −=− Given 0 lim()3, x fx + → = then 0 lim()3. x fx → =−
46. If f is an even function of x, then ()().fxfx −= Given 2 lim()7 x fx → = then 2 lim()7. x fx + →− = However, nothing can be said about 2 lim() x fx →− because we don’t know 2 lim() x fx + →
47. (5,5)55Ixδδ =+ <<+ Also, 22 555.xxx −< −< <+ Choose 2 δ = 5 lim50 x x + → −=
48. (4,4)44.Ix δδ =− −<< Also, 44422 . xxx−< −< >− Choose 2 δ = 4 lim40. x x → −=
49. As 0 x → the number x is always negative. Thus, (1)10xx x x −−< +< < which is always true independent of the value of x. Hence we can choose any 0 δ > with 0 0lim1. x x x x δ → << =−
50. Since 2 x + → we have 2 x > and 22.xx−=− Then, 22 2 2 110xx x x −=−< < which is always true so long as 2. x > Hence we can choose any 0, δ > and thus 22 x δ <<+ 2 2 1 . x x −< Thus, 2 2 2 lim1. x x x + →− =
51. (a) 400 lim400. x x + → = Just observe that if 400401, x << then 400. x = Thus if we choose 1, δ = we have for any number 0 > that 400400 x δ <<+ x4004004000. −=−=<
(b)
400 lim399 x x → = Just observe that if 399400 x << then 399. x = Thus if we choose 1, δ = we have for any number 0 > that 400400 x δ −<< x3993993990. −=−=< (c) Since 400400 limlim xx xx →→+− = / we conclude that 400 lim x x → does not exist.
52. (a) 00 lim()lim00; xx fxx →→++ === 2 00 xxx −< −<< << for x positive. Choose 2 δ = 0 lim()0. x fx + → = (b) () 2 1 00 lim()limsin 0 x xx fxx →→ == by the sandwich theorem since () 22 2 1 sin x xxx ≤≤ for all 0 x = /
Since 222 00 xxx−=−−=< whenever , x < we choose δ = and obtain () 2 1 sin0 x x −< if 0. x δ << (c) The function f has limit 0 at 0 0 x = since both the right-hand and left-hand limits exist and equal 0.
2.5 CONTINUITY
1. No, discontinuous at 2, x = not defined at 2 x =
2. No, discontinuous at 3, x = 3 1 lim()(3)1.5 x gxg → === /
3. Continuous on [ 1,3]
4. No, discontinuous at 1, x = 11 1.5lim()lim()0 xx kxkx →→−+ === /
5. (a) Yes
(b) Yes, 1 lim() 0 x fx + →− = (c) Yes
(d) Yes
6. (a) Yes, (1)1 f =
(b) Yes, 1 lim()2 x fx → = (c) No (d) No
7. (a) No
8. [ 1,0)(0,1)(1,2)(2,3) −∪∪∪
9. (2)0, f = since 22 lim()2(2)40lim() xx fxfx −+ →→ =−+==
10. (1) f should be changed to 1 2lim() x fx → =
(b) No
11. Nonremovable discontinuity at 1 x = because 1 lim() x fx → fails to exist 1 (lim()1 x fx → = and 1 lim()0) x fx + → = Removable discontinuity at 0 x = by assigning the number 0 lim()0 x fx → = to be the value of (0) f rather than (0)1. f =
12. Nonremovable discontinuity at 1 x = because 1 lim() x fx → fails to exist 11 (lim()2andlim()1). xx fxfx −+ →→ == Removable discontinuity at 2 x = by assigning the number 2 lim() 1 x fx → = to be the value of (2) f rather than (2)2. f =
13. Discontinuous only when 202xx −= = 14. Discontinuous only when 2 (2)02 xx += =−
15. Discontinuous only when 2 430(3)(1)03xxxxx −+= −−= = or 1 x =
16. Discontinuous only when 2 3100(5)(2)05 xxxxx −−= −+= = or 2 x =−
17. Continuous everywhere. (|1|sinxx −+ defined for all x; limits exist and are equal to function values.)
18. Continuous everywhere. (||10 x += / for all x; limits exist and are equal to function values.)
19. Discontinuous only at 0 x =
20. Discontinuous at odd integer multiples of 22 ,i.e.,(21), xn ππ =− n an integer, but continuous at all other x
21. Discontinuous when 2x is an integer multiple of ,i.e.,2, xn π π = n an integer 2 , n x π = n an integer, but continuous at all other x.
22. Discontinuous when 2 x π is an odd integer multiple of 222 ,i.e.,(21), x n πππ =− n an integer 21,xn =− n an integer (i.e., x is an odd integer). Continuous everywhere else.
23. Discontinuous at odd integer multiples of 22 ,i.e.,(21), xn ππ =− n an integer, but continuous at all other x
24. Continuous everywhere since 4 11 x +≥ and 2 1sin10sin1 xx≤≤ ≤≤ 2 1sin1; x +≥ limits exist and are equal to the function values.
25. Discontinuous when 230 x +< or 3 2 x <− continuous on the interval ) 3 2 , . −∞
26. Discontinuous when 3 10 x −< or 1 3 x < continuous on the interval ) 1 3 ,. ∞
27. Continuous everywhere: (21)1/3 x is defined for all x; limits exist and are equal to function values.
28. Continuous everywhere: (2)1/5 x is defined for all x; limits exist and are equal to function values.
29. Continuous everywhere since 2 (3)(2) 6 33 333 limlimlim(2)5(3) xx xx xx xxx xg −+ →→→ ==+==
30. Discontinuous at 2 x =− since 2 lim() x fx →− does not exist while (2)4. f −=
31. limsin(sin)sin(sin)sin(0)sin0, x xx π ππππ → −=−=−== and function continuous at . x π =
32. () ()2222 0 limsin(cos(tan))sin(cos(tan(0)))sincos(0)sin1, t t ππππ → ==== and function continuous at 0. t =
33. 22222 111 limsec(sectan1)limsec(secsec)limsec((1)sec) yyy yyyyyyyy →→→ −−=−=− 2 sec((11)sec1) = −= sec01, = and function continuous at 1. y =
34. () () 1/3 4444 0 limtancos(sin)tancos(sin(0))tancos(0)tan1, x x ππππ →
and function continuous at 0. x =
35. 2 42 193sec2193sec016 0 limcoscoscoscos, t t
and function continuous at 0. t =
36. () () () 6 22 1 66 3 limcsc53tancsc53tan45393, x xx π ππ → +=+=+== and function continuous at 6 x π =
37. () () () 0 222 0 limsinsinsin1, x x ee + → πππ=== and the function is continuous at x = 0.
38. () () 111 2 1 limcoslncosln1cos(0), x x → === π and the function is continuous at x = 1.
39. 2 (3)(3) 9 3(3) ()3, xx x xx gxx +− ===+ 3 3(3)lim(3)6 x xgx
40. 2 (5)(2) 310 22 ()5, tt tt tt htt +− +− ===+ 2 2(2)lim(5)7 t t ht → = =+= /
41. 2 32 3 (1)(1) 11 (1)(1)1 1 (), sss sss sss s fs ++− −++ +−+ === ( ) 2 13 12 1 1(1)lim ss s s sf ++ +
42. 2 2 (4)(4) 164 (4)(1)1 34 (), xx xx xxx xx gx +− −+ −++ === ()48 15 4 4(4)lim x x x xg + + → = == /
43. As defined, 2 3 lim()(3)18 x fx → =−= and 3 lim(2)(3)6. x aa + → = For ()fx to be continuous we must have 4 3 6 8 . aa = =
44. As defined, 2 lim()2 x gx →− =− and 2 2 lim()(2)4. x gxbb + →− =−= For ()gx to be continuous we must have 1 2 42. bb =− =−
45. As defined, 2 lim()12 x fx → = and 22 2 lim()(2)222. x fxaaaa + → =−=− For ()fx to be continuous we must have 2 12223 aaa=− = or 2. a =−
46. As defined, 0 11 0 lim() bb bb x gx ++ → == and 2 0 lim()(0). x gxbb + → =+= For ()gx to be continuous we must have 1 0 b b bb + = = or 2. b =−
47. As defined, 1 lim()2 x fx →− =− and 1 lim()(1), x fxabab + →− =−+=−+ and 1 lim()(1) x fxabab → =+=+ and 1 lim()3. x fx + → = For ()fx to be continuous we must have 2 ab=−+ and 5 2 3 aba += = and 1 2 . b =
48. As defined, 0 lim()(0)22 x gxabb → =+= and 2 0 lim()(0)33, x gxabab + → =+−=− and 2 2 lim()(2)3 x gxab → =+−= 43a b +− and 0 lim()3(2)51. x gx + → =−= For ()gx to be continuous we must have 23bab =− and 431 ab +−= 3 2 a =− and 3 2 . b =−
49. The function can be extended: (0)2.3. f ≈
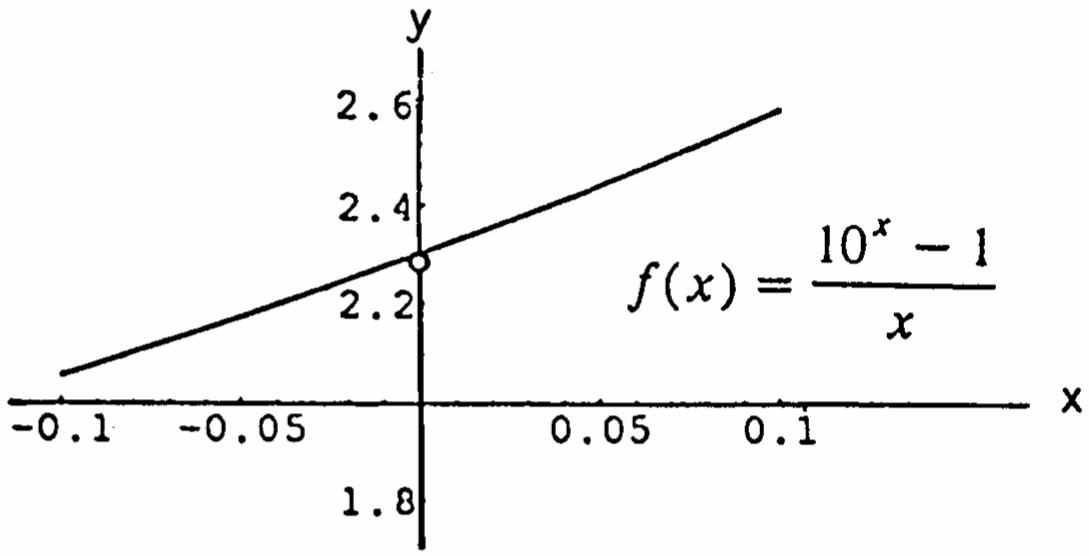
51. The function cannot be extended to be continuous at 0. x = If (0)1, f = it will be continuous from the right. Or if (0)1, f =− it will be continuous from the left.
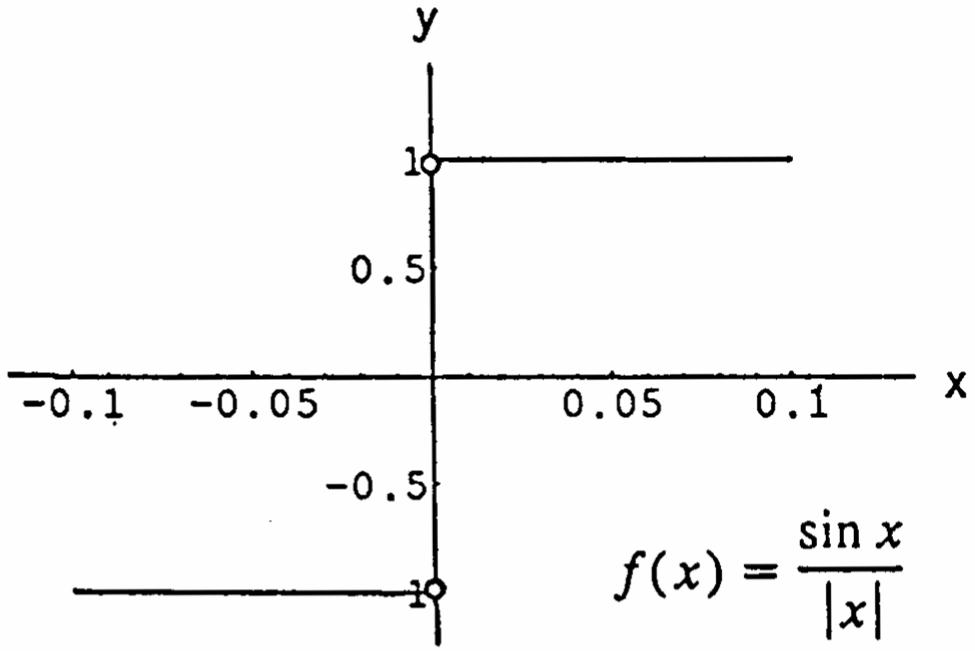
53. ()fx is continuous on [0,1] and (0)0,(1)0ff<> by the Intermediate Value Theorem ()fx takes on every value between (0) f and (1) f the equation () 0 fx = has at least one solution between 0 x = and 1. x =
50. Thefunction cannot be extended to be continuous at 0 x = If (0)2.3, f ≈ it will be continuous from the right. Or if (0)2.3, f ≈− it will be continuous from the left.
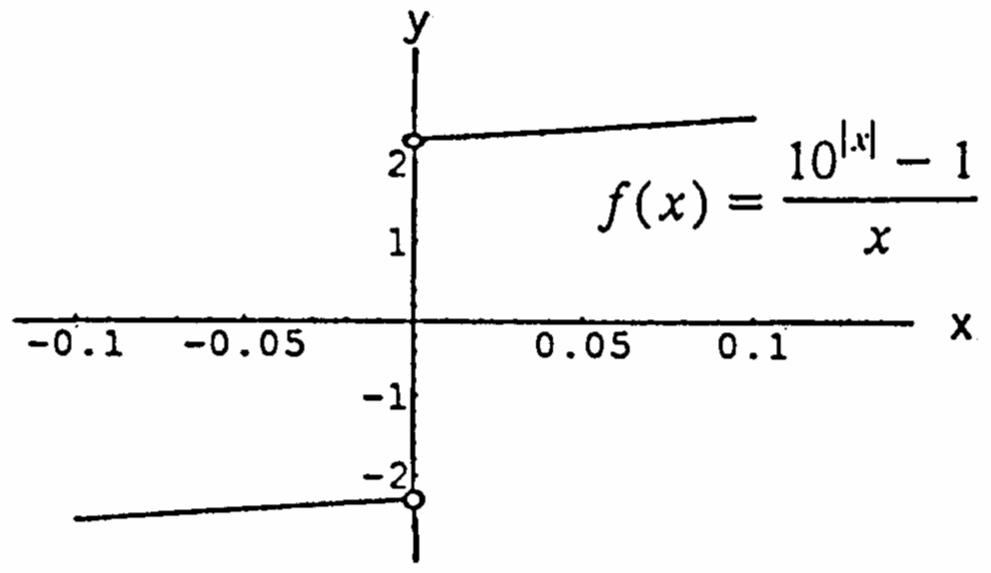
52. The function can be extended: (0)7.39. f ≈

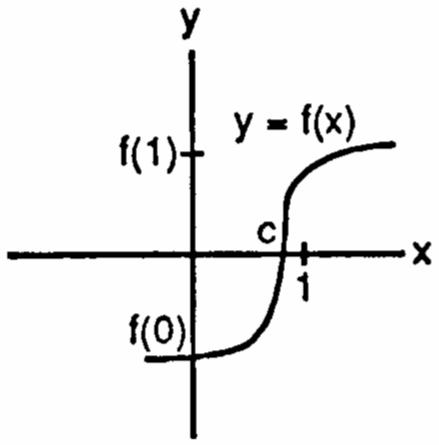
54. cos(cos)0 xxxx = −= If 2 , x π =− () ()22 cos0. ππ −−−> If 2 , x π = ()22 cos0. ππ−< Thus cos0 xx−= for some x between 2 π and 2 π according to the Intermediate Value Theorem, since the function cos xx is continuous.
55. Let 3 ()151, fxxx=−+ which is continuous on [ 4,4]. Then (4)3, f −=− (1)15, f −= (1)13, f =− and (4)5. f = By the Intermediate Value Theorem, () 0 fx = for some x in each of the intervals 41, x <<− 11, x << and 1 4. x << That is, 3 1510xx−+= has three solutions in [ 4,4]. Since a polynomial of degree 3 can have at most 3 solutions, these are the only solutions.
56. Without loss of generality, assume that .ab < Then ()()()22 Fxxaxbx =−−+ is continuous for all values of x, so it is continuous on the interval [ ,].ab Moreover () Faa = and (). Fbb = By the Intermediate Value Theorem, since 2 , ab ab + << there is a number c between a and b such that 2 (). ab Fx + =
Copyright 2016 Pearson Education, Inc.
57. Answers may vary. Note that f is continuous for every value of x
(a) 3 (0)10,(1)18(1)103.ff==−+= Since 3 10, π << by the Intermediate Value Theorem, there exists a c so that 0 1 c << and ().fc π =
(b) 3 (0)10,(4)(4)8(4)1022ff=−=−−−+=− Since 22310, <−< by the Intermediate Value Theorem, there exists a c so that 40 c << and ()3.fc =−
(c) (0)10, f = 3 (1000)(1000)8(1000)10999,992,010. f =−+= Since 105,000,000999,992,010, << by the Intermediate Value Theorem, there exists a c so that 0 1000 c << and ()5,000,000.fc =
58. All five statements ask for the same information because of the intermediate value property of continuous functions.
(a) A root of 3 ()31 fxxx=−− is a point c where ()0.fc =
(b) The point where 3 yx = crosses 31yx=+ have the same y-coordinate, or 3 31yxx==+ ()fx = 3 310.xx−−=
(c) 3 31xx−= 3 310.xx −−= The solutions to the equation are the roots of 3 ()31. fxxx=−−
(d) The points where 3 3 yxx =− crosses 1 y = have common y -coordinates, or 3 31yxx=−= ()fx = 3 310.xx−−=
(e) The solutions of 3 310xx−−= are those points where 3 ()31 fxxx=−− has value 0.
59. Answers may vary. For example, sin(2) 2 () x x fx = is discontinuous at 2 x = because it is not defined there. However, the discontinuity can be removed because f has a limit (namely 1) as 2 x →
60. Answers may vary. For example, 1 1 () x gx + = has a discontinuity at 1 x =− because 1 lim() x gx →− does not exist. 11 lim()andlim(). xx gxgx −+ →−→−
61. (a) Suppose 0x is rational 0 ()1.fx = Choose 1 2 . = For any 0 δ > there is an irrational number x (actually infinitely many) in the interval 00 (,) xx−+δδ ()0.fx = Then 0 0 || xx δ <−< but 0 | ()()|fxfx−= 1 2 1 > , = so 0 lim() xx fx → fails to exist f is discontinuous at 0x rational. On the other hand, 0x irrational 0 ()0fx = and there is a rational number x in 00 (,)()1. xxfx −+δδ = Again 0 lim() xx fx → fails to exist f is discontinuous at 0x irrational. That is, f is discontinuous at every point.
(b) f is neither right-continuous nor left-continuous at any point 0x because in every interval 00 (,) xx δ or 00 (,) xx δ + there exist both rational and irrational real numbers. Thus neither limits 0 lim() xx fx → and 0 lim() xx fx + → exist by the same arguments used in part (a).
62. Yes. Both () fxx = and 1 2 () gxx=− are continuous on [0,1]. However () () fx gx is undefined at 1 2 x = since () () 1 2() 0 fx gx g = is discontinuous at 1 2 . x =
63. No. For instance, if ()0,fx = (),gxx = then () ()00hxx== is continuous at 0 x = and ()gx is not.
64. Let 1 1 () x fx = and ()1.gxx=+ Both functions are continuous at 0 x = The composition (())fgfgx== 11 (1)1xx +− = is discontinuous at 0, x = since it is not defined there. Theorem 10 requires that ()fx be continuous at (0), g which is not the case here since (0) 1 g = and f is undefined at 1.
Copyright 2016 Pearson Education, Inc.
65. Yes, because of the Intermediate Value Theorem. If ()fa and ()fb did have different signs then f would have to equal zero at some point between a and b since f is continuous on [ ,].ab
66. Let ()fx be the new position of point x and let ()() dxfxx =− The displacement function d is negative if x is the left-hand point of the rubber band and positive if x is the right-hand point of the rubber band. By the Intermediate Value Theorem, () 0 dx = for some point in between. That is, () fxx = for some point x, which is then in its original position.
67. If (0)0 f = or (1)1, f = we are done (i.e.,0or1inthosecases). cc== Then let (0)0fa=> and (1)1fb=< because 0 ()1fx ≤≤ Define ()() gxfxxg =− is continuous on [0,1]. Moreover, (0)(0)00 gfa=−=> and (1)(1)110 gfb=−=−< by the Intermediate Value Theorem there is a number c in (0, 1) such that ()0()0 gcfcc = −= or (). fcc =
68. Let () 2 0. fc => Since f is continuous at xc = there is a 0 δ > such that ()() xcfxfc δ −< −< ()()(). fcfxfc −<<+ If ()0,fc > then 3 11 222()()()()()0 fcfcfxfcfx = << > on the interval (,). cc−+δδ
If ()0,fc < then 3 11 222()()()()() 0 fcfcfxfcfx =− << < on the interval (,). cc−+δδ

69. By Exercise 52 in Section 2.3, we have 0 lim()lim(). xch fxLfchL →→ =⇔+= Thus, ()fx is continuous at 0 lim()()lim()(). xch xcfxfcfchfc →→ =⇔=⇔+=
70. By Exercise 69, it suffices to show that 0 limsin()sin h chc → += and 0 limcos()cos h chc → +=
+=+=+
Now [] 0000 limsin()lim(sin)(cos)(cos)(sin)(sin)limcos(cos)limsin hhhh chchchchch →→→→
.
By Example 11 Section 2.2, 0 limcos1 h h → = and 0 limsin0 h h → = So 0 limsin()sin h chc → += and thus ()sin fxx = is continuous at xc = Similarly, [] 00 limcos()lim(cos)(cos)(sin)(sin) hh chchch →→ +=− 00 (cos)limcos(sin)limsin hh chch →→
=
cos .c = Thus, ()cosgx x = is continuous at .xc =
71. 1.8794,1.5321,0.3473 x ≈−−
73. 1.7549 x ≈
75. 3.5156 x ≈
77. 0.7391 x ≈
72. 1.4516,0.8547,0.4030 x ≈−
74. 1.5596 x ≈
76. 3.9058,3.8392,0.0667 x ≈−
78. 1.8955,0,1.8955 x ≈−
Copyright 2016 Pearson Education, Inc.
2.6 LIMITS INVOLVING INFINITY; ASYMPTOTES OF GRAPHS
1. (a) 2 lim()0 x fx → =
(c) 3 lim()2 x fx →− =
(e) 0 lim() 1 x fx + → =−
(g) 0 lim()doesnotexist x fx → =
(i) lim() 0 x fx →−∞ =
2. (a) 4 lim() 2 x fx → =
(c) 2 lim()1 x fx → =
(e) 3 lim() x fx + →− =+∞
(g) 3 lim() x fx →− =+∞
(i) 0 lim() x fx → =−∞
(b) 3 lim() 2 x fx + →− =−
(d) 3 lim()doesnotexist x fx → = (f) 0 lim() x fx → =+∞ (h) lim()1 x fx →∞ =
(h) 0 lim() x fx + → =+∞
(j) 0 lim()doesnotexist x fx → = (l) lim()1 x fx →−∞ =−
(k) lim()0 x fx →∞ = (b) 2 lim()3 x fx + → =− (d) 2 lim()doesnotexist x fx → = (f) 3 lim() x fx →− =+∞
Note: In these exercises we use the result / 1 lim0whenever0. mn m n x x →±∞ => This result follows immediately from
Theorem 8 and the power rule in Theorem 1: ( ) () / / / / 111 limlimlim00. mn mn mn mn xx x xxx →±∞→±∞→±∞
3. (a) 3
4. (a) π
5. (a) 1 2
6. (a) 1 8
7. (a) 5 3
8. (a) 3 4 (b) 3
9. 11sin2sin2lim0 xx xxxx x →∞ ≤≤ = by the Sandwich Theorem
10. 11coscos 3333lim0 θθ
≤≤ = by the Sandwich Theorem
11. () () sin 2 cos 1 2sin010 cos10 1 limlim1 t tt t t tt tt t t −+ −+−+ ++ + →∞→∞ ===−
12. () () sin 7sin 1 sin10 1 275sin2002 25 limlimlim r r r rr rr rr rrr + ++ +−+− +− →∞→∞→∞ ===
13. (a) 3 7 2 23 2 575 5 limlim x x x x xx + + + + →∞→∞ == (b) 2 5 (same process as part (a))
14. (a) 7 3 3 327 11 23 2 27 1 7 limlim2 x x x x x xxx xx
+
−++ →∞→∞
(b) 2 (same process as part (a))
15. (a) 11 2 23 2 1 1 3 limlim0 x x x x x xx + + + + →∞→∞ == (b) 0 (same process as part (a))
16. (a) 37 2 22 2 37 1 2 limlim0 x x x x x xx + + + →∞→∞ == (b) 0 (same process as part (a))
17. (a) 3 3239 2 77 1 36 limlim7 x x x xxx xx
== (b) 7 (same process as part (a))
18. (a) 1 4 3 4256 1 234 9 99 2 2 256 limlim x x xx xx xxx xx + + +−+ +−+ →∞→∞ == (b) 9 2 (same process as part (a))
19. (a) 1031 1 54 26 6 1031 1 limlim 0 x xx xx x xx ++ ++ →∞→∞ == (b) 0 (same process as part (a))
20. (a) 321 212 7272 11 limlim, xxxx xxxxxx +−+− →∞→∞ ==∞ since 0 and 7. n xx→+→∞
(b) 321 212 7272 11 limlim, xxxx xxxxxx +−+− →−∞→−∞ ==−∞ since 0 and 7. n xx→+→−∞
21. (a) 72413 323 35135 673673 limlim, xxxxx xxxxxx +−+− →∞→∞−+−+ ==∞ since 4 0 and 3. n xx→→∞ (b) 72413 323 35135 673673 limlim, xxxxx xxxxxx +−+− →−∞→−∞−+−+ ==∞ since 4 0 and 3. n xx→→∞
22. (a) 83325 554 529529 3434 limlim, xxxxx xxxxxx −+−+ →∞→∞+−+− ==−∞ since 3 0, 5, and the denominator4. n xx→→∞→− (b) 83325 554 529529 3434 limlim, xxxxx xxxxxx −+−+ →−∞→−∞+−+− ==∞ since 3 0, 5, and the denominator4. n xx→→−∞→−
23. 2 2 83 2 lim x xx x + →∞ = 3 2 1 8 2 lim x x x + →∞ = 3 2 1 8 2 lim x x x + →∞ = 80 20 4 2 + ==
Copyright 2016 Pearson Education, Inc.
32.
33. 2 1 1 lim x x x + + →∞ = 22 2 1/ (1)/ lim xx x xx + →∞ + = (1)/22 (1)/ lim xx xx x + + →∞ = 2 11/10 (11/)(10) lim1 x x x ++ ++ →∞ ==
34. 222 2 11/ 1 (1)/ limlimxxx x xx xx ++ + →−∞→−∞ + == (1)/22 (1)/() lim xx xx x + +− →−∞ = 2 11/10 (11/)(10) lim1 x x x ++ →∞ ==−
35. 2 3 425 lim x x x →∞ + = 2 22 (3)/ 425/ lim xx x xx →∞ + = 22 (3)/ (425)/ lim xx x xx →∞ + = 2 (13/)(10) 1 2 40 425/ lim x x x + →∞ + ==
36. 3 6 43 9 lim x x x →−∞ + = 36 66 (43)/ 9/ lim xx x xx →−∞ + = 33 66 (43)/() (9)/ lim xx x xx →−∞ + = 3 6 (4/3)(03) 10 19/ lim3 x x x −++ + →∞ + ==
37. ( ) positive 1 3positive 0 lim x x + → =∞
39. ( ) positive 3 2negative 2 lim x x → =−∞
41. ( ) negative 2 8positive 8 lim x x x + + →− =−∞
38. ( ) positive 5 2negative 0 lim x x → =−∞
40. ( ) positive 1 3positive 3 lim x x + → =∞
42. ( ) negative 3 210negative 5 lim x x x + →− =∞
43. ( ) 2 positive 4 positive (7) 7 lim x x → =∞
45. (a) 1/3 2 3 0 lim x x + → =∞
46. (a) 1/5 2 0 lim x x + → =∞
47. 2/51/52 44 () 00 limlim xxxx →→ ==∞
49. () 2 limtan x x π → =∞
51. 0 lim(1csc) θ θ → +=− ∞
44. ( ) 2 negative 1 positivepositive (1) 0 lim xx x + → =−∞ (b) 1/3 2 3 0 lim x x → =−∞ (b) 1/5 2 0 lim x x → =−∞
48. 2/31/32 11 () 00 limlim xxxx →→ == ∞
50. () 2 limsec x x π + → =∞
52. 0 lim(2cot) θ θ + → −=−∞ and 0 lim(2cot), θ θ → −=∞ so the limit does not exist
53. (a) ( ) 2 111 (2)(2)positivepositive 4 22 limlim xx x xx ++ +−⋅ →→ ==∞
(b) ( ) 2 111 (2)(2)positivenegative 4 22 limlim xx x xx +−⋅ →→ ==−∞
(c) ( ) 2 111 (2)(2)positivenegative 4 22 limlim xx x xx ++ +−⋅ →−→− ==−∞
(d) ( ) 2 111 (2)(2)negativenegative 4 22 limlim xx x xx +−⋅ →−→− ==∞
54. (a) ( ) 2 positive (1)(1)positivepositive 1 11 limlimxx xx x xx ++ +−⋅ →→ ==∞
(b) ( ) 2 positive (1)(1)positivenegative 1 11 limlimxx xx x xx +−⋅ →→ ==−∞
(c) ( ) 2 negative (1)(1)positivenegative 1 11 limlimxx xx x xx ++ +−⋅ →−→− ==∞
(d) ( ) 2 negative (1)(1)negativenegative 1 11 limlimxx xx x xx +−⋅ →−→− ==−∞
55. (a) ( ) ( ) 2 111 002negative lim0lim x xx xx ++ →→ −=+=−∞
(b) ( ) ( ) 2 111 002positive lim0lim x xx xx →→ −=+=∞
(c) ( ) 2 2/3 1/3 3 1/31/3 121 22 2 2 lim220 x x x → −=−=−=
(d) ( ) () 2 3 111 2212 1 lim x x x →− −=−=
56. (a) ( ) 2 positive 1 24positive 2 lim x x x + + →− =∞
(c) 2 (1)(1) 120 11242424 limlim0 xx x xx xx ++ +− +++ →→ ===
(d) 2 1 1 244 0 lim x x x + → =
(b) ( ) 2 positive 1 24negative 2 lim x x x + →− =−∞
Copyright 2016 Pearson Education, Inc.
57. (a) ( ) 2 322 (2)(1)negativenegative 32 positivenegative 002(2) limlim xx xx xxxxxx ++ −+ →→ ==−∞
(b) 2 3222 (2)(1) 321 1 4 2(2) 222 limlimlim, xx xxx xxxxxxxx +++ −+− →→→ === 2 x = /
(c) 2 3222 (2)(1) 321 1 4 2(2) 222 limlimlim, xx xxx xxxxxxxx −+− →→→ === 2 x = /
(d) 2 3222 (2)(1) 321 1 4 2(2) 222 limlimlim, xx xxx xxxxxxxx −+− →→→ === 2 x = /
(e) ( ) 2 322 (2)(1)negativenegative 32 positivenegative 002(2) limlim xx xx xxxxxx −+ →→ ==−∞
58. (a) 2 3 (2)(1)(1) 32 11 (2)(2)(2)2(4)8 4 222 limlimlimxxx xx xxxxx xx xxx +++ −+ −++ →→→ ====
(b) ( ) 2 3 (2)(1)(1)negative 32 (2)(2)(2)negativepositive 4 222 limlimlimxxx xx xxxxx xx xxx +++ −+ −++⋅ →−→−→− ===∞
(c) ( ) 2 3 (2)(1)(1)negative 32 (2)(2)(2)negativepositive 4 000 limlimlimxxx xx xxxxx xx xxx −+ −++⋅ →→→ ===∞
(d) 2 3 (2)(1)(1) 320 (2)(2)(2)(1)(3) 4 111 limlimlim0 xxx xx xxxxx xx xxx +++ −+ −++ →→→ ====
(e) ( ) negative 1 (2)positivepositive 0 lim x xx x + +⋅ → =−∞ and ( ) negative 1 (2)negativepositive 0 lim x xx x +⋅ → =∞ so the function has no limit as 0. x →
59. (a) 1/3 3 0 lim2 t t + →
−=−∞
60. (a) 3/5 1 0 lim7 t t + →
61. (a) 2/32/3 12 (1) 0 lim xx x + → +=∞
(c) 2/32/3 12 (1) 1 lim xx x + → +=∞
62. (a) 1/34/3 11 (1) 0 lim xx x + →
−=∞
(c) 1/34/3 11 (1) 1 lim xx x + →
−=−∞
(b) 1/3 3 0 lim2 t t →
−=∞
(b) 3/5 1 0 lim7 t t →
+=−∞
+=∞
(b) 2/32/3 12 (1) 0 lim xx x →
(d) 2/32/3 12 (1) 1 lim xx x →
+=∞
−=−∞
(b) 1/34/3 11 (1) 0 lim xx x →
−=−∞
(d) 1/34/3 11 (1) 1 lim xx x →
63. 1 1 x y = 64. 1 1 x y + =





possibility.
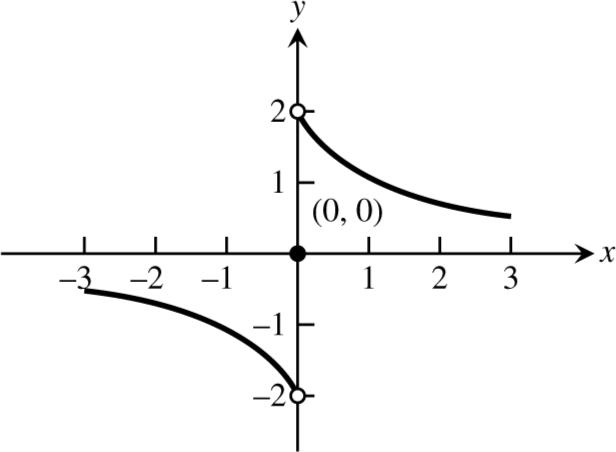
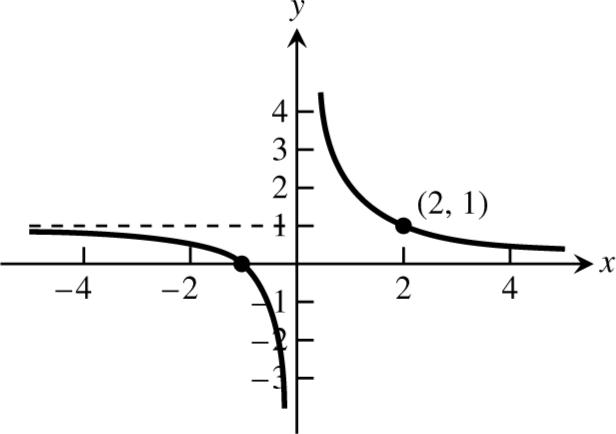
73. Here is one possibility.
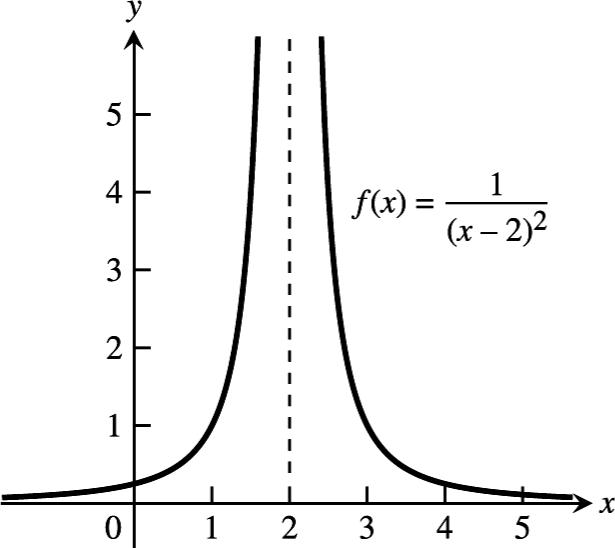
75. Here is one possibility.

74. Here is one possibility.
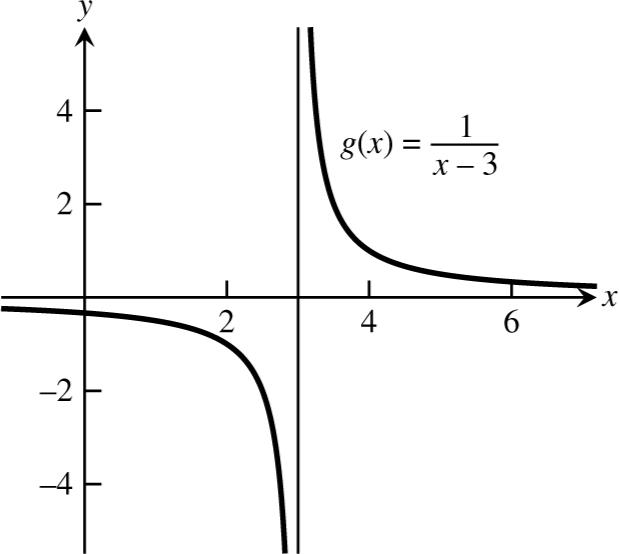
76. Here is one possibility.
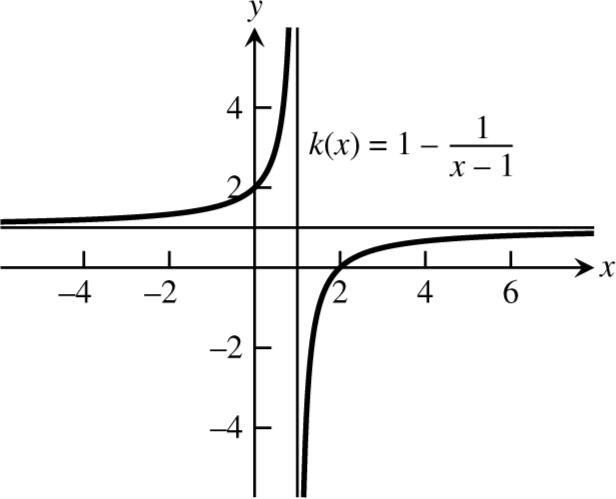
77. Yes. If () () lim 2 fx gx x →∞ = then the ratio the polynomials’ leading coefficients is 2, so () () lim2 fx gx x →−∞ = as well.
78. Yes, it can have a horizontal or oblique asymptote.
79. At most 1 horizontal asymptote: If () () lim, fx gx x L →∞ = then the ratio of the polynomials’ leading coefficients is L, so () () lim fx gx x L →−∞ = as well.
For any 0,
take 1 N = Then for all yN <− we have that ()0. fxkkk−=−=<
89. For every real number 0, B < we must find a 0 δ > such that for all x, 2 1 0 0. x xB δ <−< <− Now, 22 2 1111 00. B B xx BBxx <−<⇔>>⇔<⇔< Choose 1 , B δ = then 1 0 B xx δ << < 2 1 x B <− so that 2 1 0 lim. x x → −=−∞
90. For every real number 0, B > we must find a 0 δ > such that for all x, 1 0 0. x xB δ <−< > Now, 11 0 . B x Bx >>⇔< Choose 1 . B δ = Then 11 0 0 B x xxB δ <−< < > so that 1 0 lim. x x → =∞
91. For every real number 0, B < we must find a 0 δ > such that for all x, 2 2 (3) 0 3. x xB δ <−< <− Now, 2 2 (3) 0 x B <−<⇔ 2 2 (3) 21 2 (3) 0 x B x B >>⇔<⇔ 2 22 (3)03. BB x −<⇔<−< X Choose 2 , B δ = then 2 2 (3) 0 3 0 x xB δ <−< <−< so that 2 2 (3) 3 lim x x → =−∞
92. For every real number 0, B > we must find a 0 δ > such that for all x, 2 1 (5) 0 (5) x xB δ + <−−< > Now, 2 2 111 (5) 0(5)5. B B x Bxx + >>⇔+<⇔+< Choose 1 B δ = Then 0 (5) x δ <−−< 2 11 (5) 5 B x xB + +< > so that 2 1 (5) 5 lim x x + →− =∞
93. (a) We say that ()fx approaches infinity as x approaches 0x from the left, and write 0 lim(), xx fx → =∞ if for every positive number B , there exists a corresponding number 0 δ > such that for all x, 00 () .xxxfxB δ −<< >
(b) We say that ()fx approaches minus infinity as x approaches 0x from the right, and write 0 lim(), xx fx + → =−∞ if for every positive number B (or negative number B) there exists a corresponding number 0 δ > such that for all x, 00 (). xxxfxB δ <<+ <−
(c) We say that ()fx approaches minus infinity as x approaches 0x from the left, and write 0 lim(), xx fx → =−∞ if for every positive number B (or negative number B) there exists a corresponding number 0 δ > such that for all x, 00 (). xxxfxB δ −<< <−
94. For 0,011 . xB BBx >>>⇔< Choose 1 . B δ = Then 11 0 0 Bx xx δ << << > B so that 1 0 lim. x x + → =∞
95. For 1111 0,00. xxBB BBBxx ><−<⇔−>>⇔−<⇔−< Choose 1 . B δ = Then 1 0 B xx δ << −< 1 x B <− so that 1 0 lim. x x → =−∞
96. For 11 22 0, (2) xx BBBx ><−⇔−>⇔−− 111 22 . BBB xx < ⇔−>−⇔>− Choose 1 . B δ =
Then 22 x δ −<< 11 2 20200 Bx xxB δ <−< −<−< <−< so that 1 2 2 lim. x x → =−∞
97. For 11 2 0,02. xB BBx >>⇔<−< Choose 1 B δ = Then 1 220202 B xxx δδ <<+ <−< <−< 1 2 0 x B >> so that 1 2 2 lim. x x + → =∞
98. For 0 B > and 2 2 111 1 0 1,1(1)(1). BB x xBxxx <<>⇔−<⇔−+< Now 1 2 1 since 1. x x + << Choose 1 2 . B δ < Then 1 110xx−<<δδ −<−< () 1 1111(1)(1)22x xxxBBB δ + −<< −+<< 2 1 1 for 01and x Bx ><< 2 1 1 1 near 1lim. x x x → =∞
99. 2 1 11 1 x yxxx ==++ 100. 2 1 2 11 1 x yxxx + ==++

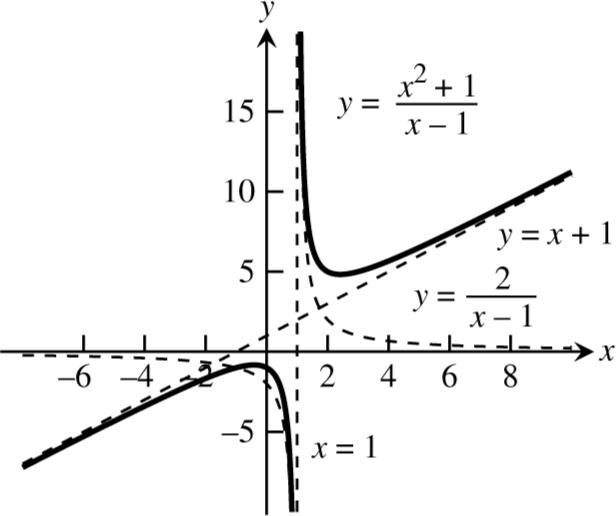
Copyright 2016 Pearson Education, Inc.
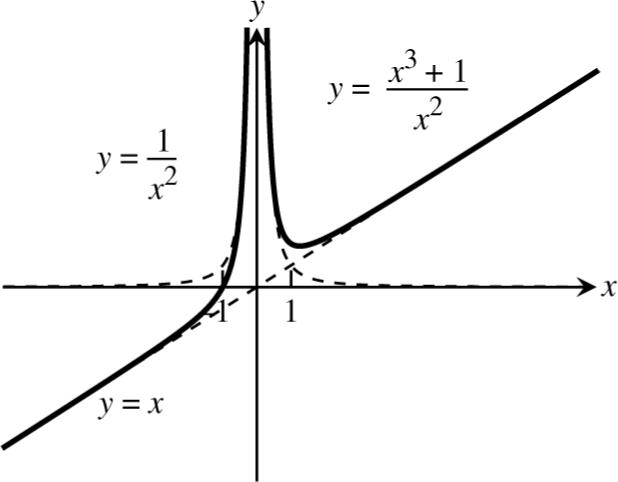
2 43 11 1 x yxxx ==+−

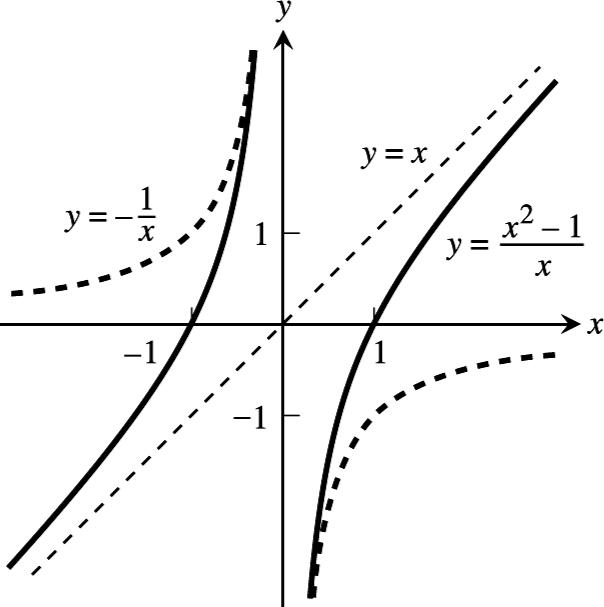

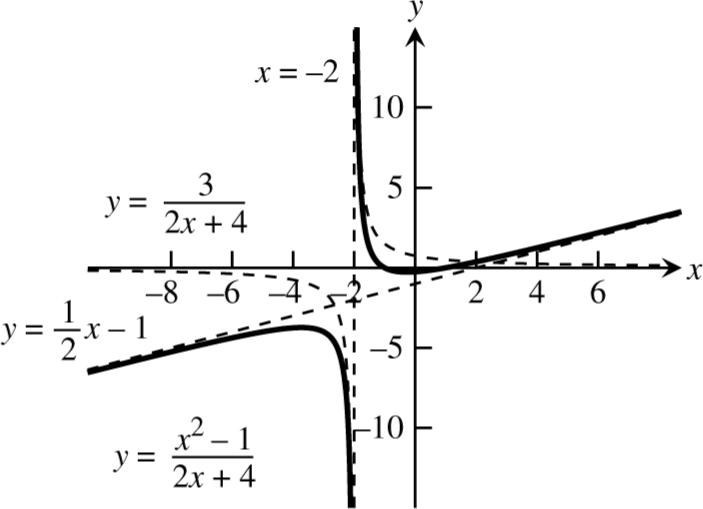
2 13 1 24224 1 x yxxx ++ ==−+

Copyright 2016 Pearson Education, Inc.
107. 1/3 2/3 1 x yx=+

109. (a) y → ∞ (see accompanying graph)
(b) y → ∞ (see accompanying graph)
(c) cusps at 1 x =± (see accompanying graph)
110. (a) 0 y → and a cusp at 0 x = (see the accompanying graph)
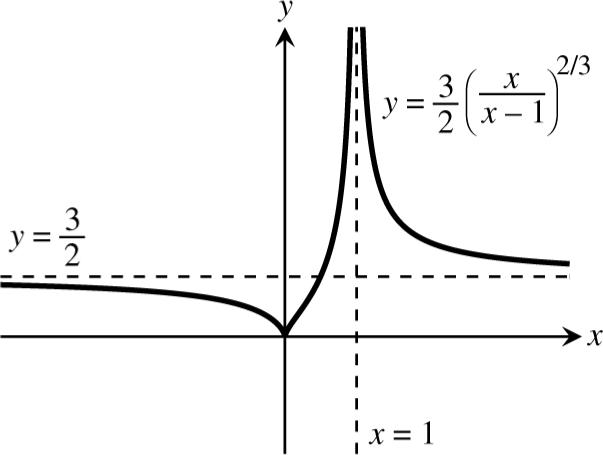
(b) 3 2 y → (see accompanying graph)
(c) a vertical asymptote at 1 x = and contains the point ( ) 3 3 24 1, (see accompanying graph)
CHAPTER 2 PRACTICE EXERCISES
1. At 11 1:lim ()lim()1 xx xfxfx →−→−−+ =−==
1 lim ()1(1) x fxf →− ==− is continuous at 1 fx =−
At 00 0:lim ()lim ()0 xx xfxfx →→−+ ===
0 lim ()0. x fx → = But 0 (0)1lim () x ffx → =≠ is discontinuous at 0. fx = If we define (0)0, f = then the discontinuity at 0 x = is removable.
At 11 1:lim ()1andlim ()1 xx xfxfx −+ →→ ==−=
1 lim()does not exist x fx → is discontinuous at 1. fx =
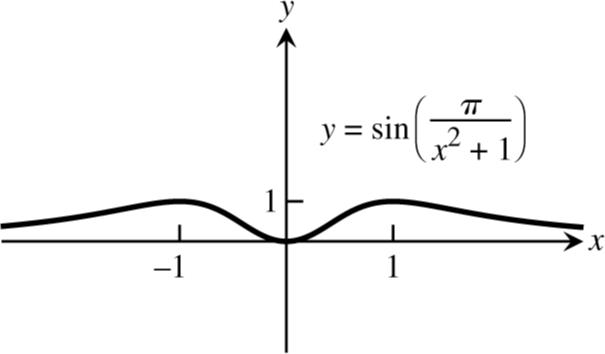
108. ( ) 2 1 sin x y π + =


2. At 11 1:lim ()0 and lim ()1 xx xfxfx −+ →−→− =−==−
1 lim () does not exist x fx →− is discontinuous at 1 fx =−
At 00 0:lim ()andlim () xx xfxfx −+ →→ ==−∞=∞
0 lim()does not exist x fx → is discontinuous at 0. fx =
At 1 11 1:lim ()lim ()1lim ()1. x xx xfxfxfx −+ → →→ === = 1 But(1)0lim () x ffx → =≠ is discontinuous at 1. fx = If we define (1)1, f = then the discontinuity at 1 x = is removable.
3. (a) 00 lim(3())3 lim ()3(7)21 t ttt ftft →→ ==−=−
(b) 00 2 lim(())lim22()(7)49 t ttt ftft →→
(c) 000 lim (()())lim ()lim ()(7)(0) 0 t ttttt ftgtftgt →→→ ⋅=⋅=−=
(d) 00 0 000 lim ()lim () () 7 ()7lim (()7)lim ()lim707 lim1 tttt tttttt ftft ft gtgtgt t t →→ →→→ → ====
(e) 00 limcos(())coslim ()cos01 t ttt gtgt →→
(f) 00 lim|()|lim ()|7|7 t ttt ftft →→ ==−=
(g) 000 lim(()())lim ()lim ()707 t ttttt ftgtftgt →→→ +=+=−+=−
(h) ( ) 0 0 1111 ()lim ()77 lim tt ftft t t → → ===−
4. (a) 00 lim()lim ()2 xx gxgx →→ −=−=−
(b) () () 2 1 22 000 lim(()())lim ()lim ()2 xxx gxfxgxfx →→→ ⋅=⋅==
(c) 1 2 000 lim (()())lim ()lim ()2 xxx fxgxfxgx →→→ +=+=+
(d) 1 2 0 111 ()lim () 0 lim 2 x fxfx x → → ===
(e) 11 22 000 lim (())lim lim ()0 xxx xfxxfx →→→ +=+=+=
(f) () 1 2 00 00 lim ()lim cos (1) ()cos 1 1lim lim 1012 0 lim xx x x fxx fxx xx x →→ →→ → ===−
5. Since 0 lim 0 x x → = we must have that x0 lim → (4())0. gx −= Otherwise, if 0 lim (4()) x gx → is a finite positive number, we would have 4() 0 lim gx x x → =−∞ and 4() 0 lim gx x x + → =∞ so the limit could not equal 1 as 0. x → Similar reasoning holds if 0 lim (4()) x gx → is a finite negative number. We conclude that 0 lim () 4 x gx → =
6. 4044 2limlim ()limlim xxxx xgxx →−→→−→− ==⋅ 0400 lim ()4limlim()4lim() xxxx gxgxgx →→−→→
(since 0 lim x → ()gx is a constant) 21 42 0 lim (). x gx → ==−
7. (a) 1/31/3 lim ()lim () xcxc fxxcfc →→ === for every real number c f is continuous on (,). −∞∞
(b) 3/43/4 lim ()lim () xcxc gxxcgc →→ === for every nonnegative real number c g is continuous on [0,). ∞
(c) 2/3 2/3 1 lim ()lim () c xcxc hxxhc →→ === for every nonzero real number c h is continuous on (,0) −∞ and (,). −∞∞
(d) 1/6 1/6 1 lim()lim () c xcxc kxxkc →→ === for every positive real number c k is continuous on (0,) ∞
8. (a) () () () 11 22,, n I nnππ ∈ −+ where I = the set of all integers.
(b) (, (1)), n I nnππ ∈ + where I = the set of all integers.
(c) (, )(, ) ππ −∞∪∞ (d) (, 0)(0, ) −∞∪∞
9. (a) 2 32 44 (2)(2) 2 (7)(2)(7) 514 000 lim limlim ,2; xx xx x xxxxx xxx xxx x −+ +−+ +− →→→ ==≠ the limit does not exist because 2 (7) 0 lim x xx x + → =∞ and 2 (7) 0 lim x xx x + + → =−∞
(b) 2 32 44 (2)(2) 2 (7)(2)(7) 514 222 limlimlim, 2, xx xx x xxxxx xxx xxx x −+ +−+ +− →→→ ==≠ and 20 (7)2(9) 2 lim0 x xx x + → ==
10. (a) 2 54332 (1) 002(21) limlim xx xx xxxxxxxx + + →→++++ = 22 1 1 00(1)(1)(1) limlim, 0 x xxxxxxx x + →→+++ = =≠ and 1. x ≠− Now 2 1 (1) 0 lim xx x + → =∞ and 2 2543 1 (1)2 0 0 limlim. xx xxxxx x x + + +++ → → =∞ =∞ (b) 2 543322 (1) 1 1112(21)(1) limlimlim, 0 xx xx xxxxxxxxxxx x + + →−→−→−+++++ ==≠ and 1. x ≠− The limit does not exist because 2 1 (1) 1 lim xx x + →− =−∞ and 2 1 (1) 1 lim. xx x + + →− =∞
11. 11 11 12 (1)(1)1 111 limlimlim xx x xxxxxx →→→−++ ===
12. 22 22 442222222 () 11 ()()2 limlimlim xa xa xaxaxaxaxaxaxaa →→→−+−+ ===
13. ()(2)22222 000 limlimlim (2)2 xhxxhxhx hh hhh xh x +−++− →→→ ==+=
14. ()(2)22222 000 limlimlim (2) xhxxhxhx hh xxx xhh +−++− →→→ ==+=
15. 11 22 2(2) 11 0002(2)424 limlimlim x x xxxxxxx + −+ →→→++ ===−
16. 332 (2)8(6128)8 2 000 limlimlim (612)12 xxxx xx xxx xx +−+++− →→→ ==++=
17. 1/32/31/3 1/3 2/31/3 (1)(1)(1) 1 1(1) (1)(1) 11 limlim xxxx x xx xxx xx −+++ +++ →→ =⋅ 2/31/32/31/3 (1)(1) 1 112 1113 (1)(1)1 11 limlim xx x xxxxxxx −+ + + ++ →→−++++ = ===
18. 1/31/3 2/3 (4)(4) 16 646488 limlim xx x xxxx −+ →→ = 1/31/32/31/3 2/31/3 (4)(4)(416)(8) 8 (8)(416) 64 lim xxxxx x xxx x −++++ +++ → = 1/31/3 2/31/32/31/3 (64)(4)(8)(4)(8)(44)(88) 8 1616163 (64)(416)416 6464 limlimxxxxx xxxxxxx −++++++ ++ →→−++++ = ===
19. tan2cos sin 2 tancos 2sin 00 limlimxx x xxxxx π →→ππ =⋅ () () ( ) () sin 2cos2 22 2cos 2sin 0 lim111 xxxx xxxx x ππ ππππ → = =⋅⋅⋅=
20. 1 sin limcsc lim x xx x ππ →→ ==∞
21. () () ()222 limsinsinsinsinsin1 x x x ππ π π → +=+==
22. limcos(tan)cos(tan)2222cos()(1)1 x xx π πππ → −=−==−=
23. sin 888 3sin 3(1)1 31 00 limlim4 x x x xx xx →→ ===
24. () cos 21cos 21cos 2 1 sinsincos 21 00 limlimxxx xxxxx −−+ + →→ ==⋅ cos22 21sin2 sin(cos 21)sin (cos 21) 00 limlimxx xxxxxx →→++ = = 2 2 4sincos 4(0)(1) cos 2111 0 lim 0 xx x x ++ → = ==
25. Let x = t 3 30 limln(3)limln tx tx →→++ −==−∞
26. () 2 1 limln2ln10 t tt → −==
27. () 1cos(/)11cos(/)cos(/) 0 1cos1lim0 eeeeeee + → −≤≤ ≤≤ ≤≤ = πθπθπθ π θ θ θθθθ by the Sandwich Theorem
28. 1/ 1/ 22 10 1/ 1 0 2 limlim2 1 z z z e zz e e ++ + + →→0 === +
29. 1/3 1/3 000 lim[4 ()]2lim4()2lim4()8, xxx gxgxgx +++ →→→ = = = since 3 28. = Then 0 lim()2. x gx + → =
30. 11 55()2 lim2lim(()) xgx xx xgx + →→ = += 11 5lim5522 ()lim ()5 xx gxgx →→ += =−
31. 2 2 31 () 111 limlim ()0 since lim (31)4 x gx xxx gxx + →→→ =∞ =+=
32. 2 2 5 () 222 lim0lim () since lim (5)1 x gx xxx gxx →−→−→− = =∞−=
Copyright 2016 Pearson Education, Inc.
33. At 2 2 (1) |1| 11 1:lim()lim xx x xx xfx →−→− =−= 2 2 (1) 1 11 limlim1,and xx x xx x →−→− ===− 22 22 (1)(1) 111|1|(1) lim()limlimxxxx xxxxx fx +++ →−→−→− ==

1 lim()(1)1.Since x x →− = −=−−= 1 lim() x fx →− ≠ 1 lim() x fx + →− 1 lim x →− ()fx does not exist, the function f cannot be extended to a continuous function at 1. x =− 2 2 (1) |1| 11 At1:lim()lim xx x xx xfx →→ == 2 2 (1) (1) 11 limlim()1,and xx x xx x →→ = =−=− 2 2 (1) |1| 11 lim()lim xx x xx fx →→++ =
2 (1) 1 1 lim xx x x + → = 1 lim1. x x + → = = 1 Againlim() x fx → does not exist so f cannot be extended to a continuous function at 1 x = either.
34. The discontinuity at 0 x = of () 1 ()sin x fx = is nonremovable because 1 0 limsin x x → does not exist.
35. Yes, f does have a continuous extension at 1: a = define 4 1 4 3 1 (1)lim x xx x f → ==

36. Yes, g does have a continuous extension at 2 : a π = () 2 5 cos 5 2424 lim . g π θ π θπ θ→ ==−

37. From the graph we see that 00 lim()lim () t t htht →→−+ ≠ so h cannot be extended to a continuous function at 0 a =
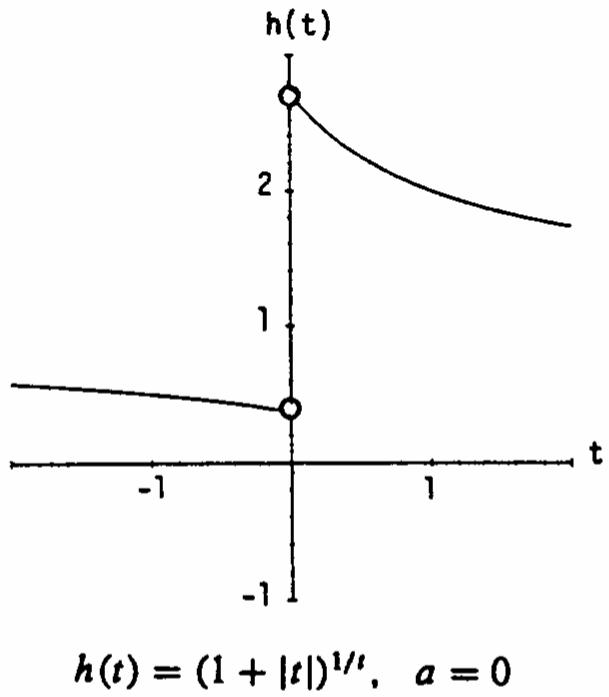
38. From the graph we see that 00 lim()lim() xx kxkx →→−+ ≠ so k cannot be extended to a continuous function at 0. a =
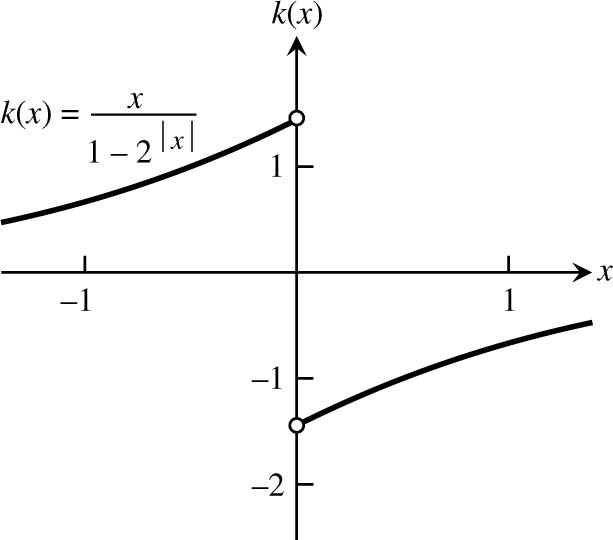
39. (a) (1)1and(2)5hasarootbetween fff −=−= 1 and 2 by the Intermediate Value Theorem. (b), (c) root is 1.32471795724
40. (a) (2)2and(0)2hasarootbetween fff −=−= 2 and 0 by the Intermediate Value Theorem. (b), (c) root is -1.76929235424
41. 3 7 2 2320 2 57505 5 limlim x x x x xx + ++ ++ + →∞→∞ ===
43. ( ) 2 323 488 14 3 333 limlim0000 xx
44. 1 2 271 2 0 1 100 1 71 limlim0 x x x xx xx −+ −+ −+ →∞→∞
45.
47. sin sin 1 limlim0 since as lim0.xx xxxxxx xx →∞→∞→∞ ≤=→∞→∞
48. cos 1cos1 2 limlim0lim0. θθ θθθ θ θθ →∞→∞→∞ ≤= =
49. sin 2 sin 1 sin 2 100 sin 10 1 limlim1 x x x x x xxx xx xx ++ ++ ++ ++ + →∞→∞ ===
50. 2/315/3 2/322 cos 2/3 110 10 cos 1 limlim1 x x xxx xx xx +++ + + →∞→∞ +
51. () 1/0 1 limcoscos(0)111 x x x ee →∞ =⋅=⋅=
52. () 1 limln1ln10 t x →∞ +==
53. 1 2 limtan x x →−∞ =− π
54. () 311 1 limsin0sin(0)000 t t t e →−∞ =⋅=⋅=
55. (a)
(b)
asymptote.
(c)
56.
(b)
and
1 3 thus y = is a horizontal asymptote.
CHAPTER 2 ADDITIONAL AND ADVANCED EXERCISES
1. (a) 0.10.010.0010.00010.00001 0.79430.95500.99310.99910.9999 x x x Apparently, 0 lim1 x x
(b)

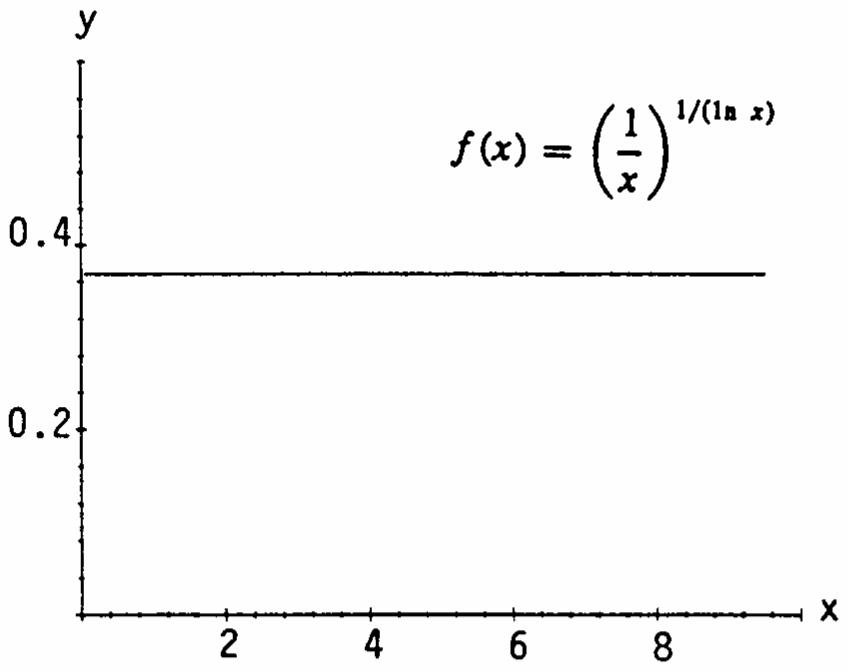
2. (a) ()1/(ln ) 1 101001000 0.36790.36790.3679 x x x Apparently, ()1/(ln ) lim0.367811 x xe x →∞ == (b)
3. 2 22 222 lim 000 limlim 111 0 vc v vc ccc v cvc LLLL → →→ =−=−=−=
The left-hand limit was needed because the function L is undefined if v c > (the rocket cannot move faster than the speed of light).
4. (a) 2210.20.210.20.8 xx −< −<−< 2 1.21.62.42.565.76 x xx < < << << (b) 2210.10.110.1 xx −< −<−< 2 0.91.11.82.23.244.84. x xx
5. 4 |10(70)1010|0.0005 t +−×−< 44 |(70)10|0.00050.0005(70)100.0005 tt −×< −<−×< 57056575Within 5F. tt −<−< °<<° °
6. We want to know in what interval to hold values of h to make V satisfy the inequality | 1000||361000|Vh π −=− 10. ≤ To find out, we solve the inequality: | 361000|101036100010 hh ππ −≤ −≤−≤ 9901010 3636 9903610108.88.9 hhh ππ π ≤≤ ≤≤ ≤≤ where 8.8 was rounded up, to be safe, and 8.9 was rounded down, to be safe. The interval in which we should hold h is about 8.98.80.1 −= cm wide (1 mm). With stripes 1 mm wide, we can expect to measure a liter of water with an accuracy of 1%, which is more than enough accuracy for cooking.
7. Show 2 11 lim ()lim (7)6(1). xx fxxf →→ =−=−=
Step 1: 22 | (7)6|1 xx −+< −<−< 2 111 1. xx −<<+ −<<+
Step 2: | 1|111 xxxδδδδδ −< −<−< −+<<+
Then 11 or 11 δδ+=−+=+ Choose { } min11,11, δ =−−+− then 0 |1| x δ <−<
2 | (7)6| x −−< and 1 lim()6 x fx →− =− By the continuity text, ()fx is continuous at 1 x =
8. Show () 11 44 11 24 lim ()lim 2. x xx gxg →→ ===
Step 1: 11111 2224242 2222. xxx x −+ −< −<−< −<<+ >>
Step 2: 1111 4444 xx δδδδδ −< −<−< −+<<+ X
Then 1111 4424424(2) , δδ ++− += =−= or 1111 4424244(2) . δ δ += =−=
Choose 4(2) , δ + = the smaller of the two values. Then 11 42 0 2 x x δ <−< −< and 1 4 1 2 lim2 x x → = By the continuity test, ()gx is continuous at 1 4 x =
9. Show 22 lim ()lim231(2). xx hxxh →→ =−==
Step 1: 231231 xx −−< −<−−<
22 (1)3(1)3 22 1231. xx −+++ −<−<+ <<
Step 2: | 2|2or22 xxxδδδδδ −< −<−<−+<<+
Then 222 (1)3(1)31(1) 22222 δδ−+−+−− += =−=
22 (1)3(1)1 22 2 +++− = −==
2 2 + Choose 2 2 , δ =− the smaller of the two values. Then, 0 |2|231, xx δ <−< −−< 2 solim231. x x → −= By the continuity test, ()hx is continuous at 2 x =
10. Show 55 lim()lim9 2(5). xx FxxF →→ =−==
Step 1: 22 92929(2)9(2). xxx−−< −<−−< −−>>−+
Step 2: 0 |5|555 xxxδδδδδ <−< −<−< −+<<+ Then 222 59(2)(2)42,δδ +=−+ =+−=+ or 222 59(2)4(2)2. δ δ +=−− =−−=−
Choose 2 2, δ =− the smaller of the two values. Then, 0 |5|92, xx δ <−< −−< so 5 lim92. x x → −=
By the continuity test, ()Fx is continuous at 5. x =
11. Suppose 1L and 2L are two different limits. Without loss of generality assume 21LL > Let 1 21 3 (). LL=− Since 0 1 lim() xx fxL → = there is a 1 0 δ > such that 011 0 |||()| xxfxL δ <−< −< 1 () fxL −<−< 1 11 33211211212 ()()()43()2. LLLfxLLLLLfxLL −−+<<−+ −<<+ Likewise, 0 2 lim() xx fxL → = so there is a 2δ such that 0222 0 |||()|() xxfxLfxL δ <−< −< −<−< 11 33212212 ()()() LLLfxLLL −−+<<−+ 21211221 23()443()2. LLfxLLLLfxLL +<<− −<−<−− If 12 min{,} δ δδ = both inequalities must hold for 0 0 ||: xx δ <−< 1212 1212 1221 4 3() 2 5()0 43()2 LLfxLL LLLL LLfxLL −<<+ −<<− −<−<−− That is, 12 0 LL−< and 12 0, LL−> a contradiction.
12. Suppose lim() xc fxL → = If 0, k = then lim()lim000 xcxc kfx →→ ===⋅ lim() xc fx → and we are done. If 0, k ≠ then given any 0, > there is a 0 δ > so that || 0 |||()||||()| k xcfxLkfxL δ <−<< −< −< |(())| kfxL −< |(())()|. kfxkL −< Thus lim()lim(). xcxc kfxkLkfx →→
13. (a) Since 333 0 0,01()0lim() x xxxxxfxx + +− → →<<< −→ 3 0 lim() where . y fyByxx → = ==− (b) Since 333 0 0,10()0lim() x xxxxxfxx −+ → →−<<< −→ 3 0 lim() where . y fyAyxx + → = ==−
(c) Since 422424 0 0,01()0lim() x xxxxxfxx + ++ → →<<< −→ 24 0 lim() where . y fyAyxx + → = ==−
(d) Since 4224 0,1001()0 xxxxxx →−<<−+ <<< −→ 24 0 lim() as in part (c). x fxxA + → −=
Copyright 2016 Pearson Education, Inc.
14. (a) True, because if lim(()()) xa fxgx → + exists then lim(()())lim()lim xaxaxa fxgxfx →→→ +−= [(()())()] fxgxfx+−= lim() xa gx → exists, contrary to assumption.
(b) False; for example take 1 () x fx = and 1 (). x gx =− Then neither 0 lim() x fx → nor 0 lim() x gx → exists, but () 11 000 lim(()())limlim00 xx xxx fxgx →→→ +=−== exists.
(c) True, because ()|| gxx = is continuous (())|()| gfxfx = is continuous (it is the composite of continuous functions).
(d) False; for example let 1,0 ()() is discontinuous at 0. However |()| 1 1,0 x fxfxxfx x −≤ = == > is continuous at 0. x =
15. Show 2 (1)(1) 1 1111(1) lim()limlim2,1. xx x xxxxxfxx +− →−→−→−++ ===−≠−
Define the continuous extension of ()fx as 2 1 1 ,1 ().We now prove the limit of () as 1 2 , 1 x x x Fxfxx x + ≠− =→− −=− exists and has the correct value.
Step 1: 2 (1)(1) 1 1(1)(2)2(1) xx x xx x +− ++ −−< −<+< −<−
2,111. xx + <≠− −−<<−
Step 2: | (1)|111. xxxδδδδδ −−< −<+< −−<<− Then 11,or11 δδδδ −=−− =−=− = Choose δ = Then 0 |(1)| x δ
Since the conditions of the continuity test are met by (),Fx then ()fx has a continuous extension to ()Fx at 1. x =−
16. Show 2 (3)(1) 23 333262(3) lim()limlim2,3. xx xx xxxxxgxx −+ →→→ ===≠
Define the continuous extension of ()gx as 2 23 26 ,3 () 2,3 xx
We now prove the limit of ()gx as 3 x → exists and has the correct value.
Step 1: 2 (3)(1) 23 262(3)22 xx xx xx −+ −< −<−< 1 2 2,33232 x xx + −<−<≠ −<<+
Step 2: | 3|333. xxxδδδδδ −< −<−< −<<+
Then, 3 322,−=−δδ = or 3322δδ +=+ = Choose 2. δ = Then 0 |3| x δ <−< 2 (3)(1) 23 262(3) 3 2lim2. xx xx xx x −+ → −< = Since the conditions of the continuity test hold for (),() Gxgx can be continuously extended to ()Gx at 3. x =
17. (a) Let 0 > be given. If x is rational, then ()|()0||0||0|; fxxfxxx = −=−<⇔−< i.e., choose δ = Then | 0||()0|xfx δ −< −< for x rational. If x is irrational, then ()0|()0|0 fxfx = −<⇔< which is true no matter how close irrational x is to 0, so again we can choose . δ = In either case, given 0 > there is a 0 δ => such that 0 |0||()0| . xfx δ <−< −< Therefore, f is continuous at 0. x = (b) Choose 0. xc=> Then within any interval (,) cc−+δδ there are both rational and irrational numbers. If c is rational, pick 2 c = No matter how small we choose 0 δ > there is an irrational number x in 2 (,)|()()||0| c ccfxfccc −+δδ −=−=>= That is, f is not continuous at any rational 0. c > On the other hand, suppose c is irrational ()0.fc = Again pick 2 c = No matter how small we choose 0 δ > there is a rational number x in (,) cc−+δδ with 3 222 | | xcxccc ε −<=⇔<< Then |()()||0| fxfcx−=− 2 || c x =>= f is not continuous at any irrational 0. c >
If 0, xc=< repeat the argument picking || 22 c c == Therefore f fails to be continuous at any nonzero value .xc =
18. (a) Let m n c = be a rational number in [0,1] reduced to lowest terms 1 (). n fc = Pick 1 2 n = No matter how small 0 δ > is taken, there is an irrational number x in the interval (,)|()()| ccfxfc −+δδ 111 2 0. nnn =−=>= Therefore f is discontinuous at ,xc = a rational number.
(b) Now suppose c is an irrational number ()0.fc = Let 0 > be given. Notice that 1 2 is the only rational number reduced to lowest terms with denominator 2 and belonging to [0,1]; 1 3 and 2 3 the only rationals with denominator 3 belonging to [0,1]; 1 4 and 3 4 with denominator 4 in [0,1]; 3 12 555 ,, and 4 5 with denominator 5 in [0,1]; etc. In general, choose N so that 1 N < there exist only finitely many rationals in [0,1] having denominator , N ≤ say 12,,,. rrrp Let min{||:1,,} i crip δ =−=… Then the interval (,) cc−+δδ contains no rational numbers with denominator . N ≤ Thus, 0 |||()()| xcfxfc δ <−< −= | ()0|fx = 1 | ()| N fx ≤< f is continuous at xc = irrational.
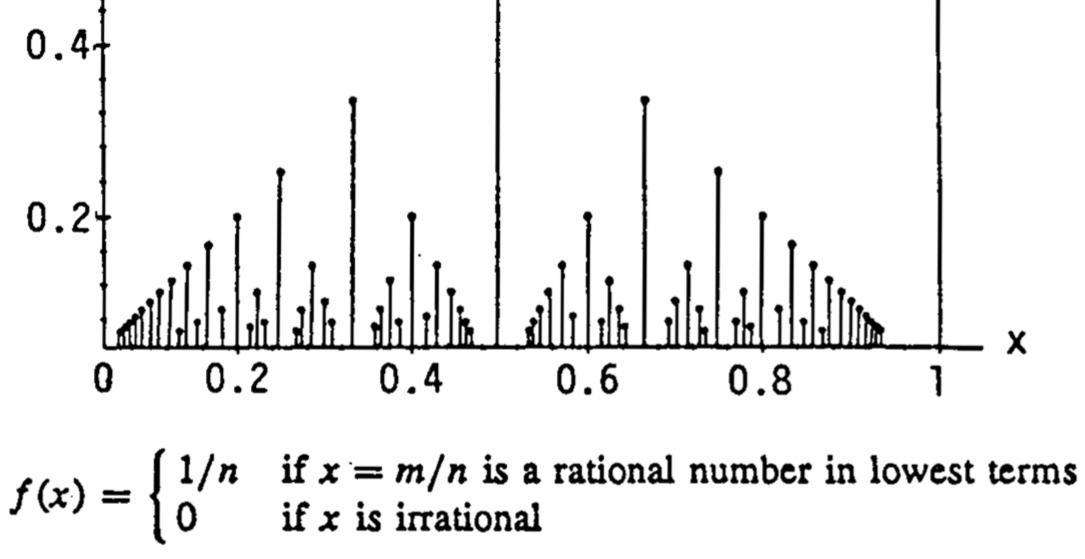
(c) The graph looks like the markings on a typical ruler when the points (,()) xfx on the graph of ()fx are connected to the -axis x with vertical lines.

19. Yes. Let R be the radius of the equator (earth) and suppose at a fixed instant of time we label noon as the zero point, 0, on the equator 0 Rπ + represents the midnight point (at the same exact time). Suppose 1x is a point on the equator “just after” noon 1 xR π + is simultaneously “just after” midnight. It seems reasonable that the temperature T at a point just after noon is hotter than it would be at the diametrically opposite point just after midnight: That is, 11 ()()0. T xTxR π −+> At exactly the same moment in time pick 2x to be a point just before midnight 2 xR π + is just before noon. Then 22 ()()0. T xTxR π −+< Assuming the temperature function T is continuous along the equator (which is reasonable), the Intermediate Value Theorem says there is a point c between 0 (noon) and Rπ (simultaneously midnight) such that ()()0; T cTcR π −+= i.e., there is always a pair of antipodal points on the earth’s equator where the temperatures are the same.
(b) At
1(1) 00(11)(11) limlim a a aaaaaa
(because the denominator is always negative); 0 lim() a ra + →
(because the denominator is always positive).
(c)
Therefore,lim() does not exist
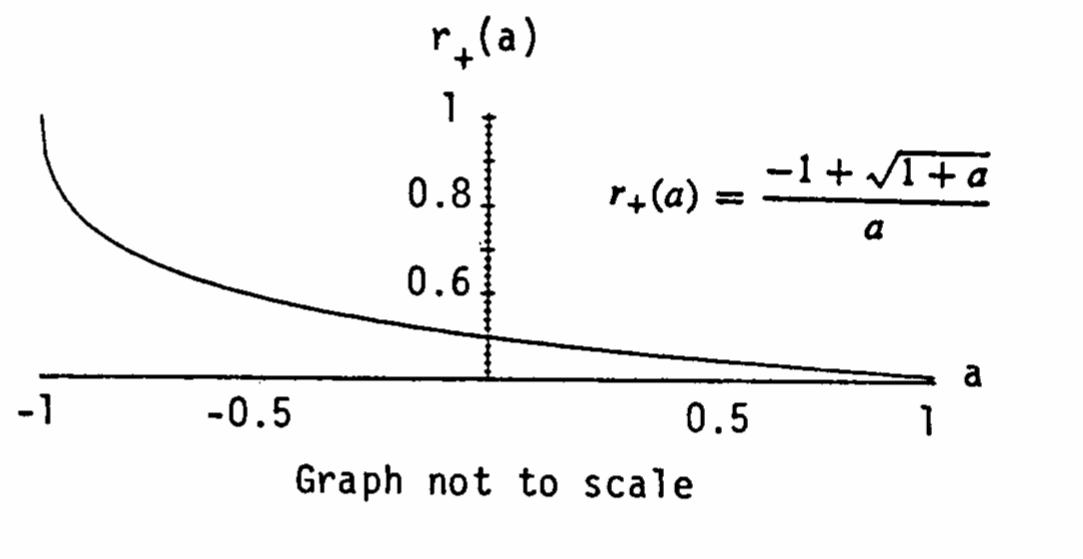
(d)
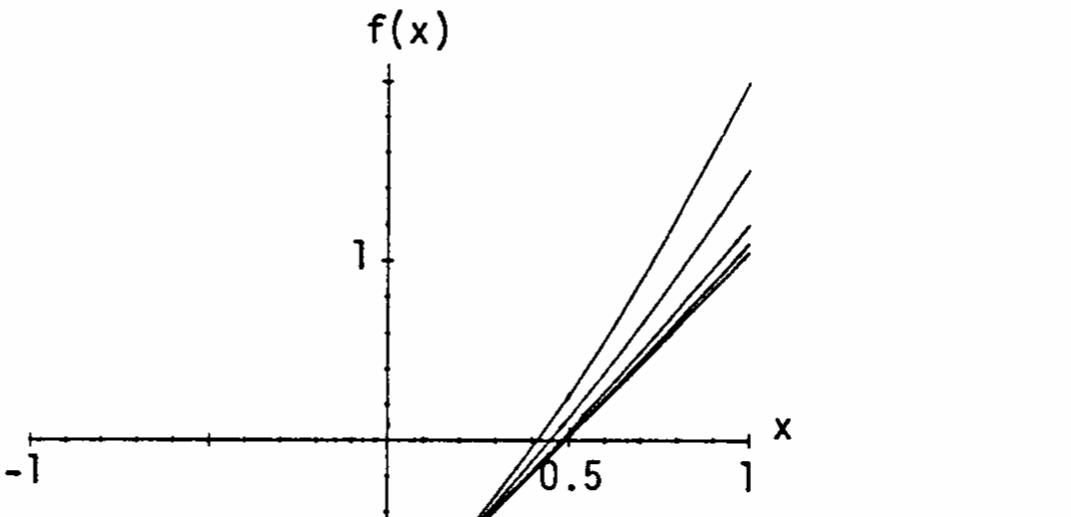
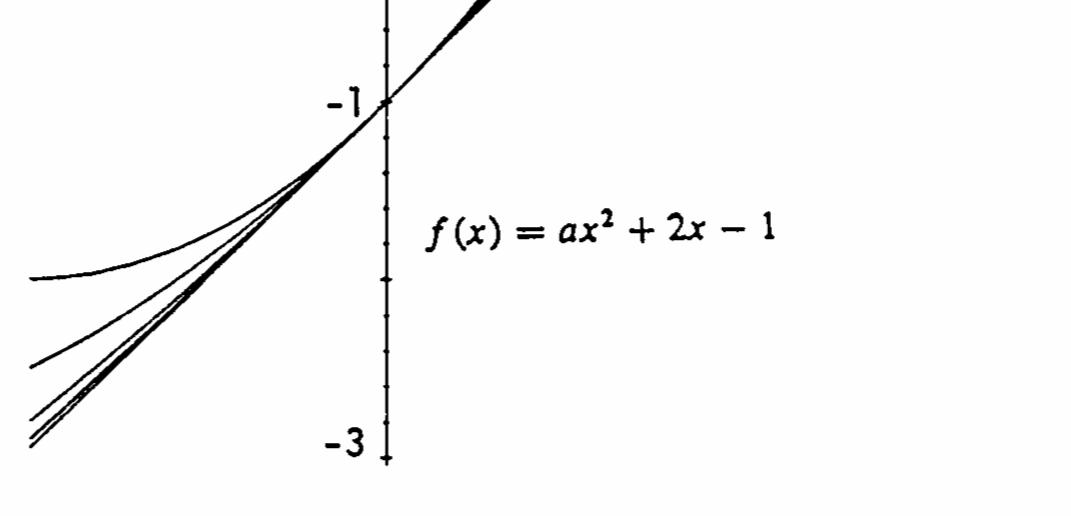


22. ()2 cos (0)02 cos 02 0 fxxxf =+ =+=> and ()2 cos()20. f ππππ −=−+−=−−< Since ()fx is continuous on [,0], π by the Intermediate Value Theorem, ()fx must take on every value between [2,2]. π Thus there is some number c in [,0] π such that ()0;fc = i.e., c is a solution to 2 cos 0. xx+=
23. (a) The function f is bounded on D if () fxM ≥ and () fxN ≤ for all x in D. This means () M fxN≤≤ for all x in D. Choose B to be max {||, ||}.MN Then | ()| .fxB ≤ On the other hand, if | ()|, fxB ≤ then ()() B fxBfxB≤≤ ≥− and ()() fxBfx ≤ is bounded on D with NB = an upper bound and M B =− a lower bound.
(b) Assume () fxN ≤ for all x and that LN > Let 2 LN = Since 0 lim () xx fxL → = there is a 0 δ > such that 0 0 |||()| xxfxL δ <−< −<⇔ 222 ()()() LNLNLN LfxLLfxLfx −−+ −<<+⇔−<<+⇔<
3 2 LN < But 2 () LN LNNNfx + > > < contrary to the boundedness assumption (). fxN ≤ This contradiction proves . LN ≤
(c) Assume () M fx ≤ for all x and that LM < Let 2 M L = As in part (b), 0 2 0 || M L xxL δ <−< 3 222 ()(), LM M LML fxLfxM −+ < <+⇔<<< a contradiction.
Copyright 2016 Pearson Education, Inc.
24. (a) If ,ab ≥ then 0||max {,}abababab −≥ −=− || 2 22222 . ab abababa a ++− = +=+== If ,ab ≤ then 0||() abababba −≤ −=−−=− || 2 22222 max{,} ab ababbab abb ++− =+=+== (b) Let || 22 min{,}. ab ab ab + =−
25. 2 sin(1cos) sin(1cos )sin(1cos ) 1cos 1cos 1cos 1cos1cos 1cos(1cos ) 0000 limlimlimlim x xx xxx xxxxxxxxxxx −+− →→→→−+−+ ==⋅⋅=⋅ () 2 sinsin sin 0 (1cos )1cos 2 00 1limlim10. xxx xxxxxx →→++ =⋅=⋅=⋅=
26. ( ) sin sin sin 1 sinsin 0000 limlim1limlim1100. x x x xxx x xxx xxxx x ++++ →→→→ =⋅⋅=⋅⋅=⋅⋅=
27. sin(sin )sin(sin )sin(sin ) sin sin sinsin 0000 limlimlimlim111 xxxxx xxxxxxxxx →→→→ =⋅=⋅=⋅=
28. 222 22 sin()sin()sin() 0000 limlim(1)limlim(1)111 xxxxxx x xxxx xxxx xx +++ ++ →→→→ =⋅+=⋅+=⋅=
29. 222 22 sin(4)sin(4)sin(4) 2 44 2222 limlim(2)limlim(2)14 4 xxx x xx xxxx xx →→→→ =⋅+=⋅+=⋅= .
30. sin(3)sin(3)sin(3)1111 96699993333 limlimlimlim1 xxx x xxxxxxxx →→→→−+−+ =⋅=⋅=⋅= .
31. Since the highest power of x in the numerator is 1 more than the highest power of x in the denominator, there is an oblique asymptote. 3/2 2233 11 2, xx xx yx +− ++ ==− thus the oblique asymptote is 2.yx =
32. As () ()111 ,0sin01sin1, xxx x →±∞→ → +→ thus as () () ()11 ,sin1sin; xx xyxxxx →±∞=+=+→ thus the oblique asymptote is .yx =
33. As 2222 ,11; xxxxx →±∞+→ +→ as 2 ,, xxx →−∞=− and as 2 ,; xxx →+∞= thus the oblique asymptotes are yx = and yx =−
34. As 2 ,22 xxxxx →±∞+→ + (2);22 as ,, xxxxxx = +→→−∞=− and as 2 ,; xxx →+∞= asymptotes are yx = and .yx =−
