Ch. 2Functions and Their Graphs
2.1Functions
1Determine Whether a Relation Represents a Function
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Determine whether the relation represents a function. If it is a function, state the domain and range. 1)
4 → 20 7 → 35 10 → 50 13 → 65
A)function domain: {4, 7, 10, 13} range: {20, 35, 50, 65}
2)
Alice Brad Carl snake cat dog
A)function domain: {Alice, Brad, Carl} range: {snake, cat, dog}
3)
Alice Brad Carl cat dog
A)function domain: {Alice, Brad, Carl} range: {cat, dog}
4){(- 2 , - 7), (0 , 5), (5 , 0), (6 , - 1)}
A)function domain: {- 2, 0, 5, 6} range: {- 7, 5, 0, - 1}
5){(5 , - 2), (1 , - 1), (1 , 0), (2 , 1), (10, 3)}
A)function domain: {5, 2, 1, 10} range: {- 2, - 1, 0, 1, 3}
6){(- 3 , 11), (- 2 , 6), (0, 2), (2 , 6), (4 , 18)}
A)function domain: {- 3, - 2, 0, 2, 4} range: {11, 6, 2, 18}
B)function domain:{20, 35, 50, 65} range: {4, 7, 10, 13}
C)not a function
B)function domain: {snake, cat, dog} range: {Alice, Brad, Carl}
C)not a function
B)function domain: {cat, dog} range: {Alice, Brad, Carl}
B)function domain: {- 7, 5, 0, - 1} range: {- 2, 0, 5, 6}
B)function domain: {- 2, - 1, 0, 1, 3} range: {5, 2, 1, 10}
B)function domain: {11, 6, 2, 18} range: {- 3, - 2, 0, 2, 4}
C)not a function
C)not a function
C)not a function
C)not a function
7){(5.88, 7.58), (5.888, - 7.6), ( 9 7 , 0), (1.29, - 5)}
A)function domain: {5.88, 5.888, 9 7 , 1.29}
range: {7.58, - 7.6, 0, - 5}
B)function domain: {7.58, - 7.6, 0, - 5}
range: {5.88, 5.888, 9 7 , 1.29}
C)not a function
Determine whether the equation defines y as a function of x.
8)y = x4
A)functionB)not a function
9)y = 1 x
A)functionB)not a function
10)y = |x|
A)functionB)not a function
11)y 2 = 6 - x2
A)functionB)not a function
12)y = ± 1 - 5x
A)functionB)not a function
13)x = y 2
A)functionB)not a function
14)y 2 + x = 2
A)functionB)not a function
15)y = 4x2 - 9x + 9
A)functionB)not a function
16)y = 5x - 1 x + 1
A)functionB)not a function
17)x2 - 4y 2 = 1
A)functionB)not a function
18)x - 4y = 5
A)functionB)not a function
19) - 9x + x2 - 97 = y
A)functionB)not a function
2Find the Value of a Function
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the value for the function.
1)Find f(- 4) when f(x) = x2 - 3x + 1. A)29B)27C)3D)5
2)Find f(1) when f(x) = x2 - 8 x - 2 . A)7B) - 9C) - 1D)7 3
3)Find f(- 9) when f(x) = |x|- 6. A)3B) - 15C)15D) - 3
4)Find f(7) when f(x) = x2 + 5x A)221 B)74 C)30 D)36
5)Find f(- x) when f(x) = 3x2 - 4x + 1. A)3x2 + 4x + 1B) - 3x2 + 4x - 1C)3x2 + 4x - 1D) - 3x2 + 4x + 1
6)Find f(- x) when f(x) = x x2 + 8 A) - x x2 + 8 B) - x x2 - 8 C) x - x2 + 8 D) - x - x2 + 8
7)Find - f(x) when f(x) = 2x2 + 5x + 2. A) - 2x2 - 5x - 2B)2x2 - 5x + 2C)2x2 - 5x - 2D) - 2x2 - 5x + 2
8)Find - f(x) when f(x) = |x| + 9. A) - |x| - 9B)| - x| + 9C) - |x| + 9D)| - x| - 9
9)Find f(x - 1) when f(x) = 5x2 + 5x - 6.
A)5x2 - 5x - 6B) - 5x2 + 5x - 6C)5x2 - 5x + 4D)5x2 - 25x + 4
10)Find f(x + 1) when f(x) = x2 - 4 x + 4 A) x2 + 2x - 3 x + 5 B) x2 + 2x + 5 x + 5 C) x2 + 2x - 3 x - 3 D) x2 - 3 x + 5
11)Find f(- x) when f(x) = 2x2 - 2x - 4.
A)2x2 + 2x - 4B) - 2x2 + 2x - 4C) - 2x2 + 2x + 4D)2x2 + 2x + 4
12)Find f(2x) when f(x) = 9x2 - 7x
A)36x2 - 14x B)29x2 - 7x C)18x2 - 14x D)18x2 - 28x
13)Find f(x + h) when f(x) = 3x2 - 4x - 3.
A)3x2 + 6xh + 3h2 - 4x - 4h - 3B)3x2 + 3h2 - 4x - 4h - 3
C)3x2 + 3h2 + 2x + 2h - 3D)3x2 + 3xh + 3h2 - 4x - 4h - 3
14)Find f(x + h) when f(x) = 4x + 9 3x + 4 .
4x + 4h + 9 3x + 3h + 4
Solve the problem.
4x + 4h + 9 3x + 4
4x + 13h 3x + 7h
15)If f(x) = 9x3 + 7x2 - x + C and f(- 2) = 1, what is the value of C?
4x + 9h 3x + 4h
A)C = 43B)C = - 5C)C = - 101D)C = - 45
16)If f(x) = x - B x - A , f(4) = 0, and f(6) is undefined, what are the values of A and B?
A)A = 6 , B = 4B)A = 4 , B = 6C)A = - 6 , B = - 4D)A = - 4 , B = - 6
17)If f(x) = x - 5A 5x + 5 and f(5) = - 15, what is the value of A?
A)A = 91B)A = - 91C)A = - 29D)A = 29
18)If a rock falls from a height of 50 meters on Earth, the height H (in meters) after x seconds is approximately H(x) = 50 - 4.9x2
What is the height of the rock when x = 1.9 seconds? Round to the nearest hundredth, if necessary. A)32.31 mB)67.69 mC)40.69 mD)32.67 m
19)If a rock falls from a height of 60 meters on Earth, the height H (in meters) after x seconds is approximately H(x) = 60 - 4.9x2
When does the rock strike the ground? Round to the nearest hundredth, if necessary. A)3.5 secB)12.24 secC)1.58 secD)2.5 sec
20)It has been determined that the number of fish f(t) that can be caught in t minutes in a certain pond using a certain bait is f(t) = 0.28t + 1, for t > 10. Find the approximate number of fish that can be caught if you fish for 38 minutes.
A)About 11 fishB)About 24 fishC)About 40 fishD)About 42 fish
21)The function P(d) = 1 + d 33 gives the pressure, in atmospheres (atm), at a depth d feet in the sea. Find the pressure at 29 feet.
A) 62 33 atmB) 29 33 atmC) 4 33 atmD) 10 11 atm
22)The function F described by F(C) = 9 5 C + 32 gives the Fahrenheit temperature corresponding to the Celsius temperature C. Find the Fahrenheit temperature equivalent to - 20°C.
A) - 4°FB) - 40°FC) - 76°FD) - 112°F
3Find the Domain of a Function Defined by an Equation
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Find the domain of the function.
1)f(x) = 3x - 5
A)all real numbersB){x|x ≥ 5}C){x|x ≠ 0}D){x|x > 0}
2)f(x) = x2 + 8
A)all real numbersB){x|x ≥ - 8}C){x|x > - 8}D){x|x ≠ - 8}
3)f(x) = x2 x2 + 4
A)all real numbersB){x|x ≠ - 4}C){x|x > - 4}D){x|x ≠ 0}
4)g(x) = x x2 - 49
A){x|x ≠ - 7 , 7}B){x|x ≠ 0}C){x|x > 49}D)all real numbers
5)h(x) = x - 2 x3 - 64x
A){x|x ≠ - 8 , 0, 8}B){x|x ≠ 0}C){x|x ≠ 2}D)all real numbers
6)f(x) = 23 - x A){x|x ≤ 23}B){x|x ≠ 23}C){x|x ≤ 23}D){x|x ≠ 23}
7) x x - 6
A){x|x > 6}B){x|x ≥ 6}C){x|x ≠ 6}D)all real numbers
4Form the Sum, Difference, Product, and Quotient of Two Functions MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
For the given functions f and g, find the requested function and state its domain.
1)f(x) = 6 - 6x; g(x) = - 2x + 6
Find f + g.
A)(f + g)(x) = - 8x + 12; all real numbersB)(f + g)(x) = - 2x + 6; {x| x ≠ 3}
C)(f + g)(x) = 4x; all real numbersD)(f + g)(x) = - 4x + 12; {x|x ≠ - 3}
2)f(x) = 4x - 8; g(x) = 8x - 3
Find f - g.
A)(f - g)(x) = - 4x - 5; all real numbersB)(f - g)(x) = - 4x - 11; {x|x ≠11 4 }
C)(f - g)(x) = 12x - 11; {x|x ≠ 1}D)(f - g)(x) = 4x + 5; all real numbers
3)f(x) = 4x + 3; g(x) = 6x - 9
Find f · g.
A)(f · g)(x) = 24x2 - 18x - 27; all real numbersB)(f · g)(x) = 24x2 + 9x - 27; {x|x ≠ - 27}
C)(f · g)(x) = 10x2 - 18x - 6; all real numbersD)(f · g)(x) = 24x2 - 27; {x|x ≠ - 27}
4)f(x) = 2x + 5; g(x) = 3x - 4
Find f g .
A) f g (x) = 2x + 5 3x - 4 ; x|x ≠ 4 3
C) f g (x) = 3x - 4 2x + 5 ; x|x ≠ 4 3
5)f(x) = 16 - x2 ; g(x) = 4 - x
Find f + g.
A)(f + g)(x) = - x2 - x + 20; all real numbers
B)(f + g)(x) = 4 + x; {x|x ≠ - 4}
C)(f + g)(x) = - x2 + x + 12; all real numbers
D)(f + g)(x) = x3 - 4x 2 - 16x + 64; all real numbers
6)f(x) = x - 3; g(x) = 3x2
Find f - g.
B) f g (x) = 2x + 5 3x - 4 ; x|x ≠5 2
D) f g (x) = 3x - 4 2x + 5 ; x|x ≠5 2
A)(f - g)(x) = - 3x2 + x - 3; all real numbersB)(f - g)(x) = 3x2 - x + 3; all real numbers
C)(f - g)(x) = - 3x2 + x - 3; {x|x ≠ 3}D)(f - g)(x) = 3x2 + x - 3; all real numbers
7)f(x) = 2x3 + 1; g(x) = 3x2 + 2
Find f · g.
A)(f · g)(x) = 6x5 + 4x3 + 3x2 + 2; all real numbers
B)(f · g)(x) = 6x6 + 4x3 + 3x2 + 2; all real numbers
C)(f · g)(x) = 6x5 + 4x3 + 3x2 + 2; {x|x ≠ 0}
D)(f · g)(x) = 2x3 + 3x2 + 2; all real numbers
8)f(x) = x ; g(x) = 5x - 4
Find f g .
A) f g (x) = x 5x - 4 ; x|x ≥ 0, x ≠ 4 5 B) f g (x) = x 5x - 4 ; x|x ≠ 4 5
C) f g (x) = x 5x - 4 ; {x|x ≠ 0}D) f g (x) = 5x - 4 x ; {x|x ≥ 0}
9)f(x) = 4 - x; g(x) = x - 3
Find f · g.
A)(f · g)(x) = (4 - x)(x - 3) ; {x|3 ≤ x ≤ 4}B)(f · g)(x) = (4 - x)(x - 3) ; {x|x ≥ 0}
C)(f · g)(x) = (4 - x)(x - 3) ; {x|x ≠ 3, x ≠ 4}D)(f · g)(x) = - x2 - 12; {x|x ≠ 12}
10)f(x) = 5x + 4 6x - 1 ; g(x) = 7x 6x - 1
Find f - g.
A)(f - g)(x) = - 2x + 4 6x - 1 ; x|x ≠ 1 6
C)(f - g)(x) = - 2x + 4 6x - 1 ; x|x ≠ 1 6 , x ≠ 2
B)(f - g)(x) = 12x - 4 6x - 1 ; x|x ≠ 1 6
D)(f - g)(x) = - 2x + 4 6x - 1 ; {x|x ≠ 0}
11)f(x) = x + 9 ; g(x) = 2 x
Find f · g.
A)(f · g)(x) = 2x + 9 x ; {x|x ≥ - 9, x ≠ 0}B)(f · g)(x) = 2x + 18 x ; {x|x ≥ - 9, x ≠ 0}
C)(f · g)(x) = 2x + 18 x ; {x|x ≥ - 9, x ≠ 0}D)(f · g)(x) = 11 x ; {x|x ≠ 0}
Solve the problem.
12)Given f(x) = 1 x and ( f g )(x) = x + 2 x2 + 3x , find the function g.
A)g(x) = x + 3 x + 2
B)g(x) = x + 2 x + 3
C)g(x) = x - 3 x - 2
D)g(x) = x - 2 x - 3
13)Find (f + g)(- 4) when f(x) = x - 6 and g(x) = x + 2. A) - 12B)0C) - 16D) - 4
14)Find (f - g)(2) when f(x) = 4x2 + 7 and g(x) = x + 3. A)18B) - 25C)24D)22
15)Find (fg)(3) when f(x) = x - 1 and g(x) = - 2x2 + 13x - 3. A)36B) - 84C)72D)90
16)Find f g ( - 5) when f(x) = 5x - 6 and g(x) = 4x2 + 14x + 3. A)31 33 B) 4 33 C) 4 19 D)0
Find and simplify the difference quotient of f, f(x + h) - f(x) h , h≠ 0, for the function.
17)f(x) = 4x - 9 A)4B)4 + - 18 h C)4 + 8(x - 9) h D)0
18)f(x) = 8x2 A)8(2x+ h)B) 16 h + x + 8hC) 8(2x2 + 2xh + h2 ) h D)8
19)f(x) = 5
A)0B)1C)1 + 10 h D)5
20)f(x) = 1 6x A) - 1 6x (x + h) B) - 1 x(x + h) C) 1 6x D)0
21)f(x) = x2 + 7x + 2
A)2x+ h + 7B) 2x2 + 2x + 2xh + h2 + h + 4 h
C)2x+ h + 2D)1
Solve the problem.
22)Express the gross salary G of a person who earns $10 per hour as a function of the number x of hours worked.
A)G(x) = 10xB)G(x) = 10 + xC)G(x) = 10 x D)G(x) = 10x2
23) Jacey, a commissioned salesperson, earns $300 base pay plus $50 per item sold. Express Jaceyʹ s gross salary G as a function of the number x of items sold.
A)G(x) = 50x + 300B)G(x) = 300x + 50C)G(x) = 50(x + 300)D)G(x) = 300(x + 50)
24)Suppose that P(x) represents the percentage of income spent on food in year x and I(x) represents income in year x. Determine a function F that represents total food expenditures in year x.
A)F(x) = (P · I)(x)B)F(x) = (P + I)(x)C)F(x) = (I - P)(x)D)F(x) = I P (x)
25)A retail store buys 65 VCRs from a distributor at a cost of $160 each plus an overhead charge of $40 per order. The retail markup is 25% on the total price paid. Find the profit on the sale of one VCR. A)$40.15B)$4015.00C)$40.00D)$39.85
26)The following graph shows the private, public and total national school enrollment for students for select years from 1970 through 2000.
i)How is the graph for total school enrollment, T, determined from the graph of the private enrollment, r, and the public enrollment, u?
ii)During which 10 - year period did the total number of students enrolled increase the least?
iii)During which 10 - year period did the total number of students enrolled increase the most?
A)i)T is the sum of r and u. ii)1970 - 1980 iii)1990- 2000
C)i)T is the sum of r and u. ii)1970 - 1980 iii)1980- 1990
B)i)T is the sum of r and u. ii)1990- 2000 iii)1970- 1980
D)i)T is the difference of r and u. ii)1970 - 1980 iii)1990- 2000
27)A firm is considering a new product. The accounting department estimates that the total cost, C(x), of producing x units will be
C(x) = 50x + 6630. The sales department estimates that the revenue, R(x), from selling x units will be R(x) = 60x, but that no more than 881 units can be sold at that price. Find and interpret (R - C)(881).
A)$2180 profit, income exceeds cost It is worth it to develop product.
C)$103,540 profit, income exceeds cost It is worth it to develop product.
B) - $2180 loss, cost exceeds income It is not worth it to develop product.
D)$1544 profit, income exceeds cost It is worth it to develop product.
28)The function f(t) = - 0.14t 2 + 0.52t + 31.9 models the U.S. population in millions, ages 65 and older, where t represents years after 1990. The function g(t) = 0.5t 2 + 12.49t + 106.8 models the total yearly cost of Medicare in billions of dollars, where t represents years after 1990. What does the function g f represent?
Find g f (10).
A)Cost per person in thousands of dollars. $12.19 thousand
B)Cost per person in thousands of dollars. $0.18 thousand
C)Cost per person in thousands of dollars. $0.08 thousand
D)Cost per person in thousands of dollars. $9.11 thousand
2.2The Graph of a Function
1Identify the Graph of a Function
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Determine whether the graph is that of a function. If it is, use the graph to find its domain and range, the intercepts, if any, and any symmetry with respect to the x -axis, the y-axis, or the origin. 1)
A)function domain: {x|x ≤ - 3 or x ≥ 3} range: all real numbers intercepts: (- 3, 0), (3, 0) symmetry: x- axis, y - axis, origin
C)function domain: {x| - 3 ≤ x ≤ 3} range: all real numbers intercepts: (- 3, 0), (3, 0) symmetry: x- axis, y - axis
B)function domain: all real numbers range: {y|y ≤ - 3 or y ≥ 3} intercepts: (- 3, 0), (3, 0) symmetry: y - axis
D)not a function
A)function domain: {x|x > 0}
range: all real numbers intercept: (1, 0) symmetry: none
C)function domain: all real numbers range: {y|y > 0} intercept: (1, 0) symmetry: none
B)function domain: {x|x > 0}
range: all real numbers intercept: (0, 1) symmetry: origin
D)not a function
A)function domain: {x| - π ≤ x ≤ π }
range: {y|- 1 ≤ y ≤ 1}
intercepts: ( - π, 0), (π 2 , 0), (0, 0), ( π 2 , 0), (π, 0)
symmetry: origin
B)function domain: {x| - 1 ≤ x ≤ 1}
range: {y|- π ≤ y ≤ π }
intercepts: ( - π, 0), (π 2 , 0), (0, 0), ( π 2 , 0), (π, 0)
symmetry: none
C)function domain: all real numbers
range: {y| - 1 ≤ y ≤ 1}
intercepts: ( - π, 0), (π 2 , 0), (0, 0), ( π 2 , 0), (π, 0)
symmetry: origin
D)not a function
-10-5510x
A)function domain: all real numbers
range: {y|y ≤ 4}
intercepts: (- 1, 0), (0, 3), (3, 0)
symmetry: none
C)function domain: all real numbers
range: {y|y ≤ 4}
intercepts: (0, - 1), (3, 0), (0, 3)
B)function
domain: {x|x ≤ 4}
range: all real numbers
intercepts: (- 1, 0), (0, 3), (3, 0) symmetry: y - axis
symmetry: none D)not a function
A)function domain: {x| - 9 ≤ x ≤ 9}
range: {y|- 9 ≤ y ≤ 9}
intercepts: (- 9, 0), (0, - 9), (0, 9), (9, 0)
symmetry: x- axis, y - axis, origin
C)function domain: {x| - 9 ≤ x ≤ 9}
range: {y|- 9 ≤ y ≤ 9}
intercepts: (- 9, 0), (0, - 9), (0, 0), (0, 9), (9, 0)
symmetry: origin
B)function domain: {x| - 9 ≤ x ≤ 9}
range: {y|- 9 ≤ y ≤ 9}
intercepts: (- 9, 0), (0, - 9), (0, 9), (9, 0)
symmetry: x- axis, y - axis
D)not a function
A)function domain: {x|x ≥ - 2} range: {y|y ≥ 0} intercepts: (- 2, 0), (0, 2), (2, 0) symmetry: none
C)function domain: all real numbers range: all real numbers intercepts: (- 2, 0), (0, 2), (2, 0) symmetry: none
B)function domain: {x|x ≥ 0} range: {y|y ≥ - 2} intercepts: (- 2, 0), (0, 2), (2, 0) symmetry: y - axis
D)not a function
A)function domain: all real numbers range: {y|y = 6 or y = 3} intercept: (0, 3) symmetry: none
C)function domain: all real numbers range: all real numbers intercept: (0, 3) symmetry: none
B)function domain: {x|x = 6 or x = 3} range: all real numbers intercept: (3, 0) symmetry: x- axis
D)not a function
2Obtain Information from or about the Graph of a Function
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
The graph of a function f is given. Use the graph to answer the question.
1)Use the graph of f given below to find f(4). 5 - 55 - 5
2)Is f(8) positive or negative? 10 - 1010 - 10 A)positiveB)negative
3)Is f(6) positive or negative?
- 1010 - 10
A)positiveB)negative
4)For what numbers x is f(x) = 0?
- 1010 - 10
A) - 6 , 7 , 10B)( - 10, - 6), (7 , 10)C)( - 6 , 7)D) - 6
5)For what numbers x is f(x) > 0?
- 1010 - 10
A)[ - 10, - 6), (7 , 10)B)( - 6 , 7)C)( - 6 , ∞)D)( - ∞ - 6)
6)For what numbers x is f(x) < 0? 50 - 5050 - 50
A)( - 30, 35)B)[ - 50, - 30), (35, 50)C)( - 30, ∞)D)( - ∞ , - 30)
7)What is the domain of f?
- 1010 - 10
A){x|- 10 ≤ x ≤ 10}B){x|- 8 ≤ x ≤ 11}C)all real numbersD){x|x ≥ 0}
8)What are the x- intercepts? 25 - 2525 - 25
A) - 15, 17.5 , 25B) - 25, - 15, 17.5 , 25C) - 15, 17.5D) - 15
9)What is the y- intercept?
- 5050 - 50
A) - 30B)35C)50D) - 40
10)How often does the line y = - 25 intersect the graph? 25 - 2525 - 25
A)onceB)twiceC)three timesD)does not intersect
11)How often does the line y = 4 intersect the graph?
- 2020 - 20
A)onceB)twiceC)three timesD)does not intersect
12)For which of the following values of x does f(x) = 40?
- 100100 - 100
A)80B)140C)100D)40
Answer the question about the given function.
13)Given the function f(x) = 3x2 - 6x - 9, is the point (1, - 12) on the graph of f?
A)YesB)No
14)Given the function f(x) = 3x2 + 6x + 4, is the point ( - 2, 10) on the graph of f? A)YesB)No
15)Given the function f(x) = 2x2 + 4x - 3, if x = - 1, what is f(x)? What point is on the graph of f?
A) - 5; (- 1 , - 5)B) - 5; (- 5 , - 1)C)3; (- 1 , 3)D)3; (3 , - 1)
16)Given the function f(x) = 5x2 + 10x - 8, what is the domain of f? A)all real numbersB){x|x ≥- 1}C){x|x ≤ - 1}D){x|x ≥ 1}
17)Given the function f(x) = x2 + 4x - 12, list the x- intercepts, if any, of the graph of f. A)( - 6 , 0), (2 , 0)B)(6 , 0), (2 , 0)C)( - 6 , 0), (1, 0)D)(6 , 0), (- 2 , 0)
18)Given the function f(x) = - 6x2 - 12x + 1, list the y - intercept, if there is one, of the graph of f. A)1B) - 11C)7D) - 17
19)Given the function f(x) = x2 - 9 x + 1 , is the point ( - 2, 5) on the graph of f?
A)YesB)No
20)Given the function f(x) = x2 - 5 x - 3 , is the point ( - 1,3 2 ) on the graph of f?
A)YesB)No
21)Given the function f(x) = x2 - 5 x + 3 , if x = 2, what is f(x)? What point is on the graph of f?
A)1 5 ; (2,1 5 )B)1 5 ; (1 5 , 2)C) 9 5 ; (2, 9 5 )D) 9 5 ; ( 9 5 , 2)
22)Given the function f(x) = x2 + 7 x + 4 , what is the domain of f?
A){x|x ≠ - 4}B){x|x ≠ 4}C){x|x ≠ 7}D){x|x ≠7 4 }
23)Given the function f(x) = x2 + 2 x - 3 , list the x- intercepts, if any, of the graph of f.
A)(2 , 0), (- 2 , 0)B)(3 , 0)C)( - 2 , 0)D)none
24)Given the function f(x) = x2 + 2 x + 9 , list the y - intercept, if there is one, of the graph of f.
A)(0, 2 9 )B)( 2 9 , 0)C)(0, - 9)D)(0, - 2)
Solve the problem.
25)If an object weighs m pounds at sea level, then its weight W (in pounds) at a height of h miles above sea level is given approximately by W(h) = m 4000 4000 + h 2 How much will a man who weighs 165 pounds at sea level weigh on the top of a mountain which is 14,494 feet above sea level? Round to the nearest hundredth of a pound, if necessary. A)164.77 poundsB)7.72 poundsC)165.23 poundsD)165 pounds
Match the function with the graph that best describes the situation.
26)The amount of rainfall as a function of time, if the rain fell more and more softly.
27)The height of an animal as a function of time.
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
Solve the problem.
28)Michael decides to walk to the mall to do some errands. He leaves home, walks 2 blocks in 8 minutes at a constant speed, and realizes that he forgot his wallet at home. So Michael runs back in 6 minutes. At home, it takes him 3 minutes to find his wallet and close the door. Michael walks 2 blocks in 8 minutes and then decides to jog to the mall. It takes him 6 minutes to get to the mall which is 2 blocks away. Draw a graph of Michaelʹ s distance from home (in blocks) as a function of time.
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
29)A steel can in the shape of a right circular cylinder must be designed to hold 650 cubic centimeters of juice (see figure). It can be shown that the total surface area of the can (including the ends) is given by S(r) = 2 π r 2 + 1300 r , where r is the radius of the can in centimeters. Using the TABLE feature of a graphing utility, find the radius that minimizes the surface area (and thus the cost) of the can. Round to the nearest tenth of a centimeter.
A)4.7 cmB)5.9 cmC)3.9 cmD)0 cm
30)The concentration C (arbitrary units) of a certain drug in a patientʹ s bloodstream can be modeled using C(t) = t 0.389t + 2.569 2 , where t is the number of hours since a 500 milligram oral dose was administered.
Using the TABLE feature of a graphing utility, find the time at which the concentration of the drug is greatest. Round to the nearest tenth of an hour.
A)6.6 hoursB)8.1 hoursC)7.4 hoursD)8.9 hours
2.3Properties of Functions
1Determine Even and Odd Functions from a Graph
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. The graph of a function is given. Decide whether it is even, odd, or neither. 1) -10-8-6-4-2246810x
A)evenB)oddC)neither
-10-8-6-4-2246810x
A)evenB)oddC)neither
A)evenB)oddC)neither
A)evenB)oddC)neither
2Identify Even and Odd Functions from the Equation
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Determine algebraically whether the function is even, odd, or neither.
1)f(x) = - 4x3
A)evenB)oddC)neither
2)f(x) = - 2x4 - x2
A)evenB)oddC)neither
3)f(x) = - 5x2 + 6 A)evenB)oddC)neither
4)f(x) = 3x3 + 8
A)evenB)oddC)neither
5)f(x) = 3 x A)evenB)oddC)neither
6)f(x) = x A)evenB)oddC)neither
7) 3 2x2 + 7
A)evenB)oddC)neither
8)f(x) = 1 x2
A)evenB)oddC)neither
9)f(x) = x x2 + 4
A)evenB)oddC)neither
10)f(x) = - x3 5x2 + 7
A)evenB)oddC)neither
11)f(x) = 5x |x|
A)evenB)oddC)neither
3Use a Graph to Determine Where a Function Is Increasing, Decreasing, or Constant MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given interval.
1)( - 5,5 2 )
A)decreasingB)increasingC)constant
2)(5 2 , 0) -55x y 5 -5
A)increasingB)decreasingC)constant
3)(0, 1)
A)decreasingB)increasingC)constant
4)(1, 5)
A)increasingB)decreasingC)constant
5)(0, 1)
A)constantB)increasingC)decreasing
- 1 , 0) -10-5510x
A)increasingB)decreasingC)constant
7)(2 , ∞) -10-5510x y 10
A)decreasingB)increasingC)constant
8)( - 2 , ∞)
A)increasingB)decreasingC)constant
A)decreasingB)increasingC)constant
10)(0.5, 3.5)
(-5,-2)(-4,-2) (0.5,2.5)(3.5,2.5) (6,-1.6)
-55x y 5 -5
A)constantB)decreasingC)increasing
11)( - 6 , - 2.5) -55x y 5 -5 (-6,2)
(-2.5,0)
(-1,-3)(0,-3) (2,0) (5,-4)
A)decreasingB)increasingC)constant
A)increasingB)decreasingC)constant
Use the graph to find the intervals on which it is increasing, decreasing, or constant. 13)
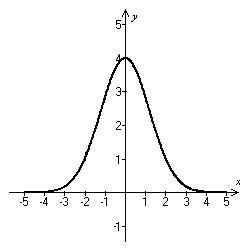
A)Increasing on (- ∞ , 0); decreasing on (0, ∞)B)Decreasing on (- ∞ , 0); increasing on (0, ∞) C)Decreasing on (- ∞ , ∞)D)Increasing on (- ∞ , ∞)
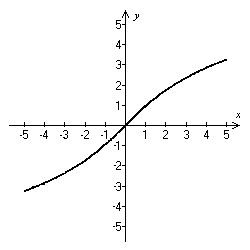
A)Increasing on (- ∞ , ∞)B)Decreasing on (- ∞ , 0); increasing on (0, ∞)
C)Decreasing on (- ∞ , ∞)D)Increasing on (- ∞ , 0); decreasing on (0, ∞)
A)Decreasing on -
B)Increasing on
C)Decreasing on - π , 0 ; increasing on 0, π
D)Increasing on (- ∞ , ∞)
A)Decreasing on (- 3, - 2) and (2, 4); increasing on ( - 1, 1); constant on ( - 2, - 1) and (1, 2)
B)Decreasing on (- 3, - 2) and (2, 4); increasing on ( - 1, 1)
C)Decreasing on (- 3, - 1) and (1, 4); increasing on ( - 2, 1)
D)Increasing on (- 3, - 2) and (2, 4); decreasing on ( - 1, 1); constant on ( - 2, - 1) and (1, 2)
4Use a Graph to Locate Local Maxima and Local Minima
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
The graph of a function f is given. Use the graph to answer the question. 1)Find the numbers, if any, at which f has a local maximum. What are the local maxima? -5-4-3-2-112345x
A)f has a local maximum at x = 0; the local maximum is 2
B)f has a local maximum at x = - 1 and 1; the local maximum is 0
C)f has a local maximum at x = 1; the local maximum is 2
D)f has no local maximum
2)Find the numbers, if any, at which f has a local minimum. What are the local minima?
A)f has a local minimum at x = - 3 and 3; the local minimum is 0
B)f has a local minimum at x = 0; the local minimum is 1
C)f has a local minimum at x = - 3; the local minimum is 0
D)f has no local minimum
3)Find the numbers, if any, at which f has a local maximum. What are the local maxima?
A)f has a local maximum at x = 0; the local maximum is 1
B)f has a local maximum at x = - π and π; the local maximum is - 1
C)f has a local maximum at - π ; the local maximum is 1
D)f has no local maximum
4)Find the numbers, if any, at which f has a local minimum. What are the local minima?
A)f has a local minimum at x = 0; the local minimum is - 2
B)f has a local minimum at x = - π and π; the local minimum is 2
C)f has a local minimum at x = - π ; the local minimum is - 2
D)f has no local minimum
Find the numbers, if any, at which f has a local maximum. What are the local maxima?
A)f
Solve the problem.
6)The height s of a ball (in feet) thrown with an initial velocity of 90 feet per second from an initial height of 6 feet is given as a function of time t (in seconds) by s(t) = - 16t 2 + 90t + 6. What is the maximum height? Round to the nearest hundredth, if necessary.
A)132.56 ftB)146.63 ftC)126.94 ftD) - 98.06 ft
5Use a Graph to Locate the Absolute Maximum and the Absolute Minimum MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. For the graph of the function y = f(x), find the absolute maximum and the absolute minimum, if it exists. 1)
A)Absolute maximum: f(5) = 6; Absolute minimum: f(2) = 1
B)Absolute maximum: f(7) = 2; Absolute minimum: f(0) = 3
C)Absolute maximum: f(6) = 5; Absolute minimum: f(1) = 2
D)Absolute maximum: f(2) = 7; Absolute minimum: f(3) = 0
A)Absolute maximum: f(3) = 6; Absolute minimum: none
B)Absolute maximum: f(3) = 6; Absolute minimum: f(5) = 1
C)Absolute maximum: f(7) = 4; Absolute minimum: f(0) = 2
D)Absolute maximum: f(3) = 6; Absolute minimum: f(0) = 2
A)Absolute maximum: none; Absolute minimum: f(1) = 2
B)Absolute maximum: f( - 1) = 6; Absolute minimum: f(1) = 2
C)Absolute maximum: f(3) = 5; Absolute minimum: f(1) = 2
D)Absolute maximum: none; Absolute minimum: none
A)Absolute maximum: none; Absolute minimum: none
B)Absolute maximum: f(4) = 7; Absolute minimum: f(1) = 2
C)Absolute maximum: none; Absolute minimum: f(1) = 2
D)Absolute maximum: f(4) = 7; Absolute minimum: none
6Use Graphing Utility to Approximate Local Maxima/Minima and to Determine Where Function Is Incrs/Decrs
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Use a graphing utility to graph the function over the indicated interval and approximate any local maxima and local minima. Determine where the function is increasing and where it is decreasing. If necessary, round answers to two decimal places.
1)f(x) = x3 - 3x + 1, (- 2, 2)
A)local maximum at (- 1 , 3) local minimum at (1, - 1) increasing on ( - 2, - 1) and (1, 2) decreasing on (- 1, 1)
C)local maximum at (- 1 , 3) local minimum at (1, - 1) increasing on ( - 1, 1) decreasing on (- 2, - 1) and (1, 2)
B)local maximum at (1 , - 1) local minimum at ( - 1, 3) increasing on ( - 2, - 1) and (1, 2) decreasing on (- 1, 1)
D)local maximum at (1 , - 1) local minimum at ( - 1, 3) increasing on ( - 2, - 1) decreasing on (- 1, 1)
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
2)f(x) = x3 - 4x2 + 6; (- 1, 4)
3)f(x) = x5 - x2 ; ( - 2, 2)
4)f(x) = - 0.3x3 + 0.2x2 + 4x - 5; (- 4, 5)
5)f(x) = 0.15x4 + 0.3x3 - 0.8x2 + 5; (- 4, 2)
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Use a graphing utility to graph the function over the indicated interval and approximate any local maxima and local minima. If necessary, round answers to two decimal places.
6)f(x) = x2 + 2x - 3; (- 5, 5)
A)local minimum at ( - 1, - 4)B)local maximum at (- 1, 4)
C)local minimum at (1, 4)D)local maximum at (1, - 4)
7)f(x) = 2 + 8x - x2; (- 5, 5)
A)local maximum at (4, 18)B)local minimum at (4, 50)
C)local minimum at ( - 4, 18)D)local maximum at (- 4, 50)
8)f(x) = x3 - 3x 2 + 1; (- 5, 5)
A)local maximum at (0, 1) local minimum at (2, - 3)
B)local minimum at (0, 1) local maximum at (2, - 3)
C)local minimum at (2, - 3)D)none
9)f(x) = x3 - 12x + 2; (- 5, 5)
A)local maximum at (- 2, 18) local minimum at (2, - 14)
B)local maximum at (- 2, 18) local minimum at (0, 0) local minimum at (2, - 14)
C)local minimum at (0, 0)D)none
10)f(x) = x4 - 5x 3 + 3x 2 + 9x - 3; (- 5, 5)
A)local minimum at ( - 0.57, - 6.12) local maximum at (1.32, 5.64) local minimum at (3, - 3)
C)local minimum at ( - 3, - 3) local maximum at (- 1.32, 5.64) local minimum at (0.57, - 6.12)
B)local minimum at ( - 1, - 6) local maximum at (1, 6) local minimum at (3, - 3)
D)local minimum at ( - 0.61, - 5.64) local maximum at (1.41, 6.12) local minimum at (3, - 3)
Solve.
11) John owns a hotdog stand. He has found that his profit is represented by the equation P(x) = - x2 + 66x + 82, with P being profits and x the number of hotdogs sold. How many hotdogs must he sell to earn the most profit?
A)33 hotdogsB)49 hotdogsC)34 hotdogsD)24 hotdogs
12)Bob owns a watch repair shop. He has found that the cost of operating his shop is given by c(x) = 4x2 - 248x + 79, where c is cost and x is the number of watches repaired. How many watches must he repair to have the lowest cost?
A)31 watchesB)40 watchesC)79 watchesD)39 watches
13)John owns a hotdog stand. His profit is represented by the equation P(x) = - x2 + 10x + 31, with P being profits and x the number of hotdogs sold. What is the most he can earn?
A)$56B)$51C)$66D)$25
14)A rock falls from a tower that is 122.5 m high. As it is falling, its height is given by the formula h(t) = 122.5 - 4.9t2 How many seconds will it take for the rock to hit the ground (h =0)? Round to the nearest tenth.
A)5 secB)11.1 secC)3100 secD)25 sec
15)A projectile is thrown upward so that its distance above the ground after t seconds is h(t) = - 16t 2 + 570t. After how many seconds does it reach its maximum height? Round to the nearest second.
A)18 secB)9 secC)28.5 secD)38 sec
16)A rock falls from a tower that is 432 ft high. As it is falling, its height is given by the formula h(t) = 432 - 16t2 . How many seconds will it take for the rock to hit the ground (h =0)? Round to the nearest tenth.
A)5.2 secB)20.8 secC)11,664 secD)27 sec
7Find the Average Rate of Change of a Function MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
For the function, find the average rate of change of f from 1 to x: f(x) - f(1) x - 1 , x ≠ 1
1)f(x) = 6x
2)f(x) = x2 - 2x A)x - 1B)x + 1C)1D)
3)f(x) = 8 x + 7
4)f(x) = x + 99
x + 99 - 10 x - 1
x + 99 + 10 x + 1
Find the average rate of change for the function between the given values.
5)f(x) = - 3x + 6; from 1 to 2 A) - 3B) - 6C)3D)6
6)f(x) = x2 + 3x; from 5 to 7
A)15B)35C) 30 7 D)10
7)f(x) = 8x3 - 2x2 + 2; from - 5 to 3
A)156B)25C)416D) 200 3
8)f(x) = 2x; from 2 to 8 A) 1 3 B)2C)7D)3 10
9)f(x) = 3 x - 2 ; from 4 to 7 A)3 10 B)2C)7D) 1 3
10)f(x) = 4x 2 ; from 0 to 7 4 A)7B)2C) 1 3 D)3 10
11)f(x) = - 3x2 - x; from 5 to 6 A) - 34B) - 2C) 1 2 D)1 6
12)f(x) = x3 + x2 - 8x - 7; from 0 to 2 A) - 2B) - 28C) 1 2 D)1 6
13)f(x) = 2x - 1 ; from 1 to 5 A) 1 2 B) - 2C) - 28D)1 6
14)f(x) = 3 x + 2 ; from 1 to 4 A)1 6 B) - 2C) - 28D) 1 2 Find an equation of the secant line containing (1, f(1)) and (2, f(2)).
15)f(x) = x3 + x A)y = 8x - 6B)y = 8x + 6C)y = - 8x - 6D)y = - 8x + 6
16)f(x) = 4 x + 3 A)y =1 5 x + 6 5
17)f(x) = x + 3
A)y = (5 - 2)x - 5 + 4B)y = (- 5 + 2)x + 5 - 4
C)y = (5 - 2)x + 5 - 4D)y = (- 5 - 2)x - 5 + 4
Solve the problem.
18)From April through December 2000, the stock price of QRS Company had a roller coaster ride. The chart below indicates the price of the stock at the beginning of each month during that period. Find the monthly average rate of change in price between June and September.
MonthPrice
April (x = 1)116
May108
June89
July100
August95
September113
October93
November86
December64
A)$8.00 per monthB) - $8.00 per month
C)$12.00 per monthD) - $12.00 per month
19)Along with incomes, peopleʹ s charitable contributions have steadily increased over the past few years. The table below shows the average deduction for charitable contributions reported on individual income tax returns for the period 1993 to 1998. Find the average rate of change between 1995 and 1997.
YearCharitable Contributions
1993$1660
1994$2350
1995$2500
1996$2780
1997$3010
1998$3120
A)$255 per yearB)$510 per yearC)$310 per yearD)$330 per year
20)A deep sea diving bell is being lowered at a constant rate. After 8 minutes, the bell is at a depth of 600 ft. After 40 minutes the bell is at a depth of 1300 ft. What is the average rate of lowering per minute? Round to the nearest hundredth is needed.
A)21.9 ft per minuteB)0.05 ft per minuteC)17.5 ft per minuteD)32.5 ft per minute
2.4Library of Functions; Piecewise-defined Functions
1Graph the Functions Listed in the Library of Functions
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Match the graph to the function listed whose graph most resembles the one given. 1)
A)square functionB)cube function C)absolute value functionD)reciprocal function
A)constant functionB)linear function
C)absolute value functionD)reciprocal function 3)
A)square root functionB)square function C)cube root functionD)cube function 4)
A)absolute value functionB)square function C)linear functionD)reciprocal function
A)linear functionB)constant function
C)absolute value functionD)reciprocal function
A)cube functionB)cube root function C)square functionD)square root function
A)reciprocal function
B)square root function
C)absolute value functionD)square function 8)
A)cube root functionB)cube function
C)square root functionD)square function
Graph the function.
9)f(x) = x
10)f(x) = x2
11)f(x) = x3
12)f(x) = x
13)f(x) = 1 x
14)f(x) = x
15)f(x) = 3 x
2Graph Piecewise -defined Functions
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Graph the function.
f(x) = x - 4if x < 1 1if x ≥ 1
f(x) = - x + 3if x < 2 2x - 3if x ≥ 2
5)
f(x) = x + 5if - 8 ≤ x < 2 - 8if x = 2 - x + 3if x > 2
-10-5510x y 10 5 -5 -10 A)
-10-5510x y 10 5 -5 -10 (-8,-3) (2,7) (2,-8) (2,1) B)
-10-5510x y 10 5 -5 -10 (-8,-3) (2,7) (2,-8) (2,1)
C)
-10-5510x y 10 5 -5 -10 (-8,-2) (2,8) (2,-8) (2,1) D)
f(x) = 1if 0 ≤ x < 5 |x|if 5 ≤ x < 8 x if 8 ≤ x ≤ 14
-10-5510x y 10 5 -5 -10 (-8,-2) (2,8) (2,-8) (2,1)
Find the domain of the function. 6)
f(x) = 4xif x ≠ 0 5if x = 0 A)all real numbersB){x|x ≠ 0}C){0}D){x|x ≤ 0}
f(x) = 1if - 8 ≤ x < - 3 |x|if - 3 ≤ x < 8
x if 8 ≤ x ≤ 28
A){x|- 8 ≤ x ≤ 28}B){x|x ≥ - 8} C){x|- 8 ≤ x < 8 or 8 < x ≤ 28}D){x|8 ≤ x ≤ 28}
Locate any intercepts of the function.
8)
f(x) = - 3x + 6if x < 1 6x - 3if x ≥ 1
A)(0, 6)B)(0, 6), (2, 0), ( 1 2 , 0)
C)(0, - 3)D)(0, - 3), (2, 0), ( 1 2 , 0)
9)
f(x) = 1if - 6 ≤ x < - 8 |x|if - 8 ≤ x < 6
x if 6 ≤ x ≤ 15
A)(0, 0)B)(0, 0), (1, 0)C)(0, 0), (0, 1)D)none
Based on the graph, find the range of y = f(x). 10)
f(x) =1 3 xif x ≠ 0 - 9if x = 0 -10-55x 10y 5 -5 -10 (0,-9)
A)( - ∞ , 0) or (0, ∞)B)( - ∞ , ∞)
C)( - 10, 10)D)( - ∞ , 0) or {0} or (0, ∞)
f(x) = 4if - 6 ≤ x < - 2 |x|if - 2 ≤ x < 4 3 x if 4 ≤ x ≤ 12
A)[0, 4)B)[0, ∞)C)[0, 3 12]D)[0, 4]
The graph of a piecewise -defined function is given. Write a definition for the function. 12)
A)
f(x) =1 2 xif - 4 ≤ x ≤ 0
xif 0 < x ≤ 3
C)
f(x) =1 2 xif - 4 < x < 0
xif 0 < x < 3
B)
f(x) = 1 2 xif - 4 < x < 0 xif 0 < x < 3
D)
f(x) = - 2xif - 4 ≤ x ≤ 0 xif 0 < x ≤ 3
-55x y 5 -5 (0,1) (3,4) (3,2) (5,3)
f(x) = x + 1if 0 ≤ x ≤ 3 1 2 x + 1 2 if 3 < x ≤ 5
f(x) = x + 1if 0 ≤ x ≤ 3
f(x) = x + 1if 0 ≤ x ≤ 3 1 2 xif 3 < x ≤ 5
= x + 1if 0 ≤ x ≤ 3
2 x1 2 if 3 < x ≤ 5
-55x y 5 -5 (-3,0) (0,4) (3,2)
f(x) = 4 3 x + 4if - 3 ≤ x ≤ 0 2 3 xif 0 < x ≤ 3
=
+ 4if
≤ x
3 x + 4if - 3 ≤ x ≤ 0
3 x + 2if 0 < x ≤ 3
f(x) = 4 3 x + 4if - 3 ≤ x ≤ 0 2 3 xif x > 0
Solve the problem.
f(x) = 3 4 x + 4if - 3 ≤ x ≤ 0 3 2 xif x > 0
16)If f(x) = int(2x), find f( - 1.8). A) - 4B) - 3C) - 1D) - 2
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
17)A gas company has the following rate schedule for natural gas usage in single- family residences:
Monthly service charge $8.80 Per therm service charge 1st 25 therms$0.6686/therm Over 25 therms$0.85870/therm
What is the charge for using 25 therms in one month?
What is the charge for using 45 therms in one month?
Construct a function that gives the monthly charge C for x therms of gas.
18)An electric company has the following rate schedule for electricity usage in single- family residences:
Monthly service charge $4.93
Per kilowatt service charge
1st 300 kilowatts$0.11589/kW
Over 300 kilowatts$0.13321/kW
What is the charge for using 300 kilowatts in one month?
What is the charge for using 375 kilowatts in one month?
Construct a function that gives the monthly charge C for x kilowatts of electricity.
19)One Internet service provider has the following rate schedule for high- speed Internet service:
Monthly service charge$18.00
1st 50 hours of usefree
Next 50 hours of use$0.25/hour
Over 100 hours of use$1.00/hour
What is the charge for 50 hours of high- speed Internet use in one month?
What is the charge for 75 hours of high- speed Internet use in one month?
What is the charge for 135 hours of high - speed Internet use in one month?
20)The wind chill factor represents the equivalent air temperature at a standard wind speed that would produce the same heat loss as the given temperature and wind speed. One formula for computing the equivalent temperature is
W(t) = t
33(10.45 + 10v - v)(33 - t ) 22.04
33 - 1.5958(33 - t) if 0 ≤ v < 1.79 if 1.79 ≤ v < 20 if v ≥ 20
where v represents the wind speed (in meters per second) and t represents the air temperature (°C). Compute the wind chill for an air temperature of 15°C and a wind speed of 12 meters per second. (Round the answer to one decimal place.)
21)A cellular phone plan had the following schedule of charges:
Basic service, including 100 minutes of calls$20.00 per month
2nd 100 minutes of calls$0.075 per minute
Additional minutes of calls$0.10 per minute
What is the charge for 200 minutes of calls in one month?
What is the charge for 250 minutes of calls in one month?
Construct a function that relates the monthly charge C for x minutes of calls.

