IntroductiontoProbability
2.2SampleSpaces,Events,andSetOperations
1.(a)Thesamplespaceis {(1, 1), (1, 2), ··· , (1, 6), ··· , ··· , (6, 1), (6, 2), ··· , (6, 6)}.
(b)Thesamplespaceis {2, 3, 4, ··· , 12}.
(c)Thesamplespaceis {0, 1, 2, , 6}
(d)Thesamplespaceis {1, 2, 3, ···}
2.(a)TheVenndiagramisshownas
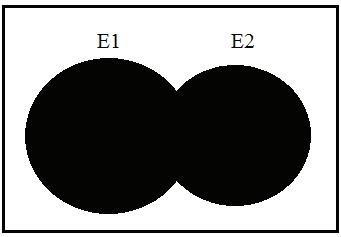
(b)TheVenndiagramisshownas
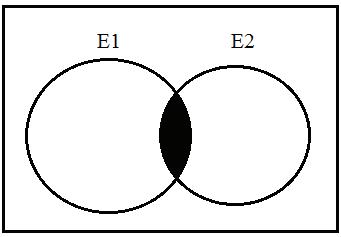
Copyright © 2016PearsonEducation,Inc.
(c)TheVenndiagramisshownas
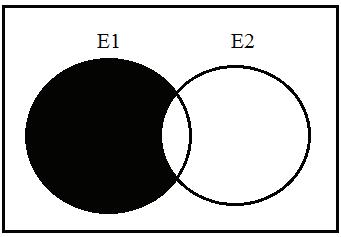
3.(a)Theeventsarerepresentedas
(i) T ∩ M
(ii) T c ∩ M c
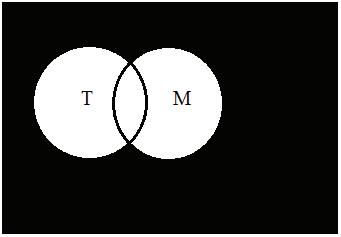
(iii)(T ∩ M c ) ∪ (T c ∩ M )
(b)TheVenndiagramsforpart(a)areshownas
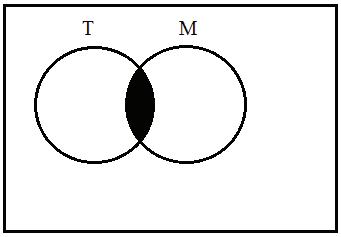
Copyright © 2016PearsonEducation,Inc.
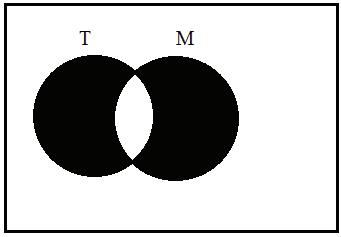
4.BothoftheVenndiagramsshouldbesimilarto
5.(a) Ac = {x|x ≥ 75},thecomponentwilllastatleast75timeunits.
(b) A ∩ B = {x|53 <x< 75},thecomponentwilllastmorethan53unitsbutless than75timeunits.
(c) A ∪ B = S ,thesamplespace.
(d)(A B ) ∪ (B A)= {x|x ≥ 75or x ≤ 53},thecomponentwilllasteitherat most53oratleast75timeunits.
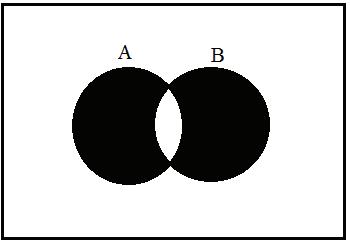
6.BothoftheVenndiagramsshouldbesimilarto
Copyright © 2016PearsonEducation,Inc.
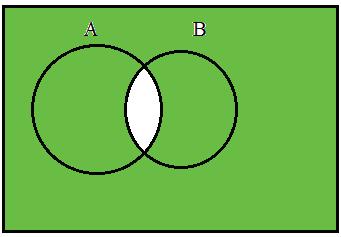
7.BothoftheVenndiagramsshouldbesimilarto
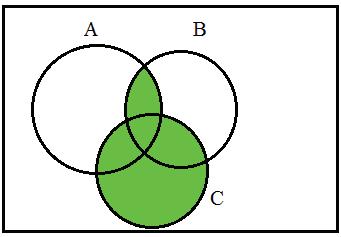
8.(a)Provethat(A B ) ∪ (B A)=(A ∪ B ) (A ∩ B ): x ∈ (A B ) ∪ (B A) ⇔ x ∈ A B or x ∈ B A
⇔ x ∈ A but x ∈ B or x ∈ B but x ∈ A
⇔ x ∈ A or x ∈ B butnotinboth
⇔ x ∈ A ∪ B and x ∈ A ∩ B
⇔ x ∈ (A ∪ B ) (A ∩ B )
(b)Provethat(A ∩ B )c = Ac ∪ B c : x ∈ (A ∩ B )c ⇔ x ∈ A ∩ B
⇔ x ∈ A B or x ∈ B A or x ∈ (A ∪ B )c ⇔ [x ∈ A B or x ∈ (A ∪ B )c ]or[x ∈ B A or x ∈ (A ∪ B )c ]
x ∈ Ac ∪ B c .
(c)Provethat(A ∩ B ) ∪ C =(A ∪ C ) ∩ (B ∪ C ):
x ∈ (A ∩ B ) ∪ C ⇔ x ∈ A ∩ B or x ∈ C
⇔ x ∈ A and x ∈ B or x ∈ C
⇔ [x ∈ A or x ∈ C ]and[x ∈ B or x ∈ C ]
⇔ x ∈ A ∪ C and x ∈ B ∪ C
⇔ x ∈ (A ∪ C ) ∩ (B ∪ C ).
9.(a)Thesamplespaceis S = {(x1 ,x2 ,x3 ,x4 ,x5 )|xi =5 3, 5 4, 5 5, 5 6, 5 7,i = 1, 2, 3, 4, 5}.Thesizeofthesamplespaceis55 =3125.
(b)Thesamplespaceisthecollectionofthedistinctaverages,(x1 + x2 + x3 + x4 + x5 )/5,formedfromtheelementsof S .TheRcommands s=c(5.3,5.4,5.5, 5.6,5.7);Sa=expand.grid(x1=s,x2=s,x3=s,x4=s,x5=s); length(table(rowSums(Sa))) return21forthesizeofthesamplespaceofthe averages.
Copyright © 2016PearsonEducation,Inc.
2.3ExperimentswithEquallyLikelyOutcomes39
10.(a)Thenumberofdisksin E1 is5+16=21,thenumberofdisksin E2 is5+9=14, andthenumberofdisksin E3 is5+16+9=30.
(b)BothoftheVenndiagramsshouldbesimilarto
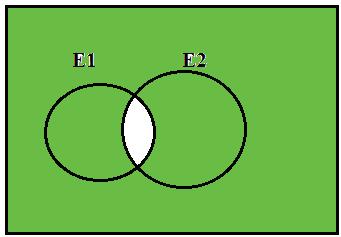
(c) E1 ∩ E2 istheeventthat“thediskhaslowhardnessandlowshockabsorption,” E1 ∪ E2 istheeventthat“thediskhaslowhardnessorlowshockabsorption,” E1 E2 istheeventthat“thediskhaslowhardnessbutdoesnothavelow shockabsorption,”and(E1 E2 ) ∪ (E2 E1 )istheeventthat“thediskhas lowhardnessorlowshockabsorptionbutdoesnothavelowhardnessandlow shockabsorptionatthesametime.”
(d)Thenumberofdisksin E1 ∩ E2 is5,thenumberofdisksin E1 ∪ E2 is30,the numberofdisksin E1 E2 is16,andthenumberofdisksin(E1 E2 ) ∪ (E2 E1 ) is25.
2.3ExperimentswithEquallyLikelyOutcomes
2.(a)Ifweselecttwowaferswithreplacement,then
(i)Thesamplespacefortheexperimentthatrecordsthedopingtypeis {(ntype,n-type),(n-type,p-type),(p-type,n-type),(p-type,p-type)} and thecorrespondingprobabilitiesare0.25,0.25,0.25,and0.25.
(ii)Thesamplespacefortheexperimentthatrecordsthenumberofn-type wafersis {0,1,2} andthecorrespondingprobabilitiesare0.25,0.50,and 0.25.
(b)Ifweselectfourwaferswithreplacement,then
(i)Thesamplespacefortheexperimentthatrecordsthedopingtypeisallof the4-componentvectors,witheachelementbeingn-typeorp-type.The sizeofthesamplespacecanbefoundbytheRcommands Copyright © 2016PearsonEducation,Inc.
G=expand.grid(W1=0:1,W2=0:1,W3=0:1,W4=0:1);length(G$W1) andtheresultis16.Theprobabilityofeachoutcomeis1/16.
(ii)Thesamplespacefortheexperimentthatrecordsthenumberofn-type waferis {0,1,2,3,4}.ThePMFisgivenby x 01234 p(x)0.06250.25000.37500.25000.0625
(iii)Theprobabilityofatmostonen-typewaferis0.0625+0.25=0.3125.
3. E1 = {6.8, 6.9, 7.0, 7.1} and E2 = {6.9, 7.0, 7.1, 7.2}.Thus, P (E1 )= P (E2 )=4/5. E1 ∩ E2 = {6 9, 7 0, 7 1} and P (E1 ∩ E2 )=3/5.E1 ∪ E2 = S and P (E1 ∪ E2 )=1. E1 E2 = {6 8} and P (E1 E2 )=1/5.Finally,(E1 E2 ) ∪ (E2 E1 )= {6 8, 7 2}, so P (E1 E2 ) ∪ (E2 E1 ))=2/5.
4.(a)IfthewaterPHlevelismeasuredoverthenexttwoirrigations,then (i)Thesamplespaceis S = {(x1 ,x2 ): x1 =6 8, 6 9, 7 0, 7 1, 7 2, and x2 = 6 8, 6 9, 7 0, 7 1, 7 2}.Thesizeofthesamplespaceis25. (ii)Thesamplespaceoftheexperimentthatrecordstheaverageofthetwo PHmeasurementsis S = {6.8, 6.85, 6.9, 6.95, 7, 7.05, 7.1, 7.15, 7.2} andthe PMFis
x 6.86.856.96.9577.057.17.157.2 p(x)0.040.080.120.160.200.160.120.080.04
(b)Theprobabilitymassfunctionoftheexperimentthatrecordstheaverageof thePHmeasurementstakenoverthenextfiveirrigationsis
x 6.86.826.846.866.886.96.92
p(x)0.000320.001600.004800.011200.022400.038720.05920 x 6.946.966.9877.027.047.06
p(x)0.081600.102400.116800.121920.116800.102400.08160 x 7.087.17.127.147.167.187.2
p(x)0.059200.038720.022400.011200.004800.001600.00032
5.(a)TheRcommandis sample(0:2,size=10,replace=T,prob=pr) andthefollowinggivesonepossibleresult:1,0,0,1,1,0,1,0,0,0.
(b)Therelativefrequencybasedon10,000replicationsis 012 0.68970.27990.0304
(c)Thehistogramoftherelativefrequenciesandlinegraphoftheprobabilitymass functionisgivenonthenextpage.
Copyright © 2016PearsonEducation,Inc.
Thisfigureshowsthatallrelativefrequenciesaregoodapproximationsto correspondingprobabilitiesandwehaveempiricalconfirmationofthelimiting relativefrequencyinterpretationofprobability.
6.(a)Thenumberofwaystofinishthetestis25 =32.
(b)Thesamplespacefortheexperimentthatrecordsthetestscoreis S = {0, 1, 2, 3, 4, 5}.
(c)ThePMFof X isgivenby
7.Thenumberofassignmentsis
8.Theprobabilityis
9.(a)Thenumberofpossiblecommitteesis
(b)Thenumberofcommitteesconsistingof2biologists,1chemist,and1physicist is
.
(c)Theprobabilityis120/495=0.2424.
10.(a)Thenumberofpossibleselectionsis 10 5 =252
(b)Thenumberofdivisionsofthe10playersintotwoteamsof5is252/2=126.
(c)Thenumberofhandshakesis
11.(a)Inordertogofromthelowerleftcornertotheupperrightcorner,weneedto totallymove8steps,with4stepstotherightand4stepsupwards.Thus,the totalnumberofpathsis
8 4 =70.
(b)Wedecomposethemoveastwostages:stage1isfromlowerleftcornerto circledpoint,whichneeds5stepswith3stepstotherightand2stepsupwards; stage2isfromthecircledpointtotheupperrightcorner,whichneeds3steps with1steptotherightand2stepsupwards.Thus,thetotalnumberofpaths passingthecircledpointis
.
(c)Theprobabilityis30/70=3/7.
12.(a)Inordertokeepthesystemworking,thenonfunctioningantennascannotbe nexttoeachother.Thereare8antennasfunctioning;thus,the5nonfunctioningantennasmustbeinthe9spacescreatedbythe8functioningantennas. Thenumberofarrangementsis
9 5 =126.
(b)Thetotalnumberofthe5nonfunctioningantennasis 13 5 =1287.Thus,the requiredprobabilityis126/1287=0.0979.
Copyright © 2016PearsonEducation,Inc.
13.(a)Thetotalnumberofselectionsis 15 5 =3003
(b)Thenumberofselectionscontainingthreedefectivebusesis 4 3 11 2 =220
(c)Theaskedprobabilityis220/3003=0.07326.
(d)Theprobabilityallfivebusesarefreeofthedefectiscalculatedas
14.(a)Thenumberofsamplesofsizefiveis 30 5 =142506
(b)Thenumberofsamplesthatincludetwoofthesixtaggedmooseis 6 2 24 3 = 30360
(c)
(i)Theprobabilityis
=0.213.
(ii)Theprobabilityis
15.(a)Theprobabilityis
(b)Theprobabilityis
(c)Theprobabilityis
16.Thetotalnumberofpossibleassignmentsis 10 2,2,2,2,2 =113400
17.(a)Thereare315 =14348907waystoclassifythenext15shinglesintowthree grades.
Copyright © 2016PearsonEducation,Inc.
(b)Thenumberofwaystoclassifyintothreehigh,fivemediumandsevenlow gradesis
15 3, 5, 7 =360360.
(c)Theprobabilityis360360/14348907=0.0251.
18.(a)
(b)
2.4AxiomsandPropertiesofProbabilities
1. P (A ∩ B )= P (A)+ P (B ) P (A ∪ B )=0.37+0.23 0.47=0.13.
2.(a) P (A1 )= ··· = P (Am )=1/m. (b)If m =8, P (A1 ∪ A2 ∪ A3 ∪ A4 )= P (A1 )+ P (A2 )+ P (A3 )+ P (A4 )=4 × 1/m = 1/2.
3.(a)TheRcommandsare Copyright © 2016PearsonEducation,Inc.
t=c(50,51,52,53);G=expand.grid(X1=t,X2=t,X3=t);attach(G) table((X1+X2+X3)/3)/length(X1)
TheresultingPMFis x 5050.3350.675151.33 p(x)0.0156250.0468750.0937500.1562500.187500 x 51.675252.3352.6753 p(x)0.1875000.1562500.0937500.0468750.015625
(b)Theprobabilitythattheaveragegasmileageisatleast52MPGis0.156250+ 0 093750+0 046875+0 015625=0 3125
4.(a)
(i) E1 = {5, 6, 7, 8, 9, 10, 11, 12} P (E1 )=4/36+5/36+6/36+5/36+4/36+ 3/36+2/36+1/36=5/6
(ii) E2 = {2, 3, 4, 5, 6, 7, 8} P (E2 )=1/36+2/36+3/36+4/36+5/36+ 6/36+5/36=13/18
(iii) E3 = E1 ∪ E2 = {2, ··· , 12}, P (E3 )=1. E4 = E1 E2 = {9, 10, 11, 12}, P (E4 )=4/36+3/36+2/36+1/36=5/18. E5 = E c 1 ∩ E c 2 = ∅, P (E5 )=0.
(b) P (E3 )= P (E1 ∪ E2 )= P (E1 )+ P (E2 ) P (E1 ∩ E2 )=30/36+26/36 (4/36+ 5/36+6/36+5/36)=1.
(c) P (E5 )= P (E c 1 ∩ E c 2 )= P ((E1 ∪ E2 )c )= P (E c 3 )=1 P (E3 )=1 1=0.
5.(a)
(i) E1 = {(> 3,V ), (< 3,V )}, P (E1 )=0.25+0.3=0.55.
(ii) E2 = {(< 3,V ), (< 3,D ), (< 3,F )}, P (E2 )=0.3+0.15+0.13=0.58. (iii) E3 = {(> 3,D ), (< 3,D )}, P (E3 )=0.1+0.15=0.25. (iv) E4 = {(> 3,V ), (< 3,V ), (< 3,D ), (< 3,F )}, P (E4 )=0.25+0.3+ 0.15+0.13=0.83. E5 = {(> 3,V ), (< 3,V ), (< 3,D ), (< 3,F ), (> 3,D )}, P (E5 )=0 25+0 3+0 15+0 13+0 1=0 93.
(b) P (E4 )= P (E1 ∪ E2 )= P (E1 )+ P (E2 ) P (E1 ∩ E2 )=0 55+0 58 0 3=0 83. (c) P (E5 )= P (E1 ∪ E2 ∪ E3 )= P (E1 )+ P (E2 )+ P (E3 ) P (E1 ∩ E2 ) P (E1 ∩ E3 ) P (E2 ∩ E3 )+ P (E1 ∩ E2 ∩ E3 )=0 55+0 58+0 25 0 3 0 0 15+0=0 93
6.(a)Theprobabilitythat,inanygivenhour,onlymachineAproducesabatchwith nodefectsis
(b)Theprobability,inthatanygivenhour,onlymachineBproducesabatchwith nodefectsis P (E2 ∩ E c 1 )= P (E2 ) P (E1 ∩ E2 )=0 92 0 88=0 04 Copyright © 2016PearsonEducation,Inc.
(c)Theprobabilitythatexactlyonemachineproducesabatchwithnodefectsis
(d)Theprobabilitythatatleastonemachineproducesabatchwithnodefectsis
7.Theprobabilitythatatleastoneofthemachineswillproduceabatchwithno defectivesis
8.(a)
(b)Theprobabilitymassfunctionfortheexperimentthatrecordsonlytheonline monthlyvolumeofsalescategoryisgivenas
OnlineSales012
Probability0.160.440.4
9.Let
E4 = {atleasttwooftheoriginalfourcomponentswork}, and
E5 = {atleastthreeoftheoriginalfourcomponentswork} ∪{twooftheoriginalfourcomponentswork andtheadditionalcomponentworks}
Then E4 ⊂ E5 because
B ={exactlytwooftheoriginalfourcomponentswork andtheadditionalcomponentdoesnotwork}, whichispartof E4 ,isnotin E5 .Thus, E4 ⊂ E5 and,hence,itisnotnecessarily truethat P (E4 ) ≤ P (E5 ).
10.(a)Iftwodicearerolled,thereareatotalof36possibilities,amongwhich6are tied.Hence,theprobabilityoftieis6/36=1/6.
Copyright © 2016PearsonEducation,Inc.
(b)Bysymmetryofthegame P (A wins)= P (B wins)and P (A wins)+P (B wins)+ P (tie)=1.Usingtheresultof(a),wecansolvethat P (A wins)= P (B wins)= 5/12.
11.(a) A>B = {dieAresultsin4}, B>C = {dieCresultsin2}, C>D = {dieCresultsin6,ordieCresultsin2anddieDresultsin1}, D>A = {dieDresultsin5,ordieDresultsin1anddieAresultsin0}.
(b) P (A>B )=4/6, P (B>C )=4/6, P (C>D )=4/6, P (D>A)=4/6.
12.(a)Iftheparticipantstickswiththeoriginalchoice,theprobabilityofwinningthe bigprizeis1/3.
(b)Iftheparticipantchoosestoswitchhis/herchoice,theprobabilityofwinning thebigprizeis2/3.Thisisbecausethatifthefirstchoicewasactuallythe minorprize,then,afterswitching,he/shewillwinthebigprize.Ifthefirst choicewasactuallythebigprize,afterswitchinghe/shewillwintheminor prize.Whilethefirstchoicebeingtheminorprizehasaprobabilityof2/3, consequently,switchingleadstoaprobabilityof2/3towinthebigprize.
13.Toprovethat P (∅)=0,let E1 = S and Ei = ∅ for i =2, 3, ···
isasequenceofdisjointevents.ByAxiom3,wehave
whichimpliesthat
Toprove(2)ofProposition2.4-1,let
isasequenceofdisjointeventsand
whichiswhattobeproved.
2.5ConditionalProbability
1.Theprobabilitycanbecalculatedas
2.Let B = {systemre-evaluationoccurs} and C = {acomponentisindividuallyreplaced}. Consideranewexperimentwithreducedsamplespace A = B ∪ C .Thedesired probabilityistheprobabilityof B inthisnewexperiment,whichiscalculatedas
3.(a) P (A)=0.132+0.068=0.2.
(b) P (A ∩ B )=0.132, thus P (B |A)= P (A ∩ B )/P (A)=0.132/0.2=0.66.
(c) P (X =1)=0.2, P (X =2)=0.3, P (X =3)=0.5.
4.Welet B1 ,B2 ,BO betheeventthattheTVisbrand1,brand2,andotherbrand, respectively.Let R betheeventthattheTVneedswarrantyrepair.
(a) P (B1 ∩ R )= P (B1 )P (R|B1 )=0 5 × 0 1=0 05
(b)Thetreediagramis
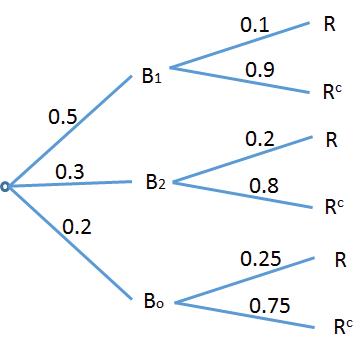
(c)Usingthediagram
(R )= P (B1 )P (R|B1 )+ P (B2 )P (R|B2 )+ P (BO )P (R|BO ) =0 5 × 0 1+0 3 × 0 2+0 2 × 0 25=0 16
5.(a)Theprobabilityis0.36 × 0.58=0.2088.
(b)Thetreediagramis
Copyright © 2016PearsonEducation,Inc.
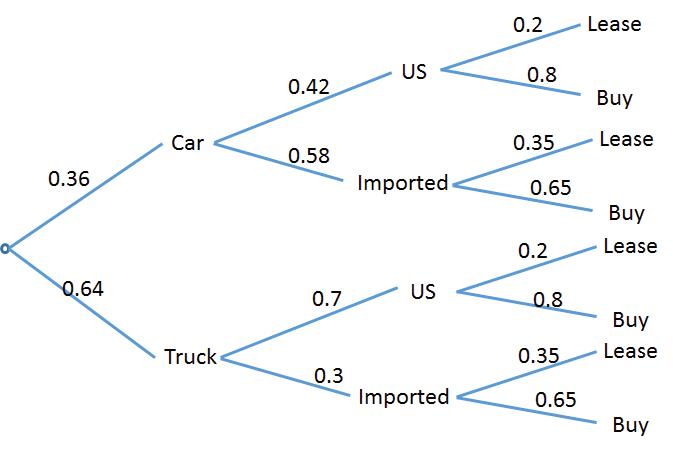
(c)Byusingthetreediagram,theprobabilitythatthenextconsumerwilllease his/hervehicleis
0 36 × 0 42 × 0 2+0 36 × 0 58 × 0 35+0 64 × 0 7 × 0 2+0 64 × 0 3 × 0 35=0 26
6.(a) P (nodefect ∩ A)= P (nodefect|A)P (A)=0 99 × 0 3=0 297
(b)P (nodefect∩B )= P (nodefect|B )P (B )=0.97×0.3=0.291, and P (nodefect∩ C )= P (nodefect|C )P (C )=0.92 × 0.3=0.276.
(c) P (nodefect)= P (nodefect ∩ A)+ P (nodefect ∩ B )+ P (nodefect ∩ C )= 0 297+0 291+0 276=0 864
(d) P (C |nodefect)= P (nodefect ∩ C )/P (nodefect)=0.276/0.864=0.3194.
7.(a)Thetreediagramis
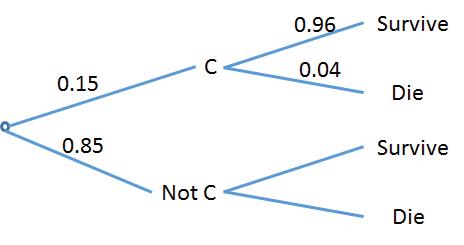
(b)Fromthegiveninformation,wehave P (survive)=0 15 × 0 96+0 85 × P (Survive|NotC-section)=0 98
Solvingthisequationgivesus P (Survive|NotC-section)=0.984.
8.Let B betheeventthatthecreditcardholdsmonthlybalance,then P (B )=0 7 and P (B c )=0.3.Let L betheeventthatthecardholderhasannualincomeless than $20,000,then P (L|B )=0.3and P (L|B c )=0.2.
Copyright © 2016PearsonEducation,Inc.
(a) P (L)= P (L|B )P (B )+ P (L|B c )P (B c )=0.3 × 0.7+0.2 × 0.3=0.27.
(b) P (B |L)= P (L|B )P (B )/P (L)=0 3 × 0 7/0 27=0 778
9.Let A betheeventthattheplantisaliveandlet W betheroommatewatersit. Then,fromthegiveninformation, P (W )=0.85and P (W c )=0.15; P (A|W )=0.9 and P (A|W c )=0 2.
(a) P (A)= P (A|W )P (W )+ P (A|W c )P (W c )=0 9 × 0 85+0 2 × 0 15=0 795
(b) P (W |A)= P (A|W )P (W )/P (A)=0 9 × 0 85/0 795=0 962
10.Let D1 betheeventthatthefirstisdefectiveand D2 theeventthatthesecondis defective.
(a) P (nodefective)= P (D c 1 ∩ D c 2 )= P (D c 2 |D c 1 )P (D c 1 )=6/9 × 7/10=0 467 (b) X canbe0,1,or2.Wealreadycalculated P (X =0)= P (nodefective)= 0.467. P (X =2)= P (D1 ∩ D2 )= P (D2 |D1 )P (D1 )=2/9 × 3/10=0.067. Thus, P (X =1)=1 P (X =0) P (X =2)=0 466.
(c) P (D1 |X =1)= P (D1 ∩ D c 2 )/P (X =1)= P (D c 2 |D1 )P (D1 )/P (X =1)= 7/9 × 0.3/0.466=0.5.
11.Let L1 ,L2 ,L3 ,L4 betheeventthattheradartrapsareoperatedatthe4locations, then P (L1 )=0 4,P (L2 )=0 3,P (L3 )=0 2,P (L4 )=0 3.Let S betheperson speedingtowork,then P (S |L1 )=0.2,P (S |L2 )=0.1,P (S |L3 )=0.5,P (S |L4 )= 0 2.
(a) P (S )= P (S |L1 )P (L1 )+ P (S |L2 )P (L2 )+ P (S |L3 )P (L3 )+ P (S |L4 )P (L4 )= 0.2 × 0.4+0.1 × 0.3+0.5 × 0.2+0.2 × 0.3=0.27. (b) P (L2 |S )= P (S |L2 )P (L2 )/P (S )=0 1 × 0 3/0 27=0 11
12.Let D betheeventthattheaircraftwillbediscovered,and E betheeventthat ithasanemergencylocator.Fromtheproblem, P (D )=0.7and P (D c )=0.3; P (E |D )=0 6and P (E |D c )=0 1.
(a) P (E ∩ D c )= P (E |D c )P (D c )=0 1 × 0 3=0 03. (b) P (E )= P (E |D c )P (D c )+ P (E |D )P (D )=0 1 × 0 3+0 6 × 0 7=0 45. (c) P (D c |E )= P (E ∩ D c )/P (E )=0.03/0.45=0.067.
13. R.H.S.= P (E1 ) P (E1 ∩ E2 ) P (E1 )
(E1 ∩ E2 ∩···∩ En 1 ∩ En ) P (E1 ∩ E2 ∩···∩ En 1 ) = P (E1 ∩ E2 ∩···∩ En 1 ∩ En )=L.H.S. Copyright © 2016PearsonEducation,Inc.
2.6IndependentEvents
1.Fromthegiveninformation P (E2 )=2/10and P (E2 |E1 )=2/9,thus P (E2 ) = P (E2 |E1 ).Consequently, E1 and E2 arenotindependent.
2.Wecancalculatefromthetablethat P (X =1)=0.132+0.068=0.2and P (Y = 1)=0.132+0.24+0.33=0.702,thus P (X =1)P (Y =1)=0.2 × 0.702= 0 1404 =0 132= P (X =1,Y =1).Thus,theevents[X =1]and[Y =1]arenot independent.
3.(a)Theprobabilityis0 910 =0 349
(b)Theprobabilityis0.1 × 0.99 =0.0387.
(c)Theprobabilityis10 × 0.1 × 0.99 =0.387
4.Atotalof8fusesbeinginspectedmeansthatthefirst7arenotdefectiveandthe 8thisdefective,thustheprobabilityiscalculatedas0 997 × 0 01=0 0093
5.Assumingthecarsassembledoneachlineareindependent,alsoassumethatthe twolinesareindependent.Wehave
(a)Theprobabilityoffindingzerononconformanceinthesamplefromline1is 0 84 =0 410.
(b)Theprobabilityoffindingzerononconformanceinthesamplefromline1is 0.93 =0.729.
(c)Theprobabilityis0 84 × 0 93 =0 2986
6.Yes.Bythegiveninformation, P (T |M )= P (T ),weseethat T and M areindependent.Thus, T and F = M c arealsoindependent;thatis, P (T |F )= P (T ).
7.(a)Thecompletedtableisgivenas
(b)Let B betheeventthatthestudentprefersbasketball,then P (F |B )= P (F ∩ B )/P (B )=0 28/0 5=0 56
(c) F and B arenotindependentbecause P (F |B )=0 56 =0 35= P (F ).
8.Wecanwrite E1 = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}, E2 = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)},
Copyright © 2016PearsonEducation,Inc.
and E3 = {(1, 4), (2, 4), (3, 4), (4, 4), (5, 4), (6, 4)}.
Thus, E1 ∩ E2 = E1 ∩ E3 = E2 ∩ E3 = {(3, 4)},and E1 ∩ E2 ∩ E3 = {(3, 4)}.Hence, P (E1 )= P (E2 )= P (E3 )=1/6,and P (E1 ∩ E2 )= P (E1 ∩ E3 )= P (E2 ∩ E3 )= 1/36,thisshowsthat E1 ,E2 ,E3 arepairwiseindependent.But P (E1 ∩ E2 ∩ E3 ) = P (E1 )P (E2 )P (E3 ).
9.Since E1 ,E2 ,E3 areindependent,wehave P (E1 ∩ (E2 ∪ E3 ))= P ((E1 ∩ E2 ) ∪ (E1 ∩ E3 ))= P (E1
E2 )+ P (E1 ∩ E3 ) P (E1 ∩ E2 ∩ E3 ) = P (E1 )P (E2 )+ P (E1 )P (E3 ) P (E1 )P (E2 )P (E3 ) = P (E1 )[P (E2 )+ P (E3 ) P (E2
E3 )]= P (E1 )P (
2 ∪ E3 ), whichprovestheindependencebetween E1 and E2 ∪ E3 .
10.Let E1 ,E2 ,E3 ,E4 betheeventsthatcomponents1,2,3,4function,respectively, then
(systemfunctions)=
11.Let A denotetheeventthatthesystemfunctionsand Ai denotetheeventthat component i functions, i =1, 2, 3, 4.Inmathematicalnotations
