Solutions for Intermediate Algebra With Applications And Visualization 3rd Us Edition by Rockswold by 6alsm

Chapter 2: Linear Equations and Inequalities

Section 2.1 Introduction to Equations

1. solution

2. true

3. false

4. solution set

5. solutions

6. Equivalent

7. bc +

8. subtraction

9. bc

10. division

11. equivalent

12. given

13. 22

14. 1 6

15. 3

16. 1 4

17. 505505055; xxxx +=⇒+−=−⇒+=−⇒=− To check your answer, substitute 5 for x in the original equation, 550.−+= This statement is true. Thus, the solution 5 x =− is correct.

18. 373373044; xxxx +=⇒+−=−⇒+=⇒= To check your answer, substitute 4 for x in the original equation, 437. += This statement is true. Thus, the solution 4 x = is correct.

19. 1231212312099 aaaa −=−⇒−+=−+⇒+=⇒=

20. 191119191119088 aaaa −=−⇒−+=−+⇒+=⇒=

21. 9898881701717 yyyyy =−⇒+=−+⇒=+⇒=⇒=

22. () 9723972323231200120 yyyy =−+⇒+=+−+⇒=+⇒=

23. 131333171717 0 525222101010 zzzzz =−⇒+=−+⇒=+⇒=⇒=

24. 31331355 0 42442444 zzzz ⎛⎞⎛⎞ +=−⇒+−+=−+−⇒+=−⇒=− ⎜⎟⎜⎟ ⎝⎠⎝⎠

25. 0.84.30.80.84.30.805.15.1 tttt −=⇒−+=+⇒+=⇒= 26. 1.230.021.231.230.021.2301.211.21 yyyy −=−⇒−+=−+⇒+=⇒=

27. 414414033 xxxx +=⇒−+=−⇒+=−⇒=−

28. 162161621601818 xxxx +=−⇒−+=−−⇒+=−⇒=−

29. 1111222 110 3333333 yyyyy =+⇒−=−+⇒=+⇒=⇒=

30. 77111111 22220 22222 yyyyy =−+⇒+=−++⇒=+⇒=⇒=

31. a

32. a

33. 1 5

34. 3 4

35. 6

36. 0.2

37. 515 5153 55 x xx =⇒=⇒=

38. 28 284 22 x xx −=⇒=⇒=−

39. 70 700 77 x xx −=⇒=⇒=

40. 250 2500 2525 x xx =⇒=⇒=

41. 355 35577 55 a aaa −=−⇒=⇒=⇒=

42. 324 32488 44 a aaa −=−⇒=⇒=⇒=

43. 183 18366 33 a aaa −=⇒=⇒−=⇒=−

44. 7010 701077 1010 a aaa −=⇒=⇒−=⇒=−

45. 132132 3 221221 xxx =⇒⋅=⋅⇒=

46. 3543545 4834836 xxx =⇒⋅=⋅⇒=

47. 12515255 25222544 zzzz =⇒⋅=⋅⇒=⇒=

48. 313881 66 484118 zzzz ⎛⎞⎛⎞ −=−⇒−⋅−=−⋅−⇒=⇒= ⎜⎟⎜⎟ ⎝⎠⎝⎠

49. 0.53.5 0.53.57 0.50.5 t tt =⇒=⇒=

50. 2.29.99.9 2.29.94.5 2.22.22.2 t ttt =−⇒=⇒=−⇒=−

51. 1.70.2 1.70.28.58.5 0.20.2 x xxx −=⇒=⇒−=⇒=−

52. 6.41.6 6.41.644 1.61.6 x xxx =⇒=⇒=⇒=

53. a

54. a

55. (a) See Figure 55.

(b) Let R represent total rainfall and let x represent the number of hours past noon. Start with 3 inches of rain and then add 1 , 2 or 0.5, inches per hour after noon, 30.5, or equivalently 0.53.xRRx +==+

(c) At 3 pm, 3. x = Substituting x with 3 in the formula, 0.5334.5 inches. RR=⋅+⇒= This answer agrees with the table from part (a).

(d) At 2:15 pm, 2.25. x = Substituting x with 2.25 in the formula, 0.52.2534.125 inches. RR =⋅+⇒=

Figure 55

56. (a) See Figure 56.

Figure 56

(b) Let T represent the temperature and let x represent the number of hours past midnight. Since the temperature increases 10ºF per hour, 10.Tx =

(d) At 2:45 am, 2.75. x = Substituting x with 2.75 in the formula, 102.7527.5ºF.TT=⋅⇒=

57. (a) Let L be the length of the football fields and x be the number of fields. Because each field x contains 300 feet, 300.Lx =

(b) Substitute L with 870. Then 870300. x =

58. (a) Let A represent the number of acres and let S represent the number of square feet. Because each acre contains 43,560 square feet, let 43,560. SA = (b) Substitute S with 871,200. Then, 871,20043,560. A =

59. The formula for this scenario is 0.3 Tx = where x is in days and T is in millions. To find the number of days needed for Twitter to add 15 million new accounts, replace the variable T in the formula with 15. 150.3 0.3150.350 0.30.3 x Txxx =⇒=⇒=⇒= At this rate it takes 50 days to add 15 million accounts.

60. The formula for this scenario is 14,000 Wx = where x is in days and W is the number of visitors. To find the number of days for the Web site to add 98,000 new visitors, replace the variable W in the formula with 98,000. 98,00014,000 14,00098,00014,0007 14,00014,000 x Wxxx =⇒=⇒=⇒= At this

rate it takes 7 days to add 98,000 new visitors.

61. a) The latitude of Winnipeg to the nearest degree is 50 N

b) The sun at the equator will be approximately 325 5.7 57 ≈ times as intense as they are in Winnipeg on March 21st.

62. a) The latitude of Columbus, Ohio to the nearest degree is 40 N

b) The sun in Limon, Costa Rica will be approximately 275 1.4 199 ≈ times as intense as they are in Columbus on June 21st

63. Let x represent the cost of the car to obtain the equation 0.071750. x = Then the solution is 0.0717501750 25,000. 0.070.070.07 x xx =⇒=⇒= Thus, the cost of the car is $25,000.

64. Let S represent the employee’s current salary to obtain the equation 1.0658,300. S = Then the solution is 1.0658,30058,300 55,000. 1.061.061.06

S SS =⇒=⇒= Thus, the employee’s current salary is $55,000.

Section 2.2 Linear Equations

1. constant

2. 0 axb+=

3. Exactly one

4. numerically

5. addition, multiplication

6. LCD

7. None

8. Infinitely many

9. 370 is a linear equation. 3 and 7. xab −===−

10. 214 is a linear equation. x −+= 21421444230. xxx −+=⇒−+−=−⇒−−= 2 and 3. ab=−=−

11. 11 0 is a linear equation. and 0. 22 xab ===

12. 33 0 is a linear equation. and 0. 44 xab −==−=

13. 2 4611 x −= is not a linear equation because it cannot be written in the form 0. axb+= It has a non-zero term containing 2 x

14. 2 24 xx −+= is not a linear equation because it cannot be written in the form 0. axb+= It has a non-zero term containing 2 . x

15. 6 42 x −= is not a linear equation because it cannot be written in the form 0. axb+= It has the variable x in the denominator.

16. 210 x −= is not a linear equation because it cannot be written in the form 0. axb+= It has a nonzero term containing . x

17. 1.10.91.8 is a linear equation. 1.10.91.81.10.91.81.81.81.10.90.1.1 and 0.9. x xxxab += +=⇒+−=−⇒−===−

18. 5.73.46.8 is a linear equation.

5.73.46.85.73.46.86.86.85.73.40.5.7 and 3.4. x xxxab −−=− −−=⇒−−+=−+⇒−+==−=

19. () 230 x −= is a linear equation. Use the distributive property to obtain 260. 2 and 6. xab −===−

20. () 1 40 2 x += is a linear equation. Use the distributive property to obtain 11 20. and 2. 22 xab +===

21. 321 x += is not a linear equation because it cannot be written in the form 0. axb+= It has a nonzero term containing . x

22. 3 34xx = is not a linear equation because it cannot be written in the form 0. axb+= It has a nonzero term containing 3 . x

23. For 1, substitute 1 for and solve:134. xx =−−−−=− For 0, substitute 0 for and solve:033. xx =−=− For 1, substitute 1 for and solve:132. xx =−=− For 2, substitute 2 for and solve:231. xx =−=− For 3, substitute 3 for and solve:330. xx =−=

See Figure 23. From the table, we see that the equation 31 is true when 2. xx −=−= Therefore, the solution to the equation 31 is 2. xx−=−=

Figure 23

Figure 24

24. () For 2, substitute 2 for and solve:224. xx =−−−−= () For 1, substitute 1 for and solve:212. xx =−−−−= ()

For 0, substitute 0 for and solve:200. xx =−= ()

For 1, substitute 1 for and solve:212. xx =−=− ()

For 2, substitute 2 for and solve:2274. xx =−+=−

See Figure 24. From the table, we see that the equation 20 is true when 0. xx −== Therefore, the solution to the equation 20 is 0. xx −==

25. () For 0, substitute 0 for and solve:307077. xx =−+=+= ()

For 1, substitute 1 for and solve:317374. xx =−+=−+= () For 2, substitute 2 for and solve:327671. xx =−+=−+= () For 3, substitute 3 for and solve:337972. xx =−+=−+=− () For 4, substitute 4 for and solve:3471275. xx =−+=−+=−

See Figure 25. From the table, we see that the equation 371 is true when 2. xx −+== Therefore, the solution to the equation 371 is 2. xx −+==

Figure 25

Figure 26

26. () For 1, substitute 1 for and solve:512527. xx =−−−−=−−=− () For 0, substitute 0 for and solve:502022. xx =−=−=− () For 1, substitute 1 for and solve:512523. xx =−=−= () For 2, substitute 2 for and solve:5221028. xx =−=−= () For 3, substitute 3 for and solve:53215213. xx =−=−=

See Figure 26. From the table, we see that the equation 523 is true when 1. xx −== Therefore, the solution to the equation 523 is 1. xx−==

27. () For 2, substitute 2 for and solve:422448. xx =−−−−=+= () For 1, substitute 1 for and solve:421426. xx =−−−−=+= () For 0, substitute 0 for and solve:420404. xx =−=−=

For 1, substitute 1 for and solve:421422. xx =−=−=

For 2, substitute 2 for and solve:422440. xx =−=−=

See Figure 27. From the table, we see that the equation 426 is true when 1. xx −==− Therefore, the solution to the equation 426 is 1. xx −==−

Figure 27

Figure 28

28. () For 2, substitute 2 for and solve:923918. xx =−−−−+=−=

For 1, substitute 1 for and solve:913927. xx =−−−−+=−=

For 0, substitute 0 for and solve:903936. xx =−+=−=

For 1, substitute 1 for and solve: 913945. xx =−+=−=

For 2, substitute 2 for and solve: 923954. xx =−+=−=

See Figure 28. From the table, we see that the equation () 934 is true when 2. xx −+==

Therefore, the solution to the equation () 934 is 2. xx −+==

29. 1133 113 111111 x xx =⇒=⇒=

30. 515 5153 55 x xx −=⇒=⇒=−

31. 185181851823 xxx −=⇒−+=+⇒=

32. 33 853855533311 33 x xxxxx =+⇒−=−+⇒=⇒=⇒=⇒=

33. 1111 1131113114221428 2222 x xxxx −=⇒−+=+⇒=⇒⋅=⋅⇒=

34. 1111 393393644624 4444 x xxxx +=⇒+−=−⇒=⇒⋅=⋅⇒=

35. 11511 65565555115 555 x xxxx −=+⇒−−=+−⇒−=⇒=⇒=−

36. 357 31743147443575 77 x xxxx =−−⇒+=−−+⇒=−⇒=⇒=−

37. 32532252373727 zzzzzzzzzzz +=−⇒+−=−−⇒=−⇒−=−−⇒=−⇒ 277 222 z z =⇒=−

38. 5535553552555242 zzzzzzzzzzz −=−⇒−+=−+⇒=+⇒−=−+⇒−=⇒ 421 442 z z =⇒=−

39. 12633126633612391239 yyyyyyyyyy −=−⇒−+=+−⇒=−⇒+=−+⇒ 1339 13393 1313 y yy =⇒=⇒=

40. 1322231322222313203 yyyyyy −+=−⇒−+−=−−⇒−=−⇒ 1020 133203310202 1010 y yyyyyy −+=−+⇒−=⇒=⇒=−

41. () 499 4154454445449 444 x xxxxx −=⇒−=⇒−+=+⇒=⇒=⇒=

42. () 415 2271414141414114415 44 x xxxx −+=⇒−−=⇒−−+=+⇒−=⇒=⇒ 15 4 x =−

43. () 131513153535 xxxxxxxxxx −+=−⇒−−=−⇒−=−⇒−+=−+⇒ 255 25 222 x xx −=⇒=⇒=−

44. ()() 62710336214103928193 xxxxxx +−=−−⇒+−=−+⇒−=−⇒ 23819335819588198527 xxxxxxx +−=−+⇒−=⇒−+=+⇒=⇒ 52727 555 x x =⇒=

45. ()() 5621256222562452662264 tttttttttt −=++⇒−=++⇒−=+⇒−−+=−++⇒

31010

310 333 t tt =⇒=⇒=

46. ()() 27552145539539959 tttttt −−−+=⇒−+−−=⇒−+=⇒−+−=−⇒ 344 34 333 t tt −=−⇒=⇒=

47. ()()() 3412221123242210722 zzzzzzzz −−+=+⇒−−−=+⇒−=+⇒ 10772271029 zzzz −+=++⇒=+⇒ 899 10222989 888 z zzzzzz −=−+⇒=⇒=⇒=

48. ()()()43121431222322 zzzzzzzz −+++=−+⇒−−++=−−⇒−=−−⇒ 2332232212222141 zzzzzzzzz −+=−−+⇒=−+⇒+=−++⇒=⇒ 411 444 z z =⇒=

49. 7.37.3 7.31.75.67.31.71.75.61.77.37.31 7.37.3 x xxxx −=⇒−+=+⇒=⇒=⇒=

50. 8.551 5.53518.5516 8.58.5 x xxxx +=⇒=⇒=⇒=

51. 9.50.0510.51.059.510.50.0510.510.51.05 xxxxxx −−=+⇒−−−=−+⇒ 201.1 200.051.05200.050.051.050.05201.1 2020 x xxx −−=⇒−−+=+⇒−=⇒=⇒ 0.055 x =−

2.2: Linear Equations

52. 0.040.030.020.10.040.020.030.020.020.1 xxxxxx +=− 0.020.030.1 x +=−⇒

0.020.030.030.10.030.020.13 xx +−=−−⇒=−⇒ 0.020.13 6.5 0.020.02 x x =⇒=−

53. 1351335311 42428 2222222222 xxxxx −=⇒−+=+⇒=⇒⋅=⋅⇒=

54. () () 153155351212 442 444444444444 xxxxx ⎛⎞ −+=⇒−+−=−⇒−=−⇒−⋅−=−⋅−⇒= ⎜⎟ ⎝⎠

55. 31131131 84884888 xxx −+=⇒−=−+⇒−=−⇒ 83181 38833 xx⎛⎞⎛⎞⎛⎞⎛⎞ −−=−−⇒= ⎜⎟⎜⎟⎜⎟⎜⎟ ⎝⎠⎝⎠⎝⎠⎝⎠

56. 11111141141111 34634634634464 xxxxxxxx +=−⇒++=−+⇒+=⇒+−=−⇒ 41341331 312431244816 xxxx =−⇒⋅=−⋅⇒=−⇒=−

57. () 421042202202220222 yyyyyyy −+=⇒−−=⇒−=⇒−+=+⇒=⇒ 22 1 22 y y =⇒=

58. () 15205510102051010102051010 yyyyyyyyy +−=−⇒+=−⇒++=−+⇒ 20153 202052020205202015 20204 y yyyy +=⇒+−=−⇒=−⇒=⇒=−

59. 00 axbaxbbb +=⇒+−=− axb⇒=− axb aa ⇒= b x a ⇒=−

60. 11 00 xbxbbb aa −=⇒−+=+ 1 xb a ⇒= 1 axab a ⇒⋅=⋅ xab⇒=

61. 5515555101 xxxxxx =+⇒−=−+⇒=

Because the equation 01 = is always false, there are no solutions.

62. () 2326262622622666 xxxxxxxx −=−⇒−=−⇒−−=−−⇒−=−

Since the equation 66−=− is always true, there are infinitely many solutions.

63. 80 800 88 x xx =⇒=⇒= Thus, there is one solution.

64. 811 919181 888 x xxxxxxxx =+⇒−=−+⇒=⇒=⇒= Thus, there is one solution.

65. () 45345154415444415015 xxxxxxxxxxxx =+−⇒=+−⇒=+⇒−=−+⇒=

Because the equation 015 = is always false, there are no solutions.

66. () 515275152145215221471 xxxxxxxxx =−+⇒=−−⇒+=−+−⇒=⇒ 711 777 x x =⇒= Thus, there is one solution.

67. ()() 527105301035105303030 xxxx +−+=⇒+−−=⇒=

Since the equation 3030 = is always true, there are infinitely many solutions.

68. ()() 42223104846108610210 xxxx +−+=⇒+−−=⇒−=⇒=

Because the equation 210 = is always false, there are no solutions.

69. ()321523215222152 xxxxxxxx −+=−⇒−−=−⇒−−=−⇒ 2221522215 xxxx −+−=−+⇒−=

Because the equation 215−= is always false, there are no solutions.

70. () 2552555555 xxxxxxxxxxxx −+=−⇒−−=−⇒−=−⇒−−=−−⇒ 55−=− Since the

equation 55−=− is always true, there are infinitely many solutions.

71. (a) See Figure 71.

(b) Let D represent the distance from home and x represent the number of hours. Then 48. Dx =+

(d) Using the formula 48, Dx =+ substitute 22 for D. Then, 2248. x =+ Then, solving for x: 1889 2244481882.25 hours. 884 x xxxx −=−+⇒=⇒=⇒=⇒= Thus, the bicyclist is 22 miles from home after 2 hours and 15 minutes.

Figure 71

72. (a) Let D represent distance from home and x represent hours. Note that each hour spent running decreases the distance from home by 6 miles. Thus, set the formula to 166. Dx =−

(b) Using the formula, substitute 1.5 for x and solve for D () 1661.51697 miles. DDD =−⇒=−⇒=

(c) Substitute 5.5 for D and solve for x. 5.51665.5161616610.56 xxx =−⇒−=−−⇒−=−⇒ 10.56 1.751.75 66 x xx =⇒=⇒= Thus, the athlete is 5.5 miles from home after 1 hour and 45 minutes of running.

73. Using the formula, substitute 1730 for I and solve for x. 1730241482,440 x =−⇒ 1730482,440241482,440482,440 x +=−+

484,170241 484,1702412009 241241 x xx ⇒=⇒=⇒≈

74. Using the formula, substitute 970 for N and solve for x. 9704283,19797083,1974283,19783,197 xx =−⇒+⇒−+

84,16742 84,167422004 4242 x xx ⇒=⇒=⇒≈

75. Using the formula, substitute 1.5 for N and solve for x 1.50.0358.621.558.620.0358.6258.62 xx =−⇒+=−+

60.120.03 60.120.032004 0.030.03 x xx ⇒=⇒=⇒=

76. Using the formula, substitute 6.6 for C and solve for x. 6.60.35684 x =−⇒

690.60.35 6.66840.35684684690.60.351973.143 0.350.35 x xxx +=−+⇒=⇒=⇒≈⇒

1973.143 x ≈ Thus, the cost reached $6.6 billion sometime in the year 1973.

77. Using the formula, substitute 2841 for H and solve for x. 28413369,105 x =−+⇒ 6626433 284169,1053369,10569,10566264332008 3333 x xxx −=−−+⇒−=−⇒=⇒=

Thus, the number of hospitals reached 2841 in 2008.

78. Using the formula, substitute 2504 for F and solve for x. 25043465,734 x =−⇒ 68,23834 250465,7343465,73465,73468,238342007 3434 x xxx +=−+⇒=⇒=⇒=

Thus, the average home size reached 2504 square feet in 2007.

Checking Basic Concepts Sections 2.1 and 2.2

1. (a) 3 420 x −= is not linear because it cannot be written in the form 0. axb+= It has a non-zero term containing 3 x (b) () 214 x += is a linear equation. Use the distributive property to obtain 224, x += then 22444 x +−=− 220. x ⇒−= 2 a = and 2. b =−

2. For 3, x = substitute 3 for x and solve: () 4331239 −=−=

For 3.5, x = substitute 3.5 for x and solve: () 43.5314311 −=−=

For 4, x = substitute 4 for x and solve: () 44316313 −=−=

For 4.5, x = substitute 4.5 for x and solve: () 44.5318315 −=−=

For 5, x = substitute 5 for x and solve: () 45320317 −=−=

See Figure 2. To solve 4313, x −= the table tells us that when 4, 4313.xx=−=

Figure 2

3. (a) 126121261218 xxx −=⇒−+=+⇒=

To check the answer, substitute 18 for x in the original equation 126. x −= 1812666. −=⇒= Since this is true 18 x = is correct.

(b) 31431441 483483246 zzzz =⇒⋅=⋅⇒=⇒=

(d) ()() 5223452412392123 xxxxxx −−=−⇒−+=−⇒−=−⇒ 9231233912991293 xxxxxxx −+=−+⇒+=⇒−+=−⇒=

4. (a) 55 5656551. 55 x xxxxxxxx −=⇒−−=−⇒−=⇒=⇒−= Thus, the equation has one solution.

(b) () 25102210102221010221010 xxxxxxxx −−=−⇒−+=−⇒−++=−+⇒=

Since 1010 = is always true, the equation has infinitely many solutions.

Since this is never true, the equation has no solutions.

5. (a) Let D represent distance from home and x represent hours driven. Note that the driver is initially 300 miles from home and that each hour driven the driver gets closer to home by 75 miles. Thus, the formula is 30075. Dx =−

(b) Since the distance from home, when the driver is home, is 0, use the formula and set D equal to 0. Thus, 030075. x =−

(c)

75 300 0300750753007575753004 hours. 7575 x xxxxxx =−⇒+=−+⇒=⇒=⇒=

Section 2.3 Introduction to Problem Solving

1. Check your solution.

2. +

3. =

4. 1 and 2 nn++

5. 100 x

6. 0.01

7. left

8. right

9. 100 BA A

10. increase; decrease

11.rt

12. distance; time

13. Let t represent the number. 2122212210 ttt +=⇒−+=−⇒=

14. 22 27927797221 22 x xxxx +=⇒+−=−⇒=⇒=⇒=

15. () 24552451205551204120 55 xx xxxxxxxxx =−⇒⋅=−⇒=−⇒−=−−⇒−=−⇒ 4120 30 44 x x =⇒=

16. 25125 251255 2525 x xx =⇒=⇒=

17. 55 7272514551459 22 xx xxx ++ =⇒⋅=⋅⇒+=⇒+−=−⇒=

18. ()() 85885831133 xxxxx −=⇒−−=−⇒−=−⇒−−=−−⇒=

19. 17217234 22 xx x =⇒⋅=⋅⇒=

20. 595 59519 55 x xx =⇒=⇒=

21. Let the smallest natural number be represented by x ()()12963396xxxx ++++=⇒+=⇒ 393 33396339331 33 x xxx +−=−⇒=⇒=⇒= Thus, the numbers are 31, 32 and 33.

22. Let x represent the smallest integer, ()()1212333123xxxx ++++=−⇒+=−⇒ 3126 3331233312642 33 x xxx +−=−−⇒=−⇒=⇒=−

Thus, the numbers are 42, 41 and 40.

23. 3102 310234 33 x xx =⇒=⇒=

24. 1821821818 xxxxxxxx +=⇒−+=−⇒=⇒=

25. 324 52245222243248 33 x xxxxxxxx =+⇒−=−+⇒=⇒=⇒=

26. 218 3183182189 22 x xxxxxxxx =−⇒−=−−⇒=−⇒=⇒=−

27. 666126 187187612621 7766 xxx xx =⇒⋅=⋅⇒=⇒=⇒=

28. 2222 45452220222202222 55 xx xxx =⇒⋅=⋅⇒−=⇒−+=+⇒=⇒ 222 11 22 x x =⇒=

29. Let x represent the child’s current age. 10231023103 xxxxxxx +=+⇒−+=−+⇒=+ 1033377 xxx ⇒−=+−⇒=⇒=

30. Let x be the age of the daughter then 215 x + is the age of the mother. The equation is 49215. x =+

342 4921549152151534217and21549 22 xxxxxx =+⇒−=+−⇒=⇒=⇒=+=

31.Let x be the previous weight of the individual. () 11 301103303110 33 xxxx −=+⇒−=+⎛⎞

390330390330 xxxxxx ⇒−=+⇒−−=−+⇒

2903302909033090 xx −=⇒−+=+ 2420 2420210lb 22 x xx ⇒=⇒=⇒=

32. Let x be the person’s weight before gaining 25 pounds. The equation is 252115xx+=− 2521152511525115115115140 xxxxxxx −+=−−⇒=−⇒+=−+⇒= pounds

33. Let x be the number of waste sites in Washington. 2422242222262 xxx =−⇒+=−+⇒= 262 1313 22 x xx ⇒=⇒=⇒=

34. Let x be the number of unhealthy air quality days in San Diego. 993 1003110013119933333 33 x xxxxx =+⇒−=+−⇒=⇒=⇒=⇒=

35. Let x be the number of reptiles on the endangered species list. 802 922129212212128024040 22 x xxxxx =+⇒−=−+⇒=⇒=⇒=⇒=

36. 844 8438442121and363 44 x xxxxxx =+⇒=⇒=⇒=⇒==

There are 63,000 millionaires in Kentucky and 21,000 millionaires in Rhode Island.

37. 15622501562156225015621812 xxx −=⇒−+=+⇒= million

38. 5002 311218931118921891895002250 22 x xxxx =−⇒+=−+⇒=⇒=⇒=⇒

250 x = billion kilowatt-hours

39. 274 247024470427437 22 x xxxx −=⇒−+=+⇒=⇒=⇒=

There were 37,000 cosmetic surgeries performed on persons under age 18.

40. 368132236822132222 xx =−⇒+=−+ 39013 390133030 1313 x xxx ⇒=⇒=⇒=⇒= thousand

41. 1062(5)210621021064101061041010 964 9642424 44 xxxxxx x xxx =++⇒=++⇒=+⇒−=+−⇒ =⇒=⇒=⇒=

42. 24(4)(2)2436246366183 183 66 33 xxxxxx x xx =++++⇒=+⇒−=+−⇒=⇒ =⇒=⇒=

43. 6222(7)62221462414621441414 484 4841212and719 44 xxxxxx x xxxx =++⇒=++⇒=+⇒−=+−⇒ =⇒=⇒=⇒=+=

The length is 19 inches and the width is 12 inches.

44. 102(15)(6)1023211022132121 1233 12334141,635,and1526 33 xxxxx x xxxxx =+−+−⇒=−⇒+=−+⇒ =⇒=⇒=⇒=−=−=

The measures are 26, 35, and 41 feet.

45. 170(210)1703101701031010 1803 18036060and210110 33 xxxx x xxxx =+−⇒=−⇒+=−+⇒ =⇒=⇒=⇒=−=

Therefore, Facebook had 60 million users and MySpace had 110 million users.

46. 225400225225400225175 xxx +=⇒+−=−⇒=

There were 175 million Facebook users in February 2009.

47. 248,000(52,000)248,000252,000248,00052,0002 300,0002 300,0002150,000150,000and 52,00098,000 22 xxxx x xxxx =+−⇒=−⇒+=⇒ =⇒=⇒=⇒=−=

In 2003 there were 150,000 troops and in 2010 there were 98,000 troops.

48. 64(12)64212641221212 762 7623838and1226 22 xxxx x xxxx =+−⇒=−⇒+=−+⇒ =⇒=⇒=⇒−−=

In 1980 there were 38 million acres and in 2009 there were 26 million acres.

49. 37 37% 100 = 37%370.010.37 =×=

50. 5213413 52% 10025425 === ⋅ 52%520.010.52 =×=

51. 14837437 148% 10025425 === 148%1480.011.48 =×=

52. 25263463 252% 10025425 === 252%2520.012.52 =×=

53. 6.96.91069 6.9% 100100101000 ==⋅= 6.9%6.90.010.069 =×=

54. 8.18.11081 8.1% 100100101000 ==⋅= 8.1%8.10.010.081 =×=

55. 0.050.051005151 0.05% 10010010010,000200052000 ==⋅=== 0.05%0.050.010.0005 =×=

56. 0.120.1210012343 0.12% 10010010010,000250042500 ==⋅=== 0.12%0.120.010.0012 =×=

57. 0.450.45100%45% =×=

58. 0.080.08100%8% =×=

59. 1.81.8100%180% =×=

60. 2.972.97100%297% =×=

61. 0.0060.006100%0.6% =×=

62. 0.00010.0001100%0.01% =×=

63. 2 0.40.4100%40% 5 ==×=

64. 1 0.3330.333100%33.3% 3 ==×=

65. 3 0.750.75100%75% 4 ==×=

66. 7 0.350.35100%35% 20 ==×=

67. 5 0.8330.833100%83.3% 6 ==×=

68. 53 1.061.06100%106% 50 ==×=

69. Let B represent voters in 2008 and let A represent voters in 1980. Then, the percent change in the number of voters is 132.686.546.1 0.533 or about 53.3%. 86.586.5 BA A

70. Let B represent the number of master’s degrees received in 2010 and let A represent the number of master’s degrees received in 2005. Then, the percent change in the number of master’s degrees received is 659,000594,00065,000 0.109or about 10.9%. 594,000594,000

71. Calculate the value of 4% of 950, then add the value to 950. Thus, () 4% of 950.0495038. == Then, 95038$988 per credit. +=

72. Calculate the value of 8% of 125, then add the value to 125. Thus, () 8% of 125.0812510. == Then, 12510$135 per credit. +=

73. To calculate the total area of Wisconsin, let x represent the unknown number and note that 13.6 is 38% of the unknown number. Then, 0.3813.6 0.3813.635.8. 0.380.38 x xx =⇒=⇒≈ Thus, the total area of Wisconsin is about 35.8 million acres.

74. Let x be the number of female military personnel in 2008. 1.0038203,375 0.0038203,3751.0038203,375202,605. 1.00381.0038 x xxxxx +=−⇒=⇒=⇒≈

75. The percent change from $1.20 to $1.50 is, 1.501.20 10025 1.20 ⋅= Thus, the percent change from $1.20 to $1.50 is 25%. The percent change from $1.50 to $1.20 is 1.201.50 10020 1.50 ⋅=− Thus, the percent change from $1.50 to $1.20 is 20%.

76. Given the percent change is 30% when the amount increases from 1A to 2 , A then 21

So the percent charge is not 30%, it is about

77. 428 miles drtdd =⇒=⋅⇒=

78. 702.5175 miles drtdd =⇒=⋅⇒=

79. 100050 100050 2020 feetsecond 5050 r drtrrr =⇒=⋅⇒=⇒=⇒=

80. 12505 12505250250 milesday 55 r drtrrr =⇒=⋅⇒=⇒=⇒=

81. 20040 2004055 hours 4040 t drtttt =⇒=⇒=⇒=⇒=

82. 170010 170010170170 seconds 1010 t drtttt =⇒=⇒=⇒=⇒=

83. Given that the distance traveled (d) is 255 and that the time spent traveling (t) is 4.25 hours, calculate the speed of the car (r).

Then, 2554.25 2554.256060 mileshour. 4.254.25 r drtrrr =⇒=⋅⇒=⇒=⇒=

84. Given the distance and the time, calculate the speed. Then, 7155.5 7155.5 5.55.5 r r =⋅⇒=⇒ 130130 mileshour. rr =⇒=

85. Let the slower runner be standing still. Then, the faster runner will be traveling at 02 mph. + Then, this problem is equivalent to solving how long it takes the faster runner to travel 3 4 of a mile. Using the drt = formula: 3312133 2. 4421288 tttt =⇒⋅=⋅⇒=⇒= So, in 3 8 hour the faster runner will be 3 4 mile ahead of the slower runner.

86. Since the athlete runs 1 3 of an hour at 6 mph, the athlete runs 1 62 3 ⋅= miles in the first 1 3 of an hour. Since the athlete runs a total of 8 miles, the athlete runs 826 −= miles in the remaining 12 1 33 −= of an hour. Using the formula: drt = 2323 6699. 3232 rrrr =⋅⇒⋅=⋅⋅⇒=⇒=

Therefore, the second speed is 9 miles/hour.

87. Let t represent the amount of time spent running 5 mph. Since the total time spent running was 1.1 hours, then 1.1 t represents the amount of time running at 8 mph. Using the drt = formula, the distance run will equal the sum of () 5 and 81.1.tt

Thus, () 7581.1758.8878.83 ttttt =+−⇒=+−⇒=−⇒

378.833378.83778.8731.80.6. 3 ttttttt +=−+⇒+=⇒+−=−⇒=⇒==

Therefore, the athlete ran at 5 mph for 0.6 hour and ran at 8 mph for () 1.10.60.5 hour. −=

88. The distance the bus travels is 160295455 += miles. The bus travels at 70 mph. Then, 45570 455706.56.5. 7070 t ttt =⇒=⇒=⇒= Therefore, it will take the bus 6.5 hours to be 295 miles west of the border.

89. Since the plane is already 300 miles west of Chicago, it will have to fly 21753001875 −= miles to be 2175 miles west of Chicago. The plane is traveling at 500 mph. Then, 1875500 18755003.753.75. 500500 t ttt =⇒=⇒=⇒= Therefore, it will take the plane 3.75 hours to be 2175 miles west of Chicago.

90. Let x represent the speed of the slower car and 6 x + represent the speed of the faster car. Then, the distance of 171 miles will equal the speed of the slower car multiplied by the time added to the speed of the faster car multiplied by the time. Therefore, ()()() 1711.561.51711.51.59 xxxx =++⇒=++⇒ 1623 17139171939916235454. 33 x xxxxx =+⇒−=+−⇒=⇒=⇒=⇒= Thus, 54 mph is the speed of the slower car and 54660 += mph is the speed of the faster car.

91. Let x represent the amount of water that should be added. Note that there is no salt in pure water and that we will add the amount of pure water to the 3% salt solution to obtain a 1.2% solution. Therefore, set up the equation so that the amount of salt on both sides of the equation is equal. Thus, ()()()() 0.00200.03200.0120.000.60.0120.24 xxxx+=+⇒+=+⇒

0.360.012 0.60.240.0120.240.240.360.0123030. 0.0120.012 x xxxx −=+−⇒=⇒=⇒=⇒= Therefore, 30 ounces of water should be added.

92. Let x represent the amount of water that should be added. Note that there is no hydrochloric acid in pure water and that we will add the amount of pure water to the 15% solution to obtain a 2% solution. Therefore, set up the equation so that the amount of hydrochloric acid on both sides of the equation is equal. Thus, ()()()() 0.00500.15500.020.007.50.021 xxxx+=+⇒+=+⇒

7.510.0211 x −=+−⇒

6.50.02 6.50.02325325. 0.020.02 x xxx =⇒=⇒=⇒= Therefore, 325 ml of water should be added.

93. Let x represent the amount of the loan at 6% and let 1000 x + represent the amount of the loan at 5%. The total interest for one year is $215 and this is the sum of the interest paid on the two loans. Therefore: () 0.060.0510002150.060.0550215 xxxx ++=⇒++=⇒

0.11505021550 x +−=−⇒ 0.11165 0.111651500. 0.110.11 x xx =⇒=⇒= Therefore, the amount of the loan at 6% interest is $1500 and the amount of the loan at 5% interest is 15001000$2500. +=

94. Let x represent the interest rate for the $3000 loan and let 0.03 x represent the interest rate for the $5000 loan. The total interest cost for the year will equal the sum of the interest for each loan. Therefore: () 300050000.0355030005000150550 xxxx +−=⇒+−=⇒

8000150150550150 x −+=+⇒

8000700 80007000.0875. 80008000 x xx =⇒=⇒= Therefore, the interest rate for the $3000 loan is 8.75% and the interest rate for the for the $5000 loan is 0.08750.030.0575 or 5.75%. −=

95. Let x represent the amount of 70% antifreeze. Then, the 45% antifreeze mixture is the sum of the 70% mixture and the 30% mixture. Therefore, ()()() 0.7100.3100.45 xx +=+⇒

0.730.454.5 xx+=+⇒ 0.7330.454.53 xx +−=+−⇒

0.70.451.50.70.450.450.451.5 xxxxxx =+⇒−=−+⇒ 0.251.5 0.251.56. 0.250.25 x xx =⇒=⇒= Therefore, 6 gallons of 70% antifreeze should be mixed with 10 gallons of 30% antifreeze to obtain the 45% mixture.

96. Since there is a total of 50 gallons of mixture, let x represent the gallons of 65% antifreeze. Then 50 x represent the 20% antifreeze. Then: ()() 0.650.2050500.56 xx+−=⇒

0.65100.2028 xx+−=⇒ 0.4510102810 x +−=−⇒

0.4518

0.451840. 0.450.45 x xx =⇒=⇒=

Therefore, 40 gallons of 65% antifreeze should be mixed with 10 gallons of 20% antifreeze.

97. Let x represent the amount of 2.5% cream. Then, the 1% cream is the sum of the 2.5% cream and the base cream ()0%.Therefore ()()() 0.025150150.01 xx+=+⇒

0.0250.010.150.0250.010.010.010.15 xxxxxx =+⇒−=−+⇒

0.0150.15

0.0150.1510. 0.0150.015 x xx =⇒=⇒= Therefore, 10 grams of 2.5% hydrocortisone cream should be mixed with the base to obtain the 1% cream.

98. Let x represent the balance on the card with the 1.75% interest rate. Then the balance on the other card is 600. x The total interest for the month will equal the sum of the interest for each card.

Therefore: () 0.01750.01560049.50 xx+−= 0.01750.015949.50 xx ⇒+−=⇒

0.0325949.500.03259949.509 xx −=⇒−+=+⇒

0.032558.50

0.032558.501800. 0.03250.0325 x xx =⇒=⇒= Therefore, the balance on the 1.75% card is $1800 and the balance on the 1.5% card is $1800$600 $1200. =

Group Activity Working with Real Data

1. ()()()()() 2 Area length width . Then, 1211132 cm. AlwAlw =×===

2. ()()()()()()() 3 Volume length width height . Then, 12115660 cm. VlwhVlwh =××===

3. The area of the bottom of the box is 50 square centimeters and the formula for area is .Alw = Thus, 50. lw = Since 10050 1005022 cm. 5050 h Vlwhhhh =⇒=⇒=⇒=⇒=

4. Because one cubic centimeter weighs 2.7 grams, 3 5.4 2 cm. 2.7 = Thus, the volume of the aluminum foil is 3 2 cm.

5. Because the sheet of foil weighs 5.4 grams, from the previous problem the volume of the foil is 3 2 cm. Then, insert this information into the volume formula .Vlwh = Thus, ()() 2502021000 Vlwhhh =⇒=⇒=⇒ 2100022 0.002 cm. 1000100010001000 h hh =⇒=⇒==

Section 2.4 Formulas

1. formula

2. lw

3. 1 2 bh

4. 1 360

5. 360

6. 180

7. lwh

8. 222 lwwhlh ++

9. 2 rπ

10. 2 rπ

11. 2 rhπ

12. () 1 2 abh +

13. 2 . Thus, 6318 ft. AlwA==⋅=

14. 2 . Thus, 42.510 yd. AlwA==⋅=

15. 2 11 . Thus, 63 9 in. 22 AbhA==⋅⋅=

16. 2 113 . Thus, 31 mi. 222 AbhA==⋅⋅=

17. 222 . Thus, 41650.3 cm. ArA=π=π=π≈

18. 222 . Thus, 3928.3 km. ArA=π=π=π≈

19. () () () 2 111 . Thus, 56211211 mm. 222 AabhA =+=+==

20. () () () 2 111 . Thus, 432727 ft. 222 AabhA =+=+==

21. 2 . Thus, 13791 in. AlwA==⋅=

22. 2 11 .Thus,972324 cm. 22 AbhA==⋅⋅=

23. Convert yards to feet in order to keep the units consistent. Therefore, 7 yards7321 feet. =⋅= Alw = Thus, 2 215105 ft. A =⋅= Or, convert feet to yards to obtain 5 3 yards. Then 2 535 7 yd. 33 Alw==⋅=

24. 2 11 . Thus, 12636 mm. 22 AbhA==⋅⋅=

25. 2.Cr =π Because the circle has a diameter of 8 inches, the radius is 8 4 inches. 2 == Thus, 224825.1 inches. Cr=π=π=π≈

26. 222 . Thus, 981254.5 ft. ArA=π=π=π≈

27. The total area of the lot is the sum of the area of the square and the area of the triangle. The area of the square is 2 52522704 ft. lw =⋅= The area of the triangle is 2 11 73521898 ft. 22 bh =⋅⋅= Thus, the area of the lot is 2 189827044602 ft. +=

28. The total area of the lot is the sum of the area of the rectangle and the areas of the two triangles. The area of the rectangle is 2 60201200 yd. lw =⋅= The area of the triangle on the left is

2 11 1020100 yd. 22 bh =⋅⋅= The area of the triangle on the rights is

2 11 3020300 yd. 22 bh =⋅⋅= Thus, the total area is 2 12001003001600 yd. ++=

29. The sum of the angles of a triangle is 180º. Let the unknown angle be represented by x. Then, 754018075407540180754065. xxx ++=⇒++−−=−−⇒= Thus, the third angle is 65º.

30. The sum of the angles of a triangle is 180º. Let the unknown angle be represented by x. Then, 3025180302530251803025125. xxx ++=⇒++−−=−−⇒= Thus, the third angle is 125º.

31. The sum of the angles of a triangle is 180º. Let the unknown angle be represented by x. Then, 237618023762376180237681. xxx ++=⇒++−−=−−⇒= Thus, the third angle is 81º.

32. Because there are three angles in any triangle and because the measures of the angles in an equilateral triangle are equal, 3180 180318060. 33 x xxxxx ++=⇒=⇒=⇒= Thus, the measure of each angle is 60º.

33. Because the sum of the angles of a triangle is 180, 5180 221805180 55 x xxxx ++=⇒=⇒=⇒

36. x = Thus, the value of x is 36º.

34. 18180 34111801818010. 1818 x xxxxx ++=⇒=⇒=⇒= Thus, the value of x is 10º.

35. Let x represent the largest angle. Then, 115351803 180180 3335315 xxxxx ++=⇒=⇒⋅=⋅⇒ 540 108. 5 xx=⇒= Thus, the largest angle has a measure of 108º and the two small angles each have measure 1108108 36º. 313 ⋅==

36. Let x represent the largest angle. Then, 10 x represents the second largest angle and 50 x represents the smallest angle. Then, ()()10501801050180xxxxxx +−+−=⇒+−+−=⇒ 3240 3601803606018060324080. 33 x xxxx −=⇒−+=+⇒=⇒=⇒= Thus, the largest angle has measure 80º, the second largest angle has measure 801070º −= and the smallest angle has measure 805030º. −=

37. 2.Cr =π Since the diameter of the circle is 12 inches, the radius is 12 6 inches. 2 = Then,

261237.7 inches. C =π=π≈ Then, 222 636113.1 in. Ar=π=π=π≈

38. 2.Cr =π Then, 55 27.9 feet. 42 C ⎛⎞ =π=π≈

39. 2.Cr =π Then, set C equal to 2 π and solve for r 22 2211 inch. 22 r rrr ππ π=π⇒=⇒=⇒= ππ Then, 2 . Ar =π Because 1, substitute 1 for and solve for .rrA = ()2 1. A =π=π Thus, the area is equal to π, which is approximately equal to 2 3.14 in.

40. 2.Cr =π Then, set C equal to 13π and solve for r. 1321313 132 2222 r rrr πππ π=π⇒=⇒⋅=⇒=⇒ πππ 13 2 r = Thus, the radius is 13 6.5 feet. 2 = Then, ()2 22 . Thus, 6.542.25132.7 ft. ArA=π=π=π≈

41. 3 . Thus, V2212102640 in. Vlwh==⋅⋅= Surface area equals 222. lwlhwh ++ Thus, 2 2221222210212105284402401208 in. S =⋅⋅+⋅⋅+⋅⋅=++=

42. 3 . Thus, 53690 ft. VlwhV==⋅⋅= Surface area equals 222. lwlhwh ++ Thus, 2 253256236306036126 ft. S =⋅⋅+⋅⋅+⋅⋅=++=

43. Convert yards to feet. Then, 3 2223 yard32 feet. Then, 22 ft. 3332 Vlwh =⋅===⋅⋅= Surface area equals 222. lwlhwh ++ Thus, 2 2323882 2222262810 ft. 3232333 S =⋅⋅+⋅⋅+⋅⋅=++==

44. 3 . Thus, 1.20.80.60.576 m. VlwhV==⋅⋅= Surface area equals 222. lwlhwh ++ Thus, 2 21.20.821.20.620.80.61.921.440.964.32 m. S =⋅⋅+⋅⋅+⋅⋅=++=

45. 223 . Thus, 254520 in. VrhV=π=π⋅=π⋅⋅=π

46. 2 23 13133 . Thus, in. 22428 VrhV ⎛⎞⎛⎞⎛⎞⎛⎞ =π=π=π=π

47. Convert feet to inches to obtain 12inches 2 feet2feet24 inches. 1oot h f ==⋅= Then, 22 . Thus, 524 VrhV=π=π⋅= 3 2524600 in. π⋅⋅=π

48. Convert yards to feet to obtain 3feet 1.5 yards1.5yards4.5 feet. 1yard h ==⋅= Then,

49. (a) 2 2 3 35954545 . Thus, 4.4 in. 421623232 VrhV

(b) Because there is about 4.4 cubic inches of volume in the can, the number of fluid ounces is ()() 4.40.5542.4 fl oz. ≈

50. The volume formula for a cylindrical container is given by 2 .Vrh =π Because the diameter of the barrel is 37177 1 feet, the radius is feet. Thus, 44248

() () 2 2 749147 33 86464 Vrh

51. 369 936993693692332 333 yx xyxxyxyxyxyx +=⇒−+=−⇒=−⇒=−⇒=−⇒=−+

52. 2102 22102221022102 222 55 yx xyxxyxyx yxyx −−=⇒−+−=+⇒−=+⇒=+⇒ =−−⇒=−−

53. 3124 43124431243124 333 44 44 33 yx xyxxyxyx yxyx +=⇒−+=−⇒=−⇒=−⇒ =−⇒=−+

54. 2225 52225522252225 222 55 1111 22 yx xyxxyxyx yxyx −=⇒−−=−⇒−=−⇒=−⇒ =−+⇒=−

55. The formula is given as .Alw = To solve for w, proceed as follows: AlwA Alww lll =⇒=⇒=

56. The formula is given as 1 2 Abh = To solve for b, proceed as follows: () 11 22 22 AbhAbh =⇒=⇒

22 2. AbhA Abhb hhh =⇒=⇒=

57. The formula is given as 2 Vrh =π To solve for h, proceed as follows: 2 2 22 Vrh Vrh rr π =π⇒=⇒ ππ 2 V h r = π

58. The formula is given as 2 1 . 3 Vrh =π To solve for h, proceed as follows:

1122 33 33 VrhVrh =π⇒=π⇒ 2 2 222 33 3. VrhV Vrhh rrr π =π⇒=⇒= πππ

59. The formula is given as () 1 2 Aabh =+ To solve for a, proceed as follows: () 1 2 Aabh=+⇒

1222 222 2 abh AAA AabhAabhabbabb hhhh + =+⇒=+⇒=⇒=+⇒−=+−⇒ 2 . A ab h =−

60. The formula is given as 2.Cr =π To solve for r, proceed as follows: 2 2. 222 CrC Crr π =π⇒=⇒= πππ

61. The formula is given as .Vlwh = To solve for w, proceed as follows: Vlwh Vlwh lhlh =⇒=⇒ V w lh =

62. 222 22222222 222 PlwPl PlwPlllwPlww =+⇒−=−+⇒−=⇒=⇒=

63. 2222 22 abcabc sssabcsacabcac ++++ =⇒=⋅⇒=++⇒−−=++−−⇒

22 sacbbsac −−=⇒=−−

64. 333333 33 xyxy tttxytyxyytyxxty =⇒=⋅⇒=−⇒+=−+⇒+=⇒=+

65. () 11acacbbacbbac bbbb ⎛⎞ −=⇒−=⇒−=⇒=− ⎜⎟ ⎝⎠

66. 55555xzxz yyxzyxxzyxzyx yyyy ⎛⎞ +=⇒+=⇒+=⇒−+=−⇒=−

67. () abcdadabadcdadadabadcdabdcd =+⇒−=+−⇒−=⇒−=⇒ () () () abdcdcd a bdbdbd =⇒=

68. 22222222222 SlwlhwhSlhlwlhwhlhSlhlwwh =++⇒−=++−⇒−=+⇒ () () 22 222 222 (22)(22)(22)(22) wlh SlhSlhSlh Slhwlhww lhlhlhlh + −=+⇒=⇒=⇒= ++++

69. Because the perimeter equals the lengths of the four sides, 22. PWL =+ Thus, 22 PWL=+⇒ () 230 402524010240101021023015 22 L LLLLL =+⇒=+⇒−=+−⇒=⇒=⇒= Thus, the length of the rectangle is 15 inches.

70. Let x represent the length of the third side. Thus, 572157572157 xx ++=⇒++−−=−−⇒

9. x = Thus, the length of the third side is 9 feet.

71. The formula for GPA is given by 432 . abcd abcdf +++ ++++

()()()() 43034521214 120135244283 2.98. 304512449595 +++ +++ ==≈ ++++ Thus, the GPA is 2.98.

72. The formula for GPA is given by 432 . abcd abcdf +++ ++++

()()()() 4703352510 280105100395 3.59. 7035500110110 +++ +++ ==≈ ++++ Thus, the GPA is 3.59.

73. The formula for GPA is given by 432 . abcd abcdf +++ ++++

()()()() 40360280110 018016010350 2.24. 06080106156156 +++ +++ ==≈ ++++ Thus, the GPA is 2.24.

74. The formula for GPA is given by 432 . abcd abcdf +++ ++++

()()()() 43352810 121516043 1.13. 3580223838 +++ +++ ==≈ ++++ Thus, the GPA is 1.13.

75. To convert Celsius to Fahrenheit temperature, the formula given is 9 32. 5 CF +=

() 9225160385

253277ºF. 5555 FFFF +=⇒+=⇒=⇒=

76. To convert Celsius to Fahrenheit temperature, the formula given is 9 32. 5 CF +=

() 99001601060

10032212ºF. 5555 FFFF +=⇒+=⇒=⇒=

77. To convert Celsius to Fahrenheit temperature, the formula given is 9 32. 5 CF +=

() 9360160200

403240ºF. 5555 FFFF −+=⇒+=⇒=⇒=−

78. To convert Celsius to Fahrenheit temperature, the formula given is 9 32. 5 CF +=

() 90160160 03232ºF. 5555 FFFF +=⇒+=⇒=⇒=

79. To convert Fahrenheit to Celsius temperature, the formula given is () 5 32. 9 CF=−

() () 5545

233295ºC. 999 CCCC =−⇒=−⇒=⇒=−

80. To convert Fahrenheit to Celsius temperature, the formula given is () 5 32. 9 CF=−

() () 55333

98.63266.637ºC. 999 CCCC =−⇒=⇒=⇒=

81. To convert Fahrenheit to Celsius temperature, the formula given is () 5 32. 9 CF=−

() () 55180

4323620ºC. 999 CCCC =−−⇒=−⇒=⇒=−

82. To convert Fahrenheit to Celsius temperature, the formula given is () 5 32. 9 CF=−

() () 55315

31326335ºC. 999 CCCC =−−⇒=−⇒=⇒=−

83. The formula for calculating gas mileage is , D M G = where D is the distance and G is the gasoline used. Therefore, 88,04387,625418 11 mpg. 3838 MMM =⇒=⇒=

84. The formula for gas mileage is , D M G = where D is the distance and G is the gasoline used. Therefore, 578578 343434578 GGG GG ⎛⎞ =⇒=⇒= ⎜⎟ ⎝⎠ 34578 17 gal. 3434 G G ⇒=⇒=

85. 12 55 x DD=⇒=⇒ 2 22.4 miles. 5 D ==

86. 2.5 55 xx D =⇒=⇒ () 52.5512.512.5 seconds. 5 x xx =⋅⇒=⇒=

Checking Basic Concepts Sections 2.3 and 2.4

1. (a) 336 33612 33 x xx =⇒=⇒= (b) ()() 35433535433581818 xxxxx −=⇒−−=−⇒−=⇒−=−⇒=−

2. ()()12933393333933396 xxxxxx ++++=−⇒+=−⇒+−=−−⇒=−⇒

396 32. 33 x x =⇒=− The three consecutive integers are 32,31,30.

3. 9.5%0.095 =

4. 51 11.25125% 44 ===

5. Convert 38.8% to the decimal 0.388 and let x represent the unknown rate. Therefore, 0.38846,357.xx−= Thus, 0.38846,3570.61246,357xxx −=⇒=⇒

0.61246,357 75,747. 0.6120.612 x x =⇒≈ Thus, the rate in 2009 was about 75,747.

6. Use the formula , Drt = where D is distance, r is the speed and t is the time. Thus, 39060t =⇒

39060 6.5. 6060 t t =⇒= Thus, the travel time is 6.5 hours.

7. Let x represent the amount of the loan at 7% and 2000 x + represent the amount of the loan at 6%. Thus, () 0.070.0620005100.070.06120510 xxxx ++=⇒++=⇒

0.13120120510120 x +−=−⇒

0.13390 0.133903000. 0.130.13 x xx =⇒=⇒= Thus, the loan at 7% was $3000 and the loan at 6% was $5000.

8. The formula for gas mileage is , D M G = where D is the distance and G is the gasoline used.

Therefore, 50450428504 28282850418 gal. 2828 G GGGG GG ⎛⎞ =⇒=⇒=⇒=⇒= ⎜⎟

9. The area of a triangle is given by 1 2 Abh = Thus, () 11363 366363 2233 h Abhhh =⇒=⇒=⇒=⇒ 12. h = Thus, the height of the triangle is 12 inches.

10. The area of a circle is given by 2 Ar =π Thus, ()2 22 3928.3 ft. ArAA =π⇒=π⇒=π≈ The circumference of a circle is given by 2.Cr =π Thus, 223618.8 feet. CrCC =π⇒=π⇒=π≈

11. 6180 231806180 30. 66 x xxxxx ++=⇒=⇒=⇒= Thus, the value of x is 30º.

12. 22 22222 ArrlAr ArrlArrrrlArrll rrr −ππ−π =π+π⇒−π=π−π+π⇒−π=π⇒=⇒= πππ

Section 2.5 Linear Inequalities

1. ;;; <≤>≥

2. greater than; less than 3. solution

4. equivalent

5. True

6. True

7. number line

8. > 9. < 10. > 11. 12. 13. 14. 15. 16. 17. 18.

19. 0 x <

20. 2 x ≥−

21. 3 x ≤

22. 5 x >−

23. 10 x ≥

24. 20 x <−

25. [ ) 6, ∞

26. () ,3−∞

27. () 2, −∞

28. [ ) 1, ∞

29. ( ] ,7−∞

30. () ,5−∞−

31. Substitute x with 4 in order to test the inequality. Thus, 5545595. x +>⇒+>⇒> Because this inequality statement is true, 4 x = is a solution.

32. Substitute x with 2 in order to test the inequality. Thus, 3(2)868 −−≤−⇒≤− . Because this inequality statement is not true, 2 x =− is not a solution.

33. Substitute x with 5 in order to test the inequality. Thus, 5(5)252525. ≥⇒≥ Because this inequality statement is true, 5 x = is a solution.

34. Substitute y with 3 in order to test the inequality. Thus,4(3)351235155 −−≤⇒−−≤⇒−≤

Because this inequality statement is true, 3 y =− is a solution.

35. Substitute y with 3 in order to test the inequality. Thus, 3(3)5895848 −+≥−⇒−+≥−⇒−≥−

Because this inequality statement is true, 3 y =− is a solution.

36. Substitute z with 2 in order to test the inequality. Thus, ()() 27362(9)3(4)912 −+>−⇒−>⇒−>

Because this inequality statement is not true, 2 z = is not a solution.

37. Substitute z with 4 in order to test the inequality. Thus, () 5413(4)75(3)1271519 −+<−−⇒−<−−⇒−<− Because this inequality statement is not true, 4 z =− is not a solution.

38. Substitute t with 3 5 in order to test the inequality. Thus, 331391539524222 1 2525102551010510555

Because this inequality statement is true, 3 5 t = is a solution.

39. 2 x >−

40. 2 x ≥

41. 1 x <

42. 3.8 x ≤

43. To complete the table, insert the x value into 26 x −+ whenever there is a missing value in the table. Thus, () 26226462; x −+⇒−+⇒−+= () 26236660; x −+⇒−+⇒−+= 262(4)6862. x −+⇒−+⇒−+=− Thus, the missing values in the table are 2, 0 and 2.

See Figure 43.

From the table, we see that 260 whenever 3. Thus, the solution to the inequality is 3. xxx −+≤≥≥

Figure 43

Figure 44

44. To complete the table, insert the x value into 31 x whenever there is a missing value in the table. Thus, () 31311312; x −⇒−⇒−= () 31321615; x −⇒−⇒−= ()()31331918; 3134112111.xx −⇒−⇒−=−⇒−⇒−= Thus, the missing values in the table are 2, 5, 8 and 11. See Figure 44.

From the table, we see that 318 whenever 3. Thus, the solution to the inequality is 3. xxx −<<<

45. To complete the table, insert the x value into 5 and 7 xx −+ whenever there is a missing value in the table. ()()()5527; 5516; 5505.xxx −⇒−−=−⇒−−=−⇒−=

Thus, the missing values in the table that correspond to 5 x are 7, 6 and 5. ()()()7275; 7176; 7077. xxx +⇒−+=+⇒−+=+⇒+=

Thus, the missing values in the table that correspond to 7 x + are 5, 6 and 7. See Figure 45. From the table, we see that 57 xx −>+ whenever 1. x <− The solution to the inequality is 1. x <−

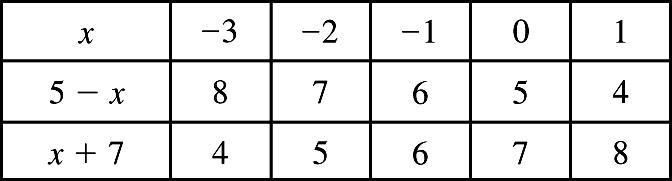
Figure 45

Figure 46

46. To complete the table, insert the x value into ()23 x and ()32 x whenever there is a missing value in the table. ()() () ()()() () () 232322510; 23231248;xx −⇒−−⇒=−⇒−−⇒= ()()() ()()()() 23 230236; 23231224;xx −⇒−⇒=−⇒−⇒= ()()() 23232212. x −⇒−⇒= Thus, the missing values that correspond to ()23 x are 10, 8, 6, 4 and 2. ()()()()()() 323223412; 32312339;xx −−⇒−−−⇒−−=−−⇒−−−⇒−−= ()()()()()() 32302326; 32312313;xx −−⇒−−⇒−−=−−⇒−−⇒−−= ()()() 32322300. x −−⇒−−⇒−= Thus, the missing values that correspond to ()32 x are 12, 9, 6, 3 and 0. See Figure 46. From the table, we see that 2(3)3(2) xx −≥−− whenever 0. x ≥ Thus, the solution to the inequality is 0. x ≥

47. 3033033.xxx −>⇒−+>+⇒> See Figure 47.

Figure 47

48. 6366363.xxx +<⇒+−<−⇒<− See Figure 48.

Figure 48

49. 35355522. yyyyyy −≤⇒−−+≤−+⇒−≤⇒≥− See Figure 49.

Figure 49

Figure 50

50. 810810101022. yyyyyy −≥⇒−−+≥−+⇒−≥⇒≤− See Figure 50.

51. 1241244488. zzzz <+⇒−<−+⇒<⇒> See Figure 51.

Figure 51

52. 21721717. zzzzzzz ≤+⇒−≤−+⇒≤ See Figure 52.

Figure 52

53. 521051022101025 ttttttt −≥−⇒−−+≥−−+⇒−≥⇒ 5. t ≤− See Figure 53.

Figure 53

Figure 54

Chapter 2 Linear Equations and Inequalities

54. 231233311. ttttttt −>−+⇒−+>−++⇒> See Figure 54.

55. 210 2105. 22 x xx <⇒<⇒< See Figure 55.

Figure 55

56. 39 393. 33 x xx >⇒>⇒> See Figure 56.

57. 11 12212. 22 ttt −≥⇒−⋅≤−⋅⇒≤− See Figure 57.

Figure 57

58. 566 56. 555 t tt −≤−⇒≥⇒≥ See Figure 58.

59. 3 4 335313 55. 44554520 y yyyy ⎛⎞ >−⇒−<⇒>⇒>⋅−⇒>− ⎜⎟

Figure 56

Figure 58

See Figure 59.

Figure 59

Figure 60

60. 1171107 101070. 771711 yyyy ⎛⎞⎛⎞ ≥−⇒−≤⇒−−≥−⇒≥− ⎜⎟⎜⎟ ⎝⎠⎝⎠ See Figure 60.

61. 2112712714 377317313 zzzz ⎛⎞⎛⎞ −≤⇒≥−⇒≥−⇒≥− ⎜⎟⎜⎟ ⎝⎠⎝⎠

Figure 61

62. 310310110 1111. 1031033 zzz ⎛⎞⎛⎞ −<⇒−−>−⇒>− ⎜⎟⎜⎟ ⎝⎠⎝⎠

63. { }67667611 xxxxx +>⇒+−>−⇒>⇒>

64. { }41441433 xxxxx +<⇒+−<−⇒<−⇒<−

65. {} 321 32177 33 x xxxx −≤⇒≥⇒≥−⇒≥−

66. {} 420 42055 44 x xxxx ≥−⇒≥⇒≥−⇒≥−

See Figure 61.

Figure 62

See Figure 62.

67. 212 23923393212 22 x xxx −<⇒−+<+⇒<⇒< { }66xxx ⇒<⇒<

68. 5444544444540 xxx −+<⇒−+−<−⇒−< {} 540 88 55 x xxx ⇒>⇒>−⇒>−

2.5: Linear Inequalities

69. 321 31223112213217 33 x xxxx +<⇒+−<−⇒<⇒<⇒<

70. 55 45944594551 55 x xxxx +≤⇒−+≤−⇒≤⇒≤⇒≤

71. 3334344 56556511 4443433 xxxxx ⎛⎞⎛⎞ −≥⇒−−≥−⇒−≥⇒−−≤−⇒≤− ⎜⎟⎜⎟ ⎝⎠⎝⎠

72. 22252550 10010100101010 5552522 xxxxx ⎛⎞⎛⎞ −>⇒−−>−⇒−>−⇒−−<−−⇒<⇒ ⎜⎟⎜⎟ ⎝⎠⎝⎠ 25 x <

73. 23939 45626245662456239 222 x xxxxx >−⇒−<⇒−−<−⇒−<⇒>⇒>−

74. 1166 6931131169331169311666 1111 x xxxxx ≥−⇒−≤⇒−−≤−⇒−≤⇒≥⇒≥−

75. 52315323312212221223 xxxxxxxxx −≤+⇒−−≤−+⇒−≤⇒−+≤+⇒≤⇒ 233 222 x x ≤⇒≤

76. 12125312312533151251511251 xxxxxxxx +<−⇒++<−+⇒+<⇒+−<−⇒ 15248 1524 15155 x xx <⇒<⇒<

77. 2423242322423224242324 xxxxxxxx −+<+⇒−−+<−+⇒−+<⇒−+−<−⇒ 211 21 2 22 x xx −<−⇒>⇒>

78. 6416416516651655 xxxxxxxxx −≤+⇒−−≤−+⇒−≤⇒−−≤−⇒−≤−⇒ 55 1 55 x x ≥⇒≥

79. ()()13213631336416 xxxxxxxxx −+≥−⇒−−≥−⇒−−−≥−−⇒−−≥−⇒ 455 4116145 444 x xxx −−+≥−+⇒−≥−⇒≤⇒≤

80. ()() 52235102652102267106 xxxxxxxxx +>−−⇒+>−+⇒++>−++⇒+>⇒ 744 7101061074 777 x xxx +−>−⇒>−⇒>⇒>−

81. ()() 321536353633533335 xxxxxxxxx +>−−⇒+>−+⇒−+>−+−⇒+>−⇒ 388 3335338 333 x xxx +−>−−⇒>−⇒>⇒>−

82. () 43721421614620466620 xxxxxxxxxx ≥−−+⇒≥−++⇒≥−⇒−≥−−⇒ 220 22010 22 x xx −≥−⇒≤⇒≤

Chapter 2 Linear Equations and Inequalities

83. 1.60.40.41.60.40.40.40.41.20.40 xxxxxxx +≤⇒−+≤−⇒+≤⇒ 1.20.41 1.20.40.400.41.20.4 1.21.23 x xxx +−≤−⇒≤−⇒≤⇒≤−

84. 5.11.10.10.15.10.11.10.10.10.151.10.1 xxxxxxx −+<−⇒−++<−+⇒−+<⇒ 511 51.11.10.11.151 555 x xxx −+−<−⇒−<−⇒>⇒>

85. 0.80.510.50.80.50.510.80.50.50.50.51 xxxxxxxxx −<+−⇒−<+⇒−−<−+⇒ 0.31.5 0.30.510.30.50.510.50.31.55 0.30.3 x xxxx −<⇒−+<+⇒<⇒<⇒<

86. () 0.110.10.20.50.10.10.10.20.50.10.20.5 xxxxxx +−≤−⇒+−≤−⇒≤−⇒

0.10.5 0.10.20.20.20.50.10.55 0.10.1 x xxxxxx −≤−−⇒−≤−⇒≥⇒≥

87. 12114 42220 23333 xxxxxxxxx⎛⎞ −+≥⇒−−≥⇒−−−≥−⇒−−≥⇒ ⎜⎟ ⎝⎠ 443433 220222 334342 xxxx ⎛⎞⎛⎞ −−+≥+⇒−≥⇒−−≤−⇒≤− ⎜⎟⎜⎟

88. 4108888158 51058588 53333333 xxxxxxxxxx ⎛⎞ −>+⇒−>+⇒−−>−+⇒−−>⇒ ⎜⎟ ⎝⎠ 23323324 88 32332323 xxx ⎛⎞⎛⎞ −>⇒−−<−⇒<− ⎜⎟⎜⎟ ⎝⎠⎝⎠

89. 3215312115425 7771477777147714 xxxxxxx +>−−⇒++>−+−⇒+>−⇒ 4225245449749763 777147714147144714456 xxxxx ⎛⎞⎛⎞ +−>−−⇒>−−⇒>−⇒>−⇒>−⇒ ⎜⎟⎜⎟ ⎝⎠⎝⎠ 9 8 x >−

90. 51155151515551 1 633663183631818183 xxxxxxxx ⎛⎞ −≥−−⇒−≥−+⇒−+≥−++⇒ ⎜⎟ ⎝⎠ 56515115511512511 61818361836618361866182 xxxxxx −+≥⇒−≥⇒−−≥−⇒−≥−⇒−≥−⇒ 181118 9 11821 xx⎛⎞⎛⎞ −−≤−−⇒≤ ⎜⎟⎜⎟ ⎝⎠⎝⎠

91. () 522527272744 6674 3636636363777 xxxxxxx xx ⎛⎞ +≤⇒+≤⇒≤⇒≤⇒≤⇒≤⇒≤ ⎜⎟ ⎝⎠

92. () 332 1114144 424444 xxxxxx x ⎛⎞ −<⇒−<⇒<⇒<⇒< ⎜⎟ ⎝⎠

93. 616111618711 11111 73733373212121 xxxxxxx xxxx <+⇒−<−+⇒−<⇒−<⇒<⇒ () 11112121 211211121 21111111 xx xx ⎛⎞ <⇒<⇒<⇒< ⎜⎟ ⎝⎠

94. ()()() 5356 888888641641 848888 xxxxxx xx ⎛⎞ −≤⇒−≤⇒≤⇒≤⇒−≤⇒−−≥−⇒ ⎜⎟ ⎝⎠ 64 x ≥−

95. 60 x >

96. 60 x ≤

97. 21 x ≥

98. 21 x <

99. 40,000 x >

100. 40,000 x ≤

101. 70 x ≤

102. 70 x ≥

103. () 2525021025041050410105010 xxxxxx ++<⇒++<⇒+<⇒+−<−⇒ 440 44010 feet. 44 x xx <⇒<⇒<

104. The area of a triangle is 1 2 bh Substitute 12 for h and solve. () 11 12012120 22 bhb<⇒<⇒ 6120 612020. 66 b bb <⇒<⇒< Thus, the base of the triangle must be less than 20 inches.

105. Let x represent the unknown test score. Then, () 7474 80280274160 22 xx x ++⎛⎞≥⇒≥⇒+≥⇒ ⎜⎟ ⎝⎠ 74741607486. xx −+≥−⇒≥ Thus, the student needs a score of 86 or more to maintain an average of at least 80.

106. Let x represent the unknown test score. Then, () 65826582 703703 33 xx ++++⎛⎞≥⇒≥⇒ ⎜⎟ ⎝⎠ 658221014721014714721014763. xxxx ++≥⇒+≥⇒−+≥−⇒≥ Thus, the student needs a score of 63 or more to maintain an average of at least 70.

107. Let x represent the number of hours parked after the first half hour. We see that there is a $2.00 cost for the first half hour and $1.25 cost for each hour after that. Therefore, 21.258221.25821.256 xxx +≤⇒−+≤−⇒≤⇒ 1.256 4.8. 1.251.25 x x ≤⇒≤ This result would indicate that the student can park for as long as 4.8 hours beyond the first half hour for $8.00. However, because a partial hour of parking is charged as a full hour, the longest amount of time that the student could park beyond the first hour is 4 hours for a total of 4.5 hours.

108. Let x represent the number of parking hours in the student lot and y represent the number of parking hours in the nearby lot. Examine the first question and compare the results for x and y. Therefore, 2.5015 x +≤⇒ 2.502.5052.502.50. xx −+≤−⇒≤ Because a partial hour is charged as a full hour, the student could park in the lot for 3 hours. Then, 1.255 1.2554. 1.251.25 y yy ≤⇒≤⇒≤

Therefore, the student could park in this lot for 4 hours. Thus, for $5.00, the student could park for a longer time in the nearby lot. Now, examine the second question, 2.501112.502.50112.508.50. xxx +≤⇒−+≤−⇒≤ Because a partial hour is charged as a full hour, the student could park in the lot for 9 hours. Then, 1.2511 1.25118.8. 1.251.25 y yy ≤⇒≤⇒≤

Because a partial hour is charged as a full hour, the student could park in this lot for 8 hours. Thus, for $11.00, the student could park for a longer time in the first lot.

109. Let x represent the number of days. Then, () 250.20902002518200 xxxx +≤⇒+≤⇒

43200 x ≤⇒ 43200 4.65. 4343 x x ≤⇒≤ Because the car can not be rented for a partial day, the person can rent the car for 4 days.

110. Let x represent the number of miles. Then, 37200.25372020200.25 xx <+⇒−<−+⇒ 170.25 170.256868. 0.250.25 x xxx <⇒<⇒<⇒> Therefore, for more than 68 miles per day, the second rental agency is a better deal.

111. (a) 1.52000Cx=+ (b) 12 Rx = (c) () 121.5200010.52000PxxPx =−+⇒=−

(d) To yield a positive profit, revenue must be greater than cost. Then, 121.52000 xx>+⇒ 10.52000 121.51.51.5200010.52000190.476. 10.510.5 x xxxxxx −>−+⇒>⇒>⇒> Thus, 191 or more compact discs must be sold to yield a profit.

112. (a) 100,000890 Cx =+ (b) 1520 Rx =

(d) To yield a positive profit, revenue must exceed cost. Then, 1520100,000890 xx >+⇒

630100,000 1520890100,000890890630100,000158.73. 630630 x xxxxxx −>+−⇒>⇒>⇒>

Thus, 159 or more laptop computers must be sold to yield a positive profit.

113. (a) Set the distances equal and then solve for x. Then, 11 2434848. 68 xxxxx =+⇒=+⇒=

Thus, at 48 minutes the athletes are the same distance from the parking lot.

(b) 11 2434848. 68 xxxxx >+⇒>+⇒> Thus, after more than 48 minutes, the first athlete is farther from the parking lot than the second athlete.

114. 5.829 655.83665655.836655.8295. 5.85.8 x xxxx −>⇒−−>−⇒−>−⇒<⇒< Thus, at altitudes less than 5 miles, the dew point is greater than 36ºF.

115. Because 9019, Tx =− set an inequality statement with T equal to 4.5 and solve. Then, 1985.5 90194.59090194.5901985.54.5. 1919 x xxxx −<⇒−−<−⇒−<−⇒>⇒>

Thus, at altitudes more than 4.5 miles, the air temperature is less than 4.5ºF.

116. (a) 0.9614.47.20.9614.47.214.40.9614.414.421.60.96 Wxxxx =−⇒=−⇒+=−+⇒=⇒

21.60.96

22.522.5. 0.960.96 x xx =⇒=⇒= Thus, the length of bass is likely to be 22.5 inches. (b)

0.9621.6

0.9614.47.20.9614.414.47.214.40.9621.6 0.960.96 x xxx −<⇒−+<+⇒<⇒<⇒

22.5. x < Thus, bass less than 22.5 inches in length are likely to weigh less than 7.2 pounds

Checking Basic Concepts Section 2.5

2. 1 x <

3. Substitute 3 into the inequality. Thus 4(3)5151255151715. −−≤−⇒−−+≤−⇒−≤− Thus, 3 is a solution to the inequality.

4. () When 2, then 522549; x =−−−=+= () When 1, then 521527; x =−−−=+= () When 0, then 520505; x =−=−= () When 1, then 521523. x =−=−= Therefore, the numbers that complete the table are 9, 7, 5 and 3. See Figure 4.

Figure 4

From the table, we see that 527 whenever 1. xx −≤≥− Thus, the solution to the inequality is 1. x ≥−

5. (a) 5855853xxx +>⇒+−>−⇒>

(b) 5757175 252535 75755 xxxx ⎛⎞⎛⎞ −≤⇒−−≥−⇒≥−⇒≥− ⎜⎟⎜⎟ ⎝⎠⎝⎠

6. 12 x ≤

Chapter 2 Linear Equations and Inequalities

7. Let l represent length and w represent width. Then, 25.lw=+ Therefore, () 225288 ww++>⇒

41028861088610108810678 wwwww ++>⇒+>⇒+−>−⇒>⇒ 678 13. 66 w w >⇒>

Thus, the possible widths must be more than 13 inches.

Chapter 2 Review Exercises

1. 9399396xxx +=⇒+−=−⇒=− Check: 69333 −+=⇒=

2. 4244242 xxx −=−⇒−+=−+⇒= Check: 24222 −=−⇒−=−

3. 333333639 424424444 xxxx −=⇒−+=+⇒=+⇒= Check: 9336333 4424222 −=⇒⇒⇒=

4. 1 0.500.50.500.50.5 2 xxxx +=⇒+−=−⇒=−⇒=− Check: 1 0.500.50.5000 2 −+=⇒−+=⇒=

5. 412 4123 44 x xx =⇒=⇒= Check: 4(3)121212 =⇒=

6. 377 37 333 x xx =−⇒=⇒=− Check: 7 3777 3 ⎛⎞−=−⇒−=−

7. 0.51.25 0.51.252.5 0.50.5 x xx −=⇒=⇒=− Check: 0.5(2.5)1.251.251.25 −−=⇒=

8. 173173217 36136162 xxxx ⎛⎞⎛⎞ −=⇒−−=−⇒=−⇒=− ⎜⎟⎜⎟ ⎝⎠⎝⎠ Check: 17777 32666 ⎛⎞ −−=⇒= ⎜⎟ ⎝⎠

9. The equation 432 is linear. x −+= 43243222410; xxx −+=⇒−+−=−⇒−+= 4, 1 ab=−=

10. The equation 2 31 84 xx−= is not a linear equation because it cannot be written in the form 0. axb+=

11. 48 45345535482. 44 x xxxx −=⇒−+=+⇒=⇒=⇒= To check the solution, substitute 2 for x in the original equation: () 4534253853. x −=⇒−=⇒−= Because this statement is true, the solution checks.

12. 11121112 7477471122. 2221211 xxxxx ⎛⎞⎛⎞ −=−⇒−−=−−⇒−=−⇒−−=−−⇒= ⎜⎟⎜⎟ ⎝⎠⎝⎠ To check the solution, substitute 22 for x in the original equation: () 11 7472247114. 22 x −=−⇒−=−⇒−=− Because this statement is true, the solution checks.

13. () 52727 531251512515151215527. 555 x xxxxx −=⇒−=⇒−+=+⇒=⇒=⇒= To check the solution, substitute 27 5 for x in the original equation: 272715 5312512 555 ⎛⎞⎛⎞−=⇒−=⇒ ⎜⎟⎜⎟ ⎝⎠⎝⎠ 1260 51212. 55 ⎛⎞ =⇒= ⎜⎟ ⎝⎠ Because this statement is true, the solution checks.

14. 32432434 xxxxxxx +=−⇒+−=−−⇒=− 344477. xxx ⇒+=−+⇒=⇒=

To check the solution, substitute 7 for x in the original equation: () 32437274 xx +=−⇒+=− 101441010.⇒=−⇒= Because this statement is true, the solution checks.

15. ()() 214322412 xxxx −=+⇒−=+ 22242122212 xxxxx ⇒−−=−+⇒−=+ 142 21221212142 22 x xx ⇒−−=+−⇒−=⇒= 77. xx ⇒−=⇒=−

To check the solution, substitute 7 for x in the original equation: ()()()() 2143271473 xx−=+⇒−−=−+ ()() 28441616.⇒−=−⇒−=− Because this statement is true, the solution checks.

16. () 13621362462462 xxxxxxxxxx −−=+⇒−+=+⇒−=+⇒−+=++⇒ 2322 4634666323. 3333 x xxxxx =+⇒−=−+⇒−=⇒=⇒−=⇒=− To check the solution, substitute 2 3 for x in the original equation: 22 1362 33 ⎛⎞⎛⎞ −−−=+−⇒ ⎜⎟⎜⎟

2422

13644. 3333 ++=−⇒= Because this statement is true, the solution checks.

17. 3.4450.63.444540.63.490.6 xxxxxx −=−⇒−+=+−⇒=−⇒ 499 3.40.690.60.649. 444 x xxxxxx +=−+⇒=⇒=⇒= To check the solution, substitute 9 4 for x in the original equation: ()() 99 3.4450.63.42.25450.62.25 44 ⎛⎞⎛⎞−=−⇒−=−⇒ ⎜⎟⎜⎟

7.65451.353.653.65. −=−⇒= Because this statement is true, the solution checks.

18. ()() 1 36211221211 3 xxxxxx −−=−++⇒−+=−−+⇒−=−−⇒ 30 2111122300. 33 x xxxxxxxxxx −+=−−+⇒=−⇒+=−+⇒=⇒=⇒=

To check the solution, substitute 0 for x in the original equation: () () () 1 360021 3 −−=−++⇒ () 1 32111. 3 −=−+⇒−=− Because this statement is true, the solution checks.

Chapter 2 Linear Equations and Inequalities

19. 21521151252273273 36123661263121231223122 xxxxx⎛⎞⎛⎞ −=⇒−+=+⇒=+⇒=⇒=⇒ ⎜⎟⎜⎟ ⎝⎠⎝⎠

217 . 248 xx=⇒= To check the solution, substitute 7 8 for x in the original equation: 2715 38612

144101010 2424242424 −=⇒= Because this statement is true, the solution checks.

20. () 23252635565565 yyyyyyyyyyyy −−=+⇒−+=+⇒−=+⇒−−=+−⇒ 41111 46546656411. 444 y yyyy −=⇒−+=+⇒=⇒=⇒= To check the solution, substitute 11 4 for y in the original equation: 11111122332011 23256 4444444

22243320113131 4444444 −+=+⇒= Because this statement is true, the solution checks.

21. First, solve for x: ()() 4322651281210 xxxx −=+⇒−=+⇒ 12128121210 xxxx −−=−+⇒ 810.−= Because this statement is not true, the equation has no solutions.

22. First, solve for x: () 531155155155. xxxx −=−⇒−=− Because this statement is true for any value of x, the equation has infinitely many solutions.

23. First, solve for x: 85388. xxxxx =+⇒= Because this statement is true for any value of x, the equation has infinitely many solutions.

24. First solve for x: 928298288222 xxxxxxx −=−⇒−−=−−⇒−=−⇒ 22220.xx −+=−+⇒= Thus, there is one solution to the equation.

25. () When 1.0, then 21.03231; x =−+=−+=

() When 2.0, then 22.03431; x =−+=−+=−

() When 1.5, then 21.53330; x =−+=−+=

() When 2.5, then 22.53532; x =−+=−+=− Thus, the missing values in the table are 1, 0, 1 and 2. See Figure 25. From the table we see that when 1.5, x = the value of 23 x −+ is 0.

Figure 25

Figure 26

26. () When 2, then 2132134; x =−−−++=−+=

() When 0, then 0130132; x =−++=−+=

() When 1, then 1131133; x =−−−++=−+=

() When 1, then 113231; x =−++=−+=

() When 2, then 213330; x =−++=−+= Thus, the missing values in the table are 4, 3, 2,1 and 0 See Figure 26. From the table we see that when 0, x = the value of ()13 x −++ is 2.

27. 672 67212 66 x xx =⇒=⇒=

28. 18231818231841 xxx +=−⇒+−=−−⇒=−

29. 2542554529299 xxxxxxxxxxx −=+⇒−+=++⇒=+⇒−=−+⇒=

30. 4334332402440424 xxxxxxxxx +=⇒−+=−⇒−+=⇒−+−=−⇒−=−⇒ 24 2 22 x x =⇒=

31. 535315 159 35351 xx x =⇒⋅=⋅⇒=

32. ()()121533315333315333156xxxxxx ++++=−⇒+=−⇒+−=−−⇒=−⇒ 3156 52. 33 x x =⇒=− The numbers are 52, 51 and 50.

33. 8517 85%; 85%0.85 10020 ===

34. 5.6567 5.6%; 5.6%0.056 1001000125 ====

35. 0.033 0.03%; 0.03%0.0003 10010,000 ===

36. 342171 342%; 342%3.42 10050 ===

37. 0.8989% =

38. 0.0050.5% =

39. 2.3230% =

40. 1100% =

41. () 8324 miles. drtdd =⇒=⇒=

42. () 70553850 feet. drtdd =⇒=⇒=

43. () 50020500 5002025 ydsec. 202020 drtrrrr =⇒=⇒=⇒=⇒=

44. 1251512525 12515 hours. 1515153 t drtttt =⇒=⇒=⇒=⇒=

45. The area of a triangle is ()() 1 baseheight. 2 Thus, ()() ()() 2 11 537.5 m. 22 Abh===

46. The area of a circle is 2 rπ where r represents radius. Thus, () 222 636113.1 ft. Ar=π=π=π≈

47. The area of a rectangle is given as length (l) times width (w). Thus, ()() 22 3624864 in or 6 ft. Alw===

48. 22 Plw =+ where P represents perimeter, l represents the length of the base and w represents the width. Thus, ()() 2221327261440 in. Plw=+=+=+=

49. The circumference of a circle is 2, rπ where r represents radius. Thus, () () 11 diameter189. 22 r === () 2291856.5 feet. Cr=π=π=π≈

50. 2 , Ar =π where A represents area and r represents radius. Thus, () 222 52578.5 in. Ar=π=π=π≈

51. The angles in a triangle must add up to 180º. Let x represent the unknown angle. Thus, 904018013018013013018013050º. xxxx ++=⇒+=⇒−+=−⇒=

52. The angles in a triangle must add up to 180º. Thus, 8180 341808180 88 x xxxx ++=⇒=⇒=⇒

22.5º. x =

53. () ()()() 223 52525256251963.5 in. Vrh=π=π=π=π≈

54. First, convert height (h) and base (b) to inches. 12inches 5 feet60 inches and 1foot h =⋅= 12inches 3 feet36 inches. 1foot b =⋅=

Then, () () ()() 2 111 361860546027601620 in. 222 Aabh=+=+=== Or, convert the base in inches to feet. 1foot 18 inches1.5 feet. 12inches b =⋅= Then, () () ()() 2 111 31.554.552.25511.25 ft. 222 Aabh=+=+===

55. The total area of the figure is the sum of the area of the triangle and the area of the rectangle. The area of the triangle is 2 11 8624 in. 22 bh =⋅⋅= The area of the rectangle is 2 256150 in. lw =⋅= Thus, the total area is 2 24150174 in. +=

56. The total area of the figure is the sum of the area of the rectangle and the area of a circle. The area of the rectangle is 2 12448 ft. lw =⋅= The area of the circle is

Thus, the total area is about 2 4812.660.6 ft. +=

57. 35355535 xyxyxy =+⇒−=−+⇒−=

58. 1622 162216222216228 22 xy xyxxxyxyxy =+⇒−=−+⇒−=⇒=⇒−=⇒ 8 yx=−+

59. 2 2 2222 zxyzz zxyyy xxxx =⇒=⇒=⇒=

60. 3333 33 abcabc SSSabcSacabcac ++++ =⇒=⋅⇒=++⇒−−=++−−⇒

33 SacbbSac −−=⇒=−−

61. 12431243 1212121243 34121212121212

abTabTab TTab ⎛⎞⎛⎞⎛⎞ =+⇒=+⇒=+⇒=+⇒

1243124124 1244431243 3333 TabTaTa TaaabTabbb −=−+⇒−=⇒=⇒=⇒=

62. () cdabbccdbcabbcbccdbcabcdbab =+⇒−=+−⇒−=⇒−=⇒ () () () cdbabab c dbdbdb =⇒=

63. The formula for GPA is given by 432abcd abcdf +++ ++++

4(20)3(25)2(12)48075244183 2.82. 202512446565 ++++++ ==≈ ++++

64. The formula for GPA is given by 432 . abcd abcdf +++ ++++

Thus, the GPA is 2.82.

4(64)3(32)2(20)10256964010402 3.12. 643220103129129 ++++++ ==≈ ++++

Thus, the GPA is 3.12.

65. To convert Celsius to Fahrenheit temperature, the formula given is 9 32. 5 CF += 9135 (15)3232273259F. 55 FFFF +=⇒+=⇒+=⇒=°

66. To convert Fahrenheit to Celsius temperature, the formula given is 5 (32). 9 CF=− 55405 (11332)(81)45C. 999 CCCC =−⇒=⇒=⇒=°

67.

68.

69.

70.

71. 3 x <

72. 1 x ≥−

73. Substitute 2 for x and check for accuracy: ()() 131232112 xx −+≥⇒−−+≥−⇒−≥−⇒

02. ≥− Because this statement is true, 2 x =− is a solution to the inequality.

74. Substitute 1 for x and check for accuracy: ()()()() ()41541151 xx+<−−⇒−+<−−−⇒ ()() 40606. <−⇒<− Because this statement is not true, 1 x =− is not a solution to the inequality.

75. When 1, then 5514;xx=−=−= When 2, then 5523;xx=−=−= When 3, then 5532;xx=−=−= When 4, then 5541;xx=−=−=

Thus, the missing values in the table are 4, 3, 2 and 1. See Figure 75. From the table we see that 53, x −> when 2. x <

Figure 75

Figure 76

76. () When 1.5, then 2521.55352;xx=−=−=−=− () When 2, then 25225451;xx=−=−=−=− () When 2.5, then 2522.55550;xx=−=−=−= () When 3, then 25235651;xx=−=−=−=

Thus, the missing values in the table are 2, 1, 0 and 1. See Figure 76. From the table we see that 250 when 2.5. xx −≤≤

77. 3033033xxx −>⇒−+>+⇒>

78. 210 2105 22 x xx −≤⇒≥⇒≥−

79. 22 52755275221 22 x xxxx −≥⇒−−≥−⇒−≥⇒≤⇒≤−

80. () 32323 31203320333203323 333 x xxxxx −<⇒−<⇒−+<+⇒<⇒<⇒<

81. () 911 5342534254344291 999 x xxxxxxxxxx ≤−+⇒≤−−⇒+≤−+−⇒≤⇒≤⇒≤

82. () 324138215881859 xxxxxxxxxx −−≥+⇒−+≥+⇒−+≥++⇒≥+⇒ 499 5949 444 x xxxxxx −≥−+⇒≥⇒≥⇒≥

83. 50 x <

84. 45,000 x ≤

85. 16 x ≥

86. 1995 x < or 1994 x ≤

87. (a) See Figure 87. (b) 3 2 4 Rx =+ (c) () 315233 At 5 PM, 5; 2525 inches. 4444 xR==+=+== This value does agree with the table.

(d) 333154532457713 At 3:45 PM, 3.75; 23224 inches. 44441616161616 xR

Figure 87

88. Let x represent the cost of the laptop.

Figure 89

0.05106.25 0.05106.252125. 0.050.05 x xx =⇒=⇒= Thus, the cost of the laptop is $2125.

89. (a) See Figure 89.

(b) 5010 Dx =−

(d) 1030 20. Thus, 50102050501020501030 1010 x Dxxx ≥−≥⇒−−≥−⇒−≥−⇒≤⇒

3. x ≤ Thus, the bicyclist was at least 20 miles from home when he had traveled for 3 or fewer hours, or from noon to 3 PM.

90. First, subtract the smaller number from the larger to obtain the difference between them: 625,000468,500156,500. −= Then, determine what percentage 156,500 is of 468,500 Do this by dividing the smaller number by the larger: 156,500 0.334. 468,500 ≈ Thus, there was about an 33.4% change in master’s degrees received between 2001 and 2008.

91. Use the ()()() distance rate time formula. drt =× Determine how long it takes the faster car to be 2 miles ahead of the slower car, let () 12 r + be the rate of the faster car and r be the rate of the slower car. () 21211 212212 hour,or 10 minutes. 12 1266 t drtrrtttt =⇒=+−⇒=⇒=⇒=⇒=

92. ()()()() Perimeter 2width 2length . Then, 102102112PWLWLLL =×+×=−⇒−+=⇒ 4132 220211222020211220413233. 44 L LLLLLL −+=⇒−++=+⇒=⇒=⇒= Because the length is 33, the width is ()1023. L −= Thus, the dimensions are 33 by 23 inches.

93. Let x represent the amount of water. The amount of salt on one side of the equation must equal the amount of salt on the other side. Thus, ()()()() 1000.030.001000.023020.02 xxx +=+⇒+=+⇒ 10.02 32220.0210.025050. 0.020.02 x xxxx −=−+⇒=⇒=⇒=⇒= Thus, 50 ml of water must be added.

94. Let x represent the higher interest rate. Then, ()() 8005000.0255 xx+−=⇒ 8005001055 xx+−=⇒ 130065 1300101055101300650.05. 13001300 x xxx −+=+⇒=⇒=⇒=

Thus, the interest rate on the $800 loan is 5% and the interest rate on the $500 loan is 3%.

95. () ()() () 1111 Area of a triangle is base height . Thus, 22221008100AbhAbhbhb××=⇒≤⇒≤⇒ 4100 410025. 44 b bb ≤⇒≤⇒≤ Therefore, the base must be 25 inches or less.

96. Let x represent the unknown test score. Then, 7591166 8080 33 xx+++ ≥⇒≥⇒

() 166 338016624016616624016674. 3 x xxx + ⎛⎞ ≥⇒+≥⇒−+≥−⇒≥ ⎜⎟ ⎝⎠ Thus, the student must score 74 or more.

97. Let x represent the unknown number of hours after the first hour. Then, 2.251.259 x +=⇒

1.256.75 2.252.251.2592.251.256.755.4. 1.251.25 x xxx −+=−⇒=⇒=⇒= Because each partial hour is charged as a full hour, the person can park for 156 += hours.

98. (a) 150,00085 Cx =+ (b) 225 Rx =

(c) () 225150,00085140150,000PxxPx =−+⇒=− (d) 140150,0000140150,000150,0000150,000140150,000 xxx −<⇒−+<+⇒<⇒ 140150,000 1071.43. 140140 x x <⇒< Therefore, if 1071 or fewer DVD players are sold, there will be a loss.

Chapter 2 Test

1. ()()() 939333661166 xxxxxx =−⇒−=−−⇒=−⇒−=−−⇒−=⇒=−

To check the solution: () 93699. The solution checks. =−−⇒=

2. 4105 43743373410 442 x xxxx −=⇒−+=+⇒=⇒=⇒=

To check the solution: 520614 4377777. 2222 ⎛⎞ −=⇒−=⇒=⇒= ⎜⎟ ⎝⎠ The solution checks.

3. ()() 423264261852618 xxxxxxxx −−=−+⇒−+=−−⇒−=−−⇒ 522618256165666161116 xxxxxxxxx −+=−−+⇒=−−⇒+=−+−⇒=−⇒ 111616 111111 x x =⇒=− To check the solution: 161616 42326 111111

−−−−=−−+⇒ ⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟ ⎝⎠⎝⎠⎝⎠⎝⎠⎝⎠ 64161664221696198102102 2618. 11111111111111111111 ⎛⎞ −−−=−−−⇒−−−=−⇒−=− ⎜⎟ ⎝⎠ The solution checks.

4. 121311231112311 123243123861263866 xxxxxxxx ⎛⎞ −=−⇒−=−⇒+−=−+⇒ ⎜⎟ ⎝⎠ 322323916325123122530025 . 1233831224241224312324726 xxxxx ⎛⎞⎛⎞ −+=+⇒=+⇒=⇒=⇒== ⎜⎟⎜⎟ ⎝⎠⎝⎠

To check the solution: 125213125254812750 12632436727223636

−=−⇒−=−⇒ ⎜⎟ ⎜⎟⎜⎟⎜⎟ ⎝⎠⎝⎠⎝⎠ ⎝⎠ 231232323 722367272 ⎛⎞ −=−⇒−=− ⎜⎟ ⎝⎠ The solution checks.

5. First, solve for x: ()() 6214331261212 xxxx −=−−⇒−=−+⇒ 12126121212 xxxx −−=−+−⇒ 612.−=− Because this statement is not true, there are no solutions.

6. First, solve for x: () 421848484 xxxx −=−⇒−=−⇒ 8844884400 xxxx −−+=−−+⇒=

Because this statement is always true, there are infinitely many solutions.

7. () When 1, then 626214;xx=−=−= () When 2, then 626222;xx=−=−= () When 3, then 626230;xx=−=−= () When 4, then 626242;xx =−=−=−

Thus, the missing values in the table are 4, 2, 0 and 2. See Figure 7. From the table we see that 620, x −= when 3. x =

Figure 7

8. ()7676776713xxxx +−=⇒−=⇒−+=+⇒=

9. 26726767667613 xxxxxxxxx +=−⇒−+=−−⇒+=−⇒+−=−−⇒=−

10. ()()123363333633333633333 xxxxxx ++++=⇒+=⇒+−=−⇒=⇒ 3333 111. 33 x x =⇒= Thus, the three numbers are 111, 112 and 113.

11. 3.2321684 3.2%0.032;3.2% 1001000500250125 ======

12. 0.34534.5% = 13. 200 200450 4 drtrr =⇒=⋅⇒== Thus, 50 ft/sec

14. () ()() ()() 2 111 Area base height . Thus, 537.5 in. 222 AbhAbh =××===

15. Circumference of a circle is given as () 30 2. Then, 222153094.2 inches. 2 CrCr ⎛⎞ =π=π=π=π=π≈ ⎜⎟

Area of a circle is given as ()2 222 . Then, 15225706.9 in. ArAr =π=π=π=π≈

16. The angles in a triangle must add up to 180º. Then, 6180 23180618030. 66 x xxxxx ++=⇒=⇒=⇒= Thus, the angles are 30º, 60º and 90º.

17. 3 333 3333 zyxyzyyz zyxyzyyyxyzyxyxx yyyy =−⇒−=−−⇒−=−⇒=⇒=⇒=

18. 204 20542045 455 xyRy RRxyRyxx =+⇒=+⇒−=⇒=

19.

20. x > 0

21. 3915399159324324 xxxxxxxxxx −+≥−⇒−+−≥−−⇒−≥−⇒−−≥−− 424 4246 44 x xx ⇒−≥−⇒≤⇒≤

22. () 365201815201818152018152 xxxxxxxx −<−⇒−<−⇒−−<−−⇒−<−⇒ 1421 152142 14147 x xxxxxx −+<−+⇒−<⇒>⇒>−

23. (a) 52, where represents hours past noon. Sxx =+ (b) () 8. Thus, 52821 inches. xS==+= (c) () 6.25. Thus, 526.2517.5 inches. xS ==+=

24. The amount of acid on the left side of the equation must equal the amount of acid on the right side of the equation. Let x represent the unknown amount of water. Then, ()()()() 10000.45010000.15 xx +=+⇒ 4501500.154501501501500.15 xx =+⇒−=−+⇒ 3000.15 3000.15 0.150.15 x x =⇒=⇒ 20002000. xx =⇒= Thus, 2000 ml of water must be added.

25. Subtract the lesser amount from the larger amount and then calculate the percentage difference as compared to the smaller amount. Then, 20 957520; 0.26726.7%. 75 −=≈⇒ Therefore, there will be a 26.7% increase in cost from 2010 to 2015.

Chapters 2 Extended Discovery Exercises

1. For the first hour, the distance traveled was drt = such that ()()50150 miles. d == For the second hour, the distance traveled was ()() such that 70170 miles. drtd=== Thus, for the two hours such that d r t = 7050120 60. 112 r + === + Thus, the average speed of the car was 60 mph.

2. Uphill, 11 such that of an hour. 55 d tt r === Downhill, 11 such that of an hour. 1010 d tt r === Thus, the average speed 3 11 51010 11220 is 6.6 mph. 3 d rr t + ===== + Answersmayvary

3. For the first two miles, 21 such that of an hour. 84 d tt r === For the third mile, such that d t t =

t == of an hour. Thus, the average speed of the athlete is

4. Choose a distance of 400 miles as the distance between the two cities (the distance is arbitrary because any distance gives the same average speed). Then, the pilot flew at 200 mph for 1 hour and at 100 mph for 2 hours. Then, 400400 133.3. 123 d r t ==== + Thus, the average speed is 133.3 mph.

5. The lighter coin can be found in two weighings as follows: Place two coins on each pan of the balance and set three coins off to the side. Case 1: The pans balance and the lighter coin is one of the three coins that were set off to the side. Case 2: The pans do not balance and the lighter coin is one of the two coins on the higher pan. To find the lighter coin in Case 1, work only with the three remaining coins. Place one coin on each side of the balance and set one coin off to the side. If the pans do not balance, the lighter coin is the one on the higher pan. To find the lighter coin in Case 2, work with only the two coins from the higher pan. Place one coin on each side of the balance. The lighter coin is on the higher pan.

6. (a) ()()2 22 Surface area 443960197,060,797 mi. Ar=π=π≈ (b) () 2 0.71197,060,797139,913,166 mi. ≈

(d) They would be flooded.

(e) Divide the volume of the Antarctic ice cap by the surface area of the oceans: 6,300,000 0.045 miles. 139,913,166 ≈ To convert 0.045 miles to feet: 5280feet 0.045mile237.7 feet. 1mile ⋅≈

Chapters 1 and 2 Cumulative Review Exercises

1. The number 45 is a composite number because it has factors other than itself and 1; 45335 =××

2. The number 37 is a prime number because its only factors are itself and 1.

3. 43431211211211 1 38382421221222 ⋅====⋅=⋅=

4. 22621212121211 61 331363618929299 ⋅⋅ ÷=÷=⋅====⋅=⋅=

5. 113112331123322922913 128122831228324242424 ⋅⋅− −=⋅−⋅=−=−== ⋅⋅

6. 212513251310310313 353553355315151515 ⋅⋅+ +=⋅+⋅=+=+==

7. 1 is a rational number, and is an integer.

8. 3 is an irrational number.

9. 154315123 −⋅=−=

10. 30625210 ÷⋅=⋅=

11. 2 23422316223815 −÷=−÷=−=

12. 314 11111129 642 + −=−=−=

13. 3333 5(51)4 xxxx −=−=

14. 4213412341(23)35 xxxxxx +−+=−++=−++=+

15. 3113311314 xxx −=⇒−+=+⇒=

16. 416 46224662264164 44 x xxxx −=−⇒−+=−+⇒=−⇒=⇒=−

17. 5(62)255(6)5(2)2530102530101025103015 yyyyy +=⇒+=⇒+=⇒+−=−⇒=⇒ 30 151 30302 y y =⇒=

18. 11(2)351123511235 yyyyyy −+=+⇒−−=+⇒−−=+ 935935945 yyyyyyy ⇒−=+⇒−+=++⇒=+ 44 95455441 44 y yyy ⇒−=+−⇒=⇒=⇒= 1 y ⇒=

19. First, solve for x: 622(31)626266266222. xxxxxxxx +=+⇒+=+⇒−+=−+⇒= Because this statement is true for any value of x, the equation has infinitely many solutions.

20. First, solve for x: 2(34)6(1)686666866686. xxxxxxxx −=−⇒−=−⇒−−=−−⇒−=− Because this statement is not true, the equation has no solutions.

21. Let x represent the first integer. Then 1 x + and 2 x + represent the other two integers. The sum of the integers is 12,xxx++++ 12903390333903387 xxxxxx ++++=⇒+=⇒+−=−⇒= 387 29,130,231. 33 x xxx ⇒=⇒=+=+= The integers are 29, 30, and 31.

22. 4.747 4.7%0.047 1001000 ===

23. 0.170.17100%17% =×=

24. Given that the distance traveled (d) is 325 miles and that the time spent traveling (t) is 5 hours, calculate the speed of the car (r).

Then, 3255 32556565 miles/hour. 55 r drtrrr =⇒=⋅⇒=⇒=⇒=

25. The sum of the measures of the angles of a triangle is 180°. Then 9180 234180(234)180918020 99 x xxxxxx ++=⇒++=⇒=⇒=⇒=

26. Since the diameter of the circle is 10 inches, the radius is 10 5 inches. 2 = Then, 222 525 in. Ar=π=π=π≈78.5

27. 434 34434443 333 axya axyaxyaxyx yyy ++ =−⇒+=−+⇒+=⇒=⇒=

28. 3333 33 AxyzxyzAAxyzAyzxyyzz++++⎛⎞ =⇒=⇒=++⇒−−=+−+−⇒

3 Ayzx −−=

29. 33 7347734734(7)331 33 x xxxxx −>⇒−−>−⇒−>+−⇒−>−⇒<⇒<

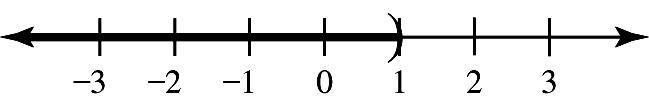
30. 65(9)659614614 xxxxxxxxxx ≤−−⇒≤−+⇒≤−⇒+≤−+ 714 7142 77 x xx ⇒≤⇒≤⇒≤

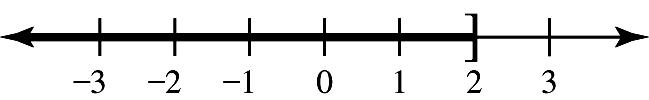
31. 36 IY =

32. Start with the initial balance, subtract the amounts withdrawn and add the amounts deposited: 46814200732158454200732158 −+−−+=+−−+= 6547321 58581215856058$618 +=−+=+=

33. Let x represent the amount of 4% acid. Then, the 6% acid solution is the sum of the 4% acid and the 10% acid. Therefore 0.040.10(150)0.06(150) xx +=+ 0.04150.069 xx ⇒+=+

0.040.04150.060.049 xxxx ⇒−+=−+ 150.0291590.029960.02 xxx⇒=+⇒−=+−⇒= 60.02 300 0.020.02 x x ⇒=⇒=

300 mL of 4% acid solution should be mixed with the 10% acid solution to dilute it to a 6% acid solution.

34. Let x represent the 2009 production level and the equation is 2188356 x −= . 2544 218835621881883561882544272 22 x xxxx −=⇒−+=+⇒=⇒=⇒=

The 2009 production level was 272 billion kilowatt-hours.