Solutions for Elements Of Electromagnetics 7th Us Edition by Sadiku by 6alsm

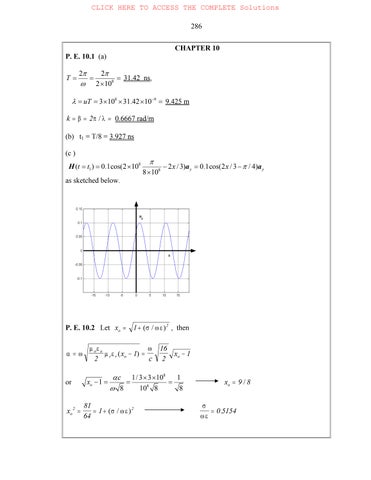
P. E. 10.1 (a)

CHAPTER 10

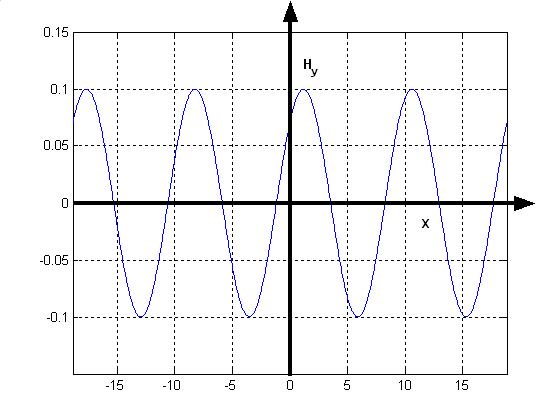
Att=2ns,y=1m, 0.9425 30cos(220.96/4)2.844zz e

1 106 1 09425 1 06  ln(/.) . ln . 542mm (d) 2 /60 ||188.11 11.002[1(0.09)] 4

P. E. 10.8

P. E. 10.12 (a)

(b)  122  oo,/ E isparalleltotheplaneofincidence.Since  12  o , wemayusetheresultofProb.10.42,i.e.

(c)11sincos rryrz   kaa .Oncekrisknown,Erischosensuchthat 11 .0or.0.Let (cossin)cos(sincos) rrr rorryrzrr Etyz  

Onlythepositivesignwillsatisfytheboundaryconditions.Itisevidentthat

(cossin)cos(24)ioiiyizEtyz   Eaa

Since ri  ,

EE orroii coscos. ////  102946

EEorroii sinsin. ////  51473

 1124sin,cosrr 

i.e.

Eaatyz ryz  (..)cos() 2946147324 

1(105)cos(24)(2.9461.473)cos(24) iryzyztyztyz   EEEaaaa V/m

(d)22sincos ttytz   kaa .Since

Eaa

 22212220  r sinsin,cos  tit  1 2 1 25 9 20

2220 19 20 8718cos. t 

EEottoit coscos.. //  06474125 19 20 7055

EEottoit sinsin.. //  06474125 1 20 16185

Hence 2(7.0551.6185)cos(28.718) tyztyz  EEaa V/m

(d)tan. ////     BB o  2 1 26343

P.E. 10.13

Si= 104 104 14 06   . . . . =2.333 So= 102 102 12 08   .. =1.5

Prob. 10.1 (a)Wavepropagatesalong+ax (b)

Thesearesketchedbelow.

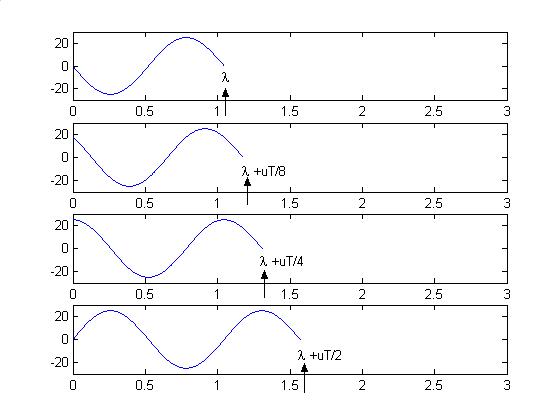
Prob. 10.2 (a) 8 3106510m 60 c

8 6 310 150m 210

8 6 310 2.5m 12010

8 9 310 0.125m 2.410

Prob. 10.3

Prob. 10.4

Prob.

Assumingthat1,weincludeuptothesecondpowerinand neglecthigher-orderterms.

(d)Thephasedifferenceis2.74

Prob. 10.14

Prob. 10.18 (a)Along-xdirection.

Prob. 10.20

Prob. 10.22

Prob. 10.25 Foragoodconductor,

No,notconducting.

Yes,conducting.

Prob. 10.26

(seeTable10.2).

Prob. 10.36 y (25)sin()

TheratioE/remainsthesameastchanges.Hencethewaveislinearlypolarized

Prob. 10.37

Hence,wehavecircularpolarization.

Hence,wehaveellipticalpolarizatio

Prob. 10.38

(a)Wecanwrite x Re()(4060)cos(10)

SinceE/doesnotchangewithtime,thewaveislinearlypolarized.

(b)Thisisellipticallypolarized.

Prob.

Prob. 10.40 Wecanwrite Esas 12 1 2 12 ()() where 1 ()() 2 1 ()() 2

Werecognizethatandarecircularlypolarizedwaves.Theproblemisthereforeproved. s

Prob. 10.41 (a) 12 When0, (,)()cos()

Thetwocomponentsareinphaseandthewaveislinearlypolarized.

When/2, cos(/2)sin()

Wecancombineandtoshowthatthewaveisellipticallypolarized. zoo xz

When,

Thus,thewaveislinearlypolarized.

Prob.

Similarly,

Prob.

.or0.1716 (Notethatthesevaluesaremutualreciprocals,reflectingtheinherentsymmetryofthe problem.)

Thefractionoftheincidentpowerreflectedis

Thetransmittedfractionis

Prob. 10.68 (a)

Prob.10.72

From

From  kHE , kHE  aaa

Prob. 10.73

Similarly,

2 2222 cossin sincos(sincos)sincos(sincos)

2 cossin (sincossincos)(coscossinsin)

it ittiitit

 2 cossin sin()cos()

Fromthefigure, rrzzryy

Hence,43ryz  kaa

17.46,12cos0.9539,120,/260ttoo  21 // 21 coscos(0.9539)(0.8)20.253 coscos(0.9539)(0.8)

But k ioo  1 k k tkk i ti  2210

kkkk tytttztt  cos.,sin, 95393

kaa tyz 95393

Notethat kkk izrztz  3

But ()(sincos)6.256(0.30.9539) tyytzztotytzyz EEE   

Hence,

Prob. 10.76

Prob. 10.78

Prob. 10.79

(a)2.111.45

Prob.10.80

Microwaveisused:

(1)Forsurveyinglandwithapieceofequipmentcalledthe tellurometer. Thisradar systemcanpreciselymeasurethedistancebetweentwopoints.

(2)Forguidance.Theguidanceofmissiles,thelaunchingandhomingguidanceof spacevehicles,andthecontrolofshipsareperformedwiththeaidofmicrowaves.

(3)Insemiconductordevices.Alargenumberofnewmicrowavesemiconductor deviceshavebeendevelopedforthepurposeofmicrowaveoscillator, amplification,mixing/detection,frequencymultiplication,andswitching. Withoutsuchachievement,themajorityoftoday’smicrowavesystemscouldnot exist.

Prob.10.81

(a)IntermsoftheS-parameters,theT-parametersaregivenby T11=1/S21,T12=-S22/S21,T21=S11/S21,T22=S12-S11S22/S21

(b)T11=1/0.4=2.5,T12=-0.2/0.4, T21=0.2/0.4,T22=0.4-0.2x0.2/0.4=0.3 Hence,

T = 2.50.5 0.50.3

Prob. 10.82

SinceZL=Zo,  L=0.

 i=S11=0.33–j0.15

 g=(Zg-Zo)/(Zg+Zo)=(2–1)/(2+1)=1/3

 o=S22+S12S21  g/(1-S11  g)

=0.44–j0.62+0.56x0.56x(1/3)/[1–(0.11–j0.05)]

=0.5571-j0.6266

Prob. 10.83 Themicrowavewavelengthsareofthesamemagnitudeasthecircuit components.Thewavelengthinairatamicrowavefrequencyof300GHz,forexample, is1mm.Thephysicaldimensionofthelumpedelementmustbeinthisrangetoavoid interference.Also,theleadsconnectingthelumpedelementprobablyhavemuchmore inductanceandcapacitancethanisneeded.

Prob. 10.84

CHAPTER 12

P. E. 12.1 (a)ForTE10,fc=3GHz, 11315096 22  (/)(/). ff c ,  

60084261588 (.).  P. E. 12.2 (a)Since E z  0,thisisaTMmode

j Exye h

y x  1254050 .tancot

P. E. 12.3 IfTE13modeisassumed,fcand  remainthesame.

fc=28.57GHz,  =1718.81rad/m,    j

Form=1,n=3,thefieldcomponentsare:

Ez=0

Ez=0,

P. E. 12.4

Forn=0,m=1,

2(/)sin(/)cos(/) z yso EjaHxaybe h 

2(/)sin(/)cos(/) z xso HjaHxaybe h

yso HjbHxaybe h

Fortheelectricfieldlines,

Forthemagneticfieldlines

Noticethat()() E E H H y x y x  1

showingthattheelectricandmagneticfieldlinesaremutuallyorthogonal.Thefield linesareasshowninFig.12.14.

P. E. 12.8

P. E. 12.9

(a)BySnell’slaw,n1sin  1=n2sin  2.Thus  2=90osin  2=1 sin  1=n2/n1,  1=sin–1n2/n1=sin–11.465/1.48=81.83o (b)NA= nn 1 2 2 2 =148146522=0.21

P. E. 12.10  l=10logP(0)/P(l)=0.2X10=2 P(0)/P(l)=100.2,i.e.P(l)=P(0)10-0.2=0.631P(0) i.e.63.1%

Thefollowingmodesaretransmitted

Prob.

Usingthisformula,weobtainthecutofffrequenciesforthegivenmodesasshownbelow.

(b)10 Sincef=12GHz,onlyTEmodewillpropagate.

Prob. 12.5 a/b=3a=3b f u ac102  '8 9 10 '310 221810 c u a f  

Adesigncouldbea=9mm,b=3mm.

Prob. 12.6 Forthedominantmode,

8310 18.75MHz 228 c fc a 

m=0.833cm

(a)ItwillnotpasstheAMsignal,(b)itwillpasstheFMsignal.

Prob. 12.7 (a)ForTE10mode, f u a c  ' 2

Or 8 9 '310 3cm 22510 c u a f  

ForTE01mode, f u cb  ' 2 Or 8 9 '310 1.25cm 221210 c bu f

(b)Sincea>b,1/a<1/b,thenexthighermodesarecalculatedasshownbelow.

Modefc(GHz)

TE105 *TE2010 TE3015 TE4020

*TE0112 TE0224

*TE1113 TE2115.62

Thenextthreehighermodesarestarredones,i.e.TE20,TE01,TE11

m/s

ForTE11modes,

(d)ForTEmode,

Prob.

Prob. 12.18 Infreespace,

1||1.5667 1|| s  

Prob. 12.19 Substituting ERZ z   intothewaveequation,

Dividingby RZ  , 1 2 22 R d d Rk Z Z k z

i.e.2''0 z ZkZ 1 20 22 R d d Rkk z    (') '' ()  

   R d d Rkkk z (')() '' 2222   or

''  k  20

 d d RkkR (')()2220 ,where kkk z  222  .Hence  22220 RRkkR '''() 

Prob. 12.20

TheMATLABcodeandtheplotofthephaseandgroupvelocitiesarepresentedbelow.

% Plot U_p and U_g versus frequency f (10<f<100) in GHz

c=3*10^8; for k=1:91

f(k)=9+k

fac = sqrt( 1 - (8/f(k))^2 );

up(k) = c/fac; ug(k) = c*fac; end

plot(f,up, 'r', f, ug, 'k') xlabel('frequency f') ylabel('phase vel (red) & group vel (black)')

Prob.

ForTM

TheMATLABcodeisshownbelow

k=10^(-5)/(30*sqrt(5.8/2.25)); fc=10^10; forn=1:1000 f(n)=fc*(n/100+1); fn=f(n); num=sqrt(fn)*(1+(fc/fn)^2); den=sqrt(1-(fc/fn)^2); alpha(n)=k*num/den; end plot(f/10^9,alpha) xlabel('frequency(GHz)') ylabel('attenuation') grid

Theplotofattenuationversusfrequencyisshownbelow.

Prob. 12.35 Thecutofffrequencyofthedominantmodeis

Prob. 12.39 ForTE10mode,

wherekisaconstant.

Forminimumvalue, d df c

 0 .Thisleadstof=2.962fc

Prob. 12.40 FortheTEmodetoz,

asrequired.

FromMaxwell’sequation,

0 ss xsys jxyz EE

Prob. 12.41 Maxwell’sequationcanbewrittenas

Hj h E yh H x xs zszs 

Forarectangularcavity, hkkmanb xy 22222 (/)(/) 

ForTMmode,Hzs=0and

EEmxanybpzc zso  sin(/)sin(/)cos(/)  Thus 2 zs xs HjE hy

asrequired.

FromMaxwell’sequation,

Prob. 12.42

f u rmanbpc  ' (/)(/)(/) 2 222

whereforTMmodetoz,m=1,2,3,…,n=1,2,3,….,p=0,1,2,….

andforTEmodetoz,m=0,1,2,3,…,n=0,1,2,3,….,p=1,2,3,…,()0 mn .

(a)Ifa<b<c,1/a>1/b>1/c,

ThelowestTMmodeisTM110with f u rab  ' 2 11 22

ThelowestTEmodeisTE011with2222 '11'11 22 r fuubcab 

HencethedominantmodeisTE011.

(b)Ifa>b>c,1/a<1/b<1/c,

ThelowestTMmodeisTM110with f u rab  ' 2 11 22

ThelowestTEmodeisTE101with2222 '11'11 22 r fuuacab 

HencethedominantmodeisTM110.

(c)Ifa=c>b,1/a=1/c<1/b,

ThelowestTMmodeisTM110with f u rab  ' 2 11 22

ThelowestTEmodeisTE101with f u ac u rab  '' 2 11 2 11 2222

HencethedominantmodeisTE101.

Prob. 12.45

9.48500.250.111=5.701GHz

9.48500.250.444=7.906GHz

9.48500.250.999=10.61GHz

9.485010.111=10GHz

Thus,thefirstfiveresonantfrequenciesare:

5.701GHz(TE)

7.906GHz(TE)

10GHz(TEandTE)

10.61GHz(TEorTM)

11.07GHz(TEorTM)

Prob. 12.46

Prob.

ThisisaTMmodetoz.FromMaxwell’sequations,

Prob. 12.52

(8.7)(3.6)

(10.2)(8.7)(3.6)

Prob. 12.56

2 d Vnn V N

17.17or17modes

Prob. 12.57

(a)NA=sin  a= nn 1

=153145 22 = 0.4883  a=sin–10.4883=29.23o

(b)P(l)/P(0)=10- l /10=10-0.4X5/10=0.631

i.e.63.1%

Prob. 12.58 /100.50.85/10

Prob. 12.59

AsshowninEq.(10.35),log10P1/P2=0.434lnP1/P2, 1Np=20log10e=8.686dBor1Np/km=8.686dB/km, or1Np/m=8686dB/km.Thus, 1210 8686

0.40.4dB/km=Np/km 8.686

30.79230.392dB76.98km 0.4dB/km

Prob. 12.61

P(0)=P(l)10  l/10=0.2x100.4x30/10mW=3.1698mW

Prob. 12.62 Seetext.

CHAPTER 2 P. E. 2.1

(a)AtP(1,3,5),x=1,y=3,z=5,  xy 22 =10,z=5,11tan/tan371.6 o yx   P( ,,)(,tan,)(.,.,) zPPo 103531627165 1

Sphericalsystem:

222 12211 355916 105063253231 . tantantan..  (,,)(5.916,32.31,71.57)PrP   

AtT(0,-4,3),x=0y=-4,z=3; 

xyzyx TzT 22114340270 42703 ,,tan/tan/ (,,)(,,).

Sphericalsystem: rxyzz TrT

 222115435313 55313270 ,tan/tan/.. (,,)(,.,).

AtS(-3-4-10),x=-3,y=-4,z=-10; 22145,tan233.1 3 (,,)(5,233.1,10).

Sphericalsystem: 222 11 5511.18. 5 tantan153.43; 10 (,,)(11.18,153.43,233.1). rxyz z SrS

(b)InCylindricalsystem,22;sin, xyyzz

2222 sin ;0;;xyz QQQz zz

Note,thatthemagnitudeofvectorQ=2.53inall3casesabove.

Prob. 2.1

Prob. 2.2 (a) 11 cos2cos301.732; sin2sin301; 5; (,,)(1.732,1,5). x

(b) 22 1cos900;1sin901;3. (,,)(0,1,3). xyz

(c)

33 sincos10sin(/4)cos(/3)3.535; sinsin10sin(/4)sin(/3)6.124; cos10cos(/4)7.0711 (,,)(3.535,6.124,7.0711).

(d) 44 4sin30cos601 4sin30sin601.7321 cos4cos303.464 (,,)(1,1.7321,3.464).

Prob.

Prob. 2.4 (a)

HenceQ(5.099,78.69,120)

Prob. 2.5 (,,)10,60,30 sincos10sin60cos307.5 sinsin10sin60sin304.33 cos10cos605 (,,)(7.5,4.33,5) sin10sin608.66 (,,)(8.66,30,5)

Prob.

Prob. 2.9

cossin02 sincos03 0014 AtP,2,/2,1

2cos3sin2cos903sin903

2sin3cos2sin903cos902 4 Hence,324

Prob. 2.10

2 z Az  Hence, 222 yzxyz Aaa

(b)

Prob.

Prob. 2.12

sincoscoscossinsin coscoscossincos0 cossin0cos sincossincos,sincoscoscos sincos

Prob. 2.14

Insphericalsystem:

aa aa aa aa

Hence, sincos; coscos; sinsin; cossin; cos; sin; xr x yr y zr z aa aa

 aaaaaa aaaa aaaaa aaaaa

Prob. 2.15 (a) 22 cossin,sincos cossin0 sincos0(cossin) 001 sincos cossin0 sincos0 cossin 001 xyxy zz zxy zxy 

 

 

 



 

(b) 2222 sincossinsincos coscoscossinsin sincos sincossinsincos coscoscossinsin (sinsincossin)(coscossincos) (sincossincossinco rxyz xyz xy

 aaaa aaaa aaa aa aa ssincos) sincos z xy     a aaa

22 sincos0 sincossinsincos coscoscossin(sinsinsincos) coscoscossinsin coscoscossinsin sincos0 sincossinsin(coscoscossin)

Prob. 2.16

Prob. 2.18

Prob.

Prob. 2.21

Prob. 2.24

99.1189.956. d d

 2223 1052(10)(5)coscos2(10)(5)sinsincos(7) 464644 125100(0.7071)(0.866)100(0.7071)(0.5)(0.2334) 12561.2335.3399.118

Prob. 2.25

Usingeq.(2.33), 222 121212121221 2coscos2sinsincos() 16362(4)(6)cos30cos902(4)(6)sin30sin90cos(180) 1636048(0.5)(1)(1)522476

8.718

Prob. 2.26

coscoscossinsin2cotsin sincos0sin sincos2cossi

ncossin sincos3cossin coscos2cotcossinsinsin sincos2cotsincos [sincos3cossin] [coscos2cotcossinsinsin] sincos(2cotcos) r

Prob. 2.31

(a)Aninfinitelineparalleltothez-axis.

(b)Point(2,-1,10).

(c)Acircleofradius r sin   5,i.e.theintersectionofaconeandasphere.

(d)Aninfinitelineparalleltothez-axis.

(e)Asemi-infinitelineparalleltothex-yplane.

(f)Asemi-circleofradius5inthey-zplane.

Prob. 2.32 ()() sincoscoscossin. At(2,/2,3/2), ln2. Pxx xr P d

Prob. 2.33

AtP,2,60,1 4(1/4)2(3/4)11.52.5 x o x H z H

Prob. 2.34

10||22 001 acylinderofinfinitelength zxy xyz