Chapter 2: Fractions
Prep Test
1. 20
2. 120
3. 9
4. 10
5. 7
6. 2r3 3063 60 3
7. 1, 2, 3, 4, 6, 12
8. 8 · 7 356 359
9. 7
10. <
Section 2.1
Concept Check
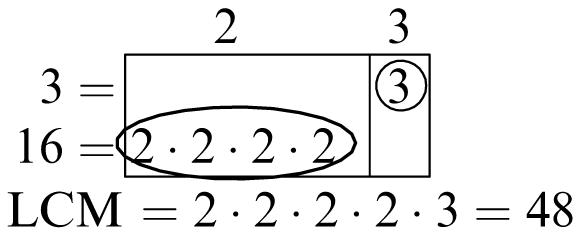
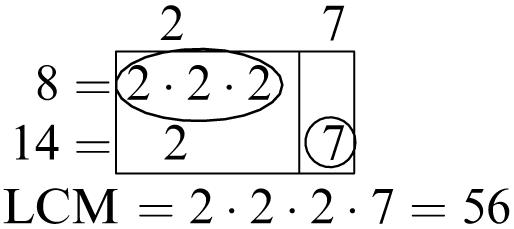
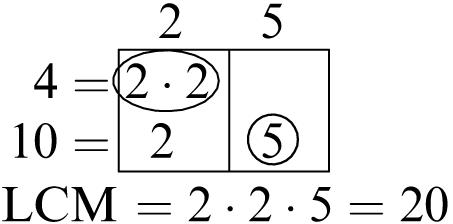
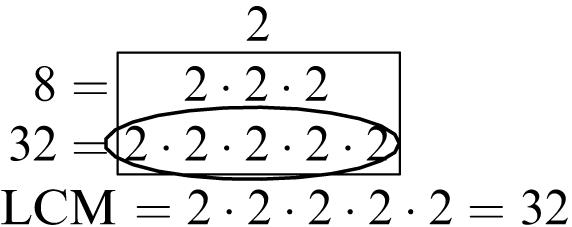
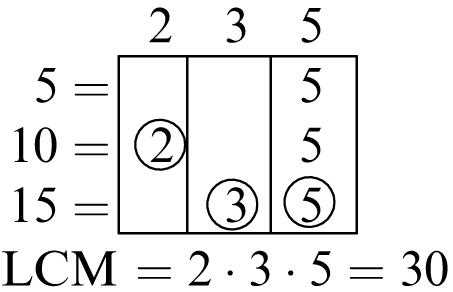
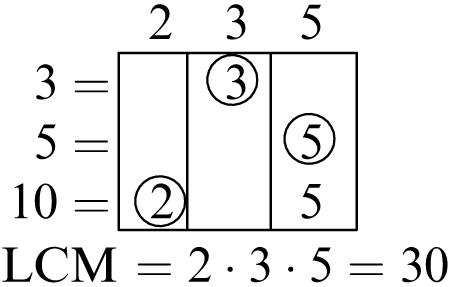
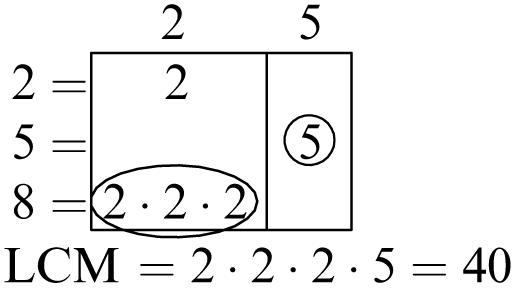
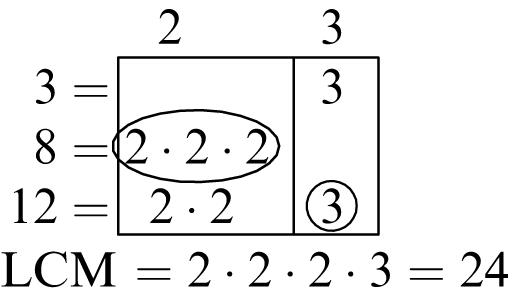
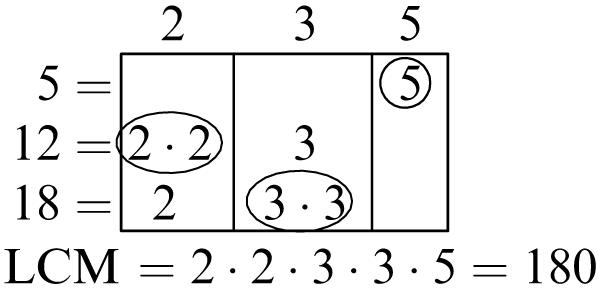
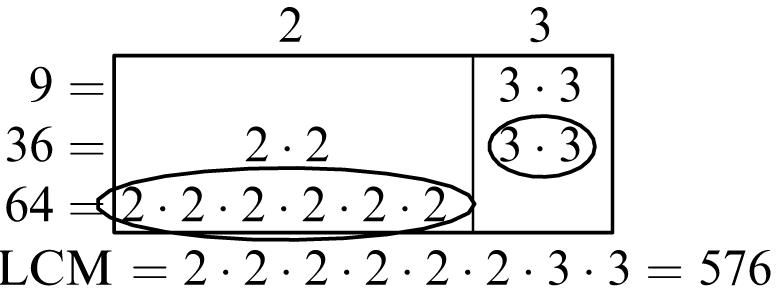
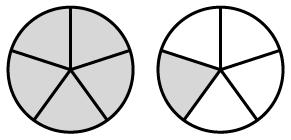
1. 5, 10, 15, 20
2. 7, 14, 21, 28
3. 10, 20, 30, 40
4. 15, 30, 45, 60
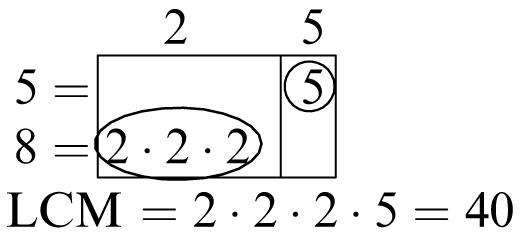
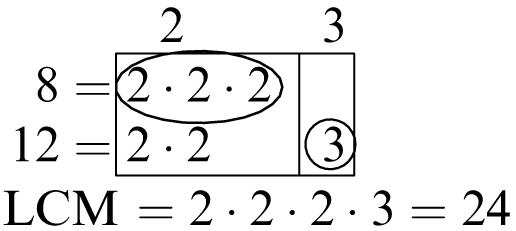
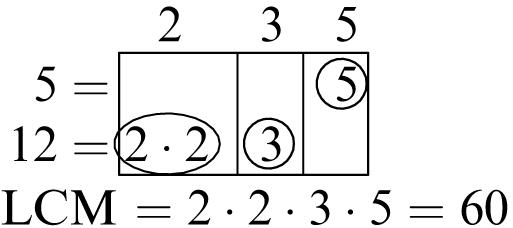
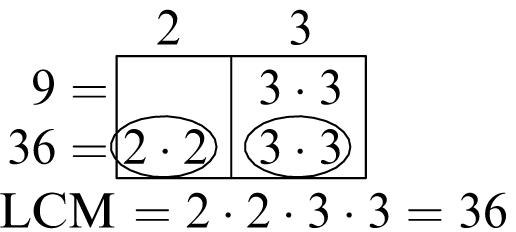
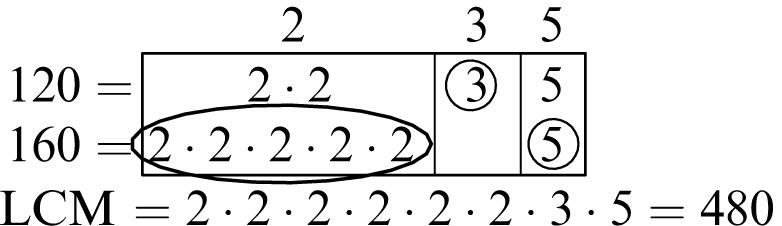
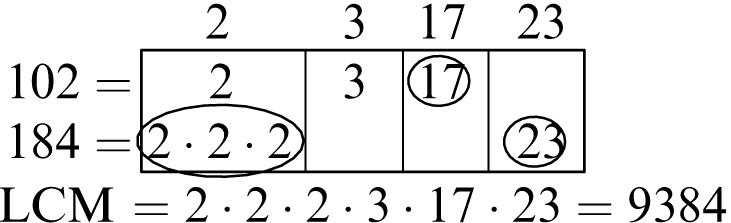
5. Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80
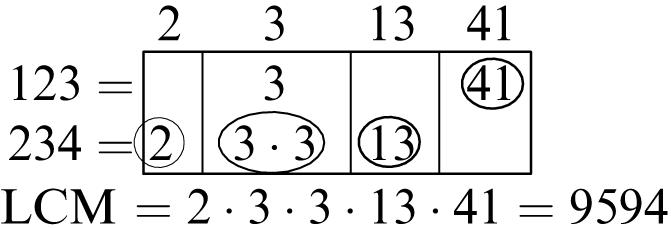
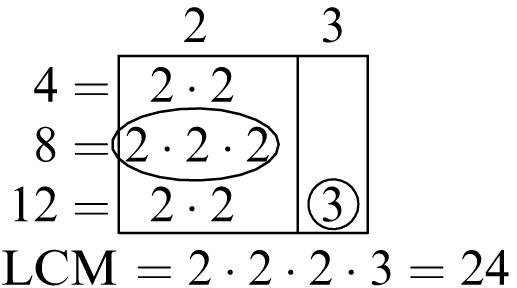
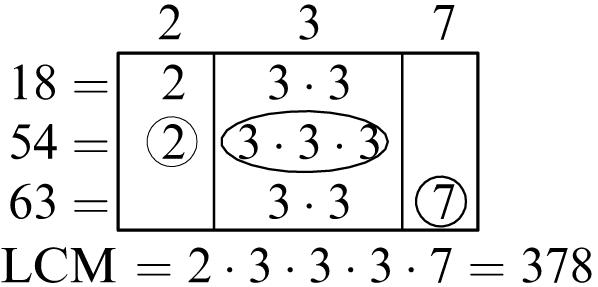
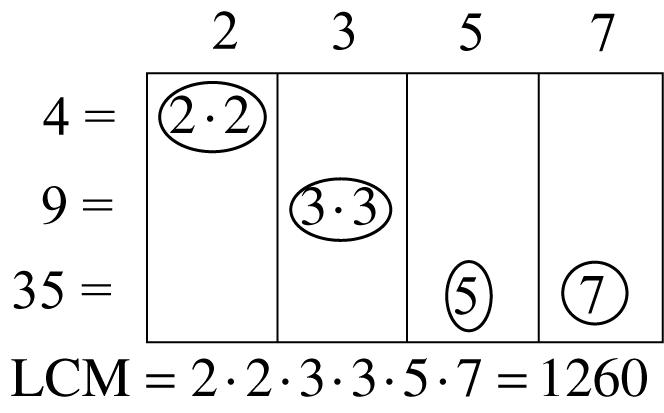
Common multiples: 24, 48
Least common multiple: 24
6. 1, 2, 3, 4, 6, 12
7. 1, 2, 4, 5, 10, 20
8. 1, 23
9. 1, 2, 4, 7, 14, 28
10. Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
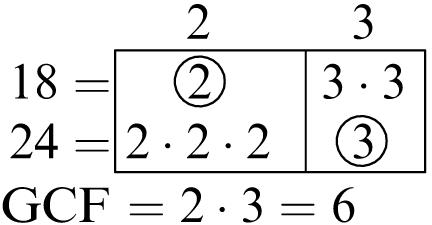
Common factors: 1, 2, 3, 6
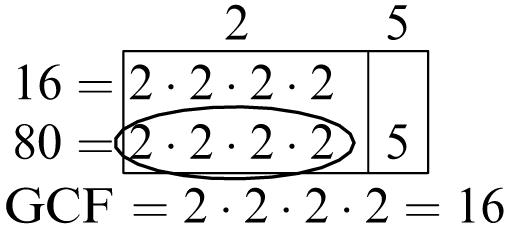
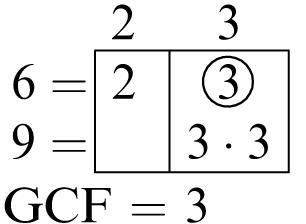
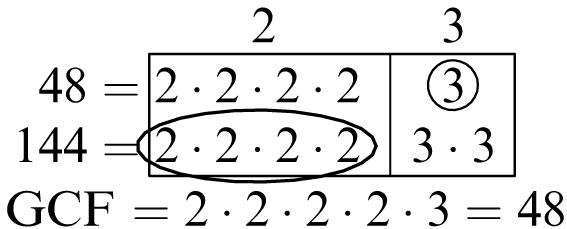
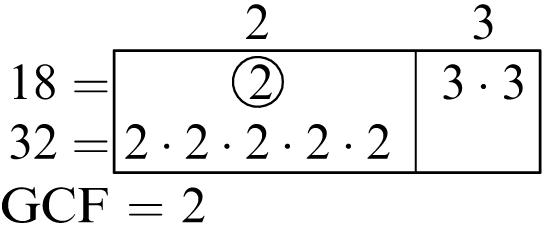
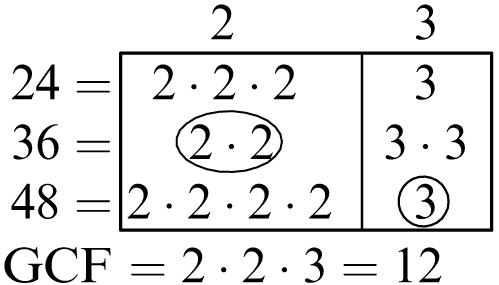
Greatest common factor: 6
Objective A Exercises
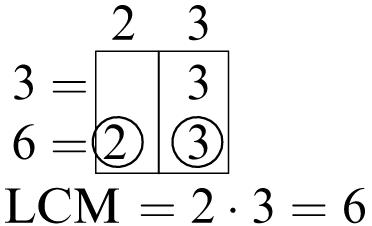
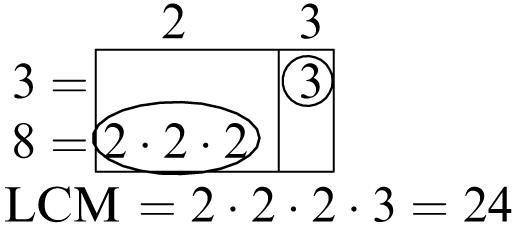
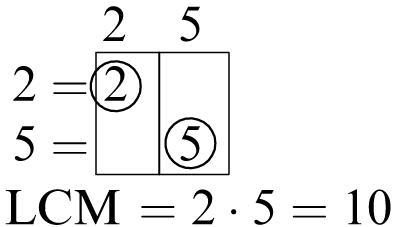
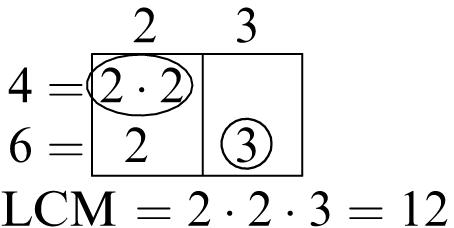
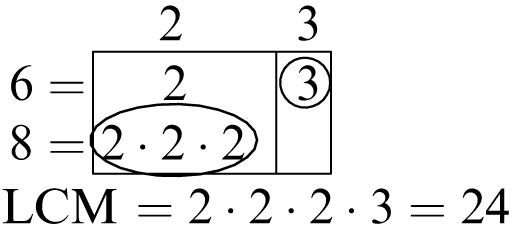
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part


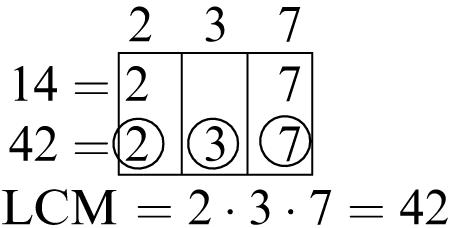

© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part

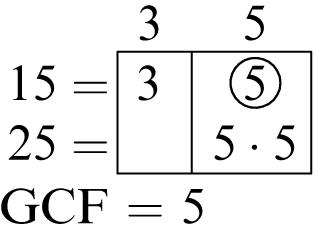
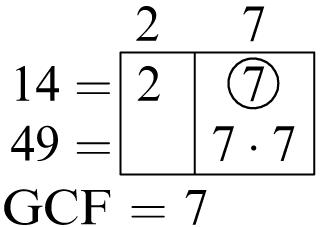
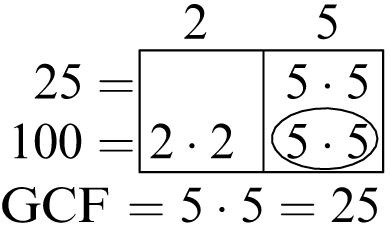
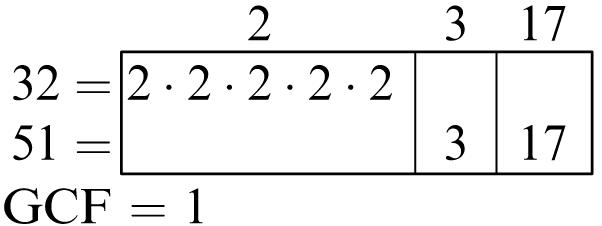
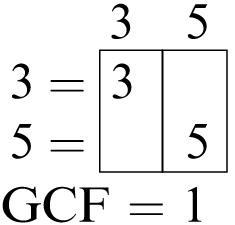
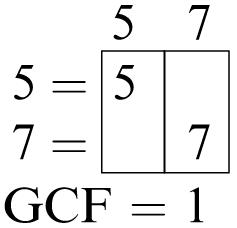
B Exercises

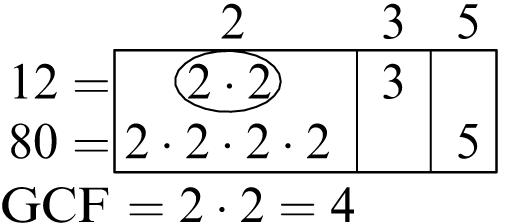


© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
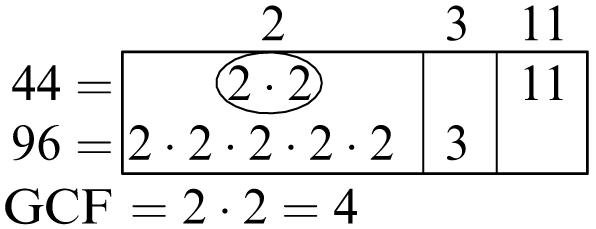
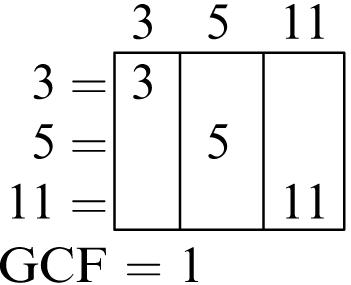
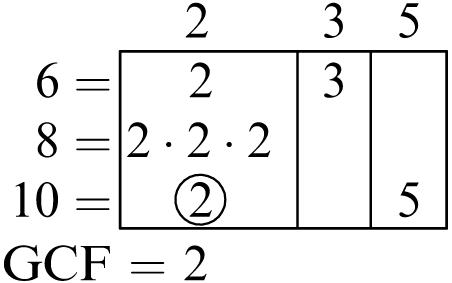

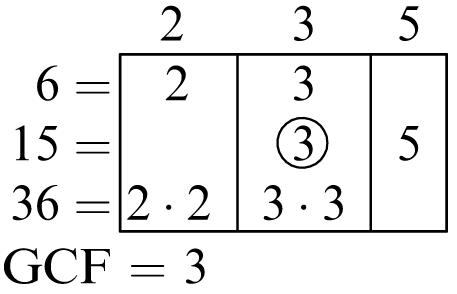

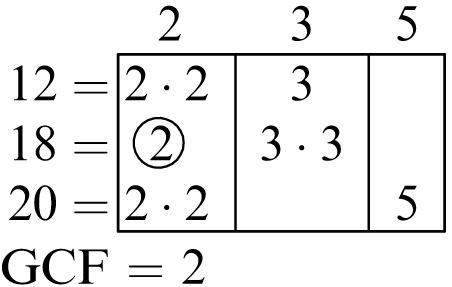
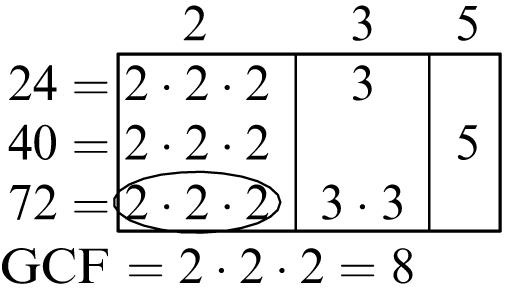
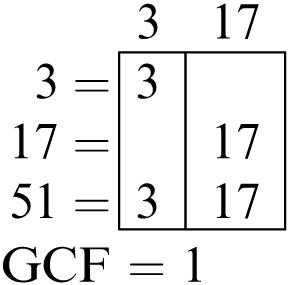
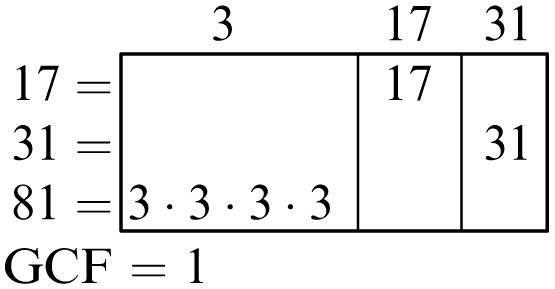
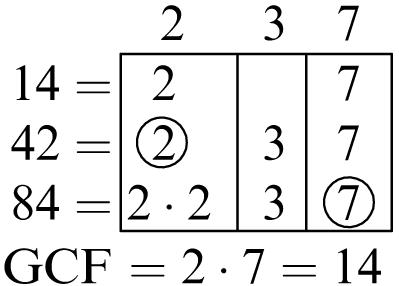
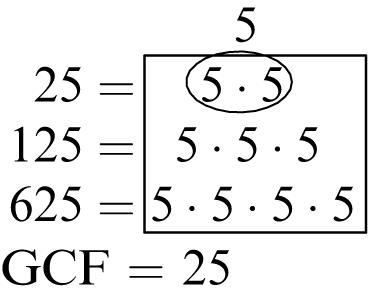
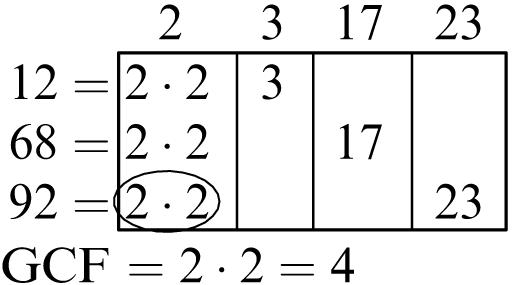
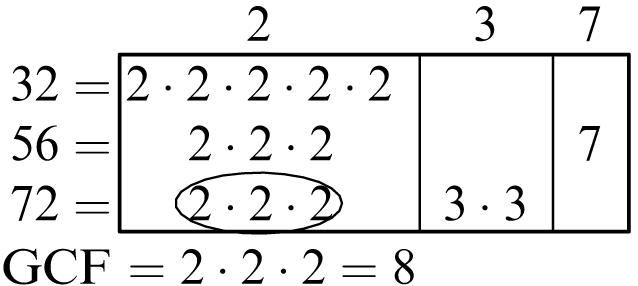
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
Critical Thinking
75. Joe has a 4-day cycle (3 workdays + 1 day off). Raya has a 6-day cycle (5 workdays + 1 day off). The least common multiple of 4 and 6 is 12. After Joe and Raya have a day off together, they will have another day off together in 12 days.
76. The LCM of 2 and 3 is 6. The LCM of 5 and 7 is 35. The LCM of 11 and 19 is 209. The LCM of two prime numbers is the product of the two numbers. The LCM of three prime numbers is the product of the three numbers.
77. The GCF of 3 and 5 is 1. The GCF of 7 and 11 is 1. The GCF of 29 and 43 is 1. Because two prime numbers do not have a common factor other than 1, the GCF of two prime numbers is 1. Because three prime numbers do not have a common factor other than 1, the GCF of three prime numbers is 1.
Projects or Group Activities
78. 4, the GCF of 20, 36, and 60
79a. No; the GCF of 48 and 50 is 4. 48 and 50 are not coprime.
b. Yes; 2555 and 362233, so their GCF is 1.
c. Yes; 22211 and 27333, so their GCF is 1.
d. Yes; 71 and 73 are both prime numbers, so their GCF is 1.
Section 2.2
Concept Check
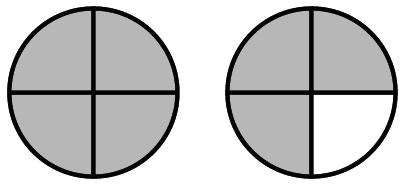
1. Improper fraction; greater than 1
2. Mixed number; greater than 1
3. Proper fraction; less than 1
4. Improper fraction; equal to 1
Objective A Exercises
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
8 3
9 4
27 8
18 5
23.
38. 71 2 2 33 37 6 1
39. 94 1 = 1 55 59 5 4
40. 16 = 16 16 1 116 1 06 6 0
41. 23 23 =23 1 123 2 03 3 0
42. 171 2 2 88 817 16 1
43. 3115 1 = 1 1616 1631 16 15
44. 122 2 2 55 512 10 2
45. 191 6 = 6 33 319 18 1
46. 9 1 1 9 99 9 0
47. 40 5 = 5 8 840 40 0
48. 72 9 9 8 872 72 0
49. 3 1 = 1 3 33 3 0
50. 1617 2 333
51. 212214 4 333
52. 112113 6 222
53. 224226 8 333
54. 536541 6 666
55. 356359 7 888
56. 136137 9 444
57. 124125 6 444
58. 120121 10 222
59. 11201121 15 888
60. 172173 8 999
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
61.
536541 3 121212
62. 355358 5 111111
63.
727734 3 999
64.
516521 2 888
65.
236238 12 333
66.
58513 1 888
67.
335338 5 777
68.
1991100 11 999
69.
360363 12 555
70.
324327 3 888
71.
536541 4 999
72.
778785 6 131313
73.
51125117 8 141414
74. True Critical Thinking
75. Students might mention any of the following: fractional parts of an hour, as in three-quarters of an hour; lengths of nails, as in 3 4 -inch nail; lengths of fabric, as in
5 8 1 yards of material; lengths of lumber, as
in 1 2 2 feet of pine; ingredients in a recipe, as in 1 2 1 cups sugar; or innings pitched, as in four and two-thirds innings.
Projects or Group Activities
76. To write improper fractions that represent the numbers 1, 2, 3, and 4, write the first four multiples of 5 in the numerators: 5101520 ,,, 5555
77. Answers will vary. For example, 17 8
Section 2.3
Concept Check
1. No. 5 does not divide into 7 evenly.
2. 1
Objective A Exercises
3. 1 · 55 1025; 2 · 510 4. 1644; 1 · 44 4 · 416
5. 48163; 3 · 39 16 · 348 6. 8199; 5 · 945 9 · 981 7. 3284; 3 · 412 8 · 432
8. 33113; 3 7 · 21 11 · 333
9. 51173; 3 · 39 17 · 351
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
10. 90109; 9 7 · 63 10 · 990
11. 1644; 3 · 412 4 · 416
12. 3284; 4 5 · 20 8 · 432
13. 919; 3 · 927 1 · 99
14.
25125; 25 5 · 125 1 · 2525
15. 60320; 1 · 2020 3 · 2060
16. 48163; 3 1 · 3 16 · 348
17.
60154; 11 · 444 15 · 460
18. 300506; 6 3 · 18 50 · 6300
19. 1836; 2 · 612 3 · 618
20. 3694; 4 5 · 20 9 · 436
21. 4977; 5 · 735 7 · 749
22. 3284; 4 7 · 28 8 · 432
23. 1892; 5 · 210 9 · 218
24. 36123; 3 11 · 33 12 · 336
25. 313; 7 · 321 1 · 33
26. 414; 4 9 · 36 1 · 44
27. 4595; 7 · 535 9 · 545
28. 4267; 7 5 · 35 6 · 742
29. 64164; 15 · 460 16 · 464
30. 54183; 3 11 · 33 18 · 354
31. 98147; 3 · 721 14 · 798
32. 144624; 24 5 · 120 6 · 24144
33. 4886; 5 · 630 8 · 648
34. 96128; 8 7 · 56 12 · 896
35. 42143; 5 · 315 14 · 342
36. 42314; 14 2 · 28 3 · 1442
37. 144246; 17 · 6102 24 · 6144
38. 1
Objective
B Exercises
39. 11 11 42·21 122·2 · 33
40. 1 1 82·2·24 222·11 11
41. 11 11 222·111 442·2·112 / /
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
74. 1
Critical Thinking
75. Answers will vary. For example, are 4681012 , , , , and 69121518 fractions that are equal to 2 3 76. 155 248
Projects or Group Activities
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part 68.
77a. Five provinces and territories begin with the letter N: Northwest Territories, Nunavut, Newfoundland and Labrador, Nova Scotia, New Brunswick. The fraction of provinces and territories that begin with the letter N is 5 13
b. Five provinces and territories end with a vowel: British Columbia, Alberta, Manitoba, Ontario, Nova Scotia. The fraction of provinces and territories that end with a vowel is 5 13 .
Section 2.4
Concept
Check
1. 25257 9999 2. 131341 88882 3. 8 4. 12
18
21. 4 15 7 15 11 15 227 1 1515
22. 5 7 4 7 5 7 14 2 7
23. 5111175 1 1212121212
24. 537157 1 88888
25. A whole number other than 1
26. A mixed number
27. The number 1
28. A proper fraction
Objective B Exercises 29. 13 26 24 36 71 1 66
30. 28 312 13 412 11 12 31. 33 1414 510 714 13 14 32. 36 510 77 1010 133 1 1010
33. 832 1560 721 2060 53 60 34. 13 618 714 918 17 18 35. 321 856 936 1456 571 1 5656 36. 520 1248 515 1648 35 48 37. 39 2060 714 3060 23 60
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
525 1260 714 3060 3913 6020 39.
16 318 515 618 714 918 3517 1 1818 40.
28 312 510 612 77 1212 251 2 1212
540 648 14 1248 515 1648 5911 1 4848 42.
270 9315 7147 15315 460 21315 277 315 43. 240 360 112 560 735 1260 87279 11 606020
345 460 448 560 735 1260 12882 22 606015
280 3120 372 5120 7105 8120 25717 2 120120
345 10150 14140 15150 954 25150 23989 1 150150
248 372 545 872 756 972 1495 2 7272
2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
48. 124 372 216 972 763 872 10331 1 7272
49. 315 840 324 540 39 40
50. 520 936 721 1236 415 1 3636
51. 39 824 520 624 714 1224 4319 1 2424
52. 136 272 545 872 756 972 13765 1 7272
53. (ii)
2 Fractions
Objective C Exercises
54. 24 22 510 33 33 1010 7 5 10
55.
16 44 212 77 55 1212 131 910 1212
56.
36 33 816 55 22 1616 11 5 16
4 2 5 7 2 9 7
8 6 9 12 8 18 9
520 77 1248 927 22 1648 47 9 48
60. 111 99 222 36 33 1122 17 12 22
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
61. 6 3 2 13 3 8 13
62. 21 8 40 6 21 14 40
63. 29116 88 30120 1133 77 40120 14929 1516 120120
64. 515 1717 1648 1122 33 2448 37 20 48
65. 315 1717 840 714 7 7 2040 29 24 40
66. 749 1414 1284 1352 2929 2184 10117 4344 8484
67. 721 5 5 824 510 2727 1224 317 3233 2424
68. 515 77 618 510 33 918 257 1011 1818
69.
520 77 936 721 22 1236 415 910 3636 70.
16 33 212 39 22 412 510 11 612 251 68 1212
71. 16 22 212 28 33 312 13 44 412 175 910 1212
72. 135 33 3105 121 77 5105 115 22 7105 71 12 105
73. 145 33 290 118 33 590 110 88 990 73 14 90
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
74.
520 66 936 515 66 1236 510 22 1836 4591 141515 36364
75.
318 22 848 728 44 1248 515 33 1648 6113 910 4848
76.
12 1111 24 33 44 51 1112 44 The distance is 1 12 4 inches.
77. 2 3 8 2 3 8 1 1 2 1 4 8 3 7 8 The pole is 7 3 8 metres long.
78.
416 22 936 721 55 1236 371 78 3636
79. 520 5 = 5 624 39 3 = 3 824 295 8 = 9 2424
80.
39 44 412 14 99 312 131 1314 1212
81. 816 4 = 4 918 13 9 = 9 618 191 13 = 14 1818
82. 22 545 44 872 216 22 972 61 8 72
83. 515 1 = 1 824 33 77 7 = 7 2424 2211 11 = 11 2412
84. Yes
85. No
Objective D Exercises
86. Strategy To find the shaft length, add the three distances.
Solution 36 816 1111 1616 14 416 215 1 1616 The shaft length is 1 5 16 cm.
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
87. Strategy To find shaft length, add the lengths of the three parts.
Solution 55 = 1616 714 6 = 6 816 36 1 = 1 816 259 7 = 8 1616 The shaft length is 9 8 16 centimetres.
88. Strategy To find the total thickness, add the table-top thickness to the veneer thickness.
Solution 12 11 816 33 1616 5 1 16
The total thickness is 5 1 16 centimetres.
89. The sum represents the height of the table.
90a. Strategy To find the total number of hours worked, add the five amounts. Solution 55 39 33 412 14 22 312 13 11 412 28 77 312 24 1820 12
A total of 20 hours was worked.
b. Strategy To find the week’s total salary, multiply the hours worked (20) by the pay for 1 hour ($11).
Solution 11 20 220 Your total salary for the week is $220.
91. Strategy To find the total course length, add the three sides.
Solution 33 4 = 4 1010 77 3 = 3 1010 15 2 = 2 210 151 9 = 10 102 The total course length is 10 1 2 km.
92. Strategy To find the thickness of the wall, add the thickness of the stud to the thickness of the dry wall on each side of the stud.
The total thickness of the wall is 5 4 8 in.
93. Strategy To find the thickness of the wall, add the thickness of the stud to the thickness of the dry wall on each side of the stud.
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
The total thickness of the wall is 5 6 8 in.
94. Strategy To find the thickness of the wall, add the thickness of the stud to the thickness of the dry wall on each side of the stud.
Critical Thinking
96. 11112 + + + + 368125 4020151048 + + + + 120120120120120 13313 = = 1 120120 No, this is not possible. The total cannot be greater than 1, which represents all the people surveyed.
Projects or Group Activities
97. 111 ,, 234
98. There is no smallest unit fraction. No matter how small the unit fraction is, we can always add 1 to the denominator to make it even smaller.
99. 74311 12121234
The total thickness of the wall is 7 4 8 in.
95. Strategy To find the minimum length of bolt needed, add the thickness of each piece of wood to the thickness of the washer and the thickness of the nut. Solution 18 = 216
100. 118311 24242438
101. 53211 12121246
Section 2.5
Concept Check 1. 53532 11111111 2. 747431 99993 3. 11 18 4. 1 3
bolt must be 3 1 8 in. long.
2 Fractions
Objective B Exercises
21. 24 36 11 66 31 62
22. 714 = 816 55 = 1616 9 16
23.
535 856 216 756 19 56 24. 535 = 642 318 = 742 17 42
25. 510 714 33 1414 71 142
26. 525 = 945 721 = 1545 4 45 27. 832 1560 721 2060 11 60
28. 714 = 918 13 = 618 11 18
29. 918 = 1632 1717 = 3232 1 32
30. 2958 60120 39 40120 49 120
31. 1155 = 1260 336 = 560 19 60
32. 1133 1545 525 945 8 45 33. 1133 = 2472 728 = 1872 5 72 34.
927 1442 55 4242 2211 4221
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
49.
721 2323 824 216 1616 324 5 7 24
50.
13 17 16 13 88 7 7 1313 5 9 13
51. 5 6 = 5 5 33 4 = 4 55 2 1 5
52.
1428 232322 62424 399 151515 82424 19 7 24
55.
126 292928 244 333 777 444 3 21 4
The distance is 3 21 4 inches.
56.
1210 232322 488 333 191919 888 7 3 8 The distance is 7 3 8 inches.
57.
3323 232322 202020 31212 7 7 7 52020 11 15 20
58.
53.
4826 404039 91818 51515 242424 61818 11 15 18
54.
51569 121211 185454 112222 111111 275454 47 54
3933 12 1211 82424 51010 7 7 7 122424 23 4 24
59. 52570 10 = 10 = 9 94545 113333 5 = 5 = 5 154545 37 4 45
60.
1520 665 31515 399 333 51515 11 2 15
61. No
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
Objective D Exercises
62. Strategy Subtract the larger segment of the shaft 7 7 feet 8
from the total length of the shaft
The missing dimension is 19 8 24 feet.
63. Strategy Subtract the larger shaft segment 7 2 inches 8
from the total shaft length 3
The horses run 1 16 mile farther in the Queen’s Plate than in the Preakness Stakes.
Strategy To find how much farther the horses run, subtract the distance run in the Preakness Stakes 3 1 miles 16
from the distance run in the Belmont Stakes 1 1 miles 2
The missing dimension is 1 9 inches 2
64. Strategy To find how much farther the horses run in the Queen’s Plate than in the Preakness Stakes, subtract the distance run in the Preakness Stakes 3 1miles 16
from the distance run in the Queen’s Plate 1
The horses run 5 16 mile farther in the Belmont Stakes than in the Preakness Stakes.
65. Strategy To find the difference in the desk heights, subtract the shorter desk height 3 56 centimetres 4
from the taller desk height 1 58 centimetres 2
. Solution 126 585857 244 333 565656 444 3 1 4
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
The new desk is 3 1 4 centimetres shorter than a desk of standard height.
66a. Strategy Add the distance from the starting point to the first checkpoint to the distance from the first checkpoint to the second checkpoint.
The distance is 17 7 24 kilometres.
b. Strategy To find the distance, subtract the distance from the starting point to the second checkpoint 17 7 kilometres 24
from the total distance (12 kilometres). Solution 24 12 11 24 1717 7 7 2424 7 4 24
The distance from the second checkpoint to the finish line is 7 4 kilometres 24
67a. Strategy Add the distance to be travelled the first day 3 7kilometres 8
to the distance to be travelled the second day 1 10kilometres 3
Solution 39 77 824 18 1010 324 17 17 24
The distance to be travelled during the first two days is 17 17 24 kilometres.
b. Strategy To find the distance, subtract the miles hiked 17 17 24
from the
On the third day, 19 9 24 kilometres remain.
68. The difference represents the distance that will remain to be travelled after the first day.
69. The difference represents how much farther the hikers plan to travel on the second day than on the first day.
70. Strategy To find how much weight must be lost during the third month:
• Add the weight lost during the first month 1 4kilograms 4
to the amount lost during the second month 1 5kilograms. 2
• Subtract the total lost during the first two months from the total goal (15 kilograms).
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
• Subtract the smaller total thickness from the larger total thickness.
The patient has
71a. The wrestler lost 3 2 kilograms 4 in week 1 and 1 2 kilograms 4 in week 2, or 4 kilograms total. Since less than 6 kilograms needs to be lost, the wrestler can attain the weight class by losing under 2 kilograms. Yes, this is less than the 1 2 kilograms 4 lost in the second week.
b. Strategy To find how much weight must be lost:
• Add the amounts of weight lost during the first two weeks.
• Subtract the current weight loss total from the required
kilograms.
73. The electrician’s income is 1, that is, 100%.
The wrestler needs to lose 3
72. Strategy To find the difference:
• Find the thickness of each wall by adding the thickness of each stud to the thickness of two pieces of dry wall for each wall.
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
Critical Thinking
74.
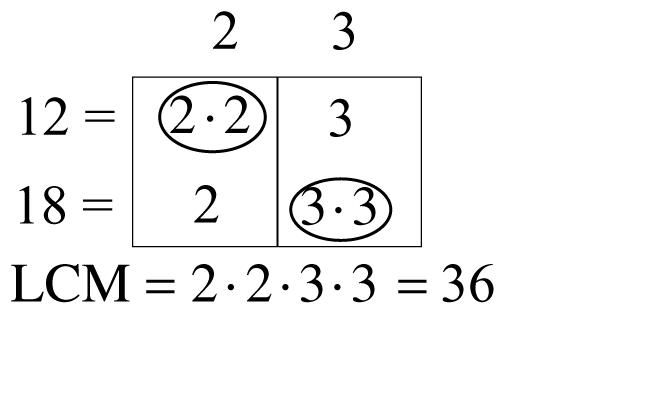
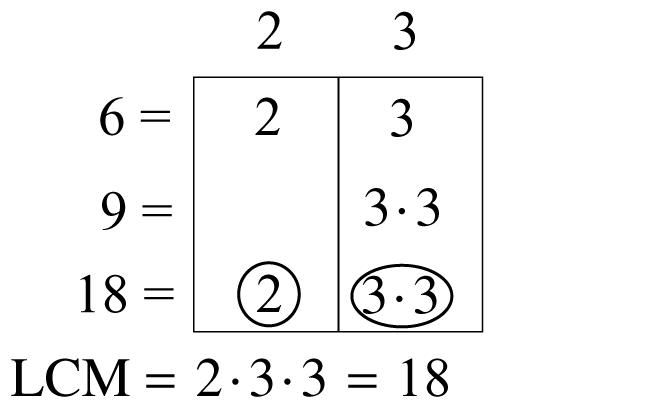


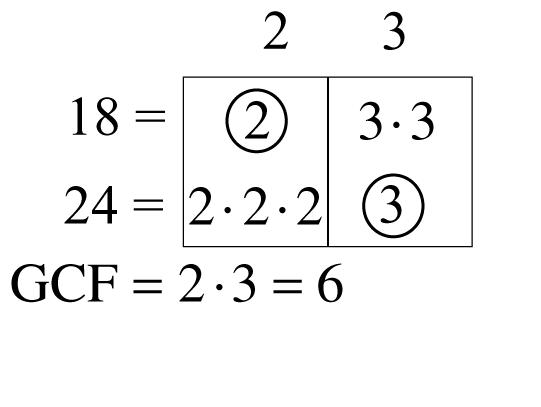

Chapter 2 Fractions
20. 312 520 15 420 17 20
21. 13 22 1030 12 77 1530 51 99 306
22. 48 1111 918 13 77 618 11 18 18
23.
612 77 714 17 11 214 5 6 14
24. 1326 33 2856 17 11 856 19 2 56
1315 887 41212 51010 555 61212 5 2 12
Section 2.6
Concept Check 1. 525210 939327 2. 664243 43 77177
25. 816 55 918 515 77 618 3113 1213 1818 26. 315 99 420 36 77 1020 211 1617 2020 27. 4 98 4 33 55 44 1 3 4
3. Yes 4. Less than Objective A Exercises
2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
1111 111 151615 163 5 2 2 2 2 10 838 32 2 2
11 1 1 545 45·2·2 6156 152·3·3·5
11141 2 24 1 33333 39
11 1 1 2·5 5·2
2125 21 5252
1111 11 11 741543 5 2 21 1 8158152 2 2 3 52 51. 1511511 2 522522 1 5 1 5 1 211 1 1 2
1910 9330 313
11533 5 3453 236 7717 177
· · ·
11 11 3·7·2·2·2 2·2·1
1218 5842 441
· 3·1 211511 5551 3518 331 33
1 1 ·19·3 3··1
23832382 4312 991333
58.
59.
5157552 21 73737·33
64. 208080 020 313133
65. ·0
14949 6000 888
66. 5221173
111 1111 318316832·2·2 55 1631632·2·2·2·3 832 27 33 68.
11 11 / 1126402·13·2·2·2·5 5316 5135135·13 /
1 1 331543 32 420420 3·5·43 2·2·2·2·5 1291 8 1616
11 11 3363103·3·7·2·5 12118 57575·7
11 11 / 13131613·2·2·2·2 618 2132132·1/3
343545 4 8585
1 71 3 22 The height is 1 3 2 inches. 73. 14272 413 212
1 2333 2 1 54
The distance is 54 metres.
74. True
11 1 1 135185 2 3 3 239 25252 5
76.
11 1 1 3335185·7·2·3·3 43 85852·2·2·5 633 15 44
77. 1517517 2 817817
1 5 22217
1 5 8 78.
11 11 2762100 123 531531 / 2·31·2·2·5·5 5·3/1 40
Objective C Exercises
81. Less than $35, because 2 3 4 3
82. Less than 4 feet, because 1 3 of 9 feet is approximately 3 feet; therefore, 1 3 of 1 9 4 feet is approximately 3 feet.
83. Strategy To find the cost of the salmon, multiply the amount of salmon
by the cost per kilograms ($12).
85. Strategy To find the length cut, multiply the length of the board
The length of the board cut off is
86. Strategy To find the perimeter of the square, multiply the length of 1 side 1 16centimetres 4
The perimeter of the square is 66 centimetres.
87. Strategy To find the area of the square, multiply the length of one side
The salmon costs $33.
84. Strategy To find how far a person can walk in 1 3 hour, multiply the distance walked in 1 hour 1 2kilometres
of the square is
88. Strategy To find the area of the rectangle, multiply the length by the width.
Solution 1 1 232233 43 510510 2·11·3·11 5·2·5 36313 14 2525
The area of the rectangle is 13 14 25 square centimetres.
89. Strategy To find the number of acres turned into ethanol, multiply the total number of acres planted each year (3 million) by 6 10
Solution 636 3 10110 361894 1 1101055
4 1 5 million acres of corn are turned into ethanol each year.
90. 13 6× 2 133397 2 8281616
The weight of the 1 6 2 -foot steel rod is 7 2 16 pounds.
91. 7115113196319 12454 1231233636
The weight of the 7 12-foot 12 steel rod is 19 54 36 pounds.
92. 257 10 32
5169534525 8110 84843232 314352157 10226 424288 2528 261026 83232 5321 3637 3232
The total weight is 21 37 32 pounds.
93. Strategy To find the total cost of the capes, multiply the amount of material each cape requires by the cost of 1 yard and by the number of capes needed.
Solution 13 112221222 22 31222 2 792 396 2
The total cost is $396.
94. Strategy To find the distance from the wall to the centre of the drain, multiply the distance of the front face of the cabinet from the wall 1 23 inches 2 by 1 2
Solution 11471 23 2222 47147 224 3 11 4
The distance is 3 11 4 inches.
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
Critical Thinking
95. 1 2 ; Any number multiplied by 1 is the number.
96. Student explanations should include the idea that every 4 years we must add 1 day to the usual 365-day year.
97. A. The product of any two positive rational numbers, each less than 1, is less than either of the two numbers.
Projects or Group Activities
98. 235 349 111 11
2 4189 More than one answer is possible.
Section 2.7 Concept Check
11 11 1051072·5·72 2172153·7·53
1 1 11142 2 2 24212
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
11 11 525535 31 939253 3 5 515
111 111 53585·2·2·25 1681632·2·2·2·36
1 1 21232 3 2 33313
11 11 41492·2·3·3 4 99913·3
1 1 52575 751 2 77727 222
1 1 51595·3·3151 7 69612·322
11 1 1 22292 3 3 3 39323 2
1 11 73747 2 271 1 84832 2 2 366
11 11 73747·2·27 1241232·2·3·39
1 1 535145 2 7101 3 714737 333
1 1 696322·3·2·2·2·2·2 113211911·3·3 6431 1 3333
39. True 40. True Objective B Exercises
1 1 2432 2 3 46 3122
1 1 22121 4 3343·2·26
1 1 33131 3 2232 32
1 1 3323·2 32 2133
1 1 55151 25 66252 3 5 530
56. 11 11 7171374 3 8484813 7·2·27 2·2·2·1326
59.
11 11 1121120119 2 1891891820 11 3 311 2 3 3 2 2 540
60.
111 1 11 21321332110 3 401040104033 3·7·2·57 2·2·2·5·3·1144 61.
1 1 11335332 22 162162165 3 11 233 2 2 2 2 540
62. 3738193812 71 512512519 219
1 24 5 4 4 5
63. · ·
235358 1 383833 5 2 2 240 3 39 4 4 9
·
1 1 1845349 15 3939353 2 2 3 312 3 5353
70. 2 130 3 Division by zero is undefined.
1 3141319141310 8219 5105105191 7 59 2 582662 4 5 191191191 72.
3228152281 4515 551515 2·2·3·19761 3 5·3·52525
1 1 110231022 1021 21213 23172 68 3 74. 17 0300 22 75. 25858582 81118 77777 76.
111111 1111 11 931053510532 61 163216321635 3 5 7 2 2 2 2 2 6 2 2 2 2·5·7
11 11 81380498018 82 918918949 2 2 2 2 5 2 3 3 3 3 7 7 16013 3 4949
11 11 1751175110 101 510510517 / 3·17·2·5 6 5·1/7 79.
1111 11 11 3275959932 71 832832859 / 59·2·2·2·2·2 4 2·2·2·59 / 80. ·
11 111 757035706 75 9696935 2 5 7 2 41 1 3 3 5 733
81. / /
111 11 1 32311551132 21 432432435 11·2·2·2·283 1 2·2·5·1155
84. False 85. False
Objective C Exercises
86. Greater than 22, because
87. Less than 16, because
88. Strategy To find how many boxes can be filled with 22 cups of cereal, divide 22 by the amount per box
There are 5 15 8 servings in 400 grams of cereal.
90. Strategy To find the cost of a similar diamond weighing 1 karat, divide the cost of the purchased diamond ($1200) by its weight 5 karat.
89. Strategy To find the number of servings in 400 grams of cereal, divide 400 by the amount in each
The cost of a similar diamond weighing 1 karat is $1920.
91. Strategy To find the cost of each acre, divide the total cost ($200 000) by the number of acres 1
92. Strategy To find how many kilometres the car can travel on 1 litre of gasoline, divide the distance (440 kilometres) by the amount of gasoline used 47 1 2 litres
94a. Strategy To find the number of acres, subtract the number of acres set aside 1 1 2
from the total number of acres 3 9. 4
The car can travel 5 9 19 kilometres on 1 gallon of gasoline.
93. Strategy To find the number of turns, divide the distance for the nut to move 4 4 centimetres 5
by the distance the nut moves for each turn
8 4 acres are available for housing.
b. Strategy To find the number of parcels, divide the number of acres available 1 8 4
by the number of acres in one parcel 1 . 4
33 parcels of land can be sold.
95a. Strategy To find the total weight of the fat and bone, subtract the weight after trimming 1 4 kilograms 3
from the original weight 3 5 kilograms. 4
The nut will make 12 turns in moving 4 4
The total weight of the fat and bone was 5 1 12 kilograms.
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
b. Strategy To find the number of servings, divide the weight after trimming 4 1 3 kilograms
by the weight of one serving 1 3 kilogram
97. Strategy To find the distance between each post:
• Find the total distance taken up by the five posts 1 1 inches each 4
• Subtract that sum from the total distance between the posts 3 22 inches 4
The chef can cut 13 servings from the roast.
96. Strategy To find the length of the remaining piece:
• Divide the total length (5 metres) by the length of each shelf 1 1 metres 6
• Multiply the fraction left over by the length of one shelf.
• Divide the remaining distance by 6, the number of spaces between each of the five inserted posts and the end posts.
The length of the remaining piece is 1
each
98. Strategy To find the distance between each post:
• Find the total distance taken up by the 10 posts 1 1 inches each 2
• Subtract that sum from the total distance between the posts 1 42 inches 2
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
• Divide the remaining distance by 11, the number of spaces between each of the ten inserted posts and the end posts.
107. Strategy To find the bank-recommended maximum monthly house payment, multiply your monthly income ($4500) by 1 . 3 Solution 14500 4500 = = 1500 33 The bank would recommend that your maximum monthly house payment be $1500.
108. Strategy To find how much higher the grass plots were mowed for the study 3 inch 20 than the more common heights used in tournaments 11 inch or inch, 108 subtract each of the shorter heights from the higher height. Solution 31321 2010202020 31651 208404040
The grass plots in the study are 1 20 inch or 1 40 inch higher.
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
109. Strategy Multiply the length of one side (28 centimetres) by 1 2 and multiply the thickness 7 centimetre 8 by 2.
Solution 1 28 = 14 2 centimetres on one side.
The thickness is 773 21 844 centimetres. The other dimension (28 centimetres) remains the same.
The dimensions of the board when it is closed are 28 centimetres by 14 centimetres by 1 3 4 centimetres.
110. Strategy To find the number of miles:
• Find out how many units of 1 2 centimetre there are in 3 4 10 centimetres.
• Multiply by 60 kilometres.
Solution 3143243 4units 1021015
Then, because each unit represents 60 kilometres, 4360 516 51
The distance is 516 kilometres.
111. First, find the spacing between the three columns. 2224 2centimetre 5515
Second, find the remaining space for the columns.
1458158 181817 2510101010 7 17centimetres 10
Third, divide that space among the three columns.
7177117727 1735 101033030 9 5centimetres 10
Projects or Group Activities
112. Internet Explorer: 9 25
Firefox: 7 25
Chrome: 9 50
9791814941 25255050505050 41 50 of the market
113. Safari: 3 50 Opera: 1 50 313 5050 50 1 50 1 3 1 3 times more people
114. 99 2 50 50 2 2 2 9 billion, 125 or 360 000 000, or 360 million
93179 5050502525 931141845 505050505050 45504551 1 5050505010
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
Section 2.8
Concept Check
1. Equal to
2. Greater than
3. Less than
4. (ii)
Objective A Exercises
5. 1119 4040
6. 9219 > 103103
7. 21451525 ,, 32172137
8. 21631523 = , = , > 54084058
9. 51571457 ,, 8241224812
10. 113317341117 = , = , < 164824481624
11. 7281133711 ,, 9361236912
12. 52572857 = , = , < 126015601215
13. 133919381319 ,, 144221421421
14. 1326721137 ,, 183612361812
15. 7351144711 ,, 24120301202430
16. 135219571319 ,, 36144481443648
17. 4 5 is larger.
Objective B Exercises
18. 2 3339 88864
19. 2 55525 121212144
20. 3 22228 9999729
22. 4 1 1 2121111 · ···· 3232222 2·1·1·1·11
2·2·2·5·58 5·5·5·7·7245
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
26. 112322 233663 12 63 14 66 5 6
27. 232432 +=+ 510310103 72 103 2120 3030 1 30
28. 113123 324314 23 34 89 1212 175 1 1212
29. 314424 715555 61 1 55
30. 72478 935915 3524 4545 11 45
31. 51252 883824 152 2424 17 24
1 4 1 1 5 2 1
134113 35923
2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part
31175322215 4128164242416
43. 2 11371197 +=+ 16412161612 27 + 1612 17 + 812 314 + 2424 17 24
3413161
55. 22 2 531532 642644
56a. 2533 9645
b. 2533 9645
Critical Thinking
57a.
More people choose location.
b.
125 Food Quality 4100 1326 Location 50100 416 Menu 25100
The criterion that was cited by most people was location.
Projects or Group Activities
© 2016 Nelson Education Ltd. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part












