Chapter 1 Graphs
Section 1.1
1. 0
2.
3. x-coordinate; y-coordinate;quadrants
4. False;pointsthatlieinQuadrantIVwillhavea positive x-coordinateandanegative y-coordinate. Thepoint 1,4liesinQuadrantII.
5. d
6. c
7. (a)QuadrantII (b) x-axis (c)QuadrantIII (d)QuadrantI (e) y-axis (f)QuadrantIV
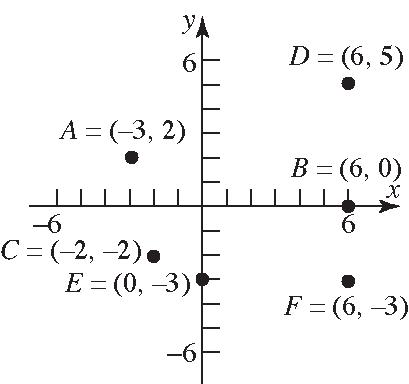
8. (a)QuadrantI (b)QuadrantIII (c)QuadrantII (d)QuadrantI (e) y-axis (f) x-axis
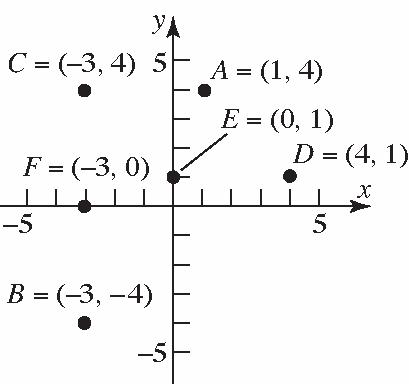
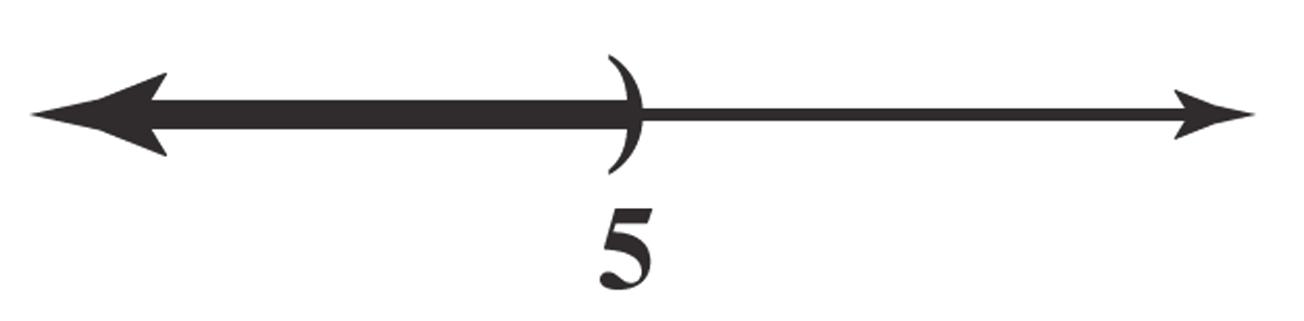
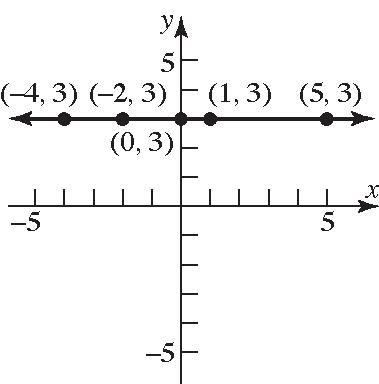
9. Thepointswillbeonaverticallinethatistwo unitstotherightofthe y-axis.
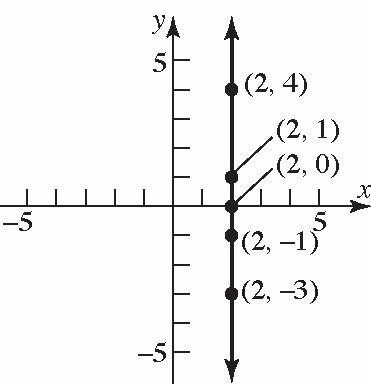
10. Thepointswillbeonahorizontallinethatis threeunitsabovethex-axis.
11. 1,4;QuadrantII
12. (3,4);QuadrantI
13. (3,1);QuadrantI
14. 6,4;QuadrantIII
15. min11 max5
scl1 min3 max6 scl1 X X X Y Y Y
16. min3 max7 scl1 min4 max9 scl1 X X X Y Y Y
17. min30 max50 scl10 min90 max50 scl10 X X X Y Y Y
18. min90 max30 scl10 min50 max70 scl10 X X X Y Y Y
19. min10 max110 scl10 min10 max160 scl10 X X X Y Y Y
20. min20 max110 scl10 min10 max60 scl10 X X X Y Y Y
21. min6 max6 scl2 min4 max4 scl2 X X X Y Y Y
22. min3 max3 scl1 min2 max2 scl1 X X X Y Y Y
23. min6 max6 scl2 min1 max3 scl1 X X X Y Y Y
24. min9 max9 scl3 min12 max4 scl4 X X X Y Y Y
25. min3 max9 scl1 min2 max10 scl2 X X X Y Y Y
26. min22 max10 scl2 min4 max8 scl1 X X X Y Y Y
27.
28.
(0,0)and(1,–1)areonthegraphofthe equation.
29. 229yx
30.
(0,1)and(–1,0)areonthegraphofthe equation.
31. 224xy 22 024 44
(0,2)and2,2areonthegraphofthe equation.
32. 2244xy 22 0414 44 22 2404
(0,1)and(2,0)areonthegraphoftheequation.
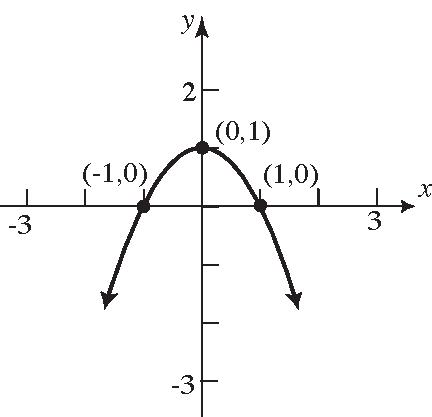
33. (–1,0),(1,0)
34. (0,1)
35. ,0,,0,(0,1)22
36. (–2,0),(2,0),(0,–3)
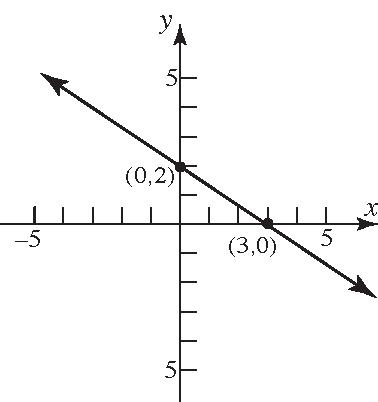
37. 1,0, 0,2, 0,2
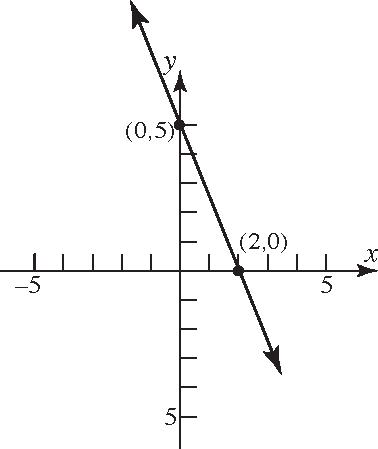
38. (2,0),(0,2),(–2,0),(0,–2)
39. (–4,0),(–1,0),(4,0),(0,–3)
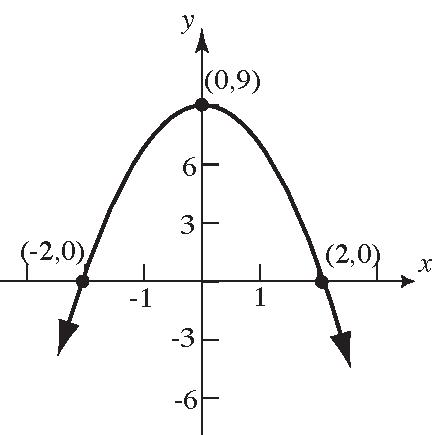
40. (–2,0),(2,0),(0,3)
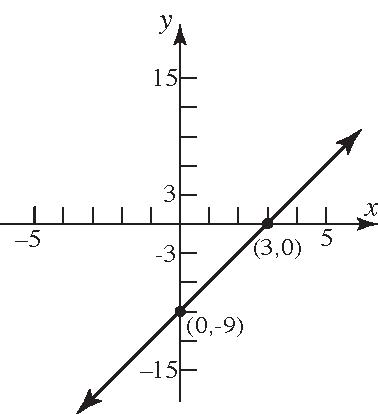
41. 2 yx 42. 6 yx
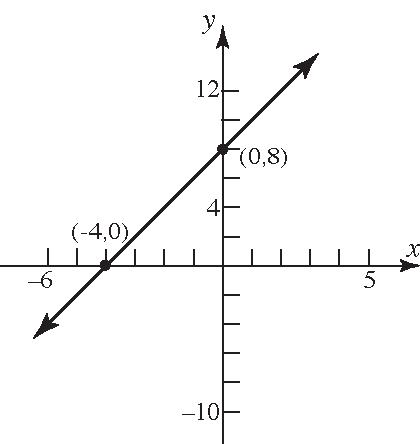
43. 28yx
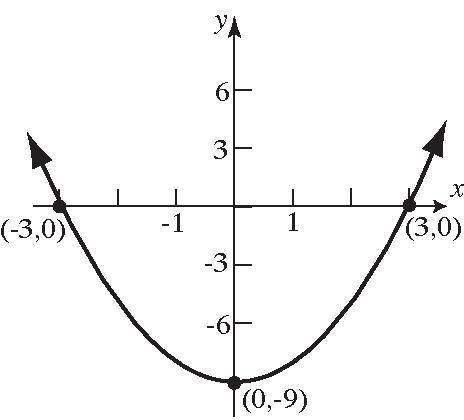
51. 2 9436 xy
52. 2 44 xy
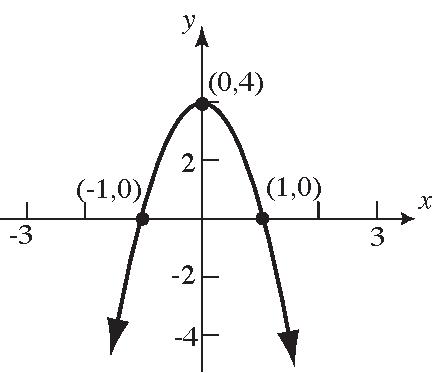
53. 213yx
Section1.1: Graphing Utilities; Introduction to Graphing Equations
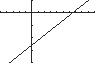
54. 314yx
Thex-interceptis4.67 x andthey-interceptis 14 y .
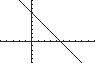
55. 2 215yx
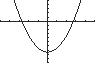
Thex-interceptis6.5 x andthey-interceptis 13 y
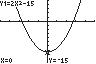
Thex-interceptsare2.74 x and2.74 x They-interceptis15 y
56. 2 319yx
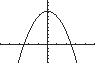
59. 2 25375337or 3 x xyy
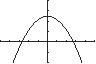
Thex-interceptsare2.52 x and2.52 x
They-interceptis19 y .
57. 3243343 or 2 x xyy
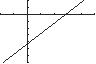
Thex-interceptis14.33 x andthey-intercept is21.5 y
58. 4582482 or 5 x xyy
Thex-interceptis20.5 x andthey-interceptis 16.4 y
Thex-interceptsare2.72 x and2.72 x They-interceptis12.33 y .
60. 2 22352335or 3 x xyy
Thex-interceptsare4.18 x and4.18 x They-interceptis11.67 y .
61. If 2,5isshifted3unitsrightthenthex coordinatewouldbe23 .Ifitisshifted2units downthenthey-coordinatewouldbe5(2)
Thusthenewpointwouldbe 23,5(2)(5,3) .
62. If 1,6isshifted2unitsleftthenthex coordinatewouldbe1(2) .Ifitisshifted4 unitsupthenthey-coordinatewouldbe64
Thusthenewpointwouldbe 1(2),64(3,10)
63. a. 25feet
b. 23.2ft;34.1ft
c. (0,6),Theshotisreleasedataheightof6 feet;(48.7,0),theshothitsthegroundafter travelingahorizontaldistanceof48.7feet.
64. a. 20meters
b. 12seconds;36meters
c. (0,2),Thediscusisreleasedataheightof2 meters;(18,0),thediscushitstheground after18seconds.
65. a. $19.95;$19.95
b. $182.45
c. (0,19.95),Themembershipplancosts $19.95permonth.
66. a. 1.5miles
b. 1mile
c. (0,2),Caleb’sfriendlives2milesfromhis house;(28,0),ittakesCaleb28minutesto ridehome.
67. (1,0),(1,0),(0,1),(0,1)
68. (2,0),(3,0),(0,2),(0,0),(0,2)
69. Answerswillvary
70. a.
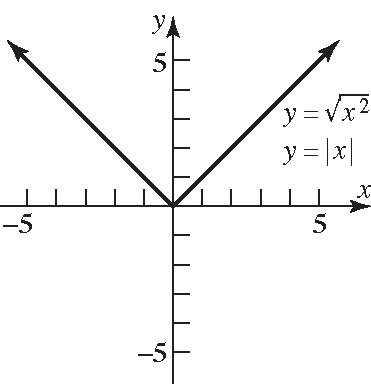
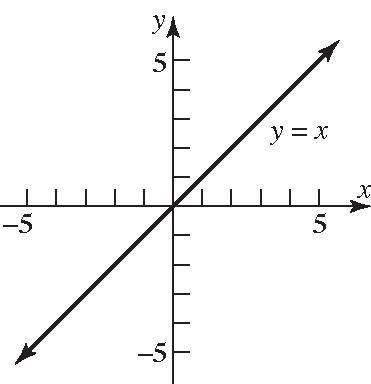
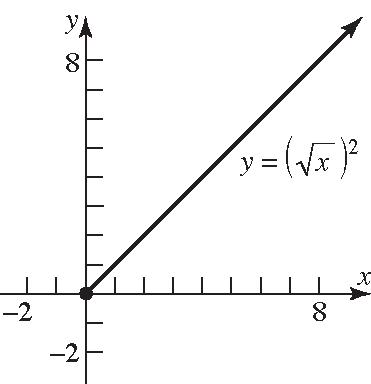
b. Since2 x x forall x ,thegraphsof 2and y xyx arethesame.
c. For 2 yx ,thedomainofthevariable x is0 x ;for yx ,thedomainofthe variable x isallrealnumbers.Thus, 2 onlyfor0.xxx
d. For2 yx ,therangeofthevariable y is 0 y ;for yx ,therangeofthevariable y isallrealnumbers.Also, 2onlyif0. xxx
71. Answerswillvary
72. Answerswillvary.Acompletegraphpresents enoughofthegraphtotheviewersotheycan “see”therestofthegraphasanobvious continuationofwhatisshown.
73. Answerswillvary.
Section 1.2
1. 5388
2. 22 34255
3. 222 11601213600372161
Sincethesumofthesquaresoftwoofthesides ofthetriangleequalsthesquareofthethirdside, thetriangleisarighttriangle.
4. 0,0
5. 1 2 bh
6. true
7. midpoint
8. False;thedistancebetweentwopointsisnever negative.
9. True;1212 , 22
10. a
22 12 22 (,)(20)(10) 21415
12. 22 12 22 (,)(20)(10) (2)1415
319110 dPP
16.
22 12 22 (,)(53)44 2846468217 dPP
22 12 22 (,)2140 34916255 dPP
dPP
17. 22 12 22 (,)4(7)(03) 11(3)1219130
18.
22 12 22 (,)422(3) 2542529 dPP
19. 22 12 22 (,)(65)1(2) 131910
20.
dPP
22 12 22 (,)6(4)2(3) 10510025 12555 dPP
21.
dPP
22 12 22 (,)2.3(0.2)1.1(0.3) 2.50.86.250.64 6.892.62
22.
dPP
22 12 22 (,)0.31.21.12.3 (1.5)(1.2)2.251.44 3.691.92
23. 22 12 2222 (,)(0)(0) ()() dPPab abab
24. 22 12 22 222 (,)(0)(0) ()() 22 dPPaa aa aaaa
Section1.2: The Distance and Midpoint Formulas
25. (2,5),(1,3),(1,0)ABC
22 22 22 22 22 22 (,)1(2)(35) 3(2)9413 (,)11(03) (2)(3)4913 (,)1(2)(05) 1(5)12526 dAB dBC dAC
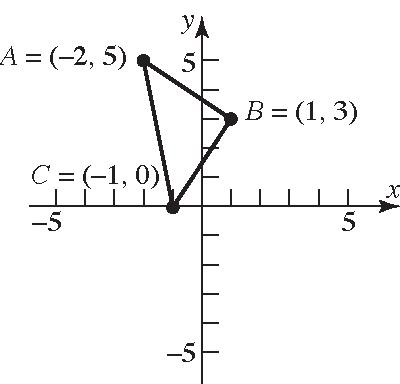
Verifyingthat ∆ ABCisarighttrianglebythe PythagoreanTheorem:
222 222 (,)(,)(,) 131326 131326 2626 dABdBCdAC
Theareaofatriangleis1 2 A bh .Inthis problem,
1(,)(,) 2 11131313 22 13squareunits 2 A dABdBC
26. (2,5),(12,3),(10,11)ABC 22 22 22 22 22 22 (,)12(2)(35) 14(2) 1964200 102 (,)1012(113) (2)(14) 4196200 102 (,)10(2)(115) 12(16) 144256400 20 dAB dBC dAC
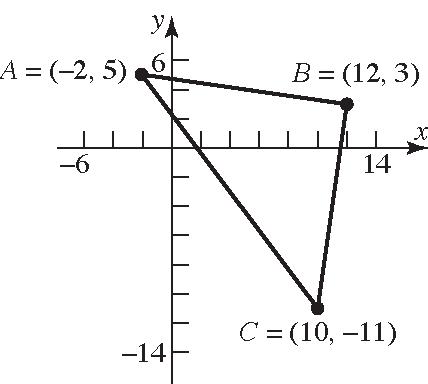
Verifyingthat ∆ ABCisarighttrianglebythe PythagoreanTheorem:
222 222 (,)(,)(,) 10210220 200200400 400400 dABdBCdAC
Theareaofatriangleis1 2 A bh .Inthis problem,
1(,)(,) 2 1102102 2 11002100squareunits 2 AdABdBC
27. (5,3),(6,0),(5,5)ABC
dAB
130 (,)56(50) (1)5125
dBC dAC
(,)5(5)(53) 1021004
22 22 22 22 22 22 (,)6(5)(03) 11(3)1219
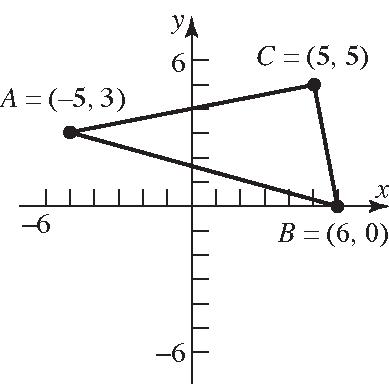
Verifyingthat ∆ ABCisarighttrianglebythe PythagoreanTheorem:
222 222 (,)(,)(,) 10426130 10426130 130130 dACdBCdAB Theareaofatriangleis1 2 A bh .Inthis problem, 1(,)(,) 2 110426 2 122626 2 1226 2 26squareunits A dACdBC
28. (6,3),(3,5),(1,5)ABC 22 22 22 22 22 22 (,)3(6)(53) 9(8)8164 145 (,)13(5(5)) (4)1016100 116229 (,)1(6)(53) 52254
29 dAB dBC dAC
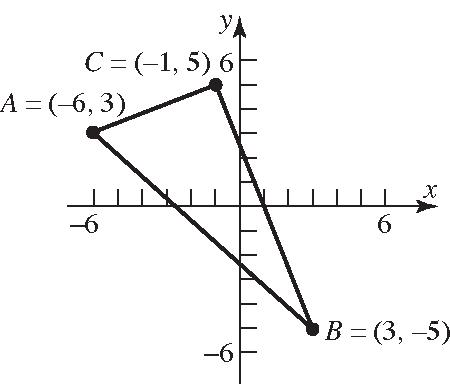
Verifyingthat ∆ ABCisarighttrianglebythe PythagoreanTheorem:
222 222 (,)(,)(,) 29229145 29429145 29116145 145145 dACdBCdAB
Theareaofatriangleis1 2 A bh .Inthis problem,
1(,)(,) 2 129229 2 1229 2 29squareunits A dACdBC
29. (4,3),(0,3),(4,2)ABC
22 22 22 22 22 22 (,)(04)3(3) (4)0160 16 4 (,)402(3) 451625 41 (,)(44)2(3) 05025 25 5
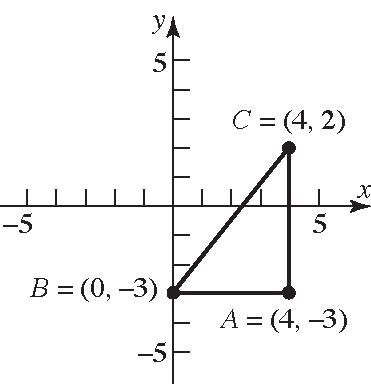
Verifyingthat ∆ ABCisarighttrianglebythe PythagoreanTheorem: 222 222 (,)(,)(,) 4541 162541 4141 dABdACdBC
Theareaofatriangleis1 2 A bh .Inthis problem,
1(,)(,) 2 145 2 10squareunits A dABdAC
Section1.2: The Distance and Midpoint Formulas
30. (4,3),(4,1),(2,1)ABC
22 22 22 22 22 22 (,)(44)1(3) 04 016 16 4 (,)2411 (2)040 4 2 (,)(24)1(3) (2)4416 20 25 dAB dBC dAC
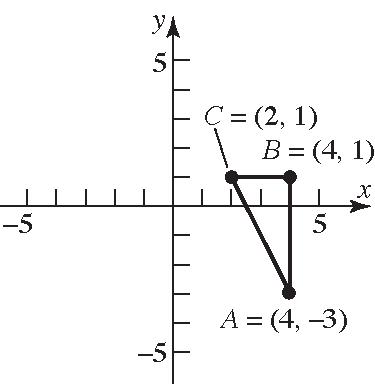
Verifyingthat ∆ ABCisarighttrianglebythe PythagoreanTheorem:
222 222 (,)(,)(,) 4225 16420 2020 dABdBCdAC Theareaofatriangleis1 2 A bh .Inthisproblem,
1(,)(,) 2 142 2 4squareunits A dABdBC
31. Thecoordinatesofthemidpointare:
xyy xy
1212(,),22 3544 , 22
80 , 22 (4,0)
32. Thecoordinatesofthemidpointare:
1212(,),22 2204 , 22 04 , 22 0,2
33. Thecoordinatesofthemidpointare: 1212(,),22 1840 , 22 74 , 22 7,2 2
34. Thecoordinatesofthemidpointare: 1212(,),22 2432 , 22 61 , 22 3,1 2 x xyy
35. Thecoordinatesofthemidpointare: 1212(,),22 7951 , 22 164 , 22 (8,2)
x xyy
36. Thecoordinatesofthemidpointare: 1212(,),22 4232 , 22 21 , 22 1,1 2 x xyy xy
37. Thecoordinatesofthemidpointare: 1212(,),22 00 , 22 , 22 x xyy xy ab ab
38. Thecoordinatesofthemidpointare: 1212(,),22 00 , 22 , 22 x xyy xy aa
39.
121,3;5,15PP
22 12 22 ,51153 412 16144 160410
Thecoordinatesofthemidpointare: 1212(,),22 15315 , 22 618 , 22 (3,9)
x xyy xy
Section1.2: The Distance and Midpoint Formulas
40. 128,4;2,3PP
22 12 22 ,2834 107
Thecoordinatesofthemidpointare: 1212(,),22 8243 , 22 61 , 22 3,1 2
124,6;4,8PP
x xyy xy 41.
22 12 22 ,4486 814 64196
Thecoordinatesofthemidpointare:
1212(,),22 446(8) , 22 02 , 22 (0,1)
Thecoordinatesofthemidpointare: 1212(,),22 036(8) , 22 32 , 22 3,1 2
43. a. Ifweusearighttriangletosolvethe problem,weknowthehypotenuseis13unitsin length.Oneofthelegsofthetrianglewillbe 2+3=5.Thustheotherlegwillbe:
222 2 2 513 25169 144 12 b b b b
Thusthecoordinateswillhaveanyvalueof 11213 and11211 .Sothepoints are 3,11and 3,13.
b. Considerpointsoftheform 3, y thatarea distanceof13unitsfromthepoint 2,1
22 2121 22 22 2 2 3(2)1 51 2512 226 dxxyy y y yy yy
2 2 22 2 2 13226 13226 169226 02143 01113 yy yy yy yy yy 110 11 y y or130 13 y y
Thus,thepoints 3,11and 3,13area distanceof13unitsfromthepoint 2,1
44. a. Ifweusearighttriangletosolvethe problem,weknowthehypotenuseis17unitsin length.Oneofthelegsofthetrianglewillbe 2+6=8.Thustheotherlegwillbe: 222 2 2 817 64289 225 15 b b b b
Thusthecoordinateswillhaveanxvalueof 11514 and11516 .Sothepointsare 14,6and 16,6.
b. Considerpointsoftheform ,6 x thatare adistanceof17unitsfromthepoint 1,2.
2 2 22 2 2 17265 17265 289265 02224 01416 xx xx xx xx xx
140 14 x x or160 16 x x Thus,thepoints 14,6and 16,6area distanceof13unitsfromthepoint 1,2
45. Pointsonthe x-axishavea y-coordinateof0.Thus, weconsiderpointsoftheform ,0x thatarea distanceof6unitsfromthepoint 4,3.
22 2121 22 22 2 2 430 1683 1689 825 dxxyy x xx xx xx
2 2 22 2 2 2 6825 6825 36825 0811 (8)(8)4(1)(11) 2(1) 864448108 22 863 433 2
433 x or433 x Thus,thepoints 433,0 and 433,0are onthe x-axisandadistanceof6unitsfromthe point 4,3.
46. Pointsonthe y-axishavean x-coordinateof0. Thus,weconsiderpointsoftheform 0, y that areadistanceof6unitsfromthepoint 4,3
22 2121 22 22 2 2 403 496 1696 625 dxxyy y yy yy yy
2 2 22 2 2 2 6625 6625 36625 0611 (6)(6)4(1)(11) 2(1) 63644680 22 645 325 2 yy yy yy yy y
325 y or325 y
Thus,thepoints 0,325 and 0,325
areonthe y-axisandadistanceof6unitsfromthe point 4,3.
47. Forthe x coordinateof B
Thus,thepoint B is
48. Letthecoordinatesofpoint B be ,x y .Using themidpointformula,wecanwrite
18 2,3, 22 x y
Thisleadstotwoequationswecansolve.
Section1.2: The Distance and Midpoint Formulas
49.
Point B hascoordinates
ThemidpointofACis:
ThemidpointofBCis:
22 22 (,)04(34) (4)(1)16117 dCD
22 22 (,)26(20) (4)2164 2025 dBE
22 22 (,)(20)(50) 25425 29 dAF
52. Let12(0,0),(0,4),(,) PPPxy 22 12 22 1 22 22 22 2 22 22 ,(00)(40) 164 ,(0)(0) 4 16 ,(0)(4) (4)4 (4)16 dPP dPPxy xy xy dPPxy xy xy
Therefore,
Chapter1: Graphs
22 22 4 816 816 2 yy yyy y y whichgives 22 2 216 12 23 x x x Twotrianglesarepossible.Thethirdvertexis 23,2or23,2
53. 22 12 22 (,)(42)(11) (6)0 36 6 dPP
22 23 22 (,)4(4)(31) 0(4) 16 4 dPP
22 13 22 (,)(42)(31) (6)(4) 3616 52 213 dPP
Since 222 122313 (,)(,)(,) dPPdPPdPP , thetriangleisarighttriangle.
22 13 22 (,)4(1)(54) 5(9) 2581 106 dPP
Since 222 122313 (,)(,)(,) dPPdPPdPP , thetriangleisarighttriangle.
Since 1223 ,, dPPdPP ,thetriangleis isosceles. Therefore,thetriangleisanisoscelesright triangle. 55.
22 12 22 (,)0(2)7(1) 2846468 217 dPP
22 23 22 (,)30(27) 3(5)925 34 dPP
22 13 22 (,)3(2)2(1) 53259 34 dPP
Since2313 (,)(,) dPPdPP ,thetriangleis isosceles.
Since 222 132312 (,)(,)(,) dPPdPPdPP , thetriangleisalsoarighttriangle. Therefore,thetriangleisanisoscelesright triangle.
54. 22 12 22 (,)6(1)(24) 7(2) 494
53 dPP
22 23 22 (,)46(52) (2)(7) 449
53 dPP
56.
55 dPP
22 12 22 (,)4702 (11)(2) 1214125
100 10 dPP
22 23 22 (,)4(4)(60) 866436
Copyright©2021PearsonEducation,Inc.
Since 222 132312 (,)(,)(,) dPPdPPdPP , thetriangleisarighttriangle.
57. UsingthePythagoreanTheorem: 222 2 2 9090 81008100 16200 16200902127.28feet
58. UsingthePythagoreanTheorem: 222 22 6060 360036007200 720060284.85feet
59. a. First:(90,0),Second:(90,90), Third:(0,90) (0,0)
(90,0) (90,90) X Y
Section1.2: The Distance and Midpoint Formulas
b. Usingthedistanceformula: 22 22 (31090)(1590) 220(75)54025 52161232.43feet
d
c. Usingthedistanceformula: 22 22 (3000)(30090) 300210134100 30149366.20feet d
60. a. First:(60,0),Second:(60,60) Third:(0,60) (0,0) (0,60) (60,0) (60,60) x y
b. Usingthedistanceformula: 22 22 (18060)(2060) 120(40)16000 4010126.49feet
d
c. Usingthedistanceformula: 22 22 (2200)(22060) 22016074000 20185272.03feet
d
61. TheFocusheadingeastmovesadistance60t after t hours.Thetruckheadingsouthmovesa distance40t after t hours.Theirdistanceapart after t hoursis:
22 2 (60)(45) 36002025 5625
62. 15miles5280ft1hr22ft/sec 1hr1mile3600sec
63. a. Theshortestsideisbetween1(2.6,1.5) P and2(2.7,1.7) P .Theestimateforthe desiredintersectionpointis:
12122.62.71.51.7 ,, 2222
b. Usingthedistanceformula: 22 22 (2.651.4)(1.61.3) (1.25)(0.3) 1.56250.09
64. Let1(2014,110.21) P and 2(2018,138.43) P .Themidpointis:
1212 ,,22 20142018110.21138.43 , 22 4032248.64 , 22 2016,124.32
Theestimatefor2016is$124.32billion.The estimatenetsalesofCostcoWholesale Corporationin2016ishigherthanthereported valueof$116.07billion.
65. For2010wehavetheorderedpair 2010,22113andfor2018wehavetheordered pair 2018,25465.Themidpointis
year,201020182211325465 $,22
402847578 , 22 2014,23789
Usingthemidpoint,weestimatethepoverty levelin2014tobe$23,789.Thisislowerthan theactualvalue.
66. Let 10,0P , 2,0Pa ,and 3 3 , 22 aa P .Then 22 122121 222 , 000 dPPxxyy aaa
22 232121 22 222 2 , 3 0 22 34 444 dPPxxyy aa a aaa aa
22 132121 22 222 2 , 3 00 22 34 444 dPPxxyy aa aaa aa
Sincethelengthsofthethreesidesareallequal,
thetriangleisanequilateraltriangle. Themidpointsofthesaidsare
Sincethelengthsofthesidesofthetriangle formedbythemidpointsareallequal,the triangleisequilateral.
Section1.2: The Distance and Midpoint Formulas
67. Let 10,0P , 20, Ps , 3,0Ps ,and
4, Pss betheverticesofthesquare.
Thepoints1 P and4 P areendpointsofone diagonalandthepoints2 P and3 P arethe endpointsoftheotherdiagonal. 14 00 ,, 2222
PP s sss M 23 00 ,, 2222
Themidpointsofthediagonalsarethesame. Therefore,thediagonalsofasquareintersectat theirmidpoints.
68. Let ,2 Paa .Then
2222 2222 22 521424 521424 56265832 626832 26 3
aaaa aaaa aaaa aa a a Then(3,6) P
69. Arrangetheparallelogramonthecoordinate planesothattheverticesare
12340,0,(,0),(,)and(,) PPaPabcPbc Thenthelengthsofthesidesare: 22 12 2 (,)000 dPPa aa 22 23 22 (,)()0 dPPabac bc
22 34 2 (,)() dPPbabcc aa and y x (0,)s (0,0) (,0) s (,) ss
Chapter1: Graphs
dPPbc bc
22 14 22 (,)00
13 and PP aretheendpointsofonediagonal,and 24 and PP aretheendpointsoftheother diagonal.Thelengthsofthediagonalsare
5. y-axis
6. 4 7. 3,4
8. True
dPPabc aabbc and 22 24 222 (,)()0 2
22 13 222 (,)()00 2
dPPbac aabbc
Sumofthesquaresofthesides: 22222222 222 ()() 222 abcabc abc
Sumofthesquaresofthediagonals:
aabbcaabbc abc
22 222222 222 22 222
Section 1.3
1. 2317 236 33 6 x x x x
Thesolutionsetis 6.
2. 2 2 90 9 93 x x x
Thesolutionsetis 3,3.
3. intercepts
4. 0 y
9. False;the y-coordinateofapointatwhichthe graphcrossesortouchesthe x-axisisalways0. The x-coordinateofsuchapointisan x-intercept.
10. False;agraphcanbesymmetricwithrespectto bothcoordinateaxes(insuchcasesitwillalsobe symmetricwithrespecttotheorigin).
Forexample:221 xy 11. d 12. c
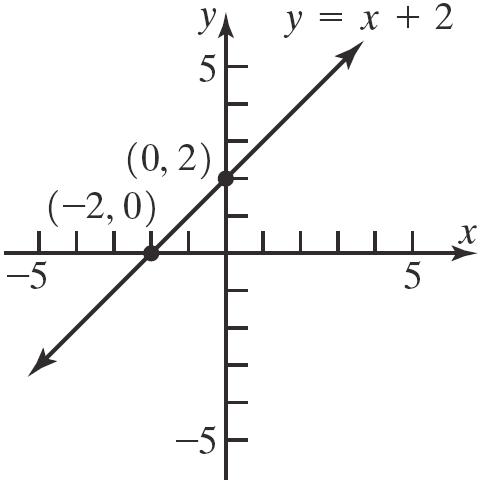
13. 2 yx x-intercept: y-intercept: 02 2 x x 02 2 y y
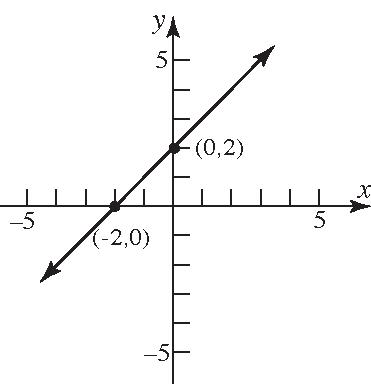
Theinterceptsare 2,0and 0,2.
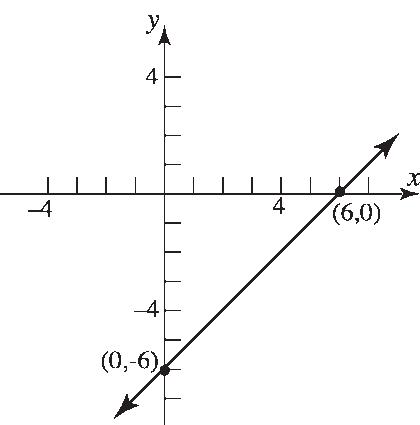
14. 6 yx x-intercept: y-intercept: 06 6 x x 06 6 y y
Section1.3: Intercepts; Symmetry; Graphing Key Equations
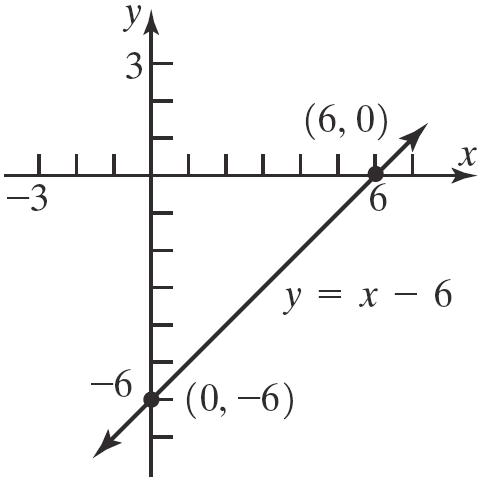
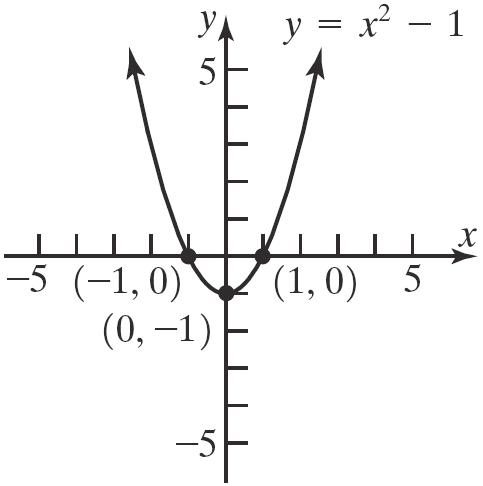
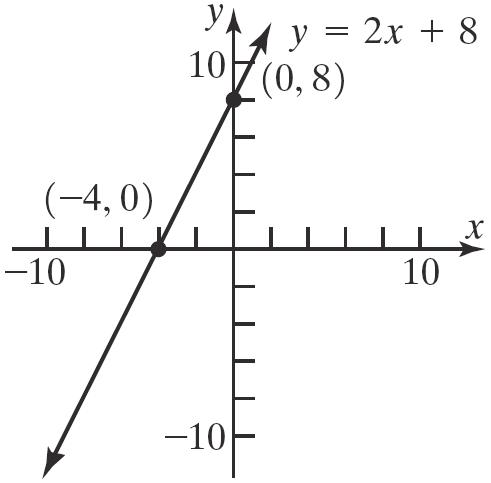
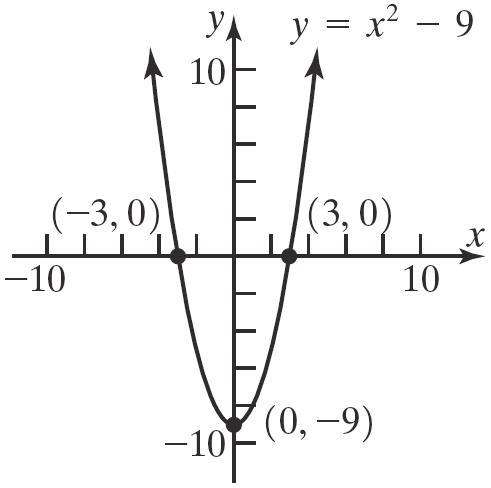
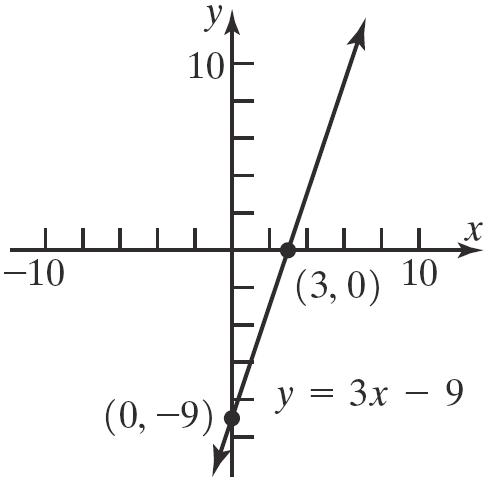
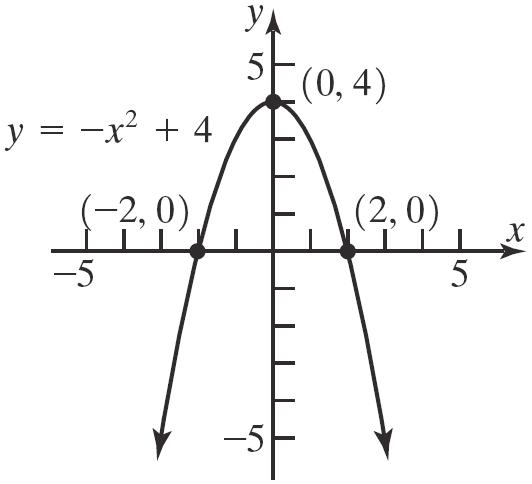
Theinterceptsare 2,0, 2,0,and 0,4
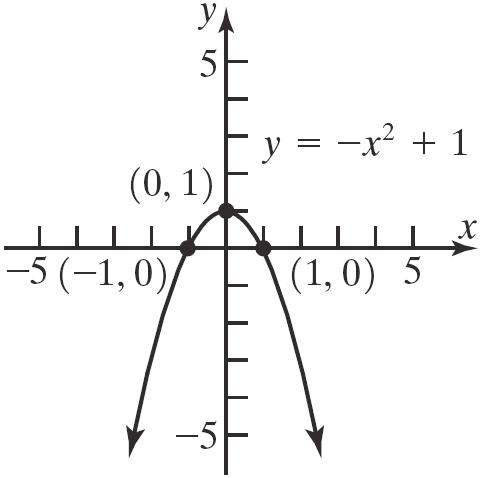
20. 21 yx
x-intercepts: y-intercept: 2 2 01 1 1 x x x
Theinterceptsare
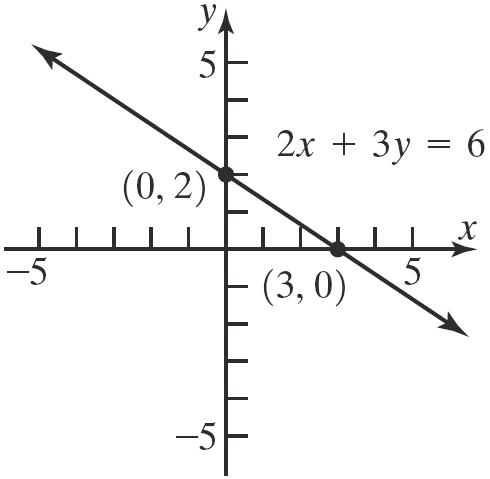
21. 236 xy
x-intercepts: y-intercept:
2306 26 3 x x x
Theinterceptsare
22. 5210 xy x-intercepts: y-intercept: 52010 510 2 x x x
Theinterceptsare 2,0and 0,5
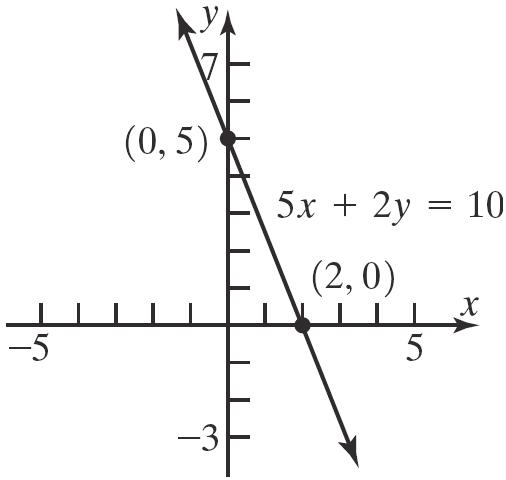
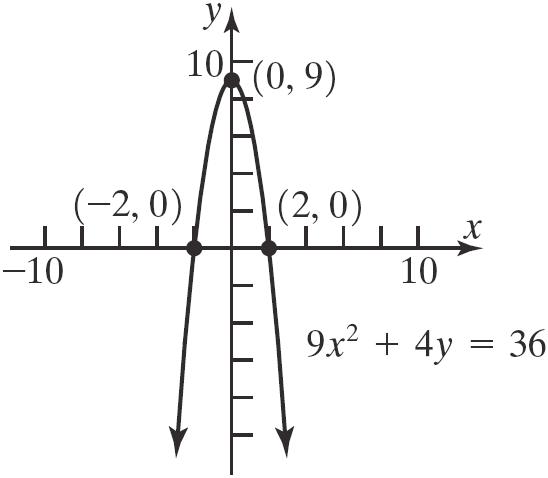
23. 2 9436 xy
x-intercepts: y-intercept:
2 2 2 94036 936 4 2 x x x x
2 90436 436 9 y y y
Theinterceptsare 2,0, 2,0,and 0,9.
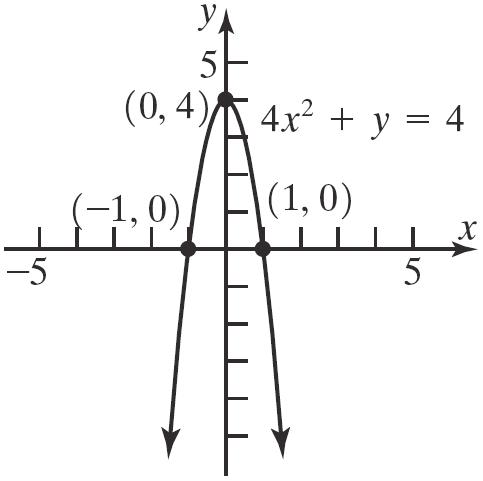
24. 2 44 xy
x-intercepts: y-intercept: 2 2 2 404 44 1 1 x x x x
2 404 4 y y
Theinterceptsare 1,0, 1,0,and 0,4
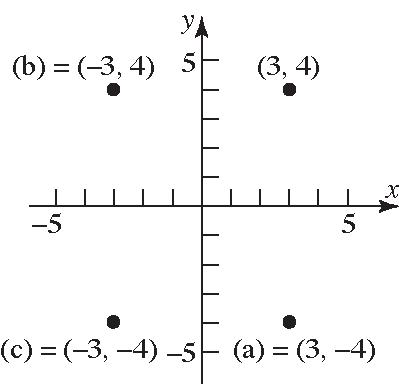
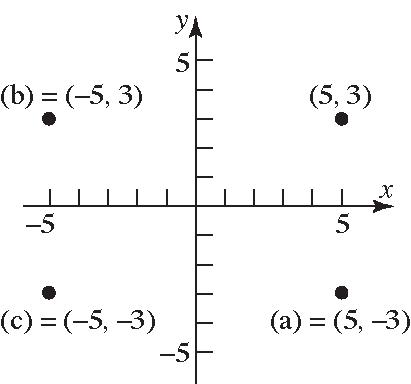
Section1.3: Intercepts; Symmetry; Graphing Key Equations
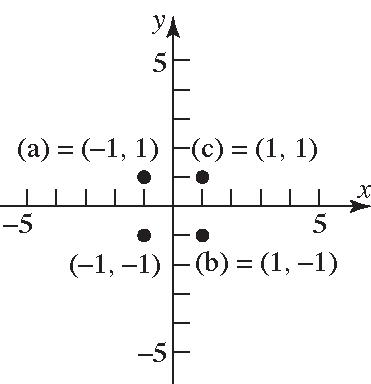
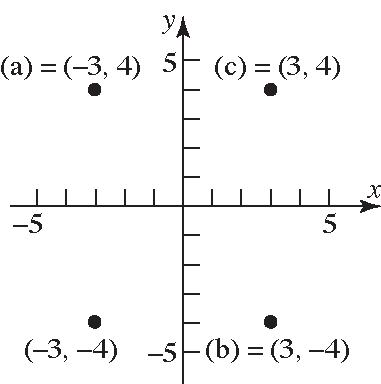
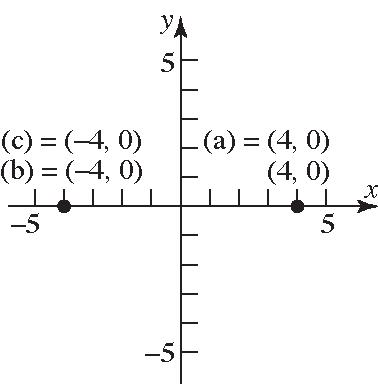
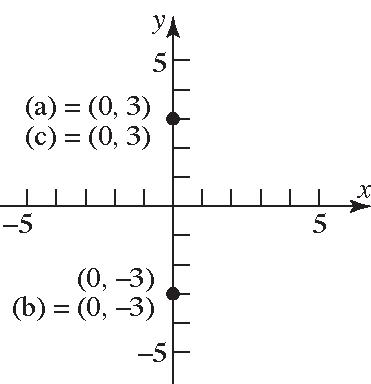
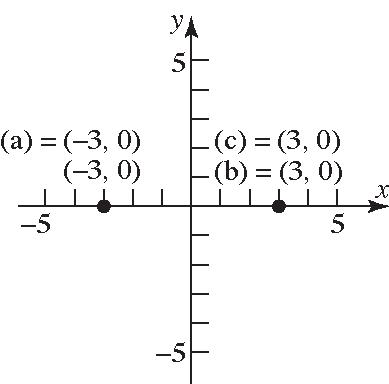
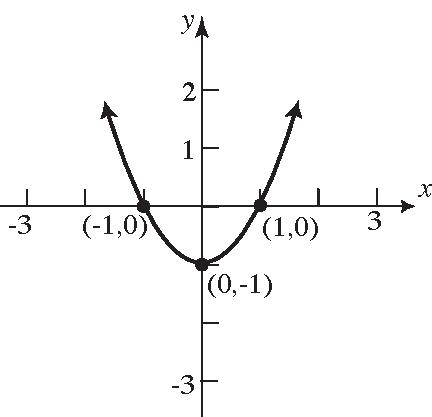
35. a. Intercepts: 1,0and 1,0
b. Symmetricwithrespecttothe x-axis, y-axis, andtheorigin.
36. a. Intercepts: 0,1
b. Notsymmetrictothe x-axis,the y-axis,nor theorigin
37. a. Intercepts: 20 , , 0,1,and 2,0
b. Symmetricwithrespecttothe y-axis.
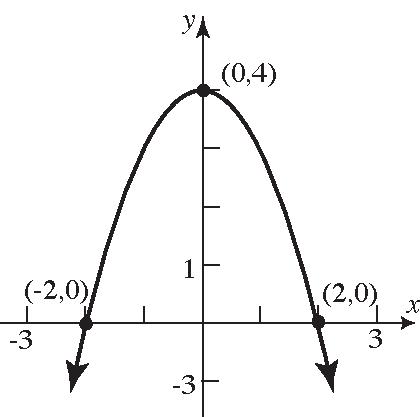
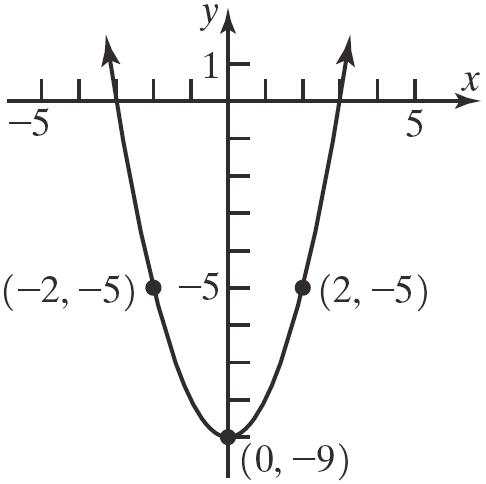
38. a. Intercepts: 2,0, 0,3,and 2,0
b. Symmetricwithrespecttothe y-axis.
39. a. Intercepts: 0,0
b. Symmetricwithrespecttothe x-axis.
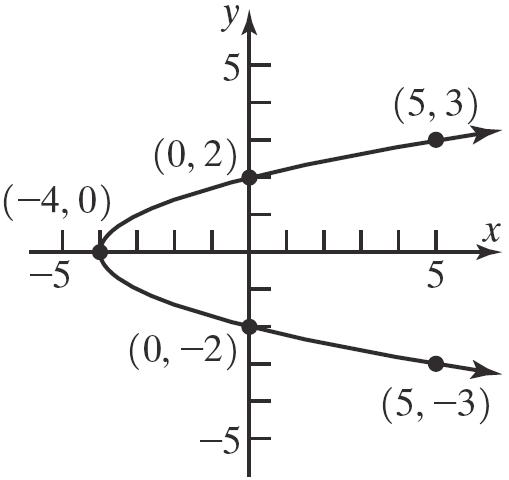
40. a. Intercepts: 2,0, 0,2, 0,2,and 2,0
b. Symmetricwithrespecttothe x-axis, y-axis, andtheorigin.
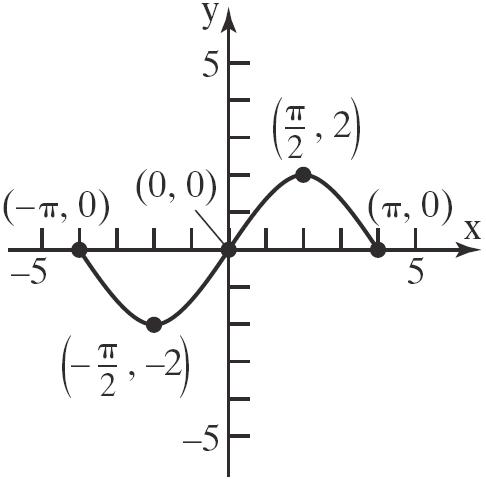
41. a. Intercepts: 2,0, 0,0,and 2,0
b. Symmetricwithrespecttotheorigin.
42. a. Intercepts: 4,0, 0,0,and 4,0
b. Symmetricwithrespecttotheorigin.
43. a. x-intercepts: 2,1, y-intercept0
b. Notsymmetricto x-axis, y-axis,ororigin.
44. a. x-intercepts: 1,2, y-intercept0
b. Notsymmetricto x-axis, y-axis,ororigin.
45. a. Intercepts:none
b. Symmetricwithrespecttotheorigin.
46. a. Intercepts:none
b. Symmetricwithrespecttothe x-axis.
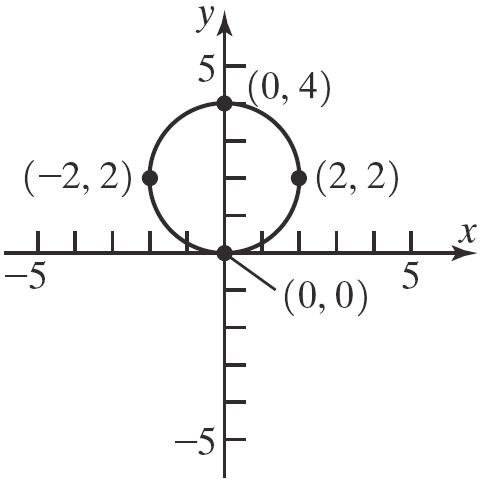
51. 216 yx
x-intercepts: y-intercepts: 2 016 16 x x 2 2 016 16 4 y y y
Theinterceptsare 16,0, 0,4and 0,4.
Test x-axissymmetry:Let yy
2 2 16 16same
yx yx
Test y-axissymmetry:Let x x 216 yx different
Testoriginsymmetry:Let x x and yy
yx yx
2 2 16 16different
Therefore,thegraphwillhave x-axissymmetry.
52. 29yx
x-intercepts: y-intercepts: 2 (0)9 09 9 x x x
2 2 09 9 3 y y y
Theinterceptsare 9,0, 0,3and 0,3.
Test x-axissymmetry:Let yy 2 2 9 9same yx yx
Test y-axissymmetry:Let x x 29yx different
Testoriginsymmetry:Let x x and yy 2 2 9 9different yx yx
Therefore,thegraphwillhave x-axissymmetry.
53. 3 y x
x-intercepts: y-intercepts: 03 0 x x 300 y
Theonlyinterceptis 0,0.
Test x-axissymmetry:Let yy 3differentyx
Section1.3: Intercepts; Symmetry; Graphing Key Equations
Test y-axissymmetry:Let x x 33differentyxx
Testoriginsymmetry:Let x x and yy 33 3same y xx yx
Therefore,thegraphwillhaveoriginsymmetry.
54. 5 y x
x-intercepts: y-intercepts: 03 0 x x 500 y
Theonlyinterceptis 0,0
Test x-axissymmetry:Let yy 5differentyx
Test y-axissymmetry:Let x x 55differentyxx
Testoriginsymmetry:Let x x and yy 55 5same y xx yx
Therefore,theissymmetricwithrespecttothe origin.
55. 290xy x-intercepts: y-intercepts: 2 2 90 9 3 x x x
Theinterceptsare 3,0, 3,0,and 0,9.
Test x-axissymmetry:Let yy 290differentxy
Test y-axissymmetry:Let x x
2 2 90 90same xy xy
Testoriginsymmetry:Let x x and yy
2 2 90 90different xy xy
Therefore,thegraphhas y-axissymmetry.
56. 240xy
x-intercepts: y-intercept: 2 2 040 4 2 x x x
Theinterceptsare 2,0, 2,0,and 0,4
Test x-axissymmetry:Let yy
2 2 40 40different xy xy
Test y-axissymmetry:Let x x
2 2 40 40same xy xy
Testoriginsymmetry:Let
2 2 40 40different xy xy
Therefore,thegraphhas y-axissymmetry.
57. 22 254100 xy x-intercepts: y-intercepts:
22 2
Theinterceptsare 2,0, 2,0, 0,5,and 0,5.
Test x-axissymmetry:Let yy
22 22 254100 254100same
xy xy
Test y-axissymmetry:Let x x 22 22 254100 254100same xy xy
Testoriginsymmetry:Let x x and yy 22 22 254100 254100same xy xy
Therefore,thegraphhas x-axis, y-axis,and originsymmetry.
58. 22 44 xy x-intercepts: y-intercepts: 22 2 2 404 44 1 1 x x x x
Theinterceptsare
0,2.
22 2 404 4 2 y y y
0,2,and
Test x-axissymmetry:Let yy
22 22 44 44same xy xy
Test y-axissymmetry:Let x x
22 22 44 44same xy xy
Testoriginsymmetry:Let x x and yy
22 22 44 44same xy xy
Therefore,thegraphhas x-axis, y-axis,and originsymmetry.
59. 364yx
x-intercepts: y-intercepts: 3 3 064 64 4 x x x 3 064 64 y y
Theinterceptsare 4,0and 0,64
Test x-axissymmetry:Let yy 364different yx
Test y-axissymmetry:Let x x 3 3 64 64different
yx yx
Testoriginsymmetry:Let x x and yy 3 3 64 64different yx yx
Therefore,thegraphhasnosymmetry.
60. 41 yx
x-intercepts: y-intercepts: 4 4 01 1 1 x x x
Theinterceptsare
4
Section1.3: Intercepts; Symmetry; Graphing Key Equations
Test x-axissymmetry:Let yy 24different yx
Test y-axissymmetry:Let x x 2 2 4 4same yx yx
0,1
Test x-axissymmetry:Let yy 41different yx
Test y-axissymmetry:Let x x
4 4 1 1same yx yx
Testoriginsymmetry:Let x x and yy
4 4 1 1different yx yx
Therefore,thegraphhas y-axissymmetry.
61. 228 y xx
x-intercepts: y-intercepts:
Testoriginsymmetry:Let x x and yy
2 2 4 4different yx yx
Therefore,thegraphhas y-axissymmetry.
63. 2 4 16 x y x
x-intercepts: y-intercepts: 2 4 0 16 40 0
2 400 0 01616
Theonlyinterceptis 0,0.
xx xx x x
2 028 042 4or2
2 0208 8
Theinterceptsare 4,0, 2,0,and 0,8
Test x-axissymmetry:Let yy 228different
yxx
Test y-axissymmetry:Let x x
yxx yxx
2 2 28 28different
Testoriginsymmetry:Let x x and yy
yxx yxx
2 2 28 28different
Therefore,thegraphhasnosymmetry.
62. 24 yx
x-intercepts: y-intercepts: 2 2 04 4 norealsolution x x
2 04 4 y y
Theonlyinterceptis 0,4.
Test x-axissymmetry:Let yy 2 4 different 16 x y x
Test y-axissymmetry:Let x x 2 2 4 16 4 different 16
x y x x y x
Testoriginsymmetry:Let x x and yy
2 2 2 4 16 4 16 4 same 16
x y x x y x x y x Therefore,thegraphhasoriginsymmetry.
Testoriginsymmetry:Let
Theinterceptsare
Therefore,thegraphhasoriginsymmetry.
norealsolution
Therearenointerceptsforthegraphofthis equation.
Therefore,thegraphhasoriginsymmetry.
Test
Testoriginsymmetry:Let
Therefore,thegraphhasoriginsymmetry.
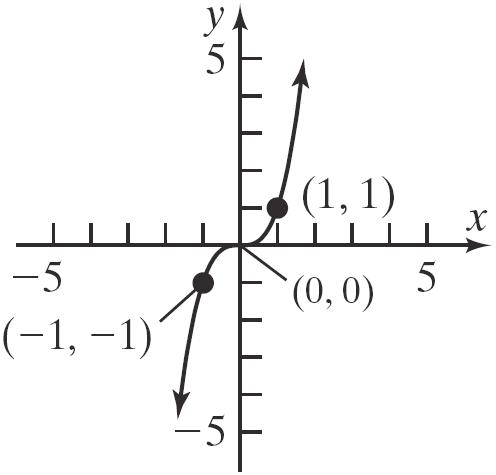
67. 3 y x
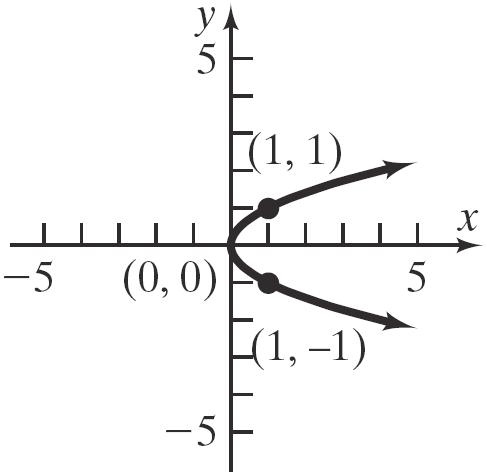
68. 2 x y
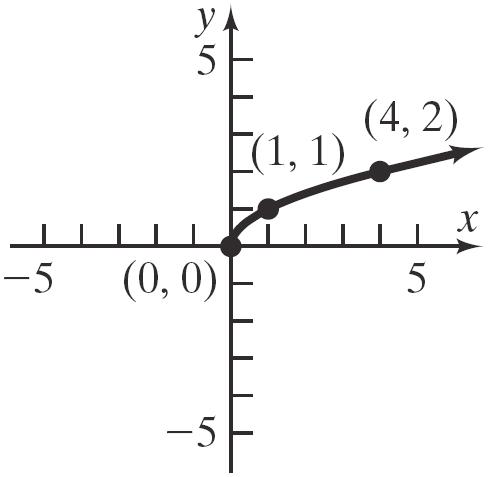
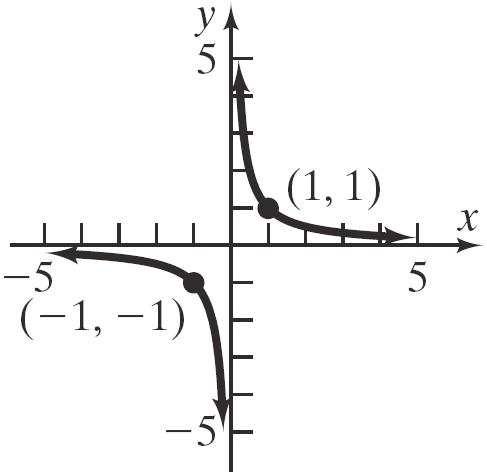
69. y x
70. 1 y x
Section1.3: Intercepts; Symmetry; Graphing Key Equations
71. Ifthepoint ,4 a isonthegraphof 23 y xx ,thenwehave
2 2 43 034 041 aa aa aa
40 4 a a
or10 1 a a
Thus,4 a or1 a
72. Ifthepoint ,5 a isonthegraphof 26 y xx ,thenwehave
2 2 56 065 051 aa aa aa
50 5 a a
or10 1 a a
Thus,5 a or1 a
73. a. 2 2 05 5 5 x x x
Thex-interceptsare5 x and5 x .
2 055 y
They-interceptis5 y
Theinterceptsare 5,0, 5,0,and 0,5
b. x-axis(replace y by y ): 2 2 5 5different yx yx
y-axis(replace x by x ):
2255yxx same origin(replace x by x and y by y ):
2 2 5 5different yx yx
Theequationhasy-axissymmetry.
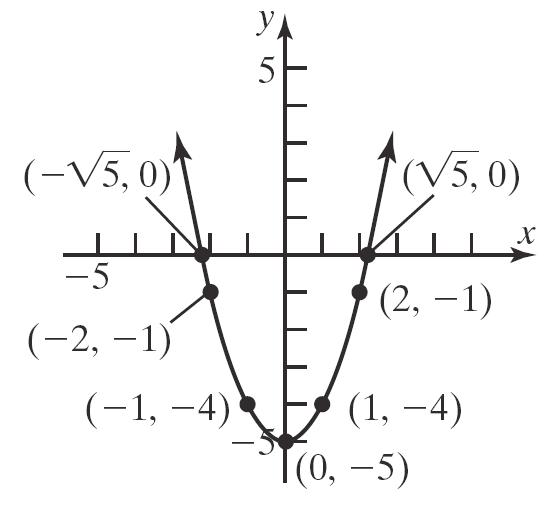
c. 25 yx
Additionalpoints:
Chapter1: Graphs
2 2 2 5, 11541,4 1fromsymmetry1,4 22512,1 2fromsymmetry2,1 xyxxy
74. a. 2 2 08 8 22 x x x
Thex-interceptsare22 x and 22 x .
2 088 y
They-interceptis8 y
Theinterceptsare 22,0, 22,0,and
0,8
b. x-axis(replace y by y ): 2 2 8 8different yx yx
y-axis(replace x by x ):
2288yxx same
origin(replace x by x and y by y ): 2 2 8 8different yx yx
Theequationhasy-axissymmetry.
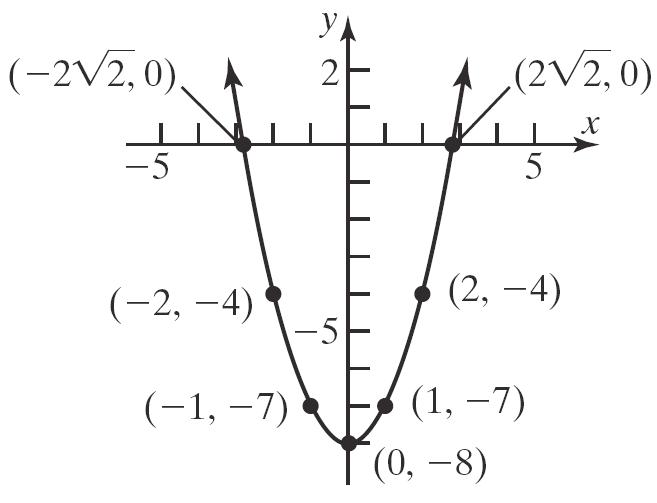
c. 28 yx
Additionalpoints:
2 2 2 5, 11871,7 1fromsymmetry1,7 22842,4 2fromsymmetry2,4 xyxxy y y
75. a. 2 09 9 x x
Thex-interceptis9 x
2 2 2 09 9 93 y y yy
They-interceptsare3 y and3 y
Theinterceptsare 9,0, 0,3,and 0,3.
b. x-axis(replace y by y ):
2 2 9 9same xy xy y-axis(replace x by x ): 2 2 9 9different xy xy
origin(replace x by x and y by y ): 2 2 2 9 9 9different xy xy xy
Theequationhasx-axissymmetry.
c. 29 xy or 29 xy
Additionalpoints:
2 2 9, 22955,2 2fromsymmetry5,2 yxyxy x
5 5 52
76. a. 2 04 4 x x
Thex-interceptis4 x .
2 2 04 42 y yy
They-interceptsare2 y and2 y
Theinterceptsare 4,0, 0,2,and 0,2
b. x-axis(replace y by y ): 2 2 4 4same xy xy
y-axis(replace x by x ): 2 2 4 4different xy xy
origin(replace x by x and y by y ):
2 2 2 4 4 4different xy xy xy
Theequationhasx-axissymmetry.
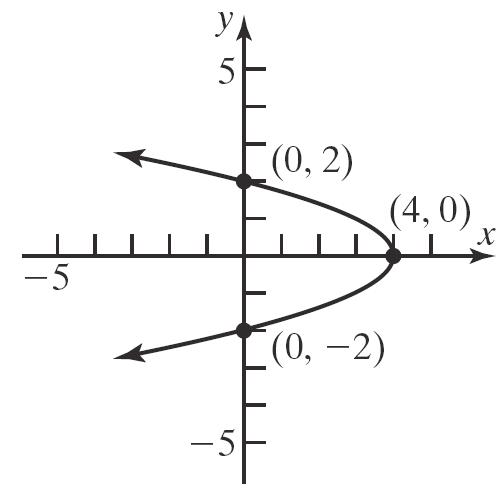
c. 24 xy or 42 x y
Additionalpoints:
Section1.3: Intercepts; Symmetry; Graphing Key Equations
2 2 4, 14133,1 1fromsymmetry3,1 yxyxy x
77. a. 22 2 09 9 3 x x x
Thex-interceptsare3 x and3 x
22 2 09 9 3 y y y
They-interceptsare3 y and3 y
Theinterceptsare 3,0, 3,0, 0,3, and 0,3
b. x-axis(replace y by y ): 22 22 9 9same xy xy
y-axis(replace x by x ):
22 22 9 9same xy xy
origin(replace x by x and y by y ):
22 22 9 9same xy xy
Theequationhasx-axissymmetry,y-axis symmetry,andoriginsymmetry.
c. 229xy
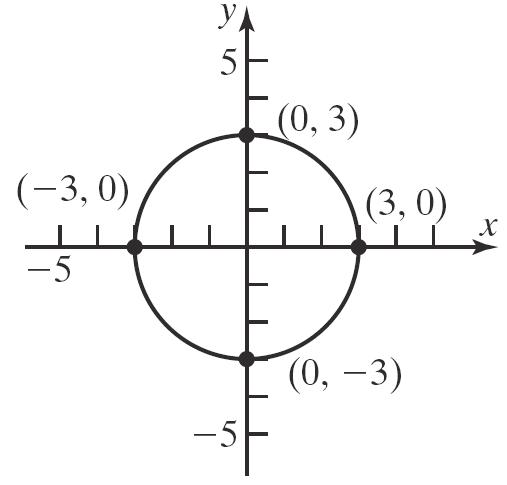
78. a. 22 2 016 16 4 x x x
Thex-interceptsare4 x and4 x .
22 2 016 16 4 y y y
They-interceptsare4 y and4 y
Theinterceptsare 4,0, 4,0, 0,4, and 0,4.
b. x-axis(replace y by y ):
22 22 16 16same xy xy
y-axis(replace x by x ):
22 22 16 16same xy xy
origin(replace x by x and y by y ):
22 22 16 16same xy xy
Theequationhasx-axissymmetry,y-axis symmetry,andoriginsymmetry.
c. 2216xy
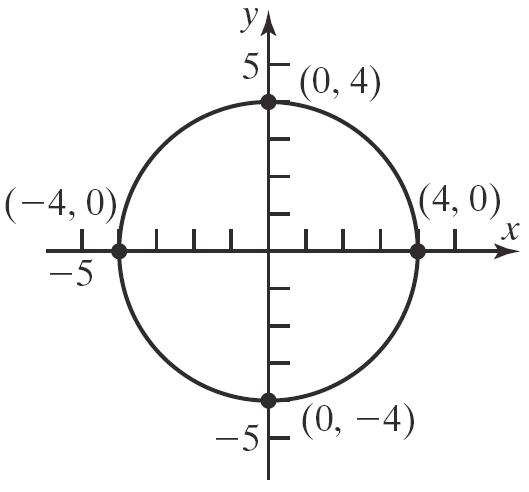
79. a. 3 2 04 04 x x xx 0 x or 2 2 40 4 2 x x x
Thex-interceptsare0 x ,2 x ,and 2 x 3 0400 y
They-interceptis0 y
Theinterceptsare 0,0, 2,0,and 2,0
b. x-axis(replace y by y ): 3 3 4 4different yxx yxx y-axis(replace x by x ): 3 3 4 4different yxx yxx
origin(replace x by x and y by y ):
3 3 3 4 4 4same y xx yxx yxx
Theequationhasoriginsymmetry.
c. 34 y xx
Additionalpoints: 3 3 4, 114131,3 1fromsymmetry1,3 x yxxxy y
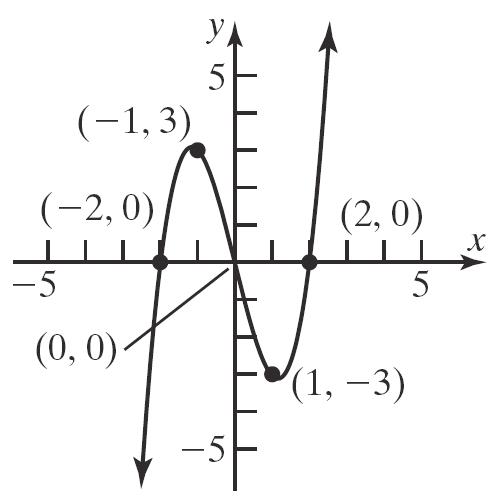
80. a.
3 2 0 01 x x xx
0 x or 2 2 10 1 1 x x x
Thex-interceptsare0 x ,1 x ,and 1 x
3 000 y
They-interceptis0 y
Theinterceptsare 0,0, 1,0,and 1,0
b. x-axis(replace y by y ): 3 3different yxx yxx
y-axis(replace x by x ):
3 3different yxx yxx
origin(replace x by x and y by y ):
3 3 3 same y xx yxx yxx
Theequationhasoriginsymmetry.
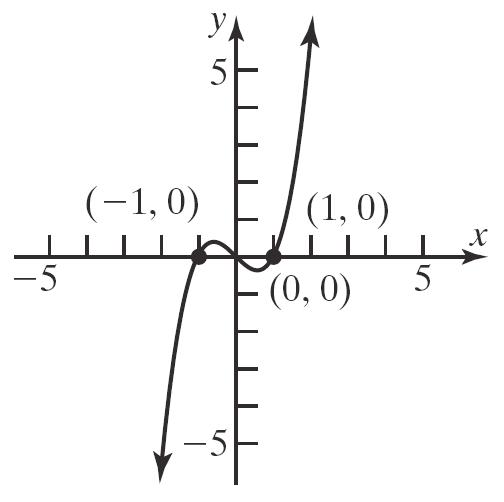
c. 3 y xx
Additionalpoints:
3 3 4, 22262,6 2fromsymmetry2,6 xyxxxy y
Section1.3: Intercepts; Symmetry; Graphing Key Equations
81. Foragraphwithoriginsymmetry,ifthepoint , ab isonthegraph,thensoisthepoint , ab .Sincethepoint 1,2isonthegraph ofanequationwithoriginsymmetry,thepoint 1,2mustalsobeonthegraph.
82. Foragraphwith y-axissymmetry,ifthepoint , ab isonthegraph,thensoisthepoint , ab .Since6isan x-interceptinthiscase,the point 6,0isonthegraphoftheequation.Due tothe y-axissymmetry,thepoint 6,0must alsobeonthegraph.Therefore,6isanother xintercept.
83. Foragraphwithoriginsymmetry,ifthepoint , ab isonthegraph,thensoisthepoint , ab .Since4isan x-interceptinthiscase, thepoint 4,0isonthegraphoftheequation. Duetotheoriginsymmetry,thepoint 4,0 mustalsobeonthegraph.Therefore,4is another x-intercept.
84. Foragraphwith x-axissymmetry,ifthepoint , ab isonthegraph,thensoisthepoint , ab .Since2isa y-interceptinthiscase,the point 0,2isonthegraphoftheequation.Due tothe x-axissymmetry,thepoint 0,2must alsobeonthegraph.Therefore,2isanother yintercept.
85. a. 2 2222 x yxxy x-intercepts:
Theinterceptsare
b. Test x-axissymmetry:Let yy
Test y-axissymmetry:Let x
Testoriginsymmetry:Let x x and yy
Thus,thegraphwillhave x-axissymmetry. 86. a. 2 16120225 yx
y-intercepts:
2 2 2 161200225 16225 225 16 norealsolution y y y
x-intercepts: 2 160120225 0120225 120225 22515 1208 x x x x
Theonlyinterceptis15,0 8
b. Test x-axissymmetry:Let yy
2 2 16120225 16120225same yx yx
Test y-axissymmetry:Let x x
2 2 16120225 16120225different yx yx
Testoriginsymmetry:Let x x and yy
2 2 16120225 16120225different yx yx
Thus,thegraphhas x-axissymmetry.
87. Let y =0. 222222 422 422 222 222 22 (0)(0) () 0 ()0 0or()0 0or ,
xax xax xax xxa xxa xxa xaa Let x =0. 222222 422 422 222 (0)(0) () 0 ()0 0 yay yay yay yya y (Notethatthesolutionsto220 ya arenot real)
Sotheinterceptsareare(0,0),(a,0)and(-a,0). Test x-axissymmetry:Replace y by-y 222222 222222 (())(()) ()()equivalent
xyaxy xyaxy
Section1.3: Intercepts; Symmetry; Graphing Key Equations
Test y-axissymmetry:replace x by-x 222222 222222
(())(()) ()()equivalent
xyaxy xyaxy
Testoriginsymmetry:replace x by-x and y by -y 222222 222222
89. Answerswillvary.Oneexample: y x
(()())(()()) ()()equivalent
x yaxy xyaxy
Thegraphissymmetricbyrespecttothe xaxis,the y-axis,andtheorigin.
88. Let y =0.
90. Answerswillvary.
Case1:Graphhas x-axisand y-axissymmetry, showoriginsymmetry.
222222 432222 2 (0)(0) 20 (()(()0 0or or
xaxbx xaxaxbx xxabxab x xab xab
Let x =0. 222222
yaby yby yybyb yybyb
Sotheinterceptsare(0,0),(a-b,0),(a+b,0), (0,-b),(0, b).
Test x-axissymmetry:replace y by-y 2 22222 222222 ()() ()()Equivalent
xyaxbxy xyaxbxy
Test y-axissymmetry:replace x by-x 2 22222 222222 ()()() ()()Notequivalent
xyaxbxy xyaxbxy
Testoriginsymmetry:replace x by-x and y by -y 2 22222 222222 ()()()()() ()()Noequivalent
x yaxbxy xyaxbxy
Thegraphissymmetricwithrespecttothe x-axisonly.
,ongraph,ongraph (from-axissymmetry) xyxy x
,ongraph,ongraph from-axissymmetry xyxy y
Sincethepoint ,x y isalsoonthegraph,the graphhasoriginsymmetry.
Case2:Graphhas x-axisandoriginsymmetry, show y-axissymmetry.
,ongraph,ongraph from-axissymmetry xyxy x
,ongraph,ongraph fromoriginsymmetry xyxy
Sincethepoint ,x y isalsoonthegraph,the graphhas y-axissymmetry.
Case3:Graphhas y-axisandoriginsymmetry, show x-axissymmetry.
,ongraph,ongraph from-axissymmetry xyxy y
,ongraph,ongraph fromoriginsymmetry xyxy
Sincethepoint ,x y isalsoonthegraph,the graphhas x-axissymmetry.
91. Answersmayvary.Thegraphmustcontainthe points 2,5, 1,3,and 0,2.Forthe graphtobesymmetricaboutthe y-axis,thegraph mustalsocontainthepoints 2,5and 1,3 (notethat(0,2)isonthe y-axis).
Forthegraphtoalsobesymmetricwithrespect tothe x-axis,thegraphmustalsocontainthe
Chapter1: Graphs
points 2,5, 1,3, 0,2, 2,5,and 1,3.Recallthatagraphwithtwoofthe symmetries(x-axis,y-axis,origin)will necessarilyhavethethird.Therefore,ifthe originalgraphwithy-axissymmetryalsohasxaxissymmetry,thenitwillalsohaveorigin symmetry.
Section 1.4
1.
2.
2 2520 2120 xx xx
210 21 1 2 x x x
Thesolutionsetis 1 2, 2
23411 23441 2343 233 26 3 xx xx xx x x x
Thesolutionsetis
3. ZERO(ROOT)
4. False;exactsolutionsareobtained,ingeneral,if thesolutionisarationalnumber.Forirrational solutions,approximateanswersaretypically given,thoughsomeutilitiescanexpresscertain irrationalexpressionsinexactform.
5. 3420xx ;UseZERO(orROOT)onthe graphof3142 yxx
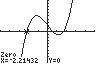
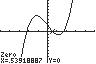
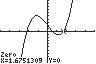
Thesolutionsetis 2.21,0.54,1.68.
6. 3810xx ;UseZERO(orROOT)onthe graphof3181y xx .
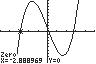
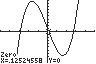
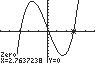
Thesolutionsetis 2.89,0.13,2.76.
7. 4 2532 xx ;UseINTERSECTonthe
graphsof4125yx and232 yx
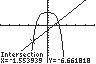
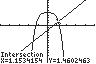
Thesolutionsetis 1.55,1.15
8. 42123xx ;UseINTERSECTonthe
graphsof411yx and2223yx
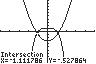
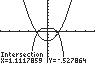
Thesolutionsetis 1.11,1.11
9. 432310xxx ;UseZERO(orROOT)on thegraphof431231y xxx
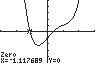
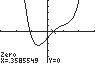
Thesolutionsetis 1.12,0.36
10. 432 3450 xxx ;UseZERO(orROOT) onthegraphof4321345 yxxx
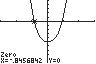
Thesolutionsetis
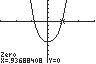
0.85,0.94
Section1.4: Solving Equations Using a Graphing Utlilty
11. 325720 32 xxx ; UseZERO(orROOT)onthegraphof 32 15/37/22 yxxx .
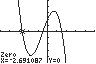
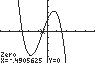
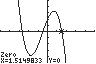
Thesolutionsetis
2.69,0.49,1.51.
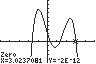
12. 432715 320 32 xxxx ;UseZERO(or ROOT)onthegraphof
432 137/315/22 yxxxx
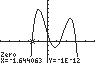
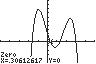
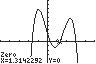
13. 432 2521 2 3232 xxxx UseINTERSECTonthegraphsof
43 12/325/2 yxxx and 2 2(2/3)1/2 yx .
Chapter1: Graphs
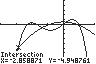
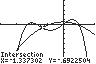
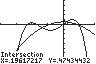
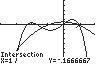
Thesolutionsetis 2.86,1.34,0.20,1.00
14. 321154 45 xxx
UseINTERSECTonthegraphsof 3 1/45y xx and22/54yx anda standardviewingwindow(10to10forboth x and y).
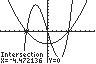
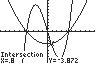
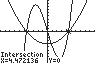
Thesolutionsetis 4.47,0.80,4.47
15. 4252110xxx UseZERO(orROOT)onthegraphof 42 15211 yxxx
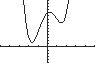
Therearenorealsolutions.
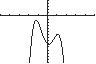
16. 42 38290 xxx UseZERO(orROOT)onthegraphof 42 13829 yxxx . Therearenorealsolutions.
17. 2(32)3(4) xx 64312 6463126 4318 433183 18 xx xx xx x xxx x
Thesolutionsetis 18.
18. 3(2)21 x x 6321 636216 327 32272 57 57 55 7 5 xx xx xx x xxx x x x
Thesolutionsetis 7 5
19. 821313 821313 61313 6113131 6312 633123 312 xxx xxx xx xx xx x xxx x
312 33 4 x x Thesolutionsetis 4.
20. 52110 52110 2610 262102 610 6101010 4 xx xx xx x xxx x x x
Thesolutionsetis
21.
125 37 12 2121215 37 7736105 xx
Thesolutionsetis46 5
22. 21163 3 x x 21 31633 3 21489 2499 249292 497 497 77 7 x x xx xx x
Thesolutionsetis
23. 543 93 yy y 1 91 3 1 93 991 93 3 y y y y
Thesolutionsetis 3.
24. 418 5 2 418252 2 yy yy yy
81018 8108188 1010 1010 1010 1 y y y y y
Thesolutionsetis 1
25.
26.
27.
Thesolutionsetis
23280 7428 xx xx
Thesolutionsetis 4,7.
28.
27180 920 xx xx
90 9 x x
29.
2 2 5136 51360 5230 xx xx xx
520 52 2 5 x x x
or30 3 x x
Thesolutionsetis 2 ,3 5 31.
32 32 2 2 440 440 1410 140 1220 xxx xxx xxx xx xxx
10 1 x x or20 2 x x or20 2 x x
Thesolutionsetis 2,1,2
32.
or20 2 x x
Thesolutionsetis 2,9
2 2 344 3440 3220 xx xx xx
320 32 2 3 x x x
or20 2 x x
Thesolutionsetis 2 ,2 3
33.
32 32 2 2 29180 29180 2920 290 2330 xxx xxx xxx xx xxx
20 2 x x or30 3 x x or30 3 x x
Thesolutionsetis 3,2,3.
22 14 14 116 11161 15 x x x x x
Check: 1514 164 44 T
Thesolutionsetis 15.
34.
23
Thesolutionsetis
35. 238 215xx
MultiplybothsidesoftheequationbytheLCD. Thisyieldstheequation
Section 1.5
1. a. 2;2;1 b. -2 c. 0 d. ii,iv e. ii 2. undefined;0 3. 3;2 x-
4. True 5. False;theslopeis32. 235 35 22 yx yx
True;
12. d
13. a. 101 Slope202
b. If x increasesby2units, y willincrease by1unit.
14. a. 101 Slope202
b. If x increasesby2units, y willdecrease by1unit.
15. a. 121 Slope1(2)3
b. If x increasesby3units, y willdecrease by1unit.
16. a. 211 Slope2(1)3
b. If x increasesby3units, y willincrease by1unit.
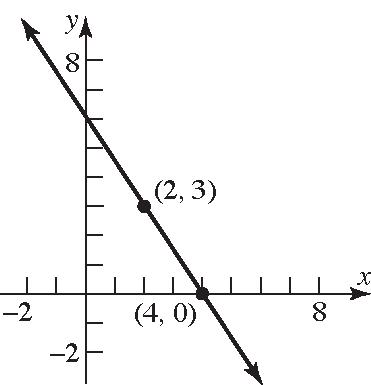
17. 21 21 033 Slope422 yy xx
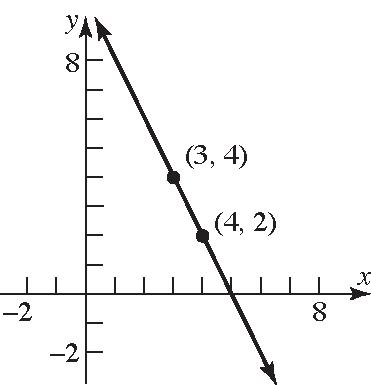
18. 21 21 422 Slope2 341 yy xx
19. 21 21 1321 Slope2(2)42 yy xx
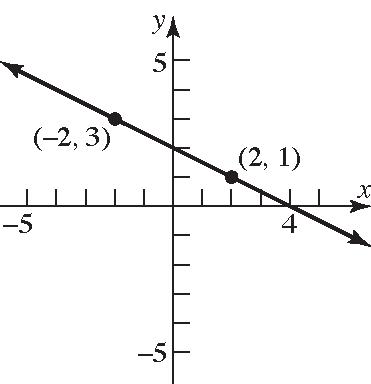
20. 21 21 312 Slope2(1)3 yy xx
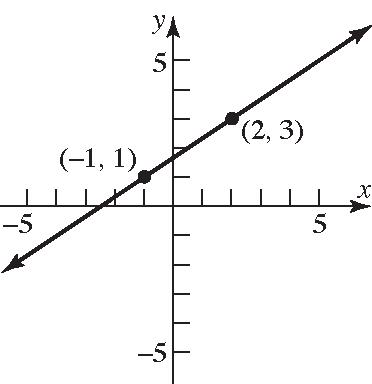
21. 21 21 1(1)0 Slope0 2(3)5 yy xx
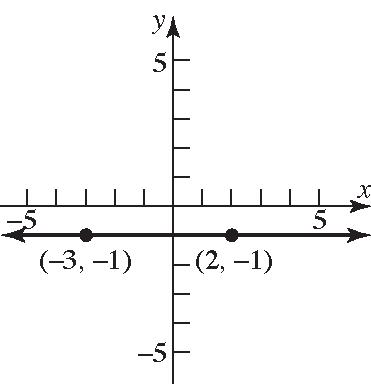
22. 21 21 220 Slope0 549 yy xx
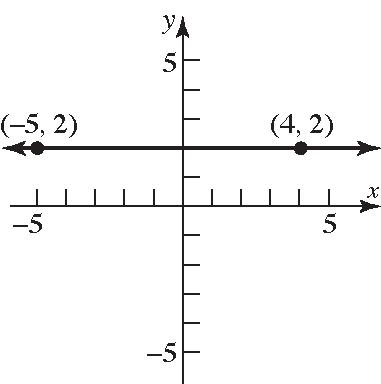
Section1.5: Lines
23. 21 21 224 Slopeundefined. 1(1)0 yy xx
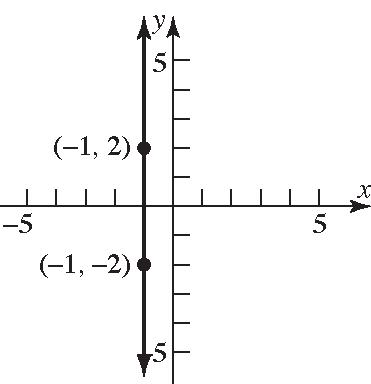
24. 21 21 202 Slopeundefined. 220 yy xx
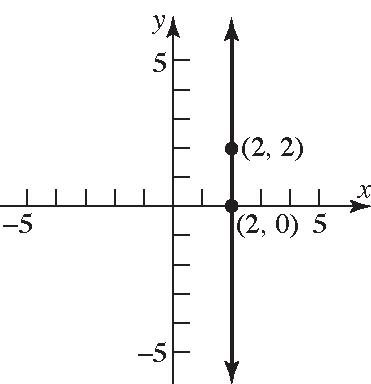
25. 1,2;3Pm
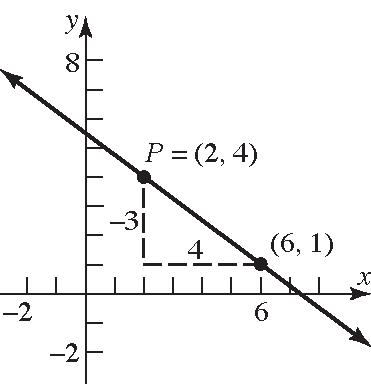
28. 2 1,3; 5 Pm 29. 1,3;0Pm 30. 2,4;0Pm
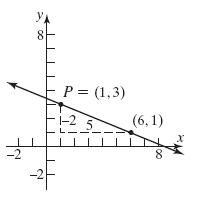
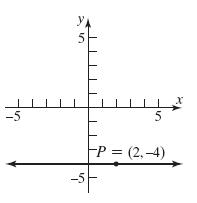
26. 2,1;4Pm 27. 3 2,4; 4 Pm
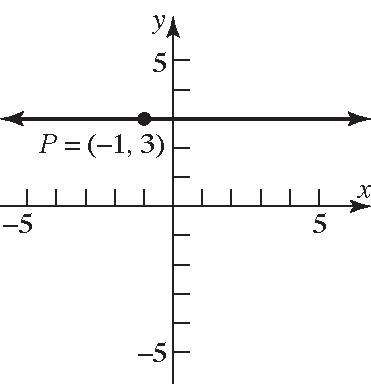
31. 0,3;slopeundefined P
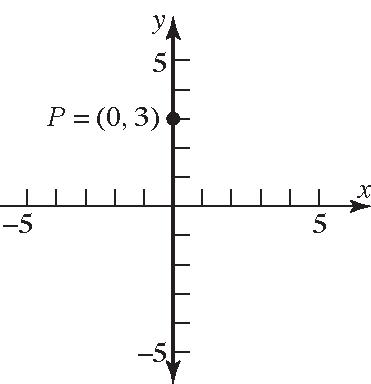
(note:thelineisthe y-axis)
32. 2,0;slopeundefined P
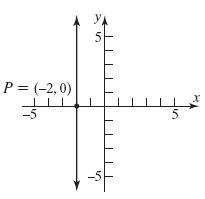
33. 1,2;3Pm ; 23(1)yx
34. 2,1;4Pm ; 14(2)yx
35. 3 2,4; 4 Pm ; 3 4(2) 4 yx
36. 2 1,3; 5 Pm ; 2 3(1) 5 yx
37. 1,3;0Pm ; 30 y
38. 2,4;0Pm ; 40 y
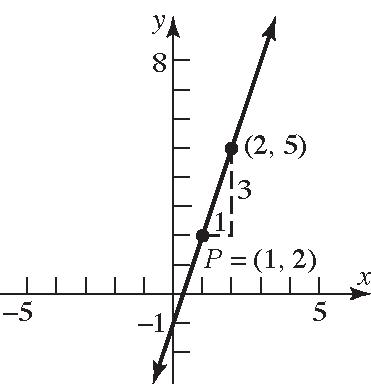
39. 4 Slope41 ;point: 1,2
If x increasesby1unit,then y increasesby4 units.
Answerswillvary.Threepossiblepointsare:
112and246 2,6 213and6410 3,10 314and10414 4,14 xy xy xy
40. 2 Slope21 ;point: 2,3
If x increasesby1unit,then y increasesby2 units.
Answerswillvary.Threepossiblepointsare:
211and325 1,5 110and527 0,7 011and729 1,9 xy xy xy
41. 33 Slope22 ;point: 2,4
If x increasesby2units,then y decreasesby3 units.
Answerswillvary.Threepossiblepointsare:
224and437 4,7 426and7310 6,10 628and10313 8,13 xy xy xy
42. 4 Slope3 ;point: 3,2
If x increasesby3units,then y increasesby4 units.
Answerswillvary.Threepossiblepointsare:
330and246 0,6 033and6410 3,10 336and10414 6,14 xy xy xy
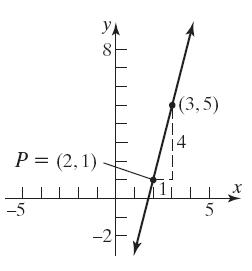
43. 2 Slope21 ;point: 2,3
If x increasesby1unit,then y decreasesby2 units.
Answerswillvary.Threepossiblepointsare:
44. 1 Slope11 ;point: 4,1
If x increasesby1unit,then y decreasesby1 unit.
Answerswillvary.Threepossiblepointsare:
45. (0,0)and(2,1)arepointsontheline. 101 Slope202
-interceptis0;using: yymxb 1 0 2 2 02 1 20or 2 yx
46. (0,0)and(–2,1)arepointsontheline. 1011 Slope2022
1 0 2 2 20 1 20or 2 yx yx xy x yyx
47. (–1,3)and(1,1)arepointsontheline. 11 132 Slope1 1(1)2
Using() yymxx
11(1) 11 2 2or2 yx yx yx xyyx
48. (–1,1)and(2,2)arepointsontheline. 11 211 Slope2(1)3
Using() yymxx
1 1(1) 3 1 1(1) 3 11 1 33 14 33 14 34or 33 yx yx yx yx xyyx
49. 11(),2yymxxm 32(3) 326 23 23or23 yx yx yx xyyx
50. 11(),1yymxxm 21(1) 21 3 3or3 yx yx yx xyyx
51. 11 1 (),2yymxxm 1 2(1) 2 11 2 22 15 22 15 25or 22 yx yx yx xyyx
52. 11(),1yymxxm 11((1)) 11 2 2or2 yx yx yx xyyx
53. Slope=3;containing(–2,3) 11() 33((2)) 336 39 39or39 yymxx yx yx yx xyyx
54. Slope=2;containingthepoint(4,–3) 11() (3)2(4) 328 211 211or211 yymxx yx yx yx xyyx
55. Slope= 1 2;containingthepoint(3,1) 11() 1 1(3) 2 13 1 22 11 22 11 21or 22 yymxx yx yx yx xyyx
56. Slope= 2 3;containing(1,–1) 11() 2 (1)(1) 3 22 1 33 21 33 21 231or 33 yymxx yx yx yx xyyx
57. Containing(1,3)and(–1,2) 2311 1122 m 11() 1 3(1) 2 11 3 22 15 22 15 25or 22 yymxx yx yx yx xyyx
58. Containingthepoints(–3,4)and(2,5) 541 2(3)5 m
11() 1 5(2) 5 12 5 55 123 55 123 523or 55 yymxx yx yx yx xyyx
59. Slope=–3; y-intercept=3 33 33or33 ymxb yx xyyx
60. Slope=–2; y-intercept=–2 2(2) 22or22 ymxb yx xyyx
61. x-intercept=–4; y-intercept=4 Pointsare(–4,0)and(0,4) 404 1 0(4)4 m 14 4 4or4 ymxb yx yx xyyx
62. x-intercept=2; y-intercept=–1 Pointsare(2,0)and(0,–1) 1011 0222 m
63. Slopeundefined;containingthepoint(2,4) Thisisaverticalline.
2Noslope-interceptform. x
64. Slopeundefined;containingthepoint(3,8) Thisisaverticalline.
3Noslope-interceptform. x
65. Horizontallineshaveslope0 m andtakethe form yb .Therefore,thehorizontalline passingthroughthepoint 3,2is2 y .
66. Verticallineshaveanundefinedslopeandtake theform x a .Therefore,theverticalline passingthroughthepoint 4,5is4 x
67. Parallelto2 y x ;Slope=2 Containing(–1,2) 11() 22((1)) 22224 24or24 yymxx yx yxyx xyyx
68. Parallelto3 y x ;Slope=–3;Containingthe point(–1,2) 11() 23((1)) 23331 31or31 yymxx yx yxyx xyyx
69. Parallelto25 xy ; 1 Slope;Containingthepoint0,0 2 11() 11 0(0)22 1 20or 2 yymxx yxyx xyyx
70. Parallelto22 xy ;Slope=2 Containingthepoint(0,0) 11() 02(0) 2 20or2 yymxx yx yx x yyx
71. Parallelto5 x ;Containing(4,2) Thisisaverticalline. 4Noslope-interceptform. x
72. Parallelto5 y ;Containingthepoint(4,2) Thisisahorizontalline.Slope=0 2 y
73. Perpendicularto 1 4; 2 yx Containing(1,–2)
Slopeofperpendicular=–2 11() (2)2(1) 2222 20or2 yymxx yx yxyx xyyx
74. Perpendicularto23 yx ;Containingthe point(1,–2) 1 Slopeofperpendicular2 11() 1 (2)(1) 2 1113 2 2222 13 23or 22 yymxx yx yxyx xyyx
75. Perpendicularto25 xy ;Containingthe point(0,4) Slopeofperpendicular=–2 24 24or24 ymxb yx xyyx
Chapter1: Graphs
76. Perpendicularto22 xy ;Containingthe point(–3,0) 1 Slopeofperpendicular2 11() 113 0((3))222 13 23or 22
77. Perpendicularto8 x ;Containing(3,4) Slopeofperpendicular=0(horizontalline) 4 y
78. Perpendicularto8 y ; Containingthepoint(3,4) Slopeofperpendicularisundefined(vertical line).3 x Noslope-interceptform.
79. 23yx ;Slope=2; y-intercept=3
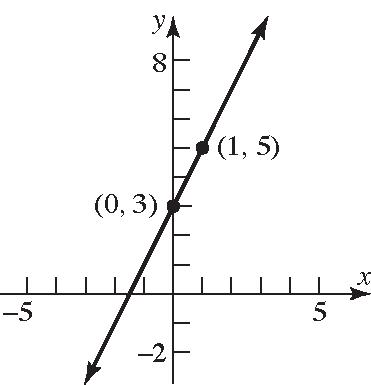
80. 34yx ;Slope=–3; y-intercept=4
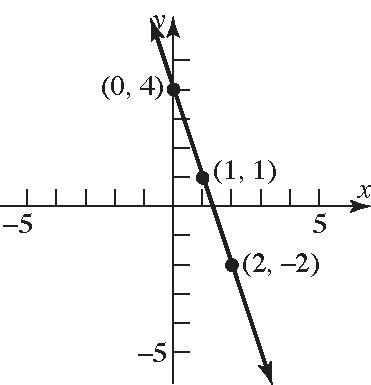
81. 1 1 2 yx ;22 yx Slope=2; y-intercept=–2 82. 1 2 3 xy ; 1 2 3 yx
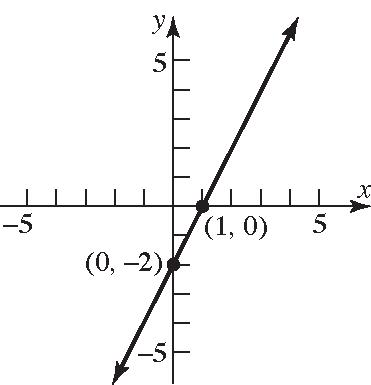
1 Slope3 ; y-intercept=2
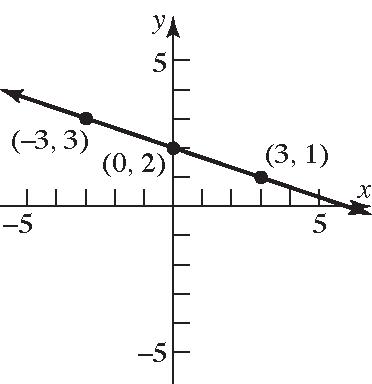
1 2 2 yx ; 1 Slope2 ; y-intercept=2 84. 1 2 2 yx ;Slope=2; 1 -intercept2 y
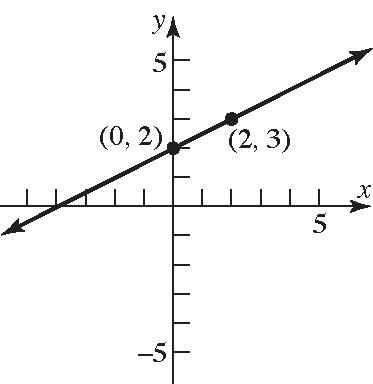
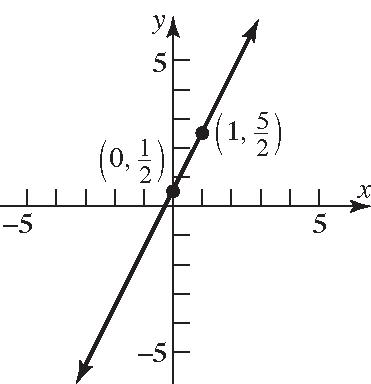
85. 24xy ; 1 242 2 yxyx 1 Slope2 ; y-intercept=2
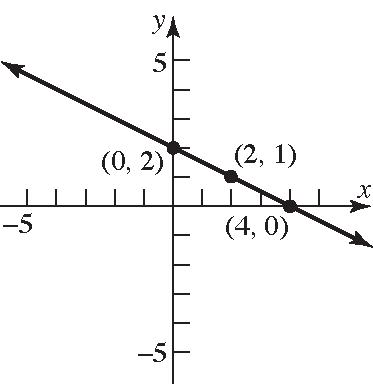
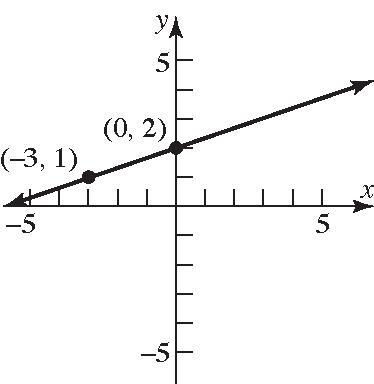
86. 36xy ; 1 362 3 yxyx
1 Slope3 ; y-intercept=2
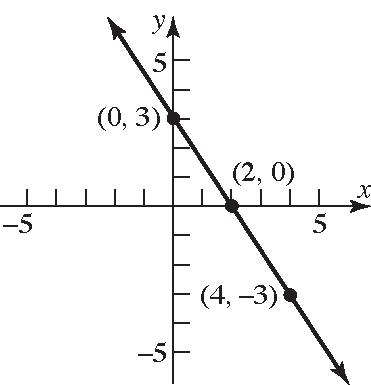
87. 236 xy ; 2 3262 3 yxyx
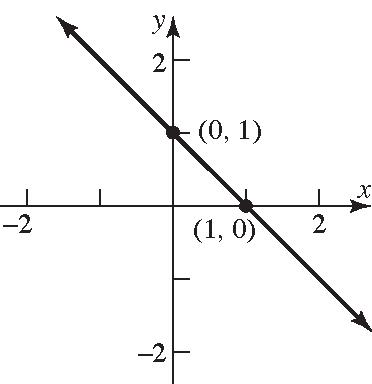
89. 1 xy ;1 y x
Slope=–1; y-intercept=1
90. 2 xy ;2 yx
Slope=1; y-intercept=–2
Section1.5: Lines
2 Slope3 ; y-intercept=–2 88. 326 xy ; 3 2363 2 yxyx
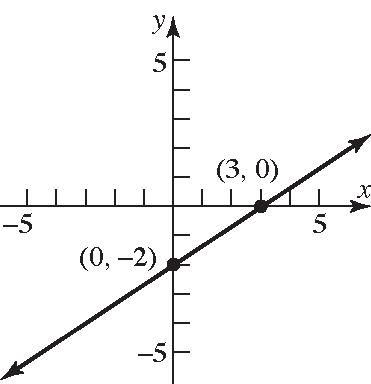
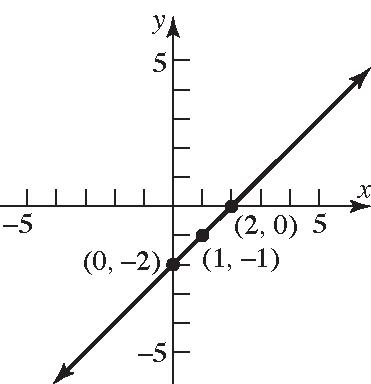
91. 4 x ;Slopeisundefined y-intercept-none
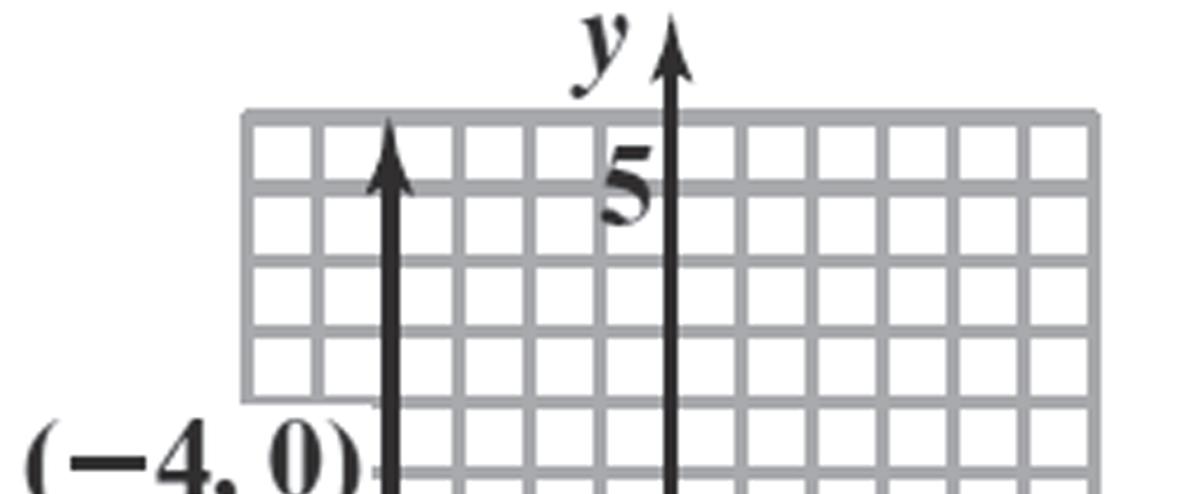
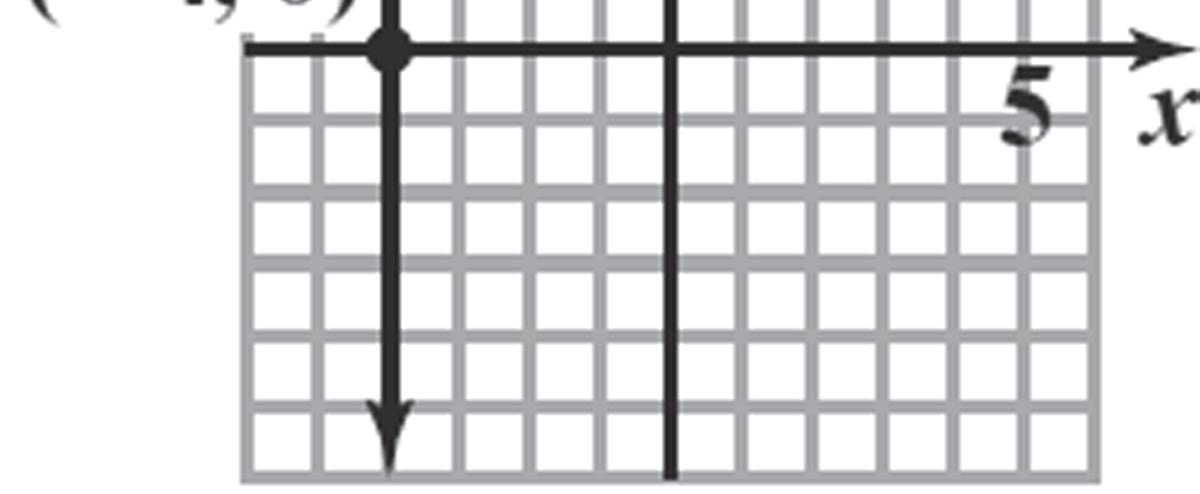
Chapter1: Graphs
92. 1 y ;Slope=0; y-intercept=–1
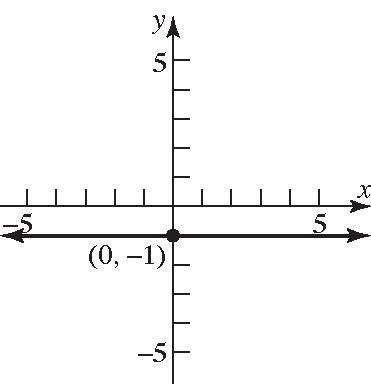
93. 5 y ;Slope=0; y-intercept=5
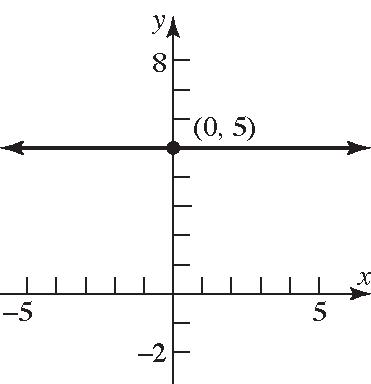
94. 2 x ;Slopeisundefined y-intercept-none
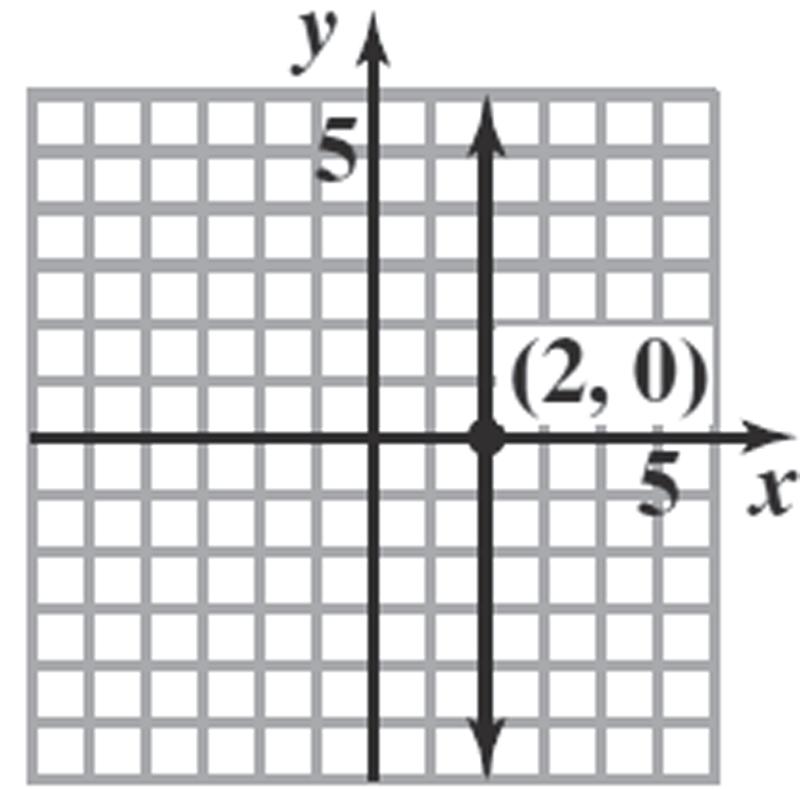
95. 0 yx ; yx Slope=1; y-intercept=0
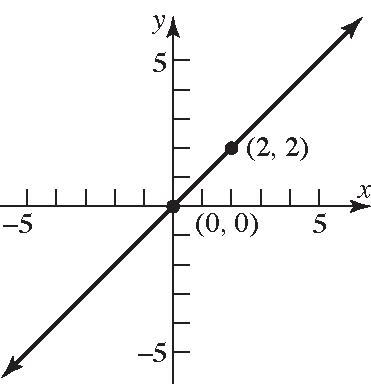
96. 0 xy ; yx Slope=–1; y-intercept=0
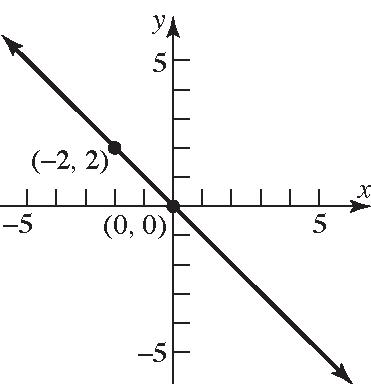
97. 230 yx ; 3 23 2 yxyx 3 Slope2 ; y-intercept=0
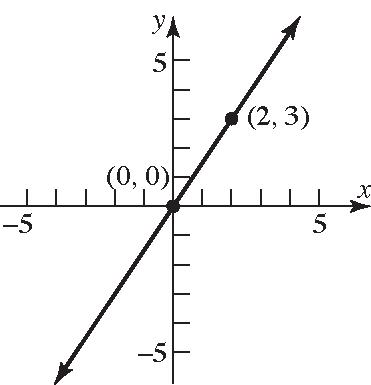
98. 320 xy ; 3 23 2 yxyx 3 Slope2 ; y-intercept=0 99. a. x-intercept:
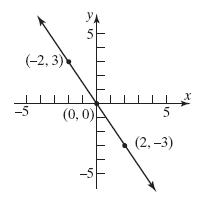
Thepoint 3,0isonthegraph.
Thepoint 0,2isonthegraph.
b.
100. a. x-intercept:
3206
Thepoint 2,0isonthegraph.
intercept:
Thepoint 0,3isonthegraph.
b.
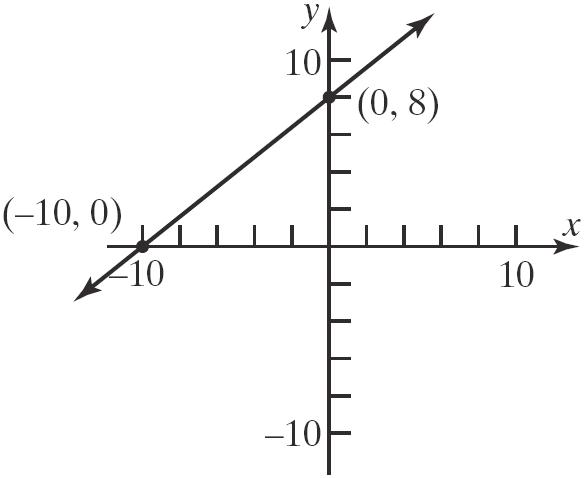
101. a. x-intercept: 45040 440 10 x x
Thepoint 10,0isonthegraph. y-intercept: 40540 540 8 y y y
Thepoint 0,8isonthegraph. b.
102. a. x-intercept: 64024 624 4 x x x
Thepoint 4,0isonthegraph.
y-intercept: 60424 424 6 y y y
Thepoint 0,6isonthegraph.
b.
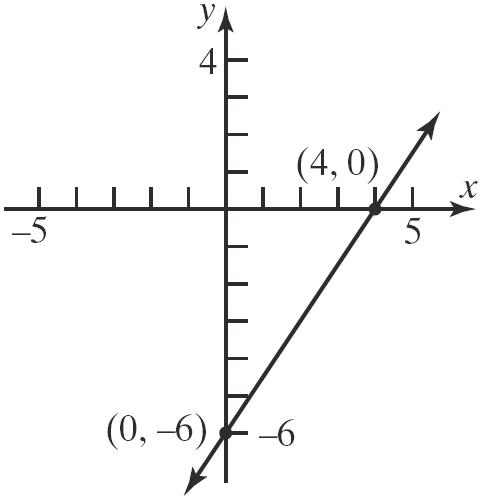
103. a. x-intercept: 72021 721 3 x x x
Thepoint 3,0isonthegraph.
y-intercept: 70221 221 21 2 y y y
Thepoint 21 0, 2 isonthegraph.
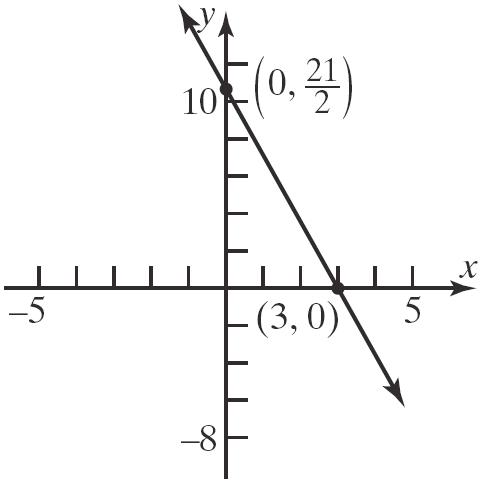
104. a. x-intercept: 53018 518 18 5 x x x
Thepoint18,0 5 isonthegraph.
y-intercept: 50318 318 6 y y y
Thepoint 0,6isonthegraph. b.
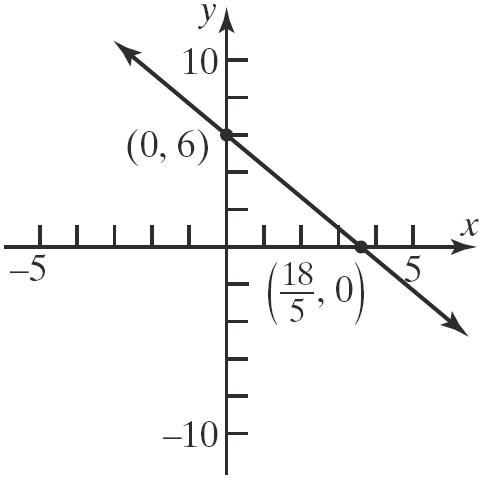
105. a. x-intercept: 11 01 23 1 1 2 2 x x x
Thepoint 2,0isonthegraph.
y-intercept: 11 01 23 1 1 3 3 y y y
Thepoint 0,3isonthegraph.
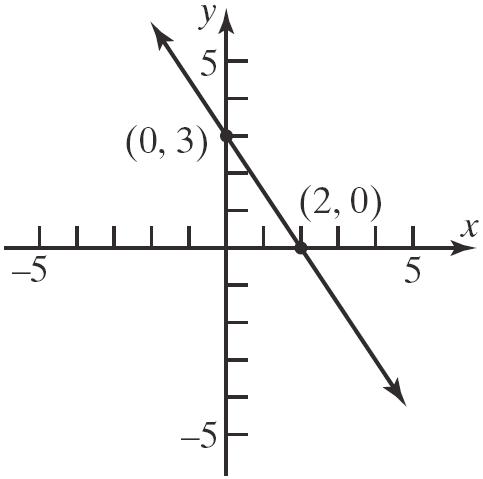
106. a. x-intercept: 2 04 3 4 x x
Thepoint 4,0isonthegraph.
y-intercept: 2 04 3 2 4 3 6 y y y
Thepoint 0,6isonthegraph.
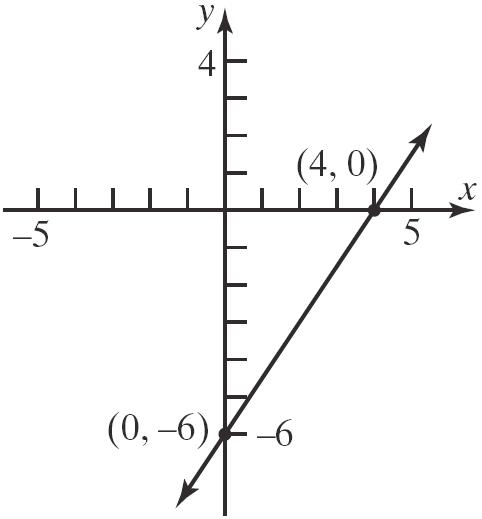
107. a. x-intercept: 0.20.501 0.21 5 x x x
Thepoint 5,0isonthegraph.
y-intercept: 0.200.51 0.51 2 y y y
Thepoint 0,2isonthegraph.
Section1.5: Lines
b.
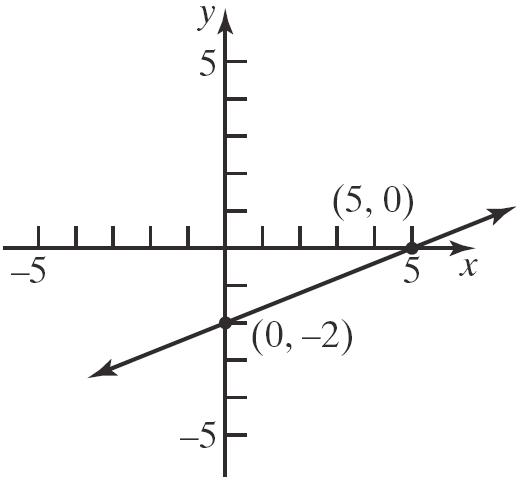
108. a. x-intercept: 0.30.401.2
Thepoint 4,0isonthegraph.
b.
Thepoint 0,3isonthegraph.
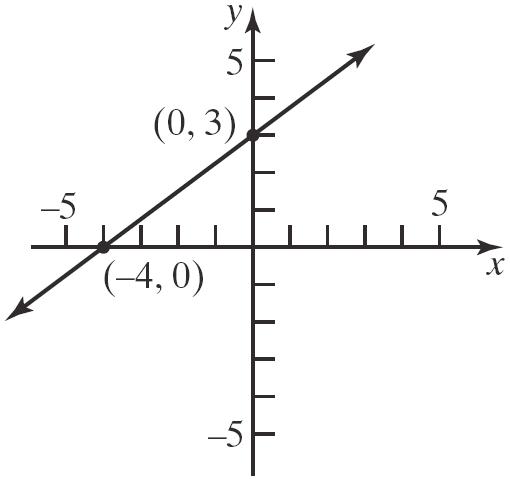
109. Theequationofthe x-axisis0 y .(Theslope is0andthe y-interceptis0.)
110. Theequationofthe y-axisis0 x .(Theslope isundefined.)
111. Theslopesarethesamebutthe y-interceptsare different.Therefore,thetwolinesareparallel.
112. Theslopesareopposite-reciprocals.Thatis,their productis1.Therefore,thelinesare perpendicular.
113. Theslopesaredifferentandtheirproductdoes notequal1.Therefore,thelinesareneither parallelnorperpendicular.
114. Theslopesaredifferentandtheirproductdoes notequal1(infact,thesignsarethesameso theproductispositive).Therefore,thelinesare neitherparallelnorperpendicular.
115. Intercepts: 0,2and 2,0.Thus,slope=1. 2or2yxxy
116. Intercepts: 0,1and 1,0.Thus,slope=–1. 1or1yxxy
117. Intercepts: 3,0and 0,1.Thus,slope= 1 3 1 1or33 3 yxxy
118. Intercepts: 0,1and 2,0.Thus, slope= 1 2 1 1or22 2 yxxy 119.
Since121 mm ,thelinesegments12 PP and 23PP areperpendicular.Thus,thepoints1 P ,2 P , and3 P areverticesofarighttriangle.
Eachpairofoppositesidesareparallel(same slope)andadjacentsidesarenotperpendicular. Therefore,theverticesareforaparallelogram.
Oppositesidesareparallel(sameslope)and adjacentsidesareperpendicular(productofslopes is1).Therefore,theverticesareforarectangle.
22 1210301910d
22 2341239110 d
22 3434121910 d
22 1430109110d
Oppositesidesareparallel(sameslope)and adjacentsidesareperpendicular(productof slopesis1).Inaddition,thelengthofallfour sidesisthesame.Therefore,theverticesarefora square.
123. Let x =numberofmilesdriven,andlet C =cost indollars.
Totalcost=(costpermile)(numberofmiles)+ fixedcost
0.6039Cx
When x =110, 0.6011039$105.00 C
When x =230, 0.6023039$177.00 C
124. Let x =numberofpairsofjeansmanufactured, andlet C =costindollars.
Totalcost=(costperpair)(numberofpairs)+ fixedcost 201200Cx
When x =400, 204001200$9200 C .
When x =740, 207401200$16,000 C
125. Let x =numberofmilesdrivenannually,and let C =costindollars.
Totalcost=(approxcostpermile)(numberof miles)+fixedcost 0.144252Cx
126. Let x =profitindollars,andlet S =salaryin dollars.
Weeklysalary=(%shareofprofit)(profit)+ weeklypay 0.05525Sx
127. a. 0.09058.28Cx ;01000 x
b.
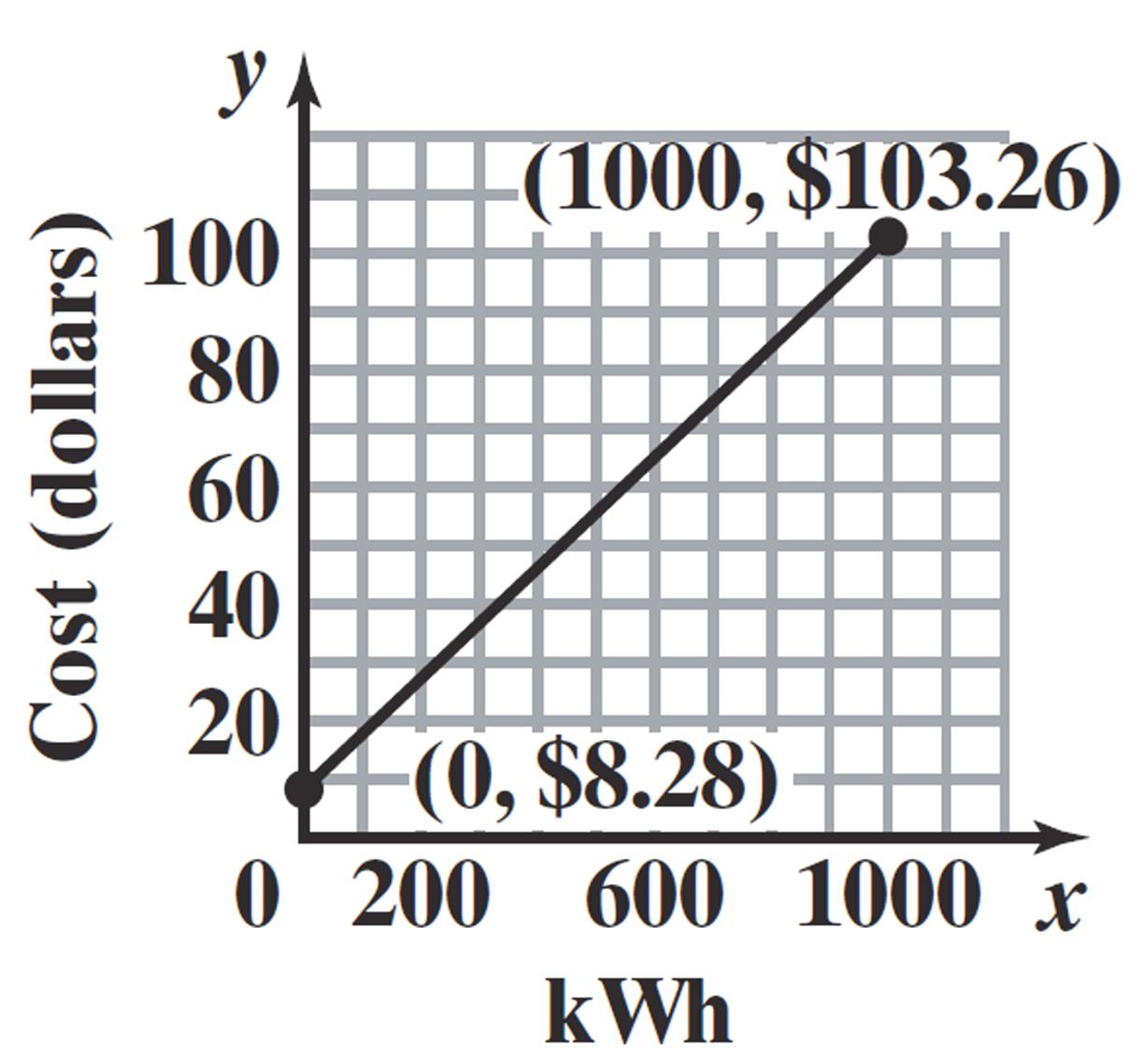
c. For200kWh, 0.09052008.28$26.38 C
d. For500kWh, 0.09055008.28$53.53 C
e. Foreachusageincreaseof1kWh,the monthlychargeincreasesby$0.0905 (thatis,9.05cents).
128. a. 0.62320.26Cx
b. For90therms, 0.6239020.26$76.33 C
c. For150therms, 0.62315020.26$113.71 C
d.
e. Foreachusageincreaseof1thermthe monthlychargeincreasesby$0.623 (thatis,62.3cents).
129. (,)(0,32);(,)(100,212) CFCF slope212321809 10001005 9 32(0) 5 9 32() 5 5(32) 9 FC FC CF
If70 F ,then 55 (7032)(38)99 21.1 C C
130. a. º273KC
b. 5 º(º32) 9 CF 5 9(32)273 5160 º273 99 52297 º 99 KF KF KF
131. a. The y-interceptis(0,30),so b =30.Since therampdrops2inchesforevery25inches ofrun,theslopeis 22 2525 m .Thus, theequationis 2 30 25 yx .
b. Let y =0. 2 030 25 2 30 25 25225
The x-interceptis(375,0).Thismeansthat therampmeetsthefloor375inches(or 31.25feet)fromthebaseoftheplatform.
c. No.Frompart(b),therunis31.25feetwhich exceedstherequiredmaximumof30feet.
d. First,designrequirementsstatethatthe maximumslopeisadropof1inchforeach 12inchesofrun.Thismeans1 12 m
Section1.5: Lines
Second,therunisrestrictedtobenomore than30feet=360inches.Forariseof30 inches,thismeanstheminimumslopeis 301 36012 .Thatis,112 m .Thus,the onlypossibleslopeis112 m .The diagramindicatesthattheslopeisnegative. Therefore,theonlyslopethatcanbeusedto obtainthe30-inchriseandstillmeetdesign requirementsis112 m .Inwords,for every12inchesofrun,therampmustdrop exactly 1inch.
132. a. Let x representthepercentofinternetad spending.Let y representthepercentof printadspending.Thenthepoints (0.19,0.26)and(0.35,0.16)areontheline. Thus, 162610 0.625 351916 m .Using thepoint-slopeformulawehave 260.625(19) 260.62511.875 0.62537.875
yx yx yx
60.6
b. x-intercept:00.62537.875 37.8750.625
x x x y-intercept:0.625(0)37.875 37.875 y Theinterceptsare(60.6,0)and(0,37.875).
c y-intercept:WhenInternetadsaccountfor 0%ofU.S.advertisementspending,print adsaccountfor37.875%ofthespending. x-intercept:WhenInternetadsaccountfor 60.6%ofU.S.advertisementspending,print adsaccountfor0%ofthespending.
d.Let x =39.2.
0.625(39.2)37.87513.4% y
133. a. Let x =numberofboxestobesold,and A =money,indollars,spentonadvertising. Wehavethepoints 11 (,)(100,000,40,000); xA
Chapter1: Graphs
22 (,)(200,000,60,000) xA
slope60,00040,000 200,000100,000 20,0001 100,0005 1 40,000100,000 5 1 40,00020,000 5 1 20,000 5 Ax Ax Ax
b. If x =300,000,then
1300,00020,000$80,000 5 A
c. Eachadditionalboxsoldrequiresan additional$0.20inadvertising.
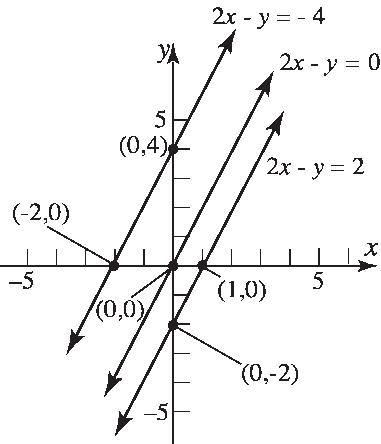
134. 2 x yC
Graphthelines: 24 20 22 xy xy xy
Allthelineshavethesameslope,2.Thelines areparallel.
135. Puteachlinearequationinslope/interceptform. 2523400 25324 1524 2233
xyxyaxy yxyxyax yxyx Iftheslopeof yax equalstheslopeofeither oftheothertwolines,thennotriangleisformed. So, 11 22 aa and 22 33 aa
Alsoifallthreelinesintersectatasinglepoint,
xx x x
thennotriangleisformed.So,wefindwhere 1524 and 2233 yxyx intersect. 1524 2233 77 66 1 15 (1)222
Thetwolinesintersectat(1,2).If yax also containsthepoint(1,2),then 212 aa
Thethreenumbersare 12 ,,and-2. 23
136. Theslopeofthelinecontaining , ab and , ba is 1 ab ba
Theslopeoftheline yx is1.
Thetwolinesareperpendicular. Themidpointof(,)and(,) abba is , 22 abba M
Sincethe x and y coordinatesof M areequal,M liesontheline yx
Note: 22 abba
137. Thethreemidpointsare 0000 ,,0,,, 2222222
aaabcabc and00,, 2222
bcbc
1from(0,0)to,22 0 2; 0 2 0(0)
1
abc Line c c m ab ab c yx ab c yx ab
bc Line cc c m bba ba a c yxa ba c yxa ba
2from(a,0)to,22 0 22 22 22 0() 2 2()
a Linebc cc m a ba b ca yx ba ca yx ba
3from,0to(,) 2 02 2 2 2 0 22 2 22
Substituteintoline1:
So,line1andline2intersectat,. 33
Showthatline3containsthepoint,33
cabacbac y baba So thethreelinesintersectat,. 33
138. RefertoFigure43.Assume121 mm .Then 222 12 2 12 22 1122 22 12 22 12 (,)(11)() () 2 2(1) 2
dABmm mm mmmm mm mm
Now, 2222 11 2222 22 (,)(10)(0)1 (,)(10)(0)1
dOBmm dOAmm , So
dOBdOAmm mmdAB
2222 12 222 12 (,)(,)11 2(,)
BytheconverseofthePythagoreanTheorem, AOB isarighttrianglewithrightangleat vertex O.ThuslinesOAandOBare perpendicular.
139. (b),(c),(e)and(g) Thelinehaspositiveslopeandpositive y-intercept.
140. (a),(c),and(g) Thelinehasnegativeslopeandpositive y-intercept.
141. (c)
Theequation2 xy hasslope1and yintercept(0,2).Theequation1 xy hasslope 1and y-intercept(0,1).Thus,thelinesare parallelwithpositiveslopes.Onelinehasa positive y-interceptandtheotherwithanegative yintercept.
142. (d)
Theequation22 yx hasslope2and yintercept(0,2).Theequation21 xy has slope 1 2 and y-intercept 1 0,. 2
Thelines areperpendicularsince 1 21 2
.Oneline hasapositive y-interceptandtheotherwitha negative y-intercept.
143 – 145. Answerswillvary.
146. No,theequationofaverticallinecannotbe writteninslope-interceptformbecausetheslope isundefined.
147. No,alinedoesnotneedtohavebothan xinterceptanda y-intercept.Verticaland horizontallineshaveonlyoneintercept(unless theyareacoordinateaxis).Everylinemusthave atleastoneintercept.
148. Twolineswithequalslopesandequal y-interceptsarecoincidinglines(i.e.thesame).
149. Twolinesthathavethesame x-interceptand yintercept(assumingthe x-interceptisnot0)are thesamelinesincealineisuniquelydefinedby twodistinctpoints.
150. No.Twolineswiththesameslopeanddifferent xinterceptsaredistinctparallellinesandhaveno pointsincommon.
AssumeLine1hasequation1 ymxb andLine 2hasequation2 ymxb ,
Line1has x-intercept1 b m and y-intercept1 b .
Line2has x-intercept2 b m and y-intercept2 b
AssumealsothatLine1andLine2haveunequal x-intercepts.
Ifthelineshavethesame y-intercept,then12 bb . 1212 12 bbbb bb
Line1andLine2havethe same x-intercept,whichcontradictstheoriginal assumptionthatthelineshaveunequal x-intercepts. Therefore,Line1andLine2cannothavethesame y-intercept.
151. Yes.Twodistinctlineswiththesame y-intercept, butdifferentslopes,canhavethesame x-intercept ifthe x-interceptis0 x
AssumeLine1hasequation1ymxb andLine 2hasequation2ymxb ,
Line1has x-intercept 1 b m and y-intercept b
Line2has x-intercept 2 b m and y-intercept b
AssumealsothatLine1andLine2haveunequal slopes,thatis12 mm . Ifthelineshavethesame x-intercept,then 12 bb mm
12 21 210 bb mm mbmb mbmb
2112 1212 But00 0 or0 mbmbbmm b mmmm
Sinceweareassumingthat12 mm ,theonlyway thatthetwolinescanhavethesame x-interceptis if0. b
152. Answerswillvary.
153. 21 21 4263 1342 yy m xx
Itappearsthatthestudentincorrectlyfoundthe slopebyswitchingthedirectionofoneofthe subtractions.
Section 1.6
1. add; 12 21025
2. 2 29 29 23 23 x x x x
Thesolutionsetis{1,5}.
3. a. Center:(0,0);radius1;221 xy
b. 229 xy
c. 2225 xy
d. Center:(2,1); 22 2(1)9xy
e. Center:(2,1); 22 2(1)9xy
f. Center:(2,2); 22 2(2)9xy
g. Center:(5,7);radius6
4. a. Center:(4,0); 22 49xy ;No yintercepts; x-intercepts:1,7
b. Center:(4,3); 22 4(3)9xy ;No y-intercepts; x-intercepts:4
c. 22 4(4)9xy ;No y-intercepts;No x-intercepts
d. One x-intercept
e. No y-intercepts
5. False.Forexample,222280 xyxy isnotacircle.Ithasnorealsolutions.
6. radius
7. True;293 rr
8. False;thecenterofthecircle 22 3213xy is 3,2.
9. d
10. a
11. Center=(2,1)
Radiusdistancefrom(0,1)to(2,1) (20)(11)42
22
Equation:22(2)(1)4 xy
12. Center=(1,2)
Radiusdistancefrom(1,0)to(1,2) (11)(20)42
22
Equation:22(1)(2)4 xy
13. Center=midpointof(1,2)and(4,2)
14225 222,,2 2 2 5 Radiusdistance2from,2to(4,2)
593 4(22)242
Equation: 2 2 59 (2) 24xy
14. Center=midpointof(0,1)and(2,3) 0213 ,1,2 22
22 Radiusdistancefrom1,2to(2,3) 21(32)2
Equation: 22 1(2)2xy
15. 222()() x hykr 222 22 (0)(0)2 4 xy xy
Generalform:2240 xy
16. 222()() x hykr 222 22 (0)(0)3 9 xy xy
Generalform:2290 xy
Chapter1: Graphs
17. 222()() x hykr 222 22 (0)(2)2 (2)4 xy xy
Generalform:22 22 444 40 xyy xyy
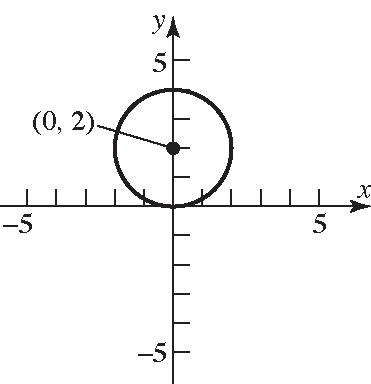
18. 222()() x hykr 222 22 (1)(0)3 (1)9 xy xy
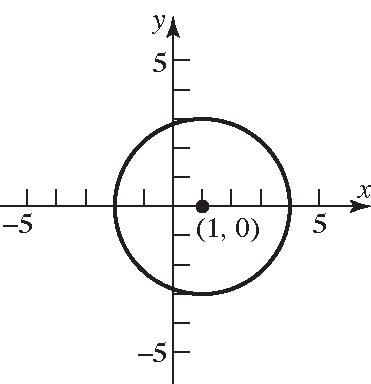
Generalform:22 22 219 280 xxy xyx
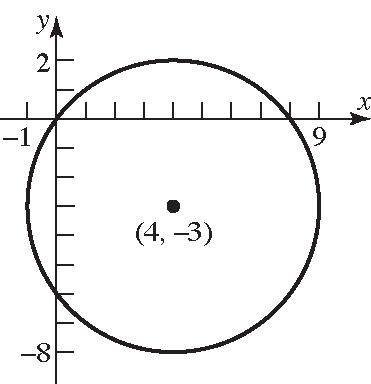
19. 222()() x hykr 222 22 (4)((3))5 (4)(3)25 xy xy
Generalform: 22 22 8166925 860 xxyy xyxy
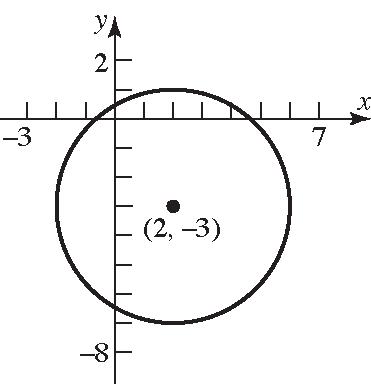
20. 222()() x hykr 222 22 (2)((3))4 (2)(3)16 xy xy
Generalform:22 22 446916 4630 xxyy xyxy
21. 222()() x hykr 222 22 (2)(1)4 (2)(1)16 xy xy
Generalform:22 22 442116 42110 xxyy xyxy
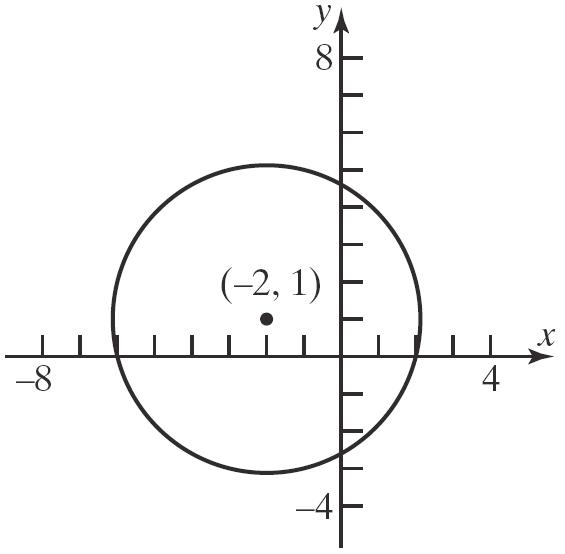
22. 222()() x hykr 222 22 (5)((2))7 (5)(2)49 xy xy
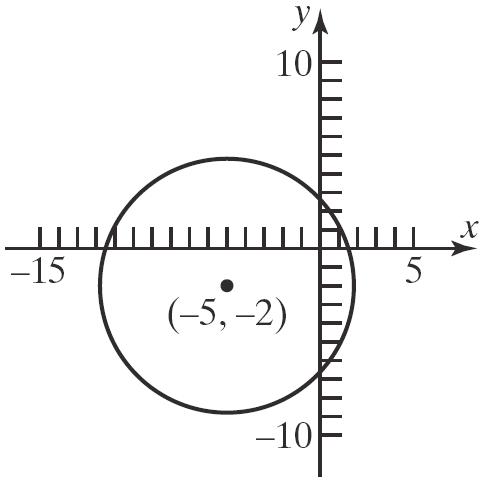
23.
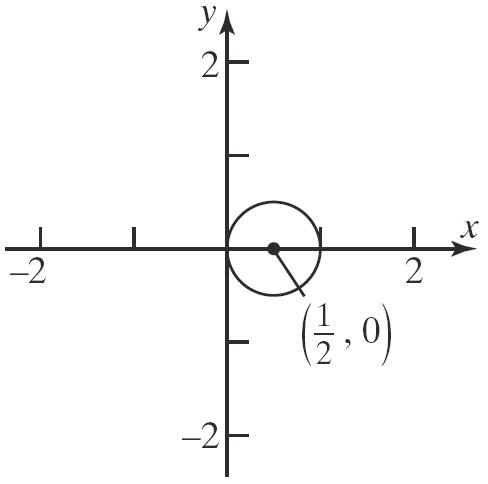
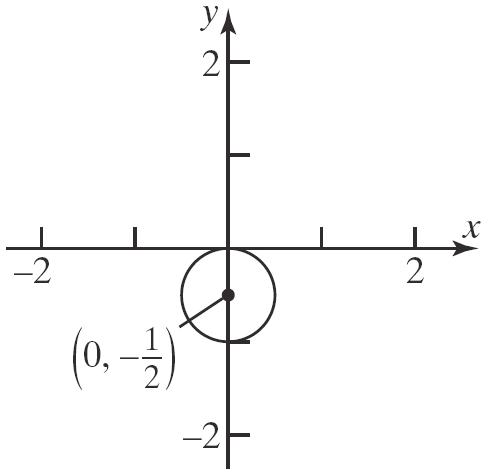
25. 222()() x hykr
222 22 (5)((1))13 (5)(1)13
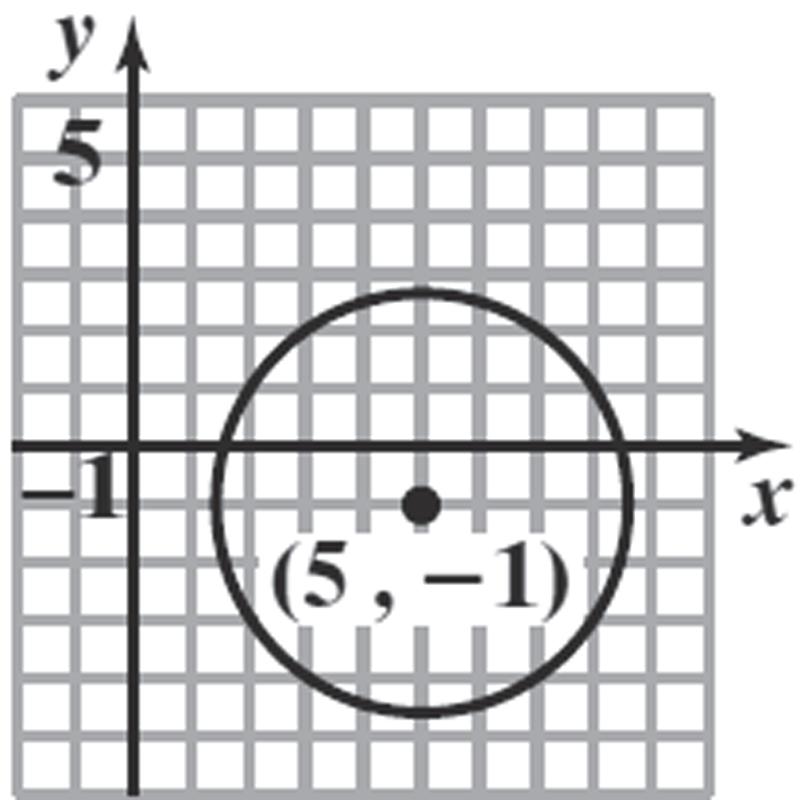
26. 222()() x hykr
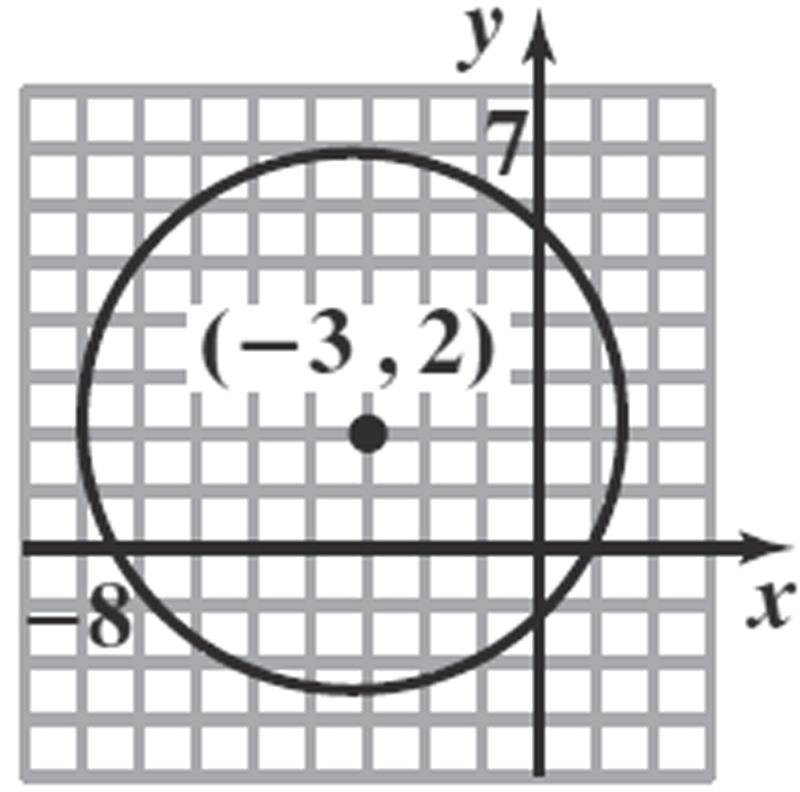
222 22 (3)(2)25 (3)(2)20
Generalform:22 22 694420 6470
27. 224xy
222 2 xy
a. Center:(0,0);Radius2
b.
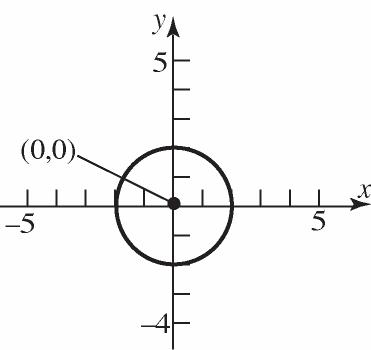
c. x-intercepts: 22 2 04 4 42 x x x y-intercepts: 22 2 04 4 42 y y y
Theinterceptsare 2,0,2,0, 0,2, and 0,2.
28. 22(1)1xy 222 (1)1xy
a. Center:(0,1);Radius1
b.
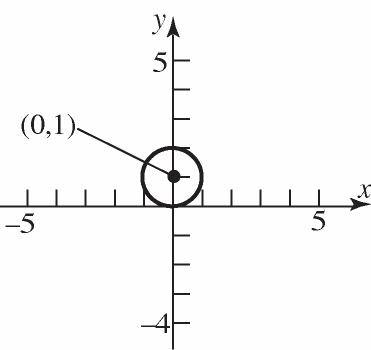
c. x-intercepts:22 2 2 (01)1 11 0 00 x x x x y-intercepts: 22 2 0(1)1 (1)1 11 11 11 y y y y y
2or0yy
Theinterceptsare 0,0and 0,2.
29. 22 2328 xy 22 34xy
a. Center:(3,0);Radius2
b.
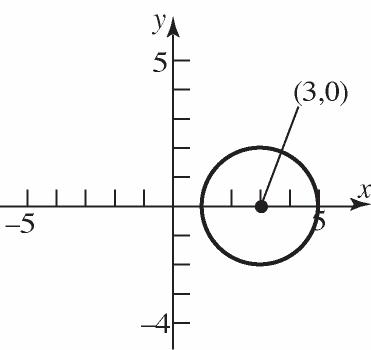
c. x-intercepts: 22 2 304 34
32 x x x x x 5or1 x x
30. 22 31316 xy
a. Center:(–1,1);Radius=2
b.
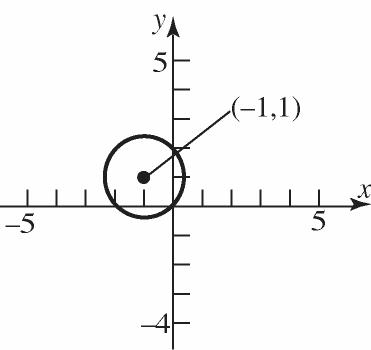
c. x-intercepts:
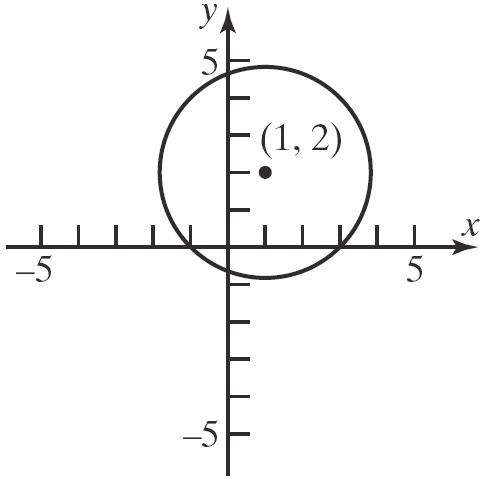
c. x-intercepts:
y-intercepts:
(01)(2)3 (1)(2)3
222
Theinterceptsare 15,0,15,0, 0,222,and 0,222.
32. 2242200 xyxy 22 22 222 4220 (44)(21)2041 (2)(1)5 xxyy xxyy xy
a. Center:(–2,–1);Radius=5
b.
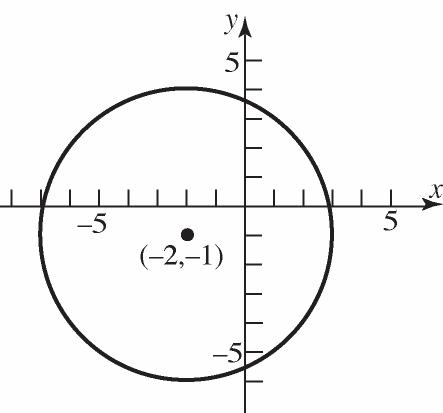
c. x-intercepts:222 2 2 (2)(01)5 (2)125 (2)24 224 226 226 x x x x x x
y-intercepts:222 2 2 (02)(1)5 4(1)25 (1)21 121 121 y y y y y
Theinterceptsare 226,0, 226,0, 0,121,and 0,121.
33. 22 22 22 222 4410 441 (44)(44)144 (2)(2)3 xyxy xxyy xxyy xy
a. Center:(–2,2);Radius=3
b. y
c. x-intercepts:222 2 2 (2)(02)3 (2)49 (2)5 25 25 x x x x x
y-intercepts:222 2 2 (02)(2)3 4(2)9 (2)5 25 25 y y y y y
Theinterceptsare 25,0,
25,0,
0,25,and 0,25. 34. 22 22 22 222 6290 629 (69)(21)991 (3)(1)1 xyxy xxyy xxyy xy
a. Center:(3,–1);Radius=1
b.
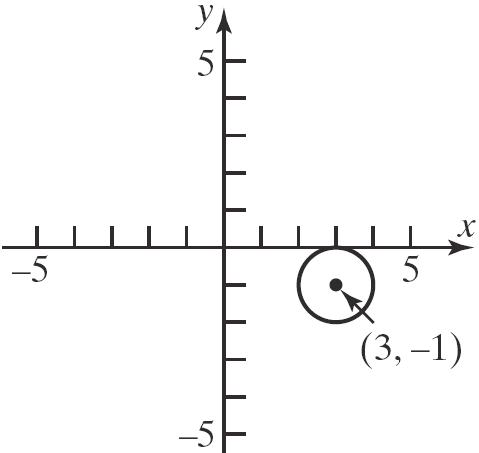
c. x-intercepts: 222 2 2 (3)(01)1 (3)11 30 30 3 x x x x x
y-intercepts: 222 2 2 (03)(1)1 9(1)1 18 y y y Norealsolution.
Theinterceptonlyinterceptis 3,0
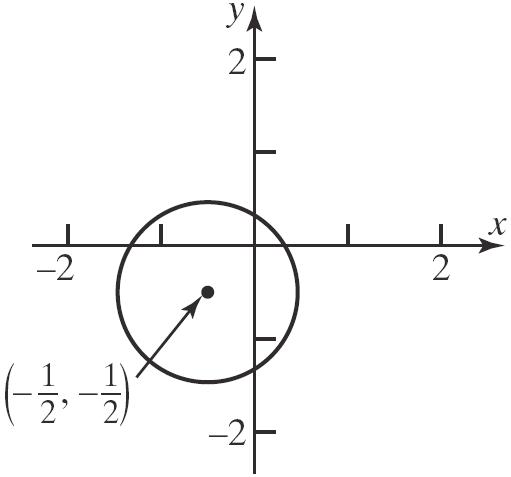
b.
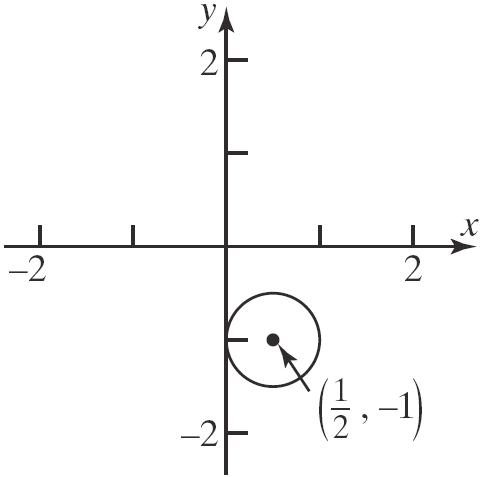
c.
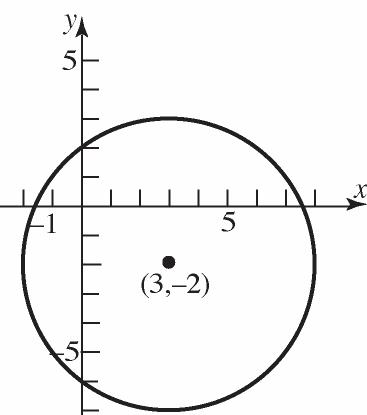
c. x-intercepts:
Center:(–2,0);Radius= 2 2
39.
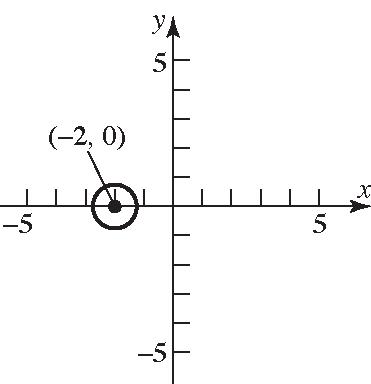
c. x-intercepts:
Norealsolutions.
Theinterceptsare 2 2,0 2
and 2 2,0. 2
22 22 22 222 2820 40 4404 22 xxy xxy xxy xy
a. Center: 2,0;Radius:2 r
b.
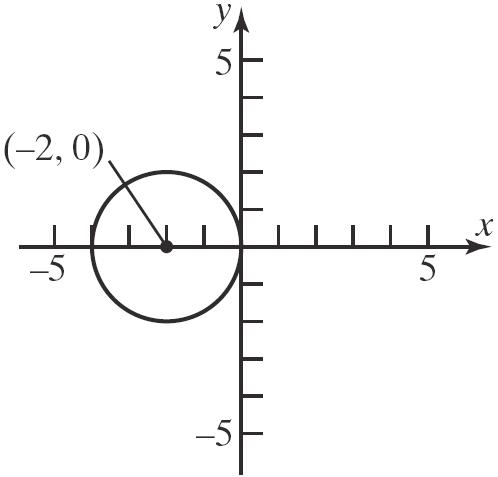
c. x-intercepts:
40. 22 22 22 22 33120 40 4404 24 xyy xyy xyy
a. Center: 0,2;Radius:2 r
b.
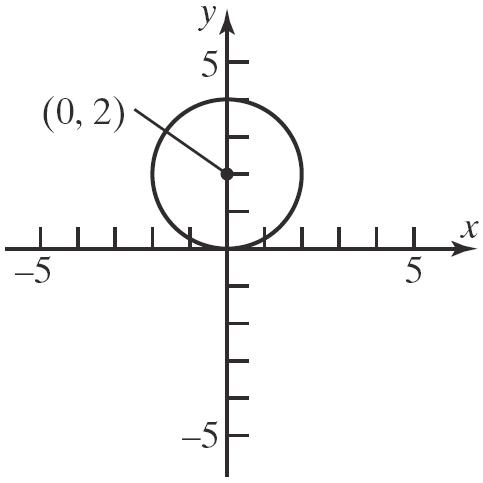
c.
Section1.6: Circles
41. Centerat(0,0);containingpoint(–2,3).
22 20304913 r
Equation: 222 22 (0)(0)13 13 xy xy
42. Centerat(1,0);containingpoint(–3,2).
22 31201642025 r
Equation: 222 22 (1)(0)20 (1)20 xy xy
43. Endpointsofadiameterare(1,4)and(–3,2). Thecenterisatthemidpointofthatdiameter:
Center: 1(3)42,1,3 22
Radius:22(1(1))(43)415 r
Equation: 222 22 ((1))(3)5 (1)(3)5 xy xy
44. Endpointsofadiameterare(4,3)and(0,1). Thecenterisatthemidpointofthatdiameter:
Center: 4031 ,2,2 22
Radius:22(42)(32)415 r
Equation: 222 22 (2)(2)5 (2)(2)5 xy xy
45. 2 162 8 Cr r r 222 22 (2)((4))8 (2)(4)64 xy xy
46. 2 492 7 A r r r
222 22 ((5))(6)7 (5)(6)49
xy xy
47. (c);Center: 1,2;Radius=2
48. (d);Center: 3,3;Radius=3
49. (b);Center: 1,2;Radius=2
50. (a);Center: 3,3;Radius=3
51. Thecentersofthecirclesare:(4,-2)and(-1,5). Theslopeis5(2)77 1455 m .Usethe slopeandonepointtofindtheequationofthe line.
53. Considerthefollowingdiagram:
Therefore,thepathofthecenterofthecirclehas theequation2 y
54. Considerthefollowingdiagram:
7 (2)(4) 5 728 2 55 510728 7518
yx yx yx xy
52. Findthecentersofthetwocircles: 22 22 22 4640 (44)(69)449 (2)(3)9 xyxy xxyy xy
Center: 2,3 22 22 22 6490 (69)(44)994 (3)(2)4 xyxy xxyy xy
Center: 3,2
Findtheslopeofthelinecontainingthecenters: 2(3)1 325 m
Findtheequationofthelinecontainingthe centers: 1 3(2) 5 5152 513 5130 yx yx xy xy
Thereforethepathofthecenterofthecirclehas theequation7 x .
55. Lettheupper-rightcornerofthesquarebethe point ,x y .Thecircleandthesquareareboth centeredabouttheorigin.Becauseofsymmetry, wehavethat x y attheupper-rightcornerof thesquare.Therefore,weget
Thelengthofonesideofthesquareis2 x .Thus, theareais
56. Theareaoftheshadedregionistheareaofthe circle,lesstheareaofthesquare.Lettheupperrightcornerofthesquarebethepoint ,x y Thecircleandthesquarearebothcenteredabout theorigin.Becauseofsymmetry,wehavethat x y attheupper-rightcornerofthesquare. Therefore,weget
Thelengthofonesideofthesquareis2 x .Thus, theareaofthesquareis 2 23272 square units.Fromtheequationofthecircle,wehave 6 r .Theareaofthecircleis
squareunits. Therefore,theareaoftheshadedregionis
squareunits.
57. ThediameteroftheFerriswheelwas250feet,so theradiuswas125feet.Themaximumheight was264feet,sothecenterwasataheightof 264125139 feetabovetheground.Sincethe centerofthewheelisonthe y-axis,itisthepoint (0,139).Thus,anequationforthewheelis:
222 22 0139125 13915,625
58. Thediameterofthewheelis520feet,sothe radiusis260feet.Themaximumheightis550 feet,sothecenterofthewheelisataheightof 550260290 feetabovetheground.Since thecenterofthewheelisonthe y-axis,itisthe point(0,290).Thus,anequationforthewheel is:
222 22 0290260 29067,600
59.
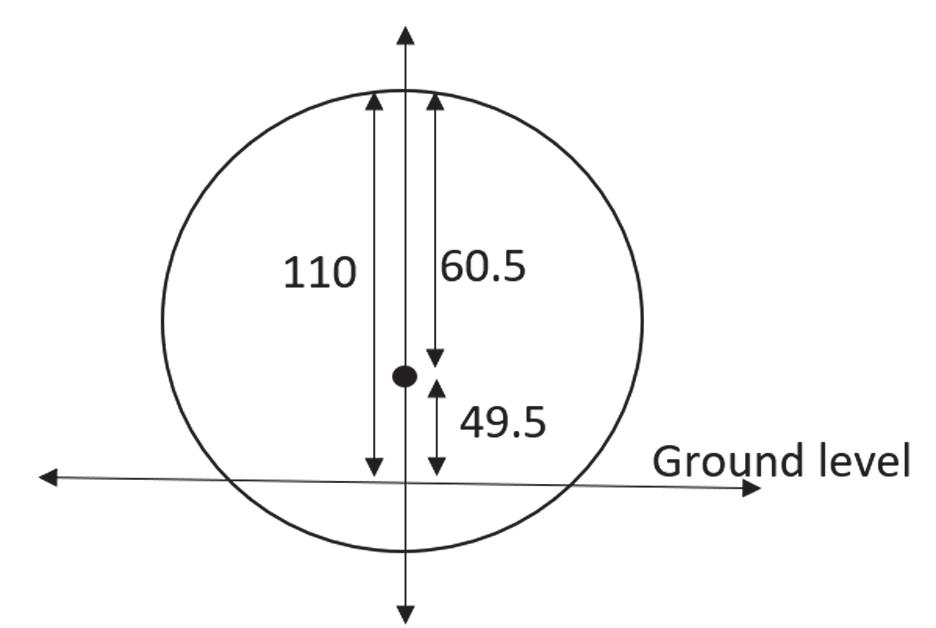
Refertofigure.Sincetheradiusofthebuilding is60.5mandtheheightofthebuildingis110m, thenthecenterofthebuildingis49.5mabove theground,sothey-coordinateofthecenteris 49.5.Theequationofthecircleisgivenby 222(49.5)60.53660.25 xy
60. Completethesquaretofindtheequationofthe circlerepresentingtheformulaforthebuilding. 22 222 781521184315213364 (39)58
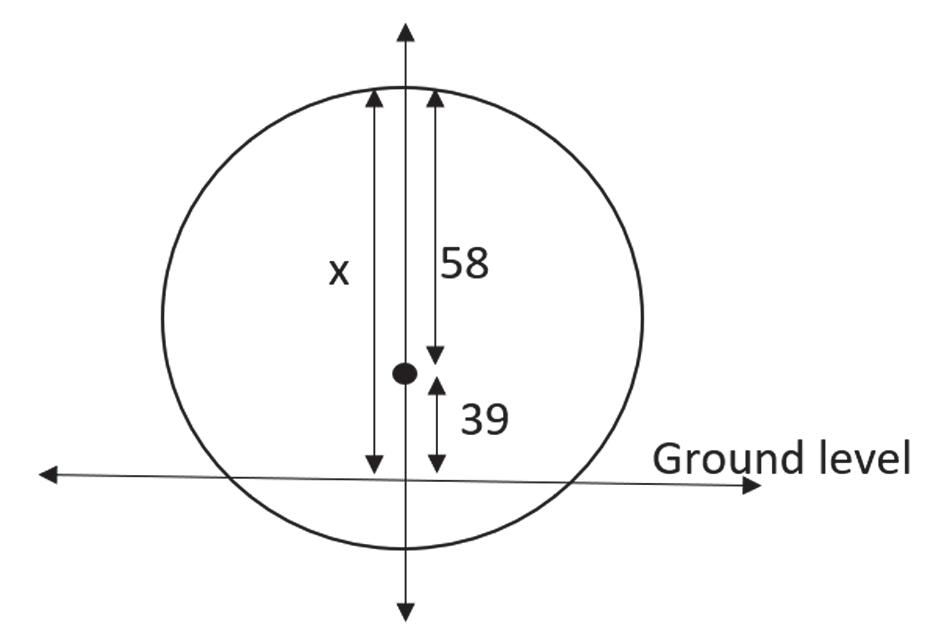
Refertofigure.Theycoordinateofthecenteris 39.Theradiusis58.Thustheheightofthe buildingis58+39=97m.
61. Centerat(2,3);tangenttothe x-axis.
3 r
Equation:222 22 (2)(3)3 (2)(3)9 xy xy
62. Centerat(–3,1);tangenttothe y-axis.
3 r
Equation:222 22 (3)(1)3 (3)(1)9 xy xy
63. Centerat(–1,3);tangenttotheline y =2. Thismeansthatthecirclecontainsthepoint (–1,2),sotheradiusis r =1.
Equation:222 22 (1)(3)(1) (1)(3)1 xy xy
64. Centerat(4,–2);tangenttotheline x =1. Thismeansthatthecirclecontainsthepoint (1,–2),sotheradiusis r =3. Equation:222
(4)(2)(3) (4)(2)9 xy
65. a. Substitute222 into: y mxbxyr
2222 () 2 (1)20 x mxbr x mxbmxbr mxbmxbr
Thisequationhasonesolutionifandonlyif thediscriminantiszero.
b. Frompart(a)weknow 2222 (1)20 mxbmxbr .Usingthe quadraticformula,sincethediscriminantis zero,weget:
2 2(1) bmbmbmrmr x b mb b r mr ymb b mrmrbr b bbb
2
Thepointoftangencyis
c. Theslopeofthetangentlineis m . Theslopeofthelinejoiningthepointof tangencyandthecenter(0,0)is: 2 2 22 0 1 0
Thetwolinesareperpendicular.
66. Let(,) hk bethecenterofthecircle. 240 24 1 2 2 xy yx yx
Theslopeofthetangentlineis 1 2.Theslope from(,) hk to(0,2)is–2. 2 2 0 22 k h kh
Theothertangentlineis27 yx ,andithas slope2.
Theslopefrom(,) hk to(3,–1)is 1 2 . 11 32 223 21 12 k h kh kh hk
Solvethetwoequationsinandhk : 22(12) 224 30 0 kk kk k k
12(0)1 h
Thecenterofthecircleis(1,0).
67. Theslopeofthelinecontainingthecenter(0,0) and 1,22is 220 22 10 .Thentheslopeofthetangent lineis 12 224
Sotheequationofthetangentlineis: 2 221 4 22 22 44 48222 2492
yx yx yx xy
68. 224640 xyxy 22 22 (44)(69)449 (2)(3)9 xxyy xy
Center:(2,–3) Theslopeofthelinecontainingthecenterand
69. Thecenterofthecircleis1212 , 22
Thentheslopeofthetangentlineis: 12 224 So,theequationofthetangentlineis
2 223(3) 4 232 223 44 48212232 2411212
70. Completethesquaretoget
Chapter1: Graphs
71. (b),(c),(e)and(g)
Weneed,0 hk and 0,0onthegraph.
72. (b),(e)and(g)
Weneed0 h ,0 k ,and hr
73. Answerswillvary.
74. Thestudenthasthecorrectradius,butthesigns ofthecoordinatesofthecenterareincorrect.The studentneedstowritetheequationinthe
Chapter 1 Review
1. 0,0,4,2
a. 22distance4020 16420 25
b.
040242 midpoint,,2,1 2222
c. 2021 slope4042 y x
d. When x increasesby2units, y increasesby 1unit.
2. 1,1,2,3
a.
22distance2131 916255
b. 1213 midpoint,22 121 ,,1 222
22 222 3216 324 xy xy
Thus, ,3,2hk and4 r
c. 3144 slope2133 y x
d. When x increasesby3units, y decreasesby 4units.
3. 4,4,4,8
a. 22distance4484 014414412
b. 4448midpoint,22 84 ,4,2 22
c. 8412 slope,undefined 440 y x
d. Undefinedslopemeansthepointslieona verticalline,inthiscase4 x .
4. 2,1,3,1
a. 22distance321(1) 250255
b. 231(1)midpoint,22 121 ,,1 222
c. 1(1)0 slope0 325 y x
d. Slope=0meansthepointslieona horizontalline,inthiscase1 y
5. 4,0,0,0,2,0, 0,2,0,0,0,2
6. 215 yx
Theinterceptsare 0,15, 3.87,0,and 3.87,0
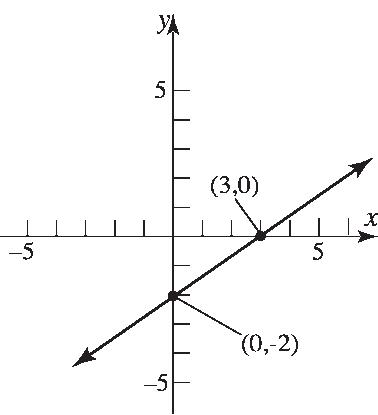
7. 236 326 2 2 3 xy yx yx
2306 26 3 x x
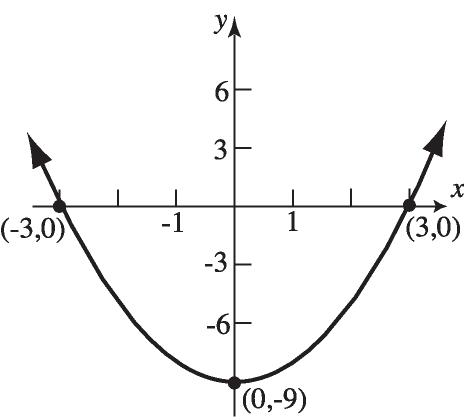
8. 29 yx x-intercepts:y-intercept:
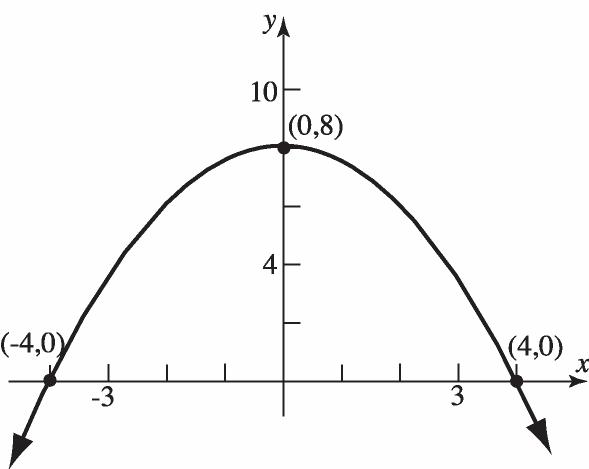
10. 232 x y
x-axis: 2 2 23 23same xy xy
y-axis: 2 2 23 23different xy xy
origin: 2 2 23 23different xy xy
Therefore,thegraphoftheequationhasx-axis symmetry.
11. 22416xy
x-axis: 22 22 416 416same xy xy y-axis: 22 22 416 416same xy xy
origin: 22 22 416 416same xy xy
Therefore,thegraphoftheequationhasx-axis, y-axis,andoriginsymmetry.
12. 4234yxx x-intercepts: y-intercepts:
Theinterceptsare(2,0),(2,0),(0,4),and (0,2).
Test x-axissymmetry:Let yy 42 42 34 34different yxx yxx
Test y-axissymmetry:Let x x
42 42 34 34same yxx yxx
Testoriginsymmetry:Let x x and yy
42 42 42 34 34 34different yxx yxx yxx
Therefore,thegraphwillhave y-axissymmetry.
13. 3 y xx
x-axis: 3 3different yxx yxx
y-axis: 3 3different yxx yxx
origin: 3 3 3 same yxx yxx yxx
Therefore,theequationofthegraphhasorigin symmetry.
14. 2220 xxyy
x-axis: 22 22 20 20different xxyy xxyy
y-axis: 22 22 20 20different xxyy xxyy
origin:
22 22 20 20different xxyy xxyy
Therefore,thegraphoftheequationhasnoneof thethreesymmetries.
16. 3530xx
UsetheZerooptionfromtheCALCmenu.
Thesolutionsetis
17. 4321 x x
UsetheIntersectoptionontheCALCmenu.
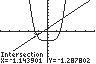
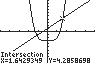
Thesolutionsetis 1.14,1.64
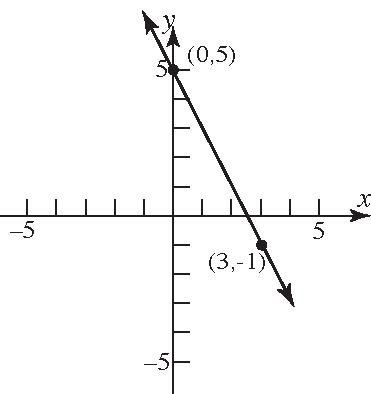
18. Slope=–2;containing(3,–1) 11() (1)2(3) 126 25 25or25 yymxx yx yx yx xyyx
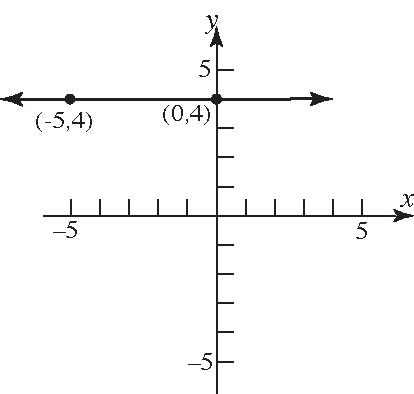
19. Slope=0;containingthepoint(–5,4) 11() 40((5)) 40 4 yymxx yx y y
Chapter1: Graphs
20. Slopeundefined;containing(–3,4). Thisisaverticalline. 3 x Noslope-interceptform. 5 (3,0) (3,4) 5 5 y x 5
21. x-intercept=2orthepoint(2,0); Containingthepoint(4,–5) 5055 4222
11 5 02 2 5 5 2 5 5210or5 2 yymxx yx yx xyyx
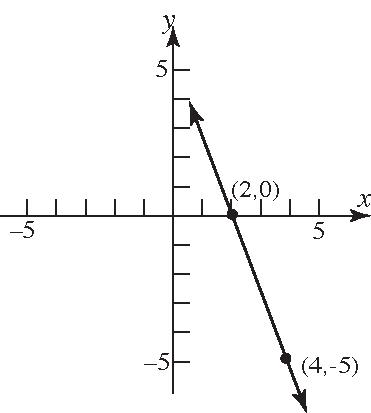
22. y-intercept=–2;containing(5,–3) Pointsare(5,–3)and(0,–2) 2(3)11 0555 m
1 2 5 1 510or2 5 ymxb yx xyyx
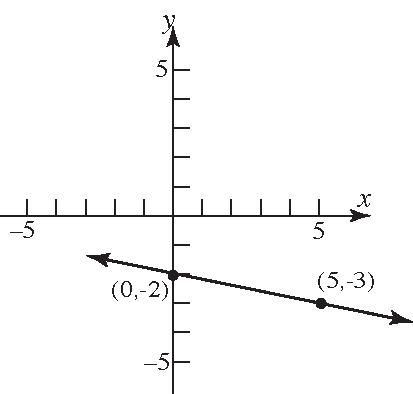
23. Containingthepoints(3,–4)and(2,1) 1(4)55 231 m
11 (4)53 4515 511 511or511 yymxx yx yx yx xyyx
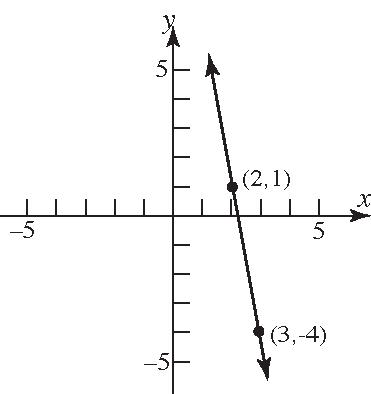
24. Parallelto234 xy ; 2 Slope;containing(–5,3) 3 11() 22103((5))3333 219 33 219 2319or 33 yymxx yxyx yx xyyx
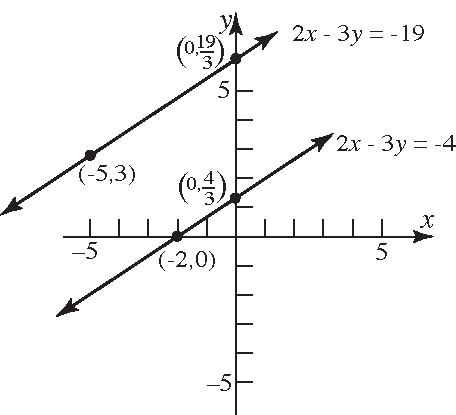
25. Perpendicularto34 xy ; 1 Slopeofperpendicular3
Containingthepoint(–2,4) 11() 1 4((2)) 3 12 4 33 110 33 110 310or 33 yymxx yx yx
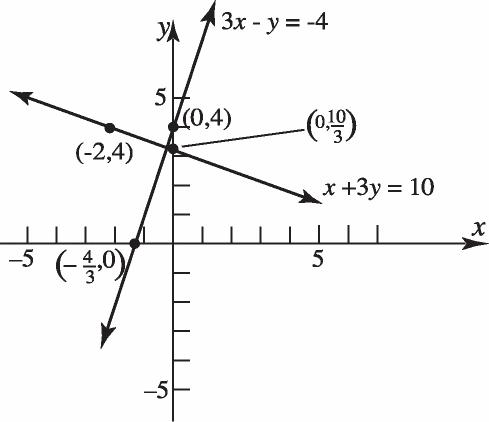
26. 222()() x hykr
222 22 234 2316 xy xy
27. 222()() x hykr
222 22 121 121 xy xy
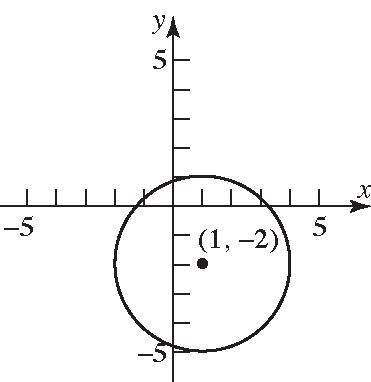
28. 222440 xyxy 22 22 22 222 244 (21)(44)414 (1)(2)9 (1)(2)3 xxyy xxyy xy xy Center:(1,–2)Radius=3
22 2 024040 240 xx xx
2 22414220 212 225 15 2 x
22 2 020440 440 yy yy
2 44414432 212 442 222 2 y
Intercepts: 15,0, 15,0 , 0,222,and 0,222
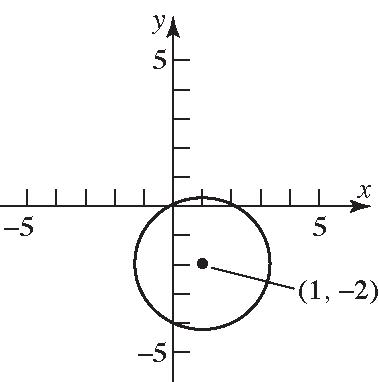
29. 22 336120 xyxy
22 22 22 22 222 240 240 (21)(44)14 (1)(2)5 (1)(2)5 xyxy xxyy xxyy xy xy
Center:(1,–2)Radius=5
22 2 33061200 360 320 xx xx xx
xx
22 2 30360120 3120 340 yy yy yy
0or4yy
Intercepts:
0,0, 2,0,and 0,4
30. Giventhepoints (2,0),(4,4),(8,5)ABC .
a. Findthedistancebetweeneachpairof points. 22 22 22 ,(4(2))(40) 4162025 ,(8(4))(54) 1441145 ,(8(2))(50) 1002512555
dAB dBC dAC
222 20125145 20125145 145145
ThePythagoreanTheoremissatisfied,so thisisarighttriangle.
b. Findtheslopes: 4042 4(2)2 541 8412 5051 82102 AB BC AC m m m
1 21 2 mmABAC
Sincetheproductoftheslopesis–1,the sidesofthetriangleareperpendicularand thetriangleisarighttriangle.
31. slope15of1; 62 slope11of1 86 AB BC
Sincelines AB and BC areparallel,and haveapointincommon(B),theyarethe sameline.Therefore, A , B ,and C are collinear.
32. Acirclewithcenter 1,2hasequation
22212 x yr
point2,42142 9413
point3,53152 4913 Ar rr Br rr Cr rr
Thereforethepoints A, B and C lieonacircle withcenterpoint 1,2andradius=13.
33. Endpointsofthediameterare(–3,2)and(5,–6). Thecenterisatthemidpointofthediameter: Center:
Radius:22(1(3))(22)1616 3242 r
Equation:
222 22 22 (1)(2)42 214432 24270 xy xxyy xyxy
34. Usingthedistanceformulaonthepoints(–3,2) and(5, y)yields
222 (5(3))(2)64(2)dyy Nowset10andsolvefor. dy
2 2 22 2 2 1064(2) 1064(2) 10064(2) 36(2) 62 so268 and264 y y y y y yy yy
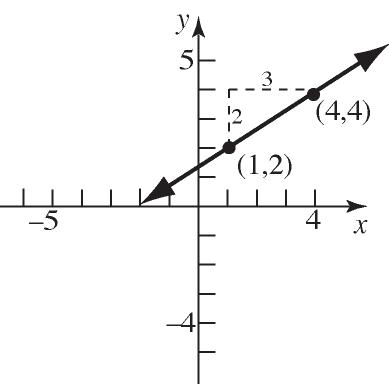
35. slope= 2 3,containingthepoint(1,2)
36. Answerswillvary.
37. a. 0 x isaverticallinepassingthroughthe origin,thatis,0 x istheequationofthe y-axis.
b. 0 y isahorizontallinepassingthrough theorigin,thatis,0 y istheequationof the x-axis.
c. 0 xy impliesthat yx .Thus,the graphof0 xy isthelinepassing throughtheoriginwithslope=–1.
d. 0 xy impliesthateither0 x ,0 y ,or bothare0.0 x isthey-axisand0 y is thex-axis.Thus,thegraphof0 xy isa graphconsistingofthecoordinateaxes.
e. 220xy impliesthatboth0 x and 0 y .Thus,thegraphof220 xy isa graphconsistingofasinglepoint-the origin.
Chapter 1 Test
1. a.
22 2121 22 22 4253 68 3664 100 10
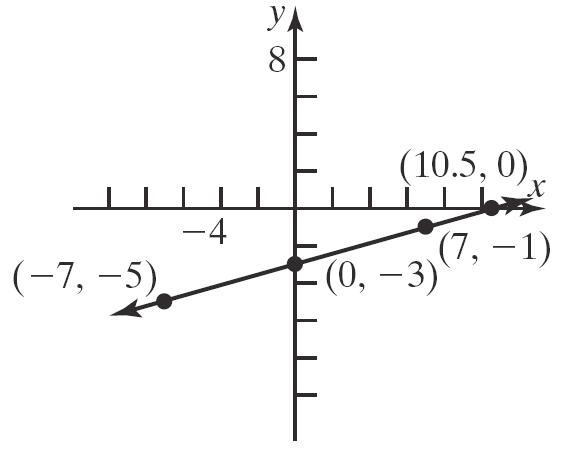
25 yx
33543,4 11541,4
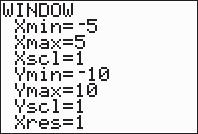
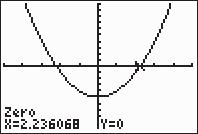
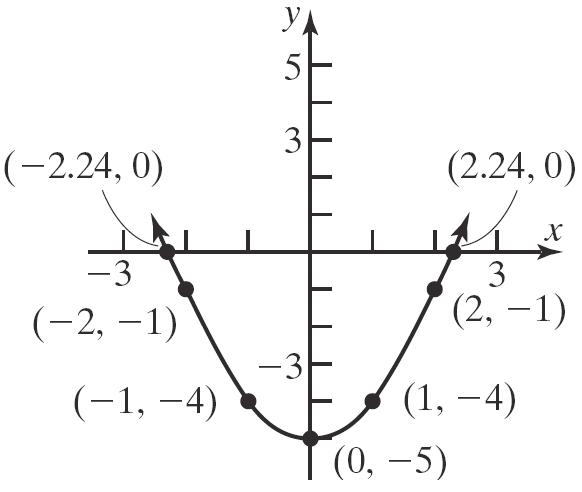
4. 32 2210 xxx
Sincethisequationhas0ononeside,wewill usetheZerooptionfromtheCALCmenu.Itwill beimportanttocarefullyselectthewindow settingssoasnottomissanysolutions.
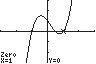
Thesolutionstotheequationare1,0.5,and1.
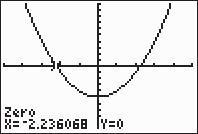
5. 42580xx
Sincethisequationhas0ononeside,wewill usetheZerooptionfromtheCALCmenu.
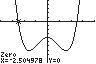
Thesolutions,roundedtotwodecimalplaces, are2.50and2.50.
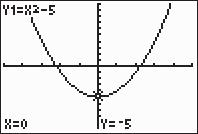
6. 327233xxxx
Sincetherearenonzeroexpressionsonboth sidesoftheequation,wewillusetheIntersect optionfromtheCALCmenu.Entertheleftside oftheequationinY1andtherightsideinY2.
Thesolutions,roundedtotwodecimalplaces, are2.46,0.24,and1.70
7. a.
b. If x increasesby3units, y willdecrease by2units.
8. 2 y x y
9. 29xy x-intercepts: y-intercept: 2 2 09 9 3 x
Test x-axissymmetry:Let yy
2 2 9 9different xy xy
Test y-axissymmetry:Let x x
2 2 9 9same xy xy
Testoriginsymmetry:Let x x and yy
2 2 9 9different xy xy
Therefore,thegraphwillhave y-axissymmetry.
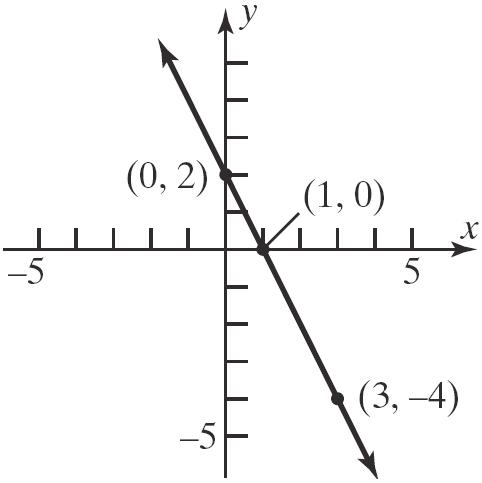
10. Slope=2;containing(3,4) 11() (4)2(3) 426 22 yymxx yx yx yx
11. 222()() x hykr 222 22 4(3)5 4325 xy xy
Generalform: 22 22 22 4325 8166925 860 xy xxyy xyxy
Chapter1: Graphs
12. 22 22 22 222 4240 424 (44)(21)441 (2)(1)3 xyxy xxyy xxyy xy
Center:(–2,1);Radius=3 y
Parallelline
Anylineparallelto236 xy hasslope
Chapter 1 Project
Internet-based Project
Perpendicularline
Anylineperpendicularto236
