Chapter 1 Graphs, Equations, and Inequalities
Section 1.1
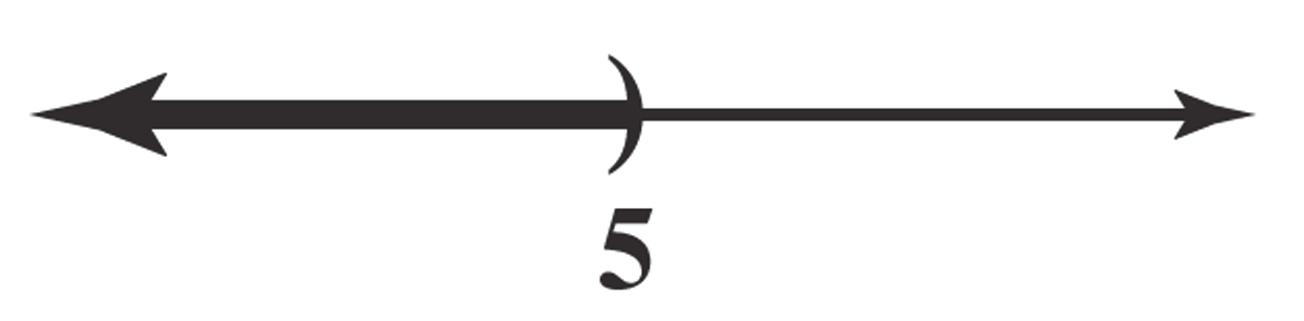
0
3. x-coordinate; y-coordinate;quadrants
4. False;pointsthatlieinQuadrantIVwillhavea positive x-coordinateandanegative y-coordinate. Thepoint 1,4liesinQuadrantII.
5. d 6. c
7. (a)QuadrantII (b) x-axis
(c)QuadrantIII (d)QuadrantI (e) y-axis (f)QuadrantIV
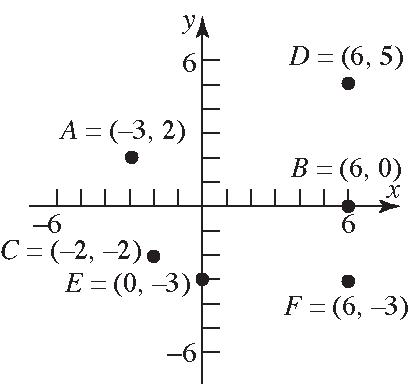
8. (a)QuadrantI (b)QuadrantIII (c)QuadrantII (d)QuadrantI (e) y-axis (f) x-axis
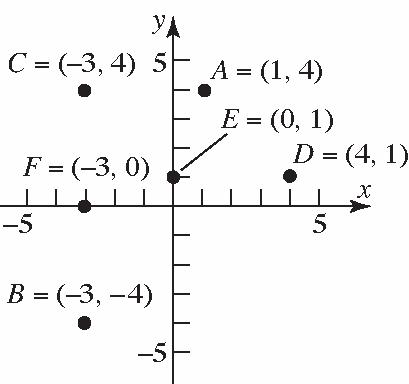
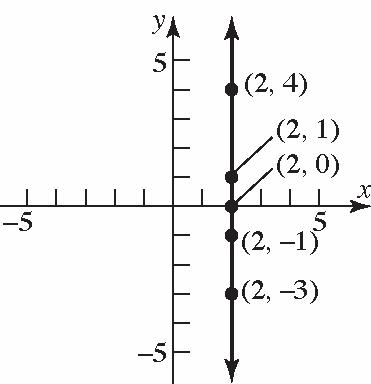
9. Thepointswillbeonaverticallinethatistwo unitstotherightofthey-axis.
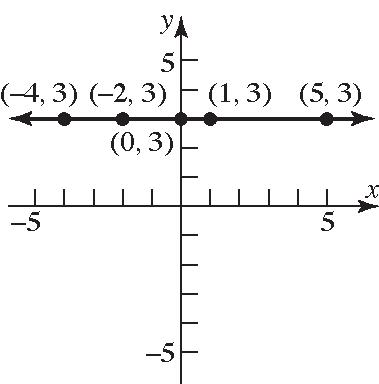
10. Thepointswillbeonahorizontallinethatis threeunitsabovethex-axis.
11. 1,4;QuadrantII
12. (3,4);QuadrantI
13. (3,1);QuadrantI
14. 6,4;QuadrantIII
15. min11 max5 scl1 min3 max6 scl1 X X X Y Y Y
16. min3 max7 scl1 min4 max9 scl1 X X X Y Y Y
17. min30 max50 scl10 min90 max50 scl10 X X X Y Y Y
18. min90 max30 scl10 min50 max70 scl10 X X X Y Y Y
19. min10 max110 scl10 min10 max160 scl10 X X X Y Y Y
20. min20 max110 scl10 min10 max60 scl10 X X X Y Y Y
21. min6 max6 scl2 min4 max4 scl2 X X X Y Y Y
22. min3 max3 scl1 min2 max2 scl1 X X X Y Y Y
23. min6 max6 scl2 min1 max3 scl1 X X X Y Y Y
24. min9 max9 scl3 min12 max4 scl4 X X X Y Y Y
25. min3 max9 scl1 min2 max10 scl2 X X X Y Y Y
26. min22 max10 scl2 min4 max8 scl1 X X X Y Y Y
Chapter 1: Graphs, Equations, and Inequalities
27. 4 y xx
(0,0)isonthegraphoftheequation.
28. 32 y
(0,0)and(1,–1)areonthegraphofthe equation.
29. 229yx 22 309
30. 31
(0,1)and(–1,0)areonthegraphofthe equation.
31. 224xy 22 024 44
(0,2)and2,2areonthegraphofthe equation.
32. 2244xy 22 0414 44 22 2404 44 22 1 2 244 54 (0,1)and(2,0)areonthegraphoftheequation.
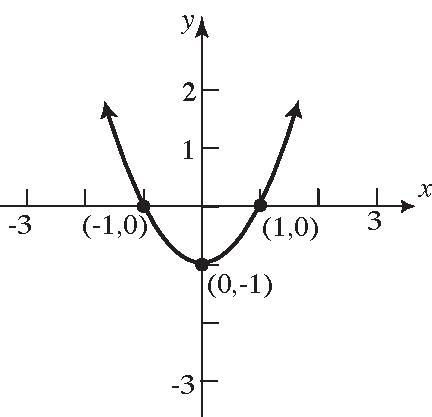
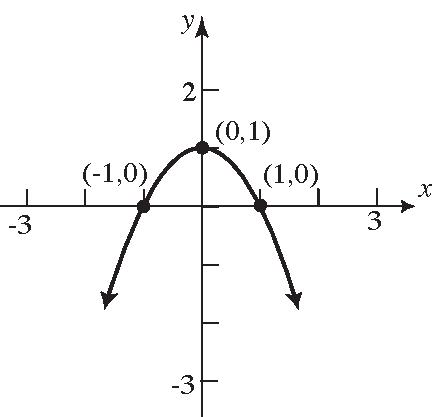
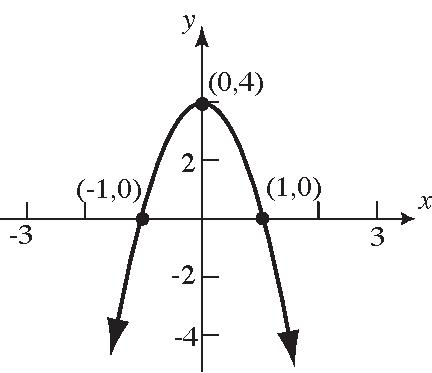
33. (–1,0),(1,0)
34. (0,1)
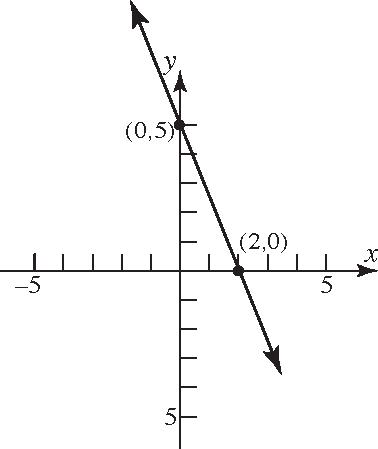
35. ,0,,0,(0,1)22
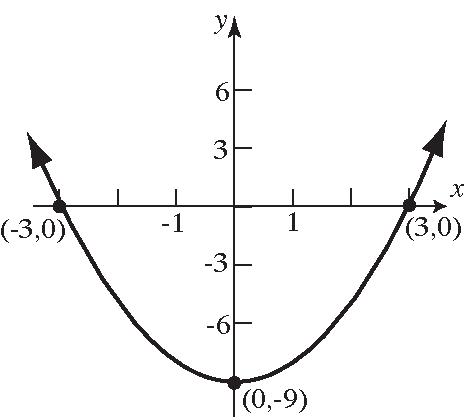
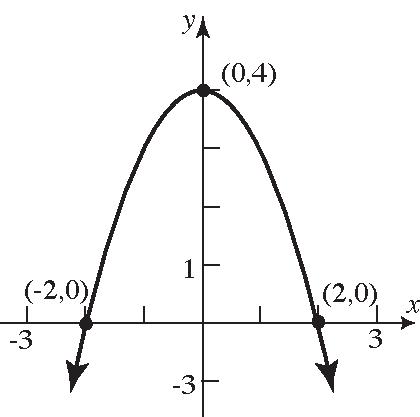
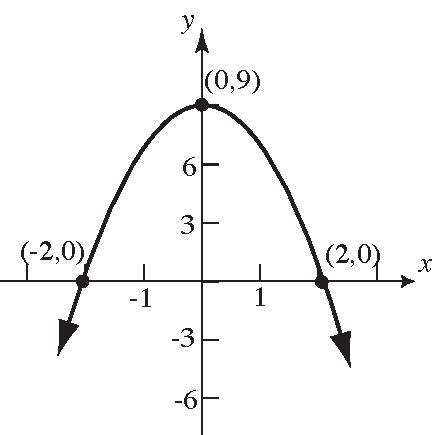
36. (–2,0),(2,0),(0,–3)
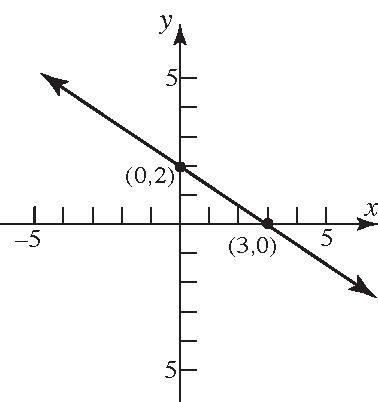
37. 1,0, 0,2, 0,2
38. (2,0),(0,2),(–2,0),(0,–2)
39. (–4,0),(–1,0),(4,0),(0,–3)
40. (–2,0),(2,0),(0,3)
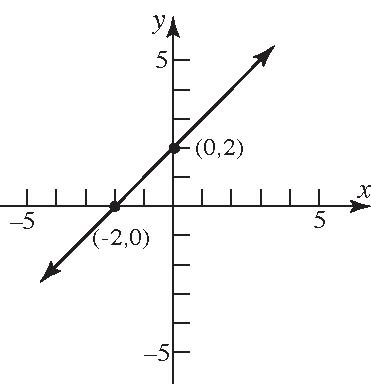
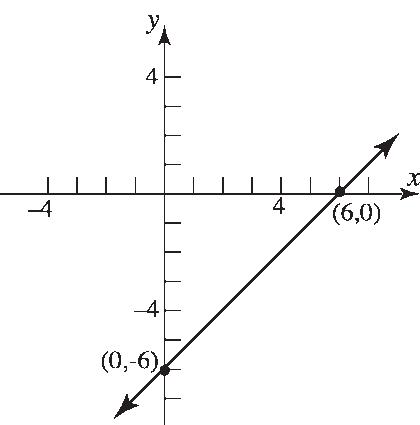
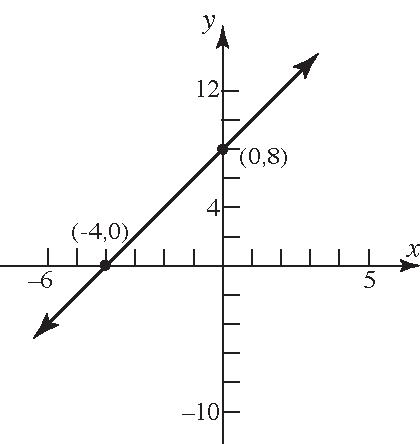
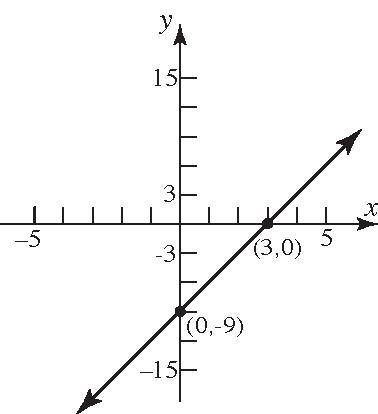
41. 2 yx 42. 6 yx
Chapter 1: Graphs, Equations, and Inequalities
2 9436 xy
2 44 xy
53. 213yx

Thex-interceptis6.5 x andthey-interceptis 13 y
54. 314yx
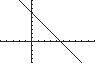
Thex-interceptis4.67 x andthey-interceptis 14 y .
55. 2 215yx
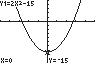
Thex-interceptsare2.74 x and2.74 x They-interceptis15 y
56. 2 319yx
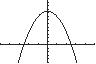
Section 1.1: Graphing Utilities; Introduction to Graphing Equations
59. 2 25375337or 3 x xyy
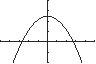
Thex-interceptsare2.52 x and2.52 x They-interceptis19 y .
57. 3243343 or 2 x xyy
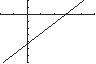
Thex-interceptis14.33 x andthey-intercept is21.5 y
58. 4582482 or 5 x xyy
Thex-interceptis20.5 x andthey-interceptis 16.4 y
Thex-interceptsare2.72 x and2.72 x They-interceptis12.33 y .
60. 2 22352335or 3 x xyy
Thex-interceptsare4.18 x and4.18 x They-interceptis11.67 y .
61. If 2,5isshifted3unitsrightthenthex coordinatewouldbe23 .Ifitisshifted2units downthenthey-coordinatewouldbe5(2)
Chapter 1: Graphs, Equations, and Inequalities
Thus the new point would be
( ) 23,5(2)(5,3) ++ - =
( ) 1,61(2)- +64 +
62. If is shifted 2 units left then the x coordinate would be . If it is shifted 4 units up then the y-coordinate would be . Thus the new point would be .
( ) 1(2),64(3,10)- + - += -
63. a. 25 feet
b. 23.2 ft; 34.1 ft
c. (0,6), The shot is released at a height of 6 feet; (48.7, 0), the shot hits the ground after traveling a horizontal distance of 48.7 feet.
64. a. 20 meters
b. 12 seconds; 36 meters
c. (0, 2), The discus is released at a height of 2 meters; (18, 0), the discus hits the ground after 18 seconds.
65. a. $19.95; $19.95
b. $182.45
c. (0, 19.95), The membership plan costs $19.95 per month
66. a. 1.5 miles
b. 1 mile
c. (0, 2), Caleb’s friend lives 2 miles from his house; (28, 0), it takes Caleb 28 minutes to ride home.
67.
68.
(1,0),(1,0),(0,1),(0,1) (2,0),(3,0),(0,2),(0,0),(0,2)
69. Answers will vary.
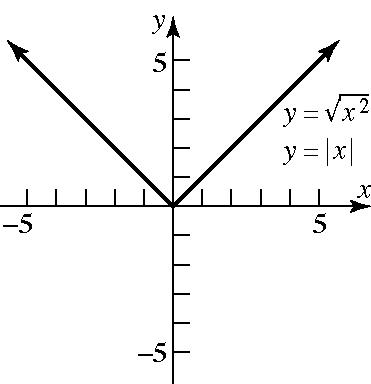
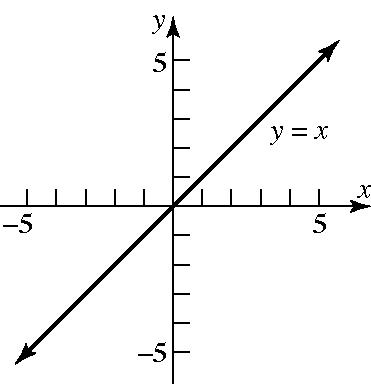
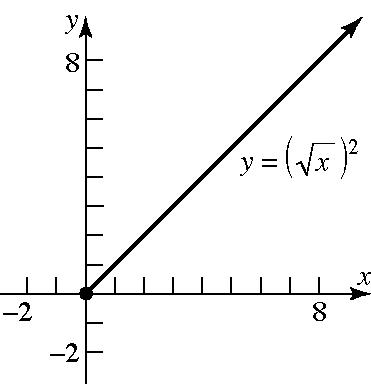
b. Since for all , the graphs of are the same.
c. For , the domain of the variable is ; for , the domain of the variable is all real numbers. Thus,
2 xx = x 2 and yxyx == ( ) 2 yx = x 0 x ³ yx = x ( ) 2 only for 0. xxx = ³
d. For , the range of the variable is ; for , the range of the variable is all real numbers. Also,
2 yx = y 0 y ³ yx = y 2 only if 0. xxx = ³
71. Answers will vary.
Section 1.2: Solving Equations Using a Graphing Utility; Linear and Rational Equations
72. Answerswillvary.Acompletegraphpresents enoughofthegraphtotheviewersotheycan “see”therestofthegraphasanobvious continuationofwhatisshown.
73. Answerswillvary.
Section 1.2
1. Usingthedistributiveproperty:
2. 23512(3)35[(3)1] 635(4)6320 31017 xx
3. No,4 x isnotinthedomainof3 4 x because itmakesthedenominatorequal0.
4. LCM= 2 1323 x xxx
5. b
6. identity
7. linear;first-degree
8. d
9. True;equationsthatarecontradictionshaveno solution.
10. False;whenusingagraphingutility,weoften obtaindecimalapproximationstosolutions.
11. Dividebothsidesby7.Thesolutionsetis 3
12. Dividebothsidesby6.Thesolutionsetis 4
13. Subtract35frombothsides,thendivideboth sidesby5.Thesolutionsetis 7
14. Subtract18frombothsides,thendivideboth sidesby6.Thesolutionsetis 3.
15. Add3tobothsides,thendividebothsidesby2. Thesolutionsetis 3 2
16. Subtract4frombothsides,thendivideboth sidesby3.Thesolutionsetis 4 3
17. Multiplybothsidesby4.Thesolutionsetis7 5
18. Multiplybothsidesby3 2 .Thesolutionsetis27 4
19. 3420xx ;UseZERO(orROOT)onthe graphof3142 yxx
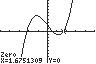
Thesolutionsetis 2.21,0.54,1.68
20. 3810xx ;UseZERO(orROOT)onthe graphof3181y xx .
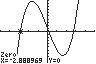
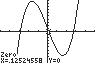
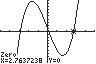
Thesolutionsetis 2.89,0.13,2.76
21. 4 2532 xx ;UseINTERSECTonthe graphsof4125yx and232 yx .
.
Chapter 1: Graphs, Equations, and Inequalities
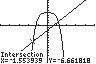
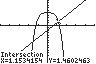
Thesolutionsetis 1.55,1.15
22. 42123xx ;UseINTERSECTonthe graphsof411yx and2223yx
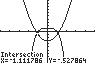
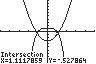
Thesolutionsetis 1.11,1.11.
23. 43 25840 xxx ;UseZERO(orROOT) onthegraphof4312584 yxxx
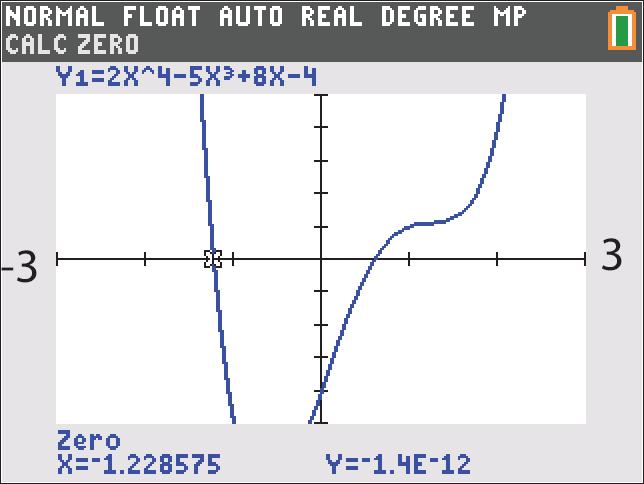
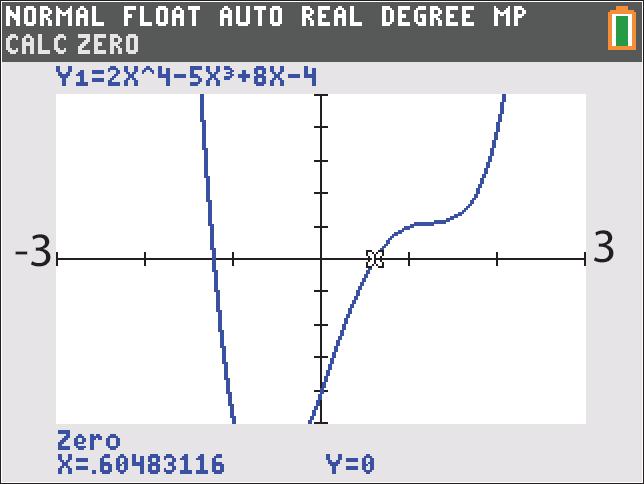
Thesolutionsetis 1.23,0.60.
24. 432 3450 xxx ;UseZERO(orROOT) onthegraphof4321345 yxxx
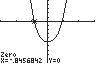
Thesolutionsetis 0.85,0.94.
25. 325720 32 xxx ; UseZERO(orROOT)onthegraphof 32 15/37/22 yxxx
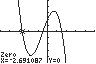
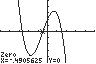
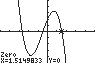
Thesolutionsetis 2.69,0.49,1.51
26. 432715 320 32 xxxx ;UseZERO(or ROOT)onthegraphof
432 137/315/22 yxxxx
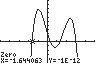
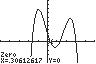
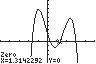
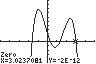
Thesolutionsetis 1.64,0.31,1.31,3.02
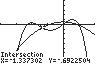
27. 432 2521 2 3232 xxxx
UseINTERSECTonthegraphsof 43 12/325/2 yxxx and 2 2(2/3)1/2 yx
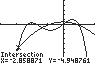
Section 1.2: Solving Equations Using a Graphing Utility; Linear and Rational Equations
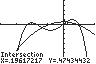
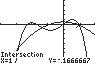
Thesolutionsetis 2.86,1.34,0.20,1.00
28. 321154 45 xxx
UseINTERSECTonthegraphsof 3 1/45y xx and22/54yx anda standardviewingwindow(10to10forboth x and y).
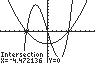
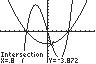
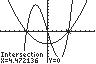
Thesolutionsetis 4.47,0.80,4.47
29. 4252110xxx
UseZERO(orROOT)onthegraphof 42 15211 yxxx
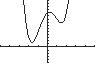
Therearenorealsolutions.
30. 42 38290 xxx UseZERO(orROOT)onthegraphof 42 13829 yxxx
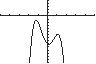
Therearenorealsolutions.
31. 34 3444 34 34 24 24 22 2 xx xx xx x xxx x x x
Thesolutionsetis 2
32. 295 29959 259 25595 39 39 33 3 xx xx xx x xxx x x x
Thesolutionsetis 3
33. 263tt 26636 29 29 39 39 33 3 tt tt tttt t t t
Thesolutionsetis 3
34. 5618 y y 566186 524 524 624 624 66 4 yy yy yyyy y y y
Thesolutionsetis 4.
Chapter 1: Graphs, Equations, and Inequalities
35. 629 66296 23 2232 33 33 33 1 xx xx xx x xxx x x x
Thesolutionsetis 1
36.
322 32323 21 21 1 111 1 xx xx xx x xxx x x x
Thesolutionsetis 1.
37. 3(53)8(1) xx 15988 159158815 9823 988238 23
xx xx xx x xxx x
Thesolutionsetis 23.
38. 3(2)21 x x 6321 636216 327 32272 57 57 55 7 5 xx xx xx x xxx x x x
Thesolutionsetis 7 5
39. 832310 832310 52310 5223102 538 53383 28 xxx xxx xx xx xx x xxx x
28 22 4 x x
Thesolutionsetis 4.
40. 72110 72110 2810 288108 22 22 22 1 x x x x x x x
Thesolutionsetis 1
41. 2356334556 610618121556 12282018 82818 810 5 4 xxxx xxxx xx x x x
Thesolutionsetis5 4
.
42. 52231412 5106248 1247 6124 616 8 3 x xxx x xxx xx x x x
Thesolutionsetis8 3
43.
45. 211 323 pp
Thesolutionsetis 2.
46. 114 233 p 11466 233 328 32383 25 25 22 5 2 p p p p p p
Thesolutionsetis 5 2
47. 0.20.90.5 mm 0.20.50.90.50.5 0.30.9 0.30.9 0.30.3 3
mmmm m m m
Thesolutionsetis 3
48. 0.91tt 0.91 0.11 0.11 0.10.1 10 tttt t t t
Thesolutionsetis 10
49. 122 37 12 2121212 37 773642 xx xx xx
101342 1013134213 1029 1029 1010 29 10 x x x x x
Thesolutionsetis29 10
Chapter 1: Graphs, Equations, and Inequalities
53. 123 24 12344 24 283 28232 8or8 x xx x xx xxxx xx
Thesolutionsetis 8. 54. 311 36 31166 36 182 18222 183 183 33 6or6 x xx x xx xxxx x x xx
Thesolutionsetis 6
55. 7(1)(1)2xxx 22 22 2222 7721 6721 6721 6721 672212 471 47717 48 482 44 xxxxx xxxx x xxxxx xx xxxx x x x x x
Thesolutionsetis 2
Thesolutionsetis
56.
Section 1.2: Solving Equations Using a Graphing Utility; Linear and Rational Equations
59. 23 33 3333 312 312 312 312 312 33 4
ppp ppp ppppp p p p
Thesolutionsetis 4
60. 23 33 48 48 48 2 www www w w
Thesolutionsetis
57. (23)(21)(4) xxxx 22 2222 23274 2322742 374 37747 44 441 44 xxxx x xxxxx xx xxxx x x x
Thesolutionsetis 1.
58. (12)(21)(2) xxxx 22 2222 2252 222522 52 5525 62 621 663 xxxx x xxxxx xx xxxx x x x
Thesolutionsetis 1 3 .
61.
Thesolutionsetis 2.
32 22 2322 22 322 362 462 48 2 x xx x xx xx xx xx x x x
Thissolutionisnotinthedomainofthevariable soitmustbediscarded.Theequationhasno solution.Thesolutionsetis or .
62.
262 33 26 332 33 2623 2626 2212 412 3 x xx x xx xx xx xx xx x x
Thissolutionisnotinthedomainofthevariable soitmustbediscarded.Theequationhasno solution.Thesolutionsetis or .
Chapter 1: Graphs, Equations, and Inequalities
63.
22 22 22 243 442 24344 442 2432 2436 2103 510 2 x x xx x xx x xx xx xx xx x x
Thissolutionisnotinthedomainofthevariable soitmustbediscarded.Theequationhasno solution.Thesolutionsetis or .
64.
Thissolutionisnotinthedomainofthevariable soitmustbediscarded.Theequationhasno solution.Thesolutionsetis or
65. 3 22 232 236 6 6 x x xx xx x x
Thesolutionsetis 6
66. 32 1 321 322 2 x x xx xx x
Thesolutionsetis 2
67.
72 3103 732310 721620 7641 41
xx xx xx xx x Thesolutionsetis 41.
68. 43 46 4634 424312 4312 12 12 xx xx xx xx x x
Thesolutionsetis 12
69. 6738 4124 67243841 tt tt tttt 22 22 12142428123238 12102812298 1028298 102920 3920 20 39 20 39 tttttt tttt tt tt t t t
Thesolutionsetis 20 39 .
70.
22 22 8543 10757 855743107 4025563540302821 408135405821 ww ww wwww wwwwww wwww
81355821 815814 13914 14 139 ww ww w w
Thesolutionsetis 14 139
Section 1.2: Solving Equations Using a Graphing Utility; Linear and Rational Equations
411 231231 xx
Chapter 1: Graphs, Equations, and Inequalities
2 22 22 43103 7121030 7121030
Thesolutionsetis 14 76. 222 143 232 xx xxxxxx
Thesolutionsetis
77. 54 254 25 2 5 yx a a a
78. 2 2 3 23(2)4610 yxx b
79. 236 xy 236 326 22 3 ab ba ba
80. 0(2) 5(0)5 ymxb mb mbb Therefore, 025 25 5 2 m m m
81. ,0axbca axbbcb axcb axcb aa bc x a
82. 1,0 axba 111 1 1 11 axb axb ax b aa bb x aa
Section 1.2: Solving Equations Using a Graphing Utility; Linear and Rational Equations
83. ,0,0, xx cabab ab () () xx ababc ab bxaxabc x ababc xab abc abab abc x ab
84. ,0 ab cc xx ab x xc xx abcx abcx cc ab x c
suchthat ab
85. 112 1 x axax MultiplybothsidesbytheLCD, 1 xaxax ,toget:
bxcxabacbxcxabac bxcxabacbxbxcxabacbx
2 2 22 22 22 cxabaccxabac cxabaccxcxabaccx cxabacabac cxabacabacabacabac cxab cxab cc ab x c
where0,0 ac ,and bc
87. 2166 x aaxa when4 x : 421646 421646 42162 412 3 aaa aaa aa a a
88. 242 x bxbx when2 x :
222422 22244 2224 42 42 2 bb bb bb b bb
89. SolvingforR: 12 1212 12 1221 1221 1221 2121 12 12 111 111 () () RRR RRRRRR RRR RRRRRR RRRRR RRRRR RRRR RR R RR
Chapter 1: Graphs, Equations, and Inequalities
90. Solvingfor r : (1) A Prt A PPrt APPrt Prt
91. SolvingforR: 2
92. SolvingforT:
93. Solvingfor r:
94. Solvingfor t: 0 000 0 0 00 or vgtv vvgtvv vvgt vv gt gg vvvv tt g g
95. Let x =amountinvestedinbonds. InvestedinCDs:3000 x 3,00020,000 23,00020,000 223,000 11,500 xx x x x
$11,500willbeinvestedinbondsand$8,500 willbeinvestedinCD's.
96. Let x =amountthatSeanreceives. AmountforGeorge:3000 x 3,00010,000 23,00010,000 213,000 6,500 xx x x x
Seanwillreceive$6,500andGeorgewillreceive $3,500.
97. Let x Sandra’sregularhourlywage. 401.58910 4012910 52910 91017.50 52 xx xx x x Sandra’sregularhourlywageis$17.50.
98. Let x =Leigh’sregularhourlywage. 4061.5421083 40981083 571083 108319 57
xxx xxx x x Leigh’sregularhourlywageis$19.00.
99. Letx=finalexamscore. Computethefinalaverageandsetequalto80. 1808371619580 7 xx
Nowsolvefor x:
Brookeneedstoscorean85onthefinalexamto getanaverageof80inthecourse.
100. Let x =finalexamscore.
Mikemustscore78onthefinaltoearnaB. Followingthesameapproachasabove,weget
34081290 34081080 8740
Mikemustscore93onthefinaltoearnanA.
101. Let x representtheoriginalpriceofthephone. Then0.15 x representsthereductionintheprice ofthephone. originalprice–reduction=newprice 0.15799 0.85799 940
xx x x Theoriginalpriceofthephonewas$940. Theamountofthesavingsis 0.15($940)=$141.
102. Let x representtheoriginalpriceofthecar. Then0.12 x representsthereductionintheprice ofthecar. originalprice–reduction=newprice 0.1228,160 0.8828,160 32,000 xx x x Theoriginalpriceofthecarwas$32,000.
Theamountofthesavingsis $32,000–$28,160=$3,840.
103. Let x representthepricethetheaterpaysforthe candy. Then2.75 x representsthemarkuponthecandy. Thesellingpriceofthecandyis$3.00. suppierpricemarkupsellingprice 2.754.50 3.754.50
Thetheaterpaid$1.20forthecandy.
104. Let x representthedealer'scostofthenewcar. 0.85($34,000)$28,900 x Ifthedealeraccepts$100overcost,thenyou willpay $28,900+$100=$29,000.
105. Let a =numberofadultpatrons. Childpatrons:5200 a 8.506.00520032,200 8.5031,2006.0032,200 2.5031,20032,200 2.501,000 2.501,000 2.502.50 400 aa aa a a a a
Thetheaterhad400adultpatrons.
106. Let x =originalpriceoftheboots. Discount:0.3 x originalpricediscountsaleprice 0.3399 0.7399 0.7399 0.70.7 570 xx x x x
Theoriginalpriceofthebootswas$570.
107. Let w =width. Length:8 lw Perimeter:22Plw 2260 2(8)260 216260 41660 444 11 lw ww ww w w w
Chapter 1: Graphs, Equations, and Inequalities
Therectanglehasawidthof11feetandalength of19feet. 108.Let w =width.
Length:2lw
Perimeter:22Plw
Therectanglehasawidthof7metersanda lengthof14meters.
109. Let x =thetotalnumberofpeoplewhoowneda smartphonein2019.Then0.534 x represents thenumberofpeoplewhoownedasmartphone thatrantheGoogleAndroidOS. 0.534124.4 124.4 233 0.534
x x
Therewereabout233millionpeoplewhoowned asmartphonein2019.
110. LetTbethepercentagethatusedTwitter.Then: 6729
Therefore,38%ofU.S.adultsaged18-29used Twitter.
111. Let x =amountthatScottgets.
AmountforAlice:3 4 x
AmountforTricia:1 2 x
Scottreceives$400,000;Alicereceives $300,000;Triciareceives$200,000.
112. Let x =amountthatJudypays. AmountTompays:2 3 x
Judypays$10.80andTompays$7.20.
113. Anisoscelestrianglehasthreeequalsides. Therefore:410240318 xxx .Solve eachsetseparately: 410240 230 15 410318 8 240318 22 22
x x xx x xx x x Since22isthelargestofthenumbersthenthe largestperimeteris: 422102224032218266
114. 311114 316 4524205 313134 1 41058025
xxx xxx MultiplybothsidesbytheLCD80toclear fractions. 608488012064 1087258 10716 16 107
115. Ifahexagonisinscribedinacirclethenthesides ofthehexagonareequaltotheradiusofthe circle.LettheP=6rbetheperimeterofthe hexagon.Letrbetheradiusofthecircle. 610 510 2
Thusr=2inchesistheradiusofthecirclewhere theperimeterofthehexagonis10inchesmore thantheradius.
116. Inordertosolve58 3 33 x xx ,wemultiply eachtermbytheexpression“3 x ”toget
58 333 33 x xx xx
Now,provided3 x ,wecancancelthe denominatorstoget
5338 5398263 xx xxxx
However,wealreadystatedthat3 x .Sowe haveacontradiction.
117. Answerswillvary.Oneexampleis 3136 xx
118. Answerswillvary.Ingeneral,‘solve’meansto findvaluesforavariablethatmaketheequation true,‘evaluate’meanstopluginaspecificvalue foravariableinanexpressionandsimplify,and ‘simplify’meanstocollectliketermsandwrite anexpressioninasimplerform.
Ex:Solve 328 xx .
Ex:Evaluate 32
119. Inobtainingstep(7)wedividedbyx–2.Since x=2fromstep(1),weactuallydividedby0.
Section 1.3: Quadratic Equations
Section 1.3
1. 25661 xxxx
2. 2 23231 xxxx
3. 5,3 3
4. True
5. 2 2 2 2 1552525 5;;5 22244 255 5 42 xx xxx
6. discriminant;negative
7. False;aquadraticequationmayhavenoreal solutions.
8. False;If2 x p then x couldalsobenegative.
9. b 10. d
11. 290 90 xx xx 0or90 0or9 xx xx Thesolutionsetis{0,9}.
12. 240 (4)0 xx xx 0or40 0or4 xx xx Thesolutionsetis{–4,0}.
13. 2250 (5)(5)0 x xx 50or50 5or5 xx xx Thesolutionsetis{–5,5}.
Chapter 1: Graphs, Equations, and Inequalities
14. 290 (3)(3)0 x xx 30or30 3or3 xx xx
Thesolutionsetis{–3,3}.
15. 260 (3)(2)0 zz zz
30or20 3or2 zz zz
Thesolutionsetis{–3,2}.
16. 2760 (6)(1)0 vv vv 60or10 6or1 vv vv
Thesolutionsetis{–6,–1}
17. 2 2530 (21)(3)0 xx xx
210or30 1or3 2 xx xx
Thesolutionsetis 1,3 2
18. 2 3520 (32)(1)0 xx xx 320or10 2 or1 3 xx xx
Thesolutionsetis 1,2 3
19. 2 2 51800 5(36)0 5(6)(6)0
w w ww 60or60 6or6 ww ww
Thesolutionsetis{–6,6}.
20. 2 2 2500 2(25)0 2(5)(5)0 y y yy 50or50 5or5 yy yy
Thesolutionsetis{–5,5}.
21. 2 3100 3100 (2)50
xx xx xx 20or50 2or5 xx xx
Thesolutionsetis 5,2.
22. 2 (4)12 4120 (6)(2)0 xx xx xx 60or20 6or2 xx xx
Thesolutionsetis 6,2.
23. 2 2 2 4912 41290 (23)0 230 3 2 x x xx x x x
Thesolutionsetis 3 2
24. 2 2 2 251640 2540160 (54)0 540 4 5 x x xx x x x
Thesolutionsetis 4 5 .
25. 2 2 2 6(1)5 665 6560 (32)(23)0 pp pp pp pp
320or230 23 or 32 p p p p
Thesolutionsetis23 , 32
26. 2 2 2(24)30 4830 (21)(23)0 uu uu uu
210or230 13 or 22 uu uu
Thesolutionsetis13 , 22
27.
2 2 6 65 6 65 656 6560 (32)(23)0 x x x xx x xx xx xx
320or230 23 or 32 x x x x
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis23 , 32
28. 2 2 12 7 12 7 127 7120 (3)(4)0 x x x xx x x x xx xx
29.
Section 1.3: Quadratic Equations
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis{3,4}.
4233 33 423333 33 x xx xx x xxxx xx xx
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis
Chapter 1: Graphs, Equations, and Inequalities
32. 236 36 6 x x x
Thesolutionsetis 6,6
33. 2 14 14 12 12or12 3or1 x x x xx xx
Thesolutionsetis 1,3
34. 2 21 21 21 21or21 1or3 x x x xx xx
Thesolutionsetis 3,1
35. 12416 3 1416 3 144 3 1144or44 33 110or8 33 0or24
h h h hh hh hh
Thesolutionsetis 24,0 36. 2 324 324 322 322or322 34or30 4or0 3
Thesolutionsetis 0,4 3
37. 2 2 2 421 44214 225 225 25 25 3or7 xx xx x x x x xx
Thesolutionsetis7,3.
38. 2 2 2 613 69139 322 322 322 xx xx x x x
Thesolutionsetis322,322.
39. 2 2 2 2 130 216 13 216 1131 2161616 11 44 xx xx xx x
111 442 11 42 31 or 44 x x xx The13 solutionsetis,. 44
40. 2210 33 xx
Section 1.3: Quadratic Equations
The317317 solutionsetis,. 44
43. 2420xx 2 1,2,13 (2)(2)4(1)(13)2452 2(1)2 2562214114 22
Thesolutionsetis114,114.
44. 2420xx 2 1,4,2 444(1)(2)4168 2(1)2 48422 22 22 abc x
Thesolutionsetis22,22.
45. 2410xx 2 1,4,1 (4)(4)4(1)(1)4164 2(1)2
42042525 22 abc x
Thesolutionsetis25,25.
Chapter 1: Graphs, Equations, and Inequalities
46. 2610xx 2 1,6,1 664(1)(1)6364 2(1)2 632642 322 22
abc x
Thesolutionsetis322,322.
47. 2 2530 xx 2 2,5,3 (5)(5)4(2)(3) 2(2) 525245151 444 5151 or 44 64 or 44 3or1 2 abc x xx xx xx
The3 solutionsetis1,. 2
48. 2 2530 xx 2 2,5,3 554(2)(3) 2(2) 525245151 444 5151 or 44 46 or 44 13 or 2 abc x xx xx xx
The3solutionsetis,1. 2
49. 2 420 yy 2 4,1,2 (1)(1)4(4)(2) 2(4) 1132131 88 abc y
Norealsolution.
50. 2 410 tt 2 4,1,1 114(4)(1) 2(4) 1116115 88 abc t
Norealsolution.
51. 2 2 985 9850 xx xx 2 9,8,5 884(9)(5) 2(9) 8641808244 1818 8261461 189
abc x
Thesolutionsetis461461,.99
52. 2 2 212 2210 x x xx
abc x
2 2,2,1 224(2)(1)248 2(2)4 21222313 442
Thesolutionsetis1313,.22
53. 2 2 49 490 (49)0 x x xx xx
0or490 09 or 4 xx xx
Thesolutionsetis 9 0,. 4
54. 2 2 54 045 0(45) xx x x xx
0or450 05 or 4 xx xx
Thesolutionsetis 5 0,. 4
55. 2 9610 tt 2 9,6,1 (6)(6)4(9)(1) 2(9) 63636601 18183 abc
Thesolutionsetis 1 . 3
56. 2 4690 uu 2 4,6,9 (6)(6)4(4)(9) 2(4) 6361446108 88 abc u
Norealsolution.
57.
2 2 2 3110 442 311 440 442 320 xx xx xx
3,1,2abc
Section 1.3: Quadratic Equations
2 11432 23 112412515 666 1515 or 66 64 or 66 12 or 3 x xx xx xx
The2solutionsetis,1. 3 58. 2230 3 xx
2 33429 22 397238139 444 3939 or 44 126 or 44 33 or 2 x xx xx xx
The3solutionsetis,3. 2
Chapter 1: Graphs, Equations, and Inequalities
59. 2 2 2 2 51 33 5133 33 531 5310 xx xx xx xx
Thesolutionsetis329329 , 1010
2 3,5,1 55431 23 52512537 66 abc x
Thesolutionsetis537537 , 66
61. 2 2(2)3 2430 xx xx
2 2,4,3 444(2)(3)41624 2(2)4 4404210210 442 abc x
Thesolutionsetis210210,.22
62. 2 3(2)1 3610 xx xx 2 3,6,1 664(3)(1)63612 2(3)6 648643323 663 abc x
Thesolutionsetis323323,.33
63. 2 22 2 2 11 40 11 40 410 x x xx x x x x
4,1,1abc
2 11441 24 1116117 88 x
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis 117117 , 88
64. 2 83 20
x x
xx x x xx abc x
22 2 2 2 83 20 2830 2,8,3 88423 22 86424840 44 8210410 42
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis 410410 , 44
65. 2 22 2 314 2 31(2)4(2) 2 3()(2)48 3248 092 x xx x xxxx xx x xxxx x xxx xx
1,9,2abc 2 (9)(9)4(1)(2) 2(1) 9818973 22 x
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis 973973 , 22
66. 2 22 2 214 3 21(3)4(3) 3 2()(3)412 23412 02133 x xx x xxxx xx x xxxx x xxx
(13)(13)4(2)(3) 2(2) 131692413145 44 x
Neitherofthesevaluescausesadenominatorto equalzero,sothesolutionsetis 1314513145 , 44
67. 24.12.20xx
Thesolutionsetis 0.63,3.47
Section 1.3: Quadratic Equations
68. 23.91.80xx
2 1,3.9,1.8 3.93.9411.8 21 3.915.217.23.98.01 22 0.53or3.37 abc x x x
Thesolutionsetis 3.37,0.53.
69. 2330xx
2 1,3,3 33413 21 3312315 22 1.07or2.80 abc x xx
Thesolutionsetis 2.80,1.07
70. 2220xx
2 1,2,2 22412 21 228210 22 0.87or2.29 abc x xx
Thesolutionsetis 2.29,0.87.
71. 20xx 2 2 ,1, 114 2 114 2 1.17or0.85 abc x x x
Thesolutionsetis 0.85,1.17.
Chapter 1: Graphs, Equations, and Inequalities
72. 220xx
2 2 ,,2 42 2 8 2 0.44or1.44 abc x x x
Thesolutionsetis 1.44,0.44
73. 2 2670 xx
22 2,6,7 4(6)4(2)7365620 abc bac
Sincethe240, bac theequationhasnoreal solution.
74. 2470xx
22 1,4,7 4(4)4(1)7162812 abc bac
Sincethe240, bac theequationhasnoreal solution.
75. 2 930250 xx
22 9,30,25 4(30)4(9)259009000 abc bac
Since240, bac theequationhasone repeatedrealsolution.
76. 2 252040 xx 22 25,20,4 4(20)4(25)44004000 abc bac
Since240, bac theequationhasone repeatedrealsolution.
77. 2 3580 xx
22 3,5,8 4(5)4(3)82596121 abc bac
Since240, bac theequationhastwo unequalrealsolutions.
78. 2 2370 xx 22 2,3,7 4(3)4(2)795665 abc bac
Since240, bac theequationhastwo unequalrealsolutions.
79. 2 2 50 5 5 x x x Thesolutionsetis5,5.
80. 2 2 60 6 6 x x x Thesolutionsetis6,6.
81.
2 16810 41410 410 1 4 xx xx x x
Thesolutionsetis 1 . 4
82.
2 91240 32320 320 2 3 xx xx x x
Thesolutionsetis 2 . 3
83.
2 1019150 53250 xx xx 530or250 35 or 52 xx xx
Thesolutionsetis 35 ,.52
84.
2 67200 34250 xx xx 340or250 45 or 32 xx xx
Thesolutionsetis 54 ,.23
85.
86.
87.
2 (22)(22)4(2)1 2(2) 22882216 44 22422 42 x
2 2 2 2 121 2 1210 2 1 22120 2 2220 x x xx xx xx
Section 1.3: Quadratic Equations
Thesolutionsetis22,22.
89. 2 2 4 40 xx xx
2 (1)(1)414 2(1) 1116117 22
The117117 solutionsetis,. 22
90. 2 2 1 10 xx xx 1,1,1abc
2 (1)(1)411 2(1) 11415 22 x
The1515 solutionsetis,. 22
Chapter 1: Graphs, Equations, and Inequalities
(2)(1)(2)(1)21(2)(1) (1)2(2)71 2471 3471 450 (1)(5)0
Thevalue1 x causesadenominatortoequalzero,sowedisregardit.Thus,thesolutionsetis{5}. 92. 2 3147 212 x x
310or20 1or2 3 xx xx
Thevalue2 x causesadenominatortoequalzero,sowedisregardit.Thus,thesolutionsetis 1 . 3
93. Sincethisisarighttrianglethenwecanusethe PythagoreanTheorem.So 222 222 2 2 (23)(25)(7) 4129420251449 129674 01865 0(5)(13) xxx xxxxxx xxx xx xx
50or130 5or13 xx xx
Thismeansthereare2possiblethatmeetthese requirements.Substituting x intothegivensides gives: When x =5:5m,12m,13m When x =13:20m,21m,29m Thusthereare2solutions.
94. Sincethisisarighttrianglethenwecanusethe PythagoreanTheorem.So 222 222 2 2 (45)(313) 164025978169 6381440 2(31972)0 2(38)(9)0
Thismeansthereare2possiblesolutionsthat meettheserequirements.Substituting x intothe givensidesgives: When x =9:41m,40m,9m When x = 8 3atleastonesideofthetriangle hasanegativemeasurementwhichisimpossible. Thusthereisonly1trianglepossible
95. Let w representthewidthofwindow. Then2 lw representsthelengthofthe window.
Sincetheareais143squarefeet,wehave:
2 (2)143 21430 (13)(11)0 ww ww ww
13 w or11 w
Discardthenegativesolutionsincewidthcannot benegative.Thewidthoftherectangular windowis11feetandthelengthis13feet.
96. Let w representthewidthofwindow. Then1 lw representsthelengthofthe window.
Sincetheareais306squarecentimeters,we have:(1)306 ww 23060 (18)(17)0 ww ww
18 w or17 w
Discardthenegativesolutionsincewidthcannot benegative.Thewidthoftherectangular windowis17centimetersandthelengthis18 centimeters.
97. Let l representthelengthoftherectangle. Let w representthewidthoftherectangle. Theperimeteris26metersandtheareais40
squaremeters. 2226 13so13 lw lwwl
2 2 40 (13)40 1340 13400 (8)(5)0 lw ll ll ll ll
8or5 58 ll ww
Thedimensionsare5metersby8meters.
98. Let r representtheradiusofthecircle. Sincethefieldisasquarewitharea1250square feet,thelengthofasideofthesquareis 1250252 feet.Thelengthofthediagonal is2r . UsethePythagoreanTheoremtosolvefor r :
222 2 2 2 (2)252252 412501250 42500 625 25 r r r r r
Theshortestradiussettingforthesprinkleris25 feet.
99. Let x =lengthofsideoforiginalsheetinfeet. Lengthofbox:2 x feet Widthofbox:2 x feet Heightofbox:1foot
0or4xx Discard0 x sincethatisnotafeasiblelength fortheoriginalsheet.Therefore,theoriginal sheetshouldmeasure4feetoneachside.
Chapter 1: Graphs, Equations, and Inequalities
100. Let x =widthoforiginalsheetinfeet.
Lengthofsheet:2 x
Lengthofbox:22 x feet
Widthofbox:2 x feet
Heightofbox:1foot
Discard0 x sincethatisnotafeasiblelength fortheoriginalsheet.Therefore,theoriginal sheetis3feetwideand6feetlong.
101. a. Whentheballstrikestheground,the distancefromthegroundwillbe0. Therefore,wesolve
2 2 2 9680160 1680960 560 610 tt tt tt
Discardthenegativesolutionsincethetime offlightmustbepositive.Theballwill strikethegroundafter6seconds.
b. Whentheballpassesthetopofthebuilding, itwillbe96feetfromtheground.Therefore, wesolve
2 2 2 96801696 16800 50 50 tt tt tt tt
Theballisatthetopofthebuildingattime 0
whenitisthrown.Itwillpassthetop ofthebuildingonthewaydownafter5 seconds.
102. a. Tofindwhentheobjectwillbe15meters abovetheground,wesolve 2 2 4.92015 4.920150 tt tt 4.9,20,15abc
0.99or3.09tt Theobjectwillbe15metersabovethe groundafterabout0.99seconds(ontheway up)andabout3.09seconds(ontheway down).
b. Theobjectwillstrikethegroundwhenthe distancefromthegroundis0.Therefore,we solve 2 4.9200 4.9200 tt tt 0 t or4.9200 4.920 4.08 t t t
Theobjectwillstrikethegroundafterabout 4.08seconds.
c. 2 2 4.920100 4.9201000 tt tt 4.9,20,100abc
2 202044.9100 24.9 201560 9.8 t
Thereisnorealsolution.Theobjectnever reachesaheightof100meters.
103. Let x representthenumberofcentimetersthe lengthandwidthshouldbereduced. 12 x =thenewlength,7 x =thenewwidth. Thenewvolumeis90%oftheoldvolume.
2 2 2 (12)(7)(3)0.9(12)(7)(3) 357252226.8 35725.20 198.40 xx xx xx xx
2 (19)(19)4(1)(8.4)19327.4 2(1)2
0.45or18.55 x xx
Since18.55exceedsthedimensions,itis discarded.Thedimensionsofthenewchocolate barare:11.55cmby6.55cmby3cm.
104. Let x representthenumberofcentimetersthe lengthandwidthshouldbereduced. 12 x =thenewlength,7 x =thenewwidth. Thenewvolumeis80%oftheoldvolume. 2 2 2 (12)(7)(3)0.8(12)(7)(3) 357252201.6 35750.40 1916.80 xx xx
2 (19)(19)4(1)(16.8)19293.8 2(1)2 0.93or18.07 x xx
Since18.07exceedsthedimensions,itis discarded.Thedimensionsofthenewchocolate barare:11.07cmby6.07cmby3cm.
105. Let x representthewidthoftheborder measuredinfeet.Theradiusofthepoolis5 feet.Then5 x representstheradiusofthe circle,includingboththepoolandtheborder. Thetotalareaofthepoolandborderis (5)2 T Ax
Theareaofthepoolis2(5)25 AP
Section 1.3: Quadratic Equations
106. Let x representthewidthoftheborder measuredinfeet.Theradiusofthepoolis5 feet.Then5 x representstheradiusofthe circle,includingboththepoolandtheborder. Thetotalareaofthepoolandborderis (5)2 T Ax Theareaofthepoolis2(5)25 AP . Theareaoftheborderis 2 (5)25
BTP AAAx . Sincetheconcreteis4inches=13footthick,the volumeoftheconcreteintheborderis 112 33(5)25 B Ax
Solvingthevolumeequation:
2 2 2 1(5)2527 3 10252581 10810 x xx xx
2 2 10(10)4()(81) 2()
2.13or12.13 x xx
31.42100324
6.28
Discardthenegativesolution.Thewidthofthe borderisapproximately2.13feet.
107. Let x representthewidthoftheborder measuredinfeet.
Thetotalareais(62)(102) AT xx
BTP AAAx
Theareaoftheborderis 2 (5)25
Sincetheconcreteis3inchesor0.25feetthick, thevolumeoftheconcreteintheborderis
2 0.250.25(5)25 B Ax
Solvingthevolumeequation:
2 2 10(10)4()(108) 2() 31.42100432 6.28 2.71or12.71 x xx
Discardthenegativesolution.Thewidthofthe borderisroughly2.71feet.
Theareaofthegardenis61060 AG . Theareaoftheborderis (62)(102)60
BTG AAAxx Sincetheconcreteis3inchesor0.25feetthick, thevolumeoftheconcreteintheborderis
0.250.25(62)(102)60 B Axx Solvingthevolumeequation: 2 2 2 0.25(62)(102)6027 6032460108 4321080 8270 xx xx xx xx
2.56or10.56 x xx
2 884(1)(27)8172 2(1)2
Discardthenegativesolution.Thewidthofthe borderisapproximately2.56feet.
Chapter 1: Graphs, Equations, and Inequalities
108. Let x =thewidthand2x =thelengthofthe patio.Theheightis13footandtheconcrete availableis 827216 cubicfeet.. 2 2 1 (2)216 3 2216 3
Vlwhxx x xx Thedimensionsofthepatioare18feetby36 feet.
109. Let x =thelengthofa12.9-inchiPadProina 16:94:3format.
Then 9 16 x =thewidthoftheiPad.Thediagonal ofthe12.9-inchiPadis9.7inches,sobythe Pythagoreantheoremwehave:
Sincethelengthcannotbenegative,thelengthof theSurfaceProis10.23inchesandthewidthis 21361.61 6.82 313 inches.Thus,theareaofthe 12.3-inch3:2formatSurfaceProis 1361.611361.61 2 13313 69.83squareinches.
TheiPadProformathasthelargerscreensince itsareaislarger.
110. Let x =thelengthofa7.9-inchiPadMiniina 4:3format.
Then3 4 x =thewidthoftheiPad.Thediagonal ofthe7.9-inchiPadis7.9inches,sobythe Pythagoreantheoremwehave:
Sincethelengthcannotbenegative,thelengthof theiPadis42600.96337inchesandthewidthis
42600.96 337 9 6.32 16
inches.Thus,theareaofthe iPadis42600.96942600.963371633771.11
square inches.
Let y =thelengthofa12-inch3:2format MicrosoftSurfacePro.Then 2 3 y =thewidthof theSurfacePro.Thediagonalofa12-inch SurfaceProis12inches,sobythePythagorean theoremwehave:
Sincethelengthcannotbenegative,thelengthof theiPadis6.32inchesandthewidthis 3 6.324.74 4 inches.Thus,theareaofthe iPadis(6.32)(4.74)29.9568 squareinches. Let y =thelengthofa8-inch16:10format AmazonFireHD8™.Then 10 16 y =thewidthof theFire.Thediagonalofa8-inchFireis8 inches,sobythePythagoreantheoremwehave:
Section 1.3: Quadratic Equations
113. Wewillsetg=2.97andsolveforhusingthe QuadraticFormula.
0.00060.0153.04
Sincethelengthcannotbenegative,thelengthof theFireis 16384 6.78399 356 inchesandthe widthis 1016384 4.240 16356 inches.Thus,thearea oftheAmazonFireis
TheiPadMini™4:3formathasthelargerscreen sinceitsareaislarger.
111. Let h be1.1.Then
1.10.000250.04
00.000250.041.1
0.04(0.04)4(0.00025)(1.1) 2(0.00025)
35.3ftor124.7ft
xx xx x 124.7ftdoesnotmakesenseinthecontextof theproblem,sotheansweris35.3ft.
112. Sincedisexpressedin1000’swewillsetd=15 andsolveforxusingtheQuadraticFormula. 2 2 2 2 0.828(0.828)4(0.012)(9.25) 2(0.012) 0.828.241584 0.024 0.0120.82815.750 250.0120.82815.750 00.0120.8289.25
54.98or14.02
Sothenearestyearwhenthedifferencewas $25,000occurredabout14yearsafter1980or 1994.Thevalue55hasnomeaningsinceitisin thefuture.
2.970.00060.0153.04
00.00060.0150.07 29or4.02 gxx
0.015(0.015)4(0.0006)(0.07) 2(0.0006)
0.0150.000393 0.0012
Sotheestimatednumbersofhoursworkedbya studentwithaGPAof2.97is29hours.The value-4.02hasnomeaningsinceitisnegative.
114. Letxbethenumbersofmembersinthe fraternityandsbethesharepaidbyeach member.Then1470 s x . Ifthereare7 memberswhocannotcontributethentheshare goesupby$5.Sowehavethefollowing equation: 51470 7 s x or 571470sx
Solvingthesetwoequationstogether:
2 5714701470 and 1470571470 10290 14705351470 10290 5350 535102900 sxs x x x x x x x xx
2 2 535102900 720580 (42)(49)0 42or49 xx xx xx xx
Sincexisthenumberofmembers,itmustbe positivesothenumberofmembersis49.
Chapter 1: Graphs, Equations, and Inequalities
115. Let a betheagetheindividualisabletostart savingmoney.Thenweneedtofindwherethe modelsareequal.Solvingthesetwoequations together:
2 2240(2240)4(25)(38540) 2(25)
22401163600 50 252400307001607840 252240385400
22401078.7 50
22401078.722401078.7 or 5050
66.4or23.2
Since x istheagetostartsaving,itmakessense thattheanswerisapproximateatage23.
116.Wewillsettheequationequalto10andsolve:
0.0030.0348.08610
0.0030.0341.9140
2(0.003)
0.034.024124 0.006
0.034.15532 0.006
0.0340.155320.0340.15532 or 0.0060.006 20.22
x or31.55 x Thepercentagewillreach10%approximately32 yearsafter1960whichis1992.
Sincethenumberofconsecutiveintegerscannot benegative,wediscardthenegativevalue.We mustadd37consecutiveintegers,beginningat1, inordertogetasumof703. 118.
2 1365 2 3130 31300 13100 nn nn nn nn
13or10nn Sincethenumberofsidescannotbenegative,we discardthenegativevalue.Apolygonwith65 diagonalswillhave13sides.
2 1 380 2 3160 31600 nn nn nn
2 33411603646 212 n
Neithersolutionisaninteger,sothereisno polygonthathas80diagonals.
119. Therootsofaquadraticequationare
120. Therootsofaquadraticequationare
121. Inordertohaveonerepeatedsolution,weneed thediscriminanttobe0.
122. Inordertohaveonerepeatedsolution,weneed thediscriminanttobe0.
Section 1.3: Quadratic Equations
bbac x cc bbacbbac c bbac bbac ac cbbaccbbac a bbac x
123. For20 axbxc : 24 2
For20 axbxc :
125. If x =originalwidthand y =originallength,then 11 or xyx y .Theratioofsidelengthsis
2 1 x y y .Foldingalongthelongestsideresults insidesoflength1and2 y x y whoseratiois
2 2 12 y y y Equatingtheratiosgives
Chapter 1: Graphs, Equations, and Inequalities
3.
126. a. 29 x and3 x arenotequivalent becausetheydonothavethesamesolution set.Inthefirstequationwecanalsohave 3 x
b. 9 x and3 x areequivalentbecause 93
c. 1212xxx and21 x x are notequivalentbecausetheydonothavethe samesolutionset.
Thefirstequationhasthesolutionset 1 whilethesecondequationhasnosolutions.
127. Answerswillvary.Methodsmayincludethe quadraticformula,completingthesquare, graphing,etc.
128. Answerswillvary.Knowingthediscriminant allowsustoknowhowmanyrealsolutionsthe equationwillhave.
129. Answerswillvary.Onepossibility:
Twodistinct:23180 xx
Onerepeated:214490 xx Noreal:240 xx
130. Answerswillvary.
Section 1.4
1. Integers: 3,0
Rationals: 3,0,6 5
2. True;thesetofrealnumbersconsistsofall rationalandirrationalnumbers.
4. real;imaginary;imaginaryunit
5. False;theconjugateof25i is25i
6. True;thesetofrealnumbersisasubsetoftheset ofcomplexnumbers.
7. False;if23i isasolutionofaquadratic equationwithrealcoefficients,thenits conjugate,23i ,isalsoasolution.
8. b
9. a
10. c
11. (23)(68)(26)(38)85 iiii
12. (45)(82)(4(8))(52) 47 iii i
13. (32)(44)(34)(2(4)) 76 iii i
14. (34)(34)(3(3))(4(4)) 606 iii i
15. (25)(86)(28)(56) 611 iii i
16. (84)(22)(82)(4(2)) 106 iii i
17. 3(26)618 ii
18. 4(28)832 ii
19. 2 3(76)21182118(1) 1821 iiiii i
Section 1.4: Complex Numbers; Quadratic Equations in the Complex Number System
20. 2 3(34)912912(1)129 iiiiii
21. (34)(2)63842 654(1) 105 iiiii i i
28. 2 2 222 222 2(1)121 2(1)22 iiiii iii i i i i
22. (53)(2)105632 103(1) 13
iiiii i i
23. (5)(5)25552 25(1) 26
24. (3)(3)9332 9(1) 10 iiiii
25. 2 1010343040 3434349121216 30403040 916(1)25 3040 2525 68 55 ii iii iii ii i i
26. 2 1313512 512512512 65156 256060144 6515665156 25144(1)169 65156 169169 512 1313 i iii i iii ii i i
27. 2 2 222 2(1)1212 (1)1 ii iii iii i i i i
29. 2 2 66166 1111 67(1)5757 1(1)222 iiiiii iii iii i i i
30. 2 2 232312233 1111 253(1)1515 1(1)222 iiiiii iii iii i i i
31. 2 1311332 2 224224 13313 (1) 42422 iii ii
32. 2 3133112 2 224224 33113 (1) 42422 iii ii
33. 22 (1)1212(1)2 iiiii 34. 22 (1)1212(1)2 iiiii
11 2322122211 (1) iiiiiiii
36.
7 1427(1)1 ii
37. 20 2020210 10 111 () 111 (1)1
i iii
38. 23 2322122211 112 1111 () 111 (1)(1) i iiiiii iii i iii ii
Chapter 1: Graphs, Equations, and Inequalities
39.
3 62355(1)5156ii
40. 32 444(1)4 iiiii
41. 3532 2 64(64) (64(1))1(10)10 iiii iiii
42. 3222 421421 4(1)2(1)1 421 34 iiiii i i i
43. 32 2 (1)(1)(1)(1)(12)(1) (121)(1)2(1) 2222(1) 22 iiiiiii iiii iii i
44. 44 (3)181181(1)182 ii
45. 7277 (1)(1(1))(0)0 iiii
46. 42 2(1)2(1)(1(1))2(0)0 ii
47. 432 86422222 432 (1)(1)(1)1 1111 0
iiiiiiii
48. 32 753222 32 (1)(1)(1) 0 iiiiiiiiiii iiii iiii
54. 189232 ii
55. 2001002102 ii
56. 459535 ii
57. 2 (34)(43)1291612 916(1) 25 5 iiiii i
58. 2 (43)(34)1216912 169(1) 25
5 iiiii i
59. 2 2 40 4 4 2 x x x x i
Thesolutionsetis 2,2. ii
60. 240 x
(2)(2)0 2or2 Thesolutionsetis2,2. xx xx
61. 2160 x 440 4or4
Thesolutionsetis4,4. xx xx
62. 2250 x 225 255 Thesolutionsetis5,5. x xi ii
63. 26130xx
Thesolutionsetis32,32.
64. 2480xx
.
65. 26100xx 22 1,6,10 4(6)4(1)(10)36404 (6)4623 2(1)2 abc bac i xi
Thesolutionsetis 3,3ii
66. 2250xx 22 1,2,5 4(2)4(1)(5)42016 (2)162412 2(1)2
abc
bac i xi
Thesolutionsetis 12,12 ii .
67. 2 251020 xx 22 25,10,2 4(10)4(25)(2)100200100 (10)100101011 505055
abc bac i xi
Thesolutionsetis 1111 , 5555 ii
68. 2 10610 xx 22 10,6,1 464(10)(1)36404 646231 2(10)201010 abc bac i x i
Thesolutionsetis 3131 , 10101010 ii
69. 2 2 512 5210 x x xx 22 5,2,1 424(5)(1)42016 (2)162412 2(5)1055 abc bac i xi
Thesolutionsetis 1212 , 5555 ii
70. 2 2 1316 13610 x x xx 22 13,6,1 4(6)4(13)(1)365216 (6)166432 2(13)261313 abc bac i xi
Thesolutionsetis 3232 , 13131313 ii
71. 210xx 1,1,1,abc 22414(1)(1)143 131313 2(1)222
bac i x i
Thesolutionsetis1313 , 2222 ii
72. 210xx 1,1,1abc 224(1)4(1)(1)143 (1)31313 2(1)222 bac i x i
Thesolutionsetis1313 , 2222 ii .
Chapter 1: Graphs, Equations, and Inequalities
73. 3640 x 2 2 (4)4160 404 or4160
abc bac i x i
xxx xx xx 22 1,4,16 444(1)(16)166448 448443 223 2(1)2
Thesolutionsetis 4,223,223. ii
74. 3270 x
2 2 (3)390 303 or390 xxx xx xx
22 1,3,9 4(3)4(1)(9)93627 (3)27333333 2(1)222 abc bac i x i
Thesolutionsetis3333333,,. 2222 ii
75. 4 4 16 160 x x
22 2 440 (2)(2)40 xx xxx
2 2 20or20or40 2or2or4 2or2or42 xxx xxx x xxi
Thesolutionsetis 2,2,2,2. ii
76. 4 4 1 10 x x
22 2 110 (1)(1)10 xx xxx
77. 4213360xx 22 22 22 940 90or40 9or4 9or4 3or2 xx xx xx xx x ixi
Thesolutionsetis 3,3,2,2. iiii
78. 42340xx 22 2 140 (1)(1)40 xx xxx
2 2 10or10or40 1or1or4 1or1or42 xxx xxx x xxi
Thesolutionsetis 1,1,2,2. ii
79. 2 3340 xx 22 3,3,4 4(3)4(3)(4)94839 abc bac
Theequationhastwocomplexsolutionsthatare conjugatesofeachother.
80. 2 2410 xx 22 2,4,1 4(4)4(2)(1)1688 abc bac
Theequationhastwounequalrealnumber solutions.
81. 2 2 234 2340 xx xx 22 2,3,4 434(2)(4)93241 abc bac
Theequationhastwounequalrealsolutions.
82. 2 2 62 260 x x xx
22 1,2,6 4(2)4(1)(6)42420 abc bac
Theequationhastwocomplexsolutionsthatare conjugatesofeachother.
2 2 10or10or10 1or1or1 1or1or1 xxx xxx x xxi
Thesolutionsetis 1,1,,. ii
Section 1.4: Complex Numbers; Quadratic Equations in the Complex Number System
83. 2 91240 xx 22 9,12,4 4(12)4(9)(4)1441440 abc bac
Theequationhasarepeatedrealsolution.
84. 2 41290 xx 22 4,12,9 4124(4)(9)1441440 abc bac
Theequationhasarepeatedrealsolution.
85. Theothersolutionis2323. ii
86. Theothersolutionis44. ii
87. 343434346zziiii
88. 8383 83(83) 8383 066 wwii ii ii ii
89. 2 (34)(34) (34)(34) 9121216 916(1)25 zzii ii iii
90. 34(83) 3483 57 57 zwii ii i i
91. 2 2 181834 343434 54723454754 9121216916 5075 23 25 Viii Z Iiii iiii iii i i
Theimpedanceis23i ohms.
92. 12 2 11111(43)(2) 243(2)(43) 626262 8643823112 ii Z ZZiiii iii ii iii
So, 2 2 11211262 626262 662212466104 3612124364 701071 4044 iii Z iii iiii iii i i
Thetotalimpedanceis71 44 i ohms.
93. ()() 2 zzabiabi abiabi a
() () 2 zzabiabi abiabi abiabi bi
94. zabiabiabiz
95. ()() ()() ()() ()() zwabicdi acbdi acbdi abicdi abicdi zw
96. 2 ()() ()() ()() zwabicdi acadibcibdi acbdadbci acbdadbci
2 ()() ()() zwabicdi abicdi acadibcibdi acbdadbci
97. 22 2222 222222 2222 2()2() 22 22
abiabi aabibiaabibi aabibiaabibi aabibaabib
Chapter 1: Graphs, Equations, and Inequalities
2222 22 22 () 2()0
abab ab abba
Anycomplexnumberoftheform aai or aai willwork.
98. Let32 u in320 x sothat330 xu
uuu x uuuu ii
Then,22()()0 xuxuxu .Fromthefirst factorwefind32 xu .Fromthesecond factor,usethequadraticformulatoget 22 233 ()()41 21 33223 22222
Thesolutionsetis: 33 3223 2,22
99. 2 (5)(5)(); x yxy let5 ux (so 5 xu and5 vy so5 yv
Substitutinggives2 () uvuv or 220 uuvv whichisquadraticinu.Using thequadraticformulagives
223 41 212 vv vvv x .Since x isarealnumber, u mustalsobearealnumber. Thisisonlypossibleifv=0whichthenmakes u =0.Therefore,055 x and 055 y ,so5510 xy
100 – 102. Answerswillvary.
103. Answerswillvary.Acomplexnumberisthe sumordifferenceoftwonumbers(realand imaginarypartsofthecomplexnumber)justasa binomialisthesumordifferenceoftwo monomialterms.Wemultiplytwobinomialsby usingtheFOILmethod,anapproachwecanalso usetomultiplytwocomplexnumbers.
104. Althoughthesetofrealnumbersisasubsetof thesetofcomplexnumbers,notallrulesthat workintherealnumbersystemcanbeusedin thelargercomplexnumbersystem.Therulethat allowsustowritetheproductoftwosquare rootsasthesquarerootoftheproductonly worksintherealnumbersystem.Thatis, abab onlywhen a and b arereal
numbers.Inthecomplexnumbersystemwe mustfirstconverttheradicalstocomplexform. Inthiscasethismeansweneedtowrite9as 19913i .Thenwecanmultiplyto get
2 99339919 iii
1.5 1. True
33 x x
322 2 4936494 49 433 xxxxxx xx xxx
5. Thedistancefromtheoriginto4onareal numberlineis4units.
6. False;youcanalsousetheQuadraticFormulaor completingthesquare.
7. quadraticinform
8. True
9. a 10. c 11. 64 y 2264 61610 y yy Check:223255 Thesolutionsetis 22
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
12. 37 t
2237 34952 t tt
Check:523497
Thesolutionsetis52.
13. 211 t
22211 211221 t
Check:2(1)111
Thesolutionsetis1.
14. 342 t
22342 344300 t
Check:3(0)442
Thesolutionsetis{0}.
15. 346 t
Sincetheprincipalsquarerootisnevernegative, theequationhasnorealsolution.
16. 532 t
Sincetheprincipalsquarerootisnevernegative, theequationhasnorealsolution.
17. 31230 x
3 333 123 123 122722613 x x xxx
Check:3312(13)32730
Thesolutionsetis{13}.
18. 31210 x
3 333 121 121 121200 x x xxx
Check:3312(0)1110
Thesolutionsetis{0}.
19.
20.
4 444 542 542 5416 520 4 x x x x x
Check: 44544162 T
Thesolutionsetis 4.
5 555 231 231 231 22 1 x x x x x
Check: 5521311 T
Thesolutionsetis 1.
21.
22.
52 5 55 2 2 2 2 21 21 21 210 10 10 1 xx xx xx xx x x x
Check: 52551211211 T
Thesolutionsetis 1
42 444 2 2 2 165 165 1625 9 3 x x x x x
Chapter 1: Graphs, Equations, and Inequalities
Thesolutionsetis
Thesolutionsetis
Check–5:152(5)25 55
Check3:152(3)933
Thesolutionsetis{3}.
26. 12 x x
22 22 12 12120 (4)(3)04or3 xx xxxx xxxx
Check–4:12(4)16 44
Check3:123933
Thesolutionsetis{3}.
27.
28.
22 2 2 3(10)4 3(10)4 3(10)(4) 330816 0514 0(7)(2) 7or2 xx xx xx xxx xx xx xx
Check7:3(710)49417
Check2:3(210)436422
Discard7 x asextraneous.
Thesolutionsetis{2}.
22 2 2 132 15 1(5) 11025 01124 0(3)(8) 3or8 xx xx xx xxx xx xx xx
Check3:1(3)33211
Check8:1(8)38206
Discard8 x asextraneous. Thesolutionsetis{-3}.
29. 242 xxx
222 22 42 444 858 5 xxx xxxx x x
Check:
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
2 88842 555 6482 4 2555 42 255 22 55
Thesolutionsetis 8 5
30. 285 xxx
2 22 22 85 81025 1133 3 xxx xxxx x x
Check:
2 33835 93835 42 22
T
Thesolutionsetis 3.
31. 331 x x
22 2 2 313 31(3) 3169 098 0(1)(8) 1or8 xx xx xxx xx xx xx
32. 2122 x x
22 2 2 1222 122(2) 12244 028 (2)(4)0 2or4 xx xx xxx xx xx xx
Check2:2+122(2)21662
Check4:2122(4)2444
Discard2 x asextraneous.
Thesolutionsetis{4}
33. 3572 xx
22 22 2 2 2 2 3527 3527 354477 21647 (216)47 46425616(7) 46425616112 4801440 20360 (2)(18)02or18 xx xx xxx xx xx xxx xxx xx xx xxxx
Check2:3(2)527 191322
Check18:3(18)5187
49257522
Discard2 x asextraneous.
Check1:33(1)13451
Check8:33(8)132588
Discard1 x asextraneous.
Thesolutionsetis 8.
Thesolutionsetis 18
Chapter 1: Graphs, Equations, and Inequalities
34. 3721 xx
22 22 2 2 3712 3712 371222 2422 22 (2)2 442 320 (1)(2)0 1or2 xx xx xxx xx xx xx xxx xx xx xx
Check–1:3(1)712 412131
Check2:3(2)722 101011
Discard1 x asextraneous.
Thesolutionsetis 2.
35. 3112 xx
22 22 2 2 2 3121 3121 314411 2241 (22)41 48416(1) 2144 650 (1)(5)01or5 xx xx xxx xx xx xxx xxx xx xxxx
Check1:3(1)111 402022
Check5:3(5)151 1644222
Thesolutionsetis 1,5
36. 2311 xx
22 22 2 2 2 2311 2311 231211 121 (1)21 214(1) 2144 230 (1)(3)01or3 xx xx xxx xx xx xxx xxx xx xxxx
Check–1:2(1)311101 Check3:2(3)331321
Thesolutionsetis 1,3
37. 22 32 32 32 23 xx x x xx xx
22 2 2 23 469 0109 091 xx xxx xx xx 1or9xx Check: 3211 321 11 11 T 3299 3233 33
Discard9 x asextraneous.Thesolutionsetis {1}
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
41. 1/3 522 x 3 1/33522 5285102 x xxx
Check: 1/3 1/3 5222 82 22
Thesolutionsetis{2}.
42. 1/3 211 x 3 1/33211 211221 x xxx
Check:
Discard4 x asextraneous.Thesolutionsetis
39. 1/2 314 x
1/2 1/2 3514 164 44
T
Thesolutionsetis{5}
40. 1/2 352 x 2 1/22352 354393 x xxx
Check:
1/2 1/2 3352 42 22 T
Thesolutionsetis{3}
1/3 1/3 2111 11 11
Thesolutionsetis 1.
43. 21/295 x
21/222 22 95 92516 4or4 x xx xx
Check:
21/2 1/2 495 255 55
Thesolutionsetis 4,4.
21/2 1/2 495 255 55
Chapter 1: Graphs, Equations, and Inequalities
Thesolutionsetis
240hasnorealsolution t ,soweonlyneed toconsider 20 2 t t
Thesolutionsetis 2,2
46. 440 y
22 2 22 220 2220 202,whichisimpossible or2202 yy yyy yy yyy
Thesolutionsetis 2,2.
47. 42540xx
22 22 410 40or10 2or1 xx xx xx
Thesolutionsetis 2,1,1,2.
48. 4210240xx
22640xx 2 2 60 6 6 x x x or 2 2 40 4 2 x x x
Thesolutionsetis 6,2,2,6.
49. 42 6510 xx
22 22 2 6110 610or10
61,whichisimpossible or1
xx xx x x Thesolutionsetis 1,1.
50. 42 25120 xx
22 22 2 2340 230or40
23,whichisimpossible or2 xx xx x x
Thesolutionsetis 2,2.
51. 63780xx
33 33 3 3 810 80or10 82 or11 xx xx xx x x
Thesolutionsetis 2,1.
52. 63780xx
33 33 3 3 810 80or10 82 or11 xx xx xx x x
Thesolutionsetis 1,2.
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
53. 2 272120xx
22 2 22 7120 340 30or40 3235 or4246 letpxpx pp pp pp pxx pxx
Thesolutionsetis 6,5.
54. 2 252560 xx
22 2 2525 60 320 3020 32531 22527 2 letpxpx pp pp porp pxx orpxx
Thesolutionsetis 7 2,1.
55. 2 21513 ss
22 2 2 11 253 2530 2130 210or30 113 1 222 or3132 letpsps pp pp pp pp pss pss
Thesolutionsetis 3,2. 2
56. 2 315120 yy 22 2 11 3520 3210 320or10 225 1 333 or1112 letpypy pp pp pp pyy pyy
Thesolutionsetis 5,2. 3
57. 40xx
22 22 4 4 16016 0160 or16016 xx xx x xxx xxx x x
Check: 0:0400 00 16:164160 16160 00 x x
Thesolutionsetis 0,16 58. 80xx
22 22 8 8 64064 0640or64 xx xx xxxx xxxx
Check: 0:0800 00
64:648640 64640 x x
Thesolutionsetis 0,64
Chapter 1: Graphs, Equations, and Inequalities
59. 20 xx 2
62. 1/21/4210tt
2 2 20 200 540 50or40 5=5non-real or4=4=16
letpxpx pp pp pp pp px pxx
Check: 16:161620 16420 x
Thesolutionsetis 16.
60. 6 xx
1/421/2 2 1/4 210 110 10 111 letptpt pp pp p ptt
Check: 1:1/21/412110 121000 t
Thesolutionsetis 1
2
letpxpx pp pp pp pp px pxx
2 2 6 60 320 30or20 3=3non-real or2=24
Check:
4:446 426 x
Thesolutionsetis 4
61. 1/21/4440zt
1/421/2 2 1/4 440 220 20 2216 letpzpz pp pp p pzz
Check:
16:1/21/41641640 484000 z
Thesolutionsetis 16.
63. 1/21/4 4940 xx 1/421/2 2 4 1/4 let 4940 98164917 88 917917 88 pxpx pp p xx
Check:
1/21/444 2 2 2 917917 494 648 64064 917917 4940 88 917917 4940 88 917917 4940 648
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
Check:
2 121 22 2:112
64. 1/21/4320xx
Check:
1/21/4 1/21/4 16:1631620 462000 1:13120 132000 x x
Thesolutionsetis 1,16.
65. 2 112 11 x x
2 2 22 let11 11 220 1201or2 1 11112 1 or 1122122 12 pp xx pppp pppp pxx x pxx x
2/3 2/33/23/2 3/2 22 2 2whichisnotarealnumber px x x
Check:
4/32/333 99 11 93 3520 3520 1520 33 00
4/32/333 99 11 93 3520 3520 1520 33 00
Thesolutionsetis33 , 99
.
71. 235 x 235or235 22or28 1or4 xx xx xx
Thesolutionsetis{–4,1}.
72. 312 x 312or312 33or31 11 or 3 xx xx xx
Thesolutionsetis 1,1 3
Chapter 1: Graphs, Equations, and Inequalities
73. 14813145 tt 145or145 44or46 13 or 2 tt tt tt
Thesolutionsetis 1,3 2
74. 1269123 zz 123or123 22or24 1or2 zz zz zz
Thesolutionsetis 1,2
75. 721 x 721or721 3or3
xx xx
Thesolutionsetis{–3,3}.
76. 1 x 1or1xx Thesolutionsetis{–1,1}.
77. 42321 xx 21or21 11 or 22 xx xx
Thesolutionsetis 11 , 22 .
78. 11532 22 x x 112or2 22 4or4 xx xx
Thesolutionsetis 4,4
79. 83 7 x 212121 or 888 xxx
Thesolutionsetis 2727 , 22 .
80. 39 4 x 1212or12xxx Thesolutionsetis{–12,12}.
81. 22 35 x 222or2 3535 5630or5630 524or536 2436 or 55 xx xx xx xx
Thesolutionsetis 3624 , 55 .
82. 11 23 x 111or1 2323 326or326 38or34 84 or 33 xx xx xx xx
Thesolutionsetis 48 , 33 .
83. 21 2 u impossible,sinceabsolutevaluealwaysyieldsa non-negativenumber.
84. 21 v impossible,sinceabsolutevaluealwaysyieldsa non-negativenumber.
85. 290 x 2 2 90 9 3 x x x
Thesolutionsetis 3,3.
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
86. 2160 x 2 2 160 16 4 x x x
87. 223xx
88. 212xx
22 22 12or12 120or120 3401148 or 2 147norealsol. 2 3or4 xxxx xxxx xxx xx
Thesolutionsetis 4,3.
89.
3 2 90 90 330 xx xx xxx
0 x
Thesolutionsetis
90.
42 22 2 810 810 990 xx xx xxx
20 0 x x or90 9 x x or90 9 x x
Thesolutionsetis 9,0,9
91.
92.
32 2 200 200 540 xxx xxx xxx 0 x or50 5 x x or40 4 x x
Thesolutionsetis 5,0,4
32 2 670 670 710 xxx xxx xxx 0 x or70 7 x x or10 1 x x
Thesolutionsetis 7,0,1
93.
32 2 2 10 1110 110 1110 xxx xxx xx xxx 10 1 x x or10 1 x x Thesolutionsetis 1,1
94. 32 2 2 440 4140 410 4110 xxx xxx xx xxx
40 4 x x or10 1 x x or10 1 x x Thesolutionsetis 4,1,1.
95.
32 2 2 316480 31630 3160 3440 xxx xxx xx xxx 30 3 x x or40 4 x x or40 4 x x Thesolutionsetis 4,4,3
Chapter 1: Graphs, Equations, and Inequalities
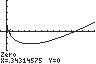
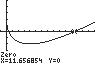
100. 2/31/3420xx ;UseZERO(orROOT)on thegraphof2/31/3142 yxx
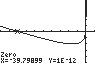
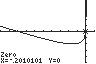
Thesolutionsetis 39.80,0.20
101. 42330xx ;UseZERO(orROOT)on thegraphof42133 yxx
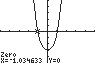
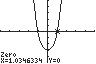
Thesolutionsetis 1.03,1.03
102. 42220xx ;UseZERO(orROOT)on thegraphof42122 yxx .
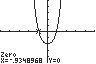
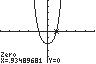
Thesolutionsetis 0.93,0.93
103. 2 37200 3540 xx xx 350 35 5 3 x x x or40 4 x x
Thesolutionsetis5 4, 3
.
108. 13 23 42 236 x
or236 23 3 2 x x x
Thesolutionsetis39 , 22
109. 433 4123 315 5 ww ww w w
Thesolutionsetis 5.
110. 63212 618212 46 3 2 kk kk k k
Thesolutionsetis3 2
.
Chapter 1: Graphs, Equations, and Inequalities
7 u
or1 u
Gobackintermsof y andsolve: 7 1 77 67 7 6 y y yy y y
115.
Thesolutionsetis15 , 53
22 2 2 251 251 251 2521 40 220 xx xx xx x xx x xx
2 x or2 x
Check:
22521 121 31
Thesolutionsetis 2.
116.
22521 921 11
T
22 2 2 3126 3126 3126 3142436 427350 4750 xx xx xx xxx xx xx
Thesolutionsetis
Check: 77 3126 44 57 6 22 16
Thesolutionsetis 5
351256 4106 66
T
Section 1.5: Radical Equations; Equations Quadratic in Form; Absolute Value Equations; Factorable Equations
117. 2 2 361 3610
118.
Check:
Thesolutionsetis
119.
2 2 322 340 410 4or1 xx xx xx xx
Sinceanevenrootcannotbenegative,wecan exclude1asasolution. Check:
Thesolutionsetis
Chapter 1: Graphs, Equations, and Inequalities
4 22 160 440 t tt
Thesolutionsetis
2 2 390 1,3,9 33419 21 327333 22 zz abc z i
2 2 10 1,1,1 11411 21 1313 22 zz abc z i
Thesolutionsetis33313,,2222 ii
33313 ,,3,1 2222 ii
127. 2212120kkkk
430kk 4 34 3 3412 315 5 k x x xx x x
or3 33 3 339 3 2 k x x xx x
Andsinceneitherofthese x valuescausesa denominatortoequalzero,thesolutionsetis
3,5 2
128. 223283280kkkk
Andsinceneitherofthesexvaluescausesa denominatortoequalzero,thesolutionsetis
129. 8327
Thesolutionsetis 3,1
130. 53124 x x 53124 54123 99 1 x x xx x x
or53(124) 53124 54123 15 x x x x xx x
Thesolutionsetis 1,15.
131. Graphtheequations1/4/1100 yxx and 24y ;thenuseINTERSECTtofindthe x-coordinateofthepointsofintersection: 300 5 0 0
Thedistancetothewater'ssurfaceis approximately229.94feet.
132. 2 4 25 LH T
Let4 T and10 H ,andsolvefor L
Thecrushingloadis64tons.
133. 2 32 l T
Let16.5 T andsolvefor l 22 2 2 16.52 32 16.5 232 16.5
Thelengthwasapproximately221feet. 134.
Chapter 1: Graphs, Equations, and Inequalities
Sincex>2,thenegativesolutionisextraneous.
136.
Thesolutionsetis
xxx xxx xxx xx
Tosolve1 2 121330 xx ,let1 2 ux 11 22 Then2121330 (43)(31)0 31 or 43 91 169
uu uu uxx xx
Thesolutionsetis 910,,169
137. 63 33 22 28270 (27)(1)0 (3)(39)(1)(1)0
zz zz zzzzzz 30or10 3or1 zz zz 2 2 1,3,9 33419 2 327333 22 , 1,1,1 11411 2 1313 22
abc x i Also abc x i Thesolutionsetis133333,1,,. 22
138. Answerswillvary,oneexampleis11 x
139. Answerswillvary,oneexampleis 20 xx
140. Answerswillvary.
141. x representsthedistancefrom x totheorigin. Sincedistanceisnevernegative,2 x hasno realsolution.
142. Janedidnotcheckhersolutionsandincludedthe extraneoussolution,1 x
2 2 2 2 230 23 23 23 230 310 3or1 xx xx x x xx xx xx x x
Check:
Section 1.6: Problem Solving: Interest, Mixture, Uniform Motion, Constant Rate Job Applications
Thesolutionsetis 3.
Section 1.6
1. mathematicalmodeling
2. interest
3. uniformmotion
4. False;theamountchargedfortheuseof principalistheinterest.
5. True;thisistheuniformmotionformula.
6. a
7. b
8. c
9. Let A representtheareaofthecircleand r the radius.Theareaofacircleistheproductof π timesthesquareoftheradius:2 A r
10. Let C representthecircumferenceofacircle and r theradius.Thecircumferenceofacircle istheproductof π timestwicetheradius: 2 Cr
11. Let A representtheareaofthesquareand s the lengthofaside.Theareaofthesquareisthe squareofthelengthofaside:2 A s
12. Let P representtheperimeterofasquareand s thelengthofaside.Theperimeterofasquareis fourtimesthelengthofaside:4Ps
13. Let F representtheforce, m themass,and a theacceleration.Forceequalstheproductofthe masstimestheacceleration: F ma
14. Let P representthepressure, F theforce,and A thearea.Pressureistheforceperunitarea: F P A
15. Let W representthework, F theforce,and d thedistance.Workequalsforcetimesdistance: WFd
16. Let K representthekineticenergy, m themass, and v thevelocity.Kineticenergyisone-half theproductofthemassandthesquareofthe velocity:2 1 2 K mv
17. C totalvariablecostindollars, x number ofdishwashersmanufactured:150Cx
18. R totalrevenueindollars, x numberof dishwasherssold:250Rx
19. Let x representtheamountofmoneyinvestedin bonds.Then50,000 x representstheamount ofmoneyinvestedinCD's.Sincethetotal interestistobe$6,000,wehave:
0.150.07(50,000)6,000 1000.150.07(50,000)6,000100 157(50,000)600,000 15350,0007600,000 8350,000600,000 8250,000 31,250 xx xx xx xx x x x
$31,250shouldbeinvestedinbondsat15%and $18,750shouldbeinvestedinCD'sat7%.
20. Let x representtheamountofmoneyinvestedin bonds.Then50,000 x representstheamount ofmoneyinvestedinCD's.Sincethetotal interestistobe$7,000,wehave:
0.150.07(50,000)7,000 1000.150.07(50,000)7,000100 157(50,000)700,000 15350,0007700,000 8350,000700,000 8350,000 43,750 xx xx xx xx x x x
$43,750shouldbeinvestedinbondsat15%and $6,250shouldbeinvestedinCD'sat7%.
Chapter 1: Graphs, Equations, and Inequalities
21. Let x representtheamountofmoneyloanedat 8%.Then12,000 x representstheamountof moneyloanedat18%.Sincethetotalinterestis tobe$1,000,wehave:
0.080.18(12,000)1,000
1000.080.18(12,000)1,000100
818(12,000)100,000
8216,00018100,000
10216,000100,000 10116,000 11,600
$11,600isloanedat8%and$400isat18%.
22. Let x representtheamountofmoneyloanedat 16%.Then1,000,000 x representstheamount ofmoneyloanedat19%.Sincethetotalinterest istobe$1,000,000(0.18),wehave:
0.16190,0000.19180,000
0.03190,000180,000 0.0310,000
0.160.19(1,000,000)1,000,000(0.18) 10,000 0.03 $333,333.33
Wendycanlend$333,333.33at16%.
23. Let x representthenumberofpoundsofEarl Greytea.Then100 x representsthenumberof poundsoforangepekoetea. 64(100)5.50(100) 64004550 2400550 2150 75
xx xx x x x 75poundsofEarlGreyteamustbeblendedwith 25poundsoforangepekoe.
24. Let x representthenumberofpoundsofthe firstkindofcoffee.Then100 x representsthe numberofpoundsofthesecondkindofcoffee. 2.755(100)4.10(100) 2.755005410 2.25500410 2.2590 40
xx xx x x x 40poundsofthefirstkindofcoffeemustbe blendedwith60poundsofthesecondkindof coffee.
25. Let x representthenumberofpoundsof cashews.Then60 x representsthenumberof poundsinthemixture. 94.50(60)7.75(60) 92707.75465
1.25195 156
xx xx x x 156poundsofcashewsmustbeaddedtothe60 poundsofalmonds.
26. Let x representthenumberofcaramelsinthe box.Then30 x representsthenumberof cremesinthebox.
RevenueCostProfit
12.500.250.45(30)3.00
12.500.2513.50.453.00
12.5013.50.203.00
12.5013.500.203.00 1.000.203.00 0.204.00 20 xx xx x x x x x
Theboxshouldcontain20caramelsand10 cremes.
27. Let r representthespeedofthecurrent.
RateTimeDistance
Upstream16
Downstream16 r r r r
2016 1 6033 1516 1 6044
Sincethedistanceisthesameineachdirection: 1616 34
4(16)3(16) 644483 167 162.286 7 rr rr rr r
Thespeedofthecurrentisapproximately2.286 milesperhour.
28. Let r representthespeedofthemotorboat.
RateTimeDistance
Upstream3553
Downstream32.52.53 rr rr
Thedistanceisthesameineachdirection:
5(3)2.5(3) 5152.57.5 2.522.5
Thespeedofthemotorboatis9milesperhour.
29. Let r representthespeedofthecurrent.
(25)(25)4(12)(75)
Sincethetotaltimeis1.5hours,wehave:
10(15)10(15)1.5(15)(15) 15010150101.5(225)
3001.5(225) 200225 250 (5)(5)0 5or5
Speedmustbepositive,sodisregard5
Thespeedofthecurrentis5milesperhour.
30. Let r representtherateoftheslowercar.Then 10 r representstherateofthefastercar.
RateTimeDistance
Slowercar3.53.5 Fastercar103310
3.53(10) 3.5330 0.530 60 rr
Theslowercartravelsatarateof60milesper hour.Thefastercartravelsatarateof70miles perhour.Thedistanceis(70)(3)=210miles.
31. Let r representKaren’snormalwalkingspeed.
RateTimeDistance
With50walkway2.550 2.5
Against50walkway2.550 2.5
Sincethetotaltimeis48seconds:
Karen’normalwalkingspeedisapproximately 3.75feetpersecond.
32. Let r representthespeedoftheairportwalkway.
RateTimeDistance
Walking280with1.5280 1.5
Walkingwiththewalkwaytakes60secondsless timethanstandingstillonthewalkway:
Speedmustbepositive,sodisregard7 2 r
Thespeedoftheairportwalkwayis2metersper second.
33. Let w representthewidthofaregulationdoubles tenniscourt.Then26 w representsthelength. Theareais2808squarefeet:
Chapter 1: Graphs, Equations, and Inequalities
Thewidthmustbepositive,sodisregard39 w
Thewidthofaregulationdoublestenniscourtis36 feetandthelengthis2(36)+6=78feet.
34. Let t representthetimeittakestheBrotherHLL8350CDWtocompletetheprintjobalone. Then9 t representsthetimeittakestheXerox VersaLinkC500tocompletetheprintjobalone.
todojobinoneminute
Timemustbepositive,sodisregard5 t . TheBrotherHL-L8350CDWtakes36minutesto completethejobalone,printing144040 36 pagesperminute.XeroxVersaLinkC500takes 36+9=45minutestocompletethejobalone, printing144032 45 pagesperminute.
35. Let t representthetimeittakestodothejob together.
Lois20
Workingtogether,thejobcanbedonein12 minutes.
36. Let t representthetimeittakesApriltodothe jobworkingalone. 1 10 1 1 6
todojobinonehour
Aprilwouldtake15hourstopainttherooms.
37. l lengthofthegarden w widthofthegarden
a. Thelengthofthegardenistobetwiceits width.Thus,2lw . Thedimensionsofthefenceare4 l and 4 w . Theperimeteris46feet,so: 2(4)2(4)46 2(24)2(4)46 482846 61646 630 5 lw ww ww w w w
Thedimensionsofthegardenare5feetby 10feet.
b. Area51050 lw squarefeet
c. Ifthedimensionsofthegardenarethesame, thenthelengthandwidthofthefenceare alsothesame(4) l .Theperimeteris46 feet,so:
Section 1.6: Problem Solving: Interest, Mixture, Uniform Motion, Constant Rate Job Applications
2(4)2(4)46 282846 41646 430 7.5 ll ll l l l
Thedimensionsofthegardenare7.5feetby 7.5feet.
d. Area7.5(7.5)56.25 lw squarefeet.
38. l lengthofthepond w widthofthepond
a. Thepondistobeasquare.Thus, lw . Thedimensionsofthefencedareaare6 w oneachside.Theperimeteris100feet,so: 4(6)100 424100 476 19 w w w
Thedimensionsofthepondare19feetby 19feet.
b. Thelengthofthepondistobethreetimes thewidth.Thus,3lw .Thedimensionsof thefencedareaare6and6 wl .The perimeteris100feet,so: 2(6)2(6)100 2(6)2(36)100 212612100 824100 876 9.5 3(9.5)28.5 wl ww
Thedimensionsofthepondare9.5feetby 28.5feet.
c. Ifthepondiscircular,thediameteris d and thediameterofthecirclewiththepondand thedeckis6 d d 3 3
Theperimeteris100feet,so:
Thediameterofthepondis25.83feet. d. 2 square Area19(19)361ft lw
. 2 rectangle Area28.5(9.5)270.75ft lw
. 2 22 circle 25.83 Area=524ft 2 r
Thecircularpondhasthelargestarea.
39. Let t representthetimeittakesforthedefensive backtocatchthetightend.
Def. Back TimeRate
1002525 1233
Tight12sec End 10sec1010 tt tt
100 10 TimetorunDistance 100yards
Sincethedefensivebackhastorun5yards farther,wehave:
Thedefensivebackwillcatchthetightendatthe 45yardline(15+30=45).
40. Let x representthenumberofhighwaymiles traveled.Then30,000 x representsthenumber ofcitymilestraveled.
30,000900 4025
30,000 200200900 4025 5240,0008180,000 3240,000180,000 360,000 20,000
x x x
Thereseisallowedtoclaim20,000milesasa businessexpense.
41. Let x representthenumberofgallonsofpure water.Then1 x representsthenumberof gallonsinthe60%solution.
Chapter 1: Graphs, Equations, and Inequalities
2 3gallonofpurewatershouldbeadded.
42. Let x representthenumberofliterstobe drainedandreplacedwithpureantifreeze.
%liters%liters%liters
5litersshouldbedrainedandreplacedwithpure antifreeze.
43. Let x representthenumberofouncesofwater tobeevaporated;theamountofsaltremainsthe same.Therefore,weget 2 3 0.04(32)0.06(32) 1.281.920.06
0.060.64
0.64643210 0.0663 x x x x
2 3 1010.67 ouncesofwaterneedtobe evaporated.
44. Let x representthenumberofgallonsofwater tobeevaporated;theamountofsaltremainsthe same.
0.03(240)0.05(240) 7.2120.05 0.054.8 4.896 0.05 x x x x
96gallonsofwaterneedtobeevaporated.
45. Let x representthenumberofgramsofpure gold.Then60 x representsthenumberof gramsof12karatgoldtobeused.
12(60)(60)23
300.540 0.510 20 xx xx x x
20gramsofpuregoldshouldbemixedwith40 gramsof12karatgold.
46. Let x representthenumberofatomsofoxygen. 2 x representsthenumberofatomsofhydrogen. 1 x representsthenumberofatomsofcarbon. 2145 444 11 xxx x x
Thereare11atomsofoxygenand22atomsof hydrogeninthesugarmolecule.
47. Let t representthetimeittakesforMiketo catchupwithDan.Sincethedistancesarethe same,wehave: 11(1) 69 322 2 tt
MikewillpassDanafter2minutes,whichisa distanceof1 3 mile.
48. Let t representthetimeofflightwiththewind. Thedistanceisthesameineachdirection: 330270(5) 3301350270 6001350 2.25 tt tt
Thedistancetheplanecanflyandstillreturn safelyis330(2.25)=742.5miles.
49. Let t representthetimetheauxiliarypump needstorun.Sincethetwopumpsareemptying onetanker,wehave: 31 49 27436 49 92.25 4 t t t
Theauxiliarypumpmustrunfor2.25hours.It mustbestartedat9:45a.m.
50. Let x representthenumberofpoundsofpure cement.Then20 x representsthenumberof poundsinthe40%mixture.
54. Let r representthespeedoftheeastbound cyclist.Then5 r representsthespeedofthe westboundcyclist.
RateTimeDistance Eastbound66 Westbound566(5) rr rr
5poundsofpurecementshouldbeadded.
51. Let t representthetimeforthetubtofillwith thefaucetsonandthestopperremoved.Since onetubisbeingfilled,wehave: 1 1520 4360 60
60minutesisrequiredtofillthetub.
52. Let t bethetimethe5horsepowerpumpneeds toruntofinishemptyingthepool.Sincethetwo pumpsareemptyingonepool,wehave:
The5horsepowerpumpmustrunforan additional1.75hoursor1hourand45minutesto emptythepool.
53. Let t representthetimespentrunning.Then 5 t representsthetimespentbiking.
RateTimeDistance Run66 Bike25525(5) tt tt
Thetotaldistanceis87miles: 625(5)87 61252587 1912587 1938 2 tt tt
Thetimespentrunningis2hours,sothe distanceoftherunis6(2)12 miles.The distanceofthebicycleraceis25(52)75 miles.
Thetotaldistanceis246miles: 66(5)246 6630246 1230246 12216 18 rr rr r r r
Thespeedoftheeastboundcyclistis18miles perhour,andthespeedofthewestboundcyclist is18523 milesperhour.
55. Burke'srateis10012meters/sec.In9.81seconds, Burkewillrun100(9.81)81.75 12 meters.Bolt wouldwinby100-81.75=18.25meters.
56. 2 22 A rrh .Since58.9 A square inchesand6.4 h inches, 2 2 2 22(6.4)58.9 212.858.90 212.858.90 rr rr rr 2 12.8(12.8)4(2)(58.9) 2(2) 12.8635.04 4 3.1or9.5 r rr . Theradiusofthecoffeecanis3.1inches.
57.Lettheindividualtimestocompletetheproject beEforElaine,BforBrian,andDforeither daughter.Usingtherespectiveratesgives 1111111 , 22 EBEDD (or121 2 ED ), and111 4 BD .Fromthefirsttwoequations, 12 BD .Substitutingintothethirdequation gives211 4 DD or 3112hours. 4 D D Then1213hours 122 E E and
Chapter 1: Graphs, Equations, and Inequalities
1116hours. 124 B B Thecombinedrate ofElaine,Brian,andoneoftheirdaughtersis 1117 361212
projectperhour,soitwilltake them127hourstocompletetheproject.
58. If x =litersoforiginalsolution,thentherewere originally0.2x litersofsaltand0.8litersofpure water.Overtime,thesolutionloses
0.25(0.8)0.2 x x litersofpurewater.Sheadds 20litersofsaltsothetotalamountofsaltis 0.220 x liters.Shealsoadds10litersofpure water,sothetotalamountofpurewateris 0.80.2100.610 xxx liters.Theresulting concentrationis331/3%whichmeans 0.22010.2201 or 0.2200.61030.8303
xx xxx or 0.6600.830150 xxx .Therewere initially150litersofsolutioninthevat.
59. Thespeedofthetrainrelativetothemanis30–4=26milesperhour.Thetimeis 5551 secminhh. 603600720
Thefreighttrainisabout190.67feetlong.
60. Answerswillvary.
61. Let x betheoriginalsellingpriceoftheshirt. ProfitRevenueCost 40.4020240.6040 xxxx
Theoriginalpriceshouldbe$40toensurea profitof$4afterthesale.
Ifthesaleis50%off,theprofitis: 400.50(40)204020200
At50%offtherewillbenoprofit.
62. Let12 and tt representthetimesforthetwo segmentsofthetrip.SinceAtlantaishalfway betweenChicagoandMiami,thedistancesare equal.
TheaveragespeedforthetripfromChicagoto Miamiis49.5milesperhour.
63. Thetimetraveledwiththetailwindwas: 9191.67091hours 550 t
Sincetheywere20minutes 1 3hourearly,the timeinstillairwouldhavebeen:
1.67091hrs20min1.670910.33333hrs 2.00424hrs
Thus,withnowind,thegroundspeedis 919458.53 2.00424 .Therefore,thetailwindis 550458.5391.47knots
64. Itisimpossibletomixtwosolutionswitha lowerconcentrationandendupwithanew solutionwithahigherconcentration.
AlgebraicSolution: Let x =thenumberoflitersof25%solution.
Section 1.7
1. 2 x
2. True;theabsolutevalueofanumberisthe distancethenumberliesfrom0onarealnumber line.Negativenumberslietotheleftof0ona realnumberline,butstillhaveapositive distancefrom0.
3. ,,,,,,, A Babcdeiou
4. negative
5. closedinterval
6. aua
7. (,] a
8. True;thisfollowsfromtheadditionpropertyfor inequalities.
9. True;thisfollowsfromthemultiplication propertyforinequalities.
10. False;sincebothsidesoftheinequalityarebeing dividedbyanegativenumber,thesense,or direction,oftheinequalitymustbereversed. Thatis, ab cc
11. a
12. c
Section 1.7: Solving Inequalities
13. Interval: 0,2 Inequality:02 x
14. Interval: 1,2
Inequality:12 x
15. Interval: 2, Inequality:2 x
16. Interval: ,0 Inequality:0 x
17. Interval: 0,3 Inequality:03 x
18. Interval: 1,1 Inequality:11 x
19. a. 35 3353 68
b. 35 3555 20
c. 35 3335 915
d. 35 2325 610
20. a. 21 2313 54
b. 21 2515 34
c. 21 3231 63
Chapter 1: Equations and Inequalities
21 2221 42
21. a. 212 21323 245 x x x
b. 212 21525 243 x x x
c.
d.
212 32132 636 x x x
212 22122 424 x x x
22. a. 125 12353 428 x x x
b. 125 12555 240 x x x
c. 125 31235 3615 x x x
d. 125 21225 2410 x x x
23. [0,4]
24. (–1,5)
25. [4,6)
41. If4,then40. xx
42. If6,then60. xx
43. If4,then312. xx
44. If3,then26. xx
45. If6,then212. xx
46. If2,then48. xx
47. If840,then5. xx
48. If312,then4. xx
49. If13,then6. 2 xx
50. If11,then4. 4 xx
51. 372 39 3 x x x 3or(3,) xx
52. 251 24 2 x x x 2or(2,) xx
53. 3518 515 3 x x x 3or[3,) xx
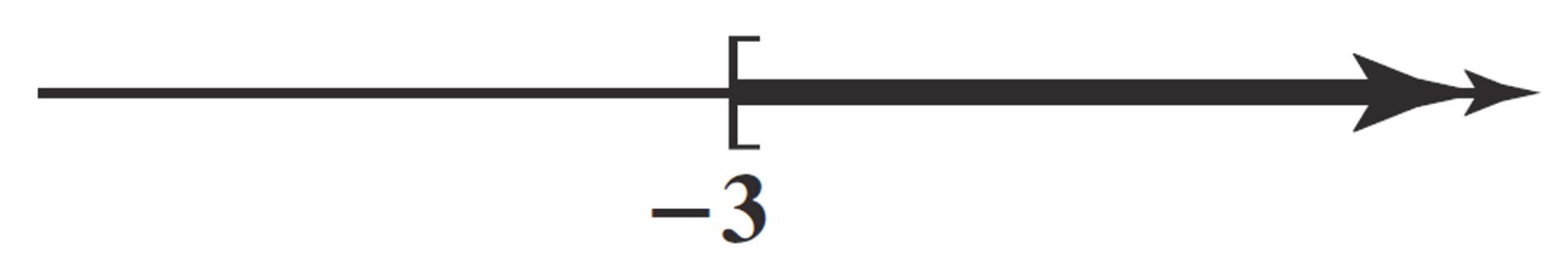
54. 235 33 1 x x x 1or[1,) xx
55. 313 24 2 x x x x
Section 1.7: Solving Inequalities
2or[2,) xx
56. 223 5 x x x
5or[5,) xx
57. 2(3)8 268 214 7 x x x x
7or(7,) xx
58. 3(1)12 3312 315 5 x x x x 5or(,5) xx
59. 43(1)3 4333 313 32 2 3 x x x x x 22 or, 33 xx
2 3
Chapter 1: Equations and Inequalities
60. 84(2)2 8842 42 60 0 x x x x x x x x
65. 5432 932 32 3 x x x
223or,333 xx
61. 1(4)8 2
62. 1 34(2) 3 3412 33 9122 814 7 4 xx xx xx
33or3,3xx
67. 21 30 4 12210 1121 111 22 x x x x
111111 or, 2222 xx
1 2 11 2
68. 32 04 2 0328 236 22 3 x x x x
63. 1375 6312 24
x x x
xx 64. 42210 228 14 x x x
44or2,4

222or,233 xx
2 3
69. 1 114 2 1 03 2
06or60 x x xx
70. 1 011 3 1 10 3 30or03 x x xx
03or0,3xx
71. 22 (2)(3)(1)(1) 61 61 5 5 xxxx xxx x x x
5or,5 xx
72. 22 (1)(1)(3)(4) 112 112 11 11 xxxx xxx x x x
11or,11 xx
73. 28 x 828 44 x x 44or4,4xx
74. 315 x 15315 55 x x
55or5,5xx
75. 742 x 742or742 6or6 xx xx
Section 1.7: Solving Inequalities
6or6or,66, xxx

76. 26 x 26or26 3or3 xx xx 3or3or,33,xxx
77. 324 t 4324 236 22 3 t t t 222or,233 tt
2 3
78. 257 u 7257 1222 61 u u u 61or6,1uu
79. 223 21 x x 121 13 x x 13or1,3xx
80. 435 42 x x 242 62 x x 62or6,2xx
Chapter 1: Equations and Inequalities
81. 32 x 32or32 1or5 xx xx
82. 42 x 42or42 6or2 xx xx
83. 527 527
33 122 or1, xx
3 2
86. 1241 123 x x 3123 422 42 22 21or12 x x x xx
12or1,2xx
87. 952 x Nosolutionsinceabsolutevalueisalwaysnonnegative.

1or6or,16, xxx 84. 231 231 x x
231or231 33or31 11 or 3 xx xx xx
11or1or,1,33 xxx
88. 340 x Allrealnumberssinceabsolutevalueisalways non-negative.
or, xx
89. 3411 48 2 x x x
|2xx or 2,
90. 137 36 2 x x x |2xx or 2,
335 244 335 444 244 635 38 x x x x
2 22 4321 43441 1 1 xxx x xxx x x
2 22 9531 95961 561 1 xxx x xxx xx
Chapter 1: Equations and Inequalities
99. 1 327 2 1 39 2 x x 11 39 22 1719 3 22 1719 66 x x x
1719 |66xx
or 1719 , 66
17 6 19 6 100. 1 4111 4 1 412 4 x x
11 412 44 4749 4 44 4749 1616 x x x
4749 |1616xx
or 4749 , 1616
49 16 47 16 101. 35211 826 43 34 x x x x
|34xx or 3,4
102. 23218 23228 2128 127 17 22 71 22 x x x x x x
71 |22xx
7 2 1 2
103. 714 13 13 313 24 x x x x x
|24xx or 2,4
104. 935 34 34 434 71 x x x x x
|71xx
or7,1
105. 352 x x 35 8 8 x x x
and52 5 5 x x x x Weneedboth8 x and5 x .Therefore, 5 x issufficienttosatisfybothinequalities. |5xx or 5,
106. 232 x x 23 5 5 x x x and32 3 3 x x x x
Weneedboth5 x and3 x .Therefore, 5 x issufficienttosatisfybothinequalities.
|5xx or 5,
107. 2215 x xx 221 21 3 3 x x x x x
and215 310 31 1 3 x x x x x
Weneedboth1 3 x and3 x .Therefore, 3 x issufficienttosatisfybothinequalities.
|3xx or 3,
108. 213557 xxx 2135 15 6 6 x x x x x and3557 257 212 6 xx x x x
Weneedboth6 x and6 x .Therefore, 6 x issufficienttosatisfybothinequalities.
|6xx or 6,
109. 20.5 x 0.520.5 0.520.52 1.52.5 x x x
Solutionset:1.52.5 xx
110. 11 x 111 111 1111 20 x x x x
Solutionset:20 xx
111. 32 x 32or32 32or32 5or1 xx xx xx
Solutionset:5or1 xxx
112. 23 x 23or23 1or5 xx xx
Solutionset:1or5 xxx
113. 21<youngadult'sage<30
114. 40 ≤ middle-aged<60
115. Atemperature x thatdiffersfrom98.6 Fbyat least1.5F .
98.61.5
98.61.5or98.61.5
97.1or100.1 x xx xx
Thetemperaturesthatareconsideredunhealthy arethosethatarelessthan97.1˚Forgreaterthan 100.1˚F,inclusive.
116. ThelengthLmustbewithin0.0025of5.375 inches..
5.3750.0025
0.00255.3750.0025
5.37255.3775
Thelengthsmustbebetween5.3725and5.3775 inches,inclusive.
117. Thepercentagemustbewithin3.9percentage pointsof64percent.Theinequalitythat representsthiswouldbe:
643.9
3.9643.9 60.167.9 x x x
Theactualpercentageislikelytofallbetween 60.1%and67.9%inclusive.
118. Thespeed x variesfrom707mphbyupto55 mph.
a. 70755 x
Chapter 1: Equations and Inequalities
b. 5570755 5570755 652762 x x x
Thespeedofsoundisbetween652and762 milesperhour,dependingonconditions.
119. a. Let x =ageatdeath.
122. Let C representthecommission. Calculatethecommissionrange: 250.4(200)250.4(3000) 1051225 C C
Thecommissionsareatleast$105andatmost $1225.
3051.7
81.7 x x
Therefore,theaveragelifeexpectancyfora 30-year-oldmalein2019willbegreater thanorequalto81.7years.
b. Let x =ageatdeath.
123. Let W =weeklywagesand T =taxwithheld. Calculatingthewithholdingtaxrange,giventhe rangeofweeklywages:
3055.5
85.5 x x
Therefore,theaveragelifeexpectancyfora 30-year-oldfemalein2019willbegreater thanorequalto85.5years.
c. Bythegiveninformation,afemalecan expecttolive85.581.73.8 yearslonger.
120. 20 VT
80º120º
80º120º 20 16002400 T V V
Thevolumerangesfrom1600to2400cubic centimeters,inclusive.
121. Let P representthesellingpriceand C representthecommission. Calculatingthecommission:
45,0000.25(900,000)
45,0000.25225,000
0.25180,000
P P
Calculatethecommissionrange,giventheprice range:
225,000180,0000.25180,000275,000180,000 900,0001,100,000
0.25(900,000)0.250.25(1,100,000) 225,0000.25275,000
45,00095,000 P P P P C
Theagent'scommissionrangesfrom$45,000to $95,000,inclusive.
45,000 900,000 0.055% to95,0001,100,0000.0868.6%, inclusive.
Asapercentofsellingprice,thecommission rangesfrom5%to8.6%,inclusive.
14.9687.340.2283287.3458.9687.34 9001100 9008328321100832 68832268
0.22(68)0.228320.22(268) 14.960.2283258.96 102.3146.3
W W W W W W T
Theamountwithheldvariesfrom$102.30to $146.30,inclusive.
124. Let x representthelengthoftimeSueshould exerciseontheseventhday. 20040450502535300 200195300 5105 x x x
SuewillstaywithintheACSMguidelinesby exercisingfrom5to105minutes.
125. Let K representthemonthlyusageinkilowatthoursandlet C representthemonthlycustomer bill.
Calculatingthebill:0.093630 CK
Calculatingtherangeofkilowatt-hours,given therangeofbills: 137.64221.88
137.64300.0936221.88
107.640.0936191.88 11502050
C W K K
Theusagevariesfrom1150.00kilowatt-hoursto 2050.00kilowatt-hours,inclusive.
126. Let W representtheamountofsewer/waterused (inthousandsofgallons).Let C representthe customercharge(indollars).
Calculatingthecharge: 23.550.40 CW
Calculatingtherangeofwaterusage,giventhe rangeofcharges:
30.3536.75
30.3523.550.4036.75 6.80.4013.2 1733
Therangeofwaterusagerangedfrom17,000to 33,000gallons.
127. Youhavealreadyconsumed21gramsoffat. LetCrepresentthenumberofcookies.Thenwe havethefollowingequation: 21546 525 5
Youmayeatupto5cookiesandkeepthetotal fatcontentofyourmealnotmorethan46g.
128. Youhavealreadyconsumed150gramsof sodium.Let H representthenumberof hamburgers.Thenwehavethefollowing equation: 1503801290 3801140 3
Youmayeatupto3hamburgersandkeepthe totalsodiumcontentofyourmealnotmorethan 1290g.
129. a. Let T representthescoreonthelasttestand G representthecoursegrade.
Calculatingthecoursegradeandsolvingfor thelasttest: 68828789 5 326 5 5326 5326 T G T G GT TG
Calculatingtherangeofscoresonthelast test,giventhegraderange: 8090 4005450 745326124 74124 G G G T
TogetagradeofB,youneedatleasta74 onthefifthtest.
b. Let T representthescoreonthelasttestand G representthecoursegrade. Calculatingthecoursegradeandsolvingfor thelasttest:
688287892 6 3262 6 163 3 3163 T G T G T G TG
Calculatingtherangeofscoresonthelast test,giventhegraderange: 8090 2403270 773163107 77107 G G G T
TogetagradeofB,youneedatleasta77 onthefifthtest.
130. Let T representthetestscoresofthepeoplein thetop2.5%. 1.96(12)100123.52 T Peopleinthetop2.5%willhavetestscores greaterthan123.52.Thatis,123.52 T or (123.52,).
131. Since ab , and 2222 and 22222222 and 22 abab aaababbb abab ab
So,2ab ab .
132. Fromproblem131,2ab ab ,so 2 ,2222 daaababababa and 2 ,2222 dbbababbabba Therefore,2ab isequidistantfrom a and b.
133. If0,then ab
22 22 22 0and0 and and ababab ababab ababab
Therefore, aabb
Chapter 1: Equations and Inequalities
134. Showthat 2 ab ab
2 12 22 10,since. 2 ab abaabb abab
135. For1111 0,2 ab hab
11 2 11 2 2 ba hh hab ba h ab ab h ab
22() 2 ()0 abaab ab haa abab abaababa abab aba ab
22
Therefore, ha
22 2()2 2 ()0 babab ab bhb abab abbabbab abab bba ab
Therefore, hb
,andwehave ahb
136. Showthat
2 (geometric2 mean) arithmeticmean1() 2 ab
2 1111 2 211 2 2 1() 2 hab ba habab hab ab ab ab h ab ab
137. 4235 3 312695 31269and695 33514 114 4
Thisisequivalentto14 1 5 x .Thesolution set,inintervalnotation,is14 1,5
138. Thelargestvalueof223 x occursatthelargest valuefor x 259 34 43 34or43
x x x xx
Thelargestvaluefor223 x is 2 2(4)332329 .
139. Answerswillvary.Onepossibility: Nosolution: 46252 x xx Onesolution: 35231321 xxx
140. Answerswillvary.
141. Since20 x ,wehave 2 2 101 11 x x Therefore,theexpression21 x canneverbe lessthan5
142. Answerswillvary.
Chapter 1 Review Exercises
Chapter 1 Review Exercises
1. 28 3 624 18 x x x
Thesolutionsetis 18
2. 2(53)845 106845 6245 6 x x x x x x x
Thesolutionsetis 6
3. 1 5 31 4312 941 51 xx xx x x
Thesolutionsetis 1 5
4. 6 15 566 6 x x xx x
Since x =6doesnotcauseadenominatorto equalzero,thesolutionsetis{6}.
5. 2 2 (1)6 6 06 xx xx xx
2241416 12423 bac
Therefore,therearenorealsolutions.
6. 1361 432 1361 1212 432 3(13)4(6)6 394246 1327 27 13 xx xx xx xx x x
Thesolutionsetis 27 13 7. 2 2 (1)(23)3 233 260 (23)(2)03or2 2 xx xx xx xxxx
Thesolutionsetis 2,3 2 8. 2 2 234 0423 2448252 88 2213113 84 xx xx x
Thesolutionsetis113113 , 44
9.
32 333 2 2 2 12 12 18 93 x x x xx
Check:3 x Check:3 x
32 3 3 312 912 82 22
Thesolutionsetis 3,3
10. 2 (1)20 20 11817 22 xx xx x Norealsolutions.
11. 2 310 1112111 66 xx x Norealsolutions.
Chapter 1: Equations and Inequalities
12.
42 22 22 540 410 40or10 2or1 xx xx xx xx
Thesolutionsetis 2,1,1,2
13. 2 2 233 233 2396 8120(2)(6)0 2or6 xx xx xxx xxxx xx
Check2: 2(2)32123
Check6: 2(6)369693 x x
Thesolutionsetis 2 14.
4 444 232 232 2316 213 13 2 x x x x x
444
Check13: 2 13 23133162 2 x
Thesolutionsetis
22 +1121 +1121 12+11121 22+1121 2+111 xxx xxx xxxxx xxxx xx
Check5: 2 555 +1121 222 1.798907439951.79890743995
Check5: 2 555 +1121, 222 x x
Thesecondsolutionisnotpossiblebecauseit makestheradicandnegative.
Thesolutionsetis5
Thesolutionsetis
19.
Thesolutionsetis
222 222 102360 5180 5920 axabxb axabxb axbaxb
590 59 9 5 axb axb b x a or20 2 2 axb axb b x a
Check1:
20.
Thesolutionsetis 92 5,,0. bb a aa
22 22 22 22 222 2 373920 37392 37392 37394394 66439 xxxx xxxx xxxx xxxxxx xxx
22 2 22 22 61439 36211639 3672361648144 xxx xxxx xxxx
2 2 20241080 56270 59309or3 5 xx xx xxxx
Chapter 1: Equations and Inequalities
Check9:
Thesolutionsetis{–5,2}.
22. 2329 237 x x
237 35 5 3 x x x
23.
or237 39 3 x x x
Thesolutionsetis 5,3 3
32 32 2 2 23 230 230 00 2303 2 xx xx xx xx xx
Thesolutionsetis 0,3 2
24.
32 2 2 2 258200 254250 2540 250or40 5or2 2 xxx xxx xx xx xx
Thesolutionsetis 5,2,2 2
25.
2 1311 122 23111 1212 23111 23311 4111 412 3 xx xx xx xxxx xx xx x x x
Since3doesnotmakeanydenominatorequalto 0,thesolutionsetis 3
26. 2 29 29 23 23 x x x x 5 x or1 x
Thesolutionsetis 1,5.
27. 3530xx UsetheZerooptionfromtheCALCmenu.
Thesolutionsetis 2.49,0.66,1.83.
28. 4321 x x UsetheIntersectoptionontheCALCmenu.
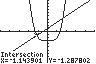
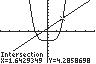
Thesolutionsetis 1.14,1.64
29. 23 2 52
2(23)10(2)5 46205 14 14 x x x x x x x x

30. 23 97 4 362328 33231 3331 22 3133 22 x x x x x
31333133 or, 2222 xx

31. 33 26 12 243372 21369 723 x x x x
237or23,7xx

32. 1 34 2 11 34 22 97 3 22 37 26 x x x x
3737 or, 2626

Chapter 1: Equations and Inequalities
38. 2 3339393 33310 933 93 1010 iii iii iii i
39.


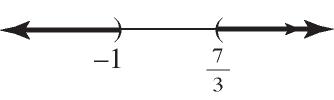
40.
12 504824212111 iiiii
32 2 2 232323 412923 51223 10152436 469 iii iii ii iii i
41. 210xx
22 1,1,1, 41411143 131313 21222 abc bac i x i
Thesolutionsetis 1313 , 2222 ii
42. 2 220 xx
22 2,1,2, 4142211617 117117 224 abc bac x
Thesolutionsetis 117117 , 44
43. 23 x x
2 22 30 1,1,3, 4141311211 111111111 21222 xx abc bac i x i
Thesolutionsetis 111111 , 2222 ii
44. (1)2xx 220 (2)(1)02or1 xx xxxx
Thesolutionsetis
45. 215 yx
46. 4,0,0,0,2,0 , 0,2,0,0,0,2 x-intercepts:4,0,2 y-intercepts:2,0,2
47. 236 326 22 3 xy yx yx
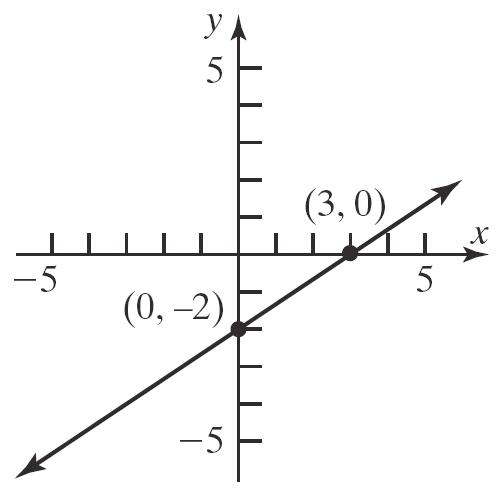
48. 29 yx
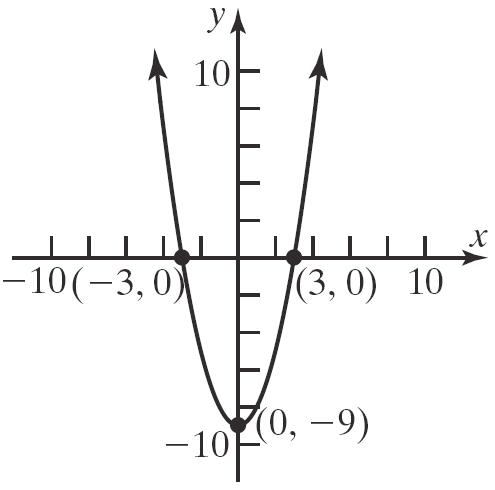
49. 2 2 2 216 216 18 2 xy yx yx
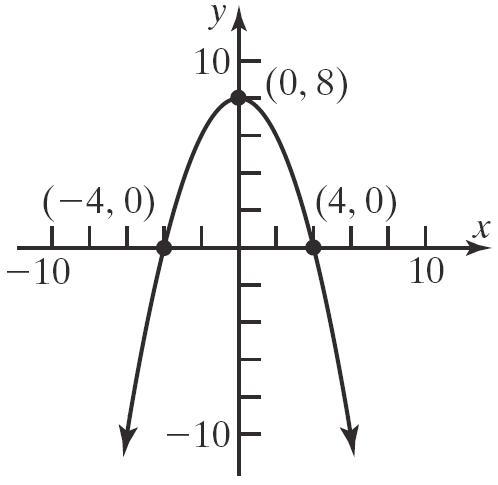
50. 22 plw 51.
90000.071$630
52. Let x representtheamountofmoneyinvestedin bonds.Then70,000 x representstheamount ofmoneyinvestedinCD's. Sincethetotalinterestistobe$5000,wehave:
Chapter 1: Equations and Inequalities
0.080.05(70,000)5000
1000.080.05(70,000)5000100
$50,000shouldbeinvestedinbondsat8%and $20,000shouldbeinvestedinCD'sat5%.
53. Using s vt ,wehave3and1100 tv .
Findingthedistance s infeet: 1100(3)3300 s Thestormis3300feetaway.
54. 16003600 I
RaftHelicopter Rate590 Time Dist.590 tt tt
Sincethetotaldistanceis150miles,wehave: 590150 95150 1.58hours1hourand35minutes tt t t
Thehelicopterwillreachtheraftinabout1hour and35minutes.
57. Let d representthedistanceflownbythebee travelingat3meterspersecond.
(Timesneededtomeetareequal.) 150 35 54503 8450
56.25 56.25meters18.75seconds 3 dd dd d dt
Thebeesmeetforthefirsttimeafter18.75 seconds.
Therangeofdistancesisfrom0.5metersto0.75 meters,inclusive.
55. Let s representthedistancetheplanecantravel. 22 WithwindAgainstwind
Rate2503028025030220 Time(/2)(/2) 280220
Dist. ss ss
Sincethetotaltimeisatmost5hours,wehave:
/2/2 5 280220 5 560440 11145(6160) 2530,800 1232 ss ss ss s s
Theplanecantravelatmost1232milesor616 milesonewayandreturn616miles.
56. Let t representthetimeittakesthehelicopterto reachtheraft.
Thebeeswillmeetasecondtimeonthesecond lap.Thefirstbeewillhavetraveled 150+ x metersandthesecondbeewillhave traveled150+(150– x)meters. Solvingfortime,wehave: 150150(150) 35 150300 35 75059003 8150 18.75metersintothesecondlap 168.7556.25seconds 3 x x xx xx x x t
Thebeesmeetthesecondtimeafter56.25 seconds(37.5secondslater).
58. Giventhat2 12803216 s tt , a. Theobjecthitsthegroundwhen0 s
2 2 012803216 2800 108010,8 tt tt tttt
Theobjecthitsthegroundafter8seconds. b. After4seconds,theobject’sheightis 2 1280324164896 s feet.
59. Let t representthetimeittakesClarissato completethejobbyherself.
ClarissaShawna Timetodo5 jobalone Partofjob11 done5 in1day Timeonjob66 (days) Partofjob66 donebyeach5 person
Sincethetwopeoplepaintonehouse,wehave:
x
62. Letthelengthofleg1= x. Thenthelengthofleg2=17– x BythePythagoreanTheoremwehave
222 22 2 2 1713 34289169 2341200 17600 125012or5 xx xxx xx xx xxxx
thelegsare5cmand12cmlong.
63. a. Considerthefollowingdiagram:
IttakesClarissa10daystopaintthehousewhen workingbyherself.
60. Let x representtheamountofthe$8-per-pound coffee.
4650
Thepaintingis6.5inchesby6.5inches. 612.5 s ,sotheframeis12.5inchesby 12.5inches.
b. Considerthefollowingdiagram: w
Add263poundsof$8/lbcoffeetoget2 263 poundsof$5/lbcoffee.
61. Let x representtheamountofwaterevaporated.
12 33 41221250 626 26428 6 ww w wlw
Thepaintingis283inchesby143inches. Theframeis2143inchesby1103inches.
Chapter 1: Equations and Inequalities
64. Let t representthetimeittakesthesmaller pumptofinishfillingthetank. 3hpPump8hpPump Timetodo128 jobalone Partofjob11 done128 in1hr Timeonjob44 (hrs) Partofjob44 donebyeach128 pump
Sincethetwopumpsfillonetank,wehave: 441
Ittakesthesmallpumpatotalof2more hourstofillthetank.
65. Let4 w .Solveforthelength:
Thelengthoftheplasterboardshouldbecut toalengthofapproximately6.47feet.
66. Let x representthenumberofpassengersover 20.Then20 x representsthetotalnumberof passengers,and150.1x representsthefarefor eachpassenger.Solvingtheequationfortotal cost,$482.40,wehave:
the114.Therefore,201636 peoplewenton thetrip;eachpersonpaid 150.116$13.40 .
67. Let rS representScott'srateandlet rT represent Todd'srate.ThetimeforScotttorun95meters isthesameasforToddtorun100meters.
95100
0.95 0.950.95 ST ST SsTT rr rr dtrtrd
IfToddstartsfrom5metersbehindthestart: 105
0.950.95(105)99.75 T ST d dd
a. Theracedoesnotendinatie.
b. Toddwinstherace.
c. Toddwinsby0.25meters.
d. Toendinatie: 1000.95(100) 100950.95
50.95 5.263meters x x x x
e. 95=0.95(100)Therefore,theraceendsina tie.
f,g,h. Raceisatie.
68. Ineachproblem,weneedtousetheLeast CommonMultipleoftheexpressions 22and4xx ,namely24. x
a. Weuse24 x astheLCDinorderto combinethegivenexpressions.
b. Wemultiplyeachsideoftheequationby 24 x inordertoclearoutthe denominatorsbeforesolvingtheequation.
c. Weuse24 x astheLCDinorderto combinethetermsonthelefthandside beforesolvingtheinequality.
Sincethecapacityofthebusis44,wediscard
Chapter 1 Test
1.
2.
Sinceneithersolutionisarestrictedvalue,the solutionsetis
4. 58416 58446 58410 918 2 xx xx xx x x
Thesolutionsetis 2. 5. 53278 53215 323 b b b
323 20 0 b b b or323 26 3 b b b
Thesolutionsetis 0,3.
6. 422 42 38 280 xxx xx
Let2 ux .Then 2 224 uxx ,andwehave
2280 420 uu uu
4or2uu
Sincewearesolvingfor x,weget 24 2 x x or 22 2 norealsolution x x
Thesolutionsetis 2,2.
7. 2420 1,4,2 xx abc 2 2 4 2 44412 21 4168 2 48 2 422 2 22 bbac x a
Thesolutionsetis 22,22
Chapter 1: Equations and Inequalities
8. 2 22 2 2172 2172 630 xxxx xxxx xx
Thesolutionsetis
9. 2721 7221 23 7 xy yx yx
2 7 2 7 2 7 3, 77357,5 00330,3 2 77317,1 7 x yxxy y y y
Theinterceptsare
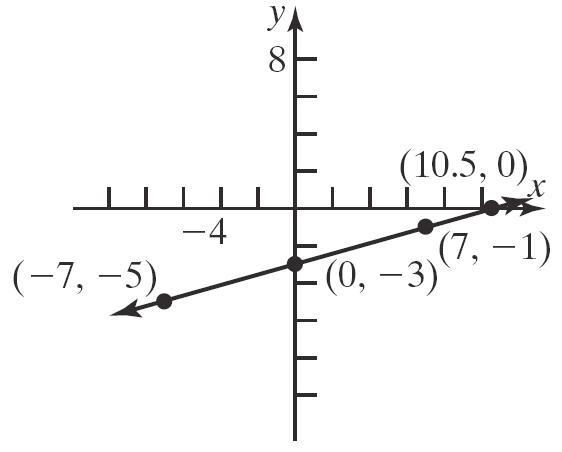
2 2 2 2 2 2 5, 33543,4 11541,4 00550,5 11541,4 33543,4 x yxxy y y y y y
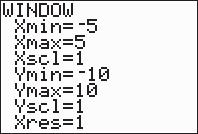
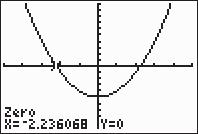
Theinterceptsare
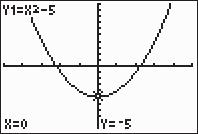
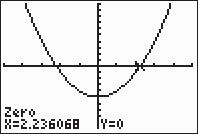
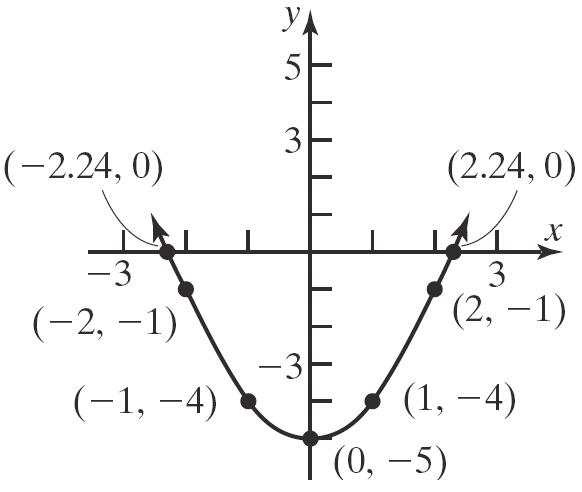
11. 32 2210 xxx Sincethisequationhas0ononeside,wewill usetheZerooptionfromtheCALCmenu.Itwill beimportanttocarefullyselectthewindow settingssoasnottomissanysolutions.
Thesolutionstotheequationare1,0.5,and1.
12. 42580xx
Sincethisequationhas0ononeside,wewill usetheZerooptionfromtheCALCmenu.
Thesolutions,roundedtotwodecimalplaces, are2.50and2.50.
13. 327233xxxx
Sincetherearenonzeroexpressionsonboth sidesoftheequation,wewillusetheIntersect optionfromtheCALCmenu.Entertheleftside oftheequationinY1andtherightsideinY2.
15. 2343 234434 237 x x x
237 210 5 x x x or237 24 2 x x x
Solutionset: |5or2xxx
Interval: ,52,
16. 7358 7335383 1055 1055 555 21 12 x x x x x x
Solutionset: |12xx
Interval:
1,2
Thesolutions,roundedtotwodecimalplaces, are2.46,0.24,and1.70
14.
17. 348 8348 1234 44 3 x x x x
44 3 xx
or 4,4 3
4 3
18. 237411614411 641411 225 iiii ii i
19. 2 310838108 2438010 2483101 1483 iiiii iii i i
22. Wecanuseatabletosummarizethegiven information. minutesper#ofcust.in
Since8565204.63 27 ,itwilltakeJamieand Scottabout204.63minutes(3.41hours)tocheck out65customersworkingtogether.
23. Let x =poundsofbananachips.Thenthetotal poundsofthemixwillbe40 x Sincethereistobenolossinrevenue,weget
newcher. newmixbananacherrymix ban. pricelbspricelbspricelbs 4100 25 revenuerevenuerevenue 6.75402.759.2540 6.752702.75370
Theretailerneedstomix25poundsofbanana chipswiththe40poundsoftheoriginalmix.
24. Let x =saleprice.Weknowthatthediscountis 0.42275.00115.50 .Therefore, salepriceoriginalpricediscount 275115.50 159.50 x x
Thesalepriceis$159.50.
25. Hereweneedthesimpleinterestformula, I Prt .Inthiscasewehave0.04 r , 3months1 12yr months/yr4 t ,and10,000 P 1 10,0000.044 100
IPrt Glennwillearn$100.00ininterestafter3 months.
Chapter 1 Projects
Project I
Internet-based Project
Project II
1. ,3,5,1,0.2 331 0.23510.660.22 n TnLMC CnpLM T ppp
2. Allofthetimesgiveninproblem1werein seconds,so T =0.1boardpersecondneedsto usedasthevaluefor T intheequationfoundin problem1.
3. T =0.15boardpersecond
Thus,only23partsperboardwillwork.
Forproblems4–6, C isrequested,sosolvefor C first:
n T CnpLM CnpLMTn CnpTLTMTn CnpTnLTMT
4. T =0.06, n =3, p =100, M =1, L =5
350.0610.06 0.147sec 31000.06 C
5. T =0.06, n =3, p =150, M =1, L =5
350.0610.06 0.098sec 31500.06 C
6. T =0.06, n =3, p =200, M =1, L =5
350.0610.06 0.073sec 32000.06 C
7. Asthenumberofpartsperboardincreases,the tacttimedecreases,ifalltheotherfactorsremain constant.