Chapter 1
EQUATIONS AND INEQUALITIES
Section 1.1 Linear Equations
1. Anequationisastatementthattwo expressionsareequal.
2. Tosolveanequationmeanstofindall numbersthatmaketheequationatrue statement.
3. Alinearequationisafirst-degreeequation becausethegreatestdegreeofthevariableis 1.
4. Anidentityisanequationsatisfiedbyevery numberthatisameaningfulreplacementfor thevariable.
5. Acontradictionisanequationthathasno solution.
6. True.Replacing x with8in253 xx yieldsatruestatement.Therefore,thegiven statementistrue.
7. True.Theleftsidecanbewrittenas
5858558 540540,
whichisthesameastherightside.Therefore, thestatementisanidentity.
8. False.If x =0,thentheequationistrue.A contradictionisfalseforallvaluesof x
9. False.Solvingtheliteralequation 1 2 Abh for h gives 1 2 2 2 Abh Abh A h b
10. Bcannotbewrittenintheform0. axb Acanbewrittenas1570or x
1570, x Ccanbewrittenas 20or200, xx andDcanbewrittenas 0.040.40or x 0.040.40. x
11. 5434 244 284 xx x xx
Solutionset: 4
12. 91171 2111 2105 xx x xx
Solutionset: 5
13. 63181014 18681014 1862210 28622 28281 xx xx xx x xx
Solutionset: 1
14.
421624 84624 84102 4106 661 xx xx xx x xx Solutionset: 1
15. 545 2 633 545 626 633 512810 7810 2 72 7 xx xx xx x xx
Solutionset: 2 7
16. 7134 4525 7134 2020 4525 3543016 4516 5 512 12 xx xx xx xx xx
Solutionset: 5 12
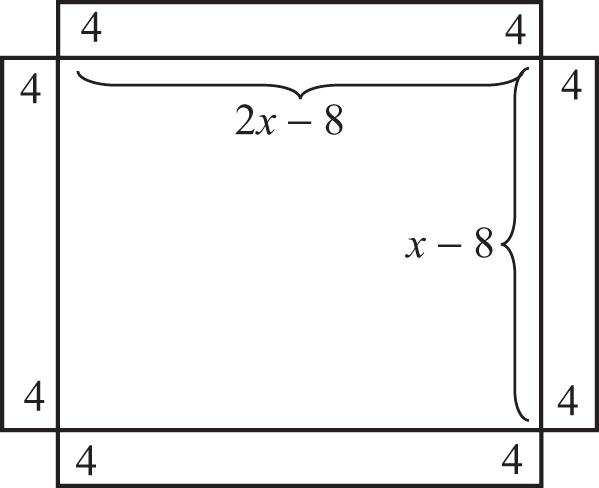
17.
355167 355567 267 77 87 88 xxx xxx xx xx
Solutionset: 7 8
18.
5343242 51543242 91226 11126 66 116 1111 xxx xxx xx x xx
Solutionset:
6 11
19.
242322 242322 2122 2222 242 44 1 xxx xxx xx xx x x x
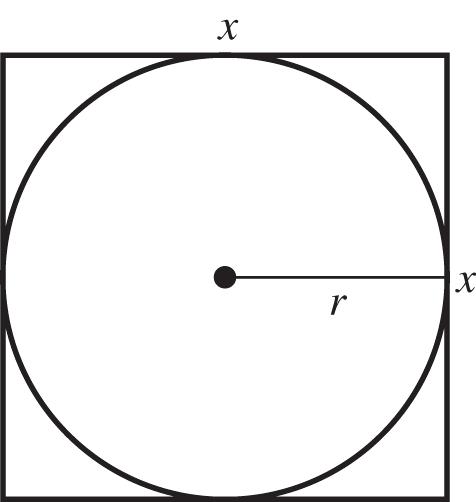
Solutionset:{1}
20.
21.
Solutionset:{2}
110 32 1410 110 703270 1410 532710 1510770 81070 88010 x x x x xx xx x xx
Solutionset:{10}
22.
12 25 159 12 452545 159 32552 615510 15105 x x x x xx xx xx
Solutionset:{5}
23. 0.20.50.17 100.20.5100.17 2570 570 75 xx xx xx x x Solutionset:{75}
24. 0.013.12.032.96 1000.013.11002.032.96 310203296 310202296 6062023 xx xx xx x xx Solutionset: 3
25.
4268524 8248624 24624 060 xxxx xxx x xx
Solutionset: 0
26. 8346484 243264324 1832832 322632 0260 xxxx xxxx xx x xx
Solutionset: 0
27. 4 0.510 3 14 10 23 14 6610 23 38660 11660 56012 xxx xxx xxx xxx xx xx
Solutionset: 12
28.
2 0.252 3 21 2 34 21 12122 34 831224 111224 2424 xxx xxx xxx xxx xx xx
Solutionset: 24
29.
30.
Solutionset: 50
Solutionset: 20
31.
427222322 82822266 828828 282800 xxx xxx xx
32. 1 620423 2 310426 310310 101000 xxx xxx xx
identity; allrealnumbers
33. 28316 216316 16160 xx xx xx
conditionalequation; 0
34.
85858 8408540 8401340 54040 50 0 xxx xxx xx x x x
conditionalequation;{0}
35.
4721221 42822422 428426 2826 xxx xxx xx
contradiction;
36.
contradiction;
62134151 126312151 156151 61 xxx xxx xx
0.320.520.20.4 100.320.52100.20.4 325224 3651024 2424 00 xxx xxx xxx xxx xx
100.650.86100.21.8 6586218 630848218 218218 00 xxx xxx xxx xxx xx
39. Vlwh Vlwh whwh lV wh
41. Pabc Pabc cPab
42. 22 22 22 22 2 22 Plw Plw Plw PlP wl
43.
1 2 1 22 2 2 2 2 2 22 hBb hBb hBb Bhbh bhBh bhBh hh bh Bb hh
49.
51. 3 33 33 33 3 3 3 3 axbxa axbxa abxax abax ab x a ab x a
53.
52. 43 43 43 43 43 aaxbbx abbxax abbax ab x ba ab x ba
2 2 2 2 2 3 1 113 1 33 33 331 33 1 33 1 x ax a x aaax a xaxaax aaxaxx aaax a x aa a x aa
55.
xaa aa x aa
22 22 2 2 32 32 2 3 axxa axa a x a
56.
22 22 22 22 22 axbbxa abbxax abbax ab x ba ab x ba
3214 3284 425 425 4 25 4 25 xxm xxmxm mxmx mmx m x m m x m
58.
59. (a) Here, r =0.04, P =3150,and 61(year).
Theinterestis$63.
(b) TheamountMiguelmustpayJulioatthe endofthesixmonthsis
$3150+$63=$3213.
60. (a) Here, r =0.055, P =30,900,and 183(year). 122 t
Shemustpaythebank $30,900+$2549.25=$33,449.25.
(b) Theinterestis$2549.25.
61. 9 32 5 9 2032363268 5 FC F
Therefore,20°C=68°F.
62. 9 32 5 9 2003236032392 5 FC F
Therefore,200°C=392°F.
63.
5 32 9 55 50321810 99 CF C
Therefore,50°F=10°C.
64.
5 32 9 55 77324525 99 CF C
Therefore,77°F=25°C.
65. 5 32 9 55 100326837.8 99 CF C Therefore,100°F 37.8°C.
66. 5 32 9 55 35032318176.7 99 CF C Therefore,350°F 176.7°C.
67. 5 32 9 55 86732835463.9 99 CF C Therefore,865°F 463.9°C.
FC F
68. 9 32 5 9 89.432160.9232128.9 5
Therefore,–89.4°C –128.9°F.
69. 5 32 9 55 113328145 99 CF C
Therefore,113°F=45°C.
70. 9 32 5 9 28.13250.583282.6 5 FC F
Therefore,28.1°C 82.6°F.
Section 1.2 Applications and Modeling with Linear Equations
1. Distance=rate×time,sotime=distance÷ rate.Divide400milesby50mphtoobtain8 hours.
2. 15minutesis14ofanhour,somultiply80 mphby14togetadistanceof20mi.
3. 2%is0.02,somultiply$500by0.02andby4 yrstogetinterestof$40
4. Multiply40half-dollarsby$0.50toget$20; multiply200quartersby$0.25toget$50. Together,themonetaryvalueis$70.
5. 75%is34,somultiply120Lby34,toget90L acid.
6. ExpressionD, x 0.60doesnotrepresentthe salesprice. x 0.60represents x dollars discountedby60cents,not x dollars discountedby60%.Alloftheotherchoices areequivalentandrepresentthesalesprice.
7. ConcentrationA,24%,cannotpossiblybethe concentrationofthemixturebecauseitisless thanboththeoriginalconcentrations.
8. A 9. D
10. BandCcannotbecorrectequations.
InB,
17 9 27552 235752 93552 917 xx xx x xx butthelengthofarectanglecannotbe negative.
InC,
52510 510510 1010101000 xx xx xxx
butthelengthofarectanglecannotbezero.
11. Intheformula22, Plw let 294and57.Pw 2942257 2942114 180290 l l ll
Thelengthis90cm.
12. Let w =widthoftherectangularstorageshed. Then w +6=thelengthofthestorageshed. Usetheformulafortheperimeterofa rectangle.
22 442(6)2 442122 44412 3248 Plw ww ww w ww
Thewidthis8ftandthelengthis 8+6=14ft.
13. Let x =thelengthoftheshortestside. Then2x =thelengthofeachofthelonger sides.
Theperimeterofatriangleisthesumofthe measuresofthethreesides. 22305306xxxxx Thelengthoftheshortestsideis6cm.
14. Let w =thewidthoftherectangle. Then2w 2.5=thelengthoftherectangle. Usetheformulafortheperimeterofa rectangle.
22 40.6222.52 40.6452 40.66545.667.6
Plw ww ww www Thewidthis7.6cm.
15. Let x =thelengthoftheshortestside. Then2x 200=thelengthofthelongestside andthelengthofthemiddlesideis (2x 200)200=2x 400. Theperimeterofatriangleisthesumofthe measuresofthethreesides.
220024002400 220024002400 56002400 53000600 xxx xxx x xx
Thelengthoftheshortestsideis600ft.The middlesideis2600400 1200400 800ft. Thelongestsideis2600200 12002001000ft.
16. Let w =thewidthofthecake. Then w +0.39=thelengthofthecake. Usetheformulafortheperimeterofa rectangle. 22
17.022(0.39)2 17.0220.782 17.0240.78 16.2444.06
Plw ww ww w ww
Thewidthofthecakewas4.06mandthe lengthwas4.06+0.39=4.45m.
17. Let h =theheightofbox. Usetheformulaforthesurfaceareaofa rectangularbox.
Slwwhhl hh hh h hh
222 496218828218 4962881636 49628852 208524
Theheightoftheboxis4ft.
18. Thevolumeofarightcircularcylinderis 2 Vrh 2 2 1446 14436 14436 4 3636 Vrh h h h h
Theheightofthecylinderis4in.
19. Let x =thetime(inhours)spentonthewayto thebusinessappointment. rtd
Morning50 x 50 x Afternoon401 4 x 1 404 x
Thedistanceonthewaytothebusiness appointmentisthesameasthereturntrip,so
1 50404 504010 10101 xx xx xx
Becauseshedrove1hr,herdistancetraveled wouldbe50150mi.
20. Let x =time(inhours)ontripfromDenverto Minneapolis. rtd
Going50 x 50 x Returning5532 x 5532 x Thedistancegoingandreturningarethesame, sowehave
505532 50176055 105176016.76 xx xx xx
Becausehetraveledapproximately16.8hrto Minneapolis,thedistancewouldbeabout 5016.8840mi.
21. Let x =David’sspeed(inmph)onbike. Then4.5 x =David’sspeed(inmph) driving. rtd
Car x +4.51 203minhr 1 34.5 x
Bike x 3 454minhr 3 4 x
Thedistancebybikeandcararethesame,so
13 34 13 34 4.5 124.512 44.59 4189 18 185 5 xx xx xx xx xx
Becausehisrateis185(or3.6)mph,David travels
31827 45102.7mi towork.
22. Let x =rate(inmph)theSanDiegobound planetravels.Then x +50=rate(inmph)the SanFranciscoboundplanetravels. rtd
SanDiego x 1 2 1 2 x
San Francisco50 x 1 2
Thedistancetraveledbythetwoplanesis275 miles.TherateoftheSanDiegoboundplane canbefoundbysolving 11 2250275. xx
50275 2502275 50550250550 2500250 xx xx xxx xx
TheSanDiegoboundplanetravelsat250mph, andtheSanFranciscoboundplanetravelsat 25050300 mph.
23. Let x =time(inhours)ittakesforRussand Janettobe1.5miapart. rtd
Mary7 x 7 x
Janet5 x 5 x
BecauseMary’srateisfasterthanJanet’s,she travelsfartherthanJanetinthesameamount oftime.TohavethedifferencebetweenMary andJanettobe1.5mi,solvethefollowing equation.
751.521.50.75 xxxx Itwilltake0.75hr=45minforMaryand Janettobe1.5miapart.
24. Let x =time(inhours)Maryruns.Because Janethasaten-minutestartand10minutesis 1 6hr,Janet’stimerunningis1 6 x hr.
Mary7 x 7 x
Janet51 6 x
1 56 x
BecauseMarymusttravelthesamedistanceas Janet,wemustsolvethefollowingequation.
Itwilltake55 1212hr60min25min for MarytocatchupwithJanet.
25. Weneedtodeterminehowmanymetersarein 26miles.
265,280ft1mmi41,840.9m 1mi3.281ft
UsainBolt’srateinthe100-mdashwouldbe 100 9.69meterspersecond. d r t
Thus,thetimeitwouldtakeforUsaintorunthe 26-mimarathonwouldbe
Becausethereare60secondsinoneminute and60603,600 secondsinonehour, 4054sec1360076034sec or1hr,7min,34sec.Thisisabout12the worldrecordtime.
26. Weknow26mi41,840.9m fromexercise 25.UsainBolt’srateinthe100-mdashwould be100meterspersecond. 9.58 d r t Thus,the timeitwouldtakeforUsaintorunthe26-mi marathonwouldbe
4008sec1360066048sec or1hr,6 min,48sec.Thisisabout12theworldrecord time.
27. Let x =speed(inkm/hr)ofCallie’sboat. WhenCallieistravelingupstream,thecurrent slowsherdown,sowesubtractthespeedof thecurrentfromthespeedoftheboat.When sheistravelingdownstream,thecurrent speedsherup,soweaddthespeedofthe currenttothespeedoftheboat.
Upstream5 x 1
Becausethedistanceupstreamand downstreamarethesame,wemustsolvethe followingequation.
28. Let x =speed(inmph)ofthewind.WhenJoe istravelingagainstthewind,thewindslows himdown,sowesubtractthespeedofthe windfromthespeedoftheplane.Whenheis travelingwiththewind,thewindspeedshim up,soweaddthespeedofthewindtothe speedoftheplane.
Against wind180 x 3
3180 x With wind180 x
Becausethedistancegoingandcomingarethe same,wemustsolvethefollowingequation.
2.81803180
5042.85403
5045.8540 5.8366.2 xx xx x xx
Thespeedofthewindisabout6.2mph.
29. Let x =theamountof5%acidsolution(in gallons).
Strength Gallons of Solution
5% x 0.05 x 10%50.1050.5 7%5 x 0.075 x
Thenumberofgallonsofpureacidinthe5% solutionplusthenumberofgallonsofpure acidinthe10%solutionmustequalthe numberofgallonsofpureacidinthe7% solution.
1 2 0.050.50.075 0.050.50.070.35
0.50.020.35
0.150.02
0.15 0.027.57gal xx xx x x xx 1 72gallonsofthe5%solutionshouldbe added.
ThespeedofCallie’sboatis35kmperhour.
30. Let x =theamountof5%hydrochloricacid solution(inmL).
Strength Milliliters of Solution Millilitersof Hydrochloric Acid
5% x 0.05 x 20%600.206012 10% x +60 0.1060 x
Thenumberofmillilitersofhydrochloricacid inthe5%solutionplusthenumberof millilitersofhydrochloricacidinthe20% solutionmustequalthenumberofmilliliters ofhydrochloricacidinthe10%solution.
0.05120.1060
0.05120.106 120.056 60.05 6600 120mL 0.055 xx xx x x
120mLof5%hydrochloricacidsolution shouldbeadded.
31. Let x =theamountof100%alcoholsolution (inliters).
Strength
Thenumberoflitersofpurealcoholinthe 100%solutionplusthenumberoflitersof purealcoholinthe10%solutionmustequal thenumberoflitersofpurealcoholinthe30% solution.
0.70.307 0.70.302.1
0.70.72.1 0.71.4 1.414 2L 0.77
2Lofthe100%solutionshouldbeadded.
32. Let x =theamountof100%alcoholsolution (ingallons).
Thenumberofgallonsofpurealcoholinthe 100%solutionplusthenumberofgallonsof purealcoholinthe15%solutionmustequal thenumberofgallonsofpurealcoholinthe 25%solution.
2 3 30.2520 30.255 0.7535 0.752
2 23gallonsofthe100%solutionshouldbe added.
33. Let x =theamountofwater(inmL).
0.048 x
Thenumberofmillilitersofsaltinthe6% solutionplusthenumberofmillilitersofsalt inthewater(0%solution)mustequalthe numberofmillilitersinthe4%solution.
0.4800.048 0.480.320.04 0.160.04 0.1616 4mL 0.044 x x x xx
Toreducethesalineconcentrationto4%, 4mLofwatershouldbeadded.
34. Let x =theamountof100%acid(inliters).
Strength Liters of Solution LitersofPure Acid 100% x 1xx
30%180.30185.4 50%18 x 0.5018 x
Thenumberoflitersofacidinthepureacid (100%)plusthenumberoflitersofacidinthe 30%solutionmustequalthenumberofliters ofacidinthe50%solution.
5.40.5018 5.40.509 0.55.49 0.53.6 3.636 7.2L 0.55 xx xx x x x 7.2Lpureacidshouldbeadded.
35. Let x =amountoftheshort-termnote.Then 240,000– x =amountofthelong-termnote. Note Amount Interest Rate Time (years)InterestPaid
x 2%1 x(0.02)(1)
240,000 x 2.5%1(240,000 x)(0.025)(1) 5500
Theamountofinterestfromthe2%noteplus theamountofinterestfromthe2.5%note mustequalthetotalamountofinterest.
0.020.025240,0005500
0.0260000.0255500
38. Let x =amountinvestedat3%. Then4x =amountinvestedat2.75%.
Amountin Account InterestRateInterest
x 3%0.03x 4 x 2.75%0.0275(4x)=0.11x 2800
Theamountofinterestfromthe3%account plustheamountofinterestfromthe2.75% accountmustequalthetotalamountof interest.
0.030.0275(4)2800
0.00560005500 0.005500 100,000
x x x
Theamountoftheshort-termnoteis$100,000 andtheamountofthelong-termnoteis $240,000–$100,000=$140,000.
36. Let x =amountpaidforthefirstplot.Then 120,000– x =amountpaidforthesecondplot.
LandPriceRateofReturnProfitorLoss
x 15%0.15 x 120,000 x 10% 0.10120,000 x 120,0005,500
0.150.10120,0005500
0.1512,0000.105500
0.2512,0005500
0.2517,500
$70,000
Rogerpaid$70,000forthefirstplotand 120,00070,000=$50,000forthesecond plot.
37. Let x =amountinvestedat2.5%. Then2x =amountinvestedat3%.
Amountin Account InterestRateInterest
x 2.5%0.025x 2 x 3%0.03(2x)=0.06x 850
Theamountofinterestfromthe2.5%account plustheamountofinterestfromthe3% accountmustequalthetotalamountof interest.
0.0250.03(2)850 0.0250.06850 0.085850$10,000 xx xx xx
Janetdeposited$10,000at2.5%and 2($10,000)=$20,000at3%.
0.030.112800 0.142800$20,000
xx xx
Thechurchinvested$20,000at3%and 420,000 $80,000at2.75%.
39. 30%of$200,000is$60,000,soafterpaying herincometax,Lindahad$140,000leftto invest.Let x =amountinvestedat1.5%.
Then140,000– x =amountinvestedat4%.
Amount Invested Interest RateInterest x 1.5%0.015x 140,000 x 4%0.04(140,000 x) 140,0004350
0.0150.04140,0004350 0.01556000.044350 0.02556004350 0.0251250
$50,000 xx
x x x
Lindainvested$50,000at1.5%and $140,000–$50,000=$90,000at4%.
40. 28%of$48,000is$13,440,soafterpayingher incometax,Beckyhad$34,560lefttoinvest. Let x =amountinvestedat3.25%.
Then34,560– x =amountinvestedat1.75%.
Amount Invested Interest RateInterest
x 3.25%0.0325x 34,560 x 1.75%0.0175(34,560 x) 34,560904.80
0.03250.017534,560904.80 0.0325604.800.0175904.80 0.015604.80904.80 0.015300
$20,000 xx xx x x x
Beckyinvested$20,000at3.25%and $34,560–$20,000=$14,560at1.75%.
41. (a) 1000.02 1000.02(2400)1004852 yx y
Theannualcostis$52.
(b) 501000.02 500.02 2500 x x x
Theannualcostofmembershipwillbe $50iftheclubpurchasesare$2500.
(c) 01000.02 1000.02 5000 x x x
Theannualcostofmembershipwillbe$0 iftheclubpurchasesare$5000.
42. (a) 500.016 500.016(1500)502426 yx y
Theannualcostis$26.
(b) 0500.016 500.016 3125 x x x
Theannualcostofmembershipwillbe$0 iftheclubpurchasesare$3125.
(c) Iftheannualclubpurchasesaremore than$3125,thenthemodelwouldyielda negativevaluefor y,theactualannual costofmembership.Essentially,thecashbackrewardexceedstheinitialfeeof $50,creatingapositivegainforthe member.
43. (a) Let x =thenumberofhours.Then F =100(140)x =14,000x
(b) Because3 33 gft causesirritation,the roomwouldneed3380026,400 g tocauseirritation. 14,000 26,40014,000 26,400 14,000 1.9hr Fx x x x
Itwilltakeabout1.9hoursfor concentrationstoreach3 33. gft
44. (a) Becauseeachstudentneeds153fteach minuteandthereare60minutesinan hour,theventilationrequiredby x studentsperhourwouldbe V =60(15x)=900x
(b) Thenumberofairexchangesperhouris
900 0.06. 15,000 Axx
(c) If x =40,then0.06402.4ach. A
(d) Theventilationshouldbeincreasedby 1 3 5010 3 153 times.(Smokingareas requiremorethantripletheventilation.)
45. (a) In2018, x =4. 0.314321.95 0.3143421.9523.2072 yx y
Theprojectedenrollmentforfall2018is approximately23.2million.
(b) 0.314321.95
240.314321.95 2.050.3143 2.05 6.52 0.3143 yx x x x
2014+6=2020
Enrollmentisprojectedtoreach24 millionduringtheyear2020.
(c) Theyarequiteclose.
(d) Theyear2000isrepresentedby x =14.
0.314321.95 0.31431421.9517.5 yx y
Accordingtothemodel,theenrollment wasapproximately17.5million
(e) Answerswillvary.Sampleanswer:When usingthemodelforpredictions,itisbest tostaywithinthescopeofthesample data.
46. (a) Theyear1952correspondsto x =6. 2.8370140.83 2.83706140.83157.852 yx y
Accordingtothemodel,theU.S. populationonJuly1,1952was157.852 millionor157,852,000.
(b) 2.8370140.83 1502.8370140.83 9.172.8370 9.17 3.2 2.8370 yx x x x
Accordingtothemodel,theU.S. populationreached150millionduring 1949.
Section 1.3 Complex Numbers
1. Bydefinition, i =1,andtherefore,21. i
2. If a and b arerealnumbers,thenanynumber oftheform a + bi isacomplexnumber.
3. Thenumbers6+5i and6–5i,whichdiffer onlyinthesignoftheirimaginaryparts,are complexconjugates.
4. Theproductofacomplexnumberandits conjugateisalwaysarealnumber.
5. Tofindthequotientoftwocomplexnumbers instandardform,multiplyboththenumerator andthedenominatorbythecomplexconjugate ofthedenominator.
6. True.252515i
7. True.2492366 iii
8. True.
3 124311 ii
9. False.
10. False.
22 2 2 5352533 25309 25309 1630 iii ii i i
11. 4isrealandcomplex.
12. 0isrealandcomplex.
13. 13i iscomplex,pureimaginary,andnonreal complex.
14. 7i iscomplex,pureimaginary,andnonreal complex.
15. 5 i iscomplexandnonrealcomplex.
16. 62i iscomplexandnonrealcomplex.
17. isrealandcomplex.
18. 24isrealandcomplex.
19. 255i iscomplex,pureimaginary,and nonrealcomplex.
20. 366i iscomplex,pureimaginary,and nonrealcomplex.
21. 25255 ii
22. 36366 ii
23. 1010 i
24. 1515 i
25. 2882881442122 iii 26. 5005001005105 iii
18189232 iii
28. 808016545 iii
22 13131313 1311313
32933923
2444
53.
25342 232541 110110 iii i ii
42345 42413510 iii ii
2264252 2652422 1342 iii i
54.
37474275 374727145 372 iii i i
2 232 232232 6432621 628 ii iiii iiii ii
57.
58.
2 2342 24223432 8412681661 8166216 ii iiii iiii ii
2 2413 21234143 2641222121 2212142 ii iiii iiii ii
2 1325 12153235 256152151 21517 ii iiii iiii ii
59. 22 2 3232322 9124512 iii ii
60. 2222222244 44134 iiiii ii
61. 22 3339(1)10 iii
62. 22 55525126 iii
63. 222 23232349 49113 iiii
64.
2 22 2 14514532 323232 42281510 32 4213101421310 94941 52135213 9413 5213 4 1313 iii iii iii i ii i ii ii
22 22 222222 2222 4413434 41555 iiiii iiii ii i
22 22 2 2 43434342433 43434343 16249162491 1691691 16249724724 169252525 iiiii iiii iii i ii i
2 22 131 13133 1111 1431143 112 2424 12 222 ii iiii iiii ii i ii
78.
79.
2 22 342 346384 2222 6541654 415 105105 2 555 ii iiii iiii ii i ii
2 5 55 55 5or05 11 ii iiii ii ii
80.
81.
2 6 66 66 6or06 11 ii iiii ii ii
2 888 88 8or08 11 ii iiii ii ii
82.
2 121212 1212 12or012 11 ii iiii ii ii
83.
2 23 266 33391 9 622 or0 933 iii iiii i ii
Note:Intheabovesolution,wemultipliedthe numeratoranddenominatorbythecomplex conjugateof3i,namely–3i.Becausethereisa reductionintheend,thesameresultscanbe achievedbymultiplyingthenumeratorand denominatorby–i.
84.
2 59 54545 999811 81 4555 or0 8199 iii iiii i ii
85. 2 57,64 (57)(64) 5(6)5(4)7(6)7(4) 30204228 306228 262 IiZi EIZ Eii iiii iii i i
86. 2 2012,105 (2012)(105) 20(10)20(5)12(10)12(5) 20010012060 2002060 26020 IiZi EIZ Eii iiii iii i i
87. 104,88128 88128(104) IiEi EIZ iiZ
22 88128 104 88128104 104104 88(10)88(4)128(10)128(4) 104 i Z i ii Z ii iiii Z i
88035212805122 100(16) 8803521280512 116 1392928 128 116 iii Z ii Z i Zi
88.
5767,95 576795 EiZi EIZ iIi
22 2 5767 95 576795 9595 57(9)57(5)67(9)67(5) 95 513285603335 81(25) 513318335 106 848318 83 106 i I i ii I ii iiii I i iii I i I i Ii
6 252446 1 iiiiiii
90.
7 292847 1 iiiiiii
5 22202451111 iiii
92.
6 26242461111 iiii
2 2222 22211 2 44422 1111 1 2222 i ii iiii iii
313312 22424 31331 1 22424 iii ii
31331 22424 3123 2242 ii ii
2 2 3113 2222 31331113 22222222 3313 4444 34333 1 44444 ii iii iii iii
104. Weneedtoshowthat 3 31 22 ii
(continued)
105. If–2+ i isasolutionoftheequation,then substitutingthatvaluefor x makesatrue statement.
2 2 2 450 24250 448450 4418450 00 xx ii iii ii
106. If–2– i isasolutionoftheequation,then substitutingthatvaluefor x makesatrue statement.
2 2 2 450 24250 448450 4418450 00 xx ii iii ii
107. If–3+4i isasolutionoftheequation,then substitutingthatvaluefor x makesatrue statement.
2 2 2 6250 34634250 924161824250 924161824250 00 xx ii iii ii
108. If–3–4i isasolutionoftheequation,then substitutingthatvaluefor x makesatrue statement.
2 2 2 6250 34634250 924161824250 924161824250 00 xx ii iii ii
Section 1.4 Quadratic Equations
1. G;225255 xx
2. A;225255 xxi
3. C;2250555 xxxi
4. E;225055xxx
5. H;2202025 xxi
6. B;2202025 xx
7. D; 505xx
8. F;505 xx
9. Distheonlyonesetupfordirectuseofthe zero-factorproperty. 3170 xx 1 3 310or70 or7 xx xx
Solutionset: 1 3,7
10. Bistheonlyonesetupfordirectuseofthe squarerootproperty. 2 257257 57 257 2 xx xx
Solutionset: 57 2
11. CistheonlyonethatdoesnotrequireStep1 ofthemethodofcompletingthesquare.
22 111 224 2 211 44 1249 24 149 24 7711 2222 Note: 1 12 12 xx xx x x xx 787611 2222224and3
Solutionset: 4,3
12. Aistheonlyonesetupsothatthevaluesof a, b,and c canbedeterminedimmediately. 2 31760 xx yields a =3, b =–17,and c =–6.
13.
Solutionset: 2,3
14. 2280 420 xx xx 404or202 xxxx
Solutionset: 4,2
15. 2 5320 5210 xx xx 2 5205or101 xxxx Solutionset: 2 5,1
16. 2 2150 2530 xx xx 5 2502or303 xxxx
Solutionset: 5 2,3
17.
2 2 43 043 0431 xx xx xx
3 4304or101 xxxx
Solutionset: 3 4,1
18.
2 2 6710 067100 06520 xx xx xx 5 6506or202 xxxx
Solutionset: 5 6,2
19.
21000 10100 x xx 10010or10010 xxxx Solutionset:{10,10}
20.
2640 880 x xx 808or808 xxxx Solutionset:{8,8}
21. 2 2 1 2 4410 210 21021 xx x xxx
Solutionset: 1 2
22.
2 2 2 3 91240 320 32032 xx x xxx
Solutionset: 2 3
23. 2 2 3 5 253090 530 53053 xx x xxx
Solutionset: 3 5
24. 2 2 5 6 3660250 650 65065 xx x xxx
Solutionset: 5 6
25. 216 164 x x
Solutionset: 4
26. 2121 12111 x x
Solutionset: 11
27. 2 2 270 27 2733 x x x
Solutionset: 33
28. 2 2 480 48 4843 x x x
Solutionset: 43
29. 281 819 x xi
Solutionset: 9i
30. 2400 40020 x xi
Solutionset: 20 i
31. 2 3112 3112 123 3123 3 x x xx
Solutionset: 123 3
32. 2 4120 4120 125 4125 4 x x xx
Solutionset: 125 4
33. 2 53 53 53 53 x x xi xi
Solutionset: 53 i
34. 2 45 45 45 45 x x xi xi
Solutionset: 45 i
35. 2 533 533 533 533 3333 555 x x xi xi i xi
Solutionset: 33 55 i
36. 2 258 258 2522 2522 5225 2 22 x x xi xi i xi
Solutionset: 5 22 i 37.
122 2 2 2 2 Note: 4 430 443442 21 21 21 21 xx xx x x x x
211and213 Solutionset: 1,3
38.
2217 22 49 4 2 24949 44 721 24 71 24 71 22 71 22 Note: 7120 7127 xx xx x x x x
7678 11 2222223and4 Solutionset: 3,4
39.
1 2 22 1111 22416 2 21 2 2111 21616 12225 416 1225 416 115 44 115 44 Multiplyby. Note: 2280 140 14 xx xx xx x x x x
15715161141 4442444and4
Solutionset: 7 2,4
40.
22 1339 24864 2 2310 44 235 42 23959 464264 2 3169 864 316913 8648 313 88 Note: 43100 0 0 xx xx xx xx x x x
31310531316 8884888and2
Solutionset: 5 4,2
41.
44.
Note: 210 5 5 xx xx xx x x x x
22 1111 22416 2 21 2 2111 21616 1281 416 181 416 19 44 19 44
91059811 4442444and2
Solutionset: 5 2,2
Note: 325 xx xx xx x x x x
22 1211 2339 2 25 2 33 25211 3939 1216 39 116 39 14 33 14 33
531414 333333and1
Solutionset: 5 3,1
45.
42.
Solutionset: 13
46.
122 2 2 23 2 23 2 25 2 510 22 10210 22 Note: 211 2430 20 211 1 1 1 xx xx xx x x x
Solutionset: 210 2
122 2 2 25 3 25 3 28 3 82426 333 26326 33 Note: 211 3650 20 211 1 1 1 xx xx xx x x x
Solutionset: 326 3
48.
2 27 4 2722 41 2 23 4 33 42 3 2 487 2 Note: 211211 1 1 1 i xx xx xx x x xi
22 139 224 2 27 3 29792827 4341212 321 212 312233 1 21212126 33 26 Note:3 397 3 3 i xx xx xx x xii xi
Solutionset: 33 26 i
49. Franciscoisincorrectbecause c =0andthe quadraticformula, 24 2, bbac x a can beevaluatedwith1,8,and0. abc
50. Francescaisincorrectbecause b =0andthe quadraticformula, 24 2, bbac x a can beevaluatedwith1,0,and19. abc
51. 210xx Let1,1,and1. abc
2 2 4 2 11411 21 11415 22 bbac x a
Solutionset:
52. 2320xx Let1,3,and2. abc
2 2 4 2 33412 21 398317 22 bbac x a
Solutionset: 317 2
53. 2 2 67 670 xx xx Let1,6,and7. abc
2 2 4 2 6641763628 212 68622 32 22 bbac x a
Solutionset: 32
54. 2 2 41 410 xx xx Let1,4,and1. abc 2 2 4 2 444114164 212 412423 23 22 bbac x a
Solutionset: 23
55. 2 2 25 250 xx xx Let1,2,and5. abc
2 2 4 2 22415 21 242021624 12 222 bbac x a i i
Solutionset: 12i
56. 2 2 210 2100 xx xx
Let1,2,and10. abc
59.
2 11 24 2 11 24 2 30 4340 2120 xx xx xx
bbac x a i i
2 2 4 2 224110 21 244023626 13 222
Solutionset: 13i
57. 2 2 41211 041211
xx xx
Let4,12,and11. abc
bbac x a
Let2,1,and12. abc 224114212 222 1196197 44
Solutionset: 197 4
60.
2 2 422123 8822 4 2 12124411 24 121441761232 88 1242 8
bbac x a i ii
Solutionset: 32 22 i
58. 2 2 632 0632 xx xx
Let6,3,and2. abc
22433462 226 3948339339 121212 bbac x a i
33939 1 1212412 xii
Solutionset: 139 412 i
61.
2 21 34 2 21 34 2 2 3 12123 8336 83360 xx xx xx xx
bbac x a
Let8,3,and36. abc 2 2 4 2 334836391152 2816 3116133129 1616
Solutionset: 33129 16
2 2 2 0.20.40.30 100.20.40.3100 2430 xx xx xx
Let2,4,and3. abc
bbac x a
2 2 4 2 4442341624 224 4404210210 442
Solutionset: 210 2
62. 2 2 2 2 0.10.10.3 100.10.1100.3 3 30 xx xx xx xx
Let1,1,and3. abc
2 2 4 2 11413 21 1112113 22
Solutionset: 113 2
63. 22 (41)(2)4 47244320 xxx xxxxx
22433442 224 3932341 88
Solutionset: 341 8
64. 2 2 (32)(1)3 323 3420 xxx xxx xx
2 2 4 2 44432 23 41624440 66 4210210 63 bbac x a
Solutionset: 210 3
65. 2 2 (9)(1)16 10916 10250 xx xx xx
Let a =1, b =10,and c =25.
2 10104125 21 10100100100 5 22 x
Solutionset:{5}
66. Answerswillvary.Multiplyingthefirst equationby–1producesthesecondequation, andthus,theequationsareequivalent.
22 2 236012360 2360 xxxx xx
Therefore,thetwoequationshavethesame solutionset.
67.
3 33 2 80 20 2240 x x xxx 202xx or 2240 1,2,and4 xx abc
2 2 4 2 224142416 212 212223 13 22 bbac x a i i
Solutionset: 2,13i
68.
3 33 2 270 30 3390 x x xxx
303xx or 2390 1,3,and9 xx abc
2 2 4 2 334193936 212 327333333 2222 bbac x a i i
Solutionset: 3333,22 i
69.
3 33 2 270 30 3390 x x xxx
1,4,and16 xx abc
x a i i
2 2 4 2 44411641664 212 448443 223 22
Solutionset:
i
74. 2 2 2 2 2 222 ek E r Erek ErErErk ee kkk
75.
2 0 2 0 2 0 02 00 1 2 1 2 2 2 22 rrat rrat rrat rr t a rrarr t aa
76. 2 0 2 0 2 2 00 00 0 ssgtk sskgt sskssk gtt ggg tssksskg ggg sskg t g
77. 0 0 2 00 2 00 2 00 16,, 16 160 160 abv chs htvts tvths tvths
2 2 000 2 000 2 000 4 2 416 216 64 32 6464 32 bbac t a vvhs vvhs vvhs
78.
2 22 22 22 2 2 2 22 4 2 444931 29 4163631 18 41610836 18 412436 18 44319 18 42319 18 23192319 99 bbac x a yyy yyy yyy yy yy yy yyyy
2,4,and232abycy
2 22 22 22 2 2 2 2 4 2 444322 23 4161222 6 4162424 6 44024 -6 44106 6 42106 6 2106 3 bbac x a xxx xxx xxx xx xx xx xx
22 22 5621 56210 xxyy xxyy a. Solvefor x intermsof y. 22 56210 xyxy 5,6,and221abycy
2 22 22 22 22 22 4 2 664521 25 6362021 10 6364020 10 6204645 1010 62535 105 bbac x a yyy yyy yyy yyyy yyyy
b. Solvefor y intermsof
83. 28160
2248411664640bac
Onerationalsolution(adoublesolution)
84. 2440xx 1,4,and4abc
224441416160bac
Onerationalsolution(adoublesolution)
85. 2 3520 xx 3,5,and2abc
222 45432252411bac Twodistinctrationalsolutions
86. 2 2 8143 81430 xx xx 8,14,and3abc
22 2 414483 1969610010 bac Twodistinctrationalsolutions
87. 2 2 463 4630 xx xx
4,6,and3abc
2246443364884bac Twodistinctirrationalsolutions
88. 2 2410 xx 2,4,and1abc
22444211688bac Twodistinctirrationalsolutions
89. 2 91140 xx 9,11,and4abc
2241149412114423bac Twodistinctnonrealcomplexsolutions
90. 2 2 345 3450 xx xx 3,4,and5abc
2244435166044bac Twodistinctnonrealcomplexsolutions
91. 2 8720 x 8,0,and72abc
222 404872230448bac
Twodistinctrationalsolutions
92. Answerswillvary.
2 25320 xx 2,5,and32abc
22454232 25122252449 bac No,thisdoesnotcontradictthediscussionin thissectionbecauseaconditionthatisplaced onthequadraticequationisthatithasinteger coefficientsinordertoinvestigatethe discriminant.
93. No,itisnotpossibleforthesolutionsetofa quadraticequationwithintegercoefficientsto consistofasingleirrationalnumber. Additionalresponseswillvary.
94. No,itisnotpossibleforthesolutionsetofa quadraticequationwithrealcoefficientsto consistofonerealnumberandonenonreal complexnumber.Answerswillvary.
Inexercises9598,thereareotherpossibleanswers.
95. 4or5 40or50 xx xx
2 2 450 54200 9200 xx xxx xx
1,9,and20abc
96. 3or2 30or20 xx xx
97.
98. or 0or0 xixi xixi
1,0,and1abc
Chapter 1 Quiz (Sections 1.1 1.4)
1. 3(5)21(42) 3152142 31332 5133 5102 xx xx xx x xx
Solutionset{2}
2. (a) 452(32)3 45643 4543 53 xx xx xx
contradiction;solutionset: (b) 595(2)1 591051 5959 xx xx xx
identity;solutionset:{allrealnumbers} or ,
(c) 2211 84 543(6) 54183 8418 822 xx xx x xx conditionalequation;solutionset: 11 4
3. 25 3 3(1) 3(1) 3 1 ayxyx ayxy xyayya xya x y a
4. Let x =theamountdepositedat2.5%interest. Then2x =theamountdepositiedat3.0% interest.Theinterestearnedonxdollarsat 2.5%is0.025x,andtheinterestearnedon2x at3.0%is(2x)(0.03)=0.06x.Thetotalearned is$850,sowehave 0.0250.06850 0.08585010,000 xx xx
$10,000wasinvestedat2.5%,and$20,000 wasinvestedat3.0%.
5. Substitute2008for x intheequation: 0.128(2008)250.436.59 y So,themodelpredictsthattheminimum hourlywagefor2008was$6.59.Themodel predictsawagethatis$0.04greaterthanthe actualwage.
6. 424446 88 42616 8824 i i
7. 72722414284(8) 2424244(16) 63263238 202020105 iiiii iii i ii
8. 22 31310 xxxx Usethequadraticformula. a =3, b =1, c =1 2 (1)(1)4(3)(1)111111 2(3)666 i
Solutionset: 111 66 i
9. 222902929 xxx
Solutionset: 29
Section 1.5 Applications and Modeling with Quadratic Equations
1. A.Thelengthoftheparkingareais2x +200, whilethewidthis x,sotheareais(2x +200)x. Settheareaequalto40,000toobtain x(2x +200)=40,000.
2. C.Thediagonalofthisrectangleisthe hypotenuseofarighttrianglewithlegs r feet and s feet.BythePythagoreantheorem,the lengthofthediagonalis22. rs
3. D.UsethePythagoreantheoremwith a = x, b =2x –2,and c = x +4.
222 (22)(4)xxx
4. B.Thelengthofthepictureis34–2x,while thewidthis21–2x,givinganareaof (34–2x)(21–2x).Usetheformulaforthe areaofarectangle, A = lw,andsetthearea equalto600toobtain (342)(212)600. xx
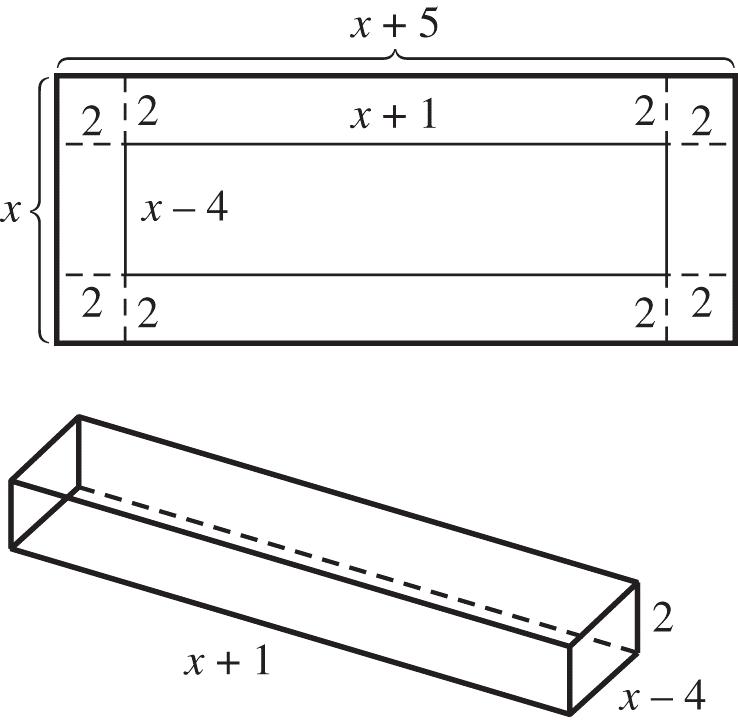
5. A.Let x =thewidth,so x +5=thelength.If2 in.arecutfromeachcorner,thenthewidthof theboxis x –4andthelengthoftheboxis x +5–4or x +1.Theheightoftheboxis2.
8. C.Theyear2010correspondsto x =10.We areseekingthevalueofthemodelfor x =10, sothecorrectequationis 2 0.0538100.807108.84. S
9. Let x =thefirstinteger.Then x +1=thenext consecutiveinteger. 2
2 (1)5656
560(8)(7)0 808or707 xxxx xxxx xxxx
If x =8,then x +1=7.If x =7,then x +1=8.Sothetwointegersare8and7,or 7and8.
10. Let x =thefirstinteger.Then x +1=thenext consecutiveinteger.
2
2 (1)110110
1100(11)(10)0 11011or 10010 xxxx xxxx xx xx
If x =11,then x +1=10.If x =10,then x +1=11.Sothetwointegersare 11and10,or10and11.
11. Let x =thefirsteveninteger.Then x +2=the nextconsecutiveeveninteger.
xxxx xxxx xx xx
2 2 (2)1682168
21680(14)(12)0 14014or 12012
If x =14,then x +2=12.If x =12,then x +2=14.so,thetwoevenintegersare 14and12,or12and14.
12. Let x =thefirsteveninteger.Then x +2=the nextconsecutiveeveninteger.
2 2 (2)2242224 22240(16)(14)0 16016or 14014 xxxx xxxx xx xx
If x =16,then x +2=14.If x =14,then x +2=16.So,thetwoevenintegersare 16and14,or14and16.
14264.Vxx
Then,thevolumeoftheboxisrepresentedby
6. C.Theheightisgiventobe40ftandweare seeking t.Thus,2401660 tt isthe correctequation.
7. B.Weareseekingtheheightgiventhetime t =2seconds.Therefore,thecorrectequation is 2 162452. s
13. Let x =thefirstoddinteger.Then x +2=the nextconsecutiveoddinteger.
2 2 (2)63263 2630(9)(7)0 909or 707 xxxx xxxx xx xx
If x =9,then x +2=7.If x =7,then x +2=9.so,thetwooddintegersare 9and7,or7and9.
14. Let x =thefirstoddinteger.Then x +2=the nextconsecutiveoddinteger. 2 2 (2)1432143
21430(13)(11)0 13013or 11011 xxxx xxxx xx xx
If x =13,then x +2=11.If x =11,then x +2=13.so,thetwooddintegersare 13and11,or11and13.
15. Let x =thefirstoddinteger.Then x +2=the nextconsecutiveoddinteger. 22 22 22 22 2202 44202 244202241980 229902990 (11)(9)0 11011or 909 xx xxx xxxx xxxx xx xx xx
If x =11,then x +2=9.If x =9,then x +2=11.Sothetwointegersare 11and9,or9and11.
16. Let x =thefirsteveninteger.Then x +2=the nextconsecutiveeveninteger.
2240(6)(4)0 606or 404 xx xxxxx xxxx xxxx xx xx
22 222 22 2 252 445224452 2448022240
If x =6,then x +2=4.If x =4,then x +2=6.Sothetwoevenintegersare6and 4,or4and6.
17. Let x =thefirsteveninteger.Then x +2=the nextconsecutiveeveninteger.
22 22 284 44844484 48020 xx xxxx xx
If x =20,then x +2=22.Thetwointegersare 20and22.
18. Let x =thefirstoddinteger.Then x +2=the nextconsecutiveoddinteger.
22 22 232 44324432 4287 xx xxxx xx
If x =7,then x +2=9.Sothetwointegersare 7and9.
19. Let x =thelengthofoneleg, x +2=thelength oftheotherleg,and x +4=thelengthofthe hypotenuse.(Rememberthatthehypotenuseis thelongestsideinarighttriangle.)The Pythagoreantheoremgives
222 222 2 24 44816 4120620 606or 202 xxx xxxxx xxxx xx xx
Lengthcannotbenegative,sorejectthat solution.If x =6,then x +2=8and x +4=10.Thesidesoftherighttriangleare 6,8,and10.
20. Let x =thelengthofoneleg, x +1=thelength oftheotherleg,and x +2=thelengthofthe hypotenuse.(Rememberthatthehypotenuseis thelongestsideinarighttriangle.)The Pythagoreantheoremgives
222 222 22 2 12 2144 22144 230 310 303or 101 xxx xxxxx xxxx xx xx xx xx
Lengthmustbeapositivenumber,soreject x =1.If x =3,then x +1=4and x +2=5. Thesidesoftherighttriangleare3,4,and5.
21. Let x =thelengthofthesideofthesmaller square.Then x +3=thelengthofthesideof thelargersquare.
22 222 2 3149 69149261400 3700(7)(10)0 707or 10010 xx xxxxx xxxx xx xx
Lengthcannotbenegative,sorejectthat solution.If x =7,then x +3=10.Thelength ofthesideofsmallersquareis7in.,andthe lengthofthesideofthelargersquareis10in.
22. Let x =thelengthofthesideofthesmaller square.Then x +5=thelengthofthesideof thelargersquare.
22 22 595 102595 10259510707 xx xxx xxx
If x =7,then x +5=12.Thelengthoftheside ofthesmallersquareis7in.,andthelengthof thesideofthelargersquareis12in.
23. Usethefigureandequation A fromExercise1.
2 2 2 220040,000 220040,000 220040,0000 10020,0000 (100)(200)0 100or200
Thenegativesolutionisnotmeaningful.If x =100,then2x +200=400.Thedimensions ofthelotare100ydby400yd.
24. Usetheformulafortheareaofarectangle. 2 2 5000(150) 5000150 15050000(100)(50)0 1000100or 50050
If x =100,then150– x =50.If x =50,then 150– x =100.Thedimensionsofthegarden are50mby100m.
25. Let x =thewidthofthestripofflooraround therug.
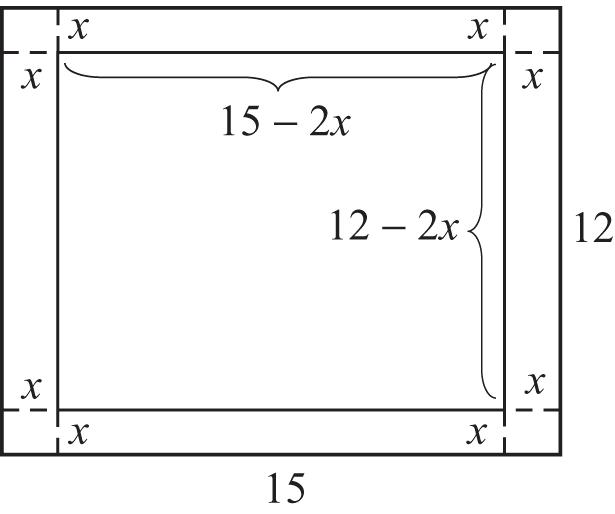
Thedimensionsofthecarpetare15–2x by 12–2x.Because, Alw theequationforthe carpetareais(15–2x)(12–2x)=108.Put thisequationinstandardformandsolveby factoring.
2 2 152122108 18030244108 180544108 454720 227360 (23)(12)0 xx xxx xx xx xx xx
3 230 2 12012 xx xx
Thesolutionsofthequadraticequationare3 2 and12.Weeliminate12asmeaninglessin thisproblem.If x = 3 2,then15–2x =12and 12–2x =9.Thedimensionsofthecarpetare 9ftby12ft.
26. Let x =thewidthoftheborder.
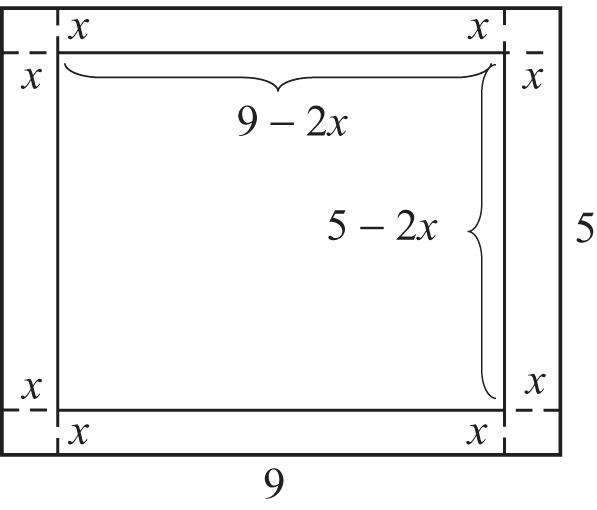
Thedimensionsofthecenterplotare9–2x by 5–2x Thetotalareais5945 sqft.The borderareais24sqft,sotheareaofthecenter plotis45–24=21sqft.Applytheformula fortheareaofarectangletothecenterplot. 2 2 (92)(52)21 451810421 4528421 Alw xx xxx xx
22 428240760 (6)(1)0606or 101 xxxx xxxx xx
Thesolutionsare1and6.Weeliminate6as meaninglessinthisproblem.Thebordercan be1ftwide.
27. Let x =thewidthofthemetal.Thedimensions ofthebaseoftheboxare x –4by x +6.
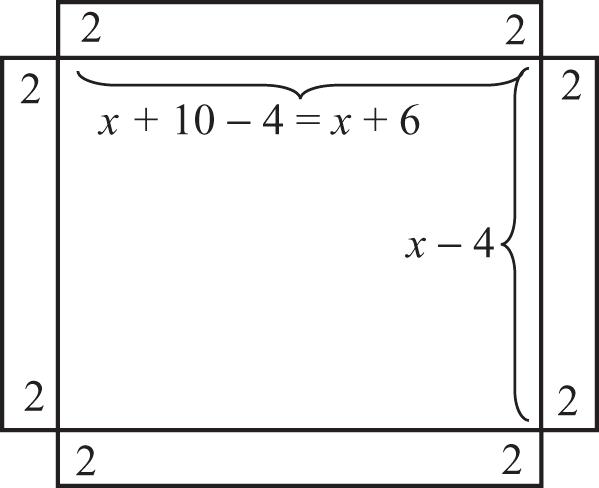
Becausetheformulaforthevolumeofaboxis ,Vlwh wehave
2 2 2 642832 64416 4624416 224416 2440022200 22022or 20020 xx xx xxx xx xxxx xx xx
Thenegativesolutionisnotmeaningful.If x =20,then x +10=30.Thedimensionsof thesheetofmetalare20inby30in.
28. Let x =thewidthofthemetal.Thedimensions ofthebaseoftheboxare8 x by28. x
Becausetheformulaforthevolumeofaboxis
,Vlwh wehave
Thenegativesolutionisnotmeaningful.If x =20,then2x =40.Thedimensionsofthe sheetofmetalare20inby40in.
29. Let h =heightand r =radius.
Surfacearea=2πrh +2πr2
8π =2πr(3)+2πr2
rr rr rrrr rrrr
2 2 2 862 0268 0234041 404or101
The r representstheradiusofacylinder,so4 isnotreasonable.Theradiusofthecircular topis1ft.
30. Let h =heightand r =radius.Volume= πr2h 222 1 3 3303 0310or310 rrrrrr rrrrr
Acirclemusthavearadiusgreaterthan0.The radiusofthecirculartopis13ftor4in.
31. Let x =lengthofsideofsquare.Area=2 x andperimeter=4x 2244040xxxxxx x =0or x =4
Wereject0because x mustbegreaterthan0. Thesideofthesquaremeasures4units.
32. Let x =widthofrectangle. Then2x =lengthofrectangle. Area= lw andPerimeter=22lw
22 22 22222 2242226 2122120 260200or 606 xxxx xxxxx xxxx xxxx xx
Wereject0because x mustbegreaterthan0. Thewidthoftherectanglemeasures6units. Thelengthoftherectanglemeasures12units.
33. Let h =heightand r =radius.
Areaofside=2πrh andAreaofcircle= πr2
Surfacearea=areaofside+areaoftop+area ofbottom
Surfacearea=2πrh + πr2+ πr2=2πrh +2πr2
371=2πr(12)+2πr2 2 2 371242 0224371
rr rr a =2π, b =24π,and c =–371 2 2 2 4 2 24(24)4(2)(371) 2(2) 245762968 4 15.753.75
bbac rr a rorr
Thenegativesolutionisnotmeaningful.The radiusofthecirculartopisapproximately 3.75cm.
34. Let x =height,then x –3.2=length,and 2.3=width. Vlwx
2 2 180.43.22.3 180.42.37.36 02.37.36180.4 xx xx xx a =2.3, b =–7.36,and c =–180.4 2 2 4 2 (7.36)(7.36)4(2.3)(180.4) 2(2.3) 7.361713.84967.3641.40 4.64.6 10.6or7.4
bbac x a x
Aboxcannothaveanegativeheight,soreject –7.4asasolution.Theheightisabout10.6in. andthelengthis10.6–3.2=7.4in.
35. Let h =theheightofthedock. Then2h +3=thelengthoftheropefromthe boattothetopofthedock. ApplythePythagoreantheoremtothetriangle showninthetext.
222 2 22 22 2 2 12(23) 1442263 1444129 0312135 04450(9)(5) 909or505 hh hhh hhh hh hhhh hhhh
Thenegativesolutionisnotmeaningful.The heightofthedockis5ft.
36. Let x =thehorizontaldistance ApplythePythagoreantheoremtotheright triangleshowninthetext.
222 222 222 22 2 2 (10)50 210102500 201002500 22024000 1012000 (40)(30)0 40040or 30030 abc xx xxx xxx xx xx xx xx xx
Thenegativesolutionisnotmeaningful. Thekite’shorizontaldistanceis30ftandthe verticaldistancefromthegroundis 40ft+5ft=45ft.
37. Let r =radiusofcircleand x =lengthofside ofsquare.Theradiusis12thelengthofthe sideofthesquare.Area=2 x 2 800800202 102 xx r
Theradiusis102feet.
38. Letx=lengthofshortleg. Then2x =lengthoflongleg. ApplythePythagoreantheorem. 222 222 22 2 2 26(2) 6764 6765 135.2 135.2 cab xx xx x x x
Thenegativesolutionisnotmeaningful.The shortlegshouldbe135.211.6 in.andthe longlegshouldbe2135.223.3 in.
39. Let x =lengthofladder
Distancefrombuildingtoladder=8+2=10. Distancefromgroundtowindow=13 ApplythePythagoreantheorem. 222 2222 2 1013100169 269269 abc xx xx
x ≈ –16.4or x ≈ 16.4
Thenegativesolutionisnotmeaningful.The workerwillneeda16.4-ftladder.
40. Let x =thenumberofhourstheycantalkto eachotheronthewalkie-talkies.
Use d = rt todeterminehowfareachboy walksin x hours.Then2.5x =thenumberof milesTannerwalksnorthand3x =thenumber ofmilesSheldonwalkseast.Thisformsa righttrianglewithlegsoflength2.5x and3x, andlengthofthehypotenuseisthedistance betweentheboys.Wewanttofind x whenthe lengthofthehypotenuseis4mi.
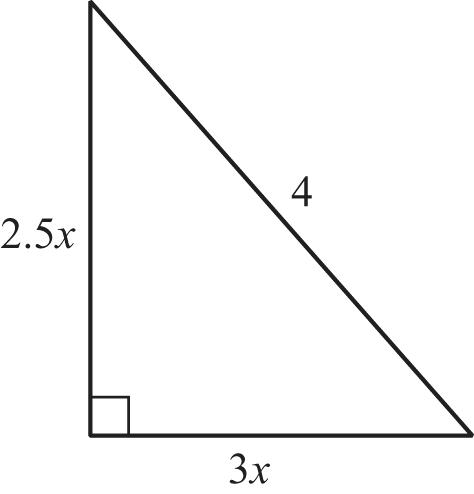
22222 22 (2.5)(3)46.25916 15.25161.0491.02 abc xxxx xxx
Thenegativesolutionisnotmeaningful. 1.02hr1.02(60min)61min
Theywillbeabletotalkforabout61min.
41. Let x =lengthofshortleg, x +700=lengthof longleg,and x +700+100or x +800=lengthofhypotenuse.
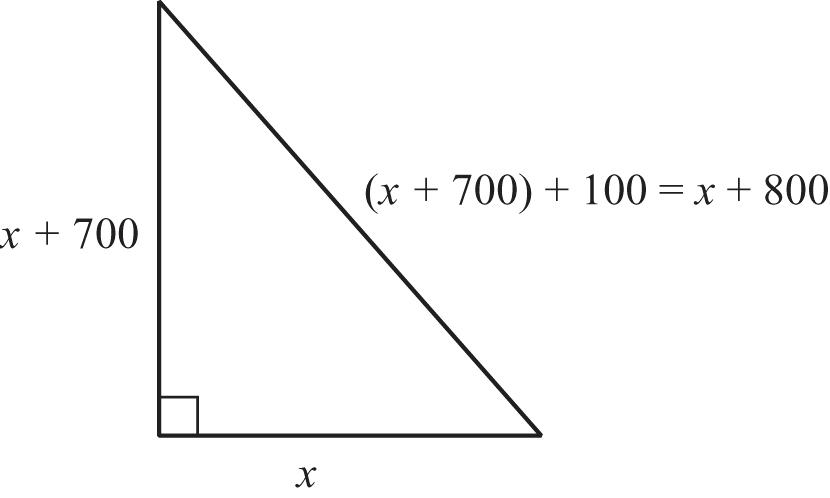
ApplythePythagoreantheorem.
222 222 2 22 2 (800)(700) 1600640,000 1400490,000 0200150,000
0(300)(500) 3000300or 5000500 cab xxx xx xxx xx xx xx xx
Thenegativesolutionisnotmeaningful. 500=lengthofshortleg
500+700=1200=lengthoflongleg 1200+100=1300=lengthofhypotenuse 500+1200+1300=3000=lengthof walkway.Thetotallengthis3000yd.
42. Let x =heightofthebreak.Then10 x =the lengthofhypotenuse.
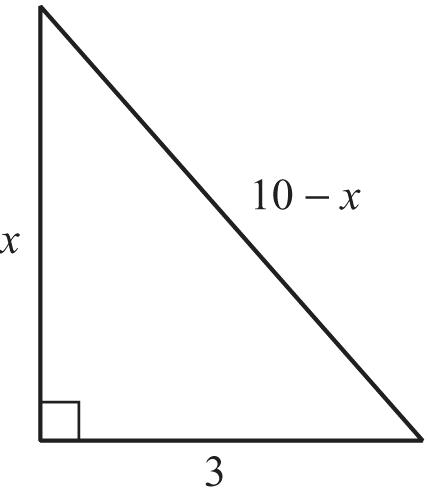
ApplythePythagoreantheorem. 222 222 22 (10)3 100209 10020920914.55 cab xx xxx xxx
Theheightofthebreakis4.55ft.
43. (a) 2 0 2 2 2 16 1696 801696 1696800 stvt stt tt tt
a =16, b =–96and c =80
2 2 4 2 96964(16)(80) 2(16) bbac t a 9692165120 32 9640969664 3232 t 96649664 1or5 3232 tt Theprojectilewillreach80ftat1secand 5sec.
(b) 2 2 1696 01696 0166 stt tt tt 1600or606 tttt Theprojectilewillreturntotheground after6sec.
44. (a) 2 0 2 2 2 2 16 16128 8016128 16128800 850 stvt stt tt tt tt a =1, b =–8and c =5
bbac t a
4110.68or 4117.32 t t
2 2 4 2 884(1)(5) 2(1) 864208448211 222 411
Theprojectilewillreach80ftat0.68sec and7.32sec.
(b)
2 2 16128 016128 0168 stt tt tt
1600or808 tttt Theprojectilewillreturntotheground after8sec.
45. (a) 2 0 2 2 2 2 16 1632 801632 1632800 250 stvt stt tt tt tt
a =1, b =–2and c =5
309004(2.7)(5.5)30840.6 2(2.7)5.4 t
30840.630840.6 10.92or0.19 5.45.4
Therefore,theballreaches12ftfirstafter 0.19sec(onthewayup),thenagainafter 10.92sec(onthewaydown).
bbac t a i i
2 2 4 2 224(1)(5) 2(1) 242021624 222 12
Theprojectilewillnotreach80ft. (b)
2 2 1632 016320162 1600or202 stt tttt tttt
Theprojectilewillreturntotheground after2sec.
46. (a) 2 0 2 2 22 16 1616 801616 161680050 stvt stt tt tttt
a =1, b =–1and c =5
2 2 4 2 114(1)(5) 2(1) 1120119119 222 bbac t a i
Theprojectilewillnotreach80ft. (b) 2 2 1616 016160161 1600or101 stt tttt tttt Theprojectilewillreturntotheground after1sec.
47. Theheightoftheballisgivenby 2 2.7306.5.stt
(a) Whentheballis12ftabovethemoon’s surface, s =12.Set s =12andsolvefor t 2 2 122.7306.5 2.7305.50 tt tt Usethequadraticformulawith a =2.7, b =–30,and c =5.5.
(b) Whentheballreturnstothesurface, s =0.
2 02.7306.5 tt Usethequadraticformulawith a =–2.7, b =30,and c =6.5. 309004(2.7)(6.5) 2(2.7)
30970.2 5.4
30970.2 11.32 5.4
30970.2 0.21or 5.4
Thenegativesolutionisnotmeaningful. Therefore,theballhitsthemoon’ssurface after11.32sec.
48. Whenthequadraticformulaisappliedtothe equation22.7306.5100 tt 2 2.73093.50, tt thediscriminant,
2243042.793.5 9001009.8109.8 bac
isnegative.Becausethisequationhasnoreal solution,theballwillneverreachaheightof 100ft.
49. (a) Theyear2007correspondsto x =13. 2 2 0.23132.60035.17 0.2313132.6001335.17 108.0597
yxx y
In2007,theNFLsalarycapwas approximately$108.1million. (b) Wemustsolvefor x when y =90. 2 2 900.23132.60035.17 00.23132.60054.83 xx xx
Usethequadraticformulawith a =0.2313, b =2.600,and c =–54.83. (continuedonnextpage)
(continued)
50. (a)
(b)
2 2 4 2
2.60057.4887 0.4626 10.8,22.0 bbac x a x
2.6002.60040.231354.83 20.2313
Thenegativesolutionisnotmeaningful. Therefore,thesalarycapreached90million dollarsduring2004.
2 2 0.02581.3023.3 0.025811.30123.3 22.0258 yxx y
Aplayerchosenfirstwillearnabout$22.0 million.
2 2 0.02581.3023.3 0.0258101.301023.3 12.88 yxx y
Aplayerchosententhwillearnabout$12.9 million.
51. (a) Let x =50. 2 0.00787(50)1.528(50)75.8919.2 T
Theexposuretimewhen x =50ppmis approximately19.2hr.
(b) Let T =3andsolvefor x 2 30.007871.52875.89 xx 2 0.007871.52872.890 xx
Usethequadraticformulawith a =0.00787, b =–1.528,and c =72.89. 2 (1.528)(1.528)4(0.00787)(72.89) 2(0.00787)
1.5280.0402068 0.01574 x
1.5282.3347842.2945772 0.01574
1.5280.0402068 109.8 0.01574 or 1.5280.0402068 84.3 0.01574
Werejectthepotentialsolution109.8 becauseitisnotintheinterval[50,100]. So,84.3ppmcarbonmonoxide concentrationisnecessaryforapersonto reachthe4%to6%CoHblevelin3hr.
52. (a) Let x =600andsolvefor T 2 2 0.00020.316127.9 0.0002(600)0.316(600)127.9 10.3
Theexposuretimewhen x =600ppmis 10.3hr.
(b) Let T =4andsolvefor x 2 40.00020.316127.9 xx 2 0.00020.316123.90 xx Usethequadraticformulawith a =0.0002, b =–0.316,and c =123.9. 2 0.316(0.316) 4(0.0002)(123.9) 2(0.0002)
0.3160.0998560.09912 0.0004 0.3160.000736 857.8or722.2 0.0004 x
857.8isnotintheinterval[500,800].A concentrationof722.2ppmisrequired.
53. (a) 2014isrepresentedby x =6.Substitute x =6intotheequationtofind y:
2 2 0.04299.73606 0.042969.736606 549.2milliontons yxx y
In2014,emissionswereabout549.2million tons.
(b) Let y =500andsolvefor x 2 2 5000.04299.73606 0.04299.731060 xx xx
Usethequadraticformulawith a =0.0429, b =–9.73,and c =106. 2 9.739.7340.0429106 20.0429 9.7376.4833 11.5or215.3 0.0858
Themodelpredictsthattheemissionswill reach500milliontonsabout11.5yearsafter 2008,whichisduring2019.
Copyright©2017PearsonEducation,Inc.
54. Let y =8605andsolvefor x 2 2 86054.065370.13450 4.065370.151550
Usethequadraticformulawith a =4.065, b =370.1,and c =5155. 2 370.1370.14(4.065)(5155) 2(4.065)
370.1220,794.31 8.130
370.1469.89 8.130 103.3or12.3
Reject103.3becauseitgivesayearbefore 2000.Basedonthismodel,thecostwas$8605 about12.3yearsafter2000orin2012.
55. Theyear2010isrepresentedby x =3.
In2010,therevenuefromInternetpublishing andbroadcastingwasabout$42,795million.
56. Theyear2012isrepresentedby x =5.
Accordingtothemodel,cableTV’stop internetspeedin2012wasabout299.43MBS.
57. Foreach$20increaseinrentover$300,one unitwillremainvacant.Therefore,for x $20 increases, x unitswillremainvacant. Therefore,thenumberofrentedunitswillbe 80– x.
58. x representsthenumberof$20increasesin rent.Therefore,therentwillbe300+20x dollars.
59. 300+20x istherentforeachapartment,and 80– x isthenumberofapartmentsthatwillbe rentedatthatcost.Therevenuegeneratedwill thenbetheproductof80– x and300+20x, sothecorrectexpressionis
2 2 (80)(30020) 24,000160030020 24,000130020. Rxx xxx xx
60. Settherevenueequalto$35,000.Thisgives theequation 2 35,00024,000130020, xx where x representsthenumberofvacantapartments. Rewritethisequationinstandardformand thensolve.
2 2 20130011,0000 655500 5510055,10 xx xx xxx
If x =55,thenonly25apartmentswillbe rented.Thisdoesnotmeettherestriction,so wedisregardthissolution.If x =10,then70 apartmentswillberented.Thismeetsthe restriction.
61. Let x =numberofpassengersinexcessof75. Then225–5x =thecostperpassenger(in dollars)and75+ x =thenumberof passengers. (Costperpassenger)(Numberofpassengers)= Revenue
2 2 22557516,000 16,875225375516,000 16,875150516,000 xx xxx xx
2 2 05150875 0301750(35)(5) 35035or505 xx xxxx xxxx
Thenegativesolutionisnotmeaningful. Becausethereare5passengersinexcessof 75,thetotalnumberofpassengersis80.
62. Let x =thenumberofunsoldseats.Thenthe numberofpassengersis100 x.Therevenue isgivenby y =(40+2x)(100 x).
2 2 2 5950402100 59504000402002 019501602 0280975 01565 xx xxx xx xx xx
15015 65065 xx xx Theremustbenomorethan50unsoldseats, soonly x =15isvalid.Thereare10015= 85passengers.
63. Let x =numberofweeksthemanagershould wait.Then100+5x =numberofpoundsand 0.400.02 x =costperpound (Costperpound)(Numberofpounds)= Revenue
Thenegativesolutionisnotmeaningful.The farmershouldwait4weekstogetanaverage revenueof$38.40pertree.
64. Let x =numberofdaysthescoutsshouldwait. Then40.1x thepricethescoutswill receiveperhundredpounds,and1204 x = thenumberofhundredsofpoundsofcansthe scoutscancollect.
(Priceperhundredpounds)(Numberof pounds)=Revenue
Thescoutsshouldwait5daysinorderto receive$490fortheircans.
Section 1.6 Other Types of Equations and Applications
1. Arationalequationisanequationthathasa rationalexpressionforoneormoreterms.
2. Proposedsolutionsforwhichanydenominator equals0areexcludedfromthesolutionssetof arationalequation.
3. Ifajobcanbecompletedin4hours,thenthe rateofworkis1/4ofthejobperhour.
4. Whenthepowerpropertyisusedtosolvean equation,itisessentialtocheckallproposed solutionsintheoriginalequation.
5. Anequationsuchas328 x isanequation witharationalexponentbecauseitcontainsa variableraisedtoanexponentthatisarational number. 6. B 7. D 8. C 9. E 10. A 11. 51 0 236 xx 3 2302 xx and606 xx
12. 23 0 152xx 101xx and2 5205 xx
13. 2 313 212xxxx 313 or 21(2)(1)xxxx 202xx and101 xx
14. 2 255 3123xxxx or 255 31(3)(1)xxxx 303xx and101 xx
15. 12 3 4 xx 400 xx
16. 52 6 2 xx 200 xx
17. 253 22 xx x x
Theleastcommondenominatoris 22, x whichisequalto0if x =2.Therefore,2 cannotpossiblybeasolutionofthisequation.
22 253 2222 22 2252322 25410624 510410 xx xxx x xxxxx xxxxxx xxx
Therestriction2 x doesnotaffectthe result.Therefore,thesolutionsetis 10.
18. 432 41 xx x x
Theleastcommondenominatoris 41, x whichisequalto0if x =1.Therefore,–1 cannotpossiblybeasolutionofthisequation. (continuedonnextpage)
(continued)
Therestriction1 x doesnotaffectthe result.Therefore,thesolutionsetis 3 5
19. 3 3 33 x xx
Theleastcommondenominatoris x 3, whichisequalto0if x =3.Therefore,3 cannotpossiblybeasolutionofthisequation.
3 333 33 333 339 36263 x xx xx xx xx xxxx
Theonlypossiblesolutionis3.However,the variableisrestrictedtorealnumbersexcept3. Therefore,thesolutionsetis:
20. 4 4 44 x xx
Theleastcommondenominatoris x 4, whichisequalto0if x =4.Therefore,4 cannotpossiblybeasolutionofthisequation.
4 444 44 444 4416 412 3124 x xx xx xx xx xx xx
Theonlypossiblesolutionis4.However,the variableisrestrictedtorealnumbersexcept4. Therefore,thesolutionsetis:.
21.
2 2312 or 339 2312 3333 xxx xxxx
Theleastcommondenominatoris
33,xx
whichisequalto0if x =3or x =3.Therefore,–3and3cannotpossiblybe solutionsofthisequation.
23 33 33 12 33 33 xx xx xx xx
233312 263912 15123 xx xx xx
Theonlypossiblesolutionis3.However,the variableisrestrictedtorealnumbersexcept–3 and3.Therefore,thesolutionsetis:. 22.
2 3112 or 224 3112 2222 xxx xxxx
Theleastcommondenominatoris
22,xx whichisequalto0if 2or2.xx Therefore,2and2cannot possiblybesolutionsofthisequation.
31 22 22 12 22 22 xx xx xx xx
32212 36212 4412 482 xx xx x xx
Theonlypossiblesolutionis2.However,the variableisrestrictedtorealnumbersexcept2 and2.Therefore,thesolutionsetis:.
23.
222 412 or 6456 412 322223 xxxxx xxxxxx
Theleastcommondenominatoris
322,xxx whichisequalto0if 3or2xx or2. x Therefore,3and 2and2cannotpossiblybesolutionsofthis equation.
322 41 3222 2 322 23 xxx xxxx xxx xx
(continuedonnextpage)
(continued)
25.
Therestrictions3,2,and2 xxx do notaffecttheresult.Therefore,thesolutionset is 9.
Theleastcommondenominatoris
whichisequalto0if
or2.
Therefore,–1and1 and–2cannotpossiblybesolutionsofthis equation.
2312271 612271 662477 4277 237 933 xxx xxx xxx xx x xx
Therestrictions1,1,and2 xxx
do notaffecttheresult.Therefore,thesolutionset is 3.
2 2136 or 22 2136 22 x xxxx x xxxx
Multiplyeachtermintheequationbytheleast commondenominator, 2, xx assuming 0,2. x
2 2 2 2136 22 22 21326 2366 2466 240220 x xxxx xxxx xxx xxx xx xxxx
200or202 xxxx Becauseoftherestriction0, x theonly validsolutionis2.Thesolutionsetis 2.
26.
2 43214321 or 111 xx xxxxxx xx
Multiplyeachtermintheequationbytheleast commondenominator, 1, xx assuming 0,1. x
2 22 4321 11 11 43211 43221 45214510 4110 x xxxx xxxx xxx xxx xxxx xx
1 4 410or101 xxxx Becauseoftherestriction1, x theonly validsolutionis14.Thesolutionsetis
1 4.
2 12 or 111 12 1111 x xxx x xxxx
Multiplyeachtermintheequationbytheleast commondenominator,
11,xx assuming1. x
1 11 11 2 11 11 x xx xx xx xx
2 22 11212 1210 110101or 101 xxxxxx xx xxxx xx
Becauseoftherestriction1, x thesolution setis
28.
Multiplyeachtermintheequationbytheleast commondenominator,
31. 2 31 2 2121 xx
Multiplyeachtermintheequationbytheleast commondenominator, 2 21, x assuming
Becauseoftherestriction1, x thesolution setis:
29. 2 543 18 xx
Multiplyeachtermintheequationbytheleast commondenominator,2, x assuming0. x
22 2 22 5 2 1 9 543 18 54318018435 02591 250or 910 xx xx xxxx xx xx xx
Therestriction0 x doesnotaffecttheresult. Therefore,thesolutionsetis 51 29,.
30. 2 719 6 xx
Multiplyeachtermintheequationbytheleast commondenominator,2, x assuming0. x
22 2 2 2 719 6 7196 06197 03127 xx xx xx xx xx
Therestriction0 x doesnotaffecttheresult. Therefore,thesolutionsetis 17 32,.
Therestriction1 2 x doesnotaffecttheresult. Thereforethesolutionsetis
3 4,1. 32. 2 73 6 2323 xx
Multiplyeachtermintheequationbytheleast commondenominator, 2 23, x assuming 3 2. x
22 2 73 23623 2323 xx xx
2 2 2 2 2 641297233 24725414213 2472541418 2486720 21243360249340 xxx xxx xxx xx xxxx
94 43490or340 xxxx Therestriction3 2 x doesnotaffecttheresult. Therefore,thesolutionsetis 94 43,.
33. 252 3 xx x Multiplyeachtermintheequationbytheleast commondenominator,3, x assuming0. x
2 2 252 33 3 32526152 0815(3)(5) xx xx x xxxxxx xxxx
303or505 xxxx Therestriction0 x doesnotaffecttheresult. Therefore,thesolutionsetis{3,5}.
34. 41 23 xx x
Multiplyeachtermintheequationbytheleast commondenominator,6x,assuming x ≠ 0.
2 2 41 66 23 3421 31222 02512 0(23)(4) xx xx x xxx xxx xx xx
3 2 230or404 xxxx
Therestriction0 x doesnotaffecttheresult. Thereforethesolutionsetis
35. 242 5 22 xx xx
Multiplyeachtermintheequationbytheleast commondenominator, x –2,assuming x ≠ 2.
2 2 2 2 24 (2)(2)522 2524 25104 04310 0245 xx xx xx xxx xxx xx xx
36. 32 2 11 xx xx
5 2,4.
Multiplyeachtermintheequationbytheleast commondenominator, x 1,assuming x ≠ 1.
37. Let x =theamountoftime(inhours)ittakes JoeandSamtopaintthehouse. rt Partofthe Job Accomplished
Joe1 3 x 1 3
Sam1 5 x 1 5 x
BecauseJoeandSammustaccomplish1job (paintingahouse),wemustsolvethe followingequation.
38. Let x =theamountoftime(inhours)ittakes JoeandSamtopaintthehouse.
BecauseJoeandSammustaccomplish1job (paintingahouse),wemustsolvethe followingequation.
39. Let x =theamountoftime(inhours)ittakes plantAtoproducethepollutant.Then2x =the amountoftime(inhours)ittakesplantBto producethepollutant.
RateTime
BecauseplantAandBaccomplish1job (producingthepollutant),wemustsolvethe followingequation.
PlantBwilltake23978
hrtoproducethe pollutant.
40. Let x =theamountoftime(inhours)thefirst (faster)pipeoperates.Then3x =thesecond (slower)pipeoperates.
Firstpipe1 x 1212 x
Becausethetwopipesareworkingtogether, wemustsolvethefollowingequation. 1212361248
Thefasterpipecanfillthepondin16hours workingalone.
41. Let x =theamountoftime(inhours)tofillthe poolwithbothpipesopen.
RateTime Partofthe Job Accomplished
Inletpipe1 5 x 1 5 x
Outletpipe1 8 x 1 8 x
Fillingthepoolis1wholejob,butbecausethe outletpipeemptiesthepool,itscontribution shouldbesubtractedfromthecontributionof theinletpipe. 11 58 11 58 1 3 1 404018540 40 34013hr 3 xx xxxx xx
Ittook1133hrtofillthepool.
42. Weneedtodeterminehowmuchofthepool wasfilledafter1hour.Todothis,weevaluate 11 58xx when1 x .After1hour, 1111853 5858404040 11
ofthepool hasbeenfilled.Whatremainstobefilledis 340337 140404040
.Ifwenowlet x bethe amountoftimeittakestocompletefillingthe pool,wemustsolvethefollowing.
373711 540540 375 88 55 4hr xx x
Itwilltake548hrmoretofillthepool.
43. Let x =theamountoftime(inminutes)tofill thesinkwithbothpipesopen.
Tap1 5 x 1 5 x Drain110 x 1 10 x Fillingthesinkis1wholejob,butbecausethe sinkisdraining,itscontributionshouldbe subtractedfromthecontributionofthetaps.
11 510 11 510 1 1010121010 xx xxxxx
Itwilltake10minutestofillthesinkifMark forgetstoputinthestopper.
44. Weneedtodeterminehowmuchofthesink wasfilledafter1minute.Todothis,we evaluate11 510xx when1 x .After1 minute,1111211 510510101010 11 of thesinkhasbeenfilled.Whatremainstobe filledis109 11 110101010 .Ifwenowlet x betheamountoftimeittakestocomplete fillingthesink,wemustsolvethefollowing.
19 510 9 11 5102 45 554min 10 x xx Itwilltake142minmoretofillthesink.
45.
xx xxxx xxxx xxxx
46.
47.
Check1. x
22 22 230 2323 23230 1301or3
xx
? 230 12130 1230 11011020
Thisisafalsestatement.1isnotasolution.
Check3. x
xx
? 230 32330 3630 39033000
Thisisatruestatement.3isasolution.
Solutionset: 3
Check2. x ? 3735 3(2)73(2)5 6765 1111 xx
Thisisafalsestatement.2isnotasolution.
Check1 x ? 3735 3(1)73(1)5 3735 4222 xx
Thisisatruestatement.1isasolution.
Solutionset: 1
xx xxxx xxxx xxxx
22 22 3180 318318 3183180 3603or6
Check3. x
xx
? 3180 333180 39180 39033060
Thisisafalsestatement.–3isnotasolution.
Check6. x
xx
? 3180 636180 618180 636066000
Thisisatruestatement.6isasolution
Solutionset: 6
22 2 2 2 3735 3735 3793025 092718 0932921 xx xx xxx xx xxxx
2or1xx
48. 22 2 2 2 41321 41321 413441 04812 0423 0413 xx xx xxx xx xx xx
1or3xx
Check1. x
xx
? 41321 4113211 41321 9333
Thisisafalsestatement.1isnotasolution. Check3. x
xx
? 41321 4313231 121361 25555
Thisisatruestatement.3isasolution.
Solutionset: 3
49.
22 2 2 2 456211 4525 4525 4542025 042420 0465415 1or5 xx xx xx xxx xx xxxx xx
(continuedonnextpage)
(continued)
Check1. x
xx
? 456211 41562111 456211 969 36939
Thisisafalsestatement.1isnotasolution.
Check5. x
xx
? 456211 45562511 20561011 256156111
Thisisatruestatement.5isasolution.
Solutionset: 5
50.
22 2 2 6797 672 672 6744 02313 xx xx xx xxx xxxx
1or3xx
Check1. x ? 6797 617917 6710 11011000 xx
Thisisatruestatement.1isasolution.
Check3. x
xx
? 6797 637937 18794 259459444
Thisisatruestatement.3isasolution.
Solutionset: 1,3
51.
52.
22 2 2 430 43 43 469 0109(1)(9) 1or9 xx xx xx xxx xxxx xx
Check1. x
? 430 41130 4130 213040 xx
Thisisafalsestatement.1isnotasolution.
Check9. x
? 430 49930 36930 693000 xx
Thisisatruestatement.9isasolution.
Solutionset: 9
22 2 2 240 24 24 2816 01016(2)(8) 2or8 xx xx xx xxx xxxx xx
Check2. x
? 240 22240 4240 224040 xx
Thisisafalsestatement.2isnotasolution.
Check8. x
? 240 28840 16840 484000 xx
Thisisatruestatement.8isasolution.
Solutionset: 8
Chapter 1 Equations and Inequalities
53.
22 22 51 1515 1255 254425 2525 459 xx xxxx xxx xxxx xx xx
Check9. x ? 51 9951 34132111 xx
Thisisatruestatement. Solutionsetis: 9
54.
22 22 122 212212 441212 41288412 212212 41216 xx xxxx xxx xxxx xx xx
Check16. x ? 122 1616122 44242222 xx
Thisisatruestatement.
Solutionset: 16
55.
22 22 734 734 76794 671646720 37103710 97100963100 37 937 9 xx xx xxx xxxx xx xx xx
37 Check9. x ? 3737 99 37633736 9999 734 734 3 xx
Thisisafalsestatement. Solutionset:
56.
57.
1001 99 1010919111 3333333 3 3
22 22 521 521 54541 94514510 255255 452542025 5 45 4 xx xx xxx xxxx xx xx xx
5 Check4. x ? 55 44 52054 4444 251 44 5911 2222 521 521 2 2 2 xx
Thisisafalsestatement. Solutionset:
22 22 2 2 2 2521 2521 2521 252221 25322 222 222 4442 4448 04 0222 xx xx xx xxx xxx xx xx xxx xxx x xxx
Check2. x
xx
? ? ? ? 2521 225221 4541 941 32111
Thisisatruestatement.2isasolution.
(continuedonnextpage)
(continued)
Check2. x
? ? ? ? 2521 225221 4501 101 10111 xx
Thisisatruestatement.2isasolution.
Solutionset:
22 4112 4112 4112 411414 41341 3241 xx xx xx xxx xxx xx
22 2 2 2 10 9 3241 9124161 91241616 92820091020 or2 xx xxx xxx xxxx xx
10 Check9. x ? 1010 99 40109 999 4112 4112 12 xx 4094911 99993 7677 1 33333 22
Thisisatruestatement.109isasolution.
Check2. x ? 4112 421212 8112 91233 xx
Thisisatruestatement.2isasolution.
Solutionset: 109,2
59.
22 222 2 3511 3511 3512511 352251 25122511 5115112 0303 0or3 xx xx xxx xxx xxxx xxxxx xxxx xx
Check0. x
? 3511 305011 0011011 01100 xx
Thisisatruestatement.0isasolution. Check3. x
xx
? 3511 335311 915113161 34133
Thisisatruestatement.3isasolution. Solutionset:{0,3}
60.
22 22 2 2 2 2 23122 23122 231243124 23164312 431216 431216 1631232256 4819232256 01664 0(8)8
xx xx xxx xxx xx xx xxx xxx xx xx
Check8. x
xx
? 23122 2838122 1624122 436246244
Thisisatruestatement. Solutionset:{8}
61.
62.
22 22 22 2137 2(137) 2123737 238237 23726 23723 373373 3769032 021 2or1 xx xx xxx xxx
Check2. x
? 2137 221327 0167 011 01100
Thisisatruestatement.2isasolution.
Check1. x
? 2137 121317 1137 114 11211 xx
Thisisafalsestatement. 1isnotasolution. Solutionset:{2}
22 22 2 2 2 2522 2522 254422 25242 742 742 1449162 14491632 308103270 3or27 xx xx xxx xxx xx xx xxx xxx xxxx xx
Check3. x
? 2522 235232 6521 12113 xx
Thisisafalsestatement.3isnotasolution.
Check27. x
? 252272 22752272 545225 492577 x
Thisisatruestatement.27isasolution. Solutionset:{27} 63.
22 22 2 2 2 2 9 27232 27232 27232 27232 4729124 2889124 09164 0922 or2 xx xx xx xx xxx xxx xx xx xx
2 Check9. x
xx
? 22 99 142 93 186142 9933 4424 9333 27232 27232 222 2 22
323424 33 333 23232323 33333
Thisisatruestatement. 2 9isasolution.
Check2. x
xx
? 27232 2722322 214262
2168 2422 8222222
Thisisatruestatement.2isasolution.
Solutionset: 2 9,2
22 22 2 2 2 3 25 32356 32356 32356 32356 923256036 1827256036 025789 02533 or3 xx xx xx xx xxx xxx xx xx xx
3 Check25. x
? 33 2525 63 255 675330 252555 32356 32356 336 3
8127927 25555 27335 555 27315 55 335315315315 55555 33 i i ii
Thisisafalsestatement.325isnotasolution.
Check3. x
? 32356 3233536 363156 xx
399 3339333
Thisisatruestatement.3isasolution Solutionset: 3 65.
22 22 2 2 323 323 9623 128 128 1442464 401440 364036or4 xx xx xxx xx xx xxx xx xxxx
Check36. x
? 323 3362363 36263 31233933 xx
Thisisafalsestatement.36isnotasolution. Check4. x
? 323 34243 32223 1431111 xx
Thisisatruestatement.4isasolution. Solutionset: 4 66.
22 22 22 247 247 4447 33 990 900or9 xx xx xxx xxxx xxxx xxxx
Check0. x ? 247 02470 02470 2402422 xx
Thisisatruestatement.0isasolution. Check9. x ? 247 92479 32473 542152555
xx
Thisisatruestatement.9isasolution. Solutionset: 0,9
67.
33 3333 4321 4321 4321242 xx xx xxxx
Check2. x 33 ? 3333 4(2)32(2)1 5555
Thisisatruestatement.2isasolution. Solutionset:{–2}
68.
333333 252252 2 25232 3 xxxx xxxx
2 Check3. x
323 333 23 22 4 3 398 398 39831080 3420or2 xxx xxx xxxxx xxxx
69.
2233 33 ?10106 443333 33333 333 44 33 3333 3 3333 33 252 2 4936 393 36493636 333 39
Thisisatruestatement.
Solutionset: 2 3
323 323 333 23 2 2 2 5 5620 562 562 562 5720 5210or1 xxx xxx xxx xxx xx xxxx
2 Check5. x
323 2?3222 3 555 412233 2555 10 412233 5555 2233 55 5620 5620 520 0 000 xxx
4
Check3. x
xxx
333 33 33 33333 33 323 2? 3444 3 333 49361616 33 933 39 163636 3124 3 33333 49363636 39333 398 398 31284
Thisisatruestatement.43isasolution. Check2. x
323 32?3 33 3333 398 329282 341882 1210222 xxx
Thisisatruestatement.2isasolution. Solutionset: 4 3,2
71.
Thisisatruestatement.25isasolution.
Check1. x 323 2?33 3 3 3 5620 5161210 516210 56210 11011000
xxx
Thisisatruestatement.1isasolution.
Solutionset: 2 5,1
72.
4444 152152 151631 xx xx
Check31. x 44? 4 15231152 16222 x Thisisatruestatement. Solutionset: 31
4 444 311 311311 300 x xx xx Check0. x
4? 4 44 3113011 0111111 x Thisisatruestatement. Solutionset: 0
73.
4444 2244 22 2323 23230 3103or1 xxxx xxxx xxxx
Check3. x
424 42?4 4444 23 3233 96333 xx
Thisisatruestatement.3isasolution.
Check1. x 424 42?4 4444 23 1213 12333
Thisisatruestatement.1isasolution.
Solutionset:{3,1}
74.
4 44224 22 6262 6166160 8208or2 xxxx xxxx xxxx
Check8. x
xx
42 42? 44 62 8682 6448216222
Thisisatruestatement.8isasolution.
Check2. x
xx
42 42? 44 62 2622 412216222
Thisisatruestatement.2isasolution.
Solutionset: 8,2
75.
32 23 3223 2 125 125 525 x x x
Check x =25. 32 32? 125 25125 125125 x
Thisisatruestatement.25isasolution.
Solutionset:{25}
76.
54 45 5445 4 32 32 216 x x x
Check x =16. 54 54? 32 1632 3232 x
Thisisatruestatement.16isasolution. Solutionset:{16}
77. 1/44 21/424 22 (24)3243 248124810 (27)(3)027027or 303 xxxx xxxx xxxx xx
Check27. x
21/4 21/4? 1/4 1/4 (24)3 2724273 7296483 81333 xx
Thisisatruestatement.–27isasolution. Check3. x
21/4 21/4? 1/41/4 (24)3 32433 972381333 xx
Thisisatruestatement.3isasolution. Solutionset:{–27,3}
78.
1/41/44 224 22 64 3 35243524 3522563522560 36440or4 xxxx xxxx xxxx
64 Check3. x
21/4 21/4?6464 33 1/4 40963328 93 409633281/4 33 7681/4 3 1/4 3524 3524 34 4 4 256444 xx Thisisatruestatement. 643isasolution. (continuedonnextpage)
(continued)
Check4. x
21/4 21/4? 1/4 3524 345244 3162084 xx
1/4 1/4 482084 256444
Thisisatruestatement.4isasolution.
Solutionset: 643,4
79. 25 255252 34 34 332 33235 33229 x x x xx xx
Check x =35.
25 25? 25 34 3534 32444 x
Thisisatruestatement.35isasolution.
Check x =29.
25 25? 25 2 34 2934 324 2444 x
Thisisatruestatement.29isasolution. Solutionset:{29,35}
80.
23 233232 20036 20036 200216 20021616 200216416 x x x xx xx
Check x =16.
23 23? 23 20036 1620036 216363636 x Thisisatruestatement.16isasolution.
81.
Check x =416.
23 23? 23 2 20036 41620036 21636 6363636 x
Thisisatruestatement.416isasolution. Solutionset:{416,16}
1313 1313 331313 3 2 25610 2561 2561 2561 46 xx xx xx xx x x
Check3 2 x
1313 1313?33 22 1313 25610 25610 88000
Thisisatruestatement.32isasolution.
Solutionset: 3 2
1313 1313 331313 37420 3742 3742 3742 5 xx xx xx xx x
Check x =5.
1313 1313? 1313 37420 3574520 2222000
Thisisatruestatement.5isasolution. Solutionset:{5}
2/31/3
83.
Thisisatruestatement.14isasolution.
Check1. x
2/31/32/3?1/3 2/32/3 (21)2111 2111111 xx
Thisisatruestatement.1isasolution.
Solutionset: 1 4,1
2/51/5 552/51/5
2 2 (3)4 (3)4 (3)4 694 1090 1901or9 xx xx xx xxx xx xxxx
Check1. x
2/51/5
2/5?1/5
2/51/5
21/51/55555 (3)4 (13)41 24 244444 xx
Thisisatruestatement.1isasolution.
Check9. x
2/51/5
2/5?1/5
2/51/521/55 1/5555 (3)4 (93)49 636636 36363636 xx
Thisisatruestatement.9isasolution.
Solutionset: 1,9
332/31/32/31/3 22 22 88080 0or8 xxxx xxxxxx xx Check0. x
2/31/3 ? 2/31/3 2 02002000 xx
Thisisatruestatement.0isasolution. Check8. x
? 2/31/32/31/3 1/3 21/3 2828 82264444 xx Thisisatruestatement.8isasolution. Solutionset: 0,8
443/41/23/41/2 3232 21 81 33 81810 81100or xxxx xxxx xxxx Check0. x
3/41/2 3/4?1/2 3 30030000 xx
Thisisatruestatement.0isasolution. 1 Check81. x
3/41/2 3/41/21/43 ? 1111 8181819 3 111111 3927999 3 33 33 xx
Thisisatruestatement.181isasolution.
Solutionset: 1 0,81 87. 42 2750 xx Let2 ux ;then24 ux .Withthis substitution,theequationbecomes 2 2750 uu 2 5 2 27501250 1or uuuu uu
Tofind x,replace u with2 x 2 51022 55 222 22 11orxx xx
Solutionset: 101,2
88. 42 4830 xx
Let2 ux ;then24 ux .
2 483021230 uuuu . 1 2 u or3 2 u
Tofind x,replace u with2 x 3622 33 222 22 222 111 222 22 or xxx xxx
Solutionset: 62 22 ,
89. 422150xx
Let2; ux then24 ux
22150350 3or5 uuuu uu
Tofind x,replace u with2 x . 2 2 33or 555 xx xxi
Solutionset: 3,5 i
90. 42 310250 xx
Let2; ux then24 ux
2 3102505350 uuuu . 5 53 or uu
Tofind x,replace u with2 x 2 25315 55 333 33 555orxxi xxx
Solutionset: 155,3 i
91. 2/31/3 (1)(1)120 xx
Let 1/3 1. ux Then
2 21/32/3 11.uxx
2120430 uuuu
4or3uu
Tofind x,replace u with 1/3 1. x
3 1/31/33 1414 16463or xx xx
1/31/333 1313 12728 xx xx
Check63. x
xx
2/31/3 2/31/3? 2/31/3 1/32 2 (1)(1)120 (631)(631)120 (64)(64)120 (64)4120 44120 16412000
Thisisatruestatement.63isasolution. Check28. x 2/31/3 2/31/3? 2/31/3 1/32 2 (1)(1)120 (281)(281)120 2727120 273120 33120 9312000 xx
Thisisatruestatement.28isasolution. Solutionset: 63,28
92. 2/31/3 (21)2(21)30 xx
Let 1/3 21.ux Then 2 21/32/3 2121.uxx
2230310 uuuu 3or1uu
Tofind x,replace u with 1/3 21. x
3 1/31/33 213213 212722613or xx xxx 1/31/333 211211 211221 xx xxx
Check13. x
xx
2/31/3 2/31/3? 2/31/3 2/31/3 1/32 2 (21)2(21)30 2(13)122(13)130 (261)2(261)30 (27)2(27)30 (27)2330 3630 9630 00
Thisisatruestatement.13isasolution. (continuedonnextpage)
(continued)
Check1. x
xx
2/31/3 2/31/3? 2/31/3 2/31/3 (21)2(21)30 2(1)122(1)130 (21)2(21)30 12(1)30 12130 1230 00
Thisisatruestatement.1isasolution
Solutionset: 13,1
93. 2/51/5 (1)3(1)20 xx
Let 1/5 1. ux Then
2 21/52/5 11.uxx
1or2uu
Tofind x,replace u with 1/5 1. x
1/51/555 1111 110 xx xx
1/51/555 1212 13231 xx xx
Check0. x 2/51/5
xx
2/51/5?
2/51/5 (1)3(1)20 (01)3(01)20 13(1)20 13(1)2000
Thisisatruestatement.0isasolution.
Check31. x
2/51/5
xx
2/51/5?
2/51/5 1/52 2 (1)3(1)20 (311)3(311)20 323(32)20 (32)3(2)20 2620 462000
Thisisatruestatement.31isasolution.
Solutionset: 0,31
94. 2/31/3 (5)(5)200 xx
Let 1/3 5. ux Then
2 21/32/3 55.uxx
2200540 uuuu 5or4uu Tofind x,replace u with 1/3 5. x
3 1/31/33 5555 5125130or xx xx
1/31/333 5454 56459 xx xx Check130. x
2/31/3 2/31/3? 2/31/3 (5)(5)200 (1305)(1305)200 125125200 255200 00 xx
Thisisatruestatement.130isasolution. Check59. x 2/31/3 2/31/3? 2/31/3 (5)(5)200 (595)(595)200 6464200 164200 00 xx
Thisisatruestatement.59isasolution. Solutionset:{130,59}
95. 42 42 411319 4113190 xx xx
Let2(1).ux Then24(1).ux
2 9 4 41390 4910or1 uu uuuu
Tofind x,replace u with2 (1) x
293 42 351 222 11 1or xx xxx
2 1111 112or0 xx xxx
Besuretocheckallpossiblesolutionsinthe originalequation.
Solutionset: 51 22 ,2,0,
96.
42 42 255116564 2551165640 xx xx
Let 2 5. ux Then 245. ux
2 16 25 25116640 251640or4 uu uuuu
Tofind x,replace u with 2 5. x 2164 255 42129 555 55 5or xx xxx
2 5452 527or3 xx xxx
Besuretocheckallpossiblesolutionsinthe originalequation.
Solutionset: 2129 55 3,,,7 97. 42 42 6(2)11(2)4 6(2)11(2)40 xx xx
Let2(2);ux then24 (2).ux 2 61140(34)(21)0 uuuu 41 32 or uu
Tofind x,replace u with2 (2) x 223 44 333 2323623 6 3333 (2)2 2 xx x
(2)2 2 xx x
or 22 11 222 2242 4 2222
Solutionset: 62342 32 ,
98. 42 42 8(4)10(4)3 8(4)10(4)30 xx xx
99. 21 103370 xx
Let1 ux ;then22. ux 2 103370(27)(51)0 uuuu 71 25 or uu
Tofind x,replace u with1 x 11721 275or5xxxx
Solutionset: 2 7,5
100. 21 71080 xx
Let1 ux ;then22. ux 2 71080(74)(2)0 uuuu 4 7or2uu
Tofind x,replace u with1 x 11 7 41 742 or2 xxxx
Solutionset: 71 42 ,
101. 2/31/360xx
Let1/3; ux then 2 21/32/3 uxx 260(3)(2)0 uuuu 3or2uu
Tofind x,replace u with1/3. x
3 1/31/333 11 327 33xx xx
or
3 3 1/31/33 11 28 22xx xx 1 Check27. x
2/31/3 2/31/3?11 2727 2/31/3 60 60 (27)(27)60 xx
(4)4 4 xx x
Let u = 2 (4); x then24 (4).ux 2 8103021430 uuuu 1 2 u or3 4 u 22 11 222 2282 8 2222
or 23 33 442 3383 8 2222 (4)4 4 xx x
Solutionset: 8283 22 ,
1/32 2 27360 3360 936000
Thisisatruestatement. (continuedonnextpage)
(continued)
1 Check8. x
2/31/3 2/31/3?11 88 2/31/3 1/32 2 60 60 8860 8260 2260 426000 xx
Thisisatruestatement.
Solutionset: 11 278 ,
102. 2/51/5 210 xx
Let1/5; ux then
2 21/52/5 uxx 2 210(21)(1)0 uuuu 1 2or1uu
Tofind x,replace u with1/5 x
1/51 2 1/555 1 2 32 x x x
5 or1/51/55111xxx
Solutionset:{32,1}
103. 42 166540 xx
Let2 ux ;then24 ux .Solvethe resultingequationbyfactoring:
2 1 16 16654041610 4or uuuu uu
Find x byreplacing u with2 x : 2211 42 22 1 16 4 164 xxx xxx
Check1 2 x
4211 22 42? 166540 16265240 161665440 25626040 00
Thisisatruestatement,so12isasolution.
Check1 2 x
4211 22 42? 166540 16265240 161665440 25626040 00
Thisisatruestatement,so12isasolution. Check x =4
42 42?11 44 11 25616 165 1616 16465440 166540 166540 40 00
Thisisatruestatement,so4isasolution. Check x =4
42 42?11 44 11 25616 165 1616 16465440 166540 166540 40 00
Thisisatruestatement,so4isasolution. Solutionset: 1 2,4
104. 42 62512540 xx
Let2 ux ;then24 ux .Solvethe resultingequationbyfactoring:
2 41 2525 62512540 2542510or uu uuuu
Find x byreplacing u with2. x 22255 4 2542 22 1 25255 xxx xxx
Check5 2 x
42?55 22 4222 55 164 62525 62512540 62512540 62512540 16204000
Thisisatruestatement,so52isasolution.
(continuedonnextpage)
(continued)
Check5 2 x
42?55 22 4222 55 164 62525 62512540 62512540 62512540 16204000
Thisisatruestatement,so52isasolution.
Check x =5
42? 4211 55 11 62525 6255125540 62512540 62512540 154000
Thisisatruestatement,so5isasolution.
Check x =5
42?
4211 55 11 62525 6255125540 62512540 62512540 154000
Thisisatruestatement,so5isasolution.
Solutionset:
5 2,5
105. dkh for h d h k 2 2 d h k
So, 2 2. d h k 106.
2/32/32/3
2/32/32/3
332/32/32/3 22/32/33
2/32/33 2/32/33/2 for () xyay yax yax yax yax yax
107. 3/43/4
3/43/4 1for 1 mnm mn Raisebothsidestothe43power.
3/44/33/44/3
3/44/3 ()(1) (1) mn mn
108. 12 121212 12 12 1221 1221 12 21 111 for 111 Multiplybothsidesby. R Rrr RrrRrrRrr Rrr Rrr rrRrRr rrRrr rr R rr
So,12 12 =. rr R rr
109. for Multiplybothsidesby. () ERr e er ERr erer er er EreRer EreRr Er e Rr
So, Er e Rr
110. 222 222 22 for abcb bca bca
111. 120 xx
Let ux ;then2ux .Solvetheresulting equationbyfactoring. 2120(4)(3)0 uuuu u =4or u =–3
Tofind x,replace u with x 22 4416xxx or 22 339xxx
But93
Sowhen u =–3,thereisnosolutionfor x. Solutionset:{16}
112. 120 xx
Solvebyisolating x ,thensquaringboth sides.
222 2 12 (12)()24144
251440(16)(9)0 xx xxxxx xxxx
x =16or x =9
Check x =16. ? 120 1616120 16412000
Thisisatruestatement. Check x =9. ? 120 991209312060 xx
Thisisafalsestatement.9doesnotsatisfythe equation.
Solutionset:{16}
113. Answerswillvary.
114. 3280 xx Solvebysubstitution.
Let ux ;then2ux .Solvetheresulting equationbyfactoring.
2 3280(34)(2)0 uuuu 4 3or2uu
Tofind x,replace u with x 4 3 x hasnosolution,becausetheresult ofasquarerootisneveranegativereal number.
24xx Check x =4.
? 3280 342480 342280 1248000
Thisisatruestatement. Solutionset:{4}
Summary Exercises on Solving Equations
1. 4323233 263 xxx xx Solutionset: 3
2.
563222 56344 2644242 221 xx xx xxx xx
Solutionset: 1.
3. 22 6969690xxxxxx Solvebycompletingthesquare.
2 122 2 2 6999
Note:639 318318 332332 xx xx xx
Solvebythequadraticformula. Let1,6,and9. abc
2 2 4 2 66419 21 63636672 22 662 332 2 bbac x a
Solutionset: 332 4. 228128120xxxx Solvebyfactoring.
28120260 2or6 xxxx xx Solvebycompletingthesquare.
2 122 2 2 8161216 Note:8416 4444 4242 422or426 xx xx xx xx
Solvebythequadraticformula. Let1,8,and12. abc
2 2 4 2 884112 21 bbac x a
8644881684 42 222 x 422or426xx Solutionset: 2,6
5.
Check25. x ? 1414 2525 503751414 25252525 36361625193119 252555555 2515 2515 5 5 xx
Thisisafalsestatement.Solutionset: 6.
2 563 or 326 563 3232 xxxx xxxx
Theleastcommondenominatoris
32,xx whichisequalto0if 3or2.xx Therefore,3and2cannot possiblybesolutionsofthisequation.
Therestrictions3and2 xx donotaffect theresult.Therefore,thesolutionsetis{31}.
7. 342 33 xx x x
Theleastcommondenominatoris 33, x whichisequalto0if3. x Therefore,3 cannotpossiblybeasolutionofthisequation.
22 342 3333 33 3343233 34912639 xx xxx x xxxxx xxxxxx
22 3111239 11129 1226 xxxx xx xx
Therestriction3 x doesnotaffectthe result.Therefore,thesolutionsetis 6.
8.
44 5665 2323 3863011630 5306
xx xxxx xxxxx xx
Solutionset: 6
9. 2 21 50 xx
Theleastcommondenominatoris2, x which isequalto0if0. x Therefore,0cannot possiblybeasolutionofthisequation. 222 2 21 505210xxxx xx
Solvebycompletingthesquare.
Note: xx xx x x xixi
1 5 221 55 22111 525525 22 1211 25525 25 114 5252525 14 525 1212 5555 0Multiplyby.
Solvebythequadraticformula. Let5,2,and1. abc
2 2 4 2 22451 25 2420216 1010 242412 10101055 bbac x a i ii Therestriction0 x doesnotaffecttheresult. Therefore,thesolutionsetis 12 55. i
10. 2 219219213 13 213 2 xxx xx 134132 2or1 2222 xx
Solutionset: 2,1
11. 2/51/52150xx
Let1/5 ux ;then
Tofind x,replace u with1/5. x
5 1/51/555 11 3243
2/51/5 2/51/511 243243 2/51/5 1/52 2 2150 2150? (243)2(243)150 24323150 361509615000
Thisisatruestatement.1243isasolution. 1 Check3125. x
2/51/5 2/51/5?11 31253125 2/51/5 1/52 2 2150 2150 (3125)2(3125)150 312525150 510150 251015000
Thisisatruestatement.13125isasolution. Solutionset: 11 2433125 , 12.
Check1. x ? 2126 121216 11262422 xx
Thisisatruestatement.
Solutionset: 1
13. 42340xx Let2 ux ;then24 ux
2340140 1or4 uuuu uu
Tofind x,replace x with2 x 2 2 11or 442 xxi xx
Solutionset: ,2 i
14. 1.20.30.70.9 101.20.3100.70.9 12379539 5122.4 xx xx xxx xx
Solutionset: 2.4
15. 333333 219219 219284 xx xxx
Check4. x
? 333 3 3333 2192419 81999 x
Thisisatruestatement. Solutionset:{4}
16. 22 3213210 xxxx Solvebycompletingthesquare. 2 2211 333 22111 3939 22 1211 2339 23 112 3999 12 39 2211 3333 321 Multiplyby.
Note: xx xx xx x x xixi
Solvebythequadraticformula. Let3,2,and1. abc (continuedonnextpage)
(continued)
Solutionset:
2/3 2/333 2 2 2 2 (142)4 [(142)]4 (142)64 19656464 4561320 414330 431103or11 x x x xx xx xx xxxx
Check3. x
Solutionset:
22 22 2 2 2 111 111 2111 3111310 310 910020 010029 029100 0425 4or25 xx xx xxx xxxx xx xxx xx xx xx xx
Check4. x ? 111 41114 211123933
xx
Thisisatruestatement.
Check25. x ? 111 2511125 5111566
xx
Thisisafalsestatement. Solutionset: 4
2/3 2/3? 2/32/3 2 1/32 (142)4 14234 146484 842444 x
Thisisatruestatement. Check11. x
2/3 2/3? 2/32/3 2 1/32 (142)4 142114 1422484 842444 x
Thisisatruestatement.
Solutionset: 3,11
20. 21 21 21 21 210 210 xx xx xx
Let1 ux ;then22. ux 22210(1)01uuuu
Tofind x,replace u with1 x 111xx
Solutionset: 1
21. 33 33xx
Theleastcommondenominatoris 3 x whichisequalto0if3. x Therefore,3 cannotpossiblybeasolutionofthisequation.
Solutionset: |3xx .
22. 222 22222 for abca acbacb
Section 1.7 Inequalities
1. F.Theinequality x <–6includesallreal numberslessthan6notincluding6.The correctintervalnotationis ,6.
2. J.Theinequality6 x includesallreal numberslessthanorequalto6,soitincludes6. Thecorrectintervalnotationis
,6.
3. A.Theinequality26 x includesallreal numbersfrom–2to6,notincluding–2,but including6.Thecorrectintervalnotationis (–2,6].
4. H.Theinequality20 x includesallreal numbersbecausethesquareofanyreal numberisgreaterthanorequalto0.The correctintervalnotationis
,.
5. I.Theinequality6 x includesallreal numbersgreaterthanorequalto–6,soit includes–6.Thecorrectintervalnotationis
6,.
6. D.Theinequality6 x includesallreal numbersgreaterthanorequalto6,soit includes6.Thecorrectintervalnotationis
6,.
7. B.Theintervalshownonthenumberline includesallrealnumbersbetween–2and6, including–2,butnotincluding6.Thecorrect intervalnotationis[–2,6).
8. G.Theintervalshownonthenumberline includesallrealnumbersbetween0and8,not including0or8.Thecorrectintervalnotation is(0,8).
9. E.Theintervalshownonthenumberline includesallrealnumberslessthan3,not including3,andgreaterthan3,notincluding 3.Thecorrectintervalnotationis
,33,,
10. C.Theintervalincludesallrealnumbersless thanorequalto–6,soitincludes–6,The correctintervalnotationis
,6.
11. Answerswil1vary.Sampleanswer:Asquare bracketisusedtoshowthatanumberispart ofthesolutionset,whileaparenthesisisused toindicatethatanumberisnotpartofthe solutionset.
12. D.810 x means8 x and10, x whichisequivalentto8 x and10. x Thereisnorealnumberthatissimultaneously totherightof–8andtotheleftof–10ona numberline.
13. 2816288168 28 284 22 xx x xx
Solutionset: 4,
14. 38738878 315 3155 33 xx x xx
Solutionset: 5,
15. 221 22212 2323 33 331 33 xx xx xxxx x xx
Solutionset: 1,
16. 432 43323 4545 55 551 55 xx xx xxxx x xx
Solutionset: ,1
17. 35153 315153165 xx xx Theinequalityistruewhen x isanyreal number.
Solutionset: ,
18. 62345 623454345 44345435 xxx xxxxx xxxx
Theinequalityistruewhen x isanyreal number.
Solutionset: ,
19. 83227 52214 5222142 3214322142 312 3124 33 xxx xx xxxx xx x xx
Solutionset: ,4
20.
15 7 245162 2455612 3612 366126 7312733123 715 715 77 xxx xxx xx xxxx xx x xx
21.
22.
11 5 47 25 3 47 3325 3 47615 4766156 10715 10771571022 1022 1010 x x x x xx xxxx x xx x x
25 1 8 25 881 8 2588
1 2 658 6558563 63 66 x xx x x
23.
48 7 1211 3 35210 1211 30330 35210 10121533 101215453 7453 74545345 748 748 77 xxx xxx xxx xxx x x x x x
Solutionset:
4,
25. C =50x +5000; R =60x
Theproductwillatleastbreakevenwhen
RC Set RC andsolvefor x 60505000105000500 xxxx
Thebreak-evenpointisat x =500. Thisproductwillatleastbreakevenifthe numberofunitsofpictureframesproducedis intheinterval
500,.
26. C =100x +6000; R =500x Theproductwillatleastbreakevenwhen RC Set RC andsolvefor x 5001006000400600015 xxxx
Thebreak-evenpointis x =15.
Theproductwillatleastbreakevenwhenthe numberofunitsofbaseballcapsproducedis intheinterval 15,.
27. C =105x +900; R =85x
Theproductwillatleastbreakevenwhen RC Set RC andsolvefor x 851059002090045 xxxx Theproductwillneverbreakeven.
28. C =70x +500; R =60x Theproductwillatleastbreakevenwhen . RC Set RC andsolvefor x. 60705001050050 xxxx Theproductwillneverbreakeven.
29. 55211 55525115 1026 1026 222 53 x x x x x
Solutionset: 5,3
30. 7235 7223252 933 933 333 31 x x x x x
Solutionset:(3,1)
31. 102416 104244164 6212 6212 222 36 x x x x x
Solutionset:[3,6]
32. 3 2 66321 63633213 9618 9618 666 3 x x x x x
Solutionset:32,3
33. 113117 111311171 12318 12318 333 46 x x x x x
Solutionset:(4,6)
34. 1 6 2633 2363333 166 166 666 1 x x x x x
Solutionset:
35.
1 45 2 1 24225 2 8110 8111101 99 x x x x x
Solutionset:[9,9]
36. 3 51 3 3 35331 3 1533 1533333 126 x x x x x
Solutionset:[12,6]
37.
1619 33 34 34 5 34 53554 5 153420 154344204 19316 x x x x x x
Solutionset: 1619 33 , 38.
45 19 2 45 21229 2 24518 25455185 3413 3413133 44444 x x x x x x x
Solutionset: 133 44 ,
39. 260xx−−>
Step1:Findthevaluesof x thatsatisfy 260.xx
260230 xxxx 202or303 xxxx Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,260. xx
IntervalTestValue Is260 xx TrueorFalse? A: ,2 3 2? 3360 60 True (continuedonnextpage)
(continued)
IntervalTestValue Is260 xx TrueorFalse?
B: 2,30 2? 0060 60 False
C: 3, 4 2? 4460 60 True
Solutionset:
,23,
40. 27100xx
Step1:Findthevaluesof x thatsatisfythe correspondingequation.
27100 250 xx xx 202or505 xxxx
Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,27100. xx
IntervalTestValue Is27100 xx TrueorFalse?
A: ,2 0
2? 070100 100 True
B: 2,53 2? 373100 20 False
C: 5, 6 2? 676100 40 True
Solutionset:
41. 2 2918 xx
Step1:Findthevaluesof x thatsatisfythe correspondingequation.
2 2 2918 29180 2360
xx xx xx 3 2 230or606 xxxx
Step2:Thetwonumbersdivideanumberline intothreeregions. Step3:Chooseatestvaluetoseeifitsatisfies theinequality,22918 xx
IntervalTestValue Is22918 xx TrueorFalse?
A: 3 ,2 2 2? 229218 2618 False
B: 3 2,60 2? 209018 018 True
C: 6, 7
Solutionset:32,6
42. 2 34 xx
2? 279718 3518 False
Step1:Findthevaluesof x thatsatisfythe correspondingequation. 22 34340 3410 xxxx xx 4 3 340or101 xxxx
Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,234 xx
IntervalTestValue Is234 xx TrueorFalse?
A: 4 ,3 2
B: 4 3,10
2? 3224 104 False
2? 3004 04 True
C: 1, 2 2? 3224 144 False
Solutionset:43,1
43. 2463xx
Step1:Findthevaluesof x thatsatisfythe correspondingequation.
2 2 463 430 310 xx xx xx
Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,2463 xx
IntervalTestValue Is2463 xx TrueorFalse? A:
2? 44463 63
True
B: 3,12
2? 24263 23
2? 04063 63
True
Solutionset:(,–3][–1,)
44. 26168xx
Step1:Findthevaluesof x thatsatisfythe correspondingequation.
2 2 6168 680 420 xx xx xx
404or202 xxxx
Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,26168. xx
IntervalTestValue Is26168 xx
A: ,4 5
B: 4,23
C: 2, 0
TrueorFalse?
2 565168 118 False
2 363168 78
True
2 060168 168
False
Solutionset: 4,2
45. 22 16660xxxxxx
Step1:Findthevaluesof x thatsatisfy 260.xx
260 230 xx xx 202or303 xxxx
Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality, 16. xx
IntervalTestValue Is 16 xx TrueorFalse?
A: ,2 3 ? 3316 126 False
B: 2,30 ? 0016 06 True
C: 3, 4 ? 4416 126 False
Solutionset: 2,3
46. 22 112112 12120 xxxx xxxx
Step1:Findthevaluesof x thatsatisfy 2120.xx
2120 430
xx xx
404or303 xxxx
Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality, 112. xx
IntervalTestValue Is 112 xx TrueorFalse?
A: ,4 5 ? 55112 2012 False
B: 4,30 ? 00112 012 True
C: 3, 4 ? 44112 2012 False
Solutionset: 4,3
47. 29 x
Step1:Findthevaluesof x thatsatisfy29 x 2 2 9 90 330 x x xx
Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,29. x
IntervalTestValue Is29 x TrueorFalse?
A: ,3 4 2? 49 169 False
B: 3,30 2? 09 09 True
C: 3, 4 2? 49 169 False
Solutionset:[–3,3]
48. 2216160xx
Step1:Findthevaluesof x thatsatisfy 2160 440 x xx
404or404 xxxx
Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,216. x
IntervalTestValue Is216 x TrueorFalse?
A: ,4 5 2? 516 2516 True
B: 4,40 2? 016 016 False
C: 4, 5 2? 516 2516 True
Solutionset:(–,–4)(4,)
49. 2570xx
Step1:Findthevaluesof x thatsatisfy 2570.xx
Usethequadraticformulatosolvethe equation.
Let a =1, b =5,and c =7.
Step2:Thenumberlineisoneregion,
,
Step3:Becausetherearenorealvaluesof x thatsatisfy2570, xx 257xx is eitheralwayspositiveoralwaysnegative.By substitutinganarbitraryvaluesuchas0, x weseethat257 xx willbepositiveand thusthesolutionsetis.
IntervalTestValue Is2520 xx TrueorFalse?
A: , 0 2? 05070 70 False
Solutionset:
50. 2 4310 xx
Step1:Findthevaluesof x thatsatisfy 2 4310. xx
Usethequadraticformulatosolvethe equation.Let4,3,and1. abc
Step2:Thenumberlineisoneregion,

Step3:Becausetherearenorealvaluesof x thatsatisfy24310, xx 2 431 xx is eitheralwayspositiveoralwaysnegative.By substitutinganarbitraryvaluesuchas0, x weseethat2431 xx willbepositiveand thusthesolutionsetis
IntervalTestValue Is24310 xx TrueorFalse?
A: , 0 2? 403010 10
Solutionset:
51. 2221210xxxx
Step1:Findthevaluesof x thatsatisfy 2210.xx Usethequadraticformulatosolvethe equation.
Let1,2,and1. abc
2 2 4 2 22411 21 24428222 12 222 bbac x a 120.4or122.4 Step2:Thetwonumbersdivideanumberline intothreeregions. Step3:Chooseatestvaluetoseeifitsatisfies theinequality,221. xx
IntervalTestValue Is221 xx TrueorFalse?
A: ,12 1 2? 1211 31 False
B: 12,12 0 ? 2 020101 True
C: 12, 3 ? 2 323131 False
Solutionset:12,12
52. 2241410xxxx
Step1:Findthevaluesof x thatsatisfy 2410.xx
Usethequadraticformulatosolvethe equation.Let1,4,and1. abc
233.7or0.3 bbac x a xx
Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,241. xx
IntervalTestValue Is241 xx TrueorFalse?
A: ,23 4
B: 23,23 1
C: 23, 0
Solutionset:
2? 4441 01
True
2? 1411 31 False
? 2 0401 01
True
,2323,
53. A.2 (3) x isequaltozerowhen3 x .For anyotherrealnumber,2 (3) x ispositive.
2 (3)0 x hassolutionset ,.
54. D.2 (87) x isnevernegative,so
2 (87)0 x hassolutionset
55. 3 0 5 x x
Becauseonesideoftheinequalityisalready0, westartwithStep2. Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0.
303or505 xxxx Thevalues–5and3dividethenumberline intothreeregions.Useanopencircleon–5 becauseitmakesthedenominatorequal0.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,30. 5 x x
IntervalTestValue Is350 x x TrueorFalse?
A: ,5 6 ? 63 650 90False B: 5,30 ? 03 05 3 5 0 0True
C: 3, 4 ? 43 45 1 9 0 0False
IntervalBsatisfiestheinequality.Theendpoint 5isnotincludedbecauseitmakesthe denominator0.
Solutionset:(–5,3]
56. 1 0 4 x x
Becauseonesideoftheinequalityisalready 0,westartwithStep2.
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0.
101or404 xxxx Thevalues–1and4dividethenumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality, 1 0. 4 x x (continuedonnextpage)
(continued)
IntervalTestValue Is140 x x TrueorFalse?
A: ,1 2 ? 21 24 1 6 0 0True
B: 1,40 ? 01 04 1 4 0 0False
C: 4, 5 ? 51 540 60True
Solutionset:(–,1)(4,)
57. 1 1 2 x x
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside. 11 11 22 112 100 222 1(2)1200 22 3 0 2
Step2:Becausethenumeratorisaconstant, determinethevaluesthatwillcause denominatortoequal0.
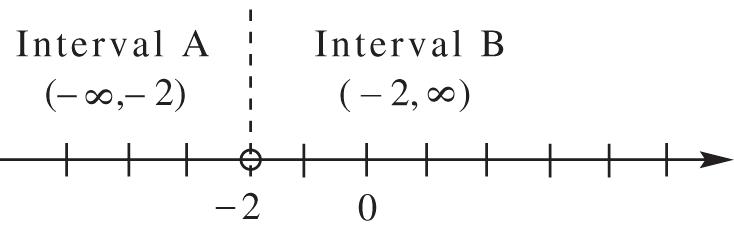
202xx Thevalue–2dividesthenumberlineintotwo regions. Step3:Chooseatestvaluetoseeifitsatisfies theinequality, 1 1 2 x x
IntervalTestValue Is121 x
,2
3
B: 2, 1
Solutionset:
True orFalse?
13? 321 21True
11? 121 21False
58. 6 1 2 x x
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside. 66 11 22 662 100 222 6224 00 22
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 2402or202 xxxx Thevalues–2and2dividethenumberlineinto threeregions.
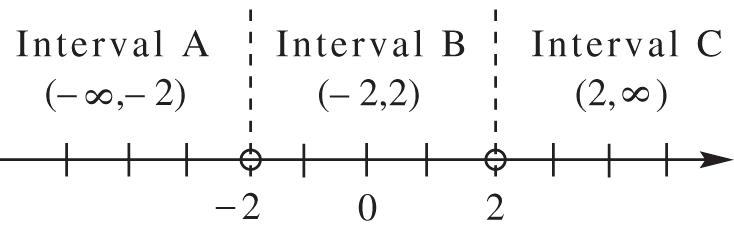
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,61 2 x x
IntervalTest
Value Is621 x x TrueorFalse?
A: ,2 3 6(3)?321 91False
B: 2,20 ? 60 021 31True
C: 2, 3 ? 63 32 3 5 1 1False
Solutionset:(–2,2) 59. 3 2 6 x
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside.
3326 200 666 3263212 00 66 152 0 6 x xxx xx xx x x
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 15 2 1520or606 xxxx (continuedonnextpage)
(continued)
Thevalues6and152dividethenumberline intothreeregions.Useanopencircleon6 becauseitmakesthedenominatorequal0.
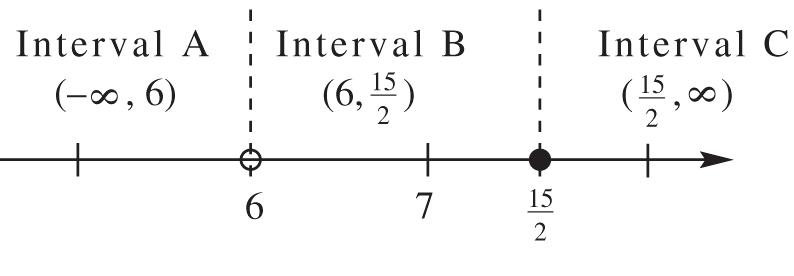
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,32. 6 x
IntervalTestValue Is362 x TrueorFalse?
IntervalTest
Value Is321 x TrueorFalse?
A: ,2 0 ? 3 02 3 2 1 1True
B: 2,53 ? 3 321 31False
C: 5, 6 ? 3 62 3 4 1 1True
Solutionset: ,25, 61. 4 5 1 x
Step1:Rewritetheinequalitytocomparea singlefractionto0:
44 550 11 451451 00 111 45595 00 11 xx xx xxx xx xx
IntervalsAandCsatisfiytheinequality.The endpoint6isnotincludedbecauseitmakes thedenominator0.
Solutionset:
60. 3 1 2 x
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside.
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 505or202 xxxx Thevalues2and5dividethenumberlineinto threeregions.
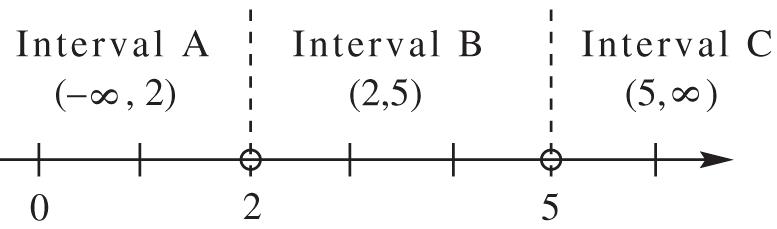
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,31. 2 x
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 9 5 950or101 xxxx Thevalues1and95dividethenumberlineinto threeregions.
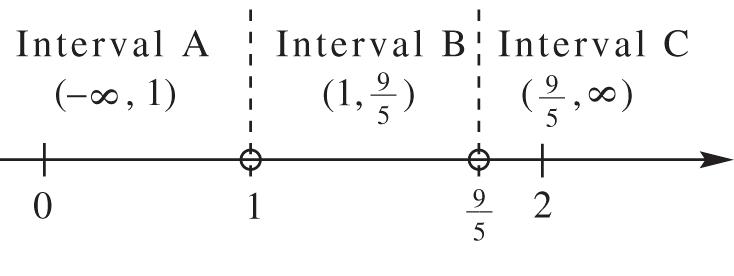
Step3:Chooseatestvaluetoseeifitsatisfies theinequality, 4 5 1 x
IntervalTestValue Is415 x TrueorFalse?
A: ,1 0 ? 4 105 45True
B: 9 1,56 5 6 5 ? 4 1 5 205False
C: 9 5, 2 ? 4 125 45True
Solutionset: 9 (–,51),
62. 6 2 35 x
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside.
66235 20 353535 62356610 00 3535 64 0 35 x xxx xx xx x x
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 25 33640or350 xxxx
Thevalues23and53dividethenumberline intothreeregions.Useanopencircleon5 3 becauseitmakesthedenominatorequal0.
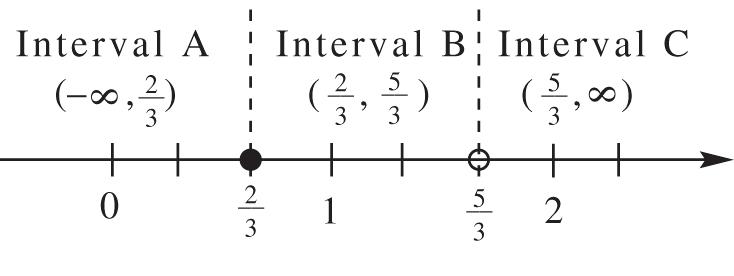
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,62. 53 x
IntervalTestValue Is6532 x True orFalse?
A: 2 ,3 0 ?
Step1:Rewritetheinequalitysothat0isonone sideandthereisasinglefractionontheother side.
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 13 221050or320 xxxx
Thevalues32and12dividethenumberline intothreeregions.Useanopencircleon3 2 becauseitmakesthedenominatorequal0.
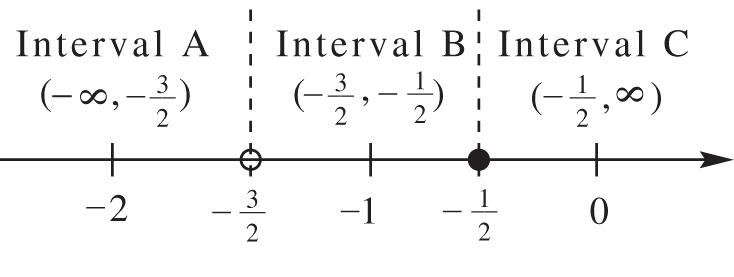
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,105. 32 x
IntervalTestValue Is10325 x TrueorFalse?
IntervalsAandCsatisfytheinequality.The endpoint53isnotincludedbecauseitmakes thedenominator0.
Solutionset:
25 ,33,
IntervalsAandCsatisfytheinequality.The endpoint32isnotincludedbecauseitmakes thedenominator0.
Solutionset:
31 22 ,,
64. 1 3 2 x
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside.
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0.
Thevalues–2and53dividethenumberline intothreeregions.Useanopencircleon–2 becauseitmakesthedenominatorequal0.
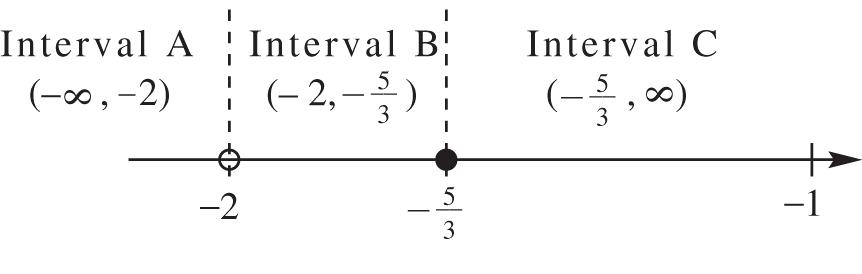
Step3:Chooseatestvaluetoseeifitsatisfies
IntervalTest
IntervalBsatisfiestheinequality.Theendpoint –2isnotincludedbecauseitmakesthe denominator0.
Solutionset: 5 2,3
65. 71 22
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside. 716 00 222
Step2:Becausethenumeratorisaconstant, determinethevaluethatwillcausethe denominatortoequal0. 202xx
Thevalue2dividesthenumberlineinto tworegions.Useanopencircleon–2because itmakesthedenominatorequal0.

Step3:Chooseatestvaluetoseeifitsatisfies theinequality,7122
IntervalTestValue Is7122xx
,2
TrueorFalse?
3 ? 71 3232 71False
B: 2, 0 ? 71 0202 71 22True
IntervalBsatisfiestheinequality.Theendpoint 2isnotincludedbecauseitmakesthe denominator0.
Solutionset: 2,
66. 512 11xx
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside.
5127
00 111xxx
Step2:Becausethenumeratorisaconstant, determinethevaluethatwillcausethe denominatortoequal0.
101xx Thevalue1dividesthenumberlineinto tworegions. Step3:Chooseatestvaluetoseeifitsatisfies theinequality,512. 11xx (continuedonnextpage)
(continued)
IntervalTestValue Is51211xx TrueorFalse?
A: ,1 2 ? 512 2121 512True
B: 1, 0 ? 512 0101 512False
Solutionset: ,1 67. 34 21xx
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside.
34 0 21 3421 0 2121 3421 0 21 384114 00 2121 xx xx xxxx xx xx xxx xxxx
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 4 11 1 2 1140or0or 210 xxx xx
Thevalues0,411,and12dividethenumber lineintofourregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,34. 21xx
IntervalTestValue Is34 21xx TrueorFalse? A:
,0 1 ? 34 2111 14False
B: 4 0,11111 11
C: 41 112 , 9 22 99 2222 ?? 33388 4 2129 17 29 or 169False
D: 1 2, 1 3?4 2111 34True
Solutionset:
41 0,112,
68. 55 32xx
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside.
55 0 32 5532 0 3232 5532 0 32 515102010 00 3232 xx xx xxxx xx xx xxx xxxx
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 12 23 20100or0or320 or0or xxx xxx
Thevalues23, 1 2,and0dividethe numberlineintofourregions.Useanopen circleon0and23becausetheymakesthe denominatorequal0.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,55 32xx (continuedonnextpage)
(continued)
IntervalTest
D:
IntervalsAandCsatisfytheinequality.The endpoints23and0arenotincludedbecause theymakethedenominator0.
Solutionset:
69. 43 21xx
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,43 21xx
IntervalTestValue Is3 4 21xx TrueorFalse?
A: ,2 3 ? 43 2313 3 44True
B: 2,10 ? 43 2010 23False
C: 1,21.5 ? 43 21.511.5 86True
D: 2, 3 ? 43 2313 3 42False
IntervalsAandCsatisfytheinequality.The endpoints1and2arenotincludedbecause theymakethedenominator0.
Solutionset:
,21,2 70. 42 13xx Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside.
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 202or202or 101 xxxx xx
Thevalues–2,1,and2dividethenumberline intofourregions.Useanopencircleon1and 2becausetheymakethedenominatorequal0.
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 21005or101or 303 xxxx xx
Thevalues–5,3,and1dividethenumber lineintofourregions.
(continuedonnextpage)
(continued)
Step3:Chooseatestvaluetoseeifitsatisfies theinequality, 42 13xx
IntervalTestValue Is4213xx TrueorFalse?
A:
,5 6 ?? 4242 616353 1210 1515 or True
B:
5,34 ? 42 4143 4 32False
C: 3,12 ? 42 2123 42True
D: 1, 0 ? 42 0103 2 3 4False
Solutionset:
71. 3 1 5 x x
,53,1
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside. 335 100 555 3(5)3500 55 8 0 5 xxx
Step2:Becausethenumeratorisaconstant, determinethevaluethatwillcausethe denominatortoequal0.
505xx
Thevalue5dividesthenumberlineintotwo regions.Useanopencircleon5becauseit makesthedenominatorequal0.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,31. 5 x x
IntervalTest
Value Is351 x x
TrueorFalse? A: ,5 0 ? 03 05 3 5 1 1True
B: 5, 6 ? 63 651 91False
IntervalAsatisfiestheinequality.The endpoint5isnotincludedbecauseitmakes thedenominator0.
Solutionset: ,5
72. 2 5 32 x x
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside.
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 133 913092 or320 xxxx
Thevalues32and139dividethenumber lineintothreeregions.Useanopencircleon 3 2becauseitmakesthedenominatorequal 0.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality, 2 5. 32 x x (continuedonnextpage)
(continued)
IntervalTestValue Is2
IntervalsAandCsatisfytheinequality.The endpoint32isnotincludedbecauseitmakes thedenominator0.
Solutionset:
73. 2 23 0 1 x x
Becauseonesideoftheinequalityisalready 0,westartwithStep2.
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0.
3 2dividesthenumberlineintotwointervals.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,2 23 0. 1 x x
IntervalTestValue Is223 1 0 x x TrueorFalse?
74. 2 98 0 425 x x
Becauseonesideoftheinequalityisalready 0,westartwithStep2. Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 8 9 2 980or 4250,whichhasnorealsolutions xx x Thevalue89dividesthenumberlineintotwo intervals.
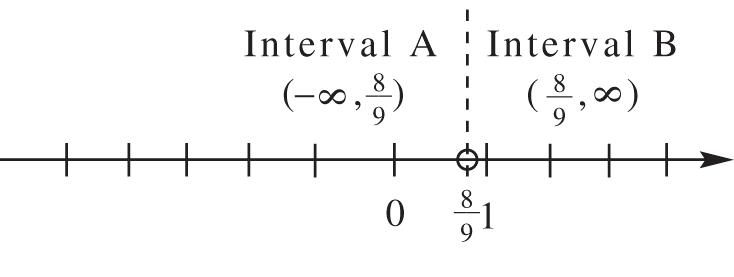
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,2 98 0. 425 x x
IntervalTestValue Is298 425 0 x x TrueorFalse?
A: 8 ,9 0 2 908? 4025 8 25 0 0True
B: 8 9, 1 2 918? 4125 1 29 0 0False
Solutionset: 8 ,9
75. 2 3 53 0 25 x x
Becauseonesideoftheinequalityisalready 0,westartwithStep2. Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal 0.
55 32530or250xxxx Thevalues53and52dividethenumberline intothreeintervals.
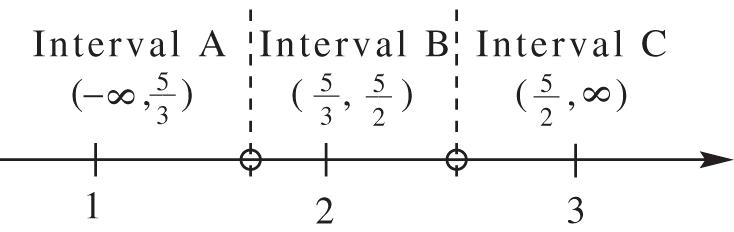
Step3:Chooseatestvaluetoseeifitsatisfies theinequality, 2 3 53 0. 25 x x (continuedonnextpage)
(continued)
IntervalTestValue Is 2 3 53 25 0 x x TrueorFalse?
A: 5 ,3 0 2 3 530? 205 1 5 0 0False
B: 55 32,2 2 3 532? 225 0 10False
C: 5 2, 3 2 3 533? 235 0 160True
Solutionset: 5 2, 76.
3 2 53 0 258 x x
Becauseonesideoftheinequalityisalready 0,westartwithStep2. Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 325 53058 or2580 xxxx
Thevalues35and258dividethenumberline intothreeintervals.Useanopencircleon25 8 becauseitmakesthedenominatorequal0.
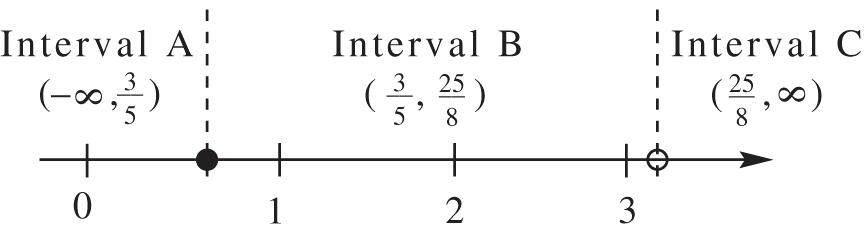
Step3:Chooseatestvaluetoseeifitsatisfies
theinequality, 3 2 53 0. 258 x x
IntervalTestValue Is 3 2 53 258 0 x x TrueorFalse?
A:
3 ,5 0
325 58,2
3 2 503? 2580 27 625 0 0True
IntervalTestValue Is 3 2 53 258 0 x x TrueorFalse?
C: 25 8, 4 3 2 543? 2584 4913 49 0 0False
Solutionset: 3 ,5
3 2338 0 6 xx x
Becauseonesideoftheinequalityisalready 0,westartwithStep2.
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 38 23 230or380or60 oror6
Thevalues83, 3 2,and6dividethenumber lineintofourintervals.Useanopencircleon6 becauseitmakesthedenominatorequal0.
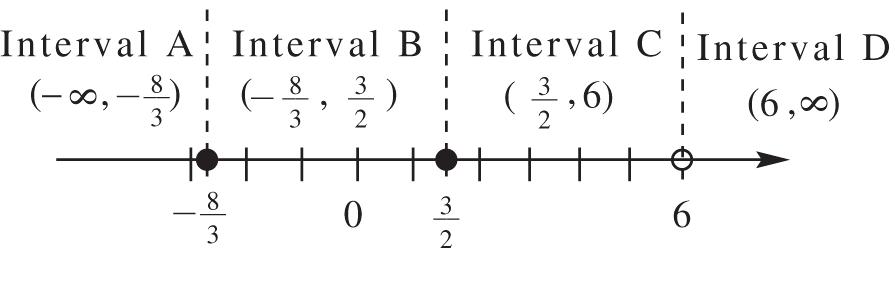
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,
3 2338 0. 6 xx x
IntervalTestValue Is
3 2338 6 0 xx x TrueorFalse? A: 8 ,3 3 3 233338? 36 1 81 0 0False
B: 83 32,0 3 203308? 06 1 9 0 0True
C: 3 2,62
D: 6, 7
Solutionset:
Copyright©2017PearsonEducation,Inc.
3 223328? 26 7 32 0 0False
3 273378? 76 0 3190True
83 32,6,
78.
3 91127 0 38 xx x
Becauseonesideoftheinequalityisalready 0,westartwithStep2.
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 1178 923 9110or270or380 oror xxx
Thevalues72, 119,and83dividethenumber lineintofourintervals.
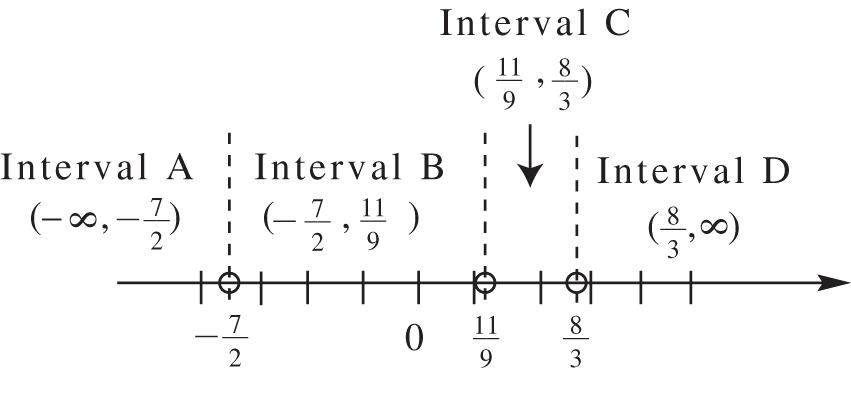
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,
IntervalTestValue
711 29,0
118 93,2
D: 8 3, 3
Solutionset:
3 9211227? 328 77 8 0 0False
3 9311237? 338 0 2080True
78 11 293,,
79. (a) Let R =7.6andthensolvefor x 0.28445.5357.6 0.28442.0657.3 x xx Themodelpredictsthatthereceipts exceeded$7.6billionabout7.3years after1993,whichwasin2000.
(b) Let R =10andthensolvefor x 0.28445.53510 0.28444.46515.7 x xx
Themodelpredictsthatthereceipts exceeded$10billionabout15.7years after1993,whichwasin2008.
80. (a) Let W =34andsolvefor x 0.3333.1Wx 0.3333.134 0.330.92.7(approx) x xx
Accordingtothemodel,thepercentof wasterecoveredfirstexceeded34%about 2.7yearsafter2007,whichwasin2009.
(b) Solvefor x forvaluesbetween33.9and 34.5. 33.90.3333.134.5 0.80.331.42.44.2 x xx
Accordingtothemodel,thepercentof wasterecoveredwasbetween33.9%and 34.5%about2.4yearsafter2007,which wasin2009,until4.2yearsafter2007, whichwasin2011.
81. 2 16220624 tt
Step1:Findthevaluesof t thatsatisfy 2 16220624. tt
22 2 16220624016220624 0455156 04439 tttt tt tt 394044or43909.75tttt
Step2:Thetwonumbersdivideanumberline intothreeregions,where0. t
Step3: Chooseatestvaluetoseeifitsatisfies theinequality,216220624. tt
IntervalTestValue Is216220624 tt TrueorFalse?
A: 0,41 2? 1612201624 204624False
B: 4,9.755 2? 1652205624 700624True
C: 9.75, 10 2? 161022010624 600624False
Theprojectilewillbeatleast624feetabove groundbetween4secand9.75sec(inclusive).
82. 2 16220744 tt
Step1:Findthevaluesof t thatsatisfy 2 16220744. tt
22 2 16220744016220744 0455186 06431 tttt tt tt
316064or43107.75tttt
Step2:Thetwonumbersdivideanumberline intothreeregions,where0. t
Step3: Chooseatestvaluetoseeifitsatisfies theinequality,216220744 tt
IntervalTestValue Is216220744 tt TrueorFalse?
A: 0,61 2? 1612201744 204744False
B:
6,7.757 2? 1672207744 756744True
C: 7.75, 10 2? 161022010744 600744False
Theprojectilewillbeatleast744feetabove groundbetween6secand7.75sec(inclusive).
83. 2 1644432 tt
Step1:Findthevaluesof t thatsatisfy 2 1644432. tt 2 2 2 1644432 1644280 41170 4710 tt tt tt tt
7 4 470=1.75or101 tttt
Step2:Thetwonumbersdivideanumberline intothreeregions,where0. t
Step3: Chooseatestvaluetoseeifitsatisfies theinequality,21644432 tt
IntervalTest
Value Is21644432 tt TrueorFalse?
A: ,1 0 2? 160440432 432False
B: 1,1.751.5 2? 161.5441.5432 3432True
C: 1.75, 2 2? 162442432 2832False
Thebaseballwillbeatleast32feetabove groundbetween1secand1.75sec(inclusive).
84. 2 1644428 tt
Step1:Findthevaluesof t thatsatisfy 2 1644428. tt 2 2 2 1644428 1644240 41160 4320 tt tt tt xx
3 4 4300.75or 202 tt tt
Step2:Thetwonumbersdivideanumberline intothreeregions,where0. t
Step3: Chooseatestvaluetoseeifitsatisfies theinequality,21644428 tt
IntervalTestValue Is21644428 tt TrueorFalse?
A: 0,0.750.5 2? 160.5440.5428 2228False
B: 0.75,21.5 2? 161.5441.5428 3428True
C: 2, 3 2? 163443428 828False
Thebaseballwillbegreaterthan28feetabove groundbetween0.75secand2sec.
85. 2 25120 tt
Step1:Findthevaluesof t thatsatisfy
2 25120. tt
2 251202340 tttt
3 2 2301.5or 404 tt tt
Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,225120. tt
IntervalTestValue Is225120 tt TrueorFalse?
A:
2? 2252120 60 False
B: 1.5,40 2? 2050120 120 True
C: 4, 5 2? 2555120 130 False
Thevelocitywillbenegativebetween–1.5sec and4sec.
86. 2 318240 tt
Step1:Findthevaluesof t thatsatisfy 2 318240. tt
2 3182403240 tttt 202or404 tttt
Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,2318240. tt
IntervalTest
Value Is2318240 tt TrueorFalse?
A: ,2 0 2? 30180240 240 False
B: 2,43 2? 33183240 30 True
C: 4, 5 2? 35185240 90 False
Thevelocitywillbenegativebetween2sec and4sec.
87. (3x –4)(x +2)(x +6)=0 Seteachfactortozeroandsolve. 4 3403or202or 606 xxxx xx
Solutionset: 4 3,2,6
88. Plotthesolutions–6,–2,and43onanumber line.

89. IntervalTest Value Is(34)(2)(6)0 xxx TrueorFalse? A: ,6 –10
? 3104102 1060 10880
True
B: 6,2–4
? 34442 460 640
False C: 4 2,30
? 30402060 480
True D: 4 3, 4
? 34442460 4800
90. (a)
(b) Solutionset: 4 ,62,3
91. (23)(2)(3)0 xxx
Step1:Solve(23)(2)(3)0. xxx Seteachfactortozeroandsolve.
3 2302or202or 303 xxxx xx
Solutionset: 3 2,2,3
Step2:Plotthesolutions32,2,and3ona numberline.

Step3:Chooseatestvaluetoseeifitsatisfies theinequality,(23)(2)(3)0. xxx
IntervalTestValue Is(23)(2)(3)0 xxx
3 2,20
53420xxx
Step1:Solve
53420.
Seteachfactortozeroandsolve. 4 5053or340or 202 xxxx xx
Solutionset: 4 5,2,3
Step2:Plotthesolutions4 5,2,3andona numberline.

Step3:Chooseatestvaluetoseeifitsatisfies theinequality,
53420.xxx
IntervalTestValue Is
53420xxx TrueorFalse? A:
25324 220 560
Solutionset:
93. 3 40 xx
4 3 5,2,
Step1:Solve340. xx
32 4040 220 xxxx xxx
Seteachfactortozeroandsolve. 0or202or 202 xxx xx
Solutionset: 2,0,2 Step2:Thevalues2,0,and2dividethe numberlineintofourintervals.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,340. xx
IntervalTestValue Is340 xx TrueorFalse? A: ,2 3 3? 4330 150 True
B: 2,01 3? 4110 30 False
(continuedonnextpage)
(continued)
IntervalTestValue Is340 xx TrueorFalse?
C: 0,21 ? 3 4110 30 True
D: 2, 3 ? 3 4330 150 False
Solutionset: ,20,2
94. 3 160 xx
Step1:Solve3160. xx
32 160160 440 xxxx xxx
Seteachfactortozeroandsolve. 0or404or 404 xxx xx
Solutionset: 4,0,4
Step2:Thevalues4,0,and4dividethe numberlineintofourintervals.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,3160. xx
IntervalTestValue Is3160 xx Trueor False?
A: ,4 5
3? 16550 450True
B: 4,01 3? 16110 150False
C: 0,41 ? 3 16110 150True
D: 4, 5 ? 3 16550 450False
Solutionset:
95.
2 130xx
Step1:Solve 2 130.xx Seteachdistinctfactortozeroandsolve. 101or303 xxxx
Solutionset: 1,3
Step2:Thevalues1and3dividethenumber lineintothreeintervals.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality, 2 130.xx
IntervalTestValue Is 2 130xx TrueorFalse?
A: ,1 2 2? 21230 50True
B: 1,30 2? 01030 30True
C: 3, 4 2? 41430 250False
Solutionset:
,11,3 96. 2 510xx
Step1:Solve 2 510.xx
Seteachdistinctfactortozeroandsolve. 505or101 xxxx
Solutionset: 1,5
Step2:Thevalues1and5dividethenumber lineintothreeintervals.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality, 2 510.xx
IntervalTestValue Is 2 510xx TrueorFalse?
A: ,1 2 2? 25210 490True
B: 1,50 2? 05010 250False
C: 5, 6 2? 65610 70False
Solutionset: ,1
97. 324936xxx
Step1:Solve324936xxx
32 32 2 2 4936 49360 4940 490 4330 xxx xxx xxx xx xxx
Seteachfactortozeroandsolve. 303or404or 404 xxxx xx
Solutionset: 4,3,4
Step2:Thevalues4,3,and4dividethe numberlineintofourintervals.
Seteachfactortozeroandsolve.
404or303or 303 xxxx xx
Solutionset: 4,3,3
Step2:Thevalues4,3,and3dividethe numberlineintofourintervals.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,324936xxx
IntervalTestValue Is324936xxx
,4 5
32? 5459536 2036
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,3231648.xxx
IntervalTestValue Is3231648.xxx TrueorFalse?
A: ,4 5
True B: 4,33.5
32 ? 535 16548 3048
2 31648 316480 31630 3160 3440 xxx xxx xxx xx xxx
C: 3,40
32? 03016048 048 True
D: 4, 5 32 53516548 12048 False
Solutionset: ,43,4 99. 2240 xx
Step1:Solve 2240. xx
Seteachdistinctfactortozeroandsolve. 0or404xxx
Solutionset: 4,0
Step2:Thevalues4and0dividethe numberlineintothreeintervals.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality, 2240. xx
IntervalTestValue Is 2240 xx TrueorFalse? A: ,4 5 22? 5540 250True (continuedonnextpage)
(continued)
IntervalTestValue Is 2240 xx TrueorFalse?
B: 4,01 22? 1140 90True
C: 0, 1 22? 1140 250True
Solutionset: ,
100. 22230xx
Step1:Solve 22230.xx Seteachdistinctfactortozeroandsolve. 23 002 or230 xxxx
Solutionset: 3 0,2
Step2:Thevalues30and2dividethenumber lineintothreeintervals.
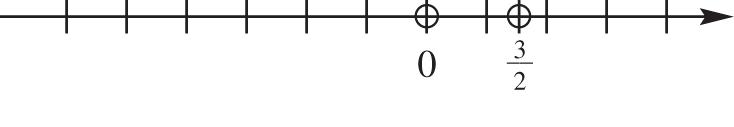
Step3:Chooseatestvaluetoseeifitsatisfies theinequality, 22230.xx
IntervalTestValue Is 22230xx TrueorFalse? A: ,0 1
Section 1.8 Absolute Value Equations and Inequalities
1. F.Thesolutionsetincludesanyvalueof x whoseabsolutevalueis7;thus x =7or x =–7 arebothsolutions.
2. B.Thereisnosolutionbecausetheabsolute valueofanyrealnumberisnevernegative.
3. D.Thesolutionsetisallrealnumbersbecause theabsolutevalueofanyrealnumberis alwaysgreaterthan–7.Thegraphshowsthe entirenumberline.
4. E.Thesolutionsetincludesanyvalueof x whoseabsolutevalueisgreaterthan7;thus x >7or x <–7.
5. G.Thesolutionsetincludesanyvalueof x whoseabsolutevalueislessthan7;thus x mustbebetween–7and7,notincluding–7or 7.
6. A.Thesolutionsetincludesanyvalueof x whoseabsolutevalueisgreaterthanorequal to7;thus x ≥ 7or x ≤ –7.
7. C.Thesolutionsetincludesanyvalueof x whoseabsolutevalueislessthanorequalto7; thus x mustbebetween–7and7,including–7 and7.
8. H.Thesolutionsetincludesanyvalueof x whoseabsolutevalueisnotequalto7;thus, x canequalallrealnumbersexcept–7and7.
9. 312 x 1 3 312331or 31231 xxx xxx
Solutionset: 1 3,1
10. 425 x 3 4 7 4 42543or 42547 xxx xxx
Solutionset: 73 44 , 11. 533 x 2 3 8 3 53323or 53383 xxx xxx
Solutionset: 28 33 , 12. 4 3 10 3 733 73334or 733310 x xxx xxx
Solutionset: 410 33 , 13. 4 5 2 4 541014or 2 4 54106 2 x x xx x xx
Solutionset:{–6,14}
Solutionset:
Solutionset: 17 88 , 17. 61 3 1 x x 4 3 2 9 61 13613(1) 613334or 61 13613(1) 613392 x xx x xxxx x xx x xxxx
Solutionset: 42 39 , 18. 23 1 34 x x
1 5 23 123134 34 23347or 23 123134 34 233451 x xx x xxx x xx x xxxx
Solutionset: 1 5,7
19. 2354 xx 7 3 11 77 235473or 23(54)2354 71 xxxx xxxx xx
Solutionset: 71 37 , 20. 113 113400or 1(13)113 221 xx xxxx xxxx xx
Solutionset:{0,1}
21. 4323 432342Falseor 43(23)4323 661 xx xx xxxx xx
Solutionset:{1}
22. 3252xx 325235Falseor 32(52)3252 842 xx xxxx xx Solutionset:{2}
23. 5225 xx 42 5225104105or 52(25)5225 00True xxxx xxxx
Solutionset: ,
24. Answerswillvary.Sampleanswer:If x is negative,then3x willalsobenegative. Becausetheoutcomeofanabsolutevaluecan neverbenegative,anegativevalueof x isnot possible.
25. Answerswillvary.Sampleanswer:If x is positive,then–5x willbenegative.Because theoutcomeofanabsolutevaluecanneverbe negative,apositivevalueofxisnotpossible.
26. (a) xx x willequalitsownoppositeonlyif x =0.
Solutionset:{0} (b) xx Anynumberanditsoppositehavethe sameabsolutevalue.
Solutionset: ,
(c) 2 xx Solutionset:{–1,0,1}
(d) 9 x 9 x isnevertrue. Solutionset:
27. 253 3253 822 41 x x x x
Solutionset: 4,1
28. 342 x 2 3 2342 236 2 x x x
Solutionset: 2 3,2
29. 253 x 253284or 253221 xxx xxx
Solutionset: ,41,
30. 342 x 2 342323or 342362 xxx xxx
Solutionset:
31. 1 22 x
2 3 ,2,
1 2 1 2 53 22 22 22222 4124 523 x x x x x
Solutionset: 35 22 ,
32. 3 51 x
3 5 3 5 82 55 11 51551 5355 852 x x x x x
Solutionset: 82 55 ,
33. 431233 330or336 xx xxxx Solutionset:(,0)(6,)
34. 511012 123or121 xx xxxx Solutionset:(,3)(1,)
35. 2 3 537 5373124or 53732 x xxx xxx
Solutionset: 2 3 –,4,
36. 11 3 734 734311or 734331 x xxx xxx
Solutionset: 11 3 –,1,
37. 537 x 2 3 2 3 7537 1232 4 4 x x x x
Solutionset:23,4
38. 734 x 11 3 11 3 4734 1133 1 1 x x x x
Solutionset:11 1,3
39. 211 326 x
1211 6326 1211 6326 1 2 666 1431 442 1 x x x x x
Solutionset:1 1,2
Copyright©2017PearsonEducation,Inc.
40. 512 329 x
551212 329329 34 9 551212 329329 26 9 1818 3094934or 1818 3094926 xx xxx xx xxx
Solutionset: 2634 ,99,
41. 0.0110.01 x
0.010.0110.01 11001 10199 x x x Solutionset:(101,99)
42. Because 22 , xx 2 xx forallvaluesof x.Theequationisanidentity.
43. 4321431 xx 21 4314242or 431441 xxx xxx Solutionset: 1 1,2
44. 8332831 xx 7 831373or 831393 xxx xxx
Solutionset: 7 3,3
45. 6213622 xx 622242or 622284 xxx xxx
Solutionset: 2,4
46. 4424442 xx 21 42 63 42 44242or 44246 xxx xxx
Solutionset: 13 22 ,
47. 3112313 xx 42 33 3313 432 x x x
Solutionset: 42 33 ,
48. 5223525 xx 73 55 5525 753 x x x
Solutionset: 73 55 ,
49. 11 22 52557 xx 1 2 1 2 1513313 1010210 757 272527 1410114 151013 x x x x xx
Solutionset: 313 210 ,
50. 11 33 21423 xx
1 3 1 3 108 66 54 33 323 333233 9619 1068 x x x x x x
Solutionset: 54 33 ,
51. 104151044 xx 147 42 63 42 1044414 or 104446 xxxx xxxx
Solutionset: 37 22 ,,
52. 126391266 xx 12666183or 1266661 xxx xxx
Solutionset: ,13,
53. 3712373 xx Anabsolutevaluecannotbenegative. Solutionset:
54. 5746572 xx Anabsolutevaluecannotbenegative. Solutionset:
55. Becausetheabsolutevalueofanumberis alwaysnonnegative,theinequality 1044 x isalwaystrue.Thesolutionset is ,.
56. Becausetheabsolutevalueofanumberis alwaysnonnegative,theinequality 12912 x isalwaystrue.Thesolutionset is ,.
57. Thereisnonumberwhoseabsolutevalueis lessthananynegativenumber.Thesolution setof6311 x is
58. Thereisnonumberwhoseabsolutevalueis lessthananynegativenumber.Thesolution setof1833 x is
59. Theabsolutevalueofanumberwillbe0if thatnumberis0.Therefore850 x is equivalentto850, x whichhassolution set 5 8
60. Theabsolutevalueofanumberwillbe0if thatnumberis0.Therefore720 x is equivalentto720, x whichhassolution set 7 2
61. Anynumberlessthanzerowillbenegative. Thereisnonumberwhoseabsolutevalueisa negativenumber.Thesolutionsetof 4.39.80 x is
62. Anynumberlessthanzerowillbenegative. Thereisnonumberwhoseabsolutevalueisa negativenumber.Thesolutionsetof 1.5140 x is.
63. Becausetheabsolutevalueofanumberis alwaysnonnegative,210 x isnevertrue, so210 x isonlytruewhen210. x 1 210210212 xxxx
Solutionset: 1 2
64. Becausetheabsolutevalueofanumberis alwaysnonnegative,320 x isnevertrue, so320 x isonlytruewhen320. x 2 320320323 xxxx
Solutionset: 2 3
65. 320 x willbefalseonlywhen 320, x whichoccurswhen2 3 x So thesolutionsetfor320 x is
22 33 ,,.
66. 430 x willbefalseonlywhen 430, x whichoccurswhen3 4 x So thesolutionsetfor430 x is
33 44 ,,.
67. 2 pq ,whichisequivalentto2 qp , indicatesthatthedistancebetween p and q is2 units.
68. 6 rs ,whichisequivalentto6 sr , indicatesthatthedistancebetween r and s is6 units.
69. “m isnomorethan2unitsfrom7”meansthat m is2unitsorlessfrom7.Thusthedistance between m and7islessthanorequalto2,or 72. m
70. “z isnolessthan5unitsfrom4”meansthat z is5unitsormorefrom4.Thus,thedistance between z and4isgreaterthanorequalto5, or45 z
71. “p iswithin0.0001unitof9”meansthat p is lessthan0.0001unitfrom9.Thusthedistance between p and9islessthan0.0001,or 90.0001. p
72. “k iswithin0.0002unitof10”meansthat k is lessthan0.0002unitfrom10.Thusthe distancebetween k and10islessthan0.0002, or100.0002. k
73. “r isnolessthan1unitfrom29”meansthat r is1unitormorefrom29.Thusthedistance between r and29isgreaterthanorequalto1, or291. r
74. “q isnomorethan8unitsfrom22”meansthat q is8unitsorlessfrom22.Thusthedistance between q and22islessthanorequalto8,or 228. q
75. Becausewewant y tobewithin0.002unitof 6,wehave60.002 y or 5160.002. x 550.002 0.002550.002
4.99855.002 0.99961.0004 x x x x
Valuesof x intheinterval 0.9996,1.0004 wouldsatisfythecondition.
76. Becausewewant y tobewithin0.002unitof 6,wehave60.002 y or 10260.002. x 1040.0020.0021040.002 3.998104.002 0.39980.4002 xx x x
Valuesof x intheinterval 0.3998,0.4002 wouldsatisfythecondition.
77. 8.21.5 1.58.21.5 6.79.7 x x x
Therangeofweights,inpounds,is[6.7,9.7].
78. 8456 C 56845614028 CC
IndegreesCelsius,therangeoftemperatureis theinterval[–140,–28].
79. 780is50morethan730and680is50less than730,soallofthetemperaturesinthe acceptablerangearewithin50°of730°.That is73050 F
80. Let x =thespeedofthekite.148is25more than123,and98is25lessthan123,soallthe speedsarewithin25ftpersecof123ftper sec,thatis,12325. x
Let x =speedofthewind.26is5morethan 21,and16is5lessthan21,sothewind speedsarewithin5ftpersecof21ftpersec, thatis,215. x
81. 26.751.42
1.4226.751.42
25.3328.17
82. Becausethereare225studentsand and LERR areindividualrates,thetotal amountsofcarbondioxideemittedwouldbe 225and225. LLEE TRTR Thus, (225)(25.33)(225)(28.17) 5699.256338.25 (225)(36.58)(225)(40.92) 8230.59207 L L E E
83. 6andtheoppositeof6,namely–6
84. 26xx
260230 202or303 xxxx xxxx
Solutionset: 2,3
85. 22660xxxx
Thequadraticformula, 24 2 bbac x a , canbeevaluatedwith a =1, b =–1,and c =6.
2 2 4 2 114161124 212 123123123 2222 bbac x a i i
Solutionset: 123 22 i
86. 1232,3,22 i
87. 222 314314or314 xxxxxx
2 2 7 3 314 3140 3720 370 202 xx xx xx xx xx
22 3143140 xxxx Wemustusethequadraticformulawith a =3, b =1,and c =14. 2 2 4 2 1143141167 236 11671167 666 bbac x a x ii
Solutionset: 7167 1 366 ,2, i
88. 222 235235or235 xxxxxx
2 2 5 2 235 2350 2510 250 101 xx xx xx xx xx
2 2 235 2350 xx xx Wemustusethequadraticformulawith a =2, b =3,and c =5.
2 2 4 2 33425331 224 331331 444 bbac x a x ii
Solutionset: 5331 2441,, i
89. 2 42360 xx
Because0andtheoppositeof0representthe samevalue,onlyoneequationneedstobe solved.
2 423604160 xxxx 1 4 410or60 or6 xx xx
Solutionset: 1 4,6
90. 32 62370 xxx
Because0andtheoppositeof0representthe samevalue,onlyoneequationneedstobe solved. 32 2 62370 62370 27310 xxx xxx xxx
7 2 1 3 0or270or 310 xxx xx
Solutionset: 71 23,,0
91. 2120xx 22 22 2 12012 12210 10101or xxxx xxxx xxx
222 1221010 101 xxxxx xx
Solutionset: 1,1 92. 2 22 211 0 3 211211 0 33 x x xx xx
22 22 2 211211 33 33 32113611 311603230 xx xx xx xxxx xxxx
2 3 320or303 xxxx or
2 2 22 2 211 3 211 33 3 32113611 311603230 x x x xx x xxxx xxxx
2 3203or303 xxxx
Solutionset: 22 33 3,,,3
93. Anynumberlessthanzerowillbenegative. Thereisnonumberwhoseabsolutevalueisa negativenumber.Thesolutionsetof 42210xx is.
94. Anynumberlessthanzerowillbenegative. Thereisnonumberwhoseabsolutevalueisa negativenumber.Thesolutionsetof 2100 x is.
95. 4 0 31 x x
Thisinequalitywillbetrue,exceptwhere 4 31 x x isundefined.Thisoccurswhen 310, x or13. x
Solutionset: 11 33 ,,
96. 9 0 78 x x
Thisinequalitywillbetrue,exceptwhere 9 78 x x isundefined.Thisoccurswhen 780, x or78. x Solutionset:
77 88 ,,
Chapter 1 Review Exercises
1. 2832826 xxxx Solutionset:{6}
2. 111 6122 1 xx
MultiplyeachtermbytheLCD,12,to eliminatethefractions.Thensolvefor x.
Solutionset:{5}
3. 524321 528633863 11 833113 3 xxx xxxxx xxx
Solutionset: 11 3
4. 911()(1) 91111 101111 (10)1111 111111() 1010 xkpxa xkpaxx xaxkp axkp kpkp x aa
5. 24 (1) Af Bp for f (approximateannual interestrate) 24 (1)(1)(1) (1)24 (1) 24 (1) 24 BpABpf Bp ABpf ABpf fABp
6. BandCcannotbeequationstosolvea geometryproblem.Thelengthofarectangle mustbepositive.
A. 22220 22420 44204164 xx xx xxx
B. 2252 21022 41024123 xx xx xxx
C. 82416 816416 1216161200 xx xx xxx
D. 22310 22610 46104164 xx xx xxx
7. AandBcannotbeequationsusedtofindthe numberofpenniesinajar.Thenumberof penniesmustbeawholenumber.
A. 8 5311585 xxx B. 105 126 12641210 xx x
C. 100503 10050150501503 xx xxxx
D. 6424 62424 52424500 xx xx xxx
8. Let l =thelengthofthecarry-on(ininches).
Let w =thewidthofthecarry-on(ininches).
Let h =theheightofthecarry-on(ininches). Linearinches= lwh
(a) Linearinches 9122142in lwh No;allairlinesonthelistwillallowthe Samsonitecarry-onbag.
(b) Linearinches 10142246in lwh Thecarry-onisallowedonAlaskaand Southwest.
9. Let x =theoriginallengthofthesquare(in inches).Becausetheperimeterofasquareis4 timesthelengthofoneside,wehave
1 2 44410. xx Solvethisequationfor x todeterminethelengthofeachsideofthe originalsquare.
416210 2161022613 xx xxx
Theoriginalsquareis13in.oneachside.
10. Let x =rateofBeckyridingherbiketolibrary. Then x –8=rateofBeckyridingherbike home. To rtd
Library x 1 203minhr 1 3 x
Home8 x 1 302minhr
1 28 x
Becausethedistancegoingtothelibraryisthe sameasgoinghome,wesolvethefollowing.
1111 32328668 2382324 2424 xxxx xxxx xx
Tofindthedistance,substitute x =24into 1 3 dx Because13(24)8, d Beckylives 8mifromthelibrary.
11. Let x =theamountof100%alcoholsolution (inliters).
Thenumberoflitersofpurealcoholinthe 100%solutionplusthenumberoflitersof purealcoholinthe10%solutionmustequal thenumberoflitersofpurealcoholinthe 30%solution.
0.71.23.6 0.72.4
3 7 1.20.3012 1.20.303.6
12. Let x =amountborrowedat5.5%. Then90,000– x =amountborrowedat6%. Amount Borrowed InterestRateInterest x 5.5%0.055 x 90,000 x 6%
0.0690,000 x 90,0005125
Theamountofinterestborrowedat5.5%plus theamountofinterestborrowedat6%note mustequalthetotalamountofinterest.
0.0550.0690,0005125 0.05554000.065125 0.00554005125 0.005275 55,000
x x x
Theamountborrowedat5.5%is$55,000and theamountborrowedat6%is $90,000–$55,000=$35,000.
13. Let x =time(inhours)themotherspent drivingtomeetplane. BecauseMaryLynnhasbeenintheplanefor 15minutes,and15minutesis14hr,shehas beentravelingbyplanefor1 4 x hr. drt
MaryLynnbyplane4201 4 x Motherbycar2040 x ThetimedrivenbyMaryLynn’smothercan befoundby120402hr. xx Mary Lynn,therefore,flewfor 11213 24444hr. TherateofMary Lynn’splanecanbefoundby 3 4 420 d r t
4 4203 560 kmperhour.
14. Let x =numberofhoursforslowerplant (PlantII)toreleasethatamount.Then1 2 x = numberofhoursforfasterplant(PlantI)to releasethatamount.(Iftheplantistwiceas fast,ittakeshalfthetime.)
RateTimePartoftheJob
Accomplished
PlantII1 x 3 13 3 xx
PlantI1 2 12 xx 3 26 3 xx
BecausePlantIandPlantIIaccomplish1job (releasingtoxicwaste)wemustsolvethe followingequation. (continuedonnextpage)
(continued)
Ittakestheslowerplant(PlantI)9hoursto releasethatsameamount.
15. (a) Inoneyear,themaximumamountoflead ingestedwouldbe
0.05mglitersdays 2365.25 literdayyear
36.525mg. year
Themaximumamount A oflead(in milligrams)ingestedin x yearswouldbe A =36.525x.
(b) If x =72,then A =36.525(72)=2629.8mg.TheEPA maximumleadintakefromwaterovera lifetimeis2629.8mg.
16. In2018, x =8.
40.892150.53 40.8928150.53477.67 yx y
Basedonthemodel,retaile-commercesales willbeapproximately$477.67billionin2018.
17. (a) Using1956for x =0,thenfor1990, x =34.
0.11320.4609 0.1132340.46094.31 yx y
Accordingtothemodel,theminimum wagein1990was$4.31.Thisis$0.51 morethantheactualvalueof$3.80.
(b) Let y =$5.85andthensolvefor x 0.11320.4609
18. (a)
(b) ThenumberofAmericanslivinginNew YorkStateisincreasing.
6726712 133133 iii ii
153211311152 1413 iii i
64826248 4444 iii ii
2 534535434 152034 151741 151741917 iiiiii iii i ii
2 821 818212 882281021 8102610 ii iiii iiii ii
25. 22 2 Productofthe sumanddifference oftwoterms 511511511 25121 251211 25121146 iii i
5.850.11320.4609
5.38910.1132
47.6 yx x x x
Themodelpredictstheminimumwageto be$5.85about47.6yearsafter1956, whichismid-2003.Thisisclosetothe minimumwagechangingto$5.85in 2007.
1980:226.5million(0.078) ≈ 17.7 million
1990:248.7million(0.072) ≈ 17.9 million
2000:281.4million(0.068) ≈ 19.1 million
2010:308.7million(0.063) ≈ 19.4 million
2014:318.9million(0.062) ≈ 19.8 million
26. 22 2 2 Squareofa4342433binomial 16249 162491 16249724 iii ii i ii
27. 222 2 535323 5961 5864030 403014030 3040 iiiii ii iiii ii i
2 2 42528202 8202 1684020 1684020 3236 iiiiii ii iii ii i
37. 2 (7)57575 xxx
Solutionset:{75}
38. 2 (23)8 x 2382322 222 2223 3 xx xx
Solutionset: 222 3
39. 2 2150 3250 xx xx 5 303or2502 xxxx
Solutionset: 5 3,2
40. 22 128112810 61210 xxxx xx 11 62610or210 xxxx
Solutionset: 11 62 ,
41. 22 2 21121211210 2112102370 xxxx xxxx 3 2 230or707 xxxx
Solutionset: 3 2,7
42. 2 22 325325 32503250 xxxx xxxx Solvebycompletingthesquare.
2 25 2 33 25211 3939 22 1211 2339 2 114 39 114 39 114 33 114 33 3250 0 Note: xx xx xx x x xi xi
Solvebythequadraticformula. Let3,2,and5. abc 2 2 2141421 6633 4 2 22435 23 2460256 66 2214 6 bbac x a i ii
Solutionset: 114 33 i
43. 2 22 2 214284 2742840 420 xxxxxxx xxxxx xx
Solvebycompletingthesquare.
2 2 122 2 2 420 4424 Note:424 262626 xx xx xxx
(continuedonnextpage)
(continued)
Solvebythequadraticformula. Let1,4,and2. abc
2 2 4 2 444124168 212 424426 26 22 bbac x a
Solutionset: 26
44. 2 2420 xx
Usingthequadraticformulawouldbethemost directapproach.
2,4,and2abc
2 2 4 2 4(4)422 22 41684842222 2222222 222222 21 222
Solutionset:{21}
45. 2510xx
Usingthequadraticformulawouldbethe mostdirectapproach.
1,5,and1abc
46.
Solutionset:
2 2 122 2 2 480 4484 Note:424 2424 2222 xx xx xx xixi
Solveusingthequadraticformula. Let1,4,and8. abc
22444418 221 41632416 22 44 22 2 bbac x a i i
Solutionset: 22i
47. D.Theequation2(74)11 x hastworeal, distinctsolutionsbecausethepositivenumber 11hasapositivesquarerootandanegative squareroot.
48. (a) BandCaretheequationsthathave exactlyonerealsolutionbecausethe positiveandnegativesquarerootof0 representthesamenumber.
(b) A.Theequation2(34)9 x hastwo imaginarysolutionsbecausethenegative number–9hastwoimaginarysquare roots.
49. 22 6236230 xxxx a =6, b =2,and c =3
22424(6)(3)47276bac
Theequationhastwodistinctirrational solutionsbecausethediscriminantispositive butnotaperfectsquare.
50. 22 8268260 xxxx a =8, b =2,and c =6
22424(8)(6)4192188bac
Theequationhastwodistinctnonrealcomplex solutionsbecausethediscriminantisnegative.
51. 22 810708107 xxxx a =8, b =10,and c =7
224(10)4(8)(7) 100224124 bac
Theequationhastwodistinctnonrealcomplex solutionsbecausethediscriminantisnegative.
52. 22 16326162630 xxxx
a =16, b =26,and c =3 22 2 4264(16)(3) 67619248422 bac
Theequationhastwodistinctrational solutionsbecausethediscriminantisa positiveperfectsquare.
53. 2 2 961961 9610 xxxx xx
a =9, b =6,and c =1 22464(9)(1)36360bac
Theequationhasonerationalsolution(a doublesolution)becausethediscriminantis equaltozero.
54. 2 251101210 xx a =25, b =110,and c =121 2241104(25)(121) 12,10012,1000 bac
Theequationhasonerationalsolution(a doublesolution)becausethediscriminantis equaltozero.
55. Theprojectilewillbe750ftabovetheground whenever216220750. tt Solvethisequationfor t
2 2 2 2 16220750 162207500 162207500 81103750 4252150 tt tt tt tt tt
Theprojectilewillbe750fthighat6.25sec andat7.5sec.
56. Let x =widthoftheframe. Then x +3=lengthoftheframe. Setupanequationthatrepresentstheareaof theunframedpicture.
2 2 370 370 3700 7100 xx xx xx xx
Wedisregardthenegativesolution.
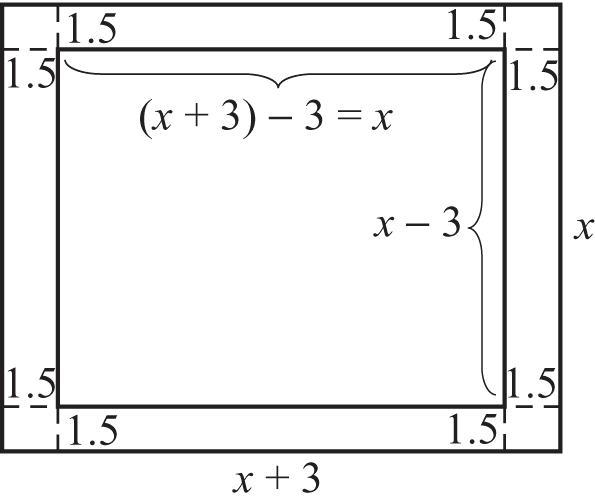
Because x representsthewidthoftheframe, theframeis10inwideand10+3=13in. long.
57. Let x =widthofborder. Applytheformula A = LW toboththeoutside andinsiderectangles. Insidearea=Outsidearea–Borderarea
122102121021 xx
2 2 2 2 1202420412021 12044499 44412099 444210 (221)(21)0 xxx xx xx xx xx
211 22 1 2 22110or 210 xx xx
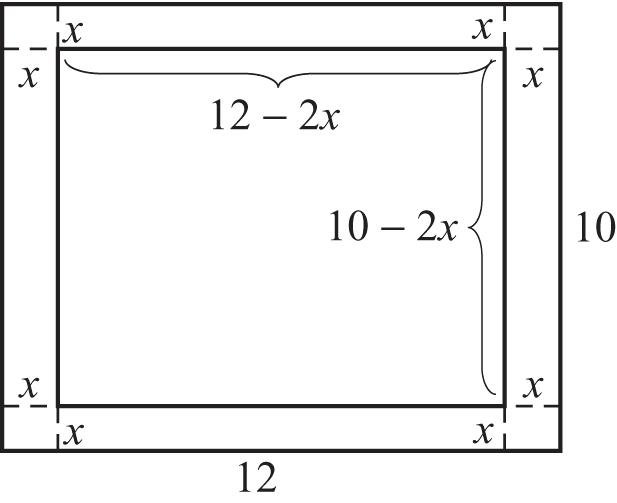
Theborderwidthcannotbe1102becausethis exceedsthewidthoftheoutsiderectangle,so rejectthissolution.Thewidthoftheborderis1 2 ft.
58. 2 2 2 2 2 0.1322 8000.1322 00.13778 100100.13778 0307780 Dss ss ss ss ss
Solveusingthequadraticformula. Let a =1, b =–30,and c =–7780.
2 2 4 2 3030417780 21 3090031,1203032,020 22 bbac s a (continuedonnextpage)
(continued)
3032,02074.5or 2 3032,020104.5 2 s s
Wedisregardthenegativesolution.The appropriatelandingspeedwouldbe approximately104.5ftpersec.
59. In2009, x =19.
Accordingtothemodel,in2009theU.S. governmentspentapproximately$801.9 billiononmedicalcare.
60. Let x =thelengthofthemiddleside. Then x –7=thelengthoftheshorterside and x +1=thelengthofthehypotenuse. UsethePythagoreantheorem. 222 222 2 (7)(1) 144921 16480 (12)(4)012or4 xxx xxxxx xx xxxx
If x =12,then x –7=5and x +1=13. If x =4,then x –7=–3,whichisnotpossible. Thesidesare5inches,12inches,and13 incheslong.
61. 42 4310 xx
Let224 ;then uxux Withthissubstitution,theequationbecomes 2 4310 uu Solvethisequationbyfactoring.
1410uu 1 114 or410 uuuu
Tofind x,replace u with2 x 2 2111 442 11orxxxi xxx
Solutionset: 1 ,2 i
62. 242220120xxxx 2000 xxx or 22 2 11 22 122 222 12012 xx xx xx
Solutionset: 20,2
63. 243 8 3 xxx 7 24 243 338 3 64249 2249 724 xx xxx x x xx
Solutionset: 7 24
64. 2 53 2 xx
22 2 2 2 53 2 253 2530 2130 xx xx xx xx xx
1 2102or303 xxxx
Solutionset: 1 2,3
65.
101101 441411 11 10101 4111411 xxxx xxxx
Multiplyeachtermintheequationbytheleast commondenominator,4(x –1),assuming 1. x
101 4141 411 104140 xx xx
Thisisafalsestatement,thesolutionsetis.
Alternatesolution:
101101 or 441411 xxxx
Multiplyeachtermintheequationbytheleast commondenominator, 411, xx assuming1. x
10 411 41 1 411 1 10141 101044 10144 1414 1 xx x xx x xx xx x x x
Becauseoftherestriction1, x thesolution setis
66. 2 132 10 xx
Multiplybothsidesbytheleastcommon denominator,
210, xx assuming0. x
67.
Therestriction0 x
doesnotaffectthe result.Therefore,thesolutionsetis 5 2,4.
25 25525 5212
55 43or43 42434243 239247 xx xx xx
Solutionset:{–239,247}
68.
214 144 24 2 2 62 6216 616 6160 2802,8 xx xx xx xx xxxx
Solutionset:{–2,8}
69.
2313 332313 2 2 2 (2) (2) (2) 44 540 (4)(1)0 xx xx xx xxx xx xx
Check1. x
2/31/3 2/31/32/3 1/322 (2) (12)1(1)1 11(1)111 xx
Thisisatruestatement.1isasolution.
Check4. x 2/31/3
2/31/32/31/3 1/3 21/31/31/3 (2) (42)4(2)4 2444
xx
Thisisatruestatement.4isasolution. Solutionset:{1,4}
70. 22 2 2 2 232 232 2344 021 01 xx xx xxx xx x 101xx
Check1. x 232 2(1)312 231 11 11 xx
Thisisatruestatement. Solutionset: 1
71.
222 2 2222 22244 032021 xxxx xxxxx xxxx
202or101 xxxx Check2. x
22 2222 0000
xx Thisisatruestatement.–2isasolution. Check1. x
xx
22 1221? 1111
Thisisatruestatement.–1isasolution. Solutionset:{–2,–1}
73.
Check1. x 31 1131? 141 121 11
Thisisatruestatement. Solutionset:{1}
22 4231 4231 4231 21 3 xx xx xx x x
Check3. x 4231 4(3)23(3)1 12291 1010
Thisisatruestatement. Solutionset:{3}
74.
Check3. x
51512 5315312 151542 022 022 22
Thisisafalsestatement.3isnotasolution. Check8. x
51512 5815812 401592 2532 532 22 xx
Thisisatruestatement.8isasolution. Solutionset: 8
22 22 2 2 33101 31310 31310 312310310 33112310 282310 4310 4310 816310 560(2)(3)0 xx xx xx xxx xxx xx xx xx xxx xxxx
303or202 xxxx Check3. x
33101 3333101 09101 011 01111 xx
Thisisafalsestatement.–3isnotasolution. Check2. x
33101 2332101 16101 141 12111 xx
Thisisafalsestatement.–2isnotasolution. Becauseneitheroftheproposedsolutions satisfiestheoriginalequation,theequation hasnosolution.Solutionset:
76.
55 5555 232 232 23222 xx xx xxxx
Check2. x
55 55 55 55 55 232 22322 462 44 44 xx
Thisisatruestatement.
Solutionset: 2
77. 33 33 3333 6240 624 624 624221 xx xx xx xxxx
Check1. x
33 33 33 33 33 6240 612410 6240 440 44000 xx
Thisisatruestatement. Solutionset:{–1}
78.
2 2 222 22 320 3232 34340 140 xx xxxx xxxx xx
101or404 xxxx
Check4. x 2 2 320 43420 161220 420 220 00
Thisisatruestatement.4isasolution.
Check1. x
2 2 320 13120 1320 420 220 00 xx
Thisisatruestatement.1isasolution. Solutionset: 4,1 79.
2 12 3 22 12 3 22 x xxxx x xxxx
Multiplyeachtermintheequationbytheleast commondenominator, 2, xx assuming 0,2. x
2 22 2 2 12 232 22 2322 2362 4722 470470 x xxxx xxxx xxxx xxxx xx xxxx
7 0or4704xxx
Becauseoftherestriction0, x theonlyvalid solutionis74Thesolutionsetis 7 4 80.
2 214 2468 214 2442 xxxx xxxx Theleastcommondenominatoris
42,xx whichisequalto0if 4or2.xx Therefore,4and2 cannotpossiblybesolutionsofthisequation.
21 42 24 4 42 42 xx xx xx xx
2424 2824362 xx xxxx
Theonlypossiblesolutionis–2.However,the variableisrestrictedtorealnumbersexcept–4 and–2.Therefore,thesolutionsetis:.
81. 2/31/3 (23)(23)60 xx
Let1/3 (23)ux .Then 21/322/3 [(23)](23)uxx . Withthissubstitution,theequationbecomes 260.uu Solvebyfactoring.
320uu
303or202 uuuu
Tofind x,replace u with1/3 (23) x .
3 1/31/33 1/31/333 5 2 233233 232723015or 232232 23825 xx xxx xx xxx
Check15. x
2/31/3 2/31/3 2/31/3
2/31/3 1/32 2 (23)(23)6 2(15)32(15)36 (303)(303)6 (27)(27)6 (27)36 336 93666 xx
Thisisatruestatement.–15isasolution.
5 Check2. x
2/31/3 2/31/3 55 22 2/31/3 2/31/3 1/32 2 (23)(23)6 23236 (53)(53)6 886 826 226 42666
Thisisatruestatement.52isasolution. Solutionset: 5 15,2
2/31/3 2/31/3 3233 32330 xx xx Let
31/3 ux ;then
2 21/32/3 33.
2230(1)(3)0 uuuu 1or3uu
Tofind x,replace u with 1/3 3. x
3 3 3 1/31/33 11 11 1/31/333 11 327 818011 27272727 3131 3314 or 3333 33 3 xx xxx xx xx x
2/31/3 2/31/3 2/31/3 2/31/3 2 1/31/3 2 32330 4324330 12130 12130 12130 12130 1230 00
Thisisatruestatement.4isasolution. 80 Check27. x
2/31/3 2/31/38080 2727 2/31/380818081 27272727 2/31/311 2727 2/31/3 1/321/3 2 32330 32330? 230 230 2722730 2722730 32330 9630 00
Thisisatruestatement.8027isasolution. Solutionset: 80 4,27
Copyright©2017PearsonEducation,Inc.
83. 7 13 93410 137 xx x x
Solutionset: 7 13,
84. 8 9 1124 1128 98 xx xx x x
Solutionset: 8 9,
85. 543(25) 54615 11415 1111 1 xx xx x x x
Solutionset: ,1
86.
42 105 72352 726105 56105 10610 104 xxx xxx xx x x xx
Solutionset: 2 ,5
87. 5237 8210 45 x x x
Solutionset:[4,5]
88. 7 3 7 3 83512 337 1 1 x x x x
Solutionset: 7 3,1
89. 2340xx
Step1:Findthevaluesof x thatsatisfy 2340.xx 2340 410 xx xx 404or101 xxxx
Step2:Thetwonumbersdivideanumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,2340. xx
IntervalTestValue Is2340 xx TrueorFalse?
A: ,4 5 2? 53540 60
False
B: 4,10 ? 2 03040 40 True
C: 1, 2 ? 2 23240 60 False
Solutionset: 4,1
90. 24210xx
Step1:Findthevaluesof x thatsatisfy 24210.xx
24210 730 xx xx 707or303 xxxx
Step2:Thetwonumbersdivideanumberline intothreeregions.
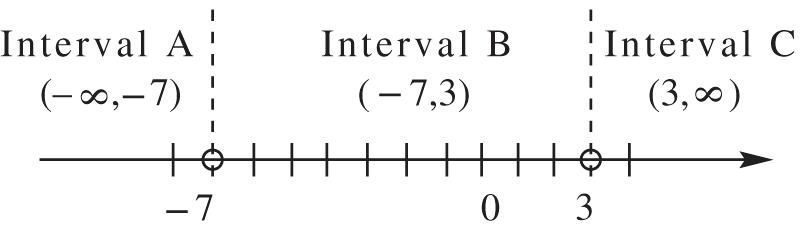
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,24210 xx
IntervalTestValue Is24210 xx TrueorFalse?
A: ,7 8 2? 848210 110 True
B: 7,30 2? 040210 210 False
C: 3, 4 2? 444210 110 True
Solutionset: ,73,
91. 2 61110 xx
Step1:Findthevaluesof x thatsatisfy 2 61110 xx 2 2 61110 611100 (32)(25)0 xx xx xx 25 32320or250 xxxx
Step2:Thetwonumbersdivideanumberline intothreeregions.
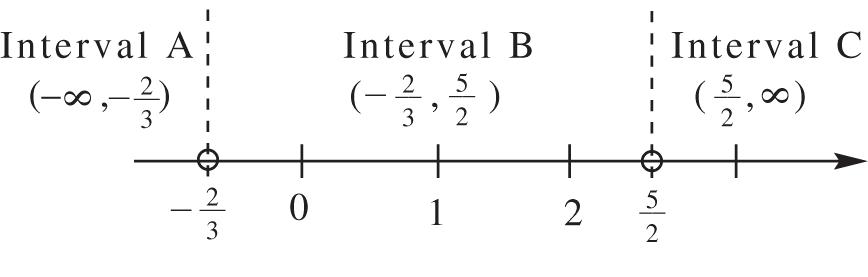
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,261110 xx
IntervalTestValue Is261110 xx TrueorFalse?
A: 2 ,3 1
2? 6111110 1710 False
B: 25 32,0 2? 601101010 1010 True
C: 5 2, 3 2? 631131010 1110 False
Solutionset: 25 32 , 92. 235xx
Step1:Findthevaluesof x thatsatisfy 2235350xxxx Usethe quadraticformulaLet 1,3,and5.abc
2 2 4 2 33415 21 3920329 22 329329 1.2or4.2
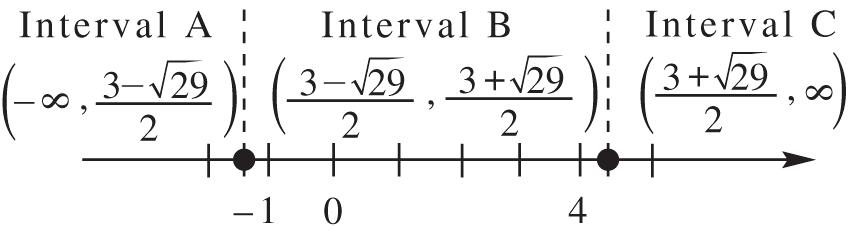
Step2:Thetwonumbersdivideanumberline intothreeregions. Step3:Chooseatestvaluetoseeifitsatisfies theinequality,235 xx
IntervalTestValue Is235 xx TrueorFalse?
A: 329 ,2 2 2? 2325 105 True
B: 329329 22 , 0 2? 0305 05 False
C: 329 2, 5 2? 5355 105 True
Solutionset: 329329 ,22,
93. 3160xx Step1:Solve3160. xx
32160160 440 xxxx xxx
Seteachfactortozeroandsolve. 0or404or 404 xxx xx
Step2:Thevalues4,0,and,4dividethe numberlineintofourintervals.
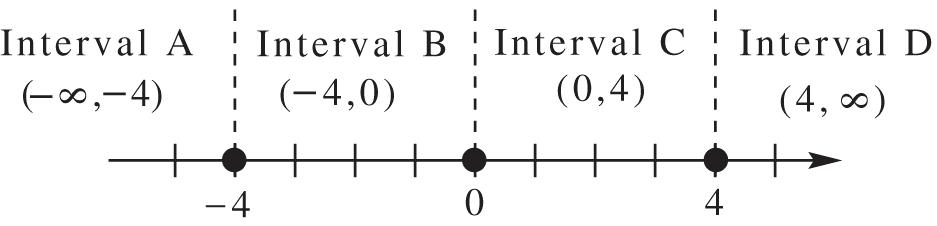
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,3160. xx
IntervalTestValue Is3160 xx TrueorFalse?
A: ,4 5 3? 51650 450 True
B: 4,01 3? 11610 150 False
(continuedonnextpage)
(continued)
IntervalTestValue
C: 0,41
Is3160 xx TrueorFalse?
3? 11610 150 True
D: 4, 5 3? 51650 450 False
Solutionset:
94. 32 2350 xxx Step1:Solve322350. xxx
322 23502350 1250 xxxxxx xxx Seteachfactortozeroandsolve. 5 2 0or10or250 0or1or xxx xxx
Step2:Thevalues51,0,and,2dividethe numberlineintofourintervals.
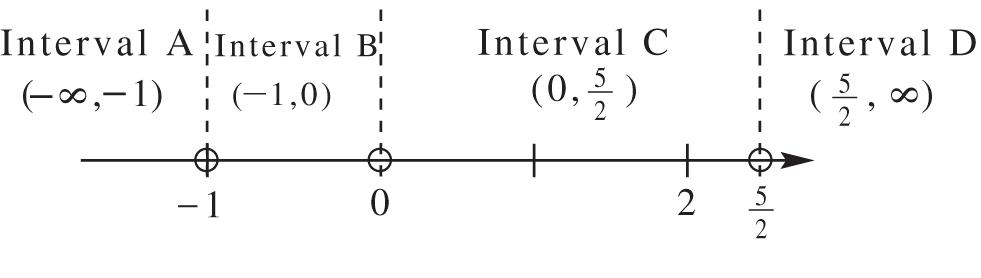
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,322350. xxx
IntervalTestValue Is322350 xxx TrueorFalse? A: ,1 2
32? 2232520 180 True
B: 1,00.5 32? 20.530.550.50

95. 36 0 5 x x Becauseonesideoftheinequalityisalready 0,westartwithStep2. Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 3602or505 xxxx Thevalues–2and5todividethenumberline intothreeregions. Step3:Chooseatestvaluetoseeifitsatisfies theinequality,360. 5 x x
IntervalTestValue Is3650 x x TrueorFalse? A: ,2
3
336? 35 3 8 0 0
B: 2,50 306? 05 6 5 0 0
C: 5, 6
Solutionset:
False
366?650 240
True
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside.
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 1 606or2102 xxxx Thevalues12and6dividethenumberline intothreeregions.Useanopencircleon1 2 becauseitmakesthedenominatorequal0. (continuedonnextpage)
(continued)
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,71 21 x x
IntervalTest
IntervalsAandCsatisfytheinequality.The endpoint12isnotincludedbecauseitmakes thedenominator0.
Solutionset:
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside. 32324 400 3242
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0.
202or0xxx
Thevalues–2and0dividethenumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,3240 x x .
IntervalTest
Value Is3240 x x TrueorFalse?
A: ,2 3 332? 3 1 3 40 0 False
B: 2,01 312? 140 10 True
C: 0, 1 312?140 30 False
Solutionset:(–2,0) 98. 52 10 x x
Step1:Rewritetheinequalitytocomparea singlefractionwith0. 5252 100 5262 00 xxx xxx xxx xx
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 1 3 620or0 xxx
Thevalues13and0dividethenumberline intothreeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,5210. x x
IntervalTest
Value
Is5210 x x TrueorFalse?
A: 1 ,3 1 512? 110 40 False
B: 1 3,00.1 50.12?0.110 140 True
C: 0, 1 512?110 80 False
Solutionset: 1 3,0
99. 35 13xx
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside. 35 0 13 3(3)5(1)0 (1)(3)(3)(1) 3(3)5(1)0 (1)(3) 3955 0 (1)(3) 214 0 (1)(3) xx xx xxxx xx xx xx xx x xx
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 21407or101or 303 xxxx xx
Thevalues–3,1and7dividethenumberline intofourregions.Useanopencircleon3 and1becausetheymakethedenominator equal0.
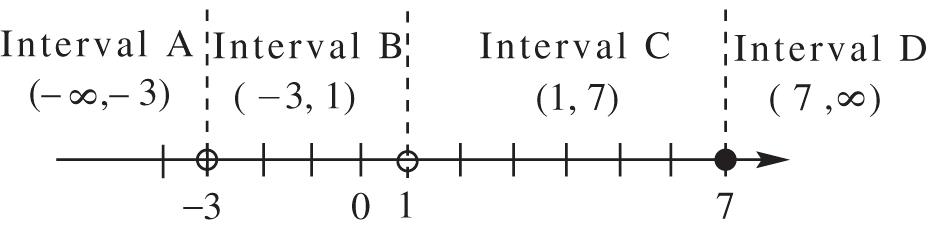
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,3513xx
IntervalTestValue Is3513xx TrueorFalse?
A: ,3 4 ? 35 4143 3 55 False
B: 3,10 ? 35 0103 5 33
True
C: 1,72 ? 35 2123 31 False
D: 7, 8 ? 35 8183 ? 35 711 3335 7777 True
IntervalsBandDsatisfytheinequality.The endpoints3and1arenotincludedbecause theymakethedenominator0. Solutionset:(3,1)[7,)
100. 32 24xx Step1:Rewritetheinequalitytocomparea singlefractionwith0. 32 0 24
3(4)2(2)0 (2)(4)(4)(2) 3(4)2(2)0 (2)(4) 31224 0 (2)(4) 16 0 (2)(4) xx xx xxxx xx xx xx xx x xx
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 16016or202or 404 xxxx xx
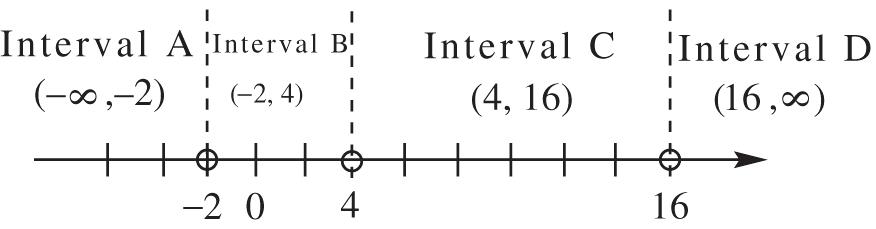
Thevalues–2,4and16dividethenumberline intofourregions. Step3:Chooseatestvaluetoseeifitsatisfies theinequality,32. 24xx
IntervalTestValue Is3224xx TrueorFalse?
A: ,2 3 3?2 3234 2
B: 2,40 3?2 0204 31 22 True
C: 4,165 3?2 5254 3 72 False
D: 16, 17 3?2 172174 3?2 1913 3938 247247
Solutionset: 2,416,
101. (a) Let x =theozoneconcentrationafterthe Purafilairfilterisused.
1400.4314079.8 x TheozoneconcentrationafterthePurafil airfilterisusedis79.8ppb.
Copyright©2017PearsonEducation,Inc.
(b) Let x =themaximuminitialconcentration ofozone.
0.43500.5750 87.7(approximately) xxx x
Thefilterwillreduceozoneconcentrations thatdon’texceed87.7ppb.
102. C =3x +1500, R =8x Thecompanywillatleastbreakevenwhen R ≥ C. 83150051500300 xxxx
Thebreak-evenpointisat x =300.The companywillatleastbreakevenifthe numberofunitsproducedisintheinterval 300,.
103. 2 16320st
(a) When s =0,theprojectilewillbeat groundlevel. 22 2 016320163200 200(20)0 tttt tttt t =0or t =20
Theprojectilewillreturntotheground after20sec.
(b) Solve s >576for t. 2 2 2 32016576 016320576 02036 tt tt tt
Step1:Findthevaluesof t thatsatisfy
220360.tt
2203602180 tttt
202or18018 tttt
Step2:Thetwonumbersdivideanumber lineintothreeregions.
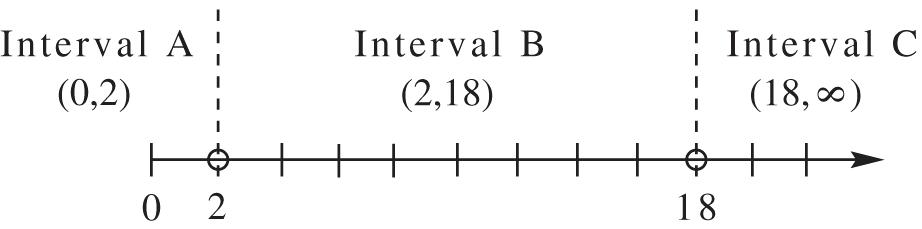
Step3:Chooseatestvaluetoseeifit satisfiestheinequality, 2 32016576. tt
IntervalTestValue Is232016576 tt TrueorFalse?
A: 0,21
True
IntervalTestValue Is232016576 tt TrueorFalse?
C: 18, 20 2? 320201620576 0576 False
Theprojectilewillbemorethan576ftabove thegroundbetween2and18sec.
104. 35.7486yx 35.7486800 35.7314
8.8(approximately) x x x
Basedonthemodel,theamountpaidbythe governmentfirstexceeds$800billionabout 8.8yearsafter2004,whichisin2012.Thisis veryclosetothegraph.
105. Answerswillvary.3cannotbeinthesolution setbecausewhen3issubstitutedinto1493, x x divisionbyzerooccurs.
106. Answerswillvary.4mustbeinthesolution setbecausewhen4issubstitutedinto421, x x theresultiszero,whichmakesthenonstrict inequalitytrue.
107. 47 473or4711 x xxxx
Solutionset:{–11,3}
108. 2323 231or235 xx xxxx
Solutionset:{–1,5}
109. 77 909 2323 xx 1111 2727 7 23979(23)71827 1127or xx x xxx
2525 2727 7 23979(23) 718272527 x x xxxx
Solutionset: 1125 2727 ,
Copyright©2017PearsonEducation,Inc.
110. 81 70 32 x x 15 13 8181 707 3232 817(32)812114 113141513or xx xx xxxx xxx
13 29 81 327817(32) 81211429114 2913 x xx x xxx xx
Solutionset: 1513 1329 ,
111. 5123 xx
4 3 2 7 512331334 or 51235123 71372 xxxxx xxxx xxx
Solutionset: 24 73 ,
112. 1011xx 1 2 10111011False or 10111011 2101121 xx xxxx xxx
Solutionset: 1 2
113. 293 x 3293 1226 63 x x x
Solutionset: 6,3
114. 852 x 6 852565or 8525102 xxx xxx
Solutionset:
6 5
115. 734 x 1 734717or 734771 xxx xxx
Solutionset:
116. 12 233 x
12 23 12 23 2214 33 33 63663 183418 22314 x x x xx
Solutionset: 2214 33 , 117. 37553710 xx 17 3 103710 1733 1 x x x
Solutionset: 173,1
118. 7863783 xx 11 7 5 7 783711or 78375 xxx xxx
Solutionset: 115 77 ,,
119. Becausetheabsolutevalueofanumberis alwaysnonnegative,theinequality 4123 x isalwaystrue.Thesolutionset is ,.
120. Thereisnonumberwhoseabsolutevalueis lessthanorequaltoanynegativenumber.The solutionsetof729 x is
121. Becausetheabsolutevalueofanumberis alwaysnonnegative,240 xx isnever true,so240 xx isonlytruewhen 240.xx 22404040 0or40 0or4 xxxxxx xx xx
Solutionset: 4,0
122. 240xx willbefalseonlywhen 240,xx whichoccurswhen 4or0xx (seelastexercise).Sothe solutionsetfor240 xx is ,44,00,.
123. “k is12unitsfrom6”meansthatthedistance between k and6is12units,or612 k or 612. k
124. “p isatleast3unitsfrom1”meansthat p is3 unitsormorefrom1.Thus,thedistance between p and1isgreaterthanorequalto3, or13 p or13. p
125. “t isnolessthan0.01unitfrom5”meansthat t is0.01unitormorefrom5.Thus,the distancebetween t and5isgreaterthanor equalto0.01,or50.01 t or50.01. t
Chapter 1 Test
1. 3(4)5(2)2(24) 312510224 22222 2222
Solutionset:{0}
2. 21 44 32 xxx
21 6464 32 434624 4312624
Solutionset: 12
3. 2 61170 21370 xx xx
17 23210or370 xxxx
Solutionset: 17 23 ,
4. 2 (31)8 31822 122 3122 3 x x xx
Solutionset: 122 3
5. 2 322 xx Solvebycompletingthesquare.
2 2 22222121 333939 322 3220 0 xx xx xxxx
22 1211 2339 25511 3939 5511 3333
Note: xx xixi
Solvebythequadraticformula. Let3,2,and2. abc
2 2 25521 6633 4 2 224322424 236 220225 66 bbac x a i ii
Solutionset:
15 33 i
2 1223 933 1232 3333 xxx xxxx
Multiplyeachtermintheequationbytheleast commondenominator, 33xx assuming3,3. x
123 33 333 2 33 3 123323 123926 3326 363 xx xxx xx x xx xx xx xx
Theonlypossiblesolutionis3.However,the variableisrestrictedtorealnumbersexcept–3 and3.Therefore,thesolutionsetis
Multiplyeachtermintheequationbytheleast commondenominator, x(x –2)assuming 0,2.
Becauseoftherestriction0, x theonlyvalid solutionis34.Thesolutionsetis
3 4.
8.
22 2 2 345213424 3424 3441616 041912 0434 xxxx xx xxx xx xx
3 4 430or404 xxxx
3 Check4. x
33 44 95255 4242 55155 2222 34521 34521 455 5 xx
Thisisafalsestatement.34isanotsolution.
Check4. x
34521 3445241 124581 16581 45999 xx
Thisisatruestatement.4isasolution. Solutionset:{4} 9.
22 2333 2333 2333 239633 231263 3963 xx xx xx xxx xxx xx
22 2 2 2 323 323 6943 69412 230310 xx xx xxx xxx xxxx
303or101 xxxx
Check3. x
2333 233333 6303 903 30333 xx
Thisisatruestatement.–3isasolution.
Check1. x 2333 213133 2343 123 12333 xx
Thisisatruestatement.1isasolution. Solutionset:{–3,1}
10.
33 3333 3894 3894 3894864 1262 xx xx xxx xx
Check2. x
xx
33 33 33 3333 3894 328924 68184 14141414
Thisisatruestatement.
Solutionset:{–2}
11. 4217160xx Let224 ;then uxux Withthissubstitution,theequationbecomes 217160uu Solvethisequationbyfactoring.
1160uu 101or16016 uuuu Tofind x,replace u with2 x 2 2 111or 16164 xxx xxx
Solutionset: 1,4
12. 2/31/3 3360xx
Let 31/3 ux .Then
2 21/32/3 33.uxx 260(3)(2)0 uuuu 303or202 uuuu Tofind x,replace u with 1/3 3. x
3 1/31/33 1/31/333 3333 32730or 3232 385 xx xx xx xx
(continuedonnextpage)
(continued)
Check30. x
2/31/3
xx
2/31/3
2/31/3 1/32 2 3360 30330360 272760 27360 3360 936000
Thisisatruestatement.–30isasolution.
Check5. x
2/31/3
2/31/3
2/31/3 1/32 2 3360 535360 8860 8260 2260 426000
Thisisatruestatement.5isasolution.
Solutionset: 30,5
13. 437 x 105 42 437441or 437410 xxx xxx
Solutionset: 5 2,1
14. 4 3 215 21531534 or 21(5)2156 xx xxxxx xxxxx
Solutionset: 4 6,3
15. 222 222 2(22) 2 22 2 22 SHWLWLH SLHHWLW SLHWHL SLH W HL SLH W HL
17. (a)
22 2 2 8382833 64489 644891 644895548 iii ii i ii
2 2 2 319(319)(13) 13(13)(13) 391957 13 31057131057 19191 60106010 6 1910 iii iii iii i ii i ii i
10 424024101111 iiii
8 313248 1 iiiiiii
18. (a) Minimum: galminhrgal11206012806,400minhrdayday
Theequationthatwillcalculatethe minimumamountofwaterpumpedafter x dayswouldbe806,400. Ax
(b) 806,400 Ax when30 x wouldbe 806,4003024,192,000 A gal.
(c) Becausetherewouldbegal 806,400day
minimumandeachpoolrequires20,000 gal,therewouldbeaminimumof 806,40040.32 20,000 poolsthatcouldbe filledeachday.Theequationthatwill calculatetheminimumnumberofpools thatcouldbefilledafter x dayswouldbe 40.32. Px Approximately40pools couldbefilledeachday.
(d) Solve40.32Px where1000. P 1000 40.32 100040.3224.8days. xx Aminimumof1000poolscouldbefilled in25days.
19. Letwidthofrectangle. w Then 220lengthofrectangle. w Usetheformulafortheperimeterofa rectangle.
22 62022202 6204402 6206406606110 Plw ww ww www
Thewidthis110mandthelengthis
21102022020200 m.
20. Let x =amountofcashews(inpounds).Then 35– x =amountofwalnuts(inpounds). Costper Pound Amountof
Cashews7.00 x 7.00 x Walnuts5.5035 x
5.5035 x Mixture6.5035356.50 Solvethefollowingequation.
35350701 1.51533 7.005.5035356.50 7192.55.5227.5 1.5192.5227.5 1.535 23
Thefruitandnutstandownershouldmix 1 233lbsofcashewswith12 33352311 lbs ofwalnuts.
21. Let x =averagespeedupriver. Then x +5=averagespeedonreturntrip. rtd Upriver x 1.21.2 x Downriver5 x 0.9 0.95 x
Becausethedistanceupriveranddownriver arethesame,wesolvethefollowing.
1.20.9(5) 1.20.94.50.34.515 xx xxxx Theaveragespeedoftheboatupriveris15 mph.
22. 0.4616.32yx
(a) Theyear2014isrepresentedby x =10. 0.461106.321.71 y
Accordingtothemodel,in2014about 1.7%ofcollegefreshmensmoked.
(b) 4.90.4616.32 1.420.4613.1 x xx
Accordingtothemodel,4.9%of freshmansmokedabout3.1yearsafter 2004orin2007.
23. 2 1696 stt (a) Let s =80andsolvefor t. 22 8016961696800 tttt 2650 (1)(5)0 tt tt
101or505 tttt Theprojectilewillreachaheightof80ft at1secand5sec.
(b) Let s =0andsolvefor t. 2 01696 016(6) tt tt 0or606ttt Theprojectilewillreturntothegroundat 6sec.
24. 211221 221222 21022 4102 412 3 xx xx xx x x x
Solutionset: 3,
25.
1 323 2 1 232223 2 646 102 x x x x
Solutionset:[–10,2]
26. 2 23 xx
Step1:Findthevaluesof x thatsatisfy 2 23. xx 2 2 23 230 (1)(23)0 xx xx xx 3 101or2302 xxxx
Step2:Thetwonumbersdivideanumberline intothreeregions.
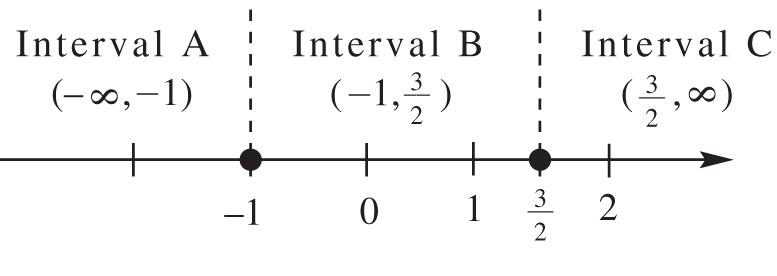
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,223 xx
(continuedonnextpage)
(continued)
IntervalTestValue Is223 xx TrueorFalse?
Step1:Rewritetheinequalitysothat0ison onesideandthereisasinglefractiononthe otherside.
Step2:Determinethevaluesthatwillcause eitherthenumeratorordenominatortoequal0. 41604or303 xxxx Thevalues3and4dividethenumberlineinto threeregions.
Step3:Chooseatestvaluetoseeifitsatisfies theinequality,135. x x
IntervalTestValue Is135 x x TrueorFalse?
A: ,3 0 01? 03 1 3 5 5 True
B: 3,43.5 3.51? 3.535 95 False
C: 4, 5 51? 535 35 True Solutionset:(,3)(4,)
28. 259 9259 4214 27 x x x x Solutionset:(–2,7)
29. 211102111 xx 2111or2111 212210 6or5 xx xx xx Solutionset:(,–6][5,)
30. 7 3703703 xxx
However,if73, x then370, x and 37 x isnotdefined.Thus,thesolutionset of370 x is 7 3
