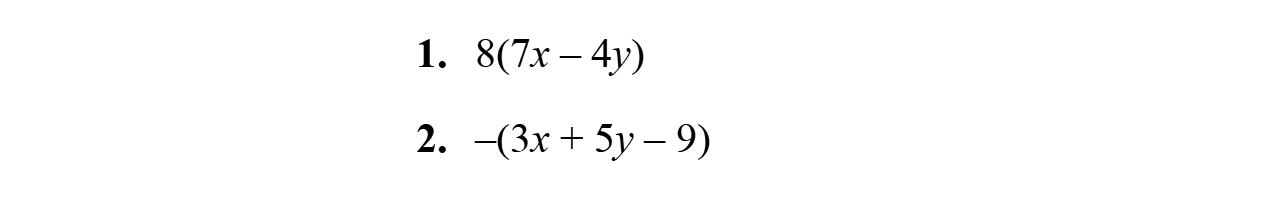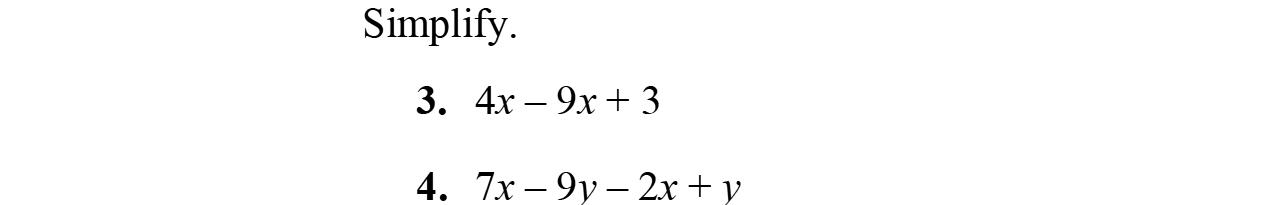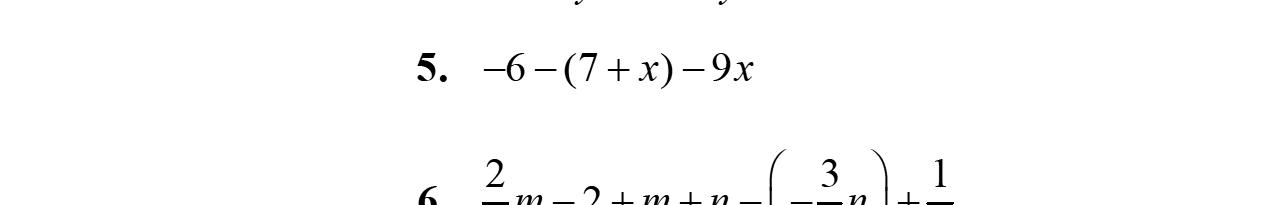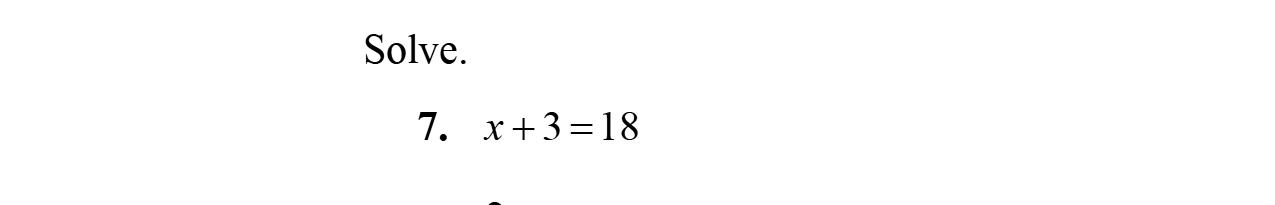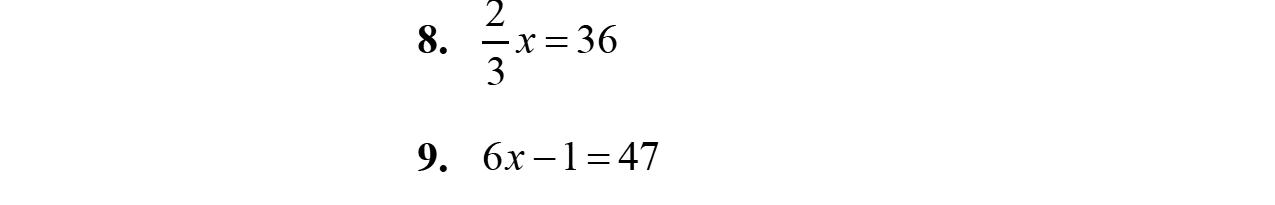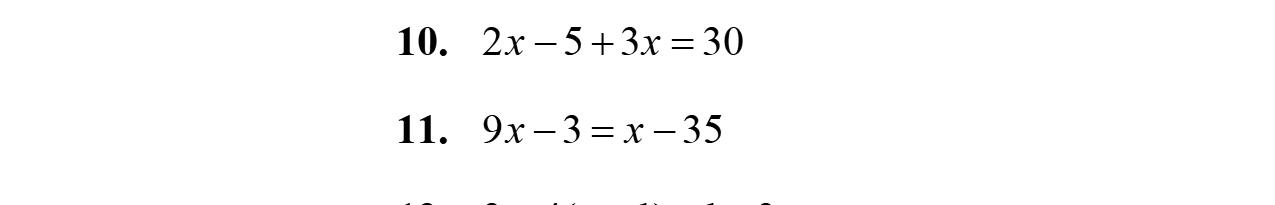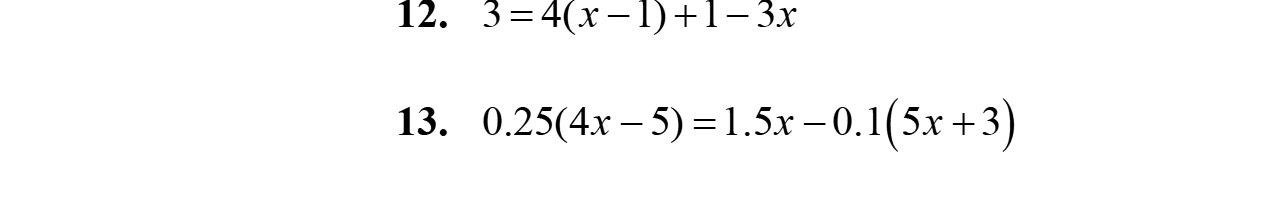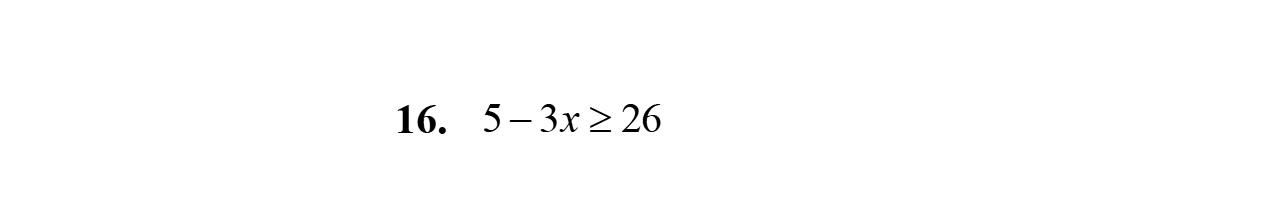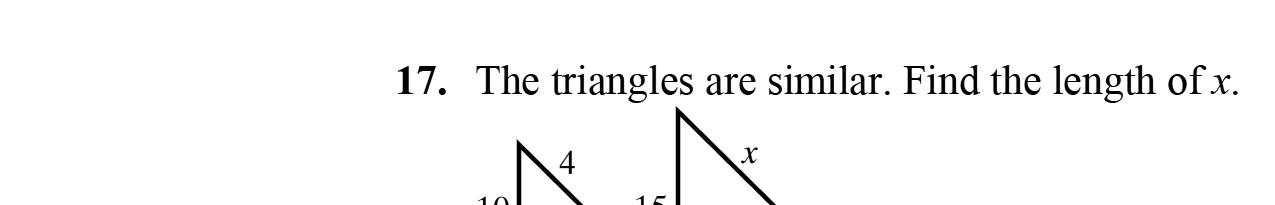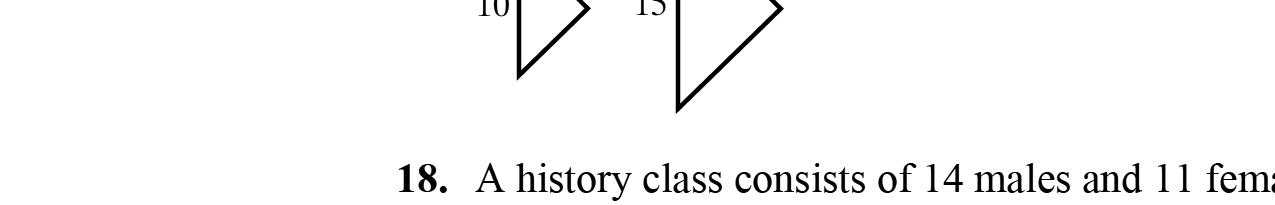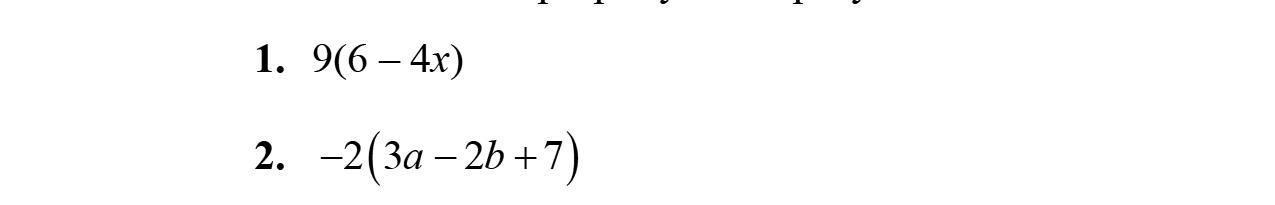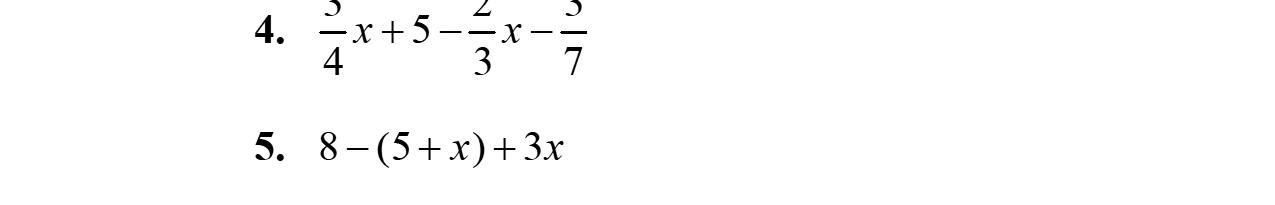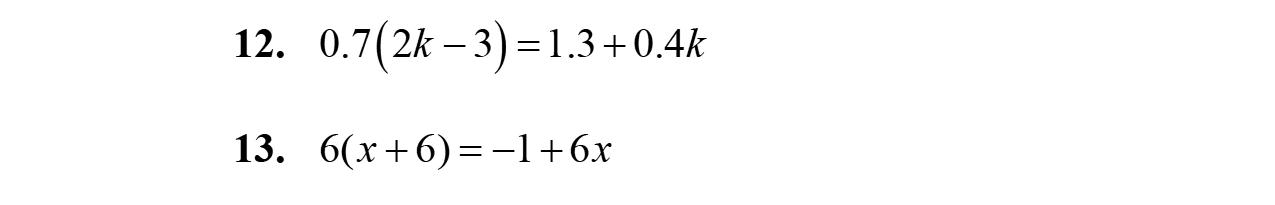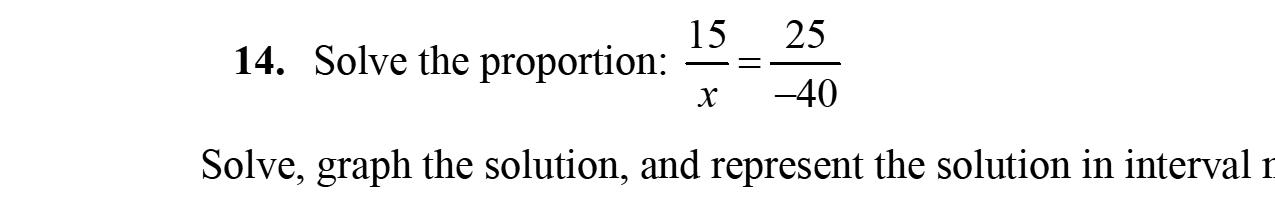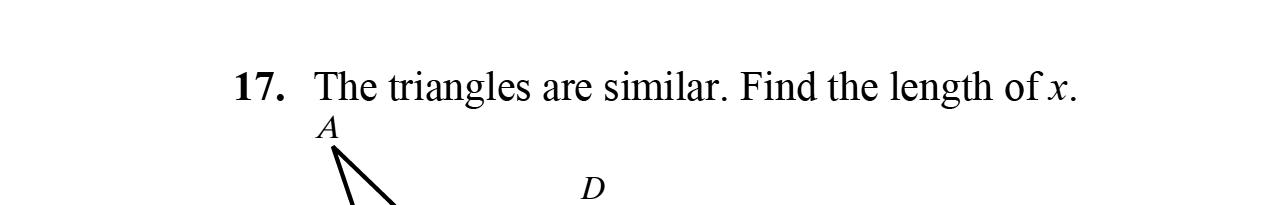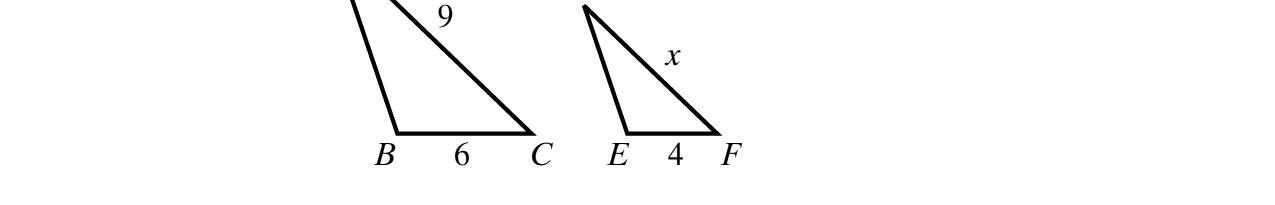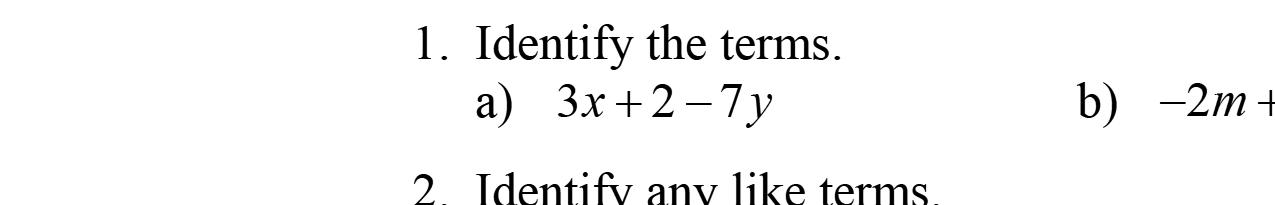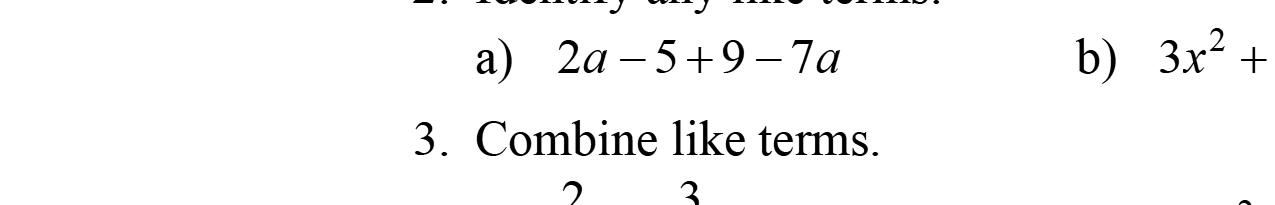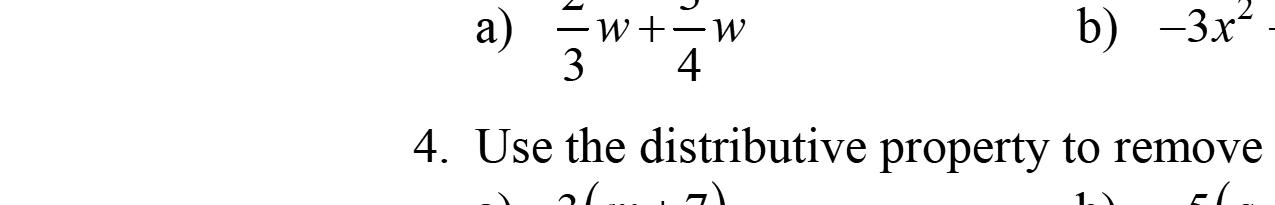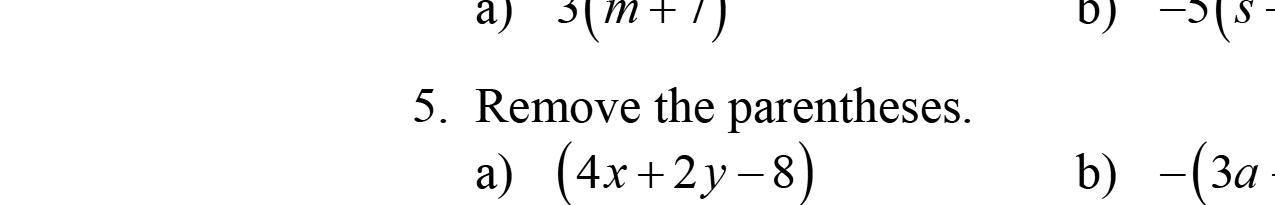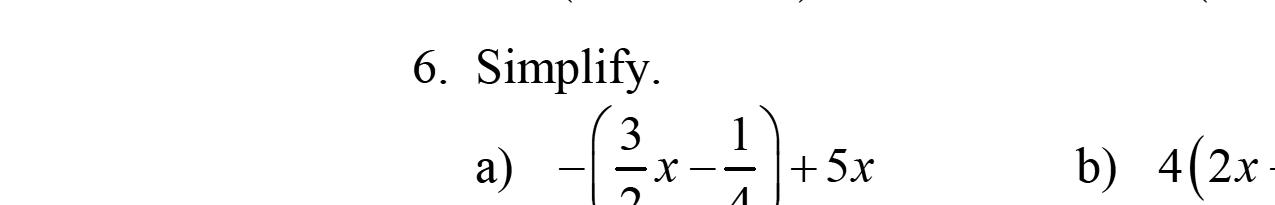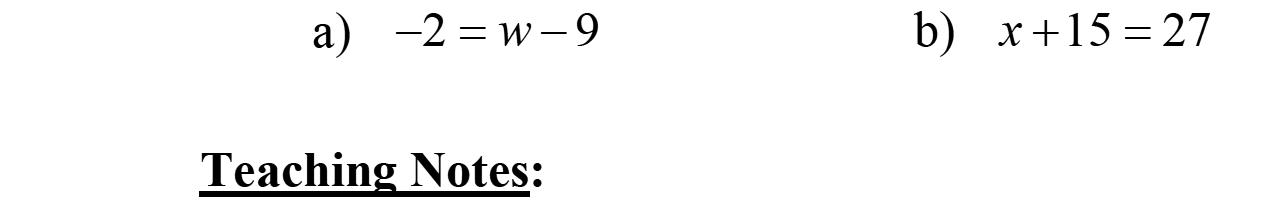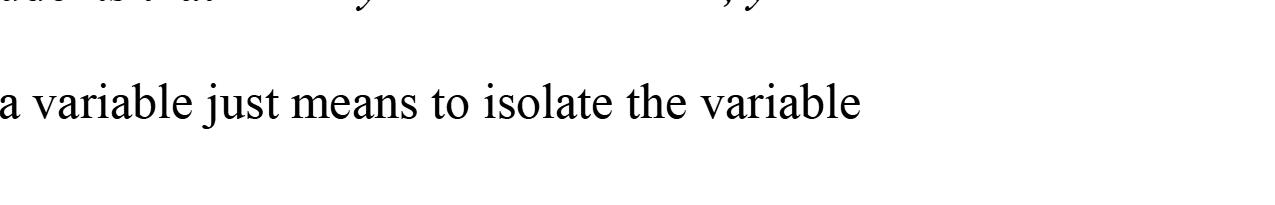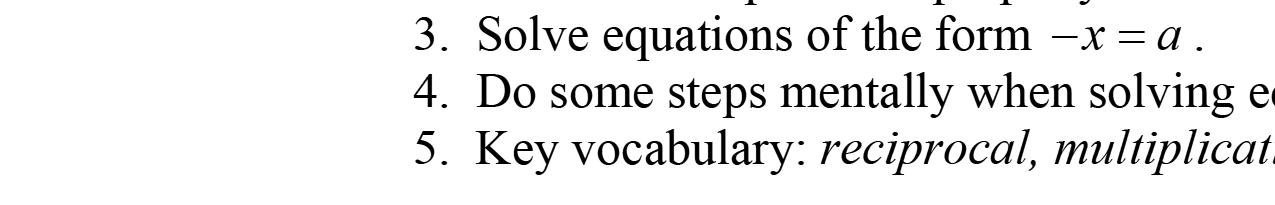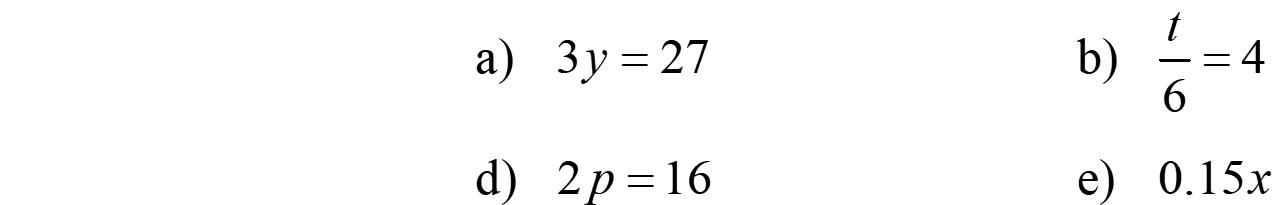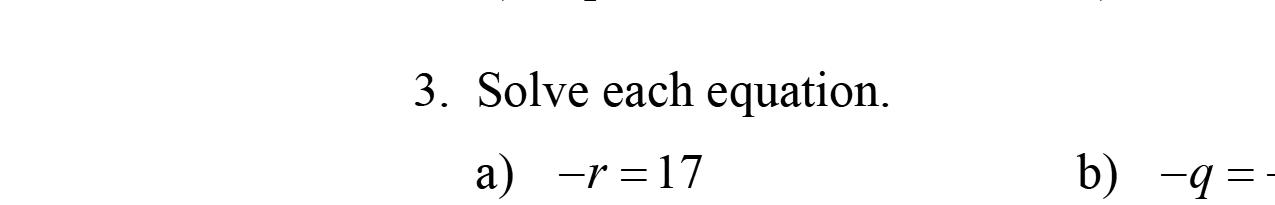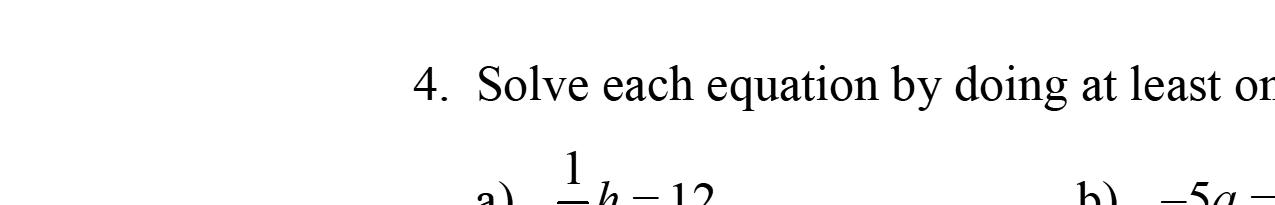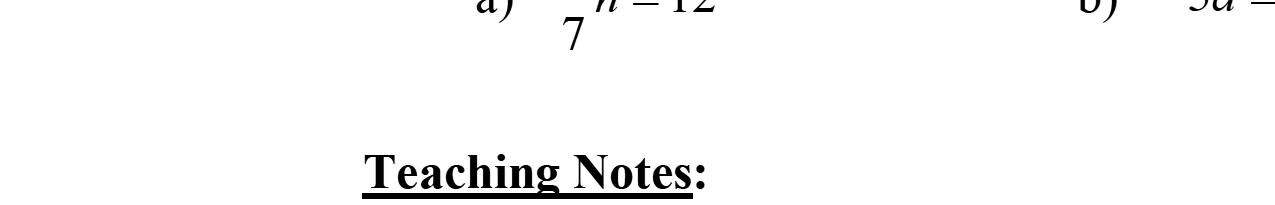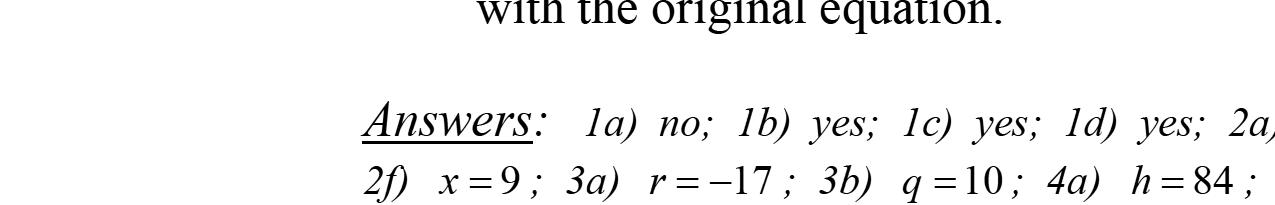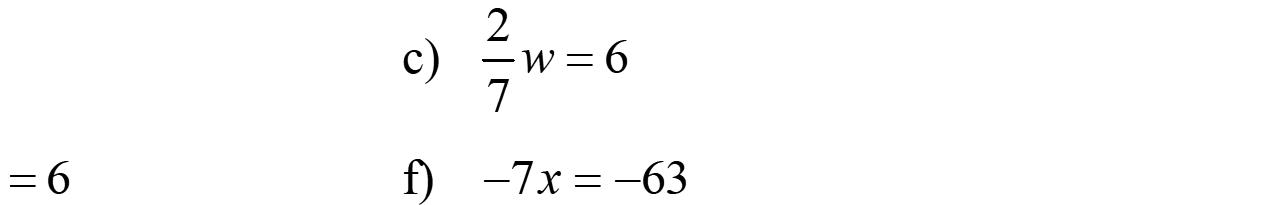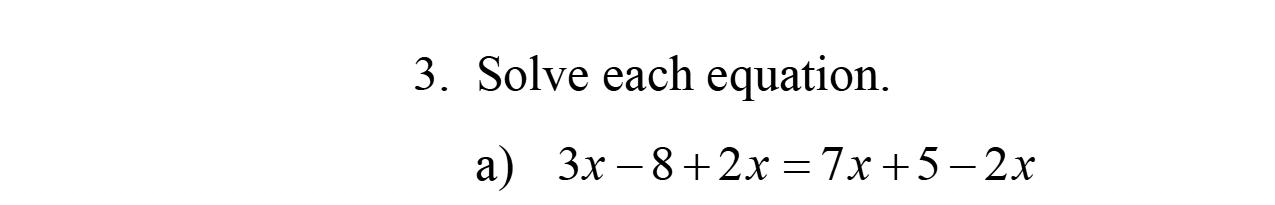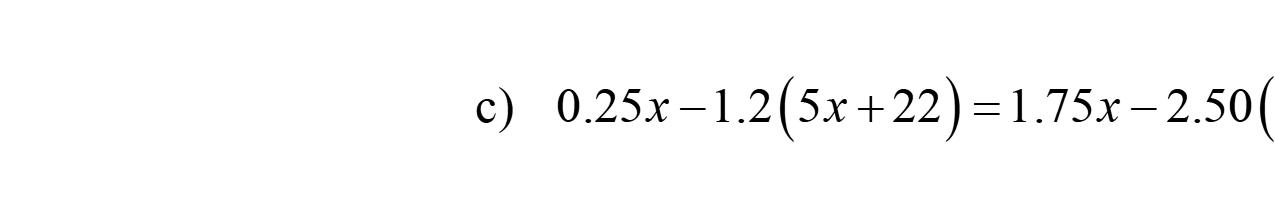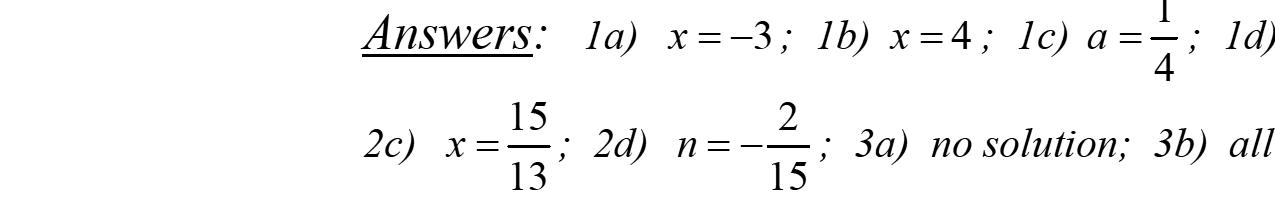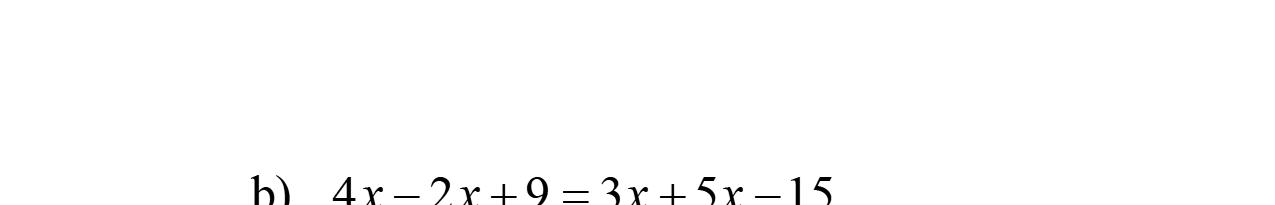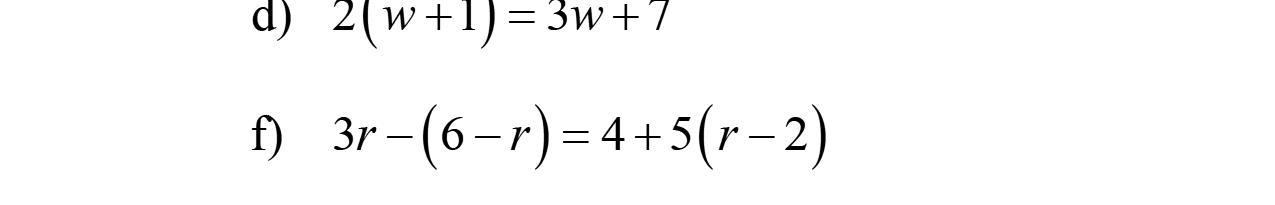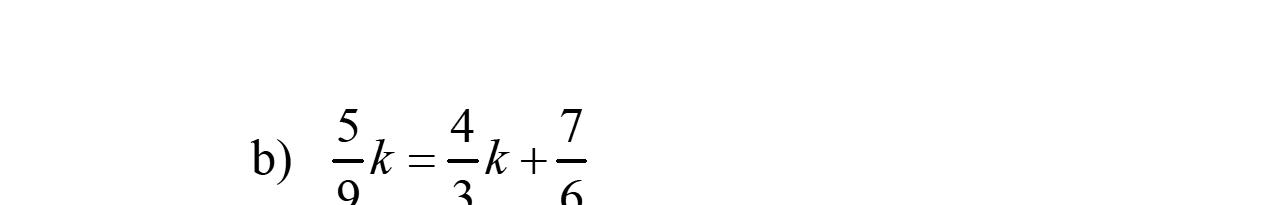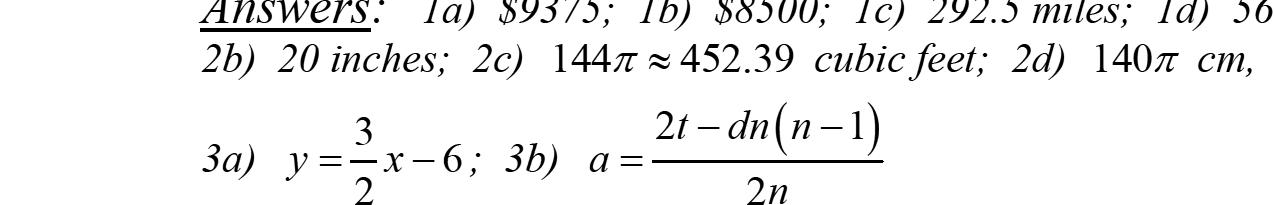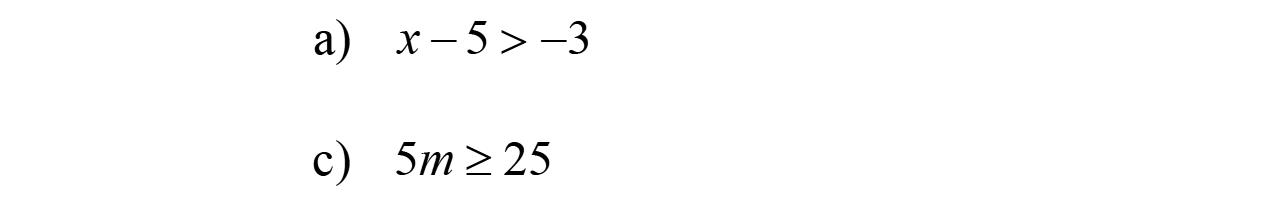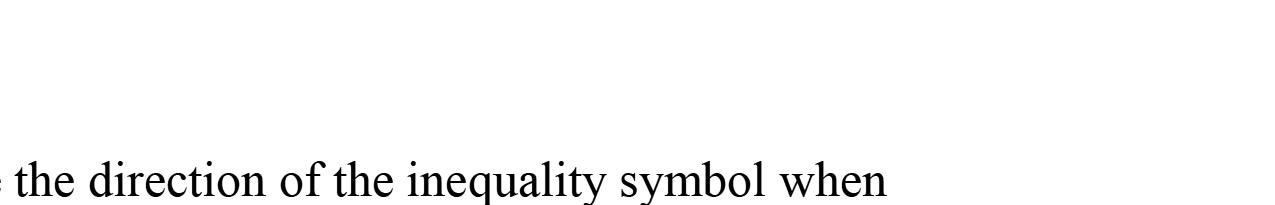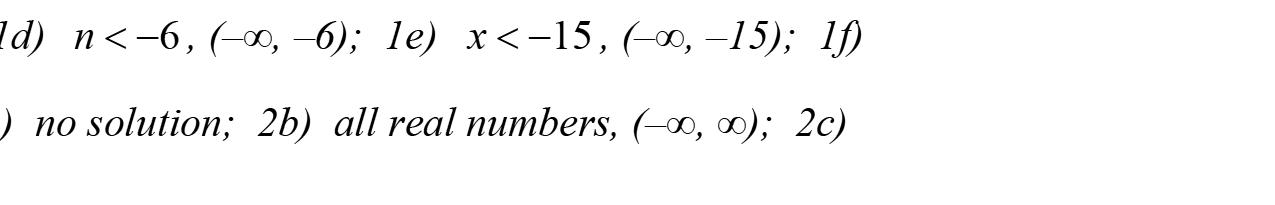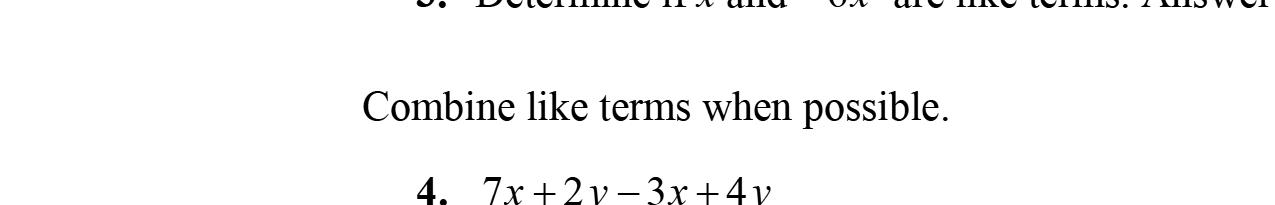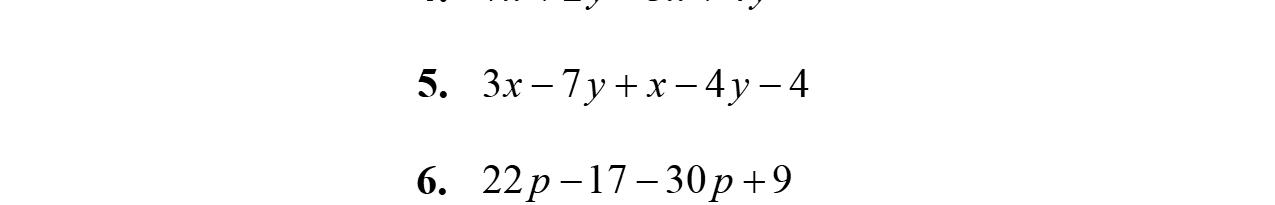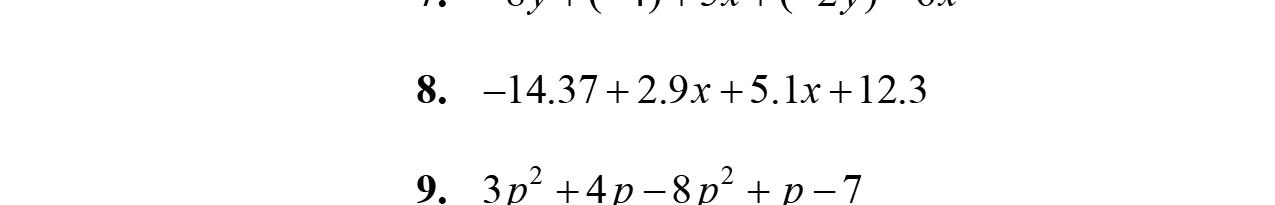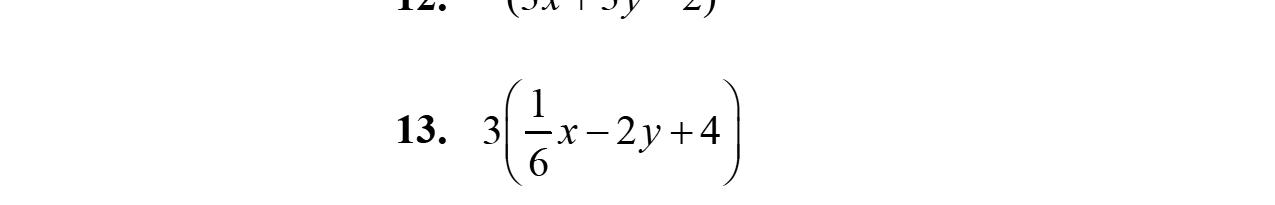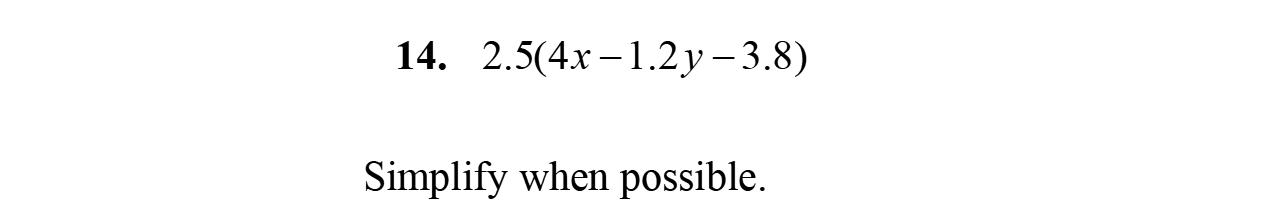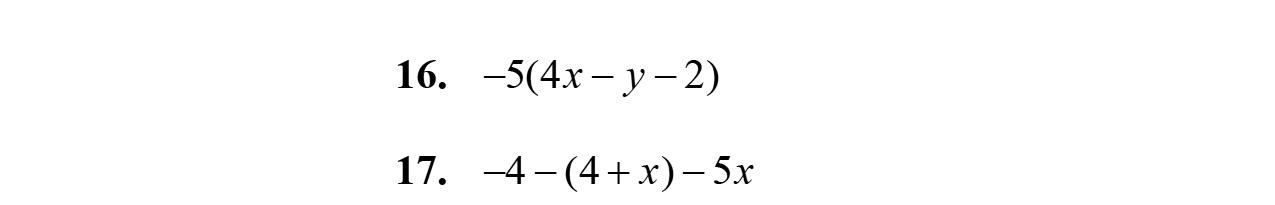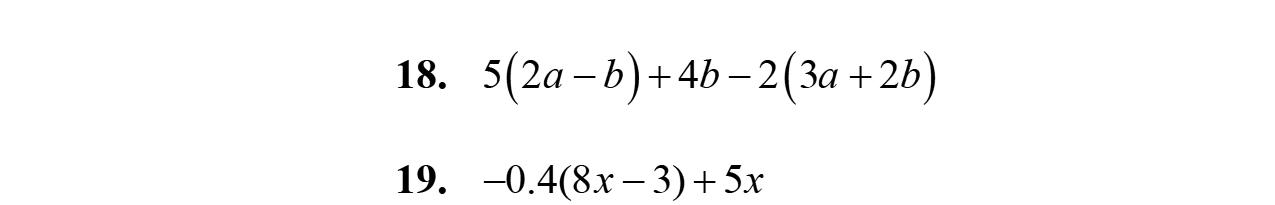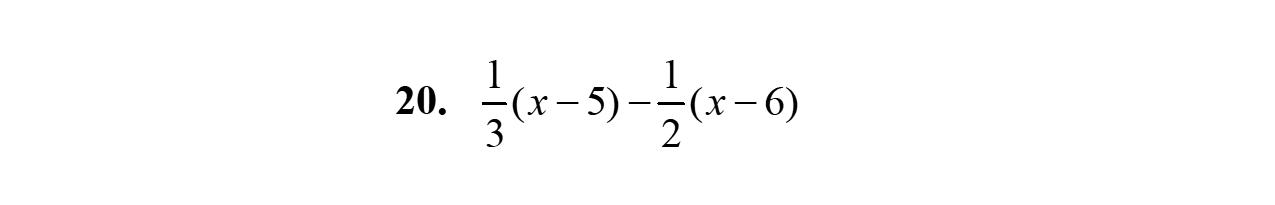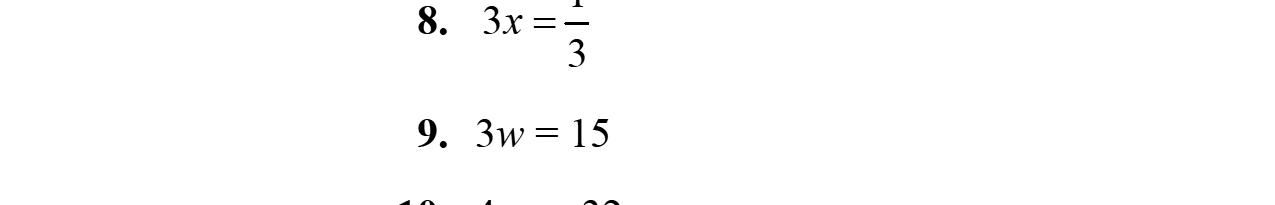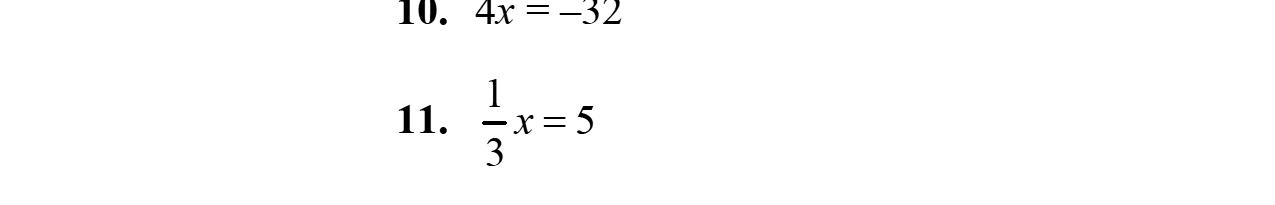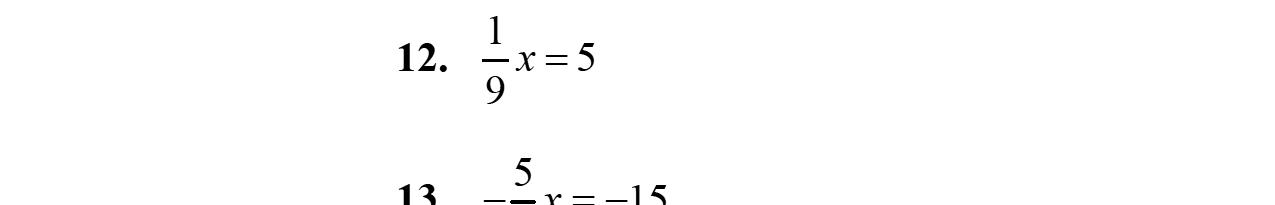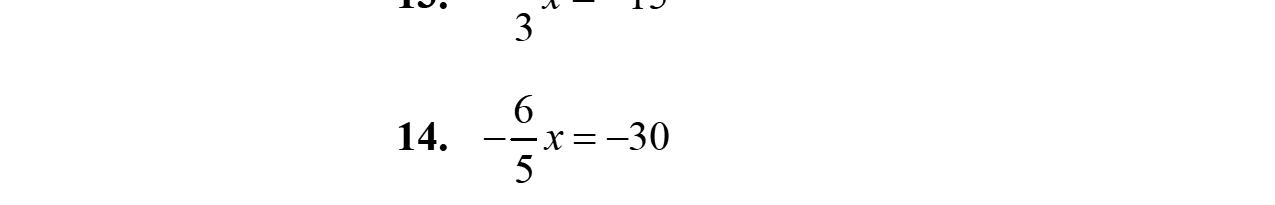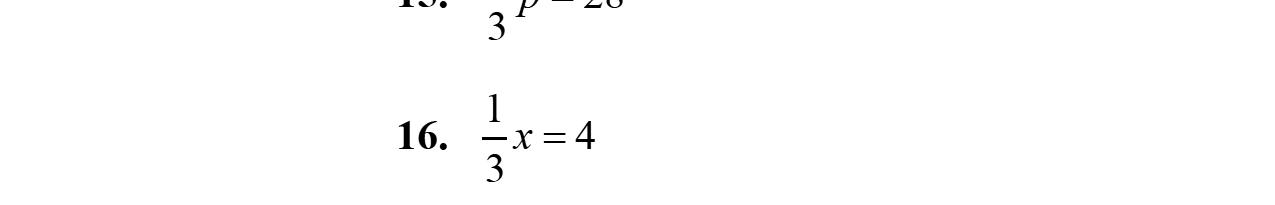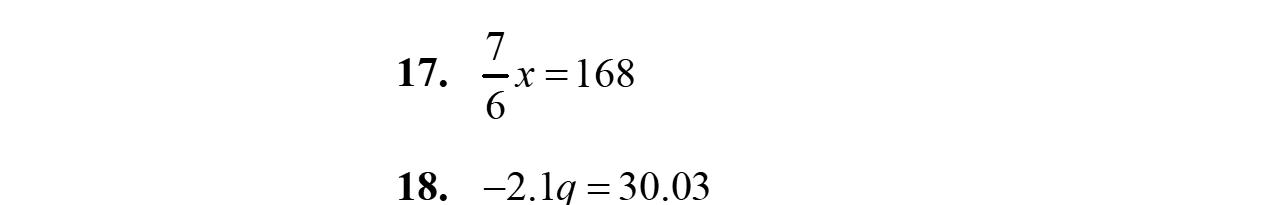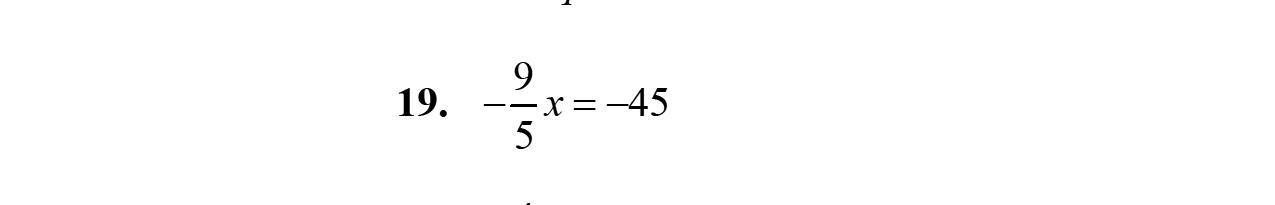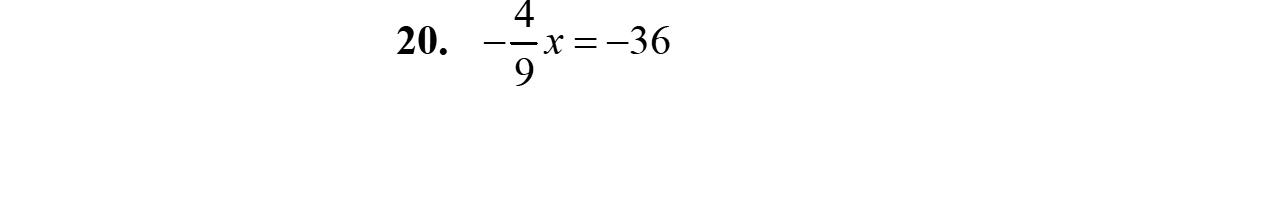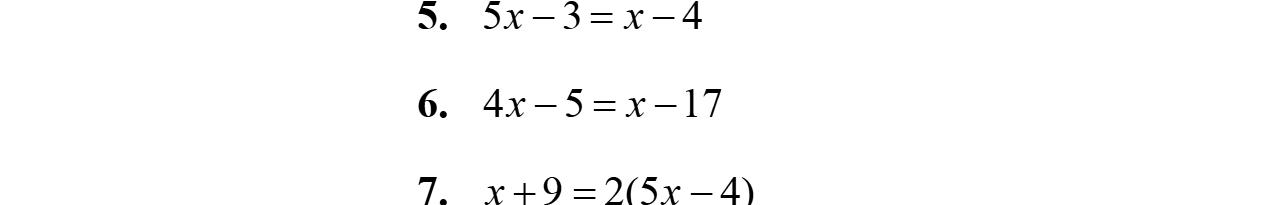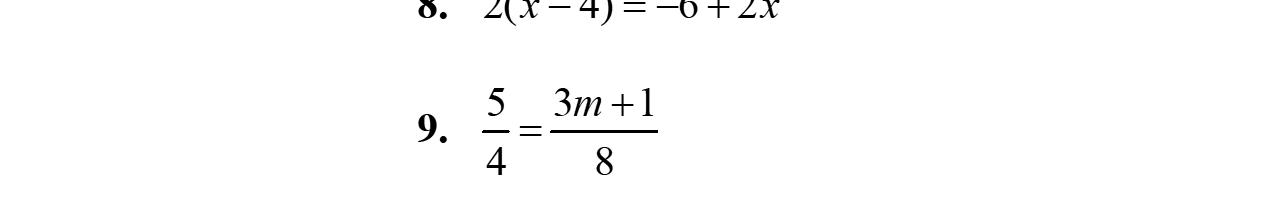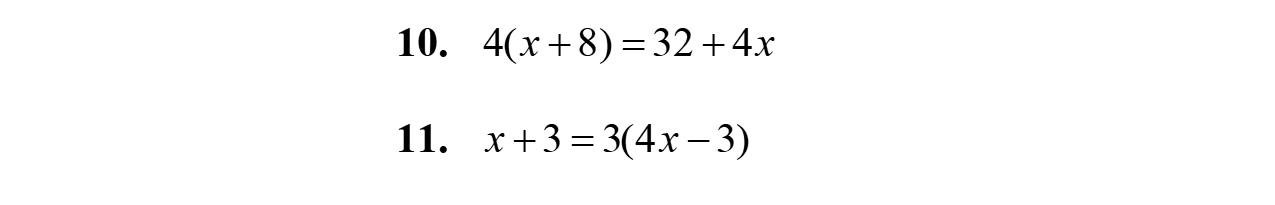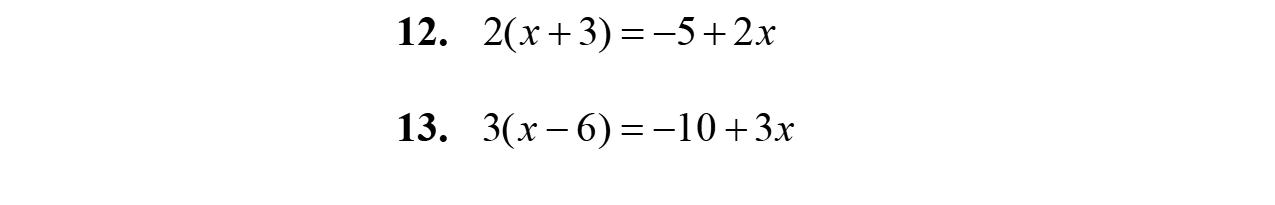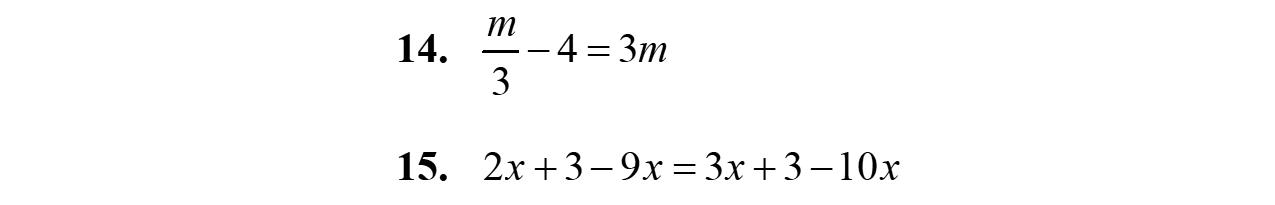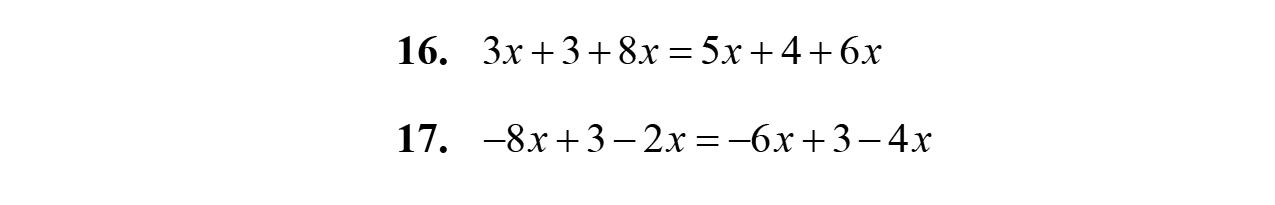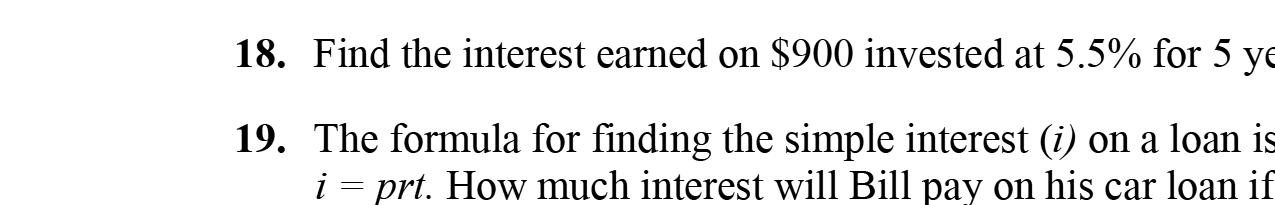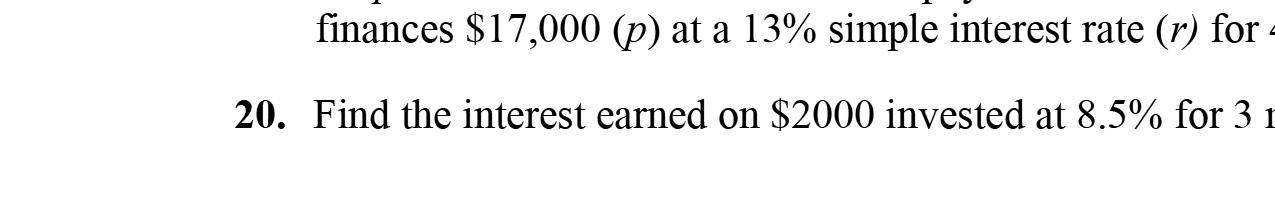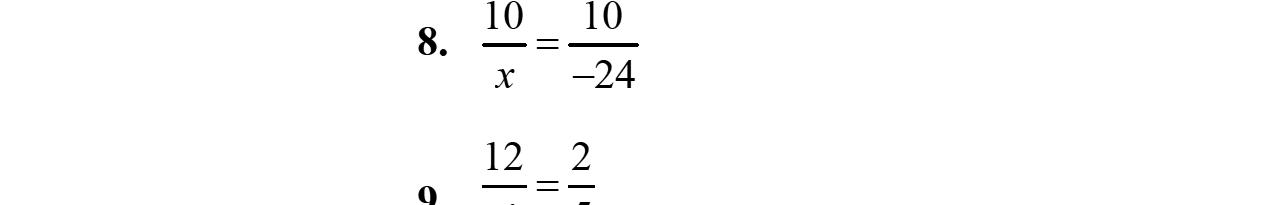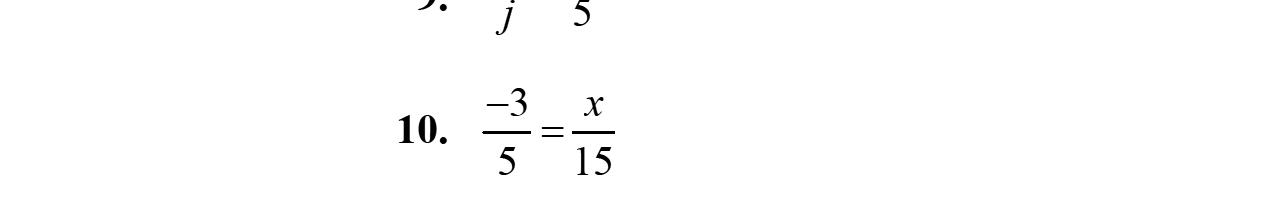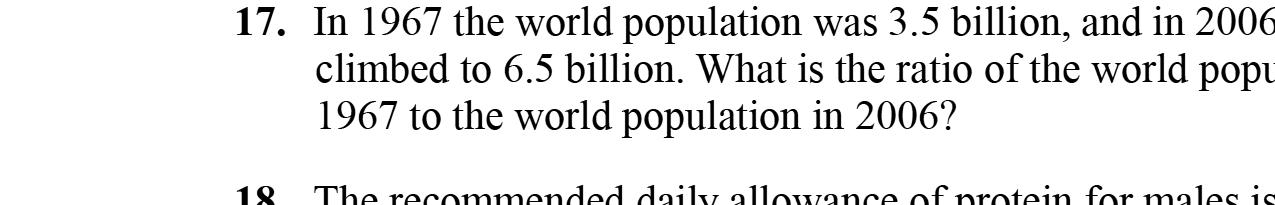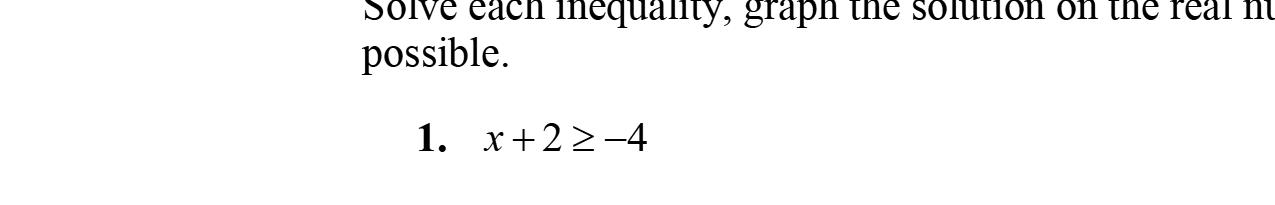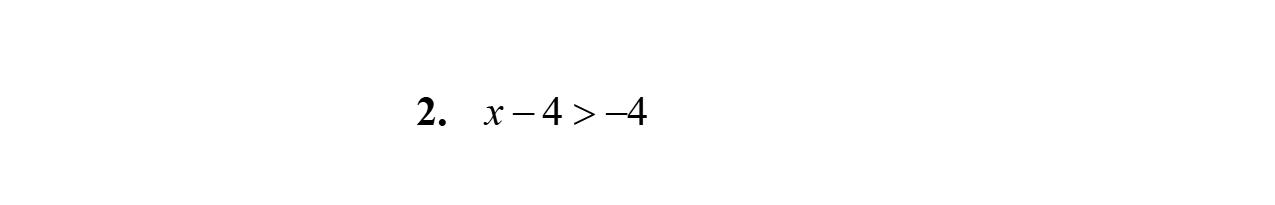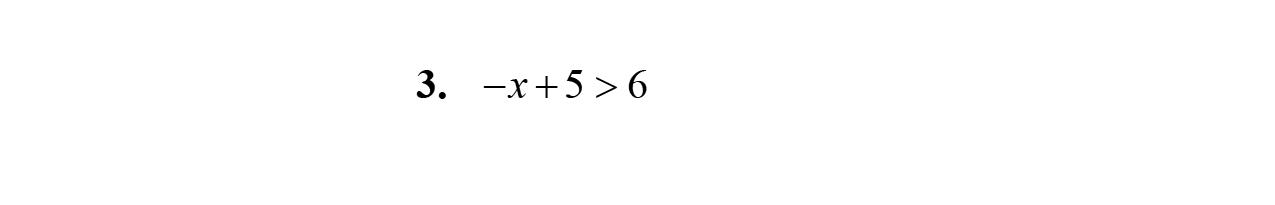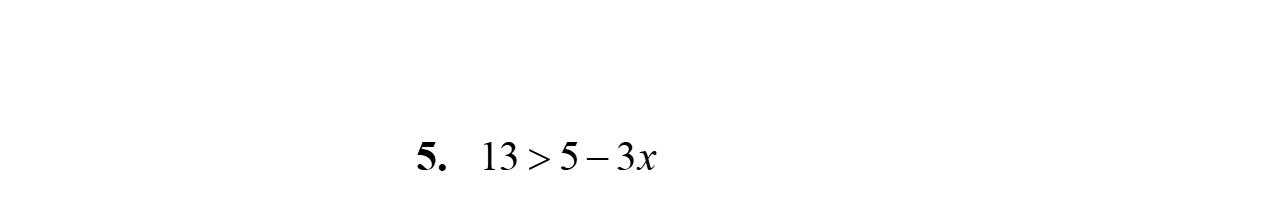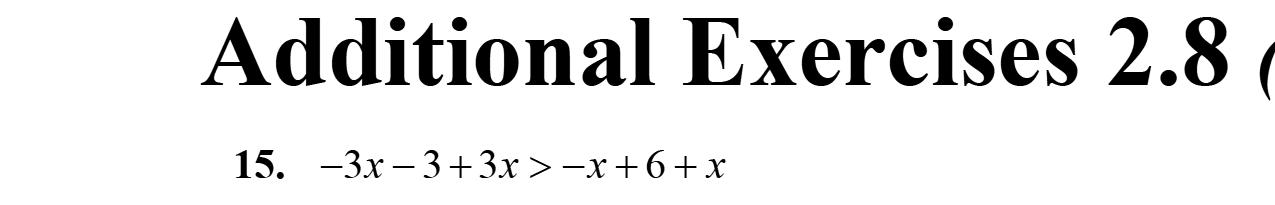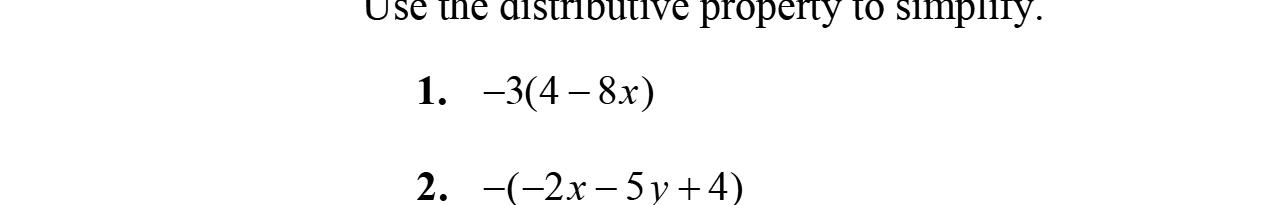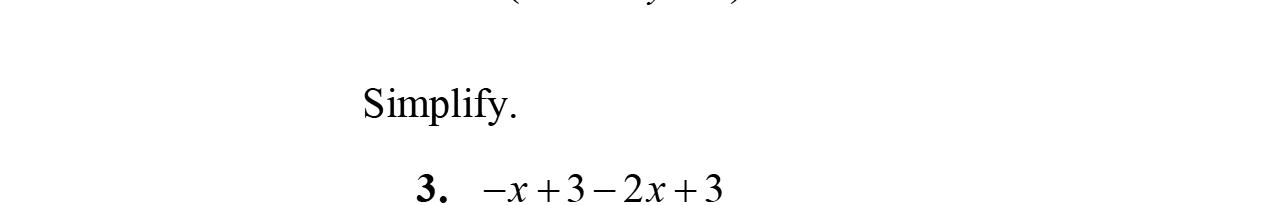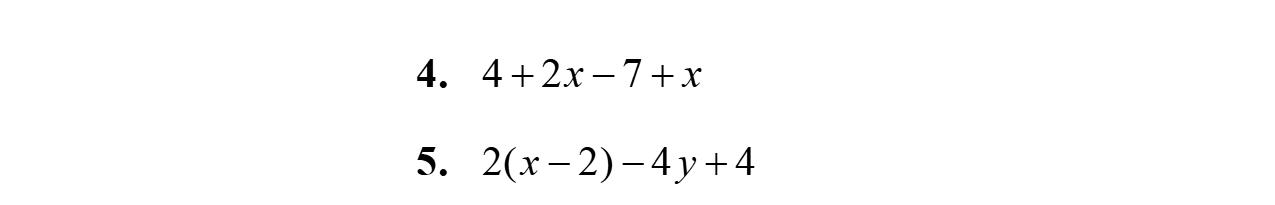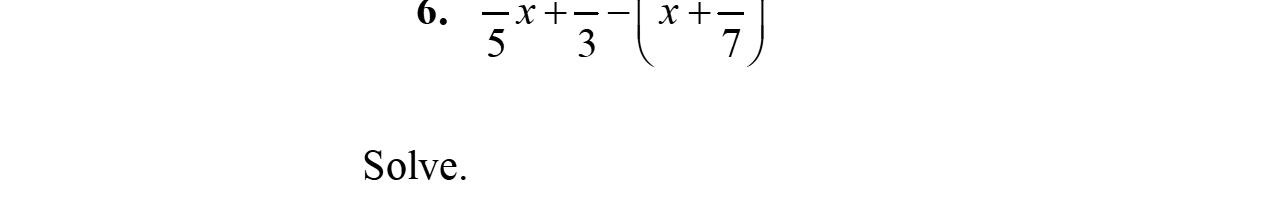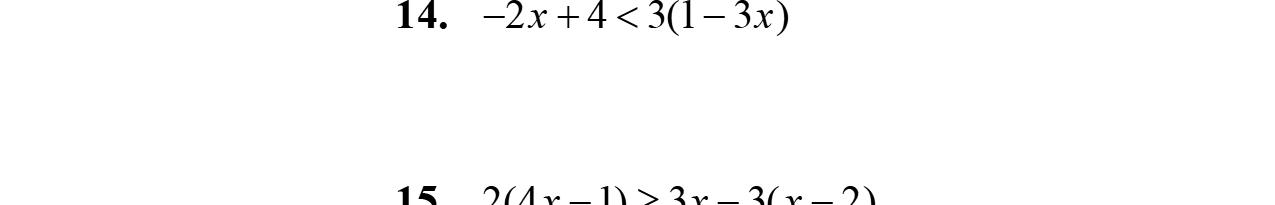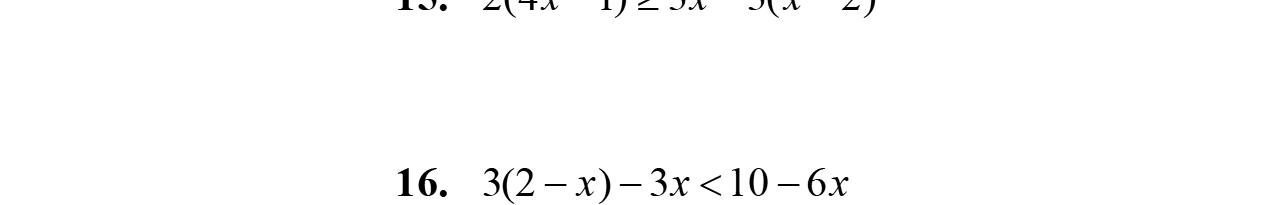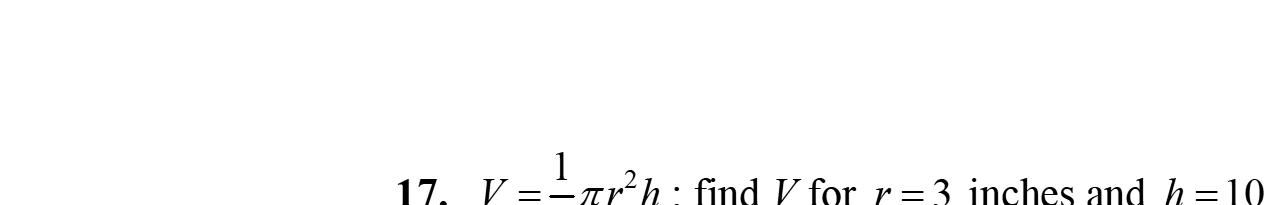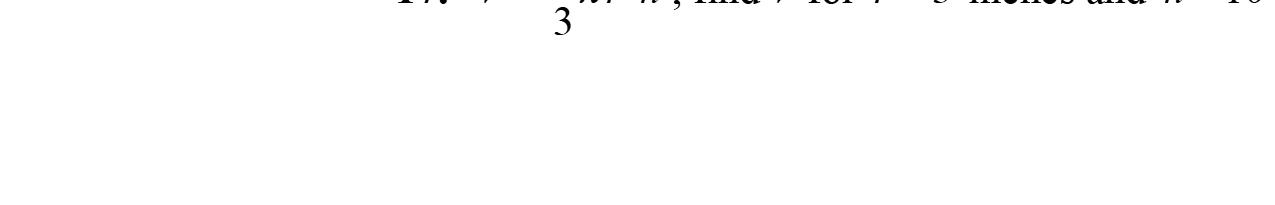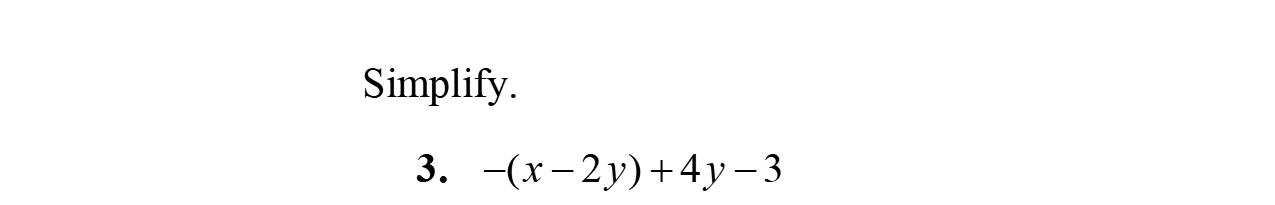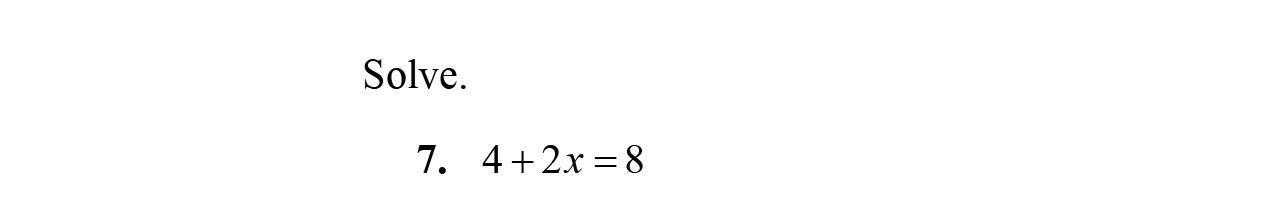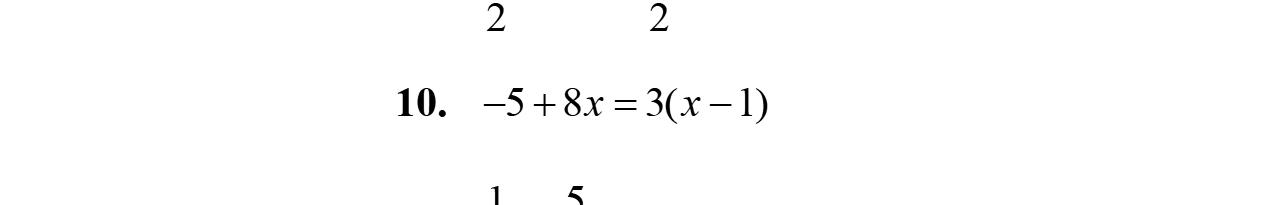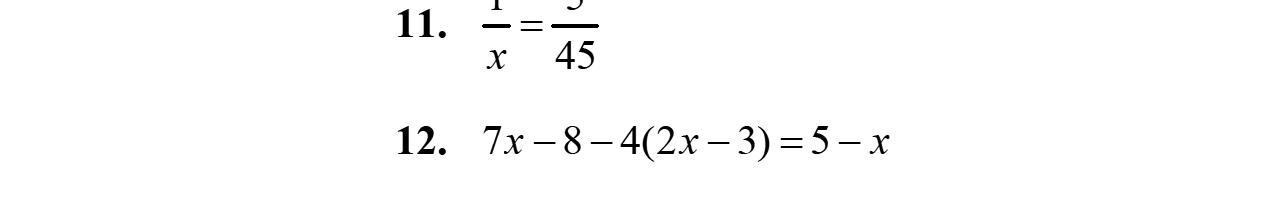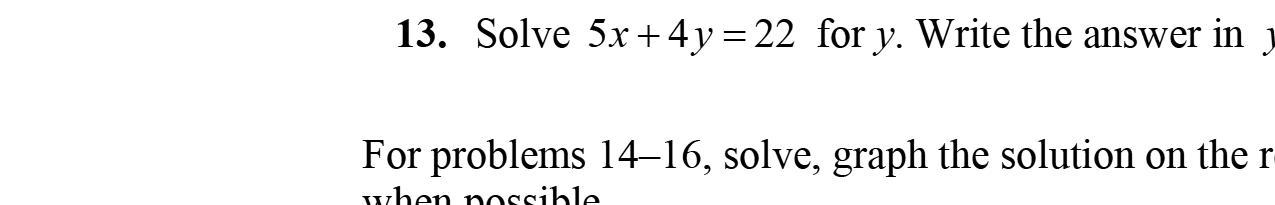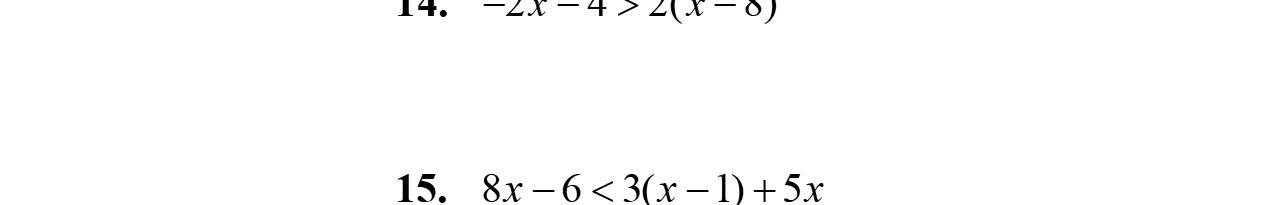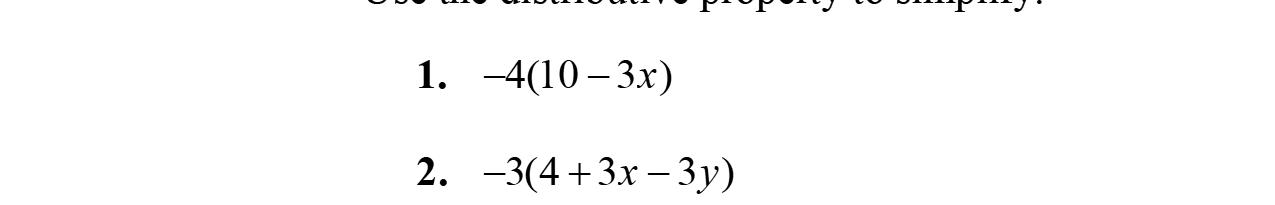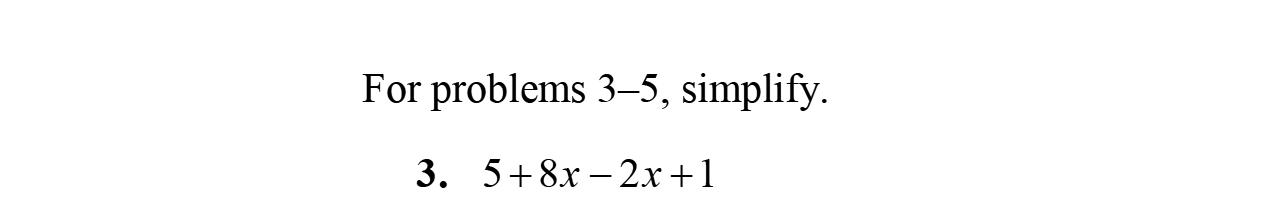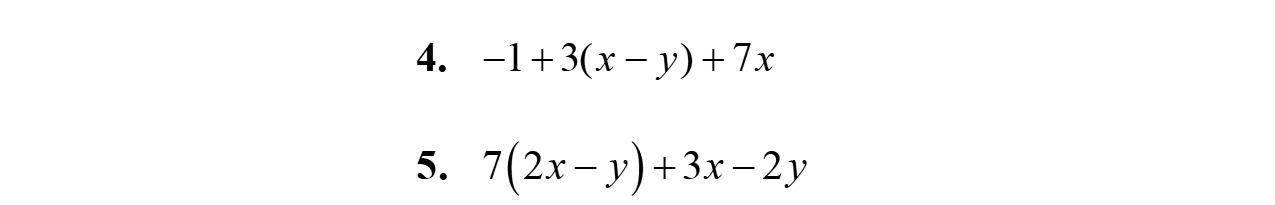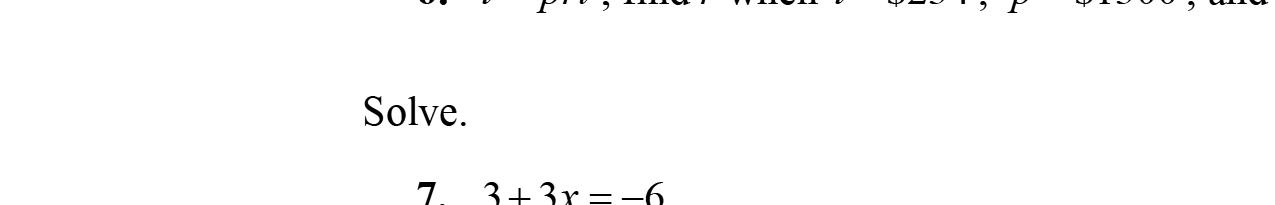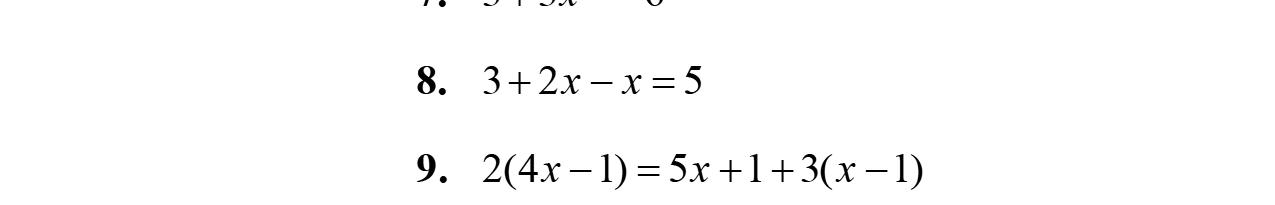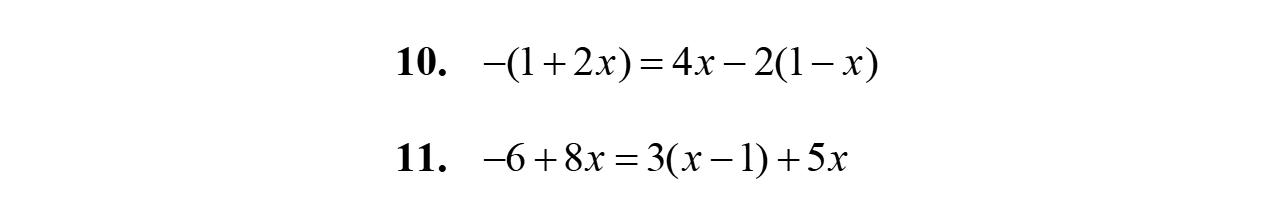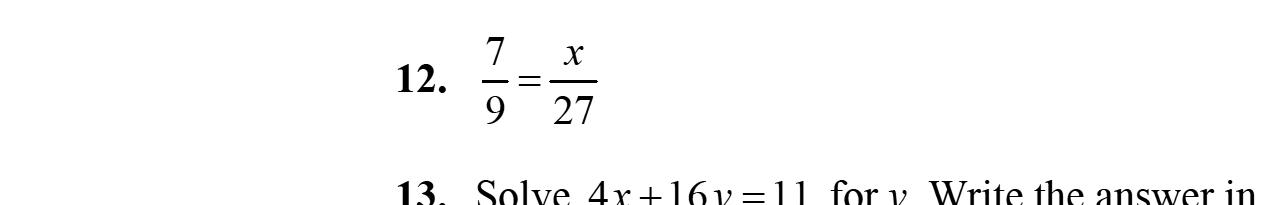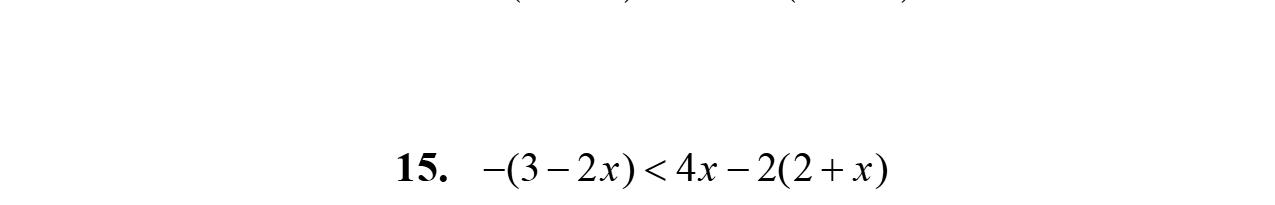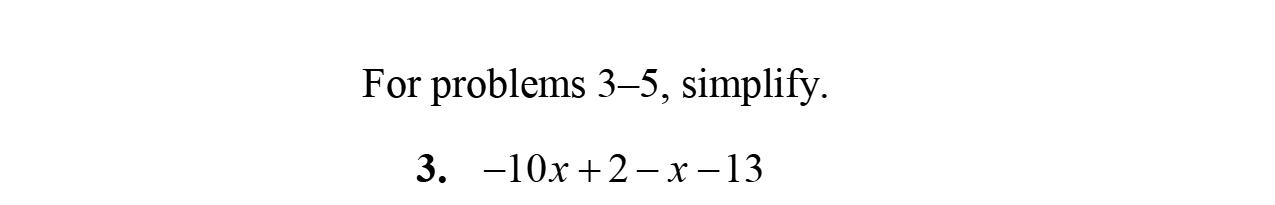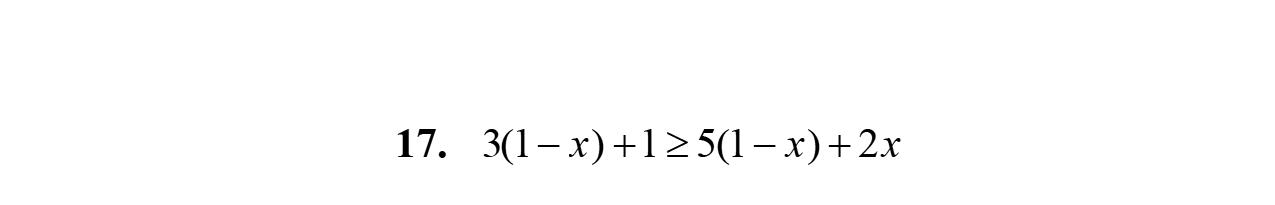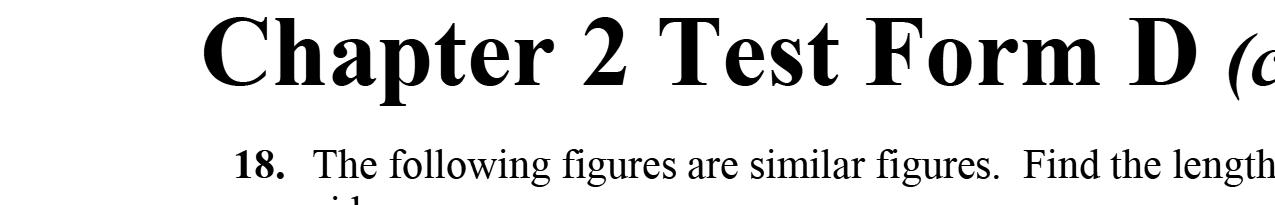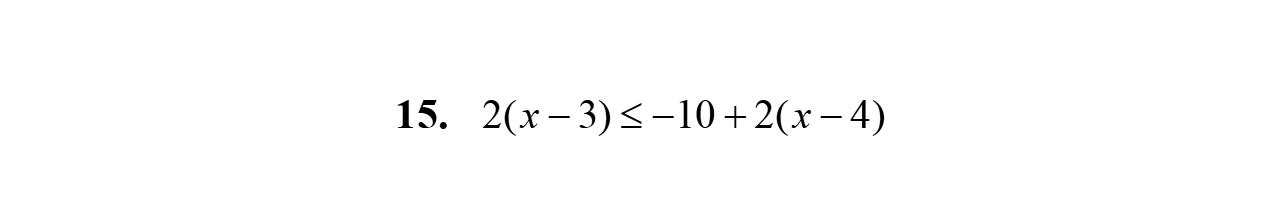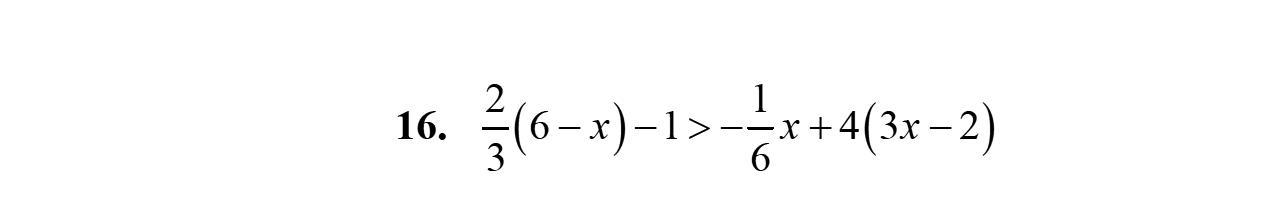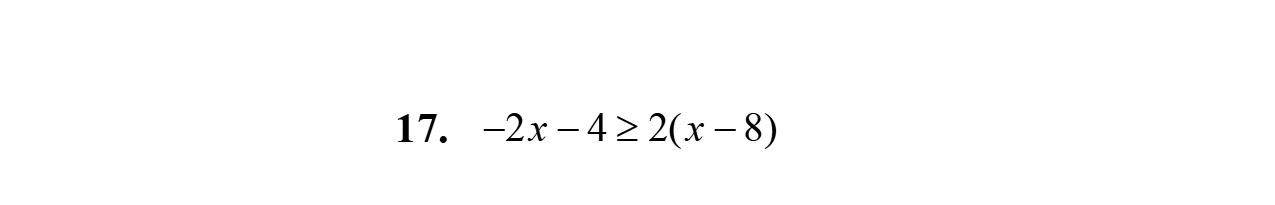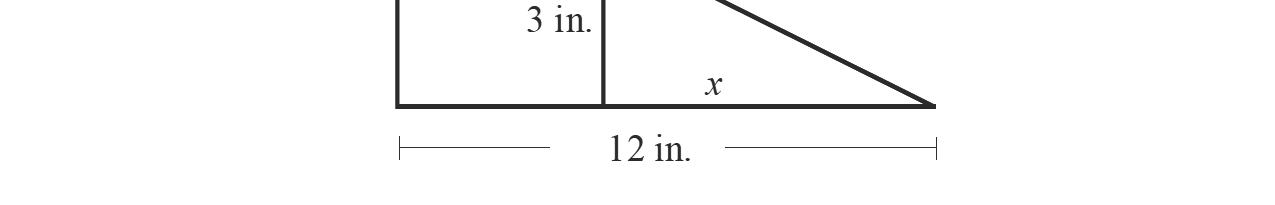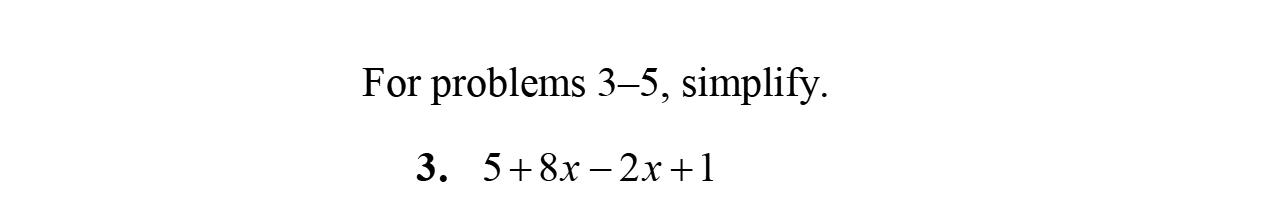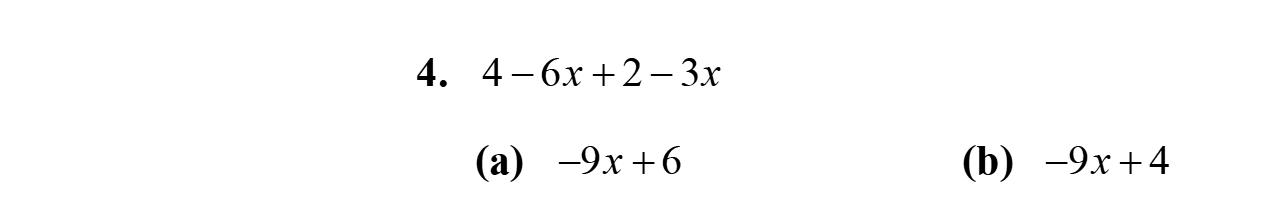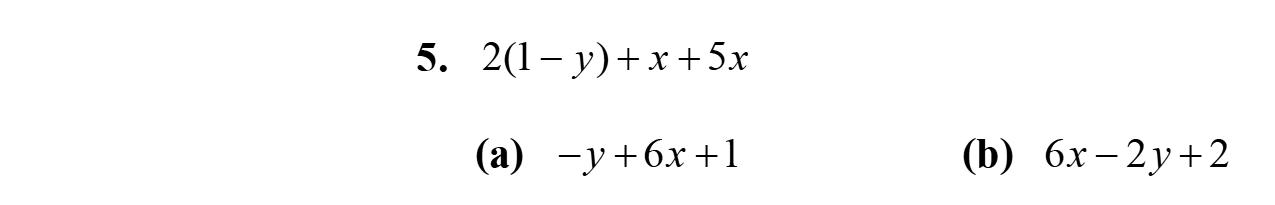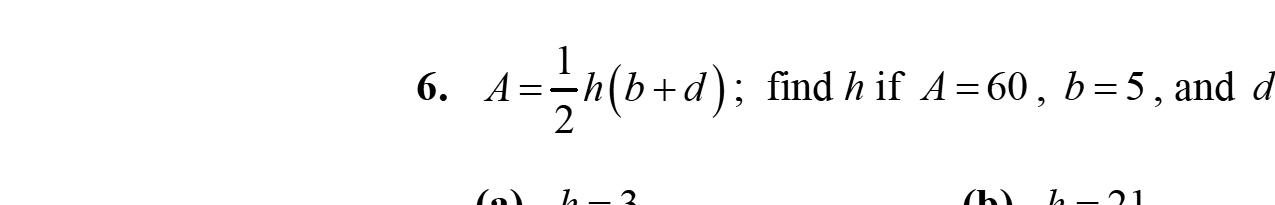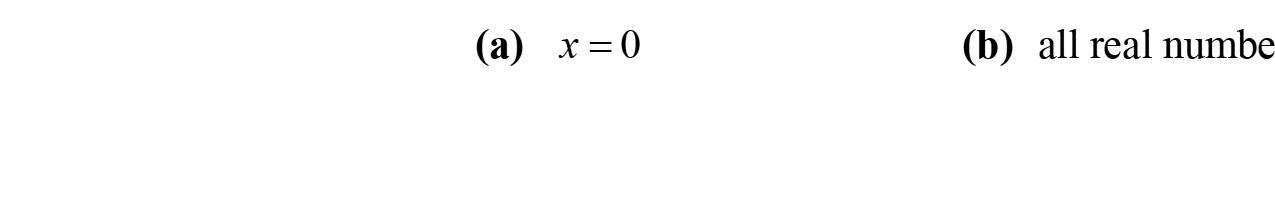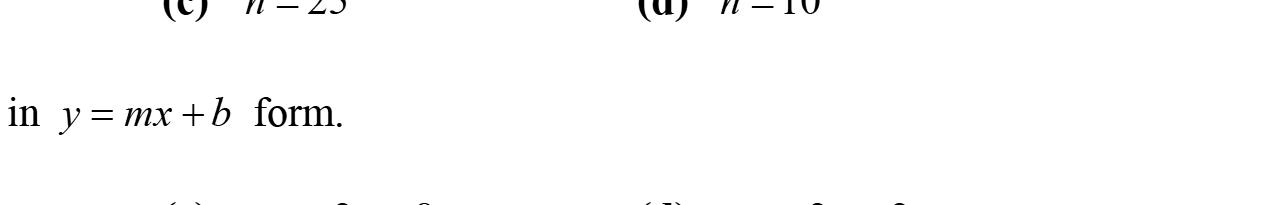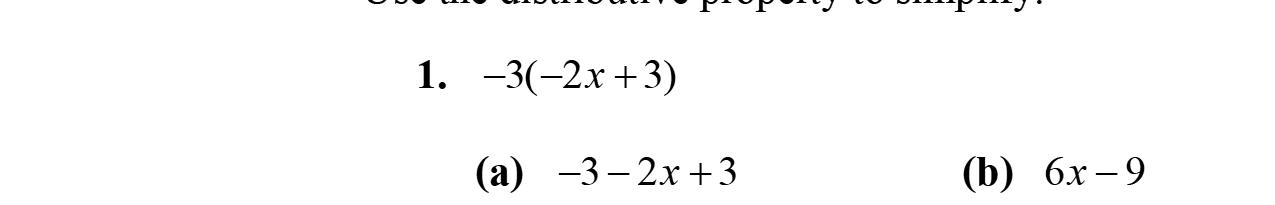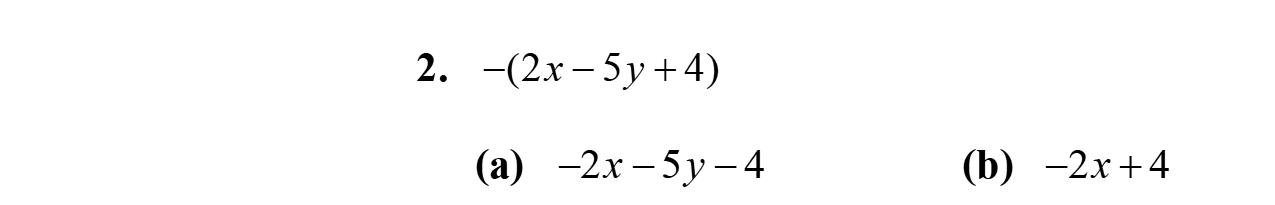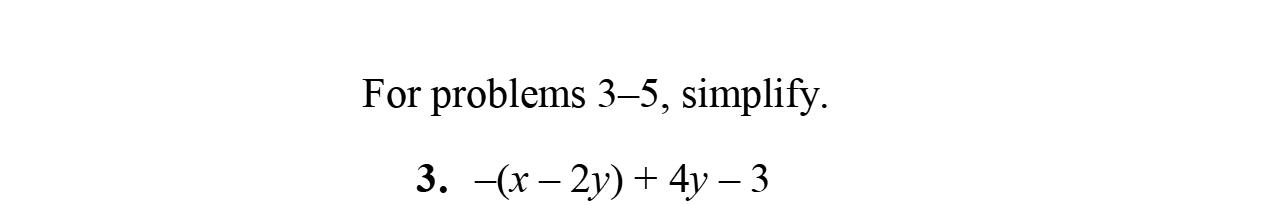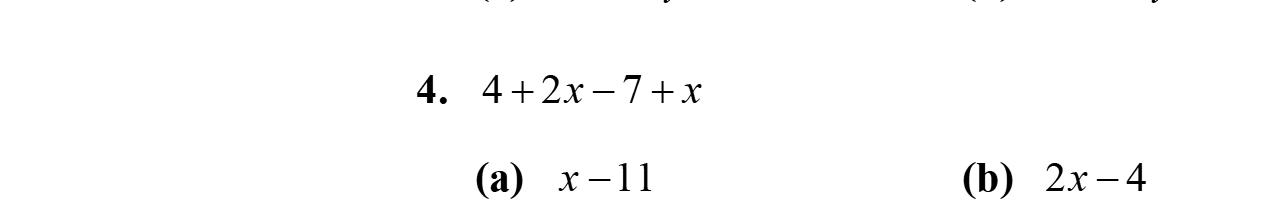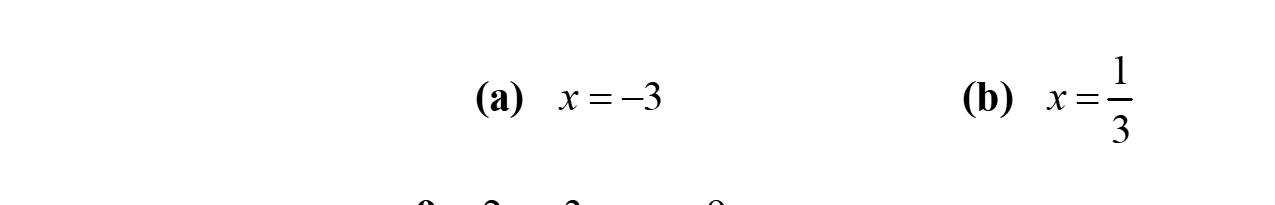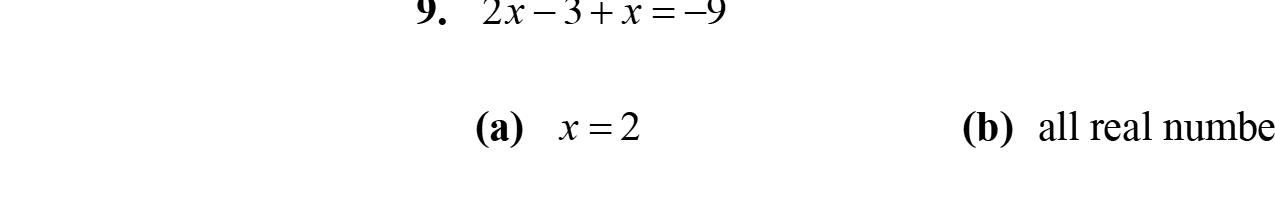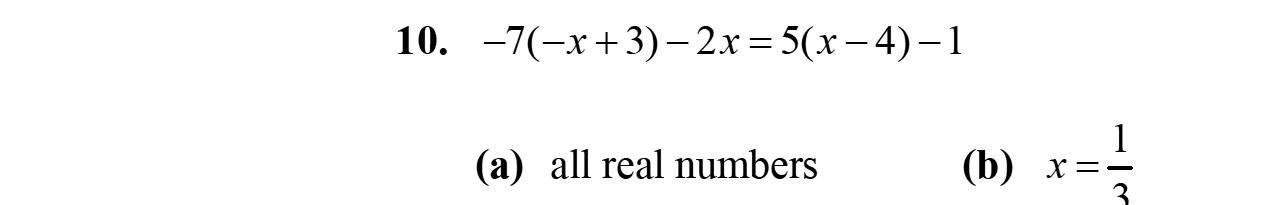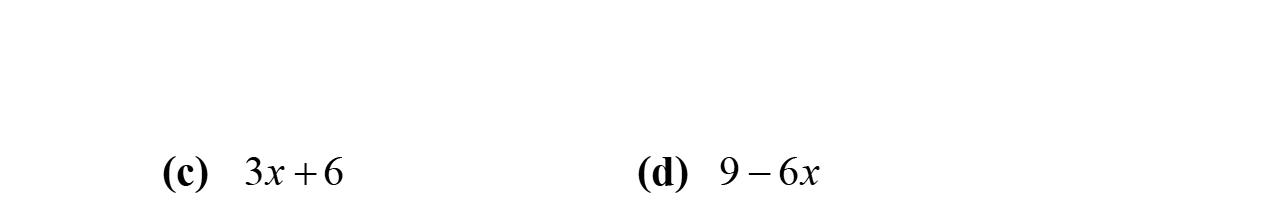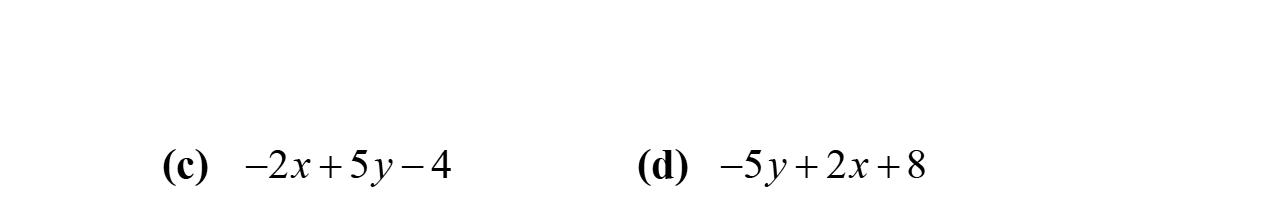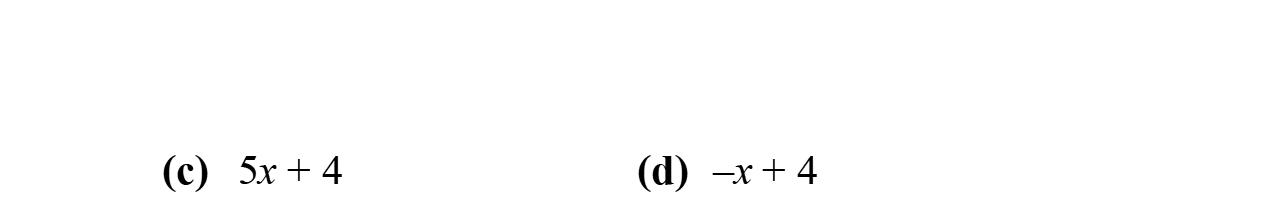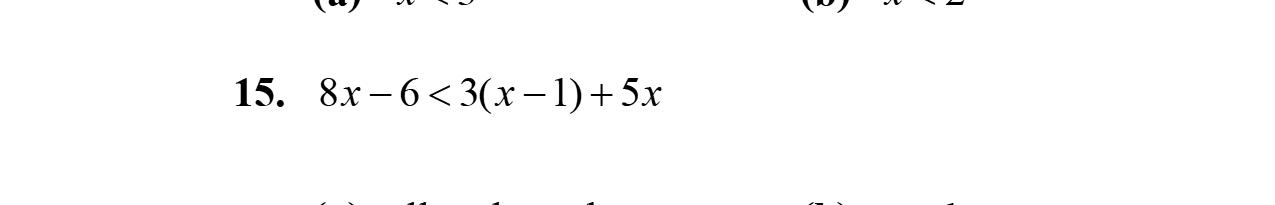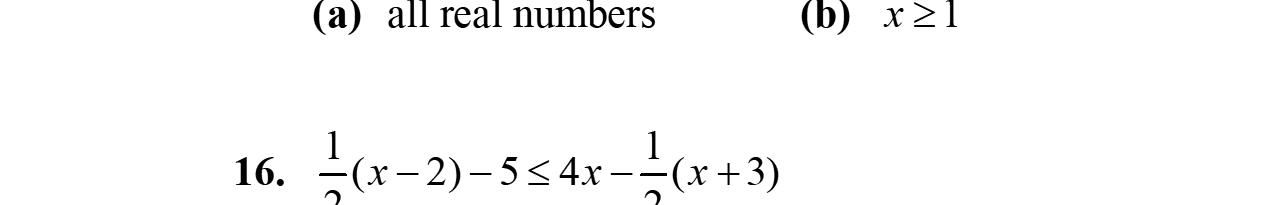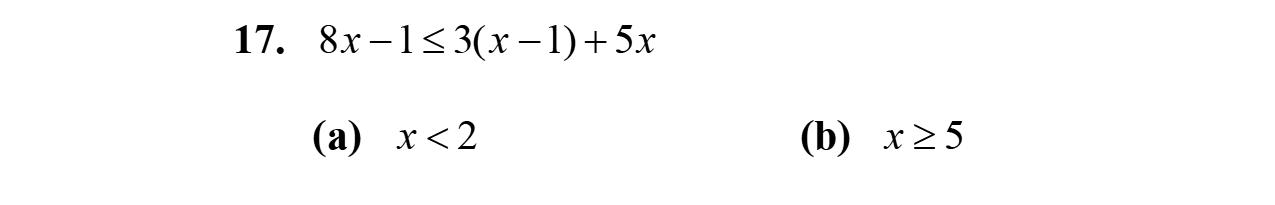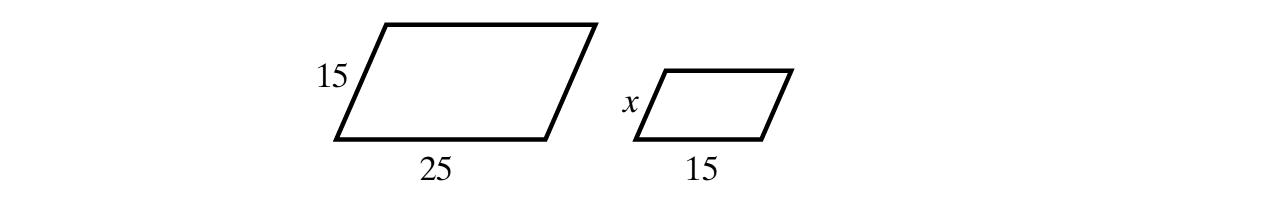Chapter 2
Exercise Set 2.1
1. Intheexpression5x –3y +17–2x,17iscalleda constantterm.
2. Whenweapplythedistributivepropertyto–2(2x –3y –9),weobtain–4x +6y +18.
3. Intheexpression5x –3y +17–2x,5x and–2x arecalledliketerms.
4. Intheexpression5x –3y +17–2x,–3iscalled thecoefficientofthesecondterm.
5. Intheexpression5x –3y +17–2x,5x and–3y arecalledunliketerms.
6. Intheexpression12x +17,12and x arefactorsof thefirstterm.
7. Intheexpression4x2+17x –90,theparts–4x2 , 17x,and–90arecalledterms.
8. Intheexpression17x, x iscalledavariable.
9. 3912 xxx
10. 5813 yyy
11. Therearenoliketerms. 36 x
12. Therearenoliketerms. 43xy
13. 3443 53 yyyy y
14. 47434 xxx
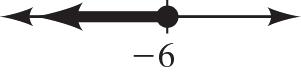
15. –2w –3w +5=–5w +5
16. 847127 yyy
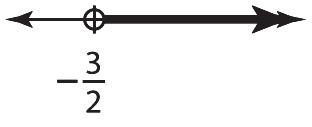
17. 35745 abaab
18. 54234 cdccd
19. 2222 2 xxxx x
20. 3431333413 9 aaaa
21. 3+6x –3–6x =6x –6x +3–3=0
22. 57755577 0 yyyy
23. 5241624516 221 tttt t
24. 71355713 46 dddd d
25. 4p –6–16p –2=4p –16p –6–2 =–12p –8
26. –6t +5+2t –9=–6t +2t +5–9 =–4t –4
27. –2x +4x –8=2x –8
28. 448448 34 xxxx x
29. 27522572 35 xyxyxxyy xy
30. 37943479 716 xxxx x
31. 222 2 xxyxy
32. 2222 2 163316 27 xxxx x
33. Therearenoliketerms.
32 523 www
34. Therearenoliketerms.
32 3772 mmm
35. 2222 2222 22 39752 37952 10107 xyxy xxyy xy
36. 22 22 2 46361 43661 775 xyxy xxyy xy
37. 22 2 43923249 3213 nnnn nn
38. 2222 2 513531 81 xxxxxx xx
Chapter 2: Solving Linear Equations and Inequalities
39. 363324 4114444 9 44
aaaa a
40. 32218 472828 13 28
bb
41. 3203 4 555 23 5
42. 33 22 44 34 2 44 7 2 4
43. Therearenoliketerms. 251 399 xy
44. Therearenoliketerms. 311 474 pq
45. 3737 3232 5454 1235 5 2020 23 5 20 xxxx
46. 131311 44 245425 352 4 41010 33 4 410 yxyxyy xyy
47. 5.16.424.35.14.36.42 0.86.42 nnnn n
48. 2.538.19.12.539.18.1 11.638.1 cccc c
49. 13.41.28.314.68.3 xxx
50. 22 43.15.248.3 xx
51. 19.3640.0212.2518.3 40.0218.319.3612.25 21.727.11 xx xx x
52. 3.413.011.0917.3 3.41.0913.0117.3 4.494.29 kk kk k
53. 332332 32 252522 72 zzzzzzzz zzz
54. 32233322 32 74255427 427 cccccccc cc
55. 22 2255235 xxxxx
56. x2–3xy –2xy +6= x2–5xy +6
57. 322 322 32 26231 26231 251 aaaaa aaaaa aaa 58 322 322 32 336224 332624 344 bbbbb bbbbb bbb
59. 52552 510 xx x
60. 54554 520 xx x
61. 3413431 123
62.
xx x
bb b b b
725725 7275 1435 1435
63. 2342324 68 cc c
64. 5925952 4510
dd d
vv v v v
65. 434434 4344 1216 1216
66.
825825 8285 1640 1640
67. 3273237 621
68. 9589598 4572
69.
532532 5352 1510
70.
867867 8687 4856
71.
2392329 618 618
5435453 2015 2015
467467 4647 2428
77.
1 11 pqpq pq pq
24–8124(–8) 12141–8 2–48 2–48 xyxy xy xy xy
32373[23(7)] 3(2)(3)3(3)7 6921 abab ab ab
2952595 1045 xyxy xy
8178717 567 bb b
3243(3)2(3)4 3(6)(12) 3612 xyxy xy xy
86. 4(238)4(2)(4)(3)(4)(8) 81232 mnmn mn
335335 38 tt t
93. 62496818 1418 xxxx x
32332
2232223
96.
653653
42334812312 831212 5 cccc cc
98. 53264515102430 15241030 3940 dddd dd d
99. 8383 73 xxxx x
100. 534534 354 49 xxxx xx x
101. (34)2342 342 46 ssss ss s
102. 622356465 4566 wwww ww w
103.
412344412324 44624 42464 22 xxxx xx xx x
104.
432546 43425546 1285206 1265208 6512 bcb bcb bcb bbc bc
105. 43412443412 412412 441212 0 mmmm mm mm
106. 323233(2)332 3636 3366 0 abababab abab aabb
107. 43454345 3445 35 xx x x
108. 2623266(2)3 26123 415 yyyy yy y
109.
110.
111.
112.
3224636286 32686 146 20 tttt tt t t
113. 3131 22 4343 31 2 43 381 443 51 43 xxxx xx xx x
114. 7171 33 8282 71 3 82 7241 882 311 82 xxxx xx x
41431 31 57577 28151 35357 431 357 xxxx xx x
117. 0.450.620.450.62 0.450.62 6 yy y y
1.0380.80.031.2 1.0380.80.031.2 0.81.21.0380.03 27 aa aa aa a
119.
0.2640.4 0.260.2440.4 1.20.241.6 0.241.21.6 0.242.8 xy xy xy xy xy
120. 1.054641.53.05 4.26.3612.2 4.266.312.2 4.265.9 xy xy xy xy
121. 111336 336 232233 13 2 22 13 2 22 1234 2222 37 22 xxxx xx xx xx x
122. 212414 24 323322 214 2 323 4346 6633 110 63 rrrr rr rr r
123. 23
Chapter 2: Solving Linear Equations and Inequalities
124. 24
125. 232 xyxyy xxyyy xy
126. 222 222 26 xy xy xy
127. 118,29,36 positivefactors:1,2,3,6,9,18
128. 124,212,38,46
positivefactors:1,2,3,4,6,8,12,24
129. a. Toremovetheparentheses,multiplytheterms insidetheparenthesesby–1.Thesignsofall termsinsidetheparentheseschangewhenthe parenthesesareremoved.
b. –(x –8)=–1(x)–1(–8)=–x +8
130. a. Liketermsaretermsthathavethesame variablewiththesameexponent.
b. 3x and4y arenotliketermsbecausethe variablesaredifferent.
c. 7and–2areliketermsbecausetheyareboth constants.
d. 5x2and5x arenotliketermsbecausethe variableshavedifferentexponents.
e. 4x and–5xy arenotliketermsbecausethe variablesaredifferent.
131.
234523 2342023
11 32126 43 11 32226 43 11 128 43 1281 4433 2118 4343 yy yy yy yy yy
32332 661212 129 612 y y
77
161616
137. 413(6)4136 176 11
138. Answerswillvary.Theanswershouldinclude thattheorderisparentheses,exponents, multiplicationanddivisionfromlefttoright,and additionandsubtractionfromlefttoright.
139. Substitute–1foreach x intheexpression.
22561516 156 66 12
Exercise Set 2.2
1. Tosolvetheequation6= x –2,firstadd2toboth sidesoftheequation.
2. Numbers,whichwhensubstitutedforthevariable, maketheequationatruestatement,arecalled solutions.
3. Thestrategyforsolvingalinearequationinone variableincludesaprocesstoisolatethevariable.
4. Thesymbol ? isusedwhencheckingthesolution inthegivenequation.
5. Theequation x –3=–19isanexampleofalinear equationinthevariable x.
6. Twoequationswiththesamesolutionsarecalled equivalentequations.
7. Astatementofequalitybetweentwoexpressions, like x +7=19,iscalledanequation.
8. Tosolvetheequation x –6=–2,firstadd6to bothsidesoftheequation.
9. Whensolvingtheequation x + a = b,theopposite of a isaddedtobothsides.
10. (TrueorFalse)Theequations x +19=–14and x +60=27areequivalentequations.True
11. Substitute2for x =2.
435 4235 835 55True x
Sinceweobtaintruestatement,2isasolution.
12. Substitute5for x,5 x .
x
61713 651713 301713 1313True
Sinceweobtainatruestatement,5isasolution.
13. Substitute–3for x, x =–3.
2552 235532 6551 115False
Sinceweobtainafalsestatement,–3isnota solution.
14. Substitute–7for q,7 q
31175 3711775 318495 54495 55False
Sinceweobtainafalsestatement,–7isnota solution.
15. Substitute–15for p, p =–15.
25710 215515710 305810 304010 1010True pp
Sinceweobtainatruestatement,–15isa solution.
16. Substitute–2for k, k =–2.
5618 526218 10638 10188 88True kk
Sinceweobtainatruestatement,–2isasolution.
17. Substitute3for m,3 m .
347535 33473535 377235 211435 3535False
mm
Sinceweobtainafalsestatement,3isnota solution.
18. Substitute4for n,4 n .
8163424 841634424 83612424 246824 244824 2424False
nn
Sinceweobtainafalsestatement,4isnota solution.
19. Substitute1 2 for x, 1 2 x . 4422 11 4422 22 2412 21False xx
Sinceweobtainafalsestatement,1 2 isnota solution.
Chapter 2: Solving Linear Equations and Inequalities
20. Substitute 2 3 for x, 2 3 x . 61125 22 61125 33 1224 15 33 4185
Sinceweobtainatruestatement, 2 3 isasolution.
21. Substitute3.4for x, x =3.4.
Sinceweobtainatruestatement,3.4isasolution.
22. Substitute5.5for x,5.5 x
35.5355.5418 38.551.518 25.57.518 1818True
Sinceweobtainatruestatement,5.5isasolution.
23. x +2=7 2272 05 5 x x x
Check:27 527 77True x
24. x +6=14 66146 08 8 x x x
Check:614 8614 1414True x
25. –6= x +1 x +1=–6 1161 07 7 x x x
Check:16 716 66True x
26. –5= x +4 x +4=–5 4454 09 9 x x x
Check:45 945 55True x
27. 48 x 4484 04 4 x x x
Check:48 448 88True x
28. p –5=–12 55125 07 7 p p p
Check:512 7512 1212True p
29. t +9=52 99529 043 43 t t t
Check:952 43952 5252True
ISM: Elementary Algebra
30. x +8=17 817 88178 09 9 x x x x
Check:817 9817 1717True x
31. –6+ w =9 6696 015 15 w w w
Check:69 6159 99True w
32. –10+ n =5 1010510 015 15 n n n
Check:1015 10155 55True n
33. 27= x +16 27161616 110 11 x x x
Check:2716 271116 2727True x
34. 50= x –35 50353535 850 85 x x x
Check:5035 508535 5050True x
35. 1814 x 18141414 40 4 x x x
Check:1814 18414 1818True x
2: Solving Linear Equations and Inequalities
36. –4= w +5 4555 90 9 w w w
Check:45 495 44True w
37. 94 x 9949 05 5 x x x
Check:94 9(5)4 44True x
38. 12+ w =9 1212912 03 3 w w w
Check:129 1239 99True w
39. 4+ x =–8 4484 012 12 x x x
Check:48 4128 88True x
40. 7+ z =–3 7737 010 10 z z z
Check:73 7103 33True z
41. 7+ r =–23 723 77237 030 30 r r r r
Check:723 7(30)23 2323True r
Chapter 2: Solving Linear Equations and Inequalities
42. 7+ v =–7 7777 014 14 v v v
Check:77 7147 77True v
43. 8=8+ v 8888 00 0 v v v
Check:88 880 88True v
44. –5=–5+ m 5555 00 0 m m m
Check:55 550 55True m
45. 750 x 77507 057 57 x x x
Check:750 75750 5050True x
46. –5+ c =–23 55235 018 18 c c c
Check:523 51823 2323True
47. 1216 x 12161616 40 4 x x x
Check:1216 12164 1212True x
48. 62= z –15 62151515 770 77 z z z
Check:6215 627715 6262True z
49. 15+ y =–50 15155015 065 65 y y y
Check:1550 156550 5050True y
50. 204 x 20444 240 24 x x x
Check:204 20424 2020True x
51. 1515 x 15151515 00 0 x x x
Check:1515 15015 1515True x
52. 77 x 7777 00 0 x x x Check:77 707 77True x
53. 512 x 5121212 170 17 x x x Check:512 51712 55True x
54. 8= x –9 8999 170 17 x x x
55. 5024 x 50242424 260 26 x x x
Check:5024 502624 5050True x
56. 3712 x 37121212 250 25 x x x
57. 43=15+ p 43151515 280 28 p p p
Check:4315 431528 4343True p
58. 2574 x 25747474 990 99 x x x
Check:2574 257499 2525True x
a a
59. 71 88 a 7717 8888 6 0 8 3 4
Check:71 88 371 488 671 888 11 True 88
60. 51 66 b 5515 6666 4 0 6 2 3
b b b
Check:51 66 251 366 451 666 11 True 66
Chapter 2: Solving Linear Equations and Inequalities
61. 15 96 c 1151 9969 152 0 1818 17 18
64. 3.4111 t 3.413.41113.41 07.59 7.59 t t t
65. –5.9= x +4.01 –5.94.014.014. 9.910 01 9.91 x x x
Check:5.94.01 5.99.914.01 5.95.9True x
66. –13.7= x +7.28 13.77.287.287.28 20.980 20.98 x x x
Check:13.77.28 13.720.987.28 13.713.7True x
67. No;therearenorealnumbersthatcan make12 xx
68. Yes;infinitenumber;theequation44 xx is truenomatterwhatrealnumberissubstitutedfor x
69. Toisolatethevariable,usepropertiesthatallow ustogetthevariablebyitselfononesideofthe equation.
Forexample,intheequation x +8=–12,you wouldsubtract8frombothsidessothatthe variable x remainsontheleftbyitself.
70. Allthreeequationshavethesamesolution,where x =1.
71. x x
72.
73.
74.
75. a. yes b. yes c. yes d. yes e. Sincetheleftsideoftheequationisequalto therightsideoftheequation,2x +6=2x +6, thesolutionisallrealnumbers.
76. 751425142511 15630303030
77.
229 11322931 12824242424
4325743657 43567
Exercise Set 2.3
1. Theexpression1 3 x canberewrittenas 3 x
2. Tosolvetheequation3x =5,multiplybothsides oftheequationby1 3
3. Tosolvetheequation7 3 x ,wemultiplyboth sidesoftheequationby3.
4. Thestrategyforsolvingalinearequationinone variableincludesaprocesstoisolatethevariable.
5. Thesymbol ? isusedwhencheckingthesolution inthegivenequation.
6. Anothernameforthereciprocalofanumberis themultiplicativeinverse.
7. Thereciprocalof7 x is7 x .
8. Twonumbersequaltotheirownreciprocalare1 and–1.
9. 520 520 55 4 x x x
Check:520 5420 2020True x
10. 550 550 55 10 x x x
Check:550 51050 5050True x 11. 412 412 44 3 x x x
Check:412 4312 1212True x
65. a. In5+ x =10,5isaddedtothevariable, whereasin5x =10,5ismultipliedbythe variable.
66. a. In3+ x =6,3isaddedtothevariable,whereas in3x =6,3ismultipliedbythevariable.
Elementary Algebra
67. Multiplyingby32iseasierbecausetheequation involvesfractions.
68. Multiplyingby1 4 is easierbecausetheequationinvolvesafraction.
69. Multiplyingby73iseasierbecausetheequation involvesfractions.
70.
b. Dividebothsidesoftheequationby
c.
71.
b. Dividebothsidesoftheequationby
c.
b. Multiplybothsidesoftheequationby
75. 23 42636168636 164836 16166 06 6
76. Associativepropertyofaddition
Exercise Set 2.4
1. Themultiplicationpropertyofequalityallowsus tomultiplyordividebothsidesofanequationby thesamenonzeronumber.
2. Theadditionpropertyofequalityallowsustoadd orsubtractthesamenumberfrombothsidesofan equation.
3. Intheequation0.51.21.8 x wecaneliminate thedecimalnumbersbymultiplyingbothsidesof theequationby10.
4. Intheequation0.02175335.25 x wecan eliminatethedecimalnumbersbymultiplying bothsidesoftheequationby100.
5. Wecaneliminatefractionsfromanequationby multiplying both sidesoftheequationbytheleast commondenomination(LCD)ofthefractions withintheequation.
6. Intheequation255 386 x wecaneliminatethe decimalnumbersbymultiplyingbothsidesofthe equationby24.
7. 3612
2921
5619
578
5210
y y y y y
14. 359 35595 314 314 33 14 3
15. 5919 599199 510 510 55 2 k k k k k
16. 7620 766206 714 714 77 2
z z z z z
17. 125 1212512 7 (1)()(1)(7) 7 x x x x x
18.
138 1313813 21 1121 21 x x x x x
19. 8319 883198 311 311 33 11 3 x x x x x
ISM: Elementary Algebra
20. 5818 558185 813 813 88 13 8 x x x x x
21. 16514 1655145 1619 1619 1616 19 16 x x x x x
x x x x x
22. 13827 1388278 1319 1319 1313 19 13
23. 959 99599 50 50 55 0 x x x x
24. 241624 2424162424 160 160 1616 0 x x x x x
25. 7162 71616216 714 714 77 2 r r r r r
26. 248 24484 212 212 22 6 w w w w w
27. 6059 609599 515 515 55 51 5 s s s s s
28. 4568 458688 536 536 66 53 6 v v v v v
29. 14583 14538 1428 148288 62 62 22 3 xx xx x x x x x
30. 15633 15633 1593 153933 189 189 99 2 xx xx x x x x x
31. 2.39.346.3 2.39.349.346.39.34 2.315.64 2.315.64 2.32.3 6.8 x x x x x
Chapter 2: Solving Linear Equations and Inequalities
32. 1.51.053.9 1.51.051.053.91.05 1.54.95 1.54.95 1.51.5 3.3 q q q q q
33. 0.0716.05
1.0716.05 1.0716.05 1.071.07 15
34. 0.0817.28 1.0817.28 1.0817.28 1.081.08 16 xx x x x
38.
1 23 5 1 525(3) 5 215 22152 17 x x x x x
39. 3 9 7 3 77(9) 7 363 33633 60 d d d d d
35. 0.912.250.015.85
0.910.012.255.85
0.902.255.85
0.902.252.255.852.25
0.903.60 0.903.60 0.900.90 4 yy yy y y y y y
36. 0.150.051.350.20
40. 6 2 5 6 55(2) 5 610 66106 16 m m m m m
0.150.050.201.35
0.150.151.35
0.151.350.151.351.35
1.500.15
1.500.15
0.150.15 10 xx xx x x x x x
1 64 7 1 7674 7 628 66286 22 x x x x x
1 77 3 1 373(7) 3 721 77217 14 t t t t t
1 97 5 5195(7) 15 935 99359 26
3 512 4 434 512 343 516 55165 11 x x x x x
44.
47. 42 77 42 77 77 42 4424 2 x x x x x
51.
554 62 t 554 66 62 53(54) 51512 512151212 1715 1715 1515 17 15 t t t t t t t
7(1)14 7114 77 1121 3
x x x x 52. 3(2)12 3612 366126 318 318 33 6 x x x x x x
53. 2(3)26 2626 266266 220 220 22 10 x x x x x x
60. 2(8)51 21651 2211 22121121 222 222 22 11 x x x x x x x
qq qq q q q q
61. 25(7)13 253513 735351335 722 722 77 22 7
62. 34211 34811 7811 788118 719 719 77 19 7 rr rr r r r r r
63. 53479 479 47797 416 416 44 4 xxx x x x x x
64. 7421126 51126 511112611 515 515 55 3 xxx x x x x x
65. 0.7(3)1.4
0.72.11.4
0.72.12.11.42.1
0.73.5 0.73.5 0.70.7 5 x x x x x x
66.
0.596.5 0.596.5 0.50.5 913 99139 4 x x x x x
68. 0.15(61)4.8
0.90.154.8
0.90.150.154.80.15
69. 32(3)21 32621 23621 211 21111 22 22 22 1 x x x x x x x x
70. 734536 7312536 3712536 32436 324243624 312 312 33 4 x x x x x x x x
cc cc cc c c c
71. 3(5)713 35713 35713 886138 65 66 5 6
72. 64513 64513 56413 41013 xx xx xx x
410101310 43 43 44 3 4 x x x x
73. 4.856.41.1125.8 6.44.851.1125.8 6.45.9625.8 6.45.965.9625.85.96 6.419.84 6.419.84 6.46.4 3.1 x x x x x x x
Chapter 2: Solving Linear Equations and Inequalities
Chapter 2: Solving Linear Equations and Inequalities
90.
73 5 168 7315 1688 7315 1616 1688 7630 73063030 h h h h h
95. 313 564 313 6060 564 361045 3610101045 2645 q q q q q
2645 4545 26 45 q q
96. 315 564 315 6060 564 361075 3610101075 2675 2675 7575 m m m m m m
97. a. Bysubtractingfirst,youwillnothavetowork withfractions.
b. 3211 322112 39 39 33 3 x x x x x
98. a. Byaddingfirst,youwillnothavetoworkwith fractions. b. 5312
102. - = @
100.
103. a. Let x =costofoneboxofstationery 3x +6=42
b. 3642 366426 336 12 x x x x
Aboxofstationerycosts$12.00.
104. a. Let x =costofonerollofcandy. 3x +0.5=2.75 b. 30.52.75 30.50.52.750.5 32.25 0.75 x x x x Arollofcandycosts$0.75.
105. False.2isarealnumberbutisirrational.
106.
107. Tosolveanequation,weneedtoisolatethe variableononesideoftheequation.
108. Tosolvetheequation,wedividebothsidesofthe equationby–4.
Mid-Chapter Test: Sections 2.1 – 2.4
1. 5912476 5794126 256 xyyx
2. 231231 88 542542 815161 202022 715 202
6. Substitute2forinthefollowingequation
Sinceweobtainedatruestatement,2isasolution.
7. 2 Substituteforinthefollowingequation 5
Sinceweobtainedafalsestatement,2 5 isnota solution.
20. 89462 893662 983662 9222 920 20 9 y y y y y y
Exercise Set 2.5
1. Ourgoalinsolvingalinearequationistoisolate thevariable.
2. Toeliminatedecimalnumbersfromanequation wecanmultiplybothsidesoftheequationbya poweroften.
3. Toeliminatefractionsfromanequationwecan multiplybothsidesoftheequationbytheleast commondenominatorofthefractionsinthe equation.
4. Aconditionalequationistrueforaspecificvalue orvaluesofthevariable.
5. Anidentityistrueforallvaluesofthevariable.
6. Acontradictionisnottrueforanyvalueofthe variable.
7. Whenwehaveanidentity,wewillstatethe solutionisallrealnumbers.
8. Whenwehaveacontraction,wewillstatethat thereisnosolution.
9. Whensolvinganequationandweobtainan equationthatisalwaystrue,wewritetheanswer as allrealnumbers
10. Whensolvinganequationandweobtainan equationthatisnevertrue,wewritetheansweras nosolution
11.
13. 3210 322210 510 510 55 2 xx xxxx x x x
14. 356 35556 26 26 22 3 xx xxxx x x x
15. 74225 722442254 31 31 33 1 3
16. 93272 927337723 41 41 44 1 4
17. 21632 216 21666 217 217 77 3 ppp pp pppp p p p
Chapter 2: Solving Linear Equations and Inequalities
18. 30859 3088598 306 306 66 5
qqq qqqqq q q q
19. 2836 228326 86 8666 2 xx xxxx x x x
20. 83450 8334350 8750 85075050 427 427 77 6 xx xxxx x x x x x
21. 62986 6292 622922 69False yyy yy yyyy
Sinceafalsestatementisobtained, thereisnosolution.
22. 78325 78352 7882 788882 72False yyy yyy yy yyyy
Sinceafalsestatementisobtained, thereisnosolution.
23. 5326 53212 5232212 3312 333123 39 39 33 3 xx xx xxxx x x x x x
24. 1432 1436 1436 1426 146266 202 202 22 10 xx xx xxxx x x x x x
25. 4281953 4825193 42516 4425416 2916 21691616 189 yyy yyy yy yyyy y y y
189 99 2 y y
26. 359249 395429 125411 12454411 8511 855115 816 xxx xxx xx xxxx x x x
816 88 2 x x
27. 22462 24426 2426 224226 46False xxx xxx xx xxxx
Sinceafalsestatementisobtained, thereisnosolution.
28.
952716 925776 75713 7757713 513False xxx xxx xx xxxx
Sinceafalsestatementisobtained, thereisnosolution.
29.
30.
3174 3174 33174344 132 132 22 13 2
31.
3255313 6155313 620313 66203613 20913 201391313
32. 7353106 mm 21353018 212135301821 35303 353030303 53 53 33 5 3 mm mmmm m m m m m
33. 124.89.44.832.5 124.89.49.44.89.432.5 124.814.232.5 124.832.514.232.532.5 92.314.2 92.314.2 14.214.2 6.5 xx xxxx x x x x x
34. 90.54.58.5
90.50.54.50.58.5 958.5 98.558.58.5 xx xxxx x x 0.55 0.55 55 0.5 5 0.1 x x x x
35. 0.620.659.752.63 0.622.630.659.752.632.63 3.250.659.75
3.250.650.659.750.65
3.2510.4 3.2510.4 3.253.25 3.2 xx xxxx x x x x x
36.
7 2 23 7 662 23 21212 2122122 2114 2114 1414 x x x x xx xxxx x x
5 2 73 5 21212 73 33542 342354242 x x x x xx xxxx
45350 453535035 4535 4535 4545 7 9 x x x x x
43. 511 842 511 88 842 524 52242 52 52 22 aa aa aa aaaa a a
44. 573 632 bb 573 66 632 5149 551495 144 144 44 7 2 bb bb bbbb b b b
45. 0.1100.34 0.110.34 0.10.110.30.14 140.244 50.2 50.2 0.20.2 25 xx xx xxxx x x x x
46. 0.3514.32 1.50.34.32 1.520.34.322 0.50.34.3
0.50.30.34.30.3 0.54 0.54 0.50.5 8 xx xx xxxx x x x x x
47. 244325 284325 2828 xxx xxx xx
Sincetheleftsideoftheequationisidenticalto therightside,theequationistrueforallvaluesof x.Thusthesolutionisallrealnumbers.
48. 319865 33936 3636 yyy yy yy
Sincetheleftsideoftheequationisidenticalto therightside,theequationistrueforallvaluesof x.Thusthesolutionisallrealnumbers.
49. 5332546 15151086 1515168 15151516158 158 15888 23 nnn nnn nn nnnn n n n
6217324 12621144 1212614214121414 205 205 55 4
mmm mmm mmmmm m m m 51.
323 323 32223 333 33333 30 30 33 0 pp pp pppp p p p p p
Chapter 2: Solving Linear Equations and Inequalities
52. 3773 3773 33777733 06 06 66 0
53. 1695373 1695219 169169
Sincetheleftsideoftheequationisidenticalto therightside,theequationistrueforallvaluesof z.Thusthesolutionisallrealnumbers.
54.
3821138 3168138 138138 yyy yyy yy
Sincetheleftsideoftheequationisidenticalto therightside,theequationistrueforallvaluesof y.Thusthesolutionisallrealnumbers.
55. 3521743 70357283 70351028 701035101028 603528 6035352835 6063 xxx xxx xx xxxx x x x
6063 6060 21 20 x x
56. 24217523 482435143 482435314 484824384814 241014 xxx xxx xxx xxxx x
2414101414 3810 3810 1010 19 5 x x x x
0.40.280.62.52
0.40.40.280.60.42.52 0.280.22.52 0.282.520.22.522.52 2.80.2 2.80.2 0.20.2 14 xx xx xxxx x x x x x
58. 0.5(68)1.4(5)0.2 341.470.2 341.47.2 31.441.41.47.2 1.647.2 1.6447.24 1.63.2 1.63.2 1.61.6 xx xx xx xxxx x x x x
2 x
59. 31 2 52 31 10210 52 620105 66201065 2045 205455 154 xx xx xx xxxx x x x
154 44 15 4 x x
1090 10109010 xx xxxx
354371 3541277 3547127 35319 3553519 xxx xxx xxx xx xxxx
3219 31921919 222 222 22 11 x x x x x
69. 752363 7526618 12412 121241212 424 44424 524 yyy yyy yy yy yy yyyy y
524 55 24 5 y y
70. 3427521 34214105 7210145 7819 788819 7919 ccc ccc ccc cc cccc c
779197 912 912 99 4 3 c c c c
71. 32 635 53 31810 2 553 31810 15152 553 9543050 995430950 542150 5450215050 xx xx xx xx xxxx x x
421 421 2121 4 21 x x x
72.
11 2444 23 44 2 33 44 323 33 3644 336434 64 dd d d d d dd dddd
73.
32536 53 61536 53 61536 1515 53 3615536 18451530 181545151530 34530
345453045 315 315 33 5
74.
34523 43 3121015 43 3121015 1212 43 331241015 9364060 993640960 363160 xx xx xx xx xx xxxx x
3660316060 2431 2431 3131 24 31 x x x x
75.
21 54341 72 1083 21 772 1083 1 772 1083 14141 772 20162114 202016212014 xx xx xx xx xx xxxx
1614 16141414 30 x x x
521 221 1236 510421 1212336 510421 1212 1212336 5101682 5101610 551016510 xx xx xx xx xx xxxx
101110 1010111010 x x
x
614141614
79. a. Oneexampleis12 xxx b. Ithasasinglesolution.
c. Answerswillvary.Forequationgiveninpart a): 12 212 212 12 1121 1 xxx xx xxxx x x x
80. a. Oneexampleis21 xxx .
b. Ithasasinglesolution.
c. Answerswillvary.Forequationgiveninpart a): 21 221 221 21 2111 1 xxx xx xxxx x x x
81. a. Oneexampleis121 xxx
b. Bothsidessimplifytothesameexpression.
c. Thesolutionisallrealnumbers.
82. a. Oneexampleis2x +1= x + x +1.
b. Bothsidessimplifytothesameexpression.
c. Thesolutionisallrealnumbers.
83. a. Oneexampleis122 xxx
b. Itsimplifiestoafalsestatement.
c. Thesolutionisthatthereisnosolution.
84. a. Oneexampleis221 xxxx
b. Itsimplifiestoafalsestatement.
c. Thesolutionisthatthereisnosolution.
85. 5145 55195 14 14 44 1 4
86. 2435 2425 224225 45False
Nosolution
87. 3525 3535
Theleftsideoftheequationisidenticaltothe rightside.Thesolutionisallrealnumbers.
88.
89.
28 28 22 4 x x x
90. a. Let x bethecostofonechocolatebar. 2x = x +6
b. 2x = x +6 2x – x = x +6 x =6 Achocolatebarcosts$6.00.
91. a. |4|=4
b. |–7|=7
c. |0|=0
92. a abab b x xxx x
93. Factorsareexpressionsthataremultiplied together;termsareexpressionsthatareadded together.
94.
23442644
23440 26440 7100 71010010
Exercise Set 2.6
1. Anequationusedtoexpressaspecific relationshipmathematicallyiscalledaformula.
2. Theprocessofsubstitutingvaluesandperforming indicatedoperationsonaformulaiscalled evaluatingit.
3. Afour-sidedfigureiscalledaquadrilateral.
4. Twicetheradiusofacircleisthediameterofthe circle.
5. Simpleinterestisfoundbymultiplyingthe principal,therate,andthetime.
6. Whencalculatingsimpleinterest,therateshould beexpressedasadecimalnumber.
7. Thecircumferenceofacircleisfoundby multiplying2πbytheradius.
8. Distanceisfoundbymultiplyingtheratebythe time.
9. Apossibleunitofmeasureforvolumeiscubic feet.
10. Apossibleunitofmeasureforareaissquare inches.
11. Substitute75for r and3for t
12. Substitute6for s
13.
17. Substitute10for
20. Substitute6for r and7for h.
2 2 1 3 1 67 3 263.89 Vrh V V
21. Substitute16for m and56for n
22. Substitute72for a,81for b,and93for c. 3 728193 3 246 3 82 abc A A A A
23. Substitute100for x,80for m,and10for s 10080 10 20 2
24. Substitute135for s and100for d. 135100 100 0.35 sd m d
25. Substitute56for P
26. Substitute28for P and6for w
27. Substitute678.24for V and6for r 2 2
678.24(6)
678.2436
678.2436 3636
28. Substitute188.5for V and6for r
29. a)Substitute3for s
30. a)Substitute7for s
As A A
2 2 2 7 49mi
b)Substitute7fors.
4 47 28mi Ps P P
31. a)Substitute11for l and7for w 2 117 77yd Alw A A
b)Substitute11for l and7for w
22 21127 2214 36yd Plw P P P
32. a)Substitute7for l and15for w
2 715 105mm Alw A A
b)Substitute7for l and15for w
Plw P P P
22 27215 1430 44yd
33. a)Substitute17for l and12for h
2 1712 204m Alh A A
b)Substitute17for l and13for w
Plw P P P
22 217213 3426 60m
34. a)Substitute7for l and3for h. 2 73 21mm Alh A A
b)Substitute7for l and5for w
22 2725 1410 24mm Plw P P P
35. a)Substitute4for h,4for b and10for d
Ahbd A A A A
2 1 2 1 4410 2 1 414 2 1 56 2 28cm
Chapter 2: Solving Linear Equations and Inequalities
b)Substitute5for a,4for b,5for c,and10for d 54510 24cm
36. a)Substitute12for h,12for b and22for d.
Ahbd A A A A
b)Substitute13for a,12for b,13for c,and22 for d 13121322 60yd
37. a)Substitute10for b and12for h
39. a)Substitute3for r 2 2 2 3 928.27m Ar A A
r 2 23 618.85m Cr C C
40. a)Substitute 8 4 2 for r 2 2 2 4 1650.27ft Ar A A
Substitute 8 4 2 for r
41. a)Substitute147 2 for r
Ar A A
2 2 2 7 49153.94m
b)Substitute147 2 for r
2 24 825.13ft
b)Substitute13for a,10for b,and13for c. 131013 36ft
Pabc P P
38. a)Substitute19for b and5for h
Abh A A A
2 27 1443.98m
42. a)Substitute9for r.
Ar A A
2 2 2 9 81254.47in.
b)Substitute9for r
Cr C C
2 29 1856.55in.
Pabc P P
b)Substitute8.6for a,19for b,and13for c 8.61913 40.6m
43. Substitute4for l,3for w,and5for h V = lwh V =(4)(3)(5) V =60ft3
ISM: Elementary Algebra
44. Substitute7for l,2for w,and5for h
2: Solving Linear Equations and Inequalities
49. Substitute6for r
45. Substitute4for r and9for h
V =πr2h
V =π(4)2(9)
V =π(16)(9)
V =144π≈452.39cm3
46. Substitute 12 6 2 for r and12for h
50. Substitute126 2 for r
47. Substitute4for
and8for h.
51. Substitute50for F
Theequivalenttemperatureis10°C.
52. Substitute86for F.
48. Substitute73.5
Theequivalenttemperatureis30°C.
53. Substitute25for C.
9 32 5 9 2532 5 4532
Theequivalenttemperatureis77°F.
Chapter 2: Solving Linear Equations and Inequalities
54. Substitute–40for C
62. 4525 445254 5254 5254 55 254425 55 mn mmnm nm nm mm n
63. 32 3323 23 23 22 33 22 rn rn rn rn nn r
64. 75 7757 57 pq pq pq
pq q p q p q p
57 55 7 5 17 15 7 5
65.
Chapter 2: Solving Linear Equations and Inequalities
74. 396 39996 396 33963 xy xyyy xy xxyx
75. 5103 5103 55 103 55 3 2 5 3 2 5 yx yx x y yx yx
76. 7219 7219 77 219 77 9 3 7 yx yx x y yx
77. 1536 1536 66 153 66 51 22 15 22 xy xy x y xy yx
78. 2318 2318 22 318 22 3 9 2 yx yx x y yx
79. 1 34 3 14 3 33 14 333 33 149 333 15 33 yx yx yx yx yx
80. 2 34 3 28 3 33 28 333 33 289 333 217 33 yx yx yx yx yx
81. 11 2 53 12 2 53 1121 2 5535 103 2 1515 13 2 15 yx yx yx yx yx
82. 31 5 42 33 5 48 33 555 48 3340 488 337 48 yx yx yx yx yx
83. a)
15,0000.04542700
Hewillpay$2700interest. b)15,000270017,700 pi
Hewillpayatotalof$17,700.
84. a)
35,0000.03755 6562.50
Shewillpay$6562.50interest. b)35,0006562.5041,562.50 pi Shewillpayatotalof$41,562.50.
85. iprt
4500.033 4500.09 4500.09 0.090.09 5000 p p p p Sheplaced$5000inthesavingsaccount.
86. iprt
84060000.035 840210 840210 210210 4 t t t
Hismoneyhadbeenintheaccountfor4years.
87. 7630.02 15.26 drt d d Thecartravels15.26mi.
88. 3.42 6.8 drt d d
Shewalked6.8mi.
89. 1803 60 drt r r Heraveragespeedwas60mph.
90.
39000.3 13,000 drt r r Theaveragespeedwas13,000mph.
91. a)
20090 18,000 Alw A A
Theareaofthepastureis18,000squareyards. b)
22 2200290 400180 580 Plw P P P
Shewillneed580yardsoffencing.
92. a) 3557.4 2009 Alw A A
Theareais2009squareinches. b)
22 235257.4 70114.8 184.8 Plw P P P
Theperimeteris184.8inches.
93. a) 2 30 2 2 215 94.25
Cr C C C
Hewillneedapproximately94.25feetoffencing. b) 2 152 225706.86 Ar A A
Theareaofthecoverisapproximately706.86 squarefeet.
Theareaofthehelipadisapproximately4071.50 squarefeet.
Thecircumferenceofthehelipadisapproximately 226.19feet. 95. 2 62.832
Theradiusofthegardenisapproximately10.00 feet.
Theradiusofthetabletopisabout3.00feet.
Thediameteristwicetheradius,so d =2(3.00)=6.00
Thediameterofthetabletopisabout6.00feet.
97. Totalarea=Areaoftoptriangle+areaofbottom triangle
TotalArea=0.5b1h1+0.5b2h2
TotalArea=0.5(2)(1)+0.5(2)(2)
TotalArea=1+2=3
Theareaofthekiteis3squarefeet.
98. 1 2 1 2(36)(31)558
Abh A
Theareais558in.2
100. 17146 1428 Vlwh V V
Thevolumeofthecarryingcaseis1428in.3 .
101.V =πr2h =π(4)2(3) =π(16)(3) =48π≈150.80
Thevolumeofwaterinthehottubisabout 150.80ft3 .
102. 2 Vrh
Theradiusis1 2 thediameteror
1 24in.12in.1foot. 2 2 (1)(4)412.57 V
Thevolumeofthedrumisabout12.57ft3
103. 1 2 Ahbd 1 243 2 1 27 2 17 7 A
Theareaofthesignis7ft2 .
104. 1 2 Ahbd
1 10080200 2 1 100280 2 50280 14,000 A
Theseatingareais14,000ft2 .
99. 60301.5 2700
Vlwh V V
Thevolumeofsandis2700cubicfeet.
105. Theradiusishalfthediameter. 3 3 4 3 49 32 381.7 Vr V V
Thevolumeofthebasketballisabout381.7in.3
106. Theradiusishalfthediameter.
32 32 183 18737 6174147 6027 Vxx V
Volumeis6027cm3 . c.
Thevolumeoftheballisabout904.78ft
107. Theradiusishalfthediameter.
Thevolumeoftheconeisabout18.85cubicfeet. 108.
d.
2 2 548 54787 264656 2590 Sxx S
Surfaceareais2590cm2 .
112. Whenusingthedistanceformula,iftherateis doubledandthetimeishalved,thedistancestays thesame.Todoubletherate,multiply r by2.To halvethetime,divide t by2.
2 2 22 drt trt drrt
113. Whenusingthesimpleinterestformula,ifthe principalandratearedoubledandthetimeis halved,simpleinterestdoubles.Todoublethe principal,multiply p by2.Todoubletherate, multiply r by2.Tohalvethetime,divide t by2.
4 222 22 Iprt Itprtprprt
114 Whenusingtheformulaforareaofasquare,ifthe sideofthesquareisdoubled,thenthearea becomes4timesaslarge.Todoubletheside length,multiply s by2.
2 2222224 As Asss
115. Whenusingtheformulaforvolumeofacube,if thesideofthecubeisdoubled,thenthevolume becomes8timesaslarge.Todoubletheside length,multiply s by2.
3 3333228 Vs Vsss
Chapter 2: Solving Linear Equations and Inequalities
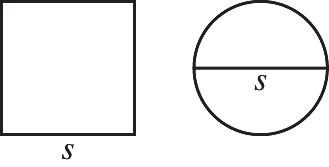
Therefore,asquarewithsidelength s incheshasa greaterareathanacirclewithdiameter s inches. 117.
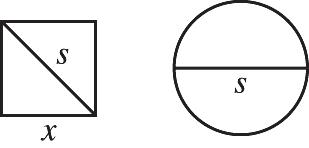
Firstfindthesidelength x ofthesquareinterms of s.UsethePythagoreantheoremtosolve.Then comparetheareasofthesquareandcircle.
Therefore,acirclewithdiameter s incheshasa greaterareathanasquarewithdiagonallength s inches.
a. 2 B b. 2 A c. 22AB d. 2 AC e.
Exercise Set 2.7
1. Aproportionisastatementofequalityoftwo ratios.
2. Intheproportion ap bq , a and q arecalled extremes.
3. Intheproportion ap bq , b and p arecalled means.
4. Amethodforsolvingproportionsiscross multiplying.
5. Twofiguresthathaveequalcorrespondingangles andhavetheircorrespondingsidesinproportion arecalledsimilarfigures.
6. Anotherwayofexpressingtheratio c d is c : d
7. Whensolvinganappliedprobleminvolving proportions,itiscrucialthatthetworatioshave thesameunits.
8. Thequotientoftwoquantitiesiscalledaratio.
9. 6:9=2:3
Elementary Algebra
10. 6:4=3:2
11. 6:24=1:4
12. 9:24=3:8
13. GradesbetterthanC=6+4=10
RatioofgradesbetterthanCtototal grades=10:24=5:12
14. GradesbetterthanC6410
GradeslessthanC=3+2=5
RatioofgradesbetterthanCtogradeslessthan C=10:5=2:1
15. 7:4
16. 3:47
17. 5:15=1:3
18. 18:24=3:4
19. 3hours360180 minutes
Ratiois1806 301 or6:1.
20. 7minutes760420seconds Ratiois42028 151 or28:1.
21. 3feet31236inches Ratiois369 82 or9:2.
22. 4yardsis4312 feet
Ratiois61 122 or1:2.
23. 12quartersis 5 1230 2
dimes
Ratiois7:30.
24. 5quarters5525nickels
Ratiois27 25 or27:25.
25. Gearnumberofteethondrivinggear ratio numberofteethondrivengear 408 51
Gearratiois8:1.
26. Gearnumberofteethondrivinggear ratio numberofteethondrivengear 3015 84
Thusthegearratiois15:4.
Dividingbothpartsoftheratioby4,ratiocanalso beexpressedas3.75:1.
27. Gearnumberofteethondrivinggear ratio numberofteethondrivengear 455 182
Thusthegearratiois5:2.
Dividingbothpartsoftheratioby2,ratiocanalso beexpressedas2.5:1.
28. Gearnumberofteethondrivinggear ratio numberofteethondrivengear 567 162
Thusthegearratiois7:2.
Dividingbothpartsoftheratioby2,ratiocan alsobeexpressedas3.5:1.
29. a) 663,000:1200=1105:2
b)Dividingbothpartsoftheratioby2,ratiocan alsobeexpressedas552.5:1.
30. a. 270:75=18:5
b. Dividingbothpartsoftheratioby5,ratiocan alsobeexpressedas3.6:1.
31. a. 2320:1450=8:5
b. Dividingbothpartsoftheratioby5,ratiocan alsobeexpressedas1.6:1.
32. a. 19,320:7850=1932:785
b. Since1932÷785≈2.46,1932:785≈2.46:1.
33. a. 35:17
b. 25:19
34. a. 2500:2200=25:22
b. 3500:2500=7:5
35. a. 40:32or5:4
b. 15:11
36. a. 80:11
b. 1:5
Thusthesideis11.2feetinlength.
1626
53.
54.
Thusthesideis19.5inchesinlength.
Thusthesideis5.6inchesinlength.
55. Let x =numberofloadsonebottlecando. 4flounces100flounces 1loadloads 4100 1 4100 25 x x x x
Onebottlecando25loads.
56. Let x =amountoftimeittakestolaycablein hours. 42feet252feet 1hourhours 42252
Itwilltakethem6hours.
57. Let x =numberofmilesthatcanbedrivenwitha fulltank.
25miles 1gallon21.1gallons
Itcantravel527.5milesonafulltank.
58. Let x =numberofsharesthatcanbepurchased.
2sharesshares $38.25$344.25 2 38.25344.25 2344.2538.25 688.538.25 18 x x x x x
18sharescanbepurchased.
59. Let x =lengthofmodelinfeet. 1footmodelfootmodel 20foottrain30foottrain 1 2030 2030 1.5 x x x x
Themodelshouldbe1.5feetlong.
60. Let x =Jane’spropertytax.
$1000assessedvalue$333,716assessedvalue $15.9933taxdollarstax 1000333,716 15.9933 100015.9933333,716 10005,337,220.103 5337.22 x x x x x ThusJane’spropertytaxis$5337.22.
61. Let x =numberofteaspoonsneededforsprayer. 3teaspoonsteaspoons 1gallonwater8gallonswater 3 18 381 24 x x x x
Thus24teaspoonsareneededforthesprayer.
Chapter 2: Solving Linear Equations and Inequalities
62. Let x =numberofpoundsoffertilizerneeded.
5000squarefeet26,000squarefeet 40poundsfertilizerpoundsfertilizer
500026,000 40
50004026,000
50001,040,000 208 x x x x x
Thus208poundsoffertilizerareneededfor 26,000squarefeet.
63. Let x =actualdistanceinmiles. 1inch3.75inches 4milesmiles 13.75 4 143.75 15 x x x x
Theactualdistanceis15miles.
64. Let x =lengthonamapininches. 0.5inchesinches 22miles55miles 0.5
66. Let x =timeinhoursitwilltakeKarentoreadthe entirenovel. 72pages656pages 1.3hourshours
72656 1.3 720.3656 72852.8 11.84 x x x x x
Itwilltakeherabout11.84hours.
67. Let x =lengthofthemodelbullinfeet. 2.95feetmetalbull28feetmetalbull 1feetrealbullxfeetrealbull 2.9528 1 2.95128 2.9528 9.49 x x x x
Themodelbullisabout9.49feetlong.
68. Let x =time,inminutes,itwilltaketo removethewater. 3inches12inches 30minutesminutes
Thelengthonthemapwillbe1.25inches.
65. Let x =numberofcupsneeded. 1 2 3 2 1cupscups 6servings15servings 615 3 615 2 622.5 3.75 x x x x x
3.75cupsofonionsareneeded.
Itwilltake120minutesor2hours.
69. Let x =numberofmilliliterstobegiven. 1millilitermilliliter 400micrograms220micrograms 1 400220 1220400 220400
0.55 x x x x x x
Thus0.55millilitershouldbegiven.
70. Let x =numberofgramsofmeprobanate tobegiven.
1sqmbodysurface0.6sqmbodysurface 0.7gramsgrams
Thus0.42gmeprobamateshouldbegiven.
71. Let x =numberofminutestoreadentirebook.
40pages760pages 30minutesminutes 40760 30 4030760 4022,800
Thusitwilltakeher570minutesor 9hours30minutestoreadtheentirebook.
72. Let x =time,inminutes,ittakesJasontoswim30 laps.
3laps30laps 2.3minutesminutes
Itwilltakehim23minutes.
73. Let x =numberofchildrenbornwithPrader-Willi Syndrome.
12,000births4,315,000births 1babywithsyndromebabieswithsyndrome
74. Let x =timeittakeshertocompletethe scrapbook. 4pages36pages 20.5minutesminutes
Thus,about360childrenwerebornwithPraderWilliSyndrome.
Itwilltakeher184.5minutesor3hr.4min.30 sec.tocompletethescrapbook.
75. 12inches78inches 1footfeet 1278
Thus78inchesequals6.5feet.
76. 1milemiles 5280feet22,704feet 1 528022,704 22,7045280 22,704 5280 4.3
Thus22,704feetequals4.3miles.
77. 9squarefeet26.1squarefeet 1squareyardsquareyards 926.1 1 926.1
Thus26.1squarefeetequals2.9squareyards.
Chapter 2: Solving Linear Equations and Inequalities
78. 1poundpounds 16ounces146.4ounces 1 16146.4 146.416 146.4 16 9.15 x x x x x
Thus146.4ouncesequals9.15pounds.
79. 2.54cm50.8cm 1inchinches 2.5450.8 1 2.5450.8 50.8 20 2.54 x x x x
Thusthelengthofthenewbornis20inches.
80.
1mile520miles 1.6kilometerskilometers 1520 1.6 1.6520 832 x x x x
ThusthedistancefromSanDiegotoSan Franciscois832kilometers.
81. $41.08$513.50 1gramgrams 41.08513.5 1 41.081513.5 41.08513.5 513.5 12.5 41.08
Briecanpurchase12.5gramsofgold.
82. $31.08$1359.75 1gramgrams
31.081359.75 1
31.0811359.75 31.081359.75 1359.75
Jacquecanpurchase43.75gramsofplatinum.
Timneeds7 1 8cupsofsugar. 84. 1 2teaspoonofcayenneteaspoonsofcayenne 3avocados8avocados
Anthonyneeds1 1 3teaspoonsofcayennepepper.
85. $1.00U.S.$U.S. $1.33Canadian$1995Canadian 1 1.331995 19951.33 19951.33 1.331.33 1500 x x x x x
Willywillneed$1500U.S.dollars.
86. $1.00U.S.$400U.S. 0.92euroseuros 1400 0.92 10.92400 368
x x x x Andrewwillreceive368euros.
87. TheratioofJavier’stotalcholesteroltohigh densitycholesterolis17556.Ifwedivide175by56
weobtain3.125.ThusJavier’sratioisequivalent to3.125:1.Thereforehisratioislessthanthe desired3.5:1ratio.
88. a. TheratioofCameron’stotalcholesteroltohigh densitycholesterolis21648.Ifwedivide216by
48weobtain4.5.ThusCameron’sratiois equivalentto4.5:1.Thereforehisratioisnot lessthanorequaltothedesired3.5:1ratio.
89. In ac bd ,if b and d remainthesamewhile a increases,then c increasesbecause ad=bc.If a increases,then ad increasesso bc mustincrease byincreasing c.
90. In ac bd ,if a and c remainthesamewhile d decreases,then b decreasesbecause ad = bc.If d decreases,then ad decreasesso bc mustdecrease bydecreasing b
91. Let x =numberofmilesremainingonthelifeof eachtire.
Inchesremainingonthelifeofeachtire:
0.310.060.25
0.03inches0.25miles
5000milesmiles
0.030.25
5000
0.0350000.25
Thetireswilllastabout41,667moremiles.
92. Let x representtheamountoftheingredientthat shouldbeused.
3cupofflourshouldbeused.
nutmeg:
2 3teaspoonofcinnamonshouldbeused. salt:1
Chapter 2: Solving Linear Equations and Inequalities
1cupofsugarshouldbeused.
93. Let x =numberofcubiccentimetersoffluid needed.
0.625cubiccentimetersoffluidshouldbedrawn upintoasyringe.
94. a. – d. Answerswillvary.
95. Answerswillvary.
96. commutativepropertyofaddition
97. associativepropertyofmultiplication
98. distributiveproperty
99.
Sinceatruestatementisobtained,thesolution isallrealnumbers.
100. ymxb ybmxbb ybmx ybmx xx yb m x
Exercise Set 2.8
1. Amathematicalstatementthatincludesthe symbols<,>, ,or≥iscalledaninequality.
2. Wheneverwemultiplyordividebothsidesofan inequalitybyanegativenumberwemustchange thedirectionoftheinequalitysymbol.
3. Whenrepresentingasolutiononanumberline,an opencircle, ,indicatesthattheendpointisnot includedinthesolution.
4. Whenrepresentingasolutiononanumberlinea closedcircle, ,indicatesthattheendpointis includedinthesolution.
5. Whenwearesolvinganinequalityandweobtain aninequalitythatis always truethenwestatethat thesolutionisallrealnumbers.
6. Whenwearesolvinganinequalityandweobtain aninequalitythatis never truethenwestatethat thereisnosolution.
7.

12. 62 6626 4

13. 39 3393 6 x

14. 73 7737 4

4,
15.
16.
38 3383 5 115 5 x x x x x

5,
42 4424 6 116 6 x x x x x
,6
17. 82 8222 6 (1)(6)(1)() 6 6 r r r r r r

,6
18. 1512 1512 3 131 3 3
s s s s s s

,3








31. 162169 16221692 161611 1616161611 011False ss ss ss ssss
Sinceafalsestatementisobtained,thereis nosolution.
32. 5357 537577 5105 551055 100False tt tt tt tttt
Sinceafalsestatementisobtained,thereis nosolution.
33.
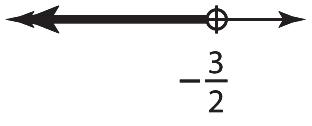

Chapter 2: Solving Linear Equations and Inequalities
8361 2494 249949 2413 24242413 013 xx xx xx xx xxxx
Since0isalwayslessthan13,thesolutionisall realnumbers


Since3isalwayslessthan4,thesolutionisall realnumbers.



Since4isalwaysgreaterthanorequalto–3,the solutionisallrealnumbers.

,
41. 63215 186215 1815621515 362 36626 38 38 88 xx xx xx xx xxxx x x

Sinceatruestatementisobtained,thesolutionis allrealnumbers.
Elementary Algebra Chapter 2: Solving Linear Equations and Inequalities
42. 2346 6246 626 66266 212 212 22 6 xx xx x x x x x

43. 4445 44420 4444420 420 xx xx xxxx
Since–4isneverlessthan–20,thereisno solution.
44.
25324 102364 102210 10222210 1010 xxx xxx xx xxxx
Since10isnevergreaterthan10,thereisno solution.
45. 523622 1015622 10158 101515815 107 107 117 xxx xxx xx xx xx xxxx x
117 1111 7 11 x x
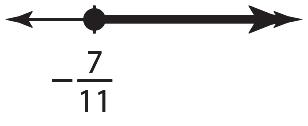
7 11,
46. 3212426 636486 636414 64364414 103614 1036361436 1022 xx xx xx xxxx x x x

1022 1010 11 5 x x 11 ,5
47. 1.23.13.53.8 1.21.23.13.51.23.8 3.12.33.8 3.13.82.33.83.8 6.92.3 6.92.3 2.32.3 3 3 xx xxxx x x x x x x

3, 48. 5.36.72.36.5 5.36.56.72.36.56.5 1.26.72.3 1.26.76.72.36.7 1.29.0 1.29.0 1.21.2 7.5 rr rrrr r r r r r 7.5,

Chapter 2: Solving Linear Equations and Inequalities
49.
1.234.621.7
1.23.69.24.61.7
1.23.610.94.6
1.24.63.610.94.64.6
5.83.610.9
5.83.63.610.93.6
5.814.5 mm mm mm mmmm m m m

50.
4.642.430.2

18.44.62.47.20.2
18.44.62.47.4
18.44.62.42.42.47.4
18.42.27.4
18.418.42.27.418.4 2.211.0 xx xx xx xxxx x x x
2.211.0 2.22.2 5 x x

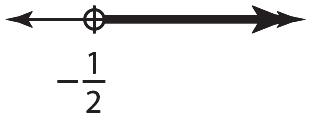


55.



59. a. Theaveragehightemperaturewasgreaterthan 65°FinMay,June,July,August,and September.
b. Theaveragehightemperaturewaslessthanor equalto59°FinJanuary,February,March, April,November,andDecember.
c. Theaveragelowtemperaturewaslessthan 29°FinJanuary,February,andDecember.
d. Theaveragelowtemperaturewasgreaterthan orequalto58°FinJune,July,andAugust.
60. a. KoreaandMexico
b. MexicoandtheUnitedStates
c. UnitedStatesandFrance
d. UnitedStates
61. ≠
62. Thedirectionoftheinequalitysymbolwasnot changedwhenbothsidesoftheinequalitywere dividedby–4.
63. Wecannotdividebothsidesofaninequalityby y becausewedonotknowthat y ispositive.If y is negative,wemustreversethesignofthe inequality.

Chapter 2: Solving Linear Equations and Inequalities
64.
69. Let x =numberofkilowatt-hoursofelectricity used. $0.174$87 1kilowatt-hourkilowatt-hours 0.17487 1 0.17487 87 500 0.174 x
ThustheVega'sused500kilowatt-hoursof electricityinJuly.
Review Exercises
67. Substitute–5for x
5.
5252 552 510 510 xx x x x
24224 28 28 xx x x
212 112 2 2 xx x x x
818 118 8 mm m m
6.
4444 444 164 xx x x
5555 555 255 255 pp p p p
8.
9.
11. 111 (24)(2)(4) 222
13.
32573257 323537 61521 61521 abab ab ab ab
15. 10m –6m =4m
16. 533353 38 yy y
17. 13215 51 xxx x
18. 2333 xxyxy
19. 42464426 88 mnmnmmnn mn
20. Therearenoliketerms. 932 xy cannotbefurthersimplified.
21. 6236436 xxyxy
22. 893993 3 xxxxx 23. 222 483123 xxx
24. 2222 22 234686868 6688 0 aaaa aa
25. 234523125 57 xxxx x
26. 4232464 23 32 bbbb b b
27. 67676767 7766 0 xxxx xx
28. 225104410104 44 xx x
29. 6431842418184 1842418 2242 xxxx xx x
30. 2 2 2 2 4.0321.661.09 4.0323.261.09 64.0323.21.09 62.032.11 xxx xxx xxx xx
31. 1313 2525 4545 512 7 2020 7 7 20 dddd dd d
32. 33 3 3 abababab aabb
33. 5152 262 6363 54 2 66 1 2 6 xxxx xx x
326 366 36666 312 312 33 4 x x x x x x
45. 12328 12624 122462424 126 126 66 2 x x x x x x
46.
4620 2480 24248024 824 824 88 3 x x x x x x
47. 6260 460 46606 46 46 44 63 42 nn n n n n n
48. 3346 3346 316 36166 31 31 11 3 ww ww w w w w w
49. 62346 62346 63246 366 33663 63 63 66 nn nn nn n n n n
50. 62343213 121812813 121218813 1013False xx xx xx
Sinceafalsestatementisobtained,thereisno solution.
51. 531311 533331 3232 332332 22True xx xx xx xxxx
Thesolutionisallrealnumbers.
52. 8.46.36.32.1
8.42.16.36.32.12.1
6.36.36.3
6.36.36.36.36.3
6.312.6 6.312.6 6.36.3 2 rr rrrr r r r r r
53. 1.12.340.091.7 1.10.092.340.090.091.7 1.012.341.7 1.012.342.341.72.34 1.014.04 1.014.04 1.011.01 4 xx xxxx x x x x x
0.3550.454 0.351.750.451.8 0.350.351.750.450.351.8 1.750.101.8 1.751.80.101.81.8 3.550.10 3.550.10 0.100.10 35.5 cc cc cccc c c c c c
0.260.321 0.21.20.60.3 0.20.61.20.60.60.3 0.81.20.3 0.81.21.20.31.2 0.80.9 0.80.9 0.80.8 1.125 xx xx xxxx x x x x x
2.383.74 2.318.43.714.8 2.32.318.43.72.314.8 18.46.014.8 18.414.86.014.814.8 3.66.0 3.66.0 6.06.0 0.6 xx xx xxxx x x x x x
61. 85419 8454419 12519 1255195 1224 1224 1212 2 xx xxxx x x x x x
2236 2612 21261212 106 106 107 ww ww ww ww wwww w
63. 26393 2636 226326 66 6666 0 xx xx xxxx x x x
64. 53210 531021010 572 55725 77 77 77 1 aa aa aa aaaa a a a
65.
52236 52612 5526512 212 2121212 10 pp pp pppp p p p
66. 312249 9249 992499 024False xxx xx xxxx
Sinceafalsestatementisobtained,thereisno solution.
67.
423488 812488 8888 xx xx xx
Sincetheequationistrueforallvaluesof x,the solutionisallrealnumbers.
68.
424334 486312 54312 5343312 2412 244124 28 ccc ccc cc cccc c c c
69.
27694 214694 21429 2214229 149False xxx xxx xx xxxx
Sinceafalsestatementisobtained,thereisno solution.
70. 5(34)6209 15206209 15201520 xx xx xx
Thestatementistrueforallvaluesof x,thusthe solutionisallrealnumbers.
71.
4350 41250 3170 31717017 317 317 33 17 3 xx xx x x x x x
72.
24623 826123 82912 812291212 2029 202292 207 xxx xxx xx xx xx xxxx x
207 77 20 7 x x
73. 3 22 232 262 22622 60False xx xx xx xxxx Sinceafalsestatementisobtained,thereisno solution.
74. 5 72 275 2735 277735 535 535 55 7 yy yy yy yyyy y y y
Chapter 2: Solving Linear Equations and Inequalities
78. 1 3 462 3 4622 3 1212 4622 32618 5618 566618 118 xx x xxx xxx xxx xx xxxx x
21 222 56 4222 5566 4211 5533 4211 1515 5533 12655 1266565 xx xx xx xx xx xxxx
125 12555 7 x x x
79. Substitute7for y,2for x,and1for b.Thensolve for m.
721 721 71211 62 62 22 3 ymxb m m m m m
80. Substitute12for h,3for b,and5for d.Then solvefor A
1 2 1 1235 2 1 128 2 48 Ahbd A A A
2 1 2 1 83 2 12cm Abh A A
82.
83.
85.
87.
Hetraveled308.5miles.
88.
Theareaoftheflowergardenis240ft2 .
2 2 3 22 825.13in. Vrh V V
89. 15:20=3:4
90. 80ounces805 16 pounds
Theratioof80ouncesto12poundsisthus5:12. 91. 4minutes=240seconds
Theratioof4minutesto40secondsis2406 401
Theratiois6:1.
92. 8 416 1684 1632 32 2 16 x x x x
93. 5 2080 20805 20400 400 20 20 x x x x
94. 315 45 34515 13515 135 15 9 t t t t
95. 2015 45 201545 20675 675135 204 q q q q
96. 612 5 6125 660 60 10 6 x x x x
103. 410414 44104414 10814 101481414 248 248 88 3 3 aa aaaa a a a a a a

,3
104. 53215 515321515 1032 103323 105 105 55 2 2 rr rr rr rrrr r r r r

105. 2425 2825 228225 85 xx xx xxxx Since8isneverlessthanorequalto–5,thereis nosolution.
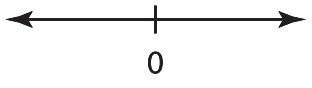
106. 23644 26644 2624 226224 64 xxx xxx xx xxxx Since6isalwaysgreaterthan4,theanswerisall realnumbers.






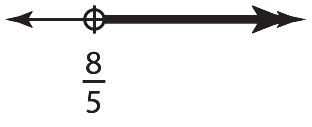
Chapter 2: Solving Linear Equations and Inequalities
112. Let t =thetimeitwilltakeinhourstomakethe boattrip. 40miles140miles 1.8hourshours 40140 1.8 401.8140 40252 40252 4040 6.3
Itwilltaketheboat6.3hourstotravel140miles.
113. Let x =numberofdisheshecanwashin21 minutes. 12dishesdishes 3.5minutes21minutes 12 3.521 12213.5 2523.5 2523.5 3.53.5 72 x x x x x x
Hecanwash72dishesin21minutes.
114. Let x =numberofpagesthatcanbecopiedin22 minutes. 1minutes22minutes 20pagespages 122 20 12220 440 x x x x
440pagescanbecopiedin22minutes.
115. Let x =numberofinchesrepresenting380miles. 60miles380miles 1inchinches 60380 1 603801 60380 3801 6 603 x x x x x
1 6 3inchesonthemaprepresent380miles.
116. Let x =sizeofactualcarinfeet 1inch10.5inches 1.5feetfeet 110.5 1.5 11.510.5 15.75 x x x x
Thesizeoftheactualcaris15.75ft.
117. Let x =thevalueof1pesointermsofU.S. dollars.
$1U.S.dollars 20.52pesos1peso
x x x x x 1pesoequalsabout$0.049.
118. Let x =numberofbottlesthemachinecanfilland capin2minutes. 2minutes=120seconds 50seconds120seconds 80bottlesbottles
50120 80 5080120 509600 9600 192 50 x x x x x
Themachinecanfillandcap192bottlesin 2minutes.
Practice Test
4. 42362346
5.
6.
12
Sinceafalsestatementisobtained,thereisno solution.
3232317 69627 6969 xx xx xx
Sincetheequationistrueforallvaluesof x,the solutionisallrealnumbers.
13.0 0 axbyc axbybycby axcby axccbyc axbyc axbyc aa byc x a
14 652 66526 562 562 55 62 55 62 55 xy xxyx yx yx x y yx
Chapter 2: Solving Linear Equations and Inequalities
15
17. a. Anequationthathasexactlyonesolutionisa conditionalequation.
b. Anequationthathasnosolutionisa contradiction.
c. Anequationthathasallrealnumbersasits solutionisanidentity.
18. 24410 241041010

19. 34512 312512 3121251212 3245 332453 242 242 22 xx xx xx xx xxxx x x

20. 43263 412263 61263 6612663 123 xxx xxx xx xxxx
Since12isneverlessthan–3,theanswerisno solution.
21. 23412 23442 4242True xxx xxx xx Thisequationistrueforallrealnumbers.

, 22. 38 4 348 332 32 3 x x x x Thelengthofside x is322 feetor10 33 feet.
23. Let r =thesimpleinterestrate.
Theinterestratewas4%.
24. Let C=thecircumferenceofthepie.
Thecircumferenceofthepieis28.27in.
25. Let x =numberofminutesitwilltake. 25miles125miles 35minutesminutes
Itwouldtake175minutesor2hours55minutes.
8. Substitute–2foreach x
9. distributiveproperty 10. 824842 12 xyxyxxyy xy
11. 2332 916916 3443 98 25 1212 1 25 12 xxxx xx x
12. 734 73343 77 77 77 1 t t t t t


19. LetA=theareaofthetrampoline.
Theareaofthetrampolineis380.13ft2
20. Let x =amountheearnsafter8hours.
2hours8hours
Heearns$42after8hours.