Solutions for Calculus Early Transcendentals 3rd Us Edition by Briggs by 6alsm

Chapter2

Limits

2.1TheIdeaofLimits

2.1.1 Theaveragevelocityoftheobjectbetweentime t = a and t = b isthechangeinpositiondividedby theelapsedtime: vav = s(b) s(a) b a

2.1.2 Inordertocomputetheinstantaneousvelocityoftheobjectattime t = a,wecomputetheaverage velocityoversmallerandsmallertimeintervalsoftheform[a,t],usingtheformula: vav = s(t) s(a) t a .We let t approach a.Ifthequantity s(t) s(a) t a approachesalimitas t ! a,thenthatlimitiscalledthe instantaneousvelocityoftheobjectattime t = a.

2.1.3 Theaveragevelocityis s(3) s(2) 3 2 =156 136=20.

2.1.4 Theaveragevelocityis s(4) s(1) 4 1 = 144 84 3 = 60 3 =20.

2.1.5

a. s(2) s(0) 2 0 = 72 0 2 =36.

b. s(1.5) s(0) 1.5 0 = 66 0 1.5 =44

c. s(1) s(0) 1 0 = 52 0 1 =52.

d. s(.5) s(0) .5 0 = 30 0 .5 =60.

2.1.6

a. s(2 5) s( 5) 2 5 5 = 150 46 2 =52.

b. s(2) s(.5) 2 5 = 136 46 1 5 =60

c. s(1 5) s( 5) 1 5 5 = 114 46 1 =68.

d. s(1) s(.5) 1 .5 = 84 46 .5 =76.

2.1.7 s(1 01) s(1) 01 =47 84,while s(1 001) s(1) 001 =47 984and s(1 0001) s(1) 0001 =47 9984.Itappears thattheinstantaneousvelocityat t =1isapproximately48.

2.1.8 s(2.01) s(2) .01 = 4 16,while s(2.001) s(2) .001 = 4 016and s(2.0001) s(2) .0001 = 4 0016.Itappears thattheinstantaneousvelocityat t =2isapproximately 4.

2.1.9 Theslopeofthesecantlinebetweenpoints(a,f (a))and(b,f (b))istheratioofthedi↵erences f (b) f (a)and b a.Thus msec = f (b) f (a) b a .

2.1.10 Inordertocomputetheslopeofthetangentlinetothegraphof y = f (t)at(a,f (a)),wecompute theslopeofthesecantlineoversmallerandsmallertimeintervalsoftheform[a,t].Thusweconsider f (t) f (a) t a andlet t ! a.Ifthisquantityapproachesalimit,thenthatlimitistheslopeofthetangent linetothecurve y = f (t)at t = a

2.1.11 Bothproblemsinvolvethesamemathematics,namelyﬁndingthelimitas t ! a ofaquotientof di↵erencesoftheform g (t) g (a) t a forsomefunction g .

2.1.12 Notethat f (2)=64.

a. i. f (0.5)=28.Sotheslopeofthesecantlineis

ii. f (1 9) ⇡ 63 84.Sotheslopeofthesecantlineisabout

iii. f (1 99) ⇡ 63 9984.Sotheslopeofthesecantlineisabout 63 9984 64 1 99 2 =0 16.

iv. f (1.999) ⇡ 63.999984.Sotheslopeofthesecantlineisabout 63 999984 64 1 999 2 =0.016.

v. f (1 9999) ⇡ 63 99999984.Sotheslopeofthesecantlineisabout 63 99999984 64 1 9999 2 =0 0016.

b. Agoodguessisthatthelimitis0.

c. Theslopeofthetangentlineisthelimitoftheslopesofthesecantlines,soitisalso0.

2.1.13

a. Over[1, 4],wehave

b. Over[1, 3],wehave vav = s(3) s(1) 3

c. Over[1, 2],wehave vav = s(2) s(1) 2 1 = 192 112 1 =80.

d. Over[1, 1+ h],wehave

2.1.14

a. Over[0, 3],wehave vav = s(3) s(0) 3 0 = 65.9 20 3 =15 3.

b. Over[0, 2],wehave vav = s(2) s(0) 2 0 = 60.4 20 2 =20 2.

c. Over[0, 1],wehave vav =

d. Over[0,h],wehave

2.1.15

Theslopeofthesecantlineisgivenby s(2) s(0 5) 2 0.5 = 136 46 1.5 =60 Thisrepresents theaveragevelocityoftheobjectoverthetime interval[0.5, 2].

2.1.16

Theslopeofthesecantlineisgivenby s(0 5) s(0) 0.5 0 = 1 0.5 =2 Thisrepresentstheaveragevelocityoftheobjectoverthetimeinterval [0, 0.5].

2.1.17

Theinstantaneousvelocityappearstobe96ft/s.

2.1.18

Theinstantaneousvelocityappearstobe10.4m/s.

2.1.19

Theinstantaneousvelocityappearstobe4ft/s.

2.1.20

Theinstantaneousvelocityappearstobe0ft/s.

2.1.21

TimeInterval [3, 3.1] [3, 3.01] [3, 3.001] [3, 3.0001]

AverageVelocity 17 6 16 16 16 016 16 002

Theinstantaneousvelocityappearstobe 16ft/s.

2.1.22

Theinstantaneousvelocityappearstobe 20ft/s.

2.1.23

Theinstantaneousvelocityappearstobe80ft/s.

2.1.24

AverageVelocity 10 18 1818 19 802 19 98 Theinstantaneousvelocityappearstobe 20ft/s.

2.1.25

Theslopeofthetangentlineappearstobe8. 2.1.26

2.1.27

Theslopeofthetangentlineappearstobe1.

Theslopeofthetangentlineappearstobe2.

2.1.29

a. Notethatthegraphisaparabolawithvertex(2, 1).

b. At(2, 1)thefunctionhastangentlinewith slope0.

Theslopeofthetangentlineat(2, 1)appearstobe0.

2.1.30

a. Notethatthegraphisaparabolawithvertex(0, 4).

b. At(0, 4)thefunctionhasatangentlinewith slope0.

c. Thisistrueforthisfunction–becausethe functionissymmetricaboutthe y -axisand wearetakingpairsofpointssymmetrically aboutthe y axis.Thus f (0+ h)=4 (0+ h)2 =4 ( h)2 = f (0 h).Sotheslopeof anysuchsecantlineis 4 h2 (4 h2 ) h ( h) = 0 2h =0.

2.1.31

a. Notethatthegraphisaparabolawithvertex(4, 448).

b. At(4, 448)thefunctionhastangentlinewith slope0,so a =4.

c. x Interval [4, 4 1] [4, 4 01] [4, 4 001] [4, 4 0001] SlopeoftheSecantLine 1.6 .16 .016 .0016 Theslopesofthesecantlinesappeartobe approachingzero.

d. Ontheinterval[0, 4)theinstantaneousvelocityoftheprojectileispositive.

e. Ontheinterval(4, 9]theinstantaneousvelocityoftheprojectileisnegative.

2.1.32

a. Therockstrikesthewaterwhen s(t)=96.Thisoccurswhen16t2 =96,or t2 =6,whoseonlypositive solutionis t = p6 ⇡ 2.45seconds.

b. t Interval [p6 .1, p6] [p6 .01, p6] [p6 .001, p6] [p6 .0001, p6]

Whentherockstrikesthewater,itsinstantaneousvelocityisabout78.38ft/s.

2.1.33 Forline AD ,wehave

Forline AC ,wehave mAC = yC yA xC xA = f (⇡ /2+ 5) f (⇡ /2) (⇡ /2+ 5) (⇡ /2) = cos(⇡ /2+ 5) 5 ⇡ 0.958851.

Forline AB ,wehave mAB = yB yA xB xA = f (⇡ /2+ 05) f (⇡ /2) (⇡ /2+ 05) (⇡ /2) = cos(⇡ /2+ 05) 05 ⇡ 0 999583

Computingonemoreslopeofasecantline:

sec = f (⇡ /2+ .01) f (⇡ /2) (⇡ /2+ .01) (⇡ /2) = cos(⇡ /2+ .01) .01 ⇡ 0 999983

Conjecture:Theslopeofthetangentlinetothegraphof f at x = ⇡ /2is1.

2.2DeﬁnitionofaLimit

2.2.1 Supposethefunction f isdeﬁnedforall x near a exceptpossiblyat a.If f (x)isarbitrarilyclosetoa number L whenever x issucientlycloseto(butnotequalto) a,thenwewritelim x!a f (x)= L

2.2.2 False.Forexample,considerthefunction f (x)= 8 < : x2 if x =0 4if x =0

Thenlim x!0 f (x)=0,but f (0)=4.

2.2.3

a. h(2)=5

b. lim x!2 h(x)=3

c. h(4)doesnotexist.

d. lim x!4 f (x)=1.

e. lim x!5 h(x)=2.

2.2.5

a. f (1)= 1.

b. lim x!1 f (x)=1.

c. f (0)=2.

d. lim x!0 f (x)=2.

2.2.7

a. x 1.9

f (x)= x2 4 x 2 3.9 3.99

b. lim x!2 f (x)=4.

2.2.4

a. g (0)=0.

b. lim x!0 g (x)=1.

c. g (1)=2.

d. lim x!1 g (x)=2.

2.2.6

a. f (2)=2.

b. lim x!2 f (x)=4.

c. lim x!4 f (x)=4.

d. lim x!5 f (x)=2.

2.2.8

a. x

f (x)= x3 1 x 1

b. lim x!1 x3 1 x 1 =3

2.2.9

a. t

g (t)= t 9 pt 3

b. lim t!9 t 9 pt 3 =6.

2.2.10

a. x 0.01

b. lim x!0(1+ x)1/x ⇡ 2 718.

c. lim x!0(1+ x)1/x = e.

2.2.11 Supposethefunction f isdeﬁnedforall x near a butgreaterthan a.If f (x)isarbitrarilycloseto L for x sucientlycloseto(butstrictlygreaterthan) a,thenwewritelim x!a+ f (x)= L

2.2.12 Supposethefunction f isdeﬁnedforall x near a butlessthan a.If f (x)isarbitrarilycloseto L for x sucientlycloseto(butstrictlylessthan) a,thenwewritelim x!a f (x)= L

2.2.13 Itmustbetruethat L = M .

2.2.14

b. lim x!2 g

2.2.15

f (1)=0.

d. lim x!1 f (x)doesnotexist,sincethetwoone-sidedlimitsaren’tequal.

2.2.16 Becausegraphingutilitiesgenerallyjustplotasamplingofpointsand“connectthedots,”theycan sometimesmisleadtheuserinvestigatingthesubtletiesoflimits.

2.2.17

a. f (1)=3. b. lim x!1 f (x)=2. c. lim x!1+ f (x)=2.

d. lim x!1 f (x)=2. e. f (3)=2.

lim x!3 f (x)=4. g. lim x!3+ f (x)=1.

lim x!3 f (x)doesnotexist. i. f (2)=3. j. lim x!2 f (x)=3.

lim x!2 f (x)=3.

2.2.18 a. g (2)=3.

lim x!2 g (x)=2.

d. lim x!2 g (x)doesnotexist. e. g (3)=2.

lim x!2+ g (x)=3.

lim x!3 g (x)=3. g. lim x!3+ g (x)=2. h. g (4)=3.

2.2.19

f ( 1)=2,lim x!1 f (x)=2,lim x!1+ f (x)=3,lim x!1 f (x)doesnotexist.

2.2.20

f (2)isundeﬁned.lim x!2 f (x)=1,lim x!2+ f (x)=1,andlim x!2 f (x)=1.

lim x!4 g (x)=3.

2.2.21

2.2.22

2.2.25

2.2.26

Fromthegraphandthetable,thelimitappearstobe0.

2.2.28

Fromboththegraphandthetable,thelimitappearstobe2.

2.2.29

(x) 1.993342 1.999933 1.999999 1.999999 1.999933 1.993342

Fromboththegraphandthetable,thelimitappearstobe2.

2.2.30

Fromboththegraphandthetable,thelimitappearstobe3.

2.2.31

x 1 1 1 01 1 001 0 999 0 99 0 9 f (x) 0 9983342 0 9999833 0 9999998 0 9999998 0 9999833 0 9983342

Fromboththegraphandthetable,itappearsthatthelimitdoesnotexist.

2.2.32

)

Fromboththegraphandthetable,itappearsthatthelimitdoesnotexist.

2.2.33

a. False.Infactlim x!3 x2 9 x 3 =lim x!3(x +3)=6.

b. False.Forexample,if f (x)= 8 < : x2 if x =0; 5if x =0 andif a =0then f (a)=5butlim x!a f (x)=0.

c. False.Forexample,thelimitinpartaofthisproblemexists,eventhoughthecorrespondingfunction isundeﬁnedat a =3. Copyright c 2019PearsonEducation,Inc.

d. False.Itistruethatthelimitof px as x approacheszerofromtherightiszero,butbecausethe domainof px doesnotincludeanynumberstotheleftofzero,thetwo-sidedlimitdoesn’texist.

e. True.Notethatlim x!⇡ /2 cos x =0andlim x!⇡ /2 sin x =1,solim x!⇡ /2

2.2.34

a. Notethat H ispiecewiseconstant.

b. lim x!0 H (x)=0,lim x!0+ H (x)=1,andso lim x!0 H (x)doesnotexist.

2.2.35

a. Notethatthefunctionispiecewiseconstant.

b. lim w !2 3 f (w )= 89.

c. lim w !3+ f (w )=1 1correspondstothefact thatforanypieceofmailthatweighsslightly over3ounces,thepostagewillcost$1.1 cents.lim w !3 f (w )=$0 89correspondsto thefactthatforanypieceofmailthatweighs slightlylessthan3ounces,thepostagewill cost89cents.Becausethetwoone-sidedlimitsarenotequal,lim w !3 f (w )doesnotexist.

2.2.36

h)1/h

lim h!0 (1+2h)1/h 2e2+h = 1 2

2.2.37

lim x!⇡ /2 cot3x cos x =3.

lim x!1 18( 3 px 1) x3 1 =2.

2.2.39

18( 3 px 1) x3 1

lim x!1 9p2x x4 3 px 1 x3/4 =16.

2.2.40

6x 3x x ln16

lim x!0 6x 3x x ln16 = 1 4

2.2.41 h 0.01

) h

lim h!0 ln(1+ h) h =1.

2.2.42

4h 1 h ln(h+2)

lim h!0 4h 1 h ln(h +2) =2.

2.2.43

f (x)=sin(1/x) 1 1 1 1 1 1

If xn = 2 (2n+1)⇡ ,then f (xn )=( 1)n where n isanon-negativeinteger.

b. As x ! 0,1/x !1.Sothevaluesof f (x)oscillatedramaticallybetween 1and1.

c. lim x!0 sin(1/x)doesnotexist.

2.2.44

a. x

f (x)=tan(3/x) 1 1 1 1 1 1

Wehavealternating1’sand 1’s.

b. tan3x alternatesbetween1and 1inﬁnitely manytimeson(0,h)forany h> 0.

c. lim x!0 tan(3/x)doesnotexist. 2.2.45

2.2.50

a. Notethat f (x)= |x| x isundeﬁnedat0,and lim x!0 f (x)= 1andlim x!0+ f (x)=1.

b. lim x!0 f (x)doesnotexist,sincethetwoonesidelimitsaren’tequal.

2.2.51

a. lim x!1 bxc = 2,lim x!1+ bxc = 1,lim x!2 bxc =1,lim x!2+ bxc =2.

b. lim x!2 3 bxc =2,lim x!2 3+ bxc =2,lim x!2 3bxc =2.

c. Ingeneral,foraninteger a,lim x!a bxc = a 1andlim x!a+ bxc = a

d. Ingeneral,if a isnotaninteger,lim x!a bxc =lim x!a+ bxc = bac.

e. lim x!a bxc existsandisequalto bac fornon-integers a

2.2.52

a. Notethatthegraphispiecewiseconstant.

b. lim x!2 dxe =2,lim x!1+ dxe =2,lim x!1 5dxe =2.

c. lim x!a dxe existsandisequalto dae fornonintegers a.

2.2.53

a. Becauseofthesymmetryaboutthe y axis,wemusthavelim x!2+ f (x)=8.

b. Becauseofthesymmetryaboutthe y axis,wemusthavelim x!2 f (x)=5. Copyright c 2019PearsonEducation,Inc.

2.2.54

a. Becauseofthesymmetryabouttheorigin,wemusthavelim x!2+ g (x)= 8.

b. Becauseofthesymmetryabouttheorigin,wemusthavelim x!2 g (x)= 5.

2.2.55

2.2.56 a.

lim x!0 sin x x =1.

lim x!0 sin2x x =2.

lim x!0 sin3x x =3.

b. Itappearsthatlim x!0 sin(px) x = p

lim x!0 sin4x x =4.

2.2.57

For p =8and q =2,itappearsthatthelimitis4.

For p =12and q =3,itappearsthatthelimitis4.

For p =4and q =16,itappearsthatthelimitis1/4.

For p =100and q =50,itappearsthatthelimitis2. �

Conjecture:lim x!0 sin px sin qx = p q

2.3TechniquesforComputingLimits

2.3.1 If p(x)=

= an (lim x!a x)n + an 1 (lim x!a x)n 1 + + a1 lim x!a x +lim x!a a0

an an + an 1 an 1 + + a1 a +

= p(a)

2.3.2 lim x!1(x 3 +3x 2 3x +1)=1+3 3+1=2.

2.3.3 Forarationalfunction r (x),wehavelim x!a r (x)= r (a)exactlyforthosenumbers a whichareinthe domainof r .(Whicharethoseforwhichthedenominatorisn’tzero.)

2.3.4 lim x!4 ✓ x2 4x 1 3x 1 ◆ = 16 16 1 12 1 = 1 11 .

2.3.5 Because x 2 7x+12 x 3 = (x 3)(x 4) x 3 = x 4(for x =3),wecanseethatthegraphsofthesetwofunctions arethesameexceptthatoneisundeﬁnedat x =3andtheotherisastraightlinethatisdeﬁnedeverywhere. Thusthefunction x 2 7x+12 x 3 isastraightlineexceptthatithasa“hole”at(3, 1).Thetwofunctionshave thesamelimitas x ! 3,namelylim x!3 x2 7x +12 x 3 =lim x!3(x 4)= 1.

2.3.6 lim x!5 4x2 100 x 5 =lim x!5 4(x 5)(x +5) x 5 =lim x!5 4(x +5)=40.

2.3.7 lim x!1 4f (x)=4lim x!1 f (x)=4 · 8=32.ThisfollowsfromtheConstantMultipleLaw.

2.3.8 lim x!1 f (x) h(x) = lim x!1 f (x) lim x!1 h(x) = 8 2 =4.ThisfollowsfromtheQuotientLaw.

2.3.9 lim x!1(f (x) g (x))=lim x!1 f (x) lim x!1 g (x)=8 3=5.ThisfollowsfromtheDi↵erenceLaw.

2.3.10 lim x!1 f (x)h(x)=lim x!1 f (x) lim x!1 h(x)=8 2=16.ThisfollowsfromtheProductLaw.

2.3.11 lim x!1 f (x) g (x) h(x) = lim x!1 f (x) lim x!1[g (x) h(x)] = lim x!1 f (x) lim x!1 g (x) lim x!1 h(x) = 8 3 2 =8.Thisfollowsfromthe QuotientandDi↵erenceLaws.

2.3.12 lim x!1 3 pf (x)g (x)+3= 3 q lim x!1(f (x)g (x)+3)= 3 q lim x!1 f (x) lim x!1 g (x)+lim x!1 3= 3 p8 3+3= 3 p27= 3.ThisfollowsformtheRoot,Product,SumandConstantLaws.

2.3.13 lim x!1 f (x)2/3 = ⇣ lim x!1 f (x)⌘2/3 =82/3 =22 =4.ThisfollowsfromtheRootandPowerLaws.

2.3.14 If p(x)isapolynomial,thenlim x!a p(x)=lim x!a+ p(x)= p(a).

2.3.15 lim x!0 g (x)=lim x!0(2x +1)=1,while g (0)=5.

2.3.16 lim x!3 f (x)=lim x!3 4=4,andlim x!3+ f (x)=lim x!3+ (x +2)=5.Becausethetwoone-sidedlimitsdi↵er, thetwo-sidedlimitdoesn’texist.

2.3.17 If p and q arepolynomialsthenlim x!0 p(x) q (x) = lim x!0 p(x) lim x!0 q (x) = p(0) q (0) .Becausethisquantityisgiventobe

equalto10,wehave p(0) 2 =10,so p(0)=20.

2.3.18 Byadirectapplicationofthesqueezetheorem,lim x!2 g (x)=5.

2.3.19 lim x!4(3x 7)=3lim x!4 x 7=3 4 7=5.

2.3.20 lim x!1( 2x +5)= 2lim x!1 x +5= 2 · 1+5=3.

2.3.21 lim x!9(5x)=5lim x!9 x =5 · 9= 45.

2.3.22 lim x!6 4=4.

2.3.23 lim x!1(2x 3 3x 2 +4x +5)=lim

2(1)3 3(1)2 +4 1+5=8.

2.3.24 lim t!2(t2 +5t +7)=lim t!2 t2 +lim t!2 5t +lim t!2 7= ✓ lim t!2

2.3.25 lim x!1 5x2 +6x +1 8x 4 = lim x!1(5x 2 +6x +1) lim x!

2.3.26

2.3.30

2.3.31

2.3.32 lim h!0 100 (10h 1)11 +2 = 100 ( 1)11 +2 = 100 1 =100.

2.3.33 lim x!1 x2 1 x 1 =lim x!1 (x +1)(x 1) x 1 =lim x!1(x +1)=2.

2.3.34

2.3.35 lim x!4 x2 16 4 x =lim x!4 (x +4)(x 4) (x 4) =lim x!4[ (x +4)]= 8.

2.3.36 lim t!2 3t2 7t +2 2 t =lim t!2 (t 2)(3t 1) (t 2) =lim t!2[ (3t 1)]= 5.

2.3.37 lim x!b (x b)50 x + b x b =lim x!b (x b)50 (x b) x b =lim x!b (x b)((x b)49 1) x b = lim x!b[(x b)49 1]= 1.

2.3.38 lim x!b (x + b)7 +(x + b)10 4(x + b) =lim x!b (x + b)((x + b)6 +(x + b)9 ) 4(x + b) =lim x!b

2.3.39 lim x!1 (2x 1)2 9 x +1 =lim x!1 (2x 1 3)(2x 1+3) x +1 =lim x!1 2(x 2)2(x +1) x +1 =lim x!1 4(x 2)=4 ( 3)= 12

2.3.40 lim h!0 1 5+h 1 5 h =lim h!

2.3.41

2.3.43

2.3.44 Expandinggives

Nowbecause t 3= (3 t),wehave

2.3.45

2.3.46

) x a = (a + a)(pa + pa)=4a 3/2 .

2.3.47 lim h!0 p16+ h 4 h =lim h!0 (p16+ h 4)(p16+ h +4) h(p16+ h +4) =lim h!0 (16+ h) 16 h(p16+ h +4) =lim h!0 h h(p16+ h +4) =lim h!0 1 (p16+ h +4) = 1 8 .

2.3.48 lim x!c x2 2cx + c2 x c =lim x!c (x c)2 x c =lim x!c x c = c c =0.

2.3.49 lim x!4 1 x 1 4 x 4 =lim x!4 4 x 4x x 4 =lim x!4 4 x 4x(x 4) = lim x!4 1 4x = 1 16

2.3.50 lim x!3 1 x2 +2x 1 15 x 3 =lim x!3 15 (x 2 +2x) 15(x2 +2x) x 3 =lim x!3 15 (x2 +2x) 15(x2 +2x)(x 3) =lim x!3 15 2x x2 15(x2 +2x)(x 3) =lim x!3 (3 x)(5+ x) 15(x2 +2x)(x 3) =lim x!3 (5+ x) 15(x2 +2x) = 8 225 .

2.3.51 lim x!1 p10x 9 1 x 1 =lim x!1 (p10x 9 1)(p10x 9+1) (x 1)(p10x 9+1) =lim x!1 (10x 9) 1 (x 1)(p10x 9+1) =lim x!1 10(x 1) (x 1)(p10x 9+1) =lim x!1 10 (p10x 9+1) = 10 2 =5.

2.3.52 lim x!2 ✓ 1 x 2 2 x2 2x ◆ =lim x!2 ✓ x x(x 2) 2 x(x 2) ◆ =lim x!2 ✓ x 2 x(x 2) ◆ =lim x!2 1 x = 1 2

2.3.53 lim h!0 (5+ h)2 25 h =lim h!0 25+10h + h2 25 h =lim h!0 h(10+ h) h =lim h!0(10+ h)=10.

2.3.54 Wehave lim w !k w 2 +5kw +4k 2 w 2 + kw =lim w !k (w +4k )(w + k ) (w )(w + k ) =lim w !k w +4k w = k +4k k = 3 If k =0,wehavelim w !k w 2 +5kw +4k 2 w 2 + kw =lim w !0 w 2 w 2 =1. Copyright c 2019PearsonEducation,Inc.

2.3.55 lim x!1 x 1 px 1 =lim x!1 (x 1)(px +1) (px 1)(px +1) =lim x!1 (x 1)(px +1) x 1 =lim x!1(px +1)=2.

2.3.56 lim x!1 x 1 p4x +5 3 =lim x!1 (x 1)(p4x +5+3) (p4x +5 3)(p4x +5+3) =lim x!1 (x 1)(p4x +5+3) 4x +5 9 =lim x!1 (x 1)(p4x +5+3) 4(x 1) =lim x!1 (p4x +5+3) 4 = 6 4 = 3 2

2.3.57 lim x!4 3(x 4)px +5 3 px +5 =lim x!4 3(x 4)(px +5)(3+ px +5) (3 px +5)(3+ px +5) =lim x!4 3(x 4)(px +5)(3+ px +5) 9 (x +5) =lim x!4 3(x 4)(px +5)(3+ px +5) (x 4) =lim x!4[ 3(px +5)(3+ px +5)]=( 3)(3)(3+3)= 54

2.3.58 Assume c =0. lim

2.3.59 lim x!0 x cos x =0 1=0.

2.3.60 lim x!0 sin2x sin x =lim x!

2.3.61 lim x!0 1 cos x cos2 x 3cos x +2 =lim x!0 1 cos x (cos x 2)(cos x 1) = lim x!

2.3.62 lim x!0 cos x 1 cos2 x 1 =lim x!0 cos x 1 (cos x 1)(cos x +1) =lim x!0 1 cos x +1 = 1 2

2.3.63 lim x!0 x2 x |x| =lim x!0 x(x 1) x = lim x!0 (x 1)=1.

2.3.64 lim w !3 |w 3| w 2 7w +12 =lim w !3 3 w (w 3)(w

2.3.65 lim t!2+ |2t 4| t2 4 =lim t!2+ 2(t 2) (t 2)(t +2) = 2 4 = 1 2 .

2.3.66 lim x!1 g (x)=lim x!1 x2 1 x +1 =lim x!1 (x +1)(x 1) x +1 =lim x!1 (x 1)= 2.Also,lim x!1+ g (x)= lim x!1+ ( 2)= 2.Therefore,lim x!1 g (x)= 2.

2.3.67 lim x!3+ x 3 |x 3| =lim x!3+ x 3 x 3 =lim x!3+ 1=1.Ontheotherhand,lim x!3 x 3 |x 3| =lim x!3 x 3 3 x = lim x!3 ( 1)= 1.Therefore,lim x!3 x 3 |x 3| doesnotexist. Copyright c 2019PearsonEducation,Inc.

2.3.68 lim x!5+ |x 5| x2 25 =lim x!5+ x 5 (x 5)(x +5) =lim x!5+ 1 x +5 = 1 10 .Ontheotherhand,lim x!5 |x 5| x2 25 = lim x!5 5 x (x 5)(x +5) = lim x!5+ 1 x +5 = 1 10 .Therefore,lim x!5 |x 5| x2 25 doesnotexist.

2.3.69 Becausethedomainof f (x)= x 3 +1 px 1 istheinterval(1, 1),thelimitdoesn’texist.

2.3.70 lim x!1+ x 1 px2 1 =lim x!1+ x 1 (x 1)1/2 (x +1)1/2 =lim x!1+ (x 1)1/2 (x +1)1/2 = 0 p2 =0.

2.3.71

a. False.Forexample,if f (x)= 8 < : x if x =1; 4if x =1, thenlim x!1 f (x)=1but f (1)=4.

b. False.Forexample,if f (x)= 8 < : x +1if x  1; x 6if x> 1, thenlim x!1 f (x)=2butlim x!1+ f (x)= 5.

c. False.Forexample,if f (x)= 8 < : x if x =1; 4if x =1, and g (x)=1,then f and g bothhavelimit1as x ! 1, but f (1)=4 = g (1).

d. False.Forexamplelim x!2 x2 4 x 2 existsandisequalto4.

e. False.Forexample,itwouldbepossibleforthedomainof f tobe[1, 1),sothattheone-sidedlimit existsbutthetwo-sidedlimitdoesn’tevenmakesense.Thiswouldbetrue,forexample,if f (x)= x 1.

2.3.72

a. lim x!4 g (x)=lim x!4 (5x 15)=5.

b. lim x!4+ g (x)=lim x!4+ p6x +1=5.

c. Becausethetwoone-sidedlimitsbothexistandareequalto5,lim x!4 g (x)=5.

2.3.73

a. lim x!1 f (x)=lim x!1 (x 2 +1)=( 1)2 +1=2.

b. lim x!1+ f (x)=lim x!1+ px +1= p 1+1=0.

c. Becausethetwoone-sidedlimitsdi↵er,lim x!1 f (x)doesnotexist.

2.3.74

a. lim x!5 f (x)=lim x!5 0=0

c. lim x!5 f (x)=0.

e. lim x!5+ f (x)=lim x!5+ 3x =15.

2.3.75 Copyright c

b. lim x!5+ f (x)=lim x!5+ p25 x2 = p25 25=0.

d. lim x!5 f (x)=lim x!5 p25 x2 = p25 25=0

f. lim x!5 f (x)doesnotexist.

a. lim x!2+ px 2= p2 2=0.

b. Thedomainof f (x)= px 2is[2, 1).Thus,anyquestionaboutthisfunctionthatinvolvesnumbers lessthan2doesn’tmakeanysense,becausethosenumbersaren’tinthedomainof f .

2.3.76

a. Notethatthedomainof f (x)= q x 3 2 x is(2, 3].lim x!3 r x 3 2 x =0.

b. Becausethenumberstotherightof3aren’tinthedomainofthisfunction,thelimitas x ! 3+ of thisfunctiondoesn’tmakeanysense.

2.3.77 lim x!10 E (x)=lim x!10 4 35 xpx2 +0 01 = 4 35 10p100.01 ⇡ 0.0435N/C.

2.3.78 lim t!200 d(t)=lim t!200 (3 0.015t)2 =(3 (0.015)(200))2 =(3 3)2 =0.Astimeapproaches200 seconds,thedepthofthewaterinthetankisapproaching0.

2.3.79 lim S !0+ r (S )=lim S !0+ (1/2) r100+ 2S ⇡ 10! =0.

Theradiusofthecircularcylinderapproacheszeroasthesurfaceareaapproacheszero.

2.3.80

a. L(c/2)= L0 q1 (c/2)2 c2 = L0 p1 (1/4)= p3L0 /2.

b. L(3c/4)= L0 p1 (1/c2 )(3

c. Itappearsthatthattheobservedlength L oftheshipdecreasesastheshipspeedincreases.

d. lim x!c L0 p1 (⌫ 2 /c2 )= L0 0=0.Asthespeedoftheshipapproachesthespeedoflight,theobserved lengthoftheshipshrinksto0.

2.3.81

a. Thestatementwearetryingtoprovecanbestatedincasesasfollows:For x> 0, x  x sin(1/x)  x, andfor x< 0, x  x sin(1/x) x

Nowforall x =0,notethat 1  sin(1/x)  1(becausetherangeofthesinefunctionis[ 1, 1]). Wewillconsiderthetwocases x> 0and x< 0separately,butineachcase,wewillmultiplythis inequalitythroughby x,switchingtheinequalitiesforthe x< 0case. For x> 0wehave x  x sin(1/x)  x,andfor x< 0wehave x x sin(1/x) x,whichareexactly thestatementswearetryingtoprove.

c. Becauselim x!0 |x| =lim x!0 |x| =0,and because |x|  x sin(1/x)  |x|, theSqueezeTheoremassuresusthat lim x!0[x sin(1/x)]=0aswell.

2.3.82

b. Notethatlim x!0 1 x2 2 =1=lim x!0 1.So because1 x 2 2  cos x  1,thesqueeze theoremassuresusthatlim x!0 cos x =1as well.

2.3.83 a.

b. Notethatlim x!0 1 x2 6 =1=lim x!0 1.So because1 x 2 6  sin x x  1,thesqueeze theoremassuresusthatlim x!0 sin x x =1as well.

2.3.84 a.

b. Notethatlim x!0( |x|)=0=lim x!0 |x|.So because |x|  x2 ln x2  |x|,thesqueeze theoremassuresusthatlim x!0(x 2 ln x 2 )=0 aswell.

2.3.85 Usingthedeﬁnitionof |x| given,wehavelim x!0 |x| =lim x!0 ( x)= 0=0.Also,lim x!0+ |x| =lim x!0+ x = 0.Becausethetwoone-sidedlimitsareboth0,wealsohavelim x!0 |x| =0.

2.3.86

If a> 0,thenfor x near a, |x| = x.Sointhiscase,lim x!a |x| =lim x!a x = a = |a| If a< 0,thenfor x near a, |x| = x.Sointhiscase,lim x!a |x| =lim x!a ( x)= a = |a|,(because a< 0).

If a =0,wehavealreadyseeninapreviousproblemthatlim x!0 |x| =0= |0|

Thusinallcases,lim x!a |x| = |a|.

2.3.87 lim x!3 f (x)=lim x!3 x2 5x +6 x 3 =lim x!3 (x 3)(x 2) x 3 =lim x!3(x 2)=1.So a =1.

2.3.88 Inorderforlim x!2 f (x)toexist,weneedthetwoone-sidedlimitstoexistandbeequal.Wehave lim x!2 f (x)=lim x!2 (3x + b)=6+ b,andlim x!2+ f (x)=lim x!2+ (x 2)=0.Soweneed6+ b =0,sowerequire that b = 6.Thenlim x!2 f (x)=0.

2.3.89 Inorderforlim x!1 g (x)toexist,weneedthetwoone-sidedlimitstoexistandbeequal.Wehave lim x!1 g (x)=lim x!1 (x 2 5x)=6,andlim x!1+ g (x)=lim x!1+ (ax 3 7)= a 7.Soweneed a 7=6,so werequirethat a = 13.Thenlim x!1 f (x)=6.

2.3.90 lim x!2 x5 32 x 2 =lim x!2 (x 2)(x4 +2x3 +4x2 +8x +16) x 2 =lim x!2(x 4 +2x 3 +4x 2 +8x +16)=16+16+ 16+16+16=80.

2.3.91 lim x!1 x6 1 x 1 =lim x!1 (

2.3.92 lim x!1 x7 +1 x

2.3.94

2.3.95

b. Theslopeofthesecantlinebetween(0, 1) and(x, 2x )is 2x 1 x

2.3.96

2.3.98

b. Theslopeofthesecantlinebetween(0, 1) and(x, 3x )is 3x 1 x

2.3.101 Let f (x)= x 1and g (x)= 5 x 1 .Thenlim x!1 f (x)=0,lim x!1

2.3.102 Let f (x)= x2 1.Thenlim x!1 f (x) x 1 =lim x!1 x2 1 x 1 =lim x!1(x +1)=2.

2.3.103 Let p(x)= x2 +2x 8.Thenlim x!2 p(x) x 2 =lim x!2 (x 2)(x +4) x 2 =lim x!2(x +4)=6.

Theconstantsareunique.Weknowthat2mustbearootof p (otherwisethegivenlimitcouldn’t exist),soitmusthavetheform p(x)=(x 2)q (x),and q mustbeadegree1polynomialwithleading coecient1(otherwise p wouldn’thaveleadingcoecient1.)Sowehave p(x)=(x 2)(x + d),butbecause lim x!2 p(x) x 2 =lim x!2(x + d)=2+ d =6,weareforcedtorealizethat d =4.Therefore,wehavededucedthat theonlypossibilityfor p is p(x)=(x 2)(x +4)= x2 +2x 8.

2.3.104 Becauselim x!1 f (x)=4,weknowthat f isnear4when x isnear1(butnotequalto1).Itfollows thatlim x!1 f (x 2 )=4aswell,becausewhen x isnearbutnotequalto 1, x2 isnear1butnotequalto1. Thus f (x2 )isnear4when x isnear 1.

2.3.105 As x ! 0+ ,(1 x) ! 1 .Solim x!0+ g (x)=lim (1 x)!1 f (1 x)=lim z !1 f (z )=6. (Where z =1 x.)

As x ! 0 ,(1 x) ! 1+ .Solim x!0 g (x)=lim (1 x)!1+ f (1 x)=lim z !1+ f (z )=4. (Where z =1 x.)

2.3.106

a. Suppose0 < ✓ < ⇡ /2.Notethatsin ✓ > 0,so | sin ✓ | =sin ✓ .Also,sin ✓ = |AC | 1 ,so |AC | = | sin ✓ |

Nowsupposethat ⇡ /2 < ✓ < 0.Thensin ✓ isnegative,so | sin ✓ | = sin ✓ .Wehavesin ✓ = |AC | 1 , so |AC | = sin ✓ = | sin ✓ |

b. Suppose0 < ✓ < ⇡ /2.Because AB isthehypotenuseoftriangle ABC ,weknowthat |AB | > |AC | Wehave | sin ✓ | = |AC | < |AB | < thelengthofarc AB = ✓ = |✓ | If ⇡ /2 < ✓ < 0,wecanmakeasimilarargument.Wehave | sin ✓ | = |AC | < |AB | < thelengthofarc AB = ✓ = |✓ |

c. If0 < ✓ < ⇡ /2,wehavesin ✓ = | sin ✓ | < |✓ |,andbecausesin ✓ ispositive,wehave |✓ |  0 < sin ✓ Puttingthesetogethergives |✓ | < sin ✓ < |✓ |

If ⇡ /2 < ✓ < 0,then | sin ✓ | = sin ✓ .Fromthepreviouspart,wehave | sin ✓ | = sin ✓ < |✓ |. Therefore, |✓ | < sin ✓ .Nowbecausesin ✓ isnegativeonthisinterval,wehavesin ✓ < 0  |✓ |.Putting thesetogethergives |✓ | < sin ✓ < |✓ |.

d. If0 < ✓ < ⇡ /2,wehave

0  1 cos ✓ = |OB | |OC | = |BC | < |AB | < thelengthofarc AB = ✓ = |✓ |

For ⇡ /2 < ✓ < 0,wehave

0  1 cos ✓ = |OB | |OC | = |BC | < |AB | < thelengthofarc AB = ✓ = |✓ |.

e. Usingtheresultofpartd,wemultiplythroughby 1toobtain |✓ |  cos ✓ 1  0,andthenadd1 toallparts,obtaining1 |✓ |  cos ✓  1,asdesired.

2.3.107

2.4InﬁniteLimits

2.4.1 As x approaches a fromtheright,thevaluesof f (x)arenegativeandbecomearbitrarilylargein magnitude.

2.4.2 As x approaches a (fromeitherside),thevaluesof f (x)arepositiveandbecomearbitrarilylargein magnitude.

2.4.3 Averticalasymptoteforafunction f isaverticalline x = a sothatoneormoreofthefollowingare true:lim x!a f (x)= ±1,lim x!a+ f (x)= ±1

2.4.4 No.Forexample,if f (x)= x2 4and g (x)= x 2and a =2,wewouldhavelim x!2 f (x) g (x) =4,even though g (2)=0. Copyright c

2.4.5

Fromthedatagiven,itappearsthatlim x!1 f (x)= 1

2.4.6

2.4.7

lim x!2 f (x)doesnotexist.

2.4.8

lim x!4 g (x)= 1

2.4.9

x!4+ g (x)= 1

lim x!4 g (x)= 1

a. lim x!2 h(x)= 1 b. lim x!2+ h(x)= 1. c. lim x!2 h(x)= 1 d. lim x!3 h(x)= 1. e. lim x!3+ h(x)= 1. f. lim x!3 h(x)doesnotexist.

2.4.10

a. lim x!2 p(x)= 1 b. lim x!2+ p(x)= 1 c. lim x!2 p(x)= 1

d. lim x!3 p(x)= 1. e. lim x!3+ p(x)= 1. f. lim x!3 p(x)= 1.

2.4.11

a. lim x!0 1 x2 x = 1.

b. lim x!0+ 1 x2 x = 1.

c. lim x!1 1 x2 x = 1.

d. lim x!1+ 1 x2 x = 1. - �� - �� - �� - � � �

2.4.12

a. lim x!2+ e x x(x +2)2 = 1

b. lim x!2 e x x(x +2)2 = 1.

c. lim x!0 e x x(x +2)2 = 1

d. lim x!0+ e x x(x +2)2 = 1.

2.4.13 Becausethenumeratorisapproachinganon-zeroconstantwhilethedenominatorisapproaching zero,thequotientofthesenumbersisgettingbig–atleasttheabsolutevalueofthequotientisgettingbig. Thequotientisactuallyalwaysnegative,becauseanumbernear100dividedbyanegativenumberisalways negative.Thuslim x!2 f (x) g (x) = 1.

2.4.14 Usingthesamesortofreasoningasinthelastproblem–as x ! 3thenumeratorisﬁxedat1,but thedenominatorisgettingsmall,sothequotientisgettingbig.Itremainstoinvestigatethesignofthe quotient.As x ! 3 ,thequantity x 3isnegative,sothequotientofthepositivenumber1andthissmall negativenumberisnegative.Ontheotherhand,as x ! 3+ ,thequantity x 3ispositive,sothequotient of1andthisnumberispositive.Thus:lim x!3 1 x 3 = 1,andlim x!3+ 1 x 3 = 1

2.4.15 Notethatlim x!1 x2 4x +3 x2 3x +2 =lim

2 1 =2.Sothereis not avertical asymptoteat x =1.Ontheotherhand,lim x!2+ x2 4x +3 x2 3x +2 =lim x!2+ (x 3)(x 1) (x 2)(x 1) =lim x!2+ x 3 x 2 = 1,so thereisaverticalasymptoteat x =2.

2.4.16 Notetheat x ! 0thenumeratorhaslimit1whilethedenominatorhaslimit0,sothequotientis growingwithoutbound.Notealsothatthedenominatorisalwayspositive,becauseforall x,cos x  1so 1 cos x 0.

2.4.17

2.4.19 Both a and b aretruestatements.

2.4.20 Both a and c aretruestatements. Copyright c

2.4.21

a. lim x!2+ 1 x 2 = 1

b. lim x!2 1 x 2 = 1

c. lim x!2 1 x 2 doesnotexist.

2.4.22

a. lim x!3+ 2 (x 3)3 = 1

b. lim x!3 2 (x 3)3 = 1.

c. lim x!3 2 (x 3)3 doesnotexist.

2.4.23

a. lim x!4+ x 5 (x 4)2 = 1

b. lim x!4 x 5 (x 4)2 = 1

c. lim x!4 x 5 (x 4)2 = 1

2.4.24

a. lim x!1+ x |x 1| = 1

b. lim x!1 x |x 1| = 1.

c. lim x!1 x |x 1| = 1

2.4.25

a. lim x!3+ (x 1)(x 2) (x 3) = 1.

b. lim x!3 (x 1)(x 2) (x 3) = 1

c. lim x!3 (x 1)(x 2) (x 3) doesnotexist.

2.4.26

a. lim x!2+ (x 4) x(x +2) = 1

b. lim x!2 (x 4) x(x +2) = 1

c. lim x!2 (x 4) x(x +2) doesnotexist.

2.4.27

a. lim x!2+ x2 4x +3 (x 2)2 = 1.

b. lim x!2 x2 4x +3 (x 2)2 = 1

c. lim x!2 x2 4x +3 (x 2)2 = 1

2.4.28

a. lim x!2+ x3 5x2 +6x x4 4x2 =lim x!2+ x(x 2)(x 3) x2 (x 2)(x +2) =lim x!2+ x 3 x(x +2) = 1

b. lim x!2 x3 5x2 +6x x4 4x2 =lim x!2 x(x 2)(x 3) x2 (x 2)(x +2) =lim x!2 x 3 x(x +2) = 1

c. Becausethetwoone-sidedlimitsdi↵er,lim x!2 x3 5x2 +6x x4 4x2 doesnotexist.

d. lim x!2 x3 5x2 +6x x4 4x2 =lim x!2 x 3 x(x +2) = 1 8

2.4.29

a. lim x!2+ 1 px(x 2) = 1.

b. lim x!2 1 px(x 2) doesnotexist.Notethatthedomainofthefunctionis(1, 0) [ (2, 1).

c. lim x!2 1 px(x 2) doesnotexist.

2.4.30

a. lim x!1+ x 3 px2 5x +4 doesnotexist.Notethat x2 5x +4=(x 4)(x 1)sothedomainofthefunction is(1, 1) [ (4, 1).

b. ]lim x!1 x 3 px2 5x +4 = 1

c. lim x!1 x 3 px2 5x +4 doesnotexist.

2.4.31

a. lim x!0 x 3 x4 9x2 =lim x!0 x 3 x2 (x 3)(x +3) =lim x!0 1 x2 (x +3) = 1

b. lim x!3 x 3 x4 9x2 =lim x!3 x 3 x2 (x 3)(x +3) =lim x!3 1 x2 (x +3) = 1 54

c. lim x!3 x 3 x4 9x2 =lim x!3 x 3 x2 (x 3)(x +3) =lim x!3 1 x2 (x +3) ,whichdoesnotexist.

2.4.32

a. lim x!0 x 2 x5 4x3 =lim x!0 x 2 x3 (x 2)(x +2) =lim x!0 1 x3 (x +2) ,whichdoesnotexist.

b. lim x!2 x 2 x5 4x3 =lim x!2 x 2 x3 (x 2)(x +2) =lim x!2 1 x3 (x +2) = 1 32

c. lim x!2 x 2 x5 4x3 =lim x!2 x 2 x3 (x 2)(x +2) =lim x!2 1 x3 (x +2) ,whichdoesnotexist.

2.4.33 lim x!0 x3 5x2 x2 =lim x!0 x2 (x 5) x2 =lim x!0(x 5)= 5.

2.4.34 lim t!5 4t2 100 t 5 =lim t!5 4(t 5)(t +5) t 5 =lim t!5[4(t +5)]=40.

2.4.35 lim x!1+ x2 5x +6 x 1 =lim x!1+ (x 2)(x 3) x 1 = 1.(Notethatas x ! 1+ ,thenumeratorisnear2,while thedenominatorisnearzero,butispositive.Sothequotientispositiveandlarge.)

2.4.36 lim z !4 z 5 (z 2 10z +24)2 =lim z !4 z 5 (z 4)2 (z 6)2 = 1.(Notethatas z ! 4,thenumeratorisnear 1 whilethedenominatorisnearzerobutispositive.Sothequotientisnegativewithlargeabsolutevalue.)

2.4.37 lim x!6+ x 7 px 6 = 1.(Notethatas x ! 6+ thenumeratorisnear 1andthedenominatorisnear zerobutispositive.Sothequotientisnegativewithlargeabsolutevalue.)

2.4.38 lim x!2 x 1 p(x 3)(x 2) = 1.Notethatas x ! 2 thenumeratorisnear1andthedenominatoris nearzerobutispositive.Sothequotientispositivewithlargeabsolutevalue.)

2.4.39 lim ✓ !0+ csc ✓ =lim ✓ !0+ 1 sin ✓ = 1

2.4.40 lim x!0 csc x =lim x!0 1 sin x = 1.

2.4.41 lim x!0+ 10cot x =lim x!0+ 10cos x sin x = 1.(Notethatas x ! 0+ ,thenumeratorisnear 10andthe denominatorisnearzero,butispositive.Thusthequotientisanegativenumberwhoseabsolutevalueis large.)

2.4.42 lim ✓ !(⇡ /2)+ 1 3 tan ✓ =lim ✓ !(⇡ /2)+ sin ✓ 3cos ✓ = 1.(Notethatas ✓ ! (⇡ /2)+ ,thenumeratorisnear1and thedenominatorisnear0,butisnegative.Thusthequotientisanegativenumberwhoseabsolutevalueis large.)

2.4.43 lim ✓ !0 2+sin ✓ 1 cos2 ✓ = 1.(Notethatas ✓ ! 0,thenumeratorisnear2andthedenominatorisnear0, butispositive.Thusthequotientisapositivenumberwhoseabsolutevalueislarge.)

2.4.44 lim ✓ !0 sin ✓ cos2 ✓ 1 =lim ✓ !0 sin ✓ sin2 ✓ = lim ✓ !0 1 sin ✓ = 1

2.4.45

a. lim x!5 x 5 x2 25 =lim x!5 1 x +5 = 1 10 ,sothereisn’taverticalasymptoteat x =5.

b. lim x!5 x 5 x2 25 =lim x!5 1 x +5 = 1,sothereisaverticalasymptoteat x = 5.

c. lim x!5+ x 5 x2 25 =lim x!5+ 1 x +5 = 1.Thisalsoimpliesthat x = 5isaverticalasymptote,aswe alreadynotedinpartb.

2.4.46

a. lim x!7 x +7 x4 49x2 =lim x!7 x +7 x2 (x +7)(x 7) =lim x!7 1 x2 (x 7) = 1,sothereisaverticalasymptote at x =7.

b. lim x!7+ x +7 x4 49x2 =lim x!7+ x +7 x2 (x +7)(x 7) =lim x!7+ 1 x2 (x 7) = 1.Thisalsoimpliesthatthereisa verticalasymptoteat x =7,aswealreadynotedinparta.

c. lim x!7 x +7 x4 49x2 =lim x!7 x +7 x2 (x +7)(x 7) =lim x!7 1 x2 (x 7) = 1 686 .Sothereisnotavertical asymptoteat x =7.

d. lim x!0 x +7 x4 49x2 =lim x!0 x +7 x2 (x +7)(x 7) =lim x!0 1 x2 (x 7) = 1.Sothereisaverticalasymptoteat x =0.

2.4.47 f (x)= x2 9x +14 x2 5x +6 = (x 2)(x 7) (x 2)(x 3) .Notethat x =3isaverticalasymptote,while x =2appears tobeacandidatebutisn’tone.Wehavelim x!3+ f (x)=lim x!3+ x 7 x 3 = 1 andlim x!3 f (x)=lim x!3 x 7 x 3 = 1, andthuslim x!3 f (x)doesn’texist.Notethatlim x!2 f (x)=5.

2.4.48 f (x)= cos x x(x +2) hasverticalasymptotesat x =0andat x = 2.Notethatcos x isnear1 when x isnear0,andcos x isnear 0 4when x isnear 2.Thus,lim x!0+ f (x)=+1,lim x!0 f (x)= 1, lim x!2+ f (x)= 1,andlim x!2 f (x)= 1

2.4.49 f (x)= x +1 x3 4x2 +4x = x +1 x(x 2)2 .Thereareverticalasymptotesat x =0and x =2.Wehave

lim x!0 f (x)=lim x!0 x +1 x(x 2)2 = 1,whilelim x!0+ f (x)=lim x!0+ x +1 x(x 2)2 = 1,andthuslim x!0 f (x)doesn’t exist.

Alsowehavelim x!2 f (x)=lim x!2 x +1 x(x 2)2 = 1,whilelim x!2+ f (x)=lim x!2+ x +1 x(x 2)2 = 1,andthus lim x!2 f (x)= 1 aswell.

2.4.50 g (x)= x3 10x2 +16x x2 8x = x(x 2)(x 8) x(x 8) .Thisfunctionhasnoverticalasymptotes.

2.4.51

a. lim x!(⇡ /2)+ tan x = 1.

b. lim x!(⇡ /2) tan x = 1

c. lim x!( ⇡ /2)+ tan x = 1

d. lim x!( ⇡ /2) tan x = 1.

2.4.52

2.4.53

a. lim x!(⇡ /2)+ sec x tan x = 1

b. lim x!(⇡ /2) sec x tan x = 1.

c. lim x!( ⇡ /2)+ sec x tan x = 1

d. lim x!( ⇡ /2) sec x tan x = 1

a. False.lim x!

b. True.Forexample,lim

c. False.Forexample

2.4.54

2.4.55 Weareseekingafunctionwithafactorof x 1inthedenominator,butthereshouldbemorefactors of x 1inthenumerator,andthereshouldbeafactorof(x 2)2 inthedenominator.Thiswillaccomplish thedesiredresults.So

2.4.56

2.4.57 Oneexampleis f (x)= 1 x 6

2.4.58 f (x)= x2 1 (x2 1)(x2 +1) = 1 x2 +1 (for x = ±1).Therearenoverticalasymptotes,becauseforall a,

lim x!a f (x)= 1 a2 +1 .

2.4.59 f (x)= x2 3x +2 x10 x9 = (x 2)(x 1) x9 (x 1) f hasaverticalasymptoteat x =0,becauselim x!0+ f (x)= 1 (andlim x!0 f (x)= 1.)Notethatlim x!1 f (x)= 1,sothereisn’taverticalasymptoteat x =1.

2.4.60 g (x)=2 ln x2 hasaverticalasymptoteat x =0,becauselim x!0(2 ln x 2 )= 1

2.4.61 h(x)= ex (x +1)3 hasaverticalasymptoteat x = 1,because lim x!1+ ex (x +1)3 = 1 andlim x!1 h(x)= 1

2.4.62 p(x)=sec(⇡ x/2)= 1 cos(⇡ x/2) hasaverticalasymptoteon( 2, 2)at x = ±1.

2.4.63 g (✓ )=tan(⇡✓ /10)= sin(⇡✓ /10) cos(⇡✓ /10) hasaverticalasymptoteateach ✓ =10n +5where n isaninteger. Thisisduetothefactthatcos(⇡✓ /10)=0when ⇡✓ /10= ⇡ /2+ n⇡ where n isaninteger,whichisthesame as {✓ : ✓ =10n +5,n aninteger}.Notethatatallofthesenumberswhichmakethedenominatorzero,the numeratorisn’tzero.

2.4.64 q (s)= ⇡ s sin s hasaverticalasymptoteat s =0.Notethatthisistheonlynumberwheresin s = s.

2.4.65 f (x)= 1 px sec x = cos x px hasaverticalasymptoteat x =0.

2.4.66 g (x)= e1/x hasaverticalasymptoteat x =0,becauselim x!0+ e 1/x = 1.(Notethatas x ! 0+ , 1/x !1,so e1/x !1 aswell.)

2.4.67

a. Notethatthenumeratorofthegivenexpressionfactorsas(x 3)(x 4).Soif a =3orif a =4the limitwouldbeaﬁnitenumber.Infact,lim x!3 (x 3)(x 4) x 3 = 1andlim x!4 (x 3)(x 4) x 4 =1.

b. Foranynumberotherthan3or4,thelimitwouldbeeither ±1.Because x a isalwayspositive as x ! a+ ,thelimitwouldbe+1 exactlywhenthenumeratorispositive,whichisfor a intheset (1, 3) [ (4, 1).

c. Thelimitwouldbe 1 for a intheset(3, 4).

2.4.68

a. Theslopeofthesecantlineisgivenby f (h) f (0) h = h1/3 h = h 2/3

b. lim h!0 1 3 ph2 = 1.Thistellsusthattheslopeofthetangentlineisinﬁnite–whichmeansthatthe tangentlineat(0, 0)isvertical.

2.4.69

a. Theslopeofthesecantlineis f (h) f (0) h = h2/3 h = h 1/3 .

b. lim h!0+ 1 h1/3 = 1,andlim h!0 1 h1/3 = 1.Thetangentlineisinﬁnitelysteepattheorigin(i.e.,itisa verticalline.)

2.5LimitsatInﬁnity

2.5.1 As x< 0becomesarbitrarilylargeinabsolutevalue,thecorrespondingvaluesof f approach10.

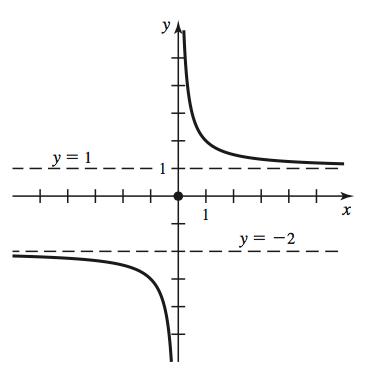
2.5.2 lim x!1 f (x)= 2andlim x!1 f (x)=4.

2.5.3 lim x!1 x 12 = 1.Notethat x12 ispositivewhen x> 0.

2.5.4 lim x!1 3x 11 = 1.Notethat x11 isnegativewhen x< 0.

2.5.5 lim x!1 x 6 =lim x!1 1 x6 =0.

2.5.6 lim x!1 x 11 =lim x!1 1 x11 =0.

2.5.7 lim t!1 ( 12t 5 )=lim t!1 12 t5 =0.

2.5.8 lim x!1 2x 8 =lim x!1 2 x8 =0.

2.5.9 lim x!1 (3+10/x2 )=3+lim x!1 (10/x2 )=3+0=3.

2.5.10 lim x!1 (5+1/x +10/x2 )=5+lim x!1 (1/x)+lim x!1 (10/x2 )=5+0+0=5.

2.5.11 If f (x) ! 100, 000as x !1 and g (x) !1 as x !1,thentheratio f (x) g (x) ! 0as x !1.(Because eventually thevaluesof f aresmallcomparedtothevaluesof g .)

2.5.12 lim x!1 3+2x +4x2 x2 =lim x!1 3 x2 +lim x!1 2x x2 +lim x!1 4x2 x2 =0+lim x!1 2 x +lim x!1 4=0+0+4=4

2.5.13 lim t!1 e t = 1,lim t!1 e t =0,andlim t!1 e t =0.

2.5.14 As x !1,wenotethat e 2x ! 0,whileas x !1,wehave e 2x !1

2.5.15 Becauselim x!1 3 1 x2 =3andlim x!1 3+ 1 x2 =3,bytheSqueezeTheoremwemusthavelim x!1 g (x)=3. Similarly,becauselim x!1 3 1 x2 =3andlim x!1 3+ 1 x2 =3,bytheSqueezeTheoremwemusthave lim x!1 g (x)=3.

2.5.16 lim x!1 g (x)=3,lim x!1 g (x)= 1,lim x!2 g (x)= 1,lim x!2+ g (x)= 1.

2.5.17 lim ✓ !1 cos ✓ ✓ 2 =0 Notethat 1  cos ✓  1,so 1 ✓ 2  cos ✓ ✓ 2  1 ✓ 2 .Theresultnowfollowsfromthe SqueezeTheorem.

2.5.18 Notethat 5t2 + t sin t t2 canbewrittenas5+ sin t t .Also,notethatbecause 1  sin t  1,wehave 1 t  sin t t  1 t ,so sin t t ! 0as t !1 bytheSqueezeTheorem.Therefore, lim t!1 5t2 + t sin t t2 =lim t!1 ✓5+ sin t t ◆ =5+0=5.

2.5.19 lim x!1 cos x5 px =0.Notethat 1  cos x5  1,so 1 px  cos x 5 px  1 px .Becauselim x!1 1 px =lim x!1 1 px = 0,wehavelim x!1 cos x5 px =0bytheSqueezeTheorem.

2.5.20 lim x!1 ✓5+ 100 x + sin4 (x3 ) x2 ◆ =5+0+0=5.Forthislastlimit,notethat0  sin4 (x3 )  1,so

0  sin4 (x3 ) x2  1 x2 .TheresultnowfollowsfromtheSqueezeTheorem.

2.5.21 lim x!1 (3x 12 9x 7 )= 1.

2.5.22 lim x!1 (3x 7 + x 2 )= 1

2.5.23 lim x!1 ( 3x 16 +2)= 1.

2.5.24 lim x!1 (2x 8 +4x 3 )=0+lim x!1 4x 3 = 1

2.5.25 lim x!1 (14x3 +3x2 2x) (21x3 + x2 +2x +1) · 1/x3 1/x3 =lim x!1 14+(3/x) (2/x2 ) 21+(1/x)+(2/x2 )+(1/x3 ) = 14 21 = 2 3

2.5.26 lim x!1 (9x3 + x2 5) (3x4 +4x2 ) 1/x4 1/x4 =lim x!1 (9/x)+(1/x2 ) (5/x4 ) 3+(4/x2 ) = 0 3 =0.

2.5.27 lim x!1 (3x2 +3x) (x +1) 1/x 1/x =lim x!1 3x +3 1+(1/x) = 1.

2.5.28 lim x!1 (x4 +7) (x5 + x2 x) · 1/x5 1/x5 =lim x!1 (1/x)+(7/x5 ) 1+(1/x3 ) (1/x4 ) = 0+0 1+0 0 =0

2.5.29 Notethatfor w> 0, w 2 = pw 4 .Wehave lim w !1 (15w 2 +3w +1) p9w 4 + w 3 1/w 2 1/pw 4 =lim w !1 15+(3/w )+(1/w 2 ) p9+(1/w ) = 15 p9 =5

2.5.30 Notethat px8 = x4 (evenfor x< 0).Wehave lim x!1 (40x4 + x2 +5x) p64x8 + x6 · 1/x4 1/px8 =lim x!1 40+(1/x2 )+(5/x3 )

2.5.31 Notethatfor x< 0, px2 = x.Wehave lim x!1 p16x2 + x x p1/x2 1/x

2.5.32 Notethat x2 = px4 forall x.Wehave

2.5.33 lim x!1

dividethenumeratoranddenominatorby x2 togive

2.5.34 lim x!1 (x + px2 5x) 1 (x px2 5x) (x px2 5x) =lim x!1 x2 (x2 5x) x px2 5x =lim x!1 5x x px2 5x Nowdivide thenumeratoranddenominatorby x (andrecallthatfor x< 0wehave px2 = x)giving

2.5.35 Notethatbecause 1  sin x  1,wehave 1 ex  sin x ex  1 ex .Thenbecauselim x!1 ±1 ex =0,the SqueezeTheoremtellsusthatlim x!1 sin x ex =0.

2.5.36 Notethatbecause 1  cos x  1,wehave

x cos

x .Then3 ex 

x +3  ex +3. Becauselim x!1 3 ex =3andlim x!1 ex +3=3,theSqueezeTheoremtellsusthatlim x!1 ex cos x +3=3.

2.5.37 lim x!1 4x 20x +1 =lim x!1 4x 20

asymptote.

.Thisshowsthatthecurveisalso asymptotictotheasymptoteinthenegativedirection.

2.5.38 lim x

horizontalasymptote.

asymptotictotheasymptoteinthenegativedirection.

2.5.39 lim x!1 (6x2 9x +8) (3x2 +2) ·

=3.Thus,theline

=2.Similarlylim x!1 f (x)=2.The line y =2isahorizontalasymptote.

2.5.40 lim x!1 (12x8 3) (3x8 2x7 ) · 1/x8 1/x8 =lim x!1 12 3/x8 3 2/x = 12 0 3 0 =4.Similarlylim x!1 f (x)=4.Theline y =4 isahorizontalasymptote.

2.5.41 lim x!1 3x3 7 x4 +5x2 =lim x!1 3x3 7 x4 +5x2 3/x4 1/x4 =lim x!1 1/x (7/x4 ) 1+(5/x2 ) = 0 0 1+0 =0.Thus,theline y =0(the x-axis)isahorizontalasymptote. lim x!1 3x3 7 x4 +5x2 =lim x!1 3x3 7 x4 +5x2 · 3/x4 1/x4 =lim x!1 1/x (7/x4 ) 1+(5/x2 ) = 0 0 1+0 =0.Thus,thecurveis asymptotictothe x-axisinthenegativedirectionaswell.

2.5.42 lim x!1 (2x +1) (3x4 2) 1/x4 1/x4 =lim x!1

3 +1/x4 3

= 0+0 3

=0.Similarlylim x!1 f (x)=0.Theline y =0is ahorizontalasymptote.

2.5.43 lim x!1 (40x5 + x2 ) (16x4 2x) 1/x4 1/x4 =lim x!1 40x +1/x2 16 2/x3 = 1.Similarlylim x!1 f (x)= 1.Thereareno horizontalasymptotes.

2.5.44 Notethatforall x, px4 = x2 .Then lim x!±1 (6x2 +1) p4x4 +3x +1 1/x2 p1/x4 =lim x!±1 6+(1/x2 ) p4+(3/x3 )+(1/x4 ) = 6 p4 =3 So y =3istheonlyhorizontalasymptote. Copyright c 2019PearsonEducation,Inc.

2.5.45 Notethatforall x, px8 = x4 .Thenlim x!±1 1 (2x4 p4x8 9x4 (2x4 + p4x8 9x4 ) (2x4 + p4x8 9x4 ) =lim x!±1 (2x4 + p4x8 9x4 ) (4x

So y = 4 9 istheonlyhorizontalasymptote.

2.5.46 Firstnotethat px2 = x for x> 0,while px2 = x for x< 0.Thenlim x!1 f (x)canbewrittenas

However,lim x!1 f (x)canbewrittenas

2.5.47 Firstnotethat px6 = x3 if x> 0,but px6 = x3 if x< 0.Wehavelim x!1 4x3 +1 (2x3 + p16x6 +1)

. However,lim x!1 4x3 +1 (2x3 + p16

2 = 2. So y = 2 3 isahorizontalasymptote(as x !1)and y = 2isahorizontalasymptote(as x !1).

2.5.48 Firstnotethatfor x> 0wehave px2 = x,butfor x< 0,wehave x = px2 .Thenwehavelim x!1 x px2 9x =lim x!1 (x px2 9x)(

Ontheotherhand,lim x!1 x px2 9x =lim x!1 (x px2 9x)(x + px2 9x) x + px2 9x = lim x!1 9x (x + px2 9x) 1/x 1/x =lim x!1 9 1+ p1 9/x = 1. Thelastequalsignfollowsbecause p1 9/x> 1butisapproaching1as x !1.Wecanthereforeconcludethat y = 9 2 istheonlyhorizontal asymptote,andisanasymptoteas x !1

2.5.49 Firstnotethat 3 px6 = x2 and px4 = x2 forall x (evenwhen x< 0.)Wehavelim x!1 3 px6 +8 (4x2 + p3x4 +1) 1/x2 1/x2 =lim x!1 3 p1+8/x6 4+ p3+1/x4 = 1 4+ p3+0 = 1 4p3 Thecalculationas x !1 issimilar.So y = 1 4p3 isahorizontalasymptote.

2.5.50 Firstnotethat px2 = x for x> 0and px2 = x for x< 0. Wehave lim x!1 4x(3x p9x2 +1)=lim x!1 4x(3x p9x2 +1)(3x + p9x2 +1) 3x + p9x2 +1 =lim x!1 (4x)( 1) (3x + p9x2 +1) 1/x 1/x =lim x!1 4 3+ p9+1/x2 = 4 6 = 2 3 Copyright c 2019PearsonEducation,Inc.

Moreover,as x !1 wehave lim x!1 4x(3x p9x2 +1)=lim x!1 4x(3x p9x2 +1)(3x + p9x2 +1) 3x + p9x2 +1 =lim x!1 (4x)( 1) (3x + p9x2 +1) 1/x 1/x =lim x!1 4 3 p9+1/x2 = 1.

Notethatthislastequalityisduetothefactthatthenumeratoristheconstant 4andthedenominator isapproachingzero(fromtheleft)sothequotientispositiveandisgettinglarge. So y = 2 3 istheonlyhorizontalasymptote.

2.5.51

a. f (x)= x2 3 x +6 = x 6+ 33 x +6 .Theobliqueasymptoteof f is y = x 6.

Becauselim x!6+ f (x)= 1,thereisaverticalasymptoteat x = 6.Notealsothat lim x!6 f (x)= 1

2.5.52

a. f (x)= x2 1 x +2 = x 2+ 3 x +2 .Theobliqueasymptoteof f is y = x 2.

b. Becauselim x!2+ f (x)= 1,thereisaverticalasymptoteat x = 2.Notealsothat lim x!2 f (x)= 1.

2.5.53

a. f (x)= x2 2x +5 3x 2 =(1/3)x 4/9+ 37 9(3x 2) .Theobliqueasymptoteof f is y =(1/3)x 4/9.

b. Becauselim x!(2/3)+ f (x)= 1,thereisaverticalasymptoteat x =2/3.Notealsothat lim x!(2/3) f (x)= 1

2.5.54

a. f (x)= 5x2 4 5x 5 = x +1+ 1 5x 5 .Theobliqueasymptoteof f is y = x +1.

b. Becauselim x!1+ f (x)= 1,thereisaverticalasymptoteat x =1.Notealsothatlim x!1 f (x)= 1.

2.5.55

a. f (x)= 4x3 +4x2 +7x +4 1+ x2 =4x +4+ 3x 1+ x2 .Theobliqueasymptoteof f is y =4x +4.

b. Therearenoverticalasymptotes.

2.5.56

a. f (x)= 3x2 2x +5 3x +4 = x 2+ 13 3x +4 .Theobliqueasymptoteof f is y = x 2.

b. Becauselim x!( 4/3)+ f (x)= 1,thereisaverticalasymptoteat x = 4/3.Notealsothat

lim x!( 4/3) f (x)= 1

2.5.57

lim x!1 ( 3e x )= 3 0=0.lim x!1 ( 3e x )= 1

2.5.58

lim x!1 2x = 1.lim x!1 2x =0.

2.5.59

lim x!1 (1 ln x)= 1.lim x!0+ (1 ln x)= 1

2.5.60

lim x!1 | ln x| = 1.lim x!0+ | ln x| = 1.

2.5.61

y =sin x hasnoasymptotes.lim x!1 sin x and lim x!1 sin x donotexist.

2.5.62

2.5.63

a. False.Forexample,thefunction y = sin x x onthe domain[1, 1)hasahorizontalasymptoteof y =0, anditcrossesthe x-axisinﬁnitelymanytimes.

b. False.If f isarationalfunction,andiflim x!1 f (x)= L =0,thenthedegreeofthepolynomialinthe numeratormustequalthedegreeofthepolynomialinthedenominator.Inthiscase,bothlim x!1 f (x) andlim x!1 f (x)= an bn where an istheleadingcoecientofthepolynomialinthenumeratorand bn is theleadingcoecientofthepolynomialinthedenominator.Inthecasewherelim x!1 f (x)=0,then thedegreeofthenumeratorisstrictlylessthanthedegreeofthedenominator.Thiscaseholdsfor lim x!1 f (x)=0aswell.

c. True.Thereareonlytwodirectionswhichmightleadtohorizontalasymptotes:therecouldbeoneas x !1 andtherecouldbeoneas x !1,andthosearetheonlypossibilities.

d. False.Thelimitofthedi↵erenceoftwofunctionscanbewrittenasthedi↵erenceofthelimitsonly whenbothlimitsexist.Itisthecasethatlim x!1 (x 3 x)= 1

2.5.64 lim t!1 p(t)=lim t!1 2500 t +1 =0 Thesteadystateexists.Thesteadystatevalueis0.

2.5.65 lim t!1 p(t)=lim t!1 3500t t +1 =3500. Thesteadystateexists.Thesteadystatevalueis3500.

2.5.66 lim t!1 m(t)=lim t!1 200(1 2 t )=200 Thesteadystateexists.Thesteadystatevalueis200.

2.5.67 lim t!1 v (t)=lim t!1 1000e 0 065t = 1. Thesteadystatedoesnotexist.

2.5.68 lim t!1 p(t)=lim t!1 1500 3+2e 1t = 1500 3 =500 Thesteadystateexists.Thesteadystatevalueis500.

2.5.69 lim t!1 a(t)=lim t!1 2 ✓ t +sin t t ◆ =lim t!1 2 ✓1+ sin t t ◆ =2. Thesteadystateexists.Thesteadystate valueis2.

2.5.70

a. lim x!1 x2 4x +3 x 1 = 1,andlim x!1 x2 4x +3 x 1 = 1.Therearenohorizontalasymptotes.

b. Itappearsthat x =1isacandidatetobeaverticalasymptote,butnotethat f (x)= x2 4x +3 x 1 = (x 1)(x 3) x 1 .Thuslim x!1 f (x)=lim x!1(x 3)= 2.So f hasnoverticalasymptotes.

2.5.71

a. lim x!1 2x3 +10x2 +12x x3 +2x2 (1/x3 ) (1/x3 ) =lim x!1 2+10/x +12/x2 1+2/x =2.Similarly,lim x!1 f (x)=2.Thus, y =2 isahorizontalasymptote.

b. Notethat f (x)= 2x(x +2)(x +3) x2 (x +2) .Solim x!0+ f (x)=lim x!0+ 2(x +3) x = 1,andsimilarly,lim x!0 f (x)= 1.Thereisaverticalasymptoteat x =0.Notethatthereisnoasymptoteat x = 2because lim x!2 f (x)= 1.

2.5.72

a. Wehavelim x!1 p16x4 +64x2 + x2 2x2 4 (1/x2 ) (1/x2 ) =lim x!1 p16+64/x2 +1 2 4/x2 = 5 2 .Similarly,lim x!1 f (x)= 5 2 . So y = 5 2 isahorizontalasymptote.

b. lim x!p2+ f (x)=lim x!p2 f (x)= 1,andlim x!p2 f (x)=lim x!p2+ f (x)= 1 sothereareverticalasymptotesat x = ±p2.

2.5.73

a. Wehavelim x!1 3x4 +3x3 36x2 x4 25x2 +144 (1/x4 ) (1/x4 ) =lim x!1 3+3/x 36/x2 1 25/x2 +144/x4 =3.Similarly,lim x!1 f (x)=3. So y =3isahorizontalasymptote.

b. Notethat f (x)= 3x2 (x +4)(x 3) (x +4)(x 4)(x +3)(x 3) .Thus,lim x!3+ f (x)= 1 andlim x!3 f (x)= 1.Also, lim x!4 f (x)= 1 andlim x!4+ f (

2.5.74

a. Firstnotethat

)= 1.Thusthereareverticalasymptotesat x = 3and x =4.

4 = 1 8 Similarly,thelimitas x !1 of f (x)is 1 8 aswell.So y = 1 8 isahorizontalasymptote. b. f hasnoverticalasymptotes. Copyright c

2.5.75

a. lim x!1 x2 9 x2 3x (1/x2 ) (1/x2 ) =lim x!1 1 9/x2 1 3/x =1 Asimilarresultholdsas x !1.So y =1isahorizontal asymptote.

b. Becauselim x!0+ f (x)=lim x!0+ x +3 x = 1 andlim x!0 f (x)= 1,thereisaverticalasymptoteat x =0.

2.5.76

a. lim x!±1 x4 1 x2 1 =lim x!±1 (x2 1)(x2 +1) x2 1 =lim x!±1 x 2 +1= 1.Therearenohorizontalorslantasymptotes.

b. Itappearsthat x = ±1maybecandidatesforverticalasymptotes,butbecause x4 1 x2 1 = (x2 1)(x2 +1) x 1 = x 2 +1 for x = ±1therearenoverticalasymptoteseither.

2.5.77

a. Firstnotethat f (x)canbewrittens px2 +2x +6 3 x

= (x 1)(x +3) (x 1)(px2 +2x +6+3) . Thus lim x!1 f (x)=lim x!1 x +3 px2 +2x +6+3 1/x 1/x =lim x!1 1+3/x p1+2/x +6/x2

Usingthefactthat px2 = x for x< 0,wehavelim x!1 f (x)= 1.Thusthelines y =1and y = 1 arehorizontalasymptotes.

b. f hasnoverticalasymptotes.

2.5.78

a. Notethatwhen x islarge |1 x2 | = x2 1.Wehavelim x!1 |1 x2 | x2 + x =lim x!1 x2 1 x2 + x =1.Likewise lim x!1 |1 x2 | x2 + x =lim x!1 x2 1 x2 + x =1.Sothereisahorizontalasymptoteat y =1.

b. Notethatwhen x isnear0,wehave |1 x2 | =1 x2 =(1 x)(1+ x).Solim x!0+ f (x)=lim x!0+ 1 x x = 1

Similarly,lim x!0 f (x)= 1.Thereisaverticalasymptoteat x =0.

2.5.79

a. Notethatwhen x> 1,wehave |x| = x and |x 1| = x 1.Thus f (x)=(px px 1) px + px 1 px + px 1 = 1 px + px 1

Thuslim x!1 f (x)=0. When x< 0,wehave |x| = x and |x 1| =1 x.Thus f (x)=(p x p1 x) p x + p1 x p x + p1 x = 1 p x + p1 x

Thus,lim x!1 f (x)=0.Thereisahorizontalasymptoteat y =0.

b. f hasnoverticalasymptotes.

2.5.80

a. lim x!1 (3ex +10) ex 1/ex 1/ex =lim x!1 3+(10/ex ) 1 =3.Ontheotherhand,lim x!1

x +10 ex 1/ex 1/ex = lim x!1 3+(10e x ) 1 = 1 y =3isahorizontalasymptoteas x !1

b. f hasnoverticalasymptotes.

2.5.81

a. lim x!1 cos x +2px px =lim x!1 ✓2+ cos x px ◆ =2. y =2isahorizontalasymptote.

b. lim x!0+ cos x +2px px = 1.andlim x!0 cos x +2px px doesnotexist. x =0isaverticalasymptote.

2.5.82

a. lim x!1 cot 1 x =0.

b. lim x!1 cot 1 x = ⇡

2.5.83

a. lim x!1 sec 1 x = ⇡ /2.

b. lim x!1 sec 1 x = ⇡ /2.

2.5.84

a. lim x!1 ex + e x 2 = 1 lim x!1 ex + e x 2 = 1.

b. cosh(0)= e 0 +e 0 2 = 1+1 2 =1.

2.5.85

a. lim x!1 ex e x 2 = 1. lim x!1 ex e x 2 = 1 Copyright c 2019PearsonEducation,Inc.

b. sinh(0)= e 0 e 0 2 = 1 1 2 =0

2.5.86

Onepossiblesuchgraphis:

2.5.87

Onepossiblesuchgraphis:

2.5.88 lim n!1 f (n)=lim n!1 4 n =0

2.5.89 lim n!1 f (n)=lim n!1 n 1 n =lim n!1 [1 (1/n)]=1

2.5.90 lim n!1 f (n)=lim n!1 n2 n +1 =lim n!1 n 1+1/n = 1,sothelimitdoesnotexist. Copyright c 2019PearsonEducation,Inc.

2.5.91 lim n!1 f (n)=lim n!1 n +1 n2 =lim n!1 [1/n +1/n2 ]=0

2.5.92

a. Suppose m = n

= an bn .

b. Suppose m<n

2.5.93

a. No.If m = n,therewillbeahorizontalasymptote,andif m = n +1,therewillbeaslantasymptote.

b. Yes.Forexample, f (x)= x4 px6 +1 hasslantasymptote y = x as x !1 andslantasymptote y = x as x !1.

2.5.94

a. lim x!1

b. lim x!1 4ex +2e2x 8ex + e2x =lim x!1 (4ex +2e2x ) (8ex + e2x ) 1/ex 1/ex =lim x!1 4+2ex 8+ ex = 1 2

c. Thelines y =2and y = 1 2 arehorizontal asymptotes.

2.5.95 lim x!1 2ex +3 ex +1 =lim x!1 (2ex +3) (ex +1) 1/ex 1/ex =lim x!1

horizontalasymptote.Alsolim x!1

2.5.96 lim x!1 3e5x +7e6x 9e5x +14e6x =lim x!1

horizontalasymptote.Also,lim x!1

So y = 1 3 isahorizontalasymptote.

/ex 1+1/ex = 2+0 1+0 =2.Thustheline y =2isa

=3,so y =3isahorizontalasymptote.

2.5.97 Usingtherulesoflogarithms, f (x)= 6ln x 3ln x 1 .Thedomainof f is(0, 3 pe) [ ( 3 pe, 1).Weﬁrst examinetheendbehaviorofthefunction.Observethatlim x!1 6ln x 3ln x 1 =lim x!1 6 3 (1/ ln x) = 6 3 =2and

lim x!0+ 6ln x 3ln x 1 =lim x!0+ 6 3 (1/ ln x) = 6 3 =2.Sothefunctionhasahorizontalasymptoteof y =2anditis

undeﬁnedat x =0buthaslimit2as x approaches0fromtheright.Noticealsothatas x ! 3 pe + ,6ln x ! 2 and3ln x 1ispositiveandapproaches0.Therefore,lim x! 3 pe+ 6ln x 3ln x 1 = 1 andbyasimilarargument,

lim x! 3 pe 6ln x 3ln x 1 = 1

2.6Continuity

2.6.1

a. a(t)isacontinuousfunctionduringthetimeperiodfromwhenshejumpsfromtheplaneandwhen shetouchesdownontheground,becauseherpositionischangingcontinuouslywithtime.

b. n(t)isnotacontinuousfunctionoftime.Thefunction“jumps”atthetimeswhenaquartermustbe added.

c. T (t)isacontinuousfunction,becausetemperaturevariescontinuouslywithtime.

d. p(t)isnotcontinuous–itjumpsbywholenumberswhenaplayerscoresapoint.

2.6.2 Inorderfor f tobecontinuousat x = a,thefollowingconditionsmusthold:

• f mustbedeﬁnedat a (i.e. a mustbeinthedomainof f ),

• lim x!a f (x)mustexist,and

• lim x!a f (x)mustequal f (a).

2.6.3 Afunction f iscontinuousonaninterval I ifitiscontinuousatallpointsintheinteriorof I ,andit mustbecontinuousfromtherightattheleftendpoint(iftheleftendpointisincludedin I )anditmustbe continuousfromtheleftattherightendpoint(iftherightendpointisincludedin I .)

2.6.4 Thewords“hole”and“break”arenotmathematicallyprecise,soastrictmathematicaldeﬁnitioncan notbebasedonthem.

2.6.5 f isdiscontinuousat x =1,at x =2,andat x =3.At x =1, f (1)isnotdefined(sothefirstcondition isviolated).At x =2, f (2)isdefinedandlim x!2 f (x)exists,butlim x!2 f (x) = f (2)(socondition3isviolated). At x =3,lim x!3 f (x)doesnotexist(socondition2isviolated).

2.6.6 f isdiscontinuousat x =1,at x =2,andat x =3.At x =1,lim x!1 f (x) = f (1)(socondition3is violated).At x =2,lim x!2 f (x)doesnotexist(socondition2isviolated).At x =3, f (3)isnotdeﬁned(so condition1isviolated).

2.6.7 f isdiscontinuousat x =1,at x =2,andat x =3.At x =1,lim x!1 f (x)doesnotexist,and f (1)isnot deﬁned(soconditions1and2areviolated).At x =2,lim x!2 f (x)doesnotexist(socondition2isviolated).

At x =3, f (3)isnotdeﬁned(socondition1isviolated).

2.6.8 f isdiscontinuousat x =2,at x =3,andat x =4.At x =2,lim x!2 f (x)doesnotexist(socondition2 isviolated).At x =3, f (3)isnotdeﬁnedandlim x!3 f (x)doesnotexist(soconditions1and2areviolated). At x =4,lim x!4 f (x) = f (4)(socondition3isviolated).

2.6.9

a. Afunction f iscontinuousfromtheleftat x = a if a isinthedomainof f ,andlim x!a f (x)= f (a).

b. Afunction f iscontinuousfromtherightat x = a if a isinthedomainof f ,andlim x!a+ f (x)= f (a).

2.6.10 If f isright-continuousat x =3,then f (3)=lim x!3+ f (x)=6,so f (3)=6.

2.6.11 f iscontinuouson(0, 1),on(1, 2),on(2, 3],andon(3, 4).Itiscontinuousfromtheleftat3.

2.6.12 f iscontinuouson(0, 1),on(1, 2],on(2, 3),andon(3, 4).Itiscontinuousfromtheleftat2.

2.6.13 f iscontinuouson[0, 1),on(1, 2),on[2, 3),andon(3, 5).Itiscontinuousfromtherightat2.

2.6.14 f iscontinuouson(0, 2],on(2, 3),on(3, 4),andon(4, 5).Itiscontinuousfromtheleftat2.

2.6.15 Thedomainof f (x)= ex x is(1, 0) [ (0, 1),and f iscontinuouseverywhereonthisdomain.

2.6.16 Thefunctioniscontinuouson(0, 15],on(15, 30],on(30, 45],andon(45, 60].

2.6.17 Thenumber 5isnotinthedomainof f ,becausethedenominatorisequalto0when x = 5. Thus,thefunctionisnotcontinuousat 5.

2.6.18 Thefunctionisdeﬁnedat5,infact f (5)= 50+15+1 25+25 = 66 50 = 33 25 .Also,lim x!5 f (x)=lim x!5 2x2 +3x +1 x2 +5x =

33 25 = f (5).Thefunctioniscontinuousat a =5.

2.6.19 f isdiscontinuousat1,because1isnotinthedomainof f ; f (1)isnotdeﬁned.

2.6.20 g isdiscontinuousat3because3isnotinthedomainof g ; g (3)isnotdeﬁned.

2.6.21 f isdiscontinuousat1,becauselim x!1 f (x) = f (1).Infact, f (1)=3,butlim x!1 f (x)=2.

2.6.22 f iscontinuousat3,becauselim x!3 f (x)= f (3).Infact, f (3)=2andlim x!3 f (x)=lim x!3 (x 3)(x 1) x 3 = lim x!3(x 1)=2.

2.6.23 f isdiscontinuousat4,because4isnotinthedomainof f ; f (4)isnotdeﬁned.

2.6.24 f isdiscontinuousat 1becauselim x!1 f (x)=lim x!1 x(x +1) x +1 =lim x!1 x = 1 = f ( 1)=2.

2.6.25 Because p isapolynomial,itiscontinuousonallof R =(1, 1).

2.6.26 Because g isarationalfunction,itiscontinuousonitsdomain,whichisallof R =(1, 1).(Because x2 + x +1hasnorealroots.)

2.6.27 Because f isarationalfunction,itiscontinuousonitsdomain.Itsdomainis(1, 3) [ ( 3, 3) [ (3, 1).

2.6.28 Because s isarationalfunction,itiscontinuousonitsdomain.Itsdomainis(1, 1) [ ( 1, 1) [ (1, 1).

2.6.29 Because f isarationalfunction,itiscontinuousonitsdomain.Itsdomainis(1, 2) [ ( 2, 2) [ (2, 1).

2.6.30 Because f isarationalfunction,itiscontinuousonitsdomain.Itsdomainis(1, 2) [ ( 2, 2) [ (2, 1).

2.6.31 Because f (x)= x8 3x6 140 isapolynomial,itiscontinuouseverywhere,includingat0.Thus lim x!0 f (x)= f (0)=( 1)40 =1.

2.6.32 Because f (x)= ✓ 3 2x5 4x2 50 ◆4 isarationalfunction,itiscontinuousatallpointsinitsdomain, includingat x =2.Solim x!2 f (x)= f (2)= 81 16 .

2.6.33 Because x3 2x2 8x = x(x2 2x 8)= x(x 4)(x +2),wehave(aslongas x =4) r x3 2x2 8x x 4 = px(x +2).

Thus,lim x!4 r x3 2x2 8x x 4 =lim x!4 px(x +2)= p24,usingTheorem2.12andthefactthatthesquareroot isacontinuousfunction.

2.6.34 Notethat t 4=(pt 2)(pt +2),sofor t =4,wehave t 4 pt 2 = pt +2

Thus,lim t!4 t 4 pt 2 =lim t!4(pt +2)=4.ThenusingTheorem2.12andthefactthatthetangentfunctionis continuousat4,wehavelim t!4 tan ✓ t 4 pt 2 ◆ =tan ✓ lim t!4 t 4 pt 2 ◆ =tan4.

2.6.35 Because f (x)= ⇣ x+5 x+2 ⌘4 isarationalfunction,itiscontinuousatallpointsinitsdomain,including at x =1.Thuslim x!1 f (x)= f (1)=16.

2.6.36 lim x!1 ✓ 2x +1 x ◆3 =lim x!1 (2+(1/x))3 =23 =8.

2.6.37 Notethat

2.6.38 Firstnotethat

Thenbecause f (x)= x1/3 iscontinuousat1/8,wehavelim x!0 ✓ x p16x +1 1

Theorem2.12.

2.6.39

a. f isdeﬁnedat1.Wehave f (1)=12 +(3)(1)=4.Toseewhetherornotlim x!1 f (x)exists,weinvestigate thetwoone-sidedlimits.lim x!1 f (x)=lim x!1 2x =2,andlim x!1+ f (x)=lim x!1+ (x 2 +3x)=4,solim x!1 f (x) doesnotexist.Thus f isdiscontinuousat x =1.

b. f iscontinuousfromtheright,becauselim x!1+ f (x)=4= f (1).

c. f iscontinuouson(1, 1)andon[1, 1).

2.6.40

a. f isdeﬁnedat0,infact f (0)=1.However,lim x!0 f (x)=lim x!0 (x 3 +4x +1)=1,whilelim x!0+ f (x)= lim x!0+ 2x 3 =0.Solim x!0 f (x)doesnotexist.

b. f iscontinuousfromtheleftat0,becauselim x!0 f (x)= f (0)=1.

c. f iscontinuouson(1, 0]andon(0, 1).

2.6.41 f isdeﬁnedandiscontinuouson(1, 5].Itiscontinuousfromtheleftat5.

2.6.42 f isdeﬁnedandiscontinuouson[ 5, 5].Itiscontinuousfromtherightat 5andiscontinuous fromtheleftat5.

2.6.43 f iscontinuouson(1, p8]andon[p8, 1).Itiscontinuousfromtheleftat p8andfromthe rightat p8.

2.6.44 g (x)= px2 3x +2= p(x 1)(x 2)isdeﬁnedandiscontinuouson(1, 1]andon[2, 1).Itis continuousfromtheleftat1andfromtherightat2.

2.6.45 Because f isthecompositionoftwofunctionswhicharecontinuouson(1, 1),itiscontinuouson (1, 1).

2.6.46 f iscontinuouson(1, 1]andon[1, 1).Itiscontinuousfromtheleftat 1andfromtheright at1.

2.6.47 Because f isthecompositionoftwofunctionswhicharecontinuouson(1, 1),itiscontinuouson (1, 1).

2.6.48 f iscontinuouson[1, 1).Itiscontinuousfromtherightat1.

2.6.49 lim x!2 r 4x +10 2x 2 = r 18 2 =3.

2.6.50 lim x!1 ⇣x 2 4+ 3 px2 9⌘ =( 1)2 4+ 3 p( 1)2 9= 3+ 3 p 8= 3+ 2= 5.

2.6.51 lim x!⇡ cos2 x +3cos x +2 cos x +1 =lim x!⇡ (cos x +1)(cos x +2) cos x +1 =lim x!⇡ (cos x +2)=1.

2.6.52 lim x!3⇡ /2 sin2 x +6sin x +5 sin2 x 1 =lim x!3⇡ /2 (sin x +5)(sin x +1) (sin x 1)(sin x +1) =lim x!3⇡ /2 sin x +5 sin x 1 = 4 2 = 2

2.6.53 lim x!3 px2 +7= p9+7=4.

2.6.54 lim t!2 t2 +5 1+ pt2 +5 = 9 1+ p9 = 9 4 .

2.6.55 lim x!⇡ /2 sin x 1 psin x 1 =lim x!⇡ /2 (psin x +1)=2.

2.6.56 lim ✓ !0 1 2+sin ✓ 1 2 sin ✓ · (2)(2+sin ✓ ) (2)(2+sin ✓ ) =lim ✓ !0 2 (2+sin ✓ ) (sin ✓ )(2)(2+sin ✓ ) =lim ✓ !0 1 2(2+sin ✓ ) = 1 4

2.6.57 lim x!0 cos x 1 sin2 x =lim x!0 cos x 1 1 cos2 x =lim x!0 cos x 1 (1 cos x)(1+cos x) =lim x!0 1 1+cos x = 1 2

2.6.58 lim x!0+ 1 cos2 x sin x =lim x!0+ sin2 x sin x =lim x!0+ sin x =0.

2.6.59 lim x!0 e4x 1 ex 1 =lim x!0 (e2x +1)(e2x 1) ex 1 =lim x!0 (e2x +1)(ex 1)(ex +1) ex 1 = lim x!0(e 2x +1)(ex +1)=2 2=4

2.6.60 lim x!e2 ln2 x 5ln x +6 ln x 2 =lim x!e2 (ln x 2)(ln x 3) ln x 2 =lim x!e2 (ln x 3)= 1.

2.6.61 f (x)=csc x isn’tdeﬁnedat x = k ⇡ where k isaninteger,soitisn’tcontinuousatthosepoints.Soitis continuousonintervalsoftheform(k ⇡ , (k +1)⇡ )where k isaninteger.lim x!⇡ /4 csc x = p2.lim x!2⇡ csc x = 1

2.6.62 f isdeﬁnedon[0, 1),anditiscontinuousthere,becauseitisthecompositionofcontinuousfunctions deﬁnedonthatinterval.lim x!4 f (x)= e 2 .lim x!0 f (x)doesnotexist—butlim x!0+ f (x)= e 0 =1,because f is continuousfromtheright.

2.6.63 f isn’tdeﬁnedforanynumberoftheform ⇡ /2+ k ⇡ where k isaninteger,soitisn’tcontinuous there.Itiscontinuousonintervalsoftheform(⇡ /2+ k ⇡ , ⇡ /2+(k +1)⇡ ),where k isaninteger. lim x!⇡ /2 f (x)= 1.lim x!4⇡ /3 f (x)= 1 p3/2 1/2 = p3 2.

2.6.64 Thedomainof f is(0, 1],and f iscontinuousonthisintervalbecauseitisthequotientoftwo continuousfunctionsandthefunctioninthedenominatorisn’tzeroonthatinterval.

lim x!1 f (x)=lim x!1 ln x sin 1 (x) = ln1 sin 1 (1) = 0 ⇡ /2 =0.

2.6.65 Thisfunctioniscontinuousonitsdomain,whichis(1, 0) [ (0, 1).

lim x!0 f (x)=lim x!0 ex 1 ex = 1,whilelim x!0+ f (x)=lim x!0+ ex 1 ex = 1

2.6.66 Thisfunctioniscontinuousonitsdomain,whichis(1, 0) [ (0, 1).

lim x!0 f (x)=lim x!0 e2x 1 ex 1 =lim x!0 (ex +1)(ex 1) ex 1 =lim x!0(ex +1)=2.

2.6.67

a. Notethat f (x)=2x3 + x 2iscontinuouseverywhere,soinparticularitiscontinuouson[ 1, 1]. Notethat f ( 1)= 5 < 0and f (1)=1 > 0.Because0isanintermediatevaluebetween f ( 1)and f (1),theIntermediateValueTheoremguaranteesanumber c between 1and1where f (c)=0.

b. Usingagraphingcalculatorandacomputeralgebrasystem,weseethattherootof f isabout 0 835

2.6.68

a. Notethat f (x)= px4 +25x3 +10 5iscontinuousonitsdomain,soinparticularitiscontinuous on[0, 1].Notethat f (0)= p10 5 < 0and f (1)=6 5=1 > 0.Because0isanintermediate valuebetween f (0)and f (1),theIntermediateValueTheoremguaranteesanumber c between0and 1where f (c)=0.

b. Usingagraphingcalculatorandacomputeralgebrasystem,weseetherootof f (x)isatabout 834.

2.6.69

a. Notethat f (x)= x3 5x2 +2x iscontinuouseverywhere,soinparticularitiscontinuouson[ 1, 5].

Notethat f ( 1)= 8 < 1and f (5)=10 > 1.Because 1isanintermediatevaluebetween f ( 1) and f (5),theIntermediateValueTheoremguaranteesanumber c between 1and5where f (c)= 1.

Usingagraphingcalculatorandacomputeralgebrasystem,weseethatthereareactuallythree di↵erentvaluesof c between 1and5forwhich f (c)= 1.Theyare c ⇡0 285, c ⇡ 0 778,and c ⇡ 4 507.

2.6.70

a. Notethat f (x)= x5 4x2 +2px +5iscontinuousonitsdomain,soinparticularitiscontinuouson [0, 3].Notethat f (0)=5 > 0and f (3) ⇡270.5 < 0.Because0isanintermediatevaluebetween f (0) and f (3),theIntermediateValueTheoremguaranteesanumber c between0and3where f (c)=0.

b. Usingagraphingcalculatorandacomputeralgebrasystem,weseethatthevalueof c guaranteed bythetheoremisabout1.141.

2.6.71

a. Notethat f (x)= ex + x iscontinuousonitsdomain,soinparticularitiscontinuouson[ 1, 0].Note that f ( 1)= 1 e 1 < 0and f (0)=1 > 0.Because0isanintermediatevaluebetween f ( 1)and f (0),theIntermediateValueTheoremguaranteesanumber c between 1and0where f (c)=0.

b. Usingagraphingcalculatorandacomputeralgebrasystem,weseethatthevalueof c guaranteed bythetheoremisabout 0 567.

2.6.72

a. Notethat f (x)= x ln x 1iscontinuousonitsdomain,soinparticularitiscontinuouson[1,e].Note that f (1)=ln1 1= 1 < 0and f (e)= e 1 > 0.Because0isanintermediatevaluebetween f (1) and f (e),theIntermediateValueTheoremguaranteesanumber c between1and e where f (c)=0.

b. Usingagraphingcalculatorandacomputeralgebrasystem,weseethatthevalueof c guaranteed bythetheoremisabout1 76322.

2.6.73

a. True.If f isrightcontinuousat a,then f (a)existsandthelimitfromtherightat a existsandisequal to f (a).Becauseitisleftcontinuous,thelimitfromtheleftexists—sowenowknowthatthelimit as x ! a of f (x)exists,becausethetwoone-sidedlimitsarebothequalto f (a).

b. True.Iflim x!a f (x)= f (a),thenlim x!a+ f (x)= f (a)andlim x!a f (x)= f (a).

c. False.Thestatementwouldbetrueif f werecontinuous.However,if f isn’tcontinuous,thenthe statementdoesn’thold.Forexample,supposethat f (x)= 8 < : 0if0  x< 1; 1if1  x  2, Notethat f (0)=0and f (2)=1,butthereisnonumber c between0and2where f (c)=1/2.

d. False.Consider f (x)= x2 and a = 1and b =1.Then f iscontinuouson[a,b],but f (1)+f ( 1) 2 =1, andthereisno c on(a,b)with f (c)=1.

2.6.74

a. Because m isacontinuousfunctionof r on[0.04, 0.05],andbecause m(0.04) ⇡ 1193.54and m(0.05) ⇡ 1342 05,(and1300isanintermediatevaluebetweenthesetwonumbers)theIntermediateValueTheoremguaranteesavalueof r between0 04and0 05where m(r )=1300.

b. Usingacomputeralgebrasystem,weseethatthe requiredinterestrateisabout0 047.

2.6.75

a. Because A isacontinuousfunctionof r on[0, 0 08],andbecause A(0)=5000and A(0 08) ⇡ 11098 2, (and7000isanintermediatevaluebetweenthesetwonumbers)theIntermediateValueTheorem guaranteesavalueof r between0and0 08where A(r )=7000.

b. Solving5000(1+(r/12))120 =7000for r ,wesee that(1+(r/12))120 =7/5,so1+ r/12= 120p7/5, so r =12( 120p7/5 1) ⇡ 0 034.

2.6.76

a. Notethat A(0.01) ⇡ 2615.55and A(0.1) ⇡ 3984.36.BytheIntermediateValueTheorem,theremust beanumber r0 between0.01and0.1sothat A(r0 )=3500.

b. Thedesiredvalueis r0 ⇡ 0.0728or7.28%.

2.6.77 Considerthefunction f (x)=cos x 2x ontheinterval[0, 1].Notethat f (0)=1and f (⇡ /2)= ⇡ < 0.SobytheIntermediateValueTheorem,theremustbearootof f ontheinterval[0, ⇡ /2].Usinga computeralgebrasystem,weﬁndarootofapproximately0.45.

2.6.78 Let f (x)= |x|

Forvaluesof a otherthan0,itisclearthatlim x!a |x| = |a| because f isdeﬁnedtobeeitherthepolynomial x (forvaluesgreaterthan0)orthepolynomial x (forvalueslessthan0.)Forthevalueof a =0,wehave lim x!0+ f (x)=lim x!0+ x =0= f (0).Also,lim x!0 f (x)=lim x!0 ( x)= 0=0.Thuslim x!0 f (x)= f (0),so f is continuousat0.

2.6.79 Because f (x)= x3 +3x 18isapolynomial,itiscontinuouson(1, 1),andbecausetheabsolute valuefunctioniscontinuouseverywhere, |f (x)| iscontinuouseverywhere.

2.6.80 Let f (x)= x +4 x2 4 .Then f iscontinuouson(1, 2) [ ( 2, 2) [ (2, 1).So g (x)= |f (x)| isalso continuousonthisset.

2.6.81 Let f (x)= 1 px 4 .Then f iscontinuouson[0, 16) [ (16, 1).So h(x)= |f (x)| iscontinuouson thissetaswell.

2.6.82 Because x2 +2x +5isapolynomial,itiscontinuouseverywhere,asis |x2 +2x +5|.So h(x)= |x2 +2x +5| + px iscontinuousonitsdomain,namely[0, 1).

2.6.83

Thegraphshownisn’tdrawncorrectlyattheintegers.Ataninteger a,thevalueofthefunction is0,whereasthegraphshownappearstotakeon allthevaluesfrom0to1. Notethatinthecorrectgraph,lim x!a f (x)=1and lim x!a+ f (x)=0foreveryinteger a

2.6.84

Thegraphasdrawnonmostgraphingcalculatorsappearstobecontinuousat x =0,butitisn’t,of course(becausethefunctionisn’tdeﬁnedat x =0).Abetterdrawingwouldshowthe“hole”inthegraph at(0, 1).

c. Itappearsthatlim x!0 sin x x =1.

2.6.85 Withslightmodiﬁcations,wecanusetheexamplesfromtheprevioustwoproblems.

a. Thefunction y = x bxc isdeﬁnedat x =1but isn’tcontinuousthere.

b. Thefunction y = sin(x 1) x 1 hasalimitat x =1, butisn’tdeﬁnedthere,soisn’tcontinuousthere.

2.6.86 Inorderforthisfunctiontobecontinuousat x = 1,werequirelim x!1 f (x)= f ( 1)= a.Sothe valueof a mustbeequaltothevalueoflim x!1 x2 +3x +2 x +1 =lim x!1 (x +2)(x +1) x +1 =lim x!1(x +2)=1.Thus wemusthave a =1.

2.6.87

a. Inorderfor g tobecontinuousfromtheleftat x =1,wemusthavelim x!1 g (x)= g (1)= a.Wehave

lim x!1 g (x)=lim x!1 (x 2 + x)=2.Sowemusthave a =2.

b. Inorderfor g tobecontinuousfromtherightat x =1,wemusthavelim x!1+ g (x)= g (1)= a.Wehave

lim x!1+ g (x)=lim x!1+ (3x +5)=8.Sowemusthave a =8.

c. Becausethelimitfromtheleftandthelimitfromtherightat x =1don’tagree,thereisnovalueof a whichwillmakethefunctioncontinuousat x =1.

2.6.88 lim

Thereisaverticalasymptoteat x =0,andtheline y = 5isahorizontalasymptote.

2.6.89 lim x!0 2ex +10e x ex + e x = 12 2 =6.

lim x!1

Therearenoverticalasymptotes.Thelines y =2and y =10arehorizontalasymptotes.

2.6.90 Let f (x)= x3 +10x2 100x +50.Notethat f ( 20) < 0, f ( 5) > 0, f (5) < 0,and f (10) > 0. Becausethegivenpolynomialiscontinuouseverywhere,theIntermediateValueTheoremguaranteesusa rooton( 20, 5),atleastoneon( 5, 5),andatleastoneon(5, 10).Becausetherecanbeatmost3roots andthereareatleast3roots,theremustbeexactly3roots.Therootsare x1 ⇡16.32, x2 ⇡ 0.53and x3 ⇡ 5.79.

2.6.91 Let f (x)=70x3 87x2 +32x 3.Notethat f (0) < 0, f (0 2) > 0, f (0 55) < 0,and f (1) > 0. Becausethegivenpolynomialiscontinuouseverywhere,theIntermediateValueTheoremguaranteesusa rooton(0, 0 2),atleastoneon(0 2, 0 55),andatleastoneon(0 55, 1).Becausetherecanbeatmost3 rootsandthereareatleast3roots,theremustbeexactly3roots.Therootsare x1 =1/7, x2 =1/2and x3 =3/5.

2.6.92

a. Wehave f (0)=0, f (2)=3, g (0)=3and g (2)=0.

b. h(t)= f (t) g (t), h(0)= 3and h(2)=3.

c. BytheIntermediateValueTheorem,because h isacontinuousfunctionand0isanintermediatevalue between 3and3,theremustbeatime c between0and2where h(c)=0.Atthispoint f (c)= g (c), andatthattime,thedistancefromthecaristhesameonbothdays,sothehikerispassingoverthe exactsamepointatthattime.

2.6.93 Wecanargueessentiallylikethepreviousproblem,orwecanimagineanidenticaltwintotheoriginal monk,whotakesanidenticalversionoftheoriginalmonk’sjourneyupthewindingpathwhilethemonkis takingthereturnjourneydown.Becausetheymustpasssomewhereonthepath,thatpointistheonewe arelookingfor.

2.6.94

a. Because | 1| =1, |g (x)| =1,forall x

b. Thefunction g isn’tcontinuousat x =0,becauselim x!0+ g (x)=1 = 1=lim x!0 g (x).

c. Thisconstantfunctioniscontinuouseverywhere,inparticularat x =0.

d. Thisexampleshowsthatingeneral,thecontinuityof |g | doesnotimplythecontinuityof g .

2.6.95 Thediscontinuityisnotremovable,becauselim x!a f (x)doesnotexist.Thediscontinuitypicturedisa jumpdiscontinuity.

2.6.96 Thediscontinuityisnotremovable,becauselim x!a f (x)doesnotexist.Thediscontinuitypicturedis aninﬁnitediscontinuity.

2.6.97 Notethatlim x!2 x2 7x +10 x 2 =lim x!2 (x 2)(x 5) x 2 =lim x!2(x 5)= 3.Becausethislimitexists,the discontinuityisremovable.

2.6.98 Notethatlim x!1 x2 1 1 x =lim x!1 (x 1)(x +1) 1 x =lim x!1[ (x +1)]= 2.Becausethislimitexists,the discontinuityisremovable.

2.6.99 Notethat h(x)= x3 4x2 +4x x(x 1) = x(x 2)2 x(x 1) .Thuslim x!0 h(x)= 4,andthediscontinuityat x =0is removable.However,lim x!1 h(x)doesnotexist,andthediscontinuityat x =1isnotremovable(itisinﬁnite.)

2.6.100 Thisisajumpdiscontinuity,becauselim x!2+ f (x)=1andlim x!2 f (x)= 1.

2.6.101

a. Notethat 1  sin(1/x)  1forall x =0,so x  x sin(1/x)  x (for x> 0.For x< 0wewould have x  x sin(1/x) x.)Becauseboth x ! 0and x ! 0as x ! 0,theSqueezeTheoremtellsus thatlim x!0 x sin(1/x)=0aswell.Becausethislimitexists,thediscontinuityisremovable.

b. Notethatas x ! 0+ ,1/x !1,andthuslim x!0+ sin(1/x)doesnotexist.Sothediscontinuityisnot removable.

2.6.102 Because g iscontinuousat a,as x ! a, g (x) ! g (a).Because f iscontinuousat g (a),as z ! g (a), f (z ) ! f (g (a)).Let z = g (x),andsuppose x ! a.Then g (x)= z ! g (a),so f (z )= f (g (x)) ! f (g (a)),as desired.

2.6.103

a. Consider g (x)= x +1and f (x)= |x 1| x 1 .Notethatboth g and f arecontinuousat x =0.However f (g (x))= f (x +1)= |x| x isnotcontinuousat0.

b. Theprevioustheoremsaysthatthecompositionof f and g iscontinuousat a if g iscontinuousat a and f iscontinuousat g (a).Itdoesnotsaythatif g and f arebothcontinuousat a thatthecomposition iscontinuousat a

2.6.104 TheIntermediateValueTheoremrequiresthatourfunctionbecontinuousonthegiveninterval.In thisexample,thefunction f isnotcontinuouson[ 2, 2]becauseitisn’tcontinuousat0.

2.6.105

a. Usingthehint,wehave

Notethatas x ! a,wehavethatcos(x a) ! 1andsin(x a) ! 0.

So,

b. Usingthehint,wehave

2.7PreciseDeﬁnitionsofLimits

2.7.1 Notethatallthenumbersintheinterval(1, 3)arewithin1unitofthenumber2.So |x 2| < 1is trueforallnumbersinthatinterval.Infact, {x :0 < |x 2| < 1} isexactlytheset(1, 3)with x =2.

2.7.2 Notethatallthenumbersintheinterval(2, 6)arewithin2unitsofthenumber4.So |f (x) 4| < " for " =2(oranynumbergreaterthan2).

2.7.3

a. Thisissymmetricabout x =5,because 1+9 2 =5.

b. Thisissymmetricabout x =5,because 4+6 2 =5.

c. Thisisnotsymmetricabout x =5,because 3+8 2 =5.

d. Thisissymmetricabout x =5,because 4 5+5 5 2 =5.

2.7.4 Theset {x : |x a| < } istheinterval(a ,a + )and {x :0 < |x a| < } isthesetofallpoints intheinterval(a ,a + )excludingthepoint a

2.7.5 lim x!a f (x)= L ifforanyarbitrarilysmallpositivenumber ",thereexistsanumber ,sothat f (x)is within " unitsof L foranynumber x within unitsof a (butnotincluding a itself).

2.7.6 Thesetofall x forwhich |f (x) L| < " isthesetofnumberssothatthevalueofthefunction f at thosenumbersiswithin " unitsof L

2.7.7 Wearegiventhat |f (x) 5| < 0 1forvaluesof x intheinterval(0, 5),soweneedtoensurethatthe setof x valuesweareallowingfallinthisinterval. Notethatthenumber0istwounitsawayfromthenumber2andthenumber5isthreeunitsawayfrom thenumber2.Inordertobesurethatwearetalkingaboutnumbersintheinterval(0, 5)whenwewrite |x 2| < ,wewouldneedtohave =2(oranumberlessthan2).Infact,thesetofnumbersforwhich |x 2| < 2istheinterval(0, 4)whichisasubsetof(0, 5).

Ifweweretoallow tobeanynumbergreaterthan2,thenthesetofall x sothat |x 2| < would includenumberslessthan0,andthosenumbersaren’tontheinterval(0, 5).

2.7.8

lim x!a f (x)= 1,ifforany N> 0,thereexists > 0

sothatif0 < |x a| < then f (x) >N

2.7.9

a. Inorderfor f tobewithin2unitsof5,itappearsthatweneed x tobewithin1unitof2.So =1.

b. Inorderfor f tobewithin1unitof5,itappearsthatwewouldneed x tobewithin1/2unitof2.So =0 5.

2.7.10

a. Inorderfor f tobewithin1unitof4,itappearsthatwewouldneed x tobewithin1unitof2.So =1.

b. Inorderfor f tobewithin1/2unitof4,itappearsthatwewouldneed x tobewithin1/2unitof2. So =1/2.

2.7.11

a. Inorderfor f tobewithin3unitsof6,itappearsthatwewouldneed x tobewithin2unitsof3.So =2.

b. Inorderfor f tobewithin1unitof6,itappearsthatwewouldneed x tobewithin1/2unitof3.So =1/2.

2.7.12

a. Inorderfor f tobewithin1unitof5,itappearsthatwewouldneed x tobewithin3unitsof4.So =3.

b. Inorderfor f tobewithin1/2unitof5,itappearsthatwewouldneed x tobewithin2unitsof4. So =2.

2.7.13

a. If " =1,weneed |x3 +3 3| < 1.Soweneed |x| < 3 p1=1inorderforthistohappen.Thus =1willsuce.

b. If " =0 5,weneed |x3 +3 3| < 0 5.Sowe need |x| < 3 p0 5inorderforthistohappen.Thus = 3 p0.5 ⇡ 0.79willsuce.

2.7.14

a. Bylookingatthegraph,itappearsthatfor " =1, wewouldneed tobeabout0 4orless.

b. Bylookingatthegraph,itappearsthatfor " = 0 5,wewouldneed tobeabout0 2orless.

2.7.15

a. For " =1,therequiredvalueof wouldalsobe1.Alargervalueof wouldworktotherightof2, butthisisthelargestonethatwouldworktotheleftof2.

b. For " =1/2,therequiredvalueof wouldalsobe1/2.

c. Itappearsthatforagivenvalueof ",itwouldbewisetotake =min(", 2).Thisassuresthatthe desiredinequalityismetonbothsidesof2.

2.7.16

a. For " =2,therequiredvalueof wouldbe1(orsmaller).Thisisthelargestvalueof thatworkson eitherside. Copyright c 2019PearsonEducation,Inc.

b. For " =1,therequiredvalueof wouldbe1/2(orsmaller).Thisisthelargestvalueof thatworks ontherightof4.

c. Itappearsthatforagivenvalueof ",thecorrespondingvalueof =min(5/2, "/2).

2.7.17

a. For " =2,itappearsthatavalueof =1(orsmaller)wouldwork.

b. For " =1,itappearsthatavalueof =1/2(orsmaller)wouldwork.

c. Foranarbitrary ",avalueof = "/2orsmallerappearstosuce.

2.7.18

a. For " =1/2,itappearsthatavalueof =1(orsmaller)wouldwork.

b. For " =1/4,itappearsthatavalueof =1/2(orsmaller)wouldwork.

c. Foranarbitrary ",avalueof2" orsmallerappearstosuce.

2.7.19 Forany " > 0,let = "/8.Thenif0 < |x 1| < ,wewouldhave |x 1| < "/8.Then |8x 8| < ", so |(8x +5) 13| < ".Thislastinequalityhastheform |f (x) L| < ",whichiswhatwewereattempting toshow.Thus,lim x!1(8x +5)=13.

2.7.20 Forany " > 0,let = "/2.Thenif0 < |x 3| < ,wewouldhave |x 3| < "/2.Then |2x 6| < ", so | 2x +6| < ",so |( 2x +8) 2| < ".Thislastinequalityhastheform |f (x) L| < ",whichiswhatwe wereattemptingtoshow.Thus,lim x!3( 2x +8)=2.

2.7.21 Firstnotethatif x =4, f (x)= x 2 16 x 4 = x +4.

Nowif " > 0isgiven,let = ".Nowsuppose0 < |x 4| < .Then x =4,sothefunction f (x)can bedescribedby x +4.Also,because |x 4| < ,wehave |x 4| < ".Thus |(x +4) 8| < ".Thislast inequalityhastheform |f (x) L| < ",whichiswhatwewereattemptingtoshow.Thus,lim x!4 x2 16 x 4 =8.

2.7.22 Firstnotethatif x =3, f (x)= x 2 7x+12 x 3 = (x 4)(x 3) x 3 = x 4.

Nowif " > 0isgiven,let = ".Nowsuppose0 < |x 3| < .Then x =3,sothefunction f (x)canbe describedby x 4.Also,because |x 3| < ,wehave |x 3| < ".Thus |(x 4) ( 1)| < ".Thislast inequalityhastheform |f (x) L| < ",whichiswhatwewereattemptingtoshow.Thus,lim x!3 f (x)= 1.

2.7.23 Let " > 0begivenandassumethat0 < |x 0| < where = ".Itfollowsthat ||x| 0| = |x| = |x 0| < = ".Wehaveshownthatforany " > 0, ||x| 0| < " whenever0 < |x 0| < ,provided0 <  "

2.7.24 Let " > 0begivenandassumethat0 < |x 0| < where = " 5 .Itfollowsthat ||5x| 0| = 5|x 0| < 5 =5 " 5 = ".Wehaveshownthatforany " > 0, ||5x| 0| < " whenever0 < |x 0| < , provided0 <  " 5

2.7.25 Let " > 0begivenandassumethat0 < |x 7| < where = "/3.If x< 7, |f (x) 9| = |3x 12 9| = 3|x 7| < 3 =3("/3)= ";if x> 7,then |f (x) 9| = |x +2 9| = |x 7| < = "/3 < ".We’veshownthat forany " > 0, |f (x) 9| < " whenever0 < |x 7| < ,provided0 <  "/3.

2.7.26 Let " > 0begivenandassumethat0 < |x 5| < where = "/4.If x< 5, |f (x) 4| = |2x 6 4| = 2|x 5| < 2 =2("/4)= "/2 < ";if x> 5,then |f (x) 4| = | 4x +24 4| = | 4(x 5)| =4|x 5| < 4 = 4("/4)= ".We’veshownthatforany " > 0, |f (x) 4| < " whenever0 < |x 5| < ,provided0 <  "/4.

2.7.27 Let " > 0begiven.Let = p".Thenif0 < |x 0| < ,wewouldhave |x| < p".Butthen |x2 | < ", whichhastheform |f (x) L| < ".Thus,lim x!0 f (x)=0.

2.7.28 Let " > 0begiven.Let = p".Thenif0 < |x 3| < ,wewouldhave |x 3| < p".Butthen |(x 3)2 | < ",whichhastheform |f (x) L| < ".Thus,lim x!3 f (x)=0.

2.7.29 Let " > 0begivenandassumethat0 < |x 2| < where =min{1, "/8}.Byfactoring x2 +3x 10, weﬁndthat |x2 +3x 10| = |x 2||x +5|.Because |x 2| < and  1,wehave |x 2| < 1,whichimplies that 1 <x 2 < 1,or1 <x< 3.Itfollowsthat |x +5| = x +5  8.Wealsoknowthat |x 2| < "/8 because0 < |x 2| < and  "/8.Therefore |x2 +3x 10| = |x 2||x +5| < ("/8) 8= ".Wehave shownthatforany " > 0, |x2 +3x 10| < " whenever0 < |x 2| < ,provided0 <  min{1, "/8}

2.7.30 Let " > 0begivenandassumethat0 < |x 4| < where =min{1, "/14}.Observethat |2x2 4x +1 17| = |2x2 4x 16| =2|x 4||x +2|.Because |x 4| < and  1,wehave |x 4| < 1 whichimpliesthat 1 <x 4 < 1or3 <x< 5.Itfollowsthat |x +2| = x +2  7.Wealsoknowthat |x 4| < "/14because0 < |x 4| < and  "/14.Therefore |2x2 4x +1| =2|x 4||x +2| < 2("/14) · 7= " Wehaveshownthatforany " > 0, |2x2 4x +1 17| < " provided0 <  min{1, "/14}

2.7.31 Let " > 0begivenandassumethat0 < |x ( 3)| < where = "/2.Usingtheinequality ||a| |b||  |a b| with a =2x and b = 6,itfollowsthat ||2x| 6| = ||2x| | 6||  |2x ( 6)| = 2|x ( 3)| < 2 =2("/2)= " andtherefore ||2x| 6| < ".Wehaveshownthatforany " > 0, ||2x| 6| < " whenever0 < |x ( 3)| < ,provided0 <  "/2.

2.7.32 Let " > 0begivenandassumethat0 < |x 25| < where =min{25, 5"}.Because |x 25| < and  25,wehave |x 25| < 25,whichimpliesthat 25 <x 25 < 25or0 <x< 50.Because x> 0,we have px +5 > 5anditfollowsthat 1 px+5 < 1 5 .Therefore |px 5| = |x 25| p

Wehaveshownthatforany " > 0, |px 5| < ",provided0 <  min{25, 5"}.

2.7.33 Assume |x 3| < 1,asindicatedinthehint.Then2 <x< 4,so 1 4 < 1 x < 1 2 ,andthus 1 x < 1 2 Alsonotethattheexpression

canbewrittenas

Nowlet " > 0begiven.Let =min(6", 1).Nowassumethat0 < |x 3| < .Then

Thuswehaveestablishedthat

2.7.34 Notethatfor x =4,theexpression x 4 px 2 = x 4 px 2 px+2 px+2 = px +2.Alsonotethatif |x 4| < 1, then x isbetween3and5,so px> 0.Thenitfollowsthat px +2 > 2,andtherefore 1 px+2 < 1 2 .Wewill usethisfactbelow.

Let " > 0begiven.Let =min(2", 1).Supposethat0 < |x 4| < ,so |x 4| < 2".Wehave |f (x) L| = |px +2 4| = |px 2| =

2.7.35 Assume |x (1/10)| < (1/20),asindicatedinthehint.Then1/20 <x< 3/20,so 20 3 < 1 x < 20 1 ,and thus 1 x < 20.

Alsonotethattheexpression 1 x 10 canbewrittenas 10x 1 x .

Let " > 0begiven.Let =min("/200, 1/20).Nowassumethat0 < |x (1/10)| < .Then |f (x) L| = 10x 1 x < |(10x 1) 20|

 |x (1/10)|· 200 < " 200 200= ".

Thuswehaveestablishedthat 1 x 10 < " whenever0 < |x (1/10)| < . Copyright c

2.7.36 Multiplyingbothsidesoftheinequality | sin 1 x |  1by |x|,wehave |x sin 1 x |  |x|.Let " > 0begiven andassumethat0 < |x 0| < where = ".Wehave |x sin 1 x 0| = |x sin 1 x |  |x|  |x 0| < = " Thereforeitasbeenshownthatforany " > 0, |x sin 1 x 0| < " whenever0 < |x 0| < ,provided0 <  "

2.7.37 Let " > 0begivenandassumethat0 < |x 0| < where =min{1, p"/p2}.Because |x 0| < , wehave |x| < 1and |x| < p"/p2,whichimpliesthat x2 < 1and x2 < "/2.Itfollowsthat |x2 + x4 0| = x2 + x4 = x2 (1+ x2 )  " 2 · 2= ".Wehaveshownthatforany " > 0, |x2 + x4 0| < " whenever0 < |x 0| < , provided0 <  min{1, p"/p2}

2.7.38 Let f (x)= b.Let " > 0begivenandassumethat0 < |x a| < where =1(oranyotherpositive number).Then |f (x) b| = |b b| =0 < ".Wehaveshownthatforany " > 0, |b b| < " whenever 0 < |x a| < ,provided equalsanypositivenumber.

2.7.39 Let m =0,thentheproofisasfollows:Let " > 0begivenandassumethat0 < |x a| < where =1(oranyotherpositivenumber).Then |f (x) b| = |b b| =0 < ".Wehaveshownthatforany " > 0, |b b| < " whenever0 < |x a| < ,provided equalsanypositivenumber. Nowassumethat m =0.Let " > 0begivenandassumethat0 < |x a| < where = "/|m|.Then |(mx + b) (ma + b)| = |m||x a| < |m| = |m|("/|m|)= "

2.7.40 Let " > 0begivenandassumethat0 < |x 3| < where =min{1, "/37}.Byfactoring x3 27,we ﬁndthat |x3 27| = |x 3||x2 +3x +9|.Because |x 3| < and  1,wehave |x 3|  1,whichimpliesthat 1 <x 3 < 1or2 <x< 4.Itfollowsthat |x2 +3x +9| = x2 +3x +9  42 +3(4)+9=37.Wealsoknowthat |x 3| < "/37because0 < |x 3| < and  "/37.Therefore |x3 27| = |x 3||x2 +3x +9|  ("/37) · 37= " Wehaveshownthatforany " > 0, |x3 27| < " whenever0 < |x 3| < ,provided0 <  min{1, "/37}

2.7.41 Let " > 0begivenandassumethat0 < |x 1| < where =min ⇢ 1 2 , 8" 65 .Observethat |x4 1| = |(x2 1)(x2 +1)|

.Because

and  1 2 ,wehave |x 1| < 1 2 , whichimpliesthat 1 2 <x 1 < 1 2 ,or 1 2 <x< 3 2 .Itfollowsthat |x +1|

 5 2 .Also x 2

9 4 ,so |x2 +1| = x2 +1  13 4 .Wealsoknowthat |x 1| < 8" 65 because |x 1| < and  8" 65 .Therefore |x 4 1| = |

" >

2.7.42 Notethatif |x 5| < 1,then4 <x< 6,sothat9 <x +5 < 11,so |x +5| < 11.Notealsothat 16 <x2 < 36,so 1 x2 < 1 16

Let " > 0begiven.Let =min(1, 400 11 ").Assumethat0 < |x 5| < .Then

2.7.43 Let " > 0begiven.

Becauselim x!a f (x)= L,weknowthatthereexistsa 1 > 0sothat |f (x) L| < "/2when0 < |x a| < 1

Also,becauselim x!a g (x)= M ,thereexistsa 2 > 0sothat |g (x) M | < "/2when0 < |x a| < 2 .

Nowlet =min(1 , 2 ).

Thenif0 < |x a| < ,wewouldhave |f (x) g (x) (L M )| = |(f (x) L)+(M g (x))|  |f (x) L| + |M g (x)| = |f (x) L| + |g (x) M |  "/2+ "/2= ".Notethatthekeyinequalityinthis sentencefollowsfromthetriangleinequality.

2.7.PreciseDeﬁnitionsofLimits139

2.7.44 Firstnotethatthetheoremistriviallytrueif c =0.Soassume c =0. Let " > 0begiven.Becauselim x!a f (x)= L,thereexistsa > 0sothatif0 < |x a| < ,wehave |f (x) L| < "/|c|.Butthen |c||f (x) L| = |cf (x) cL| < ",asdesired.Thus,lim x!a cf (x)= cL.

2.7.45 Let N> 0begiven.Let =1/pN .Thenif0 < |x 4| < ,wehave |x 4| < 1/pN .Taking thereciprocalofbothsides,wehave 1 |x 4| > pN ,andsquaringbothsidesofthisinequalityyields 1 (x 4)2 >N .Thuslim x!4 f (x)= 1

2.7.46 Let N> 0begiven.Let =1/ 4 pN .Thenif0 < |x ( 1)| < ,wehave |x +1| < 1/ 4 pN .Takingthe reciprocalofbothsides,wehave 1 |x +1| > 4 pN ,andraisingbothsidestothe4thpoweryields 1 (x +1)4 >N . Thuslim x!1 f (x)= 1

2.7.47 Let N> 1begiven.Let =1/pN 1.Supposethat0 < |x 0| < .Then |x| < 1/pN 1,and takingthereciprocalofbothsides,weseethat1/|x| > pN 1.Thensquaringbothsidesyields dsfrac1x2 >N 1,so 1 x2 +1 >N .Thuslim x!0 f (x)= 1

2.7.48 Let N> 0begiven.Let =1/ 4 pN +1.Thenif0 < |x 0| < ,wewouldhave |x| < 1/ 4 pN +1. Takingthereciprocalofbothsidesyields 1 |x| > 4 pN +1,andthenraisingbothsidestothe4thpowergives 1 x4 >N +1,so 1 x4 1 >N .Nowbecause 1  sin x  1,wecansurmisethat 1 x4 sin x>N aswell, because 1 x4 sin x 1 x4 1.Hencelim x!0 ✓ 1 x4 sin x◆ = 1.

2.7.49

a. False.Infact,ifthestatementistrueforaspeciﬁcvalueof 1 ,thenitwouldbetrueforanyvalueof < 1 .Thisisbecauseif0 < |x a| < ,itwouldautomaticallyfollowthat0 < |x a| < 1

b. False.Thisstatementisnotequivalenttothedeﬁnition–notethatitsays“foranarbitrary there existsan "”ratherthan“foranarbitrary " thereexistsa .”

c. True.Thisisthedeﬁnitionoflim x!a f (x)= L

d. True.Bothinequalitiesdescribethesetof x’swhicharewithin unitsof a

2.7.50

a. Wewantittobetruethat |f (x) 2| < 0.25.Soweneed |x2 2

Thereforeweneed |x 1| < p0 25=0 5.Thusweshouldlet =0 5.

b. Wewantittobetruethat |f (x) 2| < ".Soweneed |x2 2x +3 2|

|x2 2x

1)2 < " Thereforeweneed |x 1| < p".Thusweshouldlet = p"

2.7.51 Becauseweareapproaching a fromtheright,weareonlyconsideringvaluesof x whicharecloseto, butalittlelargerthan a.Thenumbers x totherightof a whicharewithin unitsof a satisfy0 <x a< .

2.7.52 Becauseweareapproaching a fromtheleft,weareonlyconsideringvaluesof x whicharecloseto, butalittlesmallerthan a.Thenumbers x totheleftof a whicharewithin unitsof a satisfy0 <a x< . Copyright c 2019PearsonEducation,Inc.

2.7.53

a. Let " > 0begiven.let = "/2.Supposethat0 <x< .Then0 <x< "/2and |f (x) L| = |2x 4 ( 4)| = |2x| =2|x| =2x< "

b. Let " > 0begiven.let = "/3.Supposethat0 < 0 x< .Then <x< 0and "/3 <x< 0,so " > 3x.Wehave |f (x) L| = |3x 4 ( 4)| = |3x| =3|x| = 3x< ".

c. Let " > 0begiven.Let = "/3.Because "/3 < "/2,wecanarguethat |f (x) L| < " whenever 0 < |x| < exactlyasintheprevioustwopartsofthisproblem.

2.7.54

a. Thisstatementholdsfor =2(oranynumberlessthan2).

b. Thisstatementholdsfor =2(oranynumberlessthan2).

c. Thisstatementholdsfor =1(oranynumberlessthan1).

d. Thisstatementholdsfor = 5(oranynumberlessthan0 5).

2.7.55 Let " > 0begiven,andlet = "2 .Supposethat0 <x< ,whichmeansthat x< "2 ,sothat px< ".Thenwehave |f (x) L| = |px 0| = px< " asdesired.

2.7.56

a. Supposethatlim x!a f (x)= L andlim x!a+ f (x)= L.Let " > 0begiven.Thereexistsanumber 1 so that |f (x) L| < " whenever0 <x a< 1 ,andthereexistsanumber 2 sothat |f (x) L| < " whenever0 <a x< 2 .Let =min(1 , 2 ).Itimmediatelyfollowsthat |f (x) L| < " whenever 0 < |x a| < ,asdesired.

b. Supposelim x!a f (x)= L,andlet " > 0begiven.Weknowthata existssothat |f (x) L| < " whenever 0 < |x a| < .Inparticular,itmustbethecasethat |f (x) L| < " whenever0 <x a< andalso that |f (x) L| < " whenever0 <a x< .Thuslim x!a+ f (x)= L andlim x!a f (x)= L

2.7.57

a. Wesaythatlim x!a+ f (x)= 1 ifforeachpositivenumber N ,thereexists > 0suchthat f (x) >N whenever a<x<a + .

b. Wesaythatlim x!a f (x)= 1 ifforeachnegativenumber N ,thereexists > 0suchthat

f (x) <N whenever a <x<a.

c. Wesaythatlim x!a f (x)= 1 ifforeachpositivenumber N ,thereexists > 0suchthat

f (x) >N whenever a <x<a.

2.7.PreciseDeﬁnitionsofLimits141

2.7.58 Let N< 0begiven.Let = 1/N ,andsupposethat1 <x< 1+ .Then1 <x< N 1 N ,so 1 N N < x< 1,andtherefore1+ 1 N N < 1 x< 0,whichcanbewrittenas 1 N < 1 x< 0.Taking reciprocalsyieldstheinequality N> 1 1 x ,asdesired.

2.7.59 Let N> 0begiven.Let =1/N ,andsupposethat1 <x< 1.Then N 1 N <x< 1,so 1 N N > x> 1,andtherefore1+ 1 N N > 1 x> 0,whichcanbewrittenas 1 N > 1 x> 0.Taking reciprocalsyieldstheinequality N< 1 1 x ,asdesired.

2.7.60 Let M< 0begiven.Let = p 2/M .Supposethat0 < |x 1| < .Then(x 1)2 < 2/M ,so 1 (x 1)2 > M 2 ,and 2 (x 1)2 <M ,asdesired.

2.7.61 Let M< 0begiven.Let = 4 p 10/M .Supposethat0 < |x +2| < .Then(x +2)4 < 10/M ,so 1 (x +2)4 > M 10 ,and 10 (x +2)4 <M ,asdesired.

2.7.62 Let N> 0begivenandlet N1 =max{1,N c}.Becauselim x!a f (x)= 1 thereexists > 0such that f (x) >N1 whenever0 < |x a| < .Itfollowsthat f (x)+ c>N1 + c N c + c = N .Soforany N> 0,thereexists > 0suchthat f (x)+ c>N whenever0 < |x a| <

2.7.63 Let N> 0begiven.Becauselim x!a f (x)= 1,thereexists 1 > 0suchthat f (x) > N 2 whenever 0 < |x a| < 1 .Similarly,becauselim x!a g (x)= 1,thereexists 2 > 0suchthat g (x) > N 2 whenever

0 < |x a| < 2 .Let =min{1 , 2 } andassumethat0 < |x a| < .Because =min{1 , 2 },  1 and  2 .Itfollowsthat0 < |x a| < 1 and0 < |x a| < 2 andtherefore f (x)+ g (x) > N 2 + N 2 = N .So forany N> 0,thereexists > 0suchthat f (x)+ g (x) >N whenever0 < |x a| <

2.7.64 Let " > 0begiven.Let N = 10 " .Supposethat x>N .Then x> 10 " so0 < 10 x < ".Thus, | 10 x 0| < ",asdesired.

2.7.65 Let " > 0begiven.Let N =1/".Supposethat x>N .Then 1 x < ",andso |f (x) L| = |2+ 1 x 2| < ".

2.7.66 Let M> 0begiven.Let N =100M .Supposethat x>N .Then x> 100M ,so x 100 >M ,as desired.

2.7.67 Let M> 0begiven.Let N = M 1.Supposethat x>N .Then x>M 1,so x +1 >M ,and thus x2 + x x >M ,asdesired.

2.7.68 Let " > 0begiven.Becauselim x!a f (x)= L,thereexistsanumber 1 sothat |f (x) L| < " whenever 0 < |x a| < 1 .Andbecauselim x!a h(x)= L,thereexistsanumber 2 sothat |h(x) L| < " whenever

0 < |x a| < 2 .Let =min(1 , 2 ),andsupposethat0 < |x a| < .Because f (x)  g (x)  h(x)for x near a,wealsohavethat f (x) L  g (x) L  h(x) L.Nowwhenever x iswithin unitsof a (but x = a),wealsonotethat " <f (x) L  g (x) L  h(x) L< ".Therefore |g (x) L| < ",asdesired.

2.7.69 Let " > 0begiven.Let N = b(1/")c +1.Byassumption,thereexistsaninteger M> 0sothat |f (x) L| < 1/N whenever |x a| < 1/M .Let =1/M Nowassume0 < |x a| < .Then |x a| < 1/M ,andthus |f (x) L| < 1/N .Butthen

asdesired.

2.7.70 Supposethat " =1.Thennomatterwhat is,therearenumbersintheset0 < |x 2| < sothat |f (x) 2| > ".Forexample,when x isonlyslightlygreaterthan2,thevalueof |f (x) 2| willbe2ormore.

2.7.71 Let f (x)= |x| x andsupposelim x!0 f (x)doesexistandisequalto L.Let " =1/2.Theremustbe avalueof sothatwhen0 < |x| < , |f (x) L| < 1/2.Nowconsiderthenumbers /3and /3,both ofwhicharewithin of0.Wehave f ( /3)=1and f ( /3)= 1.However,itisimpossibleforboth |1 L| < 1/2and | 1 L| < 1/2,becausetheformerimpliesthat1/2 <L< 3/2andthelatterimplies that 3/2 <L< 1/2.Thuslim x!0 f (x)doesnotexist.

2.7.72 Supposethatlim x!a f (x)existsandisequalto L.Let " =1/2.Bythedeﬁnitionoflimit,theremust beanumber sothat |f (x) L| < 1 2 whenever0 < |x a| < .Nowineverysetoftheform(a,a + )there arebothrationalandirrationalnumbers,sotherewillbevalueof f equaltoboth0and1.Thuswehave |0 L| < 1/2,whichmeansthat L liesintheinterval( 1/2, 1/2),andwehave |1 L| < 1/2,whichmeans that L liesintheinterval(1/2, 3/2).Becausethesebothcan’tbetrue,wehaveacontradiction.

2.7.73 Because f iscontinuousat a,weknowthatlim x!a f (x)existsandisequalto f (a) > 0.Let " = f (a)/3. Thenthereisanumber > 0sothat |f (x) f (a)| <f (a)/3whenever |x a| < .Thenwhenever x liesin theinterval(a ,a + )wehave f (a)/3  f (x) f (a)  f (a)/3,so2f (a)/3  f (x)  4f (a)/3,so f is positiveinthisinterval.

2.7.74 Usingthetriangleinequality,wehave |a| = |(a b)+ b|  |a b| + |b|.Thisimpliesthat |a|  |a b| + |b| or |a| |b|  |a b|.Asimilarargumentshowsthat |

|.Becausetheexpression ||

| |

|| is equaltoeither |a| |b| or |b| |a|,itfollowsthat

ChapterTwoReview

a. False.Becauselim x!1 x 1 x2 1 =lim x!1 1 x +1 = 1 2 , f doesn’thaveaverticalasymptoteat x =1.

b. False.Ingeneral,thesemethodsaretooimprecisetoproduceaccurateresults.

c. False.Forexample,thefunction f (x)=

hasalimitof0as x ! 0,but f (0)=1.

d. True.Whenwesaythatalimitexists,wearesayingthatthereisarealnumber L thatthefunction isapproaching.Ifthelimitofthefunctionis 1,itisstillthecasethatthereisnorealnumberthat thefunctionisapproaching.(Thereisnorealnumbercalled“inﬁnity.”)

e. False.Itcouldbethecasethatlim x!a f (x)=1andlim x!

f. False.

g. False.Forexample,thefunction f (x)= 8 < : 2if0 <x< 1; 3if1  x< 2, iscontinuouson(0, 1),andon[1, 2),but isn’tcontinuouson(0, 2).

h. True.lim x!a f (x)= f (a)ifandonlyif f iscontinuousat a

2 s(1)=48and s(1.5)=60,sotheaveragevelocityoverthetimeperiodis

3 Forvariousvaluesof b,wecalculate vavg = s(b) s(1 5) b 1.5

Weestimatethattheinstantaneousvelocityis12. 4

f ( 1)=1

(

)=1. d. lim x!1 f (x)doesnotexist. e. f (1)=5.

g. lim x!2 f (x)=4.

j. lim x!3 f (x)doesnotexist.

lim x!3 f (x)=3.

lim x!1 f (x)=5.

lim x!3+ f (x)=5.

5 Thisfunctionisdiscontinuousat x = 1,at x =1,andat x =3.At x = 1itisdiscontinuousbecause lim x!1 f (x)doesnotexist.At x =1,itisdiscontinuousbecauselim x!1 f (x) = f (1).At x =3,itisdiscontinuous because f (3)doesnotexist,andbecauselim x!3 f (x)doesnotexist. 6

a. Thegraphdrawnbymostgraphingcalculatorsand computeralgebrasystemsdoesn’tshowthediscontinuitieswheresin ✓ =0.

b. Itappearstobeequalto2

c. Usingatrigonometricidentity,lim ✓ !0 sin2✓ sin ✓ = lim ✓ !0 2sin ✓ cos ✓ sin ✓ .Thiscanthenbeseentobe lim ✓ !0 2cos ✓ =2

Truegraph,showingdiscontinuities wheresin ✓ =0.

Graphshownwithoutdiscontinuities.

Thelimitappearstobeapproximately1.4142.

Thereareinﬁnitelymanydi↵erentcorrectfunctionswhichyoucoulddraw.Oneofthemis:

d. Thecostoftherentaljumpsby$15exactly at t =3.Arentallastingslightlylessthan 3dayscost$55andrentalslastingslightly morethan3dayscost$70.

e. Thefunction f iscontinuouseverywhereexceptattheintegers.Thecostoftherental jumpsby$15ateachinteger.

Factoringthenumeratorasthedi↵erenceofsquares,wehave

x +1)+(3

+1))

19 lim x!3 1 x 3 ✓ 1 px +1 1 2 ◆ =lim x!3 2 px +1 2(x 3)px +1 (2+ px +1) (2+ px +1) =lim x!3 4 (x +1) 2(x 3)(px +1)(2+ px +1) =lim x!3 (x 3) 2(x 3)(px +1)(2+ px +1) =lim x!3 1 2px +1(2+ px +1) = 1 16

20 lim t!1/3 t 1 3 (3t 1)2 =lim t!1/3 3t 1 3(3t 1)2

/3 1 3(3t 1) ,whichdoesnotexist. 21 lim x!3 x4 81 x 3 =lim x!3 (x 3)(x +3)(x2 +9) x 3 =lim x!3(x +3)(

26 Thedomainof f (x)= r x 1 x 3 is(1, 1]and(3, 1),solim x!1+ f (x)doesn’texist. However,wehavelim x!1 f (x)=0.

27 lim x!5 x 7 x(x 5)2 = 1

28 lim x!5+ x 5 x +5 = 1.

29 lim x!3 x 4 x2 3x =lim x!3 x 4 x(x 3) = 1

30 lim x!0+ u 1 sin u = 1.

31 lim x!1+ 4x3 4x2 |x 1| =lim x!1+ 4x2 (x 1) x 1 =lim x!1+ 4x 2 =4

32 Theexpression2x 4=2(x 2)isnegativefor x< 2,so |2x 4| = 2(x 2).Therefore, lim x!2 |2x 4| x2 5x +6 =lim x!2 2(x 2) (x 2)(x 3) =lim x!2 2 x 3 =2.

33 lim x!0 2 tan x = 1.

34 Firstnotethatforall x, px4 = x2 .Thenwehave lim x!1 (4x2 +3x +1) p8x4 +2 1/x2 1/px4 =lim x!1 4+(3/x)+(1/x2 ) p8+(2/x4 ) = 4 p8 = 2 p2 = p2.

35 lim x!1 2x 3 4x +10 =lim x!1 2 (3/x) 4+(10/x) = 2 4 = 1 2

36 lim x!1 x4 1 x5 +2 =lim x!1 (1/x) (1/x5 ) 1+(2/x5 ) = 0 0 1+0 =0.

37 Notethatfor x< 0, x = px2 .Thenwehave lim x!1 (3x +1) pax2 +2 1/x

38 Wehave lim x!1 px2 + ax px2 b =lim x!1 (px2 + ax px2 b

Nownotingthat x = px2 for x> 0wehave

39 Wemultiplythenumeratoranddenominatorbytheconjugateofthedenominator(i.e.,theexpression px2 ax + px2 x).Thisgives

Wenowmultiplyby 1/px2 1/x toobtain

40 lim z !1

lim x!1

e 2z + 2 z

1 x +2)=

lim x!1 ( 3x 3 +5)=

er =0.

47 lim r !1 (2e4r +3e5r ) (7e4r 9

48 Because 1  sin x  1, ex  ex sin x  ex .Becauselim x!1 ex =lim x!1 ex =0,wecanconcludethat lim x!1 ex sin x =0bytheSqueezeTheorem.

49 Weknowthat0  cos4 x  1.Dividingeachpartofthisinequalityby x2 + x +1andthenadding5,we have5  5+ cos4 x x2 + x +1  5+ 1 x2 + x +1 .Notethatlim x!1 5=5andlim x!1 ✓5+ 1 x2 + x +1 ◆ =5,sobythe SqueezeTheoremwecanconcludethatlim x!1 ✓5+ cos4 x x2 + x +1 ◆ =5.

50 Recallthat 1  cos t  1,andthat e3t > 0forall t.Thus 1 e3t  cos t e3

.Becauselim t!1 1

3t = lim t!1 1 e3t =0,wecanconcludelim t!1 cos t e3t =0bytheSqueezeTheorem.

51 lim x!1 x ln x = 1

52 Notethatlim x!0(sin2 x +1)=1.Thusif1  g (x)  sin2 x +1,theSqueezeTheoremassuresusthat lim x!0 g (x)=1aswell.

b. Becauselim x!0 cos x =lim x!0 1 cos x =1,theSqueeze

Theoremassuresusthatlim x!0 sin x x =1aswell. 54

Firstnotethat f (x)= x 2 5x+6 x2 2x = (x 3)(x 2) x(x 2)

a. lim x!0 f (x)=lim x!0 (x 3)(x 2) x(x 2) = 1.

lim x!0+ f (x)=lim x!0+ (x 3)(x 2) x(x 2) = 1.

lim x!2 f (x)=lim x!2 x 3 x = 1 2

lim x!2+ f (x)=lim x!2+ x 3 x = 1 2

b. Bytheabovecalculationsandthedeﬁnitionof verticalasymptote, f hasaverticalasymptoteat x =0.

c. Notethattheactualgraphhasa“hole”atthe point(2, 1/2),because x =2isn’tinthedomain, butlim x!2 f (x)= 1/2.

55 lim x!1 4x3 +1 1 x3 =lim x!1 4+(1/x3 ) (1/x3 ) 1 = 4+0 0 1 = 4.Asimilarresultholdsas x !1.Thus, y = 4isa horizontalasymptoteas x !1 andas x !1

56 Notethat px12 = x6 forall x.Wehavelim x!±1 (x6 +1) p16x14 +1 · 1/x6 1/px12 =lim x!±1 1+(1/x6 ) p16x2 +(1/x12 ) =0.

57 lim x!1 (1 e 2x )=1,whilelim x!1 (1 e 2x )= 1 y =1isahorizontalasymptoteas x !1.

58 lim x!1 1 ln x2 =0,andlim x!1 1 ln x2 =0,so y =0isahorizontalasymptoteas x !1 andas x !1

59 lim x!1 (6ex +20) (3ex +4) 1/ex 1/ex =lim x!1 6+(20/ex ) 3+(4/ex ) = 6 3 =2. lim x!1 6ex +20 3ex +4 = 0+20 0+4 =5.

60 Firstnotethat

Ontheotherhand,lim

So y = 1 3 isahorizontalasymptoteas x !1,and y = 1 3 isahorizontalasymptoteas x !1

Bylongdivision,weseethat

x!1

b. Becausethereisahorizontalasymptote,thereisnotaslantasymptote.

63 a.

b. Bylongdivision,wecanwrite

asymptote.

b. Becausethedegreeofthenumeratorofthisrationalfunctionistwomorethanthedegreeofthe denominator,thereisnoslantasymptote.

b. Bylongdivision,wecanwrite 4x3 + x2 +7 x2 x +1 =4x +5+ x +2 x2 x +1 .Therefore y =4x +5isaslant asymptote.

66 Notethat f (x)= 2x2 +6 2x2 +3x 2 = 2(x2 +3) (2x 1)(x +2)

Wehavelim x!1 f (x)=lim x!1 2+6/x2 2+3/x 2/x2 =1.Asimilarresultholdsas x !1.

lim x!1/2 f (x)= 1.lim x!1/2+ f (x)= 1

lim x!2 f (x)= 1.lim x!2+ f (x)= 1

Thus, y =1isahorizontalasymptoteas x !1 andas x !1.Also, x = 1 2 and x = 2arevertical asymptotes.

67 Recallthattan 1 x =0onlyfor x =0.Theonlyverticalasymptoteis x =0.

lim x!1 1 tan 1 x = 1 ⇡ /2 = 2 ⇡ lim x!1 1 tan 1 x = 1 ⇡ /2 = 2 ⇡ .So y = 2 ⇡ isahorizontalasymptoteas x !1 and y = 2 ⇡ isahorizontal asymptoteas x !1

68 Bylongdivision,wecanwrite 2x2 7 x 2 =2x +4+ 1 x 2 ,so y =2x +4isaslantasymptote.Also, lim x!2+ 2x2 7 x 2 = 1,so x =2isaverticalasymptote.

69 Observethat f (x)= x + xex +10ex 2(ex +1) = x(1+ ex )+10ex 2(ex +1) = 1 2 x + 5ex ex +1 . Becauselim x!1 5ex ex +1 =lim x!1 5 1+(1/ex ) =5,thegraphof f andtheline y = 1 2 x +5approacheachotheras x !1.Similarly,lim x!1 5ex ex +1 = 0 0+1 =0andthereforethegraphof f andtheline y = 1 2 x approach eachotheras x !1

70 Observethatlim x!0+ x2 + x +3 |x| =lim x!0+ x2 + x +3

x!0+ x +1+(3/x)= 1 andlim x!0 x2 + x +3 |x| = lim x!0 x2 + x +3 x = lim x!0 (x +1+(3/x))= 1.For x> 0,wehave f (x)= x2 + x +3 x = x +1+ 3 x , so y = x +1isaslantasymptoteas x !1.For x< 0,wehave f (x)= x2 + x +3 x = x 1 3 x ,so

y = x 1isaslantasymptoteas x !1.Sothefunctionhasoneverticalasymptote x =0andtwo slantasymptotes, y = x +1and y = x 1.

71 Thefunction f isnotcontinuousat5because f (5)isnotdeﬁned.

72 g isdiscontinuousat4becauselim x!4 g (x)=lim x!4 (x +4)(x 4) x 4 =8 = g (4).

73 Observethat h(5)= 2(5)+14=4.Becauselim x!5 h(x)=lim x!5 ( 2x +14)=4andlim x!5+ h(x)= lim x!5+ px2 9= p25 9=4,wehavelim x!5 h(x)=4.Thus f iscontinuousat x =5.

74 Observethat g (2)= 2andlim x!2 g (x)=lim x!2 x3 5x2 +6x x 2 =lim x!2 x(x 2)(x 3) x 2 =lim x!2 x(x 3)= 2. Therefore g iscontinuousat x =2.

75 Thedomainof f is(1, p5]and[p5, 1),and f iscontinuousonthatdomain.Itisleftcontinuous at p5andrightcontinuousat p5.

76 Thedomainof g is[2, 1),anditiscontinuousonthatdomain.Itiscontinuousfromtherightat x =2.

77 Thedomainof h is(1, 5),( 5, 0),(0, 5),(5, 1),andlikeallrationalfunctions,itiscontinuouson itsdomain.

78 g isthecompositionoftwofunctionswhicharedeﬁnedandcontinuouson(1, 1),so g iscontinuous onthatintervalaswell.

79 Inorderfor g tobeleftcontinuousat1,itisnecessarythatlim x!1 g (x)= g (1),whichmeansthat a =3.Inorderfor g toberightcontinuousat1,itisnecessarythatlim x!1+ g (x)= g (1),whichmeansthat a + b =3+ b =3,so b =0.

80 a. Becausethedomainof h is(1, 3]and[3, 1),thereisnowaythat h canbeleftcontinuousat3.

b. h isrightcontinuousat3,becauselim x!3+ h(x)=0= h(3).

Onesuchpossiblegraphispicturedtotheright.

a. Considerthefunction f (x)= x5 +7x +5. f iscontinuouseverywhere,and f ( 1)= 3 < 0while f (0)=5 > 0.Therefore,0isanintermediatevaluebetween f ( 1)and f (0).BytheIntermediate ValueTheorem,theremustanumber c between0and1sothat f (c)=0.

b. Usingacomputeralgebrasystem,onecanﬁndthat c ⇡0 691671isaroot.

a. RewriteTheequationas x cos x =0andlet f (x)= x cos x.Because x andcos x arecontinuous onthegiveninterval,sois f .Because f (0)= 1 < 0and f (⇡ /2)= ⇡ /2 > 0,itfollowsfromthe IntermediateValueTheoremthattheequationhasasolutionon(0, ⇡ /2).

b. Usingacomputeralgebrasystem,onecanﬁndthat c ⇡ 0.739085isaroot.

84 Temperaturechangesgradually,soitisreasonabletoassumethat T isacontinuousfunctionandtherefore f isalsocontinuous.Becausef (0)= 33 < 0and f (12)=33 > 0,itfollowsfromtheIntermediateValue Theoremthatthereisavalue t0 in(0, 12)satisfying f (t0 )=0..Therefore, T (t0 ) T (t0 +12)=0,or T (t0 )= T (t0 +12).

a. Notethat m(0)=0and m(5) ⇡ 38 34and m(15) ⇡ 21 2.Thus,30isanintermediatevaluebetween both m(0)and m(5),and m(5)and m(15).Notealsothat m isacontinuousfunction.BytheIVT, theremustbeanumber c1 between0and5with m(c1 )=30,andanumber c2 between5and15with m(c2 )=30.

b. Alittletrialanderrorleads c1 ⇡ 2 4and c2 ⇡ 10 8.

c. No.Thegraphofthefunctiononagraphingcalculatorsuggeststhatitpeaksatabout38.5

86 Let " > 0begiven.Let = "/5.Nowsupposethat0 <

Then

87 Let " > 0begiven.Let = ".Nowsupposethat0

Then

88 Let " > 0begiven.Let = " 4 andassumethat0 < |x 3| < .For x< 3, |f (x) 5| = |3x 4 5| =3|x 3| < 3 =3 · " 4 < " For x> 3, |f (x) 5| = | 4x +17 5|

,provided0 <  " 4 .

89 Let " > 0begiven.Let =min{1, "/15} andassumethat0 < |x 2| < .Then |3x2 4 8| = 3|x2 4| =3|x 2||x +2|.Because0 < |x 2| < and  1, 1 <x 2 < 1andso1 <x< 3.Itfollows that x +2 < 5.Therefore |3x2 4 8| =3|x 2||x +2| < 3 " 15 5= ".Sowe’veshownthatforany " > 0, |3x2 4 8|

90 Let " > 0begiven.Let = " 2 4 andassumethat0 <x 2 < .Then |p4x 8 0| =2px 2 < 2p =2q "2 4 = ".Sowe’veshownthatforany " > 0, |p4x 8 0| < " whenever0 <x 2 < ,provided 0 <  " 2 4

91 Let N> 0begiven.Let =1/ 4 pN .Supposethat0 < |x 2| < .Then |x 2| < 1 4 pN ,so 1 |x 2| > 4 pN , and 1 (x 2)4 >N ,asdesired.

a. Assume L> 0.(If L =0,theresultfollowsimmediatelybecausethatwouldimplythatthefunction f istheconstantfunction0,andthen f (x)g (x)isalsotheconstantfunction0.)Assumethat 1 isa numbersothat |f (x)|  L for |x a| < 1 .

Let " > 0begiven.Becauselim x!a g (x)=0,weknowthatthereexistsanumber 2 > 0sothat |g (x)| < "/L whenever0 < |x a| < 2 .Let =min(1 , 2 ). Then |f (x)g (x) 0| = |f (x)||g (x)| <L " L = ", whenever0 < |x a| <

b. Let f (x)= x2 x 2 .Then

Thisdoesn’tviolatethepreviousresultbecausethegivenfunction f isnotboundednear x =2.

c. Because |H (x)|  1forall x,theresultfollowsdirectlyfromparta)ofthisproblem(using L =1, a =0, f (x)= H (x),and g (x)= x).

Guided Project 2: Constant rate problems

Topicsandskills:Algebra

Continuing with the theme of problem solving, we now give you an opportunity to apply Pólya’s method (see Guided Project 1: Problem-solvingskills) to a specific type of problem. Constant rate problems require only algebra (solving problems that involve variable rates is a major reason for studying calculus). Exercises 1−16 below involve constant speeds. Constant speed problems use the fact that Distance traveled = speed × time elapsed or d = s × t Exercises 17−25 deal with more general constant rates, such as work rates and flow rates; but the same ideas may be used. If a problem involves a quantity Q (such as gallons of water or number of bagels) and its rate of change is the constant r, the constant rate formula is

Amount of Q = rate of change of Q × time elapsed or Q = r × t

Write out complete solutions to the following problems and discuss whether and how Pólya’s method was useful.

Problem-Solving Exercises

Constant speed problems

1. A car went 4 miles up a hill at 40 mi/hr and 6 mi down the back of the hill at 60 mi/hr. What was the average speed of the round trip?

2. A one-mile-long train went through a one-mile-long tunnel at 15 mi/hr. How long did it take the entire train to pass through the tunnel?

3. If a lady walks to work and drives home, it takes one and a half hours. When she drives both ways, it takes half an hour. At the same speeds, how much time does a round trip while walking require?

4. At full speed, a motor boat can go upstream 10 mi (against the current) in 15 min and downstream 10 mi (with the current) in 9 min. At full speed, how much time is required for the boat to go 10 mi with no current?

5. Two trains travel toward each other on parallel tracks. Train A is 0.5 mi long and travels at 20 mi/hr. Train B is 1/3 mi long and travels at 30 mi/hr. How long does it take the trains to pass each other completely (from the instant the engines meet to the instant that the cabooses pass each other)?

6. At midnight a train left Denver bound for Omaha, a distance of 500 mi, at a speed of 80 mi/hr and another train left Omaha bound for Denver at a speed of 100 mi/hr. When the trains passed each other, what fraction of its trip had the Denver train completed?

7. At midnight a train left Denver bound for Chicago and another train left Chicago bound for Denver, both traveling at constant speeds on adjacent tracks. The first train took 12 hr to complete the trip and the second train took 16 hr to complete the trip. At what time did the trains pass each other?

8. A train left Denver bound for Omaha, a distance of 500 mi, at a speed of 80 mi/hr. Two hours later, another train left Omaha bound for Denver at a speed of 100 mi/hr. When the trains passed each other, how far had the Denver train traveled?

9. A train left Boston for New York, a distance of 220 mi, at 70 mi/hr. One hour later, a train left New York for Boston at 60 mi/hr. How far apart were the trains one hour before they met?

10. Two cyclists racing on parallel roads maintain constant speeds of 30 mi/hr and 25 mi/hr. The faster cyclist crosses the finish line one hour before the slower cyclist. How long was the race (in miles)?

11. Because Boat A travels 1.5 times faster than Boat B, Boat B was given a 1.5-hr head start in a race. How long did it take Boat A to catch Boat B?

12. A plane flew into a headwind and made the outbound trip in 84 min. It turned around and made the return trip with a tailwind in 9 min less than it would have taken with no wind. Assuming that the plane's ground speed and the wind speed are constant, what are the possible times for the return trip?

13. A woman usually takes the 5:30 train home from work, arriving at the station at 6:00 where her husband meets her to drive her home. One day she left work early and took the 5:00 train, arrived at the station at 5:30, and began walking home. Her husband, leaving home at the usual time, met his wife along the way and brought her home 10 min earlier than usual. How long did the woman walk?

14. Bob was traveling 80 km/hr behind a truck traveling 65 km/hr. How far behind the truck was Bob one minute before the crash?

15. At his usual rate Bernie can row 15 mi downstream in five hr less time than it takes him to row 15 mi upstream. If he doubles his usual rate, his time downstream is only one hour less than the time upstream. What is the rate of the current in miles per hour?

16. A cyclist began at the tail of a parade that is 4 km long and rode in the direction that the parade was moving. By the time the cyclist reached the head of the parade and returned to the tail, the parade had moved 6 km. Assuming that the cyclist and the parade moved at constant (but different) speeds, how far did the cyclist ride?

Solution to Guided Project 2: Constant rate problems

Constant speed problems

1. The car traveled 10 miles in 9 minutes (3/20 hr) for an average speed of 160 53.3 3  mi/hr.

2. When the front of the train enters the tunnel, the end of the train has two miles to travel before exiting the tunnel. Dividing this distance by the speed of 15 mi/hr gives that the train takes 2/15 hr or 8 minutes to pass through the tunnel.

3. Driving one way takes 15 minutes, so walking one way takes one and a quarter hours. The round trip walking takes two and one half hours.

4. Upstream, the boat travels 40 mi/hr. Downstream, it travels 200/3 mi/hr. These speeds are the boat speed minus the current speed and the boat speed plus the current speed, respectively. Combining these facts gives that the speed of the boat alone is 160/3 mi/hr. Therefore, traveling 10 mi with no current takes 3/16 hr or 11.25 min.

5. Consider the point at which the engines meet to be the origin. Then the position of the caboose of Train A after t hr is 1/220t  and the position of the caboose of Train B is 1/330t . These positions are equal at time 1/60 t  hr, meaning the trains completely pass each other after one minute.

6. Consider Denver to be the origin. After t hr, the train bound for Omaha is at position 100t. At that same time, the train bound for Denver is at position 50080t . These positions are equal when 25/9 t  , at which point the train bound for Denver will have traveled (25/9)·80 mi, which is 4/9 of its trip.

7. Consider Denver to be the origin. After t hr, the first train is at position (/12)· dt , where d is the distance between Denver and Chicago. At that same time, the second train is at position (/16)· ddt . The trains meet at 48/76.86 t  hr, meaning the trains passed each other at approximately 6:51 a.m.

8. Consider Denver to be the origin. After t hours, the Omaha-bound train is at position 80t . For 2 t  , the Denver-bound train’s position is 500100(2) t . Therefore, the trains meet at time 35/9 t  hr, meaning the Omaha-bound train had traveled (35/92)·100(17/9)·100189

mi.

9. Consider Boston to be the origin. After t hours, the New York train is at position 70t . For 1 t  , the Boston train is at position 22060(1) t . Therefore, the trains meet at time 28/13 t  hr. One hour prior, the distance between the trains is 130 mi.

10. Let x be the length of the race (in miles). The first cyclist completes the race in /30 x hr, while the second requires /25 x hr. We are given that /301/25xx  , which implies 150 x  mi.

11. Let the speed of Boat B be s mi/hr. After t hr, Boat B has traveled st mi. Boat A has traveled 15(15) st mi t hr after Boat B started. Therefore, Boat A overtakes Boat B 4.5hr after Boat B began, so it took Boat A 3 hr to catch Boat B.

12. Let g be the plane’s ground speed, w the wind speed, and d the distance the plane travels (one way). From the outbound trip, we have 84()gwd  , so /84 wgd  . For the return trip, we have ()(/9) gwdgd  . Substituting for w and solving for g gives that /21 gd  or /72 gd  . The time for the return trip is /9dg , so it must be either 12 minutes or 63 minutes.

13. Let w t be the time the woman spent walking and c t the time spent in the car on this day. Let t be the usual amount of time it takes her husband to drive her home from the train station. Since she left 30 minutes early but only got home 10 minutes early, 20 wc ttt  . Since her husband left at the usual time but got home 10 minutes early, 2210 c tt . Combining these facts, we see that 25 w t  minutes.

14. At time t hr before the crash, the truck is 65t km away from the crash site and Bob is 80t km away from the crash site. Here 1/60 t  , and so the distance between these positions is 1/4 km.

15. Let r be Bernie’s usual rowing rate and c the speed of the current. The relationship at his usual rowing rate gives that 15()(15/()5) rcrc  . At double his usual rate, we have 15(2)(15(2)1) rcrc  . Combining and solving for c gives /2 cr  . Substituting this, we are able to solve for r and find 4 r  miles per hour, so 2 c  miles per hour.

16. Let p be the rate at which the parade moves and c the rate at which the cyclist moves. Fixing the origin at the point where the back of the parade began, before the cyclist turns around, the cyclist’s position is ct and the front of the parade is at 4 pt  . The cyclist turns around at time 0 4/() tcp  . For 0 tt  , the cyclist’s position is 0 ctct . The back of the parade is at 0 ptpt  . Therefore, the cyclist reaches the back of the parade when 00 ctctptpt  . Solving for t, we find that the cyclist reaches the back of the parade 1t hours after the turnaround where 1 4/() tcp  . Since the parade moves 6 km in time 01tt  , we have 01 ()6ptt , and therefore   132/3cp  . The distance the cyclist rode is 01 ()421311.21ctt km.

Solutions for Calculus Early Transcendentals 3rd Us Edition by Briggs

Chapter2

Limits

2.1TheIdeaofLimits

2.2DeﬁnitionofaLimit

2.3TechniquesforComputingLimits

2.4InﬁniteLimits

2.5LimitsatInﬁnity

2.6Continuity

2.7PreciseDeﬁnitionsofLimits

ChapterTwoReview

Guided Project 2: Constant rate problems

Solution to Guided Project 2: Constant rate problems

Constant speed problems

The Idea of Limits

Figure 2.1

Figure 2.2 (a)

Figure 2.2 (b)

Figure 2.3

Table 2.1

Figure 2.4

Figure 2.5

Figure 2.6 (1 of 3)

Figure 2.6 (2 of 3)

Figure 2.6 (3 of 3)

Definitions of Limits

Figure 2.7

Table 2.2

Figure 2.11 (a & b)

Figure 2.12 (a & b)

Table 2.3

Table 2.4

Techniques for Computing Limits

Figure 2.19 (a)

Figure 2.19 (b)

Table 2.5

Infinite Limits

Table 2.7

Figure 2.24 (a)

Figure 2.24 (b)

Figure 2.26 (a & b) continued…

Figure

Limits at Infinity

Continuity

Figure 2.46 (a)

Figure 2.46 (b)

Figure 2.50 (a)

Figure 2.50 (b)

Precise Definitions of Limits

Figure 2.60 (a)

Figure 2.60 (b)

Figure 2.61 (a)

Figure 2.61 (b)

Figure 2.67 (a)

Figure 2.67 (b)

Figure 2.68 (a)

Figure 2.68 (b)