Chapter2
Graphs,Functions,andApplications
ExerciseSet2.1
RC2. 4y 3x =0
4y =3x y = 3 4 x
Theansweris(b).
RC4. 3y +4x = 12 3y = 4x 12 y = 4 3 x 4
Theansweris(c).
2. 4.
Parallelogram
A = bh =9 4=36squareunits
6. t =4 3s 4?4 3 3 4 9 5FALSE
Since4= 5isfalse,(3, 4)isnotasolutionof t =4 3s
8. 4r +3s =5 4 2+3 ( 1)?5Substituting2for r and |−1for s 8 3 (alphabeticalorderof | variables) 5
Since5=5istrue,(2, 1)isasolutionof4r +3s =5. 10. 2p 3q = 13 2( 5) 3 1? 13Substituting 5for p and | 1for q 10 3 13
Since 13= 13istrue,( 5, 1)isasolutionof2p 3q = 13.
12. y = x 3 2?5 3 2TRUE y = x 3 4? 1 3 4TRUE
Plotthepoints(5, 2)and( 1, 4)anddrawtheline throughthem.
Thelineappearstopassthrough(0, 3)aswell.Wecheck toseeif(0, 3)isasolutionof y = x 3. y = x 3
3?0 3 3TRUE
(0, 3)isasolution.Othercorrectanswersinclude ( 3, 6),( 2, 5),(1, 2),(2, 1),(3, 0),and(4, 1).
14. y = 1 2 x +3 5? 1 2 · 4+3 2+3 5TRUE y = 1 2 x +3 2? 1 2 ( 2)+3 1+3 2TRUE
Plotthepoints(4, 5)and( 2, 2)anddrawthelinethrough them.
Thelineappearstopassthrough(2, 4)aswell.Wecheck
toseeif(2, 4)isasolutionof y = 1 2 x +3. y = 1 2 x +3
4? 1 2 · 2+3 1+3 4TRUE
(2, 4)isasolution.Othercorrectanswersinclude( 6, 0), ( 4, 1),(0, 3),and(6, 6).
16. 4x 2y =10 4 0 2( 5)?10 0+10 10 TRUE 4x 2y =10 4 4 2 3?10 16 6 10 TRUE
Plotthepoints(0, 5)and(4, 3)anddrawthelinethrough them.
4224 4 2 2 4 531135 5 3 1 1 3 5 x y (2,4) (4,5) (2,2) 4224 4 2 2 4 531135 5 3 1 1 3 5 x y (4,3) (2,1) (0,5)
Thelineappearstopassthrough(5, 5)aswell.Wecheck
toseeif(5, 5)isasolutionof4x 2y =10.
4x 2y =10
4 5 2 5?10 20 10 10 TRUE
(5, 5)isasolution.Othercorrectanswersinclude(1, 3), (2, 1),and(3, 1).
18. x y 2 1 1 0 0 1 1 2 2 3 3 4
50.
52.
54. 2x 5 ≥−10 or 4x 2 < 10 2x ≥−5 or 4x< 12 x ≥− 5 2 orx> 3
Thesolutionsetis {x|x> 3},or( 3, ∞).
56. 13 < 3x +5 < 23 18 < 3x< 18
6 <x< 6
Thesolutionsetis {x|− 6 <x< 6},or( 6, 6).
58. Let h =theheightofthetriangle,infeet.
Solve: 1 2 · 16 · h =200 h =25ft
60. Let x =thesellingpriceofthehouse.Then x 100, 000= theamountthatexceeds$100,000.
Solve:
0 07(100, 000)+0 04(x 100, 000)=16, 200 x =$330, 000
62.
64.
66. Each y -coordinateis3timesthecorresponding x-coordinate,sotheequationis y =3x
68. Each y -coordinateis5lessthesquareofthecorresponding x-coordinate,sotheequationis y =5 x2
ExerciseSet2.2
RC2. f (0)=3
RC4. f (3)=0
2. Yes;eachmemberofthedomainismatchedtoonlyone memberoftherange.
4. No;amemberofthedomain(6)ismatchedtomorethan onememberoftherange.
6. Yes;eachmemberofthedomainismatchedtoonlyone memberoftherange.
8. Yes;eachmemberofthedomainismatchedtoonlyone memberoftherange.
10. Thiscorrespondenceisafunction,sinceeachpersonina familyhasonlyoneheight,ininches.
12. Thiscorrespondenceisnotafunction,sinceeachstatehas twosenators.
14. a) g (0)=0 6= 6
b) g (6)=6 6=0
c) g (13)=13 6=7
d) g ( 1)= 1 6= 7
e) g ( 1 08)= 1 08 6= 7 08
f) g 7 8 = 7 8 6= 5 1 8
16. a) f (6)= 4 6= 24
b) f 1 2 = 4 1 2 =2
c) f (0)= 4 0=0
d) f ( 1)= 4( 1)=4
e) f (3a)= 4 3a = 12a
f) f (a 1)= 4(a 1)= 4a +4
18. a) h(4)=19
b) h( 6)=19
c) h(12)=19
d) h(0)=19
e) h 2 3 =19
f) h(a +3)=19
20. a) f (0)=3 02 2 0+1=1
b) f (1)=3 12 2 1+1=3 2+1=2
c) f ( 1)=3( 1)2 2( 1)+1=3+2+1=6
d) f (10)=3 102 2 10+1=300 20+1=281 Copyright c 2017PearsonEducation,Inc.
e) f ( 3)=3( 3)2 2( 3)+1=27+6+1=34
f) f (2a)=3(2a)2 2(2a)+1=3 4a2 4a +1= 12a2 4a +1
22. a) g (4)= |4 1| = |3| =3
b) g ( 2)= |− 2 1| = |− 3| =3
c) g ( 1)= |− 1 1| = |− 2| =2
d) g (100)= |100 1| = |99| =99
e) g (5a)= |5a 1|
f) g (a +1)= |a +1 1| = |a|
24. a) f (1)=14 3=1 3= 2
b) f ( 1)=( 1)4 3=1 3= 2
c) f (0)=04 3=0 3= 3
d) f (2)=24 3=16 3=13
e) f ( 2)=( 2)4 3=16 3=13
f) f ( a)=( a)4 3= a4 3
26. In1980, h =1980 1945=35.
A(35)=0 059(35)+53 ≈ 55 1years
In2013, h =2013 1945=68
A(68)=0 059(68)+53 ≈ 57 0years
28. T (5)=10 5+20=50+20=70◦ C
T (20)=10 · 20+20=200+20=220◦ C
T (1000)=10 · 1000+20=10, 000+20=10, 020◦ C
30. C (62)= 5 9 (62 32)= 5 9 30= 50 3 =16 2 3 ◦ C
C (77)= 5 9 (77 32)= 5 9 45=25◦ C
C (23)= 5 9 (23 32)= 5 9 ( 9)= 5◦ C 32.
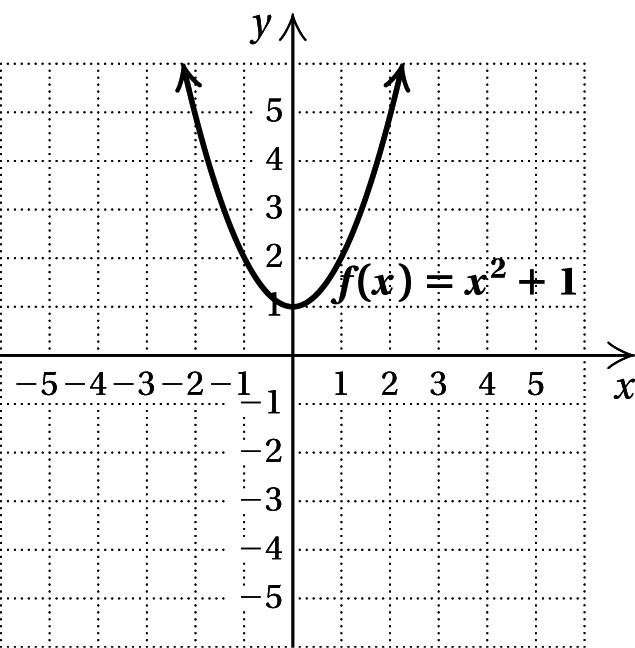
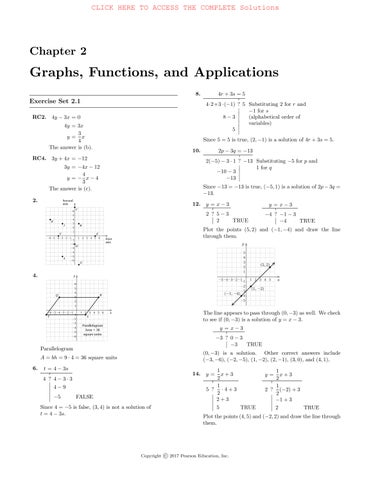
46. x y 5 0 4 3 3 4 2 3 1 0 0 5 1 12
48.
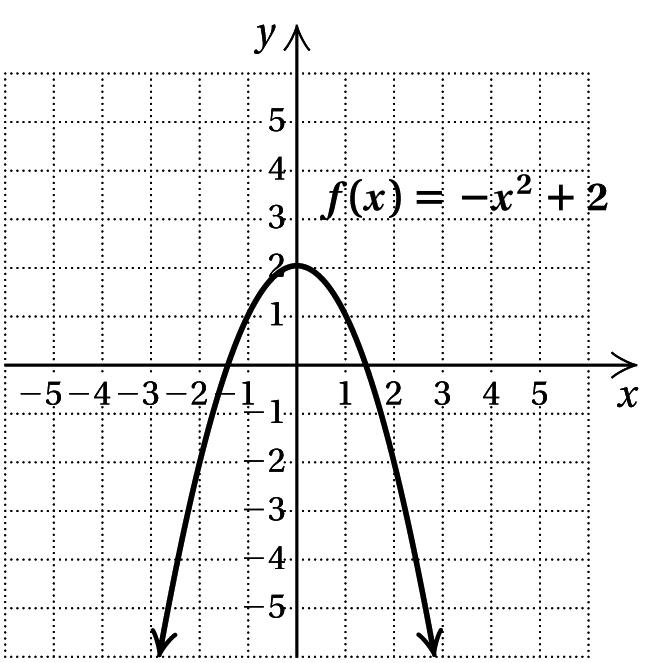
50. x f (x)
52. No;itfailstheverticallinetest.
54. Yes;itpassestheverticallinetest.
56. Yes;itpassestheverticallinetest.
58. No;itfailstheverticallinetest.
60. About1.3millionchildren
62. About280,000pharmacists
64. 6x 31=11+6(x 7) 6x 31=11+6x 42
6x 31=6x 31 31= 31 Wegetatrueequation,soallrealnumbersaresolutions.
66. 2 3 (4x 2) > 60 4x 2 > 90 4x> 92 x> 23 {x|x> 23},or(23, ∞)
68. 4(x 5)=3(x +2) 4x 20=3x +6 x =26
70. 1 2 x +10 < 8x 5 15 < 15 2 x 2 <x {x|x> 2},or(2, ∞)
72. 1 16 x +4= 5 8 x 1 5= 9 16 x 80 9 = x
74. x +5=3when x = 2.Find h( 2). h( 2)=( 2)2 4=4 4=0
76. g ( 1)=2( 1)+5=3,so f (g ( 1))= f (3)= 3 · 32 1=26. f ( 1)=3( 1)2 1=2,so g (f ( 1))= g (2)=2 2+5=9.
ExerciseSet2.3
RC2. 5 x =0for x =5,sothedomainis
{x|x isarealnumber andx =5}.Theansweris(b).
RC4. |x 5| =0for x =5,sothedomainis
{x|x isarealnumber andx =5}.Theansweris(b).
RC6. x +5=0for x = 5,sothedomainis
{x|x isarealnumber andx = 5}.Theansweris(d).
2. a) f (1)=1
b) Thesetofall x-valuesinthegraphis
{−3, 1, 1, 3, 5}.
c) Theonlypointwhosesecondcoordinateis2is(3, 2), sothe x-valueforwhich f (x)=2is3.
d) Thesetofall y -valuesinthegraphis
{−1, 0, 1, 2, 3}.
4. a) f (1)= 2
b) Thesetofall x-valuesinthegraphis
{x|− 4 ≤ x ≤ 2},or[ 4, 2].
c) Theonlypointwhosesecondcoordinateis2isabout ( 2, 2),sothe x-valueforwhich f (x)=2isabout 2.
d) Thesetofall y -valuesinthegraphis
{y |− 3 ≤ y ≤ 3},or[ 3, 3].
6. a) f (1)= 1
b) Noendpointsareindicatedandweseethatthe graphextendsindefinitelybothhorizontallyand vertically,sothedomainisthesetofallrealnumbers.
c) Theonlypointwhosesecondcoordinateis2is ( 2, 2),sothe x-valueforwhich f (x)=2is 2.
d) Therangeisthesetofallrealnumbers.(Seepart (b)above.)
8. a) f (1)=3
b) Noendpointsareindicatedandweseethatthe graphextendsindefinitelyhorizontally,sothedomainisthesetofallrealnumbers.
c) Therearetwopointsforwhichthesecondcoordinateis2.Theyareabout( 1 4, 2)and(1 4, 2),so the x-valuesforwhich f (x)=2areabout 1 4and 1.4.
d) Thelargest y -valueis4.Noendpointsareindicated andweseethatthegraphextendsdownwardindefinitelyfrom(0, 4),sotherangeis {y |y ≤ 4},or (−∞, 4].
10. f (x)= 7 5 x
Solve:5 x =0 x =5
Thedomainis {x|x isarealnumber andx =5},or (−∞, 5) ∪ (5, ∞).
12. f (x)=4 5x
Wecancalculate4 5x foranyvalueof x,sothedomain isthesetofallrealnumbers.
14. f (x)= x2 2x +3
Wecancalculate x2 2x +3foranyvalueof x,sothe domainisthesetofallrealnumbers.
16. f (x)= x 2 3x +4
Solve:3x +4=0 x = 4 3
Thedomainis x|x isarealnumber andx = 4 3 ,or
−∞, 4 3 ∪ 4 3 , ∞
18. f (x)= |x 4|
Wecancalculate |x 4| foranyvalueof x,sothedomain isthesetofallrealnumbers.
20. f (x)= 4 |2x 3|
Solve: |2x 3| =0 x = 3 2
Thedomainis x|x isarealnumber andx = 3 2 ,or
−∞, 3 2 ∪ 3 2 , ∞ .
22. g (x)= 11 4+ x
Solve:4+ x =0 x = 4
Thedomainis {x|x isarealnumber andx = 4},or (−∞, 4) ∪ ( 4, ∞).
24. g (x)=8 x2
Wecancalculate8 x2 foranyvalueof x,sothedomain isthesetofallrealnumbers.
26. g (x)=4x3 +5x2 2x Wecancalculate4x3 +5x2 2x foranyvalueof x,sothe domainisthesetofallrealnumbers.
28. g (x)= 2x 3 6x 12
Solve:6x 12=0 x =2
Thedomainis {x|x isarealnumber andx =2},or (−∞, 2) ∪ (2, ∞).
30. g (x)= |x| +1
Wecancalculate |x| +1foranyvalueof x,sothedomain isthesetofallrealnumbers.
32. g (x)= x2 +2x |10x 20|
Solve: |10x 20| =0 x =2
Thedomainis {x|x isarealnumber andx =2},or (−∞, 2) ∪ (2, ∞).
34. {x|x isaninteger}
36. |x| = 8
Sinceabsolutevaluemustbenonnegative,thesolutionset is {} or ∅.
38. |2x +3| =13 2x +3= 13 or 2x +3=13
2x = 16 or 2x =10 x = 8 orx =5
Thesolutionsetis {−8, 5}
40. |5x 6| = |3 8x| 5x 6=3 8xor 5x 6= (3 8x) 13x =9 or 5x 6= 3+8x
x = 9 13 or 3x =3
x = 9 13 orx = 1
Thesolutionsetis 1, 9 13
42. |3x 8| =0
3x 8=0
3x =8 x = 8 3
Thesolutionsetis 8 3
44. Grapheachfunctiononagraphingcalculator,anddeterminetherangefromthegraph.
ForthefunctioninExercise22,therangeis
{x|x isarealnumber andx =0},or (−∞, 0) ∪ (0, ∞).
ForthefunctioninExercise23,therangeis
{x|x ≥ 0},or[0, ∞).
ForthefunctioninExercise24,therangeis
{x|x ≤ 8},or(−∞, 8].
ForthefunctioninExercise30,therangeis
{x|x ≥ 1},or[1, ∞).
46. Wemusthave2 x ≥ 0,or2 ≥ x.Thus,thedomainis
{x|x ≤ 2},or(−∞, 2].
ExerciseSet2.4
RC2. (f g )(x)= f (x) g (x)
= x2 1 (x +3)
= x2 1 x 3
= x2 x 4
Answer(c)iscorrect.
RC4. (g f )(x)= g (x) f (x)
= x +3 (x2 1)
= x +3 x2 +1
= x2 + x +4
Answer(e)iscorrect.
2. Since f (4)= 2 4+3= 8+3= 5and g (4)=42 5= 16 5=11,wehave
f (4)+ g (4)= 5+11=6.
4. Since f (2)= 2 2+3= 4+3= 1and g (2)=22 5= 4 5= 1,wehave
f (2) g (2)= 1 ( 1)= 1+1=0.
6. Since f ( 1)= 2( 1)+3=2+3=5and g ( 1)= ( 1)2 5=1 5= 4,wehave
f ( 1) g ( 1)=5( 4)= 20.
8. Since f (3)= 2 3+3= 6+3= 3and g (3)=32 5= 9 5=4,wehave
f (3)/g (3)= 3 4 = 3 4
10. Since g ( 3)=( 3)2 5=9 5=4and f ( 3)= 2( 3)+3=6+3=9,wehave
g ( 3)/f ( 3)= 4 9 .
12. (f g )(x)= f (x) g (x) = 2x +3 (x2 5) = 2x +3 x2 +5 = x2 2x +8
14. (g/f )(x)= g (x)/f (x) = x2 5 2x +3
16. Since F (a)= a2 2and G(a)=5 a,wehave (F + G)(a)= F (a)+ G(a) = a2 2+5 a = a2 a +3
Or(F + G)(x)= F (x)+ G(x) = x2 2+5 x = x2 x +3,
so(F + G)(a)= a2 a +3
18. Since F (2)=22 2=4 2=2and G(2)=5 2=3,we have
(F G)(2)= F (2) G(2) =2 3= 1
Or(F G)(x)= F (x) G(x) = x2 2 (5 x) = x2 2 5+ x = x2 + x 7, so(F G)(2)=22 +2 7=4+2 7= 1
20. (G · F )(x)= G(x) · F (x) =(5 x)(x2 2) =5x2 10 x3 +2x, or x3 +5x2 +2x 10
22. (G F )(x)= G(x) F (x) =5 x (x2 2) =5 x x2 +2 = x2 x +7
24. Since F ( 1)=( 1)2 2= 1and G( 1)= 5 ( 1)=6, wehave(F/G)( 1)= F ( 1)/G( 1)= 1 6 = 1 6 Alternatively,wecouldfirstfind(F/G)(x).
(F/G)(x)= F (x)/G(x)= x2 2 5 x Then(F/G)( 1)= ( 1)2 2 5 ( 1) = 1 6 = 1 6
26. Since G(6)=5 6= 1,wehave
(G G)(6)= G(6) G(16)= 1( 1)=1.
Alternatively,wecouldfirstfind(G G)(x).
(G G)(x)= G(x) G(x) =(5 x)(5 x) =25 10x + x2
Then(G G)(6)=25 10 6+62 =25 60+36=1.
28. (r/t)(x)= r (x)/t(x) = 5 x2 3 2x = 5 x2 2x 3 = 5 2 x / x / x 3 = 10 3x
30. (r + t)(x)= r (x)+ t(x) = 5 x2 + 3 2x = 10 2x2 + 3x 2x2 = 10+3x 2x2
32. (t r )(x)= t(x) r (x) = 3 2x 5 x2 = 3x 2x2 10 2x2 = 3x 10 2x2
34. 0 8+2 9=3 7million
36. 21 11=10
38. f (x)=5x 1, g (x)=2x2
Domainof f =Domainof g = {x|x isarealnumber}, soDomainof f + g =Domainof f g =Domainof f · g = {x|x isarealnumber}
40. f (x)=3x2 , g (x)= 1 x 9
Domainof f = {x|x isarealnumber}
Domainof g = {x|x isarealnumber andx =9}
Domainof f + g =Domainof f g =Domainof f · g = {x|x isarealnumber andx =9}
42. f (x)= x3 +1, g (x)= 5 x
Domainof f = {x|x isarealnumber}
Domainof g = {x|x isarealnumber andx =0}
Domainof f + g =Domainof f g =Domainof f g = {x|x isarealnumber andx =0}
44. f (x)=9 x2 , g (x)= 3 x +6
Domainof f = {x|x isarealnumber}
Domainof g = {x|x isarealnumber andx = 6}
Domainof f + g =Domainof f g =Domainof f g = {x|x isarealnumber andx = 6}
46. f (x)= 5 3 x , g (x)= 1 4x 1
Domainof f = {x|x isarealnumber andx =3}
Domainof g = x|x isarealnumber andx = 1 4
Domainof f + g =Domainof f g =Domainof f · g = x|x isarealnumber andx =3 andx = 1 4
48. f (x)=2x3 , g (x)=5 x
Domainof f =Domainof g = {x|x isarealnumber} and g (5)=0,soDomainof f/g = {x|x isarealnumber andx =5}
50. f (x)=5+ x, g (x)=6 2x
Domainof f =Domainof g = {x|x isarealnumber} and g (3)=0,soDomainof f/g =
{x|x isarealnumber andx =3}
52. f (x)= 1 2 x , g (x)=7+ x
Domainof f = {x|x isarealnumber andx =2}
Domainof g = {x|x isarealnumber } andwehave g ( 7)=0.
Domainof f/g = {x|x isarealnumber andx =2 andx = 7}
54. f (x)= 7x x 2 , g (x)=3x +7
Domainof f = {x|x isarealnumber andx =2}
Domainof g = {x|x isarealnumber} and g 7 3 =0
Domainof f/g = x|x isarealnumber andx =2 andx = 7 3
56. (F G)(6)= F (6) G(6)=0(3.5)=0 (F G)(9)= F (9) G(9)=1 2=2
58. (F/G)(3)= F (3)/G(3)= 2 1 =2 (F/G)(7)= F (7)/G(7)= 1 4 = 1 4
60. Domainof F = {x|0 ≤ x ≤ 9}; F (6)=0and F (8)=0
Domainof G = {x|3 ≤ x ≤ 10}
Domainof F G =Domainof F · G = {x|3 ≤ x ≤ 9}
Domainof G/F = {x|3 ≤ x ≤ 9 andx =6 andx =8}
62. Let p =thenumberofpointsIsaiahscored.Then p 5= thenumberofpointsTerrencescored.
Solve: p + p 5=27 p =16,soTerrencescored p 5=16 5=11points.
64. 7x +16=5x 20 2x = 36 x = 18
66. fx)= 3x 2x +5 , g (x)= x4 1 3x +9
Domainof f = x|x isarealnumber andx = 5 2
Domainof g = {x|x isarealnumber andx = 3}
g (x)=0when x4 1=0orwhen x =1 orx = 1
Domainof f/g = x|x isarealnumber and x = 5 2 andx = 3 andx =1 andx = 1
68. Theinputsthatareinthedomainsofboth f and g are 2, 1,0,and1,soDomainof f + g =Domainof f g =
Domainof f g = {−2, 1, 0, 1}.
g ( 1)=0,soDomainof f/g = {−2, 0, 1}.
Chapter2Mid-ChapterReview
1. True;afunctionisaspecialtypeofrelationinwhicheach memberofthedomainispairedwithexactlyonemember oftherange.
2. False;seethedefinitionofafunctiononpage85ofthe text.
3. True;forafunction f (x)= c,where c isaconstant,all theinputshavetheoutput c
4. True;seethevertical-linetestonpage90ofthetext.
5. False;forexample,seeExercise3above.
6. Wesubstitute 2for x and 1for y (alphabeticalorder ofvariables.)
5y +6=4x 5( 1)+6?4( 2) 5+6 8 1 FALSE
Thus,( 2, 1)isnotasolutionoftheequation.
7. Wesubstitute 1 2 for a and0for b (alphabeticalorderof variables.)
8a =4 b
8 1 2 ?4 0 4 4TRUE
Thus, 1 2 , 0 isasolutionoftheequation.
8. Yes;eachmemberofthedomainismatchedtoonlyone memberoftherange.
9. No;thenumber15inthedomainismatchedto2numbers oftherange,25and30.
10. Thesetofall x-valuesonthegraphextendsfrom 3 through3,sothedomainis {x|− 3 ≤ x ≤ 3},or[ 3, 3]. Thesetofall y -valuesonthegraphextendsfrom 2 through1,sotherangeis {y |− 2 ≤ y ≤ 1},or[ 2, 1].
11. g (x)=2+ x g ( 5)=2+( 5)= 3
12. f (x)= x 7 f (0)=0 7= 7
13. h(x)=8 h 1 2 =8
14. f (x)=3x2 x +5 f ( 1)=3( 1)2 ( 1)+5=3 · 1+1+5=3+1+5=9
15. g (p)= p4 p3 g (10)=104 103 =10, 000 1000=9000
16. f (t)= 1 2 t +3 f ( 6)= 1 2 ( 6)+3= 3+3=0
17. Noverticallinewillintersectthegraphmorethanonce. Thus,thegraphisthegraphofafunction.
18. Itispossibleforaverticallinetointersectthegraphmore thanonce.Thus,thegraphisnotthegraphofafunction.
19. Noverticallinewillintersectthegraphmorethanonce. Thus,thegraphisthegraphofafunction.
20. g (x)= 3 12 3x
Since 3 12 3x cannotbecalculatedwhenthedenominator is0,wefindthe x-valuethatcauses12 3x tobe0: 12 3x =0 12=3x 4= x
Thus,thedomainof g is {x|x isarealnumber andx =4}, or(−∞, 4) ∪ (4, ∞).
21. f (x)= x2 10x +3
Sincewecancalculate x2 10x +3foranyrealnumber x, thedomainisthesetofallrealnumbers.
22. h(x)= x 2 x +2
Since x 2 x +2 cannotbecalculatedwhenthedenominatoris 0,wefindthe x-valuethatcauses x +2tobe0: x +2=0 x = 2
Thus,thedomainof g is {x|x isarealnumber andx = 2},or(−∞, 2) ∪ ( 2, ∞). Copyright c 2017PearsonEducation,Inc.
23. f (x)= |x 4|
Sincewecancalculate |x 4| foranyrealnumber x,the domainisthesetofallrealnumbers.
24. y = 2 3 x 2
Wefindsomeorderedpairsthataresolutions.
When x = 3, y = 2 3 ( 3) 2=2 2=0.
When x =0, y = 2 3 · 0 2=0 2= 2.
When x =3, y = 2 3 3 2= 2 2= 4. x y 3 0 0 2 3 4
Plotthesepoints,drawthelinetheydetermine,andlabel it y = 2 3 x 2.
25. f (x)= x 1
Wefindsomeorderedpairsthataresolutions.
f ( 3)= 3 1= 4.
f (0)=0 1= 1.
f (4)=4 1=3.
x f (x) 3 4 0 1 4 3
Plotthesepoints,drawthelinetheydetermine,andlabel it f (x)= x 1.
When x =2, y =2 2+ 1 2 =4+ 1 2 =4 1 2
Plotthesepoints,drawthelinetheydetermine,andlabel it h(x)=2x + 1 2
27. g (x)= |x|− 3
26. h(x)=2x + 1 2
Wefindsomeorderedpairsthataresolutions.
When x = 2, y =2( 2)+ 1 2 = 4+ 1 2 = 3 1 2
When x =0, y =2 0+ 1 2 =0+ 1 2 = 1 2 .
Wefindsomeorderedpairsthataresolutions.
g ( 4)= |− 4|− 3=4 3=1
y x 2 3 y x 2 y x f (x ) x 1 y x 1 2 h (x ) 2x y x g ( x ) |x | 3
g ( 1)= |− 1|− 3=1 3= 2
g (0)= |0|− 3=0 3= 3
g (2)= |2|− 3=2 3= 1
g (3)= |3|− 3=3 3=0 x g (x) 4 1 1 2 0 3 2 1 3 0
Plotthesepoints,drawthelinetheydetermine,andlabel it g (x)= |x|− 3.
28. y =1+ x2
Wefindsomeorderedpairsthataresolutions.
When x = 2, y =1+( 2)2 =1+4=5.
When x = 1, y =1+( 1)2 =1+1=2.
When x =0, y =1+02 =1+0=1.
When x =1, y =1+12 =1+1=2.
When x =2, y =1+22 =1+4=5.
x y 2 5 1 2 0 1 1 2 2 5
Plotthesepoints,drawthelinetheydetermine,andlabel it y =1+ x2
Domainof f + g =Domainof f g =Domainof f g = {x|x isarealnumber}
Since g (x)=0when x = 4,wehaveDomainof f/g = {x|x isarealnumber andx = 4}
34. f (x)= 7 x 9 , g (x)=6 x
Domainof f = {x|x isarealnumber andx =9}
Domainof g = {x|x isarealnumber}
Domainof f + g =Domainof f g =Domainof f · g = {x|x isarealnumber andx =9}
Since g (x)=0when x =6,wehaveDomainof f/g = {x|x isarealnumber andx =9 andx =6}
35. No;sinceeachinputhasexactlyoneoutput,thenumber ofoutputscannotexceedthenumberofinputs.
29. f (x)= 1 4 x Wefindsomeorderedpairsthataresolutions.
f ( 4)= 1 4 ( 4)=1
f (0)= 1 4 0=0
f (4)= 1 4 · 4= 1 x f (x) 4 1 0 0 4 1
Plotthesepoints,drawthelinetheydetermine,andlabel it f (x)= 1 4 x.
y x y 1 x 2 y x f (x ) x 1 4
30. (f g )(x)= f (x) g (x) =3x 1 (x2 +2)
=3x 1 x2 2 = x2 +3x 3
31. f ( 2)=3( 2) 1= 6 1= 7
g ( 2)=( 2)2 +2=4+2=6
f ( 2) g ( 2)= 7 6= 42
32. (g/f )(a)= g (a)/f (a)= a2 +2 3a 1
33. f (x)=5x2 , g (x)= x +4
Domainof f =Domainof g = {x|x isarealnumber}
36. When x< 0,then y< 0andthegraphcontainspoints inquadrantIII.When0 <x< 30,then y< 0andthe graphcontainspointsinquadrantIV.When x> 30,then y> 0andthegraphcontainspointsinquadrantI.Thus, thegraphpassesthroughthreequadrants.
37. Theoutput 3correspondstotheinput2.Thenumber 3intherangeispairedwiththenumber2inthedomain. Thepoint(2, 3)isonthegraphofthefunction.
38. Thedomainofafunctionisthesetofallinputs,andthe rangeisthesetofalloutputs.
ExerciseSet2.5
RC2. m = 3 0 3 ( 2) = 3 1 =3
Theansweris(b).
RC4. Thisisahorizontalline,sotheslopeis0.Theanswer is(c).
RC6. m = 1 ( 2) 1 3 = 3 4 = 3 4
Theansweris(a).
2. Slopeis 5; y -interceptis(0, 10).
4. Slopeis 5; y -interceptis(0, 7).
6. Slopeis 15 7 ; y -interceptis 0, 16 5
8. Slopeis 3 1; y -interceptis(0, 5).
10. 8x 7y =24
7y =8x +24
y = 8 7 x 24 7
Slopeis 8 7 ; y -interceptis 0, 24 7
12. 9y +36 4x =0
9y =4x 36 y = 4 9 x 4
Slopeis 4 9 ; y -interceptis(0, 4).
14. 5x = 2 3 y 10
5x +10= 2 3 y 15 2 x +15= y
Slopeis 15 2 ; y -interceptis(0, 15).
16. 3y 2x =5+9y 2x 6y =5
y = 5 6 , or0x 5 6
Slopeis0; y -interceptis 0, 5 6
18. Wecanuseanytwopointsontheline,suchas( 3, 4) and(0, 3).
m = changein y changein x = 3 ( 4) 0 ( 3) = 1 3
20. Wecanuseanytwopointsontheline,suchas(2, 4)and (4, 0).
m = changein y changein x = 0 4 4 2 = 4 2 = 2
22. Slope= 1 7 2 8 = 8 6 = 4 3
24. Slope= 15 ( 12) 9 17 = 3 26 = 3 26
26. Slope= 17 6 ( 7 8) 12 5 14 4 = 9 8 26 9 = 98 269
28. m = 43 33 1238 = 7 200 ,orabout3.5%
30. m = 7 11 =0 63=63 63%
32. Rateofchange= 16 5 4 2050 2011 = 10 6 39 ≈ 0 27
Therateofchangeisabout0.27million,or270,000people peryear.
34. Wecanusethecoordinatesofanytwopointsontheline. We’lluse(0, 100)and(9, 40).
Slope= changein y changein x = 40 100 9 0 = 60 9 = 20 3 , or 6 2 3 mpersecond
36. Rateofchange= 41 33 2012 2002 = 8 10 =0 8
Therateofchangeis0.8million,or800,000peopleper year.
38. 9{2x 3[5x +2( 3x + y 0 2)]}
=9{2x 3[5x +2( 3x +1 2)]} (y 0 =1)
=9{2x 3[5x +2( 3x 1)]}
=9{2x 3[5x 6x 2]}
=9{2x 3[ x 2]}
=9{2x +3x +6}
=9{5x +6}
=45x +54
40. 54 ÷ 625 ÷ 52 · 57 ÷ 53
=1 ÷ 52 57 ÷ 53
=5 2 57 ÷ 53
=55 ÷ 53
=52 , or25
42. |5x 8|≥ 32 5x 8 ≤−32 or 5x 8 ≥ 32 5x ≤−24 or 5x ≥ 40 x ≤− 24 5 orx ≥ 8
Thesolutionsetis x x ≤− 24 5 orx ≥ 8 ,or
−∞, 24 5 ∪ [8, ∞).
44. |5x 8| =32
5x 8= 32 or 5x 8=32
5x = 24 or 5x =40 x = 24 5 orx =8
Thesolutionsetis 24 5 , 8
ExerciseSet2.6
RC2. False;the y -interceptof y = 2x +7is(0, 7).
RC4. True
RC6. False;seepage209inthetext.
2.
18. y = 2 5 x 4
Slope: 2 5 ; y -intercept:(0, 4)
Startingat(0, 4),findanotherpointbymoving2units upand5unitstotherightto(5, 2).
Startingat(0, 4)again,move2unitsdownand5units totheleftto( 5, 6).
20. y = 2 5 x +3
Slope: 2 5 ; y -intercept:(0, 3)
Startingat(0, 3),findanotherpointbymoving2unitsup and5unitstotherightto(5, 5).
Startingat(0, 3)again,move2unitsdownand5unitsto theleftto( 5, 1).
22. x 3y =6
3y = x +6 y = 1 3 x 2
Slope: 1 3 ; y -intercept:(0, 2)
Startingat(0, 2),findanotherpointbymoving1unit upand3unitstotherightto(3, 1).
From(3, 1),move1unitupand3unitstotheleftagain to(6, 0).
24. 2x +6y =12
6y = 2x +12 y = 1 3 x +2
Slope: 1 3 ; y -intercept:(0, 2)
Startingat(0, 2),findanotherpointbymoving1unitup and3unitstotheleftto( 3, 3).Startingat(0, 2)again, move1unitdownand3unitstotherightto(3, 1).
26. g (x)= 0 25x +2
Slope: 0 25,or 1 4 ; y -intercept:(0, 2)
Startingat(0, 2),findanotherpointbymoving1unitup and4unitstotheleftto( 4, 3).Startingat(0, 2)again, move1unitdownand4unitstotherightto(4, 1).
28. 3 f (x)=4x +6 f (x)= 4 3 x +2
Slope: 4 3 ; y -intercept:(0, 2)
Startingat(0, 2),findanotherpointbymoving4unitsup and3unitstotherightto(3, 6).Startingat(0, 2)again, move4unitsdownand3unitstotheleftto( 3, 2).
30. Theslopeisnotdefined.
32. Theslopeis0.
34. Theslopeis0.
36. Theslopeisnotdefined.
4224 4 2 2 4 531135 5 3 1 1 3 5 x y x 0
38. 4 g (x)+3x =12+3x 4 g (x)=12 g (x)=3
4224 4 2 2 4 531135 5 3 1 1 3 5 x y 4 g (x) 3x 12 3x
Theslopeis0.
40. 3 f (x)=2 1= f (x)
4224 4 2 2 4 531135 5 3 1 1 3 5 x y 3 f (x) 2
Theslopeis0.
42. Writebothequationsinslope-interceptform.
y =2x 7(m =2)
y =2x +8(m =2)
Theslopesarethesameandthe y -interceptsaredifferent, sothelinesareparallel.
44. Writebothequationsinslope-interceptform.
y = 6x 8(m = 6)
y =2x +5(m =2)
Theslopesarenotthesame,sothelinesarenotparallel.
46. Writebothequationsinslope-interceptform.
y = 7x 9(m = 7)
y = 7x 7 3 (m = 7)
Theslopesarethesameandthe y -interceptsaredifferent, sothelinesareparallel.
48. Thegraphof5y = 2,or y = 2 5 ,isahorizontalline;the graphof 3 4 x =16,or x = 64 3 ,isaverticalline.Thus,the graphsarenotparallel.
50. Writebothequationsinslope-interceptform.
y = 2 5 x + 3 5 m = 2 5
y = 2 5 x + 4 5 m = 2 5 2 5 2 5 = 4 25 = 1,sothelinesarenot perpendicular.
52. y = x +7(m = 1) y = x +3(m =1) 1 1= 1,sothelinesareperpendicular.
54. y = x (m =1) y = x (m = 1) 1( 1)= 1,sothelinesareperpendicular.
56. Sincethegraphsof 5y =10,or y = 2,and y = 4 9 are bothhorizontallines,theyarenotperpendicular.
58. Movethedecimalpoint5placestotheright.Thenumber issmall,sotheexponentisnegative.
0 000047=4 7 × 10 5
60. Movethedecimalpoint7placestotheleft.Thenumber islarge,sotheexponentispositive.
99, 902, 000=9.9902 × 107
62. Theexponentispositive,sothenumberislarge.Movethe decimalpoint8placestotheright.
9 01 × 108 =901, 000, 000
64. Theexponentisnegative,sothenumberissmall.Move thedecimalpoint2placestotheleft.
8 5677 × 10 2 =0 085677
66. 12a +21ab =3a(4+7b)
68. 64x 128y +256=64(x 2y +4)
70.
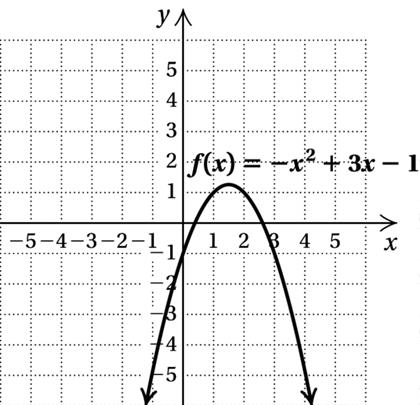
72. x +7y =70
y = 1 7 x +10 m = 1 7 y +3= kx y = kx 3(m = k )
Inorderforthegraphstobeperpendicular,theproduct oftheslopesmustbe 1. 1
7 k = 1 k =7
74. The x-coordinatemustbe 4,andthe y -coordinatemust be5.Thepointis( 4, 5).
76. Allpointsonthe y -axisarepairsoftheform(0,y ).Thus anynumberfor y willdoand x mustbe0.Theequation is x =0.Thegraphfailsthevertical-linetest,sothe equationisnotafunction.
78. 2y = 7x +3b 2( 13)= 7 0+3b 26=3b 26 3 = b
ExerciseSet2.7
RC2. y = 5isahorizontalline,soitsslopeis0. a)0
b)notdefined
RC4. y = 5 6 x + 4 3 a) 5 6 b) 6 5
RC6. 10x +5y =14
5y = 10x +14
y = 2x + 14 5
a) 2 b) 1 2
2. y =5x 3
4. y = 9 1x +2
6. f (x)= 4 5 x +28
8. f (x)= 7 8 x 7 11
10. Usingthepoint-slopeequation:
y y1 = m(x x1 )
y 2=4(x 5)
y 2=4x 20
y =4x 18
Usingtheslope-interceptequation:
y = mx + b
2=4 5+ b
18= b
y =4x 18
12. Usingthepoint-slopeequation:
y y1 = m(x x1 )
y 8= 2(x 2)
y 8= 2x +4
y = 2x +12
Usingtheslope-interceptequation:
y = mx + b
8= 2 2+ b
12= b
y = 2x +12
14. Usingthepoint-slopeequation:
y y1 = m(x x1 )
y ( 2)=3(x ( 2))
y +2=3(x +2)
y +2=3x +6 y =3x +4
Usingtheslope-interceptequation:
y = mx + b
2=3( 2)+ b
4= b
y =3x +4
16. Usingthepoint-slopeequation:
y y1 = m(x x1 )
y 0= 3(x ( 2))
y = 3(x +2)
y = 3x 6
Usingtheslope-interceptequation:
y = mx + b
0= 3( 2)+ b
6= b
y = 3x 6
18. Usingthepoint-slopeequation:
y y1 = m(x x1 )
y 4=0(x 0)
y 4=0
y =4
Usingtheslope-interceptequation:
y = mx + b
4=0 · 0+ b
4= b
y =0x +4,or y =4
20. Usingthepoint-slopeequation:
y y1 = m(x x1 )
y 3= 4 5 (x 2)
y 3= 4 5 x + 8 5
y = 4 5 x + 23 5
Usingtheslope-interceptequation:
y = mx + b
3= 4 5 2+ b 23 5 = b
y = 4 5 x + 23 5
22. m = 7 5 4 2 = 2 2 =1
Usingthepoint-slopeequation:
y y1 = m(x x1 )
y 5=1(x 2)
y 5= x 2
y = x +3
Usingtheslope-interceptequation:
y = mx + b
5=1 · 2+ b
3= b
y =1 x +3,or y = x +3
24. m = 9 ( 1) 9 ( 1) = 10 10 =1
Usingthepoint-slopeequation:
y y1 = m(x x1 )
y 9=1(x 9)
y 9= x 9
y = x
Usingtheslope-interceptequation:
y = mx + b
9=1 9+ b
0= b
y =1 x +0,or y = x
26. m = 0 ( 5) 3 0 = 5 3
Usingthepoint-slopeequation:
y y1 = m(x x1 )
y 0= 5 3 (x 3)
y = 5 3 x 5
Usingtheslope-interceptequation:
y = mx + b 5= 5 3 0+ b
5= b
y = 5 3 x 5
28. m = 1 ( 7) 2 ( 4) = 6 2 =3
Usingthepoint-slopeequation:
y y1 = m(x x1 )
y ( 7)=3(x ( 4))
y +7=3(x +4)
y +7=3x +12
y =3x +5
Usingtheslope-interceptequation:
y = mx + b 7=3( 4)+ b 5= b
y =3x +5
30. m = 7 0 4 0 = 7 4
Usingthepoint-slopeequation:
y y1 = m(x x1 )
y 0= 7 4 (x 0)
y = 7 4 x
Usingtheslope-interceptequation:
y = mx + b
0= 7 4 0+ b
0= b
y = 7 4 x +0,or y = 7 4 x
32. m = 5 6 3 2 3 2 3 = 4 6 11 3 = 2 11
Usingthepoint-slopeequation:
y y1 = m(x x1 )
y 5 6 = 2 11 (x ( 3))
y 5 6 = 2 11 (x +3)
y 5 6 = 2 11 x + 6 11
y = 2 11 x + 91 66
Usingtheslope-interceptequation:
y = mx + b 5 6 = 2 11 ( 3)+ b 91 66 = b
y = 2 11 x + 91 66
34. 2x y =7Givenline
y =2x 7 m =2
Usingtheslope,2,andthe y -intercept(0, 3),wewritethe equationoftheline: y =2x +3.
36. 2x + y = 3Givenline
y = 2x 3 m = 2
Usingthepoint-slopeequation:
y y1 = m(x x1 )
y ( 5)= 2(x ( 4))
y +5= 2(x +4)
y +5= 2x 8
y = 2x 13
Usingtheslope-interceptequation:
y = mx + b
5= 2( 4)+ b 13= b
y = 2x 13
38. 5x +2y =6Givenline
y = 5 2 +3 m = 5 2
Usingthepoint-slopeequation:
y y1 = m(x x1 )
y 0= 5 2 (x ( 7))
y = 5 2 (x +7)
y = 5 2 x 35 2
Usingtheslope-interceptequation:
y = mx + b 0= 5 2 ( 7)+ b
35 2 = b
y = 5 2 x 35 2
40. x 3y =9Givenline
y = 1 3 x 3 m = 1 3
Usingthepoint-slopeequation:
y y1 = m(x x1 )
y 1= 3(x 4)
y 1= 3x +12
y = 3x +13
Usingtheslope-interceptequation:
y = mx + b 1= 3 4+ b
13= b
y = 3x +13
42. 5x 2y =4Givenline
y = 5 2 x 2 m = 5 2
Usingthepoint-slopeequation:
y y1 = m(x x1 )
y ( 5)= 2 5 (x ( 3))
y +5= 2 5 (x +3)
y +5= 2 5 x 6 5
y = 2 5 x 31 5
Usingtheslope-interceptequation:
y = mx + b 5= 2 5 ( 3)+ b
31 5 = b
y = 2 5 x 31 5
44. 3x +6y =2Givenline
y = 1 2 x + 1 3 m = 1 2
Usingthepoint-slopeequation:
y y1 = m(x x1 )
y ( 4)= 2(x ( 3))
y +4= 2(x +3)
y +4= 2x 6
y = 2x 10
Usingtheslope-interceptequation:
y = mx + b 4= 2( 3)+6 10= b
y = 2x 10
46. a) C (t)=24 95t +165 b)
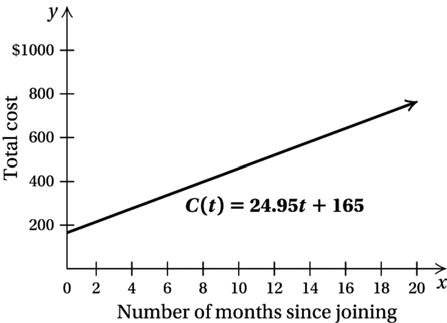
c) C (14)=24 95(14)+165=$514 30
48. a) V (t)=3800 50t b)
c) V (10.5)=3800 50(10.5)=$3275
50. a) Thedatapointsare(0, 174)and(5, 245).
m = 245 174 5 0 = 71 5 =14 2
Usingtheslopeandthe y -intercept,wewritethe function:
D (x)=14 2x +174,where x isthenumberofyears since2007and D (x)isinbillionsofdollars.
b) In2010, x =2010 2007=3.
D (3)=14 2(3)+174=$216 6billion
In2015, x =2015 2007=8.
D (8)=14 2(8)+174=$287 6billion
52. a) Thedatapointsare(0, 46 8)and(40, 43 8).
m = 43 8 46 8 40 0 = 3 40 = 0 075
Usingtheslopeandthe y -intercept,wewritethe function R(x)= 0 075x +46 8.
b) R(73)= 0 075(73)+46 8=41 325sec
R(76)= 0.075(76)+46.8=41.1sec
c) Solve: 0 075x +46 8=40 x ≈ 91
Therecordwillbe40secabout91yrafter1930,or in2021.
54. a) Thedatapointsare(0, 79 27)and(8, 89 73).
m = 89 73 79 27 8 0 = 10 46 8 ≈ 1 308
Usingtheslopeandthe y -interceptwewritethe function:
E (t)=1 308t +79 27,where t isthenumberofyears since2003.
b) In2016, t =2016 2003=13.
E (13)=1 308(13)+79 27 ≈ 96 27years
56. |2x +3| =51
2x +3=51 or 2x +3= 51
2x =48 or 2x = 54
x =24 orx = 27
Thesolutionsetis {24, 27}
58. 2x +3 ≤ 5x 4 7 ≤ 3x 7 3 ≤ x
Thesolutionsetis x x ≥ 7 3 ,or 7 3 , ∞
60. |2x +3| = |x 4|
2x +3= x 4 or 2x +3= (x 4)
x = 7 or 2x +3= x +4
x = 7 or 3x =1
x = 7 orx = 1 3
Thesolutionsetis 7, 1 3
62. 12 ≤ 2x +3 < 51
15 ≤ 2x< 48 15 2 ≤ x< 24
Thesolutionsetis x 15 2 ≤ x< 24 ,or 15 2 , 24
64. Firstfindtheslopeofthelinethrough( 1, 3)and(2, 9). m = 9 3 2 ( 1) = 6 3 =2
Thentheslopeofalineperpendiculartothislineis 1 2
Nowwefindtheequationofthelinewithslope 1 2 passing through(4, 5).
y y1 = m(x x1 )
y 5= 1 2 (x 4)
y 5= 1 2 x +2
y = 1 2 x +7
Chapter2VocabularyReinforcement
1. Thegraphof x = a isavertical linewith x-intercept(a, 0).
2. Thepoint-slope equationofalinewithslope m andpassing through(x1 ,y1 )is y y1 = m(x x1 ).
3. Afunction isacorrespondencebetweenafirstset,called thedomain,andasecondset,calledtherange,suchthat eachmemberofthedomain correspondstoexactlyone memberoftherange
4. Theslope ofalinecontainingpoints(x1 ,y1 )and(x2 ,y2 ) isgivenby m =thechangein y /thechangein x,also describedasrise/run.
5. Twolinesareperpendicular iftheproductoftheirslopes is 1.
6. Theequation y = mx + b iscalledtheslope-intercept equationofalinewithslope m and y -intercept(0,b).
7. Linesareparallel iftheyhavethesameslopeanddifferent y -intercepts.
Chapter2ConceptReinforcement
1. False;theslopeofaverticallineisnotdefined.See page123inthetext.
2. True;seepage113inthetext.
3. False;parallellineshavethesameslopeand different yintercepts.Seepage124inthetext.
Chapter2StudyGuide
1. Amemberofthedomainismatchedtomorethanone memberoftherange,sothecorrespondenceisnotafunction.
2. g (x)= 1 2 x 2
g (0)= 1 2 0 2=0 2= 2
g ( 2)= 1 2 ( 2) 2= 1 2= 3
g (6)= 1 2 · 6 2=3 2=1
3. y = 2 5 x 3
Wefindsomeorderedpairsthataresolutions,plotthem, anddrawandlabeltheline.
When x = 5, y = 2 5 ( 5) 3= 2 3= 5.
When x =0, y = 2 5 0 3=0 3= 3.
When x =5, y = 2 5 5 3=2 3= 1.
x y 5 5 0 3 5 1
y x (5,5) (0,(5,1) 3) 2 5 y x 3
4. Noverticallinecancrossthegraphatmorethanonepoint, sothegraphisthatofafunction.
5. Thesetofall x-valuesonthegraphextendsfrom 4 through5,sothedomainis {x|− 4 ≤ x ≤ 5},or[ 4, 5].
Thesetofall y -valuesonthegraphextendsfrom 2 through4,sotherangeis {y |− 2 ≤ y ≤ 4},or[ 2, 4].
6. Since x 3 3x +9 cannotbecalculatedwhen3x +9is0,we solve3x +9=0. 3x +9=0
3x = 9 x = 3
Thus,thedomainof g is {x|x isarealnumber and x = 3},or(−∞, 3) ∪ ( 3, ∞).
7. f (x)=2x2 +3, g (x)=1 x
a) (f + g )(x)= f (x)+ g (x) =2x2 +3+1 x =2x2 x +4
b) f ( 4)=2( 4)2 +3=2 · 16+3=32+3=35
g ( 4)=1 ( 4)=1+4=5 (f g )( 4)=35 5=30
c) f (6)=2 62 +3=2 36+3=72+3=75
g (6)=1 6= 5
(f/g )(6)= 75 5 = 15
d) f (1)=2 12 +3=2+3=5 g (1)=1 1=0
(f g )(1)=5 0=0
8. f (x)= 6 4x +3 , g (x)= x 2
Wehave4x +3=0when x = 3 4 ,soDomainof
f = x|x isarealnumber andx = 3 4
Domainof g = {x|x isarealnumber}
Domainof f + g =Domainof f g =Domainof f g = x|x isarealnumber andx = 3 4
Since g (x)=0when x =2,wehaveDomainoff/g = x x isarealnumber andx = 3 4 andx =2
9. m = 8 2 2 ( 3) = 10 5 = 2
10. 3x = 6y +12 3x 12= 6y 1 2 x +2= y Dividingby 6
Theslopeis 1 2 ,andthe y -interceptis(0, 2).
11. 3y 3= x
Tofindthe y -intercept,let x =0andsolvefor y 3y 3=0
3y =3 y =1
The y -interceptis(0, 1). Copyright c 2017PearsonEducation,Inc.
Tofindthe x-intercept,let y =0andsolvefor x 3 · 0 3= x 0 3= x 3= x
The x-interceptis( 3, 0).
Weplotthesepointsanddrawtheline.
Wefindathirdpointasacheck.Let x =3.
3y 3=3
3y =6 y =2
Weseethatthepoint(3, 2)isontheline.
12. y = 1 4 x 3
Firstweplotthe y -intercept(0, 3).Thenweconsiderthe slope 1 4 .Startingatthe y -intercept,wefindanotherpoint bymoving1unitupand4unitstotheright.Wegetto thepoint(4, 2).Wecanalsothinkoftheslopeas 1 4
Weagainstartatthe y -interceptandmovedown1unit and4unitstotheleft.Wegettoathirdpoint( 4, 4). Weplotthepointsanddrawthegraph.
14. x = 5 2
Allpoints 5 2 ,y aresolutions.Thegraphisavertical linethatintersectsthe x-axisat 5 2 , 0
13. y =3
Allorderedpairs(x, 3)aresolutions.Thegraphisahorizontallinethatintersectsthe y -axisat(0, 3).
y x (3,0) (3,2) (0,1) 3y 3 x y x (4,4) (4,2) (0,3) 1 4 y x 3 y x y 3 y x 5 2 x
15. Wefirstsolvefor y anddeterminetheslopeofeachline.
3x +8y = 8
8y =3x 8 y = 3 8 x 1
Theslopeof 3x +8y = 8is 3 8 .
8y =3x +40
y = 3 8 x +5
Theslopeof8y =3x +40is 3 8
Theslopesarethesameandthe y -intercepts,(0, 1)and (0, 5)aredifferent,sothelinesareparallel.
16. Wefirstsolvefor y anddeterminetheslopeofeachline.
5x 2y = 8
2y = 5x 8
y = 5 2 x +4
Theslopeof5x 2y = 8is 5 2
2x +5y =15
5y = 2x +15
y = 2 5 x +3
Theslopeof2x +5y =15is 2 5
Theslopesaredifferent,sothelinesarenotparallel.The productoftheslopesis 5 2 2 5 = 1,sothelinesare perpendicular.
17. y = mx + b Slope-interceptequation
y = 8x +0 3
18. Usingthepoint-slopeequation:
y ( 3)= 4 x 1 2
y +3= 4x +2
y = 4x 1
Usingtheslopeinterceptequation:
3= 4 1 2 + b
3= 2+ b 1= b
Then,substitutingin y = mx + b,wehave y = 4x 1.
19. Wefirstfindtheslope:
m = 3 7 4 ( 2) = 10 6 = 5 3
Weusethepoint-slopeequation.
y 7= 5 3 [x ( 2)]
y 7= 5 3 (x +2)
y 7= 5 3 x 10 3
y = 5 3 x + 11 3
20. Firstwefindtheslopeofthegivenline:
4x 3y =6
3y = 4x +6
y = 4 3 x 2
Alineparalleltothislinehasslope 4 3
Weusetheslope-interceptequation.
5= 4 3 (2)+ b
5= 8 3 + b 23 3 = b
Thenwehave y = 4 3 x 23 3
21. FromExercise20aboveweknowthattheslopeofthe givenlineis 4 3 .Theslopeofalineperpendiculartothis lineis 3 4
Weusethepoint-slopeequation.
y ( 5)= 3 4 (x 2)
y +5= 3 4 x + 3 2
3. g (x)= 2x +5
g (0)= 2 0+5=0+5=5
g ( 1)= 2( 1)+5=2+5=7
4. f (x)=3x2 2x +7
f (0)=3 02 2 0+7=0 0+7=7
f ( 1)=3( 1)2 2( 1)+7=3 1 2( 1)+7=3+2+7=12
5. C (t)=309 2t +3717 7
C (10)=309 2(10)+3717 7=3092+3717 7=6809 7 ≈ 6810
Weestimatethattheaveragecostoftuitionandfeeswill beabout$6810in2010.
6. y = 3x +2
Wefindsomeorderedpairsthataresolutions,plotthem, anddrawandlabeltheline.
When x = 1, y = 3( 1)+2=3+2=5.
When x =1, y = 3 1+2= 3+2= 1
When x =2, y = 3 · 2+2= 6+2= 4.
x y (x,y )
1 5 ( 1, 5)
1 1 (1, 1)
2 4 (2, 4)
7. y = 5 2 x 3
Wefindsomeorderedpairsthataresolutions,usingmultiplesof2toavoidfractions.Thenweplotthesepoints anddrawandlabeltheline.
When x =0, y = 5 2 0 3=0 3= 3.
When x =2, y = 5 2 · 2 3=5 3=2.
When x =4, y = 5 2 4 3=10 3=7.
x y (x,y )
0 3 (0, 3)
2 2 (2, 2)
4 7 (4, 7)
y x y 3x 2 y x 5 2 y x 3 Chapter2SummaryandReview:ReviewExercises67
y = 3 4 x 7 2
Chapter2ReviewExercises
1. No;amemberofthedomain,3,ismatchedtomorethan onememberoftherange.
2. Yes;eachmemberofthedomainismatchedtoonlyone memberoftherange.
8. y = |x 3|
Tofindanorderedpair,wechooseanynumberfor x and thendetermine y .Forexample,if x =5,then y = |5 3| = |2| =2.Wefindseveralorderedpairs,plotthem,and connectthem.
14. g (x)= x x2
9. y =3 x2
Tofindanorderedpair,wechooseanynumberfor x and thendetermine y .Forexample,if x =2,then3 22 = 3 4= 1.Wefindseveralorderedpairs,plotthem,and connectthemwithasmoothcurve.
y x y x 3 y x y 3 x 2
10. Noverticallinewillintersectthegraphmorethanonce. Thus,thegraphisthegraphofafunction.
11. Itispossibleforaverticallinetointersectthegraphmore thanonce.Thus,thisisnotthegraphofafunction.
12. a) Locate2onthehorizontalaxisandthenfindthe pointonthegraphforwhich2isthefirstcoordinate. Fromthatpoint,looktotheverticalaxistofindthe corresponding y -coordinate,3.Thus, f (2)=3.
b) Thesetofall x-valuesinthegraphextendsfrom 2 to4,sothedomainis {x|− 2 ≤ x ≤ 4},or[ 2, 4].
c) Todeterminewhichmember(s)ofthedomainare pairedwith2,locate2ontheverticalaxis.From therelookleftandrighttothegraphtofindany pointsforwhich2isthesecondcoordinate.One suchpointexists.Itsfirstcoordinateappearstobe 1.Thus,the x-valueforwhich f (x)=2is 1.
d) Thesetofall y -valuesinthegraphextendsfrom1 to5,sotherangeis {y |1 ≤ y ≤ 5},or[1, 5].
13. f (x)= 5 x 4
Since 5 x 4 cannotbecalculatedwhenthedenominatoris 0,wefindthe x-valuethatcauses x 4tobe0: x 4=0
x =4Adding4onbothsides
Thus,4isnotinthedomainof f ,whileallotherreal numbersare.Thedomainof f is {x|x isarealnumber andx =4},or(−∞, 4) ∪ (4, ∞).
Sincewecancalculate x x2 foranyrealnumber x,the domainisthesetofallrealnumbers.
15. (f/g )(x)= f (x)/g (x)= x2 3x x +10
16. (f g )(x)= f (x) g (x) = x2 3x (x +10) = x2 3x x 10 = x2 4x 10
(f g )( 2)=( 2)2 4( 2) 10=4+8 10=2
17. f (x)= 2x2 , g (x)= x +6
Domainof f =Domainof g = {x|x isarealnumber}
Domainof f + g =Domainof f g =Domainof f · g = {x|x isarealnumber}
Since g (x)=0when x = 6,wehaveDomainof f/g = {x|x isarealnumber andx = 6}
18. f (x)= 3 7 x , g (x)=5 x
Since7 x =0when x =7,wehaveDomainof f = {x|x isarealnumber andx =7}
Domainof g = {x|x isarealnumber}
Domainof f + g =Domainof f g =Domainof f g = {x|x isarealnumber andx =7}
Since g (x)=0when x =5,wehaveDomainof f/g = {x|x isarealnumber andx =7 andx =5}
19. f (x)= 3x +2
f (x)= mx + b
Theslopeis 3,andthe y -interceptis(0, 2).
20. Firstwefindtheslope-interceptformoftheequationby solvingfor y .Thisallowsustodeterminetheslopeand y -intercepteasily.
4y +2x =8
4y = 2x +8
4y 4 = 2x +8 4 y = 1 2 x +2
Theslopeis 1 2 ,andthe y -interceptis(0, 2).
21. Slope= changein y changein x = 4 7 10 13 = 11 3 = 11 3
22. 2y + x =4
Tofindthe x-interceptwelet y =0andsolvefor x
2y + x =4
2 0+ x =4 x =4
The x-interceptis(4, 0).
Tofindthe y -interceptwelet x =0andsolvefor y
2y + x =4
2y +0=4
2y =4 y =2
The y -interceptis(0, 2).
Weplotthesepointsanddrawtheline.
y x (0,2) (4,0)
Weuseathirdpointasacheck.Wechoose x =4and solvefor y 2y =6 3 4
2y =6 12 2y = 6 y = 3
Weplot(4, 3)andnotethatitisontheline.
24. g (x)= 2 3 x 4
Firstweplotthe y -intercept(0, 4).Wecanthinkofthe slopeas 2 3 .Startingatthe y -interceptandusingthe slope,wefindanotherpointbymoving2unitsdownand 3unitstotheright.Wegettoanewpoint(3, 6).
Weuseathirdpointasacheck.Wechoose x = 2and solvefor y .
2y +( 2)=4
2y =6 y =3
Weplot( 2, 3)andnotethatitisontheline.
23. 2y =6 3x
Tofindthe x-interceptwelet y =0andsolvefor x
2y =6 3x
2 0=6 3x 0=6 3x
3x =6 x =2
The x-interceptis(2, 0).
Tofindthe y -interceptwelet x =0andsolvefor y .
2y =6 3x
2y =6 3 0
2y =6 y =3
The y -interceptis(0, 3).
Weplotthesepointsanddrawtheline.
2y x 4 y x (0,3) (2,0)
Wecanalsothinkoftheslopeas 2 3 .Weagainstartat the y -intercept(0, 4).Wemove2unitsupand3unitsto theleft.Wegettoanothernewpoint( 3, 2).Weplot thepointsanddrawtheline.
2y 6 3x y x 2 3 g (x ) x 4 y x 5 2 f (x ) x 3
25. f (x)= 5 2 x +3
Firstweplotthe y -intercept(0, 3).Thenweconsiderthe slope 5 2 .Startingatthe y -interceptandusingtheslope, wefindanotherpointbymoving5unitsupand2unitsto theright.Wegettoanewpoint(2, 8).
Wecanalsothinkoftheslopeas 5 2 .Weagainstartat the y -intercept(0, 3).Wemove5unitsdownand2units totheleft.Wegettoanothernewpoint( 2, 2).We plotthepointsanddrawtheline.
26. x = 3
Since y ismissing,allorderedpairs( 3,y )aresolutions. Thegraphisparalleltothe y -axis.
30. Wefirstsolveeachequationfor y anddeterminetheslope ofeachline.
4y + x =3
4y = x +3
27. f (x)=4
Since x ismissing,allorderedpairs(x, 4)aresolutions. Thegraphisparalleltothe x-axis.
y x x 3 y x f (x ) 4
28. Wefirstsolveeachequationfor y anddeterminetheslope ofeachline.
y +5= x y = x 5
Theslopeof y +5= x is 1.
x y =2
x = y +2
x 2= y
Theslopeof x y =2is1.
Theslopesarenotthesame,sothelinesarenotparallel. Theproductoftheslopesis 1 · 1,or 1,sothelinesare perpendicular.
29. Wefirstsolveeachequationfor y anddeterminetheslope ofeachline.
3x 5=7y 3 7 x 5 7 = y
Theslopeof3x 5=7y is 3 7
7y 3x =7
7y =3x +7
y = 3 7 x +1
Theslopeof7y 3x =7is 3 7
Theslopesarethesameandthe y -interceptsaredifferent, sothelinesareparallel.
y = 1 4 x + 3 4
Theslopeof4y + x =3is 1 4
2x +8y =5
8y = 2x +5
y = 1 4 x + 5 8
Theslopeof2x +8y =5is 1 4 .
Theslopesarethesameandthe y -interceptsaredifferent, sothelinesareparallel.
31. x =4isaverticallineand y = 3isahorizontalline,so thelinesareperpendicular.
32. Weusetheslope-interceptequationandsubstitute4.7for m and 23for b.
y = mx + b
y =4.7x 23
33. Usingthepoint-slopeequation:
Substitute3for x1 , 5for y1 ,and 3for m
y y1 = m(x x1 )
y ( 5)= 3(x 3)
y +5= 3x +9
y = 3x +4
Usingtheslope-interceptequation:
Substitute3for x, 5for y ,and 3for m in y = mx + b andsolvefor b.
y = mx + b
5= 3 3+ b
5= 9+ b
4= b
Thenweusetheequation y = mx + b andsubstitute 3 for m and4for b
y = 3x +4
34. Firstfindtheslopeoftheline:
m = 6 3 4 ( 2) = 3 2 = 3 2
Usingthepoint-slopeequation:
Wechoosetousethepoint( 2, 3)andsubstitute 2for x1 ,3for y1 ,and 3 2 for m
y y1 = m(x x1 )
y 3= 3 2 (x ( 2))
y 3= 3 2 (x +2)
y 3= 3 2 x 3
y = 3 2 x
Usingtheslope-interceptequation:
Wechoose( 2, 3)andsubstitute 2for x,3for y ,and 3 2 for m in y = mx + b.Thenwesolvefor b.
3= 3 2 ( 2)+ b
3=3+ b
0= b
Finally,weusetheequation y = mx + b andsubstitute 3 2 for m and0for b
y = 3 2 x +0,or y = 3 2 x
35. Firstsolvetheequationfor y anddeterminetheslopeof thegivenline.
5x +7y =8Givenline
7y = 5x +8
y = 5 7 x + 8 7
Theslopeofthegivenlineis 5 7 .Thelinethrough (14, 1)musthaveslope 5 7 .
Usingthepoint-slopeequation:
Substitute14for x1 , 1for y1 ,and 5 7 for m.
y y1 = m(x x1 )
y ( 1)= 5 7 (x 14)
y +1= 5 7 x +10
y = 5 7 x +9
Usingtheslope-interceptequation:
Substitute14for x, 1for y ,and 5 7 for m andsolvefor b
y = mx + b
1= 5 7 14+ b
1= 10+ b
9= b
Thenweusetheequation y = mx + b andsubstitute 5 7 for m and9for b
y = 5 7 x +9
36. Firstsolvetheequationfor y anddeterminetheslopeof thegivenline.
3x + y =5Givenline
y = 3x +5
Theslopeofthegivenlineis 3.Theslopeoftheperpendicularlineistheoppositeofthereciprocalof 3.Thus, thelinethrough(5, 2)musthaveslope 1 3
Usingthepoint-slopeequation:
Substitute5for x1 ,2for y1 ,and 1 3 for m
y y1 = m(x x1 )
y 2= 1 3 (x 5)
y 2= 1 3 x 5 3
y = 1 3 x + 1 3
Usingtheslope-interceptequation:
Substitute5for x,2for y ,and 1 3 for m andsolvefor b
y = mx + b
2= 1 3 5+ b
2= 5 3 + b 1 3 = b
Thenweusetheequation y = mx + b andsubstitute 1 3 for
m and 1 3 for b.
y = 1 3 x + 1 3
37. a) Weformpairsofthetype(x,R)where x isthe numberofyearssince1972and R istherecord.We havetwopairs,(0, 44 66)and(40, 43 94).Theseare twopointsonthegraphofthelinearfunctionwe areseeking.
Firstwefindtheslope:
m = 43 94 44 66 40 0 = 0 72 40 = 0 018.
Usingtheslopeandthe y -intercept,(0, 44 66) wewritethefunction: R(x)= 0 018x +44 66, where x isthenumberofyearsafter1972.
b) 2000is28yearsafter1972,sotoestimatetherecord in2000,wefind R(28): R(28)= 0.018(28)+44.66 ≈ 44 16
Theestimatedrecordwasabout44.16secondsin 2000.
2010is38yearsafter1972,sotoestimatetherecord in2010,wefind R(38): R(38)= 0.018(38)+44.66 ≈ 43 98
Theestimatedrecordwasabout43.98secondsin 2010.
38. f (x)= x +3 x 2
Wecannotcalculate x +3 x 2 whenthedenominatoris0,so wesolve x 2=0. x 2=0 x =2
Thus,thedomainof f is(−∞, 2) ∪ (2, ∞).AnswerCis correct.
39. Firstwefindtheslopeofthegivenline.
3y 1 2 x =0
3y = 1 2 x y = 1 6 x
Theslopeis 1 6 .Theslopeofalineperpendiculartothe givenlineis 6.Weusethepoint-slopeequation.
y 1= 6[x ( 2)]
y 1= 6(x +2)
y 1= 6x 12
y = 6x 11, or 6x + y = 11
AnswerAiscorrect.
40. Thecostof x jarsofpreservesis$2 49x,andtheshippingchargesare$3 75+$0 60x.Thenthetotalcostis $2 49x +$3 75+$0 60x,or$3 09x +$3 75.Thus,alinear functionthatcanbeusedtodeterminethecostofbuying andshipping x jarsofpreservesis f (x)=3.09x +3.75.
41. Aline’s x-and y -interceptsarethesameonlywhenthe linepassesthroughtheorigin.Theequationforsucha lineisoftheform y = mx
42. Theconceptofslopeisusefulindescribinghowaline slants.Alinewithpositiveslopeslantsupfromleftto right.Alinewithnegativeslopeslantsdownfromleft toright.Thelargertheabsolutevalueoftheslope,the steepertheslant.
43. Findtheslope-interceptformoftheequation.
4x +5y =12
5y = 4x +12 y = 4 5 x + 12 5
Thisformoftheequationindicatesthatthelinehasa negativeslopeandthusshouldslantdownfromleftto right.Thestudentapparentlygraphed y = 4 5 x + 12 5
44. For R(t)=50t +35, m =50and b =35;50signifiesthat thecostperhourofarepairis$50;35signifiesthatthe minimumcostofarepairjobis$35.
45. m = changein y changein x Aswemovefromonepointtoanotheronaverticalline, the y -coordinatechangesbutthe x-coordinatedoesnot. Thus,thechangein y isanon-zeronumberwhilethe changein x is0.Sincedivisionby0isundefined,the slopeofaverticallineisundefined.
Aswemovefromonepointtoanotheronahorizontal line,the y -coordinatedoesnotchangebutthe x-coordinate does.Thus,thechangein y is0whilethechangein x isa non-zeronumber,sotheslopeis0.
46. Usingalgebra,wefindthattheslope-interceptformof theequationis y = 5 2 x 3 2 .Thisindicatesthatthe yinterceptis 0, 3 2 ,soamistakehasbeenmade.It appearsthatthestudentgraphed y = 5 2 x + 3 2
Chapter2Test
1. Yes;eachmemberofthedomainismatchedtoonlyone memberoftherange.
2. No;amemberofthedomain,LakePlacid,ismatchedto morethanonememberoftherange.
3. f (x)= 3x 4
f (0)= 3 0 4=0 4= 4
f ( 2)= 3( 2) 4=6 4=2
4. g (x)= x2 +7
g (0)=02 +7=0+7=7
g ( 1)=( 1)2 +7=1+7=8
5. h(x)= 6
h( 4)= 6
h( 6)= 6
6. f (x)= |x +7|
f ( 10)= |− 10+7| = |− 3| =3
f ( 7)= |− 7+7| = |0| =0
7. y = 2x 5
Wefindsomeorderedpairsthataresolutions,plotthem, anddrawandlabeltheline.
When x =0, y = 2 0 5=0 5= 5.
When x = 2, y = 2( 2) 5=4 5= 1.
When x = 4, y = 2( 4) 5=8 5=3.
8. f (x)= 3 5 x
Wefindsomefunctionvalues,plotthecorresponding points,anddrawthegraph.
f ( 5)= 3 5 ( 5)=3
f (0)= 3 5 0=0
f (5)= 3 5 5= 3
9. g (x)=2 −|x|
Wefindsomefunctionvalues,plotthecorresponding points,anddrawthegraph.
g ( 4)=2 −|− 4| =2 4= 2
g ( 2)=2 −|− 2| =2 2=0
g (0)=2 −|0| =2 0=2
g (3)=2 −|3| =2 3= 1
g (5)=2 −|5| =2 5= 3
10. f (x)= x2 +2x 3
Wefindsomefunctionvalues,plotthecorresponding points,anddrawthegraph.
f ( 4)=( 4)2 +2( 4) 3=16 8 3=5
f ( 3)=( 3)2 +2( 3) 3=9 6 3=0
f ( 1)=( 1)2 +2( 1) 3=1 2 3= 4
f (0)=02 +2 0 3= 3
f (1)=12 +2 1 3=1+2 3=0 f (2)=22 +2 2 3=4+4 3=5
11. y = f (x)= 3
Since x ismissing,allorderedpairs(x, 3)aresolutions. Thegraphisparalleltothe x-axis.
12. 2x = 4 x = 2
Since y ismissing,allorderedpairs( 2,y )aresolutions. Thegraphisparalleltothe y -axis.
13. a) In2005, x =2005 1990=15.Wefind A(15). A(15)=0 233(15)+5 87=9 365 ≈ 9 4
Themedianageofcarsin2005wasabout9.4yr.
b) Substitute7.734for A(t)andsolvefor t 7 734=0 233t +5 87 1 864=0 233t 8= t
Themedianageofcarswas7.734yr8yearsafter 1990,orin1998.
14. Noverticallinewillintersectthegraphmorethanonce. Thus,thegraphisthegraphofafunction.
15. Itispossibleforaverticallinetointersectthegraphmore thanonce.Thus,thisisnotthegraphofafunction.
16. f (x)= 8 2x +3
Since 8 2x +3 cannotbecalculatedwhenthedenominator is0,wefindthe x-valuethatcauses2x +3tobe0: 2x +3=0
2x = 3 x = 3 2
Thus, 3 2 isnotinthedomainof f ,whileallotherreal numbersare.Thedomainof f is x x isarealnumber andx = 3 2 ,or −∞, 3 2 ∪ 3 2 , ∞ .
17. g (x)=5 x2
Sincewecancalculate5 x2 foranyrealnumber x,the domainisthesetofallrealnumbers.
18. a) Locate1onthehorizontalaxisandthenfindthepoint onthegraphforwhich1isthefirstcoordinate.From thatpoint,looktotheverticalaxistofindthecorresponding y -coordinate,1.Thus, f (1)=1.
b) Thesetofall x-valuesinthegraphextendsfrom 3 to4,sothedomainis {x|− 3 ≤ x ≤ 4},or[ 3, 4].
c) Todeterminewhichmember(s)ofthedomainare pairedwith2,locate2ontheverticalaxis.From therelookleftandrighttothegraphtofindany pointsforwhich2isthesecondcoordinate.Onesuch pointexists.Itsfirstcoordinateis 3,sothe x-value forwhich f (x)=2is 3.
d) Thesetofall y -valuesinthegraphextendsfrom 1 to2,sotherangeis {y |− 1 ≤ y ≤ 2},or[ 1, 2].
19. f (x)= 4x +3,g (x)= x2 1
f ( 2)= 4( 2)+3=8+3=11
g ( 2)=( 2)2 1=4 1=3
(f g )( 2)= f ( 2) g ( 2)=11 3=8
(f/g )(x)= f (x)/g (x)= 4x +3 x2 1
20. f (x)= 4 3 x , g (x)=2x +1
Domainof f = {x|x isarealnumber andx =3}
Domainof g = {x|x isarealnumber}
Domainof f + g =Domainof f g =Domainof f g = {x|x isarealnumber andx =3}
Since g (x)=0when x = 1 2 ,wehaveDomainof f/g = x|x isarealnumber andx =3 andx = 1 2
21. f (x)= 3 5 x +12
f (x)= mx + b
Theslopeis 3 5 ,andthe y -interceptis(0, 12).
22. Firstwefindtheslope-interceptformoftheequationby solvingfor y .Thisallowsustodeterminetheslopeand y -intercepteasily.
5y 2x =7
5y =2x +7
5y 5 = 2x +7 5 y = 2 5 x 7 5
Theslopeis 2 5 ,andthe y -interceptis 0, 7 5
23. Slope= changein y changein x = 2 3 2 6 = 5 8 = 5 8
24. Slope= changein y changein x = 5 2 5 2 4 4 ( 3 1) = 0 1 3 =0
25. Wecanusethecoordinatesofanytwopointsonthegraph.
We’lluse(10, 0)and(25, 12).
Slope= changein y changein x = 12 0 25 10 = 12 15 = 4 5
Theslope,orrateofchangeis 4 5 km/min.
26. 2x +3y =6
Tofindthe x-interceptwelet y =0andsolvefor x
2x +3y =6
2x +3 0=6
2x =6 x =3
The x-interceptis(3, 0).
Tofindthe y -interceptwelet x =0andsolvefor y
2x +3y =6
2 0+3y =6
3y =6 y =2
The y -interceptis(0, 2).
Weplotthesepointsanddrawtheline.
y x 2x 3y 6 y-intercept (0,2) x-intercept (3,0)
Weuseathirdpointasacheck.Wechoose x = 3and solvefor y 2( 3)+3y =6
6+3y =6
3y =12 y =4
Weplot( 3, 4)andnotethatitisontheline. Copyright c 2017PearsonEducation,Inc.
27. f (x)= 2 3 x 1
Firstweplotthe y -intercept(0, 1).Wecanthinkofthe slopeas 2 3 .Startingatthe y -interceptandusingthe slope,wefindanotherpointbymoving2unitsdownand 3unitstotheright.Wegettoanewpoint(3, 3).
Wecanalsothinkoftheslopeas 2 3 .Weagainstartat the y -intercept(0, 1).Wemove2unitsupand3units totheleft.Wegettoanothernewpoint( 3, 1).Weplot thepointsanddrawtheline.
y x 2 3 f (x ) x 1
28. Wefirstsolveeachequationfor y anddeterminetheslope ofeachline.
4y +2=3x 4y =3x 2
y = 3 4 x 1 2
Theslopeof4y +2=3x is 3 4
3x +4y = 12
4y =3x 12
y = 3 4 x 3
Theslopeof 3x +4y = 12is 3 4
Theslopesarethesameandthe y -interceptsaredifferent, sothelinesareparallel.
29. Theslopeof y = 2x +5is 2. Wesolvethesecondequationfor y anddeterminethe slope.
2y x =6
2y = x +6
y = 1 2 x +3
Theslopesarenotthesame,sothelinesarenotparallel. Theproductoftheslopesis 2 1 2 ,or 1,sothelinesare perpendicular.
30. Weusetheslope-interceptequationandsubstitute 3for m and4.8for b.
y = mx + b
y = 3x +4 8
31. y = f (x)= mx + b
f (x)=5 2x 5 8
32. Usingthepoint-slopeequation:
Substitute1for x1 , 2for y1 ,and 4for m
y y1 = m(x x1 )
y ( 2)= 4(x 1)
y +2= 4x +4
y = 4x +2
Usingtheslope-interceptequation:
Substitute1for x, 2for y ,and 4for m in y = mx + b andsolvefor b
y = mx + b
2= 4 1+ b
2= 4+ b
2= b
Thenweusetheequation y = mx + b andsubstitute 4 for m and2for b
y = 4x +2
33. Firstfindtheslopeoftheline:
m = 6 15 4 ( 10) = 21 14 = 3 2
Usingthepoint-slopeequation:
Wechoosetousethepoint(4, 6)andsubstitute4for x1 , 6for y1 ,and 3 2 for m
y y1 = m(x x1 )
y ( 6)= 3 2 (x 4)
y +6= 3 2 x +6
y = 3 2 x
Usingtheslope-interceptequation:
Wechoose(4, 6)andsubstitute4for x, 6for y ,and 3 2 for m in y = mx + b.Thenwesolvefor b
y = mx + b
6= 3 2 · 4+ b
6= 6+ b
0= b
Finally,weusetheequation y = mx + b andsubstitute 3 2 for m and0for b.
y = 3 2 x +0,or y = 3 2 x
34. Firstsolvetheequationfor y anddeterminetheslopeof thegivenline.
x 2y =5Givenline
2y = x +5
y = 1 2 x 5 2
Theslopeofthegivenlineis 1 2 .Thelinethrough(4, 1)
musthaveslope 1 2
Usingthepoint-slopeequation:
Substitute4for x1 , 1for y1 ,and 1 2 for m
y y1 = m(x x1 )
y ( 1)= 1 2 (x 4)
y +1= 1 2 x 2
y = 1 2 x 3
Usingtheslope-interceptequation:
Substitute4for x, 1for y ,and 1 2 for m andsolvefor b
y = mx + b
1= 1 2 (4)+ b
1=2+ b
3= b
Thenweusetheequation y = mx + b andsubstitute 1 2 for m and 3for b
y = 1 2 x 3
35. Firstsolvetheequationfor y anddeterminetheslopeof thegivenline.
x +3y =2Givenline
3y = x +2
y = 1 3 x + 2 3
Theslopeofthegivenlineis 1 3 .Theslopeoftheperpendicularlineistheoppositeofthereciprocalof 1 3 .Thus, thelinethrough(2, 5)musthaveslope3.
Usingthepoint-slopeequation:
Substitute2for x1 ,5for y1 ,and3for m
y y1 = m(x x1 )
y 5=3(x 2)
y 5=3x 6
y =3x 1
Usingtheslope-interceptequation:
Substitute2for x,5for y ,and3for m andsolvefor b
y = mx + b
5=3 2+ b
5=6+ b
1= b
Thenweusetheequation y = mx + b andsubstitute3for m and 1for b
y =3x 1
36. a) Notethat2010 1970=40.Thus,thedatapoints are(0, 23 2)and(40, 28 2).Wefindtheslope.
m = 28 2 23 2
40 0 = 5 40 =0.125
Usingtheslopeandthe y -intercept,(0, 23 2),we writethefunction: A(x)=0 125x +23 2
b) In2008, x =2008 1970=38.
A(38)=0 125(38)+23 2=27 95years
In2015, x =2015 1970=45.
A(45)=0 125(45)+23 2=28 825years
37. Usingthepoint-slopeequation, y y1 = m(x x1 ),with x1 =3, y1 =1,and m = 2wehave y 1= 2(x 3). Thus,answerBiscorrect.
38. Firstsolveeachequationfor y anddeterminetheslopes.
3x + ky =17
ky = 3x +17
y = 3 k x + 17 k
Theslopeof3x + ky =17is 3 k
8x 5y =26
5y = 8x +26
y = 8 5 x 26 5
Theslopeof8x 5y =26is 8 5
Ifthelinesareperpendicular,theproductoftheirslopes is 1.
3 k · 8 5 = 1 24 5k = 1
24=5k Multiplyingby 5k 24 5 = k
39. Answersmayvary.Onesuchfunctionis f (x)=3.