CHAPTER 2 LIMITS AND CONTINUITY
2.1 RATES OF CHANGE AND TANGENTS TO CURVES
1. (a) (3)(2) 289 321 19 fff x
2. (a) (3)(1)() 3 1 312 2 ggg x
3. (a)
3 44 3 442 114
4. (a) ()(0)(21)(21) 2 00 ggg t
5. (2)(0) 811 31 2022 1 RRR
6. (2)(1)(81610)(145) 211 22 0 PPP
7. (a) 22 2 ((2)5)(25) 4451yhhh xhh
(1)(1) 20 1(1)2 1 fff x
(4)(2) 88 4(2)6 0 ggg x
26 263 0333
()()(21)(21) ()2 0 ggg
at (2,1) P the slope is 4. (b) (1)4(2)148
8. (a) 22 2 (7(2))(72) 7443yhhh
9. (a)
22 ((2)2(2)3)(22(2)3)yhh xh
13. (a) 33 (1)12(1)(112(1))yhh xh
As 0, h 2 93hh 9 at (1,11) P the slope is 9 (b) (11)(9)(1)119 yxyx
14. (a) 3232 (2)3(2)4(23(2)4)yhh xh
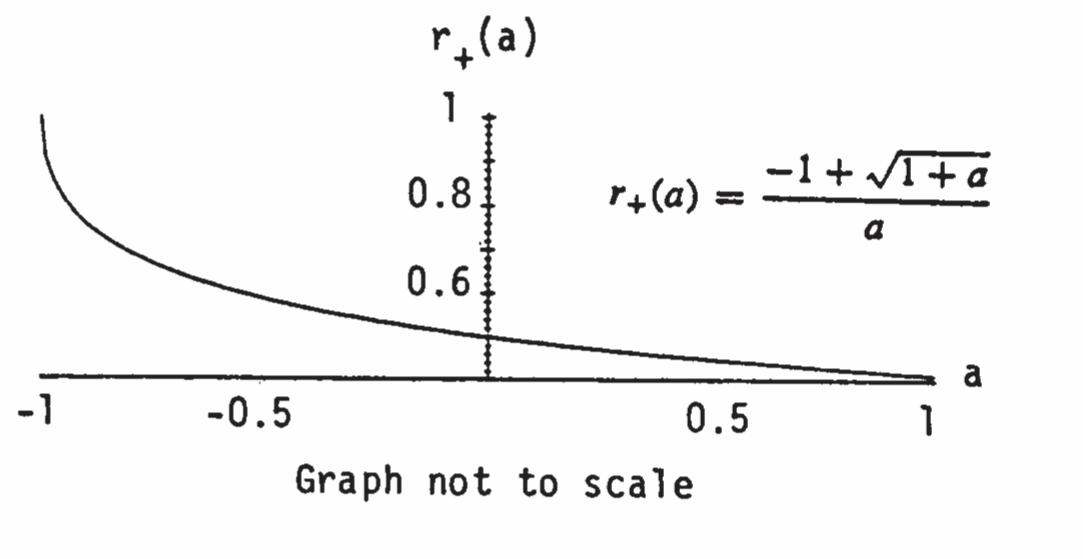
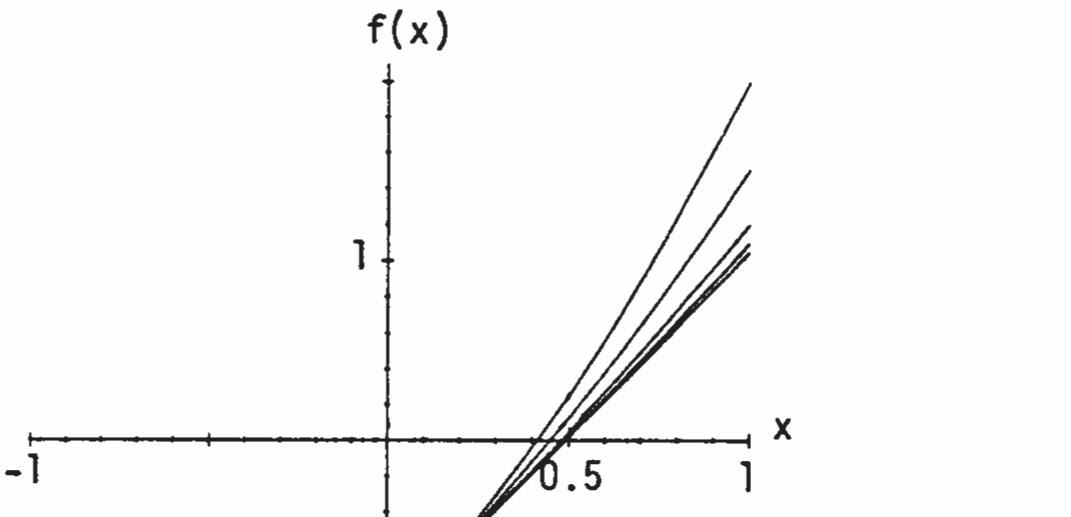
15. (a) 11 22 2(2) 11 2(2)2(2)
11111 24242 ((2)) yxyx
16. (a)
(4) 4 2(4)24 42(2) 4 21111 21222 .
17. (a) (4)4 444242 1 42(42)42
(b) 111 444 2(4)211
18. (a) 7(2)7(2) (9)9 939393 1 93(93)93 h yh
As 0, h 111 6 9393 , h at (2,3) P the slope is 1 6 (b) 8 1111 3((2))366363 yxyxyx
19. (a) Q Slope of p t PQ
1 (10,225) Q 650225 2010 42.5m/sec 2 (14,375) Q 650375 2014 45.83m/sec
3 (16.5,475) Q 650475 2016.5 50.00m/sec 4 (18,550) Q 650550 2018 50.00m/sec (b) At 20, t the sportscar was traveling approximately 50 m/sec or 180 km/h.
20. (a) Q Slope of p t PQ
1 (5,20) Q 8020 105 12m/sec 2 (7,39) Q 8039 107 13.7m/sec
3 (8.5,58) Q 8058 108.5 14.7m/sec
4 (9.5,72) Q 8072 109.5 16m/sec
(b) Approximately 16 m/sec
21. (a)
(b) 17462 112 201420122 56 p t
thousand dollars per year
(c) The average rate of change from 2011 to 2012 is 6227 20122011 35 p
thousand dollars per year.
The average rate of change from 2012 to 2013 is 11162 20132012 49
thousand dollars per year.
So, the rate at which profits were changing in 2012 is approximately 1 2 (3549)42 thousand dollars per year.
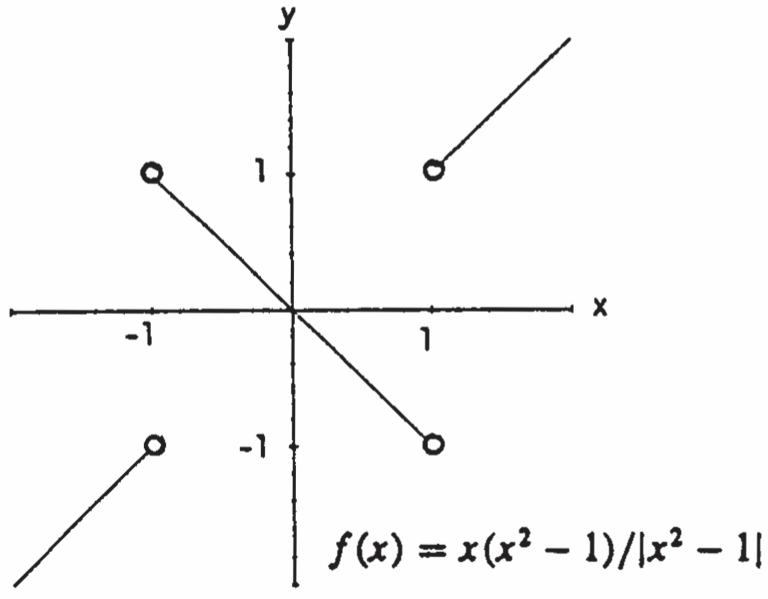
22. (a) ()(2)/(2)Fxxx
1
3
(b) The rate of change of ()Fx at 1 x is 4
23. (a) (2)(1) 21 2121 0.414213 ggg x
(1)(1) 11 (1)1 gghgh xhh
(b) () gxx
(c) The rate of change of ()gx at 1 x is 0.5.
(d) The calculator gives 11 1 2 0 lim. h hh
24. (a) i) 111 326 (3)(2) 1 32116 ff
(c) The table indicates the rate
(d)
NOTE: Answers will vary in Exercises 25 and 26. 25. (a) 150
(b) At 1 2 ,7.5: P Since the portion of the graph from 0 t to 1 t is nearly linear, the instantaneous rate of change will be almost the same as the average rate of change, thus the instantaneous speed at 1 2 t is 157.5 10.5 15mi/hr. At (2,20): P Since the portion of the graph from 2 t to 2.5 t is nearly linear, the instantaneous rate of change will be nearly the same as the average rate of change, thus 2020 2.52 0mi/hr. v For values of t less than 2, we have
Q Slope of s t PQ
1 (1,15) Q 1520 12 5mi/hr
2 (1.5,19) Q 1920 1.52 2mi/hr
3 (1.9,19.9) Q 19.920 1.92 1mi/hr
Thus, it appears that the instantaneous speed at 2 t is 0 mi/hr. At (3,22) : P
Q Slope of s t PQ
1 (4,35) Q 3522 43 13mi/hr
2 (3.5,30) Q 3022 3.53 16mi/hr
3 (3.1,23) Q 2322 3.13 10mi/hr
Thus, it appears that the instantaneous speed at 3 t is about 7 mi/hr.
(c) It appears that the curve is increasing the fastest at 3.5. t Thus for (3.5,30) P
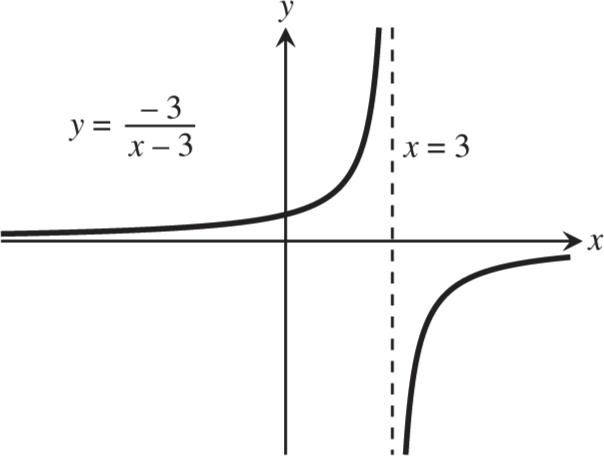
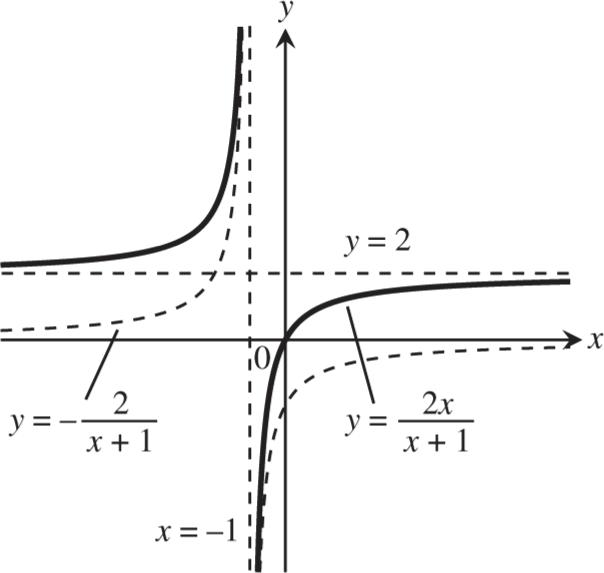
Q Slope of s t PQ
1 (4,35) Q 3530 43.5 10mi/hr
2 (3.75,34) Q 3430 3.753.5 16mi/hr
3 (3.6,32) Q 3230 3.63.5 20mi/hr
26. (a) gal 1015 30day [0,3]:1.67; A
(b) At (1,14): P Q Slope of A t PQ
Slope of s t PQ 1 (3,22) Q 2230 33.5 16mi/hr
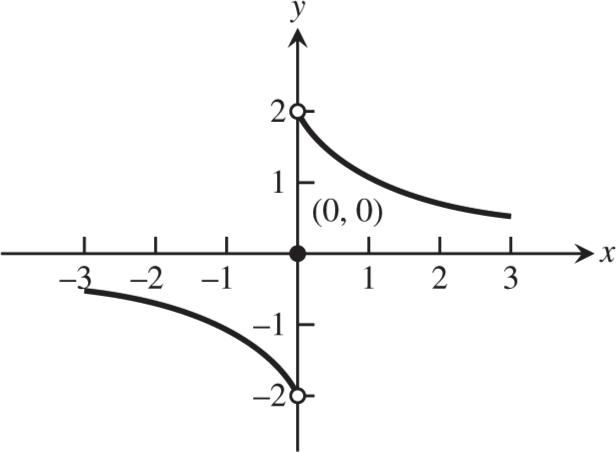
2 (3.25,25) Q 2530 3.253.5 20mi/hr 3 (3.4,28) Q 2830 3.43.5 20mi/hr
Thus, it appears that the instantaneous speed at 3.5 t is about 20 mi/hr.
(1.1,13.85)
Thus, it appears that the instantaneous rate of consumption at 1 t is about 1.45gal/day. At (4,6): P Q Slope of A t PQ 1 (5,3.9) Q
Q Slope of A t PQ 1 (0,15) Q 1514 01 1gal/day 2 (0.5,14.6) Q 14.614 0.51 1.2gal/day 3 (0.9,14.86) Q 14.8614 0.91 1.4gal/day Q Slope of A t PQ 1 (3,10) Q 106 34 4gal/day
2 (3.5,7.8) Q 7.86 3.54 3.6gal/day 3 (3.9,6.3) Q 6.36 3.94 3gal/day
Thus, it appears that the instantaneous rate of consumption at 1 t is 3gal/day.
(solutioncontinuesonnextpage) Q Slope of s t PQ 1 (2,20) Q 2022 23 2mi/hr 2 (2.5,20) Q 2022 2.53 4mi/hr 3 (2.9,21.6) Q 21.622 2.93 4mi/hr
Copyright 2018 Pearson Education, Inc.
At (8,1) : P
1 (9,0.5) Q
of
Slope of A t PQ
1 (7,1.4) Q 1.41 78 0.6gal/day
2 (7.5,1.3) Q 1.31 7.58 0.6gal/day
3 (7.9,1.04) Q 1.041 7.98 0.6gal/day
Thus, it appears that the instantaneous rate of consumption at 1 t is 0.55gal/day. (c) It appears that the curve (the consumption) is decreasing the fastest at 3.5. t Thus for (3.5,7.8) P
of
Slope of s t PQ
1 (2.5,11.2) Q 11.27.8 2.53.5 3.4gal/day
2 (3,10) Q 107.8 33.5 4.4gal/day
3 (3.4,8.2) Q 8.27.8 3.43.5 4gal/day
Thus, it appears that the rate of consumption at 3.5 t is about 4gal/day
2.2 LIMIT OF A FUNCTION AND LIMIT LAWS
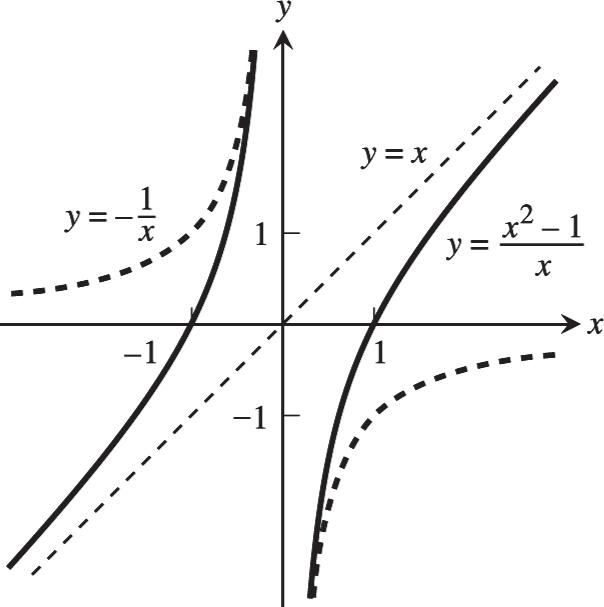
1. (a) Does not exist. As x approaches 1 from the right, ()gx approaches 0. As x approaches 1 from the left, ()gx approaches 1. There is no single number L that all the values ()gx get arbitrarily close to as 1 x (b) 1 (c) 0 (d) 0.5
2. (a) 0 (b) 1
(c) Does not exist. As t approaches 0 from the left, ()ft approaches 1. As t approaches 0 from the right, ()ft approaches 1. There is no single number L that ()ft gets arbitrarily close to as 0 t (d) 1
3. (a) True
(b) True (c) False (d) False (e) False (f) True (g) True (h) False (i) True (j) True (k) False
4. (a) False
(b) False (c) True (d) True (e) True (f) True (g) False (h) True (i) False
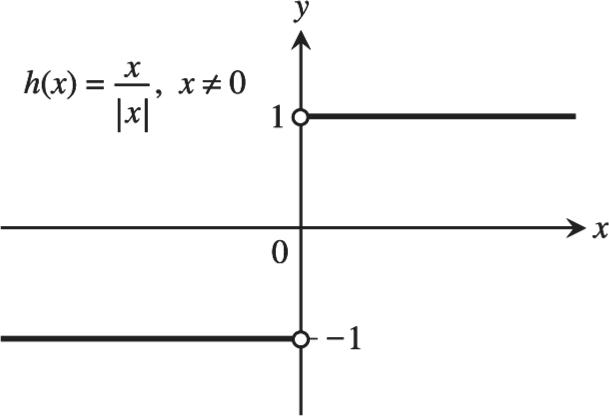
5. || 0 lim x xx does not exist because || 1 xx xx if 0 x and || 1 xx xx if 0. x As x approaches 0 from the left, || x x approaches 1. As x approaches 0 from the right, || x x approaches 1. There is no single number L that all the function values get arbitrarily close to as 0 x
6. As x approaches 1 from the left, the values of 1 1 x become increasingly large and negative. As x approaches 1 from the right, the values become increasingly large and positive. There is no number L that all the function values get arbitrarily close to as 1, x so 1 1 1 lim xx does not exist.
7. Nothing can be said about ()fx because the existence of a limit as 0xx does not depend on how the function is defined at 0x In order for a limit to exist, ()fx must be arbitrarily close to a single real number L when x is close enough to 0x That is, the existence of a limit depends on the values of ()fx for x near 0 , x not on the definition of ()fx at 0x itself.
8. Nothing can be said. In order for 0 lim() x fx to exist, ()fx must close to a single value for x near 0 regardless of the value (0) f itself.
9. No, the definition does not require that f be defined at 1 x in order for a limiting value to exist there. If (1) f is defined, it can be any real number, so we can conclude nothing about (1) f from 1 lim()5. x fx
10. No, because the existence of a limit depends on the values of ()fx when x is near 1, not on (1) f itself. If 1 lim() x fx exists, its value may be some number other than (1)5. f We can conclude nothing about 1 lim(), x fx whether it exists or what its value is if it does exist, from knowing the value of (1) f alone. 11. 22 3
13. 6 lim8(5)(7)8(65)(67)8
15. 33 2(2)5 25 1111(2) 2
2241 3333 2/3
25. 2 (5)(2) 310 55 555 limlimlim xxxx xxxxx
26. 2 (5)(2) 710 22 222
223
28. 2 2 (2)(1) 322 (2)(1)2 2 111
29. 3222 2(2)
30. 322 42222 58(58)58 316(316)316 000
32 (1)(1)(1) 1 1(1)(1) 111 limlimlim uuuu uuuuuuu
34. 2 3 42 (2)(24) 8 16(2)(2)(4) 222 limlimlim vvvv vvvvvvv
2 2 243 44412 (4)(8)328 (2)(4)
35. 33 111 96 999(3)(3)393 limlimlim xx xxxxxxx
36. 2 (4)(2)(2) 4 222 444 limlimlimxxxxxxx xxxx xx
37.
(1)32 1 32 3232 111 limlimlim xx x xxxxxx
22 2 2 8383 83 1 11 (1)83
4
43. 0 lim(2sin1)2sin01011 x x
45. 111 coscos01 00 limseclim1 xx
47. 1sin10sin0100 1 3cos3cos033 0 lim xx xx
48. 22 0 lim(1)(2cos)(01)(2cos0) x xx
49. lim4cos()lim4lim xxx xxx
50. 22 00 lim7seclim(7sec) xx xx
51. (a) quotient rule
2 222 00 limsinlimsin(sin0)00 xx xx
(b) difference and power rules (c) sum and constant multiple rules
52. (a) quotient rule
(b) power and product rules (c) difference and constant multiple rules
53. (a) lim()()lim()lim() xcxcxc fxgxfxgx
(b) lim2()()2lim()lim() xcxcxc fxgxfxgx
(c) lim[()3()]lim()3lim() xcxcxc
(d) lim() () 55 ()()lim()lim()5(2)7 lim
54. (a) 444 lim[()3]lim()lim3330 xxx gxgx
(b) 444 lim()limlim()(4)(0)0 xxx xfxxfx
(c) 2 22 44 lim[()]lim()[3]9 xx gxgx
(d) 4 44 lim() () 3 ()1lim()lim101 4 lim3 x xx gxgx xfxfx
55. (a) lim[()()]lim()lim() xbxbxb fxgxfxgx
(b) lim()()lim()lim() xbxbxb fxgxfxgx
(c) lim4()lim4lim()(4)(3) xbxbxb gxgx
58. 22 2 (2)(2) 444 000 limlimlim hhh hh hhh
59. [3(2)4][3(2)4] 3 00 limlim3 hh hhhh
60.
61.
11 2 22 2 1 2(2) 00022(2) limlimlimhhh hhhhhhh
7777 77 77 00 limlimhhh hhhhh
63. 22 0 lim5252(0)5 x x
64. 2 0 lim(2)202 x x
65. (a)
and 0 lim x
and 0 lim2cos x x
2 0 66 0 lim11 1 x x
by the sandwich theorem, 0 lim()5 x fx
2(1)2; by the sandwich theorem, 0 lim()2 x gx
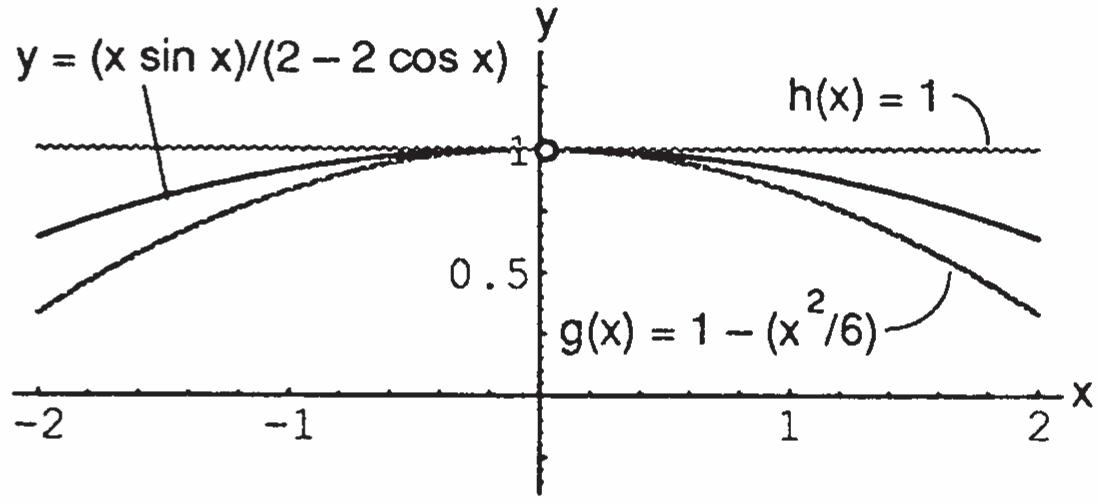
and 0 lim11; x by the sandwich theorem, sin 22cos 0 lim1 xx xx
(b) For 0,(sin)/(22cos) xyxxx lies between the other two graphs in the figure, and the graphs converge as 0 x
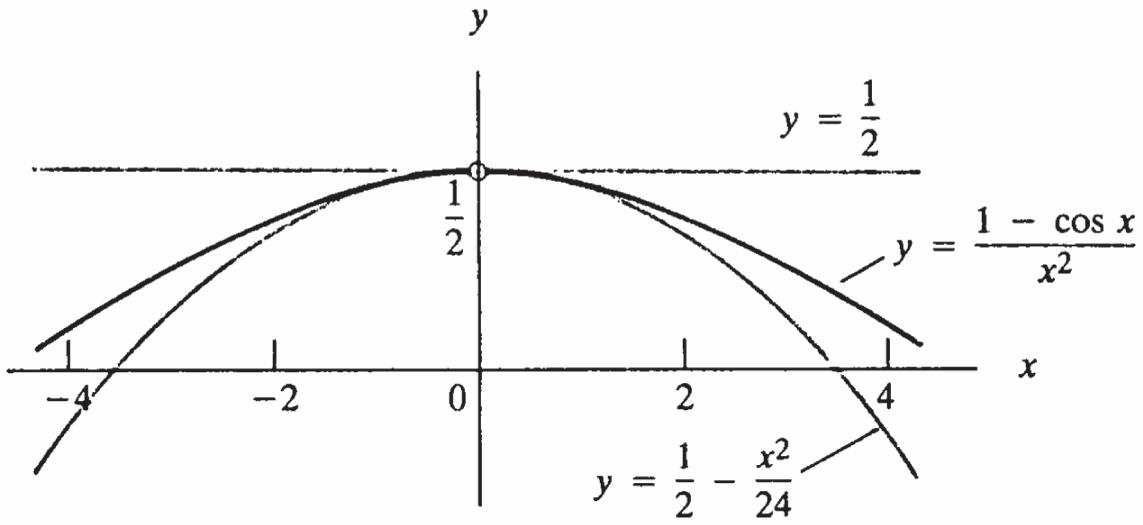
66. (a) 22 1111 00022422422 limlimlim0 xx
(b) For all 0, x the graph of 2 ()(1cos)/ fxxx lies between the line 1 2 y and the parabola 2 1 2 /24, yx and the graphs converge as 0. x
67. (a) 2 ()(9)/(3) fxxx
The estimate is 3 lim()6. x fx (b)
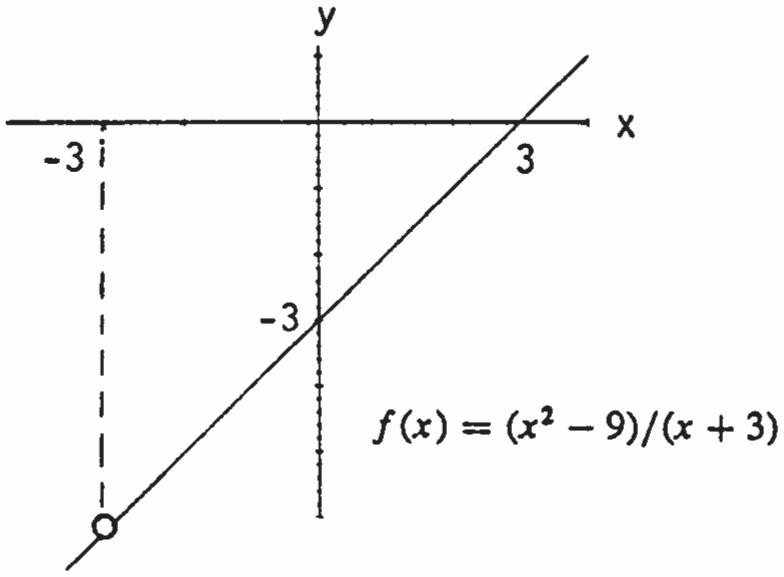
(c) 2 (3)(3) 9 33 ()3 xxxfxxxx
68. (a) 2 ()(2)/2 gxxx x
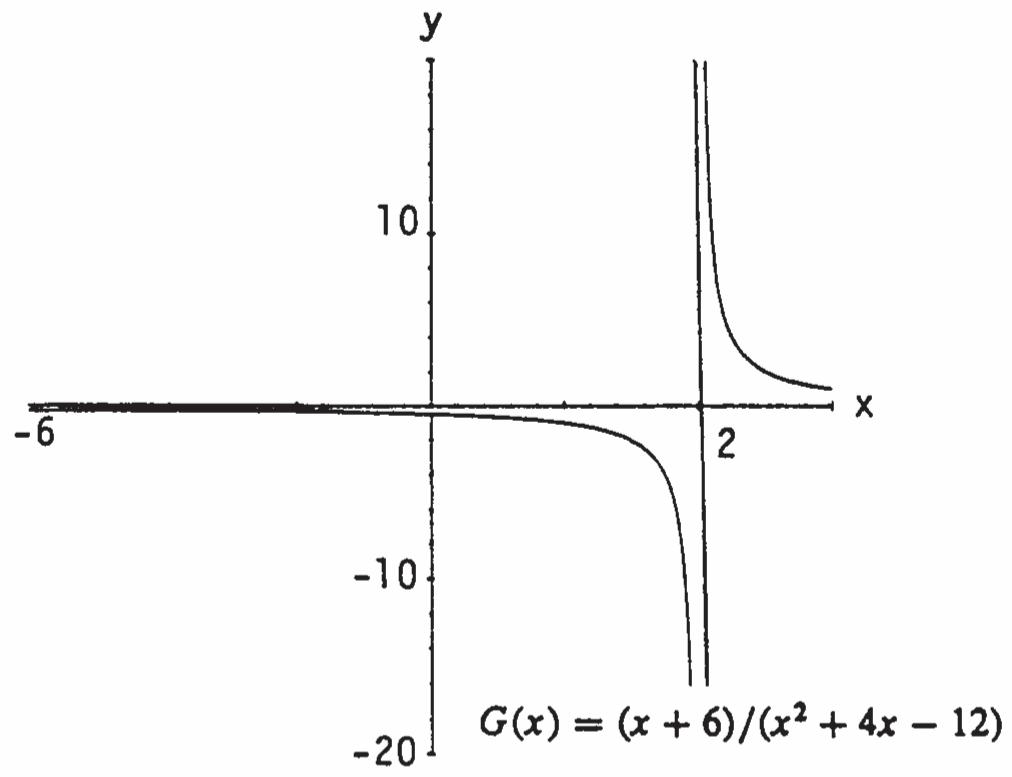
70. (a) 22 ()(23)/(43) hxxxxx x 2.9
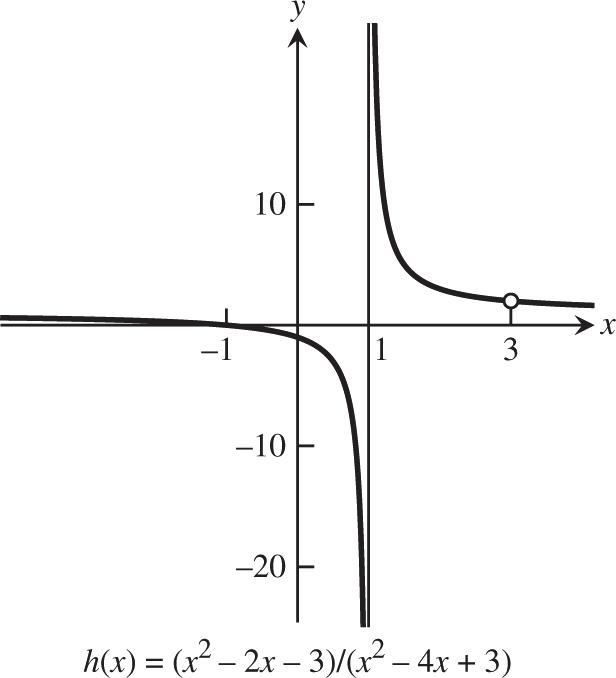
(b) (c) 2 2 (3)(1) 231 (3)(1)1 43 () xxxxx xxxx x hx
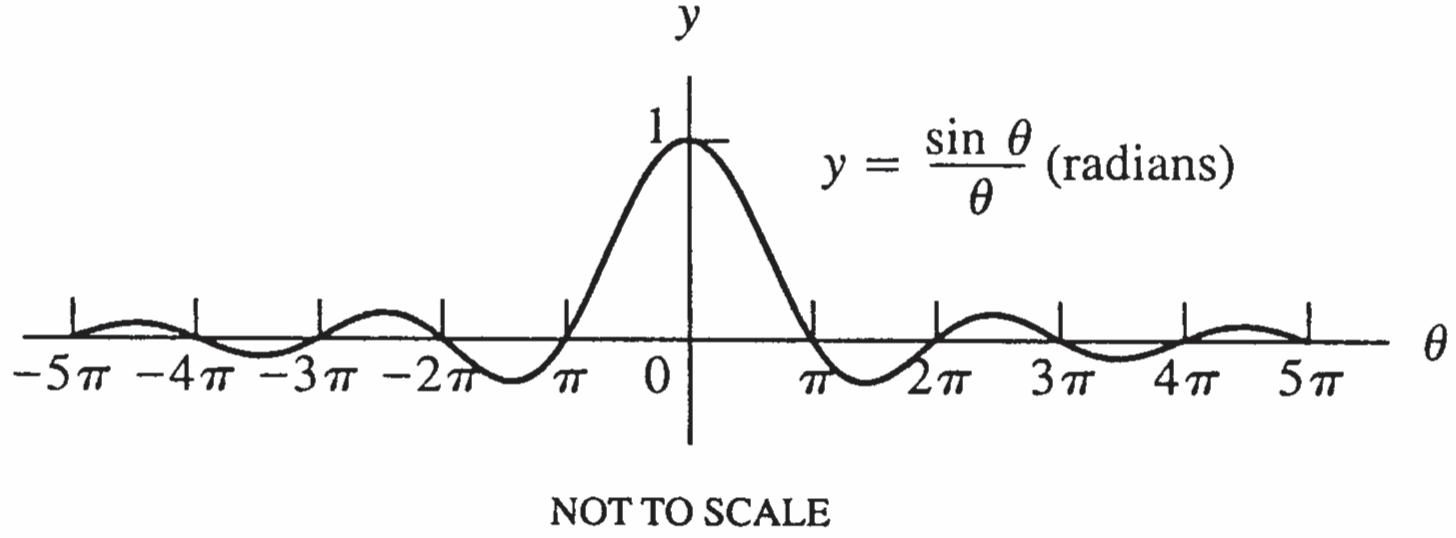
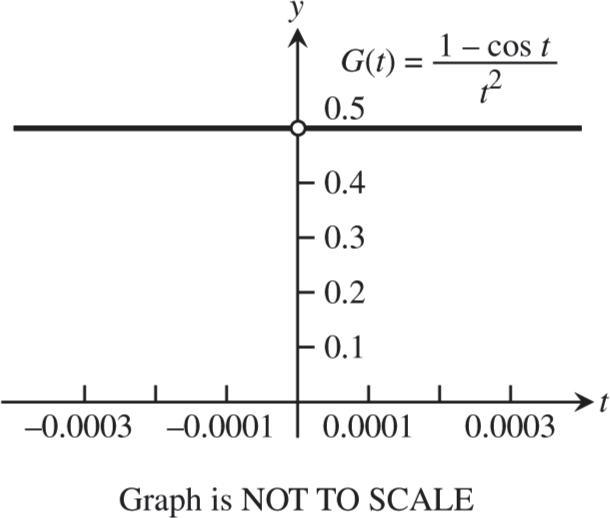
74. (a) 2 ()(1cos)/ Gttt
t
Gt
Gt
(b)
75. (a) 1/(1) () fxxx
x
x fx
(b)
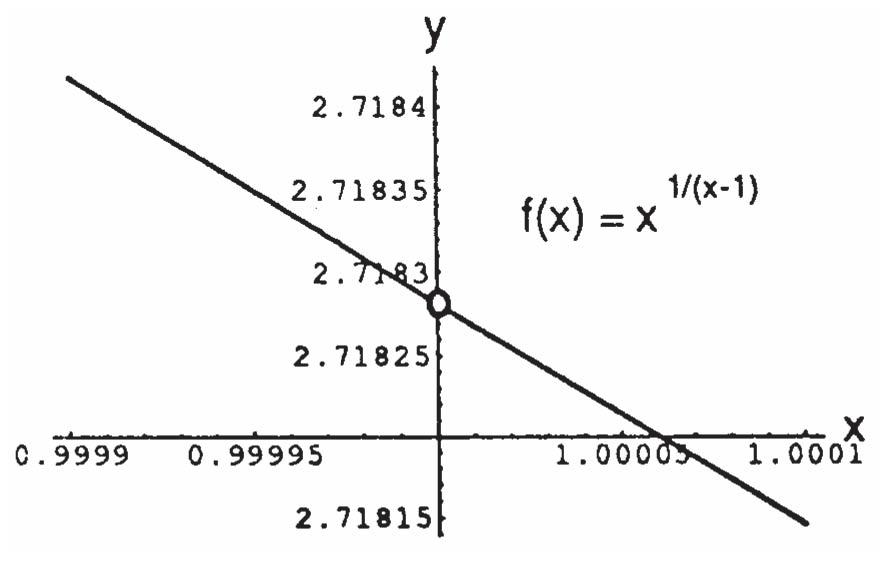
Graph is NOT TO SCALE. Also, the intersection of the axes is not the origin: the axes intersect at the point (1, 2.71820).
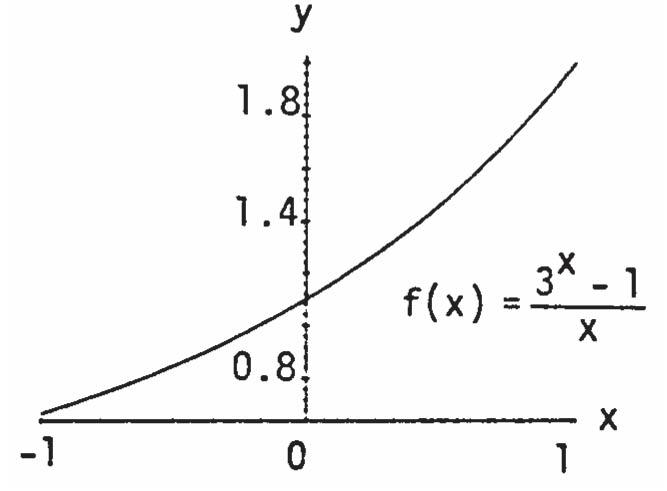
76. (a) ()(31)/ x fxx
77. lim() xc fx exists at those points c where 4
78. Nothing can be concluded about the values of ,,fg and h at 2 x Yes, (2) f could be 0. Since the conditions of the sandwich theorem are satisfied, 2 lim()50. x fx
79. 444 44 lim()lim5lim()5 ()5
80. (a) 22 22 2 lim()lim() () 4 lim 2 1 lim xx x fxfxfx xxx
83. (a) 1 0 limsin0 xx x
(b)
1sin1
84. (a)
by the sandwich theorem; 11
by the sandwich theorem.
(b)
85–90. Example CAS commands: Maple:
f:x-(x^416)/(x2); x0:2;
plot(f(x),xx0-1..x01,colorblack,
title"Section 2.2,85(a); #" )
limit(f(x),xx; 0 )
In Exercise 87, note that the standard cube root, x^(1/3), is not defined for x<0 in many CASs. This can be overcome in Maple by entering the function as f:x-(surd(x1,3)1)/x.
Mathematica: (assigned function and values for x0 and h may vary)
Clear[f,x]
322 f[x_]:(xx5x3)/(x1) x01;h0.1;
Plot[f[x],{x,x0h,x0h}]
Limit[f[x],xx0]
2.3 THE PRECISE DEFINITION OF A LIMIT
1.

Step 1: 55xx
55 x
Step 2: 572, or 514.
The value of δ which assures 51 x 7 x is the smaller value, 2.
2.

Step 1: 22xx 22 x
Step 2: 211, or 275.
The value of which assures 2 x 1 7 x is the smaller value, 1.
3.

Step 1: (3)3xx 33 x
Step 2: 7 1 22 3,
or 1 2 3
The value of which assures (3) x
4.
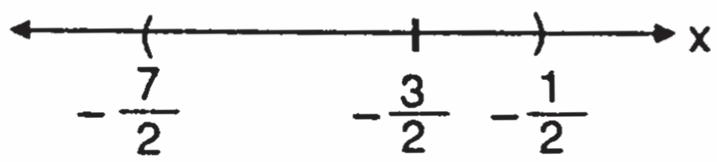
Step
5.
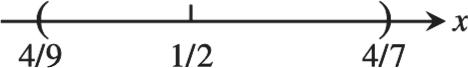
Step
The
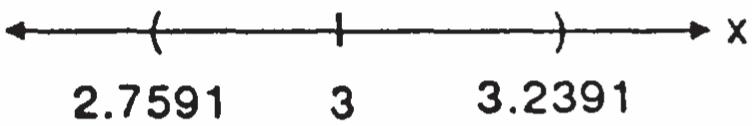
Step 1: 33xx
Step 2: 32.75910.2409, or 33.23910.2391.
The value of which assures 3 x 2.75913.2391 x is the smaller value, 0.2391.
7. Step 1: 55xx 55 x
Step 2: From the graph, 54.90.1, or 55.10.1; thus 0.1 in either case.
8. Step 1: (3)3xx 33 x
Step 2: From the graph, 33.10.1,
or 32.90.1;
thus 0.1.
9. Step 1: 11xx
Step 2: From the graph, 97 1616 1,
or 259 1616 1;
thus 7 16
10. Step 1: 33xx
Step 2: From the graph, 32.610.39,
or 33.410.41;
thus 0.39.
11. Step 1: 22xx
Step 2: From the graph,
12. Step 1: (1)1xx
Step 2: From the graph, 5 2 1
13. Step 1: (1)1xx
Step
14. Step
Step 2: From the graph, 111 22.012
15. Step 1: (1)50.0140.01 xx
Step 2: 44
16. Step 1: (22)(6)0.02240.02
Step 2: (2)2
17. Step 1:
18. Step 1:
Step 2: 11 44xx
Then 1 4 0.160.09 1 4 or0.360.11;thus0.09.
19. Step 1: 193111931 xx
219441916 xx 41916153 xx or 3 15 x
Step 2: 1010xx 1010. x
Then 1037, or 1015 5; thus 5.
20. Step 1: 7411741xx 3759725 xx
Step 2: 2323xx
23x23.
21. Step 1: 1111440.050.050.05xx
Step 2: 44xx
22. Step 1: 2230.10.130.1
Step 2: 33xx
23. Step 1: 2240.50.540.5
4.53.5, x for x near 2
Step 2: (2)2xx
24. Step 1: 11(1)0.10.110.1 xx
Step 2: (1)1xx
Then 10 1 99 1,
25. Step 1: 22 (5)111161
Step 2: 44xx 44. x
Then 415415
or 1010 911 x
0.1270, or 417174
0.1231; thus 1740.12.
26. Step 1: 120120120 511514 xxx 11 41206 63020 xx or 20 30. x
Step 2: 2424xx 2424. x
Then 24204, or 24 306; thus 4.
27. Step 1: 20.030.0320.03mxmmxm 0.0320.032 mmxm 0.03 22 m x 0.03 m
Step 2: 22xx 22. x
Then 0.030.03 22, mm or 0.030.03 22. mm In either case, 0.03 . m
28. Step 1: 33 mxmccmxmc 33 cmmxcm 33cc mm x
Step 2: 33xx 33. x
Then 33, cc mm or 3 3 cc mm In either case, c m
29. Step 1: 22 () mmmxbbccmx 22 mmccmxc 11 22 cc mm x
Step 2: 11 22xx 11 22 x
Then 11 22 , cc mm or 1 2 1 2 cc mm In either case, c m
30. Step 1: 0.050.05 ()()0.050.050.050.050.05 11. mm mxbmbmxmmmxm x
Step 2: 11xx
Then 0.050.05 11, mm
Step 1: (32)(3)0.020.0262 xx
Step 2: 033 xx
32. 1 lim(32)(3)(1)21 x x
Step 1: (32)10.030.0333 xx
Step 2: (1)1xx
Step 1:
Step 2: 22xx
34. 2 (x5)(x1) x6x5 x5x5x5(x5) limlim
Step 1: 2 65 5 (4)0.05 xx x
Step 2: (5)5xx
Then 55.050.05,
35. 3 lim1515(3)164 x x
Step 1: 1540.50.515 xx
11.25519.253.852.25. xx
Step 2: (3)3xx
Then 33.850.85,
36. 44 2 2 lim2 xx
38. Step 1: (37)239
39. Step 1: 525xx
Then
40. Step 1: 4242 xx
Step 2: 0.
41. Step 1:
Step 2:
Then 1111,
that is, the smaller of the two distances.
42. Step 1: For 22 2,44xxx
Step 2:
43. Step 1: 1111
48. Step 1: 0:2020xxx 2 0; x 2 0:002. x xx Step 2: 0.xx Then 22 , or 2 2. Choose 2
49. By the figure, 1 sin x xxx for all 0 x and 1 sinfor0. x xxxx Since 0 lim() x x 0 lim0, x x then by the sandwich theorem, in either case, 1 0 limsin0. xx x
50. By the figure, 222 1 sin x xxx for all x except possibly at 0. x Since 2 0 lim() x x 2 0 lim0, x x then by the sandwich theorem, 2 1 0 limsin0. xx x
51. As x approaches the value 0, the values of ()gx approach k. Thus for every number 0, there exists a 0 such that 00 x ().gxk
52. Write xhc Then 0 xc , xc ()xchc , c , hcch 0 h 00. h Thus, lim() xc fxL for any 0, there exists 0 such that () fxL whenever 0 xc () fhcL whenever 0 00lim(). h hfhcL
53. Let 2 ().fxx The function values do get closer to 1 as x approaches 0, but 0 lim()0, x fx not 1 The function 2 () fxx never gets arbitrarily close to 1 for x near 0.
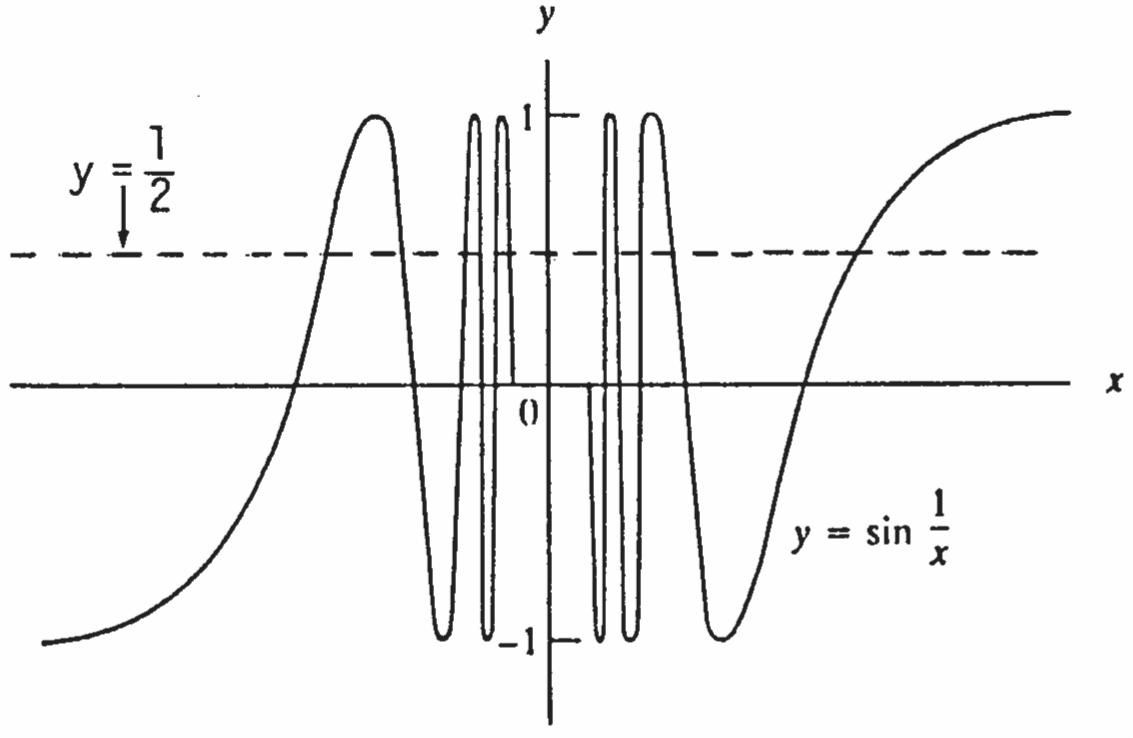
54. Let 1 0 2 ()sin,,and0 fxxLx There exists a value of x 6 (namely) x for which 1 2 sin x for any given 0. However, 0 limsin0, x x 1 2 not. The wrong statement does not require x to be arbitrarily close to 0x As another example, let 11 2 ()sin,, x gxL and 0 0. x We can choose infinitely many values of x near 0 such that 11 2 sin x as you can see from the accompanying figure. However, 1 0 limsin xx fails to exist. The wrong statement does not require all values of x arbitrarily close to 0 0 x to lie within 0of L 1 2 Again you can see from the figure that there are also infinitely many values of x near 0 such that 1 sin0. x If we choose 1 4 we cannot satisfy the inequality 11 2 sin x for all values of x sufficiently near 0 0. x 55.
228.999.01 x or3.3843.387. x To be safe, the left endpoint was rounded up and the right endpoint was rounded down.
56.
To be safe, the left endpoint was rounded up and the right endpoint was rounded down.
57.
(b) 0111() xxfx
Then ()1(1)1 fxxx 1 x That is, ()11fx no matter how small is taken when 1 1 1lim x x ()1.fx (c) 1011(). xxfxx Then ()1.51.51.5 fxxx 1.510.5. Also, 011xx 1()1. fxx
Then ()1.5fx (1)1.50.5 xx
0.510.50.5 x Thus, no matter how small is taken, there exists a value of x such that 1 x but 1 2 ()1.5fx 1 lim()1.5. x fx
58. (a) For 22()2()42. xhxhx Thus for 2,()4 hx whenever 22 x no matter how small we choose 2 0lim()4. x hx
(b) For 22()2()31 xhxhx Thus for 1,()3 hx whenever 22 x no matter how small we choose 2 0lim()3. x hx
(c) For 2 22()xhxx so 2 ()22.hxx No matter how small 0 is chosen, 2 x is close to 4 when x is near 2 and to the left on the real line 2 2 x will be close to 2. Thus if 1,()2 hx whenever 22 x no matter how small we choose 2 0lim()2. x hx
59. (a) For 3 3()4.8()40.8.xfxfx Thus for 0.8,()4 fx whenever 3 3 x no matter how small we choose 3 0lim()4. x fx
(b) For 3 3()3()4.81.8xfxfx Thus for 1.8,()4.8 fx whenever 3 3 x no matter how small we choose 3 0lim()4.8. x fx
(c) For 3 3()4.8()31.8xfxfx Again, for 1.8,()3 fx whenever 3 3 x no matter how small we choose 3 0lim()3. x fx
60. (a) No matter how small we choose 0, for x near 1 satisfying 11, x the values of ()gx are near 1 ()2gx is near 1. Then, for 1 2 we have 1 2 ()2gx for some x satisfying 11, x or 1 01lim()2. x xgx (b) Yes, 1 lim()1 x gx because from the graph we can find a 0 such that ()1gx if 0(1). x 61–66. Example CAS commands (values of del may vary for a specified eps): Maple: f:x-(x^4-81)/(x-3);x0:3; plot(f(x),xx0-1..x01,colorblack, # (a) title"Section 2.3,#61(a)"); L:limit(f(x),xx0); # (b) epsilon:0.2; # (c) plot([f(x),L-epsilon,Lepsilon],xx0-0.01..x00.01, colorblack, linestyle[1,3,3],title"Section 2.3, #61(c)");
q:fsolve(abs(f(x)-L )epsilon, xx0-1..x01); #(d)
delta:abs(x0-q); plot([f(x),L-epsilon,Lepsilon],xx0-delta..x0delta,colorblack,title"Section 2.3,#61(d)"); for eps in [0.1,0.005,0.001]do #(e)
q:fsolve(abs(f(x)-L)eps,xx0-1..x01);
delta:abs(x0-q); head:sprintf("Section 2.3,#61(e)\n epsilon%5f,delta%5f\n",eps,delta); print(plot([f(x),L-eps,Leps],xx0-delta..x0delta, colorblack,linestyle[1,3,3],titlehead)); enddo:
Mathematica (assigned function and values for x0, eps and del may vary): Clear[f,x] y1:Leps;y2:Leps;x01; 2 f[x_]:(3x(7x1)Sqrt[x]5)/(x1)
Plot[f[x],{x,x00.2,x00.2}] L:Limit[f[x],xx0] eps0.1;del0.2;
Plot[{f[x],y1,y2},{x,x0del,x0del}, PlotRange{L2eps, L2eps}]
2.4 ONE-SIDED LIMITS
1. (a) True (b) True (c) False (d) True (e) True (f) True (g) False (h) False (i) False (j) False (k) True (l) False
2. (a) True (b) False (c) False (d) True (e) True (f) True (g) True (h) True (i) True (j) False (k) True
3. (a) 2 2 2 lim()12, x fx 2 lim()321 x fx
(c) 4 2 4 lim()13, x fx
(b) No, 2 lim() x fx does not exist because 22 lim()lim() xx fxfx
lim()13 x fx
(d) Yes, 4 lim()3 x fx because 44 3 lim()lim() xx fxfx
4. (a) 2 2 2 lim()1, x fx 2 lim()321,(2)2 x fxf
(b) Yes, 2 lim()1 x fx because 22 1 lim()lim() xx fxfx
(c) 1 lim()3(1)4, x fx 1 lim()3(1)4 x fx
(d) Yes, 1 lim()4 x fx because 11 4 lim()lim() xx fxfx
5. (a) No, 0 lim() x fx does not exist since 1 sin x does not approach any single value as x approaches 0
(b) 00 lim()lim00 xx fx
(c) 0 lim() x fx does not exist because 0 lim() x fx does not exist
Copyright 2018 Pearson Education, Inc.
6. (a) Yes, 0 lim()0 x gx by the sandwich theorem since () xgxx when 0 x
(b) No, 0 lim() x gx does not exist since x is not defined for 0 x
(c) Yes, 0 0 lim()lim()0 xx gxgx since 0 x is a boundary point of the domain
7. (a) (b) 11 lim()1lim() xx fxfx
(c) Yes, 1 lim()1 x fx since the right-hand and left-hand limits exist and equal 1
8. (a) (b) 11 lim()0lim() xx fxfx
9. (a) domain: 02 x range: 01 y and 2 y (b) lim() xc fx exists for c belonging to (0,1)(1,2)
(c) 2 x (d) 0 x
10. (a) domain: x range: 11 y (b) lim() xc fx exists for c belonging to (,1)(1,1)(1,)
(c) none (d) none 11. 20.523/2 10.511/2 0.5
(c) Yes, 1 lim()0 x fx since the right-hand and left-hand limits exist and equal 0
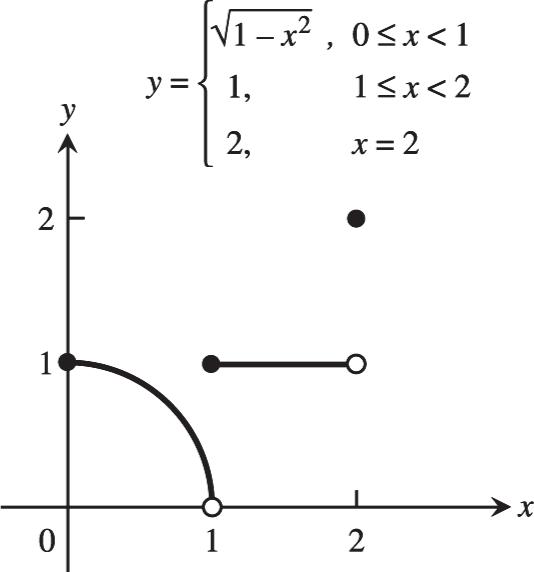
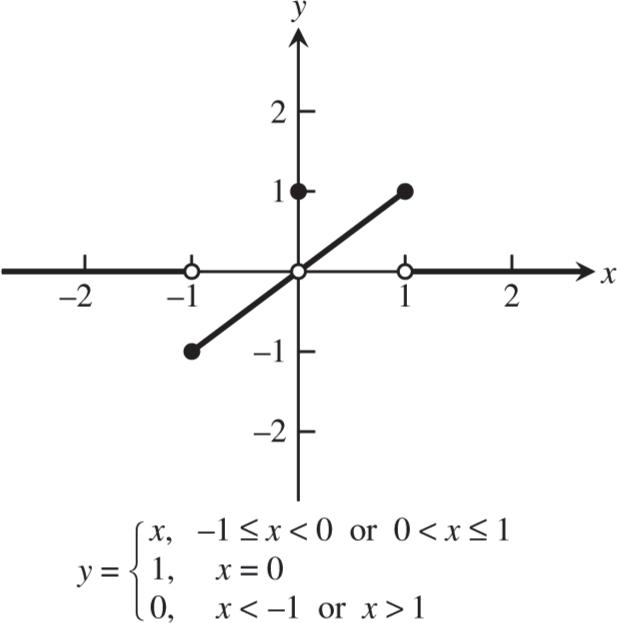
18. (a) 2(1)2(1) (1) 1 11 limlimxxxx xx xx
(b) 2(1)2(1) (1) 1 11 limlimxxxx xx xx
(|1|(1)for1) xxx 1 lim22 x x
19. (a) If 2 0, x then sin0, x so that sin sin sinsin 000 limlimlim11 xx xx xxx
(b) If 2 0, x then sin0, x so that sin sin sinsin 000 limlimlim11 xx xx xxx
20. (a) If 2 0, x then cos1, x so that 1cos1cos1cos (cos1)1cos cos1 0000 limlimlimlim11 xxx xxx xxxx
(b) If 2 0, x then cos1, x so that cos1cos1 (cos1) cos1 000 limlimlim11 xx xx
21. (a) 3 3 3 lim1
25.
csc2211111 cos5sin2cos52sin2cos522 0000 limlimlimlim1(1)
31.
coscos 1 sincossincossincossincossin 0000 limlimlimlim xxxxxxxx xxxxxxxxxx xxx
sinsin 111 cos 000 limlimlim(1)(1)12 xx xx x xxx
32.
33. 22 (1cos)(1cos) 1cos1cossin sin2(2sincos)(1cos)(2sincos)(1cos)(2sincos)(1cos) 0000 limlimlimlim
sin0 (2cos)(1cos)(2)(2) 0 lim0
34.
xxxxx xx xxxx
(1cos) 1cos 1 1cos 1 2 9 9909 222222 sin3 sin3sin3 2 33 9 0 lim (0) (1cos) cos sin3sin31 0000 lim limlimlimlim 0 xxx x
35. sin(1cos) sin 1cos 00 limlim1since1cos0as 0 t tt
36. sin(sin) sin sin 00 limlim1sincesin0as 0 h hhhh
sinsin2sin2111 sin2sin222sin222 000 limlimlim11
sin5sin5455sin5455 sin4sin45445sin444 000 limlimlim11 xxxxx xxxxxx
40. cos2cos2cos2 1 0000sin22sincos2cos2 limsincot2limsinlimsinlim
41.
tan3sin3sin383 11 sin8cos3sin8cos3sin838 000 limlimlimxxxx xxxxxxx xx
42.
sin3cot5sin3sin4cos5sin3sin4cos5345 000cot4cos4sin5cos4sin5345 limlimlimyyyyyyyyy yyyyyyyyyy yy
sin3sin45cos5 34 1212 34sin5cos4555 0 lim1111 yyyy yyyyy
43. sin cos 222 cos3 sin3 tansinsin3 000cot3coscos3 limlimlim
000 limlimlim1
45. 22 1cos31cos31cos31cos3sin33sin3sin3 221cos32(1cos3)2(1cos3)231cos3 00000 limlimlimlimlimxxxxxxx xxxxxxxxx
3sinsin30 21cos211
46. 22 2 22222 coscoscos1cos(cos1)cos(cos1)cos(cos1)cos(sin) cos1 00000(cos1)(cos1) limlimlimlimlimxxxxxxxxxxx x xxxxxxxxxxxx
xxx xxx
sinsincos 11 cos1112
47. Yes. If lim()lim(), xaxa fxLfx then lim(). xa fxL If lim()lim(), xaxa fxfx then lim() xa fx does not exist.
48. Since lim() xc fxL if and only if lim() xc fxL and lim(), xc fxL then lim() xc fx can be found by calculating lim(). xc fx
49. If f is an odd function of x, then ()(). fxfx Given 0 lim()3, x fx then 0 lim()3. x fx
50. If f is an even function of x, then ()().fxfx Given 2 lim()7 x fx
then 2 lim()7. x fx
However, nothing can be said about 2 lim() x fx because we don’t know 2 lim() x fx
51. (5,5)55Ix
52. (4,4)44Ix
Also, 22 555.
Also, 44422
53. As 0 x the number x is always negative. Thus, (1)10xx xx
which is always true independent of the value of x. Hence we can choose any 0
with
54. Since 2 x we have 2 x and 22.xx Then, 22 2 2 110xx xx
which is always true so long as 2 x Hence we can choose any
and thus 22 x
55. (a)
400 lim400. x x
Just observe that if 400401, x
then 400 x
Thus if we choose 1, we have for any number 0
that 400400 x
(b) 400 lim399. x
any number 0
Just observe that if 399400 x
then 399. x
that 400400 x
(c) Since 400400 limlim
we conclude that 400 lim x x
does not exist. 56. (a) 00 lim()lim00; xx fxx
for x positive. Choose 2
(b)
0 lim()0. x fx
2 1 00 lim()limsin0 x xx fxx by the sandwich theorem since
22 2 1 sin x xxx for all 0. x
Since 222 00 xxx whenever , x we choose and obtain
2 1 sin0 x x
if 0. x (c) The function f has limit 0 at 0 0 x since both the right-hand and left-hand limits exist and equal 0.
2.5 CONTINUITY
1. No, discontinuous at 2, x not defined at 2 x
2. No, discontinuous at 3, x 3 1 lim()(3)1.5 x gxg
3. Continuous on [ 1,3]
4. No, discontinuous at 1, x 11 1.5lim()lim()0 xx kxkx
5. (a) Yes (b) Yes, 1 lim() 0 x fx (c) Yes (d) Yes
6. (a) Yes, (1)1 f
(b) Yes, 1 lim()2 x fx (c) No (d) No
7. (a) No (b) No
8. [ 1,0)(0,1)(1,2)(2,3)
9. (2)0, f since 22 lim()2(2)40lim() xx fxfx
10. (1) f should be changed to 1 2lim() x fx
11. Nonremovable discontinuity at 1 x because 1 lim() x fx fails to exist 1 (lim()1 x fx and 1 lim()0) x fx
Removable discontinuity at 0 x by assigning the number 0 lim()0 x fx to be the value of (0) f rather than (0)1. f
12. Nonremovable discontinuity at 1 x because 1 lim() x fx fails to exist 11 (lim()2andlim()1). xx fxfx
Removable discontinuity at 2 x by assigning the number 2 lim()1 x fx to be the value of (2) f rather than (2)2 f
13. Discontinuous only when 202xx 14. Discontinuous only when 2 (2)02 xx 15. Discontinuous only when 2 430(3)(1)03xxxxx
or 1 x
16. Discontinuous only when 2 3100(5)(2)05 xxxxx or 2 x
17. Continuous everywhere. (|1|sinxx defined for all x; limits exist and are equal to function values.)
18. Continuous everywhere. (||10 x for all x; limits exist and are equal to function values.)
19. Discontinuous only at 0 x
20. Discontinuous at odd integer multiples of 22 ,i.e.,(21), xn n an integer, but continuous at all other x
21. Discontinuous when 2x is an integer multiple of ,i.e.,2, xn n an integer 2 , xn n an integer, but continuous at all other x.
22. Discontinuous when 2 x is an odd integer multiple of 222 ,i.e.,(21), xn
n an integer 21,xn n an integer (i.e., x is an odd integer). Continuous everywhere else.
23. Discontinuous at odd integer multiples of 22 ,i.e.,(21), xn n an integer, but continuous at all other x
24. Continuous everywhere since 2 1sin10sin1 xx 2 1sin1; x limits exist and are equal to the function values.
25. Discontinuous when 230 x or 3 2 x continuous on the interval 3 2 , .
26. Discontinuous when 3 10 x or 1 3 x continuous on the interval 1 3 ,.
27. Continuous everywhere: (21)1/3 x is defined for all x; limits exist and are equal to function values.
28. Continuous everywhere: (2)1/5 x is defined for all x; limits exist and are equal to function values.
29. Continuous everywhere since 2 (3)(2) 6 33 333 limlimlim(2)5(3) xxxx xxxxx xg
30. Discontinuous at 2 x since 2 lim() x fx does not exist while (2)4. f
31. Discontinuous at 1; x 2 1 lim(2)3, x x but 1 lim, x x ee so that 1 lim() x fx does not exist while (1); fe and 00 lim(1)1lim, x xx xe so that 0 lim()1(0) x fxf
32. Discontinuous at ln2, x since 202lnln2ln2 xxx eeex
33. limsin(sin)sin(sin)sin(0)sin0, x xx
34.
and function continuous at x
2222 0 limsin(cos(tan))sin(cos(tan(0)))sincos(0)sin1, t t and function continuous at 0. t
35. 22222 111 limsec(sectan1)limsec(secsec)limsec((1)sec) yyy yyyyyyyy
2 sec((11)sec1) sec01, and function continuous at 1. y
36.
1/3 4444 0 limtancos(sin)tancos(sin(0))tancos(0)tan1, x x
37. 2 42 193sec2193sec016 0 limcoscoscoscos, tt
38.
and function continuous at 0. t
6 22 1 66 3 limcsc53tancsc53tan45393, x xx
39.
0 222 0 limsinsinsin1, x x ee
40.
111 2 1 limcoslncosln1cos(0), x
41. 2 (3)(3) 9 3(3) ()3, xxx xx gxx
42. 2 (5)(2) 310 22 ()5, tttt tt htt
43. 2 32 3 (1)(1) 11 (1)(1)1 1 (), ssssss fsssss
44. 2 2 (4)(4) 164 (4)(1)1 34 (), xx xx xxxx x gx
45. As defined, 2 3 lim()(3)18 x fx
For ()fx to be continuous we must have 4 3
46. As defined, 2 lim()2 x gx
and 2 2 lim()(2)4. x gxbb
For ()gx to be continuous we must have 1 2 4 2.bb
47. As defined, 2 lim()12 x fx
For ()fx to be continuous we must have 2 12223 aaa
48. As defined, 0 11 0 lim() bb bb x gx
49. As defined, 1 lim()2 x fx
and 1 lim()(1), x fxabab
and 1 lim()(1) x fxabab and 1 lim()3. x fx For ()fx to be continuous we must have 2 ab and 5 2 3 aba and 1 2 . b
50. As defined, 0 lim()(0)22 x gxabb and 2 0 lim()(0)33, x gxabab
and 2 2 lim()(2)3 x gxab 4 3ab and 0 lim()3(2)51. x gx
For ()gx to be continuous we must have 23bab and 4 31 ab 3 2 a and 3 2 . b
51. The function can be extended: (0)2.3. f
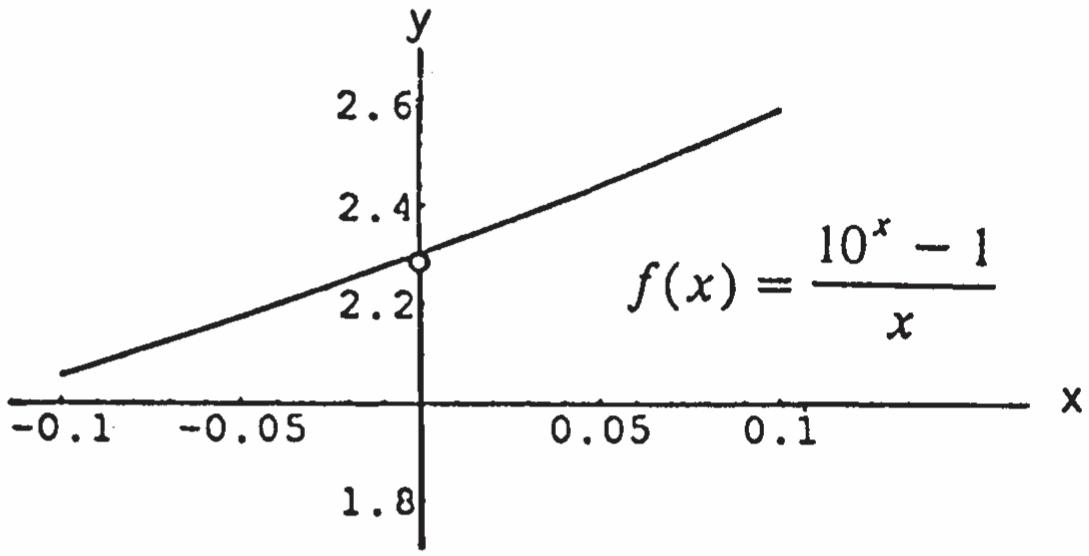
53. The function cannot be extended to be continuous at 0. x If (0)1, f it will be continuous from the right. Or if (0)1, f it will be continuous from the left.
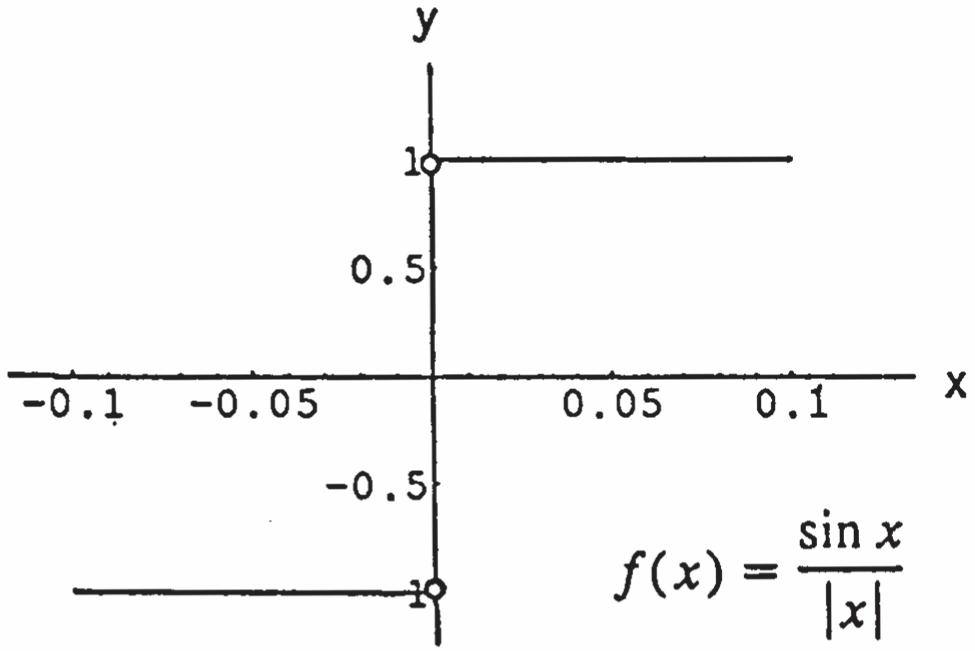
52. The function cannot be extended to be continuous at 0. x If (0)2.3, f it will be continuous from the right. Or if (0)2.3, f it will be continuous from the left.
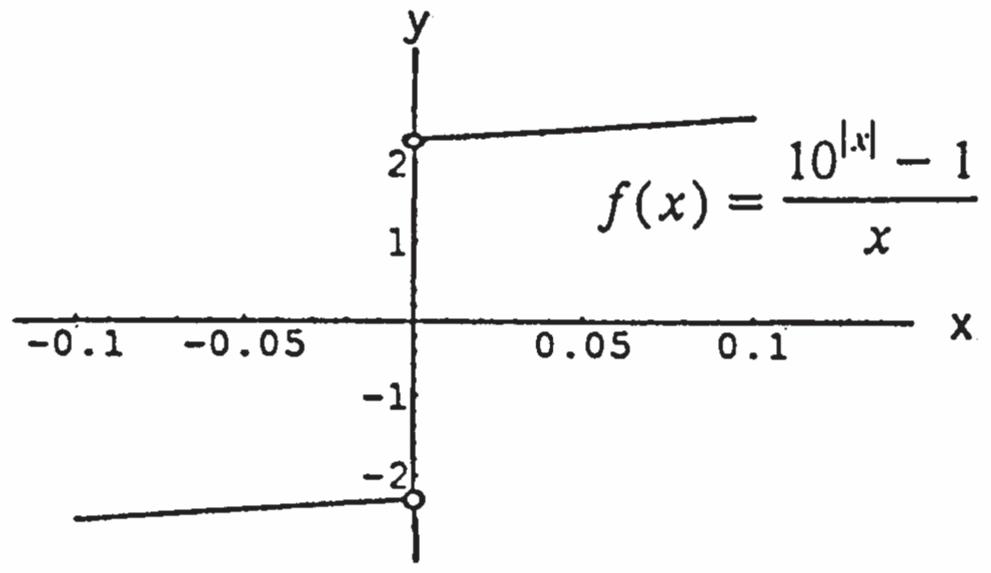
54. The function can be extended: (0)7.39. f
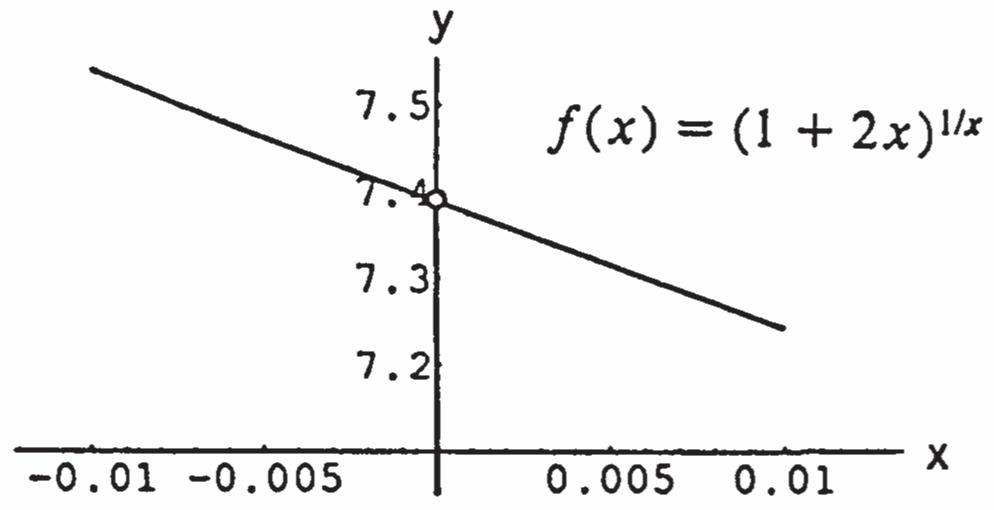
55. ()fx is continuous on [0,1] and (0)0,(1)0ff by the Intermediate Value Theorem ()fx takes on every value between (0) f and (1) f the equation ()0fx has at least one solution between 0 x and 1 x
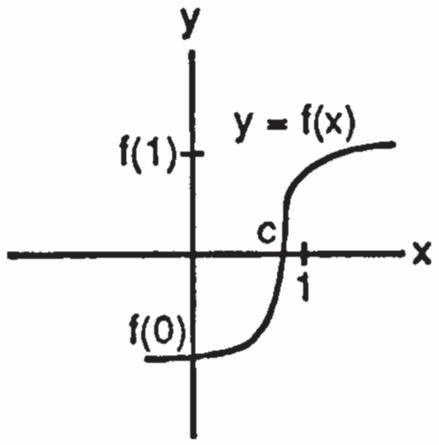
56. cos(cos)0. xxxx If 2 , x
22 cos0. If 2 , x
22 cos0. Thus cos0 xx for some x between 2 and 2 according to the Intermediate Value Theorem, since the function cos xx is continuous.
57. Let 3 ()151, fxxx which is continuous on [ 4,4]. Then (4)3, f (1)15, f (1)13, f and (4)5. f By the Intermediate Value Theorem, ()0fx for some x in each of the intervals 41, x 11, x and 1 4. x That is, 3 1510xx has three solutions in [ 4,4]. Since a polynomial of degree 3 can have at most 3 solutions, these are the only solutions.
58. Without loss of generality, assume that ab Then ()()()22 Fxxaxbx is continuous for all values of x, so it is continuous on the interval [ ,].ab Moreover () Faa and (). Fbb By the Intermediate Value Theorem, since 2 , ab ab there is a number c between a and b such that 2 ().Fab x
59. Answers may vary. Note that f is continuous for every value of x. (a) 3 (0)10,(1)18(1)103.ff Since 3 10, by the Intermediate Value Theorem, there exists a c so that 01 c and ().fc
(b) 3 (0)10,(4)(4)8(4)1022.ff Since 22310, by the Intermediate Value Theorem, there exists a c so that 40 c and ()3.fc
(c) (0)10, f 3 (1000)(1000)8(1000)10999,992,010. f Since 105,000,000999,992,010, by the Intermediate Value Theorem, there exists a c so that 01000 c and ()5,000,000.fc
60. All five statements ask for the same information because of the intermediate value property of continuous functions.
(a) A root of 3 ()31 fxxx is a point c where ()0.fc
(b) The point where 3 yx crosses 31yx have the same y-coordinate, or 3 31yxx ()fx 3 310.xx
(c) 3 31xx 3 310.xx The solutions to the equation are the roots of 3 ()31. fxxx
(d) The points where 3 3 yxx crosses 1 y have common y-coordinates, or 3 31yxx ()fx 3 310.xx
(e) The solutions of 3 310xx are those points where 3 ()31 fxxx has value 0.
61. Answers may vary. For example, sin(2) 2 () x fxx is discontinuous at 2 x because it is not defined there. However, the discontinuity can be removed because f has a limit (namely 1) as 2 x
62. Answers may vary. For example, 1 1 () gxx has a discontinuity at 1 x because 1 lim() x gx does not exist. 11 lim()andlim(). xx gxgx
63. (a) Suppose 0x is rational 0 ()1.fx Choose 1 2 For any 0 there is an irrational number x (actually infinitely many) in the interval 00 (,) xx ()0fx Then 0 0|| xx but 0 |()()| fxfx 1 2 1 , so 0 lim() xx fx fails to exist f is discontinuous at 0x rational.
On the other hand, 0x irrational 0 ()0fx and there is a rational number x in 00 (,)()1. xxfx Again 0 lim() xx fx fails to exist f is discontinuous at 0x irrational. That is, f is discontinuous at every point.
(b) f is neither right-continuous nor left-continuous at any point 0x because in every interval 00 (,) xx or 00 (,) xx there exist both rational and irrational real numbers. Thus neither limits 0 lim() xx fx and 0 lim() xx fx exist by the same arguments used in part (a).
64. Yes. Both () fxx and 1 2 () gxx are continuous on [0,1]. However () () fx gx is undefined at 1 2 x since () 1 2() 0 fx ggx is discontinuous at 1 2 x
65. No. For instance, if ()0,fx (),gxx then
()00hxx
is continuous at 0 x and ()gx is not.
66. Let 1 1 () fxx and ()1.gxx Both functions are continuous at 0. x The composition (())fgfgx 11 (1)1xx is discontinuous at 0, x since it is not defined there. Theorem 10 requires that ()fx be continuous at (0), g which is not the case here since (0) 1 g and f is undefined at 1.
67. Yes, because of the Intermediate Value Theorem. If ()fa and ()fb did have different signs then f would have to equal zero at some point between a and b since f is continuous on [ ,].ab
68. Let ()fx be the new position of point x and let ()() .dxfxx The displacement function d is negative if x is the left-hand point of the rubber band and positive if x is the right-hand point of the rubber band. By the Intermediate Value Theorem, ()0dx for some point in between. That is, () fxx for some point x, which is then in its original position.
69. If (0)0 f or (1)1, f we are done (i.e.,0or1inthosecases). cc Then let (0)0fa and (1)1fb because 0()1. fx Define ()() gxfxxg is continuous on [0,1]. Moreover, (0)(0)00 gfa and (1)(1)110 gfb by the Intermediate Value Theorem there is a number c in (0, 1) such that ()0()0 gcfcc or (). fcc
70. Let () 2 0. fc Since f is continuous at xc there is a 0 such that ()() xcfxfc ()()(). fcfxfc If ()0,fc then 3 11 222()()()()()0 fcfcfxfcfx on the interval (,). cc If ()0,fc then 3 11 222()()()()() 0 fcfcfxfcfx on the interval (,). cc
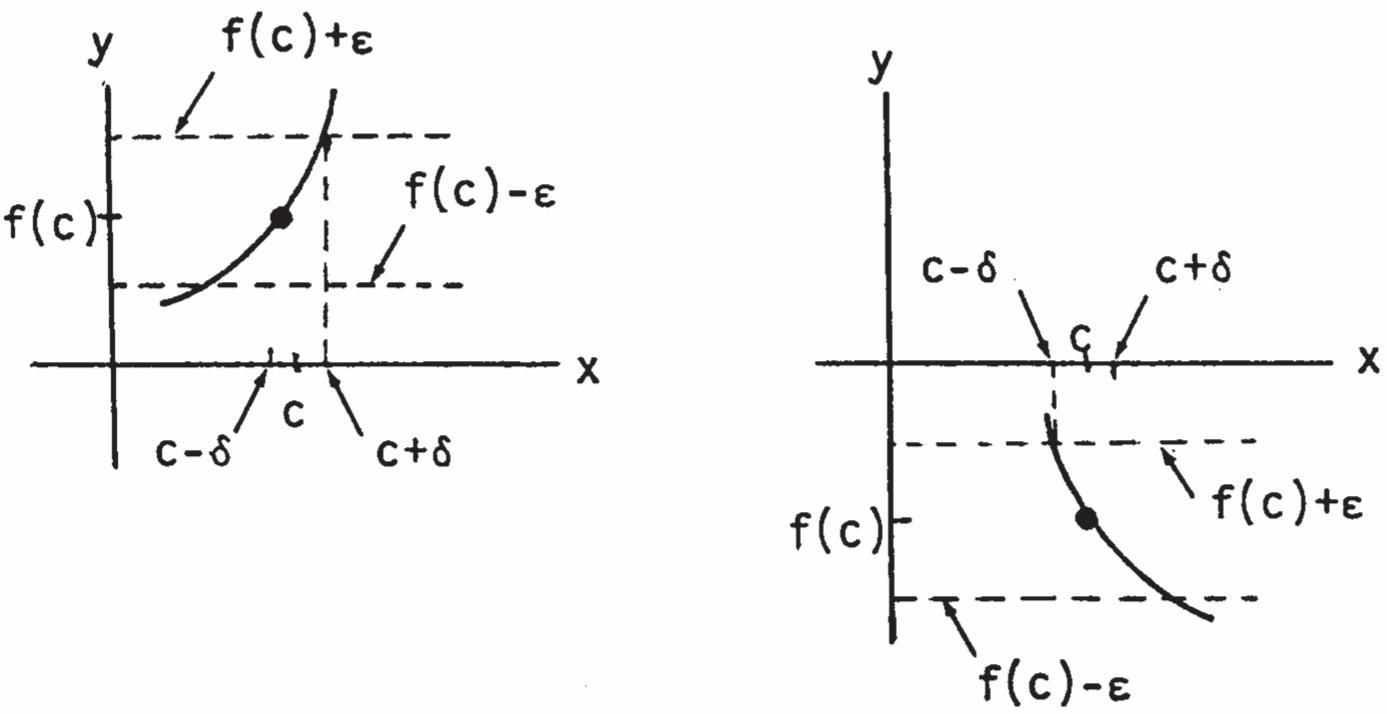
71. By Exercise 52 in Section 2.3, we have 0 lim()lim(). xch fxLfchL Thus, ()fx is continuous at 0 lim()()lim()(). xch xcfxfcfchfc
72. By Exercise 71, it suffices to show that 0 limsin()sin h chc and 0 limcos()cos . h chc Now 0000 limsin()lim(sin)(cos)(cos)(sin)(sin)limcos(cos)limsin hhhh chchchchch
. By Example 11 Section 2.2, 0 limcos1 h h and 0 limsin0. h h So 0 limsin()sin h chc and thus ()sin fxx is continuous at xc Similarly,
00 limcos()lim(cos)(cos)(sin)(sin) hh chchch 00 (cos)limcos(sin)limsin hh chch
cos c Thus, ()cos gxx is continuous at xc
73. 1.8794,1.5321,0.3473 x
75. 1.7549 x
77. 3.5156 x
79. 0.7391 x 74. 1.4516,0.8547,0.4030 x 76. 1.5596 x 78. 3.9058,3.8392,0.0667 x 80. 1.8955,0,1.8955 x
2.6 LIMITS INVOLVING INFINITY; ASYMPTOTES OF GRAPHS
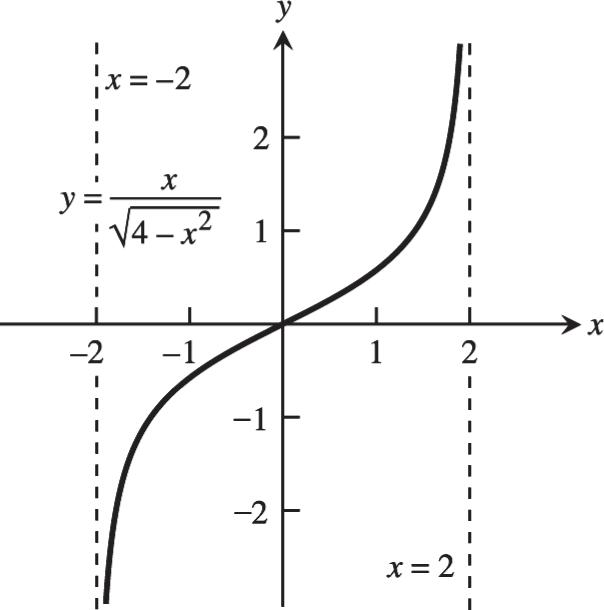
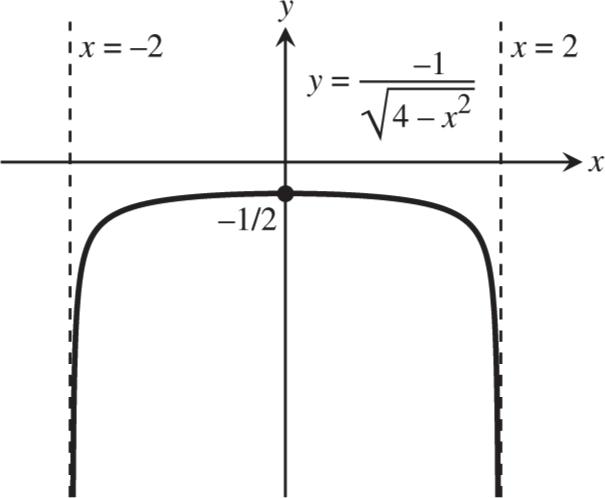
1. (a)
2 lim()0 x fx (c) 3 lim()2 x fx
0 lim()1 x fx
(g) 0 lim()doesnotexist x fx
(i) lim()0 x fx
2. (a) 4 lim()2 x fx
(c) 2 lim()1 x fx
(e) 3 lim() x fx
lim() x fx
lim() x fx
(b) 3 lim()2 x fx
(h) lim()1 x fx
Note: In these exercises we use the result / 1 lim0whenever0.
15. (a)
16. (a)
17. (a) 3 3239 2 77 1 36 limlim7 x x x xxx
18. (a) 1 4 3 4256 1 234 9 99 2 2 256 limlim x xxx xx xxx xx
19. (a) 1031 1 54 26 6 1031 1
0 (same process as part (a))
7 (same process as part (a))
21.
22.
(b) 72413 323 35135 673673
(a) 83325 554 529529 3434
(b) 83325 554 529529 3434
53. (a)
(c)
and 0 lim(2cot),
(1) 0 lim xxx
1/3 2 3 0 lim xx
1/5 2 0 lim xx
2/31/32 11 () 00 limlim xxx x
2 limsec x x
so the limit does not exist
2 111 (2)(2)positivepositive 4 22 limlim xxx
2 111 (2)(2)positivenegative 4 22 limlim xxxxx
2 111 (2)(2)positivenegative 4 22 limlim xxxxx
2 111 (2)(2)negativenegative 4 22 limlim xxxxx
(b) 2 3222 (2)(1) 321 1 4 2(2) 222 limlimlim, xx xxx xxxxxx xx
(c) 2 3222 (2)(1) 321 1 4 2(2) 222 limlimlim, xx xxx xxxxxx xx
(d) 2 3222 (2)(1) 321 1 4 2(2) 222 limlimlim, xx xxx xxxxxx xx
2 322 (2)(1)negativenegative 32 positivenegative 002(2) limlimxxxx xxxxx x
(a) 2 3 (2)(1)(1)
(2)(1)(1)negative
(2)(1)(1)negative
(d) 2 3 (2)(1)(1) 320 (2)(2)(2)(1)(3) 4 111 limlimlim0 xxxxx xxxxxxxx xx
(a)
61. (a) 2/32/3 12 (1) 0 lim xxx
(c) 2/32/3 12 (1) 1 lim xxx
62. (a) 1/34/3 11 (1) 0 lim xxx
(b) 1/3 3 0 lim2 tt
(b) 3/5 1 0 lim7 tt
2/32/3 12 (1) 0 lim xxx
2/32/3 12 (1) 1 lim xxx
(b) 1/34/3 11 (1) 0 lim xxx
70. domain(,1)(1, 1)(1, );
77. Here is one possibility.
Here is
Here is one possibility. 79. Here is one possibility.
81. Here is one possibility.
82. Here is one possibility.
83. Yes. If () () lim2 fx xgx then the ratio the polynomials’ leading coefficients is 2, so () () lim2 fx xgx as well.
84. Yes, it can have a horizontal or oblique asymptote.
85. At most 1 horizontal asymptote: If () () lim, fx xgx L then the ratio of the polynomials’ leading coefficients is L, so () () lim fx xgx L as well.
86.
93.
94. For any 0, take 1. N Then for all yN we have that ()0.
95. For every real number 0, B we must find a 0 such that for all x, 2 1 00. x xB Now, 22 2 1111 00. xBB x BBxx
Choose 1 , B then 1 0 B xx
2 1 x B so that 2 1 0 lim. xx
96. For every real number 0, B we must find a 0 such that for all x, 1 00. x xB Now, 11 0 xB Bx
so that 1 0 lim. xx
97. For every real number 0, B we must find a 0 such that for all x, 2 2 (3) 03. x xB Now, 2 2 (3) 0 x B
2 2 (3) 21 2 (3) 0 x xB B 2 22 (3)03. xBB X Choose 2 , B then 2 2 (3) 030 x xB so that 2 2 (3) 3 lim . xx
98. For every real number 0, B we must find a 0 such that for all x, 2 1 (5) 0(5) x xB Now, 2 2 111 (5) 0(5)5. xBB Bxx Choose 1 . B Then 0(5) x 2 11 (5) 5 Bx xB so that 2 1 (5) 5 lim xx
99. (a) We say that ()fx approaches infinity as x approaches 0x from the left, and write 0 lim(), xx fx if for every positive number B, there exists a corresponding number 0 such that for all x, 00 () .xxxfxB
(b) We say that ()fx approaches minus infinity as x approaches 0x from the right, and write 0 lim(), xx fx if for every positive number B (or negative number B) there exists a corresponding number 0 such that for all x, 00 (). xxxfxB
(c) We say that ()fx approaches minus infinity as x approaches 0x from the left, and write 0 lim(), xx fx if for every positive number B (or negative number B) there exists a corresponding number 0 such that for all x, 00 (). xxxfxB
100. For 11 0,0. BxB Bx Choose 1 B Then 11 00xxBx B so that 1 0 lim. x x
101.
103.
115. (a) y (see accompanying graph)
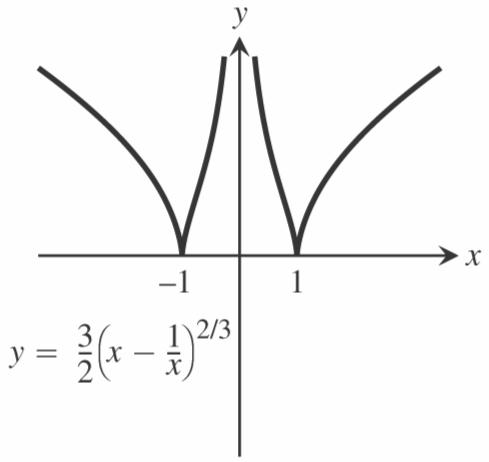
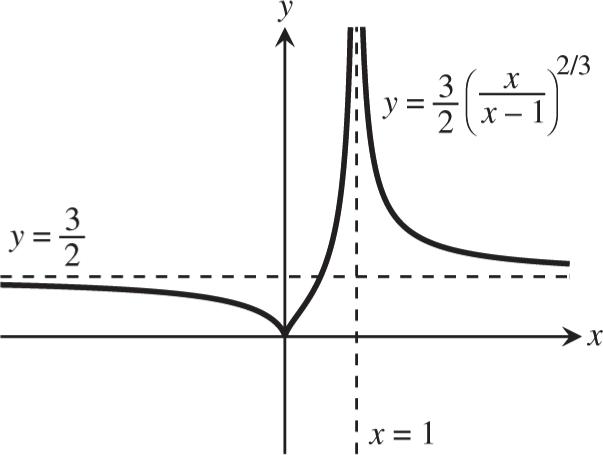
(b) y (see accompanying graph)
(c) cusps at 1 x (see accompanying graph)
116. (a) 0 y and a cusp at 0 x (see the accompanying graph)
(b) 3 2 y (see accompanying graph)
(c) a vertical asymptote at 1 x and contains the point
3 3 24 1, (see accompanying graph)
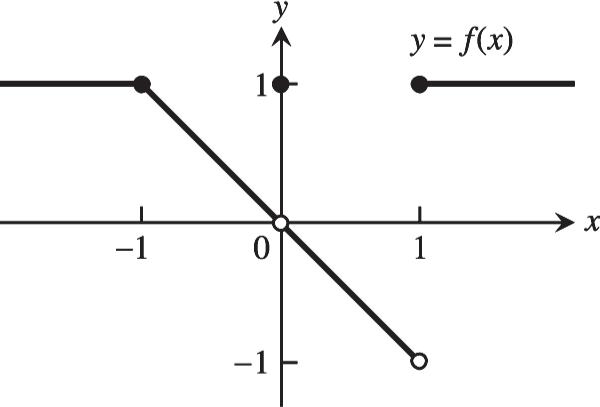
CHAPTER 2 PRACTICE EXERCISES
1. At 11 1:lim ()lim()1 xx xfxfx
1 lim ()1(1) x fxf
is continuous at 1 fx
xfxfx
At 00 0:lim ()lim ()0
lim ()0. x fx
But 0 (0)1lim () x ffx is discontinuous at 0. fx
If we define (0)0, f then the discontinuity at 0 x is removable.
At 11 1:lim ()1andlim ()1 xx xfxfx
1 lim()does not exist x fx
is discontinuous at 1. fx
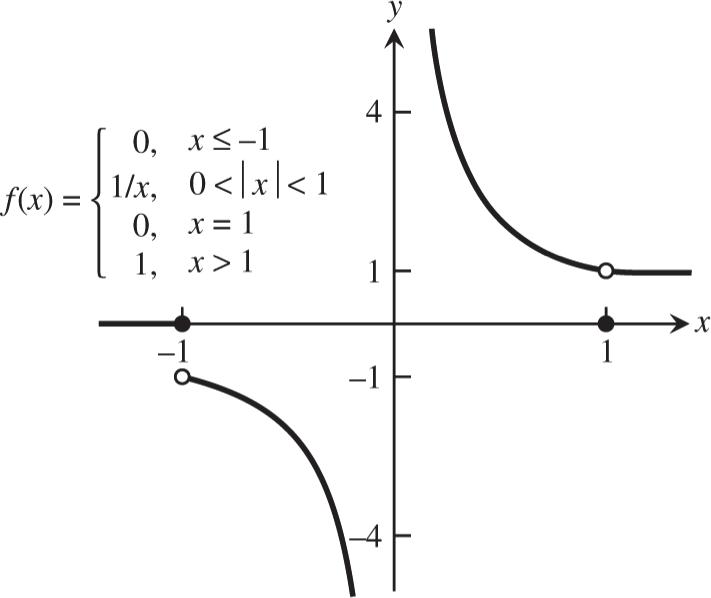
2. At 11 1:lim ()0 and lim ()1 xx xfxfx
1 lim () does not exist x fx
is discontinuous at 1 fx
At 00 0:lim ()andlim () xx xfxfx
0 lim()does not exist x fx
is discontinuous at 0. fx
At 1 11 1:lim ()lim ()1lim ()1. xx x xfxfxfx
1 But(1)0lim () x ffx
is discontinuous at 1. fx
If we define (1)1, f then the discontinuity at 1 x is removable.
(a) 00 lim(3())3 lim ()3(7)21 tttt ftft
(b) 00 2 lim(())lim22()(7)49 tttt ftft
(c) 000 lim (()())lim ()lim ()(7)(0)0 tttttt ftgtftgt
(d) 00 0 000 lim ()lim () () 7 ()7lim (()7)lim ()lim707 lim1 tttt tttttt ftftft tgtgtgt
(e) 00 limcos(())coslim ()cos01 tttt gtgt
(f) 00 lim|()|lim ()|7|7 tttt ftft
(g) 000 lim(()())lim ()lim ()707 tttttt ftgtftgt
(h)
0 0 1111 ()lim ()77 lim tt tftft
4. (a) 00 lim()lim ()2 xx gxgx
5. Since 0 lim 0 x x we must have that x0 lim (4())0. gx Otherwise, if 0 lim (4()) x gx is a finite positive number, we would have 4()
so the limit could not equal 1 as 0 x Similar reasoning holds if 0 lim (4()) x gx is a finite negative number. We conclude that 0 lim () 4 x gx .
6. 4044 2limlim ()limlim xxxx xgxx
(since 0 lim x ()gx is a constant) 21 42 0 lim (). x gx
7. (a) 1/31/3 lim ()lim () xcxc fxxcfc for every real number cf is continuous on (,).
(b) 3/43/4 lim ()lim () xcxc gxxcgc
for every nonnegative real number cg is continuous on [0,).
(c) 2/3 2/3 1 lim ()lim () xc cxc hxxhc for every nonzero real number ch is continuous on (,0) and (,)
(d) 1/6 1/6 1 lim()lim () xc cxc kxxkc for every positive real number ck is continuous on (0,)
8. (a) 11 22,, nI nn where I the set of all integers.
(b) (, (1)), nI nn where I the set of all integers.
(c) (, )(, ) (d) (, 0)(0, )
9. (a) 2 32 44 (2)(2) 2 (7)(2)(7) 514 000 lim limlim ,2; xxxxx xxxxxxxxx xx x the limit does not exist because 2 (7) 0 lim x xx x and 2 (7) 0 lim x xx x
(b) 2 32 44 (2)(2) 2 (7)(2)(7) 514 222 limlimlim, 2, xxxxx xxxxxxxxx xx x
10. (a) 2 54332 (1) 002(21) limlimxxxx xxxxxxx x
and 20 (7)2(9) 2 lim0 x
11. 11 11 12 (1)(1)1 111 limlimlim xx xxxxx xx
12. 22 22 442222222 () 11 ()()2 limlimlim xaxa xxaxaxaxaa axaxa
13. ()(2)22222 000 limlimlim (2)2 xhxxhxhx hh hhh xhx
14. ()(2)22222 000 limlimlim (2) xhxxhxhx xhhxx xhh
15. 11 22 2(2) 11 0002(2)424 limlimlim xx xxxxxxx
16. 332 (2)8(6128)8 2 000 limlimlim (612)12 xxxx xxxxx xx
17. 1/32/31/3 1/3 2/31/3 (1)(1)(1) 1 1(1) (1)(1) 11 limlimxxxxx xxxxxx
18. 1/31/3 2/3 (4)(4) 16 646488 limlimxxx xxx x
2/31/32/31/3 (1)(1) 1 112 1113 (1)(1)1 11 limlimxxx xxxxxx x
1/31/32/31/3 2/31/3 (4)(4)(416)(8) 8 (8)(416) 64 lim xxxxx xxxxx
1/31/3 2/31/32/31/3 (64)(4)(8)(4)(8)(44)(88) 8 1616163 (64)(416)416 6464 limlimxxxxx xxxxxx x
19. tan2cos sin 2 tancos 2sin 00 limlimxx x xxxx x
20. 1 sin limcsc lim x xx x
222 limsinsinsinsinsin1 x
22. limcos(tan)cos(tan)2222cos()(1)1 x xx
23. sin 888 3sin 3(1)1 31 00 limlim4 x x x
24.
cos 21cos 21cos 2 1 sinsincos 21 00 limlimxxx xxxx x
2 4sincos 4(0)(1) cos 2111 0 lim 0 xx
25. Let x = t 3 30 limln(3)limln tx tx
26.
2 1 limln2ln10 t tt
cos22 21sin2 sin(cos 21)sin (cos 21) 00 limlimxx xxxxx x
30. 11 55()2 lim2lim(()) xxgxxxgx
31. 2 2 31 () 111 limlim ()0 since lim (31)4 x xgxxxgxx
32. 2 2 5 () 222 lim0lim () since lim (5)1 x xgxxx gxx
33. (a) (1)1and(2)5hasarootbetween fff
1 and 2 by the Intermediate Value Theorem. (b), (c) root is 1.32471795724
34. (a) (2)2and(0)2hasarootbetween fff
2 and 0 by the Intermediate Value Theorem. (b), (c) root is 1.76929235424
35. At
2 (1) 1 11 limlim1,and xx x xx
lim() x fx
()fx does not exist, the function f cannot be extended to a continuous function at 1. x
does not exist so
cannot be extended to a continuous function at 1 x
either. 36. The discontinuity at 0 x of 1 ()sin fxx is nonremovable because 1 0 limsin xx does not exist.
37.
38.
39.
40.
47. sin sin 1 limlim0 since as lim0.xx xxxxxx xx
48. cos 1cos1 2 limlim0lim0
50. 2/315/3
51.
52.
1/0 1 limcoscos(0)111 x xx ee
1 limln1ln10 xt
53. 1 2 limtan x x
54.
311 1 limsin0sin(0)000 t tt e
55. (a) 222 444 333 33 is undefined at 3:lim and lim xxx xxx xx yx
(b) 22 22 22 2121 1 is undefined at 1:lim xxxx
, thus 3 is a vertical asymptote.
57. domain[4,2)(2,
58. Since
CHAPTER 2 ADDITIONAL AND ADVANCED EXERCISES
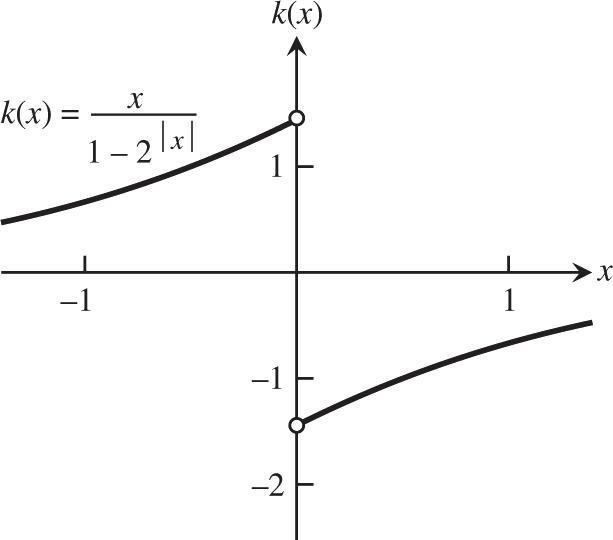
1.
2. (a)
(b)
3.
The left-hand limit was needed because the function L is undefined if vc (the rocket cannot move faster than the speed of light).
4. (a)
5.
6. We want to know in what interval to hold values of h to make V satisfy the inequality |1000||361000| Vh 10. To find out, we solve the inequality: |361000|101036100010 hh
where 8.8 was rounded up, to be safe, and 8.9 was rounded down, to be safe. The interval in which we should hold h is about 8.98.80.1 cm wide (1 mm). With stripes 1 mm wide, we can expect to measure a liter of water with an accuracy of 1%, which is more than enough accuracy for cooking.
7. Show 2 11 lim ()lim (7)6(1). xx fxxf
Step 1: 22 |(7)6|1
Step 2: |1|111. xxx
Then 11 or 11
Choose
min11,11,
then 0|1| x 2 |(7)6| x and 1 lim()6 x fx By the continuity text, ()fx is continuous at 1. x
8. Show
11 44 11 24 lim ()lim 2. x xx gxg
Step 1: 11111 2224242 2222. xxx x
Step 2: 1111 4444 . xx
X Then 1111 4424424(2) ,
Choose 4(2) ,
or 1111 4424244(2)
the smaller of the two values. Then 11 42 02 x
By the continuity test, ()gx is continuous at 1 4 . x
9. Show 22 lim ()lim231(2). xx hxxh
Step 1: 231231
Step 2: |2|2or22.
10. Show 55 lim()lim9 2(5).
Step 2: 0|5|555 xxx
Then 222 59(2)(2)42,
or 222 59(2)4(2)2
Choose 2 2, the smaller of the two values. Then, 0|5|92, xx
so 5 lim92. x x
By the continuity test, ()Fx is continuous at 5. x
11. Suppose 1L and 2L are two different limits. Without loss of generality assume 21.LL Let 1 21 3 (). LL Since 0 1 lim() xx fxL
1 () fxL
1 11 33211211212 ()()()43()2. LLLfxLLLLLfxLL
21211221 23()443()2. LLfxLLLLfxLL
If 12 min{,} both inequalities must hold for 0 0|| : xx 1212 1212 1221 4 3() 2 5()0 43()2 LLfxLLLLLL LLfxLL
That is, 12 0 LL and 12 0, LL a contradiction.
12. Suppose lim() xc fxL If 0, k then lim()lim000 xcxc kfx
lim() xc fx and we are done. If 0, k then given any 0, there is a 0 so that || 0|||()||||()| k xcfxLkfxL
kfxL
Thus lim()lim(). xcxc kfxkLkfx
Since
(b) Since 333
(c) Since 422424
0,01()0lim()
(d) Since 4224 0,1001()0 xxxxxx
24 0 lim() as in part (c). x fxxA
14. (a) True, because if lim(()()) xa fxgx exists then lim(()())lim()lim xaxaxa fxgxfx [(()())()] fxgxfx lim() xa gx exists, contrary to assumption.
(b) False; for example take 1 () fxx and 1 ().gxx Then neither 0 lim() x fx nor 0 lim() x gx exists, but 11 000 lim(()())limlim00 xxxxx fxgx exists.
(c) True, because ()|| gxx is continuous (())|()| gfxfx is continuous (it is the composite of continuous functions).
(d) False; for example let 1,0 ()() is discontinuous at 0. However |()|1 1,0 x fxfxxfx x
is continuous at 0. x
15. Show 2 (1)(1) 1 1111(1) lim()limlim2,1. xxx xxx xx fxx
Define the continuous extension of ()fx as 2 1 1 ,1 ().We now prove the limit of () as 1
exists and has the correct value.
Step 1: 2 (1)(1) 1 1(1)(2)2(1) xxx
Step 2: |(1)|111 xxx
Copyright 2018 Pearson Education, Inc.
Then 11,or11
Since the conditions of the continuity test are met by (),Fx then ()fx has a continuous extension to ()Fx at 1.
Define the continuous extension of ()gx as
exists and has the correct value.
Step 1: 2 (3)(1) 23 262(3)22 xxxx xx
Step 2: |3|333. xxx
Then, 3 322,
or 3322
We now prove the limit of ()gx as 3
Choose 2. Then 0|3| x 2 (3)(1) 23 262(3) 3 2lim2.xxxx xx x Since the conditions of the continuity test hold for (),()Gxgx can be continuously extended to ()Gx at 3. x
17. (a) Let 0 be given. If x is rational, then ()|()0||0||0|; fxxfxxx i.e., choose . Then |0||()0| xfx for x rational. If x is irrational, then ()0|()0|0 fxfx which is true no matter how close irrational x is to 0, so again we can choose . In either case, given 0 there is a 0 such that 0|0||()0| xfx Therefore, f is continuous at 0. x
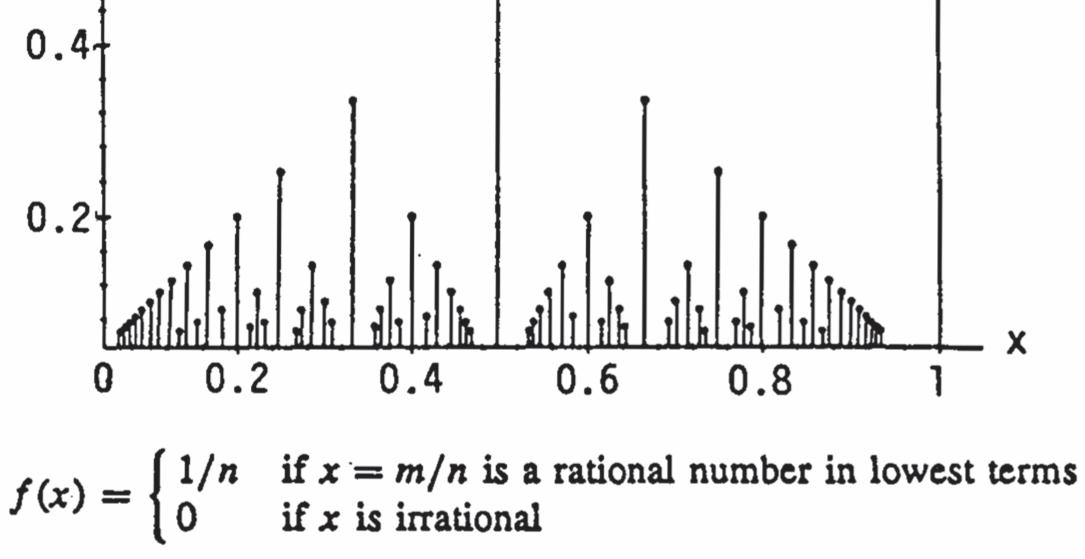
(b) Choose 0. xc Then within any interval (,) cc there are both rational and irrational numbers. If c is rational, pick 2 c No matter how small we choose 0 there is an irrational number x in 2 (,)|()()||0|. ccfxfcccc That is, f is not continuous at any rational 0. c On the other hand, suppose c is irrational ()0.fc Again pick 2 c No matter how small we choose 0 there is a rational number x in (,) cc with 3 222 ||. cccxcx Then |()()||0| fxfcx 2 ||xc f is not continuous at any irrational 0. c If 0, xc repeat the argument picking || 22 . cc Therefore f fails to be continuous at any nonzero value .xc 18. (a) Let m n c be a rational number in [0,1] reduced to lowest terms 1 ().fcn Pick 1 2 . n No matter how small 0 is taken, there is an irrational number x in the interval (,)|()()| ccfxfc 111 2 0. nnn Therefore f is discontinuous at ,xc a rational number.
(b) Now suppose c is an irrational number ()0.fc Let 0 be given. Notice that 1 2 is the only rational number reduced to lowest terms with denominator 2 and belonging to [0,1]; 1 3 and 2 3 the only rationals with denominator 3 belonging to [0,1]; 1 4 and 3 4 with denominator 4 in [0,1]; 3 12 555 ,, and 4 5 with denominator 5 in [0,1]; etc. In general, choose N so that 1 N there exist only finitely many rationals in [0,1] having denominator , N say 12,,,. prrr Let min{||:1,,}. i crip Then the interval (,) cc contains no rational numbers with denominator . N Thus, 0|||()()| xcfxfc |()0| fx 1 |()|fxN f is continuous at xc irrational.
Copyright 2018 Pearson Education, Inc.
(c) The graph looks like the markings on a typical ruler when the points (,()) xfx on the graph of ()fx are connected to the -axis x with vertical lines.

19. Yes. Let R be the radius of the equator (earth) and suppose at a fixed instant of time we label noon as the zero point, 0, on the equator 0 R represents the midnight point (at the same exact time). Suppose 1x is a point on the equator “just after” noon 1 xR is simultaneously “just after” midnight. It seems reasonable that the temperature T at a point just after noon is hotter than it would be at the diametrically opposite point just after midnight: That is, 11 ()()0. TxTxR At exactly the same moment in time pick 2x to be a point just before midnight 2 xR is just before noon. Then 22 ()()0 TxTxR Assuming the temperature function T is continuous along the equator (which is reasonable), the Intermediate Value Theorem says there is a point c between 0 (noon) and R (simultaneously midnight) such that ()()0;TcTcR i.e., there is always a pair of antipodal points on the earth’s equator where the temperatures are the same. 20.
(c)
(d)
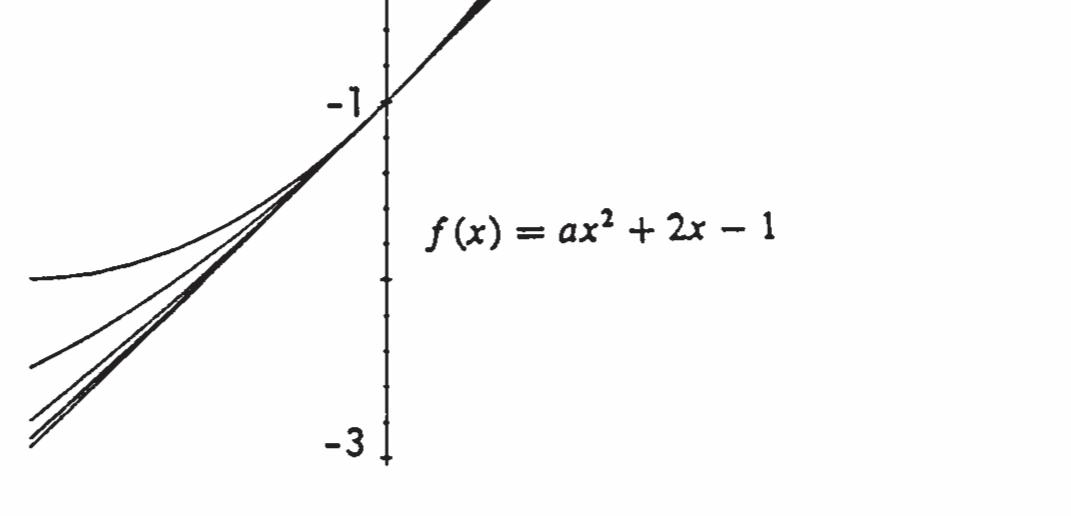
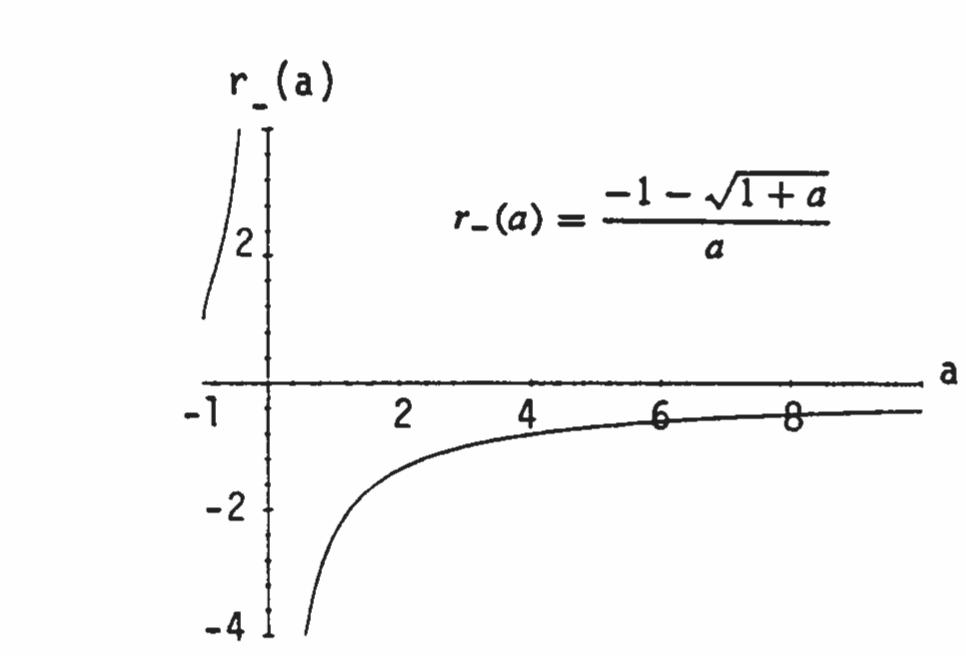
22. ()2 cos (0)02 cos 02 0 fxxxf and ()2 cos()20. f Since ()fx is continuous on [,0], by the Intermediate Value Theorem, ()fx must take on every value between [2,2]. Thus there is some number c in [,0] such that ()0;fc i.e., c is a solution to 2 cos 0. xx
23. (a) The function f is bounded on D if () fxM and () fxN for all x in D. This means () MfxN for all x in D. Choose B to be max {||, ||}.MN Then |()|. fxB On the other hand, if |()|, fxB then ()() BfxBfxB and ()() fxBfx is bounded on D with NB an upper bound and MB a lower bound. (b) Assume () fxN for all x and that . LN Let 2 . LN Since 0 lim () xx fxL there is a 0 such that 0 0|||()| xxfxL 222 ()()()LLNLNLNfxLLfxLfx 3 2 LN But 2 () LLNNNNfx contrary to the boundedness assumption (). fxN This contradiction proves . LN (c) Assume ()Mfx for all x and that LM Let 2 ML As in part (b), 0 2 0||xxLML 3 222 ()(), MLM fLML xLfxM a contradiction.
24. (a) If ,ab then 0||max {,}abababab || 2 22222 ab abababaa If ,ab then 0||() abababba || 2 22222 max{,} ab ababbab abb
(b) Let || 22 min{,}. ababab
25. 2 sin(1cos) sin(1cos )sin(1cos ) 1cos 1cos 1cos 1cos1cos 1cos(1cos ) 0000 limlimlimlim xxxxxx xxxxxxxxxxx
2 sinsin sin 0 (1cos )1cos 2 00 1limlim10. xxx xxxxxx
Copyright 2018 Pearson Education, Inc.
26.
sin sin sin 1 sinsin 0000 limlim1limlim1100. x x x xxx x xxx xxxx x
27. sin(sin )sin(sin )sin(sin ) sin sin sinsin 0000 limlimlimlim111. xxxxx xxxxxx xxx
28. 222 22 sin()sin()sin() 0000 limlim(1)limlim(1)111 xxxxxx xxxxxxxxx xx
29. 222 22 sin(4)sin(4)sin(4) 2 44 2222 limlim(2)limlim(2)14 4 xxx xxxxxxx xx
30. sin(3)sin(3)sin(3)1111 96699993333 limlimlimlim1 xxx xxxxxx xxx
31. Since the highest power of x in the numerator is 1 more than the highest power of x in the denominator, there is an oblique asymptote. 3/2 2233 11 2, xx xx yx thus the oblique asymptote is 2.yx
32. As
111 ,0sin01sin1, xxx x thus as
11 ,sin1sin; xx xyxxxx thus the oblique asymptote is yx
33. As 2222 ,11; xxxxx as 2 ,, xxx and as 2 ,; xxx thus the oblique asymptotes are yx and .yx
34. As 2 ,22 xxxxx (2);22 as ,, xxxxxx and as 2 ,; xxx asymptotes are yx and yx
35. Assume 1 ab and 2 1 ()() a xxbxaxbxxbx 2 ()()()0; fxaxbxxbx f is continuous for all x-values and (0)0,fab 22 ()()() fabaabaab 22 () () ()0.aaabab
Thus, by the Intermediate Value Theorem there is at least one number ,c 0, cab so that ()0fc 2 1 ()()0. a ccbacbccbcc
36. (a) 1"1" 0 0 lim, abxa x x
so 10 1, aa
2 11 0 lim24 bb xbx
then (1)1 1111 0011(11) limlimbxbxbx xbxxbxxx
Chapter 2 Limits and Continuity
