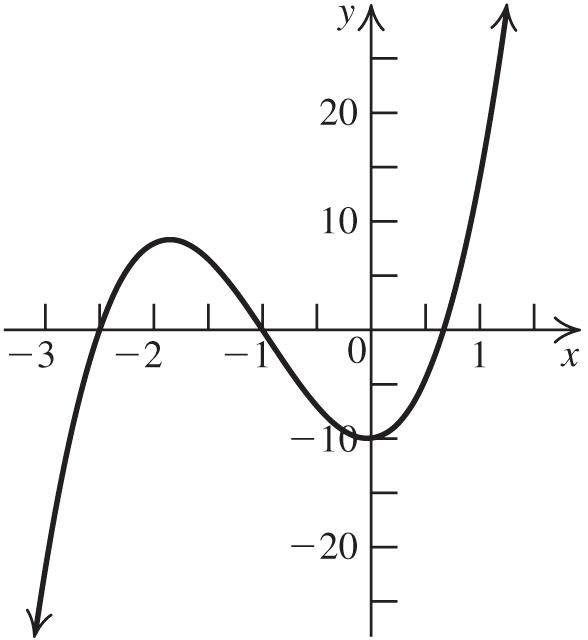
Chapter 2 Polynomial and Rational Functions
2.1 Quadratic Functions
2.1 Practice Problems
1. Substitute 1 for h, 5 for k, 3 for x, and 7 for y in the standard form for a quadratic equation to solve for a: 2 7(31)5745 aa
3 a . The equation is 2 315.yx Since a = 3 > 0, f has a minimum value of 5 at x = 1.
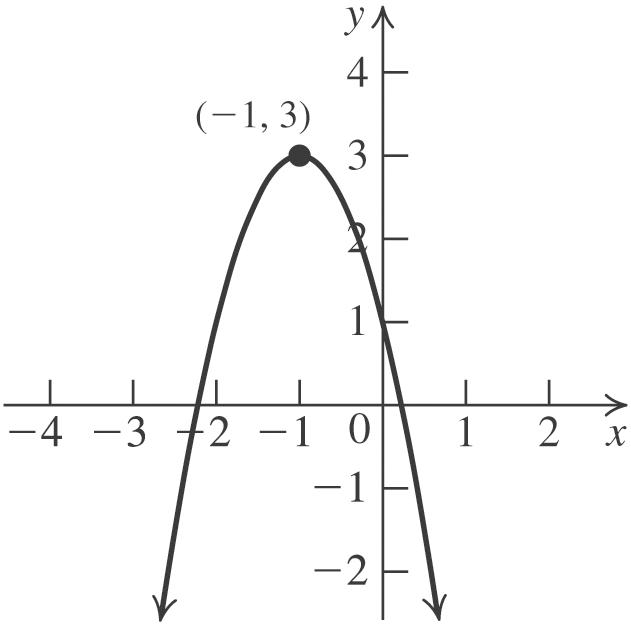
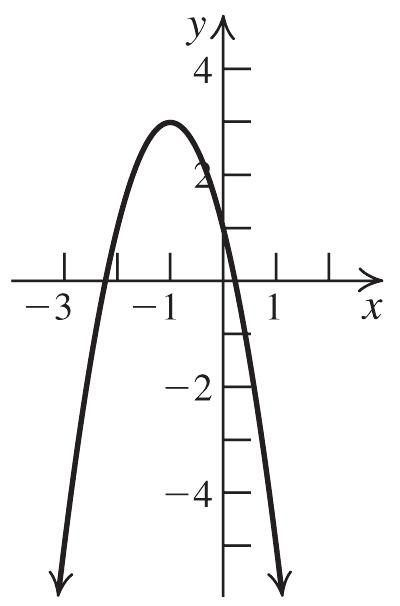
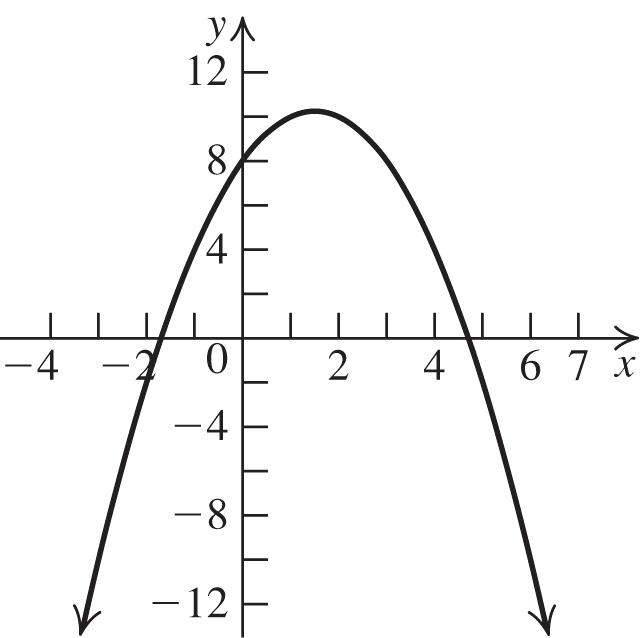
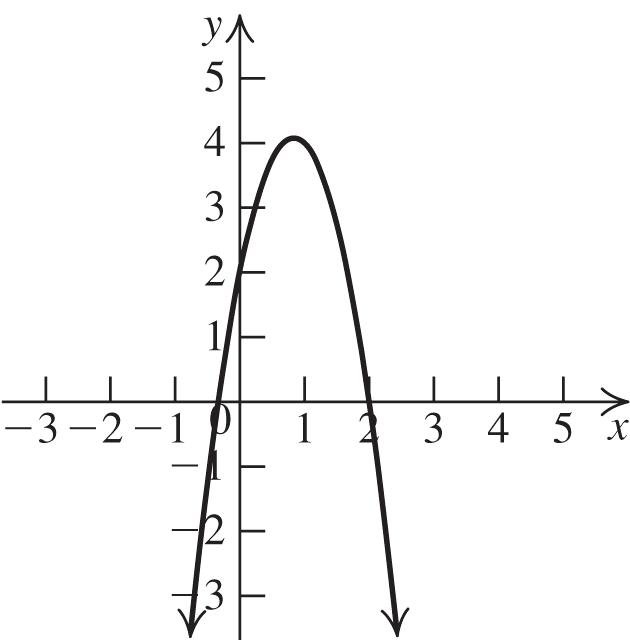
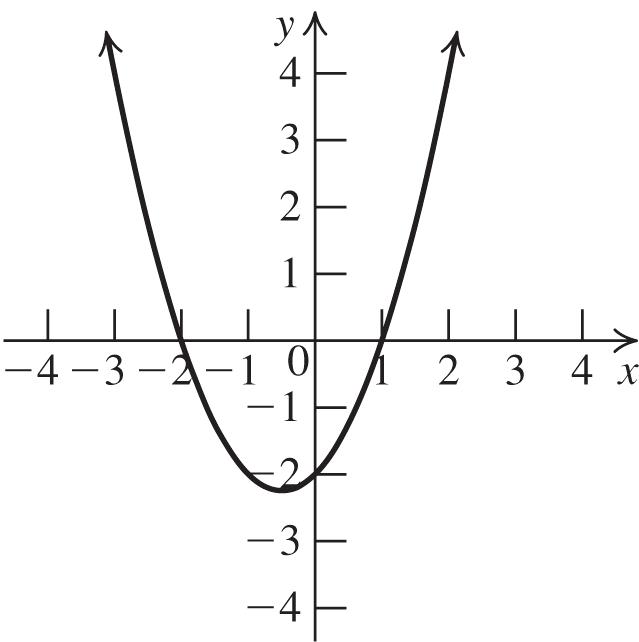
2. The graph of 2 213fxx is a parabola with a = 2, h = 1 and k = 3. Thus, the vertex is ( 1, 3). The parabola opens down because a < 0. Now, find the x-intercepts:
22 0213213 xx
2 333 111 222 xxx
0.22 or 2.22 xx . Next, find the y-intercept: 2 020131 f
. Plot the vertex, the x-intercepts, and the y-intercept, and join them with a parabola.
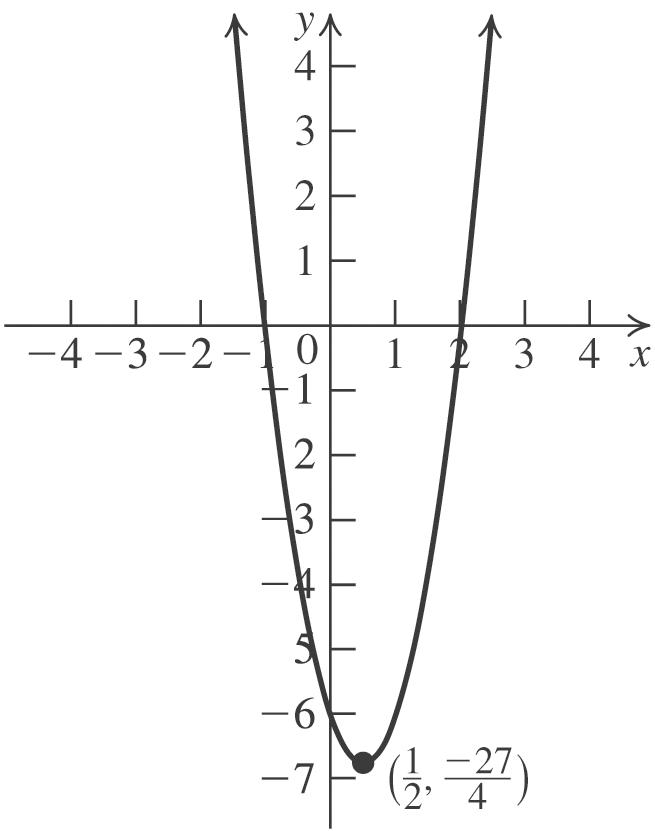
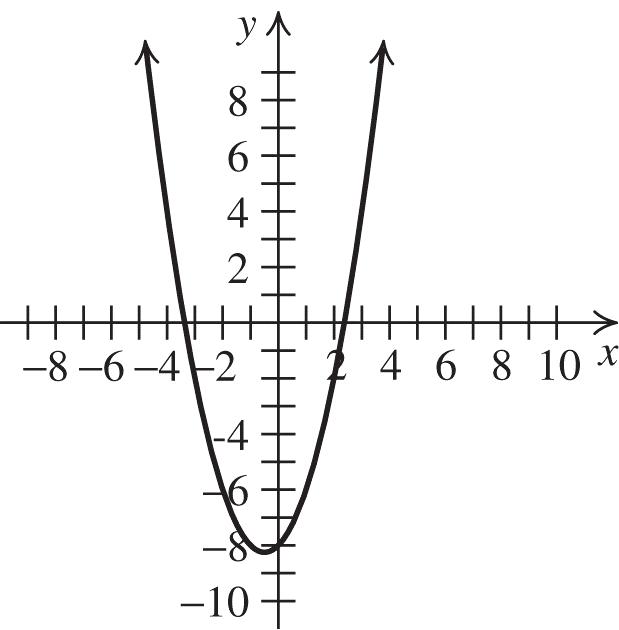
3. The graph of 2 336fxxx is a parabola with a = 3, b = 3 and c = 6. The parabola opens up because a > 0. Now, find the vertex: 31 22(3)2 b h a
2 11127 336 2224
Thus, the vertex (h, k) is 127 , 24
. Next, find the x-intercepts:
Now, find the y-intercept:
2 0303066 f
Thus, the intercepts are ( 1, 0), (2, 0) and (0, 6). Use the fact that the parabola is symmetric with respect to its axis, 1 2 , x to locate additional points. Plot the vertex, the x-intercepts, the y-intercept, and any additional points, and join them with a parabola.
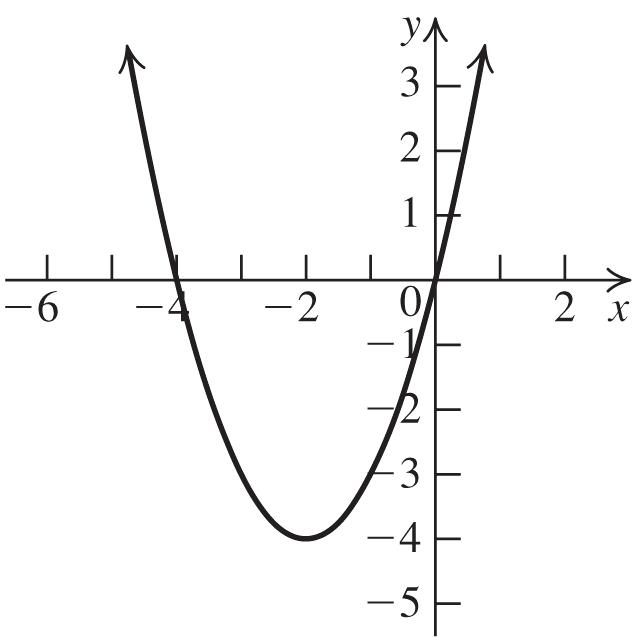
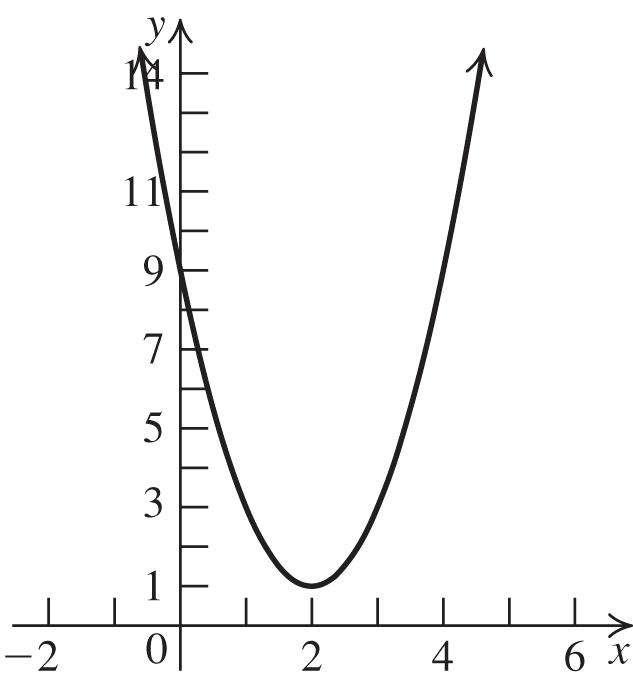
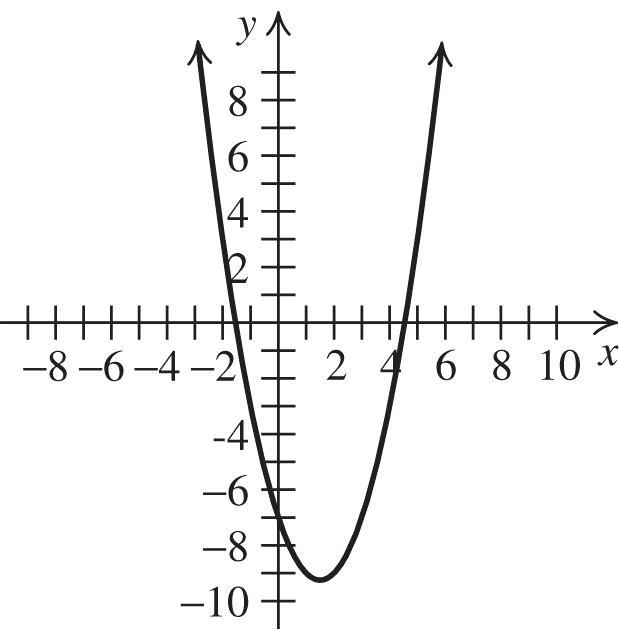
4. The graph of 2 361fxxx is a parabola with a = 3, b = 6 and c = 1. The parabola opens up because a > 0. Complete the square to write the equation in standard form:
22 361321gxxxgxxx 2 2 32113314gxxxx
Thus, the vertex is ( 1, 4). The domain of f is , and the range is 4,.
Next, find the x-intercepts: 22 4 03141 3 xx 2323 112.15 or 33 xxx
0.15 x . Now, find the y-intercept: 2 0306011 f . Use the fact that the parabola is symmetric with respect to its axis, x = 1, to locate additional points. Plot the vertex, the x-intercepts, the y-intercept, and any additional points, and join them with a parabola. (continuedonnextpage)
(continued)
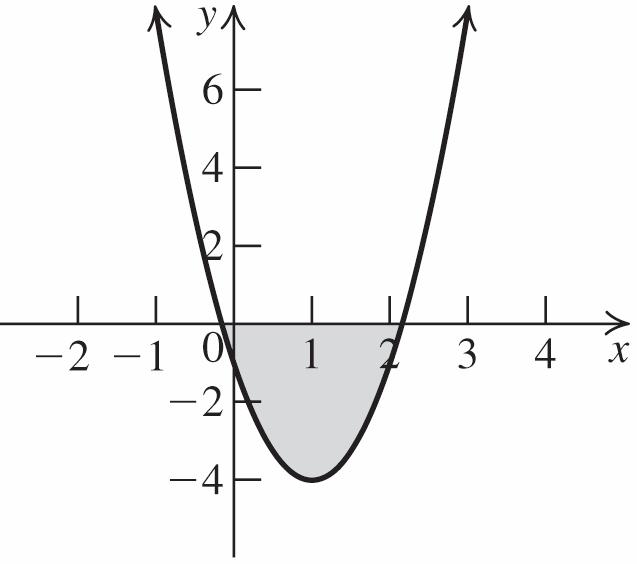
The graph of f is below the x-axis between the x-intercepts, so the solution set for 2 3610gxxx is 2323 1,133
or 323323 33,.
5. 2 00 2 E g httvth 2 0 32 fts,100 ft, max height244 ft E gh
a. Using the given values, we have 2 0 2 0 32 100 2 16100 httvt tvt
Using the formula for the vertex of a parabola gives 00 . 21632 vv t This is the time at which the maximum height h(t) = 244 ft is attained. Thus,
0 2 00 0 222 000 244 32 16100 3232 100100 643264 v hth vv v vvv
Solving for 0 v yields 22 00 2 00 244100144 6464 144641446412896 vv vv
Thus, 2 1696100.httt
b. Using the formula for the vertex of a parabola gives 9696 3. 21632 t
The ball reached its highest point 3 seconds after it was released.
6. Let x = the length of the playground and y = the width of the playground. Then 21000500 xyxy 500. yx
The area of the playground is 2 500500. Axxyxxxx
The vertex for the parabola is (h, k) where 500 250 21 h and 2 50025025062,500. k
Thus, the maximum area that can be enclosed is 62,500 ft2. The playground is a square with side length 250 ft.
2.1 Exercises
Concepts and Vocabulary
1. The graph of 2 ,0,fxaxbxca is a parabola.
2. The vertex of the graph of 2 ,0,fxaxhka is (h, k).
3. The graph of 2 ,0,fxaxhka is symmetric with respect to the vertical line x = h.
4. The x-coordinate of the vertex of 2 ,0,fxaxbxca is given by 2 . b a x
5. True.
6. False. The graph of 2 2 fxx is the graph of 2 gxx compressed horizontally by a factor of 2.
7. False. If a > 0, then the parabola opens up and has a minimum.
8. True Building Skills
9. f 10. d 11. a 12. e
13. h 14. b 15. g 16. c
17. Substitute 8 for y and 2 for x to solve for a: 2 8(2)2. aa The equation is 2 2.yx
Copyright © 2018 Pearson Education Inc.
18. Substitute 3 for y and –3 for x to solve for a: 2 1 3(3). 3 aa The equation is 2 1 . 3 yx
19. Substitute 20 for y and 2 for x to solve for a: 2 20(2)5. aa The equation is 2 5.yx
20. Substitute –6 for y and –3 for x to solve for a: 2 2 6(3). 3 aa The equation is 2 2 . 3 yx
21. Substitute 0 for h, 0 for k, 8 for y, and –2 for x in the standard form for a quadratic equation to solve for a: 2 8(20)084 aa
2. a The equation is 2 2.yx
22. Substitute 2 for h, 0 for k, 3 for y, and 1 for x in the standard form for a quadratic equation to solve for a: 2 3(12)03. aa
The equation is 2 3(2).yx
23. Substitute –3 for h, 0 for k, –4 for y, and –5 for x in the standard form for a quadratic equation to solve for a: 2 4(5(3))01. aa
The equation is 2 (3).yx
24. Substitute 0 for h, 1 for k, 0 for y, and –1 for x in the standard form for a quadratic equation to solve for a: 2 0(10)11. aa
The equation is 2 1. yx
25. Substitute 2 for h, 5 for k, 7 for y, and 3 for x in the standard form for a quadratic equation to solve for a: 2 7(32)52. aa
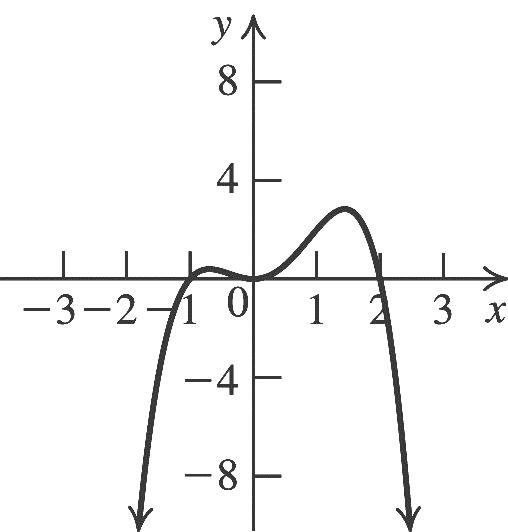
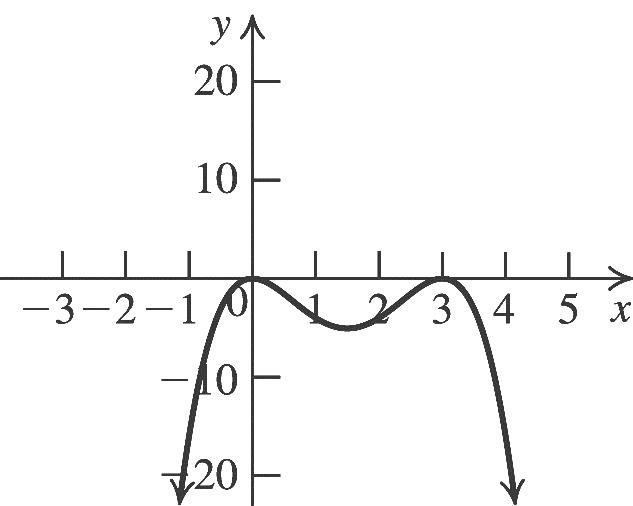
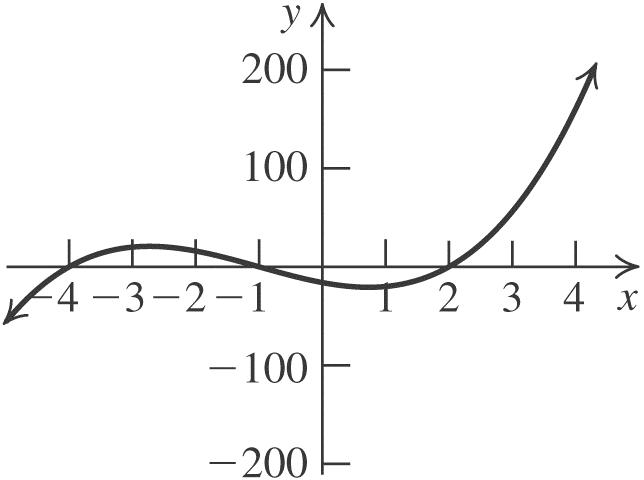
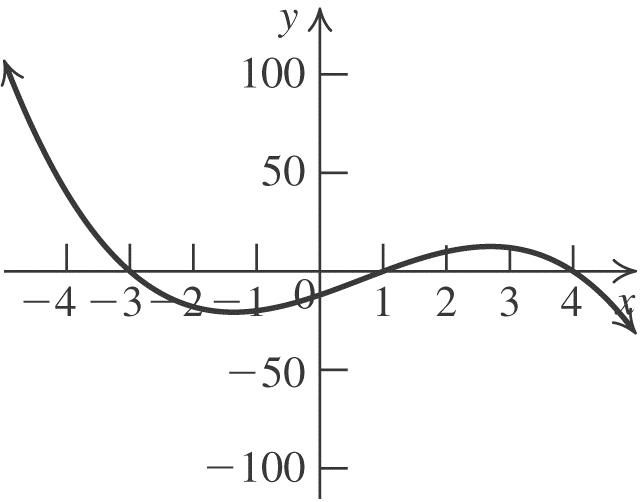
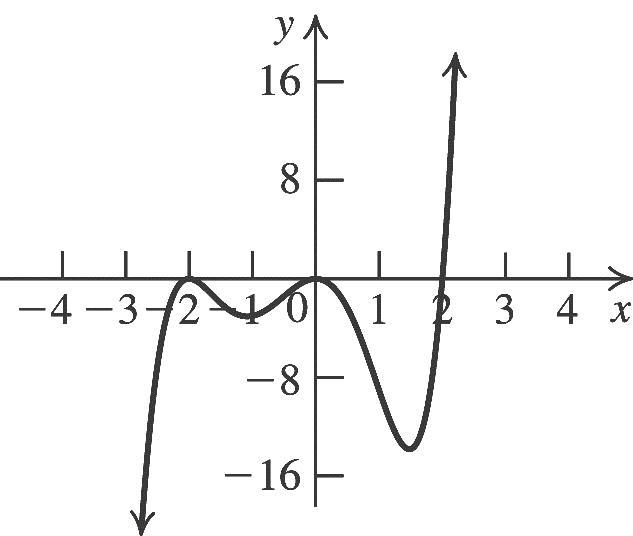
The equation is 2 2(2)5.yx
26. Substitute –3 for h, 4 for k, 0 for y, and 0 for x in the standard form for a quadratic equation to solve for a: 2 4 0(0(3))4. 9 aa
The equation is 2 4 (3)4. 9 yx
27. Substitute 2 for h, –3 for k, 8 for y, and –5 for x in the standard form for a quadratic equation to solve for a: 2 11 8(52)3. 49 aa
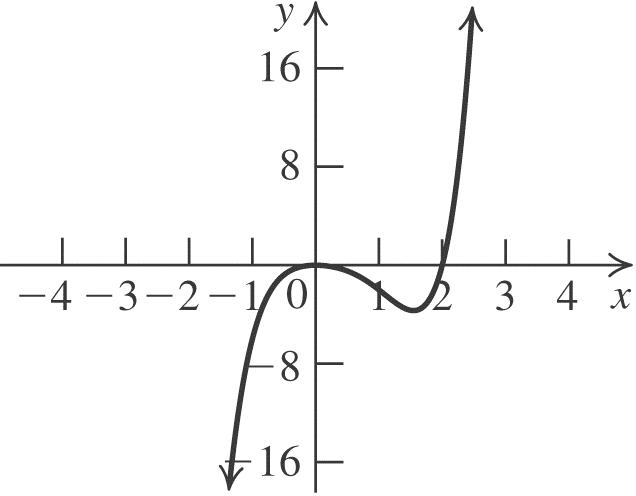
The equation is 2 11 (2)3. 49 yx
28. Substitute –3 for h, –2 for k, –8 for y, and 0 for x in the standard form for a quadratic equation to solve for a: 2 2 8(0(3))2. 3 aa
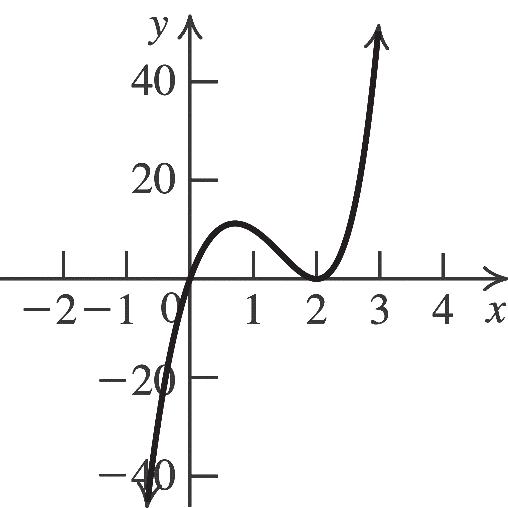
The equation is 2 2 (3)2. 3 yx
29. Substitute 1 2 for h, 1 2 for k, 1 4 for y, and 3 4 for x in the standard form for a quadratic equation to solve for a: 2 1311 12. 4422 aa
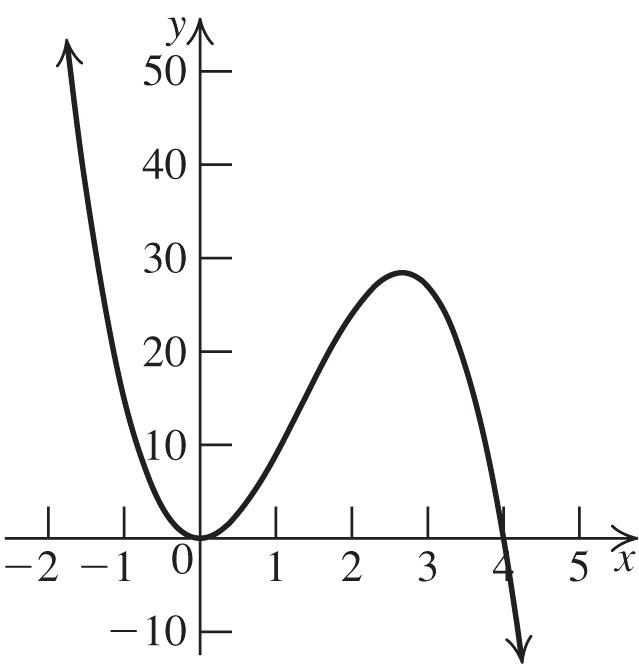
The equation is 2 11 12. 22 yx
30. Substitute 3 2 for h, 5 2 for k, 55 8 for y, and 1 for x in the standard form for a quadratic equation to solve for a: 2 55353 1. 8222 aa
The equation is 2 335 222yx
31. The vertex is (–2, 0), and the graph passes through (0, 3). Substitute 2 for h, 0 for k, 3 for y, and 0 for x in the standard form for a quadratic equation to solve for a: 2 3 3(0(2))0. 4 aa
The equation is 2 3 2. 4 yx
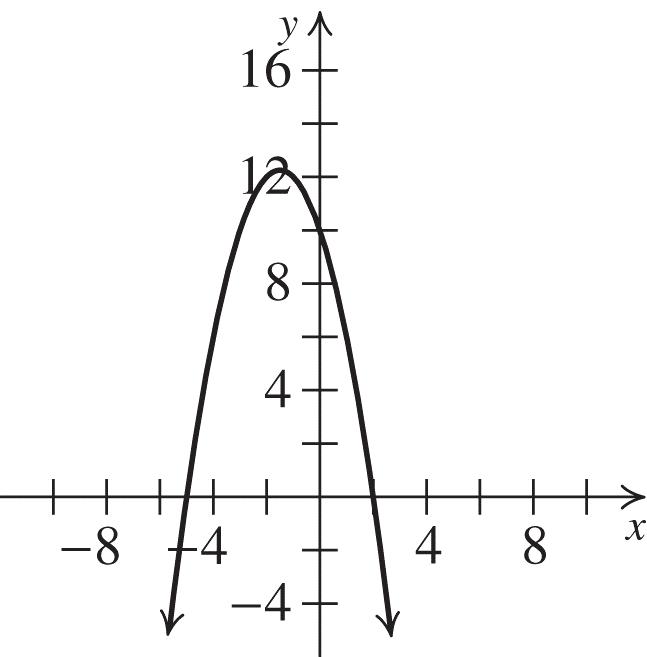
32. The vertex is (3, 0), and the graph passes through (0, 2). Substitute 3 for h, 0 for k, 2 for y, and 0 for x in the standard form for a quadratic equation to solve for a: 2 2 2(03)0. 9 aa
The equation is 2 2 3. 9 yx
33. The vertex is (3, –1), and the graph passes through (5, 2). Substitute 3 for h, –1 for k, 2 for y, and 5 for x in the standard form for a quadratic equation to solve for a: 2 3 2(53)1. 4 aa
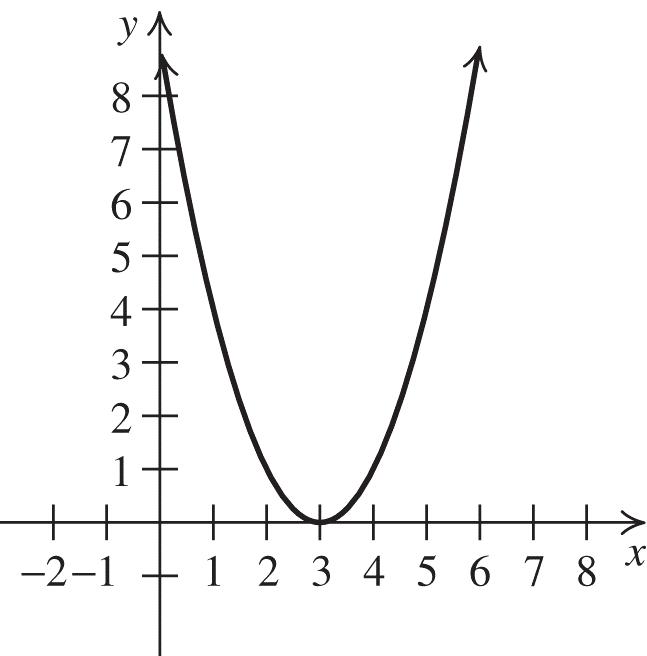
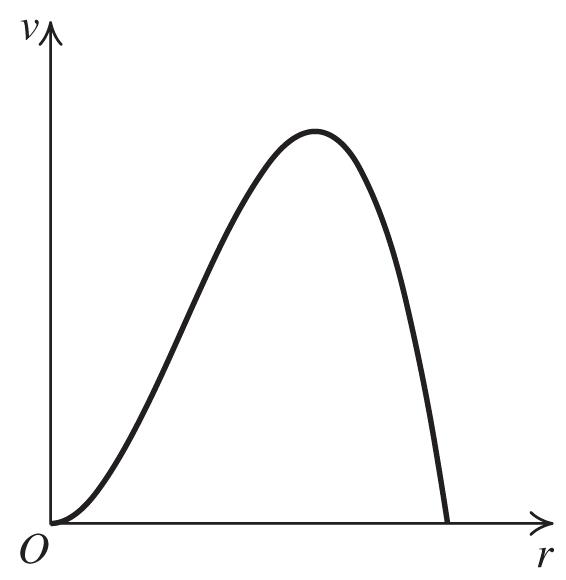
The equation is 2 3 31. 4 yx
34. The vertex is (3, –1), and the graph passes through (0, 3). Substitute 3 for h, –1 for k, 3 for y, and 0 for x in the standard form for a quadratic equation to solve for a: 2 4 3(03)194. 9 aaa
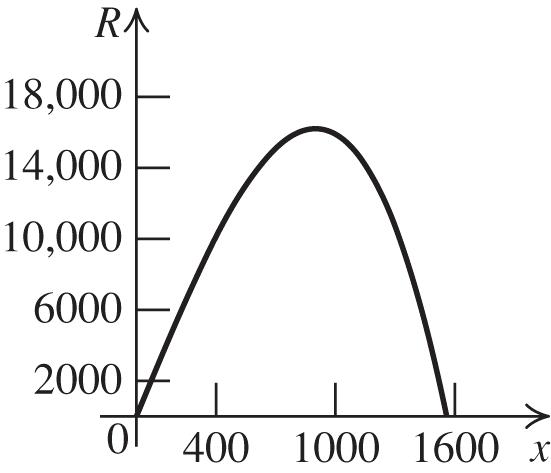
The equation is 2 4 31. 9 yx
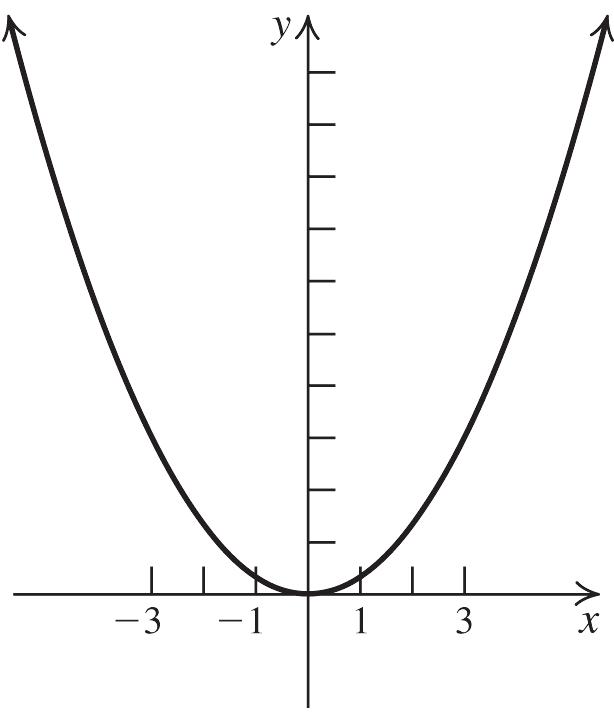
35. 2 3 fxx
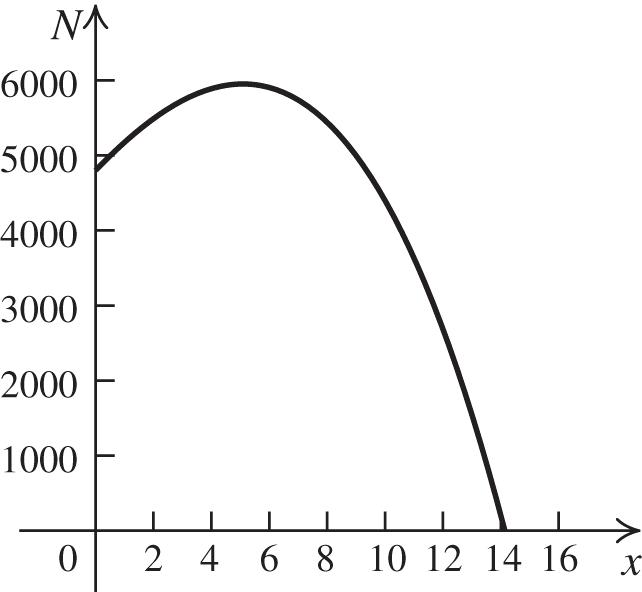
Stretch the graph of 2 yx vertically by a factor of 3.
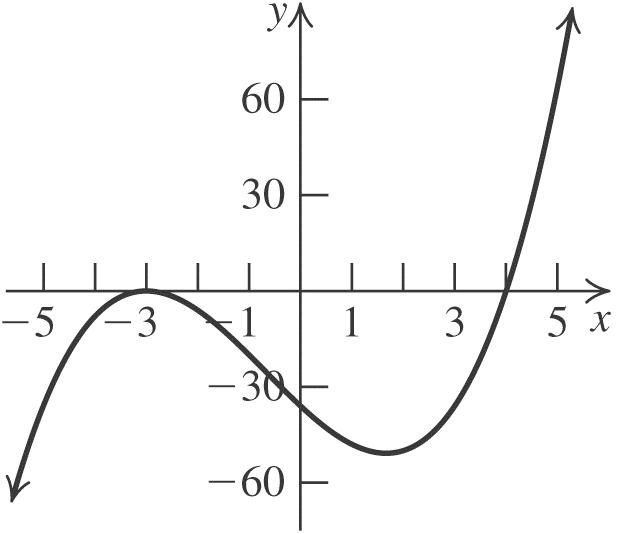
36. 2 1 3 fxx
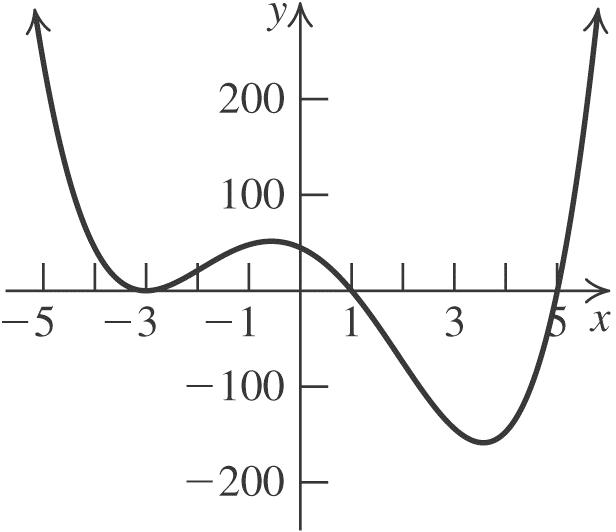
Compress the graph of 2 yx vertically by a factor of 13.
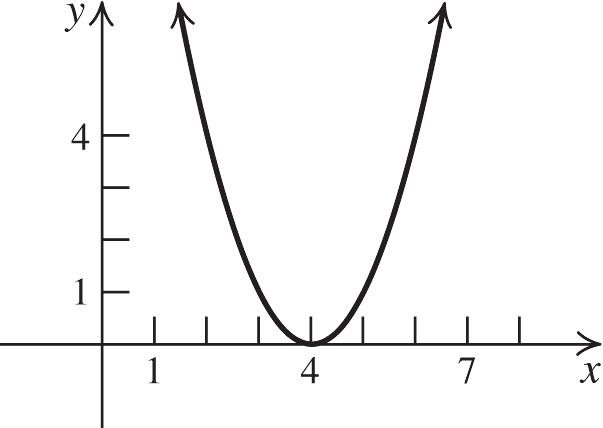
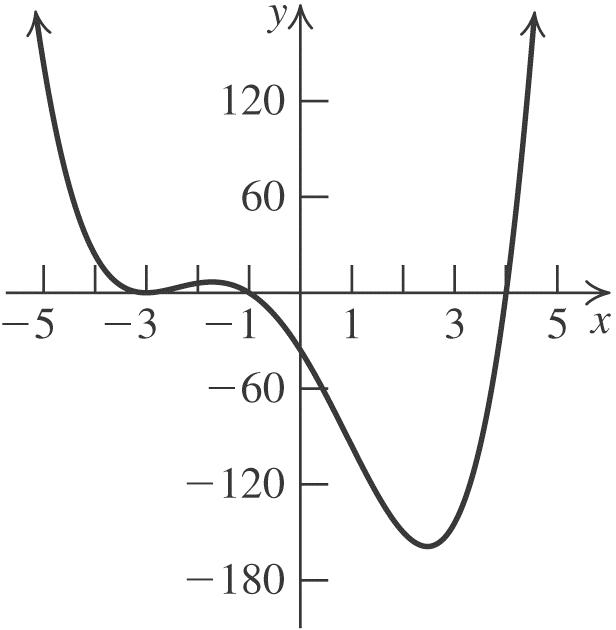
37. 2 4 gxx
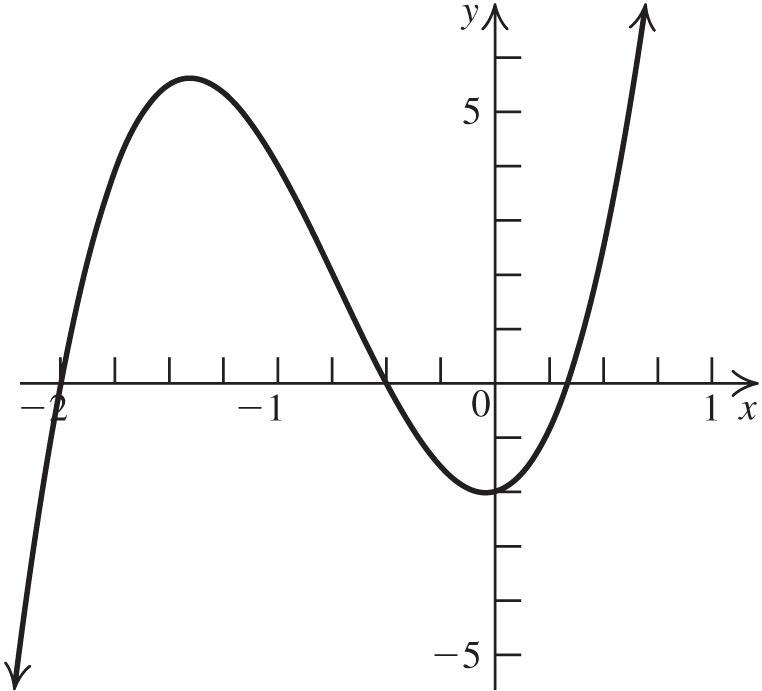
Shift the graph of 2 yx right four units.
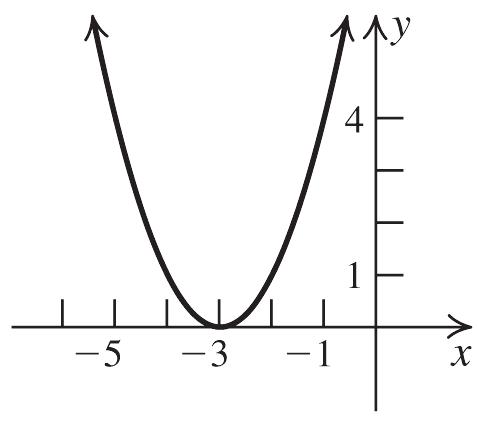
38. 2 3 gxx
Shift the graph of 2 yx left three units.
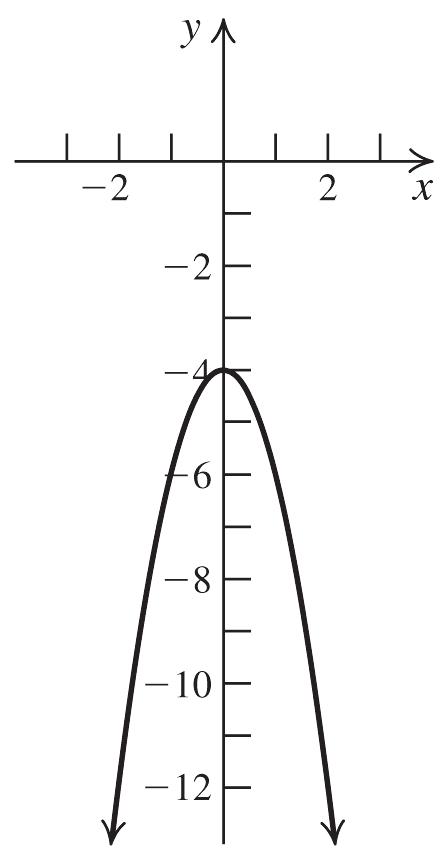
39. 2 24fxx
Stretch the graph of 2 yx vertically by a factor of 2, reflect the resulting graph in the x-axis, then shift the resulting graph down 4 units.
40. 2 3 fxx
Reflect the graph of 2 yx in the x-axis, then shift the resulting graph up 3 units.
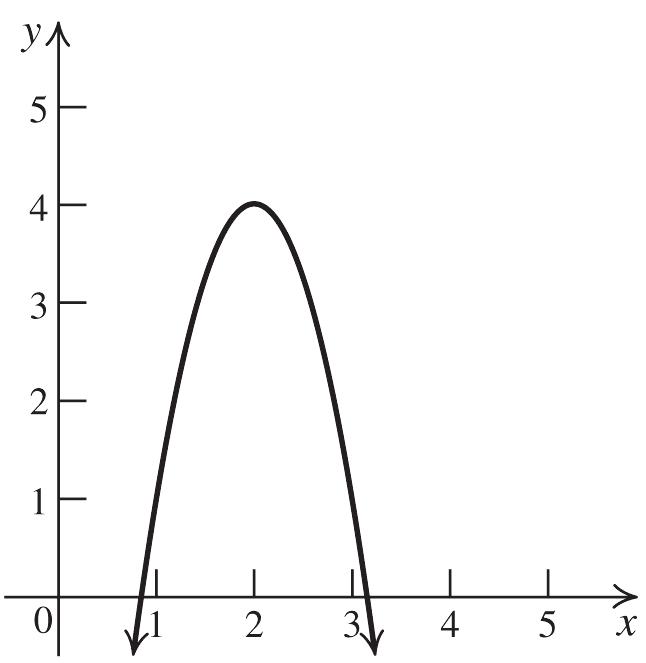
41. 2 32 gxx
Shift the graph of 2 yx right three units, then shift the resulting graph up two units.
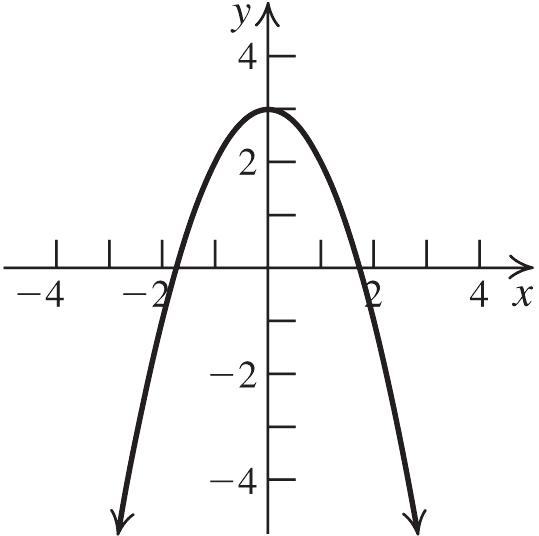
42. 2 13 gxx
Shift the graph of 2 yx left one unit, then shift the resulting graph down three units.
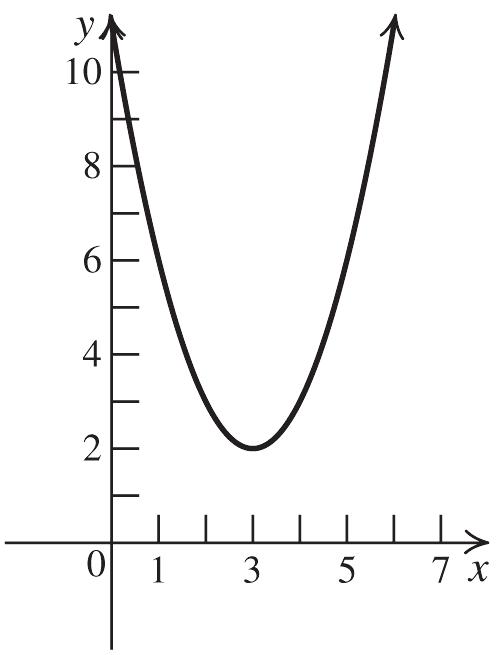
43. 2 324fxx
Shift the graph of 2 yx right two units, stretch the resulting graph vertically by a factor of 3, reflect the resulting graph about the x-axis, and then shift the resulting graph up four units.
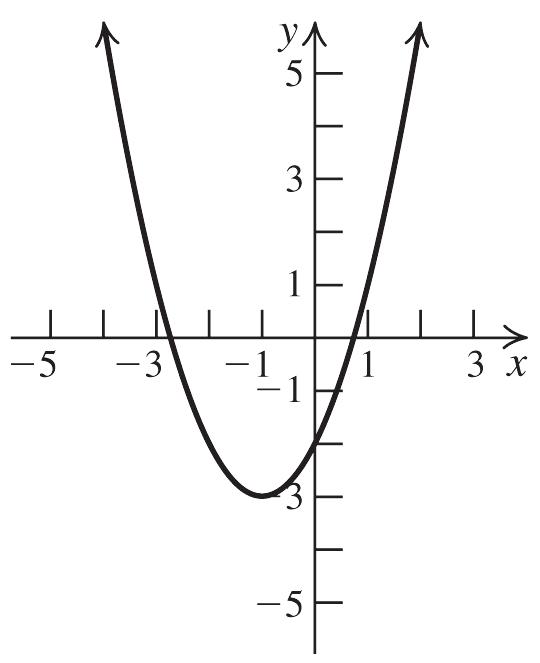
44. 2 213fxx
Shift the graph of 2 yx left one unit, stretch the resulting graph vertically by a factor of 2, reflect the resulting graph about the x-axis, and then shift the resulting graph up three units.
45. Complete the square to write the equation in standard form: 2 4 yxx 22 444(2)4.yxxyx This is the graph of 2 yx shifted two units left and four units down. The vertex is (–2, –4). The axis of symmetry is 2. x To find the x-intercepts, let y = 0 and solve 2 0(2)4 x
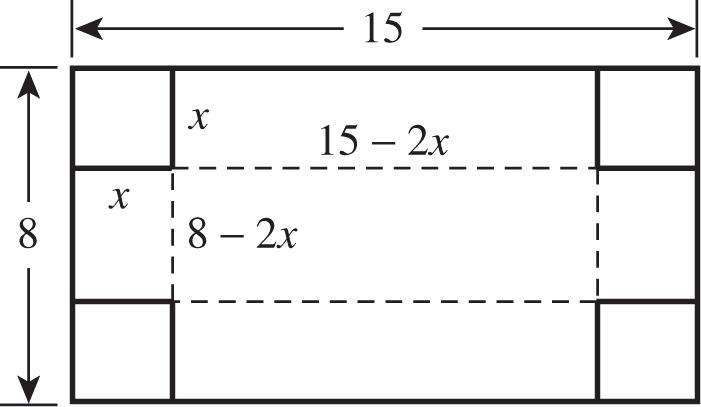
2 (2)4 x 224 or 0. xxx To find the y-intercept, let x = 0 and solve 2 (02)40.yy
46. Complete the square to write the equation in standard form: 2 22yxx
22 1(21)2(1)1.yxxyx This is the graph of 2 yx shifted one unit right and one unit up. The vertex is (1, 1). The axis of symmetry is 1. x To find the x-intercepts, let y = 0 and solve 2 0(1)1 x
2 (1)1 x there is no x-intercept. To find the y-intercept, let x = 0 and solve 2 (01)12.yy
47. Complete the square to write the equation in standard form:
22
22 610(610) 9(69)10(3)1. yxxyxx yxxyx
This is the graph of 2 yx shifted three units right, reflected about the x-axis, and then shifted one unit down. The vertex is (3, –1). The axis of symmetry is 3. x To find the x-intercepts, let y = 0 and solve 2 0(3)1 x
2 1(3) x there is no x-intercept. To find the y-intercept, let x = 0 and solve 2 (03)110.yy
48. Complete the square to write the equation in standard form:
22 83(38)yxxyxx 2 99 38 44yxx
2 341 . 24
This is the graph of 2 yx shifted 32 units right, reflected about the x-axis, and then shifted 41 4 units up. The vertex is 341 , 24
. The axis of symmetry is 3 2 x To find the x-intercepts, let y = 0 and solve 22 341341 0 2424
To find the y-intercept, let x = 0 and solve 2 341 08. 24 yy
49. Complete the square to write the equation in standard form: 22 2892(4)9yxxyxx
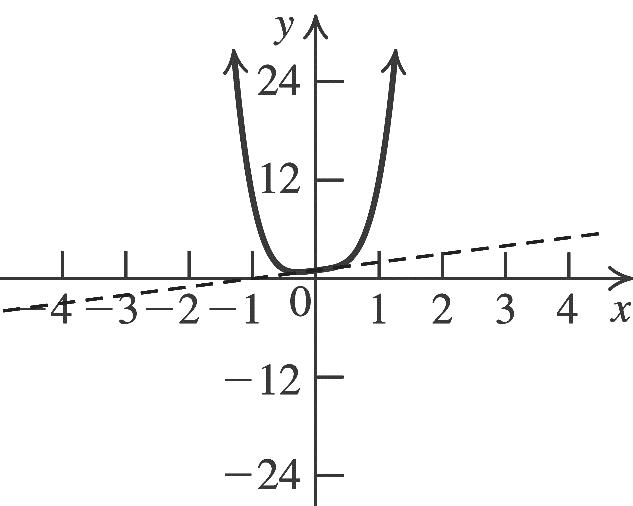
22 82(44)92(2)1. yxxyx
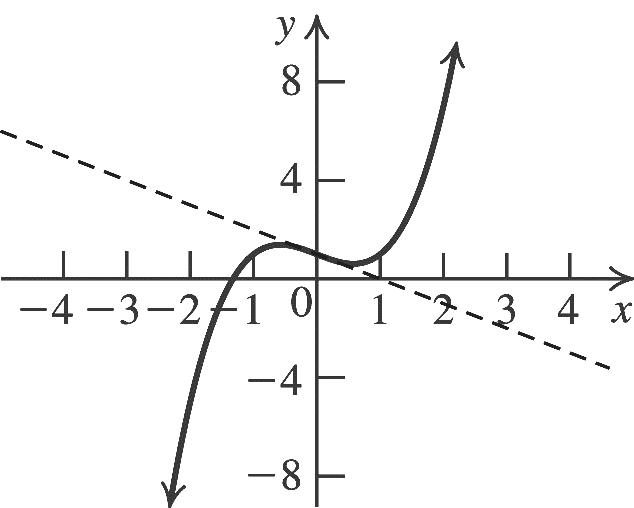
This is the graph of 2 yx shifted 2 units right, stretched vertically by a factor of 2, and then shifted one unit up. The vertex is (2, 1). The axis of symmetry is 2. x To find the x-intercepts, let y = 0 and solve
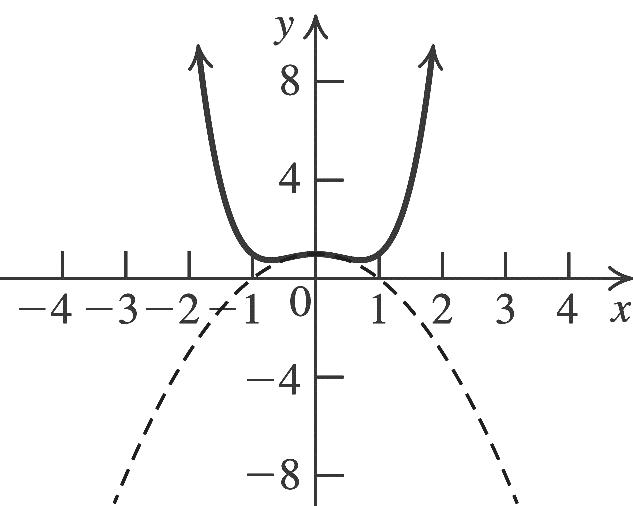
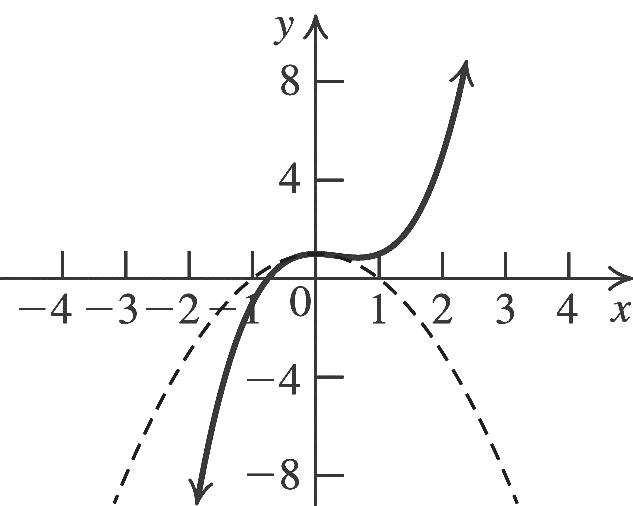
2 02(2)1 x 2 1 (2) 2 x there is no x-intercept. To find the y-intercept, let x = 0 and solve 2 2(02)19.yy
50. Complete the square to write the equation in standard form: 22 31273(4)7yxxyxx 22 123(44)73(2)19. yxxyx
This is the graph of 2 yx shifted 2 units left, stretched vertically by a factor of 3, and then shifted 19 units down. The vertex is (–2, –19). The axis of symmetry is x = 2. To find the x-intercepts, let y = 0 and solve
2 03(2)19 x
2 1919 33(2)2 xx
571
2257. 33 xx (continuedonnextpage)
(continued)
To find the y-intercept, let x = 0 and solve 2 3(02)197.yy
51. Complete the square to write the equation in standard form:
22 318113(6)11yxxyxx
2 273(69)11yxx
2 3(3)16.yx This is the graph of 2 yx shifted three units right, stretched vertically by a factor of three, reflected about the x-axis, and then shifted 16 units up. The vertex is (3, 16). The axis of symmetry is x = 3.
To find the x-intercepts, let y = 0 and solve 2 03(3)16yx
2 1643 33(3)3 xx
4
33. 3 x To find the y-intercept, let x = 0 and solve 2 3(03)1611. yy
52. Complete the square to write the equation in standard form:
22 520135(4)13yxxyxx
2 205(44)13yxx
2 5(2)33yx
This is the graph of 2 yx shifted two units left, stretched vertically by a factor of five, reflected about the x-axis, and then shifted 33 units up. The vertex is (–2, 33). The axis is x = 2. To find the x-intercepts, let y = 0 and solve 22 33 05(2)33(2) 5 xx
331 22165. 55 xx To find the y-intercept, let x = 0 and solve 2 5(02)3313.yy
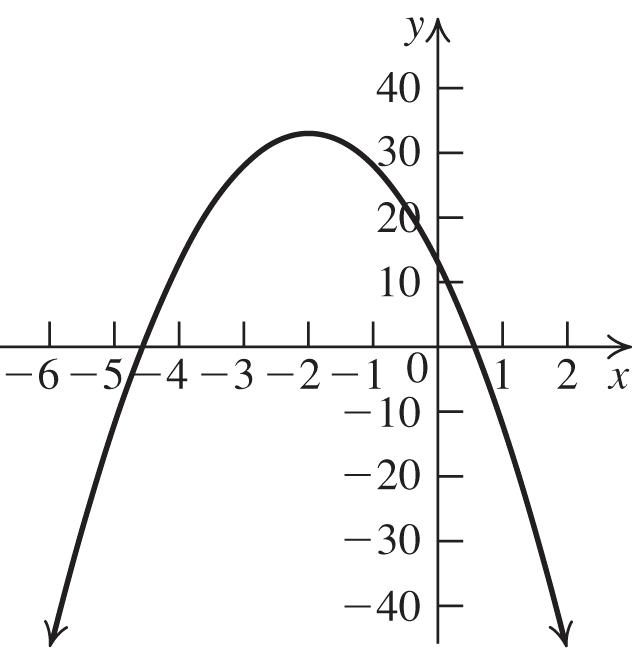
53. a. a = 1 > 0, so the graph opens up.
b. The vertex is 88 2(1)2(1),(4,1). f
c. The axis of symmetry is x = 4.
d. To find the x-intercepts, let y = 0 and solve 2 08150(3)(5) xxxx 3 or 5. xx To find the y-intercept, let x = 0 and solve 2 08(0)1515.yy
e.
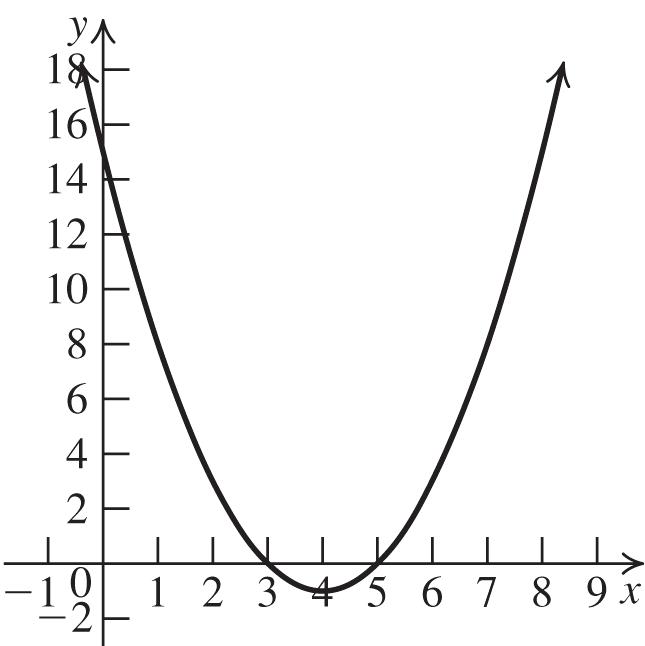
54. a. a = 1 > 0, so the graph opens up.
b. The vertex is 88 2(1)2(1),(4,3). f
c. The axis of symmetry is x = –4.
2 Polynomial and Rational Functions
d. To find the x-intercepts, let y = 0 and solve 2 2 884(1)(13) 0813 2(1) xxx 812 43. 2 x To find the y-intercept, let x = 0 and solve 2 08(0)1313. y
e.
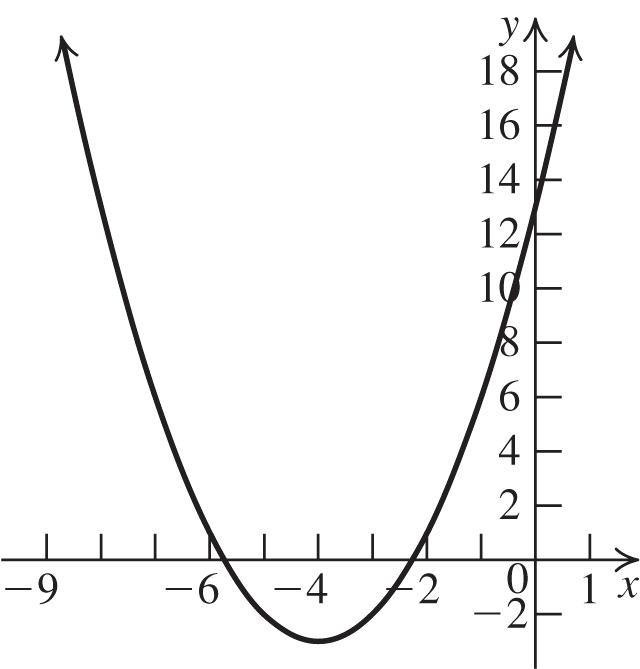
55. a. a = 1 > 0, so the graph opens up.
b. The vertex is 11125 2(1)2(1)24,,. f
c. The axis of symmetry is 1 2 x
d. To find the x-intercepts, let y = 0 and solve 2 060(3)(2)3 xxxxx or 2. x To find the y-intercept, let x = 0 and solve 2 0(0)66.yy
e.
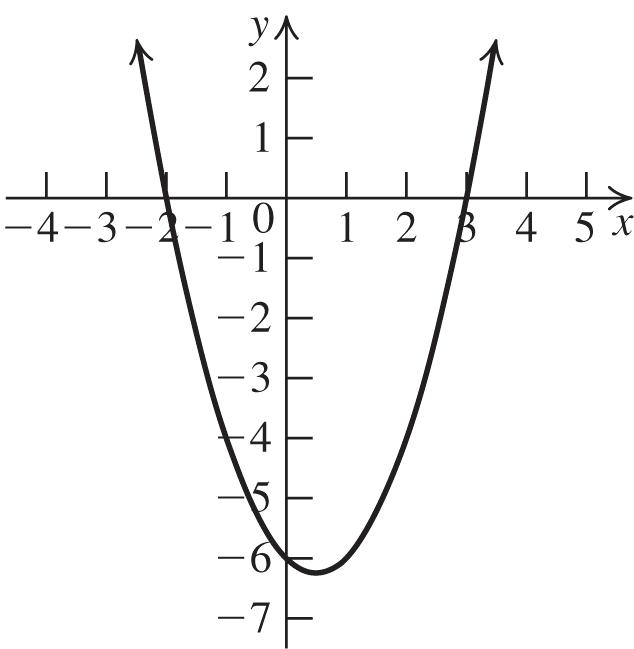
56. a. a = 1 > 0, so the graph opens up.
b. The vertex is 1119 ,,. 2(1)2(1)24 f
c. The axis of symmetry is 1 . 2 x
d. To find the x-intercepts, let y = 0 and solve 2 020(1)(2) xxxx 1 or x 2. x
To find the y-intercept, let x = 0 and solve 2 0(0)22.yy
e.
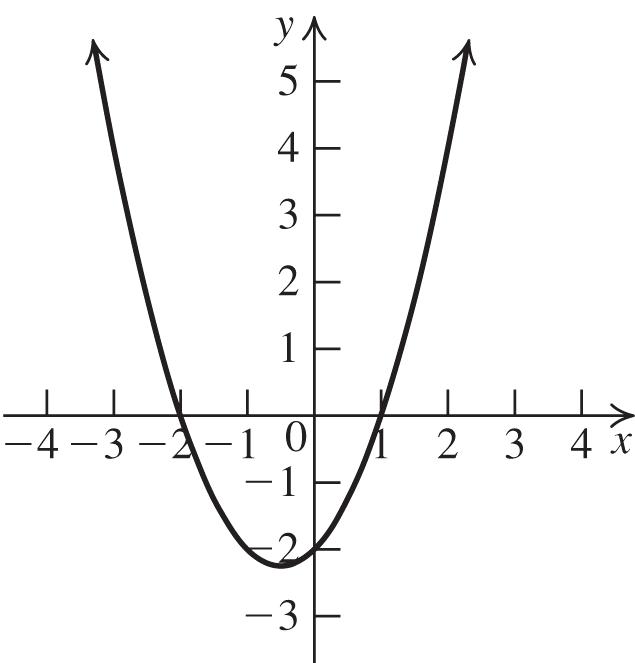
57. a. a = 1 > 0, so the graph opens up.
b. The vertex is 22 2(1)2(1),1,3. f
c. The axis of symmetry is 1. x
d. To find the x-intercepts, let y = 0 and solve 2 024 xx 2 (2)(2)4(1)(4) 2(1) x 212 2 x there are no x-intercepts.
To find the y-intercept, let x = 0 and solve 2 02(0)44.yy
e.
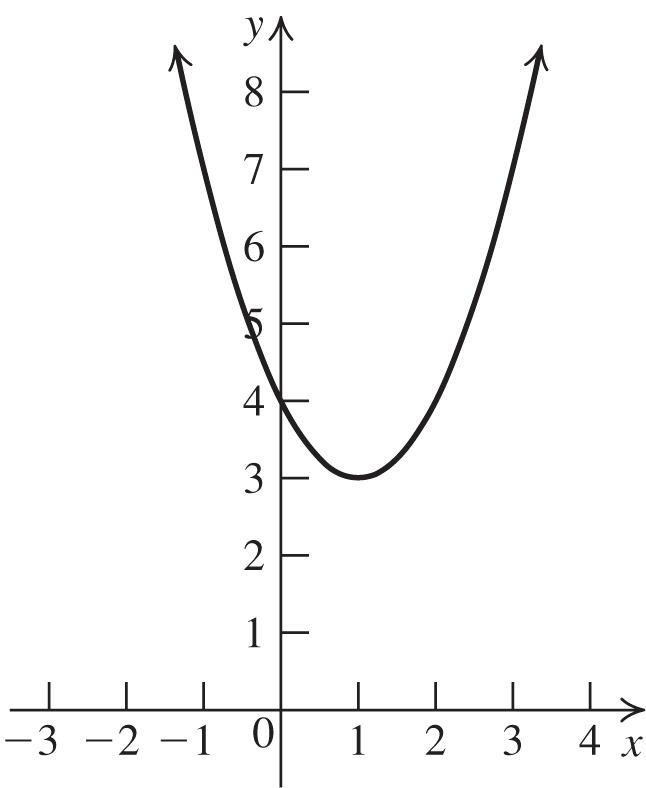
58. a. a = 1 > 0, so the graph opens up.
b. The vertex is 44 2(1)2(1),2,1. f
c. The axis of symmetry is 2. x
Copyright © 2018 Pearson Education Inc.
d. To find the x-intercepts, let y = 0 and solve
2 045 xx
2 (4)(4)4(1)(5) 2(1) x
44 2 x there are no x-intercepts. To find the y-intercept, let x = 0 and solve
2 04(0)55.yy
e.
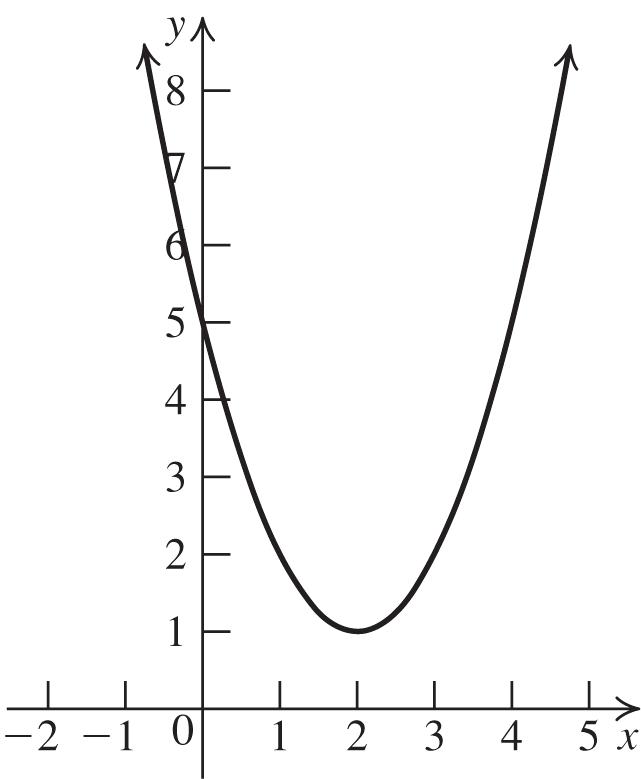
59. a. a = –1 < 0, so the graph opens down.
b. The vertex is
c. The axis of symmetry is 1. x
d. To find the x-intercepts, let y = 0 and solve
2 062 xx 2 (2)(2)4(1)(6) 228 2(1)2 xx
17. x
To find the y-intercept, let x = 0 and solve
2 62(0)06.yy
e.
60. a. a = –3 < 0, so the graph opens down.
b. The vertex is 55549 ,,. 2(3)2(3)612 f
c. The axis of symmetry is 5 . 6 x
d. To find the x-intercepts, let y = 0 and solve 22 02530(352) xxxx 1 0(31)(2) or 2. 3 xxxx To find the y-intercept, let x = 0 and solve 2 25(0)3(0)2.yy
e.
61. a. a = 1 > 0, so the graph opens up and has a minimum value. Find the minimum value by finding the vertex:
44 2(1)2(1),2,1
The minimum value is –1.
b. The range of f is [1,).
62. a. a = –1 < 0, so the graph opens down and has a maximum value. Find the maximum value by finding the vertex:
66 2(1)2(1),3,1
The maximum value is 1.
b. The range of f is (,1].
63. a. a = –1< 0, so the graph opens down and has a maximum value. Find the maximum value by finding the vertex:
44 2(1)2(1),2,0
The maximum value is 0.
b. The range of f is (,0].
Copyright © 2018 Pearson Education Inc.
64.
a. a = 1 > 0, so the graph opens up and has a minimum value. Find the minimum value by finding the vertex:
2(1)2(1),3,0
The minimum value is 0.
b. The range of f is [0,).
65.
a. a = 2 > 0, so the graph opens up and has a minimum value. Find the minimum value by finding the vertex:
2(2)2(2),2,5
The minimum value is –5.
b. The range of f is [5,).
66. a. a = 3 > 0, so the graph opens up and has a minimum value. Find the minimum value by finding the vertex:
The minimum value is –17.
b. The range of f is [17,).
67. a. a = –4 < 0, so the graph opens down and has a maximum value. Find the maximum value by finding the vertex: 12123
2(4)2(4)2,,16 f
The maximum value is 16.
b. The range of f is (,16].
68. a. a = –2 < 0, so the graph opens down and has a maximum value. Find the maximum value by finding the vertex:
88 2(2)2(2),2,3
The maximum value is 3.
b. The range of f is (,3].
In exercises 69–82, the x-intercepts are the boundaries of the intervals.
69. 2 40 x
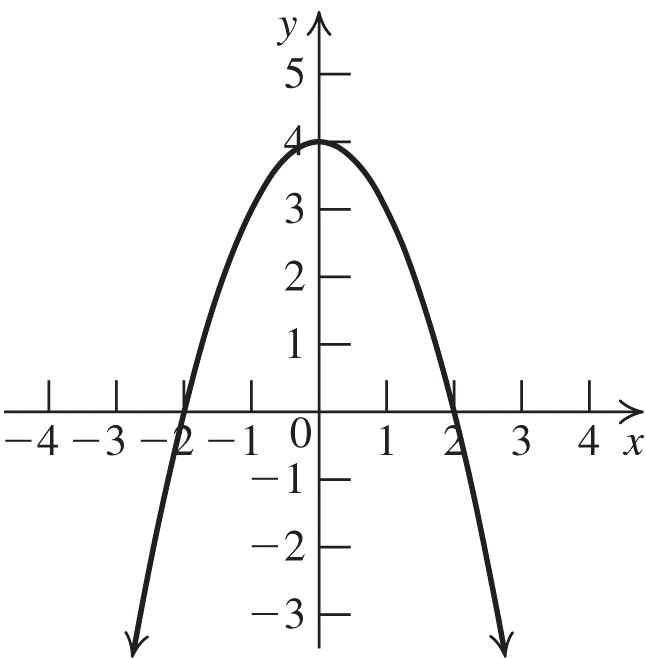
Vertex: (0, –4); x-intercepts: –2, 2
Solution: [–2, 2]
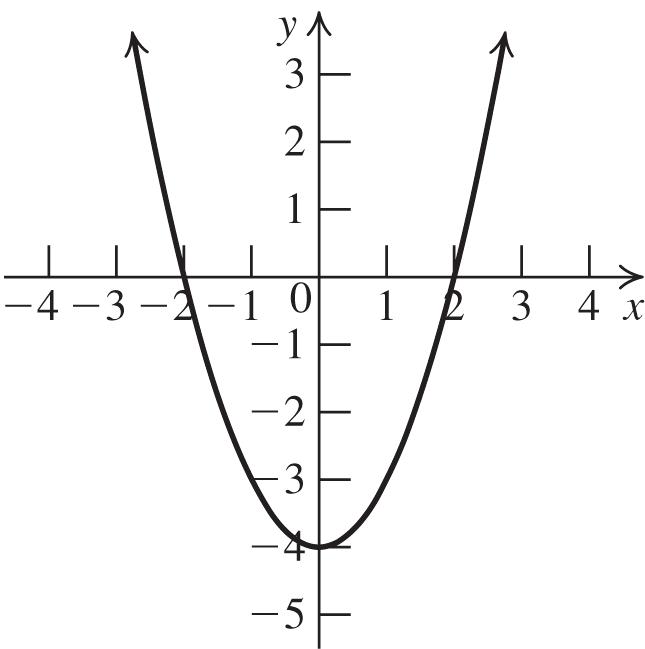
70. 2 40 x Vertex: (0, 4); x-intercepts: –2, 2
Solution: [–2, 2]
71. 2 430xx
Vertex: (2, –1); x-intercepts: 1, 3
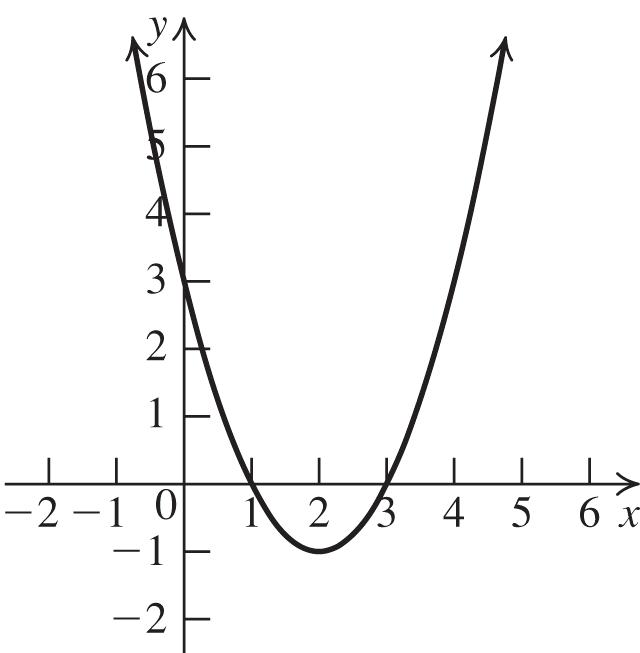
Solution: 1,3
72. 2 20 xx
Vertex: 19 24,,
x-intercepts: –2, 1
Solution:
73. 2 370xx
Vertex: 337 , 24
To find the x-intercepts, use the quadratic equation to solve 2 370.xx
2 33417 337 212 x
The solution of the inequality 2 370xx is 337337 ,,. 2222
74. 2 80 xx
Vertex: 133 , 24
To find the x-intercepts, use the quadratic equation to solve 2 80. xx
2 11418 133 212 x
The solution of the inequality 2 80 xx is 133133 2222,.
75. 2 490xx
Vertex: (2, 5)
To find the x-intercepts, use the quadratic equation to solve 2 490.xx
2 44419 420 212 x
There are no x-intercepts.
Solution: ,
76. 2 690xx
Vertex: (3, 0); x-intercept: (3, 0)
Solution: {3}
77. 2 220xx
Vertex: (1,–1)
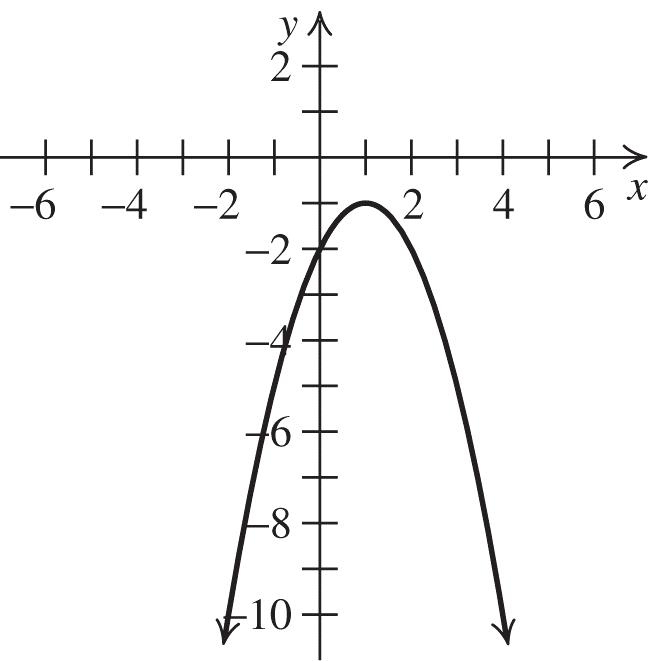
Solution:
78. 2 690xx
Vertex: (3, 0); x-intercept: (3, 0)
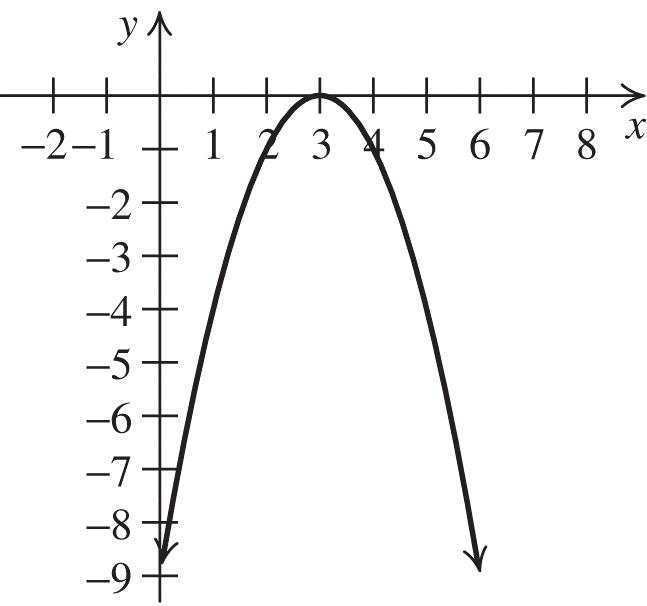
Solution: ,33,
79. 2 3100xx
Vertex: 349 , 24
x-intercepts: –5, 2
Solution: [–5, 2]
80. 2 120 xx
Vertex: 149 , 24
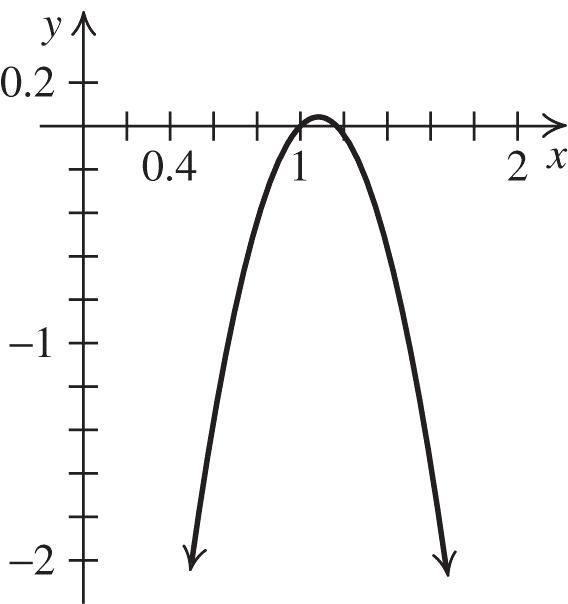
x-intercepts: –4, 3
Solution: ,43,
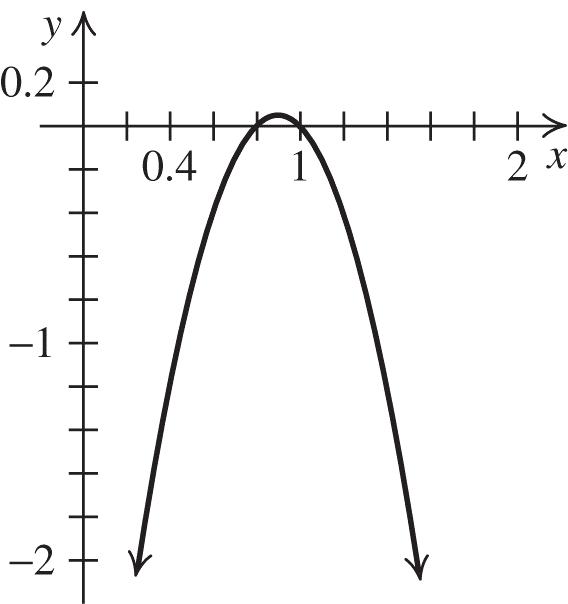
81. 2 61370 xx
Vertex: 131 , 1224
x-intercepts: 1, 7 6
Solution: 7 ,1, 6
82. 2 5940 xx
Vertex: 91 , 1020
x-intercepts: 4 ,1 5
Solution: 4 ,1 5
Copyright © 2018 Pearson Education Inc.
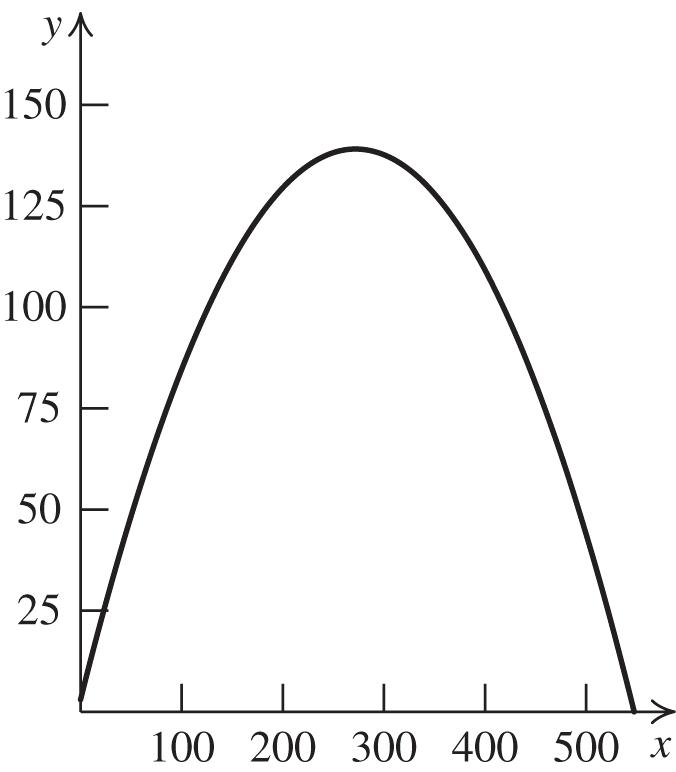
a. Using the graph, we see that the ball traveled approximately 550 ft horizontally.
b. Using the graph, we see that the ball went approximately 140 high.
c.
Thus, the ball traveled approximately 547 ft horizontally. The ball reached its maximum height at the vertex of the function,
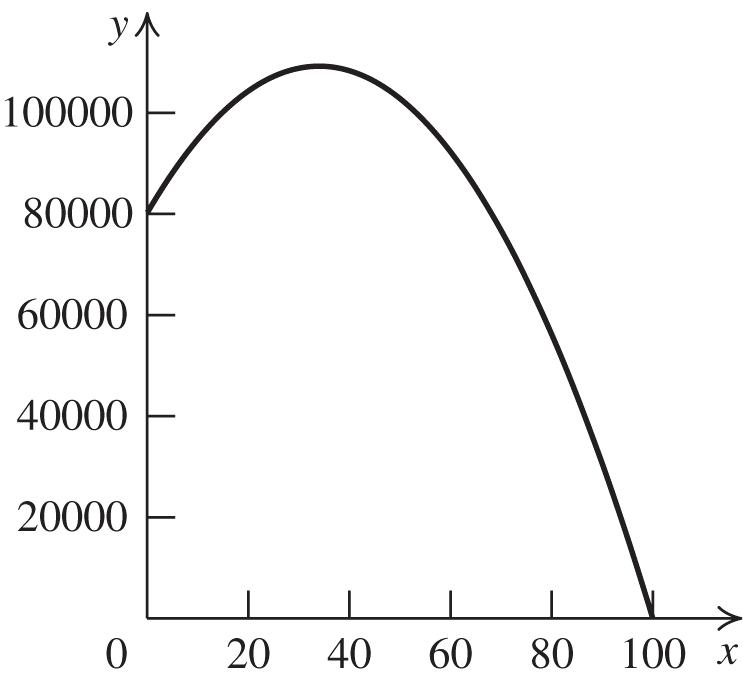
a. Using the graph, we see that the maximum revenue from the apartments is approximately $110,000
b. Using the graph, we see that the maximum revenue is generated by about 35 $25 increases.
c. The maximum revenue is at the vertex of the function, 22,. bb
2 34253417003480,000 108,900 R
The maximum revenue of $108,900 is reached at 34 $25 increases.
85. The vertex of the function is 114114 2(3)2(3),(19,1098). f
The revenue is at its maximum when x = 19.
86. 2 2004()2004. pxRxxx
The vertex of the revenue function is 200200 2(4)2(4),(25,2500).
The revenue is at its maximum when x = 25.
87. 5050 2(1)2(1),(25,425). f
The total cost is minimum when x = 25.
88. 2 100()100. pxRxxx Profit = revenue – cost
2 ()100502 Pxxxx
2 ()9850. Pxxx Now find the vertex of the profit function: 9898 , 2(1)2(1)
49,2351. So the maximum profit occurs when x = 49. The maximum profit is $2351.
89. Let x = the length of the rectangle. Then 802 40 2 x x the width of the rectangle.
The area of the rectangle = (40)xx
2 40 xx . Find the vertex to find the maximum value: 4040 2(1)2(1),(20,400).
The rectangle with the maximum area is a square with sides of length 20 units. Its area is 400 square units.
90. The fence encloses three sides of the region. Let x = the width of the region. Then 120 – 2x = the length of the region. The area of the region = 2 (1202)1202. xxxx
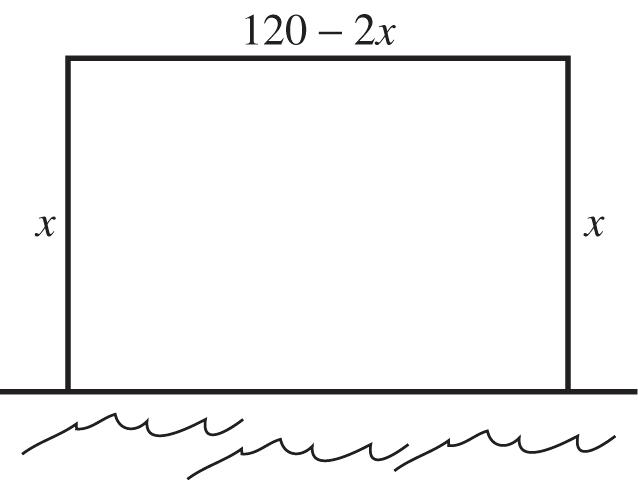
Find the vertex to find the maximum value: 120120 2(2)2(2),(30,1800).
The maximum area that can be enclosed is 1800 square meters.
91. Let x = the width of the fields. Then, 60033 300 22 x x the length of the two fields together. (Note that there is fencing between the two fields, so there are three “widths.”)
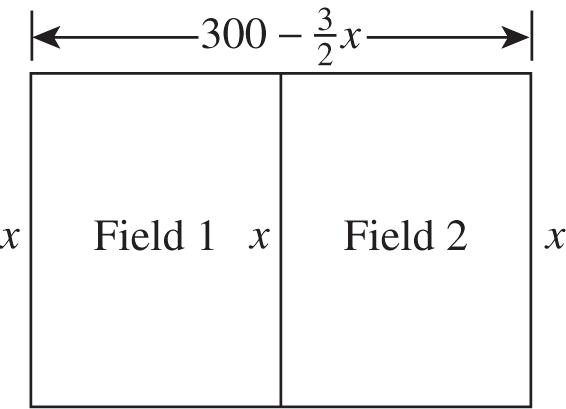
The total area = 2 33 300300. 22 xxxx
Find the vertex to find the dimensions and maximum value: 300300 2(32)2(32),(100,15,000).
So the width of each field is 100 meters. The length of the two fields together is 300 – 1.5(100) = 150 meters, so the length of each field is 150/2 = 75 meters. The area of each field is 100(75) = 7500 square meters.
92. Let x = the amount of high fencing. Then 8x = the cost of the high fencing. The cost of the low fencing = 2400 – 8x, and 24008 6002 4 x x = the amount of low fencing. This is also the width of the enclosure. So 2(6002)512005 600 222 xxx x the length of the enclosure.
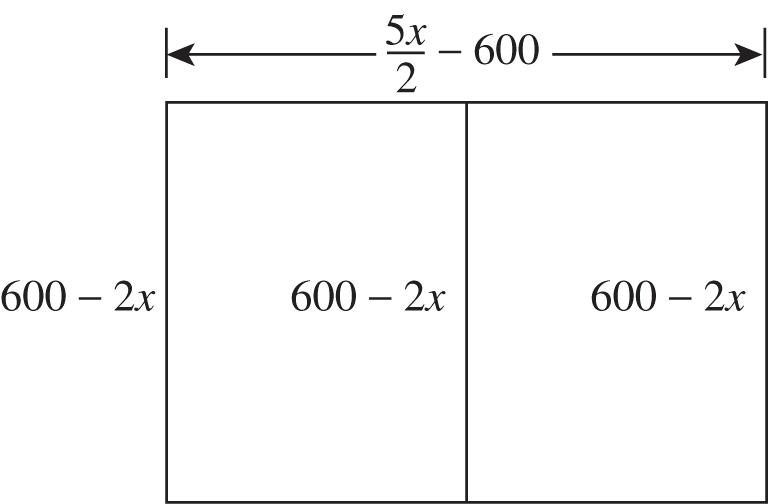
The area of the entire enclosure is 2 5 (6002)60052700360,000. 2 xxxx
Use the vertex to find the dimensions and maximum area: 27002700 2(5)2(5),(270,4500)
. So the area of the entire enclosure is 4500 square feet. There are 270 feet of high fencing, so the dimensions of the enclosure are 5(270) 60075 2 feet by 6002(270)60 feet. The question asks for the dimensions and maximum area of each half of the enclosure, so each half has maximum area 2250 sq ft with dimensions 37.5 ft by 60 ft.
Copyright © 2018 Pearson
93. The yield per tree is modeled by the equation of a line passing through (26, 500) where the x-coordinate represents the number of trees planted, and the y-coordinate represents the number of apples per tree. The rate of change is –10; that is, for each tree planted the yield decreases by 10. So, 50010(26)10760.yxyx
Since there are x trees, the total yield = 2 (10760)10760. xxxx Use the vertex to find the number of trees that will maximize the yield:
So the maximum yield occurs when 38 trees are planted per acre.
94. Let x = the number of days. The original price is $1.50 per pound and the price decreases $0.02 per pound each day, so the price per pound is (1.5 – 0.02x). The weight of the steer after x days is 300 + 8x. So the selling price = number of pounds times price per pound (3008)(1.50.02). xx The original cost of the steer is 1.5(300) = $450, and the daily cost of the steer is x, so the total cost of the steer after x days is x + 450. The profit is selling price – cost
2 (3008)(1.50.02)(450) (0.166450)(450) xxx xxx
2 0.165. xx
The maximum profit occurs at the x-coordinate of the vertex: 5 15.625. 2(0.16)
The maximum profit occurs after 16 days.
95. If 20 students or less go on the trip, the cost is $72 per students. If more than 20 students go on the trip, the cost is reduced by $2 per the number of students over 20. So the cost per student is a piecewise function based on the number of students, n, going on the trip:
72if 20 () 722(20)1122if 20 fnn nnn
The total revenue is 2 72if 20 () (1122)1122if 20 nn nfn nnnnn
The maximum revenue is either 1440 (the revenue if 20 students go on the trip) or the maximum of 2 1122. nn Find this by using the vertex: 112112 (2)(2)(2)(2),(28,1568).
The maximum revenue is $1568 when 28 students go on the trip.
96. Assume that m bytes per inch can be put on any track. Let x = the radius of the innermost track. Then the maximum number of bytes that can be put on the innermost track is 2. mx So, each track will have 2 mx bytes.
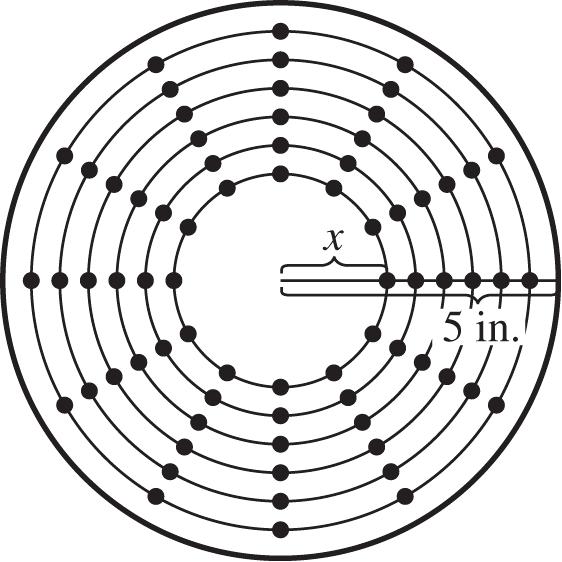
The total number of bytes on the disk is the number of bytes on each track times the number of tracks per inch times the radius (in inches): 2 2((5))2(5) mxpxmpxx 2 210mpxmpx . The maximum occurs at the x-coordinate of the vertex: 1010 2.5 22(2)4 bmp amp inches.
97. 2 00 2 M g httvth 2 0 1.6ms,5 m, max height25 m M gh
a. Using the given values, we have 22 00 1.6 50.85 2 httvttvt
Using the formula for the vertex of a parabola gives 00 20.81.6 vv t This is the time at which the height h(t) = 25 m is attained. Thus, 0 2 00 0 222 000 25 1.6 0.85 1.61.6 55 3.21.63.2 v hth vv v vvv
(continuedonnextpage)
(continued)
b. Using the formula for the vertex of a parabola gives 88 5. 20.81.6
The ball reached its highest point 5 seconds after it was released.
a. Using the given values, we have
Using the formula for the vertex of a parabola gives 00 20.81.6 vv t This is the time at which the height h(t) = 52 m is attained. Thus,
Thus,
b. Using the formula for the vertex of a parabola gives
The ball reached its highest point 7.5 seconds after it was released.
99. a. The maximum height occurs at the vertex: 6464 2(16)2(16),(2,64), f
so the maximum height is 64 feet.
b. When the projectile hits the ground, h = 0, so solve 2 0166416(4)0 tttt 0 or 4. tt
The projectile hits the ground at 4 seconds.
100. a. The maximum height occurs at the vertex: 6464 2(16)2(16),(2,464).
The maximum height is 464 feet.
b. When the projectile hits the ground, h = 0, so solve 2 01664400 tt 22 16(425)04250 tttt 2 4(4)4(1)(25) 4116 2(1)2 tt
2293.39 or 7.39. ttt Reject the negative solution (time cannot be negative). The projectile hits the ground at 7.39 seconds.
101. Let x = the radius of the semicircle. Then the length of the rectangle is 2x. The circumference of the semicircle is , x so the perimeter of the rectangular portion of the window is 18. x
The width of the rectangle = 182 2 xx
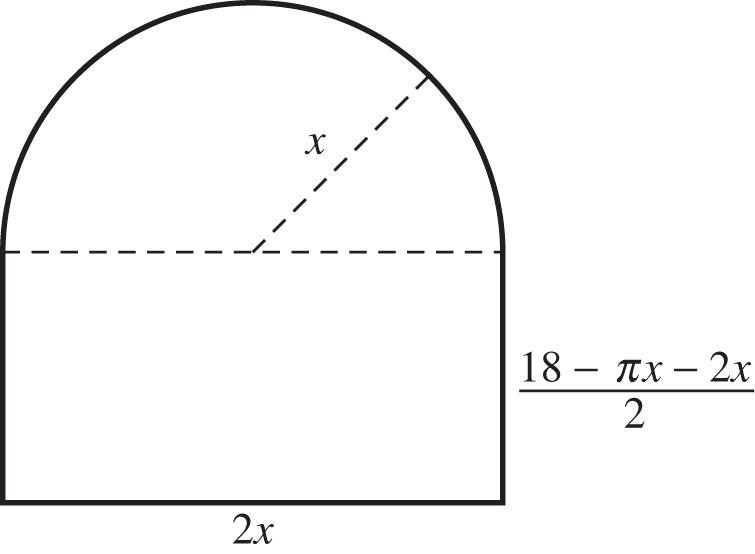
The area of the semicircle is 2 2, x and the area of the rectangle is 182 2 2 xx x
22 182. xxx So the total area is 22 222 182182 22 xx xxxxx 2 182. 2 xx
The maximum area occurs at the x-coordinate of the vertex: 181818 44 22 2
(continuedonnextpage)
(continued)
This is the radius of the semicircle. The length of the rectangle is 1836 2 44
ft. The width of the rectangle is 1818 182
102. a.
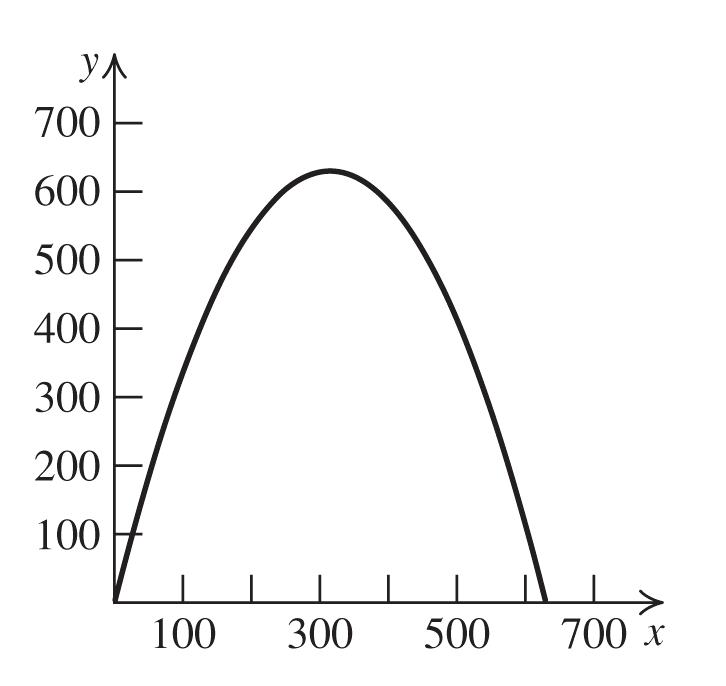
b. The width of the arch is the difference between the two x-intercepts:
2 00.006354xx 04(0.00158751)0 or xxx
629.92. x The arch is 629.92 feet wide.
c. The maximum height occurs at the vertex of the arch. Since we know that the arch is 629.92 feet wide, the vertex occurs at x = 629.92/2 = 314.96. 2 (314.96)0.00635(314.96)4(314.96) f 629.92 feet.
103. a. 1.181.18 , 2(0.01)2(0.01) (59,36.81)
b. 2 00.011.182 xx 2 1.181.184(0.01)(2) 2(0.01) 1.181.47241.181.21 0.020.02 1.5 or 119.5. Reject the negative answer x
and round the positive answer to the nearest whole number. The ball hits the ground approximately 120 feet from the punter.
c. The maximum height occurs at the vertex. Since we know that the ball hits the ground at 120, x the vertex occurs at 60. x 2 (60)0.01(60)1.18(60)236.8. f
The maximum height is approximately 37 ft.
d. The player is at x = 6 feet. 2 (6)0.01(6)1.18(6)28.72. f
The player must reach approximately 9 feet to block the ball.
e. 2 2 2 70.011.182 00.011.185
1.181.184(0.01)(5)
2(0.01)
1.181.1924 0.02 4.4 feet or 113.6 feet
104. The maximum height occurs at the vertex: 303015225 2(16)2(16)1616,,.
The maximum height is approximately 14 feet, so it will never reach a height of 16 feet.
105. 2 1.510.220.029 fxxx
a. We must complete the square to write the function in standard form.
b. Sales were at a minimum at 3.79, x or during year 4 (2010). This fits the original data.
c. The year 2011 is represented by x = 5.
2 51.510.2250.02951.135
In 2011, there were about 1.14 million vehicles sold.
106.
a. We must complete the square to write the function in standard form.
b. Foreclosure filings were at a maximum during year 4, 2010. This fits the original data.
c. The year 2013 is represented by x = 7. 2 70.8220.89670.1171.7 f
There were about 1.7 million foreclosure filings in 2013.
Beyond the Basics
107. 22 2 3(2)33(44)3 31215 yxyxx yxx
108. Substitute the coordinates (1, 5) for x and y and (–3, –2) for h and k into the standard form 2 () yaxhk to solve for a: 2 7 5(13)2716 16 aaa
The equation is 2 7 ()(3)2 16 yfxx 2 72131 16816yxx
109. The y-intercept is 4, so the graph passes through (0, 4). Substitute the coordinates (0, 4) for x and y and (1, –2) for h and k into the standard form 2 () yaxhk to solve for a:
2 4(01)26. aa The x-coordinate of the vertex is 112. 22(6) bb b a
The y-intercept = c, so the equation is 2 ()6124. fxxx
110. The x-coordinate of the vertex of the graph is halfway between the x-intercepts:
26 4. 2 h Substitute the coordinates of one of the x-intercepts and the x-coordinate of the vertex into the standard form 2 () yaxhk to find an expression relating a and k:
2 0(24)4. akak
Now substitute the coordinates of the y-intercept, the x-coordinate of the vertex, and the expression for k into the standard form
2 () yaxhk to solve for a:
2 24(04)4 aa 241642. aaa
Use this value to find k: 4(2)8. k
The equation is 22 2(4)821624.yxyxx
111. The x-coordinate of the vertex is 3. Substitute the coordinates of the x-intercept and the xcoordinate of the vertex into the standard form
2 () yaxhk to find an expression relating a and k: 2 0(73)16. akak Now substitute the coordinates of the y-intercept, the x-coordinate of the vertex, and the expression for k into the standard form 2 () yaxhk to solve for a: 2 14(03)162. aaa
Use this value to find k: 16(2)32. k The equation is 22 2(3)3221214.yxyxx
112. First, write 2 22yxx in standard form by completing the square: 22 1(21)2(1)1.yxxyx
Move the curve three units to the right by subtracting 3 from x + 1; move the curve two units down by subtracting 2 from 1: 22 (13)(12)(2)1yxx 2 43.yxx
113. The x-coordinate of the vertex is 26 2. 2
Substitute the coordinates of one of the xintercepts and the x-coordinate of the vertex into the standard form 2 () yaxhk to find an expression relating a and k: 2 0(22)16. akak
Now substitute the coordinates of the other x-intercept, the x-coordinate of the vertex, and the expression for k into the standard form 2 () yaxhk to solve for a: 2 0(62)161. aaa Use this value to find k: 16(1)16. k So one equation is 22 (2)16412.yxxx The graph of this equation opens upward. To find the equation of the graph that opens downward, multiply the equation by –1: 2 412.yxx
114. The x-coordinate of the vertex is 35 1. 2
Substitute the coordinates of one of the x-intercepts and the x-coordinate of the vertex into the standard form 2 () yaxhk to find an expression relating a and k: 2 0(31)16. akak Now substitute the coordinates of the other x-intercept, the x-coordinate of the vertex, and the expression for k into the standard form 2 () yaxhk to solve for a: 2 0(51)161. aaa Use this value to find k: 16(1)16. k So one equation is 22 (1)16215.yxxx The graph of this equation opens upward. To find the equation of the graph that opens downward, multiply the equation by –1: 2 215.yxx
115. The x-coordinate of the vertex is 71 4. 2
Substitute the coordinates of one of the x-intercepts and the x-coordinate of the vertex into the standard form 2 () yaxhk to find an expression relating a and k: 2 0(74)9. akak
Now substitute the coordinates of the other x-intercept, the x-coordinate of the vertex, and the expression for k into the standard form 2 () yaxhk to solve for a: 2 0(14)91. aaa Use this value to find k: 9(1)9. k So one equation is 22 (4)987.yxxx The graph of this equation opens upward. To find the equation of the graph that opens downward, multiply the equation by –1: 2 87.yxx
116. The x-coordinate of the vertex is 210 6. 2
Substitute the coordinates of one of the x-intercepts and the x-coordinate of the vertex into the standard form 2 () yaxhk to find an expression relating a and k: 2 0(26)16. akak Now substitute the coordinates of the other x-intercept, the x-coordinate of the vertex, and the expression for k into the standard form 2 () yaxhk to solve for a: 2 0(106)161. aaa Use this value to find k: 16(1)16. k So one equation is 22 (6)161220.yxxx The graph of this equation opens upward. To find the equation of the graph that opens downward, multiply the equation by –1: 2 1220.yxx
117. First, complete the squares on x and y.
Now, consider the two functions 2 21fx and 2 34. gy
The minimum of f is 0 and the minimum of g is 4, so the minimum of f + g = 4.
Copyright © 2018 Pearson Education
118. First, complete the squares on x and y
22 22 22 22 22 312211 312211 34211 3442111121 3212 xyxy xxyy xxyy xxyy xy
Now consider the two functions 2 32fx and 2 12. gx The maximum of f is 0 and the maximum of g is 2, so the maximum of f + g = 2.
Critical Thinking/Discussion/Writing
119. 2 2 2 2 22 22 ()()() ()()() ()() ()() ()() 2 2 422. (We can divide by because 0.)Since 0,2 fhpahpbhpc fhpahpbhpc fhpfhp ahpbhpc ahpbhpc ahahpapbhbpc ahahpapbhbpc ahpbpahb ppaah
2 b b h a
120. Write 2 289yxx in standard form to find the axis of symmetry: 22 28982(44)9yxxyxx 2 2(2)1.yx
The axis of symmetry is 2. x
Using the results of exercise 119, we know that (2)(1)(2). fpffp 21 p 3, so 22(3)5.pp
The point symmetric to the point (–1, 19) across the axis of symmetry is (5, 19).
121. a.
This is the equation of a parabola. The x-coordinate of the vertex is
22 2 22 22 or abmahmambh amam bhhb mm
The y-coordinate of the vertex is
2 2 2 2 22 2222 22 22 2 2 2 2242 2 hbhb amabmahm mm abahbk ahbabhhb abahbahk ahahbabababhah abahbahk k
The vertex is ,. hb k m
2 2 22 22 2 2 gfxgaxhk maxhkb maxahxahkb maxmahxmahmkb
This is the equation of a parabola. The x-coordinate of the vertex is 2 2 mah h ma
The y-coordinate of the vertex is 222 2 mahmahmahmkbmkb
The vertex is ,.hmkb
122. If the discriminant equals zero, there is exactly one real solution. Thus, the vertex of yfx lies on the x-axis at 2 b x a
If the discriminant > 0, there are two unequal real solutions. This means that the graph of yfx crosses the x-axis in two places. If a > 0, then the vertex lies below the x-axis and the parabola crosses the x-axis; if a < 0, then the vertex lies above the x-axis and the parabola crosses the x-axis. If the discriminant < 0, there are two nonreal complex solutions. If a > 0, then the vertex lies above the x-axis and the parabola does not cross the x-axis (it opens upward); if a < 0, then the vertex lies below the x-axis and the parabola does not cross the x-axis (it opens downward).
Copyright © 2018 Pearson Education Inc.
123. Start by writing the function in standard form.
The minimum value of this function is 2 . 2 a
Now, rewrite the function as
This is the same function, so
124. Start by writing the function in standard form.
The maximum value of this function is 2 . 4
Now, rewrite the function as
129. 222 31239 3 4444 xxx
4444 2323 42 3535 11 35 xxxx xxxx xxx
2 492323 xxx
2 2 693xxx
2 1511123453 xxxx
2 14322172 xxxx
2214141 221 xxxxx
2 2 9272527 92527 353527 xxx xx xxx
2.2 Polynomial Functions
2.2 Practice Problems
1. a. 2 1 1 fxx x is not a polynomial function because its domain is not ,
b. 72 2517gxxx is a polynomial function. Its degree is 7, the leading term is 7 2 x , and the leading coefficient is 2.
2. 32 3 23 42517 2517 4 Pxxxx x xxx
When |x| is large, the terms 2 25 ,, xx and 3 17 x are close to 0. Therefore, 33 40004. Pxxx
3. Use the leading-term test to determine the end behavior of 42 253yfxxx . Here n = 4 and 20 n a . Thus, Case 2 applies. The end behavior is described as as yx and as . yx
4. First group the terms, then factor and solve 0 fx :
32 32 22 2 2346 2436 2232 232 fxxxx xxx xxx xx
2 2 0232 3 023 or 2 02 (no real solution) xx xx x
The only real zero is 3 2
5. 3 236fxxx
17 f
and
24 f . Since
1 f and
2 f have opposite signs, by the Intermediate Value Theorem, f has a real zero between 1 and 2.
as yx and as . yx
Now find the zeros of the function:
4242 22 22 054054 41 04 or 01 2or 1 xxxx xx xx xx
There are four zeros, each of multiplicity 1, so the graph crosses the x-axis at each zero.
Next, find the y-intercept: 42 0544fxx
Determine symmetry:
42 42 54 54 fxxx xxfx
6. 2 2 1350 10 or 30 or 50 1 or 3 or 5 fxxxx xxx xxx
fx has three distinct zeros.
7.
2 2 1350 10 or 30 or 50 1 (multiplicity 2) or 3 (multiplicity 1) or 5 (multiplicity 1)
8. 4232fxxx has at most three turning points. Using a graphing calculator, we see that there are indeed, three turning points.
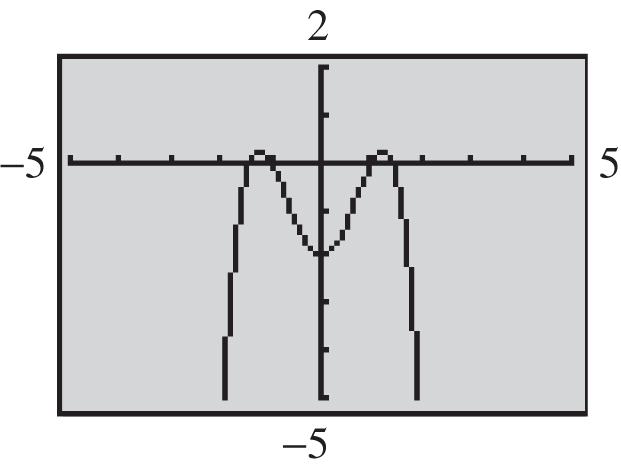
9. 4254fxxx
Since the degree, 4, is even and the leading coefficient is 1, the end behavior is as shown:
So f is an even function and its graph is symmetric with respect to the y-axis. Now find the intervals on which the graph lies above or below the x-axis. The four zeros divide the x-axis into five intervals, ,2,
2,1,1,1,1,2, and 2,. Determine the sign of a test value in each interval
Interval
Test point Value of fx Above/below x-axis
,2 3 40 below
2,1 1.5 2.1875 above
1,1 0 4 below
1,2 1.5 2.1875 above 2, 3 40 below
Plot the zeros, y-intercepts, and test points, and then join the points with a smooth curve.
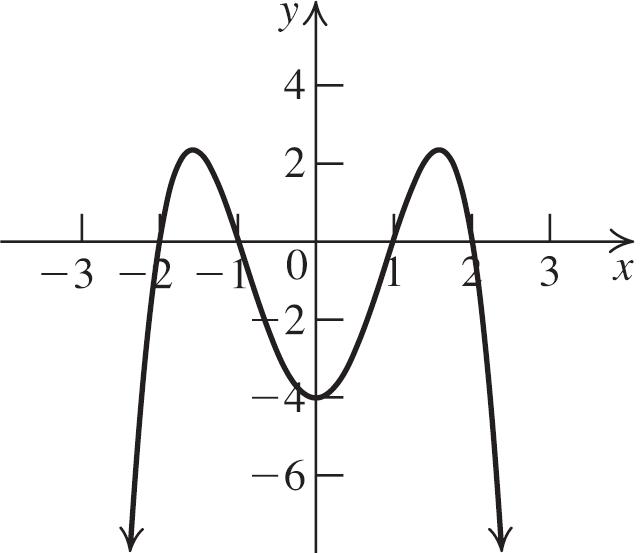
First, find the zeros of the function.
32 210 02010 21 xxx xxx xx
The function has three distinct zeros, –2, 1, and 0. The zero x = –2 has multiplicity 3, so the graph crosses the x-axis at –2, and near –2 the function looks like
323 2221182.fxxx
The zero x = 0 has multiplicity 1, so the graph crosses the x-axis at 0, and near 0 the function looks like
32 02018. fxxx
The zero x = 1 has multiplicity 2, so the graph touches the x-axis at 1, and near 1 the function looks like 322 1121271.fxxx
We can determine the end behavior of the polynomial by finding its leading term as a product of the leading terms of each factor.
32 326 21 fxxxxxxxx
Therefore, the end behavior of fx is Case 1:

Now find the intervals on which the graph lies above or below the x-axis. The three zeros divide the x-axis into four intervals, ,2,
2,0,0,1,and 1,. Determine the sign of a test value in each interval
Interval
Test point
Value of
fx Above/below x-axis
,2 3 48 above
2,0 1 –4 below
above
1, 2 128 above
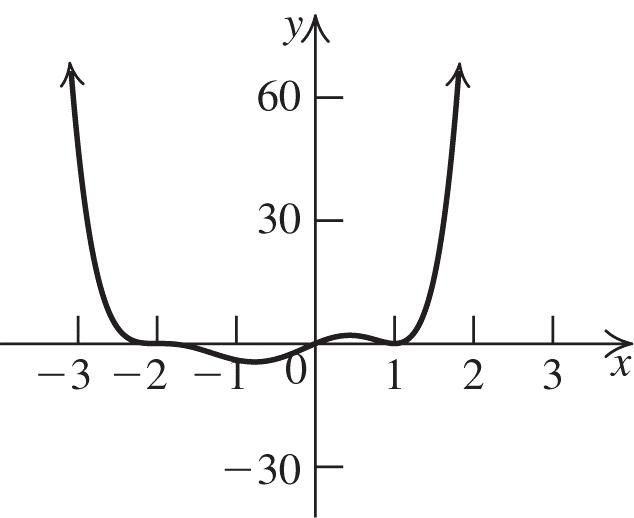
Plot the zeros, y-intercepts, and test points, and then join the points with a smooth curve.
11. 333 7207.378 dm 3333 207.378 L
2.2
Exercises
Concepts and Vocabulary
1. Consider the polynomial 54 236. xxx
The degree of this polynomial is 5, its leading term is 5 2 x , its leading coefficient is 2, and its constant term is 6.
2. A number c for which 0 fc is called a zero of the polynomial function f.
3. If c is a zero of even multiplicity for a polynomial function f, then the graph of f touches the x-axis at c.
4. If c is a zero of odd multiplicity for a polynomial function f, then the graph of f crosses the x-axis at c
5. False. The graph of a polynomial function is a smooth curve. That means it has no corners or cusps.
6. True
7. False. The polynomial function of degree n has, at most, n zeros.
8. True
Building Skills
9. Polynomial function; degree: 5; leading term: 5 2; x leading coefficient: 2
10. Polynomial function; degree: 4; leading term: 4 7; x leading coefficient: –7
11. Polynomial function; degree: 3; leading term: 3 2 ; 3 x leading coefficient: 2 3
12. Polynomial function; degree: 3; leading term: 3 2; x leading coefficient: 2
13. Polynomial function; degree: 4; leading term: 4 ; x leading coefficient:
14. Polynomial function; degree: 0; leading term: 5; leading coefficient: 5
15. Not a polynomial function (the graph has sharp corners; not a smooth curve; presence of x )
16. Not a polynomial function (the domain is restricted)
17. Not a polynomial function because the domain is not
18. Not a polynomial function (the graph is not continuous)
19. Not a polynomial function (presence of x )
20. Not a polynomial function (noninteger exponent)
21. Not a polynomial function because the domain is not
22. Not a polynomial function (negative exponent)
23. Not a polynomial function (graph is not continuous)
24. Not a polynomial function (the domain is restricted)
25. Not a polynomial function (the graph is not continuous)
26. Not a polynomial function (the graph has sharp corners; not a smooth curve)
27. Not a polynomial function (not the graph of a function)
28. Not a polynomial function (the graph has sharp corners; not a smooth curve)
29. c 30. f 31. a
32. e 33. d 34. b
3 fxxx
The
32 221fxxx
The leading term is 3 2, x so fx as x and fx as . x
37. 43 421fxxx
The leading term is 4 4, x so fx as
x and fx as x
38. 43 3 fxxxx
The leading term is 4 , x so fx as x and fx as x
39. 2 221fxxx
The leading term is 23 22,xxx so
fx as x and fx as x
40. 3 221fxxx
The leading term is 34 22,xxx so
fx as x and fx as . x
41. 2 24 fxxx
The leading term is 23 , xxx so
fx as x and fx as . x
42.
3 32 fxxx
The leading term is 34 , xxx so
fx as x and fx as x
43. 3123fxxxx
Zeros: –2, 1, 3
x = –2: multiplicity: 1, crosses the x-axis
x = 1: multiplicity: 1, crosses the x-axis
x= 3: multiplicity: 1, crosses the x-axis
44. 5123fxxxx
Zeros: –2, –1, 3
x = –2: multiplicity: 1, crosses the x-axis
x = –1: multiplicity: 1, crosses the x-axis
x = 0: multiplicity: 1, crosses the x-axis
45. 2 221fxxx
Zeros: –2, 1 2
x = –2: multiplicity 2, touches but does not cross the x-axis
1 2 : x multiplicity 1, crosses the x-axis
46.
3 221fxxx
Zeros: 1 2 ,2
1 2 : x multiplicity 1, crosses the x-axis
x = 2: multiplicity 3, crosses the x-axis
47.
3 22 932fxxxx
Zeros: 2 3 3,,0,3
x = –3: multiplicity 1, crosses the x-axis
2 3 : x multiplicity 3, crosses the x-axis
x = 0: multiplicity 2, touches but does not cross the x-axis
x = 3: multiplicity 1, crosses the x-axis
48.
2 32 432fxxxx
Zeros: 2 3 2,0,,2
x = –2: multiplicity 1, crosses the x-axis
x = 0: multiplicity 3, crosses the x-axis
2 3 : x multiplicity 2, touches but does not cross the x-axis
x = 2: multiplicity 1, crosses the x-axis
49.
2 2 132fxxx
Zero: 2 3 , multiplicity 2, touches but does not cross the x-axis
50.
2 112fxxxx
Zeros: –1, 2
x = –1: multiplicity 1, crosses the x-axis
x = 2; multiplicity 1, crosses the x-axis
51. 43 (2)22102; f 43 (3)331044 f
Because the sign changes, there is a real zero between 2 and 3. The zero is approximately 2.09.
52. 42 (1)112(1)57; f 42 (2)222(2)53. f
Because the sign changes, there is a real zero between 1 and 2. The zero is approximately 1.87.
53. 52 (2)29(2)1519; f 52 (3)39(3)15147. f
Because the sign changes, there is a real zero between 2 and 3. The zero is approximately 2.28.
54. 5432 (0)05(0)8(0)4(0)055; f 5432 (1)15(1)8(1)4(1)1512. f
Because the sign changes, there is a real zero between 0 and 1. The zero is approximately 0.68.
55. The least possible degree is 3. The zeros are –2, 1, and 3, each with multiplicity 1. The end behavior is fx as x and fx as , x so the leading coefficient is 1. The polynomial with smallest possible degree is
213.xxx
56. The least possible degree is 3.The zeros are –1, 1, and 3, each with multiplicity 1. The end behavior is fx as x and fx as , x so the leading coefficient is –1. The polynomial with smallest possible degree is
113.xxx
57. The least possible degree is 3.The zeros are –3 (multiplicity 1) and 2 (multiplicity 2). The end behavior is fx as x and fx as , x so the leading coefficient is 1. The polynomial with smallest possible degree is 2 32.xx
58. The least possible degree is 3.The zeros are –1 (multiplicity 2) and 2 (multiplicity 1). The end behavior is fx as x and fx as , x so the leading coefficient is –1. The polynomial with smallest possible degree is 2 12.xx
59. The least possible degree is 4. The zeros are –1 (multiplicity 2) and 2 (multiplicity 2). The end behavior is fx as x and fx as , x so the leading coefficient is 1. The polynomial with smallest possible degree is 22 12.xx
60. The least possible degree is 4. The zeros are –2 (multiplicity 2) and 2 (multiplicity 2). The end behavior is fx as x and fx as , x so the leading coefficient is –1. The polynomial with smallest possible degree is 22 22.xx
61. The zeros are –2 (multiplicity 2), 2 (multiplicity 1), and 3 (multiplicity 1), so the least possible degree is 4. The end behavior is fx as
x and fx as , x so the leading coefficient is 1. The polynomial with smallest possible degree is 2 223.xxx
62. The zeros are –3 (multiplicity 1), 0 (multiplicity 2), and 2 (multiplicity 1), so the least possible degree is 4. The end behavior is fx as
2 12fxxxx
2 32.xxx
x and fx as , x so the leading coefficient is –1. The polynomial with smallest possible degree is
For exercises 63–74, use the procedure shown on pages 163–164 of the text to graph the function. 63.
2124fxxxx
2322fxxx
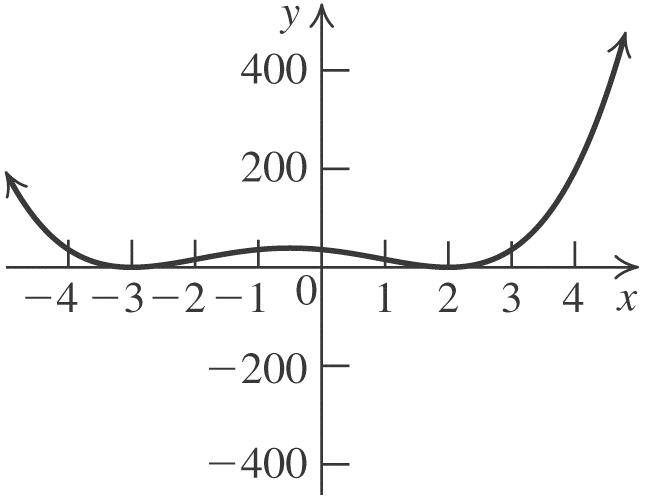
23 123fxxxx
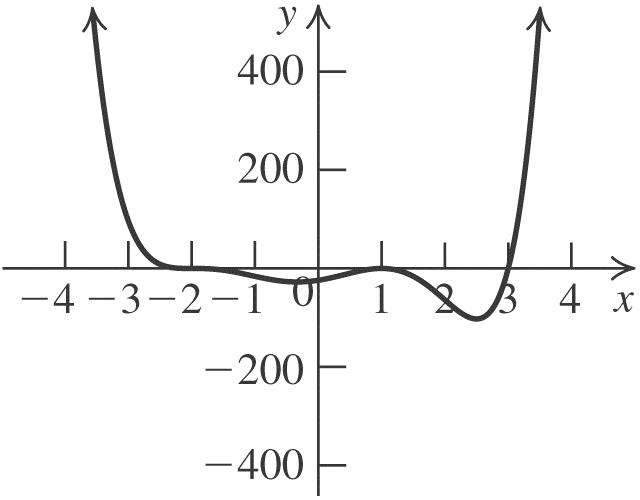
32 113fxxxx
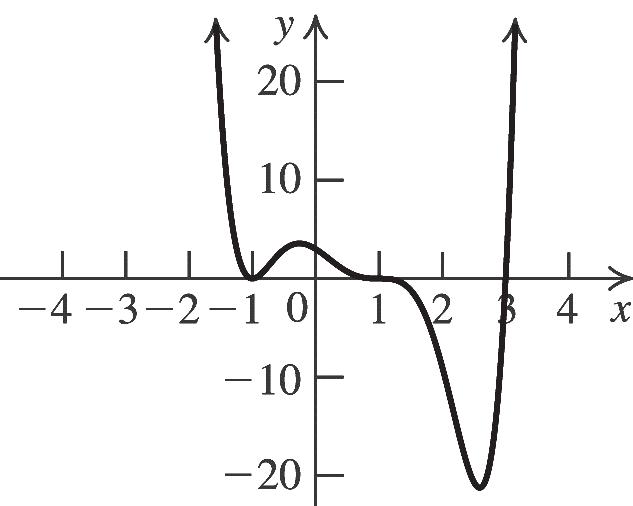
22 11fxxxx
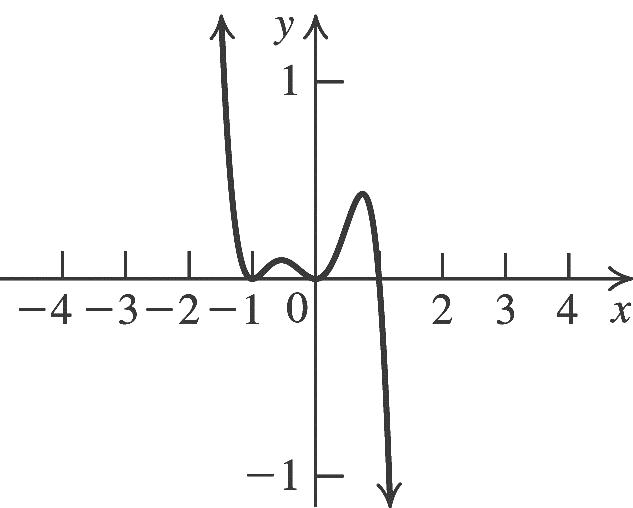
22 42fxxxx
22 12
2 2 92fxxxx
Applying the Concepts
75. a. 3 0.04825 404.14 hp 746 P
b. 3 0.04825 6517.76 hp 746 P
c. 3 0.04825 8033.12 hp 746 P d.
76. a. 4 128001.75120,050J
It reduced
77. a. 2 3(4)00 or 4. xxxx x = 0, multiplicity 2; x = 4, multiplicity 1.
b.
c. There are 2 turning points.
d. Domain: [0, 4]. The portion between the x-intercepts is the graph of R(x).
78.
R(x) is a maximum at x ≈ 2.67.
79. a. Domain [0, 1]
b.
80.
v is a maximum when r ≈ 0.67.
81. a. 2 3 ()272730090,000 xx Rxxx
b. The domain of R(x) is the same as the domain of p 0 p when 9003. p
The domain is 0,9003.
c.
82. a.
About 900 pairs of slacks were sold.
b. $16,200
83. a. 2 ()124002 Nxxx
b. The low end of the domain is 0. (There cannot be fewer than 0 workers.) The upper end of the domain is the value where productivity is 0, so solve N(x) = 0 to find the upper end of the domain. 2 22 (12)(4002)012 (reject this) or 40020200 xxx xx
102 (reject the negative solution). x The domain is [0,102].
c.
84. a.
The maximum number of oranges that can be picked per hour is about 5950.
b. The number of employees = 12 + 5 = 17.
85. a. ()(82)(152) Vxxxx
b.
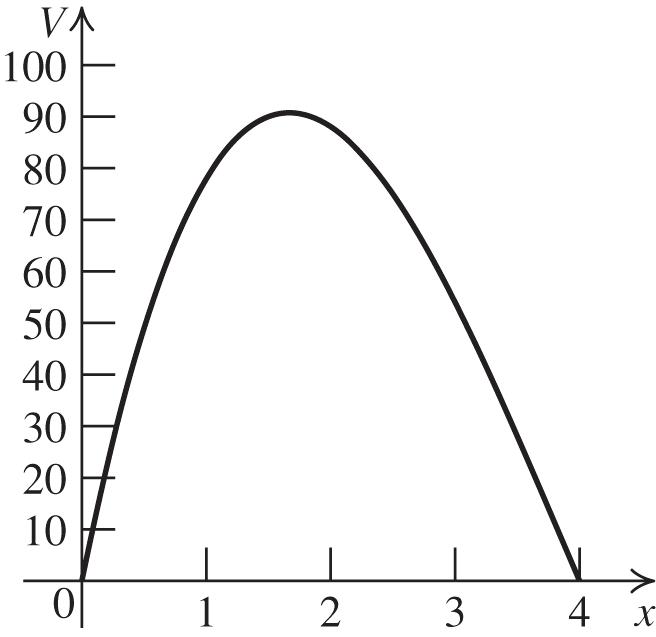
Copyright © 2018 Pearson Education Inc.
86.
The largest possible value of the volume of the box is 90.74 cubic units.
87. a. 2 ()(1084) Vxxx b.
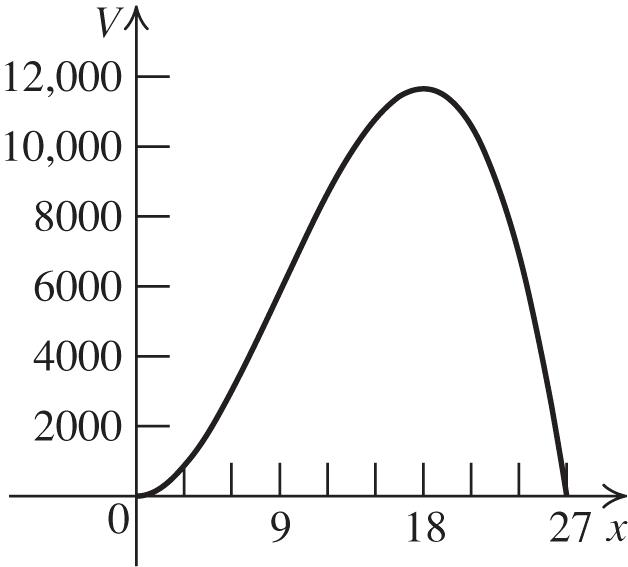
88.
The largest possible volume of the box is 11,664 cubic inches.
89. a. 2 ()(622) Vxxx b.
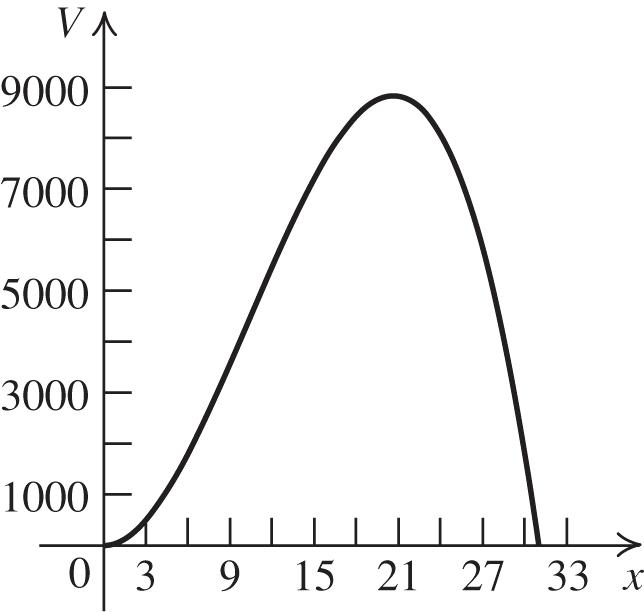
90.
The volume is greatest when x ≈ 20.67, so the dimensions of the suitcase with the largest volume are approximately 20.67 in. × 20.67 in. × 20.67 in.
91. a. 2 ()2(453) Vxxx
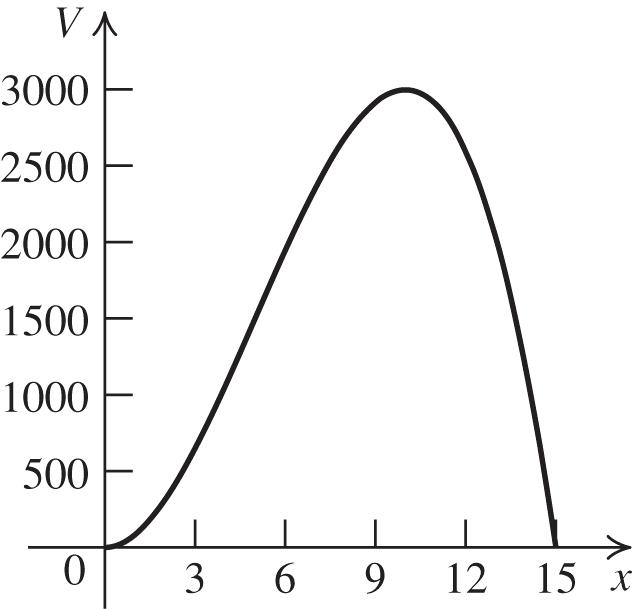
The volume is greatest when x = 10, so the width of the bag is 10 inches, the length is 2(10) = 20 inches, and the height is 45 – 20 – 10 = 15 inches.
A worker is most efficient approximately five hours after 6:00 a.m. or 11:00 a.m. 95. 0.9630.880.1920.011723 fxxxx
a. The year 2015 is represented by x = 7.
71.73 trillion f
[–2, 12] by [–2, 2.5]
It appears that there is one zero and two turning points.
Copyright © 2018 Pearson Education Inc.
c.
[0, 8] by [–0.5, 2.5]
The maximum occurs at 3.27, x which is during 2011. This fits the original data.
96. 2 3 0.230.00810.0002 0.000002 fxxx x
a. The year 2025 is represented by x = 120.
1201.32 f
b.
[0, 120] by [–0.5, 1.5]
It appears that there is one zero and no turning points.
c.
[0, 8] by [–0.5, 2.5]
The zero occurs at 65, x which is the year 1970. This fits the original data.
Beyond the Basics
97. The graph of 4 ()(1)fxx is the graph of 4 yx shifted one unit right.
4 (1)01 xx . The zero is x = 1 with multiplicity 4.
98. The graph of 4 ()(1)fxx is the graph of 4 yx shifted one unit left and then reflected across the x-axis. 4 (1)01 xx . The zero is x = –1 with multiplicity 4.
99. The graph of 4 ()2fxx is the graph of 4 yx shifted two units up.
4 4 202.xx There are no zeros.
100. The graph of 4 ()81fxx is the graph of 4 yx shifted 81 units up.
4 4 81081.xx There are no zeros.
Copyright © 2018 Pearson Education Inc.
101. The graph of 4 ()(1)fxx is the graph of 4 yx shifted one unit right and then reflected across the x-axis. 4 (1)01. xx The zero is x = 1 with multiplicity 4.
102. The graph of 4 1 ()(1)8 2 fxx is the graph of 4 yx shifted one unit right, compressed vertically by a factor of 2, and then shifted eight units down. 4 1 (1)80 2 x
4 (1)16123 or 1. xxxx Both zeros have multiplicity 1.
103. The graph of 5 ()1fxx is the graph of 5 yx shifted one unit up. 5 10 x 5 11.xx The zero is –1 with multiplicity 1.
104. The graph of 5 ()(1)fxx is the graph of 5 yx shifted one unit right. 5 (1)0 x 1. x The zero is 1 with multiplicity 5.
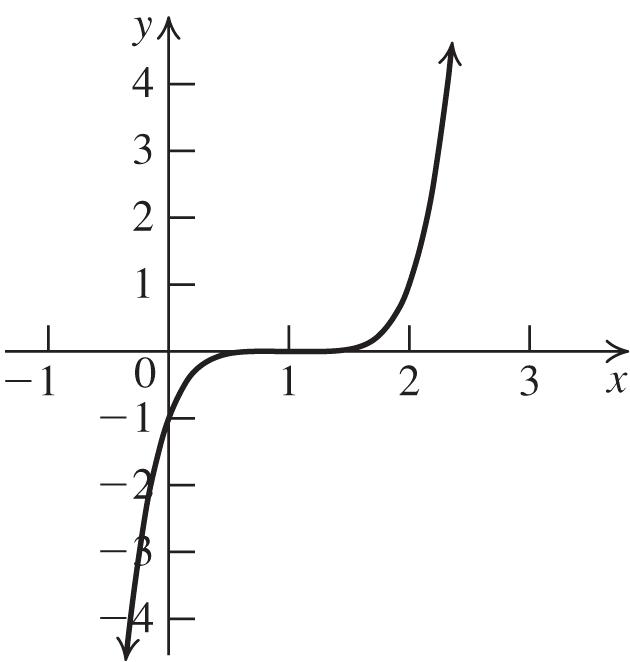
105. The graph of 5 (1) ()8 4 fxx is the graph of 5 yx shifted one unit left, compressed vertically by one-fourth, reflected in the x-axis, and then shifted up eight units.
55 (1)(1) 808 44 xx
5 (1)32121. xxx The zero is 1 with multiplicity 1.
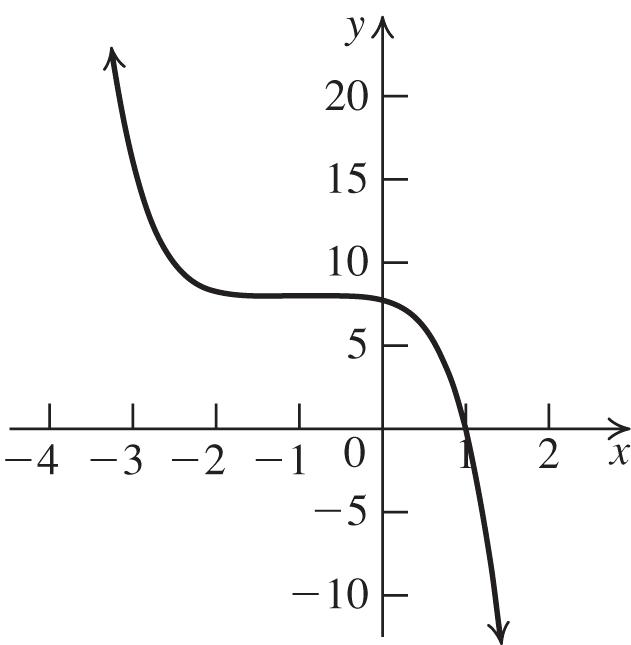
Copyright © 2018 Pearson Education Inc.
106. The graph of 5 (1) ()81 3 fxx is the graph of 5 yx shifted one unit left, compressed vertically by one-third, and then shifted up 81 units. 55 (1)(1) 81081 33 xx
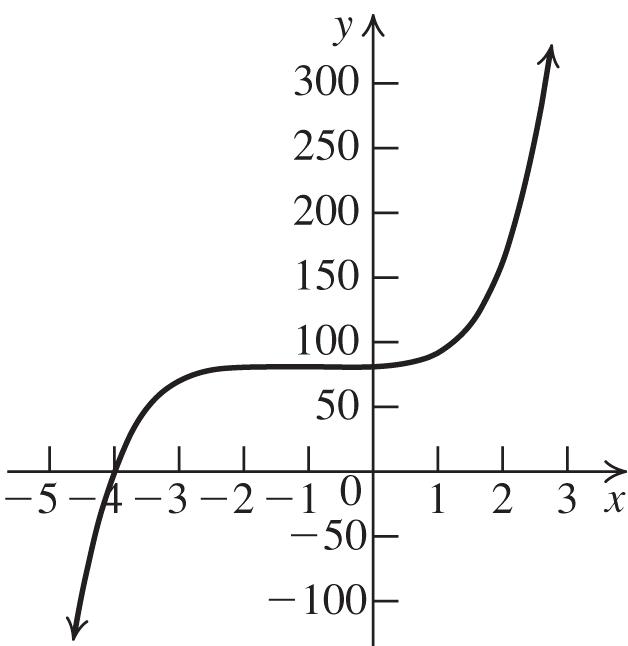
5 (1)243134. xxx The zero is –4 with multiplicity 1.
107. If 0 < x < 1, then 2 1. x Multiplying both sides of the inequality by 2 x , we obtain 42 xx Thus, 42 0. xx
108. If x > 1, then 2 1. x Multiplying both sides of the inequality by 2 x , we obtain 42 xx Thus, 42 1. xx
109.
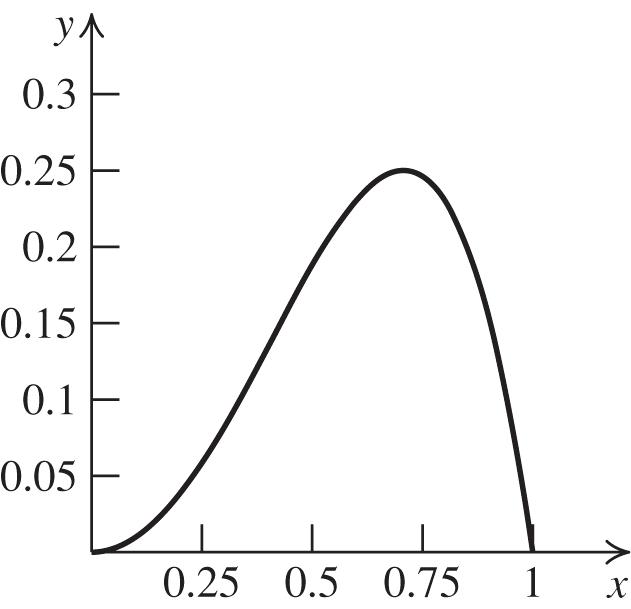
The graph of 24 yxx represents the difference between the two functions 2 yx and 4 , yx so the maximum distance between the graphs occurs at the local maximum of 24 yxx . The maximum vertical distance is 0.25. It occurs at x ≈ 0.71.

110. The graph of 35 yxx represents the difference between the two functions 3 yx and 5 , yx so the maximum distance between the graphs occurs at the local maximum of 35 yxx . The maximum vertical distance is 0.19. It occurs at x ≈ 0.77.
Answers will vary in exercises 111–114. Sample answers are given.
111. 2 ()(1)fxxx
112. ()(1)(1) fxxxx
113. 4 ()1 fxx
114. 2 ()(1)(1) fxxxx
115. The smallest possible degree is 5, because the graph has five x-intercepts and four turning points.
116. The smallest possible degree is 5, because the graph has four turns.
117. The smallest possible degree is 6, because the graph has five turning points.
118. The smallest possible degree is 6, because the graph has five turning points.
Copyright © 2018 Pearson Education Inc.
119. 4 101fxxx
For large values of x, 4 10.fxx For small values of x, 1. fxx
120. 3 1 fxxx
For large values of x, 3 fxx For small values of x, 1. fxx
121. 42 1 fxxx
For large values of x, 4 fxx For small values of x, 2 1. fxx
122. 32 1 fxxx
For large values of x, 3 . fxx For small values of x, 2 1. fxx
Critical Thinking/Discussion/Writing
123. If a human is scaled up by a factor of 20, then the total weight will increase 3 208000 times but the bone strength will increase only 2 20400 times. The bones would probably break under the increased weight.
124. If a human is scaled down by a factor of 70, then the body surface area will decrease 2 704900 times while the volume will decrease 3 70343,000 times. The body will rapidly lose heat and will have a very hard time maintaining body temperature unless its metabolic rate increases drastically.
125. It is not possible for a polynomial function to have no y-intercepts because the domain of any polynomial function is (,), which includes the point x = 0.
126. It is possible for a polynomial function to have no x-intercepts because the function can be shifted above the x-axis. An example is the function 2 1. yx
127. It is not possible for the graph of a polynomial function of degree 3 to have exactly one local maximum and no local minimum because the graph of a function of degree 3 rises in one direction and falls in the other. This requires an even number of turning points. Since the degree is 3, there can be only zero or two turning points. Therefore, if there is a local maximum, there must also be another turning point, which will be a local minimum.
128. It is not possible for the graph of a polynomial function of degree 4 to have exactly one local maximum and exactly one local minimum because the graph rises in both directions or falls in both directions. This requires an odd number of turning points. Since the degree is 4, there can be only one or three turning points. If there were exactly one local maximum and exactly one local minimum, there would be two turning points.
129. If 1 110 mm mm Pxaxaxaxa and 1 110 , nn nn Qxbxbxbxb
PQxabxbxbxbabxbxbxb abxbxbxba
1 11 1101110 1 11100 , mm nnnn mnnmnn nn nn
which is a polynomial of degree .mn
130. If 1 110 mm mm Pxaxaxaxa and
1 11 1101110 1 11100 , mm nnnn mnnmnn
Getting Ready for the Next Section
2.3 Dividing Polynomials and the Rational Zeros Test
2.3 Practice Problems 1. 232 32 2 2 34 01347 ()303 427 ()404 23 x xxxxx xxx xx xx x
Quotient: 3x + 4; remainder: 2x + 3
2. 32705 639 2134
The quotient is 2 23, xx remainder 4 or 2 4 23. 3 xx x
3. 321187 6219 2732
The quotient is 2 273, xx remainder 2.
4. 11057 112151254 F
, so the remainder when 1105725Fxxx is divided by x 1 is 4.
5. 21010220 242852 12142632
The remainder is 32, so (2)32. f
6. Since 2 is a zero of the function 32 32012, xxxx + 2 is a factor. Use synthetic division to find the depressed equation. 2312012 61412 3760
Thus,
322 320122376 xxxxxx
Now solve 2 3760 xx to find the two remaining zeros:
2 37603320 2 30 or 3203 or 3 xxxx xxxx
The solution set is 2 2,,3. 3
7.
32 0.234.2550.34541.05 310310 103 Cxxxx CCxxQx CxxQx
So, 3 is zero of C(x) 10 = 32 0.234.2550.34531.05 xxx
We need to find another positive zero of C(x) 10. Use synthetic division to find the depressed equation.
30.234.2550.34531.05
0.6910.69531.05
0.233.56510.350
Solve the depressed equation 2 0.233.56510.350 xx using the quadratic formula: 2 3.565(3.565)4(0.23)(10.35) 2(0.23) 18 or2.5 x
The positive zero is 18. Check by verifying that C(18) = 10.
8. The factors of the constant term, 8, are 1,2,4,8 , and the factors of the leading coefficient, 2, are 1,2 . The possible rational zeros are 1 ,1,2,4,8. 2 Use synthetic division to find one rational root: 22368 428 2140
The remainder is 0, so 2 is a zero of the function. 322 2368224 xxxxxx
Now find the zeros of 2 24 xx using the quadratic formula: 2 1(1)4(2)(4) 133 2(1)2 x , which are not rational roots. The only rational zero is { 2}.
9.
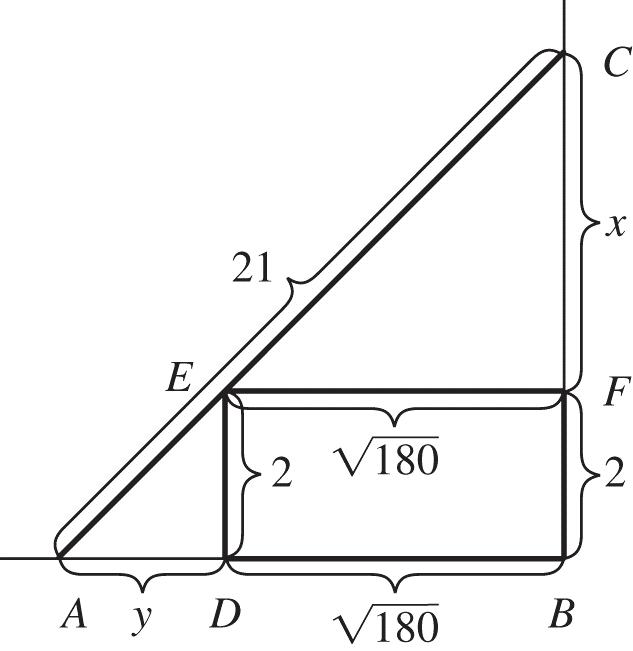
From the similar right triangles EFC and , ABC we have 180180 , 2 y xx or 2 180180. x y x
Using the Pythagorean theorem in right triangle ABC gives 2 2 2 218021.xy Now substitute.
2 2 2 2 218021. x x x
Multiply both sides by 2 x to eliminate the fraction.
2 2 222 2180221 xxxx Now expand and simplify. 2222 43222 432 4418044441 44180720720441 42577207200 xxxxxx xxxxxx xxxxPx
(continuedonnextpage)
Copyright © 2018 Pearson Education Inc.
(continued)
Use the factorization of 42 720235 to check for all possible rational zeros of the polynomial.
1,2,3,4,5,6,8,9,10, 12,15,18,20,24,30,36, 40,48,60,72,80,90,120, 144,180,240,360,720
We know that x must be a positive number less than 21 Using synthetic division, we see that x = 4 is a zero of . Px 414257720720 432900720 182251800
So, the remainder is
328225180.Qxxxx
Using synthetic division again, we see that x = 12 is another zero. 1218225180 12240180 120150
There are no other real zeros.
432 2 4257720720 4122015 Pxxxxx xxxx
Since the height = x + 2, the top of the ladder touches the wall at either 6 feet above the ground or 14 feet above the ground.
2.3 Exercises Concepts and Vocabulary
1. Consider the equation 3235145. xxxxx If both sides are divided by 2 1, x then the dividend is 3 35,xx the divisor is 2 1, x the quotient is ,x and the remainder is 45. x
2. Consider the division 2 4 12 226.xx xx x The dividend is 2 4,xx the divisor is 2, x the quotient is 6, x and the remainder is 12.
3. The Remainder Theorem states that if a polynomial ()Fx is divided by () xa , then the remainder R = F(a).
4. The Factor Theorem states that () xa is a factor of a polynomial ()Fx if and only if F(a) = 0.
5. True
6. True
7. False. The possible rational zeros of 32 991Pxxxx are 11 93,,1.
8. False. The remainder is a constant.
Building Skills
9. 2 2 32 2162 (63) 42 (42) 0 x xxx xx x x
10. 2 32 32 2 2 7 22 2 23423 (46) 4 (46) 73 21 7 2 15 2 xx xxxx xx xx xx x x
In exercises 9–14, insert zero coefficients for missing terms.
11. 32 432 43 32 32 2 2 3336 130637 (33) 36 (33) 33 (33) 67 (66) 13 xxx xxxxx xx xx xx xx xx x x
Copyright © 2018 Pearson Education Inc.
12.
13.
14.
15.
16. First, arrange the terms in order of descending powers. 2 2432 432 32 32 2 2 232 356111310 (6210) 9913 (9315) 6210 (6210) 0 xx xxxxxx xxx
17. 11172 107 1075
The quotient is 2 7 x and the remainder is 5. 18. 22312 41426 271324
The quotient is 2 2713 xx and the remainder is 24.
19. 214710 2422 121112
The quotient is 2 211xx and the remainder is 12.
20. 311132 3123 1411
The quotient is 2 41xx and the remainder is 1.
21. 213245 2208 110413
The quotient is 32 4 xx and the remainder is 13.
22. 1153010 1477 14773
The quotient is 32477 xxx and the remainder is 3.
23. 51 24 13 24 1 2431 2 1 25
The quotient is 2 1 25 2 xx and the remainder is 3 4
24. 4 3 7 3 1 3811 3 13 394
The quotient is 2 394 xx and the remainder is 7 3 .
25. 1 2532 2 133 2661
The quotient is 2 266 xx and the remainder is 1.
26. 1 3282 3 113 3391
The quotient is 2 339 xx and the remainder is 1.
27. a. 11301 144 1445
The remainder is 5, so (1)5. f b. 11301 122 1223
The remainder is 3, so (1)3. f
c. 1 1301 2 177 248 7715 1 248
The remainder is 15 8 , so 115 28 f
d. 101301 101301300 1131301301
The remainder is 1301, so (10)1301. f
28. a. 22301 41428 271427
The remainder is –27, so (2)27. f
b. 12301 255 2554
The remainder is –4, so (1)4. f
c. 1 2301 2 121 2420
The remainder is 0, so 1 0. 2 f
d. 72301 1477539 21177540
The remainder is 540, so (7)540. f
29. a. 1153020 1633 163317
The remainder is –17, so (1)17. f
b. 1153020 1477 147727
The remainder is –27, so (1)27. f
c. 2153020 261836 1391856
The remainder is –56, so (2)56. f
d. 2153020 2142244 17112224
The remainder is 24, so (2)24. f
30. a. 0.110.50.3020 0.10.060.0240.0024 10.60.240.02420.0024
The remainder is –20.0024, so (0.1)20.0024. f
Copyright © 2018 Pearson Education Inc.
b. 0.510.50.3020
0.50.50.10.05
11.00.20.119.95
The remainder is –19.95, so (0.5)19.95. f
c. 1.710.50.3020
1.73.745.8489.9416
12.23.445.84810.0584
The remainder is 10.0584 , so (1.7)10.0584. f
d. 2.310.50.3020
2.34.148.83220.3136
11.83.848.8320.3136
The remainder is 0.3136 , so (2.3)0.3136. f
31. 32 (1)2(1)3(1)6(1)10 f 1 x is a factor of 32 2361. xxx Check as follows: 12361 251 2510
32. 32 (3)3(3)9(3)4(3)1203 fx is a factor of 32 39412. xxx Check as follows: 339412 9012 3040
33. 432 (1)5(1)8(1)(1) f 2(1)40
1 x is a factor of 432 5824. xxxx Check as follows: 158124 5324 53240
34. 432 (3)3(3)9(3)4(3) f 9(3)90
3 x is a factor of 432 39499. xxxx Check as follows: 339499 90129 30430
35. 432 (2)22221802 fx is a factor of 432 18. xxxx Check as follows: 2111118 261018 13590
36. 542 (3)(3)3(3)(3) f 8(3)150
3 x is a factor of 5423815. xxxx Check as follows: 31301815 300315 100150
37. 6543 (2)(2)(2)7(2)(2) f 2 8(2)5(2)20
2 x is a factor of 654327852. xxxxxx Check as follows: 21171852 262642 1313210
38. 6543 (2)2(2)5(2)4(2)(2) f 2 7(2)7(2)20
2 x is a factor of 65432 254772. xxxxxx Check as follows: 22541772 4241062 2125310
39. 32 (1)0(1)3(1)(1) 011 fk kk
40. 32 (1)014(1)(1)210 1 fkk k
41. 32 (2)02(2)(2)22 14207 fkk kk
42. 22 2 (1)03(1)2(1)6 560(3)(2)0 3 or 2 fkkk kkkk kk
In exercises 43–46, use synthetic division to find the remainder.
43. 22449 408 2041
The remainder is 1, so 2 x is not a factor of 32 2449. xxx
Copyright © 2018 Pearson Education Inc.
44. 339512 9015 3053
The remainder is –3, so 3 x is not a factor of 32 39512. xxx
45. 249314 8222 41116
The remainder is 6, so 2 x is not a factor of 432 4934. xxxx
46. 338573 932493 3183190
The remainder is 90, so 3 x is not a factor of 432 38573. xxxx
47. The factors of the constant term, 5, are 1,5 , and the factors of the leading coefficient, 3, are 1,3 . The possible rational zeros are 15 33,1,,5.
48. The factors of the constant term, 1, are 1 , and the factors of the leading coefficient, 2, are 1,2 . The possible rational zeros are 1 ,1. 2
49. The factors of the constant term, 6, are 1,2,3,6 , and the factors of the leading coefficient, 4, are 1,2,4 .The possible rational zeros are 1133 ,,,1,, 4242 2,3,6.
50. The factors of the constant term, –35, are 1,5,7 , and the factors of the leading coefficient, 6, are 1,2,3,6 . The possible rational zeros are 11553515 ,,1,,,5,7,,,, 6232236 7773535 ,,,,,35. 63263
51. The factors of the constant term, 4, are 1,2,4 , and the factors of the leading coefficient, 1, are 1 . The possible rational zeros are 1,2,4 . Use synthetic division to find one rational root: 11144
104 1040
So, 32244(1)(4) (1)(2)(2) xxxxx xxx the rational zeros are {–2, 1, 2}.
52. The factors of the constant term, 2, are 1,2 , and the factors of the leading coefficient, 1, are 1 . The possible rational zeros are 1,2 . Use synthetic division to find one rational root: 11122 102 1020
So, 32222(1)(2) xxxxx the rational zero is {–1}.
53. The factors of the constant term, 6, are 1,2,3,6 , and the factors of the leading coefficient, 1, are 1 . The possible rational zeros are 1,2,3,6 . Use synthetic division to find one rational root: 11416 156 1560
So, 32246(1)(56) (1)(2)(3) xxxxxx xxx
the rational zeros are {–1, 2, 3}.
54. The factors of the constant term, 6, are 1,2,3,6 , and the factors of the leading coefficient, 1, are 1 . The possible rational zeros are 1,2,3,6 . Use synthetic division to find one rational root: 31326 306 1020
So, 322326(3)(2) xxxxx the rational zero is {–3}.
Copyright © 2018 Pearson Education Inc.
55. The factors of the constant term, 6, are 1,2,3,6 , and the factors of the leading coefficient, 2, are 1,2 . The possible rational zeros are 13 22,1,,2,3,6
Use synthetic division to find one rational root: 221136 4106 2530
322 2136(2)(253) (2)(3)(21) xxxxxx xxx the rational zeros are 1 3,,2 2
56. The factors of the constant term, –2, are 1,2 , and the factors of the leading coefficient, 3, are 1,3 . The possible rational zeros are 12 33,,1,2 . Use synthetic division to find one rational root: 2 3232 3 202 3030
322 2 3232(33) 3 xxxxx
the rational zero is 2 3
57. The factors of the constant term, –2, are 1,2 , and the factors of the leading coefficient, 6, are 1,2,3,6 . The possible rational zeros are 1112 6323,,,,1,2 . Use synthetic division to find one rational root: 261312 1222 6110
322 6132(2)(61) (2)(21)(31) xxxxxx xxx
the rational zeros are 11 2,,23
58. The factors of the constant term, 6, are 1,2,3,6 , and the factors of the leading coefficient, 2, are 1,2 . The possible rational zeros are 13 22,1,,2,3,6
Use synthetic division to find one rational root: 3 2346 2 306 2040
322 3 2346(24) 2 xxxxx
the rational zero is 3 2
59. The factors of the constant term, 2, are 1,2 , and the factors of the leading coefficient, 3, are 1,3 . The possible rational zeros are 12 33,,1,2
.
Use synthetic division to find one rational root: 1 3782 3 122 3660
322 1 3782(366) 3 xxxxxx
the rational zero is 1 3
60. The factors of the constant term, 4, are 1,2,4 , and the factors of the leading coefficient, 2, are 1,2 . The possible rational zeros are 1 ,1,2,4 2 . Use synthetic division to find one rational root. 1 2184 2 104 2080
322 1 284(28) 2 xxxxx
the rational zero is 1 2
Copyright © 2018 Pearson Education Inc.
61. The factors of the constant term, –2, are 1,2 , and the factors of the leading coefficient, 1, are 1 . The possible rational zeros are 1,2 . Use synthetic division to find one rational root: 111112 1212 12120
So, –1 is a rational zero. Use synthetic division again to find another rational zero:.
432322(1)(22) xxxxxxxx 21212 202 1010 43222(1)(2)(1) xxxxxxx
the rational zeros are {–1, 2}.
62. The factors of the constant term, –4, are 1,2,4 , and the factors of the leading coefficient, 2, are 1,2 . The possible rational zeros are 1 ,1,2,4
. Use synthetic division to find one rational root: 123834 2174 21740
So, –1 is a rational zero. Use synthetic division again to find another rational zero:
63. The factors of the constant term, 12, are 1,2,3,4,6,12 , and the factors of the leading coefficient, 1, are 1 . The possible rational zeros are 1,2,3,4,6,12 . Use synthetic division to find one rational root: 31113112 312312 14140
So, –3 is a rational zero. Use synthetic division again to find another rational zero: 432 32 1312 (3)(44) xxxx xxxx 11414 154 1540
So, –1 is also a rational zero. 432 2 1312 (3)(1)(54) (3)(1)(4)(1) xxxx xxxx xxxx
the rational zeros are {–3, –1, 1, 4}.
64. The factors of the constant term, –2, are 1,2 , and the factors of the leading coefficient, 3, are 1,3. The possible rational zeros are 12 33,,1,2 . Use synthetic division to find one rational root: 235152 6262 31310
So, –2 is a rational zero. Use synthetic division again to find another rational zero: 432 32 3552 (2)(331) xxxx xxxx
1 3131 3 101 3030 432 2 2 3552 1 (2)(33) 3 1 3(2)(1) 3 xxxx xxx xxx
the rational zeros are 1 2, 3
.
65. The factors of the constant term, 1, are 1 , and the factors of the leading coefficient, 1, are 1 . The possible rational zeros are 1 . Use synthetic division to find one rational root: 1121011 1198 11989
The remainder is 9 so, 1 is not a rational zero. Try 1: 1121011 131314 13131415
The remainder is 15 so, 1 is not a rational zero. Therefore, there are no rational zeros.
66. The factors of the constant term, 2, are 1,2 , and the factors of the leading coefficient, 1, are 1 .The possible rational zeros are 1,2 . Testing each value (2), f (1),(1),(2)fff shows that none cause the value of the function to equal zero, so there are no rational zeros.
67. 32582fxxxx
The possible rational zeros are 1,2. 11582 162 1620
So, 1 is a zero. Now solve the depressed equation 2 620.xx
636412 644
The solution set is 1,311.
68. 32753fxxxx
The possible rational zeros are 1,3. 11753 183 1830
So, 1 is a zero. Now solve the depressed equation 2 830.xx
864413 852 212 413 x
The solution set is 1,413.
69. 43331fxxxx
The possible rational zeros are 1. 113031 1221 12210
So, 1 is a zero. Now find a zero of the depressed equation 32221.gxxxx 11221 131 1310
So, 1 is a zero. Now solve the depressed equation 2 310xx
39411 35 212 x
The solution set is 35 1,. 2
70. 432675418fxxxxx
The possible rational zeros are 1,2,3,6,9,18. 31675418 394818 131660
So, 3 is a zero. Now find a zero of the depressed equation 323166.gxxxx 313166 3186 1620
So, 3 is a zero. Now solve the depressed equation 2 620xx
636412 628 37 212 x
The solution set is 3,37.
Copyright © 2018 Pearson Education Inc.
71. 32 2961fxxxx
The function has degree 3, so there are three zeros, one or three possible positive zeros; no possible negative zeros.
The possible rational zeros are 1 1,. 2
1 2961 2 141 2820
So, 12 is a zero. Now solve the depressed equation 2 2820 xx
2 88422 848 224 23 x
Solution set: 1 23,,23. 2
72. 32 2341fxxxx
The function has degree 3, so there are three zeros, one possible positive zero; zero or two possible negative zeros.
The possible rational zeros are 1
So, 12 is a zero. Now solve the depressed equation 2 2420 xx
Solution set: 1 12,,12. 2
73. 432536fxxxxx
The function has degree 4, so there are four zeros, zero or two possible positive zeros; zero or two possible negative zeros. The possible rational zeros are
111536 1236 12360
So, 1 is a zero. Now find a zero of the depressed equation 322360. xxx 21236 206 1030
So, 2 is a zero. Now solve the depressed equation 2 30. x
223033 xxx
Solution set: 2,3,1,3
74. 4322546fxxxxx
The function has degree 4, so there are four zeros, zero or two possible positive real zeros; zero or two possible negative real zeros. The possible rational zeros are 1,2,3,6. 312546 3366 11220
So, 3 is a zero. Now find a zero of the depressed equation 32 220.xxx 11122 102 1020
So, 1 is a zero. Now solve the depressed equation 2 20. x 222022 xxx
Solution set: 2,1,2,3
75. 32 252fxxxx
The possible rational zeros are 1 2 ,1,2.
Using synthetic division, we find that x = 1 is a zero. 12512 232 2320
Now factor 2 232.Qxxx 2 232212 xxxx
So, the complete factorization of Px is
1212.xxx
76. 32 243fxxxx
The possible rational zeros are 3 1 22,,1,3.
Using synthetic division, we find that x = –1 is a zero.
12143 213 2130
Now factor 2 23.Qxxx
2 23231 xxxx
So, the complete factorization of Px is 2 123.xx
77. 32 231730fxxxx
The possible rational zeros are 35 1 222 1,2,3,5,6,,,.
Using synthetic division, we find that x = –2 is a zero.
2231730 4230 21150
Now factor 2 215.Qxxx
2 215253 xxxx
So, the complete factorization of Px is
2253.xxx
78. 32 232312fxxxx
The possible rational zeros are 3 1 22 1,2,3,4,6,12,,.
Using synthetic division, we find that x = 4 is a zero.
4232312 82012 2530
Now factor 2 253.Qxxx 2 253213 xxxx
So, the complete factorization of Px is
4213.xxx
79. 4329116fxxxxx
The possible rational zeros are 1,2,3,6.
Using synthetic division, we find that x = 2 is a zero.
2119116 22146 11730
So, 2 is a zero. Now find a zero of the depressed function 32 73.Qxxxx 31173 363 1210
So, 3 is a zero. Now find the zeros of the depressed function 2 21xx using the quadratic formula. 2 22411 28 212 222 12 2 x
So, the complete factorization of Px is
231212,xxxx or
231212.xxxx
80. 4326308fxxxxx
The possible rational zeros are 1,2,4,8.
Using synthetic division, we find that x = –2 is a zero.
2161308 216348 181740
So, –2 is a zero. Now find a zero of the depressed function 328174.Qxxxx 418174 4164 1410
So, 4 is a zero. Now find the zeros of the depressed function 2 41xx using the quadratic formula.
2 44411 412 212 423 23 2 x
So, the complete factorization of Px is
242323,xxxx or
242323.xxxx
Copyright © 2018 Pearson Education Inc.
For exercises 81–88, use synthetic division to find the zeros of each function and then use the methods shown in Section 2.2 to complete the graph.
81. 3221920fxxxx
Zeros: –5, –1, 4
82. 32 1424fxxxx
Zeros: –3, –2, 4
83. 32 1620fxxxx
Zeros: –2 (multiplicity 2), 5
84. 3221536fxxxx
Zeros: –3 (multiplicity 2), 4
85. 42222445fxxxx
Zeros: –3 (multiplicity 2), 1, 5
86. 4323135136fxxxxx
Zeros: –3 (multiplicity 2), –1, 4
87. 32 6132fxxxx
Zeros: 11 2,,23
88. 32 61710fxxxx
Zeros: 52 ,1, 23
Copyright © 2018 Pearson Education Inc.
Applying the Concepts
91. a.
4030004030000RR and
6030006030000.RR Thus, 40 and 60 are zeros of
3000. Rx Therefore,
2 30004060 1002400 Rxaxx axx Since (30, 2400) lies on R(x), we have
2400300030403060 60010302 a aa Thus 2 300024060 22004800 Rxxx xx
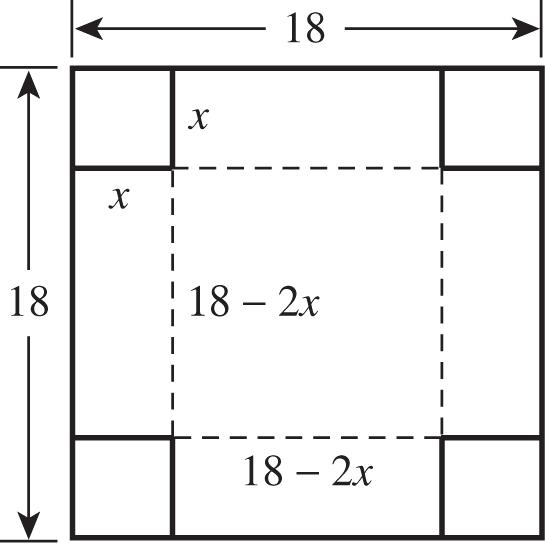
b. 2 2 300022004800 22001800 Rxxx Rxxx
c. The maximum weekly revenue occurs at the vertex of the function, 22,. bb R aa
The maximum revenue is $3200 if the phone is priced at $50.
92. a.
84725847250.RR and
1247251247250.RR Thus, 8 and 12 are zeros of 4725. Rx Therefore,
2 4725812 2096 Rxaxx axx Since (6, 4125) lies on R(x), we have
4125472568612 6002650 a aa Thus,
2 472550812 5010004800 Rxxx xx
b. 2 2 47255010004800 50100075 Rxxx Rxxx
c. The maximum weekly revenue occurs at the vertex of the function, 22,. bb R aa
2 1000 10 2 250 0501010001075 4925 b a R The maximum revenue is $4925 if tickets are priced at $10 each.
93. Since t = 11 represents 2002, we have (11)97.6()(11)()97.6 CCxxQx ()97.6(11)(). CttQt So
0.00060.06132.082982.904973232.60.00060.06132.082914.6960 (11)(). tttttt xQx
Use synthetic division to find Q(x):
110.00060.06132.082914.6960
0.00660.746914.6960
0.00060.06791.33600
Now solve the depressed equation to find another zero: 2 2 0.06790.06794(0.0006)(1.3360) 0.00060.06791.33600 2(0.0006)
0.06790.007816810.06790.0884 130.26 or 17.0939. 0.00120.0012
Since we must find t greater than 0, t = 17, and the year is 1991 + 17 = 2008.
94. Since t = 1 represents 1999, we have (1)737.7()(1)()737.7 ssttQt ()737.7(1)(). sttQt
So 3232 0.17792.829242.0240698.6831737.70.17792.829242.024039.0169 (1)() tttttt tQt
Use synthetic division to find Q(t): 10.17792.829242.024039.0169
0.17793.007139.0169
0.17793.007139.01690
Now solve the depressed equation to find another zero: 2 2 3.0071(3.0071)4(0.1779)(39.0169) 0.17793.007139.01690 2(0.1779) 3.007136.8071 25.5030 or 8.5997 0.3558
Since t must be positive, t ≈ 9, and the year is 1998 + 9 = 2007.
95. 32 0.00270.36815.8645195.2782Mtttt Since 2185.0, M
We must find two other zeros of 32 32 1850.00270.36815.8645195.2782185
ttt
0.00270.36815.864510.2782
Because 2 is a zero of F(t), use synthetic division to find Q(t). 20.00270.36815.864510.2782
0.00540.725410.2782
0.00270.36275.13910
Now use the quadratic formula to solve the depressed equation.
2 0.36270.362740.00275.1391 0.36270.0760 16.1 or 118 20.00270.0054 ttt
Thus, the model shows that the Marine Corps had about 186,000 when t ≈ 16, or in the year 1990 + 16 = 2006.
Copyright © 2018 Pearson Education Inc.
96.
We must find two other zeros of
FtUtttt ttt
0.03740.59342.05530.9522
Because 6 is a zero of F(t), use synthetic division to find Q(t).
60.03740.59342.05530.9522
0.22442.21400.9522
0.03740.36900.15870
Now use the quadratic formula to solve the depressed equation.
2 0.36900.369040.03740.1587 0.36900.1599 0.41 or 10.3 0.0748 20.0374 ttt
Reject the negative solution.
According to the model, there was a 7.7% unemployment level in 2002 + 10 = 2012.
97. Use synthetic division to solve the equation 32 62836108100 xxx 32 361085280. xxx The factors of the constant term, 528, are {1,2,3,4,6,8,11,48,66,88, 132,176,264,528}.
The factors of the leading coefficient, 3, are {1,3}. Only the positive, whole number possibilities make sense for the problem, so the possible rational zeros are {1, 2, 3, 4, 6, 8, 11, 16, 22, 44, 48, 66, 88, 132, 176, 264, 528}.
436108528 1224528 361320
Thus, x = 4.
98. The demand function is 2 ()33010 pxxx the revenue function is 23 33010. xxx
Profit = revenue – cost = 2332 910(33010)(36108100) xxxxxx 32 910416222100 xxx 32 04162221010. xxx The factors of the constant term, –1010, are {1,2,5,10,101,202,505,1010}. The factors of the leading coefficient, –4, are 1,2,4 .
Find the zero using synthetic division: 54162221010 20201010 442020
Thus, x = 5.
99. The cost function gives the result as a number of thousands, so set it equal to 125: 3215550125 xxx 32155750. xxx The factors of the constant term, –75, are {1,3,5,15, 25,75}. The factors of the leading coefficient, 1, are 1 . Only the positive solutions make sense for the problem, so the possible rational zeros are {1, 3, 5, 15, 25, 75}. Use synthetic division to find the zero: 15115575 15075 1050
The total monthly cost is $125,000 when 15 hundred (1500) units are produced.
100. The demand function is 74 ()33pxx x , so the revenue function is 2 ()3374.xpxxx
The break-even point occurs when revenue – cost = 0: 232 32 32 22 2 (3374)(15550)0 122240 (2)(1224)0 (2)12(2)0 (12)(2)0 12 xxxxx xxx xxx xxx xx x
So 1200 printers must be sold to break even.
101. Let x represent the edge of the taller box. Then x – 3 represents the edge of the shorter box. The volume of the taller box is 3 , x and the volume of the shorter box is 3 3. x We must solve 3 3 31843. xx
There are many possible rational zeros, so we start with an educated guess. The edge must be greater than 3 and less than 12. (Note that 3 121728, which is close to the total volume of the two boxes.) The possible rational zeros between 3 and 12 are 5, 10, 11, and 11 2 Using synthetic division, we find that 11 is a zero. 1129271870 221431870 2131700
Using the quadratic formula to find the zeros of 2 213170 xx , we have
2 131342170 131191 , 224 x
which is not a real number. Thus, there are no other real zeros. Therefore, the taller box has edge 11 inches and the shorter box has edge 11 – 3 = 8 inches.
102. Let x represent the width of the pool. Then the volume of the deep water section is 3 , x and the volume of the shallow water section is 3. x The total volume is 536 cubic meters, so we have 33353635360. xxxx
There are many possible rational zeros, so we start with an educated guess. The edge must be greater than 1 and less than 9. (Note that 3 9729, which is more the total volume of the pool.) The possible rational zeros between 1 and 8 are 2, 4, 8. Using synthetic division, we find that 8 is a zero.
8103536 864536 18670
Using the quadratic formula to find the zeros of 2 867xx , we have
2 884167 8204 , 212 x which is not a real number. Thus, there are no other real zeros.
Therefore, the dimensions of the deep water section are 8 m8 m8 m.
103. The length and width of the box are 18 – 2x, and the height is x, so the volume is 2 (182).xx
2 432(182) xx 32 432472324 xxx 32 4723244320. xxx
The factors of the constant term, 432, are {1,2,3,4,6,8,9,12, 16,18,24,27,36,48,54, 72,108,144,216,432}.
The factors of the leading coefficient, 4, are 1,2,4 . There are many possible rational zeros, but the only ones that make sense for the problem are 1133 4242,,,1,,2,3,4,6,8.
Use synthetic division to find the zero: 3472324432 12180432 4601440
The corners should be 3 inches by 3 inches.
Copyright © 2018 Pearson Education Inc.
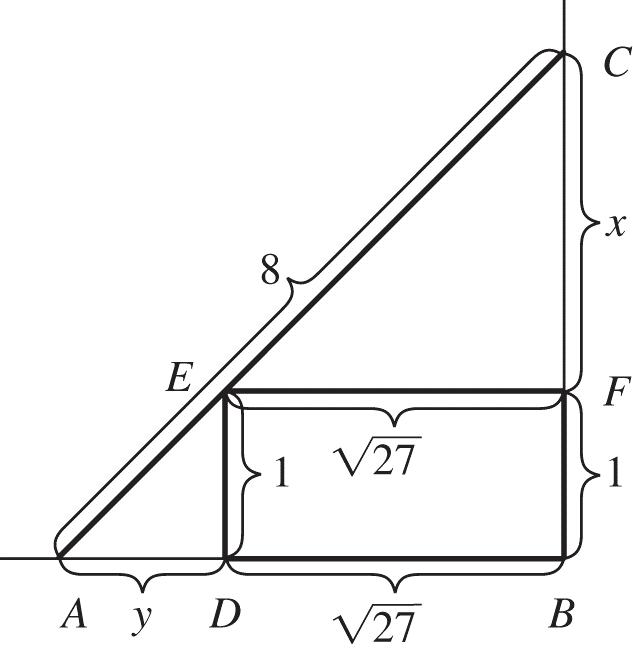
From the similar right triangles EFC and , ABC we have 2727 , 1 y xx or 1 2727. x y x
Using the Pythagorean theorem in right triangle
ABC gives 2 2 2 1278.xy
Now substitute.
2 2 2 1 1278. x x x
Multiply both sides by 2 x to eliminate the fraction.
2 2 222 12718 xxxx
Now expand and simplify.
2222 43222 432 21272164 227542764 23654270 xxxxxx xxxxxx xxxxPx
The possible rational zeros of the polynomial are 1,3,9,27.
We know that x must be a positive number less than 8 Using synthetic division, we see that x = 3 is a zero of . Px 312365427 3156327 152190
So, the remainder is 325219.Qxxxx
There are no other real zeros.
432 32 2365427 35219 Pxxxxx xxxx
The possible rational zeros of Qx are 1,3,9. Using synthetic division, we see that x = 3 is a zero of . Qx 315219 3249 1830
Thus, 432 2 2 2365427 383 Pxxxxx xxx
Since the height = x + 1, the top of the ladder touches the wall at 3 + 1 = 4 feet above the ground.
Beyond the Basics
105. Divide 32 48113 xxx by 1 : 2 x
1248113 253 41060
Now divide 2 4106 xx by 1 : 2 x
124106 26 4120
Since 1 2 x does not divide 412 x , 1 2 x
is a root of multiplicity 2 of 32 48113 xxx
106. Divide 32 9384 xxx by 2 : 3 x
239384 624 9360
Now divide 2 936 xx by 2 : 3 x
23936 66 990
Since 2 3 x does not divide 9x – 9, 2 3 x
is a root of multiplicity 2 of 32 9384 xxx
107. Let x represent b. Then we can use synthetic division to divide 33 xa by x – a. 3 23 2 100 10 aa aaa aa
Then 3322 xaxaxaxa or 3322 . babababa
Copyright © 2018 Pearson Education Inc.
108. Let x represent b. Then we can use synthetic division to divide 44 xa by x – a. 4
109. If 2 1 x is a factor of 10 4, xax then so are x – 1 and x + 1. Use synthetic division to show that one or the other is not a factor.
Now see if x + 1 is a factor of
x + 1 is not a factor, so there is no real number a such that 2 1 x is a factor of 10 4. xax
110. If 22ba divides 22 , nnba then b – a and b + a, must divide 22nnba Let x represent b. Then we can use synthetic division to divide 22nn xa by x – a and by x + a
Thus, 22ba divides 22nnba
The
113. 43213 2220 22 xxxx
432 44430. xxxx The factors of the constant term, –3, are 1,3. The factors of the leading coefficient are 1,2,4 . So, the possible rational zeros are 1133 ,,,1,,3. 4242
Use synthetic division to find one zero:
So, 1 2 is a rational zero and
3 2 x is another rational zero.
114. i. Simplifying the fraction if necessary, we can assume that p q is in lowest terms. Since p q is a zero of F, we have 0. Fp q
ii. Substitute p q for x in the equation ()0.Fx
iii. Multiply the equation in (ii) by . n q
iv. Subtract 0 n aq from both sides of the equation.
v. The left side of the equation in (iv) is
11 11 121 11 nnn nn nnn nn apapqapq papapqaq Therefore p is a factor.
vi. ab ab pp
vii. Since p and q have no common prime factors, p must be a factor of 0 . a
viii. Rearrange the terms of the equation in (iii).
ix. The left side of the equation in (viii) is
11 110 121 110 nnn n nnn n apqapqaq qapapqaq
Therefore q is a factor.
x. . ab ab qq
xi. Since p and q have no common prime factors, q must be a factor of n a
Critical Thinking/Discussion/Writing
115. 3 2 fxxcx
Possible rational zeros are 1,2.
Use synthetic division to see which zeros lead to an integer value of c. 1102 111 1110 c c c
2101 cc 1102 111 1110 c c c
2103 cc 2102 2428 1240 c c c
22805 cc 2102 2428 1240 c c c
22803 cc
The values of c for which 3 2 fxxcx has at least one rational zero are –1, 3, and 5.
116. 3 6 fxxcx
Possible rational zeros are 1,2,3,6.
Use synthetic division to see which zeros lead to an integer value of c. 1106 111 1110 c c c
6107 cc (continuedonnextpage)
(continued) 1106 111 1110 c
6106 6366216 16360 c
66216035 cc 6106 6366216 16360 c c c
66216037 cc
The values of c for which 3 6 fxxcx has at least one rational zero are –5, 1, 7, 11, 35, and 37.
117. Let 22 3330.xxx The only possible rational zeros of this equation are 1 and 3 . Because 3 is neither of these, it must be irrational.
118. 3 3333 4440.xxx
The only possible rational zeros of this equation are 1,2,4 . Since 3 4 is not in the set, it must be irrational.
119. 2 3232962 xxxx 2 670.xx The possible rational zeros of this equation are 1,7 . Since 32 is not in the set, it must be irrational.
120. 3 2/332/33 99810.xxx The possible rational zeros of this equation are {1,3,9,27, 81}. Since 23 9 is not in the set, it must be irrational.
121. a. xa is a factor of nn xa if n is an odd integer. The possible rational zeros of nn xa are 23 {,,,,}. n aaaa Since xa is a factor means that –a is a root, then ()0()nnnn aaaa only for odd values of n.
b. xa is a factor of nn xa if n is an even integer. The possible rational zeros of nn xa are 23 {,,,,}. n aaaa Since xa is a factor means that –a is a root, then ()0()nnnn aaaa only for even values of n.
c. There is no value of n for which xa is a factor of nn xa . The possible rational zeros of nn xa are 23 {,,,,}. n aaaa If xa is a factor, then a is a root, and 0 nnnn aaaa , which is not possible.
d. xa is a factor of nn xa for all positive integers n. The possible rational zeros of nn xa are 23 {,,,,}. n aaaa If xa is a factor, then a is a root, and 0 nn aa , which is true for all values of n. However, if n is negative, then 11 nn nn xa xa and xa is not a factor.
122. a. According to exercise 121d, xa is a factor of nn xa for any positive integer n. Using this result with x = 7, a = 2, and n = 11, we find that 7 – 2 = 5 is a factor of 1111 72. Therefore, 721111 is divisible by 5.
b. 202010101010 191019101910.
According to exercises 121b and 121d, xa is a factor of nn xa if n is an odd integer, and xa is a factor of nn xa for any positive integer n. Using these results with x = 19, a = 10, and n = 10, we find that 19 – 10 = 9 and 19 + 10 = 29 are both factors of 1010 1910, and therefore, 19102020 is divisible by 9 and 29. Since 9 and 29 have no common factors, 19102020 must be divisible by their product, 9(29) = 261.
Getting Ready for the Next Section
Rational Functions
Practice Problems 1. 2 3 () 45 fxx xx
The domain of f consists of all real numbers for which 2 450xx 2 450(5)(1)0 5 or 1 xxxx xx
Thus, the domain is (,1)(1,5)(5,)
2. a. 3 2 gx x Let 1 fx x Then 31 332. 22 gxfx xx
The graph of 2 yfx is the graph of yfx shifted two units to the right. This moves the vertical asymptote two units to the right. The graph of 32yfx is the graph of 2 yfx stretched vertically three units. The domain of g is ,22,. The range of g is ,00,. (continuedonnextpage)
Copyright © 2018 Pearson Education Inc.
(continued)
The vertical asymptote is x = 2. The horizontal asymptote is y = 0. b. 25 1 hxx x 2 125 22 3 xx x
253 2 11 hxx xx
1 fx x Then
253 2231. 11 x hxfx xx
The graph of yhx is the graph of
yfx shifted one units to the left and then stretched vertically three units. The graph is then shifted two units up. This moves the vertical asymptote one unit to the left. The horizontal asymptote is shifted two units up. The domain of h is
,11,. The range of h is
,22,. The vertical asymptote is x = 1. The horizontal asymptote is y = 2.
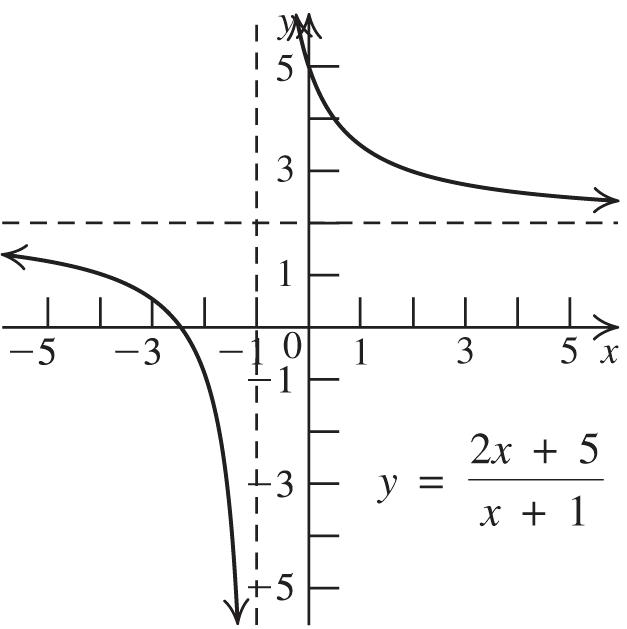
3. 2 1 () 310 fxx xx
The vertical asymptotes are located at the zeros of the denominator.
2 3100(5)(2)0 5 or 2 xxxx xx
The vertical asymptotes are x = 5 and x = 2.
4. 2 3(3)1 () (3)(3)3 9 303 fxxx xxxx xx
The vertical asymptote is x = 3.
5. a. 25 () 34fxx x
Since the numerator and denominator both have degree 1, the horizontal asymptote is 2 3 y
b. 2 3 () 1 x gx x
The degree of the numerator is greater than the degree of the denominator, so there are no horizontal asymptotes.
6. 2 2 () 1 fxx x
First find the intercepts: 2 2 00 1 x x x
The graph passes through the origin. Find the vertical asymptotes: 2 10(1)(1)0 1 or 1 xxx xx
Find the horizontal asymptote: The degree of the numerator is less than the degree of the denominator, so the horizontal asymptote is the x-axis.
Test for symmetry: 22 2()2 ()() ()11 fxxxfx xx
f is an odd function and is symmetric with respect to the origin.
Use test numbers to determine where the graph of f is above and below the x-axis. (continuedonnextpage)
Copyright © 2018 Pearson Education Inc.
Interval
The zero of 2 Rxx is 2 and the zeros of 2 23231Dxxxxx are
2 x and x = 1.
Use test numbers to determine where the graph of f is above and below the horizontal asymptote y = 1.
Interval
7. 2 2 21 () 23 fxx xx
First find the intercepts: 2 2 212 0 2 23 x x xx ; 1 (0) 3 f
Find the vertical asymptotes: 2 230(23)(1)0 3 or 1 2 xxxx xx
Find the horizontal asymptote: The degree of the numerator is the same as the degree of the denominator, so the horizontal asymptote is 2 1 2 y
Test for symmetry: 22 2()121 () 2()()323 () and () fxxx xxxx fxfx
f is neither even nor odd, so there is no symmetry with respect to the y-axis or the origin.
Test point Value of
fx Above/below x-axis 3 , 2
Notice that the graph crosses the horizontal asymptote at (2, 1).
First find the intercepts:
x xi
there is no x-intercept.
Find the vertical asymptotes: 2 202xxi there is no vertical asymptote. Find the horizontal asymptote: The degree of the numerator is the same as the degree of the denominator, so the horizontal asymptote is 1 1 1 y
(continuedonnextpage)
(continued)
Test for symmetry: 22 22 ()11 ()() ()22 fxxxfx xx
f is an even function and is symmetric with respect to the y-axis.
2 22 11 1 22 fxx xx
Neither R(x) = 1 nor 2 2 Dxx have real zeros. Since 2 1 2 x is negative for all values of x, the graph of fx is always below the line y = 1.
9. 2 2 () 1 fxx x
First find the intercepts: 2 2 02 1 x xi x there is no x-intercept. (0)2 f
Find the vertical asymptotes: 101xx
Find the horizontal asymptote: The degree of the numerator is greater than the degree of the denominator, so there is no horizontal asymptote. However, there is an oblique asymptote: 2 23 11 is the oblique 11 x xyx xx asymptote.
The graph is above the line y = x + 1 on 1, and below the line on ,1.
Test for symmetry: 22 ()22 ()() 11 and () fxxxfx xx fx f is neither even nor odd, so there is no symmetry with respect to the y-axis or the origin.
The intervals determined by the zeros of the numerator and of the denominator of
2 23 11 11 x fxxx xx
divide the x-axis into two intervals, ,1 and 1,.
Use test numbers to determine where the graph of f is above and below the x-axis.
Interval Test point Value of fx Above/below y = x + 1
2 6 above 10. (100) () 20 xx Rx x a. 10(10010) (10)30 1020 R billion dollars.
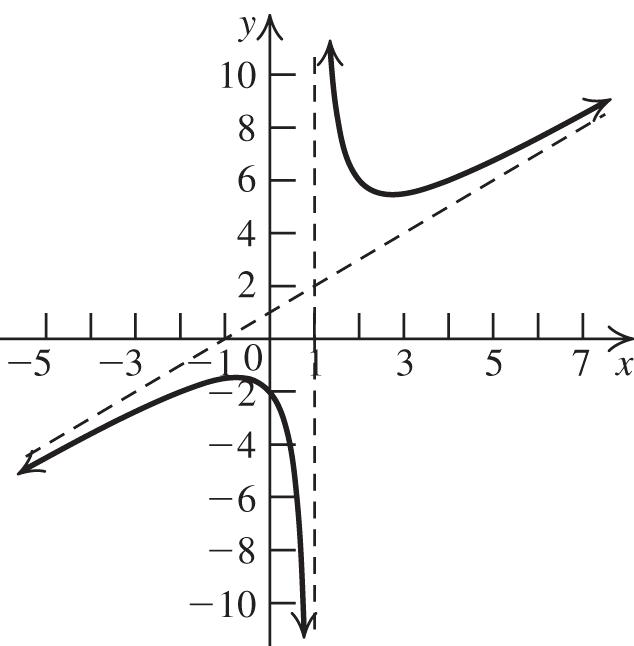
This means that if income is taxed at a rate of 10%, then the total revenue for the government will be 30 billion dollars. Similarly, R(20) = $40 billion, R(30) = $42 billion, R(40) = $40 billion, R(50) ≈ $35.7 billion, R(60) = $30 billion.
b.
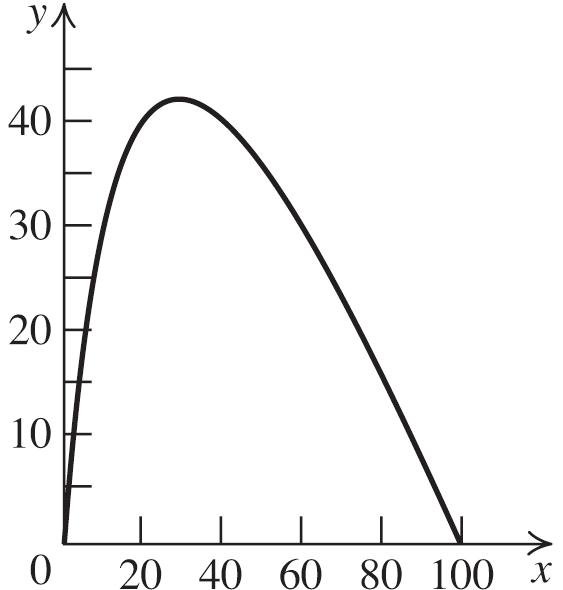
Copyright © 2018 Pearson Education Inc.
From the graphing calculator screen, we see that a tax rate of about 29% generates the maximum tax revenue of about $42.02 billion.
2.4 Exercises
Concept and Vocabulary
1. A function f is rational if it can be expressed in the form Nx Dx where N(x) and D(x) are polynomials.
2. A line x = a is called a vertical asymptote of the rational function f if ()fx as xa or as xa
3. A line y = k is called a horizontal asymptote of the rational function f if () fxk as x or as x .
4. If a is a zero of denominator Dx of the rational function
Nx fxDx
expressed in lowest terms, then x = a is a vertical asymptote of f
5. True
6. False. The graph of a rational function can cross its horizontal asymptote.
7. True
8. False Building Skills
9. (,4)(4,)
13. 2 60(3)(2)02,3xxxxx
The domain of the function is (,2)(2,3)(3,).
14. 2 670(7)(1)01,7xxxxx
The domain of the function is (,1)(1,7)(7,).
15. 2 680(4)(2)02,4xxxxx
The domain of the function is (,2)(2,4)(4,).
16. 2 320(2)(1)01,2xxxxx
The domain of the function is (,1)(1,2)(2,).
17. As 1,().xfx
18. As 1,().xfx
19. As 2,().xfx
20. As 2,().xfx
21. As ,()1.xfx
22. As ,()1.xfx
23. The domain of f is (,2)(2,1)(1,).
24. There are two vertical asymptotes.
25. The equations of the vertical asymptotes of the graph are x = –2 and x = 1.
26. The equation of the horizontal asymptote of the graph is y = 1.
27.
Domain: (,4)(4,)
Range: (,0)(0,)
Vertical asymptote: x = 4
Horizontal asymptote: y = 0
Domain: (,3)(3,)
Range: (,0)(0,)
Vertical asymptote: x = 3
Horizontal asymptote: y = 0
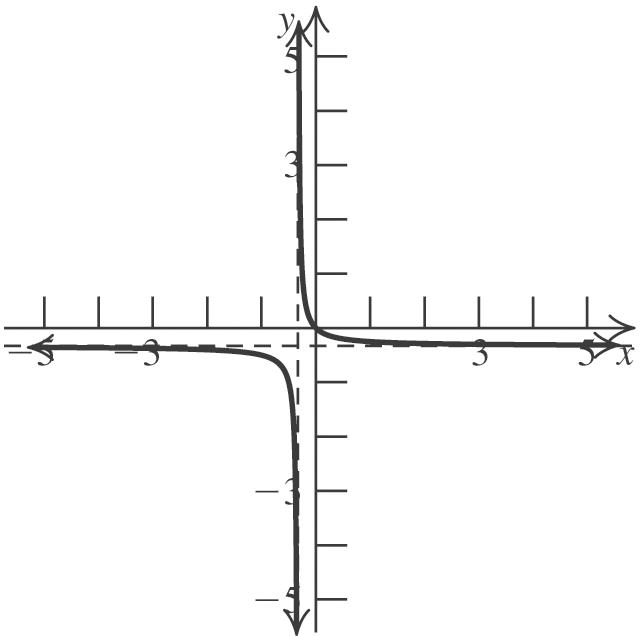
Domain:
Range:
Horizontal
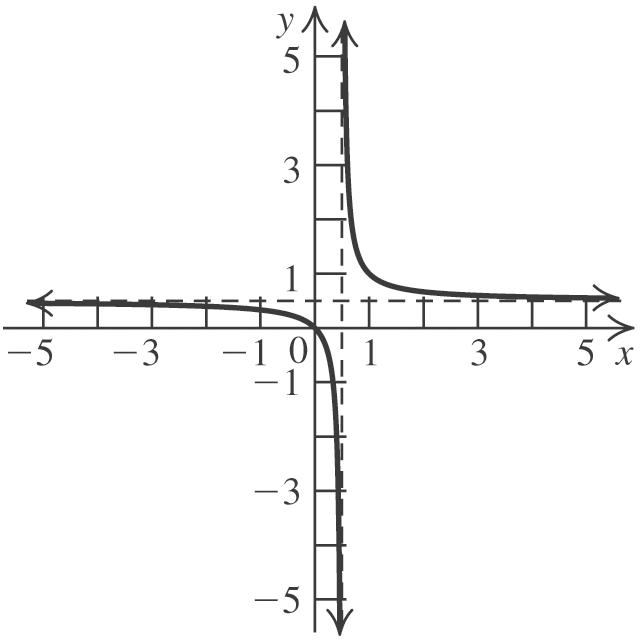
Domain:
Range:
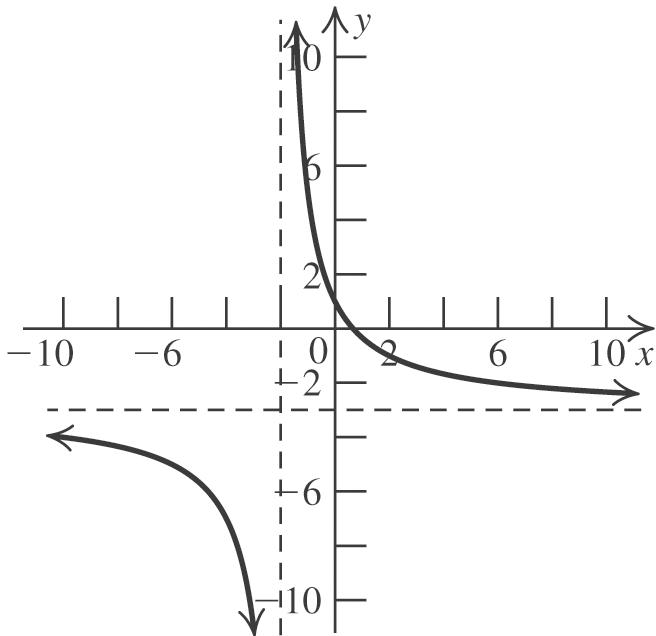
Domain: (,2)(2,)
Range: (,3)(3,)
Vertical asymptote: x = 2
Horizontal asymptote: y = 3
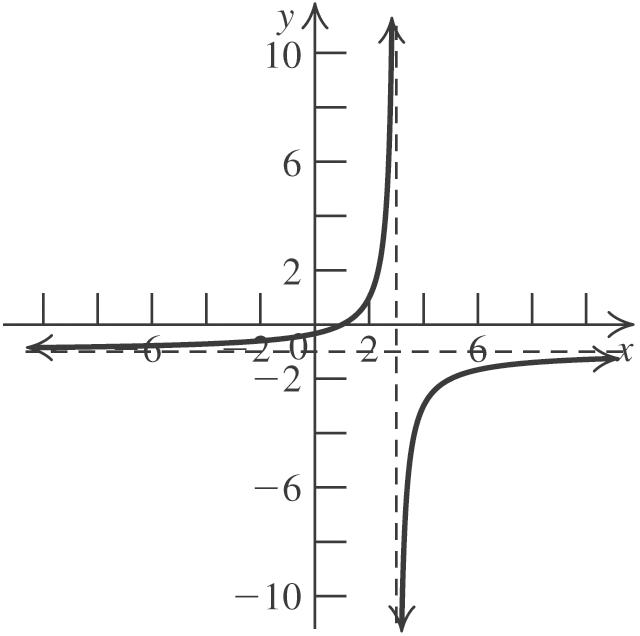
Domain: (,3)(3,)
Range: (,1)(1,)
Vertical asymptote: x = 3
Horizontal asymptote: y = 1
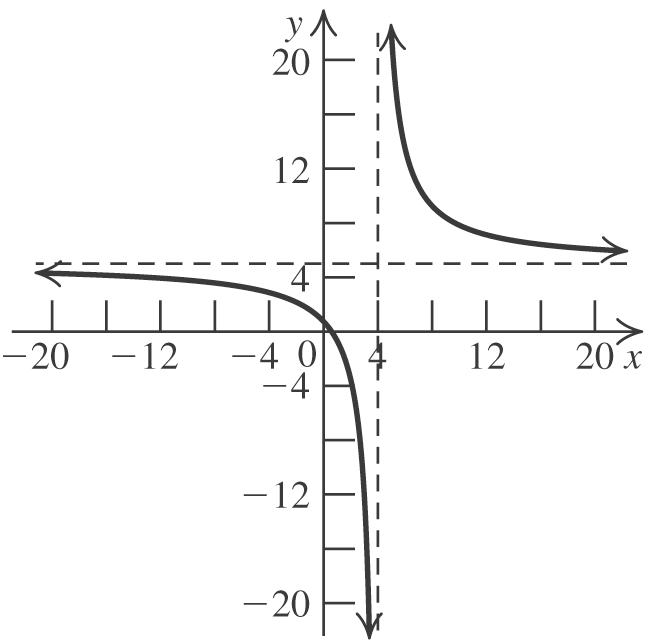
Domain: (,4)(4,)
Range: (,5)(5,)
Vertical asymptote: x = 4
Horizontal asymptote: y = 5
Domain: (,5)(5,)
Range: (,2)(2,)
Vertical asymptote: x = 5
Horizontal asymptote: y = 2
In exercises 35 44, to find the vertical asymptotes, first eliminate any common factors in the numerator and denominator, and then set the denominator equal to zero and solve for x
35. 1 x 36. 2 x
37. 4,3xx 38. 34 , 23 xx
39. 2 2 1(1)(1) (). (2)(3) 6 hxxxx xxxx
The equations of the vertical asymptotes are 3 and 2.
40. 2 2 4(2)(2) (). (34)(1) 34 hxxxx xxxx
The equations of the vertical asymptotes are 4 and 1. 3
41. 2 2 68(4)(2) (). (4)(3) 12 fxxxxx xxxx
Disregard the common factor. The vertical asymptote is 3. x
42. 2 3 9(3)(3) (). (2)(2) 4 fxxxx xxxxx
The equations of the vertical asymptotes are 0,2, and 2. xxx
43. There is no vertical asymptote.
44. There is no vertical asymptote.
For exercises 45 52, locate the horizontal asymptote as follows:
• If the degree of the numerator of a rational function is less than the degree of the denominator, then the x-axis (y = 0) if the horizontal asymptote.
• If the degree of the numerator of a rational function equals the degree of the denominator, the horizontal asymptote is the line with the equation n m a yb , where n a is the coefficient of the leading term of the numerator and mb is the coefficient of the leading term of the denominator.
• If the degree of the numerator of a rational function is greater than the degree of the denominator, then there is no horizontal asymptote.
45. 0 y 46. 0 y 47. 2 3 y 48. 3 4 y
49. There is no horizontal asymptote.
50. 0 y 51. 0 y
52. There is no horizontal asymptote.
53. d 54. f 55. e
56. b 57. a 58. c
59. 2 00 3 x x x is the x-intercept. 2(0) 00 03 y is the y-intercept. The vertical asymptote is x = 3. The horizontal asymptote is y = 2. 2()2 ()() ()33 fxxxfx xx and ()fxfx there are no symmetries. The intervals to be tested are (,3) and (3,). The graph is above the horizontal asymptote on (3,) and below the horizontal asymptote on (,3).
60. 00 1 x x x is the x-intercept.
0 00 01 y is the y-intercept. The vertical asymptote is x = 1. The horizontal asymptote is y = –1. () () ()3fxx x () and() 3 xfxfx x there are no symmetries. The intervals to be tested are (,1), and (1,). The graph is above the horizontal asymptote on (,1) and below the horizontal asymptote on (1,).
61. 2 00 4 x x x is the x-intercept.
2 0 00 04 y is the y-intercept. The vertical asymptotes are x = –2 and x = 2. The horizontal asymptote is the x-axis.
22 ()() ()44 xx fxfx xx the function is odd, and the graph is symmetric with respect to the origin. The intervals to be tested are (,2),(2,0),(0,2) and (2,). The graph is above the x-axis on (2,0)(2,) and below the x-axis on (,2)(0,2).
62. 2 00 1 x x x is the x-intercept.
2 0 00 10 y is the y-intercept. The vertical asymptotes are x = –1 and x = 1. The horizontal asymptote is the x-axis.
22 ()() 1()1 xx fxfx xx the function is odd, and the graph is symmetric with respect to the origin. The intervals to be tested are (,1),(1,0),(0,1) and (1,). The graph is above the x-axis on (,1)(0,1) and below the x-axis on (1,0)(1,).

63. 2 2 2 00 9 x x x is the x-intercept.
2 2 0 00 04 y is the y-intercept. The vertical asymptotes are x = –3 and x = 3. The horizontal asymptote is y = –2.
22
22 () ()() ()99 xx fxfx xx the function is even, and the graph is symmetric with respect to the y-axis. The intervals to be tested are (,3),(3,3), and (3,). The graph is above the horizontal asymptote on (3,3) and below the horizontal asymptote on (,3)(3,)
Copyright © 2018 Pearson Education
64. 2 2 4 02 x x x is the x-intercept.
2 2 40 0 there is no y-intercept. The vertical asymptote is the y-axis. The horizontal asymptote is y = –1. 22
22 4()4 ()() () xx fxfx xx the
function is even, and the graph is symmetric with respect to the y-axis. The intervals to be tested are (,0),and (0,). The graph is above the horizontal asymptote on (,0)(0,).

65. 2 2 0 2 x there is no x-intercept.
2 2
01 02 y is the y-intercept. The
vertical asymptotes are 2 x . The horizontal asymptote is the xaxis.
22 22 ()() ()22 fxfx xx the function is even, and the graph is symmetric with respect to the y-axis. The intervals to be tested are (,2),(2,2) and (2,).
The graph is above the x-axis on ,2 2, and below the x-axis on 2,2 .

66. 2 2 0 3 x there is no x-intercept.
2 22 0 3 03 y is the y-intercept. The vertical asymptotes are 3 x . The horizontal asymptote is the x-axis.
22 22 ()() ()32 fxfx xx the function is even, and the graph is symmetric with respect to the y-axis. The intervals to be tested are (,3),(3,3) and (3,).
The graph is above the x-axis on 3,3 and below the x-axis on
,33,
67. 1 01 (2)(3) x x xx is the x-intercept. 0111 (02)(03)66 y is the y-intercept. The vertical asymptotes are x = –3 and x = 2. The horizontal asymptote is the x-axis. ()1 ()() (()2)(()3)fxxfx xx and ()fx there are no symmetries. The intervals to be tested are (,3),(3,1), (1,2), and (2,). The graph is above the x-axis on (3,1)(2,) and below the x-axis on (,3)(1,2).
68. 1 01 (1)(2) x x xx is the x-intercept.
0111
(01)(02)22 y is the y-intercept.
The vertical asymptotes are x = –1 and x = 2. The horizontal asymptote is the x-axis. ()1 ()() and (()1)(()2) x fxfx xx ()fx there are no symmetries. The intervals to be tested are (,1),(1,1), (1,2), and (2,). The graph is above the x-axis on (1,1)(2,) and below the x-axis on (,1)(1,2).
69. 2 2 32 fxx xx 2 2 0200 32 x xx xx is the x-intercept. 2 20 00 0302 y is the y-intercept. 2 32121,2xxxxxx are the vertical asymptotes. The horizontal asymptote is the x-axis. 2 2 2 32 2 or 32 x fx xx xfxfx xx
There are no symmetries. The intervals to be tested are (,2),(2,1), (1,0)and (0,).
The graph is below the x-axis on (,2)(1,0) and above the x-axis on (2,1)(0,).
70. 2 2 68 fxx xx 2 2 0200 68 x xx xx is the x-intercept.
2 20 00 0608 y is the y-intercept.
2 68242,4xxxxxx are the vertical asymptotes. The horizontal asymptote is the x-axis.
2 2 2 68 2 or 8 x fx xx xfxfx xx
There are no symmetries. The intervals to be tested are (,0),(0,2), (2,4)and (4,). The graph is below the x-axis on (,0)(2,4) and above the x-axis on (0,2)(4,).
Copyright © 2018 Pearson Education
71.
2 1 1 fxx xx 2 1
0101 1 x xx xx is the x-intercept.
2 01 001 is undefined, so there is no y-intercept. 2 100,1xxxx are the vertical asymptotes. The horizontal asymptote is the x-axis.
2 2 1 1 1 or 1 fxx xx xfxfx xx
There are no symmetries. The intervals to be tested are (,1),(1,0), (0,1)and (1,). The graph is above the x-axis on (,1)(1,) and below the x-axis on (1,0)(0,1).
72. 2 1 1 fxx xx
2 1 0101 1 x xx xx
is the x-intercept.
2 01 001 is undefined, so there is no y-intercept.
2 100,1xxxx are the vertical asymptotes. The horizontal asymptote is the x-axis.
2 1 or 1 fxxfxfx xx
There are no symmetries. The intervals to be tested are (,1),(1,0), (0,1)and (1,). The graph is below the x-axis on (0,1) and above the x-axis on (,1)(1,0)(1,).
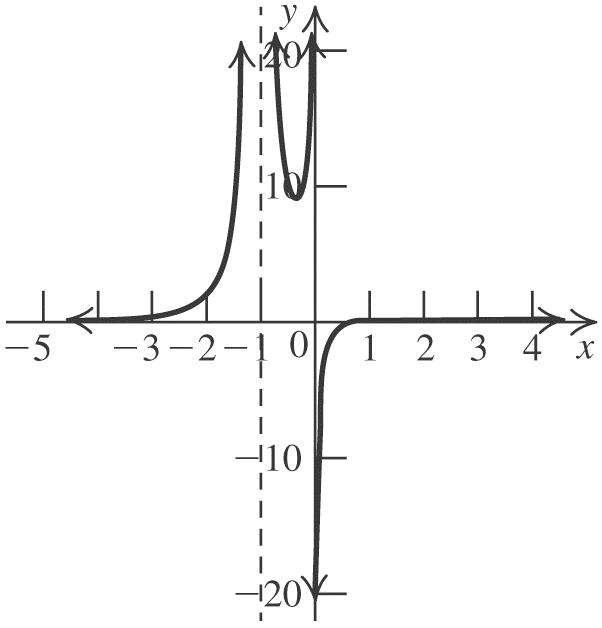
73. 2 3 712 fxx xx
2 331 0 344 712 xx xxxxx
there is no x-intercept. 2 031 4 07012 is the y-intercept.
There is a hole at (3, –1) and x = 4 is the vertical asymptote. The horizontal asymptote is the x-axis.
2 2 3 712 3 or 712 fxx xx xfxfx xx
There are no symmetries. The intervals to be tested are (,3),(3,4), and (4,). The graph is below the x-axis on (,1)(3,4) and above the x-axis on (4,).
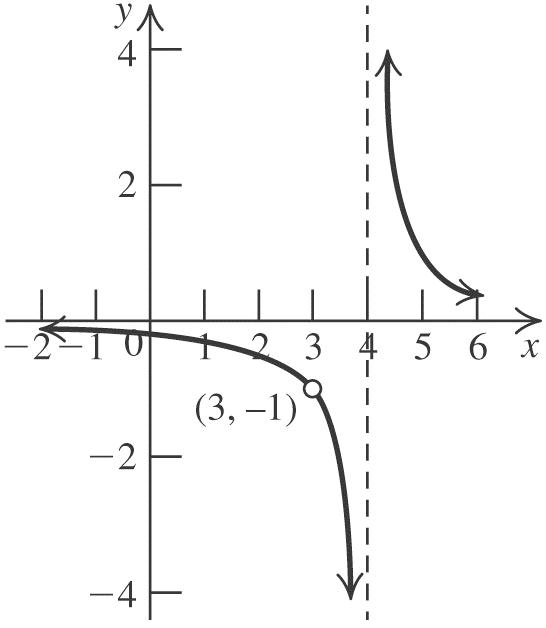
74. 2 2 6 fxx xx
2 221 0 233 6 xx xxxxx there is no x-intercept. There is a hole at 1 5 2,.
2 021 3
006 is the y-intercept. x = 3 is the vertical asymptote. The horizontal asymptote is the x-axis.
2 2 2 6 2 or 6 fxx xx xfxfx xx
There are no symmetries. The intervals to be tested are (,2),(2,3), and (3,). The graph is below the x-axis on (,2)(2,3) and above the x-axis on (3,).
75. 2 2 00 1 x x x is the x-intercept.
2 2 0 00 01 y is the y-intercept. There is no vertical asymptote. The horizontal asymptote is y = 1. 22 22 () ()() ()11 xx fxfx xx the function is even, and the graph is symmetric with respect to the y-axis. The intervals to be tested are (,0) and (0,). The graph is above the x-axis on (,0)(0,) and below the horizontal asymptote on ,.
76. 2 2 2 00 4 x x x is the x-intercept.
2 2 2(0) 00 04 y is the y-intercept. There is no vertical asymptote. The horizontal asymptote is y = 2. 22 22 2() ()() ()44 xx fxfx xx the function is even, and the graph is symmetric with respect to the y-axis. The intervals to be tested are (,0) and (0,). The graph is above the x-axis on (,0)(0,) and below the horizontal asymptote on ,. 77.
02fxx are the x-intercepts.
2 322 322 2 4 44044 9 9909 9 xx xxx xxx xx 4 9 is the y-intercept. However, there is a hole at 4 0, 9
since
3 0900
2 90330xxxx x = –3 and x = 3 are the vertical asymptotes.
(continuedonnextpage)
(continued)
The degree of the numerator is the same as the degree of the denominator, so the horizontal asymptote is y = 1.
3 33 333 4 44 () 99 9 () the function is even, and the fxxxxxxx xxxxxx fx
graph is symmetric with respect to the y-axis. The intervals to be tested are (,3),(3,0), (0,3), and (3,). The graph is above the horizontal asymptote on (,3)(3,) and below the horizontal asymptote on
3,00,3.
2 2 2 32 032 8 x x x there are no x-intercepts.
2 2 03232 4 8 08 y is the y-intercept. However, there is a hole at (0, 4) since 3 0800. Since there is no real solution for 2 80, x there are no vertical asymptotes. The horizontal asymptote is y = 1 since the degrees of the numerator and the denominator are equal and the leading coefficients are the same.
even, and the graph is symmetric with respect to the y-axis. The intervals to be tested are (,0) and (0,). The graph is above the horizontal asymptote on (,0)(0,)
() the function is
79. 2 (2) 0 2 x x there is no x-intercept. (There is a hole at x = 2.)
2 (02) 22 02 y is the y-intercept. There are no vertical asymptotes. There are no horizontal asymptotes.
2 (2)
()() and() 2 x fxfxfx x
there are no symmetries. The intervals to be tested are (,2) and (2,). The graph is above the x-axis on (2,) and below the x-axis on (,2) .
80. 2 (1) 0 1 x x there is no x-intercept. (There is a hole at x = 1.)
2 (01) 11 01 y is the y-intercept. There are no vertical asymptotes. There are no horizontal asymptotes.
2 (1) ()() and() 1 x fxfxfx x there are no symmetries. The intervals to be tested are (,1) and (1,). The graph is above the x-axis on (1,) and below the x-axis on (,1)
(continuedonnextpage)
(continued)
81. The x-intercept is 1 and the vertical asymptote is x = 2. The horizontal asymptote is y = 2, so the degree of the numerator equals the degree of the denominator, and the ratio of the leading terms of the numerator and the denominator is 2.
Thus, the equation is of the form 1 2 x ya
The y-intercept is 1, so we have 01 12.
Thus, the equation is
82. The x-intercept is 2 and the vertical asymptote is x = 1. The horizontal asymptote is 1 2 y , so the degree of the numerator equals the degree of the denominator, and the ratio of the leading terms of the numerator and the denominator is 1 2 . Thus, the equation is of the form 2 1 x ya x
The y-intercept is 1, so we have 021 1. 012
Thus, the equation is
2 21fxx x
83. The x-intercepts are 1 and 3, and the vertical asymptotes are x = 0 and x = 2. The horizontal asymptote is y = 1, so the degree of the numerator equals the degree of the denominator, and the ratio of the leading terms of the numerator and the denominator is 1. Thus, the equation is of the form
There is no y-intercept, so the equation is
84. The x-intercepts are 2 and 3. The vertical asymptotes are x = 1 and x = 2. The horizontal asymptote is y = 1, so the degree of the numerator equals the degree of the denominator, and the ratio of the leading terms of the numerator and the denominator is 1. Thus, the equation is of the form
The y-intercept is 3, so we have
0203 31. 0102 aa Thus, the equation is
85. 2 211 2. x x xx
The oblique asymptote is 2.yx
86. 2 11 . x x xx
The oblique asymptote is yx
87. 3 22 11 . x x xx
The oblique asymptote is yx
88. 32 22 211 21. xx x xx
The oblique asymptote is 21.yx 89. 2 2 2 11 21 22 3 x xxx xx x
The oblique asymptote is 2. yx
90. 2 2 21 1232 22 2 1 1 x xxx xx x x
The oblique asymptote is 21.yx 91. 232 3 2 2 2 1201 21 22 1 x xxxx xx xx x x
The oblique asymptote is y = x 2. Note that there is a hole in the graph at x = 1. 92. 232 3 4001 4 41 x xxxx xx x
The oblique asymptote is .yx
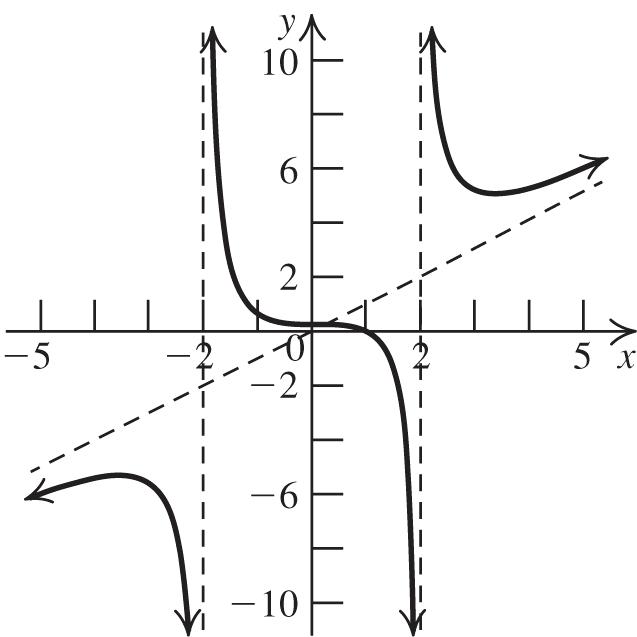
Applying the Concepts
93. a. ()0.52000Cxx b. ()0.5()0.520002000 Cxx Cx xxx
c. 2000 (100)0.520.5 100 2000 (500)0.54.5 500 2000 (1000)0.52.5 1000
These show the average cost of producing 100, 500, and 1000 trinkets, respectively.
d. The horizontal asymptote of ()Cx is 0.5 y . It means that the average cost approaches the fixed daily cost of producing each trinket as the number of trinkets approaches .
94. a. 2 0.00267000 () 7000 0.0026 Cxxx x x x
b. 7000 (100)0.002(100)675.8 100 7000 (500)0.002(500)619 500 7000 (1000)0.002(1000)611 1000
These show the average cost of producing 100, 500, and 1000 CD players, respectively.
c. The oblique asymptote is 0.0026.yx For large values of x, this is a good approximation of the average cost of producing x CD players.
95. a.

b. 4(50)1 (50)4 min 10050 f
4(75)1 (75)12 min 10075 f 4(95)1 (95)76 min 10095 f
4(99)1 (99)397 min 10099 f
c. (i) As 100,().xfx
(ii) The statement is not applicable because the domain is x < 100.
d. No, the bird doesn’t ever collect all the seed from the field.
96. a. 1000 (50)20 10050 1000 (75)40 10075 1000 (90)100 10090 1000 (99)1000 10099
These show the estimated cost (in millions of dollars) of catching and convicting 50%, 75%, 90%, and 99% of the criminals, respectively.
b.
c. As 100,().xCx
d. 1000 303000301000 100 20003066.67% x x xx
97. a. 2 3(50)50 (50)$3.02 billion 50(10050) C
b.
Copyright © 2018 Pearson Education Inc.
c. 22 2 22 2 350350 30 (100) 100 300030350 333000500 xx xxxx xxx xx
2 300030004(33)(50) 2(33) 30008,993,40030002998.9 6666 90.89 or 0.017 x
Reject the negative solution. Approximately 90.89% of the impurities can be removed at a cost of $30 billion.
98. a. The horizontal asymptote is y = aa is called the saturation level because as the concentration of the nutrient is increased, the growth rate is pushed close to a
b. () 22 kka gkaakkk
99. a. 8(0)16 (0)16 thousand16,000 2(0)1 P
b. The horizontal asymptote is 4. y This means that the population will stabilize at 4000.
100. a.

b. The horizontal asymptote is 0. y This means that, as time passes, the concentration of the drug approaches 0.
c.
The concentration of the drug in the bloodstream is maximal at 1 hour after the injection.
d. 2 2 5 22520 1 1 (21)(2)0 or 2 2 t tt t txtt
The concentration level equal 2 ml/l at 1 2 hr and 2 hr after the injection.
101. a. 10200,000 () 2500 fxx x b. 10(10,000)200,000 (10,000)$40 10,0002500 C
c. 10200,000 20 2500 2050,00010200,000 10250,00025,000 x x xx xx
More than 25,000 books must be sold to bring the average cost under $20.
d. The vertical asymptote is x = 2500. This represents the number of free samples. The horizontal asymptote is y = 10. This represents the cost of printing and binding one book.
102. a. (1)(1)111 (1) 1 qppqpq p qppq p
b.
c. 0.25 0.3333.33% 10.25 q
Copyright © 2018 Pearson Education Inc.
Beyond the Basics
103. Stretch the graph of 1 y x vertically by a factor of 2, and then reflect the graph about the x-axis.
104. Shift the graph of 1 y x two units right, and then reflect the graph about the x-axis.
105. Shift the graph of 2 1 y x two units right.
106. Shift the graph of 2 1 y x one unit left.
107. Shift the graph of 2 1 y x one unit right and two units down.
108. Shift the graph of 2 1 y x two units left and three units up.
109. Shift the graph of 2 1 y x six units left.
110. 22 2 22 22 2 222 3 6931828 31827 1 318283(69)1
Shift the graph of 2 1 y x three units left and three units
111. 22 2 1 2122 21 1 xxxx xx
22 22 2 222 22(21)1 2121 2111 1 2121(1) xxxx xxxx xx xxxxx
Shift the graph of 2 1 y x one unit right and one unit up.
112. 22 2 22 22 2 222 2 21243 242 5 2432(21)5 2121 2(21)55 2 2121(1) xxxx xx xxxx xxxx
Shift the graph of 2 1 y x one unit left, stretch the graph vertically by a factor of 5, reflect it in the x-axis, and shift it two units up.
113. a. If c is a zero of f(x), then x = c is a vertical asymptote because c is not a factor of the numerator.
b. Because the numerators are positive, the signs of f(x) and g(x) are the same.
c. If the graphs intersect for some value x, then f(x) = g(x).
2 1
d. If f(x) increases (decreases, remains constant), then the denominator of g(x) increases (decreases, remains constant). Therefore, g(x) decreases (increases, remains constant).
114.
115. 1 1 ()23() and 23 23 becomes 23 fxxfx x yxxy
Thus, the functions are different.
116. 1 1 12 ()() and 21 11 becomes 22 2121 (1)21 2121 (). 11 xxfxfx xx xy yx xy xyxyxyyx yxx xx yyfx xx
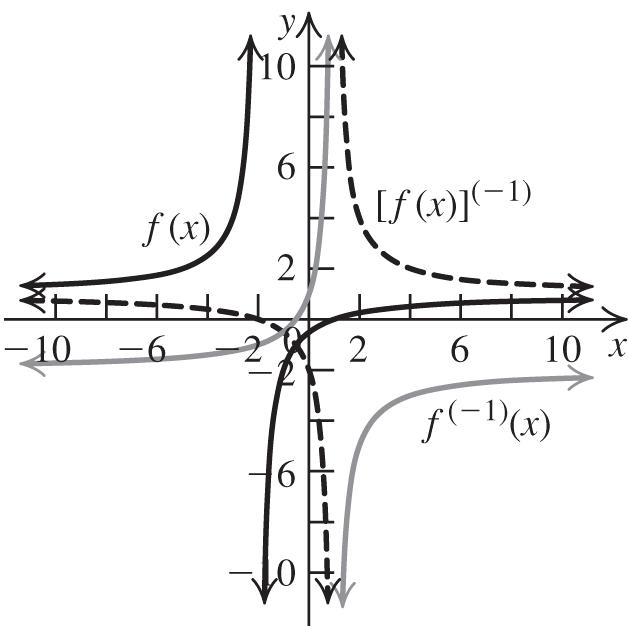
117. g(x) has the oblique asymptote 23yx . () as , and () as . gxxgx x
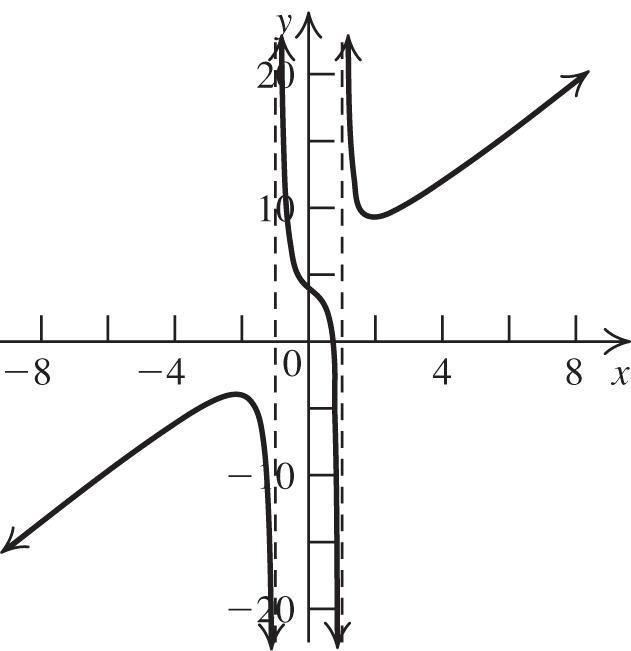
118. f(x) has no oblique asymptote. ()fx as , and ()as . xfxx For large |x|, the graph behaves like the graph of 2 . yx
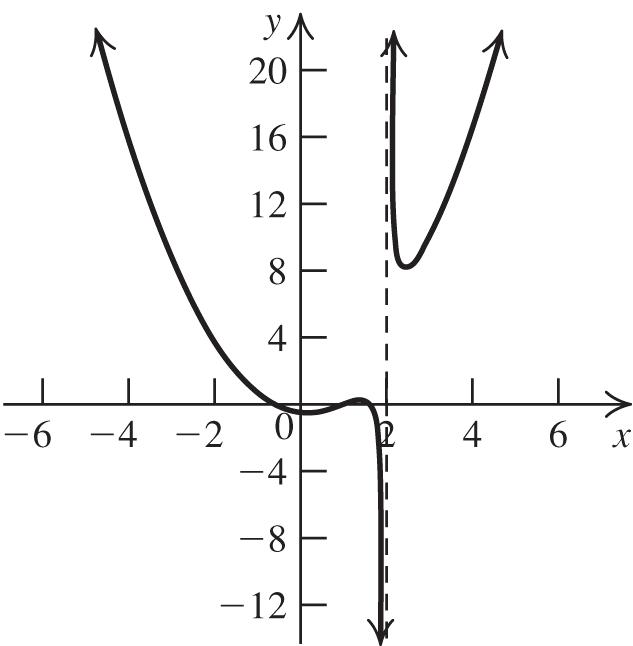
119. The horizontal asymptote is y = 1. 2 22 2 2 1223 23 xx xxxx xx
1 31. 3 xx The point of intersection is 1 ,1. 3
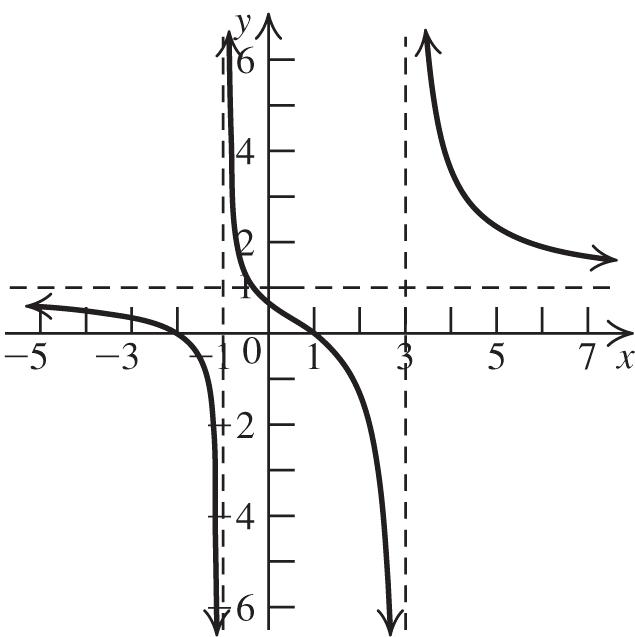
120. The horizontal asymptote is 1 . 2 y
1. x The point of intersection is 1 1,. 2
121. Vertical asymptote at 3 x the denominator is 3 x . Horizontal asymptote at 1 y the ratio of the leading coefficients of the numerator and denominator = 1. The x–intercept = 2 the numerator is x 2. So the equation is of the form 22 or . 33 fxxx xx
122. Vertical asymptotes at x = 1 and x = 1 the denominator is 11xx . Horizontal asymptote at 1 y the degrees of the numerator and denominator are the same. The x–intercept = 0 the numerator is 2 x . So the equation is of the form
22 2 . 11 1 fxxx xxx
123. Vertical asymptote at 0 x the denominator is x. The slant asymptote y = x the degree of the numerator is one more than the degree of the denominator and the quotient of the numerator and the denominator is . The x-intercepts 1 and 1 the numerator is
11.xx So the equation is of the form
2 2 1 1 x xx x
However, the slant asymptote is y = x, so a = 1 and the equation is
124. Vertical asymptote at 3 x the denominator is x 3. The slant asymptote y = x + 4 the degree of the numerator is one more than the degree of the denominator, and the quotient of the numerator and the denominator is x + 4. Thus, (x 3)(x + 4) + a is the numerator.
Therefore, the equation is
125. Vertical asymptote at 2 x the denominator is x 2. Horizontal asymptote at 1 y the degrees of the numerator and denominator are the same and the leading coefficients of the numerator and denominator are the same. So the numerator is xa , where a is chosen so that 4 (0)2(). 2 ffxx x
126. Vertical asymptotes at 2 and 1 xx the denominator is (2)(1) xx . Horizontal asymptote at 0 y the degree of the numerator < the degree of the denominator. So the numerator is xa , where a is chosen so that 4 (0)2. (2)(1)ffxx xx Verify that the x-intercept is 4:
44 40. 4241 f
127. () as 1 and () as 1 the denominator is zero if 1. fxxfx xx Since 1 x from both directions, the denominator is 2 (1). x ()4 as fx
x the horizontal asymptote is 4. So the leading coefficient of the numerator is 4 and the degree of the numerator is the same as the degree of the denominator. The numerator is 2 4 xa , where a is chosen so that 2 2 412 1 01. 2 121 a fa
So, 2 2 41 (). (1) fxx x
128. No vertical asymptotes the denominator has no real zeros. ()fx symmetric about the yaxis ()fx is an even function. So the degree of the numerator and the degree of the denominator can equal 2. Then a possible denominator is 2 1. x ()2 as fx
x the horizontal asymptote is 2. So the numerator is 2 2 xa where a is chosen so that (0)00. fa 2 2 2 (). 1 fxx x
129. Vertical asymptote at 1 x the denominator could be 1. x Because the oblique asymptote is 32,yx the numerator is (32)(1), xxa where a can be any number (no x-intercepts or function values are given). Let a = 1. So. (32)(1)1 () 1fxxx x 2 31 1 xx x
130. A rational function cannot have both a horizontal asymptote and an oblique asymptote because there would values of x which are mapped to two different function values. In that case, it wouldn’t be a function.
Critical Thinking/Discussion/Writing
131. 2 12 111 ,5 T R RRR a. 11 111 55 1111 555 T TT RR R RRRRR
b. 1 1 1 5 0 5 R R R is the x-intercept.
1 1 5 5(0) 00 505 R Ry is the y-intercept. The vertical asymptote is x = –5. The horizontal asymptote is y = 5.
11 1 11 55 () 55 T RR RRfx RR and ()fxfx there are no symmetries. The intervals to be tested are (,5),(5,0) and (0,). The graph is above the horizontal asymptote on (,5) and below the horizontal asymptote on (5,0)(0,). The graph is below the x-axis on (–5, 0) and above the x-axis on (,5)(0,).
c. 1R must be greater than 0, so 05. TR The horizontal asymptote is 5, TR so as
1 ,5. TRR 132. 2 ,2 1 Kcc
a. 2 2 0 1 K is the x-intercept.
2 20 00 10 K is the y-intercept. The vertical asymptote is 1. The degree of the numerator is greater than the degree of the denominator, so there is an oblique asymptote.
2 22 22 11
The oblique asymptote is 22. K
2 2 2 2 () 11 fx and ()fxfx there are no symmetries.
Use the intervals determined by the zeros of the numerator and of the denominator of 2 22 2222 11 K
to create a sign graph. The numerator 2 has no zero and the denominator has one zero, 1. The intervals to be tested are (,1),and (1,). The graph is above the oblique asymptote on (,1) and below the oblique asymptote on (1,).
b. As 0 (meaning as approaches 0 from the right), 0. K In other words, is a positive number that is becoming smaller and smaller. As it approaches 0, 2 2. K
c. As 1 (meaning as approaches 1 from the left), . K In other words, is a positive number > 0 that is becoming closer and closer to 1. As it approaches 1, the denominator approaches 0, so Ostwald’s law cannot hold for strong elctrolytes.
133. Answers may vary. Sample answers are given:
134. Answers may vary. Sample answers are given:
Copyright © 2018 Pearson Education Inc.
135. Since y = ax + b is the oblique asymptote, we know that
. rx Rxaxb Dx We are told that the graph of Rx intersects the asymptote at the points
1122 ,,,,,, nncRccRccRc so Rxaxb when
0. rx Dx Thus,
Recall that the numerator of a rational function must have degree greater than that of the denominator in order for there to be an oblique asymptote, so the denominator,
, Dx can be any polynomial whose degree is greater than or equal to n + 2. Thus, a possible rational function is
where
Dx is a polynomial of degree n + 1 and none of its zeros are at 12,,,. n ccc
Getting Ready for the Next Section
c.
The
For exercises 141–144, instead of graphing the function to determine the solution set as shown in Section 2.1, we use test points.
141.
120xx
The zeros occur at x = –2 and x = 1, so the intervals to be tested are
,2,2,1, and 1,.
Interval Test point
Value of fx Result
,2 –3 4 +
2,1 0 –2 –
1, 2 4 +
120xx for
,21,.
142. 240xx
The zeros occur at x = –2 and x = –4, so the intervals to be tested are
,4,4,2, and
1,.
Interval Test point Value of
,4 –5 3 +
4,2 –3 –1 –
2, 0 8 +
143.
2 3100520xxxx
The zeros occur at x = –5 and x = 2, so the intervals to be tested are ,5,5,2, and
2,.
Interval Test point
,5
Value of
fx Result
2.5 Polynomial and Rational Inequalities
2.5 Practice Problems 1. 322 32 25214215 49360 xxxxx xxx
Now solve 3249360. xxx
The possible rational zeros are 1,2, 3,4,6,9,12,18,36.
Using synthetic division, we see that x = 3 is a factor. 314936 32136 17120
32249363712 3340 xxxxxx xxx
So, the zeros are x = –4, x = –3, and x= 3, and the intervals to be tested are ,4, 4,3,3,3, and 3,.
Interval Test point
144.
2 670710xxxx
The zeros occur at x = –1 and x = 7, so the intervals to be tested are ,1,1,7, and
7,.
Interval Test point
of
7, 10 33 + 2 670xx for 1,7.
Value of Px Result
,4 –5 –16 –
4,3 3.5 1.625 + 3,3 0 –36 – 3, 5 144 +
Solution set: 4,33,.
2.
2 210xxx
The boundary points are x = 0, x = –2, and x = 1, so the intervals are ,2,2,0,
0,1, and 1,. The leading term of 22 4 21, Pxxxxxxxx so the end behavior of the graph is fx as x and fx as . x Because 0 and 1 are zeros of odd multiplicity, the graph of Px crosses the x-axis at these points. Because –2 is a zeros of even multiplicity, the graph touches but does not cross the x-axis at x = –2.
(continuedonnextpage)
(continued)
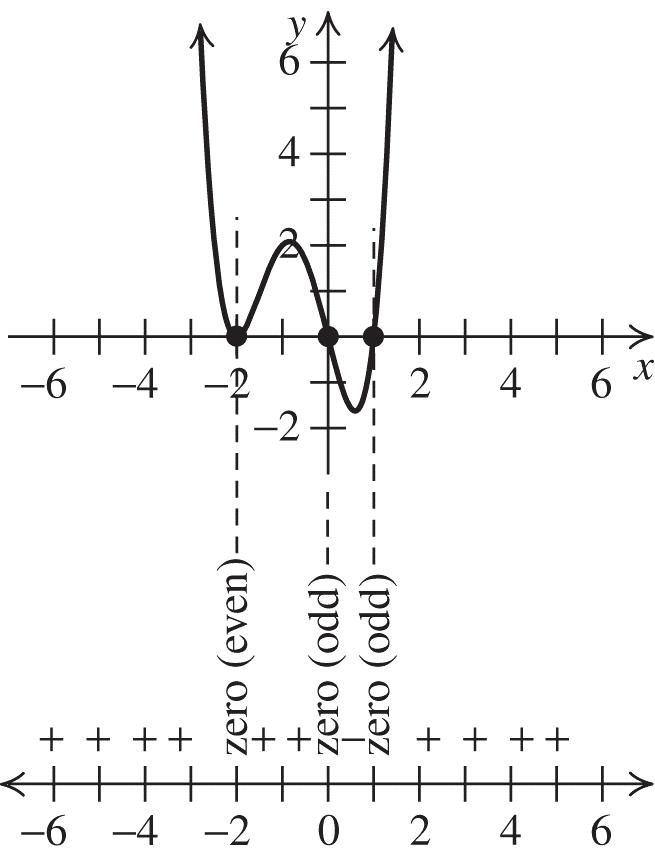
To solve the inequality, examine the graph to find the intervals on which Px is positive. The solution set is
,22,01,.
3.
2 2220xxxx
Note that the quadratic term 2 22xx has no real zeros and is always positive. The real zeros of
2 222xxxx are x = 0 and x = 2.
So, the intervals are ,0,0,2, and
2, 3 51 + [–6, 6] by [–6, 6]
We can verify the solution by examining the graph. Solution set: ,02,. 4.
numerator: 21206 xx
The boundary points are 0, 4, and 6. The lines x = 0 and x = 4 are the vertical asymptotes of
. Rx The intervals are
,0,0,4,
4,6, and 6,. Note that 0 and 4 are not included in the intervals to be tested because they cause the denominator of Rx to equal 0.
Interval Test point
[–10, 10] by [–10, 10]
We can verify the solution by examining the graph. Solution set:
,04,6.
5151 330 33 5533 24 0 33 xx xx xxx Rx xx numerator: 2402 xx denominator : 303xx
The boundary points are 2 and 3. The line x = 3 is the vertical asymptote of Rx The intervals are ,3,3,2, and 2,.
Note that –3 is not included in the intervals to be tested because it causes the denominator of Rx to equal 0. To determine the sign of , Rx form the corresponding polynomial
243.Pxxx The signe rule says that Px has the same sign as Rx on the intervals listed above. Px is a quadratic polynomial with leading coefficient 2 20. a
(continuedonnextpage)
(continued)
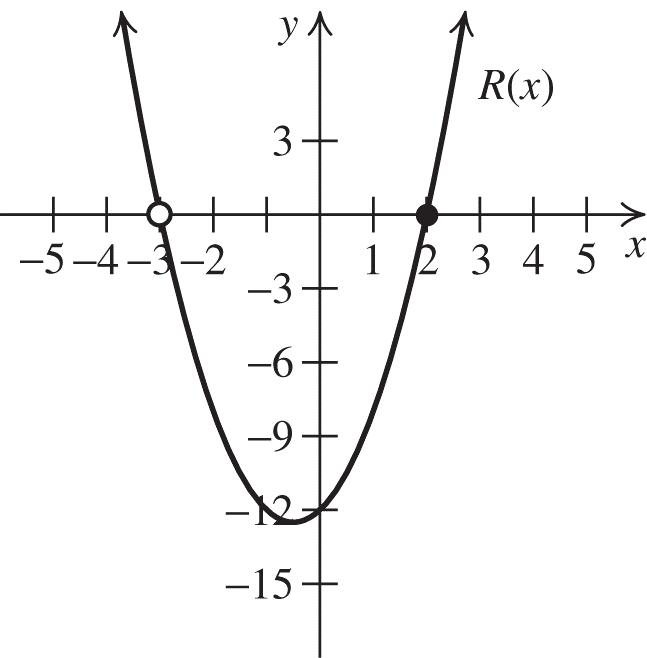
From the graph, it is clear that 0 Rx when 32. x Thus, the solution set is 3,2.
6.
2 2 0 31 xx Rx xx
numerator: 2 200,2xxxx
denominator: 3103,1xxxx
The lines x = –3 and x = 1 are the vertical asymptotes of Rx The intervals to be tested are
,3,3,2,2,0,0,1, and
1,. Note that –3 and 1 are not included in the intervals to be tested because they cause the denominator of Rx to equal 0.
Interval Test point
,3
Value of Rx Result
2.5 Exercises
Concepts and Vocabulary
1. For the polynomial inequalities 0 Px or 0, Px the zeros of the polynomial function Px are always included in the solution set.
2. For the polynomial inequalities 0 Px or 0, Px the zeros of the polynomial function
Px are always excluded from the solution set.
3. To solve a rational inequality, we begin by locating all zeros and vertical asymptotes (if they exist).
4. For the rational inequalities 0, Rx
0,0,RxRx or 0, Rx the zeros of the denominator of the rational function Rx (vertical asymptotes or holes) are always excluded from the solution set.
5. True
6. False. A polynomial function does not change sign at its zero if its graph touches, but does not cross the x-axis. A polynomial function changes sign at its zero if its graph crosses the x-axis.
7. False
8. True
Building Skills
9. From the graph, 0 Px on 2,13,.
10. From the graph 0 Px on 2,03,.
11. From the graph, 0 Px on 3,22,.
12. From the graph, 0 Px on 2,.
13. From the graph, 0 Px on ,22,23,.
14. From the graph, 0 Px on 2,11,3.
[–10, 10] by [–10, 10]
We can verify the solution by examining the graph. Solution set: 3,22,01,
or
3,01,.
15. From the graph, 0 Px on 3,2.
16. From the graph 0 Px on
,31,.
17.
340xx
The zeros are x = 3 and x = 4. So, the intervals to be tested are
,3,3,4, and
4,.
Interval Test point
18.
250xx
The zeros are x = –2 and x = 5. So, the intervals to be tested are
,2,2,5,
Interval Test point
and
Value of
Px Result
,2 –5 30 +
2,5 0 –10 –
5, 6 8 + Solution set:
2,5
19.
180xx
The zeros are x = –1 and x = 8. So, the intervals to be tested are ,1,1,8, and
Interval Test point
8,.
Value of Px Result
,1 –2 10 +
1,8 0 –8 –
8, 10 22 +
Solution set:
,18,
20.
460xx
The zeros are x = –4 and x = –6. So, the intervals to be tested are
,6,6,4, and 4,.
Interval Test point
Value of Px Result ,6 –10 24 +
6,4 –5 –1 – 4, 0 24 +
Solution set: 6,4
21.
21530 xxx
The zeros are x = 1, x = –5, and x = 3. So, the intervals to be tested are
,5,5,1,
1,3, and 3,.
Interval Test point
Value of Px Result ,5 –6 –126 –
5,1 0 30 +
1,3 2 –14 –
3, 6 330 +
Solution set: ,51,3
22.
31240 xxx
The zeros are x = –1, x = 2, and x = 4. So, the intervals to be tested are ,1,1,2, 2,4, and 4,.
Interval Test point
Value of Px Result
,1 –2 –72 – 1,2 0 24 +
2,4 3 –12 –
4, 5 54 +
Solution set: 1,24,
23. 1470 xxx
The zeros are x = 1, x = 4, and x = –7. So, the intervals to be tested are ,7,7,1,
1,4, and 4,.
Interval Test point Value of Px Result
,7 –10 462 +
7,1 0 –28 –
1,4 2 18 +
4, 5 –48 –
Solution set: 7,14,
24.
2450xxx
The zeros are x = –2, x = 4, and x = –5. So, the intervals to be tested are ,5,5,2,
2,4, and 4,.
Interval Test point
Value of Px Result ,5 –6 40 +
5,2 –4 –16 –
2,4 0 40 +
4, 5 –70 –
Solution set: ,52,4
25. 2 210xxx
The zeros are x = 0, x = –2, and x = 1. So, the intervals to be tested are ,2,2,0, 0,1, and 1,.
Interval Test point
Value of Px Result
,2 –3 36 + 2,0 –1 –2 –
0,1 0.5 –0.3125 –
1, 2 16 +
Solution set: 2,00,1
26. 2 2160xxx
The zeros are x = –2, x = 1, and x = 6. So, the intervals to be tested are ,2,2,1, 1,6, and 6,.
Interval Test point Value of Px Result
,2 –3 144 +
2,1 0 –12 –
1,6 2 –16 – 6, 7 324 +
Solution set: ,26,
27. 2 130xxx
The zeros are x = 0, x = 1, and x = 3. So, the intervals to be tested are ,0,0,1, 1,3, and 3,.
Interval Test point
Value of Px Result
,0 –1 8 +
0,1
+
1,3 2 –4 – 3, 5 200 +
Solution set:
,00,13,,13,
28. 2 4310xxx
The zeros are x = –4, x = 3, and x = 1. So, the intervals to be tested are ,4,4,1,
1,3, and 3,.
Interval Test point
Value of Px Result
,4 –5 384 +
4,1 0 –36 –
1,3 2 6 +
3, 5 144 + (continuedonnextpage)
(continued)
Note that 2 4310xxx when x = 3, so include that value in the solution set.
Solution set: 4,13
29. 2 2110 xxx
The real zeros are x = 0 and x = 1. So, the intervals to be tested are ,0,0,1, and
1,.
Interval Test point
Value of Px Result
,0 –1 8 +
0,1 0.5 –0.625 –
1, 2 20 +
Solution set: ,01,
30. 2 3230 xxx
The real zeros are x = 0 and x = –2. So, the intervals to be tested are ,2,2,0, and 0,.
Interval Test point
Value of Px Result
,2 –3 –108 –
2,0 –1 12 +
0, 1 –36 –
Solution set: 2,0
31. 22220 210 xxxx xx
The zeros are x = 2 and x = –1. So, the intervals to be tested are ,1,1,2, and 2,.
Interval Test point
Value of Px Result
,1 –3 10 + 1,2 0 –2 –
2, 3 4 +
The zeros are x = –5 and x = 4. So, the intervals to be tested are ,5,5,4, and 4,.
Interval Test point Value of
Px Result
,5 –6 –10 –
5,4 0 20 +
4, 5 –10 –
Solution set: 5,4
33. 221033100 xxxx 2 310Pxxx cannot be factored, so there are no rational zeros. We must examine the graph. This is a parabola that opens upward and with vertex
331 2224,,. bb aa P
[–10, 10] by [0, 20]
The graph is always greater than 0, so the solution set is ,.
Solution set: ,12, 32. 22 2 20200 200540 xxxx xxxx
34. 2242240 xxxx 2 34Pxxx cannot be factored, so there are no rational zeros. We must examine the graph. This is a parabola that opens upward and with vertex
22,1,1. bb aa P
[–10, 10] by [0, 20]
The graph is never less than or equal to 0, so the solution set is .
Copyright © 2018 Pearson Education
35. 32460xxx
The possible rational zeros are 1,2,3,6.
Using synthetic division, we find that x = 1 is a zero.
11416 156 1560
So,
32246156 123 xxxxxx xxx
Interval Test point Value of Px Result
1,2 1.5 –1.375 – 2, 3 14 +
Solution set: ,41,2
37. 33121612160 xxxx
The possible rational zeros are 1,2,4,8,16.
Using synthetic division, we find that x = –2 is a zero.
,3,3,2,
The zeros are x = –2, x = –3, and x = 1. So, the intervals to be tested are
2,1, and
Interval
3,2 –2.5 0.875 +
2,1 0 –6 –
1, 2 20 +
Solution set:
36. 32 1080xxx
The possible rational zeros are 1,2,4,8.
Using synthetic division, we find that x = 1 is a zero.
111108 128 1280 So,
322108128 124 xxxxxx xxx
The zeros are x = –4, x = 1, and x = 2. So, the intervals to be tested are
,4,4,1,
1,2, and 2,.
Interval Test point Value of Px Result ,4 –5 –42 –
4,1 0 8 +
2101216 2416 1280 So,
321216228 224 xxxxx xxx
The zeros are x = –2 and x = 4. So, the intervals to be tested are ,2,2,4, and 4,.
Interval
Test point
Value of Px Result
,2 –3 –7 – 2,4 0 –16 – 4, 5 49 +
Note that 3 1216xx when x = –2, so include that value in the solution set.
Solution set: 24,
38. 33 3 32320 320 xxxx xx
The possible rational zeros are 1,2.
Using synthetic division, we find that x = –2 is a zero. 21032 242 1210
So, 32 2 32221 21 xxxxx xx
The zeros are x = –2 and x = 1. So, the intervals to be tested are ,2,2,1, and 1,.
(continuedonnextpage)
(continued)
Interval Test point Value of Px Result ,2 –3 16 + 2,1 0 –2 – 1, 2 –4 –
Solution
39. 322 32 33523 5280 xxxxx xxx
The possible rational zeros are 1,2,4,8.
Using synthetic division, we find that x = 2 is a zero. 21528 268 1340
So,
322528234 241 xxxxxx xxx
The zeros are x = –1, x = 2, and x = 4. So, the intervals to be tested are ,1,1,2, 2,4, and 4,.
Interval Test point Value of Px Result
,1 –2 –24 –
1,2 0 8 +
2,4 3 –4 –
4, 5 18 +
Solution set: ,12,4
The possible rational zeros are 1,2,3,4,6,12.
Using synthetic division, we find that x = 1 is a zero. 1121112 1112 11120
32221112112 143 xxxxxx xxx
The zeros are x = –3, x = 1, and x = 4. So, the intervals to be tested are ,3,3,1, 1,4, and 4,.
Interval Test point Value of Px Result
,3 –4 –40 – 3,1 0 12 + 1,4 3 –12 –
4, 5 32 +
Solution set: 3,14,
424222 2 33030 330 xxxxxx xxx
The zeros are 3,0.
So, the intervals to be tested are
Note that 42 3 xx when x = 0, so include that value in the solution set.
Solution set:
42.
The zeros are 2,0.
So, the intervals to be tested are
,2,2,0,
0,2,
and
43. From the graph,
44. From the graph,
45. From the graph,
46. From the graph, 0 Rx on 1,00,1.
47. From the graph, 0 Rx on 1,02,.
48. From the graph, 0 Rx on ,01,2.
49. From the graph, 0 Rx on ,11,01,.
50. From the graph, 0 Rx on 1,00,11,.
For exercises 51–76, verify your answers by graphing the function.
51. 1 0 2 x x numerator: 101xx denominator: 202xx
The line x = –2 is the vertical asymptote of , Rx so –2 is not included in the intervals to be tested The boundary points are –2 and 1. The intervals are ,2,2,1, and 1,.
Interval Test point
Solution set: ,21,
52. 3 0 4 x x
numerator: 303xx denominator: 404xx
The line x = 4 is the vertical asymptote of
, Rx so 4 is not included in the intervals to be tested. The boundary points are –3 and 4. The intervals are ,3,3,4, and 4,.
Interval Test point
Value of Rx Result
,3 –4 1 8 +
3,4 0 3 4 –
4, 5 8 +
Solution set: 3,4
53. 2 0 8 x x
numerator: 202xx
denominator : 808xx
The line x = 8 is the vertical asymptote of , Rx so 8 is not included in the intervals to be tested. The boundary points are –2 and 8. The intervals are ,2,2,8, and 8,.
Interval Test point
Value of Rx Result ,2 –4 1 6 + 2,8 0 1 4 –
8, 10 6 +
Solution set: ,28,
54. 5 0 1 x x
numerator: 505xx
denominator : 101xx
The line x = 1 is the vertical asymptote of , Rx so 1 is not included in the intervals to be tested. The boundary points are –5 and 1. The intervals are
,5,5,1, and 1,.
Interval Test point Value of Rx Result
55. 32 0 43 x x numerator: 2 3 320xx
The line 4 3 x is the vertical asymptote of
56. 12 0 32 x x numerator: 1 2 120xx denominator : 3 2 320xx
The line 3 2 x is the vertical asymptote of , Rx so 3 2 is not included in the intervals to be tested. The boundary points are 1 2 and 3 2
The intervals are
Solution set: 3 1 22 ,
57. 12 0 1 xx x
numerator: 1202,1xxxx denominator : 101xx
The line x = –1 is the vertical asymptote of , Rx so –1 is not included in the intervals to be tested. The boundary points are –2, –1, and 1. The intervals are
Interval Test point Value of
58. 3 0 2 xx x
numerator: 300,3xxxx
denominator : 202xx
The line x = –2 is the vertical asymptote of , Rx so –2 is not included in the intervals to be tested. The boundary points are –2, 0, and 3. The intervals are
,2,2,0,0,3, and
3,.
Interval Test point
Solution set:
59.
Value of
Rx Result
60. 1 0 4 xx x numerator: 100,1xxxx denominator : 404xx The line x = –4 is the vertical asymptote of , Rx so –4 is not included in the intervals to be tested. The boundary points are –4, 0, and 1. The intervals are ,4,4,0, 0,1 and 1,.
Interval Test point
52 0 3 xx x numerator: 5205,2xxxx denominator : 303xx
The line x = –3 is the vertical asymptote of , Rx so –3 is not included in the intervals to be tested. The boundary points are –5, –3, and 2. The intervals are
3,2 and 2,.
,5,5,3,
,5 –8 –6 –
Value of Rx Result
,4 –5 –30 – 4,0 –2 3 +
0,1 1 2 1 18 –
1, 4 3 2 +
Solution set: ,40,1
2 11 0 43 xx xx
numerator: 2 1101,1xxxx denominator : 4304,3xxxx
The lines x = –4 and x = 3 are the vertical asymptotes of , Rx so –4 and 3 are not included in the intervals to be tested. The boundary points are –4, –1, 1, and 3. The intervals are ,4,4,1, 1,1, 1,3, and 3,.
Interval Test point
Value of Rx Result
,4 –5 –12 –
4,1 –2 3 10 +
1,1 0 1 12 +
1,3 2 3 2 –
3, 5 8 +
Solution set: 4,11,13,4,13,
62.
2 42 0 21 xx xx
numerator: 4204,2xxxx
denominator : 2 2101,2xxxx
The lines x = 1 and x = 2 are the vertical asymptotes of , Rx so 1 and 2 are not included in the intervals to be tested. The boundary points are –4, –2, 1, and 2. The intervals are ,4,4,2,
2,1,
1,2, and
Interval Test point Value of Rx Result
1,2 3 2 154 +
Solution set:
4,21,22,
63. 3 23 0 1 xx x
numerator: 3 2302,3 xxxx
denominator : 101xx
The line x = –1 is the vertical asymptote of , Rx so –1 is not included in the intervals to be tested. The boundary points are –1, 2, and 3. The intervals are ,1,1,2, 2,3, and 3,.
Interval Test point Value of Rx Result
1,2 0 –24 –
2,3 5 2 1 56 +
Solution set:
64.
3 41 0 2 xx x
numerator: 3 4101,4xxxx
denominator : 202xx
The line x = 2 is the vertical asymptote of
, Rx so 2 is not included in the intervals to be tested. The boundary points are 1, 2, and 4. The intervals are ,1,1,2, 2,4, and 4,.
Interval Test point Value of Rx Result
,1 0 2 +
65.
Solution set: 1,24,
5959 440 44 5944 7 00 44 xx xx xxx xx
numerator: 707xx
denominator : 404xx
The line x = 4 is the vertical asymptote of , Rx so 4 is not included in the intervals to be tested. The boundary points are –7 and 4. The intervals are ,7,7,4 and 4,.
Interval Test point
Value of Rx Result
,7 –8 1 12 + 7,4 0 7 4 –
4, 5 12 +
Solution set: ,74,
66.
217217 330 55 21735 2 00 55 xx xx xxx xx
numerator: 202xx
denominator : 505xx
The line x = 5 is the vertical asymptote of , Rx so 5 is not included in the intervals to be tested. The boundary points are –2 and 5. The intervals are ,2,2,5 and 5,.
Interval Test point
Value of Rx Result
,2 –3 1 8 –
2,5 0 2 5 +
Solution set: ,25, 67.
88 220 33 823 2 00 33 xx xx xxx xx
numerator: 202xx denominator : 303xx
The line x = –3 is the vertical asymptote of
, Rx so –3 is not included in the intervals to be tested. The boundary points are –3 and 2. The intervals are ,3,3,2, and
2,.
Interval Test point Value of Rx Result
,3 –4 –6 –
numerator: 0 x
denominator : 303xx
The line x = 3 is the vertical asymptote of , Rx so 3 is not included in the intervals to be tested. The boundary points are 0 and 3. The intervals are ,0,0,3 and 3,.
,0 –3 1 2 +
0,3 1 1 2 –
3, 4 4 +
Solution set: 0,3 69.
2121 0 3232 223 7 00 3232 xxxx xxx xxxx
numerator: 707xx denominator : 3202,3xxxx
The lines x = –2 and x = 3 are the vertical asymptotes of , Rx so –2 and 3 are not included in the intervals to be tested. The boundary points are –7, –2, and 3. The intervals are
,7,7,2,
Interval
Solution
Copyright © 2018 Pearson Education
2,3, and 3,.
numerator: 909xx
denominator :
The lines x = –2 and x = 5 are the vertical asymptotes of , Rx so –2 and 5 are not included in the intervals to be tested. The boundary points are –9, –2, and 5. The intervals are
,9,9,2,
2,5, and
,9 –10 1 120 +
The lines x = –2 and x = 5 are the vertical asymptotes of , Rx so –2 and 5 are not included in the intervals to be tested. The boundary points are –2, 1 4 , and 5. The intervals are
numerator: 1 3 310xx denominator :
133,1xxxx
The lines x = –3 and x = –1 are the vertical asymptotes of , Rx so –3 and –1 are not included in the intervals to be tested. The boundary points are –3, –1, and 1 3 The intervals are
1 3 ,.
,3,3,1, 1 3 1,, and
Solution set:
73. 2 8868 6600 xx xx xxx
numerator:
denominator : 0 x
The line x = 0 (the y-axis) is the vertical asymptote of , Rx so 0 is not included in the intervals to be tested. The boundary points are 0, 2, and 4. The intervals are
,0,0,2,
and
Interval Test point Value of
Rx Result
75. 2 3 0 4 x x numerator: 300 xx denominator : 2 402xx
The lines x = –2 and x = 2 are the vertical asymptotes of , Rx so –2 and 2 are not included in the intervals to be tested. The boundary points are –2, 0, and 2. The intervals are ,2,2,0, 0,2, and 2,.
Interval Test point Value of Rx Result ,2 –4 –1 –
2,0 –1 1 +
0,2 1 –1 –
2, 4 1 +
Solution set: 2,02,
Solution set:
,02,4
74. 2 121212 1100 xx xx xxx
numerator:
denominator : 0 x
The line x = 0 (the y-axis) is the vertical asymptote of , Rx so 0 is not included in the intervals to be tested. The boundary points are –3, 0, and 4. The intervals are ,3,
3,0,0,4, and 4,.
Interval Test point Value of Rx Result
,3 –4 –2 –
3,0 –1 10 +
0,4 1 –12 – 4, 6 3 +
Solution set: 3,04,
76. 2 2 1 0 4 x x
numerator: 2 10 x has no real solutions. denominator : 2 402xx
The lines x = –2 and x = 2 are the vertical asymptotes of , Rx so –2 and 2 are not included in the intervals to be tested. The boundary points are –2 and 2. The intervals are
,2,2,2, and 2,.
Interval Test point Value of Rx Result
,2 –3 2 +
2,2 0 1 4 –
2, 3 2 +
Solution set: 2,2
Applying the Concepts
77. 2 0.05 dvv 2 0.05252556.25 d
In a 25-mile-per-hour zone, the stopping distance is about 56.25 feet, so the driver was going over the speed limit because it took over 75 feet to stop.
78. 2 2 163295110 1632150 tt tt
2 323241615 216 3264328 3232 4024 1.25 or 0.75 3232
The height of the stone will be at least 110 feet between 0.75 second and 1.25 seconds.
79. 3218111020QQQ
The possible rational zeros are 1,2,3,6,17,34,51,102.
Using synthetic division, we find that 3 is a factor. 311811102 345102 115340
The zeros are Q = –2, Q = 3, and Q = 17. Because we are looking for an amount, it is not necessary to test any negative values. So, the intervals to be tested are 0,3, 3,17, and 17,.
Interval Test point Value of Px Result
The company will make a profit if they sell between 3000 and 17,000 units of lip gloss. 80.
The length of the box is 9 –2x, the width is 6 – 2x, and the height is x. Then, the volume is given by 9262.Vxxx
32 32 926220 4305420 43054200 xxx xxx xxx
The possible rational zeros are 1,2,4,5,10,20.
Using synthetic division, we find that 2 is a factor.
24305420 84420 422100
32 2 2 4305420 242210 222115 22215 xxx xxx xxx xxx
The zeros are 1 2 ,2, and 5. Because we are looking for a length, it is not necessary to test any negative values. The maximum value of x cannot be 3 or greater because that would eliminate the entire width. So, the intervals to be tested are 11 22 0,,,2, and 2,3.
If 0.52, x the volume of the resulting open-top box will be at least 20.
81. We want to find the value of Q that makes . ABTCTC 322 32 6141052034 1134240 QQQQQ QQQ
The possible rational zeros are 1,2,3,4,6,8,12,24.
Using synthetic division, we find that 1 is a factor. 11113424 11024 110240 (continuedonnextpage)
(continued)
32 2 113424 11024 146
The zeros are Q = 1, Q = 4, and Q = 6. Because we are looking for an amount, it is not necessary to test any negative values. So, the intervals to be tested are
0,1,1,4,4,6, and 6,.
Note that 400 3 133.3.
The likelihood that the next card dealt will be a jack, queen, king, or ace will be greater than 50% if between 134 and 208 cards are dealt.
83. The speed of the ferry against the current is v – 2, and the speed of the ferry with the current is v + 2. The time going against the current is 40 2 , v and the time going with the current is 40 2 v So, we have
It is more cost effective to produce headphones at company A when between 0 and 1000 headphones are produced and when between 4000 and 6000 headphones are produced.
640.2640.2 0.50.50 208208 640.20.5208 0 208 640.21040.5400.3 00 208208 xx xx xx x xxx xx
numerator: 400 3 400.30xx
denominator : 2080208 xx
The line x = 208 is the vertical asymptote of , Rx so 208 is not included in the intervals to be tested. The boundary points are 400 3 and 208.
Because we are looking for an amount, it is not necessary to test any negative values. There are 208 cards in four decks, so it is not necessary to test values greater than 208. The intervals are
400 3 0, and 400 3 ,208. Interval Test
numerator:
denominator : 222,2vvvv
The lines v = –2 and v = 2 are the vertical asymptotes of , Rv so –2 and 2 are not included in the intervals to be tested. Because we are looking for a speed, it is not necessary to test values less than or equal to 0. The boundary points are 0, 2, and 18. The intervals are 0,2, 2,18, and 18,.
Interval Test point
Value of Rv Result
0,2 1 –31.17 –
2,18 5 14.55 +
18, 20 –0.46 –
The ferry should travel at least 18 miles per hour to limit the round trip to at most 4.5 hours.
Copyright © 2018 Pearson Education Inc.
4 3 12340,12tttt
denominator : 2 160 t has no real zeros. Because we are looking for an amount, it is not necessary to test any negative values. The boundary points are 4 3 and 12. The intervals to be tested are
44 33 0,,,12,
and
12,.
Interval Test point Value of
4 3 0,
Rx Result
2 1 +
12, 13 –0.19 –
The drug concentration is least 3 mg/dl for 4 3 hr12 hr, t or between 1 hr 20 min and 12 hr, inclusive.
85. We are looking for the values of I that make . ABPP
numerator: 2 4400,4IIIIII denominator : 5205,2 IIII
The lines I = –5 and I = –2 are the vertical asymptotes of , RI so –5 and –2 are not included in the intervals to be tested. Because we are looking for an amount, it is not necessary to test any negative values. The boundary points are 0 and 4. The intervals to be tested are 0,4 and 4,.
Interval
Test point
Value of Rx
Result
0,4 1 1 6 –
4, 5 1 14 +
ABPP for 04. I 86.
00 11 0.4252 0 1 0.4212 0 1 xx
1 2 0.42120,2 xxxx
denominator : 2 1 x has no real zeros
Because we are looking for an amount, it is not necessary to test any negative values. The boundary points are 1 2 and 2. The intervals to be tested are 11 22 0,,,2, and 2,.
Interval Test point Value of
The efficiency of this rocket is at least 80% for 1 2 2. x
We want to know when 1.4. fx Graph fx and y = 1.4 in the window [0, 20] by [–1, 7], and then find the intersection.
Vinyl sales exceeded 1.4 million between 13.5 years after 1993, or during 2007, and 2013.
88. 25.2691.24050.0640.00103623 fxxxx
We want to know when 17.65. fx Graph fx and y = 17.65. Use the window [0, 40] by [17, 19] to be able to see the intersections clearly.
91.
The intervals to be tested are
,5,5,3, and 3,.
Interval Test point
The intersections occur at 13.3, x which is during 1988, 18.3, x which is during 1993, and at 30.2, x which is during 2005. The price of a music album was less than $17.65 between the years 1988 and 1993, and between 2005 and 2014.
Beyond the Basics
89. 2 412fxxx
The domain consists of those values of x for which 2 4120.xx
2 4120620 6,2 xxxx xx
The intervals to be tested are ,2,2,6, and 6,.
Interval Test point Value of Px Result
,2
–3 9 +
2,6 0 –12 –
6, 7 9 +
The domain is ,26,.
90. 2 152 fxxx
The domain consists of those values of x for which 2 1520. xx
2 1520530 5,3 xxxx xx
Value of Px Result
,5 –6 –9 – 5,3 0 15 +
3, 4 –9 –
The domain is 5,3.
3 4 fxxx
The domain consists of those values of x for which 3 40. xx 3 40220 0,2,2 xxxxx xxx
The intervals to be tested are
,2,2,0,0,2, and 2,.
Interval Test point Value of Px Result ,2 –3 15 + 2,0 –1 –3 –
0,2 1 3 +
2, 3 –15 –
The domain is ,20,2.
92. 4 8 fxxx
The domain consists of those values of x for which 4 80. xx 43 2 8080 22400,2 xxxx xxxxxx
The intervals to be tested are
,2,2,0, and 0,.
Interval Test point
Value of Px Result
,2 –3 57 +
2,0 –1 –7 –
0, 1 9 +
The domain is ,20,.
Copyright © 2018 Pearson Education
93. 2 5 fxx x
The domain consists of those values of x for which 2 0. 5 x x
numerator: 202 xx
denominator : 505xx
The line x = –5 is the vertical asymptote of , Rx so –5 is not included in the intervals to be tested. The boundary points are –5 and 2. The intervals to be tested are ,5,5,2, and 2,.
Interval Test point
Value of Px Result
,5 –6 –8 –
5,2 0 2 5 +
2, 3 1 8 –
The domain is 5,2.
94. 3 2 fxx x
The domain consists of those values of x for which 3 0. 2 x x numerator: 303xx denominator : 202xx
The line x = 2 is the vertical asymptote of , Rx so 2 is not included in the intervals to be tested. The boundary points are –3 and 2. The intervals to be tested are
,3,3,2, and 2,.
Interval Test point
Value of Px Result
,3 –6 3 8 +
The domain is
,32,.
95. 12 1 33fxx xx
The domain consists of those values of x for which 12 10. 33 x xx
numerator: 202xx denominator : 303xx
The line x = 3 is the vertical asymptote of , Rx so 3 is not included in the intervals to be tested. The boundary points are 2 and 3. The intervals to be tested are ,2,2,3, and 3,.
Interval Test point
Value of Px Result
,2 0 2 3 +
3, 4 2 +
The domain is ,23,.
25311 311 2 55 1 5 fxxxx xx x x
The domain consists of those values of x for which 3111 20. 55 xx xx numerator: 101xx denominator : 505xx
The line x = –5 is the vertical asymptote of , Rx so –5 is not included in the intervals to be tested. The boundary points are –5 and –1. The intervals to be tested are
,5,5,1, and 1,.
Interval Test point
Value of Px Result
,5 –6 –5 –
5,1 –3 1 + 1, 0 1 5 –
The domain is 5,1.
97. 2 22 31 1 44 fxx xx
The domain consists of those values of x for which 2 22 31 10. 44 x xx
numerator: 2 101xx
denominator : 2 402xx
The lines x = –2 and x = 2 are the vertical asymptotes of , Rx so –2 and 2 are not included in the intervals to be tested. The boundary points are –2, –1, 1 and 2. The intervals to be tested are ,2,2,1, 1,1,1,2, and 2,.
Interval Test point Value of
Px Result
,2 –4 5 4 +
2,1 –1.5
The domain is
,21,12,.
98. 2 15252 22 fxxxx xx
The domain consists of those values of x for which 2 15252 0. 22 xx x xx numerator: 2 1 2 25202120 ,2 xxxx xx denominator : 200 xx The line x = 0 (the y-axis) is the vertical asymptotes of , Rx so 0 is not included in the intervals to be tested. The boundary points are 0, 1 2 , and 2. The intervals to be tested are ,0, 11 22
The domain is
3221112,Pxxxx range [–10, 18]
We must solve
10 Px and 18. Px
First inequality: 32 32 2111210 211220 xxx xxx
Possible rational zeros: 1,2,11,22
Using synthetic division, we find that 2 is a factor.
2121122 2022 10110
32221122211 21111 xxxxx xxx
The zeros are x = 2, 11, x and 11. x
The intervals to be tested are ,11, 11,2,
2,11,
and
11,.
Note that 113.32.
Interval Test point Value of Px Result
,11 –4 –30 –11,2
–2 28 + 2,11
4 10 +
The solution set for the first inequality is
Copyright © 2018 Pearson Education
(continuedonnextpage)
(continued)
Second inequality: 32 32 2111218 21160 xxx xxx
Possible rational zeros: 1,2,3,6 Using synthetic division, we find that –2 is a factor. 212116 286 1430
Use the quadratic formula to find the zeros of 2 43.xx
Verify graphically by graphing 1 , yPx 2 10, y and 3 18, y and then finding the intersections.
[–10, 10] by [–20, 20] 100. 323420,Pxxxx range [8, 14]
We must solve 8 Px and 14. Px
The zeros are x = –2, 27, x and 27. x The intervals to be tested are
,2, 2,27, 27,27, and 27,.
Interval Test point Value of Px Result
,2 –3 –18 –
2,27 –1 2 + 27,27, 0 –6 –
27, 5 14 +
The solution set for the second inequality is
,227,27,
,20.65,4.65.
Now we must see where the two solution sets intersect. To make the work easier, use the decimal equivalents.
3.32,23.32, ,20.65,4.65 3.32,20.65,23.32,4.65 11,227,211,27
The number line below shows the overlap.
First inequality: 32 32 34208 34120 xxx xxx
Possible rational zeros: 1,2,3,4,6,12 Using synthetic division, we find that 2 is a factor. 213412 2212 1160
322341226 232 xxxxxx xxx
The zeros are x = –2, x = 2 and x = 3 The intervals to be tested are ,2,
2,2, 2,3, and 3,.
Interval Test point Value of Px Result
,2 –3 –30 –
2,2 0 12 +
2,3 2.5 –1.125 – 3, 4 12 +
The solution set for the first inequality is 2,23,.
Second inequality: 32 32 342014 3460 xxx xxx
Possible rational zeros: 1,2,3,6 (continuedonnextpage)
(continued)
Using synthetic division, we find that 1 is a factor.
Use the quadratic formula to find the zeros of 2 26.
The zeros are 17,1,xx and 17. x
The intervals to be tested are
Interval
Test point
Value of
Px Result ,17 –2 –6 –17,1 0 6 + 1,17
The solution set for the second inequality is
,1.651,3.65.
Now we must see where the two solution sets intersect. To make the work easier, use the decimal equivalents.
2,171,23,17
2,23,,1.651,3.65
2,1.651,23,3.65
The number line below shows the intersection.
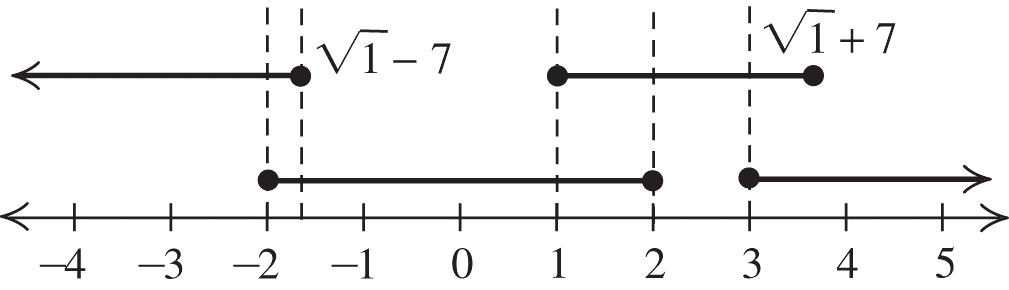
Verify graphically by graphing 1 , yPx 2 10, y and 3 18, y and then finding the intersections.
[–10, 10] by [–2, 22]
101. 2 , 3 x Rx x range [2, 6]
We must solve 2 Rx and 6. Rx
First inequality: 22 220 33 223 8 00 33 xx xx xxx xx
numerator: 808xx denominator : 303xx
The line x = 3 is the vertical asymptote of , Rx so 3 is not included in the intervals to be tested. The boundary points are 3 and 8. The intervals to be tested are ,3,3,8, and 8,. Interval
The solution set for the first inequality is 3,8.
Second inequality:
22 660 33 263 520 00 33 xx xx xxx xx
numerator: 52004 xx denominator : 303xx
The line x = 3 is the vertical asymptote of , Rx so 3 is not included in the intervals to be tested. The boundary points are 3 and 4. The intervals to be tested are ,3,3,4, and 4,.
(continuedonnextpage)
(continued)
Interval Test point
Value of Px Result
,3 2 –10 –
3,4 3.5 5 +
4, 8 –4 –
The solution set for the second inequality is
,34,. Now we must see where the two solution sets intersect.
3,8,34,4,8
The number line below shows the intersection.
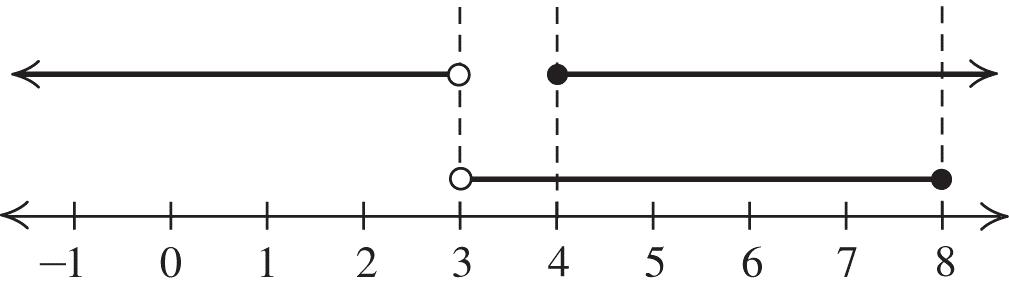
Verify graphically by graphing 1 , yRx
2 10, y and 3 18, y and then finding the intersections.
[–4, 16] by [–10, 10]
102. 3 , 7 x Rx x range [1, 3]
We must solve 1 Rx and 3. Rx
First inequality:
numerator: 21005 xx denominator : 707xx
The line x = 7 is the vertical asymptote of , Rx so 7 is not included in the intervals to be tested. The boundary points are 5 and 7. The intervals to be tested are
,5,5,7,
and 7,.
Interval Test point
Value of Px Result
7, 8
The solution set for the first inequality is 5,7. Second inequality:
numerator: 42406 xx denominator : 707xx
The line x = 7 is the vertical asymptote of , Rx so 7 is not included in the intervals to be tested. The boundary points are 6 and 7. The intervals to be tested are ,6,6,7, and
The solution set for the second inequality is ,67,. Now we must see where the two solution sets intersect. 5,7,67,5,6
The number line below shows the intersection.
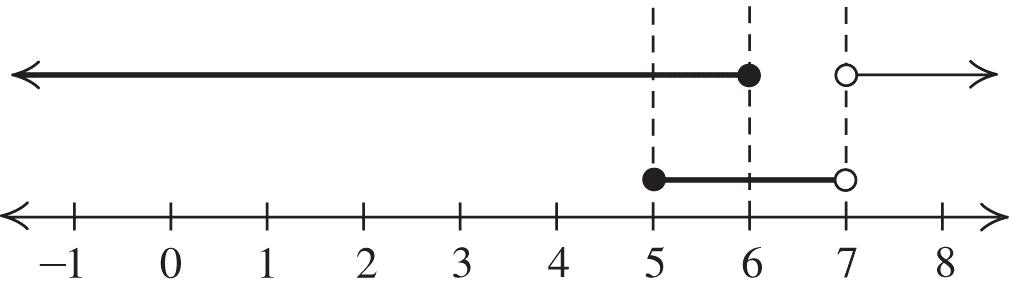
Verify graphically by graphing 1 , yRx 2 1, y and 3 3, y and then finding the intersections.
[–4, 16] by [–10, 10]
Copyright © 2018 Pearson Education
103. 2 5 , 1 x Rx x range [0, 1]
We must solve 0 Rx and 1. Rx
First inequality: 2 5 0 1 x x
numerator: 505 xx
denominator : 2 101xx
The lines x = –1 and x = 1 are the vertical asymptotes of , Rx so –1 and 1 are not included in the intervals to be tested. The boundary points are –1, 1, and 5. The intervals to be tested are
,1,1,1,1,5, and
5,.
Interval Test point Value
Px Result
The solution set for the first inequality is
Second inequality:
numerator:
denominator : 2 101xx
The lines x = –1 and x = 1 are the vertical asymptotes of , Rx so –1 and 1 are not included in the intervals to be tested.
The boundary points are –3, –1, 1, and 2. The intervals to be tested are ,3,3,1,
1,1,1,2, and 2,.
The solution set for the second inequality is
,31,12,. Now we must see where the two solution sets intersect.
,11,5 ,31,12, ,32,5
The number line below shows the intersection.
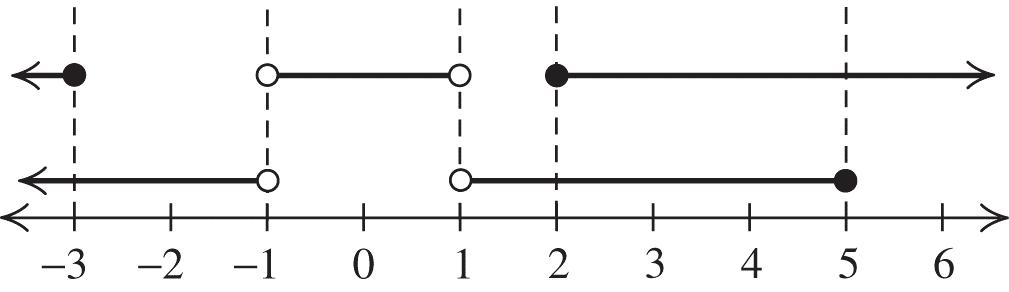
Verify graphically by graphing 1 , yRx
2 1, y and 3 3, y and then finding the intersections.
[–10, 10] by [–10, 10]
104. 2 21 , 4 x Rx x range [0, 1]
We must solve 0 Rx and 1. Rx
First inequality:
2 21 0 4 x x
numerator: 1 2 210xx
denominator : 2 402xx
The lines x = –2 and x = 2 are the vertical asymptotes of , Rx so –2 and 2 are not included in the intervals to be tested.
(continuedonnextpage)
Copyright © 2018 Pearson
(continued)
The boundary points are –2, 1 2 , and 2. The intervals to be tested are
Interval Test point
The solution set for the first inequality is
denominator : 2 402xx
The lines x = –2 and x = 2 are the vertical asymptotes of , Rx so –2 and 2 are not included in the intervals to be tested. The boundary points are –2, –1, 2, and 3. The intervals to be tested are ,2,2,1,
1,2,2,3, and 3,.
Interval Test point Value of Px Result
The solution set for the second inequality is ,21,23,. Now we must see where the two solution sets intersect.
1 2 1 2 2,2, ,21,23, 1,3,
The number line below shows the intersection.
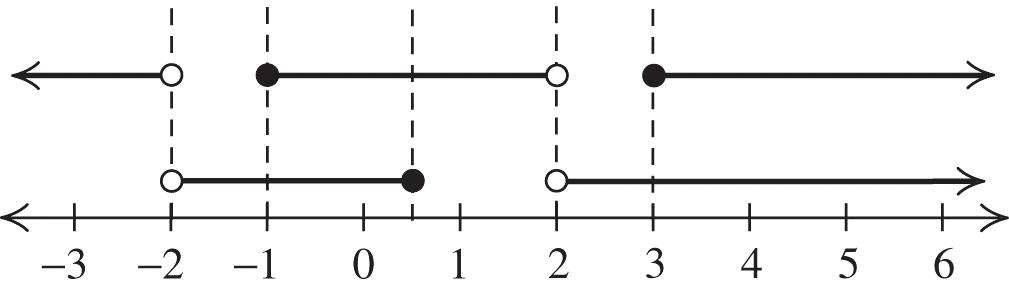
Verify graphically by graphing 1 , yRx 2 1, y and 3 3, y and then finding the intersections.
[–6, 6] by [–6, 6]
105. 2 1121 2200 xx xx xxx
numerator: 2 2 210101xxxx
denominator : 0 x
The boundary points are 0 and 1, so the intervals to be tested are ,0, 0,1, and 1,.
Interval Test point
Value of Px Result ,0 –1 –4 – 0,1 0.5 1 2 + 1, 2 1 2 +
Solution set: 0,
106.
4444 432 22220 282432140 xxxx xxxx
From the hint, we know that 2 1 x is a factor. After using long division or synthetic division twice, we have
there are no real zeros. The intervals to be tested are
,1 and
The solution set is
Therefore, the inequality is true for all real numbers. 107.
22 114114 0 4 0 44 0 xaxaxaxa aaxaxxax axax aaxx axax
denominator : 00, axaxxxa
The boundary points are 0, 2 , a and a. The intervals to be tested are 2 ,0,0,, a
and
,.a
Substitute the test values for x in
22 44 aaxx axax
Interval Test point
The solution set is
Therefore, x is a positive number less than a
332323 2 23320 20 xaxaxxaa axax
The zeros of Px are x = a and x = –2a
Because x is positive, it is not necessary to test negative values. Substitute the test values for x in 2 2.axax
Interval Test point Value of Px Result
0, a 2 a 3 5 8 a +
, a a + 1 3a + 1 +
The solution set is 0,,0,. aa
Therefore, x is a positive number.
Critical Thinking/Discussion/Writing
For exercises 109–114, answers will vary. Verify your answer by graphing.
109. 4,5 450xx
110. ,24, 240xx
111. 1,23, 1230xxx
112. 2 3,14 3140xxx
113. 1,04,5 1450xxxx
114.
,20,14, 2140xxxx
For exercises 115–120, answers will vary. Verify your answer by graphing.
115.
2,6 2 0 6 x x
119.
1,23, 3 0 12 x xx
121. If
0, Px then
Px could be
2 213.xxx
Solving 2 2130xxx leads to the solution set
,21,33,,21,.
Thus, 2 213Pxxxx satisfies both conditions.
122. Use the graphing transformation rules to find the solution sets.
a. ,64,2 Px
b. 21,23,Px
c. 1 2 4,812, Px
123. 10 xax
For 1, a the solution set is
,1,. a For a = 1, the solution set is
,. For a > 1, the solution set is
,1,. a
124. 0 1 xa x
For 1, a the solution set is
,1,. a
For a = 1, the solution set is
,11,. For a > 1, the solution set is
,1,. a
125. 110xaxx
For 1, a the solution set is ,11,. a For a = –1, the solution set is 11,. For –1 < a < 1, the solution set is 1,1,. a For a = 1, the solution set is
1,. For a > 1, the solution set is 1,1,. a
126. 0 11 xa xx
For a < –1, the solution set is ,11,. a
For a = –1, the solution set is 1,.
For –1 < a < 1, the solution set is
1,1,. a For a = 1, the solution set is
1,11,. For a > 1, the solution set is
1,1,. a
127. P has to be a polynomial of odd degree, and its degree has to be less than or equal to 21. k An example is 1,12,46, is the solution set of
112460.Pxxxxxx
The solution set has k = 2 open intervals of the form , ab and one interval of the form
,.c Px has degree 5 = 2k + 1.
128. P has to be a polynomial of even degree, and its degree has to be greater than or equal to 2. k An example is 3,21,12,4 is the solution set of
3211240. Px xxxxxx
The solution set has 3 k open intervals of the form ,.ab Px has degree 6 = 2k.
Getting Ready for the Next Section
129.
130.
222211xixixixx
222 2 52522542541 254 xixixix x
2.6 Zeros of a Polynomial Function 2.6 Practice Problems
1. 52 ()2351 fxxxx
There is one sign change in ()fx , so there is one positive zero. 52 52 ()2()3()5()1 2351 fxxxx xxx
There are two sign changes in ()fx , so there are either 2 or 0 negative zeros.
2. 32 ()44 fxxxx
The possible rational zeros are 1,2,4.
There are two sign changes in ()fx , so there are either 2 or 0 positive zeros.
32 32 ()()()4()4 44 fxxxx xxx
There is one sign change in ()fx , so there is 1 negative zero. Testing each positive possibility shows that 2 is an upper bound. Testing the negative values shows that –2 is a lower bound. 21144 224 1120 21144 264 1320
3. a. ()3(2)(1)(1)(1) 3(2)(1)(1)(1) Pxxxxixi xxxixi
b. 2 32 432 432 ()3(2)(1)(1)(1) 3(2)(1)22 3(2)342 3264 3361812 Pxxxxixi xxxx xxxx xxxx xxxx
4. Since 2 3i is a zero of multiplicity 2, so is 2 + 3i. Since i is a zero, so is i. The eight zeros are 3, 3, 2 3i, 2 3i, 2 + 3i, 2 + 3i, i, and i.
5. The function has degree four, so there are four zeros. Since one zero is 2i, another zero is 2i
So 2 (2)(2)4 xixix is a factor of ()Px .
Now divide to find the other factor:
So, 432 2 ()36128 (2)(2)(32) (2)(2)(2)(1) Pxxxxx xixixx xixixx
The zeros of () are 1,2,2, and 2.Pxii
6. 432 ()8222816 fxxxxx
The function has degree 4, so there are four zeros. There are three sign changes, so there are either 3 or 1 positive zeros.
Now find the zeros of 2 22xx using the quadratic formula: 2 2(2)4(1)(2) 24 1 2(1)2
The zeros are 2, 4, 1 + i, and 1 i.
2.6 Exercises
Concepts and Vocabulary
1. If the nonzero terms of a polynomial are written in descending order, then a variation of sign occurs when the sign of two consecutive terms differ.
2. The number of positive zeros of a polynomial function P(x), is either equal to the number changes of sign of P(x) or less than that number by an even integer.
3. The Fundamental Theorem of Algebra states that a polynomial function of degree 1 n has at least one complex zero.
4. If P is a polynomial function with real coefficients and if z = a + bi is a zero of P, then zabi is also a zero of P(x).
5. True.
6. False. If 2 + 3i is a zero of P(x) with real coefficients, then so is 2 3i
7. True
432 43 ()()8()22()28()16 8222816 fxxxxx xxxx
There are no sign changes in ()fx , so there are no negative zeros. The possible rational zeros are 1,2,4,8,16. Using synthetic division to test the positive values, we find that one zero is 2: 218222816 2122016 161080
The zeros of the depressed function 326108 xxx are also zeros of P
The possible rational zeros of the depressed function are 1,2,4,8. Examine only the positive possibilities and find that 4 is a zero: 416108 488 1220
So, 4328222816 xxxx 2 (2)(4)(22) xxxx .
8. False. 164i
Building Skills
9. 32 32 32 ()5234; ()5()2()3()4 5234 fxxxx fxxxx xxx
There are two sign changes in ()fx , so there are either 2 or 0 positive zeros. There is one sign change in ()fx , so there is one negative zero.
10. 32 32 32 ()393; ()3()()9()3 393 gxxxx gxxxx xxx
There is one sign change in ()gx , so there is one positive zero. There are two sign changes in ()gx , so there are either 2 or 0 negative zeros.
11. 32 32 32 ()252; ()2()5()()2 252 fxxxx fxxxx xxx
There are two sign changes in ()fx , so there are either 2 or 0 positive zeros. There is one sign change in ()fx , so there is one negative zero.
12. 432 432 432 ()38523; ()3()8()5()2()3 38523 gxxxxx gxxxxx xxxx
There are three sign changes in ()gx , so there are either 3 or 1 positive zeros. There is one sign change in ()gx , so there is 1 negative zero.
13. 532 532 532 ()25321 ()2()5()3()2()1 25322 hxxxxx hxxxxx xxxx
There are three sign changes in ()hx , so there are either 1 or 3 positive zeros. There are two sign changes in ()hx , so there are either 2 or 0 negative zeros.
14. 643 643 643 ()5721; ()5()7()2()1 5721 Fxxxx Fxxxx xxx
There are three sign changes in ()Fx , so there are either 3 or 1 positive zeros. There is one sign change in ()Fx , so there is 1 negative zero.
15. 432 432 432 ()34537; ()3()4()5() 3()7 34537 Gxxxxx Gxxxx x xxxx
There are three sign changes in ()Gx , so there are either 3 or 1 positive zeros. There is one sign change in ()Gx , so there is 1 negative zero.
16. 532 532 532 ()53274; ()5()3()2() 7()4 53274 Hxxxxx Hxxxx x xxxx
There are three sign changes in ()Hx , so there are either 3 or 1 positive zeros. There are two sign changes in ()Hx , so there are 0 or 2 negative zeros.
17.
42 42 42 24 2424 fxxx fxxxxx
There are no sign changes in f(x), nor are there sign changes in f( x). Therefore, there are no positive zeros and no negative zeros.
18.
42 42 42 356 356356 fxxx fxxxxx
There are no sign changes in f(x), nor are there sign changes in f( x). Therefore, there are no positive zeros and no negative zeros.
19.
53 53 53 23 23 23 gxxxx gxxxx xxx
There are no sign changes in g(x), nor are there sign changes in g( x). Therefore, there are no positive zeros and no negative zeros.
20.
53 53 53 245 245 245 gxxxx gxxxx xxx
There are no sign changes in g(x), nor are there sign changes in g( x). Therefore, there are no positive zeros and no negative zeros.
21.
53 53 53 24 24 24 hxxx hxxx xx
There is one sign change in h(x), and no sign changes in g( x). Therefore, there is one positive zero and there are no negative zeros.
22.
53 53 53 231 231 231 hxxx hxxx xx
There are no sign changes in h(x), and one sign change in g( x). Therefore, there are no positive zeros and there is one negative zero.
23. The possible rational zeros are 1 ,1,3. 3
There are three sign changes in ()fx , so there are either 3 or 1 positive zeros. There are no sign changes in ()fx , so there are no negative zeros. Testing each positive possibility shows that 13 is an upper bound. Testing the negative values shows that 13 is a lower bound.
24. The possible rational zeros are 13721 ,1,,3,,7,21.
There are two sign changes in ()gx , so there are either 2 or 0 positive zeros. There is one sign change in ()gx , so there is one negative zero. Testing each positive possibility shows that 72 is an upper bound. Testing the negative values shows that –3 is a lower bound.
25. The possible rational zeros are 17
There are no sign changes in ()Fx , so there are no positive zeros. There are three sign changes in ()Fx , so there are either 3 or 1 negative zeros. Because there are no positive zeros, the smallest positive possible zeros, 13 , is an upper bound. Verify this with using synthetic division. Testing the negative values shows that 73 is a lower bound.
26. The possible rational zeros are 1,2,4.
There is one sign change in ()Gx , so there is one positive zero. There are two sign changes in ()Gx , so there are either 2 or 0 negative zeros. Testing each positive possibility shows that 1 is an upper bound. Testing the negative values shows that –4 is a lower bound.
27. The possible rational zeros are 1,31.
There are two sign changes in ()hx , so there are either 2 or 0 positive zeros. There are two sign changes in ()hx , so there are either 2 or 0 negative zeros. Testing each positive possibility shows that 31 is an upper bound. Testing the negative values shows that –31 is a lower bound.
311315931
31105432,209998,200 134103932,200998,231
311315931
3186826,443820,012 12885326,452820,043
28. The possible rational zeros are 113 33,1,,13.
There are three sign changes in ()Hx , so there are either 3 or 1 positive zeros. There is one sign change in ()Hx , so there is one negative zero. Testing each positive possibility shows that 13 is an upper bound. Testing the negative values shows that –1 is a lower bound.
13320281913
39247357546,722 319275359446,709 1320281913 3235132 323513219
29. The possible rational zeros are 111777 ,,,1,,,,7. 632632 There are two sign changes in ()fx , so there are either 2 or 0 positive zeros. There are two sign changes in ()fx , so there are either 2 or 0 negative zeros. Testing each positive possibility shows that 72 is an upper bound. Testing the negative values shows that 72 is a lower bound.
7 614377 2 2177119392 62234112399 (continuedonnextpage)
(continued) 7 614377 2 1891421 2170 24 2031449 62027 24
30. The possible rational zeros are 111555 ,,,,1,,,5. 632632 There is one sign change in ()gx , so there is one positive zero. There are three sign changes in ()gx , so there are either 3 or 1 negative zeros. Testing each positive possibility shows that 12 is an upper bound. Testing the negative values shows that 5 is a lower bound. 1 6232595 2 313195 62638100 56232595 30353001545 67603091540
31. 22250255 xxxi
32. 22 164 9160 93 xxxi
33. 22 (2)90(2)9 2323 xx xixi
34. 22 (1)270(1)27 133133 xx xixi
35. 22449(2)9 2323 xxx xixi
36. 222116(1)16 1414 xxx xixi
37. 32 2 80(2)(24)0 224(1)(4) 2 or 2(1) 2416212 13 22 xxxx xx i
The solution set is 2,13 i .
38. 422 2 10(1)(1)0 (1)(1)(1)01 or 1 or xxx xxxxx xi
39. (2)(3)(3)02 or 3 xxixixxi
40. (1)(2)(26)(26)0 1 or 2 or 3 xxixixi xxixi
41. The remaining zero is 3. i
42. The remaining zero is 2. i
43. The remaining zero is 2. i
44. The remaining zeros are i and 1. i
45. The remaining zeros are i and 3. i
46. The remaining zeros are 2,4, ii and 1. i
47. 432 ()2((5))((5))(3)(3) 22070180468 Pxxixixixi xxxx
48. 432 ()3((23))((23)) ((14))((14)) 318114282663 Pxxixi xixi xxxx
49. 2 5432 ()7(5)(1)((3))((3) 71197772415 35001750 Pxxxxixi xxxx x
50. 3 6543 ()4(3)((23))((23)) 428100156 Pxxxxixi xxxx
51. The function has degree four, so there are four zeros. Since one zero is 3, i another zero is 3. i So 2 (3)(3)9 xixix is a factor of ()Px Now divide to find the other factor: 2 2432 42 3 3 999 9 9 9 0 xx xxxxx xx xx xx
432 2 ()99 (3)(3)() (3)(3)(1) the zeros of Pxxxxx xixixx xixixx
() are1,0,3,3. Pxii
52. The function has degree four, so there are four zeros. Since one zero is 1, i another zero is 1. i So 2 ((1))((1))22 xixixx is a factor of ()Px . Now divide to find the other factor:
((1))((1))(1) ((1))((1))(1)(1)
53. The function has degree five, so there are five zeros. Since one zero is 3, i another zero is 3. i So 2 ((3))((3))610 xixixx is a factor of ()Px . Now divide to find the other factor: 32 25432 543 432 432
5432
2 ()522220 ((3))((3))(2) ((3))((3))(2) ((3))((3))(2)(1) Pxxxxxx xixixxx xixixxx xixixxx
the zeros of () are2,0,1,3,3. Pxii
54. The function has degree five, so there are five zeros. Since one zero is i, another zero is –i. So 2 ()()1 xixix is a factor of ()Px . Now divide to find the other factor: 32 25432 53 432 42 32 3 2 2 211176 12111917176 22 111717 1111 17617 1717 66 66 0 xxx xxxxxx xx xxx xx xxx xx x x 5432 32 ()2111917176 ()()(211176) Pxxxxxx xixixxx
Now find the zeros of 32 211176. xxx
There are either three or one positive, rational zeros. The possible zeros are 13 22,1,,2,3,6.
Using synthetic division, we find that x = 2 is one of the zeros: 2211176 4146 2730 5432 32 2 ()2111917176 ()()(211176) ()()(2)(273) ()()(2)(21)(3) Pxxxxxx xixixxx xixixxx xixixxx
the zeros of 1 () are ,2,3,,. 2 Pxii
55. The function has degree 3, so there are three zeros. There are three sign changes, so there are 1 or 3 positive zeros. The possible rational zeros are 1,17. Using synthetic division we find that one zero is 1: 1192517 1817 18170 32292517(1)(817). xxxxxx
Now solve the depressed equation 2 8170xx 2 8(8)4(1)(17) 84 2(1)2 xx
4.xi The zeros are 1,4. i
56. The function has degree 3, so there are three zeros. There are two sign changes, so there are either 2 or 0 positive zeros. There is one sign change in ()fx , so there is one negative zero.
The possible rational zeros are 1,13. Using synthetic division, we find that one zero is 1: 115713 1613 16130 3225713(1)(613). xxxxxx
Now solve the depressed equation 2 2 6130 6(6)4(1)(13) 616 2(1)2
32. xi The zeros are 1,32. i
57. The function has degree 3, so there are three zeros. There are two sign changes, so there are either 2 or 0 positive zeros. There is one sign change in ()fx , so there is one negative zero.
The possible rational zeros are 12
Using synthetic division to test the negative values we find that one zero is
58. The function has degree 3, so there are three zeros. There are three sign changes, so there are either 3 or 1 positive zeros. There are no sign changes in ()fx , so there are no negative zeros. The possible rational zeros are
4 ,2,4. 3
Using synthetic division to test the positive values we find that one zero is 1 3 :
322 1 3124(312) 3 xxxxx
2 11 3(4)3(2)(2). 33 xxxxixi
The zeros are 1 ,2. 3 i
59. The function has degree 4, so there are four zeros. There are two sign changes, so there are 4, 2, or 0 positive zeros. There are no sign changes in ()fx , so there are no negative zeros. The possible rational zeros are 139 ,1,,3,,9. 222
Using synthetic division to test the positive values we find that one zero is 1: 121023249 28159 281590
The zeros of the depressed function 32 28159 xxx are also zeros of P. The possible rational zeros are 139 ,1,,3,,9. 222
Using synthetic division to test the positive values we find that one zero is 1: 128159 269 2690
Thus, 432 21023249 xxxx 2 2 1269.xxx Now solve the depressed equation 2 2690. xx (continuedonnextpage)
(continued) 2 6(6)4(2)(9) 636 2(2)4
6633 422 ii x The zeros of P are 33 1,. 22 i
60. The function has degree 4, so there are four zeros. There are two sign changes, so there are either 2 or 0 positive zeros. There are two sign change in ()fx , so there are either 2 or 0 negative zeros. The possible rational zeros are 12142848 ,,,,,,1,,2,, 99393933
4,8. Using synthetic division to test the negative values we find that one zero is –2: 293014168 1824208 9121040
The zeros of the depressed function 32 912104 xxx are also zeros of P. The possible rational zeros are 121424 ,,,,,1,,2,4. 993933
Using synthetic division to test the negative values we find that one zero is –2: 2912104 18124 9620
Now solve the depressed equation 2 2 9620 6(6)4(9)(2) 636 2(9)18 xx xx
6611 1833 i xi The zeros are 11 2,. 33 i
61. The function has degree 4, so there are four zeros. There are three sign changes, so there are either 3 or 1 positive zeros. There is one sign change in ()fx , so there is one negative zero. The possible rational zeros are 1,2,3,5,6,10,15,30. Using synthetic division to test the negative values, we find that one zero is –3: 31453830 3214830 1716100
The zeros of the depressed function 3271610 xxx are also zeros of P. The possible rational zeros of the depressed function are 1,2,5,10. Since we have already found the negative zero, we examine only the positive possibilities and find that 1 is a zero: 1171610 1610 16100 432453830 xxxx 2 (3)(1)(610) xxxx . Now solve the depressed equation: 2 2 6(6)4(1)(10) 6100 2(1) xxx
The zeros are –3, 1, 3. i
62. The function has degree 4, so there are four zeros. There is one sign change, so there is one positive zero. There are three sign changes in ()fx , so there are either 3 or 1 negative zeros. The possible rational zeros are 1,2,3,6,9,18. Using synthetic division to test the positive values we find that one zero is 1: 1117918
12918
129180
The zeros of the depressed function 322918 xxx are also zeros of P. We can factor by grouping to find the next zero: 3222918(2)9(2) xxxxxx 2 (2)(9). xx So –2 is a zero, as are 3. i
The zeros are –2, 1, 3. i
63. The function has degree 5, so there are five zeros. There are five sign changes, so there are either 5, 3, or 1 positive zeros. There are no sign changes in ()fx , so there are no negative zeros. The possible rational zeros are 13 22,1,,2,3,6. Using synthetic division to test the positive values, we find that one zero is 1 2 : (continuedonnextpage)
(continued)
1 2111917176 2 15756 2101410120
The zeros of the depressed function 432 210141012 xxxx are also zeros of P. Use synthetic division again to find the next zero, 2: 2210141012 412412 26260 5432 2111917176 xxxxx
32 1 (2)(2626) 2 xxxxx
32 1 2(2)(33). 2 xxxxx
Use factoring by grouping to factor 3233xxx : 32233(3)1(3) xxxxxx 2 (1)(3) xx . So the remaining zeros are 3 and i The zeros are 1 ,2,3,. 2 i
64. The function has degree 5, so there are five zeros. There are four sign changes, so there are either 4, 2, or 0 positive zeros. There is one sign change in ()fx , so there is one negative zero. The possible rational zeros are 1,2,4.
Using synthetic division to test the negative values, we find that one zero is –2: 21218104 2814124 147620
The zeros of the depressed function 4324762 xxxx are also zeros of P Use synthetic division again to find the next zero, 1: 114762 1342 13420
543228104 xxxxx 32 (2)(1)(342) xxxxx
The zeros of the depressed function 32342 xxx are also zeros of P. Use synthetic division again to find the next zero, 1: 11342 122 1220
543228104 xxxxx 32 (2)(1)(342) xxxxx 2 (2)(1)(1)(22). xxxxx
Now solve the depressed equation: 2 220xx 2 2(2)4(1)(2) 24 1. 2(1)2 xi The zeros are 2,1 (multiplicity 2),1. i
65. Since one zero is 3i, 3i is another zero. There are two zeros, so the degree of the equation is at least 2. Thus, the equation is of the form
2 339.fxaxixiax The graph passes through (0, 3), so we have 2 1 309. 3 aa Thus, the equation of the function is 2 1 9. 3 fxx
66. Since one zero is i, another zero is i. From the graph, we see that 3 is another zero. There are three zeros, so the degree of the equation is at least 3. Thus, the equation is of the form
2 331fxaxxixiaxx
The graph passes through (0, 3), so we have 2 303011. aa Thus, the equation of the function is 2 31.fxxx
67. Since i and 2i are zeros, so are i, and 2i. From the graph, we see that 2 is also a zero. There are five zeros, so the degree of the equation is at least 5. Thus, the equation is of the form
22 222 142 fxaxixixixix axxx
The graph passes through (0, 4), so we have
22 1 4010402. 2 aa
Thus, the equation is
22 1 142 2 fxxxx or
22 1 142. 2 fxxxx
Copyright © 2018 Pearson Education
68. Since 2i is a zero, so is 2i. From the graph, we see that 1, 0, and 1 are also zeros. There are five zeros, so the degree of the equation is at least 5. Thus, the equation is of the form
The y-intercept is (0, 0), so we have
22 000401 a which is true for all values of a. Thus, the equation is
Beyond the Basics
69. There are three cube roots. We know that one root is 1. Using synthetic division, we find 32 01(1)(1) xxxx :
Solve the depressed equation 2 2 114(1)(1) 10 2(1)
So, the cube roots of 1 are 1 and 13 . 22 i
70. The solutions of the equation and the zeros of the polynomial are the same. There are n roots.
71. The polynomial has degree 6, so there are six zeros. There are no sign changes in ()Px , nor are there sign changes in ()Px , so according to Descartes’s Rule of Signs, there are neither positive nor negative zeros. Therefore, all six zeros must be complex.
72. The polynomial has degree 5, so there are five zeros. There are no sign changes in ()Px , while there is one sign change in ()Px . According to Descartes’s Rule of Signs, there is one negative zero, and the remaining four zeros must be complex.
73. The polynomial has degree 7, so there are seven zeros. There are no sign changes in ()Px , while there is one sign change in ()Px . According to Descartes’s Rule of Signs, there is one negative zero, and the remaining six zeros must be complex.
74. The polynomial has degree 3, so there are three zeros. There is one sign change in ()Px , while there are no sign changes in ()Px . According to Descartes’s Rule of Signs, there is one positive zero, and the two remaining zeros must be complex.
75. Since 1 + 2i is a zero, so is 1 2i. The equation is of the form
21212 225 fxaxxixi axxx
2
The y-intercept is 40, so we have 2 400202054 aa
Thus, the equation is
2 4225.fxxxx Because a < 0, as yx and as . yx
76. Since 2 3i is a zero, so is 2 + 3i. The equation is of the form
2 12323 1413 fxaxxixi axxx
The y-intercept is 26, so we have
2 2601040132 aa
Thus, the equation is 2 21413.fxxxx Because a > 0, as yx and as . yx
77. Since 3 + i is a zero, so is 3 i. The equation is of the form
22 1133 1610 fxaxxxixi axxx
The y-intercept is 20, so we have 22 2001060102 aa
Thus, the equation is
22 21610.fxxxx Because a < 0, as yx and as . yx
78. Since 1 2i and 3 2i are zeros, so are 1 + 2i and 3 + 2i. The equation is of the form
22 1212 3232 25613 fxaxixi xixi axxxx
(continuedonnextpage)
(continued)
The y-intercept is 130, so we have
Thus, the equation is
22 1300205060132 aa
22 225613.fxxxxx
Because a > 0, as yx and as . yx
79. 2 22, Pxxixixi 122 2 120 iii ii 2 222xixixix
80. 2 32,2 Pxxixxi 2132 22 10 ii i i
2 322 xixxixi
81. 323434, Pxxixixixi
13434 34 1340 iiii iii
32234343441 xixixixxxixxxi
82. 32427814,2 Pxxixixixi
21427814 2814 1470 iiii iii
322427814472 xixixixxxi
Now solve 2 470xx to find linear factors.
Thus,
32242781447223232 23232 xixixixxxixxxi xixixi
Critical Thinking/Discussion/Writing
83. Factoring the polynomial, we have 1 110 nn nn axaxaxa 12 ()()(). nn axrxrxr Expanding the right side, we find that the coefficient of 1 n x is 12 nnnn ararar and the constant term is 12 (1) n nn arrr . Comparing the coefficients with those on the left side, we obtain 112(). nnn aarrr
Because 0, n a 1 12 n n n a rrr a and 0 12 (1). n n n a rrr a
Copyright © 2018 Pearson Education Inc.
84. Because 1r and 2r are roots of the equation, we have
85. a. 336206200. xxxx There is one sign change, so there is one positive root. There are no sign changes in ()fx , so there are no negative roots. Therefore, there is only one real solution.
b. Substituting vu for x and remembering that 33 20 and 2, vuuv we have 332233322 3333 ()6()336()()(33)6() ()3()6()()(63)() 20(63(2))()20 vuvuvvuvuuvuvuvuvuvu vuvuvuvuvuuvvu vu
Therefore, xvu is the solution.
c. To solve the system 33 20,2vuvu , solve the second equation for v, and substitute that value into the first equation, keeping in mind that u cannot be zero, so division by u is permitted: 3 3333 3 3 3 28 2020 8 200. vuuu uu u u
3 2 Let, so 8 2002080 ua aaa a
d. If q is positive, then, according to Descartes’s Rule of Signs, the polynomial 3 xpxq has one positive zero and no negative zeros. If q is negative, then it has no positive zeros and one negative zero. Either way, there is exactly one real solution. From (b), we have 33 vuq , , 3 p vu and .xvu
Substituting, we have 33 3223 3322 33 33 ()() 33() ()(33)() ()3()() ()(3)() 3 3 xpxvupvu vvuvuupvu vuvuvupvu vuvuvupvu vupuvvu p qpxq
is the xvu solution. Solving the system 33 vuq , , 3 p vu we obtain 3 3333 33 3 3 pp vuquuq uu
Let, so we have 00 33 ua pp aqaqa a (continuedonnextpage)
86. 32610806,10,8 xxxabc
Substituting 6 2 3 xyy as in (1e), we have 32 (2)6(2)10(2)80 yyy 322 (6128)(62424) 102080 yyyyy y 3324024. yyyy Then, using the results of (1d), we have 23 3 23 3 442 223 442 223
Using a calculator, we find that y = –2. So 224. x Now use synthetic division to find the depressed equation: 416108 488 1220 3226108(4)(22)0. xxxxxx 2 2 224(1)(2) 220 2(1) 2422 1 22 xxx i i
The solution set is 4,1. i
Getting Ready for the Next Section
87. a. 22 3535 33 2221 53 3333 yxyx yxyx
b. 21 11 33 y 88. a. The slope of the line 456 xy 46 546 55yxyx is 4 . 5 The slope of the line perpendicular to this line is 5 4 The equation we are seeking is
5 32 4 yx
5 32 4 5551 23. 4442 yx yxyx
2.7 Variation
2.7 Practice Problems
1.
2.
A battery of 275 volts is needed to produce 60 amperes of current.
3. 22 2 48(2)12 12(5)300 ykxkk y
4. 1260 5 60 20 3 kk Ak B A
5.
6. Mars 12 22 Mars Mars 2 Mars mmmM FGmgG rR M gG R
Note that the radius of Mars is given in kilometers, which must be converted to meters.
2.7 Exercises Concepts and Vocabulary
1. y varies directly as x if y = kx
2. y varies inversely as x if . k yx
3. y varies directly as the nth power of x if n ykx
4. z varies jointly as x and y if z = kxy
5. True
6. False. A varies directly as the second power of r
7. False.
8. True Building Skills
9. 11 ;1530;(28)14 22xkykkx
10. ;32;(7)3321 222ykxkky
11. 222 ;64216;5(16)400sktkks
12. 33 3 ;270310; 80102 ykxkk xx
13. 33 ;333;99 1113 kk rkr u
14. 4 ;244;4 161 kk yky z
15. 333 81 ;18; 8 24 kk BkB A
16. 3 3 3 3 3 3 ;10102; 2 10220001 4040 32 kk yk x x xx
17. ;42(2)(3)7;562(7) 4 zkxykky y
18. 1137(1)1 ;1; 226142 kqk mkm p
19. 222 ;3242;2(5)50zkxkkz
20. 333 721 ;972; 3 26 kk uku t
21. 22 2 1 ;36(17)(6); 17 1324 (4)(9) 1717 PkTQkk P
22. 1 ;91381; 13 115 (5)9 1313 akbckk a
23. 22 2 16 ;2454 3 54 2724 2 kxk zk y x xx
24. 33 22 3 22 4(3)1 ;9; 3 2 1 (27)(2) 72 3 883 kuvk zk w w ww
25. 168 6 12 y y
26. 17 85 22110 z z
27. 00 100 200 2 y y xx
28. 23981 24 9 yy y
Applying the Concepts
29. yHx , where y is the speed of the galaxies and x is the distance between them.
30. RkP , where k is a constant.
31. a. 30.5 yx , where y is the length in centimeters and x is the length in feet.
b. (i) 30.5(8)244 cm y
(ii) 1 30.55162.67 cm 3 y
c. (i) 5730.51.87 ft xx (ii) 12430.54.07 ft xx
32. a. 2.2 yx , where y is the weight in pounds and x is the weight in kilograms.
b. (i) 2.2(0.125)0.275 lb y (ii) 2.2(4)8.8 lb y (iii) 2.2(2.4)5.28 lb y
c. (i) 272.212.27 kg xx (ii) 1602.272.73 kg xx
33. 77 ;720;(100)35 g 2020PkQkkP
34. ;6004015;Wkhkk 15(25)$375. W The constant of proportionality is the hourly wage.
35. 222 ;64216;916 0.75 sec dktkkt t
36. 55 ;104;(6)15 lb 22 FkxkkF
37. 2 ;206000; 300 6000 60 lb/in. 100 kk Pk V P
38. 9 2609 ;36;1355 KK kTT k PkP VV
a. 3 9(300) 4013.5 in. 5 V V b. 2 9(280) 12.92 lb/in. 5(39) P
39. a. The astronaut is 6000 + 3960 miles from the Earth’s center.
2 22 2 2 ;120120(3960) 3960 120(3960) 18.97 lb (60003960) kk Wk d W
b. 2 2 2 2 200200(3960) 3960 200(3960) 201.01 lb 3950 k k W
Copyright © 2018 Pearson Education Inc.
40. You should buy at the higher altitude because an object weighs less the further it is from the Earth’s center.
41. 1740 km = 1,740,000 m = 6 1.74010 m
(6.67)(7.4)(10) 1.63 m/sec 1.74010 M
42. 696,000 km = 696,000,000 m = 6.96108 m
(6.67)(2)(10) 2.7510 m/sec 6.9610 M gG R
43. a. 22 2 ;32032,000 10 32,000 1280 candla 5 kk Ik d I
b. 2 2 32,000 400808.94 ft dd d from the source.
44. a. ;489626 26 skdkk sd
b. (i) 26(60)37.95 mph s (ii) 26(150)60 mph s (iii) 26(200)69.28 mph s
c. 2 7026635 6351225204.17 ft dd dd
45. 22 24 pklkppp lll the length is quadrupled if the period is doubled.
46. 3 ;4001004 4(120)480 cm VkAkk V
47. a. 2 HkRN
b. 22 (2)44 kRNkRNH the horsepower is multiplied by 4 if the radius is doubled.
c. 22 (2)22 kRNkRNH the horsepower is doubled if the number of pistons is doubled.
d. 2 22 2 (2) 2422 RkRNkRNH kN
the horsepower is halved if the radius is halved and the number of pistons is doubled.
48. Convert the dimensions given in inches to feet. 2 2 2 11 32 ;576172,800 25 15 172,800 26 3000 lb 20 k kwd sk l s
Beyond the Basics
49. a. 23Eklv
b. 23 3 1920(10)(8)0.0375 80 kk
c. 23 0.0375(8)(25)37,500 watts E
d. 2323 (2)88 klvklvE
e. 2323 (2)44 klvklvE f. 2323 (2)(2)4(8)32 klvklvE
50. a. 22 1002 ;20.08 25 2 d kIk Ik d
b. The distance from the bulb to the point on the floor is 22 2313 m. 2 2 0.08(200) 1.23 watts/m 13 d I
c. If the bulb is raised by 1 meter, then the distance from the bulb to the point on the floor is 22 3332 m.
2 2 0.08(200) 0.89 watts/m 32 d I
51. a. 3434 4 ;75(75) 352.94 mkwk k
b. 34 2.94(450)287.25 watts m
c. 34343434 (4)42.832.83m kwkwkw
52.
The gravitational attraction between the sun and the Earth is approximately 168.92 times as strong as the gravitational pull between the Earth and the moon.
53. a. 23 2 12 4 () r T
b. Because gravity is in terms of cubic meters per kilogram per second squared, convert the distance from kilometers to meters: 811 1.510km1.510m
4(1.510) (3.1510) 6.6710 4(3.375)10 9.922510 6.6710 M M
24 sun 1114 30 133.2410 6.67109.922510 2.0110
54. Because gravity is in terms of cubic meters per kilogram per second squared, convert the distance from kilometers to meters: 8 384,000km3.8410m . 27.3 days 27.3(24)(60)(60) sec 2,358,720 sec 283 2 11 Earth 283 Earth 112 24 Earth 4(3.8410) 2,358,720 6.6710 4(3.8410) 6.67102,358,720 6.0210 kg M M M
55. a. (),RkNPN where k is the constant of proportionality.
b. 6 451000(9000)510 kk
c. 6 510(5000)(5000)125 R people per day.
d. 6 2 100510(10,000) 20,000,00010,000 NN NN
2 27 10,00020,000,0000 10,00010,0004(1)(210) 2(1) 10,00020,000,000 2764 or 7236 2 NN N
Critical Thinking/Discussion/Writing
56. 1.31.56 the voltage 1.2 kV IIRkV R kV IIRkV R must increase by 56%.
57. a. 2 vkw . The diamond is cut into two pieces whose weights are 2 5 w and 3 5 w The value of the first piece is 4 (1000)$160 25
, and the value of the second piece is 9 (1000)$360 25 . The two pieces together are valued at $520, a loss of $480.
b. The stone is broken into three pieces whose weights are 59 25525,, www and 11 . 25 w So, the values of the three pieces are 2 1 (25,000)$1000, 5
2 9 (25,000)$3240, 25
and 2 11 (25,000)$4840, 25
respectively. The total value is $9,080, a loss of $15,920.
c. The weights of the pieces are 23 ,,, 1515155 wwww 45 , and , 15153 www respectively. If the original value is x, then 222 22 121 85,000 15155 41 153 11 85,000$112,500 the 45 xxxx xx xxx
original value of the diamond. A diamond whose weight is twice that of the original diamond is worth 4 times the value of the original diamond = $450,000.
58. ()pkdnf 80(40)(30) and kf
180(60)(35). kf
Solving the first equation for k we have
Substitute that value into the second equation and solve for f: 2 180(60)(35) 30 4200120 180 30 54001804200120 12006020 ff f f ff ff
59.
60. 24;202442 0242144. The greatest number skwkk ww
Getting Ready for the Next Section 61. 3 28
2 2 11 3
3 63. 3 3 3 111 28 2
64. 4 4 1 216 2
65.
13 132 22224 xxxx
66.
233 233 5555 xxxxx
67. 32 325 23 5 2 22 2 x xxx x
68.
2 1 1 222 xxxxxx
Chapter 2 Review Exercises
Building Skills
1.(i) opens up (ii) vertex: (1, 2)
(iii) axis: x = 1
(iv) 22 0(1)22(1) there xx are no x-intercepts.
(v) 2 (01)23 is the yy y-intercept.
Copyright © 2018 Pearson Education Inc.
(vi) The function is decreasing on (,1) and increasing on (1,).
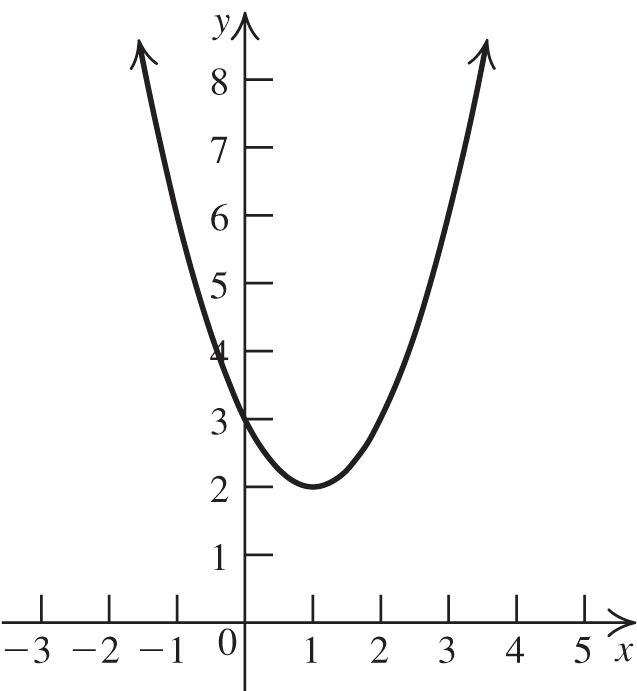
2.(i) opens up (ii) vertex: (–2, –3)
(iii) axis: x = –2
(iv) 22 0(2)33(2)
23 are the -intercepts. xx xx
(v) 2 (02)31 is the yy y-intercept.
(vi) The function is decreasing on (,2) and increasing on (2,).
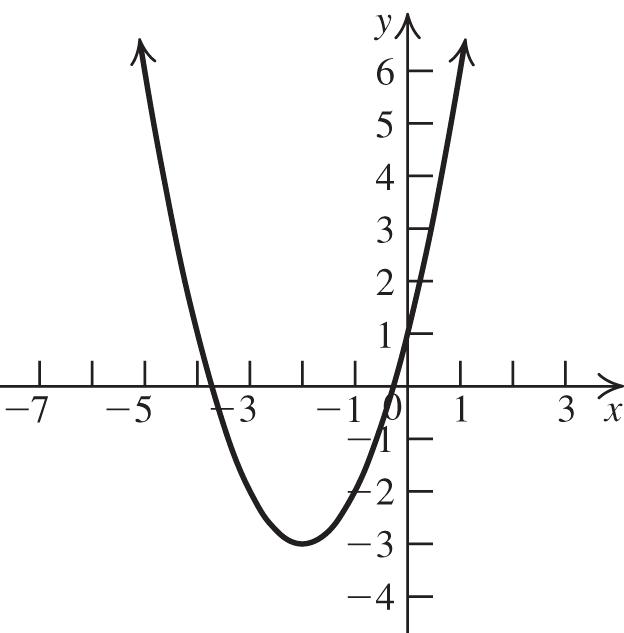
3.(i) opens down
(ii) vertex: (3, 4)
(iii) axis: x = 3
(iv) 22 02(3)42(3)
32 are the -intercepts.
(v) 2 2(03)414 is the yy y-intercept.
(vi) The function is increasing on (,3) and decreasing on (3,).
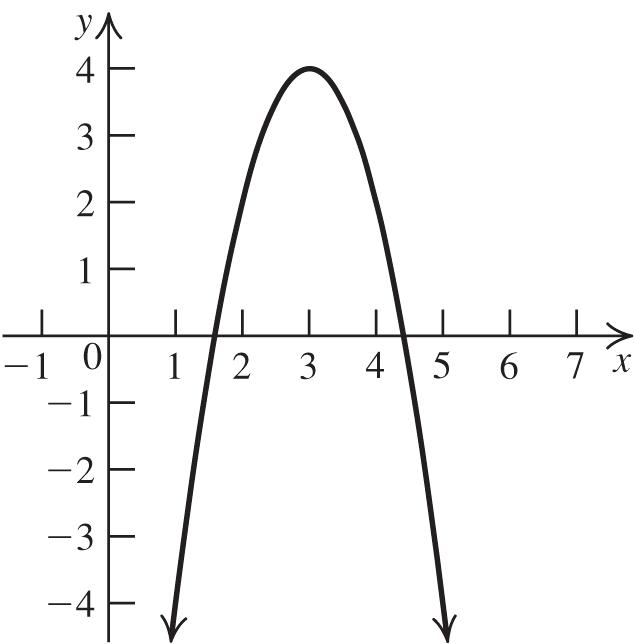
4.(i) opens down
(ii) vertex: (–1, 2) (iii) axis: x = –1
(iv) 22 1 0(1)24(1) 2 3 and 1 are the -intercepts. xx xxx
(v) 2 13 (01)2 is the 22yy y-intercept.
(vi) The function is increasing on (,1) and decreasing on (1,).
5.(i) opens down (ii) vertex: (0, 3)
(iii) axis: x = 0 (y-axis)
(iv) 22 3 023 2 6 are the -intercepts. 2 xx xx
(v) 2 2(0)33 is the yy y-intercept.
Copyright © 2018 Pearson Education Inc.
(vi) The function is increasing on (,0) and decreasing on (0,).
6.(i) opens up
(ii) To find the vertex, write the equation in standard form by completing the square: 2 2 2 241 122(21) 2(1)3 the vertex is (1,3).
(iii) axis: x = –1
(iv) 2 2 0241 444(2)(1) 424 2(2)4 6 1 are the -intercepts. 2 xxx xx
(v) 2 2(0)4(0)11 is the yy y-intercept.
(vi) The function is decreasing on (,1) and increasing on (1,).
7.(i) opens up
(ii) To find the vertex, write the equation in standard form by completing the square: 2 2 2 243 322(21) 2(1)1 the vertex is (1,1). yxx yxx yx
(iii) axis: x = 1
(iv) 2 2 0243 4(4)4(2)(3) 48 2(2)4 xx x
there are no x-intercepts.
(v) 2 2(0)4(0)33 is the yy y-intercept.
(vi) The function is decreasing on (,1) and increasing on (1,).
8.(i) opens down
(ii) To find the vertex, write the equation in standard form by completing the square: 2 2 2 23 111 32 8216 125 2 48 125 the vertex is 48,. yxx yxx yx
(iii) axis: 1 4 x
(iv) 2 023 3 0(23)(1) and 2 1 are the -intercepts. xx xxx xx
(v) 2 2(0)033 is the yy y-intercept.
Copyright © 2018 Pearson Education Inc.
(vi) The function is increasing on 1 , 4
and decreasing on 1 ,. 4
9.(i) opens up
(ii) To find the vertex, write the equation in standard form by completing the square.
2 2 2 321 121 13 339 1212 3 the vertex is 3333,. yxx yxx yx
(iii) axis: 1 3 x
(iv) 2 2 0321 2(2)4(3)(1) 28 2(3)6
there are no x-intercepts.
(v) 2 3(0)3(0)11 is the yy y-intercept.
(vi) The function is decreasing on 1 , 3
and increasing on 1 ,. 3
10.(i) opens up
(ii) To find the vertex, write the equation in standard form by completing the square: 2 2 2 354 25525 43 12336 523 3 612 523 the vertex is 612,. yxx yxx yx
(iii) axis: 5 6 x
(iv) 2 2 0354 5(5)4(3)(4) 523 2(3)6 xx x
there are no x-intercepts.
(v) 2 3(0)5(0)44 is the yy y-intercept.
(vi) The function is decreasing on 5 , 6
and increasing on 5 ,. 6
In exercises 11–14, find the vertex using the formula 22,. bb f aa
11. 0 a the graph opens up, so f has a minimum value at its vertex. The vertex is 44 2(1)2(1),(2,1).
12. 0 a the graph opens down, so f has a maximum value at its vertex. The vertex is 88 2(4)2(4),(1,1).
Copyright © 2018 Pearson Education Inc.
13. 0 a the graph opens down, so f has a maximum value at its vertex. The vertex is
14. 0 a the graph opens up, so f has a minimum value at its vertex. The vertex is
15. Shift the graph of 3 yx one unit left and two units down.
16. Shift the graph of 4 yx one unit left and two units up.
17. Shift the graph of 3 yx one unit right, reflect the resulting graph about the y-axis, and shift it one unit up.
18. Shift the graph of 4 yx three units up.
19.(i) () as () as fxx fxx
(ii) Zeros: x = –2, multiplicity 1, crosses the x-axis; x = 0, multiplicity 1, crosses the x-axis; x = 1, multiplicity 1, crosses the x-axis.
(iii) x-intercepts: –2, 0, 1; 0(01)(02)0 is the yy y-intercept.
(iv) The intervals to be tested are (2,0) , (0,1),(1,2), and (2,). The graph is above the x-axis on (2,0)(1,) and below the x-axis on (,2)(0,1).
(v) ()(1)(2)() fxxxxfx f is not even.
()((1)(2))() fxxxxfx f is not odd. There are no symmetries.
(vi)
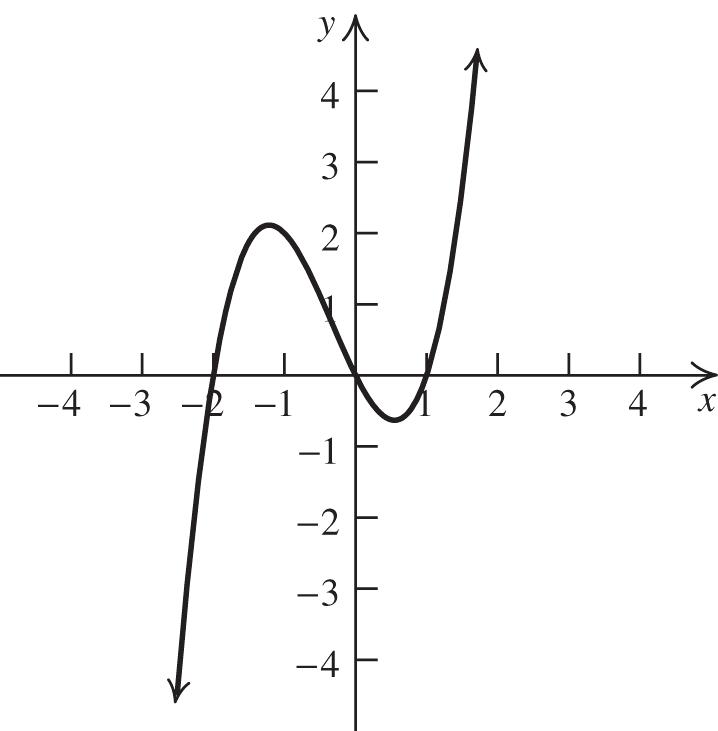
20.(i) () as () as fxx fxx
(ii) 32 ()(1) fxxxxx (1)(1).xxx Zeros: x = –1, multiplicity 1, crosses the x-axis; x = 0, multiplicity 1, crosses the x-axis; x = 1, multiplicity 1, crosses the x-axis.
(iii) x-intercepts: –1, 0, 1; 3 000yy is the y-intercept.
(iv) The intervals to be tested are (,1) , (1,0),(0,1), and (1,). The graph is above the x-axis on (1,0)(1,) and below the x-axis on (,1)(0,1).
(v) ()()()33 fxxxxx
()fx f is odd. f is symmetric with respect to the origin.
(vi)
21.(i) () as () as fxx fxx
(ii) Zeros: x = 0, multiplicity 2, touches but does not cross the x- axis; x = 1, multiplicity 2, touches but does not cross the x- axis.
(iii) x-intercepts: 0, 1; 22 0(01)0 is the yy y-intercept.
(iv) The intervals to be tested are (,0) , (0,1), and (1,). The graph is below the x-axis on (,0)(0,1)(1,).
(v) 2 2 ()()(1) (1)() or () fxxx xxfxfx
()fx f is neither even nor odd. There are no symmetries. (vi)
22.(i) () as () as fxx fxx
(ii) Zeros: x = 0, multiplicity 3, crosses the x-axis; x = 2, multiplicity 2, touches but does not cross the x-axis.
(iii) x-intercepts: 0, 2; 32 0(02)0 is the yy y-intercept.
(iv) The intervals to be tested are (,0) , (0,2), and (2,). The graph is above the x-axis on (,0) and below the x-axis on (0,2)(2,).
(v) 3 3 ()()(2) (2)() or () fxxx xxfxfx
f is neither even nor odd. There are no symmetries.
(vi)
23.(i) () as () as fxx fxx
(ii) Zeros: x = –1, multiplicity 1, crosses the x-axis; x = 0, multiplicity 2, touches but does not cross; x = 1, multiplicity 1, crosses the x-axis.
(iii) x-intercepts: –1, 0, 1; 22 0(01)0 is the yy y-intercept.
(iv) The intervals to be tested are (,1) , (1,0),(0,1), and (1,). The graph is above the x-axis on (1,0)(0,1) and below the x-axis on (,1)(1,).
(v) 22 22 ()()(()1) (1)() fxxx xxfx
f is even, and f is symmetric with respect to the y-axis.
Copyright © 2018 Pearson Education Inc.
(vi)
24.(i) () as () as fxx fxx
(ii) Zero: x = 1, multiplicity 2, touches but does not cross.
(iii) x-intercept: 1; 22 (01)(01)1 is the yy y-intercept.
(iv) The intervals to be tested are (,1) and (1,). The graph is below the x-axis on (,1)(1,).
(v) 22 ()(1)(()1)() or fxxxfx ()fx f is neither even nor odd. There are no symmetries.
(vi)
xxxxx xx xx xx xx xx x x
28. 232 32 2 2 1 26347 26 27 26 413 x xxxxx xxx xx xx x
29. 310123 399 1336
Quotient: 2 33xx remainder –6.
30. 64350 24126786 421131786
Quotient: 2 421131 xx remainder –786.
31. 12357165 251017 251017182
Quotient: 32 251017 xxx remainder 182.
32. 2320116132 616326292 38163146224
Quotient: 432 38163146 xxxx remainder –224.
33.(i) 32 (2)23(2)11(2)2911 f (ii) 2131129 2218 11911
The remainder is –11, so f(2) = –11.
34.(i) 32 (2)2(2)(2)15(2)216 f (ii) 221152 4618 23916
The remainder is 16, so f(–2) = 16.
35.(i) 42 (2)(3)2(3)5(3)1088 f (ii) 3102510 392178 1372688
The remainder is 88, so f(–3) = 88.
36.(i) 5 (1)123 f (ii) 1100002 11111 111113
The remainder is 3, so f(1) = 3.
37. 217148 2108 1540
The remainder is 0, so 2 is a zero. Now find the zeros of the depressed function
2 54xx (4)(1) xx 4 and 1 are also zeros. So the zeros of 327148 xxx are 1, 2, and 4.
38. 223124 4144 2720
The remainder is 0, so –2 is a zero. Now find the zeros of the depressed function 2 272 xx : 2 7(7)4(2)(2) 2(2) x 733 4
So the zeros of 32 23124 xxx are –2 and 733 4
39. 1 314136 3 156 315180
The remainder is 0, so 1 3 is a zero. Now find the zeros of the depressed function 2 315183(2)(3) xxxx –2 and –3 are also zeros. So the zeros of 32 314136 xxx are –3, –2, and 1 3 .
40. 1 419132 4 152 42080
The remainder is 0, so 14 is a zero. Now find the zeros of the depressed function 2 2 20204(4)(8) 4208 2(4) 20433533 . 82 xx
So the zeros of 32 419132 xxx are 533 2 and 1 4
41. The factors of the constant term are 1,2,3,6 , and the factors of the leading coefficient are 1. The possible rational zeros are 1,2,3,6
42. The factors of the constant term are 1,2,4,8,16 , and the factors of the leading coefficient are 1,3,9. The possible rational zeros are 121 993,,, 4284168 ,,,1,,,2,,4, 939393 16 ,8,16. 3
43. 32 32 32 ()5112; ()5()11()2() 5112 fxxxx fxxxx xxx
There are no sign changes in ()fx , so there are no positive zeros. There are two sign changes in (),fx so there are 2 or 0 negative zeros.
322 5112(5112) (51)(2) xxxxxx xxx 1 the zeros are 2,,0. 5
Copyright © 2018 Pearson Education Inc.
44. 32 32 32 ()256 ()()2()5()6 256 fxxxx fxxxx xxx
There is one sign change in ()fx , so there is one positive zero. There are two sign changes in (),fx so there are 2 or 0 negative zeros. The possible rational zeros are 1,2,3,6 . Use synthetic division to find one zero: 31256 336 1120
The remainder is 0, so –3 is a zero. Now find the zeros of the depressed function.
2 2(2)(1)xxxx –1 and 2 are also zeros. So the zeros of 32256 xxx are –3, –1, and 2.
45. 32 32 32 ()3412 ()()3()4()12 3412 fxxxx fxxxx xxx
There is one sign change in ()fx , so there is one positive zero. There are two sign changes in (),fx so there are 2 or 0 negative zeros. The possible rational zeros are 1,2,3,4, 6,12. Use synthetic division to find one zero: 313412 3012 1040
The remainder is 0, so –3 is a zero. Now find the zeros of the depressed function
2 4(2)(2)xxx –2 and 2 are also zeros. So the zeros of 323412 xxx are –3, –2, and 2.
46. 32 32 32 ()29125; ()2()9()12()5 29125 fxxxx fxxxx xxx
There are three sign changes in (),fx so there are 3 or 1 positive zeros. There are two sign changes in (),fx so there are 2 or 0 negative zeros. The possible rational zeros are 15 22,1,,5.
Use synthetic division to find one zero: 129125 275 2750
The remainder is 0, so 1 is a zero. Now find the zeros of the depressed function 2 275(25)(1)52 xxxx and 1 are also zeros. The zeros of 32 29125 xxx are 52 and 1 (multiplicity 2).
47. The function has degree three, so there are three zeros. Use synthetic division to find the depressed function: 21076 246 1230
Now find the zeros of the depressed function 2 23(3)(1)3 and 1 are xxxx zeros. The zeros of the original function are –3, 1, 2.
48. The function has degree four, so there are four zeros. Since 1 is a zero of multiplicity 2, 2 (1) x is a factor of 43232. xxxx
Use synthetic division twice to find the depressed function: 111312 1212 12120 11212 132 1320
Alternatively, divide 43232 xxxx by 22 (1)21 xxx . Now find the zeros of the depressed function 2 32(2)(1)xxxx 2 and 1 are zeros. The zeros of the original function are –2, –1, and 1.
49. The function has degree four, so there are four zeros. Use synthetic division twice to find the depressed function: 11261827 13927 139270 313927 3027 1090
Alternatively, divide 432261827 xxxx by 2 (1)(3)23. xxxx Now find the zeros of the depressed function 2 93 xi are zeros. The zeros of the original function are –1, 3, and 3i
50. The function has degree three, so there are three zeros. Since one zero is 2 – i, another zero is 2 + i. Divide 32 4193215 xxx by 2 ((2))((2))45 xixixx to find the depressed function:
Now find the zeros of the depressed function: 3 430. 4 xx Alternatively, find the possible rational zeros, and then use synthetic division to find the zero. The zeros of the original function are 3 ,2, and 2. 4 ii
51. The function has degree four, so there are four zeros. Since one zero is –1 + 2i, another zero is –1 – 2i. Divide 43229820 xxxx by 2 ((12))((12))25 xixixx to find the depressed function: 2 2432 432 2 2 4 2529820 25 4820 4820 0
Now find the zeros of the depressed function: 2 402. xxi The zeros of the original function are 2 and 12. ii
52. The function has degree five, so there are five zeros. Since two zeros are 2 + 2i, 2 – 2i are also zeros. Divide 54327243264 xxxx by 2 22 ((22))((22))(48) xixixx 4328326464 xxxx to find the depressed function. (Note it may be easier to divide by 2 48xx and then to divide the quotient by 2 48xx .) The quotient is 1, x so –1 is a zero. The zeros of the original function are 1 and 22. i
53. The function has degree three, so there are three zeros. The possible rational zeros are 1,2,4. Using synthetic division, we find that one zero is 1: 11144 104 1040
Now find the zeros of the depressed function: 2 402.xx
The solution set is {–2, 1, 2}.
54. The function has degree three, so there are three zeros. The possible rational zeros are 13 22,1,,2,3,6.
Using synthetic division, we find that one zero is 12 : 1221126 106 20120
Now find the zeros of the depressed function: 2 21206. xx
The solution set is 12,6.
55. The function has degree three, so there are three zeros. The possible rational zeros are 1133 ,,,1,,3. 4242 Using synthetic division, we find that one zero is –1: 14073 443 4430
Now find the zeros of the depressed function: 2 4430(23)(21)0 xxxx 32 or 12. xx
The solution set is 12,1,32
56. The function has degree three, so there are three zeros. The possible rational zeros are 1,2,3,6. Using synthetic division, we find that one zero is –3: 31186 366 1220
xx x
Now find the zeros of the depressed function: 2 2 220 2(2)4(1)(2) 212 13. 2(1)2
The solution set is 3,13
Copyright © 2018 Pearson Education Inc.
57. The function has degree four, so there are four zeros. The possible rational zeros are 1,2. Using synthetic division, we find that one zero is 2: 211112 2222 11110
Now find the zeros of the depressed function:
32 10. xxx Again using synthetic division, we find that one zero is –1: 11111
101 1010
The zeros of the depressed function
2 10 x are .i The solution set is 1,2, i
58. The function has degree four, so there are four zeros. The possible rational zeros are 1,2, 3,4,6,12. Using synthetic division, we find that one zero is 2: 11113112 101312 1013120
Now find the zeros of the depressed function:
3 13120.xx Again using synthetic division, we find that one zero is –1: 1101312 1112 11120
2 120(4)(3)04xxxxx or x = 3. The solution set is 3,1,1,4 .
59. The only possible rational roots are 1,2. None of these satisfies the equation.
60. The only possible rational roots are 5 1 33,1,,5. None of these satisfies the equation.
61. 32 (1)16(1)2821 f
32 (2)26(2)284 f
Because the sign changes, there is a real zero between 1 and 2. The zero is approximately 1.88.
62. 32 (1)13(1)3(1)76 f 32 (2)23(2)3(2)77 f
Because the sign changes, there is a real zero between 1 and 2. The zero is approximately 1.60.
63. 1 101 x x is the x-intercept. There is no y-intercept. The vertical asymptote is the y-axis (x = 0). The horizontal asymptote is y = 1. 1 ()1() and(),fxfxfx x so there are no symmetries. Testing the intervals (,0), and (0,), we find that the graph is below the horizontal asymptote on (,0) and above the horizontal asymptote on (0,).
64. 2 02 x x x is the x-intercept. There is no y-intercept. The vertical asymptote is the y-axis (x = 0). The horizontal asymptote is y = –1.
2 ()() and(), fxxfxfx x so there are no symmetries. Testing the intervals (,0), and (0,), we find that the graph is above the horizontal asymptote on (0,) and below the horizontal asymptote on (,0). (continuedonnextpage)
65. 2 00 1 x x x is the x-intercept.
2 0 00 01 y is the y-intercept. The vertical asymptotes are x = 1 and x = –1. The horizontal asymptote is the x-axis.
2 ()() and(), ()1 fxxfxfx x so there is symmetry with respect to the origin. Testing the intervals (,1),(1,0), (0,1), and (1,), we find that the graph is above the x-axis on (,1)(0,) and below the x-axis on (1,0)(0,1).
Exercise 65
66.
Exercise 66
2 2 9 03 4 x x x are the x-intercepts.
2 2 0999 44 04 y is the y-intercept. The vertical asymptotes are x = 2 and x = –2. The horizontal asymptote is y = 1.
2
2 ()9 ()() ()1 x fxfx x the function is even and the graph is symmetric with respect to the y-axis. Testing the intervals (,2), (2,2), and (3,), we find that the graph is above the horizontal asymptote on (2,2) and below the al asymptote on (,2)(2,).
67. 3 2 00 9 x x x is the x-intercept.
3 2 0 00 09 y is the y-intercept. The vertical asymptotes are x = 3 and x = –3. There is no horizontal asymptote.
3
2 () ()() but()(), ()9 fxxfxfxfx x so there is symmetry with respect to the origin.
3 2 9, 9 x xx x so the oblique asymptote is y = x.
Testing the intervals (,3),(3,0),(0,3), and (3,), we find that the graph is above the oblique asymptote on (3,0) (3,) and below the oblique asymptote on (,3)(0,3).
68.
2 1 01 28 x x xx is the x-intercept.
2 0111 88 02(0)8 y is the y-intercept. The vertical asymptotes are x = 4 and x = –2. The horizontal asymptote is the x-axis.
2 ()1 ()() and(), ()2()8 fxxfxfx xx so there are no symmetries. Testing the intervals (,2),(2,1),(1,4), and (4,), we find that the graph is above the x-axis on (2,1)(4,)) and below the x-axis on (,2)(1,4). (continuedonnextpage)
Copyright © 2018 Pearson Education Inc.
69. 4 2 00 4 x x x is the x-intercept.
4 2 0 00 04 y is the y-intercept. The vertical asymptotes are x = 2 and x = –2. There is no horizontal asymptote.
4 2 () ()() ()4 fxxfx x , so the function is even, and the graph is symmetric with respect to the y-axis.
Testing the intervals (,2), (2,0),(0,2), and (2,), we find that the graph is above the x-axis on (,2)(2,) and below the x-axis on (2,0)(0,2).
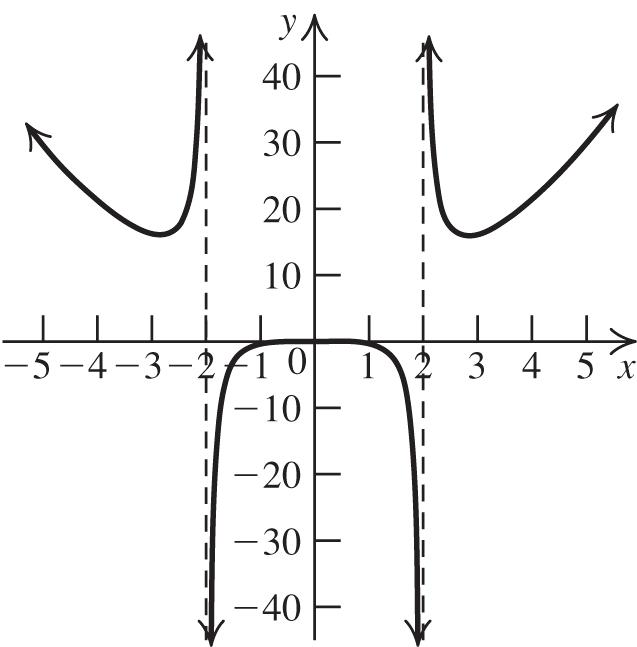
70. 2 2 6 02 12 xx x xx is the x-intercept.
2 2 00611 22 0012 y is the y-intercept. The vertical asymptote is x = 4. The horizontal asymptote is y = 1.
2 2 ()()6 ()() and ()()12 xx fxfx xx (),fx so there are no symmetries.
Testing the intervals (,3),(3,4), and (4,), we find that the graph is above the horizontal asymptote on (4,) and below the horizontal asymptote on (,3)(3,4).
71. 2320xxx
The real zeros are x = –2, x = 2, and x = 3. So, the intervals to be tested are ,2, 2,2,2,3, and 3,.
Interval Test point
Value of Px Result
,2 –3 –30 –
2,2 0 12 +
2,3 2.5 –1.125 –
3, 4 12 +
Solution set: ,22,3
72. 2 1120xxx
The real zeros are x = –2, x = –1, and x = 1. So, the intervals to be tested are ,2,
2,1,1,1, and 1,.
Interval Test point
Value of Px Result
,2 –3 16 +
2,1 –1.5 –0.3125 –
1,1 0 –2 –
1, 2 36 +
Solution set: ,211,
73. 322 32 4774 5730 xxxx xxx
The possible rational zeros are 1,3
Using synthetic division, we find that x = 3 is a zero.
31573 363 1210
322 2 573321 31 xxxxxx xx
The zeros are x = 1 and x = 3. So, the intervals to be tested are
,1,1,3, and
Interval Test point Value of
3,.
3, 4 9 +
Solution set:
74. 322 32 24832 5280 xxxxx xxx
The possible rational zeros are 1,2,4,8.
Using synthetic division, we find that x = 2 is a zero. 21528 268 1340
322528234 241 xxxxxx xxx
The zeros are x = –1, x = 2 and x = 4. So, the intervals to be tested are
,1,1,2,
2,4 and
4,.
Interval Test point Value of
Px Result
1,2 0 8 +
2,4 3 –4 –
Solution set:
13 0 2 xx x
numerator: 1301,3xxxx denominator : 202xx
The line x = –2 is the vertical asymptote of , Rx so –2 is not included in the intervals to be tested. The boundary points are –3, –2, and 1. The intervals are ,3, 3,2, 2,1, and 1,.
Interval Test point Value of Rx Result
,3 –5 –4 –
1, 2 5 4 +
Solution set: 3,21,
76. 2 14 0 2 xx x
numerator: 2 1401,4xxxx
denominator : 202xx
The line x = 2 is the vertical asymptote of , Rx so 2 is not included in the intervals to be tested. The boundary points are –1, 2, and 4. The intervals are ,1, 1,2, 2,4, and 4,.
Interval Test point
Value of Rx Result ,1 –2 3 2 + 1,2 0 2 + 2,4 3 –16 –
4, 5 12 +
Solution set: 12,4 (Remember to include –1 in the solution set because it is a zero.)
77.
2323 330 44 2334 15 00 44 xx xx xxx xx
numerator: 15015xx
denominator : 404xx
The line x = –4 is the vertical asymptote of , Rx so –4 is not included in the intervals to be tested. The boundary points are –15 and –4. The intervals are
,15,15,4
and
Interval Test point Value of
Rx Result
–12 –
Solution set:
,154,
2323 0
numerator: 12012xx
denominator : 400,4xxxx
The lines x = –4 and x = 0 are the vertical asymptotes of , Rx so –4 and 0 are not included in the intervals to be tested. The boundary points are –12, –4, and 0. The intervals are ,12,12,4, 4,0, and 0,.
,12 –13 1 117 +
12,4 –6 1 2 –
4,0 –3 3 +
0, 1 13 5 –
Solution set: ,124,0
Applying the Concepts
79. ;1243;3(5)15ykxkky
80. 12 ;412;3 34 kk pkp q
81. 222 ;2025;3(5)45sktkks
82. 222 192 ;3192;124 8 kk ykx xx
83. The maximum height occurs at the vertex, 2020 (100,1000). 2(110)2(110) f
The maximum height is 1000. To find where the missile hits the ground, solve 2 1 2000 or 200. 10 xxxx
The missile hits the ground at x = 200.
84. Let x = the length of one piece, and the area of the square formed by that piece is 2 x . Then 20 x the length of the other piece, 2 (20) x the area of the square formed by that piece. The total area is 222(20)240400. xxxx The minimum is at the x-coordinate of the vertex, 40 10. 2(2) Each piece must be 10 cm long.
85. The area of each section is 400 square feet. Since the width is x, 400 y x The total amount of fencing needed is 2400 4. x x Using a graphing calculator, we find that this is a minimum at 24.5 feet. x So 400 16.3 feet. 24.5 y The dimensions of each pen should be approximately 24.5 ft by 16.3 ft. (continuedonnextpage)
(continued)
86. Since x = the width, 400 y x Then 2400
6 y x the length of the heavy fencing.
The farmer needs 2400 2 x x feet of heavy fencing, so it will cost 240012,000 5210. xx xx
The low fencing will cost 3(2)6. xx The total cost of the fencing is 12,000 16. x x
Using a graphing calculator, we find this is a minimum when 27.4 x .
87. a.
So 400 14.6 27.4 y . The cost will be minimized when the dimensions of each pen are 27.4 ft by 14.6 ft.

b.
2 2 2 425800105,000 0 50 271503350 0 50 xx x xx x
numerator: 2715033500 xx 150350 73 , xx
denominator: 2 50050 xx
The line x = –50 is the vertical asymptote of , Rx so –50 is not included in the intervals to be tested. In the context of this problem, x > 0, so it is not necessary to test negative values. The boundary points are 0, 150 7 , and 350 3 The intervals are
150150350 773 0,,,, and 350 3 ,.
Interval Test point
Value of Rx Result
150 7 0, 10 128 9 – 150350 73 , 50 8 + 350 3 , 200 –10 –
The power absorbed by the circuit is greater than 42 for 150350 73 x
c.
The maximum occurs at x = 50.
88. a. The total area of the paper is 100 square inches. If the width of the paper is x, then the length is 100 x . The width of the printed area is x –2(1) = x – 2, and the length of the printed area is 1003100 2 23. xx The area of the printed region is 100 23. x x (continuedonnextpage)
Copyright © 2018 Pearson Education Inc.
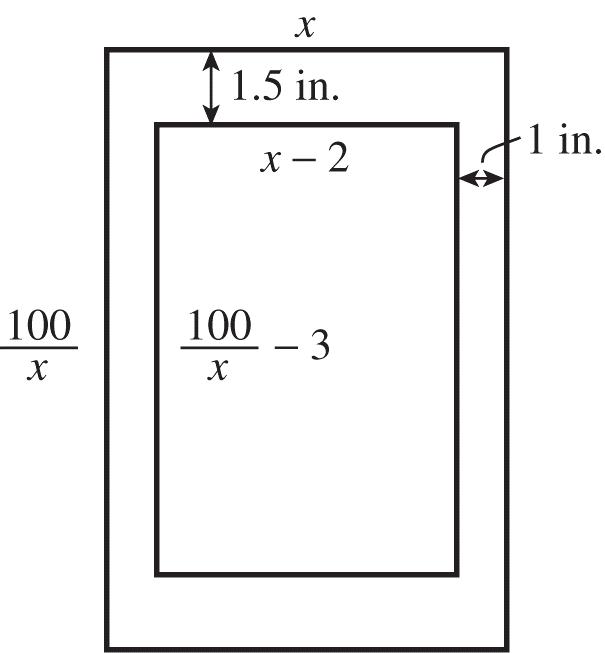
We want to solve 100 2356. x x
2 100 2356 100 23560 200 3106560 200 3500 350200 0 x x x x x x x x xx x
numerator: 2 3502000 xx
20 3 10320010,xxx
denominator: x = 0
Test intervals:
2020 33 0,,,10,10,
Interval Test point Value of Rx Result
20 3 0, 5 –5 –20 3 ,10 8 1 + 10, 12 8 3 –The width of the paper should be between 20 3 6.67 in. and 10 in.
b. The area of the printed region is given by 100 23. x Ax [0, 30] by [0, 100]
Copyright © 2018 Pearson Education Inc. (continued)
The maximum value of x, the width, is about 8.16 in., so the maximum length is 100 8.16 12.25 in. The maximum area of the printed region is about 57.01 in2
89. a. The revenue is 24x. Profit = revenue – cost, so 2 3 ()241503.9 1000 Pxxxx
2 3 20.1150. 1000 xx
b. The maximum occurs at the x-coordinate of the vertex: 3 1000 20.1 3350 2 c. 2 3 1000 3.9150 () () 3150 3.9 1000 Cxxx Cx xx x x
90. a. 19,340 19,340 feet3.66 miles 5280 69.1 11.59 inches 3.662.3 p
b. 69.1 0069.1, 2.3 a which is impossible. So there is no altitude at which the pressure is 0.
91. 280407;7(35)$245 kks
92. 22 2 1 ;2530 36 1 (66)121 feet 36 dkskk s
93. 2 , ki I d where I = illumination, i = intensity, and d = distance from the source. The illumination 6 inches from the source is 6 2 300 , 6 k I while the illumination x inches from the source is 2 300 x k I x . 6 2 IIx
Chapter 2 Practice Test A
1. 2 2 6(6)4(1)(2) 620 2(1) xxx 628 37 2 x are the x-intercepts
94. 1.2 ;1.2295 295 1.2 (310)1.26 cubic feet. 295 VkTkk V
95. ;309000 300 kk Ik R
a. 9000 36 amp 250 I
b. 9000 60150 ohms R R
96. 22 2 4 ;201440 12 14403 24.94 tons 10
97. ()Rkipi
a. 6 255(0.15)(20,000)(0.85)(20,000) 1 510 200,000 k
b. 1 (10,000)(10,000) 200,000 500 people per day R
c. 2 1 95(20,000) 200,000 20,00019,000,0000 (1000)(19,000)01000 or 19,000 xx xx xxx x
98. 2 12 () Fkqqd . If the distance is quadrupled, then the force is 1212 new 22 . (4)16 Fkqqkqq dd So the original force is divided by 16: 96 6 16 units.
3. The vertex is at , 22 bb f aa
1414 2(7)2(7),(1,10).
4. The denominator is 0 when x = –4 or x = 1. The domain is (,4)(4,1)(1,).
5. Using either long division or synthetic division, we find that the quotient is 2 43xx and the remainder is 0. 21256 286 1430
6.
7. The function has degree three, so there are three zeros. Since 2 is a zero, use synthetic division to find the depressed function: 22288 448 2240
Now find the zeros of 2 224: xx 22 2242(2)2(2)(1) xxxxxx the zeros are x = –2 and x = 1. The zeros of the original function are –2, 1, 2.
8.
9. Using synthetic division to find the remainder, we have (2)53. P 2157917 262670 13133553
10. The function has degree three, so there are three zeros. There are two sign changes in ()fx , so there are either 2 or 0 positive zeros. There is one sign change in ()fx , so there is one negative zero. The possible rational zeros are 1,2,4,5,10,20. Using synthetic division, we find that –2 is a zero: 215420 21420 17100
Now find the zeros of the depressed function 22710:710(5)(2) xxxxxx the zeros are x = 2 and x = 5. The zeros of the original function are –2, 2, 5.
11. The function has degree four, so there are four zeros. Factoring, we have 432 15 xxx 22(15)xxx 0 is a zero of multiplicity
2. Now find the zeros of 2 15: xx 2 114(1)(15) 161 2(1)2 x
The zeros of the original function are 0 and 161 2
12. The factors of the constant term, 9, are 1,3,9 , while the factors of the leading coefficient are 1,2. The possible rational zeros are 139 ,1,,3,,9. 222
13. () as ;() as . fxxfxx
14. 22 2 ()(4)(2) (2)(2)(2) fxxx xxx the zeros are –2 (multiplicity 3) and 2 (multiplicity 1).
15. There are two sign changes in ()fx , so there are either two or zero positive zeros. There is one sign change in ()fx , so there is one negative zero.
16. The zeros of the denominator are x = 5 and x = –4, so those are the vertical asymptotes. The degree of the numerator equals the degree of the denominator, so the horizontal asymptote is y = 2.
17.
numerator: 21407 xx denominator:
4204,2xxxx
The intervals to be tested are ,7,
7,4,4,2, and 2,.
Interval Test point Value of Rx Result
Solution set:
7,42, 18. 2 2 8 63 2 kx y t k k 2 312 4 3 y
19. The minimum occurs at the x-coordinate of the vertex: 30 15 2(1) thousand units.
20. (172)(82) Vxxx
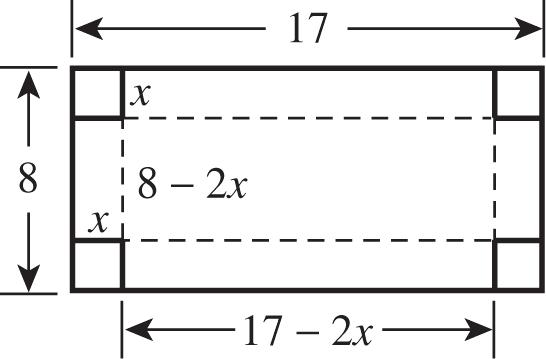
Chapter 2 Practice Test B
1. B 2 2 530 554(1)(3) 513 2(1)2 xx x
2. D. The graph of 2 ()4(2)fxx is the graph of 2 () fxx shifted two units right, reflected across the x-axis, and then shifted 4 units up
3. A 1212 ,, 222(6)2(6) (1,11) bb ff aa
4. B. The denominator is 0 when x = –3 or x = 2.
5. D 31086 393 1313
6. C 433 ()2(2). Pxxxxx So the zeros are 0 (multiplicity 3) and –2 (multiplicity 1).
7. C 33266130 95130 317100 The zeros of the depressed function 2 31710 xx are 2 and 5. 3 xx
8. B 2 32 32 2 2 534 2310211712 1015 617 69 812 812 0 xx xxxx xx xx xx
9. C 31471015 33126 114221 (3)21. P
10. A. The polynomial has degree three, so there are three zeros. The possible rational zeros are 1,2,3,4,6,12. Using synthetic division, we find that one zero is 3: 311812 31212 1440
The zeros of the depressed function 2 44xx are x = 2 (multiplicity 2).
11. A. The polynomial has degree three, so there are three zeros. Factoring, we have 32230(30)(6)(5) xxxxxxxxx
12. D. The factors of the constant term, 60, are 1,2,3,4,5,6,10,12,15,20, 30,60. Since the leading coefficient is 1, these are also the possible rational zeros.
13. C 14. B 22 2 (1)(1)(1)(1)(1). xxxxx
15. C. There are three sign changes in ()Px , so there are 3 or 1 positive zeros. There are two sign changes in ()Px , so there are 2 or 0 negative zeros.
16. C. The zeros of the denominator are x = 3 and x = –4, so those are the vertical asymptotes. The degree of the numerator equals the degree of the denominator, so the horizontal asymptote is y = 1.
Copyright © 2018 Pearson Education Inc.
17. C
numerator: 707
18. B
19. B. The minimum occurs at the x-coordinate of the vertex: 24 12. 2(1)
20. D. (102)(122) Vxxx
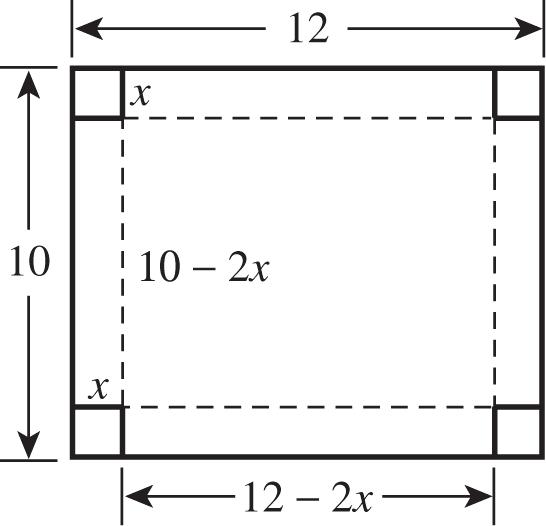
Cumulative Review Exercises Chapters 1–2
1. 2 2121 22 123513
2. 1212 , 22 2(8)5(3),3,4 22 Mxxyy
3. 2 2 028042 404 or 202 002088 xxxx xxxx f
The x-intercepts are ( 2, 0) and (4, 0), and the y-intercept is (0, 8).
4. Write the equation in slope-intercept form: 1 360362 3 xyyxyx
The slope is 1 3 , and the y-intercept is (0, 2). 3(0)60606,xxx so the x-intercept is (6, 0).
5. Write the equation in slope-intercept form: 1 26623 2 xyxyxy
The slope is 1 2 , and the y-intercept is (0, 3).
The x-intercept is x = 2(0) 6 = 6. (continuedonnextpage)
6. 22 (2)(3)16 xy
7. 22 22 22 2440 (2)(4)4 (21)(44)414 xyxy xxyy xxyy
22 (1)(2)9 xy
The center is (–1, 2). The radius is 3.
8. 23(1)35yxyx
9. 25 235 33xyyx the slope is 2 3 2211 3(1)333yxyx
10. 3 230. 2 xx
The domain is 33 ,, 22
11. 4202. xx The domain is (,2).
12. 2 2 2 22 22 (2)(2)2(2)311; (3)32(3)36; ()()2()3 2223 2(1)23 f f fxhxhxh xxhhxh xhxhh
222 2 22 ()() (2(1)23)(23) 2(1)22 222222 22 fxhfx h xhxhhxx h hxxhh h hxxxhhhhxh hh hx
13. a. 2 1 fgxx
b. 2 11gfxxx
c. 4 ffxxx
d.
2 2421122ggxxxx
14. a. (1)3(1)25;(3)4(3)111; (4)6 ff f
b.
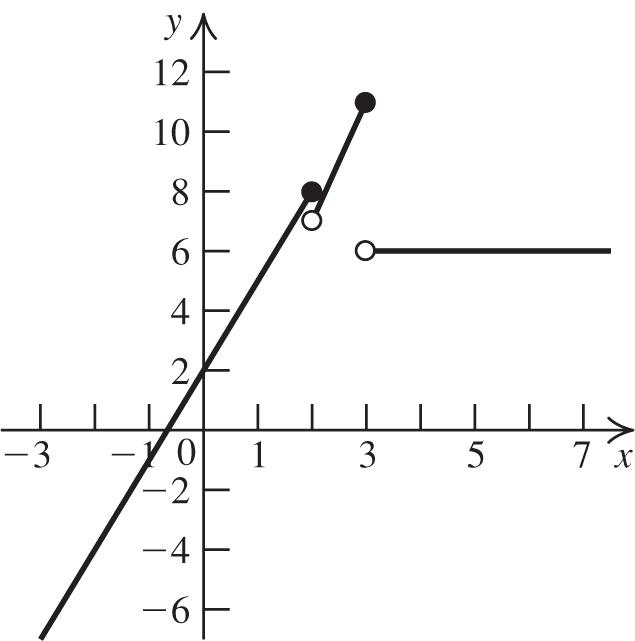
15. 23.yx Interchange x and y, and then solve for y 1 313 23(). 222 x xyyxfx
16. a. Shift the graph of yx two units left.
b. Shift the graph of yx one unit left, stretch vertically by a factor of two, reflect about the x-axis, and then shift up three units.
17. The factors of the constant term, –6, are 1,2,3,6 , and the factors of the leading coefficient, 2, are 1,2. The possible rational zeros are 13 22,1,,2,3,6.
18. a.
b. 2 2410 xx
Use the quadratic formula to find the zeros.
20. a.
The intervals to be tested are ,1, 1,3, and 3,. From the graph in part (a), we see that the solution set is 1,3.
b. 2 2 120 1201,2 xx xxx
The intervals to be tested are ,2, 2,1, and 1,. From the graph in part (a), we see that the solution set is 2,11,2,.
Interval Test point
21. a.
b. 2 2 1 0 4 x x
numerator: 2 101xx denominator: 2 402xx
The intervals to be tested are ,2, 2,1,1,1,1,2, and 2,. From the graph in part (a), we see that the solution set is ,21,12,.
22. Since one zero is 1 + i, another zero is 1 i So 2 ((1))((1))22 xixixx is a factor of ()fx . Now divide to find the other factor:
432 2 ()3224 ((1))((1))(2) ((1))((1))(2)(1) fxxxxx xixixx xixixx
the zeros of () are1,2,1,1. fxii
23. ;643;399ykxkky
24. Profit = revenue – cost 2 2 150(0.021003000) 0.02503000. xxx xx The maximum occurs at the vertex: 5050 , 2(0.02)2(0.02) (1250,$28,250).
25. 100.0248.8299025,000 0.249025,000 0.024925000 Now solve the depressed equation 2 0.024925000. xx 2 49494(0.02)(2500) 2(0.02) 4926014951 50 or 0.040.04 x x 2500 x . There cannot be a negative amount of units sold, so another break-even point is 50.
