MathematicalModelsofSystems
Exercises
E2.1 Wehavefortheopen-loop y = r 2 andfortheclosed-loop e = r y and y = e 2
So, e = r e2 and e2 + e r =0 .
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGUREE2.1
Plotofopen-loopversusclosed-loop.
Forexample,if r =1,then e2 + e 1=0impliesthat e =0 618.Thus, y =0.382.Aplot y versus r isshowninFigureE2.1.
E2.2 Define
when R0 =10, 000Ω.Thus,thelinearapproximationiscomputedby consideringonlythefirst-ordertermsintheTaylorseriesexpansion,and isgivenby
R = 135∆T.
E2.3 Thespringconstantfortheequilibriumpointisfoundgraphicallyby estimatingtheslopeofalinetangenttotheforceversusdisplacement curveatthepoint y =0.5cm,seeFigureE2.3.Theslopeofthelineis K
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
y=Displacement (cm) For ce (n) Spring compresses Spring breaks
FIGUREE2.3
Springforceasafunctionofdisplacement.
CHAPTER2MathematicalModelsofSystems
E2.4 Since R(s)= 1 s wehave Y (s)= 6(s +50) s(s +30)(s +10)
Thepartialfractionexpansionof Y (s)isgivenby
where
UsingtheLaplacetransformtable,wefindthat
Thefinalvalueiscomputedusingthefinalvaluetheorem: lim t→∞ y(t)=lim s→0 s 6(s +50) s(s2 +40s +300) =1
E2.5 ThecircuitdiagramisshowninFigureE2.5.
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGUREE2.5 Noninvertingop-ampcircuit.
Withanidealop-amp,wehave vo = A(vin v ),
Exercises 25 where A isverylarge.Wehavetherelationship
v = R1 R1 + R2 vo
Therefore, vo = A(vin R1 R1 + R2 vo), and solvingfor vo yields
vo = A 1+ AR1 R1+R2 vin
Since A ≫ 1,itfollowsthat1+ AR1 R1 +R2 ≈ AR1 R1 +R2 .Thentheexpressionfor vo simplifiesto
E2.6 Given
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
vo = R1 + R2 R1 vin
y = f (x)= ex andtheoperatingpoint xo =1,wehavethelinearapproximation y = f (x)= f (xo)+ ∂f ∂x x=xo (x xo)+ ·· · where f (xo)= e, df dx x=xo=1 = e, and x xo = x 1
Therefore,weobtainthelinearapproximation y = ex
E2.7 TheblockdiagramisshowninFigureE2.7.
FIGUREE2.7 Blockdiagrammodel.
CHAPTER2MathematicalModelsofSystems
Startingattheoutputweobtain I(s)= G1(s)G2(s)E(s).
But E(s)= R(s) H(s)I(s),so I(s)= G1(s)G2(s)[R(s) H(s)I(s)] .
Solvingfor I(s)yieldstheclosed-looptransferfunction
E2.8 TheblockdiagramisshowninFigureE2.8.
FIGUREE2.8
Blockdiagrammodel.
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
Startingattheoutputweobtain
Substituting
and with E(s)= R(s) Y (s)and Z(s)= sY (s)thisreducesto
Y (s)=[ G1(s)G2(s)(H2(s)+ H1(s)) G1(s)H3(s) 1 s G1(s)G2(s)K]Y (s)+ 1 s G1(s)G2 (s)KR(s)
Solvingfor Y (s)yieldsthetransferfunction
Y (s)= T (s)R(s), where
T (s)= KG1(s)G2 (s)/s 1+ G1(s)G2(s)[(H2(s) + H1(s)]+ G1(s)H3(s)+ KG1(s)G2(s)/s
E2.9 FromFigureE2.9,weobservethat
Ff (s)= G2(s)U (s) and
FR(s)= G3(s)U (s)
Then,solvingfor U (s)yields
U (s)= 1 G2(s) Ff (s) and itfollowsthat
FR(s
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
Again,consideringtheblockdiagraminFigureE2.9wedetermine
But,fromthepreviousresult,wesubstitutefor FR(s)resultingin
Solvingfor Ff (s)yields
CHAPTER2MathematicalModelsofSystems
FIGUREE2.9
Blockdiagrammodel.
E2.10 TheshockabsorberblockdiagramisshowninFigureE2.10.Theclosedlooptransferfunctionmodelis
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
Piston travel measurement
FIGUREE2.10
Shockabsorberblockdiagram.
E2.11 Let f denotethespringforce(n)and x denotethedeflection(m).Then K = ∆f ∆x . Computingtheslopefromthegraphyields:
(a) xo = 0.14m → K =∆f/∆x =10n/0.04m=250n/m
(b) xo =0m → K =∆f/∆x =10n/0.05m=200n/m
(c) xo =0.35m → K =∆f/∆x =3n/0.05m=60n/m
E2.12 ThesignalflowgraphisshowninFig.E2.12.Find Y (s)when R(s)=0. Y(s) -1 K 2 G(s) -K 1 1 Td(s)
FIGUREE2.12
Signalflowgraph.
Thetransferfunctionfrom Td(s)to Y (s)is Y (s)= G(s)Td(s) K1K2G(s)Td(s) 1 ( K2G(s)) = G(s)(1 K1K2)Td(s) 1+ K2G(s)
Ifweset K1K2 =1 , then Y (s)=0forany Td(s).
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
E2.13 Thetransferfunctionfrom R(s), Td(s),and N (s)to Y (s)is Y (s)= K s2 +10s + K R(s)+ 1 s2 +10s + K Td(s) K s2 +10s + K N (s) Therefore,wefindthat Y (s)/Td(s)= 1 s2 +10s + K and Y (s)/N (s)= K s2 +10s + K
E2.14 Sincewewanttocomputethetransferfunctionfrom R2(s)to Y1(s),we canassumethat R1 =0(applicationoftheprincipleofsuperposition). Then,startingattheoutput Y1(s)weobtain
Consideringthesignal W (s)(seeFigureE2.14),wedeterminethat
CHAPTER2MathematicalModelsofSystems
FIGUREE2.14 Blockdiagrammodel. or
Substitutingtheexpressionfor W (s)intotheaboveequationfor Y1(s) yields
E2.15 Forloop1,wehave
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
Andforloop2,wehave
E2.16 Thetransferfunctionfrom R(
)to P (
TheblockdiagramisshowninFigureE2.16a.Thecorrespondingsignal flowgraphisshowninFigureE2.16bfor
FIGUREE2.16
(a) Blockdiagram,(b)Signalflowgraph.
E2.17 Alinearapproximationfor f isgivenby
f = ∂f
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
= k
where xo =1/2,∆f = f (x) f (xo),and∆x = x xo
E2.18 Thelinearapproximationisgivenby ∆y = m∆x where m = ∂y ∂x x=xo
(a) When xo =1,wefindthat yo =2 4,and yo =13 2when xo =2.
(b)Theslope m iscomputedasfollows: m = ∂y ∂x x=xo =1+ 4 2x 2 o Therefore, m =5 2at xo =1,and m =18 8at xo =2.
CHAPTER2MathematicalModelsofSystems
E2.19 Theoutput(withastepinput)is Y (s)= 28(s +1) s(s +7)(s +2)
Thepartialfractionexpansionis Y (s)= 2 s 4 8 s +7 + 2 8 s +2 .
TakingtheinverseLaplacetransformyields
E2.20 Theinput-outputrelationshipis Vo V = A(K 1) 1+ AK where K = Z1 Z1 + Z2
Assume A ≫ 1.Then,
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
Therefore,
E2.21 Theequationofmotionofthemass mc is
TakingtheLaplacetransformwithzeroinitialconditionsyields
So,thetransferfunctionis
E2.22 Therotationalvelocityis ω(s)= 2(s +4) (s +5)(s +1)2 1 s .
Expandinginapartialfractionexpansionyields
(
TakingtheinverseLaplacetransformyields
E2.23 Theclosed-looptransferfunctionis
(s) R(s) = T (s)= K1K2 s2 +(
.
E2.24 Let x =0.6and y =0.8.Then,with y = ax3,wehave 0.8= a(0.6)3 .
Solvingfor a yields a =3 704.Alinearapproximationis y yo =3ax 2 o(x xo) or y =4x 1 6,where yo =0 8and xo =0 6.
E2.25 Theclosed-looptransferfunctionis Y (s) R(s) = T
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
E2.26 Theequationsofmotionare
TakingtheLaplacetransform(withzeroinitialconditions)andsolving for X2(s)yields X2(s)= k (m
Then,with m1 = m2 = k =1,wehave
CHAPTER2MathematicalModelsofSystems
E2.27 Thetransferfunctionfrom Td(s)to Y (s)is
.
E2.28 Thetransferfunctionis
E2.29 (a)If
)= 1 s2 +15s +50 and H(s)=2s +15 , thentheclosed-looptransferfunctionofFigureE2.28(a)and(b)(in Dorf&Bishop)areequivalent.
(
(b)Theclosed-looptransferfunctionis T (s)= 1 s2 +17s +65
E2.30 (a)Theclosed-looptransferfunctionis
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGUREE2.30 Stepresponse.
(b) Theoutput Y (s)(when R(s)=1/s)is
Y (s)= 0 5 s + 0 25+ 0 1282j s +2 5 4 8734 + 0 25 0 1282j s +2 5+4 8734j or
Y (s)= 1 2 1 s s +5 s2 +5s +30
(c)Theplotof y(t)isshowninFigureE2.30.Theoutputisgivenby y(t)=0 5(1 1 1239e 2 5t sin(4 8734t +1 0968));
E2.31 Thepartialfractionexpansionis
V (s)= a s + p1 + b s + p2
where p1 =4 22j and p2 =4+22j.Then,theresiduesare a = 11 37jb =11 37j.
TheinverseLaplacetransformis v(t)= 11 37je( 4+22j)t +11 37je( 4 22j)t
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
Problems
P2.1 Theintegrodifferentialequations,obtainedbyKirchoff’svoltagelawto eachloop,areasfollows:
P2.2 Thedifferentialequationsdescribingthesystemcanbeobtainedbyusing afree-bodydiagramanalysisofeachmass.Formass1and2wehave
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
Usingaforce-currentanalogy,theanalagouselectriccircuitisshownin FigureP2.2,where Ci → Mi ,L1 → 1/k1 ,L12 → 1/k12 , and R → 1/b.
FIGUREP2.2
Analagouselectriccircuit.
P2.3 Thedifferentialequationsdescribingthesystemcanbeobtainedbyusing afree-bodydiagramanalysisofeachmass.Formass1and2wehave
Usingaforce-currentanalogy,theanalagouselectriccircuitisshownin FigureP2.3,where
FIGUREP2.3
Analagouselectriccircuit.
P2.4 (a)Thelinearapproximationaround vin =0is vo =0vin,seeFigureP2.4(a).
(b)Thelinearapproximationaround vin =1is vo =2vin 1,seeFigureP2.4(b).
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGUREP2.4
Nonlinearfunctionsandapproximations.
CHAPTER2MathematicalModelsofSystems
P2.5 Given Q = K(P1 P2)1/2
Let δP = P1 P2 and δPo =operatingpoint.UsingaTaylorseries expansionof Q,wehave Q = Qo + ∂Q
Define∆Q = Q Qo and∆P = δP δPo.Then,droppinghigher-order termsintheTaylorseriesexpansionyields ∆Q = m∆P where m = K 2δP 1
P2.6 FromP2.1wehave
and
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
TakingtheLaplacetransformandusingthefactthattheinitialvoltage across C2 is10vyields
and
Rewritinginmatrixformwehave
Solvingfor I2 yields
P2.7 Considerthedifferentiatingop-ampcircuitinFigureP2.7.Foranideal op-amp,thevoltagegain(asafunctionoffrequency)is
and Z2 = R2 aretherespectivecircuitimpedances.Therefore,weobtain
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGUREP2.7
Differentiatingop-ampcircuit.
CHAPTER2MathematicalModelsofSystems
P2.8 Let
Then,
Therefore,thetransferfunctionis
FIGUREP2.8 Pole-zeromap.
Pole-zero map (x:poles and o:zeros)
Using R1 =1.0, R2 =0.5,and C =0.5,wehave T (s)= s2 +4s +8 s
The pole-zeromapisshowninFigureP2.8.
P2.9 FromP2.3wehave
.
TakingtheLaplacetransformofbothequationsandwritingtheresultin matrixform,itfollowsthat
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGUREP2.9 Pole-zeromap.
CHAPTER2MathematicalModelsofSystems or
where∆=(Ms2 + bs + k)(Ms2 +2k) k2 . So, G(s)= X1(s) F (s) =
.
When b/k =1, M =1, b2/Mk =0.04,wehave G(s)= s2 +0 04s +0 04 s4 +0.04s3 + 0.12s2 +0.0032s +0.0016
Thepole-zeromapisshowninFigureP2.9.
P2.10 FromP2.2wehave
TakingtheLaplacetransformofbothequationsandwritingtheresultin matrixform,itfollowsthat
or
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
where
So,when f (t)= a sin
,wehavethat
Formotionlessresponse(inthesteady-state),setthezeroofthetransfer functionsothat
P2.11
Thetransferfunctionsfrom Vc(s)to Vd(s)andfrom Vd(s)to θ(s)are:
and
Theblockdiagramfor θ(s)/Vc(s)isshowninFigureP2.11,where
(s)/Vc(s)= θ(s) Vd(s) V
(s) Vc(s) = K1K2K
∆(s) , where
FIGUREP2.11
Blockdiagram.
P2.12 Theopen-looptransferfunctionis
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
With R(s)=1/s,wehave Y (s)= K s(s +50) . Thepartialfractionexpansionis Y (s)= K 50 1 s 1 s +50 , andtheinverseLaplacetransformis y(t)= K 50 1 e 50t , As t → ∞,itfollowsthat y(t) → K/50.Sowechoose K =50sothat y(t)
CHAPTER2MathematicalModelsofSystems
approaches1.Alternativelywecanusethefinalvaluetheoremtoobtain
Itfollowsthatchoosing K =50leadsto y(t) → 1as t →∞.
P2.13 Themotortorqueisgivenby
Combiningtheaboveexpressionsyields
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
P2.14 Forafield-controlleddcelectricmotorwehave
Withastepinputof Vf (s)=80/s,thefinalvalueof ω(t)is
(t)t→∞ =lim s→0 sω(s)= 80Km Rf b =2.4or Km Rf b =0.03 .
Solvingfor ω(t)yields
At t =1/2, ω(t)=1,so ω(1/2)=2 4(1 e (b/J )t)=1implies b/J =1 08sec
Therefore, ω(s)/Vf (s)= 0 0324 s +1.08
P2.15 SummingtheforcesintheverticaldirectionandusingNewton’sSecond Lawweobtain x + k m x =0
Thesystemhasnodampingandnoexternalinputs.TakingtheLaplace transformyields
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
X(s)= x0s s2 + k/m ,
whereweusedthefactthat x(0)= x0 and˙x(0)=0.Thentakingthe inverseLaplacetransformyields x(t)= x0 cos k m t.
P2.16 (a)Formass1and2,wehave
(b)TakingtheLaplacetransformyields
(c)Let
FIGUREP2.16
Signalflowgraph.
CHAPTER2MathematicalModelsofSystems
G2(s)=1/p(s)
G3(s)=1/q(s)
G4(s)= sb1 , where
and
ThesignalflowgraphisshowninFigureP2.16.
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
(d)Thetransferfunctionfrom X3(s)to X1(s)is
P2.17 UsingCramer’srule,wehave
The signalflowgraphisshowninFigureP2.17.
FIGUREP2.17
Signalflowgraph.
P2.18 ThesignalflowgraphisshowninFigureP2.18.
FIGUREP2.18
Signalflowgraph.
Thetransferfunctionis
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
P2.19 (a)Assume Rg ≫ Rs and Rs ≫ R1.Then Rs = R1 + R2 ≈ R2,and vgs = vin vo , whereweneglect iin,since Rg ≫ Rs.AtnodeS,wehave vo Rs = gmvgs = gm(vin vo)or vo vin = gmRs 1+ gmRs . (b) With gmRs =20,wehave vo vin = 20 21 =0.95 .
CHAPTER2MathematicalModelsofSystems
(c)TheblockdiagramisshowninFigureP2.19. gmRsvin(s) vo(s)
FIGUREP2.19
Blockdiagrammodel.
P2.20 Fromthegeometrywefindthat
Theflowratebalanceyields A dy dt = p∆z whichimplies Y (s)= p∆Z(s) As
Bycombiningtheaboveresultsitfollowsthat
Therefore,thesignalflowgraphisshowninFigureP2.20.UsingMason’s
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGUREP2.20
Signalflowgraph.
gainformulawefindthatthetransferfunctionisgivenby
where
P2.21 (a)Theequationsofmotionforthetwomassesare
FIGUREP2.21 (a) Blockdiagram.(b)Pole-zeromap.
CHAPTER2MathematicalModelsofSystems
(b) Define a = g/L + k/4M and b = k/4M .Then
1(s)
(c) Theblockdiagramandpole-zeromapareshowninFigureP2.21.
P2.22 Foranoninvertingop-ampcircuit,depictedinFigureP2.22a,thevoltage gain(asafunctionoffrequency)is
Vo(s)= Z1(s)+ Z2(s) Z1(s) Vin(s), where Z1(s)and Z2(s)aretheimpedancesoftherespectivecircuits.In
FIGUREP2.22 (a) Noninvertingop-ampcircuit.(b)Voltagefollowercircuit.
thecaseofthevoltagefollowercircuit,showninFigureP2.22b,wehave Z1 = ∞ (opencircuit)and Z2 =0.Therefore,thetransferfunctionis
P2.23 Theinput-outputratio, Vce/Vin,isfoundtobe
P2.24 (a)Thevoltagegainisgivenby
(b) Thecurrentgainisfoundtobe
(c) Theinputimpedanceis
+ R2 , and when β1β2 isverylarge,wehavetheapproximation
P2.25 Thetransferfunctionfrom R(s)and Td(s)to Y (s)isgivenby
Thus,
(s)/R(s)= G(s) . Also,wehavethat Y (s)=0 when R(s)=0.Therefore,theeffectofthedisturbance, Td(s),iseliminated.
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
P2.26 Theequationsofmotionforthetwomassmodeloftherobotare
x + b(˙x y)+ k(x y)= F (t) m ¨ y + b(˙ y ˙ x)+ k(y x)=0 .
TakingtheLaplacetransformandwritingtheresultinmatrixformyields
Solvingfor Y (s)wefindthat
CHAPTER2MathematicalModelsofSystems
P2.27 Thedescribingequationofmotionis
Defining
(
)=
leadsto ¨ z = f (z,i) .
Theequilibriumconditionfor io and zo,foundbysolvingtheequationof motionwhen
is
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
WelinearizetheequationofmotionusingaTaylorseriesapproximation. Withthedefinitions ∆z = z zo and∆i = i io , wehave ˙ ∆z =˙ z and ¨ ∆z =¨ z.Therefore,
z = f (z,i)= f (zo,io)+
But f (zo,io)=0,andneglectinghigher-ordertermsintheexpansion yields
Usingtheequilibriumconditionwhichrelates zo to io,wedeterminethat
TakingtheLaplacetransformyieldsthetransferfunction(validaround theequilibriumpoint)
P2.28 ThesignalflowgraphisshowninFigureP2.28.
FIGUREP2.28 Signalflowgraph.
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning.
(a)ThePGBDPloopgainisequalto-abcd.Thisisa negative transmissionsincethepopulationproducesgarbagewhichincreasesbacteria andleadstodiseases,thusreducingthepopulation.
(b)ThePMCPloopgainisequalto+efg.Thisisa positive transmissionsincethepopulationleadstomodernizationwhichencourages immigration,thusincreasingthepopulation.
orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
(c)ThePMSDPloopgainisequalto+ehkd.Thisisa positive transmissionsincethepopulationleadstomodernizationandanincrease insanitationfacilitieswhichreducesdiseases,thusreducingtherate ofdecreasingpopulation.
(d)ThePMSBDPloopgainisequalto+ehmcd.Thisisa positive transmissionbysimilarargumentasin(3).
P2.29 Assumethemotortorqueisproportionaltotheinputcurrent Tm = ki.
Then,theequationofmotionofthebeamis
¨ φ = ki,
where J isthemomentofinertiaofthebeamandshaft(neglectingthe inertiaoftheball).Weassumethatforcesactingontheballaredueto gravityandfriction.Hence,themotionoftheballisdescribedby mx = mgφ bx
CHAPTER2MathematicalModelsofSystems
where m isthemassoftheball, b isthecoefficientoffriction,andwe haveassumedsmallangles,sothatsin φ ≈ φ.TakingtheLaplacetransfor ofbothequationsofmotionandsolvingfor X(s)yields
X(s)/I(s)= gk/J s2(s2 + b/m) .
P2.30 Given H(s)= k τs +1
where τ =5µs =4 × 10 6 secondsand0 999 ≤ k< 1 001.Thestep responseis
Y (s)= k τs +1 · 1 s = k s k s +1/τ
TakingtheinverseLaplacetransformyields
y(t)= k ke t/τ = k(1 e t/τ ) .
Thefinalvalueis k.Thetimeittakestoreach98%ofthefinalvalueis t =19 57µs independentof k
P2.31 Fromtheblockdiagramwehave
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
Therefore, Y1(s)=
And,computing E2(s)(with R2(s)=0)wefind
Substituting E2(s)intoequationfor Y1(s)yields
Finally,solvingfor Y1(s)yields
Similarly,for Y2(s)weobtain
P2.32
Thesignalflowgraphshowsthreeloops:
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
Thetransferfunction Y2/R1 isfoundtobe
, whereforpath1
∆1 =1
andforpath2
∆2 =1 L1
Sincewewant Y2 tobeindependentof R1,weneed Y2/R1 =0.Therefore, werequire
CHAPTER2MathematicalModelsofSystems
P2.33 Theclosed-looptransferfunctionis
(
) =
P2.34 Theequationsofmotionare
TakingtheLaplacetransformyields
Therefore,aftersolvingfor Y1(s)/X(s),wehave
P2.35 (a)WecanredrawtheblockdiagramasshowninFigureP2.35.Then,
(b)Thesignalflowgraphrevealstwoloops(bothtouching):
Therefore,
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
(c)Wewanttochoose K1 and K2 suchthat
+10)2
Therefore, K1 =100and1+ K2K1 =20or K2 =0 19.
(d)ThestepresponseisshowninFigureP2.35.
FIGUREP2.35
The equivalentblockdiagramandthesystemstepresponse.
P2.36 (a)Given R(s)=1/s2,thepartialfractionexpansionis
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
Therefore,usingtheLaplacetransformtable,wedeterminethatthe rampresponsefor t ≥ 0is
(b) Fortherampinput, y(t) ≈ 0 25at t =1second(seeFigureP2.36a).
(c)Given R(s)=1,thepartialfractionexpansionis
(s)= 30 (
Therefore,usingtheLaplacetransformtable,wedeterminethatthe
CHAPTER2MathematicalModelsofSystems
impulseresponsefor t ≥ 0is
(d) Fortheimpulseinput, y(t) ≈ 0 73at t =1seconds(seeFigureP2.36b).
(a) Ramp input
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGUREP2.36 (a) Rampinputresponse.(b)Impulseinputresponse.
P2.37 Theequationsofmotionare
When
(b) Impulse input
P2.38 Theequationofmotionforthesystemis J d2θ dt2 + b dθ dt + kθ =0 , where k istherotationalspringconstantand b istheviscousfriction coefficient.Theinitialconditionsare θ(0)= θo and θ(0)=0.Takingthe Laplacetransformyields
Therefore,
(s)= (s + b J θo) (s2 + b J s + K J ) = (s +2ζωn)θo s2 +2ζωns + ω2 n .
Neglectingthemassoftherod,themomentofinertiaisdeteminedtobe
Also,
Solvingfor θ(t),wefindthat
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
+ φ) , wheretan φ = 1 ζ 2/ζ).Therefore,theenvelopedecayis θe = θo 1 ζ 2 e ζωnt .
So,with ζωn =2 × 10 4 , θo =4000o and θf =10o,theelapsedtimeis computedas
P2.39 When t< 0,wehavethesteady-stateconditions i1(0)= 6 7 A,va(0)= 12 7 V and vc(0)= 36 7 V, where vc(0)isassociatedwiththe0.75Fcapacitor.After t ≥ 0,wehave
CHAPTER2MathematicalModelsofSystems and
TakingtheLaplacetransform(usingtheinitialconditions)yields
Solvingfor I2(s)yields I2(s)= 4s(27s2 +216s +604) 7(s +2)(60s2 +203s +14)
Then, Vo(s)=10I2(s).
P2.40 Theequationsofmotionare
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
TakingtheLaplacetransformyields (J1s 2 + bs + K)θ1(s) bsθ2(s)=
and(
),wefind that
)) ∆(s) , where∆(
P2.41 Assumethattheonlyexternaltorquesactingontherocketarecontrol torques, Tc anddisturbancetorques, Td,andassumesmallangles, θ(t). Usingthesmallangleapproximation,wehave ˙ h = Vθ
Jθ = Tc + Td , where J isthemomentofinertiaoftherocketand V istherocketvelocity (assumedconstant).Now,supposethatthecontroltorqueisproportional tothelateraldisplacement,as
Tc(s)= KH(s) , wherethenegativesigndenotesanegativefeedbacksystem.ThecorrespondingblockdiagramisshowninFigureP2.41.
FIGUREP2.41 Blockdiagram.
P2.42 (a)Theequationofmotionofthemotoris
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
J dω dt = Tm bω, where J =0 1, b =0 06,and Tm isthemotorinputtorque. (b)Given Tm(s)=1/s,and ω(0)=0 7,wetaketheLaplacetransform oftheequationofmotionyielding
sω(s) ω(0)+0.6ω(s)=10Tm or
ω(s)= 0 7s +10 s(s +0.6) Then,computingthepartialfractionexpansion,wefindthat ω(s)= A s + B s +0.6 = 16 67 s 15 97 s +0.6 Thestepresponse,determinedbytakingtheinverseLaplacetransform,is ω(t)=16.67 15.97e 0 6t ,t ≥ 0 .
CHAPTER2MathematicalModelsofSystems
P2.43 Theworkdonebyeachgearisequaltothatoftheother,therefore
Also,thetraveldistanceisthesameforeachgear,so
Thenumberofteethoneachgearisproportionaltotheradius,or
So,
and
Finally,
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
P2.44 Theinertiaoftheloadis
Also,fromthedynamicswehave
and
So,
since ω2 = nω1 .
Therefore,thetorqueatthemotorshaftis
T = T1 + Tm = n 2(JL ˙ ω1 + bLω1)+ Jm ˙ ω1 + bmω1 .
P2.45 Let U (s)denotethehumaninputand F (s)theloadinput.Thetransfer functionis
P (s)= G(s)+ KG1(s) ∆(s) U (s)+ Gc(s)+ KG1(s) ∆(s) F (s) , where
∆=1+ GH(s)+ G1KBH(s)+ GcE(s)+ G1KE(s)
P2.46 ConsidertheapplicationofNewton’slaw( F = m ¨ x).Fromthemass mv weobtain
mv ¨ x1 = F k1(x1 x2) b1(˙x1 ˙ x2)
TakingtheLaplacetransform,andsolvingfor X1(s)yields
X1(s)= 1 ∆1(s) F (s)+ b1s + k1 ∆1(s) X2(s), where
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
Fromthemass mt weobtain
1(˙x1 x2).
TakingtheLaplacetransform,andsolvingfor X2(s)yields
X2(s)= b1s + k1 ∆2(s) X1(s), where ∆2 := mts 2 +(b1 + b2)s + k1 + k2.
Substituting X2(s)aboveintotherelationshipfpr X1(s)yieldsthetransferfunction
X1(s) F (s) = ∆2(s) ∆1(s)∆2(s) (b1s + k1)2
CHAPTER2MathematicalModelsofSystems
P2.47 Usingthefollowingrelationships
h(t)= (1 6θ(t) h(t))dt
ω(t)= ˙ θ(t)
J ˙ ω(t)= Kmia(t)
va(t)=50vi(t)=10ia(t)+ vb(t)
˙ θ = Kvb
wefindthedifferentialequationis
P2.48 (a)Thetransferfunctionis
V2(s)
V1(s) = (1+ sR1C1)(1+ sR2C2) R1C2s
(b) When R1 =250 kΩ, R2 =200 kΩ, C1 =2 µF and C2 =0 1 µF ,we have
V2(s) V1(s) = 0.4s2 +20.8s + 40 s .
(c) Thepartialfractionexpansionis
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
V2(s) V1(s) =20 8 + 40 s +0 4s.
P2.49 (a)Theclosed-looptransferfunctionis T (s)= G(s) 1+ G(s) = 5000 s3 +20s2 +1000s +5000 .
(b)Thepolesof T (s)are s1 = 5.43and s2,3 = 7.28 ± j29.46.
(c)Thepartialfractionexpansion(withastepinput)is Y (s)= 1 s 1.06 s +5 43 + 0.0285+0.0904j s +7 28 j29 46 + 0.0285 0.0904j s +7 28+ j29 46 , and y(t)=1 1 06e 5 43t +0 06e 7 28t (cos29 46t 3 17sin29 46t);
(d)ThestepresponseisshowninFigureP2.49.Therealandcomplex rootsareclosetogetherandbylookingatthepolesinthes-planewe
P2.50
FIGUREP2.49 Stepresponse.
havedifficultydecidingwhichisdominant.However,theresidueat therealpoleismuchlargerandthusdominatestheresponse.
(a)Theclosed-looptransferfunctionis
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
(b)Thepolesof T (s)are s1 = 5and s2,3 = 20 ± j50
.
(c)Thepartialfractionexpansion(withastepinput)is
.
(d)ThestepresponseisshowninFigureP2.50.Therealrootdominates theresponse.
(e)Thefinalvalueof y(t)is yss =lim s→0 sY (s)=0.9655 .
CHAPTER2MathematicalModelsofSystems
FIGUREP2.50 Stepresponse.
P2.51 ConsiderthefreebodydiagraminFigureP2.51.UsingNewton’sLaw andsummingtheforcesonthetwomassesyields
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGUREP2.51 Freebodydiagram.
AdvancedProblems
AP2.1
Thetransferfunctionfrom V (s)to ω(s)hastheform
ω(s) V (s) = Km τms +1
In thesteady-state,
ss =lim s→0 s Km τms +1 5 s =5Km So, Km =70/5=14 .
Also,
where V (s)= Vm/s.Solvingfor τm yields
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
(t)= VmKm(1 e t/τm )
m = t ln(1 ω(t)/ωss)
When t =2,wehave τm = 2 ln(1 30/70) = 3 57
Therefore,thetransferfunctionis ω(s) V (s) = 14 3.57s +1
AP2.2 Theclosed-looptransferfunctionform
Ifweselect G5(s)= G2G3G
thenthenumeratoriszero,and Y2(s)/R1(s)=0.Thesystemisnow decoupled.
CHAPTER2MathematicalModelsofSystems
AP2.3 (a)Computingtheclosed-looptransferfunction:
Y (s)= G(s)Gc(s) 1+ Gc(s)G(s)H(s) R(s)
Then,with E(s)= R(s) Y (s)weobtain E(s)= 1+ Gc(s)G(s)(H(s) 1) 1+ Gc(s)G(s)H(s) R(s)
Ifwerequirethat E(s) ≡ 0foranyinput,weneed1+ Gc(s)G(s)(H(s) 1)=0or
H(s)= Gc(s)G(s) 1 Gc(s)G(s) = n(s) d(s)
Sincewerequire H(s)tobeacausalsystem,theorderofthenumerator polynomial, n(s),mustbelessthanorequaltotheorderofthedenominatorpolynomial, d(s).Thiswillbetrue,ingeneral,onlyifboth Gc(s) and G(s)areproperrationalfunctions(thatis,thenumeratoranddenominatorpolynomialshavethesameorder).Therefore,making E ≡ 0 foranyinput R(s)ispossibleonlyincertaincircumstances.
(b)Thetransferfunctionfrom Td(s)to Y (s)is
Y (s)= Gd(s)G(s) 1+ Gc(s)G(s)H(s) Td(s) .
With H(s)asinpart(a)wehave
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
(s)= Gd(s) Gc(s) Td(s) .
(c) No.Since
theonlywaytohave Y (s) ≡ 0forany Td(s)isforthetransferfunction T (s) ≡ 0whichisnotpossibleingeneral(since G(s) =0).
AP2.4 (a)With q(s)=1/s weobtain
Then,itfollowsthat
TakingtheinverseLaplacetransformyields
Qs+1/R (c)Toincreasethespeedofresponse,youwanttochoose Ct, Q, S and R suchthat
AP2.5 Consideringthemotionofeachmass,wehave
Inmatrixformthethreeequationscanbewrittenas
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
AP2.6 ConsideringthecartmassandusingNewton’sLawweobtain M x = u bx F sin ϕ where F isthereactionforcebetweenthecartandthependulum.Consideringthependulumweobtain m d2(x + L sin ϕ) dt2 = F
CHAPTER2MathematicalModelsofSystems
m d2(L cos ϕ) dt2 = F cos ϕ + mg
Eliminatingthereactionforce F yieldsthetwoequations
(m + M )¨ x + b ˙ x + mL ¨ ϕ cos ϕ mL ˙ ϕ 2 sin ϕ = u mL2 ϕ + mgL sin ϕ + mLx cos ϕ =0
Ifweassumethattheangle ϕ ≈ 0,thenwehavethelinearmodel
(m + M )¨ x + bx + mLϕ = u
mL2 ¨ ϕ + mgLϕ = mL¨ x
AP2.7 Thetransferfunctionfromthedisturbanceinputtotheoutputis
Y (s)= 1 s +40+ K Td(s)
When Td(s)=1,weobtain
y(t)= e (40+K )t
Solvingfor t when y(t) < 0.1yields t> 2.3 40+ K
When t =0.05and y(0.05)=0.1,wefind K =6.05.
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
AP2.8 Theclosed-looptransferfunctionis
T (s)= 200K(0.25s +1) (0 25s +1)(s + 1)(s +8)+200K
Thefinalvalueduetoastepinputof R(s)= A/s is
v(t) → A 200K 200K +8 .
We needtoselect K sothat v(t) → 50.However,tokeepthepercent overshoottolessthan10%,weneedtolimitthemagnitudeof K.FigureAP2.8ashowsthepercentovershootasafunctionof K.Let K =0.06 andselectthemagnitudeoftheinputtobe A =83 3.TheinverseLaplace transformoftheclosed-loopresponsewith R(s)=83.3/s is
v(t)=50+9 85e 9 15t e 1 93t (59 85cos(2 24t)+11 27sin(2 24t))
The resultis P.O. =9 74%andthesteady-statevalueoftheoutputis approximately50m/s,asshowninFigureAP2.8b.
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGUREAP2.8 (a) Percentovershootversusthegain K.(b)Stepresponse.
AP2.9 Thetransferfunctionis
CHAPTER2MathematicalModelsofSystems
Thenwecanwrite
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
DesignProblems 73
DesignProblems
CDP2.1 closelythearmature-controlleddcmotormodeldepictedinFigure2.18 inDorfandBishop.Thetransferfunctionis
Themodelofthetractiondrive,capstanroller,andlinearslidefollows
DP2.1 Theclosed-looptransferfunctionis
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
When
DP2.2 Atthelowernodewehave
Also,wehave v =24and i2 = Gv. So
CHAPTER2MathematicalModelsofSystems and
DP2.3 TakingtheLaplacetransformof
yields
Similarly,takingtheLaplacetransformoftherampinputyields
Therefore
DP2.4 Foranidealop-amp,atnodeawehave
andatnodeb
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
fromitfollowsthat
Also,foranidealop-amp, Vb Va =0.Thensolvingfor Vb intheabove equationandsubstitutingtheresultintothenodeaequationfor Va yields
or
DesignProblems
For vin(t) = At,wehave Vin(s)= A/s2,therefore vo(t)= A 2 β e βt + t 2 β
where β =1/R2C
DP2.5 Theequationofmotiondescribingthemotionoftheinvertedpendulum (assumingsmallangles)is
ϕ + g L ϕ =0
Assumingasolutionoftheform ϕ = k cos ϕ,takingtheappropriate derivativesandsubstitutingtheresultintotheequationofmotionyields therelationship
ϕ = g L .
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
Iftheperiodis T =2seconds,wecompute˙ϕ =2π/T .Thensolvingfor L yields L =0 99meterswhen g =9 81m/s2.So,tofitthependuluminto thegrandfatherclock,thedimensionsaregenerallyabout1.5metersor more.
CHAPTER2MathematicalModelsofSystems
ComputerProblems
CP2.1 Them-filescriptisshowninFigureCP2.1.
p=[1 8 12]; q=[1 2];
% Part (a)
pq=conv(p,q)
% Part (b)
P=roots(p), Z=roots(q)
% Part (c)
value=polyval(p,-1)
FIGURECP2.1
Scriptforvariouspolynomialevaluations.
CP2.2 Them-filescriptandstepresponseisshowninFigureCP2.2.
numc = [1]; denc = [1 1]; sysc = tf(numc,denc) numg = [1 2]; deng = [1 3]; sysg = tf(numg,deng)
% part (a)
sys_s = series(sysc,sysg); sys_cl = feedback(sys_s,[1])
% part (b) step(sys_cl); grid on
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGURECP2.2 Stepresponse.
CP2.3 Given
y +6˙ y +5y = u
with y(0)=˙ y =0and U (s)=1/s,weobtain(viaLaplacetransform) Y (s)= 1 s(s2 +6s +5) = 1 s(s +5)(s +1)
Expandinginapartialfractionexpansionyields
.
TakingtheinverseLaplacetransformweobtainthesolution
(t)=0.2+0.
. Them-filescriptandstepresponseisshowninFigureCP2.3.
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
n=[1]; d=[1 6 5]; sys = tf(n,d); t=[0:0.1:5]; y = step(sys,t); ya=0.2+0.05*exp(-5*t)-0.25*exp(-t); plot(t,y,t,ya); grid; title('Step Response'); xlabel('Time (s)'); ylabel('Amplitude');
FIGURECP2.3 Stepresponse.
CP2.4 Themass-spring-dampersystemisrepresentedby mx + b ˙ x + kx = f.
TakingtheLaplacetransform(withzeroinitialconditions)yieldsthe transferfunction
X(s)/F (s)= 1/m s2 + bs/m + k/m
Them-filescriptandstepresponseisshowninFigureCP2.4.
m=10; k=1; b=0.5; num=[1/m]; den=[1 b/m k/m]; sys = tf(num,den); t=[0:0.1:150]; step(sys,t)
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGURECP2.4 Stepresponse.
CP2.5 ThespacecraftsimulationsareshowninFigureCP2.5.Weseethatas J isdecreased,thetimetosettledowndecreases.Also,theoverhootfrom 10o decreasesas J decreases.Thus,theperformanceseemstogetbetter (insomesense)as J decreases.
%Part (a)
a=1; b=8; k=10.8e+08; J=10.8e+08; num=k*[1 a]; den=J*[1 b 0 0]; sys=tf(num,den); sys_cl=feedback(sys,[1]);
%
% Part (b) and (c) t=[0:0.1:100];
%
% Nominal case f=10*pi/180; sysf=sys_cl*f; y=step(sysf,t);
%
% O -nominal case 80%
J=10.8e+08*0.8; den=J*[1 b 0 0]; sys=tf(num,den); sys_cl=feedback(sys,[1]); sysf=sys_cl*f; y1=step(sysf,t);
%
% O -nominal case 50%
J=10.8e+08*0.5; den=J*[1 b 0 0]; sys=tf(num,den); sys_cl=feedback(sys,[1]); sysf=sys_cl*f; y2=step(sysf,t);
% plot(t,y*180/pi,t,y1*180/pi,'--',t,y2*180/pi,':'),grid xlabel('Time (sec)')
ylabel('Spacecraft attitude (deg)')
title('Nominal (solid); O -nominal 80% (dashed); O -nominal 50% (dotted)')
FIGURECP2.5
Stepresponsesforthenominalandoff-nominalspacecraftparameters.
CP2.6 Theclosed-looptransferfunctionis
num1=[4]; den1=[1]; sys1 = tf(num1,den1); num2=[1]; den2=[1 1]; sys2 = tf(num2,den2); num3=[1 0]; den3=[1 0 2]; sys3 = tf(num3,den3); num4=[1]; den4=[1 0 0]; sys4 = tf(num4,den4); num5=[4 2]; den5=[1 2 1]; sys5 = tf(num5,den5); num6=[50]; den6=[1]; sys6 = tf(num6,den6); num7=[1 0 2]; den7=[1 0 0 14]; sys7 = tf(num7,den7); sysa = feedback(sys4,sys6,+1); sysb = series(sys2,sys3); sysc = feedback(sysb,sys5); sysd = series(sysc,sysa); syse = feedback(sysd,sys7); sys = series(sys1,syse)
% pzmap(sys) % p=pole(sys) z=zero(sys)
7.0709 -7.0713 1.2051 + 2.0863i 1.2051 - 2.0863i 0.1219 + 1.8374i 0.1219 - 1.8374i -2.3933 -2.3333 -0.4635 + 0.1997i -0.4635 - 0.1997i
z = 0 1.2051 + 2.0872i 1.2051 - 2.0872i -2.4101 -1.0000 + 0.0000i -1.0000 - 0.0000i
where
s 2
s 1400 .
CP2.7 Them-filescriptandplotofthependulumangleisshowninFigureCP2.7. Withtheinitialconditions,theLaplacetransformofthelinearsystemis
θ(s)= θ0s s2 + g/L
To usethestepfunctionwiththem-file,wecanmultiplythetransfer functionasfollows: θ(s)= s2 s2 + g/L θ0 s , whichisequivalenttotheoriginaltransferfunctionexceptthatwecan usethestepfunctioninputwithmagnitude θ0.Thenonlinearresponse isshownasthesolidlineandthelinearresponseisshownasthedashed line.Thedifferencebetweenthetworesponsesisnotgreatsincetheinitial conditionof θ0 =30◦ isnotthatlarge.
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
L=0.5; m=1; g=9.8; theta0=30; % Linear simulation sys=tf([1 0 0],[1 0 g/L]); [y,t]=step(theta0*sys,[0:0.01:10]); % Nonlinear simulation [t,ynl]=ode45(@pend,t,[theta0*pi/180 0]); plot(t,ynl(:,1)*180/pi,t,y,' '); xlabel('Time (s)') ylabel('\theta (deg)')
function [yd]=pend(t,y) L=0.5; g=9.8; yd(1)=y(2); yd(2)=-(g/L)*sin(y(1)); yd=yd';
Plotof θ versus xt when θ0 =30◦
CHAPTER2MathematicalModelsofSystems
CP2.8 Thesystemstepresponsesfor z =5, 10,and15areshowninFigureCP2.8.
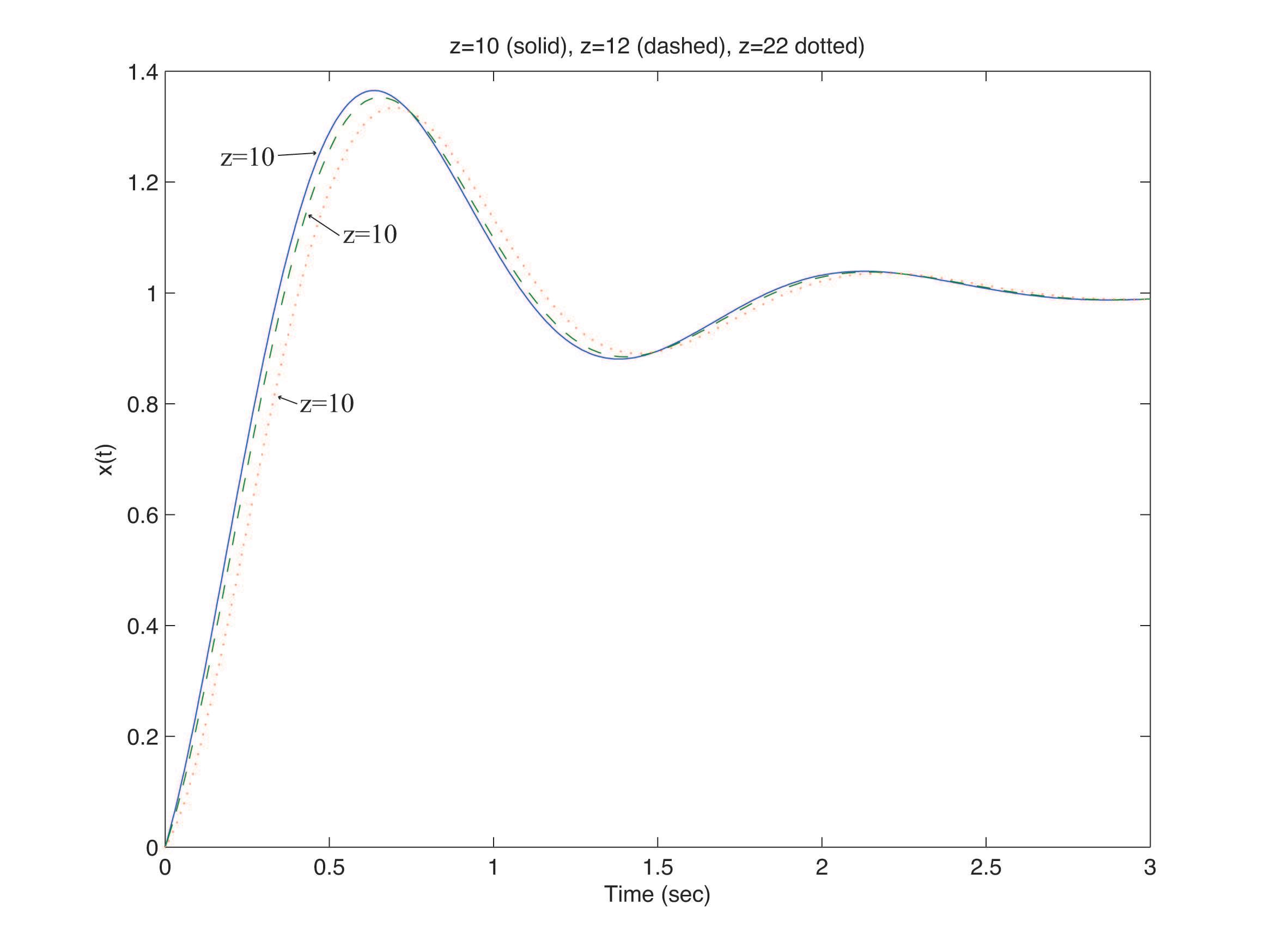
FIGURECP2.8 The systemresponse.
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
CP2.9 (a,b)Computingtheclosed-looptransferfunctionyields
T (s)= G(s) 1+ G(s)H(s) = s2 +2s +1 s2 +4s +3 .
Thepolesare s = 3, 1andthezerosare s = 1, 1. (c)Yes,thereisonepole-zerocancellation.Thetransferfunction(after pole-zerocancellation)is
T (s)= s +1 s +3
ng=[1 1]; dg=[1 2]; sysg = tf(ng,dg); nh=[1]; dh=[1 1]; sysh = tf(nh,dh); sys=feedback(sysg,sysh)
% pzmap(sys)
% pole(sys) zero(sys)
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
FIGURECP2.9 Pole-zeromap.
CP2.10 FigureCP2.10showsthesteady-stateresponsetoaunitstepinputanda unitstepdisturbance.Weseethat K =1leadstothesamesteady-state response.
K=[0.1:0.1:10]; sysg=tf([1],[1 20 20]); for i=1:length(K) nc=K(i); dc=[1];sysc=tf(nc,dc); syscl=feedback(sysc*sysg,1); systd=feedback(sysg,sysc); y1=step(syscl); Tf1(i)=y1(end); y2=step(systd); Tf2(i)=y2(end); end plot(K,Tf1,K,Tf2,'--') xlabel('K') ylabel('Steady-state response')
FIGURECP2.10
Gain K versussteady-statevalue.
ThisworkisprotectedbyUnitedStatescopyrightlaws andisprovidedsolelyfortheuseof instructorsinteachingtheircoursesandassessingstudentlearning. Dissemination orsaleofanypartofthiswork(includingontheWorldWideWeb) willdestroytheintegrityoftheworkandisnotpermitted.
