Solutions for Pathway To Introductory Statistics 1st Us Edition by Lehmann by 6alsm

Chapter2

LectureNotesandTeachingTips

Thischapterincludeschapteroverviews,section-by-sectionlecturenotes,andteachingtipsforthelecturenotes. Thelecturenotesincludehomeworkassignments.

Theteachingtipsforthelecturenotesdescribetypicalstudentdifﬁcultiesandwhataninstructorcandoto helpstudentsovercometheseobstacles.

CHAPTER1OVERVIEW

Chapter1containsalargenumberofconcepts.Ifyoucannotaffordthetimetoaddressthemall,focuson Sections1.1,1.2,and1.7becausetheycontainimportantalgebraconcepts.

Ofthesethreesections,Section1.7isthemostimportantbecauseitcontainsthekeyconceptsexponents, squareroots,orderofoperations,andscientificnotation.Exponentsandscientificnotationarepresentedsoearly becausetheyarenecessarytointerpretcalculatoroutputswhenfindingnormalprobabilitiesinSection5.4.I consideredpostponingthesetwoconceptsuntilChapter5,butIwasconcernedthatdoingsowouldbreaktheflow ofstudentslearningstatisticsinChapters2–5.

Proportions(Section1.3)shouldbediscussedbecausetheywillbeusedthroughoutChapters2–5.Converting units(Section1.3)willcomeinhandyforafewexercisesinsubsequentchapters.Theconceptchangeina quantity(Section1.5)shouldbediscussedbecausethisconceptlaysthefoundationforslopeofalineandother concepts.Ratiosandpercents(Section1.6)shouldalsobeaddressed.

Istronglyadviseobtainingdataaboutyourstudentsbyanonymouslysurveyingthem.Althoughthereare plentyofcurrent,compelling,authenticdatasetstochoosefrominthetextbook,studentswillgetakickoutof analyzingdataaboutthemselves.ThisdatacanﬁrstbeusedinChapter3.Collectingitnowwillbuyyoutimeto inputitelectronically,althoughStatCrunchandothertechnologiescandothatautomatically.

HerearequestionsItypicallyincludeinmysurvey:

1. Howmanyunitsareyoutakingrightnow?

2. Howmanyclassesareyoutakingrightnow?

3. Whatisyourmajor?(Ifyoudon’thaveone,write"undecided.")

4. Howmanyhoursdoyouworkperweekduringthissemesteronaverage?

5. Whatisyourgender?(maleorfemale)

6. Whatisthetotalnumberofpeoplelivinginyourhouseholdatthistime(includeyourself)?

7. Doyouexercise?Ifyes,howmanyminutesdoyouspendexercisingperday,onaverage?

8. Whatisyourfavoritegenreofmusic?(hiphop,rap,electronic,rock,country,classical,folk,etc) Copyright c 2016PearsonEducation,Inc.

9. Howmanynovelsdoyoureadperyearforfun(notforaclass)?

10. Whichpoliticalpartydoyoutendtobeinlinewith(e.g.Republican,Democrat,Independent,etc)?

11. Whatisyourreligiousafﬁliation(e.g.Catholic,Protestant,Mormon,etc)

12. Howmanyfriendsdidyouhaveduringyoursenioryearinhighschool?Howmanyofthosepeopleareyou stillintouchwithandconsidertostillbefriendswith?

13. Howmanycigarettesdidyousmokeinthelastmonth?

14. Doyoudriveacar?Ifyes,haveyoueverintentionallyenteredanintersectionwhenthelightwasred("run" aredlight)?

15. Howmanyhoursdoyouspendonlineonaweekday?

16. HowmanyhoursdoyouspendwatchingTVshows,movies,andvideosonaweekday?

17. Whatisyourage?

18. Whatisyourheight?

19. Howmanylanguagesdoyouspeak?

20. Whatisthetotalnumberofcarsownedbypeopleinyourhousehold?

21. Howmanytattoosdoyouhave?

22. Estimateyourprofessor’s(JayLehmann’s)age.

23. Isyourmotheralive?Ifyes,whatisherage?

24. Howmanystateshaveyoulivedin?

25. Howmanytimesdoyounottellthetruthperday?

26. Howoftendoyougotochurch?(never,onceamonth,onceaweek,twiceaweek,daily)

27. Howmanytimesdoyougotoamovietheatereachmonth?

28. DoyouhaveaFacebookaccount?Ifyes,howmanyfriendsdoyouhaveonFacebook?

29. Circlethesocialmediathatyouuse: FacebookTwitterInstagramPinterestVineSnapchat

30. Howmanytextsdoyousendonaweekday?

31. Howmanye-mailsdoyousendonaweekday?

32. Howmanytweetsdoyousendonaweekday?

33. Howmanytimesdoyoueatatarestaurant(includingfast-food)perweek?

34. Howmanytimesdoyoueatatfast-foodrestaurantsperweek?

35. Ifyoucouldhaveonesuperpower,whatwoulditbe?

36. Howmanyalcoholicdrinksdoyouhaveperweek?

Alsoconsideraddinganotherdimensiontoyourcoursebyﬁndingdataaboutyourcollege,thecollege’s neighborhood,andbreakingnewsaboutyourstate.Analysisofsuchdatawillimpressuponstudentsthatstatistics istrulyrelevant.

SECTION1.1LECTURENOTES

Objectives

1. Describethemeaningof variable and constant.

2. Describethemeaningof countingnumbers, integers, rationalnumbers, irrationalnumbers, realnumbers, positivenumbers,and negativenumbers

3. Useanumberlinetodescribenumbers.

4. Graphdataonanumberline.

5. Plotpointsonacoordinatesystem.

6. Describethemeaningof inequalitysymbols and inequality.

7. Graphaninequalityandacompoundinequalityonanumberline.

8. Useinequalitynotation,intervalnotation,andgraphstodescribepossiblevaluesofavariableforan authenticsituation.

9. Describeaconceptorprocedure.

OBJECTIVE1

Deﬁnition Variable

A variable isasymbolthatrepresentsaquantitythatcanvary.

1. Let p betheprice(indollars)toseeaModestMouseconcert.Whatisthemeaningof p =60?

2. Let t bethenumberofyearssince2010.Whatisthemeaningof t =7?of t = 5?

3. Chooseasymboltorepresentthenumberofstudentsinaclass.Explainwhythesymbolisavariable.Give twonumbersthatthevariablecanrepresentandtwonumbersthatitcannotrepresent.

Deﬁnition Constant

A constant isasymbolthatrepresentsaspeciﬁcnumber(aquantitythatdoes not vary).

4. Arectanglehasanareaof16squarefeet.Let W bethewidth(infeet), L bethelength(infeet),and A be thearea(insquarefeet).

a. Sketchthreepossiblerectanglesofarea16squarefeet.

b. Whichofthesymbols W , L,and A arevariables?Explain.

c. Whichofthesymbols W , L,and A areconstants?Explain.

OBJECTIVE2

• The countingnumbers,or naturalnumbers,arethenumbers1,2,3,4,5,....

• The integers arethenumbers..., 3, 2, 1,0,1,2,3,....

• The positiveintegers arethenumbers1,2,3, .

• The negativeintegers arethenumbers 1, 2, 3,....

• Thenumber0isneitherpositivenornegative.

• The rationalnumbers arethenumbersthatcanbewrittenintheform n d ,where n and d areintegersand d isnonzero.

• Thenumbersrepresentedonthenumberlinethatare not rationalarecalled irrationalnumbers

• The realnumbers areallofthenumbersrepresentedonthenumberline.

OBJECTIVE3

5. Graphtheintegersbetween 4 and2,inclusive,ononenumberline.

6. Graphtheintegersbetween 4 and2ononenumberline.

7. Graphallofthenumbers3, 5, 7 2 ,0, 2.7,and 1.3 ononenumberline.

OBJECTIVE4

8. Theaveragestudentdebtsperborrowerareshowninthefollowingtablefortheﬁvestateswiththelargest per-studentdebts.

AverageStudentDebt State(thousandsofdollars) Georgia30.4 Maryland30.0 Virginia28.5 SouthCarolina28.3 Florida27.9

Source: U.S.DepartmentofEducation

Let d beastate’saveragestudentdebt(inthousandsofdollars).Graphtheaveragedebtsshowninthetable onanumberline.

Whenwewritenumbersonanumberline,theyshouldincreasebyaﬁxedamountandbeequally spaced.

OBJECTIVE2(revisited)

• The negativenumbers aretherealnumberslessthan0.

• The positivenumbers aretherealnumbersgreaterthan0.

9. Let T bethetemperature(indegreesFahrenheit).Whatvalueof T representsthetemperature20degrees Fahrenheitbelow0?Graphthenumberonanumberline.

OBJECTIVE5

10. Plotthepoints (2, 5), ( 3, 1), ( 2, 4),and (6, 3) onacoordinatesystem.

OBJECTIVE6

Herearethedeﬁnitionsof inequalitysymbols:

SymbolMeaning < islessthan

≤ islessthanorequalto > isgreaterthan ≥ isgreaterthanorequalto

An inequality containsoneofthesymbols <, ≤, >,and ≥ withaconstantorvariableononesideanda constantorvariableontheotherside.

11. Decidewhethertheinequalitystatementistrueorfalse.

OBJECTIVE7

Writetheinequalityinintervalnotation,andgraphthevaluesof x. 12. x< 4 13. x ≥−3

OBJECTIVE8

2 <x ≤ 5

15. Apersonheldhisbreathforatleast50seconds.Let t bethelengthoftime(inseconds)thatheheldhis breath.Describethelengthoftimeheheldhisbreathusinginequalitynotation,intervalnotation,anda graph.

16. Let t bethetime(inminutes)ittakesforastudenttodrivetocollege.Interpretandgraphtheinequality 19 <t< 23

OBJECTIVE9

Herearesomeguidelinesonwritingagoodresponse:

• Createanexamplethatillustratestheconceptoroutlinestheprocedure.Lookingatexamplesorexercises mayjump-startyouintocreatingyourownexample.

• Usingcompletesentencesandcorrectterminology,describethekeyideasorstepsofyourexample.You canreviewthetextforideas,butwriteyourdescriptioninyourownwords.

18CHAPTER2LectureNotesandTeachingTips

• Describealsotheconceptortheprocedureingeneralwithoutreferringtoyourexample.Itmayhelpto reﬂectonseveralexamplesandwhattheyallhaveincommon.

• Insomecases,itwillbehelpfultopointoutthesimilaritiesandthedifferencesbetweentheconceptorthe procedureandotherconceptsorprocedures.

• Describethebeneﬁtsofknowingtheconceptortheprocedure.

• Ifyouhavedescribedthestepsinaprocedure,explainwhyit’spermissibletofollowthesesteps.

• Clarifyanycommonmisunderstandingsabouttheconcept,ordiscusshowtoavoidmakingcommonmistakeswhenfollowingtheprocedure.

17. Describehowinequalitynotation,intervalnotation,andgraphscanbeusedtodescribepossiblevaluesofa variableforanauthenticsituation.

HW 1,3,5,15,21,29,31,47,51,55,71,81,85,99,107

SECTION1.1TEACHINGTIPS

Thissectioncontainsalotofobjectives,butstudentshaveaneasytimewiththissection,soIadvisenotgettingtoo boggeddown.Asidefromtheobviousimportanceofvariables,it’sagoodideatofocusoninequalitiesbecause theseareusedsomuchwithprobability(Chapter5).Students’greatestchallengeinthissectiontendstobeusing intervalnotationcorrectly.

OBJECTIVE1COMMENTS

Problem2isgoodpreparationforworkingwithtime-seriesdatabecausestudentswillsometimesgetanegative valuewhenusingamodeltomakeanestimatefortheexplanatoryvariable.Moststudentsthinkthattimecannot benegativeandaresurprisedthat t = 5 representstheyear2005.

InProblem3,discussingunreasonablevaluesofthevariableisaniceprimerfortheconceptofmodelbreakdown(Section6.3).

AftercompletingProblems1–3,Iquicklymentionseveralmoreexamplesofvariables,pointingoutthat variables“areallaroundus.”Isuggestthatthroughouttherestoftheday,mystudentsshouldnoticequantities thatcanberepresentedbyvariables.Isaythatavariableisakeybuildingblockofalgebraandstatistics.

InSection2.1,akeydistinctionwillbemadebetweenhowvariablesaredeﬁnedandusedinalgebraand statistics.ButfornowIrestrictmydiscussionaboutvariablestothescopeofalgebra.

Whendiscussingconstants,Igive π andanumbersuchas5asexamples.

BeforecompletingProblem4,Idiscussthemeaningoftheareaofaﬂatsurface.Moststudentsdonotknow thatthearea(insquareinches)isthenumberofsquareinchesthatittakestocoverthesurface.Iremindmy studentsthattheareaofarectangleisequaltotherectangle’slengthtimesitswidthandexplainthisbybreaking uparectangleintounitsquares.Althoughthesearesimpleconcepts,theyarecriticaldevelopmentforthefrequent useofdensityhistogramsinChapters3–5.

OBJECTIVE2COMMENTS

WhenIdefinecountingnumbersandintegers,Imakesurethatstudentsunderstandthemeaningoftheellipsis. Iquicklydefinethevarioustypesofnumbers,givingespeciallylighttreatmenttodefiningrationalandirrational numbersbecauseeventhoughtheseterminologiesareusedinthetextbook,asuperficialunderstandingofthem willsuffice.

Comparingthedifferencesbetweentheintegersandtherealnumberscanhelppreparestudentstolearnabout discreteandcontinuousvariables(Section3.3).

OBJECTIVE3COMMENTS

Graphingnumbersonthenumberlineisgoodpreparationforconstructingdotplots,time-seriesplots,andscatterplots.Discussinghowtographdecimalnumbersisespeciallyimportantforworkwithauthenticdata(Problem8).

MoststudentsdonotunderstandhowProblems5and6differ.Thisissuewillkeepcomingupthroughoutthe course(e.g."Findtheprobabilitythatarandomlyselectedtestscoreisbetween80and89points,inclusive.").

OBJECTIVE4COMMENTS

ForProblem8,Iemphasizethatthenumber-linesketchshouldincludeatitle,thevariable"d",andtheunitsof d.Ialsoemphasizethatwhenwewritenumbersonanumberline,theyshouldincreasebyaﬁxedamountand beequallyspaced.Withoutgivingsuchawarningseveraltimes,manystudentswillmakerelatederrorswhen constructingnumberlinesandvarioustypesofstatisticaldiagrams.

TofurtherengagestudentswhendiscussingProblem8,Iaskthemtoidentifyinwhichregion(s)thestatesare located.AndIaskforsomepossiblereasonswhytheaveragestudentdebtishigherinthoseﬁvestates.ThenI generalize,suggestingthatstudentsshouldbethisengagedwhenworkingwithdatasetsthroughoutthecourse.

GROUPEXPLORATION:ReasonableValuesofaVariable

Theexplorationisagoodprimerfortheconceptofmodelbreakdown(Section6.3).

OBJECTIVE2(REVISITED)COMMENTS

Iemphasizethat0isneithernegativenorpositive.

OBJECTIVE5COMMENTS

Whenplottingapoint,Iremarkthatit’ssimilartolookingupadateonacalendar.Thisskillisaprecursorto constructingtime-seriesplots(Section3.3)andscatterplots(Section6.1).

OBJECTIVE6COMMENTS

StudentstendtohavedifﬁcultywithProblem11(b)andsometimes11(c).

OBJECTIVE7COMMENTS

Evenifstudentshaveseenintervalnotationbefore,theytendtohaveforgottenit.Understandingthemeaning oftheinequalitiesinProblems12–15willbegoodpreparationforprobabilityproblems(Sections5.1–5.3)and normaldistributionproblems(Sections5.4and5.5).Problem14alsoprovidesalead-intoconﬁdenceintervals, whosefoundationwillbefurtherdevelopedinSection8.5.

OBJECTIVE8COMMENTS

Throughoutthecourse,Ilookforeveryopportunitytohavestudentsworkwiththephrases lessthan, atmost, greaterthan,and atleast becausemanystudentsstrugglewiththeirmeaningsinintroductorystatistics.Problem15isagreatwaytogetthatprocessstarted.

AsubtleissuetoexploreforProblem15isthatananswerof (50, ∞) doesnotimplythatwebelievethe personcouldholdtheirbreathforanextremelylongtimesuchasa1000minutes.Rather,itisimpossibleto knowwhatupperlimittochoose.Forexample,itmaysurpriseyouoryourstudentsthatStigSeverinsenseta GuinnessWorldRecordbyholdinghisbreathfor22minutes.Here’salinkattheGuinnessWorldRecordssite: http://www.guinnessworldrecords.com/world-records/24135-longest-time-breath-held-voluntarily-male.

OBJECTIVE9COMMENTS

Whenaskedtodescribeconcepts,studentstendtowriteasinglesentenceortwo.Theyneedmetomodel athoroughresponse:describingaconcept’smeaning,listingbeneﬁtsanddrawbacks,comparing,contrasting, statingexceptions,andsoon.Moststudentsareastoundedbyhowmuchthereistosay.

Iwillmodelthisforstudentsseveraltimesthroughoutthecourse,butinthemeantimeItellthemtoread Example12inthetextbookandthepreceding“GuidelinesonWritingaGoodResponse”onpage12ofthe textbookathome.Studentswillbeaskedtoexplainconceptsorproceduresinmosthomeworksections.This isverymuchinlinewithintroductorystatistics,wherestudentswillhavetodescribestatisticalpracticesand interpretconceptsandresults.

SECTION1.2LECTURENOTES

Objectives

1. Describethemeaningof expression and evaluateanexpression

2. Useexpressionstodescribeauthenticquantities.

3. Evaluateexpressions.

4. TranslateEnglishphrasestoandfrommathematicalexpressions.

5. Evaluateexpressionswithmorethanonevariable.

OBJECTIVES1–3

1. Apersonisdriving3milesperhouroverthespeedlimit.Foreachspeedlimitshown,ﬁndthedivingspeed. a. 55mph b. 70mph c. s mph

Wecall s +3 isan expression

Deﬁnition Expression

An expression isaconstant,avariable,orcombinationofconstants,variables,operationsymbols,and groupingsymbols,suchasparentheses.

Herearesomeexamplesofexpressions: x +9,5, x 7, π, 20 x , xy.

2. Substitute65for s intheexpression s +3 anddiscussthemeaningoftheresult(seeProblem1).

Wesaywehave evaluatedtheexpression s +3 at s =65.

Deﬁnition Evaluateanexpression

We evaluateanexpression bysubstitutinganumberforeachvariableintheexpressionandthencalculating theresult.Ifavariableappearsmorethanonceintheexpression,thesamenumberissubstitutedforthat variableeachtime.

3. Acertaintypeofpencosts$3.

a. Completethefollowingtabletohelpﬁndanexpressionthatdescribesthetotalcost(indollars)of n pens.Showthearithmetictohelpseethepattern.

b. Evaluateyourresultfor n =10.Whatdoesitmeaninthissituation?

• Weavoidusing × forthemultiplicationoperation.

• Eachofthefollowingexpressionsdescribesmultiplying3by n: 3n, 3 n, 3(n), (3)n,and (3)(n)

OBJECTIVE4

Mathematicsisalanguage.

Deﬁnition Product,factor,andquotient

Let a and b benumbers.Then

• The product of a and b is ab.Wecall a and b factors of ab

• The quotient of a and b is a ÷ b,where b isnotzero.

4. Usephrasessuchas“2plus x”andsentencessuchas“Add2and x.”tocompletethesecondcolumnofthe followingtable.

MathematicalExpressionEnglishPhraseorSentence 2+ x 2 x 2 x 2 ÷ x

Warning:Subtracting2from7is 7 2,not 2 7

5. Let x beanumber.TranslatetheEnglishphraseintoamathematicalexpressionorviceversa,asappropriate:

a. Thedifferenceofthenumberand9 b. Theproductof5andthenumber

c. 7+ x d. x ÷ 4

6. Let x beanumber.Translatethesentence“Subtractthenumberfrom10.”intoamathematicalexpression. Evaluatetheexpressionat x =7

OBJECTIVE5

Recallthattheareaofarectangleisequaltothelengthtimesthewidthoftherectangle.

7. Let W bethewidth(infeet)and L bethelength(infeet)ofarectangle.Evaluatetheexpression LW for L =7 and W =5.Whatdoesyourresultmeaninthissituation?

8. Writethephrase"thequotientof x and y"asamathematicalexpression,andthenevaluatetheresultfor x =24 and y =3

HW 1,3,11,13,19,21,23,29,35,49,53,59,61,63,67

SECTION1.2TEACHINGTIPS

Themostimportantskillinthissectionisevaluatingexpressions,whichstudentspickuponquickly.Emphasizing translatingEnglishtoandfrommathematicshelpsbuildengagedreading,whichisakeyingredientforsuccessin introductorystatistics.

OBJECTIVES1–3COMMENTS

ForPart(a)ofProblem3,studentswanttosimplywritetheanswers,butIemphasizethatwewanttoshowthe arithmetictohelpseethepattern.Insistingthatstudentsdothisnowwillformgoodhabitssothatstudentswill beabletoﬁndmorechallengingexpressionsoftheform mx + b inSection1.7.Theformofstudents’answers willvaryforPart(a),andtheywillbereassuredtoknowthat 3n = n(3).Thecommutativelawformultiplication willbeformallydiscussedinSection8.1.

WhendiscussingProblem3,Iemphasizethatwecandescribethenumberofpensandtheirtotalcostby thevariable n andtheexpression 3n,respectively.So,bytheabstractionofalgebraweareabletorelatetwo quantities.Thisisthefundamentalideabetweenrelations(Section7.4),functions(Section7.4),andultimately regression(Chapters9and10).

GROUPEXPLORATION:ExpressionsUsedtoDescribeaQuantity

Inthisexploration,studentsworkbackwardsandﬁndanauthenticquantitythatcanbedescribedbythegiven expression.Ideally,thispromptsstudentstoreﬂectonhowexpressionsconnecttotheirworld.Infact,asa follow-uporreplacementfortheexploration,youcouldhavegroupsofstudentscreatetheirownexpressionsthat describeauthenticquantitiesthatareimportantorinterestingtothem.Thismightstumpthem,sobepreparedto modelhowtodothis.

OBJECTIVE4COMMENTS

Iemphasizethatmathematicsisalanguage.Moststudentshaveneverthoughtofmathematicsinthisway.

Moststudentsdonotknowthemeaningsof product, quotient,and ratio.Theseterminologieswillbeused extensivelyinthetextbook.Inparticular,devotingsomeattentiontoratioswillserveasagoodprimerforrate ofchangeandslope(Section7.2).Computingratiosaboutyourclass(e.g.ratioofnursingmajorstopsychology majors)andcomparingthemtoyourcollege’sstudentbodycanbeinterestingandinstructive.

Althoughstudentswon’thavetotranslateEnglishphrasestoandfrommathematicalexpressionsinintroductorystatistics,theywillhavetoreadpassagescarefullyformeaning.Thisimportantprocesscanbefosteredin partbypracticingtranslating.

Iemphasizethat“Subtracting2from7”is 7 2,not 2 7.Ipointoutthatifyoutake2CDs from 7CDs, then5CDsremain.Thismayhelpstudentsseewhywesubtractthenumbers“outoforder.”

OBJECTIVE5COMMENTS

Studentshaveaneasytimewiththisobjective.IadviseworkingwiththeareaofarectanglesuchasinProblem7 tocontinuetopreparestudentsfordensityhistograms,whichwillbeemphasizedinChapters3–5.

SECTION1.3LECTURENOTES

Objectives

1. Describethemeaningofafraction.

2. Explainwhydivisionbyzeroisundeﬁned.

3. Describetherulesfor a 1, a 1 ,and a a

4. Performoperationswithfractions.

5. Findtheprimefactorizationofanumber.

6. Simplifyfractions.

7. Findproportions.

8. Convertunitsofquantities.

OBJECTIVE1

1. Shadeaportionofacircletoillustratethemeaningof 5 8 ofapizza.

2. Usetwopizzaswith4sliceseachtoshowthat 8 4 =8 ÷ 4=2

Thefraction a b means a ÷ b.

OBJECTIVE2

Usetheconceptthatdivisionisrepeatedsubtractiontoshowwhydivisionby0isundeﬁned(seethetopofpage24 ofthetextbook).

DivisionbyZero

Thefraction a b isundeﬁnedif b =0.Divisionby0isundeﬁned.

OBJECTIVE3

• a 1= a

• a 1 = a

• a a =1,where a isnonzero

• Whenwewritestatementssuchas a 1= a,wemeanthatifweevaluate a 1 and a for any valueof a in bothexpressions,theresultswillbeequal.

• Wesaytheexpressions a · 1 and a are equivalentexpressions.

OBJECTIVE4

MultiplyingFractions

If b and d arenonzero,then a b c d = ac bd 3. 3 5 · 7 2 4. 4 9 · 5 7

OBJECTIVE5

5. Primefactor24. 6. Primefactor36.

OBJECTIVE6

Useadrawingofapizzatoshowthat 6 8 = 3 4

SimplifyingaFraction

Tosimplifyafraction.

1. Findtheprimefactorizationsofthenumeratorandthedenominator.

2. Findanequalfractioninwhichthenumeratorandthedenominatordonothavecommonpositive factorsotherthan1byusingtheproperty

where a and c arenonzero.

7. Simplify 6 8 8. Simplify 24 18 9. Simplify 7 49

OBJECTIVE4(revisited)

DividingFractions

Whenyouuseacalculatortocheckworkwithfractions,encloseeachfractioninparentheses.

14. Useadrawingofapizzatoshowthat 3 8 + 4 8 = 7 8 . Copyright c 2016PearsonEducation,Inc.

AddingFractionswiththeSameDenominator

If b isnonzero,then a b + c b = a + c b

Useadrawingofapizzatoshowthat 7

If b isnonzero,then

SubtractingFractionswiththeSameDenominator

Adding(orSubtracting)FractionswithDifferentDenominators

Toadd(orsubtract)twofractionswithdifferentdenominators,usethefactthat a a =1,where a isnonzero, towriteanequalsum(ordifference)offractionsforwhicheachdenominatoristheLCD.

Throughoutthecourse,ifaresultisafraction,itmustbesimpliﬁed.

OBJECTIVE7

Deﬁnition Proportion

Instatistics,a proportion isafractionofthewhole.Aproportioncanalsobewrittenasadecimalnumber.

Aproportionisalwaysbetween0and1,inclusive.

SumoftheProportionsEquals1

Ifanobjectismadeupoftwoormoreparts,thenthesumoftheirproportionsequals1. Wewillusecapitalletterstoemphasizethemathematicalmeaningsof"AND,""OR,"and"NOT."

22. About 3 20 of1.2millionpeoplesurveyedthinkthatFiveGuyshasthebestburgeroutofallfastfoodchains (Source: YouGov).WhatproportionofthosesurveyeddoNOTthinkFiveGuyshasthebestburgeroutof allfastfoodchains?

ProportionoftheRest

Let a b betheproportionofthewholethathasacertaincharacteristic.Thentheproportionofthewholethat doesNOThavethatcharacteristicis

23. Ofallbribesmadeinthemultinationalindustry, 1 10 ofthebribesaremadeinextraction(ofoil,coal,and soon)and 3 20 ofthebribesaremadeinconstruction(Source: OECD).Whatproportionofthebribesare madeinsectorsotherthanextractionandconstruction?

24. Atotalof1012AmericanswereaskedwhetherGodplaysaroleindeterminingwhichteamwinsasporting event.Theirresponsesaresummarizedinthefollowingtable.

GodPlaysaRoleinSportingEvents CompletelyMostlyMostlyCompletelyDon’t AgreeAgreeDisagreeDisagreeKnow/Refused Total NumberofPeople10116220351630 1012

Source: PublicReligionResearchInstitute

Findtheproportion(roundedtothethirddecimal)ofthosesurveyedwho

a. completelyagreed.

b. didNOTcompletelyagree.

c. mostlydisagreedORcompletelydisagreed.

OBJECTIVE8

Maketheindicatedunitconversions.Roundapproximateresultstotwodecimalplaces.

25. TheSearsTowerinChicagois1450feettall.Whatisitsheightinyards?

26. Ajugcontains5gallonsofwater.Howmanycupsofwaterdoesitcontain?

27. Acartravelsataspeedof65milesperhour.Whatisthecar’sspeedinfeetpersecond?

ConvertingUnits

Toconverttheunitsofaquantity,

1. Writethequantityintheoriginalunits.

2. Multiplybyfractionsequalto1sothattheunitsyouwanttoeliminateappearinonenumeratorand onedenominator.

HW 1,3,21,25,33,41,49,67,73,81,87,93,95,99,103,107

SECTION1.3TEACHINGTIPS

Becausesomestudentshavedifficultywiththismaterial,thisisagoodtimetoremindthemofyouravailability duringofficehoursandotherformsofcollegesupportsuchasmathcentertutoring.Students’greatestdifficulty isusuallywithaddingandsubtractingfractionswithdifferentdenominators.So,itiswisetogoquicklythrough therestofthematerialsoyouhaveadequatetimetofocusonthismoredifficultskill.

OBJECTIVE1COMMENTS

Somestudentswillneedareminderaboutthemeaningofafraction(seeProblem1).

OBJECTIVE2COMMENTS

Iuserepeatedsubtractiontoshowthatdivisionbyzeroisundeﬁned.Moststudentsreallyappreciatethisexplanation,becausetheyhaveneverbeentold why divisionbyzeroisundeﬁned.

OBJECTIVE3COMMENTS

Althoughtheserulesareverybasic,theyarethefoundationforperformingoperationswithfractions.

OBJECTIVE4COMMENTS

Afterwehavediscussedhowtosimplifyfractions(Objective6),wewilldiscusshowtomultiplyfractionswhich canbesimpliﬁed.

OBJECTIVE5COMMENTS

Inarithmetic,studentslearnavarietyofwaystoprimefactoranumber.AlthoughIallowstudentstouseany method,IencouragethemtousethemethodshowninExample2onpage26ofthetextbook,becausethismethod clearlyportraysthatthefactorizationisequaltotheoriginalnumber.

OBJECTIVE6COMMENTS

Moststudentscansuccessfullysimplifyafraction,butmostarenotawareoftheconceptsinvolved.Imakesure theyunderstandthatweusetheproperty a a =1,where a =0,tosimplifyafraction.Thetextbookavoidsusing theterminology“reduce,”becausemanyprofessorsthinkthatthisterminologysuggeststhatreducingafraction makesitsmaller.Thetextbookalsoavoidsusingthetechniqueof"canceling,"becausestudentsmisapplythis techniqueinamyriadofways.

OBJECTIVE4(REVISITED)COMMENTS

Oncemystudentsknowhowtosimplifyfractions,Idiscusshowtomultiplyfractionsinwhichtheresultneedsto besimpliﬁed.

Usingadrawingofapizzatoshowthat 3 8 + 4 8 = 7 8 helpsstudentsunderstandwhyitdoesn’tmakesenseto addthedenominators.

Whenaddingfractionswithdifferentdenominators,IlistmultiplesofthedenominatorstoﬁndtheLCD. Whenaddingfractionssuchas 5 6 and 3 8 (Problem18),Ishowatleastoncethatwearemultiplyingfractionsby1 togeteachdenominatortobetheLCD:

GROUPEXPLORATION:IllustrationsofSimplifyingFractionsandOperationswith

Fractions

Thisexplorationisanicewayforstudentstolearntovisualizetheirworkwithfractions.

OBJECTIVE7COMMENTS

Thepropertyaboutthesumoftheproportionsequals1isgoodpreparationforthefactthatthesumoftherelative frequenciesofallthecategoriesofacategoricalvariableequals1.Italsopreparesstudentsforthesimilarproperty aboutnumericalvariablesandultimatelythattheareaunderthenormalcurveis1.Aquickdiscussionmaysufﬁce toexplainthisconceptoryoucoulddemonstrateitbyworkingwithacategoricalvariablethatdescribesyour class.

Althoughitisabitjarringtoreadthewords AND, OR,and NOT inalluppercaseletters,thisisahelpfulsignal tostudentsthatthewordsarebeingusedinamathematicalway.Theword AND willnotbeusedinthehomework untilChapter3,butitisdiscussedbrieﬂyinthissectionforcompleteness.Thewords AND and OR willbemore carefullydescribedandcomparedinSection3.1(seepage137ofthetextbook).Ifyoupostponediscussing AND and OR untilthen,besuretoavoidassigningExercise93(aiii)andExercise94(aiii)becausetheybothincludethe word OR.

Theword NOT andtheproportionoftherestpropertyareemphasizedinthehomeworkandshouldbediscussednow.Beforeintroducingtheboxedgeneralstatementoftheproportionoftherestproperty,Iﬁrsthave studentssolveProblem22becausetheyarecapableofsolvingitwithoutmyhelp.Thenit’seasytobridgetothe generalstatement.

Ofcourse,theproportionoftherestpropertyisverysimilartothecomplementrulebutIdon’treferto itassuchbecausethecomplementrulehastodowithprobabilities.Nonetheless,studentswillhavelotsof practicewiththeproportionoftherestpropertyinChapters1,3,and4,readyingthemforthecomplementrule (Section5.2),whichwillbeespeciallyhelpfulwhenworkingwithnormaldistributions(Sections5.4and5.5).

ThereareseveralwaystosolveProblem24(b).Considerhavinggroupsofstudentssolvetheproblemand sharetheirmethodswiththeclass.

OBJECTIVE8COMMENTS

Theskillofconvertingunitswillcomeinhandyseveraltimesinthetextwhenstudentsworkwithunitswith whichtheyarenotasfamiliar.Forexample,inExercise22ofHomework6.2,studentswillconvertEarth’sescape velocityfrom11.2km/stounitsofmi/h.

JustaswithObjective7,Iprefertoproblemsolveﬁrstandthenpresenttheboxedsummarystatementbecause Idon’tbelievethesummarywillmeanmuchuntilI’vegivensomespeciﬁcexamples.

Iemphasizethatweperformconversionsbymultiplyingbyfractionsequalto1,soaconversiondescribesthe samequantity.Someequivalentunitsareshowninthemarginonpage34ofthetextbook.

SECTION1.4LECTURENOTES

Objectives

1. Findtheoppositeofanumber.

2. Findtheabsolutevalueofanumber.

3. Addtworealnumberswiththesamesign.

4. Addtworealnumberswithdifferentsigns.

5. Addrealnumberspertainingtoauthenticsituations. Copyright c 2016PearsonEducation,Inc.

OBJECTIVE1

• Twonumberarecalled opposites ofeachotheriftheyarethesamedistancefrom0onthenumberline,but areonoppositesidesof0.

• Toﬁndtheoppositeofanumber,wereﬂectthenumberacross0onthenumberline.

• Theoppositeof5is 5.Theoppositeof 5 is5.[Drawaﬁgure.]

Usereﬂectionswithanumberlinetoshowthat ( a)= a 1. ( 6)

( ( 5))

Weuseparenthesestoseparatetwooppositesymbolsoranoperationsymbolandanoppositesymbol.

OBJECTIVE2

Deﬁnition Absolutevalue

The absolutevalue ofanumberisthedistancethatthenumberisfrom0onthenumberline.[Drawa ﬁgure.]

3. |4|

OBJECTIVE3

7. a. Apersonhasacreditcardbalancewitha0dollarbalance.Ifsheuseshercreditcardtomaketwo purchasesfor$3and$4,whatisthenewbalance?

b. WriteasumthatisrelatedtothecomputationinPart(a).

c. UseanumberlinetoillustratethesumfoundinPart(b).

AddingTwoNumberswiththeSameSign Toaddtwonumberswiththesamesign,

1. Addtheabsolutevaluesofthenumbers.

2. Thesumoftheoriginalnumbershasthesamesignasthesignoftheoriginalnumbers.

OBJECTIVE4

11. a. Abrotheroweshissister$5.Ifhethenpaysherback$2,howmuchdoeshestilloweher?

b. WriteasumthatisrelatedtoyourworkinPart(a).

c. UseanumberlinetoillustratethesumyoufoundinPart(b).

AddingTwoNumberswithDifferentSigns

Toaddtwonumberswithdifferentsigns:

1. Findtheabsolutevaluesofthenumbers.Thensubtractthesmallerabsolutevaluefromthelarger absolutevalue.

2. Thesumoftheoriginalnumbershasthesamesignastheoriginalnumberwiththelargerabsolute value.

12. 9+2 13. 7+( 4)

OBJECTIVE5

19. Apersonbouncesseveralchecksandischargedservicefeessuchthatthebalanceofthecheckingaccount is 78 dollars.Thepersonthendeposits$250.Findthebalance.

20. Twohoursago,thetemperaturewas 9◦F.Ifthetemperaturehasincreasedby 4◦Finthelasttwohours, whatisthecurrenttemperature?

HW 1,3,5,15,23,25,39,45,53,59,63,67,69,71,75

SECTION1.4TEACHINGTIPS

Inthissection,studentsaddrealnumbersandﬁndexpressionstomodelauthenticquantities.Theywillusethese skillsthroughoutthecourse.

OBJECTIVE1COMMENTS

Althoughﬁndingtheoppositeofanumberisaneasytopic,Idiscussreﬂectinganumberacross0onthenumber linetosetthestageforObjective2.

TheconceptofﬁndingtheoppositeoftheoppositewillhelpstudentssubtractnumbersinSection1.5:

OBJECTIVE2COMMENTS

Absolutevaluecomesinhandywhendiscussingnotonlyhowtoaddsignednumbersbutalsotointerpreta correlationcoefﬁcient.

OBJECTIVES3and4COMMENTS

Mostofmystudentsprefertothinkofaddingrealnumbersintermsofmoney(asopposedtothenumberlineor absolutevalue).Iquicklygoovertherulesandspendmoretimehavingmystudentsdomixedsetsofproblems suchasProblems12–18.

GROUPEXPLORATION:AddingaNumberandItsOpposite

Thisexplorationisanicewayforstudentstolearnthat a +( a)=0.

OBJECTIVE5COMMENTS

WhensolvingProblems19and20,Iemphasizethattheresultsmustincludeunits.

SECTION1.5LECTURENOTES

Objectives

1. Findthechangeinaquantity.

2. Subtractrealnumbers.

3. Findachangeinelevation.

4. Determinethesignofthechangeforanincreasingordecreasingquantity.

OBJECTIVE1

1. a. Ifthepriceofabasketofstrawberriesincreasesfrom$2to$5,ﬁndthechangeintheprice.

b. WriteadifferencethatisrelatedtothecomputationinPart(a).

ChangeinaQuantity

Thechangeinaquantityistheendingamountminusthebeginningamount:

Changeinthequantity = Endingamount Beginningamount

2. TherevenuesofFacebookareshowninthefollowingtableforvariousyears.

FacebookRevenue

Source: Facebook

a. Fortheperiod2009–2013,ﬁndeachofthechangesinannualrevenuefromoneyeartothenext.

b. Fromwhichyeartothenextdidtheannualrevenueincreasethemost?

OBJECTIVE2

3. a. Thevolumeofgasolineinacar’sgasolinetankdecreasesfrom6gallonsto2gallons.Whatisthe changeinthevolumeofgasolineinthetank?

b. WriteadifferencethatisrelatedtothecomputationinPart(a).

c. FromPart(b),wefoundthat 2 6= 4.Find 2+( 6).Explainwhywecanconcludethat 2 6=2+( 6)

SubtractingaRealNumber

a b = a +( b)

7. a. Thetemperatureincreasesfrom 3◦Fto 2◦F.Findthechangeintemperature. b. WriteadifferencethatisrelatedtotheworkinPart(a).

c. FindthedifferenceobtainedinPart(b)byusingtherule a b = a +( b).

11. Translatethesentence“Subtractthenumberfrom5.”intoamathematicalexpression.Thenevaluatethe expressionfor x = 3.

OBJECTIVE3

20. ThelowestelevationinLouisianaisinEasternNewOrleans( 8 ft),andthehighestelevationisatthetop ofDriskillMountain(535ft).FindthechangeinelevationfromEasternNewOrleanstoDriskillMountain.

OBJECTIVE4

RefertoProblem2tomotivatethefollowingproperties.

ChangesofIncreasingandDecreasingQuantities

• Anincreasingquantityhasapositivechange.

• Adecreasingquantityhasanegativechange.

21. ThenumberofmoviesshotinGeorgiaareshowninthefollowingtableforvariousyears.

Source: GeorgiaFilm,Music,andDigitalEntertainmentOfﬁce

a. FindthechangeinthenumberofmoviesshotinGeorgiafrom2006to2007.

b. In2008,Georgiaincreasedthetaxincentivestoshootmoviesinthestate.Findthechangeinthe numberofmoviesshotinGeorgiafrom2008to2013.

HW 1,3,5,15,19,33,47,53,57,61,65,73,79,81,85

SECTION1.5TEACHINGTIPS

Inthissection,studentssubtractrealnumbers,askillthattheywillusethroughoutthecourse.Inthissection, studentsﬁndthechangeinaquantity.Unfortunately,thisimportantconceptisoverlookedinmostarithmeticand algebratextbooks.Thisisacentralconceptneededtounderstandthatingoingfromapoint (x1,y1) toapoint (x2,y2), y2 y1 istheverticalchangeand x2 x1 isthehorizontalchange.Thisgivesmeaningtotheslope formula m = y2 y1 x2 x1 .Anotherkeypieceofthepuzzleaboutslopewillbetodiscussthemeaningofratios inSection1.6.Understandinghowtoﬁndthechangeinaquantitywillalsohelpstudentsmakesenseofthe techniquesweusetosubtractrealnumbers.

OBJECTIVE1COMMENTS

Problem1nicelymotivatesthechangeinaquantityproperty.NotethattheresultsofPart(a)ofProblem2are ratesofchange(Section7.2)forvariousyears.

OBJECTIVE2COMMENTS

Problem3suggeststheproperty a b = a +( b).Problem7suggestshowtosubtractanegativenumber. Problems12–19serveasasummaryofSections1.4and1.5.

GROUPEXPLORATION:SubtractingNumbers

Thisactivityisanicewayforgroupsofstudentstodiscoverthat a b = a +( b).Somegroupswillneedhelp withProblems4and5ofthisexploration.

OBJECTIVE3COMMENTS

AftersolvingProblem20,Isketchaﬁguretoillustratewhytheresultmakessense.

OBJECTIVE4COMMENTS

AlthoughIaddresstheconceptsaboutthesigniﬁcanceofsignsofchangeinObjectives1and2,itisniceto reinforcetheseimportantconceptsattheendofthissection.Problem21servesasgoodpreparationforworkwith time-seriesplots(Section3.3),scatterplots(Section6.1),andratesofchange(Section7.2).

SECTION1.6LECTURENOTES

Objectives

1. Findtheratiooftwoquantities.

2. Describethemeaningof percent

3. Convertpercentagestoandfromdecimalnumbers.

4. Useproportionsandpercentagestodescribeauthenticsituations.

5. Findthepercentageofaquantity.

6. Multiplyanddividerealnumbers.

7. Describewhichfractionswithnegativesignsareequaltoeachother. Copyright c 2016PearsonEducation,Inc.

OBJECTIVE1

• Supposethatthereare8womenand4menonasoftballteam.Theratioofwomentomenis 8women 4men = 2women 1men

• Thismeansthatthereare2womento1man.Thisratioiscalleda unitratio

• A unitratio isaratiowrittenas a b oras a : b with b =1

1. Theblinkofaneyetakes400milliseconds.Onebeatofahummingbird’swingstakes20milliseconds.Find theunitratioofthetimeittakesfortheblinkofaneyetothetimeittakesforonebeatofahummingbird’s wings.Whatdoesyourresultmeaninthissituation?

2. Themediansalespricesofexistinghomesandthemedianhouseholdincomesin2011areshowninthe followingtableforfourregionsoftheUnitedStates.

MedianSalesPriceMedianHousehold ofExistingHomesIncome Region(dollars)(dollars) Northeast237,50051,862 Midwest135,40049,549 South135,20042,590 West201,30053,367

Sources: U.S.Census;FederalReserveBankofSt.Louis

a. Findtheunitratioofthemediansalespriceofexistinghomestothemedianhouseholdincomeinthe Northeast.Whatdoestheresultmean?

b. Foreachofthefourregions,ﬁndtheunitratioofthemediansalespriceofexistinghomestothe medianhouseholdincome.Takingintoaccountthemedianhouseholdincomeofeachregion,listthe regionsinorderofaffordabilityofexistinghomes,fromgreatesttoleast.

c. ApersonbelievesthatexistinghomesintheSoutharemoreaffordablethanintheMidwest,because themedianpriceofexistinghomesislowerintheSouththanintheMidwest.Whatwouldyoutell thatperson?

OBJECTIVE2

• If57of100songsarehiphop,then57%ofthesongsarehiphop.

• Percent means“foreachhundred”: a%= a 100

• Apercentisaratio.

OBJECTIVE3

ConvertingPercentagestoandfromDecimalNumbers

• Towriteapercentageasadecimalnumber,removethepercentsymbolanddividethenumberby100 (movethedecimalpointtwoplacestotheleft).

• Towriteadecimalnumberasapercentage,multiplythenumberby100(movethedecimalpointtwo placestotheright)andinsertapercentsymbol.

3. Write8%asadecimalnumber. 4. Write0.145asapercent.

Warning:8%isequalto0.08,not0.8.

OBJECTIVE4

5. About63%ofAmericansfeelthedistributionofmoneyandwealthintheUnitedStatesshouldbemore evenlydistributed(Source: CBSNewsPoll).Useaproportiontodescribethissituation.

6. TheproportionofYahooemployeeswhoareAsianis0.39(Source: Yahoo).Useapercentagetodescribe thissituation.

7. Of905surveyeddrivers,163driverssaidittakesthematleastthreetriestoparallelpark(Source: Hankook TireFallGaugeIndexsurvey).Useapercentagetodescribethesituation.

OBJECTIVE5

FindingthePercentageofaQuantity

Toﬁndthepercentageofaquantity,multiplythedecimalformofthepercentageandthequantity.

8. Of4672surveyedstudentsingrades3–5,85%knewhowtouseakeyboardtotypeanswerstoquestions (Source: Idaho’sSmarterBalancedFieldTestsurvey).Howmanyofthestudentsknewhowtousea keyboard?

9. Apersonbuyssometake-outfoodfor$8(notincludingstatemealstax)inBoston,Massachusetts,which hasastatemealstaxof6.25%.Howmuchmoneyisthestatemealstax?

OneHundredPercentofaQuantity

Onehundredpercentofaquantityis all ofthequantity.

OBJECTIVE6

Userepeatedadditiontoshowthat 4( 3)= 12

MultiplyingTwoNumberswithDifferentSigns

Theproductoftwonumberthathavedifferentsignsisnegative.

10. a. Findtheproducts 3( 4)= 12, 2( 4)= 8, 1( 4)= 4, 0( 4)=0

b. ExplainwhytheresultsofPart(a)suggestthat 1( 4)=4, 2( 4)=8,and 3( 4)=12.

c. Formatheoryaboutthesignoftheproductoftwonumbersthathavethesamesign.

MultiplyingTwoNumberswiththeSameSign

Theproductoftwonumbersthathavethesamesignispositive.

3( 8)

Therulesfordividingnumbersaresimilartothoseformultiplyingnumbers,becausetodividebyanumber, wemultiplybythereciprocalofthenumber.

MultiplyingorDividingRealNumbers

Theproductorquotientoftwonumbersthathavedifferentsignsisnegative.Theproductorquotientoftwo numbersthathavethesamesignispositive.

19. Apersonhascreditcardbalancesof 3580 dollarsonaDiscoverR accountand 1590 dollarsonaMasterCardR account.

a. FindtheunitratiooftheDiscoverbalancetotheMasterCardbalance.

b. Ifthepersonwishestograduallypayoffbothaccountsinthesameamountoftime,describehowthe resultinPart(a)canhelpguidethepersoninmakinghisnextpayment.

20. 4 ( 7) 21. 8 ÷ ( 2)

15+11

OBJECTIVE7

( 7)( 10)

5.8+2.9

Comparetheresultsof 6 3 , 6 3 ,and 6 3 tomotivatethefollowingproperty.

EqualFractionswithNegativeSigns If b =0,then

HW 1,3,9,11,15,19,27,29,35,45,55,65,69,77,83,87,89,97

SECTION1.6TEACHINGTIPS

Inthissection,studentsworkwithratios,proportions,percents,andmultiplyinganddividingrealnumbers.It maybetemptingtoskipordeemphasizeratios,butthisconcept,togetherwiththeconceptofchange,willbevery helpfulinintroducingrateofchangeandtheslopeformula m = y2 y1 x2 x1 (Section7.2).Moststudentshavelittle experienceworkingwithratios.

OBJECTIVE1COMMENTS

Moststudentshaveaneasytimecomputingratiosbuthaveahardertimethinkingaboutthesigniﬁcanceof comparingratiossuchasinProblem2.Part(c)addressestheextremelyimportantconceptinintroductorystatistics thatitusuallyismorehelpfultocompareunitratios(orproportions)thanitistocomparequantities.Thetextbook willcontinuetoemphasizethisconceptinChapters3and5.

OBJECTIVE2COMMENTS

Moststudentshaveaweakunderstandingofpercents,whichisimportantforworkwithproportions(Chapter3) andprobabilities(Chapter5).

OBJECTIVE3COMMENTS

Iusethedeﬁnitionofpercenttosuggesthowtoconvertpercentagestoandfromdecimalnumbers.

ForProblem3,somestudentsthinkthattheresultis0.8.

OBJECTIVE4COMMENTS

Problems5and6canbeabitchallengingforsomestudentsbecausetheymustchangethestructureofthe sentences.

OBJECTIVE5COMMENTS

Ifirstusethedefinitionofpercenttofindthepercentageofaquantityandthenstreamlinetheprocess.For Problems8and9,Iremindstudentstoincludeunitsintheirresults.

Studentswillneedtoknowthatonehundredpercentofaquantityisallofthequantityformanyreasons, includingrecognizingwhenmodelbreakdownhasoccurredwhenmakingpredictionswithlinearandexponential models(Chapters6–10).

OBJECTIVE6COMMENTS

Studentshaveaneasytimewiththeseskills.

Writing 4( 3)=( 3)+( 3)+( 3)+( 3)= 12 suggeststheruleformultiplyingtwonumberswith differentsigns.Problem10suggeststheruleformultiplyingtwonumberswiththesamesign.

ForProblem13,manystudentsthinkthat 0 2( 0 1)=0 2.ForProblem14,somestudentsneedtobe remindedtosimplifytheirresult.

Thetextbookincludesadetailedexplanationaboutwhythesignrulesfordivisionarethesameasformultiplication(seepages59and60ofthetextbook).Duetotimeconstraints,Iusuallyjustsaytherulesfordividing numbersaresimilartothoseformultiplyingnumbersbecausetodividebyanumber,wemultiplybythereciprocal ofthenumber.

Problem19tiesratiosinnicelywithdividingtwonegativenumbers.Manystudentswhohavecreditcarddebt coulddirectlybeneﬁtfromlearninghowtodosuchworkwithcreditcardbalances.

IbudgetplentyoftimeforstudentstocompleteProblems20–27,whichserveasagoodsummaryofSections1.3–1.6.

GROUPEXPLORATION:FindingtheProductofaPositiveNumberandaNegative

Number

Groupsofstudentscandiscoverhowtomultiplytwonumberswithdifferentsignsbycompletingthisexploration. Itellstudentsthatthemoretheycanunderstandwhypropertiesmakesense,thebettertheywillbeabletokeep themstraight.

OBJECTIVE7COMMENTS

Iemphasizetheproperty a b = a b = a b ,where b =0,becauseitwillbeusefulwhenworkingwithslope.It seemsthatnoamountofemphasisistoomuchbecausesomestudentscompletelyforgetthispropertybythetime weneedtouseitforslope(Sections7.2and7.3).

Itellmystudentstowritetheirresultswhicharenegativefractionsintheform a b ratherthan a b or a b .

SECTION1.7LECTURENOTES

Objectives

1. Describethemeaningof exponent.

2. Describethemeaningoftheexponentzero.

3. Describethemeaningofanegative-integerexponent.

4. Describethemeaningof squareroot and principalsquareroot

5. Approximateaprincipalsquareroot.

6. Usetherulesfororderofoperationstoperformcomputationsandevaluateexpressions.

7. Usetherulesfororderofoperationstomakepredictions.

8. Findtheareaofpartofanobject.

9. Usescientiﬁcnotation.

OBJECTIVE1

24 =2 2 2 2=16

Deﬁnition Exponent

43 =4 4 4=64

Foranycountingnumber n, bn = b b b ... b n factorsof b

Wereferto bn asthe power,the nthpowerof b,or b raisedtothe nthpower.Wecall b the base and n the exponent

Foranexpressionoftheoftheform bn,wecalculate bn beforetakingtheopposite.

OBJECTIVE2

Findthepowers 24 , 23 , 22,and 21 andhavestudentsguesstheresultfor 20

Deﬁnition Zeroexponent Fornonzero b, b0 =1

OBJECTIVE3

Findthepowers 22 , 21 , 20,andhavestudentsguesstheresultfor 2 1 , 2 2,and 2 3

Deﬁnition Negative-integerexponent

If n isacountingnumberand b isnonzero,then

OBJECTIVE4

Deﬁnition Principalsquareroot

If a isanonnegativenumber,then √a isthenonnegativenumberwesquaretoget a.Wecall √a the principalsquareroot of a.

• Thesymbol"√ "iscalleda radicalsign.

• Anexpressionunderaradicalsigniscalleda radicand

• Aradicalsigntogetherwitharadicandiscalleda radical

• Anexpressionthatcontainsaradicaliscalleda radicalexpression.

• Asquarerootofanegativenumberisnotarealnumber.

Findthesquareroot.

OBJECTIVE5

Statewhetherthesquarerootisrationalorirrational.Ifthesquarerootisrational,ﬁndthe(exact)value.Ifthe squarerootisirrational,estimateitsvaluebyroundingtotheseconddecimalplace. 13. √144 14. √24

OBJECTIVE6

• Wedooperationsthatliewithingroupingsymbolsbeforeweperformotheroperations.

• Theorderofoperationsdoesmatter: (4+2) 5=6 5=30 4+(2 5)=4+10=14

• Forafractionsuchas 2+5 9 4 ,thefollowinguseofparenthesesisassumed: 2+5 9 4 = (2+5) (9 4) = 7 5

• Foraradicalexpressionsuchas √16+9,thefollowinguseofparenthesesareassumed:

Warning: √16+9 does not equal √16+ √9.

(4 8)(9 2)

OrderofOperations

Weperformoperationsinthefollowingorder:

1. First,performoperationswithinparenthesesorothergroupingsymbols,startingwiththeinnermost group.

2. Thenperformexponentiations.

3. Next,performmultiplicationsanddivisions,goingfromlefttoright.

4. Last,performadditionsandsubtractions,goingfromlefttoright.

17. 3 8 ÷ 4

18. 4+( 2)3

19. 2(5 8) (4 9)

20. 3 [6 2(3+4)]

21. 33 2(3 5)2 ÷ ( 4)

OperationComputationwith10s

Exponentiation 1010 =10, 000, 000, 000 Multiplication 10 · 10=100 Addition 10+10=20

OrderofOperationsandtheStrengthsofOperations

Afterwehaveperformedoperationsinparentheses,theorderofoperationsgoesfromthemostpowerful operation,exponentiation,tothenext-most-powerfuloperations,multiplicationanddivision,totheweakest operations,additionandsubtraction.

25. (1 3)2 +(2 3)2 +(6 3)2 3 1 26. (44 35) 4 42 2 + 72 49

27. Useacalculatortoperformtheindicatedoperationsfor

28. Evaluate a b c d for a = 3, b =5, c =4,and d = 6.

29. Evaluate x t s √n for x =12, t =3, s =10,and n =25.

30. Let x beanumber.Translatethesentence“Subtract5fromtheproductofthenumberand 3.”Then evaluatetheexpressionfor x = 2

OBJECTIVE7

31. ThenumberofkneereplacementsurgeriesamongMedicareparticipantswasabout244thousandin2010 andhasincreasedbyapproximately8thousandsurgeriesperyearuntil2014(Source: JournaloftheAmericanMedicalAssociation).Completethefollowingtabletohelpﬁndanexpressionthatstandsforthe numberofsuchsurgeriesat t yearssince2010.Showthearithmetictohelpseeapattern.

NumberofKneeReplacementSurgeries YearsAmongMedicareParticipants Since2010(inthousands)

Evaluateyourresultfor t =4 anddiscusswhattheresultmeansinthissituation.

32. Thenumberofage-relatedretirementsofU.S.pilotswas226retirementsin2010,anditincreasedby20.8% in2011(Source: KitDarby.comAviationConsulting).Whatwasthenumberofage-relatedretirementsin 2011?

OBJECTIVE8

33. Usethefactthatthetotalareaofthefollowingobjectis1toﬁndtheareaoftheshadedbar.Theobjecthas notbeendrawntoscale.

OBJECTIVE9

Deﬁnition Scientiﬁcnotation

Anumberiswrittenin scientiﬁcnotation ifithastheform N × 10k,where k isanintegerandtheabsolute valueof N isbetween1and10orisequalto1.

Examples: 6 74 × 107 , 9 2 × 10 6

Writethenumberinstandarddecimalnotation.

34. 5 36 × 103 35. 8 192 × 106

ConvertingfromScientiﬁcNotationtoStandardDecimalNotation

Towritethescientiﬁcnotation N × 10k instandarddecimalnotation,wemovethedecimalpointofthe number N asfollows:

• If k is positive,wemultiply N by10 k timesandhencemovethedecimalpoint k placestothe right.

• If k is negative,wedivide N by10 k timesandhencemovethedecimalpoint k placestothe left.

Writethenumberinscientiﬁcnotation.

38. TheﬁrstevidenceoflifeonEarthdatesbackto 3.6 × 109 yearsago.

39. Thewavelengthofvioletlightisabout0.00000047meter.

ConvertingfromStandardDecimalNotationtoScientiﬁcNotation

Towriteanumberinscientiﬁcnotation,countthenumber k ofplacesthatthedecimalpointmustbemoved sothattheabsolutevalueofthenewnumber N isbetween1and10orisequalto1.

• Ifthedecimalpointismovedtotheleft,thenthescientiﬁcnotationiswrittenas N × 10k

• Ifthedecimalpointismovedtotheright,thenthescientiﬁcnotationiswrittenas N × 10 k

• Somecalculatorsrepresent 7 29 × 1026 as7.29E26.

• Somecalculatorsrepresent 5 96 × 10 23 as5.96E 23

HW 1,3,5,19,25,39,45,53,67,71,73,79,81,85,87,91,97,103,105,109,117,123,129,131

SECTION1.7DETAILEDCOMMENTS

Inthissection,studentsworkwithexponentsandusetherulesfororderofoperationstoperformcomputations andevaluateexpressions.Studentswillusethismaterialthroughoutthecourse.

OBJECTIVE1COMMENTS

Itwillbeespeciallyhelpfulforstudentstoknowthemeaningof exponent, base,and power whenworkingwith exponentialmodelsinChapter10.Manystudentsthinkthat power meansthesamethingas exponent.Explain that bn isapowerof b andthat n istheexponent.

ForProblem4,moststudentsaresurprisedthat 52 isnotequalto25.Itellstudentsthatforanexpressionof theoftheform bn,wecalculate bn beforetakingtheopposite.Italsohelpstopointoutthatthebaseof ( 5)2 is 5 andthatthebaseof 52 is5.

OBJECTIVE2COMMENTS

Manystudentsaresurprisedtolearnthat b0 isnotequalto0.

OBJECTIVE3COMMENTS

Thereasonnegative-integerexponentsareincludedinthissectionistopreparestudentsforscientiﬁcnotation,

LectureNotesandTeachingTips43 whichwillbedisplayedbycalculatorswhenstudentscomputeprobabilitiesforthenormaldistribution(Section5.4).

OBJECTIVE4COMMENTS

Squarerootsareincludedinthissectionbecausestudentswillworkwithsquarerootswhencomputingstandard deviation(Section4.2).Tokeepthingsmoving,Iskipallthedeﬁnitionsforprincipalsquareroot,radicalsign, radicand,andsoonandjustdoProblems9–12.

OBJECTIVE5COMMENTS

Ifstudentsareusingavarietyofcalculators,itcanbechallengingtotellthemallhowtoaccessthesquareroot command.Ifstudentshavetrouble,ItellthemtowaituntiltheynextworkingroupssoIcanthengoaboutthe classroomhelpingstudentsindividually.

OBJECTIVE6COMMENTS

Whendiscussingtheorderofoperations,Iemphasizethatmultiplicationanddivisionareonthesamelevelofthe hierarchy;somestudentsthinkthat“goingfromlefttoright”meansthatallmultiplicationsshouldbedonebefore alldivisions,becausetheword“multiplications”appearstotheleftoftheword“divisions”intheinstructionsfor theorderofoperations.Thesamegoesforadditionandsubtraction.

Sometimesitseemsthattheonlythingsstudentshavelearnedfrompastmathcoursesaretheacronyms "PEMDAS"and"FOIL."Idislike"PEMDAS"becauseitlacksdetailsneededforstudentstouseitcorrectly. Evenwithcommas,theacronym“P,E,MD,AS”lacksnecessarydetails.Nonetheless,Ipresent"PE,MD,AS" becauseifIdon’t,studentswillaskaboutitanyway.ThenIemphasizehowtheacronymisincomplete.

Eventhoughorderofoperationsisareviewtopicfromarithmetic,somestudentsarechallengedbyProblems17–24.Problems23,25,and27aregoodpreparationforcalculatingthemean(Section4.1),variance (Section4.2),andstandarddeviation(Section4.3),respectively.Problem28relatestocomputingslopeofaline (Section7.2).Finally,Problems26and29relatetofindingconfidencesintervals,althoughconfidencesintervals arenotaddressedinthiscourse.

WhenstudentspracticeProblem27,Iencouragethemtosavetimebycomputingtheentirenumeratorrather thancomputingandrecordingthevaluesofthethreetermsbeforeadding.

GROUPEXPLORATION:OrderofOperations

Inthisactivity,groupsofstudentsdiscoverthatitmattersinwhichorderweaddandmultiply.

OBJECTIVE7COMMENTS

InProblem31,studentscontinuetheirworkwithbuildingexpressionsbyrecognizingpatternsintheirarithmetic. AlthoughstudentswilluseadifferentmethodtoﬁndlinearmodelsinSection7.3,thetwomethodshavesome overlapandtothedegreethattheydiffertheycanserveaschecksofeachother.

OBJECTIVE8COMMENTS

IhavegroupsofstudentsworkonProblem33,whichisexcellentpreparationforthedevelopmentofdensityhistograms,whichwillbeemphasizedinChapters3–5.Althoughstudentshavealreadyworkedwiththeproportion oftherestpropertyinSection1.3,theytendtohaveatoughtimewiththisproblem.Forgroupsthatgetstuck,I askthemwhethertheycanﬁndtheareasofalltheunshadedrectangles.Whentheysayyes,Iremindthemofthe proportionoftherestproperty,whichusuallyisabigenoughhint.

OBJECTIVE9COMMENTS

Deemphasizingscientificnotationisonewaytohandlegettingthroughthislongsection.However,ifyour studentsareusingTI-84graphingcalculators,makesurethattheyknowhowtointerprettheircalculators’wayof expressingscientificnotation,becausestudentswillrunintothisnotationwhenfindingprobabilitiesfornormal distributions(Section5.4).

Onewaytomotivatescientiﬁcnotationistoaskstudentstousetheirgraphingcalculatorstocompute 250 or 2 50

Forconvertingscientiﬁcnotationtoandfromstandarddecimalnotation,studentsarenotsurewhethertomove thedecimalpointtotherightorleft.First,Idemonstratethattomultiplyby10,wemovethedecimalpointone placetotheright,andtodivideby10,wemovethedecimalpointoneplacetotheleft.ThenIbridgetopowers of10.Forexample,for 3 56 × 10 8,3.56isdividedby 108 (aproductofeight10’s),soweneedtomovethe decimalpoint8placestotheleft.

CHAPTER2OVERVIEW

Howmanytimeshaveyouquestionedthevalidityofconclusionsdrawnbythemediaorcorporationsbecauseof nonsamplingerrororsomeotherbadpracticeofstatistics?Itwouldbeapowerfullifelessonforyourstudentsto enhancetheirabilitytodothis.Ibelievethatshouldbethehighestgoalofthischapter.Infact,onecouldargue thatthisisthemostimportantobjectiveoftheentirecoursebecausesomestudentsmaynotusestatisticsmuchin theircareersbutweallaresubjecttobadpracticesofstatisticsbythemediaandadvertisements.

Thischapterisalsohugelyimportantbecauseitprovidesthebigpicturefortherestofthecourseandevenfor thesubsequentcourseinintroductorystatistics.

Inmyopinion,thesinglemostimportantconceptofthechapterisrandomness.Notonlydomanystudents havemisconceptionsaboutthisconcept,theyalsohavemuchtogainbylearningaboutconceptsrelatedtorandomnesssuchasrandomsampling,randomselection,andprobability.

AclosesecondinimportanceisthedistinctionmadebetweenexperimentsandobservationalstudiesinSection2.3.Itisthisdistinctionthatallowsstudentstodiscern,forthemostpart,whetherastudycandeterminethat thereiscausality.ThisconceptwillbeneededformanypartsofexercisesinChapters3–5.

SomeoftheHands-OnResearchexercisesandtheHands-onProjectassignmentsrequirestudentstoperform surveysorphysicalexperiments.ThesamplingmethodsdiscussedinSection2.2willexpandstudents’options ofcollectingsuchdata.AndthedescriptionsofvarioustypesofbiasinSection2.1willserveaswarningsfor collectingmeaningfuldata.

InSection2.3,bepreparedtocoachstudentsonhowtoreaddescriptionsofstudies.Iprovidesometipsin thismanualforthatsection.ThehigherreadingleveloftheexamplesandtheexercisesinSection2.3isthe naturalresultoftryingtoexpresscomplexideasaboutauthenticstudies.Ifstudentscanlearntocomprehendsuch descriptions,theywillbewellpreparedtodigestsimilardescriptionsinintroductorystatisticscoursesaswellas intheircareers.

Ifyouhavenotalreadysurveyedyourstudents,thiswouldbegoodtimetodosobecausethedatawillcome inhandyatthestartofChapter3,wheretheclasswillbegintoconstructstatisticaldiagrams.

SECTION2.1LECTURENOTES

Objectives

1. Identifythe individuals,the variables,andthe observations ofastudy.

2. Describetheﬁvestepsof statistics

3. Identifythe sample andthe population ofastudy.

4. Identify descriptivestatistics and inferentialstatistics

5. Selecta simplerandomsample

6. Identifythe samplingbias,the nonresponsebias,andthe responsebias ofastudy.

7. Identifysamplingandnonsamplingerror.

OBJECTIVE1

Individuals arethepeopleorobjectswewanttolearnabout.

Deﬁnition Variable

Instatistics,a variable isacharacteristicoftheindividualstobemeasuredorobserved.

Observations aredatathatweobserveforavariable.

1. ThenumberoflistensofcertainsongsduringtheweekendingSunday,February,2015onLast.fmare showninthefollowingtable.

SongBandGenreNumberofListens "Breezeblocks"Alt-JAlternative1436 "10Bands"DrakeHip-Hop5817 "BackseatFreestyle"KendrickLamarHip-Hop1466 "Chandelier"SiaPop3256 "BlueMoon"BeckAlternative5360

Source: Last.fm

a. Identifytheindividuals.

b. Identifythevariables.

c. Identifytheobservationsforeachvariable.

d. Ofthesongslistedinthetable,whichonewaslistenedtothemost?

OBJECTIVE2

Deﬁnition Statistics

Statistics isthepracticeofthefollowingﬁvesteps:

1. Raiseaprecisequestionaboutoneormorevariables.

2. Createaplantoanswerthequestion.

3. Collectthedata.

4. Analyzethedata.

5. Drawaconclusionaboutthequestion.

2. Motivationalenhancementtherapy (MET)isacounselingprocessthataimstomotivatedrugabusersto stopusingdrugs.SomeresearcherswantedtotestwhetherMETreallyworks.Outof70drugabusers whoparticipatedinthestudy,35receivedthestandarddrugtreatmentprovidedatahospital.Theother 35individualsreceivedMETinadditiontothestandarddrugtreatment.Afterreceivingtreatmentfor 12weeks,all70individualstookaquestionnairewhichmeasuresadrugabuser’smotivationtostopusing drugs.TheresearchersconcludedthatMETeffectivelymotivatesdrugabuserstostopusingdrugs.(Source: MotivationalEnhancementTherapyforSubstanceAbusers:AQuasiExperimentalStudy,SeemaRaniet al.).Describetheﬁvestepsofthestudy.Ifnodetailsaregivenaboutastep,sayso.

OBJECTIVE3

Deﬁnition Population

A population isthe entire groupofindividualsaboutwhichwewanttolearn.

A census isastudyinwhichdataarecollectedabout all membersofthepopulation.

Deﬁnition Sample

A sample isthepartofapopulationfromwhichdataarecollected.

Collectingdatafromasample,ratherthantheentirepopulation,savestime,money,andeffort.

3. Inapollof1000Americanadults,13%ofrespondentssaidthatconcernsaboutglobalwarmingareunwarranted.ThestudythenmadeaconclusionaboutallAmericanadults(Source: NBCNews/WallStreet Journal).

a. Deﬁneavariableforthestudy.

b. Identifythesample.

c. Identifythepopulation.

OBJECTIVE4

• Descriptivestatistics isthepracticeofusingtables,graphs,andcalculationsaboutasampletodrawconclusionsaboutonlythesample.

• Inferentialstatistics isthepracticeofusinginformationfromasampletodrawconclusionsaboutthe entire population.Whenweperforminferentialstatistics,wecalltheconclusions inferences

4. ResearcherswantedtoﬁndouthowarestricteddietwouldaffectaLabradorRetriever’slifespan.Of48 LabradorRetrieversbeingobserved,24werefedanormaldietand24werefedarestricteddiet.Thedogs’ lifetimeswererecorded.ThestudyconcludedthatatypicalLabradorRetrieveronarestricteddiettendsto livelongerthanatypicalLabradorRetrieveronanormaldiet(Source:EffectsofDietRestrictiononLife SpanandAge-RelatedchangesinDogs,RichardD.Kealy,PhD,etal.).

a. Whatquestionweretheresearcherstryingtoanswer?

b. Identifythepopulation

c. Identifythesample.

d. Identifytheconclusion.Isitpartofdescriptiveorinferentialstatistics?

OBJECTIVE5

Whenastudymakesuseofasample,itisimportantthatthesamplerepresentsthepopulationwell.

Deﬁnition Simplerandomsample

Aprocessofselectingasampleofsize n is simplerandomsampling ifeverysampleofsize n hasthesame chanceofbeingchosen.Asampleselectedbysuchaprocessiscalleda simplerandomsample

• Ifweallowanindividualtobeselectedmorethanonce,thenwearesamplingwithreplacement.

• Ifwedonotallowanindividualtobeselectedmorethanonce,thenwearesamplingwithoutreplacement.

• A frame isanumberedlistofalltheindividualsinthepopulation.

5. a. Createaframeofallthestudentsinyourclass.

b. Usetechnologytorandomlyselect6studentswithoutreplacement.

6. In2013,1523outof4270collegeswere2-yearcolleges(Source: U.S.DepartmentofEducation).

a. Whatproportionofthecollegeswere2-yearcolleges?

b. Byusingthenumbers1through1523torepresentthe2-yearcollegesandthenumbers1524through 4270torepresenttheothercolleges,theauthorusedtechnologytorandomlyselect500colleges withoutreplacement.Therewere1732-yearcollegesinthesample.Whatproportionofthesample was2-yearcolleges?

c. Ifyoudidnotknowtheproportionofthepopulationthatare2-yearcollegesandusedtheresultyou foundinPart(b)toestimateit,wouldthatbepartofdescriptivestatisticsorinferentialstatistics? Explain.

Deﬁnition Samplingerror

Samplingerror istheerrorinvolvedinusingasampletoestimateinformationaboutapopulationdueto randomnessinthesample.

7. FindthesamplingerrorfortheestimationyoumadeinProblem6.

Ifrandomsamplingisusedtoselectalargeenoughsample,thesamplingerrorwillnotbetoolarge.

OBJECTIVE6

Deﬁnition Bias

Asamplingmethodthatconsistentlyunderemphasizesoroveremphasizessomecharacteristic(s)ofthepopulationissaidtobe biased.

Ifasamplingmethodisbiased,thenanyinferencesmadewillbemisleading. Therearethreetypesofbias:

1. Samplingbias occursifthesamplingtechniquefavorsonegroupofindividualsoveranother.

2. Nonresponsebias happensifindividualsrefusetobepartofthestudyoriftheresearchercannottrack downindividualsidentiﬁedtobeinthesample.

3. Responsebias occursifsurveyedpeople’sanswersdonotmatchwithwhattheyreallythink.

GuidelinesforConstructingSurveyQuestions

Whenconstructingasurveyquestion:

• Donotincludejudgmentalwords.

• Avoidaskingayes/noquestion.

• Ifthequestionincludestwoormorechoices,switchtheorderofthechoicesfordifferentrespondents.

• Addressjustoneissue.

Foreachstudy,identifypossibleformsofbias.Also,discusssamplingerror.

8. Aliberalradiostationconductsacall-insurvey,askingcallers,"ShouldCongressdotherightthingand increasethebudgetforeducation?"Ofthe1140callers,969answeredyes.Thestationconcludesthat85% ofallAmericansthinkthatthebudgetforeducationshouldbeincreased.

9. Agroupofstudentssurveysotherstudentswhoenterandexitthegymandﬁndsthat67studentsoutof100 studentsexerciseeveryday.Thegroupconcludesthat67%ofallstudentsatthecollegeexerciseeveryday.

OBJECTIVE7

Deﬁnition Nonsamplingerror

Nonsamplingerror iserrorfromusingbiasedsampling,recordingdataincorrectly,andanalyzingdata incorrectly.

10. Ahotelrandomlyselectssomecustomerswhostayedatthehotelinthepastmonth,askingwhetherthey hadtakenclotheshangersand/ortowelsfromtheirroom.Theproportionofthesampledcustomerswho saidtheyhadtakenclotheshangersand/ortowelswas0.01.Butthepopulationproportionisactually0.12. Identifywhethersamplingerror,nonsamplingerror,orbothhavelikelyoccurred.

HW 1,3,7,11,13,19,21,23,27,33,35,41,43,58,59

SECTION2.1TEACHINGTIPS

Onecouldarguethatthemostimportanttopicofthissectionissimplerandomsamplingbecauseitistheﬁrstof severalsamplingmethodsthatwillbeaddressedinthischapter.Plus,theconceptofrandomnesswillalsocome upwhendiscussingprobability(Chapter5).ThissectionlaysthefoundationforSection2.3,whichdescribeskey featuresofanexperiment.

OBJECTIVE1COMMENTS

Studentsoftenconfusethemeaningsof individuals, variables,and observations.IprefertointroducetheterminologiesasIworkonProblem1sostudentscanseeconcreteexamples.ThenIpresentthegeneraldeﬁnitions.

Astimepasses,studentstendtoslipintothinkingthattheterminology individuals referstopeopleandnot objects,soitwillhelptoremindthemofthecorrectdeﬁnitioninafewdays.

OBJECTIVE2COMMENTS

Theﬁvestepsofstatisticslaysthefoundationnotonlyforthiscourse,whichaddressesdescriptivestatistics,but alsoforintroductorystatisticscourses,whichaddressbothdescriptiveandinferentialstatistics.Iquicklydiscuss thestepsgenerallyandthenhavegroupsofstudentscompleteProblem2,whichtheyhaveaneasytimewith.

OBJECTIVE3COMMENTS

Studentsarequicktopickuponthebasicideaofthemeaningsof population and sample,buttherearesubtleties thatcanbechallenging.

Forexample,somestudentsthinkthatindividualsinthecontrolgrouparenotpartofthesample.Itishelpful topointoutthatsuchindividualsarepartofthesamplebecausedataarecollectedfromthem.(Controlgroups willbedeﬁnedinSection2.3.)

Whenreadingstatisticalreports,itcanbedifficultforstudentstodeterminethepopulationbecauseitisoften implied.Forexample,inExercise22ofHomework2.1,astudentmightconcludethatthepopulationisall sexuallyconfidentwomen.Actually,acomparisonisbeingmadebetweenwomenwhoaresexuallyconfidentand thosewhoarenot,sothepopulationisallwomen.Also,ifallthewomeninthesamplewererandomlyselected fromtheUnitedStates,thenthepopulationwouldbeallAmericanwomenratherthanallwomenintheworld.

Anotherissueisthatsomestudentsunderstandhowtoidentifythesampleandpopulation,buttheygivevague referencestoeach.Itellthemthatstatingthenumberofindividualsinthesample(ifprovided)andusingthe word"all"whendescribingthepopulationcanhelpclarifywhichindividualsareinwhichgroups.

IprefertoassignthesimplerexercisesaboutsampleandpopulationinHomework2.1sothatstudentsgain someconﬁdence.OncewereachSection2.3,theexercisesthatcontinuetoaddresspopulationandsamplewill raisestudents’understandingtoahigherlevel.

OBJECTIVE4COMMENTS

Somestudentsstrugglewithdistinguishingdescriptivestatisticsfrominferentialstatistics.I’mnotsurewhy.To helpclarify,Igivealotofexamplesofeach.AlthoughChapters3–10willfocusondescriptivestatistics,there areexamplesofinferencessprinkledthroughoutthetextinwhichstudentsmustidentifythemassuch.

OBJECTIVE5COMMENTS

Onecouldarguethatsimplerandomsamplingisthemostimportantconceptofthissectionbecauseitisthekey ideaofformingsamples,performingrandomassignment(Section2.3),andprobability(Chapter5).

Manystudentshavemisconceptionsaboutrandomness.Somestudentsbelievesixflipsofafaircoinwould resultinthreeheadsandthreetails.Somestudentsbelievethatflipsofafaircoinwouldnotresultinstreaks. Todismantlethesemisconceptions,Iflipacoininclass20timesandrecordtheresultsontheboard.Thenwe identifythelongeststreakandalsocomparethefrequenciesofheadsandtails.Iftherehappentobe10ofeach, wecomparethefrequenciesofheadsandtailsafterthefirst n flips,where n isevenandthenumbersofheadsand tailsarenotequal.

Afterdiscussinghowtorandomlyselectpeopleusingnamesinahat,Idiscusshowtousetechnology.For exams,Itellstudentswhatnumbertouseasaseedsothatitwon’tbetoocumbersometograde,butthefact thatallstudentsthengeneratethesamerandomnumbersmuddiesthewatersaboutthemeaningofrandomness. Pointingoutthattechnology simulates randomselectioncanhelpclarify.

Anotherthingthatiscuriousaboutaseedisthatbeforewecanusetechnologytorandomlyselectsome numbers,wemustrandomlyselecttheseed.Thetextbookusesthecurrentdate,time,ortemperaturetoselecta seed,butstudentsmightthinkaseedmustalwaysbeselectedinthoseways.Tossinga10-sideddieseveraltimes togeneratethedigitsofaseedmightbethebestwaytogo.

It’sagoodideatopointoutthatinmostcases,samplesareformedusingsamplingwithoutreplacement.

OBJECTIVE6COMMENTS

Iemphasizethemeaningof samplingbias, nonresponsebias,and responsebias becausesomanybadpractices ofstatisticsstemfromthesemisuses.Mosttextbooksaddresstheseconceptsinasinglechapteranddonot revisittheminsubsequentchaptersondescriptivestatistics.In Pathway,theseconceptsareaddressedmanytimes inChapters2–5.Chapters6–10willfocusontheprevalentmisunderstandingthatastrongassociationimplies causation.

DiscussingbiasatgreatlengthwillbetterpreparestudentsforsomeoftheHands-OnResearchexercisesas wellassomeoftheHands-OnProjectsthatrequirestudentstoperformsurveys.Duetostudents’limitedtimeand money,theirsurveyswillhavebias,buttheyarerequiredtodescribethebias(seeProblems7and8oftheSurvey aboutProportionsProjectonpage123ofthetextbook).

Beforediscussingsampling,nonresponse,andresponsebias,Ihavegroupsofstudentsidentifysampling issuesinProblems8and9.ThenIgeneralizetheircommentsbyprovidingthedefinitions.Havingstudentsfirst workwithconcreteexamplespreparesthemfordigestingthegeneraldefinitions.

Whensomestudentslearnaboutsamplingbias,theyhavedistortedideasabouthowtoavoidit.Forasurvey aboutpeople’sfavoritesport,somestudentsmayseethepitfallinpollingpeopleatabasketballgamebutmay thinkthatpollingpeopleatvarioussportingeventswouldbeﬁne.Evenafteranin-depthclassroomdiscussion aboutsamplingbias,somestudentswillnotunderstandthattheonlywaytoavoidsamplingbiasistorandomly selectthesample.Asaresult,ImakesureIrevisitthisconceptseveraltimesthroughoutthecourse.

Ispendadisproportionateamountoftimediscussingresponsebiasbecauseithasmanyfacetsanditisthebias thatstudentswillbeabletocontrolthemostwhenperformingsurveysbycarefullyconstructingtheirquestions.

SamplingwillbefurtherdevelopedinSection2.2,whichdescribessystematic,stratiﬁed,andclustersampling.

OBJECTIVE7COMMENTS

Studentsoftenconfusethemeaningof samplingerror withthemeaningof nonsamplingerror probablybecause theysoundsosimilar.Oncestudentscankeepstraightwhichiswhich,theyhaveaneasytimewithnonsampling error.Samplingerrorisamuchmorechallengingconcepttograsp.Studentstendtothinkthatthevalueofa statisticisequaltothevalueoftheparameter.Themediahasintroducedoratleastreinforcedthismisconception. Grapplingwithsamplingerrorisattheheartofstatistics,butitisdifﬁculttoaddressthisconceptinthemidstof descriptivestatistics.

UsingtechnologytosolveanexamplesimilartoExample6inthetextbookisanicewaytoexploresampling error,butIemphasizethatnormallywedonotknowthevalueofaparameter.Example6isalsomisleading becauseitsuggeststhatinstatisticsweusepointestimatestoestimateparameterswheninfactweuseconfidenceintervals.Forthisreason,Iseriouslyconsideredintroducingalighttreatmentofconfidenceintervalsin Section2.1,butIdecidedthatitwouldlikelycreatetoomanymisconceptionsaboutconfidenceintervals.

Despitetheseissues,Example6doesagreatjobofclarifyingsamplingerrorbecauseitissoconcrete.

GROUPEXPLORATION:UsingSamplingMethods

Tellingstudentshowtoconstructgoodsurveyquestionsisagoodﬁrststep.Buthavingstudentsconstructtheir ownquestionsandgettingfeedbackfromyouwillgreatlyenhancetheirunderstanding.Thisisagoodtimeto warnstudentstoavoidinappropriatequestions.

Providingadiagramofthenamesofstudentsandwheretheyareseatedcanmovethingsalong.Iemphasize thatgroupsshouldrecordtheseedtheyselected.Havingthemcarryouttheirsurveyscanbechaoticandinefﬁcient unlessyouprovidesomestructure.Eachgroupcouldselectonemembertobethesurveyor.Thesurveyorscould circulatetheclassroomwhiletheotherstudentsremainseated.Classtimecouldbepreservedbyhavingthe studentsparticipateinthesurveysonline,butthiswouldrequiretimeandeffortonyourparttocoordinateposting students’questionsandresponses.

ThisexplorationisgoodpreparationfortheSurveyaboutProportionsProjectonpage123ofthetextbook.

SECTION2.2LECTURENOTES

Objectives

1. Identifyandexplain systematicsampling

2. Identifyandexplain stratiﬁedsampling.

3. Identifyandexplain clustersampling.

4. Comparesamplingmethods.

5. Describewhy conveniencesampling and voluntaryresponsesampling shouldneverbeused.

OBJECTIVE1

Deﬁnition Systematicsampling

Toperform systematicsampling,werandomlyselectanindividualoutoftheﬁrst k individualsandalso selectevery kthindividualaftertheﬁrstselectedindividual.

Warning:Once k ischosen,theresearchermustmakesurethatselectingevery kthindividualdoesnotmatch withsomepatterninthepopulation.

1. ATargetmanagerwantstosurveycustomersastheyleavethestoreonacertainday.Thereareabout 925customerseachday.Themanagerwouldliketogetfeedbackfromatleast75customers.Frompast experience,themanagerknowsthatif100customersareapproached,about75ofthemwillparticipatein thesurvey.

a. Giventhatthemanagerwantstosurveycustomersastheyleavethestore,explainwhyitwouldnotbe possibletoperformsimplerandomsampling.

b. Themanagerdecidestoperformsystematicsampling.Ifevery kthcustomerisapproached,ﬁnd k so that100customersareapproached.

c. Tofindwhichcustomershouldbefirstapproached,use822astheseedtofindarandomnumber between1and k,inclusive.

d. Listtheﬁrst5customerswhoshouldbeapproached.

Weshouldalwaysrounddownwhencalculating k forsystematicsampling. Akeybeneﬁtofsystematicsamplingisthataframeisnotrequired.

OBJECTIVE2

Deﬁnition Stratiﬁedsampling

Toperform stratiﬁedsampling,apopulationisdividedintosubgroupscalled strata (singular: stratum) andsimplerandomsamplingisperformedoneachstratum.Ineachstratum,theindividualssharesomecharacteristic.Theratiosofthenumberofindividualsselectedfromeachstratumareequaltothecorresponding ratiosofthestratumsizes.

Beneﬁtsofstratiﬁedsampling:

• Individualsinsmallstrataarenotexcluded.

• Asmallersamplecanbeselectedthanbyusingsimplerandomsampling.Thissavestime,money,and effort.

2. EmoryUniversitywantstosurveyasampleof250studentsfromtheclassof2015,askingthemwhether theyfeelliketheybelong.Thenumbersofstudentsareshowninthefollowingtableforvariousethnicities. Howmanystudentsofeachethnicityshouldbeincludedinthestudy?

EthnicityNumberofStudents

Caucasian1826

AsianAmerican800

AfricanAmerican425

Latino507

Multi-Racial155

NativeAmerican1

International855

DidNotIdentify261

Source: EmoryUniversity

3. WesternIllinoisUniversity,QuadCities,wantstosurveyitsstudentsabouttheirﬁrst-semesterexperience. Becausefemaleundergraduates,maleundergraduates,femaletransferstudents,maletransferstudents,femalegraduatestudents,andmalegraduatestudentsmayhavehaddifferentexperiences,theuniversityplans tousethesesixtypesofstudentsasstrata.Thestatasizesareshowninthefollowingtable.Iftheuniversity wantstosurvey150students,howmanystudentsineachstratashouldbesurveyed?

GenderFreshmenUndergraduateTransferFirst-TimeGraduate Female154234115 503 Male13018652 368 Total284420167 871

Source: WesternIllinoisUniversity

OBJECTIVE3

Deﬁnition Clustersampling

Toperform clustersampling,apopulationisdividedintosubgroupscalled clusters.Thensimplerandom samplingisusedtoselectsomeoftheclusters.Alloftheindividualsinthoseselectedclustersformthe sample.

Beneﬁtsofclustersampling:

• Itdoesnotrequireconstructingaframeofindividuals.

• Itsavestime,money,andeffort.

4. BostonMayorMartyWalshwantsdatacollectorstoconductin-personinterviewswithsomeBostonresidents.Ifeachcityblockistreatedasacluster,describehowclustersamplingcouldbeaccomplished.

OBJECTIVE4

SamplingMethodRequirementBeneﬁts SimpleRandomAframeofallindividuals.Worksﬁnefortelephoneande-mail surveysinwhichthereislittleriskof excludinganyone.

SystematicSelectingevery kthindividualmustNoframeisrequired. notmatchwithsomepatterninthe population.

StratiﬁedIneachstrain,individualsaresimilar.Individualsinsmallstrataarenot Aframeforindividualsineachstrata.excludedfromthesample.Cansave time,money,andeffort.

ClusterAframeofclusters.Noframeofindividualsisrequired. Cansavetime,money,andeffort.

OBJECTIVE5

Deﬁnition Conveniencesampling

Toperform conveniencesampling,wegatherdatathatareeasytocollectanddonotbotherwithcollecting themrandomly.

Althoughconveniencesamplingiseasytoperform,itshouldneverbedonebecausethesamplewill usuallynotrepresentthepopulationwell.

Deﬁnition Voluntaryresponsesampling

Toperform voluntaryresponsesampling,weletindividualschoosetobeinthesample.

Neverperformvoluntaryresponsesamplingorthemoregeneralconveniencesampling. Identifywhetherthesamplingmethodissimplerandom,systematic,stratiﬁed,cluster,orconvenience.Explain.

5. Inastudyatauniversity,250studentsareselectedfromeachoftheclassesfreshmen,sophomores,juniors, andseniors.

6. HomeDepotcreatesaframeofallofits340thousandemployeesandrandomlyselectssomeoftheemployees.

7. Abloghostsanonlinesurvey,askingrespondentswhethertheygotothemoviesatleastoncepermonth.

8. TwentyBurgerKinglocationsintheUnitedStatesarerandomlyselectedandalltheemployeesatthose locationsaresurveyed.

9. Apoliceunitstopseveryfourthcaronahighwayandtestswhetherthedriverisdrivingundertheinﬂuence ofalcohol.

HW 1,3,5,7,9,11,13,19,27,29,31,33,39,43,45

SECTION2.2TEACHINGTIPS

Studentsarechallengedbyhavingtodistinguishbetweensimplerandomsamplingandthefivesamplingmethods introducedinthissection.Someofthedifficultystemsfromusingsomeofthesamewordstodescribedifferent methods.Andeventhoughthedifferentwords strata and cluster areusedtodescribesubgroupsforstratifiedand clustersamplingmethods,studentsstilltendtostruggletokeepthetwomethodsstraightbecausesimilarsteps aretakenbutinadifferentorder.

OBJECTIVE1COMMENTS

StudentsaresoaccustomedtotheusualroutineofroundingthatImakesuretheyunderstandthatwhendetermining k forsystematicsampling,weshouldalwaysrounddown.Thispracticeinvolvessomenicecriticalthinking andwillalsoleadtocorrectanswersforhomeworkexercises,butitisnotimportantformanyactualstudiesbecausethemaximumnumberofindividualsthatmightbesurveyedormeasuredisunclear.Forexample,thetotal numberofpeoplethatmightvisitastoreinonedayisunknown.

Althoughusingsystematicsamplingforqualitycontrolofproductsonanassemblylinemightnotimpress students,theydotendtoﬁnditcompellingthattheSupremeCourtruledthatsobrietycheckpointsarelegal,but policedepartmentsmustﬁleaplanthatdescribeshowtheywillrandomlyselectdriversforsobrietytests.Infact, Exercise43describeshowamotoristarrestedfordrunkdrivingcontestedandwonhiscourtcasebecausethe policedidnotperformsystematicsamplingcorrectly.

Suchauthenticstorieswillmakethecoursecomealiveforyourstudents.Considerresearchinghowyourlocal policedepartmenthascarriedoutsobrietycheckpoints.

OBJECTIVE2COMMENTS

InsteadofusingtheethnicbreakdownatEmoryUniversityinProblem2todiscussstratiﬁedsampling,consider researchingtheethnicbreakdownatyourcollege.Oryoucouldresearchtheacademic-majorbreakdown.Itis idealifoneormoreofthecategorieshasapercentageclosetozerotoillustratethatstratiﬁedsamplingcanensure thatsuchcategoriesarerepresentedinthesample.

AlthoughthecalculationsforProblem2suggestthattheNativeAmericanshouldnotbeincludedinthe sample,youcouldpointoutthatitmightbeagoodideatoincludethestudenttohearthestudent’spossibly uniqueperspective.

Forfearofcreatingmoreconfusionthanunderstanding,Ididnotstateinthetextbookthatstratiﬁedsampling canbeusedtosurveyadisproportionateamountofcategoriesandthatthiscanbecorrectedbyusingaweighted meanorothermeasure.Thisway,thetruecompositionofcategorieswithsmallpercentagesarewellrepresented. Itisprobablynotworththetroubletoincludeweightinginyourlessonplan–thisformofstratiﬁedsamplingisnot evenaddressedinmanyintroductorystatisticstextbooks–butifyouwanttodiscussit,Iadvisewaitinguntilyou reachSection4.1,whichintroducestheconceptofarithmeticmean.

ForProblem3,studentstendtoneedclarificationwhywefindtheappropriateproportionsbydividingthecells bythegrandtotal871ratherthanthesubtotals.SomereviewersfeelthatProblem3istoodifficultforstudents, butI’vefoundmystudentscanhandleit.Therealquestioniswhetherworkingwitha single variablesuchas ethnicitysufficestogetacrosstheideaofstratifiedsampling.Onebenefitofworkingwithtwo-waytablesisthat itwillprimethepumpforstudents’workwithtwo-waytablesinChapters3–5.

OBJECTIVE3COMMENTS

IprefertodiscussExample3inthetextbooktogetacrosstheideaofclustersamplingbecausestudentscanrelate tothesituation.Iemphasizewhywedividethe1000studentsbythe smallest classsize.Thisconcept,aswell aswhyweround k downforstratiﬁedsampling,makesforgoodconceptualquestionsonquizzesandexams.I alsoemphasizethatthebeneﬁtofclustersamplingisthatnoframeofindividualsisrequiredanditcansavetime, money,andeffort.

OBJECTIVE4COMMENTS

Studentsoftenconfusestratiﬁedsamplingwithclustersampling.ReferringtoFigs.8and9onpage105ofthe textbookorcreatingyourowndiagramscanhelpyoucompareandcontrastthetwomethods.Table14onpage 105ofthetextbookprovidesanicecomparisonoftherequirementsandbeneﬁtsofthefoursamplingmethods.

Evenforstudentswhoarenotintosports,comparingclusterandstratiﬁedsamplingbyreferringtofootball teams(orsomeothersport’steams)asclusters/strataseemstogetacrossthedifferenceinthetwosampling methods.

Evenoncestudentscanidentifythevarioustypesofsamplingmethods,theirunderstandingtendstoslipaway withtime.It’sagoodideatorevisitthistopicneartheendofChapter2andtoencouragestudentstoreviewthe methodsthoroughly.

GROUPEXPLORATION:PerformingSamplingMethods

Providingadiagramofthenamesofstudentsandwheretheyareseatedcanmovethingsalong.Iemphasize thattheyshouldrecordtheseedthattheyselected.Havinggroupscarryouttheirsurveyscanbechaoticand inefﬁcient,unlessyouprovidesomestructure.Eachgroupcouldselectonemembertobethesurveyor.The surveyorscouldcirculatetheclassroomwhiletheotherstudentsremainseated.Classtimecouldbepreserved byhavingthestudentsparticipateinthesurveysonline,butthiswouldrequiretimeandeffortonyourpartto coordinatepostingquestions,respondingtoquestions,andpostingresponses.

Althoughthisexplorationmaybetootime-consuming,thephysicalactofcarryingoutthethreetypesof samplingmethodswouldenhancestudents’understandingandretentionofthethreemethods.

OBJECTIVE5COMMENTS

Ihesitatedinconstructingdefinitionboxesfor conveniencesampling and voluntaryresponsesampling forfear thatstudentswouldthinkthatthesetechniquesarevalidsamplingmethods.Forthesamereason,Iwasalso hesitanttoincludeexercisesthatrequirestudentstoidentifysuchbadsamplingpractices.However,reviewers suggestedIincludedefinitionboxessotherewouldbeaclearwaytorefertosuchbadsamplingmethods.Ifelt thiswasagoodpoint,sointheend,Iincludedthedefinitionboxes.Hopefullytheboldfacewarningsonpage106 ofthetextbookandyourverbalwarningswillimpressuponstudentsthatthesemethodsshouldneverbeused.

Groupsofstudentsarequicktopointouttheproblemswithusingaspeciﬁcformofvoluntarysamplingorthe moregeneralconveniencesampling.

SECTION2.3LECTURENOTES

Objectives

1. Identifythefollowingcomponentsofagoodstudy: treatmentgroup, controlgroup, placebo, singleblindanddouble-blind, randomassignment,andlarge-enoughsamplesize.

2. Identify experiments and observationalstudies.

3. Identify explanatoryvariables, responsevariables, association,and causation.

4. Identify lurkingvariables and confoundingvariables

5. Redesignanobservationalstudyintoanexperiment.

OBJECTIVE1

Deﬁnition Treatmentgroupandcontrolgroup

Each treatmentgroup inastudyisacollectionofindividualswhoreceiveacertaintreatment(orhavea certaincharacteristicofinterest).The controlgroup isacollectionofindividualswhodonotreceiveany treatment(ordonothavethecharacteristicsofanytreatmentgroup).

Whendesigningastudy,itisimportantthateachtreatmentgroupbeassimilartothecontrolgroupas possible,exceptforthecharacteristicofinterest.

1. Aresearcherwantstoinvestigatewhetheranewdruglowersthebloodpressureofpatientswhohavehigh bloodpressure.Describethedesignofapossiblestudy,whichincludesatreatmentgroupandacontrol group.

• The placeboeffect occurswhenthecharacteristicofinterestchangesinindividualsduetotheindividuals believingthecharacteristicshouldchange.

• A placebo isafakedrugorprocedureadministeredtothecontrolgroup.

• Ina single-blindstudy,individualsdonotknowwhethertheyareinthetreatmentgroup(s)orthecontrol group.

• Ina double-blindstudy,neithertheindividualsnortheresearcherintouchwiththeindividualsknowwho isinthetreatmentgroup(s)andthecontrolgroup.

2. ExplainhowthedesignofthestudyyoudescribedinProblem1couldbemodiﬁedsothatitwouldbe double-blindanduseaplacebo.

Deﬁnition Randomassignment

Randomassignment istheprocessofassigningindividualstothetreatmentgroup(s)andthecontrolgroup randomly.

3. Aresearcherwantstotestwhetherahigh-proteindietimprovescollegemalesprinters’performances.The researcherrandomlyselectsthe10collegemalesprintersshowninthefollowingtable.Usetheseed892to randomlyselect5ofthesprintersforthetreatmentgroup.Theother5studentswillbeinthecontrolgroup.

Inawell-designedstudy,

BennyDavidNicoAustinDaniel RyanMattMarcosCameronRandell

ComponentsofaWell-DesignedStudy

• Thereshouldbeacontrolgroupandatleastonetreatmentgroup.

• Individualsshouldberandomlyassignedtothecontrolgroupandthetreatmentgroup(s).

• Thesamplesizeshouldbelargeenough.

• Aplaceboshouldbeusedwhenappropriate.

• Thestudyshouldbedouble-blindwhenpossible.Ifthisisimpossible,thestudyshouldbesingle-blind ifpossible.

OBJECTIVE2

Deﬁnition Experimentandobservationalstudy

Inan experiment,researchersdeterminewhichindividualsareinthetreatmentgroups(s)andthecontrol group,oftenbyusingrandomassignment.Inan observationalstudy,researchersdonotdeterminewhich individualsareinthetreatmentgroup(s)andthecontrolgroup.

Identifywhetherthestudyisanexperimentoranobservationalstudy.Discusswhetherthecomponentsofa well-designedstudywereused.

4. InastudytodeterminewhetherthedruglatrepirdineimprovesthementalimpairmentofpatientswithHuntingtondisease,researchersrandomlyassigned403patientswithmildtomoderateHuntingtondiseasetoa treatmentgroupandacontrolgroup.For3timesdailyfor26weeks,latrepirdinewasorallyadministered tothetreatmentgroupandaplacebowasorallyadministeredtothecontrolgroup.Thestudyconcluded thatlatrepirdinedoesnotimprovethementalimpairmentofpatientswithHuntingtondisease(Source:A randomized,Double-Blind,Placebo-ControlledStudyofLatrepirdineinPatientswithMildtoModerate HuntingtonDisease,Kieburtzetal.).

5. Inastudytodeterminewhethereliteathleteshaveunbalancedpostures,researchersmeasuredtheposture ofthefollowingeliteathletes:29rugbyplayers,29bikers(motorcyclists),10skiers,and10judokas.The posturesof71amateurathleteswerealsomeasured.Thestudyfoundthateliterugbyplayers,eliteskiers, andelitejudokashadunbalancedposturesbutelitebikershadbalancedpostures(Source:Assessmentof BodyPlantarPressureinEliteAthletes:anObservationalStudy,G.Gobbietal.).

OBJECTIVE3

Deﬁnition Explanatoryandresponsevariables

Inastudyaboutwhetheravariable x explains(affects)avariable y,

• Wecall x the explanatoryvariable (or independentvariable).

• Wecall y the responsevariable (or dependentvariable).

Anexplanatoryvariablemayormaynotturnouttoaffect(explain)theresponsevariable.

6. Inadouble-blindstudy,40healthyforeignstudentswererandomlyassignedtotakepillsofthenatural substanceRhodiolaroseaextractSHR-5oraplacebofor20daysduringanexaminationperiod.The studyconcludedthatthesubstanceimprovespeople’smentalfatiguecausedbystress(Source:ADoubleBlind,Placebo-ControlledPilotStudyoftheStimulatingandAdaptogenicEffectofRhodiolaRoseaSHR-5 ExtractOntheFatigueofStudentsCausedbyStressDuringanExaminationPeriodwithaRepeatedLowDoseRegimen,Spasovetal).

a. Describethetreatmentandcontrolgroups.

b. Isthestudyanexperimentoranobservationalstudy?Explain.

c. Describethesampleandthepopulation.

d. Whataretheexplanatoryandresponsevariables?

e. Whatdoesitmeanthatthestudyisdouble-blind?Howcouldthatbeaccomplished?

• Thereisan association betweentheexplanatoryandresponsevariablesiftheresponsevariablechangesas theexplanatoryvariablechanges.

• Ifthechangeintheexplanatoryvariable causes achangeintheresponsevariable,wesaythereis causality.

DeterminingCausality

• Awell-designedexperimentcandeterminewhetherthereiscausalitybetweentheexplanatoryandthe responsevariables.

• Mostobservationalstudies cannot determinewhetherthereiscausalitybetweentheexplanatoryand responsevariables.Theycanonlydeterminewhetherthereisanassociationbetweenthetwovariables.

OBJECTIVE4

Deﬁnition Lurkingvariable

A lurkingvariable isavariablethatcausesboththeexplanatoryandtheresponsevariablestochangeduring thestudy.

Lurkingvariablesmustbeavoided.Wecanusuallydosobyusingrandomassignment.

Deﬁnition Confoundingvariable

A confoundingvariable isavariableotherthantheexplanatoryvariablethatcausesorhelpscausethe responsevariabletochangeduringthestudy.

Awell-designedexperimentrequirescarefulplanningsothatthereareasfewconfoundingvariablesas possible.

OBJECTIVE5

7. Aresearcherwantstodeterminewhetherwatchingtelevisionandplayingvideogamescausesattention deﬁcithyperactivitydisorder(ADHD)inchildren.Theresearcherrandomlyselects200childrenandasks theirparentshowmuchtelevisiontheirchildrenwatchdailyandwhethertheirchildrenhaveADHD.The researcheranalyzestheirresponsesandconcludesthatwatchingtelevisionandplayingvideogamescauses ADHDinchildren.

a. Describesomeproblemswiththeobservationalstudy.Includeinyourdescriptionatleastonepossible lurkingorconfoundingvariableandidentifywhichtypeitis.

b. Redesignthestudysothatitisawell-designedexperiment.

HW 1,3,5,7,11,13,15,17,19,23,29,33,41

SECTION2.3TEACHINGTIPS

ThisisthemostimportantsectionofChapter2becauseitaddressessomanyimportantfeaturesofawell-designed studyanditemphasizestheconceptofcausation,whichismisusedsooftenbythemediaandbusinesses.

Ifyouaretightontime,itisprobablynotworthdistinguishinglurkingvariablesfromconfoundingones.Itis probablyenoughforstudentsatthisleveltolearnthatawell-designedexperimentcanavoidtheimpactofsuch variables.

OBJECTIVE1COMMENTS

Afterdeﬁning treatmentgroup and controlgroup,Idiscusstheimportanceofcontrolgroups.Ialsoexplainthat individualsinthecontrolgroupareconsideredpartofthesample.

Whenﬁrstdescribingthecomponentsofagoodstudy,Ikeepthingssimpleandsticktodescribingstudies thathavejustonetreatmentgroupandacontrolgroup.Later,Iexplainthebeneﬁtsofusingmultipletreatment groups.

Studentsarequicktopickuponthemeaningandbeneﬁtofaplacebo.Studentstendtoalreadyknowthat sugarpillsareusedasplacebos,butmoststudentsdon’tknowthatplacebosincludefakeprocedures.Infact, manystudentsareshockedtolearnthatfakekneesurgerieswereusedinthestudythatisdescribednearthetopof page112ofthetextbook.ImakesurethatIsharethisstudywithstudentsbecausewhentheyhavesuchastrong emotionalresponse,theyarethatmuchmorelikelytoretaintheconcept.

Randomassignmentisacrucialconceptbecauseitisoftenwhatdistinguishesexperimentsfromobservations. Unfortunately,studentsoftenconfuserandomassignmentwithrandomsampling,soImakesureIcompareand contrastthesetwotechniquesandremindstudentsofthedistinctionbetweenthemethodsseveraltimesduringthe course.Itisworthpointingoutthatinmanyexperiments,theindividualswerenotrandomlyselectedbutthatis okayprovidedtheresearchersperformedrandomassignment.

Havinggroupsofstudentsﬁrstrandomlyselectasamplefromapopulationandthenrandomlyassignmembers ofthesampletoatreatmentgroupandacontrolgroupwouldbeaworthwhilewayforstudentstolearnthe differencebetweenselectingarandomsampleandperformingrandomassignment.Ifyoucannotaffordthetime, considerdisplayingadiagramsimilartoFig.12onpage113ofthetextbook.

Thetextbook’sdiscussionaboutsamplesizeispurposelyvague.Itisonlyoncestudentsstudyinferential statisticsthattheycanquantifyhowthesamplesizeisrelatedtotheerrorbound.Atthispointinthecourse,I saythatthelargerthesamplesize,themoreinformationwewillhavesothelowertheerrorwillbe;therefore,a relativelylargesamplesizeisdesirable.Becausewehavenotdiscussedthearithmeticmeanyet,Idonotbother tosaythat"relativelylarge"canmeanquitedifferentthingsforestimating,say,thepopulationmeanversus estimating,say,thepopulationproportion.

OnceIhavediscussedallthecomponentsofagoodstudy,Iliketodisplayanactualstudywhichconsistsof severalpagesonanoverhead.Idescribehowthestudyisstructuredandpointoutthecomponentsthatwehave discussedingeneral.Iemphasizethatstudentsmaysomedayhavetoreadsuchstudiesfortheircareers.This driveshomethepointthattheconceptswediscussinclassaretrulyrelevantandimportant.

Thegreatestchallengewiththisobjectiveisreadingcomprehension.Thehomeworkexercisesareatahigher readinglevelthanmostoftherestoftheexercisesinthebook.Thisisduetonumerousreasons,includingthe largenumberofaspectsofastudy,theintricaciesofcontrollingforconfounding,andcomplicatednamesofdrugs. Iurgestudentstoreaddescriptionsofstudiesmanytimes.Ialsosuggestthatafterreadingeachsentence,students shouldpauseandreﬂectonitsmeaninganddeterminewhythataspectofthestudyisimportant.Mostofmy studentsdonotknowhowtoperformengagedreading,andIhavetodevotemuchtimetocoachingthemonthis. Itcanbehelpfultomodelit.Forexample,Ireadasentenceoutloudandthensayoutloudallthethoughtsand questionsIhaveinresponsetothatinformation.ThenIdothesameforthenextsentenceandthenext,untilI reachtheendofthedescription.MoststudentsareamazedatthelevelofengagementIhavewithreading.

Learninghowtoreadinanengagedwaycanbeneﬁtstudentsinalloftheircoursesandlaterintheircareer. Forsomestudents,itmightbethemostpowerfullearningexperienceofthesemester.

OBJECTIVE2COMMENTS

Initially,studentshaveaneasytimedistinguishingbetweenexperimentsandobservationalstudiesbecausethey canscanthedescriptionofastudytoseewhetherthephrase"randomassignment"isincluded.However,students tendtoforgetthatrandomassignmentisthekeydistinctionunlesstheyareremindedmanytimes.Ifanobservationalstudyinvolvesexplanatoryandresponsevariablesinwhichcausationseemslikely,studentstendtoassume there is causation.

Studentsstruggletolearnwhyrandomassignmentallowsresearcherstodeterminewhetherthereiscausation. Tohelpthemunderstand,Igivealotofexamplesofwhatcangowrong(i.e.lurkingvariables)ifrandom assignmentisnotused.Explainingthisconceptcanserveasagoodconceptualquestiononaquizorexam.

OBJECTIVE3COMMENTS

Oncestudentsunderstandthattheexplanatoryvariableinvolvesthetreatmentthatthetreatmentgroupreceivesand theresponsevariableinvolvessomeresponseduetothetreatment,studentshaveafairlyeasytimeidentifying thetwovariables.ThebiggeststumblingblockisthesameaswithObjective1:readingcomprehension.The suggestionsIgaveregardingthatobjectiveapplyhere,too.

Togetacrosstheideathatthepresenceofanassociationbetweentwovariablesdoesnotguaranteecausality, IdescribetheﬁreﬁghtersituationillustratedbyFig.13onpage116ofthetextbook.Thisbringstheclassroom discussionfullcircletothefactthatwecanuseexperimentstodeterminewhetherthereiscausalitybecause experimentsemployrandomassignment.

Thereasonthetextbookstatesthat most observationalstudiescannotdeterminewhetherthereiscausation isbecauseinsomecases,causalitycanbedeterminedfrom"BigData."However,toavoidconfusion,Idon’t explainthistostudents.Evenwithoutthiscomplication,itisanuphillbattletomakesurethatallstudentslearn thepitfallsofobservationalstudiescommonlyreferredtobythemedia.Onecouldarguethatthisisthemost importantstatisticalinsightstudentscangainfromthecourse.

OBJECTIVE4COMMENTS

Studentshavetroubledistinguishingbetweenlurkingandconfoundingvariables,whichisunderstandable.AlthoughIsketchdiagramssuchasthoseinFigs.14and15onpage117ofthetextbook,Idon’tspendmuchtime makingthedistinction.Whatreallymattersisthatstudentsunderstandthatbothtypesofvariablescanwreak havoc.Iemphasizethattocontendwiththesevariables,researchersmustuserandomassignmentandtakegreat

careindesigninganexperiment.

OBJECTIVE5COMMENTS

Whendiscussinghowtoredesignanobservationalstudyintoawell-designedexperiment,Iemphasizethatakey stepistointroducerandomassignment.ThenIsuggeststudentsreadalistofcomponentsofawell-designed experimentandcheckwhethereachofthecomponentsispresentinthestudy.Ofcourse,itisimpossibleto employcomponentssuchasdouble-blindinallstudies,butdiscussingwhyacomponentcannotbeusedcanbea learningexperience,too.

GROUPEXPLORATION:DesigninganExperiment

Becausedesigninganexperimentismorechallengingthanplanningasurvey,thisexplorationismorechallenging thantheonesinSections2.1and2.2.Atthispointinthecourse,moststudentshaveonlylearnedabouta fewexperimentsanditwillbedifﬁcultforthemtothinkofanexperimentontheirown.Plus,manyorallof theexperimentsyouhavediscussedlikelyinvolveequipmentormedicationthatstudentswon’thaveaccessto. Distributingahandoutwithexamplesofsimpleexperimentsmayhelpstudentsthinkofanexperiment.Ifyou can’taffordthetimeforstudentstobrainstormideas,youcouldallowstudentstochoosefromyourexamples,but thiswouldrobthemofagreatdealofcriticalthinking.

IfyoufacilitatedtheexplorationinSection2.2,studentsshouldhaveaneasytimecarryingoutthecluster sampling.

CHAPTER3OVERVIEW

Bynowyouhaveprobablysurveyedyourstudents,butifyouhaven’tyet,Iadvisedoingsoverysoon.Youcan usethedataasearlySection3.1whenconstructingbargraphs.Andhavingaccesstorawdatamayrevealresponse and/ornonresponsebiasthatyoucanrefertoasareminderofChapter2material.

Itiseasytobecomeboggeddownwiththischapterbecauseitincludessomanytypesoftablesanddiagrams, butitisnotnecessarytohavestudentslearnaboutallofthemforseveralreasons.

First,studentsonlyneedtoknowabouttwo-waytables(Section3.2)andhistograms(Section3.4)todothe vastmajorityofexercisesinsubsequentchapters.Two-waytablesareanexcellentwayforstudentstograpplewith probability(Sections5.1–5.3)anddensityhistogramsareagreatwaytopreparestudentsfornormaldistributions (Sections5.4and5.5).ForChapters6–10,studentswillworkextensivelywithscatterplots,butthosediagrams arenotincludedinChapter3.(TheyareintroducedinSection6.1.)

Second,asidefromaquickrun-throughofmanytypesoftablesanddiagrams,themaintablesanddiagrams usedinintroductorystatisticsareonceagaintwo-waytables,histograms,andscatterplots.

Third,Idonotbelievethepointof Pathway istoaddresseverysingledescriptivestatisticstopicthatishandled inintroductorystatistics.Rather, Pathway shouldfocusonkeyconceptsthatlayafoundationsostudentscanhave surefootinginintroductorystatisticscoursesastheylearncomplexconceptssuchasthesamplingdistribution andhypothesistesting.

Forexample,itisfarmoreimportantthatstudentshaveanin-depthunderstandingofthenormalcurvethan itisforthemtoknowhowtoconstructamyriadoftypesoftablesanddiagrams.Thatiswhythetextbook emphasizestheinterpretationofdensityhistograms(Section3.4).

Whatevertablesanddiagramsyouincludeinthecourse,makesuretheemphasisisoninterpretingthem.It istheinterpretationofconceptsandresults,nottheconstructionoftablesanddiagrams,thatchallengesmost introductorystatisticsstudents.That’swhythefourcharacteristics(Sections3.3and3.4)ofanumericalvariable areintroducedinthischapterratherthaninChapter4.

Othertopicsthatarekeytothischapterarethewaysdiagramscanbeusedtopersuadeormislead(Section3.5). Somestudentswillreadstatisticalreportsintheircareers.Fewmayperformstatistics.Butallstudentscanbeneﬁt frombecomingmorecriticalofdiagramsdisplayedbybusinessesandthemedia.

SECTION3.1LECTURENOTES

Objectives

1. Identify categoricalvariables and numericalvariables

2. Constructandinterpret frequencytables and relativefrequencytables.

3. Constructandinterpret frequencybargraphs and relativefrequencybargraphs.

4. Describethemeaningsof AND and OR

5. Usearelativefrequencybargraphtoﬁndproportions.

6. Interpret multiplebargraphs

OBJECTIVE1

Deﬁnition Categoricalvariable

A categoricalvariable (or qualitativevariable)consistsofnamesorlabelsofgroupsofindividuals.

Deﬁnition Numericalvariable

A numericalvariable (or quantitativevariable)consistsofmeasurablequantitiesthatdescribeindividuals.

1. Identifywhetherthevariableiscategoricalornumerical.

a. Thesalary(indollars)ofaperson

b. Thestatewhereapersonlives

c. TheZIPcodeofahomeinIllinois

d. Avariableconsistingofzeroesandones,where0standsforafull-timestudentand1standsfora part-timestudent

OBJECTIVE2

Deﬁnition Frequencyofacategory

The frequencyofacategory isthenumberofobservationsinthatcategory.

A frequencytable foracategoricalvariableisatablethatlistsallthecategoriesandtheirfrequencies.

2. Themusicgenresofthe20top-sellingsinglesduringtheweekendingonSeptember5,2015,areshownin thefollowingtable.Constructafrequencytable.

R&BDanceElectronicPopPopDancePop PopPopPopAlternativeHip-Hop/RapDanceDance Hip-Hop/RapPopPopPopAlternativePop

Source: AT40

Deﬁnition Frequencydistributionofacategoricalvariable

The frequencydistributionofacategoricalvariable isthecategoriesofthevariabletogetherwiththeir frequencies.

ThefrequencytableweconstructedinProblem2describesthefrequencydistributionofthecategoricalvariablemusicgenre.

Deﬁnition Relativefrequency

The relativefrequencyofacategory isgiveby frequencyofthecategory totalnumberofobservations

• ForProblem2,therelativefrequencyofdancecategoryis 4 20 = 1 5

• Arelativefrequencyisaproportion.

• A relativefrequencytable ofacategoricalvariableisalistofthecategoriesandtheirrelativefrequencies.

3. RefertothefrequencytableweconstructedinProblem2.

a. Whatistherelativefrequencyofthehip-hop/rapcategory?

b. Constructarelativefrequencytable.

c. Whichcategoryhasthelargestrelativefrequency?Whatisthatrelativefrequency?Whatdoesitmean inthissituation?

Weagreetoroundrelativefrequenciesandproportionstothethirddecimalplace.

Deﬁnition Relativefrequencydistributionofacategoricalvariable

The relativefrequencydistributionofacategoricalvariable isthecategoriesofthevariabletogetherwith theirrelativefrequencies.

4. UseStatCrunchtoconstructafrequencyandrelativefrequencytableofthemusicdistribution.

SumofRelativeFrequencies

Foracategoricalvariable,thesumoftherelativefrequenciesofallthecategoriesisequalto1.

OBJECTIVE3

A frequencybargraph isagraphthatusesheightsofbarstodescribethefrequenciesofcategories.

5. Constructabargraphofthemusicdistribution.

A relativefrequencybargraph isagraphthatusesheightsofbarstodescribetherelativefrequenciesof categories.

6. Constructarelativefrequencybargraphofthemusicdistribution.

OBJECTIVE4

• When"AND"isusedwithtwocategories,thismeanstoconsidertheobservationsthatthecategorieshave incommon.

• When"OR"isusedwithtwocategories,thismeanstoconsidertheobservationsinthecategoriesalltogether.

7. ThedatesofSeptember2016areshowninthefollowingtable.

SunMonTuesWedThursFriSat 123 45678910 11121314151617 18192021222324 25262728

a. Findthedatesthatareinthefourthweek.

b. FindthedatesthatareWednesdays.

c. FindthedatesthatareinthefourthweekANDareWednesdays.

d. FindthedatesthatareinthefourthweekORareWednesdays.

OBJECTIVE5

8. Arelativefrequencybargraphofthemusicdistributionisshowninthefollowingﬁgure.

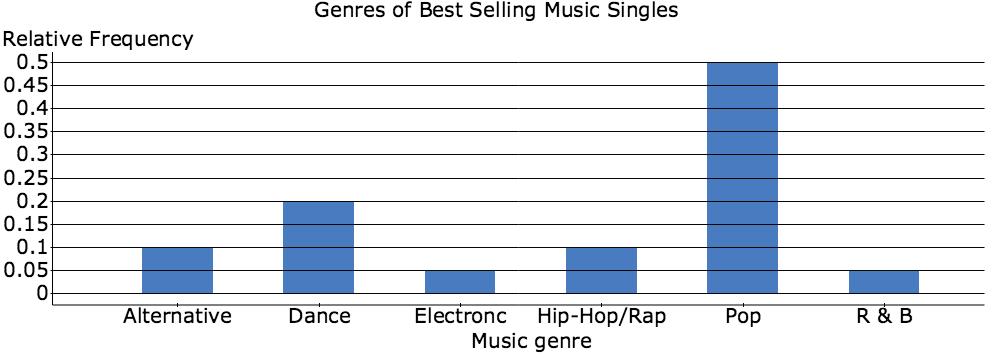
Source: AT40

Findtheproportionoftheobservationsthat

a. fallintheelectroniccategory.

b. doNOTfallinelectroniccategory.

c. fallinthealternativecategoryORfallinthepopcategory.

d. fallinthealternativecategoryANDfallinthepopcategory.

NotethatinProblem8(b),weusedtheproportionoftherestproperty(Section1.3).

ProportionoftheRest

Let a b betheproportionofthewholethathasacertaincharacteristic.Thentheproportionofthewholethat doesNOThavethatcharacteristicis

OBJECTIVE6

A multiplebargraph isagraphthathastwoormorebarsforeachcategoryofthevariabledescribedonthe horizontalaxis.

9. Inasurveyin2012,1960adultswereaskedthefollowingquestion:“Generallyspeaking,doyouusually thinkofyourselfasaRepublican,Democrat,Independent,orwhat?”Theresultsofthesurveyaredescribed bythemultiplebargraphinthefollowingﬁgure.

Relativefrequency

PoliticalParty,byGender

Politicalparty

Source: GeneralSocialSurvey

a. WhatproportionofwomenthoughtofthemselvesasDemocrats?

b. Towhichpoliticalpartydidthegreatestproportionofmenchoose?

c. ComparetheproportionofwomenwhothoughtofthemselvesasIndependentstotheproportionof menwhothoughtofthemselvesasIndependents.

d. Atotalof1081womenand879menrespondedtothesurvey.Weretheremorewomenormenwho thoughtofthemselvesasIndependents?Howisthispossible,giventherewasasmallerproportionof womenwhothoughtofthemselvesasIndependentsthanmen?

e. Onthebasisofthemultiplebargraph,astudentconcludesthat24%of all AmericanmenareRepublicans.Whatwouldyoutellthestudent?

Foramultiplebargraph,itismoremeaningfulfortheverticalaxistodescriberelativefrequencies ratherthanfrequencies.

HW 1,3,9,11,13,21,23,27,29,31,33,35,39,43,51

SECTION3.1TEACHINGTIPS

Onecouldarguethatthekeyobjectiveofthissectionisforstudentstobeabletouserelativefrequencybar graphstoﬁndproportions.Thisskillwilllaythefoundationforworkwithdensityhistograms(Section3.4)and probability(Chapter5).AclosesecondwouldbethemeaningsofANDandOR,whichwillbeaddressedinthe restofChapter3aswellasChapter5.

OBJECTIVE1COMMENTS

Studentsarequicktopickuponthedifferencebetweencategoricalandnumericalvariables,butImakesurethey understandthatnumbersaresometimesusedtorepresentthecategoriesofacategoricalvariable.Problems1(c) and1(d)areexamplesofthis.

Inthissection,thetextbookdoesnotexplainthatdiscreteandcontinuousvariablesaretwotypesofnumerical variablesbecausethissectionfocusesoncategoricalvariables.Discreteandcontinuousvariablesaredescribedin Section3.3,whichfocusesonnumericalvariables.

Distinguishingbetweendiscreteandcontinuousvariablesisimportantformanyreasons,includingthatitisa keystepindeterminingwhichtypesofstatisticaldiagramsareappropriatetouse.

OBJECTIVE2COMMENTS

Becausestudentshaveaneasytimeconstructingfrequencyandrelativefrequencytables,Imovequicklythrough

thismaterial.Thisisagoodopportunitytousedatacollectedfromsurveyingstudentsbecausetheyareusually interestedinlearningabouttheirclassmates.Plus,hopefullytheywillmaketheconnectionthatiffrequencyand relativefrequencytablescandescribecategoricalvariablesaboutthemselves,thensuchtablescouldbeusedto describemostanycategoricalvariable.

Forstarters,Iwriteontheboardasubset(about20)ofmystudents’responsestoaquestionabouttheir favoritemusicgenres,usingthecategory"other"sothattherearenottoomanycategories.Next,Iconstructa frequencyandrelativefrequencytable.ThenIdemonstratehowtouseStatCrunchtoconstructsuchatablefor allthestudentsintheclass.Finally,IdemonstratehowtouseStatCrunchtoconstructsuchatableforadataset consistingofhundredsofobservations.Thisprogressiondisplaysthepoweroftechnology.

Eachtimeanewtableordiagramisintroducedinthischapter,Irequirestudentstoconstructacoupleofthem byhandandfromthenonallowstudentstousetechnology.Thisway,studentsgettheideaofhowtoconstruct thevariousdiagramsbuttheyarenotturnedofftostatisticsbythetediumofconstructinglotsofthem.

Idescribefrequencyandrelativefrequencydistributionsofacategoricalvariablecarefully,becausetheword distribution isusedsoofteninthecourse.It’sagoodideatoremindstudentsofitsmeaningeachtimeitisused inanewcontext(e.g.frequencydistributionofanumericalvariableinSection3.3)becausemanystudentswill otherwiseforget.

IfyoutaughtfromChapter1,thenyourstudentsshouldalreadyhaveaprettygoodunderstandingofproportions.Nowyoucanemphasizethatarelativefrequencyisaproportion.Inthefuture,youcanstresshowboth proportionsandrelativefrequenciesarerelatedtopercentiles(Section3.3),areasofbarsofdensityhistograms (Section3.4),andprobabilities(Chapter5).

Ialsoemphasizethatthesumoftherelativefrequenciesofallthecategoriesofacategoricalvariableisequal to1.Thisdovetailswiththeconceptthatthesumofallthepartsisequaltothewhole(Section1.3).These conceptssetthestageforthecomplementrule,whichwillbeinformallyusedinthissectionandsubsequentones andformallyintroducedinSection5.2.Iadvisethatstudentscheckthatthesumoftherelativefrequenciessum to1whenevertheyconstructarelativefrequencytable.

WhengoingoverProblem8(b),Iﬁrstﬁndtheprobabilitybyaddingtheprobabilitiesforallthecategories exceptelectronics.ThenIasktheclassifthere’saneasierway.Studentsarequicktosuggestusingtheproportionof-the-restproperty(Section1.3).Asmuchaspossible,Ipromptstudentstobeactivelearnersintheclassroom inhopesofminimizingmemorizationwithoutunderstanding.

Tellstudentsthattheywillneedtoroundrelativefrequencies(andproportions)tothethirddecimalplacefor theiranswerstomatchtheonesinthebackofthebook(andmostlikelyinMyMathLab).

OBJECTIVE3COMMENTS

Studentshaveaneasytimeconstructingfrequencyandrelativefrequencybargraphsforthemostpart,butthere aredetailsthattheyneedcoachingon.IfyoutaughtfromSection1.1,studentswillhopefullyrememberthat theyshoulduseuniformscalingonthe(vertical)axis.Inaddition,youshouldtellthemtowrite"frequency"or "relativefrequency"ontheverticalaxis,thecategoricalvariableanditscategoriesbelowthehorizontalaxis,and atitleabovethegraph.Ideally,abargraphshouldconveythecomplete"story"ofthedata.

Iadvisestudentstoreadinstructionscarefully,especiallyontests.Weakerstudentstendtoconstructfrequency bargraphswhenaskedtoconstructrelativefrequencygraphs,orvice-versa.Studentshavesometimeseven constructedafrequencybargraphwhenrequestedtoconstructafrequencytable.

Afterstudentspracticeconstructingoneortwobargraphsbyhand,IallowthemtouseStatCrunchtoconstruct them.

InChapters3and4,thehomeworkexercisesarestructuredsothatthereisﬁrstatleastapairofexercises withabout10observations,nextatleastapairofexerciseswithabout25observations,andthenatleastapair ofexerciseswithatleast50observations.Thisstructureismeanttoofferinstructorsﬂexibilityinhavingstudentsconstructdiagramsand/orcomputemeasurementswithorwithoutstatisticaltechnology.Forexample,I wouldhavestudentsconstructabargraphforthe15observationsinExercise35byhand,the24observationsin Exercise37byhand,andthe50observationsinExercise39usingtechnology.

Thepurpleicon"DATA"ﬂagsexerciseswhosedatasetscanbedownloadedfromMyMathLabandfromthe PearsonDownloadableStudentResourcesforMath&Statisticswebsite: http://www.pearsonhighered.com/mathstatsresources.

OBJECTIVE4COMMENTS

Althoughitisabitjarringtoreadthewords AND and OR inalluppercaseletters,thisisahelpfulsignaltostudents thatthewordsarebeingusedinamathematicalway.DrawingadiagramsimilartoFig.5onpage137ofthe textbookcanhelpclarifythemeaningsof AND and OR.SuchadiagramisagentleintroductiontoVenndiagrams withoutcallingthemassuchbecausestudentsdonotneedtokeeptrackofsamplespacesandeventsyet.Venn diagramswillbeformallyintroducedinSection5.2.

Ialsodemonstratethemeaningsof AND and OR byhavingoneormorestudentsraisetheirhandsiftheyare inthe,say,secondrowORinthe,say,thirdcolumn.ThenIhaveoneormorestudentsraisetheirhandsiftheysit inthesecondrowANDthethirdcolumn.BeforeIbeginthedemonstration,Imakeitclearthattheentireclass isresponsibleforthecorrectstudentstoraisetheirhandssothateveryoneisinvolvedandalsosothatthestudent whositsinthesecondrowANDthethirdcolumndoesnotfeelputonthespot.Itrytopickarowandcolumnin whichthestudentwhositsintheintersectionisgood-humoredandwon’tmindbeingsingledout.

UsingacalendarsuchastheoneusedinProblem7isyetanothernicewaytoworkwith AND and OR. StudentswillworkwithcalendarsinasimilarmannerwhenﬁndingprobabilitiesinSections5.2and5.3.

Studentswillcontinuetoworkwith AND and OR manytimesinChapters3–5,includingtheimportantuseof AND withthemultiplicativeruleforindependentevents(Section5.3).

OBJECTIVE5COMMENTS

Whenﬁndingproportionsusingarelativefrequencybargraph,Iemphasizeusingtheproportion-of-the-restproperty(Section1.3).Ofcourse,thepropertyisequivalenttothecomplementrule,whichwillbeformallyintroduced inSection5.2.NotethatProblem8(c)isreallyanapplicationoftheadditionrulefordisjointevents.Applying bothprobabilityrulesnow(withoutcallingthemassuch)isgoodpreparationforsolvingprobabilityproblemsin Chapter5,includingworkingwiththenormaldistribution.

GROUPEXPLORATION:RelativeFrequencies

Thisexplorationcouldbeuseddirectlyafterdescribinghowtoconstructrelativefrequencybargraphsanddiscussingthemeaningof OR

OBJECTIVE6COMMENTS

Whenworkingwithmultiplebargraphs,Ihavestudentsreﬂectonthedifferencebetweencomparingfrequencies versuscomparingrelativefrequencies(Problem9d).Studentstendtodrawconclusionsbycomparingfrequencies wheninmanyofthosecasesitismoremeaningfultocomparerelativefrequencies.Directlyfollowingsucha discussion,Ipointoutthatformultiplebargraphs,itismoremeaningfulfortheverticalaxistodescriberelative frequenciesthanfrequencies.

Becausetheissueofcomparingfrequenciesversuscomparingrelativefrequenciesissoimportant,itisaddressedinmanyexercisesthroughoutthetextbook.

IalsohavestudentsreﬂectonconceptsfromChapter2(Problem9e).ExercisesscatteredthroughoutChapters3–5continuetorequirestudenttoapplyconceptsfromChapter2sothatstudentsrememberthisfoundational material.

SECTION3.2LECTURENOTES

Objectives

1. Constructandinterpret piecharts.

2. Constructandinterpret two-waytables.

3. Useatwo-waytabletocomputeproportions.

OBJECTIVE1

Thedistributionofacategoricalvariablecanbedescribedbya piechart,whichisadiskwhereslicesrepresent thecategories.Theproportionofthetotalareaforonesliceisequaltotherelativefrequencyforthecategory representedbytheslice.Therelativefrequenciesareusuallywrittenaspercentages.

1. SomeAmericansatleast12yearsofageweresurveyedaboutthemediumtheyfirstusetofindoutabout newmusic.Themediumsandthepercentagesofrespondentswhofirstusethemareshowninthefollowing table.

MediumPercent

Internet44

Radio32

Television9

Newspaper1

Other14

Source: EdisonResearch

a. UseStatCrunchtoconstructapiechart.

b. FindtheproportionoftheobservationsthatfallintheInternetcategory.

c. FindtheproportionoftheobservationsthatdoNOTfallintheInternetcategory.

d. FindtheproportionoftheobservationsthatfallintheradiocategoryORfallinthetelevisioncategory.

e. Onthebasisofthepiechart,astudentconcludesthat44%ofallAmericansatleast12yearsofage ﬁrstusetheInternettoﬁndoutaboutnewmusic.Whatwoudyoutellthestudent?

OBJECTIVE2

A two-waytable isatableinwhichfrequenciescorrespondtotwocategoricalvariables.Thecategoriesofone variablearelistedverticallyontheleftsideofthetable,andthecategoriesoftheothervariablearelistedalong thetop.

2. Inasurveyofoneoftheauthor’sstatisticsclasses,27studentsrecordedwhethertheyhaveaSnapchat account.Afewoftheresponsesareshowninthefollowingtable.

GenderHaveaSnapchataccount?

FemaleNo

MaleNo

FemaleYes

MaleYes

MaleNo

FemaleYes

Source: J.Lehmann

Constructatwo-waytablebyhandthatcomparestheresponsesandgradesoftheindividuals.

3. UseStatCrunchtoconstructatwo-waytablethatcomparestheresponsesandgradesoftheindividuals.

OBJECTIVE3

4. Thefollowingtablesummarizestheresponsesfromall27studentswhoparticipatedinthesurveyabout whethertheyhaveaSnapchataccount.

Source: J.Lehmann

a. HowmanyofthestudentshaveaSnapchataccount?

b. WhatproportionofthestudentsdoNOThaveaSnapchataccount?

c. WhatproportionofthemenhaveaSnapchataccount?

d. WhatproportionofthestudentswhohaveaSnapchataccountaremale?

5. In2012,atotalof1824adultswereaskedthefollowingquestion:“Doyoufavororopposethedeath penaltyforpersonsconvictedofmurder?”Thefollowingtablecomparestheadults’responseswiththeir ethnicities.

FavororOpposethe African DeathPenalty AmericanCaucasianOther Total Favor 128953108 1189 Oppose 14041481 635 Total 2681367189 1824

Source: GeneralSocialSurvey

a. FindtheproportionofadultsinthesurveywhoopposethedeathpenaltyORareCaucasian.

b. FindtheproportionofadultsinthesurveywhoopposethedeathpenaltyANDareCaucasian.

c. FindtheproportionofCaucasianswhoopposethedeathpenalty.

d. FindtheproportionofAfricanAmericanswhoopposethedeathpenalty.

e. AstudentsaysthatCaucasiansinthestudyaremorelikelytoopposethedeathpenaltythanAfrican AmericansinthestudybecausemoreoftheCaucasians(414)opposethedeathpenaltythanthe AfricanAmericans(140).Whatwouldyoutellthestudent?

HW 1,3,5,9,13,15,17,19,21,23,25,30,34

SECTION3.2TEACHINGTIPS

Themostimportantobjectiveofthissectionistouseatwo-waytabletocomputeproportions.Thisskillwillbe extremelyimportantwhenﬁndingprobabilities(Sections5.2and5.3).

OBJECTIVE1COMMENTS

Instructorswhodonothavemanycontacthourswithstudentsshouldconsiderskippingpiechartsbecausecategoricalvariablesaremorelikelytobedescribedbyrelativefrequencybargraphs(Section3.2)inintroductory statistics.Onesmalladvantageofpiechartsisthattheyvisuallyconveyhowacategory’srelativefrequencycomparestothewholebetterthanrelativefrequencybargraphsdo.Anotherreasontodevoteatleastbriefcoverage topiechartsisthatstudentswillusepiechartstoﬁndafewprobabilitiesinSections5.1and5.2.

Ingeneral,Ithinkitisagoodideaforstudentstoconstructacoupleofeachtypeofstatisticaldiagramby handsothattheyunderstandwhat’sinvolved,butpiechartsaretheexception.Idon’twanttotroublestudentsto obtainaprotractor,and,besides,themeaningofpiechartsisfairlyobvious.

Whenworkingwithpiecharts,Icontinuetousethecomplementruleandtheadditionrulefordisjointevents withoutcallingthemassuch.

OBJECTIVE2COMMENTS

ItisimportantthatstudentsknowhowtoconvertdatadisplayedincolumnssuchasthedatadisplayedinProblem2 toatwo-waytablebecausedataareoftenstoredincolumnsandthenconvertedbytechnologytotwo-waytables. Thebestwaytoconveytheconnectionbetweenthetwoformatsistohavestudentsconvertaverysmalldataset onceortwicebyhand.

GROUPEXPLORATION:AssociationversusCausation

Thisactivitycouldbeuseddirectlyafterdiscussinghowtoconstructatwo-waytableoritcouldbeusedto introducetwo-waytables.Problem5isanicereminderthatastrongassociationdoesnotguaranteecausation, whichisacommonstudentmisunderstanding.

OBJECTIVE3COMMENTS

Workingwithtwo-waytablesnowisgoodpreparationforusingtwo-waytablestoﬁndprobabilitiesinSections5.2 and5.3.Justaswithmultiplebargraphs,Iemphasizethatcomparingrelativefrequenciesismoremeaningful thancomparingfrequenciesinmostcases.Ialsopointoutthatbothmultiplebargraphsandtwo-waytablescan beusedtodescribetheassociationbetweentwocategoricalvariables.

Studentstendtohavetroubleknowingwhichrowsorcolumnstoworkwith.Toclarify,Imakesuretocompare andcontrasttheresultsforParts(c)and(d)ofProblem4.

Partofthereasonwhytwo-waytablesareaneffectiveformatforstudentstoﬁndprobabilitiesisthatthe intersectionofeventsdescribedbyrowsandcolumnsisapparent.Forexample,Problem5(a)isgoodpreparation forlearningthegeneraladditionruleinSection5.2.WhengoingoverProblem5(a),Iletstudentstellmethatwe shouldnotcountthefrequency414twice.

SECTION3.3LECTURENOTES

Objectives

1. Identify discretevariables and continuousvariables.

2. Constructandinterpret dotplots

3. Identify outliers ofadistribution.

4. Findpercentilesofadistribution.

5. Estimatethecenterofadistribution.

6. Constructandinterpret stemplots.

7. Constructandinterpret time-seriesplots.

OBJECTIVE1

Deﬁnition Discretevariable

A discretevariable isavariablethathasgapsbetweensuccessive,possiblevalues.

Deﬁnition Continuousvariable

A continuousvariable isavariablethatcantakeonanyvaluebetweentwopossiblevalues.

Identifywhetherthevariableisdiscreteorcontinuous.

1. thenumberofstudentsinaprestatisticscourse

2. thevolume(ingallons)ofwaterinalake

3. aperson’sheight(ininches)

4. theprice(indollars)ofacandybar

Whenidentifyingavariableasdiscreteorcontinuous,weconsiderthepossiblevaluesofthevariable before rounding.

OBJECTIVE2

Toconstructa dotplot,foreachobservation,weplotadotabovethenumberline,stackingdotsasnecessary.

5. Theendorsementsofthe15athleteswiththehighest2015endorsementsareshowninthefollowingtable.

AthleteSportEndorsement(millionsofdollars)

TigerWoodsGolf50 CristianoRonaldoSoccer27 UsainBoltTrackandField21 LebronJamesBasketball44 KobeBryantBasketball26 KevinDurantBasketball35 RoryMcllroyGolf32 RafaelNadalTennis28

MahendraSinghDhoniCricket27 RogerFedererTennis58 MariaSharapovaTennis23 NovakDjokovicTennis31 LionelMessiSoccer22 PhilMickelsonGolf44 NeymardaSilvaSantosJuniorSoccer17

Source: Opendorse

a. Constructadotplotoftheendorsements.

b. Whatobservation(s)occurredthemost?

c. Howmanyobservationsareatleast$40million?

d. Whatproportionoftheobservationsareatmost$30million?

Wetendtousedotplotstodescribedatavaluesofdiscretevariables,buttheycanbeusedtodescribe datavaluesofcontinuousvariables,too.

Deﬁnition Frequencyofanobservation

The frequencyofanobservation ofanumericalvariableisthenumberoftimestheobservationoccursin thegroupofdata.

Deﬁnition Frequencydistributionofanumericalvariable

The frequencydistributionofanumericalvariable istheobservationstogetherwiththeirfrequencies.

OBJECTIVE3

An outlier isanobservationthatisquiteabitsmallerorlargerthantheotherobservations.

6. Themaximumrecordedlifetimesofanimalsthathavethe10largestmaximumrecordedlifetimesareshown inthefollowingtable.

MaximumRecordedLifetime Animal(years)

OceanQuahog400

BowheadWhale211

RougheyeRockﬁsh205

RedSeaUrchin200

GalapagosTortoise177

ShortrackerRockﬁsh157

LakeSturgeon152

AldabraGiantTortoise152

OrangeRoughy149

WartyOrea140

Source: DiscoveryNews

a. Constructadotplot.

b. Identifyanyoutliers.

OBJECTIVE4

Forthedatadescribedbythefollowingdotplot,27pointsisatthe98thpercentile.

Deﬁnition Percentile

The kthpercentile ofsomedataisavalue(notnecessarilyadatavalue)thatisgreaterthanorequalto approximately k%oftheobservationsandislessthanapproximately (100 k)%oftheobservations.

7. FortheendorsementdatainProblem5,ﬁndthepercentileofMariaSharapova.

8. Fortheendorsementdata,ﬁndthe90thpercentile.

OBJECTIVE5

Forthischapter,wewillalwaysusethe50thpercentiletomeasurethecenterofadistribution.

9. FortheendorsementdatainProblem5,usethe50thpercentiletomeasurethecenter.

OBJECTIVE6

A stemplot (or stem-and-leafplot)breaksupeachdatavalueintotwoparts:the leaf,whichistherightmost digit,andthe stem,whichistheotherdigits.

10. Constructastemplotfortheendorsementdistribution.

A splitstem isastemplotwhichliststheleavesfrom0to4inonerowandliststheleavesfrom5to9inthe next.

11. Constructasplitstembyhandfortheendorsementdistribution.

12. UseStatCrunchtoconstructasplitstemfortheendorsementdistribution.

Stemplotsworkbestwithasmallnumberofobservationswhosevariableisdiscreteorcontinuouswith roundedvalues

OBJECTIVE7

Toconstructa time-seriesplot,weplotpointsinacoordinatesystemwherethehorizontalaxisrepresentstime andtheverticalaxisrepresentssomeotherquantity,andwedrawlinesegmentstoconnecteachpairofsuccessive dots.

13. ThenumberofnewappssubmittedtoApple’sAppStorepermonthareshowninthefollowingtablefor variousyears. NumberofApps

Source: pocketgamer.biz

a. Constructatime-seriesplotofthedata.

b. DescribehowthenumberofnewappssubmittedtoApple’sAppstorepermonthhaschangedover theyears.

c. FindthechangeinthenumberofnewappssubmittedtoApple’sAppstorepermonthfrom2009to 2015.IfthenumberofnewappssubmittedtoApple’sAppstorepermonthchangesbythatsame amountfrom2015to2021,whatwillitbein2021?Doyouhavemuchfaiththatthiswillturnoutto betrue?Explain.

Ifavariablehasincreased(ordecreased)throughoutaperiod,wecannotassumeitwillcontinueto increase(ordecrease)beforeorafterthatperiod.

HW 1,3,5,7,13,15,17,21,23,25,29,31,35,37,39

SECTION3.3TEACHINGTIPS

Studentstendtohaveanyeasytimeconstructingthediagramsdiscussedinthissection,soIstrivetokeepthe emphasisoninterpretingthediagrams,includingmeasuringthecenterandidentifyingoutliers,whicharetwoof fourcharacteristics(center,spread,shape,andoutliers)ofnumericalvariablesthatareemphasizedinChapters3 and4.

Ispendagooddealoftimediscussingpercentilesbecausestudentstendtohavemoretroublewiththisconceptthantheotherconceptsinthissection.Thisworkwilllaygoodgroundworkfortheirstudyofthenormal distribution(Sections5.4and5.5).

OBJECTIVE1COMMENTS

Studentstendtohavetroublegettingtheideaofdiscreteandcontinuousvariables.AlthoughIpresenttheformal deﬁnitions,studentstendtolearnthedistinctionbetweenthetwovariablesbetterbyseeingseveralexamples. Forsomestudents,discussingwhethertherearegapsbetweensuccessivepossiblevaluesworksﬁne.Forother students,ithelpstodiscusswhetherapossiblevaluecanhaveanynumberofdecimalplaces.

Thedistinctionbetweenthesetwotypesofvariableswillnotmatterwhenconstructinghistogramsinthis coursebecausethetextbookpresentsaone-size-ﬁts-allapproach(Section3.4).AsI’vementionedbefore,the textbook’sphilosophyistohavestudentsconstructacoupleofeachtypeofdiagramsotheyhavethegeneralidea andthenallowthemtousetechnologyfromthenon.However,thedistinction will matterwhenﬁndingpercentiles fromdensityhistograms(Section3.4).

OBJECTIVE2COMMENTS

Whenconstructingdotplots,Ipointoutthattheprocessissimilartoplottingpointsonnumberlines(Section1.1).I remindstudentsthattheyshoulduseuniformscalingonthehorizontalaxis,writethevariablebelowthehorizontal axis,andtitlethediagram.

Whenworkingwithdotplots,Itakeeveryopportunitytofindfrequenciesandrelativefrequenciesthatinvolve thephrases lessthan, greaterthan, atleast,and atmost becausestudentshavesuchdifficultywiththesephrases inintroductorystatisticscourses.Inparticular,studentsfindthephrases atleast and atmost tobethemost challenging.

Thisisagoodtimetoremindstudentsofthedifferenceinmeaningbetweenphrasessuchas between10and 20 and between10and20,inclusive (Section1.1).

Asusual,Ihavestudentsconstructoneortwodotplotsbyhandandfromthenonallowthemtousetechnology. RecallthatinChapters3and4,thehomeworkexercisesarestructuredsothatthereisﬁrstatleastapairof exerciseswithabout10observations,nextatleastapairofexerciseswithabout25observations,andthenatleast apairofexerciseswithatleast50observations.Thisstructureismeanttoofferinstructorsﬂexibilityinhaving studentsconstructdiagramsand/orcomputemeasurementswithorwithoutstatisticaltechnology.Forexample, Iwouldhavestudentsconstructadotplotforthe12observationsinExercise19byhand,the24observationsin Exercise21byhand,andthe50observationsinExercise23byusingtechnology.

Thepurpleicon"DATA"ﬂagsexerciseswhosedatasetscanbedownloadedfromMyMathLabandfromthe PearsonDownloadableStudentResourcesforMath&Statisticswebsite: http://www.pearsonhighered.com/mathstatsresources.

Justaswithfrequencydistributionsofcategoricalvariables,Iemphasizethemeaningof frequencydistribution ofanumericalvariable becausetheterminology distribution isusedsomuchinstatistics.

OBJECTIVE3COMMENTS

Atthispointinthecourse,thetextbookinformallydeﬁnesanoutliertobeanobservationthatisquiteabitsmaller

76CHAPTER2LectureNotesandTeachingTips

orlargerthantheotherobservations.AprecisedeﬁnitionisgiveninSection4.3,wheretheIQRandfencesare deﬁned.Exercises21(a)and35ofHomework3.3aremeanttopreparestudentsfortheexplanationaboutwhat shouldbedonewithoutliersthatisincludedinthegreenboxonpage185ofthetextbook.

Adotplotisabetterdiagramtoillustrateanoutlierthanahistogramorastemplotbecausetheoutlierisboth singledout(byadot)anditsdistancefromtheotherobservationsisdisplayed.

ForProblem6,studentsaresurprisedthatananimalcanliveaslongas400years.Theoceanquahogisaclam thatisnativetotheNorthAtlanticOcean.

OBJECTIVE4COMMENTS

Tointroducepercentiles,Iskipthechallengingabstractdeﬁnitionandgiveexamples.Dotplotsareaconvenient waytointroducepercentilesbecausecountingdotsissoconcrete.Displayingadotplotwith100observations suchastheoneincludedinthelecturenotesisagoodwaytogetacrosstheconceptofpercentiles.

Evenaftersuchanintroduction,studentsinitiallyhaveatoughtimewithProblem8.Somestudentsmistakenly thinktheyshouldﬁnd90%ofthelargestendorsement($58million)ratherthanthenumberofobservations(15 endorsements).

Findingpercentilesisagreatprimerforﬁndingavalueofanormalvariableforagivenprobabilitywhen workingwithanormalcurve(Section5.5).

OBJECTIVE5COMMENTS

Computingthe50thpercentileisanexcellentwaytogetstudentsthinkingaboutthecenterofadistribution.I toyedwithpostponingadiscussionaboutcenteruntilthemean,median,andmodeareintroducedinSection4.1, butIreallywantedstudentstobeengagedwiththematerialinChapter3atahigherlevelthanjustconstructing diagrams.Thisisachievedinanumberofways,butakeyoneishavingstudentsidentifythefourcharacteristics ofanumericalvariable:outliers(thissection),shape(Section3.4),center(thissection),andspread(Section3.4). Thefourcharacteristicsaresummarizedinthegreenboxonpage185ofthetextbook.

Onetechnicaldifficultywiththe50thpercentileisthatitisnotwelldefinedforreallysmalldatasetswith anoddnumberofobservations.Forexample,considerthesetofnumbers2,3,5,8,and9.Accordingtothe textbook’sdefinitionforpercentile,whichisfairlystandard,thenumbersintheinterval [3, 5) areatthe40th percentileandthenumbersintheinterval [5, 8) areatthe60thpercentile.Themedianis5,soitisabitofastretch tosaythatthe50thpercentileandthemedianarethesamething.Therootoftheproblemisthatpercentilesare meantfordatasetsthatinvolvemuchmorethan5observations.

Ialludetothisissueonpage218ofthetextbook,wherethemedianisintroduced,butIdon’tgointodetails becauseI’mmoreinterestedingettingacrossthattherearevariouswaystomeasurethecenterandwemust determinethemostappropriatemeasureforaparticulardataset.Besides,themedianandthe50thpercentileare extremelycloseorequalforlargedatasets,whichiswhenmeasuringthecenterismosthelpful.

OBJECTIVE6COMMENTS

Instructorswhodonothavemanycontacthourswithstudentsshouldconsiderskippingstemplotsbecausehistogramsareusuallyusedtodescribenumericalvariablesinintroductorystatistics.

Forthemostpart,studentshaveaneasytimeconstructingandinterpretingstemplots.Theonetasktheyﬁnd challengingisdeterminingtowhichdecimalplacethedatashouldberoundedbeforeconstructingthestemplot. Roundingsomedatavaluesto,say,theseconddecimalplaceandconstructingastemplot,andthenroundingthe samedatavaluesto,say,theﬁrstdecimalplaceandconstructingastemplotwillhelpstudentsunderstand.

Recallthattopreparestudentsforintroductorystatistics,Itakeeveryopportunitytosolveproblemswiththe phrases lessthan, greaterthan, atleast,and atmost

Tosavetime,Idonotbothershowingstudentshowtoconstructsplitstems,butIdodemonstratehowtouse StatCrunchtoconstructthemandweinterpretthediagrams.

OBJECTIVE7COMMENTS

Afterhavingconstructedsomanyotherdiagrams,studentshaveaneasytimeconstructingtime-seriesplots.This isgoodpreparationforalltheworkwithscatterplotstocomeinChapters6–10.Iemphasizethatfortimesseriesplots,timeisalwaysdescribedbythehorizontalaxis.Becauseofalltheworkstudentshavedoneonother

diagrams,afterIdrawthetwoaxes,studentsarequicktotellmetouseuniformscaling,indicatetheunitsonthe axes,andtotitlethediagram.

Whenworkingwithtime-seriesplots,Iwarnstudentsthatwecannotextrapolate,althoughIwaittointroduce theterminology extrapolate untilSection6.3,wheretheconceptisdescribedingreatdetail.

GROUPEXPLORATION:DeterminingWhichTableorDiagramtoUse

Thisexplorationhasmeritbecauseitinvolvesaformofcriticalthinkingsimilartodeterminingwhichtypeof conﬁdenceintervalorhypothesistesttouseforaparticulardataset.Avariationonthisexplorationwouldbe topresentgroupsofstudentswithactualdatasetsandhavethemdeterminewhichdiagramscouldbeusedto describethem.Oryoucouldaskthegroupstogoaheadandconstructoneormorediagramsforeachdataset.

SECTION3.4LECTURENOTES

Objectives

1. Constructandinterpret frequencyandrelativefrequencytables

2. Constructandinterpret frequencyhistograms and relativefrequencyhistograms

3. Interpret densityhistograms

4. Describethe shape ofadistribution.

5. Describethe spread ofadistribution.

6. Describethemeaningof model.

OBJECTIVE1

1. Theendorsementsofthe15athleteswiththehighest2015endorsementsareshowninthefollowingtable.

AthleteSportEndorsement(millionsofdollars) TigerWoodsGolf50 CristianoRonaldoSoccer27 UsainBoltTrackandField21 LebronJamesBasketball44 KobeBryantBasketball26 KevinDurantBasketball35 RoryMcllroyGolf32 RafaelNadalTennis28 MahendraSinghDhoniCricket27 RogerFedererTennis58 MariaSharapovaTennis23 NovakDjokovicTennis31 LionelMessiSoccer22 PhilMickelsonGolf44 NeymardaSilvaSantosJuniorSoccer17

Source: Opendorse

Constructafrequencyandrelativefrequencytablefortheendorsementdistribution.

Foraclass [a,b],the lowerclasslimit is a andthe upperclasslimit is b.Toﬁndthe classwidth ofaclass, wesubtractthelowerclasslimitofaclassfromthelowerclasslimitofthenextclass.

Deﬁnition Frequencyofaclassandrelativefrequencyofaclass

The frequencyofaclass isthenumberofobservationsintheclass.The relativefrequencyofaclass is theproportionoftheobservationsintheclass.

Whenusingclasses,the frequencydistributionofanumericalvariable aretheclassestogetherwiththeir frequenciesandthe relativefrequencydistributionofanumericalvariable aretheclassestogetherwiththeir relativefrequencies.

SumofRelativeFrequencies

Foranumericalvariable,thesumoftherelativefrequenciesofalltheclassesisequalto1.

OBJECTIVE2

2. ConstructafrequencyhistogrambyhandfortheendorsementdistributioninProblem1.

3. Constructarelativefrequencyhistogrambyhandfortheendorsementdistribution.

4. Usetechnologytoconstructafrequencyhistogramandarelativefrequencyhistogramfortheendorsement distribution.

• Histogramscanbeusedwithanynumericalvariable(discreteorcontinuous)andanynumberofobservations.

• Histogrambarscantouch,butbar-graphbarsnevertouch.

5. Thebodytemperaturesof130adultsaredescribedbythefollowingrelativefrequencyhistogram.

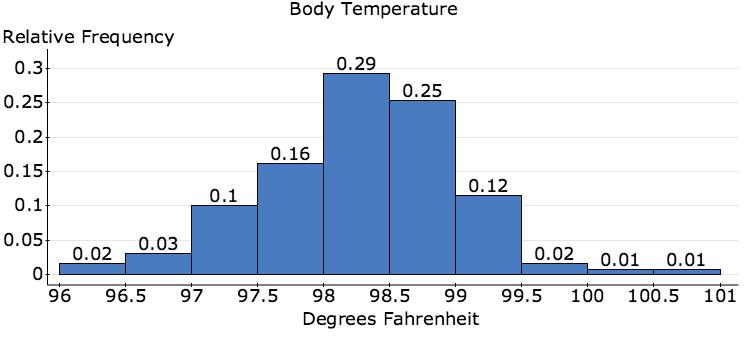
Source: AmericanStatisticalAssociation

Estimatetheproportionofobservationsthatare

a. greaterthanorequalto98degreesFahrenheitANDlessthan99degreesFahrenheit.

b. lessthan97.5degreesFahrenheit.

c. atleast99degreesFahrenheit.

OBJECTIVE3

Fora densityhistogram,theverticalaxishasunitscalled density sothatthe area ofeachbaristherelative frequencyofthebar’sclass.

6. Theaveragepricesof2014MajorLeagueBaseballR (MLB)ticketsatthestadiumsaredescribedbythe followingdensityhistogram.

Source: TeamMarketingReport

a. Findtheproportionofstadiumswhoseaveragepriceof2014MLBticketsare...

i. between$30and$39.99,inclusive.

ii. lessthan$20.

iii. atleast$20.

b. Estimatethepercentileofa$25averageticketprice.Roundtothenearestdollar.

c. TheaverageticketpriceatNationalsPark,homeoftheWashingtonNationals,isatthe83rdpercentile. Estimatetheaverageticketprice.Roundtothenearestdollar.

d. Identifytheclasswhichcontainsthe50thpercentile,whichisareasonablemeasureofthecenter.

OBJECTIVE4

Deﬁnition

Unimodal,bimodal, and multimodaldistributions

Adistributionis unimodal ifithasonemound, bimodal ifithastwomounds,and multimodal ifithas morethantwomounds.

Foraunimodaldistribution,the lefttail isthepartofthehistogramtotheleftofthe50thpercentileandthe righttail isthepartofthehistogramtotherightofthe50thpercentile

Deﬁnition

Skewed-left,skewed-right, and symmetricdistributions

• Ifthelefttailofaunimodaldistributionislongerthantherighttail,thenthedistributionis skewed left

• Iftherighttailofaunimodaldistributionislongerthanthelefttail,thenthedistributionis skewed right

• Ifthelefttailofadistributionisroughlythemirrorimageoftherighttail,thedistributionis symmetric.

Anobservationatthe50thpercentile(theapproximatecenter)ofaunimodaldistributiontendstobea typicalobservation.

OBJECTIVE5

7. Thefollowingtwodensityhistogramsdescribecalculusstudents’testscores(Source: J.Lehmann).The lefthistogramdescribesthescoresof35studentsonTest1.Therighthistogramdescribesthescoresof30 remainingstudentsonTest3.

DensityHistogramofTest1Scores

DensityHistogramofTest3Scores

a. Forthetwodistributionsidentifyanyoutliers.

b. Comparetheshapesofthetwodistributions.

c. Comparethecentersofthetwodistributions.Whatdoesthatmeaninthissituation?

d. Comparethespreadsofthetwodistributions.Whatdoesthatmeaninthissituation?

e. Givethreepossiblereasonswhythedistributionsaredifferent.

OrderofDeterminingtheFourCharacteristicsofaDistributionwithaNumericalVariable

Weoftendeterminethefourcharacteristicsofadistributionwithanumericalvariableinthefollowingorder:

1. Identifyalloutliers.

a. Foroutliersthatstemfromerrorsinmeasurementorrecording,correcttheerrors,ifpossible.If theerrorscannotbecorrected,removetheoutliers.

b. Forotheroutliers,determinewhethertheyshouldbeanalyzedinaseparatestudy.

2. Determinetheshape.Ifthedistributionisbimodalormultimodal,determinewhethersubgroupsof thedatashouldbeanalyzedseparately.

3. Estimateandinterpretthecenter.

4. Describethespread.

OBJECTIVE6

Deﬁnition Model

A model isamathematicaldescriptionofanauthenticsituation.Wesaythedescription models thesituation.

DiagramTypesofVariablesBeneﬁts

FrequencyBarGraphOnecategoricalvariableComparefrequenciesofcategories. RelativeFrequencyBarGraphOnecategoricalvariableCompareaparttothewhole. MultipleBarGraphTwocategoricalvariablesCompareaparttothewhole.

PieChartOnecategoricalvariableCompareaparttothewhole.

Two-WayTableTwocategoricalvariablesCompareaparttothewhole.

DotplotOnenumericalvariableDescribeindividualvaluesforasmall ormediumnumberofobservations.

StemplotOnenumericalvariableDescribeindividualvaluesforasmall numberofobservations.

FrequencyHistogramOnenumericalvariableComparethefrequenciesofclasses.

RelativeFrequencyHistogramOnenumericalvariableCompareaparttothewhole.

DensityHistogramOnenumericalvariableCompareaparttothewhole.

Time-SeriesPlotTwonumericalvariablesFindtheassociationbetweentwovariables.

HW 1,3,5,9,10,11,13,17,19,23,25,27,33,43,45,49

SECTION3.4TEACHINGTIPS

AlthoughObjectives1–5areallveryimportant,Iemphasizeinterpretingdensityhistogramsthemostbecauseit issuchgoodpreparationforthenormalcurve(Sections5.4and5.5).

OBJECTIVE1COMMENTS

Whenconstructingafrequencyandrelativefrequencytableforanumericalvariable,Ipointoutthattheprocess issimilartoconstructingsuchatableforacategoricalvariable,wheretheclassesactascategories.

ForthedatainTable46onpage174ofthetextbook,itishelpfultocompareTable47(thefrequencyand relativefrequencytable)withthestemplotshowninFig.62.

Becauseofthesimilaritiesdescribedintheprevioustwoparagraphs,studentshaveafairlyeasytimeconstructinghistograms.

Sometextbooksgivecomplexinstructionsabouthowtodeterminetheclasses,butIbelievethereislittle beneﬁtwithhavingstudentsgetsocaughtupinthedetails.Themainpointistohavestudentsconstructoneor twohistogramsbyhandsotheycanbetterinterpretthem.Technologycantakecareoftherest.

Eachtimestudentsarerequiredtoconstructatableand/orhistogramintheexercises,thelowerclasslimit andtheclasswidtharegiven.Thisway,theirtableand/orhistogramwillmatchtheoneintheanswersection. Supplyingthelowerclasslimitandtheclasswidthonatestmakesiteasiertogradestudents’work.

Wheneverstudentsconstructarelativefrequencytable,Iadvisethattheycheckthatthesumoftherelative frequenciessumto1.Iexplainthatthesumequals1forthesamereasonthattherelativefrequenciessumto1 whenworkingwithacategoricalvariable.

OBJECTIVE2COMMENTS

BecausehistogramswillbeusedmorethananyotherdiagraminChapters4and5(andinintroductorystatistics), Imakesurestudentshaveasolidunderstandingofhowtoconstructandinterprethistograms.Inadditionto drawingthecomparisonbetweenconstructingbargraphsandhistograms,Idemonstratethatastemplotrotated counterclockwise90degreesissimilartoahistogram(seeFigs.63and65onpage176ofthetextbook).

Toimpressuponstudentstheimportanceofhistograms,Ishowthemhistogramsfromawidevarietyof mediums,includingnewspapers,blogs,andstatisticalreports.Itisvisceraltohavestudentsinterpretahistogram thathastodowithaneventthathasjustoccurredinthepastweekorso.

Becauseofthewayhistogramsareconstructedinthetextbook,Itendtosolveproblemswiththephrases lessthan and atleast (ratherthan greaterthan and atmost).Recallthatthisisgoodpreparationforintroductory statistics.

OBJECTIVE3COMMENTS

Considerastepfunctionthatisrelatedtothetopsofadensityhistogram.Thatstepfunctionisaprobability densityfunction.Thatiswhyinterpretingdensityhistogramsisexcellentpreparationforworkingwithnormal distributions(Sections5.4and5.5).Forthatreason,IemphasizethemmorethananyotherdiagraminChapter3. ButIdon’tmentionanyofthistostudents,excepttosaythatdensityhistogramswillbeveryhelpfulinChapters4 and5.

Introductorystatisticstextbookstendtogiveshortshrifttodensityhistograms,whichisunfortunate,butthis createstheopportunityfor Pathway toofferadifferentperspectivetostudents.Learningaconceptfromtwo perspectivesisbetterthanfromone.

Itiskeythatstudentsunderstandwhytheareaofabarisequaltotherelativefrequencyofthebar’sclass. Toconveythis,IcomputetheareaofabarsimilartotheoneinFig.73onpage179ofthetextbook.ThenI buildonthisfacttoarguethatthetotalareaofthebarsofadensityhistogramisequalto1andmakegreatuseof theadditionrulefordisjointeventsandthecomplementrule(withoutcallingthemassuch).Bothruleswillbe formallyintroducedinSection5.2.

Thehomeworkexercisesdonotrequirestudentstoconstructdensityhistogramsbuttheydohavestudents interpretthem(seeExercises13–20).SelectexercisesinChapters4and5willcontinuetorequirestudentsto workwithdensityhistograms.

OBJECTIVE4COMMENTS

Whendeterminingtheshapeofadistribution,Itellstudentstonoticethegeneralpatternratherthanfocuson smalldeviationsfromtheoverallpattern.Forexample,foralmostallauthenticunimodaldistributionswewould considersymmetric,thelefthalfofthehistogramisnottheexactmirrorimageoftherighthalf.

Iemphasizethatifadistributionisbimodalormultimodal,it’sagoodideatodeterminewhethersubgroups ofthedatashouldbeanalyzedseparately.

OBJECTIVE5COMMENTS

UntilmeasuresofvariationareintroducedinSection4.2,thebestwaytohavestudentsreﬂectonspreadistohave themcomparethespreadsoftwoormoredistributionssuchasthetest-scoredistributionsdescribedinProblem7. StudentsarequicktoseethatthedistributionofTest3scoresismorespreadoutthanthedistributionofTest1 scores.

Withtheintroductionofspread,studentsnowknowthefourcharacteristicsofanumericaldistribution(outliers,shape,center,andspread).ThefourcharacteristicswillbefurtherdevelopedandemphasizedinChapter4.

OBJECTIVE6COMMENTS

Toconveytheideaofamodel,Ishowstudentsseveralhistogramsthatrepresentasingledataset,whereeach histogramhasadifferentclasswidth(seethegroupexplorationonpage186ofthetextbook).Thissetsthestage fortheconceptthatanormaldistributionisamodel(it’sextremelyrareforanauthenticdistributiontobeexactly normal).TheconceptofamodelisthemostimportantthemethatrunsthroughallofChapters3–10.

Iadvisestudentstocarefullyexaminetheoverviewoftablesanddiagrams(models)includedinTable48on page186ofthetextbook.AsImentionedearlier,theskillofidentifyingwhichtablesanddiagramsdescribea distributionwell(Exercises43–48)issimilartothekeyskillofidentifyingwhichtypesofconﬁdenceintervals andhypothesistestsareappropriatetodrawinferencesaboutapopulation.

GROUPEXPLORATION:ComparingHistogramswithDifferentClassWidths Themainpointofthisexplorationisthattheperspectivewegainfromahistogramdependsinpartontheclass

sizewechoose.Thisreinforcestheconceptthatahistogramisamodel.Theexplorationisalsoagoodprimerfor Example1ofSection3.5,whichshowsthatcertainclasswidthscanbemisleading.

SECTION3.5LECTURENOTES

Objectives

1. Explainwhyacertainclasswidthofahistogramcanemphasizeorde-emphasizeanaspectofa distribution.

2. Explainwhythestartingvalueoftheverticalaxisofabargraphoratime-seriesplotcanemphasize orde-emphasizeanaspectofadistribution.

3. Explainwhynonuniformscalingcanbemisleading.

4. Explainwhy three-dimensionalgraphs canbemisleading.

OBJECTIVE1

1. ThedailyapprovalratingsofPresidentObamaaredescribedbythefollowinghistograms.Thelefthistogramdescribesthedailyapprovalratingsin2009usingasmallerclasswidth(2percentagepoints),and therighthistogramdescribesthesameratingsusingalargerclasswidth(5percentagepoints).Whichof thesehistogramsismisleading?Explain.

Source: RasmussenReports

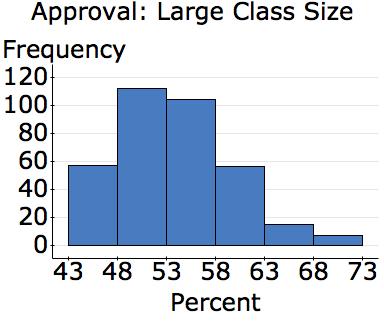
Whenviewingahistogram,keepinmindthatacertainchoiceofclasswidthcanemphasizeordeemphasizecertainaspectsofthedistribution.

OBJECTIVE2

2. ThepercentagesofveteranswhousedGIBillbeneﬁtsfrom2002through2013tocompleteeducations rangingfromvocationaltrainingtopost-graduatearedescribedbythefollowingbargraphsforvarious servicebranches.

a. IftheAirForcewantstoconvincepotentialrecruitshowmuchbettertheeducationcompletionrateis forAirForceveteransthanforveteransoftheotherfourservicebranches,whichbargraphwouldit display?Explain.

b. IftheNavywantstoconvincepotentialrecruitsthattheeducationcompletionrateforNavyveterans isveryclosetotherateforCoastGuardveterans,whichbargraphwoulditdisplay?Explain.

c. FromwhichbargraphcanyoubetterestimatetheeducationcompletionrateforCoastGuardveterans? Explain.Estimatetherate.

3. TheannualrevenuesofMicrosoftR aredescribedbythefollowingtime-seriesplotsforvariousyears.If Microsoftwantstoemphasizethegrowthofitsrevenue,whichtime-seriesplotwoulditwanttodisplay? Explain.

Iftheverticalaxisofatime-seriesplotdoesnotstartat0,thechangesinthevariabledescribedbythat axisarebeingemphasized.

4. NorthwesternUniversitytuitionsaredescribedbythefollowingtime-seriesplotsforvariousyears,where thestartingyearoftheacademicyearisshownonthehorizontalaxis.IfNorthwesternwantstodeemphasizehowmuchitstuitionhasincreased,whichtime-seriesplotwoulditwanttodisplay? Copyright c 2016PearsonEducation,Inc.

Iftheverticalaxisofatime-seriesplotstartsat0,beawarethatthechangesinthevariabledescribed bythataxisarebeingde-emphasized.

OBJECTIVE3

5. Therevenues(inbillionsofdollars)oftheWaltDisneyCompanyR aredescribedbythefollowingbar graphsforvariousyears.IfWaltDisneywantedtoemphasizeitsgrowthinrevenue,whichbargraphwould bemoreconvincing?Whyisthatbargraphmisleading?Whattypeofgraphwouldcontainthesame informationbutnotbemisleading?

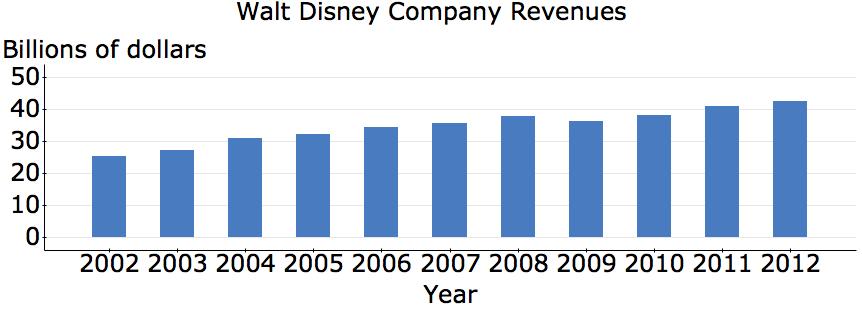
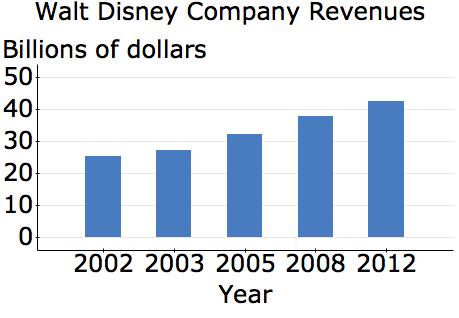
Source: WaltDisneyCompany

Ifthecategoriesforabargrapharevariousyearsandthoseyearsdonotincreasebythesameamount, thebargraphcanbemisleading.Atime-seriesplotwouldbeabettergraphtouse.

OBJECTIVE4

6. Atotalof2059randomlyselectedadultswereaskedwhichschoolsubjecthasbeenthemostvaluableto themintheirlives.Theirresponsesaredescribedbythefollowingthree-dimensionalgraph.

Source: TheGallupOrganization

a. Whatisconfusingaboutthisgraph?

b. Determineabettertypeofgraphanddrawit.

c. Whichsubjectreceivedthemostvotes?Whatpercentageofadultsvotedforit?

HW 1,3,5,7,9,11,13,15,17,20,22

SECTION3.5TEACHINGTIPS

Onecouldarguethatthisisthemostimportantsectionofthetextbecausethemediaandbusinessesoftenuse statisticaldiagramsinmisleadingways.

OBJECTIVE1COMMENTS

Togetacrosshowahistogramisimpactedbyitsclasswidth,youcoulduseStatCrunchtodisplayhistograms withvariousclasswidthsforthesamedataset.Oryoucouldhavegroupsofstudentscompletetheexplorationon page186ofthetextbookorProblem1inthelecturenotes.

Infact,youcouldhavegroupsofstudentsworkonallofProblems1–6becausetheyaresointuitive.

OBJECTIVE2COMMENTS

Theimpactofthestartingvalueontheverticalaxisofabargraphortime-seriesplotmightbethemostimportant conceptofthissectionbecausecorporationsandthemediausethistacticsooften.Ipointoutthateventhough thepracticemaybeusedtopersuadeorevenmislead,thereisnothingmathematicallywrongwithit.Iemphasize thatstudentsshouldcarefullyinspectbothaxestomakesuretheyinterpretadiagramcorrectly.

GROUPEXPLORATION:UsingtheVerticalAxistoPersuade

Studentstendtoreallyengageinthisexploration,probablybecausetheyseetheycandirectlybeneﬁtfrombeing criticalconsumersofstatistics.Problems3–5areaniceintroductiontolinearmodelingissuesthatwillbefurther developedinChapters6–9.Problems3–5arealsogoodpreparationforExercises9(d),10(d),11(d),and12(d).

OBJECTIVE3COMMENTS

WhenIlectureonProblem5orfacilitategroupworkonit,Itellstudentsthatthemediaoftenusesbargraphs whentime-seriesplotswouldbemoreappropriate.SimilartomywarningregardingObjective2,Iemphasizethat studentsshouldcarefullyinspectthehorizontalaxisofabargraph.

OBJECTIVE4COMMENTS

Considerﬁndingthree-dimensionalgraphsinyourlocalnewspaperorothermediatoshowyourstudents.Have themdeterminewhetherthegraphsareconfusing,misleading,orboth.

CHAPTER4OVERVIEW

ThemainpaththroughChapters2–5culminatesinthenormaldistribution(Sections5.4and5.5).Andtheintroductionofthemean(Section4.1),thestandarddeviation(Section4.2),andtheEmpiricalRule(Section4.2)are threesigniﬁcantstepstowardthatgoal.

Nomatterhowmuchtimeisdevotedtomeasuresofvariabilityinintroductorystatisticscourses,students tendtohaveasketchyunderstandingofthisconcept,soIadvisefacilitatingplentyofactivitiesthatenhancetheir understandingofit.

Thischapterofferscopiousamountsofcritical-thinkingopportunities,especiallyintheformofcomparisons:

• Studentscomparethemeanwiththemedianforskewed-left,symmetric,andskewed-rightdistributions.

• Studentsidentifywhichofthemeasuresmean,median,andmodeisthebestmeasureofthecenterfora givendataset.

• Studentsidentifywhichofthemeasuresstandarddeviation,IQR,andrangeisthebestmeasureofthe variabilityforagivendataset.

• Studentscompareandinterpretthecentersoftwogroupsofdata.

• Studentscompareandinterpretthevariabilityoftwogroupsofdata.

Manyoftheseconceptscanbediscoveredbyhavinggroupsofstudentscompletetheexplorationsorbyhaving themﬁndsolutionsfortextbookexamples.

It’sagoodideatocontinueusingdataaboutyourstudents.Iftheyseemedtoespeciallyenjoyacertaindata setthatyouworkedwithinChapter3,considerreturningtothatdatasettonowmeasurethecenter,measurethe variability,andconstructaboxplot(Section4.3).

ConstructingboxplotsisabitmoretechnicalthanthediagramsdiscussedinChapter3,somakesurethat studentsdonotgetsoinvolvedwiththecalculationsthattheylosesightofaboxplot’smanyadvantages:to visualizethecenter(median),thevariability(theIQRandrange),andoutliers.

SECTION4.1LECTURENOTES

Objectives

1. Computethe median ofsomedata.

2. Describethemeaningof sigmanotation

3. Computethe arithmeticmean ofsomedata.

4. Comparethemeansoftwogroupsofdata.

5. Comparethemeanandthemedianofsomedata.

6. Findthemeansandmediansofbimodalandmultimodaldistributions.

7. Findthe mode ofsomedata.

OBJECTIVE1

Deﬁnition median

The median ofsomedataisthe50thpercentile.

FindingtheMedianofaDistribution

Toﬁndthemedianofsomedatavalues,ﬁrstlisttheobservationsfromsmallesttolargest.

• Ifthenumberofobservationsisodd,thenthemedianisthemiddleobservation.

• Ifthenumberofobservationsiseven,thenthemedianistheaverageofthetwomiddleobservations.

1. ThepercentagesofadultswhoexercisefrequentlyareshowninthefollowingtableforNortheasternstates andMountainstates.

NortheasternStatePercentMountainStatePercent Connecticut54Arizona53 Maine55Colorado60

Massachusetts53Idaho58

NewHampshire54Montana60

NewJersey48Nevada55 NewYork49NewMexico57 Pennsylvania50Utah54

RhodeIsland48Wyoming54 Vermont65

Source: TheGallupOrganization

a. FindthemedianpercentfortheNortheasternstates.Whatdoesitmeaninthissituation?

b. FindthemedianpercentfortheMountainstates.Whatdoesitmeaninthissituation?

c. ComparetheresultsyoufoundinParts(a)and(b).Whatdoesthismeaninthissituation?

d. AstudentsaysthattheresultyoufoundinPart(a)shouldbegreaterthantheresultyoufoundin Part(b)becausetherearemoreNortheasternstatesthanMountainstates.Whatwouldyoutellthe student?

OBJECTIVE2

Deﬁnition SummationNotation

Let x1, x2, x3,..., xn besomedatavalues.The summationnotation Σxi standsforthesumofthedata values:

2. TheTVserieswiththetopfivemost-watchedfinalesandthefinaleviewershipsareshowninthefollowing table.Let xi bethefinaleviewership(inmillions)listedinthe ithrowofthetable.

a. Findthevaluesof x1, x2, x3, x4,and x5

b. Find Σxi.Whatdoesitmeaninthissituation?

FinaleViewership

TVSeries(inmillions)

M*A*S*H105.9

Cheers80.4

Seinfeld76.3

Friends52.5

Magnum,p.i.50.7

Source: USAToday,Reuters,TVGuide,ABC

OBJECTIVE3

Deﬁnition Mean

The arithmeticmean (or mean)of n

• Remembertoalwaysincludetheunitsofthemean.

• A formula isanequationthatcontainstwoormorevariables.

3. Thenumbersofteaspoonsofsugarin12ﬂuidouncesofvariousbeveragesareshowninthefollowingtable. Findthemeannumberofteaspoonsofsugarinthebeverages.Thenconstructadotplotandverifythatthe meanisareasonablemeasureofthecenter.

Source: Thecompanies

MeanisaMeasureoftheCenter

Ifadistributionisunimodalandapproximatelysymmetric,themeanisareasonablemeasureofthecenter. Inthiscase,wesaythemeanisatypicalvalue.

4. Thestudentsinoneoftheauthor’sprestatisticsclassesestimatedhisage.Theirestimatesareshowninthe followingtable.

4845454140444744

5035455438404650 3842474349454343 49

Source: J.Lehmann

a. Determinewhetherthemeanshouldbeareasonablemeasureofthecenterofthedistribution.

b. Computethemean.Whatdoesittellusinthissituation?

c. Astudentcalculatesthemeanestimatetobe44.4yearsandconcludesthatatypicalestimatebyall studentsatthecollegewherethesurveywasperformedis44.4years.Whatwouldyoutellthestudent?

Whencomputingthemeanorothermeasuresofdata,wewillroundtoonemoredecimalplacethanthe data.

OBJECTIVE4

5. ThepricesofhotdogsateachofthestadiumsforthebaseballteamsintheNationalLeagueCentral(NLC) andtheNationalLeagueWest(NLW)areshowninthefollowingtable.

NLCHotDogPriceNLWHotDogPrice Team(dollars)Team(dollars) ChicagoCubs5.50ArizonaDiamondbacks2.75 CincinnatiReds1.00ColoradoRockies4.75 MilwaukeeBrewers3.50LosAngelesDodgers5.50 PittsburghPirates3.25SanDiegoPadres4.00 St.LouisCardinals4.25SanFranciscoGiants5.25

Source: TeamMarketingReport

a. DeterminewhetherthemeanhotdogpriceoftheNLCdistributionshouldbeareasonablemeasureof thecenterofthedistribution.DothesamefortheNLWdistribution.

b. FindthemeanhotdogpricefortheNLC.

c. FindthemeanhotdogpricefortheNLW.

d. WhatdoyourresultsinParts(b)and(c)meaninthissituation?

6. a. Computethemeanforthenumbers3,4,and5.

b. Computethemeanforthenumbers3,4,5,and4.

c. AstudentssaysthattheresultyoufoundinPart(b)shouldbelargerthantheresultyoufoundin Part(a)becausetherearemoreobservationsinPart(b).Whatwouldtellthestudent?Includeinyour explanationadiscussionaboutdivisionaswellasacomparisonofdotplotsofthetwodatasets.

OBJECTIVE5

7. Thefollowingdataarethesavings(inthousandsofdollars)ofﬁveadults:15,9,11,6,and3.

a. Findthemeansavings.

b. Findthemediansavings.

c. Supposethattheadultwhohad$15thousandinsavingswins$800thousand(aftertaxes)fromthe lottery.So,theadult’snewsavingsis$815thousand.Findthemeansavingsoftheﬁveadultsafter thelotterywin.

d. Findthemediansavingsoftheﬁveadultsafterthelotterywin.

e. Describehowmuchtheoutlier$815thousandaffectedthemeanandthemedian.

TheEffectofOutliersontheMeanandtheMedian

• Themeanissensitivetooutliers.

• Themedianisresistanttooutliers.

8. Thetop-paidfemaleCEOsandtheircompensationsareshowninthefollowingtable.

Compensation CEOCompany(inbillionsofdollars) IreneRosenfeldMondelez21.0 VirginiaRomettyIBM19.3 SafraAdaCatzOracle37.7 PhebeNovakovicGeneralDynamics19.3 CarolMeyrowitzTJK28.7 IndraNooyiPepsiCo22.5 MegWhitmanHewlett-Packard19.6 DebraReedSempra16.9 MarissaMayerYahoo42.1 UrsulaBurnsXerox22.2 MarillynHewsonLockheedMartin33.7 MaryBarraGM16.2

Source: S&PCapitalIQ,USAToday,BespokeInvestmentGroup

a. Findthemeancompensation.

b. Findthemediancompensation.

c. Constructafrequencyhistogramandindicatethemeanandthemedianonit.Describetheshape.

d. Whichmeasuresthecenterbetter,themeanorthemedian?Explain.

e. Explainwhyitmakessensethatthemeanislargerthanthemedian.

HowtheShapeofaDistributionAffectstheMeanandtheMedian

• Ifadistributionisskewedleft,themeanisusuallylessthanthemedianandthemedianisusuallya bettermeasureofthecenter.

• Ifadistributionissymmetric,themeanisapproximatelyequaltothemedianandbotharereasonable measuresofthecenter.

• Ifadistributionisskewedright,themeanisusuallygreaterthanthemedianandthemedianisusually abettermeasureofthecenter.

OBJECTIVE6

9. a. ConsiderhowmanydayseachpresidentoftheUnitedStateshasservedinofﬁce.Whatshapewould thedistributionhave?

b. ThenumbersofdaysservedbythepresidentsaredescribedbythedotplotinFig.2.1.Themeanand medianareshowninFig.2.2.Howdothemeanandthemedianrelatetothedistribution?Howwell dotheydescribeatypicalobservation?

DaysServedbyU.S.Presidents

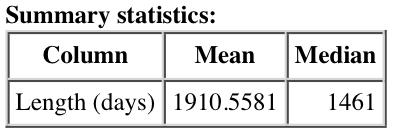
Figure2.2: NumbersofdaysservedbyU.S.presidents

NumberofDays

Figure2.1: NumbersofdaysservedbyU.S. presidents(Source: WorldAlmanacandBookof Facts2014)

c. Whatwouldbeamoreusefulwaytoanalyzethissituation?

OBJECTIVE7

Deﬁnition Mode

The mode ofsomedataisanobservationwiththegreatestfrequency.Therecanbemorethanonemode, butifalltheobservationshavefrequency1,thenthereisnomode.

10. Foreachdataset,ﬁndthemode.

a. Theauthorsurveyedthestudentsinoneofhisprestatisticsclassesaboutthenumberofstatesthey havelivedin.Someoftheirresponsesareshowninthefollowingtable.

1101211

211141

Source: J.Lehmann

b. Theauthorsurveyedthestudentsinoneofhisprestatisticsclassesaboutwhatsuperpowertheywished theyhad.Someoftheirresponsesareshowninthefollowingtable.

flyteleportmindreadflyfly invisibleflyteleportinvisibleclonemyself

Source: J.Lehmann

c. Thetuitionsoftheﬁvemostexpensivecollegesareshowninthefollowingtable.

Tuition,Fees,Room,andBoard College(dollars)

SarahLawrenceCollege61,236 NewYorkUniversity59,837 HarveyMuddCollege58,913 ColumbiaUniversity58,742 WesleyanUniversity58,202

Source: CampusGrotto.com

11. Theauthorsurveyedstudentsinoneofhisstatisticsclassesaboutthehowmanytimesperweektheyeatat fast-foodrestaurants.Adotplotandthemean,median,andmodeareshowninthefollowingﬁgure.Explain whythemedianandthemean(roundedtotheonesplace)arebettermeasuresofthecenterthanthemode.

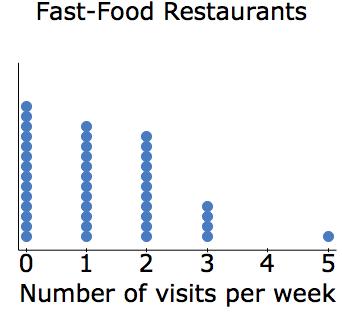
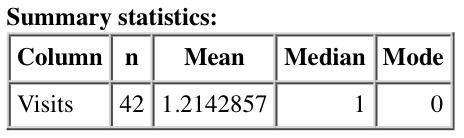
HW 1,3,5,7,15,17,19,23,27,29,35,37,43,49,53,59,63

SECTION4.1TEACHINGTIPS

Thisisanextremelyimportantsectionbecausecentraltendencyisattheheartandsoulofstatistics.Themean andthemedianarebothimportantmeasuresofthecenter,butthemodecanbede-emphasizedorskippedbecause itisrarelyusedinstatistics.

Althoughstudentshaveafairlyeasytimecomputingmeans,medians,andmodes,theyoftenconfuseonewith another.Iadvisewarningyourstudentsthattheyshoulddevotesomeoftheirstudytimetokeepingthethree measuresstraightintheirminds.

OBJECTIVE1COMMENTS

InChapter3,thetextbookusesthe50thpercentiletomeasurethecenter.InChapter4,thetextbookusesthe medianinsteadofthe50thpercentiletomeasurethecenter.

Whenﬁndingamedian,Iemphasizethatthedatavaluesmustbelistedfromsmallesttolargestbeforeidentifyingthemiddleobservationortheaverageofthetwomiddleobservations.Ialsoemphasizethatthemedianisa

measureofthecenterandthatstudentsmustindicateitsunits.

OBJECTIVE2COMMENTS

Oncestudentsrealizethat xi representsthesumoftheobservations xi,theycaneasilyﬁndcorrectresults,but Itrytomakesuretheyunderstandtheroleofthesubscriptsinhopesofbetterpreparingthemforthestandard deviationformula,whichisintroducedinSection4.2.Justlikewiththemedian,Iemphasizethatstudentsshould indicatetheunitsforthesumofsomedatavalues.

MuchmorecomplicatedsummationsareincludedinSection8.4,whichfocusesonstatisticsformulas.Ifyou donotplantouseChapter8,considerhavingstudentsworkabitwiththesummationsinSection8.4tobetter preparestudentsforintroductorystatistics.

OBJECTIVE3COMMENTS

Becausemanystudentshavecomputedaveragesinpreviousclasses,theyarerelievedtoknowthatthemeanis thesamemeasure.

AftercompletingProblem3,Isaythatifweimaginethatthehorizontalaxisofthedotplotisaseesawand thedotsarebowlingballsthatallhavethesameweight,themean(9.5teaspoons)wouldbethebalancepoint.I emphasizethatifadistributionisunimodalandsymmetric,themeanisareasonablemeasureofthecenterand wesayitisatypicalvalue.Ialsoemphasizethatstudentsshouldindicatethemean’sunits.

Itcanbeinstructivetousetechnologytoconstructahistogramthatdescribesauniform,symmetricdistribution thatinvolvesalargenumberofobservationsandhavestudentsestimatethecenterbyinspection.Thenyoucan usetechnologytocomputethemeanandcompareitwiththestudents’estimates.

Tellstudentsthattheywillneedtoroundthemeanandothermeasuresofdatatoonemoredecimalplacethan thedatasothattheiranswersmatchtheonesinthebackofthebook(andmostlikelyonMyMathLab).

OBJECTIVE4COMMENTS

Measuringthecenterofadatasetisinteresting,butcomparingthemeansof twodatasets providesextrapunch:

• Whichcarmodeltendstohavebettergasmileages?

• Studentsofwhichsectionofprestatisticstendtoperformbetterontests.

• Whichethnicgrouptendstospendmoremoneyonhip-hopmusic?

Iremindstudentsthatbeforewecomparethemeansoftwoormoredatasets,weshouldcheckthateachdistributionisunimodalandsymmetric.Ialsoremindthemthatwecannotdrawconclusionsaboutindividualsnotinthe datasets(Chapter2).

EvenafterIhavediscussedwithstudentsatgreatlengththatforunimodal,symmetricdistributionsthemean isagoodmeasureofthecenterandareasonabletypicalvalue,somestudentsthinkthatthemeanweightof 20,000randomlyselectedcatswouldbegreaterthanthemeanweightofﬁverandomlyselectedhumanadults (Exercise63).Itseemsthatsuchstudentsthinkofthemeanasasumofobservations,perhapsbecausethe formulaforthemeanincludesasummation.Ormaybetheydon’treadtheexercisecarefully.Inanycase,this misconceptioncertainlydeservessomeattention!Problem6isanicewaytoaddressthisissue.Problem6could befollowedbythecomparisonofcatsandadulthumansorseeExercise64foracomparisonofhighschooland NBAbasketballplayers’heights.

OBJECTIVE5COMMENTS

Thefundamentalconceptsforthisobjectivearethatthemeanissensitivetooutliersandthemedianisresistantto outliers.Problem7suggeststhattheseconceptsaretrue,butaftergoingoversuchanexample,Idiscuss why the conceptsmakesense(seethetwoparagraphsdirectlyafterExample6).

Thetwoconceptsleadtotheconclusionsabouthowthemeanandthemediancompareforskewed-left, symmetric,andskewed-rightdistributions(seethesolutiontoProblem5ofExample7andtheparagraphsdirectlyfollowingExample7).Itakemytimemakingtheseconnectionsbecausetheyinvolvesomanyterminologies/concepts.StudentswillneedtoapplythismaterialmanytimesinSections4.1and4.2.

GROUPEXPLORATION:ComparingtheMeanandtheMedian

Becausegroupsofstudentshaveaneasytimewiththisexplorationanditaddressesimportantconcepts,Iadvise usingthisexplorationtointroduceObjective5.

OBJECTIVE6COMMENTS

Problem9servesasanicereminderthatweoftenseparatebimodalandmultimodaldistributionsintotwoormore groupsandthenﬁndthemeanand/orothermeasuresofeachgroup.

OBJECTIVE7COMMENTS

Iwastemptedtoexcludethemodefromthetextbookbecauseitisusedsomuchlessoftenthanthemeanand themedianinstatistics,andforgoodreason.However,somereviewerswanteditsinclusion,soIdidsofor completeness.Nonetheless,ifyoudoincludethetopic,Iadviseyoutogiveitlighttreatment.Theonlyhomework sectionsinthetextbookthatincludethemodeareHomework4.1(Exercises15,16,27,28,and31),Chapter4 ReviewExercises(Exercises3and4),andChapter4Test(Exercise4).

TheparagraphsdirectlyfollowingExample9giveaniceexampleinwhichthemodeisnotareliablemeasure ofthecenter.

SECTION4.2LECTURENOTES

Objectives

1. Computethe range ofsomedata.

2. Computethe standarddeviation ofsomedata.

3. Comparethemeansandstandarddeviationsoftwogroupsofdata.

4. Applythe EmpiricalRule tosomedata.

5. Determinewhetheranobservationisunusual.

6. Comparetherangeandthestandarddeviation.

7. Computethe variance ofsomedata.

OBJECTIVE1

Deﬁnition Range

The range ofsomedatavaluesisgivenby

R = largestnumber smallestnumber

1. Thepricesof8randomlyselectedcalculatorsareshowninthefollowingtable.

Source: Amazon.com

Findtherangeinpricesandexplainwhatitmeansinthissituation.

OBJECTIVE2

Deﬁnition Standarddeviation

The standarddeviation of n datavalues x1, x2, x3,..., xn isgivenby s = (xi x)2 n 1

Thestandarddeviationmeasuresthespread.Thegreaterthespread,thegreaterthestandarddeviation willbe.

2. ThehighwaygasmileagesofdifferentversionsoftheAudiR8Spyderare23,20,22,and19,allinmiles pergallon.Findthestandarddeviationofthegasmileages.

OBJECTIVE3

3. Ahouseholdsuffersfrom foodinsecurity ifatsomepointintheyearthehouseholdeatsless,goeshungry, oreatslessnutritionalmealsbecausethereisnotenoughmoneyforfood.Thepercentagesofhouseholds sufferingfromfoodinsecuritiesareshowninthefollowingtablefortheWestNorthCentralandPaciﬁc states.

WestNorthFoodInsecurityPaciﬁcFoodInsecurity CentralState(percentofhouseholds)State(percentofhouseholds) Iowa12.7Alaska14.0 Kansas14.8California16.2 Minnesota10.7Hawaii14.2 Missouri17.1Oregon16.7 Nebraska13.4Washington15.0 NorthDakota7.7 SouthDakota12.3

Source: FeedingAmerica;U.S.DepartmentofAgriculture

a. ComparethemeanfoodinsecuritiesfortheWestNorthCentralstatesandforthePaciﬁcstates.What doesyourcomparisonmeaninthissituation?

b. ComparethestandarddeviationsofthefoodinsecuritiesfortheWestNorthCentralstatesandforthe Paciﬁcstates.Whatdoesyourcomparisonmeaninthissituation?

c. EventhoughthemeanfoodinsecurityfortheWestNorthCentralstatesislessthanthemeanfood insecurityforthePacificstates,oneoftheWestNorthCentralstates(Missouri)hasalargerpercentageofhouseholdswithfoodinsecuritythaneveryoneofthePacificstates.Explainwhythisisnot surprisingbyreferringtothestandarddeviationoffoodinsecuritiesfortheWestNorthCentralstates andthePacificstates.

OBJECTIVE4

4. Supposethat100statisticsstudents’scores(inpoints)onatestaredescribedbythefollowingdotplot.The meanis70pointsandthestandarddeviationisapproximately10points.

a. Describethedistribution.

b. Findthepercentageofthescoresthatarewithinonestandarddeviationofthemean.

c. Findthepercentageofthescoresthatarewithintwostandarddeviationsofthemean.

d. Findthepercentageofthescoresthatarewithinthreestandarddeviationsofthemean.

EmpiricalRule

Ifadistributionisunimodalandsymmetric,thenthefollowingstatementsaretrue.

• Approximately68%oftheobservationsliewithinonestandarddeviationofthemean.So,approximately68%oftheobservationsliebetween x s and x + s.

• Approximately95%oftheobservationsliewithintwostandarddeviationsofthemean.So,approximately95%oftheobservationsliebetween x 2s and x +2s.

• Approximately99.7%oftheobservationsliewithinthreestandarddeviationsofthemean.So,approximately99.7%oftheobservationsliebetween x 3s and x +3s

BeforeapplyingtheEmpiricalRuletoaparticulardistribution,wemustmakesurethedistributionis unimodalandsymmetric.Otherdistributionscanhavequitedifferentpercentages.

5. Thebodytemperaturesof130adultsaredescribedbythefollowingrelativefrequencyhistogram.Themean is 98 25◦Fandthestandarddeviationis 0 73◦F(Source: AmericanStatisticalAssociation).

Source: AmericanStatisticalAssociation

a. ExplainwhytheEmpiricalRulecanbeapplied.

b. ApplytheEmpiricalRule.

c. UsetheEmpiricalRuletoestimatethe number oftheadultswhohavebodytemperaturesbetween 97 52◦Fand 98 98◦F.Verifyyourresultbyreferringtothehistogram.

d. UsetheEmpiriicalRuletoestimatethepercentageoftheadultswhohavebodytemperatureslessthan 96 79◦FORgreaterthan 99 71◦F?

e. UsetheEmpiricalRuletoestimatethe number oftheadultswhohavebodytemperaturesgreaterthan 99.71◦F.

6. TheWechslerIQtestmeasuresaperson’sintelligence.TheIQs(inpoints)ofsomepeoplearedescribedby thefollowingdensityhistogram.Someofthebarshavebeenleftblankonpurpose.

a. Estimate M .

b. Estimate x

c. Estimate s.

OBJECTIVE5

Ifanobservationismorethantwostandarddeviationsawayfromthemean,werefertotheobservationas unusual.

7. InProblem5,the130adultshaveameanbodytemperatureof 98.25◦Fwithstandarddeviation 0.73◦F.Is abodytemperatureof 96.3◦Funusual?

OBJECTIVE6

SummaryofMeasuringCenterandSpread

• Ifadistributionisunimodalandsymmetric,thenweusuallyusethemeantomeasurethecenterand thestandarddeviationtomeasurethespread.

• Ifadistributionisskewed,thenweusuallyusethemediantomeasurethecenterandtherangeto measurethespread.

OBJECTIVE7

Deﬁnition Variance

The variance isthesquareofthestandarddeviation.

8. InProblem2,wefoundthatthestandarddeviationofthegasmileagesofdifferentversionsoftheAudiR8 Spyderis1.8257milespergallon.Findthevariance.

ThemeaningsandsymbolsofthemeasureswehavediscussedinSections4.1and4.2areshowninthe followingtable.

MeasureWhatItMeasuresSymbol meancenter x mediancenter M modecenter(nostandardsymbol) rangespread R standarddeviationspread s variancespread s2

HW 1,3,7,9,13,19,21,23,27,29,31,33,35,37,43,45,47,55

SECTION4.2TEACHINGTIPS

Standarddeviationisanextremelyimportantfoundationalconcept.Inparticular,itwillbeusedagreatdealwhen workingwithnormaldistributions(Sections5.4and5.5).Althoughvarianceservesaroleinanintroductory statisticscourse,itwillnotbeusedinsubsequentchaptersofthistext.

OBJECTIVE1COMMENTS

Studentshaveaneasytimewithﬁndingtherange.Asusual,Iemphasizethatstudentsshouldstatetheunits.

OBJECTIVE2COMMENTS

Atthebottomofpage241ofthetextbook,thereisaniceexampleoftheshortcomingofusingtherangeto measurespread.Topreparestudentsfortheforthcomingstandarddeviationformula,Iemphasizethatwhenwe subtracttwonumbers,theresultisthedistancebetweenthenumbersortheoppositeofthedistance,depending onwhichofthetwonumbersislarger.

Studentshaveatoughtimefollowingthederivationforthestandarddeviationformula.Theﬁrsttwoparagraphsonpage242ofthetextbookareanicewaytogetacrosswhywesquarethedifferences.Ratherthango intodetailaboutwhywedivideby n 1 ratherthan n,whichwouldconfusestudentsmorethanhelp,Isimply saythatitturnsouttobemoreusefultodivideby n 1.

Tocomputeastandarddeviation,Iﬁrstdemonstratehowtouseatable(seeTable22onpage243ofthe textbook).ThenIshowhowtoavoidusingatablebypressingalltheappropriatebuttonsonacalculator.Some studentspreferthetableapproachandotherspreferthelatterapproach.Iwarnstudentsthatonthenexttest theywillhavetouseoneofthesetwomethodstoﬁndthestandarddeviationforadatasetcontainingaboutfour observations.

Withallthenecessarycalculations,somestudentsforgetthatstandarddeviationmeasuresthespreadofsome observations,soIrepeatthismanytimes,remindingthemofthegeometricmeaningofdifferences.

Afterhavingstudentscalculateoneortwostandarddeviations,Ishowthemhowtocomputestandarddeviation usingStatCrunch.Asusual,Iemphasizethattheyshouldincludeunitsintheirresult.

OBJECTIVE3COMMENTS

Bycomparingthestandarddeviationoftwodatasets,studentsstarttoseehowstandarddeviationcanbehelpful. NotonlydoesProblem3demonstratemakingsuchacomparison,italsodemonstratesthesubtlepointthatwe mustconsiderthemeansandthestandarddeviationsoftwogroupsofdataifwewantsomehinttowardhowthe largest(orsmallest)observationscompare.

OBJECTIVE4COMMENTS

TheEmpiricalRuleisahighlightofthechapterandwillbeusedfrequentlyinSection4.2andwillobviouslybe animportantconceptwhendiscussingthenormaldistribution(Sections5.4and5.5).

Topreparestudentsforthegeometricsigniﬁcanceofexpressionssuchas x s and x + s intheEmpirical

100CHAPTER2LectureNotesandTeachingTips

Rule,IsketchaﬁguresimilartoFig.51onpage245ofthetextbooktogetacrossthegeometricsigniﬁcanceof thenumbers 7 ± 3.Thisisasimpleidea,butmanystudentslackthenumbersensetosortthisoutontheirown.

GROUPEXPLORATION:EmpiricalRule

ThisactivityismeanttointroducetheEmpiricalRule.IadviseusingtheexplorationbecausetheEmpiricalRule issoimportant.Becausethecalculationsaresomewhatinvolved,Iliketolisttheresultsoftheexplorationin stagessothatgroupsofstudentscanmakesurethey’reontherighttrack.

IfyouchoosetolectureontheEmpiricalRule,Iadviseworkingwithadatasetconsistingof100observations socomputingpercentageswillbeconvenient.Ialsoadviseconstructingadatasetwithameanandastandard deviationthatareeasytoperformcalculationswith,suchastheonesinExample4: x =70 and s ≈ 10.Foraﬁrst example,itishelpfultodisplaythedatawithadotplot(asopposedtoahistogram)sothatindividualobservations canbecounted.Subtractingthenumberofobservationsnotinanintervalfrom100canmovethingsalong.

OncestudentsunderstandhowtheEmpiricalRuleconnectswithadotplotofdata,itisimportanttomoveon todensityhistograms.Thisshouldgosmoothlyduetostudents’workwithdensityhistogramsinSections3.4and 4.1.TheconnectionbetweentheEmpiricalRuleanddensityhistogramswillsetasolidfoundationforthenormal distribution.

Problem5isaniceapplicationoftheEmpiricalRule.Itisharderthantheexercises,butitwillprimestudents fortacklingsuchharderproblemswhenworkingwiththenormalcurve(Sections5.4and5.5).

Problem6requiresstudentstogobackward:fromprobabilitiestoﬁndingthemeanandthestandarddeviation. Whenaconceptisimportant,studentswillgainabetterunderstandingbyhavingtogoforwardandbackward. TheEmpiricalRuleiscertainlyworththatemphasis.

OBJECTIVE5COMMENTS

Fornow,thetextbookdeﬁnesanobservationtobeunusualifitismorethan2standarddeviationsawayfromthe mean.Oncestudentscanﬁndprobabilitiesforthenormalcurvewithgreaterprecision,thetextbookwillusethe moreprecisecutoffof1.96standarddeviations(Section5.5).

OBJECTIVE6COMMENTS

Afterestablishingthatweshouldusetherangetomeasurethespreadforaskeweddistribution,Iremindstudents thattherangeisacrudewaytomeasurespreadandsaythatinSection4.3wewilllearnanothermeasureofspread (theIQR)thatwillhelpcompletethepicture.

OBJECTIVE7COMMENTS

Aftercalculatingastandarddeviation,itiseasyforstudentstoﬁndthevariance. Becauseofthepreferredunitsofstandarddeviationandtheusefulnessinusingstandarddeviationtoﬁnd z-scores,variancewillnotbeusedinsubsequentsections.

SECTION4.3LECTURENOTES

Objectives

1. Find quartiles ofsomedata.

2. Findthe interquartilerange ofsomedata.

3. Constructa boxplot todescribeadistributionwithoutoutliers.

4. Identifyoutliers.

5. Constructa boxplot todescribeadistributionwithoneormoreoutliers.

6. Comparetheboxplotsoftwogroupsofdata.

OBJECTIVE1

Deﬁnition Firstquartile,secondquartile, and thirdquartile

The ﬁrstquartile, secondquartile,and thirdquartile arethe25th,50th,and75thpercentiles,respectively.

Weusethesymbols Q1 , Q2 ,and Q3 tostandfortheﬁrst,second,andthirdquartiles,respectively.

1. Studentsinoneoftheauthor’sstatisticsclassesweresurveyedaboutthenumberofhourstheyspending watchingvideos,movies,andtelevisionshowsonaweekday.Herearetheanonymousresponses(inhours) oftenofthestudents:4,10,3,2,0,2,1,2,4,7(Source: J.Lehmann).

a. Constructahistogramtodeterminewhetherthemeanorthemedianisthebettermeasureofthecenter. Explain.

b. Find Q2 (themedian).

c. Find Q1

d. Find Q3

e. UsetechnologytoverifytheresultsyoufoundinParts(b),(c),and(d).

f. DescribethemeaningoftheresultsyoufoundinParts(b),(c),and(d).

Ifsomedatahaveanoddnumberofdatavalues,donotincludethemedianinthelowerhalfofthedata whenﬁnding Q1 .Likewise,donotincludethemedianintheupperhalfofthedatawhenﬁnding Q3 .

OBJECTIVE2

Deﬁnition InterquartileRange

The interquartilerange (IQR)isgivenby IQR = Q3 Q1

TheIQRmeasuresthespreadofthemiddle50%oftheobservations(from Q1 to Q3 ).

2. InProblem1,wefound Q1 =2, Q2 =2 5,and Q3 =4 forthedataaboutthenumberofhoursstudents spendwatchingvideos,movies,andtelevisionshowsperweekday:4,10,3,2,0,2,1,2,4,7.

a. CalculatetheIQR.

b. Calculatetherange.

c. WhatdotheIQRandtherangemeaninthissituation?

d. DiscusswhethertheIQRandtherangearesensitivetotheoutlier10hours.

TheIQRisresistanttooutliersandtherangeissensitivetooutliers.

OBJECTIVE3

3. ThenumberofannualsharkattacksinHawaiiareshowninthefollowingtablefortheyears2001–2014. 3653437 134310137

Source: FloridaMuseumofNaturalHistory

a. Constructaboxplot.

b. Whichislonger,theleftpartoftheboxortherightpart?Whichislonger,theleftwhiskerorthe rightwhisker?Assumingthedistributionisunimodal,isthedistributionskewedleft,skewedright,or symmetric?

c. Refertotheboxplottoestimatetherange.Whatdoesitmeaninthissituation?

d. RefertotheboxplottoestimatetheIQR.Whatdoesitmeaninthissituation?

Ifonewhiskerislongerthantheother,thatdoes not meanmoreobservationsarerepresentedbythe longerwhisker.Itmeansthattheobservationsrepresentedbythelongerwhiskeraremorespreadoutthan theapproximatelyequalnumberofobservationsrepresentedbytheshorterwhisker.

MeaningofBoxplotsThatDescribeDistributionswithoutOutliers

• Aboxplotthatdescribesadistributionwithoutoutliersconsistsoffourparts:theleftwhisker,the leftpartofthebox,therightpartofthebox,andtherightwhisker.Eachpartrepresents25%ofthe observations.

• ThefulllengthoftheboxisequaltotheIQR.

Thefollowingtwostatementsapplytounimodaldistributions:

• Iftheleftpartoftheboxisatleastaslongastherightpartandtheleftwhiskerisquiteabitlonger thantherightwhisker,thenthedistributionisskewedleft.

• Iftherightpartoftheboxisatleastaslongastheleftpart,andtherightwhiskerisquiteabitlonger thantheleftwhisker,thenthedistributionisskewedright.

4. Thepercentagesofresidentswhoarenonreligiousaredescribedbytheboxplotfortheﬁftystates.

Source: TheGallupOrganization

a. Itturnsoutthedistributionisunimodal.Onthebasisoftheboxplot,isthedistributionsymmetric, skewedleft,orskewedright?Explain.

b. Estimatetherange.Whatdoesitmeaninthissituation?

c. EstimatetheIQR.Whatdoesitmeaninthissituation? Copyright c 2016PearsonEducation,Inc.

OBJECTIVE4

Deﬁnition Fences

The leftfence andthe rightfence ofsomedatavaluesaregivenby

• leftfence = Q1 1 5 IQR

• rightfence = Q3 +1 5 IQR

Deﬁnition Outlier

An outlier isanobservationthatislessthantheleftfenceorgreaterthantherightfence.Wesaythatthe outlierlies outside thefences.

5. InProblems1and2,wefound Q1 =2, Q3 =4,andIQR =2 forthedataaboutthenumberofhours studentsspendwatchingvideos,movies,andtelevisionshowsperweekday:4,10,3,2,0,2,1,2,4,7. Identifyandinterpretanyoutliers.

OBJECTIVE5

6. Constructaboxplotthatdescribesthedataaboutthenumberofhoursstudentsspendwatchingvideos, movies,andtelevisionshowsperweekday:4,10,3,2,0,2,1,2,4,7.

7. Whichislonger,theleftpartoftheboxortherightpart?Whichislongertheleftwhiskerortheright whisker?Whatdoyourresponsestellyouabouttheshapeofthedistribution?

OBJECTIVE6

8. ThenumberofannualsharkattacksinCalifornia,Florida,andHawaiiaredescribedbythefollowing boxplotsfortheyears2001–2014.

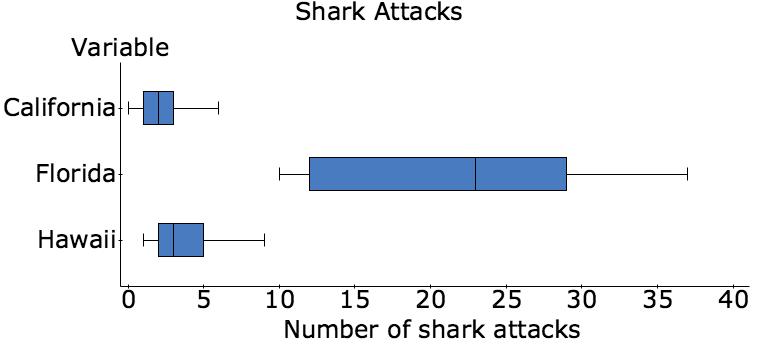
Source: FloridaMuseumofNaturalHistory

a. Comparethecentersofthethreedistributions.Whatdoesthismeaninthissituation?

b. Comparethespreadsofthethreedistributions.Whatdoesthismeaninthissituation?

c. ComparetheIQRofFlorida’sdistributiontotherangeofCalifornia’sdistribution.Whatdoesthis meaninthissituation?

HW 1,3,5,11,13,15,17,21,23,25,29,33,41,45,47

SECTION4.3TEACHINGTIPS

Thissectioncouldbeskippedbecauseboxplotswillnotbeusedinsubsequentchapters,butboxplotsareuseful inintroductorystatistics.Inparticular,theyareaconvenientwaytoidentifyoutliers.

OBJECTIVE1COMMENTS

Somestudentsthinkthatthedistancesbetweentheminimumobservationand Q1, Q1 and Q2, Q2 and Q3,andso on,areallequal.ThediagraminFig.79onpage260ofthetextbookmakesitclearthatthisisnottrue.

Ingeneral,studentsfinditeasytofindthequartiles,buttheydoneedtoberemindedthatforanoddnumber ofobservations,wedonotincludethemedianinthelowerorupperhalfwhenfinding Q1 or Q3,respectively. AlthoughtheTI-84followsthispracticeforanyoddnumberofobservations,StatCrunchfollowsthispractice onlywhenthenumberofobservationsisoneofthefollowingoddnumbers:3,7,11,15,19,....

OBJECTIVE2COMMENTS

OncestudentsunderstandhowtocomputetheIQR,Iemphasizethatifadistributionisunimodalandsymmetric, standarddeviationisabettermeasureofvariabilitythantheIQRbecausestandarddeviationtakesintoaccount alltheobservationsbuttheIQRtakesintoaccountonlytwoobservations.

Foradistributionthatisnotunimodalandsymmetric,IsuggestthatstudentscomputeboththeIQRandthe rangetomeasurethevariabilitybecauseeachmeasureinvolvesonlytwoobservations.Thismotivatesconstructing boxplots.

Asimplebutgoodcritical-thinkingquestionistoaskstudentswhytheIQRisresistanttooutliersbutthe rangeissensitivetooutliers.

OBJECTIVE3COMMENTS

Constructingboxplotsofdistributionsthatdonothaveoutliersisreallyjustasteppingstonetoconstructingboxplotsofdistributionsthatdohaveoutliers,whichisObjective5.

Itellstudentsthattheboxplotistheonlydiagramwehavediscussedwhosefeaturesallowustovisualizeall threeoffollowing:themedian,theIQR,andtherange.

Oncestudentsunderstandhowtoﬁndthequartiles,itiseasyforthemtoconstructaboxplot.Itistheinterpretationofboxplotsthatchallengessomestudents.Inparticular,somestudentsthinkthatifonepartoftheboxplot, saytheleftwhisker,isshorterthananotherpart,saytherightwhisker,thenfewerobservationsarerepresented bytheleftwhisker.DrawingaboxplotaboveadotplotsuchasinFig.85onpage263ofthetextbookcandispel thismisconception,althoughitwillbeevenclearerifyouworkwiththefollowingcontriveddatabecausenoneof theobservationsareequaltothequartiles:0,4,6,19,21,49,51,and100.Oryoucanfacilitatetheexploration, whichaddressesthisissue.

Comparingaboxplotandahistogramofthesamedatacanalsobeinstructive(seeFigs.85and86onpage 263ofthetextbook).Thiscanbefollowedupbyhavingstudentsmatchhistogramswithboxplots(Exercises5–8).

Asusual,afterstudentshaveconstructedoneortwoboxplotsbyhand,Iallowthemtousetechnology.

OBJECTIVE4COMMENTS

Oncestudentsarecomfortablecalculatingthefencesandidentifyingtheoutliers,Itrytomakesuretheyunderstandwhytheprocessmakessense.Inparticular,Idiscussthattheleftfenceisadistanceof1.5IQRtotheleftof Q1 andtherightfenceisadistanceof1.5IQRtotherightof Q3.

Afterdisplayingseveralboxplotsfordistributionsthathavejustoneortwooutliers,it’sfuntodisplaya boxplotforthedistributionofinterestratesatthewebsiteLendingClub,whichhas186outliers(Exercise11). Anotheroptionistodisplayboxplotsforthedistributionsofhighwayandcitygasmileagesofcars(Exercise28).

OBJECTIVE5COMMENTS

Whenintroducinghowtoconstructaboxplotofadistributionwithoutliers,Iﬁrstconstructaboxplotasifthere werenooutliers.ThenIerasetheappropriatewhisker(s),drawthefences,drawtheshorterwhisker(s),andplot

theoutlier(s).ThisprogressionhelpsstudentsbuildonwhattheyalreadylearnedaboutboxplotsinObjective3.

ItellstudentsthatevenifIalreadyhaveasenseofadistributionbyviewingadiagramotherthanaboxplot, Ioftenstillusetechnologytoconstructaboxplottocheckforoutliers.ThenIgeneralize,explainingthatwe cangainmuchinsightbyconstructingseveraltypesofdiagramsofonedistribution.Andthiscanbedonevery quicklywiththeuseoftechnology.

OBJECTIVE6COMMENTS

Problem5demonstratesameaningfulcomparisonofboxplots.

GROUPEXPLORATION:DeterminingtheMeaningofaBoxplot

Thisisanicewaytoconveytostudentsthatthelengthsofthepartsofaboxplotindicatethevariabilityofthe observationsandnotthenumberofobservations.

Usually,I’mafanofhavingstudentsusetechnologywhencompletingexplorationssotheycanfocusonthe conceptsandnotgetboggeddownwithconstructingdiagramsorcomputingvalues,butforthisexplorationit helpsstudentstoconstructtheboxplotsbyhandtoseewhat’sgoingon. Copyright c 2016PearsonEducation,Inc.

CHAPTER5OVERVIEW

ThischapterdrawsheavilyonconceptsaddressedinChapters1–4.Thefoundationofprobability(Chapter5) israndomness,whichwasdiscussedinChapter2.Thecomplementrule,additionrulefordisjointevents,and thegeneraladditionrule(allinSection5.2)haveallbeenaddressedwithoutcallingthemassuchwhenworking withproportionsinChapters1and3.Thenormalcurve(Section5.4and5.5)reliesoncentraltendencyconcepts (Section4.1),variationconcepts(Section4.2),anddensityhistograms(Section3.4).

Becausesomuchofthegroundworkhasbeenestablishedinpreviouschapters,youwillbepleasedhow quicklystudentspickuponmanyconceptsinthischapter.

Ifyouaretightontime,considerskippingSections5.3and5.5.Sections5.1and5.2provideimportant developmentforSection5.4,whichisthegrandfinaleofthefirstfivechapters.UponcompletionofSection5.4, studentsshouldhaveasolidfoundationforquiteabitofanintroductorystatisticscourse,includingthecrucial samplingdistribution.

SECTION5.1LECTURENOTES

Objectives

1. Computeandinterpret probabilities

2. Use simulation toestimateaprobability.

3. Usethe equallylikelyprobabilityformula toﬁndprobabilities.

4. Describepropertiesofprobability.

5. Useapiecharttoﬁndprobabilities.

6. Useadensityhistogramtoﬁndprobabilities.

7. Usethe EmpiricalRule toﬁndprobabilities.

OBJECTIVE1

• RecallfromSection2.1that ifwerandomlyselectoneitemfromagroupofitems,eachitemhasthe samechanceofbeingselected.

• Wecallaprocessthatselectsitemsrandomlya randomexperiment

Deﬁnition Probability

The probability ofanoutcomefromarandomexperimentistherelativefrequencyoftheoutcomeifthe experimentwererunaninﬁnitenumberoftimes.

1. Anexperimentconsistsofrollingasix-sideddieonce.Findandinterprettheprobabilityofrollinga5.

Aprobabilitydoesnottelluswhattoexpectifwerunanexperimentasmallnumberoftimes.

OBJECTIVE2

Usingtechnologytoimitatearandomexperimentiscalleda simulation

2. Usetechnologytosimulateﬂippingacointhegivennumberoftimes.Discusshowwelltherelativefrequencyoftailsestimatestheprobabilityofgettingtails.

a. 5times b. 100times c. 1100times d. 10,100times

Byrunningarandomexperimentalargenumberoftimes,wecanuserelativefrequencytoestimate theprobability.

OBJECTIVE3

3. Anexperimentconsistsofrollingasix-sideddieonce.Findandinterprettheprobabilityofrollinganodd number.

Deﬁnition Samplespace

The samplespace ofarandomexperimentisthegroupofallpossibleoutcomes.

Deﬁnition Event

An event issomeoftheoutcomesinthesamplespace,allofthem,ornoneofthem.

EquallyLikelyProbabilityFormula

Ifthesamplespaceofarandomexperimentconsistsof n equallylikelyoutcomesandanevent E consists of m ofthoseoutcomes,then

Iftheoutcomesofarandomexperimentarenotequallylikely,thenwecannotusetheequallylikely probabilityformula.

4. Foragroupof10studentsinoneoftheauthor’sprestatisticsclasses,thereare4sociologymajors,2 graphicdesignmajors,3communicationsmajors,and1artmajor.Noneofthestudentsaredouble-majors. Assumeonestudentisrandomlyselectedfromthegroup.UseSforsociology,Gforgraphicdesign,Cfor communications,andAforart.

a. Constructafrequencyandrelativefrequencytableofthestudents’majors.

b. Find P (S), P (G), P (C),and P (A).HowdoyourresultstieintothetableyouconstructedinPart(a)?

c. Find P (math)

d. Findtheprobabilityofrandomlyselectingasociology,graphicdesign,communications,ORartmajor.

e. Find P (S)+ P (G)+ P (C)+ P (A).Whydoestheresultmakesense?

OBJECTIVE4

• An impossibleevent doesnotcontainanyoutcomesofthesamplespace.

• A sureevent (or certainevent)containsalltheoutcomesinthesamplespace.

• Aneventthatcontainsjustoneoutcomeisa single-outcomeevent

ProbabilityProperties

• Theprobabilityofanimpossibleeventisequalto0.

• Theprobabilityofasureeventisequalto1.

• Theprobabilityofaneventisbetween0and1,inclusive.

• Thesumoftheprobabilitiesofallthesingle-outcomeeventsinthesamplespaceisequalto1.

Ifyouevercalculateaprobabilitytobenegativeorgreaterthan1,youshouldrealizethatyou’vemade anerror.

5. Astudentsurveysotherstudentsabouttheirfavoritesport.Foreachsport,thestudentcalculatestheprobabilityofrandomlyselectingthatsportfromtheresponses(seethefollowingtable).Whatwouldyoutell thestudent?

6. Astudentcalculatesthattheprobabilityofrandomlyselectingacarthathasgasmileageof25milesper gallonis 0 32.Whatwouldyoutellthestudent?

Ifasituationinvolvesaproportionorprobability,itcanbeinterpretedtoinvolvetheotheraswell.

OBJECTIVE5

7. Someadultemployeesweresurveyedabouthowoftentheyarelateforwork.Thepercentagesforvarious responsesaredescribedbythefollowingpiechart(Source: YouGov).

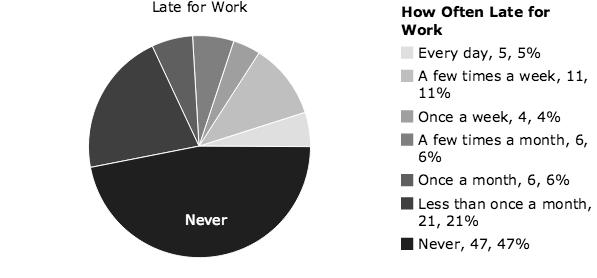
Findtheprobabilitythatapersonrandomlyselectedfromthesurveyis

a. neverlatetowork.

b. latetoworkatleastonceamonth.

c. latetoworkatmostonceamonth.

Deﬁnition Randomvariable

A randomvariable isanumericalmeasureofanoutcomefromarandomexperiment.Weoftenusea capitallettersuchas X tostandforarandomvariable.

8. Let X betheoutcomeofrollingasix-sideddieonce.Findthegivenprobability.

a. P (X =5)

b. P (X ≤ 3)

c. P (X> 3)

d. P (2 ≤ X ≤ 5)

e. P (2 <X< 5)

OBJECTIVE6

Thefollowingdensityhistogramdescribesthenumberofmammalspeciesthreatenedineachcountryintheworld. Somecountrieshaveatleast80threatenedmammalspecies,butthebarswouldnotbevisible.

ThreatenedMammalSpecies,byCountry Density

Numberofthreatenedmammalspecies

Let X bethenumberofthreatenedmammalspeciesinarandomlyselectedcountry.Findthegivenprobability.

1. P (10 ≤ X ≤ 40)

2. P (X< 30)

3. P (X ≥ 30)

InterpretingtheAreaofaBarofaDensityHistogram

Wecaninterprettheareaofabarofadensityhistogramas

• theproportionofobservationsthatlieinthebar’sclass.

• theprobabilityofrandomlyselectinganobservationthatliesinthebar’sclass.

OBJECTIVE7

9. TheWechslerIQtestmeasuresaperson’sintelligence.ThedistributionofIQscoresisunimodaland symmetric.Thetestisdesignedsothatthemeanscoreis100pointsandthestandarddeviationis15 points(Source:EssentialsofWAIS-IVAssessment,ElizabethLichtenbergeretal.).Findtheprobabilityof randomlyselectingapersonwhohasIQbetween55and145points.

HW 1,3,5,7,15,19,23,29,31,35,41,45,49,53,55,57,59,65,73

SECTION5.1TEACHINGTIPS

Akeyconceptofthischapterisrandomness.IfyouskippedSection2.1,Iadviseaddressingtherandomness conceptsincludedinSection2.1now.

OBJECTIVE1COMMENTS

ForProblem1,studentsarequicktosaythattheprobabilityis 1 6 .Butonatest,somestudentstendtothinkthe probabilityis 5 6 (andotherwronganswers),soitisworthrevisitingthisbasictypeofproblemseveraltimesonce otherconceptsinthissectionhavebeenaddressed.

OBJECTIVE2COMMENTS

IbelievecompletingasimulationlikeinProblem2isareallyeffectivewaytogetacrosshowrelativefrequencies canestimateprobabilities.

GROUPEXPLORATION:PerformingaSimulation

InsteadofgoingoverProblem2,youcouldhavegroupscompletethisexploration.Problem4oftheexploration canclarifyatypicalstudentmisconception.

OBJECTIVE3COMMENTS

CompletingProblem3isagreatprimerfordeﬁning samplespace and event.Itisalsoanicewaytointroducethe equallylikelyprobabilityformula.

ThediscussionaboutthespinnerinFig.6onpage288ofthetextbookisagreatwaytounderscorethe importancethatoutcomesmustbeequallylikelytoapplytheequallylikelyprobabilityformula.

SolvingProblem4willbegreatpreparationfordiscussingprobabilityproperties(thenextobjective).

OBJECTIVE4COMMENTS

Whendiscussingtheprobabilityproperties,IrefertotheresultswefoundforProblem4.Iemphasizethat becauseofwhatweknowaboutrelativefrequencies,itmakessensethatthesumoftheprobabilitiesofallthe single-outcomeeventsinthesamplespaceisequalto1.

Ialsoemphasizethataprobabilitymustbebetween0and1,inclusive.Otherwise,studentstendtomiss catchingthatthey’vemadesucherrorsontests.

OBJECTIVE5COMMENTS

Problem8isagoodreminderaboutinequalitynotation(Section1.1),whichsomestudentsstrugglewith.

OBJECTIVE6COMMENTS

Somestudentscontinuetostrugglewithinequalitynotation,buttheseissuesarelargelyresolveduponcompletion ofthisobjective.

OBJECTIVE7COMMENTS

Problem9isanicereminderabouttheEmpiricalRule(Section4.2),whichisgoodpreparationforthenormal

curve(Section5.4).

SECTION5.2LECTURENOTES

Objectives

1. Usethe complementrule toﬁndprobabilities.

2. Usetheadditionrulefordisjointeventstoﬁndprobabilities.

3. Usethegeneraladditionruletoﬁndprobabilities.

OBJECTIVE1

1. Foragroupof10studentsinoneoftheauthor’sprestatisticsclasses,thereare4sociologymajors,2 graphicdesignmajors,3communicationsmajors,and1artmajor.Noneofthestudentsaredouble-majors. Assumeonestudentisrandomlyselectedfromthegroup.UseSforsociology,Gforgraphicdesign,Cfor communications,andAforart.

a. Findtheprobabilityofrandomlyselectingacommunicationsmajor.

b. FindtheprobabilityofNOTrandomlyselectingacommunicationsmajor.

Deﬁnition Complement

The complement ofanevent E istheeventthatconsistsofalltheoutcomesnotin E.Wewrite“NOT E” tostandforthecomplementof E

A Venndiagram consistsofoneormoreshadedcirclesthatareallborderedbyarectangle.Theregioninside therectanglerepresentsthesamplespaceandtheregioninsideeachcirclerepresentsanevent.

ComplementRule

Foranyevent E, P (NOT E)=1 P (E)

2. ConsidertheexperimentofrandomlyselectinganAmerican.TheprobabilitythatthepersonisAfrican Americanis0.13(Source: U.S.CensusBureau).FindtheprobabilityofselectingapersonwhoisNOT AfricanAmerican.

OBJECTIVE2

Deﬁnition Disjointevents

Twoeventsare disjoint (or mutuallyexclusive)iftheyhavenooutcomesincommon.

3. Acommitteeconsistsof3Republicans,5Democrats,and2Independents.Onepersonisrandomlyselected fromthecommittee.Use R forRepublican, D forDemocrat,and I forIndependent.

a. Aretheevents R and I disjoint?Explain.

b. Find P (R).

c. Find P (I).

d. Find P (R OR I).

e. Find P (R)+ P (I)

f. ComparetheresultsofParts(d)and(e).

If E and F aredisjointevents,then

AdditionRuleforDisjointEvents

4. Aten-sideddieisrolledonce.Use F tostandforanoutcomelessthan4and E tostandforanoutcome greaterthan8.Findthegivenprobabilities.

a. P (F )

b. P (E)

c. P (F OR E)

5. Theweights(inpounds)oftype2diabetespatientsfrom2006to2007aredescribedbythefollowing densityhistogram.Theweightsareroundedtotheonesplace.

WeightsofType2DiabetesPatients Density Pounds

a. Findtheprobabilitythatapatientrandomlyselectedfromthestudywouldweighbetween150and 299pounds,inclusive.

b. Findtheprobabilitythatapatientrandomlyselectedfromthestudywouldweighlessthan150pounds ORatleast300pounds.

c. Findtheprobabilitythatapatientrandomlyselectedfromthestudywouldweighbetween150and 199pounds,inclusive,ORbetween250and299pounds,inclusive.

OBJECTIVE3

6. Atotalof1287randomlyselectedadultswereaskedthefollowingquestion.“Doyouagreeordisagree? Gaycouplesshouldhavetherighttomarryoneanother.”Theirresponsesandtheirreligiouspreferences aresummarizedinthefollowingtable.

ProtestantCatholicJewishOtherNone Total Agree 2301711246167 626

NeitherAgreeNorDisagree 713612224 154 Disagree 3089426043 507 Total 60930115128234 1287

Source: GeneralSocialSurvey

Anadultisrandomlyselectedfromthosesurveyed.Use A tostandforanadultwhoagreesand N tostand foranadultwhohasnoreligiouspreference.Findthegivenprobability.Roundtothethirddecimalplace.

Foranyevents E and F ,

GeneralAdditionRule

7. Asix-sideddieisrolledonce.Findtheprobabilityofrollinganumberthatisatmost3ORisodd.

8. Wereturntothesurveyaboutgaycouples’righttomarryversusreligiouspreference(seethefollowing table).FindtheprobabilityofrandomlyselectingasurveyedadultwhodisagreesORisCatholic.Roundto thethirddecimalplace.

ProtestantCatholicJewishOtherNoneTotal yellowAgree2301711246167626

NeitherAgreeNorDisagree713612224154 Disagree3089426043507 Total609301151282341287

Source: GeneralSocialSurvey

Ifthegeneraladditionruleisusedwithtwodisjointevents,theresultwillbethesameasusingthe additionrulefordisjointevents.

HW 1,3,5,9,13,17,23,27,35,43,47,53,55,59,65

SECTION5.2TEACHINGTIPS

Thecomplementruleandtheadditionrulefordisjointeventsareextremelyimportantpreparationforthe normaldistribution(Section5.4),whichisahighlightofthecourse.

OBJECTIVE1COMMENTS

Afterhavingworkedsomuchwiththeproportion-of-the-restproperty,studentsarequicktoﬁndthesolutionto

Problem1(b).Fromtheirperspective,thecomplementruleissimplyanothernamefortheproportion-of-the-rest property.

Becausestudentsaresoquicktopickuponthecomplementrule,theydon’treallyneedtoseeitillustrated withaVenndiagram,butIshowthemoneanywaytogetthemusedtoviewingsuchdiagrams.

OBJECTIVE2COMMENTS

WhenworkingwithdensityhistogramsandpiechartsinChapter3,studentswerebasicallyapplyingtheaddition rulefordisjointeventswithoutrealizingit,sostudentscannoweasilylearnthisrule.

HavinggroupsofstudentsworkonProblem3isanexcellentwaytointroducetheadditionrulefordisjoint events.Studentsarequicktosaythat P (R OR I) and P (R)+ P (I) are"thesamething."

Becauseofstudents’pastworkwithdensityhistograms,theyhaveaneasytimewithProblem5.

OBJECTIVE3COMMENTS

Whenworkingwithtwo-waytablesinChapter3,studentswerebasicallyapplyingthegeneraladditionrule withoutrealizingit,sotheyeasilylearnthisrulenow.Eventhoughstudentsalreadyhavetheidea,Iemphasize thatwesubtractP(EANDF)toaccountforthedouble-countingandillustratewithaVennDiagram.

GROUPEXPLORATION:GeneralAdditionRule

Thisexplorationcanbeusedtointroducethegeneraladditionrule.Evenifsomegroupsofstudentsareunableto completetheexploration,whateverportiontheyareabletocompletewillserveasagoodprimerasyougoover therestoftheexplorationandthendiscussthegeneraladditionruleingeneral.

SECTION5.3LECTURENOTES

Objectives

1. Findandinterpret conditionalprobabilities

2. Determinewhethertwoeventsare independent or dependent

3. Usethemultiplicationruleforindependenteventstoﬁndprobabilities.

OBJECTIVE1

Deﬁnition Conditionalprobability

If E and F areevents,thenthe conditionalprobability P (E | F ) istheprobabilitythatEoccurs,giventhat Foccurs.

Itisimportanttokeepstraightthedifferenceinmeaningsof P (E AND F ) and P (E | F )

1. Atotalof989randomlyselectedadultswereaskedwhethertheyareinterestedininternationalissues.The followingtablecomparestheirresponsesandtheirages.

Table2.1: InterestinInternationalIssuesversusAge

AgeGroup(years)

18–3031–4041–5556–89 Total

Veryinterested 173667106 226

Moderatelyinterested 8169128184 462

Notatallinterested 77657980 301 Total 175170274370 989

Source: GeneralSocialSurvey

Supposeapersonisrandomlyselectedfromthesurvey.

a. Find P (notatallinterested).Whatdoesthismeaninthissituation?

b. Find P (notatallinterested | ages18–30years).Whatdoesthismeaninthissituation?

c. ComparetheresultsyoufoundinParts(a)and(b).Whatdoesyourcomparisonmeaninthissituation?

2. InProblem1,weworkedwiththedatashowninthefollowingtable.

AgeGroup(years)

18–3031–4041–5556–89 Total

Veryinterested 173667106 226

Moderatelyinterested 8169128184 462

Notatallinterested 77657980 301 Total 175170274370 989

Source: GeneralSocialSurvey

a. Findtheprobabilitythatanadultrandomlyselectedfromthesurveyisbetween56and89yearsof age,giventhepersonisnotatallinterestedininternationalissues.

b. Findtheprobabilitythatanadultrandomlyselectedfromthesurveyisbetween31and40yearsof age,giventhepersonisnotatallinterestedininternationalissues.

c. ComparetheresultsyoufoundinProblems1and2.Whatdoesyourcomparisonmeaninthissituation?

InProblem1,wecomparedtwoconditionalprobabilities,whichwasquiteinstructive.InProblem2,we comparedtwootherconditionalprobabilitiesaboutthesamesituation,butthecomparisonwasnotinstructive.The mainpointisthatcareshouldbetakentounderstandthemeaningofprobabilitiesbeforejumpingtoconclusions bycomparingthem.

3. Apersonrollsasix-sideddieonce.Findtheprobabilitythattheoutcomeis

a. a5,giventhenumberisodd.

b. anoddnumber,giventhenumberisatmost3.

OBJECTIVE2

Deﬁnition Independentevents and dependentevents

Twoevents E and F are independent if P (E | F )= P (E).Theeventsare dependent if P (E | F ) and P (E) are not equal.

Determinewhetherthegivenevents E and F areindependent.

1. Experiment:Acollegestudentwhoistakingprestatisticsisrandomlychosen. Event E:Thestudentattemptseveryexerciseinthetextbook. Event F :Thestudentpassesthecourse.

2. Experiment:Apersonﬂipsacoinandrollsasix-sideddie. Event E:Thecoinlandsonheads. Event F :Thepersonrollsa2.

Iftwoeventsaredependent,thisdoesnotnecessarilymeanthatoneeventcausestheother.

4. Atotalof1310adultsweresurveyedaboutwhethertheyhadagreatdealofconfidence,onlysomeconfidence,orhardlyanyconfidenceinthepress(newspapersandmagazines).Thefollowingtablecompares theirresponsesandtheirages.

Conﬁdence CaucasianAfricanAmericanHispanicOther Total AGreatDeal 56271716 116 OnlySome 370908333 576 HardlyAny 439837521 618 Total 86520017570 1310

Source: GeneralSocialSurvey

a. Findtheprobabilitythatapersonrandomlyselectedfromthesurvey i. hadagreatdealofconﬁdenceinthepress. ii. hadagreatdealofconﬁdenceinthepress,giventhepersonisHispanic.

b. DeterminewhetherhavingagreatdealofconﬁdenceinthepressisindependentofbeingHispanic. Whatdoesthatmeaninthissituation?

OBJECTIVE3

MultiplicationRuleforIndependentEvents

If E and F areindependentevents,then

5. a. Apersonﬂipsacoinandrollsasix-sideddie.Whatistheprobabilitythatthepersonrollsa5AND thecoinlandsontails?

b. Threecoinsareﬂipped.Whatistheprobabilitythatalltheoutcomesareheads?

6. Apersonﬂipsacoin8times.

a. Findtheprobabilityofalternatingbetweengettingheadsandtails,beginningwithtails:THTHTHTH.

b. Findtheprobabilityofgettingalltails.

c. ComparetheresultsyoufoundinParts(a)and(b).

• Supposeapersonﬂipsacoin7timesandgetsalltails.Whatistheprobabilityofgettinganothertails? Therearetwowaystointerpretthequestion:

1. Whatistheprobabilityofgetting8tailsinarow?

2. Whatistheprobabilityofgettingatail,giventhattheﬁrst7outcomeswerealltails?

Manystudentsconfuseinterpretations(1)and(2).Itisimportanttounderstandthemeaningofeach.

• Beforeusingthemultiplicationruleforindependentevents,wemustcheckthattheeventsaretruly independent.

7. Forthespringsemester2014,43%ofstudentsatBellevueCollegeweremale(Source: BellevueCollege). If4studentswererandomlyselectedfromthecollegeduringthatsemester,whatistheprobabilitythatat least1ofthestudentswouldhavebeenmale?

SummaryofProbabilityRules

Let E and F beevents.

• P (NOT E)=1 P (E) Complementrule

• If E and F aredisjoint,then P (E OR F )= P (E)+ P (F ) Additionrulefordisjointevents

• P (E OR F )= P (E)+ P (F ) P (E AND F ) Generaladditionrule

• If E and F areindependent,then P (E AND F )= P (E) · P (F ) Multiplicationrulefor independentevents

HW 1,3,5,7,11,15,19,23,25,27,29,33,35,39,45,51,55,57

SECTION5.3TEACHINGTIPS

Ifyouaretightontime,youcouldskipthissectionbecauseitisnotneededforsubsequentsections.Onecould arguethattheconceptsinthissectionareatahigherlevelthantherestoftheconceptsinthetextandshouldbe ﬁrsttaughtinanintroductorystatisticscourse.

OBJECTIVE1COMMENTS

ForProblem1,somestudentsthinkthat P (notatallinterested | ages18–30years) mustbesmallerthan P (notatallinterested) becausethesamplespaceof P (notatallinterested | ages18–30years) isjustadultsages 18–30yearsinthestudywhereasthesamplespaceof P (notatallinterested) issomuchlarger(alladultsinthe study).

ForProblem2,IemphasizethatitisnotmeaningfultocomparetheresultsofParts(a)and(b)andexplain why.

EvenifallgroupsofstudentsgetcorrectanswersforProblem3(a),Iemphasizethedifferencebetween P (5 | odd), P (odd | 5), P (5),and P (odd) becausestudentsoftenconfusethesewhentakingatest.

GROUPEXPLORATION:ConditionalProbability

Becausethisactivityishands-on,studentswouldlikelygainabetterunderstandingofconditionalprobability thanbyotheractivities.InProblem5,makesurestudentsgivecarefulthoughttowhytheirresultisaconditional probability.Otherwise,theymightmissthewholepoint.

OBJECTIVE2COMMENTS

Moststudentsbelievethatiftwoeventsaredependent,thenoneeventcausestheother.Todismantlethisbelief, Ipointoutthatevenifitturnsoutthatpeoplewhodrinkorangejuiceeverydaygetsicklessoften,thatdoesnot meanthatorangejuicecausesgoodhealth.Itmightbethatpeoplewhodrinkorangejuicetendtotakebettercare ofthemselvesinallsortsofways(exercise,eathealthy,getenoughsleep,etc)andit’sreallybecauseofthese otherbehaviorsthattheygetsicklessoften.

OBJECTIVE3COMMENTS

Aperson’scell-phonebatterygoesdeadrightatthemomenttheygetstuckinanelevator.Atypicalresponse wouldbe,"Whatarethechancesofthat!"Takingthequestionliterally,itallcomesdowntohowwedeﬁnethe probability.ThebulletpointjustafterProblem6addressesthisissue.Idiscussthiscarefullywithmystudents. Oncestudentslearnthemultiplicationrule,theytendtowanttouseitregardlessofwhethertwoeventsare independent.Icautionthemtoalwayscheckwhethereventsareindependentbeforeusingthisrule.

SECTION5.4LECTURENOTES

Objectives

1. Describethemeaningofa normalcurve anda normaldistribution.

2. Computeandinterpret z-scores.

3. Use z-scoresandtablestoﬁndprobabilitiesforanormaldistribution.

4. Usetechnologytoﬁndprobabilitiesforanormaldistribution.

OBJECTIVE1

• Whenanormalcurvedescribesadistributionperfectly,wesaytherelationshipis normal or normally distributed

• Whenanormalcurvedescribesadistributionfairlywell(butnotexactly),wesaythedistributionis approximatelynormal or approximatelynormallydistributed

PropertiesofaNormalCurve

• Anormalcurveisunimodalandsymmetric.

• Themeanisequaltothemedian.Botharethecenterofthecurve.

Area-ProbabilityEqualityProperty

Theareaunderanormalcurveforanintervalisequaltotheprobabilityofrandomlyselectinganobservation thatliesintheinterval.

TotalAreaundertheNormalCurve

Thetotalareaunderanormalcurveisequalto1.

Theprobabilityofasinglevalueofanormallydistributedvariableis0.

1. Supposethataprestatisticsclasstakesaﬁrsttestandtheirscoresaredescribedwellbythefollowingnormal curve.

a. Whatistheprobabilitythatarandomlyselectedstudentscoredmorethan80points?

b. OnTest2,themeanscoreis20pointslessthanthemeanscoreonTest1,butthestandarddeviation isthesame.Assumingthescoresarestillnormallydistributed,sketchthecurvethatdescribesthe scores.

c. OnTest3,themeanscoreisthesameasonTest2,butthestandarddeviationislarger.Assumingthe scoresarestillnormallydistributed,sketchacurvethatdescribesthescores.

ComparingNormalCurveswithDifferentStandardDeviations

Anormalcurveforadistributionwithlargerstandarddeviationwillbewiderandﬂatterthananormalcurve foradistributionwithsmallerstandarddeviation.[Drawaﬁgure.]

EmpiricalRule

Ifadistributionisnormal,thentheprobabilitythatarandomlyselectedobservationlieswithin

• onestandarddeviationofthemeanisapproximately0.68.So,about68%ofthedataliebetween x s and x + s.[Drawaﬁgure.]

• twostandarddeviationsofthemeanisapproximately0.95.So,about95%ofthedataliebetween x 2s and x +2s.[Drawaﬁgure.]

• threestandarddeviationsofthemeanisapproximately0.997.So,about99.7%ofthedataliebetween x 3s and x +3s.[Drawaﬁgure.]

OBJECTIVE2

Deﬁnition z-Score

The z-score ofanobservationisthenumberofstandarddeviationsthattheobservationisfromthemean.If theobservationliestotheleftofthemean,thenits z-scoreisnegative.Iftheobservationliestotherightof themean,thenits z-scoreispositive.

z-ScoreFormula

The z-scoreofanobservation x isgivenby z = x x s

2. The2014draftpicksforNBAbasketballteamshaveheightsthatareapproximatelynormallydistributed withmean79.1inchesandstandarddeviation3.0inches(Source: nbadraft.net).ShabazzNapierwasthe shortest2014draftpickwithaheightof72inches.Findthe z-scorefor72inches.Whatdoesitmean?

StandardNormalDistribution

Ifadistributionisnormallydistributed,thenthedistributionoftheobservations’ z-scoresisalsonormally distributedwithmean0andstandarddeviation1.Wecallthedistributionof z-scoresthe standardnormal distribution

OBJECTIVES3and4

3. Findtheprobabilitythata z-scorerandomlyselectedfromthestandardnormaldistributionis

a. lessthan 2 3.

b. greaterthan1.6.

c. between0.5and2.8

Theentriesinthestandardnormaldistributiontableareareastothe left ofavalue.Wehavetosubtract anentryfrom1toﬁndtheareatotheright.

4. RecallthatscoresontheWechslerIQtestarenormallydistributedwithmean100pointsandstandard deviation15points.Let X betheIQ(inpoints)ofarandomlyselectedperson.Findtheprobabilitythata randomlyselectedpersonhasanIQ

a. lessthan90points.

b. greaterthan125points.

c. between90and125points.

5. Recallthatthe2014draftpicksforNBAbasketballteamshaveheightsthatareapproximatelynormally distributedwithmean79.1inchesandstandarddeviation3.0inches.Findtheprobabilitythatarandomly selecteddraftpickhasheight

a. lessthan72inches.

b. greaterthan81inches.

c. between77inchesand87inches.

InterpretingtheAreaUnderaNormalCurveforanInterval

Wecaninterpretthearea A underthenormalcurveforanintervalas

• theprobabilitythatarandomlyselectedobservationwilllieintheinterval.

• theproportionofobservationsthatlieintheinterval.

HW 1,3,7,9,13,23,25,29,35,43,47,49,53,55,61,65

SECTION5.4TEACHINGTIPS

Thisisacrucialsectionbecauseitlaysafoundationforthesamplingdistribution,whichisakeyfoundational conceptinanintroductorystatisticscourse.

OBJECTIVE1COMMENTS

Becauseofpastworkwiththeshapeofdistributions,studentsarequicktoobservethatthenormalcurveis unimodal,symmetric,andthemeanisequaltothemedian.Becauseofpastworkwithdensityhistogramsand probability,studentsarealsoquicktosaythattheareaunderthenormalcurveforanintervalisequaltoa probability.Theycanalsoobservethattheareaundertheentirenormalcurvemustbeequalto1becausethesum oftheareasofallthebarsofadensityhistogramisequalto1.

Becauseofpastworkwithdensityhistograms,studentshaveaneasytimewithParts(a)and(b)ofProblem1, buttheyoftenstillneedcoachingwithPart(c).

BecauseofpastworkwiththeEmpiricalRule,aquickdiscussionofthisruleinthecontextofprobabilitywill sufﬁce.

OBJECTIVE2COMMENTS

Tocircumventstudentsfromusingthe z-scoreformulawithoutunderstanding,Icarefullyconnecttheformula withourpastworkwiththeEmpiricalRule.Theuseof z-scorestocompareobservationsfromtwodifferent distributionswillbeintroducedinSection5.5.

OBJECTIVES3and4COMMENTS

Iemphasizethattheentriesgiveninthestandardnormaldistributiontablefor z-scoresareareastothe left ofa value.

Becauseofpastworkwithdensityhistograms,studentsarequicktopickuponhowtoapplythecomplement ruleforPart(b)ofProblems4and5.However,theystillhaveatoughtimewithPart(c)withbothproblems, partlybecausethesubtractiondoesnotinvolvethenumber1andpartlybecauseofthecomplexityofhavingto computetwo z-scores.

Evenaftersomepractice,somestudentstendtoskipcertaincrucialsteps.Forexample,somestudentswill skipusingthestandardnormaldistributiontable,thinkinga z-scoreisaprobability.

Toreinforcethatstudentsshouldthinkgeometricallywhenworkingwithanormalcurve,foreachexercise, Irequirethatstudentssketchanormalcurve,recordrelevantvaluesonthe X-axisandthe z-axis,andwrite appropriateareasunderthecurve.

GROUPEXPLORATION:SymmetryofaNormalCurve

Thisexplorationreinforcestheimportanceofsketchinganormalcurveandconsideringitssymmetrytoﬁnd probabilities.

SECTION5.5LECTURENOTES

Objectives

1. Findanobservationfromits z-score.

2. Use z-scorestotheﬁndvalueofanormallydistributedvariablefromaprobability.

3. Usetechnologytoﬁndthevalueofanormallydistributedvariablefromaprobability.

4. Use z-scorestocomparetherelativesizeoftwoobservationsfromdifferentgroupsofdata.

5. Identifyunusualobservations.

6. Investigatewhetheraclaimistrue.

OBJECTIVE1

FindingtheValueofanObservationfromIts z-Score

Anobservation x with z-score z isgivenby x =¯ x + zs

1. RecallthatthescoresontheWechslerIQtestarenormallydistributedwithmean100pointsandstandard deviation15points.JamesWoodsisreportedtohaveanapproximate z-scoreof z =5 33 (Source:The ChicagoTribune).WhatishisapproximateIQscore?

OBJECTIVES2and3

2. Aprofessorgivesatesttoherprestatisticsstudents.Thescoresareapproximatelynormallydistributedwith mean74pointsandstandarddeviation8points.TheprofessordecidestogiveAstoapproximately10% ofthestudentsbutnotlessthan10%.Usethestandardnormaldistributiontableortechnologytoﬁndthe cutoffscoreforanA.

• Rememberthatwheneveryouusethestandardnormaldistributiontable,youmustlookforthearea tothe left ofavalue.

• RememberthatwheneveryouuseinvNorm,youmustentertheareatothe left ofavalue.

3. AresearchermeasuredthelifetimesofsomeActivairR 13HPXbatterieswhenusedforhearingaids.The meanlifetimewas252.4hoursandthestandarddeviationwas18.4hours(Source:Measurementwith VariousLoadsonThreeSizesofZinc-AirBatteriesforHearingAids,BjörnHagerman).Assumeall Activair13HPXbatteriesarenormallydistributedwiththesamemeanandsamestandarddeviationas thosetested.

a. Explainwhyitwouldbeunwiseforthecompanytoadvertisethattheirbatterieslast252.4hours.

b. Whatshouldthecompanyadvertisethelifetimeoftheirbatteriestobesothat99%ofthebatteries wouldlastatleastthatlong?

OBJECTIVE4

JennyandErictooktestsonprobabilityintwodifferentsectionsofprestatistics.Jennyscored92pointsonatest withmean78pointsandstandarddeviation7points.Ericscored79pointsonatestwithmean67pointsand standarddeviation3points.Thetestscoresoneachtestareapproximatelynormallydistributed.

1. Findthe z-scoreforJenny’stestscore.Whatdoesitmeaninthissituation?

2. Findthe z-scoreforEric’stestscore.Whatdoesitmeaninthissituation?

3. Assumingatypicalstudentinoneclassknowsthematerialaswellasatypicalstudentintheotherclass, determinewhetherJennydidrelativelybetterthanEric.

OBJECTIVE5

Deﬁnition

Unusualobservation

Assumethatsomedataarenormallyorapproximatelynormallydistributed.Anobservationis unusual ifit ismorethan1.96standarddeviationsawayfromthemean.

4. Inastudyof1541randomlyselectedyoungmen(ages20–29years),theyoungmen’sHDLcholesterollevelsareapproximatelynormallydistributedwithmean47mg/dlandstandarddeviation12.5mg/dl(Source: NHANES).

a. SupposethatayoungmaninthestudyhasanHDLcholesterollevelof19mg/dl.Isthatanunusual observation?

b. FindtheprobabilityofrandomlyselectingayoungmanfromthestudywithanHDLcholesterolless thanorequalto19mg/dl.

c. ExplainwhyitmakessensethatyourresultinPart(b)islessthan0.025.

DeterminingWhetheranObservationisUnusual

Anobservationofanormaloranapproximatelynormaldistributionisunusualifeitherofthefollowing equivalentstatementsistrue:

• Theobservation’s z-scoreislessthan 1 96 ORgreaterthan1.96.

• TheprobabilityofrandomlyselectingtheobservationORoneonthesamesideofthemeanbuteven moreextremeislessthan0.025.

OBJECTIVE6

5. Acompanyclaimsthatitslow-saltpotatochipscontainonly83mgofsodiumperserving,onaverage. Anindependentcompanyrandomlyselectsandtestsabagofthelow-saltpotatochips,whichturnsoutto contain102mgofsodiumperserving.

a. Assumingthesodiumlevelsperservingofthelow-saltchipsareapproximatelynormallydistributed withmean83mgandstandarddeviation6mg,ﬁndtheprobabilitythatarandomlyselectedbagwould haveatleast102mgofsodiumperserving.

b. IftheassumptionsyoumadeinPart(a)aretrue,isthebagcontaining102mgofsodiumperserving anunusualevent?

c. Describeascenarioinwhichthebagcontaining102mgofsodiumperservingisnotanunusualevent.

d. Onthebasisofthebagcontaining102mgofsodiumperserving,dotheassumptionsyoumadein Part(a)seemreasonable?Shouldamorethoroughinvestigationoccur?

HW 1,3,7,9,13,15,17,19,21,23,25,29,31,37,43

SECTION5.5TEACHINGTIPS

Ifyouaretightontime,youmightconsiderskippingthissection,whichcontainsconceptsthatwillnotbeneeded insubsequentsections.Ifyourushthroughthismaterial,itmaymuddythewatersanddomoreharmthangood. However,athoroughtreatmentofthissectioncouldlayanevenstrongerfoundationforthenormalcurve,which issoimportantinanintroductorystatisticscourse.

OBJECTIVE1COMMENTS

Tointroducetheformula, x =¯ x + zs,Iﬁrstaskstudentswhattestscorecorrespondstoa z-scoreof2ifthe meanscoreis70pointsandthestandarddeviationis10points.ThenIusethecomputation 90=70+2(10) to introducetheformula.

OBJECTIVES2and3COMMENTS

WhenusingthestandarddeviationnormaltabletosolveProblem2,studentstendtolookupthearea0.1inthe middleofthetableratherthanthecorrectarea0.9eventhoughtheylearnedinSection5.4thateachentryinthe tableisanareatothe left ofavalue.StudentstendtomakeasimilarerrorwhenusinginvNormwithaTI-84. AftercompletingProblem3,Ipointoutthatitwouldbebeneﬁcialtothecompany(andconsumers)ifthe standarddeviationwerelower.

GROUPEXPLORATION:GradingonaCurve

Studentstendtoaskinstructorswhethertheygradeonacurve,butmostofthemhavenoideawhatthistruly means.Perhapsthebiggestbenefitofthisexplorationisthatstudentscanfinallylearnwhat’sinvolved.They tendtobesurprisedtolearnthatgradingonacurvecanresultinstudentsearninglowergradesthanbythegrade cutoffsusedbymostinstructors.Themostchallengingpartofthisexplorationisthatstudentsmustrealizethey needtoaddthegivenpercentagesinProblem2tofindthegradecutoffs.

OBJECTIVE4COMMENTS

Iemphasizethisconceptbecauseitisimportantthatstudentsmakemeaningfulcomparisonsbetweentwoquantitiesnotonlyinstatisticsbutintheirlives.

OBJECTIVE5COMMENTS

Section4.2statesthatanobservationisunusualifitismorethan2standarddeviationsawayfromthemean.But thisobjectivereﬁnesthecutoffto1.96standarddeviationsbecausewecannowdeterminethismoreprecisecutoff byusingthestandardnormaldistributiontableand/ortechnology.

OBJECTIVE6COMMENTS

ThisisaniceobjectivetoﬁnishupChapter5becauseitinchesupquiteclosetohypothesistesting,whichisakey techniqueusedinintroductorystatistics.

AkeyconceptrelatedtoProblem5isthatwecannotconcludethecompany’sclaimisfalsesimplybecause therandomlyselectedbagcontains102mgofsodiumperserving;thestandarddeviation(andprobability)must beconsidered.

CHAPTER6OVERVIEW

Thischapterprovidesthebigpictureforlinearmodeling,whichwillbeaddressedinChapters6–9.Chapters7 and8introducethenecessaryalgebrasothatlinearmodelingcanbeexploredatadeeperlevelinChapter9.

Thekeythemeofthefourcharacteristicsofanassociationisintroducedinthischapterandwillbedeveloped furtherinChapters7–10.

ManyconceptsinthischaptercanbetiedtoconceptsincludedinChapter2:explanatoryandresponsevariables,associations,warningsaboutcausation,lurkingvariables,andtime-seriesplots.Concernsaboutextrapolationaresimilartotheconcernsaboutmakinginferences.Andthefourcharacteristicsofanassociationaresimilar tothecenter,spread,shape,andoutliersofadistributionofonenumericalvariable.Becauseofthesesimilarities andtherelativeeasinessofthematerial,youwillbeabletotraversethischapteratafasterpacethanpreceding ones.

SECTION6.1LECTURENOTES

Objectives

1. Identifyexplanatoryandresponsevariables.

2. Constructascatterplot.

3. Determinethedirectionofanassociation.

OBJECTIVE1

Herewereviewthemeaningsof explanatoryvariable and responsevariable (Section2.3):

Deﬁnition Explanatoryandresponsevariables

Inastudyaboutwhetheravariable x explains(affects)avariable y,

• Wecall x the explanatoryvariable (or independentvariable).

• Wecall y the responsevariable (or dependentvariable).

Recallthatcallingavariabletheexplanatoryvariabledoesnotmeanforsurethatthevariableaffects (explains)theresponsevariable.Afterall,we’dhavetocarryoutthestudytoﬁndout.

1. Foreachsituation,identifytheexplanatoryvariableandtheresponsevariable.

a. Let d bethenumberofmilesapersonrunsperday,andlet T (inseconds)betheperson’sbestmile runtime.

b. Let n bethenumberofadultswhowanttobuyaniPhonethatcosts d dollars.

c. Let s beanemployee’ssalary(inthousandsofdollars)atacompany,andlet n bethenumberofyears theemployeehasworkedforthecompany.

Foranorderedpair (a, b),wewritethevalueoftheexplanatoryvariableintheﬁrst(left)positionand thevalueoftheresponsevariableinthesecond(right)position.

2. Let s bethesales(inthousands)ofavideogame,andlet b bethegame’sadvertisingbudget(inthousands ofdollars).Avideogamewitha$50-thousand-dollaradvertisingbudgethassalesof742thousandgames. Expressthisasanorderedpair.

3. Let n bethemeannumberofhoursthatastudentstudiesprestatisticsperweek,andlet p bepercentageof pointsthestudentearnsontheﬁrsttest.Astudentwhostudies15hoursperweekearns93%ofthepoints ontheﬁrsttest.Expressthisasanorderedpair.

4. Let s bethemeannumberofgramsofsugarthatanadultconsumesdaily,andlet n bethemeannumberof cavitiesthepersongetsperdecade.Whatdoestheorderedpair (76, 1.5) meaninthissituation?

5. Let p bethepercentageofAmericansatage A yearswholistentotalkradio.Whatdoestheorderedpair (59, 23) meaninthissituation?

ColumnsofTablesandAxesofCoordinateSystems

Assumethatanauthenticsituationcanbedescribedbyusingtwonumericalvariables.Then

• Fortables,thevaluesoftheexplanatoryvariablearelistedintheﬁrstcolumnandthevaluesofthe responsevariablearelistedinthesecondcolumn.[Giveanexample.]

• Forcoordinatesystems,thevaluesoftheexplanatoryvariablearedescribedbythehorizontalaxisand thevaluesoftheresponsevariablearedescribedbytheverticalaxis.[Drawaﬁgure.]

OBJECTIVE2

Acoordinatesystemwithplottedorderedpairsiscalleda scatterplot.

6. Thefatalityratesfromautomobilecrashesareshowninthefollowingtableforvariousspeeds.Let r bethe fatalityrate(deathsper1000crashes)foraspeedof s mph.

SpeedUsedtoFatality SpeedRepresentRate GroupSpeedGroup(deathsper (mph)(mph)1000crashes)

0–30152.5

30–40353.5

40–50456.1

50–605515.3 over607016.9

Source: NationalHighwayTransportationSafetyAdministration

a. Constructascatterplot.

b. Whichofthepointsinyourscatterplotislowest?Whatdoesthatmeaninthissituation?

c. Whichofthepointsinyourscatterplotishighest?Whatdoesthatmeaninthissituation?

• Recallthatthereisan association betweentheexplanatoryandresponsevariablesiftheresponsevariable changesastheexplanatoryvariablechanges.

• Anassociationof numerical explanatoryandresponsevariablesisoftencalleda correlation

• Ifthereisanassociationbetweentwovariablesthatdoes not necessarilymeanthereiscausation.

OBJECTIVE3

Deﬁnition Positiveandnegativeassociation

Assumetwonumericalvariablesaretheexplanatoryandresponsevariablesofastudy.

• Iftheresponsevariabletendstoincreaseastheexplanatoryvariableincreases,wesaythevariablesare positivelyassociated (or positivelycorrelated)andthatthereisa positiveassociation (or positive correlation).[Drawaﬁgure.]

• Iftheresponsevariabletendstodecreaseastheexplanatoryvariableincreases,wesaythevariablesare negativelyassociated (or negativecorrelated)andthatthereisa negativeassociation (or negative correlation).[Drawaﬁgure.]

Wedescribethe direction ofanassociationbydeterminingwhethertheassociationispositive,negative,or neither.

7. PercentagesofadultssurveyedwhoplantoattendaHalloweenpartythisyearareshowninthefollowing tableforvariousagesgroups.

AgeGroupAgeUsedtoRepresent (years)AgeGroup(years)Percent 18–2421.044 25–3429.534

35–4439.525

45–5449.514

55–6459.510

65orover70.06

Source: InternationalMassRetailAssociation

Let p bethepercentageofadultsatage a yearswhoplantoattendaHalloweenpartythisyear.

a. Constructascatterplot.

b. Determinewhethertheassociationispositive,negative,orneither.

8. Let t bethenumberofyearssince2000.Findthevaluesof t thatrepresenttheyears2000,2005,2010,and 2015.

9. Let n bethenumber(inthousands)ofnewappssubmittedtoApple’sAppStorepermonthat t yearssince 2010.In2015,40thousandnewappsweresubmittedtoApple’sAppStore(Source: pocketgamer.biz). Expressthisasanorderedpair.

10. Let p bethepercentageofadultsages18–24wholivewiththeirparentsat t yearssince2005.Whatdoes theorderedpair (7, 56) meaninthissituation?

11. ThenumbersofInternetsearchesusingGoogleareshowninthefollowingtableforvariousyears.

NumberofSearches

Source: Google

Let r betheannualnumber(inbillions)ofsearchesat t yearssince2005.

a. Constructascatterplot.

b. Determinewhethertheassociationispositive,negative,orneither.

HW 1,3,9,17,23,31,35,39,41,43,47,51,55,59,69

SECTION6.1TEACHINGTIPS

Studentstendtohaveaneasytimewiththissectionbecausemanyoftheconceptshavebeenaddressedin previouschaptersbutindifferentcontexts.Constructingscatterplotsisafoundationalskillthatstudentswilluse frequentlythroughouttherestofthecourse.

OBJECTIVE1COMMENTS

AlthoughstudentslearnedaboutexplanatoryandresponsevariablesinChapter2,theytendtoneedarefresher atthispointinthecourse.Iemphasizethenewinformationthatvaluesoftheexplanatoryvariablearedescribed bytheﬁrstcoordinateinanorderedpair,theﬁrstcolumnofatable,andthehorizontalaxisofacoordinate system.Evenaftercompletingtheentirechapter,theretendtobeafewstudentswhocontinuetostrugglewith thisconcept,soyoucan’temphasizeitenough.

OBJECTIVE2COMMENTS

Ipointouttomystudentsthatscatterplotsaresimilartotime-seriesplots,exceptwedonot"connectthedots" withscatterplots.

Studentstendtoconstructexcellentscatterplots,probablyduetoallthepracticetheyhavehadconstructing othertypesofdiagramsinpreviouschapters.Iremindstudentsthatunitsandvariablesshouldbedisplayedon eachaxisandatitleshouldalsobedisplayed.

Ratherthanintroducetheterminology correlation,tokeeptheamountofterminologytoaminimum,Istick withusing association becausewehavealreadyintroducedthisterminologyinChapter2.

EventhoughthedistinctionbetweenassociationandcausationwasalreadyaddressedinChapter2,Iemphasizethisdistinctionnowbecauseitissuchanimportantconcept.ThiscanbeillustratedbytheInternetassociation describedinProblem11.InSection6.2,thistopicwillberevisitedbycomparingtheU.S.per-personconsumption ofmargarineandthedivorcerateinMaine(Figure50onpage389ofthetextbook).

OBJECTIVE3COMMENTS

Studentshaveaneasytimeidentifyingthedirectionofanassociation.

Workingwithdeﬁnitionssuchas t isthenumberofyearssince2000isnewcontentandit’sworthtakingtime tocarefullydescribehowtointerpretsuchdeﬁnitionsbecausesomestudentsstrugglewiththisinitially.

GROUPEXPLORATION:AnalyzingPointsbelow,above,andonaLineContaining

PointswithEqualCoordinates

Althoughnotcrucialforthecourse,thisexplorationrequiressomegoodcriticalthinking.Problem6providesa hintofwhat’stocomewithlinearregression(Section9.3).

SECTION6.2LECTURENOTES

Objectives

1. Determinetheshapeofadistribution.

2. Determinethestrengthofadistribution.

3. Computeandinterpretthecorrelationcoefﬁcient.

4. Determinewhetherthereareanyoutliersandwhattodowiththem.

5. Determinethefourcharacteristicsofanassociationinthecorrectorder.

6. Explainwhystrong(orweak)associationdoesnotguaranteecausation.

OBJECTIVE1

• Ifthepointsofascatterplotliecloseto(oron)aline,wesaythevariablesare linearlyassociated andthat thereisa linearassociation.[Drawaﬁgure.]

• Ifthepointsofascatterplotliecloseto(oron)acurvethatisnotaline,wesaythereisa nonlinear association.[Drawaﬁgure.]

• Ifnocurvecomesclosetoallthepointsofascatterplot,wesaythereis noassociation.[Drawaﬁgure.]

Foranypairofnumericalvariables,thereiseitheralinearassociation,anonlinearassociation,ornoassociation.Wewillrefertothe shape ofanassociationasbeingoneofthesethreetypes.

1. Foreachofthefollowingscatterplots,determinewhetherthereisalinearassociation,nonlinearassociation, ornoassociation.

OBJECTIVE2

• Ifacurvepassesthroughallthepointsofascatterplot,wesaythereisan exact associationwithrespectto thecurve.[Drawaﬁgure.]

• Ifacurvecomesclosetoallthepoints,wesaythereisa strongassociation withrespecttothecurve. [Drawaﬁgure.]

• Ifacurvecomessomewhatclosetoallthepoints,wesaythereisa weakassociation withrespecttothe curve.[Drawaﬁgure.]

2. Thecarbohydrates,calories,andfatfor29pizzasmadebysixoftheleadingpizzacompaniesareshownin thefollowingtable.

Carbohydrates(g)CaloriesFat(g)Carbohydrates(g)CaloriesFat(g) 39368173534216 36308133735917 20259152629716 39348153230513 36311135349921 20249146454921 40357164241019 27279136357924 2824694339517 3027611292609 3733815372779 41367163026911 35320142928614 36329153330914 2626613

Source: Domino’s,LittleCeasar’s,PapaJohn’s,PizzaHut,DiGiornoFrozen,KashiFrozen

a. Constructascatterplotthatcomparescarbohydratesandcalories.

b. Constructascatterplotthatcomparescarbohydratesandfat.

c. Foreachofthescatterplotsyouconstructed,describetheshapeoftheassociation.

d. Comparethestrengthsofthetwoassociations.

e. Foreachofthescatterplotsyouconstructed,identifywhethertheassociationispositive,negative,or neither.

f. Useanappropriatescatterplottoestimatethecaloriccontentsofthepizzaswith20gofcarbohydrates.

g. Useanappropriatescatterplottoestimatethefatcontentofthepizzaswith20gofcarbohydrates.

OBJECTIVE3

PropertiesoftheLinearCorrelationCoefﬁcient

Assume r isthelinearcorrelationcoefﬁcientfortheassociationbetweentwonumericalvariables.Then

• Thevaluesof r arebetween 1 and1,inclusive.

• If r ispositive,thenthevariablesarepositivelyassociated.

• If r isnegative,thenthevariablesarenegativelyassociated.

• If r =0,thereisno linear association.

• Thelargerthevalueof |r|,thestrongerthelinearassociationwillbe.

• If r =1,thenthepointslieexactlyonalineandtheassociationispositive.

• If r = 1,thenthepointslieexactlyonalineandtheassociationisnegative. [Drawﬁgurestoillustratealloftheaboveconcepts.]

• If r =0,thenthereisnolinearassociationbuttheremaybea nonlinear association.

• Todeterminetheshapeandstrengthofanassociation,weshouldinspectascatterplotofthedataaswell ascompute r.Forexample,eventhough r ≈ 0 96 forthedatadescribedbythefollowingscatterplot,the pointsliemuchclosertoacurvethantheydotoaline.

OBJECTIVE4

• Foranassociationbetweentwonumericalvariables,apointisanoutlierifitdoesnotﬁttheoverallpattern ofthepointsinthescatterplot.[Drawaﬁgure.]

• Thecorrelationcoefﬁcientisverysensitivetooutliers.[Drawscatterplotstoshowhow r canchangefrom 0toapproximately0.95byaddinganoutlier.SeeFigs.43and44onpage387ofthetextbook.]

3. Ascatterplotcomparingthehighwaymileagesandcitymileagesof1195typesofcarsisdisplayedinthe followingﬁgure.

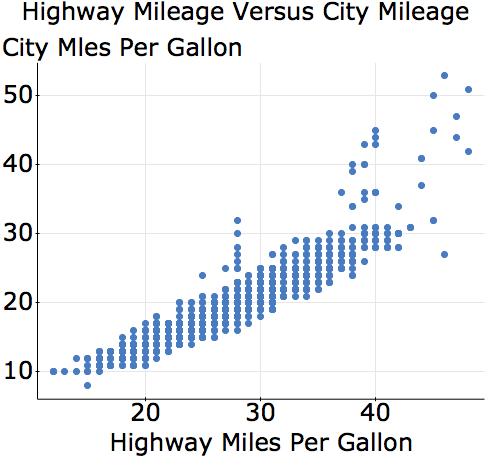
a. Identifytheoutliers.Shouldtheyberemoved?Ifyes,forwhatpurpose?

b. Assumetheoutliershavebeenremoved.Forthedatathatremain, i. determinetheshapeoftheassociation. ii. determinethestrengthoftheassociation. iii. determinewhethertheassociationispositive,negative,orneither.

OBJECTIVE5

OrderofDeterminingtheFourCharacteristicsofanAssociation

Wedeterminethefourcharacteristicsofanassociationinthefollowingorder:

1. Identifyalloutliers.

a. Foroutliersthatstemfromerrorsinmeasurementorrecording,correcttheerrorsifpossible.If theerrorscannotbecorrected,removetheoutliers.

b. Forotheroutliers,determinewhethertheyshouldbeanalyzedinaseparatestudy.

2. Determinetheshapeoftheassociation.

3. Iftheshapeislinear,thenonthebasisof r andthescatterplot,determinethestrength.Iftheshapeis nonlinear,thenonthebasisofthescatterplot,determinethestrength.

4. Determinethedirection.Inotherwords,determinewhethertheassociationispositive,negative,or neither.

OBJECTIVE6

Deﬁnition Lurkingvariable

A lurkingvariable isavariablethatcausesboththeexplanatoryandresponsevariablestochangeduring thestudy.

Astrongassociationbetweentwovariablesdoesnotguaranteethatachangeintheexplanatoryvariable willcauseachangeintheresponsevariable.

4. ThescatterplotinthefollowingﬁgurecomparesthescoresofTest4andTest5foracalculuscoursetaught bytheauthor.

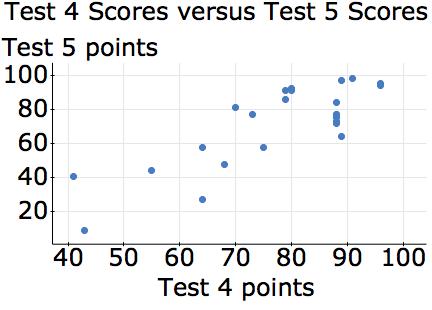
a. Describethefourcharacteristicsoftheassociation.

b. DoesahigherscoreonTest4causeahigherscoreonTest5?Ifno,describeatleastonepossible lurkingvariable.

c. Onthebasisofthefairlystrong,positiveassociationbetweenTest4andTest5scores,astudent concludesthattheremusthavebeenafairlystrong,positiveassociationbetweenanypairoftestsfor thecourse.Whatwouldyoutellthestudent?

HW 1,3,7,9,11,15,17,19,21,23,29,33,35,37,44,47

SECTION6.2TEACHINGTIPS

Althoughthissectioncontainsalotofmaterial,youcanmovefairlyquicklybecausestudentsdonottendto havemuchtroublewiththeconcepts.

OBJECTIVE1COMMENTS

Studentshaveaneasytimedeterminingtheshapeofanassociation.

OBJECTIVE2COMMENTS

Studentsarequicktopickupondescribingthestrengthofanassociation,althoughtheytendtobemorepicky atwhatqualiﬁesasastrongassociation.Anassociationthatastatisticianwouldcallstrong,astudentwouldcall weak.Thisisnotsurprisingbecauseasidefromthiscourse,studentshavelittleornoexperienceworkingwith (data)pointsthatarenotcolinear.

Ifyoudon’twanttodealwithallthedatainProblem2,youcouldworkwithasubset.Andifyouaretighton timeyoucouldjusthavestudentscompleteParts(a),(b),and(d);Part(d)isthemainpoint.

OBJECTIVE3COMMENTS

RatherthanlistallthebulletedstatementsintheboxshownforObjective3,Idrawabunchofscatterplotsalong withtheappropriatevaluesof r andverballypointoutthepropertiesastheyemerge.

Students’intuitionaboutthevalueof r becomesstrongquitequickly.Throughouttherestofthechapter,each timeIdisplayascatterplot,Iaskstudentstoguessthevalueof r andtheirguessesarequitegood.Atleastonce, wecalculatethemean(ormedian)ofseveralguessesandcompareittotheactualvalue,whichisanicereminder ofthebeneﬁtofthemeasuresofcentraltendency.

DisplayingthePricelineGroupIncscatterplot(inthelecturenotesforObjective3)andobservingthatthe associationisnonlineareventhough r ≈ 0.96 isanicewaytoemphasizethatweneedtoobserveascatterplotas wellcompute r tomakeareliabledeterminationoftheshapeandstrengthofanassociation.

GROUPEXPLORATION:ImpactofTransformingDataontheCorrelationCoefﬁcient

Thisexplorationwouldhavemorepedagogicalvalueifstudentsunderstoodhow r iscalculated,buttheystill enjoythisactivity,whichincreasestheirsenseof r

OBJECTIVE4COMMENTS

Similartotheissueofdeterminingthestrengthofanassociation,studentstendtoidentifytoomanydatapoints asoutliers.

OBJECTIVE5COMMENTS

AlthoughIdiscusstheorderofdeterminingthefourcharacteristicsasshownintheboxedpropertystatement forthisobjective,I’mquicktoaddthatsomeofthesedeterminationscanbemadesimultaneouslyandtheorder isnotsetinstone.Forexample,wemightﬁndourselvesdeterminingtheshapeanddirectionofanassociation simultaneously.

OBJECTIVE6COMMENTS

Studentstendtorememberthemeaningoflurkingvariables,whichwasdiscussedinChapter2.Studentscan drawontheirownpersonalexperienceswhenrespondingtoProblem4(b).

SECTION6.3LECTURENOTES

Objectives

1. Usealinetomodelanassociationbetweentwonumericalvariables.

2. Usealinearmodeltomakeestimatesandpredictions.

3. Describethemeaningof input and output.

4. Finderrorsinestimations.

5. Describethemeaningof interpolate, extrapolate,and modelbreakdown

6. Findinterceptsofaline.

7. Findinterceptsofalinearmodel.

8. Modifyamodel.

OBJECTIVE1

1. Let n bethenumberofbankrobberiesper100branchesat t yearssince1995.

RobberiesperRobberiesper Year100BranchesYear100Branches 199710.620076.0 19998.820096.0 200110.320115.3 20038.720124.5 20057.7

Source: FBI

a. Constructascatterplot.

b. Istherealinearassociation,anonlinearassociation,ornoassociation?

c. Compute r.Onthebasisof r andthescatterplot,determinethestrengthoftheassociation.

d. Drawalinethatcomesclosetothepointsofthescatterplot.

Deﬁnition Model

A model isamathematicaldescriptionofanauthenticsituation.Wesaythatthedescription models the situation.

Deﬁnition Linearmodel

A linearmodel isanonverticallinethatdescribestheassociationbetweentwoquantitiesinanauthentic situation.

OBJECTIVE2

2. Usetherobberymodeltoestimatethenumberofbankrobberiesper100branchesin2004.

3. Usethemodeltoestimatewhentherewere5.6bankrobberiesper100branches.

• Weconstructascatterplotofdatatodeterminewhetherthereisalinearassociation.Ifso,wedrawaline thatcomesclosetothedatapointsandusethelinetomakeestimatesandpredictions.

• Itisacommonerrortotrytoﬁndalinethatcontainsthegreatestnumberofpoints.However,ourgoalisto ﬁndalinethatcomescloseto all ofthedatapoints.

OBJECTIVE3

Deﬁnition Input,output

An input isapermittedvalueofthe explanatory variablethatleadstoatleastone output,whichisa permittedvalueofthe response variable.

4. InProblem2,identifytheinputandtheoutput.

OBJECTIVE4

The error inanestimateistheamountbywhichtheestimatediffersfromtheactualvalue.

• Foranoverestimate,theerrorispositive.

• Foranunderestimate,theerrorisnegative.

5. Usetherobberymodeltoestimatethenumberofbankrobberiesper100branchesin2001.Findtheerror intheestimate.

6. Usetherobberymodeltoestimatethenumberofbankrobberiesper100branchesin2007.Findtheerror intheestimate.

OBJECTIVE5

RefertotheestimatesandpredictionsthatyoumadeinProblems2,3,5,and6asinterpolationsorextrapolations.

Deﬁnition Interpolation,extrapolation

Forasituationthatcanbedescribedbyamodelwhoseexplanatoryvariableis x,

• Weperform interpolation whenweuseapartofthemodelwhose x-coordinatesarebetweenthe x-coordinatesoftwodatapoints.

• Weperform extrapolation whenweuseapartofthemodelwhose x-coordinatesarenotbetweenthe x-coordinatesofanytwodatapoints.

7. Usetherobberymodeltoestimatethenumberofbankrobberiesper100branchesin2002.Didyouperform interpolationorextrapolation?Explain.

8. Usetherobberymodeltoestimatethenumberofbankrobberiesper100branchesin2014.Didyouperform interpolationorextrapolation?Explain.

9. Usetherobberymodeltoestimatethenumberofbankrobberiesper100branchesin2030.Didyouperform interpolationorextrapolation?Explain.

Deﬁnition Modelbreakdown

Whenamodelgivesapredictionthatdoesnotmakesenseoranestimatethatisnotagoodapproximation, wesaythat modelbreakdown hasoccurred.

OBJECTIVE6

Deﬁnition Interceptsofaline

An intercept ofalineisanypointwherethelineandanaxis(oraxes)ofacoordinatesystemintersect. Therearetwotypesofinterceptsofalinesketchedonacoordinatesystemwithan x-axisanda y-axis:

• An x-intercept ofalineisapointwherethelineandthe x-axisintersect.[Drawaﬁgure.]

• A y-intercept ofalineisapointwherethelineandthe y-axisintersect.[Drawaﬁgure.]

10. Refertothefollowingﬁgure.

a. Findthe x-interceptoftheline.

b. Findthe y-interceptoftheline.

c. Find y when x = 6

d. Find x when y = 3.

OBJECTIVE7

11. Findthegiveninterceptoftherobberymodel.Whatdoesitmeaninthissituation?Didyouperform interpolationorextrapolation?Explain.

a. n-intercept

b. t-intercept

12. Thepercentagesofcellphoneuserswhosendorreceivetextmessagesmultipletimesperdayareshownin thefollowingtableforvariousagegroups.

AgeUsedto

Source: EdisonResearchandArbitron

Let p bethepercentageofcellphoneusersatage a yearswhosendorreceivetextmessagesmultipletimes perday.

a. Drawalinearmodelthatdescribestheassociationbetweenand a and p

b. Predictthepercentageof25-year-oldcellphoneuserswhosendorreceivetextmessagesmultiple timesperday.Didyouperforminterpolationorextrapolation?Explain.

c. Findthe p-intercept.Whatdoesitmeaninthissituation?Didyouperforminterpolationorextrapolation?Explain.

d. Findthe a-intercept.Whatdoesitmeaninthissituation?Didyouperforminterpolationorextrapolation?Explain.

OBJECTIVE8

13. Additionalresearchaboutcellphoneuserswhosendorreceivetextmessagesmultipletimesperdayyields thedatashownintheﬁrstandlastrowsofthefollowingtable.Usethisdataandthefollowingassumptions tomodifythemodelyoufoundinProblem12:

• Children3yearsoldandyoungerdonotsendorreceivetextmessagesmultipletimesperday.

• Thepercentageofcellphoneuserswhosendorreceivetextmessagesmultipletimesperdaylevels offat5%forusersover80yearsinage.

• Theageoftheoldestcellphoneusersis116years.

AgeUsedto AgeGroupRepresentAgeGroup (years)(years)Percent

12–1714.575

18–2421.076

25–3429.563

35–4439.542

45–5449.537

55–6459.517 over6470.07

Source: EdisonResearchandArbitron

HW 1,3,5,7,17,21,25,29,31,35,37,39,43,47,51

SECTION6.3TEACHINGTIPS

Thissectioncompletesthebigpictureoflinearmodeling.Inparticular,studentswillsketchlinearmodelsanduse themodelstomakepredictions.

InChapters7and8,studentswilllearnthenecessaryalgebrasotheycanrevisitlinearmodelinginamore meaningfulwayinChapter9.

OBJECTIVE1COMMENTS

ForProblem1ofthelecturenotes,somestudentsmayneedareminderofthemeaningofthephrase“at t years since1995.”Itisimportantthatthescalingoneachaxisbeginat0becausestudentswillﬁndtheinterceptsin Problems11and12.

Whendescribingthemeaningofamodel,Igiveintuitiveexamplessuchasthetextbook’sexampleabout airplanemodels(middleofpage403ofthetextbook).

InProblem1(d)ofthelecturenotes,Idemonstratethattherearemanyacceptablelinearmodels.Many studentstrytoﬁndalinethatcontainsthegreatestnumberofdatapointsratherthanalinethatcomescloseto allofthedatapoints.Toclarifythisconfusion,Icompareareasonablelinearmodelthatcomesclosetothedata pointsbutdoesnotcontainanydatapointswiththeterriblyinaccuratelinearmodelthatcontainsthedatapoints (4, 8 8) and (6, 10 3)

GROUPEXPLORATION:ModelingaLinearAssociation

Thisexplorationisagreatcollaborativeactivityforstudentstodiscoverthefundamentalideasofthissection. SomestudentswilllikelydisregardtheinstructioninProblem2anddrawa“zigzag”curveratherthanaline, unlessyouwarnthemnotto.Waitingforstudentstomakethiserrorandthenclarifyingthemeaningof“line” mightmakeamorelastingimpression.

OBJECTIVE2COMMENTS

WhencompletingProblems2and3,Idrawinput-outputarrowssimilartothoseinFig.80onpage404ofthe textbook.IrequiremystudentstousesucharrowssothatIcanbetterevaluatetheirworkonquizzesandexams. Itisdifﬁculttoawardanypartialcreditifnoarrowsaredisplayed.

Iwarnmystudentsthateventhoughtheiranswersmaydifferfromthoseintheanswerssectionofthetextbook, theiranswersmaybecorrect.Iexplainthatit’spossibletodrawreasonablelinearmodelsthataredifferentthan thereasonablemodelsthatthetextbookused.AlthoughIwantmystudentstocarefullydrawscatterplotsand linearmodels,Idon’twantthemtobeanxiousaboutgettingtheexactresults.

OBJECTIVE3COMMENTS

Thisobjectiveissettingthestagefortheconceptfunction,whichisdiscussedinSection7.4.Chapters8–10use functionnotationtoalimitedextentsoastoaccommodatebothinstructorswhouseSection7.4andthosethat don’t.

OBJECTIVE4COMMENTS

Accordingtothetextbook’sdeﬁnitionoferror,theerrorofanestimateistheoppositeofaresidual.Istruggled withwhattodowiththisdiscrepancy.Intheend,IdecidedtoletthediscrepancyexistbecauseIbelieveitmakes moresensefortheerrortobepositivewhenthemodelleadstoanoverestimateandfortheerrortobenegative whenthemodelleadstoanunderestimate.

Formanystudents,thedistinctionbetweenamodelandrealityisfoggy.Forexample,manystudentstend tothinkthattheanswerstoProblems5and6aretheactual10.3robberiesper100branchesand6.0robberies per100branches,respectively,evenifthelinearmodeldoesnotcontainthedatapoints (6, 10 3) and (12, 6 0) MakingsuchadistinctionwhilecompletingProblems5and6paysbigdividendsbothintheshortandlongrun. Foranintuitiveexplanation,Itellmystudentsthatamodelisﬁction,whichwehopeisveryclosetothetruth.

OBJECTIVE5COMMENTS

Iemphasizethatwehavelittleornofaithwhenweextrapolate.Onecouldarguethatthisisthemostimportant conceptofthesectionbecauseextrapolationissooftenmisusedbythemedia.

Problem9isanicewaytodrivehomethepointofthedangersofextrapolation.

Theconceptofmodelbreakdownisimportant,becausemostmodelsdo“breakdown.”Itellmystudentsthat whenmodelbreakdownoccurs,theymustsaysoonquizzesandexams.Evenifastudentbelievesthatnobank robberieswilloccurintheyearrepresentedbythe t-interceptinProblem11(b),thestudentshouldexplainwhy thatisreasonable.Regardlessifstudentsthinktheresultisreasonable,theyshouldalsosaytheyhavelittleorno faithinitbecausetheyperformedextrapolation.

WhenIdiscussthemodelbreakdowninProblem9,Iaskmystudentsforsuggestionsofgraphsof(nonlinear) curvesthatmightturnouttobebettermodels,whichisnicepreparationforObjective8.Ingeneral,suchquestions cangeneratesomefunandinterestingdiscussions.

GROUPEXPLORATION:IdentifyingTypesofModelingErrors

Ifyoudonotplantoassignmost(orall)oftheexplorationsinthetextbook,itwouldprobablybegoodtoomit assigningthisexplorationortoassignitforhomework.Manyoftheseideascanbetouchedonasyouproceed throughthissection.

OBJECTIVE6COMMENTS

Whenstudentsﬁndintercepts,Irequirethemtoincludebothcoordinatesasanorderedpairtoreinforcethat interceptsarepoints.

OBJECTIVE7COMMENTS

Manystudentshavetroubleﬁndinginterceptsofmodelsforavarietyofreasons.Somestudentsgetoffonthe wrongfootbywritingthevariablesonthewrongaxeswhenconstructingascatterplot.Somestudentswritethe coordinatesofaninterceptinthewrongorder,andotherswritethecoordinatesofaninterceptinthecorrectorder butinterpretthemasiftheywerewrittenintheotherorder.

OBJECTIVE8COMMENTS

Inmanycasesinwhichwecandeterminemodelbreakdownhasoccurred,itisunclearhowtomodifythemodel. Problem13isnicebecauseitincludesadditionalfactsthatsuggesthowtomodifythelinearmodelsketchedin Problem12(a).

Discussingthisobjectiveisimportantbecausestudentsshouldbeawarethateventhoughscientistsmaycurrentlybeusingacertainmodel,discoveriesmadeatalaterpointmaywarrantusingamodiﬁed(orevenacompletelydifferent)model. Copyright c 2016PearsonEducation,Inc.

CHAPTER7OVERVIEW

InSections7.1–7.3,studentswilllearnhowtographlinearequationsandhowtocomputeratesofchange. Theywillalsodiscoverthatthesetwotasksareverymuchconnected.Allofthisworkwilllayacrucialfoundation forworkwithregressionlinesinSection9.3.

ThechaptercloseswithinvestigatingfunctionsinSection7.4.Becausenotalldepartmentswillhavetimefor thisconcept,Ihaveincludedexercisesthatinvolvefunctionsinsubsequentchaptersbutnotsomuchthatitbogs downhomeworksectionsforcoursesthatdonotaddressfunctions.

Despitemoststudents’poorexperiencesinpreviousalgebracourses,youmightbesurprisedhowwellthey dointhischapter.Chapters1–6tendtobuildquiteabitofmathematicalmaturityinstudents.Plus,graphing equationsoftheform y = mx + b isfairlyeasy.Themorechallengingtaskofgraphinglinearequationsintwo variablesinwhich y isnotisolatedwillbeaddressedinSection8.4.Andstudentswillbereadyforthatchallenge bythen.

SECTION7.1LECTURENOTES

Objectives

1. Foranequationintwovariables,determinethemeaningof solution, satisfy,and solutionset

2. Describethemeaningofthe graph ofanequation.

3. Graphequationsoftheform y = mx + b

4. Describethemeaningof b inequationsoftheform y = mx + b.

5. Graphequationsoftheform y = b and x = a.

6. DescribetheRuleofFourforequations.

7. Graphanequationofalinearmodel.

OBJECTIVE1

1. Showthattheequation y = x +3 becomesatruestatementwhen2issubstitutedfor x and5issubstituted for y.

Wesay (2, 5) satisﬁes y = x +3 andthat (2, 5) isa solution of y = x +3.

Deﬁnition Solution,satisfy, and solutionset ofaequationintwovariables

Anorderedpair (a,b) isa solution ofanequationintermsof x and y iftheequationbecomesatrue statementwhen a issubstitutedfor x and b issubstitutedfor y.Wesay (a,b) satisﬁes theequation.The solutionset ofanequationisthesetofallsolutionsoftheequation.

2. Is (2, 7) asolutionof y =4x 1?

3. Is (3, 5) asolutionof y =4x 1?

OBJECTIVE2

4. a. Findﬁvesolutionsof y =2x 3 andplottheminthesamecoordinatesystem.

b. Dotheﬁvepointslieonaline?Ifso,sketchtheline.

c. Selectanotherpointonthelineandshowthatthecorrespondingorderedpairsatisﬁes y =2x 3.

d. Selectapointthatdoesn’tlieonthelineandshowthatthecorrespondingorderedpairdoesnotsatisfy y =2x 3.

WecallthelinethatwesketchedinProblem4the graph of y =2x 3

Deﬁnition Graph

The graph ofanequationintwovariablesisthesetofpointsthatcorrespondtoallsolutionsoftheequation.

• Everypointonthegraphofanequationrepresentsasolutionoftheequation.

• Everypoint not onthegraphrepresentsanorderedpairthatis not asolution.

OBJECTIVE3

Theequation y =2x 3 isoftheform y = mx + b.

Graphof y = mx + b

Thegraphofanequationoftheform y = mx + b,where m and b areconstants,isaline.

Herearesomeequationswhosegraphsarelines: y =3x +7 y = 6x +2 y =2xy = x 4 y =1

Graphtheequationbyhand.Also,ﬁndthe y-intercept.

5. y =3x 5 6. y = 2x +4 7. y = 3x 8. y = 2 3 x +1

OBJECTIVE4

Substitute0for x intotheequation y = mx + b: y = m(0)+ b =0+ b = b

The y-interceptofthegraphof y = mx + b is (0,b)

y-InterceptoftheGraphof y = mx + b

Thegraphofanequationoftheform y = mx + b has y-intercept (0,b).

For y =3x 5,the y-interceptis (0, 5) andfor y = 2x +4,the y-interceptis (0, 4).SeeProblems5and 6.

OBJECTIVE5

Findﬁvesolutionsofthegivenequation.Thengraphtheequationbyhand.

9. x =2

10. y =3

If a and b areconstants,then

EquationsforHorizontalandVerticalLines

• Thegraphof y = b isahorizontalline.[Showthegraph.]

• Thegraphof x = a isaverticalline.[Showthegraph.]

Graphtheequationbyhand.

EquationsWhoseGraphsAreLines

Ifanequationcanbeputintotheform y = mx + b or x = a,where m, a,and b areconstants,thenthe graphoftheequationisaline.Wecallsuchanequationa linearequationintwovariables

Herearesomeexamplesoflinearequationsintwovariables:

y = 5x +9 y =3x 8 y =4 x = 2

OBJECTIVE6

RuleofFourforSolutionsofanEquation

Wecandescribesomeorallofthesolutionsofanequationintwovariableswith:

1. anequation, 2. atable, 3. agraph,or 4. words.

Thesefourwaystodescribesolutionsareknownasthe RuleofFour

15. a. Listsomesolutionsof y =4x 3 byusingatable.

b. Describethesolutionsof y =4x 3 byusingagraph.

c. Describethesolutionsof y =4x 3 byusingwords.

16. Considertheequation y = x +2.

a. Substitute3for x andshowthattheinput x =3 leadstotheoutput x =5.

b. Graph y = x +2.Thenusearrowstoshowthattheinput x =3 leadstotheoutput x =5.

OBJECTIVE7

17. IntheUnitedKingdom,nervousdentalpatientsaresometimesgivenasedativetocalmthem.Toadminister thesedative,thedentistperformsa cannulation,whichinvolvesinsertingathintubeintoaveininapatient’shand.Inanexperimentinvolving20individuals,researcherstestedwhethertheamountofpainthe individualsexperiencedduringcannulationexplainsthelevelofanxietythattheindividualspredictedthey wouldexperiencebyundergoingcannulationagain.Afterundergoingcannulations,theindividualsrated theirexperiencesofpainfrom0to100andtheirpredictedanxietiesaboutundergoingcannulationsagain from0to100.Thepatients’ratingsareshowninthefollowingtable.

3750 2313 2935 6968 6370 3835 3430 143 82 6020 4148 1210 1010 3830 7570 4943 7081 4242 832 4843

Source: Pain-anxietyscatterplot(Source: Anaesthetics:ARandomised,Double-Blind,Placebo-Controlled, ComparativeStudyofTopicalSkinAnalgesicsandtheAnxietyandDiscomfortAssociatedwithVenous Cannulation,A.F.Speirsetal.)

Let a betheanxietyratingapatientpredictsforundergoinganothercannulationafterhavingundergone onewithapainratingof p.

a. Identifytheexplanatoryandresponsevariables.

b. Constructascatterplot.

c. Describeandinterpretthedirectionoftheassociation.

d. Graphthemodel a =0.91p +1.71 onthescatterplot.

e. Doesthemodelcomeclosetothedatapoints?

f. Usethemodeltopredicttheanxietyratingapatientwouldpredictaboutundergoinganothercannulationafterhavingundergoneonewithapainratingof30.

HW 1,3,7,9,19,25,27,35,39,43,47,49,51,77,81

SECTION7.1TEACHINGTIPS

Inthissection,studentswillgraphlinearequations,whichwilllaythefoundationfortherestofthechapter andultimatelypreparethemtographregressionlinesinSection9.3.Thelastobjectiveinthissection–graphing equationsoflinearmodels–willconnectnicelywithwhatstudentslearnedinSection6.3.

OBJECTIVE1COMMENTS

Iemphasizetheseterminologies,becauseIusethesewordssomuchthroughoutthecourse.

OBJECTIVE2COMMENTS

Problem4isimportant,becauseithelpsstudentsunderstandthateverypointonthegraphrepresentsasolutionof theequationandthateverypointnotonthegraphrepresentsanorderedpairthatisnotasolution.Thisimportant conceptisusedwhenﬁndingequationsoflinearequations(Sections9.1and9.2).

OBJECTIVE3COMMENTS

ForProblem5,Isuggestthatstudentsusethreepoints,becausethethirdpointcanserveasacheck.Moststudents

144CHAPTER2LectureNotesandTeachingTips

arechallengedbyProblem8.Studentswillhaveaneasiertimegraphingsuchanequationoncetheyhavelearned aboutslope.

GROUPEXPLORATION:SolutionsofanEquation

Althoughthisexplorationaddressesthemeaningofagraph(Objective2),itisbettertousethisactivityonce studentsarecomfortablegraphinglinearequations(Objective3).Thatway,studentswillbeabletoefﬁcientlydo Problem1oftheexplorationandgettothemainpointoftheexploration.

OBJECTIVE4COMMENTS

Studentswillneedtobeabletodeterminethe y-interceptofthegraphofanequationoftheform y = mx + b whentheyperformgraphinginSection7.3.

OBJECTIVE5COMMENTS

ForProblems9and10,manystudentsarethrownforaloop,becauseonlyonevariableappearsintheseequations. Onewaytoaddressthisissueistobeginwithanapplication.Let n bethenumberofstatesintheUnitedStatesat t yearssince1960.Next,createatableofnonnegativevaluesof t and n.Thendeterminethatthemodelis n =50 andgraphthemodel.Finally,discussforwhichyearsmodelbreakdownoccurs.(Hawaiibecamethe50thstate onAugust21,1959.)

Anotherwaytoaddresstheissue,whenﬁndingsolutionsoftheequation x =2 (Problem9),istousethe followingscenario:

Supposethatafamilyalwayshasexactly2carsandanotherfamilyhasvariousnumbersofcarsat varioustimes.

Thisscenariohelpsstudentsseethattheequation x =2 isrestrictingthevalueof x tobe2,butthevalueof y canbeanyrealnumber.

Forstudentswhoconfusethegraphsofequationsoftheform x = a and y = b,Isuggestthattheybuilda tableof(atleasttwo)solutionstotipthemoffwhethertheyshouldgraphahorizontalorverticalline.

OBJECTIVE6COMMENTS

TheRuleofFourwillberevisitedwhenworkingwithfunctionsinSection7.4. Problem16isimportant,becauseithelpsstudentsseetheconnectionbetweenﬁndinginputsandoutputs symbolicallyandgraphically.

OBJECTIVE7COMMENTS

InProblem17,somestudentstendtowonderhowtheequation a =0 91p +1 71 wasfound.EvenafterIsay thatwewilllearnhowtoﬁndsuchanequationinSection9.3afterwehavediscussedthenecessaryalgebra, somestudentsarenotsatisﬁed;theywanttoknownow,whichItaketobeagoodsignthattheysomuchwantto understandthereasoningbehindthings.Despitetheirdiscomfort,itisagoodideatographmodelsnowtokeep studentsthinkingaboutlinearmodeling.

WhencompletingProblem17(f),Iemphasizethattheequation a =0 91p+1 71 allowsustomakepredictions withouthavingtodrawarrows,whichistimeconsumingandimprecise.

SECTION7.2LECTURENOTES

Objectives

1. Calculatetherateofchangeofaquantitywithrespecttoanotherquantity.

2. Explaintheconnectionbetweenconstantrateofchangeandanexactlinearassociation.

3. Usearunandthecorrespondingriseofalinearmodeltoﬁndarateofchange.

4. Describetheconnectionbetweenthedirectionofanassociationandrateofchange.

5. Calculatetheslopeofaline.

6. Explainwhytheslopeofanincreasinglineispositiveandtheslopeofadecreasinglineisnegative.

7. Explainwhytheabsolutevalueoftheslopeofalinemeasuresthesteepnessoftheline.

8. Explainwhytheslopeofahorizontallineiszeroandtheslopeofaverticallineisundeﬁned.

OBJECTIVE1

1. Ifthetemperatureincreasedby 12◦Fover3hours,estimatehowmuchthetemperatureincreasedperhour.

2. Ifthetemperatureincreasedfrom 60◦Fat7A.M.to 68◦Fat11A.M.,estimatehowmuchthetemperature increasedperhour.

FormulaforRateofChange

Supposethataquantity y changessteadilyfrom y1 to y2 asaquantity x changessteadilyfrom x1 to x2 Thenthe rateofchange of y withrespectto x istheratioofthechangein y tothechangein x: changein y changein x = y2 y1 x2 x1

3. ThesalesofcigarettesintheUnitedStatesdeceasedapproximatelylinearlyfrom400billioncigarettesin 2003to280billioncigarettesin2013(Source: EuromonitorInternational).Findtheapproximaterateof changeofcigarettessales.

4. Apersonofheight132.5centimetersshoulduseaskipoleoflength90centimeters.Apersonofheight 153.0centimetersshoulduseaskipoleoflength110centimeters.Findtheapproximaterateofchangeof skipolelengthwithrespecttoaperson’sheight.

OBJECTIVE2

5. Supposethatastudenttravelsat60milesperhouronaroadtrip.Let d bethedistance(inmiles)thatthe studentcandrivein t hours.

a. Identifytheexplanatoryandresponsevariables.

b. Constructatabletodescribetheassociationbetween t and d fordrivingtimesof0,1,2,3,4,and5 hours.

c. Constructascatterplotfordrivingtimesof0,1,2,3,4,and5hours.

d. Findtheslopeofthelinearmodel.

e. Describethefourcharacteristicsoftheassociation.Computeandinterpret r aspartofyouranalysis. Ifthereisanassociation,drawanappropriatemodelonthescatterplot.

ConstantRateofChangeImpliesanExactLinearAssociation

Iftherateofchangeofonevariablewithrespecttoanothervariableisconstant,thenthereisanexactlinear associationbetweenthevariables.

6. Theamountsofmoneyastudentispaidareshowninthefollowingtableforvariousnumbersofhours worked.Let p bethestudent’spay(indollars)forworking t hours.

a. Identifytheexplanatoryandresponsevariables.

b. Describethefourcharacteristicsoftheassociation.Computeandinterpret r aspartofyouranalysis.

c. Findtherateofchangeofpayfrom2to3hours.

d. Findtherateofchangeofpayfrom0to5hours.Comparetheresultwiththeresultyoufoundin Part(c).

AnExactLinearAssociationImpliesConstantRateofChange

Ifthereisanexactlinearassociationbetweentwovariables,thentherateofchangeofonevariablewith respecttotheotherisconstant.

OBJECTIVE3

Foranylinearmodel,the run isthehorizontalchangeandthe rise istheverticalchangeingoingfromonepoint onthelinetoanotherpointontheline.

UsingRunandRisetoFindRateofChange

Assumethereisanexactlinearassociationbetweenanexplanatoryvariable x andaresponsevariable y and (x1,y1) and (x2,y2) aretwodistinctpointsofthelinearmodel.Thentherateofchangeof y withrespect to x istheratiooftherisetotheruningoingfrompoint (x1,y1) topoint (x2,y2):

rateofchangeof y withrespectto x = y2 y1 x2 x1 = rise run

7. A carat isaunitofweightforpreciousstonesandpearls.Thescatterplotandthemodelinthefollowing ﬁguredescribetheassociationbetweentheweights(incarats)ofsomediamondsandtheirvalue(inSingaporedollars).Istheassociationpositive,negative,orneither?Estimatetherateofchangeofvaluewith respecttonumberofcarats.

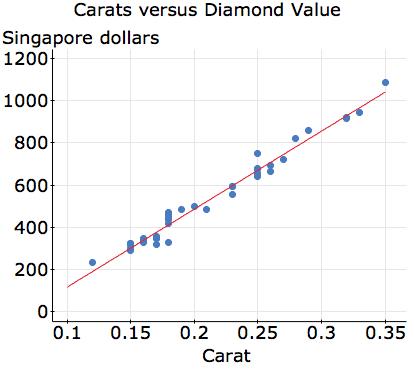
InProblem7,youlikelyfoundthatifonediamondweighs1caratmorethananotherdiamond,itwillcost approximately$3720morethantheotherdiamond.Thisdoes not meanthatthediamondscost$3720percarat.

8. Thescatterplotandthemodelinthefollowingﬁguredescribetheassociationbetweenyearsandthenumber oflargeshipslostatseaduetoﬁre,collision,storm,andmachinebreakdown.Istheassociationpositive, negative,orneither?Estimatetherateofchangeofnumberoflargeshiplosses.

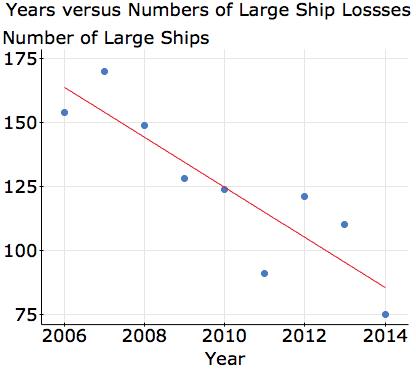
OBJECTIVE4

ConnectionbetweentheDirectionofanAssociationandRateofChange

• Ifanassociationbetweentwovariablesispositive,thentheapproximaterateofchangeofonevariable withrespecttotheotherispositive(seeProblem7).

• Ifanassociationbetweentwovariablesisnegative,thentheapproximaterateofchangeofonevariable withrespecttotheotherisnegative(seeProblem8).

OBJECTIVE5

Deﬁnition Slopeofanonverticalline

Assume (x1,y1) and (x2,y2) aretwodistinctpointsofanonverticalline.The slope ofthelineistherateof changeof y withrespectto x.Insymbols:

9. Findtheslopeofthelinethatcontainsthepoints (1, 5) and (4, 3) Itisacommonerrortomakeincorrectsubstitutionsintotheslopeformula.Carefullyconsiderwhythemiddle andright-handformulasareincorrect: CorrectIncorrectIncorrect

Findtheslopeofthelinethatcontainsthegivenpoints.

10. (1, 3) and (4, 9) 11. ( 4, 1) and (2, 3)

12. ( 5, 1) and (4, 2) 13. ( 6, 3) and ( 2, 5)

Whenworkingwithnegativecoordinates,itcanhelptoﬁrstwrite () () () () andtheninsertthecoordinatesintotheappropriateparentheses.

OBJECTIVE6

• Alinethatgoesupwardfromlefttorightis increasing.[Drawaﬁgure.]

• Alinethatgoesdownwardfromlefttorightis decreasing.[Drawaﬁgure.]

SlopesofIncreasingorDecreasingLines

• Anincreasinglinehaspositiveslope.[Drawaﬁgure.AlsorefertoProblems10and12.]

• Adecreasinglinehasnegativeslope.[Drawaﬁgure.AlsorefertoProblems11and13.]

14. Findtheapproximateslopeofthelinethatcontainsthepoints ( 2.8, 5.9) and ( 1.1, 3.7).Roundthe resulttotheseconddecimalplace.Statewhetherthelineisincreasingordecreasing.

OBJECTIVE7

15. Comparethesteepnessoftwolineswithslopes2and3.

MeasuringtheSteepnessofaLine

Theabsolutevalueoftheslopeofalinemeasuresthesteepnessoftheline.Thesteepertheline,thelarger theabsolutevalueofitsslopewillbe.

OBJECTIVE8

• Drawahorizontallineandﬁnditsslope 0 run =0

• Drawaverticallineandexplainwhyitsslope, rise 0 ,isundeﬁned.

SlopesofHorizontalandVerticalLines

• Ahorizontallinehasslopeequaltozero.[Drawaﬁgure.]

• Averticallinehasundeﬁnedslope.[Drawaﬁgure.]

ForProblems16–19,ﬁndtheslopeofthelinethatcontainsthegivenpoints.Determinewhetherthelineis increasing,decreasing,horizontal,orvertical.

16. (2, 3) and (2, 1)

17. ( 3, 2) and (2, 8)

18. ( 1, 4) and (3, 4)

19. ( 5, 2) and ( 1, 4)

20. Sketchanincreasingline,adecreasingline,ahorizontalline,andaverticalline.Foreachline,determine whethertheslopeispositive,negative,zero,orundeﬁned.

HW 1,3,7,9,13,17,21,23,25,31,39,43,53,59,63,65,67,77,83,97

SECTION7.2TEACHINGTIPS

Thissectionbeginswithrateofchange,whichisintuitiveandeasytomotivate–therearesomanyapplications! Andthetransitiontoslopeissmoothbecauseﬁndingratesofchangeoflinearmodelsleadsnicelyintodiscussing ratesofchangeoflines.

Rateofchangeandslopeofalinearecrucialtopicsforlinearregression,whichwillbefullyaddressedin Section9.3.

OBJECTIVE1COMMENTS

IfyoudiscussedthechangeofaquantityinSection1.5andunitratiosinSection1.6,yourstudentsshouldbe wellpreparedforthisobjective.Ifyoudidn’tdiscusstheseconceptsthen,spendsometimediscussingthemnow. Itellstudentsthat50milesperhourisanexampleofarateofchange.Isayarateofchangeisadescription ofhowquicklyaquantitychangesinrelationtoanotherquantitychanging.Iexplainthatweoftenusetheword “per”todescribearateofchange.Igivesomemoreexamplesofratesofchangesuchas

• Astudentearns$8perhour.

• Thealtitudeofanairplanedecreasesby2200feetperminute.

• Acollegecharges$80perunit.(Youcouldusethechargeperunit(hoursorcredits)atyourcollege.)

ThenIdiscussthematerialinthelecturenotes.WhengoingoverProblems1–4,Iemphasizethatweshould includeunitswhencomputingchangesintheexplanatoryvariableandchangesintheresponsevariable.Including unitsthroughoutthecalculationswillhelpstudentswritethecorrectunitsfortheirresult.Iemphasizethatwe dividethechangeintheresponsevariablebythechangeintheexplanatoryvariable.Studentstendtoaskme whetherthisistruebeforeImentionit,whichshowshowadepttheyhavebecomeinthinkingintermsofthe explanatoryandresponsevariables.

GROUPEXPLORATION:FindingtheMeanofRatesofChange

Althoughthisactivitydoesnotaddressacrucialtopicofthecourse,itdoesrequiresomegoodcriticalthinking. StudentstendtobeintimidatedbyProblem6;tellingthemitisn’tasdifﬁcultasitﬁrstlookscanhelp.Astronger hintwouldbetodirecttheirattentiontoeachofthedenominatorsthatequal1.Studentstendtodowellonthe otherproblems,butthechallengeisforthemtotakeinthemainpointoftheexploration(Problem7).

OBJECTIVE2COMMENTS

Thisobjectivetiesrateofchangetolinearmodels,whichisanimportanttransition,butI’musuallytightontime soinsteadofhavingstudentsworkonallpartsofProblems5and6,IjustcompletePart5(c)andpointoutthat thedatapointslieonastraightline.

OBJECTIVE3COMMENTS

ForProblems7and8,IperformthesametypesofcalculationsasinProblems2–4,butnowIemphasizethe graphicalinterpretation.Inparticular,theconceptsriseandrunareintroduced.

OBJECTIVE4COMMENTS

Toaddressthisobjective,IaskstudentswhytherateofchangeinProblem7ispositiveandwhytherateofchange inProblem8isnegative.Studentsarequicktoexplain.

Ingeneral,itisimportanttolookforsuchopportunitiestohavestudentscomeupwithanexplanationforthe nextconcepttobediscussed.Thisincreasesthechancestheywillunderstandthematerialbecausetheycameup withtheexplanationratherthanhavingpassivelyreceivedit.

OBJECTIVE5COMMENTS

ForProblem9,Iﬁndtheslopebyusingtheslopeformulabutalsoplotthepointsandlabeltheriseandtherunto keepstudentsthinkingabouttheconnectionbetweenthecomputationsandtheriseandrun.

ForProblem9,Ialsodemonstratethatwhenweusetheslopeformulawithtwopointsonaline,itdoesn’t matterwhichpointwechoosetobe (x1,y1) andwhichpointwechoosetobe (x2,y2).

Whensomeorallcoordinatesarenegative(Problems11–14),acommonstudenterroristoomitatleastone subtractionsymbolfromtheslopeformulaornegativesignfromthecoordinates.Thesuggestioninthelecture notestoﬁrstwritetheparenthesesaddressesthistypeoferror.

GROUPEXPLORATION:ForaLine,RiseoverRunisConstant

Thisexplorationhasstudentsdiscoverthattheslopeofalineisindependentofwhichpairofpointsontheline arechosentocalculatetheslope.Moststudentswon’tunderstandthisconceptunlesstheytakepartinsuchan activity.

GROUPEXPLORATION:GraphicalSigniﬁcanceof m for y = mx

Thisactivityassistsstudentsindiscoveringthegraphicalsigniﬁcanceof m foranequationoftheform y = mx, whichisakeyconceptofthecourse.Afterstudentscompletetheexploration,Ifacilitateaclassroomdiscussion inwhichstudentssharetheirresponsesforProblem4oftheexploration.Thereisalotofinformationinthis exploration,andstudentshavetroubleseeinghowitallﬁtstogether.

ThisexplorationcouldbeusedbeforediscussingObjectives6–8sostudentsdiscovertheconcepts.However, onecouldarguethatourearlierworkwithrateofchangehasalreadylaidthegroundworkforthoseobjectivesso thisexplorationshouldbeusedtosumthingsupattheendofthesection.Onedifﬁcultywitheitherplacement isthattheconnectionbetweenslopeandthecoefﬁcientof x foranequationoftheform y = mx willnotbe

establisheduntilSection7.3.So,youmayprefertousethisexplorationinthatsection.

OBJECTIVE6COMMENTS

ThisobjectivefollowsdirectlyfromthesignanalysisofrateofchangeforObjective4.Toreinforcetheconcepts, IperformasignanalysisofriseandrunasshownineachofFigs.44and45onpages451and452ofthetextbook. Or,ifyouprefer,youcouldshowasimilarsignanalysisearlierwhendiscussingrateofchange.

Acommonerrorwhencomputingtheslopeisforthesigntobeincorrect.Tocheckthesign,astudentcan quicklyplotthepointsanddeterminewhetherthelineisincreasingordecreasing.

OBJECTIVE7COMMENTS

Eventhoughthisobjectivefollowslogicallyfromtheearliertaughtfactthatslopeisarateofchange,Ipreferto sketchtwolineslikeinFig.46onpage452ofthetextbookandcomparetheirslopesandsteepnessbecausethis conceptissoimportant.

OBJECTIVE8COMMENTS

Afterdemonstratingthatahorizontallinehasaslopeequaltozero,Ipointoutthatthismatcheswithwhatwe knowaboutrateofchange.Oncestudentshaveseenhowtoshowthatahorizontallinehasslopeequaltozero, theycandiscoverthataverticallinehasundeﬁnedslope.

SECTION7.3LECTURENOTES

Objectives

1. Usetheslopeandthe y-interceptofalinetosketchtheline.

2. Describethemeaningof m foranequationoftheform y = mx + b.

3. Graphanequationoftheform y = mx + b byusingtheline’sslopeand y-intercept.

4. Findanequationofalinefromitsgraph.

5. Graphanequationofalinearmodelbyusingthemodel’sslopeandverticalintercept.

6. Usealinearmodel’sslopeandverticalintercepttoﬁnditsequation.

OBJECTIVE1

Sketchthelinethathasthegivenslopeand y-intercept.

OBJECTIVE2

4. a. UsethemethoddiscussedinSection3.1tograph y =2x +1.

b. Whatistheslopeoftheline y =2x +1?

c. Comparetheslopewiththenumbermultipliedtimes x intheequation y =2x +1 Copyright c 2016PearsonEducation,Inc.

FindingtheSlopeand y-InterceptfromaLinearEquation

Foralinearequationoftheform y = mx + b,

• theslopeofthelineis m and

• the y-interceptofthelineis (0,b).

Wesaythisequationisin slope-interceptform.

Thegraphoftheequation y = 3x +8 isalinewithslope 3 and y-intercept (0, 8)

OBJECTIVE3

Sketchthegraphoftheequationbyhand.

GraphinganEquationinSlope-InterceptForm

Tographanequationoftheform y = mx + b,

1. Plotthe y-intercept (0,b).

2. Use m = rise run toplotasecondpoint.Forexample,if m = 2 3 ,thencount3unitstotheright(fromthe y-intercept)and2unitsuptoplotanotherpoint.

3. Sketchthelinethatpassesthroughthetwoplottedpoints.

9. Graphanequationoftheform y = mx + b where m ispostiveand b isnegative.

OBJECTIVE4

10. Findanequationofalinethathasslope 5 7 and y-intercept (0, 2). 11. Findanequationofthelinesketchedbelow.

FindinganEquationofaLinefromaGraph

Toﬁndanequationofalinefromagraph.

1. Determinetheslope m andthe y-intercept (0,b) fromthegraph.

2. Substituteyourvaluesfor m and b intotheequation y = mx + b.

OBJECTIVE5

12. Let p bethepercentageofAmericanswhowatchagreaternumberofTVprogramsonchannels’websites (ratherthanonTV)at t yearssince2005(seethefollowingtable).Areasonablemodelofthesituationis p =3 7t 0 8

Source: GfK

a. Graphthemodelbyhand.

b. Predictinwhichyear36%ofAmericanswillwatchagreaternumberofTVprogramsonchannels’ websites.Didyouperforminterpolationorextrapolation?Doyouhavemuchfaithintheprediction? Explain.

OBJECTIVE6

13. Apersonearnsastartingsalaryof$30thousandatacompany.Eachyear,shereceivesa$2thousandraise. Let s betheperson’ssalary(inthousandsofdollars)aftershehasworkedatthecompanyfor t years.

a. Isthereanexactlinearassociationbetween t and s?Explain.

b. Findthe s-interceptofalinearmodel.Whatdoesitmeaninthissituation?

c. Findtheslopeofthelinearmodel.Whatdoesitmeaninthissituation?

d. Findanequationofalinearmodel.

14. Let T bethetotalone-semestercost(indollars)oftuitionplusparkingfeefor u units(creditsorhours) ofclassesatyourcollege.[Youcouldreplacetheparkingfeewithanyone-timechargesuchasastudentservicesfeeatyourcollege.]

a. Isthereanexactlinearassociationbetween u and T ?Ifso,ﬁndtheslope.

b. Findanequationofthemodel.

c. Graphthemodel.

d. Selectatotalone-semestercostandpredictthecorrespondingnumberofunits.

15. Let s beU.S.retailsales(inbillionsofdollars)ofvitaminsanddietarysupplementsat t yearssince2000 (seethefollowingtable).Areasonablemodelis s =1 23t +8 33

U.S.RetailSalesofVitamins andDietarySupplements Year(billionsofdollars) 200717.1

Source: EuromonitorInternational

a. Usetechnologytodrawascatterplotandthemodelinthesameviewingwindow.Checkwhetherthe linecomesclosetothedatapoints.

b. Whatistheslopeofthemodel?Whatdoesitmeaninthissituation?

c. Findtheratesofchangeinthenumberofretailssalesfromoneyearinthetabletothenextonelisted. ComparetheratesofchangewiththeresultyoufoundinPart(b).

d. Whatisthe s-intercept?Whatdoesitmeaninthissituation?

e. Usethemodeltoestimatetheretailsalesin2012.Didyouperforminterpolationorextrapolation? Computetheerror.

HW 1,3,7,11,19,29,41,43,51,55,63,65,69,73,77,81,85,97

SECTION7.3TEACHINGTIPS

Inthissection,studentsusetheslopeandthe y-intercepttographequationsinslope-interceptform.Afterstudents learnhowtosolveequationsinSections8.2and8.3,theywillgraphlinearequationsnotinslope-interceptform inSection8.4.Studentstendtodobetterwiththisorganization,ratherthanhavingtocontendwithgraphinglinear equationsofallformsinjustonesection.

OBJECTIVE1COMMENTS

Problems1–3providethe“bigpicture”ofthesection.

Somestudentstendtousetherunandtherisestartingfromtheoriginratherthanfromthe y-intercept.I remindthemthattherunandtherisehavetodowithgoingfromonepoint on alinetoanotherpointontheline.

ForProblem2,somestudentsareunsurewhattodowiththenegativesignoftheslope.Theywanttoknow whethertheyshouldworkwiththeslope 3 2 or 3 2 .Idemonstratethatbothwaysgivethesameresult;I emphasizethatourmaingoalistographtheline,notﬁndtwopointsontheline.

Acommonerroristowrite 3 2 = 3 2 .Ipointoutthatthisisincorrectbecause 3 2 isnegativebut 3 2 is positive.

ForProblem3,somestudentsneedareminderthat a = a 1

OBJECTIVE2COMMENTS

YoucanaddressthisobjectivebycompletingProblem4orhavinggroupsofstudentsworkonthefollowing exploration.

GROUPEXPLORATION:TheMeaningof m intheEquation y = mx + b

Thisactivityisagreatwayforstudentstodiscoverthatforanequationoftheform y = mx + b,theslopeofthe

equationis m.ManystudentswillneedhelpwithProblem4(e)oftheexploration.

OBJECTIVE3COMMENTS

Thisobjectivefollowsnicelyfromobjective1.

GROUPEXPLORATION:DrawingLineswithVariousSlopes

Thisactivityisafunwaytodrivehomethepointofthemeaningofslope.Moststudentswilluseonlyinteger valuesfortheslope.Itellthemtoalsotryvaluesbetween 1 and1(inadditionto0).

OBJECTIVE4COMMENTS

Studentshaveaneasytimewiththisobjective.Ipointoutthatthistaskisthereverseofgraphing.Iremind mystudentsabouttheRuleofFourforequations.Isaywecangofromanyoneofthesefourwaystoanother. (StudentswilllearnhowtogofromtablestoequationsinSection9.2.)

GROUPEXPLORATION:FindinganEquationofaLinefromItsGraph

Studentstendtohavefunwiththisactivity.

OBJECTIVE5COMMENTS

ForProblem12,Itellmystudentsthattheywilllearntofindlinearmodelssuchas p =3 7t 0 8 inSection9.2. Idemonstratehowtousethemethodinthissectiontosketchthemodel p =3 7t 0 8,butIalsopointoutthat itisoftenusefultofindapointfarofftotherightsuchas (10, 36.2) bysubstituting10for t.Findingsuchathird pointcanhelpstudentssketchanaccurateline,especiallywhentherunoftheirfirsttwochosenpointsissmall comparedtothelargestvalueofthescalingonthehorizontalaxis.

OBJECTIVE6COMMENTS

Althoughstudentshavefoundequationsoflinearmodelsbyrecognizingpatternsofarithmetic(Section1.7),they willinitiallyhavetroublewithﬁndingsuchanequationusingtheconceptsinthissection.

ForProblem13,theﬁrstthingIdoisusethestartingsalaryof$30thousandtoplotthe s-interceptona coordinatesystem.ThenIusethe$2thousandraiseperyeartodrawthelinearmodel.Thegraphhelpsclarify howtoapplytheconceptsofObjective4tocompleteParts(b),(c),and(d).

SECTION7.4DETAILEDCOMMENTS

Objectives

1. Describethemeaningsof relation, domain, range,and function

2. Identifyfunctionsbyusingthe verticallinetest

3. Describethemeaningof linearfunction

4. DescribetheRuleofFourforfunctions.

5. Usethegraphofafunctiontoﬁndthefunction’sdomainandrange.

6. Usefunctionnotation.

7. Usefunctionnotationtomakepredictions.

8. Determinethedomainandrangeofamodel. Copyright c 2016PearsonEducation,Inc.

OBJECTIVE1

Refertotheorderedpairs (1, 4), (2, 3), (2, 5),and (3, 1) tointroducetheconcepts relation, domain, range, input, and output

Deﬁnition Relation,domain,andrange

A relation isasetoforderedpairs.The domain ofarelationisthesetofallvaluesoftheexplanatory variable,andthe range oftherelationisthesetofallvaluesoftheresponsevariable.

• Eachmemberofthedomainisan input.

• Eachmemberoftherangeisan output.

Deﬁnition Function

A function isarelationinwhicheachinputleadstoexactlyoneoutput.

Determinewhetherthegivenrelationisafunction.

1. y = x +5 2. y =2x 3. y = ±x

4. Someorderedpairsoffourrelationsarelistedinthefollowingtable.Whichoftheserelationscouldbe functions?Explain.

Relation1Relation2Relation3Relation4 xyxyxyxy 0132205371 1183186372 2233167373 3284148374 4335129375

OBJECTIVE2

Usearrowstoshowthatthereisaninputthathastwooutputsfortherelationgraphedbelow.Concludethatthe relationisnotafunction.

VerticalLineTest

Arelationisafunctionifandonlyifeachverticallineintersectsthegraphoftherelationatnomorethan onepoint.Wecallthisrequirementthe verticallinetest

Determinewhetherthefollowinggraphrepresentsafunction.Explain.

OBJECTIVE3

Deﬁnition LinearFunction

A linearfunction isarelationwhoseequationcanbeputintotheform

y = mx + b where m and b areconstants.

Determinewhetherthegivenrelationisalinearfunction.

OBJECTIVE4

RuleofFourforFunctions

Wecandescribesomeoralloftheinput-outputpairsofafunctionbymeansof 1. anequation, 2. agraph, 3. atable,or 4. words.

9. a. Istherelation y =3x 2 afunction?

b. Listsomeinput-outputpairsof y =3x 2 byusingatable.

c. Describetheinput-outputpairsof y =3x 2 byusingagraph.

d. Describetheinput-outputpairsof y =3x 2 byusingwords.

OBJECTIVE5

10. Usethegraphofthefunctiontodeterminethefunction’sdomainandrange.

OBJECTIVE6

• Touse“f ”asthenameofthefunction y =4x +2,weuse“f (x)”torepresent y: y = f (x)

, 3)

• Wecansubstitute f (x) for y intheequation y =4x +2: f (x)=4x +2

• Toﬁnd f (3),wesaywe evaluate thefunction f at3.

• Warning:“f (x)”doesnotmean f times x

Evaluate f (x)=3x 5 atthegivenvaluesof x

11. f (4)

For f (x)= 2x +6, g(x)=3x2 4x, h(x)=

14. f (4) 15. g(2)

h(6)

(x)=5,ﬁndthefollowing:

k(3)

18. Let f (x)= 8.73x 256.Find x when f (x)=96.15.Roundyourresulttotheseconddecimalplace.

Someinput-outputpairsofafunction f areshowninthefollowingtable.

19. Find f (3)

20. Find x when f (x)=3

21. Afunction f isgraphedintheﬁgurebelow.

a. Find f ( 1)

b. Find x when f (x)= 1

c. Findthedomainof f

d. Findtherangeof f

22. Recallthatwecandescribesomeoralloftheinput-outputpairsofafunctionbymeansofanequation,a graph,atable,orwords.Let f (x)= 4x +7

a. Describeﬁveinput-outputpairsof f byusingatable.

b. Describetheinput-outputpairsof f byusingagraph.

c. Describetheinput-outputpairsof f byusingwords.

OBJECTIVE7

Deﬁnition Functionnotation

Theresponsevariableofafunction f canberepresentedbytheexpressionformedbywritingtheexplanatory variablenamewithintheparenthesesof f ():

responsevariable = f (explanatoryvariable)

23. Let T bethetotalfallsemestercost(indollars)oftuitionandfeesforpart-timestudentswhotook C credits (unitsorhours)ofcoursesatCentenaryCollege(Source: CentenaryCollege).Thesituationcanbemodeled bytheequation T =575C +15

a. Rewritetheequation T =575C +15 withthefunctionname f .

b. Find f (6).Whatdoesitmeaninthissituation?

24. ThepercentagesofAmericanadultswhosmokeareshowninthefollowingtableforvariousyears.

200023.1

201019.4

201218.0

Source: NationalCenterforHealthStatistics

Amodelis p = 0 45t +36 83,where p isthepercentageofAmericanswhosmokeat t yearssince1970.

a. Verifythatthegraphof p = 0.45t +36.83 comesclosetothedatapoints.

b. Rewritetheequation p = 0 45t +36 83 withthefunctionname g

c. EstimatethepercentageofAmericanadultswhosmokedin2005.

d. Findthe p-interceptofthemodel.Whatdoesitmeaninthissituation?

25. Let p bethepercentageofgamblingrevenueinNevadathatisfrompennyslotmachinesat t yearssince 2008.Thepercentagein2008was14%andincreasedby2.8percentagepointsperyearuntil2013(Source: NevadaStateGamingControlBoard).

a. Findanequationofamodelthatdescribesthissituation.

b. Rewriteyourequationusingthefunctionname f

c. Find f (5).Whatdoesitmeaninthissituation?

26. ThenumberofhouseholdswithcableTVsubscriptionswas61.8millionin2009anddecreasedbyabout 1.5millionperyearuntil2014(Source: IHS).Let n = g(t) bethenumber(inmillions)ofhouseholdswith cableTVsubscriptionsat t yearssince2009.

a. Findanequationof g

b. Find g(4).Whatdoesitmeaninthissituation?

OBJECTIVE8

Forthe domain and range ofamodel,weconsiderinput-outputpairsonlywhenboththeinputandoutputmake senseinthesituation.

27. Astoreisopenfrom9A.M.to5P.M.,MondaysthroughSaturdays.Let I = f (t) beanemployee’s weeklyincome(indollars)fromworking t hourseachweekat$10perhour.

a. Findanequationofthemodel f

b. Findthedomainandrangeofthemodel f

HW 1,3,5,13,19,29,33,39,47,55,57,61,65,79,81,85,89,93,95,101

SECTION7.4TEACHINGTIPS

Studentslearnabouttheconceptsofrelationandfunctioninthissection.Conceptsrelatedtofunctionswillbe neededthroughouttherestofthetextbook.Studentstendtohaveaneasytimewithfunctionconcepts,although theystruggleinitiallywithﬁndingthedomainandrangeofafunction.Theyalsohavegrowingpainslearning aboutfunctionnotation,especiallywithconfusingtheinstructionssuchas"Find f (5)"and"Find x when f (x)= 5

OBJECTIVE1COMMENTS

Togetacrosstheconceptsofrelationandfunction,Iliketodrawlotsof“relationmachines”suchastheonesin Figs.102and103onpage477ofthetextbookaswellastablessuchasTables39and40onpages476and478of thetextbook.Imakesurethatstudentsunderstandthatafunctionmayhavetwoinputsthatsharethesameoutput.

OBJECTIVE2COMMENTS

Beforediscussingtheverticallinetest,IusearrowssimilartothoseinFig.105onpage478ofthetextbooktoget studentsaccustomedtothinkingvisuallyofinputsbeingsenttooutputs.Iﬁndthatevencalculusstudentslack thisessentialperspective.Ialsousearrowswithtablesandtheircorrespondinggraphstohelpstudentsseethe connectionbetweentablesandgraphsintermsofinputsbeingsenttooutputs.

Oncestudentsseehowtodrawsucharrowswithgraphs,studentsarequicktoidentifygraphsoffunctions. Theycandothiswithouthavingbeentoldabouttheverticallinetest.Ipreferhavingstudentsdrawarrows, becausetheverticallineteststripsawaythekeyideaofafunction.Oncestudentshavemasteredusingarrowsto identifygraphsoffunctions,I’llsometimesbrieﬂydiscusstheverticallinetest.Moststudentspersistindrawing arrowsonquizzesandexams,whichItaketobeagoodsign.

GROUPEXPLORATION:UseBeforeVerticalLineTest

Thisactivitynicelymotivatestheverticallinetest.Bycompletingtheexploration,studentswillseenotonlyhow tousetheverticallinetest,butalso why itworks.

OBJECTIVE3COMMENTS

Studentshaveaneasytimewiththisobjective.

OBJECTIVE4COMMENTS

ThereareexercisesscatteredthroughoutthetextbookthatrequireconceptsrelatedtotheRuleofFourforfunctions.Forexample,seeExercises25and26ofthissectionandseeExercises59and60ofHomework9.1.

OBJECTIVE5COMMENTS

Toﬁndthedomainandrangeofafunctionfromitsgraph,Idrawarrowsindicatingabout10inputsbeingsentto

LectureNotesandTeachingTips161 correspondingoutputs(seeFigures112and113onpage481ofthetextbook).Moststudentswillthenbequick topickuponthedomainandrangeofthefunction.Iﬁndthatstudentstendtohavemuchmoresuccesswiththis approachthanwithotherstandardapproaches.

ForProblem10(c),studentswillwonderwhetherthedomainisreallythesetofallrealnumbers.Itwillhelp toexplainthemeaningofthetwodisplayedarrowsatthe"ends"ofthecurve.

Intheanswerssection,inequalitynotation(Section1.1)isusedtodescribedomainsandrangesoffunctions. Inthesecondedition,Iwilllikelyaddintervalnotation(Section1.1)totheseanswers.

OBJECTIVE6COMMENTS

Manystudentswonderwhywewouldwanttorepresent“y”bythemorecomplicatednotation“f (x).”Iemphasize thatfunctionalnotationallowsustoconvenientlynameafunction.Iexplainthatbeingabletonameafunctionis especiallyhelpfulwhenworkingwithtwomodels,suchasthemodeldescribedinProblem25andthemodelthat describesthepercentageofgamblingrevenueinNevadathatisfromblackjackat t yearssince2008.

StudentstendtobereassuredwhenItellthemthat f (x) simplystandsfor y.Later(whendiscussingObjective7)Iexplainthat,ingeneral,responsevariable = f (explanatoryvariable).

Ispendagoodchunkoftimediscussinghowtoﬁndvaluesof x or f (x),whereafunction f isdescribed byatable,agraph,oranequation.Ialsotieinfunctionnotationwithfunction-machineﬁguressuchastheone inFig.114onpage482ofthetextbook.Studentsneedtoviewfunctionsfrommultipleperspectivestoreally understandthem.

Manystudentsthinkthatthenotation f (4) meansthat y is4orthattheequation f (x)=4 meansthat x is 4.ComparingtheworkforProblem19withtheworkforProblem20andcomparingtheworkforProblem21(a) withtheworkforProblem21(b)shouldhelpaddresstheseissues.

GROUPEXPLORATION:FormulaforSlope

Thisactivitydoesnotaddressacrucialconceptofthecourse,butitdoesshedadifferentlightontheslopeformula.

OBJECTIVE7COMMENTS

StudentsdealwithfunctionnotationwellinProblems23–26,althoughsomestudentstendtocontinuetostruggle toﬁndequationsofmodelsinProblems25(a)and26(a).Theywillbechallengedbyfunctionnotationtoamuch largerdegreewhentheymustdistinguishbetweenevaluatingafunctionandsolvingforanexplanatoryvariable inSections8.3,9.2,and9.3.

OBJECTIVE8COMMENTS

Duetotimelimitations,Iusuallyskiporgivelighttreatmenttothisobjective.Inmostsituations,it’sverydifﬁcult todetermineaprecisedomainand,hence,rangeofamodel.It’sfarmoreimportanttogetacrossthemeaningsof interpolationandextrapolationandwhywehavelittleornofaithwhenweextrapolate. Copyright c 2016PearsonEducation,Inc.

CHAPTER8OVERVIEW

Inthischapter,studentswillsimplifylinearexpressionsandsolvelinearequationsinonevariable,formulas,and linearinequalities.Theskillofsolvingequationswillpreparestudentstoﬁndequationsoflinesandlinearmodels inSections9.1and9.2.Thisskillwillalsopreparestudentstolearnthederivationsofsample-sizeformulasin introductorystatistics.Theskillofsolvinginequalitieswillpreparestudentstolearnaboutthederivationof conﬁdenceintervalsinintroductorystatistics.

OnecouldarguethatSection8.4(solvingformulas)isthemostimportantsectionbecausestudentswillwork withsomanyformulasinintroductorystatistics.

StudentstendtobegreatlychallengedbySections8.3(solvingmorecomplicatedlinearequationsandlinear modeling)and8.4(solvingformulas),sobesuretoallocateenoughtimeforthesesections.

SECTION8.1LECTURENOTES

Objectives

1. Describethe commutativelaw

2. Describethe associativelaw.

3. Describethe distributivelaw.

4. Describethemeaningof equivalentexpressions.

5. Combineliketerms.

6. Simplifyexpressions.

OBJECTIVE1

Theequations 3+7=7+3 and 3 7=7 3 suggestthefollowinglaws.

CommutativeLawsforAdditionandMultiplication

Commutativelawforaddition: a + b = b + a

Commutativelawformultiplication: ab = ba

Usethecommutativelawforadditiontowritetheexpressioninanotherform. 1. 5+ x 2. 2+7k

Usethecommutativelawformultiplicationtowritetheexpressioninanotherform.

• Thereisnocommutativelawforsubtraction.

• A term isaconstant,variable,oraproductofaconstantandoneormorevariablesraisedtopowers.

• Herearesometerms: 6x, 5, w, 3pt, 4y5 w2

• Variableterms aretermsthatcontainvariables.

• Constantterms aretermsthatdonotcontainvariables.

• Weusuallywriteasumofbothvariableandconstanttermswiththevariabletermstotheleftoftheconstant terms.

6. Write 7 3x sothatthevariabletermistotheleftoftheconstantterm.

OBJECTIVE2

Theequations (3+2)+5=3+(2+5) and (3 · 2) · 5=3 · (2 · 5) suggestthefollowinglaws.

AssociativeLawsforAdditionandMultiplication

Associativelawforaddition: a +(b + c)=(a + b)+ c

Associativelawformultiplication: a(bc)=(ab)c

Useanassociativelawtowritetheexpressioninanotherform.

7. (x +4)+ y 8. b +(5+ c) 9. 8(xy) 10. (kp)w

11. Rearrangethetermsof 7 5x +3 9 sothatthenumberscanbeadded.

12. Usethecommutativeandassociativelawstoremovetheparentheses.Also,multiplyandaddnumberswhen possible. a. 2(4p) b. (3+5x)+7

OBJECTIVE3

Theequation 3(2+4)=3 2+3 4 suggeststhefollowinglaw.

DistributiveLaw

a(b + c)= ab + ac

Findtheproduct.

13. 2(x +3) 14. 4(2x +8) 15. 7(w 5) 16. 3(4x 7y)

(x 9)(2)

4(7 x)

3(2p 4t +6)

• Inapplyingthedistributivelawtoanexpressionsuchas 2(x +3),remembertodistributethe2to every termintheparentheses.

• Avoidconfusingtheassociativelawwiththedistributivelaw.We cannot applythedistributivelawtothe expression a(bc) toget (ab)(ac).

MultiplyingaNumberby 1

Removetheparentheses.

20. (x +5) 21. (8x 3y +6)

OBJECTIVE4

22. Evaluatebothoftheexpressions 2(x +3) and 2x +6 forthevalues x =0, x =1, x =2, x =3, x =4, and x =5.(Afterperformingacoupleofevaluationsbyhand,usetechnology.)

Deﬁnition Equivalentexpressions

Twoormoreexpressionsare equivalentexpressions if,wheneachvariableisevaluatedfor any realnumber (forwhichalltheexpressionsaredeﬁned),theexpressionsallgiveequalresults.

OBJECTIVE5

• The coefﬁcient ofatermistheconstantfactoroftheterm.

• Liketerms areeitherconstanttermsorvariabletermsthatcontainthesamevariable(s)raisedtoexactly thesamepower(s).

• Iftermsarenotliketerms,wesaythattheyare unliketerms

• Whenwewriteasumordifferenceofliketermsasoneterm,wesaywehave combinedliketerms. Combineliketerms.

23. 3x +5x 24. 9w 6w 25. 4b + b

CombiningLikeTerms

Tocombineliketerms,addthecoefﬁcientsofthetermsandkeepthesamevariablefactors.

OBJECTIVE6

• We simplifyanexpression byremovingparenthesesandcombiningliketerms.

• Theresultofsimplifyinganexpressionisa simpliﬁedexpression,whichisequivalenttotheoriginal expression.

Simplify.

26. 5x 2y +3x +4 6y 1

27. 7 5(b +4)

28. 4(2w 5y) 2(w + y)

29. 3(k 5) (k +2)

30. Let x beanumber.Translatethephrase“3,minus2timesthedifferenceoftwicethenumberand5”toan expression.Thensimplifytheexpression.

31. Let x beanumber.Translatetheexpression 3x 2(x 5) intoanEnglishphrase.Thensimplifythe expression.

HW 1,3,7,11,17,27,37,47,55,63,67,69,75,83,91,97,107

SECTION8.1TEACHINGTIPS

Inthissection,studentsusethecommutative,associative,anddistributivelawstosimplifyexpressions.These conceptswillbeusedthroughouttherestofthecourse.Moststudentswillhaveaneasytimewiththissection.

OBJECTIVES1–3COMMENTS

WhenIamtightontime,Igivelighttreatmenttothecommutativeandassociativelawsandemphasizethe distributivelaw.Eitherfrompastexperienceswithalgebraorbywayofintuition,studentsseemtoknowhowto applythecommutativeandassociativelawstosimplifyexpressions.Themainthingthatstudentsneedtoknow inrelationtothecommutativeandassociativelawsisthattheycanrearrangeterms.

Studentstendtohavedifﬁcultyapplyingthedistributivelawwhentheexpressionincludesnegativecoefﬁcients and/orconstantterms.

ForexpressionssuchastheonesinProblems20and21,mosttextbookssuggesttochangethesignsofthe termsintheparentheses,butstudentsdon’tseemtounderstandthistechnique.Plus,itisnotcleartostudents howthattechniqueistiedtothelawsofoperations,whereasstudentscanseethatthetechniquethatusesthefact 1a = a istiedtothedistributivelaw.Whenusingthistechnique,Ipointoutthatthedistributivelawsaysthat wecandistributeanumbersuchas 1,notanoppositesymbol.

GROUPEXPLORATION:LawsofOperations

Thisactivityhasstudentsdiscoverthethreelawsofoperationsdiscussedinthissection.Studentshaveaneasy timewiththisexploration.

OBJECTIVE4COMMENTS

ForProblem22,Iemphasizethatwhenwesimplify 2(x +3) andwrite 2(x +3)=2x +6 wemeanthatthe expressions 2(x +3) and 2x +6 areequivalent.Moststudentsthinkofsimplifyinganexpressionasataskto complete;theydonotknowthattheresultandtheoriginalexpressionareequivalent.

OBJECTIVE5COMMENTS

Tointroducehowtocombineliketermsfor 2x +3x,Iusethedistributivelawtowrite 2x +3x =(2+3)x =5x, butIalsodemonstratethat 2x +3x =(x + x)+(x + x + x)= x + x + x + x + x =5x.Thelattertechnique mightbetheclearerwayforstudentstoseethat 4b + b =5b (Problem25).

OBJECTIVE6COMMENTS

InProblem27,fortheﬁrststepintryingtosimplify 7 5(b +4),somestudentsmistakenlywrite 2(b +4).To pointouttheirerror,Iremindthemoftheorderofoperations.

ItiswithmorecomplicatedexpressionslikethoseinProblems27–29,thatstudentsaremorelikelytoforget todistributeafactortoalltermsinsideparentheses.

GROUPEXPLORATION:SimplifyingExpressions

Thisactivityessentiallywarnsgroupsofstudentsofthreetypesofcommonstudenterrors.

SECTION8.2LECTURENOTES

Objectives

1. Describethemeaningof linearequationinonevariable

2. Foranequationinonevariable,describe satisfy, solution, solutionset,and solve

3. Describe equivalentequations

4. Describethe additionpropertyofequality

5. Describethe multiplicationpropertyofequality.

6. Solvealinearequationinonevariable.

7. Solveapercentageproblem.

8. Usegraphingtosolvealinearequationinonevariable.

9. Useatabletosolvealinearequationinonevariable.

OBJECTIVE1

Deﬁnition Linearequationinonevariable

A linearequationinonevariable isanequationthatcanbeputintotheform

mx + b =0

where m and b areconstantsand m =0

OBJECTIVE2

1. Showthattheequation x +3=7 becomesatruestatementif4issubstitutedfor x

Deﬁnition Solution,satisfy,solutionset, and solve foranequationinonevariable

Anumberisa solution ofanequationinonevariableiftheequationbecomesatruestatementwhenthe numberissubstitutedforthevariable.Wesaythenumber satisﬁes theequation.Thesetofallsolutionsof theequationiscalledthe solutionset oftheequation.We solve theequationbyﬁndingitssolutionset.

2. Is2asolutionoftheequation 2 4x =3(x 4)?

3. Is5asolutionoftheequation 2 4x =3(x 4)?

OBJECTIVE3

4. Showthatthefollowingequationsallhavethesamesolutionset: x =6, x +2=6+2,and x +2=8

Equivalentequations areequationsthathavethesamesolutionset.

OBJECTIVE4

AdditionPropertyofEquality

If A and B areexpressionsand c isanumber,thentheequations A = B and A + c = B + c areequivalent.

5. Solve x 4=2

• Aftersolvinganequation,checkthatallofyourresultssatisfytheequation.

• Ourstrategyinsolvinglinearequationsinonevariablewillbetousepropertiestogetthevariablealoneon onesideoftheequation.

Solve.

OBJECTIVE5

9. Showthatthefollowingequationsallhavethesamesolutionset: x =4, 3 x =3 4,and 3x =12

MultiplicationPropertyofEquality

If A and B areexpressionsand c isanonzeronumber,thentheequations A = B and Ac = Bc are equivalent.

OBJECTIVE6

Solve.

OBJECTIVE7

17. Inasurvey,70%ofadultsansweredyestothefollowingquestion(Source: TheGallupOrganization): "Whenapersonhasanincurabledisease,shoulddoctorsbeallowedtohelpendapatient’slifebysome painlessmeansifthepatientrequestsit?"Ifthenumberofpeopleinthesurveywhosaidthisis717,what isthetotalnumberofadultssurveyed?

OBJECTIVE8

UsingGraphingtoSolveanEquationinOneVariable

Tousegraphingtosolveanequation A = B inonevariable, x,where A and B areexpressions,

1. Graphtheequations y = A and y = B onthesamecoordinatesystem.(Forexample,iftheoriginal equationis 2x +5=4x 9,thenwewouldgraphtheequations y =2x +5 and y =4x 9.)

2. Findallintersectionpoints.

3. The x-coordinatesofthoseintersectionpointsarethesolutionsoftheequation A = B

ForProblems18and19,graph y = 3 5 x +1 byhand.Usethegraphtosolvethegivenequation. 18. 3 5 x +1=4

20. Use“intersect”onaTI-84tosolve

OBJECTIVE9

21. Useatableofvaluesof y =4x 3 tosolve 4x 3=5

HW 1,3,7,11,27,39,41,55,59,65,69,71,75,79,93,95,111

SECTION8.2TEACHINGTIPS

Inthissection,studentsusesymbolicmethods,graphing,andtablestosolvelinearequationsinonevariable. TheywillusethismaterialthroughouttherestofChapter8aswellasChapter9.

OBJECTIVE1COMMENTS

IremindmystudentsthatinChapter3wegraphedequationsintwovariables.Isaywewillnowworkwithlinear equationsin one variable.Iprovideafewexamplesandthendeﬁne linearequationinonevariable. Anotheroptionistointroducethedeﬁnitionafteryouhavesolvedafewequationssothatstudentsknowwhat “putintotheform”means.

OBJECTIVE2COMMENTS

ForProblem1,Iwrite x +3=7 ontheboardandaskstudentswhat x canbe.Studentsarequicktosay x isequal to4.Isay4iscalleda solution andthatit satisﬁes theequation.ThenIdeﬁnethewordsintheboxedstatement andsaythesewordsmeanaboutthesamethingwhenappliedtoequationsintwovariables.

OBJECTIVE3COMMENTS

ThisobjectiveissettingthestageforObjective5.

OBJECTIVE4COMMENTS

Fortheadditionpropertyofequality,moststudentsthinkthattheentirepointisthat“wecanaddanumberto bothsidesofanequation.”Moststudentsdonotunderstandthatasolutionofanequationwillsatisfy all ofthe equationsthatleadtoﬁndingthesolution.Atvarioustimesinthecourse,Ireturntothistopictodeepenstudents’ understanding.

ForProblem5,Isayourobjectiveinsolvinganequationistoisolate x ononesideoftheequation.

ForProblem7,Ipointoutthatwecanstillusetheadditionpropertyofequality,becausesubtracting3from bothsidesoftheequationisthesameasadding 3 tobothsides.

GROUPEXPLORATION:LocatinganErrorinSolvinganEquation

Thisactivityisagoodreminderofthemeaningofequivalentequations.

OBJECTIVE5COMMENTS

Studentsarequicktopickuponthisconceptbecauseitissosimilartotheadditionpropertyofequality.

OBJECTIVE6COMMENTS

ForProblem10,Iﬁrstshowthattheproductofafractionanditsreciprocalisequalto1.ThenIusethemultiplicationpropertyofequalitytosolvetheequation 5 2 x =3

ForProblem11,Ipointoutthatwecanstillusethemultiplicationpropertyofequality,becausedividingboth sidesby 5 isthesameasmultiplyingbothsidesby 1 5

Whensolving t =7 (Problem12),Ishowstudentshowtosolvetheequationbydividingbothsidesofthe equationby 1 aswellasbymultiplyingbothsidesby 1.Almostallstudentspreferdividingby 1 ratherthan multiplyingby 1

ForProblem16,IaskstudentswhytheequationisdifferentthantheonesinProblems10–15.Whentheysay theequationhasvariabletermsonbothsidesoftheequation,Isaythatagoodﬁrststepistogetthevariables termsonjustonesideoftheequation.

OBJECTIVE7COMMENTS

PerhapsthehardestpartofProblem17isrealizingthatithelpstodeﬁneavariable(forthenumberofadultsin thesurvey).SuchpercentageproblemsaregoodpreparationformorechallengingonesinSection8.3.

OBJECTIVE8COMMENTS

Adiscussionaboutinputsandoutputscanbeusedtoexplainhowtousegraphingtosolveanequationinone variable.Nonetheless,moststudentswillbechallengedbysuchanexplanation.

ForProblem20,Ipointouttheadvantagesofusingtechnologytosolvesuchanequation.Itisimportant thatstudentslearnsymbolicmethodsofthecourse,butitisalsoimportantthatstudentslearnappropriateusesof technology.

OBJECTIVE9COMMENTS

AlthoughstudentsarequicktopickuponhowtosolveproblemssuchasProblem21,theymightnotreally understandwhatisgoingon.Adiscussionaboutinputsandoutputscanhelp.

SECTION8.3LECTURENOTES

Objectives

1. Usecombinationsofpropertiesofequalitytosolvealinearequationinonevariable.

2. Comparethemeaningsof simplifyanexpression and solveanequation

3. Usegraphingtosolvealinearequationinonevariable.

4. Usetwotablestosolvealinearequationinonevariable.

5. Findtheinputofalinearfunctionforagivenoutput.

6. Makeestimatesandpredictionsbysolvinglinearequations.

OBJECTIVE1

Solve.

1. 5 4(2x 3)=3(4 x)

2. 2(3x +4) (4x 1)=3(x +2) 3. 5 6 k 3 2 = 7 3 4. 4w

• Itiswisetocheckthataresult(ortheresults)ofsolvinganequationdoesindeedsatisfytheequation.

• Akeystepinsolvinganequationthatcontainsfractionsistomultiplybothsidesoftheequationbythe LCDsothattherearenofractionsoneithersideoftheequation.

5. Solve 1 96= x 21.9 3.5 .Roundanysolutionstotwodecimalplaces.

OBJECTIVE2

6. Simplify 3 8 x + 7 6 7 4 x.

7. Solve 3 8 x + 7 6 = 7 4 x

8. ComparetheﬁrststepsofyourworkinProblems6and7.

Itisincorrecttosay"solveanexpression."Itisincorrecttosay"simplifyanequation."

ResultsofSimplifyinganExpressionandSolvinganEquation

Theresultofsimplifyinganexpressionisanexpression.Theresultofsolvingalinearequationinone variableisanumber.

MultiplyingExpressionsandBothSidesofEquationsbyNumbers

Whensimplifyinganexpression,theonlynumberthatwecanmultiplytheexpressionbyorpartofitbyis 1.Whensolvinganequation,wecanmultiplybothsidesoftheequationby any numberexcept0.

OBJECTIVE3

ForProblems9and10,solvethegivenequationbyreferringtothegraphsof y = 1 3 x + 5 3 and y = 3x 5 shownbelow.

OBJECTIVE4

11. Usetablestosolvetheequation 3x 2=6 x.[Thesolutionis2.]

OBJECTIVE5

Let f (x)= 3 4 x 2.

12. Find f (8)

13. Find x when f (x)=8. NotethatinProblem12,wearetoﬁndavalueof y,butinProblem13,wearetoﬁndavalueof x.

OBJECTIVE6

14. TheTotalU.S.debitcardpurchaseswas$1.6trillionin2010andhasincreasedby$0.13trillionperyearin 2014(Source: TheNilsonReport).

a. Findamodelofthesituation.Explainwhatyourvariablesrepresent.

b. EstimatetotalU.S.debitcardpurchasesin2014.

c. EstimatewhenthetotalannualU.S.debitcardpurchaseswas$2.0trillion.

UsinganEquationofaModeltoMakePredictions

• Whenmakingapredictionabouttheresponsevariableofalinearmodel,substituteachosenvaluefor theexplanatoryvariableinthemodel.Thensolvefortheresponsevariable.

• Whenmakingapredictionabouttheexplanatoryvariableofalinearmodel,substituteachosenvalue fortheresponsevariableinthemodel.Thensolvefortheexplanatoryvariable.

15. Thenumberoftobaccofarmswas16,228farmsin2007,anditdecreasedbyabout1495farmsperyear until2015(Source: U.S.DepartmentofAgricultureNationalAgriculturalStatistics).Estimatewhenthere were6000tobaccofarms.

16. In2013,thestudent-teacherratioinU.S.publicschoolswas15.1,down5.6%from2000(Source: National CenterforEducationStatistics).Whatwastheratioin2000?

17. ManyappliancessuchastelevisionsandelectronicgadgetssuchascellphonescontainrareEarthmetals. AnnualU.S.electronicsandappliancestoressalesandannualworldwideproductionofrareEarthmetals areshowninthefollowingtablefortheperiod1992–2012.

Let p = f (s) betheannualworldwideproduction(inthousandofmetrictons)ofrareEarthmetals,andlet s betheannualU.S.electronicsandappliancestoressales(inbillionsofdollars)inthesameyear.

a. Constructascatterplot.

b. Describethefourcharacteristicsoftheassociation.

c. Graphthemodel f (s)=1.34s 16.31 inthescatterplot.Doesitcomeclosetothedatapoints?

d. Find f (100).Whatdoesitmeaninthissituation?

e. Find s when f (s)=100.Whatdoesitmeaninthissituation?

HW 1,3,5,9,15,21,31,35,41,43,51,71,77,81,85,91,95,101,107

SECTION8.3TEACHINGTIPS

Thekeyideaofthissectionissolvinglinearequationsandusingthisskillwithlinearmodelstomakepredictions. Moststudentsaregreatlychallengedbythissectionduetosolvingequationswithfractions,ﬁndingequationof linearmodels,andworkingwithfunctionnotation.

OBJECTIVE1COMMENTS

MoststudentsarechallengedbyProblems3and4.Somestudentstrytowriteallofthefractionswithacommon denominator,whichisnotincorrectbutisinefﬁcient,andusuallysuchstudentsmakeothererrorsalongtheway. SomestudentshavetroubleﬁndingtheLCD.Otherstudentshavetroublesimplifyingbothsidesoftheequation aftermultiplyingbothsidesoftheequationbytheLCD.

GROUPEXPLORATION:AnyLinearEquationinOneVariableHasExactlyOneSolution

Thisactivitynotonlyhasstudentsdeterminethenumberofsolutionsofalinearequationbutalsohasthemwork withaformula,whichisgoodwarm-upforSection8.4(solvingformulas).

OBJECTIVE2COMMENTS

Studentsusuallyhavenotroubledistinguishingwhentoapplysimplifyingtechniquesandwhentoapplysolvingtechniquesforlinearexpressionsandequations,respectively,exceptwhenitcomestothosewithfractional coefﬁcientsandconstantterms.

OBJECTIVES3and4COMMENTS

Studentsusuallyhavenotroublewiththesetwoobjectivesbecausetheybuildonsimilarobjectivesaddressedin Section8.2.

OBJECTIVE5COMMENTS

ForProblem13,studentstendtosubstitutefor8for x ratherthanfor f (x).Drawingadistinctionbetween problemssimilartoProblems12and13severaltimesinthenextfewdaysisagoodideabecausestudentstendto forget.

OBJECTIVE6COMMENTS

ForProblem14(a),studentstendtoneedareminderabouthowtoﬁndsuchalinearmodel(Section7.3).This partposesanextrachallengebecausestudentsmustdeﬁnetherelevantvariables.

ForProblem16,studentstendtothinkthatwhat’srequiredistocalculate5.6%oftheratioin2013(15.1).Encourageyourstudentstotakethenecessarytimetounderstandthesituationbeforetryingtoperformcalculations orsolveequations.

Problem17servesasagoodreminderofthefourcharacteristicsofanassociation.Italsohelpsstudentssee howthecurrentmaterialﬁtsintothebigpictureoflinearmodeling.

SECTION8.4LECTURENOTES

Objectives

1. Findaquantitybysubstitutingvaluesforallbutonevariableinaformulaandthensolvingforthe remainingvariable.

2. Findaquantitybyusingaformulawithsummationnotation.

3. Solveaformulaforoneofitsvariables.

4. Solveaformulawithasquareroot.

5. Graphalinearequationintwovariablesbysolvingfor y.

OBJECTIVE1

Recallthata formula isanequationthatcontainstwoormorevariables(Section4.1).

1. AtApple,7%ofemployeesareAfricanAmericanand18%ofemployeesareAfricanAmericanORHispanic(Source: Apple).FindtheprobabilityofrandomlyselectinganAppleemployeewhoisHispanic.

Toﬁndasinglevalueofavariableinaformula,weoftensubstitutenumbersforalloftheothervariables andthensolvefortheremainingvariable.

2. RecallthatthescoresontheWechslerIQtestarenormallydistributedwithmean100pointsandstandarddeviation15points.ActressSharonStoneisreportedtohaveanIQof154points(Source: Chicago Tribune).Usetheformula x =¯ x + zs toﬁndthe z-scoreforanIQof154points.

OBJECTIVE2

3. Substitutethefollowingvaluesintheformula µ = xiP (xi) andsolvefortheremainingvariable:

4. Substitutethefollowingvaluesintheformula MSE= [(ni 1)s2 i ] n k andsolvefortheremainingvariable:

Roundtheresulttotheﬁrstdecimalplace.

OBJECTIVE3

5. a. Solvetheformula P (A OR H)= P (A)+ P (H) for P (H)

b. Substitute0.18for P (A OR H) and0.07for P (A) intheformulafoundinProblem1.

Solvingforavariableinaformulawillnotchangetheassociationbetweenthevariablesintheformula.

6. a. Solvetheformula x =¯ x + zs for z.

b. Forstudentswhograduatedfromhighschoolin2013,theirSATmathscoreswereapproximately normallydistributedwithameanof514pointsandastandarddeviationof118points(Source: College Board).Usetheformula x =¯ x + zs ortheformulayoufoundinPart(a)toﬁndthe z-scoresforthe followingstudents’SATscores(allinpoints):621,457,555,748,242,and562.

c. Whichofthestudents’scoresgiveninPart(b)ismostunusual?Explain.

Toﬁndseveralvaluesofavariableinaformula,weusuallysolvetheformulaforthatvariablebefore wemakeanysubstitutions.

7. Let F betheFahrenheitreadingcorrespondingtoaCelsiusreadingof C degrees.Aformulathatdescribes theassociationbetween F and C is C = 5 9 (F 32).

a. SolvetheFahrenheit-Celsiusformulafor F

b. Convert 10◦CtotheequivalentFahrenheittemperature.

c. Usetechnologytoconvert 10◦C, 15◦C, 20◦C, 25◦C,and 30◦CtotheequivalentFahrenheittemperatures.

8. Solve ur = 2n1n2 n +1 for n1

OBJECTIVE4

SquaringaPrincipalSquareRoot

If x isnonnegative,then √x 2 = x

9. Inintroductorystatistics,youwilllearnabouta marginoferrorformula E = z s √n ,where E hasto dowiththeerrorinmakingacertaintypeofestimate.Solvetheformulafor n,whichisthenumberof individualsinarandomsample.

OBJECTIVE5

Determinetheslopeandthe y-intercept.Usetheslopeandthe y-intercepttographtheequationbyhand.

HW 1,3,5,13,23,29,41,43,47,61,63,65,75,87,95,101

SECTION8.4TEACHINGTIPS

Inthissection,studentswillsolveformulasandusethisskilltographlinearequationsinwhich y isnotisolated ononesideoftheequation.TheskillofsolvingformulascanbeusedinSections9.1and10.4,butitisnot essential.Theskillisimportantinintroductorystatisticsforderivingsample-sizeand z-scoreformulas.

Thissectionservesasanicereminderofpastformulasused.Itwillalsoenhancestudents’familiaritywith summationnotation(Objective2).

OBJECTIVE1COMMENTS

Sometextbooksseemtosuggestthatwealwayswanttoﬁrstsolveaformulaforavariablebeforemakingsubstitutions;thishardlymakessenseifwewanttoﬁndonlyonevalueofaquantity.

OBJECTIVE2COMMENTS

Althoughstudentshavebeenexposedtosummationnotationwhentheformulasforthemeanandthestandard deviationwereintroduced,theytendtomemorizetheprocedureswithoutreallyunderstandingthemeaningof summationnotation.Thisobjectivewillforcestudentstosortoutitsmeaning.

OBJECTIVE3COMMENTS

MoststudentshaveatoughtimewithProblems5–8.Itcanhelptosolveeachformulaalongsideasimilarequation inonevariable.Forexample,seethesolutionsofExamples5and6onpages547and548,respectively,ofthe textbook.

NotethatProblem7(a)isessentiallyhavingstudentsfindtheinversefunctionofthemodel C = 5 9 (F 32). WhencompletingPart(c),Ipointoutthatitisadvantageoustofirstsolvefor F beforesubstitutingthefivevalues for C;ifwesubstitutedbeforesolving,we’dhavefiveequationstosolve.Isaythatfirstsolvingfor F would becomeahugeadvantageifwewantedtomakehundredsofsubstitutionsfor C

GROUPEXPLORATION:DeterminingwhenIt’sBettertoSolveaFormulaforaVariable

Thisisalengthyactivity,butitmightbethebestwaytodrivehomethevalueofsolvingaformulabeforesubstitutingvaluesforthevariablesbecauseit’sonethingtotellstudentshowthispracticesavestimebutit’smore convincingforthemto experience it.

OBJECTIVE4COMMENTS

Thetextbookgiveslighttreatmenttothisobjective(Example10andExercises53and54),buttheobjective hasbeenincludedtogivestudentsabitofexposuresothey’llhaveabetterchanceoffollowingderivationsof sample-sizeformulasinintroductorystatistics.

OBJECTIVE5COMMENTS

Thisobjectiveisnotneededinintroductorystatisticsbecauselinearregressionequationsarealreadyintheform ˆ y = mx + b.ButsomereviewerswantedthisobjectiveincludedinthetextbooksoIhavedoneso.Perhapsthe bestreasonforteachingthismaterialisthatitprovidesareviewofgraphing(Section7.3).

SECTION8.5LECTURENOTES

Objectives

1. Describethe additionpropertyofinequalities.

2. Describethe multiplicationpropertyofinequalities

3. Describethemeaningof satisfy, solution,and solutionset fora linearinequalityinonevariable

4. Solvealinearinequalityinonevariable,andgraphthesolutionset.

5. Substitutevaluesforvariablesinacompoundinequality.

6. Solvea compoundinequalityinonevariable,andgraphthesolutionset.

7. Uselinearinequalitiestomakepredictionsaboutauthenticsituations.

OBJECTIVE1

Showwhathappenswhenweaddanumbertobothsidesof 5 < 7

AdditionPropertyofInequalities

If a<b,then a + c<b + c.

Similarpropertiesholdfor ≤, >,and ≥

Illustratetheadditionpropertyofinequalitiesbyusinganumberline.

OBJECTIVE2

Showwhathappenswhenwemultiplybothsidesoftheinequality 5 < 7 byanumber.

MultiplicationPropertyofInequalities

• Fora positive number c,if a<b,then ac<bc

• Fora negative number c,if a<b,then ac>bc

Similarpropertiesholdfor ≤, >,and ≥.

Illustratethatif a<b,then a> b byusinganumberline.

OBJECTIVE3

Deﬁnition Linearinequalityinonevariable

A linearinequalityinonevariable isaninequalitythatcanbeputintooneoftheforms mx + b< 0,mx + b ≤ 0,mx + b> 0,mx + b ≥ 0 where m and b areconstantsand m =0

Wesayanumber satisﬁes aninequalityinonevariableiftheinequalitybecomesatruestatementafterwe havesubstitutedthenumberforthevariable.

1. Doesthenumber2satisfytheinequality 4x 3 < 8?

2. Doesthenumber5satisfytheinequality 4x 3 < 8?

Deﬁnition Solution,solutionset, and solve foraninequalityinonevariable

Wesayanumberisa solution ofaninequalityinonevariableifitsatisﬁestheinequality.The solutionset ofaninequalityisthesetofallsolutionsoftheinequality.We solve aninequalitybyﬁndingitssolutionset.

OBJECTIVE4

Solvetheinequality.Describethesolutionsetasaninequality,inintervalnotation,andasagraph.

3. 3x 5 ≤ 7

4. 4x< 12

5. 4x< 12 6. 3x

OBJECTIVE5

12. Substitute35.2for x,1.761for t,4.7for s,and14for n inthecompoundinequality x t s √n <µ< x + t s √n toﬁndacompoundinequalitythatdescribesthevariable µ.Alsodescribethesolutionsetininterval notationandasagraph.Roundtotheﬁrstdecimalplace.

OBJECTIVE6

Solvetheinequality.Describethesolutionsetasaninequality,inintervalnotation,andinagraph.

OBJECTIVE7

16. Let B bethetotalannualboxofﬁcegrosses(inbillionsofdollars)intheUnitedStatesandCanadaat t yearssince1980(seethefollowingtable).

Sources: ACNielsenEDI,RentrakCorporation

Areasonablemodelis B =0 28t +1 98.Inwhichyearswastheannualboxofﬁcegrossgreaterthan$9.5 billion?

HW 1,3,7,17,37,47,55,59,61,65,73,77,81,85,89

SECTION8.5TEACHINGTIPS

Thissectionisgoodpreparationforintroductorystatisticsiftheinstructorplanstoderiveconﬁdenceinterval formulas.Studentswillnotneedtosolveinequalitiesintherestofthiscourse.

OBJECTIVES1and2COMMENTS

Whengoingovertheseobjectives,IemphasizethegraphicalinterpretationbecauseIbelieveitisanidealway toconveythataddinganumbertobothsidesofaninequalityormultiplyingbothsidesbyapositivenumber preservesorder.

Ialsoemphasizethatwhenwemultiplyordividebothsidesofaninequalitybyanegativenumber,wereverse theinequalitysymbol.Studentsneedseveralremindersaboutthis.

GROUPEXPLORATION:PropertiesofInequalities

Thisactivityisveryaccessibletostudents.

OBJECTIVE3COMMENTS

Ipointouttostudentsthatthemeaningsofthewords satisfy, solution,and solutionset aresimilarforequations andinequalities.

OBJECTIVE4COMMENTS

Itellstudentsthatsolvingalinearinequalityissimilartosolvingalinearequation,exceptthatcaremustbetaken toreversetheinequalitysymbolwhenappropriate.Whensayingsomethinglike,“Herewe divide bothsidesby negative 5,”I’llraisemyvoicedramaticallywhenIsay“divide”and“negative.”Althoughthisischeesy,my studentsgetthepointthattheyneedtobevigilantaboutreversingtheinequalitysymbolwhenappropriate.

Manystudentsdonotunderstandthesigniﬁcanceofthesolutionsetofaninequalityinonevariable.For example,considertheinequality 3x +1 < 11 (Problem6),whosesolutionis x> 4.Itisinstructivefor studentstoseethatnumbersgreaterthan4suchas4.1,5,and6satisfytheinequalityandnumberslessthanor equalto4suchas2,3,and4donotsatisfytheinequality.Exercises87and88addressthisissue.

GROUPEXPLORATION:MeaningoftheSolutionSetofanInequality

Althoughstudentshaveaneasytimewiththisactivity,itemphasizesaconceptthatstudentstendtolosesightof.

OBJECTIVE5COMMENTS

Thisobjectiveismeanttopreparestudentsforthecomplexityofconﬁdenceintervalformulas.

OBJECTIVE6COMMENTS

Studentswillhaveaneasytimesolvingcompoundinequalities.However,studentswillneedsomecoachingto seethataninequalitysuchas a>x>b isequivalentto b<x<a.ThisissuenaturallyarisesinProblem14, wheretheinequality 2 < 8 2x< 10 hassolution 3 >x> 1,whichisequivalentto 1 <x< 3

OBJECTIVE7COMMENTS

TosolveProblem16,Iﬁrsttranslatethephrase"annualboxofﬁcegrossgreaterthan$9.5billion:"

9 5

Somestudentshavetroubleinterpretingthemeaningofaninequalityintermsofthesituation.ForProblem16, somestudentswouldsaytheinequality t> 26 9 meansthattheannualboxofﬁcegrosswillbemorethan$9.5 billion in 2007,ratherthan after 2007.Withrepeatedwarningsaboutthisissue,farfewerstudentstendtomake thiserroronexams.Italsohelpstosketchagraphofthemodelanddiscussthesituationindetail. Copyright c 2016PearsonEducation,Inc.

CHAPTER9OVERVIEW

InSection9.1,studentsfindtheequationofalinethatcontainstwopoints.TheninSection9.2,theyuse thisskilltofindanequationofalinearmodel.Finally,inSection9.3,studentsusetechnologytofindalinear regressionmodel.

Ifyouarepressedfortime,youcouldskipSections9.1and9.2becausethemethodofusingtwopoints doesnotgeneralizetoﬁndinglinearregressionmodels.However,Sections9.1and9.2canhelpbuildstudents’ understandingoftheconnectionbetweenscatterplotsandtheequationsoflinearmodels.AndSection9.2can enhancestudents’abilitytodrawconclusionsaboutlinearmodelsandhowtousethemtomakepredictions.

Section9.3containsalargeamountofmaterialandservesasagreatreviewandextensionofChapters6–8. Mostreviewerssaidthatthissectionwouldbethelastonetheywouldincludeinthecourse.

SECTION9.1LECTURENOTES

Objectives

1. Findanequationofalinebyusingtheslope-interceptformofalinearequation.

2. Findanequationofalinebyusingthepoint-slopeformofalinearequation.

OBJECTIVE1

Recallthatanequationofalinecanbeputinslope-interceptform y = mx + b (Section7.1).

Usetheslope-interceptformtoﬁndanequationofthelinethathasthegivenslopeandcontainsthegiven point.

1. m =3, ( 4, 5)

2. m = 2, ( 3, 6)

3. m = 2 5 , ( 3, 4)

m = 4 3 , (5, 2) 5. m =0, ( 3, 2) 6. m isundeﬁned, ( 5, 1)

FindinganEquationofaLinebyUsingtheSlope,aPoint,andtheSlope-InterceptForm

Toﬁndanequationofalinebyusingtheslopeandapoint,

1. Substitutethegivenvalueoftheslope m intotheequation y = mx + b

2. Substitutethecoordinatesofthegivenpointintotheequationyoufoundinstep1andsolvefor b

3. Substitutethevalueof b youfoundinstep2intotheequationyoufoundinstep1.

4. Checkthatthegraphofyourequationcontainsthegivenpoint.

Usetheslope-interceptformtoﬁndanequationofthelinethatcontainsthetwogivenpoints.

7. (2, 3) and (4, 7) [slopeisaninteger]

8. ( 3, 4) and (2, 6) [slopeisaninteger]

9. ( 5, 3) and (2, 1) [slopeisafraction]

10. ( 6, 2) and ( 3, 7) [slopeisafraction]

FindinganEquationofaLinebyUsingTwoPointsandtheSlope-InterceptForm

Toﬁndanequationofthelinethatpassesthroughtwogivenpointswhose x-coordinatesaredifferent,

1. Usetheformula m = y2 y1 x2 x1 toﬁndtheslopeofthelinecontainingthetwopoints.

2. Substitutethe m valueyoufoundinstep1intotheequation y = mx + b.

3. Substitutethecoordinatesofoneofthegivenpointsintotheequationyoufoundinstep2andsolve for b

4. Substitutethe b valueyoufoundinstep3intoyourequationyoufoundinstep2.

5. Checkthatthegraphofyourequationcontainsthetwogivenpoints.

11. Findanapproximateequationofthelinethatcontainsthepoints ( 3.25, 8.11) and (2.67, 1.39).Round theslopeandtheconstanttermtotwodecimalplaces.

12. Findanequationofthelinethatcontainsthegivenpoints.

a. (4, 3) and (4, 2) [slopeisundeﬁned]

b. ( 5, 2) and (3, 2) [slopeis0]

OBJECTIVE2(optional)

Let (x1,y1) and (x,y) betwodistinctpointsonalinewithslope m.Usethetruestatement y y1 x x1 = m toderive thepoint-slopeform.

Point-SlopeForm

Ifanonverticallinehasslope m andcontainsthepoint (x1,y1),thenanequationofthelineis

y y1 = m(x x1)

RepeatanyofProblems1–5,7–11,and12(b).Compareyourresultswithyourearlierresults.

HW 1,3,7,15,19,25,29,43,47,51,55,57,63,69,73

SECTION9.1TEACHINGTIPS

Thissectiondiscusseshowtoﬁndequationsoflines,bothbyusingtheslope-interceptformandthepoint-slope form.Insubsequentsections,onlytheslope-interceptformwillbeusedtoﬁndsuchequations.So,thepoint-slope formisoptional.

Ihavechosentoemphasizeﬁndinglinearequationsusingtheslope-interceptformforseveralreasons:

• Mystudentshavebettersuccesswiththismethodthanwithusingthepoint-slopeform,especiallywhenthe slopeisafraction.

• Thenotionofsubstitutingapointtoﬁndtheparameter b of y = mx + b generalizestoﬁndingparameters forexponentialfunctions(Section10.4).

• Studentshaveabettersenseofwhythismethod“works”thanwithusingthepoint-slopeform.

• Usingtwoformsforlinearequationsconfusestheissueformanystudents.

TheskillofﬁndinganequationofalinethatcontainstwogivenpointswillalsobenecessaryforSection9.2, wherestudentswillﬁndequationsoflinearmodels.

OBJECTIVE1COMMENTS

ForProblem1,whenIsubstitutetheorderedpair ( 4, 5) intotheequation y =3x + b tofind b,Iremindstudents thatanorderedpairthatcorrespondstoapointonagraphsatisfiesanequationofthegraph.So,makingsucha substitutionwillgiveatruestatement,onethatwillallowustofindthevalueof b.

ForProblems3,4,9,and10,Ipreferthatstudentsusefractions,notdecimals,whenﬁndinglinearequations toremindthemofhowtoperformoperationsoffractions.Whensolvinganequationwithfractions(toﬁnd b of y = mx + b),studentstendtopreferthatwemultiplybothsidesoftheequationbytheLCDtocleartheequation offractions.

However,onecouldarguethatitsufﬁcestoallowstudentstousedecimalsratherthanfractionsbecausethat’s alltheywillneedtodowhenﬁndingequationsoflinearmodelsinSection9.2.Forthatreason,Problem11isa goodprimerforSection9.2.

GROUPEXPLORATION:DecidingwhichPointstoUsetoFindanEquationofaLine

Thisactivityrespondstothefrequentstudentquery,“Doesitmatterwhichorderedpairisusedtoﬁnd b?”and “DoesitmatterwhichtwopointsIchoosefromthegraphofalinetoﬁnditsequation?”Imakesurethatstudents understandtheinstructionsofProblem2oftheexploration,andthattheyimaginealinethatis not parallelto eitheraxis.Thisisaneasyexplorationformoststudents,anditcouldbeassignedashomework.

GROUPEXPLORATION:FindingEquationsofLines

Thisexplorationisafuncritical-thinkingactivity.Groupsofstudentscancompletethisexplorationinatimely fashioniftheydivideupthework.

OBJECTIVE2COMMENTS

Thisconceptisoptional.Seemyopeningcommentsfortheteachingtipsforthissection.

SECTION9.2LECTURENOTES

Objectives

1. Usetwopointstoﬁndanequationofalinearmodel.

OBJECTIVE1

1. Let A betheannualU.S.consumption(inbillionsofpounds)ofavocadosat t yearssince2000.Findan equationofalinearmodeltodescribethedatainthefollowingtable.

Source: CaliforniaAvocadoCommission

Itisacommonerrortoskipconstructingascatterplotwhenweﬁndanequationofamodel.

FindinganEquationofaLinearModel

Toﬁndanequationofalinearmodel,givensomedata,

1. Constructascatterplotofthedata.

2. Determinewhetherthereisalinethatcomesclosetothedatapoints.Ifso,choosetwopoints(not necessarilydatapoints)thatyoucanusetoﬁndanequationofalinearmodel.

3. Findanequationoftheline.

4. Usetechnologytoverifythatthegraphofyourequationcontainsthetwochosenpointsandcomes closetoallofthedatapointsofthescatterplot.

2. Thenumberofnew-cardealershipsareshowninthefollowingtableforvariousyears.Let n bethenumber (inthousands)ofnew-cardealershipsat t yearssince1900.

NumberofNew-CarDealerships

Source: NADAIndustryAnalysisDivision

a. Constructascatterplot.

b. Describethefourcharacteristicsoftheassociation.Computeandinterpret r aspartofyouranalysis.

c. Findanequationofalinearmodeltodescribethedata.

d. Rewritetheequationwiththefunctionname f

e. Find f (108).Whatdoesitmeaninthissituation?

3. Researcherscomparedthemeansulfurdioxideconcentrations(airpollution)andthemeandeterioration ratesofmarbletombstonesin21U.S.citiesfortheperiod1893–1993(seethefollowingtable).Amicrogram(µg)isequalto0.000001gram.

Source: MarbleTombstoneWeatheringandAirPollutioninNorthAmerica,T.C.Meierding

Let s bethemeansulfurdioxideconcentration(in µg/m3)and d bethemeandeteriorationrate(inmmper century)ofmarbletombstones,bothforthesamecity.

a. Describethefourcharacteristicsoftheassociation.Computeandinterpret r aspartofyouranalysis.

b. Findanequationofamodeltodescribethesituation.

c. Estimatethemeandeteriorationrateofmarbletombstonesduringtheperiod1893–1993inacity wherethemeansulfurdioxideconcentrationwas150 µg/m3)forthatperiod.

d. Acity’smeandeteriorationofmarbletombstonesfortheperiod1893–1993is2mm.Estimatethe city’smeansulfurdioxideconcentrationforthatperiod.

e. Becausetheassociationisstrong,astudentconcludesthatairpollutioncausestombstonedeterioration.Whatwouldyoutellthestudent?

HW 1,3,7,9,11,17,21,25,27,29,31,33

SECTION9.2DETAILEDCOMMENTS

Inthissection,studentsusetwopointstoﬁndanequationofalinearmodel.Thissectionisoptionalbecausethe algorithmdoesnotgeneralizetothemethodofminimizingthesumofsquaredresiduals(Section9.3).Butthis sectionhelpsstudentsseetheconnectionbetweendatapointsandtheequationofalinearmodel,whichisloosely relevanttoSection9.3.

OBJECTIVE1COMMENTS

Tofindanequationofalinearmodel,Ifirstconstructascatterplot.ThenInumberthedatapointsandaskmy studentswhichpairsofdatapointslieonalinethatcomesclosetotheotherdatapointsandwhichpairsdonot. Ireallyliketheavocadodataset(Problem1)becauseitillustratesthatusingthe"firstandlastpoints," (3, 0.7) and (12, 1.6),doesnotgenerateanidealmodel.Manystudentstendtoblindlyusethefirstandlastdatapoints withoutbotheringtoconstructascatterplot,sohopefullythisexamplewillserveasacautionarytale.

Studentscouldusetwonondatapointstoﬁndalinearmodel,butIdon’tbringupthisoptionforfourreasons. First,becauseusingdatapointsworksjustﬁne.Second,itiseasiertousecoordinatesofdatapointsthanto estimatecoordinatesofnondatapoints.Third,skippingthisoptionsavesmeabitofclasstime.Fourth,bynot discussinghowtousenondatapoints,IreducetheamountoftimeIspendgradingexamsbecausethereisless variationinstudents’derivedequationsofmodels.

Oncetheclasshasdeterminedtwo“goodpoints,”Ideriveanequationofthelinethatcontainsthetwopoints. AsI’vedoneinprevioussections,Istartbywritingtheequation y = mx + b andthenreplacethevariables x and

y withtheappropriatevariables.Whenfinding m and b,Iemphasizethatit’sokaytousedecimals;manystudents thinktheyneedtousefractionsbecausetheywererequiredtodosowhenfindingequationsof(non-model)lines inSection9.1.Iexplainthatit’sokaytoroundwhenfindingamodelbecausetherearealreadyvarioustypesof errorsbuiltintotheprocess,anyway(seetheexploration"Identifyingtypesofmodelingerrors"onpage412of thetextbook).Isaythatwhenmodeling,weroundthevaluesof m and b totheseconddecimalplace,unless valuesarecloseto0suchas m =0.003.

Whenverifyingamodel’sequation,explainthatthelineshouldcontainthetwochosenpoints(andcomeclose totheotherdatapoints).Encouragestudentstotakethetimetodistinguishbetweentheirchosentwopointsand theotherdatapoints.(Bytheway,moststudentsdonotrealizethatapointthatliescloseto,butnotonaline, mayappeartolie on theline.)

Forquizzesandexams,ifyourstudentsareusingtechnologytoverifytheirmodels,youcanhavethemcopy theirtechnology’sdisplayontotheirtestpapers;ifyoudon’trequirethis(bymakingitworthpoints),some studentswillresisteverlearninghowtousetechnologytoverifytheirmodels.

Thetextbook’sanswersforthissectionconsistofregressionequationsbecauseit’simpossibletoanticipate whichtwo“good”pointsstudentswillchoose.So,whenassigningthissection’shomework,warnstudentsthat theiranswerswillvaryfromtheonesinthetextbook.Remindthemthattheycanverifytheirworkusingtechnology,ifthetechnologyyouareusinghasthiscapability.

GROUPEXPLORATION:AdjustingtheFitofaModel

Thisactivityisafunreminderofthegraphicalsigniﬁcanceofslopeandtheverticalintercept.Moregenerally,the connectionbetweenafunction’sequationandgraphisreinforced.

SECTION9.3LECTURENOTES

Objectives

1. Computeandinterpretresiduals.

2. Computeandinterpretthesumofsquaredresiduals.

3. Findanequationofalinearregressionmodelanduseittomakepredictions.

4. Interpretresidualplots.

5. Usearesidualplottohelpdeterminewhetheraregressionlineisanappropriatemodel.

6. Identifyinﬂuentialpoints.

7. Computeandinterpretthecoefﬁcientofdetermination.

OBJECTIVE1

1. Theagesandaskingpricesfor8HondaAccordsatdealershipsintheBostonareaareshowninthefollowing table.

Source: Edmunds.com

Let x betheage(inyears)and y betheprice(inthousandsofdollars),bothforaHondaAccord.

a. Describethefourcharacteristicsoftheassociation.Computeandinterpret r aspartofyouranalysis.

b. Byviewingascatterplot,wecandeterminethatthelinethatcontainsthedatapoints (9, 9.9) and (5, 13.0) comesfairlyclosetothedatapoints.ByusingthetechniquediscussedinSection9.2,we canﬁndthatanequationofthelineis y = 0.78x +16.88 (tryit).Verifythatthelinecomesfairly closetothedatapoints.

c. Usethemodeltopredictthepriceofan8-year-oldHondaAccord.

d. Findthedifferenceoftheactualpriceandthepredictedpriceforan8-year-oldHondaAccord.

e. Findthedifferenceoftheactualpriceandthepredictedpricefora7-year-oldHondaAccord.

Foradatapoint (x,y),the observedvalueof y is y andthe predictedvalueof y (written ˆ y or ˆ f (x))isthe valueobtainedbyusingamodeltopredict y.

Deﬁnition Residual

Foragivendatapoint (x,y),the residual isthedifferenceoftheobservedvalueof y andthepredictedvalue of y:

Residual = Observedvalueof y Predictedvalueof y = y ˆ y

ResidualsforDataPointsAbove,Below,oronaLine Supposesomedatapointsaremodeledbyaline.

• Adatapointonthelinehasresidualequalto0.

• Adatapointabovethelinehaspositiveresidual.[Drawaﬁgure.]

• Adatapointbelowthelinehasnegativeresidual.[Drawaﬁgure.]

OBJECTIVE2

SumofSquaredResiduals

Wemeasurehowwellalineﬁtssomedatapointsbycalculatingthesumofthesquaredresiduals:

yi)2

Thesmallerthesumofsquaredresiduals,thebetterthelinewillﬁtthedata.Ifthesumofsquaredresiduals is0,thenthereisanexactlinearassociation.

2. HerewecontinuetoworkwiththeHondaAccorddata(seethefollowingtable).Let x betheage(inyears) and y betheprice(inthousandsofdollars),bothforaHondaAccord.Findthesumofsquaredresiduals forthelinearmodelweworkedwithinExample1,whichis

88.

Source: Edmunds.com

OBJECTIVE3

Deﬁnition Linearregressionfunction,line,equation,andmodel

Foragroupofpoints,the linearregressionfunction isthelinearfunctionwiththeleastsumofsquared residuals.Itsgraphiscalledthe regressionline anditsequationiscalledthe linearregressionequation, written

0 where b1 istheslopeand (0,b0) isthe y-intercept.The linearregressionmodel isthelinearregression functionforagroupof data points.

3. a. UsetechnologytoﬁndthelinearregressionequationfortheHondaAccordassociation.

b. Predictthepriceofa10-year-oldHondaAccord.

c. Whatistheslope?Whatdoesitmeaninthissituation?

d. Whatisthe y-intercept?Whatdoesitmeaninthissituation?

OBJECTIVE4

A residualplot isagraphthatcomparesdatavaluesoftheexplanatoryvariablewiththedatapoints’residuals.

4. a. ConstructaresidualplotfortheHondaAccordlinearregressionmodel.

b. Howmanydotsareabovethezeroresiduallineoftheresidualplot?Whatdotheymeaninthis situation?

c. Howmanypointsarebelowthezeroresiduallineoftheresidualplot?Whatdotheymeaninthis situation?

d. Whichpointisfarthestfromthezeroresidualline?Whatdoesthatmeaninthissituation?

e. Doestheresidualplotsupportthattheregressionlineisareasonablemodel?Explain.

OBJECTIVE5

UsingaResidualPlottoHelpDetermineWhetheraRegressionLineIsanAppropriateModel

Thefollowingstatementsapplytoaresidualplotforaregressionline.

• Iftheresidualplothasapatternwherethedotsdonotlieclosetothezeroresidualline,thenthereis eitheranonlinearassociationbetweentheexplanatoryandresponsevariablesorthereisnoassociation.

• Ifadotliesmuchfartherawayfromthezeroresiduallinethanmostoralloftheotherdots,thenthe dotcorrespondstoanoutlier.Iftheoutlierisneitheradjustednorremoved,theregressionlinemay not beanappropriatemodel.

• The vertical spreadoftheresidualplotshouldbeaboutthesameforeachvalueoftheexplanatory variable.

OBJECTIVE6

Iftheslopeofaregressionlineisgreatlyaffectedbytheremovalofadatapoint,wesaythedatapointisan inﬂuentialpoint

5. a. ThescatterplotandtheregressionlineinFig.2.3comparethehandlengthsandheightsof75women. TheresidualplotoftheobservationsisshowninFig.2.4.Identifyalloutliersforthegivensituation.

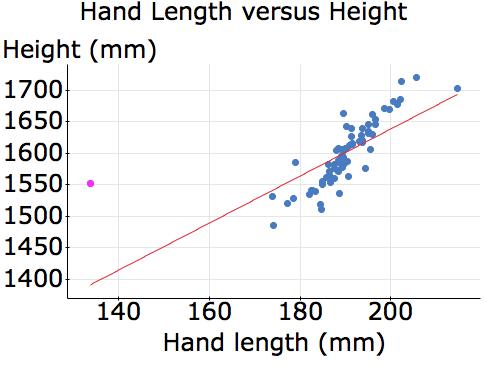
Figure2.3: Scatterplotforhand-heightdata

(Source: S.G.Sani,E.D.Kizilkanat,N.Boyan, etal.(2005)."StatureEstimationBasedonHand LengthandFootLength,"ClinicalAnatomy,Vol. 18,pp.589-596.)

Figure2.4: Residualplotforhand-heightdata

b. TheoutlieryoulikelyfoundinPart(a)hasbeenremovedandtheremainingdatapointsaredescribed bythescatterplotinFig.2.5.Istheremovedoutlieraninﬂuentialpoint?Explain.

Figure2.5: Scatterplotwithoutlierremoved

6. a. Thelengthsofcruiseshipsandthesizesofthecrewsarecomparedbythescatterplotandtheregression lineshowninFig.2.6.TheresidualplotoftheobservationsisshowninFig.2.7.Identifyalloutliers forthegivensituation.

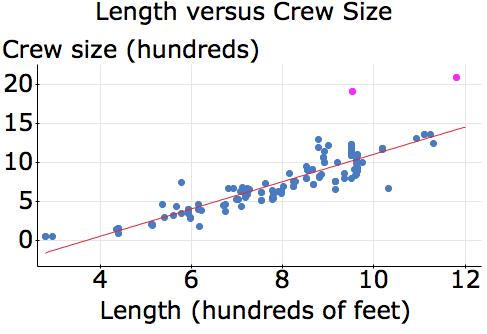
Figure2.6: Scatterplotforcruisedata(Source: TrueCruise)

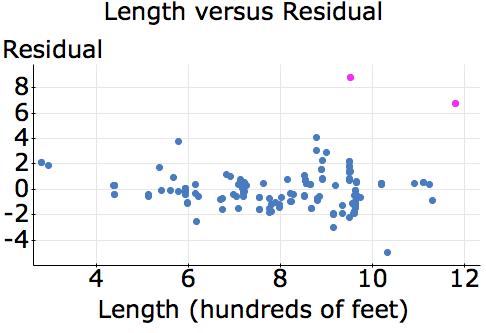
Figure2.7: Residualplotforcruisedata

b. TheoutliersyoulikelyfoundinPart(a)havebeenremovedandtheremainingdatapointsaredescribed bythescatterplotinFig.2.8.Aretheremovedoutliersinﬂuentialpoints?Explain.

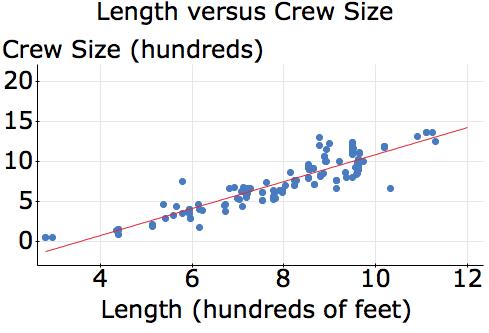
Figure2.8: Scatterplotwithoutliersremoved

Outlierstendtobeinﬂuentialpointswhentheyarehorizontallyfarfromtheotherdatapoints.

OBJECTIVE7

CoefﬁcientofDetermination

Thecoefﬁcientofdetermination, r2,istheproportionofthevariationintheresponsevariablethatisexplainedbytheregressionline.

7. ThetemperaturesandrelativehumiditiesinPhoenix,Arizona,areshowninthefollowingtableforvarious timesonJune1,2014.

(Fahrenheitdegrees)(percent)(Fahrenheitdegrees)(percent)

a. Constructascatterplot.

Source: Weatherbase

b. Findthelinearregressionmodel.Graphitonthescatterplot.

c. Computethecoefﬁcientofdetermination.Whatdoesitmeaninthissituation?

HW 1,3,5,9,13,17,21,23,25,29,33,35,43,45,47,49,51,61

SECTION9.3TEACHINGTIPS

ThissectionisthegrandﬁnaleofChapters6–9,whichaddresseslinearregression.Thefoundationalconcept istheresidual,whichleadstowardthesumofsquaredresiduals,theregressionline,andresidualplots.

OBJECTIVE1COMMENTS

Whenintroducingtheconceptofresidual,Ipointoutthataresidualistheoppositeofhowerrorwasdeﬁnedin Section6.3.(Seethelecturetipsofthatsectionformyreasoningindeﬁningerrortobetheoppositeofaresidual.) Becauseofstudents’pastworkwithcomputingerrorsinpredictions,theyquicklypickuponcomputingand interpretingresiduals.

OBJECTIVE2COMMENTS

ForProblem2,asIbuildatablesimilartoTable32onpage602ofthetextbook,Irefertothescatterplotthat weconstructedinProblem1tomakesurestudentscanpicturethegraphicalsignificanceofthecalculationsin eachcolumnofthetable.Ipointoutthatwearefindingsquaresofdifferencesforreasonssimilartowhywefind squaresofdifferencestocomputethevariance.

OBJECTIVE3COMMENTS

Afterfindingthatthesumofsquaredresidualsisequalto21.20forthemodelweworkedwithinProblem2,I remindstudentsthatourresult21.20measureshowwellthemodelfitsthedatapoints.ThenIsketchthemodel inFig.28onpage602ofthetextbookandsharewithstudentsthatthesumofsquaredresidualsis82.36.Ipoint outthatitmakessensethattheresult82.36islargerthan21.20becausethelineinFig.28doesnotfitthedata aswellasthemodelinProblem2.Ithensketchthelinearregressionmodel,explainingthatithastheleastsum ofsquaredresiduals,17.01,andconcludethatitmustfitthedatapointsthebest(seeFig.30onpage603ofthe textbook).

Parts(b),(c),and(d)ofProblem3serveasanicereviewofconceptsalreadyaddressedinSections7.1–7.3.

OBJECTIVE4COMMENTS

WhenconstructingtheresidualplotforProblem4(a),IreferbacktothescatterplotweconstructedinProblem1(a) andmakesurestudentsseetheconnectionbetweentheresidualsinthescatterplotandintheresidualplot.

GROUPEXPLORATION:MeaningofResidualPlots

Thisactivityhelpsstudentsdiscoverhowaresidualplotrelatestoascatterplotandtherelevantregressionline. StudentstendtobesurprisedthattheresidualplotsforthedatasetsdescribedbythescatterplotsinFigs.54and 55arethesame.

OBJECTIVE5COMMENTS

Foreachofthethreebulletedstatementsforthisobjective,Idisplaybothascatterplotwithamodelandthe correspondingresidualplottomakesurestudentsseetheconnectionbetweenthetwodiagrams.

OBJECTIVE6COMMENTS

Studentshaveaneasytimelearningaboutoutliersandinﬂuentialpointsbecausetheyaresuchintuitive,visual concepts.

OBJECTIVE7COMMENTS

Themostchallengingconceptinthissectionisthecoefﬁcientofdetermination.Manyintroductorystatistics textbookstrytoconveytheideabylabelingtheexplainedandunexplaineddeviationsofjustonedatapoint inascatterplot,butIdon’tbelievethisapproachiseffectivebecauseitdoesn’tgetacrossasenseofvariation. Thedetaileddescriptiononpages611and612ofthetextbooktriestoconveytheessenceofthecoefﬁcientof determinationbyillustratingrelevantvariations.

CHAPTER10OVERVIEW

Inthischapter,studentssimplifyexpressionswithexponents,graphexponentialfunctions,andperformmodeling withexponentialfunctions.

Althoughthematerialinthischapterisverychallengingformoststudents,itcreatestheopportunitytorevisit manytopicsaddressedinChapters6–9:constructingscatterplotsandresidualplots;findingequationsofmodels; graphingmodels;computingresiduals,correlationcoefficients,andcoefficientsofdetermination;identifying outliersandinfluentialpoints;andmakingpredictions.

Italsocreatestheopportunitytocomparelinearandexponentialmodels,whichshedslightonmanymodeling concepts,includingdeterminingwhichmodelbestﬁtssomedatapoints.

Althoughexponentialregressionisprobablynotpartofyourdepartment’sintroductorystatisticscourse,one couldarguethereisanotherreasontoincludethischapterinaprestatisticscourse.Assumingthatstudentswho takethiscoursearebypassingalgebra,wemustaskourselvesifthereisanyalgebracontentthattheyabsolutely mustseetohaveawell-roundededucation.Ibelievetherearetwosuchconcepts:linearandexponentialmodels. Thesearethetwomodelsmostapplicabletoourworld.

SECTION10.1LECTURENOTES

Objectives

1. Describethe productproperty forexponents.

2. Simplifyexpressionsinvolvingnonnegative-integerexponents.

3. Describethefollowingpropertiesforexponents:quotient,raisingaproducttoapower,raisinga quotienttoapower,andraisingapowertoapower.

4. Usecombinationsofpropertiesofexponentstosimplifyexpressionsinvolvingnonnegative-integer exponents.

5. Simplifyexpressionsinvolvingnegative-integerexponents.

6. Describethemeaningof exponentialfunction

7. Workwithmodelswhoseequationsinvolveintegerexponents.

OBJECTIVE1

If m and n arecountingnumbers,then

Findtheproduct.

OBJECTIVE2

SimplifyinganExpressionInvolvingNonnegative-IntegerExponents

Anexpressioninvolvingnonnegative-integerexponentsissimpliﬁedif

1. Itincludesnoparentheses.

2. Eachvariableorconstantappearsasabaseasfewtimesaspossible.Forexample,fornonzero b,we write b2b3 as b5

3. Eachnumericalexpression(suchas 32)hasbeencalculated,andeachnumericalfractionhasbeen simpliﬁed.

OBJECTIVE3

QuotientPropertyforExponents

Herewesimplify

Writequotientwithoutexponents.

Simplify:

Simplify.

Thissuggestswecansubtracttheexponents:

QuotientPropertyforExponents

If m and n arecountingnumbersand b isnonzero,then

Simplify.

Wecanwrite (bc)4 asaproductofpowers: (bc)4 =(bc)(bc)(bc)(bc) Writepowerwithoutexponents. =(

) Rearrangefactors. = b4 c 4 Simplify.

Wecangetthesameresultbyraisingeachfactorofthebase bc tothe4thpower: (bc)4 = b4 c 4

RaisingaProducttoaPower

If n isacountingnumber,then (bc)n = bncn

Performtheindicatedoperation.

Warning:Theexpression (3b)2 isequivalentto 9b2,not 3b2

RaisingaQuotienttoaPower

Herewewrite b c 3 inanotherform: b c 3 = b c · b c · b c Writepowerexpressionwithoutexponents. = b b b c · c · c Multiplynumerators;multiplydenominators. = b3 c3 Simplify.

Thissuggeststhatboththenumeratorandthedenominatorshouldberaisedtothe3rdpower:

RaisingaQuotienttoaPower

If n isacountingnumberand c isnonzero,then

Simplify.

RaisingaPowertoaPower

Herewewrite (b2)4 inanotherform: (b2)4 = b2 · b2 · b2 · b2

Writeexpressionwithoutexponent4. = b2+2+2+2 Addexponents: bmbn = bm+n = b8

Simplify.

Thissuggestswecanmultiplytheexponents: (b2)4 = b2 4 = b8

RaisingaPowertoaPower

If m and n arecountingnumbers,then (bm)n = bmn Simplify.

12. (b3)5 13. (b4)7

OBJECTIVE4

RecallfromSection1.7thatif b isnonzero,then b0 =1.Forexample, 70 =1. Simplify.

OBJECTIVE5

InSection1.7,wedeﬁnedanegative-integerexponent.

Deﬁnition Negative-integerexponent

If n isacountingnumberand b =0,then

Forexample, 2 3 = 1 23 = 1 8

Simplifyinganexpressioninvolvingnegative-integerexponentsincludeswritingitsothateachexponent ispositive. Simplify.

Herewewrite 1 b n inanotherform:

Simplify.

If n isacountingnumberand b =0,then 1

Simplify.

PropertiesofExponents

If m and n areintegers, b =0,and c =0,then

• bmbn = bm+n

• bm bn = bm n

• (bc)n = bncn

•

• (bm)n = bmn

Productpropertyforexponents

Quotientpropertyforexponents

Raisingaproducttoapower

Raisingaquotienttoapower

Raisingapowertoapower

SimplifyingExpressionsInvolvingExponents

Anexpressioninvolvingintegerexponentsissimpliﬁedif

1. Itincludesnoparentheses.

2. Eachvariableorconstantappearsasabaseasfewtimesaspossible.

3. Eachnumericalexpression(suchas 32)hasbeencalculated,andeachnumericalfractionhasbeen simpliﬁed.

4. Eachexponentispositive.

Simplify.

26. 310073 1005

27. (b5) 2

28. (6b 9c4)( 2b5c 3)

OBJECTIVE6

) 3

Deﬁnition Exponentialfunction

An exponentialfunction isafunctionwhoseequationcanbeputintotheform

f (x)= abx

where a =0, b> 0,and b =1.Theconstant b iscalledthe base

For f (x)=2x and g(x)=2(3)x,ﬁndthefollowing.

36. f (5) 37. f ( 4) 38. g(3) 39. g( 2) 40. g(0)

41. For E(x)=2x and L(x)=2x,compare E(5) with L(5).

OBJECTIVE7

42. Theweight(inpounds) f (d) ofanastronautwhen d thousandmilesfromthecenterofEarthisdescribed bytheequation f (d)=3060d 2

a. Simplifytheright-handsideoftheequation.

b. Whenatsealevel,theastronautisabout4thousandmilesfromEarth’scenter.Howmuchdoesthe astronautweighatsealevel?

c. Find f (6).Whatdoestheresultmeaninthissituation?

HW 1,3,7,13,25,33,35,55,61,67,75,87,91,97,103,105,111

SECTION10.1DETAILEDCOMMENTS

StudentslearnmanydeﬁnitionsandpropertiesofexponentsinthissectionandSection10.2,whichwillhelpthem usetwopointstoﬁndexponentialmodelsinSection10.4.

Althoughstudentsmayknowthepropertiesofexponentsfromapreviousclass,theyprobablydonotknow whytheyaretrue,whichcanhelpwithknowingwhenandhowtoapplyaproperty.

Studentsarechallengedbythissectionbecausesomuchsymbolmanipulationisrequired.

OBJECTIVE1COMMENTS

Studentshaveaneasytimewiththeproductpropertyinisolation,butoncetheraisingapowertoapowerproperty hasbeenintroduced,somestudentsconfusethetwoproperties.So,whenworkingwithanexpressionsuchas b4b3 , Iencouragestudentstoimaginestringsof b factorstohelpgroundthemwiththeconceptthattheexponentsneed tobeadded.

ForProblems2and3,Iemphasizethattheexpressionsareproducts,notdifferences.

OBJECTIVE2COMMENTS

Igooverthisobjectivequicklybecauseitwillbecomeclearaswesimplifyexpressionsthroughoutthesection.

OBJECTIVE3COMMENTS

Ialsogooverthisobjectivequicklybecausestudentstendtohaveaneasytimesimplifyingexpressionswhen onlyonepropertyisrequired.Itiswhenacombinationofpropertiesisrequired(Objective4)thatstudentstend tohavetrouble,especiallyiftheymustworkwithnegativeexponents(Objective5).

ForProblem4,Iclarifyhowthequotientpropertyforexponentscanbeusedbybreakingupthefraction 6b7 9b4 intotheproduct 6 9 b7 b4 .

ForProblem8,studentstendtoincorrectlysimplifytheexpression (2b)4 to 2b4.Iemphasizethatthecorrect resultis 16b4.Itisinterestingthatstudentstendtosimplify (bc)5 (Problem7)correctlybuthavetroublesimplifying (2b)4 correctly.Ipointoutthat2isafactorofthebase 2b of (2b)4 justlike b isafactorofthebase bc of (bc)5

Afterintroducingtheraisingapowertoapowerproperty,Icomparesimplifying (b3)2 withsimplifying b3b2 AsImentionedearlier,studentstendtoconfusetheraisingapowertoapowerpropertywiththeproductproperty.

OBJECTIVE4COMMENTS

ForProblems14–18,studentstendtoskipsteps,whichleadstoerrorsorfuzzythinkingthatgetsthemintotrouble whentheproblemsaremoredifﬁcult.Iencouragestudentstowriteallthestepsuntiltheycanpicturestepsthat theyskip.

GROUPEXPLORATION:PropertiesofPositive-IntegerExponents

Thisactivityaddressescommonstudenterrorswhensimplifyingexpressionswithpositive-integerexponents.

OBJECTIVE5COMMENTS

EventhoughnegativeintegerswerealreadyintroducedinSection1.7andtheylikelycameupagaininSections5.4 and5.5,studentsneedarefresherbythispointinthecourse.

ForProblem26,itisgoodforstudentstoﬁndoutthatmostcalculatorsgiveincorrectresults.Inparticular,it isinstructiveforthemtoreasonwhymanycalculatorsgivetheincorrectresult0for 3 1005

ForProblem30,somestudentswillmistakenlywrite

Therearemanywaystosimplifyquotientsofpowersoftheform

,ratherthancorrectlywrite

.Onewayistousetheproperty

bm n andthensimplifysothattherearenonegativeexponents.Anotherwayisto“move”thepowerwiththe smallerexponentacrossthefractionbar(andchangethesignoftheexponent).Showingmorethanonemethod usuallyconfusesstudents.Itisbesttoselectonemethodanduseitwheneverappropriate. StudentstendtobeintimidatedbyproblemsascomplicatedasProblem35,butwithpractice,theycanmaster them.

Youmayprefertointroducetheproperty a b

= b a

anduseittosimplifycertainexpressions,butI havenotincludedthispropertyinthetextbookinanattempttoavoidoverloadingstudentswithtoomanyoptions.

GROUPEXPLORATION:PropertiesofNegative-IntegerExponents

Thisactivityaddressescommonstudenterrorswhensimplifyingexpressionswithnegative-integerexponents.

OBJECTIVE6COMMENTS

AftercompletingProblem41,considercomparinginput-outputtablesof E and L tohelpstudentsbegintodistinguishexponentialfunctionsfromlinearfunctions.Or,youcouldassignExercise89ofHomework10.1andhave suchadiscussionatthenextclassmeeting.

OBJECTIVE7COMMENTS

Moststudentsknowthatanastronautisweightlessinouterspace,butfewstudentsknowthatanastronaut’s weightdeclines continuously astheastronaut’sdistancefromthecenterofEarthincreases.

SECTION10.2LECTURENOTES

Objectives

1. Describethemeaningof rationalexponents

2. Simplifyexpressionsinvolvingrationalexponents.

3. Describepropertiesofrationalexponents. Copyright c 2016PearsonEducation,Inc.

OBJECTIVE1

Arguethat

suggeststhat 161/2 =4.(Notethat 161/2 is not equalto8,whichishalfof16.)

Arguethat

suggeststhat 81/3 =2.

Deﬁnition b1/n

Forthecounting n,where n =1,

• If n isodd,then b1/n isthenumberwhose nthpoweris b,andwecall b1/n the nthrootof b

• If n isevenand b ≥ 0,then b1/n isthenonnegativenumberwhose nthpoweris b,andwecall b1/n the principal nthrootof b

• If n isevenand b< 0,then b1/n isnotarealnumber.

b1/n mayberepresentedby n √b.

OBJECTIVE2

Simplify.

Showthat 163/4 =16 1 4 3 = 161/4 3 =23 =8

Deﬁnition Rationalexponent

Forthecountingnumbers m and n,where n =1,and b isanyrealnumberforwhich b1/n isarealnumber,

• bm/n = b1/n m =(bm)1/n

• b m/n = 1 bm/n , b =0

Apoweroftheform bm/n or b m/n issaidtohavea rationalexponent.

Simplify.

For f (x)=2(27)x,ﬁndthefollowing.

OBJECTIVE3

ThepropertiesofexponentsthatwediscussedinSection10.1arevalidfor rationalexponents

PropertiesofRationalExponents

If m and n arerationalnumbersand b and c areanyrealnumbersforwhich bm , bn,and cn arerealnumbers, then

• bmbn = bm+n

• bm bn = bm n , b =0

• (bc)n = bncn

• b c n = bn cn , c =0

• (bm)n = bmn

Productpropertyforexponents

Quotientpropertyforexponents

Raisingaproducttoapower

Raisingaquotienttoapower

Raisingapowertoapower

Simplify.Assumethat b and c arepositive.

17. 8b6 4/3

18. b 5/9 b 2/9

19. b3/5b7/8

20.

HW 1,3,11,17,27,33,41,43,53,59,67,69,75,77,79,81

SECTION10.2DETAILEDCOMMENTS

Inthissection,studentslearnthemeaningofrationalexponents.Theywillusethisconceptthroughoutthechapter. Studentsalsosimplifyexpressionsinvolvingrationalexponentsinthissection.

OBJECTIVE1COMMENTS

Whenintroducingrationalexponents,Iwrite 161/2 ontheboardandsaythatwewillﬁnditsvalue,whichIwill call“hand.”Next,Iwrite 161/2 2 ontheboardandpointoutthatthisexpressionis“handsquared,”andIplace myhandoverjustthebasetoillustrate.ThenIremovemyhandandperformthefollowingcalculation:

ThenIcover 161/2 (onthefarthestleftsideoftheequation)andobservethat“handsquaredisequalto16.”Iask mystudents,“So,whatis‘hand’equalto?”Someonealwaysseesthat“hand”isequalto4(nooneevermentions 4,whichwewon’tincludeinourdeﬁnition,anyway).Finally,wediscussthat 161/2 meanstoﬁndthesquare rootof16.

ThenIuse“hand”againtoﬁndthevalueof 81/3.Afterthat,studentsarereadyformetodiscussthemeaning of b1/n ingeneral.

Forpowerswithpositiverationalexponents,Iencouragemystudentstopracticecomputingthemmentally, withoutwritingallofthesteps.Thiswillkeeptheamountofwritingtoamorereasonablelevelwhentheyare

simplifyingcomplicatedexpressions.

Moststudentshavedifﬁcultycomputingpowerswithnegativerationalexponents,especiallyaftersometime haspassed(seeProblems7,8,13,14,and16).

IdelaydiscussinghowtouseacalculatortocomputepowerswithrationalexponentsuntilI’mconﬁdentthat studentscancomputesuchpowerswithoutacalculator.Whenusingacalculatortoﬁndapowersuchas

Iemphasizethattwosetsofparenthesesmustbeused.

GROUPEXPLORATION:Deﬁnitionof b1/n

Anotherwaytointroducerationalexponentsistoassignthisactivity.Studentsmaygetmoreoutofthisexplorationthanfromalecturebecausetheyaremoreinvolvedwitheachstepofinvestigatingthemeaningofrational exponents.

OBJECTIVE3COMMENTS

Moststudentshaveatoughtimesimplifyingexpressionswithrationalexponents.Theywillcontinuetobe challengedbydeterminingwhichordertoapplythepropertiesanddeﬁnitionsofexponents.Further,studentstend toneedremindersonhowtoperformoperationswithfractions(e.g.addfractionswithdifferentdenominators). Sometimesstudentsgetpsychedoutwhentryingtosimplifysuchexpressions.Itrytoeasetheiroverwhelm bypointingoutthatwearestillperformingthesametypesofstepsasinSection10.1;itismostlyperforming operationsoffractionsthatextendsthetimetosimplifyexpressionsinvolvingrationalexponents.

Problems22–24arequitedifﬁcultandcertainlynotneededforintroductorystatistics.Ifyouaretightontime, youcouldomitdiscussingtheseproblemsandassigningthesetypesofexercises.

SECTION10.3LECTURENOTES

Objectives

1. Graphanexponentialfunction.

2. Describethe basemultiplierproperty andthe increasingordecreasingproperty

3. Findthe y-interceptofthegraphofanexponentialfunction.

4. Describethe reﬂectionpropertyforexponentialfunctions.

5. Graphanequationofanexponentialmodel.

6. Interpretthecoefﬁcientandthebaseofanexponentialmodel.

OBJECTIVE1

1. Createatableofsolutionsof f (x)=2x andgraph f byhand.

2. Createatableofsolutionsof g(x)=8 1 2 x andgraph g byhand.

OBJECTIVE2

Refertoyourtablesofsolutionsof f (x)=2x and g(x)=8 1 2 x tomotivatethebasemultiplierproperty.

BaseMultiplierProperty

Foranexponentialfunctionoftheform y = abx,ifthevalueof x increasesby1,thenthevalueof y is multipliedby b

Describethebasemultiplierpropertyasappliedtothegivenfunction.

3. f (x)=5(4)x 4. g(x)=7 2 3 x

Usethebasemultiplierpropertytoexplainthefollowingconnections:

• f (x)=2x isanincreasingfunctionand b =2 > 1 (seeProblem1).

• g(x)=8 1 2 x isadecreasingfunctionand b = 1 2 < 1 (seeProblem2).

IncreasingorDecreasingProperty

Let f (x)= abx,where a> 0.Then

• If b> 1,thenthefunction f isincreasing.Wesaythefunction growsexponentially.[Drawaﬁgure.]

• If 0 <b< 1,thenthefunction f isdecreasing.Wesaythefunction decaysexponentially.[Drawa ﬁgure.]

OBJECTIVE3

Substitute0for x inthegeneralequation y = abx toshowthefollowingproperty.

y-InterceptofanExponentialFunction

Forthegraphofanexponentialfunctionoftheform y = abx , the y-interceptis (0,a).

Findthe y-interceptofthegraphofthefunction.

5. y =8(5)x 6. y = 4 2 7 x

Warning:The y-interceptofthegraphofafunctionoftheform y = bx is (0, 1), not (0,b)

Findthe y-interceptofthegraphofthegivenfunction.Thenusethebasemultiplierpropertytographthe functionbyhand.

7. f (x)=2(3)x 8. g(x)=12 1 3 x

OBJECTIVE4

9. Sketchandcomparethegraphsof f (x)= 4(2)x and g(x)=4(2)x .

ReﬂectionProperty

Thegraphsof f (x)= abx and g(x)= abx arereﬂectionsofeachotheracrossthe x-axis.

Graphthefunctionbyhand.

10. f (x)= 3(4)x 11. g(x)= 16 1 4 x

• Thegraphofanexponentialfunctiondoesnothaveany x-interceptsandthe x-axisisahorizontalasymptote.

• Thedomainofanyexponentialfunction f (x)= abx isthesetofallrealnumbers.

• Therangeofanexponentialfunction f (x)= abx isthesetofallpositiverealnumbersif a> 0,andthe rangeisthesetofallnegativerealnumbersif a< 0.

Findthedomainandrangeofthefunction.

(x)=3(2)

OBJECTIVE5

Deﬁnition Exponentialmodel

An exponentialmodel isanexponentialfunction,oritsgraph,thatdescribesanauthenticassociation.

14. ThepricesofoneounceofgoldontheNewYorkStockExchange(NYSE)atclosingonJanuary2are showninthefollowingtableforvariousyears.IftheNYSEwasclosedonJanuary2,thentheclosingprice ontheﬁrstdateitwasopenwasused.

Source: KitcoMetals,Inc.

Let y betheprice(indollarsperounce)ofgoldonJanuary2at x yearssince2000.

a. Constructascatterplot.

b. Describetheshapeandthedirectionoftheassociation.

c. Graphthemodel ˆ y =289(1.15)x onthescatterplot.Doesthemodelcomeclosetothedatapoints?

d. Whatisthecoefﬁcientofthemodel ˆ y =289(1 15)x?Whatdoesitmeaninthissituation?

e. Whatisthebaseofthemodel ˆ y =289(1.15)x?Whatdoesitmeaninthissituation?

Ifthepointsofascatterplotliecloseto(oron)anexponentialcurve,wesaythevariablesare exponentially associated andthatthereisan exponentialassociation

OBJECTIVE6

MeaningoftheCoefﬁcientofanExponentialModel

Assumethatanassociationbetweenthevariables x and y canbedescribedexactlybytheexponentialmodel y = abx.Thenthecoefﬁcient a equalsthequantity y whenthequantity x is0.

MeaningoftheBaseofanExponentialModel

Assumethatanassociationbetweenthevariables x and y canbedescribedexactlybytheexponentialmodel ˆ y = abx,where a> 0.Thenthefollowingstatementsaretrue.

• If b> 1,thenthequantity y growsexponentiallyatarate b 1 percent(indecimalform)perunit increaseofthequantity x

• If 0 <b< 1,thenthequantity y decaysexponentiallyatarateof 1 b percent(indecimalform)per unitincreaseofthequantity x

15. Malathionisaninsecticidethathasbeensprayedfromhelicoptersonsuburbanareastocontrolmosquitoes andMediterraneanfruitﬂies.TheCaliforniaDepartmentofHealthServicesconcludedthatsomepeople maybesensitivetomalathion(seethesourceshowninthefollowingtable).Inanexperimentconducted in1993,researcherssprayedsometomatoeswithmalathionandrecordedhowmuchoftheinsecticide persisted.Themeanmalathionconcentrationsonthesurfacesoffourgroupsoftomatoesareshowninthe followingtableforvariousamountsoftime.

TimeMeanConcentration

Source: AssessmentofMalathionandMalaoxonConcentrationandPersistenceinWater,Sand,SoilandPlant MatricesUnderControlledExposureConditions,Nealetal.

Let y bethemeanmalathionconcentration(inmicrogramspercentimetersquared)onthetomatoesat x hours.

a. Constructascatterplot.

b. Describetheshapeandthedirectionoftheassociation.

c. Graphthemodel ˆ y =0 18(0 994)x onthescatterplot.Thendescribethestrengthoftheassociation.

d. Whatisthecoefﬁcientofthemodel ˆ y =0.18(0.994)x?Whatdoesitmeaninthissituation?

e. Whatisthebaseofthemodel ˆ y =0 18(0 994)x?Whatdoesitmeaninthissituation?

f. Predictthepercentageofthemalathionthatremainedonthetomatoes3daysafterspraying.

HW 1,3,5,9,15,19,25,31,33,39,51,53,59,79,87

SECTION10.3DETAILEDCOMMENTS

Studentslearntosketchgraphsofexponentialfunctionsinthissection.Conceptsrelatedtographingexponential functionswillbeveryhelpfulthroughouttherestofthischapter.Studentswillalsolearnhowtointerpretthe coefﬁcientandthebaseofanexponentialmodel.

OBJECTIVE1COMMENTS

ForProblem1,Ievaluate f at 2, 1,0,1,2,3,and4toﬁndpointstoplot.Studentscanobservethatthegraph of f isnotaline.ThenIpointoutthebasemultiplierpropertywithoutyetcallingitassuchtoﬁndotherpoints (withoutevaluating f )andsketchtheexponentialcurve.Forexample,toplotapointwith x-coordinate 3,Iplot apointabove ( 3, 0) thatishalfashighabovethe x-axisasthepoint ( 2, 1 4 ).Bythinkingintermsofhalving distancesvisuallyeachtimewemovetotheleftoneunit,studentscanseethatthecurveisgettingcloserand closertothe x-axis,butneverreachingit.Ithenintroducetheterminologyofahorizontalasymptote.

ForProblem2,Ievaluate g at0,1,2,3,and4toﬁndpointstoplot.Studentscanseethatthegraphof g isnotaline.Wecanagainusethebasemultiplierproperty(withoutnamingityet)toﬁndotherpoints(without evaluating g)andsketchtheexponentialcurve.

OBJECTIVE2COMMENTS

IrefertoProblems1and2tointroducethebasemultiplierproperty.ForProblems3and4,Idonotgraphthe functions;IwaittodomoregraphinguntilI’vediscussedﬁndingthe y-interceptofanexponentialfunction.

Ishowstudentshowtheincreasingordecreasingpropertyfollowsdirectlyfromthebasemultiplierproperty. Theconceptsofexponentialgrowthandexponentialdecaywillcomeinhandywhenperformingmodelingin Sections10.4and10.5.

OBJECTIVE3COMMENTS

Foranexponentialfunctionoftheform f (x)= bx,moststudentsthinkthatthe y-interceptofthegraphof f is (0,b).Bywriting f (x)=1(bx),studentsseethatthe y-interceptis (0, 1).Itisusuallynecessarytoremind studentsofthisatleastacoupleoftimes.

Afterdiscussingthe y-intercept,Ishowstudentshowtoefﬁcientlygraphanexponentialfunction.First,Iplot the y-intercept.ThenIusethebasemultiplierpropertytodetermineotherpointstoplot.Bythismethod,Inever havetoevaluatethefunction.Studentstendtoresistthismethod—theyinitiallypreferevaluatingthefunction. However,withsomeencouragement,moststudentswillswitchtousingthebasemultipliermethod.Ipreferthis methodnotonlybecauseitismoreefﬁcient,butalsobecauseitreinforcesthebasemultiplierpropertyandhas studentsthinkmoregeometricallythantheothermethod.

GROUPEXPLORATION:NumericalSigniﬁcanceof a and b for f (x)= abx Studentshaveaneasytimewiththisactivity.

OBJECTIVE4COMMENTS

ThebasemultipliermethodcanalsobeusedtographthefunctionsinProblem9,whichleadstodiscussingthe reflectionproperty.Togetacrosstheideaofreflection,Isaythatifamirrorwereplacedalongthe x-axis,the graphof g(x)=4(2)x would"see"thegraphof f (x)= 4(2)x asitsreflectioninthemirror.Ialsosaythatif

wepaintedthegraphof g ongraphpaperandfoldedthepaperalongthe x-axis,theblottedimagewouldbethe graphof f

Duetostudents’workwithdomainandrangeinSection7.4,moststudentshaveafairlyeasytimeﬁndingthe domainandrangeofanexponentialfunction.Areminderthatthegraphofanexponentialfunction f (x)= abx doesnotintersectthe x-axishelpsstudentsﬁndtherangeofsuchfunctions.

GROUPEXPLORATION:GraphicalSigniﬁcanceof a and b for y = abx

Thisactivityisagreatwaytoaddressthekeyconceptsofthissection.Oncegroupsofstudentsaredone,you canhaveaclassroomdiscussionaboutProblems4and5togetclosure.Functionsoftheform y = abx + c will notbeneededformodelinginthetextbook,sothisexplorationomitsinvestigationofverticaltranslation.Ifyou wantyourstudentstoexplorethegraphicalsigniﬁcanceof c,youcouldaskthemtoexploreitssigniﬁcanceatthe endoftheexploration.Agoodfollow-upquestionistoaskstudentstodescribethe y-interceptofthegraphofa functionoftheform y = abx + c.

GROUPEXPLORATION:DrawingFamiliesofExponentialCurves

Thisactivityisafunwayforstudentstoreflectonthegraphicalsignificanceofparameters a and b foranexponentialfunctionoftheform y = abx.Evenifstudentshaveexploredthegraphicalsignificanceofthebase b, studentsmaystillneedahinttousevaluesof b between0and1forProblem2.

OBJECTIVE5COMMENTS

StudentshaveaneasytimewithParts(a)and(b)ofProblem14becauseofearlierworkwithlinearmodeling.

Eventhoughthemeaningsofthecoefﬁcientandthebaseofanexponentialmodelareformallydiscussedin boxedstatementsforObjective6,theyareincludedinParts(d)and(e)ofProblem14topreparethemforthe formal,generalstatementsinthepropertyboxes.

InProblem14(d),studentshaveabitmoretroublethanexpectedtointerpretthecoefﬁcientofanexponential model,perhapsbecausetheyaresousedtoworkingwithlinearmodels.

StudentshaveevenmoretroublewithProblem14(e).Itischallengingforthemtofollowtheworkincluded onpage664ofthetextbookforthesolutiontoProblem5ofExample6.Nonetheless,theyfollowthatworkbetter thansimplysayingthatmultiplyingby1.15isequivalenttoﬁnding115%ofthepricefromthepreviousyear,so thepriceincreasesby15%peryear.

OBJECTIVE6COMMENTS

Althoughstudentsstrugglewithﬁndingbothexponentialgrowthanddecayrates,theyhaveanespeciallyhard timedeterminingdecayrates.Thisispartlybecausestudentslosesightthatthe“1”intheexpression 1 b isthe decimalformof100%.

Becauseofthepreviousworkinthissection,studentshaveaneasytimewithallpartsofProblem15except Part(e).

SECTION10.4LECTURENOTES

Objectives

1. Solveanequationoftheform abn = k forthebase b

2. Usetwopointstoﬁndanequationofanexponentialcurve.

3. Usetwopointstoﬁndanequationofanexponentialmodel.

OBJECTIVE1

Findallreal-numbersolutions.

1. b2 =9 2. b3 =27 3. 3b4 =48 4. 5b5 =95 5. b4 = 67

DiscusshowProblems1–5suggesthowtosolveequationsoftheform bn = k for b

SolvingEquationsoftheForm bn = k for b

Tosolveanequationoftheform bn = k for b,

1. If n isodd,thereal-numbersolutionis k1/n

2. If n isevenand k ≥ 0,thereal-numbersolutionsare ±k1/n

3. If n isevenand k< 0,thereisnoreal-numbersolution.

Findallreal-numbersolutions.Roundallresultstotheseconddecimalplace.

6. 2 7b4 5 3=351 9

7. 5 6 b4 3 8 = 7 12 8. b7 b2 = 83 4

OBJECTIVE2

Findanapproximateequation y = abx oftheexponentialcurvethatcontainsthegivenpairofpoints.Roundthe valueof b totwodecimalplaces.

9. (0, 7) and (6, 273)

10. (0, 95) and (3, 17)

Showthatifwedividetheleftsidesanddividetherightsidesoftheequations 5=5 and 7=7,weobtainthe truestatement 5 7 = 5 7

DividingLeftSidesandRightSidesofTwoEquations

If a = b, c = d, c =0,and d =0,then

Findanapproximateequation y = abx oftheexponentialcurvethatcontainsthegivenpairofpoints.Round thevaluesof a and b totwodecimalplaces.

11. (3, 6) and (7, 85)

OBJECTIVE3

12. (4, 47) and (9, 6)

13. ThetuitionratesatPrincetonUniversityareshowninthefollowingtablefortheacademicyearsendingin thedisplayedyear.

TuitionRate Year(thousandsofdollars) 19500.6 19601.5 19702.4 19805.6 199014.4 200024.6 201035.3 201541.8

Source: PrincetonUniversity

Let y bethetuitionrate(inthousandsofdollars)at x yearssince1950.

a. Constructascatterplot.

b. Findanequationofamodel.

c. Whatisthebase b ofthemodel ˆ y = abx?Whatdoesitmeaninthissituation?

d. Estimatethetuitionin2013.

14. ThenumbersofviewersoftheMajorLeagueBaseball(MLB)All-StarGameareshowninthefollowing tableforvariousyears.

NumbersofViewers Year(millions) 198234 198528 199024 199520 200015 200512 201012 201411

Source: NielsenMediaResearch,Inc

Let y bethenumber(inmillions)ofviewersat x yearssince1980.

a. Constructascatterplot.

b. Istheassociationpositive,negative,orneither?Whatdoesthismeaninthissituation?

c. Findanequationofamodel.

d. Whatisthecoefﬁcient a ofthemodel ˆ y = abx?Whatdoesitmeaninthissituation?

e. Whatisthebase b ofthemodel ˆ y = abx?Whatdoesitmeaninthissituation?

HW 1,3,11,15,21,33,35,45,53,55,59,61,63,73

SECTION10.4DETAILEDCOMMENTS

Inthissection,studentswillﬁndanequationofanexponentialmodelthatcontainstwogivenpoints.Although thismethoddoesnotgeneralizetoﬁndingtheexponentialregressionequation(Section10.5),interpretingthe meaningofamodelandusingittomakepredictionsisgoodpreparationforSection10.5.

OBJECTIVE1COMMENTS

Problems1–5relatenicelytopreviousworkdoneinSection10.2onrationalexponents.Studentstendtoforget thattherecansometimesbetwosolutions,soIremindthemaboutthisseveraltimes.ForProblems3,4,6,and7, Iemphasizethatweneedtoisolatethepower bn toonesideoftheequation.Problem8isexcellentpreparation fortheworkrequiredtoﬁndanexponentialequationthatcontainstwogivenpointsinwhichneitherpointisthe y-intercept.

OBJECTIVE2COMMENTS

Studentshaveaneasytimeﬁndinganexponentialequationifoneofthetwogivenpointsisthe y-intercept. Althoughitwilltakesomepractice,studentscanbecomeverysuccessfulatﬁndingequationsinwhichneither ofthegivenpointsisthe y-intercept.Ilikethismethod,becausestudentshavetherareopportunitytowitnessa meaningfulapplicationofthequotientpropertyforexponents.

ForProblem11,Itellstudentstowritethesystem

85= ab7

6= ab3

Equation1

Equation2

sothattheequationwiththelargerexponent, 85= ab7,isontop.Thatway,whenstudentslatersubtract theexponents,thedifferenceoftheexponentswillbepositive.Whenmanystudentssimplifythesidesofthe equation 85 6 = ab7 ab3 ,theywanttoperformthesameoperationwiththe85and6aswiththeexponents7and3. So,theyeitherdivide85by6anddivide7by3,ortheysubtract6from85andsubtract3from7.

Thereisawaytoavoidthesepitfalls.Insteadofdividingtheleftsidesanddividingtherightsidesofequations(1)and(2),youcansolveequation(2)for a: a = 6 b3 .Next,substitute 6 b3 for a inequation(1): 85= 6 b3 · b7 andsolvefor b.Notethatsolvingequation(2)for a ispreferable,becauseifwehadsolvedequation(1)for a,the substitutionwould’veledtotheequation 6=85b 4,whichcontainsanegativeexponent.

Studentsusuallyneedareminderonhowtousetechnologytoverifytheirwork.

Itisagoodideatocompareandcontrastequationsoftheform abn = c (e.g. 5b7 =95)withexponential functions(e.g. y =5(7)x).

GROUPEXPLORATION:UsingTrialandErrortoFindanEquationofaModel

Thisactivityservesasanicereviewofhowtointerpretthecoefﬁcientandbaseofanexponentialmodel.Italso providesthebigpictureofthissectionandhelpsstudentsdiscoverhowtheycanmakeadjustmentstomodels foundthroughoutthissection.

OBJECTIVE3COMMENTS

Whenﬁndingequationsofexponentialmodels,itcanbechallengingtoselecttwo"goodpoints"becauseitishard toimagineanexponentialcurvefromjusttwopointsthatitcontains.Usingthetrialanderrormethoddescribed inthissection’sexplorationcanhelpﬁne-tuneafoundequation.

Whenpreparingalecture,Ioften“cheat”bydetermininga“good”pairofpointsbygraphingtheregression exponentialmodelandselectingtwodatapointsthatlieclosest(oron)thecurve.However,asI’vementioned before,Irequiremystudentstoderive(nonregression)equationsofmodelsbyhand,becauseIwantstudentsto knowthosefundamentalskillsofthecourse.

Justaswithlinearmodeling,somestudentswillwanttoskipconstructingascatterplotandsimplyusetheﬁrst andlastdatapoints.Iremindstudentsthattherearetwoproblemswiththisstrategy:

• Theassociationmightnotbeexponential.

• Iftheassociationisexponential,theﬁrstandlastdatapointsmaynotbethebestpairofpointstousetoﬁnd anequationofamodel.

InProblem13,studentstendtobesurprisedhowmuchPrinceton’stuitionhasincreasedsince1950. Studentstendtoknowhowtointerpretthebaseofanincreasingexponentialmodel[Problem13(c)]bythis sectionbutcontinuetostrugglewithdoingsoforadecreasingexponentialmodel[Problem14(e)].

SECTION10.5LECTURENOTES

Objectives

1. Computeandinterpretthe exponentialcorrelationcoefﬁcient

2. Computeandinterpretresidualswhenworkingwithanexponentialmodel.

3. Findthesumofsquaredresidualsforanexponentialmodel.

4. Findanequationofan exponentialregressionmodel.

5. Usearesidualplottohelpdeterminewhetheranexponentialregressioncurveisanappropriatemodel.

6. Identifyinﬂuentialpointsforanexponentialregressionmodel.

7. Computeandinterpretthe exponentialcoefﬁcientofdetermination

OBJECTIVE1

1. ThefollowingscatterplotdescribestheassociationofdailymaximumtemperaturesinNewYorkCityversus dailymaximumozonelevels,whicharemeasuredinpartsperbillion(ppb).Let y bethemaximumozone (inppb)foradayinNewYorkCitywithmaximumtemperature x degreesFahrenheit.Describethefour characteristicsoftheassociation(Source: NAST).

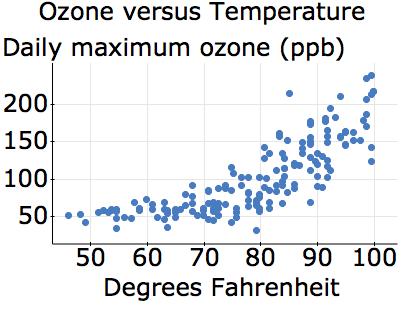
Warning:Becausethestudyisobservational,thepositiveozoneassociationdoes not meanthatanincreasein temperature causes anincreaseinozonelevel.

PropertiesoftheExponentialCorrelationCoefﬁcient

Assume r istheexponentialcorrelationcoefﬁcientfortheassociationbetweentwonumericalvariables. Then

• Thevaluesof r arebetween 1 and1,inclusive.

• If r ispositive,thenthevariablesarepositivelyassociated.

• If r isnegative,thenthevariablesarenegativelyassociated.

• If r =0,thereisnoexponentialassociation.

• Thelargerthevalueof |r|,thestrongertheexponentialassociationwillbe.

• If r =1,thenthedatapointslieexactlyonanexponentialcurveandtheassociationispositive.

• If r = 1,thenthedatapointslieexactlyonanexponentialcurveandtheassociationisnegative.

• Iftheexponentialcorrelationcoefﬁcientis0,thenthereisnoexponentialassociation,buttheremaybe someothertypeofassociation.

• Evenifanassociationisstronglylinear,theexponentialcoefﬁcientmightbequitecloseto1.So,to determinethestrengthandtypeofanassociation,weshouldinspectthescatterplotforthedataaswellas computeoneormorecorrelationcoefﬁcients.

OBJECTIVE2

2. Thenumbersofteacherswithvariousyearsofexperienceareshowninthefollowingtable.

YearsofNumberofTeachers Experience(thousands) 5185 10145 1590 2063 2554 3050 3538

Source: R.IngersollandE.Merrill,UniversityofPennsylvania,originalanalysesforNCTAFoftheSchoolsand StafﬁngSurvey

Let y bethenumber(inthousands)ofteacherswith x yearsofexperience.

a. Describethefourcharacteristicsoftheassociation.Computeandinterpretanappropriatecorrelation coefﬁcient r aspartofyouranalysis.

b. Wecanusethedatapoints (10, 145) and (25, 54) toﬁndtheexponentialmodel ˆ y =280(0.936)x . Howwelldoesthemodelﬁtthedata?

c. Usethemodeltopredictthenumberofteacherswhohave5yearsexperience.

d. FindtheresidualforthepredictionyoumadeinPart(c).Whatdoesitmeaninthissituation?What doesitmeanaboutthepositionsofthedatapointandtheexponentialcurve?

ResidualsforDataPointsAbove,Below,orOnaLine

Supposethatsomedatapointsaremodeledbyanexponentialcurve.

• Adatapointonthecurvehasresidualequalto0.

• Adatapointabovethecurvehaspositiveresidual.[Drawaﬁgure.]

• Adatapointbelowthecurvehasnegativeresidual[Drawaﬁgure.]

OBJECTIVE3

3. InProblem2,wemodeledtheteacherassociationwiththefunction ˆ y =280(0 936)x.Findthesumof squaredresidualsforthemodel.

OBJECTIVE4

Deﬁnition ExponentialRegressionModel

Foragroupofpoints,the exponentialregressionfunction istheexponentialfunctionwiththeleastsumof squaredresidualsofallexponentialfunctions.Itsgraphiscalledthe exponentialregressioncurve andits equationiscalledthe exponentialregressionequation,written

where a =0, b> 0,and b =1.The exponentialregressionmodel istheexponentialregressionfunction foragroupof data points.

4. Pointingalaserataircraft,whichcantemporarilyblindpilots,isaseriousoffensewithamaximumpunishmentof20yearsinprisonanda$250,000ﬁne.Thenumbersoflaserincidentsinvolvingaircraftareshown inthefollowingtableforvariousyears.

YearNumber 2005283 2006446 2007675 2008988 20091527 20102836

Source: FederalAviationAdministration

Let y bethenumberoflaserincidentsinvolvingaircraftintheyearthatis x yearssince2000.

a. Constructascatterplot.

b. Findaregressionequationtodescribethedata.Howwelldoesthemodelﬁtthedatapoints?

c. Whatisthe y-intercept?Whatdoesitmeaninthissituation?

d. Estimatethepercentageincreaseinlaserincidentsperyear.

OBJECTIVE5

UsingaResidualPlottoHelpDetermineWhetheranExponential RegressionFunctionisanAppropriateModel

Thefollowingstatementsapplytoaresidualplotforanexponentialregressionfunction.

• Iftheresidualplothasapatternwherethedotsdonotlieclosetothezeroresidualline,thenthere iseitheranon-exponentialassociationbetweentheexplanatoryandresponsevariablesorthereisno association.[Drawaﬁgure.]

• Theverticalspreadoftheresidualplotshouldbeaboutthesameforeachvalueoftheexplanatory variable.[Drawaﬁgure.]

OBJECTIVE6

5. Thefatalityratesfromautomobileaccidentsareshowninthefollowingtableforvariousyears.

Table2.2: YearsversusFatalityRatesFromAutomobileAccidents

FatalityRate

Year(deathsper100millionmiles) 192124.1 193015.1 194010.9 19507.2 19605.1 19704.7 19803.3 19902.1 20001.5 20101.1

Source: NationalHighwayTrafﬁcSafetyAdministration

Let y bethefatalityrate(numberofdeathsper100millionmilesdriven)at x yearssince1900.

a. Constructascatterplot.

b. Findtheequationofamodel.Doesthemodelﬁtthedatapointswell?

c. Determinewhetherthereareanyoutliersorinﬂuentialpoints.

d. Findtheexponentialdecayrateinfatalityrates.

OBJECTIVE7

ExponentialCoefﬁcientofDetermination

Let r betheexponentialcorrelationcoefﬁcientforagroupofdatapoints.Theexponentialcoefﬁcient ofdetermination, r2,istheproportionofthevariationintheresponsevariablethatisexplainedbythe exponentialregressioncurve.

Whenwereportacoefﬁcientofdetermination,itisimportantthatwestatewhetheritisforalinear regressionlineoranexponentialregressioncurve.

6. TheUniversityofMichiganoffersa$500,00lifeinsurancepolicy.Monthlyratesfornonsmokingfaculty areshowninthefollowingtableforvariousages.

AgeAgeUsedtoMonthly GroupRepresentAgeGroupRate (years)(years)(dollars)

30–343215.00

35–393718.50

40–444226.00

45–494746.00

50–545275.50

55–5957118.00

60–6462195.50

65–6967326.60

Source: UniversityofMichigan

Let y bethemonthlyrate(indollars)foranonsmokingfacultymemberat x yearsofage.

a. Constructascatterplot.

b. Findaregressionequation.Doesthegraphcomeclosetothedatapoints?

c. Describethefourcharacteristicsoftheassociation.Computeandinterpretanappropriatecorrelation coefﬁcientaspartofyouranalysis.

d. Computeandinterpretanappropriatecoefﬁcientofdetermination.

e. Predictthemonthlyratefora40-year-oldnonsmokingfacultymember.

HW 1,3,5,11,13,17,21,23,25,29,31,33,35,39,45,49,51,61

SECTION10.5TEACHINGTIPS

Inthissection,studentsuseexponentialregressionfunctionstomodeldata.Althoughthismaterialisprobably notincludedinyourintroductorystatisticscourse,therearesomanyconceptsthataresimilartothoseaddressed inSection9.3(linearregression)thatthissectionservesasagreatreinforcerofmodeling.

OBJECTIVE1COMMENTS

Problem1servesasanicereviewofthefourcharacteristicsofanassociationandmoreimportantlyintroduces theconceptofanexponentialmodel.Becausetherearesomanydatapoints,thevaluesarenotprovided.Butyou couldquicklyplotabunchofpointsthatroughlyﬁtthepatternandhavestudentsdothesame.Thenyoucould sketchacurvethatresemblestheexponentialregressioncurveshowninFig.45onpage683ofthetextbook.

Oryoucouldusedatafromanexerciseinthehomeworksection.Ifyouwouldliketoworkwithalargedata set,youcoulddownloadthedataforExercise49or50,andanalyzeitusingtechnology.

Whendiscussingtheexponentialcorrelationcoefficient,Iemphasizetheimportanceofdistinguishingitfrom thelinearcorrelationcoefficient,butIalsopointoutthesimilaritiesofthepropertiesofthetwocoefficients.

Upuntilnow,studentstendtothinkthatifthelinearcorrelationcoefﬁcientisequalto0,thenthereisno associationdespiteallwarningsIhavegiventhatallwereallyknowisthatthereisno linear association.Now thattwotypesofmodelsareontheplayingﬁeld,thisisagoodopportunitytorevisitthisissue.

Anotherissueisthatanassociationmightbeapproximatelylinearandyetthevaluesofthelinearandexponentialcorrelationcoefﬁcientsarebothcloseto1.Thesameistrueforsomeassociationsthatareapproximately exponential.

Theprevioustwoparagraphsunderscoretheimportanceofconsideringthescatterplotaswellasthecorrelation coefﬁcients.

OBJECTIVES2–4COMMENTS

Studentshaveafairlyeasytimewiththeseobjectivesbecauseoftheirpreviousworkwithlinearregressionmodels (Section9.3).

GROUPEXPLORATION:ComparingaLinearModelwithanExponentialModel

Thisexplorationisaniceactivityforstudentstocomparethegrowthpredictedbylinearandexponentialmodels. Theexplorationalsosendsasubtlemessage(whichyoucouldemphasize)thatitisfoolishtoextrapolatefrom justafewdatapoints,especiallyjusttwodatapoints!

OBJECTIVE5COMMENTS

Whendiscussingthebulletedstatementsintheboxforthisobjective,IsketchﬁguressuchasthoseinFigs.66–68 onpage691ofthetextbook.ToaddsomecontexttothediscussionyoucouldgooverExample5onpages692 and693ofthetextbook.

OBJECTIVE6COMMENTS

Studentsquicklypickupontheconceptofinﬂuentialpointsforexponentialmodelsbecauseoftheirprevious workwithinﬂuentialpointsforlinearmodels(Section9.3).

OBJECTIVE7COMMENTS

Moststudentsstrugglewithinterpretingthelinearcoefﬁcientofdetermination(Section9.3)andresorttomemorizinganinterpretation.Asaresult,moststudentsalsostrugglewiththemeaningoftheexponentialcoefﬁcient ofdetermination.Butbecauseoftherepetition,studentstendtogainatleastabitmorecomprehensionofthis challengingconcept. Copyright c 2016PearsonEducation,Inc.

Chapter 2 Designing Observational Studies and Experiments

Homework 2.1

2. A sample is the part of a population from which data are collected.

4. A sampling method that consistently underemphasizes or overemphasizes some characteristic(s) of the population is said to be biased.

6. a. Andrew Brannan, Roger Collins, Jerry Heidler, Warren Hill, and Darryl Scott.

b. County of conviction, race, age (in years), and time served (in years).

c. County of conviction: Laurens, Houston, Toombs, Lee, and Chatham. Race: Caucasian, African American, Caucasian, African American, and Caucasian. Age, all in years: 66, 55, 37, 54, and 31. Time served, all in years: 14, 37, 15, 23, and 7.

d. Andrew Brannan: 661452 −= years. Roger Collins: 553718 −= years. Jerry Heidler: 371522 −= years. Warren Hill: 542331 −= years. Darryl Scott: 31724 −= years.

e. The youngest when convicted was Roger Collins, at age 18 years.

8. a. Mars Polar Lander, Opportunity, Mars Reconnaissance Orbiter, Yinghuo-1, and Mars Orbiter Mission.

b. Mission, outcome, cost (in millions of dollars), and launch mass (in pounds).

c. Mission: lander, rover, orbiter, orbiter, and orbiter. Outcome: failure, success, success, failure, and success. Cost, all in millions of dollars: 110, 400, 720, 163, and 74. Mass, all in pounds: 640, 408, 4810, 29,100, and 2948.

d. Mars Polar Lander, 110/6400.172 = ; Opportunity, 400/4080.980 = ; Mars Reconnaissance Orbiter, 720/48100.150 = ; Yinghuo-1, 163/29,1000.006 = ; Mars Orbiter

Mission, 74/29480.025 = ; all in millions of dollars per pound.

e. Yinghuo-1, 0.006 million dollars per pound.

10. a. The variable is whether people think the Affordable Care Act goes too far.

b. The sample is the 1000 likely voters who were polled.

c. The population is all likely voters.

12. a. The variable is whether people think the United States does too much in solving the world’s problems.

b. The sample is the 1501 adults who were surveyed.

c. The population is all American adults.

14. a. The variable is whether people believe that police can protect them from violent crime.

b. The sample is the 776 Caucasians who were surveyed.

c. The population is all Caucasians.

16. a. The variable is whether parents will limit their children’s choices of college based on cost.

b. The sample is the 1000 parents who were surveyed.

c. The population is all parents with collegebound teenagers ages 16 to 18 years.

18. a. The researchers were trying to answer whether simvastatin heals ulcers.

b. The sample is the 66 ulcer patients who were tested.

c. The population is all patients with ulcers.

d. The researchers concluded that the drug heals ulcers. The study is part of inferential statistics because it uses sample data to draw a conclusion about a population.

20. a. The researchers were trying to answer whether autistic adults are less able to process social rewards than monetary rewards.

b. The sample is the 20 adults who were in the study.

c. The population is all adults.

d. The conclusion is that adults with autism are less able to process social rewards than adults without autism. It is part of inferential statistics because it uses data from a sample to make a statement about the population.

22. a. The researchers were trying to answer whether women who are more sexually confident are also more likely to achieve sexual satisfaction.

b. The sample is the 45 women who took the online survey.

c. The population is all women.

d. The conclusion is that women who are more sexually confident are also more likely to achieve sexual satisfaction. It is part of inferential statistics because it draws a conclusion about a population, based on data taken from a sample.

24. Using a TI-84: Mariah, Rani, May, and Brenton. Using StatCrunch: Rani, Brenton, Kali, and Shea.

26. a. Using a TI-84: Samuel, Paola, Joshua, Win, and Phoebe. Using StatCrunch: Win, Taja, Nathan, Samuel, and Jeffrey.

b. Using a TI-84: 3 35. 5 ÷= Using StatCrunch: 2 25. 5 ÷=

Using this result to describe the sample is part of descriptive statistics because it does not draw conclusions about a larger group.

c. Using a TI-84: Samuel, Jeffrey, Phoebe, Win, and Arnold. Using StatCrunch: Karen, Win, Monique, Arnold, and Jeffrey.

d. Using a TI-84: 3 35. 5 ÷= Using

StatCrunch: 2 25. 5 ÷=

e. Using a TI-84: Yes. Using StatCrunch: Yes. However, not all randomly selected samples of size 5 will give the same results. Because of the randomness of choosing the sample, different samples could be collected.

28. a. Using a TI-84: Dimitrios, Aksana, Jessica, Luis, Fan, Chris, and Gauri. Using StatCrunch: Gauri, Chris, Aksana, Fadi, Devin, Jose, and Julia.

b. Using a TI-84: 4 47. 7 ÷= Using

StatCrunch: 5 57. 7 ÷=

c. 9 914 14 ÷=

d. (Either technology) No. The difference between the answers in b. and c. is due to sampling error.

e. For many random samples of size 7, the proportion of students who think it is more important to improve student success would not be the same on each sample and would not all be the same as the proportion for all 14 students. This is due to sampling error.

30. a. 10571203290.520 ÷=

b. 52310000.523 ÷=

c. No, the result from part (b) does not equal the result from part (a). This is due to sampling error.

d. It would be inferential statistics because it draws a conclusion about a population based on data from a sample.

32. Do you access Facebook every day or not access Facebook every day?

34. Do you have a regular exercise program or not have one?

36. The method favors students who take evening classes, so it has sampling bias.

38. The wording of the question is not clear (since it asks whether they post daily and also if they like Facebook), so it has response bias.

40. Because 9 out of 12 subjects did not respond, the method has nonresponse bias. It also has response bias because an adult who neglects their children is unlikely to say “yes.”

42. Because 93% of those who were contacted did not give a response, the method has nonresponse bias.

44. The method has response bias because the scale of numbers for the response is not consistent.

46. This method has sampling bias because it favors cars that pass by during the morning rush hour.

48. The method has response bias because the question addresses more than one issue. It also has sampling bias, because it excludes people who do not watch this TV show.

50. a. The survey is likely to have nonresponse bias because participation is voluntary. It probably also has sampling bias, since it favors diners who want to complain about their experience.

b. The survey likely has less nonresponse bias because of the incentive. It likely has less sampling bias because of the incentive. It may have more response bias, since the future discount likely improves the customer’s satisfaction with the restaurant.

52. Using samples involves less time, less money, and less labor than taking a census.

54. Answers may vary.

56. Answers may vary.

58. Sampling error refers to the random nature of the sample; nonsampling error refers to the design of the sampling process.

Homework 2.2

2. We should always round down when calculating k for systematic sampling.

4. False. Convenience sampling should never be used because such samples usually do not represent the population well.

6. Cluster sampling is the method because the 40 blocks are randomly selected, but every adult resident of each block is surveyed.

8. Systematic sampling is the method because every 100th car fuel tank after the first selected tank is tested.

10. Convenience sampling is the method because the employee only surveys the Americans whom she can contact easily.

12. Stratified sampling is the method because registered voters are randomly sampled within each of three strata: Republicans, Democrats, and Independents.

14. Simple random sampling is the method because sample members are selected at random from the whole population.

16. The method is systematic sampling because the pollster surveys every 10th person after the first to be selected.

18. The method is simple random sampling because members are randomly selected from all the paying guests in the past month.

20. a. 420508.4; ÷= round down to 8.

b. Using a TI-84: 4. Using StatCrunch: 5.

c. Using a TI-84: 4,4812,12820,20828, 28836 +=+=+= += Using StatCrunch: 5,5813,13821,21829, 29837. +=+=+= +=

22. a. 47,756150318.4; ÷≈ round down to 318.

b. Using a TI-84: 130. Using StatCrunch: 168.

c. Using a TI-84: 130,130318448,448318766, 7663181084,10843181402 +=+= +=+=

Using StatCrunch: 168,168318486,486318804, 8043181122,11223181440. +=+= +=+=

24. From the police department, survey () 0.627043 = employees. From the fire department, survey () 0.297020 = employees. From the judicial department, survey () 0.09706 = employees. Since 4320669, ++= one more person should be selected at random from one of the three departments, also selected at random, to meet the goal of a sample size of 70.

26. The total number of students in the four schools is 1936 + 1466 + 899 + 83 = 4384. The proportions are: Franklin High School, 193643840.442; ÷= Centennial High School, 146643840.334; ÷= Fred J. Page High School, 89943840.205; ÷= Middle College High School, 8343840.019. ÷=

The numbers of students in the sample from each high school, respectively, are: () 0.4425022; ≈ () 0.3345017; ≈ () 0.2055010; ≈ () 0.019501. ≈

28. The total number of applicants to the five graduate business majors is 85 + 368 + 109 + 90 + 83 = 735. The proportions are: Accounting, 857350.116; ÷= Finance, 3687350.501; ÷= Information Risk and Operations Management, 1097350.148; ÷= Management, 907350.122; ÷= Marketing, 837350.113. ÷=

The numbers of applicants in the sample from each major, respectively, are: () 0.11610012; ≈ () 0.50110050; ≈ () 0.14810015; ≈ () 0.12210012; ≈ () 0.11310011. ≈

30. The proportions of each of the strata: Female undergraduate, 10,58829,1350.363; ÷= female graduate, 447529,1350.154; ÷= female professional, 142129,1350.049; ÷= male undergraduate, 776229,1350.266; ÷= male graduate, 373629,1350.128; ÷= male professional, 115329,1350.040. ÷=

The numbers of students in the sample from each of the strata, respectively: () 0.3631200436; ≈ () 0.1541200185; ≈ () 0.049120059; ≈ () 0.2661200319; ≈ () 0.1281200154; ≈ () 0.040120048. = Because of rounding, the sample would actually have 1201 students.

32. Using a TI-84: Republicans Reagan, Farnsworth, Biggs, Yarbrough, Yee; Democrats Tovar, Bedford, Bradley, McGuire.

Using StatCrunch: Republicans Farnsworth, Crandell, Melvin, Yee, Worsley; Democrats Bradley, Hobbs, McGuire, Gallardo.

34. The number of clusters is 75253. ÷= Using a TI-84: Red Sox, Royals, Athletics. Using StatCrunch: Royals, Tigers, Indians.

36. Stratified sampling is being used, where the strata are farmers and city or suburban residents because each of the two strata is sampled separately.

38. Cluster sampling would require the least money and effort because surveying each resident on a selected block involves less travel time than a simple random sample. The city would decide on a sample size, identify a frame of all the blocks in Los Angeles, then divide the desired sample size by the smallest number of residents per block. The required number of blocks would be randomly selected, and then every resident on the selected blocks would be surveyed.

40. Simple random sampling is the best method, since Barnes & Noble® has a frame and the surveying can be done using e-mail. The company would choose a desired sample size, then randomly select that many online customers from the frame.

42. a. If each city block is treated as a cluster, the city would decide on a sample size, identify a frame of all the city blocks in Kansas City, and then divide the desired sample size by the smallest number of residents per block. That many blocks would be randomly selected, and every resident on the selected blocks would be interviewed in person.

b. To conduct stratified sampling, the data collectors would first choose a total sample size, then identify what proportions of registered voters are Democrats, Republicans, Independents, and so on, and compute the sample size for each of the strata by multiplying the total sample size by the respective proportions. The required number for each of the strata would then be randomly selected.

c. Cluster sampling would be easier than stratified because the data collectors would only need to visit the selected blocks in person.

d. Stratified sampling would probably give better results if the sample size is small because it is more likely to get a sample that represents the whole city.

44. a. The police used systematic sampling when the traffic was heavier because they stopped every fourth car.

b. Sampling every third and fourth car is not systematic sampling because it violates the pattern of selecting every k th person, animal, or thing.

c. In lighter traffic, the police could have pulled over every other car. They would still be stopping two cars out of every four, but they would be using systematic sampling.

46. Answers may vary.

48. Answers may vary.

50. Answers may vary.

Homework 2.3

2. In a double-blind study, neither the individuals nor the researcher in touch with the individuals know who is in the treatment group(s) and who is in the control group.

4. A lurking variable is a variable that causes both the explanatory and response variables to change during the study.

6. a. The treatment groups are the second and third groups because they receive training in addition to that which the first group receives.

b. The study is an experiment because each participant is assigned to one of the treatment and control groups.

c. Random assignment means that the researchers use random sampling to decide which participants are in which groups. For example, the researchers could create a frame of all 50 older adults, randomly choose 17 of them to be in the second group, randomly choose another 17 for the third group, and assign the other 16 to the first group.

d. The sample is the 50 older adults in the study. The population is all older adults.

8. a. The explanatory variable is the type of training that participants did. The response variable is walking speed when an older person is performing a mental task at the same time.

b. The researchers concluded that the training methods for improving walking speed that include both physical and mental tasks are more effective than those used in the first group when an older adult is performing a mental task at the same time. Causality can be concluded because the participants were randomly assigned to the treatment and control groups.

c. The first group’s confidence may have increased because the group’s training was easier than that of the second and third groups.

10. a. It makes sense that the study is observational because the researchers cannot randomly assign anyone to have a major bone fracture.

b. It would be unethical to randomly assign an older adult to “treatment” when that treatment requires a major bone fracture.

c. The sample is the people whose records were studied. The population is all adults over 60.

d. The explanatory variable is whether or not the person had a major bone fracture. The response variable is the death rate.

e. The conclusion is that the death rate for older adults who have had a major fracture is higher than the death rate for older adults who have never had a major fracture. Only an association can be concluded because there was no random assignment to treatment or control groups.

12. a. The study is observational because there is no random assignment.

b. Since a placebo has no proven medical effect, it would be unethical for the doctors to administer it instead of prescribing an effective remedy for an acute cough.

c. The sample is the 241 children in the study. The population is all children with an acute cough.

d. The researchers concluded that children who took levodroprophizine recovered better from coughs than children who took other cough syrups. Only an association can be concluded because there was no random assignment to treatment and control groups.

e. Researchers could be influenced, consciously or unconsciously, by earning a salary from the company that manufactures levodroprophizine. The two researchers’ disclosing that they work for the company encourages other researchers who do not work for the company to repeat the experiment and see if they get similar results.

14. a. The treatment group is the one that received a gift card plus monetary rewards based on their class work. The control group is the one that received only a gift card.

b. The study is an experiment because the researchers randomly assigned students to the treatment and control groups.

c. Random assignment means that the researchers chose some students at random to receive the treatment and others to be the control group.

d. The sample is the 1019 students in the study. The population is all low-income community college students who are parents.

16.

a. It would be impossible to use a placebo for a monetary reward. A participant would quickly discover whether they have real or fake money.

b. In order to be double-blind, the participants would have to not know whether they will receive monetary rewards, which would remove the incentive to earn more credits.

c. The explanatory variable is whether or not students would receive an additional monetary reward based on the credits they earn. The response variable is the number of credits the students earned.

d. The researchers concluded that monetary rewards increase the number of credits earned by low-income community college students who are parents. Causality can be concluded because students were randomly assigned to the treatment and control groups.

e. Mistakenly giving monetary rewards to some of the control group introduces a possible lurking variable; believing that they will be rewarded no matter how many classes they pass could decrease students’ motivation to do well.

18. a. This is an observational study because there is no differentiation into treatment and control groups and no random assignment.

b. The sample is the 210 motorists whose behavior was observed. The population is all motorists in Chicago.

c. The explanatory variable is whether the crosswalk was marked or unmarked. The response variable is whether or not the motorist stopped.

d. The researchers concluded that motorists are more likely to follow the Must Stop law at marked than at unmarked crosswalks. Only association can be concluded because there was no random assignment into treatment and control groups.

e. We cannot assume the conclusion is also true in Prairie City because the habits of motorists could be very different in a small farm town than in a large city. Motorists are also more likely to be acquainted with the pedestrians in a small town, which could influence their behavior.

20. Using a TI-84: Lenovo ThinkPad X240, Dell Latitude 7440, Dell XPS 13, Acer Aspire S7. Using StatCrunch: Lenovo ThinkPad X240, Acer Aspire S7, Samsung ATIV Book 9, HP Spectre 13 Ultrabook.

This is an example of random assignment because the ultrabooks were randomly assigned to the treatment and control groups.

22. Using a TI-84: Palm Beach State College, Virginia Military Institute, Kean University, SUNY College at Oneonta, Angelo State University, Langston University. Using StatCrunch: Eastern Illinois University, Lander University, Boise State College, Langston University, Kean University, Oakland University.

This is an example of random assignment because the colleges were randomly assigned to the treatment and control groups.

24. a. Because this is an observational study, the student cannot conclude causality. There is likely to be response bias; people may overstate the amount of exercise they get. Also, motivation to stay healthy could be a lurking variable affecting whether or not people smoke (or quit smoking) and whether or not they exercise.

b. The student could find people who currently smoke and randomly assign the smokers to one of two groups, treatment or control. The treatment group would exercise on a regular basis, while the control group would not. It would be impossible for the study to be double-blind since the participants know what treatment they have; however, it could be a blind study if the researcher(s) in contact with the participants do not know which is in each group.

26. a. Although there is an explanatory variable, there is no control group (or random assignment). This is an observational study, and causality cannot be concluded.

There is also a confounding variable since the reward is not just monetary. Students could also be motivated to write a better project for the public honor of appearing in the newspaper.

b. The students could be randomly assigned to one of two groups, treatment or control. The control group would have the same assignment but no prize for the best project. The treatment group will be told that the best project will win a $25 prize. It could be a blind study if the projects are graded by another teacher who does not know which group the students were in.

28. a. Although there is an explanatory variable, there is no control group (or random assignment). This is an observational study and causality cannot be concluded. There could be sampling bias and response bias because the survey is online; it could favor people with greater incomes who could afford newer cars, and voluntary response could favor people whose mileage improved after using the additive. The financial state of the respondents could also be a lurking variable, since it could influence both the ability of car owners to respond online and their ability to keep the car in good running condition.

b. The magazine could select a random sample of drivers and randomly assign them to either a treatment group or a control group. The treatment group would be given the additive and asked to use it, while the control group would not. The gas mileage of each car would be recorded at the beginning of the study, and again a month afterwards.

30. Researchers could recruit a sample of volunteers who suffer from insomnia and randomly assign them to either a treatment or a control group. Volunteers in the treatment group would receive the drug, and volunteers in the control group would receive a sugar pill. The study could be double-blind, with one researcher labeling pill vials but not giving the code to the researchers in contact with the patients. The extent of insomnia would be measured at the beginning of the study and again a month later.

32. A sample of students who have the same class with the same professor could be randomly assigned to a treatment or control group. Each student could be given a recording of the professor’s lectures, but only the treatment group would be instructed to listen to the lectures while they sleep. The professor (or someone else who grades the tests) could be blind to which students are in which group.

34. With random assignment, the frame is a sample, and sampling divides the individuals into treatment group(s) and a control group. Stratified sampling does not involve treatment and control groups; it defines groups with similar characteristics (strata) that already exist in the population and creates frames for each of the strata.

36. The key difference in the designs of an experiment and an observational study is the presence of both treatment group(s) and a control group to which individuals are randomly assigned. Random assignment to one of the groups makes it possible to isolate the effects of the treatment from other factors.

38. Answers may vary.

40. The student is correct. The objects do not know whether they are in a treatment or control group.

Chapter 2 Review Exercises

1. a. The individuals are the countries: Bahrain, Iraq, Israel, Kuwait, and Saudi Arabia.

b. The variables are government, population (in millions), 2012 military expenditure (in billions of dollars), and oil production (in billions of barrels per day).

c. For the variable government: monarchy, republic, republic, monarchy, and monarchy. For the variable population, all in millions: 1.3, 31.9, 7.7, 2.7, and 26.9. For 2012 military expenditure, all in billions of dollars: 0.92, 5.69, 15.54, 5.95, and 54.22. For oil production, all in billions of barrels per day: 0.05, 2.99, 0.20, 2.69, and 9.90.

d. Bahrain, 0.920.0518.4; ÷= Iraq, 5.692.991.903; ÷= Israel, 15.540.2077.7; ÷= Kuwait, 5.952.692.212; ÷= Saudi Arabia,

54.229.905.477; ÷= all in dollars per barrel per day.

e. Israel has the greatest ratio of 2012 military expenditure to oil production, 77.7 dollars per barrel per day.

2. a. The variable is whether American adults experience a lot of happiness and enjoyment.

b. The sample is the 500 American adults who were telephoned.

c. The population is all American adults.

3. a. Using a TI-84: Antoine, Jacob, Ruben, Sandra, Dante, Jose. Using StatCrunch: Mario, Sandra, Antoine, Jacob, Alyssa, John.

b. Using a TI-84: 1 36. 2 ÷= Using StatCrunch: 1 36. 2 ÷= Using this result to describe the sample is part of descriptive statistics because it does not generalize the results of the sample to describe the population.

c. The proportion who prefer comedies is 5 0.417. 12 =

d. Using a TI-84 or Using StatCrunch: No, the sample proportion who prefer comedies does not equal the population proportion who prefer comedies. The difference is due to sampling error.

e. No, the proportion in each sample would not equal the proportion of all 12 students who prefer comedies. The difference is due to sampling error.

f. If two researchers perform the same study with different simple random samples of the same size, their inferences will not necessarily be the same because the sample data are not the same.

4. Choose the number of questions you usually ask during one hour of your prestatistics class: 0, 1, 2, 3, or more than 3.

5. The method has sampling bias; the sampling favors people who visit the militia group site.

6. The method has sampling bias, response bias, and nonresponse bias. The sampling favors people who are often in the financial district; some people may exaggerate their salary; 55 of those who were approached declined to answer.

7. Answers may vary.

8. The method is cluster sampling because the researcher selects 50 blocks at random and then surveys each adult resident of those blocks.

9. The method is simple random sampling because Human Resources creates a frame of all U.S. employees and selects at random from that frame.

10. The method is convenience sampling because the pollster only surveys people who are easy to find, without attention to any random selection.

11. The method is stratified sampling because the researchers identify two strata (people with landlines and people with cell phones), and randomly select numbers in each of the strata.

12. The method is systematic sampling because the manager surveys every eighth person leaving the store after the first person is randomly selected.

13. a. 105,000800131.25; ÷= round down to 131.

b. Using a TI-84: 57. Using StatCrunch: 47.

c. Using a TI-84: 57, 57131188; += 188131319; += 319131450; += 450131581. += Using StatCrunch: 47, 47131178; += 178131309; += 309131440; += 440131571. +=

14. The total number of employees (in thousands) is 82 + 57 + 30 + 19 + 8 + 3 = 199. The proportions are: commercial airplanes, 821990.412; ÷≈ defense, space, and security, 571990.286; ÷≈ corporate, 301990.151; ÷≈ engineering, operations, and technology, 191990.095; ÷≈ shared services group, 81990.040; ÷≈ other, 31990.015. ÷≈

The numbers of employees in the sample from each group, respectively, are: () 0.4128033; ≈ () 0.2868023; ≈ () 0.1518012; ≈ () 0.095808; ≈ () 0.040803; ≈ () 0.015801. ≈

15. Using a TI-84: Democrats Gerratana, Ayala, and Duff; Republicans Frantz and Linares. Using StatCrunch: Democrats Looney, Stillman, and Bartolomeo; Republicans Guglielmo and Welch.

16. If the clusters are city blocks, cluster sampling would require the least time and effort. The city would create a frame of all the blocks in the city, select some at random, and then survey each resident of the selected blocks.

17. a. The treatment groups are the three groups who receive the drug; the control group is the group who receives a placebo.

b. The study is an experiment because the researchers randomly assigned participants to one of the three treatment groups or to the control group.

c. Random assignment means that the researchers randomly assigned patients to one of the four groups. To accomplish the random assignment, create a frame of the 560 MDD adults. For each treatment group, randomly select 140 different MDD adults to be in the group. The remaining 140 MDD adults are the control group.

d. The sample is the 560 MDD adults in the study. The population is all adults with MDD.

18. a. The placebo could be a sugar pill.

b. Neither the study participants nor the researchers in contact with them know which treatment (or placebo) the participants receive. One researcher could have labeled the pill vials with numbers to identify the pills, but not told the code to another researcher who was in contact with the participants.

c. The explanatory variable is the dosage of the drug the person receives. The response variable is the person’s HRSD score.

d. The conclusion of the study is that Lu AA21004 successfully lowers MDD adults’ HRSD scores. The researchers can conclude causality because adults were randomly assigned to the treatment and control groups.

e. The researchers concluded that the drug tends to lower MDD adults’ HRSD scores, but that might not mean that the drug tends to reduce depression in MDD adults.

19. a. The study is observational because mothers were not randomly assigned to the group with eating disorders or the group without eating disorders.

b. It would be impossible to use random assignment in this study because mothers could not start having an eating disorder, or stop having an eating disorder, due to a researcher telling them to.

c. The sample is the mothers who were observed. The population is all mothers with first-born infants.

d. The explanatory variable is whether or not the mother has an eating disorder. The response variable is the level of negative emotions expressed toward the infants during mealtimes.

e. The conclusion of the study is that mothers with eating disorders express more negative emotions toward their first-born infants during mealtimes than mothers without eating disorders. It only describes an association; an observational study cannot conclude causality.

20. Using a TI-84: Elon University, Campbell University, Wellesley College, Columbia College, University of Mount Union. Using StatCrunch: Nichols College, Columbia College, Mills College, Rider University, Villanova University. Yes, it is an example of random assignment because the colleges were randomly assigned to the two groups.

21. a. The coordinator did not use random assignment, so she cannot conclude causality. Also, the attendance should include a time requirement because a student who attended the math center for only five minutes once in the entire semester should not be considered a

student who used the center. Motivation could be a lurking variable: students who attend the math center might be more motivated, and study harder, than other students.

b. The coordinator could randomly assign some students to a treatment group and others to a control group. The students in the treatment group would, for example, attend the math center for one hour per weekday during the entire semester, while the students in the control group would not attend the math center. After the semester is over, the coordinator could compare the proportion of the treatment group who passed their math classes that semester with the proportion of the control group who passed their math classes that semester.

22. The company could randomly assign some bald people to a treatment group and some to a control group. The treatment group would take the drug and the control group would take a sugar pill. The study could be double-blind. The company would then measure the extent of the individuals’ hair growth after 8 months.

Chapter 2 Test

1. a. The individuals are Delaware, Hawaii, Mississippi, Texas, and Wisconsin.

b. The variables are region, number of workers (in thousands), and number of workers in unions (in thousands).

c. Region: East, West, South, South, and Midwest. Number of workers: 370, 549, 1040, 10,877, and 2569, all in thousands. Number of workers in unions: 38, 121, 38, 518, and 317, all in thousands.

d. Delaware, 383700.102710.3%; ÷≈= Hawaii, 1215490.220422.0%; ÷≈= Mississippi, 3810400.03653.7%; ÷≈= Texas, 51810,8770.047624.8%; ÷≈= Wisconsin, 31725690.123412.3%. ÷≈=

e. Hawaii has the largest percentage of workers in unions, 22.0%.

2. a. The variable is whether an adult intends to buy wearable technology in the next 12 months.

b. The sample is the 2011 American adults who were surveyed.

c. The population is all American adults.

3. The study has response bias and nonresponse bias. The complex wording of the question may lead customers to give an answer that is not consistent with their opinion (response bias), and the nonresponse rate of 92% indicates nonresponse bias.

4. Using a TI-84: Jamie, Jared, Isabel, Lisa. Using StatCrunch: Jamie, Brianna, Dan, Michael.

5. The method is cluster sampling. The farmer randomly selects 8 subsections, then measures the total yield from each of those subsections.

6. a. 500806.25; k =÷= round down to 6.

b. Using a TI-84: 1. Using StatCrunch: 2.

c. Using a TI-84: 1; 1+ 6 = 7; 7 + 6 = 13; 13 + 6 = 19; 19 + 6 = 25. Using StatCrunch: 2, 2 + 6 = 8, 8 + 6 = 14, 14 + 6 = 20, 20 + 6 = 26.

7. The total number of students is given: 21,471. The proportions are: female undergraduates, 483321,4710.225; ÷≈ female graduate students, 179221,4710.083; ÷≈ male undergraduates, 972521,4710.453; ÷≈ male graduate students, 512121,4710.239. ÷≈

The numbers of students in the sample from each of the strata, respectively, are: () 0.225500113; ≈ () 0.08350042; ≈ () 0.453500226; ≈ () 0.239500119. ≈

8. a. The treatment groups are the 4 groups taking different drug dosages; the control group is the group receiving a placebo.

b. The study is an experiment because patients were randomly assigned to the treatment and control groups.

c. Random assignment means that the researchers randomly assigned the patients to the groups. To accomplish this, create a frame of the 361 patients. Then for each of the 4 treatment groups, randomly select 72 patients to be in the group. The remaining 73 adults should be in the control group.

d. The sample is the 361 patients in the study. The population is all Japanese adults with type 2 diabetes.

9. a. The placebo could be a sugar pill.

b. Neither the patients nor the researcher(s) in contact with the patients knew which patients were in each group; one researcher could have labeled the pill vials with numbers to identify the pills, but not tell the code to another researcher who was in contact with the individuals.

c. The explanatory variable is the dosage of the drug. The response variable is the glycated hemoglobin level.

d. The conclusion of the study is that the drug successfully lowers glycated hemoglobin levels in Japanese patients with type 2 diabetes. Because treatments and control were randomly assigned, the researchers can claim causality.

e. Researchers could be influenced, consciously or unconsciously, by earning a salary from the company that manufactures ipragliflozin. Reporting that they work for the company encourages other researchers who do not work for the company to repeat the experiment and see if they get similar results.

10. a. The researcher did not use random assignment. The players who run every day may also practice basketball longer and harder than players who do not run every day; motivation may be a lurking variable.

b. The researcher could randomly assign players to a treatment group and a control group. Players in the treatment group would run for one hour every day, and players in the control group would not run. The researcher could have an assistant oversee the training, so the researcher would be blind to which players are in which group. After the players have run daily for one month, the researcher would compare the scoring of the two groups in the next month, while the players in the treatment group continued to run daily.

11. The owner could randomly assign the sales force to a treatment group and a control group. The treatment group would attend a workshop about emotions for a weekend. The control group would not attend the workshop. The owner could be blind to which employees attended the workshop. One month later, the owner would compare the monthly sales by the treatment and control groups.