CHAPTER TWO SETS
Exercise Set 2.1
1. Set
2. Ellipsis
3. Description, Roster form, Set-builder notation
4. Finite
5. Infinite
6. Equal
7. Equivalent
8. Cardinal
9. Empty or null
10. {} , Æ
11. Not well defined, “best” is interpreted differently by different people.
12. Not well defined, “most interesting” is interpreted differently by different people.
13. Well defined, the contents can be clearly determined.
14. Well defined, the contents can be clearly determined.
15. Well defined, the contents can be clearly determined.
16. Not well defined, “most interesting” is interpreted differently by different people.
17. Infinite, the number of elements in the set is not a natural number.
18. Finite, the number of elements in the set is a natural number.
19. Infinite, the number of elements in the set is not a natural number.
20. Infinite, the number of elements in the set is not a natural number.
21. Infinite, the number of elements in the set is not a natural number.
22. Finite, the number of elements in the set is a natural number.
23. {} Hawaii
24. {} January, June, July
25. {} 11,12,13,14,...,177
27. {} 2,4,6,8, B =
29. {} or Æ
26. {} 4 C =
28. {} or Æ
30. {} Idaho, Oregon
31. {} 14,15,16,17,,84 E =
32. {} Alaska,Hawaii
33. {} Bangkok, London, Paris, Singapore, New York 34. {} Hong Kong, Barcelona
35. {} or Æ
36. {} Paris
37. {} 2012,2013,2014
38. {} 2010,2011
39. {} 2011
41. {} and615 or BxxNx =Î<<
{} and 714BxxNx =룣
43. {} and is a multiple of 3 CxxNx =Î
45. {} and is odd ExxNx =Î
47. {} is February Cxx =
40. {} or Æ
42. {} and 10 or AxxNx =Î<
{} and 9 AxxNx =Σ
44. {} and is a multiple of 5 DxxNx =Î
46. {} is Independence Day Axx =
48. {} {} and 14101 or and 15100 FxxNx FxxNx =Î<< =Σ£
49. Set A is the set of natural numbers less than or equal to 7.
50. Set D is the set of natural numbers that are multiples of 3.
51. Set V is the set of vowels in the English alphabet
52. Set S is the set of the seven dwarfs in SnowWhiteandtheSevenDwarfs.
53. Set T is the set of species of trees.
54. Set E is the set of natural numbers greater than or equal to 4 and less than 11.
55. Set S is the set of seasons..
56. Set B is the set of members of the Beatles.
57. {} Facebook, Twitter, LinkedIn, Pinterest
58. {} Vk, Flickr, MySpace
59. {} Twitter, LinkedIn, Pinterest
61. {} 2011,2012,2013,2014
63. {} 2007,2008, 2009, 2010
65. False; {} e is a set, and not an element of the set.
67. False; h is not an element of the set.
69. False; 3 is an element of the set.
71. True; 9 is an odd natural number.
73. ( ) 4 nA =
75. ( ) 0 nC =
60. {} Twitter
62. {} 2005
64. { 2013}
66. True; b is an element of the set.
68. True; Mickey Mouse is an element of the set.
70. False; the Amazon is a river in South America.
72. False; 2 is an even natural number.
74. ( ) 6 nB =
76. () 5 nD =
77. Both; A and B contain exactly the same elements. 78. Equivalent; both sets contain the same number of elements, 3
79. Neither; the sets have a different number of elements.
80. Neither; not all cats are Siamese.
81. Equivalent; both sets contain the same number of elements, 4.
82. Equivalent; both sets contain the same number of elements, 50.
83. a) Set A is the set of natural numbers greater than 2. Set B is the set of all numbers greater than 2.
b) Set A contains only natural numbers. Set B contains other types of numbers, including fractions and decimal numbers.
c) {} 3,4,5,6, A =
d) No; because there are an infinite number of elements between any two elements in set B, we cannot write set B in roster form.
84. a) Set A is the set of natural numbers greater than 2 and less than or equal to 5. Set B is the set of all numbers greater than 2 and less than or equal to 5.
b) Set A contains only natural numbers. Set B contains other types of numbers, including fractions and decimal numbers.
c) {} 3,4,5 A =
d) No; because there are an infinite number of elements between any two elements in set B, we cannot write set B in roster form.
85. Cardinal; 7 tells how many.
86. Ordinal; 25 tells the relative position of the chart.
87. Ordinal; sixteenth tells Lincoln’s relative position. 88. Cardinal; 35 tells how many dollars she spent.
89. Answers will vary.
90. Answers will vary. Examples: The set of elephants that can fly. The set of dogs that can talk. The set of Books that have no pages.
91. Answers will vary.
92. Answers will vary. Here are some examples.
a) The set of men. The set of actors. The set of people over 12 years old. The set of people with two legs. The set of people who have been in a movie.
b) The set of all the people in the world.
Exercise Set 2.2
1. Subset
2. Proper
3. 2 n , where n is the number of elements in the set.
4. 21 n - , where n is the number of elements in the set.
5. True; {} circle is a subset of {} square, circle, triangle
6. True; {} rain is a subset of {} rain, snow, sleet, hail
7. False; potato is not in the second set. 8. False; magazine is not in the second set.
9. True; {} cheesecake, pie is a proper subset of {} pie, cookie, cheesecake, brownie 10. True; {} elm, oak, pine is a proper subset of {} oak, pine, elm, maple
11. False; no subset is a proper subset of itself. 12. False; no set is a proper subset of itself.
13. True; spade is an element of {} diamond, heart, spade, club . 14. True; swimming is an element of {} swimming, sailing, kayaking .
15. False; {} quarter is a set, not an element. 16. False; {} is a set, not an element.
17. True; tiger is not an element of {} zebra, giraffe, polar bear
19. True; {} chair is a proper subset of {} sofa, table, chair
21. False; the set {} Æ contains the element Æ .
23. False; the set {} 0 contains the element 0
25. False; 0 is a number and {} is a set.
27. , BABA ÍÌ
29. , ABAB ÍÌ
31. , BABA ÍÌ
33. ,, ABABBA =ÍÍ
35. {} is the only subset.
37. {}{}{}{} ,cow,horse,cow,horse
39. a) {}{}{}{}{}{}{}{} ,,,,,,,,,,, abcdabacad
{}{}{}{}{} ,,,,,,,,,,,, bcbdcdabcabd {}{}{} ,,,,,,,,, acdbcdabcd
b) All the sets in part (a) are proper subsets of A except {} ,,, abcd
41.False; A could be equal to B .
43.True; every set is a subset of itself.
45.True; Æ is a proper subset of every set except itself.
47.True; every set is a subset of the universal set.
49. True; Æ is a proper subset of every set except itself and U ¹Æ .
51. True; Æ is a subset of every set.
52. False; U is not a subset of Æ .
18. True; the empty set is a subset of every set, including itself.
20. True; {}{} a,b,cc,b,a =
22. True; {} and Æ each represent the empty set.
24. True; the empty set is a subset of every set, including itself.
26. True; the elements of the set are themselves sets.
28. ,, ABABBA =ÍÍ
30. None
32. , BABA ÍÌ
34. , BABA ÍÌ
36. {}{} ,
38. {}{}{}{}{} ,steak,pork,chicken,steak, pork, {}{} steak,chicken,pork, chicken , {} steak, pork, chicken
40.a) 9 2222222222512 =´´´´´´´´= subsets
b) 9 215121511 -=-= proper subsets
42.True; every proper subset is a subset.
44.False; no set is a proper subset of itself.
46.True; Æ is a subset of every set.
48. False; a set cannot be a proper subset of itself.
50. False; the only subset of Æ is itself and U ¹Æ .
53. The number of different variations is equal to the number of subsets of cell phone holder, bluetooth radio, anchor lights, cupholders, depth guage, navigation lights, dinette table, battery charging system, ski mirror ì ü ï ï ï ï í ý ï ï ï ï î þ , which is 9 2222222222512 =´´´´´´´´= .
54. The number of different variations of the house is equal to the number of subsets of { } automatic pool cleaner, solar cover, waterfall, hot tub, fountain, slide, divingboard , which is 7 22222222128 =´´´´´´=
55. The number of options is equal to the number of subsets of {} cucumbers, onions, tomatoes, carrots, green peppers, olives, mushrooms , which is 7 22222222128 =´´´´´´=
56. The number of different variations is equal to the number of subsets of { } call waiting, call forwarding, caller identification, three-way calling, voice mail, fax line , which is 6 222222264 =´´´´´= .
57. EF = since they are both subsets of each other.
58. If there is a one-to-one correspondence between boys and girls, then the sets are equivalent.
59. a) Yes.
b) No, c is an element of set D
c) Yes, each element of {} , ab is an element of set D
60. a) Each person has 2 choices, namely yes or no. 222216 ´´´=
b) YYYY, YYYN, YYNY, YNYY, NYYY, YYNN, YNYN, YNNY, NYNY, NNYY, NYYN, YNNN, NYNN, NNYN, NNNY, NNNN
c) 5 out of 16
61. A one element set has one proper subset, namely the empty set. A one element set has two subsets, namely itself and the empty set. One is one-half of two. Thus, the set must have one element.
62. Yes
63. Yes
64. No
Section 2.3
1. Complement
2. Union
3. Intersection 4. Difference
5. Cartesian
6. Disjoint
7. mn ´
8. Four
9.
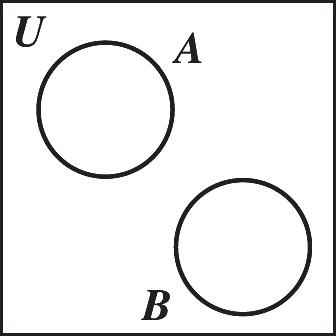
10.

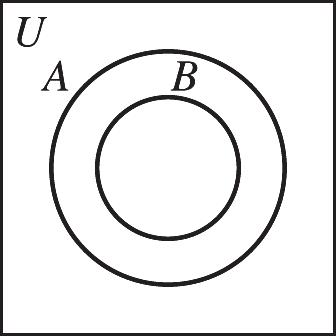

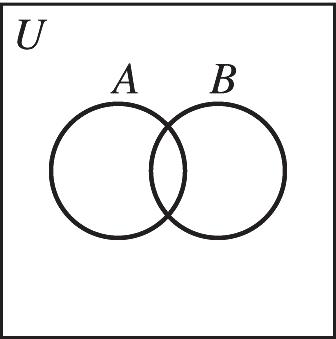
21. The set of retail stores in the United States that do not sell children’s clothing
22. The set of animals in the United States’ zoos that are not in the San Diego Zoo
23. The set of cities in the United States that do not have a professional sports team
24. The set of cities in the United States that do not have a symphony
25. The set of cities in the United States that have a professional sports team or a symphony
26. The set of cities in the United States that have a professional sports team and a symphony
27. The set of cities in the United States that have a professional sports team and do not have a symphony
28. The set of cites in the United States that have a professional sports team or do not have a symphony
29. The set of furniture stores in the U.S. that sell mattresses or leather furniture
30. The set of furniture stores in the U.S. that sell mattresses and outdoor furniture
31. The set of furniture stores in the U.S. that do not sell outdoor furniture and sell leather furniture
32. The set of furniture stores in the U.S. that sell mattresses, outdoor furniture, and leather furniture
33. The set of furniture stores in the U.S. that sell mattresses or outdoor furniture or leather furniture
34. The set of furniture stores in the U.S. that do not sell mattresses or do not sell leather furniture
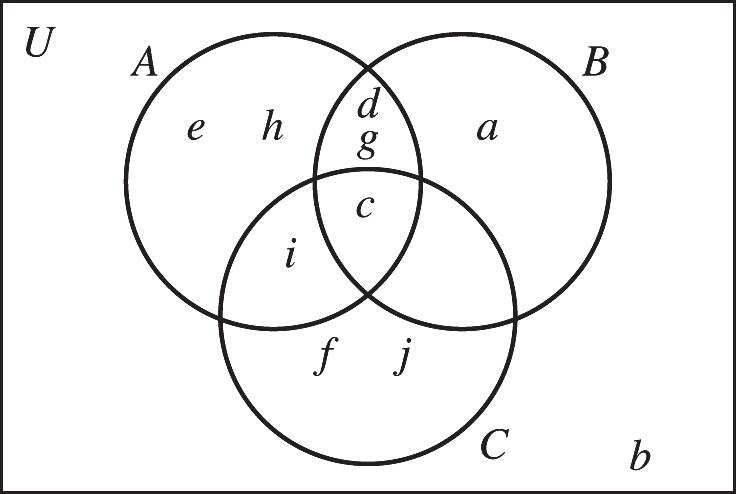
35. {} ,,,,, Aabchtw =
36. {} ,,,,,, Badfghrv =
37. {}{}{} ,,,,,,,,,,,,, ABabchtwadfghrvah Ç=Ç=
38. {} ,,,,,,,,,,,,, Uabcdfghmprtvwz =
39. {}{}{} ,,,,,,,,,,,,,,,,,,,,, ABabchtwadfghrvabcdfghrtvw È=È=
40. (){} : From #39, ,,,,,,,,,,. ABABwbctahfrdgv ¢ ÈÈ= (){}{} ,,,,,,,,,,,, ABabcdfghrtvwmpz ¢¢ È==
41. {}{}{} ,,,,,,,,,,,,,,, ABdfgmprvzbcmptwzmpz ¢¢Ç=Ç=
42. (){}(){}{} : From #37, ,. ,,,,,,,,,,,, ABABahABahbcdfgmprtvwz ¢¢¢ ÇÇ=Ç==
43. {} ,,, ABbctw -=
44. {} , ABah ¢ -=
45. {} 1,2,7,8,9 A =
46. {} 2,3,5,6,9 B =
47. {} 1,2,3,4,5,6,7,8,9,10,11 U =
48. {}{}{} 1,2,7,8,92,3,5,6,92,9 ABÇ=Ç=
49. {}{}{} 3,4,5,6,10,112,3,5,6,92,3,4,5,6,9,10,11 AB ¢ È=È=
50. {1,2,7,8,9}{1,4,7,8,10,11}{1,2,4,7,8,9,10,11} AB ¢ È=È=
51. {}{}{} 3,4,5,6,10,112,3,5,6,93,5,6 AB ¢ Ç=È=
52. (){} 4,10,11 AB ¢ È=
53. {} 4,10,11 AB ¢ -=
54. (){} 2,3,4,5,6,9,10,11 AB ¢ -=
55. {}{}{} 1,2,4,5,72,3,5,61,2,3,4,5,6,7 ABÈ=È=
56. {}{}{} 1,2,4,5,72,3,5,62,5 ABÇ=Ç=
57. (){}(){}{} From #55, 1,2,3,4,5,6,7. 1,2,3,4,5,6,78 ABABAB ¢¢¢ ÈÈ=È==
58. {}{}{}{}{} 1,2,4,5,72,3,5,63,6,81,4,7,88 AB ¢¢ ¢¢Ç=Ç=Ç=
59. ()(){}(){}{}{} : From #57, 8. 82,3,5,6 ABBABABB ¢¢¢ ÈÇÈ=ÈÇ=Ç=
60. ( ) ( ) {} = (The intersection of a set and its complement is always empty.) ABAB ¢ ÈÇÈ
61. () () ()(){} : From #57, 8. BABAABBA ¢¢¢ ¢¢ ÈÇÈÈ=È=
() () {}{}{}{}{}{} ()82,3,5,61,2,4,5,781,4,7,83,6,8 BABA æö ¢¢¢ ÷ ç ¢¢ ÈÇÈ=ÇÈ=ÇÈ ÷ ç ÷ ç èø {}{}{} 81,3,4,6,7,88=Ç=
62. (){} : From #56, 2,5. AABAB ¢ ÈÇÇ=
(){}{}{}{}{} 1,2,4,5,72,53,6,82,52,3,5,6,8 AAB ¢ ¢ ÈÇ=È=È=
63. {}()=2,3,5,6,8 AB ¢ -
64. {} 3,6 AB¢¢ -= For exercises 65-74: {}{}{}{} ,,,,,,,,,,, ,,,,,, ,,,,, ,,,, UabcdefghijkAacdfgiBbcdfgCabfij ====
65. {}{}{} ,,,,,,,,,,,,,,, BCbcdfgabfijabcdfgij È=È=
66. {}{}{} ,,,,,,,,,,, ACacdfgiabfijafi Ç=Ç=
67. {}{} ,,,,,,,,,,. AbehjkBaehijk ¢¢ == {}{}{} ,,,,,,,,,,,,,,, ABbehjkaehijkabehijk ¢¢È=È=
68. (){}(){}{} : From #66, ,,. ,,,,,,,,, ACACafiACafibcdeghjk ¢¢¢ ÇÇ=Ç==
69. ( ) ({}{}) {}{}{} {} ,,,,,,,,,,,,,,,,,,,, ,,,,,,, ABCacdfgibcdfgabfijcdfgabfij abcdfgij ÇÈ=ÇÈ=È =
70. (){}{}{} (),,,,,,,,,,,,, ACBacdfgiabfijbcdfg ¢ ¢ ÈÇ=ÈÇ
{}{} ,,,,,, acdfgibf ¢ =È {}{}{} ,,,,,,,,,,,,,,,,,,,,,, acdfgiacdeghijkacdefghijk =È=
71. () (){}{}{}{} (),,,,,,,,,,,,,,,,,, ACABacdfgiabfijacdfgibcdfg æö ¢ ÷ ç ¢ ÈÈÇ=ÈÈÇ ÷ ç ÷ ç èø ({}{}) {}{}{} ,,,,,,,,,,,,,,,,,,,,, behjkabfijcdfgabefhijkcdfg =ÈÈ=È {} ,,,,,,,,,,, or abcdefghijkU =
72. () () {} : From #70, ,.CBABCBbf ¢ ÇÇÇÇ=
() () {}{}{}{}{}{} (),,,,,,,,,,,,,,,,,,, CBABbfacdfgibcdfgbfbehjkbcdfg æö ¢ ÷ ç ¢ ÇÇÇ=ÇÇ=ÇÇ ÷ ç ÷ ç èø {}{}{} , bfbb=Ç=
73. () {,},{,,,,,,,,},{,,,,} ABaiABbcdefghjkCabfij ¢ -=-==
() {,,,,,} ABCcdeghk ¢ --=
74. () {,,},{,,,,,,,},{,,,,} CAbdjCAacefghikBbcdfg ¢ -=-==
() {,,,,} CABaehik ¢ --=
For exercises 75-80: {}{} 1,2,3and, ABab ==
75. {} (1,),(1,),(2,),(2,),(3,),(3,) ababab
76. {} (,1),(,2),(,3),(,1),(,2),(,3) aaabbb
77. No. The ordered pairs are not the same. For example ()() 1,,1 aa ¹
78. 6
79. 6
80. Yes
81. {}{}{} 1,3,5,7,92,4,6,8 ABÇ=Ç=
82. {}{}{} 1,3,5,7,92,4,6,81,2,3,4,5,6,7,8,9, or ABU È=È=
83. (){}{} ( ) {}{} 2,4,6,81,2,3,4,51,2,3,4,5,6,87,9 BC ¢ ¢ ¢ È=È==
84. {}{}{}{}{} 1,3,5,7,91,2,3,4,51,3,5,7,96,7,8,97,9 AC ¢ ¢ Ç=Ç=Ç=
85. {}{}{}{}{} 1,3,5,7,92,4,6,81,3,5,7,91,3,5,7,91,3,5,7,9, or ABA ¢ ¢ Ç=Ç=Ç=
86. (){}{} ( ) {}{} 2,4,6,81,2,3,4,52,41,3,5,6,7,8,9 BC ¢ ¢ ¢ Ç=Ç==
ACBÈÇ=ÈÇ=Ç=
87. ( ) ({}{}) {}{}{}{} 1,3,5,7,91,2,3,4,52,4,6,81,2,3,4,5,7,92,4,6,82,4
88. (){} : From #81, . ABCAB ¢ ÇÈÇ=
( ) {}{}{}{}{} 1,2,3,4,51,2,3,4,5,6,7,8,91,2,3,4,51,2,3,4,5,6,7,8,9, or ABCU ¢ ¢ ÇÈ=È=È=
89. () {}{}{} 1,3,5,7,92,4,6,81,2,3,4,5
ABC æö ¢¢ ÷ ç ¢¢ÈÇ=ÈÇ ÷ ç ÷ ç èø
({}{}) {}{}{}{} 2,4,6,81,3,5,7,91,2,3,4,51,2,3,4,5,6,7,8,91,2,3,4,51,2,3,4,5, or C =ÈÇ=Ç=
90. () (){} : From #81, . ACABAB ¢ ÇÈÇÇ=
ACAB æö ¢ ÷ ç ¢ ÇÈÇ=ÇÈ=ÇÈ ÷ ç ÷ ç èø =È=
() (){}{}{}{}{} () {} {}{}{} 1,3,5,7,91,2,3,4,52,4,6,81,2,3,4,5 2,42,4
91. A set and its complement will always be disjoint since the complement of a set is all of the elements in the universal set that are not in the set. Therefore, a set and its complement will have no elements in common. For example, if {}{}{}{} 1,2,3,1,2, and 3, then . UAAAA ¢¢ ===Ç=
92. ( ) {}{}{} 0when and are disjoint sets. For example, if 1,2,3,4,5,6,1,3, 2,4, nABABUAB Ç==== then {} ( ) . 0 ABnAB Ç=Ç=
93. Let {}{} customers who owned dogs and customers who owned cats. AB == ( ) ( ) ( ) ( ) 27381649 nABnAnBnABÈ=+-Ç=+-=
94. Let {}{} students who participated in intramurals and students who participated in student council. AB == ( ) ( ) ( ) ( ) () () ( ) 46304 4626 20 nABnAnBnAB nA nA nA È=+-Ç =+=+ =
95. a) {}{}{} ( ) ,,,,,,,,,,,,,,,, 8, ABabcdbdefghabcdefghnAB È=È=È= {}{}{} ( ) ()()() ( ) ( ) ( ) ( ) ,,,,,,,,,,2. 4628 Therefore, . ABabcdbdefghbdnAB nAnBnAB nABnAnBnAB Ç=Ç=Ç= +-Ç=+-= È=+-Ç
b) Answers will vary.
c) Elements in the intersection of A and B are counted twice in ( ) ( ) nAnB +
96. AB ¢ Ç defines Region I. AB Ç defines Region II. AB ¢ Ç defines Region III. ( ) or ABAB ¢ ¢¢ÇÈ defines Region IV.
97. {}{}{} 1,2,3,4,4,8,12,16,1,2,3,4,, or ABA È=È=
98. {}{}{} 1,2,3,4,4,8,12,16,4,8,12,16,, or ABB Ç=Ç=
99. {}{}{} 4,8,12,16,2,4,6,8,2,4,6,8,, or BCC È=È=
100. {}{}{} 4,8,12,16,2,4,6,8,4,8,12,16,, or BCB Ç=Ç=
101. {}{}{} 1,2,3,4,2,4,6,8,2,4,6,8,, or ACC Ç=Ç=
102. {}{}{}{}{} 1,2,3,4,2,4,6,8,02,4,6,8, AC ¢ ¢ Ç=Ç=Ç=
103. ()(){}{} :From #99, . 2,4,6,8,2,4,6,8, BCCBCCBCCCC ¢¢¢ ¢ ÈÈÈ=ÈÈ=È=È {} 0,1,2,3,4,, or U =
104. ()() : From #101, . . ACBACCACBCB ¢¢¢ ÇÇÇ=ÇÇ=Ç {} From #111, 2,6,10,14,18, BCCB ¢¢ Ç=Ç=
105. {} AA ¢ Ç=
107. AA ÈÆ=
109. AUU ¢ È=
111. If ABB Ç= , then BA Í .
113. If , then and are disjoint sets. ABAB Ç=Æ
Exercise Set 2.4
1. 8
2. a) V b) VI
3. a) AB¢¢ Ç b) AB¢¢ È
4. Deductive
106. AAU ¢ È=
108. A ÇÆ=Æ
110. AUA Ç=
112. If , ABB È= then AB Í
114. If , then and . ABAB È=Æ=Æ=Æ
5. '' AB Ç is represented by regions V and VI. If BC Ç contains 12 elements and region V contains 4 elements, then region VI contains 1248 -= elements.
6. AB Ç is represented by regions II and V. If AB Ç contains 9 elements and region V contains 4 elements, then region II contains 945 -= elements.


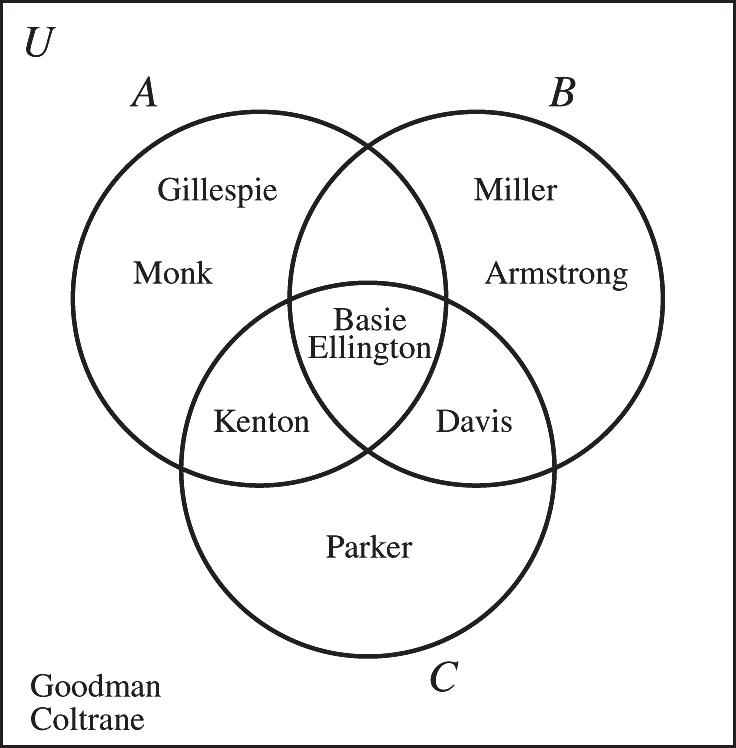
15. Canada, VI
16. United States, VII
17. Greece, V 18. China, I
19. Spain, VIII
20. Turkey, II
21. VI 22. VIII
23. III 24. IV
25. III
26. I
27. V 28. III
29. II
31. VII
30. VIII
32. VI (){} 1,2,3,7,9,10,11,12,13,14 BC ¢ Ç=
33. I 34. VII
35. VIII
37. VI
39. {} 1,3,4,5,9,10 A =
41. {} 4,5,6,8,9,11 C =
43. {} 3,4,5 ABÇ=
45. ( ) {} 1,2,3,7,9,10,11,12,13,14 BC ¢ Ç=
47. (){} 2,7,12,13,14 AC ¢ È=
49. (){} 2,3,4,5,6,7,8,11,12,13,14 AB ¢ -=
36. V
38. III
40. {} 1,2,3,4,5,6,7,8,9,10,11,12,13,14 U =
42. {} 1,2,9,10,11,13 B ¢ =
44. {} 4,5,9 ACÇ=
46. {} 4,5 ABCÇÇ=
48. {}()3,4,5,9ABCÇÈ=
50. {} 2,11,13 AB ¢ -=
51. ( ) AB ¢ Ç
AB¢¢ È
Set Regions Set Regions
A I, II A I, II
B II, III A¢ III, IV
AB Ç II B II, III
( ) AB ¢ Ç I, III, IV B ¢ I, IV
AB¢¢ È I, III, IV
Both statements are represented by the same regions, I, III, IV, of the Venn diagram. Therefore,
()ABAB ¢ Ç=È¢¢ for all sets and .AB
53. AB¢¢ È AB Ç Set Regions Set Regions
A I, II A I, II
A¢ III, IV B II, III
B II, III AB Ç II
B ¢ I, IV
AB¢¢ È I, III, IV
Since the two statements are not represented by the same regions, it is not true that ABAB ¢¢È=Ç for all sets A and B
55. AB¢¢ Ç
AB ¢ È Set Regions Set Regions
A I, II A I, II
A¢ III, IV B II, III
B II, III B ¢ I, IV
B ¢ I, IV
AB¢¢ Ç IV
AB ¢ È I, II, IV
Since the two statements are not represented by the Same regions, it is not true that ABAB ¢¢¢ Ç=È for all sets and .AB
52. ( ) AB ¢ Ç AB ¢ È Set Regions Set Regions
A I, II A I, II
B II, III A¢ III, IV
AB Ç II B II, III
( ) AB ¢ Ç I, III, IV AB ¢ È II, III, IV
Since the two statements are not represented by the same regions, it is not true that ( ) ABAB ¢ ¢ Ç=È for all sets A and B
54. AB¢¢ È ( ) AB ¢ È Set Regions Set Regions
A I, II A I, II
A¢ III, IV B II, III
B II, III ( ) AB ¢ È I, II, IV
B ¢ I, IV
AB¢¢ È I, III, IV
Since the two statements are not represented by the same regions, it is not true that ()ABAB ¢ ¢¢È=È for all sets A and B.
56. AB¢¢ Ç AB ¢ È Set Regions Set Regions
A I, II A I, II
A¢ III, IV B II, III
B II, III B ¢ I, IV
AB ¢ Ç III
( ) AB ¢ ¢ Ç I, II, IV
AB ¢ È I, II, IV
Both statements are represented by the same regions, I, II, IV, of the Venn diagram. Therefore, ( ) ABAB ¢ ¢¢ Ç=È for all sets and .AB
57. ( ) ABC ÇÈ ()ABC ÇÈ
Set Regions Set Regions
B II, III, V, VI A I, II, IV, V
C IV , V, VI, VII B II, III, V, VI
BC È II, III, IV, V, VI, VII AB Ç II, V
A I, II, IV, V C IV, V, VI, VII ( ) ABC ÇÈ II, IV, V ( ) ABC ÇÈ II, IV, V, VI, VII
Since the two statements are not represented by the same regions, it is not true that ( ) ( ) ABCABC ÇÈ=ÇÈ for all sets ,, and . ABC
58. ( ) ABC ÈÇ ( ) BCA ÇÈ
Set Regions Set Regions
B II, III, V, VI B II, III, V, VI
C IV , V, VI, VII C IV, V, VI, VII
BC Ç V, VI BC Ç V, VI
A I, II, IV, V A I, II, IV, V ( ) ABC ÈÇ I, II, IV, V, VI ( ) BCA ÇÈ I, II, IV, V, VI
Both statements are represented by the same regions, I, II, IV, V, VI, of the Venn diagram. Therefore, ( ) ( ) ABCBCA ÈÇ=ÇÈ for all sets ,, and . ABC
59. ( ) ABC ÇÈ ( ) BCA ÈÇ
Set Regions Set Regions
B II, III, V, VI B II, III, V, VI
C IV , V, VI, VII C IV, V, VI, VII
BC È II, III, IV, V, VI, VII BC È II, III, IV, V, VI, VII
A I, II, IV, V A I, II, IV, V ( ) ABC ÇÈ II, IV, V ( ) BCA ÈÇ II, IV, V
Both statements are represented by the same regions, II, IV, V, of the Venn diagram. Therefore, ( ) ( ) ABCBCA ÇÈ=ÈÇ for all sets ,, and . ABC
60. ( ) ABC ¢ ÈÇ ()ABC ¢¢ÇÈ
Set Regions Set Regions
B II, III, V, VI B ¢ I, IV, VII, VIII
C IV , V, VI, VII C IV, V, VI, VII
BC Ç V, VI
BC ¢ È I, IV, V, VI, VII, VIII
( ) BC ¢ Ç I, II, III, IV, VII, VIII A I, II, IV, V
A I, II, IV, V A¢ III, VI, VII, VIII
( ) ABC ¢ ÈÇ I, II, III, IV, V, VII, VIII ()ABC ¢¢ÇÈ VI, VII, VIII
Since the two statements are not represented by the same regions, it is not true that () ()ABCABC ¢ ¢¢ ÈÇ=ÇÈ for all sets ,, and . ABC
61. ( ) ABC ÇÈ ( ) ( ) ABAC ÇÈÇ
Set Regions Set
Regions
B II, III, V, VI A I, II, IV, V
C IV, V, VI, VII B II, III, V, VI
BC È II, III, IV, V, VI, VII AB Ç II, V
A I, II, IV, V C IV, V, VI, VII
( ) ABC ÇÈ II, IV, V AC Ç IV, V
( ) ( ) ABAC ÇÈÇ II, IV, V
Both statements are represented by the same regions, II, IV, V, of the Venn diagram. Therefore, ( ) ( ) ( ) ABCABAC ÇÈ=ÇÈÇ for all sets ,, and . ABC
62. ( ) ABC ÈÇ ( ) ( ) ABAC ÈÇÈ
Set Regions Set
Regions
B II, III, V, VI A I, II, IV, V
C IV, V, VI, VII B II, III, V, VI
BC Ç V, VI
AB È I, II, III, IV, V, VI
A I, II, IV, V C IV, V, VI, VII
( ) ABC ÈÇ I, II, IV, V, VI AC È I, II, IV, V, VI, VII
( ) ( ) ABAC ÈÇÈ I, II, IV, V, VI
Both statements are represented by the same regions, I, II, IV, V, VI, of the Venn diagram. Therefore, ( ) ( ) ( ) ABCABAC ÈÇ=ÈÇÈ for all sets ,, and . ABC
63. ( ) ( ) ABBC ÈÇÈ ( ) BAC ÈÇ
Set Regions Set Regions
A I, II, IV, V A I, II, IV, V
B II, III, V, VI C IV, V, VI, VII
AB È I, II, III, IV, V, VI AC Ç IV, V
C IV, V, VI, VII B II, III, V, VI
BC È II, III, IV, V, VI, VII ( ) BAC ÈÇ II, III, IV, V, VI
( ) ( ) ABBC ÈÇÈ II, III, IV, V, VI
Both statements are represented by the same regions, II, III, IV, V, VI, of the Venn diagram. Therefore, ( ) ( ) ( ) ABBCBAC ÈÇÈ=ÈÇ for all sets ,, and . ABC
64. ( ) ABC ¢ ÈÇ ( ) ( ) ACBC ¢¢ ÈÇÈ
Set
Regions
Set
Regions
A I, II, IV, V A I, II, IV, V
B II, III, V, VI A¢ III, VI, VII, VIII
AB È I, II, III, IV, V, VI C IV, V, VI, VII
( ) AB ¢ È VII, VIII
AC ¢ È III, IV, V, VI, VII, VIII
C IV, V, VI, VII B II, III, V, VI
( ) ABC ¢ ÈÇ VII B ¢ I, IV, VII, VIII
BC ¢ È I, IV, V, VI, VII, VIII ( ) ( ) ACBC ¢¢ ÈÇÈ IV, V, VI, VII, VIII
Since the two statements are not represented by the same regions, it is not true that () ( ) ( ) ABCACBC ¢ ¢¢ ÈÇ=ÈÇÈ for all sets ,, and . ABC
65. ( ) AB ¢ È
66. () AB ¢ Ç
67. ( ) ABC ¢ ÈÇ
68. ()() ABBC ÇÈÇ
AB AB ¢ Ç=Ç= ¢¢ ==
¢¢È=
69. a) () {3,6},{1,2,4,5,7,8} {4,5,7,8},{1,2,4,5,8}
{1,2,4,5,7,8}
Both equal {1,2,4,5,7,8} ABAB
b) Answers will vary.
¢¢ ==
71.
AbcdfBbcdefh
¢¢Ç=
Both equal {,,,} ABaeghijABbcdf
70. a) () {,,,,,},{,,,} {,,,},{,,,,,} {,,,}
ABbcdf bcdf ¢ È=È=
b) Answers will vary.
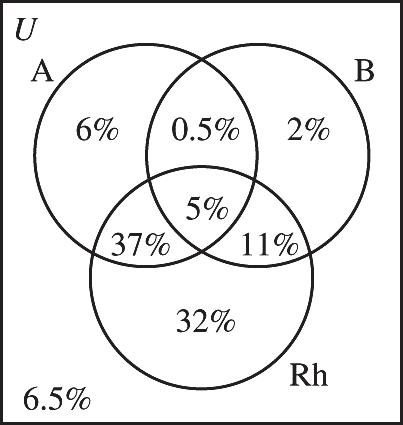
72. Region Set Region Set
I
II
III
IV
ABC ÇÇ¢¢ V
ABC ¢ ÇÇ VI
ABC ¢¢ ÇÇ VII
ABC ¢ ÇÇ VIII
ABC ÇÇ
ABC ¢ ÇÇ
ABC ¢¢ÇÇ
ABC ¢¢¢ ÇÇ
73. a) A : Office Building Construction Projects, B : Plumbing Projects, C : Budget Greater Than $300,000
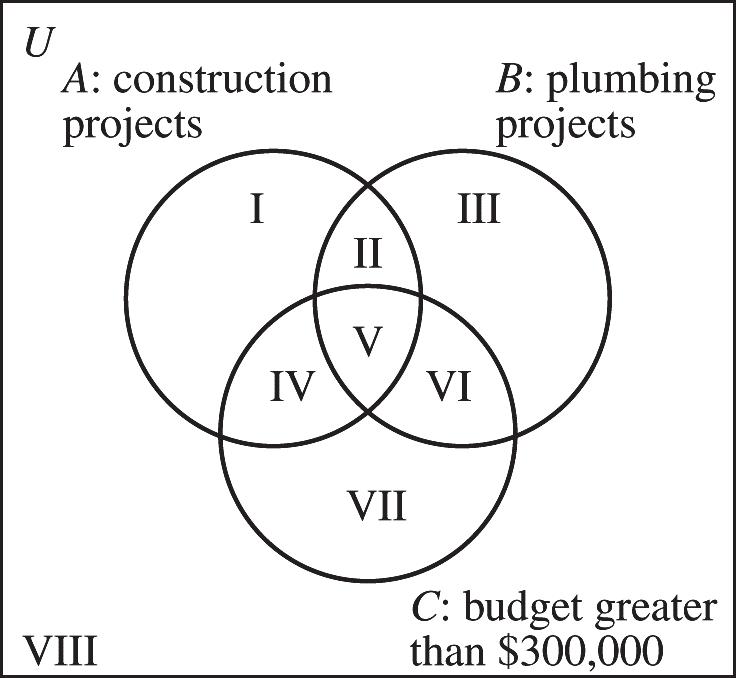
b) Region V; ABC ÇÇ
c) Region VI; ABC ¢ ÇÇ
d) Region I; ABC ÇÇ¢¢
74. ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 nABCnAnBnCnABCnABCnABCnABC ¢¢¢ ÈÈ=++-ÇÇ-ÇÇ-ÇÇ-ÇÇ
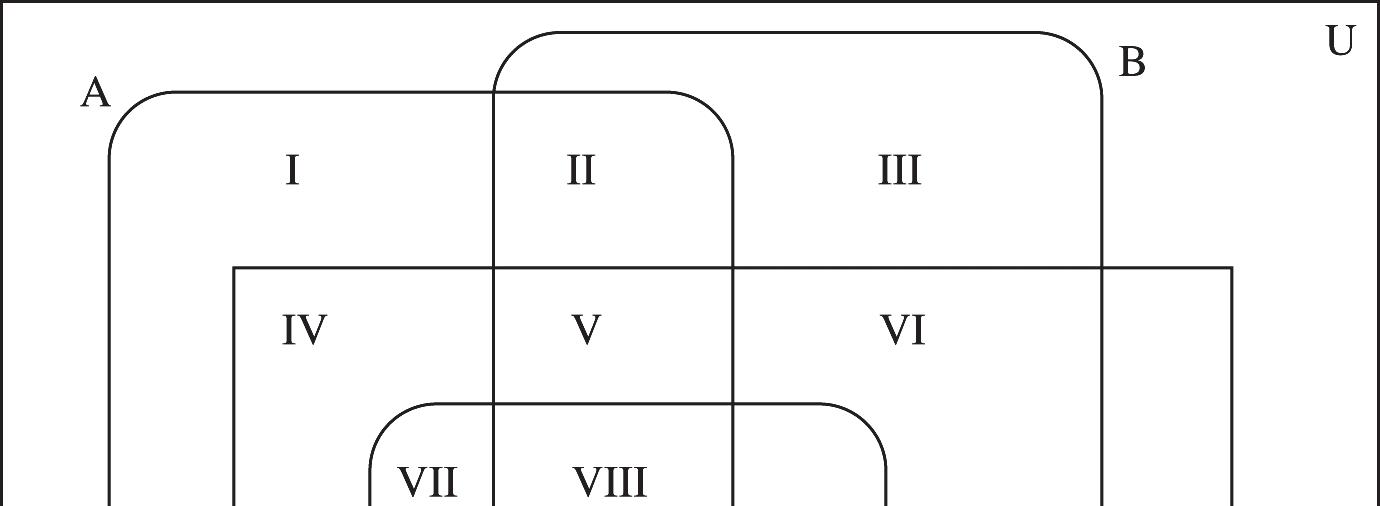
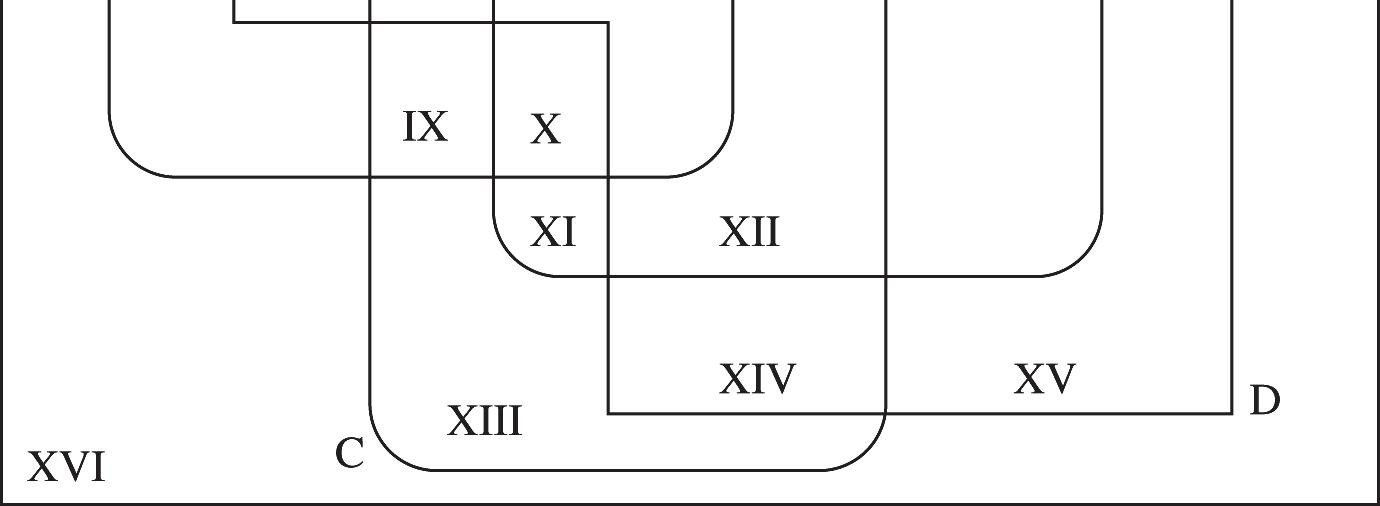
Region Set Region Set
I ABCD ÇÇÇ¢¢¢ IX
II
III
IV
V
VI
VII
VIII
Exercise Set 2.5 1. U 432219 16 Donuts Coffee a) 43 b) 19
ABCD ÇÇÇ¢¢ X
ABCD ¢¢¢ ÇÇÇ XI
ABCD ¢¢ ÇÇÇ XII
ABCD ¢ ÇÇÇ XIII
ABCD ¢¢ ÇÇÇ XIV
ABCD ¢ ÇÇÇ XV
ABCD ÇÇÇ XVI
c) 100(432219), -++ or 16
ABCD ÇÇÇ¢¢
ABCD ¢ ÇÇÇ
ABCD ¢¢ ÇÇÇ
ABCD ¢ ÇÇÇ
ABCD ¢¢¢ ÇÇÇ
ABCD ¢¢ÇÇÇ
ABCD ¢¢¢ ÇÇÇ
ABCD ¢¢¢¢ ÇÇÇ
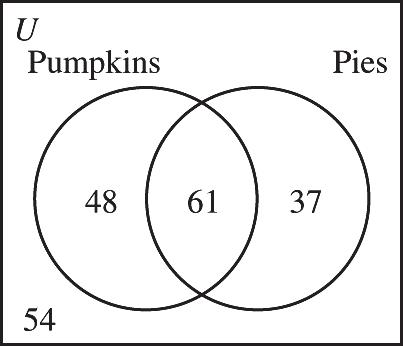
a) 48 b) 37 c) 200(486137), -++ or 54
a) 12 b) 17
c) 64, the sum of the numbers in Regions I, II, III
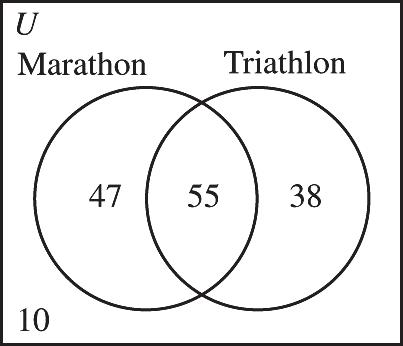
a) 47 b) 38
c) 140, the sum of the numbers in Regions I, II, III
d) 150140, - or 10.
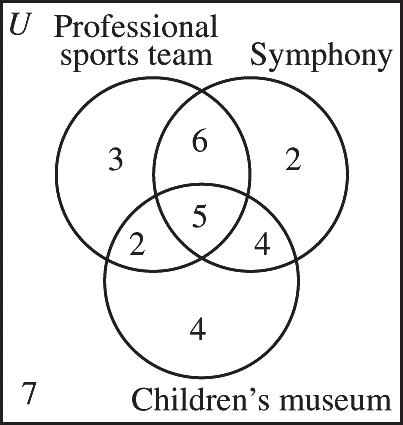
a) 3 b) 6
a) 11 b) 113016, ++ or 57
c) 11630371216, ++++++ or 85
d) 3612, ++ or 21
e) 7
c) 326524, +++++ or 22
d) 362, ++ or 11
e) 264, ++ or 12 7.

a) 20 b) 121
c) 1218340, ++ or 244
d) 163811, ++ or 65
e) 3502040, or 290

a) 22 b) 11
c) 85156, or 64
d) 221117, ++ or 50
e) 9113, ++ or 23
9.
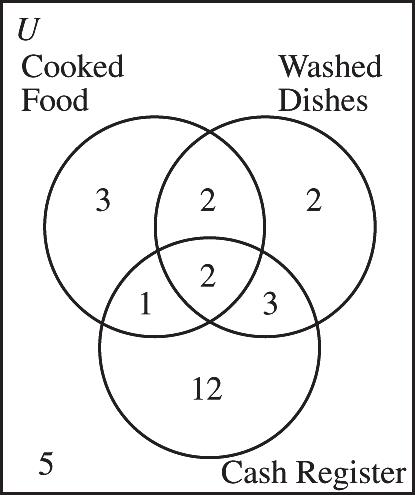
a) 3 b) 12
c) 3
d) 1232, ++ or 17 e) 1232,or8 +++
11.
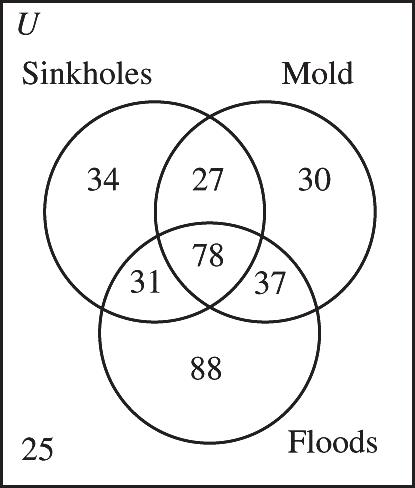
a) 3037, + or 67
b) 3502588, or 237
c) 37 d) 25
13. The Venn diagram shows the number of cars driven by women is 37, the sum of the numbers in Regions II, IV, V. This exceeds the 35 women the agent claims to have surveyed.
10. U iPad Laptop
26 Gaming system 3129 68 132 71 14 125
a) 496, the sum of the numbers in all the regions
b) 132 c) 29
d) 13212571, ++ or 328
e) 49626, - or 470
12. No. The sum of the numbers in the Venn diagram is 99. Dennis claims he surveyed 100 people.
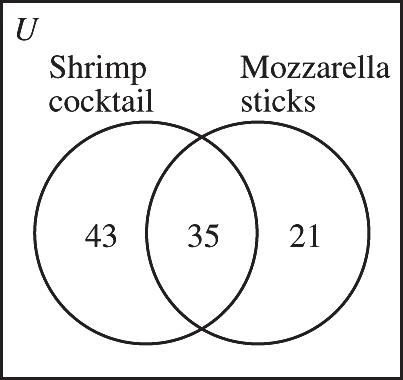
14. First fill in 15, 20 and 35 on the Venn diagram. Referring to the labels in the Venn diagram and the given information, we see that 140 125 18515170 ac bc abc += += ++=-=
Adding the first two equations and subtracting the third from this sum gives 12514017095. c =+-=
Then 45 a = and 30. b = Then 21045952050. d =---= We now have labeled all the regions except the region outside the three circles, so the number of parks with at least one of the features is 15452030955035, ++++++ or 290. Thus the number with none of the features is 300290, - or 10.
a) 290
b) 95
c) 10
d) 304550, ++ or 125.

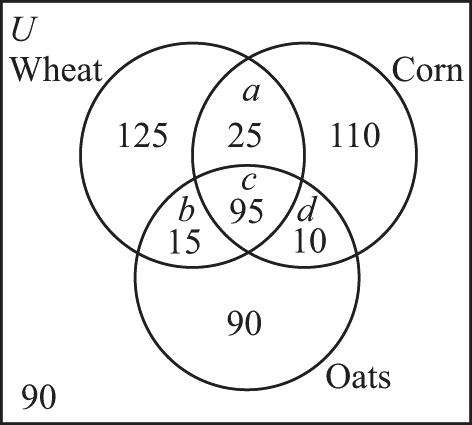
15. First fill in 125, 110, and 90 on the Venn diagram. Referring to the labels in the Venn diagram and the given information, we see that 60 50 20012575 ac bc abc += += ++=-=
Adding the first two equations and subtracting the third from this sum gives 60507535. c =+-=
Then 25 a = and 15. b = Then 180110253510. d =---= We now have labeled all the regions except the region outside the three circles, so the number of farmers growing at least one of the crops is 1252511015351090, ++++++ or 410. Thus the number growing none of the crops is 500410, - or 90.
a) 410
b) 35
c) 90
d) 152510, ++ or 50
16. 16
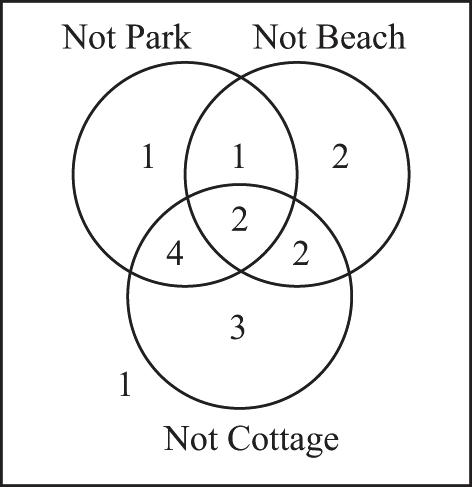
17. From the given information we can generate the Venn diagram. First fill in 4 for Region V. Then since the intersections in pairs all have 6 elements, we can fill in 2 for each of Regions II, IV, and VI. This already accounts for the 10 elements , ABC ÈÈ so the remaining 2 elements in U must be in Region VIII.
a) 10, the sum of the numbers in Regions I, II, III, IV, V, VI
b) 10, the sum of the numbers in Regions III, IV, V, VI, VIII
c) 6, the sum of the numbers in Regions I, III, IV, VI, VIII
Exercise Set 2.6
1. Infinite
2. Countable
3. {2, 3, 4, 5, 6, …, n + 1, …}
{3, 4, 5, 6, 7, …, n + 2, …}
5. {3, 5, 7, 9, 11, …, 2n + 1, …}
↓ ↓ ↓ ↓ ↓ ↓
{5, 7, 9, 11, 13, …, 2n + 3, …}
7. {5, 7, 9, 11, 13 …, 2n + 3, …}
↓ ↓ ↓ ↓ ↓ ↓ {9, 11, 13, 15, …, 2n + 5, …}
9. 111111 ,,,,,,, 2468102 n ìü ïï ïï íý ïï ïï îþ ↓ ↓ ↓ ↓ ↓ 11111 ,,,,,, 4681022 n ìü ïï ïï íý ïï + ïï îþ
4. {20, 21,22, 23, 24, …, n + 19, …}
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
{21, 22, 23, 24, 25, …, n + 20, …}
6. {10, 12, 14, 16, 18, …, 2n + 8, …}
↓ ↓ ↓ ↓ ↓ ↓
10. 11111 1,,,,,,, 2345 n ìü ïï ïï íý ïï ïï îþ ↓ ↓ ↓ ↓ ↓ ↓ 111111 ,,,,,,, 234561 n ìü ïï ïï íý ïï + ïï îþ U AB I II III 2 V IV 4 VI 2 2 2 C VII VIII
{12, 14, 16, 18, 20, …, 2n + 10, …}
8. {5, 9, 13, 17, 21, …, 4n + 1, …} ↓ ↓ ↓ ↓ ↓ ↓ {9, 13, 17, 21, 25, …, 4n + 5, …}
Copyright © 2017 Pearson Education, Inc.
11. 45673 1111111111,,,,,, n ìü + ïï ïï íý ïï ïï îþ ↓ ↓ ↓ ↓ ↓ 56784 1111111111,,,,,, n ìü + ïï ïï íý ïï ïï îþ
13. {1, 2, 3, 4, 5, …, n, …}
↓ ↓ ↓ ↓ ↓ ↓
{2, 4, 6, 8, 10, …, 2n, …}
15. {1, 2, 3, 4, 5, …, n, …}
↓ ↓ ↓ ↓ ↓ ↓
{3, 5, 7, 9, 11, …, 2n + 1, …}
17. {1, 2, 3, 4, 5, …, n, …}
↓ ↓ ↓ ↓ ↓ ↓
{2, 5, 8, 11, 14, …, 3n 1, …}
19. {1, 2, 3, 4, 5, …, n , …}
↓ ↓ ↓ ↓ ↓ ↓ 111111 ,,,,,,, 36912153n ìü ïï ïï íý ïï ïï îþ
21. { 1, 2, 3, 4, 7, …, n, …}
↓ ↓ ↓ ↓ ↓ ↓ 111111 ,,,,,,, 345672 n ìü ïï ïï íý ïï + ïï îþ
23. {1, 2, 3, 4, 5, …, n, …} ↓ ↓ ↓ ↓ ↓ ↓
{1, 4, 9, 16, 25, …, 2 n , …}
25. {1, 2, 3, 4, 5, …, n, …}
12. 6789105 ,,,,,,, 131313131313 n ìü + ïï ïï íý ïï ïï îþ ↓ ↓ ↓ ↓ ↓ ↓ 78910116 ,,,,,,, 131313131313 n ìü + ïï ïï íý ïï ïï îþ
14. {1, 2, 3, 4, 5, …, n, …}
↓ ↓ ↓ ↓ ↓ ↓
{30, 31, 32, 33, 34, …, n + 29, …}
16. {1, 2, 3, 4, 5, …, n, …}
↓ ↓ ↓ ↓ ↓ ↓ {4, 6, 8, 10, 12, …, 2n + 2, …}
18. {1, 2, 3, 4, 5, …, n, …}
↓ ↓ ↓ ↓ ↓ ↓
{7, 11, 15, 19, 23, …, 4n + 3, …}
20. { 1, 2, 3, 4, 5, …, n, …} ↓ ↓ ↓ ↓ ↓ ↓ 111111 ,,,,,,, 2468102 n ìü ïï ïï íý ïï ïï îþ
22. {1, 2, 3, 4, 5, …, n, …}
↓ ↓ ↓ ↓ ↓ ↓ 12345 ,,,,,,, 234561 n n ìü ïï ïï íý ïï + ïï îþ
24. {1, 2, 3, 4, 5, …, n, …} ↓ ↓ ↓ ↓ ↓ ↓
{2, 4, 8, 16, 32, …, 2 n , …}
26. { 1, 2, 3, 4, 5, …, n, …} ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
{3, 9, 27, 81, 243, …, 3n , …} 1 111111 ,,,,,,, 36122448 32 nìü ïï ïï íý ïï ´ ïï îþ
27. = 28. = 29. = 31. = 30. = 32. a) Answers will vary. b) No
Review Exercises
1. True
3. True
5. False; the elements 6, 12, 18, 24, … are members of both sets.
7. False; the two sets do not contain exactly the same elements.
9. True
11. True
13. True
15. {} 7,9,11,13,15 A =
17. {} 1,2,3,4,,174 C =
19. {} and 50150AxxNx =Î<< or {| in and 51 149} AxxNx =≤≤
21. {} and 7 CxxNx=Î<
2. False; the word best makes the statement not well-defined.
4. False; no set is a proper subset of itself.
6. True
8. True
10. True
12. True
14. True
16. {} Colorado, Nebraska, Missouri, Oklahoma B =
18. {} 9,10,11,12,,80 D =
20. {} and 42 BxxNx=Î>
22. {} and 2751DxxNx =룣
23. A is the set of capital letters in the English alphabet from E through M, inclusive. 24. B is the set of U.S. coins with a value of less than one dollar.
25. C is the set of the first three lowercase letters in the English alphabet.
26. D is the set of numbers greater than or equal to 3 and less than 9.
ABÇ=Ç=
27. {}{}{} 1,3,5,73,7,9,103,7
28. {}{}{}{}{} 1,3,5,73,7,9,101,3,5,71,2,4,5,6,81,2,3,4,5,6,7,8 AB ¢ ¢ È=È=È=
29. {}{}{}{}{} 1,3,5,73,7,9,102,4,6,8,9,105,7,9,109,10 AB ¢ ¢ Ç=Ç=Ç=
30. (){}{} () {}{}{} 1,3,5,73,7,9,101,7,101,3,5,7,9,101,7,10 ABC ¢ ¢¢ ÈÈ=ÈÈ=È {}{}{} 2,4,6,81,7,101,2,4,6,7,8,10=È=
31. {}{}{} 1,3,5,73,7,9,101,5 AB-=-=
32. {}{}{}{}{} ,, 1,3,5,71,7,101,3,5,72,3,4,5,6891,7 AC ¢ ¢ -=-=-=
33. {} (1,1),(1,7),(1,10),(3,1),(3,7),(3,10),(5,1),(5,7),(5,10),(7,1), (7,7),(7,10)
34. { } (3,1),(3,3),(3,5),(3,7),(7,1),(7,3),(7,5),(7,7),(9,1),(9,3),(9, 5),(9,7),(10,1),(10,3),(10,5),(10,7)
35. 4 2222216 =´´´=
36. ( ) 4 212222116115 -=´´´-=-=
Copyright © 2017 Pearson Education, Inc.
37.
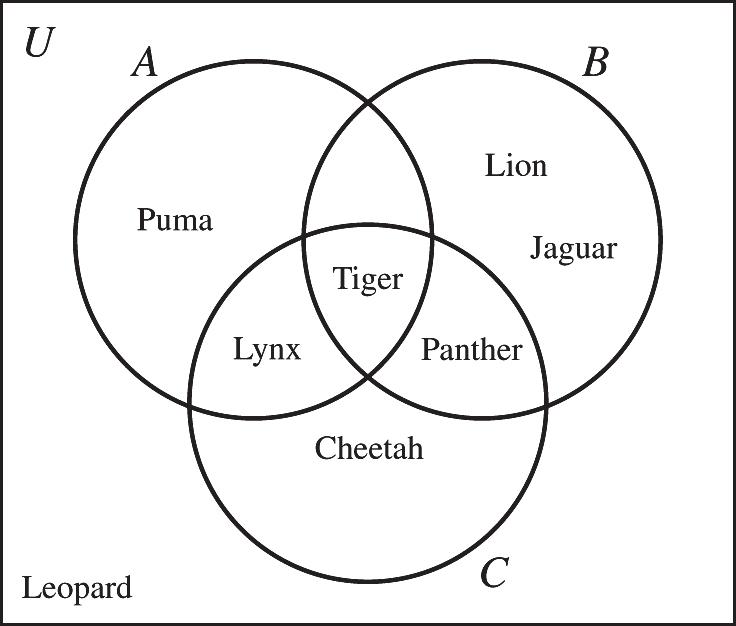
44. ( ) AB ¢ ¢¢ È AB Ç
Set Regions Set Regions
A I, II A I, II
A¢ III, IV B II, III
B II, III AB Ç II
B ¢ I, IV
AB¢¢ È I, III, IV
( ) AB ¢ ¢¢ È II
38. {} ,,,,,,, ACbcdefhkl È=
39. {} , ABek ¢ Ç=
40. {} ,,,, , ,, ,, ABCabcdefghkl ÈÈ=
41. {}ABCf ÇÇ=
42. (){} ,, ABCcef ÈÇ=
43. {} ,, ABdfl ¢ -=
Both statements are represented by the same region, II, of the Venn diagram. Therefore, ( ) ABAB ¢ ¢¢È=Ç for all sets and .AB
45. ( ) ( ) ABAC ÈÈÈ¢¢ ( ) ABC ¢ ÈÇ
Set Regions Set Regions
A I, II, IV, V B II, III, V, VI
B II, III, V, VI C IV, V, VI, VII
B ¢ I, IV, VII, VIII BC Ç V, VI
AB ¢ È I, II, IV, V, VII, VIII ( ) BC ¢ Ç I, II, III, IV, VII, VIII
C IV, V, VI, VII A I, II, IV, V
C ¢ I, II, III, VIII ( ) ABC ¢ ÈÇ I, II, III, IV, V, VII, VIII
AC ¢ È I, II, III, IV, V, VIII
( ) ( ) ABAC ÈÈÈ¢¢ I, II, III, IV, V, VII, VIII
Both statements are represented by the same regions, I, II, III, IV, V, VII, VIII, of the Venn diagram. Therefore, ( ) ( ) ()ABACABC ¢ ¢¢ ÈÈÈ=ÈÇ for all sets ,, and . ABC
46. II 47. III
48. I
50. IV
52. II
53. The company paid $450 since the sum of the numbers in Regions I through IV is 450.
54. a) 131, the sum of the numbers in Regions I through VIII
b) 32, Region I
c) 10, Region II
d) 65, the sum of the numbers in Regions I, IV, VII

55. a) 128, Region I
b) 264, the sum of the numbers in Regions I, III, VII
c) 40, Region II
d) 168, the sum of the numbers in Regions III, VI
e) 99, the sum of the numbers in Regions II, IV, VI
56. {2, 4, 6, 8, 10, …, 2n, …}
{4, 6, 8, 10, 12, …, 2n + 2, …}
58. {1, 2, 3, 4, 5, …, n, …}
{5, 8, 11, 14, 17, …, 3n + 2, …}
Chapter Test
49. IV
51. II
57. {3, 5, 7, 9, 11, …, 2n + 1, …}
{5, 7, 9, 11, 13, …, 2n + 3, …}
59. {1, 2, 3, 4, 5, …, n, …}
{4, 9, 14, 19, 24, …, 5n - 1, …}
1. True 2. False; the sets do not contain exactly the same elements.
3. True
5. False; the set has 4 2222216 =´´´= subsets.
7. False; for any set A , {} , not . AAU ¢ È=
9. {} 1,2,3,4,5,6,7,8,9,10,11 A =
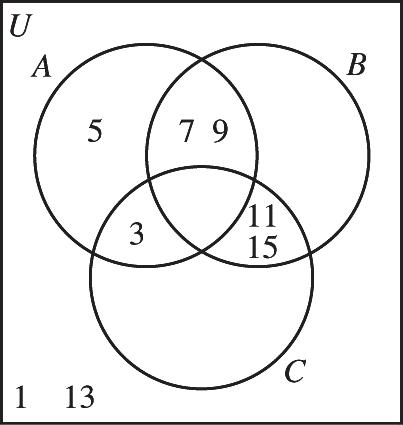
11. {}{}{} 3,5,7,97,9,11,157,9 ABÇ=Ç=
4. False; the second set does not contain the element 7.
6. True
8. True
10. Set A is the set of natural numbers less than 12.
12. {}{}{}{}{} 3,5,7,93,11,153,5,7,91,5,7,9,131,3,5,7,9,13 AC ¢ ¢ È=È=È=
13. () {}{}{} () {}{}{} 3,5,7,97,9,11,151,5,7,9,133,5,7,97,97,9 ABC ¢ ÇÇ=ÇÇ=Ç=
14. () {}{}{}{} () {} () 3,5,7,97,9,11,153,5,7,91,3,5,153,52nABnnn æö ¢ ÷ ç ¢ Ç=Ç=Ç== ÷ ç
AB-=-=
15. {}{}{} 3,5,7,97,9,11,153,5
16. { } (3,3),(3,11),(3,15),(5,3),(5,11),(5,15),(7,3),(7,11),(7,15),(9, 3),(9,11),(9,15)
17.
AC´=
18. ( ) ABC ¢ ÇÈ
Set Regions
Set
( ) ( ) ABAC ¢ ÇÈÇ
Regions
B II, III, V, VI A I, II, IV, V
C IV, V, VI, VII B II, III, V, VI
C ¢ I, II, III, VIII
AB Ç II, V
BC ¢ È I, II, III, V, VI, VIII C IV, V, VI, VII
A I, II, IV, V C ¢ I, II, III, VIII
( )
ABC ¢ ÇÈ I, II, V
AC ¢ Ç I, II
( ) ( ) ABAC ¢ ÇÈÇ I, II, V
Both statements are represented by the same regions, I, II, V, of the Venn diagram. Therefore, ( ) ( ) ( ) ABCABAC ÇÈ=ÇÈÇ¢¢ for all sets ,, and . ABC
20. {7, 8, 9, 10, 11, …, n+ 6, …}
{8, 9, 10, 11, 12, …, n + 7, …}
Copyright © 2017 Pearson Education, Inc. 19.
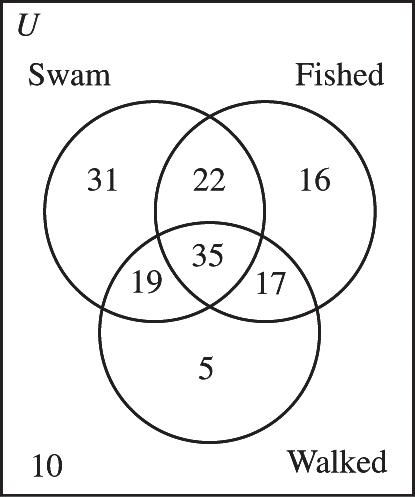
a) 58, the sum of the numbers in Regions II, IV, VI
b) 10, Region VIII
c) 145, the sum of the numbers in all regions except VIII
d) 22, Region II
e) 69, the sum of the numbers in Regions I, II, III
f) 16, Region III
