Issuu

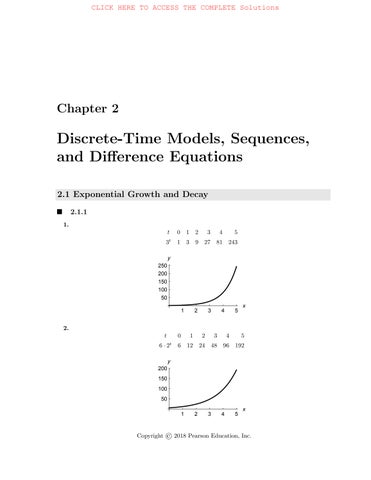
2.1ExponentialGrowthandDecay

5. Sincethepopulationdoublesevery20minutes,and20minutesistheunitoftime,theformulais Nt = N0 2t.Sincethereareinitially N0 =2individuals,weget Nt

6. Sincethepopulationdoublesevery40minutes,and40minutesistheunitoftime,theformulais Nt = N0 2t.Sincethereareinitially N0 =4individuals,weget

7. Sincethepopulationdoublesevery40minutes,but80minutesistheunitoftime,thepopulation willquadrupleinonetimeunit,sothattheformulais Nt = N0 4t.Sincethereisinitially N0 =1 individual,weget Nt =4t

8. At t =0thepopulationis20 · 40 =20;wewanttodetermine t sothat20 · 4t =2 · 20,sothatwe want4t =2.Thus t = 1 2 ,sothepopulationdoublesafter 1 2 timeunits,or1 5hours.

9. At t =0thepopulationis100 2t =100;wewanttodetermine t sothat100 2t =3 100,sothat wewant2t =3.Thus t = ln3 ln2 ≈ 1 585,sothepopulationtriplesafterabout1 585timeunits,or 1 585 · 2 ≈ 3 17hours,orabout190minutes.

10. Theinitialpopulationis10,andthepopulationtriplesinsizeeverytimeunit,sotheformulais Nt =10 3t

11. Sinceeachcellsplitsintwoeachhour,thepopulationdoubleseachhour.Sincetherewasonecell attime t =0,theformulais Nt =2t: t 012345

2t 12481632

12. Sinceeachcellsplitsintwoevery30minutes,thepopulationdoublesevery30minutes.Lettingthe timeunitbe30minutes,sincetherewasonecellattime t =0,theformulais Nt =2t.Wewant toknowthepopulationafter1,2,3,4,and5hours;thesecorrespondsto t =2, 4, 6, 8, 10:

t 0246810

2t 1416642561024

Onecouldalternativelytakethetimeunitasonehour,inwhichcasetheformulawouldbe Nt =4t .

13. Lettheunitoftimebe42minutes;thensincethedoublingtimeisoneunit,startingfromone bacteriumtheformulais Nt =2t.Then Nt =1024when2t =1024,sowhen t =10.Sinceone timeunitrepresents42minutes,thisis420minutes=7hrs.

14. Lettheunitoftimebe24minutes;thensincethedoublingtimeisoneunit,startingfromone bacteriumtheformulais Nt =2t.Then Nt =512when2t =512,sowhen t =9.Sinceonetime unitrepresents24minutes,thisis24 9=216minutes=3hrs36min.

15. Lettheunitoftimebe10minutes;thensincethedoublingtimeisoneunit,startingfrom5bacteria theformulais Nt =5 2t.Then Nt =320when5 2t =320,or2t =64,sowhen t =6.Sinceone timeunitrepresents10minutes,thisis60minutes=1hr.

16. Lettheunitoftimebe12minutes;thensincethedoublingtimeisoneunit,startingfrom10 bacteriatheformulais Nt =10 2t.Then Nt =160when10 2t =160,or2t =16,sowhen t =4. Sinceonetimeunitrepresents12minutes,thisis48minutes.

17. Sincethepopulationdoubleseveryunitoftime,theequationis Nt = N0 · 2t;sinceinitiallythere are40individuals,wehave N0 =40sothat Nt =40 2t

18. Sincethepopulationhalvesinsizeeveryunitoftime,theequationis Nt = N0 1 2 t;sinceinitially thereare1024individuals,wehave N0 =1024sothat Nt =1024 1 2

10 2

=210 t.Of course,thisisvalidonlyupto t =10,sinceafterthatwearecountingfractionalindividuals.

19. Thereproductiverateis4,sowehave

Thereforethepopulationquintupleseveryunitoftime,sotheequationis Nt = N0 5t;sinceinitially thereare20individuals,theequationis Nt =20 5t .

20. Sincethepopulationtripleseveryunitoftime,theequationis Nt = N0 3t;sinceinitiallythereare 72individuals,wehave N0 =72sothat Nt =72 3t .

21. Sincethepopulationquadrupleseveryunitoftime,theequationis Nt = N0 4t;sinceinitiallythere are5individuals,wehave N0 =5sothat Nt =5 4t

22. Sincethepopulationgrowsby50%,or 3 2 ,everyunitoftime,theequationis N

3 2 t;since initiallythereare32individuals,wehave N0 =32sothat N

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

2.1.2

23. Sincethepopulationdoubleseveryunitoftime,therecursionis Nt+1 =2Nt.(Thecorresponding equationis Nt = N0 2t;sinceinitiallythereare11individuals,wehave N0 =11sothat Nt =11 2t.)

24. Sincethepopulationtripleseveryunitoftime,therecursionis Nt+1 =3Nt.(Thecorresponding equationis Nt = N0 · 3t;sinceinitiallythereare6individuals,wehave N0 =6sothat Nt =6 · 3t.)

25. Sincethepopulationquadrupleseveryunitoftime,therecursionis Nt+1 =4Nt.(Thecorresponding equationis Nt = N0 4t;sinceinitiallythereare30individuals,wehave N0 =30sothat Nt =30 4t.)

26. Thereproductiverateis 1 3 ,sowehave

Therecursionis Nt+1 = 4 3 Nt.(Thecorrespondingequationis Nt = N0 4 3 t;sinceinitiallythere are63individuals,theequationis Nt =63 · 4 3 t.)

2.1.3

27. Thecurveisplottedbelowwiththepointssuperimposedonit:

28. Thecurveisplottedbelowwiththepointssuperimposedonit:

29. Thecurveisplottedbelowwiththepointssuperimposedonit:

30. Thecurveisplottedbelowwiththepointssuperimposedonit:

31. Nt+1 =2Nt with N0 =3,for t =0, 1, 2, 3, 4, 5. t 012345 N (t)3612244896

Ingeneral, Nt =2tN0;since N0 =3weget Nt =3 · 2t

32. Nt+1 =2Nt with N0 =5,for t =0, 1, 2, 3, 4, 5. t 012345 N (t)510204080160

Ingeneral, Nt =2tN0;since N0 =5weget Nt =5 2t .

33. Nt+1 =3Nt with N0 =2,for t =0, 1, 2, 3, 4, 5. t 012345 N (t)261854162486

Ingeneral, Nt =3tN0;since N0 =2weget Nt =2 3t

34. Nt+1 =3Nt with N0 =7,for t =0, 1, 2, 3, 4, 5. t 012345 N (t)721631895671701

Ingeneral, Nt =3tN0;since N0 =7weget Nt =7 · 3t

35. Nt+1 =5Nt with N0 =1,for t =0, 1, 2, 3, 4, 5. t 012345 N (t)15251256253125

Ingeneral, Nt =5tN0;since N0 =1weget Nt =1 5t =5t .

36. Nt+1 =7Nt with N0 =4,for t =0, 1, 2, 3, 4, 5. t 012345 N (t)4281961372960467228

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

37. Nt+1 = 1 2 Nt with N0 =640,for t =0, 1, 2, 3, 4, 5. t 012345 Nt 640320160804020

Ingeneral, Nt = 1 2 t N0;since N0 =640weget Nt =640 1 2 t

38. Nt+1 = 3 2 Nt with N0 =32,for t =0, 1, 2, 3, 4, 5. t 012345 Nt 324872108162243

Ingeneral, Nt = 3 2 t N0;since N0 =32weget Nt =32 3 2 t

39. Nt+1 = 1 3 Nt with N0 =1215,for t =0, 1, 2, 3, 4, 5. t 012345 Nt 121540513545155

Ingeneral, Nt = 1 3 t N0;since N0 =1215weget Nt =1215 · 1 3 t

40. Nt+1 = 1 3 Nt with N0 =2430,for t =0, 1, 2, 3, 4, 5. t 012345 Nt 2430810270903010

Ingeneral, Nt = 1 3 t N0;since N0 =2430weget Nt =2430 1 3 t .

41. Nt+1 = 1 5 Nt with N0 =31250,for t =0, 1, 2, 3, 4, 5. t 012345 N (t)31250625012502505010

Ingeneral, Nt = 1 5 t N0;since N0 =31250weget Nt =31250 · 1 5 t

42. Nt+1 = 1 4 Nt with N0 =8192,for t =0, 1, 2, 3, 4, 5. t 012345 N (t)81922048512218328

Ingeneral, Nt = 1 4 t N0;since N0 =8192weget Nt =8192 1 4 t = 1

43. Since Nt+1 = RNt =2Nt and N0 =2,theformulais Nt =2 2t =2t+1.Agraphof Nt+1 =2Nt in the Nt-Nt+1 plane,withthepoints(Nt,Nt+1)superimposedonitfor t =0, 1, 2,isbelow: 2 4 6 8 Nt 4 8 12 16 Nt+1

44. Since Nt+1 = RNt =2Nt and N0 =3,theformulais Nt =3 · 2t.Agraphof Nt+1 =2Nt inthe Nt-Nt+1 plane,withthepoints(Nt,Nt+1)superimposedonitfor t =0, 1, 2,isbelow:

45. Since Nt+1 = RNt =3Nt and N0 =1,theformulais Nt =3t.Agraphof Nt+1 =3Nt inthe Nt-Nt+1 plane,withthepoints(Nt,Nt+1)superimposedonitfor t =0, 1, 2,isbelow:

Nt+1

46. Since Nt+1 = RNt =4Nt and N0 =2,theformulais Nt =2 · 4t.Agraphof Nt+1 =4Nt inthe Nt-Nt+1 plane,withthepoints(Nt,Nt+1)superimposedonitfor t =0, 1, 2,isbelow:

47. Since Nt+1 = RNt = 1 2 Nt and N0 =16,theformulais Nt =16 · 1 2 t.Agraphof Nt+1 = 1 2 Nt in the Nt-Nt+1 plane,withthepoints(Nt,Nt+1)superimposedonitfor t =0, 1, 2,isbelow:

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

48. Since Nt+1 = RNt = 1 2 Nt and N0 =64,theformulais Nt =64 1 2 t.Agraphof Nt+1 = 1 2 Nt in the Nt-Nt+1 plane,withthepoints(Nt,Nt+1)superimposedonitfor t =0, 1, 2,isbelow:

49. Since Nt+1 = RNt = 1 3 Nt and N0 =81,theformulais Nt =81 1 3 t.Agraphof Nt+1 = 1 3 Nt in the Nt-Nt+1 plane,withthepoints(Nt,Nt+1)superimposedonitfor t =0, 1, 2,isbelow:

50. Since Nt+1 = RNt = 1 4 Nt and N0 =16,theformulais Nt =16 · 1 4 t.Agraphof Nt+1 = 1 4 Nt in the Nt-Nt+1 plane,withthepoints(Nt,Nt+1)superimposedonitfor t =0, 1, 2,isbelow:

51. Since Nt+1 = RNt =2Nt and N0 =2,theformulais Nt =2 · 2t.Agraphof Nt+1 Nt 1= R 1=1in the NtNt+1 Nt 1plane,withthepoint N0, N1 N0 1 superimposedonit,isbelow.Thereproductive rateisthenumberoforganismsaddedperparentfromtime t totime t +1,whichis Nt+1 Nt 1= R 1=1.

4 6 8

52. Since Nt+1 = RNt =2Nt and N0 =4,theformulais Nt =4 · 2t.Agraphof Nt+1 Nt 1= R 1=1in

the NtNt+1 Nt 1plane,withthepoint N0, N1 N0 1 superimposedonit,isbelow.Thereproductive rateisthenumberoforganismsaddedperparentfromtime t totime t +1,whichis Nt+1 Nt 1= R 1=1.

53. Since Nt+1 = RNt =3Nt and N0 =2,theformulais Nt =2 3t.Agraphof Nt+1 Nt 1= R 1=2in the NtNt+1 Nt 1plane,withthepoint N0, N1 N0 1 superimposedonit,isbelow.Thereproductive rateisthenumberoforganismsaddedperparentfromtime t totime t +1,whichis Nt+1 Nt 1= R 1=2.

54. Since Nt+1 = RNt =4Nt and N0 =1,theformulais Nt =4t.Agraphof Nt+1 Nt 1= R 1=3inthe NtNt+1 Nt 1plane,withthepoint N0, N1 N0 1 superimposedonit,isbelow.Thereproductiverate isthenumberoforganismsaddedperparentfromtime t totime t+1,whichis Nt+1 Nt 1= R 1=3.

3 4 Nt+ Nt - 1

55. Since Nt+1 = RNt = 1 2 Nt and N0 =16,theformulais Nt =16 1 2 t.Agraphof Nt+1 Nt 1= R 1= 1 2 inthe NtNt+1 Nt 1plane,withthepoint N0, N1 N0 1 superimposedonit,isbelow. Thereproductiverateisthenumberoforganismsaddedperparentfromtime t totime t +1,which is Nt+1 Nt 1= R 1= 1 2 10.20.30.40. 50. Nt -1. Nt+1 Nt - 1

56. Since Nt+1 = RNt = 1 2 Nt and N0 =128,theformulais Nt =128 · 1 2 t.Agraphof Nt+1 Nt 1= R 1= 1 2 inthe NtNt+1 Nt 1plane,withthepoint N0, N1 N0 1 superimposedonit,isbelow.

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

Thereproductiverateisthenumberoforganismsaddedperparentfromtime t totime t +1,which is Nt+1 Nt 1= R 1= 1 2

t+1 Nt - 1

100.200. 300. Nt -1.

57. Since Nt+1 = RNt = 1 3 Nt and N0 =27,theformulais Nt =27 · 1 3 t.Agraphof Nt+1 Nt 1=

R 1= 2 3 inthe NtNt+1 Nt 1plane,withthepoint N0, N1 N0 1 superimposedonit,isbelow. Thereproductiverateisthenumberoforganismsaddedperparentfromtime t totime t +1,which is Nt+1 Nt 1= R 1= 2 3 25.50.75. 100. Nt -1. Nt+1 Nt - 1

58. Since Nt+1 = RNt = 1 4 Nt and N0 =64,theformulais Nt =64 · 1 4 t.Agraphof Nt+1 Nt 1=

R 1= 3 4 inthe NtNt+1 Nt 1plane,withthepoint N0, N1 N0 1 superimposedonit,isbelow. Thereproductiverateisthenumberoforganismsaddedperparentfromtime t totime t +1,which is Nt+1 Nt 1= R 1= 3 4 .

50.100.150. 200. Nt

Forexercises59—61,whichrefertoFigure2.9,notethattheﬁrstgraphinFigure2.9describesapopulationwithaconstantreproductiverate,soitrepresentsexponentialgrowth.Inthesecondpopulation, thereproductiveratedecreasestowardszero,sothat Nt+1 Nt 1decreasestozero.Thismeansthat Nt+1 Nt decreasestowards1,sothatthepopulationeventuallybecomesconstant(atthecarryingcapacity).In thethirdgraph, Nt+1 Nt 1increasestosomeconstant,sothat Nt+1 Nt doesaswell.Thisreﬂectsapopulation thateventuallygrowsexponentiallysincethereproductiverateiseventuallyessentiallyconstant.

59. (a) Thepopulationwillgrowquicklyatﬁrst(highreproductiverate),butasitgrows,therewillbe lesssugarforeachindividual,sothegrowthratewillslowandeventuallystop;thepopulation willstabilize.Thisisthesecondgraph.

(b) Asthehabitatislarge,thepopulationwillgrowexponentially(intheabsenceofpredators), atleastuntilsomeenvironmentalconstraintsareencountered.Thisistheﬁrstgraph.

60. (a) Thispopulationwillexhibitexponentialgrowthsince(atleastintheshortterm)thereareno environmentalconstraints.Thisistheﬁrstgraph.

(b) Whilethereareasmallnumberoflionssothatpreyisplentiful,thegrowthratewillbehigh. Asthepopulationincreases,however,theamountofpreyavailableperindividualdecreases, sothepopulationlevelsoﬀatthecarryingcapacity.Thisisthesecondgraph.

61. (a) Asthepopulationofcellsgetslarger,theycanacquireadditionalresourcesthroughmetastasis, socancontinuetogrow.Thisisthethirdgraph.

(b) Thenumberofsickindividualsﬁrstexpandsrapidlyasthereisalargepoolofuninfected individuals.Asthoseresources(wellindividuals)becomescarce,thegrowthrateslowsdown andeventuallystops.Thisisgraph2.

62. (a) Therecursionis Nt+1 = 3 2 Nt,sincethepopulationgrowsby50%eachyear.Thustheformula is Nt = N1 3 2 t 1 (notethatweuse t 1ratherthan t sinceattime1wewanttohave N1 individuals).Further, N1 =16.sotheformulais Nt =16 3 2 t 1

(b) Thepopulationsizeis100when100=16 3 2 t 1,sothat 3 2 t 1 = 25 4 .Thisgives (t 1)ln 3 2 =ln 25 4 ⇒ t 1= ln25 ln4 ln3 ln2 ⇒ t =1+ ln25 ln4 ln3 ln2 ≈ 5 52years

(c) Thepopulationsizeis1000when1000=16 3 2 t 1,sothat 3 2 t 1 = 125 2 .Thisgives (t 1)ln 3 2 =ln 125 2 ⇒ t 1= ln125 ln2 ln3 ln2 ⇒ t =1+ ln125 ln2 ln3 ln2 ≈ 11 2years

(d) Accordingtothemodel,thepopulationsizeis1000000when1000000=16 3 2 t 1,sothat 3 2 t 1 =62500.Thisgives

(t 1)ln 3 2 =ln62500 ⇒ t 1= ln62500 ln3 ln2 ⇒ t =1+ ln62500 ln3 ln2 ≈ 28 2years

Themodelisunlikelytobevalidforsuchalargepopulationunlesstheislandisverylargeor thebirdsrequirelittlespace(andfood).

2.2Sequences

2.2.1

1. With an = n +1,weget n 012345 an 123456

2. With an =3n2,weget n 012345 an 0312274875

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

3. With an = n+2 n ,weget n 012345 an undeﬁned32

4. With an = n n+2 ,weget n 012345 an 0 1 3 1 2

5. WIth f (n)= 1 (1+n)2 ,wehave u 012345

6. With an = 1 √n+1 ,weget n 012345

7. With f (n)=(n +1)2,wehave n 012345 f (n)149162536

8. With f (n)=(n +4)1/3,weget n 012345

9. With an =( 1)n +( 1)n+1,notethatif k iseventhen( 1)k =1,whileif k isoddthen( 1)k = 1. Sinceexactlyoneof n and n +1isevenandtheotherisodd,thesumiszero,sothat an =0for all n

10. With an =( 1)n +1,notethatif n iseventhen( 1)n =1,whileif n isoddthen( 1)n = 1.It followsthat an =1+1=2if n isevenand an = 1+1=0if n isodd: n 012345 an 202020

11. With an = n 2 n+1 ,weget n 012345

12. With an = n3√n +1,weget n 012345

13. With f (n)= en/2,weget n 012345

14. With f (n)=log(n +1),weget n 012345 f (n)0log2log3log4log5log6

15. With f (n)= 1 3 n,wehave n 012345 f (n)1 1 3 1 9 1 27 1 81 1 243

16. With f (n)=20 2n,weget n 012345

17. Thisappearstobethesequenceofsquaresofintegers, an =(n +1)2 for n =0, 1, 2,....Then a5 =36, a6 =49, a7 =64,and a8 =81.

18. Thisappearstobethesequence an = √n,for n =0, 1, 2, 3, 4.Thusfor n =5, 6, 7, 8wehave an = √5, √6, √7, √8.

19. Thisappearstobethesequence an = 1 n+1 for n =0, 1, 2,....Then a5 = 1

20. Thisappearstobethesequence an = ( 1)n+1 (n+1)2 ,for n =0, 1, 2, 3, 4.Thusfor n =5, 6, 7, 8wehave an = 1 36 , 1 49 , 1 64 , 1 81

21. Thisappearstobethesequence an = n+1 n+2 ,for n =0, 1, 2, 3, 4.Thusfor n =5, 6, 7, 8wehave an = 6 7 , 7 8 , 8 9 , 9 10 .

22. Notethateachtermisonemorethanasquare.Thisappearstobethesequence an =(n +2)2 +1= n2 +4n +5.Thusfor n =5, 6, 7, 8wewouldget50,65,82,and101.

23. Thisappearstobethesequence an = (n +1)+ en+1,for n =0, 1, 2, 3, 4.Thusfor n =5, 6, 7, 8 wehave an = √6+ e6 , √7+ e7 ,

24. Thisappearstobesuccessivepowersof3: an =3n for n =0, 1, 2,....Then a5 =243, a6 =729, a7 =2187,and a8 =6561.

25. Thegivensequenceis a0 =0,a1 =1,a2 =2,a3 =3and a4 =4.Thuswecanguesstheexpression tobe an = n for n =0, 1, 2,...

26. Thegivensequenceis a0 =0,a1 =2,a2 =4,a3 =6and a4 =8.Thuswecanguesstheexpression tobe an =2n for n =0, 1, 2,...

27. Thegivensequenceis a0 =1,a1 =2,a2 =4,a3 =8and a4 =16.Thuswecanguessthe expressiontobe an =2n for n =0, 1, 2,...

28. Thegivensequenceis a0 =1,a1 =3,a2 =5,a3 =7and a4 =9.Thuswecanguesstheexpression tobe an =2n +1for n =0, 1, 2,....

29. Thegivensequenceis a0 =1,a1 = 1 3 ,a2 = 1 9 ,a3 = 1 27 and a4 = 1 81 .Thuswecanguessthe expressiontobe an = 1 3n for n =0, 1, 2,....

30. Thegivensequenceis a0 = 1 3 ,a1 = 2 5 ,a2 = 3 7 ,a3 = 4 9 and a4 = 5 11 .Thuswecanguessthe expressiontobe an = n+1 2n+3 for n =0, 1, 2,...

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

31. Thegivensequenceis a0 = 1,a1 =2,a2 = 3,a3 =4and a4 = 5.Thuswecanguessthe expressiontobe an =( 1)n+1(n +1)for n =0, 1, 2,...

32. Thegivensequenceis a0 =9, a1 =16, a2 =25, a3 =36,and a4 =49.Wecanguesstheexpression tobe an =(n +3)2 for n =0, 1, 2,...

33. Thegivensequenceis a0 =5, a1 =7, a2 =9, a3 =11,and a4 =13.Wecanguesstheexpression tobe an =2n +5for n =0, 1, 2,...

34. Thegivensequenceis a0 =8, a1 =18, a2 =32, a3 =50,and a4 =72.Notethat 1 2 an =(n +2)2 forthegivenvaluesof n,soweguessthesequencetobe an =2(n +2)2 for n =0, 1, 2,....

35. Thegivensequenceis a0 =2, a1 =0, a2 =2, a3 =0,and a4 =2.Recallingexercise10inthis section,wecanwritethisas an =( 1)n +1.

36. Thegivensequenceisrepetitionsofthesequence0, 1, 2.Onewayofdeﬁning an isthatitisthe remainderupondividing n by3.

2.2.2

37. Wegetthefollowingsequencefor an+1 = √an +1and a0 =1:

n 01234567891011

an 11.4141.5541.5981.6121.6161.6171.6181.6181.6181.

38. Wegetthefollowingsequencefor an+1 = 1 an+1 and a0 =2: n 012345678910

an 20.33330.750.57140.63640.61110.62070.61700.61840.61790.6181

n 111213

an 0 61800 61800 6180

39. Wegetthefollowingsequencefor an+1 = an 1 an and a0 =3:

n 012345678

an 32 6672 2921 8551 3160 557 1 240 0 4341 873

n 91011

an 1 3390 592 1 095

40. Wegetthefollowingsequencefor an+1 = an + 1 an and a0 =2:

n 012345678910

an 122 52 93 2453 5533 8344 0954 3394 5704 789

n 111213

an 4.9985.1985.390

41. Wegetthefollowingsequencefor an+1 = √an +1and a0 =6:

n 012345678910

an 6 0001 8571 5371 4971 4911 4901 4901 4901 4901 4901 490

n 1112

42. Wegetthefollowingsequencefor an+1 = an + 1 a2 n and a0 =1: n 012345678910

an 122 252 4482 6142 7612 8923 0123 1223 2243 321 n 1112 an 3 4113 497

43. Wegetthefollowingsequencefor an+1 = 1 4 an +1and a0 =0: n 012345678910

an 011 251 3131 3281 3321 3331 3331 3331 3331 333 n 11121314

an 1.3331.3331.3331.333

44. Wegetthefollowingsequencefor an+1 = a2 n +1and a0 =1: n 012345678910

an 11 4141 73222 2362 4492 6462 8283 0003 1623 317 n 111213141516 an 3.4643.6063.7423.87344.123

2.2.3

45. Weget

46. Weget

n→∞

47. Weget a0 =0, a1

sobylimitlaw4,

48. Weget a0 =0, a

.Now,

Toseetheﬁnalequality,notethatlimn→∞ 2=2andbylimitlaw9,limn

2 n =0.Sinceboth theselimitsexistandareﬁnite,limitlaw5thenimpliestheresult.Finally,bylimitlaw9,

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

49. Weget a0 =5, a1 =3, a2 = 9 5 , a3 = 7 5 , a4 = 21 17 ,and a5 = 15 13 .Now,

Bylimitlaw9,limn→∞ 4 n2+1 =0,sowecanbreakupthelimitabovebylimitlaw1:

50. Weget a0 =1, a1 = 1 √2 , a2 = 1 √3 , a3 = 1 2 , a

,bylimitlaw9weget

51. a0 isundeﬁned,and a1 = 1, a2 = 1 2 ,

andthatbylimitlaw9,limn→∞ |an| =0.Sincethe an havelimitzeroinabsolutevalue,the an themselvesmustalsohavelimitzero.

52. Weget a0 = 1 3 , a1 = 1 4 , a2 = 1 11 , a3 = 1 30 , a4 = 1 67 ,and a5 = 1 128 .Notethat |an| = 1 n3+3 , andthatbylimitlaw9,limn→∞ |an| =0.Sincethe an havelimitzeroinabsolutevalue,the an themselvesmustalsohavelimitzero.

53. Wehave a0 =0, a1 = 1 2 , a2 = 4 3 , a3 = 9 4 ,and a4 = 16 5 .Now,

Byanargumentsimilartothatgiveninthetextforﬁndinglimn→∞ n+1 n weseethatthelatter termhaslimit2,whilelimn→∞(n +1)= ∞,sothelimitofthesequenceis ∞.

54. Wehave a0 = 1 2 , a1 = 2 3 , a2 = 3 4 , a3 = 4 5 ,and a4 = 5 6 .Now,

Applyinglaws9and1giveslimn→∞ 1 1 n+2 =limn→∞ 1=1.

55. Wehave a0 =0, a1 =1, a2 = √2, a3 = √3,and a4 =2.Sincethetermsgrowwithoutboundas n →∞,weseethatlimn→∞ √n = ∞

56. Wehave a0 =3, a1 =4, a2 =7, a3 =12,and a4 =19.Sincethetermsgrowwithoutboundas n →∞,weseethatlimn→∞(n2 +3)= ∞.

57. Wehave a0 =1, a1 =2, a2 =4, a3 =8,and a4 =16.Sincethetermsgrowwithoutboundas n →∞,weseethatlimn→∞ 2n = ∞.

58. Wehave a0 =8, a1 =16, a2 =32, a3 =64,and a4 =128.Sincethetermsgrowwithoutboundas n →∞,weseethatlimn→∞ 2n+3 = ∞.

59. Wehave a0 =1, a1 =3, a2 =9, a3 =27,and a4 =81.Sincethetermsgrowwithoutboundas n →∞,weseethatlimn→∞ 3n = ∞.

60. Wehave a0 =1, a1 = 1 9 , a2 = 1 81 , a3 = 1 729 ,and a4 = 1 6561 .Further, lim n→∞ 3 2n =lim n→∞ 1 9n ; since9n growswithoutboundas n →∞,itfollowsthatlimn→∞ 9n = ∞,sobylimitlaw9, limn→∞ 3 2n =0.

61. With an = 1 n ,since n growswithoutboundas n →∞,itfollowsthatlimn→∞ an =0.Now,we needtoﬁndaninteger N suchthat 1 n 0 < =0 01whenever n>N .Solvingtheinequality

1 n 0 < 0 01forpositive n,weget 1 n < 0 01or n> 1 0 01 =100.Thusthesmallestvalueof N thatwecanchooseis N =100.Andindeed a101 = 1 101 ≈ 0.00990 < 0.01.

62. With an = 1 n ,since n growswithoutboundas n →∞,itfollowsthatlimn→∞ an =0.Now,we needtoﬁndaninteger N suchthat 1 n 0 < =0.02whenever n>N .Solvingtheinequality

1 n 0 < 0 02forpositive n,weget 1 n < 0 02or n> 1 0 02 =50.Thusthesmallestvalueof N that wecanchooseis N =50.Andindeed a51 = 1 51 ≈ 0 0196 < 0 02

63. With an = 1 n2 ,since n2 growswithoutboundas n →∞,itfollowsthatlimn→∞ an =0.Now,we needtoﬁndaninteger N suchthat 1 n2 0 < =0 01whenever n>N .Solvingtheinequality

1 n2 0 < 0 01weget 1 n2 < 0 01or n2 > 1 0 01 =100.Thisgives n> 10,sothesmallestvalueof N thatwecanchooseis N =10.Andindeed

a11 = 1 121 ≈ 0.008 < 0.01.

64. With an = 1 n2 ,since n2 growswithoutboundas n →∞,itfollowsthatlimn→∞ an =0.Now,we needtoﬁndaninteger N suchthat 1 n2 0 < =0.001whenever n>N .Solvingtheinequality

1 n2 0 < 0.001weget 1 n2 < 0.001or n2 > 1 0 001 =1000.Thisgives n> √1000 ≈ 31.62,sothe smallestvalueof N thatwecanchooseis N =31.Andindeed a32 = 1 322 = 1 1024 ≈ 0 0009766 < 0 001

65. With an = 1 √n ,since √n growswithoutboundas n →∞,itfollowsthatlimn→∞ an =0.Now,we needtoﬁndaninteger N suchthat 1 √n 0 < =0 1whenever n>N .Solvingtheinequality

1 √n 0 < 0 1weget 1 √n < 0 1or √n> 1 0 1 =10.Thisgives n> 100,sothesmallestvalueof N thatwecanchooseis N =100.Andindeed a101 = 1 √101 ≈ 0 0995 < 0 1

66. With an = 1 √n ,since √n growswithoutboundas n →∞,itfollowsthatlimn→∞ an =0.Now,we needtoﬁndaninteger N suchthat 1 √n 0 < =0 05whenever n>N .Solvingtheinequality

1 √n 0 < 0 05weget 1 √n < 0 05or √n> 1 0 05 =20.Thisgives n> 400,sothesmallestvalueof N thatwecanchooseis N =400.Andindeed a401 = 1 √401 ≈ 0 04994 < 0 05

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

67. With an = ( 1)n n ,since n growswithoutboundas n →∞,itfollowsthatlimn→∞ an =0.Now, weneedtoﬁndaninteger N suchthat ( 1)n n 0 = ( 1)n n = 1 n < =0 01whenever n>N.

Solvingtheinequality 1 n < 0 01weget n> 100,sothesmallestvalueof N thatwecanchooseis N =100.Andindeed |a101 0| = ( 1)11 11 ≈ 0.0099 < 0.01.

68. With an = e n = 1 en ,since en growswithoutboundas n →∞,itfollowsthatlimn→∞ an =0. Thuswewanttoﬁndaninteger N suchthat |e n 0| = |e n| < =0 01whenever n>N .Since e n isalwayspositive,thisisequivalenttosayingthat e n < 0 01for n>N .Takingnaturallogs gives n< ln0.01 ≈−4.61,sothat n> 4.62.Sotaking N =4(thatis, n ≥ 5)willsuﬃce.And indeed e 5 ≈ 0.0067 < 0.01.

69. With an = e 3n = 1 e3n ,since e3n growswithoutboundas n →∞,itfollowsthatlimn→∞ an =0. Thuswewanttoﬁndaninteger N suchthat e 3n 0 = e 3n < =0 001whenever n>N Since e 3n isalwayspositive,thisisequivalenttosayingthat e 3n < 0 001for n>N .Taking naturallogsgives 3n< ln 0 001 ≈−6 91,sothat n> 6 91 3 ≈ 2 30.Sotaking N =2(thatis, n ≥ 3)willsuﬃce.Andindeed e 3 3 ≈ 0 00012 < 0 001.

70. Wehave an =ln 1+ 1 n .Sincelimn→∞ 1+ 1 n =1bylimitlaws9and1,itfollowsthat limn→∞ ln 1+ 1 n =limn→∞ ln1=0.Thuswewanttoﬁndaninteger N suchthat ln 1+ 1 n 0 = ln 1+ 1 n < =0.1whenever n>N.

Since1+ 1 n > 1for n> 0,itfollowsthatln 1+ 1 n > 0,sowecanremovetheabsolutevaluesigns andsolveln 1+ 1 n < 0.1.Exponentiatebothsides,giving1+ 1 n = e0 1,sothat n = 1 e0 1 1 ≈ 9.51. Sotaking N =9(thatis, n ≥ 10)willsuﬃce.Andindeedln 1+ 1 10 ≈ 0 095 < 0 1.

71. With an =2 n = 1 2n ,since2n growswithoutboundas n →∞,itfollowsthatlimn→∞ an =0. Thuswewanttoﬁndaninteger N suchthat |2 n 0| = |2 n| < =0 01whenever n>N .Since 2 n isalwayspositive,thisisequivalenttosayingthat2 n < 0 01for n>N .Takingnaturallogs gives n ln2 < ln0 01,sothat n> ln100 ln2 ≈ 6 64.Sotaking N =6(thatis, n ≥ 7)willsuﬃce.And indeed2 7 ≈ 0.007 < 0.01.

72. Wehave an =log 1+ 2 n2 .Sincelimn→∞ 1+ 2 n2 =1bylimitlaws9and1,itfollowsthat limn→∞ log 1+ 2 n2 =limn→∞ log1=0.Thuswewanttoﬁndaninteger N suchthat log 1+ 2 n2 0 = log 1+ 2 n2 < =0.05whenever n>N.

Since1+ 2 n2 > 1for n> 0,itfollowsthatlog 1+ 2 n2 > 0,sowecanremovetheabsolutevalue signsandsolvelog 1+ 2 n2 < 0.05.Exponentiatebothsides,giving1+ 2 n2 =100 05,sothat n 2 2 = 1 100 05 1 .Solvingfor n gives n ≈ 4 05.Sotaking N =4(thatis, n ≥ 5)willsuﬃce.And indeedlog 1+ 2 25 ≈ 0.033 < 0.05.

73. Wemustshowthatforevery > 0wecanﬁnd N suchthat 3 n 0 = 3 n < whenever n>N.

Toﬁndacandidatefor N ,wesolve 3 n < forpositive n.Thisgives 3 n < ,or n> 3 .Thus N = 3 givestherequiredinequality.

74. Wemustshowthatforevery > 0wecanﬁnd N suchthat 1 n +1 0 = 1 n +1 < whenever n>N.

Toﬁndacandidatefor N ,wesolve 1 n+1 < forpositive n.Thisgives 1 n+1 < ,or n +1 > 1 ,so that n> 1 1.Thuswemaychoose N = 1 ,sincethisisclearlygreaterthan 1 1.If n>N then 1 n+1 < 1 n < 1 N =

75. Wemustshowthatforevery > 0wecanﬁnd N suchthat 1 n2 0 = 1 n2 < whenever n>N.

Toﬁndacandidatefor N ,wesolve 1 n2 = 1 n2 < forpositive n.Thisgives n2 > 1 ,or n> 1 √ Thus N = 1 √ givestherequiredinequality.

76. Wemustshowthatforevery > 0wecanﬁnd N suchthat e 2n 0 = e 2n < whenever n>N.

Toﬁndacandidatefor N ,wesolve e 2n < for n.Since e 2n > 0forall n,wecandrop theabsolutevaluesigns,giving e 2n < .Nowtakenaturallogs,giving 2n< ln ,sothat n> ln 2 = 1 2 ln 1 .Thus N = 1 2 ln 1 givestherequiredinequality.

77. Wemustshowthatforevery > 0wecanﬁnd N suchthat 2 3n 0 = 2 3n < whenever n>N.

Toﬁndacandidatefor N ,wesolve 2 3n < for n.Since2 3n > 0forall n,wecandrop theabsolutevaluesigns,giving2 3n < .Nowtakenaturallogs,giving 3n ln2 < ln ,sothat n> ln 3ln2 = 1 3ln2 ln 1 .Thus N = 1 3ln2 ln 1 givestherequiredinequality.

78. Wemustshowthatforevery > 0wecanﬁnd N suchthat n n +1 1 = 1 n +1 < whenever n>N.

Toﬁndacandidatefor N ,wesolve 1 n+1 < forpositive n.Thisgives 1 n+1 < ,or n +1 > 1 , sothat n> 1 1.Thuswemaychoose N = 1 ,sincethisisclearlygreaterthan 1 1.If n>N then 1 n+1 < 1 n < 1 N = .

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

79. Sincelimn→∞ 1 n =0andlimn→∞ 2 n2 =0bylimitlaw9(sincelimn→∞ n = ∞ andlimn→∞ n2 = ∞), limitlaw1impliesthat

80. Sincelimn→∞ 2 n =0andlimn→∞ 3 n2+1 =0bylimitlaw9(sincelimn→∞ n = ∞ andlimn→∞ n2 + 1= ∞),limitlaw1impliesthat

81. Wecanwrite n+1 n as1+1/n.Sincebothlimn→∞ 1andlimn→∞ 1 n existandareequalto1and0 respectively,wehavebylimitlaw1that

82. Wehave

Since2n1/2 increaseswithoutboundas n →∞,wehavelimn→∞(2n1/2)= ∞.Also,since √n increaseswithoutboundas n →∞,wehavelimn→∞ √n = ∞,sobylimitlaw9,limn→∞ 3 √n =0. Thusbylimitlaw5,thegivenlimitis ∞

83. Wecanwrite n 2+1 n2 as1+ 1 n2 .Sincebothlimn→∞ 1existsandisequalto1,andbylimitlaw9 limn→∞ 1 n2 existsandisequalto0,wehavebylimitlaw1that

84. Wehave

Since3n increaseswithoutboundas n →∞,wehavelimn

3n = ∞.Also,since n increases withoutboundas n →∞,wehavelimn→∞ n = ∞,sobylimitlaw9,limn→∞ 5 n =0.Thusby limitlaw5,thegivenlimitis

85. Factorthedenominatorof n+1 n2 1 ,sothat

(Notethatthisisvalidonlyif n = 1,butsinceweareinterestedinthebehavioras n →∞,we maycertainlyassumethat n = 1.)Bylimitlaw9,since n 1increaseswithoutboundas n →∞, weseethatlimn→∞ 1 n 1 existsandisequalto0.Thusbylimitlaw9

86. Wehave

Since n2 increaseswithoutboundas n →∞,wehavelimn→∞ n2 = ∞,sobylimitlaw9, limn→∞ 4 n2 =0,andthenlimitlaw1impliesthatlimn

1=1, limitlaw4applies,giving

87. Notethat 1 3 n = 1 3n ,andthat3n increaseswithoutboundas n →∞.Thuslimn→∞ 3n = ∞,so thatlimn→∞ 1 3 n =0bylimitlaw9.Further,limn→∞ 2n = ∞.Thusbylimitlaw5,

88. First,noticethattheexpression3 n 4 n canalsobewrittenas 1 3 n 1 4 n.ByExample12, weknowthatbothlimn→∞ 1 3 n andlimn→∞ 1 4 n existandareequalto0.Thusbylimitlaw1 wehave

89. First,noticethattheexpression(n +2 n)/n canalsobewrittenas1+ 1 2 n 1 n .Sincethelimits limn→∞ 1, limn→∞ 1 2 n andlimn→∞ 1 n existandareequalto1,0and0respectively,wehavethat

90. Notethat

Sincelim

=1+0 0=1.

,itfollowsfromlimitlaw9thatlim

=0, sothat

2.2.4

91. Byrepeatedlyapplyingtherecursiontotheequation an+1 =2an with a0 =1,wehave

92. Byrepeatedlyapplyingtherecursiontotheequation

93. Byrepeatedlyapplyingtherecursiontotheequation

94. Byrepeatedlyapplyingtherecursiontotheequation

95. Byrepeatedlyapplyingtherecursiontotheequation

96. Byrepeatedlyapplyingtherecursiontotheequation

97. Byrepeatedlyapplyingtherecursiontotheequation an+1 = an 1+an with a0 =1,wehave

98. Byrepeatedlyapplyingtherecursiontotheequation an+1 = √an with a0 =16,wehave

99. Byrepeatedlyapplyingtherecursiontotheequation

100. Byrepeatedlyapplyingtherecursiontotheequation

101. FollowingthemethodofExample14,herewehave f (a)= 1 2 a +2.If a isaﬁxedpoint,thenit mustsatisfytheequation a = f (a).Thentheonlyﬁxedpointis a

102. FollowingthemethodofExample14,herewehave f (a)= 1 3

+ 4 3 .If a isaﬁxedpoint,thenit mustsatisfytheequation a = f (a).Thatis,

Thustheonlyﬁxedpointis a =2.

103. FollowingthemethodofExample14,wehave

satisfytheequation a = f (a).Thatis,

Theonlyﬁxedpointis a = 5 3

104. FollowingthemethodofExample14,wehave f (a)= a2 a.If a isaﬁxedpoint,thenitmust satisfytheequation a = f (a).Thatis,

Thetwoﬁxedpointsare a =0and a =2.

105. FollowingthemethodofExample14,herewehave f (

)= 4 a .If a isaﬁxedpoint,thenitmust satisfytheequation a = f (a).Thatis,

Thustherearetwoﬁxedpoints,namely a =2and a = 2.

106. FollowingthemethodofExample14,wehave f (

)= 4 a 3 .If a isaﬁxedpoint,thenitmustsatisfy theequation a = f (a).Thatis,

Thetwoﬁxedpointsare a = 1and a =4.

107. FollowingthemethodofExample14,herewehave f (a)= 2 a+2 .If a isaﬁxedpoint,thenitmust satisfytheequation a = f (a).Thatis,

Thustherearetwoﬁxedpoints,namely a = 1+ √3and a = 1 √3.

108. FollowingthemethodofExample14,wehave f (a)= 8 √a .If a isaﬁxedpoint,thenitmustsatisfy theequation a = f (a).Thatis,

Theonlyﬁxedpointis a =4.

109. FollowingthemethodofExample14,herewehave f (a)= √5a.If a isaﬁxedpoint,thenitmust satisfytheequation a = f (a).Thatis, a = √5a ⇒ a 2 =5a ⇒ a(a 5)=0 ⇒ a =0or5

Thustherearetwoﬁxedpoints,namely a =0and a =5.

110. FollowingthemethodofExample14,wehave f (a)= √a +2.If a isaﬁxedpoint,thenitmust satisfytheequation a = f (a).Thatis,

However,notethat √a +2 ≥ 0,sothat a = 1cannotbeaﬁxedpoint.Theonlyﬁxedpointis a =2.

111. Weﬁrstcomputetheﬁxedpoints.AsinExample14,wesolvetheequation a = 1 3 a + 4 3 ,giving a =2,soweguessthatthelimitis2.Evaluating an forvariousvaluesof n supportsthatconclusion:

0123456 an 01 3331 7781 9261 9751 9921 997

112. Wefirstcomputethefixedpoints.AsinExample14,wesolvetheequation a = 1 3 a + 1 9 tofind that 2a 3 = 1 27 ,orthat a = 1 18 .Nowwhen a0 =1,then an < 1forall n =1, 2, 3,...,andsowe couldconcludethatlimn→∞ an = 1 18 ≈ 0 05556.Evaluating an forvariousvaluesof n supports thatconclusion:

n 0123456 an 10.370370.160490.090540.067220.059440.05685

113. Wefirstcomputethefixedpoints.AsinExample14,wesolvetheequation a = √2a tofindthat a(a 2)=0,whichmeansthat a =0or a =2.Nowwhen a0 =1,then an > 1forall n =1, 2, 3,... andsowecouldconcludethatlimn→∞ an =2.Evaluating an forvariousvaluesof n supportsthat conclusion:

n 0123456 an 121/2 2

114. Weﬁrstcomputetheﬁxedpoints.AsinExample14,wesolvetheequation a = 3 a+2 ,giving a =1 or a = 3.Since a1 ispositive,succeedingtermsarepositiveaswell,soweguessthatthelimitis 1.Evaluating an forvariousvaluesof n supportsthatconclusion: n 0123456 an 01 50 8571 050 9841 0050 998

115. Wefirstcomputethefixedpoints.AsinExample14,wesolvetheequation a =2a(1 a)tofind that a(2a 1)=0,whichmeansthat a =0or a = 1 2 .Nowwhen a0 =0 1,then an > 0 1forall n =1, 2, 3,... andsowemightconcludethatlimn→∞ an = 1 2 .Evaluating an forvariousvaluesof n supportsthatconclusion:

n 0123456

an 0.10.180.29520.416110.485920.49960.49999

116. Notethatif a0 =0,then an =0forall n,sinceeach ai isamultipleofthepreviousone.Thus limn→∞ an =0.

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

117. Weﬁrstcomputetheﬁxedpoints.AsinExample14,wesolvetheequation a = 1 3 a + 2 a ,giving a =1or a = 1.Since a0 ispositive,succeedingtermsarepositiveaswell,soweguessthatthe limitis1.Evaluating an forvariousvaluesof n supportsthatconclusion:

0123456 an 31 2220 9531 0170 9941 0020 999

118. Wefirstcomputethefixedpoints.AsinExample14,wesolvetheequation a = 1 2 a + 9 a tofind that a = 9 a ,orthat a = ±3.Nowwhen a0 = 1,then an < 1forall n =1, 2, 3,... soweguess thatlimn→∞ an = 3.Evaluating an forvariousvaluesof n supportsthatconclusion:

3 n=0

129. Notethateachdenominatorisﬁvegreaterthanthecorrespondingnumerator,soonewaytowrite

2.3ModelingwithRecursionRelations

Nt+1 = Nt +numberofcodfishbornduringtheyear numberofcodfishdyingofoldageduringtheyear numberofcodfishkilledbypredatorsduringtheyear numberofcodfishremovedbyfishingboatsduringtheyear

Nt+1 = Nt +numberofchildrenbornduringtheyear +numberofpeoplemovingintothetownfromothertownsduringtheyear numberofpeopledyingfromanycauseduringtheyear numberofpeopleleavingthetowntoliveinothertownsduringtheyear

Nt+1 = Nt +numberofkakapobirthsinthewildduringtheyear +numberofkakaporeintroducedintothewildfromcaptivebreedingduringayear numberofkakaporemovedforcaptivebreedingduringtheyear numberofkakapokilledbypredatorsduringtheyear numberofkakapodeathsfromdiseaseduringtheyear

Nt+1 = Nt +numberoftreesseededinthewildduringtheyear +numberoftreesplantedbypeopleduringtheyear numberoftreeskilledbydiseaseduringtheyear numberoftreescutdownbyloggersduringtheyear

Nt+1 = Nt +areaofreefrestoredorrebuiltduringtheyear areakilledbyoceanacidiﬁcationduringtheyear areakilledbyﬁshingduringtheyear

6. Notethatthenumberofrhinosborninotherparksduringtheyeardoesnotimpactthepopulation inthenationalparkunderconsideration.Neitherdoesthenumberofillorinjuredrhinos,the numberoffemalerhinos,orthenumberthatbecomepregnant(thoughthelattertwocategories arecertainlyinterestingforpopulationconsideration,theydonotdirectlyaﬀectthepopulation— onlythenumberofbirthsdoes).

Nt+1 = Nt +numberofrhinosbornintheparkduringtheyear +rhinosintroducedintotheparkfromcaptivebreedingprogramsduringtheyear +rhinosrelocatedtothisparkfromotherparksduringtheyear rhinosmovedoutofthisparktootherparksduringtheyear rhinosthatdieduringtheyear

7. Sincewearemodelingthepopulationofamœba,notthepopulationofbacteria,thenumberof bacteriaontheplate,thenumberthatareeateninonehour,andthenumberthatdivideinto twocellsinonehourareirrelevanttothemodel.Theycertainlyaﬀecttheamœbapopulationby modifyingthefoodsupply,buttheyarenotdirectinputstothemodel.

Nt+1 = Nt +numberofamœbacellsthatdivideintotwocellsinonehour numberofamœbathatdieinonehour

8. Thetotalnumberofstudentsoncampus,andthenumberwhoarenotsick,arenotdirectinputsto themodel(althoughtheydohaveaneffectontherateatwhichthediseasespreads).Thenumber ofdoctorsornursesisalsonotadirectinput,thoughittoohasaneffectonthenumberofstudents withtheflu.

Nt+1 = Nt +numberofstudentswhocatchtheflu numberofstudentswhorecoverfromthefluinoneday numberofstudentswhoreturnhometorecuperatefromthefluinoneday

9. (a) (i) Ifthereare Nt individuals,then Nt · 0 5ofthosearefemale.Ofthose,onequarterlays aneggthisyear(sinceonaverageeachfemalelaysonceeveryfouryears),sothereare Nt · 0 5 · 0 25eggs.Ofthose,only29%=0 29survivetheﬁrstyear,sothenumberof birthsthatsurvivetheﬁrstyearis Nt 0 5 0 25 0 29=0 03625Nt

(ii) Sinceoneinﬁftywilldieinagivenyear,thedeathsreducethepopulationby 1 50 Nt = 0.02Nt.

(iii) Therecursionformula,fromtheabovecalculations,is Nt+1 = Nt +0 03625Nt 0 02Nt =

1 01625Nt.Intheﬁrstﬁveyears,thepopulationisgivenbythetablebelow: t 012345 Nt 5050.851.652.553.354.2

Ofcourse,intherealworld,therewouldalwaysbeanintegernumberofindividuals,but keepingthefractionsduringthecomputationpreventserrorsfrombuildinguptooquickly.

(iv) Theformulainpart(iii)representsexponentialgrowth;since N0 =50theformulais Nt =50 · 1 01625t.Thepopulationreaches n individualswhen

n =50 1 01625t ⇒ n 50 =1 01625t ⇒ ln n 50 = t ln1 01625 ⇒ t = ln n/50 ln1 01625

Sothepopulationreaches n =100and n =200atthefollowingtimes:

n =100 t = ln 100/50 ln1 01625 = ln2 ln1 01625 ≈ 43years

n =200 t = ln 200/50 ln1 01625 = ln4 ln1 01625 ≈ 86years

(b) (i) Ifstrategy1isimplemented,thenthenumberofbirthssurvivingtheﬁrstyearbecomes Nt · 0 5 · 0 5 · 0 29=0 0725Nt,sinceonaveragehalfthefemaleswilllayeachyear.Sothe recurrencebecomes Nt+1 = Nt +0 0725Nt 0 02Nt =1 0525Nt.Thepopulationinthe nextﬁveyearsisasfollows:

t 012345

Nt 5052 655 458 361 464 6

(ii) Ifstrategy2isimplemented,thenthenumberofbirthssurvivingthefirstyearbecomes Nt · 0 5 · 0 25 · 0 75=0 09375Nt,sincethreequartersoftheeggswillsurvivetheirfirst year.Sotherecurrencebecomes Nt+1 = Nt +0 09375Nt 0 02Nt =1 07375Nt.The populationinthenextfiveyearsisasfollows:

t 012345

Nt 5053 757 661 966 571 4

(iii) Clearlythesecondstrategycausesthepopulationtoincreasemorerapidly.

10. (a) (i) Ifthereare Nt individuals,50%=0.5ofthemarefemale,sothereare0.5 Nt females. Ofthose,75%=0 75ofthemarefemalesofreproductiveage,sothereare0 75 0 5 Nt femalesofreproductiveage.Finally,ofthose,22%=0 22willgivebirthinagivenyear, sothereare0 75 · 0 5 · 0 22 · Nt =0 0825Nt birthseachyear.

(ii) 4 5%=0 045ofthe Nt individualswilldie,sothenumberofdeathsis0 045Nt

(iii) Fromthepreviousparts,therecursionrelationis Nt+1 = Nt +0 0825Nt 0 045Nt = 1 0375Nt.Thisrepresentsexponentialgrowth; Nt = N0 · 1 0375t;ifthereare300gorillas initially,theformulais Nt =300 · 1 0375t

(iv) Usingtheformulaabove,weget t 012510

Nt 300311 2322 9360 6433 5

(v) Thepopulationwilldoubleto600when600=300·1 0375t,or1 0375t =2.Takingnatural logsandsolvingfor t gives t = ln2 ln1.0375 ≈ 18 8years

(b) (i) Sincethebirthrateis0 0825,inorderforthepopulationtoremainstagnant,thedeath ratewouldhavetobethesame,or0 0825=8 25%.

(ii) Sincethenumberofdeathsis0 045Nt,inorderforthepopulationtoremainstagnant, thenumberofbirthswouldhavetobethesame,or0 045Nt.Soif r isthebirthratefor femalesofreproductiveage,wemusthave0 5 0 25 r =0 045,or r =0 36=36%.The birthrateforfemalesofreproductiveagewouldhavetobe36%.

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

(iii) Therecursionis Nt+1 =1 0375Nt;is r gorillasleaveeachyear,therecursionwould be Nt+1 =1 0375Nt r.Wewant Nt+1 = Nt,sosolving Nt =1 0375Nt r gives r =0 0375Nt.Thus3 75%ofthegorillaswouldhavetoleavetheparkeachyearforthe populationtoremainconstant.Sincethereare300gorillas,thisis0 0375 300=11 25. Soonaverage11 25gorillaswouldhavetoleaveeachyear.

11. Inthismodel, R0 =4and a = 1 30 ,sotheﬁxedpointsare N =0and N = R0 1 a = 3 1/30 =90.

12. Inthismodel, R0 =2and a = 1 60 ,sotheﬁxedpointsare N =0and N = R0 1 a = 1 1/60 =60.

13. Inthismodel, R0 =2and a = 1 90 ,sotheﬁxedpointsare N =0and N = R0 1 a = 1 1/90 =90.

14. Inthismodel, R0 =3and a = 1 100 ,sotheﬁxedpointsare N =0and N = R0 1 a = 2 1/100 =200.

15. Inthismodel, R0 =3and a = 1 30 ,sotheﬁxedpointsare N =0and N = R0 1 a = 2 1/30 =60.

16. Inthismodel, R0 =5and a = 1 240 ,sotheﬁxedpointsare N =0and N = R

17. Thepopulationsizesaregivenby

t 012345 Nt 23 927 5514 0424 6239 51

Since N0 > 0,thelimitingvalueisgivenby

18. Thepopulationsizesaregivenby N

t 012345

Nt 23.3356.6788.89

Since N0 > 0,thelimitingvalueisgivenby

19. Thepopulationsizesaregivenby

t 012345

Nt 715 5626 2534 0537 839 24

Since N0 > 0,thelimitingvalueisgivenby

20. Thepopulationsizesaregivenby

t 012345

Nt 36 9212 2716 5318 6919 54

Since N0 > 0,thelimitingvalueisgivenby

21. Thepopulationsizesaregivenby

012345 Nt 27 6225 662 4497 52113 46

Since N0 > 0,thelimitingvalueisgivenby

22. Thepopulationsizesaregivenby

012345 Nt 27.7427.4375.29133.57165.61

Since N0 > 0,thelimitingvalueisgivenby

23. Sincelim

Sincelim

25. Since Nt+1 = R(Nt)Nt = R0 1+aNt Nt,substitutingthegivenvaluesweget

26. Since Nt+1 = R(Nt)Nt = R0 1+aNt Nt,substitutingthegivenvaluesweget 40= 4 1+50a 50= 200 1+50a ⇒ 2000a +40=200 ⇒ a =0 08

2.3.3

27. Fromthediscussioninthetext, xt+1 = R0xt(1 xt)= xt(1 xt)with R0 =1.Since xt = Nt R0/b = Ntb R0 ,wehave xt = Nt1/10 1 = Nt 10 .

28. Fromthediscussioninthetext, xt+1 = R0xt(1 xt)= xt(1 xt)with R0 =1.Since xt = Nt R0/b = Ntb R0 ,wehave xt = Nt1/20 1 = Nt 20 .

29. Fromthediscussioninthetext, xt+1 = R0xt(1 xt)=2xt(1 xt)with R0 =2.Since xt = Nt R0/b = Ntb R0 ,wehave xt = Nt1/15 2 = Nt 30

30. Fromthediscussioninthetext, xt+1 = R0xt(1 xt)=2xt(1 xt)with R0 =2.Since xt = Nt R0/b = Ntb R0 ,wehave xt = Nt1/20 2 = Nt 40

31. Fromthediscussioninthetext, xt+1 = R0xt(1 xt)=2 5xt(1 xt)with R0 =2.Since xt = Nt R0/b = Ntb R0 ,wehave xt = Nt1/30 2 5 = Nt 75

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

32. Fromthediscussioninthetext, xt+1 = R0xt(1 xt)=2 5xt(1 xt)with R0 =2.Since xt = Nt R0/b = Ntb R0 ,wehave xt = Nt1/50 2 5 = Nt 125

33. Aﬁxedpointoccurswhen Nt+1 = Nt = N ,soweget N = R

)N = N (bN +1 R0)=0.Theﬁxedpointsaretherefore N =0and N = R0 1 b

34. Since Nt → 50, N =50isaﬁxedpoint,sothat50= R0 1 b = 1 b andtherefore b = 1 50 .

35. Since Nt → 40, N =40isaﬁxedpoint,sothat40= R

36. Wehave Nt+1 = R0 · Nt b · N 2 t .Substitutingthegivenvaluesgives15=2 · 10 b · 102 =20 100b, sothat b = 5 100 = 1 20

37. Wehave Nt+1 = R0 · Nt b · N 2 t .Substitutingthegivenvaluesgives30=3 · 15

2 =45 225b, sothat b = 15 225 = 1 15

38. Wehave Nt+1 = R0·Nt b·N 2 t .Substitutingthegivenvaluesgives20=15R0 1 10 ·152 =15R0 22 5, sothat R0 ≈ 2 833.

39. 5 10 15 20

40. 5 10 15 20

Discrete-TimeModels,Sequences,andDiﬀerenceEquations 50. 5 10 15 20 -1.0 -0.5

2.3.4

51. (a) Since7.7%=0.077ofthedrugiseliminatedeachhour,wehave C

(b) Therecurrencerelationexpressesexponentialdecay: Ct = C0 0 923t.Since C0 =33 8ng/ml, wehave Ct =33 8 0 923t ng/ml.

(c) Wewanttoﬁnd t suchthat Ct =0 1;then0 1=33 8 · 0 923t,sothat 0 1 33 8 =0 923t.Taking naturallogsofbothsidesandsimplifyinggives t = ln0.1 ln33.8 ln0.923 ≈ 72 67hrs

52. (a) Giventheabsorptionrate,andsince10%=0 1ofthedrugiseliminatedeachhour,wehave

(b) Startingwith a0 =0weget t 0123456 at 0101313.312.6111.6110.55

(d) Continuingthetablefrompart(b)through t =24gives t 789101112131415

at 9.538.607.746.976.285.655.084.584.12 t 161718192021222324

at 3 713 343 002 702 432 191 971 771 60

(e) Plotting at against t usingasemilogplotgivesthegraphbelow:

Semilogplot

For t largerthanabout4,thegraphisroughlylinear,indicatingexponentialdecay.

53. (a) Giventheabsorptionrate,andsince40%=0 4ofthedrugiseliminatedeachhour,wehave

(b) Startingwith a0 =0weget

0123456 at 020 0016 0010 406 403 872 33

(d) Continuingthetablefrompart(b)through t =24gives(tothreedecimalplaces) t 789101112131415 at 1.400.840.500.300.180.110.070.040.02 t 161718192021222324 at 0 010 010 01000000

(e) Plotting at against t usingasemilogplotgivesthegraphbelow.For t largerthanabout1, thegraphisroughlylinear,indicatingexponentialdecay. 4 8 12

Semilogplot

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

54. (a) Sincethedrughaszerothordereliminationkinetics,theamountremovedeachhouris20 14mg=6mg.

(b) Eachhour,6mgisremoved,soweget at+1 = at 6.

(d) Theamountofdrugpresentdropstozerowhen20 6t =0,sowhen t = 10 3 ≈ 3 33hours.

55. (a) Thepercentageremovedbetween t =0and t =1is 20 14 20 = 6 20 =0 3=30%.Sincethedrug hasﬁrstordereliminationkinetics,thispercentageisremovedeachhour.

(b) at+1 = at 0 3at =0 7at

(d) Since0 7t > 0forallvaluesof t,theamountofdrugpresentwillneverbezeroaccordingto themodel.

56. (a) Ifthedrughaszerothorderkinetics,theamounteliminatedeachhouris40 32=8mg/ml.

(b) Since8mg/mliseliminatedeachhour,wehave ct+1 = ct 8,so c2 shouldbe c1 8=24.

(d) Since20%iseliminatedeachhour,weget ct+1 = ct 0 2ct =0 8ct.Thenwewouldexpect c2 =0 8c1 =25 6.

(e) Sincetheamountfoundmatchestheamountinpart(d),weconcludethatthedrughasﬁrst orderkinetics.

57. (a) Ifthedrughaszerothorderkinetics,theamounteliminatedeachhouris50 35=15mg/ml.

(b) Since15mg/mliseliminatedeachhour,wehave ct+1 = ct 15,so c2 shouldbe c1 15=20.

(d) Since30%iseliminatedeachhour,weget ct+1 = ct 0 3ct =0 7ct.Thenwewouldexpect c2 =0 7c1 =24 5.

(e) Sincetheamountfoundmatchestheamountinpart(b),weconcludethatthedrughaszeroth orderkinetics.

58. (a) Since23%ofthedrugiseliminatedeachhour,wehave ct+1 = ct 0 23ct =0 77ct

(b) Thisrecursionexpressesexponentialdecay;sincetheinitialconcentrationis15 µg/mlat t =1, theformulais ct =15 · 0 77t 1

(d) Duringthathour,15 µg/mlenterthebloodstream,and0 23oftheamountpresentattime t =4leavesthebloodstream,sotheamountinthebloodstreamat t =5is

(e) Usingtherecursionrelation

(f) Duringtheninthhour,15 µg/mlentersthebloodstream,and0 23c8 leaves,sotheamountat t =9is

9 = c8 +15 0 23c8 =9 27+15 2 13 ≈ 22 14 µg/ml

(g) Onehourafterthe nth pillistaken,theamountinthebloodstreamis0 77timestheamount whenthepillwastaken(accountingforelimination)plus15 µg/ml.Theamountinthebloodstreamwhenthepillwastakenis0 773 timestheamountonehourafterthepreviouspillwas taken,sincethreehourselapse.Sotheamountisthebloodstreamonehourafterthe nth pill istakenis

(h) Sincepillsaretakenat t =1, 5, 9,... , C1 correspondsto t =1, C2 to t =5, C3 to t =9,and ingeneral Cn correspondsto t4n 3

(i) Seethediscussioninpart(g)fortherecursion. c1 =15sincethatistheconcentrationone houraftertheﬁrstpillwastaken.

(j) Usingtherecursionfrompart(i),weget t 123456 Ct 1520.27322.12722.77823.00723.088

(k) Theamountofincreaseineach Cn appearstobedecreasing,soitseemslikelythat Cn converges.

(l) Aﬁxedpointoftherecursionrelationisfoundbysolving C =0 774C +15=0 35

that0.65C =15and C ≈ 23.1 µg/ml.

59. Sincetheabsoluteamountbywhichtheconcentrationdecreaseschangeseachhour(itdecreases), thiscannotbezerothorderkinetics,soitmustbeﬁrstorderkinetics.Indeed,computingthe percentagedecreaseeachhourweget

, sothat25%ofthedrugiseliminatedeachhour.

60. Since2 µg/mliseliminatedeachhour,thisdrughaszerothorderkinetics.

61. Since4 µg/mliseliminatedeachhour,thisdrughaszerothorderkinetics.

62. Sincetheabsoluteamountbywhichtheconcentrationdecreaseschangeseachhour(itdecreases), thiscannotbezerothorderkinetics,soitmustbeﬁrstorderkinetics.Indeed,computingthe percentagedecreaseeachhourweget

sothat10%ofthedrugiseliminatedeachhour.

63. (a) at+1 = at +amountaddedtothebloodin tth day amounteliminatedin tth day. (b) Theamountaddedeachdayis20 µg,andtheamountremovedeachdayis4%oftheamount present(atthestartoftheday).Thus

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

(d) Solving a =0 96a +20gives0 04a =20,sothat a =500 µg.

64. (a) at+1 = at +amountaddedtothebloodin tth day amounteliminatedin tth day.

(b) Onthe tth day,10t +10mgisadded,andeachdayhalfoftheexistingamountisremoved; substitutingthisinformationgives

+10(t +1)+10mg

(d) at reaches(andbarelyexceeds)100atthestartofthesixthday.

Chapter2Review

1. Theexpression2 n canalsobewrittenas 1 2 n.Thus,fromExample12inSection2.2.2,we concludethat

2. Forsuccessivevaluesof n,thevalues1, 3, 9, 27, 81, 243,... of3n indicatethatthetermscontinue togrow.Thus3n goestoinﬁnityas n →∞,andwecanwritelimn→∞ 3n = ∞.Thiscanalsobe seenusingExample12inSection2.2.2,fromwhichweconcludethatsince R =3 > 1,

3. Theexpression40(1 4 n)canbewrittenas40 40 1 4 n.FromExample12inSection2.2.2,we knowthatlimn→∞ 1 4 n =0.Also,itisobviousthatlimn→∞ 40=40.Thus lim n→∞ 40(1 4 n)=lim n→∞

4. Theexpression 2 1+2 n canbewrittenas 2 1+(1/2)n .FromExample12inSection2.2.2,weknowthat limn→∞ 1 2 n existsandisequalto0.Thus

5. Example12inSection2.2stateswithoutproofthatthislimitis ∞.Toseethatthisistrue,choose anyrealnumber K> 0,andlet x = a 1.Since a> 1,weseethat x> 0,sothereissomepositive integer n suchthat nx>K 1.Now,usingthebinomialexpansionof(1+ x)n,weget an =(1+ x)n ≥ 1+ nx> 1+(K 1)= K, sothat an >K.Thisprovesthatnomatterwhatrealnumber K wechoose,wecanﬁndan n such that an >K,sothat an growswithoutboundas n →∞,andthuslimn→∞ an = ∞

6. Let b = 1 a .Since0 <a< 1,wehave b> 1,sothatlimn→∞ an =limn→∞ 1 bn .Bytheprevious exercise,limn→∞ bn = ∞,sothatbythelimitruleslimn→∞ an =0.

7. Notethattheexpression n(n+1) n2 1 canbewrittenas n(n+1) (n+1)(n 1) ,whichisthesameas n n 1 if n = 1. Sinceweareinterestedinthebehaviorof an as n →∞,wemayassumethat n = 1.Since limn→∞ 1 n =0wehave

(n +1)

8. Notethattheexpression n 2+n 6 n 2 canbewrittenas (n 2)(n+3) n 2 ,whichisthesameas n +3if n =2. Sinceweareinterestedinthebehaviorof an as n →∞,wemayassumethat n> 2.Recallingthat limn→∞ n doesnotexist,sincesuccessivevaluesof n growwithoutbound,wehave

9. Notethatbydividingnumeratoranddenominatorby n,theexpression √n n+1 canbewrittenas 1/√n 1+1/n Recallingthatbothlimn→∞ 1/n andlimn→∞ 1/√n existandareequalto0,wehave

10. Weﬁrstnotethattheexpression n+1 √n canbewrittenas √n + 1 √n .Now,limn→∞ 1 √n =0,but thesuccessiveterms1, √2, √3, 2, √5, √6,... of √n areclearlygrowingwithoutbound.Thatis, limn→∞ √n = ∞.Then

11. Lookingatthesequence,wecanguessthenextterms,namely, 11 12 , 13 14 , 15 16 , 17 18 , 19 20 andsoon.We thusﬁnd an = 2n +1 2n +2 for n =0, 1, 2, 3,...

12. Notethatthenumeratorof an isthesumoftheﬁrst n +1evennumbers,startingwith2,soitis twicethesumoftheﬁrst n +1positiveintegers;thissumis2 · (n+1)(n+2) 2 =(n +1)(n +2).The denominatorsarepowersoftwo.Sowecanguessthatthesequenceis an = (n +1)(n +2) 2n+1 for n =0, 1, 2, 3,...

Sothenextfewtermsofthesequencewouldbe 42 64 , 56 128 , 72 256 , 90 512 ,and 110 1024

13. Thenumeratorof an appearstobe n +1,whilethedenominatoris(n +1)2 +1,sowecanguess thatthesequenceis an = n +1 (n +1)2 +1 = n +1 n2 +2n +2 for n =0, 1, 2, 3,...

Sothenextfewtermsofthesequencewouldbe 6 37 , 7 50 , 8 65 , 9 82 ,and 10 101

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

14. Lookingatthesequence,wecanguessthenextterms,namely, 5 7 , 6 8 , 7 9 , 8 10 ,, 9 11 andsoon.Wethus ﬁnd

,...

15. (a) (i) Aplotofthepointstogetherwithaplotofthenumberofpupsbornasafunctionofthe populationsize Nt isbelow:

Thelineisareasonablygoodapproximationtothedata.

(ii) Thenumberofwolvesthatdieis0 22Nt,soputtingthattogetherwiththeapproximation frompart(i),weget

(iii) Applyingtherecursionweget

t 012345678910

(iv) Accordingtothetableabove,thepopulationsizeof220willbereachedsometimeinthe tenthyear.

(b) (i) Thepopulationincreasesbythenumberofpupsborn,whichisunchangedat0 28Nt,and alsobythenumberofnewwolvesintroduced,whichis r.Itdecreasesbythedeathrate, whichisnowonly0.30Nt.Puttingthistogethergives

(ii) For r =5, N0 =130,applyingtherecursiongives

t 012345678910

Nt 130132 4134 8137 1139 3141 5143 7145 8147 9150152

Ifweuse r =10,weget

t 012345678910

Nt 130137.4144.7151.8158.7165.5172.2178.8185.2191.5197.7

t+1 =1 06Nt +10

Computingthisrelationfor N0 =130gives t 012345678910 Nt 130147 8166 7186 7207 9230 3254 2279 4306 2334 5364 6

Apopulationof220isreachedunderthisstrategyintheﬁfthyear.However,thepopulation atthestartoftheﬁfthyearinpart(b)is165 5,whichisfartherfrom220thanthepopulation of230 3inthispart;weexpect220tobereachedsoonerusingthestrategyinthispart.

16. (a) N2 = N1 + N0 =1+1=2.

(b) N3 = N2 + N1 =2+1=3, N4 = N3 + N2 =3+2=5, N5 = N4 + N3 =5+3=8,and N6 = N5 + N4 =8+5=13.

(c) Valuesof Nk for k upto20arebelow: k 012345678910 Nk 1123581321345589 k 11121314151617181920 Nk 144233377610987159725844181676510946

(d) Therequiredsemilogplotisbelow:

Thepointsareapproximatelylinear,sotheFibonaccisequenceappearstogrowexponentially.

17. (a) Calculatingtherecurrencegives

k 01234 Nk 1019 537 167 3112

(b) Fixedpointsfortherelationaregivenbysolving N =2N 1 200 N 2,or N 2 200N =0.This gives N =0or N =200;sincethepopulationisincreasing,weseethatlimt→∞ Nt =200.

(c) Weneedtoﬁndﬁxedpointsof N =2N 1 200 N 2 pN .Simplifyinggives N 2 +200(p 1)N =0 → N (N +200(p 1))=0 → N =0or N =200(1 p)

Thelimitingpopulationis200(1 p).

(d) Sincetheobservedpopulationlimitis160,solving160=200(1 p)gives1 p =0 8,sothat p =0 2.

Semilogplot

Discrete-TimeModels,Sequences,andDiﬀerenceEquations

18. (a) Since42%ofthedruginthegutleavesthegut(intotheblood),wegetarecursionrelation at+1 = at 0 42at =0 58at, a0 =10.

(b) Therecursionexpressesexponentialdecaywithaninitialvalueof10: at =10 0.58t .

(d) Theamountofdrugenteringthebloodattime t is0 42at,andtheamountleavingisthe amounteliminated,whichis0.06bt,so

(e) Substitutingtheexplicitformulafor at intotheabove,weget

Calculatingvaluesgives k 0123456 bk 04.206.387.417.797.807.

Themaximumamountofdruginthebloodisabout7 80,intheﬁfthorsixthhour.

(f) Continuingthetablefromthepreviouspart,weget k 789101112131415

bk 7 316 966 606 235 885 545 214 904 61 k 161718192021222324 bk 4.334.073.833.603.383.182.992.812.64

Aplotofthesevaluesisbelow:

(g) (i) Ifthedrugimmediatelyenteredthebloodstream,thennomorewouldcomeinafter theinitialbolus,buteachhour6%ofitwouldbeeliminated,sothatwewouldhave bt+1 = bt 0 06bt =0 94bt

(ii) Themodelaboveisexponentialdecaywithinitialvalue10,sowehave bt =10 · 0 94t Setting t =24gives b24 ≈ 2 265mg.

(iii) Theamountintheblood24hourslaterislowerwithimmediateabsorption.