Chapter 2 Graphs
Section 2.1
1. 0
2. () 5388 −−==
3. 22 34255 +==
4. 222 11601213600372161 +=+==
Since the sum of the squares of two of the sides of the triangle equals the square of the third side, the triangle is a right triangle.
5. 1 2 bh
6. true
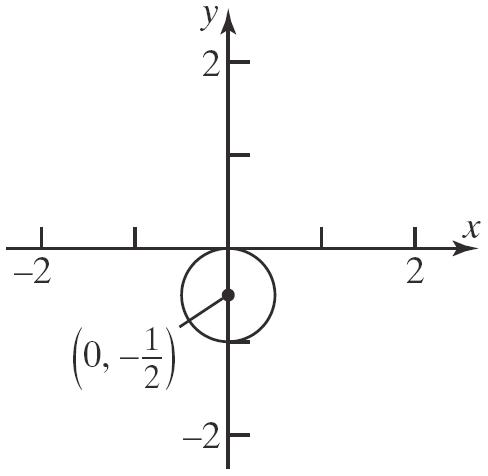
7. x-coordinate or abscissa; y-coordinate or ordinate
8. quadrants
9. midpoint
10. False; the distance between two points is never negative.
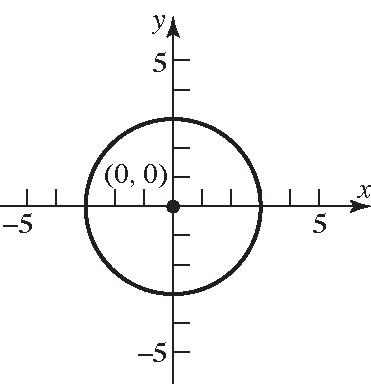
11. False; points that lie in Quadrant IV will have a positive x-coordinate and a negative y-coordinate. The point () 1,4 lies in Quadrant II.
12. True; 1212 , 22 x xyy M ++ =
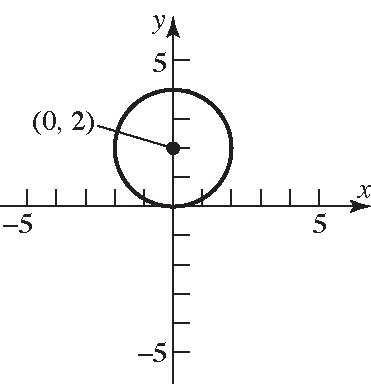
13. b
14. a
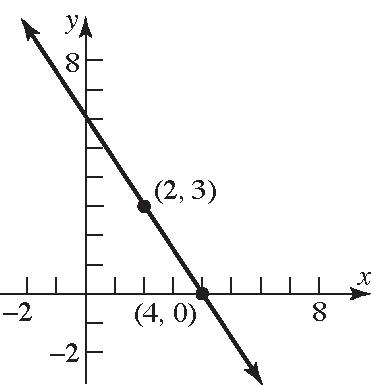
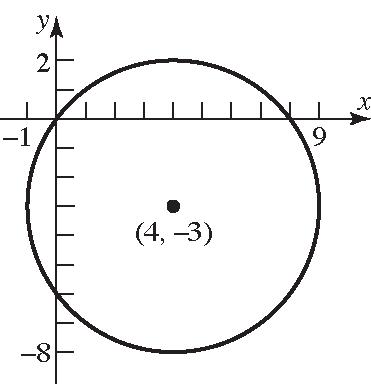
15. (a) Quadrant II (b) x-axis
(c) Quadrant III (d) Quadrant I (e) y-axis
(f) Quadrant IV
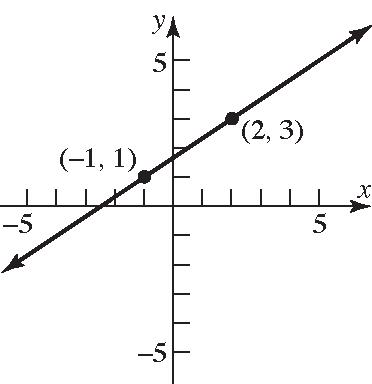
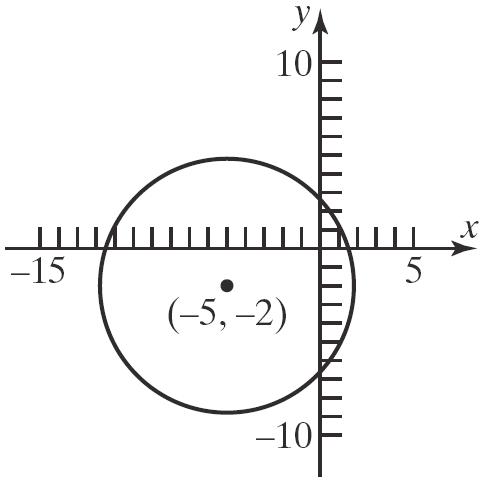
16. (a) Quadrant I (b) Quadrant III (c) Quadrant II
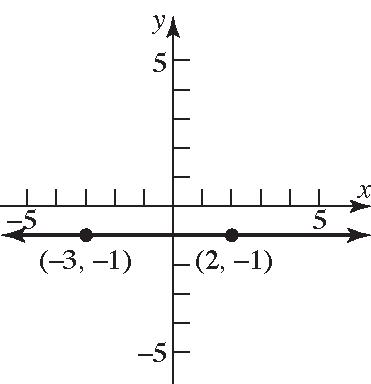
(d) Quadrant I (e) y-axis (f) x-axis

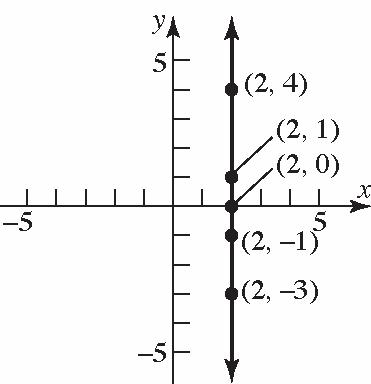
17. The points will be on a vertical line that is two units to the right of the y-axis.
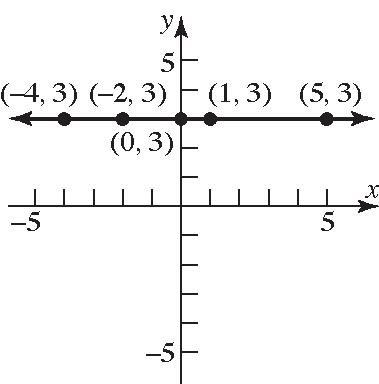
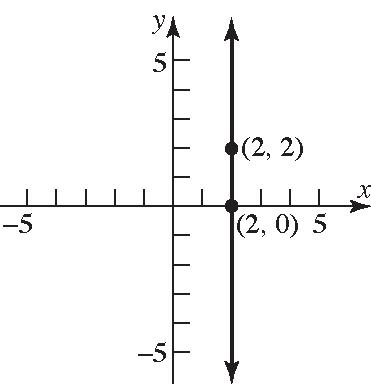
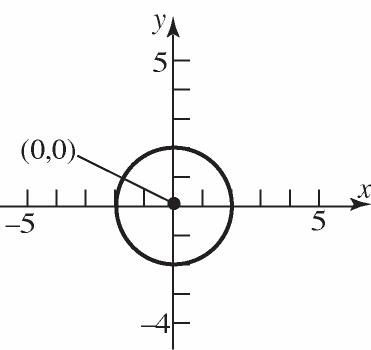
18. The points will be on a horizontal line that is three units above the x-axis.
19. 22 12 22 (,)(20)(10) 21415 dPP =−+− =+=+=
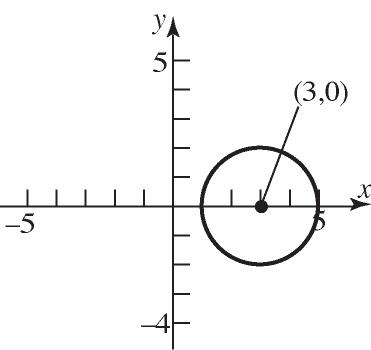
20. 22 12 22 (,)(20)(10) (2)1415 dPP =−−+− =−+=+=
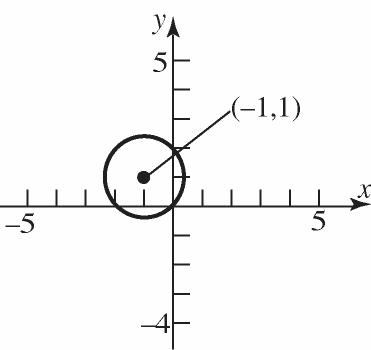
21. 22 12 22 (,)(21)(21) (3)19110 dPP =−−+− =−+=+=
22. () 2 2 12 22 (,)2(1)(21) 319110 dPP =−−+− =+=+=
23. () () () 2 2 12 2 2 (,)(53)44 2846468217 dPP =−+−− =+=+==
24. () ()() () 2 2 12 2 2 (,)2140 34916255 dPP =−−+− =+=+==
25. () 2 2 12 22 (,)6(3)(02) 9(2)81485 dPP =−−+− =+−=+=
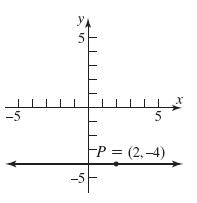
26. ()() 22 12 22 (,)422(3) 2542529 dPP =−+−− =+=+=
27. () 2 2 12 22 (,)(64)4(3) 2744953 dPP =−+−− =+=+=
28. ()() 22 12 22 (,)6(4)2(3) 10510025 12555 dPP =−−+−− =+=+ ==
29. 22 12 2222 (,)(0)(0) ()() dPPab abab =−+− =−+−=+
30. 22 12 22 222 (,)(0)(0) ()() 22 dPPaa aa aaaa =−+− =−+− =+==
31. (2,5),(1,3),(1,0)ABC =−==− () () () 2 2 22 2 2 22 2 2 22 (,)1(2)(35) 3(2)9413 (,)11(03) (2)(3)4913 (,)1(2)(05) 1(5)12526 dAB dBC dAC =−−+− =+−=+= =−−+− =−+−=+= =−−−+− =+−=+=
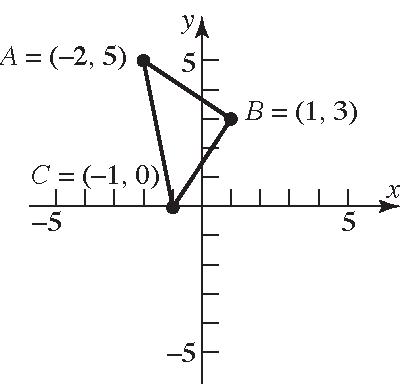
Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem: [][][] ()()() 222 222 (,)(,)(,) 131326 131326 2626 dABdBCdAC += += += =
The area of a triangle is 1 2 A bh =⋅ . In this problem,
[][] 1 (,)(,) 2 11131313 22 13 square units 2 A dABdBC=⋅ ⋅ =⋅=⋅ ⋅ =
32. (2,5),(12,3),(10,11)ABC =−==−
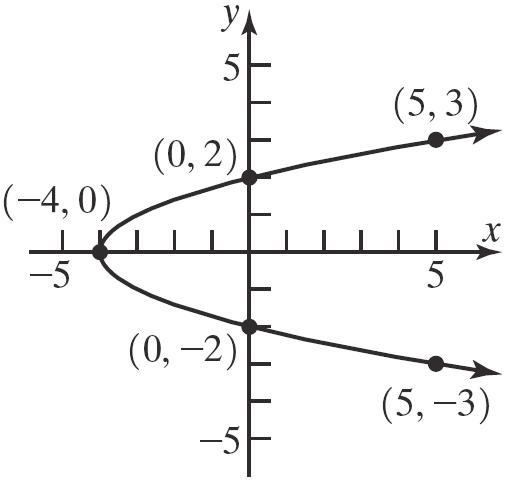
2 2 22 2 2 22 2 2 22 (,)12(2)(35) 14(2) 1964200 102 (,)1012(113) (2)(14) 4196200 102 (,)10(2)(115) 12(16) 144256400 20 dAB dBC dAC =−−+− =+− =+= = =−+−− =−+− =+= = =−−+−− =+− =+= =
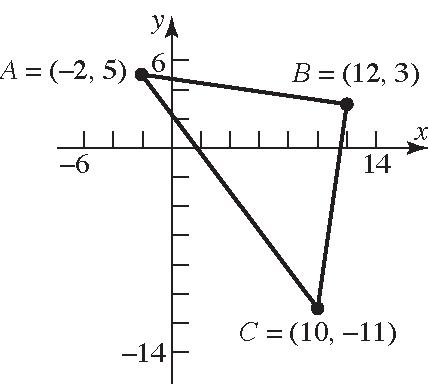
Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem: [][][] ()()() 222 22 2 (,)(,)(,) 10210220 200200400 400400 dABdBCdAC += += += =
Section2.1: The Distance and Midpoint Formulas
The area of a triangle is 1 2 A bh = . In this problem, [][] 1 (,)(,) 2 1 102102 2 1 1002100 square units 2 AdABdBC =⋅⋅ =⋅⋅ =⋅⋅=
33. (5,3),(6,0),(5,5)ABC =−== () () () 2 2 22 2 2 22 2 2 22 (,)6(5)(03) 11(3)1219 130 (,)56(50) (1)5125 26 (,)5(5)(53) 1021004 104 226 dAB dBC dAC =−−+− =+−=+ = =−+− =−+=+ = =−−+− =+=+ = =
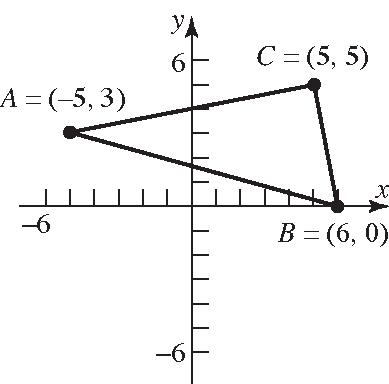
Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem: [][][] ()()() 222 222 (,)(,)(,) 10426130 10426130 130130 dACdBCdAB += += += =
The area of a triangle is 1 2 A bh = . In this
Chapter2: Graphs
problem, [][] 1 (,)(,) 2 1 10426 2 1 22626 2 1 226 2 26 square units A dACdBC=⋅⋅ =⋅⋅ =⋅⋅ =⋅⋅ =
34. (6,3),(3,5),(1,5)ABC =−=−=− () () () 2 2 22 2 2 22 2 2 22 (,)3(6)(53) 9(8)8164 145 (,)13(5(5)) (4)1016100 116229 (,)1(6)(53) 52254 29
dAB dBC dAC =−−+−− =+−=+ = =−−+−− =−+=+
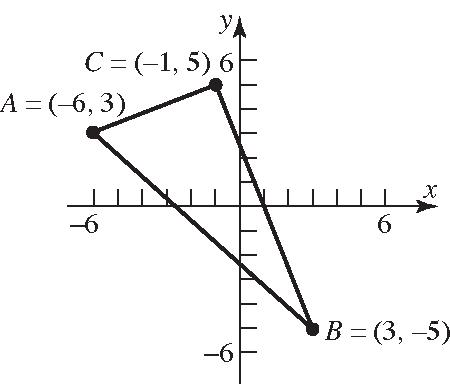
Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem: [][][] ()()() 222 222 (,)(,)(,) 29229145 29429145 29116145 145145 dACdBCdAB += += +⋅= += = The area of a triangle is 1 2 A bh = . In this
problem, [][] 1 (,)(,) 2 1 29229 2 1 229 2 29 square units A dACdBC=⋅⋅ =⋅⋅ =⋅⋅ = 35. (4,3),(0,3),(4,2)ABC =−=−= () ()() () 2 2 22 22 22 2 2 22 (,)(04)3(3) (4)0160 16 4 (,)402(3) 451625 41 (,)(44)2(3) 05025 25 5 dAB dBC dAC =−+−−− =−+=+ = = =−+−− =+=+ = =−+−− =+=+ = =
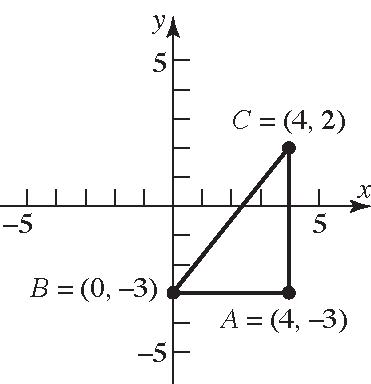
Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem: [][][] () 222 2 22 (,)(,)(,) 4541 162541 4141 dABdACdBC += += += =
The area of a triangle is 1 2 A bh = . In this
problem, [][] 1 (,)(,) 2 1 45 2 10 square units A dABdAC=⋅⋅ =⋅⋅ =
36. (4,3),(4,1),(2,1)ABC =−==
(,)(44)1(3)
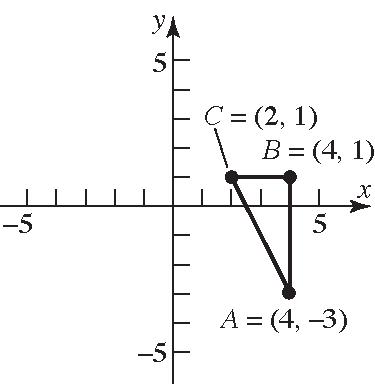
Verifying that ∆ ABC is a right triangle by the Pythagorean Theorem: [][][] () 222 2 22 (,)(,)(,) 4225 16420 2020 dABdBCdAC += += += =
Section2.1: The Distance and Midpoint Formulas
The area of a triangle is 1 2 A bh = . In this problem, [][] 1 (,)(,) 2
37. The coordinates of the midpoint are: (,),1212 22 44 35 , 22 80 , 22 (4,0) x xyy xy ++ = +−+ = = =
38. The coordinates of the midpoint are: () (,),1212 22 2204 , 22 04 , 22 0,2 x xyy xy ++ = −++ =
= =
39. The coordinates of the midpoint are: (,),1212 22 3620 , 22 32 , 22 3 ,1 2 x xyy xy ++ = −++ =
= =
40. The coordinates of the midpoint are: (,),1212 22 2432 , 22 61 , 22 1 3, 2 x xyy xy ++ = +−+ =
=
=−
41. The coordinates of the midpoint are: (,),1212 22 4631 , 22 2 10 , 22 (5,1) x xyy xy ++ = +−+ =
42. The coordinates of the midpoint are: (,),1212 22 42 32 , 22 21 , 22 1 1, 2 x xyy xy ++ =
43. The coordinates of the midpoint are: (,),1212 22 00 , 22 , 22 x xyy xy ab ab ++
44. The coordinates of the midpoint are: (,),1212 22 00 , 22 , 22 x xyy xy aa aa ++ = ++
45. The x coordinate would be 235 += and the y coordinate would be 523 −= . Thus the new point would be () 5,3
46. The new x coordinate would be 123−−=− and the new y coordinate would be 6410 += . Thus the new point would be () 3,10
47. a. If we use a right triangle to solve the problem, we know the hypotenuse is 13 units in length. One of the legs of the triangle will be 2+3=5. Thus the other leg will be:
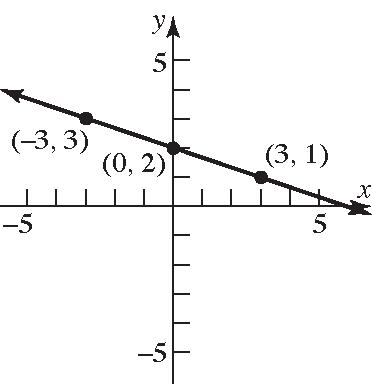
222 2 2 513 25169 144 12 b b b b += += = = Thus the coordinates will have an y value of 11213−−=− and 11211−+= . So the points are () 3,11 and () 3,13
b. Consider points of the form () 3, y that are a distance of 13 units from the point () 2,1 .
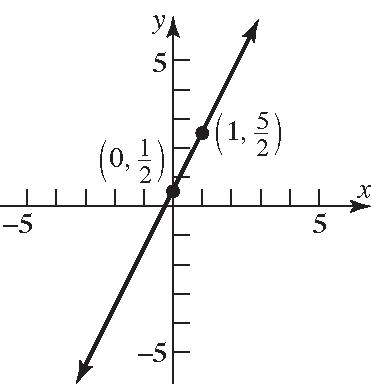
or 130 13 y y += =−
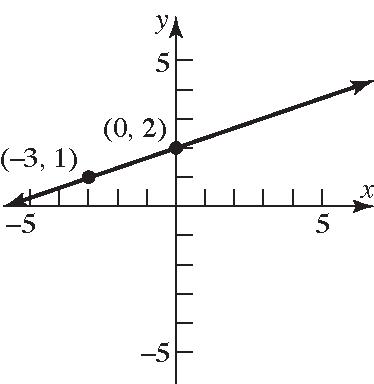
Thus, the points () 3,11 and () 3,13 are a distance of 13 units from the point () 2,1
48. a. If we use a right triangle to solve the problem, we know the hypotenuse is 17 units in length. One of the legs of the triangle will be 2+6=8. Thus the other leg will be:
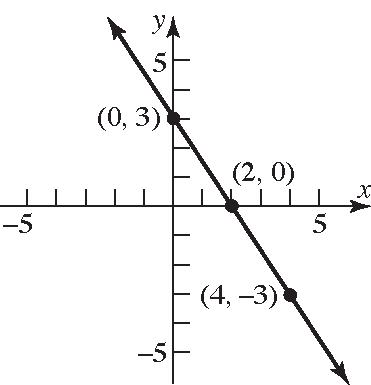
Thus the coordinates will have an x value of 11514 −=− and 11516 += . So the points are () 14,6 and () 16,6
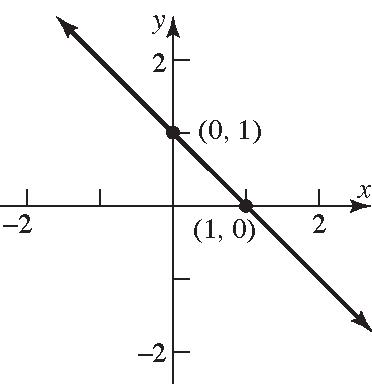
b. Consider points of the form () ,6 x that are a distance of 17 units from the point () 1,2 . ()() ()() () () 22 2121 2 2 2 2 2 2 126 218 2164 265 dxxyy x xx xx xx =−+− =−+−− =−++ =−++ =−+ () ()() 2 2 22 2 2 17265 17265 289265 02224 01416 xx xx xx xx xx =−+ =−+ =−+ =−− =+− 140 14 x x += =− or 160 16 x x −= =
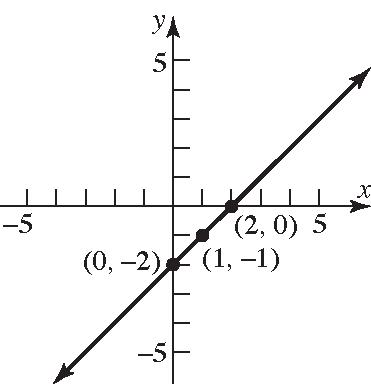
Thus, the points () 14,6 and () 16,6 are a distance of 13 units from the point () 1,2
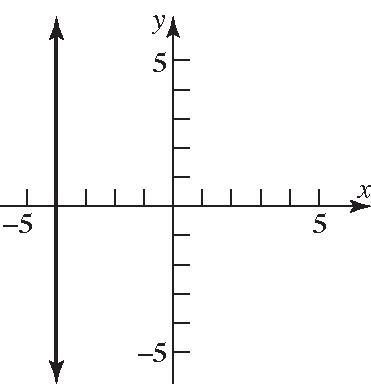
49. Points on the x-axis have a y-coordinate of 0. Thus, we consider points of the form () ,0x that are a distance of 6 units from the point () 4,3 ()() ()() () 22 2121 22 2 2 2 2 430 1683 1689 825 dxxyy x xx xx xx =−+− =−+−− =−++− =−++ =−+ () 2 2 22 2 2 2 6825 6825 36825 0811 (8)(8)4(1)(11) 2(1) 864448108 22 863 433 2 xx xx xx xx x =−+ =−+ =−+ =−− −−±−−− = ±+± == ± ==±
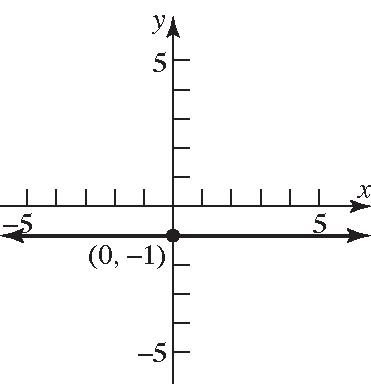
Section2.1: The Distance and Midpoint Formulas
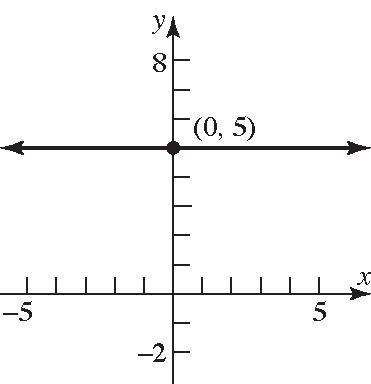
433 x =+ or 433 x =−
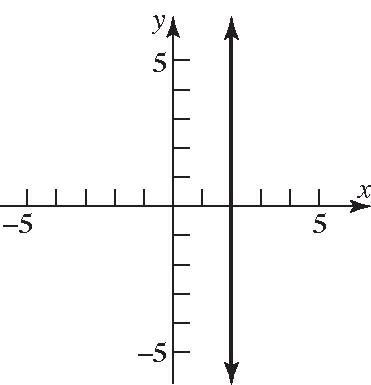
Thus, the points () 433,0 + and () 433,0 are on the x-axis and a distance of 6 units from the point () 4,3
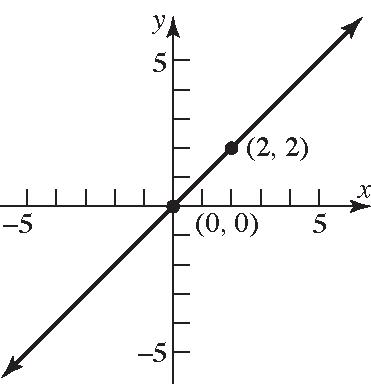
50. Points on the y-axis have an x-coordinate of 0. Thus, we consider points of the form () 0, y that are a distance of 6 units from the point () 4,3 . ()() ()() 22 2121
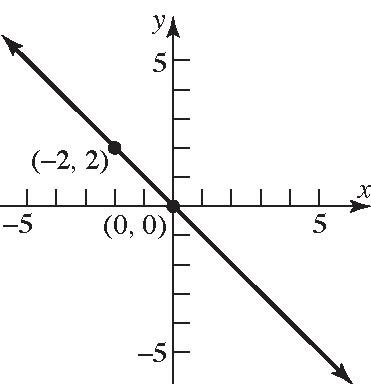
325 y =−+ or 325 y =−−
Thus, the points () 0,325 −+ and () 0,325 are on the y-axis and a distance of 6 units from the point () 4,3
51. a. To shift 3 units left and 4 units down, we subtract 3 from the x-coordinate and subtract 4 from the y-coordinate.
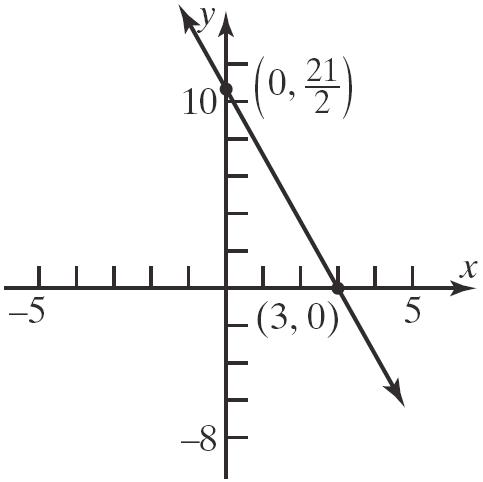
()() 23,541,1 −−=−
b. To shift left 2 units and up 8 units, we subtract 2 from the x-coordinate and add 8 to the y-coordinate.
()() 22,580,13 −+=
52. Let the coordinates of point B be () ,x y . Using the midpoint formula, we can write () 18 2,3, 22 x y −++ =
This leads to two equations we can solve. 1 2 2 14 5 x x x
Point B has coordinates () 5,2 .
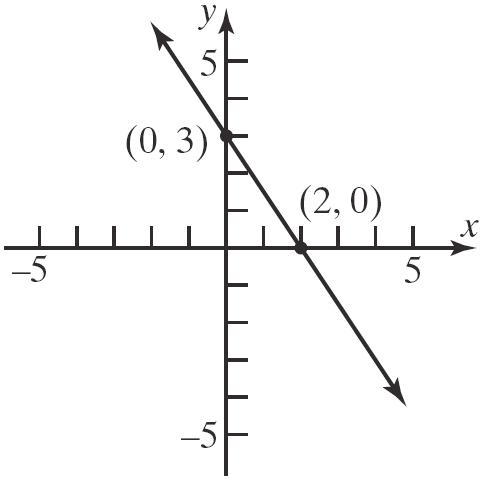
53. () 1212 ,,22 x xyy Mxy ++ == . () 111,(3,6) Pxy==− and (,)(1,4) xy =− , so 12 2 2 2 2 3 1 2 23 1 x x x x x x + =
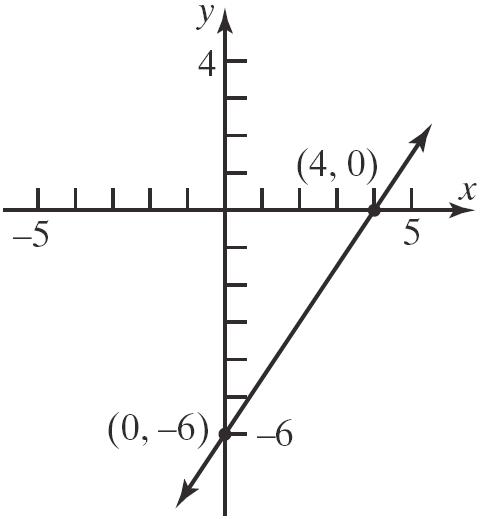
Thus, 2 (1,2) P =
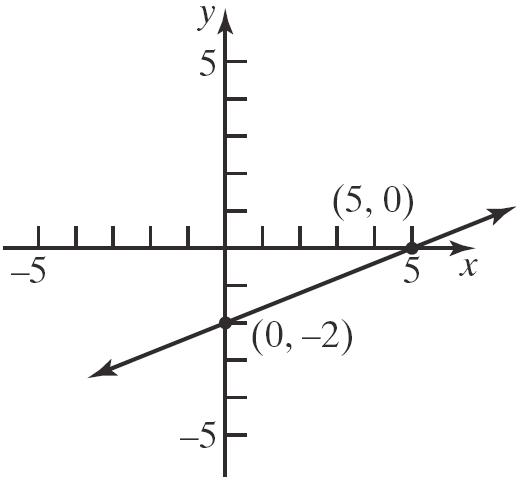
54. () 1212 ,,22 x xyy Mxy ++ == . () 222,(7,2)Pxy==− and (,)(5,4) xy =− , so
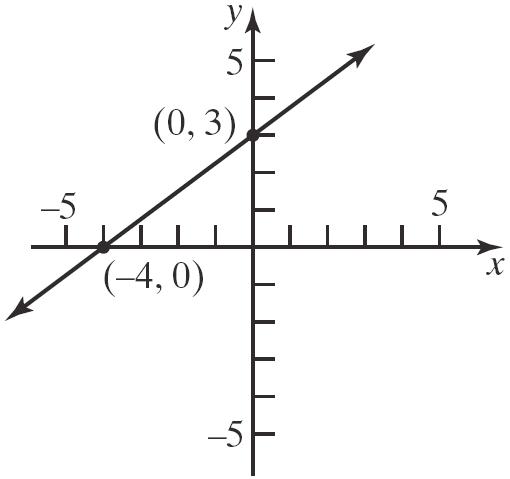
Thus, 1 (3,6) P =−
55. The midpoint of AB is: () 0600 , 22 3,0 D ++ = = The midpoint of AC is: () 0404 , 22 2,2 E ++ =
= The midpoint of BC is: () 6404 , 22 5,2 F ++ = = () 2 2 22 (,)04(34) (4)(1)16117 dCD =−+− =−+−=+= () 2 2 22 (,)26(20) (4)2164 2025 dBE =−+− =−+=+ == 22 22 (,)(20)(50) 25425 29 dAF =−+− =+=+ =
56. Let 12(0,0),(0,4),(,) PPPxy === () () () 22 12 22 1 22 22 22 2 22 22 ,(00)(40) 164 ,(0)(0) 4 16 ,(0)(4) (4)4 (4)16 dPP dPPxy xy xy dPPxy xy xy =−+− == =−+− =+= →+= =−+− =+−= →+−=
Therefore, () 2 2 22 4 816 816 2 yy yyy y y =− =−+ = = which gives 22 2 216 12 23 x x x += = =±
Two triangles are possible. The third vertex is ()() 23,2 or 23,2 .
57. Let () 1 0,0 P = , () 2 0, Ps = , () 3 ,0 Ps = , and () 4 , Pss = .
y x (0, )s (0, 0) (, 0) s (, )ss
The points 1P and 4P are endpoints of one diagonal and the points 2P and 3P are the endpoints of the other diagonal.
00 ,, 2222 s sss M ++
1,4
00 ,, 2222 s sss M ++
2,3
The midpoints of the diagonals are the same. Therefore, the diagonals of a square intersect at their midpoints.
58. Let () 1 0,0 P = , () 2 ,0Pa = , and 3 3 , 22 aa
. To show that these vertices form an equilateral triangle, we need to show that the distance between any pair of points is the same constant value.
Section2.1: The Distance and Midpoint Formulas
Since all three distances have the same constant value, the triangle is an equilateral triangle. Now find the midpoints:
Since the sides are the same length, the triangle is equilateral.
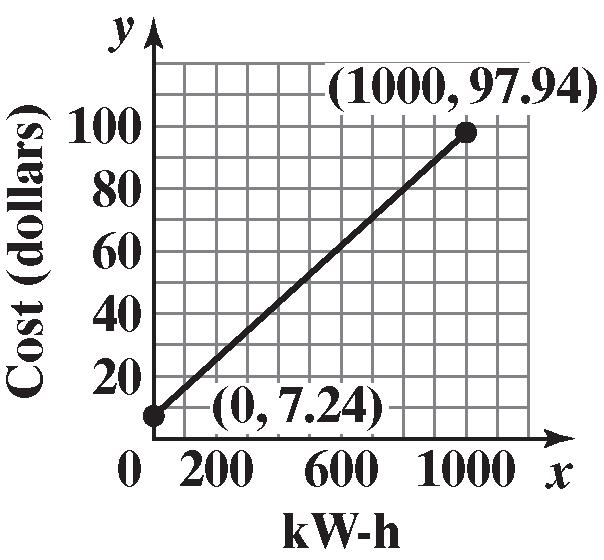
Chapter2: Graphs
59. 22 12 22 (,)(42)(11) (6)0 36 6 dPP =−−+− =−+ = = () 2 2 23 22 (,)4(4)(31) 0(4) 16 4 dPP =−−−+−− =+− = = 22 13 22 (,)(42)(31) (6)(4) 3616 52 213 dPP =−−+−− =−+− =+ = =
Since [][][] 22 2 122313 (,)(,)(,) dPPdPPdPP += , the triangle is a right triangle.
60. () 2 2 12 22 (,)6(1)(24) 7(2) 494 53 dPP =−−+− =+− =+ = () 2 2 23 22 (,)46(52) (2)(7) 449 53 dPP =−+−− =−+− =+ = () 2 2 13 22 (,)4(1)(54) 5(9) 2581 106 dPP =−−+−− =+− =+ =
Since [][][] 22 2 122313 (,)(,)(,) dPPdPPdPP += , the triangle is a right triangle. Since ()() 1223 ,, dPPdPP = , the triangle is isosceles. Therefore, the triangle is an isosceles right triangle.
61. ()() 22 12 22 (,)0(2)7(1) 2846468 217 dPP =−−+−− =+=+= = () 2 2 23 22 (,)30(27) 3(5)925 34 dPP =−+− =+−=+ = ()() 22 13 22 (,)3(2)2(1) 53259 34 dPP =−−+−− =+=+ = Since 2313 (,)(,) dPPdPP = , the triangle is isosceles.
Since [][][] 22 2 132312 (,)(,)(,) dPPdPPdPP += , the triangle is also a right triangle. Therefore, the triangle is an isosceles right triangle.
62. ()() 22 12 22 (,)4702 (11)(2) 1214125
55 dPP =−−+− =−+− =+= = () 2 2 23 22 (,)4(4)(60) 866436 100 10 dPP =−−+− =+=+ = = ()() 22 13 22 (,)4762 (3)4916 25 5 dPP =−+− =−+=+ = =
Since [][][] 22 2 132312 (,)(,)(,) dPPdPPdPP += , the triangle is a right triangle.
63. Using the Pythagorean Theorem: 222 2 2 9090 81008100 16200 16200902127.28 feet
64. Using the Pythagorean Theorem: 222 22 6060 360036007200 720060284.85 feet
65. a. First: (90, 0), Second: (90, 90), Third: (0, 90) (0,0) (0,90) (90,0) (90,90) X Y
b. Using the distance formula: 22 22 (31090)(1590) 220(75)54025 52161232.43 feet d =−+−
c. Using the distance formula: 22 22 (3000)(30090) 300210134100 30149366.20 feet d
Section2.1: The Distance and Midpoint Formulas
66. a. First: (60, 0), Second: (60, 60) Third: (0, 60) (0,0) (0,60) (60,0) (60,60) x y
b. Using the distance formula: 22 22 (18060)(2060) 120(40)16000 4010126.49 feet d =−+−
c. Using the distance formula: 22 22 (2200)(22060) 22016074000 20185272.03 feet d =−+− =+=
67. The Focus heading east moves a distance 30t after t hours. The truck heading south moves a distance 40t after t hours. Their distance apart after t hours is: 22 22 2 (30)(40) 9001600 2500 50 miles dtt tt
68. 15 miles5280 ft1 hr 22 ft/sec 1 hr1 mile3600 sec ⋅⋅= () 2 2 2 10022 10000484 feet dt
69. a. The shortest side is between 1 (2.6,1.5) P = and 2 (2.7,1.7) P = . The estimate for the desired intersection point is:
xxyy++++
1212
,, 2222
, 22
b. Using the distance formula: 22 22 (2.651.4)(1.61.3) (1.25)(0.3) 1.56250.09 1.6525 1.285 units d =−+−
70. Let 1 (2007,345) P = and 2 (2013,466) P = . The midpoint is: () () 1212 ,,22
20072013345466 , 22 4020811 , 22 2010,405.5 xxyy xy ++ = ++ = = = The estimate for 2010 is $405.5 billion. The estimate net sales of Wal-Mart Stores, Inc. in 2010 is $0.5 billion off from the reported value of $405 billion.
71. For 2003 we have the ordered pair () 2003,18660 and for 2013 we have the ordered
pair () 2013,23624 . The midpoint is () () 200320131866023624 year, $,22 401642284 , 22
2008,21142 ++ = = =
Using the midpoint, we estimate the poverty level in 2008 to be $21,142. This is lower than the actual value.
72. Answers will vary.
73. To find the domain, we know the denominator cannot be zero. 250 25 5 2 x x x −= = =
So the domain is all real numbers not equal to 5 2 or {} 5 | 2 xx ≠
74. 2 37200 (35)(4)0 (35)0 or (4)0 5 or 4 3 xx xx xx xx −−= +−= +=−= =−=
So the solution set is: 5 ,4 3
75. 2 (73)(12i)71436 7116(1) 7116 1311 iiii i i i +−=−+− =−−− =−+ =−
76. 5(3)26(23)7 515212187 7151225 510 2 xxx xxx xx x x −+≥−− −+≥−− −≥− −≥− ≤
Section2.2: Graphs of Equations in Two Variables; Intercepts; Symmetry
Section 2.2
1. () () 2317 236 33 6 x x x x +−=− +=− +=− =−
The solution set is {} 6
2. 2 2 90 9 93 x x x −= = =±=±
The solution set is {} 3,3 .
3. intercepts
4. 0 y =
5. y-axis
6. 4
7. () 3,4
8. True
9. False; the y-coordinate of a point at which the graph crosses or touches the x-axis is always 0.
The x-coordinate of such a point is an x-intercept.
10. False; a graph can be symmetric with respect to both coordinate axes (in such cases it will also be symmetric with respect to the origin).
For example: 22 1 xy+=
11. d
12. c
13. 4 y xx=−
The point (0, 0) is
14. 3
The points (0, 0) and (1, –1) are on the graph of the equation.
15. 22 9 yx=+ 22 309 99 =+ = 22 039 018 =+ ≠ 22 0(3)9 018 =−+ ≠
The point (0, 3) is on the graph of the equation.
16. 3 1 y
The points (0, 1) and (–1, 0) are on the graph of the equation.
17. 22 4 xy+= 22 024 44 += = 22 (2)24 84 −+=
() (0,2) and 2,2 are on the graph of the equation.
18. 2244xy+= 22 0414
The points (0, 1) and (2, 0) are on the graph of the equation.
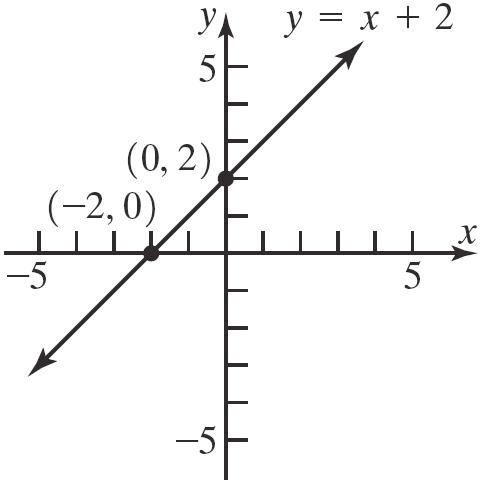
19. 2 yx=+ x-intercept: y-intercept: 02 2 x x =+ −= 02 2 y y =+ =
The intercepts are () 2,0 and () 0,2
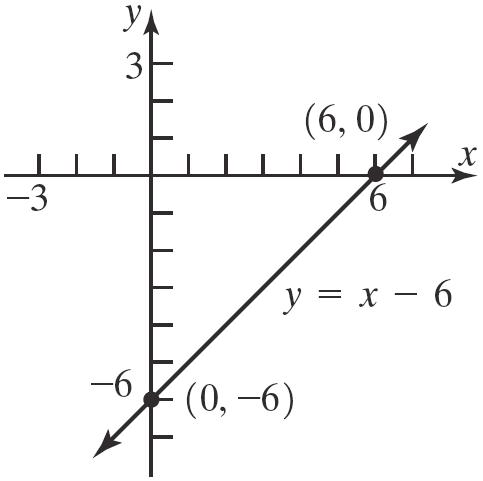
20. 6 yx=− x-intercept: y-intercept: 06 6 x x =−
Chapter2: Graphs
The intercepts are () 6,0 and () 0,6
21. 28yx=+
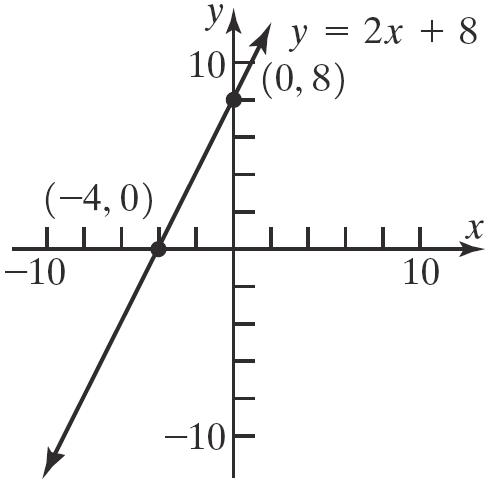
x-intercept: y-intercept: 028 28 4 x x x =+ =− =− () 208 8 y y =+ =
The intercepts are () 4,0 and () 0,8
22. 39yx=−
x-intercept: y-intercept: 039 39 3 x x x =− = = () 309 9 y y =− =−
The intercepts are () 3,0 and () 0,9
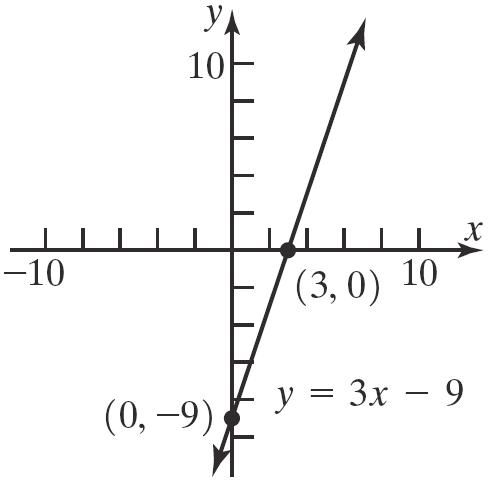
23. 2 1 yx=−
x-intercepts: y-intercept: 2 2 01 1 1 x x x =− = =± 2 01 1 y y =− =−
The intercepts are () 1,0 , () 1,0 , and () 0,1
24. 2 9 yx=−
x-intercepts: y-intercept: 2 2 09 9 3 x x x =− = =± 2 09 9 y y =− =−
The intercepts are () 3,0 , () 3,0 , and () 0,9

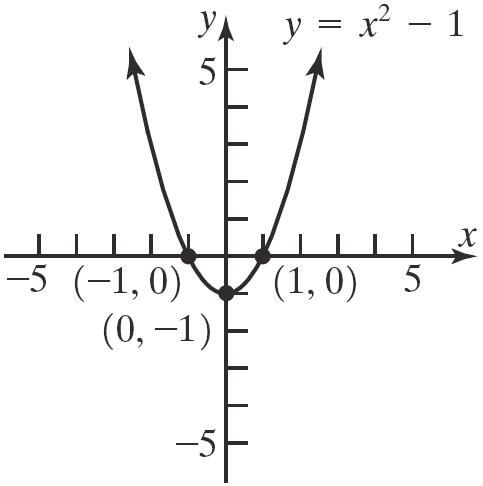
25. 2 4 yx=−+
x-intercepts: y-intercepts: 2 2 04 4 2 x x x =−+ = =± () 2 04 4 y y =−+ =
Section2.2: Graphs of Equations in Two Variables; Intercepts; Symmetry
The intercepts are () 2,0 , () 2,0 , and () 0,4

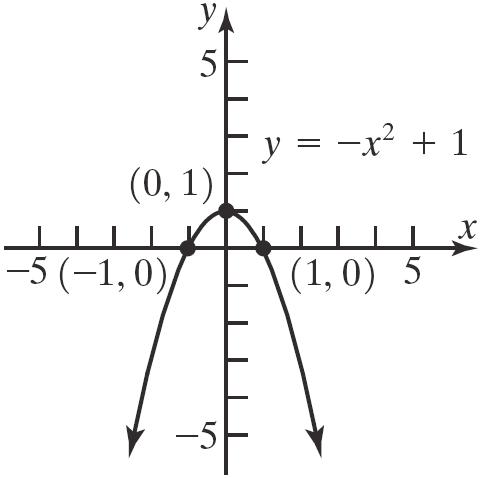
26. 2 1 yx=−+
The intercepts are () 1,0 , () 1,0 , and () 0,1
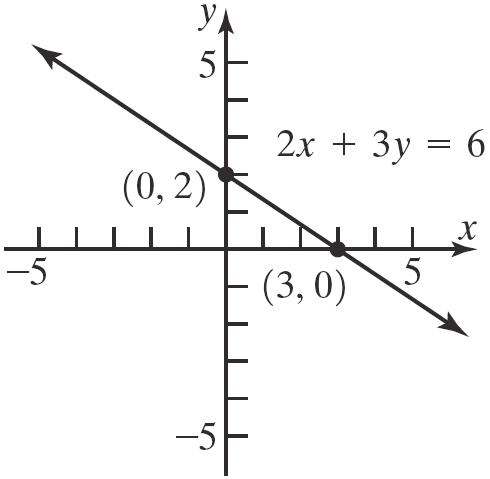
27. 236 xy+= x-intercepts: y-intercept:
The intercepts are () 3,0 and () 0,2 .
5210 xy+=
The intercepts are () 2,0 and () 0,5
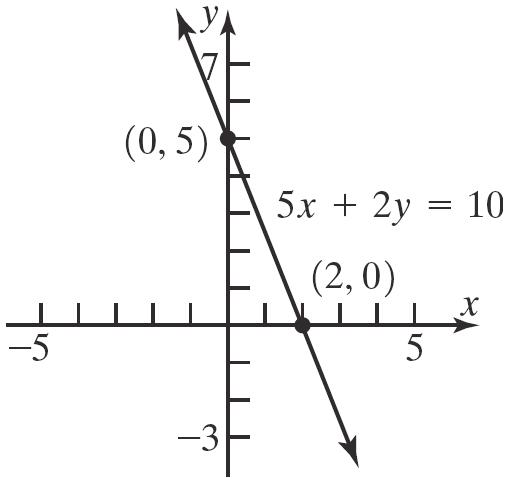
29. 2 9436 xy+= x-intercepts: y-intercept:
The intercepts are () 2,0 , () 2,0 , and () 0,9 .

44 xy+=
Chapter2: Graphs
The intercepts are () 1,0 , () 1,0 , and () 0,4


= (5, 2)
= (5, 2)
= (5, 2) (5,−2)


Section2.2: Graphs of Equations in Two Variables; Intercepts; Symmetry
41. a. Intercepts: () 1,0 and () 1,0
b. Symmetric with respect to the x-axis, y-axis, and the origin.
42. a. Intercepts: () 0,1
b. Not symmetric to the x-axis, the y-axis, nor the origin
43. a. Intercepts: () 2 0 , π , () 0,1 , and () 2 ,0 π
b. Symmetric with respect to the y-axis.
44. a. Intercepts: () 2,0 , () 0,3 , and () 2,0
b. Symmetric with respect to the y-axis.
45. a. Intercepts: () 0,0
b. Symmetric with respect to the x-axis.
46. a. Intercepts: ()2,0, ()0,2, ()0,2, and () 2,0
b. Symmetric with respect to the x-axis, y-axis, and the origin.
47. a. Intercepts: () 2,0 , () 0,0 , and () 2,0
b. Symmetric with respect to the origin.
48. a. Intercepts: () 4,0 , () 0,0 , and () 4,0
b. Symmetric with respect to the origin.
49. a. x-intercept: [] 2,1 , y-intercept 0
b. Not symmetric to x-axis, y-axis, or origin.
50. a. x-intercept: [] 1,2 , y-intercept 0
b. Not symmetric to x-axis, y-axis, or origin.
51. a. Intercepts: none
b. Symmetric with respect to the origin.
52. a. Intercepts: none
b. Symmetric with respect to the x-axis.

Chapter2: Graphs
57. 2 4 yx=+
x-intercepts: y-intercepts:
2 04 4 x x =+ −= 2 2 04 4 2 y y y =+ = =±
The intercepts are () 4,0 , () 0,2 and () 0,2 .
Test x-axis symmetry: Let yy =−
() 2 2 4 4 same yx yx −=+ =+
Test y-axis symmetry: Let x x =−
2 4 yx=−+ different
Test origin symmetry: Let x x =− and yy =−
() 2 2 4 4 different yx yx −=−+ =−+
Therefore, the graph will have x-axis symmetry.
58. 2 9 yx=+
x-intercepts: y-intercepts:
2 (0)9 09 9 x x x =−+ =−+ = 2 2 09 9 3 y y y =+ = =±
The intercepts are () 9,0 , () 0,3 and () 0,3 .
Test x-axis symmetry: Let yy =−
() 2 2 9 9 same yx yx −=+ =+
Test y-axis symmetry: Let x x =−
2 9 yx=−+ different
Test origin symmetry: Let x x =− and yy =−
() 2 2 9 9 different yx yx −=−+ =−+
Therefore, the graph will have x-axis symmetry.
59. 3 y x = x-intercepts: y-intercepts:
3 0 0 x x = = 3 00 y ==
The only intercept is () 0,0 .
Test x-axis symmetry: Let yy =−
3 different yx−=
Test y-axis symmetry: Let x x =−
33 different yxx =−=−
Test origin symmetry: Let x x =− and yy =−
33 3 same y xx yx −=−=− =
Therefore, the graph will have origin symmetry.
60. 5 y x = x-intercepts: y-intercepts:
3 0 0 x x = = 5 00 y ==
The only intercept is () 0,0
Test x-axis symmetry: Let yy =−
5 different yx−=
Test y-axis symmetry: Let x x =− 55 different yxx =−=−
Test origin symmetry: Let x x =− and yy =−
55 5 same y xx yx −=−=− =
Therefore, the graph will have origin symmetry.
61. 2 90 xy+−= x-intercepts: y-intercepts: 2 2 90 9 3 x x x −= = =± 2 090 9 y y +−= =
The intercepts are () 3,0 , () 3,0 , and () 0,9
Test x-axis symmetry: Let yy =−
2 90 different xy−−=
Test y-axis symmetry: Let x x =−
() 2 2 90 90 same xy xy −+−= +−=
Test origin symmetry: Let x x =− and yy =−
() 2 2 90 90 different xy xy −−−= −−=
Therefore, the graph will have y-axis symmetry.
Section2.2: Graphs of Equations in Two Variables; Intercepts; Symmetry
62. 2 40 xy−−=
x-intercepts: y-intercept: 2 2 040 4 2 x x x −−= = =± 2 040 4 4 y y y −−= −= =−
The intercepts are () 2,0 , () 2,0 , and () 0,4
Test x-axis symmetry: Let yy =− () 2 2 40 40 different xy xy −−−= +−=
Test y-axis symmetry: Let x x =− () 2 2 40 40 same xy xy −−−= −−=
Test origin symmetry: Let x x =− and yy =− ()() 2 2 40 40 different xy xy −−−−= +−=
Therefore, the graph will have y-axis symmetry.
63. 22 9436 xy+= x-intercepts: y-intercepts: () 2 2 2 2 94036 936
The intercepts are () 2,0 , ()2,0, ()0,3, and () 0,3 .
Test x-axis symmetry: Let yy =−
() 2 2 22 9436 9436 same xy xy +−= +=
Test y-axis symmetry: Let x x =− () 2 2 22 9436 9436 same xy xy −+= +=
Test origin symmetry: Let x x =− and yy =− ()() 22 22 9436 9436 same xy xy −+−= +=
Therefore, the graph will have x-axis, y-axis, and origin symmetry.
64. 22 44 xy+= x-intercepts: y-intercepts: 22 2 2 404 44 1 1 x x x x += = = =± () 2 2 2 404 4 2 y y y += = =±
The intercepts are () 1,0 , () 1,0 , () 0,2 , and () 0,2 .
Test x-axis symmetry: Let yy =− () 2 2 22 44 44 same xy xy +−= +=
Test y-axis symmetry: Let x x =− () 2 2 22 44 44 same xy xy −+= +=
Test origin symmetry: Let x x =− and yy =− ()()22 22 44 44 same xy xy −+−= +=
Therefore, the graph will have x-axis, y-axis, and origin symmetry.
65. 3 27 yx=−
x-intercepts: y-intercepts: 3 3 027 27 3 x x x =− = = 3 027 27 y y =− =−
The intercepts are () 3,0 and () 0,27
Test x-axis symmetry: Let yy =− 3 27 different yx −=−
Test y-axis symmetry: Let x x =− ()3 3 27 27 different yx yx =−− =−−
Test origin symmetry: Let x x =− and yy =− ()3 3 27 27 different yx yx −=−− =+
Therefore, the graph has none of the indicated symmetries.
Chapter2: Graphs
66. 4 1 yx=−
x-intercepts: y-intercepts: 4 4 01 1 1 x x x =− = =± 4 01 1 y y =− =−
The intercepts are () 1,0 , () 1,0 , and () 0,1
Test x-axis symmetry: Let yy =− 4 1 different yx −=−
Test y-axis symmetry: Let x x =− () 4 4 1 1 same yx yx =−− =−
Test origin symmetry: Let x x =− and yy =− () 4 4 1 1 different yx yx
Therefore, the graph will have y-axis symmetry.
67. 2 34yxx=−−
x-intercepts: y-intercepts: ()() 2 034 041 4 or 1 xx xx x x =−− =−+ ==− () 2 0304 4 y y =−− =−
The intercepts are () 4,0 , () 1,0 , and () 0,4
Test x-axis symmetry: Let yy =− 2 34 different yxx −=−−
Test y-axis symmetry: Let x x =− ()() 2 2 34 34 different yxx yxx =−−−− =+−
Test origin symmetry: Let x x =− and yy =− ()() 2 2 34 34 different yxx yxx −=−−−− −=+−
Therefore, the graph has none of the indicated symmetries.
68. 2 4 yx=+
x-intercepts: y-intercepts: 2 2 04 4 no real solution x x =+ =− 2 04 4 y y =+ =
The only intercept is () 0,4
Test x-axis symmetry: Let yy =− 2 4 different yx −=+
Test y-axis symmetry: Let x x =− () 2 2 4 4 same yx yx =−+ =+
Test origin symmetry: Let x x =− and yy =− () 2 2 4 4 different yx yx −=−+ −=+
Therefore, the graph will have y-axis symmetry.
69. 2 3 9 x y x = +
x-intercepts: y-intercepts: 2 3 0 9 30 0 x x x x = + = = () 2 30 0 0 9 09 y === +
The only intercept is () 0,0 .
Test x-axis symmetry: Let yy =− 2 3 different 9 x y x −= +
Test y-axis symmetry: Let x x =− () () 2 2 3 9 3 different 9 x y x x y x = −+ =− +
Test origin symmetry: Let x x =− and yy =− () () 2 2 2 3 9 3 9 3 same 9 x y x x y x x y x −= −+ −=− + = +
Therefore, the graph has origin symmetry.
Section2.2: Graphs of Equations in Two Variables; Intercepts; Symmetry
70. 2 4 2 x y x =
x-intercepts: y-intercepts: 2 2 2 4 0 2 40 4 2 x x x x x = −= = =± () 2 044 200 undefined y ==
The intercepts are () 2,0 and () 2,0
Test x-axis symmetry: Let yy =− 2 4 different 2 x y x −=
Test y-axis symmetry: Let x x =−
2 2 4 2 4 different 2 x y x x y x = =−
Test origin symmetry: Let x x =− and yy =−
2 2 2 4 2 4 2 4 same 2 x y x x y x x y x −=
Therefore, the graph has origin symmetry.
71. 3 2 9 x y x =
x-intercepts: y-intercepts: 3 2 3 0 9 0 0 x x x x
The only intercept is () 0,0
Test x-axis symmetry: Let yy =− 3 2 3 2 9 different 9 x y x x y x
Test y-axis symmetry: Let x x =− () () 3 2 3 2 9 different 9 x y x x y x = =
Test origin symmetry: Let x x =− and yy =− () () 3 2 3 2 3 2 9 9 same 9 x y x x y x x y x
Therefore, the graph has origin symmetry.
72. 4 5 1 2 x y x + = x-intercepts: y-intercepts: 4 5 4 1 0 2 1 x x x + = =− () 4 5 011 0 20 undefined y + == no real solution
There are no intercepts for the graph of this equation.
Test x-axis symmetry: Let yy =− 4 5 1 different 2 x y x + −=
Test y-axis symmetry: Let x x =− () () 4 5 4 5 1 2 1 different 2 x y x x y x −+ = + =
Test origin symmetry: Let x x =− and yy =− () () 4 5 4 5 4 5 1 2 1 2 1 same 2 x y x x y x x y x −+ −= + −= + =
Therefore, the graph has origin symmetry.
3 y x =
2 x y =
y x =
1 y x =
77. If the point () ,4 a is on the graph of 2 3 y xx=+ , then we have ()() 2 2 43 034 041 aa aa aa =+ =+− =+−
40 4 a a += =− or 10 1 a a −= = Thus, 4 a =− or 1 a = .
78. If the point () ,5 a is on the graph of 2 6 y xx=+ , then we have
50 5 a a += =− or 10 1 a a += =− Thus, 5 a =− or 1 a =−
79. For a graph with origin symmetry, if the point () , ab is on the graph, then so is the point () , ab . Since the point () 1,2 is on the graph of an equation with origin symmetry, the point () 1,2 must also be on the graph.
80. For a graph with y-axis symmetry, if the point () , ab is on the graph, then so is the point () , ab . Since 6 is an x-intercept in this case, the point () 6,0 is on the graph of the equation. Due to the y-axis symmetry, the point () 6,0 must also be on the graph. Therefore, 6 is another xintercept.
81. For a graph with origin symmetry, if the point () , ab is on the graph, then so is the point () , ab . Since 4 is an x-intercept in this case, the point () 4,0 is on the graph of the equation. Due to the origin symmetry, the point () 4,0 must also be on the graph. Therefore, 4 is another x-intercept.
82. For a graph with x-axis symmetry, if the point () , ab is on the graph, then so is the point () , ab . Since 2 is a y-intercept in this case, the
Section2.2: Graphs of Equations in Two Variables; Intercepts; Symmetry
point () 0,2 is on the graph of the equation. Due to the x-axis symmetry, the point () 0,2 must also be on the graph. Therefore, 2 is another yintercept.
83. a. () 2 2222 x yxxy+−=+
x-intercepts: () ()() () () 2 2222 2 22 4322 43 3 00 2 20 20 xxx xxx xxxx xx xx +−=+ −= −+= −= −= 3 0or20 02 xx xx =−= ==
y-intercepts: () ()() () () 2 2222 2 22 42 42 22 000 0 10 yy yy yy yy yy +−=+ = = −= −= 22 2 0or10 0 1 1 yy y y y =−= == =±
The intercepts are ()0,0, ()2,0, ()0,1, and () 0,1
b. Test x-axis symmetry: Let yy =− () ()() () 2 2222 2 2222 same xyxxy xyxxy +−−=+− +−=+
Test y-axis symmetry: Let x x =− ()() ()() () 2 2222 2 2222 different xyxxy xyxxy −+−−=−+ ++=+
Test origin symmetry: Let x x =− and yy =− ()()() ()()() () 2 2222 2 2222 different xyxxy xyxxy −+−−−=−+− ++=+
Thus, the graph will have x-axis symmetry.
84. a. 2 16120225 yx=−
x-intercepts: () 2 2 2 161200225 16225 225 16 no real solution y y y =− =− =−
y-intercepts: () 2 160120225 0120225 120225 22515 1208 x x x x =− =− −=− == The only intercept is 15 ,0 8
b. Test x-axis symmetry: Let yy =− () 2 2 16120225 16120225 same yx yx −=− =−
Test y-axis symmetry: Let x x =− () 2 2 16120225 16120225 different yx yx =−− =−−
Test origin symmetry: Let x x =− and yy =− ()() 2 2 16120225 16120225 different yx yx −=−− =−−
Thus, the graph will have x-axis symmetry.
85. a.
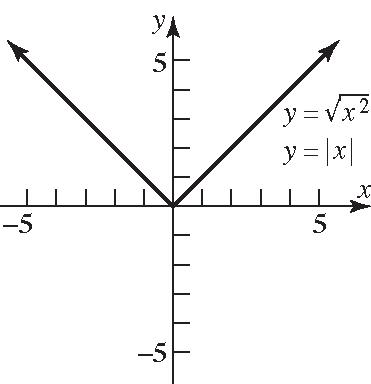
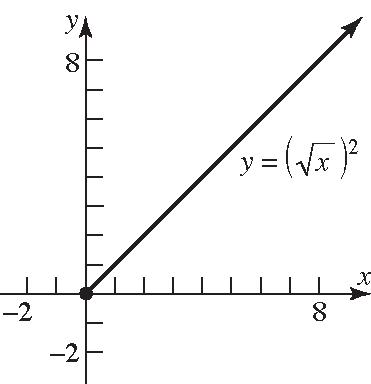
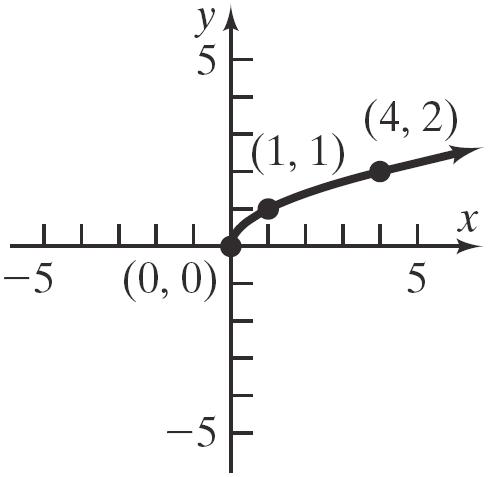
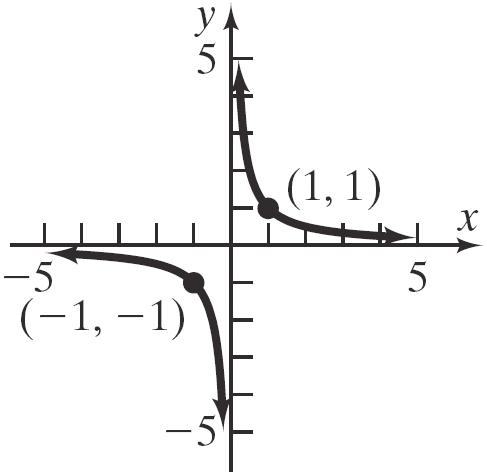
b. Since 2 x x = for all x , the graphs of 2 and y xyx== are the same.
c. For () 2 yx = , the domain of the variable x is 0 x ≥ ; for yx = , the domain of the variable x is all real numbers. Thus, () 2 only for 0. xxx=≥
d. For 2 yx = , the range of the variable y is 0 y ≥ ; for yx = , the range of the variable y is all real numbers. Also, 2 x x = only if 0 x ≥ . Otherwise, 2 x x =−
86. Answers will vary. A complete graph presents enough of the graph to the viewer so they can “see” the rest of the graph as an obvious continuation of what is shown.
87. Answers will vary. One example: y x
88. Answers will vary
89. Answers will vary
90. Answers will vary.
Case 1: Graph has x-axis and y-axis symmetry, show origin symmetry.
()() , on graph, on graph (from -axis symmetry) xyxy x →−
()() () , on graph, on graph from -axis symmetry xyxy y −→−−
Since the point () , x y is also on the graph, the graph has origin symmetry.
Case 2: Graph has x-axis and origin symmetry, show y-axis symmetry.
()() () , on graph, on graph from -axis symmetry xyxy x →−
()() () , on graph, on graph from origin symmetry xyxy −→−
Since the point () , x y is also on the graph, the graph has y-axis symmetry.
Case 3: Graph has y-axis and origin symmetry, show x-axis symmetry.
()() () , on graph, on graph from -axis symmetry xyxy y →−
()() () , on graph, on graph from origin symmetry xyxy −→−
Since the point () , x y is also on the graph, the graph has x-axis symmetry.
91. Answers may vary. The graph must contain the points () 2,5 , () 1,3 , and () 0,2 . For the graph to be symmetric about the y-axis, the graph must also contain the points () 2,5 and () 1,3 (note that (0, 2) is on the y-axis).
For the graph to also be symmetric with respect to the x-axis, the graph must also contain the points () 2,5 , () 1,3 , () 0,2 , () 2,5 , and () 1,3 . Recall that a graph with two of the symmetries (x-axis, y-axis, origin) will necessarily have the third. Therefore, if the original graph with y-axis symmetry also has x-
axis symmetry, then it will also have origin symmetry.
92. 6(2)41 6(2)82 +− ==
93. 2 2 2 33075 3(1025) 3(5)(5)3(5) xx xx xxx −+= −+= −−=−
94. 196(1)(196)14i −=−=
95. () 2
Section 2.3
1. undefined; 0
2. 3; 2 x-intercept: 23(0)6 26 3 x x x += = = y-intercept: 2(0)36 36 2 y y y += = =
3. True
4. False; the slope is 3 2 . 235 35 22 yx yx =+ =+
5. True; ()() ? ? 2124 224 44 True += += =
Section2.3: Lines
6. 12mm = ; y-intercepts; 12 1 mm⋅=−
2 8. 1 2
9. False; perpendicular lines have slopes that are opposite-reciprocals of each other. 10. d 11. c
12. b
13. a. 101 Slope 202 ==
b. If x increases by 2 units, y will increase by 1 unit.
14. a. 101 Slope 202 ==−
b. If x increases by 2 units, y will decrease by 1 unit.
15. a. 121 Slope 1(2)3 ==−
b. If x increases by 3 units, y will decrease by 1 unit.
16. a. 211 Slope 2(1)3 ==
b. If x increases by 3 units, y will increase by 1 unit.
17. 21 21 033 Slope 422 yy xx ===−
18. 21 21 422 Slope2 341 yy xx ====−

19. 21 21 1321 Slope 2(2)42 yy xx ====−

20. 21 21 312 Slope 2(1)3 yy xx ===
21. 21 21 1(1)0 Slope0 2(3)5 yy xx ====
22. 21 21 220 Slope0 549 yy xx ====
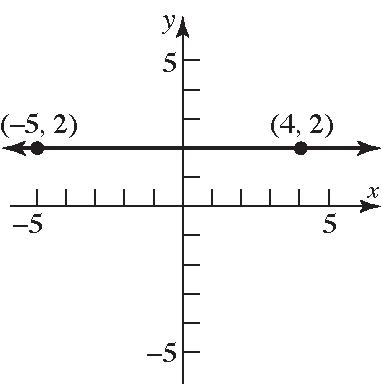
23. 21 21 224 Slope undefined. 1(1)0 yy xx ===

24. 21 21 202 Slope undefined. 220 yy xx ===
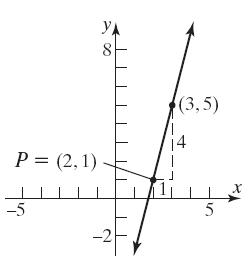
25. ()1,2;3Pm== ; 23(1)yx−=−

26. ()2,1;4Pm== ; 14(2)yx−=−
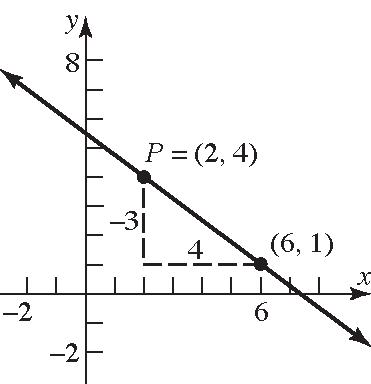
27. () 3 2,4; 4 Pm==− ; 3 4(2) 4 yx−=−−
28. () 2 1,3; 5 Pm==− ; 2 3(1) 5 yx−=−−

29. ()1,3;0Pm=−= ; 30 y −=

30. ()2,4;0Pm=−= ; 4 y =−
31. ()0,3; slope undefined P = ; 0 x =

(note: the line is the y-axis)
32. ()2,0; slope undefined P =− 2 x =−

33. 4 Slope4 1 == ; point: () 1,2
If x increases by 1 unit, then y increases by 4 units.
Answers will vary. Three possible points are: () () () 112 and 246 2,6 213 and 6410 3,10 314 and 10414 4,14 xy xy xy =+==+=
34. 2 Slope2 1 == ; point: () 2,3
If x increases by 1 unit, then y increases by 2 units.
Answers will vary. Three possible points are: () () () 211 and 325 1,5 110 and 527 0,7 011 and 729 1,9 xy xy xy =−+=−=+=
35. 33 Slope 22 =−= ; point: () 2,4
If x increases by 2 units, then y decreases by 3 units.
Answers will vary. Three possible points are: () () () 211 and 325 1,5 110 and 527 0,7 011 and 729 1,9 xy xy xy =−+=−=−−=− =−+==−−=− =+==−−=−
38. 1 Slope1 1 =−= ; point: () 4,1
If x increases by 1 unit, then y decreases by 1 unit.
Answers will vary. Three possible points are: () () () 224 and 437 4,7 426 and 7310 6,10
628 and 10313 8,13 xy xy xy =+==−−=− =+==−−=− =+==−−=−
36. 4 Slope 3 = ; point: () 3,2
If x increases by 3 units, then y increases by 4 units.
Answers will vary. Three possible points are: () () () 330 and 246 0,6 033 and 6410 3,10 336 and 10414 6,14 xy xy xy =−+==+=
37. 2 Slope2 1 =−= ; point: () 2,3
If x increases by 1 unit, then y decreases by 2 units.
Answers will vary. Three possible points are: () () () 415 and 110 5,0 516 and 011 6,1 617 and 112 7,2 xy xy xy =+==−= =+==−=− =+==−−=−
39. (0, 0) and (2, 1) are points on the line. 101 Slope 202 -intercept is 0; using : yymxb == =+ 1 0 2 2 02 1 20 or 2 yx yx xy x yyx =+ = =− −==
40. (0, 0) and (–2, 1) are points on the line. 1011 Slope 2022 -intercept is 0; using : yymxb ===− =+ 1 0 2 2 20 1 20 or 2 yx yx xy x yyx =−+ =− += +==−
41. (–1, 3) and (1, 1) are points on the line.
11 132 Slope1 1(1)2
Using ()yymxx ===− −=− 11(1) 11 2 2 or 2 yx yx yx xyyx −=−− −=−+ =−+ +==−+
42. (–1, 1) and (2, 2) are points on the line.
11 211 Slope 2(1)3
Using ()yymxx == −=− () 1 1(1) 3 1 1(1) 3 11 1 33 14 33 14 34 or 33 yx yx yx yx xyyx −=−− −=+ −=+ =+ −=−=+
43. 11(),2yymxxm −=−= 32(3) 326 23 23 or 23 yx yx yx xyyx −=− −=− =− −==−
44. 11(),1yymxxm −=−=− 21(1) 21 3 3 or 3 yx yx yx xyyx −=−− −=−+ =−+ +==−+
45. 11 1 (), 2 yymxxm −=−=− 1 2(1) 2 11 2 22 15 22 15 25 or 22 yx yx yx xyyx −=−− −=−+ =−+ +==−+
46. 11(),1yymxxm −=−= 11((1)) 11 2 2 or 2 yx yx yx xyyx −=−− −=+ =+ −=−=+
47. Slope = 3; containing (–2, 3) 11() 33((2)) 336 39 39 or 39 yymxx yx yx yx xyyx −=− −=−− −=+ =+ −=−=+
48. Slope = 2; containing the point (4, –3) 11() (3)2(4) 328 211 211 or 211 yymxx yx yx yx xyyx −=− −−=− +=− =− −==−
49. Slope = 2 3 ; containing (1, –1) 11() 2 (1)(1) 3 22 1 33 21 33 21 231 or 33 yymxx yx yx yx xyyx −=− −−=−− +=−+ =−− +=−=−−
50. Slope = 1 2 ; containing the point (3, 1) 11() 1 1(3) 2 13 1 22 11 22 11 21 or 22 yymxx yx yx yx xyyx −=− −=− −=− =− −==−
Chapter2: Graphs
51. Containing (1, 3) and (–1, 2) 2311 1122 m === 11() 1 3(1) 2 11 3 22 15 22 15 25 or 22 yymxx yx yx yx xyyx −=−
52. Containing the points (–3, 4) and (2, 5) 541 2(3)5 m == 11() 1 5(2) 5 12 5 55 123 55 123 523 or 55 yymxx yx yx yx xyyx
53. Slope = –3; y-intercept =3 33 33 or 33 ymxb yx xyyx =+ =−+ +==−+
54. Slope = –2; y-intercept = –2 2(2) 22 or 22 ymxb yx xyyx =+ =−+− +=−=−−
55. x-intercept = 2; y-intercept = –1 Points are (2,0) and (0,–1) 1011 0222 m === 1 1 2 1 22 or 1 2 ymxb yx x yyx =+ =− −==−
56. x-intercept = –4; y-intercept = 4
Points are (–4, 0) and (0, 4) 404 1 0(4)4 m === 14 4 4 or 4 ymxb yx yx xyyx =+ =+ =+ −=−=+
57. Slope undefined; containing the point (2, 4) This is a vertical line.
2 No slope-intercept form. x =
58. Slope undefined; containing the point (3, 8) This is a vertical line.
3 No slope-intercept form. x =
59. Horizontal lines have slope 0 m = and take the form yb = . Therefore, the horizontal line passing through the point () 3,2 is 2 y =
60. Vertical lines have an undefined slope and take the form x a = . Therefore, the vertical line passing through the point () 4,5 is 4 x =
61. Parallel to 2 y x = ; Slope = 2 Containing (–1, 2) 11() 22((1)) 22224 24 or 24 yymxx yx yxyx xyyx −=−
−=−−
−=+→=+
−=−=+
62. Parallel to 3 y x =− ; Slope = –3; Containing the point (–1, 2) 11() 23((1)) 23331 31 or 31 yymxx yx yxyx xyyx −=−
−=−−−
−=−−→=−−
+=−=−−
63. Parallel to 22 xy−=− ; Slope = 2
Containing the point (0, 0) 11() 02(0) 2 20 or 2 yymxx yx yx x yyx −=− −=− =
64. Parallel to 25xy−=− ; () 1 Slope; Containing the point 0,0 2 = 11() 11 0(0)22 1 20 or 2 yymxx yxyx xyyx −=−
65. Parallel to 5 x = ; Containing (4,2)
This is a vertical line.
4 No slope-intercept form. x =
66. Parallel to 5 y = ; Containing the point (4, 2)
This is a horizontal line. Slope = 0 2 y =
67. Perpendicular to 1 4; 2 yx=+ Containing (1, –2)
Slope of perpendicular = –2 11() (2)2(1) 2222 20 or 2 yymxx yx yxyx xyyx
68. Perpendicular to 23yx=− ; Containing the point (1, –2) 1
Slope of perpendicular 2 =− 11() 1 (2)(1) 2 1113 2 2222 13 23 or 22 yymxx yx yxyx xyyx
69. Perpendicular to 22 xy+= ; Containing the point (–3, 0) 1
Slope of perpendicular 2 = 11() 0((3))113 222 13 23 or 22 yymxx yxyx xyyx −=− −=−−→=+ −=−=+
70. Perpendicular to 25xy−=− ; Containing the point (0, 4)
Slope of perpendicular = –2 24 24 or 24 ymxb yx xyyx =+ =−+ +==−+
71. Perpendicular to 8 x = ; Containing (3, 4)
Slope of perpendicular = 0 (horizontal line) 4 y =
72. Perpendicular to 8 y = ; Containing the point (3, 4)
Slope of perpendicular is undefined (vertical line). 3 x = No slope-intercept form.
73. 23yx=+ ; Slope = 2; y-intercept = 3
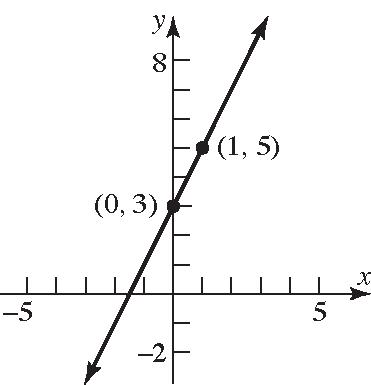
74. 34yx=−+ ; Slope = –3; y-intercept = 4
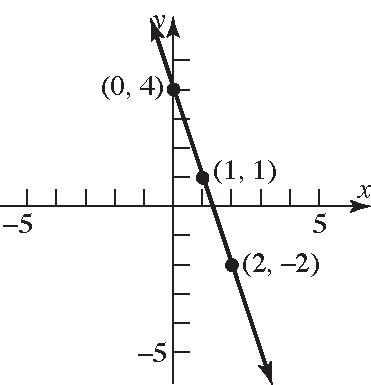
Chapter2: Graphs
75. 1 1 2 yx=− ; 22yx=−
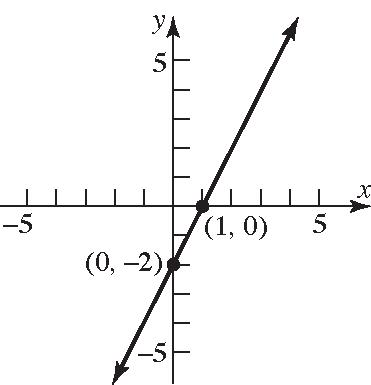
Slope = 2; y-intercept = –2
76. 1 2 3 xy+= ; 1 2 3 yx=−+ 1 Slope 3 =− ; y-intercept = 2
77. 1 2 2 yx=+ ; 1 Slope 2 = ; y-intercept = 2

78. 1 2 2 yx=+ ; Slope = 2; 1 -intercept 2 y =
79. 24xy+= ; 1 242 2 yxyx =−+→=−+ 1 Slope 2 =− ; y-intercept = 2

80. 36xy −+= ; 1 362 3 yxyx =+→=+ 1 Slope 3 = ; y-intercept = 2
81. 236 xy−= ; 2 3262 3 yxyx −=−+→=− 2 Slope 3 = ; y-intercept = –2

82. 326 xy+= ; 3 2363 2 yxyx =−+→=−+ 3 Slope 2 =− ; y-intercept = 3
83. 1 xy+= ; 1 y x =−+
Slope = –1; y-intercept = 1
84. 2 xy−= ; 2 yx=− Slope = 1; y-intercept = –2
85. 4 x =− ; Slope is undefined y-intercept - none
86. 1 y =− ; Slope = 0; y-intercept = –1
87. 5 y = ; Slope = 0; y-intercept = 5
88. 2 x = ; Slope is undefined y-intercept - none
89. 0 yx−= ; yx = Slope = 1; y-intercept = 0
Chapter2: Graphs
90. 0 xy+= ; yx =− Slope = –1; y-intercept = 0
91. 230 yx−= ; 3 23 2 yxyx =→=
3 Slope 2 = ; y-intercept = 0

92. 320 xy+= ; 3 23 2 yxyx =−→=−
3 Slope 2 =− ; y-intercept = 0
93 a. x-intercept: () 2306
26 3 x x x += = =
The point () 3,0 is on the graph.
y-intercept: () 2036
36 2 y y y += = =
The point () 0,2 is on the graph.
b. y x 5 5 5
5 (3,0) (0,2)
94. a. x-intercept: () 3206
36 2 x x x −= = =
The point () 2,0 is on the graph.
y-intercept: () 3026
26 3 y y y −= −= =−
The point () 0,3 is on the graph.
b. (0,−3) y x 5 5 5
5 (2,0)
Section2.3: Lines
95. a. x-intercept: () 45040
440 10 x x x −+= −= =−
The point () 10,0 is on the graph.
b.
y-intercept: () 40540
540 8 y y y −+= = =
The point () 0,8 is on the graph.

96. a. x-intercept: () 64024
b.
624 4 x x x −= = =
The point () 4,0 is on the graph.
y-intercept: () 60424
424 6 y y y −= −= =−
The point () 0,6 is on the graph.

97. a. x-intercept: () 72021
b.
721 3 x x x += = =
The point () 3,0 is on the graph.
y-intercept: () 70221
221 21 2 y y y += = =
The point 21 0, 2 is on the graph.
98. a. x-intercept: () 53018 518 18 5 x x x += = =
The point 18 ,0 5 is on the graph.
b.
y-intercept: () 50318
318 6 y y y += = =
The point () 0,6 is on the graph.

Chapter2: Graphs
99. a. x-intercept: () 11 01 23 1 1 2 2 x x x += = =
The point () 2,0 is on the graph.
y-intercept: () 11 01 23 1 1 3 3 y y y += = =
The point () 0,3 is on the graph. b.
100. a. x-intercept: () 2 04 3 4 x x −= =
The point () 4,0 is on the graph. y-intercept: () 2 04 3 2 4 3 6 y y
The point () 0,6 is on the graph. b.
101. a. x-intercept: () 0.20.501 0.21 5 x x x −= = =
The point () 5,0 is on the graph. y-intercept: () 0.200.51 0.51 2 y y y −= −= =−
The point () 0,2 is on the graph.
102. a. x-intercept: () 0.30.401.2 0.31.2 4 x x x −+= −= =−
The point () 4,0 is on the graph. y-intercept: () 0.300.41.2 0.41.2 3 y y y −+= = =
The point () 0,3 is on the graph.
103. The equation of the x-axis is 0 y = . (The slope is 0 and the y-intercept is 0.)
104. The equation of the y-axis is 0 x = . (The slope is undefined.)
105. The slopes are the same but the y-intercepts are different. Therefore, the two lines are parallel.
106. The slopes are opposite-reciprocals. That is, their product is 1 . Therefore, the lines are perpendicular.
107. The slopes are different and their product does not equal 1 . Therefore, the lines are neither parallel nor perpendicular.
108. The slopes are different and their product does not equal 1 (in fact, the signs are the same so the product is positive). Therefore, the lines are neither parallel nor perpendicular.
109. Intercepts: () 0,2 and () 2,0 . Thus, slope = 1. 2 or 2 yxxy=+−=−
110. Intercepts: () 0,1 and () 1,0 . Thus, slope = –1. 1 or 1 yxxy =−++=
111. Intercepts: () 3,0 and () 0,1 . Thus, slope = 1 3 1 1 or 33 3 yxxy =−++=
112. Intercepts: () 0,1 and () 2,0 . Thus, slope = 1 2 1 1 or 22 2 yxxy =−−+=−
113. () 1 2,5 P =− , () 2 1,3 P = : 1 5322 2133 m ===− () 2 1,3 P = , () 3 1,0 P =− : () 2 303 112 m == Since 12 1 mm⋅=− , the line segments 12PP and 23PP are perpendicular. Thus, the points 1P , 2P , and 3P are vertices of a right triangle.
114. () 1 1,1 P =− , () 2 4,1 P = , () 3 2,2 P = , () 4 5,4 P = () 12 11 2 413 m == ; 24 41 3 54 m == ; 34 422 523 m == ; () 13 21 3 21 m ==
Each pair of opposite sides are parallel (same slope) and adjacent sides are not perpendicular. Therefore, the vertices are for a parallelogram.
115. () 1 1,0 P =− , () 2 2,3 P = , () 3 1,2 P =− , () 4 4,1 P = () 12 303 1 213 m === ; 24 13 1 42 m ==− ; () 34 12 3 1 413 m === ; () 13 20 1 11 m ==−
Opposite sides are parallel (same slope) and adjacent sides are perpendicular (product of slopes is 1 ). Therefore, the vertices are for a rectangle.
116. () 1 0,0 P = , () 2 1,3 P = , () 3 4,2 P = , () 4 3,1 P =− 12 30 3 10 m == ; 23 231 413 m ==− ; 34 12 3 34 m == ; 14 101 303 m ==− ()() 22 12 10301910 d =−+−=+= ()() 22 23 41239110 d =−+−=+= ()() 22 34 34121910 d =−+−−=+= ()() 22 14 30109110 d =−+−−=+=
Opposite sides are parallel (same slope) and adjacent sides are perpendicular (product of slopes is 1 ). In addition, the length of all four sides is the same. Therefore, the vertices are for a square.
117. Let x = number of miles driven, and let C = cost in dollars.
Total cost = (cost per mile)(number of miles) + fixed cost 0.6039Cx=+
When x = 110, ()() 0.6011039$105.00 C =+=
When x = 230, ()() 0.6023039$177.00 C =+= .
118. Let x = number of pairs of jeans manufactured, and let C = cost in dollars.
Total cost = (cost per pair)(number of pairs) + fixed cost 8500Cx=+
When x = 400, ()()8400500$3700 C =+=
When x = 740, ()()8740500$6420 C =+=
119. Let x = number of miles driven annually, and let C = cost in dollars.
Total cost = (approx cost per mile)(number of miles) + fixed cost 0.174462Cx=+
120. Let x = profit in dollars, and let S = salary in dollars.
Weekly salary = (% share of profit)(profit) + weekly pay 0.05375Sx=+
121. a. 0.082115.37Cx=+ ; 0800 x ≤≤
b.

c. For 200 kWh, 0.0821(200)15.37$31.79 C =+=
d. For 500 kWh, 0.0821(500)15.37$56.42 C =+=
e. For each usage increase of 1 kWh, the monthly charge increases by $0.0821 (that is, 8.21 cents).
122. a. 0.09077.24Cx=+ ; 01000 x ≤≤
b.
c. For 200 kWh, () 0.09072007.24$25.38 C =+=
d. For 500 kWh, () 0.09075007.24$52.59 C =+=
e. For each usage increase of 1 kWh, the monthly charge increases by $0.0907 (that is, 9.07 cents).
123. (,)(0,32);(,)(100,212) CFCF °°=°°= 212321809 slope 10001005 9 32(0) 5 9 32() 5 5 (32) 9 FC FC CF === °−=°− °−=° °=°− If 70 F °= , then 55(7032)(38) 99 21.1 C C °=−= °≈°
124. a. º273KC=+ b. 5 º(º32) 9 CF=− 5 (32)273 9 5160 º273 99 52297 º 99 KF KF KF =°−+ =−+ =+
125. a. The y-intercept is (0, 30), so b = 30. Since the ramp drops 2 inches for every 25 inches of run, the slope is 22 2525 m ==− . Thus, the equation is 2 30 25 yx=−+ .
b. Let y = 0. () 2 030 25 2 30 25 25225 30 2252 375 x x x x =−+ =
=
=
The x-intercept is (375, 0). This means that the ramp meets the floor 375 inches (or 31.25 feet) from the base of the platform.
c. No. From part (b), the run is 31.25 feet which exceeds the required maximum of 30 feet.
d. First, design requirements state that the maximum slope is a drop of 1 inch for each 12 inches of run. This means 1 12 m ≤ Second, the run is restricted to be no more than 30 feet = 360 inches. For a rise of 30 inches, this means the minimum slope is 301 36012 = . That is, 1 12 m ≥ . Thus, the only possible slope is 1 12 m = . The diagram indicates that the slope is negative. Therefore, the only slope that can be used to obtain the 30-inch rise and still meet design requirements is 1 12 m =− . In words, for every 12 inches of run, the ramp must drop exactly 1 inch.
126. a. The year 2000 corresponds to x = 0, and the year 2012 corresponds to x = 12. Therefore, the points (0, 20.6) and (12, 9.3) are on the line. Thus,
9.320.611.3 0.942 12012 m ==−=− . The yintercept is 20.6, so b = 20.6 and the equation is 0.94220.6yx=−+
b. x-intercept: 00.94220.6 0.94220.6 21.9 x x x =−+ = = y-intercept: () 0.942020.620.6 y =−+= The intercepts are (21.9, 0) and (0, 20.6).
c. The y-intercept represents the percentage of twelfth graders in 2000 who had reported daily use of cigarettes. The x-intercept represents the number of years after 2000 when 0% of twelfth graders will have reported daily use of cigarettes.
d. The year 2025 corresponds to x = 25. () 0.9422520.62.95 y =−+=−
This prediction is not reasonable.
127. a. Let x = number of boxes to be sold, and A = money, in dollars, spent on advertising. We have the points 11 (,)(100,000,40,000); xA =
Section2.3: Lines
22 (,)(200,000,60,000) xA = () 60,00040,000 slope 200,000100,000 20,0001 100,0005 1 40,000100,000 5 1 40,00020,000 5 1 20,000 5 Ax Ax Ax = == −=− −=− =+
b. If x = 300,000, then () 1 300,00020,000$80,000 5 A =+=
c. Each additional box sold requires an additional $0.20 in advertising.
128. Find the slope of the line containing () , ab and () , ba : slope1 ab ba ==−
The slope of the line yx = is 1.
Since 111−⋅=− , the line containing the points (,) and (,)abba is perpendicular to the line yx =
The midpoint of (,) and (,)abba is , 22 abba M ++ = .
Since the coordinates are the same, the midpoint lies on the line yx =
Note: 22 abba ++ =
129. 2 x yC−= Graph the lines: 24 20 22 xy xy xy −=− −= −=
All the lines have the same slope, 2. The lines
Chapter2: Graphs
are parallel.

130. Refer to Figure 47. () () () 2 1 2 2 12 length of ,1 length of ,1 length of , OAdOAm OBdOBm ABdABmm ==+ ==+ ==−
Now consider the equation ()()() 22 2 22 111212 mmmm +++=−
If this equation is valid, then AOBΔ is a right triangle with right angle at vertex O ()()() 22 2 22 1212 2222 121122 2222 121122 11 112 22 mmmm mmmmmm mmmmmm +++=− +++=−+ ++=−+
But we are assuming that 12 1 mm =− , so we have () 2222 1212 2222 1212 221 22 00 mmmm mmmm ++=−−+ ++=++ =
Therefore, by the converse of the Pythagorean Theorem, AOBΔ is a right triangle with right angle at vertex O. Thus Line 1 is perpendicular to Line 2.
131. (b), (c), (e) and (g)
The line has positive slope and positive y-intercept.
132. (a), (c), and (g)
The line has negative slope and positive y-intercept.
133. (c)
The equation 2 xy−=− has slope 1 and yintercept (0,2). The equation 1 xy−= has
slope 1 and y-intercept (0,1). Thus, the lines are parallel with positive slopes. One line has a positive y-intercept and the other with a negative y-intercept.
134. (d)
The equation 22yx−= has slope 2 and yintercept (0,2). The equation 21xy+=− has slope 1 2 and y-intercept 1 0,. 2
The lines are perpendicular since 1 21 2
. One line has a positive y-intercept and the other with a negative y-intercept.
135 – 137. Answers will vary.
138. No, the equation of a vertical line cannot be written in slope-intercept form because the slope is undefined.
139. No, a line does not need to have both an xintercept and a y-intercept. Vertical and horizontal lines have only one intercept (unless they are a coordinate axis). Every line must have at least one intercept.
140. Two lines with equal slopes and equal y-intercepts are coinciding lines (i.e. the same).
141. Two lines that have the same x-intercept and yintercept (assuming the x-intercept is not 0) are the same line since a line is uniquely defined by two distinct points.
142. No. Two lines with the same slope and different xintercepts are distinct parallel lines and have no points in common.
Assume Line 1 has equation 1ymxb =+ and Line 2 has equation 2ymxb =+ ,
Line 1 has x-intercept 1b m and y-intercept 1b .
Line 2 has x-intercept 2b m and y-intercept 2b
Assume also that Line 1 and Line 2 have unequal x-intercepts. If the lines have the same y-intercept, then 12bb = .
But 12 bb mm
Line 1 and Line 2 have the same x-intercept, which contradicts the original assumption that the lines have unequal x-intercepts. Therefore, Line 1 and Line 2 cannot have the same y-intercept.
143. Yes. Two distinct lines with the same y-intercept, but different slopes, can have the same x-intercept if the x-intercept is 0 x =
Assume Line 1 has equation 1 ymxb =+ and Line 2 has equation 2 ymxb =+ ,
Line 1 has x-intercept 1 b m and y-intercept b
Line 2 has x-intercept 2 b m and y-intercept b
Assume also that Line 1 and Line 2 have unequal slopes, that is 12mm ≠ . If the lines have the same x-intercept, then 12 bb
Since we are assuming that 12mm ≠ , the only way that the two lines can have the same x-intercept is if 0. b =
144. Answers will vary.
145. () 21 21 4263 42 13 yy m xx ====−
It appears that the student incorrectly found the slope by switching the direction of one of the subtractions. 146. 23222 45453 2 28 2 28 416 1 1 xyx xyxyy xy xy x y
The solution set is: {} 326,326 −+ . 149. 25710 253 3253 228 14 x x x x x −+< −< −<−< << <<
The solution set is: {} |14xx<< . Interval notation: () 1,4 Section 2.4 1. add; () 2 1 2 1025 ⋅= 2. () 2 29 29 23 23 x x x x −= −=± −=± =± 5 or 1 xx==−
The solution set is {1,5}.
3. False. For example, 22 2280xyxy++++= is not a circle. It has no real solutions.
4. radius
5. True; 2 93rr=→=
6. False; the center of the circle ()() 22 3213xy++−= is () 3,2 .
7. d
8. a
9. Center = (2, 1)
Radiusdistance from (0,1) to (2,1) (20)(11)42 = =−+−==
22
Equation: 22 (2)(1)4 xy−+−=
10. Center = (1, 2)
Radiusdistance from (1,0) to (1,2) (11)(20)42 = =−+−==
22
Equation: 22 (1)(2)4 xy−+−=
11. Center = midpoint of (1, 2) and (4, 2) ()() 1422 5 222,,2 ++ == () 2 2 5 2
Radiusdistance from ,2 to (4,2) 4(22)593 242 = =−+−==
Equation: 2 2 59 (2) 24xy −+−=
General form: 22 40 xy+−=
14. ()()222 x hykr −+−= 222 22 (0)(0)3 9 xy xy −+−= +=
General form: 22 90 xy+−=
15. ()()222 x hykr −+−= 222 22 (0)(2)2 (2)4 xy xy −+−= +−=
General form: 22 22 444 40 xyy xyy +−+= +−=
12. Center = midpoint of (0, 1) and (2, 3) () 0213 ,1,2 22 ++ == () () 2 2
Radiusdistance from 1,2 to (2,3) 21(32)2 = =−+−=
Equation: () 2 2 1(2)2xy−+−=
13. ()()222 x hykr −+−= 222 22 (0)(0)2 4 xy xy −+−= +=
16. ()()222 x hykr −+−= 222 22 (1)(0)3 (1)9 xy xy −+−= −+=
General form: 22 22 219 280 xxy xyx −++= +−−=

17. ()()222 x hykr −+−= 222 22 (4)((3))5 (4)(3)25 xy xy −+−−= −++=
General form: 22 22 8166925 860 xxyy xyxy −++++= +−+=
18. ()()222 x hykr −+−= 222 22 (2)((3))4 (2)(3)16 xy xy −+−−= −++=
General form: 22 22 446916 4630 xxyy xyxy −++++= +−+−=

19. ()()222 x hykr −+−= () 222 22 (2)(1)4 (2)(1)16 xy xy −−+−= ++−=
Section2.4: Circles
General form: 22 22 442116 42110 xxyy xyxy +++−+= ++−−=

20. ()()222 x hykr −+−= () 222 22 (5)((2))7 (5)(2)49 xy xy −−+−−= +++=
General form: 22 22 10254449 104200 xxyy xyxy +++++= +++−=
21. ()()222 x hykr −+−= 22 2 2 2 11 (0) 22 11 24 xy xy −+−=
−+=
General form: 22 22 11 44 0 xxy xyx −++= +−=

22. ()()222 x hykr −+−= () 2 2 2 2 2 11 0 22 11 24 xy xy
23. 22 4 xy+= 222 2 xy+=
a. Center: (0,0); Radius2 =
b.
c. x-intercepts: () 2 2 2 04 4 42 x x x += = =±=±
y-intercepts: () 2 2 2 04 4 42 y y y += = =±=±
The intercepts are ()() 2,0,2,0, ()0,2, and ()0,2.
24. 22(1)1xy+−= 222 (1)1xy+−=
a. Center:(0,1); Radius1 = b.

c. x-intercepts: 22 2 2 (01)1 11 0 00 x x x x +−= += = =±=
y-intercepts: () 2 2 2 0(1)1 (1)1 11 11 11 y y y y y +−= −= −=± −=± =± 2 or 0 yy==
The intercepts are () 0,0 and ()0,2.
25. () 2 2 2328 xy−+= () 2 2 34xy−+=
a. Center: (3, 0); Radius 2 =
Section2.4: Circles
c. x-intercepts: ()() () 22 2 304 34 34 32 32 x x x x x −+= −= −=± −=± =± 5 or 1 x x ==
y-intercepts: () () 2 2 2 2 2 2 034 34 94 5 y y y y −+= −+= += =− No real solution. The intercepts are () 1,0 and ()5,0.
26. ()() 22 31316 xy++−= ()() 22 112xy++−=
a. Center: (–1,1); Radius = 2
b.
c. x-intercepts: ()()
-intercepts:
2 or 0
The intercepts are ()() 2,0,0,0, and ()0,2.
27. 22 2440xyxy+−−−= 22 22 222 244 (21)(44)414 (1)(2)3 xxyy xxyy xy −+−= −++−+=++ −+−=
a. Center: (1, 2); Radius = 3 b.

c. x-intercepts:
(1)(02)3 (1)(2)3
Chapter2: Graphs
y-intercepts: () () 222 222 2 2 (01)(2)3 (1)(2)3 129 28 28 222 222 y y y y y y y −+−= −+−= +−= −= −=± −=± =±
The intercepts are ()() 15,0,15,0, −+ () 0,222, and () 0,222. +
28. 22 42200xyxy+++−= 22 22 222 4220 (44)(21)2041 (2)(1)5 xxyy xxyy xy +++= +++++=++ +++=
a. Center: (–2,–1); Radius = 5 b.
c. x-intercepts: 222 2 2 (2)(01)5 (2)125 (2)24 224 226 226 x x x x x x +++= ++= += +=± +=± =−± y-intercepts: 222 2 2 (02)(1)5 4(1)25 (1)21 121 121 y y y y y +++= ++= += +=± =−±
The intercepts are () 226,0, () 226,0, −+() 0,121, and () 0,121. −+
29. 22 22 22 222 4410 441 (44)(44)144 (2)(2)3 xyxy xxyy xxyy xy ++−−= ++−= +++−+=++ ++−=
a. Center: (–2, 2); Radius = 3 b. y x −55 5 −5 (−2,2)
c. x-intercepts: 222 2 2 (2)(02)3 (2)49 (2)5 25 25 x x x x x ++−= ++= += +=± =−± y-intercepts: 222 2 2 (02)(2)3 4(2)9 (2)5 25 25 y y y y y ++−= +−= −= −=± =±
The intercepts are () 25,0, () 25,0, −+() 0,25, and () 0,25. +
30. 22 22 22 222 6290 629 (69)(21)991 (3)(1)1 xyxy xxyy xxyy xy +−++= −++=− −++++=−++ −++=
a. Center: (3, –1); Radius = 1 b.
Section2.4: Circles
c.
a.
b.
33. 22
a. Center: (3,–2); Radius = 5 b.

c. x-intercepts:
The intercepts are () 321,0, () 321,0, + ()0,6, and ()0,2.
34. a. 22 22870 xyx+++=
No
solutions.
and 2 2,0. 2
35. () 22 22 22 2 22 2820 40 4404 22 xxy xxy xxy xy ++= ++= +++=+ ++=
a. Center: () 2,0 ; Radius: 2 r = b.
c. x-intercepts: ()() () 22 2 2 2 202 (2)4 24 22 22 x x x x x ++= += +=± +=± =−± 0 or 4 xx==−
y-intercepts: () 2 22 2 2 022 44 0 0 y y y y ++= += = =
The intercepts are () 4,0 and ()0,0.
36. () 22 22 22 2 2 33120 40 4404 24 xyy xyy xyy xy +−= +−= +−+=+ +−=
a. Center: () 0,2 ; Radius: 2 r =
b.
c. x-intercepts: () 2 2 2 2 024 44 0 0 x x x x +−= += = = y-intercepts: () () 2 2 2 024 24 24 22 22 y y y y y +−= −= −=± −=± =± 4 or 0 yy==
The intercepts are () 0,0 and ()0,4.
Section2.4: Circles
37. Center at (0, 0); containing point (–2, 3). ()() 22 20304913 r =−−+−=+=
Equation: () 2 22 22 (0)(0)13 13 xy xy −+−= +=
38. Center at (1, 0); containing point (–3, 2). ()() 22 31201642025 r =−−+−=+==
Equation: () 2 22 22 (1)(0)20 (1)20 xy xy −+−= −+=
39. Center at (2, 3); tangent to the x-axis. 3 r =
Equation: 222 22 (2)(3)3 (2)(3)9 xy xy −+−= −+−=
40. Center at (–3, 1); tangent to the y-axis.
3 r =
Equation: 222 22 (3)(1)3 (3)(1)9 xy xy ++−= ++−=
41. Endpoints of a diameter are (1, 4) and (–3, 2). The center is at the midpoint of that diameter:
Center: ()1(3)42,1,3 22 +−+ =−
Radius: 22 (1(1))(43)415 r =−−+−=+=
Equation: () 2 22 22 ((1))(3)5 (1)(3)5 xy xy −−+−= ++−=
42. Endpoints of a diameter are (4, 3) and (0, 1). The center is at the midpoint of that diameter: Center: () 4031 22,2,2 ++ =
Radius: 22 (42)(32)415 r =−+−=+=
Equation: () 2 22 22 (2)(2)5 (2)(2)5 xy xy −+−= −+−=
43. Center at (–1, 3); tangent to the line y = 2. This means that the circle contains the point (–1, 2), so the radius is r = 1.
Equation: 222 22 (1)(3)(1) (1)(3)1 xy xy ++−= ++−=
44. Center at (4, –2); tangent to the line x = 1. This means that the circle contains the point (1, –2), so the radius is r = 3.
Equation: 222 22 (4)(2)(3) (4)(2)9 xy xy −++= −++=
45. (c); Center: () 1,2 ; Radius = 2
46. (d) ; Center: () 3,3 ; Radius = 3
47. (b) ; Center: () 1,2 ; Radius = 2
48. (a) ; Center: () 3,3 ; Radius = 3
49. Let the upper-right corner of the square be the point () ,x y . The circle and the square are both centered about the origin. Because of symmetry, we have that x y = at the upper-right corner of the square. Therefore, we get
The length of one side of the square is 2 x . Thus, the area is
square units.
50. The area of the shaded region is the area of the circle, less the area of the square. Let the upperright corner of the square be the point () ,x y . The circle and the square are both centered about the origin. Because of symmetry, we have that x y = at the upper-right corner of the square. Therefore, we get
The length of one side of the square is 2 x . Thus, the area of the square is () 2 23272 ⋅= square units. From the equation of the circle, we have 6 r = . The area of the circle is () 2 2 636 r πππ == square units. Therefore, the area of the shaded region is 3672 A π =− square units.
51. The diameter of the Ferris wheel was 250 feet, so the radius was 125 feet. The maximum height was 264 feet, so the center was at a height of 264125139 −= feet above the ground. Since the center of the wheel is on the y-axis, it is the point (0, 139). Thus, an equation for the wheel is: ()() () 22 2 2 2 0139125 13915,625 xy xy −+−= +−=
52. The diameter of the wheel is 520 feet, so the radius is 260 feet. The maximum height is 550 feet, so the center of the wheel is at a height of 550260290 −= feet above the ground. Since the center of the wheel is on the y-axis, it is the point (0, 290). Thus, an equation for the wheel is: ()() () 22 2 2 2 0290260 29067,600 xy xy −+−= +−=
53. 22 2440910xyxy+++−= ()() 22 22 22 2440910 214440915 124096 xxyy xxyy xy +++−= +++++=+ +++=
The circle representing Earth has center () 1,2 and radius = 409664 = So the radius of the satellite’s orbit is 640.664.6 += units. The equation of the orbit is ()()() 222 22 1264.6 244168.160 xy xyxy +++= +++−=
54. a. 222 22222 2222 () 2 (1)20 x mxbr x mxbmxbr mxbmxbr ++= +++= +++−=
There is one solution if and only if the discriminant is zero. 2222 22222222 2222 2222 222 (2)4(1)()0 444440 4440 0 (1) bmmbr bmbrbmmr brmr brmr rmb −+−= −+−+= −++= −++= +=
b. Using the quadratic formula, the result from part (a), and knowing that the discriminant is zero, we get: 2222 (1)20 mxbmxbr +++−= 22 22 2 2 2 222222 2 2(1) bmbmbmrmr x b mb b r mr ymb b mrmrbr b bbb ====
c. The slope of the tangent line is m . The slope of the line joining the point of tangency and the center is: 2 2 2 2 0 1 0 r b rb
Therefore, the tangent line is perpendicular to the line containing the center of the circle and the point of tangency.
55. 22 9 xy+=
Center: (0, 0)
Slope from center to () 1,22 is 22022 22 101 ==
Slope of the tangent line is 12 4 22 =−
Equation of the tangent line is:
56. 22 4640xyxy+−++= 22 22 (44)(69)449 (2)(3)9 xxyy xy −++++=−++ −++=
Center: (2, –3)
Slope from center to () 3,223 is 223(3)22 22 321 ==
Slope of the tangent line is: 12 4 22 =− Equation of the tangent line:
57. Let (,) hk be the center of the circle. 240 24 1 2 2 xy yx yx −+= =+ =+
The slope of the tangent line is 1 2 . The slope from (,) hk to (0, 2) is –2. 2 2 0 22 k h kh =− −=
The other tangent line is 27yx=− , and it has slope 2.
Chapter2: Graphs
The slope from (,) hk to (3, –1) is 1 2 . 11 32 223 21 12 k h kh kh hk =− +=− =− =−
Solve the two equations in and hk : 22(12) 224 30 0 kk kk k k −=− −=− = = 12(0)1 h =−=
The center of the circle is (1, 0).
58. Find the centers of the two circles: 22 22 22 4640 (44)(69)449 (2)(3)9 xyxy xxyy xy +−++= −++++=−++ −++=
Center: () 2,3 22 22 22 6490 (69)(44)994 (3)(2)4 xyxy xxyy xy ++++= +++++=−++ +++=
Center: () 3,2
Find the slope of the line containing the centers: 2(3)1 325 m ==−
Find the equation of the line containing the centers: 1 3(2) 5 5152 513 5130 yx yx xy xy +=−− +=−+ +=− ++=
59. Consider the following diagram: (2,2)
Therefore, the path of the center of the circle has the equation 2 y = .
60. 2 62 62 22 3 Cr r r r π ππ ππ ππ = = = =
The radius is 3 units long.
61. (b), (c), (e) and (g)
We need ,0hk > and () 0,0 on the graph.
62. (b), (e) and (g)
We need 0 h < , 0 k = , and hr >
63. Answers will vary.
64. The student has the correct radius, but the signs of the coordinates of the center are incorrect. The student needs to write the equation in the standard form ()() 22 2 x hykr −+−= . ()() () ()() 22 2 2 2 3216 324 xy xy ++−= −−+−=
Thus, ()() ,3,2hk =− and 4 r = .
65. 2 2 2 (13) 169 cm 2 2(13) 26 cm Ar Cr π π π π π π = = = = = =
66. 2322 32 (32)(23)369246 38136 xxxxxxxx xxx −−+−+−+− = =−+−
67. () 2 2 2 22 2 2311 2311 23121 20 (2)(1)0 2 or 1 xxx xxx xxxx xx xx xx +−=+ +−=+ +−=++ +−= +−= =−=
We need to check each possible solution:
Section 2.5 1. ykx = 2. False. If y varies directly with x, then ,ykx = where k is a constant.
3. b 4. c
Section2.5: Variation
Chapter2: Graphs
11. () 22zkxy =+
12. ()() 2 3 Tkxd =
14. () 32zkxy =+
24. ()8.991000 0.00899 pkB k k = = = Therefore we have the linear equation 0.00899 pB = If 175000 B = , then () 0.00899175000$1573.25 p ==
25. () 2 2 161 16 s kt k k = = =
Therefore, we have equation 2 16. s t =
If t = 3 seconds, then () 2 163144 s == feet.
If s = 64 feet, then 2 2 6416 4 2 t t t = = =±
Time must be positive, so we disregard 2. t =− It takes 2 seconds to fall 64 feet.
26. ()642 32 vkt k k = = =
Therefore, we have the linear equation 32.vt = If t = 3 seconds, then () 32396 v == ft/sec.
27. ()320 3 20 EkW k k = = =
Therefore, we have the linear equation 3 20 EW =
If W = 15, then () 3 152.25 20 E == .
28. 256 48 12,288 k R l k k = = =
Therefore, we have the equation 12,288 . R l =
Section2.5: Variation
If 576, R = then 12,288 576 57612,288 12,28864 inches 5763 l l l = = == 29. ()47.4012 3.95 Rkg k k = = = Therefore, we have the linear equation 3.95 Rg = If 10.5 g = , then ()() 3.9510.5$41.48 R =≈ .
30. ()23.755 4.75 CkA k k = = = Therefore, we have the linear equation 4.75. CA = If 3.5 A = , then ()() 4.753.5$16.63 C ==
31. k D p = a. 156 D = , 2.75 p = ; 156 2.75 429 k k = = So, 429 D p = . b. 429 143 bags of candy 3 D ==
32. k t s = a. 40 t = , 30 s = ; 40 30 1200 k k = = So, we have the equation 1200 t s = . b. 1200 30 minutes 40 t ==
33. k V P = 600,150VP== ;
Chapter2: Graphs
600 150 90,000 k k = =
So, we have the equation 90,000 V P =
If 200 P = , then 3 90,000 450 cm. 200 V ==
34. k i R =
If 30,8iR== , then 30 and 240 8 k k ==
So, we have the equation 240 i R =
If 10, R = then 240 24 amperes 10 i ==
35. 2 k W d =
If 125,3960Wd== then 2 125 and 1,960,200,000 3960 k k ==
So, we have the equation 1,960,200,000 W d =
At the top of Mt. McKinley, we have 39603.83963.8 d =+= , so () 2 1,960,200,000 124.76 pounds. 3963.8 W =≈
36. 2 2 55 3960 862,488,000 k W d k k = = =
So, we have the equation 2 862,488,000 W d = If =3965, d then 2 862,488,000 54.86 pounds. 3965 W =≈
37. 2 Vrh =π
38. 2 3 Vrh π =
39. 2 k I d = If 0.075,2Id== , then 2 0.075 and 0.3 2 k k ==
So, we have the equation 2 0.3 I d = If 5, d = then 2 0.3 0.012 foot-candles. 5 I ==
40. 2 2 11(20)(22) 119860 111 9680880 FkAv k k k = = = ==
So, we have the equation 2 1 880 F Av = If 47.125 A = and 36.5 v = , then ()() 2 1 47.12536.571.34 pounds. 880 F =≈
41. 3 36(75)(2)3 36600 0.06 hksd k k k = = = =
So, we have the equation 3 0.06.hsd = If 45 h = and 125, s = then 3 3 3 3 45(0.06)(125) 457.5 6 61.82 inches d d d d = = = =≈
42. (300) 100 15 10020 5 kT V P k k k = = = =
So, we have the equation 5T V P =
If 80 V = and 310, T = then 5(310) 80 801550 1550 19.375 atmospheres 80 P P P = = ==
43. 2 2 1250(25)(10) 12502500 0.5 Kkmv k k k = = = =
So, we have the equation 2 0.5. K mv = If 25 m = and 15, v = then ()() 2 0.525152812.5 K == Joules
44. () 2 2 432 1.24 (4) 1.2427 1.24 27 kl R d k k k = = = =
So, we have the equation 2 1.24 . 27 l R d = If R = 1.44 and d = 3, then 2 1.24 1.44 27(3) 1.24 1.44 243 349.921.24 349.92 282.2 feet 1.24 l l l l = = = =≈
45. (25)(5) 100 0.75 75125 0.6 kpd S t k k k = = = =
So, we have the equation 0.6 pd S t = If 40, 8, pd== and 0.50, t = then 0.6(40)(8) 384 psi. 0.50 S == 46. 2 (4)(2)2 750 8 7502 375 kwt S l k k k = = = =
Section2.5: Variation
So, we have the equation 2 375 . wt S l = If 10, 6, lw== and 2, t = then 2 375(6)(2) 900 pounds. 10 S == 47 – 50. Answers will vary. 51. 32 32 2 2 32512100 (325)(12100) (325)4(325) (4)(325) (2)(2)(325) xxx xxx xxx xx xxx +−− =+−+
2 2 (3)(4) 5252 33(3)(4) 712 5(4) (3)(4) 5(4)(2) (3)(4) 5202 (3)(4) 618 (3)(4) 6(3)6 (3)(4)(4) x xx xx xxxx xx x xx xx xx xx xx x xx x xxx ++ +=+ ++++ ++ + =+
53. 3 31 22 3 44 2525 28 5125 = =
54. The term needed to rationalize the denominator is 72 +
Chapter2: Graphs
Chapter 2 Review Exercises
1. ()()12 0,0 and 4,2 PP==
a. ()()() 2212,4020 1642025 dPP =−+− =+==
xxyy xy ++ =
b. The coordinates of the midpoint are: () (,),1212 22 040242 ,,2,1 2222
c. 2021 slope 4042 y x Δ− ==== Δ−
d. For each run of 2, there is a rise of 1.
2. ()()12 1,1 and 2,3 PP=−=−
a. ()()() () 2 2 12,2131 916255 dPP =−−+−− =+==
b. The coordinates of the midpoint are: () (,),1212 22 12 13 , 22 121 ,,1 222 x xyy xy ++ =
+− −+ =
c. ()31 44 slope 2133 y x Δ ====− Δ−−−
d. For each run of 3, there is a rise of 4.
3. ()()12 4,4 and 4,8 PP=−=
a. ()()() () 2 2 12,4484 014414412 dPP =−+−− =+==
b. The coordinates of the midpoint are: () (,),1212 22 444884 ,,4,2 2222 xxyy xy ++
=
c. ()84 12 slope,undefined 440 y x Δ === Δ−
d. An undefined slope means the points lie on a vertical line. There is no change in x
4. 2 4 yx=+ y x −55 9 −1 (0,4) (1,5) (2,8) (−1,5) (−2,8)
5. x-intercepts: 4,0, 2 ; y-intercepts: 2,0,2 Intercepts: (4,0), (0,0),(2,0),(0,2),(0,2)
6. 2 23 x y =
x-intercepts: y-intercepts: 2 23(0) 20 0 x x x = = = 2 2 2(0)3 0 0 y y y = = =
The only intercept is (0,0).
Test x-axis symmetry: Let yy =− 2 2 23() 23 same xy xy =−
Test y-axis symmetry: Let x x =− 2 2 2()3 23 different xy xy
Test origin symmetry: Let x x =− and yy =− . 2 2 2()3() 23 different xy xy −=−
Therefore, the graph will have x-axis symmetry.
7. 22+4=16xy
x-intercepts: y-intercepts: () 2 2
+40=16
The intercepts are (4,0),(4,0),(0,2), and (0,2).
Test x-axis symmetry: Let yy =− () 2 2 22 4=16 4=16 same xy xy +− +
Test y-axis symmetry: Let x x =− () 2 2 22 4=16 4=16 same xy xy −+ +
Test origin symmetry: Let x x =− and yy =− ()() 22 22 4=16 +4=16 same xy xy −+−
Therefore, the graph will have x-axis, y-axis, and origin symmetry.
8. 42+2+1yxx =
x-intercepts: y-intercepts: ()() 42 22 2 2 0+2+1 011 10 1 xx xx x x = =++ += =− 42 (0)+2(0)+1 1 y = =
no real solutions
The only intercept is (0, 1).
Test x-axis symmetry: Let yy =− 42 42 21 21 different yxx yxx −=++ =−−−
Test y-axis symmetry: Let x x =− ()() 42 42 21 21 same yxx yxx =−+−+ =++
Test origin symmetry: Let x x =− and yy =− . ()() 42 42 42 21 21 21 different yxx yxx yxx −=−+−+ −=++ =−−−
Therefore, the graph will have y-axis symmetry.
9. 3 y xx=−
x-intercepts: y-intercepts: () ()() 3 2 0 01 011 xx xx xxx =− =− =+− 3 (0)0 0 y =− = 0,1,1xxx==−=
The intercepts are (1,0), (0,0), and (1,0).
Test x-axis symmetry: Let yy =− 3 3 different yxx yxx −=− =−+
Test y-axis symmetry: Let x x =− 3 3 ()() different yxx yxx =−−− =−+
Test origin symmetry: Let x x =− and yy =− 3 3 3 ()() same yxx yxx yxx −=−−− −=−+ =−
Therefore, the graph will have origin symmetry.
10. 22 20xxyy+++=
x-intercepts: 22 2 (0)2(0)0 0 (1)0 xx xx xx +++= += += 0,1xx==−
y-intercepts: 22 2 (0)020 20 (2)0 yy yy yy +++= += += 0,2yy==−
The intercepts are (1,0), (0,0), and (0,2).
Test x-axis symmetry: Let yy =− 22 22 ()2()0 20 different xxyy xxyy ++−+−= ++−=
Test y-axis symmetry: Let x x =− 22 22 ()()20 20 different xxyy xxyy −+−++= −++=
Test origin symmetry: Let x x =− and yy =− . 22 22 ()()()2()0 20 different xxyy xxyy −+−+−+−= −+−=
The graph has none of the indicated symmetries.
11. () ()() ()() 222 2 2 2 22 ()() 234 2316 x hykr xy xy −+−= −−+−= ++−=
12. () ()() () ()() 222 22 2 22 ()() 121 121 x hykr xy xy −+−= −−+−−= +++=
Chapter2: Graphs
13. () () 2 2 2 22 14 12 xy xy +−= +−=
Center: (0,1); Radius = 2

x-intercepts: () 2 2 2 2 014 14 3 3 x x x x +−= += = =±
y-intercepts: () 2 2 2 014 (1)4 12 12 y y y y +−= −= −=± =± 3 or 1 yy==−
The intercepts are ()3,0, ()3,0, ()0,1, and ()0,3.
14. ()() ()() 22 22 22 22 2 2440 244 2144414 123 xyxy xxyy xxyy xy +−+−= −++= −++++=++ −++=
Center: (1, –2) Radius = 3
x-intercepts: ()() () () 22 2 2 2 1023 149 15 15 15 x x x x x −++= −+= −= −=± =±
y-intercepts: ()() () () 22 2 2 2 0123 129 28 28 222 222 y y y y y y −++= ++= += +=± +=± =−±
The intercepts are () 15,0, () 15,0, + () 0,222, and () 0,222. −+
15. ()() ()()() 22 22 22 22 2 22 336120 240 240 214414 125 xyxy xyxy xxyy xxyy xy +−+= +−+= −++= −++++=+ −++=
Center: (1, –2) Radius = 5
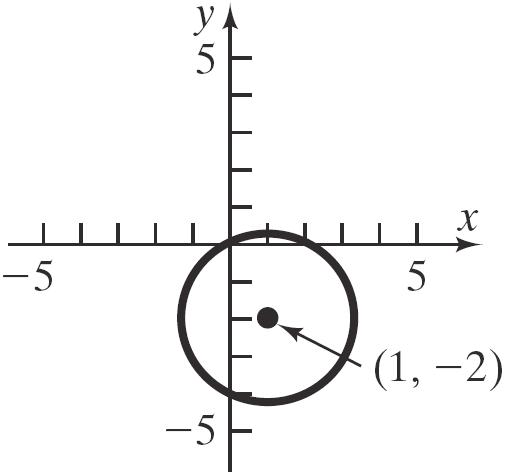
x-intercepts: ()()() () () 2 22 2 2 1025 145 11 11 11 x x x x x −++= −+= −= −=± =± 2 or 0 xx==
y-intercepts: ()()() () () 2 22 2 2 0125 125 24 22 22 y y y y y −++= ++= += +=± =−± 0 or 4 yy==−
The intercepts are ()0,0, ()2,0, and ()0,4.
16. Slope = –2; containing (3,–1) () () 11 (1)23 126 25 or 25 yymxx yx yx yxxy −=−
17. vertical; containing (–3,4)
Vertical lines have equations of the form x = a, where a is the x-intercept. Now, a vertical line containing the point (–3, 4) must have an x-intercept of –3, so the equation of the line is 3. x =− The equation does not have a slopeintercept form.
18. y-intercept = –2; containing (5,–3) Points are (5,–3) and (0,–2) 2(3)11 0555 m ===− 1 2 or 510 5 ymxb yxxy =+ =−−+=−
19. Containing the points (3,–4) and (2, 1) 1(4)5 5 231 m ===− () () 11 (4)53 4515 511 or 511 yymxx yx yx yxxy
20. Parallel to 234 xy−=− 234 324 324 33 24 33 xy yx yx yx −=− −=−− = =+ 2 Slope; containing (–5,3) 3 = () () () 11 2 3(5) 3 2 35 3 210 3 33 219 or 2319 33 yymxx yx yx yx yxxy
21. Perpendicular to 2 xy+= 2 2 xy yx += =−+
The slope of this line is 1 , so the slope of a line perpendicular to it is 1. Slope = 1; containing (4,–3) 11() (3)1(4) 4 3 7 or 7 yymxx yx yx yxxy −=− −−=− += =−−=
Chapter2: Graphs
22. 4520 5420 4 4 5 xy yx yx −=− −=−− =+ slope = 4 5 ; y-intercept = 4
x-intercept: Let y = 0. 45(0)20 420 5 x x x −=−
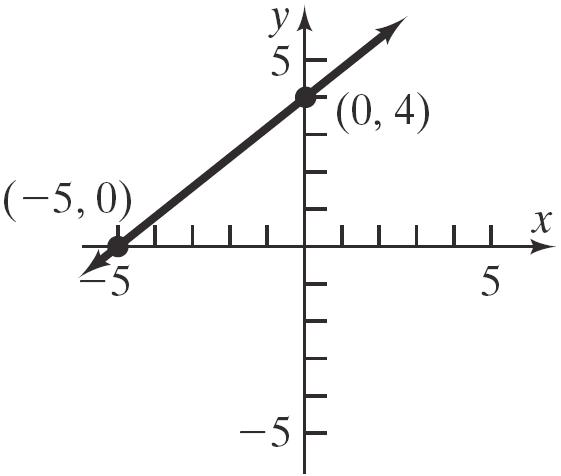
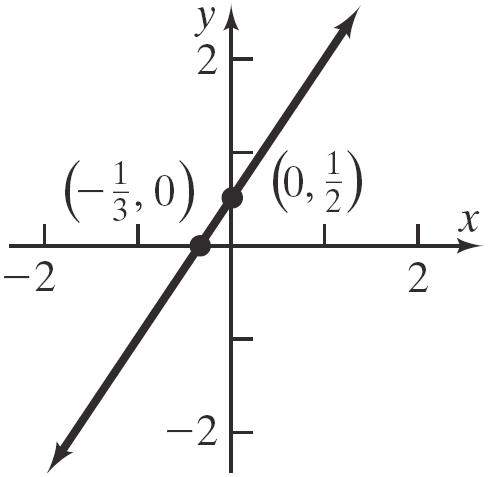
23. 111 236 111 326 31 22 xy yx yx
slope = 3 2 ; 1 -intercept 2 y =
x-intercept: Let y = 0. 111 (0) 236 11 26 1 3 x x x −=−
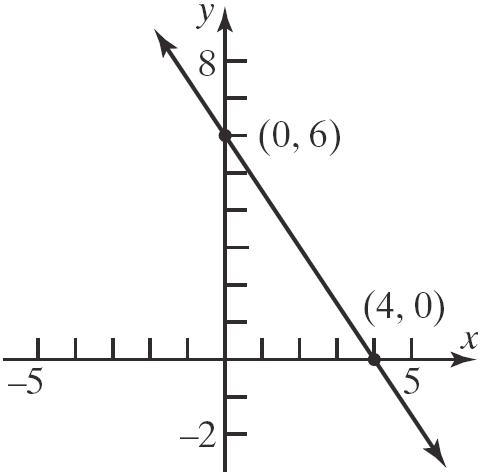
24. 2312 xy−= x-intercept: y-intercept: 23(0)12 212 6 x x x −= = = 2(0)312 312 4 y y y −= −= =− The intercepts are () 6,0 and () 0,4 .

25. 11 2 23xy+= x-intercept: y-intercept: 11 (0)2 23 1 2 2 4 x x
are () 4,0 and () 0,6
3 y x =

27. y x =
28. slope = 2 3 , containing the point (1,2)
29. Find the distance between each pair of points. 22 , 22 , 22 , (13)(14)4913 (21)(31)9413 (23)(34)25126 AB
Since AB = BC, triangle ABC is isosceles.
30. Given the points (2,0),(4,4),AB=−=− and (8,5). C =
a. Find the distance between each pair of points. () () () 22 22 22 ,(4(2))(40) 416 2025 ,(8(4))(54) 1441 145 ,(8(2))(50) 10025 12555 dAB dBC dAC =−−−+−
()()() ()()() 222 222 ,,, 20125145 20125145 145145 dABdACdBC +=
+= += =
The Pythagorean Theorem is satisfied, so this is a right triangle.
b. Find the slopes: () () 404 2 4(2)2 541 8412 5051 82102
Since 1 21 2 mmABAC⋅=−⋅=− , the sides AB and AC are perpendicular and the triangle is a right triangle.
31. Endpoints of the diameter are (–3, 2) and (5,–6). The center is at the midpoint of the diameter: Center: ()()26 35 ,1,2 22 +−
Radius: 22 (1(3))(22) 1616 3242 r =−−+−−
Chapter2: Graphs
Equation: ()()() ()() 2 22 22 1242 1232 xy xy −++= −++=
32. 15 slope of 1 62 15 slope of 1 82 AB AC ==− ==− Therefore, the points lie on a line.
33. () 854130,000 854427 130,00065,000 pkB k k = = ==
Therefore, we have the equation 427 65,000 pB = .
If 165,000 B = , then () 427 165,000$1083.92 65,000 p == .
34. 2 k w d = ()() 2 2 200 3960 20039603,136,320,000 k k = ==
Therefore, we have the equation 2 3,136,320,000 w d = . If 396013961 d =+= miles, then 2 3,136,320,000 199.9 3961 w =≈ pounds.
35. 135(7.5)(40) 135300 0.45 Hksd k k k = = = =
So, we have the equation 0.45. H sd = If 12 s = and 35, d = then ()() 0.451235189 H == BTU
Chapter 2 Test
1. ()() () 22 12 2 2 (,)5(1)13 64 3616 52213 dPP =−−+−− =+− =+ ==
2. The coordinates of the midpoint are: () (,),1212 22 3(1) 15 , 22 42 , 22 2,1 x xyy xy ++
−++−
3. a. 21 21 1342 5(1)63 yy m xx ====−
b. If x increases by 3 units, y will decrease by 2 units.
4. 2 9 yx=− 5. 2 y x = y x 10 5
6. 2 9 xy+= x-intercepts: y-intercept: 2 2 09 9 3 x x x += = =± 2 (0)9 9 y y += =
The intercepts are ()3,0, ()3,0, and ()0,9.
Test x-axis symmetry: Let yy =− () 2 2 9 9 different xy xy +−= −=
Test y-axis symmetry: Let x x =− () 2 2 9 9 same xy xy −+= +=
Test origin symmetry: Let x x =− and yy =− ()() 2 2 9 9 different xy xy −+−= −=
Therefore, the graph will have y-axis symmetry.
7. Slope = 2 ; containing (3,4) 11() (4)2(3) 426 22 yymxx yx yx yx −=− −−=−− +=−+ =−+

8. ()()222 x hykr −+−= ()() ()() 22 2 22 4(3)5 4325 xy xy −+−−= −++=
General form: ()() 22 22 22 4325 8166925 860 xy xxyy xyxy −++= −++++= +−+= 9. 22 22 22 222 4240 424 (44)(21)441 (2)(1)3 xyxy xxyy xxyy xy ++−−= ++−= +++−+=++ ++−=
Center: (–2, 1); Radius = 3 y x −55 5 −5 (−2,1) 10. 236 326 2 2 3 xy yx yx += =−+ =−+
Parallel line
Any line parallel to 236 xy+= has slope 2 3 m =− . The line contains (1,1) : 11() 2 (1)(1) 3 22 1 33 21 33 yymxx yx yx yx −=− −−=−− +=−+ =−−
Perpendicular line
Any line perpendicular to 236 xy+= has slope 3 2 m = . The line contains (0,3) : 11() 3 3(0) 2 3 3 2 3 3 2 yymxx yx yx yx −=− −=− −= =+
Chapter2: Graphs
11. Let R = the resistance, l = length, and r = radius.
Then 2 l Rk r =⋅ . Now, R = 10 ohms, when l = 50 feet and 3 610 r =× inch, so
() 2 3 2 3 6 50 10 610 610 107.210 50 k k =⋅ × × =⋅=×
Therefore, we have the equation () 6 2 7.210 l R r =× .
If 100 l = feet and 3 710 r =× inch, then ()() 6 2 3 100 7.21014.69 710 R =×≈ × ohms.
Chapter 2 Cumulative Review
1. 350 35 5 3 x x x −= = =
The solution set is 5 3
2. ()() 2 120 430 xx xx −−= −+= 4or 3 xx==−
The solution set is {} 3,4 .
3. ()() 2 2530 2130 xx xx −−= +−= 1 or 3 2 xx=−=
The solution set is 1 ,3 2
.
2 220xx−−= ()()()() () 2 22412 21 248 2 212 2 223 2 13 x −−±−−− = ±+ = ± = ± = =± The solution set is {} 13,13 −+ . 5. 2 250xx++= ()() () 2 22415 21 2420 2 216 2 x −±− = −±− = −±− = No real solutions
Check: 2(4)13? 93? 33 True += = =
The solution set is {} 4 7. 21 x −= 21 or 21 3 1 xx xx −=−=− ==
The solution set is {} 1,3
8. () 2 2 22 2 2 42 42 44 440 xx xx xx xx += += += +−= 2 444(1)(4) 41616 2(1)2 432442 222 22 x −±−−−±+ == −±−± ===−±
Check 222 x =−+ : ()() 2 22242222? 48288822? 42 True −++−+= −+−+= =
Check 222 x =−− : ()() 2 22242222? 48288822? 42 True −−+−−= ++−−= =
The solution set is {} 222,222 −−−+ .
9. 2 9 9 3 x x x i =− =±− =±
The solution set is {} 3,3ii .
10. 2 250xx−+= ()()()() () 2 22415 2420 212 21624 12 22 x i i −−±−−±− == ±−± ===±
The solution set is {} 12,12 ii−+
11. 237 210 5 x x x −≤ ≤ ≤ {}(] 5 or ,5 xx ≤−∞
12. 145 51 x x −<+< −<< {}() 51 or 5,1 xx−<<−

13. 21 121 13 x x x −≤ −≤−≤ ≤≤
{}[] 13 or 1,3 xx≤≤
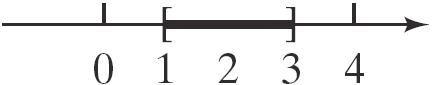
14. 23 x +> 23 or 23 5 or 1 xx xx +<−+> <−> {} 5 or 1 xxx<−> or ()() ,51, −∞−∪∞
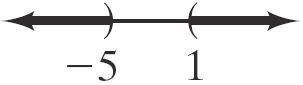
15. ()()() () ()() 2 2 22 ,1432 55 2525 5052 dPQ =−−+−− =−+ =+ == ()32 1431 Midpoint,, 2222 +−
16. 3 31 y xx =−+
a. () 2,1 : ()()() 3 23218611 −−−+=−++=−
() 2,1 is on the graph.
b. () 2,3 : ()()() 3 23218613 −+=−+= () 2,3 is on the graph.
c. () 3,1 : ()()() 3 33312791191 −+=−+=≠ () 3,1 is not on the graph.
Chapter2: Graphs
17. 3 y x =

18. The points (–1,4) and (2,–2) are on the line. 246 Slope2 2(1)3 ===− () ()
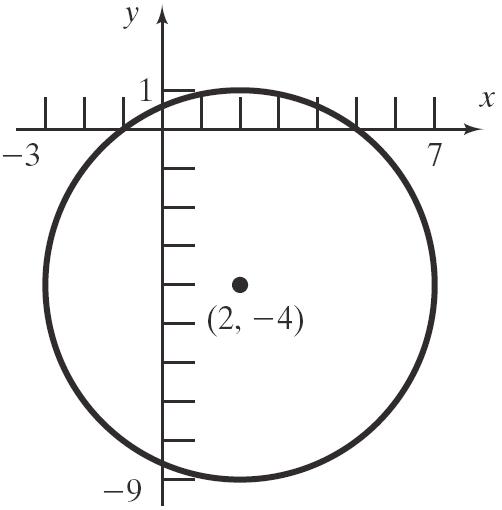
Center: (2,–4); Radius = 5
19. Perpendicular to 21 y x =+ ; Contains () 3,5 1 Slope of perpendicular = 2
Chapter 2 Project
Internet Based Project


