Chapter2
FluidStatics
2.1. Fromthegivendata: patm =101kPa, hk =0 62m,and hw =2 05m.Forwater, γw =9 79kN m3 , andforkerosene, ρk =808kg/m3,whichgives γk =7.92kN m3 (fromAppendixB.4).The absolutepressureonthebottomofthetank, pb,iscalculatedasfollows: pb = patm + γkhk + γwhw =101+7 92(0 62)+9 79(2 05)=125 98kPa
Asagaugepressure,thepressureonthebottomofthetankis125 98kPa 101kPa= 24.98kPa
2.2. (a) Taking γw =9.79kN/m3 and p =101.3kPa,thedepth, h,belowthewatersurface correspondingtoagaugepressureof101.3kPaisgivenby
= p
.3 9 79 =10 3m (b) Fromthegivendata:∆h =1.65m.Therefore,thepressuredifference,∆p,isgivenby
p =
∆h =(9.79)(1.65)=16.2kPa
2.3. Fromthegivendata:SG1 =0.98, z1 =0m,SG2 =1.07,and z2 = 12m.SinceSGvaries linearly,
Therelationshipbetweenspecificgravity(SG)andspecificweight(γ)isgivenby
(kN/m3)= g SG=9 807 SG (2)
CombiningEquations1and2givesthefollowingequationforthevariationofspecificweight withdepth,
(3)
Usingthehydrostaticpressuredistribution(Equation2.10)thedifferenceinpressurebetween z = 12mand z =0misgivenbyEquation2.11as
Thisisagaugepressure ,relativetoatmosphericpressureonthesurfaceoftheliquid.
2.4. (a) Fromthegivendata: h =12mand pA =200kPa.Forwaterat20◦C, γ =9 789kN/m3 Bydefinitionofabsolutepressure,
pA = patm + γh → 200= patm +(9.789)(12) → patm =91.5kPa
(b) Fromthegivendata:SG=0 85, ρ =850kg/m3 , γ =8 336kN/m3,and h =6m.Since thepressuredistributionishydrostatic,
pg = γh =(8.336)(6)=50.0kPa ,pA = patm + pg =91.5+50.0=141.5kPa
2.5. Fromthegivendata: h =10m.Forwaterat20◦C, γ =9.79kg/m3.Forstandardatmospheric pressure, patm =101 3kPa.Thegaugepressure, p,atthevalveisgivenby
p = γh =(9 79)(10)=97 9kPa
Theabsolutepressure, pabs,atthevalvelocationisgivenby
pabs = p + patm =97 9+101 3=199 2kPa
2.6. Fromthegivendata: p0 =14kPa,and γoil =0.80, γw =0.80(9.79)=7.83kN/m3.Hence, atadepth h =1.5mbelowthesurfaceoftheoil,thepressure, p,isgivenby
p = p0 + γoilh =14+(7.83)(1.5)=25.7kPa
2.7. Fromthegivendata: pB =5kPa,∆z1 =0.30m,and∆z2 =0.62m.Forwaterat20◦C, γ =9.789kN/m3.TheairpressuresintanksAandCareasfollows:
pA = pA + γ∆z1 =5+(9.789)(0.30)=7.94kPa
pC = pA γ∆z2 =7 94 (9 789)(0 62)=1 87kPa
2.8. Fromthegivendata: D1 =5mm, h =30m,and T =15◦C.Forwaterat15◦C, ρ = 999.1kg/m3 and γ =9798N/m3.Understandardconditions, patm =101.3kPa.Theinitial volumeofthebubble, V1,theinitialpressure, p1,andthefinalpressure, p2,aregivenby V1 = πD3 1 6 = π(0 005)3 6 =6 545 × 10 8 m3 p1 = patm + γh =101 3 × 103 +(9798)(30)=3 953 × 105 Pa p2 = patm =1 013 × 105 Pa
Applyingtheidealgaslawtotheairinthebubbleandassumingisothermalconditionsgives p1V1 = p2V2 → V2 = ( p1 p2 ) V1 = ( 3.953 × 105 1 013 × 105 ) (6 545 × 10 8)=2 554 × 10 7 m3
Therefore,thediameter, D2,atthesurfaceisgivenby D2 = [ 6V2 π ] 1 3 = [ 6(2 554 × 10 7) π ] 1 3 =0 00787m ≈ 7 9mm
2.9. Fromthegivendata:∆z =20m, patm =101 3kPa,and T =20◦C.At20◦C,thedensityof seawaterisgivenbyAppendixB.4as ρ =1023kg/m3,whichcorrespondsto γ =10 03kN/m3 Sincethepressuredistributionintheoceanishydrostaticandthepressureoftheairinside thebubbleisequaltothepressureofthewateroutsidethebubble,andthetemperatureis constant,theratioofdensitiesisgivenby
= 101 3+(10 03)(20) 101 3 =2 98
2.10. Fromthegivendata: h1 =7m, γ1 =9kN/m3 , h2 =2.3m,and pbot =92kPa.For waterat4◦C, γw =9.81kN/m3.Thespecificgravity,SG,canbederivedfromthefollowing hydrostaticpressurerelationship, pbot = γ1h1 +[SG · γw]h2 → 92=(9)(7)+[SG · (9 81)](2 3) → SG=1 3
Yes theliquidonthebottommustnecessarilybedenserthantheliquidonthetop.
2.11. Forwaterat20◦C,Table1.9gives γ =9 79kN/m3.Thepressurehead, h,correspondingto p =450kPaistherefore h = p γ = 450 9 79 =46 0m
2.12. For p =800kPa,thepressurehead, h,isgivenby h = p γw = 800 9.79 =81.7m(ofwater)
Forcrudeoilat20◦C, ρoil =856kg/m3 (fromAppendixB.4),whichgives γoil =8.40kN/m3 . For p =800kPa, h = p γoil = 800 8.40 =95.2m(ofcrudeoil)
2.13. Pressure, p1,correspondingto hw =80mmofwateris
p1 = γwhw =(9.79)(0.080)=0.783kPa
andthepressure, p2,correspondingto hf =60mmofafluidwhosespecificweightis γf = 2.90γw =2.90(9.79)=28.4kN/m3 is
p2 = γf hf =(28.4)(0.060)=1.70kPa
Thetotalpressure, p,isthereforegivenby
p = p1 + p2 =0.783+1.70=2.48kPa
andthepressurehead, hHg,inmmofmercury(taking γHg =133kN/m3)is
hHg = p γHg = 2 48 133 × 1000=18.6mmHg
2.14. For patm =101.3kPa,thepressurehead, hHg,inmmofmercury(γHg =133kN/m3)isgiven by hHg = patm γHg = 101 3 133 × 1000=762mmHg
2.15. Fromthegivendata: D =7mm,and h′ =80mm.Forwaterat20◦C, σ =72.8mN/m= 0.0728N/m,and γ =9789N/m3 (fromAppendixB.1).Forwaterandcleanglass, θ =0◦ .
(a) Theriseheight,∆h,duetosurfacetensioniscalculatedas ∆h = 4σ cos θ γD = 4(0.0728)cos0◦ (9789)(0 007) =4 45 × 10 3 m=4 45mm
(b) InaccordancewithEquation2.20,thepressurehead, h,attheattachmentpointisgiven by h = h′ ∆h =80 4.45=75.75mm ≈ 75.8mm
2.16. Whenthereservoirishalf-full,thepipelinepressureis350kPa,andtheheight, h0,ofthe mid-pointofthereservoirabovethepipelineis
Notethatthepressuresofliquidsinpipesaregenerallygivenasgaugepressuresunlessstated otherwise.Whenthepressureinthepipelineis500kPa,theheight, h1,ofthewaterinthe reservoirabovethepipelineis h1 = 500 γw = 500 9.79 =51 1m
Hencetheminimumspacebetweenthemid-pointandtopofthereservoiris51.1m 35.8m =15.3m
2.17. Fromthegivendata: x =120mmHg, y =70mmHg,∆zhead =0.5m,∆ztoe =1.5m,and ρ =1060kg/m3.Fromthegivendensity, γ =10.40kN/m3 .
(a) Thefollowingpressuredifferencescanbecalculated:
heart-head= γ ∆zhead =(10.40)(0.5)=5.20kPa=39mmHg
heart-toe= γ · ∆ztoe =(10 40)(1 5)=15 6kPa=117mmHg
Thebloodpressuresintheheadandtoesare: head= 120 39 70 39 =81/31
toes= 120+117 70+117 =237/187
(b) Themaximumpressureis p =120mmHg=16.0kPa.Therefore,theheight, h,that bloodwouldriseinthetubeisgivenby h = p γ = 16 0 10 40 =1 54m
2.18. Fromthegivendata: p =150mmHg=20 00kPa,and ρ =1025kg/m3.Taking g = 9 807m/s2,theheight h betweenarmlevelandfluidlevelisgivenby h = p ρg = 20 00 × 103 (1025)(9 807) =1 99m
2.19. Fromthegivendata:∆z =6m,and ρ =1060kg/m3.Thespecificweightofthebloodis γ =10.4kN/m3 .
(a) Whenthegiraffedrinks,thechangeinpressureinthehead,∆p,isgivenby ∆p = γ ∆z =(10.4)(6)=67.6kPa=507mmHg
(b) Thedifferenceinpressurebetweentheheadandtheheartis507mm/2=254mm. Sincethemaximumpressureattheheartlevelisgivenas280mm,thenthemaximum pressureintheheadis280mm+254mm=534mmHg .
2.20. Fromthegivendata: pair =300kPa, A1 =7cm2 =0.0007m2 , W1 =50N=0.05kN, A2 =500cm2 =0.05m2 , W2 =800N=0.8kN,∆z =1m,∆s1 =10cm, ρ =900kg/m3,and γ = ρg =8.83kN/m3
(a) Theforce, F ,exertedbythecompressedaironthepistonisgivenby F = pairA1 =(300)(0.0007)=0.21kN
(b) Let W betheweightmountedontheplatform,then
(c) If∆s2 isthedisplacementoftheplatform,then
2.21. Fromthegivendata: F1 =500N, D1 =25mm,and D2 =100mm.Iftheforceonthe100-mm pistonis F2,andnotingthatperformanceofthehydraulicsystemwillnotbecompromised ifbothpistonsexertthesamepressure,then
2.22. Fromthegivendata: z =4342m=4.342km.Forthestandardatmosphere, T0 =15◦C =288.2K, b =6.5◦C/km, p0 =101.3kPa,and g/Rb =5.26.Thestandard-atmosphere temperature, T ,atthesummitiscalculatedusingEquation2.25as T = T0 bz =15 (6.5)(4.342)= 13.2◦C =259.9K
Thestandard-atmospherepressure, p,atthesummitiscalculatedusingEquation2.26as p = p0 ( T T0 ) g Rb =101.3 ( 259.9 288 2 )5.26 =58.8kPa
Thecalculatedstandard-atmospheretemperatureandpressurearefairlyclosetothemeasured valuesof 11◦Cand58kPa.
2.23. Fromthegivendata: z1 =11km, z2 =20km, T0 = 56 5◦C=216.7K,and p1 =22.63kPa. Theaveragevalueof g is¯ g =9 769m/s2.Forair, R =287.1J/kg·K.UsingEquation2.29, thetheoreticalpressure, p2,atthetopofthestratosphereisgivenby
p2 = p1 exp [ g(z2 z1) RT0 ] =(22 63)exp [ (9 769)(20000 11000) (287.1)(216.7) ] =5 51kPa
Thestandard-atmospherepressureat z =20km(fromAppendixB.3)is5.529kPa ,sothe theoreticalandstandardvaluesareveryclose.
2.24. Fromthegivendata: b =6.5◦C/km, p0 =101 325kPa,and T0 =15◦C=288 15K.For air, R =287 1J/kg·K,whichgives g/Rb =5 255.Assumingauniformlapserateanda hydrostaticpressuredistribution,thetemperature, T ,andpressure, p,atanyelevationare givenby
Theresultsofapplyingtheseequationsandcomparingthepredictionstothestandardatmosphereisgiveninthefollowingtable.
Basesontheresultspresentedinthetheabovetable,themaximumtemperaturedifference is 0.10◦C ,andthemaximumpressuredifferenceis 0.058kPa
2.25. Takingthepressuredistributionintheatmosphereashydrostatic,
Usingtheseequations:
Fromthegivendata: p1 =101kPa, p2 =1Pa, z1 =0m, a =273+20=293K, b = 6.3 K/km= 0.0063K/m, R =287J/kg K(forair),whichyields
Rb = 9.81 (287)(0 0063) =5 426
SubstitutingintoEquation2.23gives
whichyields z2 =52,070m=52.1km
2.26. Fromthegivendata: z =2256m, T =5◦C=278K, T0 =27◦C=300K,and p0 =101kPa. Thelapserate, b,canbeestimatedas b = T0 T z = 300 278 2256 =0 00975K/m=9 75K/km
Forthestandardatmosphere, b =6.50K/km, g/Rb =5.26,andsofor b =9.75K/kmitis estimatedthat g Rb =5 26 × 6 50 9 75 =3 51
(a) Thepressure, p,atthePeakcanbecalculatedusingEquation2.26whichgives p = p0 ( T T0 ) g Rb =(101) ( 278 300 )3 51 =77 3kPa
(b) Thevaporpressureofwaterisequalto77.3kPawhenthetemperatureofthewateris 92◦C(fromAppendixB.1).Therefore,waterboilsat92◦C atthePeak.
2.27. Forthestandardatmosphere, b =6.50K/km=0.00650K/m.Forair, M =28.96g/mol= 0.02896kg/mol.Constantsare R =8.314J/mol·Kand g =9.81m/s2.Therefore, gM Rb = (9 81)(0 02896) (8.314)(0.00650) =5.26
Understandardatmosphericconditions, p0 =101.3kPaand T0 =15◦C=288.15K.InLa Paz, z =3640mandestimatedatmosphericconditionsareasfollows:
T = T0 bz =288.15 (0.00650)(3640)=264.5 K(= 8.66◦C)
p = p0 ( T T0 ) gM Rb =(101.3) ( 264 5 288.15 )5 26 =64.56kPa
Thetemperatureofwateratwhichthesaturationvaporpressureis64.56kPaisthetemperatureatwhichwaterboilsandisequaltoapproximately87.6◦C
2.28. Fromthegivendata:∆z =3000m.Forstandardair, R =287 1J/kg·K,andforastandard atmosphereatsealevel, p1 =101 325kPaand T1 =15◦C=288 15K.Assumethatthe temperatureremainsconstantat15◦Coverthedepthoftheshaft.UsingEquation2.29gives
p2 = p1 exp [ g(z2 z1) RT0 ] → p2 =(101 325)exp [ (9.807)( 3000) (287 1)(288 15) ] =145kPa
2.29. Fromthegivendata: p0 =755mm, z =829.8m=0.8298km,and T0 =35.5◦C=308.7K. Assumingstandardatmosphericconditions, b =6.5◦C/km,and g/Rb =5.26.Theestimated temperature, T ,atthetopofthebuildingiscalculatedusingEquation2.25as T = T0 bz =35 5 (6 5)(0 8298)=30 10◦C=303 3K
Thebarometricpressure, p,atthetopofthebuildingcanbeestimatedusingEquation2.26 as p = p0 ( T T0 ) g Rb =755 ( 303 3 308.7 )5 26 =688mmHg
2.30. Fromthegivendata: p1 =750mm,and p2 =690mm.Forastandardatmosphere: p0 = 760mm, T0 =15◦C=288.15K, b =6.5K/km,and g/Rb =5.26.UsingEquation2.26,
p1 = p0 [1 bz1 T0 ] g Rb → 750=(760) [1 (6.5)z1 288 15 ]5.26 → z1 =0.111km p2 = p0 [1 bz2 T0 ] g Rb → 690=(760) [1 (6 5)z1 288 15 ]5 26 → z2 =0 807km
Thereforethechangeinelevationisestimatedas0.807km 0.111km=0.696km=696m
2.31. Fromthegivendata: hair =0.3m, hg1 =1.2m, hg2 =0.8m., hg3 =1.9m,and patm = 101kPa.Forgasolineat20◦C, ρg =680kg/m3,whichgives γg =6.67kN/m3.If p0 isthe pressureattheBourdongauge,then
NotethattheBourdongaugereadsgaugepressure,andthevariationofhydrostaticpressure intheairisnegligible.
2.32. Fromthegivendata:SG1 =0.9,∆z1 =0.25m,SG2 =2.5,and∆z2 =0.25m.Thespecific weightscorrespondingtothegivenspecificgravitiesaredeterminedbytherelation γ =SG ρ0g =SG (1000)(9 807)=9807 SGN/m3 =9 807 SGkN/m3
Usingthisrelation,thespecificweightsofthelightanddensefluidsare γ1 =9.807(0.9)=8.826kN/m3,γ2 =9.807(2.5)=24.52kN/m3
(a) Assumingthatboththetopofthelightfluidandtheairabovetheliquidareatthe sameatmosphericpressure,then
(b) Sincethepressuredistributionishydrostatic,thegaugepressureonthebottomofthe tank, p0,isgivenby p0 = γ1
52)(0 25)=8 34kPa
2.33. FromFigure2.50, pA = pB γf (0.10) γw(0.15) where pB =0kPa(gaugepressure), γf =40kN/m3,and γw =9.79kN/m3.Hence, pA =0 40(0.10) 9.79(0.15)= 5.47kPa
Alternativesolution: Intermsofabsolutepressure, pB =101.33kPa, γf =40kN/m3,and γw =9.79kN/m3 Hence, pA =101 33 40(0 10) 9 79(0 15)=95 86kPa Itshouldbenotedthatthepressureofliquidsinpipesisseldomgivenintermsofabsolute pressure,so pA = 5.47kPaisthepreferredanswer.
2.34. ForSAE30oilandmercuryat20◦C: ρoil =918kg/m3,and ρHg =13550kg/m3 (from AppendixB.4).Thesevaluescorrespondto: γoil =9.00kN/m3,and γHg =133kN/m3 . Applyingthehydrostaticpressureequationgives
air +(9.00)(1) (133)(0.25)= patm → pair
2.35. FromFigure2.52,
whichsimplifiesto
=24.3kPa
2.36. Fromthegivendata: γw =9.79kN/m3 , γg =18.3kN/m3 , h1 =0.5m,and h2 =0.3m. Applyingthehydrostaticpressurerelationbetweenpoints1and2gives
2.37. Forequilibrium,
Sothepressuredifferenceis11.9kPa
2.38. Fromthegivendata: D1 =1m, D2 =10mm,∆p =200Pa,and∆s =200mm.ForSAE30 oilat20◦C, ρ =918kg/m3 and γ = ρg =9003N/m3 (fromAppendixB.4).Thefollowing preliminarycalculationsofthecross-sectionalarea, A1,ofthetankandthecross-sectional area, A2,ofthemanometerareuseful,
Let∆h bethechangeinoillevelinthereservoircorrespondingto∆p,andlet p0 beatmosphericpressure,thenthecontinuityandhydrostatic-pressurerelationshipsrequirethat
CombiningEquations1and2toeliminate∆h gives
2.39. Forawatertemperatureof15◦C, γw =9.80kN/m3.Forthegivenmanometersetup,
Notingthatsin θ =8/12=0.667,theaboveequationgives
Thereforethewaterpressureinthepipeis33.6kPa .
NEW Fromthegivendata: Ixx =8 553m4,and θ =70◦.Thegivendimensionsareshownin Figure2.1,wheretheinclineddistancefromthewatersurfacetothetopoftheplanesurface is1 5sin70◦ =1 596m.
Figure2.1:Sideviewofinclinedsurface
Forwaterat20◦C, γ =9 789kN/m3.Fromthegivendimensionsoftheplanesurface,the followinggeometricpropertiescanbecalculated:
A1 =(3)(2)=6m2 , A2 =(5)(1)=5m2
y1 =1 596+ 2 2 =2 596m, y2 =1 596+2+ 1 2 =4 096m
y = A1y1 + A2y2 A1 + A2 =3 278m,A =11m2
Usingthecalculateddata,theresultantforce, F ,andlocation, ycp,aregivenby
F = γAy sin θ =(9.789)(11)(3.278)sin70◦ =332kN
ycp =¯ y + Ixx Ay =3.278+ 8 553 (11)(3.278) =3.52m
2.40. Fromthegivendata: b =3m, d =4m, W =20kN, h =2m,and µ =0.05.Forwater, γ =9.79kN/m3.Thegeometricpropertiesofthegateare:
y = h + d 2 =2+ 4 2 =4m,A = bd =(3)(4)=12m2
Thehydrostaticforce, F ,onthegateisgivenby
F = γAy =(9 79)(12)(4)=469 9kN
Thefrictionalforce, Ff ,andthetotalforce, Flift,requiredtoliftthegatearegivenby
Ff = µF =(0 05)(469 9)=23 50kN
Flift = Ff + W =23.50+20=43.5kN
2.41. Fromthegivendata: h =4m, L =3 5m, w =0 3m,andSG=2.5.Thefollowingpreliminary calculationsareuseful:
A = Lh =(3.5)(4)=14m2,γ =SG (9.807)=24.52kN/m3 y = h 2 = 4 2 =2m, Icc = Lh3 12 = (4)(3 5)3 12 =18 67m4
Usingthegivenandderiveddata,thesupportforce, F ,andlocation, ycp,arecalculatedas follows,
F = γAy =(24 52)(14)(2)=687kN,ycp =¯ y + Icc Ay =2+ 18 67 (14)(2) =2 67m
Therefore,themagnitudeoftherequiredsupportforceoneachsideoftheformis687kN . Thissupportshouldbelocated4m 2 67m=1.33m fromthebottomofthewallsection. Thelaterallocationis L/2=3 5/2=1.75m fromtheedgeofthewallsection.
2.42. Fromthegivendata: b =2m, d =3m, θ =60◦ , htop =2.5m.Forwater, γ =9.79kN/m3
Thegeometricpropertiesofthegatearecalculatedasfollows: A = bd =(2)(3)=6m2 ,
.
◦ =2
y = ytop + d 2 =2.887+ 3 2 =4.387m,Ixx = bd3 12 = (2)(3)3 12 =4.500m4
Theresultantforce, F ,andthecenterofpressure, ycp,aregivenby F = γAy sin θ =(9 79)(6)(4 387)sin60◦ =223kN ycp =¯ y + Ixx Ay =4 387+ 4.500 (6)(4 387) =4 558m
Thecenterofpressureis4.558sin60◦ =3.95m belowthewatersurface.
2.43. Force, F ,ongategivenby F = γAy where γ =9.79kN/m3 , A = πD2/4= π(2)2/4=3.142m2,and¯ y =4m.Therefore F =(9.79)(3.142)(4)=123kN
Thelocationof F isgivenby ycp,where ycp =¯ y + Icc Ay
Foracircle Icc = πD4 64 = π(2)4 64 =0 785m4 therefore, ycp =4+ 0.785 (3 142)(4) =4 06m
MomentofhydrostaticforceaboutA, MA,istheminimummomentneededtoopenthegate, MA = F (ycp 3)=123(4 06 3)=130kN·m
2.45. Fromthegivendata: H =3m, T =1m, ρc =2800kg/m3 , ρs =1500kg/m3,and µ =0 35. Consideringaunitlengthofslurrywall(perpendiculartothepage),thefollowingpreliminary calculationsareuseful,
γc = ρcg =27.46kN/m3 , γs = ρsg =14.71kN/m3 W = γcVc =(27.46)(3 × 1)=82.38kN,Ff = µW =(0.35)(82.38)=28.83kN Fh = γsAy =(14.71)(h) ( h 2 ) =7.355h2 ,ycp =¯ y + Icc Ay = h 2 + h3/12 h h/2 = 2 3 h where W =weightofretainingwall, Ff =frictionforce,and Fh =horizontalhydrostatic force.
(a) Forshearfailure,thehorizontalhydrostaticforceisequaltothefrictionforce,which requiresthat
(b) ForoverturningaboutthepointP,thegroundreactionisequaltozeroand
Themorelikelyfailuremodeisbyshearfailure ,sincethisfailurewilloccuratwithalower slurrydepth(1.98mvs.2.56m).
2.46. Fromthegivendata: L =25m, T =5m, s =4m,SGc =2 4,and y2 =3m.Fromthegiven specificgravityofconcrete,thespecificweightofconcreteis γc =SG · g =23 53kN/m3.For waterat20◦C, γw =9 789kN/m3.TheillustrationsgiveninFigure2.2areusefulinthe calculations.
(a) Pressure distribu on
(b) Geometry of dam
Figure2.2:Definitiondiagramsforcalculations
Theslopeofthedownstreamsideofthedamismeasuredby θ,whichcanbeexpressedin termsoftheupstreamheight, h usingtherelation
Usingthesubscript“1”todesignateupstreamandthesubscript“2”todesignatedownstream, andtakingaunitlengthifthedam(perpendiculartothepage),thefollowingpreliminary calculationsareuseful:
Thecentersofpressurearecalculatedasfollows:
Thehorizontalhydrostaticforcesontheupstreamanddownstreamfacesare:
Themoment, M1,aboutthetoeofthedam(PointPinFigure2.2)causedbytheuplift pressureisobtainedwiththefollowingcalculations:
Themoment, M2,aboutthetoeofthedamcausedbytheweightoftheconcreteisobtained withthefollowingcalculations:
Attheinstantofoverturning,thegroundreactionisequaltozeroandthesumofthemoments aboutPisequaltozero,whichrequiresthat
2.48. Fromthegivendata:
(a) Thehydrostaticforcethatwouldexistonthetopsurfaceofthegateisthesameasthat whichexistsonthebottomsurfaceofthegate.Workwithatop-of-gateperspective. Therelevantgeometricpropertiesofthegateareasfollows:
Thereforetheresultantforce, F ,anditslocation, ycp,aregivenby F = γAhc =(9 79)(4 909)(1 5)=72 1kN
cp =¯ y + I Ay =2.615+ 1.918 (4 909)(2 615) =2.765m
Thelocationoftheresultantrelativetothetopofthegateis yF =2.765m 1.365m= 1 400m
(b) Whenthegateisabouttoopen,and Fb istheapplied(vertical)forceatthebottomof thegate,takingmomentsaboutthetopofthegategives,
yF + Fb (D cos θ)= W (R cos θ) (72 1)(1 400)+ Fb(2 5cos35◦)=(500)(1 25cos35◦) → Fb =201kN
2.49. Fromthegivendata: θ =50◦ , d =15m,and R =3m.Forwater, γ =9.79kN/m3.The usefulgeometricpropertiesofasemicircle(fromAppendixC)are
c = 4R 3π ,I
where,inthiscase, yc isthedistancefromtheshafttothecentroid,and Ixc isthemoment ofinertiaaboutanaxisparalleltotheshaftandpassingthroughthecentroid.Usingthese propertiesthefollowingderivedgeometricpropertiescanbecalculated:
cp =¯ y + Ixc Ay =17.85+ 8 894 (14.14)(17.85) =17.89m
Usingtheseresults,thehydrostaticforce, F ,calculatedasfollows F = γAhc =(9 79)(14 14)(13 68)=1893kN
Thedistancefromtheshafttothecenterofpressure, ycp1,isgivenby ycp1 = ycp [ d sin θ R] =17 89 [ 15 sin50◦ 3] =1 309m
Thesupportforce, FP,isderivedbyconsideringthegateasafreebodyandtakingmoments abouttheshaft,whichyields
2.50. Fromthegivendata: θ =35◦ , R =420mm,and¯ y =3m.Theforce, F ,onthehatchis F = γAy sin θ where A = πR2 = π(0 42)2 =0.554m2,andtherefore F =(9.79)(0.554)(3)sin35◦ =9.33kN
Thisforceislocatedatadistance ycp fromthesurface,where ycp =¯ y + Icc Ay
Forthecircularhatch, I
4 64 = π(0.84)4 64 =0 0244m4 hence ycp =3+ 0.0244 (0 554)(3) =3 01m
Theresultanthydrostaticforceistherefore3.01m belowthewatersurface,measuredalong theslopingwall.
2.51. Calculatetheforceonthegate: F = γAy sin θ (1) where θ =90◦ sin 1(3/5)=53 1◦,¯ y =4/ sin(53 1◦)+2 5=7 502m, A =(5)(4)=20m2 , and γ =9.79kN/m3.SubstitutingintoEquation1andalsocalculatingthecenterofpressure gives:
F =(9 79)(20)(7 502)sin(53 1◦)=1175kN ycp =¯ y + I Ay =7.502+ (4)(5)3 12 (20)(7.502) =7.780m
TakingmomentsaboutthehingeandtakingintoconsiderationthatthereactionforceatP actsnormaltothesurfacegives
[P cos(53 1◦)](5)=(7 502+2 5 7 780)(1175)
whichgives P =869kN
2.52. Fromthegivendata: W =500kg, w =5m,and θ =45◦.Taking γ =9.79kN/m3,the hydrostaticforceonthegate, Fh,isgivenby
Thecenterofpressure, ycp,isgivenby
(a) Iftheforceisappliedatthecenterofthegate,takingmomentsaboutBgives
whichgives F =522kN
(b) Theminimumforcewouldberequiredifitwereappliedatthebottomofthegate .In thiscase,takingmomentsaboutBgives
whichgives F =261kN .
2.53. Fromthegivendata: ρf =998kg/m3 , ρs =1025kg/m3,and w =100lb/m=0.4448kN/m. AsketchofthedimensionsusedinsolvingthisproblemisshowninFigure2.3.
(a) Dimensions (b) Forces on gate
Figure2.3:Gatedimensionsandforces
UsingthegivendataandreferringtoFigure2.3,
=(998)(9 81)=9 79kN/m3
γs =(1025)(9 81)=10 06kN/m3
F1 = γwAy1 sin θ =(9.79)(2 × 1)(2+1)sin30◦ =29.37kN
y1cp =¯ y1 + I Ay1 I = bd3 12 A = bd
y1cp =¯ y1 + d2 12¯ y1 =3+ 22 12(3) =3.11m
F2 = γsAy2 sin θ =(10.06)(2 × 1)[2(H 1)+1]sin30◦ =10.06(2H 1)kN
y2cp =¯ y2 + d2 12¯ y2 =(2H 1)+ 22 12(2H 1) =(2H 1)+ 0 3333 2H 1
TakingmomentsaboutA(∑ M =0)yields
29 37(1 11)+0 4448cos30◦(1)=10 06(2H 1) [1+ 0 3333 (2H 1) ] 32 99=10 06(2H 1)+3 353
whichyields H =1.97m
2.54. Thehydrostaticforce, F ,onthegateisgivenby F = γAy sin θ
Foranellipticalsurface,TableC.1inAppendixCgives A = πbh 4 where b = D =1 2m,h = D sin θ = 1 2 sin30◦ =2 4m andtherefore A = πbh 4 = π(1 2)(2 4) 4 =2 26m2
Thelocationofthecentroid,¯ y,isgivenby y = 9 sin θ = 9 sin30◦ =18m andthenethydrostaticforceonthegateis
F = γAy sin θ =(9 79)(2 26)(18)sin30◦ =199kN
Thelocationofthecenterofpressure, ycp,isgivenby ycp =¯ y + Icc Ay
whereTableC.1inAppendixCgives
Icc = πbh3 64 = π(1 2)(2 4)3 64 =0 814m4
hence ycp =18+ 0.814 (2 26)(18) =18 0m
ThemomentofthehydrostaticforceaboutP, MP ,isgivenby MP =199 [ycp (9 1 2 2 ) 1 sin30◦ ] =199 [18 0 (
Themomentrequiredtokeepthegateclosedis239kN m . 2.55. ConsidertheflapgateasafreebodyasshowninFigure2.4

Figure2.4:Flapgatefreebody
Thearea, A,ofthegateunderwaterisgivenby A =1 5 h sin86◦ =1 504h andthedistancetothecentroidofthegatefromthewatersurface,¯ y,measuredalongthe gate,isgivenby y = 1 2 h sin86◦ =0 5012h
Thehydrostaticforce, Fw,exertedbythewateris
Fw = γAy sin θ (1) where γ=9.79kN/m3 (at20◦C)and θ =86◦.Substitutingknownandderiveddatainto Equation1gives
Fw =(9 79)(1 504h)(0 5012h)sin86◦ =7 362h2 kN
Thedistance, ycp,belowthewatersurfacetothecenterofpressureisgivenby
where
CombiningEquations2and3andtaking A =1.504h and¯ y =0.5012h gives
Thedistancefromthehingetothewatersurface,measuredalongthegate(y′ inFigure2.4) isgivenby
andthehorizontaldistancefromthehingetothecenterofgravityofthegate(x′ inFigure 2.4)isgivenby x ′ =(1m)cos86◦ =0.06976m
Takingmomentsaboutthehinge,withtheweightofthegate(W )equalto8kN,yields
w · (y ′ + ycp)= W · x ′ (7 362h2)(1 75 1 002h +0 6682h)=(8)(0 06976)
whichsimplifiesto 7 362h2(1 75 0 3338h)=0 5581
Thiscubicequationhasthefollowingthreesolutions h =5 23m, 0 212m, and 0 204m
Theonlyrealisticsolutionis h =0.212m
2.56. Fromthegivendata: b =2mandtheotherdimensionsaregivenintheproblemdiagram. Take γ =9 79kN·m3.Forreference,thesketchshowninFigure2.5isuseful.
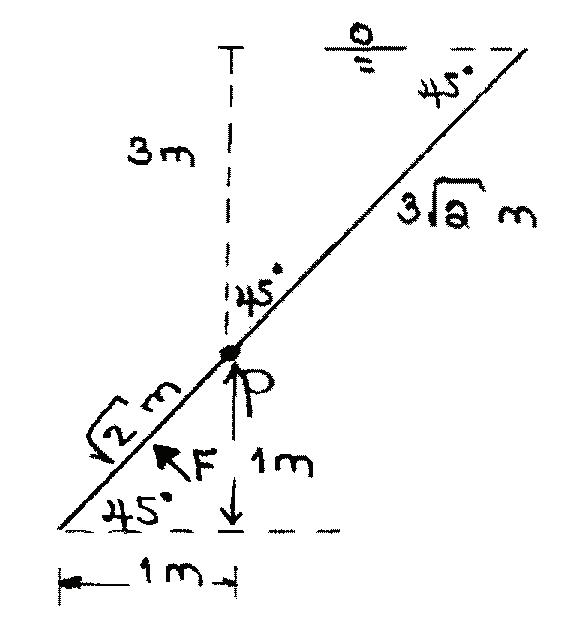
Usingthegivendata:
sin45◦ = √2, F = γAy sin θ y =3√2+ √2 2 =4 950m,F =(9 79)(√2 × 2)(4 950) ( 1 √2 ) =96 9kN
ycp =¯ y + I Ay , I = bd3 12 = (2)(√2)3 12 =0 4714m4 A =(√2)(2)=2 828m2,ycp =4 950+ 0.4714 (2 828)(4 950) =4 984m
TakingmomentsaboutPgives F (ycp 3√2)= Fs(1) → Fs =96 9 (4.984 3√2) 1 =71 8kN
2.57. Fromthegivendata: b =1 52m.Assume T =20◦C,thefluidpropertiesare: γw = 9.789kg/m3,and γsw =1.025(9.789)=10.03kg/m3.AschematicdiagramoftheimportantvariablesisshowninFigure2.6.Thecentroidaldepthonthefreshwatersideisgivenby y =0.5(3.05m)=1.525m. 0.61 m
F1 F2 3.05 m y1 y2 h
Figure2.6:Schematicdiagramofverticalgate
F1 = γwAy =(9.789)(3.05 × 1.525)(1.525)=69.21kN y1 =¯ y + I0 Ay =1.525+ (1 525)(3 05)3 12 (1 525 × 3 05)(1 525) =2.033m
F2 = γswAy =(10 03)(1 525h) ( h 2 ) =7 623h2 kN y2 =¯ y + I0 Ay = h 2 + (1 525)(h)3 12 (1 525 × h)(h/2) = 2 3 h
TakingmomentsaboutA,
whichyields h =3.002m.Therefore,thegatewillopenwhenthedepthofseawaterisless than3.00m .
2.58. Fromthegivendata: h1 =0 5m, h2 =0 7m,and w =3m.Usethesubscript“b”toindicate theportionofthegatebelowthehinge,andthesubscript“t”toindicatetheportionofthe gateabovethehinge.Thefollowingpreliminarycalculationsareuseful:
Calculatetheresultanthydrostaticforcesandtheirlocationsontheportionsofthegatebelow andabovethehinge:
Whenthegateisjustabouttoopen,thereactionofthestopperisequaltozeroandthesum ofthemomentsaboutthehingeisequaltozero.Therefore,
SubstitutingtheexpressionsfromEquations1to4intoEquation5andmaking h thesubject oftheformulayields
(a) SubstitutingthevaluesofthegivenandderivedparametersintoEquation6yields
(b) Sincethespecificweightoftheliquid, γ,doesnotappearintheexpressionfor h given byEquation6,thecalculateddepthofliquid, h doesnotdependonthespecificweight orthedensityoftheliquid.
2.59. ConsiderthesideofthetroughshownasafreebodyinFigure2.7.
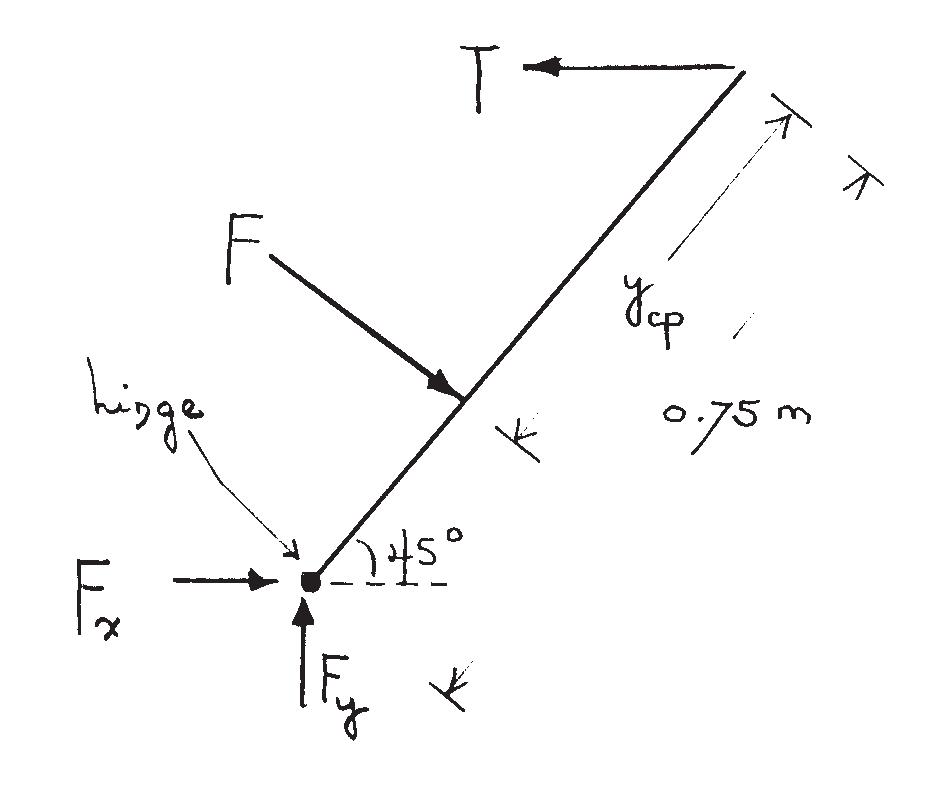
Thehydrostaticforce, F ,isgivenby F = γAy sin θ =(9 79)(0 75 × 6) ( 0 75 2 ) sin45◦ =11 68kN
Thecenterofpressure, ycp,isgivenby ycp =¯ y + Icc Ay =0 375+ 6×0 753 12 (0 75 × 6)(0 375) =0 50m
Takingmomentsaboutthehingegives
F (0 75 ycp)= T (0 75sin45◦) whichyields T = F (0 75 ycp) 0 75sin45◦ = 11 68(0 75 0 50) 0 75sin45◦ =5 51kN
2.60. Fromthegivendata: W =3m, L =2m, θ =30◦ , p0 =300kPa, d1 =2m,and d2 =1m.For waterat20◦C, γ =9 789m/s2.Thefollowingpreliminarycalculationsareuseful,
hc = d2 +[d1 + 1 2 L]sin θ =1+[2+ 1 2 (2)]sin30◦ =2 5m A = WL =(3)(2)=6m2 , y = hc sin θ = 2.5 sin30◦ =5m,Icc = WL3 12 = (3)(2)3 12 =2m4
SubstitutingthesedataintoEquations2.41and2.48gives, F =[p0 + γhc]A =[300+(9.789)(2.5)](6)=1947kN=1.947MN ycp =¯ y + γ sin θIcc [p0 + γy sin θ]A =5+ (9 789)sin30◦(2) [300+(9.789)(5)sin30◦](6) =5 005m
Thedepth, hcp,iftheresultantforcebelowthewatersurfaceisgivenby hcp = ycp sin θ =5 005sin30◦ =2 50m
2.61. Fromthegivendata: R =2m,and d =3m.Forwaterat20◦C, γ =9.79kN/m3.Using thesedata:
Ixc = Iyc =0 05488R4 =0 05488(2)4 =0 8781m4
Ixyc = 0 01647R4 = 0 01647(2)4 = 0 2635m4 A = 1 4 πR2 == 1 4 π(2)2 =3.142m2
= d + 4R 3π =3+ 4(2) 3π =3 849m x = 4R 3π = 4(2) 3π =0 849m
F = γAy =(9 79) [ 1 4 × π(2)2] (3 849)=118kN
ycp =¯ y + Ixc Ay =3 849+ 0 8781 (3 142)(3 849) =3 921m xcp =¯ x + Ixyc Ay =0.849+ 0.2635 (3.142)(3.849) =0.827m MXX = F xcp =(118) (0.827)=97.6kN m
2.62. TheellipseparametersasreferencedtothegeometricpropertiesintheAppendixare: a =1m, b/2=1m → b =2m.Fromtheothergivendata: d =2m.Forwaterat20◦C, γ = 9.789kN/m3.UsingthesedatawiththesameaxisreferencesasintheAppendix:
Iyc = 1 128 πba3 = 1 128 π(2)(1)3 =0.04909m4 Ixyc =0m4
A = 1 8 πab = 1 8 π(1)(2)=0 7854m2
y = d + a 2 =2+ 1 2 =2 500m x = 2b 3π = 2(2) 3π =0 4244m
F = γAy =(9.789)(0.7854)(2.5)=19.22kN
ycp =¯ y + Iyc Ay =2 500+ 0 04909 (0.7854)(2.500) =2 525m
xcp =¯ x + Ixyc Ay =0.4244+0=0.4244m
MXX = F xcp =(19.22) (0.4244)=8.157kN m
2.63. Fortheupperportionofthegate: AU =1m×1m=1m2 , γU =9.50kN/m3,¯ yU =2+1/2 =2.5m, IcU = bd3/12=(1)(1)3/12=0.08333m4,hence
FU = γUAUyU =(9.50)(1)(2.5)=23.75kN
ycpU =¯ yU + IcU AUyU =2 5+ 0 0833 (1)(2.5) =2 533m
Forthelowerportionofthegate,withdepthstakenrelativetotheinterface: p0 = γUhU = (9.50)(3)=28.5kPa, AL =2m×1m=2m2 , γL =9.90kN/m3,¯ yL =2/2=1m, IcL = bd3/12=(1)(2)3/12=0.6667m4,hence
Therefore,thetotalforce, F ,andlocation, ycp,aregivenby
2.64. Theparametersoftheellipse,asdescribedintheAppendix,are a =1m,and b =2m.From thegivendata: d =3m.Fortheupperportionofthegate:
U = 1 8 πab = 1 8 π(1)(2)=0 7854m2 , γU =9 40kN/m3
U = d 2b 3π =3 2(2) 3π =2.576m, IcU = 1 128 πab3 = 1 128 π(1)(2)3 =0.1963m4
=(9 40)(0 7854)(2 576)=19 02kN
0.1963 (0 7854)(2 576) =2 673m
Forthelowerportionofthegate,withdepthstakenrelativetotheinterface: p0 = γUd = (9.40)(3)=28.2kPa,and AL = AU =0 7854m2 , γ
7854)=25 41kN
Therefore,thetotalforce, F ,andlocation, ycp,aregivenby F = FU + FL =19.02+25.41=44.43kN ycp = FUycpU + FL(3+ ycpL) F = (19.02)(2.673)+(25.41)(3+0.5001) 44.43 =3.146m
NEW Forwaterat20◦C, γ =9 789kN/m3.Forthebentpartofthesurfacetheperimeterofthe quartercircleis1m,andtheradius, R,ofthequartercircleiscalculatedasfollows:
Usingthecalculatedvalueof R,thehorizontalandverticalforcesonthesurfacearegivenby
Fx = γAv1yv1 + γAv1yv1 =9 789[(2 × 3)(1 5+1)+(0 6366 × 5)(1 5+2+0 6366)] =265.8kN
Fz = γV = γ [ 1 4 πR2 +3 5R] W =9 789 [ 1 4 π(0 6366)2 +3 5(0 6366)] (5)=124 6kN
2.65. Becauseofsymmetry,thenethorizontalhydrostaticforceiszero.Thepressureatthetopof thecone, p0,isgivenby p0 =150 γw(7m)=150 (9 79)(7)=81 47kPa
Thisgivesanequivalentheightofwater, H,of H =
Therefore,theverticalforceonthecone, F ,isgivenby F = [πR2H + 1 3 πR2h] γ = [π(1)2(8 32)+ 1 3 π(1)2(4)] (9 79)=297kN
2.66. Fromthegivendata: F0 =2500kN, L =10m,and h =2.4m.Forwaterat20◦C, γ = 9 789kN/m3.Foranygivenstepheight(=width), x,thehorizontalforce, Fx,isafunction of x asfollows: Av = w(h +4x)=10(2.4+4x), yv = h +4x 2 =1.2+2x Fx = γAvyv =9.789[10(2.4+4x)](1.2+2x)
Setting Fx(x)=2500kNyields x =1.187m .Usingthisvalueof x,theverticalforceonthe dam, Fy,isgivenby
Fy = γV0 = γw(x 2 +2x 2 +3x 2 +4x 2)=(9 789)(10)(1 187)2(1+2+3+4)=1379kN
2.67. Fromthegivendata: L =5m, hf =4m, hs =2m,and R =2m.Forfreshwaterat20◦C, γf =9 789kN/m3,andforsaltwaterat20◦C, γs =10 03kN/m3 (fromAppendixB.4).The followingpreliminarycalculationsareuseful:
Af = Lhf =(5)(4)=20m2 , yf = 1 2 hf = 1 2 (4)=2m
As = Lhs =(5)(2)=10m2 , ys = 1 2 hs = 1 2 (1)=1m
V0f = L [R2 1 4 πR2] =(5) [(2)2 1
where V0f isthevolumeofthespacebetweenthetopofthewallandthefreshwatersurface. Thehorizontalandverticalcomponentsofthenethydrostaticforceonthewallaregivenby:
2.68. Fromthegivendata: R = hf =3 5m,and w =4 8m.Forfreshwaterat20◦C, γf = 9 789kN/m3,andforsaltwaterat20◦C, γs =10 03kN/m3 (fromAppendixB.4).The followingpreliminarycalculationsareuseful:
0f = Rhf w 1 4 πR2 w =(3 5)(3 5)(4 8) 1 4 π(3 5)2(4 8)=12 62m2 where V0f isthevolumeofthespacebetweenthetopofthegateandthefreshwatersurface.
(a) Forthehorizontalhydrostaticforcestobeequal, γf Avf yvf = γsAvsyvs
Substitutingthegivenandderivedrelationshipintothisequationandsolvingfor h gives
(b) Fortheverticalhydrostaticforcestobeequal,
32m3
ConsiderthegeometryofthegateshowninFigure2.8,andrecallthattheareaofa segmentofacirclewithcentralangle
Figure2.8:Segmentofacircle
Foranyheight h,thevolumeabovethegate, V0s,isequaltotheshadedareaand,using thegeometricrelationsinFigure2.8yields
Since V0s =12 32m3 whentheverticalhydrostaticforcesareequal,then
whichyields h =2.598m
2.69. Fromthegivendata: R =1m,and W =40kN/m.Forwaterat20◦C, γ =9 789kN/m3.If Fh and Fv arethehorizontalandverticalhydrostaticforcesonthegate,thenthemagnitude, F ,anddirection, θ,ofthehydrostaticforcearegivenby
Theverticalforceonthegate, Fv,isgivenby
Theresultanthydrostaticforceactsthroughthecenterofthecircularquadrant,theweight ofthegateactsverticallythroughthecentroidofthegate,andthecentroidofthegateis locatedatadistance4R/3π fromthecenterofthequadrant.Takingmomentsaboutthepin whenthegateisjustabouttoopen(i.e.,thereactionisequaltozero)andusingEquation1 gives
CombiningthisresultwithEquation2gives h =2.57m .
NEW (a) Fromthegivendata: h =2 7m, r1 =1m,and r2 =0 95m.Forwaterat20◦C, γ =9.789kN/m3.Foraunitlengthofgate, L =1mand x-and y-componentsofthe hydrostaticforceonthegate,andtheweightofthegate,aregivenby:
54kN
y = γV
2](1)=24 33kN
Thecalculatedvaluesof Fx and Fy canbeusedtodeterminethemagnitudeanddirection oftheresultantforceasfollows:
Takingmomentsaboutthehingewhenthegateisabouttoopen,yields:
(b) Considernowagatematerialwithdensity ρg =8100kg/m3.Whenthegateisfilled withwater:
W =3 004ρg + γπr 2 2L =3 004(8100)+(9 789)π(0 95)2(1)=52 08kN
sin θ = Fy F = 9 789(h 0 2146) F
Takingmomentsaboutthehingewhenthegateisabouttoopen,yields:
r1 sin θ W r1 =0 → F (1) 9 789(h 0 2146) F 52 08 (1)=0 → h =5 54m
2.70. Fromthegivendata: γ =9 79kN/m3 , Av =(3)(20)=60m2,and¯ yv =6 5m.Thehorizontal force, Fx,onviewingglassisgivenby Fx = γAvyv =(9 79)(60)(6 5)=3820kN
Thevolumeofwater, V0,abovetheviewingglassisgivenby V0 = [(8)(3) 1 4 π 4 (6)2] (20)=338 6m3
Verticalforce, Fz,ontheviewingglassisgivenby Fz = γV0 =(9.79)(338.6)=3310kN
Thenetforceontheviewingglassisgivenby
= √F 2 x + F 2 y = √(3820)2 +(3310)2 =5050kN
2.71. Determinethehydrostaticforcesontheplaneandcurvedsurfacesseparatelyandthenadd themup.Assumethat γ =9.79kN/m3.Thegeometricrelationshipsandrelevantdimensions areshowninFigure2.9.
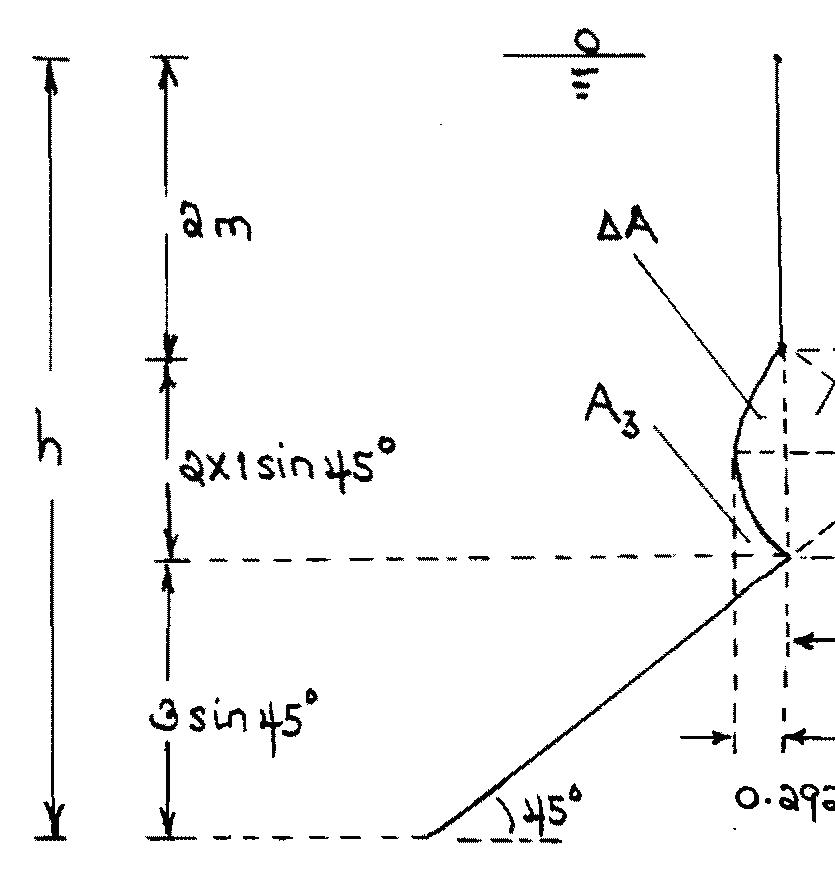
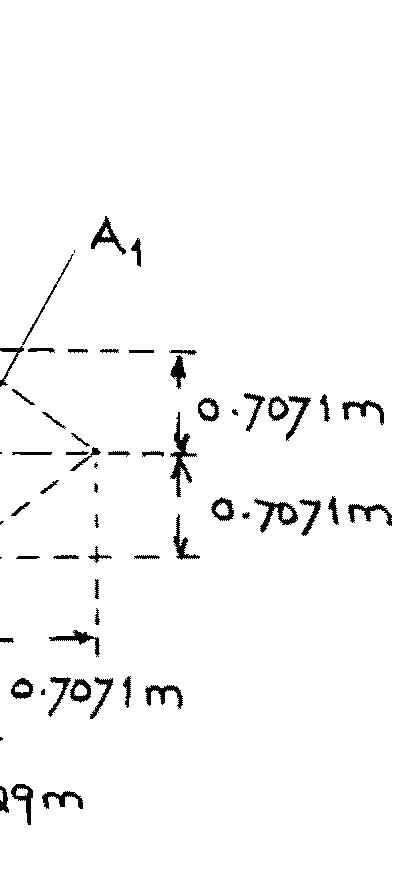
Figure2.9:GeometricRelationships
PlaneSurface: Theforcenormaltothesurface, F ,isgivenby
F = γAy sin θ
UsingthegivendataandthegeometricrelationshipsshowninFigure2.9:
A =(3)(2)=6m2 y sin θ =2+2sin45◦ + 3 2 sin45◦ =4.475m
SubstitutingtheseparametersintoEquation1gives
F =(9.79)(6)(4.475)=262.9kN
Thisforcehas x and y componentsasfollows:
Fx =262.9cos45◦ =185.9kN
Fy = 262 9sin45◦ = 185 9kN
CurvedSurface: The x-componentoftheforceonthecurvedsurfaceisgivenby
Fx = γAyv (2)
UsingthegivendataandthegeometricrelationshipsshowninFigure2.9:
A =(2 × 0 7071)(2)=2 828m2 yv =2+0 7071=2 7071m
SubstitutingtheseparametersintoEquation2gives
Fx =(9 79)(2 828)(2 7071)=74 95kN
The y componentofthehydrostaticforceontheuppercurvedsurfaceisgivenby
Fy1 = γV1 (3)
UsingthegivendataandthegeometricrelationshipsshowninFigure2.9: A1 = 1 2 (0 7071)(0 7071)=0 2500m2 A0 = π 8 r 2 = π 8 (1)2 =0 3927m2 ∆A = A0 A1 =0 3927 0 2500=0 1427m2 V1 =[(2+0.7071)(0.2929) 0.1427](2)=1.300m3
SubstitutingintoEquation3gives
Fy1 = (9.79)(1.300)= 12.73kN
The y componentofthehydrostaticforceonthelowercurvedsurfaceisgivenby Fy2 = γV2 (4)
UsingthegivendataandthegeometricrelationshipsshowninFigure2.9: A3 =(0 2929)(0 7071) ∆A =(0 2929)(0 7071) 0 1427=0 0644m2 V2 =[(2+2 × 0 7071)(0 2929) 0 0644](2)=1 871m3
SubstitutingintoEquation4gives
Fy2 =(9 79)(1 871)=18 32kN
Therefore,thenetverticalhydrostaticforceonthecurvedportionofthegateisgiven by Fy = Fy1 + Fy2 = 12.73+18.32=5.59kN
Thisforcecouldalsobedeterminedbysimplycalculatingthebuoyantforceonthegate.
TotalHydrostaticForce: The x and y componentsofthetotalhydrostaticforceareequal tothesumofthehydrostaticforcesontheplaneandcurvedportionsofthegate,so
Fx =185 9+74 95=260 9kN
Fy = 185.9+5.59= 180.3kN
2.72. Fromthegivendata:widthofthegate=5m,weightofgate=10kN.Let Rx and Ry be thereactionofthegatetothehydrostaticforce.Hence, Rx = γAvyv where γ =9.79kN/m3 , Av =3 × 5=15m2,and¯ yv =3/2=1.5m.Substitutinggives
Rx =(9 79)(15)(1 5)=220kN
Thisforceislocatedat ycp belowthewatersurface,where ycp =¯ yv + Icc Avyv where Icc = bd3 12 = 5(3)3 12 =11 25m4
andhence ycp =1.5+ 11.25 (15)(1 5) =2.0m
Theverticalreaction, Ry,isequaltotheweightofwaterabovethegate, Ry = γV =(9 79) [ π(3)2 4 ] (5)=346kN
Thisforceactsthroughthecentroidofthecirclequadrantoccupiedbythegate,whichis 4r/3π fromP,where 4r 3π = 4(3) 3π =1 27m
Thenethydrostaticforce, R,onthegateisthereforegivenby R = √R2 x + R2 y = √2202 +3462 =410kN
Themoment, M ,tendingtoopenthegateis M =346(1 27) 220(2 0) 10(1)= 10 6kN·m
Hencethemomentrequiredtoopenthegateis10.6kN m
Note: Thismomentisnumericallyequaltothemomentdueonlytotheweightofthegate. Thisisanexpectedresultsincetheresultanthydrostaticforceonacirculargatewillnecessarilyactthroughthecenterofthegate.
2.73. Fromthegivendata: H =15.25mandassume γ =9.79kN/m3.Thehorizontalcomponent oftheforceisgivenby
Theverticalforceistheweightofthefluidabovethedam.The x coordinateatthewater level, x0,isgivenby
andtheverticalforceonthedamisgivenby
Thereforetheresultantforceis √11382 +602 12 =1287kN andthisforcemakesanangle oftan 1(1138/602 1)=62.1◦ withthevertical.Thehorizontalforceactsatthecenterof pressuregivenby
Theverticalforceactsthroughthecenterofgravitygivenby
Usingthesedatagive
2.74. Consideringthenormalforceontheviewingglass, FN,andthelimitof100Nthatcanbe supportedbyeachrivet,
requiredrivets= 38450 100 =385rivets
Consideringtheshearforceontheviewingglass, FS,andthelimitof5Nthatcanbesupported byeachrivet,
requiredrivets= 2560 5 =512rivets
Therefore,atleast512rivets areneededtosupporttheweightofthewaterintheviewing glass,plusadditionalrivetstosupporttheweightoftheglassitself.Ifaflatviewingglassis usedinstead,atleast385rivets wouldberequired.
Theforceonthetophalfoftheviewingglass, FT,isgivenby
Theforceonthebottomhalfoftheviewingglass, FB,isgivenby
B = γAy = γ [ 1 2 πR2][5+ 4R 3π ] =(9.79) [ 1 2 π(0.5)2][5+ 4(0 5) 3π ] =20.04kN
Thereforetheforceratiois18.41/20.04=0.92 .Morerivetswillberequiredonthebottom
2.75. Takeone-halfofthetroughasafreebody.Thehorizontalcomponentofthehydrostatic force, Fh,isgivenby
Theverticalcomponentofthehydrostaticforce, Fv,isgivenby
Thelineofactionof Fh is yh fromthewatersurface,where
Thelineofactionof Fv is xv fromthecenterlineofthetrough,where
Takingmomentsaboutthehingegives
whichyields T =3.67kN .
2.76. LookatthegateasafreebodyasshowninFigure2.10,where2 2sin45◦ =0 586m.The nethorizontalforce, FH,isgivenby
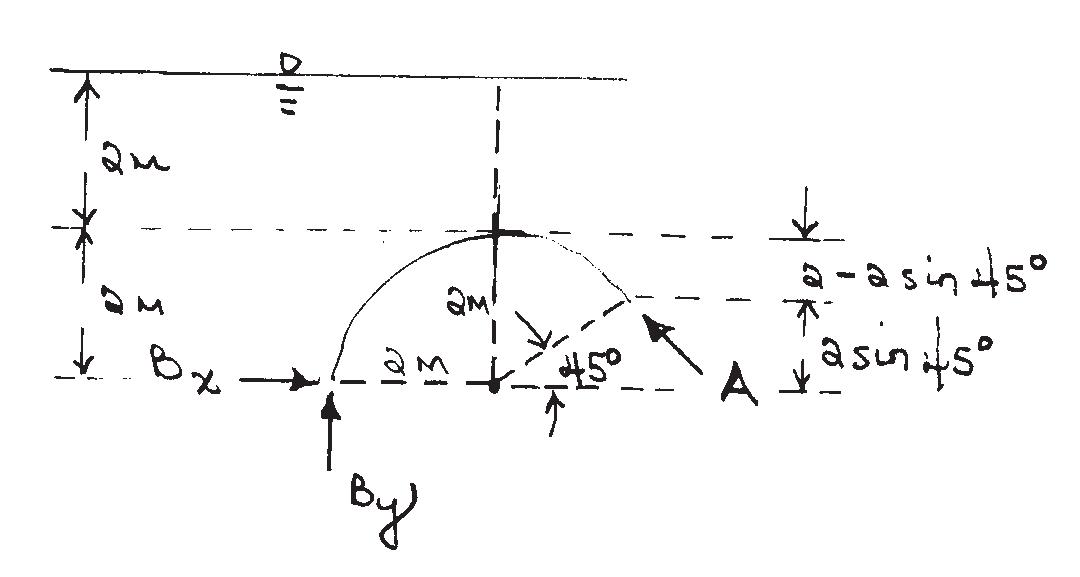
Figure2.10:GateasaFreeBody
Thenetverticalforce, FV,isgivenby Fh = γV =(10 05) [4 × 2 1 4
5kN
Thenethydrostaticforceonthegateactsthroughthecenterofthecircle.Takingmoments aboutthecenterofthecirclegives
Forequilibriuminthe x-direction,
andforequilibriuminthe y direction
CombiningEquations1to3gives
2.77. Fromthegivendata: D =400mm, t =4mm,and p =800kPa.Forequilibrium:
where σ isthecircumferentialstress,and L isanyarbitrarylengthofpipe.Substitutinggiven values:
= (800)(400) 2(4) =40000kPa=40MPa
2.78. Fromthegivendata: Wair =40N,and Wwater =25N.Forwaterat20◦C, γw =9.79kN/m3 Let γs bethedensityofthesolidobjectandlet Vs beitsvolume,then
CombiningEquations1and2yields
Thevolumeoftheobject, Vs,canthereforebeestimatedas
2.79. (a) Usethesubscript“o”todenotetheobject,“w”todenotewater,and“a”todenoteair. Thebasicequationstobeusedareasfollows:
where W representsweight,and V representsvolume.Dividingthesecondequationby thefirstequationgives
(b) Fromthegivedata: Wa =40N,and Wo =25N.Substitutingthesedataintothe derivedequationgives
1
40 =2.67
2.80. Fromthegivendata: Db =15m, Rb = Db/2=7.5m,and W =2kN.Forstandard atmosphericconditionsatsealevel, p0 =101.3kPaand T0 =15◦C=288.15K.Forair, R =287.1J/kg K.Thevolumeoftheballoon, Vb,isgivenby
Atliftoff,theweightoftheairintheballoonplustheattachedweighttobeliftedisequalto thevolumeofairdisplacedbytheballoon.If T isthetemperatureoftheairintheballoon underthiscondition,thenusingtheidealgaslawtocalculatethedensityofairgives
Therefore,thetemperatureoftheairintheballoonmustberaisedto318 1K 273 15K= 45.0◦C
2.81. Fromthegivendata: D =3m,and M =8kg.Thevolumeoftheballoonisgivenby
Theballoonstabilizeswhentheweightoftheballoonisequaltotheweightoftheairdisplaced bytheballoon,whichrequiresthat
ReferringtothestandardatmosphereinAppendixB.3,thedensityintheatmosphereisequal to0.5658kg/m3 atanelevationof7.38km.Therefore,theballoonstabilizesatanelevation of7.38km
2.82. Fromthegivendata: W =1 5kN, patm =101kPa, Ta =20◦C=293 15K, w =80g/m2,and Tb =80◦C=353 15K.Forair, R =287 1J/kg·K.Thedensityoftheatmosphericair, ρa, andthedensityoftheairintheballoon, ρb,canbederivedfromtheidealgaslawasfollows:
Understableconditions,theweightoftheballoonplustheairintheballoonplusthesupportedweightisequaltotheweightoftheairdisplacedbytheballoon,whichrequiresthat
2.83. Whenthesumoftheforcesequalzero,
whichsimplifiesto
(1) Inthiscase, γp =2.65γw =2.65(9.79)=25.9kN/m3 =25900N/m3 , γw =9.79kN/m3 = 9790N/m3 , D =2mm=0.002m,and µ =1 00 × 10 3 N·s/m2 at20◦C.Substitutinginto Equation1gives v = (25900 9790)(0 002)2 18(1.00 × 10 3) =3.58m/s
2.84. Fromthegivendata: L =10m, L1 =7m, L2 =3m, W =15m, H =4m,SG1 =1.5, andSG2 =3.0.Forfreshwaterat20◦C, γfw =9.79kN/m3.Forfreshwaterat4◦C, γw = 9.807kN/m3.Thespecificweightsofthetwopartsofthebodyarecalculatedasfollows, specificweightoflightsection, γ1 =SG1 · γw =1 5(9 807)=14 71kN/m3 specificweightofheavysection, γ2 =SG2 γw =3 0(9 807)=29 42kN/m3
Thevolumesofthesectionsofcabinarecalculatedasfollows,
volumelightsection, V1 = L1 × W × H =(7)(15)(4)=420m3
volumeofheavysection, V2 = L2 × W × H =(3)(15)(4)=180m3
volumeofentirecabin, Vc = V1 + V2 =420+180=600m3
Theforcesonvariouspartsofthebodyareasfollows, buoyantforceontheentirebody, Fc = γfwVc =(9 79)(600)=5874kN
weightoflightsection, W1 = γ1V1 =(14 71)(420)=6178kN
weightofheavysection, W2 = γ2V2 =(29 42)(180)=5296kN
Ifthesupportforceis F ,thenequilibriumofforcesintheverticaldirectionrequiresthat F = W1 + W2 Fc =6178+5296 5874=5600kN
Consideringthecabinasafreebodyandtakingmomentsaboutthecentroid,accountingfor thefactthatthebuoyantforceactsthroughthecentroidofthebody,themomentequation gives
(6178) · [ 10 7 2 ] +(5600) · x =(5296) · [ 10 3 2 ] → x =1 66m
2.85. Fromthegivendata: Lc =0 15m,and fo =0 15.Forwaterat20◦C, ρw =998 2kg/m3 (AppendixB.1),andforSAE30oilat20◦C, ρo =918kg/m3 (AppendixB.4).If ρc isthe densityofthecube,notingthatthebuoyancyforceisequaltotheweightoffluiddisplaced, thenforequilibrium,
→ ρc =(0.15)(918)+(1 0.15)(998.2)=986kg/m3
2.86. Theweight, W ,ofafloatingobjectinafluidofspecificweight γf isrelatedtothedisplacement volume, V ,bytherelation: W = γf V .Therefore,
Thisshowsthatthepercentagechangein V isthesameasthepercentagechangein W
2.87. Fromthegivendata: f =0.90, t =25mm, Wi =500N,and ρs =8000kg/m3.Forseawater, ρs =1023kg/m3 (fromAppendixB.4).Thespecificweightscorrespondingtothegiven densitiesare γs =78.56kN/m3 and γw =10.03kN/m3.If D isthe(outer)diameterofthe sphere,thenfor90%(= f )ofthespherebelowwater,puttingthebuoyantforceequaltothe weightofthesphereplustheinstrumentationgives
.9)(10.03) πD3 6 =(78.56) [ πD3 6
whichyields D =1 12m
2.88. Fromthegivendata: d1 =1m, d2 =0 1m,andSG=0 85.Assumethatthespecific gravityspecificationappliestothisobjectinthiswater.Usethesubscript“o”todenote thetotalobject,thesubscript“s”todenotetheportionoftheobjectthatissubmerged, andthesubscript“w”todenotewater.Taking L tobethelengthoftheobject,forvertical equilibrium,
ThegeometryofthepartiallysubmergedobjectisshowninFigure2.11.
Figure2.11:Geometryofpartiallysubmergedobject
Inthiscase, h = d1 d2 =1m 0 1m=0 9mandthesubmergedarea, As,isgivenby
CombiningEquations1and2andsolvingfor R (with h =0 9mandSG=0 85)yields R =0 568mandhence D =2R =1 14m.Therefore,themaximumdiameteroftheobject thatwillsatisfythegivenconstraintsis1.14m
2.89. Fromthegivendata: W1 =800Nand W2 =200N.Forwaterat20◦C, γw =9790N/m3 . Let L beanygivenloadcarriedbythecanoe,andlet V1 and V2 bethedisplacementvolumes correspondingto W1 and W2,respectively,then
SubtractingEquations1and2toeliminate L gives
2.90. Let Vt bethetotalvolumeofthebody, Va bethevolumeofthebodyabovethesurfaceof theliquid, γ1 bethespecificweightofthebody,and γ2 bethespecificweightoftheliquid. Forequilibrium,
Thefraction, fa,ofthebodythatisabovethewatersurfaceisgivenby
Inthecaseoftheiceberginseawater,SG1 =0 92andSG2 =1 03,andEquation1gives fa = 1.03 0.92 1 03 =0 11
2.91. Fromthegivendata:SG=0 8,and D =10mm.Let N =numberofbubblesperm3 , Vb = volumeofeachbubble, ρ =densityofwater,and ρb =densityofbubblywater.Usingthese definitionsandneglectingthemassofairinthebubbles,
volumeofairin1m3 = NVb
volumeofwaterin1m3 =1 NVb
massofwaterin1m3 = ρ(1 NVb)
densityofbubblywater, ρb = ρ(1 NVb)
Theshipsinkswhenthedensityofthebubblywaterisequaltothedensityoftheship,in whichcase
Fromthegivenbubblediameter, Vb = 1 6 πD3 =5 236 × 10 7 m3,andEquation1gives N = 1 0 8 5.236 × 10 7 =3.82 × 105 bubbles/m3
2.92. Forequilibrium,theweightofthepoolmustatleastequalthebuoyantforce.Letthedepth ofwaterinthepoolbe x,thenforequilibrium(seeFigure2.12)
Wt.ofpool+Wt.ofwaterinpool=Buoyantforce 500+(10 × 5 × x)(9.79)=[10 × 5 × (2.5 1.25)](9.79 500+490x =612 x =0 23m
Thereforeatleast23cm ofwatermustbemaintainedinthepool.
2.93. Whenthebargeisfullyloaded,thedraft, V ,isgivenby γswV =(20+250)kN
For S =1.03, V = 20+250 (1.03)(9.79) =26.78m3
andfromgeometry
CombiningEquations1and2gives
andsolvinggivesthedraftas y =1.34m .
2.94. Fromthegivendata: f1 =0.75,and f2 =0.90.Forwater, ρw =998kg/m3.Theaverage densityofthebody,¯ ρb,canbederivedfromEquation2.75asfollows
3
Theaveragedensityofthesolidmaterialis¯ ρs andthefractionofthebodythatisopenspace is f2.Representingthemassofthesolidby Ms andthevolumeofthesolidby Vs,then
Substitutingtheknownvaluesof f2 and¯ ρb yields
s = 1 1 0 9 (749)=7490kg/m3
2.95. Fromthegivendata: H =2m, A = LW ,SG1 =1.2,∆z1 =1.2m,andSG2 =1.6.Denote thespecificweightsofthebody,toplayer,andbottomlayerby γb, γ1,and γ2,respectively. Forverticalequilibrium,where h isthedepthofpenetrationintothebottomlayer,:
(a) Theminimumspecificgravityofthebodyforfullpenetrationofthetoplayercanbe derivedbysetting h =0inEquation1whichgives
(b) Thedepthofpenetration, h,intothebottomlayerwhenSGb =1 0canbeobtainedby substitutingdirectlyintoEquation1,whichyields
2.96. Fromthegivendata: L =3m, D =200mm=0.2m,andSG=0.6.Forseawater, γsw = 10.03kN/m3 (fromAppendixB.4).Thetherelevantforcesanddimensionsintheproblem areshowninFigure2.13,where W istheweightofthebuoy, T isthetensioninthesupport cable,and Fb isthebuoyantforce.

Let A bethecross-sectionalareaofthebuoyand Vb bethevolumeofthebuoy,then
Themagnitudesof W and Fb canbeexpressedintermsofothervariablesasfollows:
(a) Thisisthecaseofthepartiallysubmergedbuoy.Takingmomentsaboutthepointwhere thesupportcableisattachedtothebuoy,
Forverticalequilibrium,
whichsimplifiesto
CombiningEquations1and2andevaluatinggives
(b) Thisisthecaseofthefullysubmergedbuoy.Forverticalequilibrium,
2.97. Fromthegivendata: W =0.246Nand D0 =10mm=0.01m.Forpurewaterat20◦C, γw =9790N/m3.Calculatethecross-sectionalarea, A0,ofthehydrometerstemandthe volume, V0,ofthehydrometerbelowthewatermarkinpurewater:
For∆h =2cm=0.02m,thespecificgravityofthefluid,SGf ,isgivenby
2.98. Fromthegivendata: D =9mm, V0 =20cm3 =2 × 104 mm3,andSG=1.2.Thecrosssectionalarea, A0,ofthehydrometerstemisgivenby
Therelationshipbetweenthehydrometerdisplacement,∆h,andthespecificgravity,SG,is givenbyEquation2.78as
V0 V0 + A0∆h → ∆h = [ V0
Thereforethedistilled-watermarkwillbe52.4mm abovetheliquidsurface.
2.99. Fromthegivendata: D =0 70m, R = D/2=0 35m, L =0 60m,SGb =0 65,and SGℓ =0.90.Thecentroidalmomentofinertia, I00,ofthecircularareathatintersectsthe liquidsurfaceisgivenby(AppendixC.1):
Whenthecylindricalbodyisplacedintheliquid,theweightofthebodyisequaltothe weightoftheliquiddisplaced,whichrequiresthat
wheretherelation γb/γℓ =SGb/SGℓ hasbeenused.Thesubmergedheight, h,canbederived fromthebuoyancyrelationshipgiveninEquation2asfollows,
Thedistancebetweenthecenterofgravityandthecenterofbuoyancy,GB,isthereforegiven by
Themetacentricheight,GM,canbecalculatedfromEquation2.79usingtheresultsfrom Equations1to3toyield
GM= I00 Vsub GB= 1.179 × 10 2 0 1668 0 0833= 0 0127m
Sincethemetacentricheightisnegative,thecylindricalbodyisunstable attheorientation atwhichitisplacedintheliquid.
NEW Fromthegivendata: D =300mm, R = D/2=150mm=0 15m,and ρlog =512kg/m3.For waterat20◦C, ρwat =998kg/m3.Let x bethedepthofthelogbelowwaterwhentheaxisis vertical,thenforequilibrium
Atthelimitofstability,
substitutingknownquantitiesgives
NEW Fromthegivendata: rb = 1 2 (4m)=2m, hb =2m, rp = 1 2 (2m)=1m, ρw =998kg/m3,and ρb =170kg/m3.Let h betheheightofthepole.Thefollowingequationsmustbesatisfied:
GM= I00 Vsub GB, GM=0,
GB= I00 Vsub
Notingthat γw/γb =170/998=0.1703,substitutingthegivendataandcombiningtheabove equationsyieldthefollowingequationfor hp:
Afinalcheckisnecessarytoensurethatthebaseisnotsubmergedinwater.Calculating hsub gives hsub = ( γb γw ) V πr2 b =0.53m
Sincethebaseisnotsubmerged(hsub <hb)thecalculationsarevalidated.
2.100. Atthelimitofstability,themetacentricheightisequaltozero,so
GM= I00 Vsub GB → I00 Vsub GB=0 → GB= I00 Vsub
I00 = bd3 12 = 4(0.70)3 12 =0 114m4 Vsub = [ 1 2 (0.70)(0.15)+(0.3)(0.7)] (4)=1.05m3 GB= I00 Vsub = 0.114 1 05 =0 109m
Findthedistanceofthecenterofbuoyancy, zB abovethebottom:
zB = A1z1 + A2z2 A1 + A2 = (0.7 × 0.3)(0.15+0.30/2)+( 1 2 × 0.7 × 0.15)( 2×0 15 3 ) 0 21+0 0525 =0 26m
Iftheheightofthecenterofgravityabovethebottomis zG,then zG zB =0.109m → zG = zB +0.109=0.26+0.109=0.37m
Hence,thelimitofstabilityoccurswhenthecenterofgravityis0.37m abovethebottom ofthecanoe.
2.101. Fromthegivendata: D =0.3m,∆z =0.5m, ax =0,and az =1m/s2.Forkerosene at20◦C, ρ =808kg/m3 (fromAppendixB.4).ApplyingEquation2.95givesthepressure increasefrombottomtotop,∆p,asfollows
∆p = ρax∆x ρ(g + az)∆z = 808(0)(0) 808(9 81+1)(0 5)= 4367Pa= 4 37kPa
Therefore,thegaugepressureonthebottomofthecylinderis4.37kPa .Thearea, A,of thebottomofthecontainerisgivenby A = 1 4 πD2 = 1 4 π(0.3)2 =0.07069m
Hencetheforce, F ,exertedbythefluidinthecylinderontheelevatorisgivenby F = pbottomA =(4 37)(0 07069)=0 309kN=309N
2.102. Fromthegivendata:∆x =10m, D =2m, ax =2m/s2,and az =0.Forwaterat20◦C, ρ =998kg/m3.Thepressuredifference,∆p,betweenopposinglocationsatthefrontandback ofthetankisgivenbyEquation2.95as
= (998)(2)(10) 0=19960Pa=19 96kPa
Theareaofthefrontandbackofthetankis A = πD2/4=3 142m2,sotheforcedifference, ∆F ,isgivenby
F =∆p A =(19 96)(3 142)=62 7kN
2.103. Fromthegivendata: ρ =1040kg/m3.Forspillagetooccur:∆z = 0.8mfor∆x =2m, and az =0.
(a) Taking g =9.81m/s2,thelimitingacceleration, ax,isobtainedfromEquation2.96as follows
(b) Underthelimiting(spill)condition,thedepthofliquidatthefrontofthetankis 1 2m 0 8m=0 4m.InaccordancewithEquation2.23,thegaugepressure, pbf ,atthe bottomfrontofthetankisthereforegivenby
pbf = ρg(0 4m)=(1040)(9 807)(0 4)=4 08 × 103 Pa=4 08kPa
Underthelimiting(spill)condition,thedepthofliquidatthebackofthetankis2m. InaccordancewithEquation2.23,thegaugepressure, pbb,atthebottombackofthe tankisthereforegivenby pbb = ρg(2m)=(1040)(9 807)(2)=2 04 × 104 Pa=20 4kPa
2.104. Fromthegivendata: L =3m, W =0.8m, H =1.6m,and d =1.2m.Considerboth alignmentsofthetankseparately.
(a) Longsidealignedwiththedirectionoftruckmotion.Forspillagetooccur:∆z =0.4m for∆x =1.5m.Thelimitingacceleration, ax,isobtainedfromEquation2.96asfollows
2
(b) Shortsidealignedwiththedirectionoftruckmotion.Forspillagetooccur:∆z =0.4m for∆x =0.4m.Thelimitingacceleration, ax,isobtainedfromEquation2.96asfollows
Therefore,themaximumallowableaccelerationof9.81m/s2 occurswiththesideorientation .
2.105. Fromthegivendata: θ =10◦.ApplyingEquation2.96gives
2.106. Fromthegivendata:∆V =90km/h=25m/s,and∆t =10s.Sincethetruckdecelerates ataconstantrate,
5m/s2
Let θ betheslopeoftheliquidsurface,thenEquation2.96gives
2.107. Fromthegivendata: a =5m/s2 and θ =25◦.Thecomponentsoftheaccelerationare:
ax =5cos25◦ =4 532m/s2 az =5sin25◦ =2.113m/s2
Taking g =9 807m/s2 andsubstitutingintoEquation2.96gives
Theslopeofthesurfaceinthetankeristhereforeequaltotan 1(0 3802)=20.1◦ .Therefore theslopeoftheliquidinthetankislessthan theslopeoftheincline.
2.108. Underthegivenconditions,thetruckisfree-fallingdowntheinclinewith ax =0and az = g SubstitutingthesevaluesintoEquation2.96gives
Therefore,theslopeofthewatersurfaceisindeterminate .Thisresultisaconsequenceof therebeingnoeffectivegravityforcetokeeptheliquidcontainedinthetank.
2.109. Fromthegivendata: W =300mm=0.3m, H =280mm=0.28m,and patm =101kPa. Forwaterat20◦C, ρ =998kg/m3 and psvp =2.34kPa(fromAppendixB.4).
(a) Inthiscase∆z =40mmand∆x =300mm,andEquation2.96givestherequired acceleration, ax,as
(b) Inthiscase r1 =0, r2 =0.15m, z1 =0, z2 =0.28m, p1 = psvp =2.34kPa,and p2 = patm =101kPa.Therequiredrateofrotation, ω,fortheseconditionstooccurisgiven byEquation2.104asfollows:
2.110. Fromthegivendata: z1 z2 =40mm=0.04m, r1 =0.15m+0.05m=0.20m,and r2 =0.15m 0.05m=0.10m.Thecorrespondingrateofrotationcanbederivedfrom Equation2.103asfollows z1 z2 = ω2 2g (r 2 1 r 2 2) → 0 04= ω2 2(9 807) (0 22 0 12) → ω =5 114rad/s=48 8rpm
2.111. Fromthegivendata: R =0 2m, ω =450rpm=47 12rad/s,and∆=0 1m.Identify locationsinthetubeusingtheaxesshowninFigure2.83.
SincetheU-tubehasacircularshapeofradius R,then
ThepressuredistributionintheU-tubeisgivenbyEquation2.104,fromwhichthegauge pressurecanbeexpressedas
where x∗ = x-coordinatemeasuredfromtheaxisofrotation, x∗0 = x-coordinateliquidsurface thatisopentotheatmosphere,and z0 (=0)= z coordinateoftheopensurface.
(a) CombiningEquations1and2andnotingthattheaxisofrotationis∆fromtheorigin (P)gives
Thepressureisaminimumwheredpg/dx =0.DifferentiatingEquation3andsetting theresultequaltozerogives
whichsimplifiesto
Therefore,theminimumgaugepressureoccursatalocationthatis0.1026 0.1 ≈ = 0.003m totheleftoftherotationaxis.
(b) Thegaugepressureasafunctionof x isgivenbyEquation3andisplottedinFigure 2.15.
Figure2.15:GagepressureinU-tube
(c) Setting x = 0 1026minEquation3givestheminimumgaugepressureas 98 06kPa, whichcorrespondstoanabsolutepressureof101.3kPa 98.06kPa=3.24kPa .The vaporpressureofwaterat20◦Cis2.337kPa,socavitationwillnotoccur underthe givenconditions.
2.112. Fromthegivendata: D =0.5m, R = D/2=0.25m,and ω =30rad/s.Forcrudeoilat 20◦C, ρ =856kg/m3 (fromAppendixB.4).Thepressuredifference,∆p,betweenthecenter andperimeterisgivenbyEquation2.104as
2.113. Fromthegivendata: R =0 5/2=0 25m, ω =400rpm=41 89rad/s,and p0 =200kPa.For waterat20◦C, ρ =998 2kg/m3.Thepressuredistributiononthetopofthecylinderisgiven byEquation2.104,whichcanbeexpressedas
UsingEquation1,theforce, F ,onthetopsurfaceofthecylinderisgivenby
Substitutingthevaluesofthegivenandderivedparametersintotheaboveequationyields
2.114. Fromthegivendata: D =3cm, R = D/2=1.5cm=0.015m,and∆z =1cm=0.01m. InaccordancewithEquation2.108,
2.115. Fromthegivendata: D =1.5m, R = D/2=0.75m,and d =1m.
(a) InaccordancewithEquation2.108,theliquidsurfaceintersectsthebottomofthecylinderwhen
(b) Fromthegivendata: ω =40rpm=4.189rad/s.InaccordancewithEquation2.108, therequiredheight,∆z,abovethestaticwaterlevelisgivenby
Thecylindermustbeatleast1m+0.25m=1.25m hightoavoidspillage.
