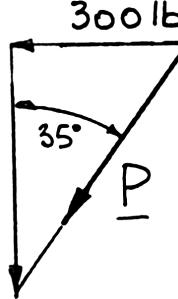
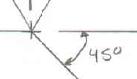
CHAPTER2


SOLUT
(a) P
(b) T W ION arallelogram l riangle rule:
e measure:
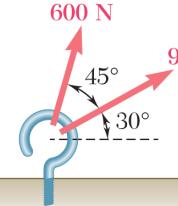
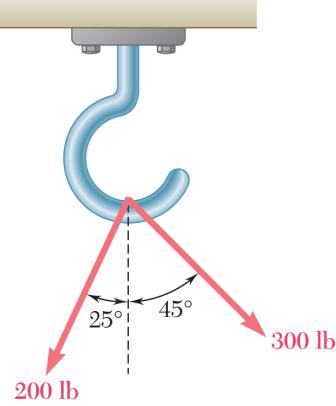
PRO Two magn (b) th law: BLEM 2.1



forces are a itude and dir e triangle rul
pplied as sho ection of thei e.
wn to a hoo r resultant us
k. Determine ing (a) the pa
graphically rallelogram la
the w,












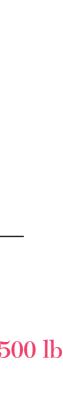
PR
OBLEM 2.2
(a) P (b) T
ION arallelogram l riangle rule:
Two grap (a) law:
forces are hically the the parallelo
applied as s magnitude gram law, (
hown to a b and directio b) the triang
racket supp n of their r le rule.
ort. Determi esultant usi
ne ng

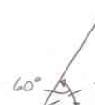









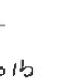




e measure:
PROBLEM 2.3
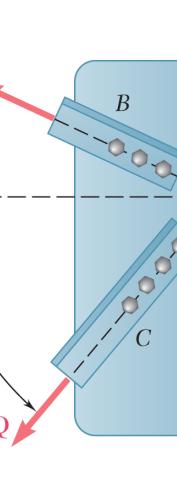
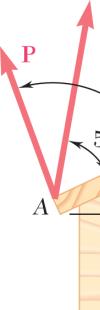
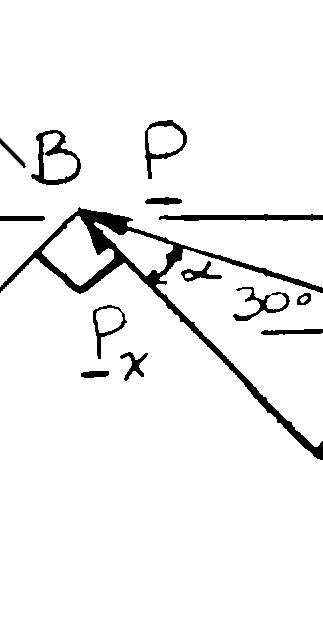
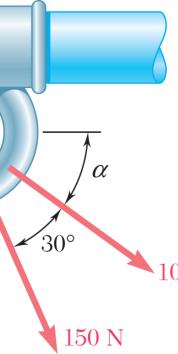
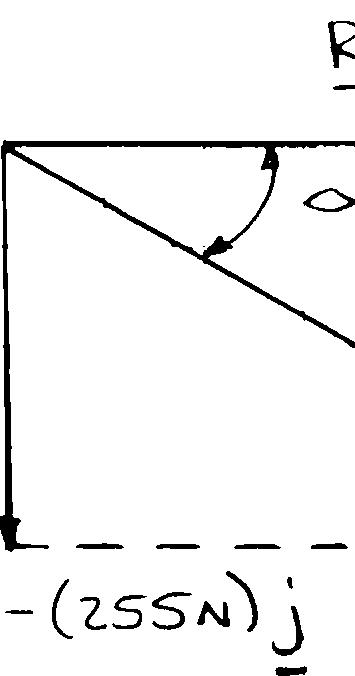
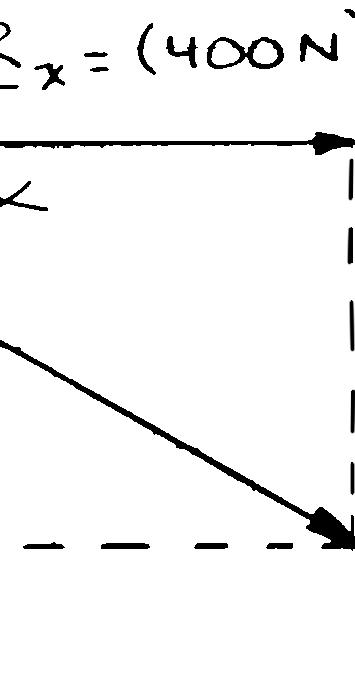
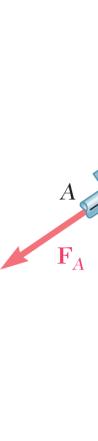
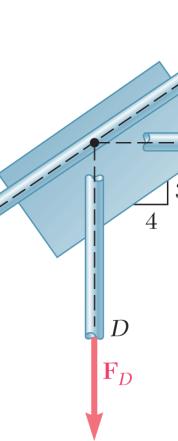
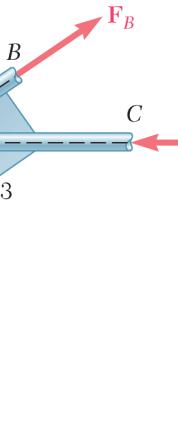
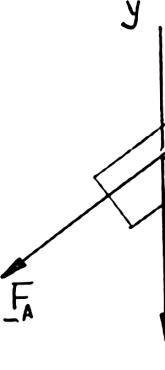
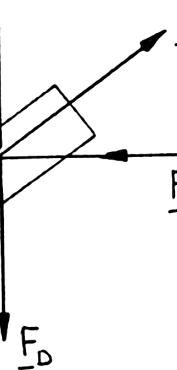
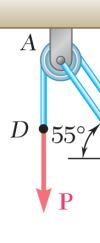
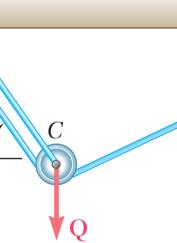
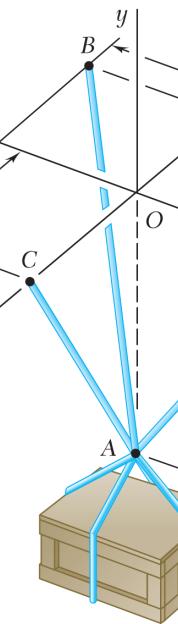
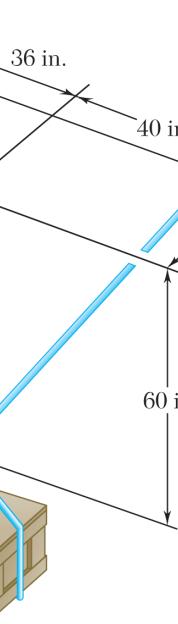
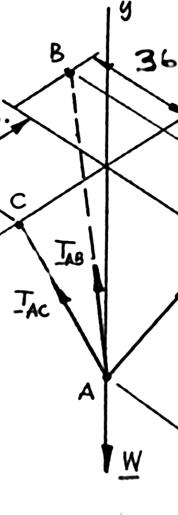
Two structural members B and C are bolted to bracket A. Knowing that both members are in tension and that P = 10 kN and Q = 15 kN, determine graphically the magnitude and direction of the resultant force exerted on the bracket using (a) the parallelogram law, (b) the triangle rule.
SOLUTION
(a) Parallelogram law:
(b) Triangle rule:


PROBLEM 2.4
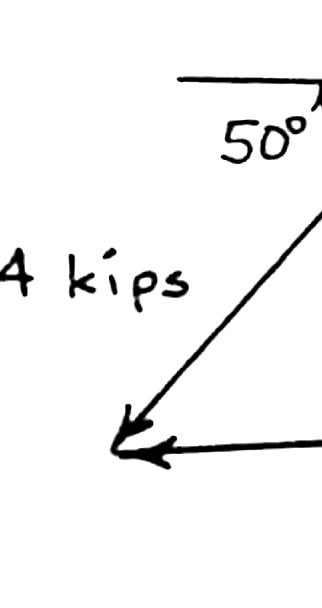
Two structural members B and C are bolted to bracket A. Knowing that both members are in tension and that P = 6 kips and Q = 4 kips, determine graphically the magnitude and direction of the resultant force exerted on the bracket using (a) the parallelogram law, (b) the triangle rule.
SOLUTION
(a) Parallelogram law:
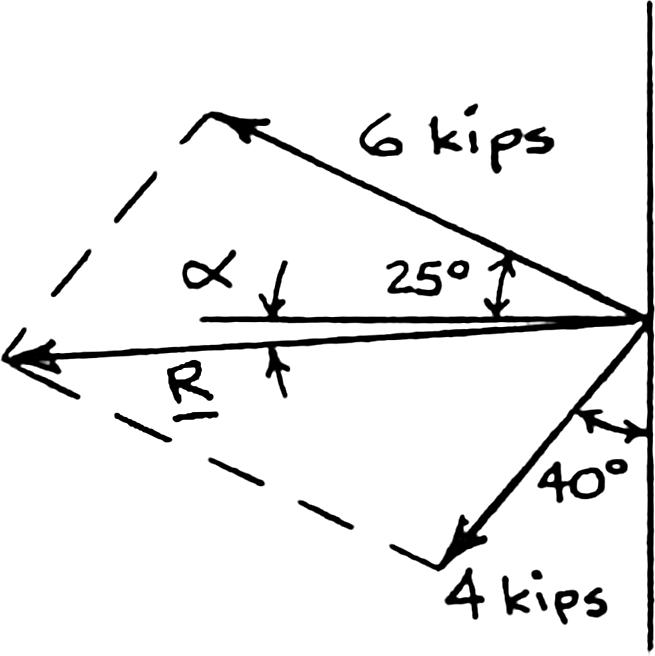
(b) Triangle rule:
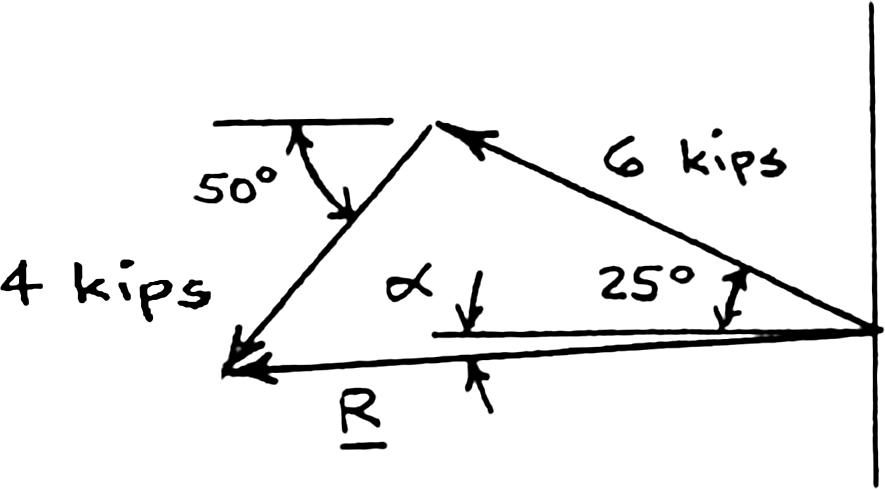

SOLUTION
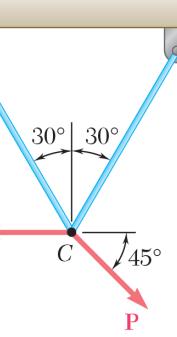
PROBLEM 2.5
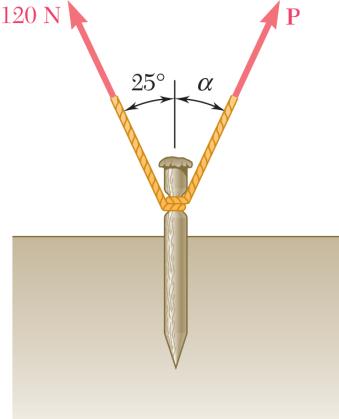
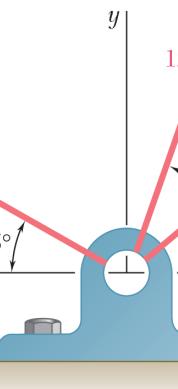
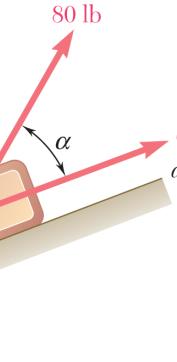
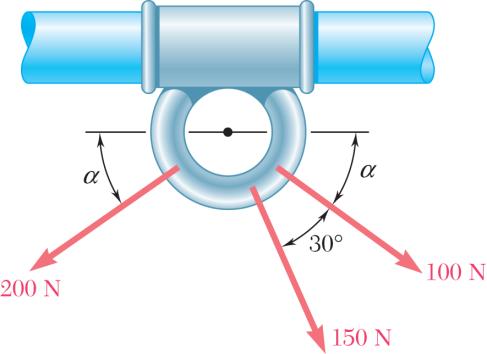
A stake is being pulled out of the ground by means of two ropes as shown. Knowing that α = 30°, determine by trigonometry (a) the magnitude of the force P so that the resultant force exerted on the stake is vertical, (b) the corresponding magnitude of the resultant.
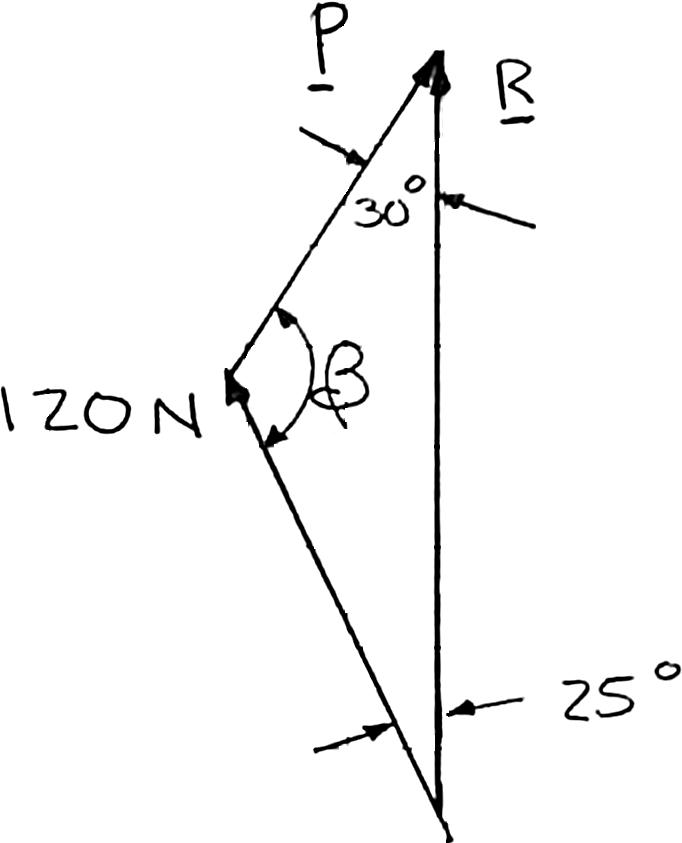
Using the triangle rule and the law of sines:
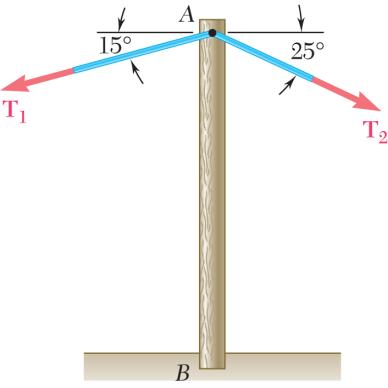
SOLUTION
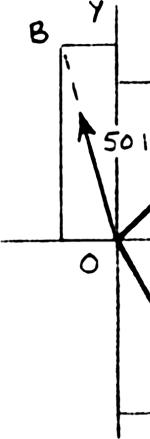
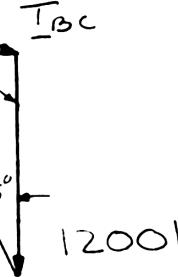
PROBLEM 2.6
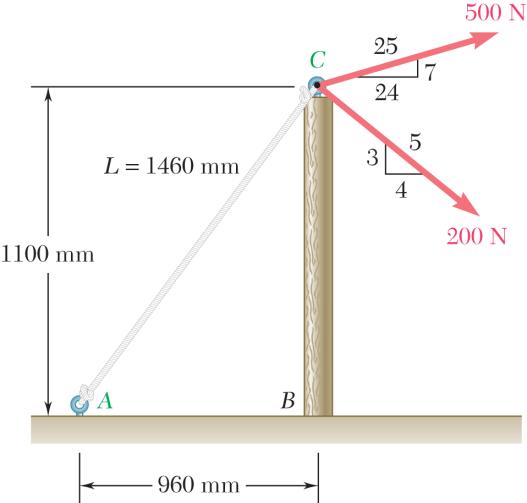
A telephone cable is clamped at A to the pole AB. Knowing that the tension in the left-hand portion of the cable is T1 = 800 lb, determine by trigonometry (a) the required tension T2 in the right-hand portion if the resultant R of the forces exerted by the cable at A is to be vertical, (b) the corresponding magnitude of R.
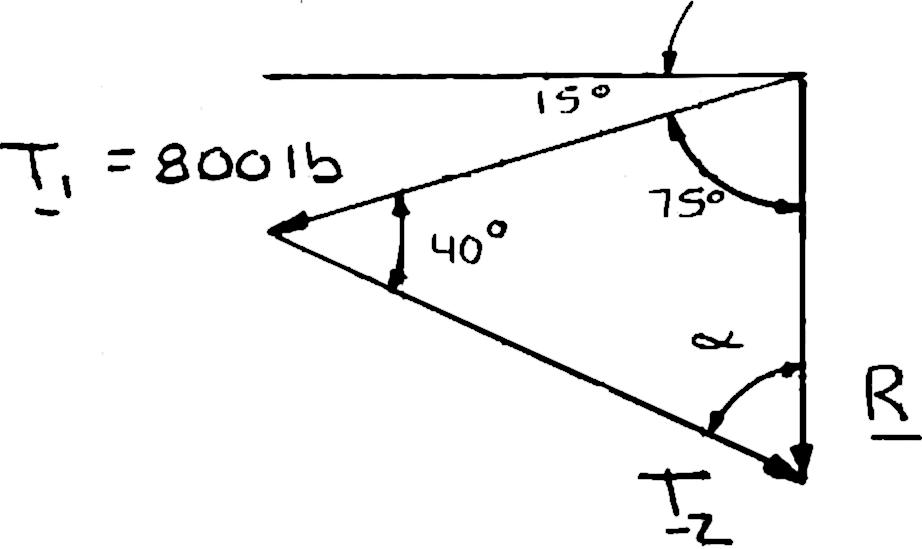
Using the triangle rule and the law of sines:

SOLUTION
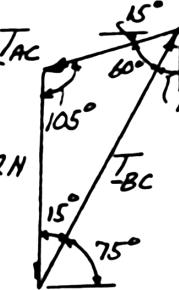
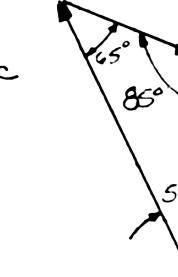
PROBLEM 2.7
A telephone cable is clamped at A to the pole AB. Knowing that the tension in the right-hand portion of the cable is T2 = 1000 lb, determine by trigonometry (a) the required tension T1 in the left-hand portion if the resultant R of the forces exerted by the cable at A is to be vertical, (b) the corresponding magnitude of R.
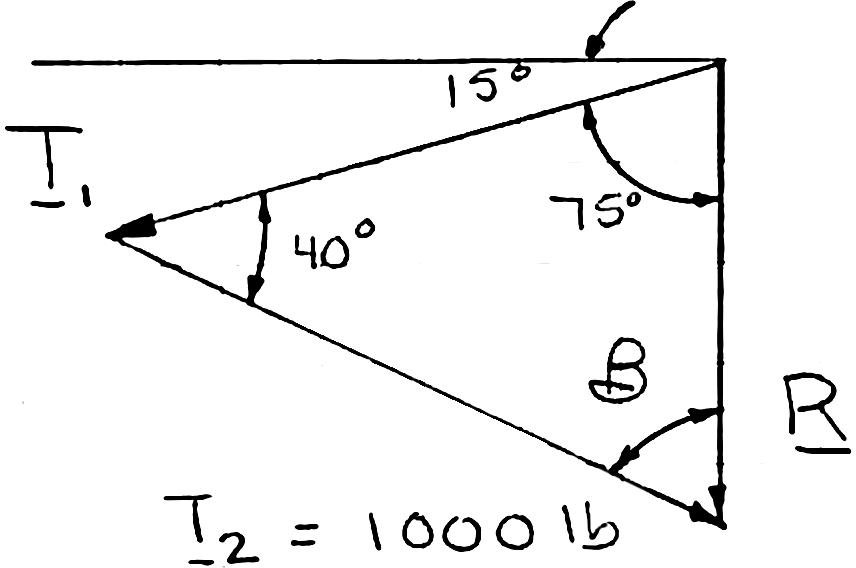
Using the triangle rule and the law of sines:
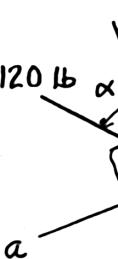
PROBLEM 2.8
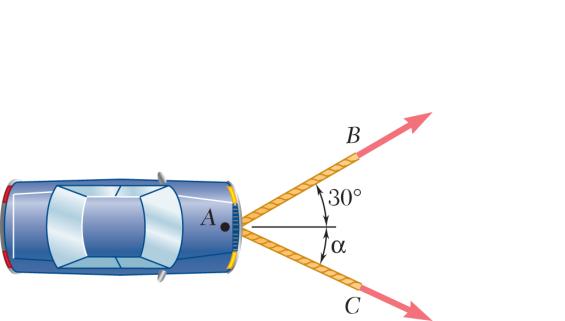
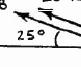
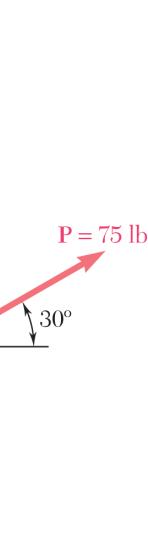
A disabled automobile is pulled by means of two ropes as shown. The tension in rope AB is 2.2 kN, and the angle α is 25°. Knowing that the resultant of the two forces applied at A is directed along the axis of the automobile, determine by trigonometry (a) the tension in rope AC, (b) the magnitude of the resultant of the two forces applied at A.
SOLUTION
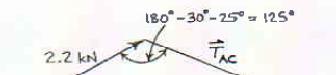
Using the law of sines:

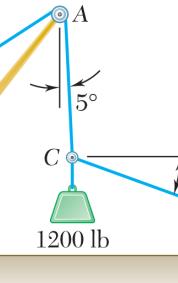
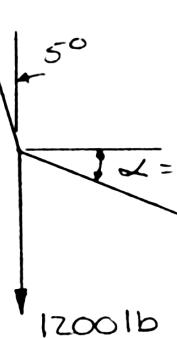
PROBLEM 2.9
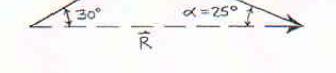
A disabled automobile is pulled by means of two ropes as shown. Knowing that the tension in rope AB is 3 kN, determine by trigonometry the tension in rope AC and the value of α so that the resultant force exerted at A is a 4.8-kN force directed along the axis of the automobile.
SOLUTION

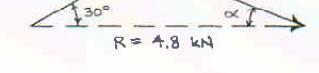


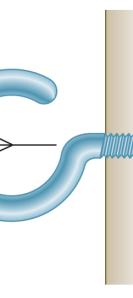
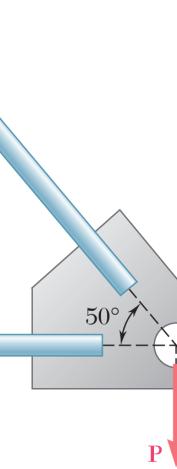
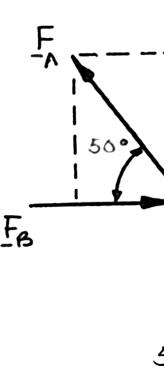
PROBLEM
Using th (a
ION e triangle rule e and law of s si 5
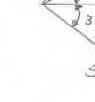
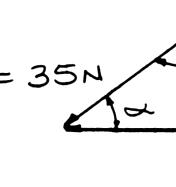
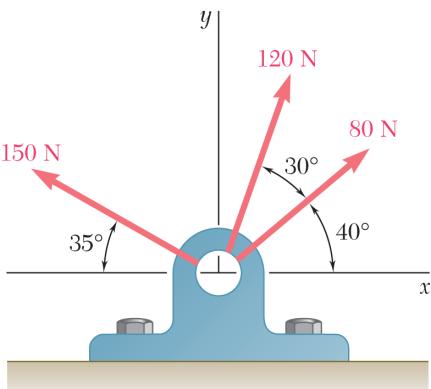
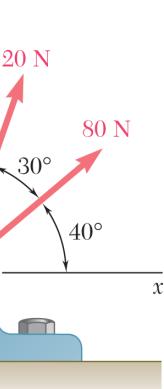
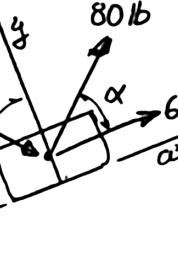
Two forces a magnitude o angle α if the be horizonta ines:
re applied as f P is 35 N, d resultant R o l, (b) the corre
shown to a ho etermine by f the two forc sponding mag ok support. K trigonometry es applied to nitude of R. nowing that (a) the requir the support is

37.1 α =°

73.2 N R = the ed to


ROBLEM
Using th (a)
e triangle rule e and the law
th m fo m of sines:
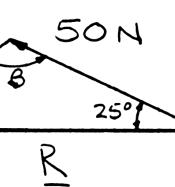
steel tank is at α = 20°, d agnitude of rces applied agnitude of R
2.11 to be position etermine by the force P i at A is to be v . ed in an excav trigonometry f the resultan ertical, (b) th ation. Knowi (a) the requir t R of the t e correspondi
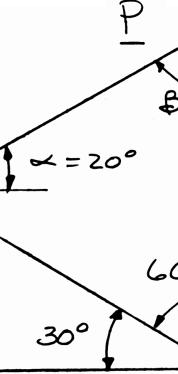
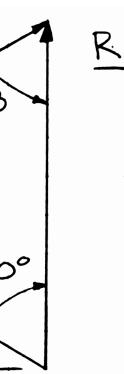
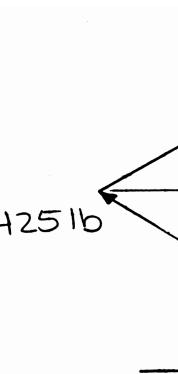
392 lb P =
346 lb R = ng ed wo ng

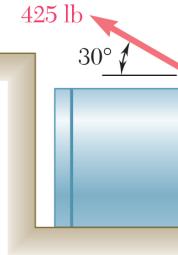

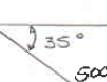
ROBLEM
2.12
Using th (a) (b)
e triangle rule e and the law ( 3 α + sin
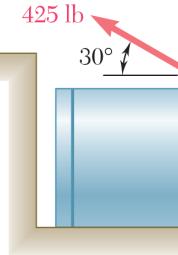
A th tr th c of sines: 30)60 sin(90) 425 lb
steel tank is at the mag igonometry ( e two force orresponding


to be position nitude of P a) the require s applied at magnitude of 30)60°−°
ed in an excav is 500 lb, d angle α if th A is to be v R. ation. Knowi determine e resultant R ertical, (b)
42.6 α =°
551 lb R = ng by of the

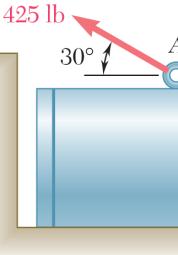
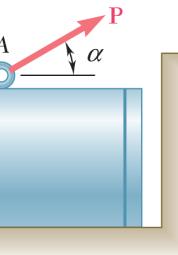

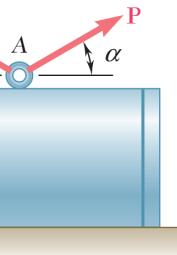
ROBLEM
The sma
(a) P
(b) R ION
llest force P w (425 lb)co = (425 lb)sin = will be perpen os30° n 30°
A D d o c dicular to R.
steel tank etermine by irection of the f the two f orresponding 2.13 is to be p trigonometr smallest forc orces applied magnitude of ositioned in y (a) the e P for which at A is v R an excavati magnitude a the resultant ertical, (b)
368 lb = P

21 R = on. nd R the 13 lb
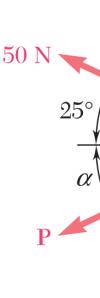
SOLUT
ROBLEM
The sma
(a) P
(b) R ION
llest force P w (50 N)sin = (50 N)cos =
F m R c will be perpen 25° 25°
or the hook s agnitude and of the two orresponding dicular to R. 2.14
upport of Pro direction of t forces appli magnitude of b. 2.10, deter he smallest fo ed to the su R
mine by trigo rce P for wh pport is hor
nometry (a) ich the result izontal, (b)
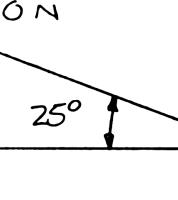
21.1 N = P
45.3 N R = the ant the
SOLUTION
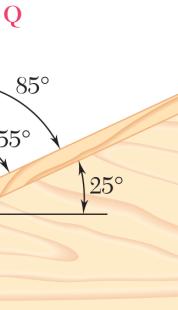
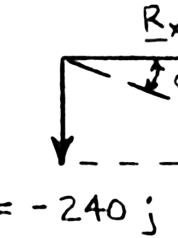
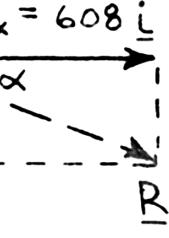
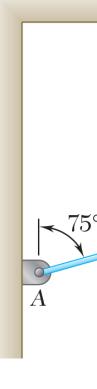
PROBLEM 2.15
For the hook support shown, determine by trigonometry the magnitude and direction of the resultant of the two forces applied to the support.
Using the law of cosines:
Using the law of sines:

PROBLEM 2.16
Solve Prob. 2.1 by trigonometry.
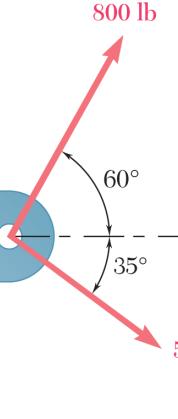
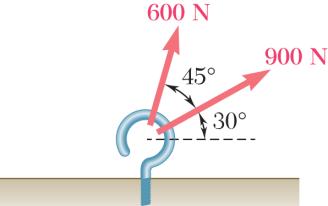
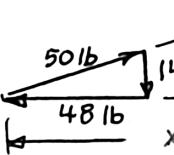
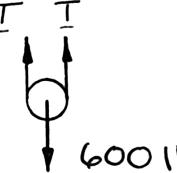
PROBLEM 2.1
Two forces are applied as shown to a hook. Determine graphically the magnitude and direction of their resultant using (a) the parallelogram law, (b) the triangle rule.
SOLUTION



Using the law of cosines:

222 (900N)(600N)
2(900N)(600 N)cos(135)
1390.57N
Using the law of sines: sin(30)sin(135)


SOLUT
Using th We hav
Then And ION e force triang e:
ROBLEM 2
lve Problem 2
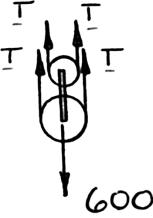
OBLEM2.4
.17 .4 by trigono
metry.
and the law
Knowing tha = 4 kips, de sultant force ) the triangle r s of cosines a (5025
Two structu t both memb termine graph exerted on th ule. nd sines:
ral members ers are in ten ically the ma e bracket usin s)(6kips)cos 1 B and C are b sion and that gnitude and g (a) the par
olted to brac P = 6 kips a direction of allelogram la
ket nd the w,
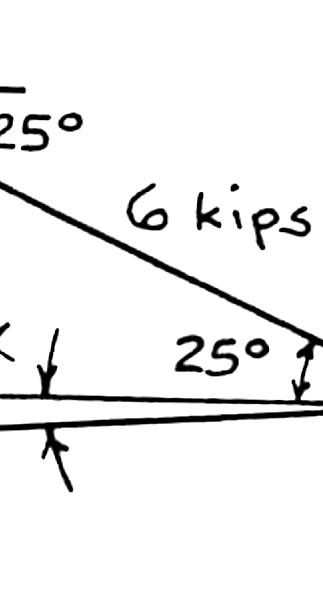



SOLUTION
PROBLEM 2.18
For the stake of Prob. 2.5, knowing that the tension in one rope is 120 N, determine by trigonometry the magnitude and direction of the force P so that the resultant is a vertical force of 160 N.
PROBLEM2.5 A stake is being pulled out of the ground by means of two ropes as shown. Knowing that α = 30°, determine by trigonometry (a) the magnitude of the force P so that the resultant force exerted on the stake is vertical, (b) the corresponding magnitude of the resultant.
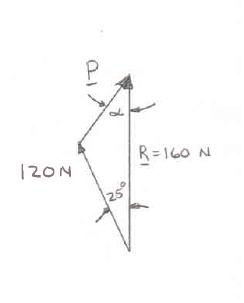
Using the laws of cosines and sines:
222(120N)(160N)2(120N)(160N)cos25 72.096N P P =+−° = And sinsin25 120N72.096N sin0.70343


SOLUT
Using th We have
Then and Hence: ION e force trianggle and the law
PROBLE
M 2.19
Two forces Knowing th the magnitu ws of cosines a
P and Q are a hat P = 48 N ude and directi and sines:
2
°+°
N) 2(48 N
(60 N) )(60 N)cos15
N
pplied to the and Q = 60 N on of the resu
lid of a storag , determine ltant of the tw
e bin as show by trigonome o forces.


SOLUT
Using th We have Then and Hence: ION e force triang
gle and the law
ROBLEM
wo forces P nowing that agnitude and s of cosines a
and Q are ap P = 60 N and direction of nd sines:
plied to the l Q = 48 N, d the resultant o id of a storag etermine by f the two forc

SOLUT
Comput
ION
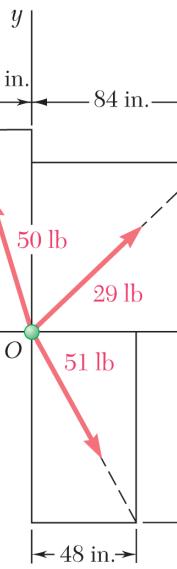
e the followin
PROB
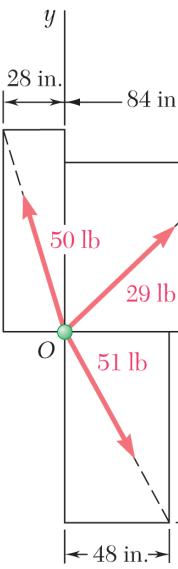
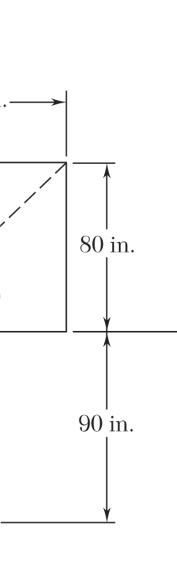
LEM 2.21
29-lb Fo 50-lb Fo
51-lb Fo
rce: rce: rce: ng distances:
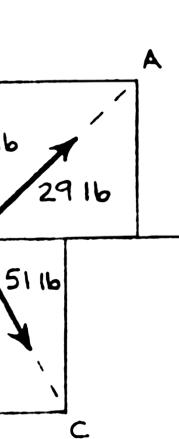

SOLUT
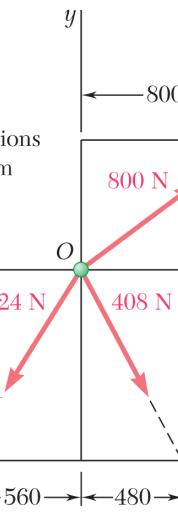
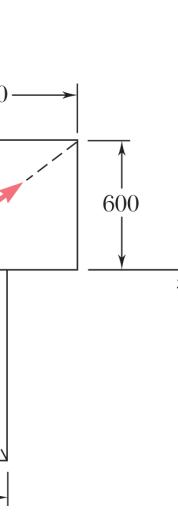
Comput
800-N F 424-N F
408-N F ION
e the followin
orce: orce: orce: ng distances:
PROBL
EM 2.22

)
) 1000 560 ) 1060 900 ) 1060 480 ) 1020 900 ) 1020 components of each of the
forces shown.
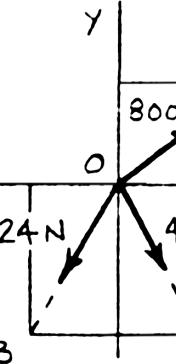
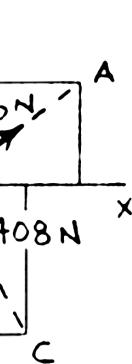
SOLUTION
PROBLEM 2.23
Determine the x and y components of each of the forces shown.
PROBLEM 2.24
Determine the x and y components of each of the forces shown. SOLUTION
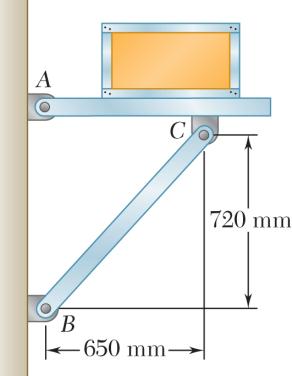
PROBLEM 2.25
Member BC exerts on member AC a force P directed along line BC. Knowing that P must have a 325-N horizontal component, determine (a) the magnitude of the force P, (b) its vertical component.
SOLUTION
(a)
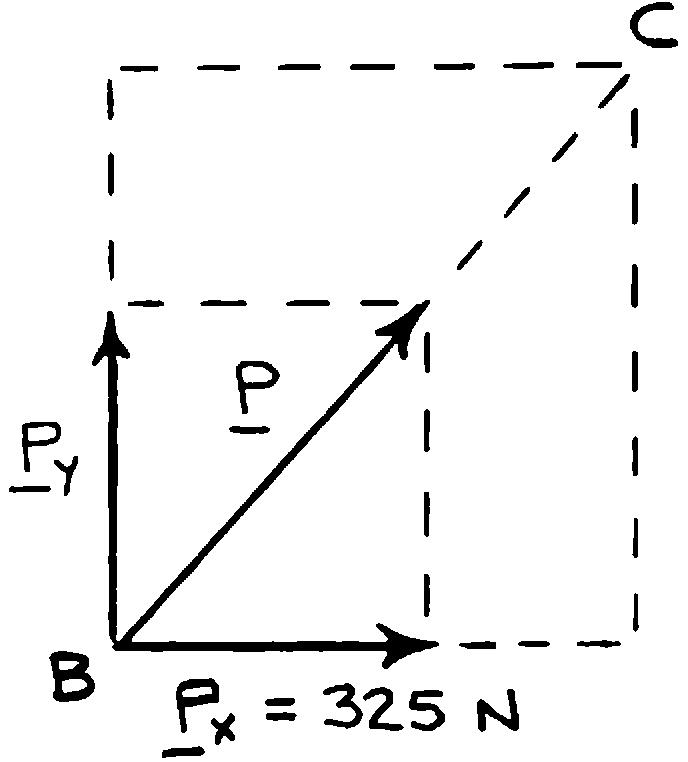
N P = (b)

PRO Memb Know magni onent
BLEM 2.26
er BD exerts ing that P mu tude of the fo
on member st have a 300rce P, (b) its v
ABC a forc lb horizontal ertical compo
e P directed component, d nent. along
etermine


OBLEM 2
e hydraulic cy ected along li ponent perp gnitude of the
linder BC ex ne BC. Know endicular to m force P, (b)
erts on memb ing that P mu ember AB, d its component er AB a force st have a 600 etermine (a) along line AB


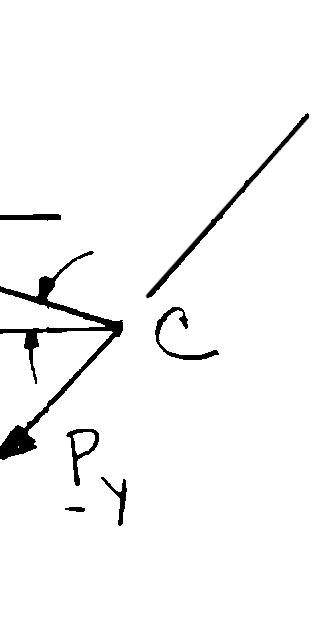

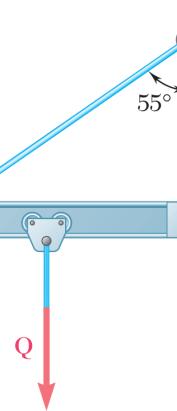

PRO Cable that P of the BLEM 2.2
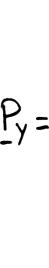
AC exerts o must have a force P, (b) cos55 y P P =
n beam AB a 350-lb vertic its horizontal
force P dire al component component. cted along lin , determine (a e AC. Knowi ) the magnitu



P Th al pe P,
ROBLEM 2
e hydraulic ong line BD rpendicular to (b) its compo
750 Nsin P = 2192 P = cos ABC PP = (219 = .29
cylinder BD e . Knowing member AB nent parallel 20° .9 N 20° 2.9 N)cos20°

xerts on mem that P must C, determine to ABC ber ABC a have a 75 (a) the magni AP
force P direc 0-N compon tude of the fo
2060 N BC = ted ent rce
2190 N P =
PROBLEM 2.30
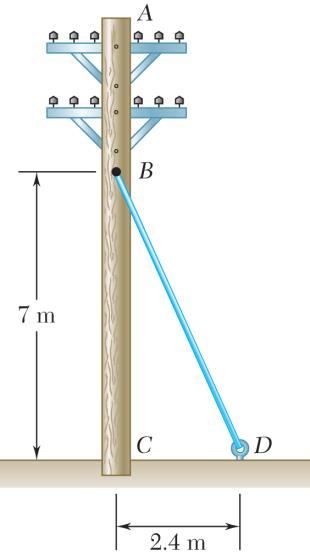
The guy wire BD exerts on the telephone pole AC a force P directed along BD. Knowing that P must have a 720-N component perpendicular to the pole AC, determine (a) the magnitude of the force P, (b) its component along line AC
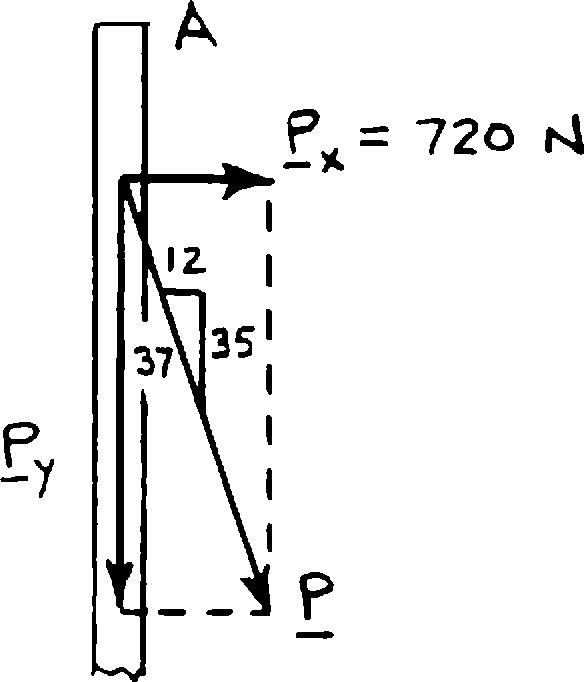

SOLUT
ION
Compon
ents of the fo
orces were dete
PROBLE
Determine t
PROBLEM forces show ermined in Pro
f the three for ine the x and
ces of Problem y componen



SOLUT
ION
Compon
ents of the fo F 1 1 orces were det orce x 80 N 20 N 50 N
PROBLE
M 2.32
Determine PROBLEM forces show ermined in Pr
f the three for ine the x and
ces of Proble y componen
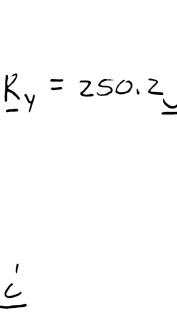


PROBL Determin
PROBLE the forces
EM 2.33
e the resultant M2.24 Dete shown.
orces of Prob and y compon






SOLUT
ION
Compon
ents of the fo
orces were det
PROBL Determine PROBLE forces sho ermined in Pr Comp. (N) +
EM 2.34
of the three f mine the x an N)
orces of Probl d y componen
em 2.22. ts of each of
the


SOLUT
100-N F 150-N F 200-N F ION orce: orce: orce:


BLEM 2.35


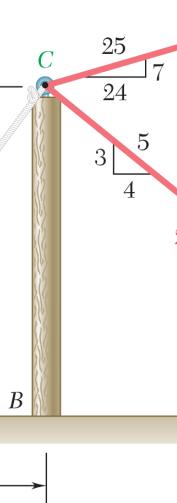

OBLEM 2.
SOLUT Determi
Cable fo 500-N F
ne force comp
rce AC:
200-N F and
orce:
orce: ponents:

Further:


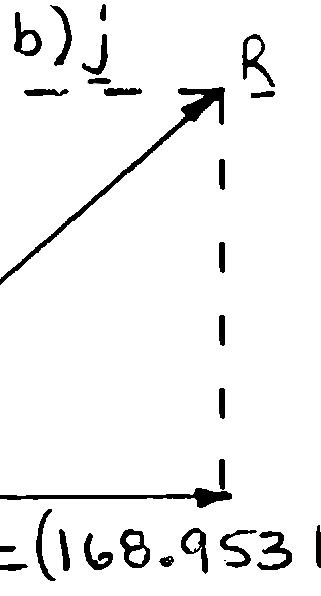
SOLUT
60-lb Fo
80-lb Fo
120-lb F and
Further: ION rce: rce: orce: (60 l (60 l x y F F = = (80 l (80 l x y F F = = (120 (12 x y F F = =−
PRO Knowi forces
b)cos604 b)sin6069




SOLUT
60-lb Fo
80-lb Fo
120-lb F Then and ION
(80lb)co (80lb)si
BLEM 2.3
ing that α = s shown.
s2056.38 n2020.52 °= °= s956.97 n9579.696 °=− °= os5119.54 in510.459 °= °= 8.953 lb 0.676 lb




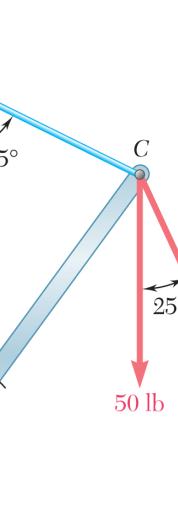
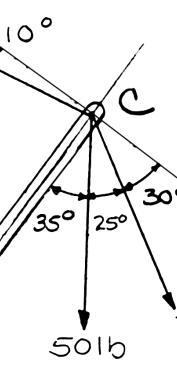
SOLUTION
PROBLEM 2.39
For the collar of Problem 2.35, determine (a) the required value of α if the resultant of the three forces shown is to be vertical, (b) the corresponding magnitude of the resultant.
(100 N)cos(150 N)cos(30)(200 N)cos (100 N)cos(150 N)cos(30)
(100 N)sin(150 N)sin(30)(200 N)sin (300 N)sin(150 N)sin(30)
(a) For R to be vertical, we must have 0. xR = We make 0 xR = in Eq. (1): 100cos150cos(30)0 100cos150(coscos30sinsin30)0
(2)
(b) Substituting for α in Eq. (2):
PROBLEM 2.40
For the post of Prob. 2.36, determine (a) the required tension in rope AC if the resultant of the three forces exerted at point C is to be horizontal, (b) the corresponding magnitude of the resultant.
(a) For R to be horizontal, we must have 0. y R = Set 0 y R = in Eq. (2):
(b) Substituting for ACT into Eq. (1) gives


SOLUT
BLEM 2.4
Using th (a) Se (b) Su
e x and y axes
t 0 y R = in E bstituting for
Dete of th BC, s shown: Eq. (2): r ACT in Eq. (1
rmine (a) the e three forces (b) the corresp
required tens exerted at P onding magn


ion in cable A oint C of boo itude of the r (50 lb)cos35 78.458 lb 5(75 lb)sin
C, knowing t m BC must b esultant.



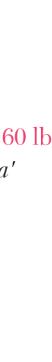
SOLUT
Select th Then and
(a) Se
(b) Su ION
e x axis to be t 0 y R = in E
D
ividing each t
PRO
BLEM 2.42
e block of P ed value of α arallel to the ultant.
roblems 2.37 if the resultan incline, (b) th
bstituting for R e along aa′. xR y R Eq. (2). (80lb term by cos α
r α in Eq. (1) 60 lb(80 x =+
For th requir to be p the res (60 l xF =Σ= (80 l y F =Σ= )sin(120 α gives: (80 gives: lb)cos56.31°
b)(80 lb)co + b)sin(120 α lb)cos0 α = lb)tan12 12 tan 8 56 α α α = = = (120lb)sin +
s(120 lb) α + lb)cos α 0 lb
lb
lb .310° 56.31204. °= and 2.38, de t of the three e correspondi sin α 22 lb termine (a) forces shown ng magnitude 56.3 α =°
204lb xR = the is of (1) (2)
PROBLEM 2.43
Two cables are tied together at C and are loaded as shown. Determine the tension (a) in cable AC, (b) in cable BC
SOLUTION



PROBLEM 2.44
Two cables are tied together at C and are loaded as shown. Knowing that α = 30°, determine the tension (a) in cable AC, (b) in cable BC
SOLUTION
Free-BodyDiagramForceTriangle
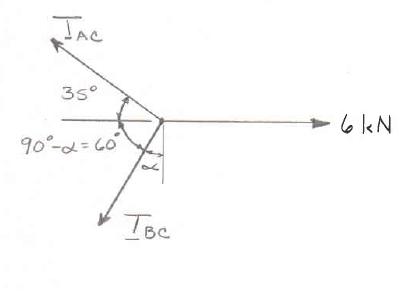
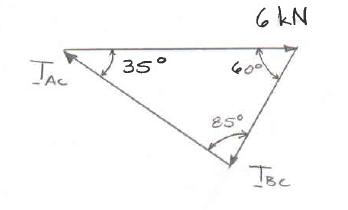
PROBLEM 2.45
Two cables are tied together at C and loaded as shown. Determine the tension (a) in cable AC, (b) in cable BC.
Free-BodyDiagram
ForceTriangle
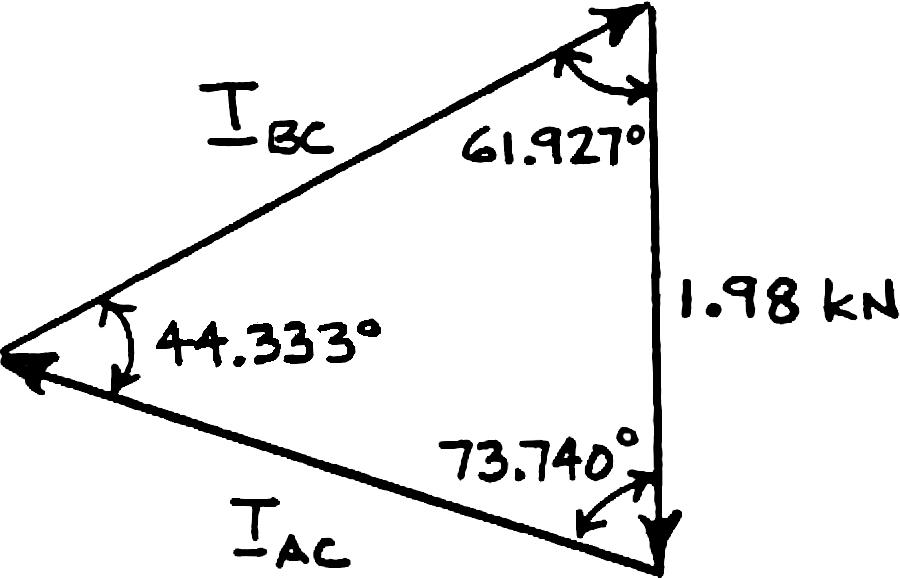
Law of sines:
SOLUT
Law of s (a) (b) ION
Free-Bod ines: yDiagram
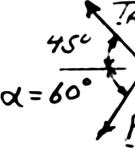
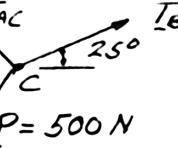

PROB
Two cab Knowing (a) in ca sin35 s A TC = ° 5 s ACT = 5 si BCT = LEM 2.46
les are tied that P = 50 ble AC, (b) in For 500 N in75sin70 BCT = ° 00N sin35 in70 ° ° 00N sin75 n70 ° °
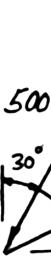
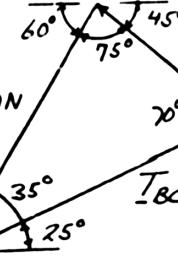
together at C 0 N and α = cable BC ceTriangle ° and are lo 60°, determin aded as show e the tension
305 N ACT =
514 N BCT = n. in

PRO
Two tensi
BLEM 2.4
Law of s
Free-Bod mg (20 196 W = = = ines:
yDiagram


00kg)(9.81m/ 62N sin
cables are tie on (a) in cabl 2 s)
d together at e AC, (b) in ca
C and are loa ble BC
orceTriang ded as shown le

. Determine
the



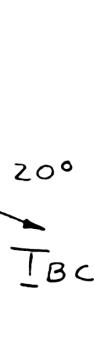




SOLUT
xFΣ For P =

y FΣ Solvin ION
0 CAT =− 200N we ha 0 = 0.8 g equations (





PRO Two Know BC. sin30 CBT + ve,
0.5 C TA co CAT
BLEM 2.49
cables are ing that P = Free-B





tied togeth 300 N, de
m









sin30cos P
0.521 CBT ++ s30co CBT °−
866030.8 CAT + 1) and (2) sim
660321 CBT ultaneously g
45200N °− = 2.13200−= s30sin4 P 2.130 = (2) ives,
er at C an termine the 0 0 (1) 50 = d are load tension in c
ed as show ables AC a



SOLUT
PRO Two Deter taut.
BLEM 2.50
cables are mine the ran
tied togeth ge of value
er at C an s of P for
Free-B




odyDiagram





xFΣ For CAT
0 CAT =−

y FΣ Adding Substitu
0 = we have, 0 = c CAT equations (1) ting for CBT =
sin30 CBT + , 0.5 CBT + cos30 c CBT °− 0.866 and (2) gives
0 = into the eq
sin30cos P
45200N °− =
0.70711 2 P os30sin P
000 = (1)
450 = ; aga
030.707 CBT , 1.36603 CT uilibrium equ
110 P = (2)
200 B = henc ations and sol
And range of
546.40 CAT = 179.315 N an
0 N , 669 P = nd 669.20 N.
0.5 0.86603 CAT .20N Thus fo
0.70711 0.70711 CA P T + r both cables
0 in setting C TA e 146.4 CBT = ving simultan 2000 0 P = = to remain ta
d are load which both 0 = yields, 10N and P = eously gives, ut, load P mu
ed as show cables rema
179.3 N
179.315N st be within << 669 N P n. in the



SOLUT
Resolvin
Substitu
In the y-
Thus, In the xThus,
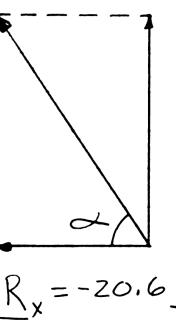
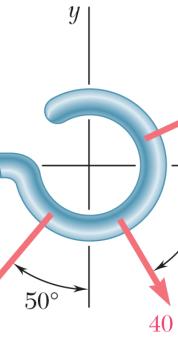
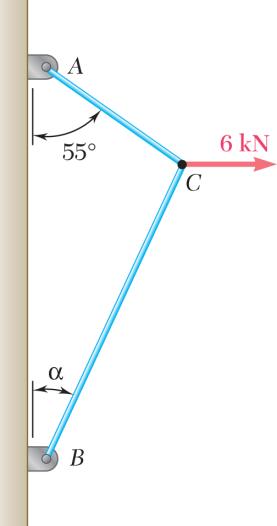
ION g the forces i ting compone direction (one direction: into x- and y-d = R ents: = R e unknown for (65 P Tw co an m irections: A ++ + PQF (500lb) [(650lb)si ( c BAFF −+ +− j i ce): 500lb(650 500lb AF + = 1302.70 = 0lb)cos50° + cos50 (1302.70 BAFF = = 419.55lb =
ROBLEM 2
o forces P a nnection. Kn d that P = agnitudes of t 0 B = F [(650lb)cos 5 n50] os50)( AF ° °+ j i lb)sin50 F °+ (650lb)sin50 sin50° lb cos 5 BAFF (650lb) c lb)cos50 °− °− .51
nd Q are ap owing that th 500 lb and he forces exer 0] sin50)0 ° °= i j sin500 A °= ° 00 °= os50 (650lb)cos50 ° plied as show e connection i 650 Q = lb, ted on the rod Free ° n to an aircr s in equilibriu determine s A and B -BodyDiagr
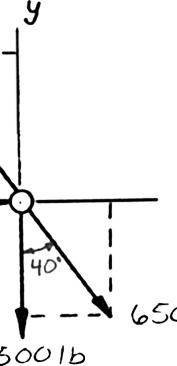
1303lb AF = 420lb BF = aft m the am




SOLUT
Resolvin
Substitu
In the x-
In the yION
g the forces i ting compone direction (one direction: into x- and y-d = RP ents: = + R e unknown for cos 5 Q P P = = = P T c e o d irections: A +++ PQFF cos50 [(750 lb)cos [(750 lb)sin PQ + j ce): 0[(750 lb) °− (750 lb 127.710 Q = = sin50 Q °+ sin50 (127.710 lb 476.70 lb Q = −° + = =
ROBLEM
wo forces P onnection. quilibrium an n rods A a etermine the 0 B = sin50 50] 50](400 lb Q °− ° ° °+ i i j cos50]400 °+ )cos5040 cos50 lb °− ° (750 lb)sin5 (750 lb)sin 5 )sin50(75 °+
2.52 and Q are ap Knowing th d that the ma nd B are F magnitudes o ) j i lb0 = 0 lb 00 °= 0 0 lb)sin50 ° ° plied as show at the con gnitudes of th 750 A = lb an f P and Q Free-Bo

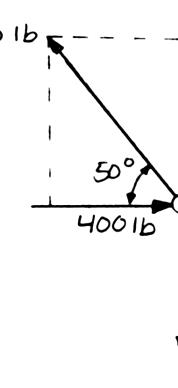
dyDiagram
477 lb; P = n to an aircr nection is e forces exer d 400 BF =
127.7 lb Q = aft in ted lb,

OBLEM 2.
elded connec four forces 16 kN, dete es.
tion is in equ shown. Kn rmine the m nnection
ilibrium und owing that agnitudes of
er the action
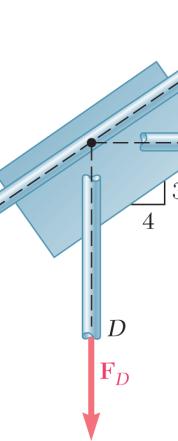

BLEM 2.54
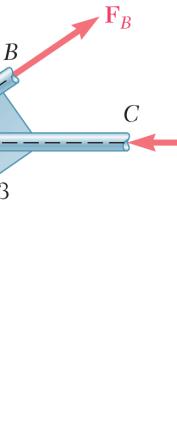
A wel four fo determ
ded connectio rces
n is in equili Knowing tha itudes of the o nnection
brium under t t 5 AF = kN ther two forc
he action of and 6 DF = k es.



ROBLEM 2
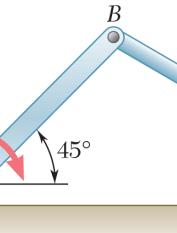
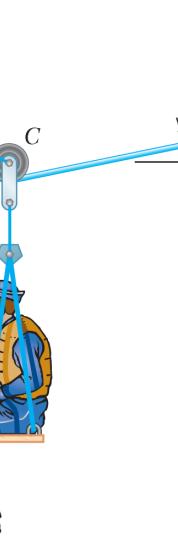
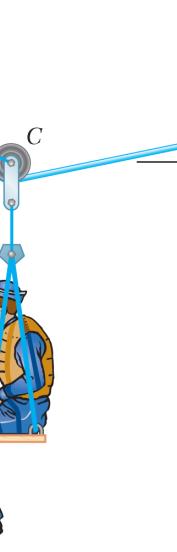
A th on co an bo de (b
sailor is be at is suspen the supp nstant spee d β = 10° oatswain’s termine the ) in the trac
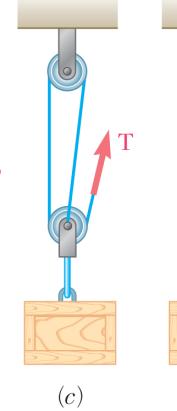
.55
ing rescued ded from a ort cable A d by cable C and that the chair and tension (a) tion cable C



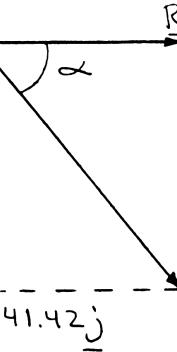
(a) Su (b) Fr ION bstitute (1) in om (1): 0: xF Σ= 0 : y F Σ= nto (2): 0.6


odyDiagram cos 3 ACBT °− 158 ACBT sin30 ACBT + 0.5 CBCD T + = .5(0.137158 T (269.46 lb)

0cos 3 CDT °− sin30 CDT °+


using a boa pulley that CB and is D. Knowin combined the sailor in the suppo D. 00 °= 0 2000°−=
tswain’s ch can roll free pulled at g that α = 3 weight of t is 200 rt cable AC 269 lb ACB = 37.0 lb CD = air ly a 0° he lb, B, (1) (2)


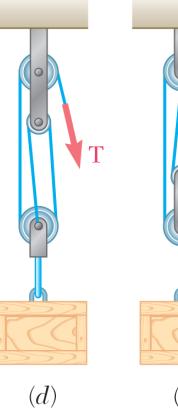
SOLUTION

ROBLEM
2.56
sailor is bein spended from ble ACB and nowing that α ble CD is 20 e boatswain’s pport cable A
odyDiagram




0: xA FTΣ= AT

0:(30 y F Σ= +
cos15 ACBT °− 304.04 l CB = 4.04 lb)sin1 (20 lb)sin25

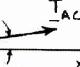
g rescued usi a pulley that is pulled at a = 25° and β lb, determin chair and th CB. cos25 ACB °− b 5(304.04 l °+ 0 215.6 W W °−= =

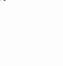
ng a boatswa can roll freel constant spe = 15° and th e (a) the com e sailor, (b) th (20 lb)cos25 b)sin25° 4 lb (a) (b) T
in’s chair that y on the supp ed by cable C at the tension bined weight e tension in 0 °=
304 lb ACB = is ort D in of the
216 lb W =
PROBLEM 2.57
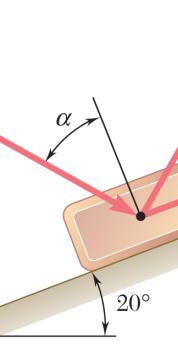
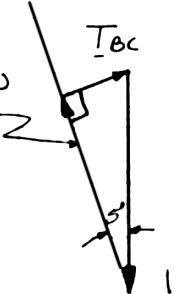
For the cables of prob. 2.44, find the value of α for which the tension is as small as possible (a) in cable bc, (b) in both cables simultaneously. In each case determine the tension in each cable.
SOLUTION
Free-BodyDiagramForceTriangle

(a) For a minimum tension in cable BC, set angle between cables to 90 degrees. By inspection,
(b) For equal tension in both cables, the force triangle will be an isosceles.
by inspection,




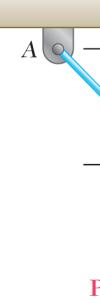


PROB
For the allowabl Determi (b) the c iagram
(a) L (b) L ION F aw of cosines aw of sines ree-BodyD 2 P P sin 600 N β β

LEM 2.58
cables of Pro e tension is 6 ne (a) the ma orresponding
2 (600)(7=+ 784.02 N = sin(25 4 784.02 N °+ = 46.0 =°
2 50)2(600 5) ° 46.0 α ∴ = °
blem 2.46, it 00 N in cabl ximum force value of α. For )(750)cos(25° 25 +° is known tha e AC and 750 P that can b ceTriangle 45)+°
t the maximu N in cable B e applied at
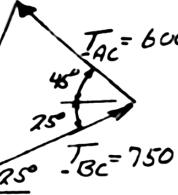

784 N P = 71.0 α =° m C C,



ROBLEM
To be sm
(a) T
(b) ION F allest, B TC m hus, ree-BodyD must be perpen α = B TC =

th as iagram dicular to the 5.00° (1200 lb)sin
or the situatio e value of α f possible, (b) direction of 5° 2.59
n described i or which the the correspon For ACT
n Figure P2.4 tension in rop ding value of ceTriangle


T 8, determine e BC is as sm the tension.
lb BC = (a) all


SOLUT
Free-Bo ION dyDiagram

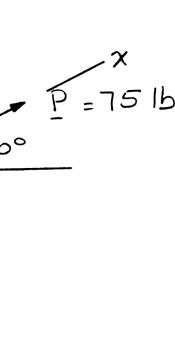
PROBLE
Two cables range of va either cable
Requireme
From Eq. (
Requireme
From Eq. ( M 2.60 tied together lues of Q for
= nt: 2): s Q nt: 1): 75 lb at C are loa which the ten co BC TQ 75 lb BCT = sin AC TQ sin AC TQ = 60 lb ACT = in6060 lb °= 69.3 Q = 60 lb BCT = cos606 Q °= 30 Q =
ded as shown sion will not s6075 lb °+ = cos60 Q −° 600 °= 60° : lb : 0lb .0lb
. Determine exceed 60 lb 0
Q ≤≤ the in (1) (2)
PROBLEM 2.61
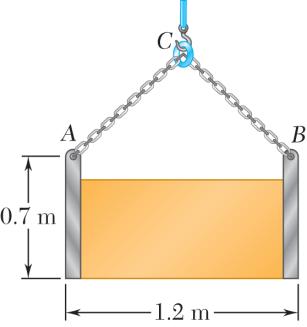
A movable bin and its contents have a combined weight of 2.8 kN. Determine the shortest chain sling ACB that can be used to lift the loaded bin if the tension in the chain is not to exceed 5 kN.
SOLUTION
Free-BodyDiagram
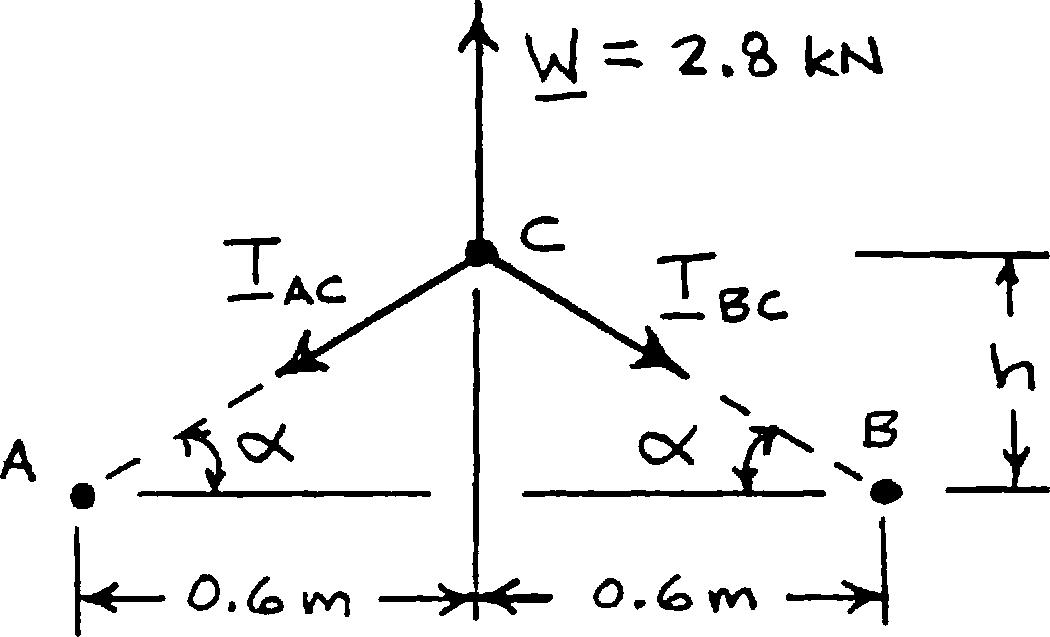
IsoscelesForceTriangle
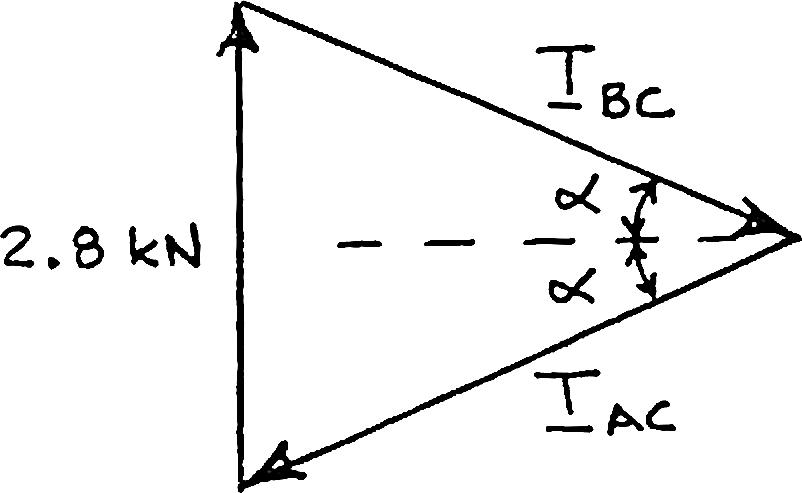
of
(0.6m)(0.175m)
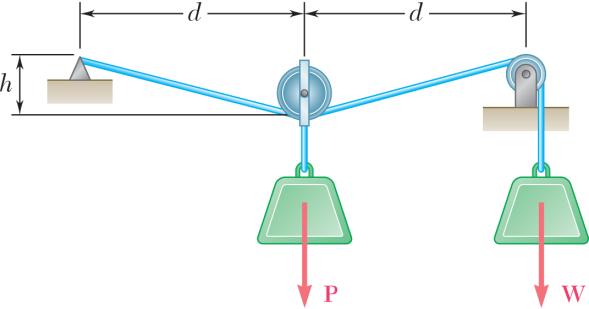
PROBLEM 2.62
For W = 800 N, P = 200 N, and d = 600 mm, determine the value of h consistent with equilibrium.
SOLUTION
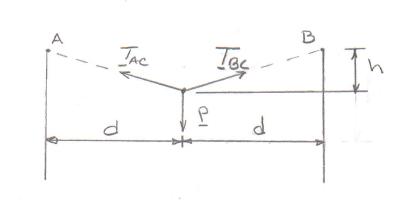
Free-BodyDiagram 800 N ACBCTT== ( ) 22 ACBChd ==+ 22 0:2(800 N) 0 y h FP hd Σ =− = + 2 8001 2 Pd h
Data: 200 N, 600 mm Pd = = and solving for h
200 N600 mm 800 N1 2 h ⎛⎞ =+
75.6 mm h =


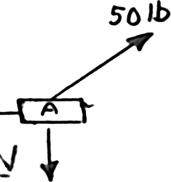
SOLUT
(a) F
(b) F ION
reeBody:Co

reeBody:Co llar A llar A
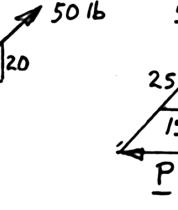
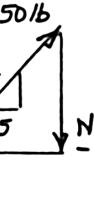
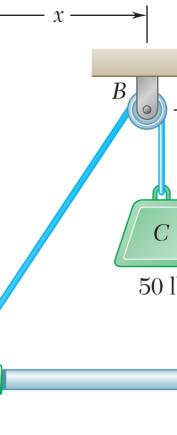
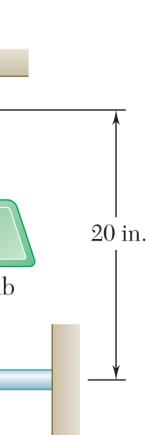
PROBLE
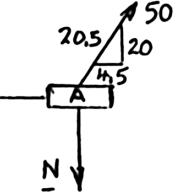
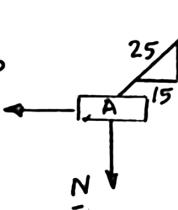
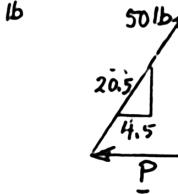
Collar A is c slide on a magnitude equilibrium 15 in. x = Forc 4.5 P Forc 15 P M 2.63 onnected as s frictionless h of the force of the colla eTriangle
50 lb 20.5 = eTriangle
50 lb 25 = hown to a 50 orizontal rod P required r when (a) -lb load and c . Determine to maintain 4.5 in., x = 10.98 lb P = 30.0 lb P = an the the (b)




PROBLEM
Similar
FreeBo Triangles dy:Collar A
Collar A is c slide on a f distance x fo P = 48 lb. F )(48)22 1 .00 lb
2 (50 14 N N = = 48 20 in.14 x =
lb lb 2.64
onnected as s rictionless ho r which the orceTriangle
hown to a 50 rizontal rod collar is in eq -lb load and c Determine uilibrium wh

68.6 in. x = an the en
PROBLEM 2.65
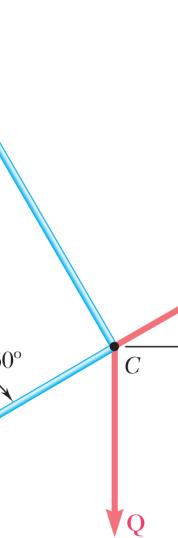
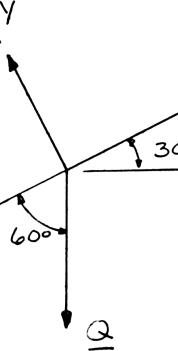
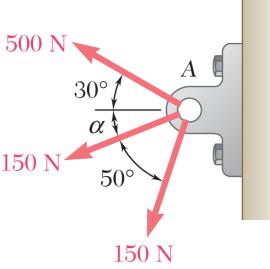
Three forces are applied to a bracket as shown. The directions of the two 150-N forces may vary, but the angle between these forces is always 50°. Determine the range of values of α for which the magnitude of the resultant of the forces acting at A is less than 600 N.
SOLUTION
Combine the two 150-N forces into a resultant force Q:
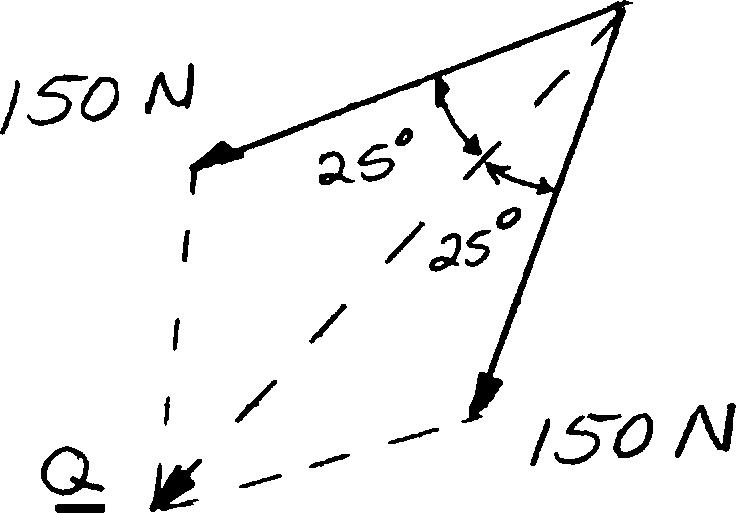
Equivalent loading at A:
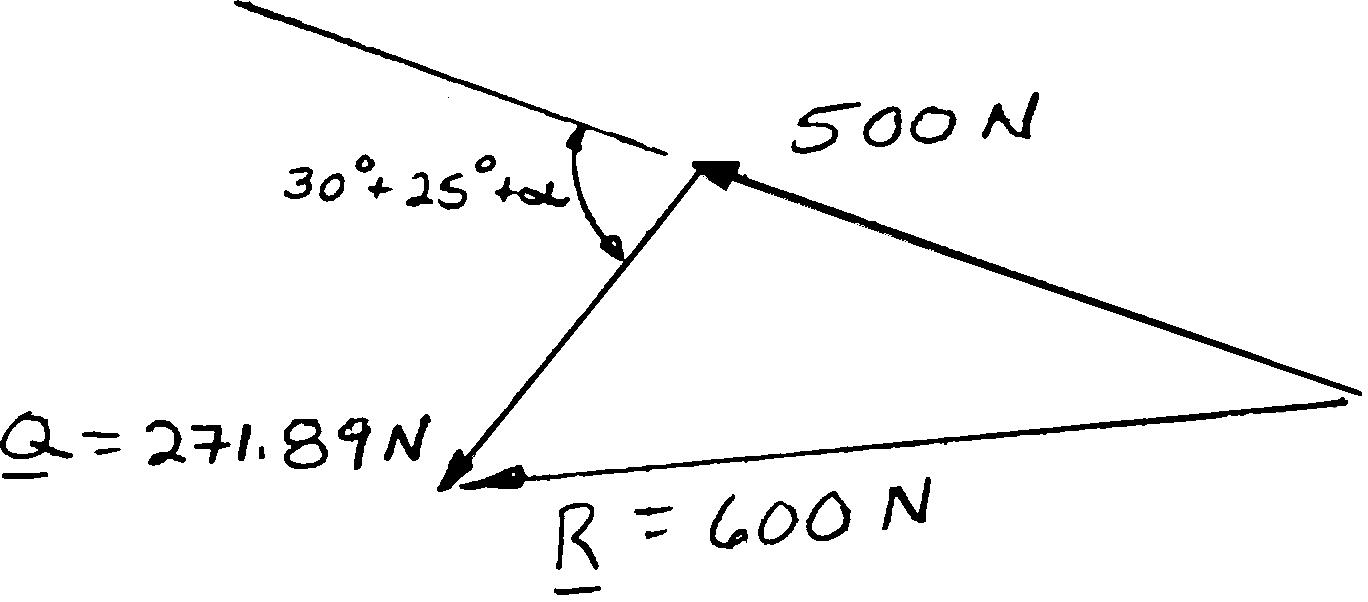
Using the law of cosines:

SOLUT
Free-Bo ION dyDiagram:
PROBL
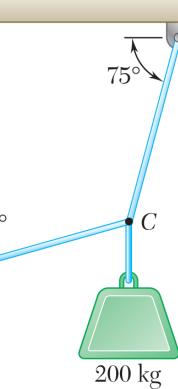
A 200-kg Determine the free en the same o Ch. 4.) :Pulley A
2.66
crate is to be the magnitu d of the rope n each side o
e supported b ude and direct to maintain e of a simple pu
y the rope-an ion of the for quilibrium. (H lley. This can
d-pulley arra ce P that mu int: The tensi be proved by
ngement show st be exerted on in the rope the methods





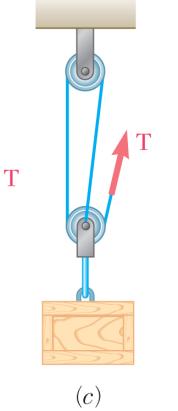
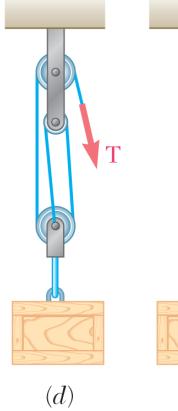
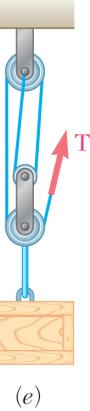
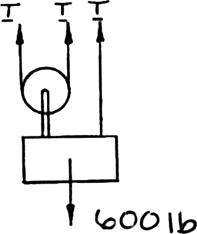
OBLEM 2
dyDiagramofPulley



00-lb crate i -pulley arrang each arrange e the hint for (600 lb) (600 lb)




600 lb) 600 lb) (600 lb) .67
s supported b ements as sh ment the tens Problem 2.66 y several rop own. Determ ion in the ro .) 300 lb
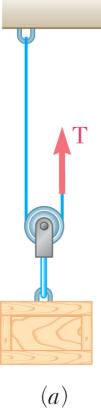
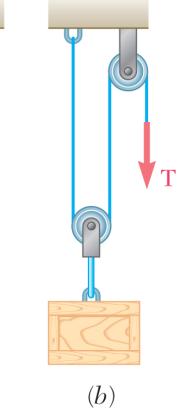

dyDiagramofPulleyandCrate
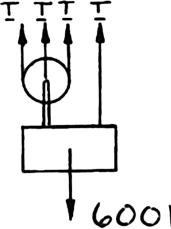

OBLEM 2.
Solv that crat PR by sho tens 2.66
e Parts b and the free end e.
d of Problem of the rope is
A 600-lb cr -and-pulley a e for each a e. (See the h 2.67, assumi attached to ate is suppor rrangements rrangement int for Probl
OBLEM2.67 several rope wn. Determin ion in the rop .) )0 1 (600 lb) 3 = =

150.0 lb T = ng the ted as the em
200 lb T =

SOLUT
Free-Bo ION dyDiagram: :Pulley C
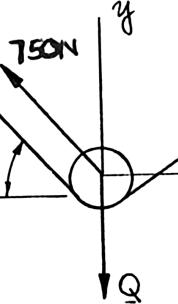
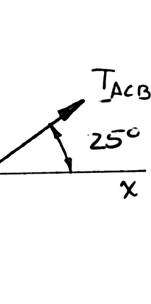

PRO A lo cable secon suppo (a) th (a) Σ Henc (b) FΣ or

BLEM 2.6
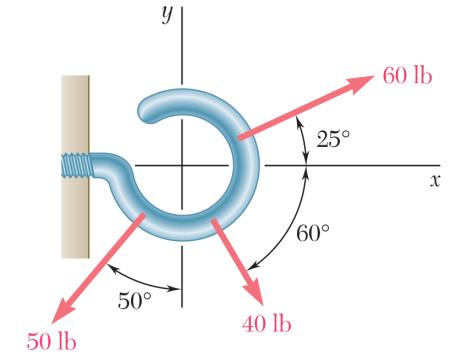
ad Q is appli ACB. The p d cable CAD rts a load e tension in c
ed to the pul ulley is held , which pa P. Knowing able ACB, (b)
129 ACBT = sin25sin5 sin25sin5 °+ °+ Q = ley C, which in the posit sses over the that 75 P = the magnitud s 55)(750 N °−
92.88 N AT 5)(750 N) 5)(750 N) °+ °+ 2219.8 N can roll on ion shown by pulley A a 0 N, determ e of load Q
= 1293 N CB = sin55 0 sin55 0 Q Q °−= °−= 2220 N Q = the a nd ine




SOLUT
Free-Bo ION dyDiagram: :Pulley C
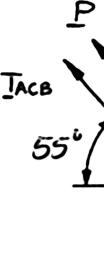
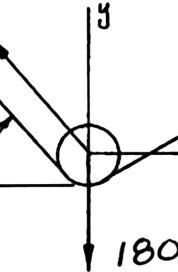
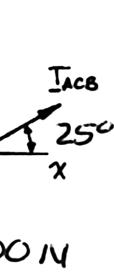


PRO
BLEM 2.7
An 1 on th a sec suppo (b) th 0 xFΣ = or y FΣ = or (a) Substit 1.24
Hence: (b) Using (
800-N load Q e cable ACB ond cable CA rts a load P e magnitude o
:(cos 2 ACBT
5cos55) °−°
0:(sin 2 ACBT
ute Equation ( 1770. ACBT + 1), 0. P = 0 is applied to The pulley is D, which p . Determine ( f load P
5sin55) °+° + 1.24177T 1) into Equat 81915(0.5801 58010(1048.3 the pulley C held in the po asses over th a) the tension cos55 0 P °= 0 P = sin551 P °−
0.81915 ACB + ion (2): 0)1800 ACBT = 1048 ACBT = AT 7 N)608.16 = , which can r sition shown e pulley A a in cable AC .58010 ACBT 800 N0 = 1800 N P = N .37 N 1048 N CB = N
608 N P = oll by nd CB, (1) (2)
PROBLEM 2.71
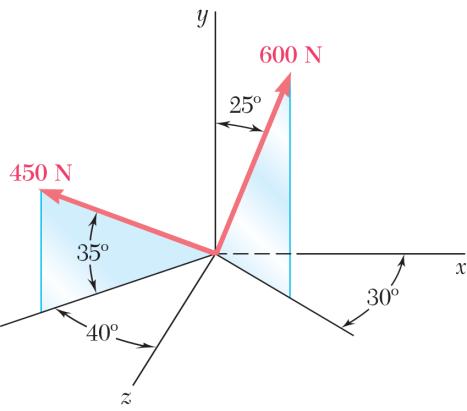
Determine (a) the x, y, and z components of the 600-N force, (b) the angles θx, θy, and θ z that the force forms with the coordinate axes.
SOLUTION (a) (600 N)sin25cos30 xF =°
xF = (600 N)cos25°
N)sin25sin30

PROBLEM 2.72
Determine (a) the x, y, and z components of the 450-N force, (b) the angles θx, θy, and θ z that the force forms with the coordinate axes.
SOLUTION
a)
N)cos35sin40
N)cos35cos40
Note: From the given data, we could have computed directly 903555, which checks with the answer obtained. yθ =−=
PROBLEM 2.73
A gun is aimed at a point A located 35° east of north. Knowing that the barrel of the gun forms an angle of 40° with the horizontal and that the maximum recoil force is 400 N, determine (a) the x, y, and z components of that force, (b) the values of the angles θx, θy, and θz defining the direction of the recoil force. (Assume that the x, y, and z axes are directed, respectively, east, up, and south.)
SOLUTION
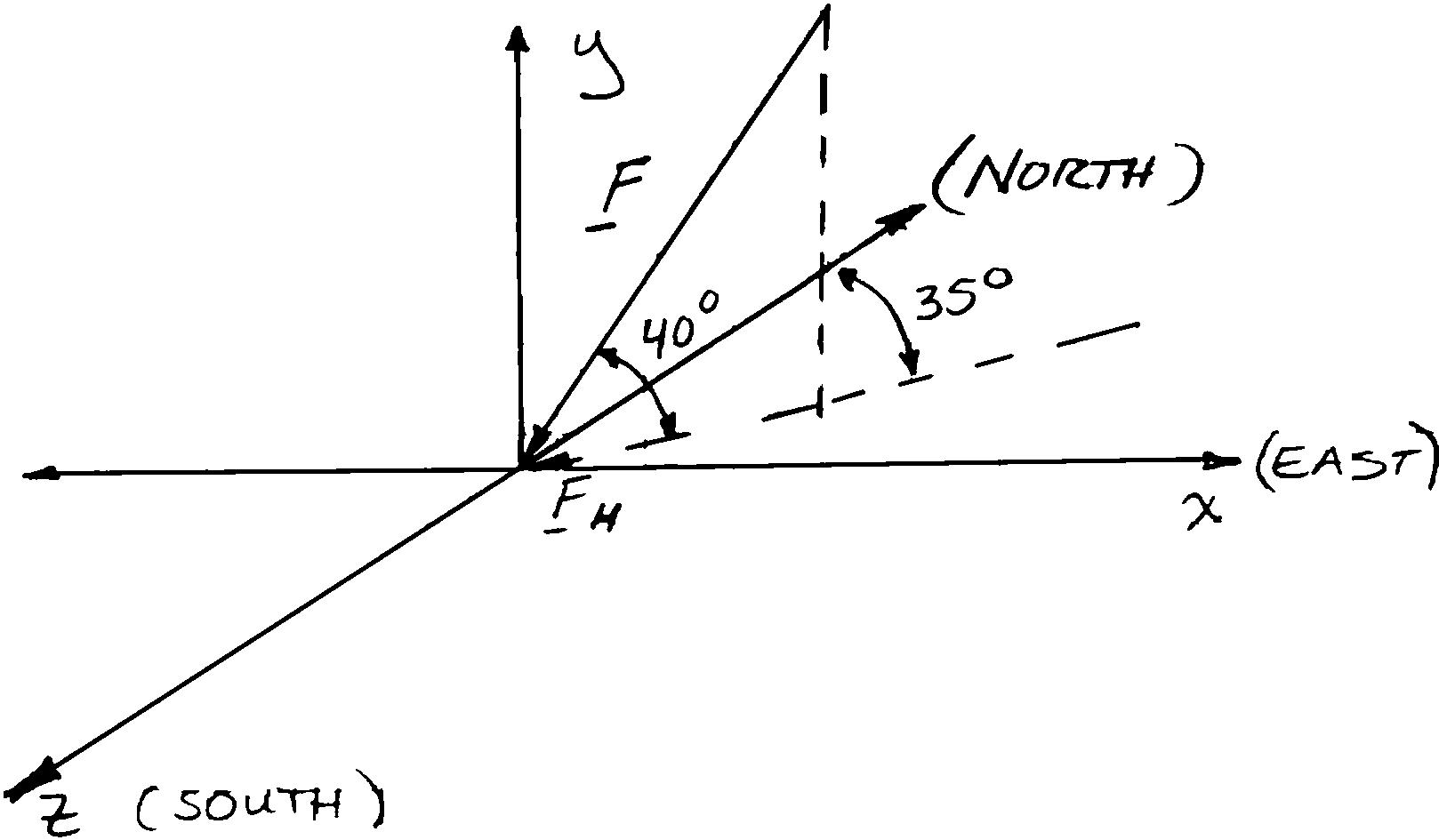
PROBLEM 2.74
Solve Problem 2.73, assuming that point A is located 15° north of west and that the barrel of the gun forms an angle of 25° with the horizontal.
PROBLEM2.73 A gun is aimed at a point A located 35° east of north. Knowing that the barrel of the gun forms an angle of 40° with the horizontal and that the maximum recoil force is 400 N, determine (a) the x, y, and z components of that force, (b) the values of the angles θx, θy, and θz defining the direction of the recoil force. (Assume that the x, y, and z axes are directed, respectively, east, up, and south.)
SOLUTION
Recoil force
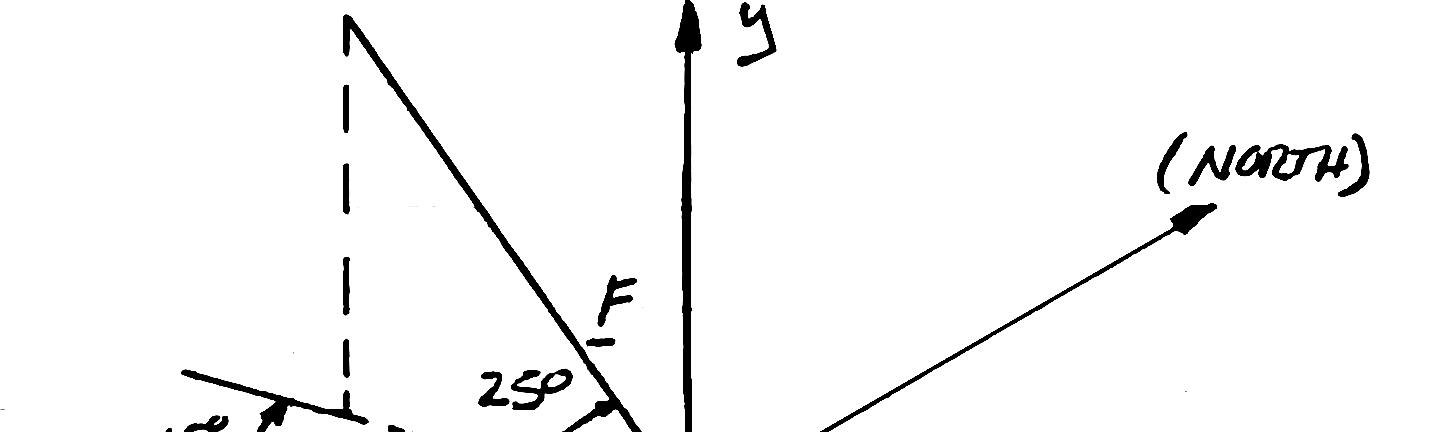

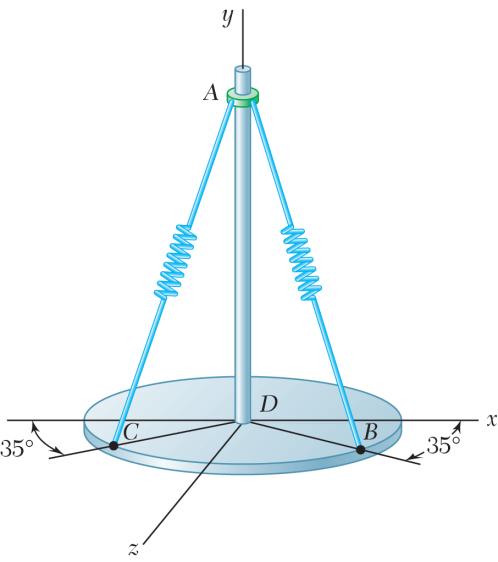
SOLUTION
PROBLEM 2.75
The angle between spring AB and the post DA is 30°. Knowing that the tension in the spring is 50 lb, determine (a) the x, y, and z components of the force exerted on the circular plate at B, (b) the angles θx, θy, and θ z defining the direction of the force at B
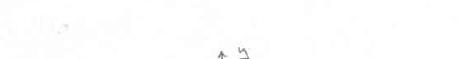





SOLUTION
PROBLEM 2.76
The angle between spring AC and the post DA is 30°. Knowing that the tension in the spring is 40 lb, determine (a) the x, y, and z components of the force exerted on the circular plate at C, (b) the angles θx, θy, and θ z defining the direction of the force at C.
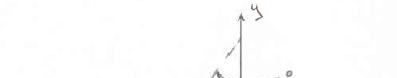


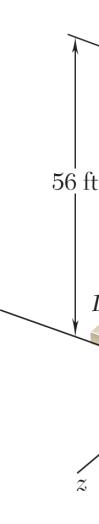

ROBLEM
able AB is etermine (a) able on the a irection of tha
65 ft long, a the x, y, and nchor B, (b) t force.
nd the tensio z component the angles θ
n in that ca s of the force ,
is 3900 exerted by
the the
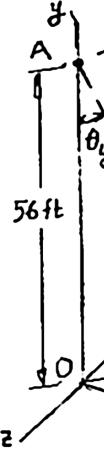
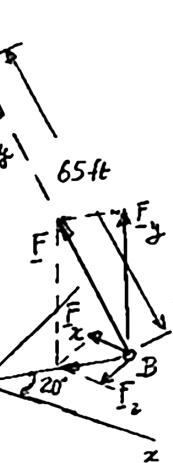
(3900 lb)(0 = )sin30.51°si
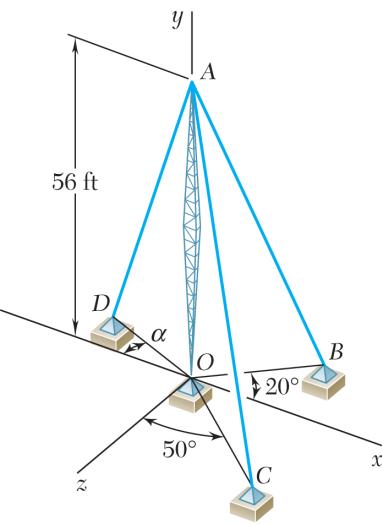
PROBLEM 2.78
Cable AC is 70 ft long, and the tension in that cable is 5250 lb. Determine (a) the x, y, and z components of the force exerted by the cable on the anchor C, (b) the angles θx, θy, and θ z defining the direction of that force.
PROBLEM 2.79
Determine the magnitude and direction of the force F = (240 N)i – (270 N)j + (680 N)k.
PROBLEM 2.80
Determine the magnitude and direction of the force F = (320 N)i + (400 N)j (250 N)k
PROBLEM 2.81
A force acts at the origin of a coordinate system in a direction defined by the angles θx = 69.3° and θ z = 57.9°. Knowing that the y component of the force is –174.0 lb, determine (a) the angle θy, (b) the other components and the magnitude of the force.
SOLUTION
(a) Since 0, y F < we choose
PROBLEM 2.82
A force acts at the origin of a coordinate system in a direction defined by the angles θx = 70.9° and θy = 144.9°. Knowing that the z component of the force is –52.0 lb, determine (a) the angle θ z, (b) the other components and the magnitude of the force. SOLUTION
PROBLEM 2.83
A force F of magnitude 210 N acts at the origin of a coordinate system. Knowing that Fx = 80 N, θ z = 151.2°, and Fy < 0, determine (a) the components Fy and Fz, (b) the angles θx and θy
SOLUTION (a) cos(210N)cos151.2zzFF θ ==°
=
Then: 2222 xyz FFFF =++
So: 2222 (210N)(80N)()(184.024N) y F =++
Hence: 222 (210N)(80N)(184.024N) y F =−−−
=−
zF =−
y F =− (b) 80N cos0.38095 210N x x F F θ ===
61.929N cos0.29490 210N y y F F θ ===−
PROBLEM 2.84
A force F of magnitude 1200 N acts at the origin of a coordinate system. Knowing that θx = 65° , θy = 40°, and Fz > 0, determine (a) the components of the force, (b) the angle θ z
(b) Since 0, zF > we choose cos0.48432, or
(a) 1200 N F = cos(1200 N) cos65 xxFF θ ==
N xF = cos(1200 N)cos40 yy FF θ ==°
N y F = cos(1200N)cos61.032zz FF θ ==°
SOLUTION
PROBLEM 2.85
A frame ABC is supported in part by cable DBE that passes through a frictionless ring at B. Knowing that the tension in the cable is 385 N, determine the components of the force exerted by the cable on the support at D.
(480 mm)(510 mm)(320 mm) (480 mm)(510 mm)(320 mm)
770 mm
385 N [(480 mm)(510 mm)(320 mm)]
770 mm (240 N)(255 N)(160 N)
240 N,255 N,160.0 N xyz FFF =+=−=+

SOLUTION
PROBLEM 2.86
For the frame and cable of Problem 2.85, determine the components of the force exerted by the cable on the support at E
PROBLEM2.85 A frame ABC is supported in part by cable DBE that passes through a frictionless ring at B. Knowing that the tension in the cable is 385 N, determine the components of the force exerted by the cable on the support at D
(270 mm)(400 mm)(600 mm) (270 mm)(400 mm)(600 mm)
770 mm
385 N [(270 mm)(400 mm)(600 mm)]
770 mm (135 N)(200 N)(300 N)
PROBLEM 2.87
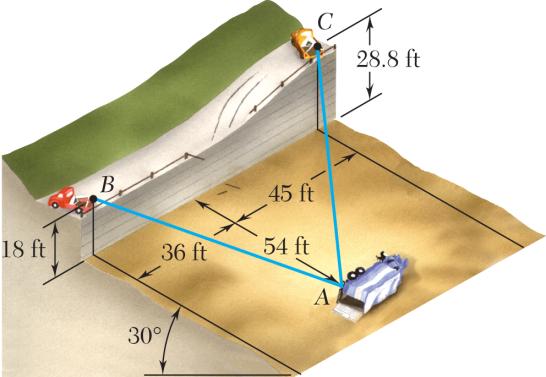
In order to move a wrecked truck, two cables are attached at A and pulled by winches B and C as shown. Knowing that the tension in cable AB is 2 kips, determine the components of the force exerted at A by the cable.
SOLUTION
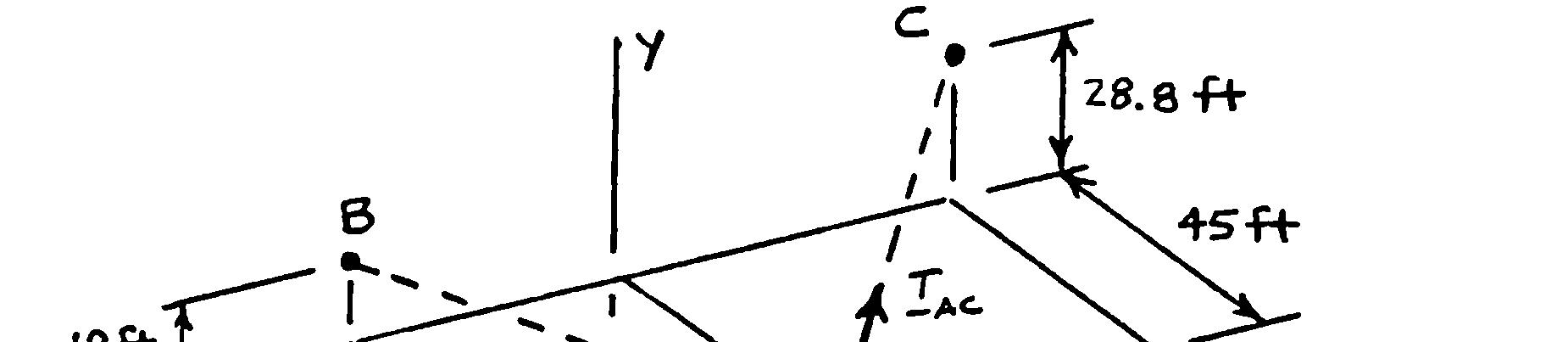
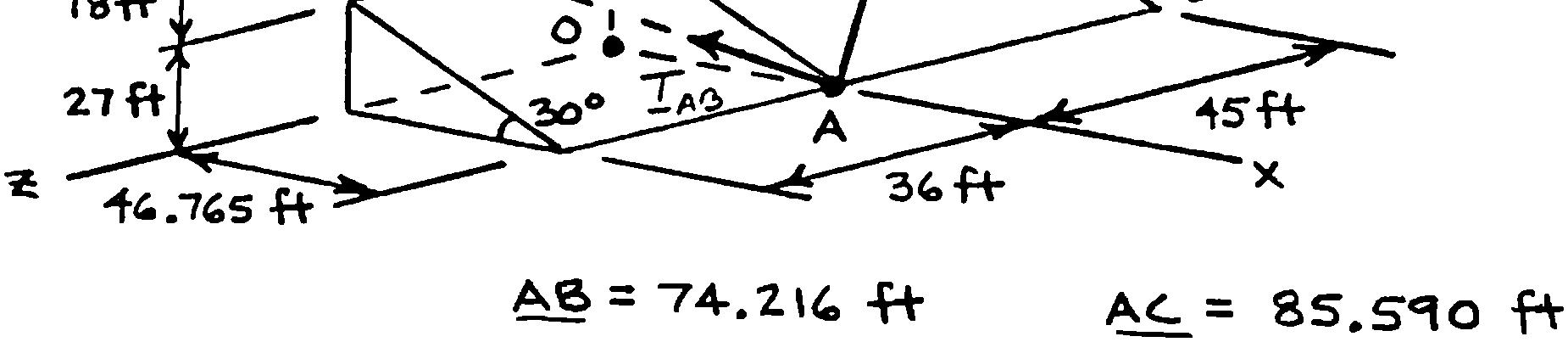
()1.260kips ABxT =−
()1.213kips AByT =+
()0.970kips ABzT =+

SOLUTION
PROBLEM 2.88
In order to move a wrecked truck, two cables are attached at A and pulled by winches B and C as shown. Knowing that the tension in cable AC is 1.5 kips, determine the components of the force exerted at A by the cable.
Cable AB:
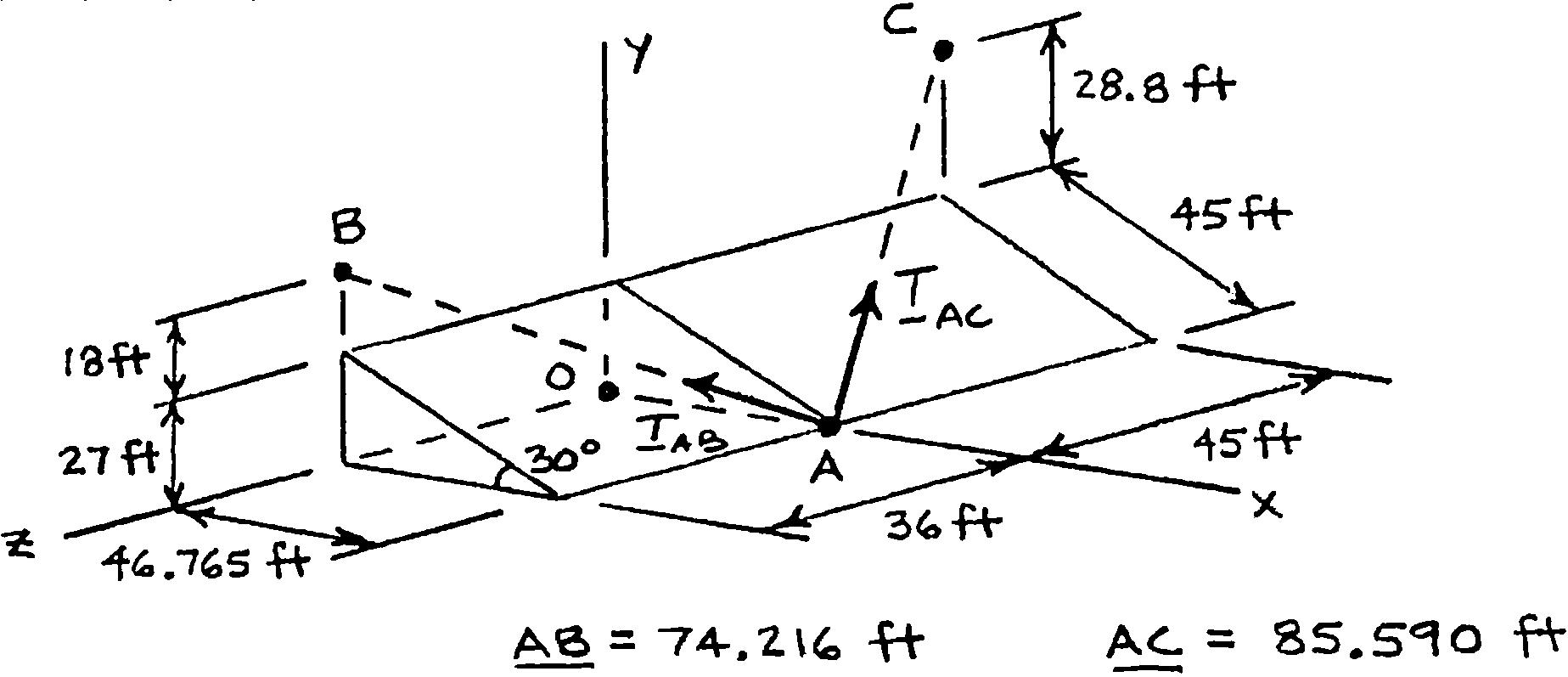
(46.765ft)(55.8ft)(45ft) 85.590ft
46.76555.845 (1.5kips)
()0.820kips ACxT =−
()0.978kips ACyT =+
()0.789kips =− ACzT
PROBLEM 2.89
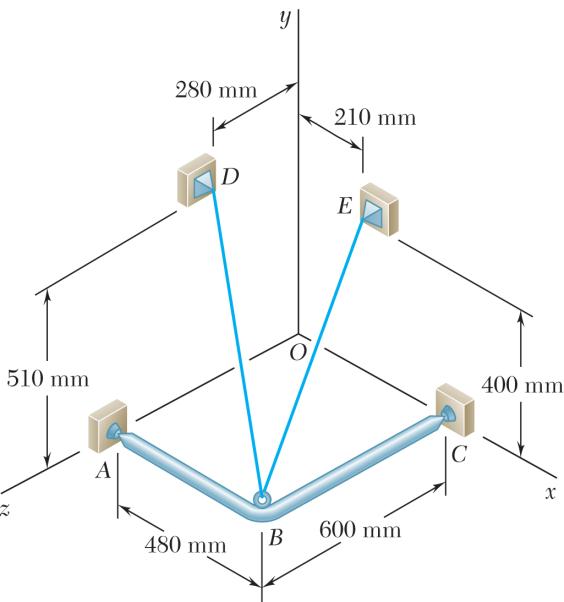
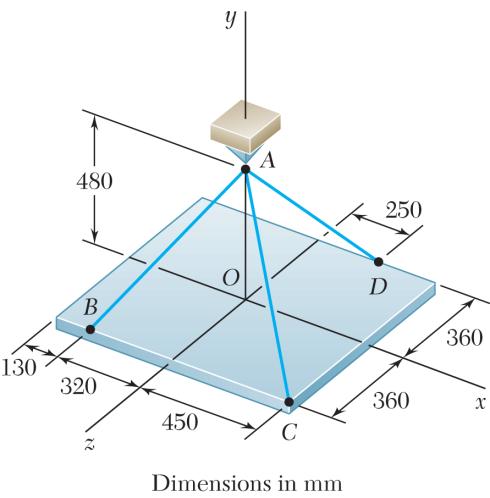
A rectangular plate is supported by three cables as shown. Knowing that the tension in cable AB is 408 N, determine the components of the force exerted on the plate at B
SOLUTION
We have:
Thus:
(320 mm)(480 mm)(360 mm)680 mm BABA =+ = i+j-k
Setting 408 N BAT = yields, 192.0 N, 288 N, 216 N xyz FFF =+ =+=−

PROBLEM 2.90
A rectangular plate is supported by three cables as shown. Knowing that the tension in cable AD is 429 N, determine the components of the force exerted on the plate at D.
SOLUTION
We have:
Thus:
(250 mm)(480 mm)(360 mm)650 mm DADA =− = i+j+k
Setting 429 N DAT = yields,
165.0 N, 317 N, 238 N xyz FFF =− =+=+
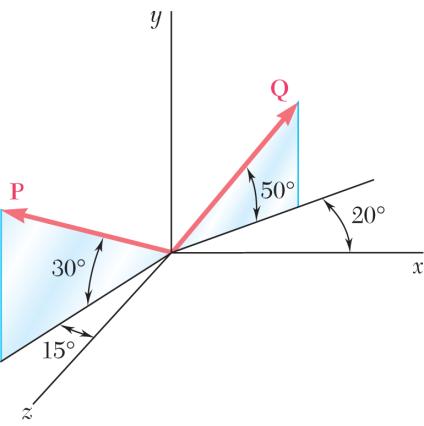
PROBLEM 2.91
Find the magnitude and direction of the resultant of the two forces shown knowing that P = 300 N and Q = 400 N.
SOLUTION
(300N)[cos30sin15sin30cos30cos15] (67.243N)(150N)(250.95N) (400N)[cos50cos20sin50cos50sin20] (400N)[0.604020.766040.21985] (241.61N)(306.42N)(87.939N) (174.
(174.367N)(456.42N)(163.011N)

PROBLEM 2.92
Find the magnitude and direction of the resultant of the two forces shown knowing that P = 400 N and Q = 300 N.
SOLUTION
(400N)[cos30sin15sin30cos30cos15] (89.678N)(200N)(334.61N) (300N)[cos50cos20sin50cos50sin20] (181.21N)(229.81N)(65.954N) (91.532N)(429.81N)(268.66N) (91.5 R
SOLUTION
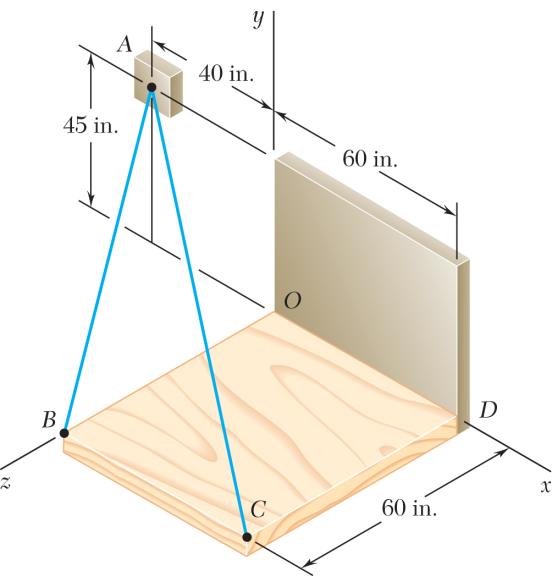
PROBLEM 2.93
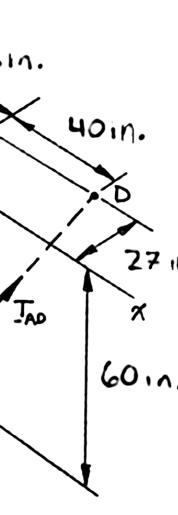
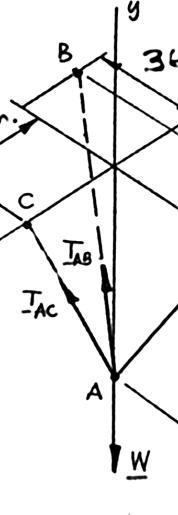
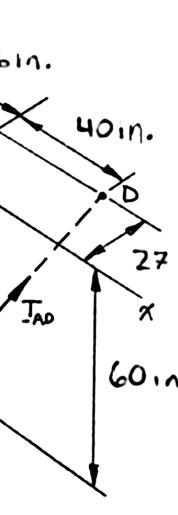
Knowing that the tension is 425 lb in cable AB and 510 lb in cable AC, determine the magnitude and direction of the resultant of the forces exerted at A by the two cables.
222
(40in.)(45in.)(60in.) (40in.)(45in.)(60in.)85in. (100in.)(45in.)(60in.) (100in.)(45in.)(60in.)125in. (40in.)(45in.)(60in.) (425lb) 85in.
(200lb)(225lb)(300lb) (100in.)(45in.)(60in.) (510lb) 125in. (408lb)(183.6lb)(244.8lb) (608)(408.6lb)(544.8lb)

SOLUTION
PROBLEM 2.94
Knowing that the tension is 510 lb in cable AB and 425 lb in cable AC, determine the magnitude and direction of the resultant of the forces exerted at A by the two cables.
222 222 (40in.)(45in.)(60in.) (40in.)(45in.)(60in.)85in. (100in.)(45in.)(60in.) (100in.)(45in.)(60in.)125in. (40in.)(45in.)(60in.) (510lb) 85in.
(240lb)(270lb)(360lb) (100in.)(45in.)(60in.) (425lb) 125in. (340lb)(153lb)(204lb) (580lb)(423lb)(564lb)
SOLUTION
PROBLEM 2.95
For the frame of Problem 2.85, determine the magnitude and direction of the resultant of the forces exerted by the cable at B knowing that the tension in the cable is 385 N.
PROBLEM2.85 A frame ABC is supported in part by cable DBE that passes through a frictionless ring at B. Knowing that the tension in the cable is 385 N, determine the components of the force exerted by the cable on the support at D
(480 mm)(510 mm)(320 mm) (480 mm)(510 mm)(320 mm)770 mm
(385 N) [(480 mm)(510 mm)(320 mm)] (770 mm)
(240 N)(255 N)(160 N)
(270 mm)(400 mm)(600 mm) (270 mm)(400 mm)(600 mm)770 mm
(385 N) [(270 mm)(400 mm)(600 mm)] (770 mm)
(135 N)(200 N)(300 N)
(375 N)(455 N)(460 N)
(375 N)(455 N)(460 N)747.83 N R

SOLUTION
We have:
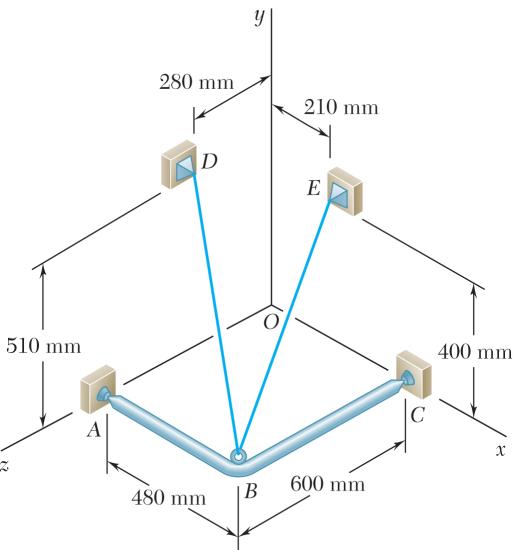
PROBLEM 2.96
For the plate of Prob. 2.89, determine the tensions in cables AB and AD knowing that the tension in cable AC is 54 N and that the resultant of the forces exerted by the three cables at A must be vertical.
(320 mm)(480 mm)(360 mm)680 mm (450 mm)(480 mm)(360 mm)750 mm (250 mm)(480 mm)360 mm650 mm
Substituting into the Eq. =Σ RF and factoring , , : ijk
PROBLEM 2.96 (Continued)
Since R is vertical, the coefficients of i and k are zero:
Multiply (1) by 3.6 and (2) by 2.5 then add:
Substitute into (2) and solve for : ADT
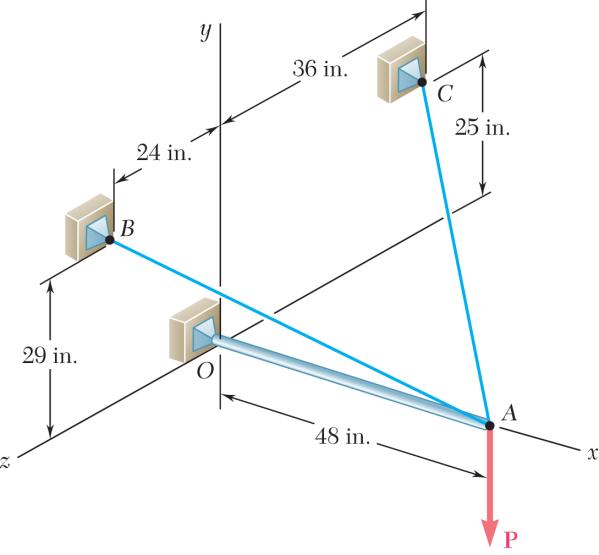
PROBLEM 2.97
The boom OA carries a load P and is supported by two cables as shown. Knowing that the tension in cable AB is 183 lb and that the resultant of the load P and of the forces exerted at A by the two cables must be directed along OA, determine the tension in cable AC.
SOLUTION
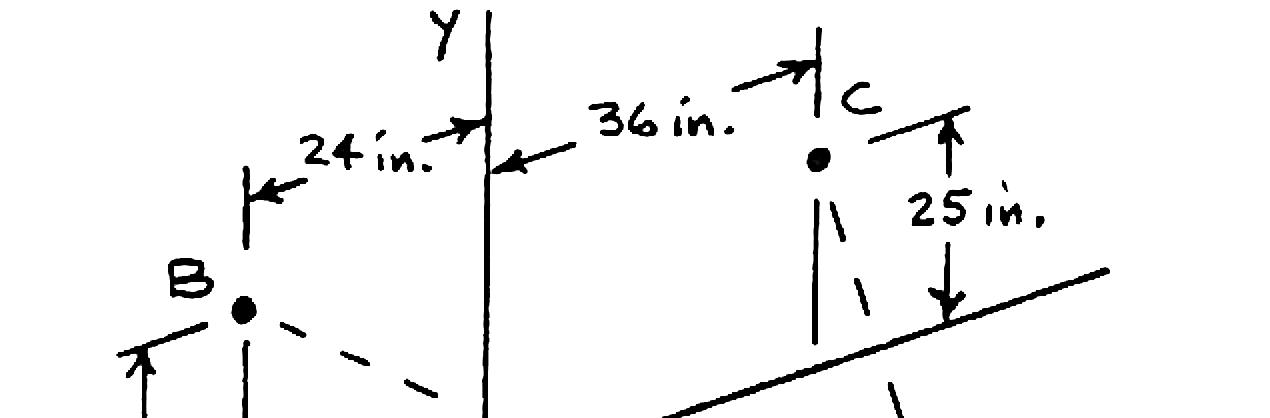
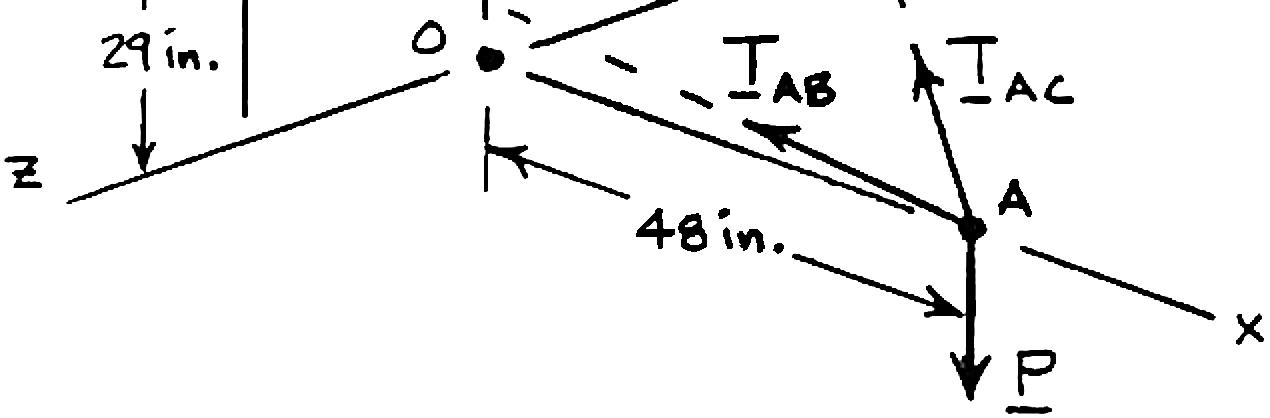
Cable AB: 183lb ABT = (48in.)(29in.)(24in.) (183lb) 61in. (144lb)(87lb)(72lb)
Cable AC: (48in.)(25in.)(36in.) 65in.
Load P: P = Pj For resultant to be directed along OA, i.e., x-axis

PROBLEM 2.98
For the boom and loading of Problem. 2.97, determine the magnitude of the load P
PROBLEM2.97 The boom OA carries a load P and is supported by two cables as shown. Knowing that the tension in cable AB is 183 lb and that the resultant of the load P and of the forces exerted at A by the two cables must be directed along OA, determine the tension in cable AC
SOLUTION
See Problem 2.97. Since resultant must be directed along OA, i.e., the x-axis, we write
ACT = from Problem 2.97.
SOLUTION
PROBLEM 2.99
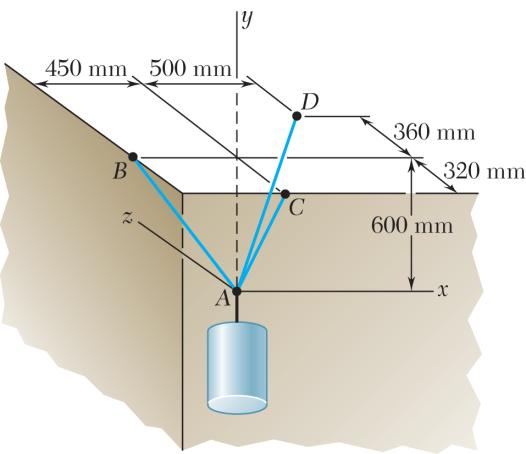
A container is supported by three cables that are attached to a ceiling as shown. Determine the weight W of the container, knowing that the tension in cable AB is 6 kN.
Free-BodyDiagramatA:
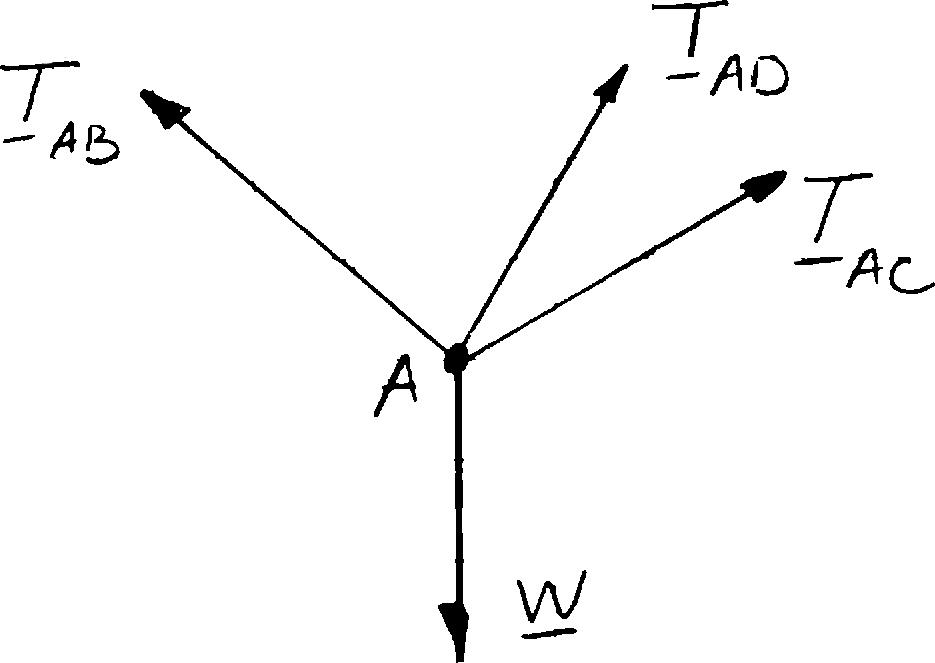
The forces applied at A are: ,,,andABACAD TTTW where W = Wj To express the other forces in terms of the unit vectors i, j, k, we write (450mm)(600mm) 750mm (600mm)(320mm) 680mm (500mm)(600mm)(360mm)860mm
and (450mm)(600mm) 750mm ABABABABAB AB TTT AB
4560 7575 AB
(600mm)(320mm) 680mm 6032 6868 (500mm)(600mm)(360mm) 860mm 506036 868686
PROBLEM 2.99 (Continued)
Equilibriumcondition: 0: 0 FABACAD Σ=∴+++= TTTW
Substituting the expressions obtained for ,,and; ABACAD TTT factoring i, j, and k; and equating each of the coefficients to zero gives the following equations:
From i: 4550 0 7586ABADTT −+=
From j: 606060 0 756886ABACAD TTTW ++−=
From k: 3236 0 6886ACADTT −+=
Setting 6kN ABT = in (1) and (2), and solving the resulting set of equations gives
W =

PROBLEM 2.100
A container is supported by three cables that are attached to a ceiling as shown. Determine the weight W of the container, knowing that the tension in cable AD is 4.3 kN. SOLUTION
See Problem 2.99 for the figure and analysis leading to the following set of linear algebraic equations:
Setting 4.3kN ADT = into the above equations gives

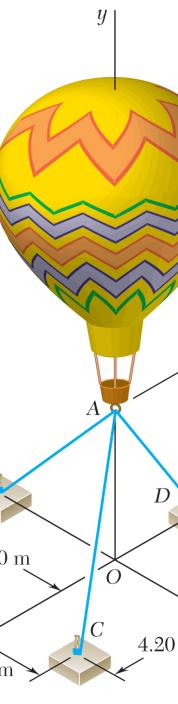

PROB
LEM 2.101
Three c the vert tension
ables are use ical force P e in cable AD i
ed to tether a exerted by the s 481 N.
The forc where P and ION es applied at A P = j To exp are: press the other
FREE-BOD , ABT forces in term (4.20m) (2.40m) ( (5.60m) i i j
YDIAGRA ,,andACADTT s of the unit (5.60m) 5.60m)(4 (3.30m) + j j k (0.6 (0.32 (0.8 C D AB AB AC AC AD AD =− = =−
A P vectors i, j, k .20m) AB AC AD k 0.8) 4320.7567
61540.507 ABT ij i j balloon as sh balloon at A k , we write 7.00m 7.40m 6.50m = = = 60.56757 69) ADT + jk k own. Determ nowing that ) ACT ine the
Equilibr
Substitu
Equating
iumcondition ting the expre ( to zero the c
: essions obtaine
ROBLEM 2
Setting
481N ADT =
0.60.3 ABT + coefficients of 0.8 ABT in (2) and (3),
0: A FBΣ= T d for , ABATT 2432) ( (0.56757 ACT + + i i, j, k: 0.6 AT 0.75676 ACT 0.56757T and solving t
AC AD T T = = .101 (Con ACAD++TT ,and CAD T an
tinued) 0 P += j d factoring i,
0.80.7 0.50769 AB AC T T 0.32432 B TT + 0.86154 ADT −+ 0.50769 AC TT he resulting se 0.26N 2.57N
56760.8 )0 AC AD T T = k
ACT =
P + =
ADT = t of equation j, and k: 6154 ) AD TP + s gives j
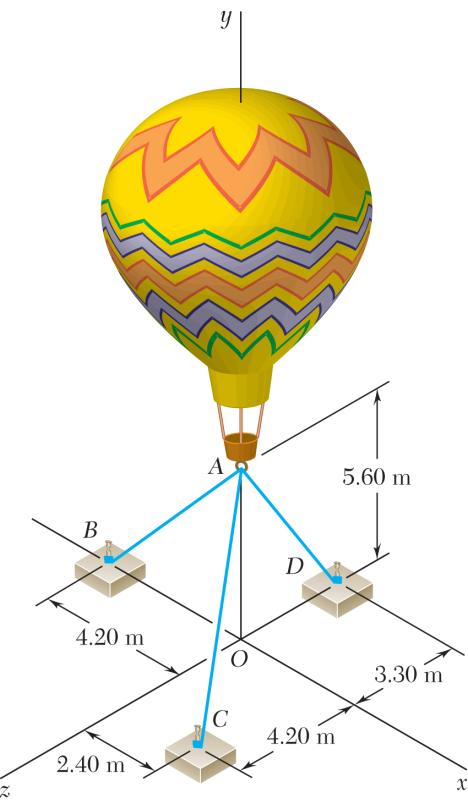
SOLUTION
PROBLEM 2.102
Three cables are used to tether a balloon as shown. Knowing that the balloon exerts an 800-N vertical force at A, determine the tension in each cable.
See Problem 2.101 for the figure and analysis leading to the linear algebraic Equations (1), (2), and (3).
0.60.324320 ABAC TT+= (1)
0.80.756760.861540 ABACAD TTTP −−−+= (2) 0.567570.507690 ACAD TT = (3)
From Eq. (1): 0.54053 ABAC TT =
From Eq. (3): 1.11795 ADAC TT =
Substituting for AB T and ADT in terms of ACT into Eq. (2) gives
0.8(0.54053)0.756760.86154(1.11795)0 ACACAC TTTP −−−+=
Substituting into expressions for AB T and ADT gives
PROBLEM 2.103
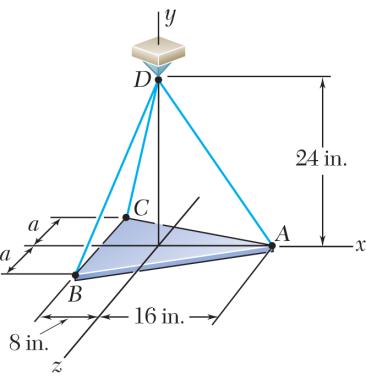
A 36-lb triangular plate is supported by three wires as shown. Determine the tension in each wire, knowing that a = 6 in.
Symmetry
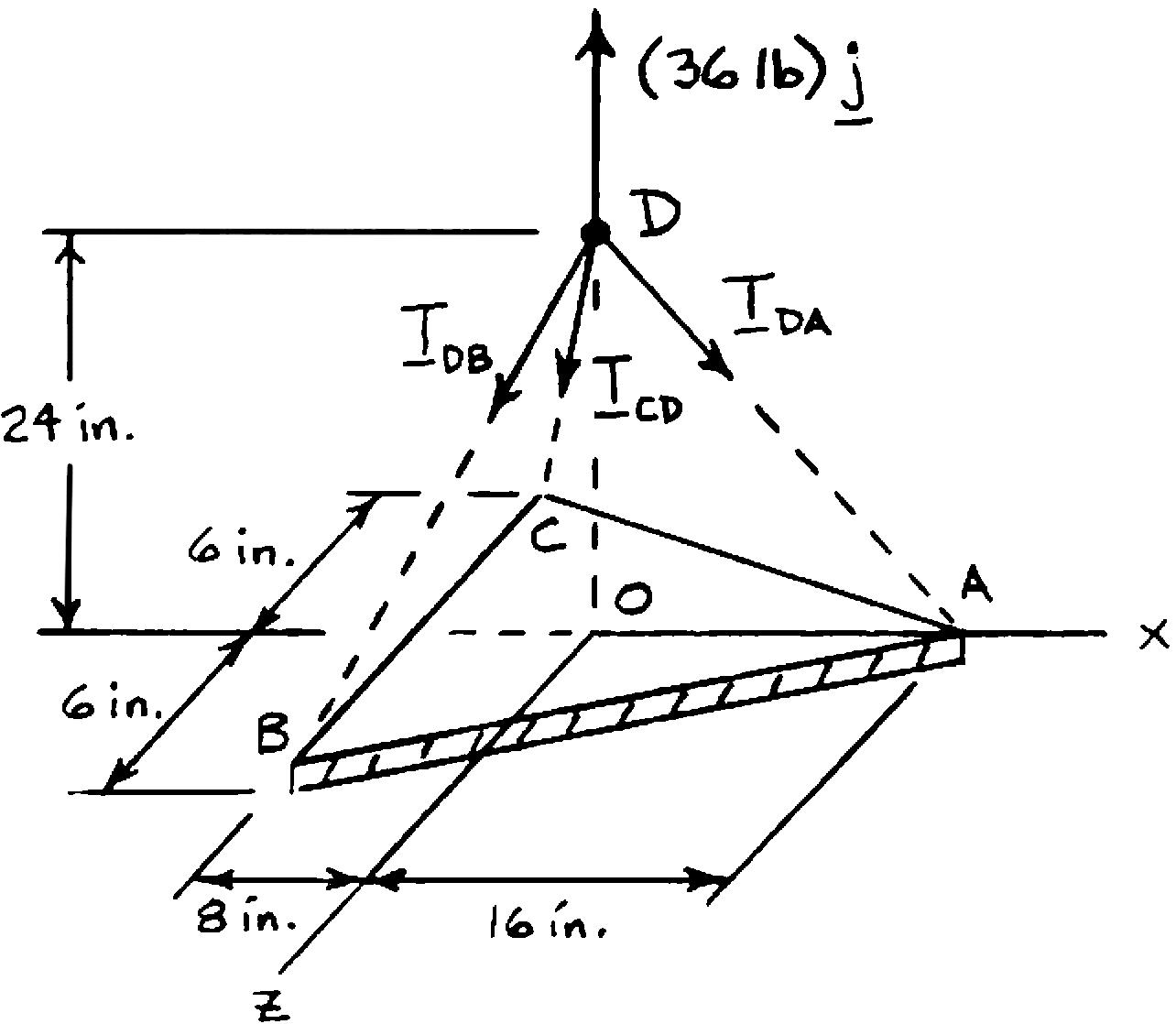
The forces applied at D are: ,,,andDBDCDA TTTP where (36 lb). P == Pjj To express the other forces in terms of the unit vectors i, j, k, we write (16in.)(24in.) 28.844in. (8in.)(24in.)(6in.)26.0in. (8 in.)(24in.)(6in.) 26.0in.
PROBLEM 2.103 (Continued)
Equilibriumcondition: 0: (36 lb)0 FDADBDC Σ=+++= TTTj
Substituting the expressions obtained for ,,and DADBDCTTT and factoring i, j, and k: (0.554710.307690.30769)(0.832060.923080.9230836 lb) (0.230770.23077)0 DADBDCDADBDC DBDC TTTTTT TT −−+−−−+ +−= ij k
Equating to zero the coefficients of i, j, k:
0.554710.307690.307690 DADBDC TTT−= (1)
0.832060.923080.9230836 lb0 DADBDC TTT −−−+= (2)
0.230770.230770 DBDC TT = (3)
Equation (3) confirms that DBDCTT = . Solving simultaneously gives, 14.42lb; 13.00lb DADBDC TTT===

SOLUTION
Symmetry
PROBLEM 2.104
Solve Prob. 2.103, assuming that a = 8 in.
PROBLEM2.103 A 36-lb triangular plate is supported by three wires as shown. Determine the tension in each wire, knowing that a = 6 in.
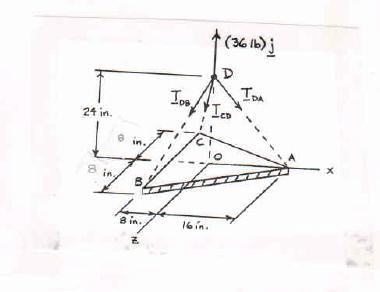
The forces applied at D are: ,,,andDBDCDA TTTP where (36 lb). P == Pjj To express the other forces in terms of the unit vectors i, j, k, we write (16in.)(24in.) 28.844in. (8in.)(24in.)(8in.)26.533in. (8 in.)(24in.)(8in.) 26.533in.
and (0.554710.83206) (0.301510.904530.30151) (0.301510.904530.30151)
PROBLEM 2.104 (Continued)
Equilibriumcondition: 0: (36 lb)0 FDADBDC Σ=+++= TTTj
Substituting the expressions obtained for ,,and DADBDCTTT and factoring i, j, and k: (0.554710.301510.30151)(0.832060.904530.9045336 lb) (0.301510.30151)0 DADBDCDADBDC DBDC TTTTTT TT −−+−−−+ +−= ij k
Equating to zero the coefficients of i, j, k:
0.554710.301510.301510 DADBDC TTT−= (1)
0.832060.904530.9045336 lb0 DADBDC TTT −−−+= (2)
0.301510.301510 DBDC TT = (3)
Equation (3) confirms that DBDCTT = . Solving simultaneously gives, 14.42lb; 13.27lb DADBDC TTT===


Solution where P and Equilibr The forces ap P = j To exp iumCondition pplied at A are press the other
forces in term (36in.) 75in. (60in.)(3 68in. (40in.)(6 77in. −+ + + i j i (0.480.8 (0.88235
OBLEM 2
crate is suppo weight of the 44 lb. and W s of the unit (60in.)(27 2in.) 0in.)(27in j k j 0.36)
rted by three crate knowin vectors i, j, k in.) .) k k
cables as sh g that the ten , we write own. Determ sion in cable A ine C
PROBLEM 2.105 (Continued)
Substituting the expressions obtained for ,,and ABACAD TTT and factoring i, j, and k: (0.480.51948)(0.80.882350.77922) (0.360.470590.35065)0 ABADABACAD ABACAD TTTTTW TTT −++++− +−+− = ij k
Equating to zero the coefficients of i, j, k:
0.480.519480 ABAD TT+= (1) 0.80.882350.779220 ABACAD TTTW ++−= (2)
0.360.470590.350650 ABACAD TTT −+−= (3)
Substituting 544lb ACT = in Equations (1), (2), and (3) above, and solving the resulting set of equations using conventional algorithms, gives:



SOLUT
The forc where P and Equilibr ION es applied at A P = j To exp iumCondition are: press the other

ROBLEM 2
D
forces in term (36in.) 75in. (60in.)(3 68in. (40in.)(6 77in.
1600-lb crat etermine the t and W s of the unit (60in.)(27 2in.) 0in.)(27in j k j
e is supporte ension in each vectors i, j, k in.) .) k k 5065) ADT k 0 = d by three c cable. , we write ables as shown.
PROBLEM 2.106 (Continued)
Substituting the expressions obtained for ,,and ABACAD TTT and factoring i, j, and k: (0.480.51948)(0.80.882350.77922) (0.360.470590.35065)0
ABADABACAD ABACAD TTTTTW TTT −++++− +−+− = ij k
Equating to zero the coefficients of i, j, k:
0.480.519480 ABAD TT+= (1)
0.80.882350.779220 ABACAD TTTW ++−= (2) 0.360.470590.350650 ABACAD TTT −+−= (3)
Substituting 1600 lb W = in Equations (1), (2), and (3) above, and solving the resulting set of equations using conventional algorithms gives,
571lb ABT =
830lb ACT =
528lb ADT =
SOLUTION
PROBLEM 2.107
Three cables are connected at A, where the forces P and Q are applied as shown. Knowing that 0, Q = find the value of P for which the tension in cable AD is 305 N.
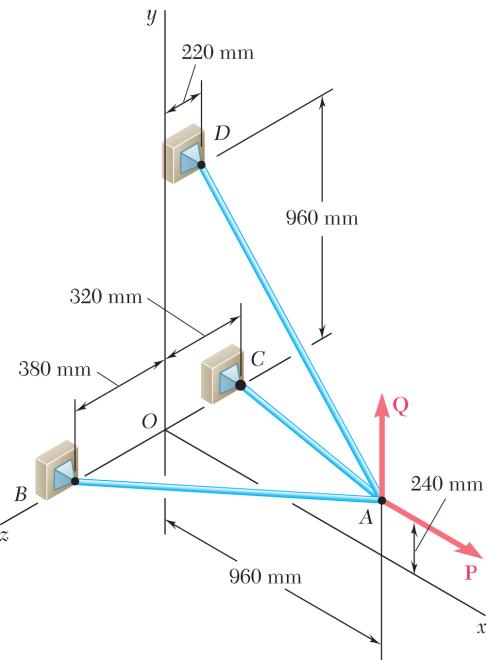
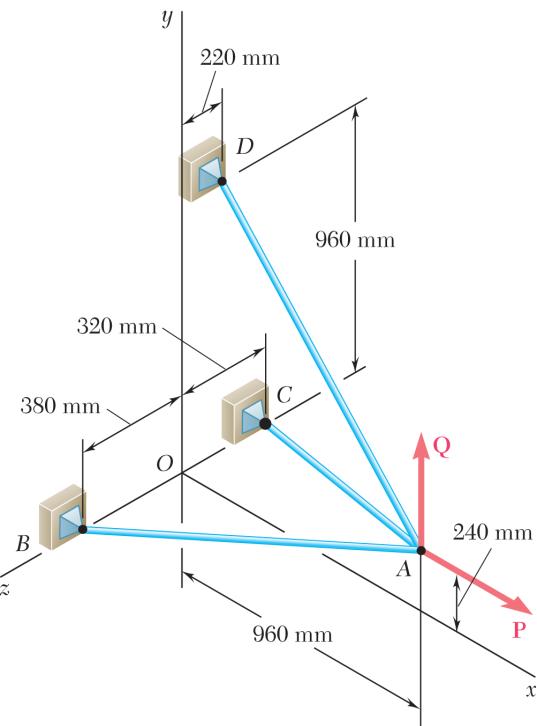
0: 0 AABACAD Σ=+++= FTTTP where P = Pi (960 mm)(240 mm)(380 mm)1060 mm (960 mm)(240 mm)(320 mm)1040 mm (960 mm)(720 mm)(220 mm)1220 mm ABAB ACAC
305 N [(960 mm)(720 mm)(220 mm)] 1220 mm (240 N)(180 N)(55 N)
Substituting into 0, A Σ= F factoring ,,,ijk and setting each coefficient equal to φ gives:
Solving the system of linear equations using conventional algorithms gives:
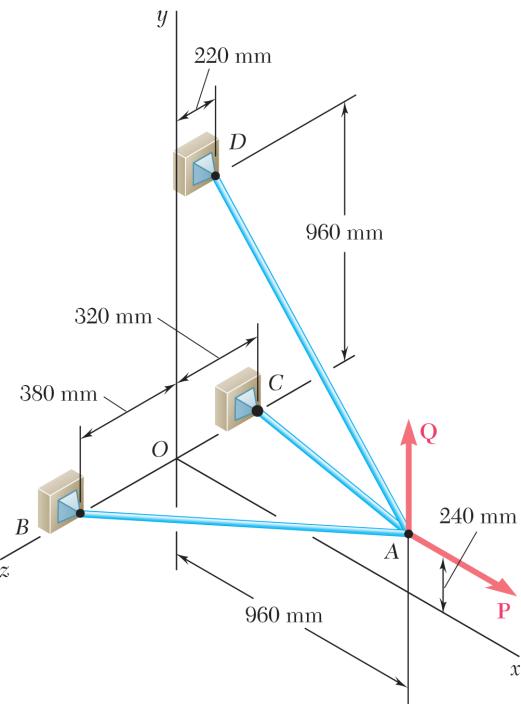
PROBLEM 2.108
Three cables are connected at A, where the forces P and Q are applied as shown. Knowing that 1200 N, P = determine the values of Q for which cable AD is taut.
SOLUTION
We assume that 0 ADT = and write
(960 mm)(240 mm)(380 mm)1060 mm (960 mm)(240 mm)(320 mm)1040 mm
Substituting into 0, A Σ= F factoring , , , ijk and setting each coefficient equal to φ gives:
Solving the resulting system of linear equations using conventional algorithms gives:
Note: This solution assumes that Q is directed upward as shown (0), Q ≥ if negative values of Q are considered, cable AD remains taut, but AC becomes slack for 460 N. Q =
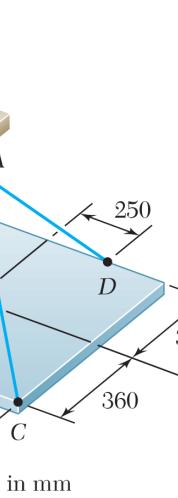
SOLUT
We note Point A. We have
Thus:
Substitu ION that the we :
ting into the E ight of the pl
PROB
LEM 2.10
A recta Knowin weight ate
angular plate ng that the te of the plate.
is supported nsion in cabl to the force
by three ca e AC is 60 N P exerted by Free
Dim
bles as show , determine the support Body A : ensions in m n. the on m

PROBLEM 2.109 (Continued)
Setting the coefficient of i, j, k equal to zero:
Making 60 N ACT = in (1) and (3):
Multiply (1′) by 9, (3′) by 8, and add:
Substitute into (1′) and solve for : ABT
Substitute for the tensions in Eq. (2) and solve for P :
N P =++ = Weight of plate 845 N P ==

PROBLEM 2.110
A rectangular plate is supported by three cables as shown. Knowing that the tension in cable AD is 520 N, determine the weight of the plate.
SOLUTION
See Problem 2.109 for the figure and the analysis leading to the linear algebraic Equations (1), (2), and (3) below:
Making 520 N ADT = in Eqs. (1) and (3):
Multiply (1′) by 9, (3′) by 8, and add:
Substitute into (1′) and solve for : AB
Substitute for the tensions in Eq. (2) and solve for P:
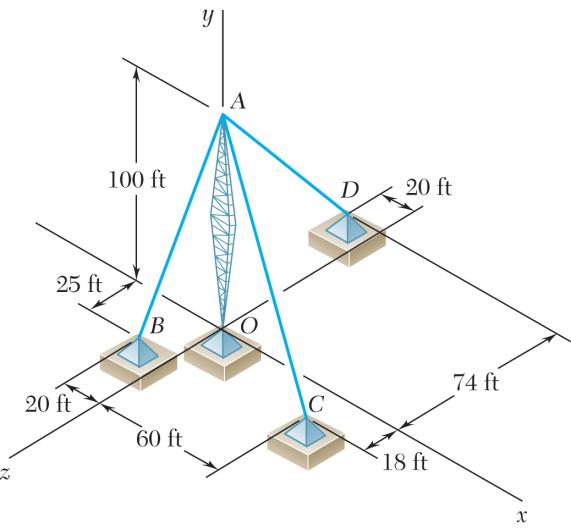
PROBLEM 2.111
A transmission tower is held by three guy wires attached to a pin at A and anchored by bolts at B, C, and D. If the tension in wire AB is 840 lb, determine the vertical force P exerted by the tower on the pin at A
PROBLEM 2.111 (Continued)

PROBLEM 2.112
A transmission tower is held by three guy wires attached to a pin at A and anchored by bolts at B, C, and D. If the tension in wire AC is 590 lb, determine the vertical force P exerted by the tower on the pin at A.
PROBLEM 2.112 (Continued)
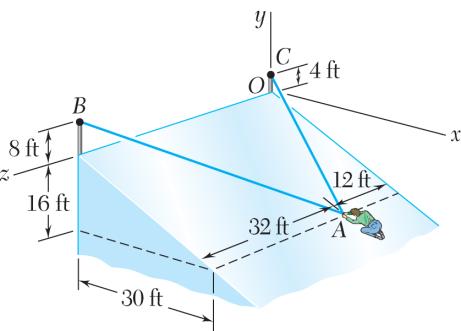
PROBLEM 2.113
In trying to move across a slippery icy surface, a 175-lb man uses two ropes AB and AC. Knowing that the force exerted on the man by the icy surface is perpendicular to that surface, determine the tension in each rope.
SOLUTION
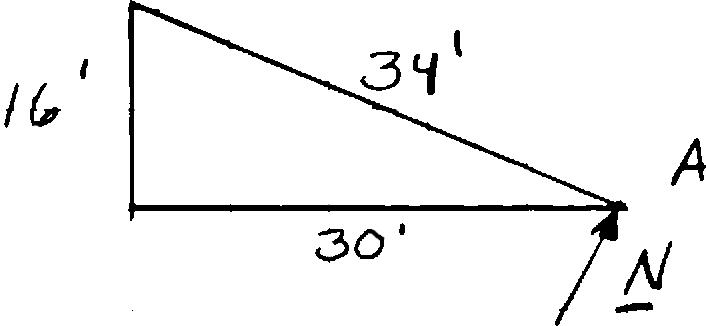
Free-BodyDiagramat A 1630 3434 N ⎛⎞ =+⎜⎟ ⎝⎠ Nij and (175lb) W ==− Wjj
(30ft)(20ft)(12ft) 38ft 15106 191919
(30ft)(24ft)(32ft) 50ft 151216 252525
PROBLEM 2.113 (Continued)
Substituting the expressions obtained for ,,,ABAC TTN and W; factoring i, j, and k; and equating each of the coefficients to zero gives the following equations:
From i: 151516 0 251934 ABAC TTN −−+=
From j: 121030 (175 lb)0 251934 ABAC TTN++−=
From k: 166 0 2519ABACTT = (3)
Solving the resulting set of equations gives:

PROBLEM 2.114
Solve Problem 2.113, assuming that a friend is helping the man at A by pulling on him with a force P = (45 lb)k.
PROBLEM2.113 In trying to move across a slippery icy surface, a 175-lb man uses two ropes AB and AC. Knowing that the force exerted on the man by the icy surface is perpendicular to that surface, determine the tension in each rope.
SOLUTION
Refer to Problem 2.113 for the figure and analysis leading to the following set of equations, Equation (3) being modified to include the additional force (45lb). = Pk
Solving the resulting set of equations simultaneously gives:

SOLUTION
PROBLEM 2.115
For the rectangular plate of Problems 2.109 and 2.110, determine the tension in each of the three cables knowing that the weight of the plate is 792 N.
See Problem 2.109 for the figure and the analysis leading to the linear algebraic Equations (1), (2), and (3) below. Setting 792 N P = gives:
Solving Equations (1), (2), and (3) by conventional algorithms gives
PROBLEM 2.116
For the cable system of Problems 2.107 and 2.108, determine the tension in each cable knowing that 2880 N P = and 0. Q =
SOLUTION 0: 0 AABACAD Σ=++++= FTTTPQ
Where P = Pi and Q = Qj
ABAB ACAC
(960 mm)(240 mm)(380 mm)1060 mm (960 mm)(240 mm)(320 mm)1040 mm (960 mm)(720 mm)(220 mm)1220 mm
481219 535353 1234 131313 483611 616161
Substituting into 0, A Σ= F setting (2880 N) P = i and 0, Q = and setting the coefficients of , , ijk equal to 0, we obtain the following three equilibrium equations:







































































































