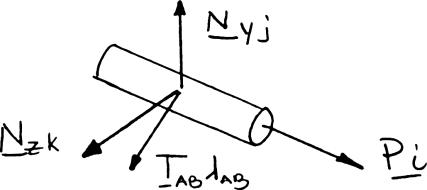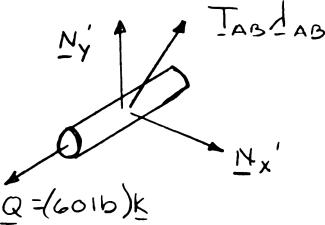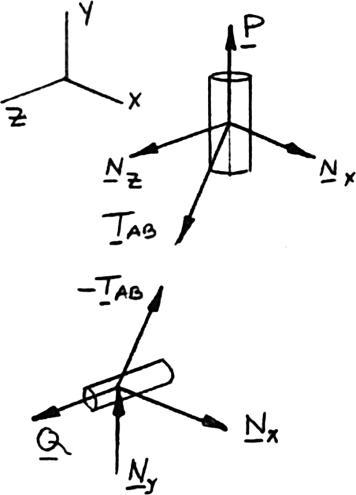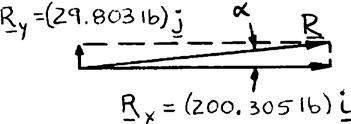
SOLUTION
(a) Parallelogram law:
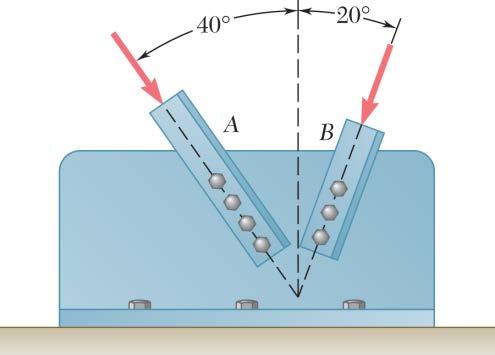
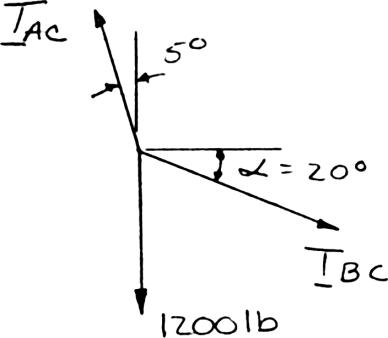
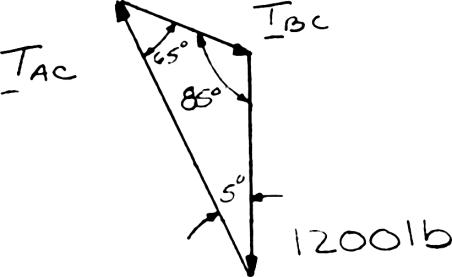
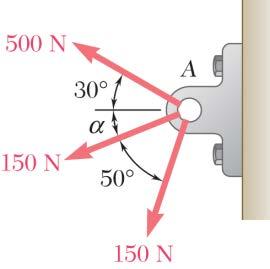
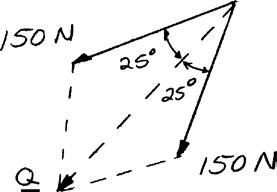
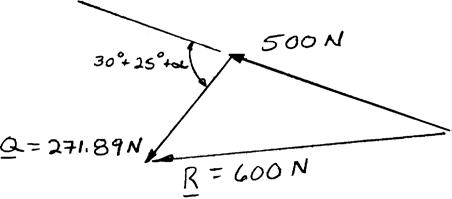
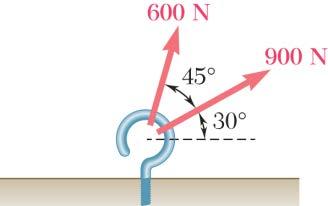
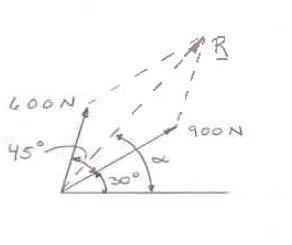
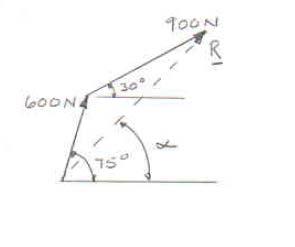
PROBLEM 2.1
Two forces are applied as shown to a hook. Determine graphically the magnitude and direction of their resultant using (a) the parallelogram law, (b) the triangle rule.
(b) Triangle rule:

Copyright © McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
SOLUTION
(a) Parallelogram law:
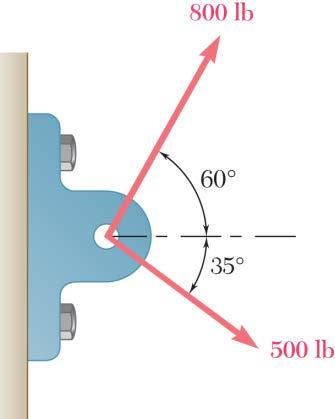
PROBLEM 2.2
Two forces are applied as shown to a bracket support. Determine graphically the magnitude and direction of their resultant using (a) the parallelogram law, (b) the triangle rule.
(b) Triangle rule:

Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
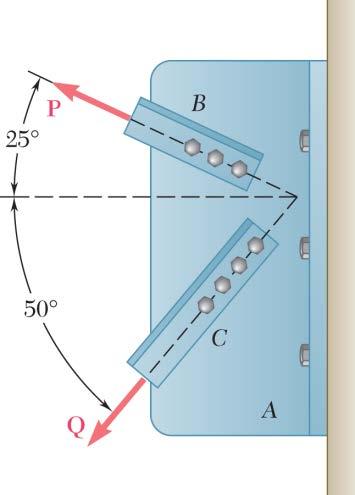
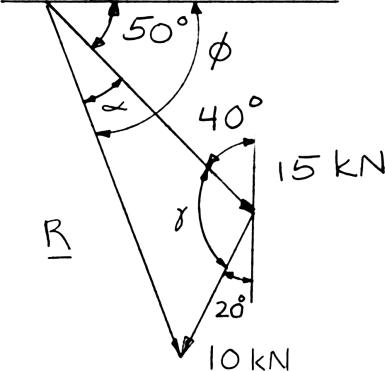
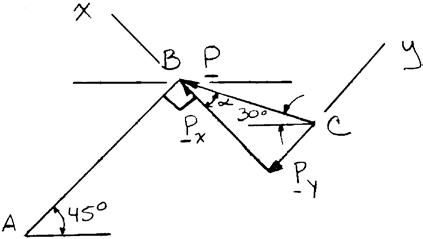
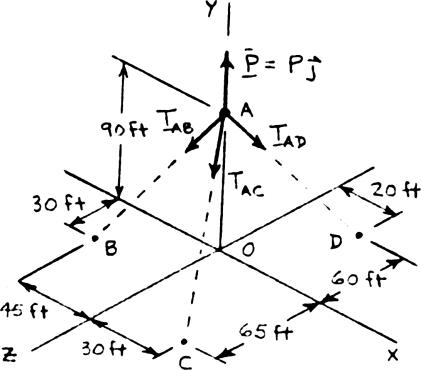
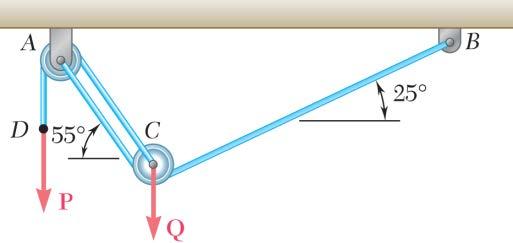
PROBLEM 2.3
Two structural members B and C are bolted to bracket A. Knowing that both members are in tension and that P = 10 kN and Q = 15 kN, determine graphically the magnitude and direction of the resultant force exerted on the bracket using (a) the parallelogram law, (b) the triangle rule.
SOLUTION
(a) Parallelogram law:
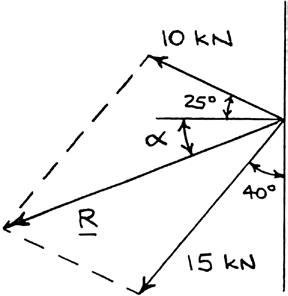
(b) Triangle rule:
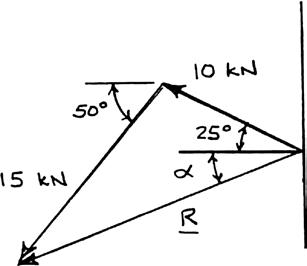
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

PROBLEM 2.4
Two structural members B and C are bolted to bracket A. Knowing that both members are in tension and that P = 6 kips and Q = 4 kips, determine graphically the magnitude and direction of the resultant force exerted on the bracket using (a) the parallelogram law, (b) the triangle rule.
SOLUTION
(a) Parallelogram law:
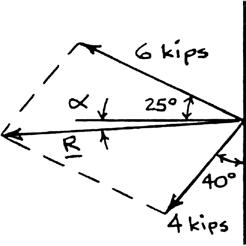
(b) Triangle rule:
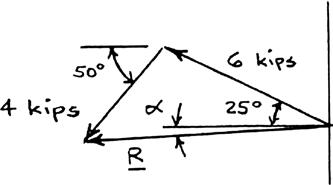
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
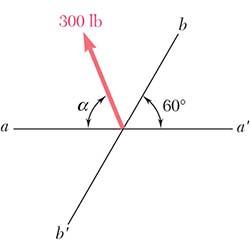
PROBLEM 2.5
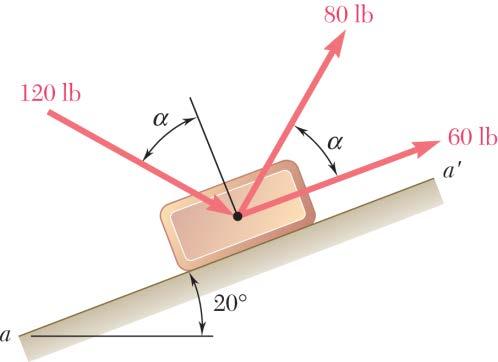
The 300-lb force is to be resolved into components along lines a-a′ and b-b′ (a) Determine the angle α by trigonometry knowing that the component along line a-a′ is to be 240 lb. (b) What is the corresponding value of the component along b-b′?
SOLUTION
(a) Using the triangle rule and law of sines:
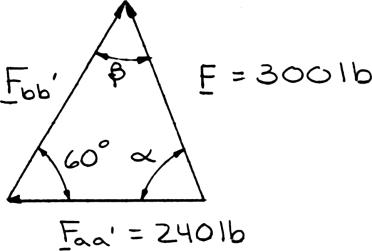
(b) Law of sines:

PROBLEM 2.6
The 300-lb force is to be resolved into components along lines a-a′ and b-b′ (a) Determine the angle α by trigonometry knowing that the component along line b-b′ is to be 120 lb. (b) What is the corresponding value of the component along a-a′?
SOLUTION
Using the triangle rule and law of sines:
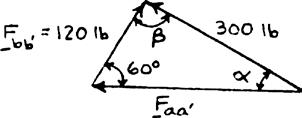
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
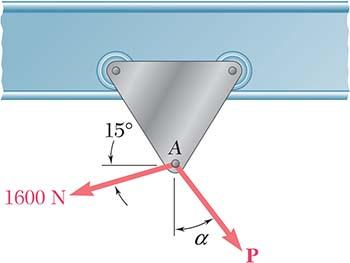
PROBLEM 2.7
A trolley that moves along a horizontal beam is acted upon by two forces as shown. (a) Knowing that α = 25°, determine by trigonometry the magnitude of the force P so that the resultant force exerted on the trolley is vertical. (b) What is the corresponding magnitude of the resultant? SOLUTION
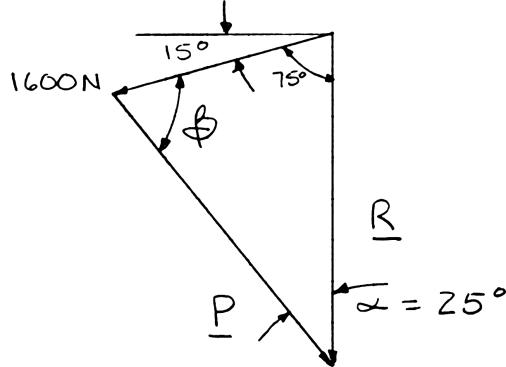
Using the triangle rule and the law of sines:
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
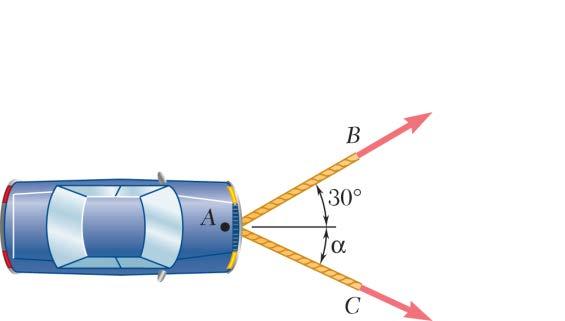
PROBLEM 2.8
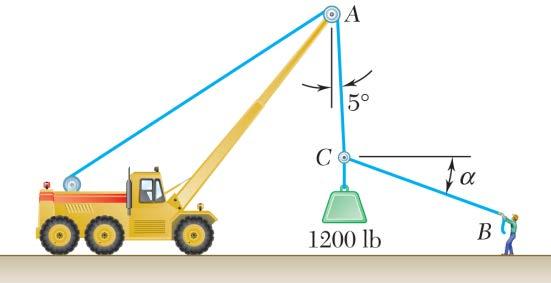
A disabled automobile is pulled by means of two ropes as shown. The tension in rope AB is 2.2 kN, and the angle α is 25°. Knowing that the resultant of the two forces applied at A is directed along the axis of the automobile, determine by trigonometry (a) the tension in rope AC, (b) the magnitude of the resultant of the two forces applied at A
SOLUTION
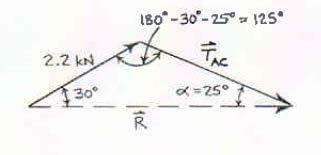
Using the law of sines:
© McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
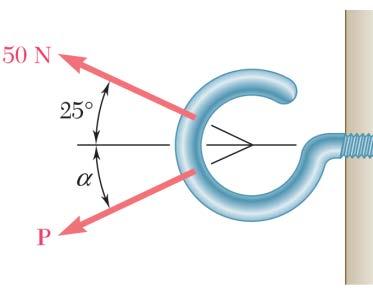
PROBLEM 2.9
Two forces are applied as shown to a hook support. Knowing that the magnitude of P is 35 N, determine by trigonometry (a) the required angle α if the resultant R of the two forces applied to the support is to be horizontal, (b) the corresponding magnitude of R
Using the triangle rule and law of sines:
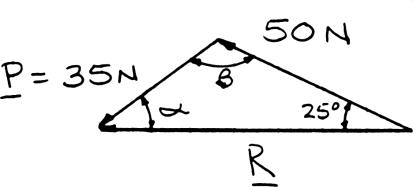
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

PROBLEM 2.10
A disabled automobile is pulled by means of two ropes as shown. Knowing that the tension in rope AB is 3 kN, determine by trigonometry the tension in rope AC and the value of α so that the resultant force exerted at A is a 4.8kN force directed along the axis of the automobile.
SOLUTION
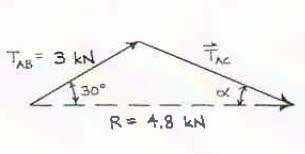
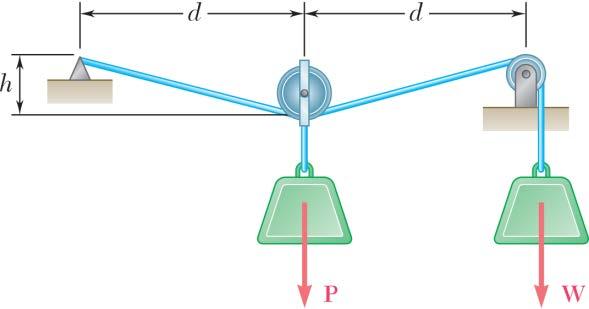
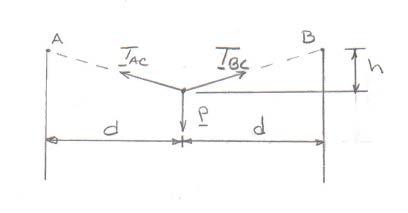
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

PROBLEM 2.11
A trolley that moves along a horizontal beam is acted upon by two forces as shown. Determine by trigonometry the magnitude and direction of the force P so that the resultant is a vertical force of 2500 N.
SOLUTION
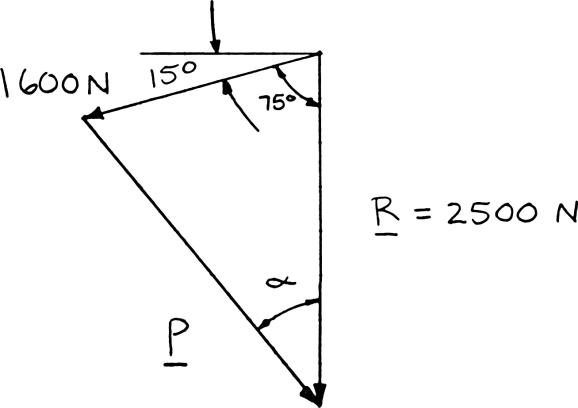
Using the law of cosines: 222 (1600 N)(2500 N)2(1600 N)(2500 N)cos 75°
Using the law of sines:
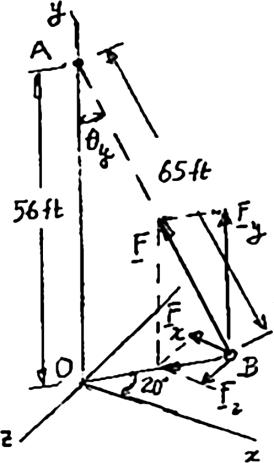
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
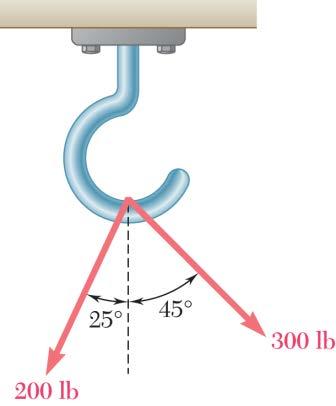
SOLUTION
PROBLEM 2.12
For the hook support shown, determine by trigonometry the magnitude and direction of the resultant of the two forces applied to the support.
Using the law of cosines:
Using the law of sines:
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

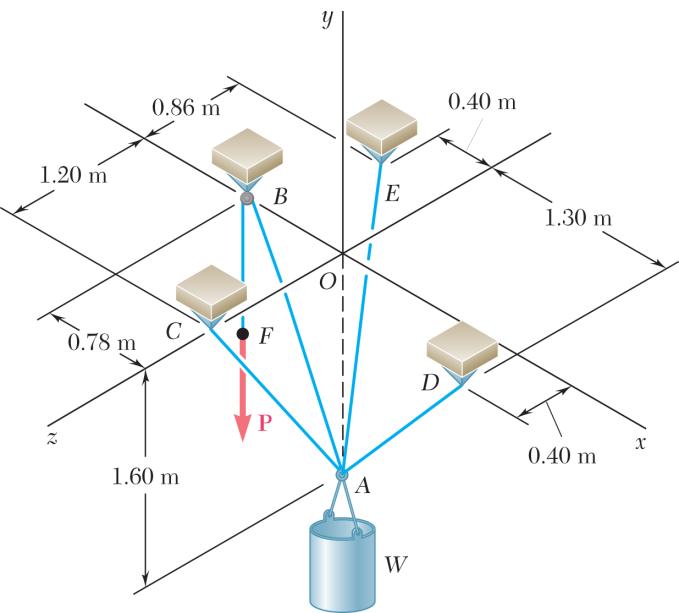
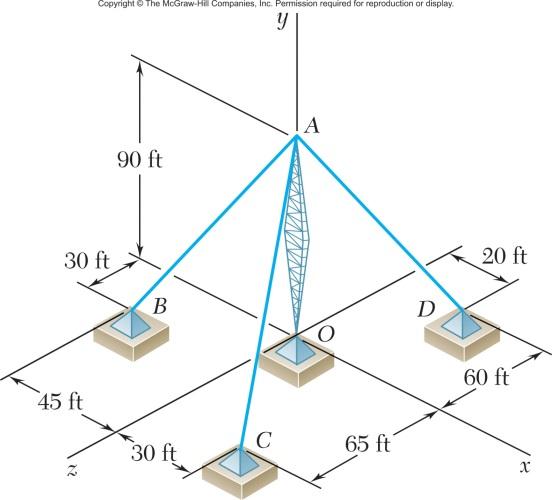
PROBLEM 2.13
The cable stays AB and AD help support pole AC. Knowing that the tension is 120 lb in AB and 40 lb in AD, determine graphically the magnitude and direction of the resultant of the forces exerted by the stays at A using (a) the parallelogram law, (b) the triangle rule.
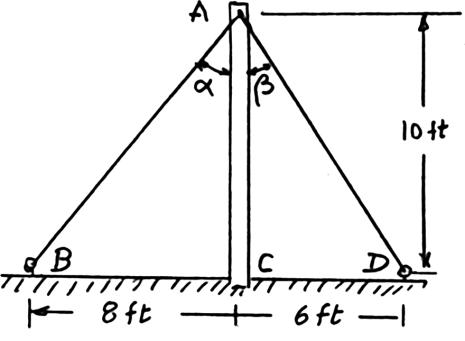

SOLUTION
PROBLEM 2.14
Solve Problem 2.4 by trigonometry.
PROBLEM2.4: Two structural members B and C are bolted to bracket A. Knowing that both members are in tension and that P = 6 kips and Q = 4 kips, determine graphically the magnitude and direction of the resultant force exerted on the bracket using (a) the parallelogram law, (b) the triangle rule.
Using the force triangle and the laws of cosines and sines: We have:
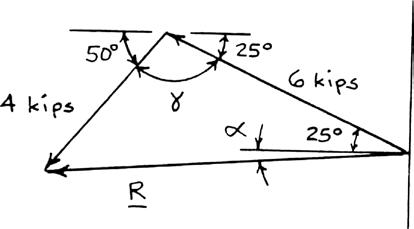
Then 222 2 (4kips)(6kips)2(4kips)(6kips)cos105 64.423kips 8.0264kips
4kips8.0264kips

SOLUTION
PROBLEM 2.15
For the hook support of Prob. 2.9, determine by trigonometry (a) the magnitude and direction of the smallest force P for which the resultant R of the two forces applied to the support is horizontal, (b) the corresponding magnitude of R
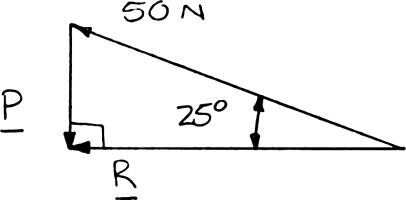
The smallest force P will be perpendicular to R
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION
Compute the following distances:
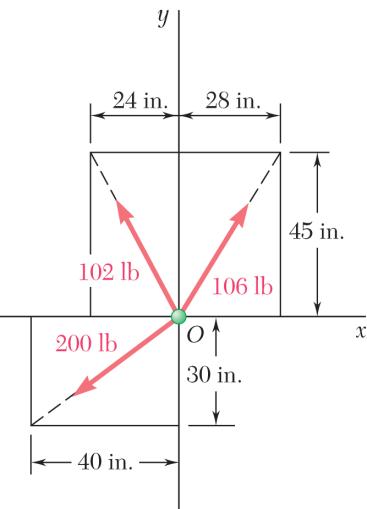
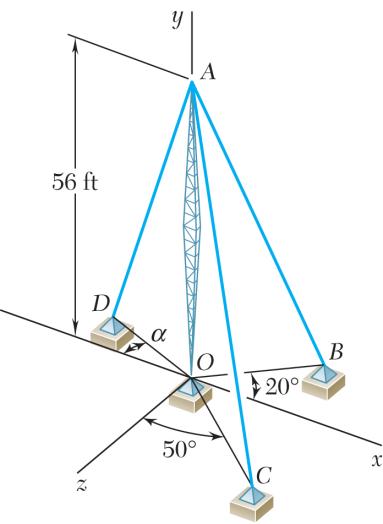
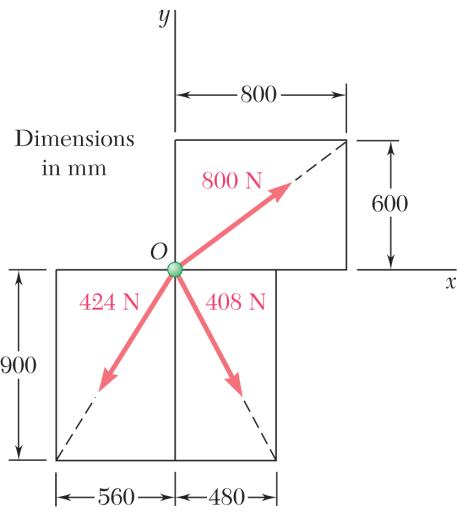
PROBLEM 2.16
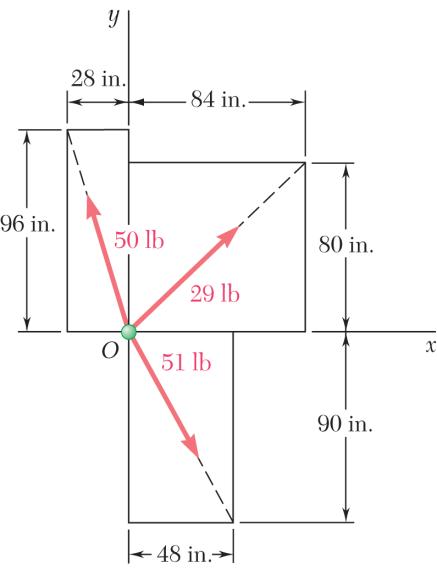
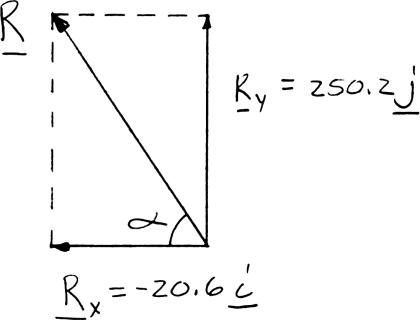
Determine the x and y components of each of the forces shown.
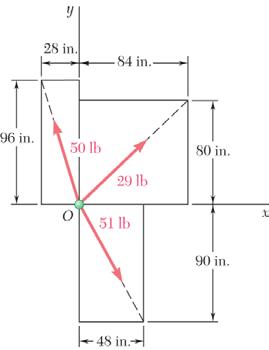
SOLUTION
Compute the following distances:
PROBLEM 2.17
Determine the x and y components of each of the forces shown.
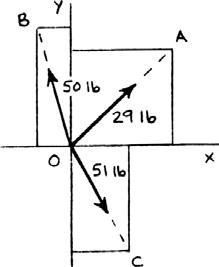
PROBLEM 2.18
Determine the x and y components of each of the forces shown.
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION
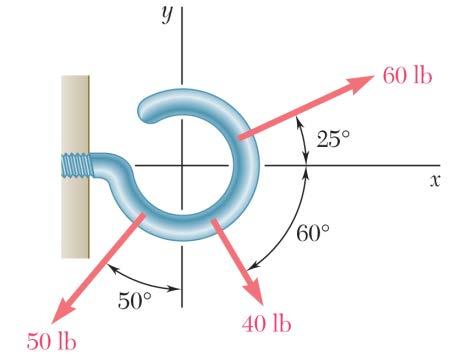
PROBLEM 2.19
Determine the x and y components of each of the forces shown.
80-N Force: (80 N)cos40 xF = +°
(80 N)sin40 y F =+°
120-N Force: (120 N)cos70 xF =
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
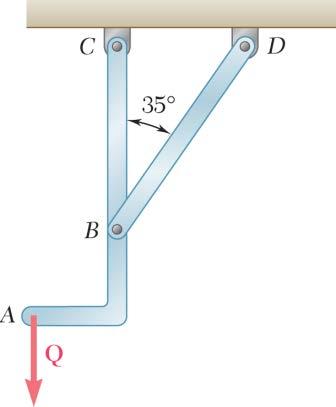
PROBLEM 2.20
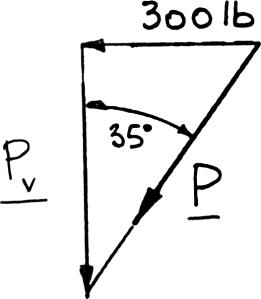
Member BD exerts on member ABC a force P directed along line BD Knowing that P must have a 300-lb horizontal component, determine (a) the magnitude of the force P, (b) its vertical component.
(b) Vertical component
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
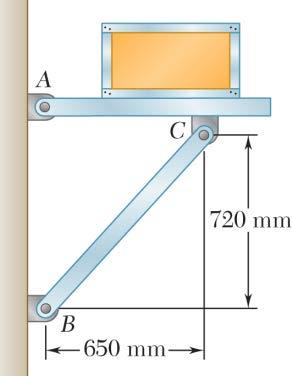
PROBLEM 2.21
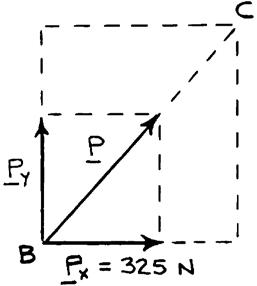
Member BC exerts on member AC a force P directed along line BC. Knowing that P must have a 325-N horizontal component, determine (a) the magnitude of the force P, (b) its vertical component. SOLUTION
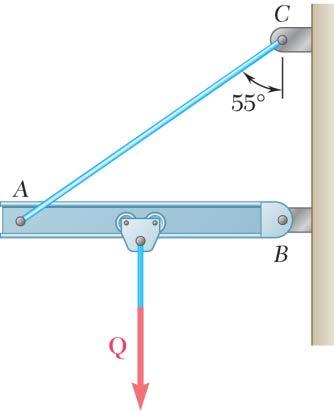
PROBLEM 2.22
Cable AC exerts on beam AB a force P directed along line AC. Knowing that P must have a 350-lb vertical component, determine (a) the magnitude of the force P, (b) its horizontal component.
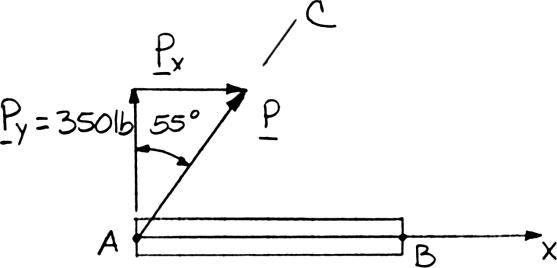
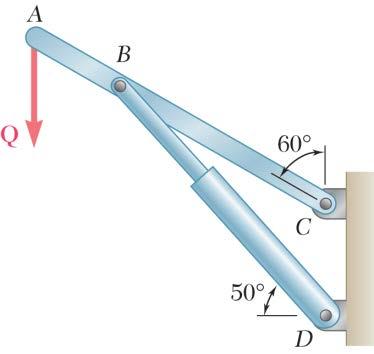
PROBLEM 2.23
The hydraulic cylinder BD exerts on member ABC a force P directed along line BD. Knowing that P must have a 750-N component perpendicular to member ABC, determine (a) the magnitude of the force P, (b) its component parallel to ABC
SOLUTION (a)
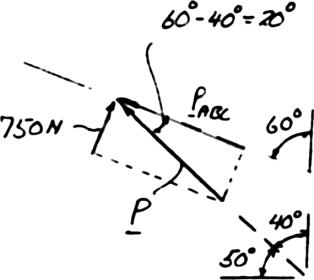
b) cos20 ABC PP=°
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

SOLUTION
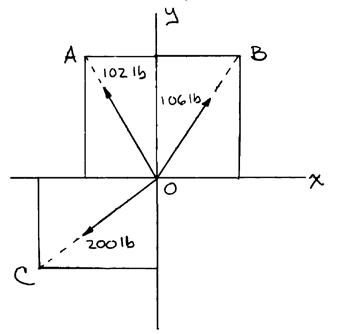
PROBLEM 2.24
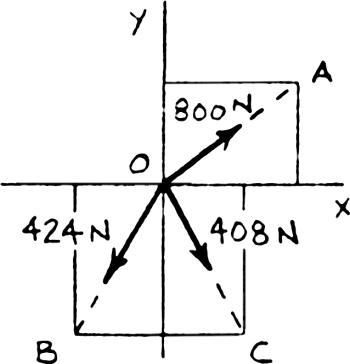
Determine the resultant of the three forces of Problem 2.16
PROBLEM2.16 Determine the x and y components of each of the forces shown.
Components of the forces were determined in Problem 2.16:
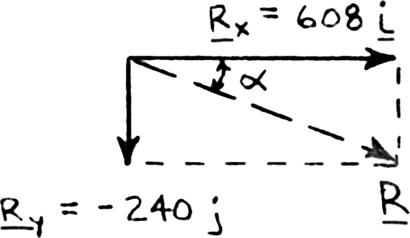
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION
PROBLEM 2.25
Determine the resultant of the three forces of Problem 2.17.
PROBLEM2.17 Determine the x and y components of each of the forces shown.
Components of the forces were determined in Problem 2.17:
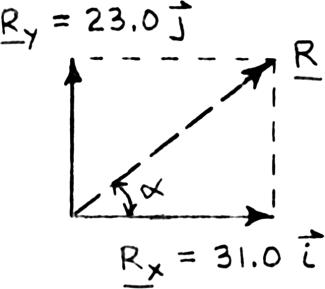

PROBLEM 2.26
Determine the resultant of the three forces of Problem 2.18.
PROBLEM2.18 Determine the x and y components of each of the forces shown. SOLUTION
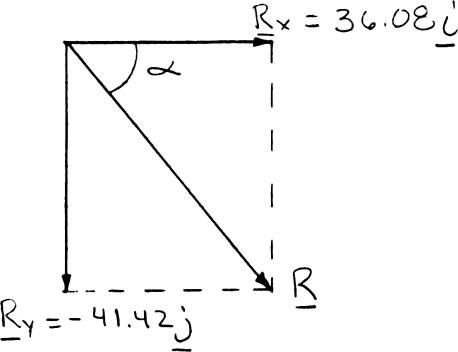

SOLUTION
PROBLEM 2.27
Determine the resultant of the three forces of Problem 2.19.
PROBLEM2.19 Determine the x and y components of each of the forces shown.
Components of the forces were determined in Problem 2.19:
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION
PROBLEM 2.28
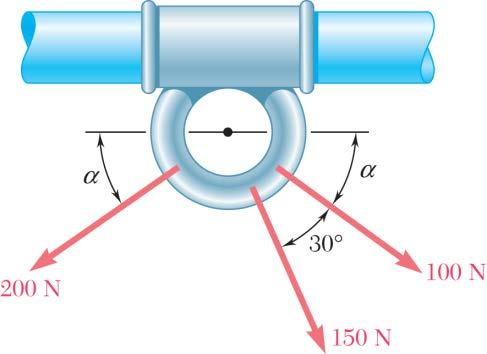
For the collar loaded as shown, determine (a) the required value of α if the resultant of the three forces shown is to be vertical, (b) the corresponding magnitude of the resultant.
(100 N)cos(150 N)cos(30)(200 N)cos (100 N)cos(150 N)cos(30)
(100 N)sin(150 N)sin(30)(200 N)sin (300 N)sin(150 N)sin(30)
(a) For R to be vertical, we must have 0. xR = We make 0 xR = in Eq. (1): 100cos150cos(30)0 100cos150(coscos30sinsin30)0
(b) Substituting for α in Eq. (2):
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
PROBLEM 2.29
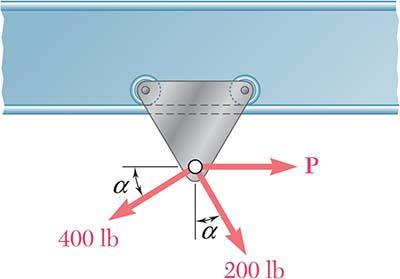
A hoist trolley is subjected to the three forces shown. Knowing that α = 40°, determine (a) the required magnitude of the force P if the resultant of the three forces is to be vertical, (b) the corresponding magnitude of the resultant.
SOLUTION
(a) For R to be vertical, we must have 0. xR = Set 0 xR = in Eq. (1)
(b) Since R is to be vertical:
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

SOLUTION
PROBLEM 2.30
A hoist trolley is subjected to the three forces shown. Knowing that P = 250 lb, determine (a) the required value of α if the resultant of the three forces is to be vertical, (b) the corresponding magnitude of the resultant.
xR = 250 lb(200 lb)sin(400 lb)cos xF Σ=+−αα 250 lb(200 lb)sin(400 lb)cos xR =+−αα (1) y R = (200 lb)cos(400 lb)sin y F Σ=+αα
(a) For R to be vertical, we must have 0. xR = Set 0 xR = in Eq. (1)
0250lb(200lb)sin(400lb)cos =+−αα
(400lb)cos(200lb)sin250lb 2cossin1.25
4cossin2.5sin1.5625 4(1sin)sin2.5sin1.5625 05sin2.5sin2.4375
Using the quadratic formula to solve for the roots gives sin0.49162 α = or
(b) Since R is to be vertical:
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
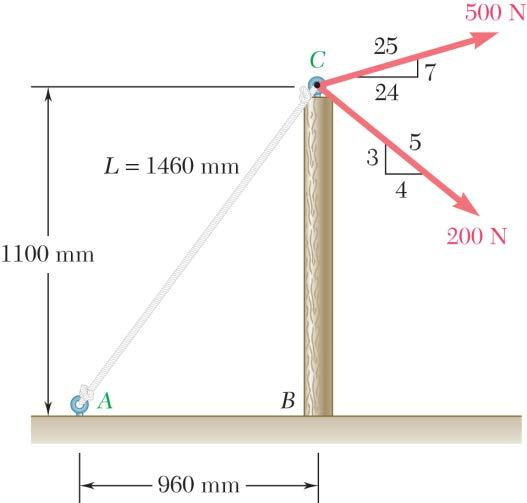
PROBLEM 2.31
For the post loaded as shown, determine (a) the required tension in rope AC if the resultant of the three forces exerted at point C is to be horizontal, (b) the corresponding magnitude of the resultant.
(a) For R to be horizontal, we must have 0. y R =
0 y R = in Eq. (2):
(b) Substituting for ACT into Eq. (1) gives
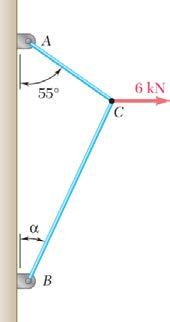
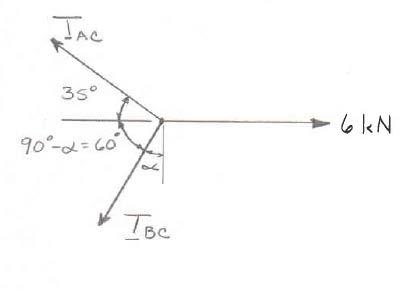
PROBLEM 2.32
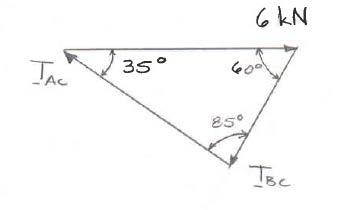
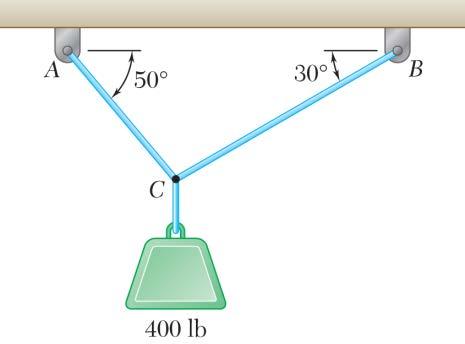
Two cables are tied together at C and are loaded as shown. Knowing that α = 30°, determine the tension (a) in cable AC, (b) in cable BC.
SOLUTION Free-BodyDiagramForceTriangle
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
PROBLEM 2.33
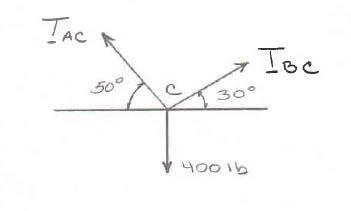
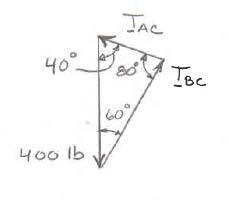
Two cables are tied together at C and are loaded as shown. Determine the tension (a) in cable AC, (b) in cable BC
SOLUTION
Free-BodyDiagramForceTriangle
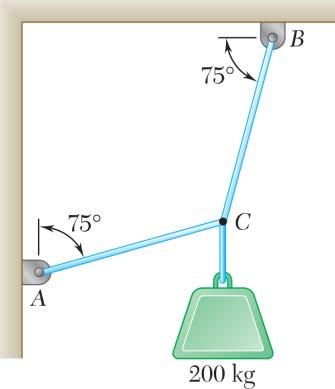
PROBLEM 2.34
Two cables are tied together at C and are loaded as shown. Determine the tension (a) in cable AC, (b) in cable BC
SOLUTION
Free-BodyDiagramForceTriangle
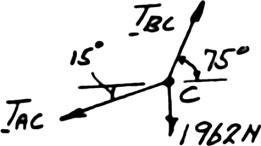
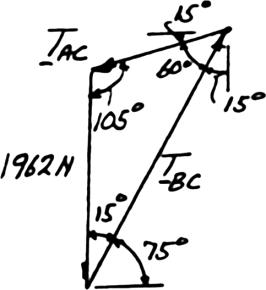
(200kg)(9.81m/s)
(1962 N) sin15 sin60
(1962 N)sin105
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
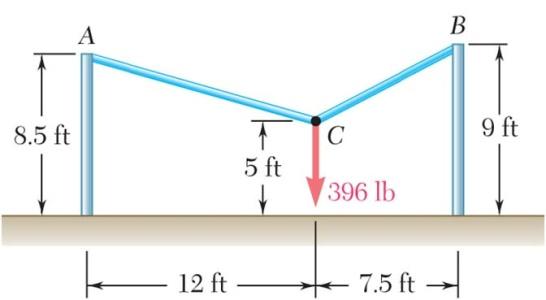
PROBLEM 2.35
Two cables are tied together at C and loaded as shown. Determine the tension (a) in cable AC, (b) in cable BC.
FreeBodyDiagramat C:
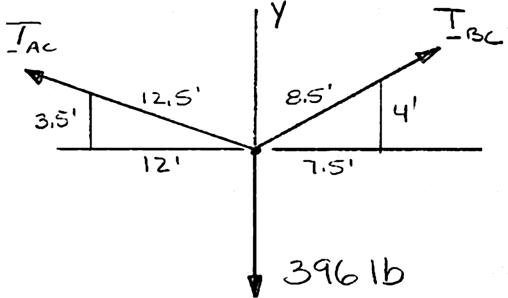
PROBLEM 2.36
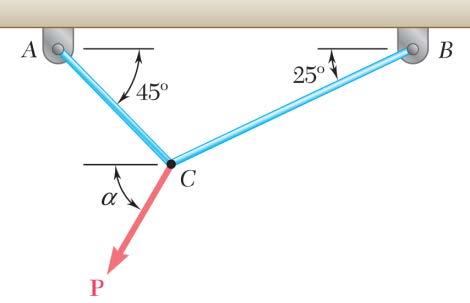
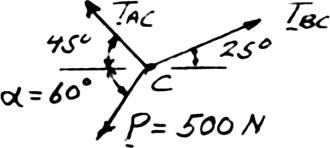
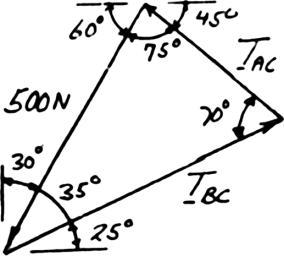
Two cables are tied together at C and are loaded as shown. Knowing that P = 500 N and α = 60°, determine the tension in (a) in cable AC, (b) in cable BC SOLUTION Free-BodyDiagramForceTriangle
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
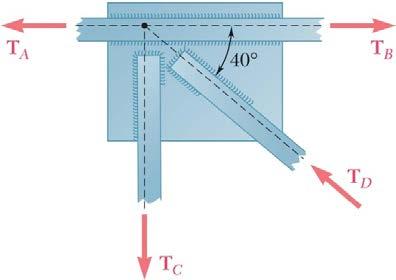
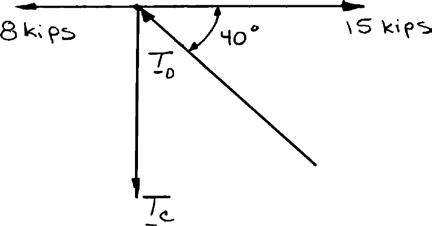
PROBLEM 2.37
Two forces of magnitude T A = 8 kips and T B = 15 kips are applied as shown to a welded connection. Knowing that the connection is in equilibrium, determine the magnitudes of the forces T C and T D . SOLUTION
Free-BodyDiagram
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
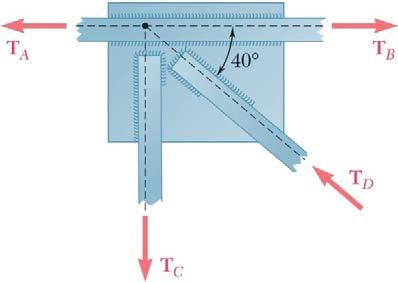
SOLUTION
PROBLEM 2.38
Two forces of magnitude T A = 6 kips and T C = 9 kips are applied as shown to a welded connection. Knowing that the connection is in equilibrium, determine the magnitudes of the forces T B and T D .
Free-BodyDiagram
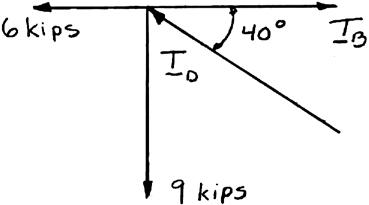
0 xF Σ= 6kipscos400BD TT−−°= (1)
0 y F Σ= sin409kips0 9kips sin40 14.0015kips D
Substituting for T D into Eq. (1) gives: 6kips(14.0015kips)cos400 16.7258kips B B T T °= = 16.73 kips BT =
kips
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
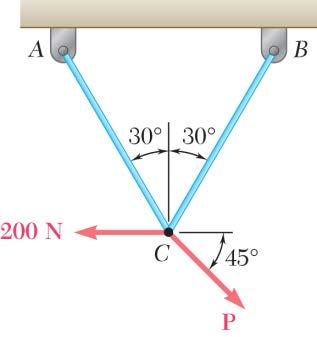
PROBLEM 2.39
Two cables are tied together at C and are loaded as shown. Knowing that P = 300 N, determine the tension in cables AC and BC
SOLUTION
Free-BodyDiagram
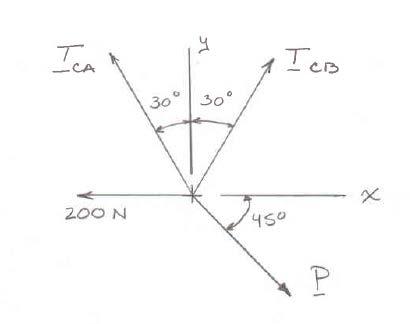
0sin30sin30cos45200N0xCACB FTTP Σ=−+−°−= AA
For 200N P = we have,
0.50.5212.132000 CACBTT −++−= (1)
0 y F Σ= cos30cos30sin450CACB TTP°−−= AA
0.866030.86603212.130 CACB TT+−= (2)
Solving equations (1) and (2) simultaneously gives,
CAT =
CBT =
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION
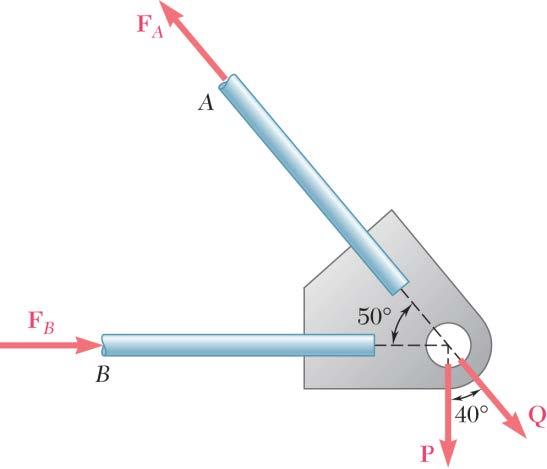
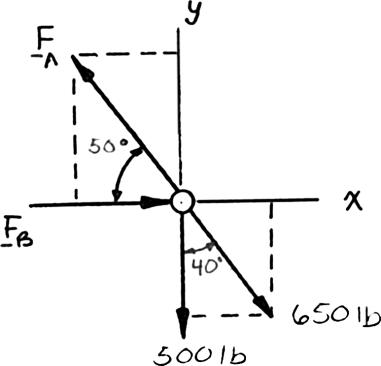
PROBLEM 2.40
Two forces P and Q are applied as shown to an aircraft connection. Knowing that the connection is in equilibrium and that 500 P = lb and 650 Q = lb, determine the magnitudes of the forces exerted on the rods A and B
Resolving the forces into x- and y-directions: 0 AB =+++=RPQFF
Substituting components: (500lb)[(650lb)cos50] [(650lb)sin50] (cos50)(sin50)0BAA FFF =−+°
In the y-direction (one unknown force):
500lb(650lb)sin50sin500 AF °+°= Thus, 500lb(650lb)sin50 sin50 AF +°
In the x-direction: (650lb)cos50cos500 BAFF °+−°= Thus, cos50(650lb)cos50 (1302.70lb)cos50(650lb)cos50
Free-BodyDiagram
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION
PROBLEM 2.41
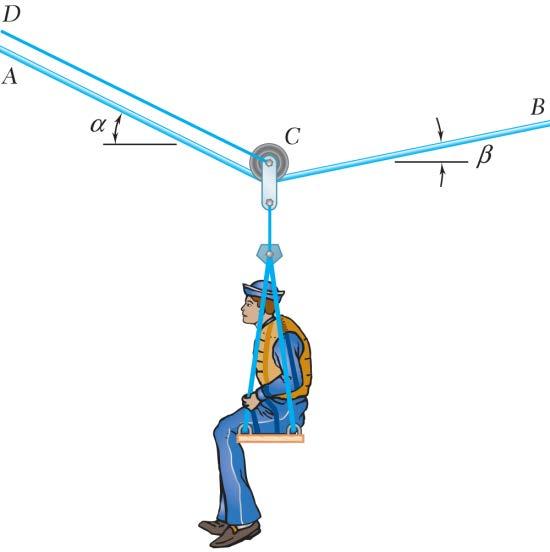
A sailor is being rescued using a boatswain’s chair that is suspended from a pulley that can roll freely on the support cable ACB and is pulled at a constant speed by cable CD. Knowing that α = 30° and β = 10° and that the combined weight of the boatswain’s chair and the sailor is 200 lb, determine the tension (a) in the support cable ACB, (b) in the traction cable CD
Free-BodyDiagram
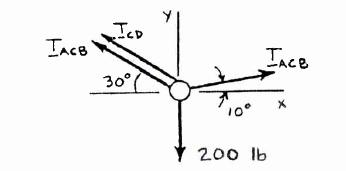
0:cos10cos30cos300 xACBACBCD FTTTΣ=
0:sin10sin30sin302000 yACBACBCD FTTTΣ= °+°+°−=
(1)
ACBCDTT+= (2) (a) Substitute (1) into (2): 0.673650.5(0.137158)200 ACBACB TT+=
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

SOLUTION
PROBLEM 2.42
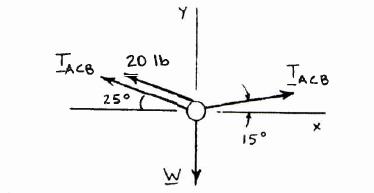
A sailor is being rescued using a boatswain’s chair that is suspended from a pulley that can roll freely on the support cable ACB and is pulled at a constant speed by cable CD. Knowing that α = 25° and β = 15° and that the tension in cable CD is 20 lb, determine (a) the combined weight of the boatswain’s chair and the sailor, (b) the tension in the support cable ACB
Free-BodyDiagram
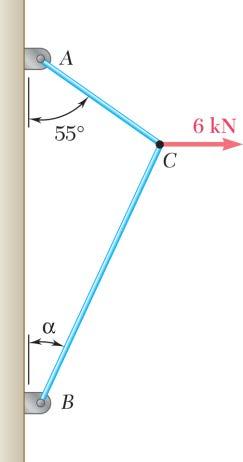
PROBLEM 2.43
For the cables of prob. 2.32, find the value of α for which the tension is as small as possible (a) in cable bc, (b) in both cables simultaneously. In each case determine the tension in each cable
SOLUTION Free-BodyDiagramForceTriangle
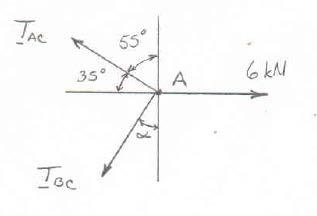
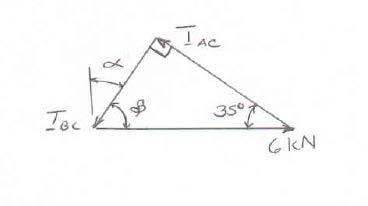
(a) For a minimum tension in cable BC, set angle between cables to 90 degrees. By inspection,
(b) For equal tension in both cables, the force triangle will be an isosceles.
by inspection,
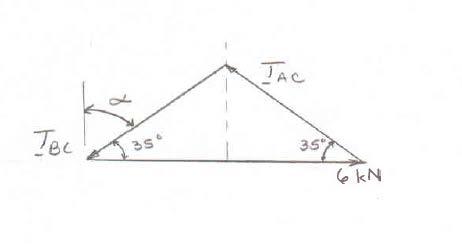
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

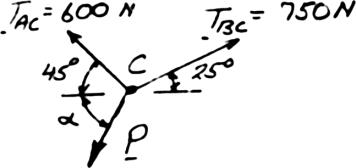
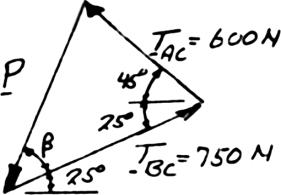
PROBLEM 2.44
For the cables of Problem 2.36, it is known that the maximum allowable tension is 600 N in cable AC and 750 N in cable BC Determine (a) the maximum force P that can be applied at C, (b) the corresponding value of α SOLUTION
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

PROBLEM 2.45
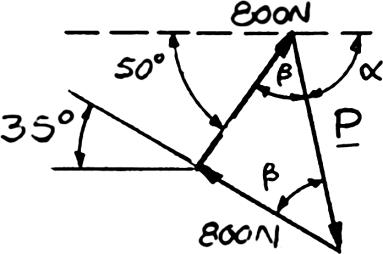
Two cables tied together at C are loaded as shown. Knowing that the maximum allowable tension in each cable is 800 N, determine (a) the magnitude of the largest force P that can be applied at C, (b) the corresponding value of α
SOLUTION
Free-BodyDiagram: C ForceTriangle
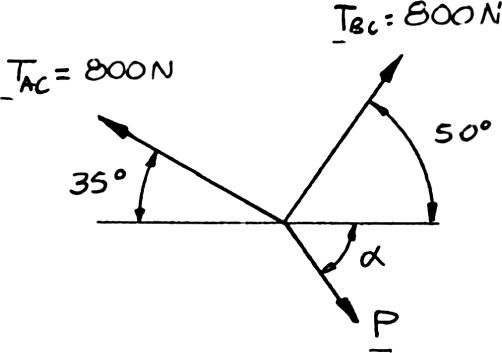
Force triangle is isosceles with
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
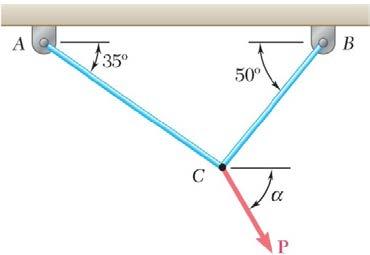
PROBLEM 2.46
Two cables tied together at C are loaded as shown. Knowing that the maximum allowable tension is 1200 N in cable AC and 600 N in cable BC, determine (a) the magnitude of the largest force P that can be applied at C, (b) the corresponding value of
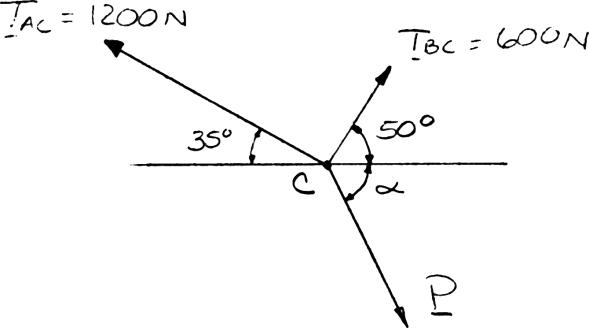
(a) Law of cosines:
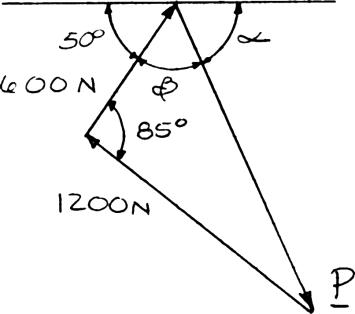
(1200 N)(600 N)2(1200 N)(600 N)cos85
Since 1200 N, P the solution is correct.
(b) Law of sines:
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION
Free-BodyDiagram
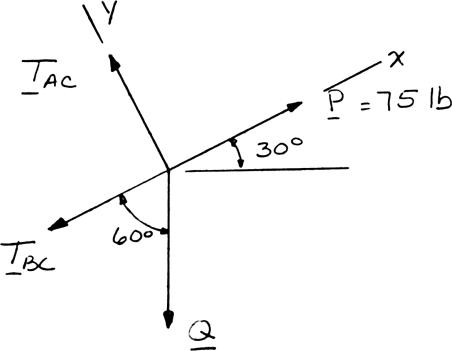
PROBLEM 2.47
Two cables tied together at C are loaded as shown. Determine the range of values of Q for which the tension will not exceed 60 lb in either cable.
0:cos6075 lb0 xBC FTQ Σ=−−°+= 75 lbcos60 BC TQ=−° (1)
0:sin600yAC FTQ Σ=−°= sin60 AC TQ=° (2)
Requirement: 60 lb: ACT = From Eq. (2): sin6060 lb Q °= 69.3 lb Q =
Requirement: 60 lb: BCT = From Eq. (1): 75 lbcos6060lb Q −°= 30.0lb Q = 30.0lb69.3lb Q ≤≤
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
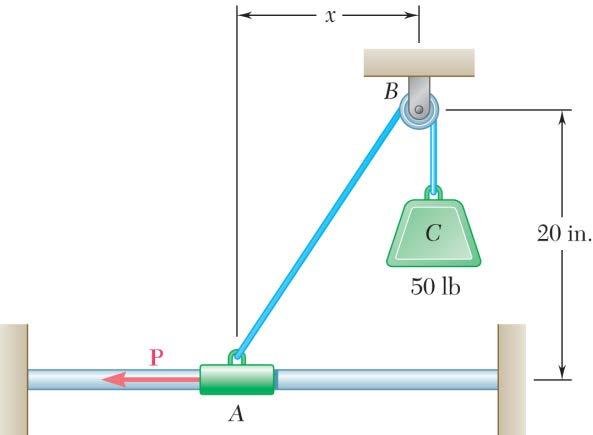
PROBLEM 2.48
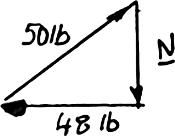
Collar A is connected as shown to a 50-lb load and can slide on a frictionless horizontal rod. Determine the magnitude of the force P required to maintain the equilibrium of the collar when (a) 4.5 in., x = (b) 15 in. x =
SOLUTION
(a) FreeBody:Collar A
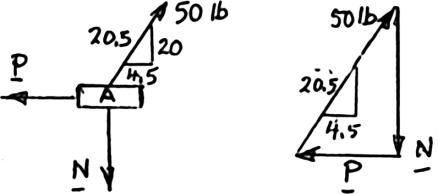
(b) FreeBody:Collar A

ForceTriangle
ForceTriangle
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

SOLUTION
FreeBody:Collar A
SimilarTriangles
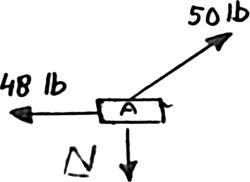
PROBLEM 2.49
Collar A is connected as shown to a 50-lb load and can slide on a frictionless horizontal rod. Determine the distance x for which the collar is in equilibrium when P = 48 lb.
ForceTriangle
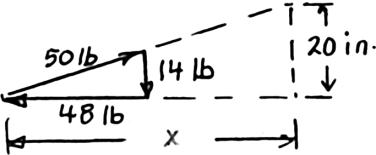
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
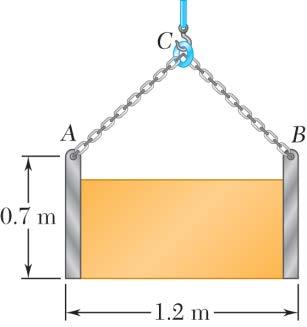
PROBLEM 2.50
A movable bin and its contents have a combined weight of 2.8 kN. Determine the shortest chain sling ACB that can be used to lift the loaded bin if the tension in the chain is not to exceed 5 kN.
SOLUTION
Free-BodyDiagram
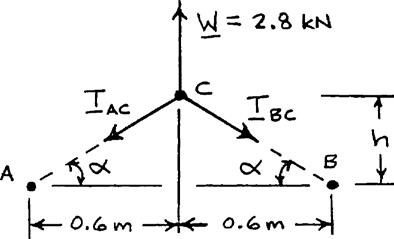
IsoscelesForceTriangle
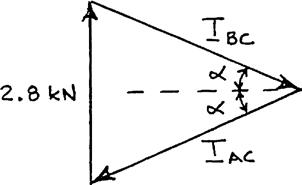
of
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION
Free-BodyDiagramofPulley
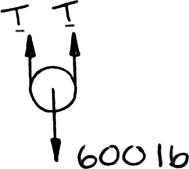
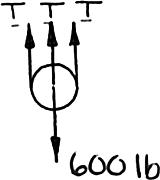
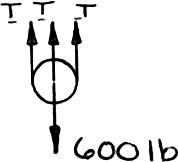
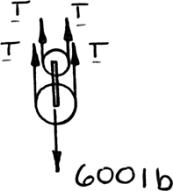
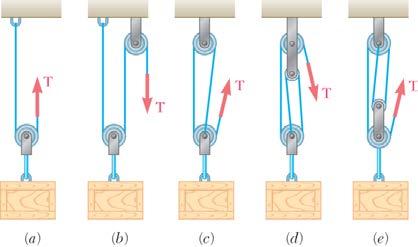
PROBLEM 2.51
A 600-lb crate is supported by several ropeand-pulley arrangements as shown. Determine for each arrangement the tension in the rope. (Hint: The tension in the rope is the same on each side of a simple pulley. This can be proved by the methods of Ch. 4.)
© McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
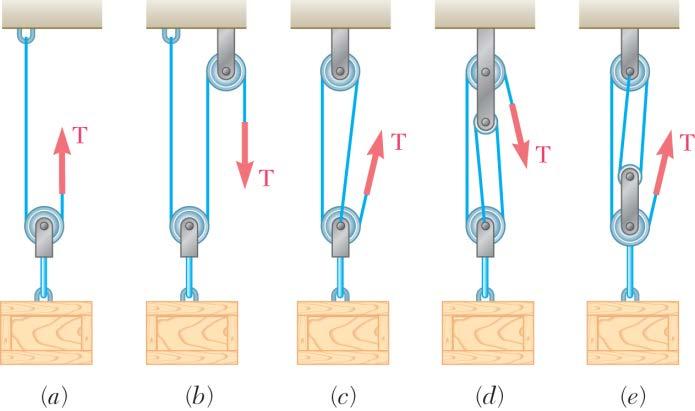
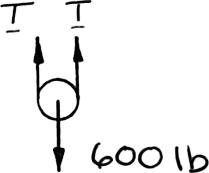
PROBLEM 2.52
Solve Parts b and d of Problem 2.51, assuming that the free end of the rope is attached to the crate.
PROBLEM2.51 A 600-lb crate is supported by several rope-and-pulley arrangements as shown. Determine for each arrangement the tension in the rope. . (Hint: The tension in the rope is the same on each side of a simple pulley. This can be proved by the methods of Ch. 4.)
SOLUTION Free-BodyDiagramofPulleyandCrate
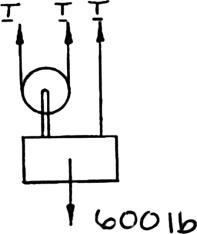
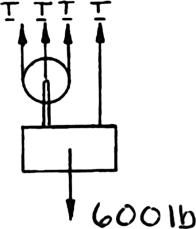
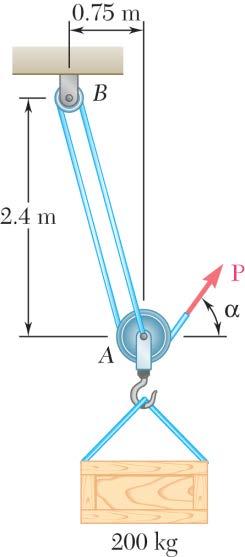
PROBLEM 2.53
A 200-kg crate is to be supported by the rope-and-pulley arrangement shown. Determine the magnitude and direction of the force P that must be exerted on the free end of the rope to maintain equilibrium. (See the hint for Prob. 2.51.)
SOLUTION
Free-BodyDiagram:Pulley A
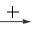
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
PROBLEM 2.54
A load Q is applied to the pulley C, which can roll on the cable ACB. The pulley is held in the position shown by a second cable CAD, which passes over the pulley A and supports a load P. Knowing that 750 N, P = determine (a) the tension in cable ACB, (b) the magnitude of load Q
SOLUTION
Free-BodyDiagram:Pulley C

b) 0:(sin25sin55)(750 N)sin550 (1292.88N)(sin25sin55)(750 N)sin550

PROBLEM 2.55
An 1800-N load Q is applied to the pulley C, which can roll on the cable ACB. The pulley is held in the position shown by a second cable CAD, which passes over the pulley A and supports a load P. Determine (a) the tension in cable ACB, (b) the magnitude of load P.
SOLUTION
Free-BodyDiagram:Pulley C
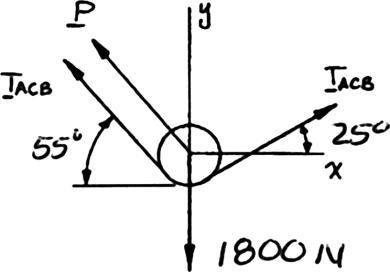
0:(cos25cos55)cos550xACB FTPΣ= °−°−°= or 0.58010 ACBPT = (1) 0:(sin25sin55)sin551800 N0 yACB FTPΣ= °+°+°−= or 1.241770.819151800 N ACB TP+= (2)
(a) Substitute Equation (1) into Equation (2): 1.241770.81915(0.58010)1800 N ACBACB TT+= Hence: 1048.37 N ACBT =
N ACBT = (b) Using (1), 0.58010(1048.37 N)608.16 N P = =
N P =
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
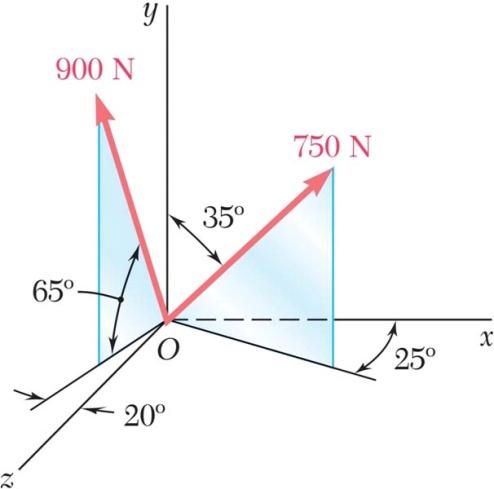
SOLUTION
PROBLEM 2.56
Determine (a) the x, y, and z components of the 900-N force, (b) the angles θx , θy , and θz that the force forms with the coordinate axes.
cos65 (900 N)cos65
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

SOLUTION
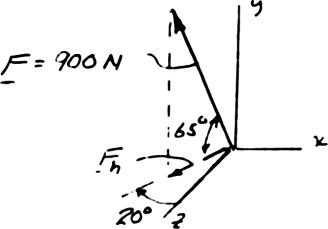
PROBLEM 2.57
Determine (a) the x, y, and z components of the 750-N force, (b) the angles θx , θy , and θz that the force forms with the coordinate axes.
sin35 (750 N)sin35
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION
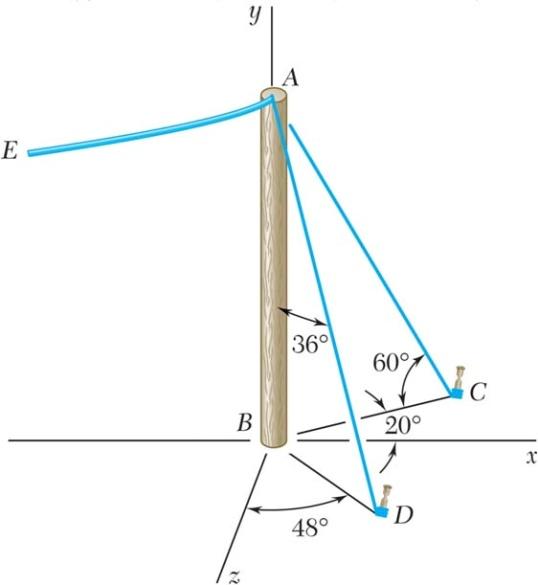
PROBLEM 2.58
The end of the coaxial cable AE is attached to the pole AB, which is strengthened by the guy wires AC and AD. Knowing that the tension in wire AC is 120 lb, determine (a) the components of the force exerted by this wire on the pole, (b) the angles θx , θy , and θz that the force forms with the coordinate axes.
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

SOLUTION
PROBLEM 2.59
The end of the coaxial cable AE is attached to the pole AB, which is strengthened by the guy wires AC and AD. Knowing that the tension in wire AD is 85 lb, determine (a) the components of the force exerted by this wire on the pole, (b) the angles θx , θy , and θz that the force forms with the coordinate axes.
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
PROBLEM 2.60
A gun is aimed at a point A located 35° east of north. Knowing that the barrel of the gun forms an angle of 40° with the horizontal and that the maximum recoil force is 400 N, determine (a) the x, y, and z components of that force, (b) the values of the angles θ x , θ y , and θ z defining the direction of the recoil force. (Assume that the x, y, and z axes are directed, respectively, east, up, and south.)
SOLUTION
Recoil

sin35 (306.42N)sin35
sin40 (400N)sin40
cos35 (306.42N)cos35
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
PROBLEM 2.61
Solve Problem 2.60, assuming that point A is located 15° north of west and that the barrel of the gun forms an angle of 25° with the horizontal.
PROBLEM2.60 A gun is aimed at a point A located 35° east of north. Knowing that the barrel of the gun forms an angle of 40° with the horizontal and that the maximum recoil force is 400 N, determine (a) the x, y, and z components of that force, (b) the values of the angles θ x , θ y , and θ z defining the direction of the recoil force. (Assume that the x, y, and z axes are directed, respectively, east, up, and south.)
SOLUTION
Recoil force
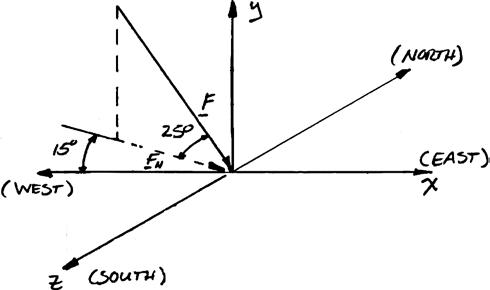
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
PROBLEM 2.62
Determine the magnitude and direction of the force F = (690 lb)i + (300 lb)j – (580 lb)k
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
PROBLEM 2.63
Determine the magnitude and direction of the force F = (650 N)i (320 N)j + (760 N)k
(650 N)(320 N)(760 N) (650 N)(320 N)(760 N)
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
PROBLEM 2.64
A force acts at the origin of a coordinate system in a direction defined by the angles θx = 69.3° and θz = 57.9°. Knowing that the y component of the force is –174.0 lb, determine (a) the angle θy , (b) the other components and the magnitude of the force.
SOLUTION
a) Since 0, y F < we choose
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
PROBLEM 2.65
A force acts at the origin of a coordinate system in a direction defined by the angles θx = 70.9° and θy = 144.9°. Knowing that the z component of the force is –52.0 lb, determine (a) the angle θz , (b) the other components and the magnitude of the force. SOLUTION
a) Since 0, z F < we choose
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
PROBLEM 2.66
A force acts at the origin of a coordinate system in a direction defined by the angles θy = 55° and θz = 45°. Knowing that the x component of the force is − 500 lb, determine (a) the angle θx , (b) the other components and the magnitude of the force.
SOLUTION
(a) We have
222222 (cos)(cos)(cos)1(cos)1(cos)(cos) xyzyyz θθθθθθ ++=⇒=−−
Since 0 xF < we must have cos0 xθ ,
Thus, taking the negative square root, from above, we have: 22 cos1(cos55)(cos45)0.41353 xθ
(b) Then:
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
PROBLEM 2.67
A force F of magnitude 1200 N acts at the origin of a coordinate system. Knowing that θx = 65° , θy = 40°, and F z > 0, determine (a) the components of the force, (b) the angle θz . SOLUTION
(b) Since 0, z F > we choose
(a)
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
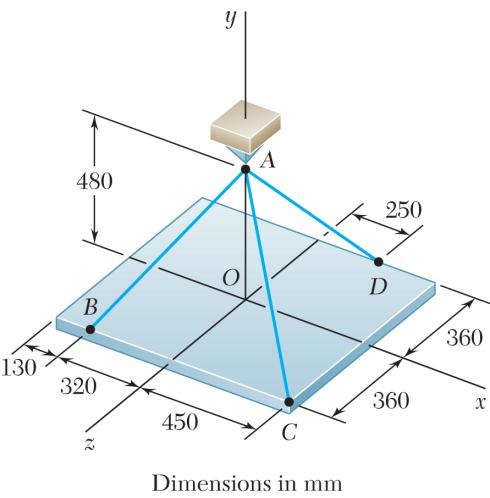
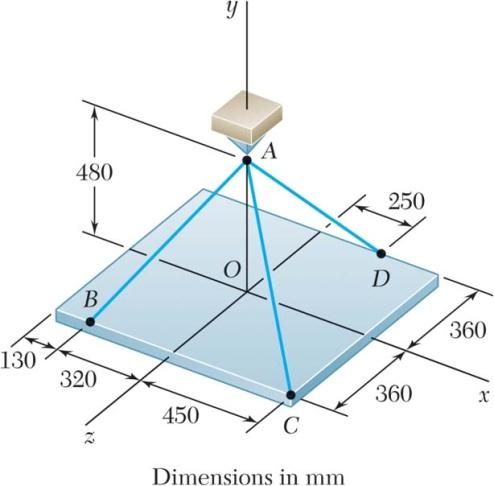
PROBLEM 2.68
A rectangular plate is supported by three cables as shown. Knowing that the tension in cable AB is 408 N, determine the components of the force exerted on the plate at B.
SOLUTION
We have: (320 mm)(480 mm)(360 mm)680 mm BABA = += i+j-k
Thus:
Setting 408 N BAT = yields,
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

PROBLEM 2.69
A rectangular plate is supported by three cables as shown. Knowing that the tension in cable AD is 429 N, determine the components of the force exerted on the plate at D
SOLUTION
We
Thus:
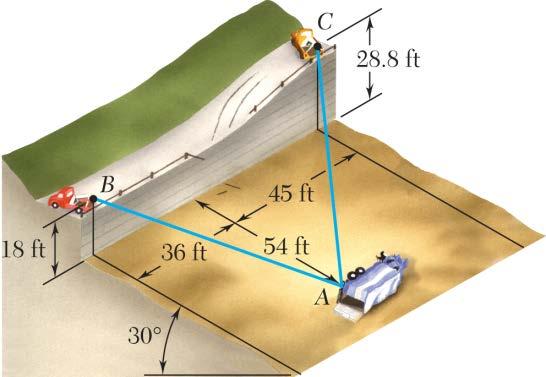
PROBLEM 2.70
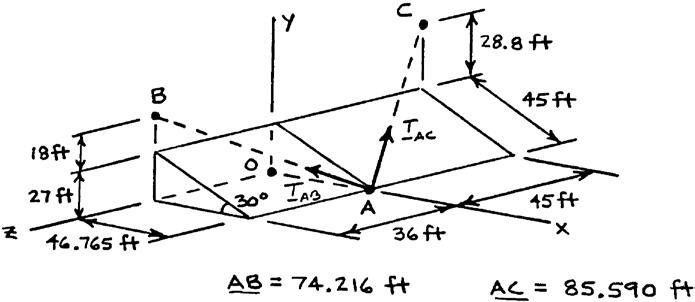
In order to move a wrecked truck, two cables are attached at A and pulled by winches B and C as shown. Knowing that the tension in cable AB is 2 kips, determine the components of the force exerted at A by the cable.
SOLUTION
()1.260kips ABxT =−
()1.213kips AByT =+
()0.970kips ABzT =+
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

SOLUTION
PROBLEM 2.71
In order to move a wrecked truck, two cables are attached at A and pulled by winches B and C as shown. Knowing that the tension in cable AC is 1.5 kips, determine the components of the force exerted at A by the cable.
Cable AB:
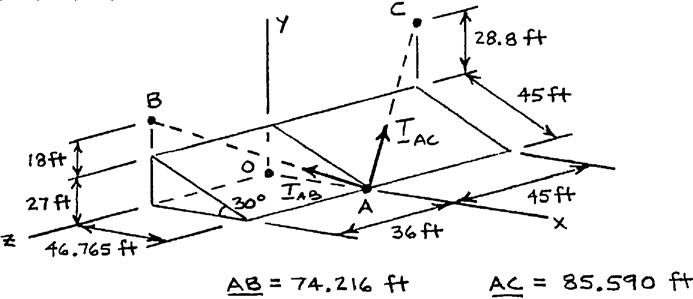
(46.765ft)(55.8ft)(45ft) 85.590ft
46.76555.845 (1.5kips)
()0.820kips ACxT =−
()0.978kips ACyT =+
()0.789kips ACzT =−
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
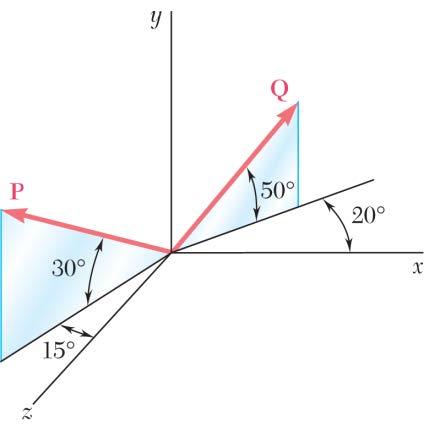
PROBLEM 2.72
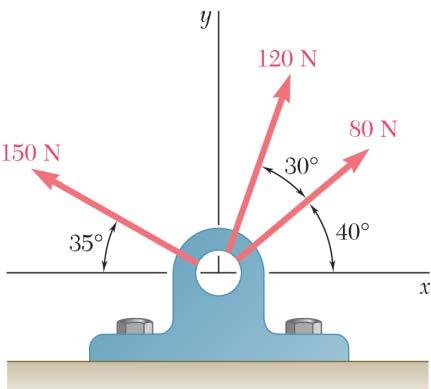
Find the magnitude and direction of the resultant of the two forces shown knowing that P = 300 N and Q = 400 N. SOLUTION
(300N)[cos30sin15sin30cos30cos15] (67.243N)(150N)(250.95N) (400N)[cos50cos20sin50cos50sin20] (400N)[0.604020.766040.21985] (241.61N)(306.42N)(87.939N) (174.
(174.367N)(456.42N)(163.011N)
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

PROBLEM 2.73
Find the magnitude and direction of the resultant of the two forces shown knowing that P = 400 N and Q = 300 N.
SOLUTION
(400N)[cos30sin15sin30cos30cos15] (89.678N)(200N)(334.61N) (300N)[cos50cos20sin50cos50sin20] (181.21N)(229.81N)(65.954N) (91.532N)(429.81N)(268.66N) (91.5 R
32N)(429.81N)(268.66N)
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
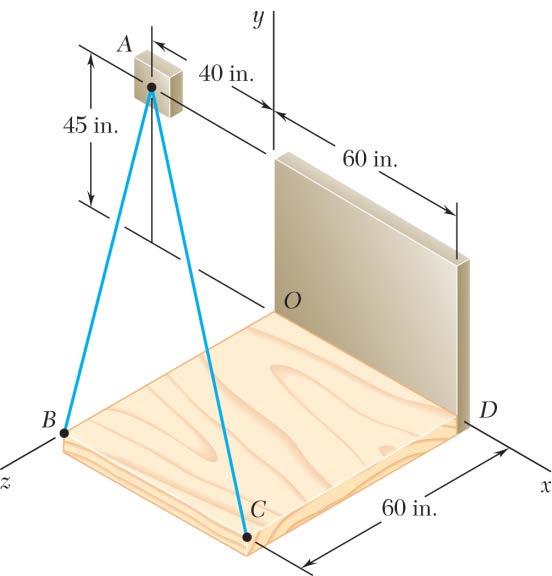
SOLUTION
PROBLEM 2.74
Knowing that the tension is 425 lb in cable AB and 510 lb in cable AC, determine the magnitude and direction of the resultant of the forces exerted at A by the two cables.
(40in.)(45in.)(60in.) (40in.)(45in.)(60in.)85in. (100in.)(45in.)(60in.) (100in.)(45in.)(60in.)125in. (40in.)(45in.)(60in.) (425lb) 85in.
(200lb)(225lb)(300lb) (100in.)(45in.)(60in.) (510lb) 125in. (408lb)(183.6lb)(244.8lb) (608)(408.6lb)(544.8lb)

SOLUTION
PROBLEM 2.75
Knowing that the tension is 510 lb in cable AB and 425 lb in cable AC, determine the magnitude and direction of the resultant of the forces exerted at A by the two cables.
(40in.)(45in.)(60in.) (40in.)(45in.)(60in.)85in. (100in.)(45in.)(60in.) (100in.)(45in.)(60in.)125in. (40in.)(45in.)(60in.) (510lb) 85in.
(240lb)(270lb)(360lb) (100in.)(45in.)(60in.) (425lb) 125in. (340lb)(153lb)(204lb) (580lb)(423lb)(564lb)
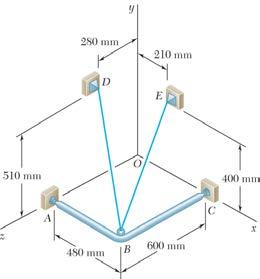
SOLUTION
PROBLEM 2.76
A frame ABC is supported in part by cable DBE that passes through a frictionless ring at B. Knowing that the tension in the cable is 385 N, determine the components of the force exerted by the cable on the support at D
(480 mm)(510 mm)(320 mm) (480 mm)(510 mm)(320 mm)770 mm
(240 N)(255 N)(160 N) BDBDBDBD BD TT BD
(385 N) [(480 mm)(510 mm)(320 mm)] (770 mm)
(270 mm)(400 mm)(600 mm) (270 mm)(400 mm)(600 mm)770 mm
(385 N) [(270 mm)(400 mm)(600 mm)] (770 mm)
(135 N)(200 N)(300 N)
(375 N)(455 N)(460 N)

SOLUTION
PROBLEM 2.77
For the plate of Prob. 2.68, determine the tensions in cables AB and AD knowing that the tension in cable AC is 54 N and that the resultant of the forces exerted by the three cables at A must be vertical.
We have: ( ) (320 mm)(480 mm)(360 mm)680 mm (450 mm)(480 mm)(360 mm)750 mm (250 mm)(480 mm)360 mm650 mm
Substituting into the Eq. =Σ RF and factoring , , : ijk
© McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION (Continued)
Since R is vertical, the coefficients of i and k are zero:
Multiply (1) by 3.6 and (2) by 2.5 then add:
Substitute into (2) and solve for : ADT
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
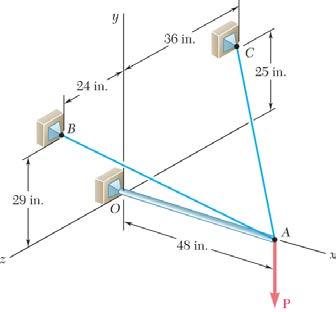
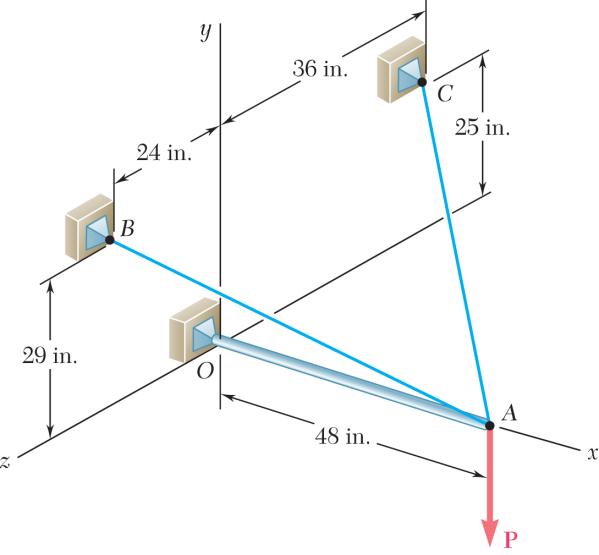
PROBLEM 2.78
The boom OA carries a load P and is supported by two cables as shown. Knowing that the tension in cable AB is 183 lb and that the resultant of the load P and of the forces exerted at A by the two cables must be directed along OA, determine the tension in cable AC SOLUTION
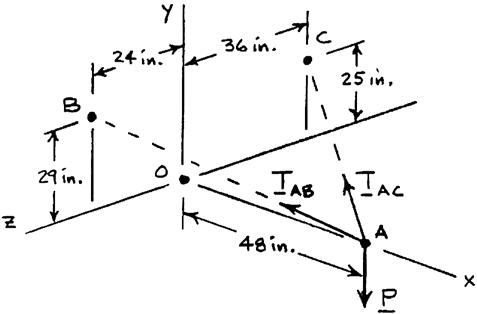
Cable AB: 183lb
(48in.)(29in.)(24in.) (183lb) 61in. (144lb)(87lb)(72lb)
Cable AC: (48in.)(25in.)(36in.) 65in.
PROBLEM 2.79
For the boom and loading of Problem. 2.78, determine the magnitude of the load P
PROBLEM2.78 The boom OA carries a load P and is supported by two cables as shown. Knowing that the tension in cable AB is 183 lb and that the resultant of the load P and of the forces exerted at A by the two cables must be directed along OA, determine the tension in cable AC
SOLUTION
See Problem 2.78. Since resultant must be directed along OA, i.e., the x-axis, we write
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION
PROBLEM 2.80
A container is supported by three cables that are attached to a ceiling as shown. Determine the weight W of the container, knowing that the tension in cable AB is 6 kN.
Free-BodyDiagramatA:
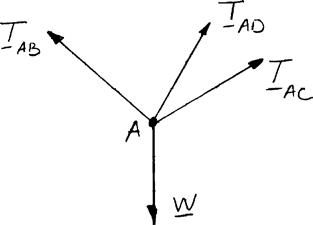
The forces applied at A are: ,,,andABACAD TTTW where . W = Wj To express the other forces in terms of the unit vectors i, j, k, we write (450mm)(600mm) 750mm (600mm)(320mm) 680 mm (500mm)(600mm)(360mm)860mm
and (450mm)(600mm) 750mm
4560 7575
(600mm)(320mm) 680mm 6032 6868 (500mm)(600mm)(360mm) 860mm 506036 868686
SOLUTION (Continued)
Equilibriumcondition: 0: 0 FABACAD Σ=∴+++= TTTW
Substituting the expressions obtained for ,,and; ABACAD TTT factoring i, j, and k; and equating each of the coefficients to zero gives the following equations:
From i: 4550 0 7586ABADTT −+=
From j: 606060 0 756886ABACAD TTTW ++−=
From k: 3236 0 6886ACADTT −+=
Setting 6kN ABT = in (1) and (2), and solving the resulting set of equations gives
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION
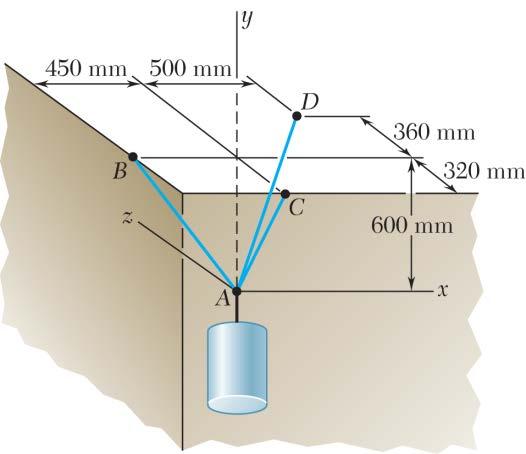
PROBLEM 2.81
A container is supported by three cables that are attached to a ceiling as shown. Determine the weight W of the container, knowing that the tension in cable AD is 4.3 kN.
Free-BodyDiagramatA:

The forces applied at A are: ,,,andABACAD TTTW where W = Wj To express the other forces in terms of the unit vectors i, j, k, we write (450mm)(600mm) 750mm (600mm)(320mm) 680mm (500mm)(600mm)(360mm)860mm
and (450mm)(600mm) 750mm
(600mm)(320mm) 680mm 6032 6868 (500mm)(600mm)(360mm) 860mm 506036 868686
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
PROBLEM 2.81 (Continued)
Equilibriumcondition: 0: 0 FABACAD Σ=∴+++= TTTW
Substituting the expressions obtained for ,,and; ABACAD TTT factoring i, j, and k; and equating each of the coefficients to zero gives the following equations:
From i: 4550 0 7586ABADTT −+=
From j: 606060 0 756886ABACAD TTTW ++−=
From k: 3236 0 6886ACADTT −+=
Setting 4.3kN ADT = into the above equations gives 4.1667kN 3.8250kN AB AC T T = = 9.71kN W =
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
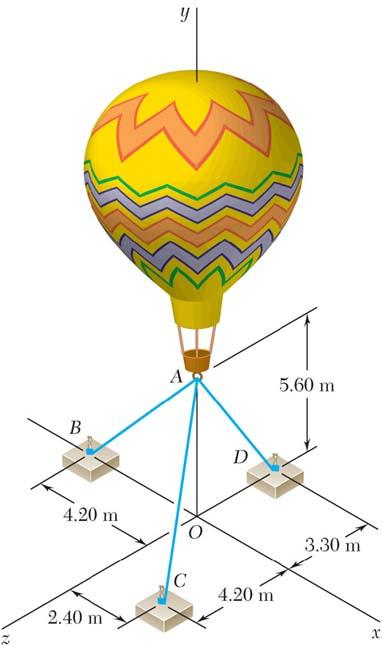
SOLUTION
PROBLEM 2.82
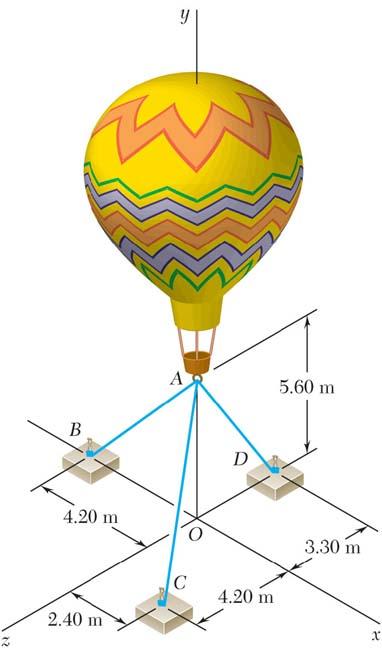
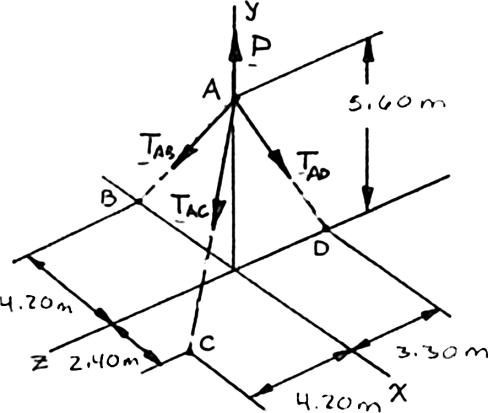
Three cables are used to tether a balloon as shown. Knowing that the balloon exerts an 800-N vertical force at A, determine the tension in each cable.
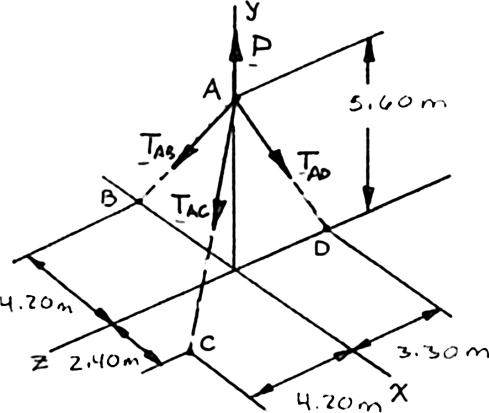
The forces applied at A are: ,,,andABACAD TTTP where P = Pj To express the other forces in terms of the unit vectors i, j, k, we write (4.20m)(5.60m) 7.00m (2.40m)(5.60m)(4.20m)7.40m (5.60m)(3.30m) 6.50m
and (0.60.8) (0.324320.756760.56757) (0.861540.50769)
PROBLEM 2.82 (Continued)
Equilibriumcondition 0: 0 ABACAD FP Σ=+++= TTTj
Substituting the expressions obtained for ,,and ABACAD TTT and factoring i, j, and k: (0.60.32432)(0.80.756760.86154) (0.567570.50769)0 ABACABACAD ACAD TTTTTP TT −+ +−−−+ +−= ij k
Equating to zero the coefficients of i, j, k:
0.60.324320 ABAC TT −+= (1)
0.80.756760.861540 ABACAD TTTP −−−+= (2)
0.567570.507690 ACAD TT−= (3)
From Eq. (1)
From Eq. (3)
0.54053 ABAC TT =
1.11795 ADAC TT =
Substituting for ABT and ADT in terms of ACT into Eq. (2) gives:
0.8(0.54053)0.756760.86154(1.11795)0 ACACAC TTTP+= 2.1523;800 N 800 N 2.1523 371.69 N AC AC TPP T == = =
Substituting into expressions for ABT and ADT gives:
0.54053(371.69 N) 1.11795(371.69 N) AB AD T T = = 201 N,372 N,416 N ABACAD TTT = = =
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
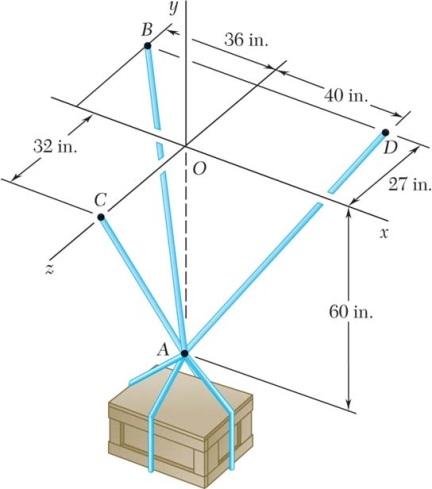
SOLUTION
The forces applied at A are:
PROBLEM 2.83
A crate is supported by three cables as shown. Determine the weight of the crate knowing that the tension in cable AD is 616 lb.
TTTW where P = Pj To express the other forces in terms of the unit vectors i, j, k, we write
(36in.)(60in.)(27in.)
75in. (60in.)(32in.)
68in. (40in.)(60in.)(27in.)
77in.
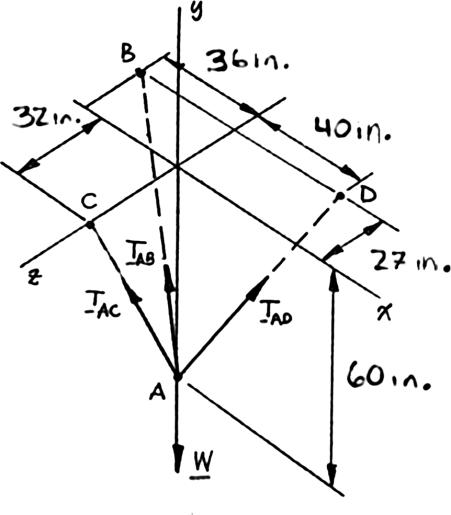
EquilibriumCondition with W =− Wj
PROBLEM 2.83 (Continued)
Substituting the expressions obtained for ,,and ABACAD TTT and factoring i, j, and k: (0.480.51948)(0.80.882350.77922) (0.360.470590.35065)0
ABADABACAD ABACAD TTTTTW TTT −++++− +−+− = ij k
0.480.519480 ABAD TT −+=
0.80.882350.779220 ABACAD TTTW ++−= 0.360.470590.350650 ABACAD TTT −+−=
Substituting 616lb ADT = in Equations (1), (2), and (3) above, and solving the resulting set of equations using conventional algorithms, gives: 667.67lb 969.00lb AB AC T T = = 1868lb W =
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
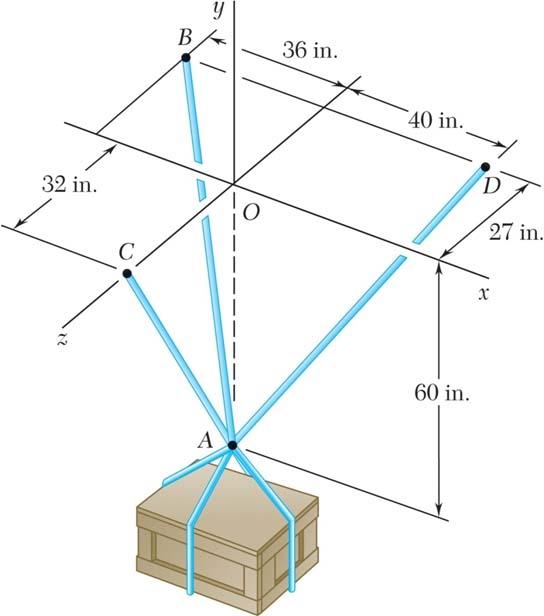
PROBLEM 2.84
A crate is supported by three cables as shown. Determine the weight of the crate knowing that the tension in cable AC is 544 lb.
SOLUTION
See Problem 2.83 for the figure and the analysis leading to the linear algebraic Equations (1), (2), and (3) below:
Substituting 544lb ACT = in Equations (1), (2), and (3) above, and solving the resulting set of equations using conventional algorithms, gives:
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

PROBLEM 2.85
A 1600-lb crate is supported by three cables as shown. Determine the tension in each cable.
SOLUTION
See Problem 2.83 for the figure and the analysis leading to the linear algebraic Equations (1), (2), and (3) below:
0.480.519480 ABAD TT −+= (1)
0.80.882350.779220 ABACAD TTTW ++−= (2)
0.360.470590.350650 ABACAD TTT −+−= (3)
Substituting 1600 lb W = in Equations (1), (2), and (3) above, and solving the resulting set of equations using conventional algorithms, gives
571lb ABT =
830lb ACT =
528lb ADT =
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
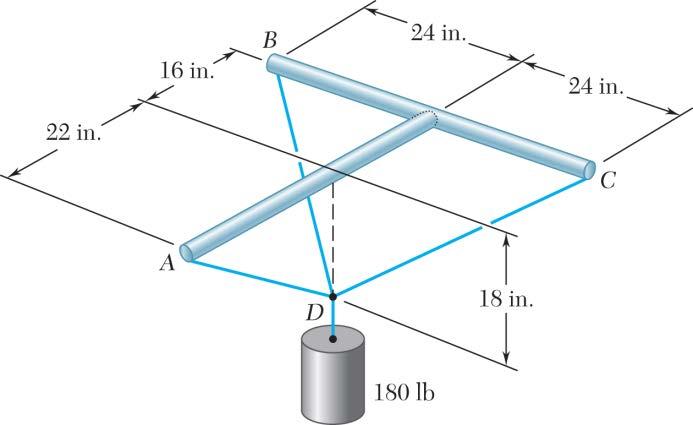
SOLUTION
PROBLEM 2.86
Three wires are connected at point D, which is located 18 in. below the T-shaped pipe support ABC. Determine the tension in each wire when a 180-lb cylinder is suspended from point D as shown.
Free-BodyDiagramofPoint D:
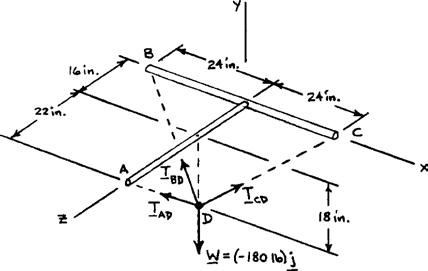
The forces applied at D are:
where 180.0 lb. =− Wj To express the other forces in terms of the unit vectors i, j, k, we write (18in.)(22in.)
28.425in. (24 in.)(18in.)(16in.)
34.0in. (24in.)(18in.)(16in.)
34.0in.
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
DADaDADa
SOLUTION (Continued) and (0.633240.77397)
(0.705880.529410.47059)
(0.705880.529410.47059)
EquilibriumCondition with W =− Wj
Substituting the expressions obtained for ,,and DADBDC TTT and factoring i, j, and k:
(0.705880.70588) (0.633240.529410.52941) (0.773970.470590.47059)
Equating to zero the coefficients of i, j, k:
0.705880.705880 DBDC TT −+= (1)
0.633240.529410.529410 DADBDC TTTW ++−= (2)
0.773970.470590.470590 DADBDC TTT−−= (3)
Substituting 180 lb W = in Equations (1), (2), and (3) above, and solving the resulting set of equations using conventional algorithms gives,
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
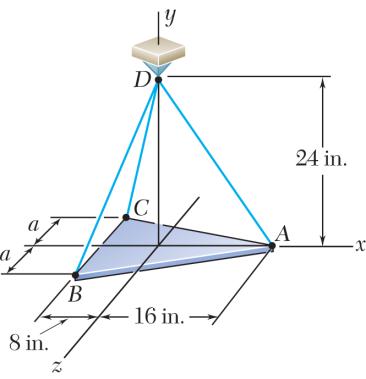
PROBLEM 2.87
A 36-lb triangular plate is supported by three wires as shown. Determine the tension in each wire, knowing that a = 6 in.
SOLUTION
By Symmetry DBDCTT = Free-BodyDiagramofPoint D:
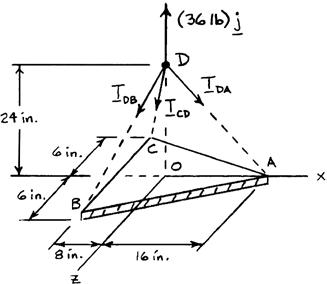
The forces applied at D are: ,,,andDBDCDA TTTP where (36 lb). P == Pjj To express the other forces in terms of the unit vectors i, j, k, we write (16in.)(24in.) 28.844in. (8in.)(24in.)(6in.)26.0in. (8 in.)(24in.)(6in.) 26.0in.
and (0.554710.83206) (0.307690.923080.23077) (0.307690.923080.23077)
SOLUTION (Continued)
Equilibriumcondition: 0: (36 lb)0 FDADBDC Σ=+++= TTTj
Substituting the expressions obtained for ,,and DADBDC TTT and factoring i, j, and k: (0.554710.307690.30769)(0.832060.923080.9230836 lb) (0.230770.23077)0 DADBDCDADBDC DBDC TTTTTT TT +−−−+ +−= ij k
Equating to zero the coefficients of i, j, k:
0.554710.307690.307690 DADBDC TTT−−= (1)
0.832060.923080.9230836 lb0 DADBDC TTT −−−+= (2)
0.230770.230770 DBDC TT−= (3)
Equation (3) confirms that DBDCTT = . Solving simultaneously gives, 14.42lb;
SOLUTION
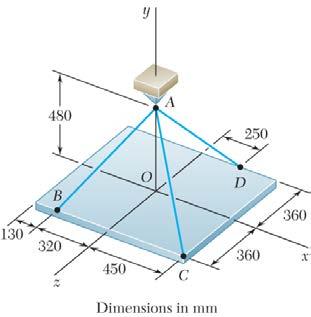
PROBLEM 2.88
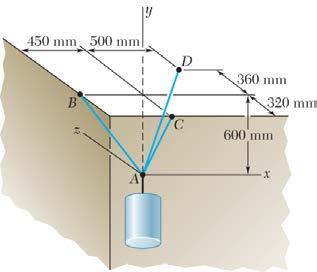
A rectangular plate is supported by three cables as shown. Knowing that the tension in cable AC is 60 N, determine the weight of the plate.
We note that the weight of the plate is equal in magnitude to the force P exerted by the support on Point A.
FreeBody A :
We have: (
(320 mm)(480 mm)(360 mm)680 mm (450 mm)(480 mm)(360 mm)750 mm (250 mm)(480 mm)360 mm650 mm
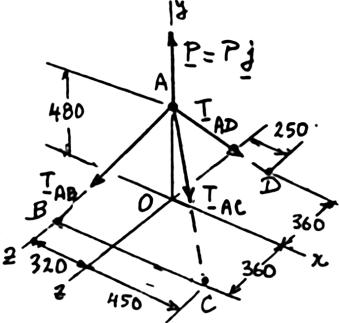
Dimensions in mm
SOLUTION (Continued)
Setting the coefficient of i, j, k equal to zero:
Making 60 N ACT = in (1) and (3):
Multiply (1′) by 9, (3′) by 8, and add:
Substitute into (1′) and solve for : AB
Substitute for the tensions in Eq. (2) and solve for P :

SOLUTION
PROBLEM 2.89
A rectangular plate is supported by three cables as shown. Knowing that the tension in cable AD is 520 N, determine the weight of the plate.
See Problem 2.88 for the figure and the analysis leading to the linear algebraic Equations (1), (2), and (3) below:
Making 520 N ADT = in Eqs. (1) and (3):
Multiply (1′) by 9, (3′) by 8, and add:
Substitute into (1′) and solve for : ABT
Substitute for the tensions in Eq. (2) and solve for P:
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
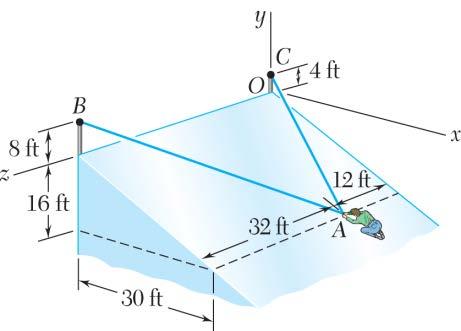
PROBLEM 2.90
In trying to move across a slippery icy surface, a 175-lb man uses two ropes AB and AC. Knowing that the force exerted on the man by the icy surface is perpendicular to that surface, determine the tension in each rope.
SOLUTION
Free-BodyDiagramat A
(30ft)(20ft)(12ft) 38ft 15106 191919
(30ft)(24ft)(32ft) 50ft 151216 252525
SOLUTION (Continued)
Substituting the expressions obtained for ,,,ABAC TTN and W; factoring i, j, and k; and equating each of the coefficients to zero gives the following equations:
From i: 151516 0 251934 ABAC TTN −−+=
From j: 121030 (175 lb)0 251934 ABAC TTN++−=
From k: 166 0 2519ABACTT−=
Solving the resulting set of equations gives:
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.

PROBLEM 2.91
Solve Problem 2.90, assuming that a friend is helping the man at A by pulling on him with a force P = (45 lb)k.
PROBLEM2.90 In trying to move across a slippery icy surface, a 175-lb man uses two ropes AB and AC. Knowing that the force exerted on the man by the icy surface is perpendicular to that surface, determine the tension in each rope.
SOLUTION
Refer to Problem 2.90 for the figure and analysis leading to the following set of equations, Equation (3) being modified to include the additional force (45lb).=− Pk
Solving the resulting set of equations simultaneously gives:
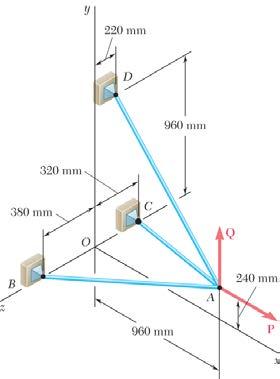
PROBLEM 2.92
Three cables are connected at A, where the forces P and Q are applied as shown. Knowing that 0, Q = find the value of P for which the tension in cable AD is 305 N.
SOLUTION
AABACAD
FTTTP where P = Pi (960 mm)(240 mm)(380 mm)1060 mm (960 mm)(240 mm)(320 mm)1040 mm (960 mm)(720 mm)(220 mm)1220 mm
481219 535353 1234 131313 305 N [(960 mm)(720 mm)(220 mm)] 1220 mm (240 N)(180 N)(55 N)
Substituting into 0, A Σ= F factoring ,,,ijk and setting each coefficient equal to φ gives: 4812
Solving the system of linear equations using conventional algorithms gives:
SOLUTION
PROBLEM 2.93
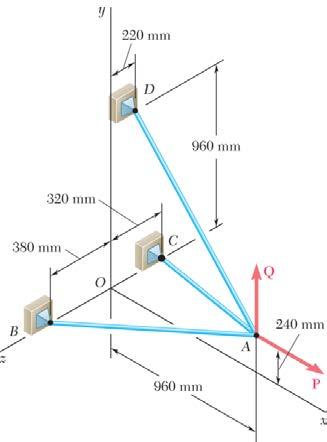
Three cables are connected at A, where the forces P and Q are applied as shown. Knowing that 1200 N, P = determine the values of Q for which cable AD is taut.
We assume that 0 ADT = and write 0: (1200 N)0 AABACQ Σ=+++= FTTji (960 mm)(240 mm)(380 mm)1060 mm (960 mm)(240 mm)(320 mm)1040 mm
Substituting into 0, A Σ= F factoring , , , ijk and setting each coefficient equal to φ gives: 4812 : 1200 N0 5313
Solving the resulting system of linear equations using conventional algorithms gives:
Note: This solution assumes that Q is directed upward as shown (0), Q ≥ if negative values of Q are considered, cable AD remains taut, but AC becomes slack for 460 N. Q =−
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education.
SOLUTION
(130
134016 454545
PROBLEM 2.94
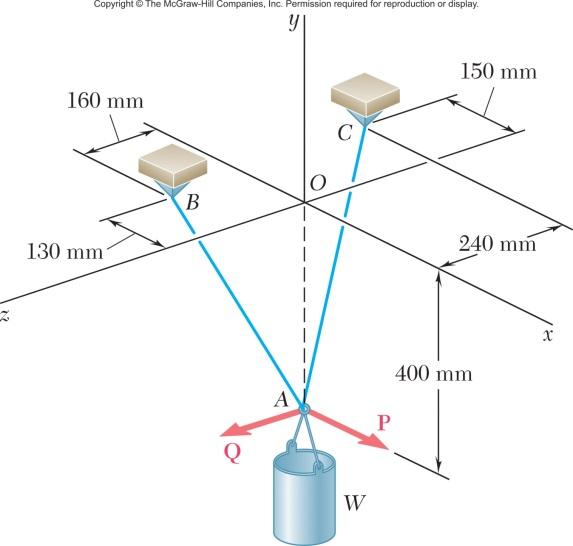
A container of weight W is suspended from ring A. Cable BAC passes through the ring and is attached to fixed supports at B and C. Two forces P = Pi and Q Q = k are applied to the ring to maintain the container in the position shown. Knowing that W 376 N, = determine P and Q. (Hint: The tension is the same in both portions of cable BAC.)
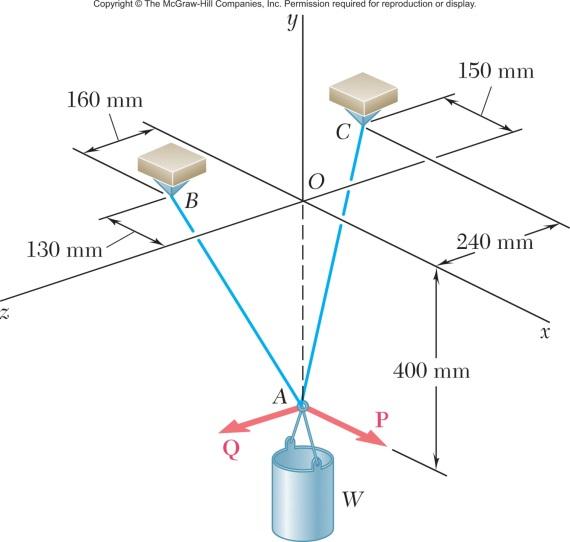
(150 mm)(400 mm)(240 mm) 490
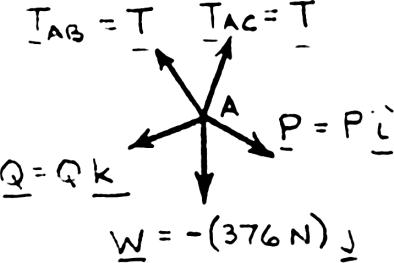
PROBLEM 2.94 (Continued)
Data: 376 N1.70521376 N220.50 N WTT = ==
N) P =
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education
SOLUTION
PROBLEM 2.95
For the system of Problem 2.94, determine W and Q knowing that 164 N. P =
PROBLEM2.94 A container of weight W is suspended from ring A. Cable BAC passes through the ring and is attached to fixed supports at B and C. Two forces P = Pi and Q = Qk are applied to the ring to maintain the container in the position shown. Knowing that W 376 N, = determine P and Q. (Hint: The tension is the same in both portions of cable BAC.)
Refer to Problem 2.94 for the figure and analysis resulting in Equations (1), (2), and (3) for P, W, and Q in terms of T below. Setting 164 N P = we have:
Eq. (1):
Eq. (2):
PROBLEM 2.96
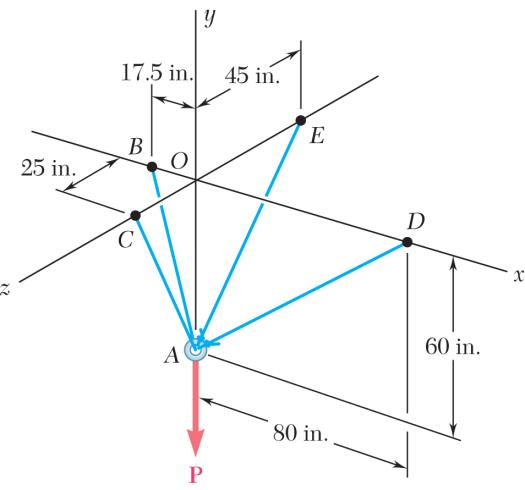
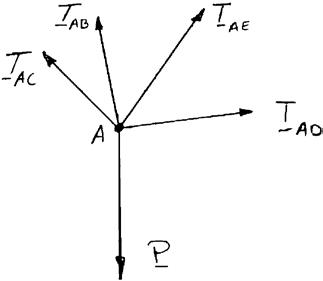
Cable BAC passes through a frictionless ring A and is attached to fixed supports at B and C, while cables AD and AE are both tied to the ring and are attached, respectively, to supports at D and E. Knowing that a 200-lb vertical load P is applied to ring A, determine the tension in each of the three cables.
SOLUTION
Since tension in BACT = cable BAC, it follows that
FreeBodyDiagramat A:
ABACBAC TTT == (17.5in.)(60in.)17.560 62.5in. 62.562.5 (60in.)(25in.)6025 65in. 6565 (80in.)(60in.)43 100in. 55
(60in.)(45in.)43 75in. 55 AE
Copyright © McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education