Central Limit Theorem

Grade: G11

Subject: Statistics

Duration: 45 minutes

Teacher: William Jung

Objective: Understand the Central Limit Theorem and use it to Find Probability

Content materials: A laptop, an interactive smart board, and whiteboard markers.

Introduce Sampling Distributions (10 minutes)

Begin the lesson by giving an example to explain the following: (Human Heights)

i Population Distribution (μ, σ)

ii. Sample Distribution (n, x)

iii Sampling Distribution (μ, σ/√n)

iv mention: the Central Limit Theorem (n>30)

v. ask: Why Sampling Distribution?

Further Explanation of the Central Limit Theorem (15 minutes)

Defining the Central Limit Theorem (CLT):

When Independent and Identically Random Variables are added, their sum tends toward a Normal Distribution, regardless of the shape of the Original Distribution

Explain that the CLT is particularly relevant when dealing with large Sample Sizes.

(The CLT states that as the sample size increases, the sampling distribution of the sample mean approaches a normal distribution, regardless of the shape of the population distribution. This allows us to approximate the sample mean's behavior using the normal distribution's properties. The normal distribution is well-studied and understood, making it easier to make statistical inferences and perform calculations.)

Continue the “Human Heights” example with the following question:

Use CLT to calculate the probability that the average height of 30 random humans is greater than 180 cm. ( μ = 167, σ = 7 )

(Review: Standard Normal Distribution, Standardization, and z-scores)

Illustrating the CLT with Simulation (15 minutes)

Show students how to use a simulation website to explore the CLT visually Provide the class with the URL of the simulation website. (https://onlinestatbook.com/stat_sim/sampling_dist/)

Instruct students to access the website on their devices (computers or tablets) Demonstrate using the simulation website by sharing a screen using a projector. Guide students through the simulation steps:

i. decide a Population Distribution

ii. choose a Sample Size

iii choose a Statistic

iv. observing the resulting Sampling Distribution

Encourage students to experiment with different Population Distributions and Sample Sizes to observe the changes in the Sampling Distribution.

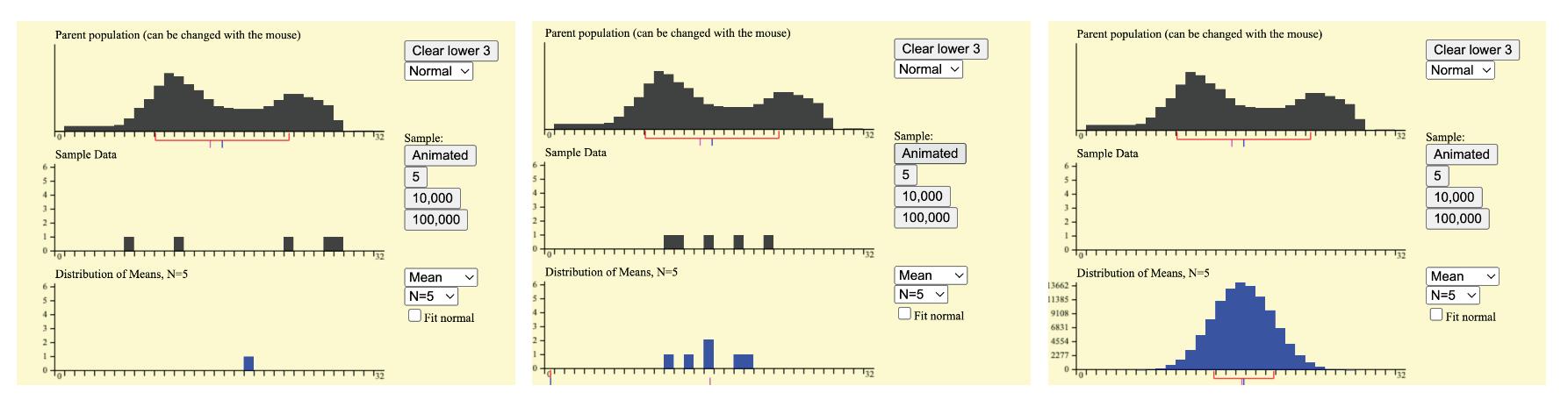
Facilitate a class discussion on the observations made during the simulation, emphasizing how the Sampling Distribution tends to approximate a Normal Distribution as the Sample Size increases.

Ask students to reflect on how the simulation aligns with the explanation of the CLT provided earlier in the lesson.

Summary and Conclusion (5 minutes)

1. Recap the main points discussed during the lesson, emphasizing the significance of the Central Limit Theorem in statistical analysis.

2 Conclude by highlighting that the Central Limit Theorem allows statisticians to make reliable inferences about a population based on a smaller Sample.