

TEST BANK TEST BANK

The title documents are available in full on the following links
Test Bank for Calculus for Business,Economics & The Social & Life Sciences 11th Edition by Laurence Hoffmann,Gerald Bradley,David Sobecki & Michael Price
Link I: https://browsegrades.net/singlePaper/416863/test-bank-for-calculus-for-businesseconomicsthe-social-life-sciences-11e-by-hoffmannbradley
Link II: https://browsegrades.net/singlePaper/416864/test-bank-for-calculus-for-businesseconomicsthe-social-life-sciences-11e-by-hoffmannbradley

1. Compute the indicated value of the given function.
Ans: 3
2 ()2 fxxx =− ; f (–1)
Difficulty: easy Section: 1.1
2. Compute the indicated value of the given function.
Ans: 1
2 ()32fxx=− ; f (–1)
Difficulty: easy Section: 1.1
3. Compute the indicated values of the given function.
f (x) = x – 3 + | x – 5| ; f (–4), f (–3), f (–2).
A) 8, 8, 8 B) –2, –2, –2 C) –6, –4, –2 D) 2, 2, 2
Ans: D Difficulty: easy Section: 1.1
4. Compute the indicated value of the given function.
f (x) = | x – 3 | + x – 5; f (2)
A) –4 B) 2 C) –2 D) 1
Ans: C Difficulty: moderate Section: 1.1
5. Compute the indicated value of the given function.
f (x) = | x + 2 | + 3| x – 1 |; f (–3)
A) 13 B) –133 C) 9 D) 23
Ans: A Difficulty: moderate Section: 1.1
6. Compute the indicated value of the given function.
2 –27if 1 () 8if 1 tt ft tt +− = +− ; f (–3)
A) 13 B) 1 C) 17 D) –1
Ans: A Difficulty: easy Section: 1.1
7. Compute the indicated value of the given function.
2 1if 1 ()3if 1 25if 1 xx fxx xx −
==
−
; f (2)
Ans: –8
Difficulty: moderate Section: 1.1

8. Compute the indicated value of the given function.
Ans: 3
2 5if 1
()4if 1
72if 1 xx fxx xx −
; f (2)
Difficulty: moderate Section: 1.1
9. Determine the domain of the given function.
2 9 () 2 x fx x = +
A) all real numbers x
B) all real numbers x except x = –2
C) all real numbers x except x = 3 and x = 7
D) all real numbers x except x = 3, x = –3, and x = –2
Ans: B Difficulty: easy Section: 1.1
10. Determine the domain of the given function.
43 ()231 fxxxx=+++
A) all real numbers x
B) all real numbers x except x = 1
Ans: A Difficulty: easy Section: 1.1
11. Determine the domain of the given function.
43 ()788 fxxxx=+++
Ans: all real numbers x
Difficulty: easy Section: 1.1
12. Determine the domain of the given function.
()23fxx=−
Ans: All real numbers x for which 3 2 x
Difficulty: moderate Section: 1.1
13. Determine the domain of the given function.
()3fxx=−
all real numbers x except x = –1
all real numbers x except x = 0
A) all real numbers x C) all real numbers x for which 3 x
B) all real numbers x except x = 3 D) all real numbers x for which 3 x −
Ans: C Difficulty: hard Section: 1.1

14. Determine the domain of the given function.
2 1 () 3 t ft t =
Ans: All real numbers t for which t 1 or t –1 except t = 3
Difficulty: hard Section: 1.1
15. Determine the domain of the given function.
2 1 () 2 t ft t =
Ans: All real numbers t for which t 1 or t –1 except t = 2 .
Difficulty: hard Section: 1.1
16. Find the composite function ( ) ( ) fgx 3 ()2fuu=+ , g(x) = x + 3
(g(x)) = 3 5 x +
(g(x)) = 3 6 x +
Ans: C Difficulty: easy Section: 1.1
17. Find the composite function ( ) ( ) fgx 1 () fuu u =− , g(x) = 2x – 3
Ans: f (g(x)) = 2 4128 23 xx x −+−
Difficulty: easy Section: 1.1
18. Find the composite function ( ) ( ) fgx 1 ()fu u = , ( ) 3 gxx=+
(g(x)) = 1 3 x +
(g(x)) = 1 3 x x ++
Ans: D Difficulty: easy Section: 1.1
(g(x)) = 3292727xxx+++
(g(x)) = 3 5 xx++
(g(x)) = 3 1 x +

19. Find the difference quotient, ( ) ( )fxhfx h +−
( ) 9 fx x = A) ( ) ( )fxhfx h +− = 1
( ) ( ) ( ) 9 fxhfx hxxh +− =− + B)
( ) ( )fxhfx h +− = 9
Ans: C Difficulty: moderate Section: 1.1
20. Find the indicated composite function.
( ) ( ) 9 fxhfx hxh +− = +
f (x + 3) where 1 ()fx x = A) f (x + 3) = 1 3 x + C) f (x + 3) = 1 3 x x ++
B) f (x + 3) = 1 3 x + D) f (x + 3) = 3 1 x +
Ans: A Difficulty: easy Section: 1.1
21. Find the indicated composite function.
f (3x – 4) where 1 () fxx x =−
Ans: f (3x – 4) = 2 –92415 34 xx x +−
Difficulty: easy Section: 1.1
22. Find functions h(x) and g(u) such that ( )()() fxghx = : 7 2 ()8025 fxxx =−−
Ans: 2 7 ()8025;() hxxxguu =−−= is one possible answer.
Difficulty: easy Section: 1.1
23. Find functions h(x) and g(u) such that ( )()() fxghx = : 5 ()34 4 fxx x =++ +
Ans: 5 ()4;()3 hxxguu u =+=+ is one possible answer.
Difficulty: easy Section: 1.1

24. An efficiency study of the morning shift at a certain factory indicates that an average worker who arrives on the job at 8:00 A.M. will have assembled 32 ()516 fxxxx =−++ transistor radios x hours later. How many radios will such a worker assemble between 10:00 and 11:00 A.M.?
A) 20 B) 22 C) 15 D) 18
Ans: B Difficulty: moderate Section: 1.1
25. To study the rate at which animals learn, a psychology student performed an experiment in which a rat was sent repeatedly through a laboratory maze. Suppose the time required for the rat to traverse the maze on the nth trial was approximately 2 24 ()5Tn nn =+− minutes. How many minutes does it take the rat to traverse the maze on the 2nd trial?
Ans: T(2) = 5 min
Difficulty: hard Section: 1.1
26. To study the rate at which animals learn, a psychology student performed an experiment in which a rat was sent repeatedly through a laboratory maze. Suppose the time required for the rat to traverse the maze on the th n trial was approximately 2 ()4816Tn nn =+− minutes. How long does it take the rat to traverse the maze in the second trial?
Ans: T(2) = 4 minutes
Difficulty: hard Section: 1.1
27. A ball is thrown upward in such a way that t seconds later, it is ( ) 2 166480Httt=−++ feet above the ground. How many seconds later does the ball hit the ground?
Ans: H(t) = 0 at t = 5 seconds
Difficulty: hard Section: 1.1
28. A ball is thrown upward in such a way that t seconds later it is ( ) 2 –156075Httt=++ feet above the ground. When does the ball hit the ground?
Ans: H(t) = 0 at t = 5 seconds.
Difficulty: hard Section: 1.1
29. At a certain factory, the total cost of manufacturing q units during the daily production run is 2 ()2297Cqqq=++ dollars. On a typical workday, q(t) = 17t units are manufactured during the first t hours of a production run. How many dollars are spent during the first 3 hours of production?
Ans: $3,000
Difficulty: hard Section: 1.1

30. At a certain factory, the total cost of manufacturing units during the daily production run is 2 ()2260Cqqq=++ dollars. On a typical day, q(t) = 15t units are manufactured during the first hours of a production run. How much is spent during the first 3 hours of production?
Ans: $2,375
Difficulty: hard Section: 1.1

W.Docs TB-Calculus for Business(11E, Hoffman)
Chapter 1: Functions, Graphs, and Limits.
31. Plot the given point in a rectangular coordinate system.
(–4, 1)
(-4, 1) x y
A)
B)
(Each gridline represents one unit.)
(-4, 1) x y
C)
(Each gridline represents one unit.)
(-4, 1) x y
(Each gridline represents one unit.)
(-4, 1) x y
D)

TB-Calculus for Business(11E, Hoffman) Chapter 1: Functions, Graphs, and Limits.
(Each gridline represents one unit.)
Ans: B Difficulty: easy Section: 1.2
32. Find the distance between the given points. (4, 8) and (–8, 7)
A) 13 D = B) D = 13 C) D = 145 D) 145 D = Ans: D Difficulty: easy Section: 1.2
33. Sketch the graph of the given function. 2 ()2fxx=+

(Tick marks are spaced one unit apart.)
A) Graph a B) Graph b C) Graph c D) Graph d Ans: D Difficulty: moderate Section: 1.2
34. Find the points of intersection (if any) of the given pair of curves. y = 3x – 1 and y = 3 – 5x Ans: 11 , 22
Difficulty: easy Section: 1.2
35. Find the points of intersection (if any) of the given pair of curves. y = x + 8 and y = 2x + 4
A) (4, 12) B) (1, –4) C) (0, 6) D) (12, 20)
Ans: A Difficulty: moderate Section: 1.2

1: Functions, Graphs, and Limits.
TB-Calculus for Business(11E, Hoffman)
36. Find the points of intersection (if any) of the given pair of curves.
y = 6x – 1 and y = 2x – 8
Ans: 723 –,–42
Difficulty: easy Section: 1.2
37. Find the points of intersection (if any) of the given pair of curves.
y = x + 3 and y = 2x + 4
A) (1, –4) B) (–1, 2) C) (0, 3) and (1, 4) D) (1, 6)
Ans: B Difficulty: moderate Section: 1.2
38. Find the points of intersection (if any) of the given pair of curves. 2 yx = and y = 3x – 2.
A) (0,0) B) There are no points of intersection. C) (2, 4) D) (1, 1), (2, 4)
Ans: D Difficulty: moderate Section: 1.2
39. If an object is thrown vertically upward with an initial speed of 128 ft/sec, its height (in feet) t seconds later is given by 2 ()16128 Httt =−+ . Graph the function H(t) and use the graph to determine when the object will hit the ground.
Ans: 8 seconds

Difficulty: hard Section: 1.2
40. A ball is thrown upward in such a way that t seconds later, it is 2 1696144stt=−++ feet above the ground. Sketch the graph of s(t) and determine the maximum height in feet attained by the ball.
Ans: 288 ft
Difficulty: hard Section: 1.2

TB-Calculus for Business(11E, Hoffman)
41. Find the slope (if possible) of the line that passes through the given pair of points. (–1, 5) and (7, 2)
Ans: 3 8
Difficulty: easy Section: 1.3
42. Find the slope (if possible) of the line that passes through the given pair of points. (5, 0) and (3, 4)
A) –2 B) 2 C) 1 2 D) 1 2
Ans: A Difficulty: easy Section: 1.3
43. Find the slope (if possible) of the line that passes through the given pair of points. (12, 0) and (16, 17)
A) 17 4 B) 4 17 C) 4 17 D) 17 4
Ans: A Difficulty: easy Section: 1.3
44. Find the slope (if possible) of the line that passes through the given pair of points. (0, 5) and (8, 7).
A) 4 B) 1 4 C) 0 D) The slope is undefined.
Ans: B Difficulty: easy Section: 1.3
45. Find the slope (if possible) of the line that passes through the given pair of points. (6, 4) and (9, –4).
Ans: 8 3
Difficulty: easy Section: 1.3
46. Find the slope of the line passing through (6, –9) and (2, 8). Round your answer to two decimal places, if necessary.
A) –4.25 B) –0.24 C) 0.24 D) 4.25
Ans: A Difficulty: easy Section: 1.3
47. Find the slope and y-intercept of the line whose equation is given. 5y = 8x
A) slope 8, y-intercept 0 C) slope 8 5 , y-intercept 0
B) slope 8, y-intercept 5 D) slope 8 5 , y-intercept 0
Ans: C Difficulty: moderate Section: 1.3

48. Find the slope and y-intercept (if they exist) of the line 7y = 2x.
A) Slope is 2 7 and y-intercept is 0.
B) Slope is 2 and y-intercept is 7.
Ans: A Difficulty: easy Section: 1.3
C) Slope is 2 and y-intercept is 0.
D)
Slope is 7 2 and y-intercept is 0.
49. Find the slope and y-intercept of the line whose equation is given. y = 2x – 5.
A) slope 2, y-intercept –5
B) slope 2, y-intercept 5
Ans: A Difficulty: easy Section: 1.3
C) slope 1 2 , y-intercept –5
D) slope 1 2 , y-intercept 5
50. Find the slope of the line whose equation is given. 3x + 5y = –7
Ans: 3 5
Difficulty: moderate Section: 1.3
51. Find the slope of the line whose equation is given. 3x – 5y = 9.
Ans: 3 5
Difficulty: moderate Section: 1.3
52. What is the slope of the line 6x + 9y = –7? Round your answer to two decimal places, if necessary.
A) –1.5 B) 1.5 C) 0.67 D) –0.67
Ans: D Difficulty: easy Section: 1.3
53. Find the slope of the line with the following equation 2x + 3y = –5.
Ans: Slope: 2 3
Difficulty: moderate Section: 1.3
54. Find the slope and y-intercept of the line 7y – 6x = 6.
Ans: Slope: 6 7 ; y-intercept: 6 7
Difficulty: moderate Section: 1.3

55. Find the slope and y-intercept of the line whose equation is given.
1 35 xy+=
Ans: Slope: 5 3 ; y-intercept: 5
Difficulty: hard Section: 1.3
56. Find the slope and y-intercept of the line whose equation is given.
1 23 xy+=
A) Slope: 3 2 ; y-intercept: 3 C) Slope: 1 2 ; y-intercept: 1
B) Slope: 3 2 ; y-intercept: 1
Ans: A Difficulty: moderate Section: 1.3
Slope: 3 2 ; y-intercept: 1 2
57. Write an equation for the line through (3, 0) with slope 2. A) y = 2x – 6 B) y = 2x – 3 C) y = 2x + 6 D) y = 2x + 3
Ans: A Difficulty: moderate Section: 1.3
58. Write an equation for the line with the given properties. Through (3, –1) with slope 2
Ans: y = 2x – 7
Difficulty: moderate Section: 1.3
59. Write an equation for the line through (5, 4) and parallel to the x-axis.
A) x = 5 B) x = –5 C) y = 4 D) y = –4
Ans: C Difficulty: easy Section: 1.3
60. Find an equation of the line parallel to the line y-axis and through the point (3, 7).
Ans: x = 3.
Difficulty: moderate Section: 1.3
61. What is the equation of the line through the points (7, –1) and (1, 15)? Round numbers to two decimal places, if necessary.
A) y = –0.38x + 17.67
B) y = –0.38x + 0.06
Ans: D Difficulty: easy Section: 1.3
C) y = –2.67x + 0.06
D) y = –2.67x + 17.67

62. Between August 29 and September 4, 2005, the price of gasoline increased steadily due to the impact of hurricane Katrina. The average price per gallon in Cincinnati on August 29 was $2.60, and on September 4 if was $3.10. Write a linear function C(x) that describes the cost per gallon of gas in Cincinnati in terms of days after August 29. Round the slope to three decimal places, if necessary. Use your function to find how much gas would have cost on October 1 if the price had continued to increase at that rate.
Ans: C(x) = 0.083x + 2.60; $5.34
Difficulty: moderate Section: 1.3
63. The cost of renting a backhoe at one distributor is $325, plus $35 per day. Write a linear function C(x) that describes the cost of renting the backhoe for x days, then use your function to find how much it would cost to rent it for 6 days.
A) ()32535;$1,985Cxx=+ C) ()32535;$535Cxx =+
B) ( ) ()632535;$3,210 Cxx =+ D) ()35319;$529Cxx=+
Ans: C Difficulty: easy Section: 1.3
64. Each unit of a certain commodity costs p = 23x + 24 cents when x units of the commodity are produced. If all units are sold at this price, express the revenue derived from the sales as a function of x
A) x(23x + 24) cents
B) 22x + 24 cents
Ans: A Difficulty: hard Section: 1.4
C) 2 2324 x + cents
D) 24x + 24 cents
65. A manufacturer's total cost consists of a fixed overhead of $250 plus production costs of $70 per unit. Express the total cost in dollars as a function of the number of units produced.
Ans: C(x) = 70x + 250
Difficulty: hard Section: 1.4
66. A manufacturer's total cost consists of a fixed overhead of $100 plus production costs of $40 per unit. Express the total cost in dollars as a function of the number of units produced.
Ans: C(x) = 40x + 100.
Difficulty: hard Section: 1.4
67. A farmer is planning to plant a rectangular garden with an area of 4,000 square yards. The garden is to be fenced on all four sides. Express the number of yards of fencing required as a function of x, the long side of the fence.
Ans: 224,000sx x
=+
Difficulty: hard Section: 1.4

68. A farmer is planning to plant a rectangular garden with an area of 6,400 square yards. The garden is to be fenced on all four sides. Express the number of yards of fencing required as a function of x, the long side of the fence.
Ans: 12,800 2x x +
Difficulty: hard Section: 1.4
69. A rectangle is constructed inside a circle of radius r with the corners of the rectangle lying on the circle. Express the area A of the rectangle as a function of the radius r if the width of one side of the rectangle is 2.
Ans: 2 41Ar=−
Difficulty: moderate Section: 1.4
70. A closed cylindrical can has a surface area of 360 square inches. Express the volume of the can as a function of its radius, r. A)
2 ()(180) π Vrrr =− cubic inches C)
2 ()360π Vrr = cubic inches B) V(r) = 180r cubic inches D)
3 ()(180) π Vrr =− cubic inches
Ans: A Difficulty: hard Section: 1.4
71. A cylindrical can is to have a volume of 36 cubic inches. The cost of the material used for the top and bottom of the can is 4 cents per square inch, and the cost of the material used for the curved side is 3 cents per square inch. Express the cost in cents of constructing the can as a function of its radius.
Ans: 2 216 8 π π Cr r =+
Difficulty: hard Section: 1.4
72. A cylindrical can is to have a volume of 27 cubic inches. The cost of the material used for the top and bottom of the can is 4 cents per square inch, and the cost of the material used for the curved side is 5 cents per square inch. Express the cost of constructing the can as a function of its radius.
Ans: 2 8270 π πr r + cents
Difficulty: hard Section: 1.4

73. A closed box with a square base is to have a volume of 40 cubic meters. The material for the top and bottom of the box costs $2 per square meter, and the material for the sides costs $1 per square meter. Express the construction cost of the box as a function of the length of its base, x. A)
2 ()1602Cxxx=++ dollars C)
2 40 ()2 Cxx x =+ dollars B)
2 2 ()24Cxx x =++ dollars D)
Ans: D Difficulty: hard Section: 1.4
2 160 ()4 Cxx x =+ dollars
74. The supply and demand functions, S(x) and D(x), respectively, for a certain commodity are given in terms of the level of production x. S(x) = 2x + 30, D(x) = 360 – x. Find the value of xe for which equilibrium occurs.
Ans: 110
Difficulty: easy Section: 1.4
75. Two car rental agencies are competing. One agency rents cars for 35 dollars per day and 35 cents a mile; the other agency rents cars for 20 dollars per day and 40 cents a mile. For a 3 day trip, how many miles must you travel to have the total cost be the same with each agency? Round to the nearest whole mile , if necessary.
A) 900 miles B) 300 miles C) 43 miles D) 38 miles
Ans: A Difficulty: hard Section: 1.4
76. Two jets bound for San Diego leave Boston 20 minutes apart. The first travels at 450 miles per hour, while the second goes 500 miles per hour. How how many hours after the second plane departs will the second plane pass the first?
Ans: 3 hours after the second plane leaves
Difficulty: hard Section: 1.4
77. Two jets bound for San Diego leave Boston 20 minutes apart. The first plane travels at 240 miles per hour, while the second plane goes 280 miles per hour. At what time will the second plane pass the first?
Ans: 2 hours after the second plane departs.
Difficulty: hard Section: 1.4
78. An appliance manufacturer can sell refrigerators for $1,500 apiece. The manufacturer's total cost consists of a fixed overhead of $30,000 plus production cost of $1,000 per refrigerator. How many refrigerators must be sold for the manufacturer to break even?
Ans: 60
Difficulty: hard Section: 1.4

79. An appliance manufacturer can sell refrigerators for $600 apiece. The manufacturer's total cost consists of a fixed overhead of $12,000 plus production cost of $400 per refrigerator. How many refrigerators must be sold for the manufacturer to break even?
Ans: 60
Difficulty: hard Section: 1.4
80. A company makes a certain product for $4 each and sells it for $8. If the company has overhead expenses of $10,000 per year, how many of its products must be made and sold to break even?
A) 10,000 B) 20,000 C) 40,000 D) 2,500
Ans: D Difficulty: hard Section: 1.4
81. If f (x) is graphed below, find 1 lim() x fx → if it exists.
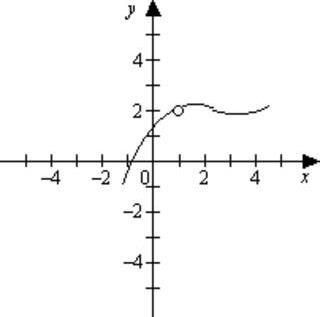
Ans: 2
Difficulty: moderate Section: 1.5

82. If f (x) is graphed below, find 1 lim() x fx → if it exists.

Ans: 1
Difficulty: moderate Section: 1.5
83. Find the indicated limit if it exists.
2 1 lim(231) x xx → −+
Ans: 0
Difficulty: easy Section: 1.5
84. Find the indicated limit if it exists. ( ) 2 1 lim641 x xx → −+
Ans: 3
Difficulty: easy Section: 1.5
85. Find the indicated limit if it exists. ( ) 3 lim4 x x → +
A) 7 B) 3 C) Does not exist D) –1
Ans: A Difficulty: easy Section: 1.5
86. Find the indicated limit if it exists.
1 21 lim 3 x x x → +
Ans: 1 4
Difficulty: easy Section: 1.5

87. Find the indicated limit if it exists.
Ans: 1 4
Difficulty: moderate Section: 1.5
88. Find the indicated limit if it exists. 2 1 lim352 21 x xx x → −+ +
Ans: 0
Difficulty: easy Section: 1.5
89. Find the indicated limit if it exists.
Ans: 1 4
90. Find the indicated limit if it exists.
Ans: 1 4
Difficulty: moderate Section: 1.5
91. Find the indicated limit if it exists.
92. Find the indicated limit if it exists.

93. Find ( ) lim x fx →+ and ( ) lim x fx →− . If the limiting value is infinite indicate whether it is + or –
94. Find ( ) lim x fx →+ and ( ) lim x fx →− . If the limiting value is infinite indicate whether it is + or –
95. Complete the table by evaluating f (x) at the specified values of x. Then use the table to estimate the indicated limit, or show that it does not exist.
2 4 ()313;lim() x fxxxfx → =− 3.93.993.99944.0014.014.1 () x fx
Ans: 3.93.993.99944.0014.014.1 ()–5.07–4.1097–4.010997 x fx 4 –3.988997–3.8897–2.87 lim()–4 x fx → = Difficulty: easy Section: 1.5
96. Complete the table by evaluating f (x) at the specified values of x. Then use the table to estimate the indicated limit, or show that it does not exist.
2 4 348 ();lim() 4 x x fxfx x →− = + 4.14.014.00143.9993.993.9 () x fx
Ans: 4.14.014.00143.9993.993.9 ()24.324.0324.003 x fx 4 23.99723.9723.7 lim()24 x fx →− =− Difficulty: easy Section: 1.5

97. Complete the table by evaluating f (x) at the specified values of x. Then use the table to estimate the indicated limit, or show that it does not exist. 6 57 ();lim() 6 x x fxfx x → + = 5.95.995.99966.0016.016.1 () x fx
Ans: 5.95.995.99966.0016.016.1 ()–365–3,695–36,995 x fx
37,0053,705375 lim()doesnotexist x fx →
Difficulty: easy Section: 1.5
98. An efficiency consultant determines that when new workers are hired to wait tables at an upscale restaurant, the average number of tables they can wait on in a 6 hour shift is given by ( ) 2 5.35014 0.10.8 xx Nx x ++ = +
where x is the number of shifts they've worked since being hired. What happens to an average waiter's productivity in the long run (as x → )?
A) It approaches 14 tables per shift. C) It approaches 53 tables per shift. B) It approaches 23 tables per shift. D) It increases without bound.
Ans: B Difficulty: moderate Section: 1.5
99. As a rumor spreads across a college campus, the number of people that have heard it can be modeled by the equation ( ) 2 2 6,0002,700 (3) tt Nt t + = +
where t is days since the rumor started spreading. What happens to the number of people that have heard the rumor in the long run (as t → )?
Ans: It approaches 6,000.
Difficulty: easy Section: 1.5
100. Find the indicated one-sided limit. If the limiting value is infinite, indicate whether it is + or –.
Ans: C Difficulty: hard Section: 1.6

101. Find the indicated one-sided limit. If the limiting value is infinite, indicate whether it is + or –
Ans: 1 12
Difficulty: hard Section: 1.6
102. Find the indicated one-sided limit. If the limiting value is infinite, indicate whether it is
103. Find the indicated one-sided limit. If the limiting value is infinite, indicate whether it is
104. Find the indicated one-sided limit. If the limiting value is infinite, indicate whether it is
105. Find the indicated one-sided limit. If the limiting value is infinite, indicate whether it is

106. Find the indicated one-sided limit. If the limiting value is infinite, indicate whether it is + or –
Ans: 3
Difficulty: hard Section: 1.6
107. Find the indicated one-sided limit. If the limiting value is infinite, indicate whether it is +
A) 7 B) 0 C) 4 D) There is none
Ans: A Difficulty: hard Section: 1.6
108. True or False:
A) True B) False
Ans: A Difficulty: hard Section: 1.6
109. Find the indicated one-sided limit. If the limiting value is infinite, indicate whether it is + or
Ans: 1
Difficulty: hard Section: 1.6
110. List all values of x for which f (x) is not continuous. 1421 () 7 x fx x =
Ans: 7
Difficulty: moderate Section: 1.6
111. List all values of x for which f (x) is not continuous. 510 () 2 x fx x =
Ans: 2
Difficulty: moderate Section: 1.6

112. List all values of x for which f (x) is not continuous.
2 51 () x fx x + =
Ans: 0
Difficulty: moderate Section: 1.6
113. List all values of x for which f (x) is not continuous.
2 21 () x fx xx + = + .
A) –1 B) 0 and –1 C) 1 2 D) None
Ans: B Difficulty: moderate Section: 1.6
114. List all values of x for which f (x) is not continuous.
2 71 () x fx x + =
Ans: 0
Difficulty: moderate Section: 1.6
115. Find all values of x for which the given function is not continuous.
2 2 32 () 43 xx fx xx ++ = ++
Ans: –1 and –3
Difficulty: hard Section: 1.6
116. Decide if the given function is continuous at the specified value of x 4if 1 ();1 41if 1 xx fxx
A) No, the function is not continuous at x = 1.
B) Yes, the function is continuous at x = 1.
Ans: B Difficulty: easy Section: 1.6
117. List all the values of x for which the given function is not continuous. 4 if 3 () 81if 3 xx fx x =
A) x = 0 B) x = 3 C) x = ±3 D) The function is continuous for all values of x. Ans: D Difficulty: easy Section: 1.6

W.Docs TB-Calculus for Business(11E, Hoffman) Chapter 1: Functions, Graphs, and Limits.
118. Find all the values of x for which the given function is not continuous.
2 4if 5 () 4if 5 xx fx x + =
Ans: 5
Difficulty: moderate Section: 1.6
119. Find all the values of x for which the given function is not continuous.
2 5if 3 () 3if 3 xx fx x + =
Ans: 3
Difficulty: moderate Section: 1.6

Chapter 2
1. The equation of the line tangent to the graph of 2 ()3 fxxx =+ at x = 2 is A) y = 7x – 4 B) y = 7x – 422 C) y = 7x – 2 D) y = 7x – 144
Ans: A Difficulty: moderate Section: 2.1
2. The equation of the line tangent to the graph of 2 ()4 fxxx =+ at x = 3 is A) y = 10x – 9 B) y = 10x – 108 C) y = 10x – 3 D) y = 10x – 27
Ans: A Difficulty: moderate Section: 2.1
3. The equation of the line tangent to the graph of ()3 fxx = at x = 1 is A)
Ans: C Difficulty: moderate Section: 2.1
4. For f (x) = 5 – x2, find the slope of the secant line connecting the points whose xcoordinates are x = –6 and x = –5.9. Then use calculus to find the slope of the line that is tangent to the graph of f at x = –6.
Ans: Slope of secant line: 11.9; Slope of tangent line: 12 Difficulty: moderate Section: 2.1
5. For 3 ()fx x =− , find the average rate of change of f (x) with respect to x as x changes from 144 to 145. Then use calculus to find the instantaneous rate of change at x = 144. Round your answer to six decimal places, if necessary.
A) Average rate of change: 0.000864; Instantaneous rate of change: –0.125
B) Average rate of change: –0.000864; Instantaneous rate of change: 0.000868
C) Average rate of change: –0.000864; Instantaneous rate of change: 0.125
D) Average rate of change: 0.000864; Instantaneous rate of change: 0.000868 Ans: D Difficulty: hard Section: 2.1
6. If f (x) represents the price per barrel of oil in terms of time, what does 00 ()() fxhfx h +− represent? What about 00 0 lim()() h fxhfx h → +− ?
Ans: The average rate of change of oil price with respect to time on the time interval [x0, x0 + h]; the instantaneous rate of change of oil price with respect to time at time x0. Difficulty: easy Section: 2.1
7. True or False: Differentiating 3 ()31 fxxx=−+ gives 2 3x A) True B) False
Ans: B Difficulty: easy Section: 2.2

8. True or False: Differentiating 6 ()42 fxxx=−+ gives 5 6x .
A) True B) False Ans: B Difficulty: easy Section: 2.2
9. Differentiate: 8 ()2fxx=+
10. Differentiate: 8 ()7fxx=+
11. True or False: Differentiating 75 1 ()298 3 fxxxx =−+− gives 6 4 7 109 3 x x −+ . A) True B) False Ans: A Difficulty: easy Section: 2.2
12. True or False: Differentiating 73 1 ()535
True B) False
13. If 3 1 () fxx x =− , differentiate f (x). Ans: 23 3 2 11 () 32 fx xx =+ Difficulty: moderate Section: 2.2
14. Differentiate: 1 () fxx x =+
15. Differentiate: 1 () fxx x =+

16. Differentiate: 6 7 () fxx x =−
Ans: –5/63/217 62 xx +
Difficulty: moderate Section: 2.2
17. Differentiate: 6 5 252 () 363 x fxxx x =−+−
Ans: 5 24/5 521 ()4 635 fxx xx =−−−
Difficulty: easy Section: 2.2
18. Differentiate: 10 9 255 () 587 fxxxx x =−+−
Ans: 9 28/9 551 4 879 x xx
Difficulty: easy Section: 2.2
19. Find the equation of the tangent line to the curve 32 ()6fxxx=−+ at the point (1, 6).
Ans: y = x + 5.
Difficulty: moderate Section: 2.2
20. Find the equation of the tangent line to the curve 32 ()1fxxx=−+ at the point (1, 1).
Ans: y = x
Difficulty: moderate Section: 2.2
21. Find the equation of the tangent to the graph of 2 ()916 fxxx=−+ at the point (1, 8).
Ans: y = –7x + 15
Difficulty: moderate Section: 2.2
22. Find the equation of the tangent to the graph of 2 ()29 fxxx=++ at the point (1, 12).
Ans: y = 4x + 8
Difficulty: moderate Section: 2.2
23. Find the equation of the tangent line to the graph of 2 ()1fxx=+ at (1, 2).
A) Not defined B) y = 2 C) x = 1 D) y = 2x
Ans: D Difficulty: moderate Section: 2.2
24. Find the equation of the tangent line to the graph of 2 ()5fxx=+ at the point (4, 21).
A) y = 8x – 11 B) Not defined C) y = 21 D) x = 4
Ans: A Difficulty: moderate Section: 2.2

25. Find the equation of the line that is tangent to the curve
25 ()53 fxxx =+− at the point (1, 7).
Ans: y = x + 6
Difficulty: moderate Section: 2.2
26. Find the equation of the line that is tangent to the curve
25 ()87 fxxx =+− at the point (1, 14).
Ans: y = 9x + 5
Difficulty: moderate Section: 2.2
27. True or False: The equation of the line tangent to the graph of ()3fxx=+ that passes through (1, 4) is y = 2x + 3.
A) True B) False
Ans: B Difficulty: moderate Section: 2.2
28. True or False: The equation of the line tangent to the graph of ()6fxx=+ that passes through (9, 9) is y = 2x + 6.
A) True B) False
Ans: B Difficulty: moderate Section: 2.2
29. Find the equation of the tangent line to the graph of
30. Find the equation of the tangent line to the graph
31. Find the equation of the tangent line to the curve 9 () fxx x =− at the point where x = 1.
Ans: y = –10x + 18.
Difficulty: moderate Section: 2.2
32. Find the equation of the tangent line to the curve 4 ()
Ans: y = –5x + 8 Difficulty: moderate Section: 2.2

33. Find the rate of change of the given function f (x) with respect for x for the prescribed value x = –2.
f (x) = x3 + 3x + 3
A) –3 B) 15 C) 18 D) 0
Ans: B Difficulty: moderate Section: 2.2
34. Find the relative rate of change of f (x) with respect to x for the prescribed value x = 1.
f (x) =5x3 + 2x2 + 2
A) 19 B) 1 19 C) 9 19 D) 19 9
Ans: D Difficulty: moderate Section: 2.2
35. The gross national product (GNP) of a certain country is 2 ()3121Nttt=++ billion dollars where t is the number of years after 1990. At what percentage rate will the GNP be changing with respect to time in 1995? Round your answer to one hundredth of a percent, if necessary.
Ans: 8.07%
Difficulty: hard Section: 2.2
36. True or False: An environmental study of a certain suburban community suggests that t years from now the average level of carbon monoxide in the air will be 2 ()0.070.22.8 Qttt=++ ppm. The rate that the carbon monoxide level will change with respect to time 2 years from now will be 0.048 ppm/yr.
A) True B) False
Ans: B Difficulty: hard Section: 2.2
37. True or False: The gross annual earnings of a certain company were 2 ()0.2930Ettt=++ thousand dollars where t is the number of years since its formation in 1990. The gross annual earnings with respect to t in 1995 are growing at 13.75%.
A) True B) False
Ans: A Difficulty: hard Section: 2.2
38. True or False: An environmental study of a certain suburban community suggests that t years from now the average level of carbon monoxide in the air will be 2 ()0.070.23.2 Qttt=++ parts per million (ppm). The rate that the carbon monoxide level will change with respect to time 3 years from now will be 0.42 ppm/yr.
A) True B) False
Ans: B Difficulty: hard Section: 2.2

39. An appliance store manager estimates that for x television ads run per day, 32 ()0.013200 Rxxxx =−+−+ refrigerators will be sold per month. Find (4) R and interpret what it tells us about sales.
A) (4) R = 203.36; they'll sell about 203 refrigerators if they run 4 ads per day.
B) (4) R = 4.52; they'll sell about 5 refrigerators if they run 4 ads per day.
C) (4) R = 4.52; sales will be increasing at about 5 refrigerators per month per ad when they're running 4 ads.
D) (4) R = 203.36; the cost of refrigerators will be rising by $203.36 if they're selling 4 per day.
Ans: C Difficulty: easy Section: 2.2
40. An efficiency study at a certain factory indicates that an average worker who arrives on the job at 8:00 A.M. will have produced 32 ()618 Qtttt =−++ units t hours later. At what rate, in units/hour, is the worker's rate of production changing with respect to time at 9:00 A.M.?
Ans: 27 units/hour
Difficulty: hard Section: 2.2
41. The displacement function of a moving object is described by 2 ()52 sttt=+− . What is the object's acceleration?
A) 2t + 5 B) 2t C) t D) 2
Ans: D Difficulty: hard Section: 2.2
42. The displacement function of a moving object is described by 2 ()54 sttt=+− . What is the acceleration of the object as a function of time?
A) 2 B) 2t + 5 C) 2t D) t
Ans: A Difficulty: moderate Section: 2.2
43. If the position of an object moving along a straight line is given by 32 ()93 stttt =−+ at time t, find the object's velocity as a function of time.
A) 2 ()393 vttt=−+ C) 2 ()93 vttt=−+
B) 2 ()18 vttt =− D) 2 ()3183 vttt=−+
Ans: D Difficulty: moderate Section: 2.2
44. The displacement function of a moving object is described by 3 ()21 sttt=+− . What is the velocity of the object as a function of t?
A) 2 3t B) 2 32 t + C) 3 D) 2
Ans: B Difficulty: easy Section: 2.2

45. An object moves along a line in such a way that its position at time t is 32 ()272313 stttt=−++ . Find the velocity and acceleration of the object at time t. When is the object stationary?
A)
B)
C)
2 ()354231 vttt=−+ ; a(t) = 6t – 54; t = 7 and 11
2 ()354231 vttt=−+ ; a(t) = 6t – 54; t = 9
2 ()318231 vttt=−+ ; a(t) = 6t – 18; t = 7
D) 2 ()354231 vttt=−+ ; a(t) = 6t – 54; t = 7
Ans: A Difficulty: moderate Section: 2.2
46. The displacement function of a moving object is described by 3 ()53 sttt=+− . What is the velocity of the object as a function of time?
A) 2 35 t + B) 2 3t C) 3 D) 2
Ans: A Difficulty: easy Section: 2.2
47. True or False: If the displacement of a moving object is 3 () stt = , the acceleration is 6t.
A) True B) False
Ans: A Difficulty: easy Section: 2.2
48. True or False: If the displacement of a moving object is 3 ()5 stt = , the acceleration is 30t.
A) True B) False
Ans: A Difficulty: easy Section: 2.2
49. If an object moves in such a way that after t seconds, the distance from its starting point is 32 ()1580 Dtttt =−+ meters, find the acceleration after 2 seconds in meters/s2 . Ans: –18 meters/s2 Difficulty: hard Section: 2.2
50. Differentiate: 2 ()(1)(3) fxxx=++
A) 2x + 1 B) 6x + 1 C) 2 361 xx++ D) 2 1 x + Ans: C Difficulty: moderate Section: 2.3
51. Differentiate: 2 ()(5)(4) fxxx=++
A) 2 385 xx++ B) 2x + 1 C) 40x + 1 D) 2 1 x + Ans: A Difficulty: moderate Section: 2.3
52. What is the rate of change of 33 () 4 t ft t = + with respect to t when t = 4?
A) 15 64 B) 15 8 C) 8 D) 7 8
Ans: A Difficulty: hard Section: 2.3

53. If 75 () 83 x fx x = + , what is ()fx ?
Ans: 2 61 () (83) fx x = +
Difficulty: moderate Section: 2.3
54. If 31 () 1 x fx x = + , what is ()fx ?
Ans: ( )2 4 1 x +
Difficulty: moderate Section: 2.3
55. Differentiate: 2 () 2 x fx x = A) 2 2 4 (2) xx x B) 2 2 4 (2) xx x + C) 2x D) –x
Ans: A Difficulty: moderate Section: 2.3
56. Differentiate: 2 () 7 x fx x = A) ( ) 2 2 14 7 xx x B) ( ) 2 2 314 7 xx x + C) 2x D) –x
Ans: A Difficulty: moderate Section: 2.3
57. If 2 3 63 () 35 x fx xx = +− , what is ()fx ?
Ans: 42 32 3273018 () (35) xxx fx xx −+− = +−
Difficulty: hard Section: 2.3
58. If 2 3 23 () 1 x fx xx = +− , what is ()fx ?
Ans: ( ) 42 2 3 3962 1 xxx xx −+− +−
Difficulty: hard Section: 2.3

59. True or False: The equation of the line that is tangent to the curve 523 ()(375)(1) fxxxxx =−++− at the point (0, –5) is y = 5x – 5.
A) True B) False
Ans: A Difficulty: hard Section: 2.3
60. True or False: The equation of the tangent line to the curve 523 ()(236)(1) fxxxxx =−++− at the point (0, –6) is y = 6x – 6.
A) True B) False
Ans: A Difficulty: hard Section: 2.3
61. Find the equation of the line that is tangent to the curve 2 3 571 () 54 xx fx x −+ = at the point (1, –1).
Ans: y = –9x + 8
Difficulty: hard Section: 2.3
62. Find the equation of the tangent line to the curve 2 3 648 () 32 xx fx x −+ = at the point (1, 10).
Ans: y = 68x – 58
Difficulty: hard Section: 2.3
63. What is the rate of change of 23 () 5 t ft t = + with respect to t when t = 5?
A) 13 100 B) 17 10 C) 10 D) 7 10
Ans: A Difficulty: hard Section: 2.3
64. What is the rate of change of 63 () 9 t ft t = + with respect to t when t = 48?
A) 1 57 B) 1 57 C) 57 D) –57
Ans: A Difficulty: hard Section: 2.3
65. Find the equation of the normal line to 3 ()2815 fxxx=−+ at the point with x-coordinate –2.
Ans: 1119 168yx=−+
Difficulty: moderate Section: 2.3

TB-Calculus for Business(11E, Hoffman)
66. Find an equation for the tangent line to the curve 1 2 5 yx =+ at the point where x = –1.
Ans: 5195 3030yx=+
Difficulty: hard Section: 2.3
67. Find ()fx , where 3 3 () 1 fx x = + .
Ans: ( ) ( ) 3 3 3 1812 1 xx x +
Difficulty: hard Section: 2.3
68. Find ()fx , where 3 ()4fxx=+ .
Ans: 6x
Difficulty: easy Section: 2.3
69. The temperature in degrees Fahrenheit inside an oven t minutes after turning it on can be modeled with the function 40070 () 1 t Ft t + = + . Find (5) F and interpret what it tells us about the temperature.
Round your answer to 2 decimal places.
Ans: (5)9.17 F = ; After 5 minutes, the temperature is increasing at the rate of 9.17 degrees per minute.
Difficulty: easy Section: 2.3
70. It is estimated that t years from now, the population of a certain suburban community will be 4 ()3073pt t =− + thousand people. At what rate will the population be growing 3 years from now?
Ans: 49 people/year
Difficulty: hard Section: 2.3
71. Find (4)()fx if 5432 ()71061011 fxxxxxx =−+−+−
(4)2()6016860fxxx=−+
(4)2()7 fxxx =− B) (4)()120168fxx=−
(4)2()710fxxx=−+
Ans: B Difficulty: moderate Section: 2.3
72. True or False: If 532 ()3725 fxxxx=−++ , then 2 ()18042fxx =−
A) True B) False
Ans: A Difficulty: moderate Section: 2.3

73. Find ()fx if 2 11 ()2 2 fx x x =−+ .
Ans: C Difficulty: moderate Section: 2.3
74. Find dy dx if 3 yu = and 4337uxx=−− .
Ans: ( ) 32 2 43 3 49 337 xx xx
Difficulty: hard Section: 2.4
75. Find dy dx if 3223yuu=+− and 2 1 uxx=+−
Ans: 5432 6158341 xxxxx ++−−−
Difficulty: hard Section: 2.4
76. Find dy dx if 3273yuu=+− and 2 6 uxx=+− .
Ans: ( )( )2 232 3216284215484 xxxxxx ++−++−−
Difficulty: hard Section: 2.4
77. Find dy dx if 3 yu = and 4326uxx=−−
Ans: 32 432/3 46 3(26) xx xx
Difficulty: hard Section: 2.4
78. Find dy dx if 1 31 y u = and 1 2 u x = +
Ans: ( )2 3 1 x
Difficulty: hard Section: 2.4

79. Find dy dx if 1 71 y u = and 1 3 u x = + .
Ans: ( )2 7 4 x Difficulty: hard Section: 2.4
80. True or False: If 3 22 (35) () (1) x fx xx = +− , then ()5(21)fxx =−+ .
A) True B) False
Ans: B Difficulty: moderate Section: 2.4
81. True or False: If 2 35 () 13 xx fx x −+ = , then 23 () 13 x fx x =
A) True B) False
Ans: B Difficulty: moderate Section: 2.4
82. True or False: An equation for the tangent line to the curve 2 ()35 fxxx =+ at the point where x = 1 is 21yx=− .
A) True B) False
Ans: B Difficulty: moderate Section: 2.4
83. An equation for the tangent line to the curve 23 (1)yxx=+− at the point where x = 1 is: A) y = 9x – 8 B) y = 9x C) y = 2x + 1 D) y = 9x – 1
Ans: A Difficulty: moderate Section: 2.4
84. Find an equation for the tangent line to the curve 23 (71)yxx=+− at the point where x = 0.
A) y = 14x + 1 B) y = 24x + 3 C) y = 3x + 1 D) y = 3x – 1
Ans: D Difficulty: moderate Section: 2.4
85. An equation for the tangent line to the curve 48 (1)yxx=+− at the point where x = 1 is A) y = 40x – 39 B) y = 40x C) y = 4x + 1 D) y = 40x – 1
Ans: A Difficulty: moderate Section: 2.4
86. An equation for the tangent line to the curve 23 (41)yxx=+− at the point where x = 0 is A) y = 3x – 1 B) y = 6x + 1 C) y = 3x + 1 D) y = 6x – 1
Ans: A Difficulty: moderate Section: 2.4

87. True or False: An equation for the tangent line to the curve 32 ()(13) fxxx =− at the point where x = –1 is y = 72x + 56.
A) True B) False
Ans: A Difficulty: moderate Section: 2.4
88. Find an equation for the tangent line to the curve 4 4 x y =+ at the point where x = –1.
Round numbers to two decimal places.
Ans: y = 0.06x + 2.00
Difficulty: hard Section: 2.4
89. Find all points on the graph of the function ( ) 3 ()624fxxx=+ where the tangent line is horizontal.
Ans: (0, 0) and (–3, –162)
Difficulty: moderate Section: 2.4
90. Find all points on the graph of the function 2 () 2 x fx x = + where the tangent line is horizontal.
A) There are none. B) (2, 1) C) (0, 0) and (–4, –8) D) (0, 0)
Ans: C Difficulty: moderate Section: 2.4
91. True or False: If ()2 fxxx =− , then ()0fx = at x = 0 and x = 2.
A) True B) False
Ans: B Difficulty: hard Section: 2.4
92. True or False: If 2 ()13 fxx =− , then 23/2 3 "() (13) fx x = .
A) True B) False
Ans: B Difficulty: moderate Section: 2.4
93. If 2 ()20 gyyy =+ represents the height in inches of a sapling y weeks after germination, find (3) g and interpret what it tells us about the height of the tree. Round your answer to 1 decimal place.
Ans: after 3 weeks, the tree is growing at 1.6 inches per week.
Difficulty: easy Section: 2.4

94. At a certain factory, the total cost of manufacturing q units during the daily production run is 2 ()0.30.8800 Cqqq=++ dollars. It has been determined that approximately 2 ()80 qttt =+ units are manufactured during the first t hours of a production run. Compute the rate at which the total manufacturing cost is changing with respect to time 2 hours after production begins.
Ans: It is increasing at $8,332.80/hour
Difficulty: hard Section: 2.4
95. When toasters are sold for p dollars apiece, local consumers will buy 57,600 ()Dp p = toasters a month. It is estimated that t months from now, the price of the toasters will be 3/2 ()0.0322.08ptt=+ dollars. Compute the rate at which the monthly demand for the toasters will be changing with respect to time 16 months from now.
Ans: Decreasing by 18 toasters/month
Difficulty: hard Section: 2.4
96. True or False: When a certain commodity is sold for p dollars per unit, consumers will buy 30,000 ()Dp p = units per month. It is estimated that t months from now, the price of the commodity will be 5/2 ()0.35.4ptt=+ dollars per unit. The monthly demand will be decreasing 40 months from now.
A) True B) False
Ans: A Difficulty: hard Section: 2.4
97. When a certain commodity is sold for p dollars per unit, consumers will buy 31,500 ()Dp p = units per month. It is estimated that t months from now, the price of the commodity will be 2/3 ()5.15ptt=+ dollars per unit. The approximate rate at which the monthly demand will be changing with respect to time in 27 months is
A) –35 units per month
B) 35 units per month
Ans: A Difficulty: hard Section: 2.4
C) –32 units per month
D) –132 units per month
98. It is estimated that t years from now, the population of a certain suburban community will be 7 ()5021pt t =− + thousand people. At what rate, in people/year will the population be growing 3 years from now?
Ans: 286 people/year
Difficulty: hard Section: 2.4

99. True or False: It is estimated that t years from now, the population of a certain suburban community will be 7 ()3021pt t =− + thousand. An environmental study indicates that the average daily level of carbon monoxide in the air will be 2 ()0.330 Cppp=++ parts per million (ppm) when the population is p thousand. The rate at which the level of pollution is changing with respect to time 3 years from now is about 0.084 ppm per year.
A) True B) False
Ans: A Difficulty: hard Section: 2.4
100. It is estimated that t years from now, the population of a certain community will be 6()143pt t =− + thousand. An environmental study indicates that the average daily level of carbon monoxide in the air will be 2 ()0.5230 Cppp=++ units when the population is p thousand. The rate at which the level of carbon monoxide will be changing 3 years from now is A) –0.078 ppm per thousand people C) 1.000 ppm per thousand people B) 0.078 ppm per thousand people D) –1.000 ppm per thousand people
Ans: B Difficulty: hard Section: 2.4
101. True or False: The function ()5 21 x fx x =− + will decrease by approximately 0.6 as x decreases from 3 to 2.7.
A) True B) False
Ans: B Difficulty: hard Section: 2.5
102. The largest percentage error you can allow in the measurement of the radius of a sphere if you want the error in the calculation of its surface area using the formula 2 4π Sr = to be no greater than 6 percent is about:
A) 6% B) 3% C) 1% D) 2%
Ans: B Difficulty: hard Section: 2.5
103. You measure the side of a cube to be 12 centimeters long and conclude that the volume of the cube is 3 121,728 = cubic centimeters. If your measurement of the side is accurate to within 4%, approximately how accurate is your calculation of this volume? Round to two decimal places, if necessary.
A) Maximum error in volume is about ±17.28 cm3
B) Maximum error in volume is about ±207.36 cm3
C) Maximum error in volume is about ±1.44 cm3
D) Maximum error in volume is about ±2,488.32 cm3
Ans: B Difficulty: moderate Section: 2.5

104. If the total cost of manufacturing q units of a certain commodity is C(q) = (3q + 1)(5q + 7), use marginal analysis to estimate the cost of producing the 19th unit, in dollars. Ans: 596 dollars
Difficulty: hard Section: 2.5
105. An efficiency study of the morning shift at a certain factory indicates that an average worker arriving on the job at 7:00 A.M. will have assembled 32 ()72 fxxxx =−+− transistor radios x hours later. Approximately how many radios will the worker assemble between 10:00 and 10:45 A.M.?
A) Approximately 13 radios
B) Approximately 585 radios
C) Approximately 10 radios
D) Approximately 30 radios
Ans: C Difficulty: moderate Section: 2.5
106. True or False: If 33 xyxy +=+ , then 2 2 31 31 dyx dxy = .
A) True B) False
Ans: B Difficulty: moderate Section: 2.6
107. Find dy dx , where 3237 xyxy −= .
Ans: B Difficulty: moderate Section: 2.6
108. Find dy dx , where xyxy +=
Ans: ( ) ( ) 21 12 yxy xxy Difficulty: moderate Section: 2.6
109. Find dy dx , where 31 5 2 xy += .
Ans: 2 2 6y x
Difficulty: moderate Section: 2.6
110. True or False: If 22315xxyy++= , then 23 dy xy dx =+ .
A) True B) False
Ans: B Difficulty: moderate Section: 2.6

111. True or False: If 22 7 xyxy+= , then 2 2 dy xyy dx =+ .
A) True B) False
Ans: B Difficulty: moderate Section: 2.6
112. True or False: If 2225xy+= , then 2 dy x dx = .
A) True B) False
Ans: B Difficulty: moderate Section: 2.6
TB-Calculus for Business(11E, Hoffman)
113. Find an equation for the tangent line to the curve 33 xxyyx ++= at the point (1, 0).
Ans: y = –2x + 2
Difficulty: hard Section: 2.6
114. Find the slope of the tangent line to the curve 2233xxyy+−= at the point (1, 1).
A) 5 B) 1 C) –5 D) 3
Ans: C Difficulty: hard Section: 2.6
115. Find an equation for the tangent line to the curve 23 1 xyxy+=+ at the point (1, –1).
Ans: 31 22yx=−+
Difficulty: hard Section: 2.6
116. Find the equation of the tangent line to the given curve at the specified point: 43 4813xyxyxy−=+− ; (0, 13)
A) 1 13 60 yx=+ B) 1 13 60 yx=−+ C) y = –60x + 13 D) y = 60x + 13
Ans: C Difficulty: moderate Section: 2.6
117. True or False: The equation for the tangent line to the curve 23 2 xxyy += at the point (1, –1) is y = –1.
A) True B) False
Ans: A Difficulty: hard Section: 2.6
118. Use implicit differentiation to find 2 2 dy dx for 5 411100 xy+=
A) 3 80x B) 3 80 11 x C) 2 6011 x + D) 2 60100 x
Ans: B Difficulty: easy Section: 2.6

119. In a certain factory, output Q is related to inputs x and y by the equation
3223352 Qxxyy =++ . If the current levels of input are x = 255 and y = 155, use calculus to estimate the change in input y that should be made to offset a decrease of 0.6 unit in input x so that output will be maintained at its current level. Round your answer to two decimal places, if necessary.
A) An increase of 0.37
B) A decrease of 0.37
C) It cannot be determined
D) No change
Ans: A Difficulty: moderate Section: 2.6
120. The output at a certain plant is 220.060.150.05 Qxxyy =++ units per day, where x is the number of hours of skilled labor used and y is the number of hours of unskilled labor used. Currently 60 hours of skilled labor and 150 hours of unskilled labor are used each day. Use calculus to estimate the change in unskilled labor that should be made to offset a 1 hour increase in skilled labor so that output will remain the same. Round your answer to two decimal places, if necessary.
A) An increase of 1.24 hours
B) A decrease of 1.24 hours
Ans: B Difficulty: hard Section: 2.6
C) It cannot be determined
D) No change
121. Suppose the output at a certain factory is 434234 +3 Qxxyy =+ units, where x is the number of hours of skilled labor used and y is the number of hours of unskilled labor. The current labor force consists of 30 hours of skilled labor and 20 hours of unskilled labor. Use calculus to estimate the change in unskilled labor y that should be made to offset a 1hour increase in skilled labor x so that output will be maintained at its current level. Round you answer to two decimal places, if necessary.
A) –0.5 hours B) –1 hours C) –2 hours D) 2 hours
Ans: A Difficulty: moderate Section: 2.6

1. Find all intervals where the derivative of the function shown below is negative.

Ans: 2 < x < 3
Difficulty: easy Section: 3.1
2. True or False: The derivative of function shown below is negative on the interval shown.
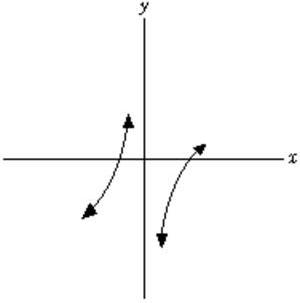
A) True B) False
Ans: B Difficulty: easy Section: 3.1
3. Find all intervals where the derivative of the function shown below is negative.
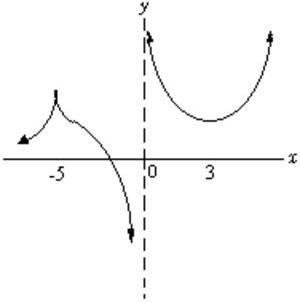
Ans: –5 < x < 0 and 0 < x < 3
Difficulty: easy Section: 3.1

4. Find the intervals of increase and decrease for the function 2 ()53 fxxx=+− .
A) Decreasing for 5 2 x − ; increasing for 5 2 x −
B) Decreasing for 5 2 x − ; increasing for 5 2 x −
C) Decreasing for all x
D) Increasing for all x Ans: A Difficulty: moderate Section: 3.1
5. Find the intervals of increase and decrease for the function 2 ()98 fxxx=+− .
A) Decreasing for 9 2 x − and increasing for 9 2 x −
B) Decreasing for 9 2 x − and increasing for 9 2 x −
C) Decreasing for all x D) Increasing for all x Ans: B Difficulty: moderate Section: 3.1
6. Find the intervals of increase and decrease for 32 ()46722 fxxxx =+−− .
A) Increasing on x –2 and x 3, decreasing on – 2 x 3
B) Increasing on x < –3 and x > 2, decreasing on –3 < x < 2
C) Increasing on –3 < x < 2, decreasing on x < –3 and x > 2
D) Increasing on x < –2, decreasing on x > 3
Ans: B Difficulty: moderate Section: 3.1
7. Find the intervals of increase and decrease for the function 53 ()410 fxxxx=−−−+ . Ans: Decreasing for all x Difficulty: moderate Section: 3.1
8. Find the intervals of increase and decrease for the function 93 ()35 fxxxx=−−−+ . Ans: Decreasing for all x Difficulty: hard Section: 3.1
9. Find the intervals of increase and decrease for 83 () 210 x fx x = −+ . Round numbers to two decimal places, if necessary.
A) Increasing on x < 5, decreasing on x > 5
B) Increasing on x < 5 and x > 5
C) Increasing on x 0.38 and on x > 5, decreasing on 0.38 < x 5
D) Increasing on 0.38 < x 5, decreasing on x 0.38 and on x > 5
Ans: B Difficulty: moderate Section: 3.1

10. Find the intervals of increase and decrease for the function 2 ()1fxx=+ .
Ans: Decreasing for x < 0; increasing for x > 0
Difficulty: hard Section: 3.1
11. Find the intervals of increase and decrease for the function 6 ()4fxx=+ .
Ans: Decreasing for x < 0, increasing for x > 0
Difficulty: hard Section: 3.1
12. Find the intervals of increase and decrease for the function 2 1 () 3 x fx x = +
Ans: Decreasing for x < –1 and x > 3; increasing for –1 < x < 3
Difficulty: hard Section: 3.1
13. Find all critical numbers of the function 34()3 fxxx =− .
Ans: 1 0, 4 x =
Difficulty: easy Section: 3.1
14. Find all the critical numbers of the function 42 ()241 fxxx=−++ .
A) 0, 1, –1 B) –1 C) 1 2 D) None
Ans: A Difficulty: moderate Section: 3.1
15. Determine the critical points of the given function and classify each critical point as a relative maximum, a relative minimum, or neither.
432 ()632483 fxxxx=−++
A) (0, 3) relative minimum; (2, 35) neither
B) (0, 2) neither; (1, 3) relative minimum
C) (0, 2) relative minimum; (1, 4) neither D) (0, 2) relative minimum; (1, 3) relative maximum
Ans: A Difficulty: moderate Section: 3.1
16. Find all the critical numbers of the function 3 ()125 fxxx=−− .
A) None B) –2, 2 C) 0, –2, 2 D) 35
Ans: B Difficulty: moderate Section: 3.1
17. Find all the critical numbers of the function 2 ()287 fxxx=−+ .
A) –7 B) 7 2 C) 2 D) None
Ans: C Difficulty: moderate Section: 3.1

18. Find all the critical numbers of the function.
2 ()463 fxxx=−+
A) –3 B) 3 4 C) 3 4 D) None
Ans: B Difficulty: moderate Section: 3.1
19. Find all the critical numbers of the function 3 ()484 fxxx=−−
A) None B) –4, 4 C) 0, –4, 4 D) 3 4
Ans: B Difficulty: moderate Section: 3.1
20. Find all critical numbers of the function 67()6 fxxx =+
Ans: 1 0, 7
Difficulty: easy Section: 3.1
21. Find all critical points of the function 2 ()22 fttt=−+ .
Ans: (1, 1)
Difficulty: hard Section: 3.1
22. Find all critical numbers of the function 2 ()28 fttt=−+ .
Ans: 1
Difficulty: hard Section: 3.1
23. Determine the critical numbers of the given function and classify each critical point as a relative maximum, a relative minimum, or neither. Round numbers to two decimal places, if necessary. 2 1 () 1016 fx xx = −+
A) x = 2, 5, 8; (5, –0.11) relative maximum
B) x = 2, 5, 8; (2, 1) relative maximum; (5, –0.11) relative minimum; (8, 1) relative maximum
C) x = 2, 8; (2, 1) relative maximum; (8, 1) relative maximum
D) x = 2, 8; (2, 1) relative maximum; (8, 1) relative minimum
Ans: A Difficulty: moderate Section: 3.1
24. Find all critical numbers of the function 2 1 () 3 x fx x = + .
Ans: x = –1, 3
Difficulty: hard Section: 3.1

25. The revenue derived from the production of x units of a particular commodity is 2 2 48 () 48 xx Rx x = + million dollars. What level of production results in maximum revenue? What is the maximum revenue? Round numbers to two decimal places, if necessary.
A) Maximum at x = 6 and maximum revenue is R(6) = 18 (million dollars)
B) Maximum at x = 6 and maximum revenue is R(6) = 2.05 (thousand dollars)
C) Maximum at x = 6 and maximum revenue is R(6) = 3 (million dollars)
D) Maximum at x = 7 and maximum revenue is R(7) = 2.05 (million dollars)
Ans: C Difficulty: moderate Section: 3.1
26. Find constants a, b, and c so that the graph of the function 2 () fxaxbxc =++ has a relative maximum at (7, 17) and crosses the y-axis at (0, 3).
Ans: B Difficulty: moderate Section: 3.1
27. True or False: The function graphed below has a positive second derivative everywhere.
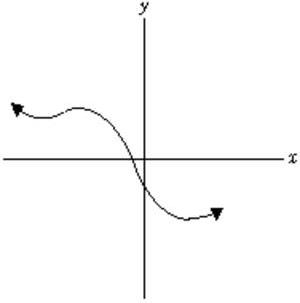
A) True B) False
Ans: B Difficulty: hard Section: 3.2

28. Determine where the second derivative in the function graphed below is positive.
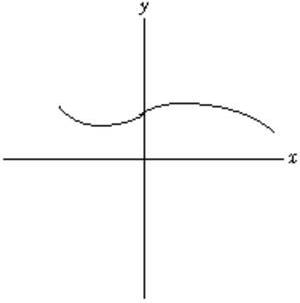
Ans: x < 0 Difficulty: hard Section: 3.2
29. True or False: The function graphed below has a negative second derivative everywhere.
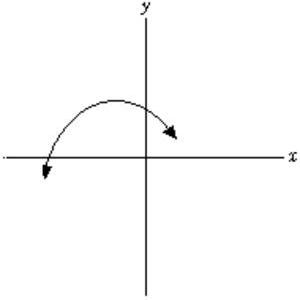
Ans: A Difficulty: moderate Section: 3.2
A) True B) False

30. Determine where the second derivative in the function graphed below is positive.
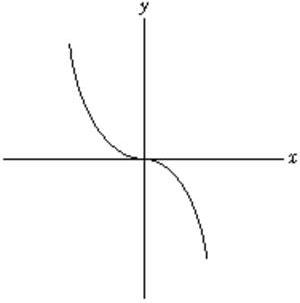
Ans: x < 0
Difficulty: hard Section: 3.2
31. Determine where the graph of 432 ()62426 fxxxx=+−+ is concave up and concave down.
Ans: Concave up for x < –4 and x > 1; concave down for –4 < x < 1
Difficulty: hard Section: 3.2
32. Determine where the graph of 2 () 3 x fx = is concave up and concave down.
Ans: Concave up for all x Difficulty: moderate Section: 3.2
33. Determine where the graph of 32 ()391 fxxxx=−−+ is concave down.
A) x > 1 B) x < 1 C) x > –1 D) x < –1
Ans: B Difficulty: hard Section: 3.2
34. Determine where the graph of 32 ()356 fxxxx=−++ is concave down.
A) For x < 1 B) For x > 1 C) For x < –1 D) For x > –1
Ans: A Difficulty: hard Section: 3.2
35. Determine where the graph of 2 () 3 x fx = is concave up and concave down.
Ans: Concave up for all x Difficulty: moderate Section: 3.2

36. True or False: The graph of 32 ()23125 fxxxx =−−− is concave down for 1 2 x .
A) True B) False
Ans: A Difficulty: moderate Section: 3.2
37. True or False: The inflection point of 32 ()613 fxxx=+− is (–2, 3).
A) True B) False
Ans: A Difficulty: moderate Section: 3.2
38. Determine where the graph of 42()6 fxxx =− is concave up.
A) for x < –1 and x > 1 B) for –1 < x < 1 C) Everywhere D) Nowhere
Ans: A Difficulty: hard Section: 3.2
39. Locate all inflection points of 432 ()62426 fxxxx=+−+ .
A) (1, 9) and (–4, –486) B) (1, 9) C) None D) (0, 26)
Ans: A Difficulty: moderate Section: 3.2
40. Determine where the graph of 42 ()543 fxxx=−+ is concave up.
A) For x < –3 and x > 3 B) For –3 < x < 3 C) Everywhere D) Nowhere
Ans: A Difficulty: hard Section: 3.2
41. True or False: The graph of 432 ()3212185 fxxxxx =−−+− is concave up for 2 3 x
A) True B) False
Ans: B Difficulty: moderate Section: 3.2
42. True or False: The graph of 43()2 gttt =+ is concave up everywhere.
A) True B) False
Ans: B Difficulty: moderate Section: 3.2
43. Determine where the graph of 2 1 () 3 gx x = + is concave up and concave down.
Ans: Concave up for x < –1 and x > 1; concave down for –1 < x < 1 Difficulty: hard Section: 3.2
44. Locate all inflection points of 2 () 1 x fx x = + .
A) 3,,(0,0),3,33 44
B) ( ) 11 0,0,1,,1, 22
C) (0, 0)
Ans: A Difficulty: moderate Section: 3.2
( ) 1 0,0,1, 2

45. True or False: The function 63 ()52 fxxx=−+ has a relative maximum at x = 1.
A) True B) False
Ans: B Difficulty: easy Section: 3.2
46. True or False: The function 2 2 () fxx x =+ has a relative minimum at x = 1.
A) True B) False
Ans: A Difficulty: easy Section: 3.2
47. Let 32 ()231213 fxxxx =−−+ . Find all critical points of f and use the second derivative test to classify each as a relative maximum, a relative minimum, or neither.
Ans: Maximum at (–1, 20); minimum at (2, –7) Difficulty: moderate Section: 3.2
48. The second derivative test reveals that 2 ()3fxx=− has
A) a relative maximum at 3 x = . C) a relative minimum at x = 0.
B) a point of inflection at 3 x = . D) a point of inflection at x = 3.
Ans: C Difficulty: easy Section: 3.2
49. Use the second derivative test to find the relative maxima and minima of the function 32 ()461443 fxxxx =+−+
A) Relative maximum at (3, 419); relative minimum at (–4, –267)
B) Relative maximum at (–4, –267); relative minimum at (–3, 381)
C) Relative maximum at (–4, –266); relative minimum at (3, 419)
D) Relative maximum at (–4, 419); relative minimum at (3, –267)
Ans: D Difficulty: moderate Section: 3.2
50. The second derivative test reveals that f (x) = x2 2 has A) a relative maximum at 2 x = C) a relative minimum at x = 0.
B) a point of inflection at 2 x = . D) nothing significant at x = 2.
Ans: C Difficulty: easy Section: 3.2
51. Find all critical points of 432 ()321218 fxxxxx =−−+ , and use the second derivative test to classify each as a relative maximum, a relative minimum, or neither.
Ans: Relative minimum at 3513 , 216
Difficulty: hard Section: 3.2

52. The second derivative test reveals that 42 ()41 fxxx=−+ has A) a relative maximum only. B) a relative minimum only.
C) a relative maximum and two relative minima.
D) neither a relative maximum nor a relative minimum.
Ans: C Difficulty: easy Section: 3.2
53. The second derivative test reveals that 42 ()23 fxxx=−+ has A) a relative maximum and two relative minima.
B) a relative maximum only.
C) a relative minimum only.
D) neither a relative maximum nor a relative minimum.
Ans: A Difficulty: easy Section: 3.2
54. A manufacturer estimates that if he produces x units of a particular commodity, the total cost will be 32 ()24350400 Cxxxx =−++ dollars. For what value of x does the marginal cost ()() MxCx = satisfy ()0Mx = ?
Ans: 8
Difficulty: hard Section: 3.2
55. A 5-year projection of population trends suggests that t years from now, the population of a certain community will be 32 ()126050 Ptttt=−+++ thousand.
a. At what time during the 5-year period will the population be growing most rapidly?
b. At what time during the 5-year period will the population be growing least rapidly?
c. At what time is the rate of population growth changing most rapidly?
A)
B)
C)
D)
a. t = 4 years
b. t = 0 years
c. t = 0 years
a. t = 0 years
b. t = 0 years
c. t = 2 years
a. t = 2 years
b. t = 1 year
c. t = 3 years
a. t = 2 years
b. t = 0 years
c. t = 2 years
Ans: A Difficulty: moderate Section: 3.2

56. Name the vertical and horizontal asymptotes of the given graph.
A) Vertical asymptotes: x = –2, x = 2; horizontal asymptote: y = 1
B) Vertical asymptotes: x = –2, x = 2; horizontal asymptotes: y = 1, y = 0
C) Vertical asymptotes: x = –2, x = 2, x = 0; horizontal asymptote: y = 1
D) Vertical asymptotes: x = –2, x = 2, x = 0; horizontal asymptotes: y = 1, y = 0
Ans: A Difficulty: easy Section: 3.3
57. Find all vertical and horizontal asymptotes of the graph of the given function. ( ) 2 2 – 7 – 6+8 xx fx xx =
A) Vertical asymptotes: x = 2, x = 4, x = 7; horizontal asymptote: y = 0
B) Vertical asymptotes: x = 2, x = 4, x = 7; horizontal asymptote: y = 1
C) Vertical asymptotes: x = 2, x = 4; horizontal asymptote: y = 7
D) Vertical asymptotes: x = 2, x = 4; horizontal asymptote: y = 1
Ans: D Difficulty: moderate Section: 3.3
58. Graph 2 ()45 fxxx=++
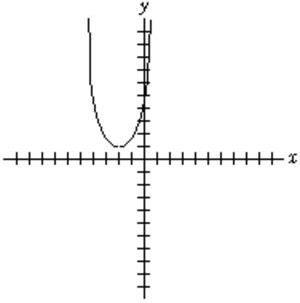
Ans: (Each tickmark represents one unit.)
Difficulty: hard Section: 3.3

59. Graph 2 ()1.20.60.2 fxxx =−+ .
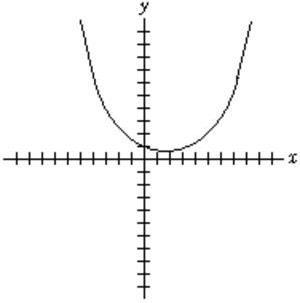
Ans: (Each tickmark represents one unit.)
Difficulty: hard Section: 3.3
60. Graph 32()24 fxxxx =+−
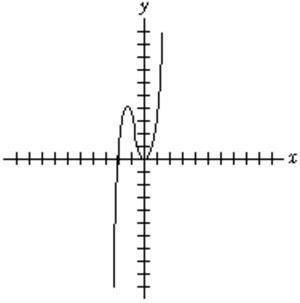
Ans: (Each tickmark represents one unit.)
Difficulty: hard Section: 3.3

61. Sketch the graph of the given function.
( ) +3 +1 x fx x =
(0, -4) x y B)
(-3, 0)
(0, -3) x y C)
(0, 2) x y
(-3, 0) (0, 3) x y D)
Ans: C Difficulty: moderate Section: 3.3
A)

62. Find A and B so that the graph of 21 () 3 Ax fx Bx = + has y = 15 as a horizontal asymptote and x = 2 as a vertical asymptote.
Ans: 453 , 22 AB==−
Difficulty: moderate Section: 3.3
63. Find the absolute maximum and minimum of 42 ()812 fxxx=−+ on the interval –1 x 2.
Ans: Maximum is 12 at x = 0, minimum is –4 at x = 2
Difficulty: easy Section: 3.4
64. Determine the absolute maximum and minimum of 42 ()25 fxxx=−+ on the interval –2 x 1.
Ans: Maximum is 13 at x = –2, minimum is 4 at x = 1 and –1
Difficulty: easy Section: 3.4
65. Find the absolute maximum and minimum of the function 32 ()2782 fxxxx=−++ on the interval 0 x 3.
Ans: Maximum is 17 at x = 3; minimum is 2 at x = 0
Difficulty: easy Section: 3.4
66. Find the absolute maximum of the function 3 () fxx = on the interval 1 1 2 x −
A) 0 B) 1 8 C) –1 D) 1
Ans: D Difficulty: easy Section: 3.4
67. Find the absolute minimum of the function 32()3 fxxx =− on the interval –1 x 3.
A) –1 B) –4 C) 0 D) 3
Ans: B Difficulty: easy Section: 3.4
68. Find the absolute minimum of the function 32()3 fxxx =− on the interval 1 x 4.
A) –4 B) 0 C) 4 D) –1
Ans: A Difficulty: easy Section: 3.4
69. Find the absolute maximum and absolute minimum of 32 ()2789 fxxxx=−++ on the interval –2 x 3.
Ans: Maximum is 24 at x = 3 and minimum is –51 at x = –2.
Difficulty: easy Section: 3.4

70. True or False: The absolute minimum of the function 32 ()8472 fxxxx =−+ on the interval 0 x 4 is 0.
A) True B) False
Ans: A Difficulty: easy Section: 3.4
71. Find the absolute maximum and minimum of the function 32 1 ()(691) 6 fxxxx =−++ on the interval 0 x 2.
Ans: Maximum is 5 6 at x = 1; minimum is 1 6 at x = 0
Difficulty: easy Section: 3.4
72. Find the absolute maximum of the function 76 () fxxx =− on the interval –1 x 1.
A) 0 B) 1 C) –1 D) –2
Ans: A Difficulty: easy Section: 3.4
73. Find the absolute maximum and absolute minimum of 42 ()816 fxxx=−+ on the interval –1 x 2.
Ans: Maximum is 16 at x = 0 and minimum is 0 at x = 2
Difficulty: easy Section: 3.4
74. Find the absolute maximum and absolute minimum of 42 ()210 fxxx=−+ on the interval –6 x 2.
Ans: Maximum is 1,234 at x = –6 and minimum is 9 at x = –1 and 1.
Difficulty: easy Section: 3.4
75. True or False: The absolute maximum of the function 42 ()23 fxxx=−+ on the interval –1 x 2 is 11.
A) True B) False
Ans: A Difficulty: easy Section: 3.4
76. True or False: The absolute maximum of the function 2 () 1 x fx x = + on the interval 0 x 1 is 1.
A) True B) False
Ans: A Difficulty: moderate Section: 3.4
77. True or False: The absolute minimum of 9 ()3fxx x =+− on the interval 1 x 9 is 1.
A) True B) False
Ans: B Difficulty: easy Section: 3.4

78. The cost of producing x units of a certain commodity is 2 ()266Cxxx=++ dollars. If the price is p(x) = (42 – x) dollars per unit, determine the level of production that maximizes profit.
A) x = 1 B) x = 2 C) x = 4 D) x = 6
Ans: D Difficulty: moderate Section: 3.4
79. A small manufacturing company estimates that the total cost in dollars of producing x radios per day is given by the formula 2 0.120500Cxx=++ . Find the number of units that will minimize the average cost.
A) 100 B) 147 C) 36 D) 71
Ans: D Difficulty: moderate Section: 3.4
80. The demand function for a certain commodity is ( ) 30 5 Dp p = + . For what values of p is the demand inelastic?
A) p > 0 B) p < 0 C) p > –5 D) p < –5
Ans: A Difficulty: hard Section: 3.4
81. Find the elasticity n of the demand function ( ) 2 3 12 Dp p = +
A) 2 6 12 n p =− + B) 2 2 4 12 p n p =− + C) n = 4p D) 3 4 np =−
Ans: B Difficulty: hard Section: 3.4
82. Suppose the total cost of producing x units of a certain commodity is 432 ()21018200167 Cxxxxx =−−++ . Determine the largest and smallest values of the marginal cost for 0 x 5.
Ans: Maximum is 270 at x = 5, minimum is 38 at x = 3
Difficulty: hard Section: 3.4
83. The total cost of producing x units of a certain commodity is 32 ()58 Cxxxx =−+
Determine the minimum average cost of the commodity.
Ans: 7 4 at 5 2 x =
Difficulty: hard Section: 3.4
84. Which non-negative number exceeds its own fourth power by the greatest amount?
Ans: 3 1 4
Difficulty: hard Section: 3.5

85. Which non-negative number exceeds its own 4th power by the greatest amount?
Ans: 3 1 4
Difficulty: hard Section: 3.5
86. Find two positive numbers whose sum is 100 and whose product is as large as possible. Ans: 50; 50
Difficulty: hard Section: 3.5
87. Find two non-negative numbers whose sum is 8 and whose product is as large as possible.
A) 2 and 6 B) 1 and 7 C) 0 and 8 D) 4 and 4
Ans: D Difficulty: hard Section: 3.5
88. Find two non-negative numbers whose sum is 12 for which the product of their squares is as large as possible.
A) 6 and 6 B) 0 and 12 C) 1 and 11 D) 4 and 8
Ans: A Difficulty: hard Section: 3.5
89. Find two non-negative numbers x and y whose sum is 10 and are such that xy2 is as large as possible.
A) 10 3 and 20 3 B) 10 and 20 C) 5 and 5 D) 9 and 1
Ans: A Difficulty: hard Section: 3.5
90. Find two non-negative numbers x and y whose sum is 14 and are such that the xy2 is as large as possible.
A) 14 3 and 28 3 B) 14 and 28 C) 7 and 7 D) 1 and 13
Ans: A Difficulty: hard Section: 3.5
91. The owner of a novelty store can obtain joy buzzers from the manufacturer for 50 cents apiece. He estimates he can sell 60 buzzers when he charges $0.90 apiece for them and that he will be able to sell 10 more buzzers for every 10 cent decrease in price. What price should he charge in order to maximize profit?
A) $0.90 B) $1.00 C) $0.80 D) $1.10
Ans: B Difficulty: moderate Section: 3.5
92. A Florida citrus grower estimates that if 70 orange trees are planted, the average yield per tree will be 300 oranges. The average yield will decrease by 3 oranges per tree for each additional tree planted on the same acreage. How many trees should the grower plant to maximize the total yield?
A) 85 trees B) 35 trees C) 15 trees D) 80 trees
Ans: A Difficulty: moderate Section: 3.5

93. A commuter train carries 600 passengers each day from a suburb to a city. It now costs $1 per person to ride the train. A study shows that 50 additional people will ride the train for each 5 cent reduction in fare. What fare should be charged in order to maximize total revenue?
A) 78 cents B) 79 cents C) 80 cents D) 85 cents
Ans: C Difficulty: hard Section: 3.5
94. A manufacturer receives an order for 5,000 items. He owns 12 machines, each of which can produce 25 items per hour. The cost of setting up a machine for a production run is $20. Once the machines are in operation, the procedure is fully automated and can be supervised by a single worker earning $4.90 per hour. Find the number of machines that should be used in order to minimize the total cost of filling the order.
A) 6 B) 7 C) 8 D) 9
Ans: B Difficulty: hard Section: 3.5
95. Find the dimensions of the rectangle of largest area that can be inscribed in a semi-circle of radius R, assuming that one side of the rectangle lies on a diameter of the semi-circle.
Ans: 2; 2 R R
Difficulty: hard Section: 3.5
96. If the cost of a commodity is 2 1 ()398 8 Cxxx=++ dollars when x units are produced and the selling price is 1 ()(75) 3 pxx =− dollars per unit, find the level of production where profit is maximized.
Ans: x = 24
Difficulty: hard Section: 3.5
97. A cable is to be run from a power plant on one side of a river 600 meters wide to a factory on the other side, 5,000 meters downstream. The cost of running cable under the water is $5 per meter, while over land is $4 per meter. What is the most economical route over which to run the cable?
A) The cable reaches the opposite bank directly across stream.
B) The cable reaches the opposite bank 800 meters downstream.
C) The cable reaches the opposite bank 5,000 meters downstream.
D) The cable reaches the opposite bank 2,500 meters downstream.
Ans: B Difficulty: moderate Section: 3.5
98. A house is located in the desert, 10 miles from a long, straight road. A man in a town 15 miles down the road arranges to be transported to the house by a company that charges $2 per mile on the road and $4 per mile on the desert. What is the minimum cost of the trip?
A) $70.53 B) $64.64 C) $74.67 D) $67.36
Ans: B Difficulty: moderate Section: 3.5

99. True or False: A dune buggy is on the desert at a point A located 40 km from the nearest point B on a long, straight road. The driver can travel at 45 km/hr on the desert and 75 km/hr on the road. He has an appointment in a town 28 km down the road from B in exactly one hour. He can make it.
A) True B) False
Ans: B Difficulty: hard Section: 3.5
100. A poster is to contain 108 cm2 of printed matter with additional margins 6 cm each at top and bottom and 2 cm on the sides. What is the minimal cost of the poster if it is to be made out of material costing 20 cents per square centimeter?
A) $59 B) $60 C) $61 D) $62
Ans: B Difficulty: hard Section: 3.5
101. If the total cost of manufacturing a commodity is 2 1 ()4200 8 Cxxx=++ dollars when x units are produced, for what value of x is the average cost the least?
A) 37 B) 38 C) 39 D) 40
Ans: D Difficulty: hard Section: 3.5
102. A store uses 900 cases of electronic parts each year. The cost of storing one case for a year is 80 cents and the ordering fee is $40 per shipment. How many cases should the store order each time to minimize total cost? Assume the orders are planned so that a new shipment arrives just as the number of cases in the store reaches zero. Also assume the parts are consumed at a constant rate.
A) 300 cases B) 600 cases C) 900 cases D) 1,000 cases
Ans: A Difficulty: hard Section: 3.5
103. A company that distributes landscape materials buys 4,000 tons of pine mulch a year. The ordering fee is $30 per shipment, the mulch costs them $20 per ton, and annual storage costs are $1.50 per ton. How many tons should be ordered in each shipment to minimize the total annual cost?
A) 2,000 tons B) 400 tons C) 200 tons D) 500 tons
Ans: B Difficulty: hard Section: 3.5
104. The owner of an appliance store expects to sell 600 toasters this year. Each toaster costs her $4 dollars to purchase, and each time she orders a shipment of toasters, it costs $30. In addition, it costs $4 a year to store each toaster. Assuming the toasters sell out at a uniform rate and that the owner never allows herself to run out of toasters, how many toasters should be ordered in each shipment to minimize the annual cost? (Round any fractional amounts.)
A) 48 B) 95 C) 33 D) 22
Ans: B Difficulty: moderate Section: 3.5

105. To raise money, a service club has been collecting used bottles that it plans to deliver to a local glass company for recycling. Since the project began 90 days ago, the club has collected 54,000 pounds of glass for which the glass company currently offers 1 cent per pound. However, because bottles are accumulating faster than they can be recycled, the company plans to reduce by 1 cent each day the price it will pay for 100 pounds of used glass. Assume that the club can continue to collect bottles at the same rate and that transportation costs make more than one trip to the glass company unfeasible. What is the most advantageous time for the club to conclude its project and deliver the bottles?
A) Today B) 55 days from now C) 15 days from now D) 5 days from now
Ans: D Difficulty: moderate Section: 3.5
106. An open box is to be made from a square piece of cardboard, 30 inches by 30 inches, by removing a small square from each corner and folding up the flaps to form the sides. What are the dimensions of the box of greatest volume that can be constructed in this way?
A) 10 inches long by 10 inches wide by 5 inches deep
B) 15 inches long by 15 inches wide by 5 inches deep
C) 5 inches long by 5 inches wide by 20 inches deep
D) 20 inches long by 20 inches wide by 5 inches deep
Ans: D Difficulty: moderate Section: 3.5

1. Evaluate the given expression. 4/3
2. Simplify 2/364 Ans: 16 Difficulty: easy Section: 4.1
3. Simplify 2/3216 . Ans: 36 Difficulty: easy Section: 4.1
4. Simplify ( ) 2 1/21/2164 Ans: 1 4 Difficulty: hard Section: 4.1
5. Simplify ( ) 2 1/21/26425 . Ans: 1 9 Difficulty: hard Section: 4.1
6. Simplify
7. Simplify

8. Simplify: 8 7 3 3
A) 3 B) 1 3 C) 153 D) 1 9
Ans: A Difficulty: moderate Section: 4.1
9. True or False: 4 6 31 39 =
A) True B) False
Ans: A Difficulty: easy Section: 4.1
10. True or False: 5 8 81 8512 =
A) True B) False
Ans: A Difficulty: easy Section: 4.1
11. Simplify: ( )1/2 710 81xy
A) 7/25 9xy B) 7/25 81 2 xy C) 13/219/2 81xy D) 58 9xy
Ans: A Difficulty: easy Section: 4.1
12. Simplify. Your answer should include only positive exponents. ( )( ) 5512634xyxy
Ans: 7 12y x
Difficulty: moderate Section: 4.1
13. Simplify. Your answer should include only positive exponents. ( ) 2 7–93 5xyz
Ans: 18 146 25 y xz
Difficulty: moderate Section: 4.1
14. Find all real numbers x that satisfy the given equation. 3x23x = 576
A) 6 B) 2 C) 8 D) 10
Ans: B Difficulty: moderate Section: 4.1

15. Find all real numbers x that satisfy the given equation.
A) 0 B) 5 –3 C) 0, 5 –3 D) 0, 5 3
Ans: D Difficulty: moderate Section: 4.1
16. Sketch the graph of ()3 xfxe =−
Difficulty: moderate Section: 4.1
17. Suppose $1,500 is invested at an annual interest rate of 8 percent compounded quarterly. Compute the balance after 12 years.
A) $3,780.61 B) $3,820.61 C) $3,880.61 D) $3,890.61
Ans: C Difficulty: hard Section: 4.1
18. How quickly will $2,000 grow to $10,000 if interest is 7% compounded quarterly? Round your answer to the nearest whole year, if necessary. A) about 20 years B) about 21 years C) about 22 years D) about 23 years
Ans: D Difficulty: hard Section: 4.1
19. How quickly will $700 grow to $2,000 if interest is 8% compounded quarterly? Round your answer to two decimal places, if necessary. A) in 13.00 years B) in 13.15 years C) in 13.20 years D) in 13.25 years
Ans: D Difficulty: hard Section: 4.1
20. If $2,000 is invested at 7 percent compounded monthly, what is the balance after 8 years? A) $3,490.51 B) $3,495.65 C) $3,521.62 D) $3,601.84
Ans: B Difficulty: hard Section: 4.1

21. If $3,000 is invested at 10% compounded continuously, what is the balance after 9 years?
A) $7,378.79 B) $7,378.81 C) $7,391.90 D) $7,342.10
Ans: B Difficulty: hard Section: 4.1
22. If $2,500 is invested at 3 percent compounded continuously, what is the balance after 14 years?
A) $1,642.62 B) $2,575.00 C) $3,804.90 D) $3,781.47
Ans: C Difficulty: hard Section: 4.1
23. True or False: If $7,000 is invested at 6% interest compounded continuously, the balance after 10 years will be $12,725.31.
A) True B) False
Ans: B Difficulty: hard Section: 4.1
24. True or False: If $7,000 is invested at 6% interest compounded monthly, the balance after 10 years will be $12,735.78.
A) True B) False
Ans: A Difficulty: hard Section: 4.1
25. True or False: If $7,000 is invested at 7% interest for 20 years, there will be $400 more if the compounding is continuous rather than quarterly.
A) True B) False
Ans: B Difficulty: hard Section: 4.1
26. How much money should be invested today at 5 percent compounded continuously so that 10 years from now it will be worth $10,000?
A) $6,065.31 B) $6,082.41 C) $6,083.43 D) $6,091.01
Ans: A Difficulty: hard Section: 4.1
27. How much money should be invested today at an annual interest rate of 9% compounded continuously so that 35 years from now it will be worth $7,000?
A) $ 6,397.52 B) $ 342.90 C) $ 163,352.45 D) $ 299.96
Ans: D Difficulty: moderate Section: 4.1
28. How much money should be invested now at a yearly rate of 3 percent compounded quarterly so that 12 years from now the account will be worth $9,000?
A) $2,177.99 B) $6,312.42 C) $8,228.14 D) $6,287.53
Ans: D Difficulty: hard Section: 4.1
29. How much money, in dollars, should be invested today at 7 percent compounded continuously so that 5 years from now it will be worth $5,000?
Ans: $3,523.44
Difficulty: hard Section: 4.1

30. Sally needs $2,000 for a trip she plans to take 3 years from now. How much, in dollars, should she invest in an account that pays 7% interest compounded continuously in order to meet her goal?
Ans: $1,621.17
Difficulty: hard Section: 4.1
31. True or False: Some amount of money is to be invested today at 7% compounded continuously so that 10 years from now the account will be worth $5,000. The amount is $2,000.
A) True B) False
Ans: B Difficulty: moderate Section: 4.1
32. Find the present value, in dollars, of $10,000 payable 8 years from now if the annual interest rate is 7% compounded continuously.
Ans: $5,712.09
Difficulty: hard Section: 4.1
33. It is projected that t years from now, the population of a certain country will be 0.07 ()70 t Pte = million. What will be the population in 40 years? Round your answer to two decimal places, if necessary.
A) 1,151.13 million C) 1,134.68 million B) 9,400.28 million D) 1,167.57 million
Ans: A Difficulty: hard Section: 4.1
34. True or False: The effective interest rate (rounded to two decimal places) if the nominal rate is 7 percent compounded quarterly is 7.30%.
A) True B) False
Ans: B Difficulty: hard Section: 4.1
35. Find the effective interest rate if the nominal rate is 6.5% compounded monthly. Round to one decimal place, if necessary.
A) 6.7% B) 6.9% C) 7.1% D) 7.3%
Ans: A Difficulty: hard Section: 4.1
36. Find the effective interest rate if the nominal rate is 8 percent compounded continuously. Round to two decimal places, if necessary.
A) 8.33% B) 7.03% C) 7.89% D) 8.21%
Ans: A Difficulty: hard Section: 4.1
37. Find the effective interest rate if the nominal rate is 7 percent compounded continuously. Round to two decimal places, if necessary.
A) 7.05% B) 7.25% C) 7.45% D) 7.55%
Ans: B Difficulty: hard Section: 4.1

38. The fraction of television sets manufactured by a certain company that are still in working condition after t years of use is approximately 0.2 () t fte = . What fraction can be expected to fail before 4 years of use? Round your answer to two decimal places, if necessary.
A) 0.45 B) 2.23 C) 0.55 D) 0.99
Ans: C Difficulty: hard Section: 4.1
39. True or False: A statistical study indicates that the fraction of the can openers manufactured by a certain company that are still in working condition after t years of use is approximately 0.3 () t fte = . The fraction that can be expected to fail during the 2nd year of use is about 19 100 .
A) True B) False
Ans: A Difficulty: hard Section: 4.1
40. The population density x miles from the center of a certain city is 0.05 ()6 x Dxe = thousand people per square mile. What is the population density 6 miles from the center of this city? Round your answer to two decimal places.
A) 8.10 thousand people per square mile C) 3.70 thousand people per square mile B) 4.44 thousand people per square mile D) 5.19 thousand people per square mile
Ans: B Difficulty: hard Section: 4.1
41. Determine the monthly car payment for a new car costing $17,188, if there is a down payment of $7,000 and the car is financed over a 9-year period at an annual rate of 5% compounded monthly.
A) $105.60 B) $197.96 C) $117.34 D) $122.31
Ans: C Difficulty: moderate Section: 4.1
42. Evaluate the expression 2ln83ln9 e without using tables or calculators. Ans: 64 729
Difficulty: easy Section: 4.2
43. True or False: Evaluation of 1/2*ln41/3*ln27 e without using tables or a calculator will show it is 6.
A) True B) False
Ans: B Difficulty: easy Section: 4.2
44. Use logarithm rules to rewrite the expression in terms of log x and log y. ( ) 1/34 log xy
Ans: 1 3log4logxy +
Difficulty: easy Section: 4.2

45. Use logarithm properties to simplify the expression. ( )5/2 5 2 2 717 log xx xx
+
Ans: ( ) ( ) 2 222 51 5loglog717log 22 xxxx +−−+
Difficulty: moderate Section: 4.2
TB-Calculus for Business(11E, Hoffman)
46. Solve for x. Give an exact answer and one rounded to two decimal places. 5x = 99
Ans: ln99 2.86 ln5 x =
Difficulty: easy Section: 4.2
47. Solve for x: 64 1 log 3 x =
A) x = 4 B) x = 64 3 C) 1 3log64 x = D) x = 8
Ans: A Difficulty: easy Section: 4.2
48. Solve for x. Round to three decimal places, if necessary. log3 x = 4
A) x = 81 B) x = 64 C) x = 1.262 D) x = 0.792
Ans: A Difficulty: easy Section: 4.2
49. Solve for x. Round to three decimal places, if necessary. 3 log4 x = A) 81 B) 64 C) 1.316 D) 1.587
Ans: A Difficulty: easy Section: 4.2
50. Solve for x if log3 x = 5. Ans: 243
Difficulty: easy Section: 4.2
51. Solve for x if 4 log3 x = . Ans: 64
Difficulty: easy Section: 4.2
52. Solve for x if ( ) 10 log23 x = Ans: 500
Difficulty: easy Section: 4.2

53. True or False: If log4 x – 2 = 5, then x = 3.161, when rounded to three decimal places.
A) True B) False Ans: B Difficulty: easy Section: 4.2
54. Solve for x if log4 (2x) = 3. Ans: 32
Difficulty: easy Section: 4.2
55. Solve for x: ( ) 2 log15 x −=
A) x = 32 B) x = 31 C) x = 33 D) x = 3,322
Ans: C Difficulty: easy Section: 4.2
56. Solve for x. Answer exactly and then round to three decimal places. ln(–6x + 28) = –5
Ans: –5 28 4.67 6 e x = Difficulty: easy Section: 4.2
57. Solve for x: 2 log(1)3 x −=
A) 9 B) 8 C) 7 D) 10
Ans: A Difficulty: easy Section: 4.2
58. True or False: If log7 (2x) = 2 , then 49 2 x = .
A) True B) False Ans: A Difficulty: easy Section: 4.2
59. True or False: If ( ) 5 log76 x = , then 15,625 7 x =
A) True B) False Ans: A Difficulty: easy Section: 4.2
60. Solve for x. Give an exact answer and then round to two decimal places, if necessary. –22 528 x+ =
No
Ans: B Difficulty: easy Section: 4.2

61. Solve for x: 24 x ab =
Ans: A Difficulty: moderate Section:
62. Solve for x: 6 5x e = A) 6 ln5 x = B) x = ln 5 C) x = 6 ln 5 D) x = 6 – ln5
Ans: A Difficulty: moderate Section: 4.2
63. Solve for x: 21 x ab =
Ans: B Difficulty: moderate Section: 4.2
64. True or False: If 0.002 3 x e = , then x is ln3 50 .
A) True B) False Ans: B Difficulty: easy Section: 4.2
65. True or False: If 0.06 1 2 2 x AAe = , then x is ln4 0.06 . A) True B) False Ans: A Difficulty: easy Section: 4.2
66. True or False: If 0.002 8 x e = , then x is ln8 500 .
A) True B) False
Ans: B Difficulty: easy Section: 4.2
67. Solve for x: 2 573 x e =− Ans: 12 ln 23
Difficulty: easy Section: 4.2
68. Solve the given equation for x –2 –4–55 x e =+ A) 5 –2e B) 5 2 e C) ln5 2 D) ln5 2
Ans: D Difficulty: moderate Section: 4.2

69. Solve the given equation for x.
70. Solve the given equation for x.
71. Solve the given equation for x. 3 547 x e =+
72. Solve for x: 6 573 x e =−
Ans: 12 ln 63
Difficulty: easy Section: 4.2
73. Solve
74. Solve for x:
75. Solve for x to two decimal places: 1 ln(ln82ln3) 5 x =+ Ans: 5.53
Difficulty: moderate Section: 4.2
76. Solve for x to two decimal places: ( ) 1 lnln62ln5 8 x =+ Ans: 3.50
Difficulty: moderate Section: 4.2

77. True or False: If ln x = 3(ln 2 – ln 7), then 1 6 x = .
A) True B) False
Ans: B Difficulty: easy Section: 4.2
78. Solve for x: 3 2x e = A) x = ln 2 B) x = 3 ln 2 C) x = 3 – ln 2 D) 3 ln2 x =
Ans: D Difficulty: moderate Section: 4.2
79. A bank compounds interest continuously. What nominal interest rate does it offer if $1,500 grows to $2,500 in 10 years? Round to two decimal places.
A) 5.00% B) 5.07% C) 5.11% D) 5.13%
Ans: C Difficulty: hard Section: 4.2
80. True or False: It takes 8 years for money to double with quarterly compounding if the annual interest rate is 8%.
A) True B) False
Ans: B Difficulty: hard Section: 4.2
81. How quickly will money triple if it is invested at 7% interest compounded continuously? Round your answer to two decimal places.
A) 15.69 years B) 15.71 years C) 15.73 years D) 15.75 years
Ans: A Difficulty: hard Section: 4.2
82. If an account that earns interest compounded continuously takes 9.5 years to double in value, how long will it take to triple? Round your answer to one decimal place, if necessary.
A) 14.3 years B) 15.1 years C) 19 years D) 12.8 years
Ans: B Difficulty: moderate Section: 4.2
83. True or False: A sum of money, A0, is invested at a certain fixed interest rate, and this interest is compounded continuously. After 7 years, the money has doubled. The balance at the end of 14 years is 0 4A .
A) True B) False
Ans: A Difficulty: hard Section: 4.2
84. True or False: A sum of money, 0A , is invested at a certain fixed interest rate, and the interest is compounded continuously. After 7 years, the money has doubled. At the end of 14 years the value is 0 2A .
A) True B) False
Ans: B Difficulty: hard Section: 4.2

85. True or False: A sum of money, 0A , is invested at a certain fixed interest rate, and this interest is compounded continuously. After 3 years, the money has doubled. The balance at the end of 6 years is 0 4A .
A) True B) False
Ans: A Difficulty: hard Section: 4.2
86. True or False: A sum of money, 0A , is invested at a certain fixed interest rate, and this interest is compounded continuously. After 10 years, the money has doubled. The balance at the end of 20 years is 0 2A .
A) True B) False
Ans: B Difficulty: hard Section: 4.2
87. True or False: Money triples in 15.50 years if it doubles in 10 years. Assume continuous compounding and rounding to two decimal places.
A) True B) False
Ans: B Difficulty: hard Section: 4.2
88. True or False: If money is compounded continuously, it will double in about 6.3 years if it triples in 10 years.
A) True B) False
Ans: A Difficulty: hard Section: 4.2
89. At what interest rate, compounded continuously, should $3,000 be invested today so that 15 years from now the account will be worth $6,000? Round your answer to two decimal places.
A) 9.24% B) 0.05% C) 2.31% D) 4.62%
Ans: D Difficulty: hard Section: 4.2
90. Suppose the number of bacteria grows from 7,000 to 10,000 in the first 15 minutes of an experiment. Assuming that the number of bacteria grows exponentially, how many bacteria will be present after 1 hour? Round to the nearest whole number.
Ans: 29,155
Difficulty: hard Section: 4.2
91. Suppose the number of bacteria grows from 4,000 to 7,000 in the first 15 minutes of an experiment. Assuming that the number of bacteria grows exponentially, how many bacteria will be present after 1 hour?Round your answer to the nearest whole number, if necessary.
Ans: 37,516
Difficulty: hard Section: 4.2

92. A radioactive substance decays exponentially. If 800 grams were present initially and 600 grams are present 100 years later, how many grams will be present after 400 years? Round your answer to two decimal places.
A) 251.93 grams B) 251.97 grams C) 252.01 grams D) 253.13 grams
Ans: D Difficulty: hard Section: 4.2
93. The amount of a sample of a radioactive substance remaining after t years is given to be a function of the form 0 () kt QtQe = . If 100 grams remain after 1,000 years and 90 grams after 2,000 years, what is the initial amount 0Q ? Round your answer to two decimal places.
A) 110.21 grams B) 110.83 grams C) 111.11 grams D) 111.49 grams
Ans: C Difficulty: hard Section: 4.2
94. Biologists estimate that the population of a biological colony at time t (in minutes) is 0 () ktPtPe = thousand, where 0P and k are positive constants. If the population is 1,000 after 20 minutes and is known to double every hour, what is the population after 40 minutes? Round to the nearest whole number.
A) 1,258 B) 1,259 C) 1,260 D) 1,261
Ans: C Difficulty: hard Section: 4.2
95. The population density x miles from the center of a city is given by a function of the form () kx QxAe = . Find this function if it is known that the population density at the center of the city is 7,000 people per square mile and the density 14 miles from the center is 4,000 people per square mile. Round numbers to six decimal places, if necessary.
A) –0.287682 ()3,000 x Qxe = C)
0.020549 ()7,000 x Qxe = B) 0.287682 ()7,000 x Qxe = D)
–0.039973 ()7,000 x Qxe =
Ans: D Difficulty: moderate Section: 4.2
96. A radioactive substance decays exponentially. If 500 grams were present initially and 300 grams are present 100 years later, how many grams will be present after 400 years? Round your answer to two decimal places, if necessary.
A) 64.8 grams B) 0.00 grams C) 63.55 grams D) 62.3 grams
Ans: A Difficulty: hard Section: 4.2
97. True or False: If the amount of a sample of radioactive substance that remains after t years is given by 0.0003 0 () t QtQe = and 500 grams of the substance remain at the end of 7,000 years, then there were about 4,083 grams present initially.
A) True B) False
Ans: A Difficulty: hard Section: 4.2

98. An economist estimates that the gross national product (GNP) of a certain country is 0 ktGGe = , where 0G and k are positive constants. If the GNP is 140 billion in 1992 and 170 billion in 1994, when will it be 300 billion? Round your answer to whole years.
A) Approximately 4 years from 1992 C) Approximately 8 years from 1992 B) Approximately 31 years from 1992 D) Approximately 3 years from 1992
Ans: C Difficulty: hard Section: 4.2
99. The gross national product (GNP) of a certain country was 150 billion dollars in 1988 and 160 billion in 1992. Assuming that the GNP grows exponentially, how much does it grow (in billions of dollars) between 1992 and the year 2000? Round your answer to two decimal places.
Ans: 22.04
Difficulty: hard Section: 4.2
100. An efficiency expert hired by a manufacturing firm has compiled the following data relating workers' output to their experience:
Experience (months) 0 6
Output (units per hour) 100 270
The expert believes that the output Q is related to experience t by a function of the form ()300 kt QtAe =− . Find the function of this form that fits the data. Round numbers to four decimal places, if necessary.
Ans: B Difficulty: moderate Section: 4.2
101. An archaeologist has found a fossil in which the ratio of 14C to 12C is 1 5 the ratio in the atmosphere. Approximately how old is the fossil? The half-life of 14C is 5,730 years. Round to the nearest whole year.
A) 13,305 years B) 13,335 years C) 14,325 years D) 28,650 years
Ans: A Difficulty: hard Section: 4.2
102. How many years old is a fossil in which the ratio of 14C to 12C is 1 7 the ratio found in the atmosphere? The half-life of 14C is 5,730 years. Round to the nearest whole year. Ans: 16,086
Difficulty: hard Section: 4.2

103. A fossil is 15,000 years old. What percentage of the ratio of 14C to 12C in the atmosphere is the ratio found in the fossil? The half-life of 14C is 5,730 years. Round your answer to one decimal place.
Ans: 16.3%
Difficulty: hard Section: 4.2
104. Evaluate the expression 2ln33ln4 e without using tables or a calculator.
Ans: 9 16
Difficulty: easy Section: 4.2
105. Differentiate the given function.
Ans: A Difficulty: easy Section: 4.3
106. Differentiate the given function. 3 () x fxe =
107. Differentiate the given function.
108. Differentiate the given function.
Ans: A Difficulty: easy Section:
109. True or False: If 3()(2) x fxxe =+ , then ()12 x fxe =− A) True B) False
Ans: B Difficulty: moderate Section: 4.3
110. True or False: If 7()(5) x fxxe =+ , then ( ) 5 x fxxe =+
A) True B) False
Ans: B Difficulty: moderate Section: 4.3
111. True or False: If 3/(1) () x fxe−+ = , then 3/(1) () x fxe−+ = .
A) True B) False
Ans: B Difficulty: easy Section: 4.3

112. Differentiate the given function. 5 ()ln fxx =
A) 5 x B) 5x C) 5 x D) 1 5x
Ans: A Difficulty: moderate Section: 4.3
113. Differentiate the given function. 7 ()ln fxx =
A) 7 x B) 7x C) 7 x D) 1 7x
Ans: A Difficulty: moderate Section: 4.3
fx
114. True or False: If 35()1 x fxe =+ , then ( ) ( )
A) True B) False
Ans: A Difficulty: moderate Section: 4.3
115. True or False: If 3 ln x yex = , then 3 3ln x dy ex dx =−
A) True B) False
Ans: B Difficulty: hard Section: 4.3
116. True or False: If ln () x x fx e = , then 1/ln () x xx fx e = .
A) True B) False
Ans: A Difficulty: moderate Section: 4.3
117. Find the derivative of ( ) 67 lnln x
.
A) 7 ln xx B) 42 ln xx C) 42 ln xx + D) 42 ln(ln) x
Ans: A Difficulty: moderate Section: 4.3
118. Differentiate the given function. 6 5 () x x fx e =
Ans: ( ) 5 5 65 x xx e
Difficulty: moderate Section: 4.3

119. Differentiate the given function.
33 () x fxxe =
Ans: ( ) 23 31 x xex
Difficulty: moderate Section: 4.3
120. Differentiate the given function.
2
3 () x x fx e =
Ans: 2 3 23 x xx e
Difficulty: moderate Section: 4.3
121. The graph of 33 xe has
A) a relative maximum at x = 0 C) a point of inflection at x = 0
B) a relative minimum at x = 0 D) nothing significant at x = 0
Ans: C Difficulty: hard Section: 4.3
122. The equation of the tangent line to ()6 xfxxe = at x = 5 is
Ans: 5536150 yexe =−
Difficulty: hard Section: 4.3
123. True or False: The equation of the tangent line to ()4 x fxe = at x = 0 is y = 4x + 4.
A) True B) False
Ans: B Difficulty: hard Section: 4.3
124. True or False: The equation of the tangent line to ()3 x fxe = at x = 0 is y = 3x + 3.
A) True B) False
Ans: B Difficulty: hard Section: 4.3
125. True or False: The equation of the tangent line to () xxfxee =− at x = 0 is y = 2x
A) True B) False
Ans: A Difficulty: hard Section: 4.3
126. True or False: The equation of the tangent line to 88 () xxfxee =− at x = 0 is y = 16x.
A) True B) False
Ans: A Difficulty: hard Section: 4.3
127. The equation of the tangent line to 3 () xfxe = at x = 5 is
A) 12512575374 yexe =− C) 125 125 ye =
B) 125 125 x ye = D) 12512575376 yexe =+
Ans: A Difficulty: hard Section: 4.3

128. True or False: The equation of the tangent line to ()3 xfxe = at x = 0 is y = 3x + 3.
A) True B) False
Ans: A Difficulty: hard Section: 4.3
129. True or False: The equation of the tangent line to ()7 xfxe = at x = 0 is y = 7x + 7.
A) True B) False
Ans: A Difficulty: hard Section: 4.3
130. The equation of the tangent line to f (x) = ln x at x = 1 is A) y = x – 1 B) y = x C) x = 1 D) y = 1
Ans: A Difficulty: hard Section: 4.3
131. The equation of the tangent line to 2 ()3ln fxx = at x = e is
Ans: B Difficulty: hard Section: 4.3
132. The equation of the tangent line to f (x) = ln x + 4 at x = 1 is A) y = x + 3 B) y = x C) x = 1 D) y = 1
Ans: A Difficulty: hard Section: 4.3
133. The equation of the tangent line to 6 ()3ln fxx = at x = e is A) 18 yx
Ans: A Difficulty: hard Section: 4.3
134. Find ()fx : 3 ()3ln(25) fxxx =−
Ans: ( ) ( ) 4 2 22 31225 25 x xx −+
Difficulty: moderate Section: 4.3
135. Use logarithmic differentiation to find dy dx , where 325 (21)(5)(1) yxxx =−+− .
Ans: 325 625 (21)(5)(1) 2151 xxx xxx
Difficulty: hard Section: 4.3

136. Use logarithmic differentiation to find ()fx . 6 87 () 24 x fx x + = + A) 84 ()() 8724 fxfx xx =− ++
Ans: B Difficulty: moderate Section: 4.3
137. Use logarithmic differentiation to find dy dx where 643 (81)(1)(6) yxxx =−+− .
Ans: 643 4843 (81)(1)(6) 8116 xxx
Difficulty: hard Section: 4.3
138. Use logarithmic differentiation to find dy dx , where 26 32 (21) (5)(47) x ex y xx = +− .
Ans: 262 323 (21)1267 2 (5)(47)21547 x exx xxxxx
Difficulty: hard Section: 4.3
139. A manufacturer can produce radios at a cost of $10 apiece and estimates that if they are sold for x dollars apiece, consumers will buy approximately 0.2 200 x e radios per month. The price at which the manufacturer should sell the radios to maximize the profit is A) $10 B) $15 C) $18 D) $20
Ans: B Difficulty: hard Section: 4.3
140. A manufacturer can produce toasters at a cost of $7 apiece and estimates that if they are sold for x dollars apiece, consumers will buy approximately 0.2 2,000 x e toasters per week. At what price should the toasters be sold in order to maximize profit?
A) $12 B) $14 C) $18 D) $22
Ans: A Difficulty: hard Section: 4.3
141. The consumer demand for a certain commodity is 0.03 ()5,000 p Dpe = units per month when the market price is p dollars per unit. Determine the market price that will result in the greatest consumer expenditure.
A) $30.31 B) $31.31 C) $33.33 D) $34.33
Ans: C Difficulty: hard Section: 4.3

142. The consumer demand for a certain commodity is 0.93 ()7,000.00 p Dpe = units per month when the market price is p dollars per unit. Express consumers' total monthly expenditure for the commodity as a function of p and determine the market price that will result in the greatest consumer expenditure.
A) $16.13 B) $7,000.00 C) $1.08 D) $8.60
Ans: C Difficulty: moderate Section: 4.3
143. It is estimated that t years from now, the population of a certain country will be 0.02 200 () 19 t Pt e = + million. When will the population be growing most rapidly? Round your answer to two decimal places.
A) 109.86 years from now C) 112.81 years from now
B) 111.92 years from now D) 113.01 years from now
Ans: A Difficulty: hard Section: 4.3
144. A certain machine depreciates so that its value after t years is 0.5 ()10,000 t Qte = dollars. At what rate is the value of the machine changing with respect to time after 3 years?
Ans: Decreasing at $1,115.65 per year
Difficulty: hard Section: 4.3
145. When a certain industrial machine is t years old, its resale value will be /4 ()4,000500 t Vte=+ dollars. How much does the resale value change between the 3rd and 4th years?
A) Decrease by $417.95 C) Decrease by $421.07
B) Decrease by $420.05 D) Decrease by $423.91
Ans: A Difficulty: hard Section: 4.3
146. Records indicate that t weeks after the outbreak of a disease, approximately 1.3 70 () 352 t Qt e = + thousand people have been infected. At what rate was the disease spreading at the end of the third week? Round your answer to two decimal places. Ans: Increasing at 5.83 thousand people per week
Difficulty: hard Section: 4.3
147. True or False: The function () xfxe = is increasing everywhere.
A) True B) False
Ans: A Difficulty: easy Section: 4.4
148. True or False: The function 7 x ye = is increasing everywhere.
A) True B) False
Ans: A Difficulty: easy Section: 4.4

149. Let /180 19 () 96 t ft e = + . Which value of t corresponds to a possible inflection point for f (t)?
A) 3ln(180) 2 B) ln3 2
Ans: C Difficulty: hard Section: 4.4
D) There is no inflection point.
150. Consider the function 2 (6)/5 () x fxe = . For what value of x does this function attain its maximum value, and what is the maximum function value? Round maximum function value to two decimal places, if necessary. A) 6 5 x = , 6 5 f
B) x = 6, f (6) = 1 D) There is no maximum. Ans: B Difficulty: moderate Section: 4.4
151. How many relative extrema does 4 x xe have on the interval (–6, 6)? Ans: 2 Difficulty: moderate Section: 4.4
152. How many relative extrema does 4 x xe have on the domain (–10, 10)? Ans: 2 Difficulty: moderate Section: 4.4
153. True or False: The function f (x) = ln x is concave downward everywhere. A) True B) False Ans: A Difficulty: easy Section: 4.4
154. Let 8 ()10240ln fxxx =− , for x > 0. Find the minimum value of f for x > 0.
A) 8 5(324ln3) B) 8 10(324ln3) C) 0 D) 30(1 – ln 3) Ans: D Difficulty: hard Section: 4.4
155. The graph of 6 ()ln fxx = has A) neither a relative minimum nor a point of inflection at x = 0 B) a relative minimum that is not an inflection point at x = 0 C) a relative maximum that is not an inflection point at x = 0 D) an inflection point that is not a relative minimum at x = 0 Ans: A Difficulty: hard Section: 4.4
156. True or False: The function y = ln 6x is concave downward everywhere. A) True B) False Ans: A Difficulty: easy Section: 4.4

157. The total number of hot dogs sold by a fast-food chain is growing exponentially. If 3 billion have been sold by 1988 and 5 billion by 1990, how many billion will be sold in the year 2000? Round your answer to one decimal place.
Ans: 64.3
Difficulty: hard Section: 4.4
158. The total number of hamburgers sold by a fast food chain is growing exponentially. If 6 billion have been sold by 1998 and 8 billion by 2000, how many will be sold in the year 2010? Round your answer to one decimal place.
Ans: 33.7 billion
Difficulty: hard Section: 4.4
159. A traffic accident was witnessed by 1 12 of the residents of a small town. The number of residents who had heard about the accident t hours later is given by a function of the form 1 kt B Ce + , where B is the population of the town. If 1 5 of the residents had heard about the accident after 4 hours, how long did it take for 1 2 of the residents to hear the news?
Round your answer to two decimal places.
A) 9.48 hours B) 4.74 hours C) 11.85 hours D) 2.37 hour
Ans: A Difficulty: moderate Section: 4.4
160. Suppose your family owns a rare book whose value t years from now will be 0.5 ()5 t Vte = dollars. If the prevailing interest rate remains constant at 6% per year compounded continuously, when will it be most advantageous for your family to sell the book and invest the proceeds? Round your answer to two decimal places.
A) 27.78 years B) 34.72 years C) 104.17 years D) 173.61 years
Ans: B Difficulty: moderate Section: 4.4

1. Evaluate ( ) 5 733xxdx −+ .
A) 6273 3 62 xx xC−++ C) 7x6 3x2 + 3x + C
B) 4 353xC −+ D) 6273 62 xx C −+
Ans: A Difficulty: easy Section: 5.1
2. Evaluate ( ) 5474 xxdx −+ .
Ans: 65 7 4 65 xx xC−++
Difficulty: easy Section: 5.1
3. Evaluate 3 (534)xxdx −+ .
4253 4 42 xx xC−++ C) 42 534xxxC −++ B) 2 153xC −+ D) 4253 42 xx C −+
Ans: A Difficulty: easy Section: 5.1
4. Evaluate 3 35 1 dx xx
−+
Ans: 2 5 3ln 2 xxC x −−+
.
Difficulty: easy Section: 5.1
5. Evaluate 2/3 5 31 5 3 xdx xx −+
Ans: 5/3 4 ln 3 3 43 x xC x +++
Difficulty: easy Section: 5.1
6. Evaluate 7 35 1 dx xx
−+
Ans: 6 5 3ln 6 x xxC −−+
.
Difficulty: easy Section: 5.1

7. True or False: 232 52551 5ln dxxC xxxx x
A) True B) False
Ans: B Difficulty: easy Section: 5.1
8. True or False: 232 62861 8ln|| dxxC xxxx x
A) True B) False
Ans: B Difficulty: easy Section: 5.1
9. Evaluate ( ) 8 2 x xedx .
Ans: 9 2 9 x x eC−+
Difficulty: moderate Section: 5.1
10. Evaluate 3 5 x edx x +
.
Ans: 3 1 5ln 3 x exC−++
Difficulty: easy Section: 5.1
11. Evaluate 7 37 x dx x
Ans: 56 37 56 C xx −++
Difficulty: moderate Section: 5.1
12. True or False: 3232 353 5ln 32 xxxxdxx x −+ =−+ + C
A) True B) False Ans: A Difficulty: easy Section: 5.1
13. Evaluate 4 23 x dx x . Ans: 23 11 xx −+ + C
Difficulty: moderate Section: 5.1

14. True or False: 3232 797 9ln|| 32 xxxxdxxC x
A) True B) False
Ans: A Difficulty: easy Section: 5.1
15. Evaluate: ( ) 3 253 xxxdx +−
16. True or False:
A) True B) False
Ans: A Difficulty: easy Section: 5.1
17. Evaluate 32 (35) xxdx −+ Ans: 4 3 5 4 x xxC−++ Difficulty: easy Section: 5.1
18. Evaluate 7 (4) x xedx . Ans: 8 2 x x eC−+ Difficulty: easy Section: 5.1
19. Evaluate 23 () tt eedt + .
Ans: 2311 23 tt eeC −+ Difficulty: easy Section: 5.1
20. A study indicates that x months from now the population of a certain city will be increasing at the rate of 1/2 (34)xx + people per month. By how much will the population increase over the next 9 months?
A) 70 people B) 80 people C) 90 people D) 100 people
Ans: C Difficulty: hard Section: 5.1

21. A study indicates that x months from now the population of a certain city will be increasing at the rate of 1/2 (43)xx + people per month. By how much will the population increase over the next 9 months?
A) 78 people B) 88 people C) 68 people D) 54 people
Ans: A Difficulty: hard Section: 5.1
22. True or False: A study indicates that x months from now the population of a town will be increasing at the rate of 35xx + people per month. The population will increase by 513 people during the next 9 months.
A) True B) False
Ans: A Difficulty: hard Section: 5.1
23. An object is moving along a straight line in such a way that after t minutes, its speed is 2 ()431 vttt=++ meters per minute. How far does the object travel during the 3rd minute?
A) 203 6 meters B) 205 6 meters C) 209 6 meters D) 211 6 meters
Ans: A Difficulty: hard Section: 5.1
24. An object is moving so that its velocity after t minutes is 2 ()489 vttt =++ meters per minute. How far does the object travel from the end of minute 5 to the end of minute 6?
A) 321 meters B) 1,267 meters C) 317 meters D) 229 meters
Ans: A Difficulty: moderate Section: 5.1
25. Specify the substitution you would choose to evaluate the integrals. 42tdt
26. Specify the substitution you would choose to evaluate the integrals.
A) 4 ut=+ B)
81tt ue ++ = C)
81utt=++ D) ( )4 ute =+ Ans: C Difficulty: easy Section: 5.2
27. Specify the substitution you would choose to evaluate the integrals.

28. Evaluate 2/7 8 7 x dx
.
9/7 49 8 97 x C
2 8 14 x xC−+
Ans: A Difficulty: moderate Section: 5.2
29. True or False: 11 10 (6) (6) 11 x xdxC + +=+
A) True B) False Ans: A Difficulty: easy Section: 5.2
30. True or False: 9 8 (7) (7) 9 x xdxC −=+
A) True B) False Ans: A Difficulty: easy Section: 5.2
31. True or False: 6 5 (3) (3) 6 x xdxC + +=−+
A) True B) False Ans: B Difficulty: moderate Section: 5.2
32. True or False: 7 6 (7) (7) 7 x xdxC + +=+
A) True B) False Ans: A Difficulty: easy Section: 5.2
33. True or False: 10 9 (1) (1) 10 x xdxC −=+
A) True B) False Ans: A Difficulty: easy Section: 5.2
34. True or False: 12 11 (2) (2) 12 x xdxC +=−+
A) True B) False Ans: B Difficulty: moderate Section: 5.2

35. Evaluate 4 6 x edx x +
.
Ans: 4 6ln|| 4 x e xC−++
Difficulty: easy Section: 5.2
36. Evaluate ( ) 82 tt eedt + .
Ans: 82 82 tt ee C −+
Difficulty: easy Section: 5.2
37. Evaluate 32 x edx .
Ans: D Difficulty: moderate Section:
38. Evaluate the following integral: 8 5 x edx
Ans: B Difficulty: moderate
39. Evaluate
Ans: A Difficulty: hard Section:
40. True or False:
A) True B) False
Ans: B Difficulty: moderate Section: 5.2
41. True or False:
A) True B) False
Ans: B Difficulty: moderate

42. Evaluate 37xdx +
Ans: ( )3 2 37 9 xC ++
Difficulty: moderate Section: 5.2
43. Evaluate 53xdx + .
Ans: 3/22(53) 15 x C + +
Difficulty: moderate Section: 5.2
44. Evaluate 3 5xdx
Ans: A Difficulty: easy Section: 5.2
45. Evaluate 3 4 dx x .
Ans: 3ln4xC −+ Difficulty: moderate Section: 5.2
46. Evaluate 2/3 1 9 3 xdx
Ans: C Difficulty: moderate Section: 5.2
47. Evaluate 3 2 x xedx .
Ans: 3 1 3 x eC + Difficulty: moderate
48. Evaluate
xeC + Ans: B Difficulty: moderate Section: 5.2

49. Evaluate 8 7 8 x xedx . A) 8 x eC + B) 9 x eC + C) 8 8 x xeC + D) 8 8 64 x xeC + Ans: A Difficulty: moderate Section: 5.2
50. Evaluate 7 68 x xedx +
Ans: 7 8 7 x e C + +
Difficulty: moderate Section: 5.2
51. Evaluate 4 3 x xedx .
Ans: 4 4 x e C +
Difficulty: moderate Section: 5.2
52. Evaluate 45 4 xxdx + A) 53/22(4) 15 x C + + B) 53/2(4)xC ++ C) 53/2(4)Cx + D) 5 4 xC ++
Ans: A Difficulty: moderate Section: 5.2
53. True or False: 23/2 2 2(2) 22 3 x xxdxC −=+ A) True B) False
Ans: A Difficulty: moderate Section: 5.2
54. Evaluate 2 4 xxdx + . A) 23/2 1 3(4)xC ++ C) 3 4 3 x xC++ B) 23/2(4)xC ++ D) 3/2 3 4 3 x C
Ans: A Difficulty: moderate Section: 5.2
55. Evaluate 2 8 xxdx + A) 23/2(8) 3 x C + + B) 23/2(8)xC ++ C) 3 8 3 x xC++ D) 23/23(8) 4 x C + +
Ans: A Difficulty: moderate Section: 5.2

56. Evaluate 2 1 xdx x + . Ans: 2 1 xC ++ Difficulty: moderate Section: 5.2
57. True or False: 23/2 2 2(1) 21 3 x xxdxC −=+ A) True B) False Ans: A Difficulty: moderate Section: 5.2
58. Evaluate 231/2 (9) xxdx + .
33/2 2 9(9)xC ++ B) 33/2(9)xC ++ C) 33/2(9)Cx + D) 3 9 xC ++ Ans: A Difficulty: moderate Section: 5.2
59. Evaluate 8 73 x xedx + . Ans: 8 3 1 8 x eC + + Difficulty: moderate Section: 5.2
60. Evaluate 3 4 2 x dx x + Ans: 4 ln2 4 x C + + Difficulty: moderate Section: 5.2
61. Evaluate 5 6 3 x dx x + Ans: 6 ln|3| 6 x C + + Difficulty: moderate Section: 5.2
62. Evaluate the indicated integral: 43 54 81288 2055 xx dx xxx ++ +++
A) 43 8ln161 5 xxC +++ C) 54 5ln2055 8 xxxC ++++ B) 54 8ln204 5 xxxC +++ D) 54 8ln2055 5 xxxC ++++
Ans: D Difficulty: moderate Section: 5.2

63. Evaluate 2 2 x dx x + .
Ans: 2 2 xC ++ Difficulty: moderate Section: 5.2
64. Solve the given initial value problem for y = f (x). 2 –4 –8 –1 dyx dxxx = where y = –7 when x = 1
Ans: C Difficulty: moderate Section: 5.2
65. The slope f (x) at each point (x, y) on a curve y = f (x) is given, along with a particular point (a, b) on the curve. Use this information to find f (x). ( ) 2 16 x fxxe = ; (4, 3)
Ans: B Difficulty: moderate Section: 5.2

66. The velocity v(t) (t)= x(t) at time t of an object moving along the x axis is given, along with the initial position x(0) of the object.
( ) ( )1/2 461xtt =−+ ; x(0) = 6
Find:
(a) The position x(t) at time t
(b) The position of the object at time t = 6.
(c) The time when the object is at x = 5.
Round answers for parts (b) and (c) to one decimal place.
A) (a) ( ) ( )3/2 458 61+ 99 xtt=−+
(b) x(6) = –93.6
(c) t = 0.2
B) (a) ( ) ( )3/2 4 61 9 xtt=−+
(b) x(6) = –100.0 (c) t = –0.2
C) (a) ( ) ( )3/2 458 61+ 99 xtt=−+
(b) x(6) = 0.0
(c) t = –70.3
D) (a) ( ) ( )3/2 4 61 9 xtt=−+
(b) x(6) = 0.8
(c) t = –76.7
Ans: A Difficulty: moderate Section: 5.2
67. Water flows into a tank at the rate of 25 t + ft3/min. If the tank is empty when t = 0, how much water does it contain 3 minutes later? Express the answer to two decimal places.
A) 0.36 ft3 B) 8.43 ft3 C) 11.89 ft3 D) 9.95 ft3
Ans: B Difficulty: hard Section: 5.2
68. In a certain section of the country, the price of chicken is currently $3 per kilogram. It is estimated that x weeks from now, the price will be increasing at a rate of 31 x + cents per kilogram. How much will chicken cost 11 weeks from now?
A) $3.81 per kilogram C) $4.81 per kilogram
B) $0.82 per kilogram D) $2.82 per kilogram
Ans: A Difficulty: moderate Section: 5.2

69. Evaluate 1 15 1 xdx .
A) 0 B) 1 15 C) 1 30 D) 1 30
Ans: A Difficulty: easy Section: 5.3
70. Evaluate 1 32 0 (35) xxdx −+ .
Ans: 17 4
Difficulty: easy Section: 5.3
71. Evaluate ( ) 2 53 2 32 xxxdx +− .
Ans: 0
Difficulty: easy Section: 5.3
72. Evaluate ( ) 1 32 0 593xxdx −+ .
Ans: 5 4
Difficulty: easy Section: 5.3
73. Evaluate ( ) 2 53 –2 885xxxdx +− .
Ans: 0
Difficulty: easy Section: 5.3
74. Evaluate 2 53 2 (32) xxxdx +− . Round answer to three decimal places, if necessary.
A) 50.123 B) 4 C) 0 D) 6.892 Ans: C Difficulty: easy Section: 5.3
75. True or False: ( ) 0 3 3 1 2 57 3 xxxdx−+=
A) True B) False Ans: B Difficulty: moderate Section: 5.3
76. Evaluate 2 3 1 35 1 dx xx −+
Ans: 233ln2 8 Difficulty: easy Section: 5.3

77. Evaluate 2 3 1 87 1 dx xx −+
.
Ans: 298ln2 8
Difficulty: easy Section: 5.3
78. Evaluate 3 4 2 23 x dx x .
Ans: 11 216
Difficulty: easy Section: 5.3
79. Evaluate 3 5 2 84 x dx x . Approximate to four decimal places.
Ans: 0.1844
Difficulty: easy Section: 5.3
80. Evaluate 3 4 1(35)xdx . Express your answer as a decimal. Approximate to one decimal place, if necessary.
A) 2,250.2 B) 2,251.6 C) 2,252.8 D) 2,253.4
Ans: C Difficulty: moderate Section: 5.3
81. Evaluate 1 3 1 5 23 dx x + . Approximate your answer to two decimal places, if necessary.
A) 6.22 B) 6.44 C) 6.88 D) 7.22
Ans: D Difficulty: hard Section: 5.3
82. True or False: 8 32 0 1116 5 1 tdt t += +
A) True B) False
Ans: A Difficulty: moderate Section: 5.3
83. Evaluate 1 22 0 (37) x dx x
A) 56 B) 1 56 C) 3 56 D) 1
Ans: B Difficulty: hard Section: 5.3
84. If ()7 b a fxdx =− and ()3 b a gxdx = , find ()() a b fxgxdx .
A) 10 B) –21 C) –10 D) –4
Ans: A Difficulty: moderate Section: 5.3

85. If 11 –5 ()–10fxdx = and 11 9 ()6fxdx = , find 9 –5 () fxdx .
Ans: –16
Difficulty: easy Section: 5.3
86. Find the area of the region under the line y = 8x + 5 over the interval 1 x 5 .
A) 134 B) 126 C) 116 D) 114
Ans: C Difficulty: moderate Section: 5.3
87. Suppose the marginal cost is 0.3 () x Cxe = , where x is measured in units of 500 items and the cost is measured in units of $1,000. Find the cost corresponding to the production interval [500, 2,000]. Round to the nearest dollar.
A) $440 B) $132 C) $1,465 D) $1,165
Ans: C Difficulty: hard Section: 5.3
88. It is estimated that t days from now a farmer's crop will be increasing at the rate of 2 0.30.61 tt++ bushels per day. By how much will the value of the crop increase during the next 4 days if the market price remains fixed at $3 per bushel?
A) $33.60 B) $45.60 C) $60.60 D) $20.40
Ans: B Difficulty: moderate Section: 5.3
89. Determine the area of the region bounded by the curve
32 22yxxx=−−+ and the line y = 2.
Ans: 37 12
Difficulty: hard Section: 5.4
90. Determine the area of the region bounded by the curves x ye = and x ye = between x = 0 and x = ln 2.
Ans: 1 2
Difficulty: hard Section: 5.4
91. Determine the area of the region bounded by the curve
3235yxxx=−++ and the line y = x + 5.
Ans: 27 4
Difficulty: hard Section: 5.4
92. Determine the area of the region bounded by the curves 2 14 yxx =+− and 2 1 yx =+ .
Ans: 8 3
Difficulty: hard Section: 5.4

93. Compute the area of the finite region bounded by the graphs of the functions 2 3 yx = , and 2 336432yxx=−−+ .
A) 3,888 B) 4,536 C) 5,832 D) 5,184
Ans: C Difficulty: hard Section: 5.4
94. Determine the area of the region bounded by the curves x ye = and x ye = between x = 0 and x = ln 9.
Ans: 64 9
Difficulty: hard Section: 5.4
95. Determine the area of the region bounded by the curve 32 22yxxx=−−+ and the line y = 2.
Ans: 37 12
Difficulty: hard Section: 5.4
96. Determine the area of the region bounded by the curves 2 44 yxx =+− and 2 4 yx =+ .
Ans: 8 3
Difficulty: hard Section: 5.4
97. True or False: The area of the region bounded by the curves 2 yx = and 4 yx = is 4 15
A) True B) False
Ans: A Difficulty: hard Section: 5.4
98. True or False: The area of the region bounded by the curve 3 16 x y = and the line y = x is 9.
A) True B) False Ans: B Difficulty: hard Section: 5.4
99. Determine the area of the region bounded by the curve 3 yx = and the line y = 3x + 2.
A) 25 4 B) 27 4 C) 29 4 D) 31 4
Ans: B Difficulty: hard Section: 5.4
100. Determine the area of the region bounded by the line y = x and the curve 3 yx = .
A) 1 2 B) 5 8 C) 3 4 D) 7 8
Ans: A Difficulty: hard Section: 5.4

101. Sketch the region R and then use calculus to find the area of R. R is the region between the curve 3 yx = and the line y = 16x for x 0.
A) 0 B) 64 C) 4 D) 16
Ans: B Difficulty: moderate Section: 5.4
102. Find the average value of 2 1 () x fx x + = over the interval 2 1 xe .
Ans: ( ) 4 2 3 21 e e + Difficulty: moderate Section: 5.4
103. Find the average value of the function 3 () 21 x fx x = + over the interval [3, 5]. Round your answer to two decimal places.
A) 1.33 B) 2.66 C) 1.67 D) 2.33 Ans: A Difficulty: hard Section: 5.4
104. Find the average value of f (x) = 2x + 3 over the interval 0 x 5. Ans: 8 Difficulty: easy Section: 5.4
105. True or False: The average value of 2 ()35 fxxx=−+ over
A) True B) False Ans: A Difficulty: easy Section: 5.4
106. True or False: The average value of () x fxxe = over the interval 0 x 3 is 3 4 3 e
A) True B) False
Ans: B Difficulty: hard Section: 5.4
107. True or False: The average value of 2 1 () 3 xx fx x ++ = + over the interval
A) True B) False
Ans: A Difficulty: hard Section: 5.4

108. Find the Gini index for the given Lorentz curve. Round your answer to four decimal places, if necessary. 2 ()0.80.1 Lxxx =+
A) 1.6333 B) 0.3667 C) 0.3143 D) 0.4400
Ans: B Difficulty: moderate Section: 5.4
109. Records indicate that t hours past midnight, the temperature at the local airport was 2 ()0.3414 fttt=−++ degrees Fahrenheit. What was the average temperature at the airport between 9:00 A.M. and noon? Round your answer to one decimal place, if necessary.
A) 166.1 degrees F B) 22.7 degrees F C) 8.7 degrees F D) 3.2 degrees F
Ans: B Difficulty: moderate Section: 5.4
110. The chief economist for a meat-packing plant estimates that if L worker-hours of labor are employed each week, the number of pounds of meat made ready for sale will be given by 3/4 ()450 QLL = . Find the average weekly output as labor varies from 500 to 800 hours. Round to the nearest pound.
A) 33,735 pounds B) 62,224 pounds C) 49,717 pounds D) 57,832 pounds
Ans: D Difficulty: moderate Section: 5.4
111. The chief economist for a meat-packing plant estimates that if L worker-hours of labor are employed each week, the number of pounds of meat made ready for sale will be given by 3/4
()600 QLL = . Find the level of labor that would result in the average production when labor varies from 500 to 700 hours. Round to the nearest whole hour.
Ans: 599 hours
Difficulty: hard Section: 5.4
112. Given a consumer's demand function, 300 () 0.76 Dq q = + dollars per unit, find the total amount of money consumers are willing to spend to get 15 units of the commodity.
A) $1.01 B) $303.48 C) $216.77 D) $433.54 Ans: D Difficulty: hard Section: 5.5
113. Find the consumer's surplus for a commodity whose demand function is 0.03 ()30 q Dqe = dollars per unit if the market price is 0 $21 p = per unit. (Hint: Find the quantity q0 that corresponds to the given price p0 = D(q0).)
A) $49.53 B) $49.81 C) $50.33 D) $53.41 Ans: C Difficulty: hard Section: 5.5
114. For the demand function 2 ()3(80)Dqq =− dollars per unit, find the total amount of money consumer's are willing to spend when q = 5 units.
A) $1,002 B) $1,053 C) $1,061 D) $1,075 Ans: D Difficulty: hard Section: 5.5

115. For the demand function 2 400 () (0.21) Dq q = + dollars per unit, find the total amount of money consumer's are willing to spend when q = 3 units.
A) $700 B) $720 C) $740 D) $750
Ans: D Difficulty: hard Section: 5.5
116. Find the consumer's surplus for a commodity whose demand function is
500 () 0.43 Dq q = + dollars per unit if the market price is 0 $100 p = per unit. (Hint: Find the quantity q0 that corresponds to the given price p0 = D(q0).)
A) $130.52 B) $138.53 C) $142.01 D) $145.43
Ans: B Difficulty: hard Section: 5.5
117. Money is transferred continuously into an account at the constant rate of $1,200 per year. The account earns interest at the annual rate of 5% compounded continuously. How much will be in the account at the end of 2 years?
A) $2,651.41 B) $65,237.76 C) $2,524.10 D) $2,400.00
Ans: C Difficulty: moderate Section: 5.5
118. An investment will generate income continuously at the constant rate of $2,100 per year for 5 years. If the prevailing annual interest rate remains fixed at 11% compounded continuously, what is the present value of the investment?
A) $8,076.41 B) $807.64 C) $80.76 D) $9,921.44
Ans: A Difficulty: moderate Section: 5.5
119. Money is transferred continuously into an account at the constant rate of $1,400 per year. Assume the account earns interest at the annual rate of 4% compounded continuously. Compute the future value of the income stream over a 12 year period.
A) $862.50 B) $43,125.21 C) $86,250.42 D) $21,562.60
Ans: D Difficulty: hard Section: 5.5
120. Given an initial population, 0 100,000 P = , a renewal rate, R = 2,000, and a survival function, .05 () t Ste = , with time t measured in years, determine the population at the end of 10 years. A)
4,000100,000e + C)
e + B)
e + D)
Ans: D Difficulty: hard Section: 5.6
e +
121. Given an initial population, 0 200,000 P = , a renewal rate, R = 251, and a survival function, 0.08 () t Ste = , with time t measured in years, determine the population at the end of 12 years.
A) 198,064 B) 78,515 C) 4,339 D) 19,421,223
Ans: B Difficulty: hard Section: 5.6

122. Given an initial population P0 = 20,000, a renewal rate 0.04 ()300 t Rte = and a survival function 0.025 () t Ste = , where t is measured in years, determine the population at the end of 18 years.
Ans: 19,292
Difficulty: hard Section: 5.6
123. Find the volume of the solid of revolution formed by rotating the region R about the xaxis.
R is the region under the line y = 8x + 5 from x = 0 to x = 2.
Ans: 1,142 π 3
Difficulty: moderate Section: 5.6
124. Find the volume of the solid of revolution formed by rotating the region R about the xaxis.
R is the region under the curve 2 64 yx =− from x = –8 to x = 8. A) 64π B) 256 π 3 C) 2,048 π 3 D) 512π
Ans: C Difficulty: moderate Section: 5.6
125. Find the volume of the solid of revolution formed by rotating the region R about the xaxis.
R is the region under the curve 2 1 y x = from x = 1 to x = 4.
Ans: 21 π 64
Difficulty: moderate Section: 5.6
126. A certain nuclear power plant produces nuclear waste in the form of strontium-90 at the constant rate of 400 pounds per year. The waste decays exponentially with a half-life of 28 years. How much of the radioactive waste from the nuclear plant will be present after 120 years? [Hint: Think of this as a survival and renewal problem.] Round to two decimal places.
A) 16,986.63 pounds C) 15,329.74 pounds B) 7,664.87 pounds D) 8,057.85 pounds
Ans: C Difficulty: moderate Section: 5.6

127. True or False: A new health club has just opened. Statistics suggest that the fraction of clients who will still be attending the club t months after their initial visit is given by 0.08 () t fte = . The club initially accepts 1,000 people for membership and plans to accept new members at the rate of 50 per month. Approximately 680 people will be in the club 2 years from now.
A) True B) False
Ans: A Difficulty: hard Section: 5.6
128. A television program currently has P0 = 19 million loyal watchers, and new people are expected to begin watching at the rate of 0.01 ()0.4 t Rte = per year. The fraction of people still watching after t years is expected to be 0.025 () t Ste = . How many watchers will there be after 5 years? Round to one decimal place.
Ans: 18.7 million
Difficulty: hard Section: 5.6
129. The population density r miles from the center of a certain city is given by the function 2 /100 ()2,000 r Dre = people per square mile. How many people live within 10 miles of the city's center?
Ans: 397,173
Difficulty: hard Section: 5.6
130. True or False: The population density r miles from the center of a city is
2 0.5 () r Drke = people per square mile. If 300,000 people live within 5 miles from the center of the city, then k is 15,000.
A) True B) False
Ans: B Difficulty: hard Section: 5.6

1. Evaluate /3 x xedx .
A) /3/3 1 3 xx xeeC −+
B) /3/311 39 xx xeeC −+
Ans: C Difficulty: hard Section: 6.1
2. Evaluate /9 x xedx .
A) /9/9981xx xeeC −+
B) /9/9981xx xeeC ++
Ans: A Difficulty: hard Section: 6.1
/3/339xx xeeC −+
/3/339xx xeeC ++
/9/9 981 xx xee C ++
/9/9 981 xx xee C −+
3. Use integration by parts to evaluate the integral (13) x xedx .
A) (14) x xeC−+
(13) x xeC−+ B) (14) x xeC++
Ans: A Difficulty: moderate Section: 6.1
4. Evaluate 2 (23) x xedx .
2 31 24 x exC −+
Ans: A Difficulty: hard Section: 6.1
5. Evaluate (3)ln(2) xxdx
2 (3)ln(2) 2 x x + C
B) 2 (6)ln(2) 3 42 xxxx x −+ + C
Ans: B Difficulty: hard Section: 6.1
6. True or False:
A) True B) False
Ans: A Difficulty: hard Section: 6.1
(14) x xeC−−+
eC−+
6(6)ln(2) 2 x xxxx −+− + C
2 (6)ln(2) 2 x xxx+− + C

7. Evaluate 9(2) xxdx A) 10 1 55(2)(10)xxC −++ C) 10 1 55(2)(51)xxC −++ B) 10 1 110(2)(52)xxC −++ D) 10 1 110(2)(101)xxC −++
Ans: C Difficulty: hard Section: 6.1
8. Evaluate 327 (3) xxdx A) 2 2829 1 16144(3)(3) x xxC −−−+ C) 2 2816(3) x xC −+ B) 2 2829 1 1672(3)(3) x xxC −−−+ D) 283(3) 24 xx C +
Ans: A Difficulty: hard Section: 6.1
9. Evaluate 8(7) xxdx +
Ans: ( ) ( ) 91011 77 990 xxxC +−++
Difficulty: hard Section: 6.1
10. Evaluate 747 (6) xxdx .
Ans: ( )( )8 44 1 436 144 xxC +−+
Difficulty: hard Section: 6.1
11. Evaluate 8(9) xxdx + .
Ans: 910(9)(9) 990 xxx C ++ −+
Difficulty: hard Section: 6.1
12. Evaluate 11611 (2) xxdx .
Ans: 6 612613 1 72936(2)(2) x xxC −−−+
Difficulty: hard Section: 6.1

13. Use integration by parts to evaluate the integral 20 x dx x + .
1/2 2 3(20)(40)xxC −++
1/2 3(20)(40) 2 xxC +−+ B) 1/2 2 3(20)(40)xxC +−+
Ans: B Difficulty: moderate Section: 6.1
3/2 2 3(20)(40)xxC +−+
14. True or False: The area of the finite region bounded by the curves x yxe = , y = 0, and x = 4 equals 4 15e .
A) True B) False
Ans: A Difficulty: hard Section: 6.1
15. Evaluate ln xxdx A) 22 ln 48 xxx + C B) x + C C) 2 ln xxC + D) 2 ln 4 xx C +
Ans: A Difficulty: hard Section: 6.1
16. Evaluate 2 ln xxdx .
Ans: 33 ln 39 xxxC −+
Difficulty: hard Section: 6.1
17. Evaluate 2 ln3x dx x
Ans: 1ln3x C xx −−+
Difficulty: hard Section: 6.1
18. Evaluate 7 ln2x dx x
Ans: 66 ln21 636 x C xx −−+
Difficulty: hard Section: 6.1
19. Evaluate ( )2 ln xxdx .
Ans: ( )2 2 22 ln ln 422 xx xxx C −++
Difficulty: hard Section: 6.1

20. Evaluate ( )2 4 ln xxdx .
Ans: ( ) 555 2 22 lnln 525125 xxxxxC −++
Difficulty: hard Section: 6.1
21. Evaluate 2 3 x xedx
Ans: ( ) 2 2 1 1 2 x xeC −+
Difficulty: hard Section: 6.1
22. Evaluate 4 7 x xedx
Ans: 4 4 4(1) x e xC −+
Difficulty: hard Section: 6.1
23. Evaluate 25 x dx x + .
Ans: ( ) 5ln25 24 x xC−++
Difficulty: hard Section: 6.1
24. Evaluate 73 x dx x +
Ans: 7493ln|73| x xC−++
Difficulty: hard Section: 6.1
25. Use the formula 1 (ln)(ln)(ln) nnn xdxxxnxdx =− to evaluate 3(ln)xdx .
Ans: ( ) ( ) 32 ln3ln6ln6 xxxxxxxC −+−+
Difficulty: moderate Section: 6.1
26. True or False: ( ) ( ) 22 lnln2ln2 xdxxxxxxC =−++ A) True B) False
Ans: A Difficulty: hard Section: 6.1

27. A manufacturer has found that marginal cost is 0.02 (21) q qe + dollars per unit when q units have been produced. The total cost of producing the first 10 units is $100. What is the total cost of producing the first 30 units?
A) $1,124.68 B) $545.39 C) $300.00 D) $635.39 Ans: D Difficulty: hard Section: 6.1
28. After t hours on the job, a factory worker can produce 0.5 70 t te units per hour. How many units does the worker produce during the first 2 hours? Round to two decimal places.
A) 206.01 units B) 73.99 units C) 486.01 units D) 125.49 units Ans: B Difficulty: moderate Section: 6.1
29. True or False: If, after t hours on the job, a factory worker can produce 0.02 10 t te units per hour, then the worker produces 130 units during the first 5 hours.
A) True B) False Ans: B Difficulty: hard Section: 6.1
30. From time t = 0 to t = 3 an object's speed is given by the function 3 () t stte = . Compute the distance travelled by the object during this time interval. Round your answer to two decimals.
A) 7,213.11 B) 7,198.98 C) 7,304.18 D) 7,202.85 Ans: D Difficulty: moderate Section: 6.1
31. An object moving in a straight line has velocity () t vtte = meters per second. Is it true that in the first 4 seconds the object will have travelled 2 412 e + meters?
A) True B) False
Ans: A Difficulty: hard Section: 6.1
32. True or False: After t seconds, an object is moving at the speed of 1 t te meters per second. If the object begins at 0 when t = 0, then the distance the object travels as a function of time is expressed 1 ()(1) t stet=−+ .
A) True B) False Ans: A Difficulty: hard Section: 6.1
33. After t weeks, a charity is raising money at the rate of 5,000 t ln(t + 1) dollars per week. How much money is raised during the first 10 weeks? Round to the nearest ten dollars.
A) $493,000 B) $493,480 C) $493,520 D) $493,550 Ans: B Difficulty: hard Section: 6.1
34. It is projected that t years from now the population of a city will be changing at the rate of 20.01t te thousand people per year. If the current population is 1 million, what will the population be 4 years from now?
A) 1,028,000 B) 1,000,022 C) 1,028,800 D) 1,021,984 Ans: D Difficulty: hard Section: 6.1

35. Given an initial population, 0 19,000 P = , a renewal rate, R = 200, and a survival function, 0.3 () t Stte = , with time t measured in years, determine the population at the end of 20 years. Round to two decimal places.
A) 1,358.95 B) 138.00 C) 9,814.35 D) 3,125.59
Ans: D Difficulty: moderate Section: 6.1
36. Find the average value of the function /6 () x fxxe = over the interval from 0 to 5. Round to two decimal places.
A) 11.65 B) 22.98 C) 1.46 D) 7.32
Ans: C Difficulty: moderate Section: 6.1
37. Evaluate 3 1 dx x
A) 0 B) 1 C) 1 3 D) Diverges
Ans: D Difficulty: hard Section: 6.2
38. Evaluate 6 1 1 dx x
A) Diverges B) 0 C) 6 5 D) 5 6
Ans: A Difficulty: hard Section: 6.2
39. Evaluate 2 5 1 dx xx . 2 111 Hint: 1 xxxx
Ans: ln5 4 Difficulty: hard Section: 6.2
40. Evaluate 2 3 (1) dx xx . Ans: Diverges Difficulty: hard Section: 6.2
41. Evaluate 5 1 x edx .
A) 5 1 5e B) 1 5e C) 5 e D) 5 5e
Ans: A Difficulty: moderate Section: 6.2

42. Given that 2 0 π 2 x edx = , evaluate 2 9 0 x edx Ans: π 6 Difficulty: hard Section: 6.2
43. Evaluate 3 1 x edx .
44. True or False: 3 0 11 (1)8 dx x = +
A) True B) False Ans: B Difficulty: hard Section: 6.2
45. Evaluate the improper integral: 2 32 2 (9) x dx x + A) 51 B) 1 34 C) 1 53 D) 1 51 Ans: D Difficulty: moderate Section: 6.2
46.
or
A) True B) False Ans: B Difficulty: hard Section: 6.2
48. Evaluate 2 1 ln dx xx
A) 0 B) 1 2ln2 C) 1 2ln2 D) Diverges
Ans: D Difficulty: hard Section: 6.2

49. Evaluate the improper integral: 10 1 (3)ln(3) dx xx
Round your answer to two decimal places, if necessary.
A) 0.67 B) 1.95 C) 2.30 D) Undefined
Ans: D Difficulty: moderate Section: 6.2
50. Evaluate the improper integral: 4 3/5 0 x xedx
Round to two decimal places, if necessary.
A) 1.88 B) 2.5 C) 1.25 D) Undefined
Ans: C Difficulty: moderate Section: 6.2
51. True or False: 3 2 0 1 3 x x dx e =
A) True B) False
Ans: A Difficulty: hard Section: 6.2
52. True or False: 3 2 0 1 3 x x dx e =
A) True B) False
Ans: A Difficulty: hard Section: 6.2
53. A certain nuclear power plant produces radioactive waste at the rate of 500 pounds per year. The waste decays exponentially at the rate of 1.5% per year. How many pounds of radioactive waste from the plant will be present in the long run? Round to two decimal places, if necessary.
Ans: 33,333.33 lbs
Difficulty: hard Section: 6.2
54. Demographic studies conducted in a certain city indicate that the fraction of the residents that will remain in the city for at least t years is /50 () t fte = . The current population of the city is 500,000, and it is estimated that new residents will be arriving at the rate of 1,000 people per year. If this estimate is correct, what will be the population in the long run?
A) 50,000 B) 40,500 C) 40,800 D) 550,000
Ans: A Difficulty: hard Section: 6.2
55. A hospital patient receives 4 units of a certain drug per hour intravenously. The drug is eliminated exponentially, so that the fraction that remains in the patients body for t hours is /12 () t fte = . If treatment is continued indefinitely, approximately how many units of the drug will be in the patient's body in the long run?
A) 44 units B) 48 units C) 52 units D) 56 units
Ans: B Difficulty: hard Section: 6.2

56. A hospital patient receives intravenously 5 units of a certain drug per hour. The drug is eliminated exponentially, so that the fraction that remains in the patients body for t hours is /14 () t fte = . If the treatment is continued indefinitely, approximately how many units of the drug will be in the patient's body in the long run? Round to two decimal places, if necessary.
A) 19 units B) 65 units C) 70 units D) 0.36 units
Ans: C Difficulty: moderate Section: 6.2
57. The long run capitalized cost of an asset that initially cost 0C dollars is given by 0 0 () rt CCAtedt =+ where A(t) is the annual cost of maintenance and r is the annual rate of interest, compounded continuously. Find the long run capitalized cost, in dollars, in the case where 0 $5,000,000 C = , A(t) = 5, 000(1 + 3t), and r = 0.08.
Ans: 7,406,250
Difficulty: hard Section: 6.2
58. Approximate the integral 2 1/ 1 x edx using (a) the trapezoidal rule and (b) Simpson's rule, both with 6 subintervals. Round your answer to five decimal places.
Ans: (a) 2.02536
(b) 2.02019
Difficulty: hard Section: 6.3
59. Approximate the integral 2 1 0 x edx using (a) the trapezoidal rule and (b) Simpson's rule, both with 4 subintervals. Round your answer to five decimal places.
Ans: (a) 1.49068 (b) 1.46371
Difficulty: hard Section: 6.3
60. Determine how many subintervals are required to guarantee accuracy to within 0.00001 for the approximation of the integral 2 2 1 ln(1)xdx + using (a) the trapezoidal rule and (b) Simpson's rule.
Ans: (a) 46 (b) 7
Difficulty: hard Section: 6.3
61. Assume a 9-year franchise is expected to generate profit at the rate of 2 3 13,000 t + dollars per year. If, over the next 9 years, the prevailing annual interest rate remains fixed at 6%, compounded continuously, what is the present value of the franchise? Use Simpson's rule with n = 6 to approximate the integral. Round your answer to two decimal places.
A) $473.20 B) $283.92 C) $946.41 D) $315.47
Ans: D Difficulty: hard Section: 6.3

62. Shortly after leaving on a road trip, two math majors realize that the car's odometer is broken. To estimate the distance they travel between 8 PM and 9 PM, they record speedometer readings every 10 minutes:
Time8:008:108:208:308:408:509:00
Speed(mph)58704065307960
Using Simpson's rule and only the information in the table, get the best possible estimate of the distance they traveled between 8 PM and 9 PM. Round your answer to one decimal place.
Ans: 61.9 miles
Difficulty: easy Section: 6.3

1. Let 2 (,)4 fxyxy =− . Compute f (2, 0).
Ans: 16
Difficulty: easy Section: 7.1
2. 2 (,)4 fxyxy =− . Compute f (3, 0).
Ans: 36
Difficulty: easy Section: 7.1
3. Let f (x, y) = 9xy. Compute f (7, 0).
Ans: 0
Difficulty: easy Section: 7.1
4. Compute f (8, 1) if 3 (,)8 fxyxy =
A) 64 B) 4,096 C) 8 D) 512
Ans: A Difficulty: easy Section: 7.1
5. Let f (x, y) = 5xy. Compute f (9, 0).
Ans: 0
Difficulty: easy Section: 7.1
6. Compute f (ln 2, ln 5) if 2 (,) xy fxye + = .
A) 20 B) 10 C) 9 D) None of the above
Ans: A Difficulty: moderate Section: 7.1
7. Let (,) y x fxy e = . Compute f (3, 0).
A) 0 B) 3 C) Undefined D) 4
Ans: B Difficulty: easy Section: 7.1
8. Compute f (7, 0) if (,) y x fxy e = .
A) 7 B) 0 C) 1 7 D) Undefined
Ans: A Difficulty: easy Section: 7.1
9. Let 2 (,)5 y fxyxe =− . Compute f (3, 0).
Ans: 44
Difficulty: easy Section: 7.1
10. Given the function of three variables f (x, y, z) = xy + xz + yz, evaluate f (–4, 7, 7).
A) 2 B) –4 C) –12 D) –7
Ans: D Difficulty: moderate Section: 7.1

11. What is the domain of 221/2 (,) (16) x fxy xy = +− ?
Ans: 22 16 xy+
Difficulty: easy Section: 7.1
12. What is the domain of ( )1/2 22 (,) 64 x fxy xy = +− ?
Ans: 22 64 xy+
Difficulty: easy Section: 7.1
13. Consider the graph of the level curve f (x, y) = C for 2 (,) fxyxy =− and C = –3. The graph is A) a parabola B) a circle C) an ellipse D) a straight line
Ans: A Difficulty: hard Section: 7.1
14. 3 (,)3 Qxyxy = is the daily production for x skilled and y unskilled workers. What is the exact change in daily production if x changes from 4 to 3 and y from 2 to 1?
Ans: –87
Difficulty: hard Section: 7.1
15. Compute y f for 3 (,)5 fxyxy = A) 5x B) 2 15xy C) 23155xyy + D) 3 y
Ans: B Difficulty: moderate Section: 7.2
16. Compute xf for 3 (,)5 fxyxy =
A) 5x B) 2 15xy C) 23155xyy + D) 3 5y
Ans: D Difficulty: moderate Section: 7.2
17. Compute fx for f (x, y) = 2x5y 5x + exy
Ans: 4 105 xyxyye −+
Difficulty: hard Section: 7.2
18. Compute xf for 6 (,)43 xyfxyxyxe =−+ .
Ans: 5 243 xyxyye −+
Difficulty: hard Section: 7.2
19. Compute y f for 8 (,)4 fxyxy =
A) 7 32xy B) 4x C) 8 4y D) 78324xyy +
Ans: A Difficulty: moderate Section: 7.2

20. Compute xf for 8 (,)4 fxyxy = .
A) 8 4y B) 7 32xy C) 4x D) 78324xyy +
Ans: A Difficulty: moderate Section: 7.2
21. Compute all first-order partial derivatives of the given function. 4(,)(48) fxyxy =+
A) 316(48) x fxy =+ , 332(48) y fxy =+
B) 516(48) x fxy =+ , 532(48) y fxy =+
C) 316(8) x fxy =+ , 332(48) y fx=+
D) 316(8) x fy = , 332(4) y fx =
Ans: A Difficulty: moderate Section: 7.2
22. Compute xf for 5 (,) xy fxye = . A)
Ans: A Difficulty: moderate Section: 7.2
23. Compute xf for (,) xyfxye = A) xye B) xyxe C) xyye D) xyxye
Ans: C Difficulty: moderate Section: 7.2
24. Compute y f for (,)8 y fxyxe = .
Ans: 8 yxe
Difficulty: moderate Section: 7.2
25. If (,) xyfxyxe = , find (2,3) y f
Ans: 4e6
Difficulty: easy Section: 7.2
26. If (,) xyfxyxe = , find (5,4) y f .
Ans: 20 25e
Difficulty: easy Section: 7.2
27. If f (y) = x ln y, find (2,1) y f .
Ans: 2
Difficulty: easy Section: 7.2
28. Find xy f for 33 (,) fxyxy =+
A) 6x B) 2233xy + C) 0 D) 6y
Ans: C Difficulty: moderate Section: 7.2

29. Let f (x, y) = x ln(1 + 2x – 5y). Find (,) xx fxy .
Ans: ( )2 4204 125 xy xy −+ +−
Difficulty: hard Section: 7.2
30. Compute yy f for
(,) xy fxye =
Ans: A Difficulty: moderate
31. Find yy f for (,) xyfxye = A) 2 xyye B) xyxye C) 2 xyxe D) xye
Ans: C Difficulty: moderate Section: 7.2
32. Let 2 5 (,) xy fxyye = . Find (,) yy fxy .
Ans: ( ) 2 225552 xy xxye
Difficulty: hard Section: 7.2
33. The weekly output for a manufacturer is 22 (,)12502 Qxyxyxy =+−+ units. Use marginal analysis to estimate the change in weekly output as a result of changing x from 20 to 21 while y remains constant at 10.
Ans: –68
Difficulty: hard Section: 7.2
34. The daily output for a manufacturer is 1/31/2 (,)10 QKLKL = units. Use marginal analysis to estimate the change in daily output as a result of changing L from 625 to 626 while K remains constant at 216. Round your answer to one decimal place, if necessary. Ans: 1.2
Difficulty: hard Section: 7.2
35. A mall kiosk sells two different models of pagers, the Elite and the Diamond. Their monthly profit from pager sales is (,)(40)(2056)(50)(3034) Pxyxxyyxy =−−++−+− where x and y are the prices of the Elite and the Diamond respectively, in dollars. At the moment, the Elite sells for $32 and the Diamond sells for $40. Use calculus to estimate the change in monthly profit if the kiosk operator raises the price of the Elite to $33 and lowers the price of the Diamond to $38.
A) Profit will increase by about $26. C) Profit will increase by about $194. B) Profit will decrease by about $310. D) Profit will stay the same.
Ans: C Difficulty: moderate Section: 7.2

36. If 22 zxy =+ , 5 xt = , and 2 ytt =− , find dz dt when t = 9.
A) –2,111 B) 10,618 C) –8,100 D) 2,473
Ans: D Difficulty: moderate Section: 7.2
37. Find the extrema (minima, maxima, saddle points), if any, for f (x, y) = (x – 1)(y + 2).
Ans: Saddle point at (1, –2)
Difficulty: hard Section: 7.3
38. Find the extrema (minima, maxima, saddle points), if any, for f (x, y) = (x – 3)(y + 9).
Ans: Saddle point at (3, –9)
Difficulty: hard Section: 7.3
39. Find the extrema (minima, maxima, saddle points), if any, for 22(,)67 fxyxy =− .
Ans: Saddle point at (0, 0)
Difficulty: hard Section: 7.3
40. Find the extrema (minima, maxima, saddle points), if any, for 22(,)56 fxyxy =− .
Ans: Saddle point at (0, 0)
Difficulty: hard Section: 7.3
41. Find the extrema (minima, maxima, saddle points), if any, for 22 (,)68 fxyxxyy =−+−
Ans: Relative minimum at (3, 4)
Difficulty: hard Section: 7.3
42. Find the critical points and classify each as being a minimum, maximum, saddle point, or other, for 23 (,)6 fxyxyxy =+− .
Ans: Saddle point at (0,0); relative minimum at (18,6)
Difficulty: moderate Section: 7.3
43. Find the extrema (minima, maxima, saddle points), if any, for 22 (,)124 fxyxxyy =−+−
Ans: Relative minimum at (6, 2)
Difficulty: hard Section: 7.3
44. Find the critical points and classify each as being a minimum, maximum, saddle point, or other, for 4422(,)22 fxyxyxy =+−− .
Ans: Relative maximum at (0,0); saddle points at (0,1), (0,–1), (1,0), (–1,0); relative minima at (1,1), (1,–1), (–1,1), (–1,–1)
Difficulty: moderate Section: 7.3

45. Find the critical points and classify each as being a minimum, maximum, saddle point, or other, for 23 (,)18 fxyxyxy =+−
Ans: Saddle point at (0, 0); relative minimum at (486, 54)
Difficulty: moderate Section: 7.3
46. Find the critical points and classify each as being a minimum, maximum, saddle point, or other, for 22 (,)55 fxyxxyyxy =+−+− .
Ans: Saddle point at (–1,–3)
Difficulty: moderate Section: 7.3
47. Find the critical points and classify each as being a minimum, maximum, saddle point, or other, for 22 (,)3030 fxyxxyyxy =+−+−
Ans: Saddle point at (–6, –18)
Difficulty: moderate Section: 7.3
48. The only grocery store in a small rural community carries two brands of frozen apple juice, a local brand that it obtains at the cost of 22 cents per can and a well-known national brand that it obtains at the cost of 40 cents per can. The grocer estimates that if the local brand is sold for x cents per can and the national brand for y cents per can, approximately 70 – 5x + 4y cans of the local brand and 80 + 6x – 7y cans of the national brand will be sold each day. How should the grocer price each brand to maximize the profit from the sale of the juice?
A) local brand (x) at 94 cents, national brand (y) at 51 cents
B) local brand (x) at 42 cents, national brand (y) at 106 cents
C) local brand (x) at 49 cents, national brand (y) at 53 cents
D) local brand (x) at 47 cents, national brand (y) at 53 cents
Ans: D Difficulty: moderate Section: 7.3
49. A manufacturer with exclusive rights to a sophisticated new industrial machine is planning to sell a limited number of the machines to both foreign and domestic firms. The price the manufacturer can expect to receive for the machines will depend on the number of machines made available. (For example, if only a few of the machines are placed on the market, competitive bidding among prospective purchasers will tend to drive the price up.) It is estimated that if the manufacturer supplies x machines to the domestic market and y machines to the foreign market, the machines will sell for 60 520 xy−+ thousand dollars apiece at home and for 50 1020 yx−+ thousand dollars apiece abroad. If the manufacturer can produce the machines at a cost of $38,000 apiece, how many should be supplied to each market to generate the largest possible profit?
A) x = 100, y = 8
B) x = 41, y = 643
C) x = 80, y = 100
D) x = 40, y = 500
Ans: C Difficulty: moderate Section: 7.3

50. Given the following points in the plane, find the corresponding least squares line: (1, 2), (2, 1), (4, 2), and (5, 1)
Ans: 19 105yx=−+
Difficulty: moderate Section: 7.4
51. Given the following points in the plane, find the slope of the least squares line: (1, 2), (2, 1), (3, 3), and (5, 18) round your answer to two decimal places, if necessary.
A) 4.23 B) 4.17 C) 4.11 D) 4.06
Ans: A Difficulty: moderate Section: 7.4
52. Given the following points in the plane, find the y-intercept of the least squares line to two decimal places: (3, 3), (5, 5), (7, 8), and (9, 21)
A) –7.85 B) –7.73 C) –9.95 D) –9.35
Ans: A Difficulty: moderate Section: 7.4
53. The following data shows the age and income for a small number of people. Age (years) 24 32 39 54 60
Find the best fit straight line of this data, rounding coefficients and constants to the nearest whole number. Let x represent age and y represent income. A) y = 1,727x – 15,776 C) y = 3,348x – 15,783 B) y = 4,072x – 15,771 D) None of the above
Ans: A Difficulty: moderate Section: 7.4
54. The accompanying table lists the high-school GPA and college GPA for a number of students:
Using the best fit straight line, predict the college GPA (to one decimal place) for a student whose high school GPA was 3.5.
A) 3.4 B) 3.3 C) 3.6 D) 3.5
Ans: A Difficulty: moderate Section: 7.4

55. The accompanying table gives the Dow Jones Industrial Average (DJIA) at the close of the first trading day of the indicated years:
Find the least squares line for the DJIA, D, as a function of the year after 1990, t Round numbers to two decimal places.
Ans: D = 693.75t + 2,131.10
Difficulty: moderate Section: 7.4
56. The accompanying table lists the Gross Domestic Product (GNP) figures for China (in billions of yuan) for the period from 1996 to 2000:
Use the best fit straight line to extrapolate the GNP to the nearest yuan in 1990?
A) 3,801 billion yuan
B) 3,876 billion yuan
Ans: A Difficulty: moderate Section: 7.4
3,942 billion yuan
3,989 billion yuan
57. A military radar is measuring the distance to a jet fighter. The radar has received the following measurements:
Using a least squares fit to the data, extrapolate to the nearest tenth of a minute when the jet will be 331 miles away?
A) 9.2 minutes B) 8.1 minutes C) 11.4 minutes D) 10.6 minutes
Ans: A Difficulty: moderate Section: 7.4
58. Find the maximum value of 2 (,) fxyxy = subject to the constraint g(x, y) = x – y = 2.
Ans: 32 27
Difficulty: hard Section: 7.5
59. Find the minimum value (if any) of 2 (,) fxyxy = subject to the constraint g(x, y) = x – y = 2.
Ans: 0
Difficulty: hard Section: 7.5

60. Find the minimum value of f (x, y) = x + 2y subject to the constraint 2 (,)8gxyxy== .
Ans: 6
Difficulty: hard Section: 7.5
61. Use Lagrange multipliers to find the maximum value of f (x, y) = 5xy subject to the constraint 3x + 3y = 9. A) 3345 , 4416 f =
B) 3345 , 224 f =
C) f (3, 3) = 45 D) f (0, 0) = 0
Ans: B Difficulty: moderate Section: 7.5
62. Find the maximum value of 2 (,) fxyxy = subject to the constraint g(x, y) = x – y = 5.
Ans: 500 27
Difficulty: hard Section: 7.5
63. Find the minimum value of 2 (,) fxyxy = subject to the constraint g(x, y) = x – y = 8.
Ans: 0
Difficulty: hard Section: 7.5
64. Find the minimum value of 22 (,)44 fxyxyy=+−+ on the hyperbola 22 4 xy−=
A) 123 B) 43 C) 6 D) No minimum, unbounded below Ans: C Difficulty: moderate Section: 7.5
65. Find the minimum and maximum value of 22 (,) fxyxy =+ on the ellipse 22 321 xy+= . A)
D) No maximum or minimum, unbounded Ans: B Difficulty: moderate Section: 7.5
66. Find the maximum value of f (x, y) = xy on the ellipse 22 4936 xy+= Ans: 3
Difficulty: moderate Section: 7.5
67. Find the maximum value of f (x, y, z) = xyz on the sphere 222 12 xyz++=
A) 8 B) 83 C) 16 D) No maximum, unbounded Ans: A Difficulty: moderate Section: 7.5

68. Use Lagrange multipliers to find the maximum value of f (x, y, z) = 3xyz subject to 4x + 4y + 1z = 48.
A) f (0, 0, 0) = 0
C) f (4, 4, 16) = 768
B) f (7, 5, 14) = 1,470 D) f (5, 2, 16) = 480
Ans: C Difficulty: moderate Section: 7.5
69. Find the maximum value of the function f (x, y, z) = 5x + 6y + 10z on the sphere 222 644 xyz++= .
A) 1,610 B) 1,127.0 C) 161 D) 322
Ans: D Difficulty: moderate Section: 7.5
70. A manufacturer is planning to sell a new product at the price of $200 per unit and estimates that if x thousand dollars is spent on development and y thousand dollars is spent on promotion, approximately 500250 48 yx yx + ++ units of the product will be sold. The cost of manufacturing the product is $170 per unit. If the manufacturer has a total of $500,000 to spend on development and promotion, how should this money be allocated to generate the largest possible profit? [Hint: Profit equals (number of units)(price per unit minus cost per unit) minus total amount spent on development and promotion.]
A)
$248,500 on development, $251,500 on promotion
B) $251,500 on development, $248,500 on promotion
C) $252,000 on development, $248,500 on promotion
D) $248,000 on development, $252,000 on promotion
Ans: D Difficulty: moderate Section: 7.5
71. Evaluate the following double integral: 94 49 –24xydydx
A) 1 4 B) 5 C) 0 D) The integral can't be evaluated.
Ans: C Difficulty: moderate Section: 7.6

72. Use inequalities to describe R in terms of its vertical and horizontal cross sections. R is the region bounded by y = x2 and y = 7x.
A) Vertical cross sections: 049 7 y y xy
Horizontal cross sections: 2 07 7 x xyx
B) Vertical cross sections: 2 07 7 x xyx
Horizontal cross sections: 049 7 y y xy
C) Vertical cross sections: 2 049 7 x xyx
Horizontal cross sections: 07 7 y y xy
D) Vertical cross sections: 07 7 y y xy
Horizontal cross sections: 2 049 7 x xyx
Ans: B Difficulty: easy Section: 7.6

73. Use inequalities to describe R in terms of its vertical and horizontal cross sections. R is the rectangle with vertices (3, –5), (5, –5), (5, –1), (3, –1).
A)
Vertical cross sections: –5–1 35 x y
Horizontal cross sections: –5–1
y
B) Vertical cross sections: 35 –5–1 x y
Horizontal cross sections: 35 –5–1 y x
C) Vertical cross sections: –5–1 35 x y
Horizontal cross sections: 35 –5–1 y x
D) Vertical cross sections: 35 –5–1 x y
Horizontal cross sections: –5–1
y x
Ans: D Difficulty: easy Section: 7.6

74. Use inequalities to describe R in terms of its vertical and horizontal cross sections. R is the region bounded by y = ex , y = 8, and x = 0.
A) Vertical cross sections: 0ln8 8 x x ey
Horizontal cross sections: 18 0ln y xy
B) Vertical cross sections: 0ln 8 x xy ey
Horizontal cross sections: 18 0ln8 y x
C) Vertical cross sections: 8 0ln8 x ex y
Horizontal cross sections: 0ln8 18 y x
D) Vertical cross sections: ln8 08 x ex y
Horizontal cross sections: 08 1ln8 y x
Ans: A Difficulty: moderate Section: 7.6
75. Evaluate the given double integral for the specified region R. 2 3 R xydA , where R is the rectangle bounded by the lines x = 2, x = 3, y = –1, and y = 0.
A) –19 B) 19 C) 5 2 D) 5 –2
Ans: C Difficulty: moderate Section: 7.6
76. Evaluate the given double integral for the specified region R. ( ) 42 R xydA + , where R is the triangle with vertices (0, 0), (1, 0), and (0, 4).
A) 188 3 B) 152 3 C) 36 D) 24
Ans: B Difficulty: moderate Section: 7.6

77. Use a double integral to find the area of R. R is the triangle with vertices (–4, 5), (4, 5), and (0, 1).
Ans: C Difficulty: moderate Section:
78. Use a double integral to find the area of R R is the region bounded by y = 13x, y = ln x, y = 0, and y = 1.
Ans: B Difficulty: moderate Section: 7.6
79. Find the volume of the solid bounded above by the graph of the function f (x, y) = 4x – y + 8 and below by the rectangular region R defined by: 0 x 2 and 0 y 1.
Ans: 23
Difficulty: hard Section: 7.6
80. Find the volume of the solid bounded above by the graph of the function f (x, y) = xy and below by the rectangular region R defined by: 0 x 3 and 0 y 4.
Ans: 36
Difficulty: hard Section: 7.6
81. Find the volume of the solid bounded above by the graph of the function (,) xfxyye = and below by the rectangular region R define by: 0 x 4 and 0 y 2.
Ans: 4 22 e
Difficulty: hard Section: 7.6
82. Use double integration to find the average value of 2 (,)18 fxyxy = over the triangle with vertices (0, 0), (0, 2), and (3, 2).
Ans: 216 5
Difficulty: hard Section: 7.6
83. Use double integration to find the average value of f (x, y) = y over the region bounded by 2 9 xy =− and the y axis.
Ans: 0
Difficulty: hard Section: 7.6

84. At a certain factory, the output Q is related to inputs x and y by the expression 4322(,)974 Qxyxxyy =++ . If 0 x 4 and 0 y 9, what is the average output of the factory? (Approximate to 2 decimal places.) A) 3,593.24 units B) 1,200.16 units C) 4,770.00 units D) 3,592.80 units
Ans: D Difficulty: moderate Section: 7.6
85. A computer-designed abstract glass sculpture is in the shape of the solid region under the graph of 2 (,) fxyxy = above the semi-circular region in the xy-plane bounded by the xaxis and 2 4 yx =− . If all measurements are in feet, what volume of glass will be needed for the sculpture?
Ans: 64 15 cubic feet
Difficulty: hard Section: 7.6

1. Find the general solution of 2 53 dy xx dx =−+ .
Ans: 32 5 3 32 xx yxC =−++
Difficulty: easy Section: 8.1
2. Find the general solution of 3 2 dy x dx =+
2 3 yxC =+
Ans: B Difficulty: easy Section: 8.1
3. Find the general solution of the given differential equation. 2 937 dy xx dx =++
432 3 3 +7 2 yxxxC =++
32 3 3 –7 2 yxxxC =++
Ans: C Difficulty: moderate Section: 8.1
4. Find the general solution of 3 7 dy x dx =+ .
Ans: A Difficulty: easy Section: 8.1
5. Find the general solution of 2 132 dy xx dx =−+
Ans: 32 13 2 32 xx xC−++ Difficulty: easy Section: 8.1
6. Find the general solution of 5 dy y dx = .
Ans: C Difficulty: moderate Section:
3 3 +7 2 yxxxC =++
2 3 +7 3 yxxxC =++

7. Find the general solution of 4 dy y dx = . A) y = 4x + C B) y = ln x + C C)
x yCe = D) 4x yeC =+
Ans: C Difficulty: moderate Section: 8.1
8. Find the general solution of x dy e dx =
yeC =+ B) xyCe = C) e x y C = D) x yxeC =+
Ans: A Difficulty: easy Section: 8.1
9. Find the general solution of 2 dyx dxy = . A) 2 3 3 2 x yC =+ B) 2 2 x yC =+ C) y = C D)
Ans: A Difficulty: hard Section: 8.1
3 (2) 3 x yC =+
10. Find the particular solution of 2x dy e dx = , given y = 1 when x = 0.
Ans: 2 3 22 x e y =−+
Difficulty: moderate Section: 8.1
11. Find the general solution of 1 x dy e dx + = .
Ans: 1 x yeC + =+
Difficulty: moderate Section: 8.1
12. The general solution of 23 x dy e dx + = is
23 2 x yeC + =+
23 2 x e yC + =+
Ans: B Difficulty: hard Section: 8.1
13. Find the general solution of 2x dy e dx = .
Ans: D Difficulty: easy Section: 8.1
23 (23) x yxeC + =++

14. The general solution of 53 x dy e dx + = is
53 53 x e yC x + =+ +
53 5 x yeC + =+
Ans: D Difficulty: hard Section: 8.1
53 (53) x yxeC + =++
53 5 x e yC + =+
15. Find the particular solution of 7x dy e dx = , given y = 6 when x = 0.
Ans: 7 43 77 x e y =−+
Difficulty: moderate Section: 8.1
16. Find the general solution of 2 x dy e dx + = .
Ans: 2 x yeC + =+
Difficulty: easy Section: 8.1
17. True or False: The general solution of 5x dy ex dx =+ is 2 5 2 x x yeC =++ .
A) True B) False Ans: B Difficulty: easy Section: 8.1
18. True or False: The general solution of 2x dyedx = is 2 2 x e yC =−+ .
A) True B) False Ans: A Difficulty: easy Section: 8.1
19. True or False: The particular solution of x dy e dx = given y = 2 when x = 0 is 2 x ye =
A) True B) False Ans: B Difficulty: easy Section: 8.1
20. True or False: The general solution of 35 x dy e dx + = is 35 x yeC + =+ .
A) True B) False Ans: B Difficulty: hard Section: 8.1

21. True or False: The general solution of 5x dy ex dx =+ is 2 5 2 x x yeC =++
A) True B) False
Ans: B Difficulty: moderate Section: 8.1
22. True or False: The general solution of 26x dy e dx = is
A) True B) False
Ans: A Difficulty: moderate Section: 8.1
23. True or False: The particular solution of x dy e dx = given y = 2 when x = 0 is 2 x ye = .
A) True B) False Ans: B Difficulty: easy Section: 8.1
24. True or False: The general solution of 27 x dy e dx + = is 27 x yeC + =+ .
A) True B) False
Ans: B Difficulty: hard Section: 8.1
25. Find the particular solution of

28. Find the particular solution of 2 7 dy x dx =+ , given y = 3 when x = 0.
Ans: 3 73 3 x yx=++
Difficulty: moderate Section: 8.1
29. True or False: The particular solution of 2 dy x dx =− given x = 1 when y = 0 is
2 3 2 22 x yx=−+ .
A) True B) False
Ans: A Difficulty: easy Section: 8.1
30. True or False: The particular solution of 10 dy x dx =− given y = 0 when x = 1 is
2 19 10 22 x yx=−+ .
A) True B) False
Ans: A Difficulty: moderate Section: 8.1
31. Find the general solution of 2 5 dyx dxy = .
Ans: A Difficulty: hard Section: 8.1
32. Find the general solution of dy xy dx = .
Ans: 2 /2 xyCe = Difficulty: hard Section: 8.1
33. Find the particular solution of 23 8 dyxy dx = , given y = 2 when x = 0.
Ans: A Difficulty: easy Section: 8.1

34. Find the particular solution of the given differential equation that satisfies the indicated condition: 32 24 dy xy dx = ; y = 2 when x = 1.
35. Find the particular solution of 23
Ans: A Difficulty: easy Section: 8.1
36. Find the general solution of 3 dy xy dx = Ans: 2 3/2 x yCe = Difficulty: hard Section: 8.1
37. True or False: The general solution of 3 dy xy dx =
A) True B) False Ans: B Difficulty: easy Section: 8.1
38. True or False: The particular solution of dy xy dx = given x = 1 when y = 1 is 2 1 22 x y =+ A) True B) False Ans: B Difficulty: hard Section: 8.1
39. True or False: The general solution of 7 dy xy dx = is 8 8 x yC =+ A) True B) False Ans: B Difficulty: moderate Section: 8.1
40. True or False: The particular solution of dy xy dx = given y = 81 when x = 9 is 2 81 22 x y =+ .
A) True B) False Ans: B Difficulty: hard Section: 8.1

41. Find the particular solution of the given differential equation that satisfies the indicated condition: 2 3 dy yx dx =− ; y = 5 when x = 3.
Ans: B Difficulty: moderate Section: 8.1
42. Write a differential equation describing the following statement: The change in surface area A of an oil drop with respect to time t is inversely proportional to its area.
Ans: , dAk dtA = where k is a constant.
Difficulty: easy Section: 8.1
43. Write a differential equation describing the given situation. Define all variables you introduce. (Do not try to solve the differential equation at this time.) An investment grows at a rate of 15% of its size.
A) Let Q denote the investment and let t denote time; 1.5 dQ Q dt =
B) Let Q denote the investment and let t denote time; 0.15 dQ Q dt =
C) Let Q denote the investment and let t denote time; 15 dQ Q dt =
D) Let Q denote the investment and let t denote time; 0.15 dQ t dt =
Ans: B Difficulty: moderate Section: 8.1
44. Write and solve a differential equation describing the given situation: One person's credit card debt grows at a rate that is 7.5% of its current size.
Ans: 0.075 dQ Q dt = where Q is the amount of the debt and t is time; 0.075t QCe =
Difficulty: moderate Section: 8.1

45. Write and solve a differential equation describing the given situation: A radioactive sample decays at a rate that is 0.02% of the current amount. Use Q to represent the amount, and t to represent time. A)
0.02; t dQ QQCe dt =−=
Ans: D Difficulty: moderate Section: 8.1
0.02;0.02 dQ QtC dt ==+
46. Write a differential equation describing the given situation: Powdered lemonade dissolves in a pitcher at a rate that is proportional to the amount of undissolved powder remaining. Let P = the total amount of powder added, D = the amount dissolved, and t = time.
A) dD kPD dt =
dD kPD dt =+− B) () dD kPPD dt =−
Ans: D Difficulty: moderate Section: 8.1
() dD kPD dt =−
47. Write a differential equation describing the given situation: The rate at which a rumor spreads across a college campus is jointly proportional to the number of people that have heard the rumor (N) and the number that have not. Assume that the total size of the student body is P, and use t to represent time.
Ans: () dN kNPN dt =−
Difficulty: moderate Section: 8.1
48. The value of a certain automobile decreases over a 12 year period at a rate that depends on its age: when it's t years old, its value is changing by 200(t – 12) dollars per year. If the initial value is $19,000, write a differential equation whose solution V(t) represents the value of the car in terms of age in years, then solve to find the function.
Ans: 2 200(12);()1002,40019,000 dV tVttt dt =−=−+
Difficulty: moderate Section: 8.1
49. Find the general solution of the given first-order linear differential equation. 9 2 dyy x dxx +=
Ans: A Difficulty: moderate Section: 8.2

50. Find the general solution of the given first-order linear differential equation. 13 14 14 x dyy xe dxx += A) 14 (1) x exC y x −+ =
1/14 x e yC x =+ B) 1/14 (1) x exC y x −+ =
1/14 (1) x yxexC =−+
Ans: B Difficulty: moderate Section: 8.2
51. Find the general solution of the given first-order linear differential equation.
32 3 dy xxy dx +=
2 C y x =− B) 2 3 C y xx =−
2 3 C y xx =−
Ans: C Difficulty: moderate Section: 8.2
2 3 yC x =−
52. Find the general solution of the given first-order linear differential equation. 7 42 42 dxx t dtt +=+ +
Ans: 2 7 (42) 9(42) tC x t + =+ +
Difficulty: moderate Section: 8.2
53. Find the particular solution of the given differential equation that satisfies the given condition.
24 24; 1when 1 dy xxyxyx dx −=== A) 3243 yxx =−
2 8485 x yxxe =−+− B) 4 887 x yxxe =−++
2 47 x yxe =−
Ans: A Difficulty: moderate Section: 8.2
54. Find the particular solution of the given differential equation that satisfies the given condition. 2 2; 6when 5 dy yxyx dx −=== A) 522(22) x yCexx =−++
2 80 22 x e y xx = ++ B) 2 802(22) x yexx =+++
Ans: D Difficulty: moderate Section: 8.2
52 802(22) x yexx =−++

55. Solve the given differential equation by separating the variables.
74 dy y dx =−
Ans: C Difficulty: easy Section: 8.2
56. Find a function ()fx whose graph passes through the point (1,1) and has the property that at each point (,) xy on the graph, the slope of the tangent line equals the difference xy of the coordinates.
Ans: 1 1 x yxe =−+
Difficulty: moderate Section: 8.2
57. The price of a certain house is currently $250,000. Suppose it is estimated that after t months, the price ()pt will be increasing at the rate of 0.02()1,000 ptt + dollars per month.
True or False: In 8 months from now, to the nearest whole dollar, the price of the house will be $327,155.
A) True B) False
Ans: A Difficulty: moderate Section: 8.2
58. Find an equation for the orthogonal trajectories of the given family of curves.
2 4xyC +=
Ans: A Difficulty: moderate Section: 8.3
59. Find an equation for the orthogonal trajectories of the given family of curves.
2 ln xyC +=
Ans: 2 ln yxC −=
Difficulty: moderate Section: 8.3
60. When placed in a container of water, sugar dissolves at a rate proportional to the amount ()Qt of undissolved sugar remaining in the container at that time. If one-quarter of the sugar has dissolved after 2 minutes, approximately how long does it take for half of the sugar to dissolve?
A) 4.28 min B) 4.82 min C) 2.68 min D) 3.56 min
Ans: B Difficulty: hard Section: 8.3

61. On a cold day, a pot of water is taken outside, where the temperature is 15F. After 10 minutes, the temperature of the water is 90F, and 10 minutes after that, its temperature is 67F. What was the original temperature of the water? Round to the nearest tenth of a degree.
Ans: 123.2F
Difficulty: moderate Section: 8.3
62. A dead body is discovered at 8:00 A M. on Tuesday in a basement where the air temperature is 60F. The temperature of the body at the time of discovery is 72F and 20 minutes later, the temperature is 71F. True or False: The time of death was 6:00 A.M. on Tuesday.
A) True B) False
Ans: B Difficulty: moderate Section: 8.3
63. The intensity of light ()Id at a depth d below the surface of a body of water changes at a rate proportional to I. If the intensity at a depth of 3 d = feet is half of the surface intensity 0, I to the nearest tenth of a foot, at what depth is the intensity 7% of 0 ? I
A) 17.3 feet B) 13.8 feet C) 11.5 feet D) 23.0 feet
Ans: C Difficulty: moderate Section: 8.3
64. Suppose a particular nutrient bed is distributed in the xy plane in such a way that the nutrient concentration is always the same along any curve of the form 223. xyC += True or False: If a chemotactic organism is introduced to the nutrient bed at the point (1,1), it follows the path 3 . yx =
A) True B) False
Ans: A Difficulty: hard Section: 8.3
65. A wooded nature preserve supports populations of silver foxes and snowshoe hares. The growth rate for each population can be modeled by this pair of differential equations:
0.240.0012
dF FFH dt
0.080.005
dH RFH dt =−+ =− where H is the number of hares and F is the number of foxes. Find equilibrium populations for this model. (Hint: These are the populations for which 0 dFdH dtdt == .)
A) 30 foxes, 220 hares C) 12 foxes, 100 hares
B) 16 foxes, 200 hares D) 12 foxes, 170 hares
Ans: B Difficulty: moderate Section: 8.3

66. A wooded nature preserve supports populations of silver foxes and snowshoe hares. The growth rate for each population can be modeled by this pair of differential equations:
dF FFH
dt
dt =−+ =−
0.240.0012
dH RFH
0.080.005
where H is the number of hares and F is the number of foxes. Using the chain rule, we can show that
If a field study indicates that there were 10 foxes and 140 hares initially, separate the variables in this equation and solve to find an implicit solution for the system. Round the constant to the nearest whole number.
Ans: 1,200ln6400ln255,761 HHFF −+=−−
Difficulty: hard Section: 8.3
67. A desert preserve in the southwest is known for its populations of coyotes and road runners. The growth rate for each population can be modeled by this pair of differential equations: 20.2 1.40.02
where C is the number of coyotes and R is the number of road runners. Find the equilibrium populations for this model. (Hint: These are the populations for which 0 dRdC
dtdt == ).
A) 70 coyotes, 10 road runners C) 60 coyotes, 15 road runners B) 15 coyotes, 60 road runners D) 10 coyotes, 70 road runners
Ans: D Difficulty: moderate Section: 8.3

68. A desert preserve in the southwest is known for its populations of coyotes and road runners. The growth rate for each population can be modeled by this pair of differential equations:
dR RRC dt
20.2 1.40.02
dC CRC dt =− =−+
where C is the number of coyotes and R is the number of road runners. Using the chain rule, we can show that 10010
dCCRC = −+
70 dRRRC
If there were 4 coyotes and 281 road runners initially, separate the variables and solve to find an implicit solution for the system. Round the constant to the nearest whole number.
Ans: 70ln100ln10212 RRCC −+=−−
Difficulty: hard Section: 8.3
69. A large pond supports two competing species of fish, sunfish and smallmouth bass. Currently, there are 2,500 of each species, and a study indicates that the growth rate for each species can be modeled by this pair of differential equations:
702 21 dS SSB dt
dB BSB dt =− =−
where S is the number of sunfish and B is the number of bass. Use the chain rule to find a single differential equation describing dS dB , then separate variables and solve to find an implicit solution for the system. Round the constant to the nearest whole number.
Ans: 702 ;21ln70ln22,117 21 dSSSB SSBB dBBSB =−=−+
Difficulty: hard Section: 8.3
70. Use Euler's method with the step size 0.2 h = to estimate the solution (2)y of the given initial value problem. Round to one decimal place. 2 ; (1)2 x yy y ==
A) 2.1 B) 2.6 C) 3.4 D) 3.1
Ans: D Difficulty: moderate Section: 8.4

71. Use Euler's method with the step size 0.2 h = to estimate the solution (1)y of the given initial value problem. Round your answer to two decimal places. ; (0)2 2 xy yy xy == +
A) 1.41 B) 0.70 C) 2.11 D) 2.82
Ans: A Difficulty: moderate Section: 8.4
72. True or False: Using Euler's method with step size 0.5 h = to estimate the solution (4)y of the initial value problem
4 1;(0)0yxyy =+= gives the value 1.056.
A) True B) False
Ans: B Difficulty: moderate Section: 8.4
73. The ferret population ()Ft in a wildlife preserve satisfies the modified logistic initial value problem
0.01(58)(54); (0)50 dF FFF dt =−−=
Use Euler's method with 1 h = to estimate (8),F the ferret population after 8 years.
Ans: 46
Difficulty: moderate Section: 8.4
74. True or False: The first five terms of the initial value problem 105; 2 nn yyy== are 2, 10, 50, 250, and 1,250.
A) True B) False
Ans: A Difficulty: easy Section: 8.5
75. True or False: The first five terms of the initial value problem 3 10 ; 3 nn yyy== are 3, 27, 54, 108, and 216.
A) True B) False
Ans: B Difficulty: easy Section: 8.5
76. Write out the first five terms of the given initial value problem.
10 ; 3 1 n n n y yy y + == +
Ans: 3, 3 4, 3 7, 3 10, 3 13
Difficulty: moderate Section: 8.5

77. Find constants A and B so that the given expression ny satisfies the specified difference equation. 23 1 42; nnn nynynnyAnB +=−=+
Ans: C Difficulty: moderate Section: 8.5
78. Solve the given first-order linear initial value problem. 10 ; 1 nn yyy + −==
Ans: D Difficulty: moderate Section: 8.5
79. Solve the given first-order linear initial value problem. 1031; 1 nn yyy=+=
Ans: A Difficulty: moderate Section: 8.5

1. Use summation notation to write the given series in compact form.
Ans: B Difficulty: moderate Section: 9.1
2. Use summation notation to write the series in compact form.
Ans:
Difficulty: easy Section: 9.1
3. Find the fourth partial sum S4 of the given series.
4. Find the fifth partial sum S5 of the given series.
Ans: D Difficulty: easy Section: 9.1
5. Determine whether the given geometric series converges, and if so, find its sum.
A) Converges to 13 28 C) Converges to 13 2
B) Converges to 15 2 D) Diverges.
Ans: C Difficulty: moderate Section: 9.1

6. Determine whether the given geometric series converges, and if so, find its sum.
1 3 7 n n =
A) Converges to 3 4 C) Converges to 3 10
B) Converges to 7 10 D) Diverges
Ans: C Difficulty: moderate Section: 9.1
7. Determine whether the given geometric series converges, and if so, find its sum.
0 8 4n n =
A) Converges to 32 3 B) Converges to 4 3 C) Converges to 32 5 D) Diverges.
Ans: A Difficulty: moderate Section: 9.1
8. True or False: the given geometric series converges.
0 9 6n n =
A) True B) False
Ans: A Difficulty: moderate Section: 9.1
9. Determine whether the given geometric series converges, and if so, find its sum.
2 5 (2)n n =
A) Converges to 10 3 B) Converges to 5 6 C) Converges to 5 3 D) Diverges
Ans: B Difficulty: moderate Section: 9.1
10. Determine whether the given geometric series converges, and if so, find its sum.
1 10 3 n n =
A) Converges to 10 13 B) Converges to 3 7 C) Converges to 10 7 D) Diverges
Ans: D Difficulty: easy Section: 9.1

11. Determine whether the given geometric series converges, and if so, find its sum.
Ans: Diverges
Difficulty: moderate Section: 9.1
12. Determine whether the given geometric series converges, and if so, find its sum.
Converges to
Ans: C Difficulty: moderate Section: 9.1
Diverges
13. True or False: the given geometric series converges. ( ) 2 2 3 2 n
True B) False
Ans: B Difficulty: moderate Section: 9.1
14. Determine whether the given geometric series converges, and if so, find its sum.
Ans: Converges to 40 3
Difficulty: moderate Section: 9.1
15. Determine whether the given geometric series converges, and if so, find its sum.
A) Converges to 1 1,792 C) Converges to 256 7
B) Converges to 1 448 D) Diverges
Ans: B Difficulty: moderate Section: 9.1

16. If 1 –3 k k a = = and 1 5 k k b = = , find ( ) 1 712kk k ab = .
A) 39 B) –39 C) –81 D) –8
Ans: C Difficulty: easy Section: 9.1
17. If
Ans: 23 –18
Difficulty: moderate Section: 9.1
18. Find the sum of the given telescoping series. ( ) 2 2 1 k kk
Ans: 2
Difficulty: easy Section: 9.1
19. Express the given decimal as a fraction. 0.454545...
A) 5 11 B) 4 11 C) 5 9 D) 4 9
Ans: A Difficulty: easy Section: 9.1
20. Express the given decimal as a fraction. 1.921921921
A) 307 333 B) 340 33 C) 1,254 1,001 D) 640 333
Ans: D Difficulty: moderate Section: 9.1
21. Suppose that nationwide, approximately 90% of all income is spent and 10% is saved. What is the total amount of spending generated by a 55 billion dollar tax rebate if savings habits do not change?
A) $61 billion B) $550 billion C) $105 billion D) $495 billion
Ans: B Difficulty: moderate Section: 9.1
22. Suppose that nationwide, approximately 95% of income income is spent and 5% is saved. If economic planners wish to generate total spending of 300 billion dollars by instituting a tax cut of N dollars, what is N?
Ans: $15 billion
Difficulty: moderate Section: 9.1

23. An investment guarantees annual payments of $1,500 in perpetuity, with the payments beginning immediately. Find the present value of this investment if the prevailing annual interest rate remains fixed at 3% compounded continuously. Round your answer to the nearest whole dollar.
A) $50,754 B) $50,000 C) $45,000 D) $49,254
Ans: A Difficulty: moderate Section: 9.1
24. An investment guarantees annual payments of $2,000 in perpetuity, with the payments beginning immediately. Find the present value of this investment if the prevailing annual interest rate remains fixed at 4.5% compounded continuously. Round your answer to the nearest whole dollar.
Ans: $45,452
Difficulty: moderate Section: 9.1
25. A patient is given an injection of 30 units of a certain drug every 24 hours. The drug is eliminated exponentially so that the fraction that remains in the patient's body after t days is (), kt fte = where k is a positive constant. If 80 units of the drug eventually accumulate in the patient's bloodstream just prior to an injection, what is k? Round your answer to two decimal places.
A) 0.32 B) 0.47 C) 0.98 D) 0.64
Ans: A Difficulty: hard Section: 9.1
26. A patient is given an injection of 21 units of a certain drug every 24 hours. The drug is eliminated exponentially so that the fraction that remains in the patient's body after t days is /5 (). t fte = If the treatment is continued indefinitely, approximately how many units of the drug will eventually be in the patient's body just prior to an injection?
A) 46.65 units B) 141.50 units C) 94.85 units D) 115.85 units
Ans: C Difficulty: moderate Section: 9.1
27. A ball is dropped from a height of 16 feet and bounces indefinitely, repeatedly rebounding to 60% of its previous height. How far does the ball travel? Round to one decimal place, if necessary.
Ans: 64 ft
Difficulty: moderate Section: 9.1
28. A ball is dropped from a height of H feet and bounces indefinitely, repeatedly rebounding to 76% of its previous height. If it travels a total distance of 80 feet, what is H? Round your answer to one decimal place.
A) 30.4 feet B) 10.9 feet C) 9.6 feet D) 19.2 feet
Ans: B Difficulty: moderate Section: 9.1

29. True or False: the given series converges. 1 2 51 k k k = +
A) True B) False Ans: B Difficulty: easy Section: 9.2
30. True or False: The given series converges.
A) True B) False
Ans: A Difficulty: moderate Section: 9.2
31. True or False: The given series converges.
A) True B) False Ans: B Difficulty: moderate Section: 9.2
32. Determine whether the given series converges or diverges. ( )2 2 1 7 3 k k k
Ans: Converges Difficulty: moderate Section: 9.2
33. True or False: The given series converges.
A) True B) False Ans: A Difficulty: moderate Section: 9.2
34. Determine whether the given series converges or diverges.
Ans: Converges Difficulty: easy Section: 9.2
35. True or False: The given series converges. 1 3 8k k k
A) True B) False
Ans: A Difficulty: moderate Section: 9.2

36. Determine whether the given series converges or diverges. ( )–8 2 ln k k k =
Ans: Converges
Difficulty: moderate Section: 9.2
37. True or False: The given series converges. 2 1 1 1 k k
A) True B) False
Ans: B Difficulty: moderate Section: 9.2
38. True or False: The given series converges.
A) True B) False
Ans: A Difficulty: moderate Section: 9.2
39. Determine whether the given series converges or diverges. 1 3 1 8k k k
Ans: Diverges
Difficulty: moderate Section: 9.2
40. Determine whether the given series converges or diverges. 2 1 (2) 4 k k
Ans: Converges
Difficulty: moderate Section: 9.2
41. Determine whether the given series converges or diverges. 2 ln 30ln10 k k k
Ans: Diverges
Difficulty: easy Section: 9.2
42. True or False: The given series converges. 1 35 57 kk kk k = + +
A) True B) False
Ans: A Difficulty: hard Section: 9.2

43. Determine whether the given series converges or diverges.
3 1 21 5 k k k + =
Ans: Converges
Difficulty: moderate Section: 9.2
44. Determine whether the given series converges or diverges. 2 5 1 1 5 k k kk
Ans: Converges
Difficulty: moderate Section: 9.2
45. Determine whether the given series converges or diverges.
Ans: Converges
Difficulty: moderate Section: 9.2
46. True or False: the given series converges. 1 ! 2k k k
A) True B) False
Ans: B Difficulty: moderate Section: 9.2
47. True or False: the given series converges.
A) True B) False Ans: A Difficulty: moderate Section: 9.2
48. Determine whether the given series converges or diverges. 1/ 1 2 k
Ans: Diverges
Difficulty: easy Section: 9.2
49. Determine the interval of absolute convergence for the given power series. 2 0 4 n n n x
A) 11 x − B) 22 x − C) 44 x − D) All real x
Ans: B Difficulty: moderate Section: 9.3

50. Determine the radius of convergence for the given power series. 2 0 2 k k kx =
A) R = 0 B) 1 R = C) 2 R = D) R =
Ans: B Difficulty: moderate Section: 9.3
51. Determine the interval of absolute convergence for the given power series.
11 33 x − B) 11 x − C) 33 x − D) All real x
Ans: C Difficulty: moderate Section: 9.3
52. Determine the interval of absolute convergence for the given power series.
53. Determine the radius of convergence for the given power series. 1 0 2 k k k kx + =
A) R = 0 B) R = 1 2 C) R = 2 D) R =
Ans: C Difficulty: moderate Section: 9.3
54. Determine the radius of convergence for the given power series. 1 0 6kk k x k = A) R = 0 B) R = 1 6 C) R = 6 D) R =
Ans: B Difficulty: moderate Section: 9.3
55. Determine the radius of convergence for the given power series. 0 2 ! kk k x k = A) R = 0 B) R = 1 2 C) R = 2 D) R =
Ans: D Difficulty: moderate Section: 9.3

56. Determine the radius of convergence for the given power series.
Ans: A Difficulty: moderate Section: 9.3
57. Find a power series for the given function.
Ans: D Difficulty: moderate Section: 9.3
58. Find a power series for the given function.
Ans: A Difficulty: hard Section: 9.3
59. Find a power series for the given function.
Ans: B Difficulty: hard Section: 9.3
60. Find a power series for the given function.
() x fxxe =
Difficulty: moderate Section: 9.3

61. Find a power series for the given function. ()ln(53) fxx =+
Ans:
Difficulty: hard Section: 9.3
62. Find a power series for the given function.
Ans: C Difficulty: hard Section: 9.3
63. Find the Taylor series for the given function at the indicated point .xa =
fxee
Ans: B Difficulty: moderate Section: 9.3
64. Find the Taylor series for the given function at the indicated point xa = 5 ();1 x fxea==
Ans: B Difficulty: moderate Section: 9.3
65. Find the Taylor series for the given function at the indicated point .xa = 8 ();5fxa x == Ans:
Difficulty: moderate Section: 9.3

66. Find the Taylor series for the given function at the indicated point .xa = 1
Ans: D Difficulty: moderate Section: 9.3
67. Find the Taylor series about 0 x = for the indefinite integral
Ans: C Difficulty: moderate Section: 9.3
68. Find the Taylor series about 0 x = for the indefinite integral
Ans: D Difficulty: moderate Section: 9.3
69. Find the Taylor series about 0 x = for the indefinite integral ( ) 244
70. Use a Taylor polynomial of specified degree n to approximate the indicated quantity. Round to four decimal places.
Ans: A Difficulty: moderate Section: 9.3

71. Use a Taylor polynomial of specified degree n to approximate the indicated quantity. Round to four decimal places.
ln1.2;4 n =
Ans: 0.1823
Difficulty: moderate Section: 9.3
72. Use a Taylor polynomial of specified degree n to approximate the indicated quantity. Round to four decimal places.
0.2;4en =
Ans: 0.8187
Difficulty: moderate Section: 9.3
73. Use a Taylor polynomial of specified degree n together with term-by-term integration to estimate the indicated definite integral. Round to six decimal places
2 0.2
0 ;6 x edxn =
A) 1.040811 B) 0.197365 C) 0.202699 D) 0.208162
Ans: B Difficulty: moderate Section: 9.3
74. Use a Taylor polynomial of specified degree n together with term-by-term integration to estimate the indicated definite integral. Round to four decimal places. 0 2 0.2 1 ;4 1 dxn x = +
A) 0.9616 B) 0.1923 C) 0.1974 D) 0.1870
Ans: C Difficulty: moderate Section: 9.3
75. Use a Taylor polynomial of specified degree n together with term-by-term integration to estimate the indicated definite integral. Round to the six decimal places.
0.3 3 0 1 ;9 1+ dxn x =
Ans: 0.298006
Difficulty: moderate Section: 9.3

1. True or False: A random variable X that counts the number of twos that come up when a die is tossed 40 times is a continuous random variable.
A) True B) False
Ans: B Difficulty: easy Section: 10.1
2. Determine whether the given random variable X is discrete or continuous. X measures the age of a randomly selected resident of your city.
Ans: Continuous
Difficulty: easy Section: 10.1
3. Determine whether the given random variable X is discrete or continuous. X measures the number of cars sold by a randomly selected auto retailer.
Ans: Discrete
Difficulty: easy Section: 10.1
4. Which of the following random variables is discrete?
A) X measures the time a randomly chosen shooting star is visible. B) X measures the body temperature of a randomly chosen person. C) X counts the number of residents in a randomly chosen home.
D) X measures the height of a randomly chosen horse.
Ans: C Difficulty: easy Section: 10.1
5. Determine whether the given random variable X is discrete or continuous. X counts the number of hairs on a randomly chosen mouse.
Ans: Discrete Difficulty: easy Section: 10.1
6. A die is rolled three times and the number of 4s that are rolled is noted. What is the sample space for this random experiment?
A) {1, 2, 3, 4} B) {0, 1, 2} C) {1, 2, 3} D) {0, 1, 2, 3}
Ans: D Difficulty: moderate Section: 10.1
7. A die is rolled four times and the number of 3s that are rolled is noted. What is the sample space for this random experiment?
A) {1; 2; 3; 4} B) {0; 1; 2; 3; 4} C) {0; 1; 2; 3; 4; 5} D) {1; 2; 3; 4; 5}
Ans: B Difficulty: moderate Section: 10.1
8. Consider the random experiment of tossing a fair coin five times, and let X denote the random variable that counts the number of times heads appears. Find (0).PX
A) 31/32 B) 29/32 C) 1/32 D) 11/32
Ans: A Difficulty: moderate Section: 10.1

9. Consider the random experiment of rolling a fair die two times, and let X denote the random variable that counts the number of times 5 appears. Find (2).PX =
A) 11/36 B) 25/36 C) 1/36 D) 1/12
Ans: C Difficulty: moderate Section: 10.1 10.
The outcomes and corresponding probability assignments for a discrete random variable X are given.
True or False: The expected value is 1.8.
A) True B) False
Ans: B Difficulty: moderate Section: 10.1
The outcomes and corresponding probability assignments for a discrete random variable X are given.
Find the variance.
Ans: 4.16
Difficulty: moderate Section: 10.1 12.
The outcomes and corresponding probability assignments for a discrete random variable X are given. Find the standard deviation of X to four decimal places.
A) 0.6944 B) 0.9258 C) 1.1573 D) 0.8571
Ans: B Difficulty: hard Section: 10.1
13. The grand prize in a lottery is $500,000. There are 3 second prizes of $50,000 and 14 third prizes of $10,000. If 1,000,000 tickets are sold, what is a fair price to pay for a ticket to this lottery?
A) $7.90 B) $5.15 C) $1.58 D) $0.79
Ans: D Difficulty: hard Section: 10.1

14. A betting wheel at a carnival has 12 blue spaces, 12 yellow spaces, and 1 black space. The spaces are equal in size. For a bet of $6, you can choose a color and spin the wheel. If the wheel lands on your color, you win $6; if not, you lose your bet. Find your expected winnings from a $6 bet on yellow.
Ans: $0.24
Difficulty: hard Section: 10.1
15. Let X represent the number of minutes spent waiting for a table at a restaurant. Suppose the probability ()PXN = that customers wait N minutes is given in the table.
What is the average wait for a table? Round to the nearest hundredth of a minute.
Ans: 3.82 minutes
Difficulty: moderate Section: 10.1
16. Let X be a geometric random variable with parameter p. True or False: If (3)0.125,then 0.25. PXp ===
A) True B) False
Ans: B Difficulty: moderate Section: 10.1
17. A factory produces MP3 players. During regular inspections, 2% of the MP3 players are found to be defective. On any particular day, what is the probability that the twentieth MP3 player inspected is the first defective player found that day? Round your answer to four decimal places.
A) 0.0136 B) 0.6812 C) 0.9864 D) 0.0134
Ans: A Difficulty: moderate Section: 10.1
18. True or False: 5 5 for 0 () 0 for 0 x ex fx x = is a probability density function.
A) True B) False
Ans: A Difficulty: moderate Section: 10.2
19. True or False: 1 for08 () 16 0 otherwise xx fx = is a probability density function.
A) True B) False
Ans: B Difficulty: moderate Section: 10.2

20. Find k so that 3 0.4for01 () 0 otherwise kxx fx + = is a probability density function.
Ans: 2.4
Difficulty: moderate Section: 10.2
21. 1 for15 () 4 0 otherwise x fx
=
Hoffman)
is a probability density function for a particular random
variable X. Use integration to find (34)Px rounded to the nearest hundredth.
A) 0.09 B) 0.75 C) 0.25 D) 0.16
Ans: C Difficulty: moderate Section: 10.2
22. 4 3 if 1 () 0 if 1 x fx x x =
is a probability density function for a particular random variable X
Use integration to find (4).PX
Ans: 1 64
Difficulty: moderate Section: 10.2
23. /2 1 if 0 () 2 0 if 0 x ex fx x
=
is a probability density function for a particular random variable
X. Use integration to find (4).PX
A) 2 e B) 2 1 e + C) 2 1 e D) 2 e
Ans: D Difficulty: moderate Section: 10.2
24. The useful life X of a particular kind of machine is a random variable with density function 2 42 if25 () 153 0 otherwise x fx x +
=
where x is the number of years a randomly selected machine stays in use.
True or False: 28 (3) 45 PX =
A) True B) False
Ans: B Difficulty: hard Section: 10.2

25. The clothes dryers at a laundromat run for 45 minutes. You arrive at the laundromat and find that all of the dryers are being used. Use an appropriate uniform density function to find the probability that a dryer chosen at random will finish its cycle within 5 minutes.
Ans: 1 9
Difficulty: hard Section: 10.2
26. Suppose the length of time, x, that it takes a chimpanzee to solve a simple puzzle is measured by a random variable X that is exponentially distributed with a probability density function
2/3 2 if 0 () 3 0 if 0 x ex fx x
where x is in minutes. Find the probability that a randomly chosen chimpanzee will take more than 6 minutes to solve the puzzle.
A) 4 1 e + B) 4 e C) 4 e D) 4 1 e
Ans: B Difficulty: moderate Section: 10.2
27. The life span of car stereos manufactured by a certain company is measured by a random variable X that is exponentially distributed with a probability density function 0.2 0.2 if 0 () 0 if 0 x ex fx x =
where x is the life span in years of a randomly selected stereo. What is the probability that the life span of a randomly selected stereo is between 5 and 13 years? Round to the nearest hundredth.
A) 0.29 B) 0.32 C) 0.26 D) 0.15
Ans: A Difficulty: moderate Section: 10.2
28. Let X be a random variable that measures the age of a randomly selected virus in a particular population. Suppose X is exponentially distributed with a probability density function for 0 () 0 otherwise kx kex fx =
where x is the age of a randomly selected virus and k is a positive constant. Experiments indicate that it is four times as likely for a virus to be less than 2 days old as it is for it to be more than 2 days old. Use this information to determine k. Ans: ln5
Difficulty: hard Section: 10.2

29. Suppose the length of time that it takes a person to complete a hedgerow maze is measured by a random variable X that is exponentially distributed with a probability density function /5 1 if 0 () 25 0 if 0 x xex fx x
where x is the number of minutes a randomly selected person takes to complete the maze. Find the probability that a randomly chosen person will take less than 20 minutes to complete the maze.
Ans: 4 15e
Difficulty: hard Section: 10.2
30. The time interval between the arrivals of successive trains at a certain station is measured by a random variable X with a probability density function
0.35 0.35 for 0 () 0 for 0 x ex fx x =
where x is the time (in minutes) between the arrivals of a randomly selected pair of successive trains. What is the probability that two successive trains selected at random will arrive within 6 minutes of one another? Round to the nearest hundredth.
A) 0.66 B) 0.44 C) 0.88 D) 0.12
Ans: C Difficulty: hard Section: 10.2
31. A 1.5-hour movie runs continuously at a local theater. You leave for the theater without first checking the show times. Use an appropriate uniform density function to find the probability that you will arrive at the theater within 12 minutes of the start of the film (before or after). Round the the nearest hundredth.
A) 0.73 B) 0.22 C) 0.16 D) 0.27
Ans: D Difficulty: hard Section: 10.2
32. Suppose the joint probability density function for the nonnegative random variables X and Y is 21.5 3if 0and 0 (,) 0 otherwise xy eexy fxy =
Find the probability that 02and13. XY Round to the nearest hundredth.
A) 0.79 B) 0.21 C) 0.42 D) 0.63
Ans: B Difficulty: hard Section: 10.2

33. Scientists are studying two bird species that interact within the same ecosystem. Let X be the random variable that measures the population of species A and let Y measure the population of species B. Research indicates that the joint probability density function for X and Y is 2 4if 0and 0 (,) 0 otherwise xy xexy fxy
What is the probability that species A outnumbers species B?
A) 5 9 B) 31 36 C) 5 18 D) 5 36
Ans: A Difficulty: moderate Section: 10.2
34. 1 if111 () 10 0otherwise x fx
=
is a probability density function for a continuous random
variable X. True or False: The expected value is 6.
A) True B) False
Ans: A Difficulty: moderate Section: 10.3
35. 2 if09 () 81 0otherwise x x fx
=
variable X
is a probability density function for a continuous random
Find the variance. Round to the nearest hundredth.
A) 4.50 B) 5.40 C) 3.60 D) 1.80
Ans: A Difficulty: moderate Section: 10.3
36. 10 9 if 1 () 0 if 1 x fx x x
=
is a probability density function for a continuous random variable X
Find the expected value.
Ans: 9 8
Difficulty: moderate Section: 10.3

37. /6 1 if 0 () 6 0 if 0 x ex fx x =
is a probability density function for a continuous random variable X Find the variance. Ans: 36
Difficulty: moderate Section: 10.3
38. The joint probability density function for two continuous random variables X and Y is /4 1 if 0and 0 (,) 4 0 otherwise xy eexy fxy
Find the expected values ()and ().EXEY
A) ()1; ()4EXEY== C) ()5; ()1EXEY==
B) ()4; ()1EXEY== D) ()1; ()3EXEY==
Ans: B Difficulty: moderate Section: 10.3
39. The joint probability density function for two continuous random variables X and Y is 3 9if 0and 0 (,) 0 otherwise xy yexy fxy
Find the expected values ()and ().EXEY A) 2 (); ()1 3 EXEY== C) 2 ()1; () 3 EXEY== B) 3 ()1; () 2 EXEY== D) 3 (); ()1 2 EXEY==
Ans: C Difficulty: hard Section: 10.3
40. The useful life X of a particular kind of machine is a random variable with density function 3 53 if36 () 162 0 otherwise x fx x
where x is the number of years a randomly selected machine stays in use.
True or False: The expected useful life of the machine is about 1 4 2 years (rounding to the nearest 1/2 year).
A) True B) False
Ans: A Difficulty: moderate Section: 10.3

41. A certain traffic light remains red for 90 seconds at a time. You arrive (at random) at the light and find it red. Use an appropriate uniform density function to find the expected waiting time for cars arriving on red at the traffic light.
Ans: 45 seconds
Difficulty: moderate Section: 10.3
42. During the evening commute, express buses run every 10 minutes from the bus stop near your work toward your neighborhood. You arrive (at random) at the bus stop and find no bus. Assuming that the buses are running on schedule, use an appropriate uniform density function to find the expected wait for rush hour commuters arriving at the stop when no bus is there.
A) 4 minutes B) 5 minutes C) 6 minutes D) 8 minutes
Ans: B Difficulty: moderate Section: 10.3
43. Suppose the time X a customer must spend waiting in line at a certain fast food restaurant is a random variable that is exponentially distributed with a density function
where x is the number of minutes that a randomly selected customer spends waiting in line. Find the expected waiting time for customers at the restaurant.
A) 7 minutes B) 14 minutes C) 3.5 minutes D) 6.5 minutes
Ans: A Difficulty: moderate Section: 10.3
44. Let X be the random variable that represents the time (in hours) between successive visits by bees to gather pollen from a particular flowering plant. Suppose X is distributed exponentially with parameter 0.8. = True or False: If a bee has just left a flower you are observing, you should expect to wait 1.25 hours for the next bee to arrive.
A) True B) False
Ans: A Difficulty: moderate Section: 10.3
45. Suppose that the time between successive hits on a popular web page can be represented by an exponentially distributed random variable X whose expected value is ()0.2EX = second. Using an appropriate probability density function, find the probability that the time between successive hits on the web page is less than 0.9 second. Round to the nearest hundredth.
Ans: 0.99
Difficulty: hard Section: 10.3

46. Suppose that during business hours, the time between successive wireless calls at a network switch can be represented by an exponentially distributed random variable X with expected value ()0.025EX = second. Using an appropriate probability density function, find the probability that the time between the arrival of successive wireless calls at the switch is between 0.03 and 0.065 second. Round to the nearest hundredth.
A) 0.77 B) 0.23 C) 0.46 D) 0.63
Ans: B Difficulty: hard Section: 10.3
47. Let the random variable X measure the time (in minutes) that a person spends in the waiting room of a doctor's office and let Y measure the time required for a complete physical examination (also in minutes). Suppose the joint probability density function for X and Y is /10/25 1 if 0and 0 (,) 250 0 otherwise xy eexy fxy
How much time would you expect to spend in the waiting room? How about during your examination?
Ans: ()10EX = minutes; ()25EY = minutes
Difficulty: hard Section: 10.3
48. The density function of a normal random variable X is 2 /8 1 () 22 x fxe =
Find the expected value ().EX
A) 1 B) 2 C) 4 D) 0
Ans: D Difficulty: moderate Section: 10.4
49. The density function of a normal random variable X is 2 (2)/8 1 () 22 x fxe =
Find the variance Var(X).
A) 2 B) 3 C) 4 D) 4.2
Ans: C Difficulty: moderate Section: 10.4
50. The density function of a normal random variable X is 2 (2)/2 1 () 2 x fxe =
True or False: ()2,Var()1, 2 EXX===
A) True B) False
Ans: B Difficulty: moderate Section: 10.4

51. Assuming that the random variable Z has a standard normal distribution, find (1.09).PZ Round your answer to four decimal places.
Ans: 0.8621
Difficulty: moderate Section: 10.4
52. Assuming that the random variable Z has a standard normal distribution, find (1.82).PZ − Round your answer to four decimal places.
A) 0.0427 B) 0.0344 C) 0.0274 D) 0.0526
Ans: B Difficulty: moderate Section: 10.4
53. Assuming that the random variable Z has a standard normal distribution, find (0.75).PZ Round your answer to four decimal places.
Ans: 0.2266
Difficulty: moderate Section: 10.4
54. Assuming that the random variable Z has a standard normal distribution, find (1.180.73).PZ− Round your answer to four decimal places.
A) 0.6483 B) 0.3517 C) 0.6167 D) 0.6670
Ans: A Difficulty: moderate Section: 10.4
55. Find the appropriate value of b for ()0.9192,PZb= assuming that the random variable Z has a standard normal distribution.
Ans: 1.4
Difficulty: moderate Section: 10.4
56. Find the appropriate value of b for ()0.1075,PZb= assuming that the random variable Z has a standard normal distribution.
Ans: 1.24
Difficulty: moderate Section: 10.4
57. Find the appropriate value of b for ()0.9070,PbZb−= assuming that the random variable Z has a standard normal distribution.
A) 1.58 B) 1.68 C) 1.78 D) 1.88
Ans: B Difficulty: hard Section: 10.4
58. Suppose X has a normal distribution with 18and 2. == True or False: (20)0.4207PX =
A) True B) False
Ans: B Difficulty: moderate Section: 10.4
59. Suppose X has a normal distribution with 20and 4. == Find (1228).PX A) 0.9544 B) 0.0456 C) 0.2736 D) 0.4772
Ans: A Difficulty: hard Section: 10.4

60. A random variable X has a normal distribution with 15and 3. == True or False: According to the empirical rule, (921)0.683.PX=
A) True B) False
Ans: B Difficulty: moderate Section: 10.4
61. Suppose that X is a Poisson random variable with parameter 2. = Give the value to three decimal places for (1).PX = Ans: 0.271
Difficulty: easy Section: 10.4
62. True or False: If X has a normal distribution with 6, = then (5.51)(6.49). PXPX=
A) True B) False
Ans: A Difficulty: moderate Section: 10.4
63. The weights of students in a sample are normally distributed with 135 = and 7 = pounds. Roughly what percent of students weigh between 121 and 149 pounds?
Ans: 95.5%
Difficulty: moderate Section: 10.4
64. The scores on a certain test are normally distributed with 73 = and 6. = Use the empirical rule to determine which one of the following ranges of scores that 68.3% of the students received.
A) between 61 and 85 C) between 67 and 79
B) between 67 and 85 D) between 61 and 79
Ans: C Difficulty: moderate Section: 10.4
65. The incomes of service workers in a particular state are normally distributed with a mean of $28,400 and a standard deviation of $2,100. Find the probability that a randomly selected worker has an income between $25,880 and $30,920. Round your answer to four decimal places.
Ans: 0.7699
Difficulty: hard Section: 10.4
66. A bakery produces loaves of bread having weights that are normally distributed with a mean weight of 2.13 pounds and standard deviation of 0.1 pound. Find the fraction of loaves that weigh less than 1.9 pounds. Round your answer to four decimal places. Ans: 0.0107
Difficulty: moderate Section: 10.4

67. The breaking strength of a certain type of fishing line is normally distributed. If the line has an average breaking strength of 50 pounds with standard deviation of 0.8 pounds, find the probability that a randomly selected piece of line will break under a strain of less than 49.5 pounds. Round your answer to four decimal places.
Ans: 0.2660
Difficulty: moderate Section: 10.4
68. The gestation period of humans follows an approximately normal distribution with a mean of 266 days and a standard deviation of 16 days. Find the probability that a gestation period is between 256 and 276 days. Round to four decimal places.
A) 0.3510 B) 0.2340 C) 0.1170 D) 0.4680
Ans: D Difficulty: hard Section: 10.4
69. The daily high temperature in a town in August has a normal distribution with a mean of 85F and a standard deviation of 3.3F. What is the probability that a daily high temperature in August is greater than 91F? round to four decimal places.
A) 0.9656 B) 0.0345 C) 0.2752 D) 0.0433
Ans: B Difficulty: moderate Section: 10.4
70. Suppose that the number of people suffering bee stings in a rural county in May follows a Poisson distribution with a mean of 0.8 bee sting per day. Find the probability that on a randomly selected day, there will be 3 bee stings. Round to three decimal places.
A) 0.015 B) 0.023 C) 0.038 D) 0.031
Ans: C Difficulty: moderate Section: 10.4
71. Suppose that the number of a certain type of bacteria in waste water follows a Poisson distribution with a mean of 5.7 bacteria per cubic millimeter of water. Find the probability that a cubic millimeter random sample of waste water contains exactly 6 bacteria. Round to three decimal places.
A) 0.159 B) 0.385 C) 0.457 D) 0.841
Ans: A Difficulty: moderate Section: 10.4
72. Suppose that the number of peanuts in a bite-sized chocolate candy follows a Poisson distribution with a mean of 3 peanuts per candy. Find the probability that a candy contains exactly 1 peanut. Round to three decimal places.
A) 0.112 B) 0.075 C) 0.037 D) 0.149
Ans: D Difficulty: moderate Section: 10.4

1. Specify the number of degrees in the indicated angle. A) 150 − B) 150 C) 210 D) 240 Ans: C Difficulty: easy Section: 11.1
2. Specify the number of radians in the indicated angle.

Ans: 7 6
Difficulty: easy Section: 11.1
3. Specify the number of radians in the indicated angle.

4. Specify the number of degrees in the indicated angle. A)

5. Specify the number of degrees in the indicated angle.

Ans: 240 −
Difficulty: easy Section: 11.1
6. Specify the number of radians in the indicated angle.

Ans: 8 3
Difficulty: easy Section: 11.1
7. Convert the indicated angle from degrees to radians. 190 −
Ans: 19 18
Difficulty: easy Section: 11.1
8. Convert the indicated angle from degrees to radians. 120 A) 3 B) 2 3 C) 4 3 D) None of the above
Ans: B Difficulty: easy Section: 11.1
9. Convert the indicated angle from radians to degrees. 11 9
Ans: 220 −
Difficulty: easy Section: 11.1
10. Convert the indicated angle from radians to degrees. 9 A) 20 B) 10 C) 40 D) None of the above
Ans: A Difficulty: easy Section: 11.1
TB-Calculus for Business(11E, Hoffman)

11. Evaluate the given expression.
sin 19 2
A) –1 B) 0 C) 1 D) Undefined
Ans: A Difficulty: moderate Section: 11.1
12. Evaluate the given expression.
cos 15 4 Ans: 2 2
Difficulty: moderate Section: 11.1
13. Evaluate the given expression. cos 7 3
Ans: D Difficulty: moderate Section: 11.1
14. Evaluate the given expression. csc 13 4
Ans: C Difficulty: moderate Section: 11.1
15. Evaluate the given expression. sec 19 6
Ans: 23 –3
Difficulty: moderate Section: 11.1
16. Evaluate the given expression.
cot 2
A) –1 B) undefined C) 1 D) 0
Ans: D Difficulty: moderate Section: 11.1

TB-Calculus for Business(11E, Hoffman) Appendix.4 The Summation Notation
17. Find cot if 3 sin. 5 = A) 4 5 B) 4 3 C) 5 4 D) 3 4
Ans: B Difficulty: moderate Section: 11.1
18. Find cot if 6 cos. 3 = A) 2 B) 2 2 C) 1 2 D) 3
Ans: A Difficulty: moderate Section: 11.1
19. True or False: 5 csc 4 = if 4 cot. 3 =
A) True B) False
Ans: B Difficulty: moderate Section: 11.1
20. Find all values of in the specified interval that satisfy the given equation. sincos2;02 = A) , 62 = B) 5 , 66 = C) 5 ,, 626 = D) 53 ,, 662 =
Ans: D Difficulty: hard Section: 11.1
21. Find all values of in the specified interval that satisfy the given equation. coscos2;02 =
Ans: 24 0,,,2 33 = Difficulty: hard Section: 11.1
22. True or False: The only value of in the interval 0 that satisfies the equation 22 cos3sin2 −=− is 3
A) True B) False
Ans: B Difficulty: moderate Section: 11.1

23. Suppose a company determines that the profit P (in hundreds of dollars) obtained from sales during week t (for 052 t ) of a particular year may be modeled by the trigonometric function (16) ()7050cos 26 t Pt −
What is the largest weekly profit?
A) $2,000 B) $12,000 C) $14,000 D) $7,000
Ans: B Difficulty: moderate Section: 11.1
24. Suppose a company determines that the profit P (in hundreds of dollars) obtained from sales during week t (for 052 t ) of a particular year may be modeled by the trigonometric function (10) ()10045cos 26 t Pt
True or False: the smallest weekly profit occurs during week 36.
A) True B) False
Ans: A Difficulty: moderate Section: 11.1
25. Suppose a company determines that the profit P (in hundreds of dollars) obtained from sales during week t (for 052 t ) of a particular year may be modeled by the trigonometric function (23) ()6050cos 26 t Pt
What is the smallest weekly profit? When does it occur?
Ans: $1,000; week 23
Difficulty: moderate Section: 11.1
26. Differentiate the given function. ()sin2cos4 fttt =−
A) 2cos24sin4 tt−+ C) 2cos24sin4 tt +
B) cos2sin4 tt D) 2sin24cos4 tt
Ans: C Difficulty: moderate Section: 11.2
27. Differentiate the given function. 55()10sin4sin gttt =−
A) 445 50sincos20cos tttt −
44 50sincos20sincos tttt −
B) 5510cos4costt D) 5510cos4costt−+
Ans: A Difficulty: moderate Section: 11.2
28. Differentiate the given function. 2 ()sin5 ftt = Ans: 10cos5sin5 tt
Difficulty: moderate Section: 11.2

29. Differentiate the given function. ( )()cos4 5 fttt =−−
Ans: ( )1sin4 55 t +−
Difficulty: moderate Section: 11.2
30. Differentiate the given function. ( ) 5tan2 yxx =−
A) ( ) 2 5sec2xx
B) ( ) ( ) 5 10tan2sec2 2 xxxx x
C) ( ) 2 5 10sec2 2 xx x
D) 1 5cot 2xx
Ans: C Difficulty: easy Section: 11.2
31. Differentiate the given function. ( ) 4 ()10tan29 fttt =−
Ans: ( ) ( ) 324 8090sec29 ttt
Difficulty: easy Section: 11.2
32. True or False: Given 2 ()tan3, ftt = 3 6sin3 (). cos3 t ft t =
A) True B) False Ans: A Difficulty: moderate Section: 11.2
33. Differentiate the given function. ()sec(25) ftt =−
TB-Calculus for Business(11E, Hoffman)
A) 5sec(25)tan(25) tt C) 2 5sec(25) t
B) 2 5tan(25) t D) 5sec(25)tan(25) tt
Ans: D Difficulty: moderate Section: 11.2
34. True or False: Given 9 ()lnsec, ftt = 9 (). sincos ft tt =−
A) True B) False
Ans: B Difficulty: moderate Section: 11.2

35. Differentiate the given function.
()lnsec2 ftt =
Ans: 2 tan 2t
Difficulty: moderate Section: 11.2
36. Find the indicated integral: ( ) 12cos5sinxxdx
A) –12sin5cosxxC −+
B) 12sin5cosxxC −+
Ans: D Difficulty: easy Section: 11.2
37. Find the indicated integral. ( ) sin5cos8ttdt
A) 11 cos5sin8 58 ttC−−+
C) –12sin5cosxxC ++
D) 12sin5cosxxC ++
C) 11 cos5sin8 58 ttC−++
B) 11 sin5cos8 58 ttC ++ D) 11 cos5sin8 58 ttC −+
Ans: A Difficulty: moderate Section: 11.2
38. Find the indicated integral: ( ) ( ) 2 1221cos27xxxdx
Ans: ( ) 2 3sin27xxC −+
Difficulty: moderate Section: 11.2
39. Find the indicated integral. ( )23 sin2 xxdx +
A) ( )3 1 sin2 3 xC++
B) ( ) 3 3 cos2 3 x xC−++
C) ( )3 1 cos2 3 xC++
D) ( )3 1 cos2 3 xC−++
Ans: D Difficulty: moderate Section: 11.2
40. Find the indicated integral: ( ) 2 7sec16sectantttdt
Ans: 7tan16secttC −+
Difficulty: easy Section: 11.2

41. Find the indicated integral. 3 sectanttdt
4 1 sec 4 tC + B) 3 1 sec 3 tC + C) 3 1 tan 3 tC + D) 2 1 sectan 2 ttC +
Ans: B Difficulty: hard Section: 11.2
42. Find the indicated integral. 2 sectanttdt
Ans: 2211 sec or tan 22 tCtC ++
Difficulty: moderate Section: 11.2
43. True or False: 2 tantanxdxxxC =−+
A) True B) False
Ans: A Difficulty: moderate Section: 11.2
44. True or False: ( ) ( ) ( ) 11 sin2sin2cos2 24 xxdxxxxC =−++
A) True B) False
Ans: B Difficulty: moderate Section: 11.2
45. Find the indicated integral: ( ) sincosttdt
3sincos 2 ttC + Ans: B Difficulty: moderate Section: 11.2
46. Find the indicated integral. 63cossinxxdx
Ans: 9711 coscos 97 xxC −+
Difficulty: hard Section: 11.2
47. Find the indicated integral. 7 sincosxxdx
Ans: 8 1 sin 8 xC +
Difficulty: moderate Section: 11.2

48. Determine the period p, the amplitude b, the phase shift d, and the vertical shift a of the given trigonometric function f(t). ( )()4+7cos1 4 ftt =+
A) 8,–7,1,4pbda ====
8,7,1,4pbda ===−= B) 4,–7,1,4pbda ====
4,7,1,4pbda ====
Ans: C Difficulty: moderate Section: 11.2
49. Determine the period p, the amplitude b, the phase shift d, and the vertical shift a of the given trigonometric function f(t). ( )()0.5–3cos3 5 ftt =−
A) 5,0.5,3,–3pbda ====
10,0.5,3,–3pbda ==== B) 10,–3,3,0.5pbda ====
Ans: B Difficulty: moderate Section: 11.2
10,3,3,0.5pbda ===−=
50. Determine the period p, the amplitude b, the phase shift d, and the vertical shift a of the given trigonometric function f(t).
()–1+5.5cos8 3 ftt
Ans: ,5.5,,–1 43 pbda ====
Difficulty: moderate Section: 11.2
51. True or False: The area between the curves cos 2 x y
and sin yx = over the interval 3 x is 1.
A) True B) False
Ans: B Difficulty: moderate Section: 11.2
52. Find the area between the given curves over the specified interval. cos2 yx = and 2sincos yxx = ; 0 8 x
Ans: 21 2
Difficulty: moderate Section: 11.2

53. Solve the given differential equation subject to the specified initial condition. cos;(0)5 5 dyt y dty ==
2 ()sin25 5 ytt=+
Ans: A Difficulty: hard Section: 11.2
()5sin 5 ytt =+
54. True or False: ()cot xtt =− is the solution to 22 sec dx xt dt = subject to the condition 1. 4 x
=−
A) True B) False
Ans: A Difficulty: moderate Section: 11.2
55. The average temperature t hours after midnight in a certain town is given by the formula
()578sin(2) 12 Ttt
.
At what rate is the temperature changing at noon? Round to one decimal place.
A) 4.0 degrees per hour C) –6.9 degrees per hour
B) –1.8 degrees per hour D) 1.0 degrees per hour
Ans: B Difficulty: moderate Section: 11.2
56. The average temperature t hours after midnight in a certain town is given by the formula ()6611sin(2) 12 Ttt =+−
.
True or False: It is getting hotter at 3 P.M.
A) True B) False
Ans: B Difficulty: moderate Section: 11.2
57. Suppose the body temperature (in F ) of a particular person t hours after midnight (for024) t is given by the function
()98.40.4sin(10) 24 Ttt =+−
.
At approximately what rate is the person's body temperature changing at noon? Round your answer to two decimal places.
Ans: 0.05 F/hr
Difficulty: moderate Section: 11.2

58. Suppose the body temperature (in F ) of a particular person t hours after midnight (for024) t is given by the function
()98.40.2sin(12) 24 Ttt =+− .
Approximately what is the person's average temperature from noon to 3 P.M.? Round your answer to two decimal places.
Ans: 98.44 F
Difficulty: moderate Section: 11.2
59. Consumers will demand (buy) x hundred units of a certain commodity when the price is ()pDx = dollars per unit, where
()2030.5sin Dxxx =−+ .
What is the average price per unit as the level of production increases from 200 units to 500 units (2 x = to 5)? x = (Round to the nearest cent.)
A) $28.82 B) $9.61 C) $14.41 D) None of the above Ans: B Difficulty: moderate Section: 11.2
60. Consumers will demand (buy) x hundred units of a certain commodity when the price is ()pDx = dollars per unit, where ()233–2.5cos Dxxx =− .
What is the average price per unit as the level of production increases from 200 units to 500 units (2 x = to 5)? x =
Ans: $12.50 per unit
Difficulty: moderate Section: 11.2
61. A manufacturer will supply x units of a certain commodity to the market when the price is ()pSx = dollars per unit, where ()293–2.5sin Sxxx =+ .
What is the average price per unit as the level of production increases from 2 x = to 5? x = (Round to the nearest cent.)
A) $38.97 per unit B) $49.47 per unit C) $39.50 per unit D) $40.03 per unit
Ans: A Difficulty: moderate Section: 11.2
62. Find the volume of the solid generated by rotating the region R about the x-axis. R is the region bounded by the x-axis, sec yx = , π 4 x =− , and π 4 x = . A) 2π B) 9π C) 9π 2 D) 45π 2
Ans: A Difficulty: moderate Section: 11.2

63. Find the volume of the solid generated by rotating the region R about the x-axis. R is the region bounded by the x-axis, 2 cossin yxx = , x = 0.6, and x = 2.5.
Ans: 0.45
Difficulty: hard Section: 11.2
64. A person 6 feet tall is watching a streetlight 16 feet high while walking toward it at a speed of 6 feet per second. At approximately what rate is the angle of elevation of the person's line of sight changing with respect to time when the person is 7 feet from the base of the light? Round to four decimal places.
A) 0.3148 radians per second
B) –0.0671 radians per second
C) 0.4027 radians per second
D) None of the above
Ans: C Difficulty: moderate Section: 11.2
65. A man sees a flag descend down a flagpole that is 15 feet away. The flag is descending at the rate of 2 feet per second. At what rate is the angle of elevation of the man's line of sight changing with respect to time when the flag is 20 feet above the man's horizontal line of sight?
Ans: 6 125 radians per second
Difficulty: moderate Section: 11.2
66. An observer watches a plane approach head-on at a speed of 475 miles per hour and at an altitude of 4 miles. At what rate is the angle of elevation of the observer's line of sight changing with respect to time t when the horizontal distance between the plane and the observer is 3 miles?
A) 57 radians per hour
B) 76 radians per hour
C) 19 radians per hour
D) None of the above
Ans: B Difficulty: moderate Section: 11.2
67. Consumers will demand (buy) x hundred units of a certain commodity when the price is ()pDx = dollars per unit, where ()302–2.5cos Dxxx =− .
True or False: The consumers' surplus when 200 units (2) x = are produced is $56.00.
A) True B) False
Ans: B Difficulty: moderate Section: 11.3
68. A manufacturer will supply x units of a certain commodity to the market when the price is ()pSx = dollars per unit, where
()202–2.5sin Sxxx =+ .
What is the producers' surplus when x = 5 units?
A) $24.68 B) $26.59 C) $25.00 D) $94.20
Ans: C Difficulty: moderate Section: 11.3

Hoffman)
69. A manufacturer will supply x units of a certain commodity to the market when the price is ()pSx = dollars per unit, where ()283–2.5cos Sxxx =+ . What is the producers' surplus when 6 x = units? Ans: $39.00
Difficulty: moderate Section: 11.3
70. A study shows that consumers in one city will buy q hundred bottles of a new perfume when the price is 308sin 3 q pq =−+
dollars per bottle. Find the consumer's surplus for this product when 22,000 bottles are demanded and produced. Round to the nearest dollar.
A) $847 B) $1,837 C) $2,311 D) $1,932 Ans: D Difficulty: hard Section: 11.3
71. Using a graphing utility, find the value of t for which the largest value of x(t) occurs for the indicated interval. Estimate to four decimal places, if necessary.
()sin32cos2for0 2 xtttt =+
A) 0 t = B) 0.8959 t
C)
t
D) None of the above Ans: C Difficulty: moderate Section: 11.3
72. Using a graphing utility, find the value of t for which the largest value of x(t) occurs for the indicated interval. Estimate to four decimal places, if necessary.
()3sin32cos5 for0 xtttt=−
A) 0.5916 t B) 2.9641 t C) t = D) None of the above Ans: A Difficulty: moderate Section: 11.3
73. Using a graphing utility, find the values of t for which the largest and smallest values of x(t) occur for the indicated interval. Estimate to four decimal places, if necessary. ()6sin23cos3 for0 xtttt=+ Ans: Maximum at 0.3990, t minimum at 2.7426 t Difficulty: moderate Section: 11.3
74. Using a graphing utility, find the value of t for which the smallest value of x(t) occurs for the indicated interval. Estimate to four decimal places, if necessary.
()(4sin33cos2)for0 t xtettt=+
A) 0 t = B) 0.2632 t C) 0.9605 t D) None of the above Ans: D Difficulty: moderate Section: 11.3

TB-Calculus for Business(11E, Hoffman)
75. True or False: The largest value of ()(sin2cos3)for0 t xtettt=− occurs when 0.8182. t
A) True B) False
Ans: A Difficulty: moderate Section: 11.3
76. A projectile is fired from a cannon at ground level at an angle of 10 with an initial velocity of 42 ft/sec. How far from the cannon does the projectile land? Round your answer to the nearest tenth of a foot.
Use the following formulas. 0 2 00 (cos) 16(sin) xvt ytvts = =−++
A) 37.7 ft B) 9.4 ft C) 9.6 ft D) 18.9 ft
Ans: D Difficulty: hard Section: 11.3
77. A projectile is fired from the top of a building 60 feet high at an angle of 26 with an initial velocity of 47 ft/sec. What is the maximum height reached by the projectile? Round your answer to the nearest tenth of a foot.
Use the following formulas.
0 2 00 (cos) 16(sin) xvt ytvts = =−++
Ans: 66.6 ft
Difficulty: moderate Section: 11.3
