
Given the number of trials and the probability of success, find the probability of:
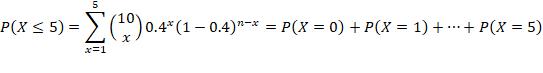
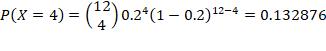
*(remember p is success and q =1-p is failure)
1. n =12, p = 0.2, r = exactly 4
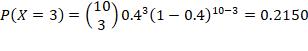
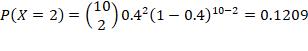
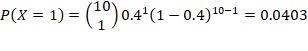
2. n =10, p = 0.4, r= at most 5
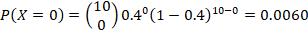
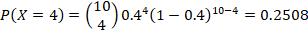
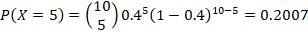
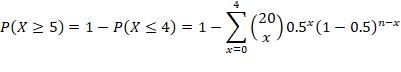
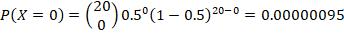
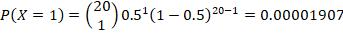
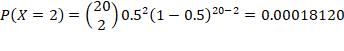
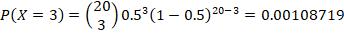
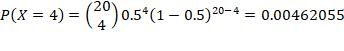
4. n =15, p = 0.9, r = at least 4 failures
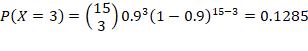
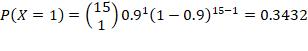
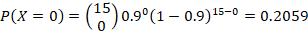
“At least 4 failures” with n =15, p = 0.9, is equivalent to “at least 4 successes” with n =15, p = 0.1
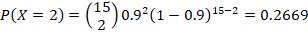
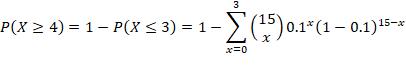
*5. n =11, p = 0.05, find P( exactly 3 failures)
Exactly 3 failures with n =11, p = 0.05 is equivalent to exactly 3 successes with n =11, p = 0.95
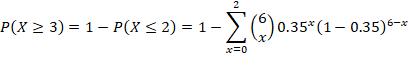
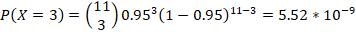
*6. n =15, p = 0.99, find P(failure) with n =15, p =0.01
7. n = 6, p = 0.35, find P(at least 3 successes)
8. n =100, p = 0.01, find P(no more than 3 successes)
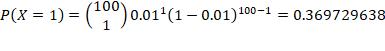
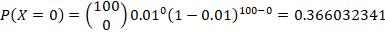
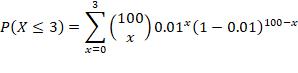
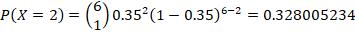
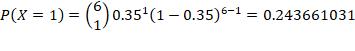
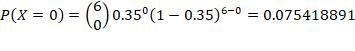
Find the probability of the Binomials given.
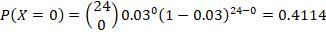
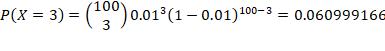
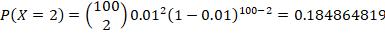
9. Approximately 3% of the eggs in a store are cracked. If you buy two dozen eggs, what is the probability that a) none of your eggs are cracked
The random variable is X: number of eggs cracked in two dozen eggs. X is distributed as binomial, with n = 24, p = 0.03 b) at least one of your eggs is cracked
c) exactly two of your eggs are cracked
10. The probability the Tim will sink a foul shot is 70%. If Tim attempts 30 foul shots, what is the probability that
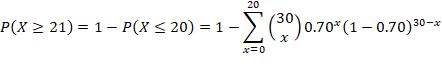
a) he sinks exactly 21 shots
The random variable is X: Number of sinks foul shots by Tim in 30 attemps. X is distributed as binomial, with n = 30, p = 0.70
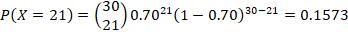
b) he sinks at least 21 shots
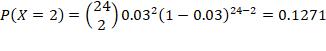
c) he sinks at most 21 shots
d) he sinks between 18 and 20 shots, inclusive.
