Engineering fundamentals an introduction to engineering si edition 5th edition moaveni solutions man by staci.farrell433

Engineering Fundamentals An Introduction to Engineering SI Edition 5th edition by Saeed Moaveni ISBN 1305105729 9781305105720

Download solution manual at:

https://testbankpack.com/p/solution-manual-for-engineeringfundamentals-an-introduction-to-engineering-si-edition-5th-edition-bysaeed-moaveni-isbn-1305105729-9781305105720/

Download full test bank at :

https://testbankpack.com/p/test-bank-for-engineeringfundamentals-an-introduction-to-engineering-si-edition-5thedition-by-saeed-moaveni-isbn-1305105729-9781305105720/

Chapter 9: Mass and Mass-Related Variables in Engineering

9.2. The density of standard air is a function of temperatureand may be approximated using the ideal gas law accordingto

 = P RT where

 = density(kg/m3)

P = standard atmospheric pressure (101.3 kPa)

R  gas constant, and its value for air is 286.9 ( J ) kg  K

T  air temperature in Kelvin

Create a table that shows the densityof air as a function of temperature in the range of 0 C (273.15 K) to 50 C (323.15 K) in increments of 5 C Also, create a graph showing the value of density as a function of temperature.

SOLUTION

9.3. Determine the specific gravity of the following materials: gold ( = 19,350 kg/m3), platinum ( = 21,465 kg/m3), silver ( = 10,475 kg/m3), sand ( = 1515 kg/m3), freshly fallen snow ( = 496 kg/m3), tar ( = 1200 kg/m3), hard rubber ( = 1192 kg/m3).

94 © 2016 Cengage Learning May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. D en sity ( k g / m 3 ) 1 35 1 30 1 25 1 20 1 15 1 10 1 05 Density of Air as a Function of Temperature 0 5 10 15 20 25 30 35 40 45 50 55 Temperature (C)

SOLUTION

We will use Equation (9.2) to answer this question.

SG = specificgravity = densityof a material density of water

9.4. Show that the specific weight and density are related according to: specific weight = (density)(acceleration due to gravity)

gold 19,350kg/m3

19.35 1000kg/m3 SGplatinum 21,465kg/m.3 =

21.47 1000kg/m3 SGsilver 10,475kg/m3 = = 10.48 1000kg/m3 SGsand 1515kg/m3 = = 1 52 1000kg/m3 SGsnow 496kg/m.3 = = 0.50 1000kg/m3 SGtar 1200kg/m3 = = 1 20 1000kg/m3 SGhard rubber 1192kg/m.3 =

1.19 1000 kg/m3

= =

SOLUTION

We will use the definition given by Equation (9.4) to show this relationship. specific weight = weight volume

weight

= (mass)(acceleration due to gravity)

volume

mass

= (density)(volume)(acceleration due to gravity) volume

= (density)(acceleration due to gravity)

9.5. Compute the values of momentum for the following situations: (a) a 90-kg football player running at 6 m/s; (b) a 1500-kg car moving at a rate of 100 km/h; (c) a 200,000 kg Boeing 777 moving at a speed of 500 km/h; (d) a bullet with a mass of 15 g traveling at a speed of 500 m/s; (e) a 140-g baseball traveling at 120 km/h; (f) a 80 kg stunt performer falling off a ten story building reaching a speed of 30 m/s.

SOLUTION

We will use Equation (9.14) to solve this problem.

(a) a 90 kg football player running at 6 m/s

L = mV = (90 kg)(6 m/s) = 540 kg m/s

(b) a 1500 kg car moving at a rate of 100 km/hr

L = mV = (1500 kg)(100 km/h)(1 h/3600 s)(1000 m/1 km) = 41,667 kg  m/s

L = mV = (200,000 kg)(500 km/h)(1 h/3600 s)(1000 m/1 km) = 27,777,777 kg  m/s

(d) a bullet with a mass of 15 g traveling at a speed of 500 m/s

L = mV = (15g)(1 kg/1000 g)(500 m/s) = 7.5 kg  m/s

(e) a 140 g baseball traveling at 120 km/hr

L = mV = (140 g)(1 kg/1000 g)(120 km/h)(1 h/3600 s)(1000 m/1 km) = 4.67 kg m/s

(f) a 80 kg stunt performer falling off a 10 story building reaching a speed of 30 m/s.

L = mV = (80 kg)(30 m/s) = 2400 kg  m/s

9.9. Determine the mass flow rate of fuel from the gasoline tank to the car's fuel injection system Assume that the gasoline consumptionof the car is 8.5 km/L when the car is moving at 90 km/h. Use the specific gravity value of 0.72 for the gasoline

SOLUTION

First, we will use Equation (9.2) to compute the densityof gasoline.

SG = specificgravity = densityof a gasoline density of water

The volume flow rate of fuel is determined from:

Next, we will use Equation (9.6) to calculate the mass flow rate of the fuel. mass flow rate = (density)(volume flow rate)

9.10. Determine the mass moment of inertia for the following objects: a thin disk, circular cylinder, and a sphere. Refer to Equations (9.10) through (9.13) for appropriate relationships. If you were to place these objects alongside of each

97 ©

Cengage Learning May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

2016

gasoline = 0.72 = densityof gasoline 1000kg/m3 → densityof gasoline = 720kg/m3

volumeflow rate = 90km/h 8.5km/L = 10.6L/h

kg L 1m.3 massflow rate

)(10.6 )(

kg/h m 3 h 1000L

= (720

) = 7.63

other on an inclined surface, which one of the object would get to the bottom first, provided that they all have the same mass and diameter?

SOLUTION

The mass moment of inertia for a thin disk, circular cylinder, and a sphere is determined from the following equations.

Provided that they all have the same mass and diameter, the sphere will get to the bottom first, because it has the smallest mass moment of inertia.

9.12. Determine the mass moment of inertia of a steel shaft that is 1-m long and has a diameter of 5 cm. Determine the mass of the shaft using the density information provided in Table 9.1.

SOLUTION

We will first calculate the mass of the shaft using Equation (9.1) For steel, we will use a density value of 7860 kg/m3 . The volume of a cylinder is given by:

To calculate the mass moment of inertia of the shaft about its longitudinal axis, we use Equation (9.11).

9.13. Determine the mass moment of inertia of steel balls used in ball bearings. Use a diameter of 2 cm.

disk: cylinder: sphere: I zz I zz I zz = 1 mR2 2 = 1 mR2 2 = 2 mR2 5

volume = (/4)(d2)(length)=(/4)(0.05 m)2(1 m) = 0.001963 m 3 density = mass volume 7860kg/m3 = mass 0.001963m3 mass = 15.43kg

I z z = 1 mR2 = 1 (15.43 kg)(0.025m)2 = 0.005 kg  m 2 2 2

SOLUTION

We will first calculate the mass of the sphere using Equation (9.1) For steel, we will use a density value of 7860 kg/m3 . The volume of a sphere is given by:

To calculate the mass moment of inertia of the sphere, we use Equation (9.12).

9.14. Determine the mass moment of inertia of the earth about its axis of rotation, going through the poles Assume the shape of the earth to be spherical Look up information such as the mass of the earth and the radius of the earth at the equatorial plane.

SOLUTION

To calculate the mass moment of inertia of the earth, we use Equation (9.12), using the following data.

theearth = 5.971024kg

earth = 12751 km

9.22. Referring to Figure 9.5, how much water is stored after 20 minutes in each of the tanks. How long will it take to fill the tanks completely provided that the volume of tank (a) is 24 m 3 and tank (b) has a volume of 36 m 3? Assume density of water is 1000 kg/m3 .

volume = 4  R3 = 4   0.02  = 4.1887910 6 m3 3 3  2    density = mass volume 7860kg/m3 = mass 4.18879 10-6 m3 mass = 0.0329kg

I z z = 2 mR2 = 2 (0.0329 kg)(0.01m)2 = 1.316 10-6 kg  m2 5 5

diameter of

I z z 2 2 1275110.3m = mR2 = (5 97 1024 kg)( )2 = 9 71037 kg  m 2 5 5 2

massof

the

SOLUTION

We will use the conservation of mass statement to solve this problem Realizing that no water leaves tank (a), we have

(2kg/s) (0) = changeof massinside thecontrol volume changein time

After 20 minutes

changeof mass insidethe control volume = (2 kg/s)(20minutes)( 60 seconds ) = 2400 kg 1 minute

To determine how long it will take to fill the tank, first we will make use of the relationship among mass, densityand volume (i.e , mass = (density)(volume))to compute how much mass each tank can hold.

For tank (a): mass = (1000 kg/m3)(24 m 3) = 24000 kg

For tank (b): mass = (1000 kg/m3)(36 m 3) = 36000 kg

By rearranging terms in the conservation of mass equation we can now solve for the time that is required to fill each tank . For tank (a)

timerequired tofill the tank = 24000kg = 12000s = 200minutes (2kg/s)

Water enters tank (b) at 2 kg/s and leaves the tank at 1 kg/s. Applying the conservation of mass to tank (b), we have

(2kg/s) (1kg/s) = change of massinside thecontrol volume changein time

After 20 minutes,

changeof mass inside the control volume = (2 kg/s) (1 kg/s)(20 minutes)( 60 seconds) = 1200 kg 1 minute

And the time that is required to fill the tank (b)

timerequired tofill the tank = 36000kg

= (2kg/s)-(1kg/s) 36000s = 600minutes

9.24. Calculate the mass moment of inertia of the thin ring shown in the accompanying diagram Express your answer in kg m 2

Note

given is a thin ring.

9.25. Determine the mass moment of inertia of a steel shaft that is 130 cm long and has diameter of 6.4 cm. Express your answer in kg·m 2 .

To calculate the mass moment of inertia of the shaft about its longitudinal axis, we use Equation (9.11).

I z z = 1 mR2 = 1 (32.85 kg)(0.032m)2 = 0.0168kg

9.26. Determine the mass moment of inertial of a steel ball with a diameter of 5 cm. Express your answer in kg m 2 .

SOLUTION

We will first calculate the mass of the steel ball using Equation (9.1). For steel, we will use a densityvalue of 7860 kg/m3 . The volume of a sphere is given by:

 m2

the object

I = mR2 = (7kg)(0.05m)2 = 0.0175kg

SOLUTION volume = (/4)(d2)(length)=(/4)(0.064 m)2(1.30 m) = 0.00418 m 3 density = mass volume 7860kg/m3 = mass 0.00418m3 mass =

32.85kg

 m 2 2 2

To calculate the mass moment of inertia of the sphere, we use Equation (9.12).

9.27. Determine the mass moment of inertia of a 100 mm (4 in.) square steel plate. Use Equation 9 13 Express your answer in kg m 2

2 5 cm

9.28. Determine the specific gravity of the following gasses by comparing their densities to air at 1.23

101 © 2016 Cengage Learning May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. volume = 4 R3 = 4  (0.025m)3 = 6.54 10 5 m 3 3 3 density = mass volume 7860kg/m3 = mass 6.54 10 5 m3 mass = 0.514kg

I = 2 mR 2 = 2 (0.514 kg)(0.025 m)2 = 0.000129kg  m 2 z z 5 5

SOLUTION Assume

volume = (0.100m)2(0.025m) = 0.00025m 3 mass = (0.00025 m 3 )(7860 kg ) = 1.96 kg m 3 I z z = 1 mW 2 = 1 (1.96 kg)(0.100 m)2 = 0.0016 kg  m2 12 12

a thickness of

Helium: 0.166 kg/m3 , Oxygen: 1.33 kg/m3 , Nitrogen: 1.16 kg/m3 , Natural gas: 0.667 kg/m3 , and Hydrogen: 0.0838 kg/m3 .

SG = specificgravity = densityof a gas densityof air

kg/m

SOLUTION

9.29. Calculate the change in the momentum of a car whose speed changes from 100 km/h to 20 km/h. The car has a mass of 1000 kg and is moving along a straight line.

102 © 2016 Cengage Learning May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. SG(Helium) = 0.166 kg m3 1.23 kg = 0.135 SG(Oxygen) = m 3 1.33 kg m 3 1.23 kg = 1.08 SG(Nitrogen) = m 3 1.16 kg m3 1.23 kg = 0.943 SG(NaturalGas) = m 3 0.667 kg m3 1.23 kg = 0.542 SG(Hydrogen) = m 3 0.0838 kg m3 1.23 kg = 0.068 m 3

SOLUTION L1 = mV = (1000 kg)(100 km/h)(1 h/3600s)(1000 m/1 km) = 27,778 kg  m/s L2 = mV = (1000 kg)(20 km/h)(1 h/3600s)(1000 m/1 km) = 5,555 kg  m/s L2 L1 = 5,555 - 27,778 = -22223 kg  m/s

9.30. Calculate the change in the momentum of a 200,000 kg Boeing 777, whose speed changes from 725 km/h to 290 km/h

9.31. Kinetic energy is another engineeringquantitythat is mass dependent. An object having a mass m and moving with a speed V has a kinetic energy, which is equal to ½ mV2 . In Chapter 13, we will explain the concept of kinetic energy in more detail after we introduce work For now, compute the kinetic energy for the following situations: a 1500 kg car moving at a speed of 100 km/h, a 200,000 kg Boeing 777 moving at a speed of 700 km/h

9.32. Rotational kinetic energy is yet another mass-dependent engineering quantity. An object having a mass moment of inertia I and rotating with angular speed of  (rad/s) has a rotational kinetic energy, which is equal to ½ I  2 . Determine the rotational kinetic energy of a steel shaft that is 2 m long and has diameter of 5 cm, and is rotating at an angular speed of 100 rpm.

104 © 2016 Cengage Learning May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. SOLUTION V1 = 725 km/h = 201 m/s; V2 = 290 km/h = 80.5 m/s L1 = mV = (200,000 kg)(201 m/s) = 40,200,000 kg  m/s L2 = mV = (200,000 kg)(80.5 m/s) =16,100,000 kg  m/s L2 L1 = 16,100,000 - 40,200,000 = -24,100,000 kg m/s

SOLUTION Vcar =100 km/h = 27.78 m/s; Vplane = 700 km/h =194.44 m/s Kinetic Energy(car) = 1 mV2 = 1 (1500 kg)(27 78 m/s)2 = 578,796 J 2 2 Kinetic Energy(plane) = 1 mV2 = 1 (200000 kg)(194 44 m/s)2 = 3 8109 J 2 2

SOLUTION volume = (/4)(d2)(length)=(/4)(0.05 m)2(2 m) = 0.00393 m 3

density = mass volume

7860 kg/m3 = mass 0.00393ft3

mass = 30.9kg

To calculate the mass moment of inertia of the shaft about its longitudinal axis, we use Equation (9.11).

1 = 2 1 = 30.9kg 0.025m 2 =0.00966kg m

and 100 rpm = 10.47 rad/s 1 1 rad = 2 = 0.00966kg∙m 2 !10.47 ( s =0.529J

9.33. Determine the change in mass moment of inertia of an object that could be modeled as a point mass m when its distance from a center of rotation is doubled.

SOLUTION

I (distanceR) = mR2

I (distance2R) = m(2R)2

I (distance2R)- I (distanceR) = 4mR2 mR2 = 3mR

9.34. A plugged dishwasher sink with the dimensions of 350 mm × 400 mm × 15 mm is being filled with water from a faucet with an inner diameter of 25 mm If it takes 220 seconds to fill the sink to its rim, estimate the mass flow of water coming out of the faucet

105 ©

Cengage Learning May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

2016

SOLUTION

3 3

s kg m3 kg mass

(1000 )(9.5510 6 ) = 0.00955 m 3 s s

Vsin k = (0.350m)(0.400m)(0.015m) = 0.0021m3

Q = volumetricflowrate = 0.0021m = 9.5510

m 220s

flow rate = ρQ = (density)(volumetric flowrate) =

9.35. Imagine the plug of the sink described in Problem 9 34 leaks If it now takes 250 seconds to fill the sink to its rim, estimate the mass-flow rate of the leak.

SOLUTION

From Problem 9.36: mass flowrate fromfaucet with no leak = 0.00955kg s

0.0021 m 3 m 3

Q-with leak = = 0.0000084 250 s s kg m 3 kg

mass flow rate with leak = (1000 )(0 00084 ) = 0 0084 m 3 s s

mass flowrate of the leak = 0 00955 0 0084 = 0 0012kg s

9.36. The tank shown in the accompanyingfigure is being filled by Pipes 1 and 2 If the water level is to remain constant, what is the mass-flow rate of water leaving the tank at Pipe 3? What is the average velocityof the water leaving the tank?

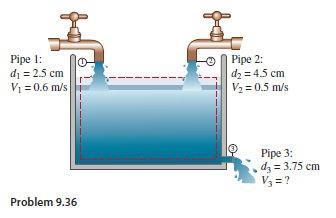
SOLUTION

Assume constant water density.

Q = volumeflowrate = (averagevelocity)(cross-sectionalarea of flow)

Q1 + Q2 = Q3 V1A1 + V2A2 = Q3 = V3A3

9.37. Imagine, the water level in the tank described in Problem 9 36 rises at a rate of 4 mm/s (0.1 in/s). Knowing the diameter of the tank is 240 mm (6 in), what is the average velocityof the water leaving the tank?

SOLUTION

The solution to this problem is similar to Problem 9.36. Realizingthat for constant water density the conservation of mass expression reduces to the balance among volumetric flow rates. Q

flow)

9.38. The density of air at a city (such as San Diego) located at sea level is 1 225 kg/m3 , while for a city (such as Denver) located at high altitude is 1.048 kg/m3 . Consider two auditoriums, each with dimensions of 30 m × 50 m × 15 m, one located in

107 © 2016 Cengage Learning May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. (0.6 m/s)( )(0.025 m)2 + (0.5 m/s)( π)(0.045 m)2 = Q = (V m/s)( )(0.0375 m)2 4 4 3 3 4

for Q3 and V3

we get: Q3 = 0 00109 m 3/s and V3= 0 987 m/s kg m. 3 kg massflow rateat3 = (1000 )(0.00109 ) = 1.09 m 3 s s

Solving

= volume

Q1 + Q2 Q3 = Atan k change in the height of water time Q1 + Q2 Atan k change in the height of water time = Q3 *06 m ,+* + 0.025m +*0.5 m ,+* + 0.045m *0.004 m ,+* + 0.240m =/0 s 4 m , s 4 s 4 =*10 s +* 4 + 0.0375m

flow rate = (average velocity)(cross-sectional area of

Solving for

and

3, we get: Q3 = 0.00091 m 3/s and V3= 0.823 m/s

108 © 2016 Cengage Learning May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. San Diego, and the other in Denver. Calculate the mass of air for each auditorium.

9.39. A rectangularduct with dimensions of 1 m × 110 cm delivers conditioned air with a density of 1.2 kg/m3 to a room at a rate of 45 m 3/min What is the mass-flow rate of air? What is the average air speed in the duct?

9.40. A rubber balloon has a mass of 10 grams. The balloon is filled with air and forms a shape that may be approximated as a sphere with a diameter of 50 cm. What is the total mass the balloon? What would be the total mass of the balloon, if it is filled with helium instead? Express your answers in grams

San Diego: kg 0 Denver: 23 =41 =!1.225 m0(

=27,560kg kg 0 3 =41 =!1.048 m0( 22,500m =23,580kg

= (30m)(50m)(15m) = 22,500m3

22,500m

SOLUTION density of air = 1.2 kg/m3 3 massflow rate = (density)(volumeflow rate) = (1.2kg/m3 )(45 m ) = 54 kg m. 3 (45 ) min h Average speed = (volumeflow rate) = min = 40.9 m crosssectional Area (1m)(1.1m) min

SOLUTION volume = 4 R3 = 4   0.5  = 0 065 m 3 3 Air:   3  2  kg 0 7 =41 =!1225 m0( 0065m total mass = 10 grams + 80 grams = 90 grams Helium:

9.41. A typical household of 4 people consume approximately300 liters (80 gallons) of water per day Express the annual consumption rate of a city with a population of 100,000 people. Express your answer in kg/year.

9.42. Lake Mead of Hoover Dam, the largest man-made lake in the United States, contains 35,000,000,000m 3 (28,537,000 acre-feet) of water. Express the mass of the water volume in kg.

9.43. Air with density of 0.45 kg/m3enters an experimental jet engine at rate of 180 m/s. The inlet area of the engine is 0.5 m 2 . After fuel is burned, the air and combustion byproducts leave the engine with a velocityof 650 m/s through an outlet area of 0.4 m 2 . What is the average density of the gas exiting the engine?

111 © 2016 Cengage Learning May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. kg 0 89 =41 =!0.166 m0( 0.065m total mass = 10 grams + 11 grams = 21 grams =0011kg=11g

SOLUTION (75 L )(100,000 people)(365.25 days) = 2.74 GL person  day year =41 =!1000 kg GL m0 (!2.74 (? kg @=2.74×10B m0 year 1000L year

SOLUTION =41 =!1000 kg( 3.5×10CDm0 =3.5×10C0 kg m0

Air Air + Combustion SOLUTION Ain = 0.5 m 2 ; Aout = 0.4 m 2

Air mass flow rate in + fuel mass flow rate in = Air + Combustion mass flow rate out

For this problem we will neglect the mass flow rate of the fuel as compared to air mass flow rate.

mass flowrate in = (density)(volumeflow rate) = (0.45 kg )(180 m/s)(0.5m2) = 40.5 kg m 3 s

mass flowrate out = (density)(volumeflow rate) = ( kg )(650 m/s)(0.4m2) = 40.5 kg m 3 s

density = 0.156 kg/m3

9.44. In a food processing (drying) application, air ( = 1.10 kg/m3 , V = 3 m/min) enters a chamber through a duct with dimensions of 500 mm × 450 mm and leaves ( = 1 10 kg/m3) through a ductwork with dimensions of 400 mm × 450 mm What is the average air speed in the exit duct? Express your answer in m/s

SOLUTION

mass flow rate in = mass flow rate out [(density)(volumeflowrate)]in = [(density)(volumeflowrate)]out

!1.1mkg(*3 0 m min + 500mm×450mm

=!11kgm0( *19G

Vexit = 3 75 m/min = 0 0625 m/s

m min+ 400mm×450mm

Note that there is no reason to convert area units. They cancel out!

9.45. To measure the fuel consumption of an experimental lawn mower, fuel is drawn from a tank that is resting on a scale as shown in the figure. The tank and the fuel have an initial total mass of 10 kg If the mass scale shows a value of 9 45 kg after 30 minutes, what is the fuel consumption of the lawn mower?

SOLUTION

density of gasoline = 720 kg/m3

10kg-9.45kg = 1 1 kg

0.5h

mass flow rate

h = [(density)(volumeflow rate)] =1.1 kg = (720 kg)(volumeflowrate) h m 3

volume flow rate = 0 001528 m 3/h = 0.4 gallons/h

9.46. In a water bottling process, one-liter bottles are filled through a system that provides filtered water to each bottle at rate of 0.3 kg/s How long would it take to fill a bottle? How many bottles can be filled in one hour, if the system can fill 20 bottles simultaneouslywith a required time of 3 seconds to move away the filled bottles and bring in the new batch of empty bottles?

SOLUTION

mass flow rate in to each bottle = 0.3 kg/s

massflow rate = [(density)(volumeflow rate)] = 0.3 kg = (1kg)( 1L )

time to fill one bottle = 3.3 seconds s L time

to fill 20 bottles simultaneously= 3.3 + 3 = 6.3 seconds/20bottles

3600 seconds h = 11,428 bottles

6.3 seconds h 20bottles

9.47. Water is available at a rate of 2000 L/min to a small apartment complex, consisting of 4 units. If at a given time, units 1, 2, and 3 are consuming9 kg/s, 7 kg/s, 8 kg/s, respectively, how much water is available to unit 4? Express your answer in m 3/s and kg/s.

SOLUTION

density of water = 1 kg/L

kg L s

/C =!9 (!1 (*60 += 540 s kg min min

kg L s

/ =!7 (!1 (*60 += 420 s kg min min kg L s

/0 =!7 (!1 (*60 += 480 s kg min min

The amount of water available to unit-4 = 2000 – 540 – 420 – 480 = 560 L/min

The amount of water available to unit-4 = 560 L/min = 0 00933 m 3/min = 9 33 kg/s.

111 ©

Cengage Learning May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

2016