Matematika 7 - Aritmetika

pro základní školy

RPZ A COVÁNO V SOULAD U S RVP PRO ZÁKLADNÍ VZDĚLÁVÁNÍ

7MATEMATIKA aritmetika

2 — 3 14 —— = — 5 15 — 7 1 1 0 1 [— + (– 0,2)] . — = — . — = 0 5 4 10 4 a : b = c : d y = k . x 1 1 % = —— = 0,01 základu 100

Zpracovali: prof. RNDr. Zden k P lpán, CSc., Mgr. Michal ihák, Ph.D., Mgr. Šárka Müllerová

Lektorovali: PaedDr. Eva Ku inová, RNDr. Václav Sýkora, CSc., Mgr. Barbora Stušová

Schválilo MŠMT . j. MSMT-30330/2020-1 dne 26. 8. 2020 k za azení do seznamu u ebnic pro základní vzd lávání jako sou ást ucelené ady u ebnic pro vzd lávací obor

Matematika a její aplikace s dobou platnosti šest let.

Gra cké zpracování obálky Michal Špatz

Ilustrace Miroslava Jakešová

Vydalo roku 2020 SPN – pedagogické nakladatelství, akciová spole nost, Ostrovní 30, 110 00 Praha 1

Odpov dná redaktorka RNDr. So a Samková

Publikaci vyrobila H.R.G., spol. s r. o., Svitavská 1203, 570 01 Litomyšl Po et stran 152

Dotisk 1. vydání

5840

© Zden k P lpán za kolektiv, 2008

Illustrations © Miroslava Jakešová, 2008

© SPN – pedagogické nakladatelství, akciová spole nost, 2008

ISBN 978-80-7235-398-9

OBSAH

OPAKOVÁNÍ

Uspořádánípřirozených čísel........................................................................................5

Číselná osa.....................................................................................................................5

Dělitelnost .....................................................................................................................6

Uspořádání desetinných čísel ........................................................................................7

Počítáme pomocí závorek ............................................................................................8

Jednotky délky, hmotnosti, obsahu aobjemu ..............................................................9

Sčítání, odčítání, násobení adělení desetinných čísel ...............................................10

I.ZLOMKY

1. Dělení celku, zlomek ...................................................................................................11

2. Rozšiřování akrácení zlomků .....................................................................................18

3. Porovnávání zlomků ....................................................................................................24

4. Sčítání zlomků

5. Odčítání zlomků ..........................................................................................................36

6. Násobení zlomků .........................................................................................................40

7. Dělení zlomků .............................................................................................................45

8. Složené zlomky ...........................................................................................................48

9. Opakování zlomků ......................................................................................................51

II. CELÁ ČÍSLA

1. Porovnávání celých čísel .............................................................................................54

2. Absolutní hodnota celého čísla ...................................................................................55

3. Sčítání celých čísel ......................................................................................................58

4. Odčítání celých čísel ...................................................................................................62

5. Násobení celých čísel ..................................................................................................66

6. Dělení celých čísel ......................................................................................................69

III. RACIONÁLNÍ ČÍSLA

1. Záporná desetinná čísla azáporné desetinné zlomky .................................................71

2. Porovnávání racionálních čísel ...................................................................................76

3. Sčítání aodčítání racionálních čísel ............................................................................78

4. Násobení adělení racionálních čísel ...........................................................................82

IV. POMĚR, PŘÍMÁ ANEPŘÍMÁ ÚMĚRNOST

1. Určení poměru .............................................................................................................85

2. Krácení arozšiřování poměru .....................................................................................87

3. Rozdělení celku vdaném poměru................................................................................89

4. Převrácený poměr ........................................................................................................90

5. Změna vdaném poměru ..............................................................................................91

6. Postupný poměr ...........................................................................................................92

7. Měřítko mapy aplánu .................................................................................................94

8. Úměra ..........................................................................................................................95

9. Pravoúhlá soustava souřadnic vrovině .......................................................................97

10. Přímá úměrnost .........................................................................................................100

11. Nepřímá úměrnost ....................................................................................................105

12. Trojčlenka .................................................................................................................109

V.PROCENTA

1. Základ (celek) ...........................................................................................................113

2. Výpočet procentové části .........................................................................................116

3. Výpočet základu .......................................................................................................121

4. Výpočet počtu procent..............................................................................................123

5. Úlohy sprocenty řešené trojčlenkou ........................................................................126

6. Jednoduché úrokování ..............................................................................................128

7. Promile .....................................................................................................................130

8. Opakování úloh sprocenty ......................................................................................133

VI. ZÁVÌREÈNÉ OPAKOVÁNÍ

Milí přátelé, dostáváte do rukou další zučebnic aritmetiky. Jejím prostřednictvím postoupíte dále vmatematických znalostech, seznámíte se například isčísly zápornými. Naučíte se je užívat stejně dobře jako čísla kladná, ato ve všech početních výkonech: při sčítání, odčítání, násobení adělení. Také budete poznávat některé vztahy mezi dvěma skupinami čísel. Klíčem bude jejich stručné vyjádření azobrazení. Snáze snad potom porozumíte některým jednoduchým vztahům mezi veličinami jak fyzikálními, tak iekonomickými. Naučíte se také chápat matematické významy nových slov jako je například procento.

Věříme, že zjistíte, jak matematika dokáže jednoduše ajednoznačně vyjádřit to, co se slovy vyjadřuje obtížně, složitě anejednoznačně.

Nezbývá než doufat, že máte hodně vůle atrpělivosti kpoznávání smyslu ikrásy matematiky. Krása je vúčelu ařádu atím matematika překypuje. Autoři

Značky použité v učebnici: –náročnější úlohy

OPAKOVÁNÍ

Uspořádání přirozených čísel

1. Seřaďte města podle jejich vzdálenosti od Prahy od nejbližšího po nejvzdálenější; nejdříve odhadněte podle mapky, pak svůj odhad zkontrolujte podle údajů znásledující tabulky:

Město

Vzdálenost od Prahy [km]

AKolín61

BBenešov45

CBrno203

DBruntál264

EOlomouc252

FPříbram61

GDěčín90

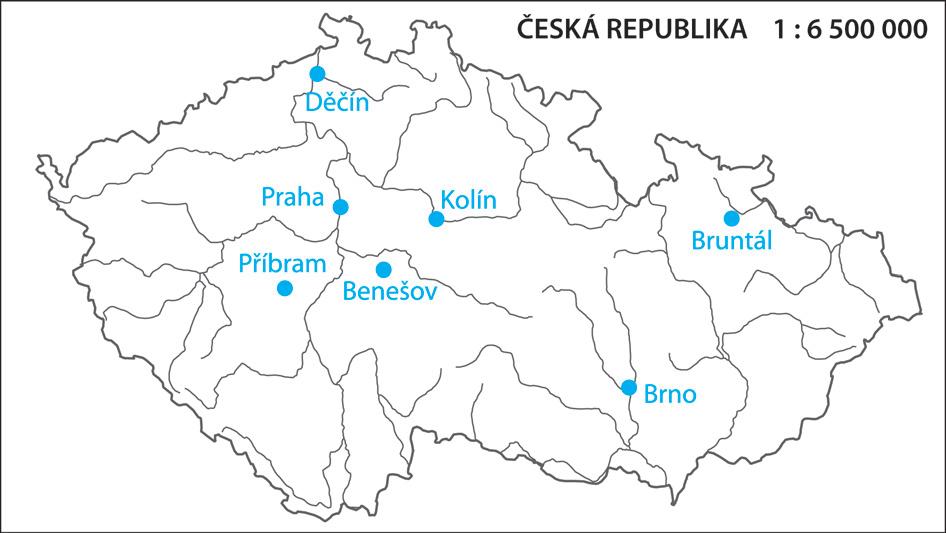
2. Zobrazte města podle vzdálenosti od Prahy na číselné ose. Místo jmen měst použijte písmena podle předchozí tabulky. Na číselné ose vyznačte také město Praha písmenem P.

3. O kolik kilometrů je od Prahy dále Olomouc než Kolín?

4. Kolikrát větší je vzdálenost Děčína od Prahy než Benešova od Prahy?

5. Kolikrát větší je vzdálenost Brna od Prahy než Benešova od Prahy?

6. Ptejte se podobně jako vúlohách 3, 4 a5 na vzdálenosti vám známých míst.

Číselná osa

1. Veschématu je vyznačena dálnice D1 zPrahy do Brna. Na trase dálnice jsou zakreslena místa R, S, T, U sčísly, která označují jejich vzdálenost od Prahy (v km). Do následující tabulky doplňte vzájemné vzdálenosti jednotlivých míst.

F

to znamená, že celek dále již nedělíme. Čitatel pak zde vyjadřuje počet celků, které zlomek představuje.

Tedy 3 1 = 3.

Zapamatujte si:

Každé přirozené číslo můžeme napsat jako zlomek se jmenovatelem 1

1 1 = 1, 2 1 = 2, 3 1 = 3, 4 1 = 4, 5 1 = 5, . . .

Cvièení

1. Zapište číslo 13 jako zlomek aspoň čtyřmi způsoby.

2. Upravte následující zlomky na základní tvar azapište, které přirozené číslo vyjadřují: a) 130 5 b) 357 21 c) 143 11 d) 364 52

3. Porovnávání zlomků

Jak porovnáváme zlomky se stejnými jmenovateli?

Pan Kubát má na 2 7 své půdy pastviny, zbytek tvoří pole. Čeho má více, pastvin, nebo polí? 2 7 …… pastvin 5 7 …… pole

Pan Kubát má více polí než pastvin.

2 7 < 5 7

Všimněte si:

Ze dvou zlomků se stejnými jmenovateli je větší ten, který má většího čitatele.

Cvièení

1. Porovnejte zlomky pomocí znaků < nebo > : a) 1 3 , 2 3 b) 7 5 , 3 5 c) 2 4 , 1 4 d) 7 8 , 9 8 e) 105 37 , 110 37 f) 7365 237 , 7499 237

7 365 , 7 499 237 237

2. Zobrazte na číselné ose následující zlomky: 1 3 , 2 3 , 5 4 , 9 4 , 7 2 , 9 2

3. Uspořádejte zlomky zpříkladu 2 od nejmenšího po největší (využijte jejich zobrazení na číselné ose).

Jak porovnáváme zlomky se stejnými čitateli?

Příklad: Porovnejte zlomky 1 3 a 1 2 .

Zlomky si znázorníme na číselné ose aporovnáme:

Na číselné ose můžeme znázornit idalší zlomky avidíme, že

Všimněte si:

Ze dvou zlomků se stejnými čitateli je větší ten, který má menšího jmenovatele

4. Odčítání celých čísel

Poušť Gobi je jednou znejsušších oblastí na světě. Nachází se na území Mongolska aČíny. Panují zde iextrémní podmínky pro teplotu vzduchu. Letní teploty vystupují až na 50 °C azimní klesají až k–40 °C. Rozdíl mezi letními azimními teplotami zde tedy někdy dosahuje 90 °C.

Všimněte si: Rozdíl letních azimních teplot zapíšeme takto: 50 – (–40) = 90

Rozdíl čísel 50 a–40 si vyznačíme na číselné ose:

rozdíl teplot

Úkol:

Vtabulce jsou uvedeny teploty naměřené na různých místech naší republiky vměsíci březnu. Určete rozdíly denních anočních teplot na jednotlivých místech.

místo noční teplota denní teplota Praha

Pomůcka: Nejprve si narýsujte číselnou osu avyznačte na ní jednotlivé teploty. Potom znázorněte aurčete rozdíly.

Putujeme autíčkem po číselné ose

Při odčítaní celých čísel můžeme opět využít autíčko vystřižené zpapíru.

Příklad 1:

Určete rozdíl 3 – (–1).

Postup:

Menšenec je číslo 3, proto umístíme autíčko nad obraz čísla 3 na číselné ose. Předek autíčka přitom musí směřovat doleva. To je jediný rozdíl oproti postupu při sčítání celých čísel, dále už postupujeme stejně. Od čísla 3 máme odečíst číslo – 1, které je záporné. Budeme proto autíčkem couvat o jeden dílek dozadu

–1 0 1 2 3 4

Nyní se autíčko nachází nad obrazem čísla 4 na číselné ose. Vypočítali jsme: 3 – (–1) = 4

Příklad 2:

Určete rozdíl (–3) – 1.

Postup:

Menšenec je číslo –3, proto umístíme autíčko nad obraz čísla –3 na číselné ose. Předek autíčka směřuje doleva. Od čísla –3 máme odečíst číslo 1, které je kladné. Autíčko proto posuneme o jeden dílek dopředu.

Autíčko se nachází nad obrazem čísla –4 na číselné ose. Vypočítali jsme: (–3) – 1 = –4

Příklad 3:

Určete rozdíl (–3) – (–1).

Postup:

Tentokrát již nebudeme celý postup popisovat, pouze jej znázorníme obrázkem:

–10 (–3) – (–1) = –2

2. Ve Školním atlase světa najděte mapu lednových teplot vzduchu. Pokuste se na ní nalézt aspoň pět měst, ve kterých jsou průměrné lednové teploty vyšší než –6 °C anižší než –4 °C. Nalezené teploty vyznačte na číselné ose. –6 –5 –4

3. Zapište čísla, jejichž obrazy jsou vyznačené na číselné ose. abc d ef g –11 –10 –9 –8

Na stole leží několik kartiček sčísly. Kristýna si nakreslila číselnou osu aumístila jednotlivé kartičky kodpovídajícím obrazům čísel na číselné ose.

–21 _ 10 –3 2 –3 4 –2 5 –0,4 –0,75 –1,5 –2,1 –2,1 –0,4 –3_2 –3_4

Přitom zjistila, že se některé kartičky překrývají (jsou umístěny kobrazu téhož čísla). Jak je to možné? –2 –1 0

Dokážete správně určit čísla na zakrytých kartičkách?

Připomínáme:

Kladná desetinná čísla umíme snadno převést na desetinné zlomky.

Příklad: 0,4 = 4 10

Takto získaný zlomek bychom ještě měli zkrátit na základní tvar: 4 10 = –2 5

Stejným způsobem můžeme převést záporná desetinná čísla na zlomky.

Příklad: –0,4 = – 4 10 = –2 5

Jinýpříklad: –0,75 = 75 100 = –3 4

Čísla– 3 2 , –3 4 , –2 5 jsou záporné zlomky.

Zlomky adesetinná čísla

Kladné zlomky umíme převést na desetinná čísla dvěma způsoby:

a) rozšířením na zlomky se jmenovatelem 10, 100, 1000, …

Příklady: 3 2 = 10 15 = 1,5 3 4 = 75 100 = 0,75

b) dělením čitatele jmenovatelem

Při tomto dělení můžeme získat dva odlišné typy výsledků:

Dělení vychází beze zbytku.

Příklady: 3 2 = 3 : 2 = 1,5 3 4 = 3 : 4 = 0,75 21 7 = 21 : 7 = 3

Výsledkem je celé číslo nebo desetinné číslosukončených desetinným rozvojem

Dělení nevychází beze zbytku, ani při dělení na libovolný počet desetinných míst. Každý zlomek nelze převést na desetinné číslo sukončeným desetinným rozvojem.

Vpodílu za desetinnou čárkou se opakuje jedna číslice, případně celá skupina číslic. Číslice nebo skupina číslic, která se opakuje, se nazývá perioda ačíslo obsahující periodu je číslo periodické. Číslici nebo skupinu číslic, která se vpodílu za desetinnou čárkou opakuje, zapíšeme jen jednou anad ní napíšeme vodorovnou čárku, které říkáme pruh

Příklady: 5 3 = 5 : 3 = 1,666... = 1,6 6 je perioda, čteme: jedna celá šest periodických

145 45 = 145 : 45 = 5,15 5 je perioda, čteme: pět celých jedna desetina pět periodických

Periodická čísla obvykle zaokrouhlujeme podle toho, jak přesné číslo potřebujeme.

Příklad: 2 3 = 2 : 3 = 0,666… 20

2 3 = · 1 přesnost na celky (vydělíme na 1 desetinné místo azaokrouhlíme na celky)

2 3 = · 0,7 přesnost na desetiny (vydělíme na 2 desetinná místa azaokrouhlíme na 1 desetinné místo)

2 3 = · 0,67 přesnost na setiny (vydělíme na 3 desetinná místa azaokrouhlíme na 2 desetinná místa)

2 3 = · 0,667 přesnost na tisíciny (vydělíme na 4 desetinná místa azaokrouhlíme na 3 desetinná místa)

Stejným způsobem můžeme záporné zlomky převést na desetinná čísla:

Příklady: –3 2 = –1,5– 3 4 = –0,75– 5 6 = –0,83 –345 99 = –3,48

Vpříkladě c) je základem celý povrch planety Země, to je přibližně 510 000000 km2

Vpříkladě d) je základem původní cena zboží.

Procenta používáme kvyjádření části celku (základu). Na obrázcích si prohlédněte, jak můžeme vyjádřit různé části celku vprocentech.

celek 1 2 celku 1 4 celku

30 % jsou 3 10 celku, nebo také 0,3 celku.90 % je 9 10 celku, nebo také 0,9 celku

1 % je 1 100 celku, nebo také 0,01 celku

Zapamatujte si:

Jedno procento (1 %) znamená jednu setinu celku (základu)

1 % = 1 100 = 0,01 základu.

Všimněte si:

Části celku můžeme vyjadřovat v procentech, zlomkem a desetinným číslem: Příklady:6 % = 6 100 = 0,06; 82 % = 82 100 = 0,82

Cvièení

1. Určete základ pro následující sdělení sprocenty:

a) Určitá politická strana získala vparlamentních volbách 23 % hlasů voličů.

b) Počet nezaměstnaných vČeské republice klesl vroce 2007 pod 7 %.

c) Od loňského ledna vzrostla cena benzinu o3 %.

d) Ve třídě 7.B je 60 % dívek a40 % chlapců.

e) Statistiky zroku 2006 uvádějí, že 70 % kuřáků vnaší republice by chtělo přestat kouřit, 40 % to každý rok zkusí, ale skutečně přestane kouřit jen 1 % –3 % kuřáků.

2. Vybarvenou část proužku zapište vprocentech, zlomkem ataké desetinným číslem. Za základ považujte celý proužek.

3. Vybarvenou část kruhu zapište vprocentech ataké zlomkem. Za základ považujte celý kruh.

4. Vybarvenou část čtverce zapište vprocentech, zlomkem ataké desetinným číslem. Za základ považujte celý čtverec.

5. Zapište vprocentech tyto části celku: a) 2

6. Zapište vprocentech tyto částicelku: a) 0,1b) 0,4c) 0,9d) 0,5 e) 0,05f) 0,33g) 0,72h) 0,99

7. Zapište vprocentech tyto části celku: a) 1 2 b) 1 4 c) 2 4 d) 3 4

Tato učebnice je druhou částí řady dvoudílných učebnic matematiky pro 2. stupeň základní školy a případně pro nižší ročníky víceletých gymnázií.

Pro každý ročník jsou vždy určeny dvě učebnice, z nichž jedna je věnována aritmetice, druhá geometrii. Praktickým a užitečným doplňkem učebnic jsou pracovní sešity ke každé z nich. Další materiály k procvičení a upevnění učiva přinášejí rovněž sbírky úloh a cvičení z matematiky, které jsou spolu s učebnicemi k dispozici.

Koncepce učebnic vychází z osvědčené praxe škol, vyhovuje však i záměrům Rámcového vzdělávacího programu pro základní vzdělávání. O tom svědčí mimo jiné i udělená schvalovací doložka MŠMT.

Celou řadu učebnic matematiky pro 6.–9. ročník ZŠ tvoří:

Matematika pro 6. ročník ZŠ – aritmetika (učebnice a pracovní sešit)

Matematika pro 6. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Matematika pro 7. ročník ZŠ – aritmetika (učebnice a pracovní sešit)

Matematika pro 7. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Matematika pro 8. ročník ZŠ – aritmetika (učebnice a pracovní sešit)

Matematika pro 8. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Matematika pro 9. ročník ZŠ – aritmetika (učebnice a pracovní sešit)

Matematika pro 9. ročník ZŠ – geometrie (učebnice a pracovní sešit)

Pro výuku matematiky na 1. stupni ZŠ je určena obdobná ucelená řada učebnic. (blíže viz www.spn.cz)