Fyzika 2

Zpracovali: PaedDr. Jiří Tesař, Ph.D., PaedDr. František Jáchim

Lektorovali: doc. PaedDr. Václav Havel, CSc., Mgr. Marie Kalivodová, doc. RNDr. Zdeněk Drozd, Ph.D., doc. RNDr. Josef Janás, CSc., PaedDr. Eva Lišáková

Schválilo MŠMT čj. MSMT-21234/2019 dne 24. července 2019 k zařazení do seznamu učebnic pro základní vzdělávání jako součást ucelené řady učebnic pro vzdělávací obor Fyzika s dobou platnosti šest let.

Tato učebnice je součástí nové ucelené řady učebnic fyziky na 2. stupni ZŠ a v nižších ročnících víceletých gymnázií.

Celá řada odpovídá požadavkům a doporučením RVP pro základní vzdělávání a tvoří ji tyto tematicky zaměřené učebnice:

Fyzika 1 (Fyzikální veličiny a jejich měření)

Fyzika 2 (Síla a její účinky – pohyb těles)

Fyzika 3 (Mechanické vlastnosti látek, Světelné jevy)

Fyzika 4 (Elektromagnetické děje)

Fyzika 5 (Energie)

Fyzika 6 (Zvukové jevy, Vesmír)

Poznámka redakce:

Snazší práci s učebnicí vám umožní malé obrázky po straně textu úloh. Co znamenají?

úloha vyžadující vaše vědomosti početní úloha úloha na procvičení dovedností a odhadu úlohy, které vás budou učit vyhledávat údaje nebo poznatky mimo učebnici domácí pokus

Fzadání pokusů prováděných ve škole

© Jiří Tesař za kolektiv, 2008, 2015

Illustrations © Karel Benetka, 2008, 2015

© SPN – pedagogické nakladatelství, a. s., 2008, 2015

ISBN 978-80-7235-560-0

Obsah

1. Gravitace 5

1.1 Jak se gravitace projevuje 5

1.2 Směr svislý a vodorovný 6

1.3 Znázornění a měření síly, tíha tělesa 9

1.4 Gravitační síla ve vesmíru 12 SHRNUTÍ 14

2. Účinky síly 15

2.1 Síla a tvar tělesa 15

2.2 Síla a pohybový stav tělesa 16 SHRNUTÍ 17

3. Tření 18

3.1 Síla, která brzdí pohyb 18

3.2 Tření – třecí síla 19

3.3 Odpor prostředí 22

3.4 Tření v technické praxi 24 SHRNUTÍ 26

4. Skládání a rozkládání sil 27

4.1 Skládání sil 27

4.2 Rozkládání sil 30 SHRNUTÍ 31

5. Newtonovy zákony 32

5.1 Zákon setrvačnosti 32

5.2 Síla zrychluje nebo zpomaluje 35 pohyb (zákon síly)

5.3 Co je akce a co reakce 37 SHRNUTÍ 39

6. Těžiště a stabilita těles 40

6.1 Těžiště 40

6.2 Stabilita těles 42 SHRNUTÍ 46

7. Otáčivé účinky síly 47

7.1 Páka 47 7.2 Užití páky 50 7.3 Páka – řešení úloh 52 7.4 Kladka pevná a její užití 54 7.5 Kladka volná a její užití 56 (rozšiřující učivo) SHRNUTÍ 59

8. Pohyb těles 60

8.1 Pohyb a klid těles 60 8.2 Rozdělení pohybů 61 8.3 Rychlost 64 8.4 Jednotky rychlosti 65 8.5 Výpočet rychlosti 67 8.6 Měření rychlosti 68 8.7 Výpočet dráhy, výpočet času 70 8.8 Grafické znázornění rychlosti pohybu 73 8.9 Grafické znázornění dráhy pohybu 75 SHRNUTÍ 76

9. Závěrečné shrnutí 77

10. Laboratorní práce 78

10.1 Laboratorní práce č. 3 78 10.2 Laboratorní práce č. 4 79 11. Náměty na projekty 81

12. Výsledky vědomostních 84 a kvantitativních úloh

Rejstřík 88

Na Galileiho výsledky navázal Angličan Isaac Newton. Zjistil, že gravitační síla působí okolo každého vesmírného tělesa, nejen kolem Země. Tato síla s rostoucí vzdáleností od příslušného tělesa klesá. Čím je těleso ve větší výšce nad povrchem Země, tím menší gravitační síla na ně působí. Newton také nalezl zákony, podle nichž se všechna tělesa ve vesmíru pohybují.

Gravitačními silami na sebe působí každá dvě tělesa. Síly působící např. mezi tělesy ve třídě jsou tak malé, že je nemůžeme našimi prostředky nijak změřit, ani jinak je nepociťujeme. Při našem výkladu se proto budeme zabývat jen gravitační silou Země.

K ZAPAMATOVÁNÍ:

Každé těleso působí na jiné gravitační silou. Gravitační síla je vždy přitažlivá a působí ve směru spojnice obou těles.

Čím větší mají tělesa hmotnost, tím větší je gravitační síla. Gravitační síla se zmenšuje s rostoucí vzdáleností mezi tělesy.

ÚLOHY

1. Na glóbu ukažte směr působení gravitační síly v různých místech Země.

Isaac Newton (1643 – 1727)

Účinek gravitace vnímají i rostliny. I na šikmém svahu rostou jejich stonky svisle. Na obrázku je strom zasazený do meze. Orbou na horním okraji meze se její sklon stále zvyšuje. Kmen stromu se zakřivuje tak, aby rostl svisle. Tomuto jevu se říká geotropizmus.

2. Na obrázku 1 jsou znázorněna stejná tělesa v různých vzdálenostech od Země. Na které těleso působí největší gravitační síla a na které nejmenší?

1. Které těleso ve sluneční soustavě má nejsilnější gravitační pole? Proč?

1.2 Směr svislý a vodorovný

Gravitační síla nám umožňuje základní orientaci v prostoru. Podle ní dovedeme rozlišit směry nahoru a dolů. V našem uchu je citlivý orgán, který vnímá směr gravitační síly a jehož prostřednictvím získáváme informace o poloze svého těla.

FNa stojan připevněte nit, na které je přivázané závaží.

Nit ukazuje směr svislý. Provedeme-li stejný pokus na různých místech Země, zaznamenáme výsledek takový, jako je na obrázku 2. Všechny závěsy ukazují ve zvoleném místě směr svislý a při prodloužení by se proťaly ve středu Země. Směr svislý je směr do středu Země. Svisle se pohybuje i volně padající těleso.

1. Tělesa v různých vzdálenostech od Země

2. Směr svislý – směr do středu Země

FNyní na stojan upevníme dva závěsy se závažími tak, jak je znázorněno na obrázku 3. Změřte označené vzdálenosti.

Zjistili jsme, že vzdálenosti závěsů jsou v obou místech stejné. To ale znamená, že závěsy jsou rovnoběžné, a pokus tedy nepotvrzuje obrázek 2. Dovedete vysvětlit, proč tomu tak je? Promyslete si, jak se bude měnit úhel mezi závěsy znázorněnými na obrázku 3, když budeme volit místa blíže k sobě. Dva závěsy při našem pokusu rovnoběžné opravdu nejsou, každý z nich směřuje do středu Země. Ovšem délka b je o tak málo menší než délka a, že naše měření to vůbec nemůže odhalit. Nedopustíme se žádné velké chyby, když budeme považovat oba závěsy za rovnoběžné.

3. Rozdíl vzdáleností mezi dvěma svislicemi je tak malý, že jej nemůžeme zjistit měřením

Když ve starověkém Egyptě stavěli pyramidy, potřebovali vytvořit velkou vodorovnou základnu (např. čtverec o straně 100 m). Postup přípravy základny pyramidy ukazuje obrázek. Okraj hladiny vody v prohlubni označil v terénu budoucí vodorovnou rovinu základny stavby.

K určování svislého směru se používá olovnice (obr. 4). Zhotovíme ji tak, že přivážeme např. kamínek na provázek. Obvykle bývá jako závaží použito kovové zašpičatělé těleso (používalo se olůvko, odtud původní název). Přiložením k hraně tabule, dveří nebo skříně můžeme zjistit, zda tyto hrany jsou svislé. Dáváme přitom pozor, aby olovnice visela volně a nedotýkala se žádných předmětů.

FDo kádinky nalijte vodu. Pozorujte hladinu. Podložte kádinku tak, aby byla nakloněna. Opět pozorujte hladinu. Výsledek pozorování zapište.

Ať nakláníme kádinku jakkoli, hladina leží stále v téže, tzv. vodorovné rovině. Libovolný směr v této rovině nazýváme směr vodorovný. Hladina kapaliny, je-li tato kapalina klidná, je vodorovná. Vodorovná je hladina rybníka, vody v louži, polévky v talíři. Na obrázku 5 máme vyznačen vodorovný směr v několika místech na Zemi. Vidíme, že i směr vodorovný je pro každé místo jiný. Mezi závěs olovnice a hladinu vody můžeme přiložit pravoúhlý trojúhelník. Směr vodorovný je kolmý na směr svislý.

5. Vodorovné směry v různých místech povrchu Země

vyhloubení místa pro staveniště

voda

označení hladiny po celém obvodu

zpevněný podklad

4. Olovnice

Každý lyžař ví, že mazáním skluznice lyží může významně ovlivnit způsob jízdy. Při jízdě z kopce bude rád, když pojede snadno a rychle, naopak při výstupu je podkluzování lyží velmi nepříjemné. Mazáním skluznic ovlivňuje tření mezi lyžemi a sněhem.

Dívka na obrázku vyšplhala po tyči a při klouzání dolů může svůj pohyb ovládat stiskem tyče, čímž vyvolává různě velkou třecí sílu mezi dlaněmi a tyčí. Třecí síla zpomaluje její pohyb dolů, jinak by se pohybovala volným pádem.

TŘENÍ

Šplh po tyči

Když vletí do zemské atmosféry těleso z kosmického prostoru (meteoroid), je třením o vzduch zpomalováno (a současně se třením zahřívá – někdy natolik, že se zcela vypaří). Někdy jeho zbytky dopadají na povrch Země, kde vytvoří kráter. Toto těleso se nazývá meteorit

3.1 Síla, která brzdí pohyb

Kromě gravitační síly se nejčastěji setkáváme se silami, které znemožňují nebo omezují pohyb těles. Lyžař, který vjede ze svahu na vodorovnou stopu, se po ujetí určité vzdálenosti zastaví. Mnohem dříve se zastaví při jízdě v neprojetém sněhu. Na svém těle pociťuje sílu působící proti směru pohybu. Tuto sílu nemůže nikdy zcela odstranit, ani když je stopa sebelépe projetá, nebo když lyže co nejlépe navoskuje. Přestaneme-li šlapat při jízdě na kole po vodorovné silnici, také se za chvilku zastavíme. Příčinou je síla vznikající na rozhraní vozovky a jízdního kola, tření v osách kol i odpor vzduchu, který můžeme vnímat. Tyto síly působí proti pohybu tělesa. Pokoušíme-li se vytáhnout vyčnívající hřebík z prkna, rukou se nám to obvykle nezdaří. Museli bychom totiž překonat poměrně velkou sílu, která vzniká mezi hřebíkem a dřevem a působí proti síle naší ruky. Nyní si ukážeme, že síla působící proti pohybu tělesa je v různém prostředí různá.

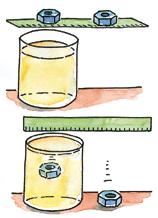
FNa skleněnou nádobu naplněnou olejem položte pravítko a na ně dvě stejné šroubové matky tak, aby jedna byla nad nádobou a druhá mimo ni. Pravítko otočte tak, aby obě matky začaly současně padat (viz obr. 19).

Co pozorujeme? Proběhl pohyb obou matek stejně? Matka padající olejem dosáhne úrovně stolu o něco později než matka padající vzduchem. Olej působí větší silou proti pohybu matky než vzduch.

19. Padající matky

Traktor táhnoucí pluh musí vyvíjet velkou sílu, aby překonal odpor, který půda lopatkám pluhu klade. Parašutista je naopak rád, že brzdné síle vzduchu vystavil svůj padák. Jinak by byl při dopadu smrtelně ohrožen. Traktor i parašutista svým pohybem přemisťují mnoho látky (země, vzduchu), toho dosáhneme působením síly. K přemisťování látky na rozhraní dvou těles dochází při každém pohybu.

FObarvěte jednu stěnu kvádru např. křídou (můžete jednu polovinu stěny obarvit červeně a druhou polovinu zeleně) a potom kvádr táhněte po stole.

Co pozorujeme? Část křídy ulpěla na stole, také na stěně kvádru došlo k rozmazání rozhraní barevných částí. Na několika příkladech jsme si ukázali existenci síly působící v prostředí proti pohybu. I tato síla podléhá fyzikálním zákonitostem, které si v dalším článku objasníme.

ÚLOHY

1. Proč automobil po vypnutí motoru po určité době zastaví?

2. Vyjmenujte některé příklady, kdy jste se setkali s třením v praxi.

3.2 Tření – třecí síla

Jestliže se pohybuje jedno těleso po druhém, vzniká odpor proti pohybu, který se nazývá tření. Síla, která vyvolává odpor proti pohybu (zpomalování pohybu), se nazývá třecí síla. Třecí síla nepůsobí pouze na pohybující se těleso, ale také na těleso v klidu, které chceme vnější silou uvést do pohybu. V tomto případě třecí síla působí proti směru vnější síly. O velikosti této síly se můžeme přesvědčit, chceme-li např. posunout stojící křeslo nebo židli po podlaze. Podle způsobu, jak se tělesa po sobě pohybují, rozeznáváme tření smykové a valivé. Nejprve se budeme zabývat třením smykovým. Příčinou vzniku smykového tření je drsnost dotýkajících se povrchů těles (obr. 20). Následující pokusy nám objasní, na čem závisí velikost třecí síly při smykovém tření.

Meteority se obvykle nazývají podle místa nálezu. V tabulce je uvedeno několik meteoritů nalezených na našem území.

Místo páduRok Celková hmotnost nalezených těles [kg] Loket1400100 Ploskovice172337 Lysá nad Labem 180810 Praskolesy18242 Bohumilce 1829 –1933 58 Broumov184724 Příbram19591,5 Ústí nad Orlicí 19631,3 Police nad Metují 19690,8

Největší sbírku meteoritů můžete vidět v Národním muzeu v Praze.

Horolezci, kteří stoupají soutěskou mezi skalními stěnami (tzv. komínem), se mohou zastavit v poloze, kterou znázorňuje obrázek. Na stěny působí tak velkou silou, že tíha horolezce je menší než třecí síla a on po stěnách nesklouzne.

20. Příčinou tření je nerovnost dotykových ploch

FPo desce lavice táhněte rovnoměrným pohybem kvádr siloměrem rovnoběžně s deskou stolu. Zapište velikost třecí síly. Pokus opakujte, posouvejte přitom kvádr po skle a po smirkovém papíru.

Napodobení horolezce

S velmi malým třením se pohybuje vznášedlo. Model vznášedla lze předvést pomůckou na obrázku.

2. Vezměte řetízek dlouhý asi 0,5 m. Položte ho na stůl, aby asi 5 cm řetízku volně viselo přes hranu stolu. Řetízek popotahujte dolů tak, až se dá sám do pohybu. Proč se řetízek dá do pohybu? Změřte délku té části řetízku, která v okamžiku samovolného pohybu ležela na stole. Je to více než polovina délky řetízku?

3. Během závodu FORMULE 1 začalo pršet. Závodníci ihned snížili rychlost jízdy. Proč?

4. Udělejte jednoduchý uzel na silnější struně do zahradní sekačky a na přibližně stejně silném provázku. Který uzel je pevnější? Proč?

5. Na jízdním kole vyhledejte všechna místa, v nichž má být co nejmenší (největší) tření. Jak je toho dosaženo?

6. Přineste takové nářadí, jehož činnost vyžaduje co největší tření.

7. Zjistěte, v jakém intervalu se musí vyměňovat olejová náplň v automobilu. K čemu tam olej slouží? Jak se vypuštěný olej likviduje?

Vzduch z nafouknutého balonku je vytlačován pod kruhovou desku, kterou nepatrně zvedá nad desku stolu. Snadno se přesvědčíte, že k pohybu tělesa ve vodorovném směru je třeba jen nepatrná síla.

• Model vznášedla podobný tomu na obrázku nahoře si snadno můžete zhotovit. Jako destička se vám hodí CD disk. S ostatním si jistě poradíte sami. Na modelu si vyzkoušejte, jak můžete ovlivnit směr pohybu vznášedla.

První vznášedlo zhotovil anglický vynálezce Ch. Cockerell (1910–1999), když začal zkoumat vlastnosti nafukovacích polštářů. Místo vzduchu z balonku vháněl vzduch z vysavače. Skutečné vznášedlo vyrobil v roce 1959 a 1. června s ním překonal kanál La Manche. Zemřel 1. června 1999 – v den 40. výročí své první cesty vznášedlem přes moře.

SHRNUTÍ

• Třecí síla působí proti pohybu – brzdí ho.

• Rozeznáváme tření smykové a valivé.

• Třecí síla vzniká v důsledku nerovností (drsnosti) dotykových ploch.

• Třecí síla závisí na materiálu a drsnosti dotykových ploch a tíze tělesa.

• Odpor prostředí se projevuje při pohybu tělesa v kapalině nebo plynu.

• Odpor prostředí závisí na tvaru tělesa, rychlosti pohybu a druhu prostředí.

• Využití tření v praxi je velmi rozsáhlé.

Motor

Vznášedlo a jeho princip

Vznášedlo – vrtulí umístěnou na zádi vznášedla se docílí pohyb ve vodorovném směru

4. SKLÁDÁNÍ A ROZKLÁDÁNÍ SIL

Znáte pohádku O veliké řepě? Děda sám nestačil na vytažení velké řepy. Přizval si proto postupně řadu pomocníků – babku, vnučku, kočku, myšku – a ti táhli jedním směrem, až řepu vytáhli. Nikdo z nich by řepu nevytáhl sám, ale působili tak, že jejich síly se sčítaly.

4.1 Skládání sil

Už jste viděli, když vlak táhnou dvě lokomotivy? Jsou zapojeny za sebe proto, aby jejich tahová síla byla větší, a mohly tak táhnout i velmi těžký vlak. V obou případech – pohádkovém i skutečném – působilo několik sil ve stejném směru. Tuto situaci si ukážeme na následujícím pokusu.

FNa siloměr zavěste deset závaží. Stejného prodloužení pružiny siloměru se snažte dosáhnout pomocí menšího počtu závaží.

Pokus ukazuje, že několik sil působících ve stejném směru můžeme nahradit menším počtem sil, které mají stejný účinek, v našem případě stejně prodlouží pružinu siloměru. Pro naše úvahy je vždy nejjednodušší, nahradíme-li několik sil silou jedinou (nazýváme ji výslednice sil) se stejnými účinky.

K ZAPAMATOVÁNÍ:

Skládat síly znamená najít jedinou sílu (výslednici), která má stejné účinky.

Součet tíh závaží je ve všech případech stejný, je roven tíze závaží (viz obr. 31). Pro každý případ můžeme celkovou sílu vyjádřit:

F1 = 0,1 N + 0,1 N + 0,1 N + 0,1 N + 0,1 N + 0,1 N + 0,1 N + 0,1 N + 0,1 N + 0,1 N = 1 N

F2 = 0,1 N + 0,1 N + 0,1 N + 0,1 N + 0,1 N + 0,5 N = 1 N

F3 = 0,5 N + 0,5 N = 1 N F4 = 1 N

Celkovou sílu, kterou nahrazujeme síly dílčí, nazýváme výslednice sil.

Některé velmi těžké vlaky jsou taženy dvěma lokomotivami buď v čele vlaku (té první se říká přípřež), nebo na obou koncích vlaku (zadní se nazývá postrk). Síly obou lokomotiv se na přímé trati v obou případech sčítají.

31. Skládání dvou sil působících ve stejném směru

K rozkladu poměrně malé síly na velké složky dochází např. u struny na kytaře. Brnknutím strunu nepatrně vychylujeme, což vyvolá dvě velké síly na místa, v nichž je struna ukotvena. I struna v klidu je napnuta silou až několik set newtonů. Konstrukce kytary musí být poměrně pevná.

Stavební konstrukcí využívající rozkládání sil je klenba. Na obrázku je její model.

4.2 Rozkládání sil

Na obrázku 34 je vozík na nakloněné rovině. I když bude poměrně těžký, není-li šikmá plocha příliš skloněna, lze vozík udržet proti možnému pohybu. Jeho tíha se rozkládá na dvě síly – složky. Jedna síla způsobuje pohyb vozíku (F1), druhá (F2) působí kolmo na plochu, na níž vozík je (způsobuje její prohnutí). Říkáme, že tíhu vozíku jsme rozložili do dvou směrů. Celková tíha vozíku je naopak výslednicí obou složek. Abychom udrželi vozík na šikmé ploše, postačí na něj působit silou F3, jíž vyrovnáme sílu F1 způsobující pohyb. Jak vidíme z obrázku, síla, kterou bychom vozík na šikmé rovině udrželi, je v tomto případě mnohem menší než jeho tíha.

K ZAPAMATOVÁNÍ:

Rozložit sílu znamená nalézt několik sil, jejichž současné působení má stejné účinky jako původní síla.

Hranoly vytvářející lomený oblouk přenášejí svisle působící zatížení do směrů klenby. Postranní pilíře musejí být dobře zajištěny proti vychýlení do stran.

Skutečná kamenná klenba pod silničním můstkem je na dalším obrázku.

Při rozkládání sil postupujeme takto:

Ø Působištěm síly, kterou rozkládáme, vedeme přímky ve směrech, do nichž se síla rozkládá.

Ø Doplníme na rovnoběžník, přičemž jeho úhlopříčkou je původní síla. Ø Sousední strany rovnoběžníka udávají velikosti složek.

Nyní si ukážeme, jak poměrně malá síla může při vhodném rozkladu vyvolávat dvě síly velké.

Jako klenba působí i skořápka vejce. Sevřete pevně do dlaně vejce (nesmí mít žádnou prasklinu ve skořápce) a pokuste se je rozmáčknout. Budete překvapeni, jak velkou sílu musíte vyvinout. Bude-li na skořápku působit síla zevnitř, snadno ji rozruší. Tak je tomu při líhnutí ptáků.

závěsné lano G

G F1 F2 F

Na obrázku 35 je síla G – tíha závaží, které chceme udržet působením sil ve směru závěsného lana. Aby závaží zůstalo v klidu, musí na něj lano působit silou F, která je stejně velká a opačně orientovaná než tíha závaží. Síla F je výslednicí, kterou rozkládáme do dvou směrů a a b svírajících poměrně velký úhel – téměř 180 o. Dokreslíme-li rovnoběžník sil, zjistíme, že složky F1 a F2 jsou mnohem větší než tíha závaží.

34. Vozík na nakloněné rovině

F2

35. Rozklad tíhy závaží na dvě síly

Mostní klenba

Model klenby

O velikosti sil F1 a F2 se můžete přesvědčit pokusem podle obrázku 36.

FNa švihadlo zavěste závaží o tíze 10 N a pokuste se švihadlo napnout tak, aby jeho prohnutí bylo co nejmenší.

36. Pokus o napnutí lana se závažím

Zjistili jste, že napnout švihadlo do přímky se nepodaří, i když budete vyvíjet co největší sílu. Z tohoto důvodu budou vždy trochu prohnuté šňůry s prádlem, dráty elektrického vedení apod.

ÚLOHY

1. Nakreslete rozložení tíhy závaží upevněného na konzole (obr. 37). Musí být vodorovná část konzoly dobře upevněna proti vytržení ze zdi?

2. Postavte se na osobní váhu a údaj zapište. Potom vezměte ještě jednu osobní váhu a postavte se tak, abyste každou nohou spočívali na jedné váze. Jaký je vztah mezi naměřenými hodnotami? Proč?

3. K rozkladu sil dochází také při tažení sáněk po vodorovné rovině (obr. 38). Do jakých směrů se rozkládá tažná síla? (Zvažte, co se stane při prudkém škubnutí za šňůru s přední částí sáněk a kam se sáňky pohybují?)

Starověcí stavitelé využívali klenbu i ve velkých stavbách. Na obrázku 30 je klenba v koloseu v tuniském městě El Jem. Stavba amfiteátru, jehož součástí klenby jsou, pochází ze 3. století. Do kruhové stavby s obvodem 427 metrů se vešlo 27 000 diváků, kteří mohli na jevišti 64 m x 39 m sledovat gladiátorské zápasy.

38. Rozklad sil při tažení sáněk

SHRNUTÍ

• Skládání sil ve stejném směru – výslednice je určena jejich součtem.

• Skládání sil v opačném směru – výslednice je určena jejich rozdílem.

• Skládání různoběžných sil – výslednice je určena úhlopříčkou v rovnoběžníku sil.

• Rozkládání sil – nalezení několika sil, které mají stejný účinek jako původní síla.

• Zjistěte, co to bylo koloseum a k jakým účelům sloužilo? V kterých městech byly podobné stavby postaveny?

Funkci klenby mají i kovové mostní oblouky. Na obrázku je silniční most, jehož nosnou částí je horní oblouk. Na něm je zbývající konstrukce mostu zavěšena.

• Poznáte, ve kterém městě tento nový most umožňuje přepravu přes řeku Dunaj?

Klenba v koloseu

37. Těleso zavěšené na konzoli

Zákon setrvačnosti poprvé formuloval italský vědec Galileo Galilei (1564–1642). Vyvrátil tak omyl starověkých učenců, kteří tvrdili, že pokud na těleso nepůsobí síla, jeho pohyb ustane. Ti vycházeli z běžné zkušenosti. Avšak při každém pokusu (např. kutálení kuličky po vodorovné desce) působí třecí síla, kterou nelze odstranit. Galilei zákon odůvodnil na základě tzv. myšlenkového pokusu, tj. pokusu za ideálních podmínek (tedy bez tření).

ZAPAMATOVÁNÍ:

Těleso setrvává v klidu nebo se pohybuje přímočaře stále stejnou rychlostí, pokud není přinuceno vnějšími silami tento stav změnit.

Podle tohoto zákona by se kulička kutálející se např. po vodorovném skle měla pohybovat přímočaře, a to stále. Ve skutečnosti se po uražení určité vzdálenosti zastaví. Kdybychom ji kutáleli po dřevěné desce, zastavila by se dříve. A co třeba na koberci? Její dráha by byla velmi malá. Příčinou je tření, které ve všech třech případech existuje a které nemůžeme nikdy zcela odstranit. Příkladem pohybu, kdy je tření velmi malé, je např. pohyb puku po ledě nebo vlaku po vodorovných kolejích. Setrvačnost tělesa se projevuje i v klidu.

FNa sklenici položte list papíru a na něj minci. Prudkým trhnutím papíru do strany docílíte toho, že mince spadne do sklenice.

FNa stůl položte tenkou dřevěnou tyčku, aby přečnívala asi z jedné třetiny přes okraj desky stolu (viz obr. 41). Část tyčky ležící na stole překryjte velkou čtvrtkou papíru. Prudce udeřte na přečnívající část tyčky.

Provedete-li stejný pokus bez užití čtvrtky papíru, tyčka se převrátí a spadne. Nad čtvrtkou papíru je vzduch, který vlivem své setrvačnosti v klidu nemůže rychle uniknout a působí velkou odporovou silou.

ÚLOHY

1. Proč se lyžař, který vjel ze svahu na vodorovnou stopu, hned nezastaví?

2. Automobil, jedoucí příliš rychle na zledovatělé vozovce v zatáčce, vyjel ze silnice. Nakreslete směr, v jakém automobil opustil silnici.

3. Proč při zakopnutí padáte kupředu?

4. Vysvětlete, proč třepáme s mokrým kabátem, abychom ho zbavili kapek vody.

5. Proč nemůže automobil zastavit okamžitě na místě, když mu do dráhy vběhne nepozorný chodec?

41. Setrvačnost vzduchu

Galileo Galilei

Náhrobek Galilea Galilei ve Francii

6. Na obr. 42 údržbář naráží kladívko na topůrko. Popište jeho postup. Neměl by to dělat obráceně?

7. Proč se má na pohyblivé schody vstupovat z chůze, a nikoli z klidu?

8. Proč když vyskočíme, se pod námi Země malinko nepootočí?

1. Můžete při rozjíždění vlaku poznat, kterým směrem se pohybuje, aniž se budete dívat ven? Poznáte to při jeho zastavování? Jestlipak dovedete určit směr pohybu vlaku na přímé trati, pohybuje-li se stálou rychlostí?

1. Na ledové ploše se odrazte bruslí a sledujte, jak daleko se vám podaří dojet.

2. Sledujte tvar dráhy puku vystřeleného po ledě. Je obtížné docílit jeho pohyb podél celého kluziště?

3. Při cestě domovním výtahem popište, co budete pociťovat a) při rozjezdu směrem nahoru, b) během jízdy, c) při dojezdu nahoru, d) při rozjezdu směrem dolů, e) při dojezdu dolů.

4. Menší plastový kelímek opatřete dvěma otvory u okraje a připevněte k nim vlákno asi 0,5 m dlouhé podle obrázku 43. Asi do ½ kelímku nalijte vodu a na vlákně ho roztočte. Proč voda nevyteče, ani když je kelímek otočen dnem vzhůru?

Míč vyhozený vzhůru svoji rychlost zmenšuje, až se v určité výši zastaví a začne padat zpět. Při pádu naopak svoji rychlost zvětšuje. Jistě máte tuto zkušenost z házení míčem. Během pohybu stále působila na míč gravitační síla. Při pohybu vzhůru působila proti pohybu a rychlost míče zpomalovala. Při volném pádu míče působila ve směru pohybu a rychlost míče zvětšovala. Zamysleme se nyní nad případem, který si následně vysvětlíme pomocí pokusu. Automobil Škoda Fabia se vyrábí s několika různě silnými motory. S kterým motorem se toto auto rozjede na křižovatce rychleji – se slabším, nebo se silnějším?

Francouzský spisovatel

Jules Verne (1828–1905) ve svém románu Pět neděl v balonu popisuje velmi snadné cestování s balonem. Stačí vystoupit několik desítek metrů nad Zemi, počkat, až se pod námi Země pootočí (v naší zeměpisné šířce se bod na povrchu Země pohybuje rychlostí asi 300 s m ) a pak sestoupit. Kdybychom setrvali v balonu celý den, mohli bychom vykonat cestu kolem světa. Nic takového ve skutečnosti ale není možné. Spolu se Zemí se otáčí i její atmosféra. Proto i pozorovatel z vesmíru by viděl, jak se balon v ovzduší poklidně otáčí se Zemí.

Původní titulní strana románu Pět neděl v balonu

42. Upevňování kladívka s využitím setrvačnosti

43. Plastové kelímky – k pokusu

5.2 Síla zrychluje nebo zpomaluje pohyb (zákon síly)

6. TĚŽIŠTĚ A STABILITA TĚLES

• Najděte polohu těžiště smetáku např. tímto způsobem: Oba ukazováčky dejte před sebe do vzdálenosti asi 1 metr. Pomocník přes ně položí smeták. Suňte ukazováčky pomalu k sobě. V místě, kde se vzájemně dotknou, je těžiště smetáku. Vysvětlete, proč se v určitém okamžiku násada sune jen po jednom ukazováčku.

6.1 Těžiště

Znázorněte graficky gravitační sílu, která působí na plavce stojícího na skokanském bloku, víte-li, že má hmotnost 50 kg. Určit velikost působící síly je snadné (gravitační síla je přibližně rovna tíze tělesa G; G = m · g; G � 500 N). Do jakého bodu ale umístíme působiště této síly? Většinou působiště síly umisťujeme „doprostřed“ tělesa, to ale není vždy správné. Kde bude působiště gravitační síly, jestliže je plavec v předklonu připraven skočit do vody? Abychom mohli tento zadaný úkol vyřešit, provedeme nejdříve jednoduchý pokus.

FNa závěs připevněte desku nepravidelného tvaru a poté na něj zavěste olovnici (obr. 50). Ta směřuje vždy do středu Země, tj. určuje směr gravitační síly, která působí na těleso.

Postupně budeme měnit zavěšení tělesa v různých otvorech a tužkou vždy obtáhneme směr provázku olovnice. Tyto přímky nazýváme těžnice. Všechny těžnice se proťaly v jednom bodě, který budeme nazývat těžiště. Můžeme o něm říci, že je to působiště gravitační síly, která na těleso působí.

K ZAPAMATOVÁNÍ:

Těžiště tělesa je bod, ve kterém působí gravitační síla na těleso, a určíme ho jako průsečík těžnic.

50. Těžiště nepravidelného tělesa

51. Poloha těžiště v hrušce a houbě

Z výsledku pokusu je také zřejmé, že těleso má vždy pouze jedno těžiště. Těžiště však nemusí být vždy uprostřed tělesa, ale nachází se blíže k místu, kde je více látky. Například těžiště hrušky je v její spodní části, protože tam je soustředěno více látky. Naopak houba muchomůrka má zpravidla těžiště těsně pod „kloboučkem“ (obr. 51). Zamyslete se, proč tomu tak je.

Polohu těžiště určujeme převážně pokusem, jako jsme to dělali s nepravidelnou deskou, můžeme ji však také celkem dobře odhadnout. Tělesa, která se skládají ze stejné látky (nazývají se stejnorodá) a mají pravidelný tvar, mívají těžiště uprostřed. Stejnorodá tělesa, která jsou souměrná podle osy, mají těžiště vždy na této ose. Naproti tomu u nepravidelných těles, jako jsou sekera, strom, jídelní vidlička, hokejka apod., se těžiště nachází blíže k jednomu konci (k těžší části), nebo dokonce vně tělesa.

U dutých těles (trubka, hrneček, naběračka, bota, loďka, koš apod.) se těžiště většinou nenachází ve stěnách tělesa, ale v jeho dutině (obr. 52). Plavec v předklonu připravený ke skoku do vody (viz úvodní obrázek této kapitoly) má těžiště přibližně na povrchu těla v břišní krajině.

T52. Těžiště trubky je mimo těleso

ÚLOHY:

1. Uchopte volně v různých místech trojúhelník na rýsování a zjistěte, kde má těžiště. Nachází se těžiště u všech stejných trojúhelníků na stejném místě?

2. Odhadněte, kde se nachází těžiště učebnice fyziky.

3. Rozevřete učebnici tak, aby desky obalu svíraly 90° a listy byly rovnoměrně rozprostřeny v prostoru. Určete polohu těžiště. Je toto těžiště na stejném místě jako v předchozím případě?

4. Na obrázku 53 vidíte bumerang (při hodu se vždy vrací zpět). Určete jeho těžiště.

5. Kde se nachází těžiště kola bicyklu? Ovlivňuje polohu těžiště hmotnost ventilku?

6. Kam se posune těžiště našeho těla, když neseme v jedné ruce kbelík s vodou?

• Podobně najděte těžiště desky nepravidelného tvaru. Desku položte přes dvě tyčky, aby se nedotýkala stolu (obr. a). Tyčky posouvejte k sobě. Přímku, v níž se dotýkají, vyznačte na desce (obr. b). Desku pootočte a postup opakujte (obr. c). Průsečík vyznačených čar je těžiště (obr. d).

b

Let bumerangu

Tato učebnice je druhou částí šestidílné řady tematicky zaměřených učebnic fyziky pro výuku na 2. stupni ZŠ (případně v nižších ročnících víceletých gymnázií). Učebnice jsou zpracovány v souladu s požadavky RVP pro základní vzdělávání. Kladou důraz na rozlišení základního a rozšiřujícího učiva, naplňují mezipředmětové vztahy, přiměřeně zohledňují průřezová témata formulovaná v RVP. Pozornost věnují praktickému aspektu výuky, uvádějí množství úkolů a pokusů vhodných k realizaci ve školních podmínkách. Všechny díly řady vycházejí se schvalovací doložkou MŠMT. Vhodným doplňkem učebnic jsou publikace Seminář a praktikum z fyziky a Sbírka úloh z fyziky pro 6.–9. ročník ZŠ.

Celá řada je tvořena těmito tematickými učebnicemi:

Fyzika 1 (Fyzikální veličiny a jejich měření)

Fyzika 2 (Síla a její účinky – pohyb těles)

Fyzika 3 (Mechanické vlastnosti látek, Světelné jevy)

Fyzika 4 (Elektromagnetické děje)

Fyzika 5 (Energie)

Fyzika 6 (Zvukové jevy, Vesmír)

ISBN 978-80-7235-560-0