

Ellära grunder
Lik- och 1-fas växelström


Innehåll
Sida Avsnitt
Historia
Multimetern 1
Testa-dig-själv 1
Resistans & resistansmätning 2
1 Testa-dig-själv 2
1 Ledningsresistans 3
1 Testa-dig-själv 3
Spänning & spänningsmätning 4
2 Testa-dig-själv 4
2 Spänningsaggregat 5
2 Testa-dig-själv 5
2 Ström & strömmätning 6
3 Testa-dig-själv 6
3 Ohms lag 7
3 Testa-dig-själv 7
Resistans i seriekretsar 8
4 Testa-dig-själv 8
4 Spänningsdelning 9
4 Testa-dig-själv 9
4 Parallellkretsar 10
5 Testa-dig-själv 10
5 Resistans i parallellkretsar 11
5 Testa-dig-själv 11
5 Blandade serie & parallellkretsar 12
6 Testa-dig-själv 12
6 Kirchhoffs spänningslag 13
6 Testa-dig-själv 13
Belastningseffekter 14
7 Testa-dig-själv 14
7 Energi & effekt 15
7 Testa-dig-själv 15
Spänningskällor 16
8 Testa-dig-själv 1
8 Effektanpassning 17
8 Testa-dig-själv 17
9 Magnetiska grundbegrepp 18
9 Testa-dig-själv 18
9 Reläer & reläkopplingar 19
10 Testa-dig-själv 19
10 Induktion 20
10 Testa-dig-själv 20
10 Oscilloskop 21
11 Testa-dig-själv 21
11 Funktionsgeneratorn 22
11 Testa-dig-själv 22
11 Kondensatorn, upp & urladdning 23
12 Testa-dig-själv 23
12 Växelspänning 24
1 Testa-dig-själv 24
13 Facit till Testa-dig-själv-uppgifter
13 Matematiska förklaringar
Som komplement till denna lärobok finns: Mätuppgifter med facit
Instuderingsuppgifter med facit.
Extrauppgifter med facit på www.revma.se
SidaAvsnitt
Personer och händelser i elkunskapens historia
Ämnesområdet elektroteknik är redan stort, men kan likväl väntas öka i såväl omfattning som betydelse. Så har det inte alltid varit, tvärtom har det tagit mänskligheten lång tid att utveckla dagens kunskapsnivå. Flera personer och händelser har bidragit. Några av de mer betydelsefulla får inleda den orientering av ämnet som följer.
600 BC
Thales från Militos, ca 625 – 545 BC, en av greklands sju vise uppmärksammar fenomenet friktionselektricitet i samband med bärnsten, som på grekiska kallas electron.
250 BC
Bagdadbatteriet, en möjlig förhistorisk galvanisk cell daterad till perioden 250 f.Kr. Det grävdes fram vid Khujut Rabula i utkanten vid Bagdad.. Fyndet har förbryllat forskare och man har inte riktigt kunnat förstå vad det möjliga batteriet kan ha använts till, eller hur man över huvud taget kommit på idén.
1600-talet
William Gilbert, 1544 – 1603, engelsk läkare och fysiker som är känd för magnetexperiment och teorin att jorden är en stor magnet som förklaring av kompassnålars beteende. Gilbert införde också ordet electrics
1700-1800-talet:
Alessandro Volta, 1745 – 1827, italiensk fysiker som uppfann batteriet, Voltas stapel, och får enheten för spänning (volt) uppkallad efter sig. I och med tillgången till en kontinuerlig strömkälla fanns förutsättningar för att undersöka strömmens verkningar.
Hans Christian Örsted, 1777 – 1851, dansk kemist och fysiker upptäcker år 1820 att en strömförande ledare omges av ett magnetiskt fält och gav oss därmed grunden för elektromagnetismen.
George Simon Ohm, 1789 – 1854, tysk vetenskapsman som hedrats med att få enheten för resistans (ohm, ) uppkallad efter sig. Ohm utvecklade idén att det är spänning som orsakar ström i en elektrisk krets och publicerar år 1827 i Die galvanische Kette, matehe-matish bearbeit grunden för elektrisk kretsteori: Ohms lag.


















Michael Faraday, 1791 – 1867, engelsk bokbindare som ”tjuvläste” de vetenskapliga böckerna han band in. Detta ledde till Royal Institution där han utsågs till professor 1833. Under denna tid upptäcker han elektromagnetisk induktion, grunden för generatorns, transformatorns och elmotorns funktion.
Gustav Kirchhoff, 1824 – 1887, tysk fysiker som utvecklade regler för beräkning av strömmar och spänningar i elektriska kretsar, kända som Kirchoffs ström- och spänningslag.
Thomas Alva Edison, 1847 – 1931, självlärd amerikansk uppfinnare som är känd för att ha uppfunnit den första användbara mikrofonen och fonografen, den första apparaten för in- och uppspelning av ljud. Han var även först med att konstruera en användbar glödlampa och att bygga ett elnät.
Jonas Wenström, 1855 – 1893, svensk uppfinnare konstruerar den första svenska trefastransformatorn och får patent på trefassystemet. Principen användes första gången i Sverige 1893 och blev grunden för storföretaget ASEA, senare ABB.
1900-talet
Guglielmo Marconi, 1874 – 1937, italiensk forskare lyckas med trådlösa telegrafisändningar från Europa till USA och får 1909 Nobelpriset i fysik för sina insatser inom trådlös radioöverföring.






John Baird, 1888 – 1946, engelsk elektroingenjör utvecklar tysken Paul Nipkows metod att omvandla en bild till en elsignal och lyckas år 1924 överföra en TV-bild och startar därmed utvecklingen av televisionen.

















William Shochley, John Bardeen och Walter Brattain, tre amerikanska forskare publicerar 1948 sina lyckade experiment med transistorn. För sina insatser belönas forskarlaget med nobelpriset i fysik år 1956.
2000-talet
Läsaren av denna bok.




MULTIMETERN
Detta avsnitt informerar om multimetern. Ha gärna en multimeter tillhandsnärduläseravsnittet.
När du är klar skall du kunna identifiera och ställa in en multimeters olikafunktionersamtavläsamultimeternsolikaskalor
ANALOG & DIGITAL
Det finnstvåolika typer avmultimetrar,analoga och digitala.Båda typerna har mätfunktioner för resistansmätning, spänningsmätning och strömmätning. På en del modeller finns det även andra mätfunktioner somfrekvens-ochkapacitansmätning.
En analog multimeter visar mätresultatet med hjälp av en visare som rörsigöverenskala,medanendigitalmultimeter visarmätvärdetmed siffror(digitärengelskaförsiffra).



ANSLUTNING & FUNKTIONSVAL
Bilden visar exempel på typiska analoga och digitala multimetrar. Omkoppling mellan multimeterns olika mätfunktioner och mätområden görs med en funktionsomkopplare. På instrumenten ovan är det vridbara funktionsomkopplare, men det finns även multimetrar med tryckknappsomkopplare och med annan indelning.
2
RESISTANS & RESISTANSMÄTNING
Detta avsnitt informerar om begreppet resistans i anslutning till några vanliga resistortyper och om hur multimetern används vid resistansmätning.
När du är klar skall du kunna mäta resistanser, avläsa färgkoden, ange standardvärden i E6- och E12-seriern, redogöra för potentiometerns funktion och bestämma dess aktuella inställning med resistansmätning.
RESISTORER
Resistorn är en mycket vanlig komponent i elektriska kretsar. Den egen-skap som resistorer har benämns resistans och utgör i elektriska kretsaretthinderförström.
Egenskapen(storheten) betecknas med (R) ochmäts ienheten(sorten) ohm sombetecknasmeddengrekiskabokstavenomega, .
Ielritningarangesresistornmedensymbolochdessresistansvärdemed etttalföljtavett ,tex1000
Resistorsymbol
MÄRKNING AV RESISTORER
Resistorer kan seväldigt olikaut. På störreresistoreråtergesresistansvärdetoftaiklartextochpåmindremedfärgbandmedenbestämdkod.


3 LEDNINGSRESISTANS
Dettaavsnitthandlaromolikamaterialsledningsförmågaochhurman mäterochberäknarledningsresistans.
Närduärklarskalldukunnaberäknaochmätaledningsresistans.
LEDARE OCH ISOLATORER
Materialsomdetgårattledaelektriskströmigenom kallasför ledare, medanmotsatsen benämns isolatorer. Idessaär det svårt, ellernästan omöjligt,attledaelektriskström.Metallerärexempelpåledare.Keramik,gummi,glas,luftochplastärexempelpåisolatorer.
Isolatormaterial
Ledarmaterial
Ledningstråd
Beroende på hur lätt det är att leda ström genom en ledare talar man om goda eller dåliga ledare. Goda ledare har låg resistans i motsats till goda isolatorer, som har hög resistans.
RESISTIVITET
Resistansenhosledareochisolatorerberorblandannat på en materialegenskap som kallas resistivitet och som betecknas med den grekiska bokstaven (uttalas”rå”).
Lågtvärdepåresistiviteteninnebärattdetärlättatt leda ström genom materialet. Ledare ska därför ha låg resistivitet medan isolatorer ska ha hög resistivitet.
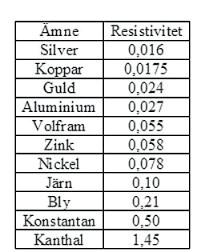
Tabellenvisarresistivitetenvid+20°Cförnågravanligaledarmaterial.
Lägg på minnet att resistiviteten för koppar. är 0,0175.Detärdet vanligasteledarmaterialeti elkablar
6
STRÖM & STRÖMMÄTNING
Detta avsnitt redogör för strömbegreppet och hur ström mäts med en multimeter.
När du är klar skall du kunna ställa in och ansluta en multimeter för strömmätning
STRÖM
Ström är elektriska laddningari rörelseroch kantill skillnad frånresistansochspänninginteexisteraensamt.Resistansfinnsochgårattmäta i resistorer, i ledningstråd och i diverse andra material. På samma sätt kanspänningexisteraibatterierochspänningsaggregat.
För att ström skall kunna existera måste det finnas en spänningskälla med elektrisk tryckskillnad, t ex ett batteri, och en sluten krets mellan spänningskällansplus-ochminuspolsomströmmenkanflytagenom.
Kopplingen visar en sluten krets med en lampa kopplad till ett batteri ochhurdettaserut iettelektrisktschema.
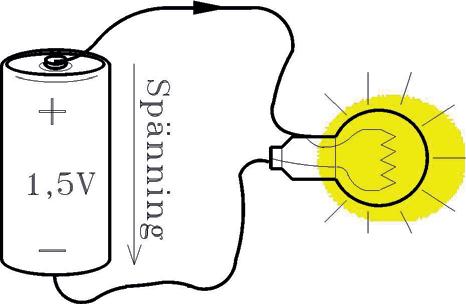
Samma koppling då lampans glödtråd gått sönder och öppnat förbindelsen mellan batteriets plus- och minuspoler.
I en öppen krets kan det inte flyta ström
Byts den trasiga lampan mot en ny med hel glödtråd börjar det genast attflytaström samtidigt ihelakretsenigen.
STRÖMSTYRKA
Inledningsvisnämndesattströmärelektriskaladdningarirörelse.Iledare är antalet laddningar som passerar ett tvärsnitt av ledaren per sekundettmåttpåströmstyrkan.
Strömbetecknasmed(I)medanenhetensomströmstyrkanmätsiheter ampere ochbetecknasmed(A).Tillföljdavdettakallasenmultimeter somärinställdförströmmätningoftaföramperemeter.
7
OHMS LAG
DettaavsnittredogörförOhmslag,grundenförelektrisktkretstänkande.
NärduärklarskadukunnaanvändaOhmslagvidberäkningaravelektriskakretsarochförattkunnaförutsägamätresultat.
Georg Simon Ohm var en tysk fysiker som levde åren 1787 till 1854. Hans upptäckt av det för elektrotekniken grundläggande sambandet mellan spänning, ström och resistans publicerades år 1827.
REFERENSPILAR & BETECKNINGAR
I de tidigare avsnitten har du bekantat dig med stoheterna spänning, ström och resistans genom att mäta och beskriva dem. Det matematiska sambandet mellan de tre storheterna är formulerat i Ohms lag, vilken introduceras i detta avsnitt.
För att Ohms lag ska få någon som helst mening måste sambandet mellan den matematiska formeln och den aktuella kretsen synliggöras med kretsscheman, referenspilar och storhetsbeteckningar så som visas i följande genomgång.
Kretsen för vårt resonomang består av en spänningskälla och en resistor kopplad mellan dess plus- och minuspol.
Vi vet att batterisymbolen innebär spänning och att det flyter ström från batteriets pluspol genom resistorn tillbaka till batteriets minuspol. Det är inte så svårt att komma ihåg när kretsen är så enkel, men vid beräkning och analys av mer komplicerade kretsar behöver tanken stöd av referenspilar och storhetsbeteckningar
Strömpilen markerar strömmen ( I ), vars riktning är från spänningskäl-lans pluspol mot dess minuspol.
Spänningsfallspilen markerar spänningen ( U ) över resistorn ( R ). Observera att referenspilen för U har en (+) och en (-) sida och att spänningen faller från ett högre till ett lägre värde i den riktning som strömmen flyter.
OHMS LAG
Med beteckningarna i bilden skrivs Ohms lag matematiskt så här:
I U R
I = strömmen i A (ampere)
U = spänningen i V (volt)
R = resistansen i (ohm)
IordkanviuttryckaOhmslagpåföljandesätt:
Strömmen genom en resistor är lika med spänningen över resistorn dividerad med med resistansen.
Exempel: Beräkna strömmen genom resistorn om resistansen är 1,5 ochspänningenöverresistornär3V.
I U R I V A 3 15 2 ,
ENHETSOMVANDLING
För att strömmen ska erhållas i grundenheten A (ampere) ska den aktuella spänningenangesi V(volt)ochresistanseni (ohm).Ibland är en eller flera av de tre storheterna angivna i under- eller överenheter,texmA(milliampere)ellerkV(kilovolt).
Förnybörjareärdetkloktattomvandlatillgrundenheterinnandesätts in i Ohms lag. Nedanstående sammanställningen visar storleksförhållandet mellan grundenheterna och de över- och underenheter som är vanligast.
Beteckningförström:I
Grundenhetär1A(ampere)
1mA, (milliampere) är en tusendels amper
1A=1000mA
1mA=0,001A
1 A, (mikroampere) är en miljondels ampere
1A=1000000 A
1 A=0,000001A
Beteckningförspänning:U
Grundenhetär1V(volt)
1kV, (kilovolt) är tusen volt
1kV=1000V
1V=0,001kV
1mV, (millivolt) är en tusendels volt
1V=1000mV
1mV=0,001V
1 V, (mikrovolt) är en miljondels volt
1V=1000000 V
1 V=0,000001V

8
RESISTANS I SERIEKRETSAR
Dettaavsnittvisarhurseriekoppladeresistorkretsarkanersättasochhur Ohmslagkananvändasförseriekretsar.
När du är klar skall du kunna förenkla kretsar med seriekopplade resistorer.
SERIEKOPPLADE RESISTORER
Antagattvi harenkretsmedtvåseriekoppladeresistorerochattvibyter ut dem mot en ensam resistor utan att strömmen eller spänningen ändrarsig.
Eftersomströmmenär2mA ochspänningen6Vbådeföre ochefterresistorbytetärdetganskauppenbartattocksåresistansenärlikastoride bådakretsarna.
Sammaresonemangkangörasförnätverkmed fleraresistorerochallmäntgällerföljanderegel:
Serikopplade resistorer kan ersättas av en enda resistor, vars resistans är lika stor som summan av de seriekopplade resistorernas värden.
Om ersättningsresistorn kallas för RS kan samma sak uttryckas matematisktsåhär:
R R R R S 1 2 3

10 PARALLELLKRETSAR
Detta avsnitt redogör för begreppet delströmmar och Kirchhoffs strömlag.
När du är klar skall du kunna beräkna och mäta delströmmar.
Gustav Robert Kirchhoff var en tysk fysiker som levde åren 1824 till 1887. Kirchhoff utförde en mängd viktiga arbeten inom fysiken, men är mest känd för sina lagar inom elektrisk kretsteori.
STRÖMMAR I PARALLELLKRETSAR
Bildenvisarenparallellkretsmedtregrenarsomviskatittanärmarepå.
Från spänningskällans pluspol flyter strömmen IT till punkten A där den delas upp i grenströmmarna I1, I2 och I3 Vid punkten B förenas de tre grenströmmarna åter till en ström med samma storlek som IT, därav den gemensamma beteckningen för strömmen som flyter från och till spänningskällan.
Här berörs en regel som gäller för alla spänningskällor och som är viktig att komma ihåg.
Strömmen som flyter från en spänningskällas pluspol är alltid lika stor som strömmen som flyter tillbaka till spänningskällans minuspol.
Riktar vi fokus mot strömmarna som flyter till, respektive från de båda grenpunkterna utan att bry oss om vad som orsakat dem eller deras storlek kan vi göra samma slutsats som Kirchhoff en gång gjorde då han fomulerade sin strömlag:
Summan av alla strömmar som flyter till och från en grenpunkt är lika med noll.

11
RESISTANS I PARALLELLKRETSAR
Dettaavsnitthandlaromersättningsresistansiparallellkoppladekretsar.
När du är klar skall du kunna beräkna och mäta ersättningsresistans i parallellkoppladeresistorkretsar.
ERSÄTTNINGSRESISTANS
Utgångspunkten för den följande diskussionen är att de tre parallella resistorernaR1,R2 ochR3 skaersättasmedenresistorsomvikankalla RP utanattströmmenIT ändras.
Det finns tre bra sätt att ta reda på hur stor ersättningsresistansen RP är.
1.En metod är att göra en resistansmätning mellan grenpunkterna A och B. Koppla i så fall bort spänningskällan först annars blir mätresultatet felaktigt.
2.Ett annat sätt är att mäta strömmen IT och spänningen U och att därefter beräkna RP med Ohms lag. R U I P T
3.Tredje sättet är att räkna fram ersättningsresistansen RP
1 1 1 1
123 RRRR P .....
I ord kan det matematiska sambandet uttryckas på följande sätt:
Inverterade totalresistansen är lika med summan av de ingående resistorernas inverterade värden.
Härledning av formeln finns i avsnittet matematiska förklaringar

12
BLANDADE SERIE & PARALLELLKRETSAR
Detta avsnitt visar hur det går till att beräkna resistans, grenströmmar ochdelspänningariblandadeserie-ochparallellkretsar.
När du är klar skall du kunna beräkna och mäta totalresistans, grenströmmarochdelspänningariblandadeserie-ochparallellkretsar.
BLANDADE KRETSAR
Kretsenhärunderkanbeskrivassomenblandadserie-parallellkretsdär resistorn R1är i serie med parallellkombinationen R2 och R3 som i sin turäriseriemedR4.
Samma metoder som vi tidigare använt för mätning och beräkning av resistans,strömmarochspänningarfungerarävenförblandadekretsar, mendetgällerattvarasystematisk.
Genom att rita om kretsen och noggrant och konsekvent sätta ut referenspilar och storhetsbeteckningar kan du klara av att beräkna ersättningsresistans,grenströmmarochdelspänningarikretsenovan.
UPPDATERING
Härärförstenuppdateringavdeformlervikommerattanvända:
Ersättningsresistansen för seriekretsar
Ersättningsresistansen för parallellkretsar
Ohms lag i alla dess former UIRI U R R U I
Observera:
Det är viktigt som tankestöd att rita om kretsen och sätta ut referenspilar och beteckningar allteftersom beräkningen genomförs.

BERÄKING AV TOTALRESISTANSEN
Totalresistansen sett från spänningskällans (+) plus- och (-) minusanslutningarberäknasgenomattkretsenstegvisförenklas.
I första steget beräknas ersättningsresistansen för parallellkombinationen R2//R3.KretsenförenklasdåtillenseriekopplingbeståendeavR1, RP ochR4. Iandrastegetreducerasseriekopplingentill densökta totalresistansenRT.
Exempel: Beräkna totalresistansen för kretsen om R1=22 , R2=18 , R3=22 och R4=15 .
R RR RR P 23 23 R P 1822 18 22 99 , RRRR TP14 R T 229915469 ,,
Exempel: Beräkna totalresistansen mellan (+) plus och (-) minusanslutningarnaomR1=100 ,R2=47 ,R3=33 ,R4=82 ochR5=82 Observeradetvåserikoppladeresistorernaiparallellkretsen!
R R R S 2 3 R S 473380
R R R RR P S S 4 4 R P 8082 80 82 405, R R R R T P 1 5 R T 100405822225 ,,
13 KIRCHHOFFS SPÄNNINGSLAG
DettaavsnitthandlaromhurKirchhoffsspänningslagkanrationalisera ström-ochspänningsberäkninginätverk.
När du är klar med avsnittet skall du kunna använda Kirchhoffs spänningslagvidberäkningochspänningsmätning.
KIRCHHOFFS SPÄNNINGSLAG
Kirchhoffsspänningslagkanformulerasolikamenändåhasammabetydelse.Utgångspunktenförvårdiskussionformulerassåhär:
Summan av alla spänningar i en sluten slinga är lika med 0 då de räknas i samma riktning
Det finns två begrepp som vi måste reda ut. Vad är en sluten slinga?
Ochvilkenriktningärdetfråganom?
KRETS MED EN SLINGA
Betrakta kretsen! Den består av en slinga med två spänningskällor och tre resistorer. Spänningskällorna har polspänningarna E1 och E2, och över resistorerna finns spänningsfallen U1, U2 och U3. Beteckning (E) harinförtsföratttydligtmarkeraskillnadenmellanspänningskällornas polspänningochspänningsfallenöverresistorerna.

Låt oss nu summera slingans spänningar med början och slut i punkten A enligt följande ordning:
Räkna de spänningspilar som pekar mot summeringsriktningen som positiva och de som pekar åt samma håll som summeringsriktningen som negativa. Då blir resultatet:
15 ENERGI & EFFEKT
Detta avsnitt redogör för begreppen energi och effekt i elektriska kretsar.
När du är klar skall du kunna beräkna och mäta effektutveckling i resistivakretsarsamtredogöraförbegreppetgränsvärden.
ENERGIPRINCIPEN
Energi ikan inte skapas eller förstöras, bara om-vandlas mellan olika energiformer.

Ett bra exempel på energiomvandlingär då lägesenergi övergår till rörelseenerginärföremålfallerfrånenhögnivåtillenlägre.
I elektriska kretsar kan energiomvandling observeras bland annat genomattdetalltidblirvärmeutvecklingvidströmtransport.
MEKANISK ENERGI
Då ett föremål flyttas under inverkan av en kraft uträttas i fysikalisk mening ett arbete. Den energi (W) som åtgår för att uträtta arbetet är inommekanikendefinieratsomproduktenavkraften(F)ochdensträcka (s)somföremåletförflyttatsikraftensriktning,(W =F s)såsomillustrerashär:
ELEKTRISK ENERGI
När det under en viss tid, under inverkan av en spänning flyter ström mellan två punkter i en ledare uträttas på liknande sätt ett arbete. Den energi som åtgår för detta arbete kan vi beräkna så här:
W U I t
W = energin i Ws (wattsekund)
U = spänningen i V
I = strömmen i A
t = tiden i s (sekunder)
16 SPÄNNINGSKÄLLOR
Detta avsnitt handlar om spänningskällors elektromotoriska kraft, inre resistansochbelastningsförmåga.
När du är klar ska du kunna beräkna och mäta inre resistans, emk och polspänninghosspänningskällor.
DET TRODDE DU INTE!
Närduhörordetspänningskällortänkerdusäkertpåbatterierochspänningsaggregat,menävenmikrofonerochTV-antennerärspänningskällormedemkochinreresistans.
IDEALA SPÄNNINGSKÄLLOR
Tänkta idealt perfekta spänningskällor har en elektromotorisk kraft (emk) som lämnar en konstant polspänning (UP), oavsett hur stor belastningsströmmen (IL) är. Bilderna nedan illustrerar sådana spänningskällor.
Polspänning UP förblir konstant 12V oberoende om belastningsströmmen IL är 1,2mA eller 4A.
VERKLIGA SPÄNNINGSKÄLLOR
Verkliga spänningskällor beter sig emellertid som om det finns en inre resistans (Ri ) mellan den konstanta emk:n och anslutningspolerna. Observera att det inte är fråga om en verklig resistor, utan ”något” som har egenskapen resistans.
20
INDUKTION
Dettaavsnitthandlaromattmagnetiskafältkanalstraenemksomkan drivaström.
När du är klar skall du kunna beskriva vad som menas med induktion ochredogöraförstorheterochenhetersomhörtillbegreppet.
INDUCERAD EMK
Bildenföreställerenspolesomiexperimentsyfteäranslutentillenvoltmetermedmittcentreradnollaochdärförkanindikeraomdetärenpositiv eller negativ spänningsom mäts.Inärheten av spolen finns också enpermanentmagnetivarsmagnetfältspolenbefinnersig.
+ -
Så länge magneten är stilla förblir voltmeterutslaget noll. Förflyttas magneten erhålles däremot ett visarutslag, det induceras (alstras) en spänning (emk) i spolen.
Experimentet antyder att flödesändringar i omgivningen av en spole orsakar en emk i lindningen.
EMK - RIKTNING
Antag nu att permanentmagneten får falla i mitten genom lindningen. Magnetflödetispolenkommerdåattväxatillsmagnetenkommithalvvägs genom spolen, för att därefter avta när den är på väg ur spolen. Observationavvoltmeternvisardåattdetinducerasenspänning(emk) sombådeändrarpolaritetochstorlek.
Är spollindningen en del av en sluten krets driver den inducerade emk:n ström som vilken spänningskälla som helst.
För den inducerade spänningens polaritetgällerföljandeviktigaregel:
Den inducerade emk:n har alltid en sådan riktning, att orsaken till dess uppkomst motverkas.

Vi prövar regeln om emk:ns riktning i anslutning till bilderna här under med följande resonomang:
För att motverka orsaken till sin egen uppkomst måste den ström som emk:n driver orsaka ett magnetflöde med motsatt riktning mot det växande flödet från permanentmagneten. När det avtar försöker emk:n däremot att förstärka flödet så att det bibehålls vid samma nivå, vilket förklarar polaritetsbytet.
Avtagande flöde
Växande flöde
Ägna lite extra uppmärksamhet åt hur referenspilarna ändrar riktning då permanentmagneten är på väg in respektive ut ur spolen. Pröva med högerhandsregeln om den angivna strömriktningen stämmer.
Noggrannare experiment visar att den inducerade emk:n i en spole är proportionell mot antalet lindningsvarv och flödesändringen i spolen.
e = den inducerade emk:n (V)
N = antalet lindningsvarv = flödesändring (Vs)
t = tiden flödesförändringen pågår
t = hastigheten i flödesändringen (Vs/s)
Exempel: Hur stor är den inducerade spänningen i en spole med 50 varv, om flödet som spolen omsluter ändrar sig från 2 till 4Vs på 2 sekunder.
21
OSCILLOSKOP
Detta avsnitt är en orientering om oscilloskopets funktion, dess kontroller och vad som kan mätas med oscilloskop. Har du tillgång till ett oscilloskopochkanprovadetsamtidigtsomduläserärdetenfördel.
När du är klar skall du kunna identifiera och ställa in standardkontrollerna på oscilloskop samt använda oscilloskopet för att mäta likspänning(växelspänningsmätningkommeriavsnitt22).
ALLMÄNT
Oscilloskopärsnabbavoltmetrarsomförutomlik-ochväxespänningar gör det möjligt att mäta frekvens och växelspänningars inbördes tidsförhållande. En av fördelarnamed oscilloskop är att devisar mätresultatet som skalenliga X / Y-grafer, ungefär som när man ritar kurvor i koordinatsystemmedx-ochy-axlar.
OSCILLOSKOPETS RITFUNKTION
Bilden ovan föreställerframsidanav ett oscilloskop. En förhållandevis stor del upptas avskärmendärde undersöktaspänningarnasvisas med enellerfleraljuspunktersom sveperöverskärmeni X-led medenvalbarhastighet.
Vid låg svephastighet kan man iaktta den lysande punkt som rör sig överskärmenfrånvänstertillhöger.Medhögresvephastighetblirljuspunktenenheldragenlinje.
Den spänning som ska undersökas påverkar ljuspunkten i Y-led med enkänslighetsomanvändarenväljer.
FUNKTIONSGENERATORN
Detta avsnitt är en introduktion i handhavandet av funktionsgeneratorer. Avsnittets mätövning behandlar även grundläggande växelspänningsmätningmedoscilloskop.
När du är klar skall du kunna ställa in en funktionsgenrators utspänning, kurvform, frekvens och att mäta den inställda växelspänningens karakteristikamedettoscilloskop.
INLEDANDE INFORMATON
För mätövningarna i växelströmskursen behövs en växelspänningskälla med varierbar utspänning, frekvens och kurvform. Funktionsgeneratorn är en variant av en sådan spänningskälla.
Med en växelspänning avses oftast en sinusformad spänning eftersom det är den vanligaste formen av växelspänning, men även andra kurvformersomfyrkant-ochsågtandsspänningärväxelspänningar.
Funktionsgeneratorer klarar att generera (alstra) alla tre kurvformerna ellerfleraformerinomettfrekvensområdepånågrationdelsHz(Hertz) tillfleraMHz.
PERIODISK VÄXELSPÄNNING
Växelspänningarsomupprepas medsamma storlek ochkurvform sägs vara periodiska. Här ser du exempel på en sinusformad spänning (a), entriangelspänning(b),ochtvåsortersfyrkantsspänningar,enmednollgenomgång(c)ochenutannollgenomgång(d).
Funktionsgenerator
a)Sinusspänning
b)Triangelspänning
c)Fyrkantsspänning med nollgenomgång
d)Fyrkantsspännining utan nollgenomgång
23 KONDENSATORN, UPP & URLADDNING
Dettaavsnitthandlaromhurkondensatorerärkonstrueradeochomhur kondensatorertaruppochlämnarifrånsigelektriskladdning.
Närduärklarskalldukunnamätakapacitans,förutsägaochmätakondensatorspänningensvärdevidupp-ochurladdningsförloppienRC-krets.
ALLMÄNT OM KONDENSATORN
Kondensatorer används i sammanhang då man behöver lagra elektrisk laddning,blockeralikströmochsläppaframväxelström.
Kondensatorer tillverkas på många olika sätt, men består i princip av tvåmetallplattormonteradeivarandrasnärhetsomibilden.
Uppladdning
Ansluts en spänning över plattorna laddas kondensatorn. Detta innebär att elektroner ”dras” från den platta som är ansluten till spänningskällans positiva pol. Samtidigt "påtrycks" den andra plattan lika många elektroner från spänningskällans negativa pol.
Den övre plattan får på detta sätt underskott på elektroner medan den nedre plattan får överskott på elektroner. Efterhand som laddningen fortgår växer spänning mellan plattorna. Laddningsförloppet fortsätter tills spänning mellan plattorna blir lika stor som den påtryckta spänningen.
Kopplas kondensatorn bort från spänningskällan då den laddats, behåller den laddningen så länge det inte finns en sluten krets mellan de båda plattorna.
Med förbindelse mellan kondensatorplattorna, t ex om en resistor ansluts över den laddade kondensatorn som i bilden här under, börjar däremot genast en laddningsutjämning.
Urladdning
24 VÄXELSPÄNNING
Dettaavsnittärenintroduktionavväxelströmsläransgrunder.
Närduärklarskadukunnamätakarakteristiskavärdenhosväxelspänningar med multimeter och oscilloskop samt relatera de uppmätta värdenatillvåg-ochvisardiagram.
VÄXELSPÄNNINGSKÄLLOR
Växelspänningen i våra vägguttag har ett effektivvärde på 230V och en frekvens på 50Hz. Observera att 230V är en livsfarlig spänningsnivå!
Vid elektriska experiment och i servicesammanhang används därför funktionsgeneratorer med inställningsmöjligheter av såväl kurvformer somspänningochfrekvens.
VÄXELSPÄNNINGSSTORHETER
Sinusformadeväxelspänningarangestillsinstorlekiallmänhetmedde beteckningarochbenämningarsomvisasi vågdiagrammet nedan. Kom också ihåg att frekvens, som är en viktig storhet i växelströmssammanhang,ärantaletperioderunderensekund.
f 1 T
Växelspänningsstorheter i ett vågdiagram
LäggmärketillattvågdiagrammetsX-axelärindeladibådegraderoch tid.PeriodtidenTmotsvarardärvid360°,halvaperiodtiden180°osv... Läggdetta påminneteftersomdu behöveromvandlatidtill graderoch tvärtomvidmätningochberäkningavväxelströmskretsar.

Ellära grunder
Lik- och 1-fas växelström
24 avsnitt går igenom likströmsläran och grundläggande växelströmslära.
Varje avsnitt omfattar en teoretisk genomgång med beräkningsexempel och testa-dig-själv-uppgifter.
Formler och matematik förklaras stegför-steg på ett sätt som ger läsaren ett aktivt eltänkande.
Till boken finns i separat utgåva instuderings- och mätuppgifter. Instuderingsuppgifterna hjälper läsaren att formulera sitt eltänkande. Mätuppgifterna ger kunnande i mätteknik och bekräftar teorin.
