Testa-dig-själv-uppgifter
5 Komplexa kretsberäkningar 5 Impedans i seriekretsar
5 Benämningen jω-metoden 5 Ström och spänning i seriekretsar
Impedans och ström i parallellkretsar 7 Komplexa effektberäkningar
Imaginära-komplexa -tal
Detta avsnitt introducerar begreppen imaginära och komplexa tal med vilka växelströmsberäkningarkanutföraspåsammasättsomilikströmsläran.Läsaresomredankännertillkomplexaberäkningarkanhoppadirekttillnästaavsnittmed växelströmstillämpningar.
Imaginära tal
Från matematiken vet vi att kvadratroten ur ett positivt tal (a), är ett positivt eller negativt tal (enrot)sommultipliceratmedsigsjälvgertalet (a).
Exempel 422 och
Både (+2) och (-2) multiplicerat med sig själv blirlikamed4.
För negativa tal existerar däremot inget tal (rot) som multiplicerat med sig själv blir talet. Inget hindrarossemellertidfrånattföreställa(imagin) och använda oss av sådana tal. För detta ändamål används beteckningen j för den imaginära enhetensomdefinierasenligt:
Förattalgebransreglerskagällaföljeratt:
Imaginä
Det imaginära talet (4 + j3) kan även representeras av absolutbeloppet (längden) för visaren (Z)tillsammansmedvinkeln( ).Beteckningen(Z)markerardärvidattvisarenharsåvälstorleksomriktning.Visarensstorlekbetecknasmed ett enkelt (Z) utan understrykning och beräknas med Pythagoras sats. Vinkeln ( ) är det komplexataletsvinkelellervinkelargumentoch beräknastrigonometriskt.
Z 4 3 22 tan 3 4
Dåvisarlängden(Z)ochvinkeln( )ärkända kanettkomplexttalirektangulärformskrivasi trigonometrisk form påföljandesätt:
Allmänt om komplexa tal
Iettkoordinatsystemplacerasdereella talenutmeddenreellatalaxelnochalladeimaginäratalen utmed en imaginär talaxel enligt bild 6-a. Uttryck som består av ett reellt tal ( a ) och ett imaginärt tal ( jb ) i formen (a + jb) kallas ett komplexttali rektangulär form.Ettexempelpå ettsådantkomplexttalär: 4+ j3
Exempel: Omvandladetkomplexatalet(3+ j2) frånrektangulärtilltrigonometriskform. 6667,0 3 2 tan 6,31323Z 22
tan
=0,6667motsvararvinkeln33,7º
Grafiskt kantaletåskådliggörassom enpunkt P med koordinaterna 4 och j3 i det komplexa talplanet enligtföljandebild.
Förkortatkantrigonometriskformskrivaspåett sättsomkallas polär form Z cos +j Z sin Z
Imaginära - komplexa -tal- testa-dig-själv
1. Beräknaa) j j b) j j j c) j4 d) j5 e) 3 j3
2. Ange i rektangulär form de komplexa tal som markerats med en punkt i bilden
Imag.
-4-2-3 +j1 -j2 -j4 -j3 1-1 -j1 234Re. +j4 +j2 +j3
3.Angetaleniuppgift2itrigomometrisk form.
4.Angetaleniexempel2ipolärform.
5.Angetaleniexempel2iexponentiellform.
6.Angeirektangulärformdekomplexatal somrepresenterasmedenvisareibilden.
Imag.
+j4 +j2 +j3
-4-2-3 +j1 -j2 -j4 -j3 -11 -j1 234Re.
7.Beräknastorlekochvinkelargumentförtaleniexempel6.
8.Beräkna(2+ j4)+(5+ j3)
9.Beräkna(7- j9)+(4+ j6)
10.Beräkna(-3-j5)+(2+ j5)+(10- j9)
11.Beräknairektangulärform(2+ j4) (5+ j3)
12.Beräknairektangulärform(7- j9)+(4+ j6)
13.Beräknaipolärform1235º 1320º
14.Beräkna1122º 1411º 1517º
15.Beräkna 42 88 6 11 º º
16.Beräkna 14 28 18 32 271814
17.Beräkna 3 4 23 j j
18.Adderavisarnaibilden.
Imag.
+j4
+j3
+j2
+j1 1234Re.
19.Beräknastorlekenochvisarargumentetför dennyavisaresom bildasgenomaddition avvisarnaiuppgift18.
20.SubtraheravisareBfrånvisareÁibilden.
Imag.
+j4
+j3
+j2
+j1 1234Re.
21.Beräknastorlekenochvisarargumentetför dennyavisaresom bildasgenomsubtraktionavvisare(A-B)iuppgift20.
22.a)Ritaettkoordinatsystemmedenimaginär-ochenreelltallinje.b)Lägginenvisaresompekarpådetkomplexatalet (5+ j4).c)Multiplicerataletmed( j ) och ritaenvisaresommotsvarardetnyatalet. d)mätvinkelnmellandebådatalvisarna medgradskiva.e)Divideratalet(5+ j4) med( j )f)Ritaenvisaresommotsvarar detnyatalet.g)Mätvinkelnmellandebåda talvisarna.
copyright
- komplexa - metoden
Komplexa kretsberäkningar
Beräkningaravväxelströmsproblemkanävenutföras med hjälp av komplexa metoden, också vanligenkallad j-ellersymboliskametoden.
Impedans i seriekretsar
Bilden visar en induktiv seriekrets med tillhörandeimpedanstriangelplaceradidetkomplexa talplanet.
j-axeln
Re-axeln
Av ovan visade bild framgår att impedansen kan skrivas som ett komplext tal:
Z = R + jXL
På motsvarande sätt kan en kapacitiv serieimpedans tecknas:
Z=R+(- j)XC
Re-axeln
(-j)-axeln
Benämningen j- metoden
Impedansen definieras därmed som en visare i det komplexa talplanet, med en reell komposant, R (), och en imaginär komposant, jXL () res-pektive (-jXC ), där XL =2f L och XC = 1 2f C
Vinkelhastigheten(2f)brukaroftaangesmed dengrekiskabokstavenomega,( =2f).Införs detta skrivsätt i de komplexa reaktansuttrycken serdeutsåsomföljer:
Impedansformlerna får därav ett utseende som förklarar benämningen j-metoden.
Z = R + jXL ⇒ Z = R + j L
Z=R+(-j)XC Z=R+ C jω 1
FörenRCL-seriekretsennedantecknasdenkomplexaimpedansenpåföljandesätt: C 1 L Z
j-axeln
Re-axeln
Ström och spänning i seriekretsar
Re-axeln Ij-axeln = j L XL j
Ovan är den induktiva seriekretsens spänningstriangel inlagd i det komplexa talplanet. Det är uppenbart att även sambandet mellan den pålagda spänningen U och delspänningarna UR och UL kan anges i komplex form.
U = UR + jUL
( UR = I R ) utgör realdelen med I och UR i fas.
( UL = I jL ) är den imaginära delen med UL fasförskjutna 90º före I eftersom multiplikation med ( j ) medför 90º posistiv fasvridning i det komplexa talplanet.
Facit till imaginära - komplexa - tal
Komplexa tal
1
a) j j = j2 =-1
b) j j j = j j2 = - j
c) j4 = j2 j2 =(-1) (-1)=1
d) j5 = j2 j2 j = (-1) (-1) j = j
e)3 j3 = 3 j2 j = 3 (-1) j = - 3j
2a)2+j3
b)-4+ j4
c)-2- j4
d)3- j3
3a)a=3,6; =56,3º . a=3,6cos56,3º+ j 3,6sin56,3º
b)b=5,7; =135º .b=5,7cos135º+ j 5,7sin135º
c)c=4,5; =234º
.c=4,5cos234º+ j 4,5sin234º
d)d=12,7; =315º
.d=12,7cos315º+ j 3,6sin315º
4a)3,6 º
b)5,7º
c)4,5º
d)12,7º
5a)3,6 e j 56,3º
b)5,7 e j 135º
c)4,5 e
d)12,7 e j 315º
6a)Z=3+ j
b)U=-3+ j2
c)I=-4- j3
d)S=2- j4
7a)Z=3,2; =15º
b)U=3,6; =146,3º
c)I=5; =216,9º
d)S=4,5; =296,6º
8)7+ j7
9) 11- j3
10)9- j9
11)-2+ j26
12)82+ j6
13)15655º
14)231053º
15)777º
16)739º
17)1,4109,4º
18)A+B=5 + j4
19)A+B=6,4; =38,7º
20)A-B = j3
21)A-B=3; =90º
22a)
90.0°
22b) 5+ j4) j =(-4+j5)
22c) Nyvisare(-4+j5)
22d) Vinkelnblir90ºmellanvisarna
22e) 5 4 j j 4j5
22f) Nyvisare(4-j5)
22g) Vinkelnblir90ºmellanvisarna
Sammanfattning lik- och 1-fas växelström
Likspänning och likström
Den elektriska kretsen
Den enklaste elektriska kretsen består av en spänningskälla ansluten till en belastningsresistans enligt schemat.
Referenspilar och storhetsbeteckningar
För att visa hur strömmen flyter och hur spänningen fördelas i kretsen används referenspilar och storhetsbeteckningar som UP för polspänningen, Ri för den inre resistansen, RL för den resistiva lasten osv.
Spänningsfallspilen pekar i den riktning som spänningen faller. Plussidan har högre spänning än minussidan.
Strömpilen pekar i den riktning som strömmen flyter.
Referenspilar och beteckningar är ett tankestöd som bör användas flitigt och noggrant både vid beräkning och analys av kretsfunktioner.
Några regler
Ström kan endast flyta om kretsen är sluten.
Strömmenflyteralltidfrånspänningskällanspluspoltilldessminuspol.
Strömmen börjar och slutar flyta i hela kretsen samtidigt.
Det flyter alltid lika mycket ström till spänningskällans minuspol som det flyter ut från dess pluspol.
En spänningskälla kan alltid betraktas som en konstant emk E i serie med en inre resistans Ri.
Polspänningen UP är beroende av det inre spänningsfallet enligt: UP = E – Ui där Ui = IL Ri
Ohms lag
Sambandet mellan strömmen som flyter genom en resistans och spänningsfallet över resistansen anges av Ohms lag.
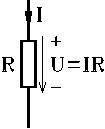
U R =
I = strömmen i A (ampere)
U = spänningen i V (volt) R = resistansen i (ohm)
Växelströmsbelastningar
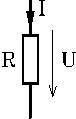
Ohms lag och fasförskjutning mellan spänning och ström för olika växelströmsbelastningar.
Resistans: Spänningen över en resistor är i fas med strömmen.
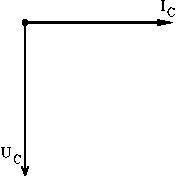
Kapacitans: Spänningen över en kapacitans ligger 90° efter strömmen.
Ideal induktans: Spänningen över en ideal induktans, med försumbar ledningsresistans, ligger 90° före strömmen
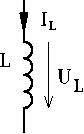
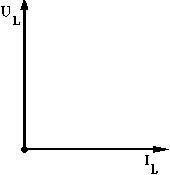
Verkliga induktansspolar: Spänningen är fasförskjuten mellan 0 och 90º före strömmen på grund av att spolen har lindningsresistans.
Verkliga induktansspolar är seriekretsar
Parallellkrets med resistans och kapacitiv reaktans
Strömtringel
Parallellkrets med resistans och induktiv reaktans
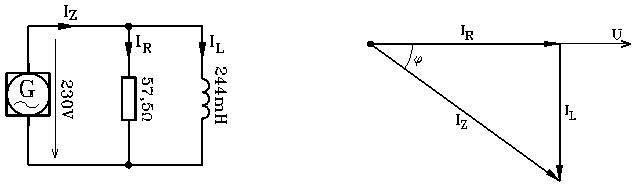
Strömtriangel
Faskompensering av induktiv belastning
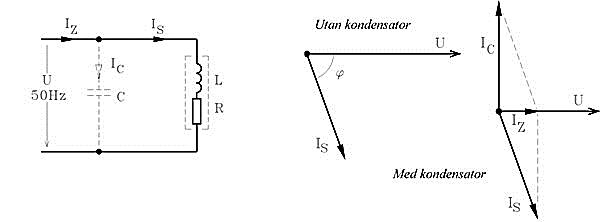
Elmotorer är exempel på induktiva belastningar som brukar faskompenseras med en kondensator för att minska matningsströmmen. Utan kondensator är matningsströmmenSZII =
Kondensatorvärdet för full faskompensering