

Innehåll
SidaAvsnitt
Historia
Multimetern 1
Testa-dig-själv 1
Resistans & resistansmätning 2
1 Testa-dig-själv 2
1 Ledningsresistans 3
1 Testa-dig-själv 3
Spänning & spänningsmätning 4
2 Testa-dig-själv 4
2 Spänningsaggregat 5
2 Testa-dig-själv 5
2 Ström & strömmätning 6
3 Testa-dig-själv 6
3 Ohms lag 7
3 Testa-dig-själv 7
Resistans i seriekretsar 8
4 Testa-dig-själv 8
4 Spänningsdelning 9
4 Testa-dig-själv 9
4 Parallellkretsar 10
5 Testa-dig-själv 10
5 Resistans i parallellkretsar 11
5 Testa-dig-själv 11
5 Blandade serie & parallellkretsar 12
6 Testa-dig-själv 12
6 Kirchhoffs spänningslag 13
6 Testa-dig-själv 13
Belastningseffekter 14
7 Testa-dig-själv 14
SidaAvsnitt
7 Energi & effekt 15
7 Testa-dig-själv 15
Spänningskällor 16
8 Testa-dig-själv 1
8 Effektanpassning 17
8 Testa-dig-själv 17
9 Magnetiska grundbegrepp 18
9 Testa-dig-själv 18
9 Reläer & reläkopplingar 19
10 Testa-dig-själv 19
10 Induktion 20
10 Testa-dig-själv 20
10 Oscilloskop 21
11 Testa-dig-själv 21
11 Funktionsgeneratorn 22
11 Testa-dig-själv 22
11 Kondensatorn, upp & urladdning 23
12 Testa-dig-själv 23
12 Växelspänning 24
1 Testa-dig-själv 24
13 FacittillTesta-dig-själv-uppgifter
13 Matematiskaförklaringar
Som komplementtill dennalärobokfinns: Mätuppgiftermedfacit Instuderingsuppgiftermedfacit.
Personer och händelser i elkunskapens historia
Ämnesområdet elektroteknik är redan stort, men kan likväl väntas öka i såväl omfattning som betydelse. Så har det inte alltid varit, tvärtom har det tagit mänskligheten lång tid att utveckla dagens kunskapsnivå. Flera personer och händelser har bidragit. Några av de mer betydelsefulla får inleda den orientering av ämnet som följer.
600 BC
Thales från Militos, ca 625 – 545 BC, en av greklands sju vise uppmärksammar fenomenet friktionselektricitet i samband med bärnsten, som på grekiska kallas electron.
250 BC
Bagdadbatteriet, en möjlig förhistorisk galvanisk cell daterad till perioden 250 f.Kr. Det grävdes fram vid Khujut Rabula i utkanten vid Bagdad.. Fyndet har förbryllat forskare och man har inte riktigt kunnat förstå vad det möjliga batteriet kan ha använts till, eller hur man över huvud taget kommit på idén.
1600-talet:
William Gilbert, 1544 – 1603, engelsk läkare och fysiker som är känd för magnetexperiment och teorin att jorden är en stor magnet som förklaring av kompassnålars beteende. Gilbert införde också ordet electrics
1700-1800-talet:
Alessandro Volta, 1745 – 1827, italiensk fysiker som uppfann batteriet, Voltas stapel, och får enheten för spänning (volt) uppkallad efter sig. I och med tillgången till en kontinuerlig strömkälla fanns förutsättningar för att undersöka strömmens verkningar.
Hans Christian Örsted, 1777 – 1851, dansk kemist och fysiker upptäcker år 1820 att en strömförande ledare omges av ett magnetiskt fält och gav oss därmed grunden för elektromagnetismen.
George Simon Ohm, 1789 – 1854, tysk vetenskapsman som hedrats med att få enheten för resistans (ohm, ) uppkallad efter sig. Ohm utvecklade idén att det är spänning som orsakar ström i en elektrisk krets och publicerar år 1827 i Die galvanische Kette, matehe-matish bearbeit grunden för elektrisk kretsteori: Ohms lag.



















MULTIMETERN
Detta avsnitt informerar om multimetern. Ha gärna en multimeter tillhands när du läser avsnittet.
När du är klar skall du kunna identifiera och ställa in en multimeters olika funktioner samt avläsa multimeterns olika skalor
ANALOG & DIGITAL
Det finns två olika typer av multimetrar, analoga och digitala. Båda typerna har mätfunktioner för resistansmätning, spänningsmätning och strömmätning. På en del modeller finns det även andra mätfunktioner som frekvens- och kapacitansmätning.
En analog multimeter visar mätresultatet med hjälp av en visare som rör sig över en skala, medan en digital multimeter visar mätvärdet med siffror (digit är engelska för siffra).



ANSLUTNING & FUNKTIONSVAL
Bilden visar exempel på typiska analoga och digitala multimetrar. Omkoppling mellan multimeterns olika mätfunktioner och mätområden görs med en funktionsomkopplare. På instrumenten ovan är det vridbara funktionsomkopplare, men det finns även multimetrar med tryckknappsomkopplare och med annan indelning.
2
RESISTANS & RESISTANSMÄTNING
Detta avsnitt informerar om begreppet resistans i anslutning till några vanliga resistortyper och om hur multimetern används vid resistansmätning.
När du är klar skall du kunna mäta resistanser, avläsa färgkoden, ange standardvärden i E6- och E12-seriern, redogöra för potentiometerns funktion och bestämma dess aktuella inställning med resistansmätning.
RESISTORER
Resistorn är en mycket vanlig komponent i elektriska kretsar. Den egenskap som resistorer har benämns resistans och utgör i elektriska kretsar ett hinder för ström.
Egenskapen (storheten) betecknas med (R) och mäts i enheten (sorten) ohm som betecknas med den grekiska bokstaven omega,
I elritningar anges resistorn med en symbol och dess resistansvärde med ett tal följt av ett , t ex 1000
Resistorsymbol
MÄRKNING AV RESISTORER
Resistorer kan se väldigt olika ut. På större resistorer återges resistansvärdet ofta i klartext och på mindre med färgband med en bestämd kod.


FÄRGKODEN
Färgerna på det första färgbandet anger den mest betydelsefulla siffran. Det andra färgbandet den därnäst mest betydelsefulla siffran. Tredje färgbandet anger värdet på det multipeltal som de båda första siffrorna skall multipliceras med. Det är detsamma som att lägga till det antal nollor som multipeltalet innehåller. Fjärde färgbandet visar resistorns tolerans.
2:dra siffran Tolerans
Multippel
1:a siffran

Färgband Siffror Multipel Tolerans
TOLERANS
Med tolerans menas en avvikelse från det nominella värde som anges på resistorn. En resistor med värdet 1000 och 10% tolerans kan ha ett resistansvärde mellan (1000 + 100 = 1100 och (1000 -100 = 900 eftersom 10% av 1000 är 100.
Exempel: Resistorn här under har från vänster till höger färgbanden rött = 2, rött = 2, orange = x 1000 och guld = 5 %

Resistorn har då ett nominelt värde av 22000 ± 22000 x 0,05 =1100 eller uttryckt i kilo-ohm: 22k ± 1,1k
4
SPÄNNING & SPÄNNINGSMÄTNING
Detta avsnitt redogör för begreppet spänning, om vanliga batterier och hur man mäter likspänning.
När du är klar skall du kunna ställa in en multimeter för likspänningsmätning och mäta spänning i serie- och parallellkopplade batterier.
SPÄNNING
Spänning kan sägas vara en elektrisk tryckskillnad som gör att det kan flyta ström i elektriska kretsar ungefär som tryckskillnaden i ett vattentorn gör att det flyter vatten i vattenledningar.
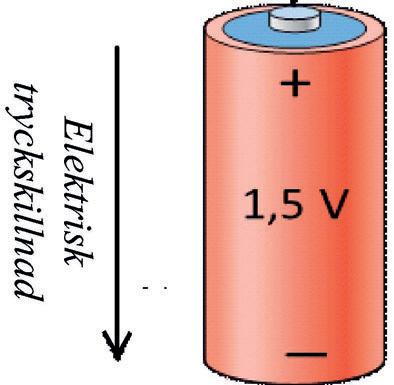
Elektrisk spänningen har storhetsbeteckningen (U) och mäts i enheten volt (V). Till följd av detta brukar en multimeter som är inställd för spänningsmätning kallas voltmeter.
Här visas hur den elektriska tryckskillnaden mellan ett batteris plus- och minussida mäts med en multimeter

Kom ihåg: Spänning mäts alltid mellan två punkter.
6
STRÖM & STRÖMMÄTNING
Detta avsnitt redogör för strömbegreppet och hur ström mäts med en multimeter.
När du är klar skall du kunna ställa in och ansluta en multimeter för strömmätning
STRÖM
Ström är elektriska laddningar i rörelser och kan till skillnad från resistans och spänning inte existera ensamt. Resistans finns och går att mäta i resistorer, i ledningstråd och i diverse andra material. På samma sätt kan spänning existera i batterier och spänningsaggregat.
För att ström skall kunna existera måste det finnas en spänningskälla med elektrisk tryckskillnad, t ex ett batteri, och en sluten krets mellan spänningskällans plus- och minuspol som strömmen kan flyta genom.
Kopplingen visar en sluten krets med en lampa kopplad till ett batteri och hur detta ser ut i ett elektriskt schema.

Samma koppling då lampans glödtråd gått sönder och öppnat förbindelsen mellan batteriets plus- och minuspoler.
I en öppen krets kan det inte flyta ström
Byts den trasiga lampan mot en ny med hel glödtråd börjar det genast att flyta ström samtidigt i hela kretsen igen.
STRÖMSTYRKA
Inledningsvis nämndes att ström är elektriska laddningar i rörelse. I ledare är antalet laddningar som passerar ett tvärsnitt av ledaren per sekund ett mått på strömstyrkan.
Ström betecknas med (I) medan enheten som strömstyrkan mäts i heter ampere och betecknas med (A). Till följd av detta kallas en multimeter som är inställd för strömmätning ofta för amperemeter.
7
OHMS LAG
Detta avsnitt redogör för Ohms lag, grunden för elektriskt kretstänkande.
När du är klar ska du kunna använda Ohms lag vid beräkningar av elektriska kretsar och för att kunna förutsäga mätresultat.
Georg Simon Ohm var en tysk fysiker som levde åren 1787 till 1854. Hans upptäckt av det för elektrotekniken grundläggande sambandet mellan spänning, ström och resistans publicerades år 1827.
REFERENSPILAR & BETECKNINGAR
I de tidigare avsnitten har du bekantat dig med stoheterna spänning, ström och resistans genom att mäta och beskriva dem. Det matematiska sambandet mellan de tre storheterna är formulerat i Ohms lag, vilken introduceras i detta avsnitt.
För att Ohms lag ska få någon som helst mening måste sambandet mellan den matematiska formeln och den aktuella kretsen synliggöras med kretsscheman, referenspilar och storhetsbeteckningar så som visas i följande genomgång.
Kretsen för vårt resonomang består av en spänningskälla och en resistor kopplad mellan dess plus- och minuspol.
Vi vet att batterisymbolen innebär spänning och att det flyter ström från batteriets pluspol genom resistorn tillbaka till batteriets minuspol. Det är inte så svårt att komma ihåg när kretsen är så enkel, men vid beräkning och analys av mer komplicerade kretsar behöver tanken stöd av referenspilar och storhetsbeteckningar
Strömpilen markerar strömmen ( I ), vars riktning är från spänningskällans pluspol mot dess minuspol.
Spänningsfallspilen markerar spänningen ( U ) över resistorn ( R ). Observera att referenspilen för U har en (+) och en (-) sida och att spänningen faller från ett högre till ett lägre värde i den riktning som strömmen flyter.
8
RESISTANS I SERIEKRETSAR
Detta avsnitt visar hur seriekopplade resistorkretsar kan ersättas och hur Ohms lag kan användas för seriekretsar.
När du är klar skall du kunna förenkla kretsar med seriekopplade resistorer.
SERIEKOPPLADE RESISTORER
Antag att vi har en krets med två seriekopplade resistorer och att vi byter ut dem mot en ensam resistor utan att strömmen eller spänningen ändrar sig.
Eftersom strömmen är 2mA och spänningen 6V både före och efter resistorbytet är det ganska uppenbart att också resistansen är lika stor i de båda kretsarna.
Samma resonemang kan göras för nätverk med flera resistorer och allmänt gäller följande regel:
Serikopplade resistorer kan ersättas av en enda resistor, vars resistans är lika stor som summan av de seriekopplade resistorernas värden.
Om ersättningsresistorn kallas för RS kan samma sak uttryckas matematiskt så här: R R R R S 1 2 3
9
SPÄNNINGSDELNING
Detta avsnitt handlar om obelastade spänningsdelare. Belastade spänningsdelare diskuteras i ett senare avsnitt.
När du är klar skall du kunna beräkna och mäta delspänningar i obelastade spänningsdelare.
DELSPÄNNINGAR
I seriekopplade resistorkretsar fördelas den totala spänningen över de ingående resistorerna och kallas därför också för spänningsdelare.
I den aktuella kretsen fördelas den odelade spänningen U=10V, så att delspänningen U1 blir 8,2V och delspänningen U2 blir 1,8V.
Detta kan enkelt visas genom att delspänningarna mäts med en multimeter, men de kan också beräknas med Ohms lag. Bra om man kan båda sätten!
U I R
RRRR S 123
Ohms lag
Seriekopplade resistorer
Gör så här:
1. De båda resistorerna kan ersättas med en tänkt resistans.
RS = 820 + 180 = 1000
2. Beräkna strömmen genom RS med Ohms lag.
I U R IA S 10 1000 001 ,
3. Strömmen genom den tänkta ersättningsresistansen RS är samma som flyter genom R1 och R2. Spänningen över R1 respektive R2 kan därför beräknas med Ohms lag så som i nästa bild.
10 PARALLELLKRETSAR
Detta avsnitt redogör för begreppet delströmmar och Kirchhoffs strömlag.
När du är klar skall du kunna beräkna och mäta delströmmar.
Gustav Robert Kirchhoff var en tysk fysiker som levde åren 1824 till 1887. Kirchhoff utförde en mängd viktiga arbeten inom fysiken, men är mest känd för sina lagar inom elektrisk kretsteori.
STRÖMMAR I PARALLELLKRETSAR
Bilden visar en parallellkrets med tre grenar som vi ska titta närmare på.
Från spänningskällans pluspol flyter strömmen IT till punkten A där den delas upp i grenströmmarna I1, I2 och I3. Vid punkten B förenas de tre grenströmmarna åter till en ström med samma storlek som IT, därav den gemensamma beteckningen för strömmen som flyter från och till spänningskällan.
Här berörs en regel som gäller för alla spänningskällor och som är viktig att komma ihåg.
Strömmen som flyter från en spänningskällas pluspol är alltid lika stor som strömmen som flyter tillbaka till spänningskällans minuspol.
Riktar vi fokus mot strömmarna som flyter till, respektive från de båda grenpunkterna utan att bry oss om vad som orsakat dem eller deras storlek kan vi göra samma slutsats som Kirchhoff en gång gjorde då han fomulerade sin strömlag:
Summan av alla strömmar som flyter till och från en grenpunkt är lika med noll.
RESISTANS I PARALLELLKRETSAR
Detta avsnitt handlar om ersättningsresistans i parallellkopplade kretsar.
När du är klar skall du kunna beräkna och mäta ersättningsresistans i parallellkopplade resistorkretsar.
ERSÄTTNINGSRESISTANS
Utgångspunkten för den följande diskussionen är att de tre parallella resistorerna R1, R2 och R3 ska ersättas med en resistor som vi kan kalla RP utan att strömmen IT ändras.
Det finns tre bra sätt att ta reda på hur stor ersättningsresistansen RP är.
1.En metod är att göra en resistansmätning mellan grenpunkterna A och B. Koppla i så fall bort spänningskällan först annars blir mätresultatet felaktigt.
2.Ett annat sätt är att mäta strömmen IT och spänningen U och att därefter beräkna RP med Ohms lag. R U I P T
3.Tredje sättet är att räkna fram ersättningsresistansen RP
1 1 1 1
123 RRRR P .....
I ord kan det matematiska sambandet uttryckas på följande sätt:
Inverterade totalresistansen är lika med summan av de ingående resistorernas inverterade värden.
Härledning av formeln finns i avsnittet matematiska förklaringar
12
BLANDADE SERIE & PARALLELLKRETSAR
Detta avsnitt visar hur det går till att beräkna resistans, grenströmmar och delspänningar i blandade serie- och parallellkretsar.
När du är klar skall du kunna beräkna och mäta totalresistans, grenströmmar och delspänningar i blandade serie- och parallellkretsar.
BLANDADE KRETSAR
Kretsen här under kan beskrivas som en blandad serie-parallellkrets där resistorn R1 är i serie med parallellkombinationen R2 och R3 som i sin tur är i serie med R4.
Samma metoder som vi tidigare använt för mätning och beräkning av resistans, strömmar och spänningar fungerar även för blandade kretsar, men det gäller att vara systematisk.
Genom att rita om kretsen och noggrant och konsekvent sätta ut referenspilar och storhetsbeteckningar kan du klara av att beräkna ersättningsresistans, grenströmmar och delspänningar i kretsen ovan.
UPPDATERING
Här är först en uppdatering av de formler vi kommer att använda:
Ersättningsresistansen för seriekretsar RRRR T
Ersättningsresistansen för parallellkretsar
Ohms lag i alla dess former UIRI U R R U I
Observera:
Det är viktigt som tankestöd att rita om kretsen och sätta ut referenspilar och beteckningar allteftersom beräkningen genomförs.
13 KIRCHHOFFS SPÄNNINGSLAG
Detta avsnitt handlar om hur Kirchhoffs spänningslag kan rationalisera ström- och spänningsberäkning i nätverk.
När du är klar med avsnittet skall du kunna använda Kirchhoffs spänningslag vid beräkning och spänningsmätning.
KIRCHHOFFS SPÄNNINGSLAG
Kirchhoffs spänningslag kan formuleras olika men ändå ha samma betydelse. Utgångspunkten för vår diskussion formuleras så här:
Summan av alla spänningar i en sluten slinga är lika med 0 då de räknas i samma riktning
Det finns två begrepp som vi måste reda ut. Vad är en sluten slinga?
Och vilken riktning är det frågan om?
KRETS
MED EN SLINGA
Betrakta kretsen! Den består av en slinga med två spänningskällor och tre resistorer. Spänningskällorna har polspänningarna E1 och E2, och över resistorerna finns spänningsfallen U1, U2 och U3. Beteckning (E) har införts för att tydligt markera skillnaden mellan spänningskällornas polspänning och spänningsfallen över resistorerna.
Låt oss nu summera slingans spänningar med början och slut i punkten
A enligt följande ordning:
Räkna de spänningspilar som pekar mot summeringsriktningen som positiva och de som pekar åt samma håll som summeringsriktningen som negativa. Då blir resultatet: E E U U U 1 2 1 2 3 0
BELASTNINGSEFFEKTER
Detta avsnitt informerar om vad som menas med belastning och om mätinstruments belastning vid spänningsmätning.
När du är klar skall du kunna beräkna och förutsäga inverkan av belastning i spänningsdelare och vid spänningsmätning.
BEGREPPET BELASTNING
Bilden visar en obelastad spänningsdelare där strömmen är lika stor i hela kretsen eftersom det inte finns några avgreningar.
U
En spänningsdelare är i sig själv inte till någon nytta. Det blir den först när ett objekt av något slag ansluts till den, t ex en resistor eller lampa som i bilden under. Den ström som då flyter från spänningsdelaren genom det aktuella objektet kallas belastningsström och brukar betecknas med IB eller IL där (L) står för last eller load.
Allmänt kan man säga, att med belastning menas objekt som ansluts till en elektrisk krets och drar ström från kretsen.
Ansluts t ex en belastningsresistor eller en lampa till spänningsdelaren, som ovan, kommer denna att dra ström från grenpunkten A och påverka strömmen och delspänningarna i kretsen.
ENERGI & EFFEKT
Detta avsnitt redogör för begreppen energi och effekt i elektriska kretsar.
När du är klar skall du kunna beräkna och mäta effektutveckling i resistiva kretsar samt redogöra för begreppet gränsvärden.
ENERGIPRINCIPEN
Enligt energiprincipen kan energi inte skapas eller förstöras, bara omvandlas mellan olika energiformer.
Ett bra exempel på energiomvandling är då lägesenergi övergår till rörelseenergi när föremål faller från en hög nivå till en lägre.
I elektriska kretsar kan energiomvandling observeras bland annat genom att det alltid blir värmeutveckling vid strömtransport.
MEKANISK ENERGI
Då ett föremål flyttas under inverkan av en kraft uträttas i fysikalisk mening ett arbete. Den energi (W) som åtgår för att uträtta arbetet är inom mekaniken definierat som produkten av kraften (F) och den sträcka (s) som föremålet förflyttats i kraftens riktning, (W = F s) så som illustreras här:
ELEKTRISK ENERGI
När det under en viss tid, under inverkan av en spänning flyter ström mellan två punkter i en ledare uträttas på liknande sätt ett arbete. Den energi som åtgår för detta arbete kan vi beräkna så här:
W U I t
W = energin i Ws (wattsekund)
U = spänningen i V
I = strömmen i A
t = tiden i s (sekunder)
16 SPÄNNINGSKÄLLOR
Detta avsnitt handlar om spänningskällors elektromotoriska kraft, inre resistans och belastningsförmåga.
När du är klar ska du kunna beräkna och mäta inre resistans, emk och polspänning hos spänningskällor.
DET TRODDE DU INTE!
När du hör ordet spänningskällor tänker du säkert på batterier och spänningsaggregat, men även mikrofoner och TV-antenner är spänningskällor med emk och inre resistans.
IDEALA SPÄNNINGSKÄLLOR
Tänkta idealt perfekta spänningskällor har en elektromotorisk kraft (emk) som lämnar en konstant polspänning (UP), oavsett hur stor belastningsström (IL) som uttages. Bilderna nedan illustrerar sådana spänningskällor. Polspänning UP förblir konstant 12V oberoende om belastningsströmmen IL är 1,2mA eller 4A.
VERKLIGA SPÄNNINGSKÄLLOR
Verkliga spänningskällor beter sig emellertid som om det finns en inre resistans (Ri ) mellan den konstanta emk:n och anslutningspolerna. Observera att det inte är fråga om en verklig resistor, utan ”något” som har egenskapen resistans.
17
EFFEKTANPASSNING
Detta avsnitt handlar om hur stor belastning som ska väljas för att erhålla maximal effektöverföring från en spänningskälla till en belastningen.
När du är klar skall du kunna redogöra för effektanpassning samt beräkna och experimentellt verifiera detta begrepp.
EFFEKTMÄTNING
Vid strömtransport genom en resistor kan effektutvecklingen beräknas på tre sätt:
P = U I
P = I 2 . R P U R 2
I alla tre effektsambanden är U spänningen över den aktuella resistorn och I den ström som flyter genom resistorn. Båda dessa storheter mäts lätt med ett par multimetrar varefter effekten kan beräknas.



Ett fjärde sätt att bestämma effekt är med en wattmeter ansluten mellan spänningskällan och belastningen. Så här kan det se det ut i ett elektriskt schema.






18 MAGNETISKA GRUNDBEGREPP
Detta avsnitt redogör för de magnetiska grundbegreppen samt för en del av de magnetiskt-elektriska sambanden.
När du är klar skall du kunna beskriva magnetiska fenomen, redogöra för skruv- och högerhandsregeln samt för den magnetiska kretsen.
PERMANENTMAGNETER
Vissa material kan magnetiseras. I huvudsak är det järn och några så kallade ferromagnetiska material som kobolt, nickel och en del legeringar som har denna egenskap. Tillverkas en stav av sådant material kallas det för en stavmagnet.
I omgivningen av en sådan magnet finns ett magnetiskt fält som utövar kraftverkan på järnföremål. Fältet kan bland annat påvisas genom att två stavmagneter närmas till varandra. Beroende av hur de är orienterade kommer de då att attrahera eller repellera varandra.
Detta beror på att magneterna har en nord- och en sydpol. Den kraftverkan en nord- och en sydpolssida utövar på varandra gör att magneterna attraherar varandra. Två lika poler, två nord- eller två sydpolssidor, har däremot en repellerande kraftverkan och stöter bort varandra.
Olika poler attraherar
Lika poler repellerar
PROVMAGNETER
För att undersöka vad som är nord- och sydpol hos en magnet används små lättrörliga provmagneter som ser ut och fungerar precis som kompasser. Placeras provmagneten i näraheten av en magnet ställer den in nordpolssidan i riktning mot den undersökta magnetens sydpolssida.
Provmagnet i omgivningen av en stavmagnet
ELEKTROMAGNETISM
På 1820-talet upptäckte den danske fysikern Hans Christian Örsted att det i omgivningen av en strömförande ledare existerade ett magnetiskt kraftfält som är cikelformat och har en riktning runt ledaren.
Denna viktiga fältbild kan beskrivas med den så kallade skruvregeln. Skruvas en högergängad skruv i en ledares strömriktning sammanfaller skruvriktningen med magnetfältets riktning runt ledaren.
Örsteds forskning visade dessutom att det mellan strömförande ledare, som befinner sig i varandras magnetfält, verkar krafter (F) som försöker föra ledarna från områden där fältlinjernas riktning sammanfaller
Lägg märke till hur strömriktningen i ledarna markeras. Krysstecknet betyder att strömmen flyter från läsaren och punkten att strömmen flyter mot läsaren. Prova gärna med skruvregeln!
Flyter strömmen åt samma håll i båda ledarna motverkar fältlinjerna varandra och då försöker ledarna att röra sig mot varandra.
Ledarna rör sig mot varandra
Örstedts upptäckt var första steget mot växelströmstekniken och allt vad det innebär av motorer, generatorer, högtalare, transformatorer, reläer med mera ............
Ledarna rör sig från varandra
RELÄER & RELÄKOPPLINGAR
Detta avsnitt redogör för funktionen hos reläer och vad de kan användas till. Reläet är ett exempel bland många elektromagnetiska tillämpningar.
När du är klar ska du kunna redogöra för reläets uppbyggnad och funktion samt använda reläer i grundläggande styrkretsar.
ALLMÄNT OM RELÄER
Reläer är elektromagnetiska strömbrytare med en eller flera kontakter. De används bland annat vid omkoppling av signalkretsar, in- och urkoppling av motorer.
Storlek, utseende och antal kontakter är faktorer som varierar med användningsområden, men i princip fungerar alla reläer på samma sätt.
ETT TYPISKT RELÄ
Bilden visar hur ett relä med tre slutande kontaktpar kan vara uppbyggt.
Anslutningar
FUNKTION
Oledande material
Järnkärnan (J) bildar tillsammans med spolen (S) en elektromagnet.
I anslutning till elektromagneten är ett ankare (A) av järn monterat.
Ankaret är rörligt kring lagringen (L), men intar ett bestämt läge på grund av spiralfjädern (F).
Kontakterna (K) är förbundna med elektriska anslutningspunkter (1, 2, 3) via bladfjädrar och står i förbindelse med ankaret och varandra via oledande ”klackar”.
För att reläer ska fungera måste de anslutas till en manöverkrets. Bilden visar principen för en sådan manöverkrets i sin enklaste form.
Ankaret attraheras och pressar ihop kontaktparen när strömbrytaren (ST) sluts och gör magnetspolen strömförande.
Reläet sägs då vara ”draget”.
När strömbrytaren åter öppnas återförs ankaret och kontakterna till viloläget av den spända spiralfjädern. Draget relä
20
INDUKTION
Detta avsnitt handlar om att magnetiska fält kan alstra en emk som kan driva ström.
När du är klar skall du kunna beskriva vad som menas med induktion och redogöra för storheter och enheter som hör till begreppet.
INDUCERAD EMK
Bilden föreställer en spole som i experimentsyfte är ansluten till en voltmeter med mittcentrerad nolla och därför kan indikera om det är en positiv eller negativ spänning som mäts. I närheten av spolen finns också en permanentmagnet i vars magnetfält spolen befinner sig.
+ -
Så länge magneten är stilla förblir voltmeterutslaget noll. Förflyttas magneten erhålles däremot ett visarutslag, det induceras (alstras) en spänning (emk) i spolen.
Experimentet antyder att flödesändringar i omgivningen av en spole orsakar en emk i lindningen.
EMK - RIKTNING
Antag nu att permanentmagneten får falla i mitten genom lindningen. Magnetflödet i spolen kommer då att växa tills magneten kommit halvvägs genom spolen, för att därefter avta när den är på väg ur spolen. Observation av voltmetern visar då att det induceras en spänning (emk) som både ändrar polaritet och storlek.
Är spollindningen en del av en sluten krets driver den inducerade emk:n ström som vilken spänningskälla som helst.
För den inducerade spänningens polaritet gäller följande viktiga regel:
Den inducerade emk:n har alltid en sådan riktning, att orsaken till dess uppkomst motverkas.
OSCILLOSKOP
Detta avsnitt är en orientering om oscilloskopets funktion, dess kontroller och vad som kan mätas med oscilloskop. Har du tillgång till ett oscilloskop och kan prova det samtidigt som du läser är det en fördel.
När du är klar skall du kunna identifiera och ställa in standardkontrollerna på oscilloskop samt använda oscilloskopet för att mäta likspänning (växelspänningsmätning kommer i avsnitt 22).
ALLMÄNT
Oscilloskop är snabba voltmetrar som förutom lik- och växespänningar gör det möjligt att mäta frekvens och växelspänningars inbördes tidsförhållande. En av fördelarna med oscilloskop är att de visar mätresultatet som skalenliga X / Y-grafer, ungefär som när man ritar kurvor i koordinatsystem med x- och y-axlar.
OSCILLOSKOPETS RITFUNKTION
Bilden ovan föreställer framsidan av ett oscilloskop. En förhållandevis stor del upptas av skärmen där de undersökta spänningarnas visas med en eller flera ljuspunkter som sveper över skärmen i X-led med en valbar hastighet.
Vid låg svephastighet kan man iaktta den lysande punkt som rör sig över skärmen från vänster till höger. Med högre svephastighet blir ljuspunkten en heldragen linje.
Den spänning som ska undersökas påverkar ljuspunkten i Y-led med en känslighet som användaren väljer.
FUNKTIONSGENERATORN
Detta avsnitt är en introduktion i handhavandet av funktionsgeneratorer. Avsnittets mätövning behandlar även grundläggande växelspänningsmätning med oscilloskop.
När du är klar skall du kunna ställa in en funktionsgenrators utspänning, kurvform, frekvens och att mäta den inställda växelspänningens karakteristika med ett oscilloskop.
INLEDANDE INFORMATON
För mätövningarna i växelströmskursen behövs en växelspänningskälla med varierbar utspänning, frekvens och kurvform. Funktionsgeneratorn är en variant av en sådan spänningskälla.
Med en växelspänning avses oftast en sinusformad spänning eftersom det är den vanligaste formen av växelspänning, men även andra kurvformer som fyrkant- och sågtandsspänning är växelspänningar.
Funktionsgeneratorer klarar att generera (alstra) alla tre kurvformerna eller flera former inom ett frekvensområde på några tiondels Hz (Hertz) till flera MHz.
PERIODISK VÄXELSPÄNNING
Växelspänningar som upprepas med samma storlek och kurvform sägs vara periodiska. Här ser du exempel på en sinusformad spänning (a), en triangelspänning (b), och två sorters fyrkantsspänningar, en med nollgenomgång (c) och en utan nollgenomgång (d).
Funktionsgenerator
a) Sinusspänning
b) Triangelspänning
c) Fyrkantspänning med nollgenomgång
d) Fyrkantspänning utan nollgenomgång
23 KONDENSATORN, UPP
& URLADDNING
Detta avsnitt handlar om hur kondensatorer är konstruerade och om hur kondensatorer tar upp och lämnar ifrån sig elektrisk laddning.
När du är klar skall du kunna mäta kapacitans, förutsäga och mäta kondensatorspänningens värde vid upp- och urladdningsförlopp i en RC-krets.
ALLMÄNT OM KONDENSATORN
Kondensatorer används i sammanhang då man behöver lagra elektrisk laddning, blockera likström och släppa fram växelström.
Kondensatorer tillverkas på många olika sätt, men består i princip av två metallplattor monterade i varandras närhet som i bilden.
Uppladdning
Ansluts en spänning över plattorna laddas kondensatorn. Detta innebär att elektroner ”dras” från den platta som är ansluten till spänningskällans positiva pol. Samtidigt "påtrycks" den andra plattan lika många elektroner från spänningskällans negativa pol.
Den övre plattan får på detta sätt underskott på elektroner medan den nedre plattan får överskott på elektroner. Efterhand som laddningen fortgår växer spänning mellan plattorna. Laddningsförloppet fortsätter tills spänning mellan plattorna blir lika stor som den påtryckta spänningen.
Kopplas kondensatorn bort från spänningskällan då den laddats, behåller den laddningen så länge det inte finns en sluten krets mellan de båda plattorna.
Med förbindelse mellan kondensatorplattorna, t ex om en resistor ansluts över den laddade kondensatorn som i bilden här under, börjar däremot genast en laddningsutjämning.
Urladdning
KONDENSATORN, UPP OCH URLADDNING
SAMMANFATTNING
1.En kondensator är i sitt enklaste utförande två metallplattor som monterats i varandras närhet.
2.Läggs en likspänning över plattorna får den sida som är ansluten till plus underskott på elektronladdningar medan den platta som är ansluten till minus får överskott på elektronladdningar.
3.Laddningsobalansen ger upphov till en spänning mellan plattorna.
4.En laddad kondensator driver ström om dess båda plattor får elektrisk förbindelse med varandra, t ex genom en resistor.
5.Kondensatorns förmåga att lagra laddning Q vid en påtryckt spänning U kallas kapacitans C. Storheternas inbördes förhållande anges i kondensatorlagen, Q=C U.
6.Grundenheten för kapacitans är F (farad). De mest använda underenheterna är F = 1 10-6F, 1pF = 1 10-12F och 1nF = 1000pF.
7.Kondensatorer märks med bokstäver eller med färgkod.
8.Polariserade kondensatorer som elektrolyt och tantalkondensatorer måste anslutas på rätt sätt till plus och minus.
9.När en kondensator laddas stiger spänningen över kondensatorn till 63,2% av den påtryckta spänningens värde under en tidskonstant T = R C
10.Vid momentan inkoppling av spänning över en kondensator kan kondensatorn betraktas som kortsluten.
11.När en kondensator urladdas minskar kondensatorspänningen 63,2% från ursprungsvärdet på en tidskonstant.
12.Kondensatorspänningens upp- och urladdningvärde kan bestämmas med generella upp- och urladdningskurvor eller matematisk.
UPPGIFTER
1.Ange a) 0,1F i F b) 10 F i nF c) 100nF i pF d) 2700pF i F
Testa-dig-själv 23
KONDENSATORN, UPP OCH URLADDNING
2.Beräkna spänningen över en kondensator på 0,1 F som en laddning av 1 10-5As. ...................................................................................................................
3.Beräkna kapacitansen hos en kondensator som laddats till 2 10-5As och då har en spänning på 22V mellan kondensatorplattorna. .................................................................................................................
4.Beräkna tidskonstanten i en RC-krets om resistansen är 15k och kapacitansen är 0,47 F.
5.Beräkna resistansen i en RC-krets om kapacitansen är 0,022 F och tidskonstanten är 12ms.
6.I en RC-krets som påtrycks en spänning på 24V har kondensatorn hunnit laddats till 8,2V, hur stor är spänningen över resistorn?
7.Hur stor är laddningsströmmen i en RC-krets precis när uppladdningen tar sin början om den påtryckta spänningen är 15V och resistansen är 150k ?
8.Hur stor är laddningsströmmen i en RC-krets som påtrycks en spänning på 24V då kondensatorn laddats till 6,2V? R = 18k och C = 1nF.
9.Beräkna med hjälp av den generella uppladdningskurvan hur stor kondensatorspänningen är efter 15,7ms i en RC-krets som laddas mot 9V om R = 56k och C = 0,56 F.
10.Beräkna med hjälp av den urladdningskurvan hur stor kondensatorspänningen är efter 9ms i en RC-krets med R=47k , C=0,39 F om kondensatorspänningen vid urladdningens början är 9V.
24
VÄXELSPÄNNING
Detta avsnitt är en introduktion av växelströmslärans grunder.
När du är klar ska du kunna mäta karakteristiska värden hos växelspänningar med multimeter och oscilloskop samt relatera de uppmätta värdena till våg- och visardiagram.
VÄXELSPÄNNINGSKÄLLOR
Växelspänningen i våra vägguttag har ett fast effektivvärde på 230V och en fast frekvens på 50Hz. Observera att 230V är en livsfarlig spänningsnivå!
Vid elektriska experiment och i servicesammanhang används därför funktionsgeneratorer med inställningsmöjligheter av såväl kurvformer som spänning och frekvens.
VÄXELSPÄNNINGSSTORHETER
Sinusformade växelspänningar anges till sin storlek i allmänhet med de beteckningar och benämningar som visas i vågdiagrammet nedan.
Kom också ihåg att frekvens, som är en viktig storhet i växelströmssammanhang, är antalet perioder under en sekund.
f 1 T
Växelspänningsstorheter i ett vågdiagram
Lägg märke till att vågdiagrammets X-axel är indelad i både grader och tid. Periodtiden T motsvarar därvid 360°, halva periodtiden 180° osv...
Lägg detta på minnet eftersom du behöver omvandla tid till grader och tvärtom vid mätning och beräkning av växelströmskretsar.

