Sofie Olsson





Sofie Olsson









Gugge träffar ankorna ________________________________ 29
INL EDNING MED GRODANS LIVSCYKEL
1 Gugge träffar ankorna ________________________________ 30 TALUPPFATTNING OCH TALS ANVÄNDNING
2 Gugge träffar hästarna ______________________________ 38
GEOME TRI – ALGEBRA
3 Gugge träffar fåren ___________________________________ 46
TALUPPFATTNING OCH TALS ANVÄNDNING
4 Gugge träffar katterna ______________________________ 54
GEOME TRI – ALGEBRA
5 Gugge träffar grisarna ________________________________ 62 TALUPPFATTNING OCH TALS ANVÄNDNING
6 Gugge träffar hundarna _____________________________ 70 GEOMETRI Träna sifferskrivning _________________________________ 78 SIFFRORNA 0–9
7 Gugge träffar hönsen _________________________________ 82 TALUPPFATTNING OCH TALS ANVÄNDNING
8 Gugge träffar kaninerna _____________________________ 90
SAMBAND O FÖRÄNDRING – SANNOLIKHET O STATISTIK
9 Gugge träffar mössen ________________________________ 98 TALUPPFATTNING OCH TALS ANVÄNDNING
10 Gugge träffar korna ________________________________ 106
GEOME TRI – ALGEBRA
KOPIERINGSUNDERLAG 114–149
Fler kopieringsunderlag finns att skriva ut från det Dig.lärarmaterialet
• Kartan över bondgården i färg och svartvit
• Gugge som klippdocka
• Planscher
• Spel
• Uppgifter på H ÖG NIVÅ, kap 1–10
• Underlag till stationsmatematiken
• Häften med arbetsblad
• Och annat berikande till din undervisning




Kapitelintroduktion Skapa nyfikenhet med sagan. Visa tillhörande bildspel via Dig.lärarmaterial. Kapitlets matematiska innehåll sätts i ett sammanhang när eleverna får prova att lösa uppgifterna tillsammans med Gugge.
Vill du undervisa om djuren kan du kopiera bilder på dem och maten de äter. Fakta till dig finns i respektive kapitel. Läs mer på nästa sida.
Nederst på sidan visas kapitlets två mål samt de begrepp som eleverna ska arbeta med i kapitlet.
Två mål i varje kapitel Uppgifterna i boken bearbetar kapitlets mål. Bilderna är kopplade till kapitlets djurfamilj, vilket ger eleverna ett tydligt sammanhang. Ofta visas påbörjade lösningar av uppgifterna. Det ökar elevernas möjligheter till självständigt arbete.
Längst ner på sidorna hittar du förslag på hur du som lärare kan konkretisera sidans innehåll ytterligare och därmed undvika vanliga missuppfattningar och fallgropar.



























Samtalsrutor När ett nytt matematiskt innehåll presenteras visas det i en samtalsruta. Dessa möjliggör resonemang och kommunikation kring nya begrepp. Här används ett tillgängligt och korrekt matematiskt språk. Samtalen skapar grunden för elevernas eget arbete med de kommande matematikuppgifterna. Skriv ut dem som planscher via Dig.lärarmaterial Spel avslutar varje kapitel och befäster elevernas kunskaper ytterligare och på ett lekfullt sätt. Om eleverna vill spela spelet fler gånger kan du skriva ut spelplanen från det Dig.lärarmaterialet.

Guggesidorna, som är placerade längst bak i boken, och som är kopplade till kapitlen, har en ökad svårighetsgrad jämfört med grundsidorna. De är till för elever som har kommit lite längre i sin matematikutveckling eller elever som behöver fler uppgifter att arbeta med. På Guggesidorna introduceras exempelvis räknesätten addition och subtraktion. Här finns också uppgifter som utmanar problemlösningsförmågan ytterligare.












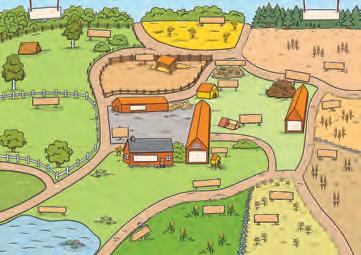

Kartan visualiserar elevernas arbete. Skriv ut den på två A3-papper från Dig.lärarmaterial, Kop.underlag: Karta över bondgården
Laminera och sätt samman till en stor affisch.
Efter varje avslutat kapitel kan djuren kopieras, klippas ut och ”flytta in” på bondgården, Kop.underlag: Djurfamilj. Kartan finns även svartvit att färglägga.
Digital elevträning innehåller enkla spel som ökar elevernas taluppfattning och befäster begrepp. Eleverna kan spela i par, enskilt eller gruppvis med lärare. Om du
med
kan spelen ingå i en station.
I processen med att skapa Mattekojan har syftet varit att underlätta för en undervisning som bygger på förståelse för matematiken. Jag som författare tror på gemensam undervisning och lärande i en social interaktion där matematiken konkretiseras, för att sedan kunna begripas abstrakt och även automatiseras. Mattekojan går fram i små steg så att alla elever kan utvecklas på sin egen nivå.
Unikt för Mattekojan FK Du kan enkelt arbeta ämnesintegrerat. NO-, Sv- och Bild-undervisningen integreras på ett naturligt sätt eftersom grodan Gugge träffar en ny djurfamilj på bondgården i varje kapitel. Här i Lärarhandledningen finns saga och fakta om djuren. Eleverna kan färglägga bilder som kopieras för respektive djur. Bilderna kan hjälpa eleverna att skapa egna faktaböcker (se föregående sida).

• Skapa lust och nyfikenhet med hjälp av sagor med fina karaktärer.
• Ge eleverna en positiv inställning till ämnet matematik.
• Inbjuda till gemensamma samtal kring begrepp, metoder och strategier via bland annat samtalsrutor

• Stärka elevernas självförtroende genom att använda ett enkelt och korrekt språk samt visa påbörjade lösningar
• Ta hänsyn till individuella förutsättningar genom att visa läraren på anpassningar som både förenklar och utmanar det fortlöpande arbetet för eleverna.
• Erbjuda elevuppgifter på olika nivåer, i aktiviteter och elevbok, som kopieringsunderlag och med stationsmatematik.
• Förstärka och utveckla lärandet med lekfullhet genom Gugge och hans vänner samt konkretisering och spel.
• Erbjuda lättillgängligt och användbart didaktiskt stöd med praktiska tips.
• Integrera flera ämnen för att skapa en helhetsbild kring lärandemålen.
Taluppfattning – grunden att bygga på
Det finns rader av studier som visar att det är brister i taluppfattning som är den grundläggande orsaken till många elevers matematiksvårigheter. I Mattekojan har vi därför lagt extra tyngd vid just detta område. Avsikten är att lyfta fram kritiska punkter, visa hållbara strategier i en inspirerande kontext och åskådliggöra hur du som lärare kan stötta med konkretiseringar och anpassningar.
Lekfullhet och fantasi – bryggan till matematiken
I serien Mattekojan synliggörs matematiken i en barnvänlig och lockande kontext. I varje nytt kapitel får du och dina elever följa med grodan Gugge och hans vänner på spännande äventyr. Gugges värld utspelar sig i fyra olika miljöer, en för varje årskurs. I Förskoleklassen lever Gugge på bondgården, i åk 1 på ängen, i åk 2 vid vattnet och i åk 3 i skogen. Naturtemat möjliggör integrering med flera ämnen och områden i undervisningen. Via sagobilden kan ni utöver matematik också diskutera etiska frågeställningar och djurens och naturens livscykler. Till förskoleklassen finns en affisch över Mattekojans bondgårdsvärld. Med den som hjälp kan klassen följa sitt lärande och får en gemensam överblick över mål och kunskaper. Från det digitala lärarmaterialet kan du skriva ut Gugge som pappersdocka. Han kan hjälpta till att visualisera och förstärka matematiska samtal.
Konkretisering – skapar förståelse och utvecklar förmågor
I Mattekojan introduceras alltid nya moment med bildstödda samtalsrutor. Vi rekommenderar att du konkretiserar det matematiska innehållet i samtalsrutorna ytterligare för att på så sätt skapa en brygga mellan det konkreta och abstrakta tänkandet. Eleverna får därigenom också uppleva matematiken med flera sinnen såsom syn, hörsel och känsel. Du underlättar dessutom för eleverna att skapa inre bilder när du till exempel synliggör specifika begrepp, beskriver iakttagelser och inför symboler. Mattekojan konkretiserar också matematiken utifrån de aktiviteter som presenteras till varje elevboksuppslag.
Individanpassning – samma bok till alla elever Våra klasser idag består av härliga elever med stort "kunskapsspann". Det finns elever som sällan har mött tal skrivna med siffror, medan andra kan utföra beräkningar i flera led med olika räknesätt. Det finns elever som inte har det svenska språket på plats än och elever som läser och förstår instruktioner. Mattekojan gör sitt allra bästa för att underlätta undervisningen och möta alla elever på den individuella nivå de befinner sig. Här är några exempel:
• Viktiga ord i instruktionerna fetas eller färgkodas.
• Elevbokens förklarande exempel på hur uppgifter ska lösas utvecklar ett självständigt arbetssätt.
• Sist i elevboken finns Guggesidor som innehåller uppgifter med högre svårighetsgrad.
• Lärarhandledningens aktiviteter utvecklar elevernas förståelse utifrån konkret material.
• Uppgifter på hög nivå utmanar elever som kommit långt i sin kunskapsutveckling.
• Lärarhandledningen ger finns tips på anpassningar i form av FÖRENKLINGAR och UTMANINGAR .
• Du får även tips på vad du kan OBSERVERA hos eleverna och hur du kan undvika MISSUPPFATTNINGAR
• Det digitala lärarmaterialet innehåller bl.a. häften att skriva ut med extra träning.
• Med övningsgeneratorn i det digitala lärarmaterialet kan du skriva ut arbetsblad med slumpmässiga uppgifter inom det räknesätt och talområde du väljer. Uppgifterna kan även räknas på skärm, då självrättande. Det senare alternativet kan vara bra i mindre grupp med lärare.
• I den digitala elevträningen finns enkla spel som befäster de viktigaste begreppen i varje mål för gemensamma samlingar eller självständigt elevarbete enskilt eller i par.
TIPS! Skriv ut Klippdockan Gugge från Dig.lärarmaterial. Placera kartong mellan Gugges fram- och baksida eller använd hård laminering. På Gugges armar kan t.ex. små, lätta korgar hängas för att konkretisera uppdelning av tal eller likhetstecknets betydelse.

Tydlig struktur – utgår från Skolverkets Hitta matematiken
Taluppfattning, vilken är en grundläggande del av matematiken, bearbetas i vartannat kapitel. Det innebär att fem av bokens tio kapitel utvecklar och stärker elevens förmåga att förstå tal, dela upp tal och göra lättare beräkningar. I övriga kapitel bearbetas områden inom geometri, algebra, samband och förändring, sannolikhet och statistik.
Som utgångspunkt för uppgifternas svårighetsgrad har jag som författare använt Skolverkets bedömningsstöd i matematik, Hitta matematiken och Nationellt bedömningsstöd i taluppfattning
Sammanställningsblankett för gruppen Gör dina anteckningar för elevens resultat vid respektive aktivitet.
resonerar om mönster.
Aktivitet Tärningsspel visar nyfikenhet och intresse för det matematiska innehållet. prövar och använder olika idéer genom att använda en metod för att addera och uppskatta. adderar antal uppskattar antal
kommunicerar och resonerar om tal och dess värden.
uppfattar antal utan att behöva räkna känner igen siffror och benämner dem storleksordnar tal visar förståelse för räkneprinciperna
Aktivitet Sanden/riset visar nyfikenhet och intresse för det matematiska innehållet. prövar och använder olika idéer för att lösa problem inom mätning. kommunicerar och resonerar om mätandets princip.
Aktivitet Lekparken visar nyfikenhet och intresse för det matematiska innehållet. prövar och använder olika idéer för att lösa problem inom rumsuppfattning. kommunicerar och resonerar om rum, perspektiv och tid.
Forskning och beprövad erfarenhet – ger trygghet
Källa: Skolverket
Innehållet i lärarhandledningen bygger på en kombination av resultat från forskning och utvecklingsarbete, samt författarens långa erfarenhet av arbete med såväl elever som lärare. Inspiration är hämtad från framför allt litteratur av Bentley & Bentley, Gelman & Gallistel, Häggblom, Johansson, McIntosh, Lunde samt Löwing.
I det här avsnittet får du veta hur, och varför, konkretisering löper som en röd tråd genom Mattekojans hela serie, från FK till åk 3. I texten hänvisar vi till flera olika laborativa material. Några går att köpa, andra kan du och eleverna tillverka själva. Du får beskrivningar här.
Du kan också läsa om taluppfattningens olika delar. Till samtliga steg i taluppfattningens uppbyggnad får du konkreta exempel på lärorika aktiviteter
Orden OBSERVERA och MISSUPPFATTNING används för att synliggöra hur du kan uppmärksamma elevernas lärarande och hur fallgropar kan undvikas.
Orden FÖRENKLA och UTMANA tipsar om användbara anpassningar på olika nivåer.
Matematik är ett ämne som ställer höga krav på att eleverna kognitivt ska förstå och ta till sig ny kunskap. Dessutom ska eleverna kunna koppla samman den nya kunskapen med det de redan kan.
Det logiska tänkandet behöver ofta ett inre bildstöd. När elever arbetar med konkret material, flyttar klossar, kopplar samman antal med talkort och så vidare, bygger de upp detta viktiga mentala bildarkiv med hjälp av olika sinnen.
I Mattekojan inleds varje nytt kapitel med en saga. Berättelsen om grodan Gugge och djurfamiljerna som han träffar fångar eleverna och via fantasin hamnar eleverna i matematikens värld.
I samtalsrutor presenteras begrepp, strategier och annat matematiskt innehåll med bilder hämtade ur den aktuella sagan. Genom att samtala kring bild och text når du de flesta eleverna i klassen, men kan du dessutom konkretisera samtalsrutornas innehåll med laborativt material, kommer ännu fler i klassen att förstå. Mattekojan visar olika förslag på hur det laborativa arbetet kan bedrivas.
När eleverna ska arbeta på egen hand i elevboken bör konkret material alltid finns nära till hands för alla elever. Om bara elever, som vanligtvis uppvisar svårigheter, har tillgång till konkreta föremål blir konkretisering inte en naturlig del av matematikundervisningen. Konsekvensen kan bli att elever som vanligtvis inte behöver laborativt stöd undviker att använda materialet, även när de stöter på problem och materialet hade varit till hjälp.
Färgkodning
Flera laborativa material som använder, såsom pärlstavar och talblock, är färgkodade för att öka den matematiska förståelsen. Vi har valt att utgå från Montessoripedagogikens färgkodning.
Talen 1–10: talet 1 färgkodas alltid rött, talet 2 ljusgrönt, talet 3 rosa, talet 4 gult, talet 5 ljusblått, talet 6 lila, talet 7 ljusgrått, talet 8 brunt, talet 9 mörkblått och talet 10 är i guld.
1 2 3 4 5 6 7 8 9 10
Räknesättet addition färgkodas rött och subtraktion grönt.
Mattekojans laborativa material
Flera av de laborativa materialen som används i Mattekojan kan du tillverka själv eller kopiera och laminera. Med start på s. 10, Om taluppfattning, visar vi den praktiska tillämpningen av materialet.
Förvara förslagsvis allt laborativt material på en eller flera hyllor som är lättillgängliga för alla. Pärlstavar, talblock och andra mindre föremål kan exempelvis läggas i transparenta myntaskar.
Ange askarnas innehåll med tydliga etiketter. Uppmana eleverna att vara varsamma om materialet och ersätt genast skadat material med nytt.

Tvåfärgade cirklar
Cirklar med olika färg på ovan och undersidan kan användas i flera olika sammanhang, exempelvis när eleverna ska träna på att dela upp tal eller göra jämförelser mellan två olika antal. I Kop.underlag: Vändbara cirklar, finns färdiga former att klistra ihop, klippa ut och laminera. VIK
Vändbara cirklar med blå ovansida och röd undersida.
Talblock
Talblock kan också hjälpa eleverna att skapa bilder av tal. Det är vanligtvis enkelt för eleverna att med en snabb blick ta fram rätt talblock då rutorna är uppdelade i två kolumner.
Kuber är utmärkta att använda för att öka förståelsen för matematiska begrepp och för att bygga mönster. En del kuber är hopfogbara på alla sex sidor och lätta att sätta ihop och ta isär.
Mulltilink-kuber är 2x2 cm stora och finns i tio färger.

Talrader och tallinjer
Vill du använda talblock under genomgångar på tavlan kan du förstora Kop.underlag: Talblock, till dubbel storlek. Laminera och klistra eventuellt magnetark på baksidan.
Även om talraden och tallinjen bara består av symboler i form av siffror kan de räcka som stöd åt elevernas tankar när de exempelvis ska lära sig att öka och minska ett antal eller bestämma skillnaden mellan två tals värden. De kan på så sätt fungera som en bro mellan det konkreta och abstrakta antalet. Om talraden inte ger tillräckligt symbolstöd kan den kompletteras med konkreta antal, t.ex. gem, stenar, pärlor, som vi i Mattekojan kallar plockisar. I kopieringsunderlaget finns talrader och tallinjer att skriva ut, se Kop.underlag: Talrader och tallinjer 0–10, 0–20. Vid behov kan talrad och/eller tallinje sättas fast på elevens bänk.
0123456789 10 -1 +1
0123456789 10 -1 +1
1 färre och 1 fler är det givna talets talgrannar på talraden.
1
3
2
4
0 1 2 3 4 5 6 7 8 9 10
När vi ökar ett antal hoppar vi till höger på tallinjen. Här visar vi addition med 2. Pilarna följer Mattekojans färgkodning för addition.
0 1 2 3 4 5 6 7 8 9 10
Mynt ger inte en visuell bild av varje antal, men kan förenkla förståelsen genom att de representerar ett visst antal. En tiokrona representerar till exempel tio ental och kan därmed underlätta förståelsen för tiotal. Mynt kan köpas in till klassens uppsättning av laborativt material. De kan också tillverkas genom att frottera en och tiokronor. Lägg ett mynt under tunt papper och rita fram myntets bild med en krita som hålls horisontellt mot pappret.
Sätt gärna talblocken med tillhörande tal på väggen, så att eleverna ser dem varje dag och kan skapa inre bilder av antalen. Skriv ut Kop.underlag: Talblock med tal från Dig.lärarmaterial
Taluppfattning kan beskrivas som en övergripande förståelse för tal samt förmågan att kunna dela upp tal och göra beräkningar i de fyra räknesätten. I begreppet ingår även förmågan att använda denna kunskap på varierande sätt för att till exempel uppskatta resultats rimlighet och utveckla hållbara beräkningsstrategier.
Det finns rader av studier som visar att det är brister i taluppfattning som är den grundläggande orsaken till många elevers svårigheter med olika delar av matematiken. I Mattekojan har vi därför lagt extra tyngd vid just detta område.
Din undervisning är viktig
Att förstå tal, kunna dela upp dem samt göra olika beräkningar är inte en egenskap som eleven har eller inte har. Studier visar att ett barns taluppfattning utvecklas successivt efter hand som barnet får utforska sin omgivning och interagera med andra. Med en väl genomtänkt och genomförd undervisning kan du som lärare stötta elevers möjlighet att utveckla en god taluppfattning. Tänk på att OBSERVERA dina elever när de arbetar i elevboken, spelar spel eller gör praktiska aktiviteter. Ju tidigare du kan hitta eventuella MISSUPPFATTNINGAR desto större är chansen att eleverna ska förstå matematiken – och även att de ska tycka att ämnet är intressant och roligt.
I Mattekojan har vi lagt stor vikt vid att utveckla god taluppfattning. Materialet är utformat för att stärka elevernas förståelse för tal och att förebygga möjliga svårigheter inom detta område.Vår målsättning är att eleverna därmed ska få en ökad förtrogenhet med tal inom ramen för mål och riktlinjer i förskolans och grundskolans läroplan och grundskolans kursplan i matematik.
Som utgångspunkt för uppgifternas svårighetsgrad har vi använt Skolverkets bedömningsstöd i Matematik för förskoleklass (Hitta matematiken) och årskurs 1–3 (Nationellt bedömningsstöd i taluppfattning). I åk 13 har vi speglat Mattekojans grundnivå mot bedömningsstödets mellannivå (M).

NATIONELLT BEDÖMNINGSSTÖD I taluppfattning Matematik
Mattekojans Guggesidor innehåller uppgifter med högre svårighetsgrad. Skriv ut Kop.underlag: Uppgifter på hög nivå till elever som behöver ytterligare stimulans.
Att förstå tal
Att förstå tal innebär att ha en god bild av och uppfattning om vad tal är. I förskoleklassen innebär det att eleven med lätthet till exempel kan uppskatta tals storlek och storleksordna tal i minst talområdet 0–6.
I Mattekojan har vi valt att beskriva elevernas förståelse för tal utifrån följande fem områden:
• Subitisering
• Tal- och sifferkunskap
• Ramsräkning • Talraden och tallinjen
• Antalsuppfattning
Subitisering
Förmågan att med synen, utan att räkna, kunna uppfatta det exakta antalet föremål i små grupper kallas subitisering, eller spontan antalsuppfattning. Elever med god spontan antalsuppfattning kan exempelvis subitisera hur många flugor det sitter på ett fönster så länge antalet inte överstiger 5–6 stycken.





Förmågan att subitisera räcker sällan till om det handlar om en grupp med ett större antal. Då måste man börja räkna för att kunna ange exakt antal. Det brukar oftast underlätta om föremålen är ordnade efter ett speciellt mönster. Det är till exempel lättare för de flesta av oss att direkt uppfatta antalet åtta, när vi ser åtta som två tärningar med fyra prickar vardera, än att se åtta föremål huller om buller, eftersom vi lärt oss att känna igen antalsmönstret.


Med hjälp av Hitta matematiken kan du som undervisar i förskoleklass under höstterminen tidigt urskilja elever som visar en indikation på att inte uppfylla de kriterier för bedömning som sen ska uppfyllas i årskurs 1 och 3 i grundskolan. Läs mer om Hitta matematiken och Nationellt bedömningsstöd i taluppfattning på Skolverkets hemsida.
EFFEKTIVARE ÄN RAMSRÄKNING
Subitisering finns i två former, perceptuell subitisering och konceptuell subitisering. Perceptuell subitisering är att direkt uppfatta antal utan att räkna föremålen, vilket beskrivs på förra sidan. Konceptuell subitisering är förmågan att dela upp ett stort antal föremål i mindre, igenkänningsbara, delar. Vi kan som exempel direkt se att det finns åtta prickar på hela dominobrickan om ena halva består av fem prickar och den andra av tre. Genom att dela upp ett antal i mindre grupper kan eleven oftast snabbare ange ett lite större antal genom subitisering än genom ramsräkning. Ett sätt att bygga upp elevernas konceptuella subitisering är att visa bilder på antal som är uppdelade på olika sätt. En äggförpackning med sex ägg kan till exempel ses som två grupper med tre ägg i varje eller tre grupper med två ägg i varje. Den konceptuella förmågan är betydelsefull inom många delar av matematiken och används bland annat när eleverna ska dela upp tal.
AVLASTA ARBETSMINNET
Det finns forskning som visar på att elever som har svårt att subitisera antal när de börjar skolan riskerar att få svårigheter i matematik under senare skolår. Det har också visat sig att förmågan att snabbt uppskatta antal avlastar arbetsminnet, vilket innebär att matematiken blir mer ansträngande för elever med dålig subitiseringsförmåga. Genom att träna in antalsmönster kan vi minska elevernas arbetsminnesbelastning och öka möjligheten för eleverna att få bättre flyt i räknandet. Se aktiviteter på s. 24, Utforska tal och ytterligare aktiviteter till kapitel 5, på s. 62–69.
Aktiviteter
P A Slå en tärning: Dela ut sex plockisar och ett halvt A4papper till varje elev. Slå en tärning och uppmana eleverna att lägga lika många plockisar som tärningen visar på pappret. (Slumptärningar finns i det Dig.lärarmaterialet/ Verktygslådan.) OBSERVERA hur eleven går tillväga när hen ska ange antalet ögon på tärningen. Om eleven inte uppfattar antalet direkt bör antalsmönster (tärningsmönster, handens fingrar, talblock och så vidare) tränas korta stunder varje dag. FÖRENKLA övningen genom att låta eleven peka på antalet på en talrad istället för att ta fram motsvarande antal plockisar

Ramsräkning
Även om små barn oftast ser räkneramsan som vilken ramsa som helst, och att den i sig inte ger någon förståelse för tals storlek och egenskaper, är den av stor betydelse för den grundläggande taluppfattningen. När barn ramsräknar uppmärksammar de hur räkneorden i ramsan är strukturerade. De lär sig tiotalen i rätt ordning och känner rytmen i ett återkommande mönster. När eleverna blir äldre är det inte ovanligt att de fortsätter att använda sig av ramsräkning vid olika typer av beräkningar – framför allt om de inte är säkra på andra beräkningsstrategier. Det är därför betydelsefullt att eleven har bra flyt i både fram och baklängesräkning.
En svårighet med den svenska talraden är att strukturen inte är lika hela vägen. Först kommer räkneorden från 1–12 som har en egen struktur, därefter följer ”ton”talen mellan 13–19, sedan räkneorden 20–29, vilka följer ytterligare ett annat mönster. Till skillnad mot det kommande mönstret från 30–99 saknas ändelsen tio i talraden från 20–29. Tjugo borde heta ”tvåtio” om det skulle stämma med de övriga tiotalen; trettio, fyrtio ... För många elever, framför allt flerspråkiga, skapar de svenska räkneordens ologiska uppbyggnad problem i inlärningen. Jämför gärna olika språks räkneramsor i klassen och diskutera likheter och skillnader.
TRE STEG I RAMSRÄKNING
Förmågan att ramsräkna i förskoleklassen kan delas upp i tre steg:
STEG 1: Eleven måste börja från 1 när hen ska ramsräkna.
STEG 2: Eleven kan starta sin ramsräkning från ett givet tal i räkneramsan.
STEG 3: Eleven kan räkna baklänges.
Öva gärna på att ramsräkna korta stunder flera gånger i veckan. Alla bör öva, oberoende av vilket steg de befinner sig på. Träna med hela klassen och låt eleverna säga räkneorden i kör. Fördelen med att öva ramsräkning i en större grupp är att elever, som är osäkra, hör räkneorden och känner rytmen. De kan därmed hänga med så gott de kan utan att känna sig utpekade.

UTMANA eleverna genom att använda två tärningar, 12 plockisar samt eventuellt en talrad från 0–12.


Grodan Gugge föds 29
1 Gugge träffar ankorna 30
TALUPPFATTNING OCH TALS ANVÄNDNING
2 Gugge träffar hästarna 38
GEOMETRI – ALGEBRA
3 Gugge träffar fåren 46
TALUPPFATTNING OCH TALS ANVÄNDNING
4 Gugge träffar katterna 54
GEOMETRI – ALGEBRA
5 Gugge träffar grisarna 62
TALUPPFATTNING OCH TALS ANVÄNDNING
6 Gugge träffar hundarna 70
GEOMETRI
Träna sifferskrivning 78–81
7 Gugge träffar hönsen 82
TALUPPFATTNING OCH TALS ANVÄNDNING
8 Gugge träffar kaninerna 90
SAMBAND O FÖRÄNDRING, SANNOLIKHET O STATISTIK
9 Gugge träffar mössen 98
TALUPPFATTNING OCH TALS ANVÄNDNING
10 Gugge träffar korna 106
GEOMETRI – ALGEBRA
”Kväk! Kväk! Kväk! En grön, liten groda tar sitt första skutt upp på land och känner fast mark under fötterna. Han tittar sig omkring med stora ögon och tänker tillbaka på allt fantastiskt han har varit med om innan han kom upp på land.
Vill du som lyssnar höra vad som hände?
Så kul! Då ska jag berätta. En dag sitter en grodhona vid strandkanten. Hennes mage är full av ägg. Då hör hon en särskilt vacker grodsång. ”Kvack, kväk, kväk, kvack”, låter det. Grodhonan följer ljudet. Plötsligt ser hon den finaste grodhanen hon någonsin sett. Hon blir kär! Grodhanen gapar stort när han får syn på henne. Han blir precis lika kär! ”Kom!” säger honan. ”Vill du bli pappa?” undrar hon. Det vill hanen väldigt gärna. Han klättrar upp på hennes rygg och håller sig fast med sina framben runt hennes kropp.
De två grodorna har så roligt tillsammans, men efter några timmar tycker honan att det är jobbigt att ha hanen på sin rygg. ”Nu är det dags att lägga äggen!” säger hon. Hanen håller sig hårt i honan medan hon kravlar fram till strandkanten. Där, i vattenbrynet, lägger hon flera tusen ägg samtidigt som hanen befruktar dem. När allt är klart går hanen av honan.




GRODANS LIVSCYKEL

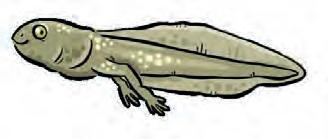
Om du skulle vara där, skulle du se att grodägg inte är några vanliga ägg med hårt skal, utan geléliknande klumpar med mörka prickar i. Äggen skimrar i solljuset.

Solen värmer vattnet. Vattnet värmer äggen. Inuti äggen händer något spännande. De små prickarna växer. Efter ungefär en vecka kommer små varelser ut. De har huvud, kropp och svans. De kallas för grodyngel och simmar omkring, leker och äter alger och växtdelar. För att få syre andas de med gälar, precis som fiskar.
Efter sju veckor börjar två ben växa ut, bak på kroppen. Några veckor senare växer även frambenen ut. I munnen utvecklas en lång tunga och i kroppen bildas lungor. Benen blir större och större. Svansen blir kortare och kortare. När cirka tre månader har gått behövs inte svansen längre. Ynglen har blivit grodor.
En av grodorna, han som Mattekojan handlar om, har ingen svans längre och andas nu med lungor. Han älskar äventyr och vill inte bara vara i vattnet. Han vill ut och se hela världen där blommorna blommar och gräset vajar. Han hoppar upp på ett näckrosblad. ”Åååååh! Världen är stor”, säger han. Sen tittar han ner i vattnet. Där simmar några av hans kompisar, som fortfarande är yngel. ”Nu ska jag ta mig upp på land”, säger han. Ynglen vinkar åt honom och önskar honom lycka till.
Han simmar till strandkanten, ser sig noga omkring och tar sitt första steg upp på land. Det är en märklig känsla att ha marken under fötterna. ”Hm, kul ... fast lite läskigt … jag är nog inte riktigt redo än, men snart ska jag ut på äventyr”, säger han till sig själv. Sen simmar han tillbaka till näckrosbladet igen.

Mål och innehåll s. 3
Mål 1 Lika många
Eleven förstår begreppet lika många och kan jämföra antalet i två mängder genom parbildning. Eleven kan även känna igen några olika representationer av antal som talbilder, t.ex. bilder av antal på tärningar.
Mål 2 Talen 0 till 5
Eleven kan koppla samman ett givet antal föremål med ett tal samt rita ett bestämt antal föremål utifrån ett givet tal.
Lärarfördjupning och didaktiska tips
I kapitlets första mål presenteras begreppet lika många. Här ska eleverna först lära sig att jämföra antalen i två mängder genom att para ihop ett föremål från den ena mängden med ett föremål från den andra mängden, den så kallade ”etttillettprincipen”. Därefter ska de para ihop två mängder som är lika stora till antalet, t.ex. en hand som visar fem fingrar och en tärning som visar fem ögon.
Att förstå begreppen lika många och olika många är betydelsefull kunskap och en förutsättning för att så småningom kunna avgöra skillnaden mellan två mängder: ”Hur många fler än …?” och ”Hur många färre än …?” (se elevbok kapitel 9).









TALUPPFATTNING OCH TALS ANVÄNDNING
I kapitlets andra mål presenteras talen 0 till 5. Här ska eleverna koppla samman ett givet antal med ett tal skrivet med siffror och vice versa.
I både mål 1 och 2 får eleverna möta olika representationer av antal, dels som bilder av fingrar på händer och ögon på tärningar, dels i form av avprickning. Syftet är att eleverna ska träna på att känna igen antalen 0 till 5 som talbilder. Det är säkert många elever i klassen som redan kan se hur många ögon det är på en tärning utan att behöva räkna tärningens ögon.




2 Talen 0 till 5 ankbonde











och INNEHÅLL
1 Lika många
Förstärk arbetet med talen 0 till 5 ytterligare med hjälp av konkreta aktiviteter. Låt exempelvis eleverna utforska talen 15 utifrån Kop.underlag: Utforska talen 1, 2, 3, 4, 5.
Läs mer om att utforska tal under rubriken Utforska tal på s. 24.



Låt gärna eleverna göra en utställning om antal, ett tal i taget, med saker som de hittar på skolan, utomhus eller tar med sig hemifrån. Läs mer under aktivitet "Antalsutställning" på s. 15.
Med Kop.underlag: Talblock kan du strukturerat visa hur antalet rutor ökar från 1 till 5.
Den lilla grodan sitter på ett stort näckrosblad i dammen. Han ser fjärilar och trollsländor dansa över vattnet. Vilken spännande värld, tänker han. Han blir lite varm i solen och dyker ner i vattnet. Då krockar han plötsligt med ett mjukt djur med stora orange fötter. Han gömmer sig snabbt i vassen.
”Lilla groda, var inte rädd”, hör han en anka kväka. ”Jag heter Anna Anka. Vad heter du?” Grodan kikar försiktigt fram. ”Jag har inget namn”, svarar han. ”Va? Alla måste ha ett namn! Hm …”, tänker Anna. ”Du är en groda, du är gullig … nu vet jag! Vad säger du om att heta Gugge?” Grodan ler med hela ansiktet. ”Hihi, det låter perfekt!”
Anna berättar om det härliga livet vid dammen, men också om farorna som lurar överallt. ”Du förstår, för att överleva måste du vara snabb.” Gugge visar hur snabb han är. ”Bra!” säger Anna. ”Och sen är det bra att kunna matematik”, fortsätter hon. ”Mate-ma-vad?” undrar Gugge. ”Matematik! Att räkna, vara klurig, se samband och mycket annat”, förklarar Anna. Gugge skruvar på sig. ”Klurig är jag nog, men allt det där andra …” Anna säger bestämt: ”Det kommer du att lära dig! Kom med mig.”
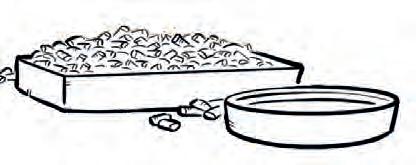
De går upp på strandkanten. Där ligger en hög med stenar och snäckskal. ”Först ska du lära dig skillnaden mellan lika många och olika många. Vi ska jämföra antal stenar med snäckskal”, undervisar Anna. ”Men …”, säger Gugge, ”… jag kan ju inte räkna.” Anna tröstar honom: ”Du behöver inte kunna räkna för att ta reda på om det är lika eller olika många.”
Anna lägger en sten bredvid ett snäckskal. ”Vi ska bilda par. Vi lägger en sten och ett snäckskal, två och två.” Sen tar hon en till sten och lägger den bredvid nästa snäckskal. Hon fortsätter tills alla stenar har parats ihop med varsitt snäckskal. ”Ser du? Det är lika många stenar som snäckskal”, säger Anna. Gugge förstår, men undrar: ”Vad händer om vi har fler stenar än snäckskal?” Anna ler och





tar fram en extra sten. ”Nu är det inte lika många, utan olika många”, förklarar hon.
Gugge vill fortsätta para ihop stenar med snäckskal. Nu får du som lyssnar hjälpa honom att ta reda på om det är lika många eller olika många. BILDSPEL, MÅL 1.
Nu säger Anna: ”Dags att lära nytt! Du ska koppla ihop antalet i en grupp med ett tal.” ”Vad kul!” säger Gugge, ”… men jag kan ju inte räkna.” Anna tröstar: ”Du får börja med att ramsräkna. Vi provar tillsammans: ett, två, tre, fyra, fem … ett, två, tre, fyra, fem …” När de tränat några gånger får Gugge försöka själv. ”Ett, två, tre, fyra, fem. Jag kan!” säger han och hoppar högt. ”Bra, då får du lära dig mer”, säger Anna och lägger fram några stenar. ”Du ska peka på en sten i taget samtidigt som du räknar. Sluta räkna när stenarna är slut.” Gugge tar ett djupt andetag: ”En … två … tre.” ”Bra!” säger Anna och ger Gugge en lapp med talet 3 på. ”Det sista räkneordet talar om hur många stenar det är.” ”Tre alltså”, säger Gugge och lägger 3:an på stenarna.
Nu får du som lyssnar hjälpa Gugge räkna antalet stenar och koppla ihop mängderna med tal. BILDSPEL, MÅL 2.
Plötsligt hörs ett förfärligt oväsen. Det är Annas familj och kompisar som kommer. Det är ankor, ankbönder och ällingar. De tjattrar för full hals. ”Göm dig snabbt under min vinge, Gugge!” utropar Anna. Gugge är blixtsnabb. Anna viskar: ”Du förstår, alla ankor, utom jag, tycker om att äta grodor. Men var inte rädd! Jag ska hjälpa dig. Håll i dig!” Gugge håller sig, hårt, hårt. Anna lyfter och flyger iväg. Till slut landar hon. ”Var är jag?” undrar Gugge. ”Du är på bondgården där resten av djuren på gården bor. Här vill ingen äta upp dig, men alla kan matematik!” ”Åh, så bra!” säger Gugge.
”Jag lovar att lära mig så mycket jag kan!”
Anna nickar stolt och flyger tillbaka till dammen.
I det Dig.lärarmaterialet finns matematiska frågor i bildspel. Bilderna förstärker även elevernas upplevelse av sagan.











































s. 4–5
SYFTE: Att eleverna får lära sig begreppet lika många.
Samtalsruta
Samtalsrutan visar tre grodyngel och lika många grå cirklar. Synliggör för eleverna att de kan låta ett föremål från den ena mängden bilda par med ett föremål från den andra mängden, den så kallade ”etttillettprincipen”, när de ska måla lika många. Läs mer om de fem antalsprinciperna under rubriken Antalsprinciper på s. 14 och 15.
FÖRSLAG PÅ FRÅGOR:
• Hur många grodyngel är det?
• Hur många cirklar har målats för att det ska vara lika många grå cirklar som grodyngel?
Aktiviteter
A Antal med rörelse: Slå en stor tärning. Låt eleverna utföra en rörelse lika många gånger som tärningen visar ögon. Om tärningen visar fyra kan eleverna t.ex. hoppa jämfota fyra gånger. Andra förslag på rörelser är att hoppa på ett ben, klappa händerna eller sätta sig ner på golvet. Använd gärna de sex korten på Gugge, Kop.underlag: Programmering – Rörelser med kroppen.

A Lika många och olika många: Samla eleverna på golvet. Lägg fram två mängder med föremål, t.ex. 4 stenar och 5 löv.









Låt eleverna fundera på hur vi ska kunna jämföra antalen föremål i de två mängderna utan att räkna dem. Kanske någon elev kommer på att vi kan låta en sten bilda par med ett löv, den så kallade ”etttillettprincipen”. Samtala om att det är lika många föremål i de två mängderna när det går att göra par av alla föremål, samt att det är olika många föremål när något föremål från den ena mängden inte kan bilda par med ett föremål från den andra mängden. Låt eleverna berätta om det finns färst/flest stenar eller löv.








Med hjälp av ”ett-till-ett-principen” ser vi att det är färst stenar och flest löv.






















s. 6–7


















SYFTE: Att eleverna får lära sig att känna igen olika representationer av antal som talbilder.
Arbete i elevboken
Visa avprickning med streck inför uppgift 5. Uppmärksamma eleverna på att det femte strecket ska dras diagonalt över de övriga fyra, likt ett "staket".
Aktiviteter
A Lika många streck som stenar: Samla eleverna i en ring. Lägg fem stenar på golvet, huller om buller. Kan någon se hur många stenar det är utan att räkna dem?





Lägg stenarna på samma sätt som ögonen på en tärning. Låt eleverna fundera på varför det är lättare att ange hur många stenar det är nu. Kanske någon elev uttrycker att de känner igen bilden för antalet 5. Läs mer om subitisering under rubriken Att förstå tal på s. 10.





Fortsätt aktiviteten med att låta en elev peka på en sten i taget samtidigt som du gör en avprickning, dvs. att du sätter ett streck för varje sten som eleven pekar på. Visa att man gör ett så kallat ”5staket” ( ) när man visar antalet 5. Samtala om varför man grupperar strecken fem och fem. Synliggör hur mycket enklare det är att ange ett stort antal när strecken är grupperade fem och fem, jämfört med när strecken står på rad utan avstånd mellan femeller tiogrupper.
A Antal bokstäver i elevernas namn: Låt eleverna skriva sina namn på varsitt papper. Uppmana dem därefter att visa antalet bokstäver i namnet med hjälp av avprickning. Ställ slutligen följande frågor:
Vem har flest antal bokstäver i sitt namn?
– Vem har färst antal bokstäver i sitt namn? – Finns det några elever som har lika många bokstäver i sina namn?

Talen 0 till 5


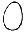

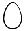
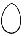

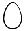
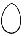
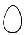


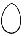
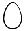
0 1 2 3 4 5 nolletttvåtrefyrafem









Tal kan skrivas med siffror eller bokstäver 012345 012345 012345 012345







s. 8–9
Dra streck till rätt tal








SYFTE: Att eleverna får lära sig att känna igen och namnge olika tal samt att koppla ett tal till ett konkret antal.
Samtalsruta
Samtalsrutan visar sex fågelbon där antalet ägg ökar med ett från vänster till höger. Under varje bo visas antalet ägg med tal skrivna med siffror (0, 1, 2, 3, 4 och 5) och som räkneord (grundtal) skrivna med bokstäver (noll, ett, två, tre, fyra och fem). Konkretisera genom att lägga talkort 0 till 5 på golvet. Se till alla elever ser korten från rätt håll. Använd
Kop.underlag: Talkort 0–12. Peka på ett tal i taget och låt eleverna lägga lika många plockisar som talet visar på en rad framför sig. Eleverna kan också visa antalet med handens fingrar eller med en tärning. Uppmärksamma eleverna på att noll är ingenting.
OBSERVERA om eleverna kan säga talens namn. Träna gärna även på ordningstalen första till femte. Visa skillnaden mellan kardinaltal (fem stenar) och ordningstal (den femte stenen). Läs mer om hur du kan utveckla arbetet med ordningstal på s. 19.
FÖRSLAG PÅ FRÅGOR:
• Hur många ägg är det i fågelboet längst till vänster/höger?
• Hur många fler ägg är det i boet med fyra ägg jämfört med boet med tre ägg?
Arbetet i elevboken
OBSERVERA om eleverna kan koppla samman de olika antalen med talen, skrivna med siffror, samt om de kan säga talens namn.
Aktiviteter
A Tal och antal, pärlstavar: Vik talkort 0 till 5 på mitten och lägg dem i en korg. Använd
Kop.underlag: Talkort 0–12. Låt en elev i taget ta en lapp ur korgen, ta upp motsvarande antal pärlor ur en skål och trä pärlorna på en piprensare. Placera pärlstaven på golvet tillsammans med talkortet. UTMANA eleverna genom att öka talområdet.
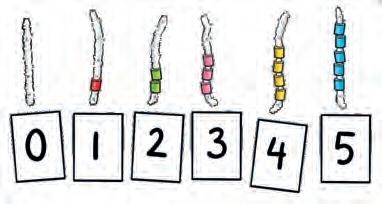
För att kunna ta upp rätt antal pärlor måste eleverna vara säkra på räkneramsan (1, 2, 3 …).
Övningar som tränar och stärker denna finns under rubriken Ramsräkning, på s. 11.






























































s. 10–11
5. Ringa in alla ägg i grupper med rätt antal i varje.


















































6. Dra streck till rätt antal













noll 2
KAPITEL 1
SYFTE: Att eleverna får lära sig att koppla samman ett tal med motsvarande antal föremål.
Arbetet i elevboken
Visa eleverna att de i uppgift 5 ska ringa in samtliga ägg på varje rad i grupper med 2, 3, 4 och 5 i varje. I uppgift 6 kan eleverna ta hjälp av färgkodningen om de inte kan läsa räkneorden (grundtalen) själva.
Aktiviteter
E Rätt antal grodor: Klipp ut sex näckrosblad i filt eller grön kartong. Skriv talen 0 till 5 på bladen. Lägg 15 grodor i en skål. Uppmana eleven att lägga lika många grodor på bladet som talet visar.





FÖRENKLA genom att rita motsvarande antal cirklar på bladen. Låt eleven lägga en groda på varje cirkel med hjälp av ”etttillettprincipen”.
UTMANA genom att utöka talområdet.

P Taltrappa 0–5: Dela ut 25 multilinkklossar till varje elevpar. Låt dem bygga en taltrappa, se nedan. Hjälp dem vid behov att skriva talen från 0 till 5. Använd Kop.underlag: Taltrappa 0 till 5
Låt eleverna bygga staplarna med multilinkkuber och/eller måla lika många rutor som talet visar.

OBSERVERA om eleverna är säkra på talens namn samt om de kan räkna fram och baklänges från 1 till 5. Om inte, finner du förslag på ramsräkningsövningar under rubriken Ramsräkning, med start på s. 11.
UTMANA genom att bygga en taltrappa från 0 till 10. Låt eleverna rita denna större taltrappa på cmrutat papper.
s. 12
Fem i rad
SYFTE: Att eleverna lär sig att känna igen olika representationer av antal som talbilder.
Material: tärning 1–6, en spelpjäs per spelare
Antal spelare: två till tre Regler: Eleverna har varsin spelplan. Spelare 1 ställer sin spelpjäs på valfri bildruta (talblock eller pärlor), slår tärningen och flyttar lika många steg som tärningen visar, medsols eller motsols. Om spelpjäsen hamnar på en ruta som visar t.ex. antalet 3, letar eleven upp talet 3 i mitten av spelplanen. Spelaren markerar talet med ett kryss och turen går över till spelare 2. Den som först får fem rutor i rad , i mitten av spelplanen, vinner spelet. Spelet kan även skrivas ut från Dig.lärarmaterial.

i rad MATERIAL: 1 5 3 4 0 4 0 2 5 1 2 1 4 3 3 3 1 5 0 2 3 4 1 5




Guggesida på lite högre nivå s. 109. Kop.underlag s. 123–132.



REGLER: Använd varsin spelplan. Ställ spelpjäsen på valfri ruta med pärlstav eller talblock. Turas om att slå tärningen. Flytta det antal steg som din tärning visar, med- eller motsols.
Räkna pärlorna eller rutorna där du hamnar.
Markera talet i mitten av spelplanen med ett kryss X på talet.
Vinnare är den som först får 5 i rad
Skriv ut Kop.underlag Uppgifter på HÖG NIVÅ från Dig,lärarmaterial .
Visa eleverna att de ska para ihop två lika tal genom att binda samman dem med raka streck. Uppmärksamma dem särskilt på att strecken inte får korsa varandra. UTMANA genom att låta eleverna göra liknande uppgifter till varandra på "prickpapper".
Låt gärna elever utforska talen 1 till 10 och/eller skapa en bok om talen. Använd Kop.underlag: Utforska talen 1-10 och/eller Representationer av antal. Se Utforska tal s. 24.

Tamankans systematik, historia och familj
Ankor tillhör understammen ryggradsdjur, klassen fåglar, ordningen andfåglar, familjen änder och släkten Anas. Tamankor är olika raser under arten gräsand.
För minst 2 000 år sedan började man föda upp änder i fångenskap. Fram till 1800talet var det i stort sett bara köttet man var intresserad av, snarare än äggen. De flesta av djurriktets drygt 50 ankraser kommer från gräsanden. Pekingankan är den ras som är vanligast i världen. I Sverige är Svensk gul anka, Blekingeanka och Svensk blå anka de tre vanligaste raserna.
Ankhanen kallas "ankbonde", "anrik" eller "andrake". Honan kallas oftast bara "anka" och ungarna "ällingar" eller "ankungar".
Hur ser tamankan ut?
Tamankors vikt varierar med ras. En medelstor tamanka väger mellan 2,5 och 5 kg. Hanen väger något mer än honan. Fjäderdräkten kan vara gul, blå, svartgrön, grå, brun, brungul, röd, vit eller brokig i någon av de färgerna. Varje fjäder är täckt med ett speciellt fett vilket gör att fjäderdräkten inte suger upp vatten när ankan tvättar sig. Tamankor ruggar (byter fjäderdräkt) som regel två gånger per år. Under ruggningen kan de inte flyga. Ankans näbb är platt, ofta orange och lite uppåtböjd. Ögonen sitter på sidan av huvudet vilket gör att den, precis som andra fåglar, kan se bra åt alla håll. Ankor har inga fungerande tårkanaler, så de behöver ha tillgång till vatten för att kunna rengöra och fukta sina ögon.
Ankfötter är platta, breda och ofta orange. Längst ut på tårna sitter små klor. Mellan tårna har den simhud vilket gör att den kan paddla sig fram i vattnet. Ankor har kalla fötter som inte värms upp så mycket av blodet i kroppen. Det gör att de kan stå på is och snö utan att frysa.
Vad äter tamankan?
Ankor är allätare, dvs. de äter olika typer av föda. Med hjälp av den böjda näbben kan ankan rota runt efter insekter, sniglar och maskar i marken och skyffla upp vatten för att komma åt växtdelar. Näsborrarna sitter nära huvudet vilket gör att de kan leta efter fiskar, grodor och alger i vattnet utan att behöva hålla andan. Till skillnad från vilda ankor dyker tamankorna inte efter mat. På land äter ankorna även nötter, bär och frön. Ankor i fångenskap äter främst kraftfoder som bland annat består av vete och korn. I närheten av utfodringsplatsen
måste det finnas vatten eftersom ankorna vill blöta upp fodret medan de äter.

Ankor har, precis som andra fåglar, mycket god syn och hörsel men ett dåligt luktsinne. Ögonens placering på var sin sida av huvudet, ger ankan ett bra vidvinkelseende, vilket gör att den snabbt kan uppfatta faror som kommer från sidorna. Ankor är väldigt sociala djur och trivs därför inte ensamma. De kommunicerar med både röst och kroppsspråk. Ljudet från framförallt honankorna kallas för kvackljud. Om någonting överraskar ankorna kan de bli väldigt högljudda.
Ankans ungar
Tamankor parar sig helst i vatten. Ett befruktat ägg kan utvecklas till en älling om det hålls varmt och fuktigt samt vänds en gång om dagen i 28 dagar. I fångenskap kläcks många ägg i äggkläckningsmaskiner. Ällingarna kan äta och simma nästan direkt efter kläckningen, men är känsliga för kyla och väta under de första levnadsveckorna eftersom de föds utan fjädrar. Läs mer om utvecklingen från ägg till kyckling i faktatexten om hönan.
Vad får vi från ankor?
I Sverige hålls tamankor framförallt i små hobbybesättningar för sällskap, avel, utställning och för bevarande av lantraser. I flera länder föds tamankor främst upp för kött, ägg och dun/fjäderproduktion.
I bland annat Kina är maträtten Pekinganka mycket populär eftersom köttet är rött och näringsrikt. I Sverige slaktas drygt 10 000 ankor varje år. Anklever är en delikatess i många länder. Eftersom ankorna behöver tvångsmatas för att levern ska bli tillräckligt fet är produktionen av anklever förbjuden i bland annat Sverige. Ankor kan lägga ett ägg om dagen, cirka 200 dagar av året. Äggen är smakrikare än hönsägg och användas bland annat till bakning.
MER ATT VETA!
På natten låser många bönder in sina ankor i ett stall för att skydda dem mot farliga fiender, t.ex. hund, räv, björn, varg och lo.
Ankor i fångenskap lever upp till 10–12 år.

Mål och innehåll s. 3
Mål 1 Geometriska former
Eleven känner igen och kan namnge de fyra grundläggande 2dimensionella formerna: rektangel, kvadrat, triangel och cirkel.
Mål 2 Mönster
Eleven förstår att ett mönster har en del som upprepas flera gånger. Eleven kan också göra klart ett påbörjat mönster samt skapa ett eget mönster med olika uttrycksformer.
Lärarfördjupning och didaktiska tips I kapitlets första mål presenteras de fyra grundläggande 2dimensionella geometriska formerna: rektangel, kvadrat, triangel och cirkel. Träna på formernas namn och uppmärksamma särskilt eleverna på att alla former kan vridas och vara olika stora utan att namnet ändras.


och INNEHÅLL
1 Geometriska former
2 Mönster






BEGREPP och ORD rektangel kvadrat triangel cirkel geometriska former hörn sida mönster mönsterdel
Här visas att namnet triangel gäller för alla dessa former oavsett om spetsen pekar uppåt, nedåt eller endera sidan.
Eleverna får också lära sig att formerna har olika egenskaper. Rektangeln, kvadraten och triangeln avgränsas med räta (raka) linjer som kallas sidor. Rektangeln och kvadraten har fyra sidor och triangeln tre. Cirkeln saknar sidor eftersom den saknar räta linjer. Den avgränsas istället av en sluten båge. Punkten där två sidor möts kallas hörn, ett begrepp som inte ska förväxlas med de 3dimensionella formernas kanter.
Skriv gärna ut de geometriska formerna som planscher från det Dig.lärarmaterial, Kop.underlag: Geometriska former Sätt upp dem i klassrummet så att eleverna kan repetera formernas namn regelbundet.
I kapitlets andra mål presenteras begreppet mönster, vilket inom matematiken betyder en exakt upprepning av en del, den så kallade mönsterdelen. I ett mönster fungerar mönsterdelen som en slinga, likt en loop i en programmering.












MÖNSTERDEL
Mönsterdelen upprepas. Mönstret består av tre mönsterdelar.
Redan i tidig ålder utforskar och skapar barn mönster med olika material. Det är viktigt att låta dem fortsätta att skapa och beskriva mönster med olika uttrycksformer, även när barnen blir äldre. På så sätt utvecklas både deras kommunikativa förmåga och deras förståelse för att se mönster i matematiken.
TIPS! I aktivitet ”Sortera med Logiska block”, som du kan läsa mer om på s. 25, får eleverna träna på att sortera fysiska former med olika färg, tjocklek och storlek.
Den röda, fina bondgården ska alltså bli mitt nya hem nu, tänker Gugge. Han ropar efter Anna Anka: ”Tack för att du räddade mitt liv!” Anna vinkar med ena vingen. Gugge suckar. Han känner sig lite ensam. Men han är i alla fall trygg ... och han är inte ensam. Fölet Fixy har hört honom och kommer galopperande. ”Iiiihhhihihi”, säger han och nosar på Gugge med sin mjuka mule. Fixy och Gugge tycker genast om varandra. Plötsligt står Fixys mamma och pappa där också. Oj, vilka stora, ståtliga djur de är, hästarna. Gugge bugar och presenterar sig. Han får veta att stoet heter Saidy och hingsten heter Hubbe.
”Vad kan vi hjälpa dig med?” undrar stoet Saidy. Gugge berättar att han inte kan bo i dammen längre utan behöver hitta en säker plats att bo på, där ingen vill äta upp honom.
”Du får stanna här så länge du vill”, säger Saidy. ”Är det något annat vi kan hjälpa dig med?” Då nickar Gugge och frågar: ”Kan ni något om matematik? Jag vill gärna lära mig mer om det.” Hela hästfamiljen blir glad. ”Såklart kan vi lära dig matematik”, svarar de.
Lilla Fixy börjar hoppa. ”Åh, kan vi inte prata om geometri?” Gugge förstår ingenting. ”Geometri?” undrar han. ”Jajaja! Det är jätteroligt!” gnäggar Fixy. Saidy lugnar honom och säger: ”Vi börjar med geometriska former Det finns många olika, men du ska först få lära dig de fyra vanligaste. Det är rektangel, kvadrat, triangel och cirkel.”
Fixy går fram till en grusplätt och börjar rita en rektangel och en kvadrat på marken med sin hov. Hingsten Hubbe står bredvid och förklarar hur man kan känna igen formerna. ”Rektangeln och kvadraten har fyra sidor. Ser du att kvadratens alla sidor är lika långa?” Gugge nickar. Fixy ritar nu en triangel och en cirkel. Hubbe fortsätter: ”Triangeln har tre sidor och cirkeln, som är helt rund, har inga sidor alls.”
Saidy lägger stenar i hörnen där sidorna möts. ”Kan du räkna hur många hörn en


rektangel har?” frågar hon Gugge. Gugge hoppar från sten till sten längs rektangelns sidor. Sedan säger han: ”Fyra stycken!” ”Det stämmer”, säger Hubbe, ”och som du ser har kvadraten lika många. Triangeln då?” Gugge svarar: ”Den har tre sidor, så den borde ha tre hörn.” Hubbe nickar. Gugge funderar. Han undrar: ”Har cirkeln några hörn?” Hubbe förklarar: ”Cirkeln har inga sidor och därför har den heller inga hörn.”
Nu får du som lyssnar hjälpa Gugge att lära sig formernas namn. BILDSPEL, MÅL 1.
Fölet Fixy viskar i Gugges öra: ”Om du kan hitta något på gården som har formen av en rektangel eller cirkel, så får du rida på min rygg, om du vågar alltså!” Spännande! Gugge sätter genast igång att leta. Det tar inte lång stund förrän han hittar formerna. ”Kolla fönstren! Hjulen! Blommorna! Staketet …” Fixy låter Gugge klättra upp längs hans hals. Det pirrar i Gugges mage, men till slut hittar han en trygg plats i Fixys man.
Högt där uppe ser han att någon har lekt med hästarnas gamla skor. Den första hästskon ligger med öppningen uppåt, den andra med öppningen nedåt och den tredje och fjärde med öppningen åt höger. Sen är resten av skorna lagda på samma sätt. ”Vem är det som lagt det fina mönstret?” undrar Gugge. Fixy svarar: ”Det var jag som kom på hur de fyra första skorna skulle ligga. Sen upprepade mamma min mönsterdel gång på gång tills skorna var slut.”
Fixy bygger nya mönster av hästskorna. En sko saknas. Nu får du som lyssnar hjälpa Gugge lista ut vilket håll skon som saknas ska ligga på. BILDSPEL, MÅL 2.

Efter den lärorika dagen är Fixy och Gugge trötta. De kommer överens om att Gugge ska sova i Fixys härliga man ända tills han ska fortsätta sin vandring. Nästa äventyr blir i hagen bredvid.
I det Dig.lärarmaterialet finns matematiska frågor i bildspel. Bilderna förstärker även elevernas upplevelse av sagan.

HÖRN
SIDA
1. Måla två former med samma namn som den första.

Tre av formerna har lika många hörn. Måla den som är olik.
3. Tre av formerna har lika många sidor. Måla den som är olik.
räknats och
räknats.
s. 14–15
SYFTE: Att eleverna får lära sig de fyra grundläggande 2-dimensionella formernas namn och egenskaper.
I samtalsrutan visas geometrins fyra grundläggande 2dimensionella former: rektangel, kvadrat, triangel och cirkel. Leta först efter föremål som har motsvarande former i klassrummet. Försök därefter tillsammans att befästa deras namn. UTMANA eleverna genom att visa att rektangeln, kvadraten och triangeln avgränsas med räta (raka) linjer som kallas sidor. Rita olika former och räkna sidorna tillsammans. Berätta gärna att en kvadrat är en speciell typ av rektangel – en rektangel med fyra lika långa sidor (och att både rektangeln och kvadraten har vinklar som är räta). Cirkeln saknar raka sidor eftersom den begränsas av en sluten båge. Visa att den punkt där två sidor möts kallas hörn (inte att förväxla med begreppet kant). Rita olika former och låt eleverna markera hörnen.
Klipp ut rektanglar med olika förhållanden mellan längd och bredd. Förtydliga att rektangeln och triangeln kan se ut på många olika sätt. Trianglar kan t.ex. ha tre lika långa sidor, två lika långa sidor eller tre olika långa sidor. Vrid på formerna för att visa att de kan ha hörnen åt olika håll.
FÖRSLAG PÅ FRÅGOR:
• Vad heter den blå/gröna/röda/gula formen?
2
• Hur många sidor/hörn har en rektangel/kvadrat/ triangel/cirkel?
• Vad finns det för likheter/skillnader mellan en rektangel och en kvadrat?
Arbete i elevboken
I uppgift 1 kan eleverna antingen använda blyertspenna eller måla formerna i samma färg som figuren de ska finna.
FÖRENKLA uppgift 2 genom att låta eleverna markera hörnen med röd penna samtidigt som de räknar dem, och i uppgift 3 måla sidorna blå.
Aktiviteter
P A Hitta formen med känselsinnet: Lägg olika 2dimensionella former i en tygpåse. Använd exempelvis Logiska block. Skicka runt påsen till en elev i taget. Säg namnet på en form och låt eleven ta upp formen som namngivits, utan att titta, bara genom att känna sig fram. Uppgiften kan även göras i par. Kamraterna turas om att säga namnet på formen, och att leta efter formen i påsen.










s. 16–17
SYFTE: Att eleverna får lära sig att rita 2-dimensionella former utifrån givna hörn.
Arbete i elevboken
I uppgift 4 är målet att eleverna ska lära sig att rita kvadrater, rektanglar och trianglar utifrån givna hörn. Låt eleverna rita sidorna på frihand eller UTMANA genom att låta dem dra streck med linjal. Visa att de kan förhindra att linjalen flyttar sig genom att trycka ner den med flera av den icke dominanta handens fingrar.
Aktiviteter
P A Geometrisk formjakt: Använd Kop.underlag: Geometrisk formjakt och dela ut det till varje elev eller elevpar. Låt eleverna leta efter föremål som har formen av en rektangel, kvadrat, triangel och cirkel, t.ex. en tavla, dörr eller klocka m.m. Uppmana dem att rita av föremålen i rätt ruta. Vilken form är enklast/svårast att hitta?
Variera aktiviteten genom att låta eleverna klippa ut och klistra in former från tidningar.
A Geometri med kroppen: Dela in eleverna i grupper med fyra i varje. Ropa ut namnet på en geometrisk form. Uppmana varje elevgrupp att skapa den geometriska formen som namngetts med sina kroppar. Hur många elever behövs för att göra t.ex. en triangel?
Variera genom att låta eleverna visa formerna med ett, cirka 6–10 m långt, hopknutet rep.
E P A Former med pinnar: Uppmana eleverna att visa kvadrater, rektanglar och trianglar med hjälp av pinnar, exempelvis glasspinnar. Låt dem sedan jämföra sina former. Kan de bygga samma form med fler, eller färre, antal pinnar?
UTMANA genom att låta eleverna bygga en särskild typ av tringel, t.ex. en liksidig, likbent eller oregelbunden, eller att bygga en form med ett visst antal pinnar.




















MÖNSTERDEL MÖNSTERDELMÖNSTERDEL













































































































s. 18–19



































SYFTE: Att eleverna får lära sig att fortsätta ett mönster genom att först ta reda på hur mönsterdelen ser ut.
Samtalsruta
Samtalsrutan visar ett mönster som är uppbyggt av äpplen i tre olika färger. Visa eleverna att ett mönster alltid har en del som upprepas flera gånger. Berätta att delen som upprepas kallas mönsterdel
En förutsättning för att kunna göra klart ett påbörjat mönster är att eleverna kan komma fram till vilken regel som gäller för mönstret, dvs. hur mönstret upprepar sig. Notera att vi har förenklat uppgifterna i elevboken genom att markera mönsterdelarna med ett mellanrum och på kommande sidor med lite tjockare streck.
Uppmärksamma eleverna på att ett tryck på en tröja inte är ett matematiskt mönster, eftersom trycket bara visas en gång och inte upprepas.
FÖRSLAG PÅ FRÅGOR:
• Var har du sett mönster förut?
Kan du beskriva det?
• Hur många äpplen är mönsterdelen i samtalsrutan uppbyggd av?
• Hur många gånger upprepas mönsterdelen?
P A Kopiera mönstret: Bygg ett mönster där mönsterdelen består av två klossar som har olika färg (t.ex. RÖD GUL). Upprepa mönsterdelen tre gånger. Uppmana eleverna att kopiera ditt mönster, dvs. att bygga ett mönster som är exakt lika, samt att därefter utöka mönstret med fyra klossar
mönsterdel
Tänk på att det är viktigt att eleverna ser mönstret från samma håll som du ser det. Bygg därefter ett nytt mönster. Den här gången med en mönsterdel som består av tre klossar i två färger (t.ex. RÖD RÖD BLÅ). Upprepa mönsterdelen två gånger. Uppmana eleverna att först kopiera ditt mönster och sen att utöka det med sex klossar.
UTMANA genom att först låta eleverna upptäcka ett mönsters upprepade struktur och därefter översätta det till ett mönster med andra föremål och material, t.ex. ett mönster med naturföremål.






SYFTE : Att eleverna får lära sig att fortsätta ett mönster samt att skapa ett eget mönster
Arbetet i elevboken
Variera uppgift 6 genom att låta klasskamraterna göra klart varandras mönster. Uppmana eleverna att, i uppgift 7, fylla i hela mönstret från vänster till höger, inte bara den del som inte är ifylld.
Aktiviteter
A Mönster med rörelser: I förskoleklass kan ett rörelsemönster bli en inledning till att bygga mönster, beskriva mönsterdelen och rita av det. Du kan själv hitta på olika rörelsemönsterdelar, t.ex. peka, hoppa, hoppa, snurra och sedan uppmana eleverna att fortsätta mönstret. Låt eleverna identifiera, visa och sätta ord på vad som är mönsterdelen i rörelsemönstret. Kop.underlag: Programmering – Rörelser med kroppen




A Mönster med symboler: Mönster kan också visas med symboler, exempelvis bokstäver eller siffror: ABBCABBCABBC 122312231223
Skriv olika mönster på tavlan med avstånd mellan mönsterdelarna. Låt eleverna identifiera mönsterdelen och fortsätta mönstret. UTMANA med mönster utan avstånd mellan mönsterdelarna.
A Växande rörelsemönster: Elever som behöver extra utmaningar kan arbeta med växande mönster. Ett exempel på ett växande mönster är att någon del ökar i antal för varje upprepning, exempelvis handklapp, knäklapp, hopp; handklapp, knäklapp, hopp, hopp; handklapp, knäklapp, hopp, hopp, hopp
Det här är en kognitivt krävande aktivitet som fordrar att eleverna kan komma ihåg mönsterdelen och samtidigt hålla reda på ordning och antal.
s. 22
Mönsterspelet
SYFTE : Att eleverna ska få ökad förståelse för mönsters uppbyggnad.
Material: tärning 16 samt en blå, en röd och en gul färgpenna per spelare Antal spelare: två till tre Regler: Eleverna spelar tillsammans i en elevbok. De väljer först varsitt mönster (1, 2 eller 3), se sidans nedre del. Sedan ställer de varsin spelpjäs i startrutan på sidans övre del. Därefter turas eleverna om att slå tärningen och flytta fram motsvarande antal steg. Om spelpjäsen hamnar på den form som passar in i mönstrets första tomma ruta, får eleven måla formen där. Detsamma gäller om spelpjäsen hamnar på en stjärna (✶ = valfri form). Om spelpjäsen hamnar på en annan form, går turen över. Den som först målat klart sitt mönster vinner. Spelet kan även skrivas ut från Dig.lärarmaterial
Utmaningar
Uppgifter på lite högre nivå: Guggesidor s. 110–111.







22
Mönsterspelet
MATERIAL:






Fortsätt ditt mönster om du landar på rätt form eller = valfri form


REGLER:
Spela på en spelplan. Välj varsitt mönster (1, 2 eller 3).
Ställ era spelpjäser på start.
Turas om att slå tärningen och flytta fram motsvarande antal steg. Om du hamnar på rätt form, eller på en stjärna, får du måla vidare på ditt mönster. Om inte, går turen över. Den som först målar klart sitt mönster vinner.
Spel befäster elevernas kunskaper på ett roligt och lärorikt sätt. Syftet
förståelsen för mönster inom matematiken. Spelplanen




s. 110
Visa eleverna att varje sudoku består av fyra rader och fyra kolumner samt att det är indelat i fyra ”lådor”. Varje rad, kolumn och ”låda” ska innehålla en rektangel, en kvadrat, en cirkel och en triangel.
s. 111
FÖRENKLA uppgift 2 genom att berätta för eleverna att de behöver samla information från hela mönstret för att lista ut mönsterdelen.
Skriv ut Kop.underlag Uppgifter på HÖG NIVÅ från Dig,lärarmaterial .

Hästens systematik, historia och familj
Hästen tillhör understammen ryggradsdjur, klassen däggdjur, ordningen uddatåiga hovdjur, familjen hästdjur och släkten hästar. Tamhästen är en underart av arten vildhästar. Det finns flera hundra olika hästraser i världen.
När isen drog sig tillbaka efter den senaste istiden, och gräs började växa i Europa, spred sig stora vildhästhjordar över landskapet. För stenåldersmänniskorna blev köttet en viktig näringskälla. Skinnet användes till kläder. Efter hand började hästarna användas som riddjur och dragdjur. Det arabiska fullblodet räknas som den absolut äldsta hästrasen som framavlats av människan.
Hästhanen kallas ”hingst”. Honan kallas ”sto” och ungen ”föl”. En kastrerad hingst kallas ”valack”.
Hur ser hästen ut?
Hästens storlek varierar mycket med ras och även mellan olika individer inom varje ras. Den lilla hästrasen Falabellan har en mankhöjd som är cirka en halv meter och vikt på ca 45 kg i vuxen ålder medan Shirehästen kan bli mer än 2 meter i mankhöjd och väga drygt 900 kg. Hästar med mankhöjd upp till 148 cm räknas som ponnyer, medan hästar över 148 cm räknas som stora hästar.
Alla hästar har en päls med en grundfärg: fux, svart eller brun. Dessa grundfärger kan sedan ändras något av olika anlag. Ett ärftligt anlag är skimmel. Skimmelhästar föds vanligtvis med en mörkare färg, som svart, brun eller fux, men deras hår ersätts gradvis med vita hårstrån.
Hästen har längre skyddshår på nacken, en så kallad man, och på svansen. Svansens långa hårstrån börjar vid roten och fortsätter till svansens spets, vilket skiljer sig från många andra djur där det längre håret främst sitter vid svansens slut som en tofs. Både svansen och manen används till att vifta bort flugor.
Hästens hovar växer hela tiden och behöver därför verkas av en hovslagare. Då tas gammalt material bort från hovarna och de jämnas till. Hästar som rids på hårt underlag behöver oftast skor för att inte hovarna ska slitas för mycket. Skorna spikas fast. Spikarna kallas sömmar. Skorna behöver bytas ungefär var åttonde vecka.
Vad äter hästen?
Hästen äter gräs i fritt tillstånd. Den äter under större delen av dygnet, och utan längre uppehåll än 3–4 timmar. Uppstallade hästar måste utfodras regelbundet med rätt och lagom mängd foder vid varje tillfälle. Under vintern, då det inte finns färskt gräs, måste hästen fodras med skördat gräs i stället, hö
eller inplastat vallfoder (hösilage eller ensilage). Dessutom behöver den fri tillgång till rent sötvatten.


Hästens sinnen och kommunikation
Hästen har samma förmåga att tolka sinnesintryck (ljud, syn, smak, doft och känsel) som människan, men de har en starkare instinkt att reagera kraftigt på oväntade stimuli, som t.ex. ljud eller rörelser, något som härstammar från deras vilda förfäder. Inom flocken sover oftast hästarna liggande, men minst en av hästarna är vaken och står upp för att hålla vakt. Hästen vill leva tillsammans med andra hästar, och i frihet lever de i flock. I fångenskap finns det en lag på att man måste ha minst två hästar på gården. Ett väldigt viktigt sätt för hästar att kommunicera med varandra är genom öronrörelser. Genom att spetsa öronen framåt, visar hästen att den är glad och nyfiken. Om hästen i stället är arg eller irriterad, lägger den öronen bakåt. Hästar kommunicerar också genom ansiktsuttryck och ljud. Att gnägga är hästens sätt att ropa på andra hästar som inte syns till. Ofta svarar de andra hästarna genom att helt enkelt gnägga tillbaka.
Hästens ungar
Hästen är dräktig i 11 månader ± 1 månad. Nästan omedelbart efter fölningen kan friska föl både stå och springa, även om de är lite ostadiga. Detta är en anpassning för att öka fölets chanser till överlevnad mot rovdjur. Föl föds utan immunförsvar och blir lätt sjuka om de inte snabbt får i sig stoets råmjölk, som är rik på antikroppar. De behöver också mjölkens livsviktiga energiinnehåll för att kunna hålla värmen och orka röra sig. I vilt tillstånd diar fölet i ca 8–10 månader. Vid cirka 10 dagars ålder får fölet tänder vilket gör att det kan börja smaka på hö och gräs redan de första veckorna.
MER ATT VETA!
Som både drag- och riddjur har hästen varit, och är på vissa platser fortfarande, ovärderlig för kommunikationer över långa avstånd. I krig var hästen också länge krigarens bästa vapen. Som draghäst har den varit bondens hjälp vid plöjning av åkern och timmersläpning i skogen.
I dagens moderna samhällen tillgodoser hästen människors behov av meningsfulla relationer, fritidsaktiviteter och sport.



















Talrader och tallinjer 0–10, 0–20
Vändbara cirklar
Talkort 0–12
Uppdelningsmodellen
Representationer av antal 1/2
Representationer av antal 2/2
talet 4
talet 5
Taltrappa 0–5
Geometrisk formjakt
Gugge visar > , < och =
Programmering – Pilkommandon
Programmering – Rörelser med kroppen
Skillnad i antal
Balansvågen – Likhetstecknets betydese
Djurfamilj – Ankorna
– Hästarna
– Fåren
Djurfamilj – Katterna
Djurfamilj – Grisarna
Djurfamilj – Hundarna
Djurfamilj – Hönsen
Djurfamilj – Kaninerna
Djurfamilj – Mössen
Djurfamilj – Korna
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20




Vik längs linjen. Klistra ihop cirklarna två och två. Klipp ut och laminera.
Laminera och klipp ut två uppsättningar talblock till varje elev. Förvara t.ex. i kuvert eller myntask.




5 9 < 6 10 = 7 11 > 1 2 3 0 4 8 12
Kopiera gärna i A3-format. Läs beskrivning på s. 41.


triangel
rektangel



















































































Mattekojan Förskoleklass lägger vikten vid lekfullhet och förståelse och utgår från Skolverkets Hitta matematiken. Vartannat kapitel bearbetar Taluppfattning Mellankapitlen behandlar övriga matematiska områden.
DIDAKTIK
Var i kunskapsutvecklingen befinner sig eleverna? Hur ska du göra för att lyfta var och en på sin nivå? Stärk din lärarroll med konkreta tips och aktiviteter för individualisering, arbete i klass samt med stationsmatematik.
ARBETET MED ELEVBOKEN
• Engagera eleverna med sagan om grodan Gugge till varje kapitel.
• Lek fram matematiken med lättarbetade laborativa aktiviteter.
• Grundlägg förståelsen med matematiska samtal.
• Bygg upp elevernas viktiga, inre matematiska bilder.
• Se vad du bör OBSERVERA , kända MISSUPPFATTNINGAR och hur du kan FÖRENKLA och UTMANA
Låt eleverna hjälpa Gugge med uppgifter kopplade till målen via sagans digitala bildspel.
KOPIERINGSUNDERLAG
Tallinjer, talblock, bilder på Gugge och djuren, uppdelningsmodell med mera. Fler kopieringsunderlag finns i det digitala lärarmaterialet, bl.a. kartan över bondgården, planscher och underlag till stationsmatematik.
UNIKT FÖR MATTEKOJAN
Integrera NO, Svenska och Bild i undervisningen. Läs om djuren med Mattekojans fakta. Skriv gemensamma texter i klassen. Kopiera bilder på djuren och maten de äter. Låt eleverna färglägga, klippa, klistra och skapa egna böcker om ett nytt djur för varje kapitel.
Sofie Olsson är aktiv lärare med många års erfarenhet av undervisning. Hon är även specialpedagog och känd för sin populära blogg Mattefixaren.
