RIK MATEMATIK FKB
LÄRARPAKET
Tryckt bok + Digital lärarlicens 36 mån

LÄS OCH PROVA
LÄRARPAKETETS
SAMTLIGA DELAR

Tryckt bok + Digital lärarlicens 36 mån


LÄS OCH PROVA
LÄRARPAKETETS
SAMTLIGA DELAR
Rik matematik är utvecklat för en undervisning där både elever och lärare är aktiva. Eleverna får resonera, diskutera och lösa problem, och utveckla en djupare förståelse för matematik.

LÄRARHANDLEDNING
I lärarhandledningen får du det stöd och de resurser du behöver för att planera och genomföra din undervisning. Det finns mer än 80 detaljerade lektionsförslag per läsår, som ger konkret stöd och tips på saker att betona, frågor att ställa och exempel att visa. Bildspelen, som hör till varje lektion, fungerar som ett stöd genom hela lektionen, både visuellt för att fånga elevernas uppmärksamhet och för att tydliggöra matematiken med pedagogiska animeringar och bilder.
I lärarhandledningen finns även avslutslappar, extra övningsblad m.m.
Det digitala lärarmaterialet är ett komplement till den trycka lärarhandledningen. Här finns alla digitala resurser samlade, samt kom igång-hjälp och annat stöd som du kan behöva.
Interaktiv version av lärarmaterialet, i vilken det går att söka, stryka under, anteckna och länka.
Fungerar på dator och surfplatta.



Andreas Ryve
Manuel Tenser
Patrik Gustafsson
Hillevi Gavel
Fredrik Blomqvist
Studentlitteratur AB
Box 141
221 00 LUND
Besöksadress: Åkergränden 1
Telefon 046-31 20 00 studentlitteratur.se
Kopieringsförbud
Detta verk är skyddat av upphovsrättslagen. Kopiering, utöver lärares begränsade rätt att kopiera för undervisningsbruk enligt Bonus Copyright Access skolkopieringsavtal, är förbjuden. Kopieringsunderlag får dock kopieras under förutsättning att kopiorna delas ut endast i den egna undervisningsgruppen. För information om avtalet hänvisas till utbildningsanordnarens huvudman eller Bonus Copyright Access.
Vid utgivning av detta verk som e-bok, är e-boken kopieringsskyddad.
Användning av detta verk för text- och datautvinningsändamål medges ej.
Den som bryter mot lagen om upphovsrätt kan åtalas av allmän åklagare och dömas till böter eller fängelse i upp till två år samt bli skyldig att erlägga ersättning till upphovsman eller rättsinnehavare.
Studentlitteraturs trycksaker är miljöanpassade, både när det gäller papper och tryckprocess.
Art.nr 46119
ISBN 978-91-44-19822-4
Upplaga 2:1
© Andreas Ryve, Rik matematik AB och Studentlitteratur 2025 © Manuel Tenser, Patrik Gustafsson, Hillevi Gavel, Fredrik Blomqvist, Rik matematik AB och Bonnierförlagen Lära 2021
Illustrationer: Jessica Svendeborn (uggla och barn), Sinnebild (alla saker och ting, förutom sol: Kolonko/Shutterstock, jordklot: LuckyVector/Shutterstock, pannkaka: NEOS1AM/Shutterstock, choklad: Paket/Shutterstock, väckarklocka: Amankris/Shutterstock, digital väckarklocka: Tatiana Popova/ Shutterstock, väggklocka: AVS-Images/Shutterstock, armbandsur: Olga Popova/Shutterstock)
Formgivare inlaga: Frangkle, Marit Messing, Go Form AB
Formgivare omslag: Marit Messing, Go Form AB
Redaktion: Mattias Ljung och Eva Skarp
Produktionsledare: Merete Lind
Printed by Eurographic Group, Poland 2025

Med Rik matematik f-klass får du som lärare ett bra stöd i att lära eleverna grundläggande matematik, samtidigt som du förbereder dem för matematikundervisningen i högre årskurser. Läromedlet ger dig stöd att bedriva en rik och varierad undervisning där eleverna får resonera, lösa problem, diskutera, tänka och räkna. På så sätt utvecklar de förståelse för matematiken samtidigt som de lär sig att räkna. Vi kallar det rik matematikundervisning.
Rik matematikundervisning är en förståelseorienterad undervisning där elever na utvecklar förståelse för matematiska begrepp i samspel med dig som lärare, och i samspel med sina klasskamrater, innan de färdighetstränar i boken för att befästa det som de har lärt sig. I rik matematikundervisning håller du som lärare ihop klassen kring samma matematiska innehåll för att kunna ha ett levande matematiskt samtal i klassrummet, samtidigt som du kan utmana elever på olika nivåer vid behov.
Lärarhandledningen har därför många detaljerade lektionsförslag med bildspel till varje lektion som hjälper dig att visualisera, förklara, utmana och resonera med eleverna om den matematik ni arbetar med. Elevboken är full av uppgifter och problem så att eleverna kan färdighetsträna. På lärarwebben finns resurser, såsom extra färdighetsträning, avslutslappar, diagnoser och kopieringsunderlag av olika slag som du kan skriva ut vid behov.
Välkommen till Rik matematik!
Så här fungerar Rik matematik f-klass
Områden och lektionsserier
Rik matematik f-klass är uppdelat i områden. Varje område fokuserar på olika delar av matematiken, såsom taluppfattning, mönster eller geometri. Varje område inleds med en områdesintroduktion, där vi går igenom vad det är för matematik som området handlar om och hur undervisningen i området är upplagd. Det är alltid bra att läsa områdesintroduktionen när ni ska börja arbeta med ett nytt område.
Ett område består av ett antal lektionsserier. En lektionsserie består av fyra detaljerade lektionsförslag, och till varje lektion finns ett färdigt bildspel. Bildspelet laddar du ned från lärarwebben där du också kan ladda ner och skriva ut andra resurser, såsom material för extra färdighetsträning och ”avslutslappar”.
En lektionsseries uppbyggnad
Varje lektionsserie har ett antal lärandemål som visar vad eleverna ska lära sig under arbetet med lektionsserien. Lärandemålen hjälper dig som lärare att planera och genomföra undervisningen, baserat på lektionsförslagen.
En lektionsserie består alltså av fyra lektionsförslag med bildspel. I den första lektionen introduceras det nya matematiska innehållet som eleverna ska arbeta med och lära sig under lektionsserien. Bildspelet ger dig som lärare stöd att visualisera, förklara och diskutera den matematik som är i fokus. I den andra och tredje lektionen får eleverna öva, ofta genom lek eller spel och genom att arbeta i elevboken. I den fjärde och sista lektionen i lektionsserien sammanfattas de viktigaste lärdomarna, och eleverna repeterar och tilllämpar dem. Här får eleverna också göra avslutslappen som ger dig stöd att bedöma elevernas kunskaper.
Lektionsförslagen och undervisningen
Lektionsförslagen ger en detaljerad bild av hur du med hjälp av bildspelet skulle kunna hålla lektionen. Tänk på att det är ett förslag, inte ett manus som du ska försöka memorera och följa till punkt och pricka.
När du har en tydlig bild av lektionen använder du bildspelet som stöd för att visualisera och förklara matematiken, men också som stöd för att du själv ska komma ihåg lektionen på ett ungefär. Det räcker för att du ska lyckas med undervisningen, så länge du har fokus på lärandemålen och använder bildspelet som stöd. En lektion blir aldrig precis så som man har tänkt sig, så var därför beredd att göra anpassningar vid behov för att ge eleverna så goda förutsättningar som möjligt för att nå lärandemålen.
I lektionsförslagen får du också konkreta uppslag på hur du kan förklara saker, frågor du kan ställa, exempel du kan visa och så vidare. Du kan ha lärarhandledningen liggandes uppslagen på katedern så att du kan snegla på lektionsförslaget under lektionen.
Lektionernas struktur
Alla lektioner har samma struktur. De inleds alltid med en uppstartsfas. Här repeterar ni det viktigaste i föregående lektion innan eleverna får möta innehållet i den nya lektionen, ofta genom en lärarledd genomgång med stöd av bildspelet.
I aktivitetsfasen sker huvudparten av lektionsarbetet. Arbetet är varierande med många olika typer av aktiviteter. Ofta har de inslag av att eleverna diskuterar och resonerar, räknar och löser problem, ofta i grupp eller i par. Här har du som lärare en viktig roll i att utmana elever, ställa frågor för att stimulera tänkande och diskussion, fånga upp och bygga vidare på elevernas egna tankar och styra mot det som eleverna ska lära sig.
I avslutsfasen sammanfattar du lektionen tillsammans med eleverna och lyfter upp det mest centrala som ni har arbetat med och lärt er.
Uppmärksamma och stötta
Sista sidan i varje lektionsserie ger dig tips och råd kring vanliga missuppfattningar och fel under rubriken Uppmärksamma och stötta. Läs detta innan ni börjar arbeta med en lektionsserie, så att du är beredd att hjälpa eleverna när du märker att de har en vanlig missuppfattning, eller gör ett klassiskt fel. Här finns också tips på hur du kan förenkla uppgifter för elever som har det behovet – eller utmana mer för de elever som behöver det.
Avslutslapparna
Varje lektionsserie avslutas med att eleverna gör en avslutslapp. Den innehåller ett litet antal noggrant uttänkta uppgifter som gör att du snabbt och enkelt kan bedöma om eleverna har nått lärandemålen. Du ser också om det är något som många i klassen har svårt för och som du behöver undervisa mer om, eller om det finns elever i klassen som behöver arbeta extra med något.
Lärartaktiker
I de detaljerade lektionsförslagen använder vi vissa nyckelord för att på ett mer effektivt sätt kommunicera instruktioner till dig. Ett sådant nyckelord kan vara återge, och det ser då ut så här: ÅTERGE
Nyckelorden är namn på olika lärartaktiker. En lärartaktik är något du kan göra för att åstadkomma ett visst resultat. Om det t.ex. står att du ska låta någon återge så betyder det att en elev ska återge vad någon annan elev just sagt, fast med egna ord. Återge är en lärartaktik som du kan använda för att signalera att det som sades är viktigt.
På lärarwebben hittar du ett ramverk med förklaringar av alla lärartaktiker.
Klassrumsnormer och Professor Uggla
Rik matematikundervisning ställer höga krav på ett gott klassrumsklimat. Det är därför viktigt att du arbetar systematiskt och enträget med att skapa bra normer i klassrummet så att eleverna vågar berätta vad de tänker, är tysta och lyssnar när någon annan har ordet, och så vidare. Vi kallar detta rika klassrumsnormer
Karaktären Professor Uggla kommer att dyka upp då och då i bildspelet och hjälpa till. Uggla kommer bland annat att förklara att en matematiker är en person som arbetar med matematik, och på matematiklektionerna så är eleverna matematiker. Professor Uggla kommer att berätta om hur matematiker tänker och arbetar, vilka regler de har att följa i matematikarbetet och varför det är viktigt att följa reglerna.
Läs mer om rika klassrumsnormer i ramverket för normer som finns på lärarwebben.
Konkret material
Ni kommer ofta att arbeta med konkret material i lektionerna. På lektionsseriernas förstasidor kan du alltid se vilket material som behövs till varje lektion. Ibland är det något som du kan skriva ut ifrån lärarwebben, ibland är det konkret material som du behöver ordna med själv, som kuber eller andra typer av plockisar.
På lärarwebben hittar du en sammanställning av vilka olika typer av material som behövs.
Förstå läromedlets grundtankar
Det är viktigt att förstå grundtankarna med det läromedel man använder. Rik matematik är designat för att ge dig stöd att bedriva rik matematikundervisning. I rik matematikundervisning ligger tyngdpunkten på att eleverna lär och utvecklas i samspel med läraren och med varandra, under lärarledd undervisning. När de arbetar i boken färdighetstränar de primärt för att befästa kunskaper och förståelse som de redan har utvecklat under den lärarledda undervisningen.
Om du tidigare har arbetat med ett läromedel där tyngdpunkten ligger vid att eleverna lär sig genom att arbeta var för sig i elevboken så kommer du förmodligen uppleva att det är väldigt annorlunda att arbeta med Rik matematik. Du får vara beredd på att delar av arbetssättet kommer att kännas lite ovana, och att du måste ge dig själv tid för att komma in i det delvis nya arbetssättet. Tänk då också på att det är vanligt att man har föreställningar, normer, rutiner och vanor som ibland kan vara ett hinder för att utveckla sin undervisning. Ta dig an Rik matematik med lite tålamod och ett öppet sinne.
Lärarens viktiga roll
I rik matematikundervisning har du som lärare en central roll för elevernas kunskapsutveckling, inte minst genom lärarledd undervisning. Du planerar undervisningen, baserat på lektionsförslagen och bildspelen, och undervisar genom att visa och förklara, utmana och ställa frågor, leda matematiska samtal och diskussioner, summera och synliggöra viktiga samband, bedöma och uppmuntra, skapa struktur och normer. Allt detta är lättare sagt än gjort, men Rik matematik är utvecklat av forskare och lärare för att ge dig förutsättningar att lyckas med det.
Lektionsförslag, inte manus
Se lektionsförslagen som just förslag, inte som manus som du ska försöka memorera och följa till punkt och pricka. Det är inte tanken, och det är heller inte möjligt. Utgå istället ifrån lärandemålen, läs lektionsförslagen för att få en god bild av lektionen och använd bildspelen som stöd för minnet när du undervisar. Gör anpassningar av lektionen vid behov, både innan och under pågående lektion, utifrån just din klass och dina elever, och styr mot den matematik som de ska lära sig.
Målfokus istället för sidfokus
I arbetet med Rik matematik är det viktigt att ha fokus på vad eleverna ska lära sig istället för hur långt de har kommit i elevboken. Det är viktigt att ha målfokus istället för ”sidfokus”. Alla elever behöver inte göra alla uppgifter, och det är viktigt att eleverna inte tror
att matematik handlar om att räkna så mycket som möjligt på så kort tid som möjligt. Matematikämnet handlar om mer än så. Eleverna ska inte bara lära sig att räkna, de ska också utveckla förståelse för matematiken så att de kan använda den i olika sammanhang.
Elevboken
Det är en vanlig missuppfattning att alla elever måste göra alla uppgifter i elevboken, under eller efter lektionen. Det är inte nödvändigt. Det räcker oftast att ha som ambition att alla gör de första grundläggande uppgifterna. Om du då har elever som är snabba går de vidare till extrauppgifterna och de mer utmanande uppgifterna. Om du bedömer att en elev har nått lärandemålen med en lektionsserie så spelar det ingen roll om eleven endast gjort uppgifter på grundläggande nivå.
När snabba elever räcker upp handen och anser sig klara med alla uppgifter måste du också kontrollera om de verkligen har löst uppgifterna med tillräcklig noggrannhet. Utmana dem att vara noggranna istället för snabba genom att låta dem göra om slarvigt eller felaktigt utförda uppgifter och uppmana dem att i fortsättningen vara noggranna från början.
Ta vara på spontana tillfällen till lärande
I vardagen dyker många tillfällen till lärande upp då du kan passa på att knyta an till matematik som ni har arbetat med tidigare eller håller på med just nu. Det kan vara när ni står i kö i matsalen, och t.ex. kan arbeta med skillnaden mellan antal och ordningstal. Det kan vara när ni ser föremål eller former som ni kan resonera om utifrån ett geometriskt perspektiv.
Arbeta långsiktigt och med tålamod
Arbeta med tålamod och långsiktighet. Stressa inte upp dig om arbetet med läromedlet inte fungerar perfekt direkt. Rik matematikundervisning är mer utmanande än att låta eleverna sitta och räkna var för sig i boken större delen av tiden. I takt med att ni – du och eleverna – lär er hur Rik matematik fungerar och kommer in i arbetssättet så kommer det att gå lättare. Ta hjälp av det stöd som finns på lärarwebben och hos Rik matematikkollegor för att snabbare komma in i arbetssättet. Skriv till oss på Rik matematik-sidan på Facebook om du behöver råd och stöd.
Problemlösning
I Rik matematik förskoleklass B kommer problemlösning att vara ett återkommande inslag. Ett problem i undervisningssammanhang är en uppgift som eleven på förhand inte vet hur hen ska kunna lösa. Det är också själva poängen, och det är därför viktigt att du som lärare stöttar eleverna att själva komma på ett sätt utan att du avslöjar eller undervisar dem om hur de kan göra och tänka för att lösa uppgiften. Tänk på att ett problem inte nödvändigtvis behöver vara så stort och omfattande. Det måste inte ta en hel lektion i anspråk, och särskilt här i förskoleklass kommer eleverna att lösa flera mindre problem av samma typ under en och samma lektion.
Syftet med problemlösningen och lärarens agerande Det finns flera syften med att arbeta med problemlösning. Ett syfte är så klart att utveckla elevernas problemlösningsförmåga. Problemlösning, särskilt i förskoleklass, handlar mycket om att du som lärare ska arbeta med att utveckla rätt mindset hos eleverna: att våga vara osäker, att se fel och misslyckade lösningar som något naturligt på vägen till kunskap och som en källa till lärande, att acceptera att man inte direkt vet hur man ska göra och att man ibland måste tänka ut det själv, att ha tålamod i sådana situationer, att orka anstränga sig för att testa och resonera sig fram, och slutligen att lita på sin egen förmåga.
I åk 1–3 blir problemen lite mer omfattande. Då kommer eleverna få lära sig professor Ugglas metod för problemlösning, ALP, som hjälper dem att mer strukturerat och systematiskt arbeta med problemlösning.
Ett annat viktigt syfte med problemlösning är att eleverna själva ska få undersöka, upptäcka och förstå särskilt viktiga aspekter av matematiken. När det gäller vissa centrala delar av matematiken så är det gynnsamt om eleverna själva får utforska, komma till insikter och utveckla förståelse. Det innebär emellertid inte att du ska vara passiv. Du styr i bakgrunden och stöttar genom att ställa öppnar frågor vid behov, utan att för den sakens skull avslöja hur man kan göra eller tänka.
Problemlösning fungerar också som variation till majoriteten av undervisningen där du som lärare på förhand visar och förklarar hur man kan göra och hur man kan förstå ett matematiskt begrepp.
Var alltså uppmärksam i lektionsförslagen på om en föreslagen undervisningssituation bygger på problemlösning och anpassa då ditt agerande till det.
Den matematiska diskussionen är avgörande En mycket viktig del av att undervisa genom problemlösning är den avslutande helklassdiskussionen. Där leder du som lärare diskussionen, men du försöker få eleverna att själva förklara de viktiga matematiska idéer som problemet har syftat till att eleverna ska upptäcka. Utan en sådan matematisk diskussion, eller om diskussionen snarare är en klassisk redovisning där alla bara visar och berättar hur de har gjort utan att läraren styr diskussionen mot den matematik de ska lära sig, riskerar problemlösningen att bli ett självändamål. En riktig matematisk diskussion där alla elever är delaktiga ger dig ett ypperligt tillfälle att bedöma elevernas kunskaper och att få syn på eventuella missuppfattningar. Tänk på att det inte innebär att alla eller ens en majoritet av eleverna pratar under varje diskussion. Däremot är det viktigt att alla lyssnar aktivt Arbeta gärna in JAG MED -tecknet. Med det kan alla som inte har ordet visa att de håller med eller har tänkt eller gjort likadant (eller motsatt, om de inte gör JAG MED tecknet). På så vis kan också de som inte pratar känna att de faktiskt är med i diskussionen och att du ser dem.
Eftersom diskussionerna alltid syftar till att eleverna ska förstå något är din uppgift att leda diskussionerna mot det målet på det sätt som du bedömer bäst i varje given situation. Ofta är det därför lämpligt att du redan innan diskussionen bestämmer dig för vilka elever, par eller grupper du tänker ge ordet, åtminstone i början av diskussionen, så att du ska kunna göra just den poäng som du vill göra. Över tid är det så klart viktigt att försöka få till en någorlunda jämn fördelning så att det inte alltid är samma elever som pratar, men det gäller inte i enskilda lektionsserier eller områden. Aktivera alla elever i alla diskussioner med JAG MED -tecknet, och variera med att då och då fråga elever som inte gör JAG MED -tecknet varför de inte håller med och om de kan berätta hur de har tänkt eller gjort annorlunda.
Det digitala stöd som hör till lärarhandledningen finns i din digitala lärarresurs. Lärarresursen når du via licensen som du får när du köper lärarhandledningen. Inloggning sker på sidan "Min bokhylla" som finns på studentlitteratur.se.
För att visa bildspelen (ppt) som inleder varje lektion, laddar du först ner dem till din dator och öppnar sedan upp dem med Powerpoint.
Bildspelen är ofta animerade. Se till att starta bildspelen så att du får en verklig bild av hur de ser ut.
Om din skola inte har en installerad version av Powerpoint kan du använda den webbaserade gratisversionen av Powerpoint.
Om du arbetar med en Chromebook kan du se filmen nedan för att lära dig om hur du då startar upp bildspelen.
Så här fungerar bildspelen i Rik matematik
Så här fungerar de webbaserade bildspelen i Rik matematik
Så här fungerar Rik matematiks bildspel med Chromebook
Ikonerna visar vilken/vilka förmågor som lektionen direkt utvecklar.
Begreppsförmåga
Kommunikationsförmåga
Metodförmåga
Problemlösningsförmåga
Resonemangsförmåga
Dessa ikoner visar i vilken konstellation en aktivitet är tänkt att genomföras i.
Undervisning under lärarens ledning
Enskilt arbete
Enskilt arbete i elevboken
Arbete i par
Arbete/diskussioner i grupp
Här kommer du direkt till bildspelet.
Ljudfil i bildspelet
Visar att det finns en särskild funktion i bildspelet och att läraren måste klicka på ett särskilt sätt för att använda funktionen.
Stanna upp innan du klickar fram svaret. Fråga hur ni kan göra.
BETÄNKETID
Film
Dokumentet kan laddas ner.
Referat av det som sägs av berättarrösten
Extra information

Guldkantslektion
RIK MATEMATIK F-klass B består av fem områden. Varje område innehåller ett antal lektionsserier. En lektionsserie består av fyra lektioner.
I område 5, Talen 1–5:s egenskaper, får eleverna lära sig mer om tal och utveckla sin taluppfattning. Det handlar framför allt om att tal kan delas upp i två nya tal och att två tal kan sättas ihop till ett nytt tal. I område 5 arbetar ni fokuserat med talet 1–5. I område 7 är fokus på talen 6–10.
I område 6, Längd, mätning och tid, får eleverna utveckla sin förståelse för vad storheten längd är och hur man kan mäta längd. Det utvecklar samtidigt deras taluppfattning eftersom de genom mätetalen kommer att få koppla ihop mätning med tal. De kommer också att få lära sig om storheten tid, våra vanligaste tidsenheter och klockan.
I område 7, Talen 6–10:s egenskaper, fortsätter arbetet ifrån område 5 med att utveckla elevernas taluppfattning, nu med fokus på talen 6–10.
I område 8, Geometri, får eleverna börja utveckla sitt grundläggande geometriska tänkande. De kommer att få undersöka, sortera och beskriva de vanligaste geometriska figurerna och kropparna utifrån egenskaper som form, antal hörn, och så vidare.
Eleverna kommer också att få lära sig de vanligaste lägesorden och riktningsorden.
I område 9, Dubbelt och hälften, får eleverna arbeta med bråk och multiplikativa relationer för första gången, även om vi inte använder just de orden. Eleverna får upptäcka att om man tar ett antal två gånger så är det dubbelt så många som det ursprungliga antalet. De får också lära sig att dubbelt och hälften är varandras motsatser: om t.ex. åtta är dubbelt så många som fyra så är fyra samtidigt hälften så många som åtta.
Eleverna får dessutom upptäcka att om man delar något i två lika stora delar så är delarna halvor, eftersom en halv är en del som är hälften så stor som den hela.
Område 5: Talen 1–5:s egenskaper
15: Längd
Ls 16: Mäta längd med föremål
17: Tid
Område 7: Talen 6–10:s egenskaper
18: Talet 10
23: Geometriska kroppar
Område 9: Dubbelt och hälften
Ls 24: Dubbelt och hälften så många
Ls 25: Halv – hälften av en hel
Talen 1–5:s egenskaper

I område 5 får eleverna lära sig mer om tal, hur de kan sättas ihop och delas upp, med särskild fokus på talen 1–5. I Område 7 fortsätter detta arbete med talen 6–10.
Sammanfattning av området
I områdets första lektionsserie får eleverna arbeta specifikt med talet 5 och upptäcka hur man kan dela upp talet 5 på flera olika sätt och sätta ihop talet 5 av andra tal på flera olika sätt. På så sätt börjar eleverna utveckla förståelse för tal som en kombination av delar, där talet 5 har en särskilt viktig roll som ankartal. När eleverna ska lära sig om andra tal underlättar det om de är väl förtrogna med talet 5 och kan sätta andra tal i relation till talet 5.
Den andra lektionsserien i området, lektionsserie 14, är uppbyggd på ungefär samma sätt med den skillnaden att fokus där ligger på talen 1–4.
Tals egenskaper – talen 1–5
När eleverna kan räkna antal är det viktigt att låta dem arbeta med och utforska tal för att de ska utveckla förståelse för tal, tals egenskaper och talens storlek i relation till varandra. Deras förståelse för talens egenskaper och storlek kommer hjälpa dem att gå från räkning av antal till att så småningom göra beräkningar med tal och lösa mer komplexa problem. Att eleverna utvecklar en grundläggande förståelse för tal och tals egenskaper är också viktiga förutsättningar för att de från åk 1 och framåt ska kunna utveckla hållbara räknestrategier och börja automatisera talkombinationer.
För att utveckla elevernas förståelse för talen 1–10, deras egenskaper och relativa storlek, så har undervisningen hittills fokuserat på talgrannar (vad 1 och 2 mer än/mindre än ett givet tal är) och ankartalen 5 och 10 (hur mycket mindre/större ett givet tal är än 5 och 10). I arbetet med det här området går undervisningen ett steg framåt och utvecklar elevernas förståelse för del-del-hel-relationer.
Del-del-hel-relationer
Undervisningen i område 5 syftar till att utveckla elevernas förståelse för del-del-hel-relationer: att kunna förstå tal som en kombination av två eller flera delar samt att kunna se tal som en sammansättning av andra tal. T.ex. kan talet 5 delas upp i bland annat 4 och 1, och 2 och 3 kan sättas samman till 5. I det här området fokuserar vi på talen 1–5. I område 7 kommer undervisningen att vara upplagd på ungefär samma sätt, men då med fokus på talen 6–10. Eleverna behöver denna förståelse för att kunna utveckla en god taluppfattning och längre fram lära sig effektiva räknestrategier för addition och subtraktion. En räknestrategi är ett sätt att tänka på för att t.ex. ta reda på vad summan av en viss addition är. Ett exempel är när eleverna i åk 1 ska lära sig addera vid tiotalsövergång. Då är det en bra strategi att använda sig av 10-kamrater och uppdelning av tal, och exempelvis tänka att 9 + 4 = 9 + 1 + 3 = 13.
Eleverna i förskoleklass kommer att få en rik och varierad undervisning för att utveckla förståelse för talens del-del-hel-relationer. I varje lektionsserie i område 5 och 7 får eleverna arbeta med del-del-hel-uppgifter som fokuserar på ett eller två specifika tal, och vi har valt att börja med talet 5. Eleverna får börja med att lösa ett problem som handlar om på hur många olika sätt fem saker kan delas upp i två grupper. Detta gör att eleverna får upptäcka talet 5:s del-del-hel-relationer. Eleverna kommer vidare att arbeta med plockisar för att dela upp ett specifikt tal i två delar, t.ex. dela upp fem objekt i en
grupp med tre och en grupp med två plockisar. Detta är en konkretisering av att 5 = 3 + 2. Eleverna får även öva på att med plockisar sätta ihop tal och t.ex se att tre och en plockisar tillsammans är fyra plockisar. Det är en konkret representation av att 3 + 1 = 4.
När eleverna arbetar med den här typen av uppgifter är det viktigt att du hjälper dem att se relationerna genom att säga saker som ”tre och två är fem tillsammans”, och dessutom uppmana dem att uttrycka sig på samma sätt. Ni kombinerar även detta med representationer i form av 10-rutor, bilder och siffror på ett sätt som visar på talens del-del-hel-relationer.
Saknad del-uppgifter
I slutet av varje lektionsserie i område 5 och 7 gör ni saknad del-uppgifter för att eleverna ska få tillämpa sina kunskaper om talens del-del-hel-relationer, som de har utvecklat för de olika tal som lektionsserierna behandlar. I t.ex. lektionsserie 13, Talet 5, gör ni övningen Hemliga facket med uppdelningsmaskinen: Du visar med bildspelet hur fem bollar rullar ned. Ett visst antal av bollarna hamnar i ett fack där man inte ser dem. Detta är det hemliga facket, ett fack där den "saknade delen" finns. Resten hamnar i ett fack där de är synliga. Genom att utgå ifrån hur många det var från början, fem stycken, och hur många som är i det genomskinliga facket får eleverna försöka resonera sig fram till hur många som finns i det hemliga facket.
Den här typen av saknad del-uppgifter gör också att du kan upptäcka elever som har svårt att automatisera talkombinationer, dvs. vilka tal som tillsammans är ett annat tal. Om en av fem bollar hamnar i det synliga facket och du i slutet av lektionsserien har elever som inte kan resonera sig fram till att det då måste ligga fyra stycken i det hemliga facket, så behöver du undersöka hur det kommer sig att de inte klarar detta. Eventuellt behöver du ge dem extra undervisning så att de får fler erfarenheter av att undersöka hur tal kan delas upp och sättas ihop.
I början kommer många elever använda en-till-enräkning för att lösa den här typen av uppgifter, men så småningom kommer de inte att behöva det längre; de kommer se att det saknas fyra bollar om det var fem från början och det är en boll i det synliga facket. Det kan vara ganska stora skillnader mellan elever när det gäller hur snabbt de utvecklar sina matematiska kunskaper, och det är därför är det viktigt att du har tålamod.
Områdets referenser
Clements, D. H., & Sarama, J. (2007). Early childhood mathematics learning. Second handbook of research on mathematics teaching and learning, 1, 461-555. Charlotte, NC: Information Age Publishing.
McIntosh, A. (2020). Förstå och använda tal: En handbok. Göteborg: Nationellt centrum för matematikutbildning.
Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2020). Elementary and middle school mathematics: Teaching Developmentally, Global Edition (uppl. 10). Pearson Education.
Område 5 | Talen 1–5:s egenskaper
Lektionsseriens syfte är att börja utveckla elevernas förståelse för tal som en kombination av delar, i den här lektionsserien med fokus på talet 5. Att kunna se tal som en sammansättning av andra tal är en mycket viktigt förutsättning för att kunna utveckla en god taluppfattning och effektiva räknestrategier. I nästa lektionsserie fortsätter vi med det detta, då med fokus på hur talen 1–4 kan ses som en kombination av delar
Lektionsseriens mål
• Eleven kan dela upp talet 5 i två tal på olika sätt och visar det genom att dela upp en grupp av fem plockisar i två nya grupper och t.ex. säga att 1 och 4 är 5.
• Eleven kan sätta samman talet 5 av två tal och visar det genom att bygga talet 5 med plockisar i två olika färger och t.ex. säga att 2 och 3 är 5
• Eleven kan uppfatta talet 5 som en sammansättning av två tal och visar det genom att identifiera den saknade delen om helheten 5 är känd och en del täcks över.
Matematiska begrepp: dela, vänster, höger
• Du repeterar hur man kan se antal i 5rutan.
• Högräkning 1–20 och 20–0.
• Eleverna arbetar i par med att komma på olika uppdelningar av fem fåglar i två grupper.
• Du leder en diskussion om hur man kan vara säker på det finns sex olika sätt och ställer frågor för att hjälpa eleverna att förklara: man placerar först alla fem i en ena gruppen och ingen i den andra, och sedan flyttar man över en i taget tills alla är i den andra gruppen.
SvA: trädgård, gräsmatta, dela upp, fack
Material och förberedelser:
Lektion 1: Ta fram fem plockisar till varje elevpar.
Lektion 2: Ta fram plockmaterial i två färger så att varje elevpar kan få fem plockisar av varje färg.
Lektion 3: Ha plockisar till hands.
Lektion 4: Skriv ut avslutslappar. Ta fram plockisar/ brickor som passar 5rutan i elevboken.
Avslutslapp – Lektionsserie 13
• Du repeterar hur man kan dela upp fem fåglar i två grupper på sex olika sätt och att man kan se det som att talet 5 kan delas upp i två delar.
• Du visar tre blå och två gröna cirklar i 5rutan och ni konstaterar att 3 och 2 är 5.
• Eleverna arbetar i par med att fylla 5rutan på olika sätt med plockisar i två färger. De tränar på att säga hur många det är av respektive färg och hur många det är tillsammans (fem).
• Du visar olika antal fingrar på en hand och eleverna tänker ut hur många fingrar som inte visas utifrån hur många som saknas för att det ska vara fem.
• Ni högräknar på följande sätt: Du ber en elev säga 1, nästa 2, och så vidare tills ni gått klassen runt. Då fortsätter ni flera varv uppåt i talområdet, eller vänder och räknar ned till 0.
• Du introducerar uppdelningsmaskinen genom att visa hur fem bollar delas upp i två grupper. Ni konstaterar att det ändå är fem bollar tillsammans.
• Du visar hur tre av fem bollar läggs i en låda. Ni konstaterar att det är två bollar utanför lådan, tre i och fem tillsammans.
• Eleverna arbetar i elevboken.
• Uppdelningsmaskinen delar upp fem bollar i en synlig och en dold grupp. Eleverna tänker ut det dolda antalet genom att tänka hur många som saknas för att det ska vara fem.
• Avslutslapp.



2 Repetition: Talet 5 5 min
Peka på 5rutan och säg: ”Man kan använda 5rutan för att lättare se hur många det är. Vi vet att den har plats för fem cirklar och därför vet vi att det är fem cirklar eftersom 5rutan är full. Vi behöver inte räkna.”
Klicka, och en cirkel försvinner. Fortsätt: ”Nu är det en cirkel färre än fem. Vi behöver inte räkna, för vi vet att det är fyra. Fyra är en färre en fem.”
Klicka, och fem cirklar visas igen. Repetera att talet 5 är ett speciellt tal för människan, bland annat eftersom människan har fem fingrar på varje hand. Återkoppla till tidigare lektionsserie när eleverna ritade exempel på talet 5 i vardagen. Låt några elever berätta vad de ritade. Ge några exempel på tillfällen då talet 5 dyker upp: skolveckan har fem dagar, 5krona, foten har fem tår, m.m.
Berätta att den här lektionsserien handlar om talet 5.
3 Högräkning
Högräkna upp till 20 och sedan nedåt från 20 till 0.
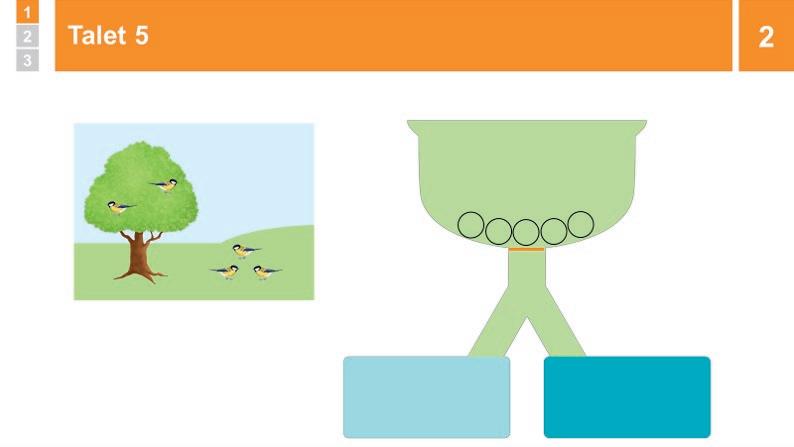
4 Parövning: Fåglar i trädgården 20 min
Berätta och visa: ”I en trädgård finns ett träd. Fem fåglar landar i trädgården. Några av fåglarna sätter sig i trädet och resten på gräsmattan. Hur många av de fem fåglarna kan det vara i trädet och hur många kan det vara på gräsmattan?”
Dela in eleverna i par, förse paren med fem plockisar vardera och låt dem slå upp sida 1 i elevboken. Säg att en plockis är en fågel och att paren ska sätta ut sina fem fåglar på valfritt sätt. Varje fågel måste landa antingen i trädet eller på gräsmattan. Påminn om att MATEMATIKER LYSSNAR, och låt dem börja när alla förstått.
CIRKULERA . Välj ut ett par.
5 Redovisning: Fåglar i trädgården
Låt det par du valt ut berätta eller visa på tavlan hur de har placerat sina fåglar. Fråga sedan om något annat par gjort på samma sätt. De kan i sådana fall svara med JAG MED
Låt ett par som gjort på ett annat sätt redovisa. Konstatera att det finns flera olika sätt som fem fåglar kan dela upp sig mellan trädet och gräsmattan.
6 Parövning: Dela upp på olika sätt
Säg: ”Vi har sett att de fem fåglarna kan placeras på olika sätt. Hur många som landar i trädet och på gräsmattan kan vara olika. Hur många olika sätt kan vi komma på? Nu ska ni försöka att ta reda på fler sätt som de fem fåglarna kan dela upp sig på mellan trädet och gräsmattan!”
Visa och förklara att det i elevboken finns små bilder med trädet och gräsmattan som paren ska använda för att dokumentera alla sätt de kommer på. Berätta att de ska rita enkla figurer istället för fåglar, som i exemplet i bildspelet.



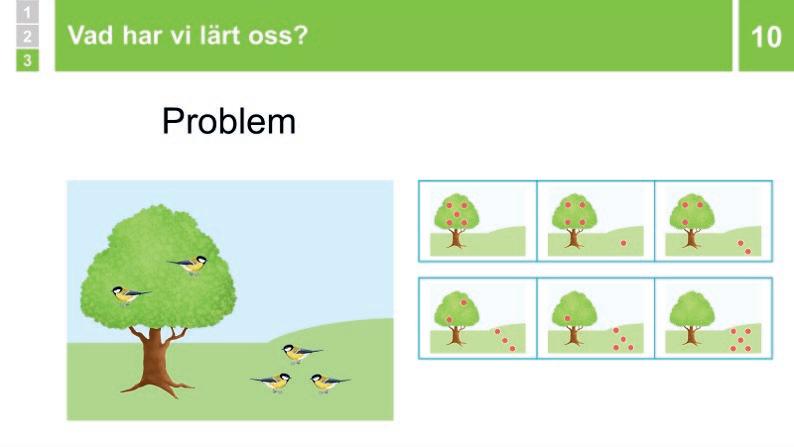
Låt paren börja när de har förstått. CIRKULERA och stötta med öppna frågor vid behov. Observera om det finns par som arbetar systematiskt, då du kan behöva bygga diskussionen i steg 8 på deras resonemang.
Om någon tror att det alltid måste finnas en fågel i antingen trädet eller gräsmattan kan du fråga: ”Kan alla fåglar sätta sig i trädet/på gräsmattan?”
Om elever säger att de är klara kan du fråga om de är säkra på att de hittat alla sätt, och hur de kan visa det för någon som inte gjort uppgiften förut.
7 Redovisning: Hur många olika sätt har vi hittat?
Repetera att paren arbetat för att försöka komma på hur många olika sätt som fem fåglar kan delas upp mellan trädet och gräsmattan. Påminn om JAG MED och be ett par visa/säga ett sätt. Låt sedan ett annat par visa/säga ett annat sätt. Fortsätt tills klassen inte kan komma på fler sätt.
8 Diskussion: Hur vet vi att det inte finns fler sätt?
Fråga: ”Hur vet vi att det inte finns fler sätt? Hur kan man göra för att vara säker på att man hittat alla sätt?” Låt paren SURRA en stund och led sedan en diskussion om detta. Låt elever komma fram och visa. Ställ frågor vid behov för att hjälpa klassen att förklara ungefär att man kan ta reda på det genom att först sätta alla fåglar i trädet och sedan flytta en fågel i taget till gräsmattan tills alla sitter där. Då finns det inget mer sätt som fåglarna kan delas upp på.
Visa i bildspelet och förklara: ”Om man först sätter alla fåglar i trädet så är det fem fåglar i trädet och noll fåglar på gräsmattan. Om man sedan flyttar en fågel till gräsmattan så är det fyra i trädet och en på gräsmattan.” Försök få eleverna att själva fortsätta resonemanget samtidigt som du visar i bildspelet, eller så förklarar du själv. Visa och konstatera att om man gör så här kan man vara säker på att det finns sex olika sätt att dela upp fem fåglar mellan trädet och gräsmattan.
9 Uggla: Mer om problem 5 min
Uggla berättar mer om vad ett problem är inom matematiken.
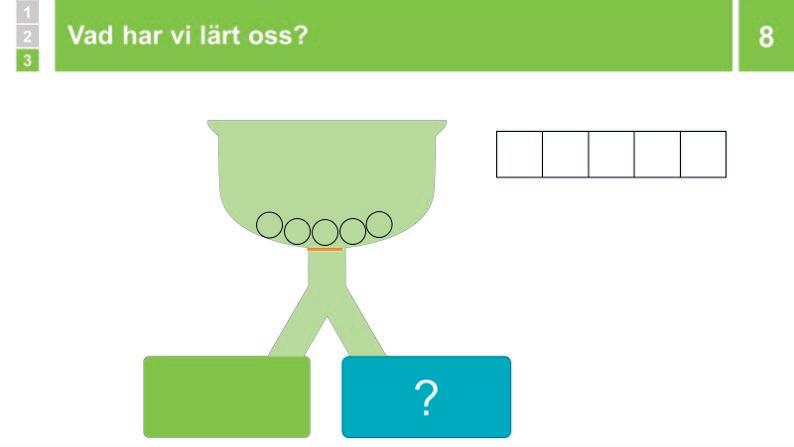
10 Sammanfattning: Vad har vi lärt oss? 5 min
Genom att först sätta alla fåglar i trädet och sedan flytta en i taget till gräsmattan tills alla sitter där istället, kunde vi vara säkra på att fem fåglar kan delas upp i två grupper på exakt sex olika sätt.
2 Repetition: Fåglar i trädgården 5 min
Påminn om förra lektionen. Säg: ”De fem fåglarna kan dela upp sig i två grupper. De kan sätta sig antingen i trädet eller på gräsmattan. På hur många på olika sätt kan de fem fåglarna delas upp i två grupper?” BETÄNKETID
Fördela ordet tills någon svarar ”sex”. Be hen förklara hur man kan vara säker på det. Visa och sammanfatta: ”Man placerar alla fåglar i trädet och flyttar sedan en i taget till gräsmattan. På så sätt kan man se att fem fåglar kan delas upp i två grupper på sex olika sätt. Man kan tänka på det som att talet 5 kan delas upp i två delar, t.ex. 3 och 2.”
3 Genomgång: Bygga 5 20 min
Klicka, och tre blå och två gröna cirklar placeras i 5rutan. Be någon räkna cirklarna, och konstatera att det är fem cirklar. Fråga: ”Hur många blå är det?” Konstatera att det är tre blå. Fråga: ”Hur många gröna är det?” Konstatera att det är två gröna. Fråga: ”Hur många är det tillsammans?” Konstatera: ”Det är fem tillsammans. 3 och 2 är 5.” Låt eleverna repetera.
4 Parövning: Bygga 5
Dela in eleverna i par. Förse paren med plockisar i två olika färger, fem i varje färg. Be eleverna slå upp sida 2 i elevboken och förklara övningen med hjälp av exemplet i bildspelet:
• En i paret fyller 5rutan med plockisar. Det kan vara en blandning av de två färgerna, och då ska de med samma färg ligga bredvid varandra, eller plockisar i en enda färg. I exemplet läggs en blå följt av fyra gröna.
• Den andra eleven säger antalen och hur många det är tillsammans, t.ex: ”1 och 4 är 5.”
Säg att de ska turas om att vara den som lägga plockisar. Låt eleverna börja när alla förstått. CIRKULERA
Var noggrann med att de säger delarna, antalet av respektive färg, innan de sedan säger helheten, alltså det totala antalet. Par som behöver utmanas kan arbeta med tre färger och t.ex. säga ”Två och två och ett är fem”.
5 Sammanfattning: Vad har vi lärt oss? 5 min
Sammanfatta: ”När 5rutan är full kan man säga att den visar talet 5. När man har fyllt 5rutan med plockisar kan man därför säga att man har byggt talet 5. I förra lektionen delade ni upp talet 5 på olika sätt. Nu har ni satt ihop talet 5 på olika sätt.
Klicka fram en ljusblå cirkel. Fråga: ”Hur många till behövs för att det ska vara fem?” BETÄNKETID . Låt någon svara. Konstatera: ”Det behövs fyra till för att det ska vara fem. 1 och 4 är 5.”

2 Repetition: Dela upp fem 5 min
Peka på lådan och bollarna. Konstatera att det är fem bollar. Klicka, och två bollar läggs ned i lådan. Säg att ni nu har delat upp de fem bollarna: några ligger i lådan och några ligger utanför lådan. Tillsammans är det fortfarande fem stycken.
Säg: ”Det är tre bollar utanför lådan. Hur många är det då inuti lådan, om det är fem bollar tillsammans?” BETÄNKETID . Låt någon svara, och konstatera att det är två bollar i lådan eftersom två och tre är fem tillsammans.

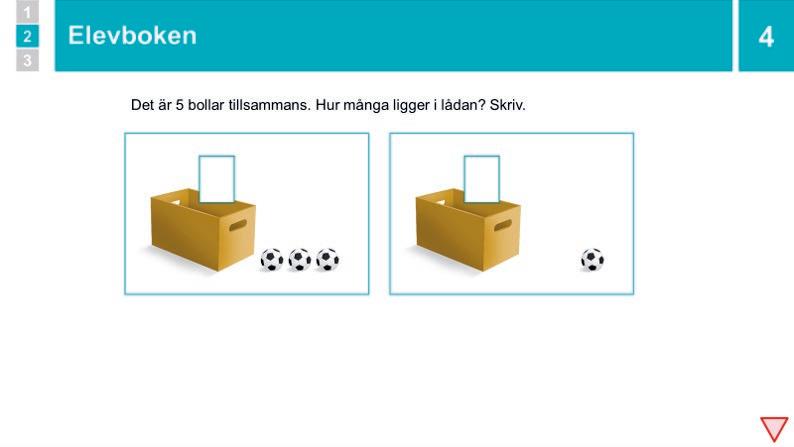
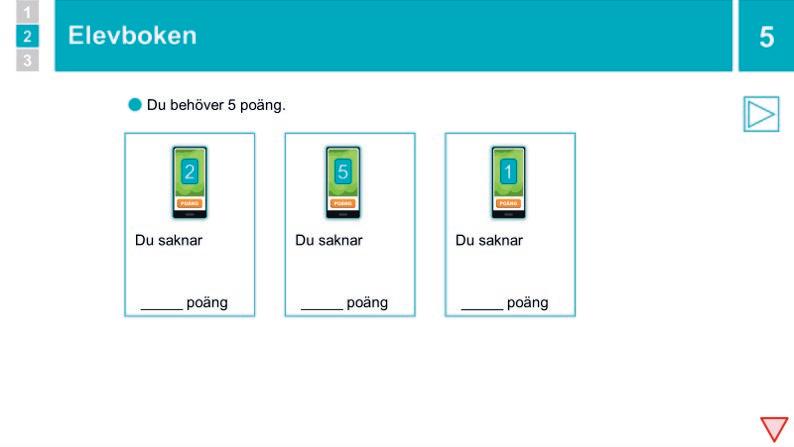

Klicka igen så att endast en boll visas utanför lådan. Säg: ”En boll ligger utanför lådan, några ligger i. Tillsammans är det fem bollar. Hur många ligger i lådan?” Ge BETÄNKETID eller låt eleverna SURRA . Fördela sedan ordet tills någon svarar ”fyra”, och be då hen förklara hur hen kom fram till det. Om hen säger ungefär att en boll tillsammans med fyra bollar är fem så låter du någon annan ÅTERGE .
Konstatera att en boll och fyra bollar är fem tillsammans genom att klicka och visa bollarna i lådan.
3 – 5 Elevboken: s. 2–4 20 min Visa vilken sida eleverna ska börja arbeta på och hur långt de som längst får arbeta under lektionen. Gå igenom den första uppgiftstypen med hjälp av exemplen i bildspelet. Låt eleverna börja när alla förstått. CIRKULERA och stötta vid behov. Om det behövs kan du låta elever SURRA när de gör de första uppgifterna.
Efter ett tag går du igenom nästa uppgiftstyp i steg 4.
Påminn om att det inte är viktigt att hinna med alla sidor. Det viktiga är att man gör sitt bästa och koncentrerar sig.
I steg 5 finns exempel till utmaningsuppgifterna i elevboken. Dessa kan du välja att arbeta med som gruppuppgifter eller i helklass. Ett annat alternativ är att låta elever som är i behov av extra utmaning arbeta med dem. Facit finns i bildspelet. Klicka på triangeln högst upp till höger för att gå direkt till nästa sida i bildspelet. Till den andra utmaningsuppgiften ges två exempel på möjliga svar. Det finns totalt 21 olika sätt som man kan lägga fem kulor i tre muggar på.
6 Sammanfattning: Vad har vi lärt oss? 5 min
Sammanfatta att antalet fem, t.ex. fem bollar eller 5 poäng, går att dela upp i två delar på flera olika sätt.
När Saga och Yosef spelade spel fick Yosef fick 4 poäng och Saga fick 1 poäng. Tillsammans fick de 5 poäng.
Nästa gång fick Yosef 0 poäng. Tillsammans fick de 5 poäng. Hur många poäng fick Saga? BETÄNKETID . Låt någon svara, fråga om klassen håller med och visa i bildspelet.
Låt elever ge förslag på andra sätt som 5 poäng kan delas upp mellan Yosef och Saga.



2 Repetition: Talet 5 10 min
Visa en hand som visar två fingrar. Fråga hur många av handens fingrar som inte visas. BETÄNKETID . Fördela ordet tills någon svarar ”tre”, och fråga hur hen kom fram till det. Ställ frågor för att hjälpa hen att förklara: handen har fem fingrar, och om två visas så finns det tre till som inte visas. Säg: ”2 och 3 är 5.”
Visa en hand som visar fyra fingrar och gör på samma sätt.
3 Högräkning
Låt klassen högräkna, utan bildstöd. Låt en elev säga ”ett”, nästa ”två”, och så vidare tills alla i klassen har sagt ett räkneord. Fortsätt upp i ett högre talområde genom att göra flera varv eller börja räkna nedåt på samma sätt.
4 Genomgång: Uppdelningsmaskinen
Peka och berätta att ni ser en uppdelningsmaskin. Be eleverna räkna bollarna i uppdelningsmaskinens övre fack. Pekräkna, och konstatera att det är fem bollar. Visa att uppdelningsmaskinen har en lucka som du kan öppna så att bollarna rullar ned och hamnar i det högra eller det vänstra facket.
Klicka, och luckan öppnar sig. Bollarna rullar ned. Peka och fråga: ”Hur många bollar är det i det vänstra facket?” Konstatera att det är två. Fråga: ”Hur många bollar är det i det högra facket?” Konstatera att det är tre. Fråga: ”Hur många bollar är det tillsammans?” BETÄNKETID . Låt någon räkna. Konstatera att det är fem tillsammans: det är fortfarande lika många bollar som det var när de låg i övre facket, men nu ligger några i det vänstra facket och några i det högra.
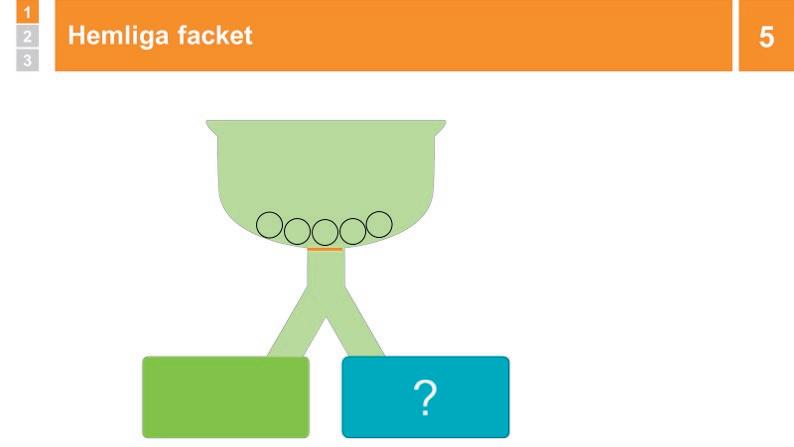
5 Genomgång: Hemliga facket
Visa att det är fem bollar i det övre facket och be eleverna titta noggrant. Klicka, och bollarna rullar ned och delas upp i de två facken. Säg: ”Det högra facket är ett hemligt fack. Vi kan inte se hur många bollar det ligger där. Kan ni lista ut det på något sätt?” BETÄNKETID
Låt eleverna SURRA en stund. Fördela sedan ordet tills någon föreslår att man kan räkna hur många det är i det vänstra facket och sedan tänka ut hur många som då måste ligga i det hemliga facket för att det tillsammans ska vara fem. Be någon annan elev ÅTERGE det sagda. Sammanfatta själv så att alla verkligen förstår. Klicka fram 5rutan med en grön cirkel. Säg: ”5rutan visar just nu hur många bollar som ligger i det vänstra facket. Eftersom det var fem bollar från början kan vi med 5rutan lista ut hur många som ligger i det hemliga facket. Hur många saknas för att det ska vara fem?” BETÄNKETID . Pekräkna högt med klassen och konstatera att det saknas fyra, alltså måste det ligga fyra bollar i det hemliga facket.
Klicka för att visa innehållet i det högra facket och visa sedan hur 5rutan fylls på med blå cirklar. Konstatera att en boll och fyra bollar tillsammans är fem bollar. 1 och 4 är 5.

6 Parövning: Hur många i det hemliga facket? 15 min
Dela in eleverna i par. Gör så här:
• Konstatera att det ligger fem bollar i det övre facket.
• Klicka så att bollarna flyttas delas upp mellan de två nedre facken.
• Säg: ”De fem bollarna har delats upp. Några ligger i det vänstra facket och några i det hemliga facket. Hur många ligger i det hemliga facket?”
• Låt paren diskutera.
• Låt något par svara. Om de säger rätt antal frågar du hur de tänkte för att komma fram till det. Ställ frågor för att hjälpa dem att förklara. Om de ger en bra förklaring låter du någon annan ÅTERGE . Påminn övriga om att göra JAG MED om de tänkt på samma sätt.
Gör fem omgångar till. I de två sista omgångarna står antalet skrivna som tal med siffror.
Om eleverna tycker det är svårt kan de använda 5-rutan i elevboken på samma sätt som du visade i steg 5. De lägger då först det kända antalet med plockisar i 5-rutan och tänker sedan ut hur många som saknas för att det ska vara fem.
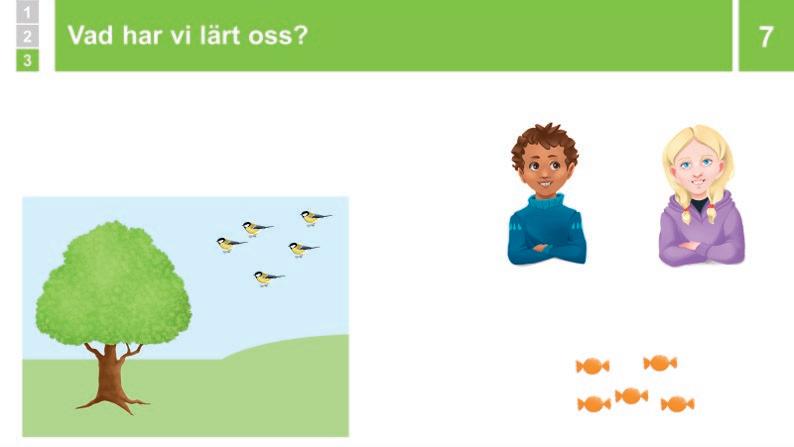
7 – 8 Sammanfattning: Vad har vi lärt oss? 5 min
Sammanfatta att man kan dela upp fem saker i två grupper på flera olika sätt. Man kan säga att talet 5 kan delas upp på olika sätt. T.ex. kan fem fåglar dela upp sig mellan trädet och gräsmattan på olika sätt. Så är det alltid med fem saker, även med fem karameller. Visa med fåglarna och karamellerna att det finns sex olika sätt att dela upp fem på.
Visa en 5ruta med fem blå cirklar och säg: ”När 5rutan är full så kan man säga att den visar talet 5. Noll gröna cirklar och fem blå är tillsammans fem cirklar. 0 och 5 är 5.” Klicka, och cirkeln till vänster blir grön. Fortsätt: ” En grön cirkel och fyra blå är fem cirklar. 1 och 4 är 5”. Klicka igen, och fortsätt tills alla cirklar är gröna.
Säg: ”Uppdelningsmaskinen har fem bollar.” Klicka, och de delas upp. Fråga: ”Till vänster syns fyra bollar. Hur många är det i hemliga facket?” BETÄNKETID. Konstatera: ”Fyra bollar och en boll är fem tillsammans. I 5rutan är det fyra cirklar. Det saknas en för att det ska vara fem. Om man vet att det var fem, och man ser fyra i den ena gruppen, då förstår man att det måste vara en i den andra gruppen.”
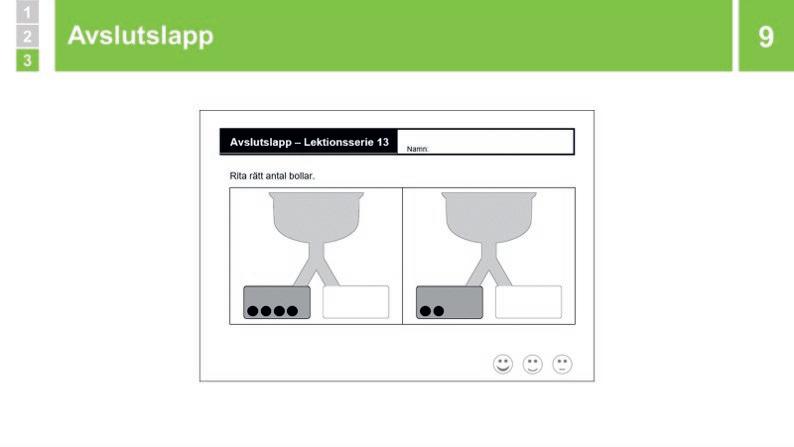
9 Avslutslapp
Säg: ”Rita bollar i högra facket så det är fem tillsammans.”
Lektionsserien går ut på att börja utveckla elevernas förståelse för tal som en kombination av delar, här med fokus på talet 5, genom att dela upp ett antal om fem objekt samt lägga ihop objekt så att de tillsammans blir fem till antalet.
Att lära sig dela upp tal och att se tal som en kombination av delar är en viktig del i att utveckla en god taluppfattning. Det är också nödvändigt för att eleverna senare ska kunna lära sig effektiva räknestrategier.1 För att eleverna ska bli skickliga på att dela upp tal och att se tal som en sammansättning av delar behöver de få undersöka hur talen kan delas upp i delar respektive sättas ihop av delar. De behöver sätta ord på detta, t.ex. att ”3 och 2 är 5”, och resonera om det: det är två bollar och det saknas tre för att det ska vara fem.
Eleverna kan ha svårt att direkt föreställa sig de gömda föremålen, t.ex. om du visar fem föremål och täcker över tre med handen och frågar hur många som är gömda. Detta är en utmaning för eleverna, då det testar om de har eller är på väg att automatisera talkamrater.
Förenkla
Elever som har svårt för uppdelning av antal kan behöva arbeta med konkret material som stöd genom hela lektionsserien. En 5- eller 10-ruta kan också vara till hjälp för att se hur talet kan delas upp. Du kan exempelvis låta dem arbeta med plockmaterial i två olika färger där den ena färgen representerar en grupp och den andra färgen den andra gruppen.
Utmana mer
Elever som behöver utmanas kan få dela upp fem föremål i tre grupper på så många sätt som möjligt. Totalt går det på 21 olika sätt (när man tillåter noll element i grupperna så att t.ex. talet 1 kan delas upp i 1 och 0 respektive 0 och 1).
Avslutslappen
Avslutslappen har två uppgifter av samma typ: eleven ser ett visst antal bollar och ska rita till så många nya bollar som behövs för att det ska vara fem bollar tillsammans. I den första uppgiften visas fyra bollar, och eleven ska alltså rita en boll. I den andra uppgift visas två bollar, och eleven ska då rita tre bollar.
Avslutslappen visar om eleven kan uppfatta talet 5 som en sammansättning av två tal. Om du har elever som ritar fel antal behöver du prata med dem för att undersöka vad som gick fel och om det är något som de inte förstår.
1 Eleverna behöver så småningom kunna dela upp talen 1–10 i två termer då det underlättar när de i lågstadiet ska göra beräkningar där de måste växla ental mot tiotal. Om eleven t.ex. ska beräkna så kan hen dela upp talet 7 i 2 och 5 och beräkna.
Lektionsseriens syfte är att fortsätta utveckla elevernas förståelse för tal som en kombination av delar, i den här lektionsserien med fokus på talen 1– 4. Att kunna se tal som en sammansättning av andra tal är en mycket viktig kunskap för att kunna utveckla en god taluppfattning och effektiva räknestrategier. I område 7 fortsätter vi arbeta med detta, då med fokus på talen 6–10.
Lektionsseriens mål
• Eleven kan dela upp talen 1– 4 i två tal på olika sätt och visar det genom att t.ex. dela upp en grupp av fyra plockisar i två nya grupper och t.ex. säga att 1 och 3 är 4.
• Eleven kan sätta samman talen 1– 4 av två tal och visar det genom att bygga t.ex. talet 3 med plockisar i två olika färger och säga att 2 och 1 är 3.
• Eleven kan uppfatta talen 1– 4 som en sammansättning av två tal och visar det genom att identifiera den saknade delen om helheten 4 är känd och en del täcks över.
Matematiska begrepp: dela
SvA: dela upp, sätta ihop
• Du repeterar hur talet 5 kan delas upp.
• Du går igenom hur talet 1 kan delas upp i 1 och 0 respektive 0 och 1.
• Eleverna SURRAR om hur talet 2 kan delas upp. Eleverna berättar alla sätt de kan komma på och SURRAR sedan om huruvida de verkligen inte kan komma på fler sätt. Du visar att 2 kan delas upp i 2 och 0, 1 och 1 samt 0 och 2.
• Eleverna arbetar i par med att komma på alla sätt som talen 3 och 4 kan delas upp på.
• Paren redovisar. Du sammanfattar och visar alla sätt.
Material och förberedelser:
Lektion 1: Ta fram fyra plockisar samt pennor i två färger till alla elevpar.
Lektion 2: Ta fram centikuber/multilink i två färger, fyra i vardera färg (en sådan uppsättning till varje par).
Lektion 3: Ha plockisar till hands.
Lektion 4: Skriv ut avslutslappar. Skriv ut kopieringsunderlagen Para ihop 3 och Para ihop 4 så att hälften av paren kan få den ena och hälften den andra. Skriv ut dubbelsidigt och skär på mitten. Du kan också skriva ut några exemplar av Para ihop 5
Para ihop 3
Para ihop 4
Para ihop 5
Avslutslapp – Lektionsserie 14
• Du repeterar hur man kan ta hjälp av uppdelningsmaskinen för att dela upp tal, och konstaterar att 1 och 3 är 4.
• Ni samlas. Du visar en centikub och säger ”Jag skulle vilja ha två. Hur många saknar jag?” Eleverna SURRAR om hur många du saknar för att det ska vara två. Ni konstaterar att 1 och 1 är 2.
• Eleverna försöker lista ut hur många bollar som ligger i uppdelningsmaskinens hemliga fack utifrån hur många bollar som syns i det andra facket.
• Eleverna arbetar i elevboken.
• Du visar den animerade genomgången som repeterar hur man kan dela upp tal med uppdelningsmaskinen.
• Högräkning.
• Du visar en uppdelning och eleverna försöker lista ut vilket hur många det är i det hemliga facket baserat på hur många som syns i det andra facket.
• Eleverna arbetar i par med aktiviteten Para ihop tal: paren får varsin spelplan med nio olika tal och ska para ihop de tal som tillsammans är talet 3 eller talet 4, beroende på vilken spelplan de har. När de är klara byter de spelplan med varandra.
• Avslutslapp.


2 Repetition: Talet 5 10 min
Repetera att talet 5 kan delas upp i två delar på flera olika sätt. T.ex. kan fem fåglar dela upp sig i två grupper.
Klicka, och uppdelningsmaskinen delar upp fem bollar. Visa och berätta att de fem bollarna nu har delats upp i två grupper med två i den ena och tre i den andra, men att de är fem tillsammans. Säg: ”2 och 3 är 5”.
3 Genomgång: Talet 1
Konstatera att det endast ligger en boll i det översta facket på uppdelningsmaskinen. Fråga: ”På vilka sätt kan bollen delas upp mellan facken när man öppnar luckan?” BETÄNKETID . Fördela ordet. Om någon säger att den antingen kan hamna i det vänstra eller högra facket så låter du någon annan ÅTERGE . Klicka, och bollen åker ner och hamnar i det vänstra facket. Konstatera att det var ett sätt. Det andra möjliga sättet var att den hamnade i det andra facket. Säg att 1 och 0 är 1, och att 0 och 1 också är 1.
4 Övning och genomgång: Talet 2
Visa att det nu ligger två bollar i det översta facket. Fråga: ”På vilka olika sätt kan två bollar delas upp?”
Låt eleverna SURRA en minut. Låt sedan ett par berätta om ett sätt som talet 2 kan delas upp på. Visa gärna genom att skriva på tavlan. Övriga elever kan delta med JAG MED. Be ett annat par berätta om ett annat sätt som två går att dela upp på. Skriv upp sättet på tavlan. Låt slutligen ett tredje par berätta om det tredje sättet (2 kan delas upp i 2 och 0, 1 och 1 samt 0 och 2, dvs. tre olika sätt).
Låt eleverna SURRA om huruvida de kan komma på fler sätt (vilket inte går). Fördela sedan ordet och ställ frågor för att hjälpa eleverna att förklara varför det inte finns fler sätt.
Klicka, och visa hur båda bollarna rullar ned i vänstra facket. Klicka fram 2rutan som har två ljusblå cirklar. Konstatera att det är två i det vänstra, ljusblå facket och noll i det högra, mörkblå facket. 2 och 0 är 2. Klicka, och en boll rullar ner i varje fack samtidigt som 2rutan nu visar en ljusblå och en mörkblå boll. Konstatera att 1 och 1 är 2. Klicka igen, och båda bollarna hamnar i det högra facket. 2rutan visar nu två mörkblå bollar. Konstatera att 0 och 2 är 2.
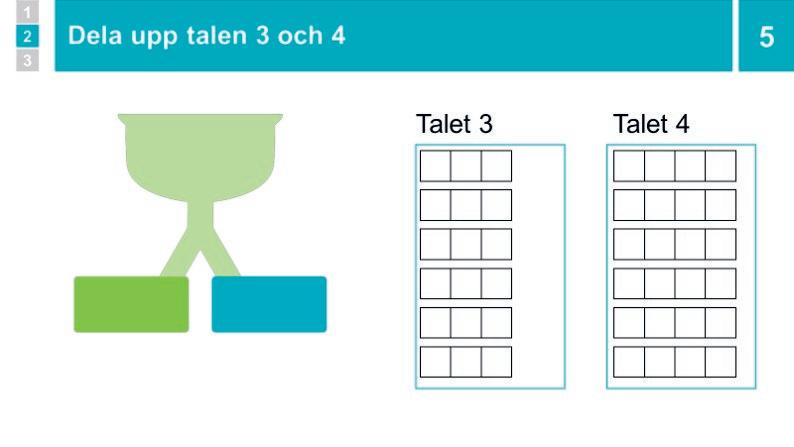
5 Parövning: Dela upp talen 3 och 4 15 min
Dela in eleverna i par. Förse hälften av paren med tre plockisar och hälften med fyra plockisar. Ge dessuom alla par en grön och en blå penna. Berätta att de som fått tre plockisar ska hitta så många olika sätt de kan att dela upp talet 3 på. De som fått fyra plockisar gör samma sak med talet 4. Be dem slå upp sida 5 i elevboken. Förklara vad paren ska göra, och visa vid behov med magneter på tavlan eller liknande:

• Paren som har talet 3 ska lägga tre plockisar i uppdelningsmaskinens övre fack och paren som har talet 4 ska lägga fyra plockisar i det övre facket.
• Paren ska dela upp sitt tal genom att dela upp plockisarna som ligger i det övre facket på valfritt sätt mellan de två nedre facken.
• Båda eleverna i paret ska säga hur många det är i det vänstra facket, i det högra facket samt hur många det är tillsammans, t.ex. 0 och 4 är 4 eller 1 och 2 är 3.
• Båda eleverna i paret ska rita av sin uppdelning med färgpennorna i 3rutan eller 4rutan. Grön färg motsvarar det vänstra facket och blå det högra. När de gjort detta börjar de om från början och upprepar punkterna ovan tills de inte kan hitta några flera uppdelningar.
Låt paren börja när alla förstått. CIRKULERA . Se till att alla i paren är aktiva, och påminn vid behov om att MATEMATIKER LYSSNAR vilket innebär att de ska lyssna på varandra.
Om något par snabbt blir klart kan du låta dem undersöka även det andra talet.
6 Redovisning: Hur kan man dela upp talen 3 och 4?
Låt ett par som har talet 3 redovisa ett sätt som de har delat upp 3 på. Påminn övriga om JAG MED. Utgå helst från elevernas egna lösningar, eller visa på tavlan eller på annat lämpligt sätt. Lösningarna finns även i bildspelet. Be paret säga hur många det är i respektive fack och hur många det är tillsammans, exempelvis: ”1 och 2 är 3 tillsammans”.
Fortsätt tills alla uppdelningar av talet 3 är redovisade och gör sedan på samma sätt med talet 4. Om ni har ont om tid kan du låta ett par redovisa alla sätt för talet 3 och ett par alla sätt för talet 4.
Avsluta med att sammanfatta och visa samtliga sätt som talet 3 och 4 delats upp på. Peka och säg t.ex. 4 och 0 är 4, för varje kombination.
7 – 8 Sammanfattning: Vad har vi lärt oss? 5 min
Visa att det är tre bollar i översta facket. Man kan se det som talet 3. Klicka, och visa att alla bollar hamnat i vänstra facket. Säg: ”3 och 0 är tillsammans 3”. Visa även med 3ruta. Klicka fram samtliga sätt som talet 3 kan delas upp på, och säg delarna och helheten.
Visa sedan att det är fyra bollar i översta facket. Man kan se det som talet 4. Klicka, och visa att alla bollar hamnat i vänstra facket. Säg: ”4 och 0 är tillsammans 4”. Visa även med fyraruta. Klicka fram samtliga sätt som talet 4 kan delas upp på, och säg delarna och helheten.
2 Repetition: Uppdelningsmaskinen 5 min
Säg att det ligger fyra bollar i översta facket och att de fyra bollarna kan ses som talet 4. Visa hur talet 4 delas upp i 1 och 3. Säg: ”Talet 4 kan delas upp på olika sätt. Här har jag delat upp 4 i 1 och 3. 1 och 3 är 4.”
3 Helklass: Jag skulle vilja ha 20 min
Samla eleverna (på samlingsmattan eller liknande). Visa en centikub i din hand och säg: ”Jag skulle vilja ha två. Hur många saknar jag?” BETÄNKETID . Påminn om JAG MED och låt någon svara. Konstatera att det saknas en för att det ska vara två.
Ta en centikub i en annan färg, sätt ihop de två kuberna och säg: ”1 och 1 är 2.”
Börja om och visa två centikuber i samma färg som sitter ihop. Säg: ”Jag skulle vilja ha fyra. Hur många saknar jag?” Låt eleverna SURRA en stund. Fördela sedan ordet tills någon svarar ”två”, och be då hen förklara hur hen kom fram till det. Om hen ger en bra förklaring, som att t.ex. visa med fingrarna, räkna upp från 2 till 4 eller säga att 2 och 2 är 4, så låter du någon annan ÅTERGE förklaringen.
Ta två centikuber i en annan färg och sätt ihop med de första två kuberna. Säg: ”2 och 2 är 4”.
Gör fler omgångar på samma sätt med olika tal mellan 1 och 4.
Testa även att hålla fram lika många som talet du önskar, så att eleverna får säga att du saknar noll. Du kan också testa med talet 5. Om eleverna förstår kan du para ihop dem och förse dem med centikuber i två färger så att de kan köra aktiviteten med varandra.
4 Sammanfattning: Vad har vi lärt oss? 5 min
Visa en stav med en grön och tre blå centikuber. Konstatera att det är fyra centikuber och att staven kan ses som talet 4. Talet 4 kan alltså sättas ihop av 1 och 3 eftersom 1 och 3 tillsammans är 4.
Visa hur staven delas upp i 1 grön och 3 blå, och säg att talet 4 kan delas upp i två delar, t.ex. i 1 och 3. Sammanfatta att tal kan delas upp och sättas ihop på olika sätt.
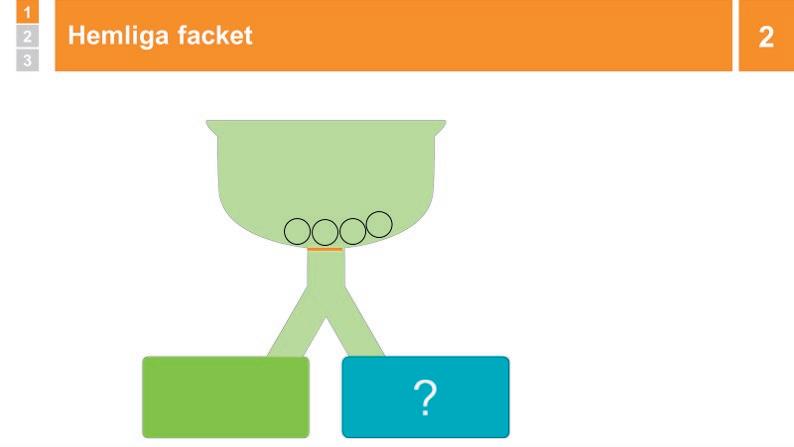
2 Repetition: Hemliga facket 5 min
Klicka, och de tre bollarna rullar ned. En hamnar i det vänstra facket och två i det hemliga facket. Fråga: ”Det låg tre bollar i det övre facket. Hur många bollar ligger i det hemliga facket?” BETÄNKETID . Låt eleverna SURRA vid behov, och fördela sedan ordet tills någon svarar ”två”. Be då eleven förklara hur hen kom fram till det. Låt någon annan ÅTERGE om eleven ger en bra förklaring.
Klicka, och konstatera att det ligger två bollar i det hemliga facket. Säg: ”1 och 2 är 3.”
Gör två omgångar till – en gång med talet 2 och en gång med talet 4.
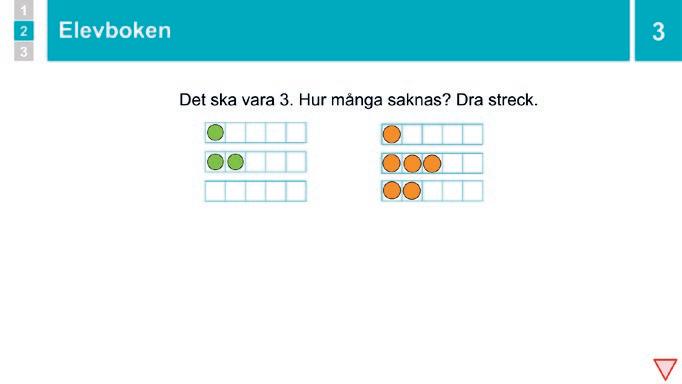
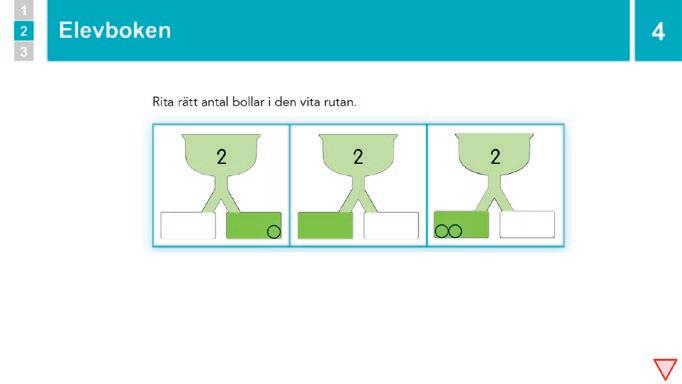


3 – 5 Elevboken s. 6–8 20 min
Visa vilken sida eleverna ska börja arbeta på och hur långt de som längst får arbeta under lektionen. Gå igenom den första uppgiftstypen i bildspelet. Låt eleverna börja när alla förstått.
CIRKULERA och stötta vid behov. Du kan låta elever SURRA när de gör de första uppgifterna.
Låt dem arbeta enskilt och CIRKULERA under tiden. Efter ett tag kan du förklara hur nästa uppgiftstyp ska gå till.
Påminn vid behov om att det inte är viktigt att hinna med alla sidor. Det viktiga är att man gör sitt bästa och koncentrerar sig.
I steg 5 finns exempel på utmaningsuppgiften i elevboken. Den kan du välja att arbeta med som en gruppuppgift eller i helklass. Ett annat alternativ är att låta elever som är i behov av extra utmaning arbeta med den. Facit finns i bildspelet. Klicka på triangeln som pekar till höger för att gå direkt till nästa sida i bildspelet.
6 Sammanfattning: Vad har vi lärt oss? 5 min
Säg att Hugo och Fatima tillsammans gjorde fyra mål i en fotbollsmatch. Fråga: ”Om Hugo gjorde tre mål, hur många gjorde då Fatima?” BETÄNKETID . Låt någon svara.
Konstatera att tal går att dela upp på olika sätt. Talet 4 kan t.ex. delas upp i 3 och 1.
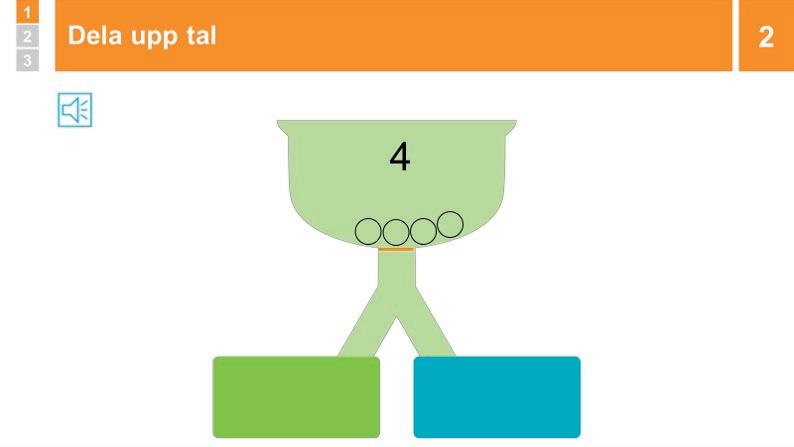

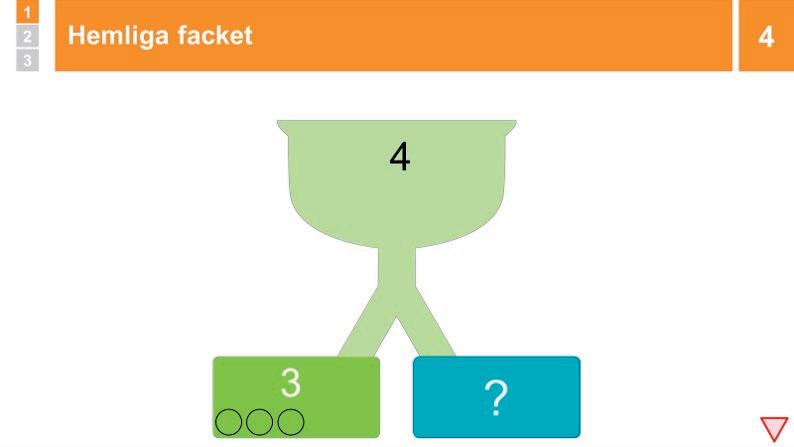
2 Repetition: Dela upp tal 10 min
Tal kan delas upp på olika sätt. Titta hur fyra bollar delas upp i två fack. Två bollar hamnade i vänstra facket och två bollar i det högra. Talet 4 kan alltså delas upp i 2 och 2, eftersom 2 och 2 tillsammans är 4.
Se hur tre bollar delas upp i uppdelningsmaskinen. En boll hamnade i det vänstra facket. Hur många hamnade då i det högra? Det saknas två bollar för att det ska vara tre, 1 och 2 är tillsammans 3. Alltså är det två bollar i det högra facket.
3 Högräkning
Låt klassen högräkna, utan bildstöd. Låt en elev säga ”ett”, nästa ”två”, och så vidare tills alla i klassen har sagt ett räkneord. Fortsätt upp i ett högre talområde genom att göra flera varv, eller räkna nedåt på samma sätt.
4 Övning: Hemliga facket
Peka på uppdelningsmaskinen och berätta att det låg fyra bollar i det översta facket innan maskinen delade upp dem i två grupper. Säg: ”Det var fyra bollar i det övre facket från början. Om det är tre i det vänstra facket, hur många är det då i det hemliga facket?” BETÄNKETID
Påminn om JAG MED och fördela ordet tills någon svarar att det måste ligga en boll i det hemliga facket. Fråga hur hen kom fram till sitt svar. Om eleven ger en bra förklaring, som att t.ex. visa med fingrarna, räkna upp från 3 till 4 eller säga att 3 och 1 är 4, så låter du någon annan ÅTERGE förklaringen. Visa innehållet i det hemliga facket och konstatera att 3 och 1 är fyra.
Gör en omgång utan bollar som konkret stöd, där talet 2 visas i det vänstra facket. Låt eleverna SURRA och resonera sig fram till vilket tal som är i det hemliga facket. Konstatera att 2 och 2 är 4.
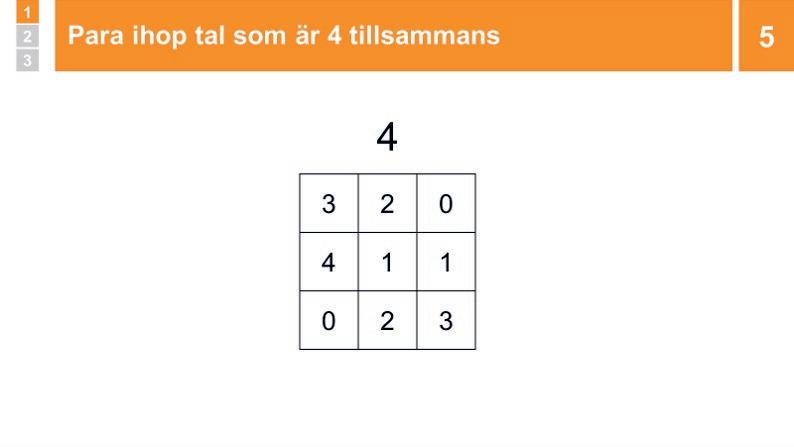
5 Genomgång: Para ihop tal som är 4 tillsammans
Säg att ni ska göra en aktivitet som kallas Para ihop tal. Peka på spelplanen i bildspelet och förklara att ni ska para ihop tal som tillsammans är 4 tills det bara finns ett ensamt tal kvar.
Fråga: ”Är det några av de här talen som tillsammans är 4?”
BETÄNKETID. Låt sedan eleverna SURRA en stund.
Påminn om JAG MED . Fördela ordet tills någon nämner två tal som tillsammans är 4. Be eleven förklara hur hen tänkte. Om eleven ger en bra förklaring låter du någon annan ÅTERGE den, annars förklarar du själv. Markera de två talen genom att klicka på dem.
Fortsätt på samma sätt med att låta elever säga tal som ännu inte markerats och som tillsammans är 4. Låt eleverna förklara hur de tänkte. När alla tal som tillsammans är 4 har markerats finns bara talet 0 kvar, omarkerat.
Rik matematik ger lärare stöd att planera, genomföra och utvärdera rik matematikundervisning. Rik matematikundervisning kännetecknas av aktiva elever och en aktiv lärare där begrepp, resonemang och problemlösning står i fokus. Förskoleklassens lärarhandledningar innehåller tillsammans mer än 80 strukturerade lektioner med bildspel. Lektionerna har tydliga inledningar och avslutningar där central matematik betonas. Med Rik matematik får läraren stöd att varje lektion bedriva en undervisning som engagerar och utvecklar elevernas matematiska tänkande.
Rik matematik är utvecklat i ett nära samarbete mellan lärare och forskare. Varje lektion är utprovad av många lärare som undervisat heltid med Rik matematik under hela läsåret.

Rik matematik Fk B omfattar 5 områden:
Område 5 – Talen 1–5:s egenskaper
Område 6 – Längd, mätning och tid
Område 7 – Talen 6–10:s egenskaper
Område 8 – Geometri
Område 9 – Dubbelt och hälften