FAVORIT MATEMATIK 6A
UTÖKAT STÖD
Lärarpaket – Tryckt + Digitalt
LÄS OCH PROVA
LÄRARPAKETETS
SAMTLIGA DELAR
FAVORIT MATEMATIK 6A UTÖKAT STÖD
Lärarpaket – Tryckt + Digitalt
Favorit matematik Utökat stöd är en kompletterande lärarhandledning för klasslärare. I Finland finns en tydlig organisation för extra hjälp till elever som behöver det. Dessutom finns speciellt framtagna läromedel att använda i arbetet.
Favorit matematik Utökat stöd kommer från Finland. Materialet har anpassats och granskats av både lärare och forskare som är verksamma i Sverige.
LÄRARHANDELEDNING
Favorit matematik Utökat stöd innehåller lektionsspecifika tips och förslag på extra hjälp framtagna med tanke på undervisning av elever som visar en lägre nivå i matematik. I de olika aktiviteterna används laborativt material. Eleven övar i sin ordinarie elevbok. Arbetet i elevboken kan också kompletteras med kopieringsunderlag för ytterligare förståelse och träning.
Kopieringsunderlagen i Favorit matematik Utökat stöd är framtagna med tanke på behoven hos de elever som behöver extra hjälp.
DIGITALA RESURSER
Med lärarhandledningens digitala resurser får du tillgång till flera praktiska verktyg för din undervisning. Introducera ett nytt moment, förklara olika begrepp, samlas kring lärorika uppgifter - tillsammans.
Interaktiv version av lärarmaterialet, där det går att söka, stryka under, anteckna och länka.
Här hittar du filmer, presentationer, kopieringsunderlag, facit, prov och mycket mer.
Favoritmatematik
UTÖKAT STÖD
Studentlitteratur AB
221 00 LUND
Besöksadress: Åkergränden 1 Telefon 046-31 20 00
studentlitteratur.se
Kopieringsförbud
Detta verk är skyddat av upphovsrättslagen. Kopiering, utöver lärares begränsade rätt att kopiera för undervisningsbruk enligt Bonus Copyright Access skolkopieringsavtal, är förbjuden. Kopieringsunderlag får dock kopieras under förutsättning att kopiorna delas ut endast i den egna undervisningsgruppen. För information om avtalet hänvisas till utbildningsanordnarens huvudman eller Bonus Copyright Access.
Vid utgivning av detta verk som e-bok, är e-boken kopieringsskyddad.
Användning av detta verk för text- och datautvinningsändamål medges ej.
Den som bryter mot lagen om upphovsrätt kan åtalas av allmän åklagare och dömas till böter eller fängelse i upp till två år samt bli skyldig att erlägga ersättning till upphovsman eller rättsinnehavare.
Studentlitteraturs trycksaker är miljöanpassade, både när det gäller papper och tryckprocess.
Art.nr 43971
ISBN 978-91-44-15267-7
Upplaga 1:1
© Författarna och Studentlitteratur 2024
Originalets titel: Tuhattaituri 6a Opettajan opas E
© Otava Publishing Company Ltd, Helsingfors 2009
Översättare: Daniela Strandberg
Kompletterande texter: Kirsti Hemmi
Illustratörer: Maisa Rajamäki, Sirkku Pitkänen
Printed by Eurographic Group, 2024
Erfarenheter från undervisning i Finland
Förord
I heterogena klasser måste läraren kunna leda alla elever framåt till nya och mer krävande områden i matematiken och samtidigt stötta de elever som har svårt att lära sig det nya och som kanske fortfarande kämpar med det mest elementära innehållet. Utan relevant material är det en svår uppgift. Favorit matematik Utökat stöd är en kompletterande lärarhandledning som hjälper lärare att på ett strukturerat sätt kontinuerligt differentiera undervisningen och ta hänsyn till de elever som behöver extra stöd. Favorit matematik Utökat stöd erbjuder redskap för både uppföljning av elevers kunskaper och valet av lämpliga stödåtgärder.
Favorit matematik Utökat stöd tillsammans med elevboken Bas Favorit matematik 6A underlättar lärares arbete att integrera elever med svårigheter i det dagliga arbetet i klassrummet och samtidigt möta elevens specifika behov av kontinuerligt och relevant stöd. Favorit matematik Utökat stöd är ett kompletterande material som används parallellt med, och inkluderat i den ordinarie undervisningen. Material går också utmärkt att använda inom specialundervisning då man kan följa det som händer i den ordinarie klassen och även förbereda elever inför nya områden. Elever med behov av stöd kan på det sättet delta i arbetet inom samma område som resten av klassen vilket bidrar till lärande och till en positiv självbild. Under höstterminen i åk 6 utökar vi kunskapen om tal i bråkform till förlängning av bråk för att kunna genomföra additioner och subtraktioner av bråk med olika nämnare. Ett korrekt språk tillsammans med lämpligt laborativt material som visar tal i olika former hjälper eleven att förstå att det är frågan om samma mängd uttryckt på olika sätt. Det är viktigt att visa eleverna varför det är nödvändigt att talen har samma nämnare när vi genomför additioner och subtraktion med tal i bråkform.
I åk 6 lär sig eleverna räkna areor av sidoytor på tredimensionella objekt samt omvandla area- och volymenheter. Vi lägger också fokus på likformighet, skala samt förstoringar och förminskningar av geometriska objekt.
Inom algebra möter eleverna enkla funktioner och deras grafer. De får också lösa problem genom att sätta upp och lösa ekvationer. Under höstterminen finns lektioner speciellt för problemlösning och eleven fördjupar sin kunskap i algebra. Vidare läggs grunden för förståelse av centrala begrepp inom statistik och sannolikhetslära. Eleven lär sig lösa kombinatoriska problem med hjälp av träddiagram.
Att kunna tänka och resonera logiskt samt att kunna koncentrera sig är grunden för all matematisk verksamhet. Det är vanligt att flera elever i åk 6 fortfarande behöver träning i koncentration i form av korta övningstillfällen som den lilla huvudräkningsstunden och hemläxan (Träna-rutan). Dessa aktiviteter förstärker även minne och ger tillfälle för lärare att kontinuerligt följa elevers framsteg och erbjuda snabb återkoppling. Detta är speciellt viktigt när det gäller elever som har det svårt med vissa områden i matematik.
Den lektionsspecifika strukturen i Favorit matematik Utökat stöd är densamma i den ordinarie lärarhandledningen, vilket underlättar planeringen. Introduktionen till nya områden och huvudräkning kan med fördel genomföras samtidigt med hela klassen. Lektionerna kan planeras olika beroende på hur du vill introducera elever till nya områden. Det går alldeles utmärkt att starta med ett problem som elever i heterogena grupper diskuterar. Flera aktiviteter lämpar sig också för hela klassen; svårighetsgraden kan lätt varieras och anpassas till olika elevers förutsättningar. Från elevboken Bas Favorit matematik kan läraren välja lämpliga uppgifter utifrån elevers olika behov. Det är dock viktigt att även elever med svårigheter i matematik, någon gång får ta del av problemlösning som förekommer på PRÖVA-sidorna och i den ordinarie lärarhandledningen.
Låt materialet fungera som en inspirationskälla när du komponerar din lektion med aktiviteter som främjar elevers lärande. Arbetet i materialet ger också möjligheter till mångsidig, formativ bedömning. På det sättet ökar din ”verktygslåda” och bidrar till professionell utveckling.
För att varje dag kunna ägna en stund åt elever som behöver stöd måste resten av klassen aktiveras med annat. På sidan 8 har jag exemplifierat hur undervisningen kan organiseras på ett sätt som underlättar det dagliga arbetet med heterogena klasser. Jag hoppas att materialet kan inspirera dig och ge dig mycket glädje då alla elever gör framsteg och får aha-upplevelser.
Kirsti Hemmi professor i de matematiska ämnenas didaktik vid Åbo Akademi
Innehåll
INLEDNING
2
räknesätten, algebra och funktioner
KAPITEL 1
KAPITEL 3
Arean för trianglar och fyrhörningar
Favoritsidor – laborativ övning
Volymen för rätblock
KAPITEL 4
38. Problemlösning, uppskatta och pröva
39. Problemlösning, rita bild
40. Problemlösning, ekvation
41. Favoritsidor
42. Kombinatorik
43. På hur många sätt?
44. Hitta mönster i talföljder
45. Historiska talsystem
46. Från tiosystemet till det binära talsystemet
47. Binära tal och datorer
48. Vad har jag lärt mig?
KAPITEL 5
49. Vi repeterar prioriteringsregler 172
50. Vi repeterar negativa tal, algebra och funktioner 174
51. Vi repeterar bråk och geometri 176
52. Vi repeterar skala, area och volym 178
Innehåll och instruktioner
INLEDNING
Favorit matematik 6A Utökat stöd
Favorit matematik 6A Utökat stöd Lärarhandledning innehåller tips, framtagna med tanke på undervisning av elever som behöver utökat stöd. Tanken är att Favorit matematik 6A Utökat stöd ska komplettera innehållet i den ordinarie lärarhandledningen Favorit matematik 6A Lärarhandledning, eftersom den ordinarie också innehåller laborativa övningar, spel och lekar som passar elever i behov av extra hjälp och stöd.
Favorit matematik 6A Utökat stöd Lärarhandledning inleds med allmän information om inlärningssvårigheter i matematik och olika metoder som du kan använda för att stödja eleven. Huvuddelen av innehållet i den kompletterande lärarhandledningen Favorit matematik 6A Utökat stöd , består i att du till varje lektion hittar enklare huvudräkningsuppgifter, tips på aktiviteter eller stöd som hör till precis det matematiska moment som lektionen behandlar. Det ingår kopieringsunderlag till varje lektion. Kopieringsunderlagen är framtagna med tanke på behoven hos de elever som visar låg nivå i matematik.
För klassläraren
Ordinarie lärarhandledning
För klassläraren
Tillägg för elever som visar låg nivå i matematik. Stöd, lektion för lektion.
För specialläraren
Tillägg för elever som behöver ännu mer stöd eller specialundervisning. Områden med fokus på det viktigaste i varje kapitel.
Inlärningssvårigheter i matematik
Inlärningssvårigheter i matematik kan ha flera orsaker. Bakom svårigheterna ligger ofta brister inom minst ett av följande delområden:
• språkliga färdigheter
• att gestalta* och minnas det man hört
• att gestalta* och minnas det man sett
• uppmärksamhet
• motorik
En del elever kan behöva ytterligare stöd utanför skolans arbete för att stärka de ovan nämnda förutsättningarna för lärande. Som lärare kan du ändå bidra till elevens kunskapsinlärning med hjälp av lämpliga pedagogiska metoder. En elev med inlärningssvårigheter i matematik behöver i högre utsträckning än sina jämnåriga:
1. stöd i form av laborativt material och bilder
2. repetition och befästande av tidigare introducerat innehåll
3. individuellt stöd/instruktioner
4. uppmuntran
5. tid att lära.
Om en elev har svårigheter med att lära sig matematik ska undervisningen innehålla praktisk verksamhet med konkreta och laborativa material . Aktiviteterna ska syfta till att tydliggöra matematiskt innehåll och stötta elevens matematikinlärning. För elever med matematik svårigheter kan det vara rörigt att använda många olika laborativa material. Det viktiga är att eleven känner till det laborativa materialet och inte behöver känna sig osäker med det. Därefter och i mycket långsam takt går vi vidare till abstrakta begrepp. Elever som inte har särskilda svårigheter med att lära sig grundbegreppen har också nytta av laborativa övningar som befäster grundläggande begrepp. Laborativa övningar breddar elevens uppfattning om vad som är matematik, samtidigt som de laborativa övningarna sammanbinder de matematiska begreppen med elevens vardag. En praktisk och laborativ form av undervisning kan också minska den ångest som en del elever upplever när det kommer till matematikinlärning, och därmed förebygga att de underpresterar. Gemensamma praktiska och laborativa övningar stärker även sammanhållningen i elevgruppen och hjälper elever som behöver särskilt stöd att känna samhörighet med resten av gruppen.
En ojämn kunskapsutveckling är typiskt för elever med matematiksvårigheter. Ibland kan det kännas som om eleven fått grepp om baskunskaperna, andra gånger kan enkla räkneuppgifter kännas helt omöjliga. De här variationerna kan hänga ihop med elevens motivation, uppmärksamhet eller minne. För att främja lärandet på bästa sätt är det viktigt med mångsidig undervisning och övningar som upprepas ofta. Kontrollera regelbundet hur väl eleverna behärskar baskunskaperna (till exempel tiokompisar, uppdelning av tal i talområdet 0 till 20 och förståelse av positionssystemet), eftersom matematikinlärningen bygger på de här kunskaperna.
* Det finska ordet hahmotus/hahmottaminen är svåröversatt. Här har vi valt att använda ordet gestalta men det kunde också stå ”skapa sig en bild av, uppfatta” eller liknande (lite beroende på situation).
Att använda olika hjälpmedel och laborativt material (till exempel tiobasmaterial och hundratavla) stöder inlärningen och gör att eleven kan skapa inre bilder och uppleva mindre oro vid uppgifter som känns svåra. Tipsa eleverna och deras vårdnadshavare om att använda hjälpmedlen och det laborativa materialet även när de löser uppgifter hemma (t.ex. Träna-uppgifterna).
I vilken grad du som klasslärare kan stödja olika typer av elever beror på flera faktorer, som du inte alltid har möjlighet att påverka (till exempel elevgruppens storlek). Med realistiska målsättningar, en uppmuntrande inställning och en varierad undervisning kan du ändå hjälpa till att ”kratta manegen” för olika elever, det vill säga ge alla de bästa förutsättningarna för inlärning. Samtidigt får du själv uppleva känslan av att lyckas!
Organisera undervisning för utökat stöd
Introduktion till nya områden och huvud räkning kan med fördel genomföras samtidigt med hela klassen. Även andra aktiviteter i Utökat stöd lämpar sig för hela klassen då aktivi teterna förstärker elevens grundläggande taluppfattning. Svårighetsgraden på aktiviteterna kan lätt varieras och anpassas till olika elevers förutsättningar.
För att varje dag kunna ägna en stund åt elever med matematiksvårigheter måste resten av klassen aktiveras med annat. Under tiden kan läraren ägna sig åt elever som behöver extra stöd.
Här är tre förslag på hur elever i klassen kan arbeta medan läraren ger stöd till elever med matematiksvårigheter.
Lärarhandledningen har många olika förslag
Den ordinarie lärarhandledningen erbjuder förslag på problem och spel som kan aktivera elever då läraren arbetar med elever som har svårigheter i matematik.
Eleverna arbetar med elevbokens uppgifter
Ett sätt kan vara att utnyttja den tid då elever arbetar med uppgifter i elevboken.
Eleverna kontrollerar och rättar sina uppgifter
Eleverna rättar och kontrollerar sina uppgifter vid en kontrollstation med ett gemensamt facit någonstans i klassrummet. Efter att eleven räknat enbart några uppgifter i ett nytt område, gör hen en kontroll för att från början se till att vara på rätt väg och inte ha missförstått något. På kontrollstationen markerar eleven de uppgifter som blivit fel. Eleven får sedan själv rätta till sina felaktiga lösningar till exempel med hjälp av laborativt material, eventuellt i samråd med en annan elev.
Kirsti Hemmi
professor i de matematiska ämnenas didaktik vid Åbo Akademi
Att förebygga matematikängslan och negativa känslor
Matematik väcker känslor hos elever. Känslor kan vara av positiv karaktär till exempel som tillfredställelse efter att eleven lyckats lösa en uppgift eller fått en aha-upplevelse gällande begrepp och deras samband. Tyvärr väcker matematik också negativa känslor och frustration. Ingen som sysslar med matematik kan undvika dessa känslor helt men vi kan lära oss att hantera dem om vi kan lita på vår förmåga att lösa uppgifter eller få hjälp i form av stöd och förklaringar från någon i vår närhet.
Enligt forskning börjar en speciell negativ känsla kopplad till matematik öka hos flera elever efter att de lämnat lågstadiet. Matematikängslan kan förekomma i olika situationer, till exempel när eleven förväntas svara inför hela klassen, när eleven får svåra eller alltför omfattande läxor, och i samband med prov. Lärarens ”genomgång” kan också orsaka ängslan hos elever. Ängslan kan leda till att eleven inte kan tänka klart och ibland glömmer allt hen lärt sig tidigare. Detta behöver inte gälla enbart elever som har svårt att lära sig matematik utan även högpresterande elever kan uppleva negativ känsla kopplad till matematik. Att uppleva ängslan och negativa känslor gentemot matematik är vanligare hos flickor men kan förekomma hos alla.
Vi vet att negativa känslor och stress stör bland annat arbetsminnet och försvårar därmed lärande och prestationer i matematik. Det leder lätt till en ond cirkel. Om eleven alltför ofta upplever negativa känslor, misslyckanden och prestationsångest finns det en risk att hen börjar undvika matematik och så småningom utvecklar en identitet med tankar som ”matematik är ingenting för mig”. Eleven är övertygad att hen aldrig kan lära sig matematik. Därför är det viktigt att vara vaksam som lärare och förebygga matematikängslan på olika sätt.
Vad kan jag göra?
Det finns en hel del som en lärare kan göra för att förebygga ängslan, stress och negativa känslor och stoppa en negativ utveckling hos eleven. Det är viktigt att lägga märke till elevens reaktioner och om hen börjar använda olika sätt att undvika matematik och olika situationer förknippade med matematik. I en stor klass kan det dock vara svårt att upptäcka allt och elever reagerar också olika på olika händelser. Därför kan det vara bra att till exempel i samband med ett prov låta elever svara på frågor om hur de upplever matematiken.
Använd laborativt material
Matematik blir naturligt mer abstrakt ju längre man kommer inom olika områden. För att förebygga stress och svårigheter är det viktigt att ständigt fortsätta exemplifiera begrepp och visa regler, samband och lösningar med hjälp av laborativt material, bilder och enkla exempel. Det är bra att undvika ensidiga snabba ”genomgångar” i början av en lektion och i stället försöka engagera alla elever i introduktionen av nya begrepp och procedurer, till exempel med hjälp av material som eleverna kan arbeta med tillsammans i par. Samtalsbilden som finns till varje lektion i elevboken är också ett trevligt sätt att tillsammans börja lära känna ett nytt innehåll.
Det är vanligt i mellanstadieåldern att inte vilja vara annorlunda jämfört med andra elever. Om laborativt material är en naturlig del av en matematiklektion, blir det inte stigmatiserande för eleven att använda det laborativa materialet som stöd för sitt tankearbete. Det blir en trygghet att arbeta med ett laborativt material som läraren har presenterat och eleven i lugn och ro, återkommande har fått lära känna. Däremot kan det sätta i gång oro om eleven behöver använda laborativt material som
är helt främmande. Många av de laborativa material som eleven har stött på tidigare under sin skoltid är fortfarande användbara på mellanstadiet. I Favorit matematik Utökat stöd 5A finns det gott om förslag på lämpligt laborativt material för att konkretisera och förklara olika matematiska innehåll.
Skapa ett positivt klassrumsklimat
Forskning visar att kommunikation och resonemang med klasskamrater kan främja en positiv atmosfär i klassrummet och Favorit matematik Utökat stöd 5A ger förslag på många kommunikativa aktiviteter. Att få arbeta tillsammans med klasskamrater som man känner ökar tryggheten. Exempel på passande aktiviteter finns för varje lektion i både den ordinarie och den kompletterande lärarhandledningen. Det är dock viktigt att tänka på gruppsammansättningar och vara uppmärksam på att elever kan ha ett olämpligt beteende mot varandra. Det är bra att repetera klassrumsregler och regler för grupparbete regelbundet.
Ett nytt inslag i Favorit matematik Utökat stöd 5A är ett spel med begreppskort som tränar aktuella matematiska begrepp. Eleverna turas om att förklara begreppet som står på sitt kort med sina ”egna” ord för de andra eleverna i laget. Spelaren får inte använda själva ordet som står på kortet. De andra spelarna försöker utifrån beskrivningen bestämma vilket begrepp som står på kortet. Avspänt samarbete och förklarande av begrepp med ”egna” ord främjar lärande och förebygger rädslor som ibland kan uppstå inför kravet att använda rätta matematiska begrepp. Att det är tillåtet och även uppmuntras att använda ”egna” ord för att förklara begrepp ökar djupare begreppsförståelse och minskar stress och prestationsångest som handlar om att använda den korrekta terminologin. I längden hjälper det även elevers aktiva användning av korrekta matematiska begrepp.
Spel och tävlingar kan vara lärorika, men även förstärka matematikängslan om de genomförs på ett olämpligt sätt. Spelen får aldrig utsätta en elev för eventuella skamkänslor eller förstärka elevens ängslan. Till exempel i de spel där elever står framför klassen och tävlar är det verkligen viktigt att välja de elever som tycker om det. De andra eleverna deltar tryggt eftersom de enbart behöver ge de tävlande uppgifter att lösa. På det sättet bidrar spelet till allas lärande.
I lektion 6 repeterar eleven hur man tydligt redovisar sin lösning på en uppgift i ett räknehäfte, vilket är mycket viktigt eftersom noggrannhet är en del av matematiskt arbete. Speciellt för elever som har svårt för matematik är det bra att vara tydlig med hur du vill att den skriftliga redovisningen av uppgiften ska vara. För dessa elever kan det också vara skönt att ha tydliga regler för hur de ska skriva tal, uttryck och svar i sina häften. Lika viktigt är att ofta och återkommande uppmuntra elever att använda lämpligt laborativt material och/eller ”kladdpapper” för att rita figurer och testa olika sätt att lösa uppgiften under tiden de funderar på hur de ska lösa ett problem. Det finns annars risk att eleven tror att hen genast ska komma på en lösning och därför bara försöker lära in en procedur för att lösa en uppgift utantill. Det leder inte till djupare förståelse, tvärtom är det lätt att eleven blir stressad och väljer fel procedur.
Alla elever behöver lära sig att hantera frustration och negativa känslor som ofta förekommer under det undersökande skedet i problemlösning. Det är också viktigt att regelbundet uppmuntra elever att kontrollera sina lösningar på olika sätt innan de skriver uttrycket, beräkningarna samt svaret för den fullständiga lösningen i sitt häfte. Allt detta är bra för elevens förståelse och minskar därmed ängslan.
Använd olika test och provsituationer
Att göra fel är en naturlig del av lärande. Med hjälp av vanliga fel och missförstånd kan man tillsammans diskutera orsaker till felen och lära sig av dem. Felen ses som ”tillgång” som öppnar upp möjligheter för gemensamt lärande. Det bidrar till avspänd atmosfär i matematikklassrummet och förebygger därmed ängslan.
Provsituationer kan vara väldigt stressande för elever som upplever matematikängslan. Läraren kan mäta elevernas kunnande på traditionellt sätt med ett prov. I så fall kan eleverna få använda konkret och laborativt material utöver kladdpapper som hjälpmedel. Läraren kan även tillåta att eleven använder elevboken som hjälp under provet. Det är också viktigt att det inte finns någon tidspress. I lärarhandledningen presenteras även alternativa metoder att följa upp elevers lärande.
Det kan fungera bra att använda kamratbedömning av vissa moment. Det är då viktigt att använda mallar och beskrivningar på vad som ska vara med i lösningen så att eleven förstår vad som bedöms. Till exempel i slutet av den lektion där elever övar att redovisa sina lösningar tydligt i räknehäften får eleverna i par utvärdera tydligheten och prydligheten i häftena, antingen muntligt eller genom att skriva något. När eleverna utvärderar arbetet i häftet ska de speciellt uppmärksamma exempelvis att skriva uttryck, uträkning, enhet och svar.
Kontakt mellan hem och skola
Läxor kan också förstärka matematikängslan, speciellt om de är omfattande eller har svåra problemlösningsuppgifter. I den ordinarie lärarhandledningen uppmuntras läraren att använda Träna-rutor som läxor. Fördelen med Träna-rutornas uppgifter är att de utgör repetition av den aktuella lektionen och ger möjlighet för eleven och läraren att efter varje lektion kontrollera att eleven ”hänger med”. Det finns alltid möjlighet att ge extra hemuppgifter för de elever som behöver svårare utmaningar.
Forskning visar att en positiv attityd ökar elevers prestationer i matematik. Vårdnadshavares attityd till matematik kan vara avgörande för vilken typ av matematikidentitet en elev utvecklar. Om en vårdnadshavare har haft negativa erfarenheter kan hen lätt förstärka sitt barns motvilja för ämnet. Därför kan det vara en bra idé att diskutera detta på ett föräldramöte och berätta hur vårdnadshavaren kan förebygga sitt barns matematikängslan och negativa känslor och undvika att förflytta sina egna eventuella negativa erfarenheter och känslor till sitt barn.
Kopplingar till elevers vardag och aktuella fenomen i samhället kan bidra till en positiv attityd hos många elever. Det är också viktigt att poängtera att vi inte alltid kan motivera allt innehåll av skolmatematik enbart från vardagens behov. Matematik kan ha oväntade tillämpningsområden och det är svårt att säga inom vilka nya innovationer våra elever i framtiden behöver använda matematik. Den tanken kan fascinera elever mer än att försöka hitta på möjliga tillämpningsområden i dagens samhälle.
AKTIVITETER FÖR GRUNDLÄGGANDE FÖRSTÅELSE
Att utveckla elevens algebraiska tänkande
Algebra är ett exempel på matematik som kan upplevas främmande och långt ifrån vardagen. Goda kunskaper i algebra är ändå nödvändiga för att kunna lära sig mer avancerad matematik som behövs för ett flertal områden i samhället. Det är inte givet att de elever som har haft det svårt i aritmetik nödvändigtvis får problem med algebraiskt tänkande. Ibland är det tvärtom. Algebra har trots det varit ett problem för många elever och bristen på algebrakunskaper har hindrat elever att gå vidare med sina matematikstudier. Därför är det viktigt att se till att alla elever har möjlighet att på olika sätt utveckla sitt algebraiska tänkande redan under de tidiga skolåren.
Film: Ekvationer
Film: Tal i bråkform
Film: Tal i bråkform på tallinjen
Under höstterminen i åk 5 arbetar eleverna med ekvationer och olikheter. Ekvationslösning syftar inte till användning av de formella metoder som elever kommer att lära sig under de senare skolåren. Det kan i stället handla om att testa med vilka olika tal som gör en likhet eller olikhet sann eller användning av olika typer av logiska slutledningar. Elever lär sig också utnyttja motsatta operationer i ekvationslösningen, vilket ytterligare förstärker elevernas förståelse för sambanden mellan olika räknesätt.
I Bas Favorit matematik 6A fördjupar eleverna sin förståelse för tal i bråkform, vilket utvecklar det proportionella tänkande som också är viktigt för algebra. Bland annat lär sig elever att förkorta tal i bråkform. Det krävs goda multiplikationskunskaper för att klara av att förlänga och förkorta tal mer effektivt. Det är därför viktigt att använda tid till repetition av multiplikationstabellerna i början av årskurs 6, om eleverna har glömt multiplikationstabellerna under sommaren.
Tal i bråkform och tal i decimalform
När eleven arbetar med tal i bråkform är det viktigt att förstå hur en hel kan delas i mindre delar. Det är bra att ge eleverna erfarenheter av helheter i olika storlek och form, till exempel cirkeln, rektangeln, tallinjen med flera. När vi funderar på storleken på olika delar kan du visa tal i bråkform med cirklar. Det är lätt att komma ihåg en hel cirkel och sektorer av lika stora cirklar är enkla att jämföra. Bråkcirklar är ett hjälpmedel för att visa tal i bråkform och jämföra storleken på olika delar.
Ett exakt språkbruk för tal i bråkform och tal i decimalform hjälper eleven att upptäcka att det är frågan om samma mängd uttryckt på två olika sätt. Använd gärna räknare för att visa sambandet mellan tal i bråkform och tal i decimalform. Påminn eleven om att bråkstrecket mellan täljaren och nämnaren symboliserar division. Med räknare kan eleverna själva pröva att omvandla tal i bråkform till tal i decimalform.
LEKTIONSSPECIFIKA INSTRUKTIONER
Innehåll till varje lektion
Lektionens innehåll
Kopieringsunderlag 3a–b
UTÖKAT STÖD 18 3. Addition och subtraktion
Kopieringsunderlag 3b finns även Favorit matematik 6A Lärarhandledning 43971_FavMat6A_U_01_Lektioner.indd
Addition och subtraktion som huvudräkning och med uppställning
Repetition av minnessiffror och växling Räkna addition och subtraktion med flera än två termer.
Frågor till samtalsbilden
1. Vad är det för skillnad på att räkna additioner med tre termer och subtraktioner med tre termer, med uppställning? (I addition med uppställning kan du räkna allt på en gång, men subtraktionen måste du räkna i två steg
2. Förklara och berätta hur du räknar additionen samtalsbilden.
3. Förklara och berätta hur du räknar subtraktionen samtalsbilden.
Huvudräkning
a. 4 800 – 700 (4 100 b. 2 500 + 3 500 (6 000 c. 2 000 – 900 (1 100 d. 1 500 + 1 500 – 1 200 (1 800)
Förslag på utökat stöd
Resonemang och kommunikation
Vilka fördelar har du av att uppskatta svaren innan du räknar? Hur kan du uppskatta svaret innan du räknar? Uppskatta svaren i till exempel uppgifterna 1a och 1b Vad har du för fördelar eller nackdelar av att kontrollera dina svar med svaren i den gröna rutan under uppgifterna?
Elevbokens uppgifter Syftet med svaren rutan längst ner på sidan i elevboken är framför allt att ge eleven omedelbar feedback på det som hen arbetar med. Eleven får direkt reda på om hen har förstått uppgiften och kan be läraren om hjälp om det behövs. Det är även lätt för eleven att korrigera eventuella fel direkt, vilket är viktigt för inlärningen.
Kopieringsunderlag Kopieringsunderlag 3a: Addition och subtraktion Kopieringsunderlag 3b: Tavelbilderna till lektionerna 3, 4 och 6
1. Lektionens innehåll
Visar vad lektionen handlar om och vad som är lektionens matematiska moment.
2. Frågor till samtalsbilden
Samtalsbilden stöder den matematik eleverna ska lära sig. Frågorna hjälper eleverna att fokusera på lektionens innehåll. Vid behov kan eleverna bygga exemplet på bilden med hjälp av olika laborativa material (stavar, kuber, pärlor, pengar).
3. Huvudräkning
Till varje lektion finns det huvudräkningsuppgifter. Du använder huvudräkningsuppgifterna bäst genom att använda dem när du har introducerat lektionens matematiska innehåll. Ovanför samtals bilden i elevboken finns tre rutor där eleven kan skriva svaren.
För alla elever, men framför allt elever som visar låg nivå i matematik, är det viktigt att du använder huvudräkningsuppgifterna på ett strukturerat sätt. Uppgifterna får inte stressa eleven för då blockeras korttidsminnet. De elever som behöver, ska ha tillgång till laborativt material.
Gör så här vid varje tillfälle:
• Först kan du enbart läsa huvudräkningsuppgiften. Då kan en del av eleverna, men inte alla, skriva svar.
• Därefter läser du uppgiften lugnt en gång till, samtidigt skriver du de aktuella talen på tavlan.
Alla elever vet från början att du kommer att upprepa uppgiften och dessutom skriva talen på tavlan.
För dig som lärare ger huvudräkningsuppgifterna en bra möjlighet för en fortsatt formativ (framåtsyftande) under visning.
För eleven kan uppgifterna vara till hjälp för reflektion över sitt eget lärande. Aktiviteten hjälper dessutom eleven att koncentrera sig i ”små portioner”, något som kan vara extra svårt för vissa elever (i början).
4. Förslag på utökat stöd
Här finns tips och aktiviteter, ofta laborativa, som förtydligar och stöttar lärandet för elever som behöver extra hjälp. Film är en symbol som talar om att här finns en film som visar en lärare och elev/elever som kommunicerar det matematiska innehållet under aktiviteten.
5. Kopieringsunderlag
Arbetsmaterial på enklare nivå än kopieringsunderlagen i den ordinarie lärarhandledningen.
6. Elevbokens uppslag
Här visas de sidor i elevboken som hör till lektionen.
1. De fyra grundläggande räknesätten
Lektionens innehåll
• De grundläggande räknesätten och tillhörande begrepp; summa, termer, differens, produkt, faktorer, kvot, täljare och nämnare.
• Sambanden mellan de grundläggande räknesätten
• Additionens och multiplikationens kommutativitet
Frågor till samtalsbilden
1. Vilka är de fyra grundläggande räknesätten? (addition, subtraktion, multiplikation och division)
2. Hur säger du multiplikationen 3 · 23 som addition? (23 + 23 + 23)
3. Med vilket räknesätt kan du kontrollera
a. subtraktion? (Addition)
b. division? (Multiplikation)
4. Vad betyder summa? (Det är additionens uttryck och svar)
5. Till vilket räknesätt hör begreppet
a. kvot? (Division)
b. differens? (Subtraktion)
c. produkt? (Multiplikation)
6. a. I vilka räknesätt kan talen byta plats i uttrycken och ändå få samma svar? (I addition och multiplikation)
b. Varför är det ibland bra att byta plats på talen? (Det kan bli lättare att räkna)
Huvudräkning
a. 36 + 24 (60)
b. 50 – 18 (32)
c. 6 · 7 (42)
d. 56 8 (7)
Förslag på utökat stöd
Det är mycket viktigt att eleverna i årskurs 6 kan multiplikationstabellerna utantill. Att t.ex. förkorta och förlänga kräver goda multiplikationstabellskunskaper.
Det lönar sig därför att använda extra tid för att repetera och träna tabellerna om en del av eleverna har glömt dem.
1. De fyra grundläggande räknesätten
Addition summa summa
46 + 23 = 69 termer
Subtraktion differens differens
69 − 23 = 46 termer
• I addition kan man byta plats på termerna. Summan är den samma.
47 + 18 + 13 = 47 + 13 + 18 = = 60 + 18 = 78
Multiplikation produkt produkt
3 · 23 = 69 faktorer
Division kvot kvot 69 ∕ 3 = 23 täljare nämnare
• I multiplikation kan man byta plats på faktorerna. Produkten är den samma.
Kommutativa lagen gäller i addition och multiplikation. Öva begreppen. Film: Förklara Film täljare nämnare 69 3 = 23 kvot
a. 24 + 26 =
b. 18 + 22 =
c. 17 + 13 =
d. 39 + 24 =
e. 18 + 18 = f. 69 − 55 = g. 46 − 22 = h. 77 −
1. Räkna i huvudet. Skriv bokstaven i rutan. 6 12 14 24 30 36 40
Taluppfattning och tals användning – centrala metoder för beräkningar i de fyra räknesätten med huvudräkning och skriftliga metoder
1. Räkna.
a. 24 + 18 + 36 + 12
Kan du förklara?
Varför är det ibland bra att byta plats på talen i uppgift 1?
b. 99 − 29 − 14 c. 5 · 5 · 4 d. 40 8 + 14 7
24 + 18 + 36 + 12 = = 60 + 30 = 90 5 · 5 · 4 = = 25 · 4 = 100
99 – 29 – 14 = = 70 – 14 = 56 40 8 + 14 7 = = 5 + 2 = 7
2. Skriv uttrycket och räkna.
a. Vad är summan, om termerna är 37 och 44?
37 + 44 = 81
c. Vad är produkten, om faktorerna är 8 och 6?
b. Vad är differensen, om termerna är 257 och 58?
2. Räkna. Skriv bokstaven i rutan. a. 80 − 21 − 50 = b. 36 +
30 − 21= 9
+ 9 = 69
· 4 = 16
– 38 = 32
– 12 = 68
3. Skriv uttrycket och räkna. Ringa in svaret.
a. Vad är summan om termerna är 43 och 46?
b. Vad är differensen om termerna är 128 och 27?
43 + 46 = 89 128 – 27 = 101
c. Vad är produkten om faktorerna är 7 och 9?
· 9 = 63
d. Vad är kvoten om täljaren är 48 och nämnaren är 8?
8 = 6
Metod – använder flera fungerande metoder för att utföra beräkningar vid huvudräkning Begrepp – använder och förstår begreppen term, summa, differens, faktor, produkt, täljare, nämnare, kvot
5. Räkna. Dra streck mellan multiplikation och motsvarande division.
6. Skolan har cirka tusen elever. Eleverna delas in i följande grupper: Ett år har: 365 dagar 52 veckor 12 månader.
A. Elever som är födda på en fredag. B. Elever som är födda den 7 januari. C. Elever som är födda i oktober.
Fundera och motivera i vilken av grupperna A till C du tror att det finns flest elever. Det finns flest elever i grupp . Varför?
d. Vad är kvoten, om täljaren är 46 och nämnaren 2?
4. Räkna. Fundera på om det är enklare att byta plats på termerna och faktorerna. Ringa in svaret i rutan.
10 50 50 + 25 = 6·10 =
a. 38 + 25 + 12 = 23 + 27 + 21 = 33 + 45
8 · 6 = 48 257 – 58 = 199 46 / 2 = 23 75 50 + 21 = 71 60
60 + 33 = 93
60 + 35 = 95 10 9 = 90 30 3 =
7. Ett papper viks fyra gånger, så att papperets mittpunkt hamnar nere till höger. När papperet vecklas ut får man en symmetrisk figur. Vilken vikning och öppnad figur hör ihop? Skriv den siffra som visar figuren som stämmer.
1. 2. 3. 4. 5. 6.
Det finns 52 fredagar på ett år, 31 dagar i oktober och en 7:e januri. A 5 6 1 3 1 365 < 31 365 < 52 365
Kopieringsunderlag 1a–b
Elevbokens uppgifter
Gör uppgift 2 och 4 tillsammans. Diskutera med eleverna hur det kan underlätta att lösa uppgiften. Det är bra att påminna eleverna att de i lugn och ro ska titta på uttrycket innan de börjar räkna. Oftast kan talen byta plats så att det är enklare att räkna.
Be eleverna att dra streck under begreppen som hör till uträkningen i uppgift 3
Det finns multiplikationstavlor på kopieringsunderlag 19b. Ge kopieringsunderlaget som stöd till de elever som behöver.
Kopieringsunderlag
Kopieringsunderlag 1a: Vi repeterar multiplikations- och divisionstabeller
Kopieringsunderlag 1b: Grundläggande räkneoperationer som huvudräkning
* Kopieringsunderlag 1a finns även i Favorit matematik 6A Lärarhandledning
Anteckningar
Kopieringsunderlag 2
2. Prioriteringsregler
Lektionens innehåll
• Repetition av prioriteringsregler
• Räkna uträkningar steg för steg
• Hitta information i en tabell som behövs till en uträkning
Frågor till samtalsbilden
1. Varför behövs prioriteringsregler? (För att alla ska räkna i samma ordning och få samma svar)
2. Vad räknar man först? (Uträkningar inom parentes)
3. Vad räknar man efter parenteserna? ( Multiplikation och division från vänster till höger )
4. I vilken ordning räknar man additioner och subtraktioner? ( Från vänster till höger )
Huvudräkning
a. 7 + 2 · 3 (13)
b. 32 (10 – 2) (4)
c. 24 + 24 4 (30)
d. (10 – 4) · (2 + 4) (36)
Förslag på utökat stöd
Hänga gubbe
Skriv ett uttryck med parenteser på tavlan så att varje siffra och tecken ersätts med ett streck. Eleverna föreslår lämpliga siffror eller tecken (en siffra i taget). Om förslaget passar in skriver du det på rätt streck. Om det finns fler av samma siffra, skriver du bara på en plats. Om förslaget är fel ritar du en del av ”den hängande gubben”. Eleverna försöker lösa uträkningen innan bilden är färdigritad. Eleverna kan även spela parvis.
Resonemang och kommunikation
Eleverna arbetar i par. Den ena eleven är turist som köper biljetter till museet och den andra eleven ”jobbar” i kassan. Biljettpriserna finns i tabellen på sidan 11 i elevboken Bas Favorit 6A
Elevbokens uppgifter
Det kan vara bra att repetera prioriteringsreglerna och träna på dem steg för steg. Eleven kan skriva siffror ovanför uttrycken i uppgifterna 1 och 4
Kopieringsunderlag
Kopieringsunderlag 2: Prioriteringsregler
Favorit 6A s. 10–13
2. Prioriteringsregler
Prioriteringsregler
1. Parenteser
2. Multiplikationer och divisioner från vänster till höger
3. Additioner och subtraktioner från vänster till höger
1. Räkna. Skriv bokstaven i rutan.
a.
ÖVA
1. Räkna.
a. (15 + 15) 5 − (16 − 11)
30 5 – 5 = 1
2. Skriv uttrycket och räkna.
2. Skriv uttrycket och räkna. Ringa in svaret i rutan.
a. Dividera summan av talen 16 och 26 med talet 7.
b. Subtrahera summan av talen 8 och 17 från talet 50.
Kan du förklara? Varför behövs prioriteringsregler?
a. Subtrahera produkten av talen 4 och 9 från talet 60. b. Addera talet 12 till produkten av talen 4 och 9. b. 45 − 2 ·
4. Gå mot uppgiften med svaret 6.
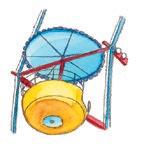
(16 + 26) 7 = 42 7 = 6
c. Räkna ut kvoten av talen 9 och 3. Addera kvoten till produkten av 9 och 3.
9 3 + ( 9 3) = 3 + 27 = 30
50 – (8 + 17) = = 50 – 25 = 25
d. Räkna ut kvoten av talen 12 och 2. Subtrahera kvoten från produkten av 12 och 2.
3. Titta i prislistan. Räkna. 6 18 20 25 30
a. Två föräldrar och två barn som är 12 år åker till museet under lågsäsong. Hur mycket kostar deras biljetter sammanlagt?
2 · 100 + 2 · 50 = = 200 + 100 = 300 300 kr
b. Hur mycket växel får en grupp på nio pensionärer om de betalar med en tusenkronorssedel?
1000 – (9 · 70) = = 1000 – 630 = 370 kr
370 kr
Svar: Svar:
c. Två vuxna och tre barn i åldern 9, 10 och 16, åker till museet. Hur mycket billigare är det för dem att köpa en gruppbiljett i stället för individuella biljetter?
2 · 100 + 3 · 50 = = 200 + 150 = 350 350 – 300 = 50 50 kr
Svar:
Biljett till museet Lågsäsong
100 kr
Vuxen
Barn (6 – 17 år) 50 kr
Barn (under 6 år) 0 kr
Grupp (två vuxna och tre barn i åldern 6 – 17 år) 300 kr Pensionär
Metod – använder enkla prioriteringsregler, t.ex. beräknar multiplikation före addition Problemlösning – använder matematisk formulering av frågeställningar utifrån vardagliga situationer
kr
978-91-44-17378-8_10_book.indd
5. Läs texten. Svara på frågorna.
Stockholm blev Sveriges huvudstad år 1634. Invånarantalet i Stockholms kommun är ungefär 924 000. Staden har en area på 187 km².
a. Hur många bor det i Stockholms kommun?
b. När blev Stockholm Sveriges huvudstad?
c. Vilken area har Stockholm?
924 000 personer år 1634 187 km2
6. Vem bor i huset och vilket husdjur har personen?
Torg Tivoli Djurpark Museum Vart kommer du? Start
60 – (4 · 9) = 60 – 36 = 24 Tivoli 45 – 10 – 28 = 7 12 + (4 9) = 12 +
Person
Husdjur
Anna Karim Lotta Sara Ville undulat hund kanin marsvin katt
• Anna och Ville har bara en granne. Anna bor i hus A. Karim bor granne med Anna.
• Ville är inte granne med Lotta.
• Lotta är granne med Sara.
• I huset bredvid Lottas hus bor ett marsvin.
978-91-44-17378-8_10_book.indd 13
• Karim har inte ett marsvin. Kaninen bor mellan hunden och marsvinet. Undulaten bor granne med hunden.
• Katten bor granne med marsvinet.
2024-10-14 15:58
Kopieringsunderlag
3. Addition och subtraktion
Lektionens innehåll
• Addition och subtraktion som huvudräkning och med uppställning
• Repetition av minnessiffror och växling
• Räkna addition och subtraktion med flera än två termer.
Frågor till samtalsbilden
1. Vad är det för skillnad på att räkna additioner med tre termer och subtraktioner med tre termer, med uppställning? (I addition med uppställning kan du räkna allt på en gång, men subtraktionen måste du räkna i två steg)
2. Förklara och berätta hur du räknar additionen i samtalsbilden.
3. Förklara och berätta hur du räknar subtraktionen i samtalsbilden.
Huvudräkning
a. 4 800 – 700 (4 100)
b. 2 500 + 3 500 (6 000)
c. 2 000 – 900 (1 100)
d. 1 500 + 1 500 – 1 200 (1 800)
Förslag på utökat stöd
Resonemang och kommunikation
Vilka fördelar har du av att uppskatta svaren innan du räknar?
Hur kan du uppskatta svaret innan du räknar?
Uppskatta svaren i till exempel uppgifterna 1a och 1b
Vad har du för fördelar eller nackdelar av att kontrollera dina svar med svaren i den gröna rutan under uppgifterna?
Elevbokens uppgifter
Syftet med svaren i rutan längst ner på sidan i elevboken är framför allt att ge eleven omedelbar feedback på det som hen arbetar med. Eleven får direkt reda på om hen har förstått uppgiften och kan be läraren om hjälp om det behövs. Det är även lätt för eleven att korrigera eventuella fel direkt, vilket är viktigt för inlärningen.
Kopieringsunderlag
Kopieringsunderlag 3a: Addition och subtraktion
Kopieringsunderlag 3b: Tavelbilderna till lektionerna 3, 4 och 6
Bas Favorit 6A s. 14–17
3. Addition och subtraktion
Addition med uppställning
3 907 + 295 + 188
1 1 2
3 9 0 7 2 9 5 + 1 8 8 4 3 9 0
Svar: 4 390
Subtraktion med uppställning 2 001 − 1 079 − 757
a. 2 750 + 250 = b. 2
Svar: 165
1. Räkna med uppställning. Ringa in svaret i rutan.
a. 2 795 + 4 586
Svar: b. 8 000 − 2 106
9 9 7 + 6 7 0 2 8 6
Svar:
Svar: e. 77 329 − 32 836 − 32 585 7 7 3 2 9 3 2 8 3 6
Svar:
TRÄNA
1. Räkna med uppställning.
a. 5 700 − 2 744
Svar: b. 7 315 + 2 968 Svar: c. 50 310 − 41 836 Svar:
2. Räkna i huvudet.
a. 25 + 13 =
d. 17 − 9 =
g. 26 + 26 = b. 80 − 32 = e. 64 + 18 = h. 84 − 23 = c. 34 + 16 = f. 42 − 15 = i. 55 + 36 = Kan du förklara? Förklara skillnaden mellan hur du räknar addition och subtraktion med uppställning. 38 8 52 48 82 61 50 27
4. Skriv uttrycket och räkna.
a. Konstmuseets samling består från början av 2 317 tavlor. Museet får sedan 969 tavlor och sedan ytterligare 677 tavlor. Hur många tavlor har museet efter det?
Samlingen = 2 317
Museet får = 969 + 677
Totalt = 2 317 + 969 + 677
Svar: 3 963 tavlor
b. Museet ska ha en ny utställning. Det finns 4 003 konstverk att välja bland. Först säger man nej till 935 konstverk, sedan säger man nej till 583 konstverk till. Hur många konstverk får vara med på utställningen?
Räkna i huvudet. Skriv bokstaven i rutan. 3. Skriv uttrycket och räkna.
Konstmuseet har 883 besökare på lördagen och 1 740 besökare på söndagen. Hur många besökare har museet sammanlagt under lördagen och söndagen?
b. På onsdagen hade museet 931 besökare och på torsdagen 85 besökare färre än på onsdagen. Hur många besökare har museet sammanlagt under onsdagen och torsdagen? 3 000 3 000 1 900 3 500 2 900 4 400 1 300 1 500 1 200 L L A H T S N O K
883 + 1 740 (931 – 85) + 931 1 7 4 0 + 8 8
Svar: 2 623 besökare
Metod – använder skriftliga och fungerande metoder för att utföra beräkningar med naturliga tal och enkla tal i decimalform Problemlösning
6. Lös uppgiften.
Från Kulla till Torp är det 14 km längs vägen. Mellan Röda huset och Kulla är det 21 km. Från korsningen är det 13 km till Röda huset. Mellan Torp och Parken är det 9 km.
a. Hur långt är det från korsningen till Kulla? till Torp?
21 km – 13 km = = 8 km
Svar: 8 km 14 km – 8 km = = 6 km
Svar: 6 km 6 5 4 1 8
978-91-44-17378-8_10_book.indd 17
5. Vilka bitar saknas i bilden? Skriv siffrorna i bilden.
4. Multiplikation
Lektionens innehåll
• Multiplikation med tio
• Multiplikation med talsorter
• Multiplikation med uppställning med tvåsiffrig faktor
Frågor till samtalsbilden
1. På vilka olika sätt kan man räkna multiplikationsuppgifter? (Till exempel med huvudräkning, genom att multiplicera talsorterna, med uppställning och med räknare)
2. Vilka multiplikationsuppgifter räknar du i huvudet?
3. Förklara hur du multiplicerar med tio.
4. Förklara och berätta hur man räknat uträkningen 70 · 80 som finns i samtalsbilden.
5. Vilka talsorter syftar förkortningarna HTE på? (Hundratal, tiotal, ental)
6. När kan det vara bra att räkna multiplikation med varje talsort? (Till exempel då den ena faktorn är ensiffrig och den andra faktorn består av flera siffror)
7. Förklara och berätta hur du räknar multiplikationen 37 · 2 018 i samtalsbilden.
Huvudräkning
a. 10 · 25 (250)
b. 60 · 80 (4 800)
c. En bussbiljett för barn kostar 13 kronor. Hur mycket kostar 10 bussbiljetter sammanlagt? (130 kr)
d. Ett äpple kostar 6 kr. Hur mycket kostar 8 äpplen sammanlagt? (48 kr)
Förslag på utökat stöd
Det är viktigt att eleverna i årskurs 6 kan multiplikationstabellerna utantill. Att till exempel förkorta och förlänga kräver goda multiplikationstabellskunskaper. Om det är utmanande för eleven att räkna multiplikation med uppställning, är orsaken sannolikt att eleven inte kan multiplikationstabellerna utantill. Eleven kan vid behov leta upp tabellsvaren från multiplikationsrutan på insidan av omslaget längst bak i boken. Om eleven är osäker på tabellerna men får tillgång till stöd kan eleven bättre koncentrera sig på att lära sig själva algoritmen.
På kopieringsunderlag 19b finns en multiplikationstavla.
Taxi eller buss?
Eleverna arbetar i grupper med 4 till 6 elever. Eleverna sitter i en cirkel. I tur och ordning säger de talraden från och med talet ett. Vid tal som är en produkt i femmans tabell säger eleven ”buss” istället för produkten och vid tal som är en produkt i sjuans tabell säger eleven ”taxi”. Forts. s. 24
Favorit 6A s. 18–21
4. Multiplikation
Huvudräkning
10 · 48 = 480 70 · 80 = 56 · 100 = 5 600
4 · 123 = 4 · 100 + 4 · 20 + 4 · 3 = = 400 + 80 + 12 = = 492
1. Räkna i huvudet. Skriv bokstaven i rutan.
Multiplikation med uppställning 37 · 2 018 Svar: 74 666 a. 10 · 13 =
Taluppfattning och tals användning – centrala metoder för beräkningar med multiplikation
978-91-44-17378-8_10_book.indd 18 2024-10-14 15:58
ÖVA
TRÄNA
1. Räkna.
a. 50 · 80 = b. 10 · 600 = c. 5 · 700 = d. 4 · 800 = e. 4 · 2 000 = f. 7 · 6 000 =
2. Räkna.
3. Skriv uttrycket och räkna.
a. En vuxenbiljett till en idrottstävling kostar 140 kronor. Barnbiljetten kostar hälften så mycket. Hur mycket kostar två vuxenbiljetter och en barnbiljett sammanlagt?
b. Det kostar 9 850 kronor att ordna kaffeförsäljning. Det säljs 612 koppar kaffe. En kopp kaffe kostar 15 kronor. Med hur mycket förlust går försäljningen?
4. Titta på bilderna en stund. Täck över bilderna. Hur många saker kommer du ihåg? Skriv en lista i ditt häfte.
2. Räkna. Ringa in svaret i rutan. a. 5 · 259
3. Skriv uttrycket och räkna.
a. En löpare springer 22 varv runt en 400 meter lång bana. Hur långt springer löparen sammanlagt?
Svar:
b. En idrottstävling har 1 507 åskådare. Ett program kostar 13 kronor. Hur mycket pengar får man in på programförsäljningen om alla åskådare köper ett program var?
22 · 400 m 8 800 m 1 507 · 13 kr 19 591 kr
Svar:
Metod – utför multiplikation med 10 och 100 – förstår och använder beräkningar i ett talområde kan utnyttjas i ett utökat talområde, t.ex. om 6 ∙ 8 = 48 så är 60 ∙ 80 = 4 800 – använder flera fungerande metoder för att utföra beräkningar i multiplikation vid huvudräkning – använder skriftliga och fungerande metoder för att utföra beräkningar i multiplikation Problemlösning – använder matematisk formulering av frågeställningar utifrån vardagliga situationer
5. Räkna. Ringa in svaret.
6. Vilka är talen?
a. Av vilka tre efterföljande heltal är summan 9?
+ = 9
b. Av vilka tre efterföljande heltal är summan 33?
+ = 33
c. Av vilka tre efterföljande heltal är summan 15?
+ = 15
d. Av vilka tre efterföljande heltal är summan 24?
+ = 24
Kopieringsunderlag 4a–b
Arbete på tavlan
Tavelbilden finns på kopieringsunderlag 3b
Kopieringsunderlag
Kopieringsunderlag 4a: Multiplikation
Kopieringsunderlag 4b: Multiplikationstävling
Anteckningar
Favoritmatematik
Utökat stöd
Lärarhand L edning
Favorit matematik är ett basläromedel i matematik med en gedigen, välfungerande och tydlig struktur. Materialet kommer från Finland där det är uppskattat för strukturen och de goda resultaten hos eleverna.
Favorit matematik 6A Utökat stöd är en kompletterande lärarhandledning för klasslärare. Här finns lektionsspecifika tips, filmer och förslag på extra hjälp till elever som har svårt att nå målen i matematik. Kopieringsunderlag som kan stötta lärandet medföljer i en bilaga men finns även som filer i den digitala lärarresursen. Den muntliga kommunikationen och det laborativa arbetet är centralt och lyfts genomgående fram i aktiviteterna.
Det beprövade och framgångsrika läromedlet har anpassats samt granskats av både lärare och forskare som är verksamma i Sverige.