

HEUREKA!
Fysik nivå 1
VÄLKOMMEN TILL HEUREKA!
De fyra krafterna
Fysiken vilar på fyra grundläggande krafter som inte bara styr de händelser som sker i vår nära omgivning, utan också, så långt vi vet, hela vårt universum. De fyra krafterna bildar en röd tråd genom all fysik. I kapitel 1 ger vi dig en första introduktion till de fyra krafterna.
Det naturvetenskapliga arbetssättet
Fysiken kan sammanfattas i teoretiska samband som tycks vara allmängiltiga naturlagar, alltså lagar som tycks gälla överallt. Men fysiken är också en experimentell vetenskap, och med nya Heureka! vill vi visa på sambandet mellan experiment och teori samt öka förståelsen för det naturvetenskapliga arbetssättet. En kortfattad beskrivning inleder kapitel 2.
Klassisk och modern fysik
Många fenomen vi möter i vår vardag kan vi förklara med den klassiska fysiken, det vill säga den fysik som beskriver till exempel kraft, rörelse och elektricitet. Flera av de tekniska apparater vi använder varje dag, som exempelvis mobiltelefonen och laserpekaren kräver för sin förklaring den moderna fysiken. Det är den fysik som har utvecklats sedan början av 1900-talet av pionjärer som Albert Einstein, Werner Heisenberg och Marie Curie. I kapitel 3 till och med kapitel 10 kommer du att få lära dig mer om den klassiska fysiken och i kapitel 12 och 13 ger vi dig en inblick i den moderna fysiken.
Energi och hållbar utveckling
Som du säkert kommer att upptäcka handlar fysik mycket om att lösa problem med matematiken som verktyg. Men ämnet fysik handlar också om samhälleliga och etiska frågor, till exempel frågor om energi och hållbar utveckling. I bokens sista kapitel, Fysikens roll i samhället – hållbar energi, belyser vi frågor om just miljö, energi och hållbar utveckling ur ett fysikaliskt perspektiv.
Läromedelserien Heureka! har funnits i över 40 år och är ett samarbete mellan erfarna lärare och etablerade fysiker. Den nya upplagan har förändrats och moderniserats. På sidan 6 kan du läsa mer om nya Heureka!
Lycka till med dina fysikstudier!
Författarna
8.2 Explosion och kollision
8.3
9.1 Varifrån kommer laddningen?
9.2 Kraftverkan mellan laddningar
9.3 Elektriska fält
9.4 Elektrisk energi och spänning
LADDNINGAR I RÖRELSE
spänning och resistans
kretsar
Uppvärmning och avsvalning
och fasövergångar
Materiens minsta beståndsdelar
13.1 Atomens kärna
13.2 Radioaktivitet
13.3 Matematisk beskrivning av sönderfall
13.4 Kärnenergi
13.5 Strålningens biologiska effekter
13.6 Strålning i medicinsk diagnostik
14.1 Energitillgångar och förbrukning
14.2 Energikällor
Så fungerar Heureka!
11.3 FASER OCH FASÖVERGÅNGAR
Ett ämnes specifika smältvärme Cs anger den energi som krävs för att smälta 1 kg av ämnet.
KONTROLL
8 Vad är skillnaden mellan avdunstning och förångning?
TÄNK TILL!
6 Efter ett härligt bad i havet är det lätt att bli lite frusen när man kommer upp. Vilka processer är inblandade i att kyla ned din kropp efter badet?
Fråga forskaren:
Vilka är rekorden i högsta och lägsta temperatur som uppnåtts på jorden?
SAMMANFATTNING
ÖVNINGAR
4.1 Krafter av olika slag
EXEMPEL 1
En kropp har massan 3,55 kg. Bestäm kroppens tyngd.
LÖSNING
F = m ∙ g = 3,55 ∙ 9,82 N = 34,861 N
Svar: 34,9 N
BLANDADE ÖVNINGAR
Varje kapitel är indelat i delkapitel.
Innehållet sammanfattas löpande i röda rutor.
Texten stöttas av Kontroll. Frågor som hjälper dig att se vad som är särskilt viktigt. Förslag på svar till frågorna hittar du i facit.
Med Tänk till! får du träna på att föra fysikaliska resonemang. Frågorna varierar från relativt enkla till riktigt svåra. De passar bra att arbeta med i grupp.
Forskning i fysik är i dag mer aktiv än någonsin tidigare. Med Fråga forskaren vill vi ge en utblick mot aktuell forskning.
I slutet av kapitlet hittar du en sammanfattning. Den ger en överblick av hela kapitlet.
Övningarna är indelade efter delkapitel och inleds med ett grundläggande exempel. Några av övningarna är mer utmanande. De är märkta med en .
Allra sist i kapitlet hittar du Blandade övningar. De är indelade i tre nivåer och blandar alla delmoment i kapitlet.
VÄRME

Jordens inre innehåller stora mängder värmeenergi, men det är värmen från solen som har skapat förutsättning för liv. Den värmen behöver vi komplettera för att livet ska bli behagligt året om.
I det här kapitlet kommer vi att beskriva begreppen värme, temperatur och inre energi. Vi kommer också att visa hur man kan beräkna den mängd energi som krävs för att värma, smälta och förånga ett ämne.
INRE ENERGI, TEMPERATUR OCH VÄRME
Solens värme är anledningen till att jorden är beboelig och att liv på jorden har kunnat utvecklas. På sommaren kan vi behöva kyla oss och vintertid är det viktigt att vi kan värma oss. Värmekällor har därför en viktig roll i vårt samhälle. Nära förknippad med värme är energiproduktion, eller mer riktigt uttryckt energiomvandlingar, i värmepumpar och i värmekraftverk av olika slag. I dagligt tal använder vi ofta begreppen värme, energi och temperatur för samma sak. Men i fysiken är de skilda begrepp och här kommer vi att gå igenom vad de betyder och hur de hänger ihop.
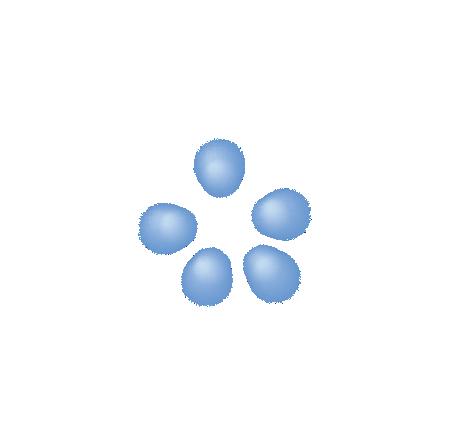
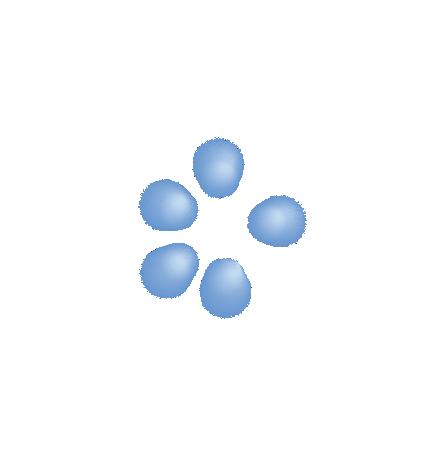

Inre energi

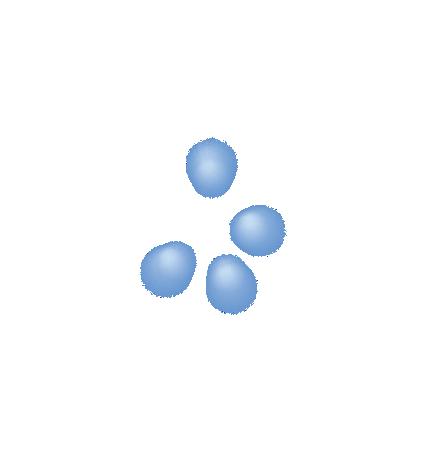
Figur 1 I ett fast ämne rör sig atomerna fram och tillbaka kring sitt jämviktsläge. De diffusa atomerna illustrerar deras rörelse, en rörelse som blir allt häftigare när temperaturen ökar.

Du vet att en kropp i rörelse har rörelseenergi. Men även inuti ett stillastående föremål finns rörelse. Atomerna i materien rör sig slumpartat i olika riktningar och har därför rörelseenergi även om föremålet inte rör sig, se figur 1. Atomen har också potentiell energi. Det är den energi som är bunden i atomernas växelverkan med varandra, som till exempel i den bindningsenergi som håller samman atomerna i en molekyl. Summan av den inre rörelseenergin och den potentiella energin är den inre energin. När vi talar om värmeenergi eller termisk energi menar vi vanligtvis energin hos atomernas och molekylernas oordnade rörelse, det vill säga den inre rörelseenergin.
All materia har inre energi men fördelningen mellan potentiell energi – atomernas växelverkan – och rörelseenergi kan variera. Ädelgaserna (helium, neon med flera) är speciella – krafterna mellan deras atomer är nämligen mycket svaga. Den inre energin hos ädelgaserna består därför nästan enbart av rörelseenergi hos atomerna. Även hos andra gaser är den potentiella energin ofta liten, medan den är större hos vätskor och fasta ämnen.
TÄNK TILL!
1 Man kan öka den inre energin genom att gnida två ämnen mot varandra. Hur varmt kan det bli? Kan det bli så varmt att det börjar brinna?

Temperatur
När vi värmer vatten, till exempel i en kastrull på en spisplatta, ökar vattnets inre energi. Samtidigt stiger temperaturen. Temperatur och inre energi har en nära koppling till varandra.
Om vi i stället för vatten har en nollgradig blandning av vatten och is i kastrullen, börjar isen smälta. Med en termometer ser vi att temperaturen inte ändras förrän all is har smält – först då stiger temperaturen. Hur kommer det sig att temperaturen inte ändras, trots att blandningens inre energi ökar?
Smältning innebär att molekylerna lossnar från sina platser i det fasta tillståndet. Då ökar deras potentiella energi, men inte nödvändigtvis deras rörelseenergier. Det tyder på att temperaturen inte beror på molekylernas potentiella energi, utan bara på deras rörelseenergi.
Temperaturen hos ett ämne ökar om den genomsnittliga rörelseenergin i ämnets molekyler ökar. Motsvarande gäller om rörelseenergin minskar – då minskar även temperaturen. Temperaturen påverkas däremot inte av att molekylernas potentiella energi ändras.
För att mäta temperatur utnyttjar man ofta en vätskas utvidgning i en vätsketermometer. Den vanligaste temperaturskalan är uppkallad efter svensken Anders Celsius (1701–1744). Vid gradering av termometern utgår man från två fixpunkter, 0 ° C vid isens smältpunkt och 100 °C vid vattnets kokpunkt vid normalt lufttryck.
KONTROLL
1 Vad är inre energi?
2 Vad händer inuti ett ämne när dess temperatur ökar?
Figur 2 Ju högre temperatur det smälta glaset har desto snabbare rör sig dess molekyler.
Helium kokar
Syre smälter Syre kokar
Figur 3 Jämförelse mellan kelvinskalan och celsiusskalan.
Torris förgasas, ammoniak smälter
Ammoniak kokar Is smälter Kalium smälter Vatten kokar Litium smälter
Hur kallt kan det bli?
Eftersom temperaturen är ett mått på den oordnade rörelseenergin hos atomer och molekyler, måste det finnas en lägsta möjlig temperatur, nämligen då all rörelse har avstannat. Denna temperatur motsvarar –273,15 °C och kallas den absoluta nollpunkten. Kallare än så kan det aldrig bli någonstans i universum!
Någon liknande gräns för hur varmt det kan bli – med allt högre fart på atomer och molekyler – finns inte. I solens inre är temperaturen flera miljoner grader, och ännu varmare kan det bli.
Kelvinskalan
Den absoluta nollpunkten, –273,15 °C, är nollpunkten för den absoluta temperaturskalan eller kelvinskalan.
SIenheten för kelvinskalan är 1 K (kelvin). Enheten 1 K är lika stor som 1 °C. Därför blir temperaturintervallet mellan vattnets fryspunkt och kokpunkt samma i båda skalorna, 100 °C respektive 100 K. Men temperaturangivelserna blir olika. Vattnets kokpunkt är 100 ° C eller 373 K. Sambandet mellan de båda skalorna framgår av figur 3. En temperaturangivelse i kelvin är 273 (noga räknat 273,15) enheter högre än i grader Celsius.
SIenheten för temperatur är 1 K (kelvin). Enheten 1 K är lika stor som 1 °C.
0 K motsvarar –273,15 °C, den absoluta nollpunkten.
Temperatur och rörelseenergi
En kropps temperatur beror på den oordnade rörelsen hos kroppens atomer eller molekyler. Vi kan uppskatta vilka farter det rör sig om för en ideal gas, det vill säga för en gas där man tänker sig att ingen annan växelverkan sker mellan molekylerna än fullständigt elastiska stötar. För en sådan gas finns en enkel relation mellan temperaturen T och molekylernas genomsnittliga rörelseenergi Ek.
där
Boltzmanns konstant k har värdet 1,38 10−23 J/K. Relationen ligger utanför den här kursen, men den ger oss en möjlighet att beräkna molekylernas hastighet.
Använder vi relationen för rörelseenergi
E mv k = 2 2 får vi
3 22 2 kT mv = eller v kT m 23 =
Låt oss beräkna molekylernas genomsnittliga fart för syrgas (O2) vid temperaturen 20 ° C. Luften vi andas består av 21 % syre och är livsviktig för oss.
En syreatom består av 8 protoner och 8 neutroner och har massan 16 ∙ 1,67 ∙ 10−27 kg, där 1,67 ∙ 10−27 kg är massan hos en proton eller en neutron. En syremolekyl, som består av två syreatomer, har dubbla massan, det vill säga 32 ∙ 1,67 10−27 kg.
EkT k = 3 2 v kT m
3313810293 3216710 23 27 , , m/s
Vid temperaturen 20 ° C, 293 K, blir molekylernas genomsnittliga fart v = 480 m/s
Molekylerna rör sig slumpartat åt alla håll med en medelfart på 480 m/s. Det är en hög fart, och visar på de stora energimängder som döljer sig i atomernas och molekylernas oordnade rörelse i materiens inre.
Figur 4 Värme flödar från en varmare kropp till en kallare kropp.

Värme
I fysiken betyder värme energi som av sig själv flödar från en varmare till en kallare kropp. Värme är en form av energiöverföring. Den energiöverföringen kan ske på olika sätt: genom strålning, som strålningen från solen till jorden, genom ledning, som till exempel från en varm spisplatta till en kastrull, eller genom strömning, som när den varma luften cirkulerar i rummet. Energiöverföringen kan pågå tills temperaturskillnaden är utjämnad.
• Inre energi är summan av den inre rörelseenergin och den potentiella energin.
• Temperatur är ett mått på molekylernas eller atomernas rörelseenergi.
• Värme är energi som överförs från en varmare kropp till en kallare.
Värmestrålning

Figur 5 Fotografiet visar den infraröda (Ir) strålningen från en hund.
Varje dag ser du ljuset från solen. Även när det är mulet är det ljuset från solen som gör att du kan se omgivningen. Du märker också att solen värmer, speciellt på sommaren, men även på vintern. Synligt ljus och värmestrålning är olika komponenter i solens strålning.
Om du värmer en metallbit, så börjar den så småningom att glöda. Först i rött, sedan kanske nästan i vitt. Det utsända ljuset beror på temperaturen. Ju varmare föremålet är, desto mer strålar det. Du strålar också. Din värmestrålning är osynlig, men den finns och den märks. Faktum är att alla föremål strålar.
TÄNK TILL!
2 Kan ett isblock stråla?

Värmeledning
Du har säkert märkt hur lätt det är att bränna sig på en varm metallbit, medan en lika varm träbit inte har samma effekt. Ett vedträ kan du faktiskt hålla i ena änden när det brinner i den andra, men en metallbit som glöder i den ena änden skall du akta dig för att röra. Metall och trä har olika förmåga att leda värme. Värmeledningsförmågan är en materialegenskap. Tabell 1 visar värmeledningsförmågan för några olika material. Ju större temperaturskillnaden är mellan olika delar av ett material, eller mellan två olika kroppar i beröring med varandra, desto fortare går överföringen och desto större blir den överförda energin.
Strömning
Värme kan också spridas genom strömning, konvektion. Om du värmer en vätska, blir temperaturen fortare jämnt fördelad om du rör om den. Stora omrörningar sker i jordens lufthav när varm luft strömmar norrut från området kring ekvatorn, eller när kall luft strömmar söderut från polartrakten. Strömning skiljer sig från värmeledning och värmestrålning genom att mediet, det ämne som tillför värme, förflyttas och inte bara energin.
TÄNK TILL!
3 Om du en kall vinterdag vidrör en metallbit med fingrarna, känns den kall, mycket kallare än till exempel en tygbit. Om du vidrör en spik eller skruv i en bastu, känns den mycket varmare än träpanelen. Hur kommer det här sig?
4 Om du skulle värmeisolera en byggnad, vilket material från tabell 1 skulle du välja?
Tabell 1 Värmeledningsförmåga för några olika material. enheten är W/(m ∙ K).
Silver 427
Koppar 398
Järn 80
Betong 1,7
Vatten 0,6 trä 0,13
Cellplast 0,037 luft 0,026
Figur 6 Fackelbärare.
11.2 UPPVÄRMNING
OCH AVSVALNING
Uppvärmning
Låt oss undersöka hur temperaturen ändras för ett ämne när vi tillför värme och den inre energin ökar. Vi använder en uppställning enligt figur 7 och häller vatten i termosen. En doppvärmare värmer vattnet med konstant effekt. Det innebär att den tillförda energin uttrycks
E = P ∙ t
Vi vill att hela den tillförda energin värmer upp vattnet och inget annat, därför utför vi experimentet i en termos. Dessutom vill vi att allt vatten i termosen värms och rör därför om hela tiden.
7
Vi gör en mätserie och antecknar temperaturen med jämna tidsmellanrum. När vi analyserar mätdata kan vi konstatera att temperaturen ökar i takt med energitillförseln. Sambandet mellan tillförd energi E och temperaturökningen ∆T kan vi skriva som
E = k1 ∙ ∆T
Det är rimligt att anta att mängden vatten påverkar hur mycket energi som behöver tillföras för att få en viss temperaturökning. I experimentet ovan är vattnets massa en kontrollerad variabel. Vi hade ju samma vattenmängd under uppvärmningen.
Vi gör en ny mätserie men nu varierar vi vattenmängden. Vi mäter massan hos olika mängder vatten och värmer dem tills temperaturökningen är 30 K. Vid denna mätserie är det alltså ∆T som är en kontrollerad variabel. Genom att analysera vår mätdata kan vi konstatera att
E = k2 ∙ m
Våra resultat kan sammanfattas till
E = c ∙ m ∙ ∆T
där c är en konstant som beror av vilket ämne vi värmer. c kallas specifik värmekapacitet och anger den energimängd som behövs för att höja temperaturen 1 K hos 1 kg av ett ämne. Enheten för specifik värmekapacitet är 1 J/(kg · K). Den enheten skrivs ibland 1 kJ/(kg · grad), eftersom temperaturskillnader är samma i kelvinskalan och i celsiusskalan.
Figur
Sambandet mellan inre energi och temperatur undersöks.
Sambandet gäller för varje ämne så länge det uppträder i samma tillstånd, det vill säga så länge det är antingen fast, flytande eller gasformigt.
Konstanten c är olika stor för olika ämnen och även för olika tillstånd av samma ämne. Se Tabell 2.
Vattens specifika värmekapacitet
Den specifika värmekapaciteten för vatten kan beräknas med data från experimentet med doppvärmaren. Men noggrannheten blir inte särskilt stor, eftersom man måste ta hänsyn till att den tillförda energin inte bara används för att värma upp vattnet utan även värmer upp doppvärmaren och termosflaskan. Ett noggrant värde är 4,19 kJ/(kg · K). Vatten har en stor specifik värmekapacitet, vilket innebär att det behövs mycket energi för att öka dess temperatur.
Avsvalning
När ett föremål svalnar, avtar den inre energin. Sambandet E = c · m · ΔT kan användas för att beräkna ändringen av den inre energin, även när det är fråga om avsvalning.
För att åstadkomma temperaturändringen ∆T hos massan m av ett ämne, måste energin E tillföras eller avges:
E = c · m · ∆T
Ämnets specifika värmekapacitet c är den energi som upptas eller avges då temperaturen hos 1 kg av ämnet ändras 1 °C eller 1 K.
Tabell 2 Värmekapacitet (kJ/(kg ∙ K)) för olika ämnen.
Järn 0,449
KONTROLL
3 Varför är det bättre att utföra det beskrivna experimentet i en termos än i en glasbägare?
4 Det går åt 2,4 kJ att värma 1,0 kg glykol 1 ˚C. Bestäm glykols specifika värmekapacitet.
5 Vilket av ämnena i tabell 2 ökar sin temperatur mest om 100 J tillförs?
6 Hur mycket energi åtgår till att värma 100 liter vatten från 25 ˚C till 45 ˚C?

Figur 8 Inre energi gör livet behagligare för den japanska snöapan.
EXEMPEL 1
Hur mycket energi behövs för att värma upp 3,0 l vatten 80 grader?
Lösning
Vi använder formeln E = c · m · ΔT, där ΔT är temperaturändringen.
Massan av 3,0 l vatten är 3,0 kg. Vi behöver också vattnets specifika värmekapacitet, som är 4,19 kJ/(kg · grad).
E = 4,19 · 3,0 · 80 kJ = 1005,6 kJ
Svar: Det behövs drygt 1 MJ.
Kommentar: Anta att du i stället använder energin 1 MJ för att värma upp 3 kg luft (omkring 2,5 m3), som har specifika värmekapaciteten
1 kJ/(kg · grad). Hur mycket skulle då luftens temperatur öka? Vi använder formeln E = c · m · ΔT, där återigen ΔT är temperaturändringen.
1000 = 1 · 3 · ΔT
ΔT = 333 grader
Det här exemplet visar att det krävs mycket mer energi att värma vatten än luft.
EXEMPEL 2
Det är stora energimängder som omsätts när föremål värms upp eller kyls av. Vi ska belysa det med ett tankeexperiment. Den energi som tillförs när man höjer temperaturen hos precis 1 kg vatten 1 grad (4,19 kJ) lagras som inre energi, dvs. som potentiell energi och kinetisk energi i den slumpmässiga molekylrörelsen. Vilken fart skulle vattnet få, om man använde lika mycket energi för att ge alla molekylerna en gemensam fart åt samma håll?
Lösning
Energin 4,19 kJ skulle bli ”vanlig” rörelseenergi hos 1 kg vatten.
Vi använder sambandet Ek = E mv k = 2 2 Ek = 4,19 ∙ 103 J ger v E m k 2241910 10 3 , , m/s90m/s
Svar: Vattnets fart skulle bli över 300 km/h!
EXEMPEL 3
Du har tappat upp 3,6 liter varmvatten med temperaturen 45 ° C i en badbalja. Hur mycket vatten med temperaturen 13 ° C ska du fylla på med för att badtemperaturen ska bli 37 ° C? Bortse från energiutbyte med omgivningen.
Lösning
Det varmare vattnet avger inre energi som upptas av det kallare. Vattnets specifika värmekapacitet kallas cvatten.
Massan av 3,6 liter vatten är 3,6 kg. Det gäller att avgiven inre energi = upptagen inre energi. Vi använder formeln
E = c · m · ΔT
där ΔT är temperaturändringen
ΔT = Tefter – Tföre
När temperaturen minskar blir ΔT negativ och energiändringen negativ, och när den ökar blir den positiv.
• Energiändringen för det varma vattnet är
cvatten · 3,6 · (37 – 45) J = –28,8 · cvatten J
Det varma vattnet avger energin 28,8 · cvatten J
• Energiändringen för det kalla vattnet är
cvatten · m · (37 – 13) J = 24 · m · cvatten J
där m är massan hos det vatten som ska tillsättas.
Det kalla vattnet upptar energin 24 · m · cvatten J
• Avgiven energi = upptagen energi ger
28,8 · cvatten J = 24 · m · cvatten J
• Vi dividerar med cvatten och löser ut m
m = 1,2 kg
Svar: 1,2 liter 13gradigt vatten ska tillsättas.

11.1 Inre energi, temperatur och värme
• Den inre energin är summan av den inre rörelseenergin och den potentiella energin.
• Temperaturen hos ett ämne är ett mått på den genomsnittliga rörelseenergin hos ämnets molekyler eller atomer.
• Värme är energi som flödar från en varmare kropp till en kallare.
11.2 Uppvärmning och avsvalning
• För att åstadkomma temperaturändringen ∆T hos massan m av ett ämne, måste energin E tillföras eller avges:
E = c · m · ∆T
Ämnets specifika värmekapacitet c är den energi som upptas eller avges då temperaturen hos 1 kg av ämnet ändras 1 °C eller 1 K. Sambandet förutsätter att ingen fasövergång sker, utan att ämnet hela tiden förblir antingen en gas, en vätska eller ett fast ämne.
11.3 Faser och fasövergångar
• När massan m av ett ämne smälter eller stelnar (utan att temperaturen ändras) omvandlas energin E:
E = cs · m
Ämnets specifika smältvärme cs är den energi som går åt för att smälta 1 kg av ämnet.
• När massan m av ett ämne förångas eller kondenseras (utan att temperaturen ändras) omvandlas energin E:
E = ck · m
Ämnets specifika ångbildningsvärme ck är den energi som går åt för att förånga 1 kg av ämnet.
11.1 Inre energi, temperatur och värme
EXEMPEL
Glykol har smältpunkten −12 °C och kokpunkten 199 °C. Beräkna skillnaden mellan dessa temperaturer, ∆T, i SIenheten för temperatur.
LÖSNING
SIenheten för temperatur är Kelvin.
Smältpunkt: (−12 + 273) K = 261 K
Kokpunkt: (199 + 273) K = 472 K
∆T = (472 – 261) K = 211 K
Svar: Skillnaden i temperatur blir 211 K.
Kommentar: En skillnad i temperatur blir lika stor om vi räknar K eller °C. Därför kan vi också uttrycka skillnaden som ∆T = (199 − (−12)) K = 211 K.
1 Bestäm temperaturen uttryckt i Kelvin.
a 22 °C
b Kokpunkten för vatten.
c Smältpunkten för kvicksilver.
2 Under ett dygn i april varierar temperaturen mellan −5 °C och 12 °C på samma plats. Hur stor var temperaturskillnaden i Kelvin?
3 Inre energin hos vattnet i en bägare kan höjas på olika sätt. Här beskrivs några:
1 En het metallkula sänks ner i vattnet.
2 En strömförande trådspiral placeras i vattnet.
3 En motordriven omrörare (med skovelhjul) får verka i vattnet.
I vilket (eller vilka) av dessa fall förmedlas energiöverföringen till vattnet av a arbete
b den process vi kallar värme?
4 När du går barfota på ett stengolv känns det kallare än när du går på ett trägolv med samma temperatur. Vilken fysikalisk egenskap ligger bakom detta? Förklara upplevelsen med fysikaliska termer.
5 När du öppnar diskmaskinen efter diskning är tallrikar och glas varma. Du ställer upp en tallrik på bänken.
a Vilken blir tallrikens temperatur efter några minuter?
b Beskriv processen när tallriken kyls av med begreppen värme och värmeledning.
6 Geir tänker “Metall har hög värmeledningsförmåga. Så dumt att min termos är gjord av metall, då svalnar min varma choklad snabbt. Det är bättre att jag tar en PETflaska eftersom plast har lägre värmeledningsförmåga.” Resonerar han riktigt?
7 Vad har störst inre energi, ett stort isberg eller en kopp varmt kaffe?
8 Du kan värma dina händer genom att hålla dem runt ett tänt ljus, men bränner dig lätt om du håller händerna rakt ovanför ljuset. Vilken typ av värmeöverföring sker i respektive fall?
11.2 Uppvärmning och avsvalning
EXEMPEL
En betongklump väger 2,5 kg och har temperaturen 79 °C. Klumpen läggs i vatten och når slutligen temperaturen 45 °C. Hur stor energi har betongklumpen avgett till vattnet?
LÖSNING
Specifik värmekapacitet för betong är c = 0,92 kJ/kg. Temperaturändringen är
∆T = (79 – 45) K = 34 K
Betongklumpen avger energin
E = m ∙
9 Jiang har feber. Hennes kroppstemperatur är 39,0 °C i stället för normala 37,0 °C. Vi antar att människan till största del består av vatten och att Jiang väger 63 kg. Hur mycket energi behövs för att höja hennes temperatur 2 °C?
10 Vid ett experiment krävdes energin 4,2 kJ för att värma upp en bit koppar från 10 °C till 25 °C. Bestäm kopparbitens massa.
11 I en termosflaska finns 500 g av en vätska med temperaturen 15,0 °C. Vätskan värms upp med en doppvärmare som avger 250 W, och då ökar temperaturen till 40,0 °C på 120 s. Hur stor är vätskans specifika värmekapacitet? Bortse från termosflaskans inverkan.
12 Luften i ett rum väger 30 kg.
a Hur stor energi behövs för att värma luften i rummet från 0 °C till 20 °C?
b Hur lång tid skulle en elektrisk kamin med effekten 1,0 kW minst behöva för att åstadkomma uppvärmningen?
13 En behållare med 10 liter vatten värms till 35 °C och får sedan svalna i rumstemperatur. När temperaturen passerar 28 °C avtar den med 0,2 °C per minut. Hur stor effekt ska en doppvärmare avge till vattnet, om temperaturen ska hållas konstant vid 28 °C under i övrigt oförändrade förhållanden?
14 I ett romerskt bad finns ett betongblock i form av en kub med sidan 0,50 m. Det har hettats upp till en temperatur av 80 °C och svalnar sedan till 20 °C på 5,0 h. Hur stor medeleffekt har denna ”värmekälla” utvecklat medan den svalnade? Betongens densitet är 2,2 g/cm3 och dess specifika värmekapacitet är 0,92 kJ/(kg · K).
15 1,00 kg järn och 1,00 kg koppar hettas upp till en gemensam temperatur av 105 °C i en ugn. De läggs sedan direkt i varsin likadan hink fylld med lika mycket rumstempererat vatten.
a I vilken hink når vattnet den högsta temperaturen? Motivera.
b Beräkna sluttemperaturen för vattnet i hinken med kopparbiten om det är 5,0 liter vatten med temperaturen 18 °C i hinken.
11.3 Faser och fasövergångar
16 a Hur stor energi behövs för att smälta det 10 cm tjocka istäcket på en helt isbelagd sjö med arean 3,0 km2? Densiteten för is är 0,92 · 103 kg/m3 och dess specifika smältvärme är 334 kJ/kg.
b Hur många kubikmeter (m3) ”eldningsolja” krävs för att åstadkomma den energi du just beräknat? Densiteten är 890 kg/m3 och energiinnehållet 43 MJ/kg.
17 I ett öppet termoskärl hålls vatten kokande med hjälp av en doppvärmare, som avger effekten 0,40 kW. Hur många gram vattenånga produceras per minut?
18 En doppvärmare med effekten 210 W glöms kvar i en tekopp med 2,0 dl vatten med temperaturen 82 °C. Hur lång tid tar det innan hälften av vattnet har kokat bort?
19 En termos innehåller nollgradigt vatten. En isbit med en temperatur som är lägre än 0 °C placeras i vattnet och ett lock läggs på. Efter en tid undersöks innehållet i termosen. Man märker att termosen fortfarande innehåller en blandning av is och vatten.
a Vilken temperatur har blandningen i termosen? Välj rätt alternativ.
A Mindre än 0 °C.
B Större än 0 °C.
C 0 °C
D Det går inte att avgöra.
b Hur har mängden is förändrats?
A Mängden har minskat.
B Mängden har ökat.
C Mängden är oförändrad.
D Det går inte att avgöra.
20 Elin och Shiva tältar vid en sjö. Det har med sig varsin burk med dryck som Elin sänker ned i det kalla vattnet så att de ska svalna. Två timmar före middag tar Shiva sin burk och hänger upp den i en blöt socka i skuggan av ett träd. När det är dags att öppna burkarna märker de att Shivas är kallare än Elins. Förklara hur det komma sig?
1
1 Rumstempererat vatten kokar om det är i vakuum. Skulle det gå att koka ägg i detta kokande vatten?
2 Spillvärmen från ett kärnkraftverk är 1,5 GW. Den bortförs med kylvatten, som därvid värms upp med 10 °C. Hur mycket kylvatten går åt på 1 s?
3 En liten guldtacka väger 12,5 kg. Hur mycket energi krävs det för att smälta en liten guldtacka med temperaturen 20,0 °C?
4 Temperaturen inne i en ugn är 200 °C. Du kan ha din hand i ugnen utan att bränna dig om du inte rör vid något. Varför är det så?
5 Hur stor energi krävs för att omvandla 1,0 kg is av temperaturen –20 °C till ånga av temperaturen 100 °C? Specifika värmekapaciteten för is är 2,2 kJ/(kg · K).
2
6 Bostäder bör ventileras så att all luft byts under en tvåtimmarsperiod. Jerkers lägenhet har arean 100 m2 och takhöjden 2,40 m. Hur stor energi krävs varje dygn för att förse lägenheten med uppvärmd friskluft om yttertemperaturen ligger 30 °C under rumstemperaturen? Vilken effekt motsvarar detta?
Luftens densitet är 1,29 kg/m3 och dess specifika värmekapacitet är 1,01 kJ/(kg · K).
7 Du tillför en mängd värme till en rumstempererad järnklump så att temperaturen fördubblas mätt i Kelvin. Hur förändras temperaturen mätt i ° C? Välj rätt alternativ.
A Den fördubblas.
B Den blir mindre än dubbelt så hög.
C Den blir mer än dubbelt så hög.
D Det går inte att besvara utan att veta hur mycket värme som överförs.
8 En elektrisk krets väger 32 mg och består till största delen av kisel. Kretsen utvecklar en effekt på 9,7 mW. Hur mycket ökar kretsens temperatur per sekund om ingen värme avges till omgivningen?
9 Vilken är den viktigaste anledningen till att det känns mycket varmare att gå in i en ångbastu (där det finns mycket vattenånga i luften) jämfört med en vanlig bastu, även om temperaturen normalt är högre i den vanliga bastun?
10 I ett termoskärl finns 150 g av en vätska. En doppvärmare med den konstanta effekten 280 W är nedsänkt i vätskan. Diagrammet visar hur vätskans temperatur ändras med tiden sedan doppvärmaren kopplats på.
01 23 4 567
a Ange vätskans kokpunkt.
b Hur stor elektrisk energi omsätts medan temperaturen ökar?
c Bestäm vätskans specifika värmekapacitet.
11 Förklara varför det är en dålig idé att mäta temperaturen av 3 cl vatten med en stor glastermometer.
12 Greg hoppar simhopp från 10,0 m. Han väger 65 kg. När han landar i vattnet värms vattnet upp lite grann. Vi gör en grov uppskattning att det är 100 l vatten som värms upp. Hur mycket ökar temperaturen på vattnet?
13 I ett fysiklaboratorium finns en ihålig tillsluten
sfär. Sfären innehåller luft och sensorer är kopplade så att man kan mäta tryck och temperatur för luften i sfären. Genom att sänka ned sfären i vatten av olika temperaturer fick man mätdata enligt diagrammet.
a Anpassa en rät linje till mätvärdena och bestäm linjens skärning med temperaturaxeln.
b Tolka linjens skärning med Taxeln fysikaliskt.
14 100 g nollgradig is blandas med 100 g vatten av temperaturen 50 °C.
a Smälter all isen?
b Vilken sluttemperatur får blandningen?
c Vilken hade sluttemperaturen blivit om vattnets temperatur varit 100 °C?
Bortse från energiutbyte med omgivningen.
15 Ett sätt att undvika att temperaturen i garaget blir för låg under nätter då utomhustemperaturen går under noll ° C är att ställa in några hinkar med vatten.
a Förklara varför detta kan vara en bra idé.
b Två tioliters hinkar ställs in i garaget kl 22.00 med rumstempererat vatten. Vi antar att de hjälper till att hålla temperaturen uppe till kl. 7.00 då allt vatten just frusit till is. Hur stor medeleffekt på ett elektriskt element krävs för att nå samma funktion?
16 Diagrammet visar sambandet mellan tillförd energi och temperatur för 1 kg vatten.
Vilka koordinater förväntar du dig att punkterna A, B och C har? Svara utan att mäta i diagrammet.
17 Amina övar prickskytte med luftpistol på grankottar som hon hängt upp i fiskelinor. Ett liten blykula med massan 0,95 g prickar en kotte som väger 22 g. Kulan har hastigheten 85 m/s när den borrar in sig i kotten och fastnar där. Efter träffen svänger kotten upp i en pendelrörelse och når på så sätt 63 cm högre upp än sin ursprungsposition. Anta att kottens temperatur är oförändrad och bestäm den högsta möjliga temperaturhöjningen i blyhaglet vid kollisionen.
Rune Alphonce
Lars Bergström
Ulf Christiansson
Tobias Eriksson
Per Gunnvald
Jenny Ivarsson
Erik Johansson
Roy Nilsson
HEUREKA!
Fysik nivå 1
Heureka! är ett komplett läromedel för gymnasieskolans fysik nivå 1 och nivå 2 samt fysik fördjupning.
I Heureka! ingår
• läroböckerna Heureka fysik nivå 1, fysik nivå 2 och fysik fördjupning
• lärarhandledningar
• ledtrådar och lösningar till övningsuppgifterna i läroböckerna
• övningsmaterial för mer problemlösning.
Heureka! finns även som digitalt läromedel.
Läs mer om Heureka! på nok.se/heureka
Inuti ett åskmoln rör sig is- och vattenpartiklar i kraftiga upp- och nedåtriktade vindar. Det medför att elektriska laddningar separeras och skapar en elektrisk spänning mellan molnet och marken. När spänningen blir tillräckligt stor sker en elektrisk urladdning – vi ser en blixt. Luften längs blixtens väg värms upp till extremt höga temperaturer och skapar en tryckvåg som når oss som en kraftig smäll –åskknallen.

