College algebra 3rd edition ratti solutions manual download by robert.king690

College Algebra 3rd Edition Ratti

Full download link at:

Test bank: https://testbankpack.com/p/test-bank-for-collegealgebra-and-trigonometry-3rd-edition-by-ratti-mcwaters-isbn0321867416-9780321867414/

Solution Manual: https://testbankpack.com/p/solution-manual-forcollege-algebra-and-trigonometry-3rd-edition-by-ratti-mcwaters-isbn0321867416-9780321867414/

4.1 Chapter 4 Exponential and Logarithmic Functions

Exponential Functions

Practice Problems ⎛1⎞ x 5. a. (0, 1) and (2, 49) f (0)=1⇒1= c a0 = c 1= c Therefore, f (x)=1⋅ ax ⇒ 49 = 1⋅ ax ⇒ 1. f (x)=⎜⎝4⎟⎠ 49 = a2 ⇒ a = 7 2 f(2)=⎜⎝4⎟⎠ = 1 16 So, f (x)= 7 x 0 b. (−2, 16) and ⎛3, 1⎞ ⎛1⎞ ⎜⎝4⎟⎠ ⎜⎝ 16 = ca 2 2⎟⎠ 1 f ( 1)=⎜⎝4⎟⎠ = 4 1 = ca3 2 ⎛5⎞ ⎛1⎞5 2 ⎛ 1 ⎞5 ⎛1⎞5 1 16 ca 2 f ⎜ ⎟=⎜ ⎟ =⎜ ⎟ =⎜ ⎟ = 1 2 = 3 ⎝2⎠ ⎝4⎠ ⎝ 4 ⎠ ⎝2⎠ 32 ca ⎛ 3⎞ ⎛1⎞ 3 2 3 32 = a 5 ⇒ a = 1 f ⎜ ⎝ = 2⎠ ⎝4⎠ = 432 =( 4) = 23 = 8 2 ⎛1⎞ 2 2. a. 3 3 = 3 8+ = 32 2+ =33 = 27 16= c ⎜⎝2 ⇒16 = 4c ⇒ 4 = c ⎛1⎞ x b. (a 8 ) = a = a = a4 So, f (x)= 4⎜⎝2⎟⎠ 2 2 2 2 2 2 8⋅ 2 f (0)= =1

4.1

6. A = P + I = P + Prt =10,000+10,000(0.075)(2) =10,000+1500 =11,500 There will be $11,500 in the account.

7. a. A = P (1+ r)t = 8000(1+ 0.075)5 ≈11,485.03 There will be $11,485.03 in the account.

b. Interest = A P =11,485.03 8000 = 3485.03

She will receive $3485.03

8. The formula for compound interest is ⎛ r ⎞ nt

4. A = P⎜⎝1+ n⎟⎠ . For each of the following, t = 1.

(i) Annual compounding (n = 1) ⎛ 0.065⎞1

A = $5000⎜⎝1+ 1 ⎟⎠ =$5325.00

(ii) Semiannual compounding (n = 2) ⎛ 0.065⎞2

A = $5000⎜⎝1+ 2

≈$5330.28

382

x 2 x −3 1 8 –2 1 4 –1 1 2 0 1 1 2 2 4 3 8 x (1 3)x −3 27 –2 9 –1 3 0 1 1 1 3 2 1 9 3 1 27

⎟⎠

20 (−∞ , ∞) and for c > 0, the range is (0,∞) .

2. The graph of f (x)= 3x has y-intercept 1 and

has no x-intercept.

y =

Carmen needs an interest rate of about 10.023%.

= Pert = $9000e(0.06)(8.25)

4. The exponential function f (x)= a is increasing if a > 1 and is decreasing if 0 < a < 1

5. The formula for compound interest at rate r

11. Shift the graph of y = ex one unit right, then compounded n times per year is reflect the graph about the x-axis. Shift the resulting graph two units down.

12. Use the exponential growth/decay formula

A(t) = A0ekt

Quarterly compounding (n = 4) Section 4.1 Exponential Functions 383 b. A( 10) = 6.08e0.016( 10) ≈ 5.1810 ⎛ 0.065⎞4 The model predicts that if the rate of A = $5000⎜⎝1+ 4 ⎟⎠ ≈$5333.01 growth is 1.6% per year, there were about (iv) Monthly compounding (n = 12) ⎛ 0.065⎞12 5.18 billion people in the world in the year 1990. A = $5000⎜⎝1+ 12 ⎟⎠ ≈ $5334.86 13. A(t) = A0e kt (v) Daily compounding (n = 365) A(6) = 22, 000e( 0.18)(6) ≈ $7471.10 ⎛ 0.065⎞365 A = $5000⎜⎝1+ 365 ⎟⎠ ≈$5335.76 4.1 Basic Concepts and Skills ⎛ r ⎞12 8 1. For the exponential function 9. 20,000 =9000⎜⎝1+ 12⎟⎠ f (x)= cax

a > 0,

≠

is ⎛

⎞96 20,000

⎜⎝1+ 12⎟⎠ = = 9000 9 r ⎛20⎞1 96

(iii)

1, the domain

1+ 12 =⎜⎝9 ⎟⎠ r ⎛20⎞1 96

12 =⎜⎝ 9 ⎟⎠ 1

⎡⎛20⎞1 96 r =12⎢⎜ ⎝ 9 ⎟ ⎠ ⎤ 1⎥≈ .10023 ⎥⎦ ⎛1⎞ ⎜⎝3⎟⎠ is the x-axis. x

3. The horizontal asymptote of the graph of A

10.

≈ $14,764.48

6. The formula continuous compound interest is

a. A(30) = 6.08e0.016(30) ≈ 9.8257

The model predicts that if the rate of growth is 1.6% per year, there will be about 9.83 billion people in the world in the year 2030.

7. False. The graphs are symmetric with respect to the y-axis.

⎛ r ⎞ nt A = P ⎜⎝1+ n⎟⎠

= Pert

8. 9.

384 Chapter 4 Exponential and Logarithmic Functions

ex +1 is obtained by

11. Not an exponential function. The base is not a constant.

28. 9 ÷ 27 =(32 ) = 32 5 3 ÷(33) = 32 = 3 ÷ 33 4.

13. Exponential function. The base is a constant, 1/2.

14. Not an exponential function. The base is not a positive constant.

29. (3 2 ) = 3 30. (2 3 ) = 2 31. (a 3 ) = a = 3 = 2 = a = a6

16. Not an exponential function. The exponent is not a variable.

positive constant.

32. a ⋅(a2 ) = a a2 = a 2+4 = a = a5 2+2

Education Inc. 5 5 5 3 5 12 36 2 ( ) ⎛1⎞ ⎜⎝2⎟⎠ ⎛2⎞ ⎛2⎞

= ex

10. False. The graph of shifting the graph of unit. 27. 8π ÷ 4π =(23)π ÷(22 )π = 23π ÷ 22π = 23π 2π = 2π

vertically one

12. Exponential function. The base is a constant,

15. Not an exponential function. The base is not a constant.

17. Not an exponential function. The base is not a

1.8. 33. a. (0, 1) and (2, 16) f (0)=1⇒1= ca0 ⇒1= c f (2)=16 ⇒16 =1 a 2 ⇒ a = 4 19. f (0) = 50 1 = 5 1 = 1 5 f (x)= 4 x 2+1 1 1 b. (0, 1) and ⎛ 2, 1⎞ 20. f ( 2) = 2 = 2 = 2 ⎝⎜ 9⎟⎠ 21. g (3.2)= 31 3.2 = 3 2.2 = 0.0892 g ( 1.2)= 31 ( 1.2) = 32.2 =11.2116 f (0)=1⇒1= ca0 ⇒1= c f 2 = 1 ⇒ 1 =1⋅ a 2 ⇒ a = 3 9 9 22. 2.8+1 g (2.8)=⎜⎝2⎟⎠ ⎛ 1 ⎞3.8 =⎜⎝2⎟⎠ = 0.0718 34. a. f (x)= 3x g ( 3.5)= ⎛1⎞ 3.5+1 ⎛1⎞ ⎜⎝2⎟⎠ 2.5 = 5.6569 (0, 3) and (2, 12) f (0)= 3 ⇒ 3 = ca0 ⇒ 3 = c f (2)=12 ⇒12 = 3 a2 ⇒ 4 = a2 ⇒ a = 2 23. 2(1.5) 1 h(1.5)=⎜⎝3⎟⎠ ⎛2⎞2 4 = ⎜⎝3⎟⎠ = 9 f (x)= 3 2 x 24. 2( 2.5) 1 h( 2.5) =⎜⎝3 ⎟⎠ f (2)= 3 52 = 22 f ( 1)= 3 5 1 = 2.8 2 2 5 5 5 5 5 6 3 5 15 3 12 2 8 8 8 2 2 =

18. Exponential function. The base is a constant,

Copyright © 2015 Pearson Education Inc. 2 12 ⎛2⎞ 6 =⎜⎝3⎟⎠ = 729 64 b. (0, 5) and (1, 15) f ( 0 ) = 5 ⇒ 5 = c a 0 ⇒ 5 = c f ( 1 ) = 1 5 ⇒ 1 5 = 5 ⋅ a 1 ⇒ a = 3 f ( x ) = 5 ⋅ 3 x 25. 3 ⋅3 = 3 2+ = 32 2 6. 7 2 3

35. a. (1, 1) and (2, 5)

f (1)=1⇒1= ca1

f (2)= 5 ⇒ 5 = ca2

ca 2 5 a 5 a f (1)=1⇒1= c 51 ⇒ c = 1

(x)= 1 (5)x

b. (1, 1) and ⎛2, 1⎞ ⎝⎜ 5⎟⎠

f (1)=1⇒1= ca1

f 2 = 1 ⇒ 1 = ca2 5 5 1 = ca1 ⇒ = 1 ⇒ 1 =

ca 2 5 a

36. a. (1, 5) and (2, 125) f (1)= 5 ⇒ 5 = ca1

f (2)=125 ⇒125 = ca2

ca1 1 = ⇒ = a 1 ⇒ 25 = a

ca2 25

f (1)= 5 ⇒ 5 = c ⋅251 ⇒ c = 1

f (x)= 1 ⋅(25)x

b. (−1, 4) and (1, 16)

f ( 1)= 4 ⇒ 4 = ca 1

f (1)=16 ⇒16 = ca1

4 = ca 1 ⇒ 1 = 2 ⇒ = 16 ca 1 4 a 2 a

f (1)=16 ⇒16 = c 21 ⇒ c = 8

x 4 x –2 1 16

Section 4.1 Exponential Functions 385 1 = ca1 ⇒ 1 = 1 ⇒ =

–1 1 4 0 1 1 4

1 10 x (3 2) x

5 5 ( ) ⎛1⎞ 5 5

37.

38.

5⎟⎠

5 ⎜⎝5⎟⎠

39.

1 5

a 5 ⎛1⎞1 f (1)=1⇒1= c ⎜⎝

(x)=

⇒ c = 5

125

40.

–4

–2

–1 3

0 1 1 2 3 2 4 9 4 16

x 7 x –2

–1 7 0 1 1 1

f (x)= 8⋅(2)x 2 1

16 x 10 x –1 1 10 –0.5 ≈ 0.32 0 1 0.5 ≈ 3.2

81 16

9 4

386 Chapter 4 Exponential and Logarithmic Functions

41.

49. g (x)= 3x 1

Shift the graph of f (x) = 3x one unit right.

Domain: (−∞ , ∞); Range: (0, ∞)

Horizontal asymptote: y = 0

50.

Shift the graph of f (x) = 3x one unit down.

Domain: (−∞ , ∞); Range: ( 1, ∞)

Horizontal asymptote: y = −1

51. g(x) = 4 x

Reflect the graph of y-axis. f (x) = 4 x about the

Domain: (−∞ , ∞); Range: (0, ∞)

Horizontal asymptote: y = 0

42.

43. 44.

45. c 46. b 47. a 48. d

x (1 4)x –2 16 –1 4 0 1 1 1 4 2 1 16 x (1 10)x –2 100 –1 10 0 1 1 0.1 2 0.01 x 1.3 x –4 ≈ 2.86 –3 ≈ 2.2 0 1 2 ≈ 0.59 4 ≈ 0.35 x 0.7 x –4 ≈ 0.24 –2 0.49 0 1 2 ≈ 2.04 4 ≈ 4.16

52. g(x) = 4 x

55. g(x) = ex 2 + 3

Shift the graph of f (x) = ex two units to the x-axis.

Reflect the graph of f (x) = 4 x about the

Domain: (−∞ , ∞); Range: (−∞, 0)

Horizontal asymptote: y = 0

right, then reflect it about the x-axis, then shift the graph three units up.

Domain: (−∞ , ∞); Range: (−∞ , 3)

Horizontal asymptote: y = 3

53. g (x)= 2 5 x 1 + 4 x

Shift the graph of f (x) = 5 one unit to the right, reflect it about the x-axis, stretch

vertically by a factor of 2, then shift four units up. Domain: (−∞ , ∞); Range: (−∞ ,4)

Horizontal asymptote: y = 4.

56. g(x) = 3 + e2 x

Reflect the graph of f (x) = ex about the x-

axis, then shift it two units to the right, then shift the graph three units up.

Domain: (−∞ , ∞); Range: (3, ∞)

Horizontal asymptote: y = 3

54. g (x)= 1 ⋅51 x 2

Reflect the graph of f (x) = 5 x about the y-

axis, then shift the graph one unit to the right, compress vertically by a factor of 2, then shift two units down.

Domain: (−∞ , ∞); Range: ( 2, ∞) .

Horizontal asymptote: y = −2.

57. The graph passes through the point (0, 3) and (1, 3.5).

58. The graph passes through (−2, 6) and (0, 3).

2 Section 4.1 Exponential Functions 387

3⇒ 3 = a0 + b ⇒ 3 =1+ b ⇒ b

f (0)=

= 2

3.5 ⇒ 3.5

2 ⇒ 1.5

f (1)=

= a

f (x)=1.5x +

(2)=1.52 + 2 = 4.25

⇒ 3

6 ⇒ 6 = a 2

2 ⇒ 4

a 2 ⇒ 1 = 4 ⇒ a = 1 a 2 2 ⎛1⎞ x

(0)= 3

+ b

+ b ⇒ b = 2f ( 2)=

Copyright © 2015 Pearson Education Inc. 2 3 ⎛1⎞ 388 Chapter 4 Exponential and Logarithmic Functions 59. The graph passes through (−2, 7) and (−1, 1). 61. y = 2 x+2 + 5 f ( 2)= 7 ⇒ 7 = a 2 + b f ( 1)=1⇒1= a 1 + b Subtract (2) from (1). (1) (2) 62. y = 3 (x 3) or ⎛1⎞ x y = 3 x+3 6 = a 2 a 1 ⇒ 6 = 1 1 ⇒ 63. y = 2⎜⎝ ⎟⎠ 5 64. y = 2 x +3 a2 a 2 6a2 =1 a ⇒ 6a2 + a 1= 0 ⇒ (2a +1)(3a 1)= 0 ⇒ a = 1 , 1 If a =− 1 , then 2 65. 66. 67. I = Prt = $5000⋅0.1⋅5 = $2500 I = Prt = $10,000⋅0.05⋅10 = $5000 I = Prt = $7800⋅0.06875⋅10.75 = $5764.69 2 ⎛ 1⎞ 1 68. I = Prt = $8670 0.04125 6 = $2384.25 3 1=⎜ ⎝ 2⎟ ⎠ 1 + b ⇒1= 2+ b ⇒ b = 3. ⎛ 0.065⎞13 If a = 3, then 69. a. A = 3500⎜⎝1+ 1 ⎟⎠ = $7936.21 ⎛1⎞ 1 1=⎜⎝3⎟⎠ + b ⇒1= 3+ b ⇒ b = 2. b. interest = $7936.21 $3500 = $4436.21 The horizontal asymptote of the given graph is ⎛ 0 075⎞12(12) y = −2, so the equation of the graph is 70. a. A = 6240⎜⎝1+ 12 ⎟⎠ = $15,305 x f (x)=⎜⎝3⎟⎠ –2. b. interest = $15,305 $6240 = $9065 ⎛1⎞2 1 17 71. a. A = 7500e0.05(10) = $12,365.41 f (2)=⎜⎝3⎟⎠ – 2 = 9 2 = 9 b. interest = $12,365.41 $7500 = $4865.41 60. The graph passes through (−1, 2.5) and (1, 1). ⎛ 0.065 ⎞365(15) f ( 1)= 2.5 ⇒ 2.5 = a 1 + b (1) 72. a. A =8000⎜⎝1+ 365 ⎟⎠ = $21,207.50 f (1)=1⇒1= a1 + b ⇒1= a + b Subtract (2) from (1). 1.5 = a 1 a ⇒1.5 = 1 a ⇒ (2) b. interest = $21,207.50 $8000 = $13,207.50 a ⎛ 0.08⎞10 10 1.5a =1 a2 ⇒ a2 + 3 a 1= 0 ⇒ 2 2a2 + 3a 2 = 0 ⇒(a + 2)(2a 1)= 0 ⇒ 73. 10,000 = P ⎜⎝1+ P = $4631.93 1 ⎟⎠ = P(1.08) ⇒ 1 ⎛ 0.08⎞4(10) 40 a = 2, 2 If a = 2, then 1= 2+ b ⇒ 3 = b. 74. 10,000 = P ⎜⎝1+ P = $4528.90 4 ⎟⎠ = P(1.02) ⇒ If a = 1 , then 1= 1 + b ⇒ 1 = b ⎛ 0.08 ⎞365(10) 2 2 2 75. 10,000 = P ⎜⎝1+ 365 ⎟⎠ ⇒ P = $4493.68

The horizontal asymptote of the given graph is y = 1/2, so the equation of the graph is 76. 10,000 = Pe0.08(10)

= $4493.29

⎛1⎞ ⎛1⎞

x f (x)=⎜⎝2⎟⎠ 2 f (2)=⎜⎝2⎟⎠ + 1 2 + 1 = 1 + 1 = 3 2 4 2 4

⇒ P

77. Reflect the graph of y = ex about the y-axis.

81. Shift the graph of y = ex one unit up.

Horizontal asymptote: y = 0

78. Reflect the graph of y = ex about the x-axis.

Horizontal asymptote: y = 1

82. Reflect the graph of y = ex about the y-axis,

then reflect it about the x-axis, and shift it two units up.

Horizontal asymptote: y = 0

79. Shift the graph of y = ex two units right.

Horizontal asymptote: y = 2

83. Shift the graph of y = ex two units right,

reflect the graph about the x-axis, and then shift it three units up.

Horizontal asymptote: y = 0

80. Reflect the graph of y = ex about the y-axis, and then shift it two units right.

Section 4.1 Exponential Functions 389

Horizontal asymptote: y = 0 Horizontal asymptote: y = 3

390 Chapter 4 Exponential and Logarithmic Functions

84. Shift the graph of y = ex two units right,

reflect the graph about the y-axis, and then shift it three units up.

89. A =80,000

90. a. I = 24(0.06)(380) = $547.20 . The total investment is $547.20 + $24 = $571.20

639,920

y = 3

4.1 Applying the Concepts

a. (i) Because t = the number of years since

t = 0.

(0) =1.6 20.1047(0) =1600 thousand = 1,600,000

(ii) t = 8, so p(8) = 1.6 20.1047(8)

≈ 2859 thousand = 2,859,000.

b. x = 2025 – 2010 = 15,

p(15) =1.6 20.1047(15) ≈ 4752.1 thousand = 4,752,100

d. A = 24e0.06(380) ≈ $191,480,886,300

91. Assume that interest is compounded annually.

d. As t →∞, e 0.28t → 0 ⇒ T → 25°C. Verify this using a graphing calculator.

⎜ ⎟

⎛ 0.15⎞1(5)

⎜⎝1 1 ⎟⎠ ≈

$35, 496.43

⎛ 0.06⎞

1(380)

⎜⎝1+ 1 ⎟⎠ ≈ $99,183,

⎛ 0.06 ⎞

b. A = 24

(380)(12)

⎜⎝1+ 12 ⎟⎠

asymptote:

c. A = 24

Horizontal

≈ $180,905,950,100

⎛ r ⎞1(54) 85. a. (i) T = 200 4 0.1(2) + 25 = 176.6°C 22,000,000 =5000⎜⎝1+ 1⎟⎠ ⇒ (ii) T = 200 4 0.1(3.5) + 25 = 148.1°C 4400 = (1+ r)54 ⇒ 44001 54 =1+ r ⇒ 1.1681≈1+ r ⇒ r ≈ 0.1681≈16.81% b. 125 = 200⋅4 0.1t + 25 ⇒100 = 200⋅4 0.1t ⇒ 5 1 = 4 0 1 t ⇒2 1 = 2 0.2t ⇒ 1= 0.2t ⇒ 92. 15,000 =12,000e10k ⇒ = e10k ⇒ 4 2 t = 5 hours k ⎛5⎞1 10 e =⎜⎝4⎟⎠ c. As t →∞ , T → 25. Verify graphically. A =15,000e10k =15,000⎛5⎞ =18,750 ⎝4⎠ [0, 50, 10] by [0, 200, 25] 86.

93. 94. a. b. c. A = 10e 0.43(10) ≈ 0.1357 mm2 T = 25 + 73e 0.28(0) = 98°C T = 25

73e 0.28(10) ≈ 29.44°C T = 25 + 73e 0.28(20) ≈ 25.27

C p

2010,

⎛ r ⎞4(12) ⎛ 0.03⎞1(5) 95. 95,600 =60,000⎜⎝1+ 4⎟⎠ ⇒ 87. A =190,000⎜⎝1+ 1 ⎟⎠ ≈

262 239 = ⎛1+ r ⎞ ⇒ 48 239 =1+ r ⇒ ⎛ 0.07 ⎞4(21) 150 ⎜⎝ 48

$220,

96. Let P represent the amount invested. Then (i) 9.7% compounded annually for one year would yield

is the number of tears. The height of the paper is

98. Because the jar is full in 60 minutes, and the number of bacteria doubles every minute, it will be half full one minute earlier, or in 59

minutes.

4.1 Beyond the Basics

Section 4.1 Exponential Functions 391 c. [ f (x)]2 [g(x)]2 =⎡(3x +3 x )⎤ ⎡(3x 3 x )⎤ A = P ⎛1+ 0.097⎞1(1)⎟ = 1.097P. ⎣ =(32x ⎦ ⎣ +3 2x + 2) (32x ⎦ +3 2x 2)= 4 ⎝ 1 ⎠ (ii) 9.6% compounded monthly for one year would yield d. [ f (x)]2 +[g(x)]2 2 2 ⎛ 0.096⎞1(12) =⎡(3x +3 x )⎤ +⎡(3x 3 x )⎤ A = P ⎜⎝1+ 12 ⎟⎠ ≈1.1003P. ⎣ =(32x ⎦ ⎣ +3 2x + 2)+(32x ⎦ +3 2x 2) (iii) 9.5%

would yield A = Pe0.095(1) ≈1.1000P. = 2(32x +3 2x ) The 9.6% investment compound monthly is the best deal. 101. S = 2+ 1 + 1 + 1 + 1 = 163 ≈ 2.71667 2! 3! 4! 5! 60 x S = S + 1 + 1 + 1 + 1 + 1 ≈ 2.7182818

10 5 6! 7! 8! 9! 10!

0.015⋅2 x . S15 = S10 + 1 + 1 + 1 + 1 + 1 11! 12! 13! 14! 15! a. 0.015⋅230 ≈16,106,127 cm ≈ 2.718281828 The sum approaches the value of e. b. 0.015 240 ≈16,492,674,420 cm c. 0.015⋅250 ≈16,888,498,600,000 cm =1.689×

102. a. b. e x + ex f x f x cosh x is even. 2 e x ex f x f x sin x is odd. 2

compounded monthly for one year

97. The number of pieces of paper is 2 , where x

1013 cm

c. cosh x +sinh x = ex + e x 2 + ex e x 2

f (x + h) f (x) ex

= 2ex = x 2 d. (cosh x)2 (sinh x)2 99. a. = = h h h ⎛ ex + e x ⎞2 ⎛ ex e x ⎞ = x (eh 1) = 2 ⎟⎠ –⎜⎝ 2 ⎟⎠ h b. f (x + y) = ex+ y = exe y = f (x) f ( y) = e 2x + 2ex x + e 2x e 2x 2ex x + e 2x 4 4 = e2x + 2 + e 2x e2x 2 + e 2x = 4 = x 1 1 1 4 4 4

x (eh 1)

Copyright © 2015 Pearson Education Inc. c. f ( x) = e = e x = f (x) ⎛ r ⎞m(1) 100. a. f (x)+ g(x) =(3x +3 x )+(3x 3 x ) 103. A = P⎜⎝1+ m⎟⎠ = P(1+ y) ⇒ = 2⋅3x ⎛ r ⎞ m ⎛ r ⎞ m b. f (x) g(x) =(3x +3 x ) (3x 3 x ) = 2 3 x ⎜⎝1+ m⎟⎠ =1+ y ⇒ y =⎜⎝1+ m ⎟⎠ 1

4.1 Critical Thinking/Discussion/Writing

109. The base a cannot be 1 because this makes the

1, then, for x < 0, cax approaches 0, so the denominator 1+ cax approaches 1 and b

112. There are four possibilities, 0 < a < 1 with c < 0, 0 < a < 1 with c > 0, a > 1 with c < 0, and a > 1 with c > 0. They are illustrated below function a constant, f (x)=1. Similarly, the base a cannot be 0 because this becomes f (x)= 0 x = 0, a constant. We rule out negative bases so that the domain can include all real numbers. For example, a cannot be −3 because f (1)=( 3)1 2 = is not a real number.

110. g (x) is defined for the set of integers. For example, g ( 2)=( 3) 2 = 1 and

Copyright © 2015 Pearson Education 3 2 9 e e e 392 Chapter 4 Exponential and Logarithmic Functions 104. a. A (t +1) A(t) A(t) = Pek (t +1) Pekt Pekt so the denominator 1+ cax b approaches 1 and = e k (t +1) ekt ekt y = 1+ ca x approaches b = ektek ekt = ekt ek 1 A(t + h) A(t) b. A(t) = Pek (t +h) Pekt Pekt = e k (t +h) ekt ekt kt kh kt = = kh

e kt e 1 y = 1+

x approaches b

For

105. y = ex → y = ex 1 → y = e2x 1 → y = 3e2x 1 denominator becomes very large, so 106. 107. 108. y = ex → y = ex+2 → y = e3x+2 → y = 2e3x+2 → y = 2e3x+2 → y = 2e3x+2 5 y = ex → y = e2+ x → y = e2+3x → y = e2 3x → y = 5e2 3x → y = 5e2 3x + 4 y = ex → y = e3+ x → y = e3+4x → y = 2e3+4x → y = 2e3+4x → y = 2e3 4x → y = b 1+ ca x approaches 0. y = 2e3 4x 1

x ≥ 0, the

g (3

111. If 0 < a < 1, then, for x < 0, the denominator becomes very large, so y = b 1+ ca x approaches 0. For x ≥ 0, cax approaches 0,

)=( 3)3 = 27.

113. The function y = 2 x is an increasing function, 123.

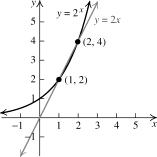
Section 4.1 Exponential Functions 393 f (x)= y = 3x + 4

so it is one-to-one. The horizontal line y = k Interchange x and y, then solve for y. for k > 0 intersects the graph of y = 2 x in x = 3y + 4 ⇒ x 4 = 3y ⇒

exactly one point, so there is exactly one solution for each value of k

x 4 = y = f 1 (x)

124.

The domain and range of f (x)= y = 1 x 5

f 1 are (−∞ , ∞).

Interchange x and y, then solve for y

x = 1 y 5 ⇒ x + 5 = 1 y ⇒ 2 x +5 = y ⇒ 2 2 y = f 1 (x)= 2x +10

114. The graphs of y = 2 x and y = x intersect in The domain and range of f 1 are (−∞ , ∞)

exactly two points: (1, 2) and (2, 4). So

125. f (x)= y = x, x ≥ 0

Interchange x and y, then solve for y x = ⇒ x2 = y = f 1 (x), x ≥ 0

126.

The domain and range of f (x)= y = x2 +1, x ≥ 0

f 1 are [0, ∞)

Interchange x and y, then solve for y

x = y2 +1⇒ x 1= y2 ⇒

The domain of x 1, x ≥1

y = f 1 (x)=

f 1 is [1, ∞). 4.1

The range of f 1 is [0, ∞)

Interchange x and y, then solve for y

The domain of f 1 is (−∞ , 0)∪(0, ∞). The

rangeof f 1 is (−∞ , 1)∪(1, ∞)

y 3 2 ( )

2 x = 2x ⇒ x =1 or 2.

Maintaining Skills

127.

115. 100 =1

f (x)= y = 1 , x ≠1 x 1 116. 10 1 = 1 = 0.1

10 117. ( 8)13 = = 2 x

1 ⇒ 118. 2512 = = 5 y =

=1+ 1

x ≠ 0 x

= y 1 ⇒ x (y

⇒ y

(

)

⎛1⎞ 2 2

3 8

Copyright © 2015 Pearson Education Inc. 18 12 3 y 119. ⎜⎝7⎟⎠ = 7 = 49 128. f (x)= y = ⎛1⎞ 1 2 1 2 Interchange x and y, then solve for y 120. ⎜⎝9⎟⎠ = 9 = = 3 x = ⇒ x3 = y = f 1 (x) 121. 1812 = = = 3 ⎛ 1 ⎞ 1 2 1 2 The domain and range of f 1 are (−∞ , ∞) 122. ⎜ ⎝12⎟ ⎠ =12 = = = 2 3 x

394 Chapter 4 Exponential and Logarithmic Functions

4.2 Logarithmic Functions

4.2 Practice Problems

210 =1024 is equivalent to log2 1024 =10 . 9 12 = 1 is equivalent to log ⎛1

= 1 Plot the ordered pairs and connect them with a

smooth curve.

c. 2.

p = q log2 64 = 6

to 26 = 64 .

2 ⇒ y = 2 Thus, log3

2. b. log 1 = y ⇒ 9 y = 1

⇒ 32y = 3 1 ⇒ y = 1

then reflect the resulting graph about the

5. Since the domain of the logarithmic function

This means that about 17.6% of the data is expected to have 2 as the first digit. is (0,∞) , the expression must be positive.

domain

1 x 1 x

is defined for (−∞,1) , so the is (−∞,1)

on the graph of y = log

9. a. y = ln 1 ⇒ e y = 1 ⇒ e y = e 1 ⇒ y = 1 e e Thus, ln 1 = 1.

2 x .

⎞

1. a. b. 3 9 ⎜⎝3⎟⎠ 2

p = aq is equivalent to loga

is equivalent

b. logv u = w is equivalent to vw = u

3. a. log3 9 = y ⇒ 3 y = 9 ⇒ 3 y = 3

9 =

9 3 3 2

Thus, log 1

1 3 2⎛1⎞ y – y 5 x-axis. c. log1 2 32 = y ⇒⎜⎝2⎟⎠ y = 5 Thus, log12 32

5. = 32⇒ 2 = 2 ⇒ 4. a. c. log5

0 7log7 5

5 b.

3 35

7. Shift the graph of y = log2 x three units right,

log

8. P2 = log3 log2 ≈ 0.176

of log10

1 x 9 x y = log2 x (x, y) 2 21 = 2 ⇒ y = log2 2 =1 (2, 1) 4 22 = 4 ⇒ y = log2 4 = 2 (4, 2) 8 23 = 8 ⇒ y = log2 8 = 3 (8, 3) x y = log2 x (x, y) 1 8 2 3 = 1 ⇒ y = log 1 = 3 8 2 8 ⎛ ⎜1 , 3⎞ ⎟ ⎝8 ⎠ 1 4 2 2 = 1 ⇒ y = log 1 = 2 4 2 4 ⎛1 ⎞ ⎝ ⎜4, 2⎠ ⎟ 1 2 2 1 = 1 ⇒ y = log 1 = 1 2 2 2 ⎛ ⎜1 , 1⎞ ⎟ ⎝2 ⎠

6. Create a table of values to find ordered pairs e

Copyright © 2015 Pearson Education Inc. b. Usin g a calcul ator, we have ln2 ≈ 0.693 10. a . I f P d o l l a r s a r e i n v e s t e d , t h e n t h e a m o u n t A = 3 P A = P ert ⇒ 3P = Pe0.065t ⇒ 3 = e0.065t ⇒ ln3= 0.065t ⇒ t = ln3 ≈16.9 0.065

will take approximately 17 years to triple your money.

The investment will triple in 5 years at the rate of 21.97%.

11. Start with equation (2) in Example 11 in the text.

T = 72+108e 0.1495317t

This equation gives the rate of cooling in a 72ºF room when the starting temperature is 180ºF. Since the final temperature is 120ºF, replace T with 120 and solve for t

e 0.1495317t

log ⎛ ⎜13⎞ ⎟= 3 11 2 ⎛11⎞

18. 5⋅2ct =11⇒ 2ct = ⇒log2 ⎜⎝ ⎟⎠= ct

120

19. 21. 23. 25 = 32 102 =100 100 =1 20. 22. 24. 72 = 49 101 =10 a0 =1 ⎛1⎞ 1 48

4 = e 0.1495317t 25. 10 2 = 0.01 26. 1 ⎝⎜5⎟⎠ = 5 9 ln ⎛4⎞ = 0.1495317t ⎝9⎠ 0.8109302 = 0.1495317t ⇒ 5.423 = t 27. 28. 3log8 2 =1⇒ log8 2 = ⇒ 813 = 2 3 1+ log1000 = 4 ⇒ log1000 = 3 ⇒103 =1000 The employees should

5.423 (realistically 5.5

deliver the coffee 29. ex = 2 30. ea = π at 120ºF.

Basic Concepts and Skills 1. The domain of the function y = log a x is 31. 32. log5125 = 3 because 53 =125 log9 81= 2 because 92 = 81 (0,∞) and it range is (−∞ , ∞) 33. log10,000 = 4 because 104 =10,000 2. The logarithmic form y = loga x is equivalent y 34. log 1 = 1 because 3 1 = 1 3 3 to the exponential form a = x . 3. The logarithm with base 10 is called the common logarithm, and the logarithm with base e is called the natural logarithm. 35. 36. log log 1 = 3 because 2 3 = 1 8 8 1 = 3 because 4 3 = 1 4. aloga x = x and loga ax = x. 4 64 64 5. False 6. True 37. log3 = 3 because 332 = 2 7. log 25 = 2 8. log ⎛1⎞ = 1 1 5 9. log 4 = 1 27 27 3 2

= 72 +108

=108e 0.1495317t

wait about

minutes) to

4.2

Copyright © 2015 Pearson Education Inc. 10. log 49 ⎜⎝7⎟⎠ 2 a 4 = 2 38. log27 3 = 3 1 because 2713 = 3 116 2 a2 39. log16 2 = 4 because 1614 = 2 11. log101= 0 12. log1010,000 = 4 3 3 2 13. log10 0.1= 1 14. log3 5 = x 40. log5 125 = 2 because 5 = 15. a2 + 2 = 7 ⇒ a2 = 5 ⇒ loga 5 = 2 41. log3 1= 0 42. log1 2 1 = 0 16. loga π = e 43. log7 7 =1 44. log 1 1 9 9 125 =1

53. Since the domain of the logarithmic function is (0,∞) , the expression x + 1 must be positive. This occurs in the interval ( 1, ∞) , so the domain of log2 (x +1) is ( 1,∞)

54. Since the domain of the logarithmic function is (0,∞) , the expression x 8 must be positive. This occurs in the interval (8,∞) , so the domain of log3 (x 8) is (8,∞)

55. Since the domain of the logarithmic function

intervals is ( 1, ∞), so the domain of g is ( 1, ∞)

59. Since the domain of the logarithmic function is (0, ∞), the expressions (x − 1) and (2 − x) must be positive. This occurs in the interval

(1, ∞) for x 2 and in the interval (−∞ , 2) for (2 − x). The intersection of the two intervals is (1, 2), so the domain of h is (1, 2).

60. Since the domain of the logarithmic function is (0, ∞), the expressions (x − 3) and (2 − x) must be positive. This occurs in the interval (3, ∞) for x − 2 and in the interval (−∞ , 2)

for (2 − x). The intersection of the two intervals is ∅, so the domain of f is ∅

61. a. F b. A

c. D d. B

e. E f. C

62. a. f (x) = log2 x b. f (x) = log3 x

c. f (x) = log1 2 x d. f (x) = log4 x

63. Shift the graph of y = log4 x three units left. is (0,∞) , the expression must be

Domain: ( 3,∞) ; range: (−∞ , ∞) ; asymptote:

positive. This occurs in the interval (1,∞) , so x = 3 the domain of log3 is (1,∞).

56. Since the domain of the logarithmic function is (0,∞), the expression must be

positive. This occurs in the interval (−∞ , 3), so the domain of log4 is (−∞ , 3)

x 1 x 1 3 x 3 x

57. Since the domain of the logarithmic function is (0,∞), the expressions (x 2) and (2x 1) must be positive. This occurs in the interval (2, ∞) for x − 2 and in the interval (1 , ∞)

64. Shift the graph of y = log1 2 x one unit right.

Domain: (1, ∞) ; range: (−∞ , ∞) ; asymptote: x =1 for (2x − 1). The intersection of the two intervals is (2, ∞), so the domain of f is (2, ∞)

49. 50. 51. 52. 2log2 7 + log5 5 3 = 7 +( 3)= 4 3log3 5 log2 2 3 = 5 ( 3)= 8 4log4 6 − log4 4 2 = 6 ( 2)= 8 10log x eln y = x y

58. Since the domain of the logarithmic function is (0,∞), the expressions and (x + 1)

must be positive. This occurs in the interval

( 5, ∞) for and in the interval

x +5 x +5

( 1, ∞) for x + 1. The intersection ofthe two

65. Reflect the graph of y = log5 x about the

69. On (0,1), reflect the graph of y = log3 x x-axis. Domain: (0,∞) ; range: (−∞ , ∞) ; asymptote: x = 0 about the x-axis. Domain: (0,∞) ; range: [0,∞) ; asymptote: x = 0

66. Stretch the graph of y = log7 x vertically by a 70. On (−∞,0), reflect the graph of y = log3 x factor of 2. Domain: (0,∞) ; range: (−∞ , ∞) ; asymptote: x = 0

about the y-axis. Domain: (−∞ ,0) ∪ (0,∞) ; range: (−∞ , ∞) ; asymptote: x = 0

67. Reflect the graph of y = log1 5 x about the y-axis. Domain: (−∞, 0) ; range: (−∞ , ∞) ; asymptote: x = 0

71. Shift the graph of y = log2 x one unit right. Domain: (1, ∞); range: (−∞ , ∞); asymptote:x =1

68. Reflect the graph of y = log1 5 x in the y-axis, and then shift it up one unit. Domain: (−∞ ,0) ; range: (−∞ , ∞) ; asymptote: x = 0

72. Reflect the graph of y = log2 x about the yaxis. Domain: (−∞, 0) ; range: (−∞ , ∞) ; asymptote: x = 0

Section 4.2 Logarithmic Functions 397

398 Chapter 4 Exponential and Logarithmic Functions

73. Shift the graph of y = log2 x three units right and then reflect it about the y-axis.

Domain: (−∞, 3); range: (−∞ , ∞);

asymptote: x = 3

74. No transformation. Domain: (0, ∞); range: (−∞ , ∞); asymptote: x = 0

77. On (−∞ ,0), reflect the graph of y = log2 x

about the y-axis. Domain: (−∞ ,0) ∪ (0,∞); range: (−∞ , ∞); asymptote: x = 0

75. Shift the graph of y = log2 x three units right,

78. On (−∞ ,0) , reflect the graph of y = log2 x

about the y-axis. On (−∞ ,0) ∪ (0,∞), stretch the graph vertically by a factor of x. then reflect it about the y-axis, and then shift it 2 units up. Domain: (−∞, 3); range: (−∞ , ∞);

asymptote: x = 3

Domain: (−∞ ,0) ∪ (0,∞); range: (−∞ , ∞);

asymptote: x = 0

76. Shift the graph of y = log2 x three units right, 79. log4(log3 81) = log4 4 =1 because 34 = 81 and 41 = 4 reflect it about the y-axis, reflect the resulting graph in the x-axis, and then shift it four units up. Domain: (−∞,3); range: (−∞ , ∞);

asymptote: x = 3

80. log4[log3(log2 8)] = log4[log3 3] = log4 1= 0 because 23 = 8,31 = 3, and 40 =1.

84. log 27=6 because ( 3)6 = 27.

85. log x = 2 ⇒102 =100 = x

86. log(x 1) =1⇒101 = x 1⇒ x =11

87. ln x =1⇒ e1 = e = x

88. ln x = 0 ⇒ e0 =1= x

89. Shift the graph of y = ln x two units left.

92. Stretch the graph of factor of 2. y = ln x vertically by a

93. Stretch the graph of y = ln x vertically by a factor of 2, reflect the resulting graph about the x-axis, and shift it three units up.

90. Shift the graph of y = ln x two units right, then reflect the graph about the y-axis.

94. Shift the graph of y = ln x one unit right, reflect the graph about the y-axis, reflect the graph about the x-axis, then shift the graph one unit up.

91. Shift the of y = ln x graph two units right, then reflect the graph about the y-axis, and then reflect the graph about the x-axis.

4.2 Applying the Concepts

3 Section 4.2 Logarithmic Functions 399

2P = Pe0.08t ⇒ 2 = e0.08t ⇒ ln 2 = 0.08t ⇒ t ≈ 8.66 years 96. 120,000 =10,000e0.1t ⇒12 = e0.1t ⇒ ln12 = 0.1t ⇒ t ≈ 24.85 years 97. 2P = Pe6k ⇒ 2 = e6k ⇒ ln2 = 6k ⇒

95.

112.33% of the population in 2000.

a. The population in 2010 was 109.7% of the population in 2000. 101. Find k using T = 50,T0 = 75,Ts = 20, t =1 minute. and 308 =1.097A0 ⇒ A0 ≈ 280.7657247 The population in 2000 was about 280.8 million. 50 = 20+(75 20)e 30 k(1) ⇒ 30 = e k ⇒ 55 b. 308 = 280.7657247e10r ⇒ ln 55 = k ⇒ 0.6061≈ k 308 280.7657247 = e10r ⇒ a. (i) T = 20 + (75 20)e 0.6061(5) ⇒ T ≈ 22.66°F ln ⎛ 308 ⎞ =10r ⇒ 0.6061(10) ⎜⎝280.7657247⎟⎠ ln( 308 ) (ii) T = 20+ (75 20)e ⇒ T ≈ 20.13°F r = 280.7657247 10 ≈ 0.009257 ≈ 0.93% (iii) T = 20 + (75 20)e 0.6061(60) ⇒ c. 400= 308e 0.0092t ⇒ 400 = e 308 0.0092t ⇒ T ≈ 20°F b. 22 = 20 + (75 20)e 0.6061t ⇒ ln ⎛400⎞ = 0.0092t ⇒ t = ln(400) ≈ 28.4 2 = e 0 6061t ⇒ ln 2 = 0.6061t ⇒ ⎝308⎠ 0.0092 55 55 years after 2010, or in the year 2039.

a. The population is 2010 was

35 =1.1233A0 ⇒ A0 ≈ 31.5819461 The population

about

2000.

T0 = 32,T

= 85, and t = 30

40 = 85+ (32 85)e 30k ⇒ 45 = e 30k ⇒ 53 ln 45 = 30k ⇒ k ≈ 0.005454 10r 35 10r 53 b. 35 = 31.2e ⇒ 31.5819461 = e ⇒ 50 = 85+ (32 85)e 0.005454t ⇒ ⎛ 35 ⎞ ⎝ 31.5819461⎠ ln 35 = 0.005454t ⇒ t ≈ 76 min 53 ln 35 r = 31.5819461 ≈ 0.011627 ≈ 1.16% 103. Find k using T =160,T0 = 50,Ts = 400, and 10 c. 70 = 35e0.011627t ⇒ 2 = e0.011627t ⇒ t = 10 minutes. 160 = 400 + (50− 400)e 10k ⇒ 240 = e 10k ⇒ ln2 = 0.011627t ⇒ 350 24 t = ln 2 0.011627 ≈ 59.614 yr or in the year ln 35 = 10k ⇒ k ≈ 0.03773 Use this value of k to find the time given 2070.

50 = 35e0.011627t ⇒ 50 = e0.011627t ⇒

99.

100.

was

31.2 million in

t ≈ 5.5 minutes 102. Find k using T = 40,

minutes.

Copyright © 2015 Pearson Education Inc. 35 ⎛50⎞ T = 220,T0 = 50, and Ts = 400. 220 = 400 + (50 400)e 0.03773t ⇒ 18 = e 0.03773t ⇒ ln 18 = 0.03773t ⇒ ln⎜⎝35⎟⎠= 0.011627t ⇒ ln(50) 35 35 t ≈17.6 minutes t = 35 ≈ 30.676 ≈ 30.7 yr or in the 104. Find k using T = 84.8,T0 = 85.7,Ts = 55, and 0.011627 year 2040. t = 30 minutes. 84.8 = 55 + (85.7 55)e k(30) ⇒ 29.8 = 30.7e k(30) ⇒ ln 29.8 = 30k ⇒ 30.7 k ≈ 0.000992 (continued on next page)

Now use this value of k to find the number of minutes that passed until the body was found.

85.7 = 55+ (98.6 55)e 0.000992t ⇒

30.7 = e 0.000992t ⇒ ln 30.7 = 0.001t ⇒

43.6 43.6

t ≈ 353 minutes

The murder occurred 353 minutes before 2:10 A.M., or at 8:17 P.M., assuming that the temperature of the live body was 98.6°F.

105. a. ( )= ( )=

A 1 0.8 0.04 0.032

c. 15,000 =1500e0.231t ⇒10 = e0.231t ⇒

ln10 = 0.231t ⇒ t = ln10 ≈10 0.231

The herd will have 15,000 sheep about 10 years from now.

108. a. In two years, there will be 8 9 the number of sharks than there are now.

8 = e2r ⇒ ln

= 2r ⇒ ln(8)

r = 9 ≈ 0.059

Using the model A(t)= A0ert , we have 2

0.032 = 0.04er ⇒ 0.8 = er ⇒ r = ln 0.8 So, in one year (12 months), the concentration of the contaminant will be

A(12)= 0.04e12ln 0.8 = .0027 = 0.27%

b. 0.0001≤ 0.04eln 0.8t ⇒ 0.0025 ≤ eln 0.8t ⇒

Thus, the function is P =150e 0.059t .

b. 150e 0.059(4) ≈118

There will be about 118 sharks four years from now.

c. 35 =150e 0.059

Thus, the function is P ≈ 1500e0.231t Alternatively, since the population doubles every three years, we have the geometric progression progression given by P =1500

have 3 as the first digit.

b. P1 = log2 log1≈ 0.3010

P2 = log3 log2 ≈ 0.1761

P3 = log4 log3≈ 0.1249

P4 = log5 log4 ≈ 0.0969

P5 = log6 log5 ≈ 0.0792

P6 = log7 log6 ≈ 0.0669

P7 = log8 log7 ≈ 0.0580

P8 = log9 log8 ≈ 0.0512

P9 = log10 log9 ≈ 0.0458

There will be about 7557 sheep in the herdseven years from now.

9 ⎝9⎠

(continued)

Section 4.2 Logarithmic Functions 401

⎛⎜

⎞⎟

t ⇒ 35 = e 0.059t ⇒ 150 ln0.0025 ≤ ln0.8t ⇒ t ≤ 26.85 months ⎛ 35 ⎞ ln( 35 ) 106. a. T (1)= 3(16,000)=12,000 ln ⎜⎝150⎟⎠= 0.059t ⇒ t = 150 0 05 9 ≈ 24.7 4 Using the model T (n)= T0ern , we have There will be 35 sharks in about 24.7 years. ⎛ 4⎞ 12,000 =16,000er ⇒ 3 = er 4 ⇒ r = ln(3 4) 109. a. P3 = log4 log3 = log⎜⎝3⎟⎠≈ 0.125 About 12.5% of the data can be expected to b. c. 107. a. So T (n)= 16,000eln(3 4)n = 16,000(3 4)n T (12)=16,000eln(3 4) 12 = 506.82 m3 0.2(16,000) =16,000eln(3 4)t ⇒ 0.2 = eln(3 4)t ⇒ ln 0.2 = ln(3 4)t ⇒ t ≈ 5.6 years 3000 =1500e3r ⇒ ln 2 = 3r ⇒ ln2

r = 3 ≈ 0.231 P1 + P2 +

3 +

⋅2t 3

e0.231

7557

b. P =1500

(7) ≈

This means that one of the digits 1 9 willappear as the first digit.

a. 2, 3, 5, 7, 11, 13, 17, 19 π (20)= 8 b. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47 π (50)=15 50 ≈ 13 ln50

110.

402 Chapter 4 Exponential and Logarithmic Functions

c. π 1,000,000 ≈ 1,000,000 ≈ 72,382 ln1,000,000

4.2 Beyond the Basics

111. Since the domain of the logarithmic function

c. = ln(log(x − 1)). Switch the variables and then solve for y: x = ln(log( y 1)) ⇒

Switch the

is (0,∞) , the expression x 2 x +1 must be variables and then solve for y: x = log(log(log( y 1))) ⇒

positive. This occurs in the interval

the domain of

112. Since the domain of the logarithmic function

∞) , the expression x + 3 must be

= 4.05% f (x) = g (h(x)). The domain of h(x) is (1,∞) ⇒ the domain of f (x) is (2,∞).

c. h(x) = log(x 1) and g(x) = ln x So,

f (x) = g (h(x)). The domain of h(x) is (1,∞) ⇒ the domain of f (x) is (2,∞).

d. h(x) = log(x 1) and g(x) = log x So,

f (x) = g (g (h(x))). The domain of h(x) is (1, ∞). The domain of g (h(x)) is (2, ∞).

(Note that log(x − 1) = 0 ⇒ x = 2.) So, the domain of g (g (h(x))) is (11,∞).

y = log2 (log3 x) . Switch the variables and

118. a. Using the simple interest formula, we find that 50,000 = P(0.05)(1) ⇒ P =1,000,000.

So we need $1,000,000 in order to earn $50,000 per year. To determine the amount in the account at age 40, we have 1,000,000 = Pe(0.05 25) ⇒ P ≈ $286,504.80.

b. Using the simple interest formula, we find

then solve for y:

( ) = 1010 3 ⎝ x + ⎟⎠1 3 ⎝ x ⎠2 ⎝2 ⎠ ⎝2 ⎠

ex = log( y 1) ⇒10e x = y 1⇒10e x +1= y d. y = log(log(log(x 1))).

(−∞

1010x x log(y 1) ⇒10 +1= y log ⎜⎛ x 2⎞

−∞

115. y = log x → y = log(x 2)→

x = log(log(y 1)) ⇒

, 1)∪(2,∞) , so

is (

, 1)∪(2,∞).

y = log⎜ ⎛1 x 2⎞ ⎟→ y = 3log⎛ ⎜1 x 2⎞ ⎟→ ⎛1 ⎞ ⎛1 ⎞ x 2 positive. This

interval (−∞ , 3)∪(2,∞),

domain of 116. y = 3log⎝ ⎜2 x 2⎟ ⎠→ y = 3log 2 x 2⎟ ⎠+ 4 y = log x → y = log(2 + x)→ log ⎜⎛ x +3⎟⎞ is (−∞ , 3)∪(2,∞) y = 4log(2 + x)→ y = 4log(2 + 3x)→ y = 4log(2 3x)→ y = 4log(2 3x)→ y = 4log(2 3x)+1 113. a. h(x) = log3 x and g(x) = log2 x So, f (x) = g (h(x)) The domain of h(x) is 117. a. P = 100,000e 0.07(20) = $24,659.69 (0,∞) ⇒ the domain of f (x) is (1,∞). b. 50,000 = 75,000e 10r ⇒ 2 = e 10r ⇒ b. h(x) = ln(x 1) and g(x) = log x So, 3 ln(2 3

⇒

≈

is (0,

occurs

the

so the

)= 10r

0.0405

114. a.

P(0.08)(1) ⇒ P = $625,000.

So we need $625,000 in order to earn $50,000 per year. To determine the amountin the account at age 40, we have

b. y = log(ln(x 1)). Switch the variables and then solve for y:

625,000 = Pe(0.08 25) ⇒ P ≈ $84,584.55.

c. Using the simple interest formula, we find that 50,000 = P(0.1)(1) ⇒ P = 500,000.

So we need $500,000 in order to earn $50,000 per year. To determine the amount in the account at age 40, we have 500,000 = Pe(0.1 25) ⇒ P ≈ $41,042.50.

4.2 Critical Thinking/Discussion/Writing

x tha

t 50, 00

x = log2(log3 y) ⇒ 2 x = log3 y ⇒ 32 = y

⇒

x = ln(y 1) ⇒

1⇒ e

x = log(ln( y 1))

e10 x = y

119. 2log2 3 − 3log3 2 = 3 2 =1

the statement is always true.

increasing property is used.

124. There are four possibilities, 0 < a < 1 with c < 0, 0 < a < 1 with c > 0, a > 1 with c < 0, and a > 1 with c > 0. They are illustrated below.

Copyright © 2015 Pearson Education Inc. 3 2 3 2 = =⎢ ⎨ln(x 1 +ln x 2 )( ) 120. log3 4 = log3 (22 )= 2log3 2 log2 9 = log2 (32 )= 2log2 3 Let x = log3 2 and let y = log2 3. (log 4 + log 9)2 −(log 4 log 9)2 = (2x + 2 y)2 (2x 2 y)2 =⎡ ⎣(2x + 2y)+(2x 2y)⎤ ⎦⋅ ⎣ ⎡(2x + 2y) (2x 2y)⎤ ⎦ = (4x)(4 y) = 16xy Note that x = log3 2 ⇒ 3x = 2 and y = log2 3 ⇒ 2 y = 3

4.2 Logarithmic Functions 403 4.2 Maintaining Skills 125. a2 ⋅ a7 = a9 126. (a2 )3 = a2 3 = a6 3xy =(3x )y = 2 y = 3⇒ 3xy = 3 ⇒ xy =1 127. =(a8)1 2 = a 8 (1 2) = a 4 Alternatively, xy = log 2⋅log 3 = log2 ⋅ log3 =1. 128. =(a6 )1 3 = a 6(1 3) = a 2 3 2 log3 log2 Therefore, 16xy = 16 1 = 16, so ⎛ 243⎞45 ⎡⎛243⎞1 5 ⎤4 ⎛3⎞4 129. 2 2 ⎜⎝ 32 ⎟⎠ =⎢ 32 ⎟⎠ ⎥ =⎜⎝2⎟⎠ (log3 4 + log2 9) –(log3 4 log2 9) = 16. ⎢⎣ ⎥⎦ 121. log3 ⎡⎣log4 (log2 x)⎤ ⎦= 0 ⇒ log 4 (log2 x)= 30 ⇒ 130. = 5 ⎛ 1 ⎞ 3 ⎛ 1 ⎞3(1 5) ⎡⎛ 1 ⎞(1 5)⎤3⎥ log4 (log2 x)=1⇒ log2 x = 4 ⇒ x = 24 =16 ⎜⎝32⎟⎠ ⎜⎝32⎟⎠ ⎢ ⎣⎜ ⎝32⎟ ⎠ ⎥ ⎦ 122. a. f (x)= log x = –log x log x if 0 < x < 1 if x ≥1 ⎛1⎞3 =⎜⎝2⎟⎠ b. g (x)= ln(x 1) + ln(x 2) = ⎧ln(x 1)− ln(x 2) ⎩ if 2 < x < 3 if x ≥ 3 131. (4.7 ×107 )(8.1×105)=(4.7 ×8 1)(107 ×105) = 38.07 ×1012 = 3.807 ×1013 123. a.

132. 7.2 ×106 = 7.2 × 106 = × 9 b.

2.4 ×10 3 2.4 10 3 3 10

133. 134. a8 3 a6 5 32 3 {

Section

Yes,

The

Copyright © 2015 Pearson Education Inc. 135. log3 81= 4 beca use 34 = 81. log3 3+ log3 27 = 1+ 3 = 4 beca use log3 3 = 1 and 33 = 27. There fore, log3 81= log3 3+ log3 27. log2 8 = 3 beca use 23 = 8. log2 128 − log2 16 = 7 4 = 3 beca use 27 = 128 and 24 = 16. log2 16 = 4 beca use 24 =16. 2log2 4 = 2⋅2 = 4 because 22 = 4. Therefore, log216 = 2log2 4.

136. log4 64 = 3 because 43 = 64. log 64 6

2 = = 3 because 26 = 64 and log2 4 2

6. a., b., Substitute (3, 3) and (9, 1) in the equation y = c + b log x to obtain

log3 (1) 1

22 = 4. Therefore, log 64 = log2 64 . Subtract equation (1) from equation (2) and

4.3 Rules of

4.3 Practice Problems

2 4 solve the resulting equation for b

2 = b log9 − b log3 = b (log9 log3)

= b log 9 = b log 3 3

Substitute the value for b into equation (1)

To find the half-life, we use the formula h = ln2 = ln2 ≈ 25.

) 15

567log234 ≈1343.345391

Since log K lies between the integers 1343 and1344, the number K requires 1344 digits to theleft of the decimal point. By definition of the common logarithm, we have K =101343.345391 =100.345391 ×101343

≈ 2.215088 ×101343

+ 2 2 15 2 2 2 404 Chapter 4 Exponential and Logarithmic Functions

= c + b

= c + b log9 (2)

Logarithms

log

a. log5 ( y z)= log5 y log5 z = 2 3 = 1 b. log5 (y2z3)= log5 (y2 )+log5 (z3)

and

for c 3 = c ⎛ 2 ⎞ log3 ⇒ 3 = c 2 ⇒ c = 5 = 2log5 y + 3log5 z = 2⋅2 + 3⋅3 =13 ⎝⎜ log3⎟⎠ Substituting the values for b and c into 2. a. ln 2x 1 = ln(2x 1) ln(x + 4) y = c + b log x 2 gives ⎛log x ⎞ x + 4 ⎛4xy ⎞1 2 1 ⎛ 4xy ⎞ y = 5 log3(log x)= 5 2⎜⎝log3⎟⎠ = 5 2log3 x b. log =log⎜⎝ 1 z ⎟⎠ = 2log⎜⎝ z ⎟⎠ 7. ln ⎛ A(t)⎞ = kt ⇒ ln( 66 )=15k ⇒ = 2 (log4xy log z) ⎝⎜ A0 ⎟⎠ 100 = 1 (log4 + log x + log y log z) = 1 (log(22 )+ log x + log y log z) ln(0.66)=15k ⇒ k = ln(0.66)

2 2 2 3. 1 ⎣ ⎡log(x +1)+log(x 1)⎤ ⎦ = 1 ⎡ ⎣log((x +1)(x 1))⎤ ⎦ = 1 log(x2 1)= log(x2 1)1 2 =

4. K =

log K =

b = 2 1. Given log5 z = 3 and log

y =

log3

solve

= log2+ 1 log x + 1 log y 1 log z k ln (0.66

log

234567

log(234567 ) log K =

4xy