professione docente materiali
e strumenti per l’insegnante
HUB Scuola
Area Primaria
Intelligenza Artificiale: istruzioni per l’uso
Dalla progettazione alla certificazione delle competenze
Programmazione
La nuova valutazione
L’insegnamento dell’Educazione civica
Se sbaglio imparo, di Federica De Gasperis (Maestra Federica)
Schede di autovalutazione di Matematica
Allenamento alla Prova nazionale INVALSI con soluzioni
Schede e verifiche multilivello
Prove strutturate per classi parallele con soluzioni
Costruire inclusione in una prospettiva universale, a cura di Erickson
Il Piano Educativo Individualizzato in prospettiva bio-psico-sociale, a cura di Erickson
Piano Didattico Personalizzato: ridare centralità alla didattica, a cura di Erickson
Calcolo facile, di Cristina Caciolo, a cura di Erickson
SOLUZIONI PER L‘INSEGNANTE NEL LIBRO DIGITALE

SCHEDE DI SCIENZE E TECNOLOGIA
Le Scienze e il lavoro di scienziati e scienziate
Le bottiglie piene d’acqua nel congelatore scoppiano
La materia e i suoi stati
La galaverna, un fenomeno emozionante, ma sconosciuto 135
L’acqua
La giornata mondiale dell’acqua
L’aria
Mongolfiere e dirigibili
Il suolo
Il compostaggio
La materia e le sostanze (Laboratorio competenze)
I viventi
Le aree naturali protette
Le piante e gli animali
L’estinzione degli animali
Identikit di piante e animali (Laboratorio competenze)
Gli invertebrati
(Laboratorio competenze)
I vertebrati
(Laboratorio competenze)
L’ecosistema
La pozza di marea
L’ecosistema bosco (Laboratorio competenze)
La catena e la rete alimentare (Laboratorio competenze)
Adattarsi

COMPITI AUTENTICI E LABORATORIO
La giornata della Terra
Costruiamo un acquedotto
PROVE STRUTTURATE PER CLASSI PARALLELE
Prova d’ingresso di Matematica
Prova intermedia di Matematica
Prova finale di Matematica
Prova d’ingresso di Matematica con soluzioni
Prova intermedia di Matematica con soluzioni
Prova finale di Matematica con soluzioni
CONTRIBUTI E PERCORSI A CURA
Costruire inclusione in una prospettiva universale
Il piano educativo individualizzato in prospettiva bio-psico-sociale
Piano didattico personalizzato: ridare centralità alla didattica
I materiali per la didattica inclusiva ne I mondi di GEA in Matematica e Scienze
Accendi la conoscenza con HUB Scuola
Nuova, intuitiva, dinamica.
HUB Scuola è la piattaforma che accompagna docenti, studentesse e studenti nel loro percorso educativo. Sempre più ricca di risorse, lezioni e strumenti per una didattica digitale efficace e coinvolgente, è l’alleata ideale per le sfide di ogni giorno.

Tutta l’autorevolezza di Mondadori Education, Rizzoli Education e Deascuola in un solo ambiente digitale: HUB Scuola rappresenta la sinergia di tre grandi editori attenti alle esigenze di una scuola in continua evoluzione.
Esplora il Sito libro, il luogo dove i tuoi libri prendono vita Qui puoi immergerti nella versione digitale dei volumi e scoprire tutti i materiali, le app e gli strumenti correlati.
Se sei docente, nelle Aree Docenti trovi l’ambiente perfetto per personalizzare le lezioni grazie a proposte, approfondimenti e strumenti specifici per ogni tua materia.
Anche la sezione Test e Verifiche è una miniera di risorse: gli studenti vi trovano materiali per esercitarsi, mentre i docenti possono attingere a vasti database e creare test per ogni materia e grado scolastico.
HUB Scuola ti offre i contenuti digitali dei tre editori, integrati in un’unica piattaforma e accessibili con un’unica email e password Entra in HUB Scuola!
Scopri di più su HUB Scuola inquadrando il QR code.
www.hubscuola.it
Scopri un mondo di risorse su misura per te

Aree Docenti
Percorsi didattici e materiali pronti all’uso per ogni materia che insegni.
Sito libro
La versione digitale del tuo libro cartaceo, con tutti i contenuti extra.
Test e Verifiche
Un ampio database di quesiti ed esercizi per creare verifiche e allenarsi.
PRESENTAZIONE DEL CORSO
Il corso
I mondi di Gea è il nuovo Sussidiario delle discipline Fabbri-Erickson, realizzato seguendo le più recenti linee guida e indicazioni ministeriali.
Il corso è nato dalla collaborazione tra Rizzoli Education ed Erickson per facilitare l’accesso all’apprendimento da parte di tutti gli alunni e tutte le alunne, anche quelli con BES, creando un punto di contatto tra la didattica di classe e la personalizzazione/ individualizzazione dell’apprendimento.
Il Sussidiario propone un percorso strutturato e completo per sviluppare le competenze e fornire un valido metodo di studio, oltre che strumenti e strategie per l’apprendimento integrati e diversificati.
Il Sussidiario I mondi di Gea è suddiviso in quattro volumi base. Più pagine, attività e approfondimenti in… uno zaino più leggero! Per ogni disciplina, infatti, la parte di Sussidiario è unita a quella del relativo eserciziario. In questo modo, ogni alunno e alunna ha a disposizione volumi completi, integrati, ma compatti. Può studiare e fare le prime attività operative, esercitarsi in maniera più approfondita… tutto senza mai cambiare strumento, con anche l’ausilio dei puntuali rimandi interni ai volumi.
Composizione del corso
Per alunne e alunni

Per l’insegnante e la classe
CLASSE 4
Matematica 4
CLASSE 5
Matematica 5
Scienze e Tecnologia 4Scienze e Tecnologia 5
Storia 4
Storia 5
Geografia 4 Geografia 5
HUB Kit + HUB Kids HUB Kit + HUB Kids
CLASSE 4
Guida professione docente - Matematica e Scienze e Tecnologia 4
Guida professione docenteStoria e Geografia 4
Che facile! Saperi di base 4
Che facile! Matematica 4
CLASSE 5
Guida professione docente - Matematica e Scienze e Tecnologia 5
Guida professione docenteStoria e Geografia 5
Che facile! Saperi di base 5
Che facile! Matematica 5
STORYTELLING
Tutte le unità sono introdotte da una doppia pagina di storytelling di Valeria Razzini, a cura di Erickson.
La narrazione favorisce l’apprendimento disciplinare. Le storie permettono di attivare quello che bambine e bambini sanno già a un livello non strutturato, coinvolgono, motivano, interessano, stimolano le emozioni. Sono un modo in più per differenziare la didattica e raggiungere il maggior numero di bambini e bambine.

PROBLEM SOLVING
In tutte le unità di lavoro sono presenti pagine speciali dedicate al PROBLEM SOLVING con le quali si pongono le basi per costruire un metodo efficace per la soluzione di problemi di ogni tipo. Viene proposto un problema esempio da risolvere passo passo e poi ci si mette alla prova con un problema simile.
MATELUDICA
Un laboratorio speciale che segue passo passo le spiegazioni classiche, ma che propone un approccio ludico alla Matematica con attività concrete e facilitanti per affrontare i vari argomenti.
Si utilizzano le metodologie del fare per capire (learning by doing) e i mateludici: diversi tipi di materiali facili da procurarsi (dalle cannucce ai mattoncini e molti altri).
SINTESI E MAPPE DI FINE UNITÀ
Al termine di ogni unità sono presenti delle sintesi o mappe a seconda dell’argomento trattato.

STEM Education
Le discipline STEM sono importantissime per la crescita e per il futuro di tutti noi e del nostro pianeta. Ne I mondi di Gea troviamo laboratori STEM e/o STEAM in tutte le materie, Matematica compresa.
CALCOLO FACILE
Un percorso a cura di Erickson che focalizza l’attenzione sulle strategie matematiche, sulla metacognizione e sul confronto tra pari, per garantire ad alunni e alunne un apprendimento di successo.
LA NUOVA EDUCAZIONE CIVICA • EDUCAZIONE FINANZIARIA
I mondi di Gea segue le più recenti linee per l’insegnamento dell’Educazione civica alla scuola primaria e introduce un breve ma esaustivo percorso dedicato all’Educazione finanziaria adattando gli argomenti all’età di alunni e alunne.
MI ESERCITO IN...
Ne I mondi di Gea l’eserciziario, integrato nel volume, è uno strumento ricco di schede e materiali adatti a tutte le esigenze della classe. Inoltre, al termine di esso trova spazio anche un percorso dedicato al Coding.
IL MIO ATLANTE • RIPASSA CON GEA
Le prime pagine dell’eserciziario sono dedicate agli schemi dei principali argomenti di Matematica da utilizzare come strumenti compensativi e per il ripasso. La sezione è a cura di Erickson.

BENVENUTI IN QUARTA • RIPASSA CON GEA
Pagine di accoglienza per ripassare e rinfrescare le conoscenze apprese nelle classi precedenti, utili come base per cominciare il nuovo percorso.
SE SBAGLIO IMPARO
Un percorso che aiuta a non commettere più errori in Matematica in alcuni particolari argomenti oggetto di errori frequenti. In ogni pagina dedicata allo sbaglio vengono forniti esempi, strategie risolutive, consigli ed esercizi per non sbagliare più.
SCHEDE ESERCIZI
Tanti esercizi dedicati a ogni argomento per mettersi alla prova e allenarsi in Matematica.
PROBLEMI AUTENTICI
In queste pagine, alunne e alunni troveranno dei problemi che li stimolano a utilizzare le loro conoscenze in problemi e situazioni reali.
VERIFICHE MULTILIVELLO
Per ogni argomento affrontato sono presenti verifichesu4livelli:PIÙFACILE,INTERMEDIA, FINALE e PROVA NON NOTA.
VERSO L’INVALSI
PerogniargomentoschedeinmodalitàINVALSI per prepararsi alla prova.
STORYTELLING
Tutte le unità sono introdotte da una doppia pagina di storytelling di Valeria Razzini, a cura di Erickson. La narrazione favorisce l’apprendimento disciplinare. Le storie permettono di attivare quello che bambine e bambini sanno già a un livello non strutturato, coinvolgono, motivano, interessano, stimolano le emozioni. Sono un modo in più per differenziare la didattica e raggiungere il maggior numero di bambini e bambine.

METODO ELS
Le Scienze utilizzano il metodo ELS (Elaborazione Logico Sperimentale) di derivazione montessoriana. L’apprendimento procede sempre per tentativi ed esperimenti. Le conoscenze che derivano dall’esperienza vengono poi elaborate e schematizzate in maniera semplice. Nelle pagine del libro, infatti, ci sono moltissime attività ed esperimenti che possono essere realizzati con materiali vari e di recupero e in diverse situazioni.
STEM Education
ÈfondamentaleinvestiresulleSTEMapartiredallascuolaprimariae
I mondi di Gea cura particolarmente le discipline STEM in Scienze con pagine dedicate a LABORATORI STEM, LABORATORI di TECNOLOGIA ed esperimenti per toccare con mano la Scienza.
METODO DI STUDIO E LIFE SKILLS
Tre percorsi operativi integrati tra loro (Imparo con metodo, Imparo con competenza, Impariamo insieme) pensati, insieme a Erickson, per far acquisire un primo metodo di studio.
Imparo con metodo è fatto di operative rubricate (parole speciali, analizzo, ricostruisco, espongo) che propongono un vero e proprio metodo per la comprensione del testo espositivo.
Imparo con competenza presenta attività su competenze disciplinari specifiche: fa lavorare, per esempio, su carte, illustrazioni, testi disciplinari, fonti.
Impariamo insieme presenta attività cooperative strutturate e guidate.
LIFE SKILLS sono attività da svolgere da soli, in coppia o piccolo gruppo che stimolano lo sviluppo delle competenze per la vita come il pensiero critico e creativo.

SINTESI E MAPPE DI FINE UNITÀ
Al termine di ogni unità si trova un apparato didattico di sintesi e verifica. Con questi strumenti ogni bambino e bambina, indipendentemente dal livello e da eventuali difficoltà, può iniziare a fissare gli apprendimenti seguendo e rispettando le proprie caratteristiche. Si inizia con una sintesi testuale accompagnata da immagini e si prosegue con una mappa da completare.
EDUCAZIONE CIVICA
I mondi di Gea seguono le nuove linee guida per l’insegnamento dell’Educazione civica. Troviamo pagine dedicate ad approfondire argomenti di Scienze dal punto di vista della sostenibilità ambientale.
MI ESERCITO IN…
Ne I mondi di Gea l’eserciziario, integrato nel volume, è uno strumento ricco di schede e materiali adatti a tutte le esigenze della classe.
IL MIO ATLANTE • RIPASSA CON GEA
Le prime pagine dell’eserciziario sono dedicate alle mappe dei principali argomenti di Scienze da utilizzare come strumenti compensativi e l’esposizione orale. La sezione è a cura di Erickson.
SCHEDE ESERCIZI
Approfondimenti ed esercizi dedicati ai vari argomenti trattati in Scienze.
VERIFICHE MULTILIVELLO
Per ogni argomento affrontato sono presenti verifiche a livelli: PIÙ FACILE, FINALE e PROVA NON NOTA.
STEM Education
Anche in Mi esercito in… trovano spazio esercitazioni laboratoriali stimolanti ed educative.
I TEMI-CHIAVE DE I MONDI DI GEA

NUOVA EDUCAZIONE CIVICA
Nel settembre 2024 il MIM ha pubblicato le nuove linee guida in materia di Educazione Civica, che sono valide a partire dall’anno scolastico 2024/2025. A partire da questo anno scolastico i curricoli di Educazione civica si riferiscono ai traguardi di apprendimento definiti a livello nazionale e indicati appunto dalle nuove linee guida. L’Educazione Civica viene individuata come disciplina trasversale, come ambito di apprendimento interdisciplinare. Al centro delle nuove linee guida ci sono i tre nuclei concettuali: Costituzione, Sviluppo economico e sostenibilità, Cittadinanza digitale. Tra tutte le tematiche viene sottolineata una particolare attenzione alla conoscenza della Costituzione, alla tutela dell’ambiente, all’educazione stradale, all’educazione finanziaria (per approfondire vedi pagg. 44-49).
In tutti i corsi Fabbri–Erickson è forte questa prospettiva interdisciplinare e trasversale dell’educazione civica. Trasversalmente sono presenti pagine dedicate, laboratori e percorsi specifici (narrativi e laboratoriali) che riguardano le tematiche più importanti (tra cui il rispetto di sé e degli altri, l’educazione finanziaria, la cittadinanza digitale).
COMPETENZE NON COGNITIVE, LIFE SKILLS
Nel novembre 2024 è stata approvata la Legge che introduce “lo sviluppo di competenze non cognitive e trasversali” nei percorsi scolastici e di formazione professionale. La sottolineatura dell’importanza delle competenze non cognitive, o Life Skills o Soft Skills, viene da lontano; già nel 1993 infatti l’OMS aveva individuato alcune life skills fondamentali per il benessere e la realizzazione delle persone. Fanno parte delle life skills competenze emotive (consapevolezza di sé e delle proprie emozioni e loro gestione), competenze relazionali (comunicazione efficace, costruzione di relazioni sane ed efficaci) e poi capacità di problem solving, pensiero critico, pensiero creativo. Sono competenze fondamentali per stare bene, costruire il proprio futuro, raggiungere l’autonomia, costruire relazioni in tutti gli ambiti dell’esistenza.
In tutti i corsi Fabbri–Erickson ci sono percorsi pensati per sviluppare le competenze non cognitive, con, per esempio, rubriche didattiche, laboratori, albi illustrati.

STEM E STEAM
STEM è un acronimo inglese riferito a diverse discipline: Science, Technology, Engineering and Mathematics, e viene usato per indicare l’insieme delle materie scientifiche-tecnologiche-ingegneristiche.
STEAM aggiunge all’acronimo la A di Arts e fa riferimento all’interdisciplinarità e alla dimensione creativa.
Già nel 2022 il MIM ha pubblicato delle linee guida sulla didattica STEM che accolgono la necessità di potenziare il processo di insegnamento–apprendimento delle discipline scientifiche e tecnologiche anche attraverso metodologie didattiche innovative e con la valorizzazione di trasversalità e interdisciplinarietà.
Potenziare le STEM è uno degli obiettivi più importanti per raggiungere il traguardo di un’istruzione di qualità che formi davvero i giovani del futuro. Uno degli obiettivi deve essere anche quello di eliminare le disparità di genere che permangono nell’ambito STEM.
I corsi Fabbri–Erickson dedicano grande attenzione all’insegnamento-apprendimento delle discipline STEM e STEAM con percorsi, laboratori, volumi dedicati, che tengono sempre in considerazione l’eliminazione delle disparità di genere.
PARITÀ DI GENERE E MULTICULTURA
Nell’ambito della parità di genere e multicultura Fabbri–Erickson porta avanti ormai da diversi anni Obiettivo Parità, un progetto nato per contrastare gli stereotipi di genere nei libri di testo che nel 2025 si è arricchito di una parte dedicata alla multiculturalità.
L’idea di base è che l’unico modo per costruire un futuro senza differenze di genere e per contrastare davvero fenomeni come la violenza di genere o qualsiasi tipo di discriminazione, sia partire dall’eliminare gli stereotipi dai libri di testo e da una corretta rappresentazione della realtà.
Obiettivo parità prevede che tutti i libri di letture vengano rivisti e supervisionati in modo che ci sia equilibrio nella scelta delle letture tra numero di autrici e autori e numero di protagonisti e protagoniste. Nella scelta delle letture ci sia una rappresentazione equilibrata della realtà. Non ci sia presenza di stereotipi, né femminili né maschili. Venga utilizzato, non solo nelle letture, ma in tutti i libri, il linguaggio di genere. Allo stesso modo, tutti i libri di letture vengono supervisionati in modo da avere una rappresentazione reale delle culture diverse in cui siamo immersi quotidianamente e che arricchiscono la nostra.

Apparato digitale per Matematica e Scienze e Tecnologia
Ne I mondi di Gea sono presenti video disciplinari (tutorial, esperimenti, approfondimenti) per stimolare la curiosità e facilitare la comprensione delle materie.
Inoltre:
• App ludico-didattiche che combinano gioco e apprendimento, aiutando i bambini a consolidare le competenze attraverso attività divertenti e coinvolgenti.
• Escape room: percorsi interattivi dove gli studenti risolvono enigmi e sfide per consolidare le conoscenze in modo coinvolgente e divertente.
• Immagini interattive per favorire l’apprendimento attraverso l’interazione e stimolare l’osservazione attiva.
• Presentazioni modificabili pronte all’uso e personalizzabili per facilitare la spiegazione o il ripasso degli argomenti.
• GeoGebra, lo strumento interattivo per esplorare concetti matematici e geometrici, che aiutano gli studenti a visualizzare e comprendere meglio teoremi e problemi.
• Esercizi interattivi e autocorrettivi integrati nel testo, da svolgere direttamente sul libro digitale per la verifica delle competenze.
Materiali per il docente
Professione docente
Le quattro guide per l’insegnante, due per l’ambito antropologico e due per quello scientifico, sono uno strumento di lavoro ricco e indispensabile, che integra i volumi per l’alunno/a.
Contengono:
• Dalla progettazione alla certificazione delle competenze, a cura di Dino Cristanini;
• Programmazione di ogni materia;
• La valutazione degli apprendimenti nella scuola primaria
• L’insegnamento dell’Educazione civica secondo la nuova normativa;
• Il Piano Educativo Individualizzato in prospettiva bio-psico-sociale, a cura di Erickson;
• Progetto CheFacile!, testi facilitati e semplificati, a cura di Erickson;
• Calcolo facile, a cura di Erickson;
• Se sbaglio imparo, di M. Federica De Gasperis
• La Mateludica di Valentina Perolio;
• Verifiche multilivello (di base, di recupero, di potenziamento);
• Prove strutturate per classi parallele con soluzioni in pagina;
• Metodo ELS, un metodo per imparare le Scienze, di Gruppo Pleiadi;
• Prova verso l’Invalsi con griglia soluzioni.

Area primaria
Lo spazio dedicato ai docenti con migliaia di risorse digitali utili all’insegnamento delle materie di primo e secondo ciclo e di religione. In questo spazio potrete trovare: escape room, app ludico didattiche, video, presentazioni modificabili, immagini interattive, itinerari con Google Earth, la cartografia digitale di HUB Maps, materiali per la verifica e molto altro ancora!
HUB Kids docente
HUB Kids per il docente, il libro digitale interattivo e multimediale, utilizzabile su computer, tablet e LIM, è arricchito da materiali aggiuntivi disponibili soltanto per l’insegnante. Inoltre il libro digitale consente di vedere le soluzioni direttamente in pagina.
HUB Kids è uno strumento indispensabile per la didattica inclusiva: permette la lettura automatica del testo, la scelta del fondino di lettura e di diversi caratteri tra cui biancoenero® (il carattere ad alta leggibilità utile per chi ha problemi di dislessia).
HUB Kit docente
Come nella versione per l’alunno, anche HUB Kit docente comprende contenuti digitali che arricchiscono ed espandono il corso.
A disposizione del docente la Guida stampabile in formato Pdf, la Programmazione e le Verifiche in Word.
HUB Test
La piattaforma di HUB Scuola per creare verifiche e mettersi alla prova, con numerosi quesiti disciplinari.
HUB INVALSI
La piattaforma di HUB Scuola per allenarsi alla Prova Nazionale INVALSI.
CHE FACILE!
Per le classi quarta e quinta, inoltre, sono disponibili su richiesta dell’insegnante i volumi CheFacile! Storia Geografia Scienze, che contengono una selezione degli argomenti principali delle tre discipline, e i volumi CheFacile! Matematica, con strumenti di facilitazione per l’apprendimento nell’area logico-matematica. I quattro volumi sono a cura di Erickson.
La Guida di Matematica e Scienze
Progettazione e certificazione delle competenze
Nella sezione Progettazione e certificazione delle competenze, a cura di Dino Cristanini, vengono fornite informazioni su come procedere nella progettazione al fine di raggiungere la certificazione delle competenze degli alunni: dai traguardi per lo sviluppo delle competenze agli obiettivi di apprendimento.
Nelle prime pagine della Guida si trovano il Quadro delle correlazioni tra i traguardi per lo sviluppo delle competenze e le competenze da certificare con il modello nazionale e le programmazioni annuali di Matematica e Scienze.

Le schede multilivello
Per ogni disciplina sono presenti delle schede multilivello sui principali argomenti.
Per ogni tematica viene presentata una scheda: • di base; • di recupero; • di potenziamento
Le schede di base e di recupero differiscono tra loro per la modalità di proposta degli esercizi. Nelle schede di recupero, infatti, gli alunni e le alunne sono maggiormente guidati nella risoluzione delle attività.
Verso la prova Invalsi con griglia delle soluzioni.
Le prove strutturate per classi parallele
Le prove strutturate per classi parallele possono essere somministrate alla classe e favoriscono il confronto e la condivisione dei criteri di valutazione, delle strategie metodologiche e delle pratiche didattiche tra insegnanti.
Vengono fornite anche le prove con le soluzioni in pagina.

I materiali per la didattica inclusiva: strategie e dettagli operativi, a cura di Erickson
In questa Guida per l’insegnante sono presenti alcuni contenuti a cura di Erickson:
• introduzione “Costruire inclusione in una prospettiva universale”;
• il Piano Educativo Individualizzato in prospettiva bio-psico-sociale;
• il Piano Didattico Personalizzato: ridare centralità alla didattica;
• descrizione dei contenuti Erickson nei volumi per l’alunno, in HUB Kids e in HUB Kit, con indicazioni per il corretto utilizzo e per lo sviluppo di materiali analoghi personalizzati/individualizzati.

INDICE CONTENUTI DIGITALI
MATEMATICA 4
Lettura espressiva delle pagine di Storytelling, lettura di tutti i testi, audio delle attività. Inoltre...
PAG.TIPOLOGIA TITOLO CONTENUTO
8Video Risolvere un problema
Video Videointervista - Martin Gardner: il giocoliere
9Documento Strategie di problem solving • Problemi con dati nascosti
12Lab I problemi
17Video Fibonacci
Video Numeri piccoli e grandi
18Video Periodi e ordini
App Carte gioco - I grandi numeri
19App Abaco
22PresentazioneTest - Grandi numeri
26Documento La numerazione nella Mesopotamia e presso gli Egizi
Documento Quanti sono i numeri?
Video La storia dei numeri
27Video La tabella dell'addizione
28Video L’addizione in colonna
PresentazioneAddizione con e senza cambio
29PresentazioneLe proprietà e la prova dell’addizione
32Video La tabella della sottrazione
34Video La sottrazione in colonna con il cambio
35PresentazioneTest - Proprietà di addizione e sottrazione
PresentazioneLa proprietà della sottrazione
40PresentazioneLa prova della sottrazione
43Video La moltiplicazione
Video La tabella della moltiplicazione
44PresentazioneMoltiplicazione con e senza cambio
45PresentazioneLe proprietà e la prova della moltiplicazione
53Video La divisione
55Video Come si esegue una divisione con un divisore a due cifre
56PresentazioneLa proprietà della divisione
58Video La divisione come scomposizione e la divisione canadese
PAG.TIPOLOGIA TITOLO CONTENUTO
Documento La divisione canadese
61PresentazioneLa prova della divisione
62PresentazioneTest - Proprietà di moltiplicazione e divisione
63Geogebra Geogebra - Multipli e divisori di un numero
65Laboratorio Le operazioni
69Geogebra Geogebra - Le frazioni
Video Le frazioni
71PresentazioneI tipi di frazione
Documento Frazioni complementari Geogebra Geogebra - Frazioni complementari
72PresentazioneUn passo alla volta - Le frazioni equivalenti
75Documento Il muretto delle frazioni
Documento Confronto di frazioni con denominatore uguale
Documento Confronto di frazioni con numeratore uguale
78Video Frazioni in musica
80PresentazioneLe frazioni decimali
82App Carte gioco - Le frazioni
Laboratorio Le frazioni
83Video Decimali in linea
PresentazioneTest - I numeri decimali
84Video Addizione e sottrazione con i decimali
85Video Moltiplicazione e divisione per 10, 100 e 1000 di un numero decimale
86Video La moltiplicazione con i numeri decimali
87PresentazioneDivisione con dividendo o divisore decimale
90Laboratorio I numeri decimali
94Video Scopriamo la misura
Video Misure ed equivalenze
PresentazioneLa storia della misura
95Geogebra Geogebra - Lunghezze equivalenti
96PresentazioneLe misure di capacità
Geogebra Geogebra - Capacità equivalenti
97PresentazioneLe misure di massa

102PresentazionePeso lordo, peso netto, tara
103PresentazioneLe misure di valore
Documento Allenati con gli euro
105Video La compravendita
Documento Capire le offerte
106PresentazioneLe misure di tempo
Geogebra Geogebra - Le misure di tempo
107App Equivalenze
109Documento La moneta
Documento Andiamo in banca
Documento Che cos'è l'economia
Documento Che cos'è la finanza
111App Carte gioco - Unità di misura
Laboratorio Le misure
114PresentazioneLa storia della geometria
Video Scopriamo lo spazio e le figure
PresentazioneLe linee
115Geogebra Geogebra - Rette parallele, incidenti e perpendicolari
Video Come si disegnano le rette parallele
Video Come si disegnano le rette perpendicolari
116Geogebra Geogebra - Classificazione angoli
Laboratorio Le linee e gli angoli
Geogebra Geogebra - Angoli e loro classificazione
PresentazioneGli angoli
117Video Misurare gli angoli
118Geogebra Geogebra - La simmetria
Video La rotazione di una figura
Video La traslazione
Video Il ribaltamento di una figura
121Documento Oggetti geometrici
Geogebra Geogebra - Poligoni e la loro classificazione
PresentazionePoligoni
123Documento Dimostrazione degli angoli interni del triangolo
PresentazioneI triangoli
Geogebra Geogebra - Angoli interni di un triangolo
PresentazioneLaboratorio dei triangoli
125PresentazioneLa famiglia dei quadrilateri
Video I quadrilateri
Documento Dimostrazione degli angoli interni dei quadrilateri
126Documento I parallelogrammi
PresentazioneLa famiglia dei parallelogrammi
127Documento I trapezi
PresentazioneI trapezi
App Carte gioco - Forme geometriche piane
128PresentazioneIl perimetro dei poligoni
Video Il perimetro
Geogebra Geogebra - Poligoni isoperimetrici
131PresentazioneTest - I perimetri
132PresentazioneLe misure di superficie
134PresentazioneLe aree dei poligoni
Video L’area
135Documento Area del romboide
Geogebra Geogebra - Area del parallelogramma a partire da quella di un rettangolo
136Documento Area del rombo
Geogebra Geogebra - Area del rombo a partire dal rettangolo
137Documento Area del trapezio
Geogebra Geogebra - Area del trapezio da quella di un triangolo
138Documento Area del triangolo
Geogebra Geogebra - Area del triangolo a partire da quella di un parallelogramma
Geogebra Geogebra - Area del triangolo
139Documento Poligoni congruenti ed equiestesi
Video Il tangram
Geogebra Geogebra - Figure equiestesetangram
140Laboratorio I poligoni e aree
142Video Videointervista - Fibonacci: la sequenza magica
146Video Scopriamo relazioni dati e previsioni
147Documento Dalla tabella ai grafici
148Geogebra Geogebra - Media e moda
149Documento Traduzione - John Venn
Documento Organizzare i dati
Geogebra Geogebra - I sottoinsiemi
Geogebra Geogebra - L'intersezione di insiemi
Geogebra Geogebra - L'unione degli insiemi
150Laboratorio Relazioni, dati e previsioni
156Documento Dado furfante
158Documento Pizza alle olive
166Documento Le trasformazioni geometriche

SCIENZE E TECNOLOGIA 4
Lettura espressiva delle pagine di Storytelling, lettura di tutti i testi, audio delle attività. Inoltre...
PAG.TIPOLOGIA TITOLO CONTENUTO
3Video Scopriamo la Scienza
Video Children's Museum di Verona
Infografica La Scienza
4Video Città della Scienza di Napoli
PresentazioneLaura Bassi
5Video Il metodo scientifico
Video Chi è Galileo Galilei
Documento One pager - Il metodo scientifico
6Bacheca Le scienziate
8App Agenda 2030
9Infografica La materia
PresentazioneLa materia
Video La materia
13Video La materia ha un peso
Video La materia occupa uno spazio
15Video Gli stati dell’acqua
Video La capillarità
Documento I passaggi di stato
App Carte gioco - Solido liquido e gassoso
Documento Punti di fusione e di ebollizione
16Video Il ciclo dell’acqua
Infografica Il ciclo dell’acqua
19Video Videolaboratorio - Una questione di livello
Bacheca L’oro blu
Documento STEAM - Il ri-ciclo dell’acqua
Infografica L'acquedotto
22Documento Il termometro
Video Videolaboratorio - Caldo o freddo?
PresentazioneIl calore
23Video L’aria ha un peso ed è elastica
Video L’aria occupa uno spazio
24Laboratorio Gli strati dell'atmosfera
28Bacheca Il cambiamento climatico e l’effetto serra
Video Videolaboratorio - I gas serra e la temperatura dell'aria
Video L’effetto serra
32Video Videolaboratorio - Che roccia!
Video La struttura interna della Terra
Video Gli strati della Terra
Laboratorio Gli strati del suolo
PAG.TIPOLOGIA TITOLO CONTENUTO
33HUB Maps Le placche tettoniche
36Video Videolaboratorio - I componenti del suolo
37Bacheca Il nostro pianeta
Video La galleria della sostenibilità del MUSE di Trento
41Video Soluzione o sospensione?
42Video La tensione superficiale
44PresentazioneMAPPA DI VERIFICA
Documento One pager - Acqua
Documento One pager - Calore
Documento One pager - Aria
Documento One pager - Suolo
47Video Gli esseri viventi
Infografica Gli esseri viventi
PresentazioneI viventi
50Infografica La cellula e gli organismi
Video La cellula
55Video Le piante
56Infografica La fotosintesi clorofilliana
Video La fotosintesi
Video Video esperimento - La fotosintesi clorofilliana
57Video Videolaboratorio - I colori delle foglie
60Laboratorio La riproduzione delle piante
Video La riproduzione delle piante
63Documento La classificazione delle piante
68Documento La classificazione degli animali
Video Videolaboratorio - Il guanto più caldo
72Documento L’uovo e il frutto hanno la stessa funzione?
74PresentazioneGli animali vertebrati e invertebrati
76PresentazioneMolluschi, echinodermi, artropodi
Documento Scheda - I principali ordini di insetti
77Video Museo di storia naturale di Milano
PresentazioneJane Goodall
82Documento Che cosa mangiano gli uccelli
Laboratorio Gli esseri viventi
App Carte gioco - I vertebrati
PAG.TIPOLOGIA TITOLO CONTENUTO
85PresentazioneMAPPA DI VERIFICA
Documento One pager - I cinque regni dei viventi e la cellula
Documento One pager - Le piante
Documento One pager - Gli animali
87Video Gli ecosistemi
PresentazioneGli ecosistemi
91Infografica Gli ecosistemi
Infografica I climi
Documento Oceani e mari nel mondo
HUB Maps Gli ambienti nel mondo
Video Gli ambienti e i biomi
94Documento Scheda - Proteggiamo le api!
Video Le api
Video Videolaboratorio - “INSECT-OMAKER”
Video Museo A come Ambiente di Torino
97Video Dentro e fuori: Gli ecosistemi
99PresentazioneMAPPA DI VERIFICA
Documento Gli ecosistemi

Materiali per l’insegnante
• Soluzioni per l’insegnate nel libro digitale.
• Schede aggiuntive e compiti di realtà.
• Guida per l’insegnante in formato digitale.
• Programmazioni annuali in word.
• Volume CheFacile! con i saperi di base di Scienze e Tecnologia disponibile in Hub Kids
• Volume CheFacile! di Matematica disponibile in Hub Kids
Intelligenza artificiale: istruzioni per l’uso!
L’Intelligenza artificiale (per comodità AI) è una rivoluzione tecnologica ma anche culturale e sociale. L’assegnazione dei Premi Nobel del 2024 sancisce in una duplice maniera questo dato di fatto.
Con il Nobel per la Fisica a John Hopfield e Geoffrey Hinton si celebra il grande sforzo che ha portato allo sviluppo delle reti neurali e dunque reso possibile l’apprendimento automatico (o machine learning), cioè la possibilità per una macchina, grazie a degli algoritmi, di migliorare e affinare le proprie capacità di elaborazione man mano che acquisisce nuovi dati, arrivando a svolgere anche compiti non assegnati all’inizio.

Da qui puoi accedere al
Con il Nobel per la Chimica a David Baker e Demis Hassabis and John Jumper si testimonia la potenzialità dell’AI di migliorare concretamente le nostre vite: la ricerca sulle proteine e la loro complessa struttura, la progettazione in laboratorio di nuove proteine e la successiva realizzazione sono di fatto il primo passo verso la comprensione e la cura (tramite nuovi farmaci e nuove terapie) di molte malattie.
L’emozione di fronte a tali importanti conseguimenti non deve lasciare spazio a un ingenuo ottimismo: accanto alle “magnifiche sorti e progressive” di questa tecnologia, esistono criticità o comunque situazioni che è bene indagare con attenzione e senza pregiudizi. A maggior ragione questo deve accadere nella Scuola, dove gli e le studenti stanno costruendo quella “cassetta degli attrezzi” che consentirà loro di essere cittadini consapevoli e professionisti capaci e, in definitiva, di vivere una vita serena.
Queste poche pagine servono dunque a questo: individuare alcune prime linee guida per impiegare con profitto l’AI a scuola, offrire dei consigli sempre pratici e costruire strategie risolutive che sappiano accogliere, senza timori, le sfide presenti e future cui l’AI ci chiama.
Un framework per l’AI a Scuola
Una strategia usata da molti esperti di fronte a problemi complessi e all’apparenza inattaccabili è quella del drill down: in parole più semplici e senza inutili tecnicismi, significa scomporre il problema in sotto-problemi più piccoli che quindi possono essere compresi e risolti con più facilità.
La stessa intuizione hanno avuto M. Ranieri, S. Cuomo e G. Biagini nello stendere il loro saggio Scuola e intelligenza artificiale: in questo valido contributo, gli autori costruiscono un framework che serve alla Scuola per scomporre il problema AI. Qui sotto ne riproponiamo una versione semplificata e, a nostro giudizio, più funzionale:
0. AI literacy (o alfabetizzazione)
1. dimensione conoscitiva
2. dimensione operativa
3. dimensione critica
0. AI literacy
“Cercando le parole, si trovano i pensieri”: così ammoniva con sagacia il filosofo francese Joseph Joubert. E quindi il punto di partenza di qualsiasi indagine non può che essere il lessico.
Ecco quindi un primo vocabolario di base:
intelligenza artificiale generativa
Si tratta di un tipo di intelligenza artificiale che è in grado di creare nuovi contenuti, come immagini, testi e suoni, che possono essere indistinguibili da quelli creati da esseri umani.
Esempio:
un software che produce nuove composizioni musicali dopo aver appreso lo stile di vari compositori classici, generando pezzi originali che rispecchiano il gusto e la complessità delle opere apprese.
intelligenza artificiale generale (agi)
Una forma di intelligenza artificiale che può comprendere, imparare ed eseguire compiti intellettuali su un livello paragonabile all’intelligenza umana. L’AGI sarebbe in grado di applicare la conoscenza e le abilità di problem solving in una vasta gamma di contesti diversi, mostrando adattabilità e comprensione del mondo su scala umana. Si ritiene che la realizzazione di un’AGI sia ancora molto lontana.
Esempio:
un sistema AGI potrebbe essere utilizzato per condurre ricerche mediche autonome, formulando ipotesi, conducendo esperimenti virtuali, analizzando dati di studi clinici, e sviluppando nuovi farmaci, adeguandosi alle scoperte emergenti e regolamenti in tempo reale, senza bisogno di direttive specifiche da parte di ricercatori umani.

Prompt: la richiesta o l’indicazione fornita a un sistema di intelligenza artificiale per guidarlo a generare un risultato.
Devoto-Oli
large language models (llms)
I modelli di linguaggio di grandi dimensioni sono sistemi di intelligenza artificiale addestrati su vasti corpus di testo che possono comprendere e generare lingua naturale in modo coerente e contestualizzato. Questi modelli sono alla base di molte applicazioni moderne, dalla traduzione automatica ai sistemi di assistenza virtuale.
Esempio:
un assistente digitale che può svolgere compiti complessi come scrivere e-mail, comporre poesie o codificare programmi, basandosi sulla sua comprensione del linguaggio acquisita tramite l’analisi di una grande quantità di testi.
chatbot
Programmi informatici avanzati capaci di condurre una conversazione con gli utenti umani, tipicamente via testo. Questi sistemi sono spesso alimentati da algoritmi di machine learning e intelligenza artificiale per migliorare la capacità di risposta e apprendere dalle interazioni precedenti.
Esempio:
un servizio di assistenza clienti online che utilizza una chatbot per rispondere alle domande frequenti dei clienti, alleggerendo il carico di lavoro del personale di supporto.
allucinazione
Un’allucinazione in un chatbot avviene quando esso fornisce una risposta non accurata o inventata, senza alcuna base nei dati reali o nelle informazioni di cui dispone.
Esempio:
un utente chiede a un chatbot “Qual è la capitale della Svizzera?” e la risposta ottenuta è “La capitale della Svizzera è Zurigo.”

1. Dimensione conoscitiva
In questa prima fase, l’AI è l’oggetto della lezione. Questo passaggio assolve, per lo meno, a un duplice compito: ➀ dare contesto e rendere conto della complessità, anche storica e sociale, di quello che in maniera riduttiva definiamo “software”; ➁ in virtù di questo contesto, rendere più consapevoli gli studenti delle potenzialità e dei limiti dello strumento che useranno in una fase successiva.
I punti di vista possono essere molteplici e ciascuno sceglierà in base alla propria sensibilità e alle proprie competenze:
a → storico: i concetti di analogico e digitale, la costruzione e trasmissione del sapere dalle enciclopedie al web semantico, la storia delle macchine “intelligenti” (una buona sintesi si legge in G. Roncaglia, L’architetto e l’oracolo);
b → storico-sociale: il rapporto uomo-macchina (si veda per esempio: A. Longo, G. Scorza, Intelligenza artificiale. L’impatto sulle nostre vite, diritti e libertà) e il ruolo della macchina nel lavoro (ottimi spunti, anche se solo in inglese, in M. Pasquinelli, The Eye of the Master: A Social History of Artificial Intelligence);
c → filosofico: i concetti di autorialità (il punto di partenza fondamentale resta l’articolo di M. Foucault, Che cos’è un autore) e di creatività (stimolante la lettura di F. D’Isa, La rivoluzione algoritmica. Arte e intelligenza artificiale);
d → giuridico: una lettura attenta del Bejing Consensus (un documento Unesco il cui tentativo è stabilire come l’intelligenza artificiale possa essere utilizzata in modo sicuro, equo ed efficace per promuovere l’educazione a livello globale) e EU AI Act (una proposta di regolamento dell’Unione europea che mira a regolamentare lo sviluppo, l’uso e la diffusione delle tecnologie di intelligenza artificiale);
e → informatico: il funzionamento dell’apprendimento automatico (o machine learning) e la sua explainability (XAI) (si può fare riferimento a N. Cristianini, La scorciatoia. Come le macchine sono diventate intelligenti senza pensare in modo umano).
Al di là delle specifiche pratiche disciplinari, ci sono due istanze di cui ogni docente dovrebbe farsi carico:
etica per l’ai fissa i principi che possono guidare l’uso degli algoritmi nella società e nelle organizzazioni: beneficenza, non maleficenza, autonomia, giustizia, esplicabilità.
etica dell’ai
definisce i problemi etici che gli algoritmi nel loro funzionamento comportano, ovvero l’equità (fairness) e l’iniquità (unfairness): un sistema di AI è considerato equo quando le sue previsioni e decisioni non sono influenzate da pregiudizi o discriminazioni verso gruppi o individui, e quando queste sono chiare, trasparenti e ugualmente applicabili a tutti.

2. Dimensione operativa
In questa seconda fase, l’AI è lo strumento della lezione: grazie a un semplice chatbot gratuito, oggi è infatti possibile generare una molteplicità di artefatti (testo, immagini, video, audio). Più che resistere a questa possibilità e dunque organizzare la propria didattica come “uno strumento di una vera e propria controcultura” (secondo l’espressione del filosofo tedesco Gernot Böhme), la Scuola otterrà maggiori e più utili risultati se insegnerà agli e alle studenti a usare con saggezza questo strumento, affidandogli i compiti per cui è progettato eppure restando sempre in controllo del processo e del prodotto. Non sarà infatti un caso che, una delle più importanti aziende informatiche del pianeta, abbia scelto per i propri servizi AI la metafora del co-pilota. Non si tratta solo di una banalità pedagogica. Si ricordi infatti ciò che sancisce quella che gli esperti hanno chiamato la legge di Kasparov (in onore del grande scacchista russo e delle sue leggendarie sfide contro il supercomputer IBM Deep Blue): una combinazione efficace di intelligenza umana e intelligenza artificiale lavora meglio di ciascuna delle due intelligenze (umana o artificiale) presa singolarmente.
Lo strumento AI più diffuso e che ciascuno di noi usa quotidianamente è un chatbot, cioè un software AI che risponde a domande e interagisce con gli utenti, adattandosi al contesto delle conversazioni.
la prima cautela ricordare che un chatbot è un motore di ragionamento (reasoning engine) e non un semplice archivio di dati (fact database): per esempio, eccelle nel brainstorming creativo, ma non sempre è attendibile nelle ricerche di dati.
la seconda cautela sapere che la qualità dell’artefatto dipenderà dalla nostra capacità di porre in modo efficiente le giuste domande (ricordate la legge di Kasparov?). Ecco quindi alcune buone pratiche per dialogare (il cosiddetto prompting) con profitto con un chatbot:
➊ esprimersi in modo grammaticalmente corretto;
➋ essere chiari e specifici;
➌ fornire contesto e vincoli;
➍ utilizzare suggerimenti ed esempi;
➎ fare una richiesta alla volta;
➏ rivedere e affinare la propria richiesta.
In termini concreti, potete chiedere al chatbot di generare un testo su qualsiasi argomento e ci sono buone probabilità che il testo che riceverete come risposta non sarà soddisfacente. Sarà importante quindi, per esempio, dare indicazioni su: la forma (un punto elenco, dialogo; perché no, una breve poesia); la lunghezza; la difficoltà oppure la competenza del destinatario (una cosa è chiedere un testo destinato agli studenti e un’altra è chiedere un testo destinato ai colleghi); il tono (formale o informale) e lo stile; la lingua (i chatbot sembrano cavarsela particolarmente bene nelle attività di traduzione, per esempio). Insomma, come scrive P.C. Rivoltella: “l’IA si può rivelare una validissima alleata nel lavoro di produzione creativa e di presa di decisione; imparare a servirsene, in una logica di co-creazione, fa parte di sicuro della nuova literacy che occorre sviluppare”.

Da quanto detto fin qui, emerge che l’AI potrà essere un valido aiuto anche per il docente, nelle molteplici attività che svolge prima della lezione, durante la lezione, dopo la lezione: (a) progettare e pianificare; (b) spiegare e presentare; (c) personalizzare e supportare; (d) erogare e gestire.
Proviamo a elencare qualche esempio: generare indicazioni sui compiti con i criteri di valutazione | sviluppare istruzioni che descrivono i ruoli e le aspettative dell’apprendimento cooperativo || produrre poster che elencano i 10 motivi per cui l’algebra è importante per il futuro degli studenti o i 20 errori di scrittura più comuni degli studenti delle scuole superiori, con brevi definizioni ed esempi | creare esempi risolti di problemi matematici, equazioni di chimica, ecc. con la spiegazione di ogni fase | costruire un organizzatore per la lettura preliminare o anticipata, estraendo il vocabolario critico e non familiare da un capitolo ed elencando le parole chiave con le relative definizioni | preparare delle flashcard con domande e risposte || semplificare la comunicazione con i genitori, i colleghi e le segreterie attraverso lettere di benvenuto alla classe, proposte di gite, programmi di assemblea e fogli di autorizzazione.
E se invece volessimo concentrarci sul monitoraggio e la valutazione:
liste di controllo: un chatbot può sviluppare una lista di attività e processi che aiuti lo studente nel percorso di metacognizione;
test: un chatbot può creare test su uno o più argomenti, con il numero e i tipi di quesiti che voi indicherete; potete richiedere anche le soluzioni con una breve spiegazione; rubriche: un chatbot sa comporre con facilità una rubrica per qualsiasi tipo di prestazione dello studente: analitica, olistica e di sviluppo; oppure suggerirvi scale e tabelle di valutazione.
3. Dimensione critica
La terza fase critica interessa infine la competenza del saper riconoscere e distinguere fra reale, verosimile e falso. La pratica del fact-checking è già in uso nelle scuole da tempo, eppure l’AI ci pone di fronte a sfideancora più complesse.
Una buona strategia è trasmettere agli studenti una semplice routine di domande (che adattiamo dal lavoro di B. Mastroianni, La disputa felice):
individuare la fonte: chi lo dice? data, luogo, circostanze: quando e dove?
verificabilità: qualcuno lo conferma?
autorevolezza: chi lo conferma?
confronto: ci sono altre versioni?
Parafrasando un valido contributo dei pedagogisti americani E.R. Mollick & L. Mollick, queste strategie promuovono una supervisione attiva e lo stimolo a combinare le capacità dell’AI con i contributi individuali, sfidando gli studenti a rimanere il “fattore umano” nel processo (human in the loop) per garantire che l’AI funzioni come uno strumento di supporto piuttosto che come un sostituto.
La valutazione dell’artefatto
La valutazione è spesso guardata con sospetto e diffidenza. Eppure è un processo che, se progettato ed eseguito con intelligenza, non è solo uno strumento diagnostico che consente al docente di evitare che le difficoltà degli studenti degenerino in insuccessi. Di più: se interpretata come relazione (e non già come la comunicazione arida di un voto), la valutazione è formazione dell’individuo che, in quanto tale, consente di conoscere sé stessi, interpretare il proprio presente e progettare il proprio futuro.
La valutazione in un processo di apprendimento arricchito dall’AI (AI-enhanced) deve possedere necessariamente alcune caratteristiche: ➀ essere formativa e integrata durante tutto il processo; ➁ offrire un feedback prospettico e costruttivo (che consenta cioè di visualizzare gli strumenti e le fasi dell’apprendimento); ➂ valorizzare la complessità di questa “prestazione epistemica” (che è quindi un insieme di informazioni disciplinari, pratiche di conoscenza, creatività).
Proponiamo qui in chiusura una semplice tabella che può servire come punto di partenza per qualsiasi pratica valutativa.
criteri descrizione punteggio *
Capacità di porre domande rilevanti

Capacità di strutturazione di ragionamenti complessi
Creatività nell’uso del chatbot
Autonomia nell’uso del chatbot
Riflessione critica
Presentazione del prodotto finale
= Non soddisfacente
La capacità di formulare domande pertinenti e ben strutturate per ottenere informazioni utili dal chatbot.
L’abilità di affinare continuamente le richieste e collegare le risposte del chatbot per costruire un discorso articolato e ben strutturato.
L’uso originale e innovativo del chatbot per esplorare soluzioni o punti di vista nuovi.
La capacità dello studente di utilizzare il chatbot in modo indipendente, senza costante supporto esterno.
L’abilità dello studente di riflettere criticamente sulle informazioni ricevute e di metterle in discussione.
La qualità della presentazione del lavoro finale derivato dall’interazione con il chatbot (chiarezza, coerenza, accuratezza).
= Adeguato
➀ ➁ ➂ ➃ ➄
➀ ➁ ➂ ➃ ➄
➀ ➁ ➂ ➃ ➄
➀ ➁ ➂ ➃ ➄
➀ ➁ ➂ ➃ ➄
➁ ➂ ➃ ➄
15 consigli per costruire prompt efficaci
11
stile
Se desideri una risposta formale, usa un linguaggio formale nel prompt; se preferisci uno stile informale o creativo, adattalo di conseguenza.

obiettivi
Prima di scrivere il prompt, è importante organizzare le idee e definire il tipo di risultato che vogliamo raggiungere. Per una richiesta sufficientemente completa, il prompt dovrà contenere almeno cinque parole.
target
Il prompt deve comunicare chiaramente ciò che si desidera ottenere: evita i convenevoli e le domande vaghe o ambigue.
istruzioni
È opportuno iniziare la richiesta utilizzando comandi diretti come “Spiega”,“Descrivi”, “Elabora”, “Indica” ecc.: questo aiuterà il modello a capire l’azione richiesta. Per ricevere risposte più elaborate, utilizza domande aperte invece di domande chiuse e inserisci istruzioni più lunghe e più complesse.
contesto
Fornisci dettagli o limitazioni per definire il contesto. Per esempio specifica l’età dei destinatari e il tipo di scuola che frequentano.
ruolo
Indica il ruolo che il bot dovrà assumere nella conversazione, per esempio un insegnante, un esperto in un argomento, un poeta.
07
dettagli
Se stai cercando una risposta basata su dati o informazioni specifiche, fornisci dettagli rilevanti come date, luoghi, nomi o simili.
formato
Se hai un formato particolare in mente per la risposta, come un elenco puntato, un paragrafo conciso o una spiegazione dettagliata, devi specificarlo nel prompt: “Elenca in formato elenco puntato…”.
esempi
lunghezza
Limita le risposte del bot a un certo numero di parole o di paragrafi. Potrebbe trattarsi di qualsiasi cosa, dal condensare le informazioni di quattro paragrafi in uno, o chiedere risposte con parole di otto caratteri o meno. Questo offre all’AI la flessibilità necessaria per generare una risposta che rientri nell’intervallo specificato.
12
limiti
Dato che esistono dei limiti precisi di input di token, quando la richiesta è particolarmente complessa, suddividila in passaggi più piccoli; per esempio, anziché chiedere “Parlami della rivoluzione industriale”, circoscrivi la richiesta in questo modo: “Spiega le cause e gli effetti della Rivoluzione industriale in Italia nel XIX secolo”.
13
remix
Tratti da: “Costruire il futuro. Linee guida sull’utilizzo dell’AI in ambito scolastico” - Rete di scuole FVG.
Fornisci esempi di testo che rispondano alla richiesta specifica. Per esempio, se vuoi generare un testo che descriva un prodotto, è utile fornirgli esempi di descrizioni di prodotti già esistenti. In questo modo, il bot capisce meglio cosa vuoi ottenere e genera un testo più preciso e pertinente.
09 sentiment
Quando è necessario, definisci i “sentiment” (cioè le emozioni, gli stati d’animo) per adattare la risposta alle emozioni richieste.
Puoi creare un prompt efficace anche ricorrendo al “copia e incolla”. Puoi chiedere al chatbot di semplificare un testo difficile, come la spiegazione di un concetto scientifico, oppure fargli tradurre un contenuto in diverse lingue, o ancora riscrivere un articolo con uno stile più accattivante.
14
coerenza
Ogni tanto l’AI perde il filo del discorso e se ricominci da zero (quindi se clicchi su new chat) tutto sarà dimenticato. Se invece resti nella stessa discussione puoi mantenere memoria di quanto è stato scritto.
15
allenamento
Un prompt efficace può richiedere pratica e adattamento per ottenere i risultati desiderati. Sperimenta e perfeziona le tue tecniche man mano che acquisisci familiarità con il modello.
Progettazione curricolare e ditattica
Certificazione delle competenze
La valutazione degli apprendimenti nella scuola primaria

dell’Educazione civica
PROGETTAZIONE CURRICOLARE
E DIDATTICA
CERTIFICAZIONE DELLE COMPETENZE
di Dino Cristanini

Le competenze come orizzonte formativo
«Le competenze chiave sono quelle di cui tutti hanno bisogno per la realizzazione e lo sviluppo personali, l’occupabilità, l’inclusione sociale, uno stile di vita sostenibile, una vita fruttuosa in società pacifiche, una gestione della vita attenta alla salute e la cittadinanza attiva» si afferma nella Raccomandazione del Consiglio dell’Unione europea del 22 maggio 2018 relativa alle competenze chiave per l’apprendimento permanente, che ha sostituito quella precedente del 18 dicembre 2006.
Le Indicazioni nazionali per il curricolo assumono le competenze chiave come l’«orizzonte di riferimento verso cui tendere», e individuano nel Profilo dello studente le competenze che un ragazzo dovrebbe avere sviluppato al termine del primo ciclo di istruzione, che saranno oggetto della certificazione prevista dall’art. 9 del D.Lgs n. 62/2017.
Si delinea così un percorso coerente tra progettazione, attività didattiche, valutazione e certificazione delle competenze, che trova concreta attuazione nelle proposte della Guida
La progettazione
Le scuole, affermano le Indicazioni nazionali, nella progettazione del curricolo assumono come riferimenti il Profilo dello studente al termine del primo ciclo di istruzione, i traguardi per lo sviluppo delle competenze e gli obiettivi di apprendimento specifici per ogni disciplina.
I traguardi, individuati nelle Indicazioni nazionali per ciascuna disciplina al termine della scuola primaria e della scuola secondaria di primo grado, descrivono lo sviluppo delle competenze che è ragionevole attendersi in corrispondenza di queste fasi evolutive. Al tempo stesso rappresentano una «garanzia dell’unità del sistema nazionale e della qualità del servizio» e perciò costituiscono «riferimenti ineludibili per gli insegnanti» e «nella loro scansione temporale, sono prescrittivi, impegnando così le istituzioni scolastiche affinché ogni alunno possa conseguirli».
Gli obiettivi di apprendimento, che nelle Indicazioni nazionali sono raggruppati per nuclei tematici, sono i mattoni con cui costruire lo sviluppo delle competenze, e definiscono le abilità e le conoscenze necessarie per il raggiungimento dei traguardi.
La progettazione dell’azione didattica ha poi il compito di individuare le scelte metodologiche e le esperienze di apprendimento più adeguate per il raggiungimento degli obiettivi e dei traguardi. Alle pagine 32-37, per evidenziare le connessioni tra tutti gli elementi della progettazione, vengono perciò allineati:
• i nuclei tematici di Matematica e Scienze in relazione ai quali sono raggruppati gli obiettivi nelle Indicazioni nazionali;
• i traguardi per lo sviluppo delle competenze previsti dalle Indicazioni nazionali al termine della scuola primaria, ciascuno connesso al nucleo maggiormente pertinente, fermo restando che alcuni traguardi possono essere connessi anche a più nuclei;
• gli obiettivi di apprendimento previsti dalle Indicazioni nazionali al termine della classe quinta della scuola primaria, correlati ai nuclei tematici pertinenti;
• i contenuti da utilizzare e le attività da svolgere per promuovere il raggiungimento degli obiettivi e dei traguardi da parte degli alunni.
La certificazione
Il modello
Il modello di certificazione per la scuola primaria adottato con D.M. n. 14 del 30 gennaio 2024 fa riferimento alle competenze chiave della Raccomandazione europea del 2018, descritte in base al Profilo dello studente declinato in relazione alla situazione attesa al termine di questo grado di scuola.
COMPETENZE CHIAVE COMPETENZE
Competenza alfabetica funzionale
Competenza multilinguistica

Competenza matematica e competenza in scienze, tecnologie e ingegneria
Padroneggiare la lingua di scolarizzazione in modo da comprendere enunciati, raccontare le proprie esperienze e adottare un registro linguistico appropriato alle diverse situazioni.
Utilizzare la lingua inglese a livello elementare in forma orale e scritta (comprensione orale e scritta, produzione scritta e produzione/interazione orale) in semplici situazioni di vita quotidiana in aree che riguardano bisogni immediati o argomenti molto familiari (Livello A1 del Quadro Comune Europeo di Riferimento per le lingue).
Avere consapevolezza che esistono lingue e culture diverse
Utilizzare le conoscenze matematiche e scientifico-tecnologiche per trovare e giustificare soluzioni a problemi reali.
Osservare comportamenti e atteggiamenti rispettosi verso l’ambiente, i beni comuni, la sostenibilità.
Competenza digitale Utilizzare con responsabilità le tecnologie digitali in contesti comunicativi concreti per ricercare informazioni e per interagire con altre persone, come supporto alla creatività e alla soluzione di problemi semplici.
Competenza personale, sociale e capacità di imparare a imparare
Competenza in materia di cittadinanza
Avere cura e rispetto di sé, degli altri e dell’ambiente; affrontare positivamente i conflitti, collaborare con altri, empatizzare.
Esprimere le proprie personali opinioni e sensibilità nel rispetto di sé e degli altri.
Utilizzare conoscenze e nozioni di base per ricercare nuove informazioni. Accedere a nuovi apprendimenti anche in modo autonomo.
Portare a compimento il lavoro iniziato, da solo o insieme agli altri.
Rispettare le regole condivise e collaborare con gli altri per la costruzione del bene comune.
Partecipare alle diverse forme di vita comunitaria, divenendo consapevole dei valori costituzionali.
Riconoscere le diverse identità, le tradizioni culturali e religiose in un’ottica di dialogo e di rispetto reciproco.
Competenza imprenditoriale
Competenza in materia di consapevolezza ed espressione culturali
Dimostrare originalità e spirito di iniziativa. Realizzare semplici progetti. Assumersi le proprie responsabilità, chiedere aiuto e fornirlo quando necessario. Riflettere sulle proprie scelte.
Orientarsi nello spazio e nel tempo, osservando e descrivendo ambienti, fatti, fenomeni e produzioni artistiche, esprimendo curiosità e ricerca di senso.
In relazione alle proprie potenzialità e al proprio talento, esprimersi negli ambiti più congeniali: motori, artistici e musicali.
Nel modello è previsto anche un ulteriore spazio, per dar modo alla scuola di evidenziare anche eventuali significative competenze manifestate dall’alunno nello svolgimento di attività scolastiche e/o extrascolastiche.
I livelli
Per ciascuna delle competenze da certificare il modello prevede quattro possibili livelli:
A AVANZATOL’alunno/a svolge compiti e risolve problemi complessi, mostrando padronanza nell’uso delle conoscenze e delle abilità; propone e sostiene le proprie opinioni e assume in modo responsabile decisioni consapevoli.
B INTERMEDIOL’alunno/a svolge compiti e risolve problemi in situazioni nuove, compie scelte consapevoli, mostrando di saper utilizzare le conoscenze e le abilità acquisite.
C BASE L’alunno/a svolge compiti semplici anche in situazioni nuove, mostrando di possedere conoscenze e abilità fondamentali e di saper applicare basilari regole e procedure apprese.
D INIZIALE L’alunno/a, se opportunamente guidato/a, svolge compiti semplici in situazioni note.
Data la dimensione promozionale e proattiva che la certificazione assume nel primo ciclo non si prevede un livello manifestamente negativo, ma si porta l’attenzione su ciò che l’alunno riesce comunque a fare.
Strumenti per valutare le competenze
Per accertare il possesso delle competenze servono strumenti diversi da quelli tradizionalmente utilizzati per la verifica dell’acquisizione di conoscenze e abilità. La letteratura scientifica in materia individua la strumentazione ottimale nell’integrazione di tre tipi di strumenti.
Compiti di realtà
Osservazioni sistematiche degli insegnanti
Narrazione dell’alunno del percorso cognitivo compiuto
Richiesta all’alunno di risolvere una situazione problematica, complessa e nuova, quanto più possibile vicina al mondo reale, utilizzando conoscenze e abilità già acquisite e trasferendo procedure e condotte cognitive in contesti e ambiti di riferimento moderatamente diversi da quelli resi familiari dalla pratica didattica.
Rilevazione dei processi, delle operazioni che l’alunno compie per interpretare e svolgere il compito.
Racconto delle operazioni compiute, degli aspetti più interessanti, delle difficoltà incontrate e del modo in cui sono state superate, delle emozioni provate, autovalutazione del prodotto e del processo adottato.
Questi strumenti vanno utilizzati durante l’intero percorso della scuola primaria per acquisire informazioni sul grado di avvicinamento degli alunni ai traguardi definiti per ciascuna disciplina e alle competenze riportate nel modello di certificazione.
Competenze e traguardi
Nelle Indicazioni nazionali si afferma che «nella scuola del primo ciclo i traguardi costituiscono criteri per la valutazione delle competenze attese». Occorre perciò individuare nell’ambito delle varie discipline i traguardi che concorrono allo sviluppo delle diverse competenze.
Per facilitare questa operazione la tabella seguente presenta il quadro delle correlazioni tra i traguardi di Scienze e Matematica e le competenze da certificare al termine della scuola primaria.
Quadro delle correlazioni tra i traguardi per lo sviluppo delle competenze di Matematica e Scienze e le competenze da certificare con il modello nazionale
COMPETENZE CHIAVE RACCOMANDAZIONE EUROPEA 2018
Competenza alfabetica funzionale

Competenza multilinguistica
Competenze da certificare Al termine della scuola primaria
• Padroneggiare la lingua di scolarizzazione in modo da comprendere enunciati, raccontare le proprie esperienze e adottare un registro linguistico appropriato alle diverse situazioni.
• Utilizzare la lingua inglese a livello elementare in forma orale e scritta (comprensione orale e scritta, produzione scritta e produzione/ interazione orale) in semplici situazioni di vita quotidiana in aree che riguardano bisogni immediati o argomenti molto familiari (Livello A1 del Quadro Comune Europeo di Riferimento per le lingue).
• Avere consapevolezza che esistono lingue e culture diverse
Competenza matematica e competenza in scienze, tecnologie e ingegneria
• Utilizzare le conoscenze matematiche e scientificotecnologiche per trovare e giustificare soluzioni a problemi reali.
• Osservare comportamenti e atteggiamenti rispettosi verso l’ambiente, i beni comuni, la sostenibilità.
Traguardi per lo sviluppo delle competenze di Matematica declinati per la classe quarta
• Analizza le situazioni problematiche, formula ipotesi risolutive, le espone argomentando nel confronto con gli altri.
• Esplicita il procedimento seguito e comprende la possibilità di utilizzazione di altre strategie.
Traguardi per lo sviluppo delle competenze di Scienze declinati per la classe quarta
• Espone in forma chiara ciò che ha sperimentato utilizzando termini specifici.
• Effettua con sicurezza calcoli scritti e mentali nell’ambito dei numeri conosciuti.
• Conosce e utilizza numeri decimali e frazioni.
• Riconosce forme geometriche presenti nell’ambiente.
• Riconosce, denomina, descrive e rappresenta figure geometriche rispettandone le caratteristiche.
• Ricerca dati, li organizza e li rappresenta graficamente.
• Interpreta i dati rappresentati in tabelle e grafici e ne ricava informazioni.
• Utilizza i più comuni strumenti per il disegno geometrico, per la misura delle lunghezze e dell’ampiezza degli angoli.
• Riconosce e quantifica semplici situazioni di incertezza.
• Individua e comprende gli aspetti logici e matematici dei testi.
• Osserva e descrive fenomeni, si pone e propone domande, formula ipotesi esplicative.
• Individua nei fenomeni somiglianze e differenze, fa misurazioni e registra dati significativi.
• Individua aspetti quantitativi e qualitativi dei fenomeni e li rappresenta graficamente.
• Riconosce le principali caratteristiche degli esseri viventi.
• Riconosce l’importanza di corrette abitudini alimentari per la cura della salute.
• Riconosce gli elementi fisici e naturali dell’ambiente, è consapevole delle relazioni tra di essi e ha consapevolezza dell’importanza della loro salvaguardia.
Progettazione e certificazione

COMPETENZE CHIAVE RACCOMANDAZIONE EUROPEA 2018
Competenze da certificare Al termine della scuola primaria
Competenza digitale
• Utilizzare con responsabilità le tecnologie digitali in contesti comunicativi concreti per ricercare informazioni e per interagire con altre persone, come supporto alla creatività e alla soluzione di problemi semplici.
Competenza personale, sociale e capacità di imparare a imparare
Competenza in materia di cittadinanza
• Avere cura e rispetto di sé, degli altri e dell’ambiente; affrontare positivamente i conflitti, collaborare con altri, empatizzare.
• Esprimere le proprie personali opinioni e sensibilità nel rispetto di sé e degli altri.
• Utilizzare conoscenze e nozioni di base per ricercare nuove informazioni.
• Accedere a nuovi apprendimenti anche in modo autonomo.
• Portare a compimento il lavoro iniziato, da solo o insieme agli altri.
• Rispettare le regole condivise e collaborare con gli altri per la costruzione del bene comune.
• Partecipare alle diverse forme di vita comunitaria, divenendo consapevole dei valori costituzionali.
• Riconoscere le diverse identità, le tradizioni culturali e religiose in un’ottica di dialogo e di rispetto reciproco.
Traguardi per lo sviluppo delle competenze di Matematica declinati per la classe quarta
• Analizza le situazioni problematiche, formula ipotesi risolutive, le espone argomentandole nel confronto con gli altri.
• Risolve problemi nei vari ambiti di contenuto utilizzando le strategie apprese.
• Esplicita il procedimento seguito e comprende la possibilità di utilizzazione di altre strategie.
• Comprende l’utilità degli strumenti matematici per risolvere problemi di vita quotidiana.
• Ricerca dati, li organizza e li rappresenta graficamente.
• Interpreta i dati rappresentati in tabelle e grafici e ne ricava informazioni.
Traguardi per lo sviluppo delle competenze di Scienze declinati per la classe quarta
• Ricerca informazioni e spiegazioni utilizzando varie fonti.
• Riconosce l’importanza e il valore del denaro e di una suo corretto utilizzo.
• Riconosce l’importanza di corrette abitudini alimentari per la cura della salute.
• Riconosce gli elementi fisici e naturali dell’ambiente, è consapevole delle relazioni tra di essi e ha consapevolezza dell’importanza della loro salvaguardia.
COMPETENZE CHIAVE RACCOMANDAZIONE EUROPEA 2018
Competenza imprenditoriale

Competenza in materia di consapevolezza ed espressione culturali
Competenze da certificare Al termine della scuola primaria
• Dimostrare originalità e sprito di iniziativa.
• Realizzare semplici progetti.
• Assumersi le proprie responsabilità, chiedere aiuto e fornirlo quando necessario.
• Riflettere sulle proprie scelte.
• Orientarsi nello spazio e nel tempo, osservando e descrivendo ambienti, fatti, fenomeni e produzioni artistiche, esprimendo curiosità e ricerca di senso.
• In relazione alle proprie potenzialità e al proprio talento, esprimersi negli ambiti più congeniali: motori, artistici e musicali.
Traguardi per lo sviluppo delle competenze di Matematica declinati per la classe quarta
Progettazione e certificazione
Traguardi per lo sviluppo delle competenze di Scienze declinati per la classe quarta
Programmazione annuale di Scienze – Classe 4a
Nuclei tematici Traguardi di sviluppo delle competenze al termine della scuola primaria (dalle Indicazioni nazionali per il curricolo)
• Sviluppa atteggiamenti di curiosità e modi di guardare il mondo che lo stimolano a cercare spiegazioni di quello che vede succedere.
Metodo

Oggetti, materiali e trasformazioni
• Trova da varie fonti (libri, Internet, discorsi degli adulti, ecc.) informazioni e spiegazioni sui problemi che lo interessano.
• Individua nei fenomeni somiglianze e differenze, fa misurazioni, registra dati significativi, identifica relazioni spazio/temporali.
• Individua aspetti quantitativi e qualitativi nei fenomeni, produce rappresentazioni grafiche e schemi di livello adeguato, elabora semplici modelli.
Traguardi declinati per la classe quarta
• Sviluppa atteggiamenti di curiosità nei confronti della realtà, si interroga sui fenomeni osservati e ricerca spiegazioni utilizzando il metodo scientifico.
• Ricerca informazioni e spiegazioni utilizzando varie fonti.
Obiettivi di apprendimento declinati per la classe quarta
• Conoscere le procedure del Metodo Scientifico d’indagine dei fenomeni.
• Utilizzare fonti di diverso tipo per ricercare possibili spiegazioni dei fenomeni osservati e risposte alle domande.
Contenuti e attività
• Analisi del Metodo Scientifico.
• Individua nei fenomeni somiglianze e differenze, fa misurazioni e registra dati significativi.
• Acquisizione dei concetti scientifici relativi a: materia, esseri viventi e tecnologia.
• Individua aspetti quantitativi e qualitativi dei fenomeni e li rappresenta graficamente.
Oggetti, materiali e trasformazioni
Osservare e sperimentare sul campo
• Esplora i fenomeni con un approccio scientifico: con l’aiuto dell’insegnante, dei compagni, in modo autonomo, osserva e descrive lo svolgersi dei fatti, formula domande, anche sulla base di ipotesi personali, propone e realizza semplici esperimenti.
• Espone in forma chiara ciò che ha sperimentato, utilizzando un linguaggio appropriato.
• Osserva e descrive fenomeni, si pone e propone domande, formula ipotesi esplicative.
• Espone in forma chiara ciò che ha sperimentato utilizzando termini specifici.
• Individuare le proprietà di acqua e aria.
• Osservare e comprendere i passaggi di stato della materia.
• Esplorare fenomeni applicando il metodo scientifico.
• Conoscere le caratteristiche dell’acqua e comprendere la sua importanza per l’ambiente e gli esseri viventi.
• Conoscere le caratteristiche dell’aria.
• Conoscere la stratificazione del suolo.
• Conoscere le principali caratteristiche dei vari elementi dell’ambiente e comprendere la loro importanza per gli esseri viventi.
• Effettuare prime classificazioni degli organismi vegetali e animali in base alle loro principali caratteristiche.
• Comprendere le relazioni tra i vari organismi.
• Attività ed esperienze finalizzate a favorire l’elaborazione del concetto di materia e individuazione della materia nell’ambiente.
• Osservazione dei passaggi di stato e analisi delle condizioni che li determinano.
• Osservazione delle caratteristiche e delle proprietà dell’acqua.
• Il ciclo dell’acqua.
• Osservazione delle caratteristiche dell’aria e attività per favorire la loro comprensione.
• Analisi della struttura del suolo.
• Attività per favorire la comprensione dell’importanza dell’acqua per gli esseri viventi.
• L’importanza dell’atmosfera per gli esseri viventi.
• Il suolo e gli esseri viventi.
Nuclei tematici Traguardi di sviluppo delle competenze al termine della scuola primaria (dalle Indicazioni nazionali per il curricolo)
• Riconosce le principali caratteristiche e i modi di vivere di organismi animali e vegetali.
• Ha consapevolezza della struttura e dello sviluppo del proprio corpo e ha cura della sua salute.
• Ha atteggiamenti di cura verso l’ambiente scolastico che condivide con gli altri; rispetta e apprezza il valore dell’ambiente sociale e naturale.
L’essere umano, i viventi e l’ambiente

Progettazione e
Traguardi declinati per la classe quarta Obiettivi di apprendimento declinati per la classe quarta Contenuti e
• Riconosce le principali caratteristiche degli esseri viventi.
• Riconosce l’importanza di corrette abitudini alimentari per la cura della salute.
• Riconosce gli elementi fisici e naturali dell’ambiente, è consapevole delle relazioni tra di essi e ha consapevolezza dell’importanza della loro salvaguardia.
• L’importanza dell’atmosfera per gli esseri viventi.
• Il suolo e gli esseri viventi.
• Analisi delle caratteristiche che distinguono gli esseri viventi e loro classificazione nei cinque Regni.
• Elaborazione di un primo modello intuitivo della cellula.
• Le parti delle piante e le loro funzioni; la fotosintesi clorofilliana.
• Analisi delle principali caratteristiche degli animali.
• Prime classificazioni degli animali; animali invertebrati e vertebrati.
• Interpretazione di reti e piramidi alimentari.
• Osservazione di un ambiente e individuazione degli elementi che lo caratterizzano.
• Il concetto di ecosistema e la necessità di salvaguardare gli ecosistemi.
Programmazione annuale di Matematica – Classe 4
Nuclei tematici

Numeri
Traguardi di sviluppo delle competenze al termine della scuola primaria (dalle Indicazioni nazionali per il curricolo)
• Si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali e sa valutare l’opportunità di ricorrere a una calcolatrice.
• Riconosce e utilizza rappresentazioni diverse di oggetti matematici (numeri decimali, frazioni, percentuali, scale di riduzione, ...).
Traguardi declinati per la classe quarta
• Effettua con sicurezza calcoli scritti e mentali nell’ambito dei numeri conosciuti.
• Conosce e utilizza numeri decimali e frazioni.
Obiettivi di apprendimento declinati per la classe quarta
• Rafforzare la consapevolezza del valore posizionale delle cifre.
• Leggere, scrivere, confrontare numeri naturali e decimali.
• Conoscere e utilizzare le proprietà delle quattro operazioni.
• Eseguire correttamente le quattro operazioni con numeri naturali e decimali.
• Acquisire i concetti di moltiplicatore e divisore di un numero.
• Acquisire il concetto di frazione, leggere e scrivere frazioni e svolgere semplici operazioni con le frazioni.
Contenuti e attività
• Riconosce e rappresenta forme del piano e dello spazio, relazioni e strutture che si trovano in natura o che sono state create dall’uomo.
• Descrive, denomina e classifica figure in base a caratteristiche geometriche, ne determina misure, progetta e costruisce modelli concreti di vario tipo.
• Utilizza strumenti per il disegno geometrico (riga, compasso, squadra) e i più comuni strumenti di misura (metro, goniometro...).
• Riconosce forme geometriche presenti nell’ambiente.
• Riconosce, denomina, descrive e rappresenta figure geometriche rispettandone le caratteristiche.
• Utilizza i più comuni strumenti per il disegno geometrico, per la misura delle lunghezze e dell’ampiezza degli angoli.
• Riconoscere linee, semirette e segmenti.
• Individuare le possibili relazioni tra rette nel piano e acquisire i concetti di perpendicolarità, parallelismo, orizzontalità, verticalità.
• Riconoscere, denominare, descrivere e classificare figure geometriche in base alle loro caratteristiche.
• Riprodurre figure geometriche, anche in scala, utilizzando strumenti idonei.
• Effettuare e riconoscere rotazioni e simmetrie.
• Riconoscere, classificare e misurare gli angoli utilizzando strumenti idonei.
• I numeri oltre il 1 000.
• Le proprietà delle quattro operazioni e il loro utilizzo.
• Esecuzione di moltiplicazioni in colonna con una o due cifre al moltiplicatore e di divisioni in colonna con una o due cifre al divisore.
• Moltiplicazioni e divisioni per 10, 100, 1 000.
• Multipli e divisori di un numero.
• Individuazione delle frazioni complementari ed equivalenti.
• Trasformazione di una frazione in numero decimale e viceversa.
• Ordinamento e confronto di numeri decimali.
• Esecuzione delle quattro operazioni con i numeri decimali.
• Calcolo della frazione di una quantità.
• Esecuzione di equivalenze e calcolo delle frazioni relative alle misure di valore.
• Riconoscimento di elementi geometrici, di figure geometriche piane.
• Analisi delle caratteristiche di semirette e segmenti.
• Disegno di rette parallele e perpendicolari.
• Esecuzione di rotazioni di segmenti.
• Riconoscimento degli angoli e della loro ampiezza.
• Analisi delle caratteristiche dei poligoni (in particolare triangoli e quadrilateri) e classificazione degli stessi.
• Determinazione e misurazione del perimetro di triangoli e quadrilateri.
• Individuazione e rappresentazione delle figure isoperimetriche.
Progettazione e certificazione

Nuclei tematici Traguardi di sviluppo delle competenze al termine della scuola primaria (dalle Indicazioni nazionali per il curricolo)
Traguardi declinati per la classe quarta
Relazioni, dati e previsioni
• Ricerca dati per ricavare informazioni e costruisce rappresentazioni (tabelle e grafici).
• Ricava informazioni anche da dati rappresentati in tabelle e grafici.
• Riconosce e quantifica, in casi semplici, situazioni di incertezza.
• Ricerca dati, li organizza e li rappresenta graficamente.
• Interpreta i dati rappresentati in tabelle e grafici e ne ricava informazioni.
• Riconosce e quantifica semplici situazioni di incertezza.
Obiettivi di apprendimento declinati per la classe quarta
• Calcolare il perimetro e l’area di triangoli e quadrilateri utilizzando le formule adeguate o altri procedimenti.
• Effettuare semplici indagini statistiche e rappresentare i dati raccolti e le loro relazioni in forma grafica.
• Leggere e interpretare i dati rappresentati in diagrammi e tabelle.
• Conoscere e utilizzare le unità di misura convenzionali.
• Confrontare misure ed eseguire equivalenze.
• Acquisire i concetti di frequenza, moda e media e applicarli ai dati esaminati, quando pertinenti.
• Effettuare valutazioni circa la probabilità di un evento di avverarsi.
Contenuti e attività
• Calcolo dell’area di triangoli e quadrilateri.
• Utilizzo delle formule inverse dell’area di rettangoli e quadrati.
• Rappresentazione di dati con grafici e tabelle.
• Effettuazione e rappresentazione di indagini statistiche.
• Conoscenza e utilizzo delle unità di misura convenzionali di lunghezza, massa (peso), capacità.
• Esecuzione di equivalenze.
• Interpretazione di dati: frequenza, moda e media.
• Calcolo della media e della probabilità.
• Conoscenza e utilizzo delle unità di misura del tempo.
• Conoscenza e utilizzo delle misure di valore nel sistema monetario corrente (euro).
• Costo unitario e costo totale.
Problemi
• Legge e comprende testi che coinvolgono aspetti logici e matematici.
• Costruisce ragionamenti formulando ipotesi, sostenendo le proprie idee e confrontandosi con il punto di vista di altri.
• Riesce a risolvere facili problemi in tutti gli ambiti di contenuto, mantenendo il controllo sia sul processo risolutivo, sia sui risultati.
• Descrive il procedimento seguito e riconosce strategie di soluzione diverse dalla propria.
• Sviluppa un atteggiamento positivo rispetto alla matematica, attraverso esperienze significative, che gli hanno fatto intuire come gli strumenti matematici che ha imparato a utilizzare siano utili per operare nella realtà.
• Individua e comprende gli aspetti logici e matematici dei testi.
• Analizza le situazioni problematiche, formula ipotesi risolutive, le espone argomentandole nel confronto con gli altri.
• Risolve problemi nei vari ambiti di contenuto utilizzando le strategie apprese.
• Esplicita il procedimento seguito e comprende la possibilità di utilizzazione di altre strategie.
• Comprende l’utilità degli strumenti matematici per risolvere problemi di vita quotidiana.
• Analizzare situazioni problematiche, tradurle e rappresentarle in termini matematici.
• Risolvere diversi tipi di problemi con più operazioni, individuando le strategie adeguate.
• Utilizzare gli strumenti della matematica per risolvere problemi relativi a situazioni di vita quotidiana.
• Esporre e argomentare la strategia adottata e il procedimento seguito per risolvere il problema.
• Analisi di problemi, individuazione della domanda o delle domande e dei dati (nascosti, inutili, mancanti, sbagliati), risoluzione.
• Risoluzione di problemi con le quattro operazioni.
• Risoluzione di problemi con peso, capacità, peso lordo, peso netto e tara.
• Risoluzione di problemi con le misure di tempo.
• Risoluzione di problemi con le misure di valore.
• Risoluzione di problemi con i perimetri.
• Risoluzione di problemi con le misure di superficie: il metro quadrato.
• Risoluzione di problemi con le aree.
• Risoluzione di problemi con le frazioni.
• Risoluzione di problemi con la compravendita.
LA VALUTAZIONE DEGLI APPRENDIMENTI NELLA SCUOLA PRIMARIA
Dino Cristanini
La valutazione, affermano le Indicazioni nazionali per il curricolo, «precede, accompagna e segue i percorsi curricolari». Si valuta nella fase d’ingresso per acquisire gli elementi di conoscenza relativi allo stato degli apprendimenti di alunne e alunni utili a definire gli obiettivi e a scegliere i metodi più adeguati in rapporto alle concrete e specifiche situazioni. Si valuta alla fine di determinati periodi per esprimere un giudizio complessivo sui processi attivati e sugli esiti conseguiti (funzione sommativa). Ma soprattutto si valuta sistematicamente in itinere (funzione formativa) sia per regolare l’azione didattica in base a quanto via via rilevato sia per restituire agli alunni e alle alunne informazioni idonee a renderli consapevoli degli apprendimenti raggiunti e delle criticità, unitamente ai suggerimenti su cosa fare per migliorare (feedback formativi).
La legge n. 150/2024 ha modificato ancora una volta le norme relative alla valutazione degli apprendimenti nella scuola primaria, compresi quelli riguardanti l’insegnamento trasversale di educazione civica, prevedendo che dall’ a.s. 2024/2025 essa venga espressa con “giudizi sintetici correlati alla descrizione dei livelli di apprendimento raggiunti”, in base a modalità definite con definite con ordinanza del Ministro dell’istruzione e del merito.
È stato perciò avviato l’iter per l’emanazione dell’ordinanza, che ha portato alla presentazione di un testo sottoposto al parere obbligatorio ma non vincolante del Consiglio Superiore della Pubblica Istruzione (CSPI), parere che è stato espresso nella seduta plenaria del 18 novembre 2024. È a questo schema di ordinanza, non essendo al momento dell’andata in stampa ancora stato emanato il testo ufficiale, che facciamo riferimento per illustrare gli elementi di novità più rilevanti e significativi.
L’entrata in vigore
L’art. 7 dello schema di ordinanza prevede che, per consentire alle scuole di effettuare le operazioni relative alla transizione nel nuovo sistema, entreranno in vigore a partire dalla valutazione finale relativa all’a.s. 2024/2025.
I NUOVI LIVELLI
I giudizi sintetici sono espressi con aggettivi riferiti a sei livelli

A. ottimo
C. ottimo
A. ottimo
B. discreto
D. sufficiente
F. non sufficiente
Si tratta di una scala ordinale, come in genere tutte o quasi le scale utilizzate nel campo scolastico, che consente di graduare i risultati di apprendimento secondo fasce distinte, ma nella quale gli intervalli tra l’una e l’altra non sono uguali e che di per sé non offre informazioni su quali sono gli apprendimenti corrispondenti a ciascun livello.
Il compito di fornire queste informazioni è affidato alle descrizioni che dovranno essere elaborate dai collegi dei docenti facendo riferimento alla tabella allegata all’Ordinanza.
Le descrizioni dei livelli di apprendimento corrispondenti ai giudizi
Il comma 5 dell’art. 3 dello schema di ordinanza prevede che «Le istituzioni scolastiche, nell’ambito dell’autonomia didattica di cui all’articolo 4, comma 4 del DPR n. 275/1999, elaborano i criteri di valutazione, da inserire nel Piano triennale dell’offerta formativa, declinando, altresì, per ciascun anno di corso e per ogni disciplina del curricolo la descrizione dei livelli di apprendimento correlati ai giudizi sintetici riportati nell’Allegato A alla presente ordinanza.»
Tabella 1 - Allegato A allo schema di ordinanza
Descrizione dei giudizi sintetici per la valutazione degli apprendimenti nella scuola primaria
L’alunno/a porta a termine con piena autonomia le attività servendosi di un’ampia varietà di risorse personali o disponibili nel contesto. Utilizza consapevolmente con continuità le conoscenze disciplinari e applica le abilità acquisite per svolgere compiti complessi e risolvere problemi anche riferiti a situazioni non affrontate in precedenza. È in grado di proporre analisi e sintesi personali in modo originale, collegando le informazioni, argomentando il proprio punto di vista ed esprimendosi con proprietà di linguaggio e in modo adeguato alla situazione.

DISTINTO
BUONO
DISCRETO
SUFFICIENTE
NON SUFFICIENTE
L’alunno/a porta a termine con piena autonomia le attività servendosi di un’ampia varietà di risorse personali o disponibili nel contesto. Utilizza consapevolmente con continuità le conoscenze disciplinari e applica le abilità acquisite per svolgere compiti complessi e risolvere problemi anche riferiti a situazioni non affrontate in precedenza. È in grado di proporre analisi e sintesi personali in modo originale, collegando le informazioni, argomentando il proprio punto di vista ed esprimendosi con proprietà di linguaggio e in modo adeguato alla situazione.
L’alunno/a porta a termine le attività servendosi di alcune risorse personali o disponibili nel contesto. Fa ricorso ad alcune conoscenze disciplinari e abilità acquisite per svolgere compiti e risolvere problemi simili ad altri già affrontati. È in grado di collegare le informazioni, esprimendosi in modo adeguato alla situazione.
L’alunno/a porta a termine le attività se guidato nell’uso delle risorse personali o disponibili nel contesto. Fa ricorso ad alcune conoscenze disciplinari e abilità acquisite per svolgere semplici compiti e risolvere problemi se già affrontati in precedenza. Si esprime in modo abbastanza adeguato alla situazione.
L’alunno/a, solo se guidato, porta a termine le attività proposte, utilizzando alcune delle risorse messe a disposizione dal docente. Applica alcune regole e procedure basilari per svolgere semplici compiti già affrontati in precedenza. Si esprime in modo semplice e legato a situazioni concrete.
L’alunno/a, anche se guidato dal docente, non porta sempre a termine le attività proposte. Anche con l’ausilio del docente non è sempre in grado di applicare procedure basilari per svolgere semplici compiti con esempi forniti. Si esprime utilizzando un linguaggio povero ed essenziale, non sempre adeguato alla situazione.
L’analisi della tabella ministeriale porta a enucleare le dimensioni dell’apprendimento prese in considerazione e i relativi descrittori di livello (v. tabella 2).
TABELLA 2 –
Dimensioni dell’apprendimento e descrittori di livello presenti nella tabella ministeriale OTTIMO
LIVELLI
DIMENSIONI
AUTONOMIA NEL PORTARE A TERMINE LE ATTIVITÀ
USO DI RISORSE PERSONALI O DISPONIBILI NEL CONTESTO
USO DELLE CONOSCENZE DISCIPLINARI E DELLE ABILITÀ ACQUISITE
COMPITI E PROBLEMI CHE RIESCE AD AFFRONTARE

PROPOSTA DI ANALISI E SINTESI PERSONALI
CAPACITÀ DI COLLEGARE LE INFORMAZIONI
CAPACITÀ DI ESPRIMERE IL PROPRIO PENSIERO
Porta a termine le attività con piena autonomia
Uso di una ampia varietà di risorse
Uso consapevole e continuo delle conoscenze e abilità
Compiti complessi e problemi anche riferiti a situazioni non affrontate in precedenza
Propone analisi e sintesi personali originali
Collega le informazioni
Porta a termine le attività con autonomia
Uso di una varietà di risorse
Uso continuo delle conoscenze e abilità
Compiti e problemi anche riferiti a situazioni non affrontate in precedenza
Propone analisi e sintesi personali
Collega le informazioni
Uso di alcune risorse
Porta a termine le attività se guidato nell’uso delle risorse
Uso delle risorse disponibili
Porta a termine le attività solo se guidato Non sempre porta sempre a termine le attività anche se guidato
Uso di alcune risorse messe a disposizione dal docente
Uso di alcune conoscenze e abilità
Uso di alcune conoscenze e abilità
Compiti e problemi simili ad altri già affrontati in precedenza
Collega le informazioni
Compiti semplici e problemi già affrontati in precedenza
Applicazione di alcune regole e procedure basilari
Compiti semplici già affrontati in precedenza
Applicazione discontinua di alcune regole e procedure basilari
Compiti semplici con esempi forniti
Argomenta il proprio punto di vista esprimendosi con proprietà di linguaggio e in modo adeguato alla situazione
Esprime il proprio punto di vista con proprietà di linguaggio e in modo adeguato alla situazione
Si esprime in modo adeguato alla situazione
Si esprime in modo abbastanza adeguato alla situazione
Si esprime in modo semplice e legato a situazioni concrete
Si esprime con un linguaggio povero ed essenziale, non sempre adeguato alla situazione.
Lo schema va perfezionato dalle scuole colmando i vuoti e graduando opportunamente le progressioni tra i livelli, ed eventualmente arricchito in base alla loro esperienza e competenza. Lo strumento così ottenuto costituirà la base per la elaborazione delle rubriche disciplinari relative alle diverse classi.
La valutazione in itinere
Nella bozza di ordinanza si ribadisce che «la valutazione in itinere resta espressa nelle forme che il docente ritiene opportune», precisando comunque che queste forme devono restituire «agli alunni, in modo pienamente comprensibile, il livello di padronanza dei contenuti verificati». Le scuole sono perciò libere di utilizzare, nella valutazione in itinere, le modalità che ritengono più opportune. Il criterio principale dovrebbe essere quello di utilizzare la valutazione come risorsa per favorire l’acquisizione degli apprendimenti. La ricerca pedagogico-didattica e la normativa degli ultimi decenni concordano infatti nel privilegiare il valore formativo della valutazione, che trova concreta attuazione nella restituzione agli alunni delle informazioni idonee a renderli consapevoli sia degli apprendimenti raggiunti sia delle criticità, unitamente ai suggerimenti su cosa fare per migliorare (feedback formativi). I feedback efficaci presentano alcune fondamentali caratteristiche: tempestività, specificità, focalizzazione sulla prestazione e non sulla persona; comprensibilità.
Fig. 1 La valutazione come risorsa per l’apprendimento
RACCOLTA CONTINUA DI INFORMAZIONI SUGLI APPRENDIMENTI DEGLI ALUNNI E DELLE ALUNNE
CHE GLI E LE INSEGNANTI UTILIZZANO PER REGOLARE L’AZIONE DIDATTICA
CHE VENGONO RESTITUITE AGLI ALUNNI E ALLE ALUNNE (FEEDBACK) PER RENDERLI CONSAPEVOLI E ATTIVI SU COSA E COME MIGLIORARE]
La valutazione esercita un notevole influsso sul senso di autostima (ossia sulla percezione di sé che l’alunno si forma) e sul senso di autoefficacia (ossia sulla convinzione di essere più o meno capace di affrontare un’attività o un compito). Per sostenere la motivazione è quindi importante anche la funzione proattiva della valutazione, che «riconosce ed evidenzia i progressi, anche piccoli, compiuti dall’alunno nel suo cammino, gratifica i passi effettuati, cerca di far crescere in lui le “emozioni di riuscita” che rappresentano il presupposto per le azioni successive».1
La valutazione periodica e finale
Gli elementi conoscitivi in ordine al raggiungimento degli obiettivi di apprendimento sono raccolti in itinere attraverso una varietà di strumenti: prove di vario genere, osservazioni, interazioni con gli alunni, analisi di materiali prodotti…
La valutazione periodica e finale costituisce non un calcolo quantitativo di una sorta di “media”, ma una sintesi interpretativa dell’insieme di elementi acquisiti nel periodo oggetto di valutazione, con l’attribuzione del livello corrispondente al giudizio descrittivo che più si avvicina a tale sintesi.
2 Il percorso di valutazione
DEFINIZIONE DEGLIOBIETTIVI DI APPRENDIMENTO

COSTRUZIONE DELLA RUBRICA VALUTATIVA DISCIPLINARE
RACCOLTA IN ITINERE DI ELEMENTI CONOSCITIVI IN RELAZIONE ALLE DIMENSIONI E AI DESCRITTORI DELLA RUBRICA VALUTATIVA DISCIPLINARE
ATTRIBUZIONE DEL GIUDIZIO SINTETICO CORRISPONDENTE AL PROFILO DESCRITTIVO PIÙ VICINO AL COMPLESSO DEGLI ELEMENTI CONOSCITIVI ACQUISITI
1 Linee guida per la certificazione delle competenze nel primo ciclo di istruzione, trasmesse dal Ministero dell’Istruzione, dell’Università e della Ricerca con nota n. 312 del 9 gennaio 2018.

L’INSEGNAMENTO DELL’EDUCAZIONE CIVICA
Il quadro normativo
La legge n. 92 del 20 agosto 2019, Introduzione dell’insegnamento scolastico dell’educazione civica, è entrata in vigore il 5 settembre 2019, con la finalità di contribuire a «formare cittadini responsabili e attivi e a promuovere la partecipazione piena e consapevole alla vita civica, culturale e sociale delle comunità, nel rispetto delle regole, dei diritti e dei doveri».
Il nuovo insegnamento, che ha sostituito quello di Cittadinanza e Costituzione introdotto da una precedente legge del 2008, è stato disciplinato nei primi anni successivi all’entrata in vigore della legge (dall’a.s. 2020/2021all’a.s.2023/2024)daldecretoministerialen.35del22giugno2020edalleLineeguidaaessoallegate. Nel frattempo la legge n. 92/2029 è stata integrata da altre norme, in particolare dalla legge n. 21/2024 che ha previsto, tra le tematiche oggetto dell’educazione civica, anche quelle dell’educazione finanziaria e assicurativa e della pianificazione previdenziale, anche con riferimento all’utilizzo delle nuove tecnologie digitali di gestione del denaro e alle nuove forme di economia e finanza sostenibile, e lo sviluppo della cultura d’impresa.
A partire dall’ a.s. 2024-2025, con decreto ministeriale n. 183 del 7 settembre 2024, sono state adottate nuove Linee guida per attuare la disposizione della legge n. 92/2019 che prevede la definizione a livello nazionale, da parte del Ministro dell’istruzione (ora Ministro dell’istruzione e del merito), dei traguardi di sviluppo delle competenze e degli obiettivi specifici di apprendimento, e per recepire le nuove tematiche introdotte dai successivi provvedimenti normativi.
La struttura delle Linee guida
Le Linee guida entrate in vigore nell’a.s. 2024-2025 sono costituite da 10 punti, tra cui i principali riguardano i principi assunti come fondamento dell’educazione civica (nel cui ambito sono definiti anche i nuclei concettuali che aggregano le tematiche di questo insegnamento), i traguardi e gli obiettivi di apprendimento per ciascun grado di scuola, l’evidenziazione del carattere trasversale dell’insegnamento dell’educazione civica, le indicazioni metodologiche di tipo generale, le modalità di valutazione degli esiti di apprendimento.
I principi fondamentali
Il principio che sta alla base di tutti gli altri è la conoscenza della Costituzione italiana, che secondo le Linee guida va riconosciuta «non solo come norma cardine del nostro ordinamento, ma anche come riferimento prioritario per identificare valori, diritti, doveri, compiti, comportamenti personali e istituzionali finalizzati a promuovere il pieno sviluppo della persona e la partecipazione di tutti i cittadini all’organizzazione politica, economica e sociale del Paese».
Altri principi importanti riguardano: la centralità della persona, con i suoi diritti e doveri nei confronti della società, la cultura del rispetto verso ogni essere umano, l’inclusione, il senso di appartenenza alla comunità nazionale e alla civiltà europea. Senza dimenticare, a nostro avviso, il fatto di appartenere comunque a una “comunità di destino planetaria”.
I nuclei concettuali e le tematiche
Le tematiche elencate nelle Linee guida sono raggruppate in base a tre nuclei concettuali. La tabella n. 1 riporta in forma sintetica tali tematiche, in relazione alle quali vanno selezionati i contenuti specifici per i diversi gradi scolastici, e, al loro interno, per i diversi livelli di classe in rapporto alle varie fasi evolutive.

NUCLEI
COSTITUZIONE
SVILUPPOECONOMICO E SOSTENIBILITÀ
CITTADINANZA DIGITALE
TEMATICHE
• Artt. 1-12 della Costituzione (Principi generali).
• Altri articoli della Costituzione (connessi con le tematiche trattate).
• Diritti e doveri che conseguono alla partecipazione alla vita della comunità nazionale ed europea.
• Ordinamento e funzioni dello Stato, delle Regioni, degli Enti territoriali e delle Organizzazioni internazionali e sovranazionali, in particolare Unione Europea e Nazioni Unite.
• Inno e bandiera nazionali.
• Inno e bandiera europei.
• Bandiera della Regione.
• Stemma del Comune.
• Concetti di legalità, di rispetto delle leggi e delle regole comuni in tutti gli ambienti di convivenza.
• Contrasto a ogni forma di discriminazione e di bullismo.
• Contrasto a ogni forma di criminalità e illegalità.
• Educazione stradale.
• Agenda ONU 2030.
• Concetti di sviluppo e di crescita economica.
• Valore del lavoro e dell’iniziativa economica, cultura d’impresa.
• Conoscenze relative al mondo del lavoro.
• Tutela della sicurezza, della salute, della dignità e della qualità della vita delle persone. Tutela della natura e protezione dell’ambiente.
• Cultura della protezione civile.
• Educazione alla salute, educazione alimentare.
• Contrasto a tutte le forme di dipendenza (droghe, fumo, alcol, doping, uso patologico del web, gaming e gioco d’azzardo).
• Rispetto per i beni pubblici e tutela del decoro urbano.
• Conoscenza e valorizzazione del patrimonio culturale, artistico e monumentale dell’Italia.
• Educazione finanziaria e assicurativa.
• Uso corretto, consapevole e responsabile degli strumenti digitali.
• Valutazione critica di dati e notizie presenti in rete.
• Intelligenza Artificiale.
I traguardi per lo sviluppo delle competenze e gli obiettivi di apprendimento per la scuola primaria
Nucleo COSTITUZIONE
Traguardi per lo sviluppo delle competenze al termine del primo ciclo di istruzione

1
Sviluppare atteggiamenti e adottare comportamenti fondati sul rispetto di ogni persona, sulla responsabilità individuale, sulla legalità, sulla consapevolezza dell’appartenenza a una comunità, sulla partecipazione e sulla solidarietà, sostenuti dalla conoscenza della Carta costituzionale, della Carta dei Diritti fondamentali dell’Unione Europea e della Dichiarazione Internazionale dei Diritti umani.
Obiettivi di apprendimento al termine della scuola primaria
• Conoscere i principi fondamentali della Costituzione e saperne individuare le implicazioni nella vita quotidiana e nelle relazioni con gli altri.
• Individuare i diritti e i doveri che interessano la vita quotidiana di tutti i cittadini, anche dei più piccoli.
• Condividere regole comunemente accettate.
• Sviluppare la consapevolezza dell’appartenenza ad una comunità locale, nazionale ed europea.
• Rispettare ogni persona, secondo il principio di uguaglianza e di non discriminazione di cui all’articolo 3 della Costituzione.
• Riconoscere, evitare e contrastare forme di violenza e bullismo presenti nella comunità scolastica.
• Curare gli ambienti, rispettare i beni pubblici e privati così come le forme di vita (piante, animali) che sono state affidate alla responsabilità delle classi.
• Aiutare, singolarmente e in gruppo, coloro che presentino qualche difficoltà per favorire la collaborazione tra pari e l’inclusione di tutti.
Interagire correttamente con le istituzioni nella vita quotidiana, nella partecipazione e nell’esercizio della cittadinanza attiva, a partire dalla conoscenza dell’organizzazione e delle funzioni dello Stato, dell’Unione europea, degli organismi internazionali, delle Regioni e delle Autonomie locali. Essere consapevoli dell’appartenenza ad una comunità, locale e nazionale.
• Conoscere l’ubicazione della sede comunale, gli organi e i servizi principali del Comune, le principali funzioni del Sindaco e della Giunta comunale, i principali servizi pubblici del proprio territorio e le loro funzioni essenziali.
• Conoscere gli Organi principali dello Stato (Presidente della Repubblica, Camera dei deputati e Senato della Repubblica e loro Presidenti, Governo, Magistratura) e le funzioni essenziali.
• Conoscere la storia della comunità locale, nazionale ed europea a partire dagli stemmi, dalle bandiere e dagli inni.
• Conoscere il valore e il significato dell’appartenenza alla comunità nazionale.
• Conoscere il significato di Patria.
• Conoscere l’Unione Europea e l’ONU.
• Conoscere il contenuto generale delle Dichiarazioni Internazionali dei diritti della persona e dell’infanzia.
• Individuare alcuni dei diritti previsti nell’ambito della propria esperienza concreta.
3 Rispettare le regole e le norme che governano la democrazia, la convivenza sociale e la vita quotidiana in famiglia, a scuola, nella comunità, al fine di comunicare e rapportarsi correttamente con gli altri, esercitare consapevolmente i propri diritti e doveri per contribuire al bene comune e al rispetto dei diritti delle persone.
• Conoscere ed applicare le regole vigenti in classe e nei vari ambienti della scuola (mensa, palestra, laboratori, cortili) e partecipare alla loro eventuale definizione o revisione.
• Conoscere il principio di uguaglianza nella consapevolezza che le differenze possono rappresentare un valore quando non si trasformano in discriminazioni.
• Conoscere i principali fattori di rischio dell’ambiente scolastico, adottare comportamenti idonei a salvaguardare la salute e la sicurezza proprie e altrui e contribuire a definire comportamenti di prevenzione dei rischi.
• Conoscere e applicare le principali norme di circolazione stradale.
4
Sviluppare atteggiamenti e comportamenti responsabili volti alla tutela della salute e del benessere psicofisico.
• Conoscere e attuare le principali regole per la cura della salute, della sicurezza e del benessere proprio e altrui, a casa, a scuola, nella comunità, dal punto di vista igienico-sanitario, alimentare, motorio, comportamentale.
• Conoscere i rischi e gli effetti dannosi delle droghe.
5

6
Traguardi per lo sviluppo delle competenze al termine del primo ciclo di istruzione
Comprendere l’importanza della crescita economica e del lavoro.
Conoscere le cause dello sviluppo economico e sociale in Italia ed in Europa, le diverse attività economiche. Sviluppare atteggiamenti e comportamenti responsabili volti alla tutela dell’ambiente, del decoro urbano, degli ecosistemi e delle risorse naturali per una crescita economica rispettosa dell’ambiente e per la tutela della qualità della vita.
Obiettivi di apprendimento al termine della scuola primaria
• Conoscere le condizioni della crescita economica. Comprenderne l’importanza per il miglioramento della qualità della vita e ai fini della lotta alla povertà.
• Individuare, con riferimento alla propria esperienza, ruoli, funzioni e aspetti essenziali che riguardano il lavoro delle persone con cui si entra in relazione, nella comunità scolastica e nella vita privata.
• Riconoscere il valore del lavoro.
• Conoscere, attraverso semplici ricerche, alcuni elementi dello sviluppo economico in Italia ed in Europa.
• Riconoscere, a partire dagli ecosistemi del proprio territorio, le trasformazioni ambientali ed urbane dovute alle azioni dell’uomo; mettere in atto comportamenti alla propria portata che riducano l’impatto negativo delle attività quotidiane sull’ambiente e sul decoro urbano.
• Individuare nel proprio territorio le strutture che tutelano i beni artistici, culturali e ambientali e proteggono gli animali, e conoscerne i principali servizi.
• Analizzare, attraverso l’esplorazione e la ricerca all’interno del proprio comune, la qualità degli spazi verdi e dei trasporti, il ciclo dei rifiuti, la salubrità dei luoghi pubblici.
Comprendere le cause dei cambiamenti climatici, gli effetti sull’ambiente e i rischi legati all’azione dell’uomo sul territorio. Comprendere l’azione della Protezione civile nella prevenzione dei rischi ambientali.
Maturare scelte e condotte di tutela dei beni materiali e immateriali.
7
8
Maturare scelte e condotte di tutela del risparmio e assicurativa nonché di pianificazione di percorsi previdenziali e di utilizzo responsabile delle risorse finanziarie.
9 Maturare scelte e condotte di contrasto all’illegalità.
• Conoscere ed attuare i comportamenti adeguati a varie condizioni di rischio (sismico, vulcanico, idrogeologico, climatico…) anche in collaborazione con la Protezione civile.
• Individuare alcune trasformazioni ambientali e gli effetti del cambiamento climatico.
• Identificare nel proprio ambiente di vita gli elementi che costituiscono il patrimonio artistico e culturale, materiale e immateriale, anche con riferimento alle tradizioni locali, ipotizzando semplici azioni per la salvaguardia e la valorizzazione.
• Riconoscere, con riferimento all’esperienza, che alcune risorse naturali (acqua, alimenti…) sono limitate e ipotizzare comportamenti di uso responsabile, mettendo in atto quelli alla propria portata.
• Conoscere e spiegare il valore, la funzione e le semplici regole di uso del denaro nella vita quotidiana.
• Gestire e amministrare piccole disponibilità economiche, ideando semplici piani di spesa e di risparmio, individuando alcune forme di pagamento e di accantonamento.
• Individuare e applicare nell’esperienza e in contesti quotidiani, i concetti economici di spesa, guadagno, ricavo, risparmio.
• Riconoscere l’importanza e la funzione del denaro.
• Conoscere le varie forme di criminalità, partendo dal rispetto delle regole che ogni comunità si dà per garantire la convivenza.
• Conoscere la storia dei vari fenomeni mafiosi, nonché riflettere sulle misure di contrasto.
• Conoscere il valore della legalità.
10
Educazione civica

Traguardi per lo sviluppo delle competenze al termine del primo ciclo di istruzione
Sviluppare la capacità di accedere alle informazioni, alle fonti, ai contenuti digitali, in modo critico, responsabile e consapevole.
11
12
Interagire con gli altri attraverso le tecnologie digitali consentite, individuando forme di comunicazione adeguate ai diversi contesti di relazione, adottando e rispettando le regole comportamentali proprie di ciascun contesto comunicativo.
Gestire l’identità digitale e i dati della rete, salvaguardando la propria e altrui sicurezza negli ambienti digitali, evitando minacce per la salute e il benessere fisico e psicologico di sé e degli altri.
Obiettivi di apprendimento al termine della scuola primaria
• Ricercare in rete semplici informazioni, distinguendo dati veri e falsi.
• Utilizzare le tecnologie per elaborare semplici prodotti digitali.
• Riconoscere semplici fonti di informazioni digitali.
• Interagire con strumenti di comunicazione digitale, quali tablet e computer.
• Conoscere e applicare semplici regole per l’utilizzo corretto di strumenti di comunicazione digitale, quali tablet e computer.
• Conoscere e applicare le principali regole di partecipazione alle classi virtuali e alle piattaforme didattiche.
• Conoscere il significato di identità e di informazioni personali in semplici contesti digitali di uso quotidiano.
• Conoscere i rischi connessi con l’utilizzo degli strumenti digitali in termini di sicurezza personale.
• Conoscere semplici modalità per evitare rischi per la salute e minacce al benessere psico-fisico quando si utilizzano le tecnologie digitali.
• Riconoscere, evitare e contrastare le varie forme di bullismo e cyberbullismo.
Carattere trasversale dell’educazione civica e unitarietà dell’azione
didattica
La trasversalità dell’educazione civica è affermata sin dalla definizione adottata dalla legge n.92/2019 («è istituito l’insegnamento trasversale dell’educazione civica») ed è stata ben illustrata nelle Linee guida del 2020 in diversi passaggi:
«La norma richiama il principio della trasversalità del nuovo insegnamento, anche in ragione della pluralità degli obiettivi di apprendimento e delle competenze attese, non ascrivibili a una singola disciplina e neppure esclusivamente disciplinari. […]»
«La norma richiama il principio della trasversalità del nuovo insegnamento, anche in ragione della pluralità degli obiettivi di apprendimento e delle competenze attese, non ascrivibili a una singola disciplina e neppure esclusivamente disciplinari. […]»
«Ogni disciplina è, di per sé, parte integrante della formazione civica e sociale di ciascun alunno. […]»
«I nuclei tematici dell’insegnamento, e cioè quei contenuti ritenuti essenziali per realizzare le finalità indicate nella Legge, sono già impliciti negli epistemi delle discipline. […]»
«L’educazione civica […] supera i canoni di una tradizionale disciplina, assumendo più propriamente la valenza di matrice valoriale trasversale che va coniugata con le discipline di studio, per evitare superficiali e improduttive aggregazioni di contenuti teorici e per sviluppare processi di interconnessione tra saperi disciplinari ed extradisciplinari.»
Anche le nuove Linee guida del 2024 dedicano un paragrafo alla trasversalità dell’educazione civica, ribadendo che «i saperi hanno lo scopo di fornire agli allievi strumenti per sviluppare conoscenze, abilità e competenze per essere persone e cittadini autonomi e responsabili, rispettosi di sé, degli altri e del bene comune», «i nuclei concettuali […] per loro natura interdisciplinari, attraversano il curricolo e possono essere considerati in ogni argomento che tutti i docenti trattano quotidianamente»
e che «si tratta dunque di far emergere all’interno dei curricoli di istituto elementi già presenti negli attuali ordinamenti e di rendere più consapevole ed esplicita la loro interconnessione, nel rispetto e in coerenza con i processi di crescita dei bambini e dei ragazzi nei diversi gradi di scuola».
Il curricolo e i percorsi di apprendimento
La progettazione dei percorsi finalizzati al perseguimento degli obiettivi di apprendimento e dei traguardi per lo sviluppo delle competenze relativi all’educazione civica richiede pertanto di:
• analizzare gli obiettivi di apprendimento previsti al termine della scuola primaria e decidere come tradurli nei vari livelli di classe;
• individuare quali sono i contributi che le discipline possono offrire al perseguimento degli obiettivi;
• definire i percorsi e le esperienze di apprendimento in base alle discipline di volta in volta coinvolte.
L’attuazione dell’insegnamento trasversale di educazione civica richiede pertanto, come del resto tutto il curricolo, una forte azione unitaria del gruppo docente, soprattutto per quanto riguarda la formazione degli atteggiamenti, che, secondo la definizione presente nella Raccomandazione relativa alle competenze chiave per l’apprendimento permanente adottata nel 2018 dal Consiglio dell’Unione europea, «descrivono la disposizione e la mentalità per agire o reagire a idee, persone o situazioni».
NUCLEI CONCETTUALI TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE AL TERMINE DELLA SCUOLA PRIMARIA
OBIETTIVI DI APPRENDIMENTO AL TERMINE DELLA SCUOLA PRIMARIA
OBIETTIVI DI APPRENDIMENTO SELEZIONATI E DECLINATI PER I VARI LIVELLI DI CLASSE INDIVIDUAZIONE DEL CONTRIBUTO DI CIASCUNA DISCIPLINA
La valutazione
L’insegnamento trasversale dell’educazione civica è oggetto delle valutazioni periodiche e finali previste dal D.Lgs. n. 62 del 13 aprile 2017. La valutazione deve ovviamente essere coerente con gli obiettivi dichiarati nella progettazione e con le attività didattiche svolte.
Per la formulazione dei giudizi occorre raccogliere in itinere gli elementi conoscitivi relativi al raggiungimento degli obiettivi e formulare il giudizio sul livello conseguito in base a una sintesi interpretativa degli stessi.

Il metodo di Matematica, Scienze e Tecnologia ne
IMONDIDIGEA

• Se sbaglio imparo
• La Mateludica
• Il metodo ELS

UN PERCORSO DI DIDATTICA
DELL’ERRORE: SE SBAGLIO IMPARO
di M. Federica De Gasperis
“Sbagliando si impara”: difficile incontrare qualcuno che non abbia mai sentito pronunciare questa frase. Si potrebbe definire un’espressione semplice ma ampia di significato e di risultati diversi al tempo stesso.
Quando è l’insegnante a usarla in primo luogo attenua l’impatto emotivo che può avere l’annuncio di un risultato scolastico non soddisfacente, per esempio un errore di calcolo o un errore ortografico; può accadere anche che venga percepita come piuttosto positiva dall’allievo/a che apprezza la propria immagine di normalissimo individuo che sta percorrendo un cammino di apprendimento verso il raggiungimento degli obiettivi che qualcuno ha programmato per lui; in secondo luogo si tratta di una frase che permette all’insegnante di gestire con meno preoccupazione il proprio compito: in fondo non sta mettendo in discussione né il proprio operato né le capacità dell’allievo/a perché l’errore, si sa, è un momento inevitabile del percorso di conoscenza di ogni discente.
Sbagli ed errori
Affinché si possa davvero imparare sbagliando è opportuno che in classe si dedichi il giusto spazio allo studio e alla riflessione sugli errori commessi e alla loro correzione consapevole al fine di evitare di rifarli.
Tuttavia è fondamentale precisare la distinzione tra sbaglio ed errore. Nonostante spesso i due termini vengano usati come sinonimi, la differenza tra i due concetti veniva già avanzata da Wiener negli anni ‘20 (Cfr. L. BINANTI, Pedagogia, epistemologia e didattica dell’errore, Rubbettino, 2001, pp.27-28): sbaglio ed errore “si possono distinguere nel senso che l’errore si basa sull’ignoranza di certi fatti essenziali per l’esatto riconoscimento, mentre lo sbaglio risulta dalla difettosa attività delle tre funzioni (attenzione, memoria e pensiero) che presiedono al compimento di ogni lavoro. Mentre dunque l’errore è una base oggettiva lo sbaglio è essenzialmente un fatto soggettivo”.
Anche analizzando l’etimologia dei termini è importante notare che errore viene da errare, inteso come movimento nel mondo del sapere e del saper fare alla scoperta di qualcosa che ancora non si conosce: l’errore in sintesi viene commesso quando ancora non si è appresa la regola o non la si è assimilata pienamente. Con pazienza, allenamento e con il feedback dell’insegnante (sull’importanza del feedback si rimanda al box di approfondimento) l’errore, una volta capito, verrà corretto con la speranza che non venga più commesso, altrimenti sarà considerato un sbaglio di applicazione della regola.
Particolare attenzione andrà inoltre prestata alla ripetizione degli sbagli per capirne le cause e per escludere che possano nascondere delle difficoltà.
É necessario, quindi, imparare a ragionare sui processi cognitivi che hanno portato a sbagliare.
L’obiettivo di Se sbaglio imparo
Obiettivo del percorso Se sbaglio imparo è dunque riconoscere e approfondire il valore formativo della didattica dell’errore, ovvero un modello di insegnamento scolastico in cui i progressi della conoscenza avvengono attraverso la scoperta e la correzione degli errori frequenti, sia propri che degli altri, al fine di non sbagliare più.
Più che un percorso di prevenzione degli errori, si configura come una raccolta di momenti di riflessione su come migliorare il rendimento: sebbene l’errore faccia parte del processo di apprendimento, è importante riconoscerlo ed eventualmente applicare strategie metacognitive di riflessione sulle proprie capacità di apprendimento.
In ogni pagina dedicata allo sbaglio vengono infatti forniti, oltre agli esempi, strategie risolutive, consigli ed esercizi per non sbagliare più.
In particolare gli errori considerati sono legati alle abilità di base:
• abilità di percezione visiva;
• abilità linguistiche;

• abilità di memoria;
• abilità logico-concettuali.
In quest’ottica anche lo sbaglio, quindi, si configura non come un ostacolo ma come un’opportunità per riflettere sulle proprie abilità e superarlo mettendo in atto capacità di riflessione su come migliorare gli apprendimenti che seguiranno.
Il percorso fornisce infatti indicazioni pratiche: usa gli strumenti, rileggi, controlla, leggi ecc. Errore e sbaglio non sono quindi nemici da evitare, ma momenti del processo di apprendimento. Se sbaglio imparo dunque… a non sbagliare più!
Contenuti SE SBAGLIO IMPARO*
MATEMATICA CLASSE 4
Il valore dello zero
La lettura dei numeri
L’incolonnamento nell’addizione
MATEMATICA CLASSE 5
La lettura dei numeri
Attenzione all’esponente
Divisioni possibili e impossibili
Attenzione alla differenza Il resto con la proprietà invariantiva
L’incolonnamento nella moltiplicazione Il resto con la proprietà invariantiva
Confronto di frazioni
Confronto di decimali
Il resto nella prova della divisione
Attenzione alla simmetria
Attenzione alla rotazione
La sequenza delle operazioni nelle espressioni
Attenzione all’unità di misura
Le misure di tempo
L’areogramma e la percentuale
E • Non • O → Enunciati logici
* Gli errori presentati sono stati prevalentemente selezionati sulla base delle richieste pervenute sui miei canali social Maestrafede_ e, in seconda battuta, desunti dall’osservazione del mio lavoro in classe.
Come può e deve essere fornito il feedback da parte dell’insegnante?
La teoria dell’apprendimento strumentale legata a Skinner spiega con il concetto di rinforzo, l’effetto positivo che il feedback relativo a un risultato soddisfacente ha sull’apprendimento.
Da ciò derivano alcune indicazioni teoriche in gran parte verificate dalla ricerca sul campo (Cfr C. PONTECORVO, Psicologia dell’educazione, Giunti, Firenze, 1999):
• la necessità di una espressione esplicita del rinforzo sotto forma di feedback sulla risposta o sulla prestazione dell’alunno/a, dal momento che una risposta rinforzata ha più probabilità di essere ripetuta;
• la necessità che il feedback sia immediato o comunque che sia dato nel più breve tempo possibile;
• la preferibilità che un feedback sia dato nella forma del prompting, cioè di istruzioni indicative che diano al discente un’informazione orientativa o un suggerimento e che, quindi, servano a impedire che l’errore sia ripetuto;
Ciò concorda con il metodo sperimentato da molti e molte insegnanti che è opportuno evitare di far sbagliare piuttosto che correggere ripetutamente gli errori e che è per questo utile fornire un feedback correttivo anticipato.
• il feedback, infine, è tanto più efficace sul discente se è completo e preciso, cioè se non si limita a informarlo sulla accettabilità del suo compito (espresso con gli avverbi bene e male) ma fornisce anche al discente una precisa informazione sul perché ha sbagliato, e gli fa conoscere così qual è la logica della risposta: il discutere i compiti fatti, lo spiegare la ragione per cui una certa affermazione è giusta o sbagliata significa anche offrire all’allievo la via per giungere da solo alla soluzione corretta.
Nell’uso del feedback è poi risultato che la correzione è efficace e valida, anche dal punto della motivazione se comincia dall’accettazione di ciò che vi è di valido e accettabile nella risposta, per portare l’allievo/a a correggere in autonomia la parte sbagliata che vi è contenuta.
Bibliografia di riferimento e approfondimento
Le difficoltà nell’apprendimento della matematica, a cura di A. Contardi e B. Piochi Erickson, 2002 Trento Pedagogia, epistemologia e didattica dell’errore, a cura di L. Binanti, Rubbettino 2001
La matematica della felicità, Rocco Dedda, Rizzoli 2023 NON SBAGLIO PIÙ!, Maestra Federica, Vallardi 2024
LA MATELUDICA

di Valentina Perolio
Studi scientifici dimostrano che i ragazzi e le ragazze a cui piace la Matematica e che si sentono competenti in questo campo sono molto pochi. Spesso il sentirsi non competenti in Matematica causa disturbi d’ansia, depressione. Inoltre l’insuccesso in Matematica è uno dei fattori che maggiormente influenzano l’impotenza appresa, e cioè la sensazione di essere inadeguati che andrà ad alimentare il circolo vizioso della demotivazione: il pensiero di non riuscire e “non essere portati” per la materia farà sperimentare ansia e disagio, questi stati d’animo faranno percepire la Matematica come difficile e noiosa e faranno diminuire notevolmente la motivazione all’impegno; meno ci si impegnerà e peggiori saranno i risultati ed ecco così che ci si sentirà ancora meno competenti e meno abili. Allora prima ancora di programmare le nostre lezioni ed entrare in classe, dobbiamo chiederci qual è la scuola che vogliamo: una scuola “che ingozza e giudica”, alleata dell’errore, che mortifica – per riprendere le parole della Dottoressa Lucangeli – oppure una scuola che stabilisce con bambine e bambini un’alleanza contro l’errore, che incoraggia e accoglie?
Gli studi nel campo delle neuroscienze hanno dato vita a un nuovo filone di ricerca chiamato warm cognition che si concentra sul rapporto fra apprendimento ed emozioni: quando apprendiamo, nella nostra mente si imprimono anche le emozioni che stiamo provando, e così, se avremo sperimentato un vissuto di ansia, paura, vergogna, demotivazione, rifuggiremo un nuovo apprendimento: se al contrario avremo appreso con gioia, curiosità, interesse, serenità, allora ricercheremo queste emozioni e la situazione che le ha generate: apprendere con gioia, piacere e allegria è 200 volte più efficace che fare la stessa cosa con tristezza, dolore e patimento. Riflettendo quindi sul cattivo rapporto di molti dei nostri allievi e delle nostre allieve con la Matematica, sulla necessità di un intervento che li aiuti a uscire dal circolo vizioso della demotivazione e sull’utilità di sperimentare sensazioni di benessere a scuola, appare evidente il forte impatto positivo che può avere un approccio didattico esperienziale e ludico, motivante perché capace di far sentire competenti alunni e alunne e di far esperire emozioni di serenità e benessere.
Tutte le attività che troverete in questi libri di testo, in particolare quelle pratiche e i giochi, come le pagine di Mateludica, garantiscono l’inclusione di tutti e tutte grazie alla possibilità di interpretare ruoli diversi, di adattare il gioco al proprio livello di competenza e grazie alle dinamiche collaborative e di peer tutoring che si innescheranno; inoltre, sono attività innovative perché permettono il superamento della lezione frontale e un apprendimento autentico in cui bambini e bambine sono protagonisti.
Voglio concludere questa breve introduzione citando di nuovo la Professoressa Daniela Lucangeli: “È difficile? Moltissimo. Ne vale la pena? Certamente.”
Fotocopia le pagg. 56-57 e gioca con la Mateludica del tuo volume a pag. 155. I materiali di pag. 59 sono utili per l’attività Il domino delle frazioni, scaricabile da HUB Kit.
IL METODO ELS

Progettare e sviluppare un percorso scientifico
Lo sviluppo di un percorso scientifico parte da un approccio pratico ed esperienziale inteso come necessaria osservazione del mondo circostante e della propria quotidianità, alla ricerca dei molteplici fenomeni che li caratterizzano.
L’obiettivo è quello di fornire un testo di accompagnamento alla formazione del percorso (e del pensiero) scientifico che, prima ancora di parlare di metodo o specifiche modalità (osservazione, ipotesi, esperimento...), trova la sua fondatezza nell’esperienza pratica.
Per quanto riguarda l’insegnamento, in fase di progettazione dell’intero anno scolastico risulta fondamentale identificare almeno 10 (o meglio 20) esperienze pratiche che i bambini e le bambine dovranno fare; non dovranno essere necessariamente esperimenti per illustrare un determinato principio ma, al contrario, potranno essere attività pratiche in cui esercitare prima l’osservazione e poi la deduzione, fino ad arrivare a sviluppare domande come “Che cosa accade se cambio x?”, dove x indica una specifica variabile (peso, volume, forza, posizione...).
Domande di questo tipo possono essere indotte nelle prime fasi per un coinvolgimento dei bambini e delle bambine per dare loro un messaggio importante: il mondo può essere “interrogato” attraverso un’attività pratica e le risposte dipendono da quello che osserviamo. Consiste in questo la grande potenza del metodo scientifico.
Connessione tra le discipline a partire dalle esperienze
Prima di arrivare a esperimenti veri e propri, occorre far sì che l’attività pratica sia parte integrante del proprio imparare, e questo non comporta strumenti specifici o elevati gradi di conoscenza. Un esempio consiste nel chiedere a ogni alunno/a di cronometrare (usando un cellulare) in quanto tempo si lava i denti, per poi lasciare il rubinetto aperto per lo stesso tempo raccogliendo l’acqua fuoriuscita. La raccolta dell’acqua consente di misurare (passando quindi attraverso il numero e l’unità di misura come elementi fondamentali per un’osservazione oggettiva) il possibile spreco dell’acqua derivante dall’azione di lavarsi i denti con o senza il rubinetto aperto.
Ma non solo... Possiamo moltiplicare la quantità (litri per esempio) di acqua per il numero di alunni/e della classe, di tutta la scuola, dell’intera città e così via... Per poi, infine, definire l’equivalente in piscine olimpioniche di acqua risparmiata o sprecata da una singola azione.
Competenze maturate nelle fasi pratiche
Le attività pratiche, che non consistono in un esperimento atto a dimostrare una legge, fanno maturare diverse competenze.
L’attività sul lavaggio dei denti, per esempio, ci permette di:
• sviluppare capacità manuali;
• coinvolgere la famiglia;
• dimostrare operativamente la potenza e le potenzialità della Matematica (e la sua relazione con il mondo quotidiano);
• sviluppare la capacità di prevedere il futuro con oggettività e agire di conseguenza;

• comprendere il “peso” del singolo nelle proprie azioni (responsabilità sociale);
• integrare il tema “acqua” con il tema “sostenibilità” e, quindi, l’Educazione civica;
• sviluppare un pensiero critico;
• legittimare una richiesta di comportamento (chiudere il rubinetto diventa un’azione non imposta, ma di senso condiviso e collettivo).
La trattazione delle STEM, il Metodo Pleiadi
Il punto di partenza
Nel trattare i diversi aspetti scientifici abbiamo essenzialmente due possibilità: una trattazione teorica con i relativi esperimenti a confermare un principio o un particolare meccanismo, oppure una serie di esperienze da cui poi dedurre un principio e una descrizione accurata.
Quello che vi vogliamo proporre è quanto abbiamo definito Elaborazione Logico Sperimentale (che va sotto il nome di Metodo Pleiadi), che consiste nel partire da un’osservazione pratica che può essere relativa alla quotidianità o un esperimento vero e proprio, ma necessariamente qualcosa che sia un’esperienza personale, fatta cioè in prima persona, in cui l’alunna/o ha potuto percepirne (toccarne) la dinamica anche negli aspetti quantitativi.
Se, per esempio, si sta parlando del vento, occorre ricreare (o rievocare se la cosa è nota) il fenomeno ma anche la sua specifica dinamica: il vento sposta le cose, non lo vedo, lo sento sulla pelle, riesce a muovere cose pesanti, può essere freddo o caldo ecc.
Il punto di partenza, quindi, non deve essere una definizione o una terminologia, ma un’esperienza (qualcosa di esterno). Definiamo quindi questa fase “E”, che sta per “Esperienza”.
In alcuni casi trovate una descrizione iniziale con relativa terminologia. Va sottolineato che quest’ultima è puramente funzionale a fornire una descrizione comune di un elemento e non consiste nel fenomeno in sé.
Le fasi della comprensione
A questa fase segue un momento deduttivo in cui gli alunni e le alunne dovranno porsi delle domande ma, soprattutto, formulare una teoria su una certa variabile del fenomeno, eventualmente suggerita dall’insegnante stesso/a (per esempio: “ma il vento può soffiare in tutte le direzioni?”). Definiamo questa fase “L”, che sta per “Logica”, durante la quale alunni e alunne sono chiamati a usare (e allenare!) le proprie capacità di pensiero ed elaborazione.
A questo punto occorre sviluppare un’attività pratica o un esperimento per verificare quanto elaborato o per comprendere una possibile risposta. Siamo di fatto giunti nuovamente a una fase sperimentale, prima definita “E”, che nel nostro esempio potrebbe consistere nel costruire una banderuola e misurare le diverse direzioni del vento.
Quanto fatto consiste nella creazione di un percorso E + L + E, che da una parte ha portato a una maggiore conoscenza del fenomeno, dall’altra ha sviluppato ulteriori competenze.
Nella trattazione di un tema, quello che abbiamo introdotto (e che invitiamo a sviluppare) è un sistema del tipo E + L + E + L + E + ... dove in alcuni casi “E” si traduce nel ricordare un’esperienza già vissuta da ogni alunna/o.
Questo tipo di modalità prende il nome di Elaborazione Logico Sperimentale, perché alterna i due elementi e tende ad affrontare le caratteristiche di ciascun fenomeno una alla volta.

Schede di autovalutazione di Matematica
Prima della prova
Stai per risolvere alcuni problemi...

Come ti senti?
Felice Tranquillo/a Un po’ agitato/a Preoccupato/a
Qual è o quali sono i passaggi nei quali ti senti più sereno o serena?
Comprensione del testo
Individuazione dei dati
Comprensione del testo
Rappresentazione
Scelta delle operazioni Controllo del risultato
Qual è o quali sono i passaggi che ti preoccupano?
Individuazione dei dati
Dopo la prova
Rappresentazione
Ora che hai provato a risolvere i problemi…
Felice: ho lavorato bene!
Scelta delle operazioni Controllo del risultato
Come ti senti?
Tranquillo/a: mi sono sembrati abbastanza semplici.
Un po’ agitato/a: non sono sicuro/a del mio lavoro.
Avevi tutte le informazioni per risolverlo? (RISORSE)
Sì. No, mi è sembrato che mancassero delle informazioni che ho dovuto ricavare.
Preoccupato/a: ho fatto molta fatica.
Sì, i dati c’erano tutti, ce n’era anche uno (o più) inutile.
Sei riuscito/a a risolverlo da solo? (AUTONOMIA)
Sì, non ho chiesto aiuti. Ho chiesto aiuto per la rappresentazione.
No, l’insegnante mi ha aiutato a ragionare e poi ho capito come risolverlo.
No, ho chiesto molti aiuti perché ero in difficoltà.
Hai riflettuto sui risultati che hai trovato? (AUTOCORREZIONE)
Sì, ho cercato di capire se avessero senso oppure no e ho corretto eventuali errori.
No, ho trovato le operazioni da risolvere, ma poi non ho riflettuto sui risultati.
No, ma quando l’insegnante mi ha consigliato di riguardare alcuni passaggi ho trovato alcuni errori.
Prima della prova
Stai per mettere alla prova le tue competenze sui numeri...
Come ti senti?

Felice
Tranquillo/a
Scrittura/lettura dei numeri
Un po’ agitato/a Preoccupato/a
Su cosa ti senti più tranquillo/a?
Composizione/scomposizione Confronto
Come mai?
Dopo la prova
Dopo aver svolto gli esercizi…
Felice: penso di non aver fatto errori, o quasi...!
Come ti senti?
Tranquillo/a: sono riuscito/a a lavorare abbastanza bene.
Scrittura/lettura dei numeri
Un po’ agitato/a: non sono sicuro/a del mio lavoro.
Quali esercizi hai svolto con più facilità?
Preoccupato/a: penso di aver fatto molti errori.
Composizione/scomposizione Confronto
In quali esercizi hai trovato maggior difficoltà?
Scrittura/lettura dei numeri
Composizione/scomposizione Confronto
Avevi già risolto esercizi simili? (SITUAZIONE NOTA/NON NOTA)
Sì, non ho trovato niente di nuovo. Alcuni sì, altri no. No, ho avuto diverse difficoltà.
Sei riuscito/a a fare tutto da solo/a? (AUTONOMIA)
Sì, non ho chiesto aiuti. L’insegnante mi ha dato qualche suggerimento. No, ho chiesto conferma qualche volta. No, ho chiesto molti aiuti perché ero in difficoltà.
Prima della prova
Stai per risolvere alcune operazioni...

Come ti senti?
Felice Tranquillo/a Un po’ agitato/a Preoccupato/a
Qual è o quali sono le operazioni nelle quali ti senti più esperto/a?
Addizione Sottrazione Moltiplicazione Divisione
Qual è o quali sono le operazioni nelle quali ti senti più esperto/a?
A mente. In colonna. Dipende.
Come mai?
Dopo la prova
Ora che le hai viste e ci hai lavorato:
Felice: penso di non aver fatto errori, o quasi...!
Come ti senti?
Tranquillo/a: sono riuscito/a a risolvere quasi tutte le operazioni.
Un po’ agitato/a: non sono sicuro/a del mio lavoro.
Preoccupato/a: penso di aver fatto molti errori.
Qual è o quali sono le operazioni che hai risolto con più facilità?
Addizione Sottrazione Moltiplicazione Divisione
Avevi già risolto operazioni simili? (SITUAZIONE NOTA/NON NOTA)
Sì, non ho trovato niente di nuovo. No, ho avuto diverse difficoltà.
Ricordavi come fare per risolverle? (RISORSE)
Sì Non ricordo come risolvere tutte le 4 operazioni. No, ho sentito una gran confusione in testa. .
Hai stimato i risultati che avresti ottenuto? (AUTOCORREZIONE)
Sì, sembra che siano venuti tutti corretti. No, non ci ho pensato.
Ci ho provato ma non sono riuscito/a in tutte le operazioni.
Prima della prova
Stai per svolgere alcuni esercizi su frazioni e numeri decimali...
Come ti senti?

Felice Tranquillo/a
Un po’ agitato/a Preoccupato/a
Su cosa ti senti più sicuro/a?
Le frazioni
Le frazioni in generale.
I numeri decimali
Su cosa invece ti senti maggiormente in difficoltà?
Le frazioni complementari e/o equivalenti.
Dopo la prova
Ora che hai eseguito la prova:
Felice: ho lavorato bene!
I tipi di frazioni.
La frazione di un numero.
Operare con i numeri decimali.
e numeri decimali
Come ti senti?
Tranquillo/a: mi è sembrata abbastanza semplice.
Un po’ agitato/a: non sono sicuro/a di aver lavorato bene.
Preoccupato/a: ho fatto molta fatica e penso molti errori.
Qual è o quali sono stati gli esercizi che ti hanno messo più in difficoltà?
Avevi già risolto esercizi simili? (SITUAZIONE NOTA/NON NOTA)
Sì, non ho trovato niente di nuovo.
Alcuni no. Scrivo quali:
C’erano tutte le informazioni per risolverli? (RISORSE)
Sì. No, ho dovuto pensare ad altri esercizi che avevamo già fatto.
No, mi sembravano tutti complicati.
No, in alcuni esercizi ho dovuto trovare io una strategia nuova.
Sei riuscito a risolverli tutti da solo? (AUTONOMIA)
Sì, non ho chiesto aiuti. Ho chiesto qualche piccolo aiuto.
No, l’insegnante mi ha aiutato a ragionare un po’.
No, ho chiesto molti aiuti perché ero in difficoltà.
Prima della prova
Stai per svolgere alcuni esercizi sulle misure di lunghezza, capacità, massa, valore e tempo...
Come ti senti?

Felice
Tranquillo/a Un po’ agitato/a Preoccupato/a
In quale tipo di attività ti senti più sicuro/a?
Scomporre e ricomporre Le equivalenze I problemi Quelle con le misure di tempo
In quali invece ti senti maggiormente in difficoltà?
Scomporre e ricomporre Le equivalenze I problemi Quelle con le misure di tempo
Dopo la prova
Ora che hai visto gli esercizi…
Felice: ho lavorato bene!
Come ti senti?
Tranquillo/a: mi sono sembrati abbastanza semplici.
Un po’ agitato/a: non sono sicuro/a di aver lavorato bene.
Qual è o quali sono stati gli esercizi che ti hanno messo più in difficoltà?
Scomporre e ricomporre. Le equivalenze. I problemi. Quelli con le misure di tempo.
Avevi già risolto esercizi simili? (SITUAZIONE NOTA/NON NOTA)
Sì, non ho trovato niente di nuovo. Alcuni no. Scrivo quali: Sei riuscito a risolverli tutti da solo/a? (AUTONOMIA)
Sì, non ho chiesto aiuti. No, l’insegnante mi ha aiutato a ragionare un po’.
Prima della prova
Stai per rispondere ad alcune domande ed esercizi sui poligoni...
Come ti senti?
Felice Tranquillo/a Un po’ agitato/a Preoccupato/a
In quale/i argomento/i ti senti più competente?

Classificazione
Classificazione
Perimetro
Area
In quale/i argomento/i ti senti più competente?
Perimetro
Area
Quale affermazione pensi che ti si addica di più?
Conosco le formule e le so applicare per risolvere i problemi di geometria.
Conosco le formule ma faccio fatica a individuare le giuste operazioni per risolvere un problema.
SCHEDA SPECIFICA PER LA VERIFICA DI PAG. 268
Dopo la verifica
Ora che hai svolto la verifica…
Felice: penso di non aver fatto errori, o quasi...!
Non ho memorizzato bene le formule, ma credo di riuscire a risolvere i problemi di geometria ragionando.
Non riesco a memorizzare le formule e sono in difficoltà quando devo risolvere un problema di geometria.
Come ti senti?
Tranquillo/a: sono riuscito/a a rispondere quasi a tutto. Un po’ agitato/a: non sono sicuro/a di ciò che ho scritto.
A quali esercizi pensi di aver risposto meglio?
A quelli sulla classificazione (1, 2, 3) Alle equivalenze (4) Al problema (5)
Avevi già svolto esercizi simili? (SITUAZIONE NOTA/NON NOTA)
Sì, non ho trovato niente di nuovo. No, mi sono trovato/a in difficoltà.
Avevi tutte le informazioni necessarie? (RISORSE)
Sì. No, ho dovuto ricordare ciò che avevo studiato. Non lo so, sono confuso/a.
Sei riuscito/a a rispondere da solo/a? (AUTONOMIA)
Sì, non ho chiesto aiuti. L’insegnante mi ha dato qualche consiglio.
No, ho chiesto conferma qualche volta.
No, ho chiesto conferma qualche volta.
Spazio e figure
SCHEDA SPECIFICA
PER LA VERIFICA DI PAG. 274
SCHEDA SPECIFICA PER LA VERIFICA DI PAGG. 286-287 Spazio
Dopo la verifica
Ora che hai svolto la verifica…
Come ti senti?

Felice: penso di non aver fatto errori, o quasi...!
Tranquillo/a: sono riuscito/a a rispondere quasi a tutto
Un po’ agitato/a: non sono sicuro/a di ciò che ho scritto.
A quali esercizi pensi di aver risposto meglio?
A quelli sulla classificazione (1, 2, 3) Alle equivalenze (4) A quelli sull’area (5 e 7)
Avevi già svolto esercizi simili? (SITUAZIONE NOTA/NON NOTA)
Sì, non ho trovato niente di nuovo. No, mi sono trovato/a in difficoltà.
Avevi già svolto esercizi simili? (SITUAZIONE NOTA/NON NOTA)
Sì No, ho dovuto ricordare ciò che avevo studiato. Non lo so, sono confuso/a.
Sei riuscito/a a rispondere da solo/a? (AUTONOMIA)
Sì, non ho chiesto aiuti.
L’insegnante mi ha dato qualche consiglio.
Dopo la verifica
Ora che hai svolto la verifica…
Come ti senti?
No, ho chiesto conferma qualche volta.
Felice: penso di non aver fatto errori, o quasi...!
Quello sulla classificazione (1)
Tranquillo/a: sono riuscito/a a rispondere quasi a tutto.
Un po’ agitato/a: non sono sicuro/a di ciò che ho scritto.
Quali esercizi pensi di aver risolto meglio?
Calcolo del perimetro (2) Equivalenze (3) Calcolo dell’area (4)
Avevi già svolto esercizi simili? (SITUAZIONE NOTA/NON NOTA)
Sì, non ho trovato niente di nuovo. No, mi sono trovato/a in difficoltà.
Avevi già svolto esercizi simili? (SITUAZIONE NOTA/NON NOTA)
Sì No, ho dovuto ricordare ciò che avevo studiato. Non lo so, sono confuso/a.
Sei riuscito/a a rispondere da solo/a? (AUTONOMIA)
Sì, non ho chiesto aiuti.
L’insegnante mi ha dato qualche consiglio.
No, ho chiesto conferma qualche volta.
NOME E COGNOME DATA CLASSE

SCHEDA SPECIFICA PER LA VERIFICA DI PAGG. 298-299
Dopo la verifica
Ora che hai svolto la verifica… Come ti senti?
Felice: penso di non aver fatto errori, o quasi...!
Il primo.
Tranquillo/a: sono riuscito/a a rispondere quasi a tutto
Un po’ agitato/a: non sono sicuro/a di ciò che ho scritto.
Quali esercizi pensi di aver risolto meglio?
Avevi già svolto esercizi simili? (SITUAZIONE NOTA/NON NOTA)
Sì, non ho trovato niente di nuovo. No, ho dovuto riflettere molto.
Sei riuscito/a a rispondere da solo/a? (AUTONOMIA)
Sì, non ho chiesto aiuti.
L’insegnante mi ha dato qualche consiglio.
No, ho chiesto conferma qualche volta. No, ho chiesto molti aiuti perché ero in difficoltà.
Prima della prova
Stai per metterti alla prova con statistica e probabilità…
Come ti senti?

Felice
Tranquillo/a
Un po’ agitato/a
Preoccupato/a
Qual è o quali sono gli argomenti nei quali ti senti più competente?
Indagine statistica
Diagrammi
Probabilità
Qual è o quali sono gli argomenti nei quali ti senti meno competente?
Indagine statistica
Dopo la verifica
Ora che hai svolto la verifica…
Felice: penso di non aver fatto errori, o quasi...!
Diagrammi
Probabilità
Indagine statistica
Indagine statistica
Come ti senti?
Tranquillo/a: sono riuscito/a a lavorare abbastanza bene.
Un po’ agitato/a: non sono sicuro/a del mio lavoro.
Quale/i esercizio/i hai trovato più facile/i?
Diagrammi
Preoccupato/a: penso di aver fatto molti errori.
Probabilità
Quale/i esercizio/i hai trovato più difficile/i?
Diagrammi
Probabilità
Avevi già svolto esercizi simili? (SITUAZIONE NOTA/NON NOTA)
Sì, non ho trovato niente di nuovo. No, ho dovuto pensare molto per capire come risolverli.
Sei riuscito/a a fare tutto da solo/a? (AUTONOMIA)
Sì, non ho chiesto aiuti. L’insegnante mi ha dato qualche suggerimento. No, l’insegnante mi ha aiutato a ragionare e poi ho capito come risolverlo.
No, ho chiesto molti aiuti perché ero in difficoltà.
Schede di Matematica

• Schede multilivello
•Compiti autentici
•Verso la Prova INVALSI
NOME E COGNOME DATA CLASSE
PROBLEMI 1
1 Leggi il testo del problema, analizza i dati e cancella con una X il dato inutile. Poi risolvi. Nella scuola di Michela ci sono 5 classi. I maschi sono 210, mentre le femmine sono 235. Qual è il numero totale degli alunni?
Dati = =
Operazione

Risposta
2 Leggi il testo del problema, sottolinea il dato nascosto e scrivi i dati. Poi risolvi. Il cartolaio ha comperato una dozzina di pacchi di quaderni a righe. Ogni pacco costa 6 euro. Quanto ha speso in tutto il cartolaio?
Dato nascosto =
Altro dato =
Operazione
Risposta
NOME E COGNOME DATA CLASSE
PROBLEMI 2
1 Leggi il testo del problema, scrivi i dati e completa il diagramma. Poi risolvi. La mamma ha comperato 2 confezioni di uova che costano € 1,85 a confezione. Quanto spende in tutto? Paga con una banconota da 10 euro. Quanto riceve di resto?
Dati = = =
Diagramma
Operazioni
Risposte
2 Leggi il testo del problema e scrivi la domanda nascosta. Poi completa il diagramma e risolvi. Le classi quarte della scuola di Samir sono andate a teatro. Gli alunni della 4a A sono 22, quelli della 4a B sono 18 e quelli della 4a C sono 20. Il biglietto costava 8 euro. Quanto hanno speso in tutto le tre classi quarte?
Domanda nascosta
Diagramma
Operazioni
Risposta
NOME

PROBLEMI 1
1 Segui le indicazioni e risolvi il problema.
L’album delle figurine dei calciatori di Mattia ha 46 pagine. Mattia ha già incollato 52 figurine sull’album e ha anche 20 figurine doppie. Quante figurine ha in tutto Mattia?
• Analizza i dati.
46 = 52 = 20 =
• Sottolinea la domanda nel testo e riscrivila qui sotto.
• Completa il ragionamento.
Devo trovare quante figurine ha in tutto Mattia: la parola chiave “in tutto” mi fa capire che devo aggiungere le figurine già incollate a quelle
• Indica con una X qual è il dato inutile.
46 pagine 52 figurine sull’album 20 figurine doppie
• Utilizza i dati utili per fare l’operazione.
• Completa la risposta. Mattia ha in tutto
Un dato è inutile quando non serve a risolvere un problema.
2 In ogni problema il dato nascosto è sottolineato. Osservalo e poi indica con una X qual è l’operazione che risolve il problema.
a. Maria ha 8 anni. Sua sorella Caterina ha il doppio degli anni di Maria. Quanti anni ha Caterina?
8 × 3 = 24
8 × 2 = 16
8 × 5 = 40
OBIETTIVI: Risolvere problemi
b. In un vaso c’è una dozzina di rose. Quanti fiori ci sono in 2 vasi?
10 × 2 = 20
6 × 2 = 12
12 × 2 = 24
Un dato nascosto è una parola che sta al posto di un numero, come “metà”, “paio”, “dozzina” ecc.
c. Ieri un atleta ha corso per 5 km in allenamento. Oggi si è allenato correndo il triplo di ieri. Quanti chilometri ha percorso oggi?
5 × 3 = 15
5 × 4 = 20
5 × 2 = 10
NOME E COGNOME DATA
PROBLEMI 2
1 Risolvi il problema in due parti.
• Prima parte
La mamma oggi ha raccolto 250 punti del supermercato. Ne aveva già 300. Quanti punti ha in tutto?
Dati Operazione
250 = Risposta
300 =

• Seconda parte
Per prendere una coppia di piatti, la mamma deve raccogliere 780 punti. Quanti punti le mancano?
Dati
Il risultato che hai trovato nella prima parte del problema serve a risolvere la seconda parte.
Operazione
= punti che la mamma ha in tutto = Risposta
2 Indica con una X qual è la domanda nascosta in ogni problema.
a. All’inizio della settimana in un supermercato è arrivato un rifornimento di pasta. In tutto c’erano 100 scatoloni contenenti ciascuno 12 pacchi di pasta. Alla fine della settimana sono rimasti sugli scaffali 18 pacchi di pasta.
Quanti pacchi sono stati venduti?
Domanda nascosta
Quanti pacchi di pasta sono arrivati in tutto?
Quanti pacchi di pasta c’erano in ogni scatolone?
A volte in un problema c’è una domanda nascosta: scoprila e risolverai il problema.
b. Nella scuola di Liù ci sono 230 maschi e 252 femmine. Oggi sono andati a teatro 180 alunni. Quanti alunni sono rimasti a scuola?
Domanda nascosta
Quanti sono gli alunni delle classi quarte?
Quanti sono gli alunni in tutto?
OBIETTIVI: Risolvere problemi utilizzando gli strumenti della Matematica.
NOME

I PROBLEMI
1 Disegna il diagramma ed esegui le operazioni in riga e in colonna per risolvere il problema. Ieri al cinema Arlecchino sono stati venduti 125 biglietti per lo spettacolo del pomeriggio e 233 biglietti per quello della sera. Il costo del biglietto è di 6 euro. Qual è stato l’incasso totale?
Dati = = = Diagramma
Operazioni
Risposta
OBIETTIVI: Risolvere problemi utilizzando gli strumenti della Matematica e mantenendo il controllo sul processo risolutivo.
NOME E COGNOME DATA
NUMERI
1 Scrivi i seguenti numeri in cifre. tremilaquattrocento = seimiladuecentosedici = quattromilacentonove = dodicimilaseicentocinquanta = trecentosettantamila = novecentoduemilaseicentotrenta =
2 Scrivi i seguenti numeri in lettere.
309 = 8 620 = 21 038 = 312 000 =
3 In ogni numero sottolinea la cifra delle decine di migliaia e cerchia quella delle decine semplici.
•
4 Componi i seguenti numeri.
9 uk 7 h 6 da 1 u =
1 dak 1 uk 2 h 3 da 1 u =
8 uk 6 h 8 da =
5 Completa con i segni > o <. 5 099 5 909 1 001 989 36 212 36 122 726 000 762 000
650 412 650 421 81 130 18 000
6 Completa la tabella.
7 Riscrivi i numeri in ordine decrescente. 8 Scrivi i numeri compresi fra 10990 e 11012. 890 • 3 400 • 2 712 • 999 • 10 348 10 990, 500 • 6 780 , 11 012.
NUMERI
1 Collega con una freccia ogni numero in parola al numero in cifre corrispondente. cinquemilaottocentosedici 899
ottocentonovantanove
ottomilatrecentonove
tremilacentocinquantadue
duemilanovecento
2 Indica il valore delle cifre sottolineate in ogni numero.
496 270 500 981 59 601 3 548 51 627
3 Scomponi i seguenti numeri.
597 = 8 304 =
4 811 = 27 102 = 9 033 = 8 150 =
4 Riscrivi i numeri in ordine crescente, cioè dal minore al maggiore.
3 152
2 900
5 816
8 309
Il valore di una cifra dipende dalla sua posizione nel numero.
hk = centinaia di migliaia dak = decine di migliaia
uk = unità di migliaia
h = centinaia
da = decine
u = unità

5 Completa con i segni > o <. > = maggiore < = minore
3 500 978 710 560 819 891
3 838 4 838
5 360 5 390
1 780 1 708
5 800 5 900
OBIETTIVI: Leggere, scrivere, confrontare e ordinare i numeri naturali.
6 Completa la tabella.
precedente = viene prima successivo = viene dopo
precedente numero successivo 764 899
3 568
7 409
9 510
NOME E COGNOME DATA CLASSE
NUMERI
1 Scrivi i seguenti numeri in cifre. quattromilatré = duecentomiladiciannove = centounmilacentonove = centosedicimilaventiquattro = settantamilatrentasei = seicentomilaotto =
2 Componi i numeri.
8 uk 9 h 1 da = 3 dak 1 uk 8 da 6 u = 5 dak 4 uk = 1 hk 2 dak 4 h 8 da = 6 hk 4 uk 9 h 7 u = 3 hk 8 dak 5 uk =
3 Riscrivi i seguenti valori in ordine crescente.

4 Completa le operazioni. Fai attenzione al valore richiesto!
4 uk + 2 uk = h 7 h + 5 h = u 3 uk + uk = 50 h 30 da + 8 da = u 4 h + h = 800 u 50 u + u = 8 da
5 dak − 3 dak = h 35 h − 15 h = uk 9 da − da = 30 u
5 Completa le relazioni con > oppure <.
6 Completa ogni relazione con un numero adatto.
5 800 > 9 000 < 49 701 > 285 999 < 2 701 < 51 678 > 56 009 > 940 607 <
7 Indica la relazione esistente tra un numero e l’altro, poi completa la serie di numeri.
1 5 9
La relazione è:
OBIETTIVI: Leggere, scrivere, confrontare e ordinare i numeri naturali.
ADDIZIONI E SOTTRAZIONI 1
1 Esegui le addizioni con la prova.
Prova Prova
345174+ 580216+ 123013= 358964=
2 Esegui le sottrazioni con la prova.
Prova Prova
398740– 834618–74026= 240327=
3 Calcola a mente.

4 Completa le tabelle.
NOME

ADDIZIONI E SOTTRAZIONI 2
1 Applica la proprietà associativa ed esegui le addizioni.
30 + 70 + 18 =
125 + 25 + 31 =
205 + 5 + 18 + 2 =
1 500 + 300 + 26 + 14 =
2 Applica la proprietà dissociativa ed esegui le addizioni.
948 + 12 =
651 + 219 =
3 600 + 117 =
2 700 + 3 385 =
3 Applica la proprietà invariantiva ed esegui le sottrazioni.
209 − 39 =
175 − 55 =
1 477 − 207 =
2 398 − 108 =
4 Completa gli schemi.
ADDIZIONI E SOTTRAZIONI 1
1 Esegui le addizioni con la prova.
Per fare la prova dell’addizione devi applicare la proprietà commutativa. Infatti se cambi l’ordine degli addendi il risultato non cambia.
Prova Prova
3243+ + 580216+ + 2155= = 358964= =
Prova Prova 157230+ + 84300+ + 23161= = 15927= =
2 Esegui le sottrazioni con la prova.
Per fare la prova della sottrazione devi utilizzare l’addizione, che è la sua operazione inversa.
Prova Prova 9584– + 8368– + 3510= = 5026= =
Prova Prova 58319– + 246308– + 16403= = 143295= =
3 Calcola le addizioni a mente.
+
=
4 Calcola le sottrazioni a mente.
− 50 =
=
ADDIZIONI E SOTTRAZIONI 2
1 Usa gli addendi sottolineati per applicare la proprietà associativa. Poi esegui le addizioni.
50 + 50 + 37 =
25 + 18 + 25 =
46 + 130 + 70 =
250 + 93 + 250 =
1 600 + 400 + 66 =
4 300 + 118 + 200 =

Proprietà associativa
Se sostituisci due o più addendi con la loro somma, il risultato non cambia.
2 Applica prima la proprietà dissociativa e poi quella associativa. Poi esegui le addizioni.
+ 70 =
50 + 20 =
20 =
+ 30 =
Proprietà dissociativa
Se sostituisci uno o più addendi con la loro scomposizione, il risultato non cambia.
+ 102 =
3 Aggiungi o togli il numero nell’etichetta per applicare la proprietà invariantiva. Poi esegui le sottrazioni.
– 28 = + 2
Proprietà invariantiva
Se aggiungi o sottrai lo stesso numero al minuendo e al sottraendo, il risultato non cambia.
– 289 = + 11
4 Indica con una X quale proprietà è stata applicata nella seguente addizione.
565 + 235 = 565 + 35 + 200 = 800
proprietà associativa proprietà dissociativa proprietà invariantiva
OBIETTIVI: Eseguire addizioni e sottrazioni a mente con i numeri naturali applicando le proprietà.
ADDIZIONI E SOTTRAZIONI
1 Completa le operazioni con i numeri mancanti.

2 Esegui le operazioni a mente e completa. 211 +
3 Indica con una X quale operazione dà come risultato 15 600.
4 Completa le addizioni con i numeri mancanti.
5 Completa le sottrazioni con i numeri mancanti. 8
MOLTIPLICAZIONI E DIVISIONI 1
1 Esegui le moltiplicazioni con la prova.

2 Esegui le divisioni con la prova.
3
3 Completa le tabelle.
4 Esegui le divisioni a mente.
NOME E COGNOME
MOLTIPLICAZIONI E DIVISIONI 2
1 Scrivi sotto ogni moltiplicazione quale proprietà è stata applicata. associativa • dissociativa • distributiva
5 × 18 = 39 × 50 × 2 =
(50 − 11) × 2 =
5 × 2 × 9 = 39 × (50 × 2) = (50 × 2) − (11 × 2) =
10 × 9 = 90 39 × 100 = 3 900
− 22 = 78
2 Applica la proprietà invariantiva ed esegui le divisioni.
490 : 70 =
250 : 5 =
180 : 90 =
800 : 20 =
3 Esegui le operazioni a mente e completa. : 10 400 : 2 × 5 × 4 :
: 9 81 × 10 × 2 : 10 × 3
4 Cerchia i multipli di 9. 16 18 60 27 99 29 81 49 45 900 34
5 Sottolinea i divisori di 40. 39 10 1 25 2 3 5 15 8 100 20
6 Scrivi i multipli di 6 compresi fra 10 e 45.
7 Scrivi tutti i divisori di 30.
8 Indica con una X i numeri primi.
OBIETTIVI: Eseguire
MOLTIPLICAZIONI E DIVISIONI 1
1 Esegui le moltiplicazioni con la prova.
Prova

Prova
Per fare la prova della moltiplicazione devi applicare la proprietà commutativa Infatti se cambia l’ordine dei fattori il risultato non cambia.
2 Esegui le divisioni con la prova.
Prova
Prova
Per fare la prova della divisione devi usare la moltiplicazione, che è la sua operazione inversa.
Prova Prova
3 Indica con una X il risultato esatto.
4 Esegui le divisioni.
MOLTIPLICAZIONI E DIVISIONI 2
1 Indica con una X quale proprietà è stata applicata nella seguente moltiplicazione.
20 × 5 × 80 = (20 × 5) × 80 = 100 × 80 = 8 000 proprietà commutativa proprietà associativa proprietà dissociativa
2 Applica prima la proprietà dissociativa e poi quella associativa. Poi esegui le moltiplicazioni.
Proprietà dissociativa
Se sostituisci un fattore con due fattori che hanno come prodotto il fattore sostituito, il risultato non cambia.
3 Applica la proprietà invariantiva ed esegui le divisioni.
490 : 70 = (490 : 10) : (70 : 10) = : =
250 : 5 =
180 : 90 =
800 : 20 =
4 Osserva le operazioni e riscrivi i risultati negli insiemi, al posto adatto.
7 × 4 = 28 30 : 6 = 5 (resto 0) 30 : 5 = 6 (resto 0)
7 × 9 = 63 30 : 10 = 3 (resto 0) 7 × 10 = 70
7 × 5 = 35 30 : 2 = 15 (resto 0) 5 × 5 = 25
Proprietà associativa
Se sostituisci due o più fattori con il loro prodotto, il risultato non cambia.
Proprietà invariantiva
Se dividi o moltiplichi il dividendo e il divisore per uno stesso numero, il risultato non cambia.
I multipli di un numero si ottengono moltiplicando un numero per qualunque altro numero.
OBIETTIVI: Eseguire moltiplicazioni e divisioni a mente con i numeri naturali applicando le proprietà. • Individuare multipli e divisori di un numero.
I divisori di un numero sono tutti i numeri che lo dividono esattamente, senza resto.
MOLTIPLICAZIONI E DIVISIONI
1 Completa le operazioni con i numeri mancanti.
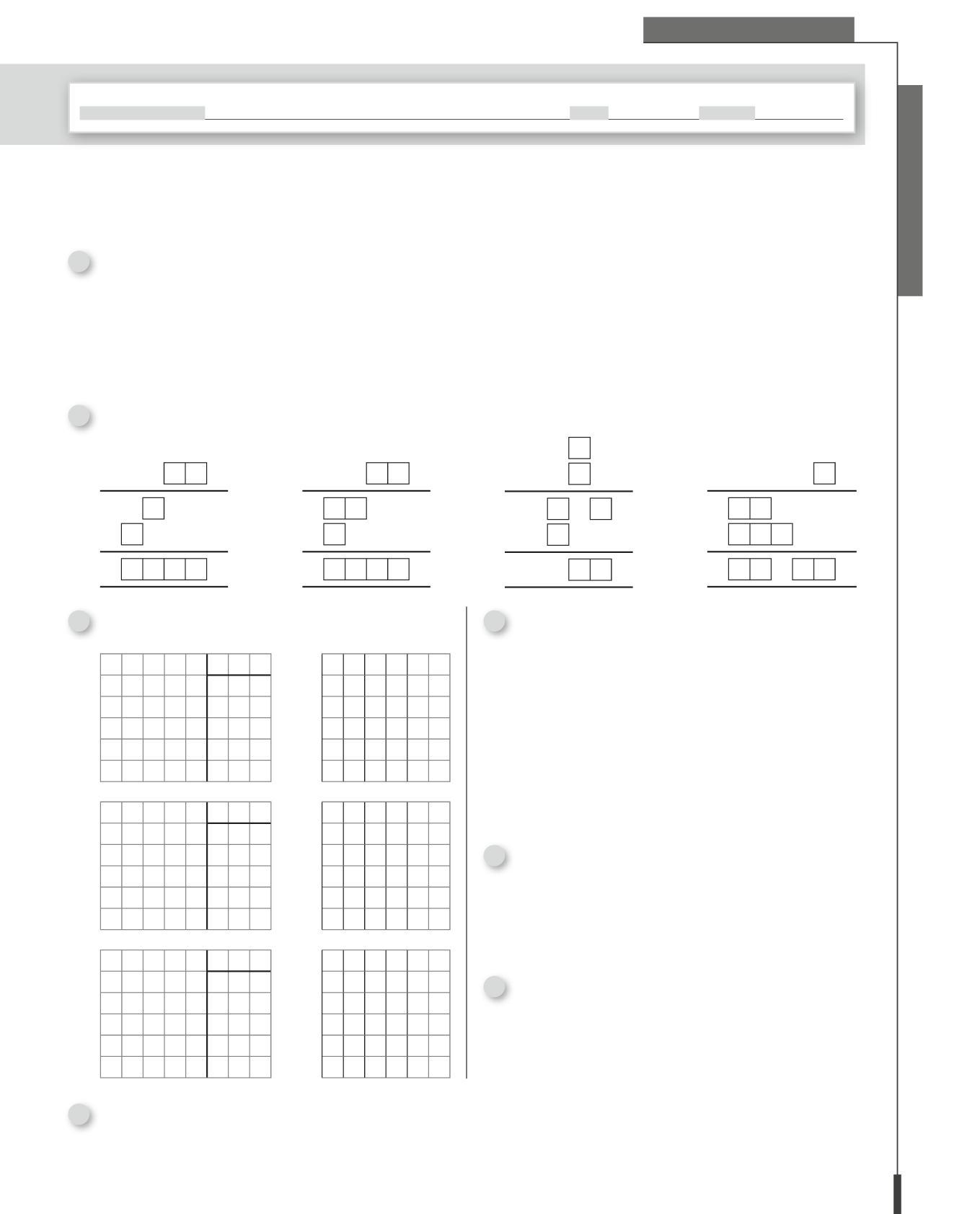
2 Completa le moltiplicazioni con i numeri mancanti e scrivi il risultato.
3 Esegui le divisioni con la prova. Prova
25806 33
4 Scrivi 10, 100, 1 000 per completare le operazioni. a. 65 × = 65 000 b.
Prova
34888 56
Prova
13689 27
5 Completa le operazioni con i numeri mancanti.
a. × 100 = 81 000 b. : 10 = 730 × 10 = 9 010 : 1 000 = 62 × 1 000 = 68 000 : 100 = 96
6 Scrivi i numeri multipli di 4 e i divisori di 3 compresi fra 40 e 60.
• Multipli di 4:
• Divisibili per 3:
7 Scrivi cinque numeri primi maggiori di 50 e minori di 100.
Eseguire
1 Colora le frazioni come indicato.
FRAZIONI 1
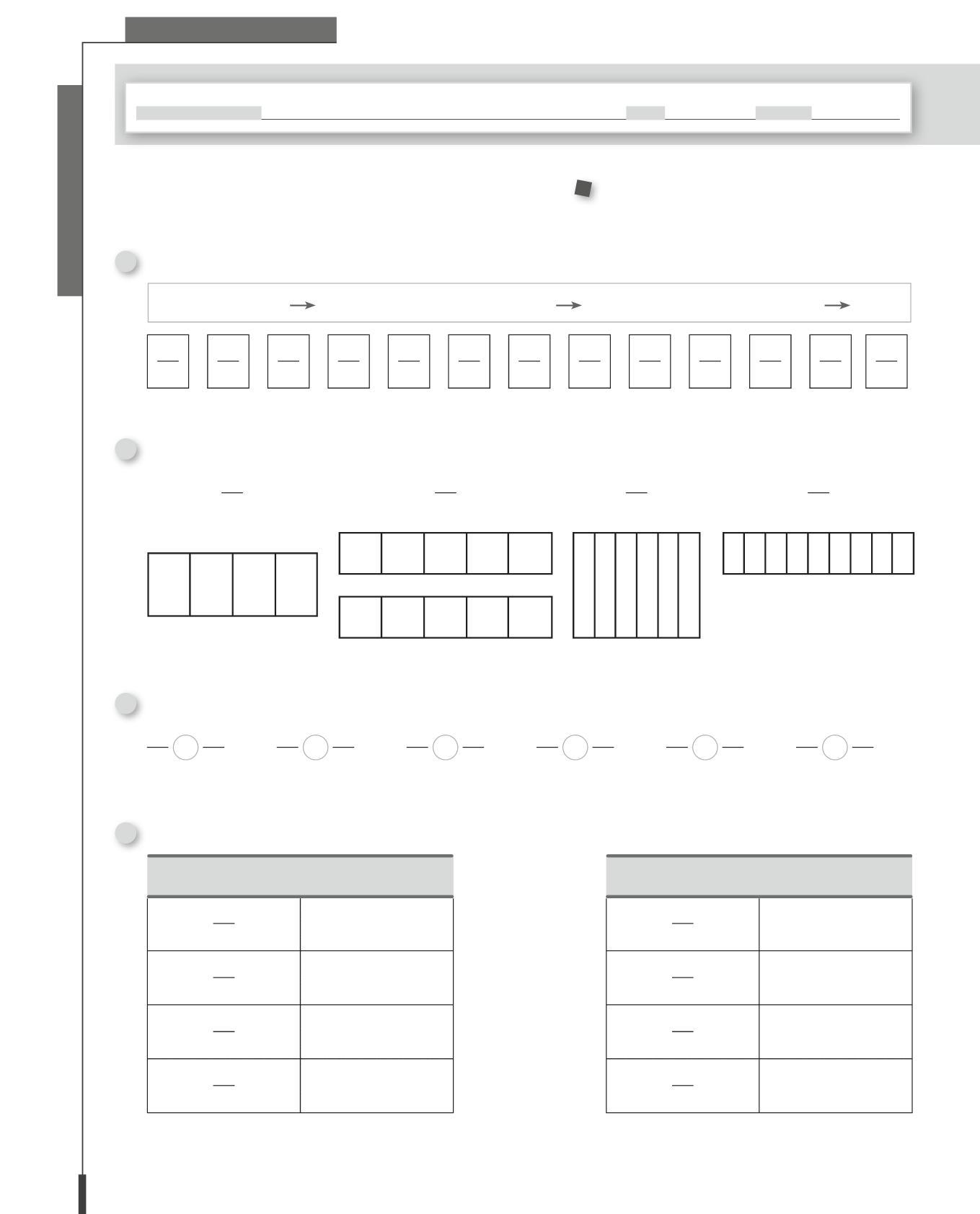
2 Colora le frazioni indicate.
3 Confronta ogni coppia di frazioni e scrivi >, < oppure =.
4 Per ogni frazione indicata scrivi quella complementare.
OBIETTIVI: Riconoscere frazioni proprie, improprie, apparenti. • Confrontare frazioni. • Calcolare la frazione complementare.
NOME E COGNOME DATA
FRAZIONI 2
1 In ogni gruppo riscrivi le frazioni in ordine crescente.
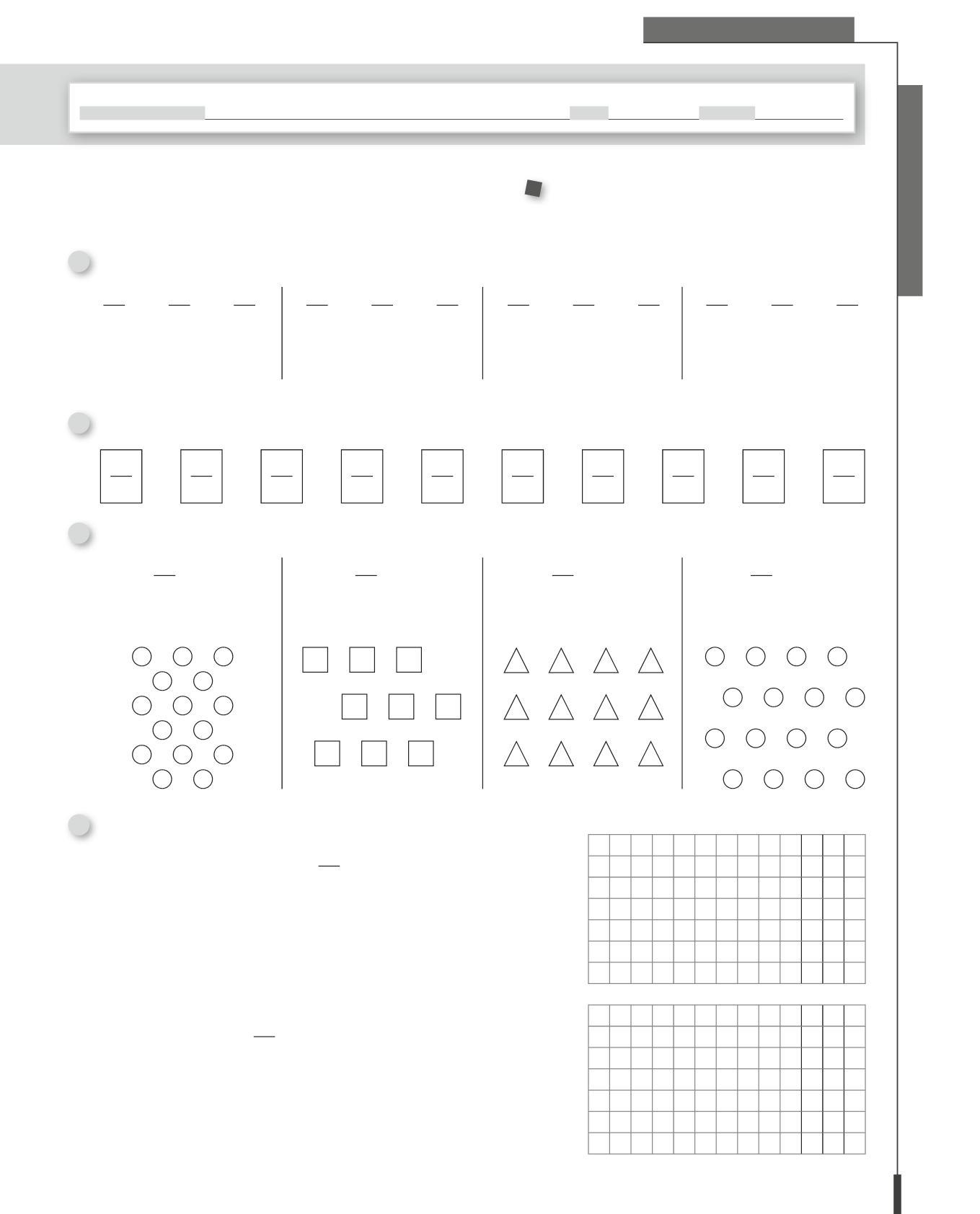
2 Colora allo stesso modo le frazioni equivalenti.
3 Calcola il valore di ogni frazione. Poi colora la quantità corrispondente. 1 5 di 15 2 3 di 9 5 6 di 12 3 8 di 16
4 Risolvi i problemi.
a. Martina ha 12 pennarelli. 1 4 dei pennarelli non scrive più. Quanti pennarelli sono? E quanti sono i pennarelli che la bambina può ancora usare per colorare?
Risposte
b. Paolo colleziona macchinine e vorrebbe arrivare ad averne 50. Ne ha 3 5 di 50.
Quante macchinine possiede?
Quante gliene mancano per completare la collezione?
Risposte
OBIETTIVI: Confrontare e ordinare frazioni. • Calcolare il valore di una frazione. • Risolvere problemi con le frazioni.
1
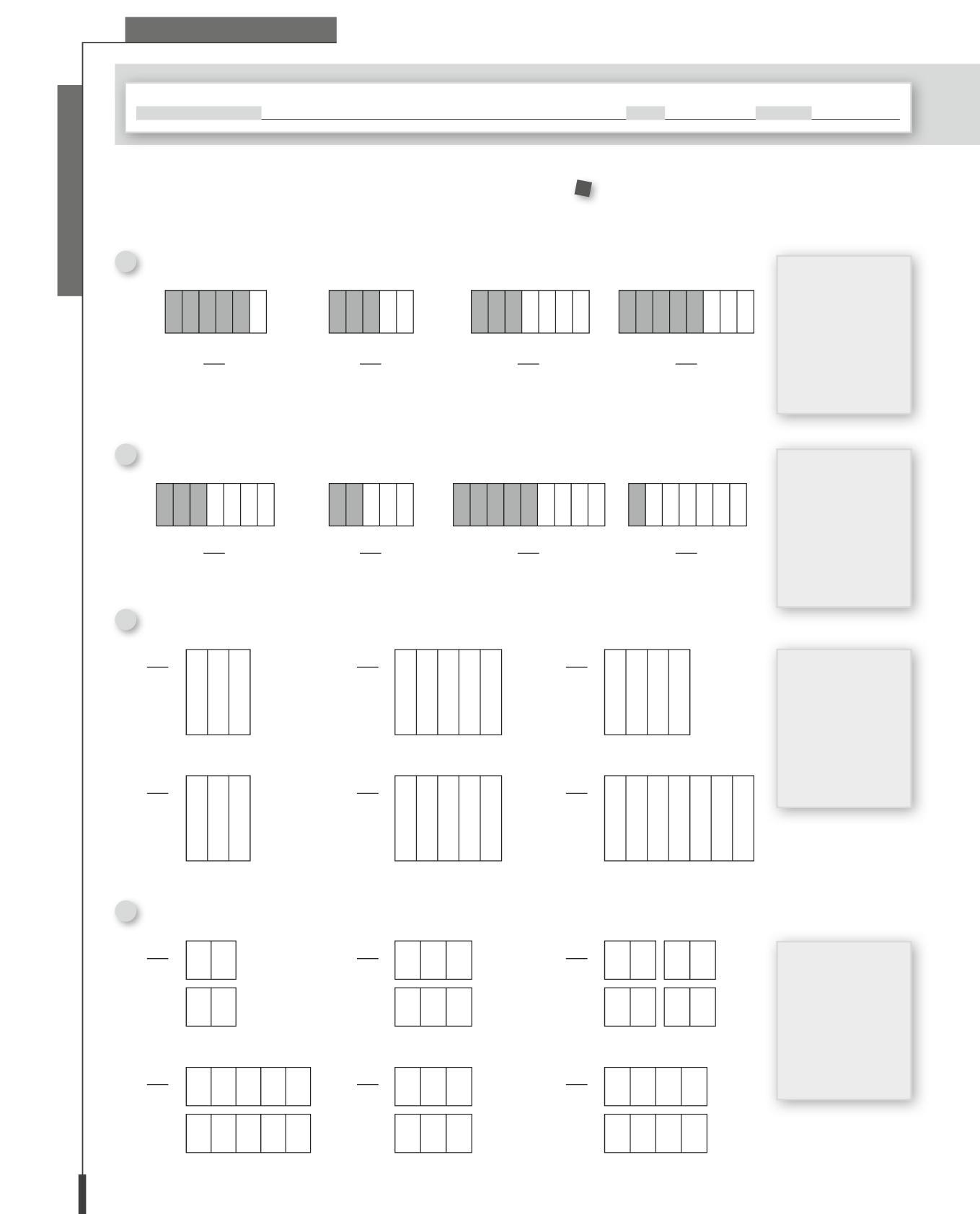
2
FRAZIONI 1
Il numeratore è scritto nella parte superiore della frazione e indica quante parti dell’intero sono da considerare. Il denominatore è scritto nella parte inferiore della frazione e indica in quante parti uguali è stato diviso l’intero.
La frazione propria indica una parte più piccola dell’intero e ha il numeratore minore del denominatore.
La frazione impropria indica una parte più grande dell’intero. Il numeratore è maggiore del denominatore.
NOME E COGNOME
FRAZIONI 2
1 Scrivi le frazioni apparenti illustrate, come nell’esempio. 4 4 = 1 = 2 = =
2 Collega ogni frazione alla figura che la rappresenta.
La frazione apparente è un intero. Il numeratore è uguale al denominatore oppure è un multiplo del denominatore.
3 Confronta le frazioni e scrivi > oppure <.
Due frazioni hanno lo stesso denominatore?
È maggiore la frazione con il numeratore maggiore.
Due frazioni hanno lo stesso numeratore?
È maggiore la frazione con il denominatore minore. 3 4
4 Indica con una X il disegno che corrisponde alla situazione descritta.
Ci sono 8 quadratini e ne coloro 1 4
FRAZIONI

1 Scrivi tre frazioni in ogni riquadro.
frazioni proprie frazioni improprie frazioni apparenti
2 Scrivi la frazione complementare e completa.
3 Calcola il valore di ogni frazione. 1 3 di 15
4 Risolvi i problemi.
a. La classe di Andrea è composta da 25 bambini. Per la festa del suo compleanno Andrea invita i suoi 24 amici. 2 3 arrivano prima delle 16:00. Quanti sono i bambini in ritardo?
Risposta b. In una scatola ci sono 20 cioccolatini assortiti. I bambini decidono di tenere da parte 1 5 dei cioccolatini per la maestra. Quanti sono i cioccolatini che rimangono da mangiare?
Risposta
NOME E COGNOME
NUMERI DECIMALI 1
1 Scomponi i seguenti numeri decimali. 4,569 = 23,512 = 465,569 = 129,74 = 0,451 = 64,109 =
2 Completa con >, < oppure =.
3 In ogni gruppo cerchia il numero maggiore e sottolinea quello minore.
4 Scrivi i numeri in colonna ed esegui le addizioni.
5 Scrivi i numeri in colonna ed esegui le sottrazioni.
−
NOME E COGNOME DATA CLASSE
NUMERI DECIMALI 2
1 Scrivi i numeri in colonna ed esegui le moltiplicazioni.
275 × 3,4 = 58,6 × 75 = 905,3 × 2,2 = 76,63 × 12,6 = 30,951 × 308 =
2 Esegui le moltiplicazioni.
67,2 × 10 = 0,84 × 100 = 1,27 × 1 000 = 17,3 × 100 = 3,2 × 1 000 = 19,77 × 10 = 6,8 × 100 = 0,891 × 1 000 = 28,36 × 100 = 1,1 × 1 000 = 5,563 × 10 = 9,688 × 100 =
3 Esegui le divisioni con divisore decimale in colonna.
486,97:2,2= 978,81:4,2= 9585 :0,45= × × × × × ×
4 Dividi per 10, 100, 1 000. : 10
OBIETTIVI: Eseguire moltiplicazioni in colonna e a mente con i numeri decimali. • Eseguire divisioni in colonna e a mente con i numeri decimali.
NUMERI DECIMALI 1
1 In ciascun numero sottolinea la parte intera e cerchia la parte decimale. 750,321 39,685 1 538,86 0,591 178,9 8,07 16,659 2 680,5
2 Scrivi i seguenti numeri decimali in cifre. venticinque virgola sette centotrentadue virgola ottantasei dodici virgola trecentoundici zero virgola novantaquattro otto virgola seicentotredici
3 Collega con una freccia ogni numero in lettere al numero in cifre corrispondente.
unità e sette decimi
unità e nove decimi
zero unità e centosedici millesimi
4 Collega con una freccia ogni numero decimale alla sua scomposizione.
unità,decimicentesimimillesimi u , d c m 3,128 3 u 6 d 13,27 3 u 1 d 2 c 8 m 3,6 1 da 3 u 2 d 7 c
5 Esegui le operazioni in colonna. Aggiungi lo zero dove serve, come nell’esempio.
375,134+ 220,718+ 957,839– 836,58–123,25 0 = 348,24= 216,41= 401,526= parte interaparte decimale 185,454
OBIETTIVI: Leggere e scrivere numeri decimali. • Eseguire addizioni e sottrazioni in colonna con i numeri decimali.
NUMERI DECIMALI 2
1 Scrivi i numeri in colonna ed esegui le operazioni.
a. 425,312 + 480,334 = • 571,48 + 218,143 = • 368,9 + 305,126 =
b. 715,365 − 203,244 = • 876,549 − 456,32 = • 985,78 − 346,257 =

• Incolonna i numeri in base al valore posizionale di ogni cifra, mettendo la virgola sotto la virgola.
• Per facilitare il calcolo, pareggia il numero di cifre nelle parti decimali, aggiungendo gli zeri necessari.
2 Esegui le moltiplicazioni in colonna.
23,12× 172,3× 34,21× 252,1× 3= 1,4= 2,5= 3,3=
3 Esegui le divisioni in colonna.
169,968 5 7,2:5,2=86,51:4,1= ×10×10 ×10×10
• Non serve incolonnare le cifre secondo il valore posizionale.
• Esegui la moltiplicazione come se fosse con i numeri interi
• Nel risultato ci devono essere tante cifre decimali quante sono in tutto quelle dei due fattori.
• Se solo il dividendo è decimale, esegui come se la divisione fosse con i numeri interi; scrivi la virgola nel risultato quando inizi a dividere la parte decimale del dividendo.
• Se sia il dividendo sia il divisore sono decimali, applica la proprietà invariantiva in modo che il divisore diventi un numero intero.
OBIETTIVI: Eseguire le quattro operazioni in colonna con i numeri decimali.
NOME E COGNOME

NUMERI DECIMALI
1 Componi i seguenti numeri decimali.
3 da 4 u 9 c =
4 da 6 u 1 d 4 m =
2 Scrivi i numeri in colonna ed esegui le operazioni.
867,95 + 4 360 + 358,148 = 7 831 − 952,84 =
5 489,73 × 9,6 = 857,968 : 0,64 =
3 Calcola a mente.
a. 12,56 + 3,2 =
50,9 + 5,05 = 30,75 + 20,14 = 10,331 + 5,045 = 25,5 + 25,4 = 130,99 + 20,1 =
b. 20,7 − 10,4 =
50,46 − 8,3 = 9,54 − 0,14 =
30,6 − 5,2 =
100,98 − 50,3 =
0,445 − 0,045 =
4 Completa le operazioni scrivendo 10, 100, 1 000.
a. 48,67 × = 4 867 17,592 × = 175,92 0,985 × = 985 65,3 × = 6 530 2,46 × = 24,6 66,85 × = 66 850 0,891 × = 89,1 13,1 × = 13 100 321,348 × = 3213,48 0,078 × = 0,78 35,9 × = 35 900 0,024 × = 24
b. 45,6 : = 4,56
5 689 : = 5,689
875,9 : = 8,759
1,5 : = 0,015
3 056 : = 3,056
5 350 : = 53,5
278 : = 0,278
45 : = 0,45
98,74 : = 9,874
76 910 : = 76,91
0,3 : = 0,03
54,1 : = 5,41
OBIETTIVI: Conoscere i numeri decimali. • Eseguire le quattro operazioni in colonna con i numeri decimali.
MISURE DI LUNGHEZZA, CAPACITÀ, MASSA
1 In ogni gruppo sottolinea la misura minore.

2 Completa le equivalenze con le misure di lunghezza. 8,27 m =
3 Completa le equivalenze con le misure di capacità.
4 Completa le equivalenze con le misure di peso (o massa).
kg = g
cg = dg
5 Scrivi le marche per completare le equivalenze. 13,65 dm = 1,365
km = 870
mm = 5,2 0,81 hℓ = 810
kg = 8 630
6 Risolvi il problema.
Una scatola piena di biscotti pesa 1,55 kg.
La scatola vuota pesa 3,9 hg.
Quanto pesano i biscotti?
Risposta 84 m 6 900 mm 2,5 km 5,6 Mg 897 hg 3 000 g
OBIETTIVI: Conoscere e utilizzare le principali misure di lunghezza, capacità e massa.
NOME E COGNOME
MISURE DI TEMPO E DI VALORE
1 Trasforma le seguenti misure di tempo. 2
= s

2 Calcola a mente e rispondi alle domande.
• Se mancano 15 minuti alle 9, che ore sono adesso?
• Un treno Frecciarossa parte da Roma alle 17:05 e arriverà a Napoli alle 18:15. Quanto tempo impiegherà per arrivare?
• Leila guarda un film alla televisione. Il film è iniziato alle 17:00 e dura 1 ora e 40 minuti. A che ora finirà?
3 Colora allo stesso modo le etichette che contengono misure equivalenti.
4 Completa la tabella.
5 Risolvi i problemi.
a. Un cartolaio ha venduto un astuccio a € 9,55. Se a lui era costato € 4,85, quanto ha guadagnato?
b. La mamma di Giovanni ha comperato 6 pacchi di pasta e ha speso € 8,52. Quanto costa un pacco di pasta?
Risposta
Risposta
NOME E COGNOME DATA CLASSE
MISURE DI LUNGHEZZA, CAPACITÀ, MASSA
1 In ogni misura sottolinea la cifra a cui si riferisce la marca.
765 cm 58,6 hm 27,345 m 0,88 km
2 569 g 3,75 kg 0,9 hg 28 dg
46,789 ℓ 13 daℓ 66 cℓ 19,57 hℓ
2 Per ogni domanda indica con una X la risposta esatta.
• Qual è la misura di lunghezza più piccola?
ettometro millimetro metro
• Qual è l’unità di misura della capacità?
decalitro decilitro litro
• Qual è la misura di peso più grande?
• Se la misura è rappresentata da un numero intero, la marca si riferisce all’ultima cifra.
• Se la misura è rappresentata da un numero decimale, la marca si riferisce all’ultima cifra prima della virgola
Megagrammo chilogrammo grammo
3 In ciascuna frase colora l’etichetta con l’unità di misura corretta.
• In una lattina l’aranciata si misura in ettolitri centilitri
• La lunghezza di un’autostrada si misura in chilometri metri
• Il peso di una sedia si misura in chilogrammi Megagrammi
• L’altezza di un palazzo si misura in decimetri metri
4 Per ogni equivalenza colora l’etichetta con il risultato esatto.
2
3 dag = 0,3 30 hg
OBIETTIVI:
g = 70 7 000 mg
NOME E COGNOME DATA CLASSE
MISURE DI TEMPO E DI VALORE
1 In ciascuna frase colora l’etichetta con l’unità di misura corretta.
• La durata del viaggio da Milano a Roma in treno si misura in giorni ore
• La durata del campionato di calcio si misura in mesi anni .
• La durata delle vacanze estive si misura in settimane decenni
• La durata di una gara dei 200 m si misura in minuti secondi .
2 Trasforma le seguenti misure di tempo.
120 s = min 60 s = min
1 min = s 3 min = s
60 min = h 180 min = h
24 h = d 48 h = d
3 d = h
4 d = h
3 Osserva, conta e scrivi il totale.
1 minuto (min) = 60 secondi (s) 1 ora (h) = 60 minuti (min) 1 giorno (d) = 24 ore (h)
4 Risolvi i problemi.
a. Il signor Carlo fa benzina e spende 35 euro. Paga con una banconota da 50 euro.
Quanto riceve di resto?
Operazione
Risposta
5 Completa la tabella.
spesa ricavo guadagno quaderno € 1,20 € 0,60
pastelli € 5,50 € 4,00
gomma € 1,10 € 1,50
OBIETTIVI: Conoscere
b. Marco riceve una mancia di 10 euro. Aveva già 12,50 euro.
Quanti soldi ha ora?
Operazione
Risposta
ricavo – guadagno = spesa ricavo – spesa = guadagno spesa + guadagno = ricavo
MISURE
1 Riscrivi le seguenti misure in ordine crescente.
• 731 m 7 km 73,1 hm 73 dam
• 9,55 hg 95 g 955 dag 9 500 dg
2 Riscrivi le seguenti misure in ordine decrescente.
• 98 ℓ 9,8 hℓ 988 mℓ 9,85 daℓ
3 Confronta le misure e scrivi >, < oppure =.
a. 65,2 dam 6,52 km 5
b. 75,68 ℓ 7 568 mℓ
c. 7,39 g 739 cg 3,5 kg
4 Completa la tabella. Esegui un’equivalenza quando è necessario.
peso lordo peso netto tara equivalenza barattolo di marmellata 372 g g 55 g
prosciutto cotto 120 g 111 g dg fette biscottate 473 g g 35 g cassetta di mele kg8,425 kg 245 g
5 Indica con una X se le frasi sono vere V o false F .
• In un anno ci sono 55 settimane. V F • In un secolo ci sono 100 anni. V F
• I mesi dell’anno sono 12. V F • Un millennio sono 5 secoli. V F
• 240 secondi formano 4 minuti. V F • 300 minuti formano 5 ore. V F
6 Risolvi il problema.
Un negoziante acquista 25 magliette a € 12,00 ciascuna. Le rivende e ricava
€ 464,75 in tutto. Quanto ha guadagnato complessivamente?

Risposta
NOME E COGNOME DATA
TRASFORMAZIONI GEOMETRICHE
1 Completa o disegna le figure in modo che siano simmetriche.
2 Esegui le traslazioni indicate dai vettori.
3 Fai un ingrandimento e una riduzione della figura in base alla scala indicata.
scala 2:1
scala 1:2
NOME
TRASFORMAZIONI GEOMETRICHE
1 Traccia l’asse di simmetria di ogni figura o coppia di figure.
2 Indica con una X in quale situazione è stata compiuta una rotazione.
90°
3 Completa la riduzione delle figure in base alla scala indicata.
scala 1:3
OBIETTIVI: Conoscere le trasformazioni geometriche: simmetria, traslazione, rotazione, riduzione.
scala 1:2
TRASFORMAZIONI GEOMETRICHE
1 In quale figura la simmetria non è corretta? Indicala con una X.

2 Esegui le rotazioni delle figure.
3 Esegui la riduzione della figura in scala 1:2.
NOME E COGNOME DATA CLASSE
LINEE, ANGOLI, POLIGONI, NON POLIGONI
1 In ogni gruppo, ripassa solo le linee parallele.

2 Completa gli angoli come indicato.
angolo retto angolo ottuso angolo acuto
3 Colora di blu i poligoni e di rosso i non poligoni.
4 Disegna i triangoli indicati.
triangolo rettangolo triangolo isoscele triangolo ottusangolo
5 Scrivi il nome di ogni poligono.
OBIETTIVI: Conoscere linee e angoli. • Conoscere poligoni e non poligoni.
NOME E COGNOME

POLIGONI: PERIMETRI E AREE
1 Esegui le seguenti equivalenze.
2 Calcola il perimetro e l’area delle seguenti figure.
AB = 20 m
BC = 26 m
CH = 24 m
P = m
A = m2
AB = 18,6 m
P = m
A = m2
AB = 36 m
BC = 20,3 m
P = m
A = m2
AB = 50 cm
BC = 47 cm
CD = 45 cm
DA = 40 cm
DH = 44 cm
= cm
= cm2
NOME E COGNOME DATA CLASSE
LINEE, ANGOLI, POLIGONI, NON POLIGONI
1 Ripassa solo le tre linee parallele.

2 Indica con una X le figure che rappresentano un poligono.
3 Collega ogni definizione al triangolo corretto.
Isoscele: due lati uguali.
Equilatero: tutti i lati uguali.
Rettangolo: un angolo retto.
Ottusangolo: un angolo maggiore di 90°.
Acutangolo: tutti angoli minori di 90°.
OBIETTIVI: Conoscere linee e angoli. • Conoscere poligoni e non poligoni. • Conoscere i triangoli.
I poligoni delimitano il piano con linee chiuse, spezzate, non intrecciate.
NOME E COGNOME

CLASSE
POLIGONI: PERIMETRI E AREE
1 Completa le equivalenze e inserisci la nuova misura nella tabella, come nell’esempio.
Per eseguire
5 m2 = 500 dm2
12 m2 = dm2
1 200 dm2 = m2
7 850 cm2 = m2
0,6 cm2 = mm2
65 m2 = dam2
2 Calcola il perimetro e l’area di ogni figura.
AB = 12 cm
BC = 11 cm
CA = 8 cm
CH = 7 cm
P = cm
A = cm2
AB = 7,2 cm
P = cm
A = cm2
AB = 25 cm
BC = 15 cm
P = cm
A = cm2
un’equivalenza dalla marca maggiore alla marca minore spostati di due caselle verso destra
Per eseguire
un’equivalenza dalla marca minore alla marca maggiore spostati di due caselle verso sinistra.
Perimetro = ℓ1 + ℓ2 + ℓ3
Area = (b × h) : 2
Perimetro = ℓ × 4
Area = (ℓ × ℓ)
Perimetro = (b + h) × 2 oppure (b × 2) + (h × 2)
Area = b × h
NOME E COGNOME

POLIGONI: PERIMETRI E AREE
1 Calcola il perimetro e l’area delle seguenti figure.
AB = 16,8 cm
AC = 24,5 cm
BD = 12,4 cm
P = cm
A = cm2
AB = 30 cm
BC = 24 cm
DH = 22 cm
P = cm
A = cm2
AB = 64 cm
BC = 42 cm
CD = 34 cm
CH = 34 cm
AD = cm
P = cm
A = cm2
2 Calcola e risolvi il problema.
Un tappeto rettangolare ha il lato maggiore di 2,9 m e il lato minore di 1,3 m. Sopra al tappeto viene messo un tavolino quadrato con il lato di 80 cm. Quanti metri quadrati misura la superficie calpestabile del tappeto?
Risposta
OBIETTIVI: Conoscere i triangoli. • Calcolare perimetri e aree dei quadrilateri.
NOME E COGNOME

RELAZIONI, DATI E PREVISIONI
1 Collega gli elementi dei due insiemi in base alle relazioni indicate.
rettili mammiferi
2 Classifica i mezzi di trasporto nel diagramma di Carroll: scrivi il loro nome al posto giusto.
monopattino automobile moto pullman quadriciclo bicicletta a motore non a motore
2 ruote
4 ruote
3 La tabella rappresenta il numero dei biglietti venduti durante la scorsa settimana in un teatro. Calcola la media.
lunedì martedì mercoledì giovedi venerdì sabato domenica
Media:
4 Indica con una frazione le probabilità di pescare i numeri della tombola indicati.
appartiene alla classe dei… 31
• Le probabilità di pescare un numero pari sono .
• Le probabilità di pescare un numero dispari sono
• Le probabilità di pescare un numero superiore a 50 sono
RELAZIONI, DATI E PREVISIONI
1 Indica con una X quale delle seguenti relazioni è sbagliata.
2 Classifica i numeri nel diagramma di Eulero-Venn.
67 5 84 90 101 16 49 78 26
3 L’istogramma rappresenta i piatti preferiti dagli alunni della 4a A. Osserva e completa le frasi con le seguenti parole.
lasagne • patatine fritte • pizza • polpette • riso mangia legge abita numeri minori di 50 numeri maggiori di 50 numeri
• Le hanno ottenuto il maggior numero di preferenze.
• Le e la hanno ottenuto lo stesso numero di preferenze.
• Il non ha ottenuto alcuna preferenza.
• Le hanno ottenuto solo due preferenze.
4 La tabella rappresenta il numero dei bambini assenti in una settimana nelle classi quarte della scuola Arcobaleno. Calcola la media. lunedì martedì mercoledì giovedi venerdì 12 15 18 11 14
Media: ( + + + + ) = : =
RELAZIONI, DATI E PREVISIONI
1 Scrivi sulla freccia qual è la relazione fra gli elementi dei due insiemi.
2 Classifica i numeri nel diagramma di Eulero-Venn.
8 9 12 16 24 27 32 33 36 40
3 Osserva la tabella di frequenza e l’ideogramma delle bottiglie d’acqua minerale vendute in un negozio di alimentari durante la settimana, poi completa dove è necessario.
lunedì 32
martedì mercoledì 74 giovedì
venerdì 96 sabato
Legenda = 10 bottiglie = 1 bottiglia
4 Disegna e colora le palline in modo che si verifichino le seguenti situazioni.
a. Le probabilità di pescare una pallina rossa sono 3 5
b. Non c’è nessuna probabilità di pescare una pallina verde. numeri multipli di 3 numeri multipli di 4 numeri multipli di 3 e 4
lunedì martedì mercoledì giovedì venerdì sabato a b
OBIETTIVI:
NOME
L’INFINITO E IL NASTRO DI MOEBIUS
Situazione iniziale
Dovete spiegare a un ’altra classe il concetto di infinito
Materiali
cartoncini • colla • pennarello
Seguite le istruzioni e costruite il nastro di Moebius.
Ritagliate una striscia rettangolare di cartoncino di 40 cm di lunghezza e 3 cm di larghezza.
Tenete ferma un’estremità della striscia e ruotate l’altra di 180°, come rappresentato. Poi incollate le due estremità.
Con un pennarello, tracciate una riga lungo tutto il nastro senza mai staccare la punta.
Che cosa succede?
Perché questo simbolo rappresenta il concetto di infinito? Discutetene in classe.
Quali altri esempi di infinito vi vengono in mente?
Situazione finale
Raccogliete le vostre idee e preparate una presentazione. Utilizzate il nastro di Moebius per spiegare il concetto di infinito.
NOME E COGNOME

LA GITA A TORINO
Situazione iniziale
Dovete organizzare il viaggio di istruzione al Museo Egizio di Torino
Materiali
fogli bianchi a quadretti • penne • matite
Prima di tutto, scegliete un giorno possibile per il viaggio, poi lavorate in gruppi di quattro e dividetevi i ruoli.
Due di voi dovranno cercare e confrontare gli orari e prezzi di pullman e treni.
Gli altri due si occuperanno di organizzare la visita al museo e di scegliere un laboratorio.
Ora confrontatevi: è necessario modificare qualcosa nelle scelte fatte da ogni coppia? Se sì, che cosa e perché?
Preparate una lettera da distribuire ai genitori con i dettagli della gita: orari, prezzi e come si svolgerà.
Usate la checklist e spuntate quello che avete già fatto.
mezzi di trasporto
Avete raccolto tutte le informazioni sui mezzi di trasporto disponibili nella vostra zona?
Avete confrontato i prezzi dei diversi trasporti disponibili?
Avete controllato gli orari dei mezzi nei giorni feriali?
Museo Egizio
Avete controllato il costo del biglietto d’ingresso al museo? C’è uno sconto per i gruppi?
Avete controllato il costo della visita guidata?
Avete controllato il prezzo e l’orario del laboratorio? Può interessare a tutti?
Situazione finale
Sistemate tutti i materiali e presentate il lavoro agli insegnanti. Ricordatevi di motivare le vostre scelte!
VERSO LA PROVA INVALSI

D1. Hanya alle 15:15 ha posteggiato la macchina in un garage a pagamento.
Prezzi parcheggio
1 ora € 3,00
Per ogni ora successiva € 1,00
All’uscita Hanya paga 6 euro. A che ora è andata via dal garage?
Risposta:
D2. Carlo esegue questa operazione con la calcolatrice:
2 768 – 564
Pigia un tasto sbagliato e digita 3 768 – 564.
Segna l’operazione che deve eseguire per correggere il risultato.
A. Sottrarre 100
B. Sommare 1 000
C. Sottrarre 1 000
B. Togliere 10
D3. Giovanni aveva 9 anni e 11 mesi il 15 gennaio 2016.
Quale età avrà il 15 febbraio 2017?
A. 11 anni e 0 mesi
B. 11 anni e 3 mesi
C. 10 anni e 11 mesi
D. 12 anni e 0 mesi
D4. Il peso totale dei cilindretti sui due piatti della bilancia è uguale.
I cilindretti del primo piatto pesano 8 kg e 3 kg. Quello grigio del secondo pesa 5 kg. Qual è il peso del cilindretto bianco?
A. 4 kg
B. 7 kg
C. 5 kg
D. 6 kg
D5. Osserva la figura.
Quanti triangoli vedi?
A. 4
B. 8
C. 3
D. 6
D6. Sulla confezione di un detersivo per bucato a mano da 600 m possiamo leggere: = 30 mℓ
30 mℓ 3 litri di acqua
50 mℓ 5 litri di acqua
a. Qual è la capacità di un solo tappo?
Risposta:
b. Quanti tappi puoi riempire con l’intera confezione?
Risposta:
c. Se riempi la bacinella con 8 litri di acqua, quanti millilitri di detersivo devi aggiungere?
Risposta:
D7. Disponi le tre cifre 5, 2 e 7 nei quadratini in modo da ottenere una addizione il cui risultato sia più vicino possibile a 80.

D8. Quanto può misurare la base di un quadernone di matematica?
A. 40 cm
B. 20 cm
C. 40 dm
D. 50 cm
D9. Per preparare gli arancini ti servono 1,7 kg di riso. Tra le confezioni disponibili quali devi scegliere?
400 g
500 g
A. Una confezione da 400 g e una da 500 g
B. Una confezione da 750 g e una da 500 g
C. Una confezione da 750 g e una da 1 000 g
D. Una confezione da 1 000 g e una da 400 g
750 g
1000 g
D10. Completa la figura in modo da ottenere un trapezio rettangolo.

D11. Osserva l’operazione:
100: = I pallini coprono numeri uguali. Quali?
Risposta: e
D12. Osserva la sequenza di rettangoli.
a. Colorane tre su quattro.
b. Potresti colorarne anche quattro su tre?
Sì
No
D.13 Annalisa, ricopiando il numero 344, ha scambiato tra loro le cifre delle centinaia e delle decine. Di quanto aumenta il valore del numero?
Risposta: di unità
Spiega come hai fatto a trovare la risposta.
D14. Osserva le due figure.
Hanno lo stesso perimetro?
Risposta:
D15. Indica qual è la metà di 2,50 euro.
A. 1,50 euro
B. 1,75 euro
C. 1,20 euro
D. 1,25 euro
D16. L’areogramma rappresenta l’andamento delle vendite di una fabbrica di moto in un anno.
Vendite
a. In quale trimestre è stato venduto il maggior numero di moto?
Risposta:
b. In quali trimestri le vendite sono state più basse?
Risposta:
D17. Osserva la tabella: inserisci nelle caselle giuste i seguenti numeri e segna la risposta corretta.
5 18 24 26 35
Multipli di 3 Multipli di 5
A. Non è possibile inserire tutti i numeri
B. Una casella rimane vuota
C. Un numero si trova in tutte e due le caselle
D. Il numero 18 si trova nella seconda casella
D18. Un gruppo di amici guarda il menu di una pizzeria.
Menu
Margherita
Capricciosa
Diavola
Rucola e parmigiano
Tricolore
D19. Osserva le figure.
€ 5
€ 6
€ 6
€ 6,50
€ 5
Ognuno di essi sceglie una pizza: una tricolore, una rucola e parmigiano e tre capricciose.
a. Quanti sono gli amici?
Risposta:
b. Quanto pagheranno in tutto?
Risposta:
1
Quale non ha assi di simmetria?
Risposta:
2
3
D20. Segna il numero che più si avvicina a 100.
A. 0,100
B. 99,9
C. 100,01
D. 100,09
D21. Scegli fra gli oggetti quello che può essere alto 80 cm.
A. una bottiglia
B. un banco
C. un cancello
D. un bicchiere
D22. Quale alternativa non indica ventimilaquattrocentotré?
A. 20 403
B. 2 × 10 000 + 4 × 100 + 3
C. 2 × 10 000 + 4 × 100 + 3 × 10
D. 20 migliaia e 403 unità
D23. Osserva i tre quadrilateri e completa la tabella. Metti una crocetta per ogni riga.
a. I tre quadrilateri hanno lo stesso perimetro
b. I tre quadrilateri hanno la stessa area
c. L’area del quadrato è minore dell’area dei rettangoli
D24. Un rigatone di pasta pesa 4,5 g.
a. In una porzione da 90 g quanti sono i rigatoni?
A. 45
B. 15
C. 20
D. 25
b. Quanti rigatoni contiene un pacco da un chilogrammo?
A. 200 circa
B. 230 circa
C. 222 circa
D. 250 circa

D25. Le torte che vedi in figura sono di peso diverso; vengono divise in porzioni da 120 g circa.
1,200 kg
kg
a. Quante porzioni si potranno ricavare dalla torta che pesa 1,200 kg ?
Risposta: porzioni
b. Da quale torta si ottengono più porzioni?
Risposta: dalla torta che pesa kg.
kg
D26. In una confezione di zuppa di riso e lenticchie, trovi scritto “da consumarsi preferibilmente entro il 18 febbraio 2023”. Oggi è il 20 dicembre 2022, entro quanti giorni bisogna cucinare la zuppa?
Risposta: giorni
D27. In una classe 4a la maestra ha chiesto alle alunne e agli alunni quale materia ritengono più difficile.

a. Quanti sono gli alunni e le alunne della classe?
Risposta:
b. Quante sono le alunne?
Risposta:
c. Quanti alunni e quante alunne non hanno risposto né Matematica né Italiano?
Risposta:
D28. Gli alunni della 3a B vengono divisi in quattro gruppi da sei per partecipare a un torneo di freccette. Gli organizzatori decidono però di ridurre solo a tre i gruppi. Quanti alunni compongono adesso un gruppo?
A. 7
B. 8
C. 9
D. 6
D29. Leggi la filastrocca:
Giro girotondo, casca il mondo, casca la terra, tutti giù per terra.
Immagina di pescare a caso da un sacchetto una delle parole della filastrocca. Metti una crocetta per ogni riga.
Certo Possibile Impossibile
Peschi una parola che inizi con la lettera zeta
Peschi un articolo
Peschi una parola che non inizi con la lettera erre
Peschi una parola della lingua francese
Le griglie di correzione della prova
Di seguito si riportano le griglie di correzione. Per ogni quesito la Griglia informa su quale sia l’Ambito che viene indagato. In HUB Kit docente sono presenti le istruzioni per svolgere la prova e le griglie di valutazione per monitorare le eventuali criticità ancora presenti nel gruppo classe.
D1 18:15
D2 C
D3 A
D4 D
D5 B
D6 a. 30 mℓ b. 20 c. 80 mℓ
D7 75 e 2 o 72 e 5
D8 B
D9 C

Numeri / Operazioni e problemi
Numeri / Operazioni
Numeri / Operazioni
Numeri / Operazioni
Spazio e figure / Riconoscimento di figure
Dati e previsioni / Dati e tabelle
Numeri / Operazioni
Spazio e figure / Misure
Numeri / Stima di misure
D10 / Spazio e figure / Composizione di figure
D11 10 e 10
D12 a. / b. no
D13 90
D14 No
D15 D
D16 a. 1° b. 3° e 4°
D17 18 e 24; 5 e 35; A
D18 a. 5 b. € 29,50
D19 Fig. 3
D20 C
D21 B
D22 C
D23 F; F; V
D24 a. C b. C
D25 a. 10 b. 2,500 kg
D26 60
D27 a. 25 b. 10 c. 9
D28 B
D29 I; P; C; I
Numeri / Operazioni
Relazioni / Successioni
Numeri / Valore posizionale
Spazio e figure / Confronto
Numeri / Decimali
Dati e previsioni / Grafici
Numeri / Tabelle
Numeri / Operazioni e problemi
Spazio e figure / Simmetrie
Numeri / Ordinamento nei decimali
Spazio e figure / Misure
Numeri / Valore posizionale
Spazio e figure / Confronto
Relazioni / Contesti vari
Numeri / Operazioni e problemi
Numeri / Operazioni e problemi
Dati e previsioni / Grafici
Numeri / Operazioni e problemi
Dati e previsioni / Dati e tabelle

Schede di Scienze e Tecnologia

• Schede multilivello
• Laboratorio competenze
• Compiti autentici

LE SCIENZE E IL LAVORO DI SCIENZIATI E SCIENZIATE
1 Scrivi il nome dello scienziato che svolge il lavoro descritto.
• Studia le sostanze e il modo in cui reagiscono tra loro.
• Studia gli esseri viventi, cerca di capire l’origine e l’evoluzione della vita.
• Studia le caratteristiche degli animali.
• Studia le caratteristiche delle piante.
• Studia i minerali, le rocce, la struttura interna della Terra e i vulcani.
• Studia i pianeti e i corpi celesti.
• Studia in modo matematico i fenomeni per trovare le leggi che li regolano.
2 Metti in ordine le fasi del metodo sperimentale. Usa i numeri.
Registra i dati e li confronta con l’ipotesi di partenza.
Cerca informazioni: qualche altro scienziato può aver trovato una spiegazione per il fenomeno prima di lui.
Formula un’ipotesi, cioè una possibile spiegazione di ciò che ha osservato.
Progetta e compie esperimenti per verificare l’ipotesi.
Formula una legge, cioè una spiegazione chiara e valida per tutti. Poi rende pubblici i risultati.
Osserva attentamente un fenomeno usando i cinque sensi o strumenti scientifici.
Si pone domande su ciò che ha osservato. Perché accade questo fenomeno? Quando accade?
3 Che cosa fa lo scienziato se la sua ipotesi non viene confermata dagli esperimenti?
LE SCIENZE E IL LAVORO DI SCIENZIATI E SCIENZIATE
1 Collega il nome di ogni scienziato al lavoro che svolge.
botanico
geologo
chimico fisico
biologo
zoologo
astronomo

Studia le sostanze e il modo in cui reagiscono tra loro.
Studia gli esseri viventi; cerca di capire l’origine e l’evoluzione della vita.
Studia le caratteristiche degli animali.
Studia le caratteristiche delle piante.
Studia i minerali, le rocce, la struttura interna della Terra e i vulcani.
Studia i pianeti e i corpi celesti.
Studia in modo matematico i fenomeni per trovare le leggi che li regolano.
2 Completa la descrizione delle fasi del metodo sperimentale. Usa le seguenti parole.
domande • esperimenti • informazioni • ipotesi • legge • osservazione • registra
• Effettua una attenta di un fenomeno usando i cinque sensi o strumenti scientifici.
• Si pone su ciò che ha osservato. Perché, quando accade questo fenomeno?
• Formula un’ , cioè una possibile spiegazione di cià che ha osservato.
• Cerca ; qualche altro scienziato può aver trovato una spiegazione per il fenomeno prima di lui.
• Progetta e compie per verificare l’ipotesi.
• i dati e li confronta con l’ipotesi di partenza.
• Formula una , cioè una spiegazione chiara e sempre alida dei risultati ottenuti, da rendere pubblica.
3 Che cosa fa lo scienziato se la sua ipotesi non viene confermata dagli esperimenti?
Indica con una X la risposta corretta.
Formula una legge senza tener conto degli esperimenti negativi.
Modifica la sua ipotesi e ricomincia da capo.
Comunica a tutti i risultati della sua ricerca.
OBIETTIVI: Conoscere il lavoro degli scienziati e le fasi del metodo sperimentale.
1 LE BOTTIGLIE PIENE D’ACQUA NEL CONGELATORE SCOPPIANO?
2 Sarà successo a molti di noi: si pone una bottiglia piena d’acqua nel congelatore per farla raffreddare più rapidamente, poi la si dimentica. Quando la si prende o il tappo è saltato e parte dell’acqua ormai ghiacciata si è sparsa nel cassetto o addirittura la bottiglia si è rotta.
3 Ma come mai accade ciò, visto che i liquidi quando si raffreddano diminuiscono il loro volume?
4 Ebbene, l’acqua rappresenta un’importantissima eccezione a questa regola. Infatti, se raffreddiamo una certa quantità di acqua sotto i 4 gradi centigradi si osserva che il suo volume, invece di diminuire, aumenta.
5 Questo comportamento anomalo è dovuto alle forze di coesione e repulsione delle molecole dell’acqua: se si riduce il movimento delle molecole, esse riescono a disporsi in posizioni più ordinate; ma poiché tali posizioni più ordinate comportano una maggior distanza tra le moleco stesse, ecco spiegata la ragione dell’aumento di volume del ghiaccio rispetto all’acqua.
6 Quindi mai mettere una bottiglia piena d’acqua nel congelatore: l’aumento di volume dell’acqua rischierebbe di farla scoppiare, perché le molecole d’acqua allo stato solido sono disposte in modo da occupare più spazio delle stesse molecole allo stato liquido.
2 Descrivi le fasi del metodo sperimentale utilizzato per scrivere questa comunicazione.
1 ipotesi 2 osservazione 3 domanda 4 esperimento
5 ricerca di informazioni
6 comunicazione
NOME E COGNOME

1 Completa le frasi.
LA MATERIA E I SUOI STATI
• La materia è tutto ciò che occupa uno e ha una .
• Le compongono la materia.
• Le sostanze sono composte da piccolissime particelle chiamate
• Gli atomi possono legarsi tra loro e formare le .
• Quando le molecole di due sostanze si mescolano perfettamente, come il sale nell’acqua, si ha una .
• Quando le molecole di due sostanze non si mescolano tra loro e mantengono le loro caratteristiche, come la farina gialla nell’acqua, si ottiene una .
2 Colora allo stesso modo lo stato della materia e tre sue caratteristiche (una per gruppo).
La materia non ha forma propria, ma prende quella del recipiente che la contiene.
stato solido
stato liquido
stato gassoso
La materia non ha una forma propria.
La materia ha una forma propria.
La materia assume la forma del recipiente che lo contiene.
La materia ha sempre la stessa forma.
La materia non ha forma e occupa sempre tutto lo spazio disponibile.
Le molecole della materia sono legate da una forza intensa e non si possono spostare.
Le molecole della materia non hanno legami tra loro e possono muoversi liberamente.
Le molecole della materia non hanno legami forti e possono scorrere l’una sull’altra.
3 Scrivi i nomi dei passaggi di stato per completare le definizioni.
• La è il passaggio dallo stato solido a quello liquido.
• L’ è il passaggio dallo stato liquido a quello gassoso.
• La è il passaggio dallo stato gassoso a quello liquido.
• La è il passaggio dallo stato liquido a quello solido.
OBIETTIVI: Conoscere gli stati della materia e le sue trasformazioni.
LA MATERIA E I SUOI STATI
1 Completa le frasi con le seguenti parole.
molecole • massa • soluzione • sospensione • sostanze • spazio • atomi
• La materia è tutto ciò che occupa uno e ha una .
• Le compongono la materia.
• Le sostanze sono composte da piccolissime particelle chiamate
• Gli atomi possono legarsi tra loro e formare le
• Quando le molecole di due sostanze si mescolano perfettamente, come il sale nell’acqua, si ha una .
• Quando le molecole di due sostanze non si mescolano tra loro e mantengono le loro caratteristiche, come la farina gialla nell’acqua, si ottiene una .
2 Collega con una freccia i tre stati della materia alle relative descrizioni.
stato solido

stato liquido
stato gassoso
La materia assume la forma del recipiente che la contiene.
La materia non ha forma e occupa tutto lo spazio disponibile.
La materia ha sempre la stessa forma.
3 Collega il nome del passaggio di stato alla sua definizione. Poi collegali all’esempio corrispondente.
fusione
evaporazione
condensazione
solidificazione
È il passaggio dallo stato gassoso a quello liquido.
È il passaggio dallo stato liquido a quello solido.
È il passaggio dallo stato solido a quello liquido.
È il passaggio dallo stato liquido a quello gassoso.
OBIETTIVI: Conoscere gli stati della materia e le sue trasformazioni.
Un cubetto di ghiaccio fuori dal congelatore.
L’acqua che bolle in una pentola diventa vapore.
Il vapore acqueo che forma goccioline sul vetro della doccia.
L’acqua messa nel congelatore.
LA GALAVERNA, UN FENOMENO EMOZIONANTE MA SCONOSCIUTO
Uno dei più spettacolari fenomeni meteorologici invernali, ma anche uno dei meno conosciuti, è la galaverna, nome che significa “nebbia che si congela”. Spesso, infatti, la nebbia provoca pioviggini cioè piogge leggere. Quando le temperature sono sotto lo zero, queste pioviggini appaiono come piccoli aghetti di ghiaccio che si posano soprattutto sull’erba, sugli alberi e nelle campagne, dando l’effetto della neve. È un fenomeno raro in Pianura Padana, ma molto frequente in montagna, sia sulle Alpi che su tutto l’Appennino.
Le piccolissime goccioline di vapore sospeso in aria, che accompagnano ogni fenomeno di nebbia, si congelano quando le temperature sono sotto lo zero, rendendo ancor più affascinante il paesaggio. Solitamente, la galaverna si posa sui fili d’erba più alti, sui rami più esterni degli alberi, ma anche sui fili stesi delle linee aeree dell’alta tensione e sulle rocce sporgenti. Arriva addirittura a posarsi sulla barba, sui capelli e sulle sopracciglia delle persone che si trovano di passaggio in mezzo a questa fredda nebbia. La comparsa della galaverna nelle zone di pianura è solitamente indice di tempo stabile, con temperature basse e assenza di nubi.

1 Indica con una X il completamento corretto per ogni frase.
• Il nome “galaverna” significa: neve d’inverno. nebbia di gala. neve gelata. nebbia che si congela.
• Le pioviggini sono: minuscole particelle di vapore che costituiscono la nebbia. piogge leggere. aghetti di ghiaccio. piogge scroscianti.
• Quando le temperature sono sotto lo zero, le pioviggini: scompaiono improvvisamente. si trasformano in aghetti di ghiaccio. diventano neve. diventano grandine.
• Il fenomeno è più frequente: nelle zone più calde. vicino al mare. nelle pianure del Meridione. sugli Appennini, sulle Alpi, nella Pianura Padana.
• Solitamente la galaverna si posa: su quasi tutti gli elementi del paesaggio. sulle nuvole. solo sugli alberi. solo sui fili d’erba.
• Nelle zone di pianura la galaverna:
è indice di tempo stabile. è indice di tempo instabile. non c’è mai. è tipica.
L’ACQUA
1 Indica con una X se le seguenti affermazioni sono vere V o false F .
• L’acqua è l’unica sostanza che in natura si trova in tutti e tre gli stati. V F
• La capillarità è la tendenza dell’acqua a scendere in rivoli sottili come capelli. V F
• L’acqua non è indispensabile per la vita. Senza di essa le persone, gli animali e le piante possono sopravvivere. V F
2 Completa il brano.
Il nostro corpo è formato per due terzi da . Anche la Terra è formata soprattutto da acqua e per questo motivo è chiamata il . L’acqua dei mari è , solo il 3 % dell’acqua sulla Terra è
L’acqua ha le seguenti caratteristiche:
• non ha un proprio;
• non ha un proprio;
• non ha un proprio.
Una delle proprietà fondamentali dell’acqua è la

3
Collega le frasi spezzate per ricostruire il ciclo dell’acqua.
Il calore del Sole fa evaporare l’acqua…
Il vapore che si forma è leggero e…
Salendo nell’aria il vapore si raffredda in piccole gocce d’acqua che…
Quando le nuvole si raffreddano le goccioline diventano pesanti e…
Se le nuvole incontrano aria gelida…
Sulla Terra una parte dell’acqua penetra nel suolo e…
Un’altra parte si raccoglie…
Da qui l’acqua evapora di nuovo e…
… ricadono a terra sotto forma di pioggia.
… si ha la caduta di neve o grandine.
… dei mari, dei fiumi, dei laghi.
… nei ghiacciai, nei laghi e nei fiumi che scorrono verso il mare.
… si disperde nell’aria.
… si uniscono e formano le nuvole.
… il ciclo ricomincia.
… si accumula nelle falde acquifere.
OBIETTIVI: Conoscere il ciclo dell’acqua in natura e le sue trasformazioni da uno stato all’altro.

L’ACQUA
1 Sottolinea le parole corrette per completare le frasi.
L’acqua è l’unica sostanza che in natura si trova in tutti e due / tre gli stati.
La liquidità / capillarità è la tendenza dell’acqua a risalire lungo i bordi del contenitore in cui viene versata.
L’acqua è indispensabile / utile per la vita. Senza acqua le persone, gli animali e le piante non possono nutrirsi / sopravvivere
2 Completa il brano con le seguenti parole: acqua • capillarità • colore • dolce • odore • Pianeta blu • salata • sapore
Il nostro corpo è formato per due terzi da . Anche la Terra è formata soprattutto da acqua e per questo motivo è chiamata il . L’acqua dei mari è , solo il 3 % dell’acqua sulla Terra è .
L’acqua ha le seguenti caratteristiche:
• non ha un proprio;
• non ha un proprio;
• non ha un proprio.
Una delle proprietà fondamentali dell’acqua è la
3 Osserva l’immagine e scrivi nelle etichette i nomi degli elementi che compongono il ciclo dell’acqua.
evaporazione • falda acquifera • fiumi • nuvole • precipitazioni
LA GIORNATA MONDIALE DELL’ACQUA
Ogni anno, il 22 marzo viene celebrata la Giornata mondiale dell’acqua per sensibilizzare la popolazione mondiale su un tema fondamentale: l’accesso alla risorsa più importante.
Ancora oggi 748 milioni di persone nel mondo non hanno accesso all’acqua potabile. L’area più colpita da questa piaga è l’Africa subsahariana, ma lo stesso problema affligge i cittadini della Cina (112 milioni senz’acqua) e dell’India (92 milioni).
Perché l’acqua a disposizione possa essere utilizzata senza rischi per la salute, è necessario che sia pulita e monitorata attraverso pozzi, reti idriche controllate, acquedotti, depuratori. Queste sono le cosiddette fonti migliorate.
In tre Paesi – Congo, Mozambico e Papua Nuova Guinea – metà della popolazione non può bere acqua da fonti migliorate e si abbevera da fonti di superficie o da sistemi che non offrono alcuna garanzia sanitaria. Secondo un rapporto congiunto di Oms e Unicef, questa condizione accomuna almeno 1,8 miliardi di individui nel mondo.
Ogni giorno milioni di persone, soprattutto donne, percorrono molta strada a piedi solo per portare una giara d’acqua a casa per bere, lavarsi e cucinare.
Nel 2012 è stato raggiunto l’obiettivo di dimezzare la percentuale di persone senza accesso all’acqua potabile. Ma molti dati continuano a essere difficili da accettare: secondo l’Unicef, circa 1000 bambini muoiono ogni giorno per diarree dovute ad acqua contaminata e assenza di servizi igienico-sanitari.
1 Indica con una X l’affermazione corretta per completare la frase.
• La giornata mondiale dell’acqua viene celebrata: per invitare tutti a bere più acqua. perché tutti possano avere accesso all’acqua potabile. per fare pubblicità all’acqua in commercio.
perché ci sia più acqua in tutto il mondo.
• Soffrono per insufficienza d’acqua: tutti i Paesi del mondo. soprattutto l’Africa a sud del Sahara, la Cina e l’India.
soltanto Congo, Mozambico e Papua Nuova Guinea.
i Paesi che hanno reti idriche controllate.

• Le fonti migliorate sono quelle in cui l’acqua viene: usata liberamente da tutti i cittadini. pulita e controllata attraverso pozzi, reti idriche, acquedotti, depuratori. condotta attraverso fontane decorate a tutte le abitazioni. offerta senza garanzie sanitarie.
• Milioni di persone per avere l’acqua per lavarsi, bere e cucinare devono: pagare molti soldi. aspettare l’arrivo di cisterne. prelevarla da pozzi profondi. percorrere molta strada a piedi perché non ci sono fonti vicine.

L’ARIA
1 Completa il testo sulle caratteristiche dell’aria.
L’aria ha una e occupa uno che però non è sempre lo stesso.
Le che la compongono non hanno legami tra loro e si muovono liberamente cercando di allontanarsi il più possibile l’una dall’altra. L’aria è e occupa tutto lo spazio disponibile. Con il calore l’aria si e verso l’alto.
2 Leggi le definizioni e scrivi i nomi dei gas che compongono l’aria corrispondenti.
• È il gas più abbondante nell’aria.
• È il gas che ci permette di respirare.
• Viene immessa nell’aria dalla respirazione dei viventi o quando si bruciano petrolio, legno o carta.
• È formato dalle invisibili goccioline dell’acqua che evapora.
• Sono presenti nell’aria insieme al pulviscolo atmosferico.
3 Completa il testo, poi osserva il disegno e scrivi nelle etichette i nomi dei diversi strati dell’atmosfera.
La Terra è avvolta da uno strato di aria, l’atmosfera, che non è uguale dappertutto ma ha caratteristiche diverse.
• La è la parte più vicina alla Terra. Qui si formano le nuvole e i fenomeni atmosferici.
• La contiene l’ozono, un gas che filtra i raggi ultravioletti che, se arrivassero direttamente sulla superficie terrestre, sarebbero molto nocivi.
• La è una zona molto fredda con temperature molto basse.
• La è invece la zona più calda, dove la temperatura è altissima.
• L’ è lo strato in cui l’atmosfera confina con lo spazio.
L’ARIA
1 Sottolinea le parole corrette per completare il testo sulle caratteristiche dell’aria.
L’aria ha / non ha una massa. Occupa uno spazio che è / non è sempre lo stesso: le molecole che la compongono non hanno legami tra loro e si muovono liberamente cercando di avvicinarsi / allontanarsi l’una dall’altra il più possibile.
L’aria è solo nello Spazio / è ovunque e occupa tutto lo spazio disponibile. Con il calore l’aria si dilata / restringe e sale / scende verso il basso / l’alto
2 Completa le frasi seguenti con i nomi dei diversi gas che compongono l’aria.
altri gas • anidride carbonica • azoto • ossigeno • vapore acqueo
• L’ è il gas più abbondante nell’aria.
• L’ è il gas che ci permette di respirare.
• L’ viene immessa nell’aria dalla respirazione dei viventi o quando si bruciano petrolio, legno o carta.
• Il è formato dalle invisibili goccioline dell’acqua che evapora.
• sono presenti nell’aria insieme al pulviscolo atmosferico.
3 Leggi il testo e sottolinea i nomi dei diversi strati dell’atmosfera.
Poi osserva il disegno e scrivi i nomi nelle etichette.
La Terra è avvolta da uno strato di aria, l’atmosfera, che non è uguale dappertutto ma ha caratteristiche diverse.
• La troposfera è la parte più vicina alla Terra. Qui si formano le nuvole e i fenomeni atmosferici.
• La stratosfera contiene l’ozono, un gas che filtra i raggi ultravioletti del Sole che se arrivassero direttamente sulla superficie terrestre sarebbero molto nocivi.
• La mesosfera è una zona molto fredda con temperature molto basse.
• La termosfera è invece la zona più calda, dove la temperatura è altissima.
• L’esosfera è lo strato in cui l’atmosfera confina con lo spazio.

OBIETTIVI: Conoscere la composizione e le proprietà dell’aria.
MONGOLFIERE E DIRIGIBILI
La mongolfiera è un aerostato che per sollevarsi da terra e volare utilizza l’aria riscaldata con un bruciatore. L’aria riscaldata, infatti, è più leggera dell’aria circostante. Se si scalda o si lascia raffreddare l’aria contenuta nel pallone, la mongolfiera può quindi salire o scendere, ma non possiede strumenti per controllare la direzione del volo, che dipende dai venti. Il nome “mongolfiera” deriva da quello dei fratelli Montgolfier, che nel 1873 in Francia riuscirono a far sollevare un pallone con aria riscaldata.
Aerostati più evoluti, in grado di sollevarsi e atterrare, ma anche di indirizzare il loro volo, sono i dirigibili. Essi hanno la forma di siluri e sono riempiti di gas come idrogeno o elio. I dirigibili si alzano in volo dopo aver scaricato la sabbia contenuta in sacchetti (detta zavorra) e aver diminuito il loro peso, e scendono a terra quando liberano il gas per mezzo di una valvola. Il volo delle mongolfiere e dei dirigibili si basa sul principio di Archimede, secondo il quale un corpo immerso in un liquido riceve una spinta dal basso verso l’alto pari al peso del liquido spostato Lo scienziato di Siracusa aveva pensato questo principio con riferimento all’acqua; si capì più tardi che questo era valido anche per l’aria.
1 Cancella in ogni frase le parole intruse. Poi riscrivile corrette.
• La mongolfiera è un aerostato che per sollevarsi da terra e volare utilizza l’aria raffreddata con un bruciatore e un motore.

• La mongolfiera può salire o scendere e possiede strumenti per controllare la direzione del volo.
• I dirigibili si alzano in volo dopo aver aumentato il loro peso scaricando la sabbia contenuta in sacchetti, e scendono a terra perché caricano sacchetti di sabbia.
• Secondo il principio di Archimede un corpo immerso in un fluido riceve una spinta dal basso verso l’alto e dall’alto verso il basso pari al peso del fluido spostato.
• I dirigibili hanno la forma di siluri, sono riempiti di gas come idrogeno o elio e di aria calda.
• Archimede applicava questo principio all’aria.
NOME E COGNOME DATA CLASSE
IL SUOLO
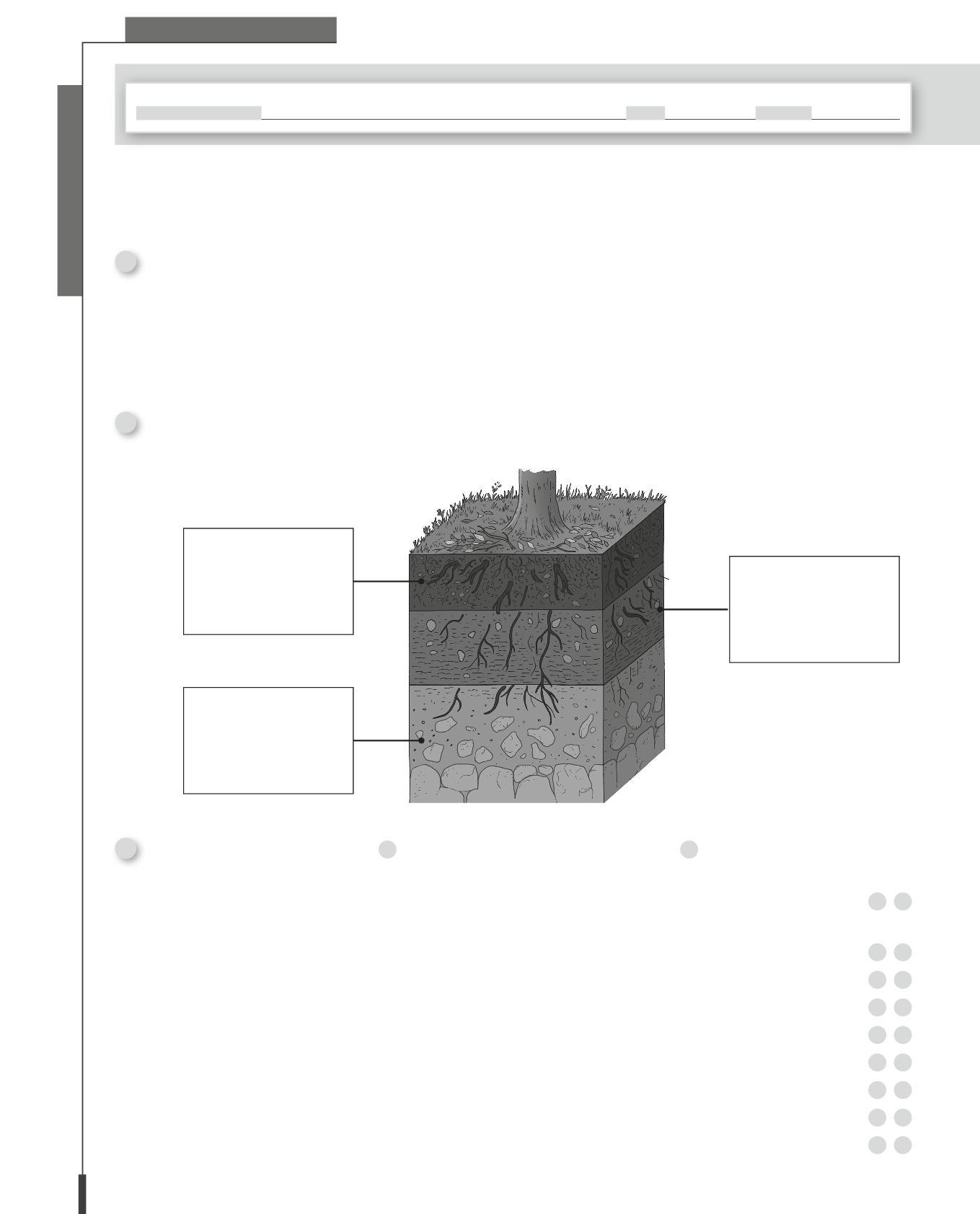
1 Completa le frasi sul suolo.
• Il suolo è
• Il suolo è formato da
• Esistono diversi tipi di suolo che si distinguono per
2 Completa il disegno con i nomi degli strati del suolo e spiega da che cosa è formato ogni strato.
3 Per ogni affermazione indica P se è riferita ai terreni permeabili o I se è riferita ai terreni impermeabili.
• L’acqua che vi passa attraverso porta via le sostanze nutritive del terreno. P I
• Le piante che vi affondano le radici non hanno tempo di assorbire le sostanze nutritive contenute nel suolo. P I
• Le sostanze nutritive in esso contenute possono essere meglio assorbite dalle piante. P I
• Sono argillosi e ricchi di humus. P I
• Sono attraversati dall’acqua con grande facilità. P I
• Sono composti da sabbia e ghiaia. P I
• Sono fertili.
• Sono poco fertili.
• Non lasciano passare rapidamente l’acqua. P I
OBIETTIVI: Conoscere la composizione e le caratteristiche del suolo.
NOME E COGNOME DATA CLASSE
IL SUOLO
1 Completa le frasi con le seguenti parole.
minerali • humus • quantità • roccia • strato • trattenere
Il suolo è lo di terreno che ricopre la superficie terrestre.
Il suolo è formato da sostanze , acqua, aria, e Esistono diversi tipi di suolo che si distinguono per la di humus, per le dimensioni dei frammenti di e per la capacità di l’acqua.
2 Colora di giallo le caratteristiche dei terreni permeabili e di verde quelle dei terreni impermeabili.
L’acqua che vi passa attraverso porta via le sostanze nutritive contenute nel terreno.

Sono argillosi e ricchi di humus.
Sono fertili.
Sono poco fertili.
Le sostanze nutritive in esso contenute possono essere meglio assorbite dalle piante.
Sono attraversati dall’acqua con grande facilità.
Le piante che vi affondano le radici non hanno tempo di assorbire le sostanze nutritive contenute nel terreno.
Non lasciano passare rapidamente l’acqua.
Sono composti da sabbia e ghiaia.
OBIETTIVI: Conoscere la composizione e le caratteristiche del suolo.

IL COMPOSTAGGIO
Il 35% dei rifiuti che si producono è rappresentato da materiale organico: fondi di caffè, bucce di frutta e verdura, gusci di uova, pane raffermo, erba tagliata, foglie secche, potature, scarti di mense, ristoranti e mercati ortofrutticoli.
Si tratta di scarti biodegradabili: alcuni batteri presenti in natura decompongono questi materiali in sostanze semplici che possono essere facilmente assorbite dal terreno. Si forma così l’humus, prezioso per la crescita delle piante. Noi possiamo riprodurre in maniera controllata e accelerata questo processo per ottenere il compost.
Il compost che si ottiene negli impianti industriali di compostaggio, oppure nel proprio giardino attraverso pratiche di compostaggio domestico, è un terriccio ricco di elementi nutritivi ottenuto dalla trasformazione dei rifiuti organici a opera di batteri. Il compost può essere impiegato per l’agricoltura o il giardinaggio.
1 Indica con una X l’affermazione corretta per ogni coppia.
Gli avanzi di cibo, l’erba tagliata, le foglie secche, gli scarti di mense, ristoranti e mercati ortofrutticoli non subiscono trasformazioni.
Gli avanzi di cibo, l’erba tagliata, le foglie secche, gli scarti di mense, ristoranti e mercati ortofrutticoli sono materiali organici biodegradabili.
Alcuni batteri presenti in natura decompongono i materiali biodegradabili in sostanze che sono assorbite dal terreno.
I materiali biodegradabili sono inattaccabili dai batteri.
Nelle nostre città è possibile riprodurre in maniera controllata e accelerata il processo di trasformazione degli scarti organici in terriccio fertile.
Nelle nostre città è impossibile riprodurre in maniera controllata e accelerata il processo di trasformazione degli scarti organici in terriccio fertile.
Il compost che si ottiene negli impianti industriali o nei propri giardini è un materiale inutilizzabile.
Il compost che si ottiene negli impianti industriali o nei propri giardini viene impiegato come terriccio fertile per le piante.
NOME E COGNOME
LA MATERIA E LE SOSTANZE
Obiettivi Riconoscere le caratteristiche di sostanze, aria, acqua, calore e suolo. Individuare, nell’osservazione di esperienze concrete, alcuni concetti scientifici: peso, presenza dell’inquinamento nell’aria.
Competenze Riconosce le principali caratteristiche della materia. Esplora i fenomeni con approccio scientifico: realizza semplici esperimenti.
1 Per ogni testo sottolinea le parole-chiave. Poi scrivi a quale degli argomenti studiati si riferisce.
È un insieme di gas diversi, tra cui l’azoto e l’ossigeno. Avvolge tutta la Terra in uno strato chiamato atmosfera.
La materia può trovarsi in tre stati: solido, liquido e gassoso. Il passaggio da uno stato all’altro avviene attraverso il riscaldamento o il raffreddamento della materia.
È formato da particelle solide, acqua, aria e humus. I terreni sabbiosi e ghiaiosi sono permeabili e meno fertili dei terreni argillosi, che sono impermeabili e ricchi di humus.
È una forma di energia chiamata energia termica. La sua principale fonte è il Sole. Uno dei suoi effetti è la temperatura, che si misura con il termometro.
Ha due caratteristiche fondamentali: occupa uno spazio e ha un peso; è formata dall’insieme di diverse sostanze. Ogni sostanza è composta da atomi e molecole.
È rinnovabile se ottenuta da Sole, vento, acqua, calore del sottosuolo; non rinnovabile se deriva da carbone, petrolio e gas metano.
Non ha colore, sapore o odore propri. È formata da idrogeno e ossigeno. In natura passa da uno stato all’altro in un ciclo che non si interrompe mai.
NOME E COGNOME DATA
2 Leggi gli esperimenti e osserva i disegni. Poi indica con una X che cosa hanno dimostrato.
PRIMO ESPERIMENTO
1 Prendete due palloncini uguali ma di colore diverso, per esempio uno rosso e uno blu.
2 Gonfiate quello rosso e legatelo a un’estremità di una gruccia.
3 Appendete quello blu, sgonfio, all’altra estremità della gruccia.
4 Mettete in equilibrio la gruccia.
Osservate che la gruccia pende dal lato del palloncino rosso gonfio.

• Questo dimostra che:
l’aria ha un colore. l’aria ha un peso. l’aria ha una forma.
SECONDO ESPERIMENTO
1 Procuratevi un pezzo di tela di cotone bianco, che l’insegnante taglierà in due parti.
2 Appendete in classe una parte e l’altra appendetela in cortile.
3 Dopo una settimana confrontate i due pezzi di stoffa.
Osservate che quello rimasto fuori dalla classe è grigio e sporco, l’altro è rimasto bianco.
• Questo dimostra che: l’aria aperta e il Sole ingrigiscono il cotone. il cotone all’aria aperta si sporca d’erba. all’esterno, l’aria è più inquinata.
I VIVENTI
1 Completa i testi con le seguenti parole.
citoplasma • cloroplasti • membrana • nucleo • parete • vacuoli
La cellula animale è avvolta da una membrana trasparente: la cellulare.
Nel il DNA contiene le informazioni per far funzionare la cellula.
Il è una sostanza gelatinosa in cui sono immersi gli organuli.
La cellula vegetale è ricoperta da un rivestimento rigido: la cellulare.
I sono organuli che contengono la clorofilla.
Nella cellula si trovano riserve d’acqua chiamate
2 Completa le frasi con i nomi dei cinque Regni.
• Regno : organismi pluricellulari capaci di produrre da soli il proprio nutrimento attraverso la fotosintesi clorofilliana.
• Regno : organismi pluricellulari che si nutrono di altri organismi.
• Regno : organismi unicellulari molto semplici.
• Regno : organismi unicellulari, più complessi delle monere.
• Regno : organismi che si nutrono assorbendo le sostanze da altri organismi; alcuni sono unicellulari, altri pluricellulari.
3 Collega correttamente le frasi spezzate.
Le funzioni vitali di piante e animali sono… … attraverso organi differenti: polmoni, branchie e stigmi.
Nelle piante la respirazione avviene… … attraverso la fotosintesi clorofilliana.
Negli animali la respirazione avviene… … mangiando altri organismi.
Le piante producono da sole il proprio nutrimento… … la respirazione, la nutrizione e la riproduzione.
Gli animali (erbivori, carnivori e onnivori) si nutrono… … attraverso gli stomi delle foglie.
Le piante e gli animali si riproducono soprattutto attraverso la fecondazione…

… cioè l’unione di una cellula sessuale maschile con una femminile.
I VIVENTI
1 Completa il testo. Se serve, aiutati con i nomi scritti sulle illustrazioni. La è la parte più piccola che compone un essere vivente.
La cellula animale è composta dal , dalla cellulare, dal e dagli organuli.
La cellula vegetale ha in più la cellulare, i e i .
2 Completa le frasi con i nomi dei cinque Regni.
degli animali • dei funghi • delle monere • delle piante • dei protisti
• Regno : organismi pluricellulari capaci di produrre da soli il proprio nutrimento attraverso la fotosintesi clorofilliana.
• Regno : organismi pluricellulari che si nutrono di altri organismi.
• Regno : organismi unicellulari molto semplici.
• Regno : organismi unicellulari, più complessi delle monere.
• Regno : organismi che si nutrono assorbendo le sostanze da altri organismi; alcuni sono unicellulari, altri pluricellulari.
3 Sottolinea le parole corrette per completare le frasi.
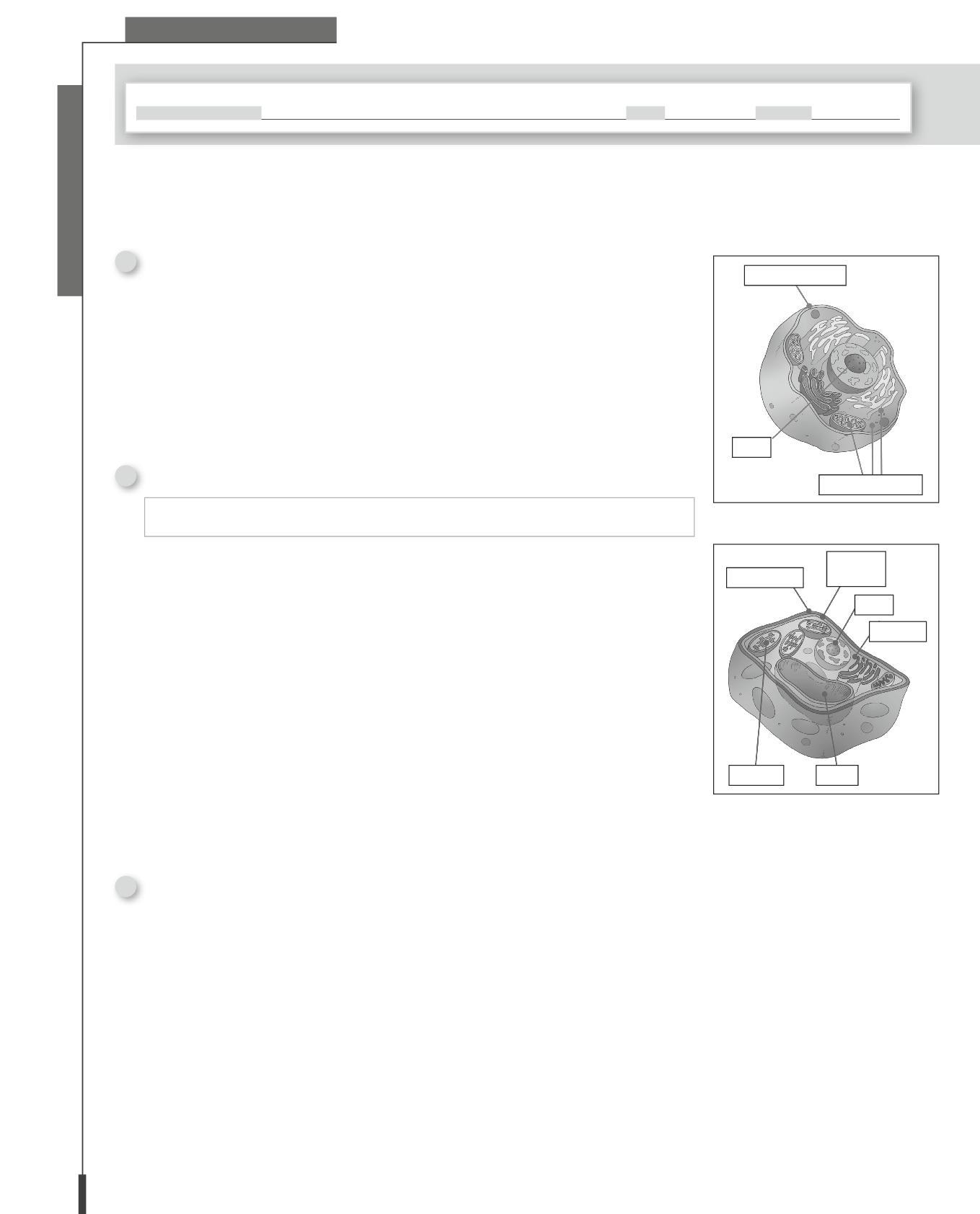
parete cellulare
e organuli
membrana cellulare nucleo
cloroplasti vacuoli
La cellula vegetale.
• Le funzioni / finzioni vitali di piante e animali sono la respirazione, la nutrizione e la riproduzione.
• Nelle piante la respirazione avviene attraverso gli steli / stomi delle foglie.
• Negli animali la respirazione avviene attraverso organi / polmoni differenti.
• Le piante producono da sole il proprio nutrimento attraverso la fotografia / fotosintesi clorofilliana.
• Gli animali (erbivori, carnivori e onnivori) si nutrono mangiando altri organismi / animali.
• Le piante e gli animali si riproducono soprattutto attraverso la fecondazione / fertilizzazione: l’unione di una cellula sessuale maschile con una cellula sessuale femminile.
OBIETTIVI: Conoscere le caratteristiche di una cellula, dei cinque Regni e del ciclo vitale di piante e animali.
LE AREE NATURALI PROTETTE
Le aree naturali protette, chiamate anche oasi o parchi naturali, sono porzioni di territorio che la legge tutela per il loro particolare interesse naturalistico, ambientale o storico-culturale.
Sono aree che contengono ecosistemi prevalentemente o largamente intatti, ambienti e paesaggi di rilievo tale da richiedere interventi per garantirne la conservazione alle future generazioni.
Il Summit mondiale per l’ambiente di Rio de Janeiro (1992) ha individuato proprio nei Parchi il principale strumento di conservazione della biodiversità, per evitare l’estinzione di un numero sempre maggiore di specie animali e vegetali. L’Italia – con i suoi quasi 3 milioni di ettari di superficie a terra, e altrettanti a mare, tra Aree naturali protette, Parchi nazionali, Riserve naturali statali, Aree naturali marine protette, i parchi sommersi e il santuario dei cetacei, Parchi naturali, Riserve naturali regionali – è uno dei Paesi che negli ultimi dieci anni ha dato il maggior contributo in Europa allo sviluppo di un sistema di aree protette, passando dal 3% a oltre il 10% di territorio tutelato.
1 Collega correttamente le frasi spezzate.
Le aree naturali protette sono...
Le aree naturali protette contengono...
Il Summit mondiale per l’ambiente di Rio de Janeiro...
È importante conservare la biodiversità...
L’Italia è uno dei Paesi che...
... ecosistemi prevalentemente o largamente intatti, ambienti o paesaggi che devono essere conservati per le future generazioni.
... ha individuato nei parchi il principale strumento di conservazione della biodiversità.
... ha dato il maggior contributo in Europa per lo sviluppo di un sistema di aree protette.
... porzioni di territorio che la legge tutela per il particolare interesse naturalistico, ambientale o storico-culturale.
... per evitare l’estinzione di un numero sempre maggiore di specie animali e vegetali.
NOME E COGNOME DATA CLASSE
LE PIANTE E GLI ANIMALI
1 Completa le frasi che descrivono come si nutrono le piante e gli animali.
PIANTE
• Le piante producono il nutrimento attraverso la
• La clorofilla serve per .
• Le piante assorbono l’anidride carbonica attraverso e l’acqua e i sali minerali attraverso
• Le piante producono come sostanza di rifiuto

ANIMALI
• Gli animali si nutrono di .
• I carnivori mangiano
• Gli erbivori mangiano
• Gli onnivori mangiano
• I carnivori hanno denti
• Gli erbivori hanno denti .
• Gli onnivori hanno denti
2 Leggi le definizioni e scrivi i termini corrispondenti.
• Nella parte bassa ha l’ovario, che contiene gli ovuli.
• È formata dai petali.
• Terminano con le antere, che contengono il polline.
3 Riconosci le diverse specie di animali dal modo in cui respirano e scrivi il loro nome.
• Respirano attraverso le branchie che si trovano ai lati della testa.
• L’aria entra nel corpo attraverso le narici e la bocca e raggiunge i polmoni.
• L’aria entra attraverso gli stigmi poi passa nelle trachee.
4 Completa le frasi sulla riproduzione degli animali.
Negli , come gli uccelli, l’embrione cresce all’interno di un , dove si trovano le sostanze necessarie al suo sviluppo.
Nei , come quasi tutti i mammiferi, l’embrione si sviluppa nel corpo della madre.
Negli , come lo squalo e la vipera, l’uovo rimane all’interno del corpo della madre fino al completo sviluppo dell’
OBIETTIVI: Conoscere i modi in cui si nutrono e respirano piante e animali.
NOME E COGNOME

LE PIANTE E GLI ANIMALI
1 Sottolinea in verde le affermazioni sulla nutrizione delle piante, in giallo quelle sulla nutrizione degli animali.
• Assorbono l’anidride carbonica che è nell’aria.
• Fabbricano il nutrimento attraverso la fotosintesi clorofilliana.
• Gli erbivori hanno denti poco appuntiti.
• Gli erbivori mangiano solo vegetali.
• Gli onnivori hanno denti adatti a mordere, a strappare, a sminuzzare.
• Gli onnivori mangiano sia vegetali sia altri animali.
• Hanno la clorofilla che cattura la luce del Sole.
• I carnivori hanno denti aguzzi.
• I carnivori si nutrono di altri animali.
• La sostanza di scarto prodotta è l’ossigeno.
• Producono da sé il nutrimento.
2 Colora nello stesso modo il termine e la sua definizione.
corolla
stami
pistillo
Nella parte bassa ha l’ovario, che contiene gli ovuli.
È formata dai petali.
Terminano con le antere, che contengono il polline.
3 Collega con una freccia le diverse specie di animali al modo in cui respirano.
insetti
Respirano attraverso le branchie che si trovano ai lati della testa. pesci
animali terrestri
L’aria entra nel corpo attraverso le narici e la bocca e raggiunge i polmoni.
L’aria entra attraverso gli stigmi poi passa nelle trachee.
4 Sottolinea le parole corrette per completare le frasi.
• Negli ovovivipari / ovipari, come gli uccelli, l’embrione cresce all’interno di un uovo / genitore, dove si trovano le sostanze necessarie al suo sviluppo.
• Nei vivipari / Negli ovipari, come quasi tutti i mammiferi, l’embrione si sviluppa nel corpo della madre.
• Nei vivipari / Negli ovovivipari , come lo squalo e la vipera, l’uovo rimane all’interno del corpo della madre fino al completo sviluppo dell’embrione / del guscio
L’ESTINZIONE DEGLI ANIMALI
L’allarme estinzione per molte specie animali e vegetali è purtroppo sempre più forte. Dagli studi biologici emerge che, attualmente, sul nostro pianeta esistono tra i 5 e i 15 milioni di specie di piante, animali, e microrganismi. Si stima che oggi siano a rischio circa 1130 specie di mammiferi, cioè il 23% del totale, e 1194 specie di uccelli, cioè il 12% del totale.
Il WWF ha redatto una classificazione delle specie più a rischio. Eccone alcune:
• la tigre indiana, la tigre siberiana, la tigre indo-cinese;
• il gorilla;
• l’orso polare;
• l’elefante;
• il rinoceronte;

• i lemuri;
• la foca monaca;
• le balene e i capodogli;
• il leopardo delle nevi;
• il bisonte europeo;
• lo scimpanzé.
A livello mondiale, la causa principale dell’estinzione è il cambiamento dell’ecosistema, che si è verificato a causa dei mutamenti del clima, del surriscaldamento della crosta terrestre e dell’inquinamento.
In Italia le specie a rischio sono concentrate maggiormente sulle montagne e sulle coste mediterranee e sono: l’orso, la lontra, lo stambecco alpino, il lupo, il capriolo italico, l’aquila del Bonelli, la pernice bianca, la tartaruga marina e molti pesci d’acqua dolce.
1 Leggi le seguenti frasi e sottolinea gli errori. Poi riscrivile corrette.
• Attualmente sul nostro pianeta esistono tra i 5 e i 15 milioni di specie di piante, animali, microrganismi a rischio.
• Le specie più a rischio sono la tigre indiana, siberiana e indo-cinese, il gorilla, il cane, l’orso polare, l’elefante, il rinoceronte, i lemuri, i capodogli, il leopardo delle nevi, la giraffa, il bisonte europeo e lo scimpanzé.
• La causa principale dell’estinzione sono i cambiamenti dell’ecosistema che si sono verificati a causa della glaciazione.
• In Italia le specie a rischio sono concentrate maggiormente sulle montagne, nelle campagne e sulle coste mediterranee.
NOME E COGNOME

IDENTIKIT DI PIANTE E ANIMALI
Obiettivi Individuare somiglianze e differenze fra i diversi esseri viventi. Classificare gli esseri viventi in base a una o più caratteristiche.
Competenze Individua aspetti quantitativi e qualitativi nei fenomeni. Espone in forma chiara ciò che ha analizzato, utilizzando un linguaggio appropriato.
1 Indica con una X l’alternativa corretta per completare le frasi. Poi completa le schede e aggiungi tutte le informazioni.
FELCE
È una pianta: Le foglie sono: semplice. larghe e sottili. complessa. strette e spesse.
Il fusto è
La felce si riproduce
Altre caratteristiche:
ABETE
È una pianta: Le foglie sono: semplice. larghe e sottili. complessa. strette e spesse.
Il fusto è
L’abete si riproduce
Altre caratteristiche:
NOME E COGNOME DATA
GIRASOLE
È una pianta: Le foglie sono: semplice. larghe e sottili. complessa. strette e spesse.
Il fusto è
Il girasole si riproduce
Altre caratteristiche:
CANE
È un animale: Nutrizione: vertebrato. erbivoro. invertebrato. carnivoro. onnivoro.
Il corpo è rivestito da: pelle. pelliccia. penne. Riproduzione: squame. oviparo. scaglie. viviparo. altro. ovoviviparo.
Altre caratteristiche:

AQUILA
È un animale: vertebrato. invertebrato.
Il corpo è rivestito da: pelle. pelliccia. penne. squame. scaglie. altro.
Nutrizione: erbivoro. carnivoro. onnivoro. Riproduzione: oviparo. viviparo. ovoviviparo.
Altre caratteristiche:
GLI INVERTEBRATI
1 Leggi il testo sulle caratteristiche degli invertebrati.
ECHINODERMI
Vivono nel mare e si muovono per mezzo di piccolissimi tentacoli. Si nutrono di molluschi e piccoli pesci. Vi appartengono le stelle marine e i ricci di mare.

MOLLUSCHI
Vivono in acqua e sulla terraferma. Hanno il corpo molle. Spesso hanno una conchiglia. I molluschi come i polpi hanno i tentacoli per muoversi e cacciare.
CELENTERATI
Vivono in acqua. Usano i tentacoli per catturare il cibo. Comprendono i coralli, ancorati al fondale, le meduse, che si lasciano trasportare dalla corrente, e gli anemoni di mare simili a fiori.
ANELLIDI
Vivono in acqua, nel terreno o nel corpo di altri animali. Possono essere cilindrici o piatti. Non hanno zampe e si muovono contraendo i muscoli e strisciando.
2 Rispondi alle seguenti domande sugli invertebrati.
Quali sono gli animali che…
• ... hanno il maggior numero di specie?
• ... vivono ancorati al fondale oppure sono trasportati dalla corrente?
• ... hanno il corpo molle, ma spesso è protetto da una conchiglia?
• ... strisciano contraendo i muscoli?
• ... si muovono nel mare con i loro piccolissimi tentacoli?
• ... si nutrono facendo passare l’acqua attraverso piccoli pori?
OBIETTIVI: Conoscere le principali caratteristiche degli invertebrati.
PORIFERI
Vivono nell’acqua, sia dolce sia salata. Filtrano l’acqua facendola passare attraverso i loro piccoli pori e in questo modo trattengono il cibo.
ARTROPODI
Comprendono i tre quarti delle specie animali. Il loro nome significa “piedi articolati”. Vi fanno parte gli aracnidi (ragni), i crostacei, i millepiedi e gli insetti.
Laboratorio
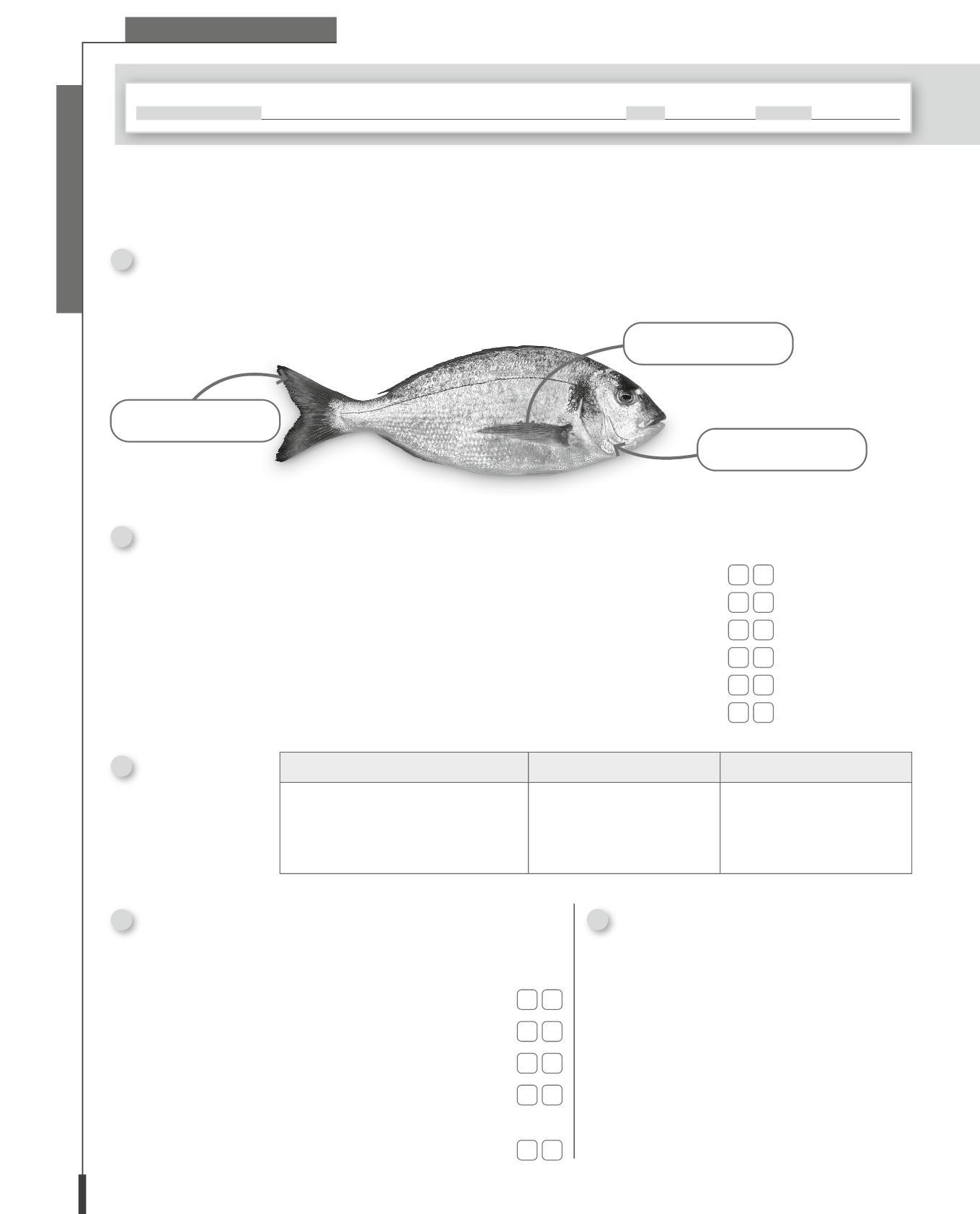
I VERTEBRATI
1 Scrivi al posto corretto nei riquadri le seguenti parti del pesce. Indica con una X se le seguenti affermazioni sugli anfibi sono vere (V) o false (F).
branchie • coda • pinna
2 Completa la tabella con le informazioni relative ai rettili.
• Vivono un periodo di vita nell’acqua e uno sulla terraferma. V F
• Si muovono grazie alle pinne. V F
• Ne fanno parte le tartarughe e gli uccelli.
V F
• Con la metamorfosi si trasformano da animali terrestri ad acquatici. V F
• Hanno generalmente quattro zampe. V F
• Quando crescono respirano attraverso i polmoni. V F
3 Completa la tabella con le informazioni relative ai rettili.
RIVESTIMENTO DEL CORPORESPIRAZIONE MOVIMENTO
4 Indica con una X se le seguenti affermazioni sugli uccelli sono vere (V) o false (F).
Mantengono costante la temperatura del corpo. V F
Depongono le uova. V F
La maggior parte riesce a volare grazie alle ali. V F
Hanno le ossa dense e pesanti. V F
Hanno le piume che servono a mantenere il corpo caldo. V F
5 Completa il testo. Scegli tra le seguenti parole.
ghiandole mammarie • peli • polmoni
I mammiferi respirano attraverso i Quasi tutti i mammiferi hanno il corpo ricoperto da Le femmine hanno le che producono il latte per i cuccioli.
OBIETTIVI: Conoscere le principali caratteristiche dei vertebrati.
NOME E COGNOME

L’ECOSISTEMA
1 Leggi le seguenti definizioni e scrivi i termini corrispondenti.
• Mostra che cosa mangiano gli organismi di un ecosistema e da chi sono mangiati.
• È la rappresentazione di un ecosistema in cui alla base si trovano i produttori. Nei gradini superiori ci sono invece i consumatori.
• È l’insieme delle caratteristiche fisiche di un ambiente, degli esseri viventi che ci vivono e delle relazioni tra loro.
• È formata da molte catene alimentari.
2 Completa la descrizione della catena alimentare.
• Le piante sono organismi perché sono capaci di produrre da sole il proprio nutrimento.
• Gli animali sono organismi consumatori perché mangiano altri organismi. Gli erbivori, che si nutrono di vegetali, sono
• I carnivori che mangiano gli animali erbivori sono .
• Infine i , come batteri e funghi, trasformano i rifiuti e i resti degli animali e dei vegetali in sostanze minerali che sono utilizzate dai vegetali per nutrirsi. E la catena alimentare ricomincia.
3 Completa le didascalie della piramide ecologica.
I sono animali come il falco, che si nutrono di consumatori di secondo grado.
I sono gli animali erbivori come la lepre, che si nutrono di vegetali.
Infine i sono le piante come il trifoglio di cui si nutrono gli erbivori. Laboratorio
Laboratorio

L’ECOSISTEMA
1 Collega con una freccia ogni termine alla sua definizione.
rete alimentare catena alimentare ecosistema
piramide ecologica
Mostra che cosa mangiano gli organismi di un ecosistema e da chi sono mangiati.
È la rappresentazione di un ecosistema in cui alla base si trovano i produttori. Nei gradini superiori ci sono invece i consumatori.
È l’insieme delle caratteristiche fisiche di un ambiente, degli esseri viventi che ci vivono e delle relazioni tra loro.
È formata da molte catene alimentari intrecciate tra loro.
2 Completa la descrizione della catena alimentare con i termini seguenti.
consumatori di primo grado • consumatori di secondo grado • consumatori di terzo grado • decompositori • produttori
• Le piante sono organismi perché sono capaci di produrre da sole il proprio nutrimento.
• Gli animali sono organismi consumatori perché mangiano altri organismi. Gli erbivori, che si nutrono di vegetali, sono
• I carnivori che mangiano gli animali erbivori sono .
• Infine i , come batteri e funghi, trasformano i rifiuti e i resti degli animali e dei vegetali in sostanze minerali che sono utilizzate dai vegetali per nutrirsi. E la catena alimentare ricomincia.
3 Completa le didascalie della piramide ecologica. Aiutati con i termini dell’esercizio precedente.
I sono animali come il falco, che si nutrono di consumatori di secondo grado.
I sono gli animali erbivori come la lepre, che si nutrono di vegetali.
I sono le piante come il trifoglio di cui si nutrono gli erbivori.

LA POZZA DI MAREA
Lungo le rive del mare è possibile osservare un piccolo ma interessante ecosistema marino: la pozza di marea. Essa è formata dall’acqua che rimane in piccole cavità della sabbia, spesso in prossimità degli scogli, quando la marea si abbassa. In questo habitat vivono creature diverse, tutte molto resistenti, perché devono sapersi adattare ai cambiamenti di temperatura e alla forza delle onde. Eccone alcune.
• Il plancton è formato da minuscoli organismi marini (frammenti di alghe e resti di piccoli animali) trasportati dalle onde; è il cibo di molti animali, tra cui gli anemoni e le cozze.
• Gli anemoni di mare sembrano colorati e meravigliosi fiori subacquei, ma in realtà sono animali e con i loro tentacoli urticanti catturano piccoli pesci e il plancton di cui si nutrono.
• I mitili, chiamati anche cozze o muscoli, si nutrono filtrando il plancton; si attaccano agli scogli e hanno le valve nere e dure; vengono mangiati dalle stelle marine.
• Le stelle marine hanno uno stomaco speciale che possono in parte far uscire dal corpo per digerire cibo più grande della loro bocca; hanno anche centinaia di piccoli piedi a forma di tubicini che usano per camminare, appendersi alle pareti rocciose e respirare; con i loro tentacoli riescono ad aprire i duri gusci delle cozze.
• Anche le stelle marine hanno nemici, come ad esempio il granchio, che è un animale onnivoro, e il gambero, noto per la sua abitudine di camminare all’indietro.
1 Stabilisci le relazioni che esistono nell’ecosistema della pozza di marea. Usa una freccia rossa per indicare la relazione “è mangiato da” e una freccia blu per indicare la relazione “si nutre di”.
Laboratorio delle

L’ECOSISTEMA BOSCO
Obiettivi Conoscere caratteristiche di un ecosistema e individuare gli aspetti che lo compongono.
Competenze Riconosce le relazioni che legano gli organismi in un ambiente.
1 Il bosco è un ecosistema dove vivono molti tipi di vegetali e di animali, legati fra loro da relazioni che cambiano con il mutare delle stagioni. Leggi i seguenti testi.
AUTUNNO
Nel bosco, in autunno, le giornate si fanno più corte e fredde. Si aggirano animali predatori come le volpi e le faine, che vanno a caccia di conigli e topi e li mangiano subito. Molti animali, invece, come gli scoiattoli, raccolgono il cibo che mangeranno durante l’inverno, quando farà freddo e non riusciranno a trovarlo facilmente. Alcuni uccelli si preparano a migrare per trovare cibo altrove e far nascere i piccoli. Alcuni alberi, come i castagni e le querce, sono coperti da foglie marroni, gialle e rosse che poi perderanno. Rimarranno spogli fino a primavera.
INVERNO
In questa stagione il clima è più freddo e molti animali non riescono a trovare cibo. Alcuni, come le donnole e i tassi, sopravvivono mangiando meno; altri, come i ricci, le marmotte e i ghiri, vanno in letargo in modo da non aver bisogno di cercare il cibo. In inverno l’ermellino cambia colore e il suo pelo diventa bianco. Si mimetizza nella neve, così gli animali suoi nemici non lo possono vedere.
Le aghifoglie, come pini e abeti, non hanno perso le foglie, al contrario di altre piante, e la loro chioma appare sempre verde. Per questo motivo sono dette sempreverdi.
PRIMAVERA ESTATE
Molti uccelli che vivono nel bosco costruiscono il loro nido sui rami più alti degli alberi. Nei nidi depongono le uova, che si schiuderanno appena i pulcini saranno pronti per nascere. Molti mammiferi, come i conigli e le volpi, partoriscono i loro piccoli. Sugli alberi spogli spuntano le prime foglioline verdi. Nel sottobosco nascono bucaneve, primule, viole e ciclamini, che attirano api, farfalle e calabroni.
Le chiome degli alberi sono verdeggianti. Le formiche ingrandiscono i loro formicai. Altri insetti, come i grilli e le cavallette, si mimetizzano con il colore verde dell’erba per non essere catturati da altri animali, come le talpe. L’ermellino cambia colore: ora ha il pelo marrone per mimetizzarsi con il bosco.
2 Scrivi sotto ogni immagine a quale stagione si riferisce.

3 Completa le schede relative al bosco nelle diverse stagioni.
AUTUNNO INVERNO
Le piante
Gli animali predatori
Gli uccelli
Altri animali
Gli animali, per sopravvivere, oppure
Alcuni animali, per nascondersi dai nemici
Le aghifoglie
Gli uccelli
PRIMAVERA
Molti mammiferi
Sugli alberi
Nel sottobosco
Le piante
Gli insetti
L’ermellino
LA CATENA E LA RETE ALIMENTARE
1 Ricomponi le frasi spezzate per ricostruire le informazioni sugli ecosistemi.
Le piante sono organismi produttori perché…
Gli animali erbivori mangiano i vegetali e…
I carnivori si alimentano di altri animali, perciò...
Alcuni animali si nutrono di altri carnivori e...
Funghi, vermi e batteri trasformano i resti e…
I viventi di un ecosistema sono legati tra loro...

… sono detti consumatori secondari.
… sono detti consumatori primari.
… sono chiamati decompositori.
… producono da sole il proprio nutrimento.
… dalle relazioni alimentari.
… sono detti consumatori terziari.
2 Osserva la piramide ecologica illustrata e completa il brano con le seguenti parole. cambiamenti • ecologica • ecosistema • equilibrio • primari • produttori
Tutti gli organismi che popolano un ecosistema sono in un numerico, rappresentato nella piramide
Gli organismi più numerosi sono i , che sono seguiti dai consumatori .
I consumatori secondari sono in numero ancora minore rispetto ai precedenti.
Se avvengono all’interno dell’ecosistema, l’equilibrio si rompe e gli organismi devono adattarsi alla nuova situazione che si è creata.
Con il passar del tempo, l’ trova un nuovo equilibrio.
NOME E COGNOME

ADATTARSI ALL’AMBIENTE
1 I viventi adottano particolari strategie per adattarsi all’ambiente circostante. Qui trovi la descrizione di alcuni comportamenti. Spiega il motivo per cui questi comportamenti si sono resi necessari, come nell’esempio.
COMPORTAMENTO
In montagna, dove la temperatura d’inverno
è molto rigida, spesso l’acqua ghiaccia e le radici non riescono ad assorbirla.
Gli alberi quindi hanno foglie ad ago e aprono gli stomi solo quando necessario per poter ridurre la traspirazione.
motivazione
Trattenere l’acqua.
COMPORTAMENTO
È difficile distinguere sulle piante l’insetto foglia, perché si mimetizza perfettamente.
motivazione
Laboratorio delle competenze
COMPORTAMENTO
Le piante da appartamento, quando la luce è scarsa, spostano i rami e le foglie verso le zone più illuminate.
COMPORTAMENTO
Durante l’inverno, il riccio, la marmotta e il ghiro dormono profondamente nelle loro tane, riducendo le funzioni vitali al minimo.
motivazione motivazione
Laboratorio delle competenze

NOME E COGNOME DATA
1 Utilizza i gruppi di parole e scrivi una didascalia per ciascuna immagine.
ambiente • esseri viventi • esseri non viventi • relazioni
consumatori primari • consumatori secondari • decompositori • produttori
catene alimentari • intreccio • rete alimentare
base • consumatori • piramide • produttori • vertice
animali • aspetto • comportamento • piante
OBIETTIVI: Riconosce le relazioni che legano gli organismi in un ambiente.
Situazione iniziale
LA GIORNATA DELLA TERRA
In Italia ci sono molti Parchi Nazionali e Aree Protette, dove vivono specie vegetali e animali a rischio di estinzione. Fate una ricerca su queste Aree e Parchi: dove sono, in quali ambienti geografici, quali specie proteggono…
Fasi di realizzazione
1. Dividetevi in “gruppi-casa” da tre persone. Un membro del gruppo si occuperà di ricercare i Parchi Nazionali delle Regioni del Nord, un altro quelli delle Regioni del Centro e il terzo membro quelli delle Regioni del Sud e delle Isole. Fate poi un elenco dei Parchi Nazionali e delle Aree Protette trovati, dividendoli per Regione e ambiente geografico.
2. Ora dividetevi in tre “gruppi-esperti”, dove si riuniscono i compagni e le compagne che si sono occupati dei Parchi Nazionali e delle Aree Protette della stessa zona d’Italia. Condividete e scrivete tutte le informazioni raccolte.
3. Terminato lo scambio, ognuno torna al proprio “gruppo-casa” e racconta ciò che ha “scoperto”.
4. Ora ogni “gruppo-casa” sceglie un Parco Nazionale o un’Area protetta da “adottare”. Ognuno si occupa di descrivere una o più specie vegetali e animali protette in quel luogo classificandole e descrivendole (ciclo vitale, caratteristiche fisiche, alimentari, riproduttive...).
5. Preparate un poster con testi, immagini e schede descrittive per presentare il vostro Parco Nazionale.

Situazione finale
Appendete i vostri poster in occasione della Giornata della Terra che ricorre il 22 aprile, per sensibilizzare il pubblico sull’importanza di proteggere il nostro bel Pianeta.
COSTRUIAMO UN ACQUEDOTTO
1 Costruisci insieme con le tue compagne e i tuoi compagni il modellino di un acquedotto.
Che cosa vi serve
bottiglie di plastica • forbici con punte arrotondate • nastro adesivo da pacco • un po’ di terra o sabbia • acqua
1 3 4 5 2
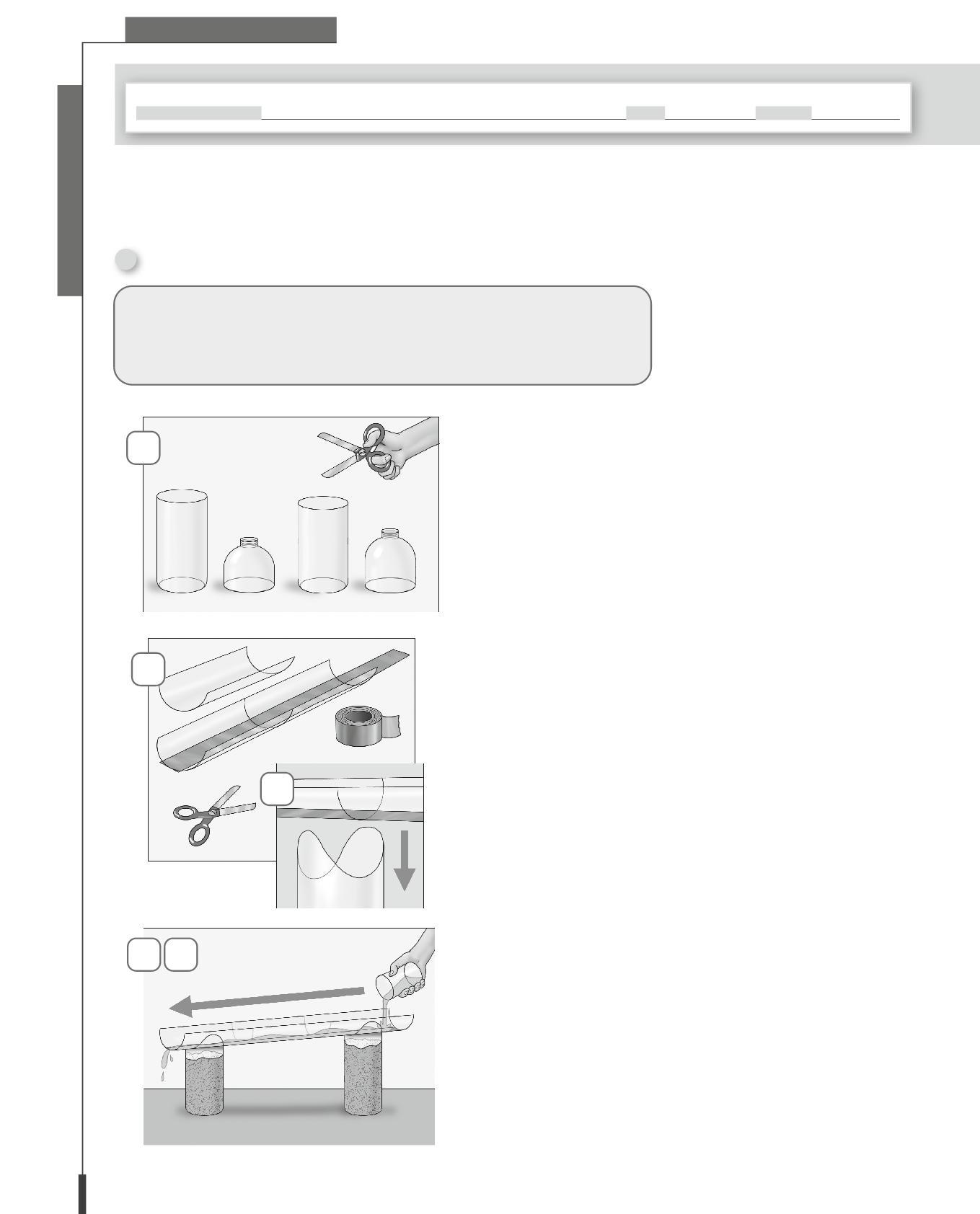
OBIETTIVI:
Fasi di lavorazione
1 Tagliate due bottiglie a metà in senso orizzontale, in modo da ottenere due colonne di appoggio di due altezze leggermente diverse (non più di 2 centimetri di differenza).
2 Tagliate tre bottiglie a metà in senso verticale, eliminando l’imboccatura. Incollate le bottiglie con una striscia di nastro adesivo una in fila all’altra, per il lato lungo. Avete formato il canale dell’acquedotto.
3 Modellate, con un taglio a semicerchio, la parte alta delle basi in modo da sostenere saldamente le bottiglie che formano il canale dell’acquedotto.
4 Riempite le basi delle bottiglie con sabbia o terra, poi appoggiate sopra il canale.
5 Versate l’acqua nel canale per vedere se scorre verso il basso: dovete regolare l’inclinazione dell’acquedotto in modo che l’acqua non ristagni, ma che non scorra nemmeno troppo veloce.

Prove strutturate per classi parallele di Matematica
PROVE STRUTTURATE PER CLASSI PARALLELE
introduzione a cura di Dino Cristanini

L’utilizzo sistematico di prove strutturate comuni è uno degli elementi che, secondo la Guida alla predisposizione del Rapporto di autovalutazione (RAV) pubblicata dal MIUR, qualificano la situazione di una scuola come eccellente nell’area Curricolo, progettazione e valutazione
Le prove comuni possono riguardare le varie fasi dello sviluppo del curricolo:
• le prove d’ingresso hanno la funzione di rilevare la situazione iniziale degli alunni in modo da calibrare opportunamente gli obiettivi di apprendimento;
• le prove intermedie svolgono soprattutto una funzione formativa, fornendo informazioni sugli obiettivi di apprendimento raggiunti dagli alunni e sulle difficoltà che invece richiedono diverse attenzioni metodologiche;
• le prove finali consentono di fare il punto al termine dell’anno scolastico.
L’uso di prove comuni a livello di classi parallele risponde a diverse esigenze.
Innanzitutto contribuiscono a migliorare l’equità dell’offerta formativa, ossia la capacità della scuola di assicurare a tutti gli alunni la stessa qualità d’istruzione. Ciò avviene attraverso una progettazione comune per classi parallele e un monitoraggio periodico sull’andamento degli apprendimenti rilevati mediante strumenti omogenei e idonei a permettere la confrontabilità, in modo da poter effettuare per tempo le opportune regolazioni nel caso di eccessivi scostamenti. Si tratta di pratiche efficaci per ridurre una criticità abbastanza diffusa per quanto riguarda gli esiti di apprendimento, ossia la varianza tra le classi della stessa istituzione scolastica.
In secondo luogo favoriscono il confronto e la condivisione tra i docenti dei criteri di valutazione, delle strategie metodologiche e delle pratiche didattiche
Infine concorrono a sviluppare una cultura della valutazione in cui i dati diventano il punto di partenza per riflessioni orientate al miglioramento.
Per tutte queste ragioni le seguenti pagine intendono offrire ai docenti un utile supporto, costituito dalla proposta di prove comuni iniziali, intermedie e finali relative alle principali discipline. Si tratta di prove strutturate che consentono di rilevare abilità e conoscenze riferite agli obiettivi di apprendimento previsti dalle Indicazioni nazionali per il curricolo.
MATEMATICA
Prova d’ingresso pag. 169 Prova d’ingresso con soluzioni pag. 181
Prova intermedia pag. 173
Prova finale pag. 177
Prova intermedia con soluzioni pag. 185
Prova finale con soluzioni pag. 189
NOME E COGNOME
PROVA D’INGRESSO DI MATEMATICA
1 Collega ogni numero in cifre al numero in parola corrispondente.

2 Indica con una X se le affermazioni sono vere V o false F .
• Il numero successivo di 1 760 è 1 761. V F
• Il numero successivo di 8 000 è 9 000. V F
• Il numero successivo di 2 909 è 2 910. V F
3 Indica con una X il precedente di ciascun numero. 1 864 2 999
A. 1 763
B. 1 863
3 000
C. 1 860 C. 2 998
D. 1 865 D. 2 098
4 Confronta i numeri scrivendo il simbolo > oppure <.
5 Indica con una X la serie di numeri scritti in ordine crescente.
A. 875 • 9 000 • 3 500 • 6 005
B. 9 000 • 875 • 3 500 • 6 005
C. 875 • 3 500 • 6 005 • 9 000
D. 875 • 3 500 • 9 000 • 6 005 905 8 000 2 326 3 079 duemilatrecentoventisei novecentocinque tremilasettantanove ottomila
5 999
2 290 B. 6 999
C. 5 000
D. 6 001
6 Indica con una X la scomposizione corretta del numero 6 042.
A. 6 k 4 h 0 da 2 u C. 6 k 4 h 2 da 4 u
B. 6 k 0 h 4 da 2 u D. 2 k 0 h 6 da 4 u
7 Quale cifra occupa il posto delle centinaia nel numero 3 705? A. 5 C. 7 B. 0
OBIETTIVI: Riconoscere numeri scritti in cifre e in parola. • Numerare in ordine crescente e decrescente. •Confrontare numeri. • Riconoscere il valore posizionale delle cifre in un numero.
8 Esegui le addizioni e le sottrazioni in colonna.
4325+ 2425+ 6598– 8390–272+ 2504+ 3106= 1164= 1301= 353=
9 Esegui le moltiplicazioni e le divisioni in colonna. 220× 126× 8422 7263 4= 3=

10 Indica con una X quale moltiplicazione dà come risultato 2 500. A. 25 × 1
11 Indica con una X quale divisione dà come risultato 8. A. 8 : 0
: 100
12 I risultati delle seguenti operazioni sono giusti? Indica SÌ oppure NO.
400 + 25 + 25 = 450 1 976 − 900 = 1 876 6 × 8 = 58
: 3 = 30 SÌ NO SÌ NO SÌ NO
13 Leggi il testo del problema, poi cerchia i dati e sottolinea la domanda. Camilla sta leggendo un libro di 192 pagine. Ha già letto 64 pagine. Quante pagine deve ancora leggere?
14 Indica con una X l’operazione da eseguire per risolvere il problema dell’esercizio precedente. A. addizione B. sottrazione C. moltiplicazione D. divisione
OBIETTIVI: Eseguire correttamente le quattro operazioni con numeri naturali. • Eseguire correttamente moltiplicazioni e divisioni per 10, 100, 1 000 con numeri naturali. • Riconoscere i dati, la domanda e l’operazione risolutiva di un problema.
NOME E COGNOME DATA
15 Collega la frazione scritta in parola a quella scritta in cifre corrispondente.

16 Indica con una X l’unità frazionaria rappresentata dal disegno.
17 Indica con una X il disegno che rappresenta la frazione 5 8 .
18 Indica con una X se le affermazioni sono vere V o false F .
• La lunghezza di un’autostrada si misura in chilometri.
• Il peso corporeo di una persona si misura in litri.
V F
V F
• Il peso dei biscotti contenuti in un pacchetto si misura in grammi. V F
• L’aranciata contenuta in una lattina si misura in centilitri. V F
19 Completa le uguaglianze con i numeri 2, 5, 10.
• 1 euro = monete da 50 cent.
• 1 euro = monete da 10 cent.
• 1 euro = monete da 20 cent. due decimi un terzo tre settimi tre quarti
20 Classifica gli angoli e scrivi al posto giusto le parole seguenti. giro • piatto • retto
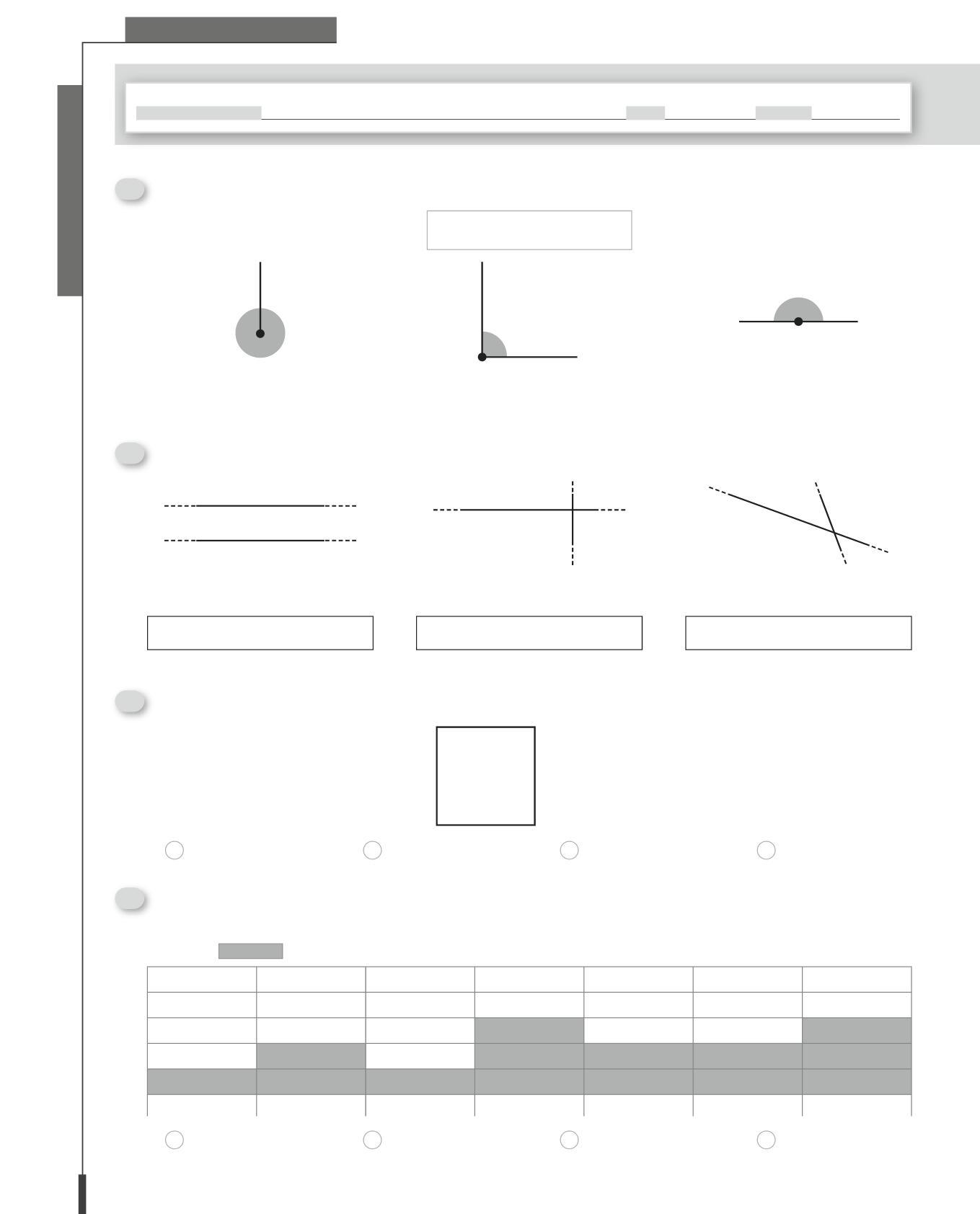
angolo angolo angolo
21 Collega ogni coppia di rette alla definizione corretta.
22 Indica con una X la misura del perimetro del quadrato. 6 cm
36 cm
12 cm
24 cm
60 cm
23 Il seguente grafico rappresenta le ore di televisione che Giorgio ha guardato in una settimana. Qual è il totale?
Legenda = 1 ora lunedì martedì mercoledì giovedì venerdì sabato domenica
12 ore
10 ore rette perpendicolari rette parallele rette incidenti
15 ore
14 ore
OBIETTIVI: Riconoscere e classificare gli angoli. • Riconoscere e classificare le rette. • Calcolare il perimetro di un quadrato. • Saper leggere un istogramma.
NOME E COGNOME
PROVA INTERMEDIA DI MATEMATICA
1 Indica con una X come si scrivono in cifre i numeri indicati. • trecentoventisettemiladuecentouno • centocinquantamilaottocentoventicinque
A. 300 201
B. 237 201
C. 327 201
D. 327 211
A. 150 855
B. 105 825
C. 510 825
D. 150 825
2 Indica con una X se il confronto è vero V o falso F .
13 013 < 13 003 V F
000 > 157 999 V F 13 103 > 13 013 V F
3 Per ogni numero indicato, scrivi il precedente e il successivo.
4 Riscrivi i numeri in ordine decrescente, dal maggiore al minore.
14 370 • 41 350 • 10 499 • 14 630 99 705 • 99 507 • 100 000 • 99 750
5 Indica con una X la scomposizione corretta del numero 5 860.
A. 5 uk 8 h 6 u 0 da C. 5 uk 8 h 6 da 0 u
B. 5 uk 8 da 6 h 0 u D. 5 h 8 uk 6 da 0 u
6 Indica con una X il valore della cifra 5 in ciascun numero.
9 508 5 736 53 697 235 120
A. u A. u A. uk A. h
B. da B. da B. dak B. hk
C. h C. h C. u C. dak
D. uk D. uk D. da D. uk 11 800 23 502
OBIETTIVI: Leggere, scrivere, ordinare e confrontare numeri naturali entro 999 999. • Individuare il valore posizionale delle cifre.
7 Calcola a mente e scrivi il risultato.
+ 19 =
– 19 =
+ 99 =
8 Indica con una X il risultato corretto di ogni operazione.
140 × 10 = 26 × 100 = 56 000 : 1 000 = 182 000 : 100 =
14
1 400
1 000
4 100
260
5 600
1 820
9 Indica con una X quale operazione rende vere le uguaglianze.
100 ? 25 = 75 48 ? 6 = 8 30 ? 3 = 90 155 ? 15 = 170
+
×
:
10 Utilizza le proprietà indicate per risolvere le operazioni.
proprietà associativa (+)
:
400 + 280 + 120 = proprietà invariantiva (−) 560 − 190 =
proprietà associativa (×)
355 × 2 × 5 = proprietà invariantiva (:) 720 : 80 =
11 Leggi il problema, poi sottolinea i dati utili e cerchia i dati inutili.
Sara compra 2 scatole di cioccolatini da dividere con 5 amiche e spende 16 euro. In ogni scatola ci sono 18 cioccolatini. Quanti sono i cioccolatini in tutto?
12 Indica con una X la domanda nascosta nel problema.
In pizzeria il papà deve pagare 3 pizze che costano 7 euro l’una e 11 euro per 3 bibite. Quanto pagherà in tutto?
A. Quanto spende in tutto per le bibite? B. Quanto spende in tutto per le pizze?
13 Quale disegno rappresenta la frazione 7 10 ?
14 Per ogni affermazione indica SÌ oppure NO.
frazione propria. SÌ NO
4 è una frazione apparente. SÌ NO
una frazione impropria. SÌ NO
è una frazione apparente. SÌ NO
15 Usa i numeri e associa ogni affermazione all’immagine corrispondente.
L’asse di simmetria è interno alla figura.
È stata eseguita una traslazione.
È stata eseguita una rotazione.
Le due figure hanno un asse di simmetria esterno.
16 Osserva i disegni e per ogni affermazione sottolinea l’alternativa corretta.
• a e b sono linee rette incidenti / perpendicolari / parallele
• c e d sono linee rette incidenti / perpendicolari / parallele.
• e e f sono linee rette incidenti / perpendicolari / parallele
• g e h sono linee rette incidenti / perpendicolari / parallele
17 Classifica i numeri nel diagramma di Carroll.
numeri multipli di 5 numeri NON multipli di 5
numeri pari
numeri dispari
18 Osserva le relazioni e indica con una X se le affermazioni sono vere V oppure false F .
La relazione è: è figlio di…
• Taro è figlio di Yoko. V F
• Marino è figlio di Aldo. V F
• Luca è figlio di Aldo. V F
OBIETTIVI: Riconoscere e classificare le linee rette. • Classificare numeri sulla base di più proprietà utilizzando adeguate rappresentazioni grafiche. • Riconoscere relazioni.
PROVA FINALE DI MATEMATICA
1 Indica con una X la frazione complementare che completa ogni uguaglianza.

2 Indica con una X la frazione equivalente a 10 20 .
3 Collega ogni frazione al numero decimale corrispondente.
4 Indica con una X come si calcola il valore 3 5 di 30.
A. (30 : 3) × 5 = 10 × 5 = 50
B. (30
5 Quale numero precede 12,601?
C. (30 : 5) × 3 = 6 × 3 = 18
6 Riscrivi i numeri in ordine crescente, dal minore al maggiore. 12,51 • 75,158 • 0,83 • 4,69 3,2 • 25,261 • 25,126 • 3,184
7 Confronta i numeri e completa con >, <, =.
8 Scrivi G (giusta) oppure S (sbagliata) accanto a ogni scomposizione. 7,512 = 7 u 5 d 1 c 2 m 2,131 = 2 u 1 d 1 c 3 m 85,06 = 8 da 5 u 6 d 0,384 = 0 u 3 d 8 c 4 m
9 Il risultato di ciascuna operazione è giusto? Indica SÌ oppure NO.
3,5 × 10 = 35 SÌ NO
× 100 = 93 SÌ
× 1
=
10 Scrivi 10, 100, 1 000 per completare le divisioni.
7 853 : = 7,853 39 : = 0,39
11 Esegui le operazioni in colonna.
2 305,173 + 831,042 + 1 242,37 = 9 461,605 − 3
=
12 Esegui le divisioni in colonna.
958,416 : 6 = 2 748,48 : 1,4 =
OBIETTIVI: Eseguire le quattro operazioni con i numeri decimali.
: = 24,1
× 7,2 =
13 Riscrivi in ordine crescente le seguenti misure di lunghezza.
5 km • 18 hm • 25 dam • 4 500 m
14 Indica con una X la misura che corrisponde a 225 ℓ .
A. 2 250 daℓ

2,25 dℓ
2,25 hℓ
22,5 cℓ
15 Il peso lordo di un barattolo di marmellata è di 470 g. Indica con una X quale potrebbe essere il peso netto della marmellata.
A. 4 kg B. 40 mg C. 4 dag
16 Indica con una X chi ha impiegato più tempo per svolgere la verifica di italiano.
A. Simone: un quarto d’ora
B. Claudia: quaranta minuti
4 hg
C. Maurizio: trenta minuti
D. Laura: mezz’ora
17 Il papà di Susanna esce di casa alle 6:50 e arriva al posto di lavoro dopo un’ora e 15 minuti. Indica con una X a che ora arriva al lavoro. A. 7:05
18 Nel borsellino della signora Camilla ci sono due banconote da € 20,00, due banconote da € 10,00, tre banconote da € 5,00, una moneta da € 2,00, due monete da € 1,00, una monetina da 20 cent e due monetine da 5 cent. Quanto ha in tutto nel borsellino la signora Camilla?
19 Indica con una X la sequenza di operazioni che risolve il problema. Ogni mattina a casa di Andrea si consumano 2 confezioni di yogurt a colazione. Ogni confezione costa € 3,00. Quale sarà la spesa complessiva di 10 giorni? A. 2 + 3 = 5
Conoscere e utilizzare le principali misure di lunghezza, capacità, peso (o massa), tempo e valore.
20 Indica con una X se le affermazioni sono vere V o false F .

• Tutte queste figure geometriche sono parallelogrammi. V F
• Tutte queste figure geometriche sono trapezi. V F
• Le figure geometriche 1 , 2 e 4 sono parallelogrammi. V F
• Le figure geometriche 3 e 4 sono parallelogrammi. V F
21 Indica con una X la formula sbagliata per calcolare la misura del perimetro del quadrato.
A. P = ℓ × 4 C. P = (ℓ + ℓ) × 2 B. P = ℓ + ℓ + ℓ + ℓ D. P = ℓ × ℓ
22 Collega ogni figura all’operazione necessaria per calcolare la sua area.
23 L’ideogramma rappresenta la presenza dei bambini alla mensa della scuola primaria Leonardo Da Vinci. Osserva il grafico e indica con una X se le affermazioni sono vere V oppure false F .
Legenda = 10 bambini = 1 bambino
lunedì
• Il giorno con il maggior numero di bambini presenti è stato il martedì. V F
• Il giorno con il minor numero di bambini presenti è stato il giovedì. V F
• Venerdì erano presenti 72 bambini. V F
• Giovedì erano presenti più bambini rispetto a mercoledì. V F
OBIETTIVI: Riconoscere le principali figure geometriche. • Conoscere le formule per calcolare perimetro e area di triangoli e quadrilateri. • Leggere e analizzare dati statistici.
NOME E COGNOME DATA
PROVA D’INGRESSO DI MATEMATICA
1 Collega ogni numero in cifre al numero in parola corrispondente.
8 000 2 326 3 079 duemilatrecentoventisei novecentocinque tremilasettantanove ottomila
2 Indica con una X se le affermazioni sono vere V o false F .
• Il numero successivo di 1 760 è 1 761.
V F
• Il numero successivo di 8 000 è 9 000. V F
• Il numero successivo di 2 909 è 2 910. V F
3 Indica con una X il precedente di ciascun numero. 1 864 2 999 6 000
A. 1 763 A. 3 000 A. 5 999
B. 1 863 B. 2 290 B. 6 999
C. 1 860
C. 2 998
D. 1 865 D. 2 098
4 Confronta i numeri scrivendo il simbolo > oppure <.
C. 5 000
6 001
5 Indica con una X la serie di numeri scritti in ordine crescente.
A. 875 • 9 000 • 3 500 • 6 005
B. 9 000 • 875 • 3 500 • 6 005
C. 875 • 3 500 • 6 005 • 9 000
D. 875 • 3 500 • 9 000 • 6 005 905
6 Indica con una X la scomposizione corretta del numero 6 042.
A. 6 k 4 h 0 da 2 u C. 6 k 4 h 2 da 4 u
B. 6 k 0 h 4 da 2 u D. 2 k 0 h 6 da 4 u
7 Quale cifra occupa il posto delle centinaia nel numero 3 705?
OBIETTIVI: Riconoscere numeri scritti in cifre e in parola. • Numerare in ordine crescente e decrescente. •Confrontare numeri. • Riconoscere il valore posizionale delle cifre in un numero.
NOME E COGNOME

8 Esegui le addizioni e le sottrazioni in colonna.
4325+ 2425+ 6598– 8390–272+ 2504+ 3106= 1164= 1301= 353= 34927226 58985282
9 Esegui le moltiplicazioni e le divisioni in colonna. 220× 126× 8422 7263 4= 3= 0442112242 8803780206 0
10 Indica con una X quale moltiplicazione dà come risultato 2 500. A. 25 × 1
11 Indica con una X quale divisione dà come risultato 8. A. 8 : 0 B. 80 : 100
: 10
12 I risultati delle seguenti operazioni sono giusti? Indica SÌ oppure NO.
400 + 25 + 25 = 450 1 976 − 900 = 1 876
13 Leggi il testo del problema, poi cerchia i dati e sottolinea la domanda. Camilla sta leggendo un libro di 192 pagine. Ha già letto 64 pagine. Quante pagine deve ancora leggere?
14 Indica con una X l’operazione da eseguire per risolvere il problema dell’esercizio precedente. A. addizione B. sottrazione C. moltiplicazione D. divisione
NOME E COGNOME DATA
15 Collega la frazione scritta in parola a quella scritta in cifre corrispondente.
due decimi un terzo tre settimi tre quarti
16 Indica con una X l’unità frazionaria rappresentata dal disegno.
17 Indica con una X il disegno che rappresenta la frazione 5 8 .
18 Indica con una X se le affermazioni sono vere V o false F .
• La lunghezza di un’autostrada si misura in chilometri.
• Il peso corporeo di una persona si misura in litri.
V F
V F
• Il peso dei biscotti contenuti in un pacchetto si misura in grammi. V F
• L’aranciata contenuta in una lattina si misura in centilitri.
19 Completa le uguaglianze con i numeri 2, 5, 10.
V F
• 1 euro = monete da 50 cent.
• 1 euro = monete da 10 cent.
• 1 euro = monete da 20 cent.
2 10 5
20 Classifica gli angoli e scrivi al posto giusto le parole seguenti. giro • piatto • retto
angolo angolo angolo
21 Collega ogni coppia di rette alla definizione corretta.
22 Indica con una X la misura del perimetro del quadrato. 6 cm
36 cm
12 cm
24 cm
60 cm
23 Il seguente grafico rappresenta le ore di televisione che Giorgio ha guardato in una settimana. Qual è il totale?
Legenda = 1 ora
10 ore rette perpendicolari rette parallele rette incidenti giro retto piatto
OBIETTIVI: Riconoscere e classificare gli angoli. • Riconoscere e classificare le rette. • Calcolare il perimetro di un quadrato. • Saper leggere un istogramma.
NOME E COGNOME DATA CLASSE
PROVA INTERMEDIA DI MATEMATICA
1 Indica con una X come si scrivono in cifre i numeri indicati. • trecentoventisettemiladuecentouno • centocinquantamilaottocentoventicinque
A. 300 201
B. 237 201
C. 327 201
D. 327 211
A. 150 855
B. 105 825
C. 510 825
D. 150 825
2 Indica con una X se il confronto è vero V o falso F .
13 013 < 13 003 V F
000 > 157 999 V F 13 103 > 13 013 V F
013 < 360 000 V F
3 Per ogni numero indicato, scrivi il precedente e il successivo.
4 Riscrivi i numeri in ordine decrescente, dal maggiore al minore.
14 370 • 41 350 • 10 499 • 14 630 99 705 • 99 507 • 100 000 • 99 750
5 Indica con una X la scomposizione corretta del numero 5 860.
A. 5 uk 8 h 6 u 0 da C. 5 uk 8 h 6 da 0 u
B. 5 uk 8 da 6 h 0 u D. 5 h 8 uk 6 da 0 u
6 Indica con una X il valore della cifra 5 in ciascun numero.
9 508 5 736 53 697 235 120
A. u A. u A. uk
h
B. da B. da B. dak B. hk
C. h C. h C. u C. dak D. uk D. uk
uk 11 800 23 502 11799118012350123503 41 35014 63014 37010 499 100 00099 75099 70599 507 X X
da
OBIETTIVI: Leggere, scrivere,
7 Calcola a mente e scrivi il risultato.
+ 19 =
– 19 =

+ 99 =
8 Indica con una X il risultato corretto di ogni operazione.
140 × 10 = 26 × 100 = 56 000 : 1 000 = 182 000 : 100 =
14
1 400
1 000
4 100
260
5 600
1 820
18 200
9 Indica con una X quale operazione rende vere le uguaglianze.
100 ? 25 = 75 48 ? 6 = 8 30 ? 3 = 90 155 ? 15 = 170 A. + A. +
:
10 Utilizza le proprietà indicate per risolvere le operazioni.
proprietà associativa (+)
400 + 280 + 120 =
proprietà invariantiva (−) 560 − 190 =
400 + (280 + 120) = 400 + 400 = 800 (560 + 10) – (190 + 10) = 570 – 200 = 370
proprietà associativa (×)
355 × 2 × 5 =
proprietà invariantiva (:) 720 : 80 =
355 × (2 × 5) = 355 × 10 = 3550 (720 : 10) : (80 : 10) = 72 : 8 = 9
11 Leggi il problema, poi sottolinea i dati utili e cerchia i dati inutili.
Sara compra 2 scatole di cioccolatini da dividere con 5 amiche e spende 16 euro. In ogni scatola ci sono 18 cioccolatini. Quanti sono i cioccolatini in tutto?
12 Indica con una X la domanda nascosta nel problema.
In pizzeria il papà deve pagare 3 pizze che costano 7 euro l’una e 11 euro per 3 bibite. Quanto pagherà in tutto?
A. Quanto spende in tutto per le bibite? B. Quanto spende in tutto per le pizze?
13 Quale disegno rappresenta la frazione 7 10 ?

14 Per ogni affermazione indica SÌ oppure NO.
è una frazione propria. SÌ NO
4 è una frazione apparente. SÌ NO
è una frazione apparente. SÌ NO
15 Usa i numeri e associa ogni affermazione all’immagine corrispondente.
L’asse di simmetria è interno alla figura.
È stata eseguita una traslazione.
È stata eseguita una rotazione.
Le due figure hanno un asse di simmetria esterno.
16 Osserva i disegni e per ogni affermazione sottolinea l’alternativa corretta.
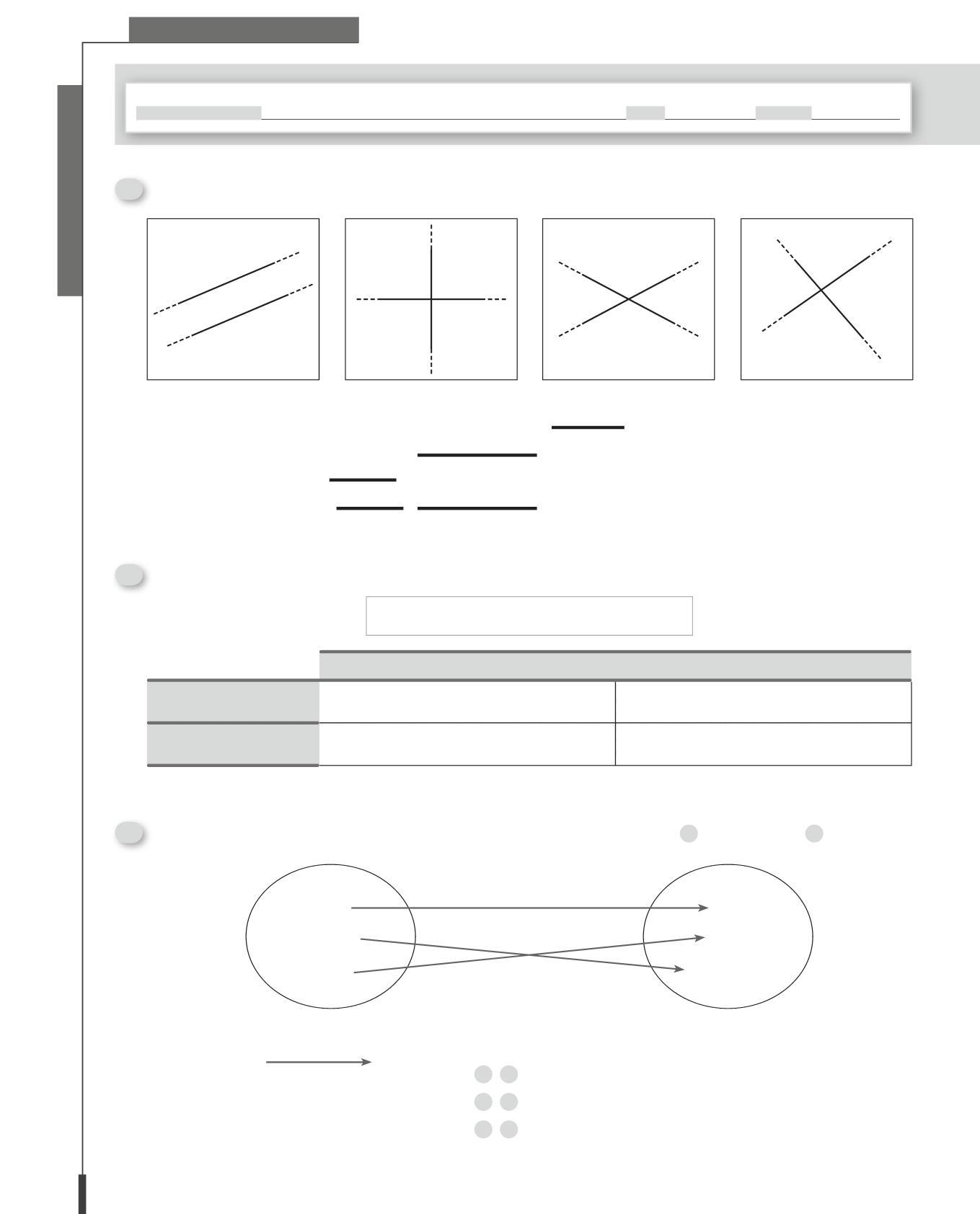
• a e b sono linee rette incidenti / perpendicolari / parallele
• c e d sono linee rette incidenti / perpendicolari / parallele.
• e e f sono linee rette incidenti / perpendicolari / parallele
• g e h sono linee rette incidenti / perpendicolari / parallele
17 Classifica i numeri nel diagramma di Carroll.
numeri multipli di 5 numeri NON multipli di 5 numeri pari numeri dispari
18 Osserva le relazioni e indica con una X se le affermazioni sono vere V oppure false F .
La relazione è: è figlio di…
• Taro è figlio di Yoko. V F
• Marino è figlio di Aldo. V F
• Luca è figlio di Aldo.
OBIETTIVI: Riconoscere e classificare le linee rette. • Classificare numeri sulla base di più proprietà utilizzando adeguate rappresentazioni grafiche. • Riconoscere relazioni.
PROVA FINALE DI MATEMATICA
1 Indica con una X la frazione complementare che completa ogni uguaglianza.
2 Indica con una X la frazione equivalente a 10 20 .
3 Collega ogni frazione al numero decimale corrispondente.
4 Indica con una X come si calcola il valore 3 5 di 30.
A. (30 : 3) × 5 = 10 × 5 = 50
B. (30 + 3) × 5 = 33 × 5 = 165
5 Quale numero precede 12,601?
C. (30 : 5) × 3 = 6 × 3 = 18
6 Riscrivi i numeri in ordine crescente, dal minore al maggiore.
• 75,158 • 0,83 • 4,69
7 Confronta i numeri e completa con >, <, =.
8 Scrivi G (giusta) oppure S (sbagliata) accanto a ogni scomposizione.
9 Il risultato di ciascuna operazione è giusto? Indica SÌ oppure NO.
3,5 × 10 = 35 SÌ NO
× 100 = 93 SÌ
10 Scrivi 10, 100, 1 000 per completare le divisioni.
7 853 : = 7,853 39 : = 0,39 241 : = 24,1
11 Esegui le operazioni in colonna.
2 305,173 + 831,042 + 1 242,37 = 9 461,605 − 3
=
× 7,2 = 2305,173+9461,605–348,56× 831,042+3620,370=7,2= 1242,370=5841,23569712+ 4378,5852439920= 2509,632
12 Esegui le divisioni in colonna.
958,416 : 6 = 2 748,48 : 1,4 = 958,416:6=159,7362748,48:1,4=1963,2 35134 5888 4444 2128 360
OBIETTIVI: Eseguire le quattro operazioni con i numeri decimali.
13 Riscrivi in ordine crescente le seguenti misure di lunghezza.
5 km • 18 hm • 25 dam • 4 500 m
14 Indica con una X la misura che corrisponde a 225 ℓ .
A. 2 250 daℓ

15 Il peso lordo di un barattolo di marmellata è di 470 g. Indica con una X quale potrebbe essere il peso netto della marmellata.
A. 4 kg B. 40 mg
4 dag
16 Indica con una X chi ha impiegato più tempo per svolgere la verifica di italiano.
A. Simone: un quarto d’ora
B. Claudia: quaranta minuti
4 hg
C. Maurizio: trenta minuti
D. Laura: mezz’ora
17 Il papà di Susanna esce di casa alle 6:50 e arriva al posto di lavoro dopo un’ora e 15 minuti. Indica con una X a che ora arriva al lavoro.
A. 7:05 B. 7:55
18 Nel borsellino della signora Camilla ci sono due banconote da € 20,00, due banconote da € 10,00, tre banconote da € 5,00, una moneta da € 2,00, due monete da € 1,00, una monetina da 20 cent e due monetine da 5 cent. Quanto ha in tutto nel borsellino la signora Camilla?
19 Indica con una X la sequenza di operazioni che risolve il problema. Ogni mattina a casa di Andrea si consumano 2 confezioni di yogurt a colazione. Ogni confezione costa € 3,00. Quale sarà la spesa complessiva di 10 giorni? A. 2 + 3 = 5
2 + 3 = 5
Conoscere e utilizzare le principali misure di lunghezza, capacità, peso (o massa), tempo e valore.
20 Indica con una X se le affermazioni sono vere V o false F .
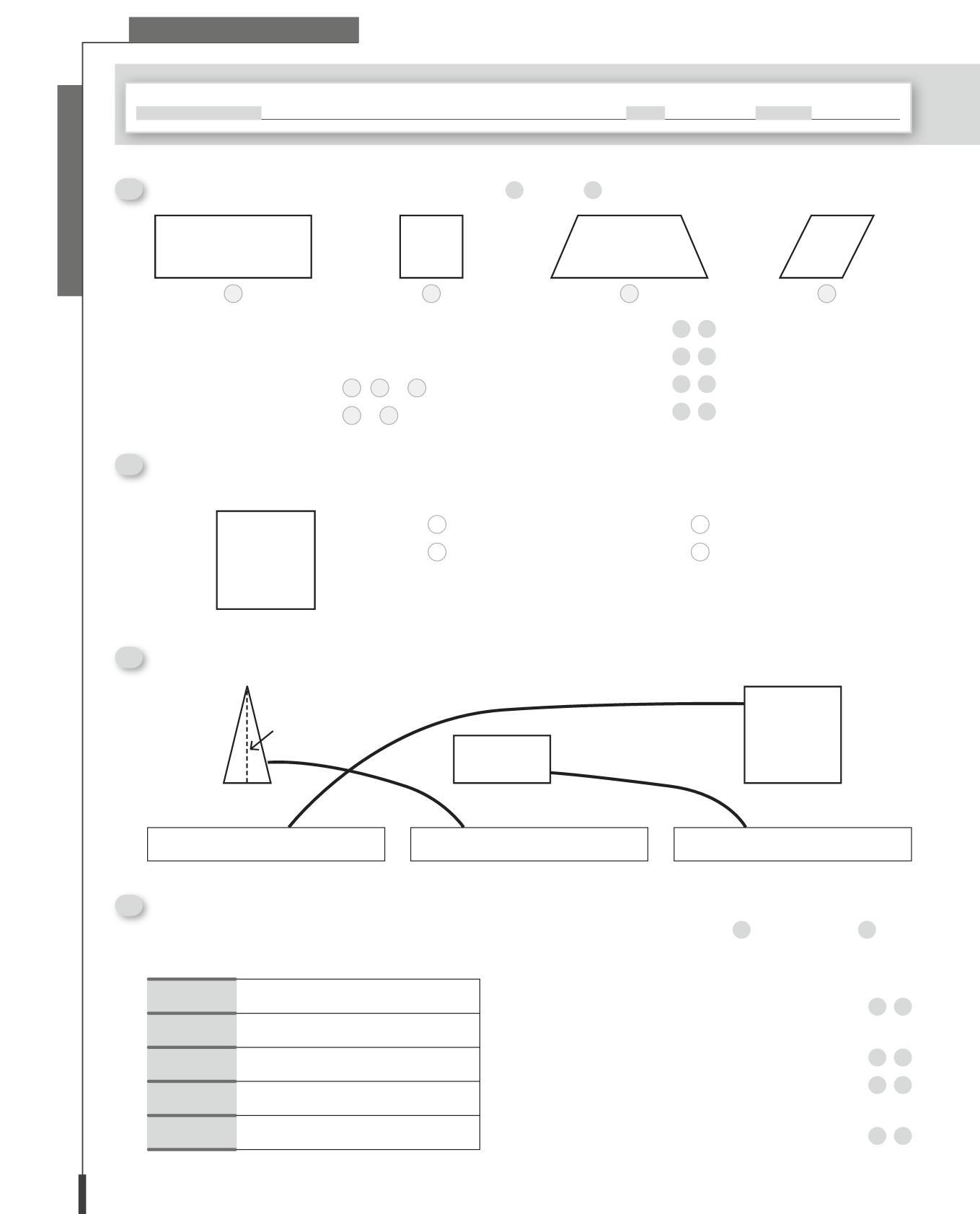
• Tutte queste figure geometriche sono parallelogrammi. V F
• Tutte queste figure geometriche sono trapezi. V F
• Le figure geometriche 1 , 2 e 4 sono parallelogrammi. V F
• Le figure geometriche 3 e 4 sono parallelogrammi. V F
21 Indica con una X la formula sbagliata per calcolare la misura del perimetro del quadrato.
A. P = ℓ × 4
C. P = (ℓ + ℓ) × 2
B. P = ℓ + ℓ + ℓ + ℓ D. P = ℓ × ℓ
22 Collega ogni figura all’operazione necessaria per calcolare la sua area.
23 L’ideogramma rappresenta la presenza dei bambini alla mensa della scuola primaria Leonardo Da Vinci. Osserva il grafico e indica con una X se le affermazioni sono vere V oppure false F .
Legenda = 10 bambini = 1 bambino
lunedì
• Il giorno con il maggior numero di bambini presenti è stato il martedì. V F
• Il giorno con il minor numero di bambini presenti è stato il giovedì. V F
• Venerdì erano presenti 72 bambini. V F
• Giovedì erano presenti più bambini rispetto a mercoledì. V F
OBIETTIVI: Riconoscere le principali figure geometriche. • Conoscere le formule per calcolare perimetro e area di triangoli e quadrilateri.
• Leggere e analizzare dati statistici.
Contributi e percorsi a cura di Ricerca e Sviluppo Erickson

• Costruire inclusione in una prospettiva universale
• Il Piano Educativo Individualizzato in prospettiva bio-psico-sociale
• Piano Didattico Personalizzato: ridare centralità alla didattica
• I materiali per una didattica inclusiva
ne I mondi di GEA – Scienze e Matematica
• Percorso Calcolo facile
• Il mio atlante • Ripassa con Gea
• Progetto CheFacile!
COSTRUIRE INCLUSIONE
IN UNA PROSPETTIVA
UNIVERSALE
Il vero significato di una scuola inclusiva
Quando parliamo di inclusione in termini generali e quando pensiamo allo sviluppo di un contesto scolastico inclusivo, dobbiamo in primis evitare un errore fondamentale: pensare all’inclusione come a qualcosa che riguarda le categorie svantaggiate. Al contrario, l’inclusione riguarda tutte le persone, tutti i membri della comunità scolastica, siano essi studenti e studentesse o docenti e altre figure professionali presenti nel contesto scolastico.
L’inclusione, infatti, si concretizza in azioni pedagogiche e didattiche nel momento in cui mira a costruire una comunità scolastica inclusiva, basata sulla valorizzazione delle differenze e sulla partecipazione sociale di tutti e tutte. Una finalità ben più ampia di quella che a volte viene indicata rispetto alle attenzioni specifiche rivolte a categorie che presentano Bisogni Educativi Speciali (BES). L’inclusione riguarda le politiche scolastiche, le scelte di indirizzo di un istituto, le relazioni tra il personale e tra docenti e il gruppo studentesco, ma anche le relazioni con le famiglie e il contesto extrascolastico. Riguarda poi ovviamente anche le scelte personali che ogni docente si trova liberamente a esercitare nella selezione delle metodologie didattiche, dei materiali, dell’organizzazione del contesto di classe, nello stile relazionale che ognuno adotta nei confronti della classe nell’esercizio della propria autorità di docente. Sono molti i gradi di libertà che ciascuno può attivare per dare forma a una didattica più inclusiva e più capace di tenere conto delle differenze individuali che formano il gruppo classe.
La finalità della didattica inclusiva
La didattica inclusiva ha come finalità il raggiungimento del maggior grado possibile di apprendimento e della partecipazione di tutti e tutte, tenendo conto delle condizioni di ciascuno. Se analizziamo queste poche parole, scopriamo già alcuni elementi di particolare importanza. Innanzitutto, vediamo subito come la didattica inclusiva contenga in sé il concetto di personalizzazione. Le “condizioni di ciascuno” ci mettono subito sulla pista delle differenze individuali, cioè il punto di partenza che non può essere ignorato. Per anni la didattica tradizionale ha cercato di eliminare questa eterogeneità, impostando la propria azione su una fantomatica “normalità” o un’altrettanto illusoria media di competenza. La didattica inclusiva riporta invece la complessità delle differenze umane al centro della propria azione. Se io docente voglio programmare la mia azione, il mio curricolo, le mie strategie e i miei strumenti, devo comprendere le condizioni di partenza del mio gruppo classe e dei singoli e monitorarle nel corso del tempo. Non solo le condizioni “speciali” (per dirla con un termine ormai desueto) di alunni e alunne con disabilità e Bisogni Educativi Speciali o con specifiche situazioni di difficoltà, ma di tutto il gruppo
Differenziazione al centro della didattica inclusiva
La definizione di inclusione ci dice anche che i traguardi e i percorsi possono essere differenti: la finalità è che tutti arrivino a sviluppare il massimo grado possibile di apprendimento e partecipazione, ma questo grado non può essere uguale per tutti, perché diverse sono le condizioni di partenza e le situazioni che possono accadere nel tempo. Questo apre la strada a un concetto chiave che è quello della differenziazione didattica.
Che cosa si intende per differenziazione?
La differenziazione è una prospettiva metodologica capace di promuovere processi di apprendimento significativi per tutti gli allievi presenti in classe, volta a proporre attività educative didattiche mirate, progettate per soddisfare le esigenze dei singoli in un clima educativo in cui è consuetudine affrontare il lavoro didattico con modalità differenti (D’Alonzo, 2017).
Riconoscere e porre al centro dell’azione educativa la differenza del singolo e del gruppo significa, infatti, differenziare i modi di fare lezione, i materiali, le modalità di lavoro e di espressione di alunni e alunne, affinché diventi normale lavorare in classe in maniera differente, utilizzando anche strumenti differenti. Come si vede nell’immagine seguente, in una scuola inclusiva gli aiuti non sono distribuiti a tutti in modo uguale (1), ma in base alle necessità e alle differenze di ogni individuo (2). Tuttavia, l’azione più efficace è quella che prevede di modificare il contesto generale eliminando le barriere e rendendo gli aiuti non sempre necessari (3).

L’evoluzione necessaria: la prospettiva universale per la piena inclusione
Partire dalla comprensione dei bisogni di tutto il gruppo classe, superare la logica dell’inclusione riferita ai soli Bisogni Educativi Speciali: una sfida certamente difficile. Sappiamo che nella quotidianità scolastica è ancora molto complesso compiere questo passo. Sappiamo che ci sono normative e figure di sistema per l’inclusione che sono riferite appunto alla tutela dei diritti di apprendimento di categorie ancora considerate svantaggiate. Se è vero che la definizione di inclusione, come abbiamo visto, si rivolge al 100% di alunni e alunne, è pur vero che la quotidianità ci mostra un panorama diverso. È necessario quindi un salto in avanti, una spinta a far evolvere le azioni didattiche per cercare la piena inclusione. Per questo motivo, è necessario assumere una prospettiva universale per programmare la propria didattica disciplinare.
La dimensione universale della didattica propone un superamento deciso della logica per cui l’inclusione sia necessaria per rispondere a bisogni specifici di alcuni e si pone, al contrario, come azione programmatica di base per la scuola in ogni situazione, per pianificare un percorso di apprendimento significativo, realmente inclusivo e fondato sulle caratteristiche del gruppo a cui si rivolge (Zambotti e Franch, 2022, p. 7)1. Come scrive Ianes, «se vogliamo davvero muoverci verso l’universalità dovremmo essere ossessionati dallo scoprire, comprendere e valorizzare in ogni modo le differenze dei nostri alunni» (Canevaro e Ianes, 2021 p. 112).
1 Zambotti F. e Franch S., in Sciapeconi I., Pigliapoco E., R&S Erickson, Didattica universale: italiano per le classi 1,2,3, Trento, Erickson, 2022.
2 Canevaro A., Ianes D., Un’altra didattica è possibile, Trento, Erickson, 2021.
Il modello DAII come azione concreta della prospettiva universale
Pianificare la propria didattica avendo come finalità l’apprendimento e la partecipazione di tutti, partendo dalle caratteristiche del gruppo classe, può essere concretizzato attraverso un modello didattico specifico.
Il modello di Didattica Aumentata per l’Inclusione e l’Innovazione (DAII), che abbiamo proposto nell’ambito della collaborazione con Rizzoli Education e di cui anche questo corso fa parte, ha lo scopo di organizzare curricoli e materiali per rispondere alle sfide che la prospettiva universale ci pone. Il modello DAII prevede infatti sette dimensioni didattiche particolarmente rilevanti per una pianificazione pienamente inclusiva e pone l’attenzione sui contesti di azione e relazione strategici per l’innovazione della didattica.
L’intreccio tra innovazione e inclusione è determinante: non c’è innovazione se non c’è un miglioramento della dimensione inclusiva, ma allo stesso tempo non si può migliorare la condizione di inclusione universale senza innovare gli stili di insegnamento, i contesti di apprendimento e l’uso significativo dei materiali didattici.
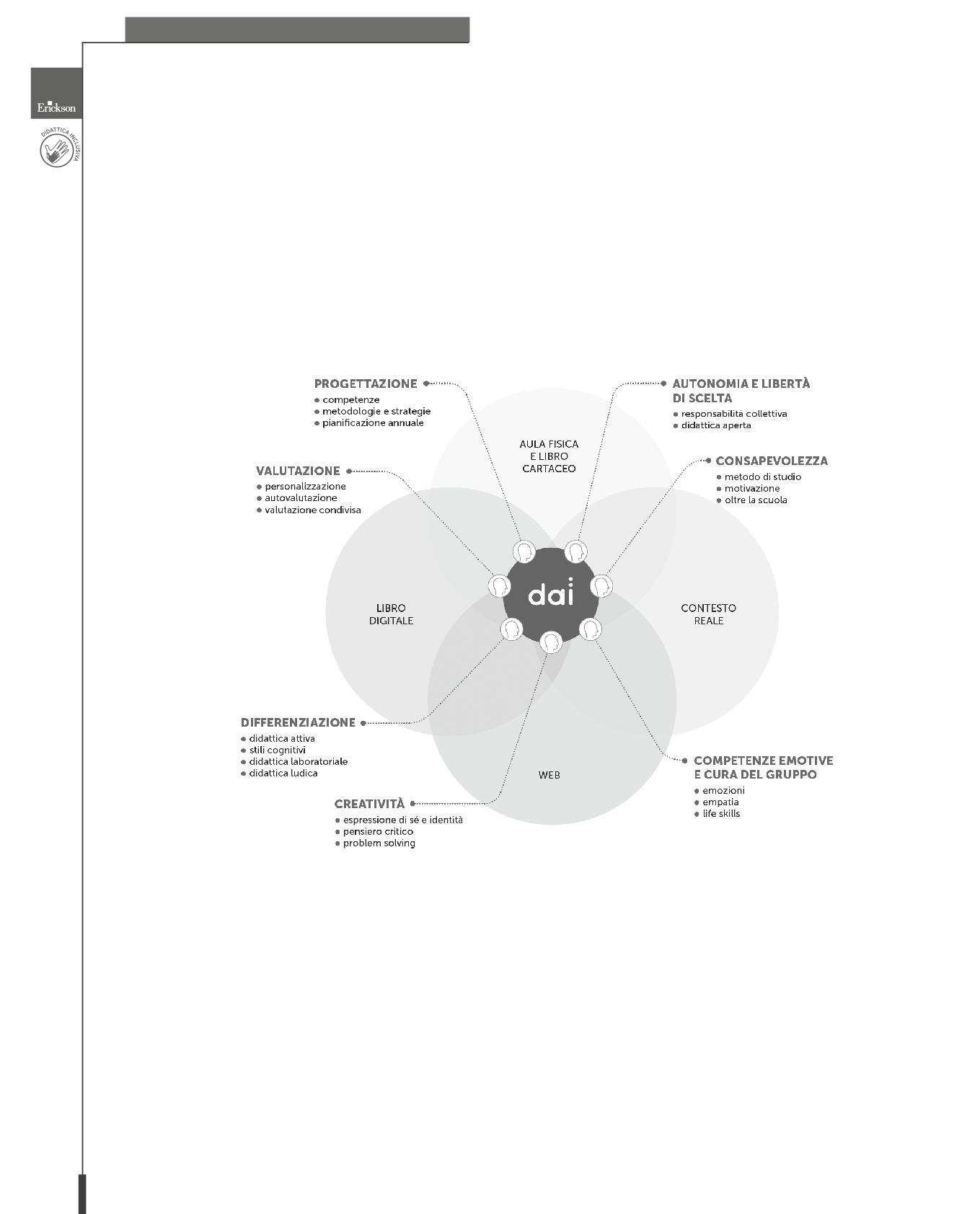
I contesti di apprendimento
Abbiamo sottolineato in primis l’importanza dei contesti:
■ spazio d’aula e spazi formali dell’istituto;
■ spazi informali dell’istituto;
■ spazi digitali di apprendimento;
■ spazi extrascolastici.
In questi quattro contesti gli alunni e le alunne interagiscono e costruiscono i propri percorsi di apprendimento e partecipazione, a volte con la mediazione dell’insegnante e dei materiali didattici, a volte in maniera indipendente, a volte con la mediazione di altre figure professionali, ma sempre nel confronto (a volte positivo, a volte negativo) con il contesto familiare.
Un libro di testo pensato in ottica universale e realmente inclusiva può attivare in maniera significativa questi diversi contesti, permettendo modalità di lavoro differenti, incentivando la collaborazione, aumentandone l’uso significativo, l’accessibilità e la personalizzazione grazie all’uso degli strumenti

digitali, incentivando la dimensione laboratoriale ed euristica dell’apprendimento. Inoltre, può aprire gli spazi dell’extrascuola, invitando alla scoperta del territorio, valorizzando il contributo di figure professionali extrascolastiche e stimolando la ricerca autonoma e condivisa.
Le sette dimensioni didattiche del DAII
Quali azioni didattiche deve mettere al centro della propria azione l’insegnante per promuovere una didattica disciplinare davvero capace di valorizzare tutte le differenze che compongono il gruppo classe?
Questa domanda chiave regge lo scheletro del modello didattico del DAII. Abbiamo individuato sette dimensioni didattiche chiave per la promozione di una didattica universale:
1. progettazione didattica;
2. didattica sensibile alle differenze;
3. valutazione, monitoraggio e autovalutazione;
4. crescita dell’autonomia, autodeterminazione e libertà di scelta;
5. crescita della consapevolezza;
6. competenze emotive e cura del gruppo;
7. sviluppo della creatività.
Le sette dimensioni didattiche del modello universale e l’attenzione ai diversi contesti di apprendimento hanno come finalità concrete due grandi miglioramenti, uno relativo all’ambiente di studio e l’altro relativo allo sviluppo delle competenze di alunni e alunne:
1. creare uno spazio didattico di insegnamento e apprendimento maggiormente flessibile; 2. sviluppare alunni e alunne maggiormente consapevoli e responsabili.
La flessibilità è la base di una didattica in cui possano concretizzarsi azioni legate alla differenziazione, alla personalizzazione e alla individualizzazione. Se impostiamo lo studio su un curricolo rigido, su un unico metodo di studio, su un unico modo di insegnare, su un unico modo di valutare, non facilitiamo lo sviluppo di un’azione inclusiva nei termini che abbiamo indicato precedentemente. Per poter essere attuata, la flessibilità richiede materiali e strumenti Per questo motivo, i nostri corsi e i materiali che li compongono mettono al centro il concetto di valorizzazione delle differenze, della molteplicità dei canali e dei codici linguistici, delle strategie metacognitive e collaborative, così come la valorizzazione delle risorse digitali e delle funzioni di personalizzazione a esse connesse. La consapevolezza è la grande sfida della scuola di oggi. Che si tratti di una maggiore consapevolezza, autonomia e capacità di organizzazione rispetto al proprio metodo di studio o che si tratti di una maggiore responsabilità nel confronto degli altri (dal gruppo classe alla collettività più estesa), questa è certamente una grande sfida che tutti sentono come urgente. Non si può parlare di apprendimento significativo se non si lavora sull’ambito della consapevolezza. Allo stesso tempo, lo sviluppo di un contesto inclusivo richiede una crescita di consapevolezza, in primis nel sapere guardare alla differenza dell’altro come valore ma anche, più concretamente, nell’assumere una maggiore responsabilità nel modo di apprendere, nelle relazioni con gli altri, nel proporre le proprie idee creative, nell’imparare a conoscersi sviluppando in modo positivo e consapevole la propria identità personale e la propria identità collettiva di gruppo. Consapevolezza e responsabilità che si sostanziano anche nel sentirsi parte della comunità scolastica partecipando attivamente e nell’essere cittadini e cittadine attive nel proprio contesto di vita.
L’attenzione ai Bisogni Educativi Speciali nella prospettiva inclusiva
Il contesto di apprendimento favorito dal modello didattico universale, anche tramite l’uso degli strumenti del DAII, consente di rispondere ai bisogni specifici di alunni e alunne con particolari caratteristiche in maniera più efficace. È infatti indubbio che un ambiente di apprendimento flessibile e consapevole favorisca i processi di individualizzazione e personalizzazione e crei un contesto di rispetto e valorizzazione reciproca in cui le differenze individuali non sono viste come un “problema”. Senza sottovalutare le difficoltà che la disabilità o le caratteristiche personali a volte comportano nella gestione del gruppo classe e nelle relazioni interpersonali, un contesto inclusivo sarà sicuramente più competente nell’affrontare la discussione, la gestione dei problemi e le relative risoluzioni, sia didattiche, sia relazionali.
Alunni con Disabilità (certificata secondo la Legge 104/92)
• Disabilità intellettiva
• Disabilità motoria
• Disabilità sensoriale
• Pluridisabilità
• Disturbi neuro-psichiatrici
prevede
Piano Educativo Individualizzato (PEI)
tiene conto del Profilo di Funzionamento stilato su base ICF da parte dell’Unità di Valutazione Multidisciplinare
è elaborato e approvato dal GLO – Gruppo di Lavoro Operativo per l’Inclusione –con la partecipazione dei genitori e delle figure professionali interne ed esterne alla scuola che interagiscono con la classe e con l’alunno con disabilità assicurando la partecipazione attiva dei genitori e dello studente/della studentessa
• individua obiettivi individualizzati nell’ambito degli apprendimenti, della socializzazione, delle autonomie e della comunicazione
• individua strumenti e strategie didattiche efficaci per la realizzazione degli stessi
• individua le modalità in cui il lavoro a scuola si coordina con il lavoro extrascolastico
ALUNNI CON BISOGNI EDUCATIVI SPECIALI (BES)
Alunni con Disturbi Specifici dell’Apprendimento (DSA, certificati secondo la Legge 170/2010)
• Dislessia evolutiva
• Disortografia
• Disgrafia
• Discalculia
Alunni con altri Bisogni Educativi Speciali (DM 27/12/2012 e CM n. 8/2013)
• Altre tipologie di disturbo non previste nella Legge 170/2010
• Alunni con iter diagnostico di DSA non ancora completato
• Alunni con svantaggio socio-economico
• Alunni con svantaggio socio-culturale
previsto sempre dalla Norma deciso dal consiglio di classe
contiene indicazioni su
• strategie compensative
• uso di strumenti compensativi digitali
o analogici
• misure compensative di adattamento di tempi e spazi
• eventuali misure dispensative
• eventuali misure rispetto alla lingua straniera
• ogni forma di personalizzazione didattica utile al miglioramento dei processi di apprendimento
In questo contesto, per il corpo docente sarà più funzionale programmare le azioni rivolte ad alunni e alunne con disabilità tramite una gestione condivisa e corresponsabile del Piano Educativo Individualizzato, così come delle azioni didattiche previste nei Piani Didattici Personalizzati previsti per persone con Disturbi Specifici dell’Apprendimento (DSA) o altre possibili situazioni di svantaggio socio-culturale. È importante quindi connettere le azioni mirate al miglioramento dell’apprendimento e della partecipazione degli alunni con BES all’ambito più ampio della didattica universale, perché la classe è il contesto in cui la scuola agisce e in cui si possono limitare i fenomeni di delega alle figure di sostegno. La classe è anche il luogo dove si possono contrastare l’isolamento e la penalizzazione di alunni e alunne che necessitano di maggiori gradi di differenziazione e di adattamento didattico. Nelle prossime pagine proponiamo quindi un approfondimento specifico sulla visione e sulle modalità esecutive relative al nuovo PEI su base ICF per le persone con disabilità, così come un approfondimento dedicato ai bisogni degli alunni con BES.
IL PIANO EDUCATIVO
INDIVIDUALIZZATO
IN PROSPETTIVA BIO-PSICO-SOCIALE
di Sofia Cramerotti, Ricerca e Sviluppo Erickson

Che cos’è il PEI?
Il Piano Educativo Individualizzato (PEI) è il documento programmatico mediante il quale viene descritto, progettato e organizzato un intervento didattico ed educativo individualizzato e multidimensionale sulla base del funzionamento dello studente con disabilità, per realizzare il diritto di istruzione e apprendimento (Legge n. 104/1992).
Il Decreto legislativo n. 66/2017 Norme per la promozione dell’inclusione scolastica degli studenti con disabilità dice che «l’inclusione scolastica è attuata attraverso la definizione e la condivisione del Piano Educativo Individualizzato (PEI), parte integrante del Progetto individuale». Il Decreto legislativo n. 66/2017 e il successivo Decreto correttivo n. 96/2019, nonché il Decreto interministeriale 182/2020 Adozione del modello nazionale di piano educativo individualizzato e delle correlate linee guida, nonché modalità di assegnazione delle misure di sostegno agli alunni con disabilità sottolineano la necessità di assunzione di una prospettiva bio-psico-sociale nella stesura del PEI (con le disposizioni correttive del DM 153/2023).
Nell’articolo 2 del Decreto legislativo n. 66/2017, Formulazione del Piano educativo individualizzato, si riporta, tra le altre cose, che il PEI:
■ tiene conto dell’accertamento della condizione di disabilità in età evolutiva ai fini dell’inclusione scolastica, con particolare attenzione all’indicazione dei facilitatori e delle barriere, secondo la prospettiva bio-psico-sociale;
■ è redatto a partire dalla scuola dell’infanzia ed è aggiornato in presenza di nuove e sopravvenute condizioni di funzionamento della persona;
■ è strumento di progettazione educativa e didattica e ha durata annuale con riferimento agli obiettivi educativi e didattici, a strumenti e strategie da adottare al fine di realizzare un ambiente di apprendimento che promuova lo sviluppo delle facoltà degli alunni con disabilità e il soddisfacimento dei bisogni educativi individuati;
■ nel passaggio tra i gradi di istruzione e in caso di trasferimento, è accompagnato dall’interlocuzione tra i docenti dell’istituzione scolastica di provenienza e i docenti della scuola di destinazione e, nel caso di trasferimento, è ridefinito sulla base delle diverse condizioni contestuali e dell’ambiente di apprendimento dell’istituzione scolastica di destinazione;
■ esplicita le modalità di sostegno didattico, le modalità di verifica, i criteri di valutazione, gli interventi di inclusione svolti dal personale docente nell’ambito della classe e in progetti specifici, la valutazione in relazione alla programmazione individualizzata, nonché gli interventi di assistenza igienica e di base, svolti dal personale ausiliario nell’ambito del plesso scolastico, e la proposta delle risorse professionali da destinare all’assistenza, all’autonomia e alla comunicazione. Questo significa che la finalità educativo-didattica dell’intervento rivolto agli studenti con disabilità ci invita a riflettere in modo interconnesso, in ottica multidimensionale e bio-psico-sociale per la valorizzazione delle capacità dello studente, non certo “classificandolo”, ma guardando al suo funzionamento all’interno dei suoi vari contesti di vita e all’influenza, positiva e/o negativa, che tali contesti esercitano. Infatti, di fronte alle oggettive difficoltà dello studente con disabilità nel seguire la programmazione rivolta alla classe e altre forme di partecipazione sociale ai vari ruoli della vita scolastica, gli insegnanti si trovano nella necessità di elaborare forme di didattica individualizzata.
Il
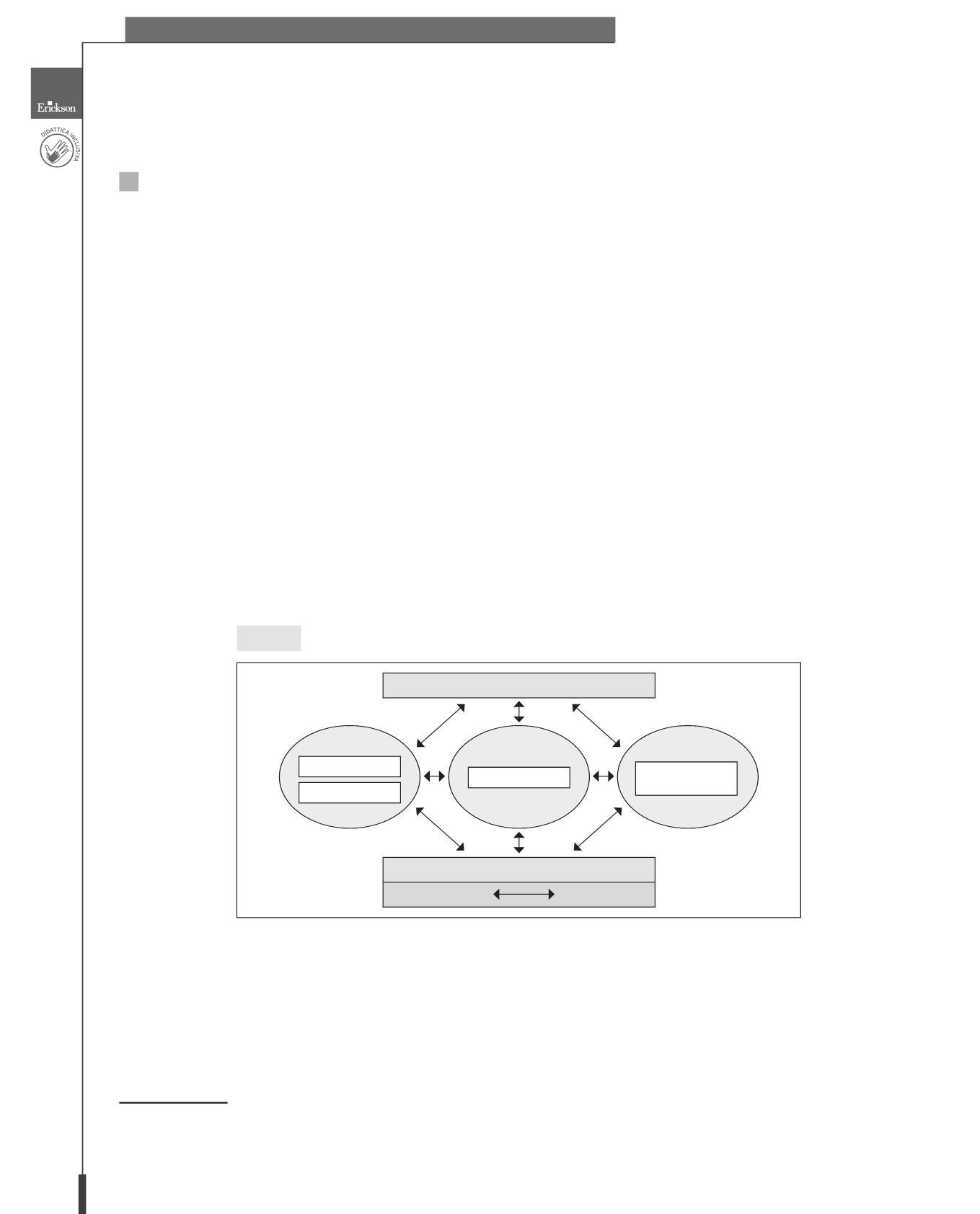
In generale, ciò significa costruire obiettivi, attività didattiche e atteggiamenti educativi “su misura” per la singola e specifica peculiarità di quello studente, ponendo particolare attenzione ai suoi punti di forza, al suo funzionamento, dai quali si potrà partire per impostare una progettualità e un lavoro efficaci.
Il PEI su base ICF
Il Profilo di funzionamento dell’alunno su base ICF1 è il documento fondamentale per la stesura del PEI. Questo documento si pone come obiettivo fondamentale la conoscenza più estesa e la comprensione più approfondita possibile dell’alunno in difficoltà. Questa conoscenza deve però essere utile alla realizzazione concreta e quotidiana di attività didattiche ed educative che devono essere appropriate, significative ed efficaci. Tramite questa conoscenza si mira a esplorare la situazione globale dell’alunno, a conoscerne i vari aspetti, le varie interconnessioni, i punti di forza e di debolezza, le risorse, i vincoli, ciò che facilita e ciò che invece ostacola. I ruoli della scuola, della famiglia e dell’alunno nel suo diritto di autodeterminazione devono essere centrali. Gli insegnanti possono ormai utilizzare una vasta gamma di strumenti di raccolta di dati e di conoscenze per la comprensione profonda e utile dell’alunno in difficoltà, attivando direttamente una regia e un coordinamento nel gruppo di lavoro a livello di scuola che integri i vari contributi che provengono dagli ambiti sanitario, familiare e sociale in un’ottica co-costruttiva e di corresponsabilità educativa. Il modello ICF offre una modalità conoscitiva dell’alunno che aiuta adeguatamente nella progettazione individualizzata. Pensare al PEI in prospettiva bio-psico-sociale significa perciò abbracciare la filosofia di ICF che ci aiuta a guardare il nostro studente secondo una visione globale, leggendo i suoi bisogni educativi in un’ottica di salute, di funzionamento e di partecipazione, frutto di relazioni tra vari ambiti (Figura 1). Infatti, la situazione di salute di una persona, nel nostro caso il suo funzionamento educativo e di apprendimento, è la risultante globale delle reciproche influenze tra i fattori rappresentati.
Fig. 1 La situazione globale di una persona (il suo “funzionamento”).
Condizioni fisiche (input biologico)
Corpo
Funzioni corporee
Strutture corporee Attività personali
Capacità Performance
Fattori contestuali (input contestuale)
Ambientali Personali
Ruoli sociali
Partecipazione sociale
L’ICF, al di là delle condizioni fisiche, individua quindi quattro componenti principali:
1. funzioni e strutture corporee; 2. attività personali;
3. partecipazione sociale;
4. fattori contestuali.
Ogni componente poi è suddivisa, in modo specifico, in vari domini.
1 ICF è la Classificazione Internazionale del Funzionamento, della Disabilità e della Salute ed è una classificazione che descrive lo stato di salute delle persone in relazione ai loro ambiti (sociale, familiare, lavorativo) al fine di cogliere tutte quelle criticità che nel contesto di riferimento possono causare difficoltà.
Il
In uno qualsiasi di questi ambiti si può generare una causa o concausa di bisogno educativo speciale, che interagisce in maniera sistemica con gli altri elementi, favorevoli o avversi (Figura 2):
1. nelle funzioni e nelle strutture corporee ci possono essere delle menomazioni;
2. nelle attività personali ci possono essere delle limitazioni alle capacità e alle performance;
3. nell’ambito della partecipazione sociale ci possono essere delle restrizioni; 4. tra i fattori contestuali (sia ambientali sia personali) ci possono essere delle barriere o dei facilitatori
Fig. 2 Interazioni tra gli elementi del modello bio-psico-sociale ICF.
PROFILO DI FUNZIONAMENTO
su base
MENOMAZIONI
Corpo
funzioni
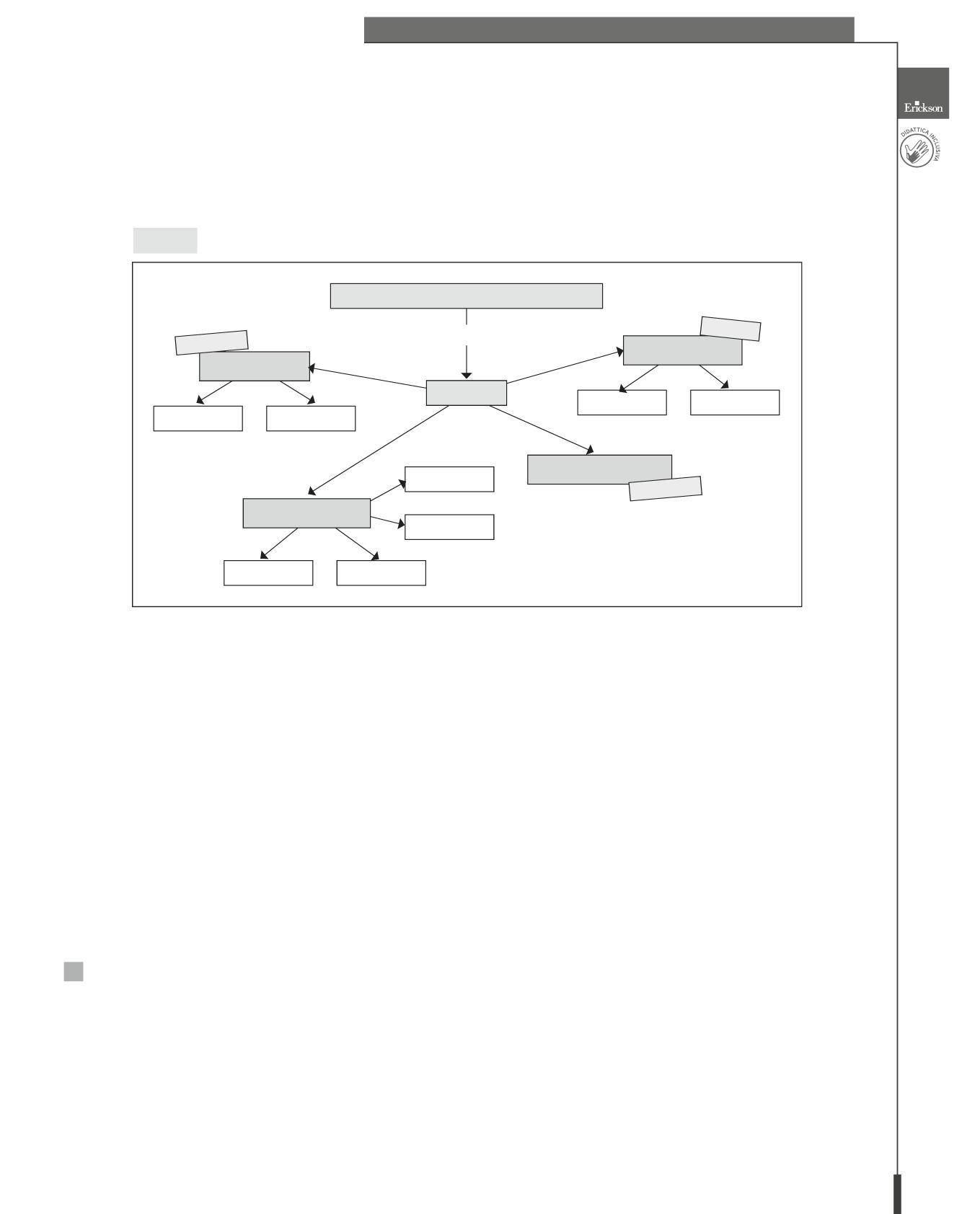
ambientali strutture personali
Fattori contestuali
facilitatori
LIMITAZIONI
Attività personali
RESTRIZIONI ICF
barriere
capacità performance
Partecipazione sociale
Attraverso queste interazioni complesse si produrrà il funzionamento educativo-apprenditivo dell’alunno. Ovviamente, il peso dei singoli ambiti varierà da alunno ad alunno, anche all’interno della stessa condizione biologica originaria.
In questo modo, adottare una prospettiva bio-psico-sociale aiuta a definire le diverse situazioni di bisogno educativo speciale degli alunni: alcune di esse saranno caratterizzate da problemi biologici, corporei e di attività personali, altre principalmente da problemi contestuali ambientali, di capacità e di partecipazione, altre primariamente da fattori contestuali ambientali, altre in misura maggiore da difficoltà di partecipazione sociale ecc. Un bisogno educativo speciale può dunque scaturire da moltissime combinazioni di fattori sfavorevoli per l’alunno.
Nel nostro caso cerchiamo quindi un modo globale, più comprensivo, più bio-psico-sociale e più rispondente a quella che è una reale situazione di bisogno educativo speciale e di difficoltà. Questo tipo di valutazione del bisogno educativo speciale serve dunque per cogliere globalmente tutte le condizioni di bisogno educativo speciale stesso, per poterci costruire una didattica realmente inclusiva, attraverso un Piano Educativo Individualizzato che guarda nella direzione del Progetto di vita.
Le quattro dimensioni del PEI
Come sottolineato nel DI 182/2020 e correttivo 153/2023, la stesura del PEI parte quindi dal raccordo con l’Unità di Valutazione Multidisciplinare (UVM) per individuare gli elementi cardine desunti dal Profilo di funzionamento dell’alunno e integrarli poi con le osservazioni a livello di scuola, necessarie per progettare e impostare gli interventi educativi di sostegno didattico. Questo lavoro è infatti propedeutico alla definizione di obiettivi educativo-didattici a lungo, medio e breve termine e all’individuazione di strategie, strumenti e modalità di lavoro per l’attuazione degli interventi didattici e metodologici più adatti e realmente efficaci per quello specifico studente (anche in riferimento al suo percorso curricolare).
Il Piano Educativo
Tutto questo si colloca all’interno di una cornice di riferimento più ampia volta alla realizzazione di un ambiente di apprendimento che sia realmente inclusivo per tutti gli alunni, non escludendo nessuno, ma dando invece a tutti pieno accesso alla partecipazione e all’apprendimento. Questo è strettamente legato all’organizzazione di un più ampio e generale progetto di inclusione in cui si individuano, assegnano, attivano e utilizzano le risorse di cui effettivamente lo studente ha bisogno.
Tutto questo è accompagnato da una continua verifica in itinere per evidenziare tempestivamente eventuali cambiamenti nel funzionamento dello studente, l’emergere di nuovi bisogni o la loro modificazione, l’adeguatezza e la significatività degli obiettivi individuati e degli interventi attuati. Ricordiamo infatti che il PEI non è un documento statico, ma un progetto dinamico, in continua evoluzione che accompagna passo passo lo studente nel suo percorso scolastico, senza dimenticarci di guardare sempre nella direzione della sua vita adulta.
Un modello di PEI in linea con i Decreti 66/17, 96/19, 182/2020 e correttivo 153/2023 fa riferimento alle quattro dimensioni fondamentali descritte in Tabella 1
Tabella 1 Le quattro dimensioni fondamentali per la stesura di un PEI.
1. Dimensione della relazione, dell’interazione e della socializzazione
2. Dimensione della comunicazione e del linguaggio
3. Dimensione dell’autonomia e dell’orientamento
4. Dimensione cognitiva, neuropsicologica e dell’apprendimento
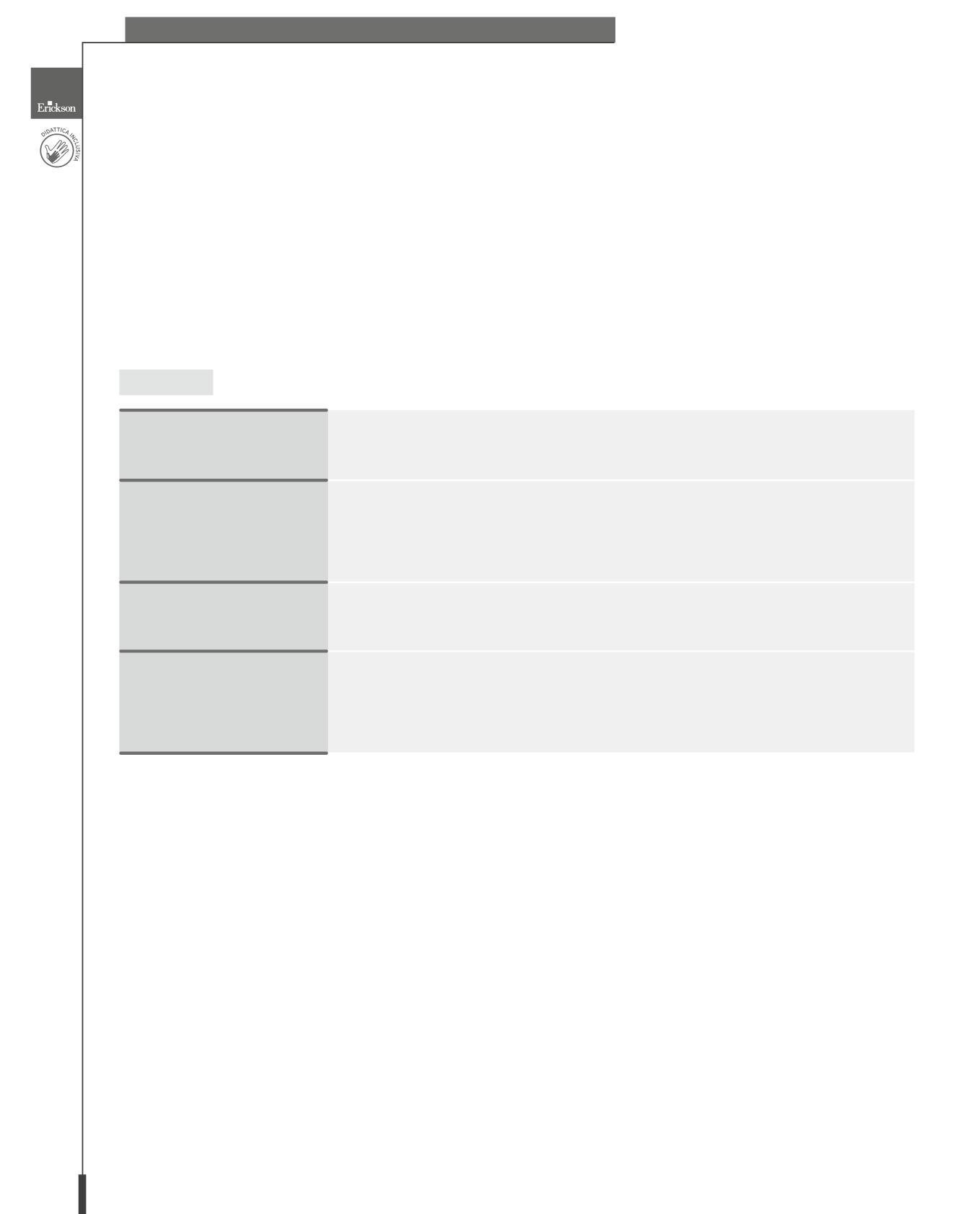
Fa riferimento alla sfera affettivo-relazionale, considerando l’area del sé, il rapporto con gli altri, la motivazione verso la relazione consapevole, anche con il gruppo dei pari, le interazioni con gli adulti di riferimento nel contesto scolastico, la motivazione all’apprendimento.
Fa riferimento alla competenza linguistica, intesa come comprensione del linguaggio orale, alla produzione verbale e al relativo uso comunicativo del linguaggio verbale o di linguaggi alternativi o integrativi, comprese tutte le forme di comunicazione non verbale, artistica e musicale. Si consideri anche la dimensione comunicazionale, intesa come modalità di interazione, presenza e tipologia di contenuti prevalenti, utilizzo di mezzi privilegiati.
Fa riferimento all’autonomia della persona e all’autonomia sociale, alle dimensioni motorio-prassica (motricità globale, motricità fine, prassie semplici e complesse) e sensoriale (funzionalità visiva, uditiva, tattile).
Fa riferimento alle capacità mnesiche, intellettive e all’organizzazione spazio-temporale, al livello di sviluppo raggiunto in ordine alle strategie utilizzate per la risoluzione di compiti propri per la fascia d’età, agli stili cognitivi, alla capacità di integrare competenze diverse per la risoluzione di compiti, alle competenze di lettura, scrittura, calcolo, decodifica di testi o messaggi.
1. Dimensione della relazione, dell’interazione e della socializzazione
Questa dimensione trova il suo collegamento più diretto con il modello bio-psico-sociale ICF, in particolare in relazione alla componente Attività personali e partecipazione sociale e al dominio Interazioni e relazioni interpersonali. Si tratta della parte che riguarda «l’esecuzione delle azioni e dei compiti richiesti per le interazioni semplici e complesse con le persone (estranei, amici, parenti, membri della propria famiglia, partner ecc.) in un modo contestualmente e socialmente adeguato» (OMS, 2007).
In questa parte vengono prese in considerazione interazioni interpersonali sia semplici – interagire con le persone in un modo contestualmente e socialmente adeguato – sia complesse – regolare le emozioni e gli impulsi, controllare l’aggressione verbale e fisica, agire in maniera indipendente nelle interazioni sociali, secondo i ruoli e le convenzioni sociali.
Nella prospettiva del Progetto di vita lo sguardo va però fin da subito allargato all’ambito della vita sociale, civile e di comunità, che riguarda le azioni e i compiti richiesti per impegnarsi nella vita sociale al di fuori di quelli più consueti che possono essere quello familiare e scolastico. Ne sono un esempio la partecipazione ad attività extrascolastiche e del tempo libero.
Infine, in riferimento ai fattori contestuali, giocano un ruolo di rilievo sia quelli ambientali, sia quelli personali.

È importante, a questo proposito, mettere in luce quella che è la rete attorno all’alunno che costituisce l’insieme delle sue relazioni e del sostegno sociale, fisico ed emotivo, ma anche dei diversi atteggiamenti presenti nel proprio contesto di appartenenza. Questa rete coinvolge i familiari, gli amici, i compagni di classe, gli insegnanti, i membri della propria comunità, i professionisti che seguono lo studente, altre persone significative del contesto extrascolastico ecc.
2. Dimensione della comunicazione e del linguaggio
Questa dimensione, in relazione a ICF, fa riferimento in primis agli aspetti delle strutture e delle funzioni corporee (Funzioni mentali del linguaggio) specificatamente coinvolti nella comprensione e produzione linguistica. La parte più consistente per una riflessione in ottica bio-psico-sociale la troviamo però nella componente Attività personali e partecipazione sociale, che riguarda «le caratteristiche generali e specifiche della comunicazione attraverso il linguaggio, i segni e i simboli, inclusi la ricezione e la produzione di messaggi, portare avanti una conversazione, usare strumenti e tecniche di comunicazione» (OMS, 2007).
Questa parte include quindi la ricezione e produzione di messaggi verbali, non verbali, scritti, uso del linguaggio dei segni, ma anche azioni come il parlare (produrre parole e frasi), raccontare o anche la vocalizzazione prelinguistica tipica dei primi anni di vita del bambino.
3. Dimensione dell’autonomia e dell’orientamento
La parte sull’autonomia personale e sociale è strettamente legata a quella delle interazioni interpersonali (che abbiamo già visto nella prima dimensione). In riferimento a ICF, essa comprende i domini:
■ mobilità: è la componente che va necessariamente letta in relazione alle corrispondenti funzioni e strutture corporee implicate nella motricità fine e grosso-motoria;
■ cura della propria persona: comprende azioni come lavarsi, prendersi cura del proprio corpo, gestire i bisogni corporali, mangiare, bere, prendersi cura della propria salute e badare alla propria sicurezza;
■ autonomia della vita domestica: prepararsi i pasti, prendersi cura del posto in cui si vive e degli oggetti in esso presenti, fare i lavori di casa ecc.;
■ partecipazione sociale: lo svolgimento dei compiti e delle azioni necessarie per la partecipazione all’interno del proprio contesto scolastico, oppure lavorativo, oppure di gioco, nonché il sapere gestire anche aspetti inerenti alla vita economica;
■ compiti e richieste generali: la capacità di intraprendere un compito singolo o articolato (con differenti gradi di complessità) completandolo in modo autonomo, con l’aiuto di un compagno o di un adulto di riferimento, oppure all’interno di un gruppo di lavoro. Questo è strettamente connesso anche alla capacità di autoregolare il proprio comportamento, approcciandosi in modo corretto alle persone e alle situazioni.
Altri aspetti molto importanti su cui focalizzarsi sono l’esecuzione e la gestione delle varie routine quotidiane, fortemente connesse anche alla capacità di adattarsi ai cambiamenti e alle diverse richieste.
4. Dimensione cognitiva, neuropsicologica e dell’apprendimento
Questa ultima dimensione comprende gli aspetti fondanti del funzionamento della persona che riguardano l’ambito cognitivo, neuropsicologico e dell’apprendimento dell’alunno e vanno esaminati attraverso il suo modo abituale e quotidiano di operare nei principali processi mentali e non solo.
Nella componente delle Funzioni mentali di ICF troviamo due domini: Funzioni mentali globali (es. funzioni della coscienza, funzioni dell’orientamento, funzioni intellettive ecc.) e Funzioni mentali specifiche (es. funzioni dell’attenzione, funzioni della memoria, funzioni percettive, funzioni del pensiero, funzioni cognitive di base e di livello superiore ecc.).
Nella componente delle Attività personali viene dato ampio spazio all’analisi dell’Apprendimento e
Il
applicazione delle conoscenze sia relativamente agli apprendimenti di base (es. copiare, imparare attraverso le azioni con gli oggetti, acquisire informazioni, imparare a leggere-scrivere-calcolare ecc.), sia relativamente all’applicazione delle conoscenze (es. focalizzare e dirigere l’attenzione, pensare, leggere, scrivere, calcolare, risolvere problemi, prendere decisioni ecc.).
In questo ambito è più che mai importante fare nostra una distinzione fondamentale all’interno dell’approccio bio-psico-sociale, ossia quella tra capacità e performance:
■ la capacità è ciò che un alunno, rispetto a un’azione, esecuzione di un compito o funzione, è in grado di fare senza alcuna influenza, positiva o negativa, di fattori contestuali ambientali o personali;
■ la performance è quello che invece il soggetto fa sotto l’influenza dei fattori contestuali (OMS, 2007; Ianes, Cramerotti e Scapin, 2019).
In conclusione, della riflessione fatta in queste pagine si sottolinea l’importanza di guardare sempre a queste quattro dimensioni in modo strettamente interconnesso e complementare, secondo una direzione circolare continua e non sequenziale per step
Questo approccio di interconnessione circolare, in cui tutti gli aspetti sono collocati sullo stesso piano, è infatti quello che ci garantisce l’assunzione e l’applicazione di un approccio bio-psico-sociale realmente funzionale nella progettazione educativo-didattica per l’alunno.

Bibliografia di riferimento e approfondimento
Cramerotti S., Ianes D., Fogarolo F. e Zagni B., PEI inclusivo (Infanzia, Primaria, Secondaria di primo grado). Trento, Erickson, 2023; 2024.
Fogarolo G. e Onger G., Inclusione scolastica: domande e risposte, Trento, Erickson, 2018.
Ianes D. e Cramerotti S., Alunni con BES, Trento, Erickson, 2013.
Ianes D., Cramerotti S. e Fogarolo F., Costruire il nuovo PEI (Infanzia, Primaria, Secondaria di primo grado, Secondaria di secondo grado), Trento, Erickson, 2021.
Ianes D., Cramerotti S. e Fogarolo F., Il Nuovo PEI in prospettiva bio-psico-sociale ed ecologica, Trento, Erickson, 2021.
Ianes D., Cramerotti S. e Fogarolo F., PEI in pratica (Infanzia, Primaria, Secondaria di primo grado, Secondaria di secondo grado), Trento, Erickson, 2022.
Ianes D., Cramerotti S., Fogarolo F. e Zagni B., PEI e classe inclusiva, Trento, Erickson, 2024.
Ianes D., Cramerotti S. e Scapin C., Profilo di funzionamento su base ICF-CY e Piano educativo individualizzato, Trento, Erickson, 2019.
OMS – Organizzazione Mondiale della Sanità, ICF-CY. Classificazione Internazionale del Funzionamento, della Disabilità e della Salute – Versione per bambini e adolescenti, Trento, Erickson, 2007.
PIANO DIDATTICO
PERSONALIZZATO: RIDARE
CENTRALITÀ ALLA DIDATTICA
Sono passati parecchi anni dall’ottobre 2010, momento in cui il Parlamento ha ratificato la Legge 170/2010 “Nuove norme in materia di disturbi specifici di apprendimento in ambito scolastico” che per la prima volta introdusse nelle prassi programmatiche della scuola la redazione di un Piano Didattico Personalizzato (PDP) rivolto agli alunni con DSA. Il 6 marzo 2013 veniva emanata una Circolare Ministeriale che estendeva la possibilità della stesura del PDP (su indicazione del Consiglio di classe) anche ad altre tipologie di BES, riconoscendone il valore didattico generale, e non solamente una misura rivolta a disturbi specifici.
In tutti questi anni la scuola si è sostanzialmente mossa tra due poli:
■ chi cerca di massimizzare il valore didattico della personalizzazione cercando di introdurre strumenti e misure che facilitino l’apprendimento di alunni e alunne tramite la riduzione di barriere e favorendo accessibilità linguistiche, esecutive e operative;
■ chi adempie l’obbligo burocratico del PDP prevendendo in maniera più o meno standardizzata un elenco di strumenti e misure uguali per tutti gli alunni con DSA, senza riconoscere il pieno valore didattico dell’attenzione ai diversi modi di apprendere.
Purtroppo, l’implementazione didattica delle norme previste dalla Legge 170 è ancora molto incostante, a macchia di leopardo sul territorio, con un grado ancora elevato di scetticismo nei confronti delle barriere e delle risorse specifiche che i DSA portano con sé, ma anche nell’efficacia delle azioni didattiche legate alla personalizzazione (per un’analisi multiprofessionale dello stato dell’arte a dieci anni dalla promulgazione della legge 170, si veda Aquino et al., 20221). La prospettiva universale che guida la nostra proposta inclusiva non può che estendere il concetto di personalizzazione all’intero gruppo classe. Cercare di garantire a ciascuno la scoperta del metodo di studio più efficace, di costruire saldamente la propria identità, è naturalmente connesso al concetto di personalizzazione didattica. La flessibilità di tempi, spazi, strumenti è alla base della differenziazione e quindi non può essere esclusivo appannaggio di alunni e alunne con BES. Tuttavia, sappiamo bene come questa prospettiva faccia fatica a concretizzarsi nella quotidianità, laddove piuttosto sono ancora negati diritti basilari di personalizzazione didattica e si fatica a ricostruire il senso didattico reale degli strumenti compensativi e delle eventuali misure dispensative.
Il reale valore didattico del PDP
Oltre dieci anni di PDP nelle scuole italiane ci portano alcune evidenze. Innanzitutto, l’efficacia degli strumenti e delle misure compensative è direttamente connessa alla didattica compensativa che i docenti sanno sviluppare in classe. Se gli strumenti e le misure compensative vengono lasciate al solo alunno o alla sola alunna con DSA e non vengono conosciute e sperimentate in classe anche dal gruppo dei pari, queste risulteranno inefficaci e verranno presto abbandonate, specie in età adolescenziale. È necessario partire da un clima realmente inclusivo in cui è “normale” che ognuno lavori in maniera differente, anche con strumenti differenti, e dove questo non vuol dire che ci siano gradi differenti di competenza. Capire perché si lavora in un certo modo per valorizzare le caratteristiche
1 Aquino G., Mammarella I.C., Trentin A., Ventriglia L., La gestione di DSA dalla Legge 170/2010 alla Linea Guida ISS 2022, Trento, Erickson, 2022.

personali è il primo passo indispensabile da compiere nel gruppo: se non viene percorso, o peggio viene nascosto, porterà solamente ad un ulteriore peggioramento delle prestazioni.
Altra evidenza è che fortunatamente la maggior parte delle misure didattiche compensative portano vantaggio all’intero gruppo classe. L’esempio più evidente è, ad esempio, quello legato agli strumenti di logica visiva, alla schematizzazione e alle mappe cognitive. Chi adempie in maniera burocratica all’obbligo di legge spesso assegna mappe come strumento di aiuto, senza valutare il valore didattico delle mappe stesse e senza approfondirne l’uso condiviso in classe. Si ritiene, in maniera peraltro stupefacente, che l’aiuto per un allievo o un’allieva in difficoltà possa arrivare in maniera automatica dall’uso di uno schema magari scaricato da Internet, senza che quest’azione sia legata al metodo di studio sviluppato in classe con il gruppo e senza che si conosca la logica di base delle mappe. Sappiamo invece come puntare sulla creazione delle mappe in classe, sulla valorizzazione delle molte e diverse tipologie di mappe presenti nei libri di testo, sulla comprensione della logica di composizione delle stesse costituisca il primo passo importante per rendere efficace questo strumento di organizzazione logica che porta vantaggi a tutti e tutte in classe e spesso in particolare ad alunni con dislessia evolutiva.
Discorso analogo potremmo fare per l’uso del computer, che spesso viene trattato non come occasione per massimizzare lo sviluppo di competenze digitali per tutti (peraltro previste dalle Indicazioni Nazionali e dalle competenze di cittadinanza europea), ma come ausilio speciale per lo studente in difficoltà. Se si accoglie l’ottica della differenziazione didattica, anche l’uso degli strumenti digitali si arricchirà di significato. Non verrà più visto come una “concessione” allo studente in difficoltà, ma come un’opportunità per tutti per esprimere la propria creatività, per approfondire il proprio metodo di studio, per avere uno strumento alternativo alla scrittura a mano libera (che non verrà mai abbandonata a scuola) e per imparare a gestire con competenza lo spazio digitale.
Questi sono solo alcuni esempi di evoluzione necessaria per tornare a dare centralità didattica alle misure di personalizzazione legate al PDP in un contesto pienamente inclusivo. Passare da una logica di strumento individuale ad una logica di condivisione e opportunità nel gruppo classe è un’evoluzione didattica significativa, che porta benefici a tutto il gruppo.
Gli strumenti di facilitazione del corso
Sono molti gli strumenti presenti nel corso che possono assumere un valore di facilitazione per gli alunni con DSA e per l’intero gruppo classe. Certamente tra questi particolare rilievo assumono le diverse forme di schematizzazioni e mappe che costellano l’intero corso. Questi elementi in particolare possono avere un duplice valore:
■ orientare lo studente/la studentessa nella costruzione logica dell’argomento. Ricostruiscono cioè in una visione unitaria la complessità dell’argomento affrontato, fornendo una vera e propria mappa per recuperare le connessioni tra i concetti, le parole chiave, i termini più importanti da ricordare, gli elementi caratteristici. Sono quindi un supporto indispensabile per comprendere, memorizzare ed esporre i contenuti delle unità.
■ essere un modello per la produzione autonoma delle proprie mappe. Imparare a produrre in autonomia le proprie mappe è sicuramente indispensabile per sviluppare un efficace metodo di studio. Si impara se si hanno a disposizione delle mappe ben strutturate e curate anche all’interno dei materiali dei libri di testo. In questo senso le mappe sono un vero e proprio modello a cui fare riferimento (anche personalizzandolo o cambiandolo) per iniziare a creare i propri schemi, le proprie mappe. Questo è tanto più significativo quanto più questo tipo di lavoro viene svolto anche in classe in maniera condivisa e quando il testo diventa un attivatore di un processo di studio che non è solo individuale a casa, ma è un’azione di co-costruzione in classe. Passare dalla mappa del libro alla mappa del gruppo è certamente una strategia efficace per imparare a studiare, per sentirsi attivi costruttori del proprio apprendimento, ma anche per rendere universale uno strumento che non è pensato solo per gli alunni con DSA.
I materiali per la didattica inclusiva ne I mondi di GEA - Scienze e Matematica
MATERIALE

Tutte le unità dei volumi di Scienze e Matematica sono introdotte da una doppia pagina di Storytelling. La narrazione permette un approccio originale all’argomento trattato e favorisce l’apprendimento disciplinare perché coinvolge, stimola le emozioni e attiva ciò che bambine e bambini già sanno a un livello non strutturato.
Le storie, inoltre, sono un modo per differenziare la didattica e raggiungere il maggior numero di bambini e bambine.
(di Valeria Razzini)
Il percorso Calcolo facile focalizza l’attenzione sugli elementi che garantiscono alla bambina e al bambino un apprendimento di successo: strategie di apprendimento, metacognizione e confronto tra pari. Il percorso si articola in più schede, ognuna delle quali è dedicata a un argomento fondamentale di Matematica.
(di Cristina Caciolo, con la supervisione scientifica di Nicoletta Perini)
Nell’eserciziario, la sezione Il mio atlante -Ripassa con Gea presenta schemi dei principali argomenti di Matematica, utili come strumenti compensativi e per il ripasso, e mappe dei principali argomenti di Scienze. La sezione è a cura di Erickson.
DOVE
Volumi Scienze e Matematica 4 e 5
Volume Matematica
Guida (pagg. 209-211)
Volumi Scienze e Matematica 4 e 5
Il volume CheFacile! Storia Geografia Scienze 4 propone testi semplificati e una struttura facilitante per l’apprendimento dei contenuti disciplinari per gli alunni e le alunne con Bisogni Educativi Speciali. Ogni argomento presenta una struttura a domanda e risposta con testi molto sintetici e chiari, corredati di illustrazioni e immagini significative, tabelle e schemi. Completano i vari argomenti domande stimolo, esercizi operativi e piccoli esperimenti/laboratori pratici per un apprendimento attivo.
(di Sara Angelicchio, Federica Biella, Alessandra Casiraghi e Silvia Riboldi, con la supervisione scientifica di Carlo Scataglini)
Il volume CheFacile! Matematica 4 presenta una selezione dei principali argomenti di Matematica e di Geometria pensati in particolar modo per alunni e alunne con Bisogni Educativi Speciali. All’interno del volume gli argomenti sono suddivisi in schede di base e schede-procedimento. Le schede di base presentano le nozioni utili alla comprensione dei saperi di base, necessarie per l’applicazione di una regola/formula.
All’interno delle schede-procedimento si trovano invece i procedimenti matematici divisi in passaggi. Il volume presenta appositi strumenti compensativi, gli “schemi” e gli “strumenti utili”, che possono essere usati per l’esposizione orale, per la verifica scritta e/o durante l’utilizzo delle schede-procedimento.
(di Cristina Caciolo)
Volume CheFacile!
Storia Geografia Scienze 4 Guida (pagg. 212-214) Hub Kids
Volume CheFacile! Matematica 4 Guida (pag. 215)
Materiali per la didattica inclusiva

Valeria Razzini, insegnante di scuola primaria, specializzata in didattica inclusiva, ha all’attivo collaborazioni con enti come formatrice e docente di Comunicazione. Ha conseguito la seconda Laurea in Scienze della formazione primaria presso l’Università di Reggio Emilia e la specializzazione in Disturbi Specifici dell’Apprendimento e Bisogni Educativi Speciali. Ha pubblicato diversi saggi sui molteplici aspetti della didattica della Matematica. Gestisce il blog e le pagine Matematica in gioco.
Cristina Caciolo, laureata in Logopedia e in Scienze e tecniche psicologiche per l’analisi e la valutazione clinica dei processi cognitivi, lavora presso la UOC di Neuropsichiatria dell’Infanzia e dell’Adolescenza dell’IRCCS Ospedale Pediatrico Bambino Gesù di Roma, dove svolge attività clinica e di ricerca. È inoltre docente del master di Neuropsicologia dei disturbi del neurosviluppo in collaborazione con l’Istituto ReTe (Roma) e il Centro Studi Erickson. Per le Edizioni Erickson ha pubblicato Percorsi di Riabilitazione-Numeri e Calcoli e Percorsi di Riabilitazione-Calcolo a mente e scritto, insieme a Manuela Pieretti, Enrica Mariani e Andrea Biancardi.
Nicoletta Perini è laureata in Psicologia clinica, specializzata in Psicologia del ciclo di vita ed esperta di Psicopatologia dell’apprendimento e di Psicoterapia cognitiva per l’età evolutiva. Ha lavorato come psicologa clinica in centri che si occupavano di diagnosi e intervento nelle difficoltà scolastiche e, con le Edizioni Erickson, ha collaborato alla progettazione di GIADA, una piattaforma multimediale per l’individuazione precoce delle difficoltà scolastiche e per la gestione di interventi didattici mirati. Svolge attività di formazione per insegnanti sulle tematiche legate ai problemi scolastici e collabora a diversi progetti editoriali e formativi con la Ricerca e Sviluppo Erickson. Sta svolgendo un dottorato di ricerca presso il Department of Mathematics Education alla Loughborough University (UK).
Sara Angelicchio, psicologa e psicoterapeuta cognitivo-comportamentale. Ha lavorato per diversi anni nell’educativa scolastica e domiciliare con bambini e ragazzi con disabilità lievi e medie. Attualmente lavora come psicoterapeuta cognitivo-comportamentale dell’adolescenza e dell’età adulta, tiene percorsi di tutoring dell’apprendimento per l’età evolutiva e percorsi di sostegno alla genitorialità.
Federica Biella, psicoterapeuta cognitivo-comportamentale, è laureata in Psicologia clinica, dello sviluppo e neuropsicologia ed è specializzata nei disturbi specifici dell’apprendimento. Ha lavorato per alcuni anni come educatrice e ha condotto diversi corsi di formazione presso alcune scuole della provincia di Monza e Brianza. Attualmente svolge attività clinica e riabilitativa presso un centro di riabilitazione per minori con disabilità e lavora come psicoterapeuta presso alcuni studi privati, dove si occupa anche di formazione.
Alessandra Casiraghi è psicologa dello sviluppo ed è specializzata in Psicoterapia cognitivo-comportamentale. Svolge attività riabilitativa e di counseling nei disturbi dello spettro autistico. Si occupa anche di formazione, di riabilitazione dei disturbi del neurosviluppo e di sostegno psicologico nelle diverse fasi del ciclo di vita.
Silvia Riboldi, laureata in Psicologia clinica, dello sviluppo e neuropsicologia, è specializzata in Analisi del comportamento e in Psicoterapia. Svolge attività clinica e riabilitativa presso un Centro di Riabilitazione per minori con disabilità e si occupa anche di sostegno psicologico, formazione e supervisione di trattamenti riabilitativi.
Carlo Scataglini è insegnante di sostegno e formatore per le strategie didattiche di facilitazione e inclusione. Per le Edizioni Erickson è autore di numerosi testi di didattica facilitata tra i quali Storia facile, Geografia facile e Scienze facili (per le classi terza, quarta e quinta), dei raccoglitori della collana “Gli Essenziali” (per le classi terza, quarta e quinta) e della Guida Facilitare e semplificare libri di testo.
CALCOLO FACILE
Un percorso per autoregolare l’apprendimento con le strategie
di Nicoletta Perini
Verso un apprendimento di successo
Un alunno di successo è un alunno che sa regolarsi all’interno del proprio processo di apprendimento: fissa obiettivi chiari, orienta il proprio comportamento al raggiungimento di tali traguardi, è sostenuto da una buona motivazione e usa differenti strategie.
In letteratura (Dignath, Buettner e Langfeldt, 20081), per riferirsi a questo insieme di comportamenti, pensieri e aspetti emotivo-motivazionali, si parla di apprendimento autoregolato, rilevando quanto risulti efficace a scuola. L’apprendimento autoregolato è caratterizzato da un’interazione tra variabili cognitive (strategie di apprendimento), metacognitive e motivazionali durante tutto il processo di apprendimento (Figura 1).
Motivazione

Strategie di apprendimento
Metacognizione
Fig. 1 Interazione tra variabili cognitive, metacognitive e motivazionali per un apprendimento di tipo autoregolato.
Ogni comportamento umano deve essere sostenuto da una buona motivazione. Per esempio, la motivazione di andare a fare una passeggiata può essere il benessere che si prova all’aria aperta; la motivazione di fare la spesa può essere la necessità di nutrirsi; la motivazione di studiare può essere il desiderio di prendere un bel voto. Lo studio, più di altro, richiede impegno e fatica, necessitando quindi di una spinta motivazionale notevole. Le motivazioni ad apprendere sono varie: il voto, il piacere di imparare, l’interesse per la materia, il sentirsi capaci, la percezione di utilità di quanto si sta apprendendo, il giudizio dei propri genitori ecc. Più lo studente fa proprie delle motivazioni personali (chiamate interne), come l’interesse e il piacere di imparare, più sarà robusta la sua motivazione: riuscirà quindi a persistere più a lungo nello studio e cercherà le modalità migliori per raggiungere i suoi obiettivi.
Per apprendere con successo è fondamentale anche avere un approccio strategico. C’è una grande differenza tra esercitare un alunno e condurlo a trovare le strategie funzionali ad apprendere. Se, ad esempio, si vuole insegnare a un bambino come risolvere i problemi matematici, diverso è proporre
1 Dignath C., Buettner G. e Langfeldt H.P. (2008), How can primary school students learn self-regulated learning strategies most effectively? A meta-analysis on self-regulation training programmes, «Educational Research Review», vol. 3, n. 2, pp. 101-129.
svariati testi e richiederne la soluzione piuttosto che suggerire una modalità per rendere evidenti le informazioni salienti e il rapporto tra i dati, pianificare le azioni da compiere e suggerire una strategia per la verifica della soluzione trovata.
Quando e come applicare le diverse strategie è un’ulteriore variabile da cui l’apprendimento autoregolato non può prescindere. Attraverso un ragionamento (spesso implicito) sul tipo di compito e sulle proprie modalità di imparare, attraverso cioè dei processi metacognitivi, l’alunno dovrebbe riuscire a capire qual è la strategia giusta rispetto a ciò che deve apprendere. Così, per memorizzare semplici combinazioni di numeri (come 50 + 50 = 100) si userà la ripetizione, mentre per risolvere un problema matematico si cancelleranno le informazioni superflue e si rappresenteranno solo quelle necessarie alla soluzione.
Sempre nell’ambito dei processi metacognitivi, risulta importante anche imparare ad autovalutare la propria preparazione per capire se il proprio processo di apprendimento va nella giusta direzione e quali eventuali strategie alternative mettere in campo.
Infine, ultimo elemento utile per un apprendimento di successo è considerare che l’alunno è inserito in una classe e che il confronto tra pari può portare notevoli vantaggi. Infatti spiegare a un compagno quanto è stato appreso permette allo studente di rendersi conto di quanto è chiaro l’argomento e ascoltare quanto il compagno dice permette di chiarire eventuali dubbi rimasti.
L’obiettivo del percorso
La Matematica richiede agli alunni di padroneggiare alcuni argomenti che permettono loro di procedere avendo basi sicure. Il percorso Calcolo facile per la classe quarta prende in considerazione questi argomenti, focalizzando l’attenzione sugli elementi che, più di altri, garantiscono all’alunno un apprendimento di successo: strategie di apprendimento, metacognizione e confronto tra pari. I contenuti del percorso sono stati ideati e realizzati da Cristina Caciolo.
La struttura del percorso
Il percorso si articola in più schede, ognuna delle quali sviluppa uno specifico argomento. Ogni scheda prevede alcuni momenti fondamentali, che richiamano le variabili descritte sopra, e si presentano sempre nello stesso ordine.
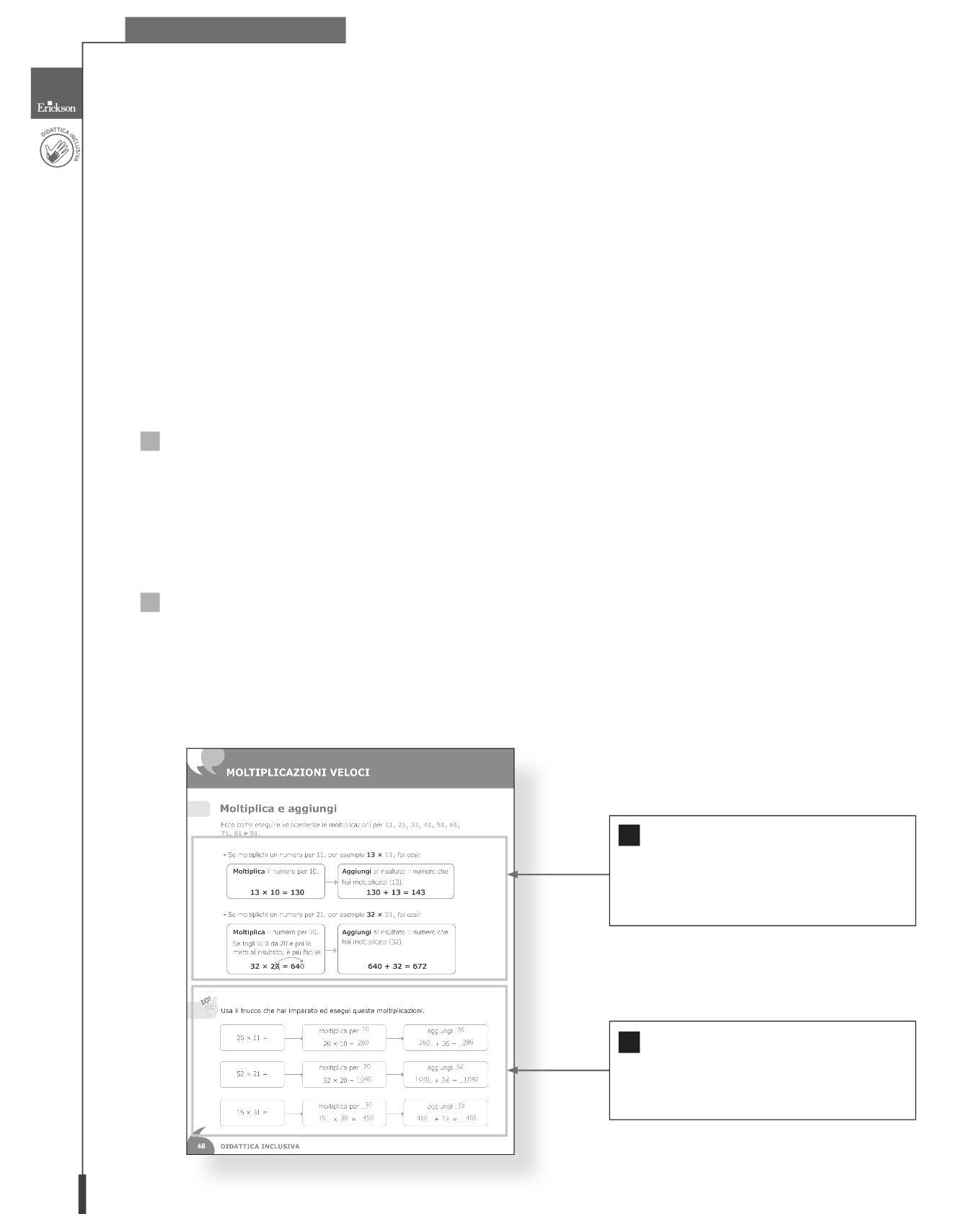
1 STRATEGIA
Ogni scheda inizia con la presentazione di una o più strategie che permettono all’alunno di far proprie alcune tecniche per affrontare gli esercizi proposti di seguito.
2 ESERCIZI INDIVIDUALI
Segue un momento in cui si chiede al bambino di sperimentare la strategia appena descritta attraverso uno o più esercizi
3 METACOGNIZIONE
Per lavorare a livello metacognitivo, attraverso un linguaggio semplice al bambino può essere chiesto di: svolgere una rapida attività per verificare se ha compreso quando e come usare la strategia; di indicare se si è trovato bene con la strategia suggerita; valutare quanto gli è piaciuta la strategia oppure, nel caso di più strategie presentate, quale ha trovato più in sintonia con il proprio modo di apprendere.
4 ESERCIZIO IN COPPIA
Apprendere significa far proprio quanto viene proposto. Per questo motivo, riuscire a spiegare a un compagno la strategia appresa ha la doppia funzione di portare lo studente a rielaborare quanto ha imparato e verificare se è tutto chiaro. Ascoltare la spiegazione del compagno, invece, può aiutare a chiarire eventuali dubbi.
I contenuti del percorso di Matematica di classe quarta
Nella tabella che segue sono riportati gli argomenti affrontati in ciascuna scheda del percorso.
Scheda 1 Addizioni veloci (pagg. 32-33)
Scheda 2 Sottrazioni veloci (pagg. 38-39)
Scheda 3 Moltiplicazioni veloci (pagg. 48-49)
Scheda 4 Moltiplicazioni in colonna (pagg. 50-51)
Scheda 5 Confronto di frazioni (pagg. 76-77)
Scheda 6 Equivalenze facili (pagg. 98-99)

STRATEGIA - Cifra + cifra
STRATEGIA - Tutti al 9 e l’ultimo al 10
STRATEGIA 1 - Moltiplica e aggiungi
STRATEGIA 2 - Moltiplica e sottrai
STRATEGIA - Frecce e colori
STRATEGIA - I mattoncini
STRATEGIA - Saltelli qua e là
PROGETTO CHEFACILE!
Saperi disciplinari di base facilitati e semplificati per migliorare l’apprendimento di tutte e tutti
Il corso I mondi di Gea è corredato dei quattro volumi del progetto CheFacile!:
• CheFacile! Saperi di base 4 e CheFacile! Saperi di base 5 (per Storia, Geografia e Scienze delle classi quarta e quinta) di Sara Angelicchio, Federica Biella, Alessandra Casiraghi e Silvia Riboldi, con la supervisione scientifica di Carlo Scataglini;
• CheFacile! Matematica 4 e CheFacile! Matematica 5 di Cristina Caciolo.
Ogni volume del progetto è pensato per facilitare l’apprendimento a partire da cinque chiavi diverse di facilitazione:
1) lessico di base e struttura sintattica semplificata, per facilitare la comprensione
2) selezione degli argomenti, dei concetti e degli eventi, per rendere subito evidenti il significato del testo e le informazioni principali
3) organizzazione delle informazioni, schematizzazione e utilizzo del codice colore, per rendere immediatamente chiari i nessi logici, i concetti chiave e gli eventi, grazie anche a un’impaginazione facilitante
4) immagini, illustrazioni e aiuti visivi semplici, per valorizzare la parte iconica del testo e renderlo più significativo
5) attività operative semplificate, mirate alla comprensione del testo e alla rielaborazione personale dell’alunno, per capire meglio gli argomenti
CheFacile! è utile per alunni e alunne con disabilità intellettiva, perché semplifica il lessico e la struttura della frase, rende più schematici gli argomenti, propone illustrazioni e aiuti visivi che facilitano la comprensione dei contenuti e la rielaborazione personale.
CheFacile! è utile per alunni e alunne con Disturbi Specifici dell’Apprendimento, perché facilita la lettura riducendo la lunghezza e la complessità dei testi, organizza al meglio i nessi logici, facilita la memorizzazione grazie all’uso di immagini significative e aiuta l’esposizione orale attraverso schemi e aiuti visivi.
CheFacile! è utile per tutta la classe, perché fornisce una base di partenza più semplice per i lavori collaborativi e di coppia, facilitando il lavoro tra compagni (anche quelli che hanno maggiori difficoltà) e realizzando un apprendimento realmente inclusivo.
I volumi CheFacile! Saperi di base
I volumi CheFacile! Saperi di base per le classi quarta e quinta sono composti da una selezione degli argomenti principali di Storia, Geografia e Scienze.

Ogni civiltà di Storia è introdotta da due pagine che indicano DOVE e QUANDO si è sviluppata, rispettivamente con delle cartine geostoriche molto pulite e una linea del tempo che identifica i principali eventi.
Gli argomenti di Geografia e Scienze, invece, si aprono ciascuno con una pagina che funge da “aggancio” alle pagine successive e dà una visione d’insieme di ciò che l’alunno studierà.
Le informazioni nelle varie pagine sono sempre molto brevi e focalizzano l’attenzione su termini e concetti chiave. Numerosi elementi visivi facilitano poi la lettura, la comprensione e lo studio. Così, il codice colore, le parole in neretto e le icone aiutano a identificare immediatamente le domande chiave e le principali informazioni da tenere a mente, mentre le immagini completano, esemplificano e approfondiscono l’argomento trattato.

Seguono le pagine che contengono le informazioni e i concetti principali di ciascun argomento, presentato utilizzando un lessico di base e una struttura sintattica semplice. Ogni concetto è introdotto da una domanda specifica (il titolo della pagina), che trova una prima breve risposta nel box con la chiave. A questa risposta seguono brevi testi, schemi, elenchi, immagini e tabelle che chiariscono l’
Ogni pagina diventa così una scheda semplice e sintetica, che l’alunno può imparare con facilità e utilizzare come strumento compensativo.
Alcune icone infine accompagnano l’alunno nello studio e lo aiutano a identificare gli elementi che può trovare nelle varie pagine.
Identifica le informazioni chiave della pagina, quelle che rispondono in modo chiaro e sintetico alla domanda del titolo.
Indica gli esercizi, semplificati e facilitati, per rendere attivo lo studio.
Rappresentano un momento di riflessione e/o di ricognizione delle conoscenze pregresse su un particolare aspetto o argomento.

Rappresentano rispettivamente uno storico/una storica, un geografo/una geografa e uno scienziato/una scienziata e introducono semplici esperimenti oppure attività pratiche legate alle tre discipline.
I volumi CheFacile! Saperi di base per le classi quarta e quinta sono dunque uno strumento innovativo ed efficace per facilitare l’apprendimento degli alunni e delle alunne con Bisogni Educativi Speciali. Un valido aiuto per organizzare al meglio lo studio e imparare con più facilità le discipline.
CheFacile! Matematica
I volumi CheFacile! Matematica presentano una selezione dei principali argomenti di Matematica e di Geometria pensati in particolar modo per alunni e alunne con Bisogni Educativi Speciali.
La semplificazione degli argomenti rappresenta il focus del progetto ed è resa possibile grazie a un lessico e a una struttura sintattica semplici. Il codice colore e le immagini, inoltre, aiutano a focalizzare l’attenzione su termini e concetti chiave.
Nei volumi CheFacile! Matematica i vari argomenti sono suddivisi in:
1. schede di base;
2. schede-procedimento;
3. schemi e strumenti utili.
1. Nelle schede di base si trovano le nozioni e le definizioni utili per la comprensione dei saperi di base, necessari per la successiva applicazione di una determinata regola o formula. Nella Matematica e nella Geometria è infatti fondamentale la padronanza del lessico per comprendere definizioni, regole e formule da applicare.
Le schede di base si aprono con le definizioni e le nozioni di base; in seguito l’alunno/a viene coinvolto/a attivamente nel processo di apprendimento grazie a degli esercizi, facilitati dal codice colore e dalla grafica.
2. All’interno delle schede-procedimento si trovano i procedimenti matematici divisi in passaggi. Accompagnare l’alunno o l’alunna “un passo alla volta” rappresenta una valida strategia per consentire una migliore comprensione di ciò che sta facendo. Frazionare il processo, infatti, consente di snellire e semplificare la pianificazione di un procedimento.
Nelle schede-procedimento, si mostra dapprima il procedimento un passo alla volta, rafforzando le informazioni grazie al codice-colore; in seguito, si chiede di applicare immediatamente il procedimento attraverso esercizi che richiedono un impegno via via maggiore.
3. Inoltre nel volume sono disponibili:
• schemi, pensati sia per avere una visione d’insieme di determinati argomenti (ad esempio, le proprietà delle operazioni) sia per consentire all’alunno o all’alunna di avere uno strumento compensativo per l’esposizione orale o per una verifica scritta. Gli schemi riassumono le nozioni principali con parole semplici e immagini chiare che riprendono gli esempi delle schede di base e delle schede-procedimento.
• strumenti utili (ad esempio, la tavola pitagorica e la tavola per le equivalenze), che sono veri e propri strumenti compensativi utilizzabili dall’alunno o dall’alunna con Bisogni Educativi speciali sia durante la lettura e lo svolgimento delle schede-procedimento, sia durante le attività curricolari. Incentivare l’utilizzo di tali strumenti consente una maggiore padronanza dello strumento stesso e un livello di autonomia maggiore nel corso delle attività richieste.

