

MATEMATICA

con SE SBAGLIO IMPARO di Maestra Federica
• Testi a cura di Valentina Perolio, Annamaria Parravicini, Claudio Riva.
• Mateludica a cura di Valentina Perolio.
• Pagine 155, 157, 158 a cura di Valentina Perolio da un’idea di Biella Cresce.
• Laboratori STEM e STEAM a cura del Gruppo Pleiadi.
• Se sbaglio imparo a cura di Federica De Gasperis.
• Schede del quaderno a cura di Annamaria Parravicini, Claudio Riva.
• Verifiche del quaderno a cura di ABC, Milano.
• Prove non note a cura di Valentina Perolio.
• Coding a cura di Monti & Russo Digital e Coder Kids.
Coordinamento editoriale: Mauro Traversa
Coordinamento redazionale: Magda Perricelli
Redazione: Silvia Zignani
Progetto grafico: Ka Communications
Impaginazione: Rossana Bernengo, Corpo4, Milano
Copertina: Ka Communications
Ideazione del personaggio Gea: Massimo Di Leo Disegni: Marco Bregolato, Valentina Magnaschi (quaderno)
Si ringrazia per la consulenza le insegnanti Antonella Ciancio e Athena Borsi
Contenuti digitali
Progettazione: Fabio Ferri, Nicola Barzagli Redazione e realizzazione: EICON s.r.l., IMMAGINA s.r.l., Isabella Spagni, Lumina Datamatics, Silvia Sferruzza
Audio: IMMAGINA s.r.l.

L’Editore è presente su Internet all’indirizzo: http://www.rizzolieducation.it
ISBN 979122310021-9
© 2025 Rizzoli Education S.p.A., Milano Tutti i diritti riservati
Prima edizione: gennaio 2025 Ristampe 2029 2028 2027 2026 2025 10 9 8 7 6 5 4 3 2 1 0
FAC-SIMILE
I contenuti per la didattica inclusiva sono a cura del gruppo di esperti della Ricerca e Sviluppo Erickson.
Storytelling: Valeria Razzini.
• Illustrazioni: Emanuela Di Donna.
• Redazione: Sabrina Del Sal.
Calcolo Facile: Cristina Caciolo.
• Redazione: ABC, Milano.
Contenuti fondamentali facilitati e semplificati di Matematica in HUB Kids e HUB Kit: Cristina Caciolo
Coordinamento editoriale: Francesco Zambotti e Chiara Golasseni. Coordinamento redazionale: Claudia Mandracchia e Milena Pellizzari.
© 2025 Edizioni Centro Studi Erickson S.p.A. Via del Pioppeto 24, 38121 Trento www.erickson.it
REFERENZE ICONOGRAFICHE
Archivio Rizzoli Education – Inoltre: Getty Images © 2025; pag. 108 Mondadori Portfolio/Fototeca Gilardi; pag. 108 Ira Berger / Alamy Stock Photo
L’Editore si scusa per eventuali omissioni o errori di attribuzione e dichiara la propria disponibilità a regolarizzare.
La realizzazione di un libro presenta aspetti complessi e richiede particolare attenzione nei controlli: per questo è molto difficile evitare completamente inesattezze e imprecisioni.
L’Editore ringrazia sin da ora chi vorrà segnalarli alle redazioni. Per segnalazioni o suggerimenti relativi al presente volume scrivere a: supporto@rizzolieducation.it
I nostri testi sono disponibili in formato accessibile e possono essere richiesti a: Biblioteca per i Ciechi Regina Margherita di Monza (http://www.bibliotecaciechi.it) o Biblioteca digitale dell’Associazione Italiana Dislessia “Giacomo Venuti” (http://www.libroaid.it).
Le fotocopie per uso personale del lettore possono essere effettuate nei limiti del 15% di ciascun volume/fascicolo di periodico dietro pagamento alla SIAE del compenso previsto dall’art. 68, commi 4 e 5, della legge 22 aprile 1941 n. 633. Le riproduzioni effettuate per finalità di carattere professionale, economico o commerciale o comunque per uso diverso da quello personale possono essere effettuate a seguito di specifica autorizzazione rilasciata da CLEARedi, Corso di Porta Romana n. 108, 20122 Milano, e-mail: autorizzazioni@clearedi.org.
Il processo di progettazione, sviluppo, produzione e distribuzione dei testi scolastici dell’editore è certificato UNI EN ISO 9001.
Stampato presso: Poligrafici Il Borgo S.r.l. – Bologna (BO)

MATEMATICA
Con
MI ESERCITO IN...
SE SBAGLIO IMPARO
LABORATORI STEM E STEAM
EDUCAZIONE FINANZIARIA
VERIFICHE A LIVELLI
MATELUDICA
STORYTELLING
CALCOLO FACILE
POSTER DELLE REGOLE E RIPASSO
Matematica 4
PROBLEMI

NUMERI E OPERAZIONI
FRAZIONI E NUMERI DECIMALI
MISURE

SPAZIO E FIGURE
RELAZIONI, DATI E PREVISIONI
Laboratorio STEM
pagg. 7, 26, 31, 95, 142
PROBLEM SOLVING
pagg. 23, 52, 64, 79, 89, 100, 141
• Il mio atlante • Ripassa con Gea
• Benvenuti in 4a • Ripassa con Gea
• Esercizi
• SE SBAGLIO IMPARO
• Verifiche più facili
• Verifiche intermedie
• Verifiche finali
• Prove non note
• Coding
EDUCAZIONE FINANZIARIA
pagg. 103, 105, 108-109
pagg. 32-33, 38-39, 48-49, 50-51, 76-77, 98-99
Testi facilitati e semplificati raccolti nel volume CheFacile! - Matematica 4, disponibile su richiesta dell’insegnante. Nella Guida per l’insegnante: strategie e dettagli operativi per la didattica inclusiva.
Problemi

A scuola di soluzioni
L’Accademia dei Talenti è una scuola come ce ne sono poche. Ecco perché i bambini e le bambine che vogliono studiare qui sono tanti!
Che cosa serve per iscriversi all’Accademia? Bisogna avere… un talento. Saper fare qualcosa o avere buona volontà, insomma.
Le materie da studiare sono tante e sempre nuove, perché ogni persona può avere un talento diverso. Ci sono Matematica, Scienze, Geografia, Storia, Grammatica… ma anche Giardinaggio, Disegno a Pennarello, Frasi d’Auguri, Gesti Gentili… Alcune lezioni durano anni, come quelle del corso Portare Pazienza, mentre il corso Cantare Sotto la Doccia è già finito dopo qualche strofa.
Per mantenere l’ordine in una scuola così, serve un tipo come l’Illustrissimo Preside Melchiorri: lui è preciso, perfezionista, pignolo e attento a ogni minimo dettaglio.
Il Preside Melchiorri è il tipo di persona che, quando all’Accademia dei Talenti va in scena la recita di fine anno, passa tutto il tempo a controllare il volume dei microfoni, le luci nella sala, i sorrisi del pubblico. E così si perde lo spettacolo, che magari è pure bellissimo! Ma al Preside va bene così. Il suo talento è risolvere i problemi.
Infatti il Preside Melchiorri, quando si trova di fronte a una domanda complicata (come per esempio: “Quanti gelati abbiamo questa settimana per ogni alunno o alunna?”), non si agita, non si preoccupa e non mordicchia la sua penna come se fosse una barretta di cioccolato.
Invece, si concentra per:
capire;
pianificare;
risolvere;
rivedere il suo lavoro.
Quando è soddisfatto del risultato che ha trovato, il Preside risponde alla domanda. Poi va da un’altra parte a controllare che tutto sia in ordine come piace a lui.

E tu, che cosa fai quando devi risolvere un problema di Matematica?
Se fai attenzione, trovi sempre la soluzione! Nelle pagine successive imparerai come risolvere qualsiasi problema.
di Valeria Razzini
PROBLEMI MATEMATICI
Un problema rappresenta una situazione in cui una persona vuole raggiungere un obiettivo, trovare una soluzione, ma non sa come fare.
Nella vita di tutti i giorni capita spesso di trovarci di fronte a problemi di vario genere. Quando per risolverli è possibile utilizzare la Matematica, ci troviamo di fronte a problemi matematici
Tra i problemi matematici, possiamo distinguere:
– problemi sempre risolvibili;
– problemi che richiedono di ragionare sulla situazione e di trovare delle strategie utili. Questi problemi non sempre sono risolvibili.
• Leggi i testi inventati da alcuni bambini e bambine, poi segna con una che tipo di problemi sono e spiega la tua risposta.
Aisha e Samuele
Katia vuole fare merenda con i suoi 5 amici e amiche. Hanno a disposizione 8 panini al formaggio, 4 al prosciutto, 6 alla marmellata e 6 con il cioccolato. Quanti panini potrà mangiare ognuno?
non-problema
problema matematico
Perché
posso trovare la soluzione svolgendo
non posso rispondere alla domanda calcoli matematici. facendo calcoli matematici.
Jordan e Maria
Oggi è il compleanno di Mirko e Giulia! Hanno invitato a casa loro amiche e amici per fare merenda. Possono scegliere tra panini al formaggio, al prosciutto e alla marmellata; inoltre hanno del succo alla pera e un po’ alla pesca. Riusciranno a fare tutti merenda?
non-problema
problema matematico
Perché

• Capovolgi il libro per scoprire le soluzioni.
un problema matematico. Quello di Jordan e Maria no.
Quello di Aisha e Samuele è
AUDIO, VIDEO E OGGETTI DIGITALI DELL’UNITÀ
Laboratorio
STELLA PITAGORICA
Pitagora è stato uno dei più importanti matematici della Storia. Nacque a Samo, una piccola isola della Grecia, nel 580 a.C.
Dopo aver viaggiato molto, arrivò a Crotone e fondò una scuola dove si insegnavano solo quattro materie: la Matematica, la Geometria, l’Astronomia e la Musica!
Il maestro Pitagora teneva delle lezioni riservate a coloro che volevano prendere il diploma di pitagorico. Noi oggi li chiameremmo studenti, ma i Greci li chiamavano matematici, che significa “apprendisti”.
La parola Matematica deriva dal greco mathematicos, che significa “colui che è desideroso di apprendere”.
Per entrare nella scuola di Pitagora serviva un simbolo segreto: una stella a 5 punte.
Sai che la stella si può disegnare anche senza staccare mai la matita dal foglio? Prova qui sotto.

Ora prova a disegnare la forma di una casetta come questa senza staccare mai la matita dal foglio.
COME SI RISOLVE UN PROBLEMA
Leggi il testo
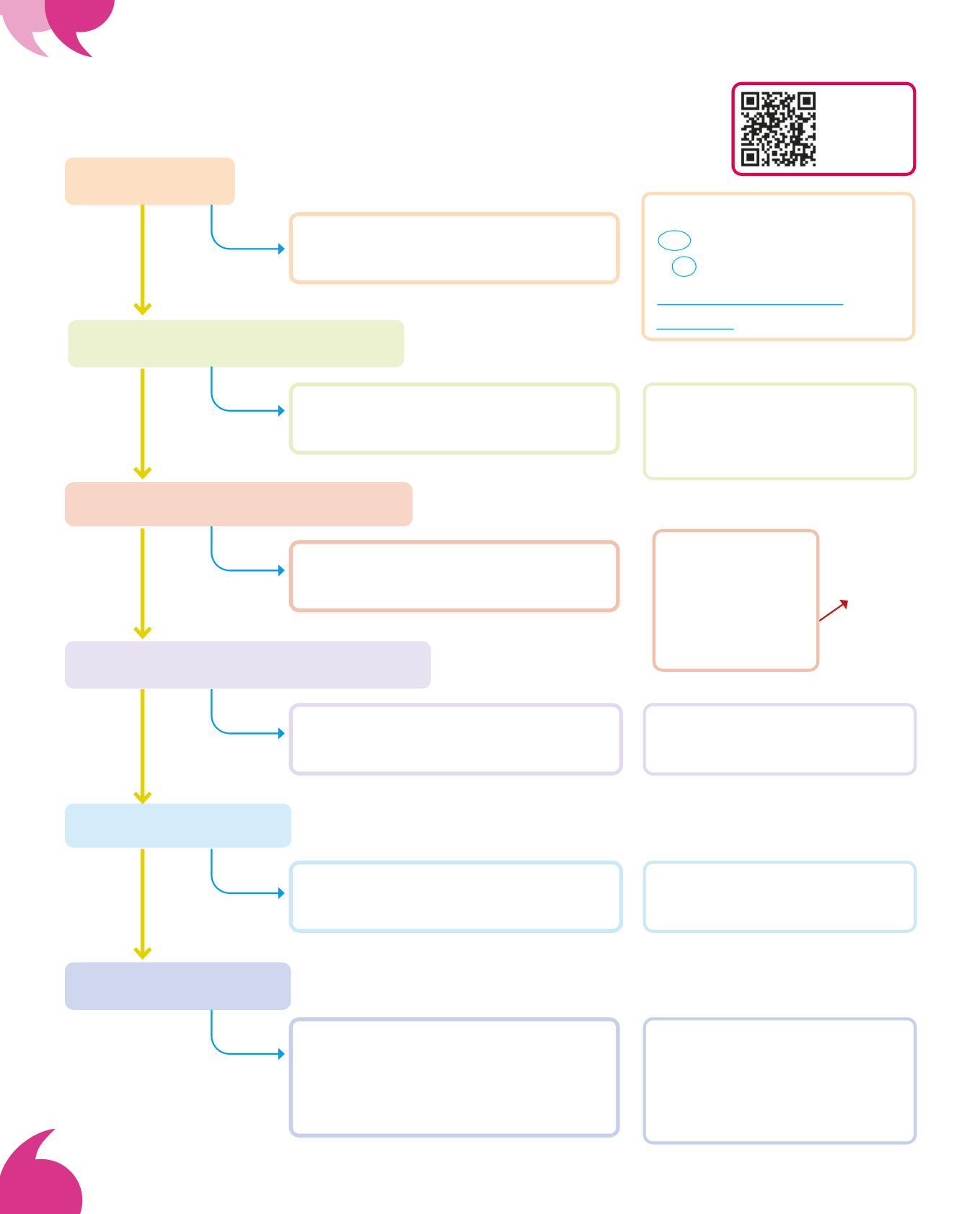
• Sottolinea la domanda;
• cerchia i dati
Riscrivi in ordine dati e domanda.
• Dati: scrivi prima il numero;
• domanda: scrivi prima il ?
Fai una rappresentazione grafica
• Scegli quella più efficace: disegni, schieramenti, barre, tabelle...
Imposta ed esegui la/le operazione/i
• Sempre prima in riga;
• solo se serve in colonna
Scrivi la/e risposta/e.
• Deve essere una frase che risponde alla domanda.
Controlla e rifletti
• Fai delle operazioni per verificare i risultati;
• rileggi la/le domanda/e: la tua risposta è possibile e sensata?
Il maestro ha preparato 110 schede da distribuire ai 22 alunni della sua classe Quante schede riceverà ciascuno?
110 schede in tutto 22 bambini/e ? schede per ogni bambino/a
110 schede
110 : 22 = (110 : 2) : (22 : 2) = = 55 : 11 = 5 schede a testa
Ogni bambino/a riceverà 5 schede.
5 × 22 = 110 schede totali
Le schede per ogni bambino/a sono molte meno delle schede totali? Sì: il risultato ha senso.
I DATI DI UN PROBLEMA
Per risolvere un problema è necessario individuare i dati, cioè le informazioni che servono per arrivare alla soluzione.
• Osserva i dati e collega ogni problema all’etichetta corrispondente.
1
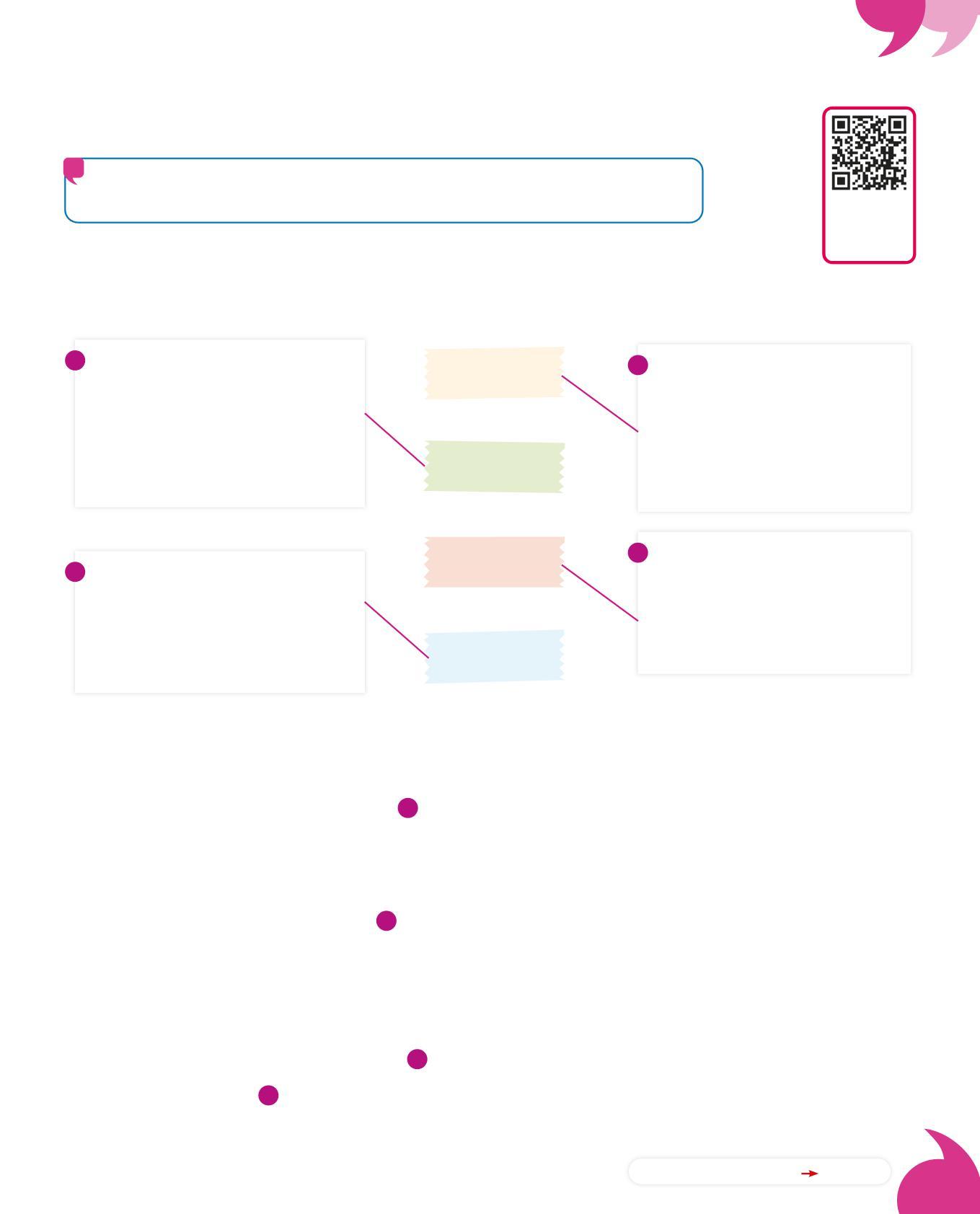
2
La mamma ha acquistato del prosciutto che è costato
€4,00 e uno yogurt al prezzo di € 2,00. Prima di pagare ha incontrato 3 amiche. Quanto ha speso in tutto?
C’È
UN DATO NASCOSTO
C’È
UN DATO INUTILE
Giacomo compra una rivista all’edicola. Paga con una banconota da €5,00 e riceve di resto €7,00. Quanto costa la rivista?
C’È
UN DATO MANCANTE
3
Per un matrimonio un fioraio ha usato 50 rose bianche e una dozzina di rose rosse per gli addobbi. Quanti fiori ha usato in tutto?
4
C’È UN DATO SBAGLIATO
Giovanni ha portato a scuola 45 pizzette da dividere in classe. Quante pizzette spettano a ognuno?
A volte i dati non sono tutti espressi con un numero; alcuni si nascondono dietro alle parole: sono dati nascosti. Bisogna trovarli e tradurli in numeri.
• Qual è il dato nascosto del problema 3 ? =
Talvolta sono presenti dati in più, che non servono per la soluzione del problema: sono dati inutili. Basta ignorarli.
• Qual è il dato inutile del problema 1 ?
dozzina 12 3 amiche
Può capitare, infine, che un problema sia impossibile da risolvere, o perché non ci sono tutti i dati che servono (dati mancanti) o perché i dati sono scorretti (dati sbagliati).
• Qual è il dato mancante del problema 4 ?
Il numero delle persone in classe.
• Perché nel problema 2 c’è un dato sbagliato?
Perché il resto non può essere maggiore del valore della banconota con cui si paga.
UNA DOMANDA E PIÙ OPERAZIONI
Quando in un problema c’è una domanda nascosta, è importante scoprirla: essa fornisce un dato necessario per arrivare alla soluzione finale.
I genitori delle classi quarte hanno regalato 90 libri, che sono stati distribuiti in parti uguali nelle 3 classi. Nella biblioteca della 4ª C c’erano già 124 libri. Quanti libri ci sono ora in tutto nella 4ª C?
1. Leggi con attenzione il testo del problema
2. Rifletti sulla domanda e sui dati.

3. Rappresenta sul quaderno.
4. Completa il diagramma ed esegui i calcoli.
5. Scrivi la risposta.
6. Controlla e rifletti: il numero che hai ottenuto è sensato? sì no
MI ESERCITO
• Quante domande ci sono nel problema?
• Hai tutti i dati che ti servono per rispondere?
• Qual è la domanda nascosta?
1 no Quanti libri ha ricevuto ogni classe?
• Per rispondere alla domanda finale devi conoscere il numero di
• Quante operazioni devi eseguire?
libri nuovi per ogni classe. 2 90 3 : 30 124 + 154
• In tutto i libri della 4ª C sono numero dei libri regalati a ogni classe numero totale dei libri della 4ª C
1. Segna con una qual è la domanda nascosta. Poi risolvi sul quaderno.
L’albergo Eden dispone di 52 camere con 2 letti ciascuna. Gli ospiti sono 81. Quanti letti sono vuoti? Quante camere ci sono? Quanti letti ci sono?
Attività nel quaderno pagg. 187, 188
PROBLEMI CON DUE DOMANDE E DUE OPERAZIONI
Nei problemi con due domande è importante seguire l’ordine stabilito: spesso il risultato dell’operazione della prima domanda ti serve per rispondere alla seconda domanda.
Nella sua pasticceria Carlo prepara 36 pasticcini al cioccolato e 44 alla crema. Quanti pasticcini prepara in tutto?
Li dispone poi su 5 vassoi, mettendo in ognuno lo stesso numero di pasticcini. Quanti pasticcini mette su ogni vassoio?
1a. Leggi la prima parte: che cosa chiede? pasticcini in tutto.
2a. Individua i dati.
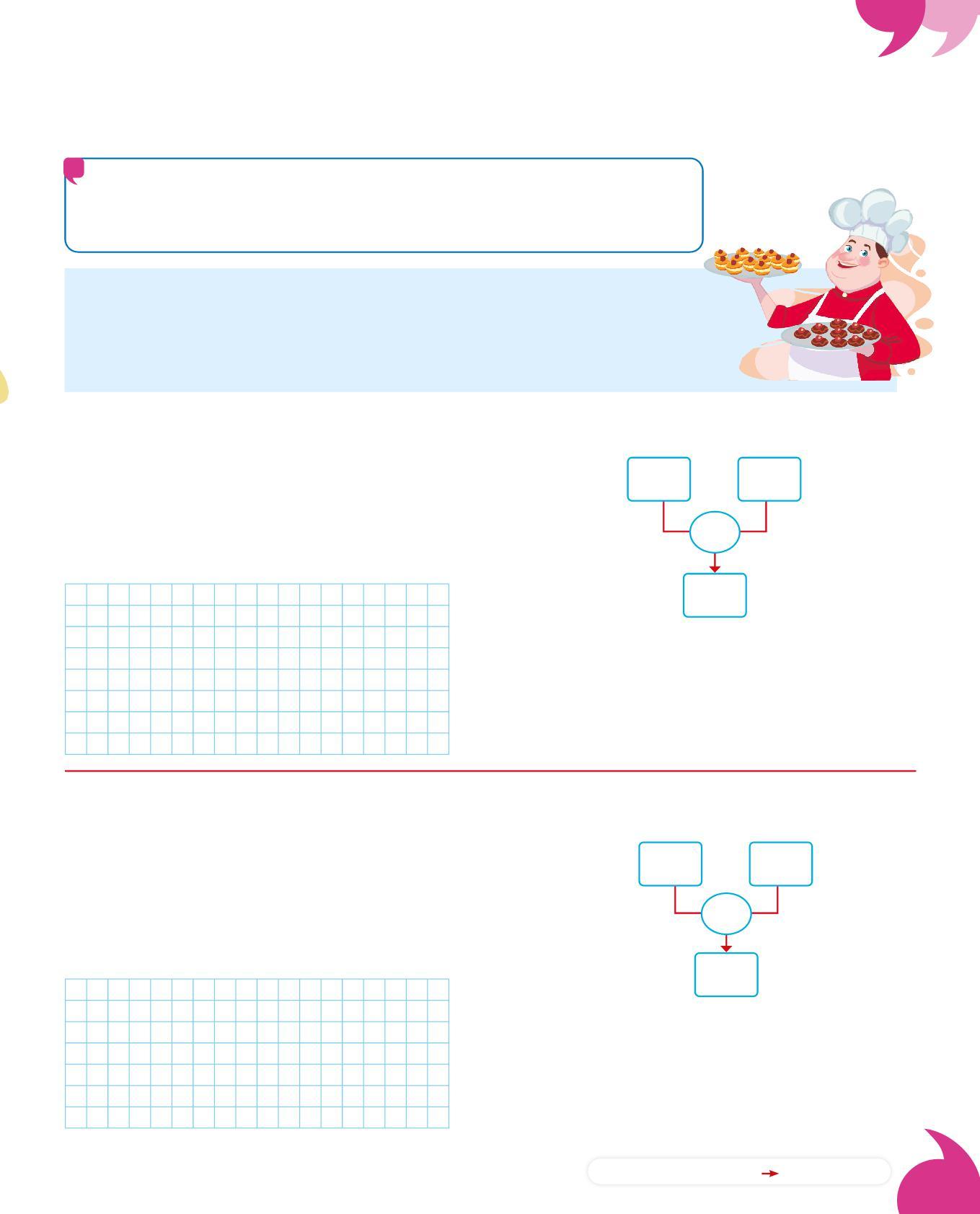
4a. Trova l’operazione:
Quanti alla crema
36 = pasticcini al cioccolato
44 = pasticcini
3a. Rappresenta.
1b. Leggi la seconda parte: che cosa chiede?
80 44 36 80 + Quanti pasticcini su ogni vassoio.
2b. Individua i dati.
vassoi
5 = Dove trovi l’altro dato che ti serve?
Uso il risultato dell’
3b. Rappresenta.
addizione della prima parte
5a. Carlo prepara in tutto
80 pasticcini
6a. Controlla e fai una verifica del risultato: – =
tot. pasticcini 36 44 numero di pasticcini in tutto alla crema al cioccolato
4b. Trova l’operazione:
numero di pasticcini su ogni vassoio
5b.
Mette 16 pasticcini su ogni vassoio.
6b. Rifletti: come puoi verificare il risultato?
Con una moltiplicazione: 16 × 5 = 80. 80 5 16 :
Attività nel quaderno pagg. 189, 190
PROBLEMI CON DISEGNI E TABELLE
A volte il testo viene sostituito o completato da un’illustrazione o da una tabella da cui si possono ricavare dati utili
Alcuni amici e amiche, adulti e bambini, si recano a pattinare alla pista di pattinaggio sul ghiaccio. All’ingresso leggono le indicazioni che vedi nel disegno.
1. Sulla pista di ghiaccio stanno pattinando 13 bambini e bambine e 9 adulti. Quante persone possono ancora entrare nella pista?
Dati utili
35 13 9 ?
capienza massima bambini/e in pista adulti in pista quanti possono entrare ancora
1ª operazione:
13 + 9 = 22
2ª operazione:
Risposta:
MI ESERCITO
Nella piscina comunale si tengono dei corsi di nuoto settimanali.
Nella tabella sono riportati i dati del numero dei bambini e delle bambine che hanno frequentato i corsi.
giornonumero bambini/e lunedì 20
martedì 18
mercoledì 32 giovedì 25
venerdì 20

1. Completa le frasi con i dati della tabella.
Il martedì hanno frequentato il corso di nuoto bambini/e.
Il venerdì hanno frequentato il corso di nuoto bambine/i, come il
Il giorno con il maggior numero di bambine/i è stato il , quando i bambini/le bambine sono stati
2.Esegui i calcoli sul quaderno, poi rispondi. Quanti bambini/e in tutto hanno frequentato i corsi di nuoto durante la settimana?
35 – 22 = 13 Possono entrare ancora 13 persone. 18 lunedì 20 mercoledì 32 115
Attività nel quaderno pag. 191
LABORATORIO I problemi
MI ESERCITO
1. Per ogni problema cerchia i dati e sottolinea la domanda. Poi risolvi sul quaderno.
a. All’hotel Miramare ci sono 25 camere da 4 posti ciascuna Qual è la capienza dell’hotel?

b. Kevin sale con 8 amici e amiche sul treno diretto a Genova. Sul treno ci sono già 140 persone, alla prima fermata ne salgono altre 64 e alla seconda 73 Quante persone sono arrivate a Genova?
2.Completa il diagramma per risolvere ogni problema.
a. Luisa compra in un grande magazzino 4 sedie uguali a € 32 ciascuna, un tavolo a € 245 e una lampada che costa € 125. Quanto spende Luisa complessivamente?
3. Risolvi i problemi sul quaderno.
a. Questa mattina al mercato del paese ho acquistato 2 kg di carote, 3 kg di zucchine e mezzo chilogrammo di pomodori. Avevo nel portafoglio una banconota da € 20 e una da € 5. Con quanti soldi sono tornata a casa?
b. Nel negozio “Il paese dei balocchi” sono stati venduti 870 giochi in scatola e 335 videogame. Quanti giochi sono stati venduti in tutto?
I giochi in vendita nel negozio erano 1465, quanti giochi sono ancora disponibili?

b. Nella vigna della zia Sandra vengono raccolti 445 grappoli di uva bianca e 399 di uva rossa. Vogliono disporli in 4 ceste che contengano lo stesso numero di grappoli. Quanti grappoli vanno in ogni cesta?
Verso l’Invalsi
Ilario, il giardiniere del parco, sta potando le piante. Sta lavorando da 2 ore e ne ha già potate 6. Osserva il disegno: quante ore impiegherà ancora per potarle tutte?
Numeri e operazioni
La lezione di motoria
Per capire bene come funzionano le lezioni all’Accademia dei Talenti devi conoscere il maestro Calatroni, l’insegnante di motoria nonché Vicepreside.
Calatroni è un gran simpaticone ed è molto amichevole: è la persona ideale per affiancare quel pignolo del Preside Melchiorri. Il talento del maestro è quello di non innervosirsi mai. Per esempio, la sua classe il mese scorso gli ha detto: – Maestro, non abbiamo le scarpe da ginnastica di ricambio.
Allora lui ha risposto: – E che problema c’è? Va benissimo così. Solo che i bambini e le bambine avevano appena terminato la lezione di Corsa nel Fango e le loro scarpe erano sporchissime… Avresti dovuto vedere le facce dei collaboratori scolastici che hanno dovuto pulire tutta la palestra, con Calatroni che diceva: – Suvvia, correre all’aperto fa bene!
Il maestro Calatroni è proprio fissato con le attività all’aria aperta e ne inventa sempre di nuove per le sue lezioni. Con lui la corsa non è solo corsa, ma Corsa Posizionale!
Calatroni scrive delle strane lettere su sei piastrelle del cortile: sono le marche del valore posizionale.

Sai scrivere in parola le marche del valore posizionale?
u da h
LETTURA ESPRESSIVA
Poi dice un numero, per esempio 400. Quando dà il via, le bambine e i bambini devono andare a posizionarsi sulle piastrelle in modo da comporre il numero, quindi 4 di loro vanno sulla piastrella delle centinaia.
– Ehi maestro – ha detto Chiara alla prima lezione – ma così oltre a fare attività fisica studiamo anche il valore posizionale!
e posiziona !





Ricorda le marche della storia: le ritroverai nelle prossime pagine!











so. propr o en usias d
Calatroni ha sorriso. È proprio entusiasta di questo esercizio.
Mettiti alla prova: conosci queste altre tre marche?
di Valeria Razzini
IL NOSTRO SISTEMA DI NUMERAZIONE
Il nostro sistema di numerazione è decimale perché raggruppiamo sempre per 10: ogni volta che abbiamo 10 elementi dobbiamo fare un cambio.
• Raggruppa per dieci e completa.
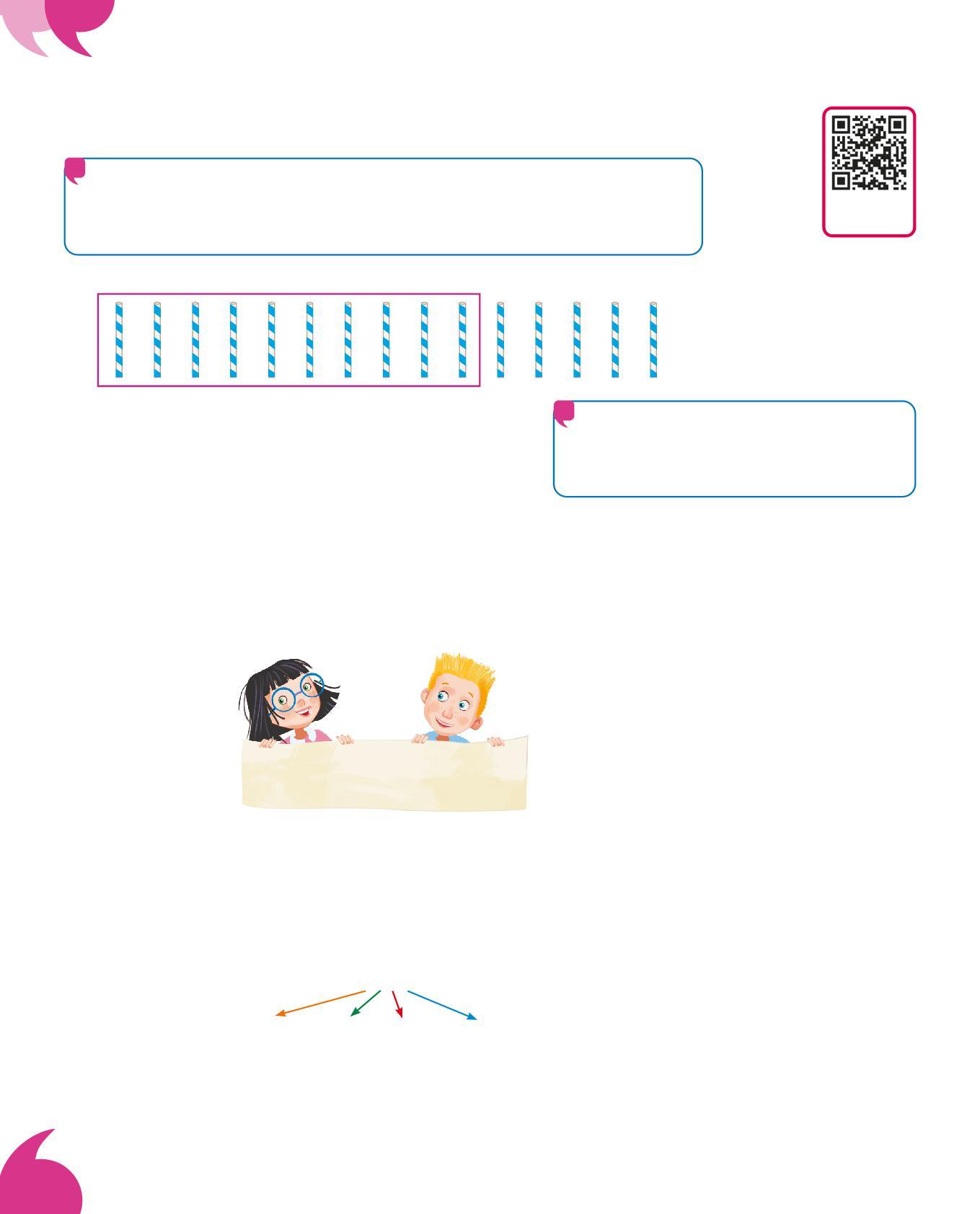
Ho formato un gruppo da cannucce; ne sono avanzate
Le cannucce sono : 1 da e 5 u
• Completa le frasi:
– 10 unità vanno raggruppate e formano una
– 10 decine vanno raggruppate e formano un
Il nostro sistema di numerazione è posizionale perché il valore di ogni cifra è dato dalla sua posizione.
– 10 centinaia vanno raggruppate e formano un .
• Osserva questo numero e completa.
1 875
– La cifra occupa la posizione delle migliaia e vale uk.
– La cifra occupa la posizione delle centinaia e vale h
– La cifra occupa la posizione delle decine e vale da
– La cifra occupa la posizione delle unità e vale u
• Lo stesso numero può essere rappresentato anche così: osserva e completa
875 uk, h, da, u
• Ora scrivi il valore di ogni cifra nei seguenti numeri.
7 h, 9 da, 2
h, 0 da, 5
AUDIO, VIDEO E OGGETTI DIGITALI DELL’UNITÀ
Il significato dello zero
• Come cambiano i numeri senza lo zero? Osserva e completa.
501 90 650
51 9 65
La cifra 0 è importante perché ci permette di indicare una posizione vuota nella composizione di un numero.
Osserva questo numero.
Se hai dubbi vai a pag. 195 SE SBAGLIO IMPARO!
2 801
2 uk 8 h 0 da 1 u
Lo zero indica una posizione vuota nelle decine: quando scrivi lo 0 in 2 801 lasci vuoto il posto occupato dalle decina.
I numeri naturali (0, 1, 2 ecc.) sono infiniti, cioè non hanno fine. Possiamo scrivere numeri sempre più grandi, composti da sempre più cifre: 8 • 32 • 546 • 1 295
MI ESERCITO
1. Scrivi tutti i numeri che puoi comporre con le seguenti cifre.
a. 2 • 4 • 8
b. 5 • 0 • 9
248, 482, 824, 842, 428, 284 509, 590, 95, 59, 905, 950
2.Scomponi i numeri.
979 = 88 = 180 = 301 =
9 h, 7 da, 9 u
8 da, 8 u
1 h, 8 da
3 h, 1 u
4.Calcola a mente e scrivi il risultato.
3. Ricomponi i numeri.
Segui l’esempio.
8 h, 5 da, 2 u = 852
2 h, 4 da, 4 u = 7 h, 0 da, 3 u = 8 da, 6 u = 1 h, 4 da, 9 u = 5 da, 0 u = 9 uk, 4 h, 0 da, 3 u = 6 uk, 0 h, 0 da, 7 u =
a. Qual è il numero più grande che puoi scrivere con le cifre: 8 • 0 • 9?
b. Qual è il numero più piccolo che puoi scrivere con le cifre 0 • 7 • 2?
c. Nella giungla la fotografa è riuscita a scattare un centinaio di foto in tutto: due decine a una tigre e le altre ai pappagalli. Quante foto ha scattato ai pappagalli?
Attività nel quaderno pag. 194 244 703 86 149 9403 6007 50
980 27 80
VIDEO Intervista a Fibonacci Numeri piccoli e grandi
NUMERI CON LE MIGLIAIA
Nei grandi numeri le cifre si raggruppano di tre in tre a partire da destra. Ogni gruppo si chiama periodo e comprende tre ordini: unità, decine e centinaia. Osserva e poi completa.
periodo delle migliaia periodo delle unità semplici centinaia di migliaia decine di migliaia

1 u = 1
10 u = 1 da 1 da = 10
10 da = 1 h 1 h = 10 = 100
10 h = 1 uk 1 uk = 10 = 100 da = 1 000
10 uk = 1 dak 1 dak = 10 uk = 100 = 1 000 da = 10 000
u u u u h h h uk
10 dak = 1 hk 1 hk = 10 dak = 100 = 1 000 = 10 000 da = 100 000 u
Per scrivere un grande numero, si contano tre cifre a partire da destra e si lascia un piccolo spazio tra un periodo e l’altro, oppure si può mettere un puntino in alto o in basso.
CON LO SPAZIO CON IL PUNTO IN ALTO CON IL PUNTO IN BASSO 318 672
Per leggere un grande numero, quando si incontra lo spazio o il punto si dice il periodo appena letto.
318 672 si legge: trecentodiciottomilaseicentosettantadue
1. Come si legge 322847?
trecentoventiduemilaottocentoquarantasette da
2.Cerchia la cifra delle unità di migliaia. 3 459 • 29 401 • 73 630 • 458 892
Se hai dubbi vai a pag. 196 SE SBAGLIO IMPARO!
3. Cerchia la cifra delle decine di migliaia. 25 318 • 49 300 • 165 927 • 830 115
4.Cerchia la cifra delle centinaia di migliaia. 468 296 • 313 280 • 121 000 • 554 300
COMPORRE E SCOMPORRE
Possiamo scomporre i numeri in diversi modi.
Osserva il numero 8349
• Lo puoi scomporre in tabella. uk h da u

• Lo puoi scomporre come somma di valori, somma di addendi o somma di prodotti
8349 significa 8 volte 10003 volte 1004 volte 109 volte 1
si può scomporre 8 uk + 3 h + 4 da + 9 u somma di valori si può anche scomporre 8000 + 300 + 40 + 9 somma di addendi si può scomporre anche 8 × 1000 + 3 × 100 + 4 × 10 + 9 × 1 somma di prodotti
• Lo puoi rappresentare con una scomposizione in u, da, h, uk, dak, hk
8 uk = 8000
3 h = 300
4 da = 40 9 u = 9
• Ora prova tu a scomporre i numeri con la tabella della scomposizione, che mostra il valore di ogni cifra, segui l’esempio.
periodo delle migliaia periodo delle unità semplici centinaia di migliaia decine di migliaia unità di migliaia centinaia semplici decine semplici unità semplici hk dak uk h da u 314 3
• Completa, segui l’esempio.
Nel numero 314 la cifra 3 rappresenta , quindi unità.
Nel numero 3295 la cifra 3 rappresenta , quindi unità.
Nel numero 382051 la cifra 3 rappresenta , quindi unità. le centinaia semplici
le unità di migliaia le decine di migliaia le centinaia di migliaia
Nel numero 30667 la cifra 3 rappresenta , quindi unità.
GIOCO L’abaco
ORDINARE I NUMERI
I numeri possono essere ordinati sulla linea dei numeri. Spostandoti verso destra trovi i numeri successivi rispetto al numero di partenza; si ottengono aggiungendo 1 (+ 1). Spostandoti verso sinistra torni indietro e incontri i numeri precedenti; si ottengono togliendo 1 (– 1)
• Osserva la linea dei numeri e completa.

La successione dei numeri può essere infinita perché se si aggiunge a un numero si ottiene sempre un numero . Non esiste un numero maggiore in assoluto, ma esiste un numero minore in assoluto: lo . Il numero precedente a 2 è e il numero successivo è .
Tutti i numeri successivi a un numero dato sono maggiori di quel numero; tutti i numeri precedenti sono minori. Tutti i numeri hanno un precedente, tranne lo zero, e un successivo.
I numeri possono essere ordinati in ordine crescente, dal minore al maggiore, o in ordine decrescente, dal maggiore al minore.
crescente
decrescente
1. Scrivi il precedente e il successivo di ogni numero in tabella.
2.Riscrivi i numeri in ordine crescente. 432 680 • 423 680 • 432 608
3. Riscrivi i numeri in ordine decrescente. 712 636 • 721 366 • 712 663
CONFRONTARE I NUMERI
Un numero si dice maggiore di un altro quando rappresenta una quantità più grande; si dice minore quando rappresenta una quantità più piccola.
Per confrontare due numeri usa i simboli > (maggiore), < (minore), = (uguale).
Osserva e completa i passaggi per farlo in modo corretto.

Ricorda: la punta di > e < va sempre verso la quantità minore.
1) Controlla il numero di cifre. Il numero con più cifre è il maggiore. 25966 2596
2) Se i due numeri hanno le stesse cifre confronta le varie cifre partendo da sinistra.
3 2 5 8 4 2 5 9
3 uk < 4 uk; dunque 3 258 4 259
3) Ora osserva questi due numeri: 2345 e 2348. Hanno lo stesso numero di cifre? sì no
La prima cifra è uguale? sì no
Allora procedi così: – parti da sinistra, confronta le cifre che hanno la stessa posizione nei due numeri e fermati quando hai trovato la cifra che vale di più.
– Se le cifre sono uguali, passa alle successive.
2 3 4 5 2 3 4 8
2 uk = 2 uk; 3 h = 3 h; 4 da = 4 da, ma 5 u < 8 u; dunque 2 345 < 2 348
1. Completa i confronti con > (maggiore), < (minore) oppure = (uguale).
2.Completa con i numeri mancanti. < 899 < 25 852 < <
MI ESERCITO
1. Collega il numero in cifre al numero in lettere corrispondente.
536 409 cinquecentosessantatremilaquattrocentonove
563 409 cinquecentotrentaseimilaquattrocentonovanta
536 490 cinquecentotrentaseimilaquattrocentonove
2. Indica il valore dello zero in ogni numero. Segui l’esempio.
507 0 da 9025

3. Indica che cosa rappresenta ciascuna cifra in rosso e scrivi il suo valore. Segui l’esempio.
3 586 5 h = 500 12790
4. Riscrivi i numeri nella tabella e poi scomponili. Segui l’esempio. hkdakukhdau
60404
350 724 350724 3 hk, 5 dak, 0 uk, 7 h, 2 da, 4 u
4 hk, 8 dak, 9 uk, 1 h, 1 da, 5 u
1 uk, 6 h, 3 da, 8 u
7 dak, 5 uk, 0 h, 2 da, 6 u
5. Indica con una se le relazioni sono vere (V) o false (F).
• 170999 è il precedente di 171000. V F
• 345150 è il successivo di 245150. V F
6. Riscrivi i numeri in ordine decrescente.
• 5601 > 5610. V F
• 75392 > 75293. V F
256730 • 265730 • 703256 • 265370 • 730255 • 345000 • 703526 • 354000
730255 • 703526 • 703256 • 354000 • 345000 • 265730 • 265370 • 256730
7. Confronta i numeri di ogni coppia e inserisci il simbolo adatto: > (maggiore) o < (minore).
Verso l’Invalsi
Segna con una perché il numero nel cartellino è scritto in maniera sbagliata.
Perché manca la cifra delle unità.
Perché è sbagliata la posizione dello spazio che separa le cifre nei periodi. 85673
PROBLEM SOLVING

Leggo il problema
Una famiglia di 4 persone è andata in vacanza a Parigi. I biglietti aerei costano
€ 150 a persona e l’appartamento € 80 a notte per 5 notti. Inoltre la famiglia spende € 10 al giorno a testa per mangiare per 6 giorni. Quanto ha speso in tutto?
Capisco il problema
• Quanti sono i membri della famiglia?
• Quanto hanno speso per ciascun biglietto aereo?
• Quanto hanno speso per 1 notte in appartamento?
• Quante notti hanno usato l’appartamento?
• Quanto hanno speso a testa al giorno per mangiare?
• Quanti giorni hanno mangiato in vacanza?
Rappresento il problema
Tipo di spesa Costo per 1 personaCosto per 4 persone Costo totale
Biglietto aereo € 150
Affitto appartamento
Cibo € 10 (per 1 giorno)
Pianifico il percorso di soluzione
€ 80 (per 1 notte)
Riordina i passaggi e poi risolvi il problema sul quaderno.
4 1 2 3
Sommo tutte le spese totali.
Calcolo la spesa totale dei biglietti aerei.
Calcolo quanto hanno speso per l’affitto dell’appartamento per 5 notti.
Calcola quanto hanno speso in tutto per il cibo i 4 membri della famiglia per 6 giorni.
MI ESERCITO
1. Risolvi un problema simile sul quaderno.
Toby, Luca e Jimmy sono andati in gita: il treno è costato € 120 a testa, l’hotel € 75 a notte per 3 notti e il mangiare € 15 a persona per 4 giorni. Quanto hanno speso in tutto?
ARROTONDAMENTO O APPROSSIMAZIONE
Arrotondare o approssimare un numero significa sostituire al numero esatto un numero “più semplice”, che gli si avvicini il più possibile.
Devi acquistare 3 confezioni di gelato che costano € 4,85 l’una e devi calcolare a mente più o meno quanto spenderai. Per farlo puoi arrotondare il costo del gelato.
• Leggi e completa.
– 4,85 è un numero più vicino a 4 o a 5?
– 3 confezioni × circa 5 euro = circa 15 euro.
In questo caso hai arrotondato per eccesso, perché per arrivare a 5 euro hai aggiunto € 0,15.
Si arrotonda per eccesso quando la cifra a destra di quella considerata è uguale o maggiore di 5
– Se invece le confezioni di gelato costano € 4,20 l’una, il numero più vicino, tra 4 e 5, sarà .
– 3 confezioni × circa 4 euro = circa 12 euro.
In questo caso hai arrotondato per difetto, perché per arrivare a € 4 hai tolto €
In entrambi i casi hai arrotondato alle unità, ma puoi arrotondare anche alle migliaia, ai decimi, ai centesimi…
Si arrotonda per difetto quando la cifra a destra di quella considerata è minore di 5
• Arrotonda alle centinaia il numero 762: collocalo sulla linea dei numeri e completa.

– Ho arrotondato per il numero 762 a , perché è il numero più vicino.

Per calcolare in modo corretto gli arrotondamenti bisogna prestare attenzione agli scarti, cioè a quanta differenza c’è tra il numero reale e quello arrotondato
• Osserva le tabelle e completa le frasi.
numeroarrotondamento alle decine scarto
18 per eccesso: 20 da 18 per arrivare a 20 c’è uno scarto di 2 18 per difetto: 10 da 18 per arrivare a 10 c’è uno scarto di 8
– Devi scegliere l’arrotondamento con lo scarto minore, quindi arrotonda per
numeroarrotondamento ai centesimi scarto
1,254 per eccesso: 1,26 da 1,254 per arrivare a 1,26 c’è uno scarto di 0,006 1,254 per difetto: 1,25 da 1,254 per arrivare a 1,25 c’è uno scarto di 0,004
– Devi scegliere l’arrotondamento con lo scarto minore, quindi arrotonda per
MI ESERCITO
1. Trasforma le affermazioni arrotondando i valori. Leggi e completa come nell’esempio.
• L’aereo arriverà tra 9 minuti e 45 secondi. L’aereo arriverà tra circa dieci minuti.
• Il cane pesa 8 kg e 220 grammi.
• Le scarpe costano 53 euro e 99 centesimi.
Il cane pesa circa 8 kg. Le scarpe costano circa 54 euro.
2.Arrotonda i numeri al valore che preferisci e completa la tabella. Segui l’esempio.
numeronumero approssimatoper eccessoper difetto approssimato a... 37 623 37 600 X centinaia semplici
75 499
91 800 56 231
75 500 92 000 56 230 centinaia semplici unità di migliaia decine semplici X X X eccesso difetto
3. Colora la casella con il valore più vicino alla somma indicata. Poi esegui le addizioni e controlla la tua ipotesi.
45,10 + 12,20 + 33,90 = 40 + 5,30 + 5,50 = 160,50 + 209 + 30,60 =
Laboratorio
LA STORIA DEI NUMERI
Gli esseri umani sanno contare fin dalla Preistoria, ma il modo di rappresentare i numeri è molto cambiato nel corso dei secoli. Osserva.
Colora dello stesso colore i numeri dello stesso valore in ogni riquadro per ricordarli meglio.
Preistoria

CONCLUSIONI
I numeri di oggi si chiamano numeri arabi perché furono insegnati agli antichi Romani dai mercanti arabi che erano molto bravi a fare i conti!
Nel passato si usavano degli strumenti chiamati abachi per contare e fare le operazioni con i numeri: addizione, sottrazione, moltiplicazione, divisione.
Gli abachi romani avevano delle pietruzze, in latino “calcoli”, che erano usate per questi scopi e che hanno dato il nome ai conti matematici.
numeri che usiamo oggi
Babilonesi
Romani
VIDEO La storia dei numeri
DOC
La numerazione in Mesopotamia ed Egitto Quanti sono i numeri?
L’ADDIZIONE
L’addizione ti serve ogni volta che devi aggiungere una quantità a un’altra quantità, oppure per unire due o più quantità.
Leggi il testo, osserva le immagini, poi rispondi e completa.
Giulio ha fatto un grosso ordine alla pasticceria “Dolci pensieri” per festeggiare la sua pensione. Il pasticciere Mario ha preparato 127 bignè alla crema e 62 cannoncini.
Quanti pasticcini ha preparato complessivamente Mario per soddisfare la richiesta di Giulio?
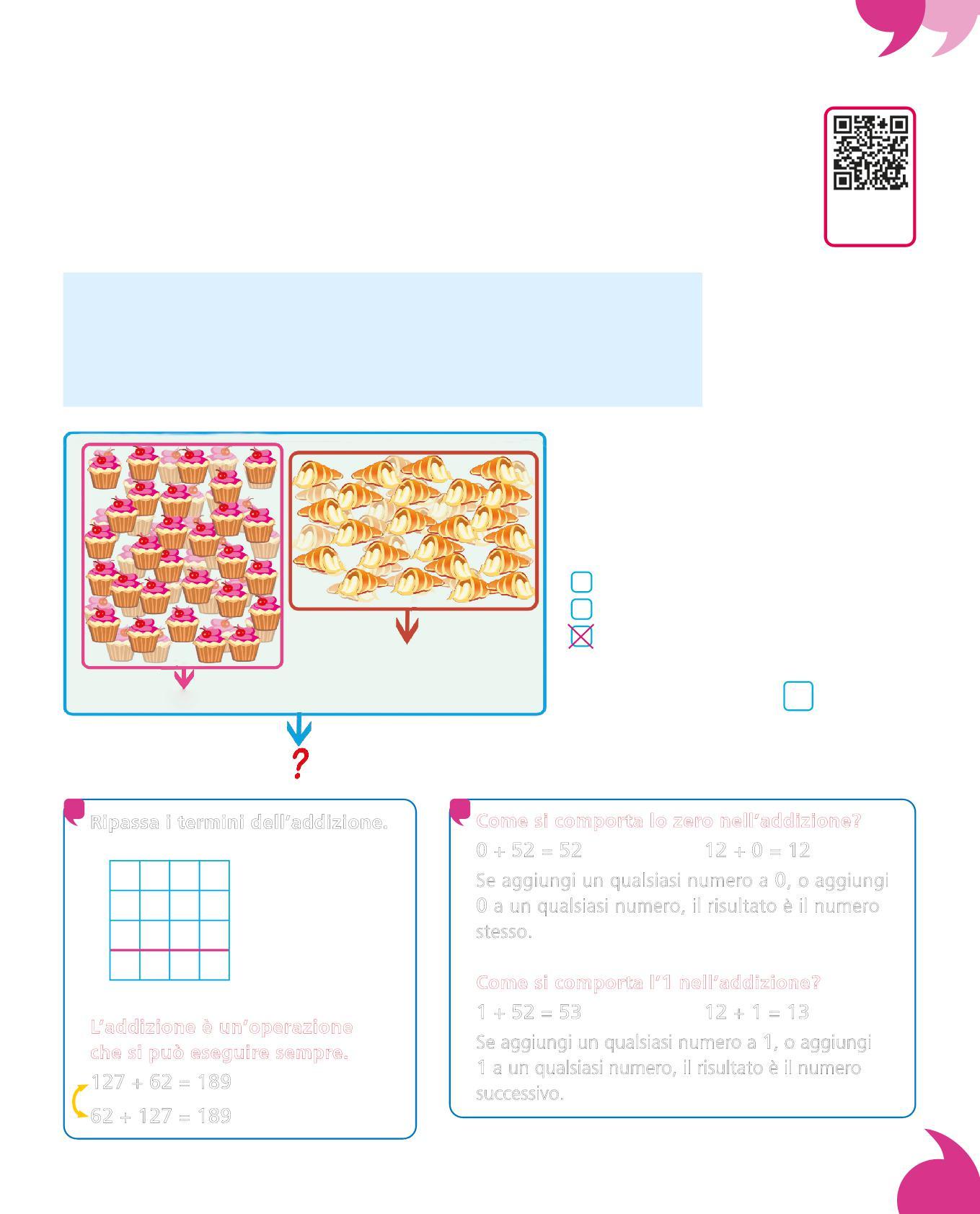
62
• Quale operazione devi usare?
addizione (+) per unire o aggiungere sottrazione (–) per togliere sottrazione (–) per calcolare una differenza
Serve : 127 62 = 127
189 un’addizione +
Ripassa i termini dell’addizione.
h da u
127 + addendo
62 = addendo
189 somma o totale
L’addizione è un’operazione che si può eseguire sempre.
127 + 62 = 189
62 + 127 = 189
Come si comporta lo zero nell’addizione?
0 + 52 = 52 12 + 0 = 12
Se aggiungi un qualsiasi numero a 0, o aggiungi 0 a un qualsiasi numero, il risultato è il numero stesso.
Come si comporta l’1 nell’addizione?
1 + 52 = 53 12 + 1 = 13
Se aggiungi un qualsiasi numero a 1, o aggiungi 1 a un qualsiasi numero, il risultato è il numero successivo.
VIDEO La tabella dell’addizione
ADDIZIONI IN RIGA O IN COLONNA?
Per eseguire addizioni semplici e veloci puoi procedere in riga. Inizia dalle unità, poi somma le decine, le centinaia, le migliaia ecc. Osserva.
256 + 123 = 379
3124 + 1732 = 4856
Per eseguire un’addizione in colonna segui questi passaggi.
• Incolonna gli addendi rispettando il valore posizionale delle cifre, cioè le unità sotto le unità, le decine sotto le decine, le centinaia sotto le centinaia ecc.
• Calcola partendo dalle unità.
• Ricordati che quando la somma è maggiore di 9 devi eseguire un cambio.
MI ESERCITO
1. Esegui le addizioni in riga o in colonna.
125 + 25 + 36 =
350 + 200 + 2435 = 46380 + 9247 = 36911 + 5246 + 12907 = 21687 + 1019 =

Vai alle pagg. 32-33 PER SCOPRIRE UN TRUCCO!
ADDIZIONE SENZA CAMBIO
345 + 52 = 397
636 + 74 = 710 ADDIZIONE CON IL CAMBIO
Se hai dubbi vai a pag. 202 SE SBAGLIO IMPARO!
VIDEO L’addizione in colonna
DOC
Addizione con e senza cambio
LE PROPRIETÀ DELL’ADDIZIONE
Le proprietà delle operazioni sono regole che permettono di rendere più semplice e veloce il calcolo a mente e di controllare il risultato dell’operazione stessa.
Proprietà commutativa: se cambi l’ordine degli addendi, il risultato non cambia.
• Osserva e completa.

45 + 32 = 32 + 45 =
Il risultato delle operazioni è lo stesso? sì no
Infatti 77 = 45 + 32 = 32 + 45.
Quale operazione è più semplice?
Proprietà associativa: se a due o più numeri sostituisci la loro somma, il risultato non cambia.
• Osserva e completa.
56 + 24 + 15 =
(56 + 24) + 15 = (80) + 15 =
Il risultato delle operazioni è lo stesso? sì no
Infatti 56 + 24 + 15 = 80 + 15
Quale operazione è più semplice?
MI ESERCITO
1. Calcola in colonna sul quaderno applicando la proprietà commutativa.
9 670 + 4 325 = 129 401 + 36 544 = 342 328 + 504 679 =
2. Calcola a mente applicando la proprietà associativa.
438 + 522 + 20 = 70 + 326 + 714 = 1 235 + 525 =
ADDIZIONI: STRATEGIE DI CALCOLO
Ci sono diverse strategie che puoi usare per calcolare velocemente le addizioni.
• Se devi aggiungere 9, 19, 29, 39… a un numero aggiungi 10, 20, 30… e togli 1!

• Se devi aggiungere 99 a un numero aggiungi 100 e togli 1.
• Se devi aggiungere 999 a un numero aggiungi 1000 e togli 1
+ 99 –
• Se devi aggiungere 11, 21, 31 a un numero aggiungi 10, 20, 30 e aggiungi ancora 1.
• Se devi aggiungere 101 a un numero aggiungi 100 e poi ancora 1
• Se devi aggiungere 1001 a un numero aggiungi 1000 e poi ancora 1
• Un’altra strategia di calcolo per l’addizione è la scomposizione degli addendi. Osserva. 155 + 15 = 170
150 + 5 + 10 + 5 = 170
MI ESERCITO
1. Calcola a mente le addizioni scegliendo la strategia migliore. 954 + 9 =
+ 999 =
+ 99 =
Laboratorio
SOMME VELOCISSIME
“Per punizione, sommate tutti i numeri da 1 a 100! Vediamo chi lo risolve per primo”.
Così tuonò il maestro Büttner, pensando di aver dato un compito lungo e difficile da risolvere ai suoi giovani alunni. Ma non aveva considerato
Carl Friedrich Gauss, studente che già a 9 anni aveva una brillante mente matematica.
Dopo solo un minuto, il giovane Carl alzò la mano, e disse: “La somma esatta dei numeri da 1 a 100 è….”

Prova anche tu a sommare i numeri da 1 a 100, ma soprattutto a trovare il metodo migliore per farlo il più velocemente possibile, proprio come ha fatto il grande matematico Gauss.
Prosegui con la lettura solo dopo averci provato, qui sotto troverai la soluzione di Gauss.
La velocità della risposta di Gauss non era dovuta a una straordinaria abilità nei calcoli, bensì alla sua capacità di trovare una soluzione… alternativa! Osserva.
Carl Gauss notò che, scrivendo i numeri da 1 a 100 su due righe, opposte nell’ordine di numerazione, la somma di ogni colonna era sempre 101! La somma di tutti i numeri in tabella era quindi 100 × 101. E poiché i numeri erano il doppio di quelli dati dal maestro, il risultato cercato era 50 × 101 = 5 050
Prova ad applicare il metodo di Gauss per calcolare la somma di un insieme di numeri a tua scelta.
Statua di Carl Gauss.
ADDIZIONI VELOCI

Cifra + cifra
Con il trucco “cifra + cifra” puoi eseguire velocemente le addizioni in riga.
1 Guarda bene l’addizione. Quanto fa…
6521 + 3427 = ?
2 Somma le cifre di ogni numero: le unità con le unità, le decine con le decine, le centinaia con le centinaia e le migliaia con le migliaia.
(6 + 3) (5 + 4) (2 + 2) (1 + 7)
6521 + 3427 = 9 9 4 8
3 Ottieni così il risultato.
6521 + 3427 = 9948
RICORDA: quando usi il trucco “cifra + cifra” e ci sono dei cambi, devi sempre aggiungerli alla cifra a sinistra. Osserva l’esempio.
1 Guarda bene l’addizione. Quanto fa…
3743 + 5532 = ?
2 Somma le cifre di ogni numero: le unità con le unità, le decine con le decine, le centinaia con le centinaia e le migliaia con le migliaia.
(3 + 5) (7 + 5) (4 + 3) (3 + 2)
3743 + 5532 = 8 12 7 5
CALCOLO FACILE

3 C’è un cambio! Devi aggiungerlo alla cifra a sinistra. (3 + 5) (7 + 5) (4 + 3) (3 + 2) 3743 + 5532 = 8 12 7 5 9 2
4 Ottieni così il risultato.
3743 + 5532 = 9275
Esercitati a usare il trucco “cifra + cifra” con queste addizioni.
3417 + 2222 = 3456 + 1335 =
Quanto sei veloce a eseguire le addizioni con il trucco “cifra + cifra”?
In coppia, scegliete un’addizione a testa e, a turno, spiegate come risolverla utilizzando il trucco appena imparato.
2572 + 1247 =
LA SOTTRAZIONE
La sottrazione ti serve quando devi calcolare il resto, la differenza tra due quantità o sapere quanto manca per raggiungere una quantità.
Leggi il testo, osserva le immagini, poi rispondi e completa.
Stamattina Maria ha preparato 198 dolci: alcuni alla fragola, altri al cioccolato. Non ricorda quanti erano quelli al cioccolato, ma sicuramente 75 erano quelli alla fragola. Quanti dolci al cioccolato ha preparato?

75 198
Ripassa i termini della sottrazione.
h da u
198 – minuendo
75 = sottraendo
123 resto o differenza
Nell’insieme dei numeri naturali, la sottrazione si può eseguire solo quando il minuendo è maggiore o uguale al sottraendo.
96 – 3 = 93 3 – 93 = non si può fare
• Quale operazione devi usare?
addizione (+) per unire o aggiungere sottrazione (–) per togliere sottrazione (–) per calcolare una differenza
Serve :
– 123 una sottrazione
198 75 =
Come si comporta lo zero nella sottrazione?
96 – 0 = 96 0 – 96 = non si può fare
Se sottrai 0 a qualsiasi numero, il risultato è il numero stesso. Lo 0 non può mai comparire al minuendo, a eccezione dell’operazione 0 – 0 = 0.
Come si comporta l’1 nella sottrazione?
52 – 1 = 51
Se togli 1 a un qualsiasi numero, il risultato è il numero precedente.
VIDEO La tabella della sottrazione
SOTTRAZIONI IN RIGA O IN COLONNA?
Per eseguire sottrazioni semplici e veloci puoi procedere in riga. Inizia dalle unità, poi sottrai le decine, le centinaia, le migliaia ecc.
Osserva.

4456 – 2234 = 2222
Per eseguire una sottrazione in colonna segui questi passaggi.
• Incolonna minuendo e sottraendo rispettando il valore posizionale delle cifre, cioè le unità sotto le unità, le decine sotto le decine, le centinaia sotto le centinaia ecc.
• Calcola partendo dalle unità.
Vai alle pagg. 38-39 PER SCOPRIRE UN TRUCCO!
SOTTRAZIONE SENZA CAMBIO 1 9 5 –78 = 117
• Ricordati che quando una cifra del minuendo è minore della cifra corrispondente del sottraendo devi eseguire un cambio 459 –36 = 423
SOTTRAZIONE CON IL CAMBIO 1 8

Se hai dubbi vai a pag. 205 SE SBAGLIO IMPARO!
MI ESERCITO
1. Esegui le sottrazioni in riga o in colonna. 3450 – 350 = 6908 – 805 = 37648 – 11749 = 56435 – 5608 =
VIDEO La sottrazione in colonna con il cambio
LA PROPRIETÀ DELLA SOTTRAZIONE
Proprietà invariantiva: se aggiungi o sottrai lo stesso numero al minuendo e al sottraendo, il risultato non cambia.
– 28 = 135
– 30 =

=
–
• Secondo te, si può utilizzare la proprietà invariantiva anche per l’addizione? sì no
• Osserva e completa, poi controlla se hai risposto bene alla domanda precedente.
57 + 39 = 57 + 39 =
La sottrazione ha una sola proprietà che può essere utile per il calcolo veloce. + 2+ 2 + 1+ 1 – 5– 5 – 7– 7
+ 40 = 57 + 39 =
+ 32 =
Il risultato delle operazioni è lo stesso? sì no
Infatti 96 ≠ 98 ≠ 82.
MI ESERCITO
1. Calcola applicando la proprietà invariantiva.
Il segno ≠ significa “diverso”.
SOTTRAZIONI: STRATEGIE DI CALCOLO
Ci sono diverse strategie che puoi usare per calcolare velocemente le sottrazioni.
• Se devi sottrarre 9, 19, 29, 39... a un numero, togli 10, 20, 30, 40... e poi aggiungi 1
• Se devi sottrarre 99, togli – 100 e aggiungi 1; per sottrarre 999, fai – 1000 + 1
– 99
– 100–
• Se devi sottrarre 11, 21, 31, 41... a un numero, togli 10, 20, 30, 40... e poi togli ancora 1
– 999
• Se devi sottrarre 101, togli – 100 e poi togli – 1; per sottrarre 1 001, fai – 1000 – 1.
– 100
• Un’altra strategia per eseguire le sottrazioni velocemente è scomporre i numeri e sottrarre le centinaia dalle centinaia, le decine dalle decine, le unità dalle unità e infine sommare i risultati. Osserva e completa.
968 – 445 = 1650 – 101
– 1001 20 523 60 40 –+ 500 900 400 –3 8 5 –
1. Calcola a mente le sottrazioni scegliendo la strategia migliore. 354 – 9 = 563 – 39 = 809 – 99 = 4 536 – 999 = 7 631 – 11 = 630 – 21 =
Tutti al 9 e l’ultimo al 10
Con questo trucco puoi eseguire velocemente alcune sottrazioni in riga.
1 Guarda la sottrazione e chiediti:
• il primo numero (minuendo) è 100, 1000, 10000 o 100000?
• il secondo numero (sottraendo) ha una cifra in meno del primo numero e finisce con 1, 2, 3, 4, 5, 6, 7, 8, 9?
10000 – 6527 = ?
2 Se la risposta alle domande è “sì”, prendi il sottraendo (6527) e scrivi:
per le prime cifre il numero che serve per arrivare a 9
3 5 cifre 4 cifre e finisce con 7
per l’ultima cifra il numero che serve per arrivare a 10
3 Ottieni così il risultato, cioè 3473.
10000 – 6527 = 3473
Usa il trucco “tutti al 9 e l’ultimo al 10” e completa le sottrazioni.
1000 – 234 = 1000 – 812 = 10000 – 3421 =
Ora usa lo stesso trucco ed esegui queste sottrazioni senza aiuti.
100 – 81 = 10000 – 4567 = 1000 – 985 =
Hai capito come funziona il trucco “tutti al 9 e l’ultimo al 10”? Segna con una × solo le sottrazioni dove puoi usarlo.
100000 – 9929
1000 – 876
100 – 7
10000 – 1240
10020 – 9199
100 – 76
1000 – 340
100000 – 65723
È stato facile capire in quali sottrazioni puoi usare il trucco “tutti al 9 e l’ultimo al 10”?
In coppia, uno o una di voi inventa una sottrazione da risolvere con il trucco appena imparato e la scrive qui sotto. Poi il compagno o la compagna spiega ad alta voce come eseguirla e, a mano a mano, scrive il risultato.
Poco
Così così Molto
LA PROVA DI ADDIZIONE E SOTTRAZIONE
Per verificare il risultato di un’operazione puoi fare la prova: esegui un’altra operazione con gli stessi numeri, ma disposti in modo diverso.
Per fare la prova dell’addizione puoi usare la proprietà commutativa Scambia l’ordine degli addendi: se le operazioni sono corrette, otterrai lo stesso risultato.

• Ti viene in mente un altro modo per verificare il risultato di questa addizione? Confrontatevi in classe.
La sottrazione è l’operazione inversa all’addizione. Per fare la prova della sottrazione procedi così:
• somma il resto al sottraendo, se ottieni il minuendo l’operazione è corretta!
• Ti viene in mente un altro modo per verificare il risultato di questa sottrazione? Confrontatevi in classe.
MI ESERCITO
1. Esegui le operazioni in colonna e con la prova sul quaderno.
a. 5 421 + 568 = 46 380 + 9 247 = 36 911 + 5 246 + 12 907 =
b. 25 645 – 18 307 = 96 801 – 7 325 = 463 040 – 20 810 =
DOC La prova della sottrazione

MI ESERCITO
1. Esegui le operazioni in colonna e con la prova sul quaderno.
a. 456789 + 345209 = 35671 + 890123 = 7499 + 89548 = 45384 + 38006 =
2.Completa scrivendo quali proprietà sono state applicate.
100 + 35 + 25 = 100 + (35 + 25) = 100 + 60 = 160
496 – 197 = (496 + 3) – (197 + 3) = 499 – 200 = 299
142 + 48 = 48 + 142 = 190
3. Calcola applicando la proprietà invariantiva, come nell’esempio.
49 – 13 = (49 – 3) – (13 – 3) = 46 – 10 = 36
– 19 =
– 99 =
associativa invariantiva commutativa (72 + 1) – (19 + 1) = 73 – 20 = 53
– 18 =
– 14 =
– 16 =
4.Calcola applicando le strategie che hai imparato alle pagg. 30 e 37.
314 + 19 =
577 + 99 = 1385 + 99 = 1378 + 199 = 3002 + 999 =
5. Risolvi i problemi sul quaderno.
455 + 101 = 1033 + 401 = 6542 + 1001 =
– 29 =
– 999 =
a. Un cartolaio ha ordinato quaderni e quadernoni: 185 sono a righe, mentre 217 sono a quadretti. Quanti sono in tutto? Se i quaderni sono 146, quanti sono i quadernoni?
c. Lea e Desiree collezionano biglie. La prima ne ha 153, la seconda 176. Quante biglie hanno in tutto? Quante biglie ha Desiree in più rispetto a Lea? 801998
b. 25645 – 18307 = 96801 – 7325 = 463040 – 20810 = 545291 – 36048 =
– 99 =
– 371 =
– 401 =
– 101 =
– 2001 =
b. Il signor Rossi ha nel portafoglio € 110. Decide di comprare una giacca che paga € 70. Quanti soldi gli restano?
(101 + 1) – (99 + 1) = 102 – 100 = 2 (42 + 2) – (18 + 2) = 44 – 20 = 24 (304 – 4) – (14 – 4) = 300 – 10 = 290 (94 + 4) – (16 + 4) = 98 – 20 = 78 402; 256 329; 23
FACCIAMO IL PUNTO • ADDIZIONE E SOTTRAZIONE

Ripassa con me!
operazione inversa: sottrazione si può sempre eseguire
termini
ADDIZIONE + 8 + 4 = 12
proprietà
commutativa
8 + 4 = 4 + 8
si usa per fare la prova
somma o totale addendi
12 – 4 = 8 sottraendo resto o differenza minuendo
LE OPERAZIONI
associativa 15 + 5 + 4 = 20 + 4 = 24
nell’insieme dei numeri naturali, si può eseguire se il minuendo è maggiore o uguale al sottraendo
termini
proprietà invariantiva
12 – 4 = (12 – 2) – (4 – 2) = 10 – 2 = 8
IL MIO ATLANTE • RIPASSA CON GEA pagg. 172-173
VERIFICA PIÙ FACILE pag. 265
VERIFICA INTERMEDIA pag. 271
VERIFICA FINALE pagg. 280-281
PROVA NON NOTA pagg. 292-293
SOTTRAZIONE
operazione inversa: addizione si usa per fare la prova
LA MOLTIPLICAZIONE
La moltiplicazione ti serve quando devi aggiungere più volte la stessa quantità.
Leggi il testo, osserva le immagini, poi rispondi e completa.
La libreria “Magie di carta” ha ricevuto 12 scatoloni contenenti 25 libri ciascuno. Quanti libri ha ricevuto in tutto?

• Quale operazione devi usare per calcolare il numero totale di libri? moltiplicazione (×) per aggiungere più volte la stessa quantità addizione (+) per unire o aggiungere sottrazione (–) per calcolare una differenza
Serve : 25 12 = fattori
300 × una moltiplicazione
Ripassa i termini della moltiplicazione
moltiplicando 57 × moltiplicatore 6 = prodotto 342
La moltiplicazione si può sempre eseguire.
Come si comporta lo zero nella moltiplicazione?
52 × 0 = 0 0 × 52 = 0
Lo 0 nella moltiplicazione annulla tutto, infatti il prodotto di qualsiasi numero per 0 è 0
Come si comporta l’1 nella moltiplicazione?
1 × 52 = 52
52 × 1 = 52
L’1 nella moltiplicazione è l’elemento neutro, perché qualsiasi numero moltiplicato per 1 non cambia (il prodotto è uguale al numero stesso).
VIDEO
La moltiplicazione
La tabella della moltiplicazione
MOLTIPLICAZIONI IN RIGA O IN COLONNA?
Per eseguire moltiplicazioni semplici e veloci puoi procedere in riga. Ricordati che la moltiplicazione è un’addizione ripetuta.

Per eseguire una moltiplicazione in colonna segui questi passaggi.
• Moltiplica le unità del moltiplicatore per il moltiplicando: ottieni il 1° prodotto parziale.
2 × 25 = 50
• Scrivi lo 0 al posto delle unità e moltiplica le decine del moltiplicatore per il moltiplicando: ottieni il 2° prodotto parziale. 1 da × 25 = 25 da = 250
• Somma i prodotti parziali (ricorda gli eventuali cambi!): ottieni così il prodotto finale
Se hai dubbi vai a pag. 208 SE SBAGLIO IMPARO! 25 × 12 = 50 25 0 300 1° prodotto parziale 2° prodotto parziale prodotto 1
1
• Se il moltiplicatore ha tre cifre, prosegui moltiplicando le centinaia del moltiplicatore per il moltiplicando e aggiungendo due 0: otterrai il 3° prodotto parziale da sommare agli altri.
1. Esegui le moltiplicazioni.
7 × 4 = 8 × 7 = 5 × 9 = 15 × 6 = 35 × 2 = 25 × 4 = 12 × 3 = 20 × 10 =
3. Risolvi il problema sul quaderno.
2. Esegui le moltiplicazioni con il moltiplicatore a tre cifre in colonna sul quaderno. 15 × 114 = 52 × 707 = 500 × 201 =
In un parcheggio di 4 piani ci sono 140 posti auto su ogni piano. Quanti posti ci sono in tutto?
LE PROPRIETÀ DELLA MOLTIPLICAZIONE
Proprietà commutativa: se cambi l’ordine dei fattori, il risultato non cambia.
• Osserva e completa: 7 × 8 = 8 × 7 =
Il risultato delle operazioni è lo stesso? sì no
Infatti 7 × 8 = 8 × 7
Quale operazione è più semplice?
PRESENTAZIONE Le proprietà e la prova della moltiplicazione
Ti ricordi? Le proprietà delle operazioni permettono di rendere più semplice e veloce il calcolo a mente e di controllare il risultato
Proprietà associativa: se a due o più numeri sostituisci il loro prodotto, il risultato non cambia.
• Osserva e completa:
4 × 5 × 10 =
4 × (5 × 10) = 4 × (50) =
Il risultato delle operazioni è lo stesso? sì no
Infatti 4 × 5 × 10 = 4 × 50
Quale operazione è più semplice?
MI ESERCITO
1. Calcola a mente applicando la proprietà commutativa quando serve.
2 × 11 =
3 × 42 = 12 × 8 = 8 × 13 = 52 × 2 = 6 × 10 =
2. Calcola a mente applicando la proprietà associativa. 6 × 5 × 2 = 4 × 2 × 11 = 94 × 20 × 5 = 37 × 50 × 2 = 20 × 4 × 2 = 12 × 5 × 2 =
Proprietà distributiva: se scomponi un numero in due o più addendi, moltiplichi ogni addendo per l’altro numero dell’operazione e poi sommi i prodotti, il risultato non cambia.
• Osserva e completa.
8 × 19 =
8 × (10 + 9) = (8 × 10) + (8 × 9) = 80 + 72 =
Il risultato delle operazioni è lo stesso?
sì no
Infatti 152 = 8 × 19 = (8 × 10) + (8 × 9).
Quale operazione è più semplice?
(8 × 10) + (8 × 9)
Quando esegui le moltiplicazioni con il moltiplicatore a più cifre stai applicando la proprietà distributiva.
Calcola i prodotti parziali e il risultato. Osserva il diagramma.

prodotto parziale (132 × 4) prodotto parziale (132 × 20) prodotto parziale (132 × 200) prodotto finale
× 224 = 528
× 200 × 20 + × 4
MI ESERCITO
1. Completa applicando la proprietà distributiva.
9 × 235 = 9 × (200 + + ) = (9 × ) + (9 × ) + (9 × ) = + + =
2. Applica la proprietà distributiva con il diagramma sul quaderno.
9 × 27 = 7 × 15 = 40 × 25 = 45 × 18 =
MOLTIPLICAZIONI:
STRATEGIE DI CALCOLO
Ci sono diverse strategie che puoi usare per calcolare velocemente le moltiplicazioni.
• Se devi moltiplicare un numero per 5, moltiplicalo per 10 e poi dividilo per 2.

• Se devi moltiplicare un numero per 9, moltiplicalo per 10 e poi sottrai il moltiplicando
• Se devi moltiplicare un numero per 11, moltiplicalo per 10 e poi aggiungi il moltiplicando.
• Se devi moltiplicare un numero per 4, moltiplicalo per 2 e poi ancora per 2.
• Se devi moltiplicare un numero per 3, moltiplicalo per 2 e poi aggiungi il moltiplicando
• Un’altra strategia di calcolo è scomporre i fattori
7 × 18 = 126 7 × 9 × 2 = 126 = (7 × 9) × 2 = 63 × 2 = 126
MI ESERCITO
1. Calcola a mente le moltiplicazioni scegliendo la strategia migliore.
Moltiplica e aggiungi
Ecco come eseguire velocemente le moltiplicazioni per 11, 21, 31, 41, 51, 61, 71, 81 e 91
• Se moltiplichi un numero per 11, per esempio 13 × 11, fai così:
Moltiplica il numero per 10.
13 × 10 = 130
Aggiungi al risultato il numero che hai moltiplicato (13).
130 + 13 = 143
• Se moltiplichi un numero per 21, per esempio 32 × 21, fai così:
Moltiplica il numero per 20.
Se togli lo 0 da 20 e poi lo metti al risultato, è più facile!
32 × 20 = 640
Aggiungi al risultato il numero che hai moltiplicato (32).
640 + 32 = 672
Usa il trucco che hai imparato ed esegui queste moltiplicazioni.
moltiplica per
26 × 11 =
52 × 21 =
15 × 31 =
26 × 10 = moltiplica per
52 × 20 = moltiplica per
× =
aggiungi + 26 = aggiungi + = aggiungi + =
CALCOLO FACILE
Moltiplica e sottrai
Puoi moltiplicare velocemente anche per 19, 29, 39, 49, 59, 69, 79, 89 e 99.
• Se moltiplichi un numero per 19, per esempio 16 × 19, fai così:
Moltiplica il numero per 20.
Se togli lo 0 da 20 e poi lo metti al risultato, è più facile!
16 × 20 = 320
Sottrai al risultato il numero che hai moltiplicato (16).
320 – 16 = 304
Usa il trucco che hai imparato ed esegui queste moltiplicazioni.
15 × 19 =
32 × 29 =
moltiplica per 15 × 20 = moltiplica per 32 × =
Quando svolgi una moltiplicazione, chiediti: Il secondo fattore è...
11, 21, 31, 41, ...?
Moltiplica e aggiungi
19, 29, 39, 49, ...?
Moltiplica e sottrai
In coppia, scegliete una moltiplicazione a testa e, a turno, spiegate quale trucco usare per eseguirla.
22 × 29 = 15 × 51 =
sottrai – 15 = sottrai – =
Frecce e colori
Ricorda i passaggi per eseguire una moltiplicazione con questo trucco.

Quanto fa 262 × 327 = ?
Aiutati con i quadretti e incolonna bene i numeri.
Segui le frecce blu ed esegui le moltiplicazioni:
7 × 2 7 × 6 7 × 2
Scrivi i cambi delle moltiplicazioni nei quadretti blu e aggiungili ai risultati. Dopo cancellali con una /.
Inserisci uno zero sotto la prima cifra che hai scritto, cioè il 4.
Poi segui le frecce rosse ed esegui le moltiplicazioni: 2 × 2 2 × 6 2 × 2
Scrivi i cambi delle moltiplicazioni nei quadretti rossi e aggiungili ai risultati. Dopo cancellali con una /.
Adesso inserisci due zeri prima di seguire le frecce viola ed eseguire le moltiplicazioni: 3 × 2 3 × 6 3 × 2
Anche in questo caso, scrivi i cambi delle moltiplicazioni nei quadretti viola e aggiungili ai risultati. Dopo cancellali con una /.
CALCOLO FACILE

1834 + 524 0 + 786 00 85674
Esegui infine l’addizione dei numeri nella parte gialla: otterrai così il risultato della moltiplicazione.
Esegui le moltiplicazioni in colonna con il trucco “frecce e colori”.
Nella prima operazione c’è qualche aiuto!
30 228
132 × 229 = 879 × 218 =
191 622
Ti è stato utile il trucco “frecce e colori” per eseguire le moltiplicazioni senza dimenticare alcun passaggio?
Poco Così così Molto
In coppia, uno o una di voi inventa una moltiplicazione, poi il compagno o la compagna spiega come eseguirla usando il trucco “frecce e colori”.
PROBLEM SOLVING
In una gara di Matematica, ci sono 12 squadre della scuola “Rodari” e ogni squadra è composta da 5 alunni/e. Inoltre ci sono 6 squadre della scuola “Collodi”, ognuna composta da 3 alunni/e. Quanti alunni/e partecipano in tutto alla gara?
Capisco il problema
• Quante scuole partecipano alla gara di Matematica?
• Quante squadre ci sono dalla scuola “Rodari”?
• Da quanti membri è composta una squadra della scuola “Rodari”?
• Quante squadre ci sono dalla scuola “Collodi”?
• Da quanti membri è composta una squadra della scuola “Collodi”?
Rappresento il problema
Numero squadre
Scuola “Rodari” 12
Scuola “Collodi”
Pianifico il percorso di soluzione
Numero alunni/e in ogni squadra

Riordina i passaggi e poi risolvi il problema sul quaderno.
Sommo gli alunni dalla scuola “Rodari” e quelli dalla scuola “Collodi”.
Calcolo quanti alunni provengono dalla scuola “Rodari”
Calcolo quanti alunni provengono dalla scuola “Collodi”.
1. Risolvi un problema simile sul quaderno. Lino ha comprato 8 bustine dell’album dei calciatori e ogni bustina contiene 5 figurine. Ha comprato anche 7 bustine dell’album degli animali e ogni bustina contiene 6 figurine. Quante figurine ha comprato Lino?
LA DIVISIONE • 1
La divisione ti serve quando devi distribuire (ripartizione) o raggruppare (contenenza) una quantità in parti uguali.
Leggi i testi seguenti, osserva le immagini, poi rispondi e completa.
La libraia Caterina decide di sistemare i 300 libri appena arrivati distribuendoli equamente su 5 scaffali. Quanti libri dovrà posizionare su ciascuno scaffale?
• Quale operazione useresti per scoprire il numero di libri per ogni scaffale?
sottrazione (–) per togliere o calcolare una differenza
divisione (:) per distribuire
divisione (:) per raggruppare
Bisogna fare una divisione in parti uguali, cioè : 300 5 =
una ripartizione
La libraia Caterina decide di sistemare i 300 libri appena arrivati: ne mette 60 su ogni scaffale. Quanti scaffali ha utilizzato?
• In questo caso, quale operazione useresti per scoprire il numero di scaffali utilizzati?
sottrazione (–) per togliere o calcolare una differenza
divisione (:) per distribuire
divisione (:) per raggruppare
una divisione per contenenza
Bisogna fare , cioè raggruppare i parti uguali: 300 : 60 =
: 60 5
LA DIVISIONE • 2

SENZA RESTO
dividendo divisore quoto
resto parziale resto
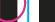
Ripassa i termini della divisione 125 5 10 25 2 5 25 0
CON IL RESTO
Come si comporta lo zero nella divisione?
24 : 0 = impossibile 0 : 24 = 0
È impossibile dividere un numero per 0.
Se lo 0 è al dividendo, invece, il risultato
è 0
Come si comporta l’1 nella divisione?
2 : 2 = 1
Se divido un numero per se stesso, il risultato è sempre 1
300 7 28 42 20 14 6
dividendo divisore quoziente resto
Nell’insieme dei numeri naturali, la divisione si può eseguire solo quando il dividendo è maggiore o uguale al divisore.
MI ESERCITO
2 : 1 = 2
L’1 al divisore lascia il dividendo invariato.
1. Segna con una se per risolvere il problema devi eseguire una divisione per ripartizione (R) o per contenenza (C). Poi svolgi l’operazione.
Martina va in edicola con 42 euro. Quanti pacchetti di figurine da 2 euro l’uno può comprare? C R
42 : 2 = 21
2. Risolvi il problema con la divisione.
Il fioraio ha potato 248 rose e le deve distribuire in 8 vasi per decorare la biblioteca. Quante rose deve mettere in ogni vaso? : dividendo divisore quoto =
31 8
DIVISIONI IN RIGA O IN COLONNA?
Per eseguire delle divisioni semplici puoi procedere in riga. 48 : 6 = 8
Conta quante volte il 6 sta nel 48: ci sta 8 volte, perché 6 × 8 = 48.
• Per eseguire le divisioni in colonna con due cifre al divisore, segui questi passaggi.
• L’1 del divisore nel 2 del dividendo sta 2 volte con il resto di 0 Il 2 del divisore sta 2 volte nell’1 del dividendo? No.
• Prova una volta di meno: l’1 del divisore sta 1 volta nel 2 del dividendo con il resto di 1
Scrivi un piccolo 1 accanto all’1 del dividendo e leggi il numero che si è formato: 11. Il 2 del divisore sta 1 volta nell’11? Sì. Scrivi 1 al risultato.
• Calcola il resto: 1 × 12 = 12, 21 – 12 = 9. Il resto è 9, abbassa il 6 del dividendo e prosegui.
• Dividi le decine 21 : 12.
• Usa la tabellina del 12 per scoprire quante volte 12 è contenuto in 21: 1 volta con il resto di 9. Infatti: 1 × 12 = 12 e 21 – 12 = 9.
Scrivi il resto di 9 sotto al 21
• Trascrivi il 6 delle unità accanto alle 9 decine e dividi le unità 96 : 12
• Usa la tabellina per vedere quante volte 12 è contenuto in 96: sono 8 volte.
• Calcola il resto: 8 × 12 = 96, 96 – 96 = 0 Il resto è 0
1. Esegui le divisioni in riga o in colonna sul quaderno.
4 750 : 12 =
8 289 : 15 =
2 500 : 50 =
1 102 : 19 =
9 984 : 32 =
2 444 : 20 =
VIDEO Come si esegue una divisione con due cifre al divisore
LA PROPRIETÀ DELLA DIVISIONE
La divisione ha una sola proprietà che può essere utile per il calcolo veloce.
Proprietà invariantiva: se moltiplichi o dividi per lo stesso numero entrambi i termini dell’operazione, il risultato non cambia.
60 : 15 =
60 : 15 =
: 5: 5
12 : 3 = 60 : 15 = 120 : 30 =
Il risultato delle operazioni è lo stesso?
sì no
In tutte il risultato è
Quale operazione è più semplice?
• Secondo te, si può utilizzare la proprietà invariantiva anche per la moltiplicazione?
sì no
• Osserva e completa, poi controlla se hai risposto correttamente alla domanda precedente.
8 × 4 = 8 × 4 =
: 2: 2
4 × 2 = 8 × 4 = 24 × 12 =
Il risultato delle operazioni è lo stesso?
sì no
Infatti 32 ≠ 8 ≠ 288

1. Calcola applicando la proprietà invariantiva.
120 : 40 =
75 : 25 = 150 : 25 = 54 : 18 =
: 5 =
: 27 =
DIVISIONI: STRATEGIE DI CALCOLO
Ci sono diverse strategie che puoi usare per calcolare velocemente le divisioni.
• Se devi dividere un numero per 4, dividilo per 2 e poi ancora per 2
• Se devi dividere un numero per 5, moltiplicalo per 2 e poi dividilo per 10
• Se devi dividere un numero per 20, dividilo per 2 e poi per 10
• Se devi dividere un numero per 25, moltiplicalo per 4 e poi dividi il risultato per 100
300 : 25 = 12
(300 × 4) : (25 × 4) = 12
1200 : 100 = 12
MI ESERCITO
1. Calcola a mente le moltiplicazioni scegliendo la strategia migliore.
: 5 =
: 20 =
: 4 =
: 20 =
: 5 =
: 25 =
DIVISIONI IN TANTI MODI
Le divisioni a due o più cifre a volte possono sembrare difficili. Ma esistono tanti metodi per renderle più semplici. Te ne presentiamo tre, scegli tu quello che ti è più utile.
Metodo della scomposizione in fattori
Con questo metodo si scompone il divisore in un prodotto di fattori (se possibile) e così si eseguono le divisioni a 1 cifra. Osserva.
2604 : 42 = ? 42 = 6 × 7
2604 : (6 × 7)
2604 : 6 = 434 434 : 7 = 62 quindi 2604 : 42 = 62
Osserva ora un esempio con il resto.
2245 : 28 28 = 4 × 7
2245 : (4 × 7)
2245 : 4 = 561 resto 1
561 : 7 = 80 resto 1
Il quoziente è 80. Il resto in questo metodo si calcola così:


resto della prima divisone + (resto della seconda divisione × il primo fattore)
1 + (1 × 4) = 5
2245 : 28 = 80 resto 5
Metodo delle prove
Con questo metodo è meglio usare una matita perché provi a scrivere il risultato, ma se non va bene provi con un altro più piccolo finché non trovi quello corretto.
Osserva.
847 : 27 = ?
• Considero le prime due cifre e vedo quante volte la prima cifra del divisore è contenuta nella prima cifra del dividendo
847 : 27 il 2 nell’8 è contenuto 4 volte e scrivo 4 (a matita) al risultato
56 1 7 01 8 0 1 2.24 5 4 24 561 05 1 resto prima divisione resto seconda divisione 84 7 27 4
• moltiplico 4 × 27 = 108; è più grande di 84, quindi provo una volta di meno cioè 3 volte, cancello il 4 e scrivo 3
• moltiplico 3 × 27 = fa 81 che è più piccolo di 84 e quindi va bene
• calcolo il resto 84 – 81 = 3, abbasso il 7, ottengo 37
• ora considero il 3 e scrivo 1 al risultato perché la prima cifra del divisore cioè il 2 è contenuta 1 volte nel 3

• moltiplico 1 × 27 = 27 che è più piccolo di 37 quindi va bene
• calcolo il resto
847 : 27 = 31 con il resto di 10
Metodo canadese
Con questo metodo si sottrae il divisore al dividendo tante volte fino a non poterlo più sottrarre. Si contano poi le volte in cui è stata possibile la sottrazione, che corrispondono al risultato della divisione e si scrive il resto se è rimasto qualcosa.
Osserva.
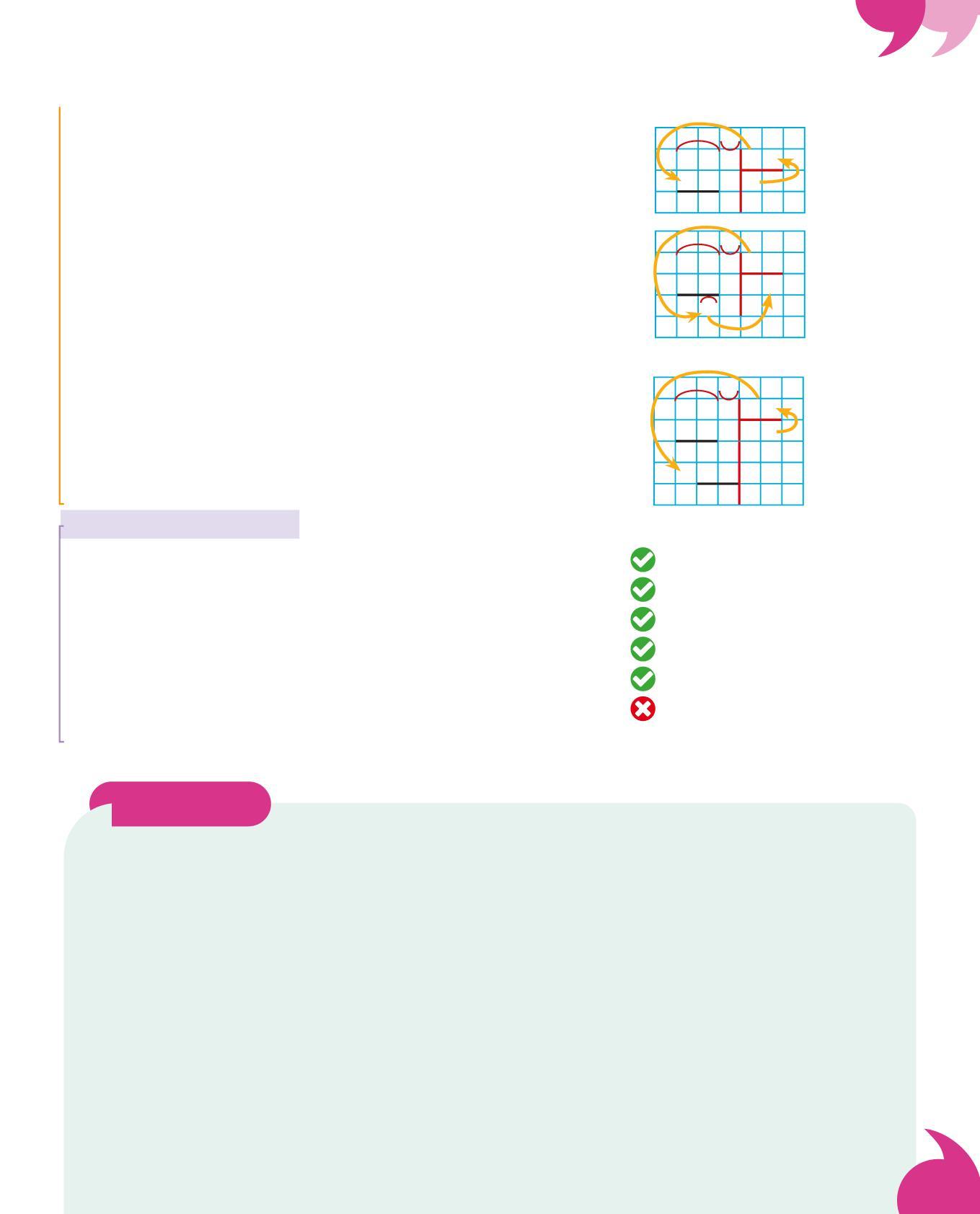
367 : 65 = ?
La sottrazione è stata fatta 5 volte con il resto di 42 quindi
367 : 65 = 5 con il resto di 42
MI ESERCITO
1. Esegui le seguenti divisioni con il metodo più adatto.
756 : 12 = 2576 : 56 =
84 7 27 81 3 //3 7 3 × 27 × 84 7 27 81 3 1 // 3 7 84 7 27
3 1 3 7 27 10 1 × 27 × –
– 65 =
: 18 = 2040 : 24 = 1344 : 24 =
: 72 = 4984 : 56 = 2415 : 35 =
: 25 = 556 : 25 = 465 : 15 =
r.6
: 27 = 6543 : 35 =
r.33
: 12 =
: 58 =
589 : 96 =
: 14 =
: 72 =
: 44 =
:
=
:
= 786 : 98 = 592 : 16 =
=
× E : 10, 100, 1 000
Moltiplicare e dividere per 10, 100, 1000 è facile.
• Osserva la tabella: se moltiplichi per 10, 100 o 1000 sposta ogni cifra a sinistra di una, due o tre posizioni, poi aggiungi a destra uno, due o tre 0 per completare la riga.
hk dak uk h da u 61
61 0 × 10 (aggiungi uno 0)
61 00 × 100 (aggiungi due 0)
61 000 × 1000 (aggiungi tre 0)
Per moltiplicare per 10, 100, 1000 aggiungi 1, 2 o 3 zeri al moltiplicando.
• Osserva la tabella: se dividi per 10, 100 o 1000 sposta ogni cifra a destra di una, due o tre posizioni togliendo uno, due o tre 0
hk dak uk h da u
230000
23000 : 10 (togli uno 0)
2300 : 100 (togli due 0)
230 : 1000 (togli tre 0)
Per dividere per 10, 100, 1000 togli 1, 2 o 3 zeri al dividendo.
MI ESERCITO
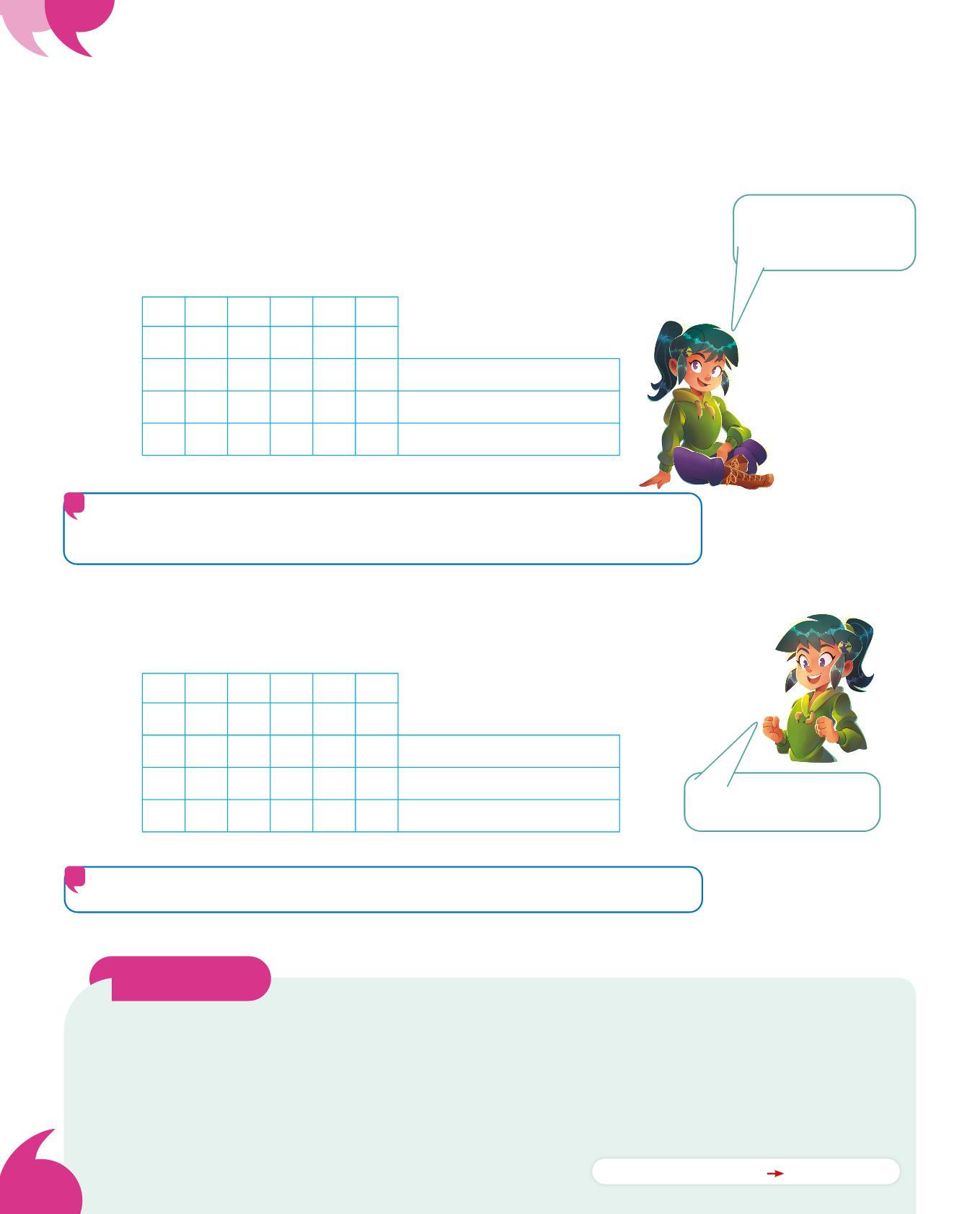
Come vedi, le cifre non cambiano, ma cambia il loro valore posizionale.
Allo stesso modo funziona anche per la divisione!
1. Risolvi le seguenti operazioni. Puoi aiutarti facendo le tabelle sul quaderno.
24 × 10 = 905 × 100 = 14 × 1 000 = 910 : 10 = 3 700 : 100 = 106 000 : 1 000 = Attività nel quaderno pagg. 209, 211
LA PROVA DI MOLTIPLICAZIONE E DIVISIONE
Per fare la prova della moltiplicazione puoi usare la proprietà commutativa Scambia l’ordine dei fattori: se le operazioni sono corrette, otterrai lo stesso risultato.

• Ti viene in mente un altro modo per verificare il risultato di questa moltiplicazione? Confrontatevi in classe.
Per fare la prova della divisione puoi usare la sua operazione inversa, cioè la moltiplicazione. Moltiplica il quoziente per il divisore: se le operazioni sono corrette, otterrai il dividendo.
Dopo aver eseguito la moltiplicazione, ricordati di aggiungere il resto (quando c’è)!
• Ti viene in mente un altro modo per verificare il risultato di questa divisione? Confrontatevi in classe.
MI ESERCITO
1. Esegui le operazioni in colonna e con la prova sul quaderno.
1. Esegui le operazioni in colonna e con la prova sul quaderno.
a. 57 × 12 = 64 × 83 =
2.Cancella con una il risultato sbagliato. 35 × 0 = 35

3. Calcola applicando la proprietà distributiva.
17 × 8 =
34 × 5 =
(10 + 7) × 8 = (10 × 8) + (7 × 8) = 80 + 56 = 136
(30 + 4) × 5 = (30 × 5) + (4 × 5) = 150 + 20 = 170
4.Segna con una le due proprietà che sono state applicate.
25 × 9 × 4 = 25 × 4 × 9 = (25 × 4) × 9 = 100 × 9 = 900 commutativa e invariantiva commutativa e associativa
5. Calcola applicando la proprietà invariantiva. Scegli quale operatore usare, come nell’esempio. : 4 × 5 : 5 × 2 : 7
150 : 25 = (150 : 5) : (25 : 5) = 30 : 5 = 6
120 : 24 =
770 : 70 =
(120 : 4) : (24 : 4) = 30 : 6 = 5 (770 : 7) : (70 : 7) = 110 : 10 = 11
: 2 = 130 : 5 =
(90 × 5) : (2 × 5) = 450 : 10 = 45 (130 × 2) : (5 × 2) = 260 : 10 = 26
6. Usa le strategie per calcolare velocemente.
64 × 4 =
26 × 3 = 12 × 9 = 48 × 5 = 63 × 11 =
7. Risolvi il problema sul quaderno.
: 4 =
: 5 =
: 20 =
: 25 =
In una fattoria sono state riempite 187 confezioni con 6 uova ciascuna e 68 confezioni con 12 uova ciascuna. Quante sono le uova in tutto?

8. Completa le tabelle, come nell’esempio.
: 10 =
: 100 =
:
MULTIPLI, DIVISORI E NUMERI PRIMI
I multipli di un numero si ottengono moltiplicando quel numero per qualsiasi altro numero. I multipli di un numero sono infiniti.
• Completa la tabella con i primi multipli di 3.

I divisori di un numero lo dividono esattamente, senza resto. Ogni numero ha una quantità limitata di divisori.
• Segna con una tutti i divisori di 20, come nell’esempio.
Un numero primo è un numero che può essere diviso (senza resto) solo per 1 e per se stesso. Il numero 1 non è un numero primo.
• Colora tutti i numeri primi fino a 100. Segui l’esempio.
Ogni numero è multiplo e divisore di se stesso. Il numero 1 è divisore di tutti i numeri. Lo 0 è multiplo di tutti i numeri.
GEOGEBRA Multipli e divisori di un numero
PROBLEM SOLVING
Leggo il problema
Giulia ha 48 ciliegie e 12 pesche che vuole dividere equamente tra i suoi 6 cugini. Quante ciliegie riceverà ciascun cugino? Quante pesche? Quanti frutti in tutto?
Capisco il problema
• Quante sono le ciliegie?
• Quante le pesche?
• Quanti sono i cugini?
• Che cosa deve fare Giulia? Prima deve e poi deve
dividere sia le ciliegie sia le pesche per i sei cugini sommare i frutti di ciascun cugino.
Rappresento il problema

Pianifico il percorso di soluzione
Riordina i passaggi e poi risolvi il problema sul quaderno.
Divido il numero delle ciliegie per il numero dei cugini.
Calcolo quanti sono i frutti in totale per ogni cugino.
Divido il numero delle pesche per il numero dei cugini.
1. Risolvi questi problemi sul quaderno.
a. Una giardiniera ha piantato 368 piantine di viole. In ogni striscia sul terreno ha collocato 16 piantine. Quante strisce di viole ha piantato?
b. Luigi sta preparando dei cestini da regalare alle sue 5 zie. Ha comprato 10 sacchettini di sali da bagno, 15 candele e 20 cioccolatini. Quanti oggetti di ogni tipo metterà in ogni cestino?
2, 3, 4
Cugini
FACCIAMO IL PUNTO • MOLTIPLICAZIONE

si può sempre eseguire
operazione inversa: divisione
Ripassa con me!
5 × 9 = 45
× prodotto
MOLTIPLICAZIONE
commutativa
5 × 9 = 9 × 5
termini proprietà
si usa per fare la prova moltiplicando fattori moltiplicatore
associativa
5 × 3 × 3 = 5 × 9
distributiva
5 × 9 = 5 × (4 + 5) = 5 × 4 + 5 × 5
LE OPERAZIONI
45 : 9 = 5
quoto o quoziente dividendo divisore
invariantiva
45 : 9 = (45 : 3) : (9 : 3) = 15 : 3
IL MIO ATLANTE • RIPASSA CON GEA pagg. 172-173
VERIFICA PIÙ FACILE pag. 265
VERIFICA INTERMEDIA pag. 271
VERIFICA FINALE pagg. 280-281
PROVA NON NOTA pagg. 292-293
termini proprietà
nell’insieme dei numeri naturali si può eseguire se il dividendo è maggiore o uguale al divisore
DIVISIONE :
operazione inversa: moltiplicazione
si usa per fare la prova
GIOCO Le quattro operazioni

Frazioni e numeri decimali
Che numeri al saggio di canto!
All’Accademia dei Talenti va in scena il saggio di canto! L’insegnante di musica Candori è molto preoccupata. – Per l’ansia ho divorato 3 4 delle merendine del distributore automatico della scuola! – dice. Così adesso oltre all’ansia ha pure il mal di pancia.
Ma perché tutta questa agitazione? Il motivo è il Preside Melchiorri: ha deciso all’ultimo minuto che il numero di Canto in coro sarà il primo del saggio.
La maestra Candori era convinta che sarebbe stato l’ultimo! Quindi è agitata, anche se nei giorni precedenti il coro ha raddoppiato le ore delle prove e tutti si sentono pronti a cantare i bbli

LETTURA ESPRESSIVA

Tutti, a parte la maestra Candori. È corsa a bere un litro di camomilla in aula insegnanti per calmarsi, ma proprio in quel momento il coro è stato chiamato sul palco!
Quando la maestra torna nell’Aula Magna dell’Accademia e vede il coro sul palco, si accorge di una cosa strana.
– Mancano 2 3 delle bambine e dei bambini! Dove sono tutti?
– Non ci stiamo! Il palco è piccolo! – spiega Francesca. Incredibile! Il precisissimo Preside Melchiorri ha calcolato male le misure del palco!
Allora la maestra Candori ha un lampo di genio: il suo talento è avere sempre buone idee.
– Facciamo così! – dice – 1 3 del coro resterà sul palco, 1 3 del coro andrà in fondo all’Aula Magna e 1 3 del coro si metterà
proprio al centro della sala, nel corridoio in mezzo alle sedie del pubblico. Canteremo in tutta l’Aula Magna! Il coro risponde – Ok, maestra! Tutti vanno ai loro posti, parte la musica e… l’esibizione è perfetta! Il pubblico applaude entusiasta. E nella foto di fine saggio la maestra Candori ha un gran sorrisone.
Per dividere una quantità, le frazioni sono di grande utilità! Scrivi le frazioni corrispondenti alle parti colorate.
di Valeria Razzini
LE FRAZIONI
Tutti i giorni hai a che fare con le frazioni. Pensa a quando parli di metà, un terzo, un quarto… di qualcosa: sono tutte parole che indicano una frazione.
Sono le 6 e un quarto.

Ho mangiato un quinto di anguria.
Frazionare significa dividere un intero in parti uguali o equiestese, cioè che hanno la stessa estensione, la stessa grandezza.
• Dividi questa barretta in 2 parti uguali. Poi colora una parte.
Hai colorato 1 2 di barretta.
• Questi bottoni sono stati divisi in tre parti uguali. Ogni parte corrisponde a un terzo. Osserva.
1 3 1 3 1 3
1. Quale frase corrisponde alla divisione dell’intero rappresentata?
Tre parti su cinque, o tre quinti.
Due parti su cinque, o due quinti.
Audio, video, oggetti digitali dell’unità
Frazioni e numeri decimali

I TERMINI DELLA FRAZIONE
Numeratore: indica quante parti dell’intero vengono prese in considerazione.
Denominatore: indica in quante parti equiestese è stato diviso l’intero. Si legge due terzi.
2
3
Linea di frazione: indica che è avvenuta una divisione.
Per leggere in modo corretto una frazione si usano:
– i numeri cardinali per il numeratore (uno, due, tre, ...);
– i numeri ordinali per il denominatore (terzo, quarto, quinto, ...).
Il numero 1 al denominatore si legge “interi”, il numero 2 si legge “mezzi”.
5 1 si legge “cinque interi”
3 2 si legge “tre mezzi”
2 5 si legge “due quinti”
MI ESERCITO
1. Scrivi in cifre e a parole la frazione corrispondente alla parte colorata di ogni figura.
5 8 Cinque ottavi Quattro quinti 4 5
2.Colora le parti indicate dalla frazione.
L’UNITÀ FRAZIONARIA
• Osserva queste frazioni e rispondi.

• Che cos’hanno in comune?
Hanno tutte il numero al numeratore. Rappresentano, cioè, delle parti in cui è diviso l’
Ogni singola parte in cui è diviso un intero si chiama unità frazionaria. È una frazione che ha sempre 1 al numeratore
L’intero di una frazione può essere diverse cose: un segmento, una figura, un oggetto o un gruppo (per esempio di oggetti, persone o animali).
Prendiamo 10 coccinelle e dividiamo l’intero in parti uguali. Osserva e completa.
Questo gruppo di 10 coccinelle è stato suddiviso in parti uguali. L’unità frazionaria che rappresenta ogni singola parte è 1
MI ESERCITO
1. Osserva la figura e completa.
2.Colora l’unità frazionaria indicata.
L’intero è stato diviso in parti uguali.
Ogni parte è dell’intero.
Frazioni e numeri decimali

FRAZIONI COMPLEMENTARI
La figura intera accanto è stata divisa in 2 parti uguali e di queste ne è stata colorata solo 1
Per completare l’intero manca 1 parte su 2, cioè 1 2 Infatti, 1 2 +
= 1 1 2 + 1 2 , quindi, formano l’intero.
Due frazioni sono complementari quando insieme formano l’intero
• Osserva e completa.
La parte che manca per completare l’intero è quella bianca.
Per completare l’intero mancano parti su 3, cioè 1 3 + = = 1
MI ESERCITO
Per completare l’intero mancano parti su 4, cioè
+ 3
= = 1
1. Osserva il disegno, scrivi la frazione complementare e completa la somma.
+
= =
2. Colora la parte indicata dalla frazione, scrivi la frazione complementare ed esegui la somma.
+ = =
+ = = 1
FRAZIONI EQUIVALENTI
Alcune frazioni che sembrano diverse in realtà hanno lo stesso valore, cioè rappresentano la stessa quantità. Osserva.
Le frazioni equivalenti rappresentano la stessa quantità
La linea di frazione rappresenta una divisione, quindi puoi applicare la proprietà invariantiva per ottenere frazioni equivalenti: moltiplica o dividi sia il numeratore sia il denominatore per uno stesso numero.
MI ESERCITO
1. Osserva le frazioni e completa con la frazione equivalente.
2. Scrivi una frazione equivalente a quella data.
FRAZIONI PROPRIE E IMPROPRIE
Anita e Alessandro preparano due torte al cioccolato usando due ricette diverse.
• Osserva e rispondi.
Nella torta di Anita ci sono 2 5 di una tavoletta di cioccolato.
Anita ha usato l’intera tavoletta di cioccolato? sì no

Le frazioni proprie rappresentano una parte minore dell’intero. Il numeratore è minore del denominatore.
Nella torta di Alessandro ci sono 7 5 di una tavoletta di cioccolato.
Quante tavolette intere ha usato Alessandro?
Quanti pezzi della seconda tavoletta ha usato?
La frazione 7 5 è maggiore dell’intero.
Le frazioni improprie rappresentano una quantità maggiore dell’intero. Il numeratore è maggiore del denominatore.
MI ESERCITO
1. Indica la frazione corrispondente a ogni figura. Poi scrivi se è propria o impropria.
FRAZIONI APPARENTI
Anita e Alessandro confrontano le ricette che hanno seguito per fare le torte al cioccolato e concludono che entrambe possono essere migliorate.
• Osserva e rispondi.
Anita decide di utilizzare 5 5 di una tavoletta di cioccolato.
Ha usato l’intera tavoletta di cioccolato? sì no
La frazione 5 5 è uguale a 1 intero.
Alessandro decide di usare 10 5 di una tavoletta di cioccolato.
Quante tavolette ha usato Alessandro?
La frazione 10 5 è uguale a interi.
Le frazioni apparenti corrispondono a uno o più interi
Il numeratore è uguale o un multiplo del denominatore.
MI ESERCITO
1. Indica la frazione apparente rappresentata da ogni figura. Poi scrivi se corrisponde a uno o due interi.

2.Di fianco a ogni frazione scrivi se è propria (P), impropria (I) o apparente (A).
CONFRONTARE LE FRAZIONI
Se confronti due o più frazioni che hanno:
• lo stesso denominatore, è maggiore quella che ha il numeratore maggiore;
• lo stesso numeratore, è maggiore quella che ha il denominatore minore.
• Confronta ogni coppia di frazioni e completa con > o <.
Il muretto delle frazioni
Se sia il numeratore sia il denominatore sono diversi tra loro, usa il muretto delle frazioni.
• Confrontiamo insieme 1 2 e 3 5 .
1. Immagina di colorare le frazioni sul muro.
2. Tieni il righello in verticale e posizionalo in corrispondenza della prima frazione da confrontare, cioè 1 2
3. Osserva: i 3 5 finiscono dopo il righello, quindi 1 2 < 3 5
Se hai dubbi vai a pag. 221
SBAGLIO IMPARO!
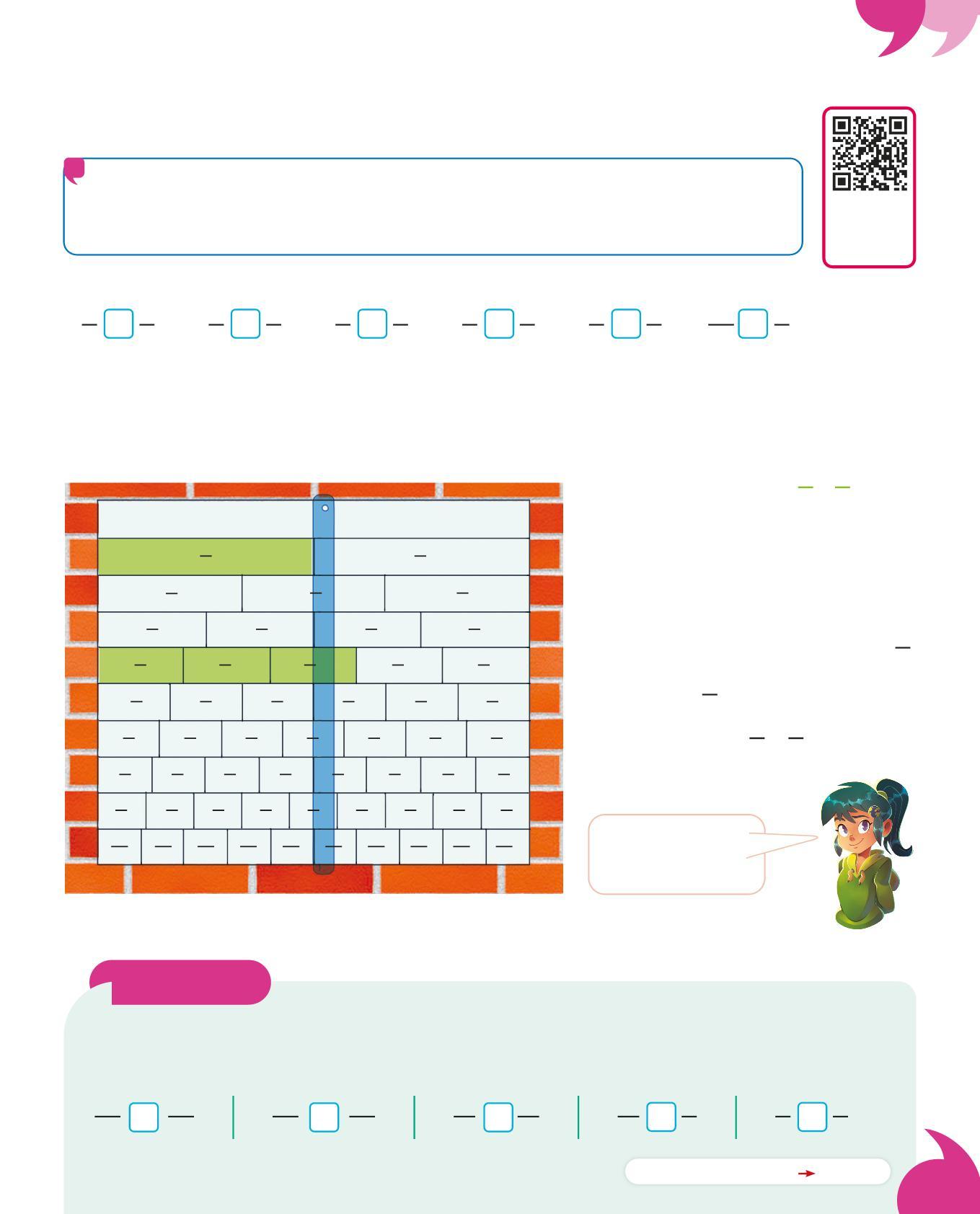
1. Confronta ogni coppia di frazioni e completa con > oppure <. Per aiutarti, puoi colorare le frazioni sul muretto.
DOC Confronto di frazioni
Il muretto delle frazioni
I mattoncini
Per confrontare due frazioni, usa il trucco dei “mattoncini”. Ora completa con >, < o =
FRAZIONI CON LO STESSO DENOMINATORE
Osserva le due frazioni: tutte e due hanno lo stesso denominatore, cioè 8

Disegna due “mattoncini” uguali. Poi dividi ogni mattoncino nelle 8 parti indicate dal denominatore.
Per ogni mattoncino, colora le parti che corrispondono al numeratore. Qual è il mattoncino più colorato?
Il mattoncino più colorato corrisponde alla frazione maggiore, cioè 7 8 .
Usa il trucco dei mattoncini e confronta le frazioni.
Disegna il mattoncino, dividilo in parti, poi colora parti.
Disegna il mattoncino, dividilo in parti, poi colora parti.
CALCOLO FACILE

Osserva le due frazioni: tutte e due hanno lo stesso numeratore, cioè 2
Disegna due “mattoncini” uguali. Poi dividi ogni mattoncino nelle parti indicate dal denominatore. In questo caso, dividi un mattoncino in 3 parti e l’altro in 6 parti
Per ogni mattoncino, colora le parti che corrispondono al numeratore. Qual è il mattoncino più colorato?
Il mattoncino più colorato corrisponde alla frazione maggiore, cioè 2 3
Dunque 2 3 > 2 6 .
Usa il trucco dei mattoncini e confronta le frazioni.
Questo trucco ti è utile per confrontare le frazioni? Sì No
Perché?
In coppia, uno o una di voi inventa due frazioni con lo stesso denominatore, la compagna o il compagno spiega come confrontarle. Poi scambiatevi i ruoli e ripetete l’esercizio inventando due frazioni con lo stesso numeratore. FRAZIONI CON LO STESSO NUMERATORE
LA FRAZIONE DI UN NUMERO
Giada ha aiutato il maestro a organizzare la festa di fine anno. Il maestro, che aveva comprato 88 biglie per i giochi da fare durante la festa, decide di regalargliene i 3 8 . Quante biglie riceverà Giada?
Per capire quante biglie dare a Giada, il maestro ha frazionato le biglie in ottavi.
Osserva: quante biglie ci sono in ogni ottavo?
11
Quale operazione ha fatto il maestro?
8 × 11
88 – 8
88 : 11
88 : 8 11 + 8
Poi il maestro ha raggruppato 3 8 delle biglie.
Quante biglie ha ricevuto Giada?
33
Quale operazione ha fatto il maestro?
addizione (+)
sottrazione (–)
moltiplicazione (×) divisione (:)
Per calcolare i 3 8 di 88 il maestro ha fatto:
88 : 8 = 11 11 × 3 = 33
che può essere scritto anche così:
(88 : 8) × 3 = 33
• Prova tu.

Per calcolare la frazione di un numero devi fare due operazioni:
• dividi il numero per il denominatore della frazione per trovare l’unità frazionaria;
• moltiplica il risultato per il numeratore, cioè per il numero di parti considerate.
Alex ha 20 figurine e ne vuole dare i 2 5 alla sua amica Elena.
Per capire quante figurine dare a Elena, Alex deve calcolare i 2 5 di 20 : 5 = × 2 =
20 4 4 8 8
I 2 5 di 20 corrispondono a figurine.
VIDEO Frazioni in musica
PROBLEM SOLVING

Leggo il problema
Alla festa di compleanno di Marco c’è un vassoio con 24 piccoli panini. Durante la festa, Marco ha mangiato 1 6 dei panini e la sua amica Lucia 1 4 Quanti panini ha mangiato Marco? Quanti Lucia? Quanti sono stati mangiati in totale da Marco e Lucia? Quanti sono rimasti?
Capisco il problema
• Quanti panini ci sono sul vassoio?
• Quanti ne ha mangiati Marco?
Rappresento il problema
• Quanti ne ha mangiati Lucia?
Pianifico il percorso di soluzione
Riordina i passaggi e poi risolvi il problema sul quaderno.
Calcolo i panini rimasti.
Calcolo quanti panini corrispondono a 1 6
Sommo i panini mangiati da Marco e quelli mangiati da Lucia.
Calcolo quanti panini corrispondono a 1 4
1. Risolvi un problema simile sul quaderno.
A cena Alice ha portato una pizza che è stata tagliata in 16 fette uguali.
Alice ha mangiato 1 8 delle fette e Luca 1 4 . Quante fette ha mangiato Alice? Quante fette Luca? Quante fette hanno mangiato in totale? Quante fette sono rimaste?
2, 4, 6, 10
LUCIA
LE FRAZIONI DECIMALI
Alcune frazioni si chiamano “decimali”; scopri perché.
L’intero è stato diviso in 10 parti uguali. Ogni parte rappresenta un decimo: 1
• Quanti decimi ci sono in un intero?
Questo è l’intero, cioè l’unità: 1
L’intero è stato diviso in 100 parti uguali. Ogni parte rappresenta un centesimo: 1
• Quanti centesimi ci sono in un intero?
Si chiamano frazioni decimali le frazioni che hanno come denominatore 10, 100, 1 000
Le frazioni decimali si possono rappresentare anche con la linea dei numeri. Qui sotto vedi il tratto compreso fra 0 e 1: è stato suddiviso in 10 parti uguali; ogni segmento vale perciò 1 10
• Scrivi al posto giusto sulla linea dei numeri:
L’intero è stato diviso in 1 000 parti uguali. Ogni parte rappresenta un millesimo: 1
• Quanti millesimi ci sono in un intero?
FRAZIONI E NUMERI DECIMALI
Le frazioni decimali si scrivono anche come numeri decimali, cioè i numeri che hanno la virgola, il segno che separa la parte intera da quella decimale
= 0 unità e 1 decimo (cioè la decima parte dell’intero)
= 0 unità, 0 decimi e 1 centesimo (cioè la centesima parte dell’intero)
parte intera , parte decimale decimicentesimimillesimi h da u d c m
, 1
parte intera , parte decimale decimicentesimimillesimi
= 0 unità, 0 decimi, 0 centesimi e 1 millesimo (cioè la millesima parte dell’intero)
intera , parte decimale decimicentesimimillesimi
Per leggere i numeri decimali, leggi prima la parte intera e poi la parte decimale.
5,7 cinque virgola sette 1,84 1 e 84 centesimi
Trasformare frazioni decimali in numeri decimali e viceversa
Per trasformare una frazione decimale in numero decimale, scrivi il numeratore, conta da destra tante cifre quanti sono gli 0 al denominatore e metti la virgola. Se le cifre non bastano, aggiungi 0 alle unità e nelle posizioni rimaste vuote.
Per trasformare un numero decimale in frazione decimale, scrivi al numeratore il numero senza virgola e al denominatore 1 seguito da tanti 0 quante sono le cifre dopo la virgola.
1. Calcola le seguenti frazioni.
2. Calcola le frazioni dei numeri. 3 5 di 25 2 9 di 27 5 6 di 30 3 9 2
(25 : 5) × 3 = 15
(27 : 9) × 2 = 6
(30 : 6) × 5 = 25
3. Trasforma sul quaderno le frazioni decimali in numeri decimali e viceversa. 5
• 19

4. Risolvi i problemi sul quaderno.
a. Dei 150 alunni e alunne delle classi quarte 3 10 vogliono fare nuoto, 1 5 basket, 1 3 calcio e il sesto rimanente ha scelto pallavolo. Quanti iscritti e iscritte ci sono per ogni sport?
45; 30; 50; 25
(120 : 12) × 4 = 40
(48 : 4) × 1 = 12
•
b. Zeno ha un album di figurine di animali. Sull’album c’è posto per 120 figurine in tutto.
Ieri ne ha incollato 1 4 e oggi ne incolla altri 2 3 del totale iniziale. Quante figurine gli mancano ancora?
(65 : 13) x 7 = 35 10
In biblioteca ci sono 360 libri. I 9 10 sono già stati presi in prestito. Quanti sono? 1 10 può ancora essere preso in prestito. Quanti libri sono?
e numeri decimali

CONFRONTARE I NUMERI DECIMALI
I numeri decimali, come i numeri interi e le frazioni, si possono confrontare e ordinare. Per farlo puoi procedere nel modo seguente.
1. Confronta prima la parte intera: è maggiore il numero con la parte intera maggiore.
9,45 > 3,12 > infatti 7 > 3
2. Se la parte intera è uguale, confronta la parte decimale: prima i decimi, poi i centesimi, infine i millesimi.


9,136 9,135 = infatti 6 > 5
Se i due numeri da confrontare hanno un numero diverso di cifre nella parte decimale, puoi pareggiare le cifre aggiungendo degli zero. 12,73 < 12,80
Puoi confrontare due numeri decimali puoi anche aiutarti posizionandoli sulla linea dei numeri. Osserva.
Se hai dubbi vai a pag. 225
MI ESERCITO
1. Scrivi questi numeri decimali in ordine crescente.
2.Completa i confronti con >, <
ADDIZIONI E SOTTRAZIONI CON I DECIMALI
Per eseguire addizioni e sottrazioni con i numeri decimali, devi incolonnare la parte decimale sotto la parte decimale, la parte intera sotto la parte intera e la virgola sotto la virgola, poi calcolare normalmente. Per i cambi ricorda che:
1 u = 10 d 1 d = 10 c 1 c = 10 m
3156,785 + 93,454 =
parte intera parte decimale
uk h da u , d c m

=
4082,64 – 527,237 =
parte intera parte decimale
uk h da u , d c m 4 0 8 2 , 6 4 0 –527,237 = 3555,403
MI ESERCITO
1. Calcola in colonna.
Se un numero ha meno decimali dell’altro, pareggiali aggiungendo tanti zeri quante sono le cifre mancanti.
a. 235,84 + 1466,513 b. 2824,103 – 283,32
2.Risolvi il problema sul quaderno.
Il papà sta preparando i biscotti. Ha usato 2,35 hg di farina per i biscotti al cioccolato e 1,8 hg per quelli allo zenzero. Quanta farina ha utilizzato in tutto?
Attività nel quaderno pagg. 224, 226-227
VIDEO
Addizione e sottrazione con i decimali
× E : 10, 100, 1 000 CON I DECIMALI
Per moltiplicare un numero decimale per 10, 100, 1000, sposta la virgola verso destra di tanti posti quanti sono gli zeri del secondo fattore. Se le cifre non bastano, aggiungi zeri a destra.
2,8 × 10 = 28
7132 1000 = 7132 0,500 × 1000 = 500

• Segui l’esempio e calcola in tabella usando le frecce per evidenziare gli spostamenti.
h da u , d c m
24 , 351
243 , 51
24,351 × 10 =
×
Per dividere un numero decimale per 10, 100, 1000, sposta la virgola verso sinistra di tanti posti quanti sono gli zeri del divisore. Se le cifre non bastano, aggiungi degli zeri a sinistra.
52,2 : 10 = 5,22
0003 : 1000 = 0,003 921,2 : 100 = 9,212
• Segui l’esempio e calcola in tabella usando le frecce per evidenziare gli spostamenti.
h da u , d c m
353 , 9 35 , 39 h da u , d c m 8 , 59 , h da u , d c m 75 , 2 , h da u , d c m
353,9 : 10 =
, , × 10 : 10
, 617 , h da u , d c m
: 1 000
MOLTIPLICAZIONI CON I DECIMALI
Quando esegui una moltiplicazione con i numeri decimali, comportati come se la virgola non ci fosse e calcola rispettando le regole valide per i numeri interi.
Alla fine metti la virgola:
– conta le cifre decimali complessive dei fattori;
– poi conta nel prodotto, a partire da destra, altrettante cifre e scrivi la virgola.
Con un fattore decimale
• Calcola, rispondi e completa.
374 × 21, 2 =
0

• Quante sono le cifre decimali del primo fattore?
• Quante sono le cifre decimali del secondo fattore?
• Le cifre decimali del prodotto devono essere
Con due fattori decimali
• Calcola, rispondi e completa.
7 3 4 8 8 382 3 9 7 2 5 0 0
63, 82 × 46, 9 =
• Quante sono le cifre decimali del primo fattore?
• Quante sono le cifre decimali del secondo fattore?
• Le cifre decimali del prodotto devono essere
1. Esegui le moltiplicazioni in colonna sul quaderno.
× 98 =
× 0,2 =
× 3,5 =
VIDEO La motiplicazione con i numeri decimali
Frazioni e numeri decimali

DIVISIONI CON I DECIMALI
Dividendo decimale
Quando esegui una divisione con il dividendo decimale, calcola come se fosse una normale divisione. Però, quando arrivi all’ultima cifra intera scrivi la virgola nel risultato prima di continuare, per indicare che ora dividi la parte decimale.
• Osserva l’esempio e continua tu.
56,9 : 13 = 4,3 resto 10 d = 1 u
Divisore decimale
Quando esegui una divisione con il divisore decimale (o con entrambi i termini decimali), devi applicare la proprietà invariantiva per rendere intero il divisore.
• Osserva l’esempio e continua tu.
o divisore decimale Se hai dubbi vai a pag. 230 SE SBAGLIO IMPARO! 4 4 1 7 8
3,64 : 2,6 = 95,04 : 0,72 =
× 10× 100× ×100 10
36, 426 1041, 4 0 950472 23013
3,64 : 2,6 = 1,4 resto 95,04 : 0,72 = resto 200,87 : 53 = resto 200, 87 53 56, 9 13 4 9 4, 3 10
MI ESERCITO
1. Esegui le divisioni in colonna sul quaderno. a. 14,4 : 12 = 354,75 : 33 = 2 763,05 : 50 = 768 : 3,2 = b. 1 188 : 2,2 = 9 982 : 4,6 = 46,71 : 2,7 = 926,2 : 2,2 =
1,2 10,75 55,261 240
NUMERI DECIMALI: STRATEGIE DI CALCOLO
Ci sono diverse strategie che puoi usare per calcolare velocemente le moltiplicazioni e le divisioni con i numeri decimali.
• Se devi moltiplicare un numero per 0,5, dividilo per 2

• Se devi moltiplicare un numero per 0,25, dividilo per 4.
• Se devi dividere un numero per 0,5, moltiplicalo per 2
• Se devi dividere un numero per 0,25, moltiplicalo per 4.
MI ESERCITO
1. Calcola a mente le moltiplicazioni scegliendo la
× 0,5 =
=
=
2. Calcola a mente le divisioni scegliendo la strategia migliore.
PROBLEM SOLVING

Leggo il problema
Giacomo è al mercato e vuole comprare delle mele. Il prezzo di una mela è di € 0,50. Giacomo ha € 5 con sé. Quante mele può comprare Giacomo?
Se Giacomo compra 6 mele, quanti euro gli rimangono?
Capisco il problema
• Quanto cosa una mela?
• Quanti soldi ha Giacomo?
€ 0,50 € 5
Rappresento il problema
1 mela 6 mele
€ 0,50 € 0,50 × = €
Pianifico il percorso di soluzione
Riordina i passaggi per risolvere il problema.
3
2
Sottraggo ai 5 euro di Giacomo il costo di 6 mele.
Calcolo il costo di 6 mele.
Calcolo quante mele può comprare Giacomo con 5 euro.
Ora risolvi il problema.
5 : 0,50 = 10
0,50 × 6 = 3
5 – 3 = 2
Se ne compra solo 6, gli restano € 2. 6 3
1 5 6
Con € 5 Giacomo può comprare 10 mele.
1. Risolvi un problema simile sul quaderno.
Giorgio vuole comprare dei pezzi di pizza da asporto.
Una fetta di pizza costa € 3,50. Giorgio ha con sé € 20
Quante fette di pizza può comprare Giorgio con € 20?
Se Giorgio compra 4 fette di pizza, quanti euro gli restano?
MI ESERCITO
1. Esegui le operazioni nelle tabelle.
2. Calcola a mente e scrivi il risultato.
2,4 + 0,3 = 5,23 + 3,16 = 26 × 12,83 = 16,5 × 17,8 = 0,57 + 0,23 = 25,8 – 0,5 = 0,62 × 3,6 =
: 3,2 =
– 29 =
– 7,9 =
: 13 =
: 2,2 =
3. Risolvi i problemi sul quaderno.
a. Una cassetta di pesche pesa 12,85 chilogrammi. La cassetta vuota pesa 0,956 chilogrammi. Quanto pesano le pesche da sole?
11,894 kg
b. Giovanni prepara una torta speciale formata da 1 3 di latte, 1 3 di farina e 1 3 di zucchero. Se il peso totale degli ingredienti è di 600 grammi, quanta farina servirà?
200 g
c. Francesca si sta allenando per la corsa di fine anno su un circuito di 3,6 km. Sapendo che ne ha percorsi i 5 9 , quanto le manca per giungere alla fine del circuito?
d. Margherita, Viola, Rosa e Iris hanno preparato dei lavoretti con materiale di recupero per il mercatino della scuola. Hanno incassato complessivamente € 222,48, che decidono di dividersi in parti uguali. Quanti soldi spettano a ciascuna di loro?
€ 55,62
e. Saad è in vacanza a Parigi con la sua famiglia e vuole portare un portachiavi a forma di Tour Eiffel come ricordo a ciascuno dei suoi 15 compagni e compagne di classe. Ogni portachiavi costa € 1,45. Quanto spenderà in tutto?
Per la gita di fine anno scolastico sono già stati pagati i 2 7 del costo del pullman e restano da pagare ancora € 525. Se i partecipanti sono 50, quanto deve pagare ancora ognuno?
€ 21,75 1,6 km € 10,50
Verso l’Invalsi
FACCIAMO IL PUNTO • FRAZIONI E NUMERI DECIMALI

Ripassa con me!
Indicano la parte di un intero diviso in parti uguali
FRAZIONI
termini tipi di frazioni
Numeratore
Linea di frazione Denominatore
parte intera parte decimale
uk h da u , d c m 1 979,276
FRAZIONI E NUMERI DECIMALI
Sono formati da una parte intera a sinistra e una decimale a destra, separate da una virgola NUMERI DECIMALI
• si ottengono con le frazioni decimali 18 100 = 0,18
• si possono formare frazioni decimali 0,18 = 18 100
• si possono eseguire le 4 operazioni
• si possono rappresentare sulla linea dei numeri
Misure

Talenti a tavola
Conosci anche tu qualcuno che ti dice sempre quanto è importante mangiare sano? All’Accademia dei Talenti ci pensa la cuoca Renata a ricordarlo a tutte e a tutti. Se incontra in corridoio qualcuno che sgranocchia caramelle quando invece sarebbe l’ora di una merenda a base di frutta, Renata lo riprende con un sonoro: – Ehi tu, mangiapasticci!
M i !

Nessuno ha il coraggio di disobbedirle e lei rimprovera persino il Preside se lo vede mangiare patatine
La cuoca dell’Accademia dei Talenti non poteva che essere un talento in cucina
Ha una ricetta infallibile anche per convincere i mangiapasticci a mangiare sano
LETTURA ESPRESSIVA
Ogni venerdì alla mensa dell’Accademia viene servito un menu speciale: il Piatto a colori.
Renata infatti crea delle ricette particolari, tutte con ingredienti dello stesso colore. Due settimane fa ha servito il Menu Viola, con tortino croccante di melanzane e budino di uva e more. Mentre venerdì scorso il Menu Verde, con pasta alle zucchine superfilanti e semifreddo al pistacchio, ha fatto il record di bis!
– E questa settimana che colore mangiamo? – chiede Luca.
Renata ha in programma il Menu Giallo, ma per prepararlo deve superare un ultimo ostacolo: la sbadataggine del suo aiuto cuoco Aristide. Aristide è bravissimo a cucinare, ma è un gran smemorato e non riesce a leggere le ricette di Renata perché non vuole indossare gli occhiali.
– Renata, quanta farina ci vuole per lo sformato di patate? 300 g o 3 hg?
– Non mi ricordo più quanto latte devo mettere nel budino di ananas… 1 o 1000 m ?
Queste sono alcune delle domande che Aristide fa spesso. Non sa proprio che cosa siano le misure equivalenti, e per questo rischia spesso di combinare qualche guaio… Meno male che Renata è sempre molto attenta!

Completa la frase con le parole UNITÀ DI MISURA • VALORE
Due quantità sono equivalenti tra loro quando sono espresse con diverse ma hanno lo stesso


In cucina serve pazienza, ma h f u ’ i l !
anche sa un’equiv
di Valeria Razzini
AUDIO, VIDEO, OGGETTI DIGITALI DELL’UNITÀ.
LE MISURE DI LUNGHEZZA
Le misure di lunghezza ci permettono di misurare lunghezze, larghezze, altezze, distanze, profondità.
L’unità di misura fondamentale della lunghezza è il metro. Il simbolo del metro è m

Equivalenze con le misure di lunghezza
Ogni misura di lunghezza può essere espressa con una marca diversa che deve seguire il valore numerico e non deve avere punti. La marca si riferisce sempre alla cifra delle unità.
Quando fai un’equivalenza per passare da un’unità di misura maggiore a una minore devi moltiplicare per 10, 100, 1000
Quando fai un’equivalenza per passare da un’unità di misura minore a una maggiore devi dividere per 10, 100, 1000
kmhmdam m dmcmmm × 10× 10× 10× 10× 10× 10 kmhmdam m dmcmmm : 10: 10: 10: 10: 10: 10
1. Osserva la marca, che corrisponde alla cifra in rosso, e scrivi il valore di ogni cifra.
12,5 m =
78,4 dam =
25,13 dm =
1,759 km =
7 hm, 8 dam, 4 m 2 m, 5 dm, 1 cm, 3 mm 1 km, 7 hm, 5 dam, 9 m 1 dam, 2 m, 5 dm
2.Componi le misure, come nell’esempio.
1 m, 8 dm = 1,8 m
3 m, 6 dm = m
5 dam, 7 m = dam
9 hm, 5 dam = hm
6 km, 3 m = km
VIDEO
Scopriamo la misura
Misure ed equivalenze PRESENTAZIONE La storia della misura
QUANTO È ALTA UNA PIRAMIDE?
Talete per molti è considerato il primo matematico della storia.
Divenne molto famoso quando provò a misurare l’altezza delle piramidi di Giza.
Visto che non esistevano particolari tecnologie e nemmeno metri così
lunghi, decise di usare la geometria, insieme al Sole e a un bastone. Provò prima con un obelisco.

Per trovare l’altezza dell’obelisco fece riferimento alla similitudine tra due triangoli rettangoli.
Vale dunque l’uguaglianza
E così fece anche per le piramidi
Altezza obelisco
Ombra obelisco = Altezza bastone
Ombra bastone
Altezza piramide = Altezza bastone
Ombra bastone × ombra piramide
Prova a misurare la tua altezza con la formula di Talete, usando il suo procedimento. E scrivi il risultato qui sotto.
Piramide
Bastone
Obelisco
LE MISURE DI CAPACITÀ
Le misure di capacità permettono di misurare la quantità di liquido contenuta in un recipiente o che un recipiente può contenere.
L’unità di misura della capacità è il litro e il suo simbolo è

Equivalenze con le misure di capacità
Ogni misura di capacità può essere espressa con una marca diversa che deve seguire il valore numerico e non deve avere punti. La marca si riferisce sempre alla cifra delle unità.
Quando fai un’equivalenza per passare da un’unità di misura maggiore a una minore devi moltiplicare per 10, 100, 1000
Quando fai un’equivalenza per passare da un’unità di misura minore a una maggiore devi dividere per 10, 100, 1000
MI ESERCITO
1. Completa la tabella, come nell’esempio, poi leggi il valore di ogni cifra.
numero h dal d c ml
875 l 8 7 5
28,7 l
734,6 dl
2 835 ml
5,729 hl
: 10: 10: 10: 10: 10
2.In ogni misura cerchia la cifra che si riferisce alla marca.

3 da • 17 • 19,4 d • 25 c • 874 m • 0,05 da • dl

3. Esegui le equivalenze.
a. 0,5 = dl
7,28 h = dal
34,25 d = cl
34,7 c = l
24,3 = dal 79 da = hl
92,8 c = m b. 1214 = hl
LE MISURE DI MASSA
Le misure di massa ci permettono di misurare la quantità di materia dei corpi. Solitamente, però, diciamo che esse ci permettono di misurare il peso.
L’unità di misura fondamentale della massa è il chilogrammo e il suo simbolo è kg
Le misure di massa seguono le regole delle misure di capacità e lunghezza quando le leggi, le scrivi e fai equivalenze.
Per misurare il peso di oggetti molto leggeri, si usano i sottomultipli del grammo.
MI ESERCITO
1. Confronta le misure e completa le relazioni con >, < o =.
Saltelli qua e là
Impara a fare le equivalenze con il trucco “saltelli qua e là”.
In una equivalenza, quando passi da una unità di misura più grande a una più piccola, spostati verso destra e moltiplica
77 hm = dm?
Passo 1 Scrivi il numero di partenza, cioè 77, nel riquadro dell’ettometro (hm).
Passo 2 Per arrivare al decimetro (dm) ti sposti verso destra di 3 posizioni, quindi moltiplichi per 1000. Ottieni il risultato: 77000.
km hm dam m dm cm mm
77
77 000 × 10 × 10 × 10 × 10 × 10 × 10
B
In una equivalenza, quando passi da una unità di misura più piccola a una più grande, spostati verso sinistra e dividi
230 mm = dm?
Passo 1 Scrivi il numero di partenza, cioè 230, nel riquadro dei millimetri (mm).
Passo 2 Per arrivare al decimetro (dm), ti sposti verso sinistra di 2 posizioni, quindi dividi per 100. Ottieni il risultato: 2,3.
: 10 : 10 : 10 : 10 : 10 : 10
CALCOLO FACILE

Ora svolgi tu le equivalenze. Aiutati con le tabelle e le frecce. Ricorda:
hg dag
6,4 g = ............ mg? 785 cg = g?
cg
× 10 × 10 × 10 × 10 × 10 × 10
: 10 : 10 : 10 : 10 : 10 : 10
Rifletti: puoi usare questo trucco anche per le misure di capacità?
Sì, perché
No, perché
mi basta sostituire la tabella di partenza con quella delle misure di capacità.
In coppia, eseguite queste equivalenze con le misure di capacità utilizzando il trucco “saltelli qua e là”. Aiutatevi con la tabella.
45 da = hl 3 = ml
PROBLEM SOLVING
Leggo il problema
Laura e Ahmed partecipano a una gara di corsa. La pista è lunga 400 m.
Se Laura corre 5 volte intorno alla pista e Ahmed 3 volte, per quanti metri corre Laura? Per quanti metri corre Ahmed? Quanti decametri in più corre
Laura rispetto ad Ahmed?
Capisco il problema
• Quanto è lunga la pista?
• Quanti giri fa Laura?

m
Rappresento il problema
lunghezza pista giri di Laura
metri percorsi da Laura
• Quanti Ahmed?
lunghezza pista giri di Ahmed
metri percorsi da Ahmed
differenza metri
Pianifico il percorso di soluzione
Riordina i passaggi e poi risolvi il problema sul quaderno.
Calcolo quanti metri corre Laura.
Calcolo quanti metri in più corre Laura.
Trasformo i metri in decametri.
Calcolo quanti metri corre Ahmed.
1. Risolvi un problema simile sul quaderno.
La classe di Carlo decide di piantare alcune piante nel giardino scolastico. Per crescere ogni pianta ha bisogno di 1,5 l d’acqua al giorno. Se la classe ha piantato 8 piante, quanti litri d’acqua sono necessari ogni giorno per tutte le piante? Se la classe dispone di un contenitore d’acqua da 240 dl, per quanti giorni potrà annaffiare le piante?
12 l, 2 giorni
MI ESERCITO
1. Scrivi la misura che corrisponde a ogni cartellino. Segui l’esempio.

2.Confronta le cifre in rosso e completa le relazioni con > o <.
5,24 m 1,16 m 35,17 hg 35,5 hg
3. Osserva le marche e riscrivi le misure di capacità in ordine crescente.
4.Per ogni misura data, colora con la stessa tinta le tre misure equivalenti.

5. Completa.
• Un chilometro (km) equivale a metri (m).
• Un ettolitro (h ) equivale a litri ( ).
• Un chilogrammo (kg) equivale a ettogrammi ( ).
• Un metro (m) è cento volte più grande di un ( ).
• Un decametro ( ) è volte più piccolo di un chilometro (km).
6. Completa con le misure equivalenti a quelle date.
PESO LORDO, NETTO, TARA
Molti dei prodotti che acquistiamo sono confezionati ed è molto importante saper distinguere tra peso lordo, peso netto e tara
• Osserva gli schemi e completa.

Il peso del prodotto + il peso della confezione si chiama LORDO
PESO NETTO TARA
PESO LORDO
• Prova tu.
Il peso del solo prodotto si chiama NETTO
PESO LORDO
TARA
PESO NETTO
Il peso della sola confezione si chiama TARA
PESO NETTO PESO LORDO
PESO NETTO
PESO LORDO PESO LORDO
PESO NETTO TARA TARA TARA
PESO NETTO TARA
MI ESERCITO
1. Risolvi i problemi sul quaderno.
PESO LORDO
a. Un pacco di biscotti pesa 540 g. Se la confezione, cioè la tara, pesa 25 g, quanto pesano i biscotti?
515 g
b. Una bustina di tè pesa 20 dg. In una scatola, che vuota pesa 3,5 g, ci sono 20 bustine. Quanti grammi pesa la confezione?
43,5 g
PRESENTAZIONE
Peso lordo, netto, tara
Educazione Finanziaria
LE MISURE DI VALORE
Il denaro è ciò che permette di misurare il valore delle merci
La moneta usata in Italia e in buona parte dell’Europa è l’euro, il cui simbolo è €

2
Leggere gli euro
L’euro e i suoi multipli seguono il sistema in base 10, mentre i sottomultipli sono espressi in centesimi: euro cent o centesimi di euro. Quando i prezzi sono espressi con i numeri decimali, vanno sempre indicati anche i centesimi, dunque i numeri vengono scritti con due cifre dopo la virgola
Anche per leggere le cifre decimali si usano i centesimi e non i decimi. Per esempio, se scrivi € 15,10 devi leggere 15 euro e 10 centesimi (cent).
MI ESERCITO
1. Colora solo le scritture corrette. 2.Completa la tabella. mercebanconotaresto
6,60
0,80 5 euro 3,00 €
7,5
2,90 10 euro
COSTO UNITARIO E COSTO TOTALE
Il costo unitario è il costo di un singolo oggetto; il costo totale è il costo complessivo di tutti gli oggetti.
• Osserva e completa.

COSTO TOTALE
COSTO UNITARIO :
COSTO UNITARIO
COSTO TOTALE :
QUANTITÀ QUANTITÀ
COSTO TOTALE QUANTITÀ COSTO UNITARIO
Quanto costa 1 bottiglia di olio?
Per rispondere, dobbiamo distinguere tra costo totale e costo unitario.
• Il costo totale è il costo complessivo di tutti gli oggetti € 45,00
• Il costo unitario è il costo di un singolo oggetto (costo di 1 bottiglia)
• Dobbiamo poi considerare il numero degli oggetti 6 bottiglie di olio
Conoscendo due tra questi valori, è sempre possibile calcolare il terzo. Nel nostro caso, per trovare il costo unitario dividiamo il costo totale per il numero degli oggetti.
€ 45,00 : 6 = € 7,50
1. Calcola e completa.
1 matita: € 0,70 10 matite: €
1 penna biro: € 1,20 10 penne biro: €
1 gomma: € 1,50 10 gomme: €
1 pennarello: € 2,40 10 pennarelli: € 1 album: € 6,90 10 album: €
Vorrei una bottiglia di olio, per favore.
Quanto costano 2 bottiglie di olio? = €
7,50 × 2 15
2. Risolvi i problemi sul quaderno.
7 12 € 14 € 16 15 24 69
a. Una libraia ha 8 copie di un nuovo libro. Se venderà tutte le copie ricaverà 112 euro. Quanto costa una copia di quel libro?
b. Il papà compera un gelato da € 3,20 a tutta la famiglia, composta da 5 persone. Qual è il prezzo che leggerà sullo scontrino?
Attività nel quaderno pag. 237
Sono .................. euro.
Educazione Finanziaria
IL COMMERCIO
Osserva come funziona il commercio.
Ho acquistato queste scarpe a 52 euro al paio.
Le rivendo a 72 euro al paio. Guadagno 20 euro al paio.
La spesa è la quantità di denaro pagata dal o dalla negoziante per comprare la merce da rivendere.
Il ricavo è la quantità di denaro che la o il negoziante incassa quando rivende la merce al o alla cliente.
Il guadagno è la quantità di denaro che la o il negoziante ottiene: è ciò che resta del ricavo una volta tolta la spesa.
Potrebbe capitare che la spesa sia maggiore del ricavo.
In questo caso, invece del guadagno si avrà una perdita: spesa – ricavo = perdita.
Calcola e completa.
LE MISURE DI TEMPO
Anche il tempo è una grandezza che si può misurare.
L’unità di misura fondamentale del tempo è il secondo e il suo simbolo è s
L’unità di misura di tempo non segue il sistema in base 10
Quando indichiamo una durata, scriviamo dopo ogni numero la sua marca. 1 h 10 min 5 s
Per indicare un orario, di solito si omettono i secondi e si separano ore e minuti con i due punti. 13:25
Per indicare periodi più lunghi si usano le seguenti misure:
settimana = 7 giorni
mese = 30 o 31 giorni
anno = 365 giorni, 52 settimane, 12 mesi
• Completa.
decennio = 10 anni
secolo = 100 anni
millennio = 1000 anni
2 d = h 3 h = min 2 min = s
4 mesi = settimane = d
3 millenni = anni = secoli
1. Rispondi.
a. Sono le 7:45. Dario entrerà in aula fra un quarto d’ora. A che ora?
8:00 17:00
b. Sono le 14:30. Ada ha lezione di pianoforte fra due ore e mezza. A che ora?
nel quaderno pag. 238
LE EQUIVALENZE
Marika compra delle pesche che costano € 4 al kg. Le pesche pesano 8 hg. Quanto pagherà Marika?
La quantità di pesche è espressa con una misura di peso (8 hg). Il prezzo del prodotto è in chilogrammi, mentre la quantità acquistata è espressa in ettogrammi, perciò occorre fare un’equivalenza. Possiamo procedere in due modi. Osserva.
Primo modo
Prima stabiliamo quanto costa 1 hg, che è la decima parte di 1 kg.

€ 4,00 : 10 = € 0,40
Poi calcoliamo quanto costano 8 hg.
Secondo modo
: 10 × 8
€ 0,40 × 8 = € 3,20
Trasformiamo 8 hg in kg e poi moltiplichiamo. 8 hg = 0,8 kg
€ 4,00 × 0,8 = € 3,20
MI ESERCITO
1. Risolvi i problemi con le misure: con entrambi i metodi.
a. Le tagliatelle sono vendute a € 4,50 al chilo. Paolo ne acquista 4 hg. Quanto spende?
€ 1,80 € 4,75
b. I biscotti “Latte & Miele” costano € 9,50 al chilo. Quanto costa un pacco da 500 g?
Educazione Finanziaria
IL DENARO
Il denaro (monete, banconote...) serve per acquistare e scambiare beni. In cambio di denaro si ottengono oggetti, come il cibo, i vestiti, le case, le automobili, i giocattoli… e servizi, come gli abbonamenti ai mezzi pubblici, l’ingresso a un museo, le visite mediche, le attività sportive…
Il baratto
Nell’antichità lo scambio di beni avveniva attraverso il baratto: cioè lo scambio di oggetti e beni dello stesso valore. Per esempio, se un contadino aveva grano in più poteva scambiare il suo bene con il vicino che produceva vino.
La
moneta
Dal V millennio a.C. gli esseri umani iniziarono a dare ad alcuni oggetti (conchiglie, sale, punte di frecce...) un valore per favorire gli scambi. Per esempio, in cambio di un sacchetto di sale si potevano ottenere oggetti o pagare un lavoro. Nacque così il commercio basato sul denaro, che divenne in seguito moneta e poi arrivò alla forma attuale.

Il metodo del baratto negli ultimi anni ha avuto un nuovo impulso, anche grazie al maggiore interesse delle persone al risparmio e alla salvaguardia ambientale. Barattare un oggetto oppure offrire in cambio un servizio di cui abbiamo bisogno è un modo semplice per ridurre gli sprechi.
Una turista giapponese offre tagli di capelli in cambio del racconto di storie personali.
Un indigeno scambia un grosso gambero per un pezzo di stoffa.
IL BARATTO OGGI PIÙ
Un’antica moneta greca.
Educazione Finanziaria
RISPARMIARE
Il denaro serve per comprare ciò di cui abbiamo bisogno, ma non cresce sugli alberi. È bene iniziare a pensare anche a risparmiare e non solo a spendere. Risparmiare, infatti, vuol dire conservare un po’ di denaro per il futuro.
Segui queste regole, per non sprecare il denaro.

Stabilisci un obiettivo Che cosa vuoi comprare o per cosa vuoi risparmiare?
Fai una lista Prima di spendere, pensa a che cosa è davvero importante. Fai una lista delle cose che ti servono e delle cose che desideri.
Dividi i soldi Prendi i tuoi soldi e dividili tra ciò che vuoi spendere subito e ciò che vuoi risparmiare.
Risparmia Metti da parte una parte dei tuoi soldi per il futuro. Risparmiare è come fare una scorta di cioccolato: sarà lì quando ne avrai voglia!
Paga con cura Quando usi i tuoi soldi, fai attenzione ai resti. Se usi una carta o un’app, controlla sempre quanto stai spendendo. Ricorda: i soldi virtuali sono reali!
Controlla i tuoi soldi Ogni tanto, conta quanti soldi hai speso e quanti ne hai risparmiato, ti aiuterà a capire se sei vicino/a al tuo obiettivo.
Imparare a gestire i tuoi soldi ti aiuterà a fare scelte intelligenti ora e in futuro. Ricorda: il denaro è uno strumento, e tu puoi imparare a usarlo nel modo migliore!
Possiedi già un salvadanaio per conservare i soldi che ricevi in regalo o con la paghetta?
LIFE SKILLS
Se impari a risparmiare con il tempo e la giusta pazienza potrai…
• soddisfare un desiderio particolare
• fare un regalo a un amico, un’amica o qualcuno a cui vuoi bene
• far fronte a spese improvvise, che non ti aspettavi di dover fare
• sostenere un’associazione benefica
Continua tu l’elenco sul quaderno.
MI ESERCITO
1. Calcola e completa le tabelle.
quantitàc. unitario c. totale
5 € 1,20
€ 2,50 € 10
4,50
2. Cerchia la misura maggiore.
4 580 m4,6 km500 dam
0,06 h 60 da 60 l
1,8 Mg1 800 g180 kg
9,6 dm96 mm100 cm
Verso l’Invalsi

3. Calcola le equivalenze.
a. 8 km = hm = dam = m 3,7 hm = km = dam = m 132,9 m = dam = cm = hm
b. 16 hg = dag = g = dg 150 g = dag = dg = hg 2000 mg = cg = dg = g c. 0,04 h = da = = dl 9 d =
La famiglia di Liù va in gita al lago in automobile. Guida la mamma, che può scegliere fra due percorsi. Osserva la tabella, calcola e rispondi.
tipo di percorsolunghezza del
A su strada provinciale su strada statale
B su strada provinciale in autostrada
• Qual è il percorso meno lungo? Perché?
• Calcola i tempi di percorrenza. A: B:
• Quale percorso richiede meno tempo di percorrenza?
• Qual è il percorso meno costoso? Perché?
A = 138,4 km; B = 129,4 km B B 1 h 52 min 1 h 27 min A = € 22,50; B = € 27,80 A
• Se tu fossi la mamma di Liù, quale percorso sceglieresti? Perché?
• Unità di misura: metro
• Multipli: dam, hm, km
• Sottomultipli: dm, cm, mm
• Ogni misura è 10 volte più piccola di quella che la segue
LUNGHEZZA

• Unità di misura: litro
• Multipli: da , hl
• Sottomultipli: d , c , m l
• Ogni misura è 10 volte più piccola di quella che la segue
l
CAPACITÀ
• unitario
• totale MISURE
VALORE
• Unità di misura: euro
VERIFICA PIÙ FACILE pag. 267
VERIFICA INTERMEDIA pag. 273
VERIFICA FINALE pagg. 284-285
PROVA NON NOTA pagg. 296-297
costo
commercio
Ripassa con me!
• Unità di misura: chilogrammo
• Multipli: 10 kg, 100 kg, Mg
• Sottomultipli: hg, dag, g
• Sottomultipli del grammo: dg, cg, mg
• Ogni misura è 10 volte più piccola di quella che la segue
s
MASSA / PESO
• spesa
• ricavo
• guadagno
• perdita
TEMPO
• Unità di misura: secondo
• Multipli: min, h, d
Spazio e figure

Imparare… ad arte
Chi ha bisogno di un momento di serenità all’Accademia dei Talenti va in un luogo preciso: l’aula di Arte.
In questa scuola speciale c’è sempre tanto da fare, quindi è importante per i bambini e le bambine prendersi un po’ di relax tra un’ora di Matematica e una di Lancio di Aeroplanini.
Nell’aula di Arte li aspetta il maestro Eustachi, che tutti chiamano maestro E. Non solo per l’iniziale del suo cognome, ma anche perché le sue caratteristiche iniziano tutte con quella lettera. Il maestro E infatti è Elegante, Energico, Equilibrato e… Estremamente Esigente. Anche il suo talento inizia per “E”: Entusiasmare la classe!
Il maestro Eustachi sa che tutti vogliono partecipare alle sue lezioni, quindi pretende il massimo impegno: a fine lezione, si pulisce l’aula insieme.
LETTURA ESPRESSIVA
STORYTELLING
di Valeria Razzini

E da pulire ce n’è, perché a volte i bambini e le bambine realizzano affreschi sul muro con musica classica in sottofondo, e altre volte lanciano schizzi di colore su una tela mentre ballano il rock. Insomma, nell’aula di Arte ci si diverte e spesso si torna a casa coperti di colore dalla testa ai piedi.
– Maestro E, ci può dare un’idea per un disegno? – chiede Ivan.
È una domanda che fa felice il maestro Eustachi. I suoi quadri preferiti sono composti da angoli e figure geometriche e non vede l’ora di farne disegnare alcuni alle bambine e ai bambini.
Ecco quindi l’esercizio che il maestro Eustachi assegna alla classe:
Disegna un pentagono, con dentro un quadrilatero, con dentro un triangolo. Colora le figure sovrapponendo i colori e… ammira la tua opera!
Prova a farlo anche tu:
Con angolo, poligono e retta la Geometria è un’arte perfetta!
AUDIO, VIDEO, OGGETTI DIGITALI DELL’UNITÀ
TANTE LINEE
• Appoggia la punta della matita e premi leggermente vicino alla lettera A qui a lato: hai disegnato il punto A.
Il punto non ha dimensioni e si indica con una lettera maiuscola dell’alfabeto (A, B, C...).
• Ora appoggia la punta della matita sotto la lettera b qui a lato e falla scorrere: hai disegnato la linea b.
La linea è formata da un insieme di punti e ha una sola dimensione: la lunghezza. Si indica con una lettera minuscola dell’alfabeto (a, b, c…).
• Osserva i diversi tipi di linea.
curva spezzata mista
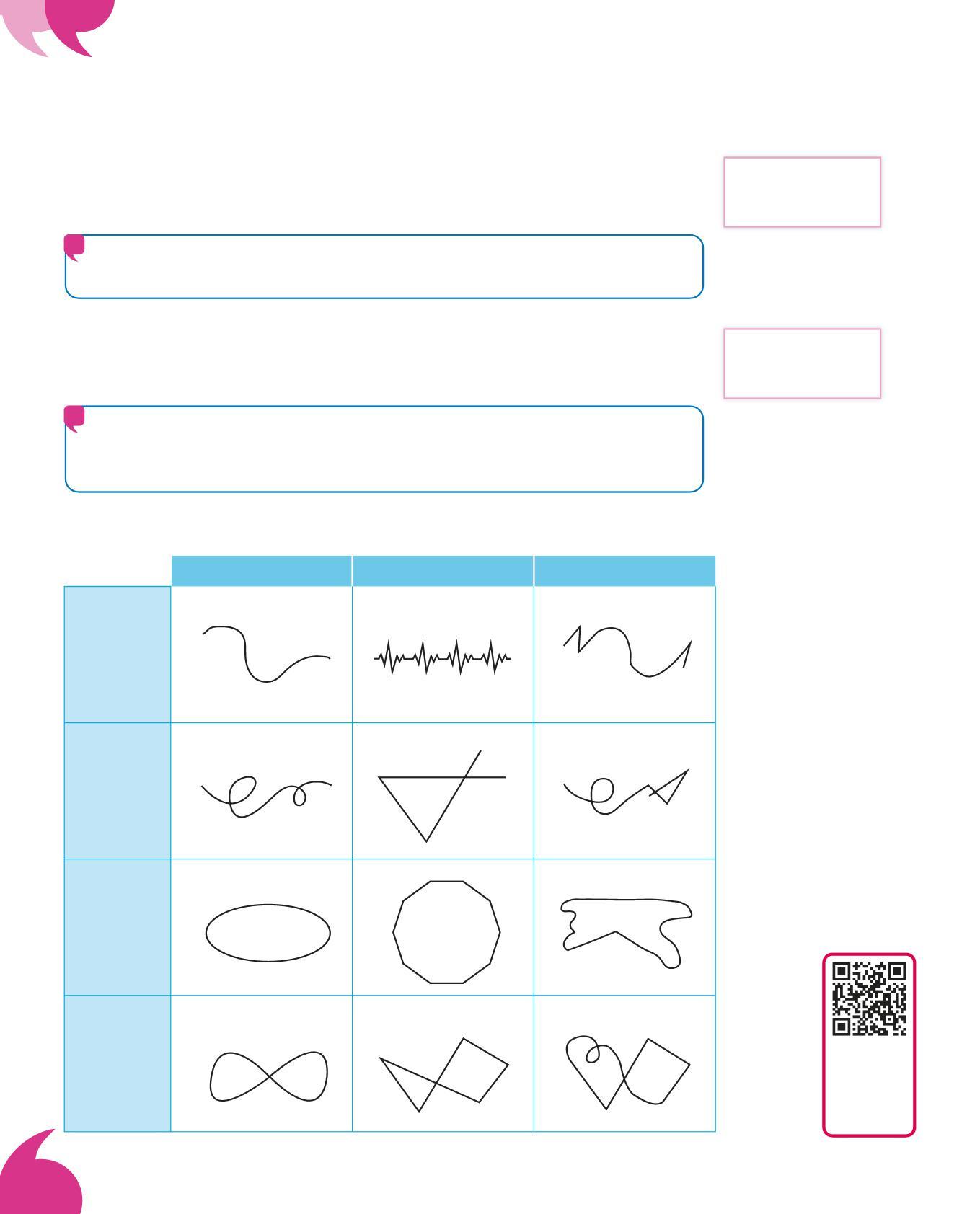
aperta semplice
aperta intrecciata
chiusa semplice
chiusa intrecciata
VIDEO Scopriamo lo spazio e le figure PRESENTAZIONE La storia della geometria Le linee
LINEE RETTE
La linea retta è un insieme infinito di punti disposti lungo la stessa direzione; non ha né origine, né fine
La semiretta è una parte di retta che ha un punto di origine, ma non una fine. Il segmento è una parte di retta compresa tra due punti: ha un inizio e una fine.

VIDEO
Come si
disegnano rette parallele
Come si
disegnano rette perpendicolari
GEOGEBRA
Rette parallele, incidenti e perpendicolari
retta semiretta segmento il tratteggio indica che la retta prosegue
In base alla posizione che occupa sul piano, una retta può essere: orizzontale verticale obliqua
Le rette su un piano possono essere: – parallele quando hanno la stessa direzione e sono equidistanti, perciò non si incontrano mai;
rette parallele
– incidenti quando si incontrano.
rette incidenti
Nel punto d’incontro le rette incidenti formano angoli uguali a due a due; se i quattro angoli sono tutti uguali, le rette si dicono perpendicolari. Due rette perpendicolari sono sempre anche incidenti.
rette perpendicolari
i punti sono indicati da lettere maiuscole a b O A B
1. Osserva le linee rette e completa. La retta di colore è perpendicolare alla retta a.
La retta di colore è parallela alla retta a
Spazio e figure rosso verde blu
La retta di colore è incidente ma non perpendicolare alla retta a. a
quaderno
TANTI ANGOLI
L’angolo è una parte del piano racchiusa tra due semirette che hanno l’origine in comune.

PRESENTAZIONE
Gli angoli
GEOGEBRA
Classificazione
angoli
Angoli e la loro
classificazione
LAB
Linee ed angoli
• Le semirette a e b hanno origine da uno stesso punto indicato con la lettera O;
• la parte di piano delimitata dalle due semirette è l’angolo; la sua ampiezza qui è colorata in giallo;
• le due semirette sono dette lati dell’angolo;
• il punto O è il vertice
Gli angoli si classificano in base alla loro ampiezza. b a O ampiezza lato lato vertice
angolo retto angolo acuto angolo ottuso
angolo piatto angolo giro angolo nullo meno ampio di un angolo retto 90° più ampio di un angolo retto
180° ampio come 2 angoli retti 360° 0°
ampio come 4 angoli retti
MISURARE L’AMPIEZZA DEGLI ANGOLI
Per misurare l’ampiezza degli angoli si usa come unità di misura il grado, indicato con il simbolo °
Un grado si ottiene dividendo l’angolo giro in 360 parti uguali
Lo strumento usato per misurare l’ampiezza degli angoli è il goniometro, che ha una scala graduata suddivisa in 360°, cioè tanto quanto un angolo giro, o in 180°, cioè tanto quanto un angolo piatto.
Ecco come si usa:
1. metti il centro del goniometro sul vertice dell’angolo;
2. fai coincidere un lato dell’angolo con lo zero;
3. leggi la misura dell’ampiezza dove si trova il secondo lato (se non riesci a vedere il lato, prolungalo in modo che arrivi al goniometro).
• Prova tu: quanto misurano questi angoli?
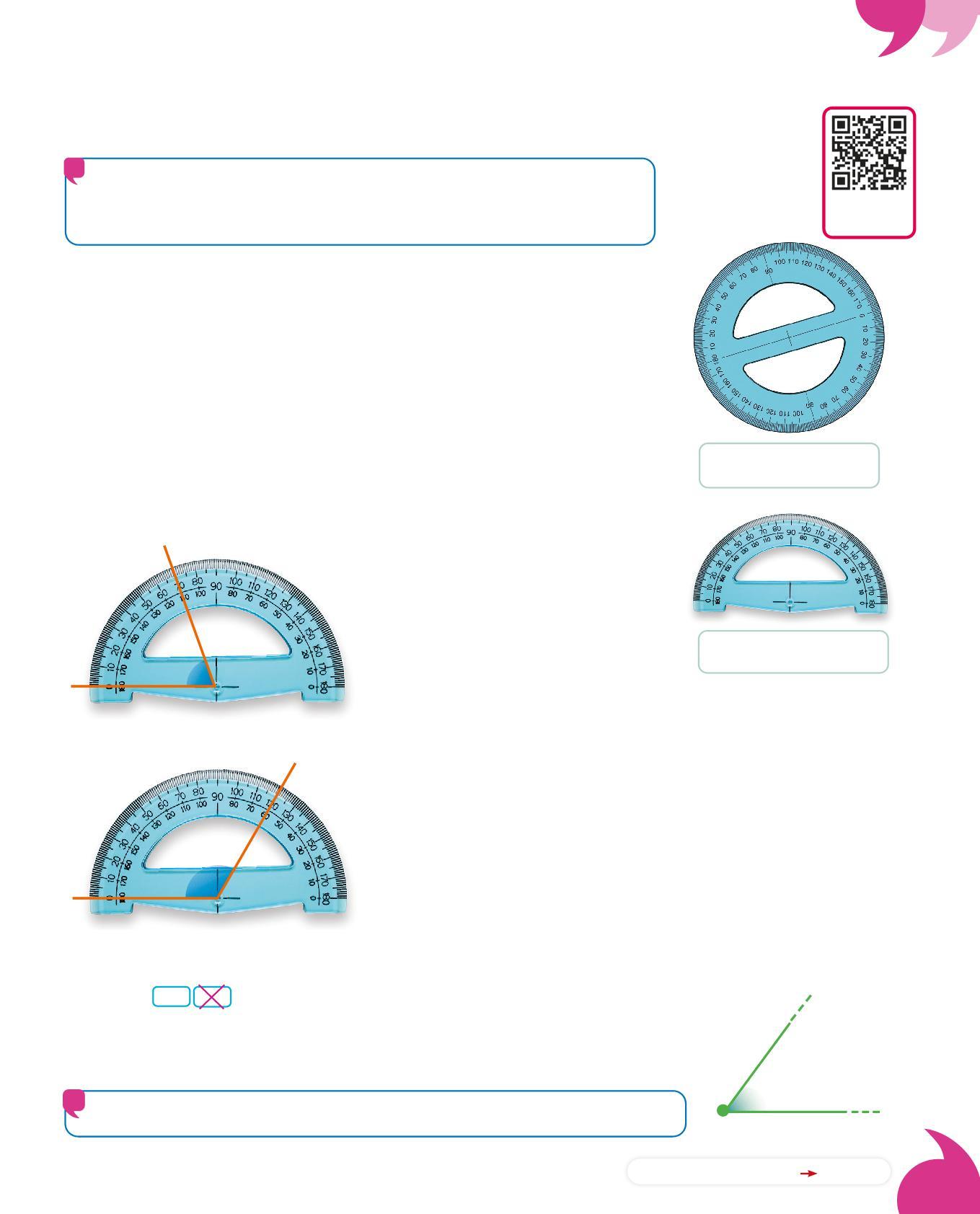
• Questo angolo misura
goniometro 360°
• Questo angolo misura
• Ora rifletti: l’ampiezza di un angolo dipende dalla lunghezza dei lati? sì no
• Misura l’angolo accanto, poi prolunga i lati e misuralo nuovamente. Che differenza c’è?
nessuna
La lunghezza dei lati non modifica l’ampiezza degli angoli.
goniometro 180°
VIDEO Misurare gli angoli
LE TRASFORMAZIONI GEOMETRICHE
Quando una figura geometrica subisce un cambiamento di posizione, di dimensioni o di forma, compie una trasformazione geometrica Esistono alcune trasformazioni che non modificano né la forma né le dimensioni delle figure, ma solo la loro posizione sul piano: sono le isometrie, parola che significa “uguale misura”.
La simmetria
Osserva questa bottiglia e questa coccinella: sono simmetriche. Possiamo infatti tracciare una linea retta che le divide in due parti uguali. Questa retta viene chiamata asse di simmetria
La simmetria è il ribaltamento di una figura attorno a una retta chiamata asse di simmetria
Come puoi vedere l’asse di simmetria può essere interno o esterno, orizzontale, verticale oppure obliquo.
In tutti i casi la trasformazione riguarda solo la posizione della figura.
• Ricopia le figure su un foglio e ritagliale. Che cosa devi fare per sovrapporle perfettamente l’una all’altra?

1. Segna con una l’unica immagine che ha un asse di simmetria.
Se hai dubbi vai a pag. 244 SE
VIDEO La rotazione di una figura La traslazione Il ribaltamento di una figura GEOGEBRA La simmetria
SBAGLIO IMPARO!
La traslazione
• Ridisegna la bottiglia in modo che tutti i punti si spostino dello stesso numero di quadretti. Hai effettuato una traslazione
• Ora confronta il tuo disegno con quello della classe. Avete traslato la bottiglia allo stesso modo.
Perché lo spostamento sia uguale, occorre definire il vettore della traslazione, cioè una freccia che indica:
– la direzione (orizzontale, verticale, obliqua);
– il verso (alto/basso, destra/sinistra);
– la misura (lunghezza) dello spostamento.
direzione verso misura
La traslazione è lo spostamento di una figura sul piano secondo il vettore indicato.
• Osserva e segna con una la risposta corretta. Con la traslazione:
– è cambiata la forma del fiore? sì no
– è cambiata la dimensione del fiore? sì no
– è cambiata la posizione del fiore? sì no
È cambiata solo la posizione: anche la traslazione, infatti, è una isometria
MI ESERCITO
1. Esegui le traslazioni delle figure secondo il vettore indicato.
e figure

La rotazione
Anche la rotazione è un’isometria
• Ritaglia da un cartoncino una figura simile a quella disegnata in nero, appoggiala su un foglio e disegna il contorno.
• Punta uno spillo sul punto O ed esegui una rotazione in senso orario di 90°, in modo che la figura raggiunga un’altra posizione.
• Disegna nuovamente il contorno.
• Le due figure hanno la stessa forma e le stesse dimensioni? sì no
La rotazione è lo spostamento di una figura su un piano definito da: un centro di rotazione, che è il punto fisso attorno al quale la figura viene ruotata; un senso di rotazione, che può essere orario o antiorario; un’ampiezza dell’angolo di rotazione
La similitudine
Gli alberelli accanto hanno tutti la stessa forma, ma...
• il disegno 2 è ingrandito di 2 quadretti ogni 1 rispetto al disegno 1: è in scala 2:1, che si legge “scala 2 a 1”;
• il disegno 3 è ridotto di 1 quadretto ogni 2 rispetto al disegno 1: è in scala 1:2, che si legge “scala 1 a 2”.
La similitudine è un ingrandimento o una riduzione di una figura secondo la scala indicata.
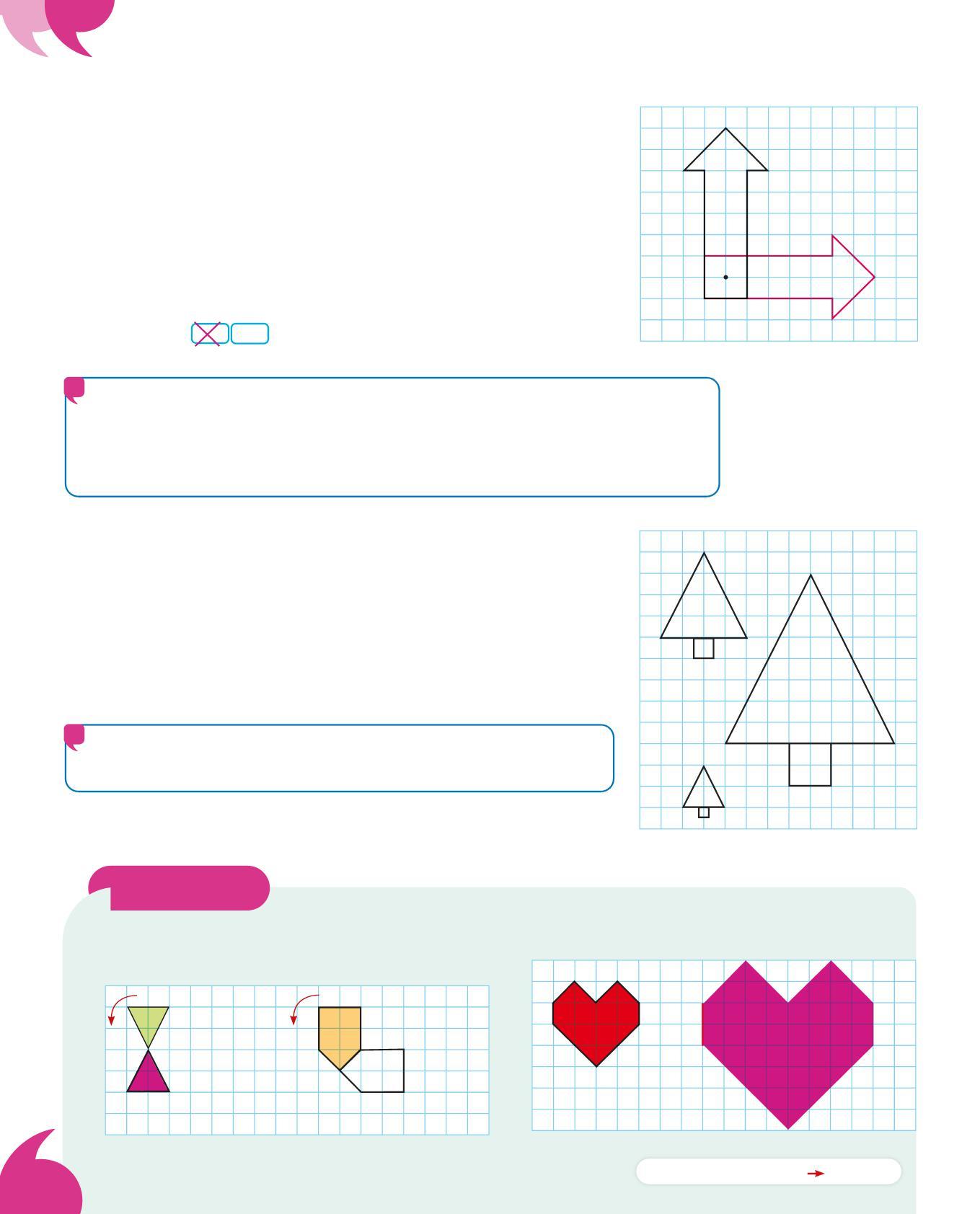
1. Finisci di colorare solo la figura che è ruotata di 180° in senso antiorario.
2. Ingrandisci il cuore in base alla scala 2:1.
LE FIGURE PIANE: I POLIGONI
Un poligono è una parte di piano delimitata da una linea spezzata chiusa semplice
I segmenti che delimitano il poligono si chiamano lati. Il lato su cui il poligono “poggia” prende il nome di base (b). Due lati consecutivi formano un angolo interno
Il punto comune a due lati consecutivi è detto vertice
Il segmento che unisce due vertici non consecutivi si chiama diagonale
Il segmento che parte da un vertice e cade perpendicolarmente sul lato opposto o sul suo prolungamento si chiama altezza (h).
Il poligono viene indicato con le lettere maiuscole dei suoi vertici (ABCD).

altezza (h)
diagonale base (b) angolo interno lato
La parola “poligono” deriva dal greco polys, “molto”, e gonon, “angolo”; significa quindi “tanti angoli”.
Il nome di ogni poligono è dato dal numero degli angoli interni, che coincide con il numero dei lati e dei vertici
• Osserva e completa.
Esistono anche poligoni con un numero maggiore di angoli, come gli esagoni (6), gli ettagoni (7), gli ottagoni (8), gli ennagoni (9), i decagoni (10) e così via. triangoli angoli lati vertici angoli lati vertici angoli lati vertici quadrilateri pentagoni
Poligoni convessi e concavi
I poligoni si suddividono in convessi e concavi
• Osserva e completa.
poligoni convessi poligoni concavi

Tutti i prolungamenti dei lati sono rispetto alla figura.
interno esterni
Almeno un prolungamento dei lati passa all’ della figura.
Tutti i segmenti che uniscono due punti del poligono sono interni al poligono stesso.
Almeno un segmento che unisce due punti del poligono è fuori dal poligono.
Un poligono convesso può essere:
• equiangolo quando ha tutti gli angoli uguali (ossia con la stessa ampiezza);
• equilatero quando ha tutti i lati uguali (ossia della stessa lunghezza);
• regolare quando è sia equiangolo sia equilatero, ossia quando ha tutti gli angoli e tutti i lati uguali.
MI ESERCITO
1. Disegna in rosso un poligono convesso e in blu un poligono concavo.
2. Colora soltanto i poligoni regolari.
I TRIANGOLI
I triangoli sono poligoni con 3 lati e 3 angoli. Non hanno diagonali perché non hanno coppie di vertici non consecutivi.
Possiamo classificare i triangoli secondo i lati o secondo gli angoli. Osserva.
secondo i lati

PRESENTAZIONE I triangoli
Laboratorio dei triangoli
DOC
Dimostrazione degli angoli interni del triangolo
GEOGEBRA
Angoli interni di un triangolo
scaleni
hanno tutti i lati diversi isosceli
acutangoli
hanno tutti gli angoli acuti
hanno due lati uguali equilateri
secondo gli angoli
hanno tutti i lati uguali
rettangoli
hanno un angolo retto ottusangoli
hanno un angolo ottuso
1. Classifica i seguenti triangoli sia in base ai lati sia in base agli angoli.
acutangolo, equilatero rettangolo, scaleno ottusangolo, isoscele
Base e altezza del triangolo
La base (b) di un triangolo è il lato su cui esso “poggia”.
Osserva: ogni lato può essere preso come base.
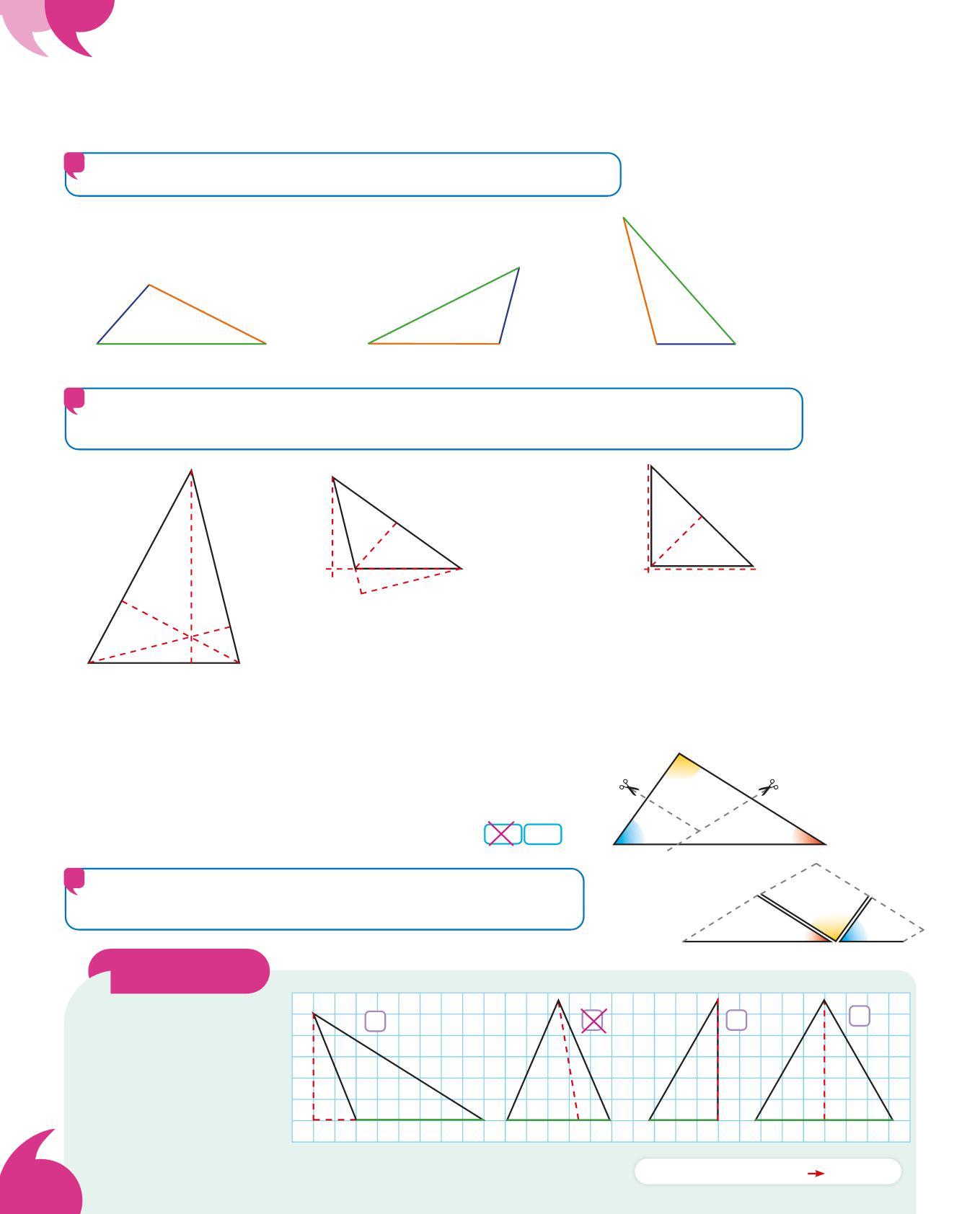
L’altezza (h) è il segmento che partendo da un vertice cade perpendicolarmente sul lato opposto o sul suo prolungamento. Ogni triangolo ha tre altezze
h h h h h h h h
Nei triangoli ottusangoli, due altezze cadono esternamente alla figura.
La somma degli angoli interni
• Disegna su un cartoncino un triangolo e colora gli angoli in modi diversi. Poi ritaglia e accosta gli angoli come nel disegno: quale angolo ottieni?
piatto
• Prova con altri triangoli: il risultato è lo stesso? sì no
La somma degli angoli interni di un triangolo è uguale a 180°, cioè un angolo piatto.
1. In quale triangolo l’altezza relativa alla base non è stata tracciata correttamente? Segnalo con una .
Nei triangoli rettangoli, due altezze coincidono con due lati.

I QUADRILATERI
Il poligono disegnato qui a fianco è un quadrilatero.
• Colora in gli angoli, fai un punto sui vertici,ripassa in i lati e in le diagonali. Poi completa la frase.
I quadrilateri sono poligoni che hanno angoli, vertici, lati e diagonali.
• Osserva la classificazione dei quadrilateri: come si chiamano i quadrilateri nell’intersezione di rombi e rettangoli?
lato vertice angolo diagonale diagonale lato lato lato
VIDEO
I quadrilateri
PRESENTAZIONE
La famiglia dei quadrilateri
DOC
Dimostrazione degli angoli interni dei quadrilateri
QUADRILATERI PARALLELOGRAMMI RETTANGOLI
I quadrilateri che hanno una coppia di lati paralleli sono detti trapezi I quadrilateri che hanno due coppie di lati paralleli e uguali sono detti parallelogrammi
La somma degli angoli interni
• Disegna su un cartoncino un quadrilatero e colora gli angoli in modi diversi. Poi ritaglia e accosta gli angoli come nel disegno: quale angolo ottieni?
4 4 4 2 quadrati giro
• Prova con altri quadrilateri: il risultato è lo stesso? sì no
La somma degli angoli interni di un quadrilatero è uguale a 360°, cioè un angolo giro.
ROMBI
TRAPEZI
QUADRATI
ROMBOIDI
I PARALLELOGRAMMI
In base ai lati e agli angoli, i parallelogrammi vengono classificati in rettangoli, romboidi, quadrati e rombi
Rettangoli e romboidi
• Costruisci un rettangolo con quattro strisce di cartoncino di due diverse lunghezze e quattro fermacampioni, poi tira verso l’esterno due vertici non consecutivi. Che cosa accade? Si forma un romboide

Il rettangolo e il romboide hanno i lati uguali e paralleli a due a due. Mentre il rettangolo ha tutti gli angoli uguali e retti (90°), il romboide ha gli angoli opposti uguali a due a due.
Quadrati e rombi
• Costruisci un quadrato con quattro strisce di cartoncino di uguale lunghezza e quattro fermacampioni, poi tira verso l’esterno due vertici non consecutivi. Che cosa accade? Si forma un rombo
Se hai dubbi vai a pag. 247 SE SBAGLIO IMPARO!
Sia il quadrato sia il rombo hanno tutti i lati della stessa lunghezza, sono quindi equilateri
Il quadrato, però, ha tutti gli angoli uguali e retti (90°), il rombo ha gli angoli opposti uguali a due a due
Il quadrato e il rombo hanno le diagonali perpendicolari, ma quelle del quadrato hanno la stessa lunghezza, quelle del rombo hanno lunghezze diverse.
1. Disegna sul quaderno un rettangolo, un romboide, un quadrato e un rombo. Poi ripassa con lo stesso colore i lati uguali e colora allo stesso modo gli angoli uguali.
Spazio e figure
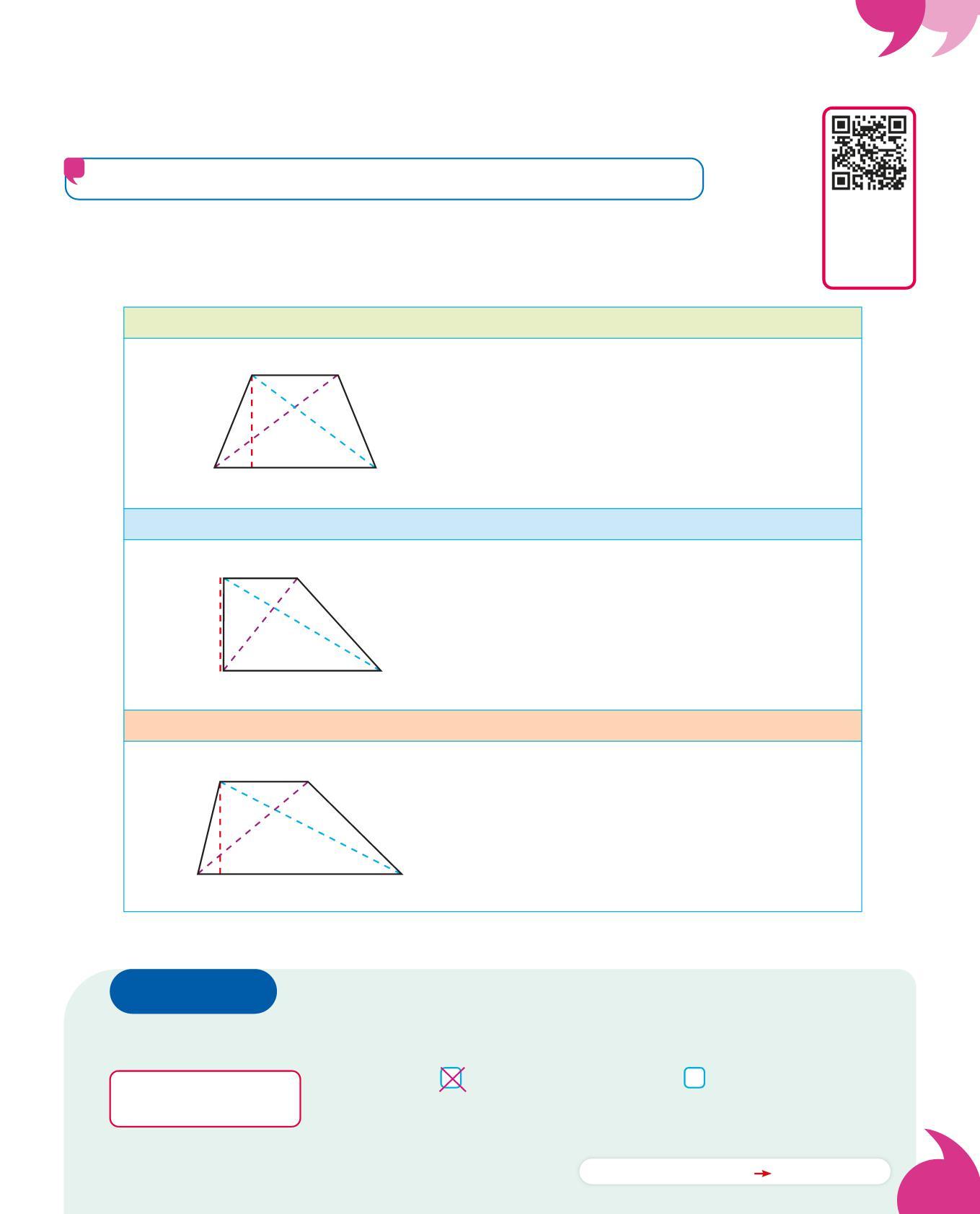
I TRAPEZI
I trapezi sono quadrilateri che hanno una coppia di lati paralleli
Tali lati vengono chiamati base maggiore (B) e base minore (b); come altezza (h) si considera la distanza tra le basi.
trapezio isoscele
Lati: i 2 lati obliqui sono uguali.
Angoli: 2 ottusi, 2 acuti, uguali a due a due.
Diagonali: uguali.
trapezio rettangolo
Lati: un lato coincide con l’altezza.
Angoli: 1 ottuso, 1 acuto, 2 retti (90°).
Diagonali: diverse.
trapezio scaleno
Lati: i lati sono tutti diversi.
Angoli: 2 ottusi, 2 acuti, tutti diversi tra loro.
Diagonali: diverse.
Perché l’affermazione di Saul è sbagliata? Segnalo con una .
Perché il trapezio ha solo due lati paralleli. Il trapezio è anche un parallelogramma.
Perché il trapezio non ha tutti i lati uguali.
nel quaderno pagg. 246, 248
IL PERIMETRO
Con cinque strisce di cartoncino e fermacampioni costruisci un poligono.

Togli un fermacampione e allinea i lati.
Ora misura la lunghezza complessiva: il dato che ottieni è il perimetro (simbolo P) del poligono.
Dunque: P = l1 + l2 + l3 + l4 + l
Il perimetro (P) di un poligono è la misura del suo contorno, cioè la somma di tutti i suoi lati
• In base alla lunghezza dei lati di questo quadrilatero, calcola il suo perimetro.
AB = 3,6 cm
BC = 4 cm
CD = 6 cm DA = 5,2 cm

Per facilitare il calcolo del perimetro di triangoli e quadrilateri ci sono delle formule.
Il perimetro dei triangoli
• Osserva e completa.
triangolo scaleno triangolo isoscele triangolo equilatero
P = l1 + l2 + l3 l2 l1 P = (l × 2) + b
l
Spazio e figure l3 3
P = l × l l l
MI ESERCITO
1. Misura con il righello i lati del triangolo scaleno, scrivi le lunghezze e infine calcola il perimetro.
AB = cm
BC = cm
CA = cm P =
2. Misura con il righello i lati del triangolo isoscele, scrivi le lunghezze e infine calcola il perimetro usando la formula adatta.
AB = cm
BC = cm
CA = cm
= = cm
Verso l’Invalsi
Se so che un triangolo equilatero ha il lato di 12 cm, posso calcolare il suo perimetro?
con una .
Sì, perché il triangolo equilatero ha tre lati uguali e posso calcolare 12 × 3.
No, perché mi manca la misura dell’altezza.
Il perimetro dei quadrilateri
• Osserva e completa.

parallelogrammi
quadrato e rombo
P = l × rettangolo e romboide
P = (l + b) × 2 o P = (l × 2) + ( × )
trapezi
trapezio isoscele
trapezio scaleno e trapezio rettangolo
P = ( × ) + B + b
MI ESERCITO
1. Calcola il perimetro delle figure usando la formula adatta.
MI ESERCITO
1. Collega con una freccia ogni figura alla formula che devi applicare per calcolare il suo perimetro.
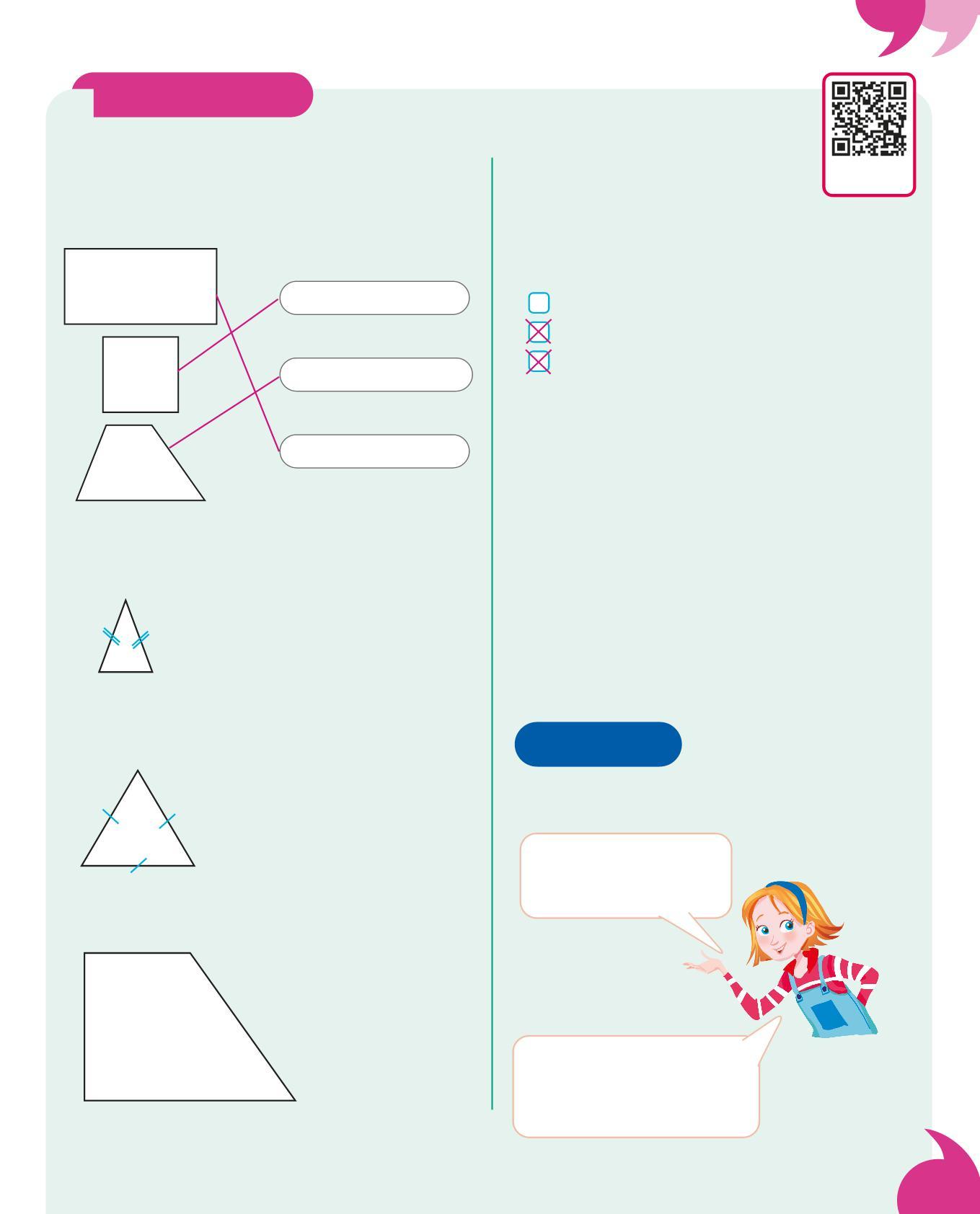
= l × 4
= l1 + B + l2 + b
= (l + b) × 2
AB = 13 cm
BC = 18 cm
CA = cm
P =
e
3. Leggi e segna con una che cosa puoi trovare nella situazione descritta.
Un’aiuola a forma di triangolo equilatero ha il lato di 3,85 m. Posso calcolare: la misura dell’altezza. la misura della base. il perimetro.
4. Risolvi i problemi sul quaderno.
a. Un tavolino quadrato ha il lato lungo 45 cm. Calcola il suo perimetro.
cm
b. La lunghezza del lato AB del rettangolo ABCD è tre volte quella del lato BC, che misura 2 m. Qual è la misura del perimetro?
m
c. Il balcone dell’appartamento di Massimo ha la forma di un rettangolo lungo 2,4 m e largo 1,2 m. Calcola il perimetro del balcone.
cm 18 49 cm
AB = 27 m
P =
m
d. Il nonno cuce un pizzo lungo il bordo di una tovaglia quadrata che ha il lato di 130 cm. Calcola la lunghezza del pizzo.
Verso l’Invalsi
Completa le frasi di Giulia in modo che le sue affermazioni siano corrette.
m 153 cm basi lato lato
AB = 50 cm
BC = 43 cm
CD = 25 cm
DA = 35 cm
P =
Posso calcolare il perimetro di un quadrato se conosco la misura di un .
Posso calcolare il perimetro di un trapezio isoscele se conosco la misura delle e di un
2. Calcola il perimetro delle figure.
MISURARE LA SUPERFICIE: IL METRO QUADRATO
In geometria la superficie di un poligono è la parte racchiusa al suo interno. La misura della superficie si chiama area (A).
L’unità di misura fondamentale della superficie è il metro quadrato, cioè un quadrato con i lati lunghi 1 m.
Il simbolo del metro quadrato è m2; il 2 scritto in alto significa che in ogni misura di superficie ci sono due dimensioni: lunghezza e larghezza.
chilometro quadrato

I multipli del metro quadrato si usano per superfici grandi, come parchi, terreni, Regioni o Stati.
Equivalenze con le misure di superficie
Come vedi, ogni unità di misura è 100 volte più grande di quella alla sua destra e 100 volte più piccola di quella alla sua sinistra. Per passare da una unità di misura all’altra devi quindi moltiplicare o dividere per 100 o multipli di 100.
1 m2 = 100 dm2
1 dm2 = 100 cm2
1 cm2 = 100 mm2
Quando leggi o scrivi una misura di superficie, ricorda che la marca si riferisce sempre alle ultime due cifre intere: decine e unità.
196,25 m2
MI ESERCITO
1. Osserva i numeri nella tabella e scrivi i numeri decimali. Segui l’esempio.

2. Completa le uguaglianze, come nell’esempio.
a. 20 dm2 + 80 dm2 = 1 m2
60 dm2 + dm2 = 1 m2
35 dm2 + dm2 = 1 m2 74 dm2 + dm2 = 1 m2
b. 38 cm2 + cm2 = 1 dm2 27 cm2 + cm2 = 1 dm2 cm2 + 50 cm2 = 1 dm2 cm2 + 79 cm2 = 1 dm2
c. 24 hm2 + hm2 = 1 km2 56 hm2 + hm2 = 1 km2 hm2 + 16 hm2 = 1 km2 hm2 + 81 hm2 = 1 km2
3. Colora l’etichetta con la marca che indica il valore delle cifre in rosso.
78 dm2
51 m2
27 hm2
2
2 cm2
2

4. Calcola le equivalenze. 10,17 km2 = hm2 = dam2
5. Esegui le equivalenze.
L’AREA DEI QUADRILATERI
L’area del rettangolo
Calcola quanti cm2 ricoprono la superficie del rettangolo. Quale operazione hai utilizzato per non contare i quadratini uno a uno?
Scrivila qui:
Sostituisci le lettere (b e h) ai numeri:
A = ×
5 × 4 = 20 b h
L’area di un rettangolo si calcola moltiplicando la base (b) per l’altezza (h).
L’area del quadrato
Il quadrato è un rettangolo speciale. Qual è la differenza tra un quadrato e un rettangolo?
Il quadrato ha tutti i lati congruenti, il rettangolo no.
La formula per calcolare l’area del quadrato è simile a quella dell’area del rettangolo, ma devi modificare le lettere: come puoi fare?
Sostituisco la base e l’altezza con il lato.
Scrivi la formula completa:
A = ×
L’area di un quadrato si calcola moltiplicando lato ( ) per lato ( ).
MI ESERCITO
1. Segna con una quale operazione risolve il problema, poi calcola. Un letto rettangolare ha il lato maggiore di 2,4 m e il lato minore di 1,8 m. Quanto misura l’area?
(2,4 + 1,8) × 2 = 2,4 × 1,8 =
2. Risolvi il problema sul quaderno.
(2,4 × 2) + 1,8 = (1,8 × 2) + 2,4 =
Un calendario quadrato ha il lato di 65 cm. Quanti cm2 misura la sua superficie?
l l 4225 cm2 4,32
L’area
del romboide
• Parti dal romboide e prova a ottenere un rettangolo tagliando e spostando una parte della figura:

• Osserva e rispondi.
Base e altezza del romboide e del rettangolo sono: diverse uguali.
La superficie:
è rimasta la stessa è cambiata.
Quindi la formula per calcolare l’area del romboide è:
A = ×
L’area di un romboide si calcola moltiplicando la base (b) per l’altezza (h).
MI ESERCITO
1. Calcola l’area dei seguenti romboidi e completa.
2. Risolvi i problemi sul quaderno.
Da un foglio di cartoncino rettangolare con il lato maggiore di 1 m e il lato minore di 60 cm, Lisa ritaglia un romboide con la base di 40 cm e l’altezza di 25 cm. Quanti m2 misura la superficie del cartoncino rimasto?
DOC Area del romboide
GEOGEBRA
Area del parallelogramma a partire da quella di un rettangolo
L’area del rombo
Puoi scomporre e ricomporre in un rettangolo anche il rombo.
• Disegna questo rombo su un foglio e ritaglialo. Sei riuscito/a?

• Osserva come ha fatto Maria.
• Rifletti e completa.
Maria ha trasformato il rombo ABCD nel rettangolo DBFE con la stessa superficie, che ha per base una diagonale (d) e per altezza metà dell’altra diagonale (D : 2).
Poi ha applicato la formula dell’area del rettangolo:
A = d × (D : 2) base altezza ×
La formula per calcolare l’area del rombo è:
A = × : oppure ×
MI ESERCITO
1. Completa i dati e calcola l’area del rombo.
L’area di un rombo si calcola moltiplicando la diagonale maggiore (D) per la diagonale minore (d), e dividendo il prodotto per 2
(D) = cm
(d) = cm
= × : = cm2
L’area del trapezio
Duplica il trapezio per ottenere un romboide (trapezio scaleno e isoscele) o un rettangolo (trapezio rettangolo).
• Disegna un trapezio uguale a quello dato, ritaglialo e accostalo al primo “a testa in giù”.

B + b = base del romboide
b b D B B B C h B + b = base del rettangolo
• Rifletti e completa.
Come vedi, il trapezio è la metà di un romboide o di un rettangolo che ha per base la somma delle basi del trapezio e per altezza l’altezza del trapezio. Quindi, per calcolare l’area del trapezio puoi applicare le formule del romboide e del rettangolo, e poi dividere il prodotto per due.
La formula per calcolare l’area del trapezio è:
A = ( + ) × : oppure A = ( + ) ×
L’area del trapezio si calcola sommando le basi, moltiplicando il risultato per l’altezza e dividendo il prodotto per 2
MI ESERCITO
1. Completa i dati e calcola l’area del trapezio.
2. Risolvi il problema sul quaderno.
La superficie di un trapezio rettangolo è la metà di quella di un rettangolo con il lato maggiore di 70 cm e il lato minore di 35,5 cm. Calcola l’area.
cm2
del trapezio
quella di un triangolo
L’AREA DEI TRIANGOLI
Osserva: puoi effettuare scomposizioni, duplicazioni e ricomposizioni per trasformare i triangoli in altri poligoni.
triangolo equilatero triangolo rettangolo scaleno
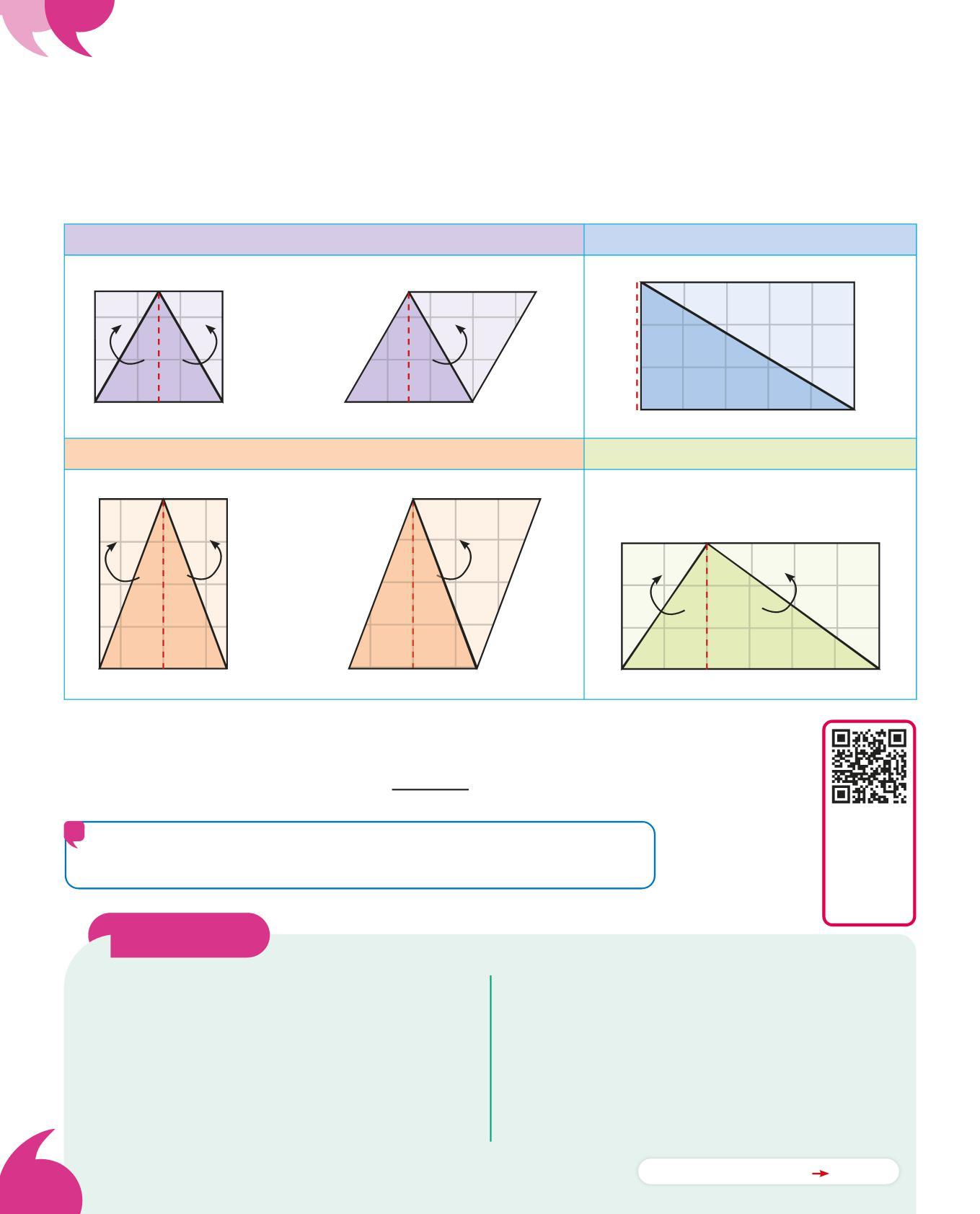
triangolo isoscele triangolo scaleno
Ogni triangolo è la metà di un rettangolo o di un parallelogramma che ha la stessa base e la stessa altezza.
A = ( × ) : 2 oppure A = ×
L’area del triangolo si calcola moltiplicando la base per l’altezza e dividendo il prodotto per 2
1. Disegna sul quaderno un triangolo rettangolo con la base di 3 cm e l’altezza di 3,5 cm. Poi completa e calcola la sua area.
(b) = cm
Area del triangolo GEOGEBRA
Area del triangolo a partire da quella di un parallelogramma
Area del triangolo
2. Risolvi il problema sul quaderno.
Lo scialle di Lucia è un triangolo isoscele con la base di 80 cm e l’altezza lunga la metà della base. Quanti m2 misura la superficie dello scialle?
m2
Attività nel quaderno pag. 251
FIGURE CONGRUENTI
Due figure sono congruenti quando sono perfettamente sovrapponibili, cioè quando hanno la stessa forma e le stesse dimensioni
• Confronta queste coppie di figure: sono congruenti?

no
FIGURE ISOPERIMETRICHE
Due figure sono isoperimetriche quando hanno lo stesso perimetro, cioè quando hanno il contorno di uguale lunghezza.
• Confronta queste coppie di figure: sono isoperimetriche?
Due figure sono equiestese quando hanno la stessa superficie, cioè quando occupano la stessa porzione di piano. sì no
FIGURE EQUIESTESE
• Confronta le coppie di figure e conta i quadretti della superficie. Poi colora allo stesso modo le coppie equiestese.
MI ESERCITO
1. Completa i disegni e calcola.

Completa il quadrato. Poi misura con il righello.
Quanto è lungo il suo lato?
Quanto misura l’area?
Completa il rettangolo. Poi misura con il righello.
Quanto è lunga la base?
Quanto è lunga l’altezza?
Quanto misura l’area?
2. Calcola sul quaderno l’area delle figure.
3. Risolvi il problema sul quaderno.
a. Una mensola ha la forma di un trapezio isoscele con la base maggiore di 3,5 m, la base minore di 2,7 m e l’altezza di 0,6 m. Quanto misura la sua superficie?
b. Per costruire un aquilone a forma di rombo Lucas incrocia due bastoncini lunghi 5,5 dm e 37 cm. Calcola l’area del tessuto che servirà per rivestire tutta la superficie dell’aquilone.
1017,5 cm2
4. Disegna tre figure equiestese, ma non isoperimetriche.
Aminah deve rifare il pavimento del balcone della sua camera. Osserva il disegno, ricava le misure del balcone e calcolane l’area sul quaderno.
Verso l’Invalsi
PROBLEM SOLVING

Leggo il problema
In un parco ci sono 5 aiuole uguali a forma di trapezio rettangolo: la base maggiore misura 1,11 m, la base minore 64 cm, il lato obliquo 86 cm e l’altezza 48 cm.
Vanno recintate con un listello in legno: quanti metri di listello servono?
In inverno l’intera superficie delle aiuole va coperta con un telo, quanti m2 serviranno?
Capisco il problema
• Quante sono le aiuole?
5
• Che forma hanno?
• Per scoprire la lunghezza del listello che cosa devi calcolare?
• Invece, per calcolare la superficie del telo?
Rappresento il problema
Per risolvere il problema disegna un’aiuola. Osserva e completa i dati:
D B C
AB = m
BC = cm
A
il perimetro del trapezio
CD = cm
DA = cm
Le misure hanno tutte la stessa unità di misura? sì no
Allora è necessario fare una o più equivalenze:
Pianifico il percorso di soluzione
Riordina i passaggi e poi risolvi il problema sul quaderno.
7 6 1
5 2 3 4 trapezio rettangolo l’area del trapezio 1,11
86 cm = 0,86 m; 64 cm = 0,64 m; 48 cm = 0,48 m
Moltiplico il perimetro calcolato per il numero delle aiuole.
Sostituisco i dati numerici alle lettere della formula.
Moltiplico l’area per il numero delle aiuole.
Scrivo la formula del perimetro del trapezio.
Sostituisco i dati numerici alle lettere della formula.
Se serve faccio una o più equivalenze.
Scrivo la formula dell’area del trapezio rettangolo.
1. Risolvi un problema simile sul quaderno.
Nella mensa ci sono 10 tavoloni congruenti di forma rettangolare che hanno bisogno di un nuovo bordo. Il lato lungo misura 1,8 m, il lato corto 70 cm. Qual è la lunghezza totale del bordo da acquistare? I tavoli vanno coperti con una tovaglia da far aderire perfettamente alla superficie: quanti m2 di tovaglia vanno acquistati?
5 m ; 1,26 m2 86
Laboratorio

LA SPIRALE AUREA
In matematica una successione è una sequenza di numeri che hanno una correlazione tra di loro.
Tra le più conosciute c’è la successione di Fibonacci, grazie alla quale è possibile costruire la famosa spirale di Fibonacci, anche detta spirale aurea. Ma come funziona?
OCCORRENTE matita • righello • foglio a quadretti
PROCEDIMENTO
1. Disegna un quadrato di lato 1, e poi un altro di lato 1 con un lato in comune come in figura.
2. Ora attacca un quadrato di lato 2 poi uno di lato 3, 5, 8, 13, proseguendo in senso antiorario fino a quando non finisce il foglio.
3. Otterrai un rettangolo ma potrai anche costruire una spirale come in figura.
CONCLUSIONI
La successione di Fibonacci si ottiene sommando i 2 numeri più a destra della sequenza. Quindi all’inizio avremo 1, 1 2, poi 1, 1, 2 3, proseguendo 1, 1, 2, 3 5 e così via. Seguendo questa regola, si ottiene la famosa spirale aurea, un tipo di rappresentazione che si trova spesso in natura, dal guscio del Nautilus alla disposizione dei semi di girasole, fino alla forma di certe tipologie di galassie.
VIDEO
Fibonacci e la sequenza magica
FACCIAMO IL PUNTO • SPAZIO E FIGURE

Ripassa con me!
Una dimensione: lunghezza
non poligoni poligoni
Possono essere
• RETTE
• SEMIRETTE
• SEGMENTI
SPAZIO E FIGURE
4 lati: quadrilateri
Due dimensioni: lunghezza larghezza
Possono essere
• RETTO 90°
• PIATTO 180°
• GIRO 360 °
• ACUTO > di 90°
• OTTUSO > di 90° ma < di 180°
3 lati: triangoli
Si possono calcolare il perimetro e l’area
Trapezio (isoscele, scaleno, rettagolo)
Romboide e rombo
Quadrato e rettangolo
Isoscele
Scaleno
Equilatero Rettangolo
Acutangolo
Ottusangolo
LINEE
FIGURE PIANE
ANGOLI

Relazioni, dati e previsioni
La Biblioteca
dell’Accademia dei Talenti
Paolo, Rino, Laura e Sandra sono gli Studiatutto dell’Accademia dei Talenti.
Questo soprannome lo ha inventato la cuoca Renata per indicare un gruppetto di bambine e bambini che discutono tra loro di cose come reticoli, fotosintesi clorofilliana, Preistoria… e che per timidezza parlano poco con il resto della classe.
Gli Studiatutto preferiscono le lezioni di Storia e Matematica a quelle di Giocoleria e Torte di compleanno. Persino d’estate amano restare in casa a leggere tutti i libri su cui riescono a mettere le mani. Il loro talento è saper trovare il libro giusto per ogni occasione.
Per questo il Preside Melchiorri ha affidato a Paolo, Rino, Laura e Sandra l’incarico di Bibliotecari e Bibliotecarie dell’Accademia dei Talenti.
Gli Studiatutto hanno accettato con entusiasmo, ma dopo una settimana erano preoccupatissimi: la Biblioteca era sempre vuota. Nonostante i quattro avessero distribuito volantini di invito a tutta la scuola, erano sempre soli tra gli scaffali. E non capivano proprio perché.
Dopo aver letto tutti i libri della sezione Grandi Misteri, Laura e Sandra hanno avuto un’idea: – Chiediamo a 100 alunni e alunne dell’Accademia che cosa amano leggere! Così capiremo il tipo di libri che vogliono trovare in Biblioteca.
Paolo e Rino, che conoscono a memoria tutti i volumi della sezione Grafici, hanno risposto: – Benissimo! Poi noi rappresenteremo i dati raccolti.
Ed ecco i voti che hanno dato i bambini e le bambine dell’Accademia.
Cosa ti piace leggere?

avventura
fantasy
manga e fumetti
libri che non ci sono in biblioteca
È bastato chiedere al Preside di acquistare un po’ di volumi nuovi e la Biblioteca si è riempita di lettrici e lettori!
Una volta raccolti i dati, per capirli vanno osservati!
Ti ricordi come si chiama il grafico qui sopra?
istogramma
AUDIO, VIDEO, OGGETTI DIGITALI DELL’UNITÀ
di Valeria Razzini
L’INDAGINE STATISTICA
Fare un’indagine statistica significa raccogliere ed elaborare dei dati per avere delle informazioni su fenomeni o preferenze.
La scuola Pascoli vuole comprare dei libri per la biblioteca. Viene deciso di fare un’indagine statistica per scoprire quali sono i generi di libri preferiti dai bambini e dalle bambine che frequentano la scuola. Per semplificare il lavoro, l’indagine viene svolta su un campione di 80 bambine e bambini che rappresenta l’insieme di tutte le persone.
Ecco il risultato dell’indagine. Ognuno degli 80 bambini e bambine ha espresso una sola preferenza che corrisponde a una
libri di fantascienza
libri fantasy
libri di avventura
libri “gialli”
libri a fumetti
• Conta i dati della tabella sopra e completa riportando il numero delle preferenze per ogni genere.
libri n. preferenze
fantascienza
fantasy avventura
“gialli”
fumetti
totale
• Qual è il genere preferito? Con quante preferenze?
fantasy, con 28 preferenze
• Qual è il genere meno richiesto?

Il numero di preferenze ottenuto da ogni genere di libro si chiama frequenza
VIDEO Scopriamo relazioni, dati e previsioni
I GRAFICI
Possiamo semplificare il risultato dell’indagine della scuola Pascoli con dei grafici.
Gli istogrammi
Nell’istogramma i dati vengono rappresentati attraverso colonne di uguale larghezza e altezza proporzionale alla frequenza, cioè al numero di preferenze.
In pratica, ogni colonna è formata da una serie di blocchi sovrapposti e ogni blocco rappresenta una o più preferenze. Deve essere sempre indicato a quante preferenze corrisponde ogni blocco.

= 1 preferenza
Gli ideogrammi
MI ESERCITO
1. In 4ª B è stata fatta un’indagine per conoscere i passatempi preferiti dalle bambine e dai bambini. Osserva la tabella di frequenza e realizza un istogramma sul quaderno che rappresenti i dati ottenuti.
= 2 bambini/e
Nell’ideogramma i dati vengono rappresentati attraverso simboli Naturalmente anche in questo caso occorre che sia spiegato il significato dei simboli.
1 bambino/a
2
fantascienza
avventura “gialli” fumetti fantasy
GLI INDICI STATISTICI
I dati raccolti nelle indagini statistiche vengono anche elaborati per ricavare alcuni indici (valori) statistici
La moda
• Osserva l’istogramma realizzato in base alle preferenze sportive in 4ª A.
– Qual è lo sport preferito?
Questo valore rappresenta la moda
La moda è il dato che si presenta con maggior frequenza
La mediana
• Osserva i dati riguardanti il numero di scarpe degli alunni e delle alunne di 4ª B. Fai attenzione: i numeri sono stati scritti in ordine crescente.
32323233333434343435363636363637373738
– Quale numero di scarpe occupa il posto centrale in questa serie di dati?
Questo valore rappresenta la mediana.
La mediana è il valore che sta al centro (cioè nel punto medio) di una serie di dati sistemati in ordine crescente
La media aritmetica
• Osserva la tabella con i gol di una squadra di calcio nelle varie partite.
La media aritmetica rappresenta i gol segnati in una partita se la squadra avesse sempre fatto lo stesso numero di gol.
Per calcolare la media aritmetica devi:
• prima sommare tutti i dati considerati;
• poi dividere la somma ottenuta per il numero dei dati
= 1 preferenza
GEOGEBRA
basket pallavolo calcio rugby hockey
CLASSIFICARE
Consideriamo questo gruppo di bambini e bambine e classifichiamoli in base a due caratteristiche: “avere gli occhiali” e “avere lo zaino”. Osserva e completa.

L’intersezione di insiemi
L’unione degli insiemi
1 2 3 4 5 6
Diagramma di Eulero-Venn
Possiamo usare un diagramma di Eulero-Venn. Dove l'insieme “universo” indica l’insieme di tutti i bambini e bambine.
Il diagramma di Eulero-Venn
è formato da una serie di linee curve chiuse accompagnate da un cartellino che indica la caratteristica considerata.
Diagramma di Carrol
Classificare significa dividere un certo numero di elementi in gruppi, in base a una o più caratteristiche. Le classificazioni si possono rappresentare in diversi modi.
universo avere lo zaino avere lo zaino e gli occhiali avere gli occhiali
Possiamo usare una tabella a doppia entrata o diagramma di Carrol.
bambini che hanno lo zaino bambini che non hanno lo zaino
Diagramma ad albero
Possiamo usare un diagramma ad albero.
bambini che hanno gli occhiali
bambini che non hanno gli occhiali
Il diagramma di Carrol viene usato per rappresentare classificazioni in base a due caratteristiche.
Nel diagramma ad albero i criteri di classificazione sono scritti sui diversi “rami“ che si leggono dall’alto al basso.
IL CALCOLO DELLE PROBABILITÀ
Calcolare le probabilità, significa calcolare quanto è probabile che accada un certo evento.

Quanti sono gli oggetti nella vasca? Marta può “pescare” qualsiasi oggetto, i casi possibili sono: 23
Quante sono le probabilità che Marta prenda un pesce rosso?
I pesci sono 8, quindi ci sono 8 casi favorevoli cioè 8 23
• Quante sono le probabilità che Marta prenda un delfino? su 23; in frazione:
• Quante che prenda una rana? E una papera?
La probabilità che un caso si verifichi dipende dai casi favorevoli su quelli possibili e si esprime con una frazione.
probabilità = casi favorevoli casi possibili
• Concludi: la probabilità più alta è quella di pescare , la probabilità più bassa è quella di pescare .
1. Indica la probabilità di pescare: un numero pari un numero dispari un numero superiore a 50
2. Colora in modo che la probabilità di pescare una pallina verde sia 5 14 .

CHE COS’È LA MATELUDICA?
La Matematica è difficile? Lo dicono in tanti, ma se mi segui scoprirai che non è così! In questo sussidiario la Matematica è facile, ed è anche un gioco! Viaggiando con me scoprirai che la Matematica può essere un racconto e poi incontrerai la Mateludica, un modo di fare Matematica diverso, giocoso, che ti permetterà di capire e imparare in maniera più semplice.
Mateludica è un percorso che ti mostra tanti modi diversi per arrivare a capire i concetti della Matematica e ad applicarli.
Per farlo utilizza… i Mateludici! Scoprirai come costruirli nella prossima pagina. È importante sceglierne solo un tipo da usare tutto l’anno.
SOMMARIO
COSTRUIRE I MATELUDICI
Che cosa ti serve?
Mateludico “striscette”: fogli a quadretti da 1 cm, forbici con la punta arrotondata, cartoncino, colla stick.
Mateludico “unità quadrata”: fogli a quadretti da 1 cm, matita, forbici con la punta arrotondata, cartoncino, colla stick.
LE STRISCETTE
Prendete i fogli a quadretti da 1 cm e incollateli su cartoncino per renderli più resistenti. Poi ritagliate delle striscioline larghe 1 quadretto e lunghe 20. Per tagliarle basta seguire il bordo dei quadretti!
DIVERTITEVI CON UNA SFIDA!
Fate a gara a chi prepara più striscette in 20 minuti.
LE UNITÀ QUADRATE
Prendete i fogli a quadretti da 1 cm e incollateli su cartoncino per renderli più resistenti. Poi ritagliate dei quadrati di lato 10 quadretti. Non serve disegnare tutto il bordo del quadrato con la matita: basterà fare un puntino in corrispondenza dei vertici per sapere fin dove tagliare.
DIVERTITEVI CON UNA SFIDA!

Mateludico “cannucce”: solo delle cannucce! Ricorda di usare cannucce biodegradabili.
Inoltre: elastici, graffette, scatoline, buste, contenitori vari…
Segui le istruzioni per realizzare i Mateludici.
Fate a gara a chi prepara più unità quadrate in 20 minuti.
LE CANNUCCE
Per usare il Mateludico “cannucce” non c’è bisogno di incollare e tagliare: l’insegnante vi dirà come procurarvi le cannucce per potervi divertire con la Matematica!
Raggruppare i Mateludici
• Osserva e completa.
Con le striscette

10 = 1 da
Con le unità quadrate
Con le cannucce
= 1 h 10 = 1
Osserva come usare i Mateludici. Un Mateludico vale 1, quindi 1 unità. Quanto vale ogni gruppo?
= 1 uk
= 1 = 1 da = 1 uk = 1 h
da h
Mateludici e simboli
= 1
uk
• Osserva. Come puoi fare per rappresentare sul quaderno i tuoi Mateludici? Puoi usare i colori che vuoi.
I NUMERI
• In gruppi di 4 o 5, unite tutti i vostri Mateludici e contate quanti ne avete.

• Confrontatevi in classe: qual è il metodo più efficace che avete trovato per contare i Mateludici? Assomiglia a uno di questi? Segna con una
Ho contato uno a uno senza raggruppare niente.
Ricorda che hai a disposizione anche elastici, graffette e scatolette!
Ho raggruppato per colore.
Ho raggruppato per decine (10) e poi per decine di decine (100).
Il metodo più efficace è quello di Lin, che raggruppa gli elementi per 10. Perché, secondo te?
Ho raggruppato i Mateludici a seconda di chi li ha portati, poi li ho sommati.
Anna
Lin
Amjad
Marco
PROBLEM SOLVING
A SCUOLA DI QUANTITÀ

Che cosa serve?
Con l’aiuto dell’insegnante, scarica i bigliettini con le scomposizioni da Hub
Scuola • mazzetti di Mateludici
Come si gioca?
1. In coppia, uno di voi interpreta l’insegnante, l’altro l’allieva o l’allievo.
2. L’insegnante porge all’allievo/a un bigliettino in modo che sia visibile la scomposizione del numero.
3. L’allieva/o rappresenta la quantità indicata con i Mateludici. Poi indovina il numero.
4. L’insegnante controlla la risposta sul retro del cartellino.
Ogni 5 bigliettini scambiatevi i ruoli. Proseguite finché i bigliettini non saranno finiti o fino allo “stop” dell’insegnante.
Dopo aver giocato
Perché è importante posizionare unità, decine e centinaia nel giusto ordine?
Perché se cambia la posizione cambia anche il valore del numero.
Riesci a capire il valore di ogni cifra in base alla sua posizione?
sì
La posizione delle cifre all’interno di un numero è importante perché ogni cifra, a seconda della posizione che occupa, assume un valore diverso.
• Osserva e completa.
584 la cifra 4 è unità
741 la cifra 4 è decine, quindi vale unità.
400
463 la cifra 4 è centinaia, quindi vale unità.
Posiziona prima le unità a destra, poi prosegui verso sinistra e rappresenta decine e centinaia.
E SOTTRAZIONE
• Le alunne e gli alunni della 4ª C stanno giocando con i Mateludici. In coppia, osservate e leggete che cosa succede.
PROBLEM SOLVING

Io sono la ladra: ho preso al collezionista dei Mateludici.
Io sono il collezionista: prima avevo 104 Mateludici e ora ne ho solo 94!
Io sono la poliziotta: devo scoprire quanti Mateludici ha preso la ladra!
• Quale operazione deve fare la poliziotta?
• In un altro gruppo, la collezionista non ricorda più quanti Mateludici aveva all’inizio! Leggete il fumetto a lato: siete d’accordo con il poliziotto? Perché?
La collezionista ora ha 78 Mateludici e il ladro ne ha presi 62. Ho capito: la collezionista aveva 78 + 62 = 140 Mateludici!
• Osservate le operazioni: che cosa notate?
78 + 62 = 140
140 – 62 = 78
GIOCO Il dado furfante
QUANTI SONO NASCOSTI?
Che cosa serve?
2 decine di Mateludici
Come si gioca?
1. In coppia, uno o una di voi decide quanti Mateludici utilizzare e li mostra all’altro o all’altra (per esempio 20).
2. Poi nasconde dietro la schiena alcuni Mateludici (per esempio 3).

Indovina quanti ne nascondo!
3. Infine mostra al compagno o alla compagna i Mateludici che non ha nascosto e dice: “Indovina quanti ne nascondo!”.
4. La compagna o il compagno prova a indovinare.
Invertite i ruoli e continuate a giocare fino allo “stop” dell’insegnante!
Dopo aver giocato
Leggi i ragionamenti dei bambini e delle bambine.
I Mateludici in tutto erano 15, io ne vedo 10. Quanti ne mancano per arrivare a 15? 5, perché 10 + 5 = 15.
!
Dai 9 Mateludici iniziali tolgo i 3 che vedo. I Mateludici nascosti sono 6, perché 9 – 3 = 6.
Entrambi i bambini hanno ragione: infatti addizione e sottrazione possono essere applicate alla stessa situazione perché sono operazioni inverse. Osserva e completa.
MOLTIPLICAZIONE E DIVISIONE
• La pizzaiola ha messo lo stesso numero di olive su ogni pizza. Osserva e rispondi.

– Quante pizze ha preparato?
– Quante olive ci sono su ogni pizza?
– Quante olive ci sono in tutto?
5 × 8 = 40
– Con quali operazioni puoi descrivere questa situazione?
• Mary e Francesco hanno scelto due operazioni diverse per descrivere la situazione.
Uso una moltiplicazione
8 × 5 = 40
• I due ragionamenti sono entrambi corretti? sì no
8 × 5 = 40
• Osserva le operazioni: che cosa noti?
40 : 5 = 8
Uso una divisione 40 : 5 = 8
GIOCO Pizza alle olive
× E : 10, 100, 1000
Osserva e completa questo trucchetto con i Mateludici per capire meglio le moltiplicazioni e le divisioni per 10, 100 e 1 000.
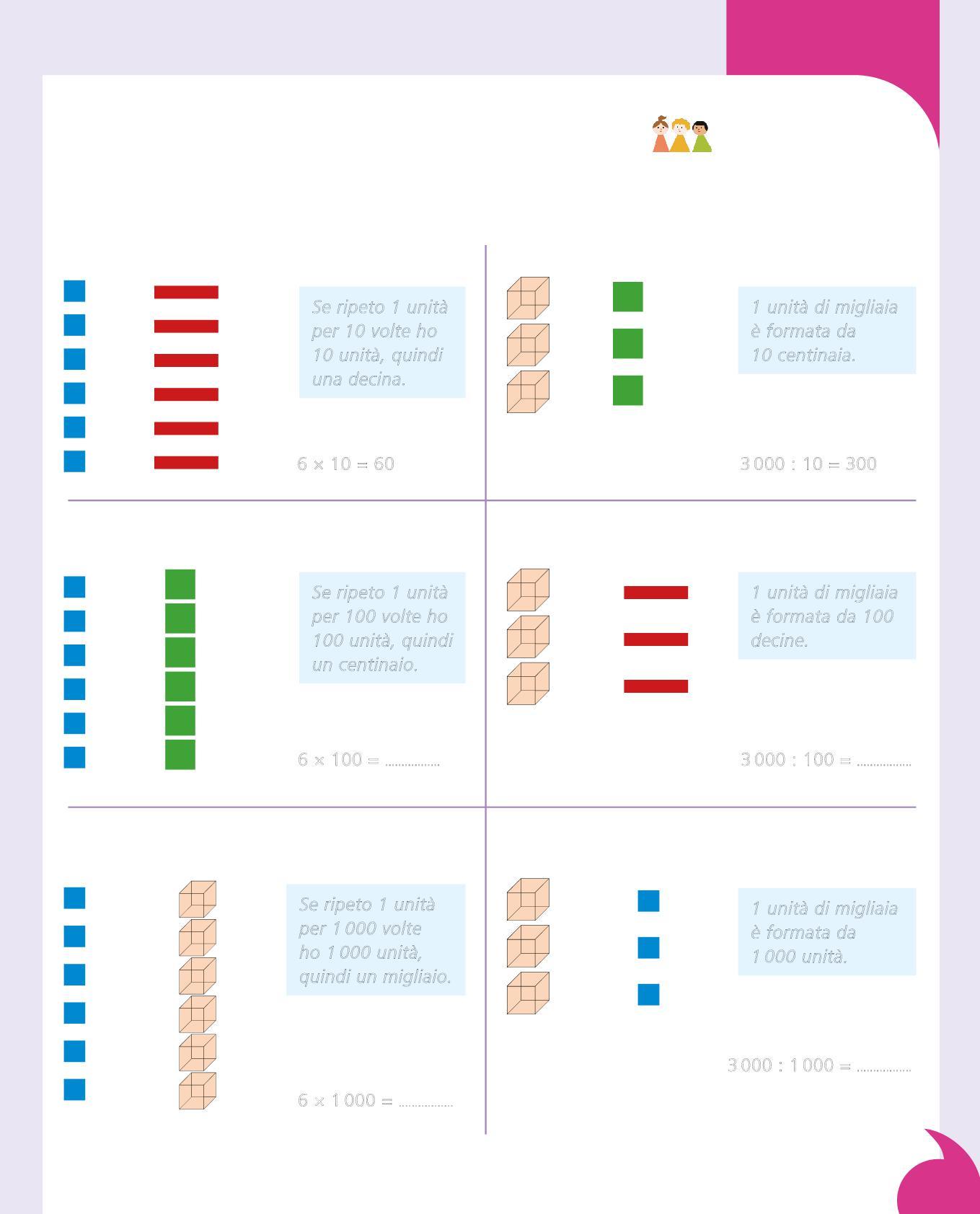
Se ripeto 1 unità per 10 volte ho 10 unità, quindi una decina.
1 unità di migliaia è formata da 10 centinaia.
Se ripeto 1 unità per 100 volte ho 100 unità, quindi un centinaio.
1 unità di migliaia è formata da 100 decine.
Se ripeto 1 unità per 1 000 volte ho 1 000 unità, quindi un migliaio.
1 unità di migliaia è formata da 1 000 unità.
FRAZIONI E DECIMALI

PROBLEM SOLVING
• A coppie, prendete un foglio a quadretti da 1 cm e disegnate un rettangolo con la base di 10 quadretti e l’altezza di 6 quadretti. Questo rettangolo rappresenta un intero
• Tagliatelo in due metà e confrontate i due pezzi che avete ottenuto con quelli dei vostri compagni e compagne, poi rispondete.
– I pezzi che avete ritagliato sono tutti uguali o hanno forme diverse?
– Ogni coppia ha diviso il rettangolo in due metà, cioè in due mezzi?
• Osservate le metà create dai bambini e dalle bambine: ognuna vale 1 2
Davide e John
Marika e Adam
Luca e Simona
e Katia
– Hanno tutte la stessa forma? sì no
– Occupano tutte lo stesso numero di quadretti? sì no
– Sono tutte metà dell’intero di partenza? sì no
– È possibile ricreare l’intero utilizzando due metà di bambini o bambine diversi? sì no
– Frazionare un intero significa: dividerlo in parti identiche. dividerlo in parti della stessa grandezza.
Per verificare le vostre risposte, disegnate le metà sul quaderno, ritagliatele e provate a ricostruire gli interi!
Giulia
FRAZIONI A CONFRONTO

Che cosa serve?
30 bigliettini di carta • quaderno • matita e colori
Come si gioca?
1. Giocate a coppie. Scrivete su ogni bigliettino una frazione che abbia come denominatore 2, 3, 4, 5, 6 o 10.
2. Pescate un bigliettino a testa.
3. Ognuno/a disegna sul quaderno un rettangolo 10 × 6 e rappresenta la frazione che ha estratto.
4. Osservate le due frazioni: quale è maggiore?
5. Scrivete sul quaderno le frazioni e completate con i simboli >, < o =.
6. Chi ha la frazione maggiore guadagna un punto. Vince chi arriva per primo a 10 punti!
Dopo aver giocato
Osserva questi turni della partita di Giorgia e Claudio e completa con >, < o =, come nell’esempio. Poi segna con una di chi è il punto.
Puoi assegnare sempre il punto? sì no Perché?
Perché 4 8 e 2 4 hanno lo stesso valore.

FRAZIONI E NUMERI DECIMALI
Usa i Mateludici per capire meglio che cosa sono i decimi, i centesimi e i millesimi
• Prendi un Mateludico, dividilo in 10 parti uguali usando le forbici con la punta arrotondata. Che cosa ottieni?
Tina usa il Mateludico dell’unità quadrata: ha frazionato l’unità in 10 parti uguali e ha ottenuto 1 10 dell’unità, cioè un decimo.
Puoi scrivere questa quantità come se fosse un numero decimale:
parte intera , parte decimale
h da u d c m
0 , 1 0,1
– Rifletti: quanti decimi ci sono in un’unità?
• Prendi un decimo e dividilo in 10 parti uguali. Che cosa ottieni?
Tina ha frazionato un decimo in 10 parti uguali e ha ottenuto 1 100 dell’unità, cioè un centesimo.
parte intera , parte decimale
h da u d c m
0 , 0 1 0,01
– Rifletti: quanti centesimi ci sono in un decimo?
Quanti centesimi ci sono in un’unità?
• Prendi un centesimo e dividilo in 10 parti uguali. Che cosa ottieni?
Tina ha frazionato un centesimo in 10 parti uguali e ha ottenuto 1
1 000 dell’unità, cioè un millesimo
parte intera , parte decimale
h da u d c m 0 , 0 0 1 0,001
– Rifletti: quanti millesimi ci sono in un centesimo?
Quanti in un decimo? E in un’unità?
PESO LORDO, PESO NETTO E TARA
• Portate in classe una bilancia da cucina, una ciotola e un sacchetto di zucchero. Mettete un po’ di zucchero nella ciotola e posizionatela sulla bilancia. Poi rispondete.
– Quanto pesa la ciotola vuota?
– Quanto pesa lo zucchero nella ciotola?
– Quanto pesa la ciotola con lo zucchero?
• Siete riusciti a rispondere a tutte le domande? sì no
Riflettete: come potete fare per trovare questi pesi?

• Confrontatevi in classe e rispondete.
– Avete risposto a tutte e tre le domande con lo stesso peso? sì no
– Perché?
– Come avete fatto a calcolare il peso dello zucchero?
– Come avete fatto a calcolare il peso della ciotola?
Quando pesiamo degli oggetti, dobbiamo sempre distinguere tra:
– il peso del prodotto senza quello del contenitore (peso netto);
– il peso del recipiente vuoto (tara);
– il peso complessivo del prodotto e del contenitore (peso lordo).
Se conosci due di questi pesi, puoi calcolare il terzo.
MISURE IN ORDINE

Che cosa serve?
21 foglietti
Come si gioca?
1. Dividetevi in 3 squadre. Ognuna sceglie una misura e prende il numero corrispondente di foglietti: lunghezza (7 foglietti), capacità (7 foglietti) oppure massa (7 foglietti)
2. Scrivete sui vostri foglietti le marche delle unità di misura e il nome completo (per esempio: l litro) e mischiateli.
3. Vince la squadra che mette in ordine decrescente i propri cartellini in meno tempo!
Dopo aver giocato
• Osserva e completa la tabella.
• Rispondi alle seguenti domande.
– Quante unità ci sono in una decina?
– Quanti metri ci sono in un decametro?
– Quante decine ci sono in un centinaio?
– Quanti decalitri ci sono in un ettolitro?
– Quanti decimi ci sono in un’unità?
– Quanti decigrammi ci sono in un grammo?
– Quanti centesimi ci sono in un euro?
IL GIOCO DELLA COMPRAVENDITA
Che cosa serve?
• 50 Mateludici raggruppati in mazzetti da 10
• 10 temperini
• 10 gomme
• 10 righelli
• 20 graffette
• 20 matite colorate
• 20 caramelle
• un vassoio e un bicchiere per ogni coppia di bambine/i
• delle monete finte con i valori dell’euro (potete anche realizzarle voi: tagliate dei cerchietti di carta e scrivete sopra il valore di ogni moneta)
Come si gioca?

LISTINO PREZZI
Mateludici: € 5 / mazzetto
Temperini: € 1,20 l’uno
Gomme: € 0,80 ognuna
Righelli: € 2,50 ciascuno
Graffette: € 0,20 ciascuna
Matite colorate: € 1 / matita
Caramelle: € 1,50 l’una
1. A coppie, il giocatore o la giocatrice A fa il o la negoziante, la giocatrice o il giocatore B fa il o la cliente. Per iniziare, i/le negozianti mettono su un grande tavolo tutta la merce del listino.
2. Ogni cliente prende un bicchiere con € 40, decide quali oggetti acquistare e li mette sul vassoio. Attenzione: il o la cliente deve spendere tutti i suoi soldi!
3. Ora scambiatevi i ruoli: – il giocatore o la giocatrice A diventa il o la cliente; ha in mano € 40 che ha incassato prima e deve spenderli; – la giocatrice o il giocatore B diventa il o la negoziante e deve rivendere la merce appena acquistata.
Dopo aver giocato
• Quanti soldi avevano all’inizio del gioco i giocatori o le giocatrici B?
• Quanti soldi hanno adesso?
• Secondo voi, hanno avuto un guadagno? sì no Le giocatrici e i giocatori B non hanno guadagnato nulla, perché alla fine del gioco si sono ritrovati con € 40, cioè la stessa somma che avevano all’inizio.
I soldi che i giocatori e le giocatrici B hanno ricevuto rappresentano il ricavo, non il guadagno.
• Che cosa avrebbero potuto fare le giocatrici e i giocatori B per avere un guadagno? Discutetene in classe.
LE TRASFORMAZIONI GEOMETRICHE
Che cosa serve?
• mattoncini colorati da costruzione
• piano d’incastro dei mattoncini
• nastro adesivo colorato

Come si gioca?
Osserva i disegni in questa pagina, riproduci delle figure posizionando i mattoncini sul piano d’incastro e divertiti a effettuare delle trasformazioni geometriche!
TRASLAZIONE
ROTAZIONE
GIOCO Le trasformazioni geometriche

LE FIGURE PIANE
• Osservate questo quadro, intitolato Kaos Quali figure riconoscete?
• In piccoli gruppi, svolgete la seguente attività.
– Prendete dei foglietti e su ognuno disegnate una tra le figure piane che avete riconosciuto. Ritagliatele e provate a raggruppare le figure per mettere un po’ di ordine... nel Kaos!
– Confrontate la vostra classificazione con quelle fatte dal resto della classe. Quale vi sembra più adatta? Discutetene insieme all’insegnante.
• Osservate la classificazione sotto: è simile alla vostra? Ci sono delle differenze? Discutetene in classe.
• Quale criterio è stato scelto per raggruppare le figure?
FIGURE PIANE
IL PERIMETRO DELLA SCUOLA
La preside della scuola primaria Giacomo Leopardi vuole cambiare i battiscopa di tutti i pavimenti, ma non sa quanti pezzi acquistare. Chiede ai bambini e alle bambine di classe quarta di aiutarla.
Carlos decide di contare i pezzi di battiscopa uno a uno, ma in questo modo impiega tantissimo tempo.
• Ogni pezzo di battiscopa è lungo un quadretto. Ti viene in mente qualche trucchetto per contare i pezzi di battiscopa più velocemente?

Trovare una strategia per calcolare il numero di pezzi di battiscopa per rivestire tutto il perimetro è complicato, ma alla fine Clara ha osservato con attenzione la pianta della scuola e ha pensato che:
– la somma dei lati verticali verdi è uguale alla somma dei lati verticali rossi, quindi è sufficiente contare i quadretti che compongono i lati verdi e trovare il doppio.
(14 + 4 + 2) × 2 = 20 × 2 = 40 pezzi di battiscopa – Il lato viola orizzontale è uguale alla somma dei due rosa: 10 × 2 = 20.
• Ora continua tu il ragionamento di Clara. Lato giallo = lati blu × 2 = I due lati arancioni sono uguali: × 2 =
12 24 4 8 20 24 8 92
• Il numero totale dei pezzi di battiscopa che servono è: 40 + + + =
L’AREA DEI PAVIMENTI DELLA SCUOLA
Alla scuola Giacomo Leopardi le bambine e i bambini di classe quarta si sono appena divertiti a scoprire la lunghezza del perimetro della loro scuola. Decidono di fare una gara: vince chi riesce a trovare più velocemente e senza errori l’area di tutta la scuola!
• I bambini e le bambine decidono di usare come unità di misura la piastrella, che nella pianta della scuola è grande un quadretto. Ti viene in mente qualche trucchetto per contare le piastrelle velocemente?

Pensando pensando, a Marco è venuta in mente una soluzione per velocizzare il calcolo: ha diviso tutta la superficie della pianta della scuola in tanti rettangoli e quadrati.
A questo punto ha sfruttato ciò che aveva imparato in classe seconda studiando le tabelline: ha moltiplicato il numero di piastrelle della prima riga per il numero di righe e ha trovato il numero totale di piastrelle. I bambini e le bambine della classe hanno iniziato a calcolare l’area A: 10 × 14 = 140 piastrelle.
• Ora continua tu.
– Area B:
– Area C:
– Area D:
– Area E:
• Ora somma tutti i prodotti che hai appena trovato: 140 + + + + = A B C D E
8 × 8 = 64
5 × 4 = 20
4 × 8 = 32
8 × 4 = 32 64 20 32 32 288
LEGGI LA MATEMATICA
La Matematica non è solo numeri, ma anche... immagini! Ripassa, approfondisci e divertiti con gli albi illustrati e i libri consigliati da Gea.

Che problema c’è? di Irene Venturi, Einaudi Ragazzi
La leggenda delle divisioni di Lorenzo Baglioni, Mondadori
Il bruco misuratutto di Leo Lionni, Babalibri
I magnifici dieci di Anna Cerasoli, Editoriale Scienza
Io conto di Anna Cerasoli, Feltrinelli Kids
Ada Lovelace & la macchina del futuro, Mondadori
Mostri in Geometria di Lorenzo Baglioni, Mondadori
Mi esercito in... Matematica 4

IL MIO ATLANTE • RIPASSA CON GEA
Le proprietà delle operazioni 172
Le frazioni 174
Perimetro e area 176
BENVENUTI IN 4a • RIPASSA CON GEA
Problemi 178
Numeri 179
Le 4 operazioni 180
Frazioni e numeri decimali 182
Misure 183
Spazio e figure 184
ESERCIZI
I dati 186
Scegli la domanda adatta 187
Un’operazione 188
Due domande e due operazioni 189
Domande nascoste 190
Le tabelle 191
PROBLEMI AUTENTICI 192
Numeri 194
SE SBAGLIO IMPARO 195
SE SBAGLIO IMPARO 196
Numeri in ordine 197
Numeri a confronto 198
Operare con le migliaia 199
Problemi 200
INVALSI • NUMERI 201
SE SBAGLIO IMPARO 202
Addizione 203
Sottrazione 204
SE SBAGLIO IMPARO 205 + e – operazioni inverse 206
Moltiplicazione 207
SE SBAGLIO IMPARO 208
Moltiplicare per 10, 100, 1000 209
Divisione 210
Dividere per 10, 100, 1000 211 × e : operazioni inverse 212
Calcoli veloci 213
Multipli 214
Divisori e numeri primi 215
Problemi 216
Altri problemi 217
INVALSI • OPERAZIONI 218
Frazioni 219
Frazioni a confronto 220
SE SBAGLIO IMPARO 221
Calcolare una frazione 222
Frazioni e numeri decimali 223
Numeri decimali 224
SE SBAGLIO IMPARO 225
Addizioni con i decimali 226
Sottrazioni con i decimali 227
Moltiplicazioni con i decimali 228
Divisioni con i decimali 229
SE SBAGLIO IMPARO 230 Problemi 231
Altri problemi 232 INVALSI • FRAZIONI E NUMERI DECIMALI 233
Misure di lunghezza 234
Misure di capacità 235
Misure di massa 236
Misure di valore 237
Misure di tempo 238 Problemi 239
Altri
ADDIZIONE
PROPRIETÀ COMMUTATIVA
Se cambi l’ordine degli addendi, il risultato non cambia.
5 + 29 + 15 = 49
5 + 15 + 29 = 49

STRATEGIA
Se sostituisci un addendo con due o più numeri la cui somma è uguale all’addendo, il risultato non cambia.
SOTTRAZIONE
PROPRIETÀ INVARIANTIVA
Se aggiungi o sottrai lo stesso numero al minuendo e al sottraendo, il risultato non cambia.
ADDIZIONE
PROPRIETÀ ASSOCIATIVA
Se sostituisci due o più addendi con la loro somma, il risultato non cambia.
13 + 25 + 45 = 83
13 + (25 + 45) = 13 + 70 = 83
16 + 23 = 39 16 + 20 + 3 = 16 + 20 + 3 = 39
MOLTIPLICAZIONE
PROPRIETÀ COMMUTATIVA
Se cambi l’ordine dei fattori, il risultato non cambia.
27 × 2 = 54
2 × 27 = 54
MOLTIPLICAZIONE
PROPRIETÀ DISTRIBUTIVA
Se scomponi un fattore in due addendi, moltiplichi ogni addendo per l’altro fattore e poi sommi i prodotti, il risultato non cambia.
7 × 8 = 56
7 × (5 + 3) =
(7 × 5) + (7 × 3) =
35 + 21 = 56
DIVISIONE :
PROPRIETÀ INVARIANTIVA
Se dividi o moltiplichi il dividendo e il divisore per uno stesso numero, il risultato non cambia.
MOLTIPLICAZIONE
PROPRIETÀ ASSOCIATIVA
Se sostituisci due o più fattori con il loro prodotto, il risultato non cambia.
5 × 2 × 5 = 50
(5 × 2) × 5 =
10 × 5 = 50
STRATEGIA DI CALCOLO • MOLTIPLICAZIONE
Se sostituisci un fattore con due o più numeri il cui prodotto è uguale al fattore, il risultato non cambia.
25 × 12 = 300
25 × (2 × 6) =
25 × 2 × 6 = 300
125 : 25 = 5
250 : 50 = 5
125 : 25 = 5
25 : 5 = 5 ×2 :5 ×2 :5
FRAZIONI PROPRIE
Una frazione propria indica una parte dell’intero, quindi il numeratore è minore del denominatore.
FRAZIONI IMPROPRIE
Una frazione impropria ha il numeratore maggiore del denominatore.

FRAZIONI APPARENTI
Una frazione è apparente quando il numeratore è un multiplo del denominatore. Quindi una frazione è apparente anche quando ha il numeratore uguale al denominatore.
Se due frazioni hanno lo stesso numeratore, è maggiore la frazione con il denominatore minore.
LE FRAZIONI

FRAZIONI COMPLEMENTARI
Due frazioni sono complementari quando sommate formano un intero.
FRAZIONI EQUIVALENTI
FRAZIONI DECIMALI 5 6 + 1 6 =
Due o più frazioni sono equivalenti se indicano la stessa quantità dell’intero.
2 4 = 4 8 = 8 16
Tutte queste frazioni rappresentano la metà dell’intero. Quindi sono equivalenti.
Le frazioni che hanno come denominatori 10, 100, 1000 si chiamano frazioni decimali.
Se due frazioni hanno lo stesso denominatore, è maggiore la frazione con il numeratore maggiore.
PERIMETRI
Il perimetro (P) è la misura di lunghezza del contorno di una figura, cioè la somma di tutti i suoi lati.
triangolo scaleno
triangolo isoscele
triangolo equilatero
rettangolo e romboide
trapezio isoscele
trapezio scaleno e trapezio rettangolo
AREA DEL RETTANGOLO E DEL ROMBOIDE
L’area del rettangolo e del romboide si ottiene moltiplicando la misura della base per quella dell’altezza.
A = b × h
AREA DEL QUADRATO
L’area del quadrato si ottiene moltiplicando la misura del lato per se stessa.
A = × l
PERIMETRO

AREA DEL ROMBO
L'area del rombo si ottiene moltiplicando la diagonale maggiore (D) per la diagonale minore (d) e dividendo il prodotto per 2.
A = D × d 2
AREA DEL TRAPEZIO
L'area del trapezio si ottiene sommando le basi, moltiplicando il risultato per l’altezza e dividendo il prodotto per 2.
A = (B + b) × h 2
AREA DEL TRIANGOLO
L’area del triangolo si ottiene moltiplicando la misura della base per quella dell’altezza e dividendo il prodotto per 2.
PROBLEMI
Di solito i numeri presenti nel testo di un problema sono dati che ti servono per risolverlo, sono DATI
UTILI. A volte però capita che ci siano anche dati che non servono alla soluzione, sono DATI INUTILI!
1 Leggi il testo del problema e rispondi alle domande.
A teatro questa sera ci sono 724 persone. 566 sono femmine. Le sedie vuote sono 84 Quanti sono gli spettatori maschi?
• Cancella con una riga il dato inutile del problema.
• Quali sono i due dati utili?
• Risolvi il problema.

Il numero di persone totali e il numero di femmine.
Leggi bene il testo, trova la domanda e cerca i dati!
Gli spettatori maschi sono 158.
Nel testo di un problema possono esserci DATI NASCOSTI, cioè numeri nascosti dentro parole come settimana (7), mese (28, 29, 30 o 31), paio (2), doppio (2 volte), triplo (3 volte), giorno (24).
2 Leggi il testo del problema e rispondi alle domande.
Un mazzo contiene una dozzina di rose. Giuliana compra 5 mazzi di rose. Quante rose compra in tutto?
• Sottolinea il dato nascosto.
• Come si traduce in numero?
dozzina = 12
• Risolvi il problema.
Compra in tutto 60 rose.
3 Risolvi i seguenti problemi.
• Lucio ha due scatole di pastelli, in una ce ne sono 12 e nell’altra il doppio. Quanti pastelli ha Lucio?
Attenzione al dato nascosto!
• Elena si sta allenando per la maratona di Chicago. In una settimana si allena per 28 ore. Quante ore si allena al giorno?
In tutto Lucio ha 36 pastelli. Elena si allena 4 ore al giorno.
NUMERI
Il nostro sistema di numerazione si chiama posizionale perché ogni cifra ha un valore diverso a seconda della posizione che occupa.
1 Indica il valore della cifra colorata. Segui l’esempio.
989 8 da 2 341 6 503
7 612 7 0
2 Completa la tabella scomponendo i numeri.

La cifra 0 si usa per indicare una posizione vuota!
3 Componi i numeri.
2 h 8 da 0 u = 3 uk 0 h 9 da 9 u = 6 da 3 u = 1 uk 4 h 0 da 8 u =
I simboli > (maggiore), < (minore), = (uguale) si usano per confrontare i numeri.
4 Completa con i simboli >, <, =.
5 Riscrivi i numeri in ordine crescente: dal minore al maggiore.
Ricorda, tra due numeri interi il maggiore è quello con più cifre!
6 Riscrivi i numeri in ordine decrescente: dal maggiore al minore.
LE 4 OPERAZIONI
I TERMINI DELL’ADDIZIONE I TERMINI DELLA SOTTRAZIONE addendo 8 + 9 = 17 addendo minuendo 17 – 8 = 9 sottraendo
1 Calcola in riga.
2 Calcola in colonna. somma o totale resto o differenza
Ricorda, l’addizione si può sempre fare!
35 + 5 = 18 + 19 = 25 + 25 + 250 = 86 + 2 + 100 = 64 + 5 + 81 = 4 + 22 + 160 =
hdau
430+

3 Calcola in riga.
35 – 5 =
– 85 =
4
127= hdau
376–151= khdau
1236–115= hdau 654+ 313= hdau
– 220 =
842–220= khdau
1358–1104= khdau 1415+ 262= hdau
419–306= khdau
1929–718= khdau 2047+ 1710= hdau 973–552=
=
Ricorda, il sottraendo deve essere minore del minuendo!
I TERMINI DELLA MOLTIPLICAZIONE I TERMINI DELLA DIVISIONE
dividendo

moltiplicando
8 × 9 = 72
moltiplicatore
prodotto o totale quoziente quoto (resto 2)
72 : 8 = 9
divisore
dividendo 14 : 3 = 4
divisore
5 Calcola in colonna.
Ricorda, la moltiplicazione è un’addizione ripetuta e si può sempre fare!
6 Calcola in colonna con il cambio.
7 Calcola in riga.
8 Calcola in colonna, attenzione al resto. 8 6

FRAZIONI E NUMERI DECIMALI
Una frazione indica una parte di intero e si scrive così:
numeratore indica le parti di un intero da considerare (colorare, prendere...)
linea di frazione indica una divisione in parti uguali
denominatore indica in quante parti uguali è stato frazionato l’intero
Numeri decimali
• Sono i numeri con la virgola. La virgola si scrive dopo le unità.
• Hanno una parte intera (prima della virgola) e una parte decimale (dopo la virgola).
1 In ogni intero osserva la parte colorata e scrivi la frazione corrispondente. Segui l’esempio.
4 k h da u,d c m parte intera parte decimale 3
2 Trasforma ogni frazione decimale in numero decimale. Segui l’esempio.
3 Trasforma ogni numero decimale in frazione decimale. Segui l’esempio.
4 Scrivi in cifre i numeri decimali rappresentati sugli abachi.
Ricorda, le frazioni decimali hanno 10, 100, 1000 come denominatore.
5 Indica il valore della cifra in colore. Segui l’esempio.
MISURE
• La marca che indica l’unità di misura si scrive con la lettera minuscola e senza il punto.
• L’equivalenza è un’uguaglianza fra due misure che hanno lo stesso valore e marche diverse.
Nelle equivalenze i multipli sono 10, 100, 1000 volte maggiori dell’unità di misura fondamentale, i sottomultipli 10, 100, 1000 volte più piccoli.

1 Completa le equivalenze.
Misure di lunghezza
3 m = dm
20 dam = m
6 km = m
9 m = cm
Misure di capacità 6 l = cl 8 l = dl
7 hl = l 3 l = ml
Misure di massa
61 dg = g
9 kg = g
3 g = mg
6000 mg = g
Il trascorrere del tempo si può misurare. L’unità di misura fondamentale del tempo è il secondo (s).
2 Quanto manca? Fai attenzione alla marca delle misure.
6,5 hg + hg = 1 kg
dl + 1450 ml = 2 l
10 dag + g = 1 hg
3 Completa le uguaglianze.
1 minuto = secondi
2 min = s
5 min = s
ora = minuti
h = min
h = min 1 giorno = ore 2 d = h
3 d = h
RETTA

SEMIRETTA
SPAZIO E FIGURE
• È dritta
• Può avere direzione orizzontale, verticale, obliqua.
• È infinita: non ha né inizio né fine.
• Si indica con una lettera minuscola dell’alfabeto.
• Ha un inizio, ma non ha una fine.
• L’inizio si indica con una lettera maiuscola dell’alfabeto.
• La semiretta si indica con una lettera minuscola dell’alfabeto.
• Ha un inizio e una fine (punti estremi).
SEGMENTO
• I punti estremi si indicano con lettere maiuscole dell’alfabeto.
DUE
SEMIRETTE
Quando hanno lo stesso inizio, formano un angolo, che è la parte di piano tra esse racchiusa.
Se le due semirette sono perpendicolari, l’angolo è retto ampiezza angolo acuto angolo giro lato lato
angolo piatto angolo ottuso
1 Colora di rosso il segmento, di viola la linea retta, di verde la semiretta.
2 Classifica gli angoli scrivendo: retto, acuto, piatto, giro, ottuso. retto ottuso acuto piatto giro
Ogni figura piana ha due dimensioni: la lunghezza e la larghezza
Il poligono:
• è una figura piana delimitata da una linea spezzata, chiusa, non intrecciata;
• prende il nome dal numero di vertici o di angoli o di lati;
• la misura del confine si chiama perimetro (somma dei lati);
• la misura della superficie si chiama area
3 Colora i vertici del triangolo, i lati del quadrilatero e gli angoli dell’esagono.

4 Segna con se le misure del perimetro e dell’area della figura sono giuste.
Perimetro = 40 Area = 70 unità di misura:
5 Calcola area e perimetro delle seguenti figure. Segui gli esempi.

I DATI
1 Individua i dati: cerchia in giallo quelli utili e in rosso quelli inutili.
a. Un meleto è composto da 64 file di 48 meli ciascuno. Quanti meli in tutto? Sapendo che ogni pianta è alta in media 2,5 m e produce 80 kg di mele, quante mele produce in tutto quel meleto?
b. Un cartolaio ha venduto 168 quaderni al prezzo di € 1,25 l’uno. Sapendo che ha dovuto spendere € 1 250 per il riscaldamento del negozio, quanto ha ricavato dalla vendita dei quaderni?
c. Gabriella ha comprato 15 scatolette di cibo per cani per la cagnolina Mia di 13 anni e 10 per la gatta Cherie di 15 anni. Quante scatolette ha comprato in tutto Gabriella?
d. Yaren ha comprato 3 piante grasse, 2 vasi con gelsomini e 1 di girasoli. In tutto ha speso 85 euro Se regala 1 gelsomino a Irene, quante piante rimangono a Yaren?
2 Individua nei seguenti problemi il dato mancante, poi aggiungilo e risolvi sul quaderno.
a. A una gita scolastica partecipano 50 alunni e alunne. Si spendono € 450 per il pranzo e 10 volte il prezzo del biglietto del museo per pagare il noleggio del pullman. Quanto costa la gita a testa?
Dato mancante:
prezzo del biglietto del museo es. € 14
b. Una commerciante acquista 6 modelli di scarpe numero 36 e le sistema nella scaffalatura della vetrina del suo negozio. Quanto spende in tutto?
Dato mancante:
c. Kim riceve in regalo un cesto di frutta. Il cesto contiene 0,5 kg di mele rosse, 0,5 kg di mele gialle, 1 kg di pere e dei mandarini. Quanto pesa in tutto la frutta contenuta nel cesto?
Dato mancante:
costo di un paio di scarpe es. € 50 peso dei mandarini es. 1 kg
3 Individua nei seguenti problemi il dato nascosto, poi scrivi a che numero corrisponde.
a. Il papà ha comprato al supermercato due confezioni da una dozzina di uova al prezzo di € 2,60 a confezione. Qual è il prezzo del singolo uovo?
Dato nascosto:
b. Lorenzo ha comprato una confezione di penne e ne ha regalato la metà a David. Se la confezione conteneva 24 penne, quante penne ha regalato a David?
Dato nascosto:
una dozzina = 12 metà = 1/2
c. Katia ha 3 decenni in meno di sua mamma. Se sua mamma ha 39 anni, quanti anni ha Katia?
Dato nascosto:
decennio = 10 anni
SCEGLI LA DOMANDA ADATTA
1 Per ciascun problema segna la domanda adatta, poi risolvi sul quaderno.
a. Mattia ha comprato una maglietta e l’ha pagata € 35. Tornando a casa vede la stessa maglia nella vetrina di un altro negozio, al prezzo di € 27,50.
Quanto ha risparmiato Mattia?
Quanto ha speso in tutto?
Quanto ha pagato in più?
b. Mauro compra una confezione di pennarelli da € 4,50 e una scatola di biro per la scuola da € 6,25. Paga con una banconota da 20 euro.
Quanto costano i pennarelli?
Quanto riceve di resto?
Quanto costa in più la scatola di biro?
2 Osserva le illustrazioni e segna una o più domande adatte ai problemi.
b. c. € 7,50 € 9,25
Quante ore resta aperto il centro commerciale alla mattina?
Quante ore resta aperto il centro commerciale di pomeriggio?
Quali sono gli orari del centro commerciale?
Quante ore al giorno resta aperto il centro commerciale?
Quanto si spende per andare al cinema?
Quanto spendono Martina e Marco?
Qual è la differenza tra un biglietto intero e uno ridotto?
Quali sono gli orari del cinema?

Quanto costano all’hg gli asciugamani?
Quanto spende ogni cliente?
Quanto costa l’asciugamano della prima bilancia?
Quanto spendono in tutto i due clienti?
Obiettivi di apprendimento Individuare la domanda di un problema.
UN’OPERAZIONE
1 Scrivi i dati, poi risolvi i problemi con una sola operazione sul quaderno.
a. Domani c’è la finale del torneo di calcio ed Enrico, il suo fratellino Giulio e i loro 2 genitori non vedono l’ora di andare a vederla. Se un biglietto costa € 7, quanto spenderà la famiglia di Enrico per assistere alla finale?
Dati:
4: membri della famiglia
€ 7: costo del biglietto
b. Durante l’intervallo le classi quarte hanno organizzato una partita di pallone. La 4ª A schiera 7 persone, la 4ª B ne schiera 6 e la 4ª C schiera lo stesso numero di persone della 4ª A. Quante persone parteciperanno alla partita?
Dati:
7: persone della 4ª A
6: persone della 4ª B

d. Durante la partita di rugby, Elena ha segnato 2 punti e Aisha ne ha segnati 3 in più di Elena.
Quanti punti ha segnato Aisha?
7: persone della 4ª C 5
c. Il nonno di Antonella ha portato in classe 34 cioccolatini per festeggiare, insieme a tutti i bambini e le bambine, l’onomastico della nipote. La classe è composta da 17 alunni e alunne. Quanti cioccolatini potrà avere ciascun bambino o bambina?
Dati:
2: punti segnati da Elena
3: punti che ha segnato Aisha in più di Elena
Dati:
34: numero dei cioccolatini
17: numero degli alunni/e in classe
Dati:
€ 28 6 92 20
e. Il maestro Federico ha distribuito 4 fogli a righe per ogni alunno e alunna. Se in classe oggi sono presenti in 23, quanti fogli ha distribuito il maestro Federico?
Dati: 2
4: numeri dei fogli per alunno/a
23: alunni/e presenti in classe
f. La 4ª C deve svolgere un compito di realtà di Matematica. Per farlo, i 24 bambini e bambine presenti oggi in classe devono dividersi in gruppi da quattro persone ciascuno.
Quante persone ci saranno in ciascun gruppo?
24: bambini/e presenti oggi
4: persone per ogni gruppo
DUE DOMANDE E DUE OPERAZIONI
1 Scrivi i dati, poi risolvi i problemi nei diagrammi e rispondi.
a. Il papà si reca alla stazione per raggiungere la famiglia al mare. Compra il biglietto del treno che costa € 7,50, poi spende € 1,10 per il caffè e € 2,00 per il giornale. Quanto spende in tutto?
Se nel portafoglio aveva € 125,75, quanto denaro gli rimane?
Dati:
€ 7,50: costo del biglietto del treno
€ 1,10: costo del caffè
€ 2,00: costo del giornale
€ 125,75: soldi nel portafoglio
Risposta 1:
Risposta 2:
In tutto spende € 10,60.
Gli rimangono € 115,15.
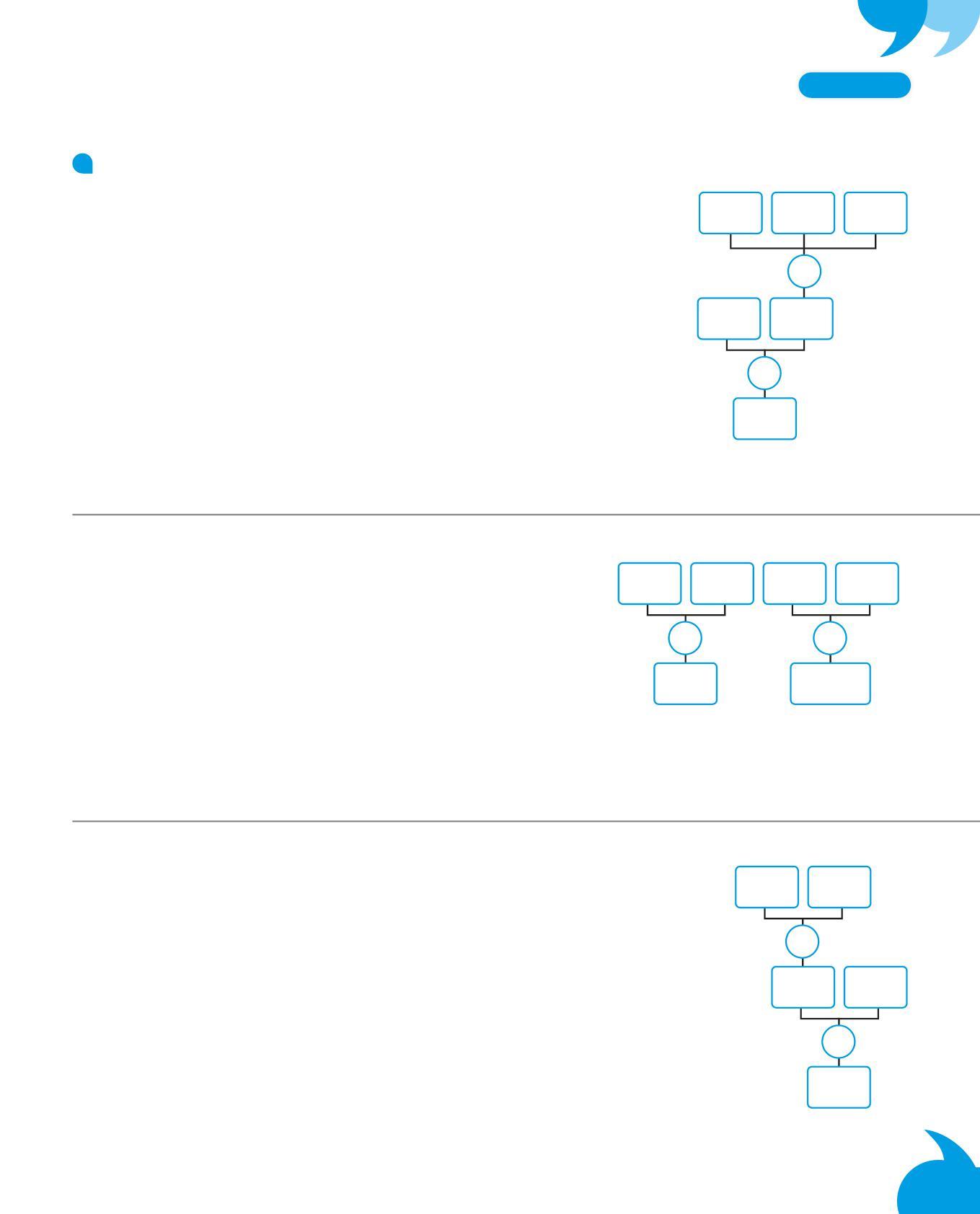
b. La scuola ha organizzato una gita al parco divertimenti. I partecipanti sono 216 e vengono distribuiti su 4 pullman. Quante persone salgono su ogni pullman? Se il biglietto d’entrata costa € 24,90, quale sarà la spesa complessiva?
Dati:
216: partecipanti alla gita
4: numero dei pullman
€ 24,90: costo del biglietto
Risposta 1:
Risposta 2:
Su ogni pullman salgono 54 persone.
La spesa complessiva è di € 5378,40.
c. La distanza tra Milano e Bologna è di 213 km se si percorre l’autostrada e di 238 km se invece si fa la strada statale. Luca sceglie l’autostrada. Quanti chilometri percorre in meno in un viaggio? E in 13?
Dati:
213 km: distanza in autostrada
238 km: distanza in strada statale
Risposta 1:
Risposta 2:
In un viaggio percorre 25 km in meno.
In 13 viaggi percorre 325 km in meno.
DOMANDE NASCOSTE
1 Completa la domanda nascosta e scrivi i dati (attenzione ai dati nascosti!).
Poi risolvi sul quaderno.
a. Un autocarro trasporta 35 sacchi di frumento che pesano ognuno 65 kg.
Durante il viaggio verso il mulino 8 sacchi cadono dall’autocarro.
Quanti sacchi ?
Quanti kg si sono persi?
Dati:

d. Per confezionare 20 sciarpe di seta si utilizzano 10 m di stoffa del costo di € 80 al metro.
A questo bisogna aggiungere la manodopera che costa 240 euro.
520 kg
35: sacchi di frumento
65 kg: peso di un sacco
8: sacchi che cadono
b. Sonia ha nel portafoglio 220 euro. Spende 38 euro per una camicetta, 65 euro per un paio di scarpe.
rimane nel portafoglio
Quanto ?
€ 117
Alla fine compra anche una cravatta per il papà.
Al ritorno a casa ha ancora € 95 nel portafoglio; quanto è costata la cravatta?
€ 22
Dati:
€ 220: soldi nel portafoglio all'inizio
€ 38: costo della camicetta
€ 65: costo delle scarpe
€ 95: i soldi nel portafoglio alla fine
c. La mamma riceve uno stipendio mensile di 1560 euro e un premio annuale di 1200 euro.
riceve in un anno
Quanto ?
€ 19920
Se le spese annuali della famiglia sono di 18 700 euro, quanto potrà risparmiare la mamma?
Dati:
€ 1220
€ 1560: stipendio della mamma
€ 1200: premio annuale
€ 18700: spese annuali della famiglia
la stoffa in tutto
Quanto costa una sciarpa?
12: confezioni nella dispensa rimangono
Quanto costa ?
€ 800
€ 52
20: sciarpe da confezionare
10 m: stoffa per 20 sciarpe
€ 80 : costo della stoffa al metro
€ 240 : costo della manodopera
Dati: e. Nella dispensa ci sono 12 confezioni di pasta che pesano 500 g ciascuna.
Quanto ?
Il papà cucina ogni giorno 300 g di pasta per tutta la famiglia, che è composta da quattro persone.
Per quanti giorni basterà la pasta della dispensa?
500 g: peso di una confezione
300 g: pasta che cucina il papà al giorno
Dati: f. Mio fratello Giovanni lavora in una pizzeria e consegna le pizze a domicilio.
Guadagna 14 euro all’ora.
Lavora 2 ore il lunedì e il martedì, 3 ore il mercoledì e il venerdì e 4 ore il giovedì.
Quante ?
20 pesa la pasta in tutto ore lavora in una settimana 14
Quanto guadagna Giovanni se lavora tutta la settimana?
€ 196
Dati:
€ 14: guadagno all’ora
2: ore di lavoro il lunedì
2: ore di lavoro il martedì
3: ore di lavoro il mercoledì
3: ore di lavoro il venerdì
4: ore di lavoro il giovedì
6000 g
1 Risolvi i problemi sul quaderno.
LE TABELLE
a. Luca si sta allenando per la corsa campestre della scuola. In tabella è registrato il numero dei giri che ha fatto ogni giorno intorno al campetto. Se ogni giro misura 310 m, quanti metri percorre Luca nel suo allenamento settimanale?

b. Liang si è iscritto a un corso di tennis e vuole acquistare tutto il necessario. Con i suoi risparmi potrà spendere al massimo 200 euro. In negozio ci sono due proposte: scegline una, calcola e verifica se i soldi basteranno a Liang e se gli avanzerà qualcosa. Motiva la tua scelta.
allenamento in una settimana giorno numero giri
lunedì 3
martedì 4
mercoledì 2
giovedì 3
venerdì 4
sabato 3
c. Al sabato il cinema Arcobaleno prevede spettacoli pomeridiani al costo di 8 euro e serali al costo di 6 euro. Osserva la tabella a fianco e calcola l’incasso totale.
La domenica, invece, il biglietto è unico per tutti gli spettacoli e costa € 6, ma per i bambini e le bambine fino a 12 anni il costo è ridotto a € 4. Osserva le presenze in tabella e calcola l’incasso della domenica.
prima proposta
nuovi prodotti
racchetta: € 115,50
tubo di palline: € 7,40 polsini: € 9,95
sabato
seconda proposta
prodotti dell’anno precedente scontati
racchetta: € 69,90
tubo di palline: € 5,55 polsini: € 7,30
spettacolo 14:0016:0020:3022:30
biglietti venduti 38 75 273104
domenica spettacolo 14:0016:0020:3022:30
biglietti adulti 41 125180 92
biglietti bambini/e sotto i 12 anni 29 60 12 0
Complessivamente, tra sabato e domenica, quanto ha incassato il cinema Arcobaleno?
5890 m € 6198 avanzano € 67,15 avanzano € 117,25 € 3166 € 3032
PROBLEMI AUTENTICI
I problemi autentici assomigliano a quelli della vita di tutti i giorni: non sono sempre risolvibili, ma comunque richiedono di ragionare sulla situazione e trovare delle strategie utili.
1 Risolvi i problemi.
a. La sorella maggiore dei gemelli David e Isacco ha appena preso la patente della moto e, come promesso, il primo giro tocca proprio a uno dei due ragazzini.
Per decidere chi dei due portare per primo, la ragazza propone loro di sfidarsi con il gioco “Pari e dispari”. David sceglie dispari e Isacco pari, ma non è molto contento. Prima di giocare a Isacco viene un’idea per avere vittoria certa e propone:
Moltiplichiamo i due numeri che usciranno anziché sommarli!
David accetta la proposta senza pensarci.
Come può Isacco essere così convinto di vincere?
Hai capito la strategia che metterà in atto?
Qualsiasi numero moltiplicato per 2 dà un numero pari, quindi a Isacco basterà proporre il numero 2 e i due numeri moltiplicati saranno sicuramente pari.

b. La classe 4a B deve preparare i costumi per lo spettacolo di Natale, ma la maestra Rosa si accorge di non aver acquistato decorazioni a sufficienza per “addobbare” tutti i bambini e le bambine che dovranno travestirsi da albero di Natale. Così Rosa chiede a Samira di andare al negozio del paese a prendere il maggior numero possibile di palline colorate. Rosa dà a Samira una banconota da € 50 per gli acquisti.
Samira va in fretta al negozio e chiede subito aiuto al signor Mattia, che è molto simpatico e gentile:
Mattia, Mattia, quante palline di Natale posso acquistare per € 50?
Il signor Mattia le risponde così:
Dipende, cara, qui ne abbiamo di due tipi: le palline più piccole sono confezionate in pacchi da 8 e ciascuna confezione costa € 5; queste invece sono un pochino più grandi, ogni confezione costa € 10 ma contiene 15 palline. Quali preferisci?
Quali palline sceglieresti tu? Perché?
I pacchi da 8, perché con 50 euro può acquistare 80 palline.
Invece scegliendo i pacchi da 15 ne potrebbe acquistare solo 75.

c. Il campo estivo organizza una gita al parco divertimenti Magic World. Appena arrivati, corrono subito tutti all’attrazione La macchina del tempo, una specie di ascensore che grazie a suoni, immagini ed effetti speciali dà l’illusione di essere trasportati nel passato e nel futuro. Vorrebbero poter salire tutti insieme, ma il cartello davanti alla giostra è chiaro, leggilo!
Massimo, l’accompagnatore, raccoglie velocemente età e pesi di chi vorrebbe salire per cercare di far stare insieme quante più persone possibili e compila questa tabella:
Francesco interviene e propone la seguente soluzione:
Possiamo salire in due gruppi: Marco, Giovanni, Lucia, Cinzia e Sophia al primo giro; Elia, Mikol, Gretel, Massimo e io al secondo turno.
Sophia però non vuole salire sulla giostra senza sua sorella Gretel o suo papà Elia.
Riesci a trovare un modo per accontentare Sophia, sempre rispettando le regole?
Elia e Gretel possono scambiare i loro posti con Lucia e Cinzia
Vai alle pagg. 16-19
NUMERI

1 Scrivi i numeri in lettere.
13 000 =
28 750=
tredicimila
ventottomilassettecentocinquanta
420 312 = 521 009 = 849 750 = 110 020 =
quattrocentoventimilatrecentododici
2 Scrivi i numeri in cifre.
cinquecentoventunomilanove
ottocentoquarantanovemilasettecentocinquanta centodiecimilaventi
cinquemilasettecento = ottomilaquattrocentodiciannove = settecentonovantacinquemila = ventiseimilaottocentosettantatré =
3 Collega i numeri scritti in cifre a quelli scritti in lettere.
42 500 quarantaduemilacinquecento
180 749 seicentoquattromilacentodue
604 102 centottantamilasettecentoquarantanove
4 Cancella con una lo 0 quando è inutile.
1 025 • 24 000 • 0 987 • 25 760 • 01 • 700 000 • 5 020 • 032 870 • 010
5 Per ogni numero indica il valore della cifra colorata. Segui l’esempio.
5 897 5 uk
6 In ogni numero sottolinea la cifra delle unità semplici e cerchia quella delle unità di migliaia.
7 Registra i numeri in tabella e poi componili. Segui l’esempio.
9 uk, 3 h, 2 da, 8 u
7 dak, 5 uk, 7 h, 3 da, 2 u
2 hk, 8 dak, 1 uk, 6 h, 9 da, 4 u
3 hk, 0 dak, 5 uk, 7 h, 1 da, 0 u
8 Completa l’esempio e scomponi i numeri.
12 563 = 1 dak + 2 uk +
5 h + 6 da + 3 u
9 563 =
9 uk + 5 h + 6 da + 3 u
342 700 =
3 hk + 4 dak + 2 uk + 7 h
Non si scrive Si scrive

Riflettendo si impara
• Se davanti non ci sono altre cifre, lo 0 non si scrive.
• Se lo 0 si trova in mezzo ad altre cifre, deve essere sempre scritto.
• Se in una scomposizione il valore di una cifra non compare, significa che la cifra è occupata dallo 0.
1 h e 3 u = 103 non serve scrivere 1 h, 0 da e 3 u
1 h e 2 da = 120 non serve scrivere 1 h, 2 da e 0 u
1uk e 4 u = 1 004 non serve scrivere 1 uk, 0 h, 0 da e 4 u
• Se ci sono numeri decimali, l’unità deve essere sempre indicata anche se è 0.
SI SCRIVE 0,75 E NON SI SCRIVE ,75
• Se si aggiungono degli zeri nella parte decimale dopo l’ultima cifra, il numero non cambia.
2,4 = 2,40 = 2,400
RICORDA: nella parte decimale a volte gli zeri vengono aggiunti per facilitare i calcoli in colonna.
METTITI ALLA PROVA
• Cancella lo zero dove non serve.


• Scomponi i seguenti numeri.
dak + 2 uk + 5
1 h + 2 da 9 hk + 8 uk + 1 h + 7 da 1 hk + 4 uk + 3 da
5 dak + 4 uk + 6 da




Non si scrive
Si scrive



Scrivendo bene si impara meglio
Se scrivi il numero staccando le cifre con uno spazietto (o un puntino) tra i diversi periodi, lo leggerai correttamente e opererai più velocemente. Per dividere in periodi:
• parti dalla cifra delle unità semplici che si trova a destra e dividi il numero in gruppi di tre cifre usando uno spazietto tra un gruppo e l’altro (o un puntino);


• partendo da sinistra leggi il numero e nomina la classe di appartenenza.
23 433 534 666 2 342
mila mila mila
RICORDA: ogni periodo è formato da tre cifre:
• unità • decine • centinaia
Il primo periodo è detto delle “unità semplici” e il secondo è quello delle “migliaia”.
Dopo le migliaia ci sono altri periodi che studierai il prossimo anno
• Dividi in periodi e scrivi il numero in lettere.
Settecentomilasettecentosettanta
Quattrocentomilaquaranta
Trentamilatre
NUMERI IN ORDINE
1 Completa ogni serie di numeri.
3 608 • 3 609 • • 5 720 • 5 721 • • • 9 000 • 9 001 • • • 41 599 • 41 598
2 Scrivi i numeri compresi fra 9 990 e 10 012. 9 990 • • •
• 10 012
3 Riscrivi i numeri in ordine crescente, dal minore al maggiore.
2 560 • 1 087 • 10 413 • 9 702 • 11 500 • 199 999 • 99 900 • 50 453 • • • • • • •
4 Riscrivi i numeri in ordine decrescente, dal maggiore al minore. 1 067 • 5 766 • 789 • 13 790 • 55 980 • 680 000 • 190 000 • 547 897
5 Completa le tabelle.
6 Scopri la regola e completa ogni serie di numeri. Segui l’esempio.
a. 15 • 20 • 25 • 30 • 35 • 40 • 45 La regola è : + 5 b. 12 • 15 • • 21 •
• La regola è : +
c. 200
190
Verso l’Invalsi
7 La frase Il numero precedente di 35 100 è 35 101 è falsa. Perché?
Perché per trovare il numero precedente si deve togliere un’unità,

NUMERI A CONFRONTO
1 In ogni gruppo di numeri sottolinea in verde il numero maggiore e in blu il mi e.
9 560 • 9 506 • 9 605
2 Completa la tabella scrivendo i numeri nella colonna giusta.
9 450 • 100 001 • 10 060
• 15 762 • 1 100 • 9 999
• 20 700 • 206 459 • 101 701
• 45 982 • 950 807 • 998
999 • 22 000 • 21 909

661 •
611 • 405 161
3 Segna con una se il confronto fra ogni coppia di numeri è vero (V) o falso (F).
398 > 99 V F
701 < 710 V F
=
4 Confronta le coppie di numeri e completa con >, < o =.
5 Completa le relazioni con > oppure <.
6 Completa scrivendo un numero adatto.
Verso l’Invalsi
7 Quale fra i seguenti numeri puoi scrivere sui puntini per completare la relazione?
996 < > 969
97 997 979
Perché?
Perché è minore di 996 ed è maggiore di 969.
Perché è maggiore sia di 996 sia di 969.
OPERARE CON LE MIGLIAIA
1 Completa le tabelle.

2 Completa le serie di numeri.
3 In ogni casella scrivi la cifra richiesta.
4 Indica il valore della cifra 2.
PROBLEMI
1 Leggi e completa la tabella degli alunni e alunne della 4ª E presenti e assenti durante la settimana.
lunedì martedìmercoledì giovedì venerdì presenti 24 22 25 assenti 1 4 2
2 Scopri i numeri! Leggi e rispondi.
• Ivan pensa a un numero, aggiunge 30 e trova 55. Quale numero ha pensato?
• Sara pensa a un numero, sottrae 50 e trova 100. Quale numero ha pensato?
• Samir pensa a un numero, aggiunge 100, poi ancora 100 e trova 300. Quale numero ha pensato?
• Carla pensa a un numero, sottrae 10, poi ancora 10 e trova 30. Quale numero ha pensato?
3 Scopri le regole delle sequenze in verticale e completa le tabelle
4 Leggi e completa la tabella con l’età dei componenti della famiglia di Annalisa.
Annalisa ha 9 anni, 2 in meno di suo fratello Gigi.
La mamma, Lucia, ha 32 anni, 8 in meno dell’età di Arturo, il papà.
L’età di nonna Giulia è la somma degli anni di Lucia e Arturo.

5 Leggi il testo del problema e segna con una la risposta corretta. A casa di Julia oggi si gioca a tombola. Per fare una cinquina, a Julia serve un numero minore di 30, maggiore di 25 e dispari. Quale numero serve a Julia per completare la cinquina?
Il numero 27 perché è dispari.
Il numero 29 perché è minore di 30.
Non possiamo sapere quale numero serve perché potrebbe essere sia il 27 sia il 29.
Annalisa
Giulia
Verso l’Invalsi
Verso l’Invalsi

NUMERI
1. Segna con una come si scrivono in lettere i seguenti numeri.
30 079 42 712
A. trentamilasettecentonove
B. trentamilasettantanove
C. tremilasettantanove
D. trentamilanovantasette
A. quarantaduemilasettecentoventuno
B. quarantaduemilasettecento
C. quarantaduemilasettecentododici
D. quarantaduemilasettantadue
2. Qual è la cifra delle decine di migliaia nel numero 327 601?
A. 2 B. 0
C. 3 D. 7
3. Segna con una il numero corrispondente a 7 dak 6 uk 9 h 4 u.
A. 7 694
B. 76 940
C. 76 904
D. 70 694
4. Qual è la scomposizione esatta del numero 9 058?
A. 9 dak 0 h 5 da 8 u
B. 9 uk 5 h 0 da 8 u
C. 9 uk 5 h 8 u
D. 9 uk 0 h 5 da 8 u
5. Segna con una quale delle seguenti affermazioni è vera.
A. 12 000 è il successivo di 11 000
B. 5 000 è il precedente di 6 000
C. 9 000 è il precedente di 9 001
D. 1 999 è il successivo di 2 000
6. Osserva la serie dei numeri e segna con una la regola corretta.
125 • 129 • 133 • 137 • 141
A. + 2
B. + 4
C. – 4
D. + 5
60 • 50 • 40 • 30 • 20
A. – 5
B. – 1
C. + 10
D. – 10
7. Segna con una quale delle seguenti relazioni è falsa.
A. 909 < 990
B. 5 550 > 5 505
C. 7 691 > 7 619
D. 20 110 < 20 101
8. Franca pensa un numero, aggiunge 22, poi ancora 10 e trova 39. Quale numero ha pensato?
A. 9
Attenzione all’incolonnamento nell’addizione imparo se sbaglio
Calcola in colonna 4 + 132 + 34 + 1 034
Non si scrive Si scrive



Riflettendo si impara
Quando devi fare un’addizione in colonna con più addendi fai attenzione al valore delle cifre.
RICORDA: puoi partire dal numero più grande e poi mettere gli altri numeri sotto in ordine decrescente (dal più grande al più piccolo) per facilitare i calcoli.
METTITI ALLA PROVA
• Metti in colonna i numeri in ordine decrescente ed esegui le addizioni.
• Calcola in colonna sul quaderno.
946 + 7459 + 9 = 8 + 65897 + 2322
Vai alle pagg. 27-29, 40
ADDIZIONE
1 Calcola applicando la proprietà associativa. Segui l’esempio.
58 + 12 + 9 =
(58 + 12) + 9 =
70 + 9 = 79
64 + 26 + 5 =
(64 + 26) + 5 =
90 + 5 = 95

105 + 15 + 7 =
(105 + 15) + 7
120 + 7 = 127
143 + 37 + 10 =
(143 + 37) + 10 =
180 + 10 = 190
439 + 41 + 20 =
(439 + 41) + 20 =
480 + 20 = 500
656 + 4 + 35 =
(656 + 4) + 35 =
660 + 35 = 695
2 Calcola applicando prima la proprietà commutativa, poi la associativa. Segui l’esempio.
413 + 227 =
(400 + 200) + (13 + 27) =
600 + 40 = 640 625 + 135 = 702 + 227 =
(600 + 100) + (25 + 35)
700 + 60 = 760
3 Esegui le addizioni in colonna con la prova sul quaderno.
a. 355 + 84 = 927 + 346 =
409 + 688 = 451 + 78 + 150 =
Verso l’Invalsi
(700 + 200) + (2 + 27) =
900 + 29 = 929
b. 96 + 709 = 830 + 2580 = 85 + 758 + 917 = 1185 + 67 + 390 =
c. 945 + 3549 = 7235 + 838 = 1406 + 815 + 1943 = 3045 + 7236 + 558 =
4 Per risolvere a mente l’addizione 340 + 60 + 27 puoi applicare la proprietà associativa. Quali numeri ti conviene associare?
+
Perché?
Perché sono i due numeri più grandi e aggiungere dopo il numero più piccolo diventa più facile.
Perché così si raggruppano due numeri alle centinaia e diventa più facile aggiungere dopo il terzo numero.
Perché nella proprietà associativa si sommano sempre i primi due numeri dell’addizione.
SOTTRAZIONE
1 Calcola a mente applicando la proprietà invariantiva. Segui e completa gli esempi.
108 – 28 = (108 – 8) – (28 – 8) = 100 – 20 = 80
(379 + 1) – (59 + 1) = 380 – 60 = 320
(433 – 3) – (103 – 3) = 430 – 100 = 330
(357 + 3) – (117 + 3) = 360 – 120 = 240
(459 – 1) – (201 – 1) = 458 – 200 = 258
148 – 38 = (148 + 2) – (38 + ) = 150 – = 379 – 59 = 433 – 103 = 357 – 117 = 459 – 201 = 821 – 311 =
(821 – 11) – (311 – 11) = 810 – 300 = 510
2 Calcola a mente e colora il quadratino di verde se l’operazione è corretta, di rosso se è sbagliata.
– 8 = 89
– 10 = 79
– 13 = 87
3 Completa con i numeri mancanti.
–
– 5 =
4 Esegui le sottrazioni in colonna con la prova sul quaderno.
a. 1 598 – 174 = 2 867 – 353 = 3 580 – 470 = 6 897 – 430 = 9 878 – 4 031 = b. 21 598 – 1 431 = 35 965 – 5 472 = 48 913 – 9 405 = 56 235
5 Completa le sottrazioni con i numeri mancanti.
– 100 = 4 000
se sbaglio
Calcola la differenza tra 805 e 850
Non si scrive
8 0 5 – 8 5 0

Attenzione alla
Si scrive
8 5 0 – 8 0 5
Riflettendo si impara
Per calcolare la differenza si svolge una sottrazione.
Osserva i numeri e rifletti: qual è il maggiore?
Nella sottrazione il numero maggiore si scrive per primo.
850 – 805
850 numero maggiore
805 numero minore
RICORDA: • numero maggiore minuendo 850
• numero minore sottraendo 805
• risultato resto o differenza 45
• Lo stesso accade con il calcolo in colonna: si parte dalle cifre del minuendo, cioè il numero che sta sopra, e si tolgono una alla volta le cifre del sottraendo, cioè del numero scritto sotto.
• Se la cifra del minuendo è più piccola, può chiedere un prestito alla cifra a sinistra.
METTITI ALLA PROVA
• Leggi la richiesta e scrivi la sottrazione.
a. Qual è la differenza tra 1265 e 1321?
1321 – 1265
b. Beatrice è nata nel 2009. Sua nonna è del 1952.
Quanti anni hanno di differenza?
c. La maestra guadagna 1400 euro. Il direttore ne guadagna 4100. Quanto guadagna di meno la maestra rispetto al direttore?
4100 – 1400 2009 – 1952
+ E – OPERAZIONI INVERSE
1 Completa gli schemi. Poi verifica facendo l’operazione inversa.

2 Scopri il comando della freccia, poi completa la tabella.
3 Completa con i numeri mancanti.
MOLTIPLICAZIONE
1 Calcola a mente applicando la proprietà associativa. Segui l’esempio.
4 × 5 × 3 = (4 × 5) × 3 = 20 × 3 = 60 3 × 3 × 9 =
(3 × 3) × 9 = 9 × 9 = 81

5 × 6 × 3 = 7 × 5 × 2 =
(5 × 6) × 3 = 30 × 3 = 90
2 × 9 × 10 = 4 × 6 × 10 =
(2 × 9) × 10 = 18 × 10 = 180 7 × (5 × 2) = 7 × 10 = 70
8 × 2 × 1 000 =
(8 × 2) × 1000 = 16 × 1000 = = 16000
× 100 × 8 =
(4 × 6) × 10 = 24 × 10 = 240 (6 × 8) × 100 = 48 × 100 = 4800
2 Calcola applicando la proprietà associativa. Segui l’esempio.
9 × 3 × 3 = 9 × 9 = 81
3 Calcola a mente applicando la proprietà distributiva. Segui l’esempio.
25 × 4 = (20 × 4) + (5 × 4) = 80 + 20 = 100
16 × 5 =
28 × 6 = 34 × 7 = 41 × 3 =
(10 × 5) + (6 × 5) = 50 + 30 = 80
(20 × 6) + (8 × 6) = 120 + 48 = 168
(30 × 7) + (4 × 7) = 210 + 28 = 238
(40 × 3) + (1 × 3) = 120 + 3 = 123
4 Completa con i numeri mancanti.
6 × = 60
5 Esegui le moltiplicazioni in colonna con la prova sul quaderno.
a. 1 523 × 4 =
9 450 × 2 = 258 × 15 = 369 × 24 = 1 803 × 25 = b. 7 019 × 5 = 3 800 × 7 = 178 × 52 = 2 079 × 29 = 8 976 × 32 = c. 12 478 × 3 =
× 18 =
× 18 =
Non si scrive
Calcola in colonna 134 × 212 134× 212= 268 134 268





Si scrive Attenzione
134 0 268 00 28408 aggiungi uno zero aggiungi due zeri
RICORDA: moltiplicando 134 moltiplicatore 212 primo prodotto parziale 268 secondo prodotto parziale 1340
terzo prodotto parziale 26800 prodotto finale 28408
Riflettendo si impara
Nella moltiplicazione in colonna le cifre del moltiplicatore vanno moltiplicate una alla volta per tutte quelle del moltiplicando.
Quando scrivi i prodotti parziali scrivi i risultati partendo dalla colonna corrispondente al valore di ogni cifra e aggiungi gli zeri a destra.
METTITI ALLA PROVA
• Calcola i prodotti parziali e fai la somma.
aggiungi uno zero
aggiungi uno zero
aggiungi uno zero aggiungi uno zero
aggiungi un altro zero
aggiungi un altro zero
MOLTIPLICARE PER 10, 100, 1 000
1 Esegui le moltiplicazioni per 10, 100, 1 000 con le tabelle, come nell’esempio.

2 Completa le moltiplicazioni con il numero mancante.
3 Segui l’indicazione e completa la serie. 4 Completa la tabella. 89
Obiettivi di apprendimento Moltiplicare per 10, 100, 1000.
DIVISIONE
1 Calcola a mente applicando la proprietà invariantiva. Segui gli esempi.
3 600 : 600 = (3600 : 100) : (600 : 100) = 36 : 6 = 6
150 : 50 = (150 × 2) : (50 × 2) = 300 : 100 = 3
125 : 25 =
(125 × 4) : (25 × 4) = 500 : 100 = 5
45 000 : 9 000 =
400 : 50 =
810 : 90 =
450 : 25 =
330 : 30 =

(45000 : 1000) : (9000 : 1000) = 45 : 9 = 5
(400 : 10) : (50 : 10) = 40 : 5 = 8
(810 : 10) : (90 : 10) = 81 : 9 = 9
(450 × 4) : (25 × 4) = 1800 : 100 = 18
(330 : 10) : (30 : 10) = 33 : 3 = 11
2 Completa le tabelle.
3 Esegui le divisioni in colonna con la prova sul quaderno.
a. 72 : 8 =
294 : 7 =
366 : 6 =
505 : 5 =
819 : 9 =
Verso l’Invalsi
4 Qual è il risultato della divisione 5 000 : 1 000? 50 5 500
Perché?
Perché il numero 5 000 diminuisce di 100 volte il suo valore.
Perché il numero 5 000 aumenta di 1 000 volte il suo valore.
Perché il numero 5 000 diminuisce di 1 000 volte il suo valore.
DIVIDERE
PER 10, 100, 1 000
1 Esegui le divisioni per 10, 100, 1 000 con le tabelle, come nell’esempio.
450 : 10 = 45
2 Completa le divisioni con il numero mancante.
3 Segui l’indicazione e completa la serie. 4 Completa la tabella.
Obiettivi di apprendimento Dividere per 10, 100, 1000.
× E : OPERAZIONI INVERSE
1 Completa gli schemi.

2 Per ogni moltiplicazione scrivi le due divisioni inverse e calcola i risultati. Segui l’esempio.
1 Completa le tabelle.
CALCOLI VELOCI
2 Scomponi e calcola a mente, come nell’esempio.
125 + 215 = (100 + 200) + (20 + 10) + (5 + 5) = 300 + 30 + 10 = 340
272 + 118 =
334 + 123 =
546 + 210 =
628 + 251 =
(300 + 100) + (30 + 20) + (4 + 3) =
(500 + 200) + (40 + 10) + (6 + 0) = 700 + 50 + 6 = 756
(600 + 200) + (20 + 50) + (8 + 1) = 800 + 70 + 9 = 879
3 Calcola a mente.
a. 58 – 9 =
– 9 = 1
– 19 =
– 99 =
–
– 999 =
– 19 = 5 450 – 999 =
–
–
– 31 =
4 Verifica se il procedimento per risolvere le moltiplicazioni è corretto.
–
–
–
=
=
=
– 91 =
Poi colora il quadratino di verde se l’operazione è corretta, di rosso se è sbagliata.
42 × 5 = (42 × 10) : 2 = 420 : 2 = 210
600 × 5 = (600 × 10) : 5 = 6 000 : 5 = 1 200
24 × 9 = (24 × 10) + 24 = 240 + 24 = 264
Verso l’Invalsi
40 × 9 = (40 × 10) – 40 = 400 – 40 = 360
× 11 = (21 × 10) + 21 = 210 + 21 =
× 11 = (32 × 10) –
5 Come puoi risolvere a mente la moltiplicazione 35 × 11?
Completa la spiegazione usando solo le parole e i numeri necessari.
100 • 10 • moltiplicare • sommare • moltiplicatore • moltiplicando
– 32 =
Per calcolare a mente quando moltiplico un numero per 11, devo quel numero per e aggiungere al prodotto ottenuto il stesso.
MULTIPLI
1 Cerchia i numeri che sono multipli sia di 5 sia di 10, poi completa la frase.
65 20 29 70 45 80 15 110
• I numeri multipli sia di 5 sia di 10 sono:
70, 80, 110
2 Cancella con una gli intrusi di ciascun insieme. 11 24 25 37 48
multipli di 2 multipli di 3 multipli di 4

3 Scrivi in ogni riquadro i multipli indicati dall’etichetta. multipli di 2 compresi fra 20 e 40 multipli di 5 compresi fra 30 e 80
4 Sottolinea i multipli di 3 e cerchia i multipli di 7. 14 •
5 Segna con una se le frasi sono vere (V) oppure false (F).
• 50 è multiplo di 5. V F
• 3 è multiplo di 15. V F
• 10 è multiplo di 5 e divisore di 50. V F
• 15 è multiplo di 5 e divisore di 50. V F
6 Leggi la richiesta e completa con dei numeri adatti.
5 multipli di 5:
5 multipli di 3:
6 multipli di 6:
10, 15, 20, 25, 30
6, 9, 12, 15, 18
12, 18, 24, 30, 36, 42
•
• 100 è multiplo di 1 000. V F
• 10 è multiplo di 2. V F
• 7 è multiplo di 49. V F
• 30 è multiplo di 3. V F
Obiettivi di apprendimento Individuare i multipli di un numero.
DIVISORI E NUMERI PRIMI
1 Completa la tabella e poi scrivi i numeri divisori di 36. Segui l’esempio.

2, 3, 4, 6, 9
• II numeri divisori di 36 sono: 1, , 36
2 Sottolinea i divisori di 24 e cerchia i divisori di 27.
• Qual è il divisore di entrambi i numeri?
3
3 Cancella con una i numeri che non sono divisori di 80.
4 Cerchia i numeri primi.
5 Segna con una se l’affermazione è vera (V) o falsa (F).
• 4 è divisore di 70. V F
• 5 è divisore di 75. V F
• 8 è un numero primo. V F
• 11 non è un numero primo. V F
6 Segna con una se le frasi sono vere (V) oppure false (F).
• 7 è divisore di 48. V F
• 9 è divisore di 81. V F
• 37 è un numero primo. V F
• 25 non è un numero primo. V F
7 Leggi la richiesta e completa con dei numeri adatti.
4 divisori di 30:
4 divisori di 48:
2, 3, 5, 10
2, 4, 6, 12
3 numeri che siano multipli sia di 2 sia di 5:
Tutti i divisori del numero 18:
I numeri primi compresi fra 10 e 20:
1, 2, 3, 6, 9, 18 10, 20, 30 11, 13, 17, 19
Obiettivi di apprendimento Individuare i divisori di un numero; individuare i numeri primi.

Vai alle pagg. 27-63
PROBLEMI
1 Nel testo di ogni problema sottolinea i dati, cerchia le parole che indicano i dati nascosti e cancella con una i dati inutili. Poi risolvi sul quaderno.
a. Il signor Rossi paga un affitto di € 400,00 al mese. Quant’è l’affitto in un anno?
€ 4800
b. La mamma compra 6 pacchetti di biscotti al supermercato spendendo in tutto € 17,00. Se paga con una banconota da € 20,00, quanto riceve di resto?
€ 3,00
c. Marco ha 20 figurine e Samir ne ha il doppio. Quante figurine ha Samir?
d. Chiara ha 42 perline e 18 braccialetti. Regala i braccialetti a 3 amici e amiche.
Quanti braccialetti riceve ciascuno?
40 6
2 Scrivi la domanda nascosta, poi risolvi i problemi sul quaderno.
a. In un supermercato la pasta viene collocata su 9 scaffali. Questa mattina su ogni scaffale c’erano 80 pacchi di pasta. Alla fine della giornata sono stati venduti 310 pacchi di pasta. Quanti pacchi sono rimasti?
410
Domanda nascosta:
Quanti pacchi
b. Il papà di Nicola va in libreria e compra 3 libri, che costano rispettivamente € 18,00, € 12,00 e € 27,00. Paga con una banconota da € 100,00. Quanto riceve di resto?
€ 43,00
Domanda nascosta:
Quanto ha speso di pasta c'erano in tutto questa mattina? in tutto?
3 Risolvi il problema sul quaderno.
Prima parte
I biglietti del cinema Apollo costano € 6,00 dal lunedì al giovedì.
Osserva la tabella delle presenze e calcola l’incasso totale.
€ 1548
Seconda parte
Da venerdì a domenica il biglietto costa € 9,00.
Osserva la tabella delle presenze e calcola l’incasso totale della settimana.
€ 6750
spettacolo lun.mar.mer.gio. biglietti venduti 38 75 41104
spettacolo ven.sab.dom. biglietti adulti 273125180
ALTRI PROBLEMI
1 Per ciascuno dei due disegni inventa il testo di un problema. Poi risolvi sul quaderno.
Ci fermeremo
una settimana!

Pagherò con una banconota da 100 euro.
2 Risolvi i problemi sul quaderno.
a. Nella scuola di Benedetta ci sono 485 alunni e alunne. 319 si fermano a mangiare in mensa. Quanti bambini e bambine mangiano a casa?
b. La scuola di Annalisa comprerà 130 libri da distribuire nelle biblioteche di classe.
Ogni libro costa € 4,00. Quanto spenderà in tutto la scuola?
c. Per trasportare 2400 lattine di aranciata si usano 50 scatoloni. Quante lattine ci sono in ogni scatolone?
d. Per la festa di Carnevale gli insegnanti delle classi quarte preparano alcuni sacchetti di caramelle.
In ogni sacchetto mettono 10 caramelle alla frutta, 5 alla liquirizia e 14 al cioccolato.
Quante caramelle metteranno in ogni sacchetto?
Gli insegnanti devono preparare in tutto 94 sacchetti.
Quante caramelle serviranno in tutto?
3 Inventa un problema per ciascuna situazione. Poi risolvi sul quaderno. Verso l’Invalsi
4 Leggi il problema e indica con una se puoi risolverlo oppure no.
Le classi quarte e quinte sono andate a teatro. Gli alunni e le alunne di quarta sono 98. Quanti alunni e alunne sono andati a teatro in tutto?
Posso risolvere il problema. Non posso risolvere il problema.
Perché?
Verso l’Invalsi

OPERAZIONI
1. Quale numero è stato cancellato dalla macchia d’inchiostro?
1 750 – = 1 500
A. 500 B. 200 C. 250 D. 1 250
2. Quale segno di operazione è stato cancellato dalla macchia d’inchiostro?
1 200 3 = 3 600
A. : B. × C. + D. –
3. Quale proprietà è stata applicata nella seguente operazione?
78 × 5 = (70 × 5) + (8 × 5) = 350 + 40 = 390
A. proprietà associativa
B. proprietà invariantiva
C. proprietà commutativa
D. proprietà distributiva
4. Se alla somma dei numeri 100 e 70 sottrai 35, quale numero ottieni?
A. 135
5. Segna con una quale moltiplicazione dà come risultato 9 010.
901 × 100
901 × 10
910 × 10
6. Segna con una quale operazione dà come risultato 75.
: 10
7. Nella sala mensa di una scuola ci sono 20 tavoli con 8 posti ciascuno. Quanti bambini e bambine possono mangiare in mensa? A. 28
80
8. Segna con una quale dei seguenti gruppi contiene i divisori di 30.
A. 7 • 9 • 11 • 19 • 29
B. 1 • 2 • 3 • 5 • 6 • 10 • 15 • 30 • 40
9. Osserva i numeri e segna se le affermazioni sono vere (V) o false (F).
• Tutti questi numeri sono multipli di 2. V F
4 13 6 18 25 12
• Tra questi numeri c’è un numero primo. V F
• Tra questi numeri ci sono dei multipli di 2. V F
• Tutti questi numeri sono numeri primi. V F
• Tra questi numeri non c’è alcun divisore di 24. V F
1 Colora la frazione propria indicata.
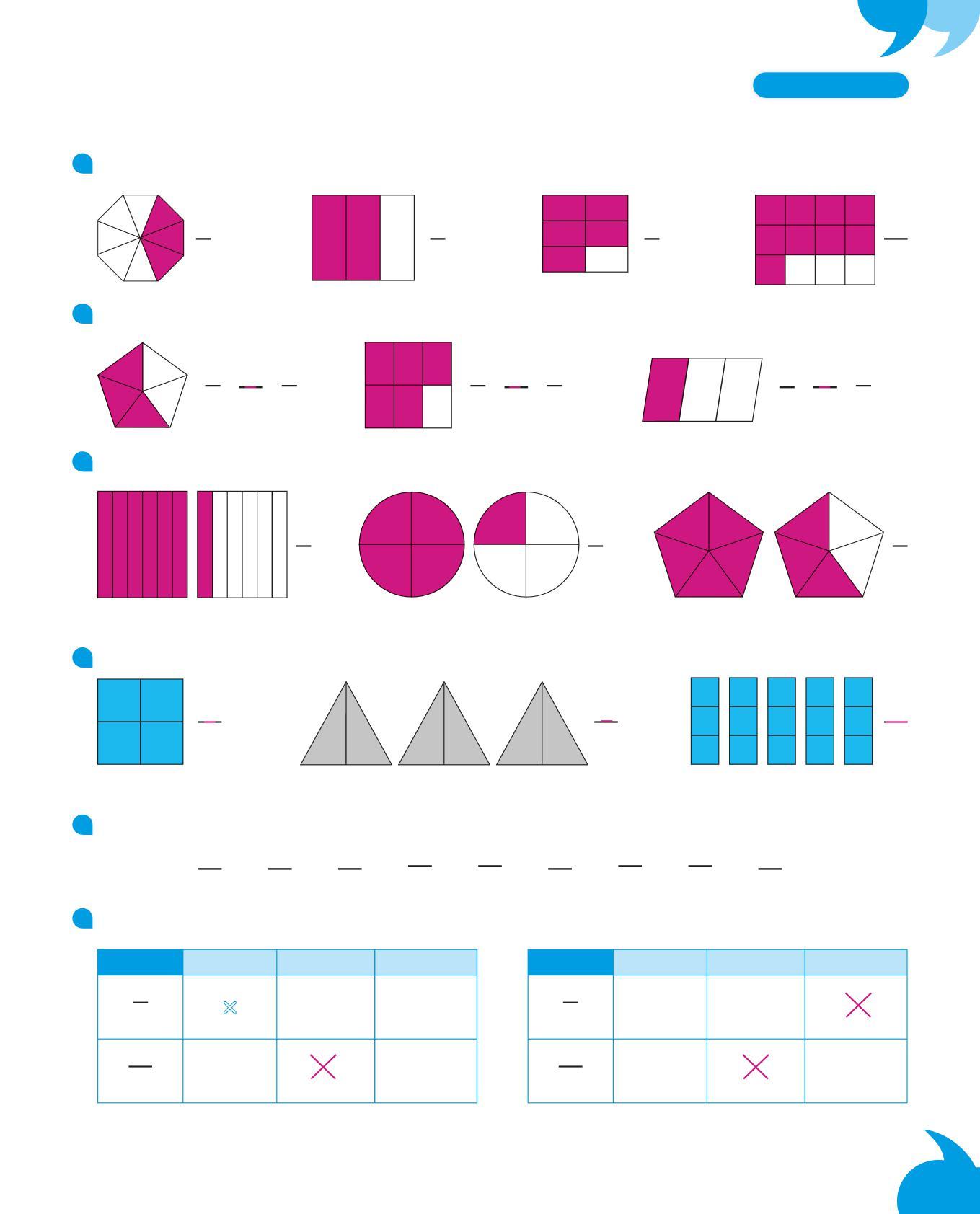
2 Colora la frazione indicata e poi scrivi la frazione complementare. 3 5 + = 5 5 = 1
3 Colora la frazione impropria indicata.
4 Scrivi la frazione apparente.
5 Completa con un numeratore o un denominatore adatto per ottenere frazioni proprie.
6 Completa le tabelle, come nell’esempio.
FRAZIONI A CONFRONTO
1 Osserva e scrivi le frazioni equivalenti.
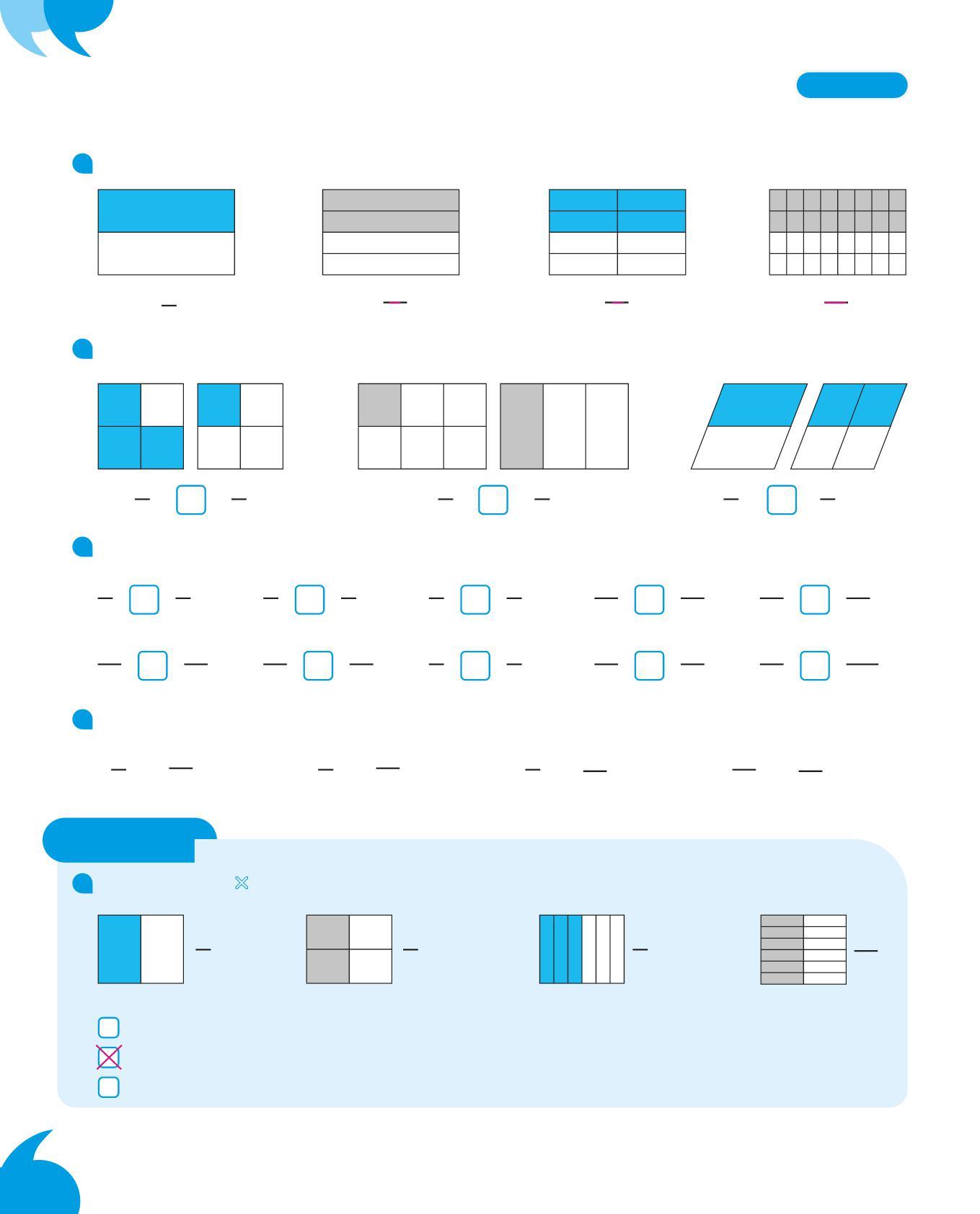
2 Confronta le coppie di frazioni e completa con >, < o =.
3 Confronta le coppie di frazioni e completa con > o <.
4 Completa ogni confronto con un numero adatto.
Verso l’Invalsi
5 Segna con una perché le seguenti frazioni sono equivalenti.
Queste frazioni sono equivalenti perché una frazione è sempre il doppio della seguente.
Queste frazioni sono equivalenti perché rappresentano la stessa quantità.
Queste frazioni sono equivalenti perché sono tutte dello stesso colore.
Obiettivi di apprendimento Riconoscere le frazioni equivalenti. Confrontare frazioni.
Confronto di frazioni
Non si scrive

Si scrive
1 8 > 1 6 / 3 6 > 2 3 1 8 < 1 6 / 3 6 < 2 3
Osservando si impara
Osserva il muretto delle frazioni a pag. 75.
Se il numeratore è uguale, la frazione con il denominatore più piccolo è maggiore perché l’intero è stato diviso in meno parti, quindi le fette sono più grandi.
TRUCCHETTO: Se denominatore e numeratore sono diversi, usa il metodo della farfalla:
Confronta le frazioni 1 8 e 1 6 3 6 e 2 3 3 × 3 = 9
• moltiplica il numeratore della prima frazione per il denominatore della seconda frazione e scrivi il risultato sul numeratore, poi moltiplica il numeratore della seconda frazione per il denominatore della prima frazione e scrivi il risultato sul numeratore
• il risultato maggiore indica la frazione maggiore.
METTITI ALLA PROVA
• Confronta le frazioni sul quaderno usando il metodo della farfalla. Inserisci il simbolo < o >.
CALCOLARE UNA FRAZIONE
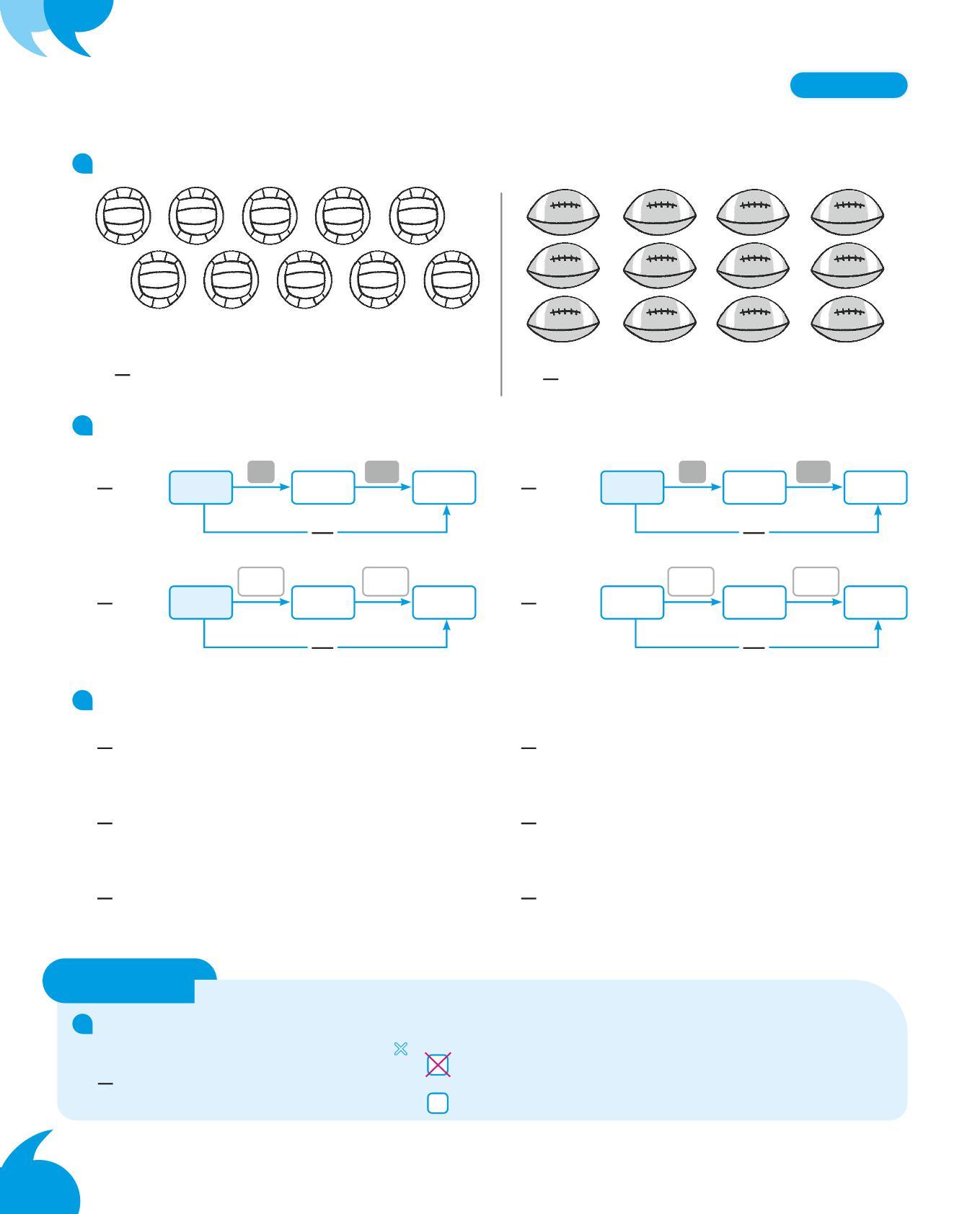
2 Completa gli schemi per calcolare le frazioni dei numeri.
3 Calcola le frazioni dei numeri. Segui l’esempio.
1 Calcola il valore di ogni frazione e colora la quantità esatta. 1 2 di 10 10 : 2 × 1 = 3 4 di 16 2 5 di 60 ➞ (60 : 5) × 2 = 12 × 2 = 24
errore. Quale? Segna con una .
3 di 6 ➞ (6 × 3) × 2 = 18 × 2 = 36
L’operazione fra parentesi doveva essere una divisione. Il risultato della seconda moltiplicazione è sbagliato.
Obiettivi di apprendimento Operare con le frazioni.
FRAZIONI E NUMERI DECIMALI
1 Trasforma le frazioni in numeri decimali. Segui l’esempio.
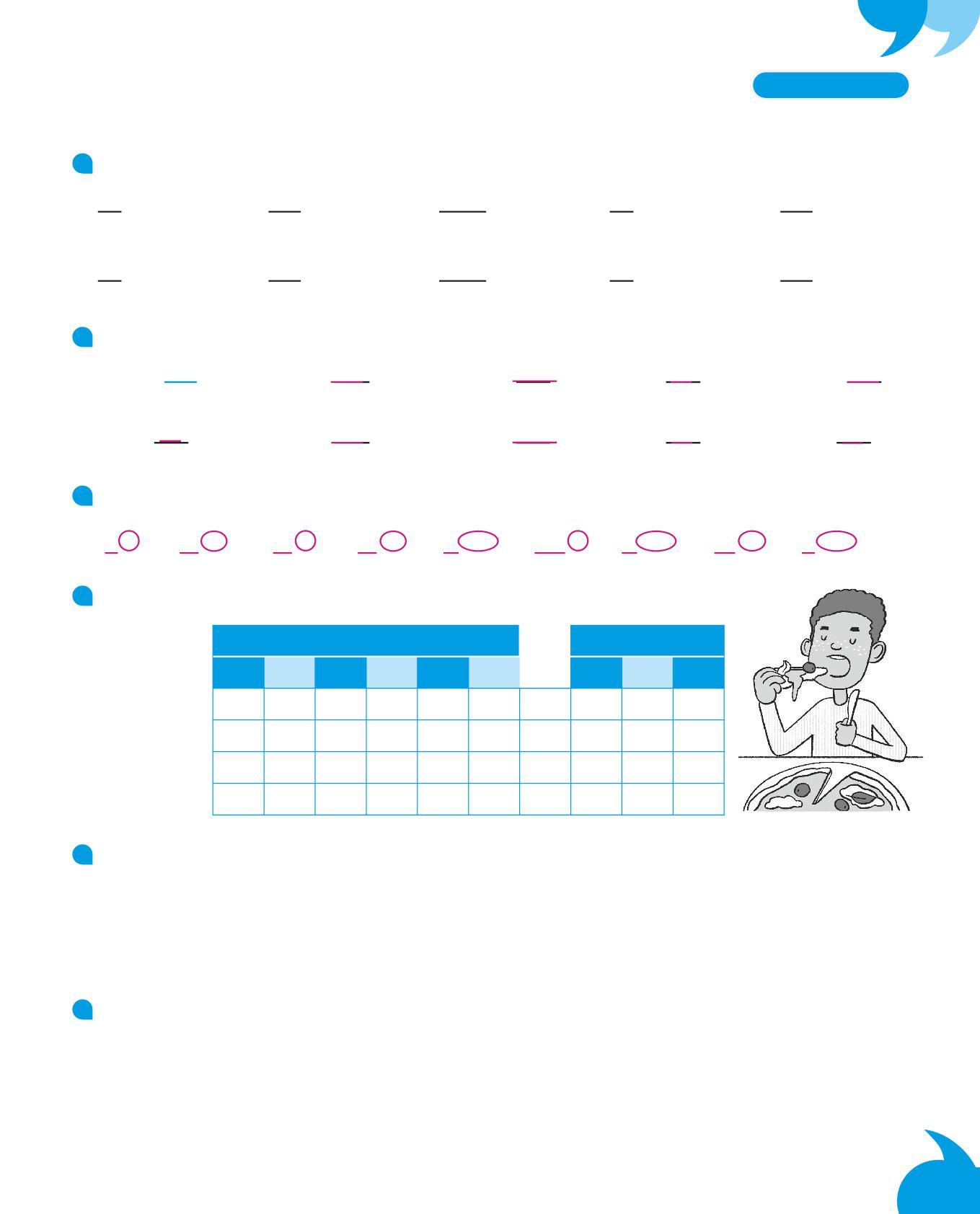
2 Trasforma i numeri decimali in frazioni. Segui l’esempio.
3 In ogni numero sottolinea la parte intera e cerchia la parte decimale.








4 Scrivi i numeri decimali in tabella.
3 345,51 23 654,329 124 871,056 253 987,709
5 Componi i seguenti numeri decimali.
3 da, 4 u, 6 d, 8 c, 9 m = 1 uk, 6 h, 4 da, 3 u, 9 c = 8 h, 9 da, 3 u,
34,689 893,05 3107,36 95,631 742,306 1643,09
6 Accanto a ogni numero indica il valore della cifra in colore. Segui l’esempio. 0,16 ➞ 6 c
69 ➞
4 ➞
NUMERI DECIMALI
1 Confronta le coppie di numeri decimali e completa con >, < o =.
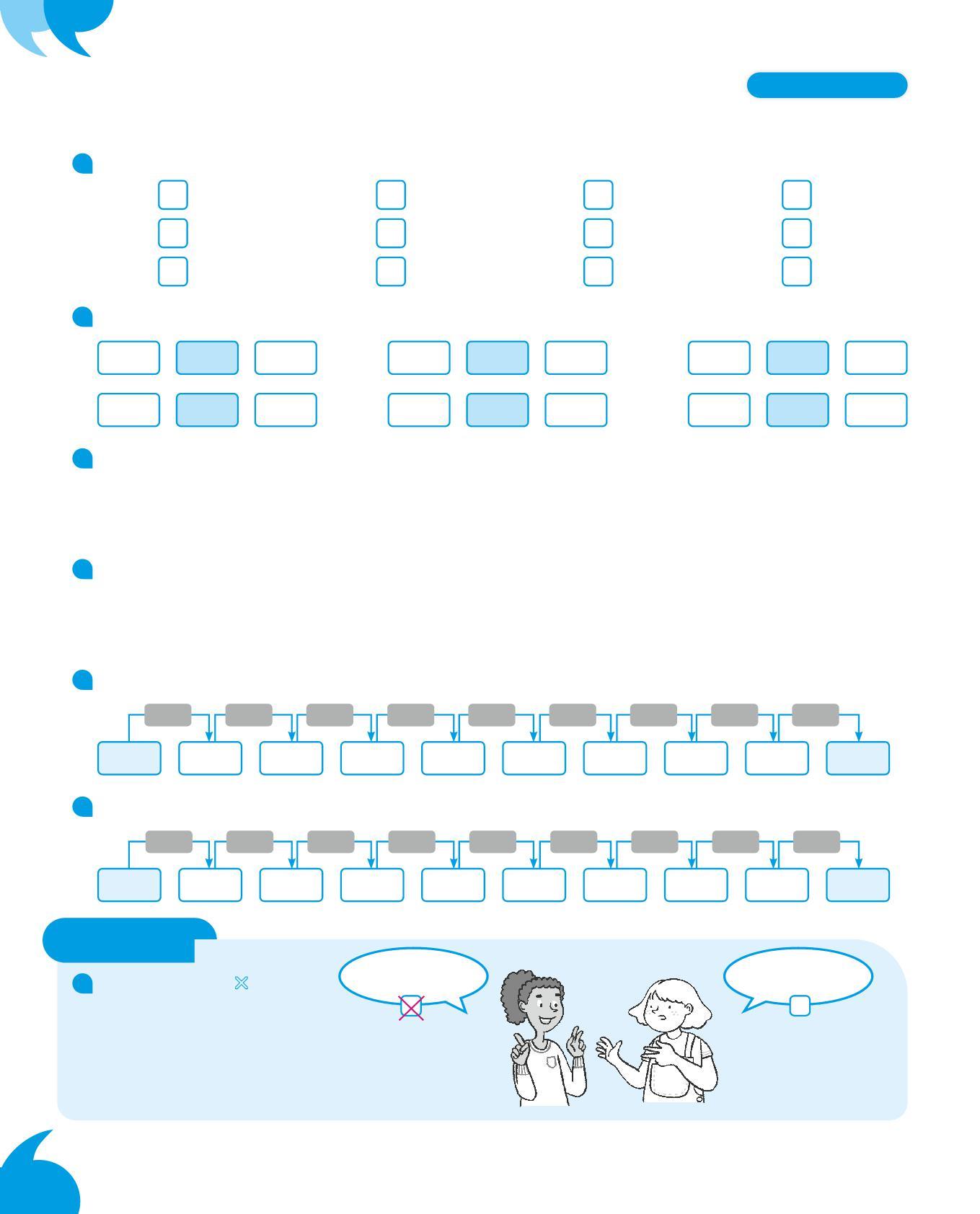
2 Scrivi il numero intero che precede il numero decimale e quello che lo segue. Segui l’esempio.
3 Riscrivi i numeri in ordine crescente.
4 Riscrivi i numeri in ordine decrescente.
5 Numera da 30 a 34,5 contando + 0,5. Segui l’esempio.
6 Numera da 80 a 78,2 contando – 0,2. Segui l’esempio.
Verso l’Invalsi
7 Segna con una quale bambina ha svolto il calcolo correttamente.
imparo se sbaglio

Confronto di decimali
Non si scrive Si scrive


Confrontando si impara
Se la parte intera è uguale, si confrontano le cifre dei decimali in ordine partendo dalla virgola e spostandosi verso destra: prima i decimi, poi i centesimi e infine i millesimi.
1,3 > 1,200 1,03 > 1,020 1,3 > 1,200 1 3 1 200 1 03 1 020
Infatti:
1,3 1 unità, 3 decimi
1,200 1 unità, 2 decimi (il posto dei centesimi e dei millesimi è occupato dallo zero)
RICORDA: dopo la virgola, se lo 0 non è seguito da altre cifre non ha valore.
METTITI ALLA PROVA
• Segna con una i confronti corretti.
600,60 > 600,6 70,07 = 70,70
>
<
>
< 702,360
ADDIZIONI CON I DECIMALI
1 Calcola a mente le seguenti addizioni.
2,5 + 0,5 = 1,7 + 0,3 = 2,2 + 0,8 = 3,4 + 1,2 = 0,3 + = 1 1,1 + = 2 1,5 + = 3
2 Completa le tabelle, come negli esempi. +

3 Esegui le addizioni a mente.
+ 10,6 =
+ 24,4 =
+
=
=
=
4 Completa le tabelle, come negli esempi.
141,22140,32140,23140,221 35,56734,66734,57734,568
9,16 9,07 9,061 72,00571,10571,01571,006 16,9 16 15,9115,901
5 Calcola a mente e colora il quadratino di verde se l’operazione è corretta, di rosso se è sbagliata. 0,5 + 0,4 = 0,9
+ 0,5 = 0,25
+ 4,5 = 6,34 1,4 + 0,4 = 0,8
+ 3,6 = 5,9
+ 5,4 = 11,5
+
= 9,5 30 + 0,7 = 30,7
+ 0,8 = 49
6 Esegui le addizioni in colonna sul quaderno e fai la prova. a. 94,2 + 33,7 = 45,31 + 7,19 =
= 9,04
SOTTRAZIONI CON I DECIMALI
1 Completa le tabelle, come negli esempi.
2 Calcola a mente e colora il quadratino di verde se l’operazione è corretta, di rosso se è sbagliata.
– 0,1 = 4
– 0,4 = 5
– 0,8 = 6
– 1 = 0,9
3 Esegui le sottrazioni a mente.
– 0,14 = 7,1
– 5 = 13
–
4 Esegui le sottrazioni in colonna.
378,986– 762,630– 407,094– 579,103–35,160 = 34,305 = 180,120 =
=
5 Esegui le sottrazioni in colonna sul quaderno e fai la prova. a. 12,89 – 2,78 = 176,659 – 5,18 = 821,053 – 98,66 = 876,3 – 67,19 = b. 998,76 – 142,54 = 1 000,99 – 980,65 = 587,41 – 111,91 = 8 879,09 – 4 536,18 = Verso l’Invalsi
6 Paolo esegue a mente la sottrazione 0,5 – 0,01 = 0,4. Perché il risultato è sbagliato? Segna con una il ragionamento corretto.
Obiettivi di apprendimento Eseguire sottrazioni con i numeri decimali a mente e in colonna. 10,11 722,393
È sbagliato perché da 5 centesimi devo togliere 1 centesimo e il risultato sarà 0,04.
È sbagliato perché da 5 decimi devo togliere 1 centesimo. 5 decimi valgono 50 centesimi, quindi il risultato sarà 0,49.
1 Moltiplica per 10, 100, 1 000.

2 Completa le tabelle.
CON I DECIMALI
3 Calcola a mente e colora il quadratino di verde se l’operazione è corretta, di rosso se è sbagliata.
0,5 × 0,5 = 0,25
0,7 × 0,4 = 28
0,11 × 0,4 = 0,4 0,12 × 0,3 = 0,036
0,9 × 5 = 4,5 0,8 × 6 = 48 0,2 × 0,4 = 0,88 0,33 × 3 = 9,9
4 Scrivi la virgola al posto corretto nei risultati delle seguenti moltiplicazioni.
a. 12,5 × 3 = 375 2,87 × 2 = 574
2,344 × 2 = 4688 25,03 × 1,5 = 37545
3,155 × 3 = 9465 24,3 × 13,2 = 32076
b. 1,6 × 2,3 = 368 2,52 × 3,8 = 9576 2,5 × 31,4 = 785 26,5 × 1,32 = 3498 3,69 × 8,1 = 29889 1,2 × 9,5 = 114
5 Esegui le moltiplicazioni in colonna sul quaderno.
a. 12,4 × 12 = 134,5 × 24 =
× 3,4 = 203,8 × 3,6 =
× 15 =
× 2,2 = 20,81 × 9 =
=
1 Dividi per 10, 100, 1 000.
2 Completa le tabelle.
968,596,859,685 15,8 1,580,158 0,9 0,090,009
3 Completa le divisioni inserendo il numero mancante.
4 Esegui le divisioni in colonna sul quaderno.
5 Qual è il risultato esatto della divisione? Segna con una e spiega il motivo della tua scelta.
1078107,810,78
146,814,681,468 12,4 1,240,124 1,2 0,120,012 0,5 0,050,005 devo spostare
Attenzione al resto nella prova della divisione imparo se sbaglio
Calcola con la proprietà invariantiva

12,5 : 0,2 = 62 con il r di 1 125 2 5 62 1

Ricordando si impara
Si scrive Non si scrive
12,5 : 0,2 = 62 con il resto di 0,1
RICORDA: per verificare i calcoli usa la moltiplicazione. Fai attenzione ad aggiungere il resto al risultato.
Quando applichi la proprietà invariantiva il resto va diviso o moltiplicato nuovamente per il numero che hai utilizzato per facilitare il calcolo. resto 1 1 : 10 = 0,1 62 × 0,2 = 124 000 12,4 + 0,1 = 12,5
METTITI ALLA PROVA
• Calcola in colonna e scrivi correttamente il resto. × 10 12,5 : 0,2 = resto 1 × 10
13,4 : 0,4 = resto 2,26 : 0,05 = resto
1 × 10 × 100 × 10 × 100 : 10 : 100
2
PROBLEMI
1 Leggi il problema, osserva lo schema e completa.
Massimiliano ha 24 macchinine.
3
4 delle macchinine sono bianche
Quante sono le macchinine bianche?
Le altre macchinine sono grigie.
Quante sono le macchinine grigie?
Calcola il valore di:
3
4 di 24 ➞ macchinine bianche
(24 : 4) × 3 =
3 =
Le macchinine bianche sono 18
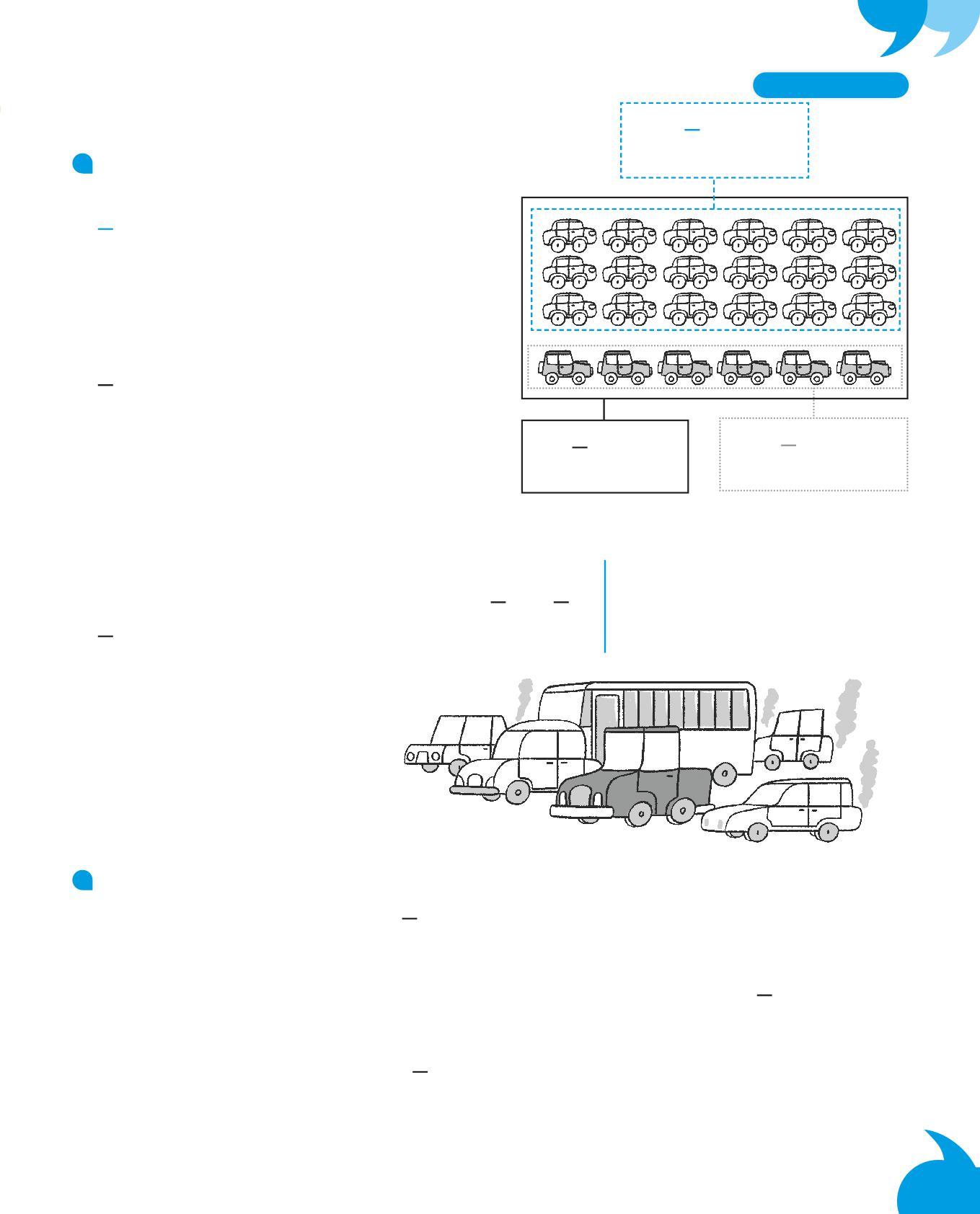
di 24 3 4
macchinine in tutto di 24 4 4 macchinine grigie di 24 1 4
Per trovare il numero delle macchinine grigie puoi operare in due modi.
PRIMO MODO
Calcola il valore della frazione complementare di 3 4, cioè 1 4.
1
4 di 24 ➞ macchinine grigie
(24 : 4) × 1 =
× 1 =
Le macchinine grigie sono 6
Esegui subito una sottrazione: 24 – = macchinine bianche
SECONDO MODO
2 Rappresenta i problemi con un disegno sul quaderno, poi risolvili.
a. Nikolas ha 50 perline. Ne utilizza i 3 5 per fare una collana. Quante perline ha la collana?
Nikolas ripone le perline avanzate in una scatola. Quante perline ci sono nella scatola?
b. La domenica il fioraio mette in vendita 80 rose. Durante la giornata ne vende i 3 4 . Quante rose ha venduto? Quante rose sono rimaste al fioraio?
c. In una cassetta ci sono 120 arance. 1 6 delle arance viene spremuto. Quante arance sono state spremute? Quante ne sono rimaste nella cassetta?
ALTRI PROBLEMI
1 Leggi il problema, osserva lo schema e completa. Dario ha 24 figurine, ma ne incolla solo 2 3 sull’album perché le altre sono doppie.
Quante sono le figurine doppie?
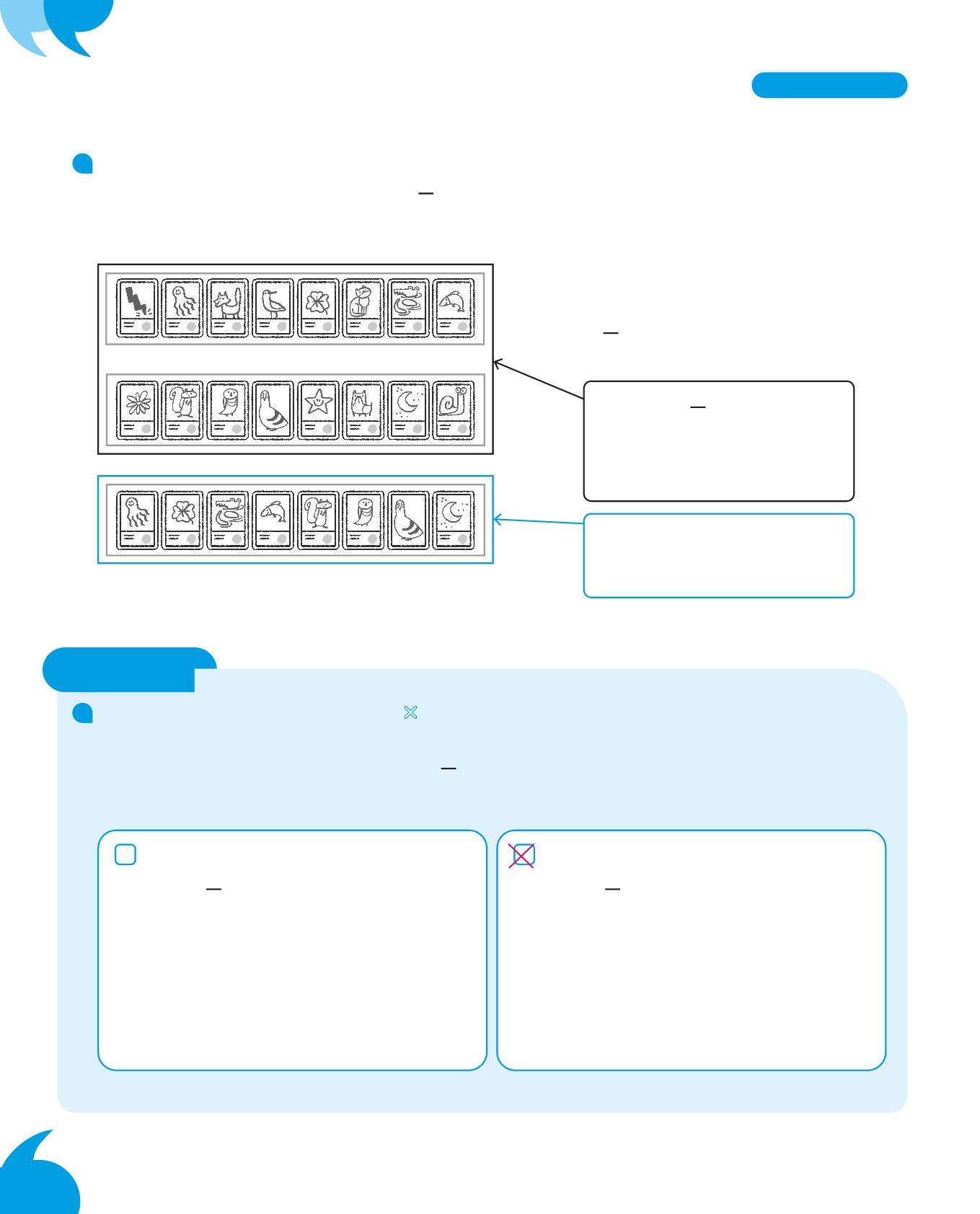
RISPOSTA
Le figurine doppie sono
8
Verso l’Invalsi
2 Leggi il problema e segna con una la soluzione corretta. Poi spiega il motivo della tua scelta.
DATI
24 = figurine di Dario
2 3 di 24 = figurine incollate sull’album
Calcolo 2 3 di 24 figurine.
(24 : 3) × 2 = × 2 =
8 16 16 8
Calcolo le figurine doppie.
24 – =
La mamma ha comperato 20 rose. Mette i 3 5 delle rose nel vaso in salotto e regala le altre a sua sorella. Quante rose ha regalato?
Soluzione A
Calcolo 3 5 di 20.
20 – 5 + 3 = 18
Le rose nel vaso sono 18
Calcolo il numero delle rose regalate.
20 – 18 = 2
Le rose regalate sono 2
• Ho scelto questa soluzione perché
Soluzione B
Calcolo 3 5 di 20.
(20 : 5) × 3 = 12
Le rose nel vaso sono 12
Calcolo il numero delle rose regalate.
20 – 12 = 8
Le rose regalate sono 8
Obiettivi di apprendimento Risolvere problemi utilizzando gli strumenti della Matematica. per calcolare il valore di una frazione devo prima dividere, poi moltiplicare.
Verso l’Invalsi
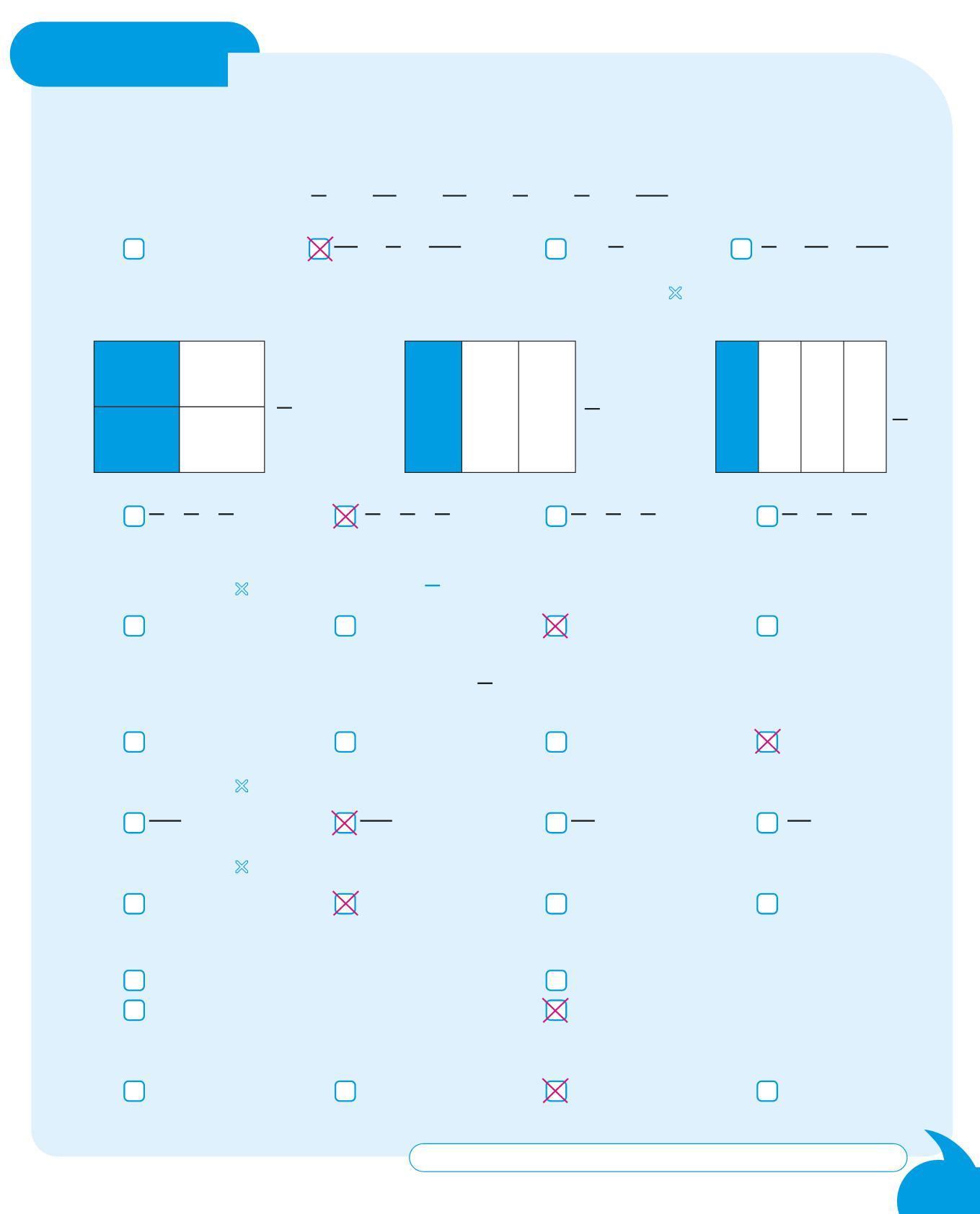
FRAZIONI E NUMERI DECIMALI
1. Quali frazioni sono proprie?
tutte
2. Osserva le figure e le frazioni corrispondenti, poi segna con una in quale gruppo le frazioni sono in ordine crescente.
3. Segna con una come si calcolano i 7 9 di 45.
A. (45 : 7) × 9 B. (9 × 7) + 45 C. (45 : 9) × 7 D. (45 : 9) + 7
4. Nella 4ª A ci sono 25 alunni e alunne. Oggi 1 5 sono assenti. Quanti alunni e alunne sono presenti in classe?
5
24
5. Segna con una l’uguaglianza corretta.
15
20
6. Segna con una come si scrive in cifre seimilatrecentodue e dodici centesimi.
6 302,012
7. Come si legge il numero 309,57?
A. trecentonove e cinquantasette decimi
B. trecentonove e cinquantasette millesimi C. trentanove e cinquantasette centesimi D. trecentonove e cinquantasette centesimi
8. Qual è la cifra dei decimi nel numero 1 560,738?
3
MISURE DI LUNGHEZZA
1 Scrivi le misure nella tabella, come nell’esempio.
57 hm 5 7
539 dam
29 651 dm
0,409 km
598,3 cm
1 234 mm
0,549 dam
2 Scomponi le misure, come nell’esempio.
5 852 m = 5 km, 8 hm, 5 dam, 2 m 7,05 km =
74 hm = 1,25 dam = 3,754 m = 579 cm =
3 Componi le misure, come nell’esempio.
1 dam, 2 m, 5 dm 7 km, 5 dam
m, 7 dm, 9
7 km, 3 hm, 5 dam, 2 m = 7 352 m 8 hm, 7 dam, 9 m = hm
6 km, 8 hm = km 3 hm, 8 m = m
4 m, 5 dm, 7 cm = cm 5 m, 4 cm, 6 mm = mm
4 Completa le equivalenze.
12 km = hm = dam = m
9,54 m = dm = cm = mm
560 m = km = hm = dam
7,5 dam = hm = m = dm
986 cm = m = dm = mm
5 Completa scrivendo le marche.
34 hm = 34 000
506 cm = 0,506
8,901 dam = 89,01
4,788 m = 4 788
470 m = 0,47
6 In ogni gruppo cerchia la misura che indica la lunghezza maggiore.
MISURE DI CAPACITÀ
1 Scrivi le misure nella tabella. h da d c m
457,6 l
9,76 hl
2 456 ml
68,44 dl
75,6 dal
7 516,3 cl
2 Scomponi le misure, come nell’esempio.
5,8 l = 5 l, 8 dl 8,65 hl = 23,45 l = 19,658 dal = 2,895 l = 320,48 dl = 547 cl = 709 ml =
2 dal, 3 l, 4 d
, 5 cl 2 l, 8 dl, 9 cl, 5 ml 8 hl, 6 dal, 5 l 1 hl, 9 dal, 6 l, 5 dl, 8 cl 3 dal, 2 l, 4 cl, 8 ml 7 dl, 9 ml 5 l, 4 dl, 7 cl
3 Completa le equivalenze. 5 l 0,06 l dl dl cl cl dal dal hl ml
4 Completa le equivalenze.
0,95 l = dl 54 cl = dl 3 hl = l 0,12 dal = cl
0,19 l = cl 128 dl = l 7,05 dal = dl 1 460 ml = l
5 Completa le tabelle, come nell’esempio. capacità in 4,97 hl 497 300 dl 47 dal 8,3 hl
l
dal
ml

in c
dl capacità in m 10,3 l 9,91 hl 3 cl 42,7 dl
Obiettivi di apprendimento Conoscere e utilizzare le principali misure di capacità.
MISURE DI MASSA
1 Scomponi le misure, come nell’esempio.
6,2 g = 6 g, 2 dg 18,768 hg = 23,76 g = 435,628 dag = 156,87 g = 1 230,64 dg = 0,005 g = 12 345 mg = 9,541 g = 6,709 kg =
2 dag, 3 g, 7 dg, 6 cg
1 hg, 5 dag, 6 g, 8 dg, 7 cg 5 mg
9 g, 5 dg, 4 cg, 1 mg
2 Completa le equivalenze.
24 kg = hg = dag = g
7,06 g = dg = cg = mg
390 g = kg = hg = dag
874 cg = g = dg = mg
1 kg, 8 hg, 7 dag, 6 g, 8 dg
4 kg, 3 hg, 5 dag, 6 g, 2 dg, 8 cg
1 hg, 2 dag, 3 g, 6 cg, 4 mg
1 dag, 2 g, 3 dg, 4 cg, 5 mg
6 kg, 7 hg, 9 g
3 Completa scrivendo le marche.
75 hg = 7 500
7,844 g = 7 844
550 g = 0,55 4,701 dag = 470,1
4 In ogni gruppo cerchia la misura che indica il peso maggiore e sottolinea la misura che indica il peso minore.
50 g 600 dg 8 dag 0,85 kg 12 hg 4000 g 7,56 g 7,5 dag 90 cg 680 g 9 dag 9 hg
5 Riscrivi le misure in ordine crescente.
6 kg • 9 hg • 13 g • 6,8 kg • 3 dag
7 Completa la tabella eseguendo le equivalenze a mente.
6 Riscrivi le misure in ordine decrescente.
85 cg • 3 g • 450 mg • 95 dag • 5 g
95 dag5 g 3 g85 cg450 mg 3 dag 13 g 9 hg 6 kg6,8 kg
Verso l’Invalsi
8 Le seguenti misure non sono scritte in ordine crescente. Perché?
13 g • 3 dag • 5 hg • 1,8 kg • 68 dag
Perché la misura 68 dag è minore di 1,8 kg.
Perché la misura 5 hg è maggiore di 1,8 kg.
Obiettivi di apprendimento Conoscere e utilizzare le principali misure di peso (o massa).
MISURE DI VALORE
1 Utilizza il minor numero possibile di monete per formare ciascuna somma di denaro. Segui l’esempio. € 1,25
€ 1,45
€ 2,75
€ 4,30
2 Calcola quanti euro ha ogni persona e completa la tabella, poi rispondi.

3 In ogni coppia cerchia la misura che indica il valore minore. Chi ha più euro? = 0,50 euro 45 cent
4 Calcola e completa le tabelle. Samir
MISURE DI TEMPO
1 Completa le tabelle, come negli esempi.
minuti secondi
2 min 120 s
3 min
mezzo min
1 min e mezzo
10 min 15 min
2 Trasforma le misure di tempo, come negli esempi.
a. 4 min = 240 s
168 h = d
180 s = min
48 h = d
120 min = h
3 d = h
3 Trasforma le misure di tempo, come nell’esempio.
4 settimane = 28 d
8 settimane = d
24 mesi = anni
Verso l’Invalsi
4 Questo foglio di calendario rappresenta il mese di maggio.
Mattia va dal dentista il 15 maggio alle 14:30 e il medico gli fissa un altro appuntamento dopo due settimane, un’ora più tardi. Suggerisci a Mattia il modo più semplice per scoprire qual è la data dell’appuntamento e in quale giorno e ora dovrà tornare dal dentista.
29 maggio alle 15:30
3 millenni = secoli 20 secoli = millenni L MaMe GVSD 123456 78910111213 14151617181920 21222324252627 28293031
PROBLEMI
1 Leggi il testo e completa la tabella. Segui l’esempio.
Lungo una strada c’è un ponte alto 3,4 m.
Quali veicoli potranno passarci sotto?
veicolo altezza ci passa?
automobile 115 cm sì
pullman 4 m
camion 3,6 m
furgone 200 cm
camper 270 cm
2 Risolvi i problemi sul quaderno.
a. Mariam si sta allenando in bicicletta su una pista lunga 400 m. Quanti giri di pista deve fare per percorrere 8 000 m?
b. Il signor Gustavo pesa 77 kg, sua moglie Giulia pesa 63,4 kg. Qual è la differenza di peso fra i due?
20 piscina coperta; 6300 l
3 Completa la tabella, poi scrivi il testo del problema e la risposta.
peso lordo 650 g
peso netto 530 g tara
4 Risolvi i problemi sul quaderno.
a. Un pattinatore si allena su una pista lunga 400 m. Dopo 36 giri, quanti chilometri ha percorso?
b. Mario deve versare 2 damigiane di olio in bottiglie da 9 dl. Ogni damigiana contiene 54 l. Quante bottiglie riempirà? Vende ciascuna bottiglia a € 4,50. Quanto ricava dalla vendita?
g
13,6 kg 14,4 km 120 bottiglie; € 540 2,95 kg
c. La piscina coperta del centro sportivo comunale ha una capacità di 25 800 l. La piscina all’aperto contiene invece 195 hl di acqua. Qual è la piscina più grande e quanta acqua contiene in più rispetto all’altra?
Problema: Risposta:
c. Flavia compra una cassetta d’arance che pesa 10,7 kg. La cassetta da sola pesa 0,9 hg. Qual è il peso delle sole arance? Se le arance costano € 2 al kg, quanto spende Flavia?
10,61 kg; € 21,22
d. Karim ed Elisa fanno una passeggiata. Nello zaino di Karim ci sono una bottiglia di aranciata che pesa 1,5 kg e un sacchetto di frutta che pesa 700 g. Nello zaino di Elisa ci sono 2 mantelle, dal peso di 2,3 hg ciascuna, e un libro che pesa 290 g. Quanti chilogrammi pesa in tutto il contenuto dei due zaini?

ALTRI PROBLEMI
1 Leggi il problema, scrivi la domanda e risolvi sul quaderno.
a. Quando è vuota, una cassetta per il trasporto della frutta pesa 480 g. Il contadino la riempie con 6,7 kg di mele.
Domanda:
Qual è il peso lordo?
b. Un barattolo di orzo solubile vuoto pesa 25 g, mentre quando è pieno pesa 2 hg.
Domanda:
Quanto pesa l'orzo solubile da solo? 7,18 kg 175 g
2 Risolvi i problemi sulle misure di valore sul quaderno.
a. Una macchina da cucire costa € 108,00. Se il negoziante l’ha pagata € 74,00, quanto vuole guadagnare dalla vendita della macchina da cucire?
€ 34
b. Un frigorifero costa al negoziante € 280,00. Dalla vendita di un frigorifero vuole guadagnare € 85,00. Quanto ricaverà dalla vendita di 12 frigoriferi?
3 Risolvi i problemi sulle misure di tempo sul quaderno.
a. Alessandra è partita da casa alle 8:06 ed è arrivata a scuola dopo 19 minuti.
A che ora è arrivata a scuola? Le lezioni sono cominciate alle 8:20.
Con quanti minuti di ritardo è arrivata?
b. La famiglia Rossi ha progettato la vacanza in montagna per la prossima estate. La vacanza durerà 2 settimane e 5 giorni. Quanti giorni durerà in tutto?
Verso l’Invalsi
4 Il signor Daniel acquista per i suoi 3 figli del materiale scolastico.
La tabella rappresenta il costo unitario di ogni oggetto e il numero degli oggetti acquistati.
Prima di arrivare alla cassa, Daniel fa i conti e dice: «Spenderò € 130,20». È vero? Ha fatto bene i conti? Per verificarlo, fai i calcoli e completa la tabella.
3
€ 4380 5 min 8:25 19 € 42 € 18 € 5,70 € 46,50
3 € 1,90 3 € 15,50 3
• Se il signor Daniel ha commesso un errore di calcolo, spiega qual è. Scegli l’ipotesi che ritieni corretta e segnala con una
Daniel ha aggiunto il costo di un astuccio, calcolando 14,00 × 4 invece di 14,00 × 3.
Daniel ha sommato due volte il costo totale dei pennarelli.
Verso l’Invalsi

MISURE
1. Lucia deve andare in biblioteca. Da casa sua può seguire quattro percorsi di lunghezze diverse. Qual è il percorso meno lungo?
A. 0,7 km B. 650 m C. 12 hm D. 80 dam
2. In quale dei seguenti gruppi le misure sono ordinate dalla maggiore alla minore?
A. 7,5 l • 4 dl • 0,9 dal • 300 cl
B. 0,9 dal • 7,5 l • 300 cl • 4 dl
C. 0,9 dal • 300 cl • 7,5 l • 4 dl
D. 0,9 dal • 7,5 l • 4 dl • 300 cl
3. Osserva i disegni: quale unità di misura è stata cancellata dalle macchie?
= 350 = 33
4. Un treno veloce è partito da Milano alle 9:00 e arriverà a Roma alle 12:00. Se sono le 11:15, quanto manca per arrivare a Roma?
A. un quarto d’ora B. 30 minuti C. 45 minuti D. un’ora
5. Segna con una se le seguenti affermazioni sono vere (V) oppure false (F).
• Per formare 1 euro occorrono 5 monete da 20 centesimi. V F
• Per formare 1 euro occorrono 15 monete da 10 centesimi. V F
• Per formare 5 euro occorrono 3 monete da 2 euro. V F
• Per formare 100 euro occorrono 5 banconote da 20 euro. V F
• Per formare 200 euro occorrono 100 monete da 2 euro. V F
6. Che cosa può comprare Giancarlo con i soldi che ha nel borsellino?
A. una scatola da 25 pennarelli: € 10,80
B. un pallone: € 9,90 C. un libro: € 14,00 D. un videogioco: € 16,99
LINEE E ANGOLI
1 Con la matita e il righello disegna due linee parallele alla linea colorata. Poi traccia una linea perpendicolare alla linea nera e una linea incidente alla linea grigia.
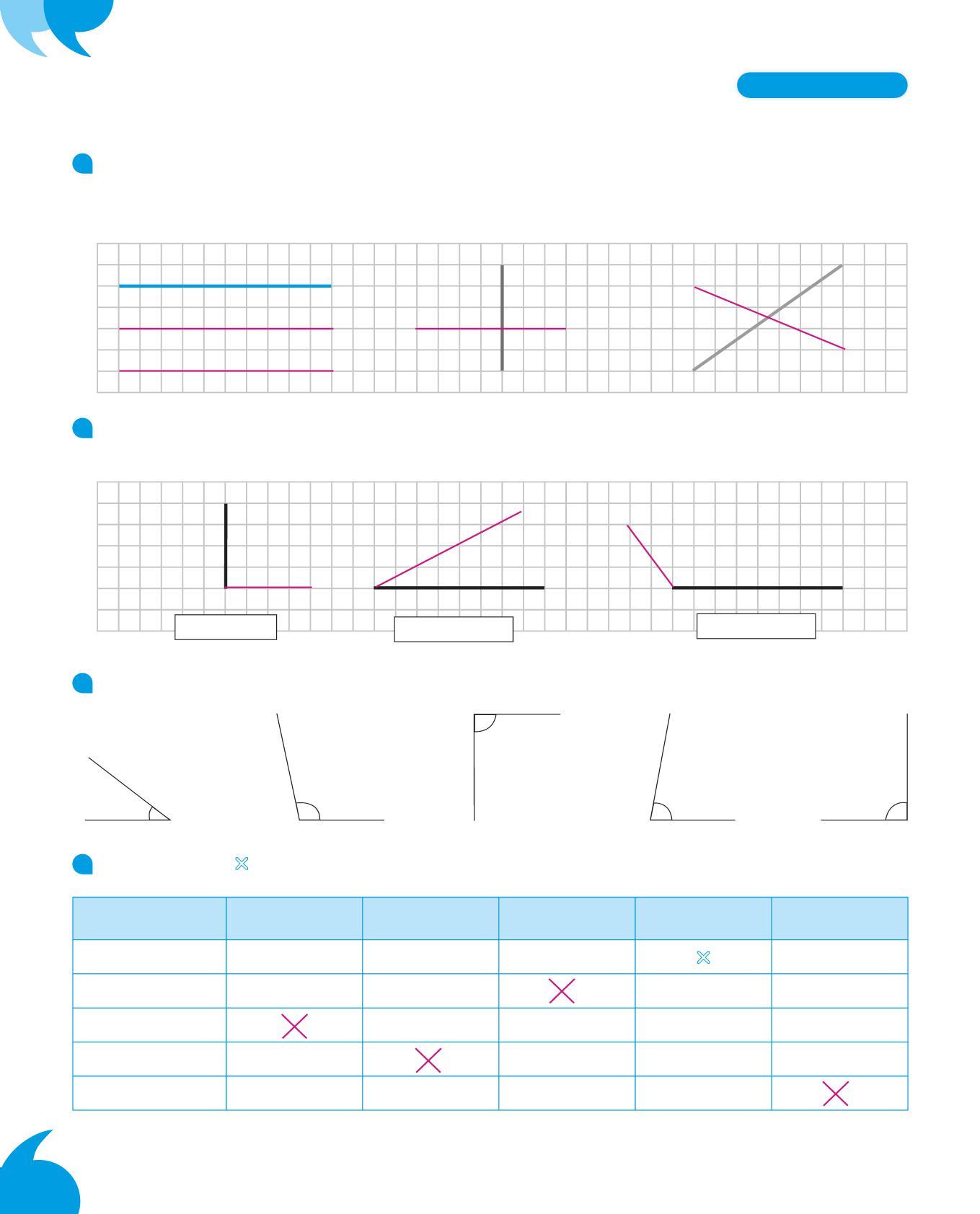
2 Con la matita e il righello completa i disegni in modo da ottenere un angolo retto, un angolo acuto e un angolo ottuso.
3 Colora in rosso gli angoli retti, in verde gli angoli ottusi e in blu gli angoli acuti. angolo retto angolo acuto angolo ottuso
acuto ottuso retto acuto retto
4 Segna con una a quale angolo corrisponde ogni misura. Segui l’esempio. ampiezza angoloangolo acutoangolo ottusoangolo rettoangolo piattoangolo giro
LA MISURA DEGLI ANGOLI
1 Leggi il goniometro e segna l’ampiezza degli angoli.
Questo angolo misura

Questo angolo misura
Questo angolo misura
Questo angolo misura
Questo angolo misura
Questo angolo misura
Questo angolo misura
Questo angolo misura
Questo angolo misura
Questo angolo misura
Attenzione alla simmetria imparo se sbaglio
Disegna la figura simmetrica a questa.

Non si scrive Si scrive
Riflettendo si impara
Nella simmetria, la figura si riflette come in un specchio rispetto all’asse di simmetria nel senso opposto.
RICORDA: immagina di piegare il foglio lungo l’asse di simmetria e di timbrare la figura nella parte opposta.
METTITI ALLA PROVA
• Indica le figure simmetriche.
Vai alle pagg. 118-120
TRASFORMAZIONI GEOMETRICHE
1 Disegna la figura simmetrica a quella data. 2 Traccia l’asse di simmetria delle due figure.

3 Esegui le traslazioni indicate dai vettori.
4 Ingrandisci o rimpicciolisci le figure seguendo la scala indicata.
Obiettivi di apprendimento Riconoscere figure riflesse e traslate. Riprodurre in scala una figura assegnata. scala 1:2 scala 2:1
POLIGONI • 1
1 Ripassa di blu la base e di rosso l’altezza di ciascun triangolo.

2 Classifica i triangoli secondo i lati.
3 Colora gli elementi del poligono come indicato.
• in blu le basi
• in rosso l’altezza
• in arancione i lati obliqui
isoscele scaleno equilatero altezza diagonali base
lato obliquo
• in verde i vertici
• in rosa gli angoli
(v) (a)
• in giallo le diagonali
4 Colora di rosso i rettangoli e di verde i romboidi.
5 Disegna le figure indicate utilizzando il righello e la squadra.
Attenzione alla rotazione imparo se sbaglio
Che figura geometrica è?

Si scrive Non si scrive
Osservando si impara
Osserva bene la figura. Ha quattro lati uguali e quattro angoli uguali, è un quadrato ma è posizionato come di solito siamo abituati a vedere un rombo: è ruotato. Il rombo non ha gli angoli uguali.
RICORDA: ruotando la figura, le sue caratteristiche non cambiano.
METTITI ALLA PROVA
• Osserva l’immagine e indica di quale figura geometrica si tratta.
• Osserva l’immagine e scrivi di quale figura geometrica si tratta.
triangolo rettangolo
triangolo equilatero X trapezio
POLIGONI • 2
1 Leggi le definizioni, osserva i disegni e scrivi i nomi dei quadrilateri.
Ha una base maggiore e una base minore.
Gli altri due lati sono obliqui, ma se è rettangolo ha un lato perpendicolare alle due basi.
Ha i lati paralleli e uguali a due a due.
Gli angoli opposti sono uguali.
Ha i lati paralleli e uguali a due a due e quattro angoli retti.
Ha quattro lati uguali, paralleli a due a due. Gli angoli opposti sono uguali.
Ha quattro lati uguali, paralleli a due a due, e quattro angoli retti.

trapezio romboide rettangolo rombo quadrato
2 Classifica ogni trapezio scegliendo tra: scaleno, rettangolo, isoscele. Poi ripassa di blu la base minore (b) e di rosso l’altezza (h) dei tre trapezi.
isoscele scaleno rettangolo
3 Il rombo e il romboide sono diversi per una caratteristica che riguarda i lati: quale?
Il rombo ha tutti i lati congruenti; il romboide ha i lati congruenti a due a due.
Obiettivi di apprendimento Riconoscere i poligoni e individuarne le caratteristiche.
Verso l’Invalsi
PERIMETRO DEI POLIGONI
1 Misura con il righello i lati e calcola il perimetro (P) di ogni triangolo.

2 Scrivi le formule per calcolare il perimetro (P) dei seguenti oggetti.
3 Calcola il perimetro (P) dei seguenti poligoni.
5 + 2,7 + 5,7 = 13,4 cm 3 + (2,6 × 2) = 8,2 cm 3,1 × 3 = 9,3, cm l × 4 b × 2 + h × 2 l × 4 16 + 12,4 + (13,2 × 2) = 54,8 cm
Verso l’Invalsi
4 Scrivi le formule per trovare i perimetri del rombo e del romboide. Poi completa per spiegare il procedimento.
= Per calcolare il perimetro del rombo
1 × 2 + l2 × 2 devo sommare due volte moltiplico il lato per 4 la lunghezza dei 2 lati diversi (numero dei lati)
calcolare il perimetro del romboide
MISURE DI SUPERFICIE
1 Trascrivi le misure nella tabella. Poi leggi a voce alta il valore di ciascuna cifra.

12,458 m2
7,09 km2
2 Completa le equivalenze.
3 Completa le tabelle, come nell’esempio.
1 Completa le tabelle.
triangoli
AREA DEI POLIGONI

2 Completa le tabelle.
3 Calcola l’area delle figure.
PROBLEMI

1 Risolvi i problemi.
a. Una contadina deve recintare con la rete metallica due campi qui sotto. Calcola il perimetro e scrivi i risultati. Poi rispondi alla domanda.
Campo del Poggio
Perimetro: m
Campo Verde
310 360
Perimetro: m
Per quale campo servirà più rete metallica?
Campo Verde
b. Calcola prima l’area totale, poi l’area di ciascuna metà del campo di calcio.
100 m
75 m
Area totale = 7500 m2
Area di metà campo = 3750 m2
2 Disegna le figure e risolvi i problemi sul quaderno.
a. Un tappetino da ginnastica di forma rettangolare è largo 50 cm e lungo 1,8 m. Quanto misura il suo perimetro? Qual è la sua area?
P = 4,6 m A = 0,9 m2
b. Un aquilone a forma di rombo ha le diagonali di 50 cm e 20 cm. Calcola la sua area.
500 cm2
3 Segna con una la risposta corretta.
In una città si è deciso di costruire un centro commerciale su un’area di 5 hm2 e di piantare degli alberi in un’altra area, vasta 1800 m2. Qual è l’area più vasta? 5 hm2
m2
ALTRI PROBLEMI
1 Risolvi il problema: calcola sul quaderno e trascrivi qui i risultati.
Il Comune di Monticello ha acquistato un terreno a forma di trapezio rettangolo.
L’area viene utilizzata per costruire la piscina comunale coperta e i suoi servizi. Lo spazio rimanente resta a prato, con una piscina più piccola scoperta. Osserva la pianta della struttura e le misure, poi calcola.
• superficie dell’intero terreno:
14850 m2
• superficie della piscina coperta:
• superficie della piscina scoperta:
• superficie dell’area verde:

4900 m2
360 m2
9590 m2
Verso l’Invalsi
2 Luca e Andrea leggono e risolvono il seguente problema.
Il giardino comunale ha una superficie di 100 dam2. Una parte che misura 1500 m2 è occupata dall’orto botanico. Quanto è esteso il resto del giardino?
La soluzione di Luca
• Dalla misura del giardino tolgo la misura dell’orto botanico.
100 dam2 – 1500 m2 =
• 100 meno 1500 non si può fare, perciò scambio di posto i numeri.
1500 m2 – 100 dam2 = 1400 m2
• Il resto del giardino è esteso 1400 m2
Chi ha risolto il problema correttamente?
Perché?
La soluzione di Andrea
• Le due misure sono espresse in dam2 e in m2, perciò eseguo un’equivalenza in modo che la marca sia sempre m2 100 dam2 = 10000 m2
• Eseguo una sottrazione.
10000 m2 – 1500 m2 = 8500 m2
• Il resto del giardino è esteso 8500 m2
Obiettivi di apprendimento Risolvere problemi utilizzando gli strumenti della Matematica. Andrea
Perché ha eseguito l’equivalenza e ha lavorato con la stessa unità di misura.
FIGURE ISOPERIMETRICHE, CONGRUENTI ED EQUIESTESE
1 Colora con lo stesso colore le figure isoperimetriche.
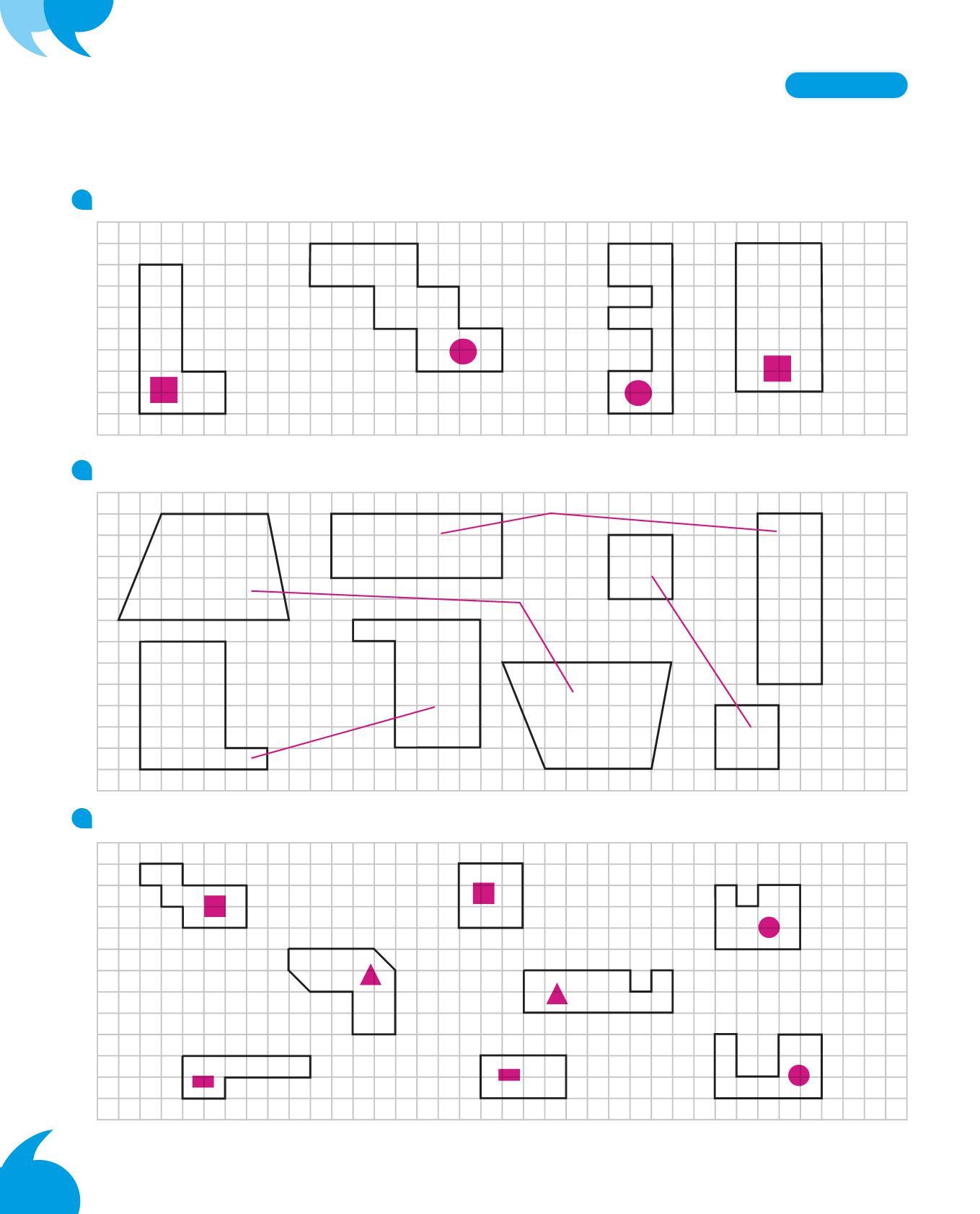
2 Unisci con una linea le figure congruenti.
3 Colora con lo stesso colore le figure equiestese. Obiettivi di apprendimento Riconoscere le figure isoperimetriche, congruenti ed equiestese.
Verso l’Invalsi
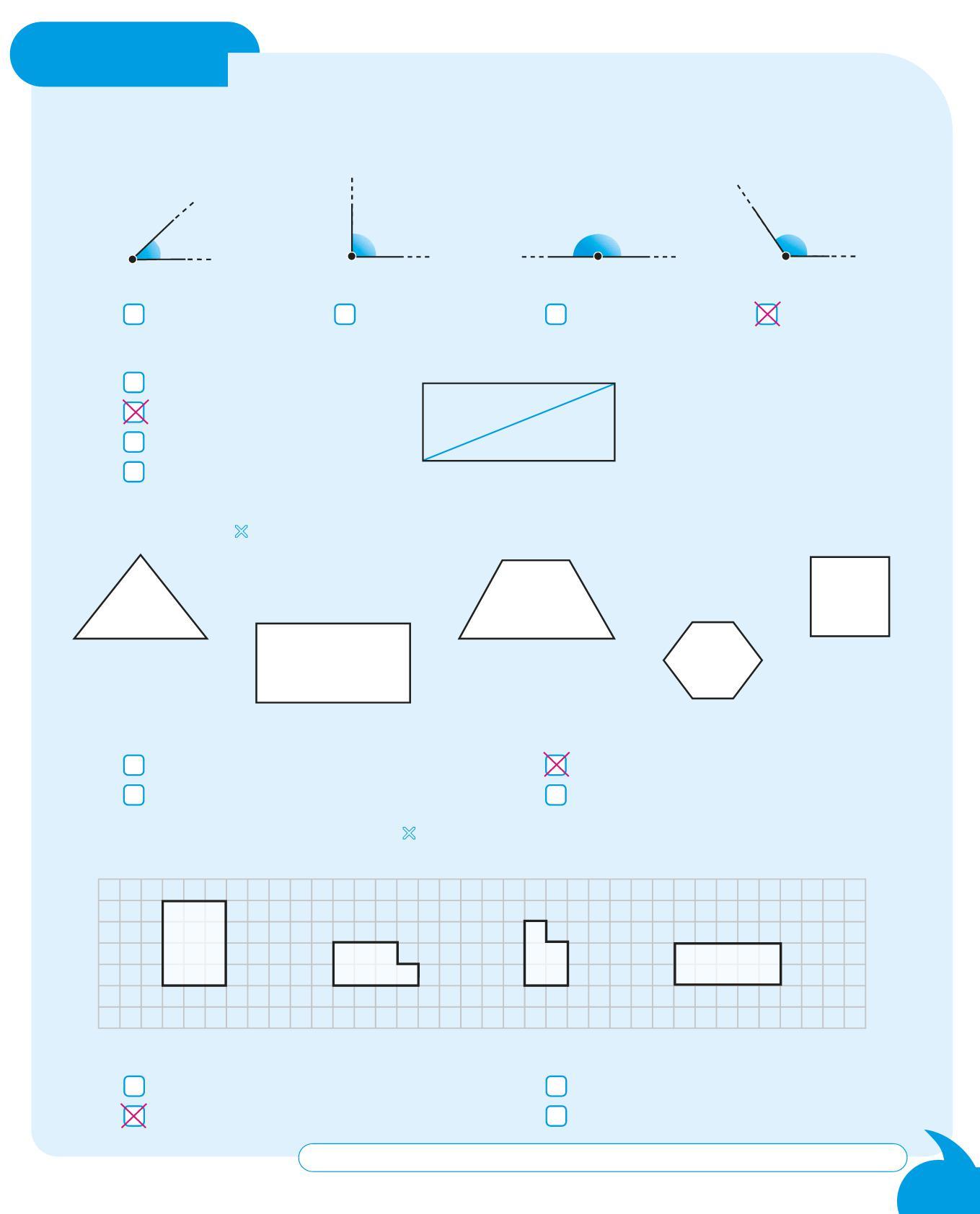
SPAZIO E FIGURE
1. Quale fra i seguenti angoli è ottuso?
A. l’angolo 1 B. l’angolo 2 C. l’angolo 3 D. l’angolo 4
2. Come si chiama il segmento AC?
A. lato
B. diagonale
C. altezza
D. base
3. Segna con una quali fra le figure sono dei parallelogrammi.
figura 1
A. le figure 2 e 3
B. solo la figura 5
figura 2
figura 3 figura 5 figura 4
C. le figure 2 e 5
D. le figure 1 e 2
4. Osserva le figure e segna con una quale alternativa le ordina dalla meno estesa alla più estesa.
figura 1 figura 2 figura 3 figura 4
A. figura 2, figura 3, figura 1, figura 4
B. figura 3, figura 2, figura 4, figura 1
C. figura 1, figura 2, figura 3, figura 4
D. figura 3, figura 2, figura 1, figura 4
L’INDAGINE STATISTICA
1 Le vacanze estive si avvicinano e i bambini e le bambine delle classi quarte, che in tutto sono 100, svolgono un’indagine statistica per conoscere quali sono le località di vacanza preferite.
Laura, Aldo, Tiziana e Lorenzo raccolgono le 100 schede e registrano i dati in un ideogramma.
LEGENDA: = 1 bambino/a
mare
montagna campagna lago
città d’arte
• Conta e finisci di registrare le frequenze, come nell’esempio.
mare montagna campagna lago
34 25 10 17
città d’arte 14
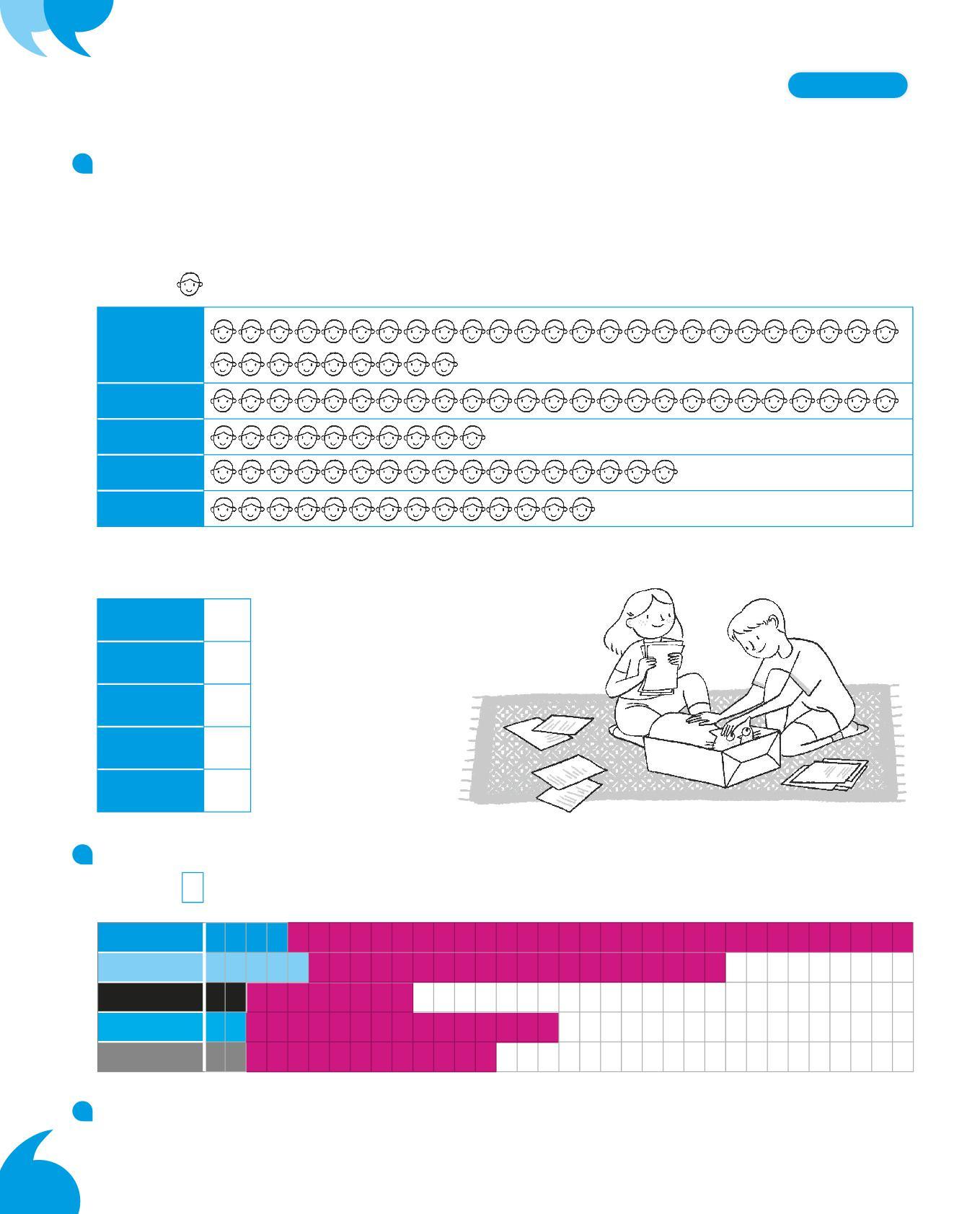
2 Usa i dati raccolti nell’esercizio precedente e completa l’istogramma.
LEGENDA: = 1 bambino/a
mare
montagna campagna lago
città d’arte
3 Disegna sul quaderno un areogramma quadrato con i dati raccolti nell’esercizio 1.
4 Nelle classi quarte della scuola Andersen è stata fatta un’indagine statistica per conoscere quali sono gli sport preferiti dalle bambine e dai bambini. Osserva l’ideogramma che riporta i risultati e segna con una se le affermazioni sono vere (V) oppure false (F).
LEGENDA: = 1 bambino/a
Sport
nuoto calcio
rugby pallacanestro pallavolo altri sport
• I bambini e le bambine che hanno partecipato all’indagine sono stati 99. V F
• Lo sport preferito dalle bambine e dai bambini delle classi quarte è il calcio. V F
• Lo sport che ha ottenuto il maggior numero di preferenze è il nuoto. V F
• Ci sono due sport che hanno ottenuto lo stesso numero di preferenze. V F
• La pallavolo ha ottenuto 20 preferenze. V F
• La pallacanestro ha ottenuto più preferenze della pallavolo. V F
• Il rugby ha ottenuto meno preferenze del nuoto. V F
Verso l’Invalsi
5 Osserva l’ideogramma dell’esercizio 4. Possiamo dire con certezza che nelle classi quarte della scuola Andersen nessuno preferisce l’atletica leggera?
Sì, perché nell’elenco degli sport che appare nell’ideogramma l’atletica leggera non c’è.
No, perché l’atletica leggera potrebbe essere compresa nella voce “altri sport” dell’ideogramma.
Obiettivi di apprendimento Leggere, interpretare e rappresentare dati statistici.
INDICI STATISTICI
1 Nelle classi quarte è stata fatta un’indagine statistica sui giochi preferiti dai maschi. Osserva l’istogramma e rispondi.

= 1 preferenza
• Quale gioco rappresenta la moda, cioè il gioco che si presenta con maggiore frequenza?
2 La tabella indica le merende preferite dagli alunni e dalle alunne della 4ª A e della 4ª B. Riscrivi i dati in ordine crescente nella tabella vuota e colora la casella della mediana, cioè del valore scritto al centro.
16
6
8
7
13
3 La tabella indica il numero delle persone che sono andate nella multisala Cinemapiù nei primi sette giorni di maggio. Calcola la media giornaliera.
6
7
8
13
16
La media giornaliera è
PROBLEMI
1 Osserva l’istogramma e risolvi il problema sul quaderno.
Nel grafico sono indicati i bambini e le bambine iscritti alla mensa. I maschi sono indicati dalla colonna grigia, le femmine sono indicate dalla colonna colorata.
Quanti sono in tutto gli iscritti e le iscritte alla mensa? Quali classi hanno il maggior numero di iscritti e iscritte e quanti sono?

classi prime classi terze classi quinte classi seconde classi quarte
2 Osserva la tabella e risolvi il problema sul quaderno.
Nella tabella sono riportati i biglietti venduti al cinema Arlecchino nella prima settimana di aprile. Se il biglietto d’ingresso costa € 6,50, quanto ha incassato il cinema Arlecchino in media al giorno?
giorni lunedì martedìmercoledìgiovedì venerdì sabatodomenica biglietti venduti
3 Osserva l’ideogramma e risolvi il problema.
Nell’ideogramma sono indicati i bambini e le bambine che ieri hanno visitato tre musei cittadini. Osserva la legenda e calcola quanti bambini e bambine hanno visitato ciascun museo.
LEGENDA: = 10 bambini/e = 1 bambino/a
Museo del giocattolo
Museo della Matematica
Museo archeologico
In ognuno dei tre musei il biglietto costa € 5,50. Quanto ha incassato ciascun museo?
Museo del giocattolo incasso: Museo della Matematica incasso: Museo archeologico incasso: Obiettivi di
CLASSIFICARE
1 Osserva il diagramma di Eulero-Venn, che rappresenta quali sport praticano alcuni bambini e bambine della 4ª A. Poi rispondi alle domande.
pattinaggio
Emanuela Gianna
Anna

Marco Gigi
Chiara
Nadia
Mario Karim
Tina
Jo
calcio
Sara Gianni
Luca
pallavolo
• Quanti sono in tutto i bambini e le bambine che praticano il calcio?
• Quanti sono in tutto i bambini che praticano la pallavolo?
• Quante sono le bambine che praticano il pattinaggio?
• Chi pratica tutti e tre gli sport?
7 3 4 Marco
• Chi non pratica né il calcio né il pattinaggio?
Nadia, Sara, Gianni
• Qual è la bambina che pratica sia il pattinaggio sia la pallavolo?
Chiara
2 Scrivi il nome dei mezzi di trasporto al posto giusto nel diagramma di Carroll. Segui l’esempio.
in cielo in terra con il motore senza il motore mongolfiera
aereo motorino treno monopattino bicicletta
3 Osserva le bandierine e completa il diagramma ad albero. Segui l’esempio.
rettangolari
bandierine bianche colorate
A, rettangolari triangolari triangolari
D, I E, H, K C, G, J, L B, F
4 Osserva i disegni e completa il diagramma di Carroll scrivendo al posto giusto le lettere corrispondenti ai cerchi.
cerchi grandi cerchi piccoli cerchi azzurri
cerchi grigi
A, E, H, K
B, I
C, G, J
D, F, L
Verso l’Invalsi
5 Se tu volessi inserire il seguente triangolo nel diagramma di Carroll dell’esercizio 4, potresti farlo? Segna con una , poi rispondi.
Posso inserirlo. Non posso inserirlo.
Perché?
Perché non è grigio.
Perché non è piccolo.
Perché non è un cerchio.
Obiettivi di apprendimento Classificare sulla base di più attributi utilizzando adeguate rappresentazioni grafiche.
CALCOLO DELLE PROBABILITÀ
1 Osserva il disegno e rispondi alle domande completando la frazione.
In un negozio ci sono i seguenti vestiti.

• Quante probabilità ha Martina di trovare un abitino a righe?
• Di trovare un abitino con le stelline?
• E quante probabilità ha di trovare un abitino a pois?
2 Osserva le carte e completa la tabella. Segui l’esempio. per pescare… casi possibilicasi favorevoliprobabilità un animale 7 5 un fiore un mammifero un insetto
Verso l’Invalsi
3 Segna con una in quale sacchetto ti conviene pescare per prendere un numero pari. Poi spiega perché.
• Ho scelto il sacchetto perché
B ci sono 6 probabilità su 9 di pescare un numero pari, mentre nel sacchetto A sono solo 3 su 9.
Obiettivi di apprendimento In una serie di eventi intuire e argomentare qual è il più probabile, dando una prima quantificazione nei casi più semplici.
Verso l’Invalsi
RELAZIONI, DATI E PREVISIONI
giallo
avventura fumetto
fantasy = 1 preferenza
In tutto hanno partecipato all’indagine alunni e alunne. Il genere preferito è il con preferenze. Il genere con il minor numero di preferenze è il . alunni e alunne hanno scelto i libri di avventura, mentre il fumetto è la lettura preferita da alunni e alunne.
2. Segna con una la media nella seguente successione di numeri.
3. Osserva la tabella delle temperature minime di una settimana di marzo. Poi rispondi alle domande.
lunedì martedì mercoledì giovedì venerdì sabato domenica
• Qual è la moda?
• Qual è la mediana?
4. Segna con una quante sono le probabilità di pescare un numero pari dal sacchetto.
1. Il grafico mostra le preferenze di lettura degli alunni e delle alunne della 4ª A. Osservalo e completa il testo. Verso
PROBLEMI
1 Leggi il problema e scegli la rappresentazione corretta.
Nell’astuccio ci sono 36 colori, di cui 16 sono pennarelli, 3 penne e un portamine. Quanti oggetti ci sono nell’astuccio?
2 Leggi il problema e segna con una le operazioni da fare.
Per il suo compleanno, Simona porta a scuola 150 pizzette. Prima ne dà una a ciascun bambino e bambina, poi distribuisce le rimanenti dandone 5 a ciascun insegnante della scuola. Quanti sono gli insegnanti?
150 : 25 = 6
150 : 5 = 30
3 Sottolinea le domande e cerchia i dati, poi risolvi sul quaderno.
Per preparare il costume di Carnevale, gli alunni e le alunne della classe 4a C usano 3 pacchi che contengono 12 rotoli di carta crespa ciascuno. Quanti rotoli hanno utilizzato in tutto? Da ogni rotolo ritagliano 45 fiori. Quanti fiori hanno a disposizione alla fine? numero dei bambini/e in ogni classe classe 1a classe
25 + 24 + 19 + 21 + 26 = 115 150 – 115 = 35 35 : 5 = 7 25 + 24 + 19 + 21 + 26 = 115 115 : 5 = 23
24 19 21 26 36; 1620 40
OPERAZIONI
1 Calcola a mente con le strategie che preferisci. 345 + 21 =
–
= ..........................
+ 99 =
2 Calcola in colonna sul quaderno (se non sei sicuro/a, verifica il risultato con la prova).
3519 + 2460 =
+ 6055 =
3 Usa la proprietà indicata ed esegui i calcoli. proprietà commutativa
proprietà associativa e/o dissociativa

4 Leggi i numeri scritti al centro di ogni fiore, poi colora di rosso i petali con i multipli di quel numero e di verde i petali con i divisori. Se il numero centrale è un numero primo, coloralo di azzurro.
5 × 3 × 4 = 20 × 3 =
(8 × 4) × 100 = 32 × 100 = 3200 (163 + 2) – (28 + 2) = 165 – 30 = 135 (505 – 7) – (107 – 7) = 498 – 100 = 398 (8400 : 100) : (400 : 100) = 84 : 4 = 21 (450 : 5) : (15 : 5) = 90 : 3 = 30 (30 × 6) + (4 × 6) = 180 + 24 = 204 (20 × 8) + (5 × 8) = 160 + 40 = 200



FRAZIONI E NUMERI DECIMALI
1 Osserva e per ogni frazione scrivi quella complementare.
2 Confronta le coppie di frazioni con i simboli maggiore >, minore < o uguale = .
3 Osserva ogni rappresentazione e calcola la frazione del numero.
4 Trasforma ogni frazione in numero decimale.
0,25 + 2,25 =
6 Calcola a mente le moltiplicazioni e divisioni per 10, 100, 1000.
× 10 =
1 Scomponi le misure in tabella.
0,12 km
3186 mm
18,9 dam

48,72 dal
5284 dag
347,89 hg
0,009 Mg
2 Esegui le equivalenze.
67 m = dm
€ 5,20 = cent
MISURE
Mg = kg
cl = dl
3 Risolvi il problema su peso netto, peso lordo e tara.
Giovanna ha abbattuto alcuni alberi che erano malati e li ha caricati sul trattore. Il carico di tronchi pesa 2850 kg e il trattore pesa 2400 kg. Quanto pesano gli alberi e il trattore insieme?
4 Risolvi il problema su costo unitario e costo totale.
Giada vuole acquistare 3 quaderni. Il prezzo di ogni quaderno è di € 1,50. Quanto spenderà in tutto?
5 Risolvi il problema su spesa, guadagno e ricavo.
Un negoziante ha acquistato dei vestiti e ha speso 230 euro. Dalla loro vendita ha guadagnato 70 euro. Qual è il ricavo?
SPAZIO E FIGURE
1 Completa le affermazioni.
– I poligoni equilateri hanno tutti i . – I poligoni equiangoli hanno tutti gli ....................................................................................................................... – I poligoni con tutti i lati e tutti gli angoli uguali sono chiamati ......................................
2 Collega con i numeri ogni triangolo alla sua definizione.
1 Il triangolo isoscele ha due lati uguali.
2 Il triangolo equilatero ha tutti i lati uguali.
3 Il triangolo scaleno ha tutti i lati disuguali.
3 Scrivi il nome di ogni quadrilatero, scegliendolo fra i seguenti. quadrato � rettangolo � rombo � romboide
4 Calcola le equivalenze.
5 Risolvi il problema sul quaderno.
lati congruenti 700 cm2 angoli congruenti regolari rettangolo quadrato romboide rombo
Il lato di una cornice quadrata misura 40 cm. Il dipinto intorno al quale si trova è anch’esso un quadrato, con il lato lungo 30 cm. Calcola l’area della cornice.
RELAZIONI, DATI E PREVISIONI
1 Nella 4a A è stata fatta un’indagine per conoscere quali sono le bevande preferite dagli alunni e dalle alunne. Osserva la tabella delle preferenze e completa l’ideogramma. Poi rispondi alle domande.
acqua minerale 3 aranciata 8
succo di frutta 4
limonata 2 tè freddo 5 chinotto 4

acqua minerale aranciata
succo di frutta
limonata tè freddo chinotto = 1 preferenza
2 Classifica i seguenti animali nel diagramma di Carroll. bevanda preferenze
- Qual è la bevanda preferita? ...............................................................................................................................
aranciata 26
- Qual è il numero di alunne e alunni che hanno partecipato? .
- Qual è la moda? . con le zampe senza zampe
capra, leone balena, delfino
lucertolaserpente gatto
3 Calcola la probabilità di pescare una caramella al limone dal sacchetto.
VERIFICA

PROBLEMI
1 Leggi il problema e rappresentalo nel modo più chiaro ed efficace possibile.
Mirko ha 3 anni in più di Cecilia, che ne ha il triplo del piccolo Sasha, che ha 5 anni. L’età del papà corrisponde esattamente alla somma dei loro anni. Quanti anni ha il papà?
Mirko
Cecilia
Sasha 5 anni
Cecilia + 3 anni = 18 anni
Triplo di Sasha = 15 anni
Papà = 38 anni
2 Leggi il problema e segna le operazioni da fare nell’ordine corretto.
Valerio e Serena raccolgono dei funghi. Valerio ne ha raccolti 16, Serena ne ha raccolti 4 in più di Valerio. Ma mentre quelli di Valerio sono tutti commestibili, solo la metà di quelli di Serena lo sono. Quanti funghi potranno essere mangiati?
16 : 2 = 8
8 + 4 = 12
16 – 12 = 4
+ 4 = 20
: 2 = 10
+ 10 = 26
– 4 = 12
: 2 = 6 6 + 4 = 10 16 + 4 = 20 16 – 4 = 12
+ 12 = 32
3 Leggi il problema, sottolinea il dato inutile e risolvi sul quaderno. Jane, Stefano e Mariaelena stanno realizzando dei braccialetti con le perline. Vogliono venderli al mercatino della scuola a € 2,00 l’uno. Hanno 90 perline rosa, 90 gialle, 80 verdi, 50 azzurre e 120 viola. Per realizzare un braccialetto servono 10 perline, quanti braccialetti riusciranno a fare?
43 Marcello
4 Leggi il problema, sottolinea il dato nascosto e risolvi sul quaderno. Miriam, Christian e Marcello hanno deciso di fare una sfida: chi riuscirà a fare più compiti delle vacanze in una settimana? Miriam decide di fare 3 pagine al giorno; Christian inizia con 4 pagine al giorno, ma gli ultimi 2 giorni riesce a farne solo 3 tra sabato e domenica; Marcello inizia con 1 pagina il primo giorno e poi aumenta di una ogni giorno fino alla fine della settimana. Chi vincerà?
1 Calcola a mente o, se è troppo difficile, in colonna sul quaderno.
a. 520 + 90 =
653 + 111 =
26 418 + 139 664 =
50 + 9 950 =
378 + 30 + 552 =
2 Calcola in colonna sul quaderno e verifica il risultato con la prova.
a. 133 925 + 18 458 =
7 946 + 63 805 =
89 457 + 251 999 =
3 Usa le proprietà e le strategie delle operazioni per calcolare velocemente.
a. 3 180 + 34 + 26 =
3180 + (34 + 26) = 3180 + 60 = 3240
57 + 325 + 23 + 75 =
8 450 + 654 =
b. 4 765 – 845 =
796 – 598 =
c. 236 × 21 =

(57 + 23) + (325 + 75) = 80 + 400 = 480 8000 + (450 + 650) + 4 = 8000 + 1100 + 4 = 9104
(4765 – 45) – (845 – 45) = 4720 – 800 = 3920
(796 + 2) – (598 + 2) = 798 – 600 = 198
(236 × 20) + 236 = 4956
5 × 45 × 20 =
324 × 8 =
d. 700 : 28 =
240 : 60 =
(5 × 20) × 45 = 100 × 45 = 4500
(300 × 8) + (20 × 8) + (4 × 8) = 2400 + 160 + 32 = 2592
(700 : 7) : (28 : 7) = 100 : 4 = 25
(240 : 10) : (60 : 10) = 24 : 6 = 4
4 Per ciascun numero scrivi almeno 2 multipli e 2 divisori, poi segna con una se è un numero primo.
FRAZIONI E NUMERI DECIMALI
1 Per ciascuna figura, scrivi la frazione corrispondente e se si tratta di una frazione propria (P), impropria (I) o apparente (A).

2 Confronta le frazioni con >, < o =.
3 Risolvi i problemi sul quaderno.
a. Francesco e Dafne stanno cercando di ricostruire un puzzle formato da 144 pezzi. Francesco ha preso i 6 8 dei pezzi. Quanti pezzi sono rimasti a Dafne?
b. Leggi la ricetta della Torta Facilina, che si prepara misurando gli ingredienti con 12 bicchieri uguali: 1 4 di latte, 3 6 di farina e la frazione rimanente di zucchero. Quanti bicchieri di zucchero servono?
4 Calcola a mente o in colonna sul quaderno.
MISURE
1 Completa le tabelle con le marche mancanti e scomponi le seguenti misure.

2 Esegui le equivalenze. 32,4 dm = mm
g = 5,46
=
cl
0,02 hl = cl 18 Mg = kg 32 cm = dam
3 Completa la tabelle.
4 Risolvi i seguenti problemi sul quaderno.
a. Sarah e Jessica sono andate a raccogliere i mirtilli. Ne hanno raccolti 6,3 kg, ma quando li pesano insieme alla cesta la bilancia indica 69 hg. Quanto
b. La libreria ha guadagnato € 67 dalla vendita di 20 copie di un libro appena uscito. Aveva pagato ogni copia € 14. Quanto è stato il ricavo?
1 Che cos’è un poligono?
SPAZIO E FIGURE

2 Colora di rosso solo i parallelogrammi.
3 Traccia di rosso una diagonale e un’altezza in ogni poligono.
4 Completa con la marca mancante.
6 m2 = 600
È una parte di piano delimitata da una linea spezzata, chiusa, semplice dm2
13,47 dm2 = 1347
58504 hm2 = 585,04
387,9 dm2 = 3,879
2078 m2 = 20,78
5 Scrivi i dati mancanti e calcola l’area.
AB = 24 cm
DC = 2 3 di AB = cm
AD = DC =
6 Risolvi il problema sul quaderno.
Il disegno illustra la pianta del cortile interno di un edificio. Partendo dalla misura del lato AB, calcola il perimetro e l’area della figura.
AB = 2 m P = m A = m2 A = ( × ) :
B
7 Completa la formula dell’area del rombo e poi calcola.
DB = 65,8 cm
AC = 35 cm A = cm2
RELAZIONI, DATI E PREVISIONI
1 Osserva la tabella dei voti di Matematica di Martino e rappresentali con un istogramma, poi rispondi alle domande.
voti frequenza
nove 6
sette 3
cinque 1

• Qual è stato il voto più frequente?
• Quanti voti ha avuto in totale?
• Qual è la media?
• Qual è la moda?
• Qual è la mediana?
2 Classifica con il diagramma di Carroll i seguenti animali secondo i criteri: vertebrato/invertebrato e con/senza ali.
vertebrati
invertebrati
con ali pettirosso, pipistrello farfalla, vespa, zanzara
senza ali salmone canguro, rana lombrico, stella marina
3 Disegna nel sacchetto delle biglie colorate verdi, gialle, rosse e viola in modo che la probabilità di pescare una biglia viola sia di 5 21 e quella di pescare una biglia verde sia di 7 21 .
PROBLEMI
1 Nei seguenti problemi cerchia solo i dati utili.
a. Ismael ha incollato su uno dei suoi quaderni 8 fotografie di cani, 7 di gatti e 3 di canarini. Sotto ogni foto ha scritto il nome degli animali con 2 matite diverse. Quante fotografie di mammiferi ha Ismael?
b. Elisabetta ha risolto 3 esercizi di Matematica. Ne deve svolgere altri 4, più altri 5 di Scienze Vuole finire presto i compiti, perché stasera vuole andare al cinema. Quanti esercizi di Matematica aveva da fare in tutto?
2 Nei seguenti problemi individua il dato mancante, poi aggiungine uno adatto.
a. L’autrice di un libro di Storia deve scrivere 2 pagine di verifica alla fine di ogni unità. Quante pagine di verifica dovrà scrivere?
Dato mancante:

b. Fra 5 giorni Elisa partirà per le vacanze. In valigia ha messo 2 romanzi e 3 fumetti. Ha preso anche dei libri per il suo fratellino Nicola. Quanti libri ha messo Elisa in valigia?
Dato mancante:
3 A quali numeri o operazioni corrispondono le seguenti parole? Completa.
dozzina: coppia o paio:
settimana:
numero delle unità: 14 libri per Nicola: 2 12 2
mese: metà: doppio:
triplo: secolo:
4 Leggi il testo dei problemi e segna con una la domanda adatta.
a. La classe di Marco ha utilizzato 400 fogli A4 per pubblicare le copie del giornalino scolastico. Ogni giornalino è formato da 10 pagine.
Quante copie del giornalino hanno preparato?
Quante copie del giornalino sono rimaste?
b. La famiglia di Sabrina è andata in pizzeria. I suoi genitori hanno preso una pizza margherita a testa, lei invece ha scelto la pizza ai quattro formaggi.
La pizza margherita costa 6 euro mentre quella di Sabrina costa € 7,50.
Quanto costa la pizza ai funghi? Quanto costano due pizze margherita?
5 Leggi il testo e le domande e colora le operazioni da fare per risolvere ogni problema.
a. Omar e Chiara giocano al tiro a segno. Omar con il primo tiro ha realizzato 150 punti, con il secondo 200. Chiara ha ottenuto prima 200 punti, poi 100.
Quanti punti ha totalizzato ognuno di loro? + – × :
Qual è la differenza tra i punteggi di Omar e Chiara? + × :
b. Sasha vuole preparare delle pizzette. Secondo la ricetta, con 500 g di farina può ottenere 25 pizzette, ma decide di raddoppiare le dosi.
Quanta farina servirà a Sasha? + – × :
Quante pizzette ha preparato in tutto? + – × :
Vuole distribuire le pizzette tra i suoi 10 amiche e amici. Quante pizzette avrà ogni amico o amica di Sasha? + – ×
6 Risolvi il problema nel diagramma, poi rispondi.
Giacomo è andato a fare la spesa al supermercato e ha comprato 5 litri di latte al prezzo di € 1,40 al litro, delle mele a € 3,55 in tutto e 2 dozzine di uova. Se ogni dozzina di uova costa € 2,30, quanto ha speso in tutto Giacomo?
Risposta:

:
7 Risolvi i problemi.
a. Li e Carlo hanno realizzato 15 braccialetti con le 195 perline che avevano a disposizione. Se vogliono preparare altri 5 braccialetti, di quante perline avranno bisogno in tutto?
Dati
Risposta:
braccialetti realizzati
195 : 15 = 13
13 × 5 = 65
Dati = = = =
Risposta: Giacomo ha speso € 15,15.
Avranno bisogno di 65 perline.
b. Per la festa di compleanno di Maha, i suoi genitori comprano 3 pizzette, 3 focaccine e 2 pasticcini per ogni invitato o invitata. Se le bambine e i bambini invitati alla festa sono 15, quante pizzette, focaccine e pasticcini hanno comprato in tutto i genitori di Maha?
pizzette per invitato/a perline usate focaccine per invitato/a braccialetti da preparare pasticcini per invitato/a bambini/e invitati alla festa
In tutto hanno comprato 120 pizzette, focaccine e pasticcini.
3 + 3 + 2 = 8
8 × 15 = 120
1 Scrivi i numeri in lettere.
738 103
30 313
451 002
390 091
2 332

NUMERI
settecentotrentottomilacentotré
trentamilatrecentotredici
quattrocentocinquantunomiladue
trecentonovantamilanovantuno
duemilatrecentotrentadue
2 Scrivi i numeri in cifre. settemilanovecentotrentatré centoventitremilanovecentosessanta ventimilatrecentotredici quattromilanovecentosettantaquattro cinquecentosettemilaottocentonovantuno
3 Registra i numeri in tabella, poi componili.
1 hk, 3 uk, 9 h, 2 da
9 dak, 1 uk, 3 h, 5 u
18 dak, 3 uk, 15 da
7 hk, 6 h, 1 da, 3 u
1 dak, 1 hk, 3 u, 2 h
9 u, 2 da, 1 uk
3 da, 1 u, 3 hk, 9 dak
4 Scomponi i seguenti numeri.
842 100
702 564
8 hk, 4 dak, 2 uk, 1 h
7 hk, 2 uk, 5 h, 6 da, 4 u
000 873 007
6 hk, 4 dak, 3 uk
8 hk, 7 dak, 3 uk, 7 u
42 802
5 Per ogni numero, indica il valore della cifra 3.
45 073
547 307
431 785
4 dak, 2 uk, 8 h, 2u u h
700
9 hk, 7 h
300 198 103 447
dak da uk hk
250 030
VERIFICA FINALE
6 Riscrivi ogni serie di numeri prima in ordine crescente, poi in ordine decrescente.
84400 • 64701 • 7405 • 593547 • 83520 • 542000 • 10250

Crescente:
64701
10250
Decrescente: 71000 • 7500 • 7400 • 7100 • 75000 • 750000 • 72500
Crescente:
Decrescente:
7405 7100 • 7400 • 7500 • 71000 • 72500 • 75000 • 750000 750000 • 75000 • 72500 • 71000 • 7500 • 7400 • 7100
7 Completa la tabella con il precedente e il successivo di ogni numero. precedente successivo 74522 65700 88598 74233 precedente successivo 101744 517490 4699 421000
8 Completa i confronti con i segni >, < o =. 85409 67480
5 hk 500 74 da, 8 u 740008
80457 8 dak, 4 h, 7 da, 5 u 48 dak 48000
9 Segna con una se le affermazioni sono vere (V) o false (F).
• Il numero precedente di 999900 è 999901. V F
• I numeri 451 000 • 452 000 • 451 500 sono stati scritti in ordine crescente. V F
• La scomposizione 4 hk, 3 dak, 3 u corrisponde al numero 430 003 V F
• Il numero 325 122 si scrive trecentoventicinquemilacentoventidue V F
• Nel numero 231 946 la cifra 2 corrisponde alle centinaia di migliaia. V F
• Nel numero 909 245 la cifra 5 corrisponde alle unità di migliaia. V F
• Ottomilanovecentotrentasette si scrive 80 937 V F
10 Per ogni riquadro, scrivi il numero maggiore e minore che puoi ottenere utilizzando tutte le cifre.
4 3 5 0 1 4 numero minore: numero maggiore:
3 1 0 0 2 numero minore: numero maggiore:
8 9 9 1 0 numero minore: numero maggiore:

OPERAZIONI
1 Applica le proprietà indicate, poi calcola le addizioni a mente.
commutativa 48 + 3 + 2 + 7 = associativa 41 + 9 + 7 =
2 Applica la proprietà della sottrazione, poi calcola a mente.
invariantiva 84 – 78 =
3 Esegui le addizioni e le sottrazioni in colonna, poi fai la prova. 876 + 165 = 1 508 + 4 769 = 1 270 – 637 = 748 – 349 =
48 + 2 + 3 + 7 = 60 (41 + 9) + 7 = 50 + 7 = 57 (84 + 2) – (78 + 2) = 86 – 80 = 6 1041 6277
4 Applica le proprietà indicate, poi calcola le moltiplicazioni a mente.
commutativa 4 × 40 × 2 = associativa 5 × 59 × 2 = distributiva 184 × 13 =
5 Applica le proprietà indicate, poi calcola le divisioni a mente.
invariantiva 4500 : 900 = distributiva 40200 : 20 =
4 × 2 × 40 = 320 (5 × 2) × 59 = 10 × 59 = 590 (184 × 20) + (184 × 3) = 1840 + 552 = 2392 (40000 : 20) + (200 : 20) = 2000 + 10 = 2010 (4500 : 100) : (900 : 100) = 45 : 9 = 5

VERIFICA FINALE
6 Esegui le moltiplicazioni e le divisioni in colonna, poi fai la prova.
873 × 13 = 2480 × 22 = 8940 : 12 = 810 : 18 =
7 Cerchia i multipli di 3 e sottolinea i divisori di 40.
9 Risolvi il seguente problema.
8 Cerchia solo i numeri primi.
Mario ha comprato 3 magliette al prezzo di 15 euro l’una, 1 paio di pantaloni a € 45,50. Se paga con una banconota da 100 euro, quanto riceve di resto?
3 € 15 1
magliette comprate
costo di 1 maglietta
pantaloni comprati
costo dei pantaloni
€ 45,50 € 100
banconota con cui paga 11349
Dati = = = = = Risolvo
3 × 15 = 45 45 + 45,50 =
Risposta:
riceve € 9,50 di resto
= 9,50
FRAZIONI E NUMERI DECIMALI
1 Segna con una se le frazioni sono proprie, improprie o apparenti.

2 Colora per ottenere una frazione complementare a quella data.
3 Colora per ottenere una frazione equivalente a quella data.
4 Completa i confronti tra frazioni con i segni >, < o =.
5 Calcola la frazione dei numeri. 8 7 di 49 = 2 11 di 121 = 3 7 di 595 = 5 6 di 84 =
6 Trasforma le frazioni in numeri decimali e viceversa. 9 10 = 20 1
= 9,4 =
7 Scomponi i seguenti numeri decimali.
=
=
7 u, 5 c, 8 m 4 da, 9 u, 7 d 5 h, 1 da, 7 d, 8 c, 4 m 9 da, 5 d, 6 m (49 : 7) × 8 = 7 × 8 = 56 (121 : 11) × 2 = 11 × 2 = 22 (595 : 7) × 3 = 85 × 3 = 255 (84 : 6) × 5 = 14 × 5 = 70
=
=
8 Completa i confronti tra numeri decimali con i segni > o <.
9 Esegui le operazioni con i numeri decimali in colonna.
10 Risolvi i seguenti problemi.
a. David compra 3 pacchetti di farina a
€ 1,25 l’uno e 2 litri di latte a € 1,45 al litro. Quanto ha speso in tutto? Se paga con una banconota da 10 euro, quanto riceve di resto?
Dati
b. La nonna vuole distribuire 10 euro ai suoi 4 nipoti. Quanto riceve in regalo ognuno?
Se poi la nonna dona un altro euro a ciascuno, quanto ha ora ogni nipote?
Dati
€ 10 soldi da distribuire pacchetti di farina comprati
€ 1,25 4 numero dei nipoti costo di un pacchetto
2 l
€ 1 soldi in più a ognuno latte comprato
€ 1,45 costo di un litro di latte
€ 10 banconota con cui paga
Ri l o

2,50 + 1 = 3,50 12,591 90,25 127,517 6,5 < < > < < > > >
3 × 1,25 = 3,75
2 × 1,45 = 2,90
3,75 + 2,90 = 6,65
10 – 6,65 = 3,35
Risposte:
3 Riceve € 3,35 di resto.

Ri l o
10 : 4 = 2,50
Risposte:
In tutto ha speso € 6,65. Ogni nipote riceve in tutto € 3,50.
Ognuno riceve in regalo € 2,50.
MISURE
1 Scomponi le seguenti misure di lunghezza.
846 m = 706,04 dm = 93,705 dam = 9 405 mm =
2 Esegui le equivalenze con le misure di lunghezza.
75 m = cm 0,807 dam = dm

070 cm =
mm = hm
3 Scomponi le seguenti misure di capacità.
50,8 l = 439,7 cl = 59,04 dal = 85,008 l =
8 hm, 4 dam, 6 m 5 da , 8 dl 4 , 3 d , 9 c , 7 ml 5 h , 9 da , 4 dl 8 da , 5 , 8 ml
4 Esegui le equivalenze con le misure di capacità.
km = m
450 ml = l 78,09 l = dal 230 dal = ml 893 hl = l 8,09 dal = hl 400 l = dl
5 Scomponi le seguenti misure di peso o massa.
300 g = 591,9 kg = 3,98 dg = 45,25 dag =
3 hg 591 kg, 9 hg 3 dg, 9 cg, 8 mg 4 hg, 5 dag, 2 g, 5 dg
6 Esegui le equivalenze con le misure di peso o massa.
1 Mg = kg 905 g = dag
dg = mg 23 hg = dg
7 Trasforma le misure di tempo come indicato.
48 h = d 3 600 s = h 4 h = min 2 min e 120 s = min
8 Calcola quanti euro ci sono nel riquadro.
€ 20,50 9 hm, 3 dam, 7 m, 5 cm 7 dam, 6 dm, 4 mm 9 m, 4 dm, 5 mm
dag = kg 305 cg = g
min = h min
s = min s
9 Risolvi i seguenti problemi.
a. Katia ha comprato una damigiana di vino rosso da 17 l. Vuole travasare il vino in bottiglie di vetro da 1,5 l ognuna. Quante bottiglie potrà riempire?
Quanto vino avanzerà?
17 l
Dati = =
capacità della damigiana
1,5 l
capacità della bottiglia
Risposte:
Riempirà 11 bottiglie.
Avanzerà 0,5 l di vino.
17 : 1,5 = 11 r. 0,5
b. La fruttivendola sta sistemando 12 cassette piene di fragole. Se ognuna contiene 2,5 kg di fragole e tutte le cassette piene pesano 32,7 kg, quant’è la tara di una cassetta?
2,5 kg
32,7 kg
Dati = = =
Risposta:
numero delle cassette
fragole in ogni cassetta
peso di tutte le cassette piene
La tara di una singola cassetta è 0,225 kg.
32,7 : 12 = 2,725
2,725 – 2,5 = 0,225
c. Mohammed è andato dal cartolaio. Ha preso 3 matite al costo di € 1,50 l’una, 6 quaderni a € 3,75 l’uno e un diario a 17 euro. Quanto spende in tutto?
12 3 numero delle matite
€ 1,50 costo di una matita
6 numero dei quaderni
€ 3,75 costo di un quaderno
€ 17 costo di un diario
Dati = = = = =
Risposta:
In tutto spende 44 euro.
3 × 1,50 = 4,50
6 × 3,75 = 22,50
4,50 + 22,50 + 17 = 44
Risolvo
Risolvo
Risolvo
SPAZIO E FIGURE
1 Leggi le misure dei lati di ogni poligono e calcola il perimetro.

2 Esegui le equivalenze con le misure di superficie.
3 Leggi le misure date di ogni poligono e calcola l’area.
4 Risolvi i seguenti problemi.
a. Una piscina quadrata è circondata da una passatoia con il lato esterno lungo 5 m. Quanto misura il perimetro esterno della passatoia? Il lato della piscina è lungo 4,5 m. Quanto misura la superficie della piscina?
Dati = =
5 m
4,5 m
Risposte:

lato della passatoia
lato della piscina
Il perimetro della passatoia è 20 m;
la superficie della piscina è 20,25 m2 .
b. Un giardino ha la forma di un trapezio isoscele. La base maggiore è lunga 15 m, quella minore 8 m e l’altezza è 5 m. Qual è la superficie del trapezio? Carla vuole recintare la parte interna, che forma un rettangolo.
Quanta rete dovrà comprare?
Dati
15 m
8 m
5 m
Risposte:
base minore altezza
5 × 4 = 20 m
4,5 × 4,5 = 20,25 m2
(15 + 8) × 5 : 2 = 57,5 m2
(8 + 5) × 2 = 26 m
La superficie è 57, 5 m2;
Carla dovrà comprare 26 m di rete.
c. Un rettangolo e un romboide sono equiestesi e hanno la stessa altezza, che misura 10 cm, e la stessa base, che è 1,7 dm. Quanto misura la loro superficie? Se il lato obliquo del romboide misura 12 cm, quanto misura il perimetro del romboide?
10 cm
1,7 dm
12 cm
Dati = = =
Risposte:
base maggiore altezza
base
lato obliquo
La loro superficie misura 170 cm2;
il perimetro del romboide misura 58 cm.
1,7 dm = 17 cm
A = 10 × 17 = 170 cm2
P = (17 + 12) × 2 = 58 cm
Risolvo
Risolvo
Risolvo
RELAZIONI, DATI E PREVISIONI
1 Osserva l’istogramma e risolvi il problema.

In 4ª B hanno fatto un’indagine su quali sono i frutti preferiti da ognuno.
• Quanti bambini e bambine ci sono in 4ª B?
• Qual è il frutto preferito?
• Quale frutto ha raccolto il minor numero di preferenze?
• Quali frutti hanno raccolto lo stesso numero di preferenze?
kiwi ciliegia e pera
2 Leggi il problema e osserva la tabella. Poi disegna un ideogramma che ne rappresenti i dati scegliendo con cura l’unità di misura. Infine rispondi.
In 4ª C gli alunni e le alunne hanno scelto lo strumento preferito con cui svolgere il compito di Matematica. La tabella riporta le preferenze espresse.
matita 3
penna blu 10
penna nera 8
matita
penna blu
penna nera
penna cancellabile
penna cancellabile5 = bambini/e
• Quanti sono gli alunni e le alunne della 4ª C?
• Qual è la moda?
penna blu penna cancellabile
• Qual è la mediana?
3 La tabella riporta il numero di ingressi al museo in una settimana. In media, quante persone hanno visitato il museo al giorno? lunedìmartedìmercoledìgiovedìvenerdìsabatodomenica
Media:
VERIFICA FINALE

4 Completa il diagramma di Eulero-Venn con i seguenti nomi.
albero • classe • aula • maestra • astuccio • amica • porta nomi che iniziano per A nomi femminili
albero astuccio aula amica classe
maestra
5 Completa il diagramma di Carroll scrivendo al posto giusto i nomi delle seguenti figure.
ha tre lati ha quattro lati
ha tutti i lati uguali ha due lati uguali
6 Osserva il disegno e rispondi alle domande sulla probabilità completando le frazioni.
triangolo equilatero quadrato triangolo isoscele trapezio isoscele porta 3 9 4 9 5 9
• Qual è la probabilità di pescare un numero multiplo di 10?
• Qual è la probabilità di pescare un numero dispari?
• Qual è la probabilità di pescare un numero pari?
PROBLEMI
1 Leggi il testo del problema, osserva l’immagine e scegli la lista di operazioni adatta per risolverlo.
Per il compleanno della sua migliore
amica Alessia, Marcello si reca nel negozio di dolciumi vicino a casa.
Decide di acquistare 10 caramelle e 3 lecca-lecca per Alessia e 2 lecca-lecca e 2 caramelle per sé.
Quanto spende in tutto?
0,60 × 10 = 6,00
3,00 + 5,00 = 8,00
5,00 + 0,60 + 0,60 = 6,20
6,00 + 8,00 + 6,20 = 20,20

+ 12,00 +
0,60 × 12 = 7,20
7,20 + 12,00 = 19,20
+ 1,20 =
2 Leggi i dati e le richieste, poi scrivi una situazione-problema adatta e risolvila.
dati
6 quaderni
€ 1,50 a quaderno
4 penne colorate
€ 20 = banconota usata per pagare
richieste
€ 1 = resto ? spesa totale ? costo di ogni penna colorata € 19,00 € 2,50
PROVA NON NOTA

3 Leggi attentamente il problema risolto da Michele, poi svolgi le attività.
Un museo di arte contemporanea si trova all’interno di un edificio disposto su 4 piani. In ogni piano ci sono 5 sale da esposizione e in ogni sala vengono esposti 3 quadri nuovi. La direttrice decide di esporre altri 20 quadri nuovi in modo che siano distribuiti equamente lungo i corridoi di ciascun piano. Quanti nuovi quadri vengono esposti in tutto?
DATI
4 piani
5 sale
3 quadri nuovi in ogni sala
20 quadri nuovi nei corridoi
DOMANDA
? quadri nuovi in tutto
OPERAZIONI
quadri per ogni sala
sale per ogni piano
quadri nelle sale
× + ×
quadri nei corridoi piani
quadri per ogni piano quadri in tutto
3 × 5 = 15 quadri nuovi in tutte le sale di un piano
15 + 20 = 35 quadri nuovi in ogni piano
35 × 4 = 140 quadri nuovi in tutto
RISPOSTA
In tutto vengono esposti nel museo 140 quadri nuovi.
• Michele ha risolto correttamente il problema? sì no
• Se hai trovato degli errori, correggili e calcola di nuovo qui sotto.
4 × 5 = 20 sale totali
20 × 3 = 60 quadri esposti nelle sale
60 + 20 = 80 quadri tra sale e corridoi
Ho svolto la prova:
Senza difficoltà e senza bisogno di aiuto.
Con qualche dubbio, ma sono riuscito/a a completarla.
Con parecchie incertezze.
Con difficoltà, quindi ho avuto bisogno di aiuto.
VALUTO LA MIA PROVA
NUMERI E OPERAZIONI
1 Chiara e Igor hanno deciso di scambiarsi i compiti di Matematica e di correggerli a vicenda. Ecco il compito di Igor. Per ogni operazione, fai la prova per controllare che i risultati siano giusti, poi correggi gli errori che Chiara non ha visto.


PROVA NON NOTA
2 Completa le seguenti operazioni con le cifre mancanti, poi scrivi l’operazione corretta in riga.
3 Completa i quadrati magici in modo che:
• in ogni griglia ci siano tutte le cifre dall’1 al 9;
• la somma di ogni riga, colonna e diagonale sia 15.
Ho svolto la prova:
Senza difficoltà e senza bisogno di aiuto.
Con qualche dubbio, ma sono riuscito/a a completarla.
Con parecchie incertezze.
Con difficoltà, quindi ho avuto bisogno di aiuto.
VALUTO LA MIA PROVA
FRAZIONI E NUMERI DECIMALI
1 Completa il crucinumero scrivendo i numeri decimali corretti.
Attenzione: le virgole vanno messe in un quadretto a sé.
ORIZZONTALI
1) Un quarto.
4) La cifra dei centesimi nel numero 813,456.
5) 7 da, 0 h, 9 u.
6) 4 da, 40 uk, 4 u.
9) 9 809 : 100.
10) Un terzo di 690.
11) 8 563 d.
13) 9,64 × 100.
VERTICALI
1) 3 m, 8 c.
2) Il doppio di 10 centinaia.
3) Cinquecentosettantaquattromilanovecentosei.
6) 1 000 × 4,92.
7) 8 c, 6 m, 40 d.
8) 2 037 1 000
12) 60 × 0,9.

2 Leggi attentamente il problema e osserva come l’hanno risolto Karim e Jasmine. Poi spiega quale procedimento ti sembra più adatto e perché.
La nonna di Angelo e il nonno di Gabriel si impegnano a preparare la merenda per i 140 bambini e bambine della scuola. La nonna di Angelo prepara una parte delle crostatine, il nonno di Gabriel i restanti 3 7 . Quante crostatine ha preparato la nonna in più del nonno?
soluzione di Karim
OPERAZIONI
140 : 7 × 3 = 20 × 3 = 60 crostatine (nonno)
140 : 7 × 4 = 20 × 4 = 80 crostatine (nonna)
80 – 60 = 20 crostatine (nonna in più del nonno)
RISPOSTA
La nonna prepara 20 crostatine in più del nonno.
OPERAZIONI
soluzione di Jasmine
140 : 7 = 20 ( 1 7 delle crostatine = differenza tra le crostatine della nonna e quelle del nonno)
RISPOSTA
Le crostatine che la nonna prepara in più sono 20.
• Chi ha usato il procedimento più adatto? Karim Jasmine
• Perché? Ha svolto correttamente il problema eseguendo il minor numero possibile di calcoli.
3 Sul pianeta Mostruoso abitano questi mostriciattoli. Il più forte è il mostro costruttore, il più veloce è un esploratore spaziale, il più intelligente un inventore. Scopri qual è e cerchia il mostriciattolo artista.

Ho svolto la prova:
Senza difficoltà e senza bisogno di aiuto.
Con qualche dubbio, ma sono riuscito/a a completarla.
Con parecchie incertezze.
Con difficoltà, quindi ho avuto bisogno di aiuto.
VALUTO LA MIA PROVA
MISURE
1 Leggi gli ingredienti necessari per preparare i muffin e completa la tabella. Poi rispondi.
INGREDIENTI PER 12 MUFFIN
260 g di farina
120 g di burro
140 g di zucchero
2 uova
120 c di latte
100 g di gocce di cioccolato
10 g di lievito per dolci

di cioccolato
Davide ha in casa 220 g di farina, 100 grammi di burro, 150 grammi di zucchero, una bustina di lievito per dolci (10 g), 1 litro di latte, 6 uova e 120 grammi di cioccolato.
Secondo te, quanti muffin potrà preparare?
solo 6 almeno 10 12
2 Idris deve riordinare i cartellini in modo che le grandezze siano in ordine crescente. Segna con una la sequenza corretta.
4; 1; 3; 2. 3; 2; 1; 4.
4; 1; 2; 3. 3; 2; 4; 1.

3 Osserva il compito svolto da Maria Sole, poi individua e correggi eventuali errori.
Spiaggia Bianca 08:15 09:05 10:15 11:20 13:00 14:48
Lido SaBBioSo 08:30 09:20 11:35 15:03
porticcioLo 08:50 09:40 10:45 13:30 15:23
• Se prendi l’autobus delle 09:05 da Spiaggia Bianca e ti devi fermare almeno un’ora e 20 minuti a Lido Sabbioso, a che ora potrai prendere l’autobus per Colle Rosso?
coLLe roSSo 09:07 11:02 12:10 13:47 15:40 11:35
Prenderò l’autobus delle 10:45 per Colle Rosso.
• E se un tuo amico, dopo pranzo, prende il primo autobus da Lido Sabbioso, a che ora vi potreste incontrare a Colle Rosso?
Ci potremmo incontrare alle 15:40 a Colle Rosso.
Ho svolto la prova:
Senza difficoltà e senza bisogno di aiuto.
Con qualche dubbio, ma sono riuscito/a a completarla.
Con parecchie incertezze.
Con difficoltà, quindi ho avuto bisogno di aiuto.
VALUTO LA MIA PROVA
SPAZIO E FIGURE
1 Adele, Bice, Carlo e Daniele hanno disegnato la piantina del proprio parco-giochi ideale. Osserva i disegni, leggi gli indizi e scopri a chi appartiene ciascuna pianta.
INDIZI
1. Il parco-giochi di Adele non è quello con il perimetro minore.
2. Il parco-giochi di Bice è quello con l’area maggiore.
3. Nel parco-giochi di Carlo la misura del perimetro corrisponde a quella dell’area.
4. L’area del parco-giochi di Daniele è più piccola di quella del parco-giochi di Carlo di 3 cm2
2 Osserva la figura e calcola l’ampiezza degli angoli A, B, C, D, E.
Se sei in difficoltà, rifletti sull’ampiezza degli angoli che conosci (angolo retto, piatto, giro) e pensa a quanto vale la somma degli angoli interni di triangoli e quadrilateri.

Ho svolto la prova:
Senza difficoltà e senza bisogno di aiuto.
Con qualche dubbio, ma sono riuscito/a a completarla.
Con parecchie incertezze.
Con difficoltà, quindi ho avuto bisogno di aiuto.
VALUTO LA MIA PROVA
RELAZIONI, DATI E PREVISIONI
1 Le alunne e gli alunni della 4ª C hanno svolto un’indagine statistica tra le classi quarte della loro scuola. Controlla che l’indagine sia corretta in ogni sua fase e, se trovi degli errori, correggili.
A • decidere l’argomento e il campione
Abbiamo deciso di scoprire qual è la materia preferita da bambini e bambine delle classi quarte.
B • raccogliere i dati

Veronica: Matematica
Alessia: Inglese
Giorgia: Matematica
Francesco: Storia
Giulia: Italiano
Leonardo: Storia
Aya: Musica
Bassirou: Inglese
Erika: Matematica
Samuele: Matematica
Giulio: Inglese
Geremia: Educazione fisica
Michelle: Educazione fisica
Lisa: Storia
Giorgio: Scienze
Giacomo: Italiano
Maria: Inglese
Tassnim: Arte e immagine
Matteo: Storia
Maria: Italiano
Giorgia: Musica
Katia: Geografia
Valentina: Matematica
Viola: Inglese
Kevin: Inglese
Luisa: Geografia
Corinne: Italiano
Pablo: Educazione civica
Margot: Musica
Chiara: Italiano
Francesca: Educazione fisica
Alessandra: Arte e immagine
Franco: Tecnologia
Vita: Matematica
Simone: Storia
Fabiola: Scienze
Angela: Matematica
Isabel: Educazione fisica
Isabella: Italiano
Lisa: Matematica
Marco: Scienze
Nicola: Geografia
Stefania: Matematica
Aurora: Educazione civica
Gemma: Italiano
Licia: Storia
Giovanna: Matematica
Luca: Storia
Cinzia: Geografia
Costantino: Musica
Yuri: Inglese
Barbara: Musica
Chiara: Inglese
Sara: Educazione civica
Gianluca: Matematica
Valeria: Inglese
Arte e immagine
Matematica
Scienze
Storia
Geografia
Italiano 5
Inglese
Musica
Educazione Fisica
Educazione Civica 2
Tecnologia
C • rappresentare i dati
Arte e immagine
Matematica
Scienze
Storia Geografia
Italiano Inglese Musica
Educazione fisica
Educazione civica
Tecnologia
0 5 10 15
• Manca qualche fase? sì no
• Se hai risposto di sì: quale manca?
• Aggiungila tu.
• La fase A è stata svolta correttamente? sì no
Perché?
• La fase B è stata svolta correttamente? sì no
Perché?
• La fase C è stata svolta correttamente? sì no
Perché?
• L'ultima fase è stata svolta correttamente? sì no
Perché?
Ho svolto la prova:
Senza difficoltà e senza bisogno di aiuto.
Con qualche dubbio, ma sono riuscito/a a completarla.
Con parecchie incertezze.
Con difficoltà, quindi ho avuto bisogno di aiuto.
VALUTO LA MIA PROVA
Coding è una parola inglese che, tradotta in italiano, significa “programmazione”.
Quando si parla di programmazione spesso ci si riferisce ai computer e alle altre macchine che popolano la nostra esistenza: per esempio gli smartphone, i frigoriferi, le lavatrici, le automobili. Tutte queste macchine si comportano allo stesso modo: non agiscono da sole, ma ogni azione da fare è stata loro spiegata nei minimi particolari Qualcuno le ha programmate, cioè ha scritto loro delle istruzioni dettagliate per raggiungere degli scopi: risolvere un problema aritmetico, ma anche... lavare i panni sporchi!
Le istruzioni vengono comunicate al computer in linguaggio informatico, un codice che le macchine possono capire.
Quando si parla di “fare coding”, però, non si intende solo la scrittura di istruzioni in linguaggio informatico. Noi facciamo coding tutti i giorni: ogni volta che dobbiamo trovare una soluzione a un problema per raggiungere uno scopo preciso Vediamo un esempio di coding applicato alle nostre azioni quotidiane
CHE COS’È IL CODING?
Per la prossima domenica, Willy vuole preparare una sorpresa ai suoi genitori: far trovare loro la tavola apparecchiata per la colazione.
Non l’ha mai fatto prima, quindi decide di scrivere una lista delle azioni da compiere perché tutto sia perfetto.
Willy sa che la domenica la sveglia suona alle 9:00, quindi imposta la sua alle 8:30 e decide di organizzarsi nel modo che puoi leggere qui a fianco.
Si rende conto, però, che rileggendo queste istruzioni qualche giorno più tardi potrebbe non ricordarsi esattamente come aveva pensato di apparecchiare la tavola.
Per evitare che succeda, divide “apparecchia la tavola” in altri passaggi più dettagliati.

vestiti
vestiti
disponi sul tavolo 3 piatti
disponi sul tavolo 3 tazze
disponi sul tavolo 3 cucchiai
disponi sul tavolo 3 tovaglioli
metti la tovaglia
apparecchia la tavola
Ora Willy è quasi soddisfatto della sua lista, ma gli sembra che qualcosa non torni.
Se dovesse seguire l’elenco delle azioni nell’ordine in cui lo ha scritto, dovrebbe mettere la tovaglia sulla tavola già apparecchiata.
Quindi sposta “metti la tovaglia” subito dopo “vestiti”.

Ora manca solo un punto fondamentale: specificare quando Willy dovrà iniziare a compiere tutte queste azioni. Per farlo, aggiunge in cima alla sua lista la frase “domenica, quando suona la mia sveglia”.
vestiti
metti la tovaglia
disponi sul tavolo 3 piatti
disponi sul tavolo 3 tazze
disponi sul tavolo 3 cucchiai
disponi sul tavolo 3 tovaglioli
domenica, quando suona la mia sveglia
vestiti
metti la tovaglia
disponi sul tavolo 3 piatti
disponi sul tavolo 3 tazze
disponi sul tavolo 3 cucchiai
disponi sul tavolo 3 tovaglioli
Avresti mai detto che qualcosa di così semplice come apparecchiare la tavola per la colazione fosse l’insieme di così tante azioni?
Pensa che ognuna di quelle azioni potrebbe essere suddivisa in gesti ancora più piccoli.
Per esempio, al posto di “vestiti” Willy avrebbe potuto scrivere:
togliti il pigiama
cambia la biancheria
metti i pantaloni
metti la maglietta
Riassumendo, “fare coding” significa:
• dividere i problemi in piccole parti per risolverli più facilmente;
• scrivere una serie di istruzioni dettagliate e ordinate per descrivere una qualsiasi azione.
LE ISTRUZIONI
Come hai visto, ogni azione può essere suddivisa in tanti piccoli passaggi. Da ora in poi chiameremo questi passaggi istruzioni Come già detto, le istruzioni devono avere due caratteristiche: essere dettagliate ed essere ordinate
Dare istruzioni dettagliate
Le istruzioni che diamo per compiere ogni azione devono essere complete, chiare e dettagliate per evitare che chi le esegue si sbagli. Per esempio, Willy ha scritto nelle sue istruzioni “metti la tovaglia”. Per essere più preciso, avrebbe potuto scrivere “metti la tovaglia arancione” oppure “metti la tovaglia che è nel primo cassetto”.
ORA PROVA TU Per ogni coppia, segna con una l’istruzione più dettagliata.
chiudi la finestra
quando sono le 20:00
vai avanti
quando ci sono più di 30 °C
metti la maglietta a righe
Dare istruzioni ordinate
chiudi la finestra della cucina
quando è ora di cena
vai avanti di un passo
quando fa caldo
metti la maglietta

Le istruzioni devono essere ordinate perché l’ordine in cui vengono disposte è fondamentale. Willy, infatti, ha dovuto cambiare l’ordine delle sue azioni per poter mettere la tovaglia sul tavolo ma non sopra le stoviglie.
ORA PROVA TU Usa i numeri e ordina le azioni da compiere per preparare una torta.
accendi il forno
inforna la torta prepara l’impasto 3 4 1 2
compra gli ingredienti
DIVERSI TIPI DI ISTRUZIONI
Le istruzioni non sono tutte uguali tra loro, ma possono essere di diverse tipologie. Nelle prossime pagine vedremo le seguenti istruzioni:
comandi Spiegano che cosa bisogna fare.

cicli Si usano per descrivere le azioni da ripetere più volte di seguito.
situazioni di partenza Specificano quando cominciare un’azione o una serie di azioni.
I comandi
se ... allora ... Indicano azioni da eseguire solo in certi casi.
Nelle istruzioni di comando si spiega che cosa bisogna fare. Queste istruzioni specificano quando, come e perché devono essere svolte le azioni. Willy nella sua lista di azioni ha utilizzato molte istruzioni di comando, per esempio:
vestiti
disponi sul tavolo 3 piatti
metti la tovaglia
Quando bisogna descrivere un procedimento, i comandi sono indispensabili. Tuttavia, non sono sufficienti a dare istruzioni davvero precise.
ESERCIZI
Scrivi il percorso che la rondine deve seguire per raggiungere il nido senza passare attraverso gli alberi.
Usa le frecce e .
Ora trasforma le frecce in istruzioni. Per descrivere il percorso della rondine usa i comandi avanti e gira a destra
avanti
avanti
gira a destra
Le situazioni di partenza
Nel dare delle istruzioni precise, è importante ricordarsi di specificare quando bisogna cominciare a eseguirle.
Per questo motivo Willy in cima alla sua lista ha specificato “domenica, quando suona la mia sveglia”.
La frase
domenica, quando suona la mia sveglia
è una situazione di partenza che dà il via a tutte le altre azioni.
Ecco altri esempi di situazioni di partenza.
alle ore 10:00 quando mi danno il “via!”
quando la maestra pone una domanda
ORA PROVA TU Se la sveglia di Willy fosse
puntata alle 9:00 del mattino, che cosa potresti scrivere come situazione di partenza? Completa.
domenica, alle 9:00

ESERCIZI
Inserisci una situazione di partenza adatta in ogni schema.
quando suona la campanella alle 22:30 quando piove
metti le penne nell’astuccio
ripeti volte
p i v l
chiudi l’astuccio
metti l’astuccio nello zaino
metti i quaderni e i libri nello zaino
chiudi lo zaino
metti il pigiama
ripeti volte
ip ti volt
lava i denti
vai a letto
spegni la luce
metti gli stivali di gomma
ripeti volte
p i vo e
prendi l’ombrello
esci di casa
apri l’ombrello
I cicli
A volte capita di dover ripetere la stessa azione per più di una volta. Quando Willy ha preparato la tavola, per esempio, ha preso 3 piatti, 3 tazze, 3 cucchiai e 3 tovaglioli.
Se Willy avesse voluto essere ancora più preciso, avrebbe potuto scrivere la sua lista nel modo seguente.
ripeti 3 volte
disponi sul tavolo 1 piatto
disponi sul tavolo 1 tazza
disponi sul tavolo 1 cucchiaio
disponi sul tavolo 1 tovagliolo
Questa tipologia di comandi si chiama ciclo, perché una volta finito ricomincia per tante volte quante ne decidiamo noi: in questo caso 3. Il ciclo racchiude al suo interno un certo numero di istruzioni: sono quelle che devono essere ripetute. Per questo motivo il ciclo nello schema ha una forma a C. Ecco una serie di cicli che potrebbero tornarti utili:
ripeti ... volte
ripeti per sempre ripeti fino a quando ...
ORA PROVA TU Scrivi il ciclo adatto per ripetere questa serie di azioni, poi rispondi alla domanda.
ripeti fino alla fine del libro
leggi la pagina sinistra
leggi la pagina destra
gira la pagina
• Qual è lo scopo dello schema qui sopra?
Leggere tutte le pagine di un libro.
Se… allora…
Se domenica mattina Willy si accorgesse che la tovaglia è tutta sporca, che cosa potrebbe fare?
Ecco quale istruzione potrebbe aggiungere alla sua lista di azioni da compiere.
se la tovaglia è sporca allora prendi una tovaglia pulita
Leggi anche i seguenti esempi.
Se pioverà, allora prenderò l’ombrello.
Se farò tutti i compiti, allora potrò andare a giocare.
Le parole “se” e “allora” collegano due frasi: se la prima frase, cioè la condizione, è vera, allora si verifica la seconda, cioè la conseguenza
È possibile che si debba decidere che cosa fare anche nel caso in cui la condizione sia falsa. In questo caso si può usare l’istruzione se … allora … altrimenti
Per esempio: Se arriverò primo, allora vincerò la gara. Altrimenti ci riproverò l’anno prossimo.
ESERCIZI

se … allora … altrimenti
Completa le sequenze di azioni per far arrivare lo scoiattolo alla tana dopo aver raccolto tutte le ghiande. Usa le seguenti istruzioni.
arrivi alla tana • avanti di 1 • raccogli la ghianda • trovi una ghianda
trovi una ghianda
ripeti fino a quando se allora avanti di 1
arrivi alla tana raccogli la ghianda
ESERCIZI DI RIEPILOGO
Scomponi ogni azione in gesti più piccoli e dettagliati, poi completa gli schemi.
apri il rubinetto
fai un passo avanti
alza un piede
sposta il piede in avanti
abbassa il piede
lava le mani
lava le mani
chiudi il rubinetto
asciuga le mani
Per ogni sequenza trova gli errori e spiega come correggeresti.
metti la castagna nel cesto raccogli una castagna
fino a quando il cesto è pieno
se il semaforo è verde allora aspetta attraversa altrimenti quando la cena è pronta
“Raccogli una castagna” deve essere all’interno del blocco RIPETI; “Quando la cena è pronta” deve essere sostituito con “Quando incontri un semaforo”; “aspetta” e “attraversa” devono essere scambiati di posto.
Completa le istruzioni per raggiungere gli obiettivi indicati.
La lampadina in giardino deve accendersi alle 19:00 e spegnersi alle 23:00.
Dai istruzioni alla sonda spaziale per cercare l’acqua su Marte ed eventualmente raccoglierne un campione.
se sono le allora
accenditi
19:00 23:00
se sono le allora
spegniti
se allora da quando atterri su esplora
trovi l'acqua Marte
raccogliene un campione
IL CODING E LA GEOMETRIA
Il re ha deciso di scavare un fossato intorno al proprio castello per difendersi dai nemici. Chiama Luigi per realizzarlo.
• Osserva come Luigi ha deciso di procedere e svolgi le attività.

• Che forma avrà il fossato?
• Completa i comandi scegliendo tra quelli qui sotto. Puoi usarli più di una volta!
• Per quante volte è necessario che Luigi ripeta i comandi? = 100 passi
ripeti volte quadrata
vai avanti di 100 passi • gira a destra • quando il re lo ordina
quando il re lo ordina
4
vai avanti di 100 passi
vai avanti di 100 passi
vai avanti di 100 passi
gira a destra
• Prova a migliorare le sequenze di istruzioni che hai creato finora. Leggi le istruzioni qui sotto, completale e riscrivile nell’ordine corretto. Un piccolo aiuto: puoi inserire un blocco “ripeti” dentro un altro blocco “ripeti”.
quando il re lo ordina
ripeti volte

ripeti volte
quando il re lo ordina ripeti 4 volte
ripeti 3 volte vai avanti di 100 passi
gira a destra
vai avanti di 100 passi
gira a destra
Ora applica ciò che hai imparato in Geometria per migliorare ulteriormente i comandi.
• Osserva il disegno di pagina 310. Di quanti gradi si deve girare Luigi per poter disegnare il lato successivo del quadrato?
• Completa la nuova istruzione.
• Scrivi le istruzioni per far costruire a Luigi un fossato a forma di triangolo equilatero. Osserva il disegno: prima di disegnare il lato successivo del triangolo, Luigi deve girare di 120°.
quando il re lo ordina = 50 passi
ripeti volte
ripeti volte
vai avanti di 50 passi
Il lavoro è terminato e il re chiede al suo manovale di fargli sapere quanto è lungo il fossato quadrato appena scavato.
quando il re lo domanda
di’ al re il perimetro del fossato
Ma come si fa a calcolare il perimetro usando le istruzioni?
Per effettuare delle operazioni matematiche, si utilizzano gli operatori matematici
Qual è il perimetro del fossato?
Questi operatori calcolano in automatico il risultato.
* /
4 + 4
Quindi scrivere equivale a scrivere:
• Qual è la formula per calcolare il perimetro del quadrato?
8
l × 4
• Completa l’operatore per calcolare in automatico il perimetro del fossato quadrato, poi calcola.
quando il re lo domanda
di’ al re che il fossato è lungo
300 × 4 = 1200 passi
4
• Qual è la formula per calcolare il perimetro del triangolo equilatero?
l × 3
• Completa l’operatore per calcolare in automatico anche il perimetro del fossato triangolare, poi calcola.
quando il re lo domanda
di’ al re che il fossato è lungo
200 × 3 = 600 passi
Nel linguaggio informatico, * indica l’operazione di moltiplicazione e / indica l’operazione di divisione.
1200 passi
Il perimetro del fossato quadrato è ......................; quello del fossato a forma di triangolo equilatero è .......................
600 passi
di’
