
Ricerca e Sviluppo Erickson in collaborazione con Cristina Caciolo


Ricerca e Sviluppo Erickson in collaborazione con Cristina Caciolo

In CheFacile! ● Matematica 4 trovi gli argomenti più importanti di Aritmetica e di Geometria che studierai durante quest’anno scolastico. Gli argomenti sono spiegati in modo breve e semplice.
Imparerai i termini, i segni delle quattro operazioni, le proprietà delle operazioni e tanto altro attraverso esempi ricchi di colori e di immagini.
Nel volume affronterai:
• Numeri e operazioni
• Misure
• Problemi
• Spazio e figure.
In ogni sezione, trovi i diversi argomenti spiegati attraverso:
1. schede di base
2. procedimenti
3. schemi.
Infine, in fondo al libro, trovi degli strumenti utili.
1. Nelle schede di base, nel riquadro arancione con la chiave trovi le definizioni. Le definizioni contengono la spiegazione di tutti gli elementi, accompagnata da esempi, e ti serviranno per capire una regola o usare una formula.
Infatti, capire perché una formula è fatta in quel modo ti permette di ricordarla meglio per quando dovrai applicarla negli esercizi.
Questo è il riquadro arancione con la definizione di addizione.
Sotto il riquadro arancione della definizione, trovi gli esempi che ti spiegano come funziona l’addizione, come si chiamano i suoi termini e il suo segno. Osserva bene i colori: ti aiuteranno a risolvere gli esercizi sotto.
Ed ecco gli esercizi.
Qui e in tutte le pagine del libro, gli esercizi sono indicati da una matita blu a fianco della consegna.
Osserva bene i colori: sono gli stessi degli esempi e ti aiutano a completare gli esercizi.
2. Nei procedimenti trovi delle istruzioni, divise in passi, che ti guidano nello svolgimento di ognuno.
Se svolgi le attività “un passo alla volta”, riuscirai a capire e ricordare meglio il procedimento per risolvere le operazioni. Come nelle schede di base, anche nei procedimenti trovi un esempio e alcuni esercizi.
Ecco i quattro passi per risolvere le addizioni senza il cambio.
Ora mettiti alla prova con gli esercizi sulle addizioni senza il cambio!
3. Gli schemi raccolgono le informazioni fondamentali sull’argomento appena affrontato. Aiutati con lo schema per prepararti a un’interrogazione o a una verifica scritta: ripassare sarà più semplice e veloce.
In fondo al libro, trovi degli strumenti utili (le tavole pitagoriche da 1 a 100 e la tavola per le equivalenze). Con l’aiuto di questi strumenti, potrai svolgere più facilmente sia gli esercizi del libro sia gli esercizi che farai in classe o a casa.

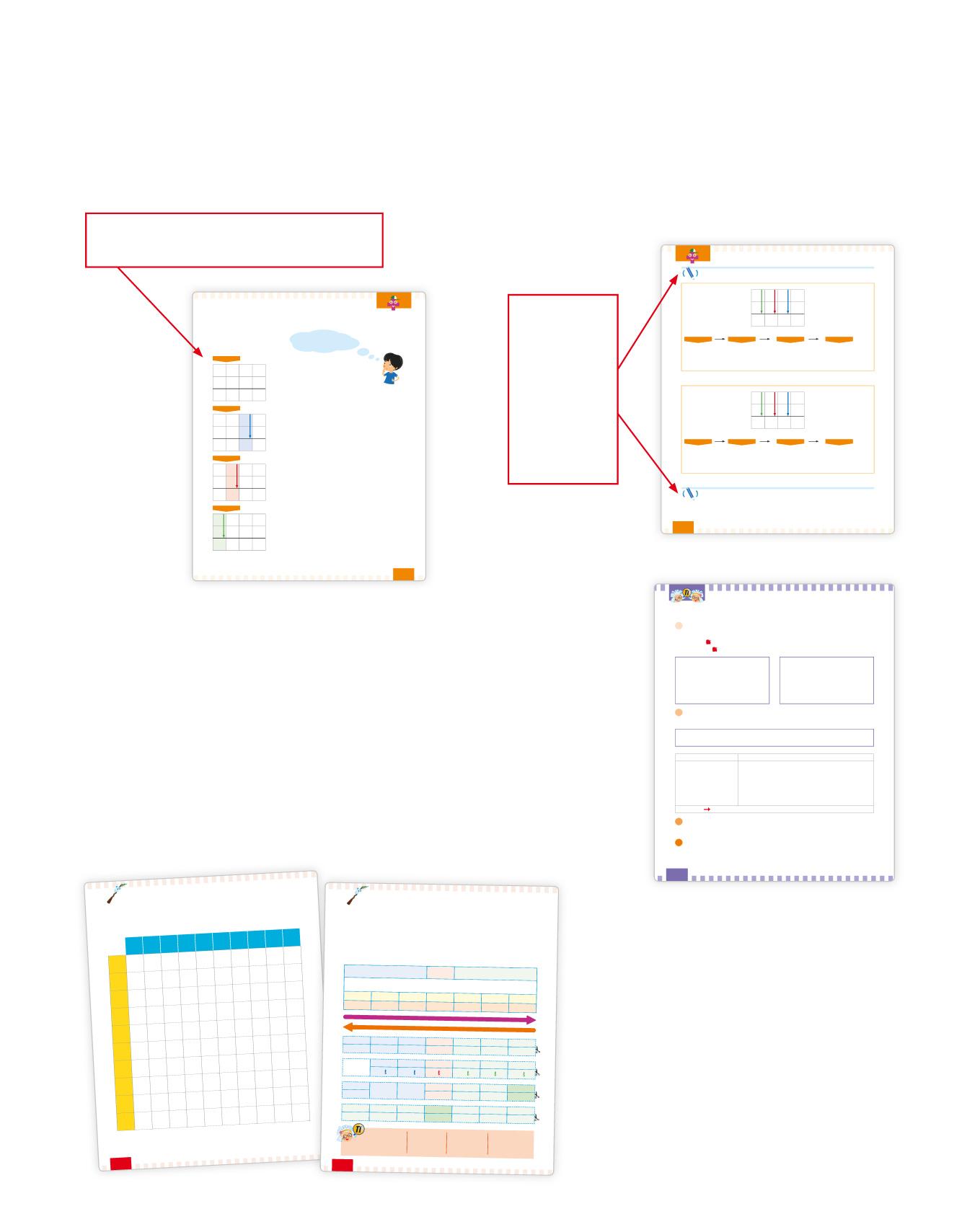
L’addizione è un’operazione che unisce più quantità o più numeri.
Osserva come funziona l’addizione...
... e quali sono i suoi termini e il suo segno.
5
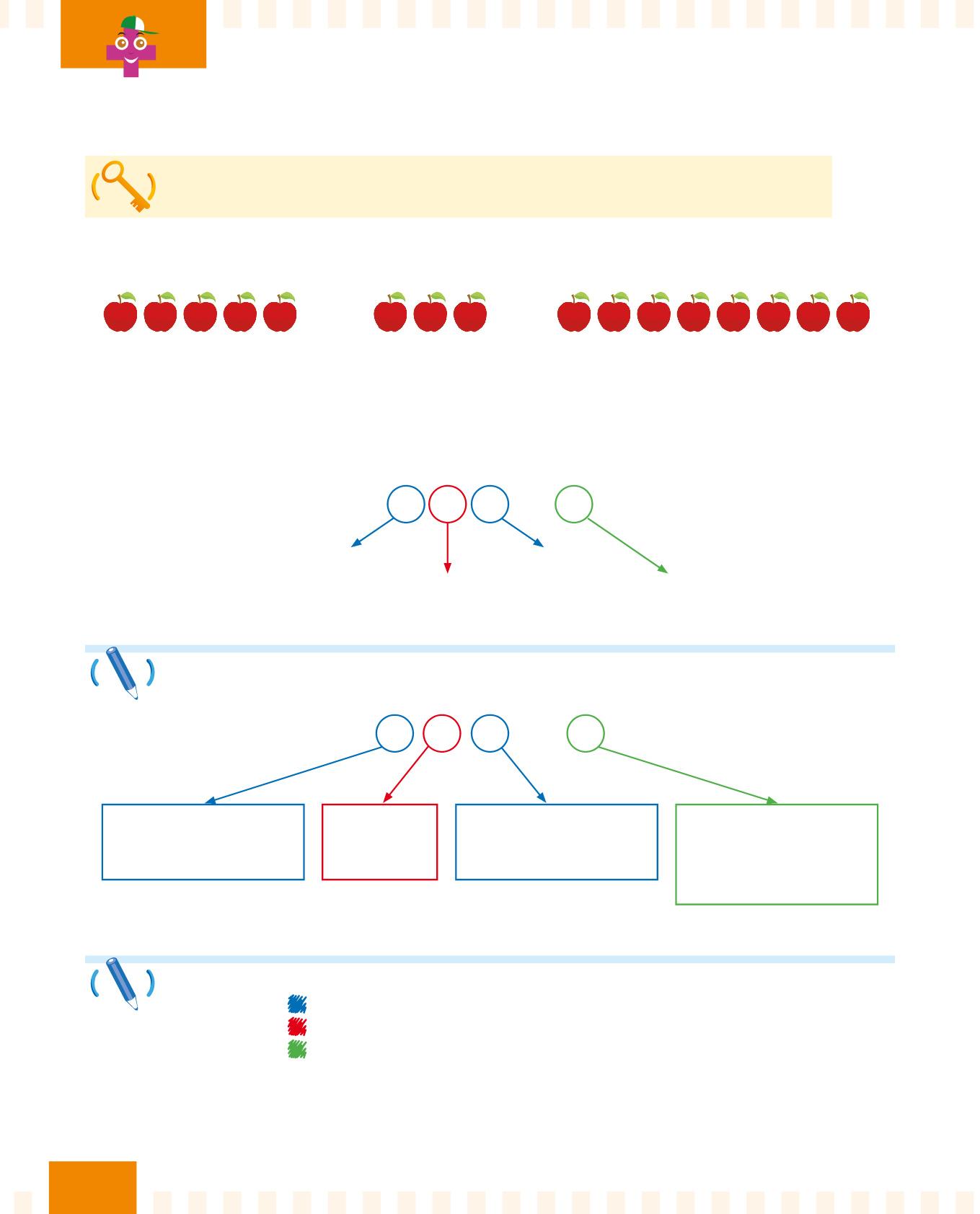
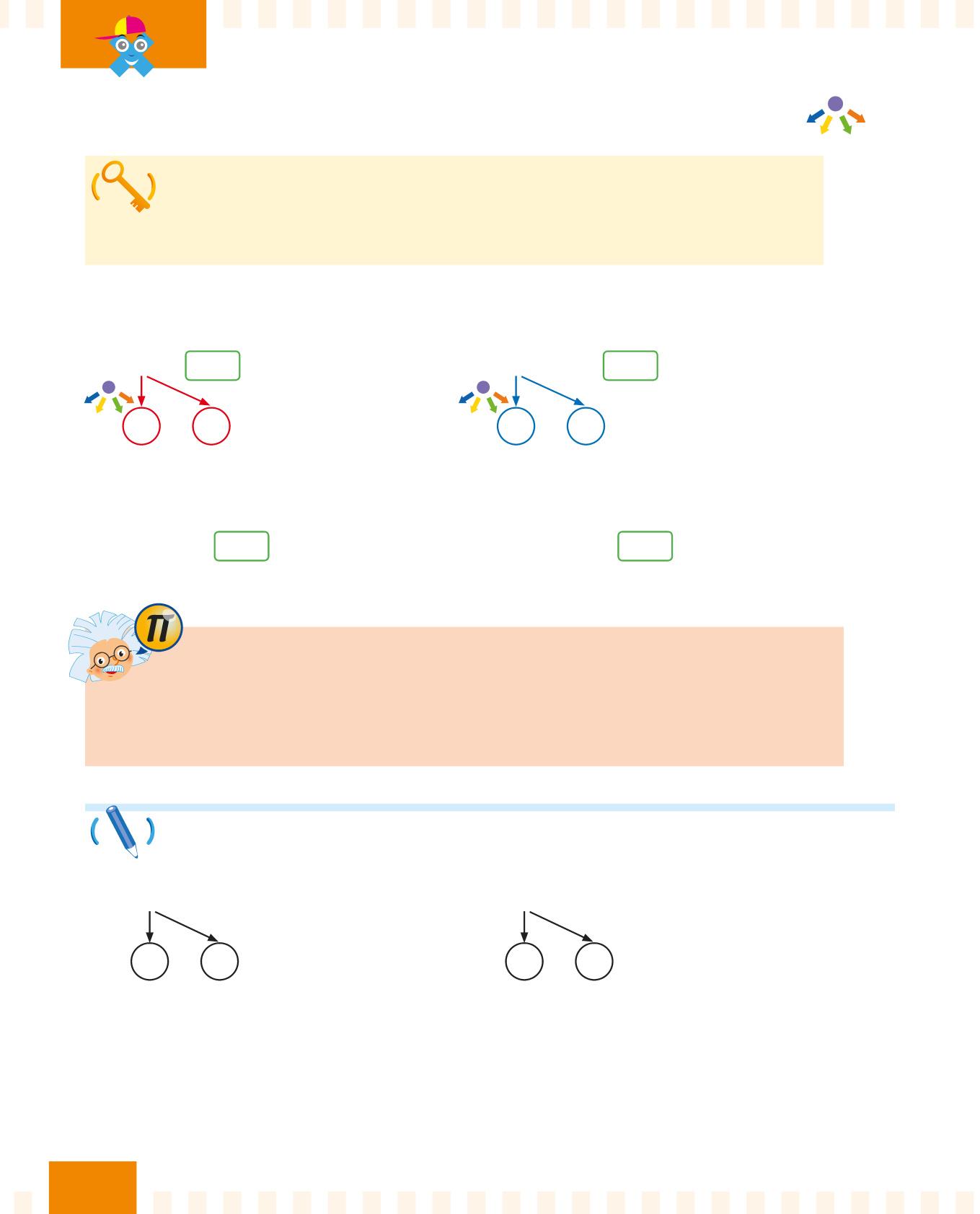
Ora scrivi tu i nomi dei termini e del segno dell’addizione.
Per ognuna delle seguenti addizioni:
• cerchia di gli addendi;
• cerchia di il segno più;
• cerchia di la somma o totale.
Se cambi l’ordine degli addendi, la somma non cambia.
Osserva come funziona la proprietà commutativa:
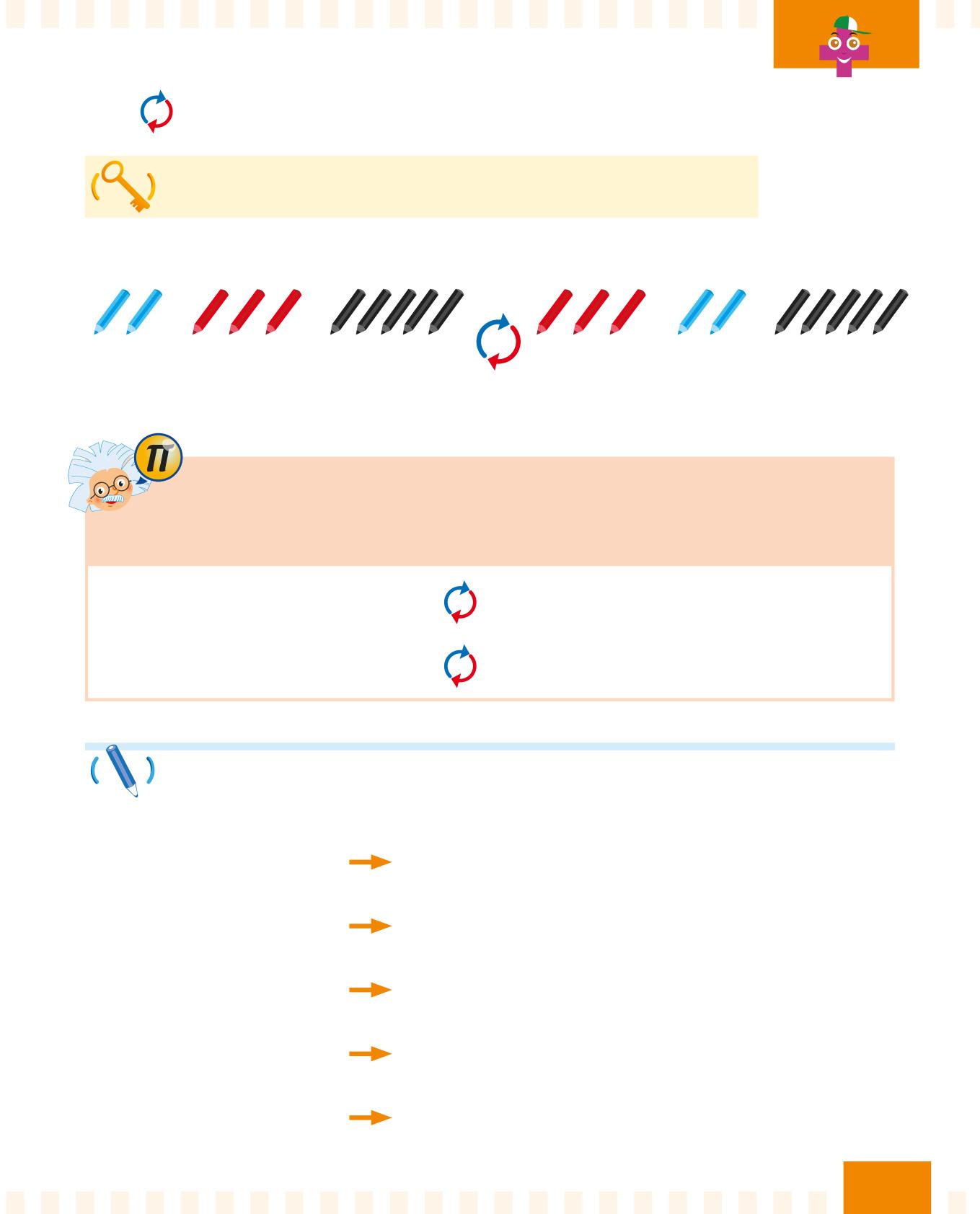
Questa proprietà è molto utile per fare i calcoli a mente!
Usala quando il primo addendo è più piccolo del secondo, così sarà più semplice calcolare la somma.
Risolvi le seguenti addizioni, poi applica la proprietà commutativa e calcola di nuovo.
Se sostituisci due o più addendi con la loro somma, il risultato non cambia.
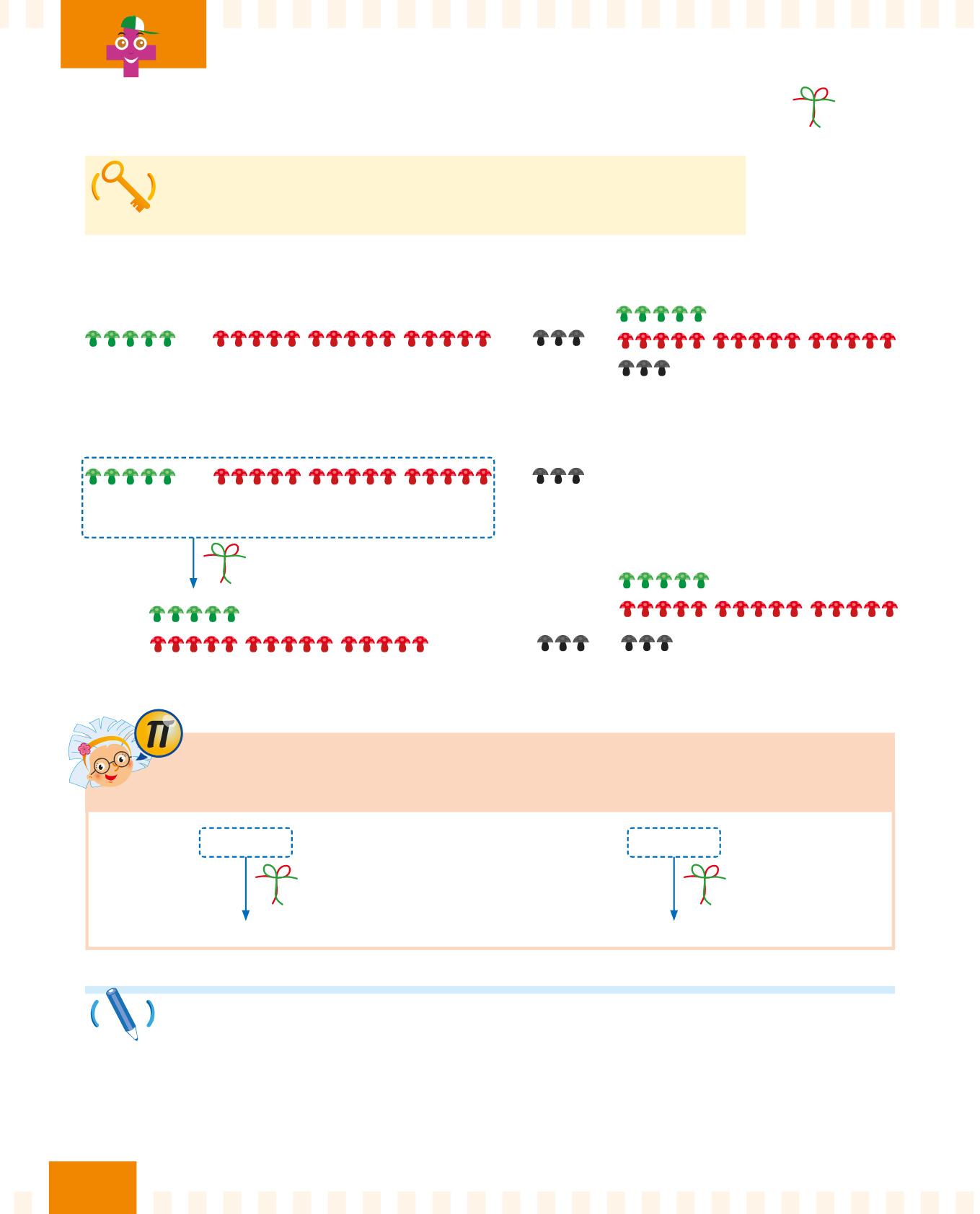
La proprietà associativa è molto utile per fare i calcoli a mente!
Se sommi gli addendi giusti, sarà più semplice calcolare la somma.
Applica la proprietà associativa e risolvi le seguenti addizioni.
Se sostituisci un addendo con due o più numeri e la somma di questi numeri è uguale all’addendo stesso, il risultato non cambia.
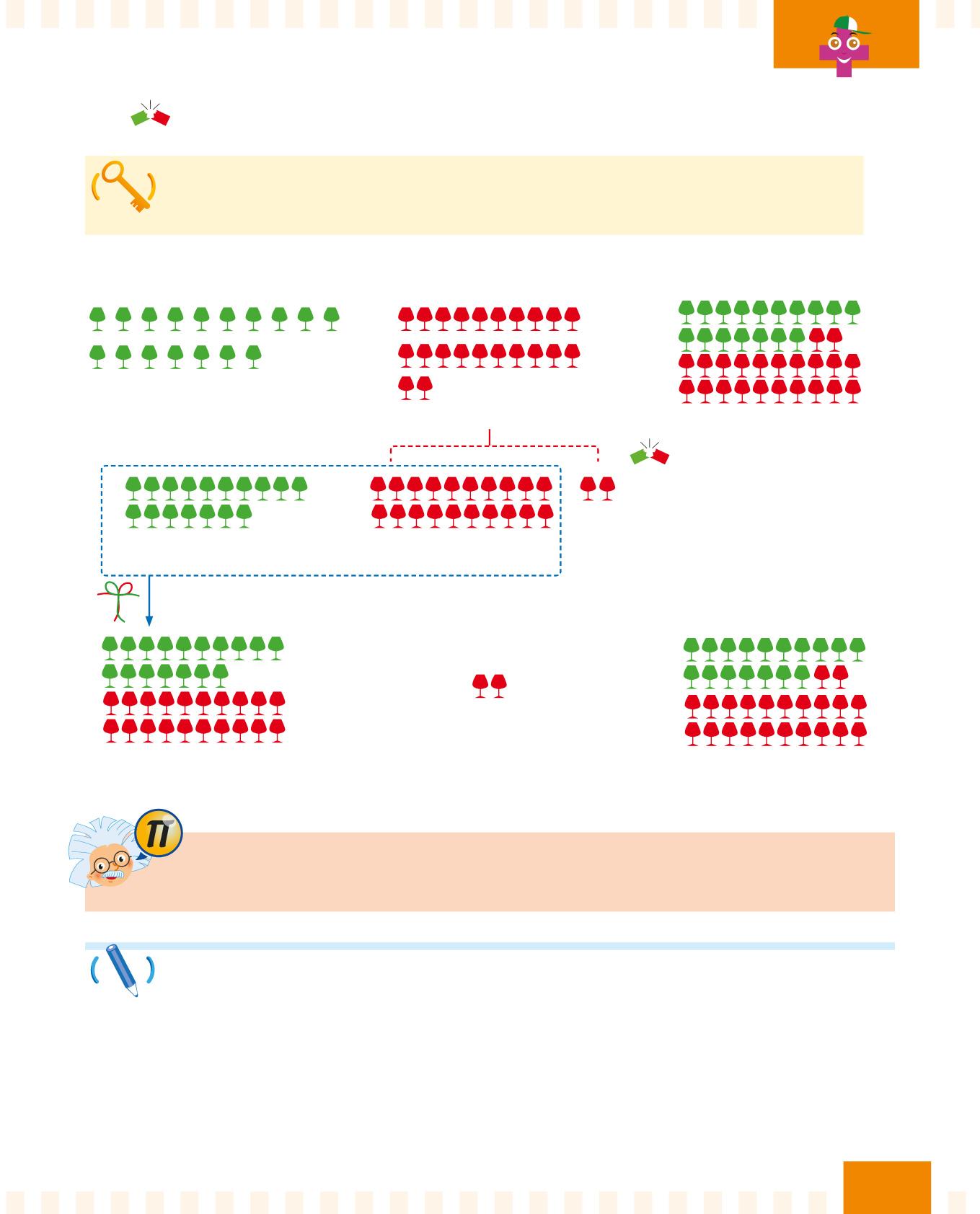
La proprietà dissociativa è molto utile per fare i calcoli a mente!
Se sostituisci l’addendo giusto, sarà più semplice calcolare la somma!
Applica prima la proprietà dissociativa, poi la proprietà associativa e risolvi le seguenti addizioni.
La sottrazione è un’operazione che toglie una quantità da un’altra.
Con la sottrazione:
ottieni una quantità più piccola di quella iniziale.
Togli 3 fiori da 4 fiori iniziali: resta 1 fiore.
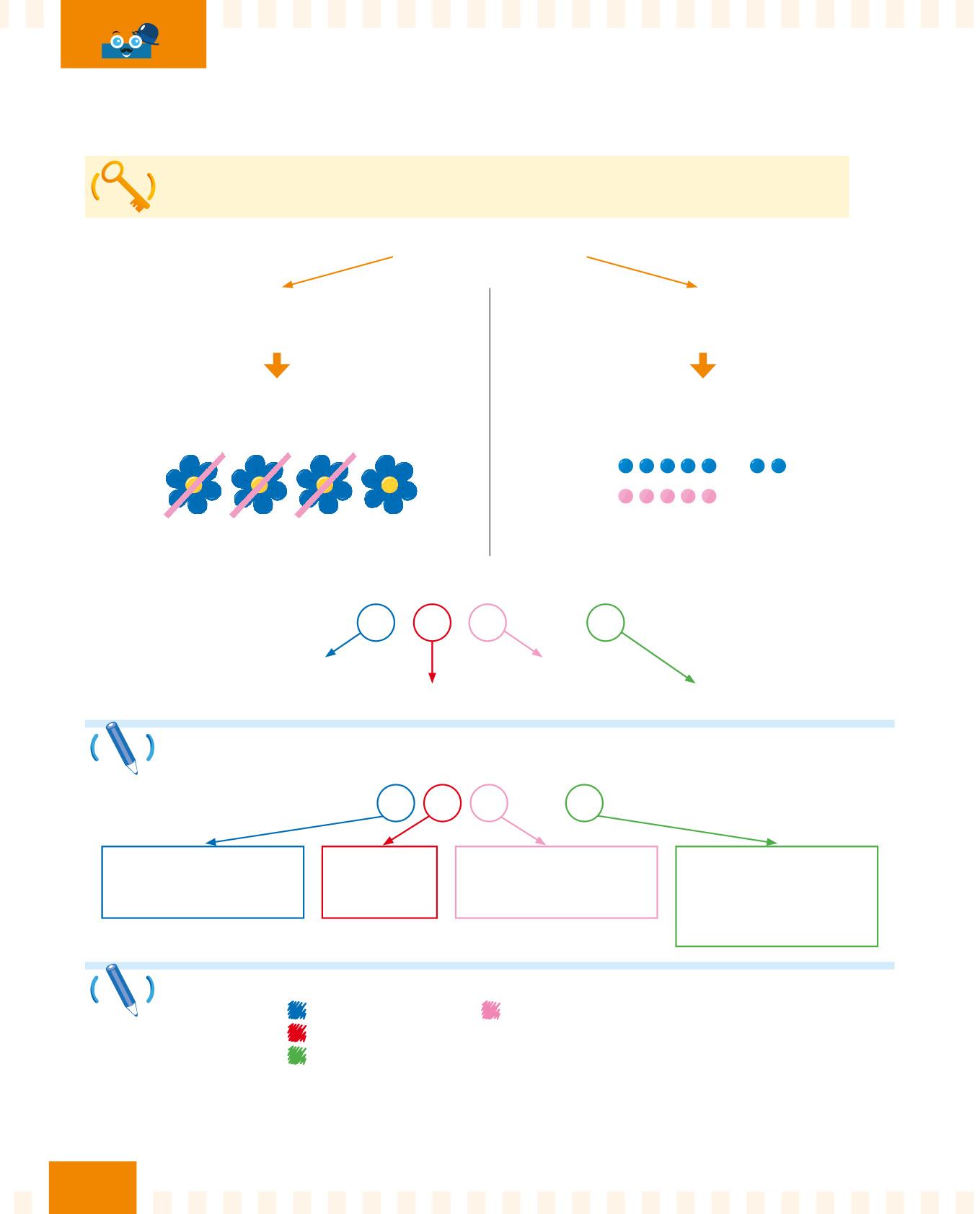
capisci quale differenza c’è tra due quantità.
Confronta le biglie blu e rosa: la differenza è di 2 biglie. 4
Osserva ora i termini e il segno della sottrazione.
MINUENDO SOTTRAENDO
MENO RESTO o DIFFERENZA
Ora scrivi tu i nomi dei termini e del segno della sottrazione.
Per ognuna delle seguenti sottrazioni:
• cerchia di il minuendo e di il sottraendo;
• cerchia di il segno meno;
• cerchia di il resto o la differenza. 25
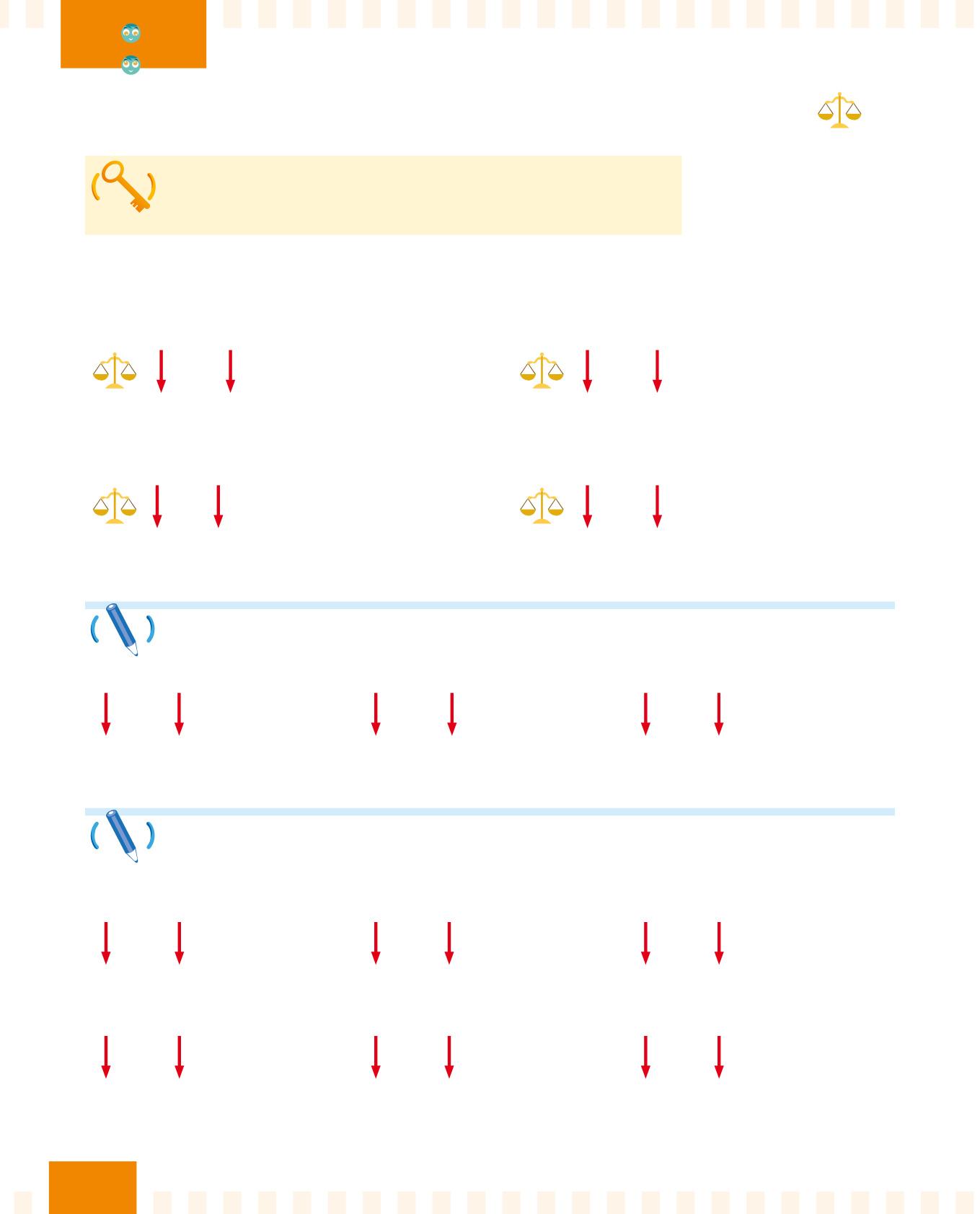
Se aggiungi o se sottrai lo stesso numero al minuendo e al sottraendo, il risultato non cambia.
Se aggiungi lo stesso numero al minuendo e al sottraendo:
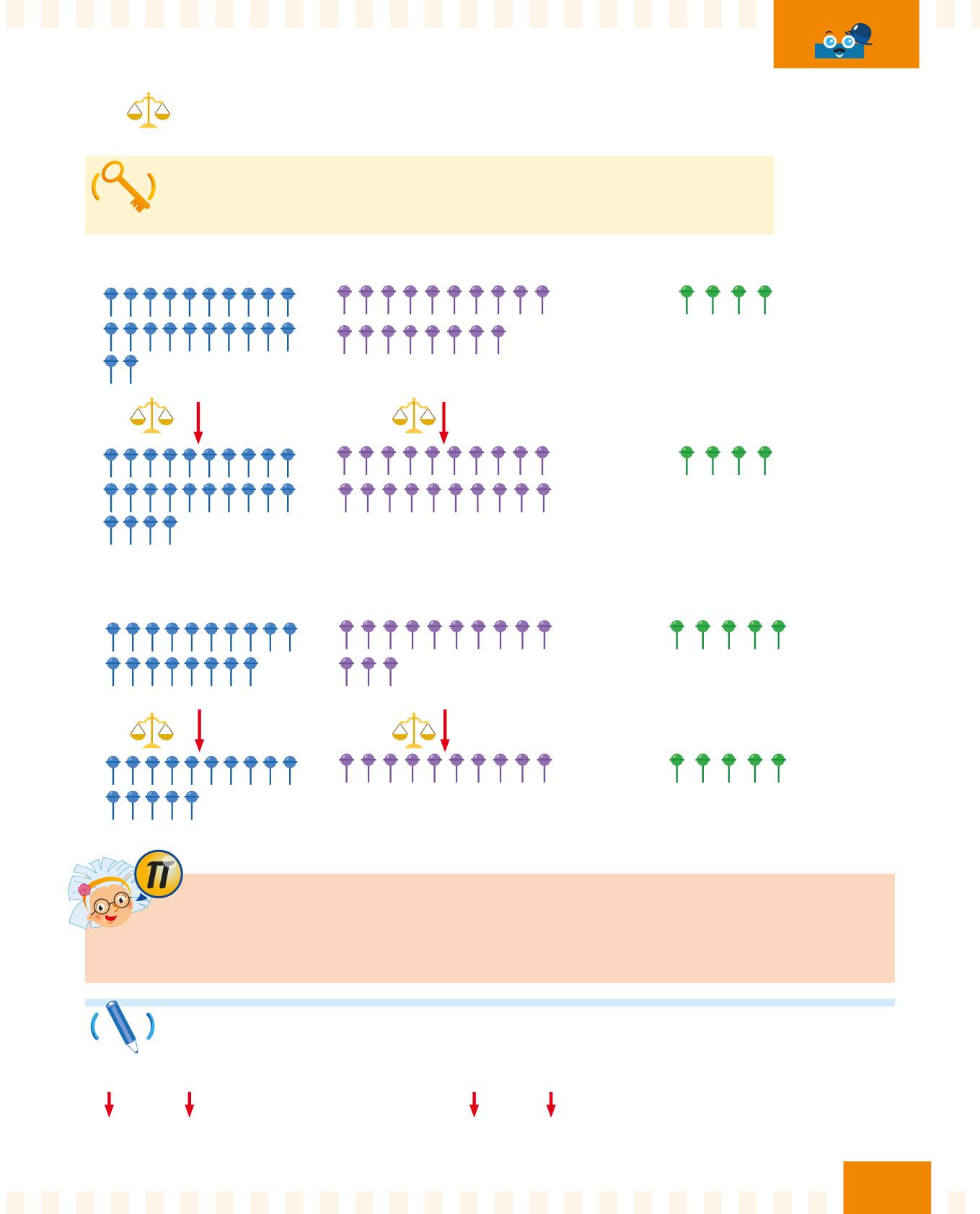
Se sottrai lo stesso numero al minuendo e al sottraendo:
La proprietà invariantiva è molto utile per fare i calcoli a mente! Scegli il numero da sottrarre o da aggiungere in modo da ottenere il sottraendo con lo zero.
Applica la proprietà invariantiva e risolvi le seguenti sottrazioni.
28 – 22 = + 8
34 – 12 = ..........
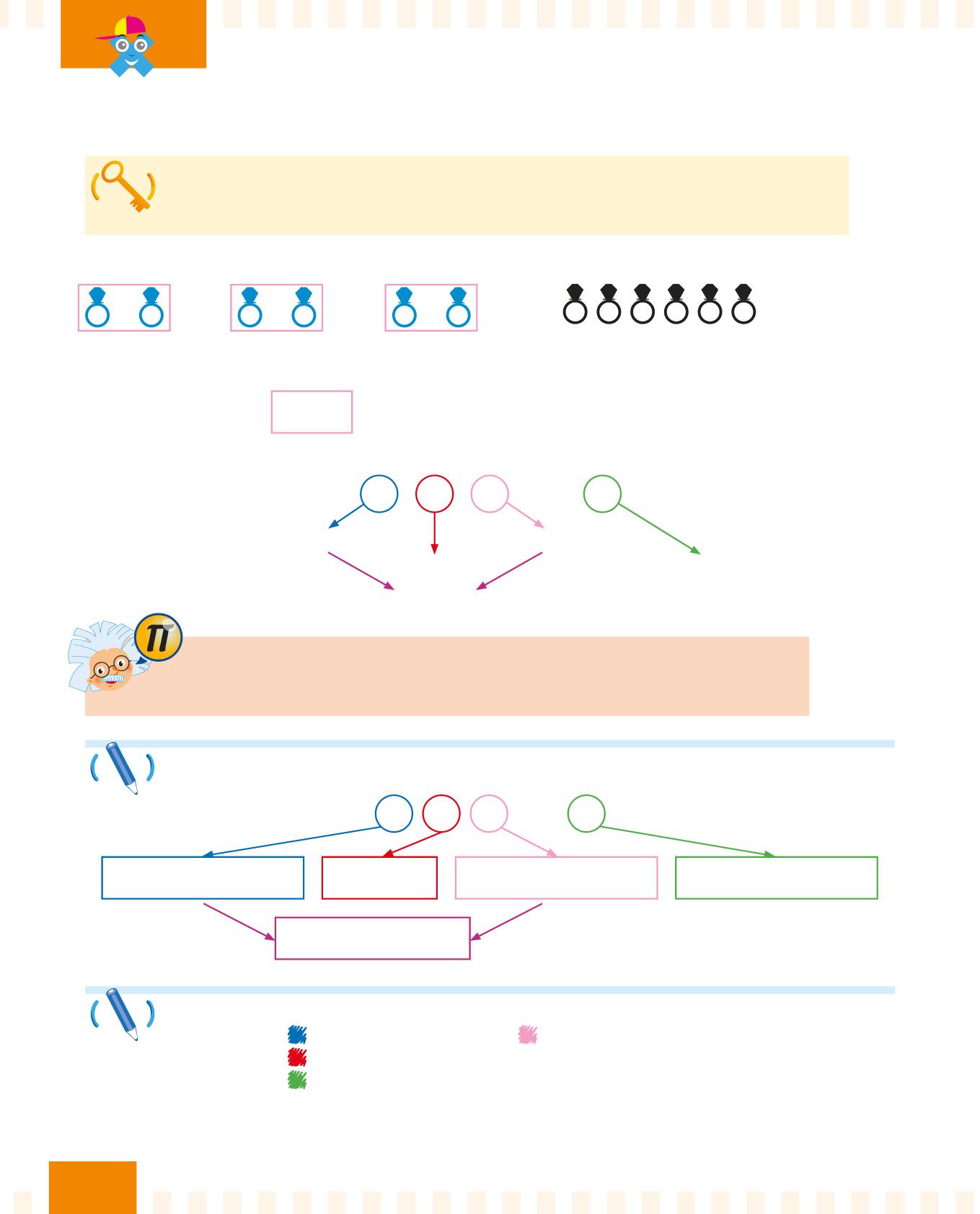
La moltiplicazione è un’operazione che unisce più volte la stessa quantità.
• cerchia di il prodotto. Osserva
Quando sommi più volte la stessa quantità, invece di usare l’addizione puoi usare la moltiplicazione!
Ora scrivi tu i nomi dei termini e del segno della moltiplicazione. 15 × 3 = 45 ... e quali sono i suoi termini e il suo segno
10
Per ognuna delle seguenti moltiplicazioni:
• cerchia di il moltiplicando e di il moltiplicatore;
• cerchia di il segno per;
12
Se cambi l’ordine dei fattori, il prodotto non cambia.
Osserva come funziona la proprietà commutativa:
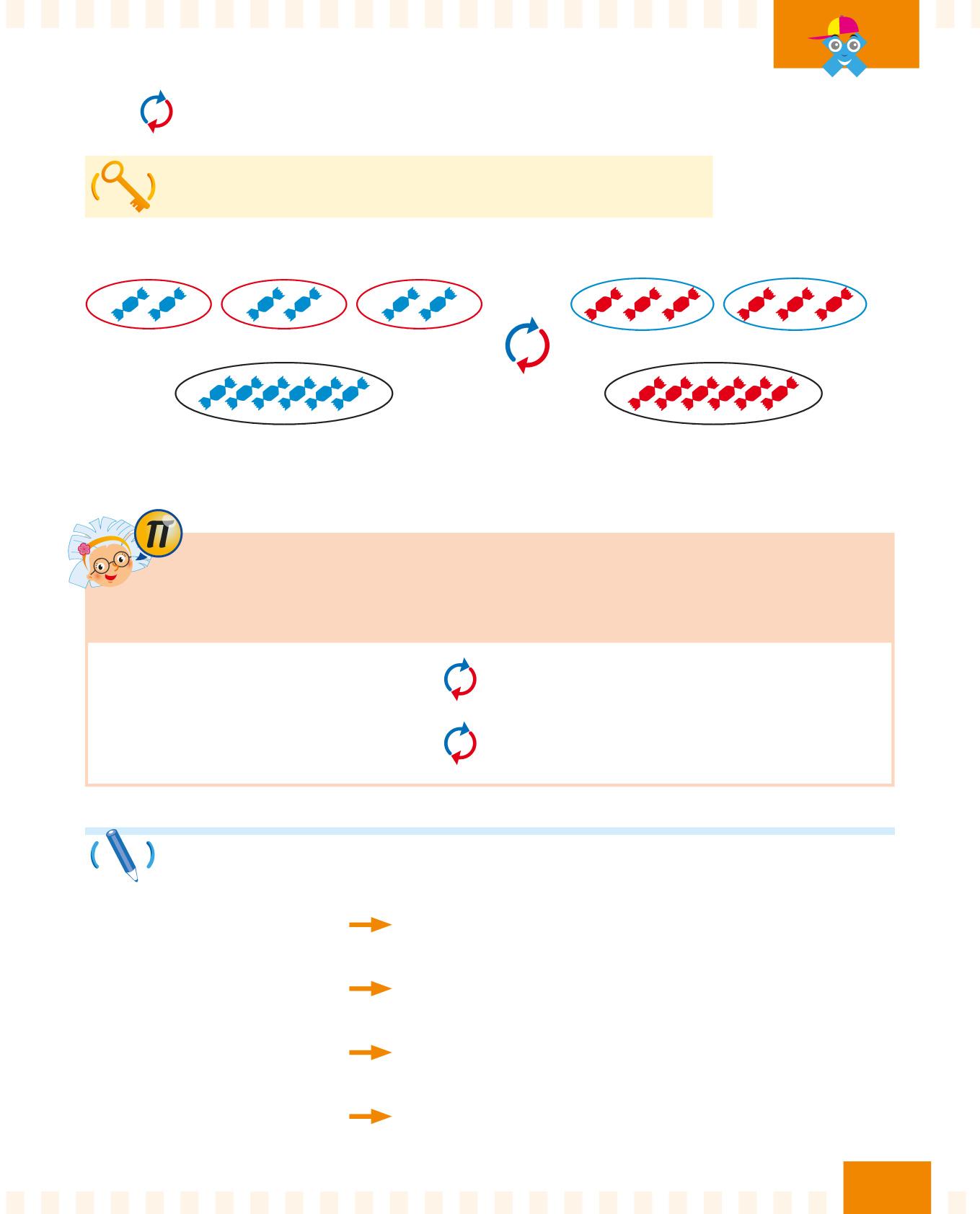
La proprietà commutativa è molto utile per fare i calcoli a mente!
Usa la proprietà commutativa quando ricordi meglio la tabellina del secondo fattore.
Risolvi le seguenti moltiplicazioni, poi applica la proprietà commutativa e calcola di nuovo. 4
Se sostituisci due o più fattori con il loro prodotto, il risultato non cambia.
Osserva come funziona la proprietà associativa: 2
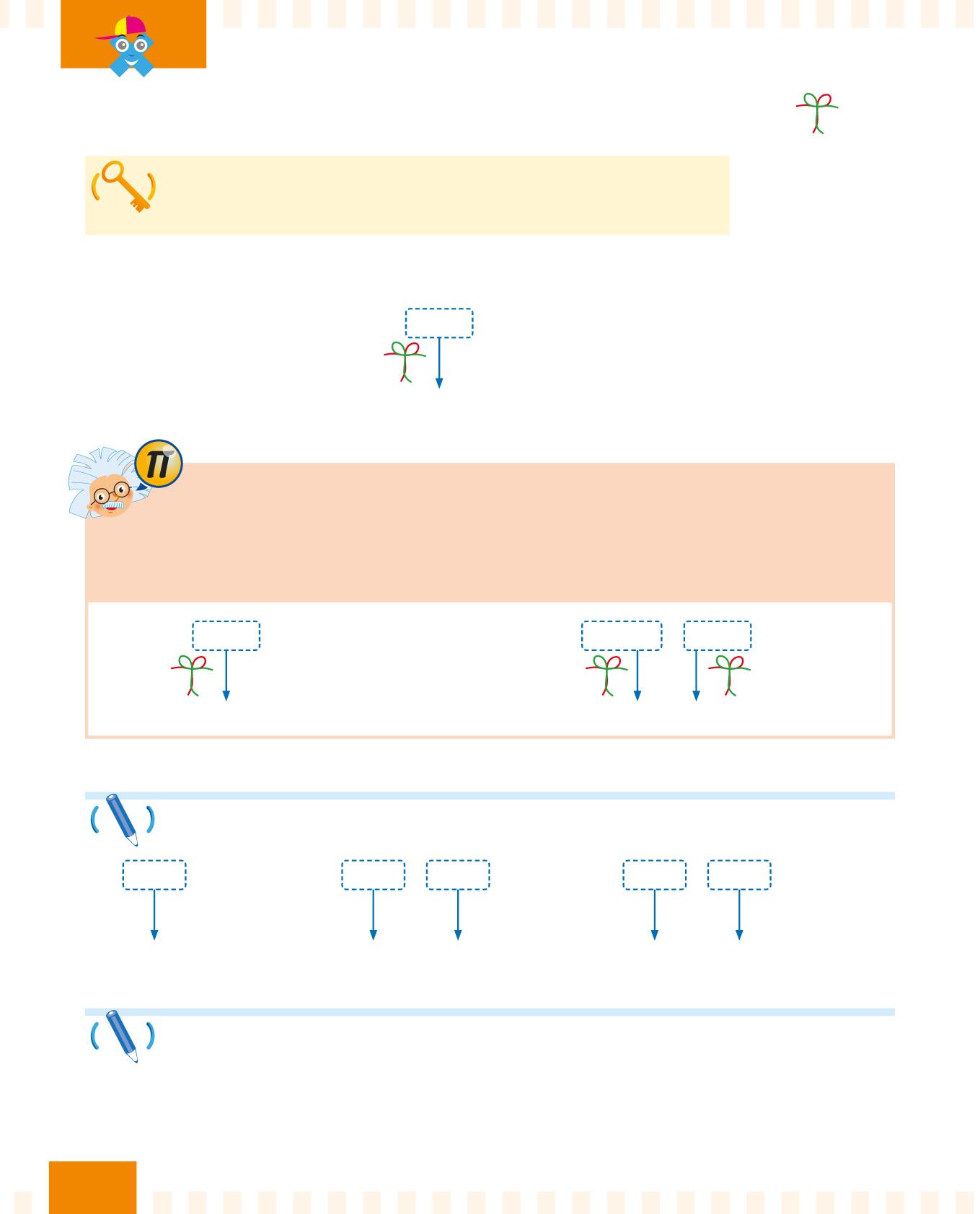
La proprietà associativa è molto utile per fare i calcoli a mente!
Usa la proprietà associativa quando hai più moltiplicazioni da fare. Se moltiplichi due fattori alla volta sarà più semplice calcolare il prodotto! 5
Applica la proprietà associativa e risolvi le seguenti moltiplicazioni.
Scegli quali fattori associare e svolgi le seguenti moltiplicazioni.
Se sostituisci un fattore con due o più numeri e il prodotto di questi numeri è uguale al fattore stesso, il risultato non cambia.
Osserva come funziona la proprietà dissociativa:
25 × 14 = 350
25 × 2 × 7 = 350
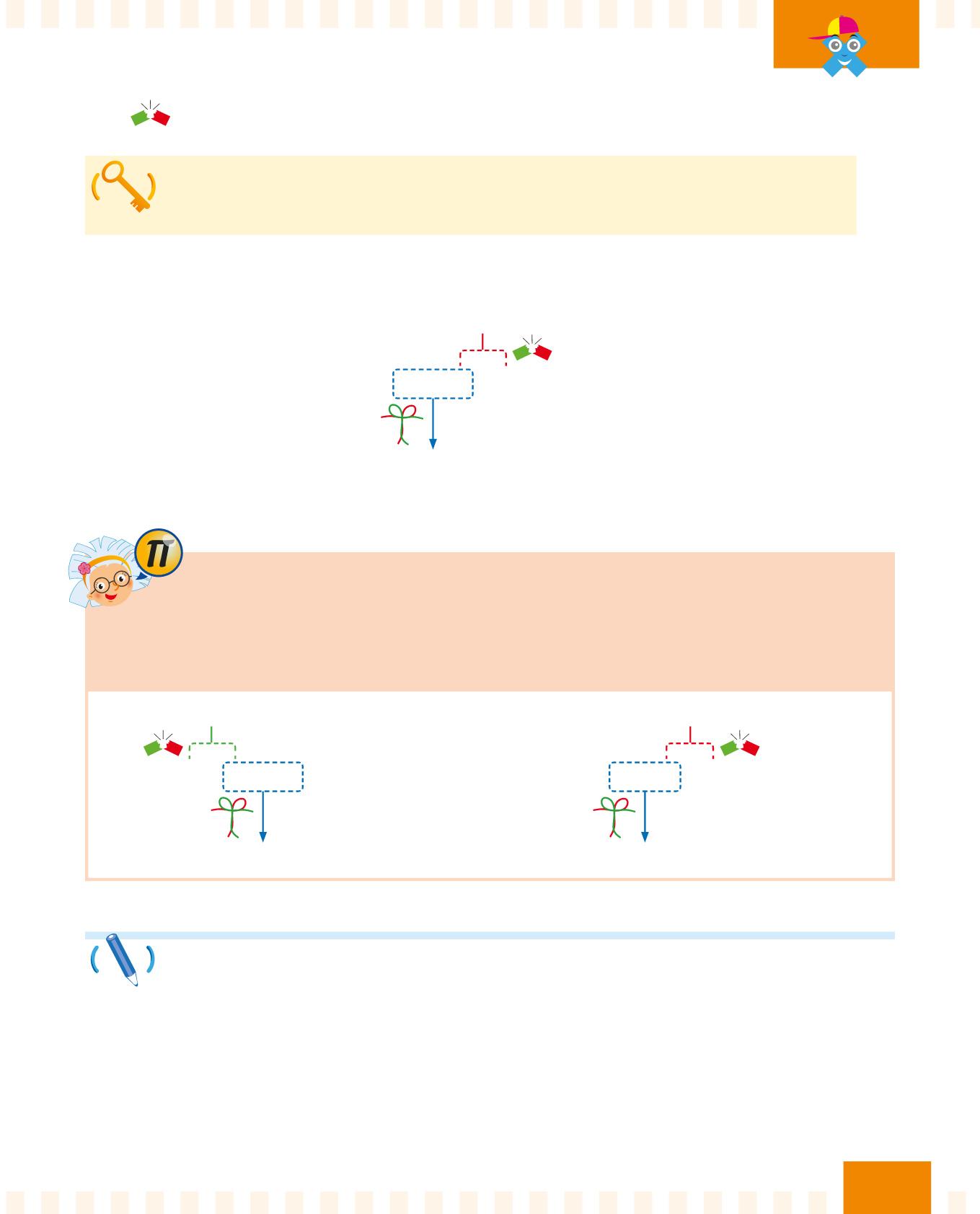
50 × 7 = 350
La proprietà dissociativa è molto utile per fare i calcoli a mente!
Usa la proprietà dissociativa quando hai moltiplicazioni con numeri grandi. Se scomponi il fattore giusto, sarà più semplice calcolare il prodotto!
12 × 25 = 300
6 × 2 × 25 = 300
6 × 50 = 300
5 × 24 = 120
5 × 6 × 4 = 120
30 × 4 = 120
35 × 12 = Applica prima la proprietà dissociativa, poi la proprietà associativa e risolvi le seguenti moltiplicazioni.
14 × 4 =
Se scomponi uno dei due fattori in due o più addendi, moltiplichi ogni addendo per l’altro fattore e infine sommi i prodotti, il risultato non cambia.
Osserva come funziona la proprietà distributiva: 6
La proprietà distributiva è molto utile per fare i calcoli a mente!
Usa la proprietà distributiva quando hai moltiplicazioni con numeri grandi. Se scomponi il fattore giusto, sarà più semplice calcolare il prodotto!
Applica la proprietà distributiva e risolvi le seguenti moltiplicazioni.
La divisione è un’operazione che divide una quantità in parti uguali.
Con la divisione raggruppi o distribuisci una quantità in parti uguali:
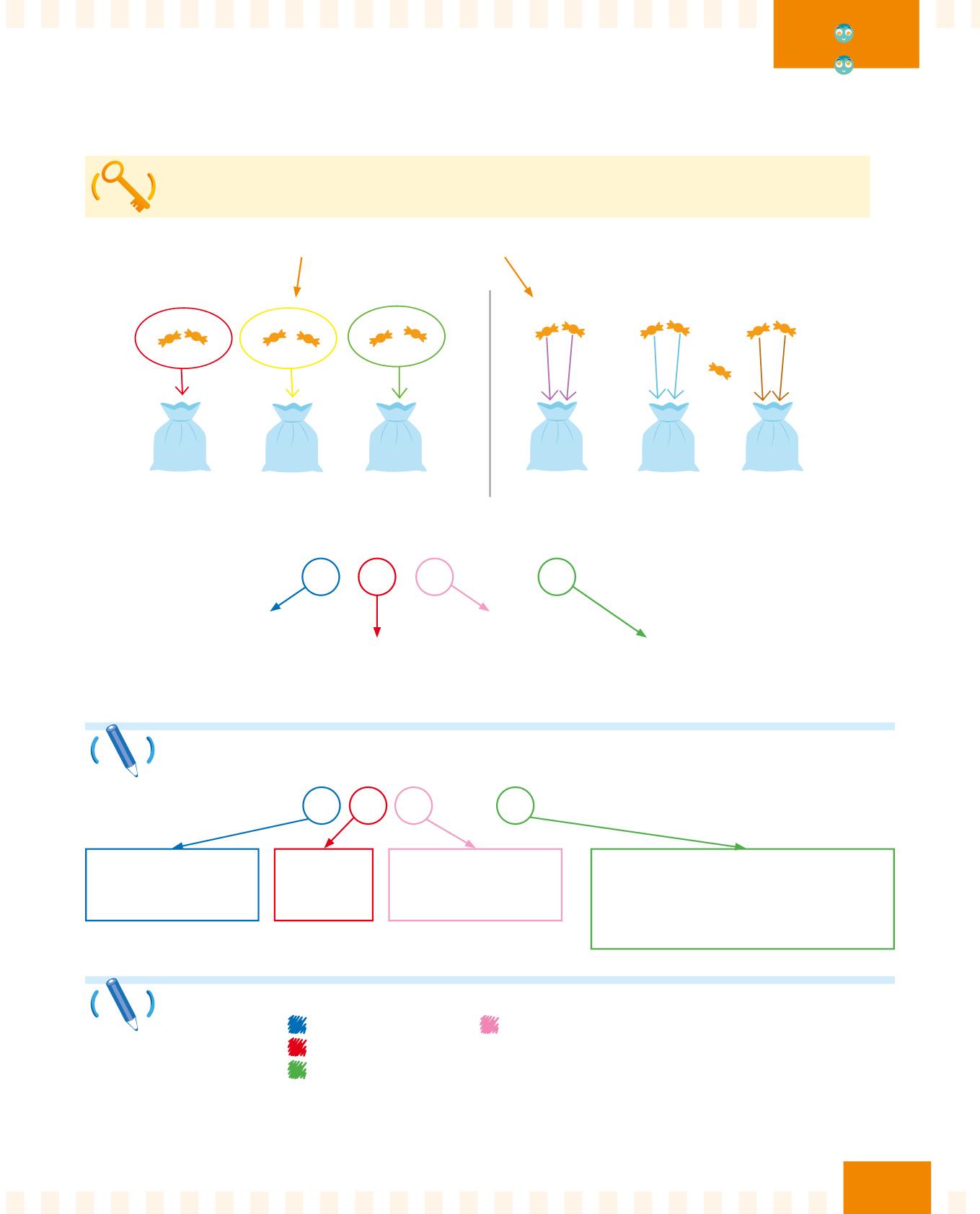
6 : 3 = 2
Osserva ora i termini e il segno della divisione.
24 : 6 = 4
DIVIDENDO DIVISORE
7 : 3 = 2 (resto 1)
DIVISO QUOTO (se il RESTO è 0)
o QUOZIENTE (se c’è il RESTO)
Ora scrivi tu i nomi dei termini e del segno della divisione.
30 : 15 = 2
Per ognuna delle seguenti divisioni:
• cerchia di il dividendo e di il divisore;
• cerchia di il segno diviso;
• cerchia di il quoto o il quoziente.
25 : 5 = 5
12 : 4 = 3
42 : 7 = 6
Se dividi o se moltiplichi per lo stesso numero il dividendo e il divisore, il risultato non cambia. Applica
Addizione (+)
Se cambi l’ordine degli addendi, il risultato non cambia.
2 + 3 = 5 3 + 2 = 5
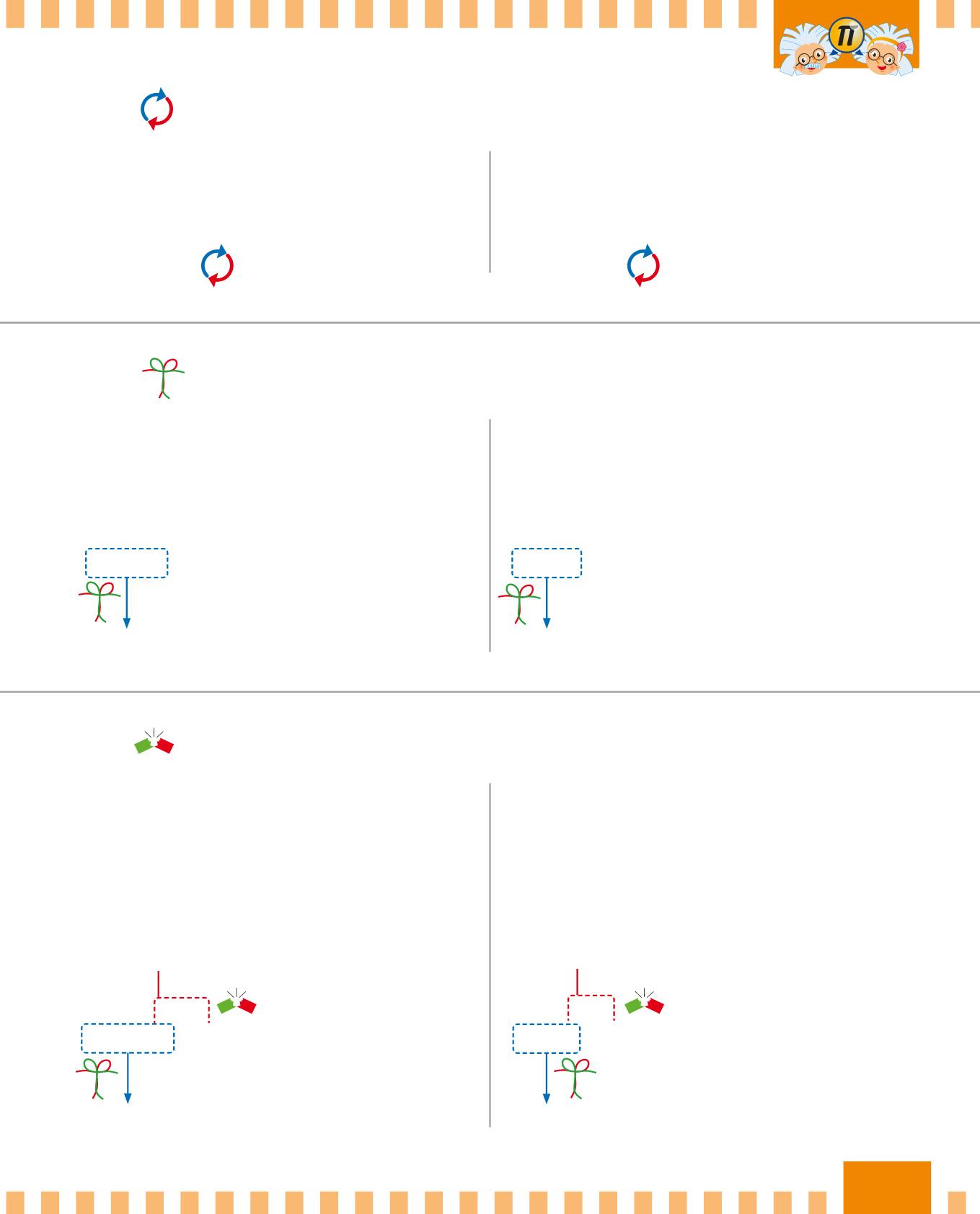
Moltiplicazione (×)
Se cambi l’ordine dei fattori, il risultato non cambia.
2 × 3 = 6 3 × 2 = 6
Addizione (+)
Se sostituisci due o più addendi con la loro somma, il risultato non cambia.
5 + 15 + 3 = 23
20 + 3 = 23
Moltiplicazione (×)
Se sostituisci due o più fattori con il loro prodotto, il risultato non cambia.
2 × 5 × 4 = 40
10 × 4 = 40
Addizione (+)
Se sostituisci un addendo con due o più numeri e la somma di questi numeri è uguale all’addendo stesso, il risultato non cambia.
10 + 15 = 25
10 + 10 + 5 = 25
20 + 5 = 25
Moltiplicazione (×)
Se sostituisci un fattore con due o più numeri e il prodotto di questi numeri è uguale al fattore stesso, il risultato non cambia.
5 × 24 = 120
5 × 6 × 4 = 120
30 × 4 = 120
Moltiplicazione (×)
Se scomponi uno dei due fattori in due o più addendi, poi moltiplichi ogni addendo per l’altro fattore e infine sommi i prodotti, il risultato non cambia. 25
Sottrazione (–)
Se aggiungi o se sottrai lo stesso numero al minuendo e al sottraendo, il risultato non cambia.
43
Divisione (:)
Se dividi o se moltiplichi per lo stesso numero il dividendo e il divisore, il risultato non cambia.

Quanto fa 345 + 123?
Svolgi le seguenti addizioni senza cambio.
Quanto fa 172 + 326?
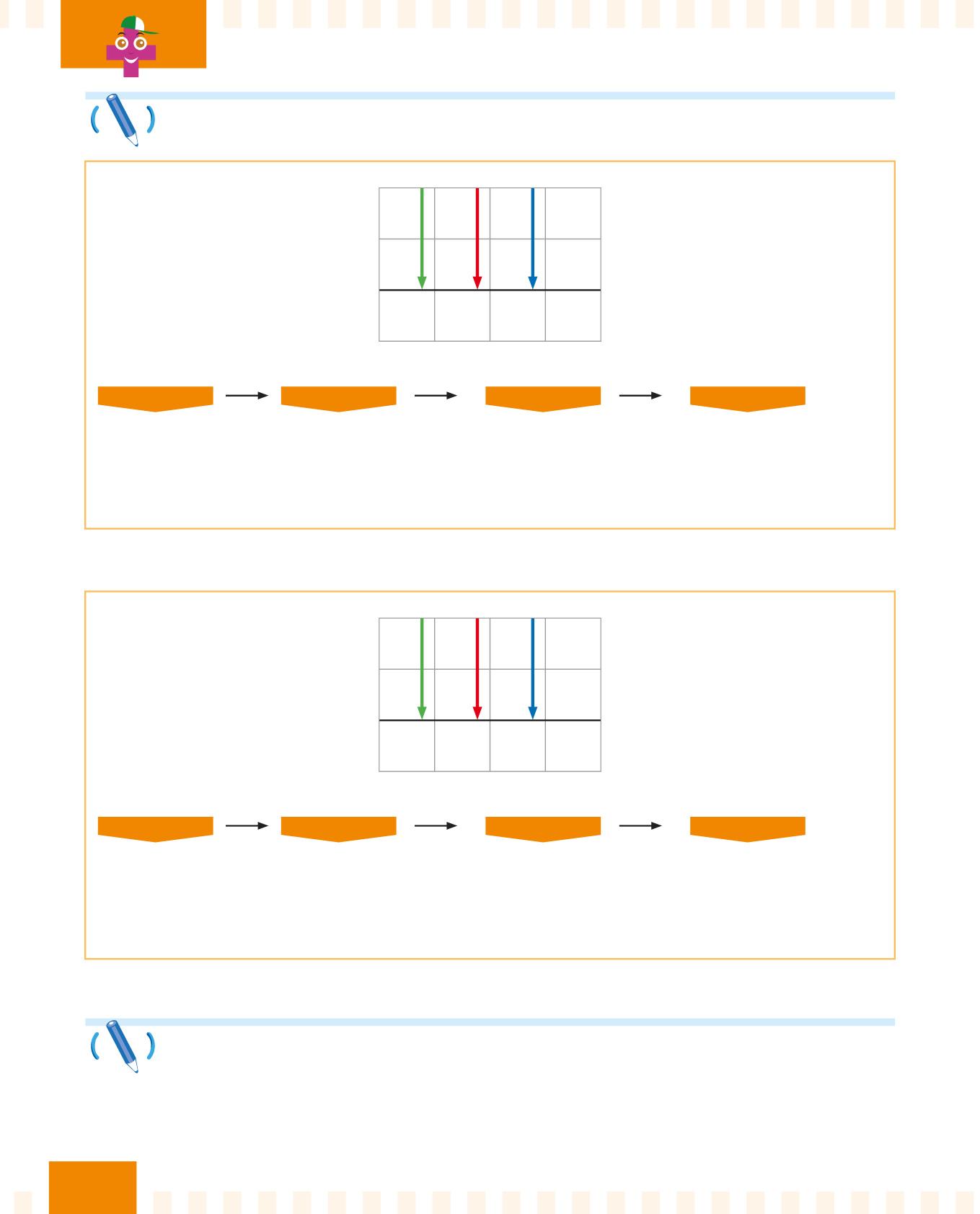
PASSO 1
Incolonna bene i numeri.
PASSO 2
Segui la freccia blu e svolgi l’addizione.
Quanto fa 235 + 34?
PASSO 3
Segui la freccia rossa e svolgi l’addizione.
PASSO 4
Segui la freccia verde e svolgi l’addizione.
PASSO 1
Incolonna bene i numeri.
PASSO 2
Segui la freccia blu.
PASSO 3
Segui la freccia rossa.
PASSO 4
Segui la freccia verde.
Usa lo stesso procedimento e svolgi le seguenti addizioni senza il cambio sul tuo quaderno.
Quanto fa 275 + 347?
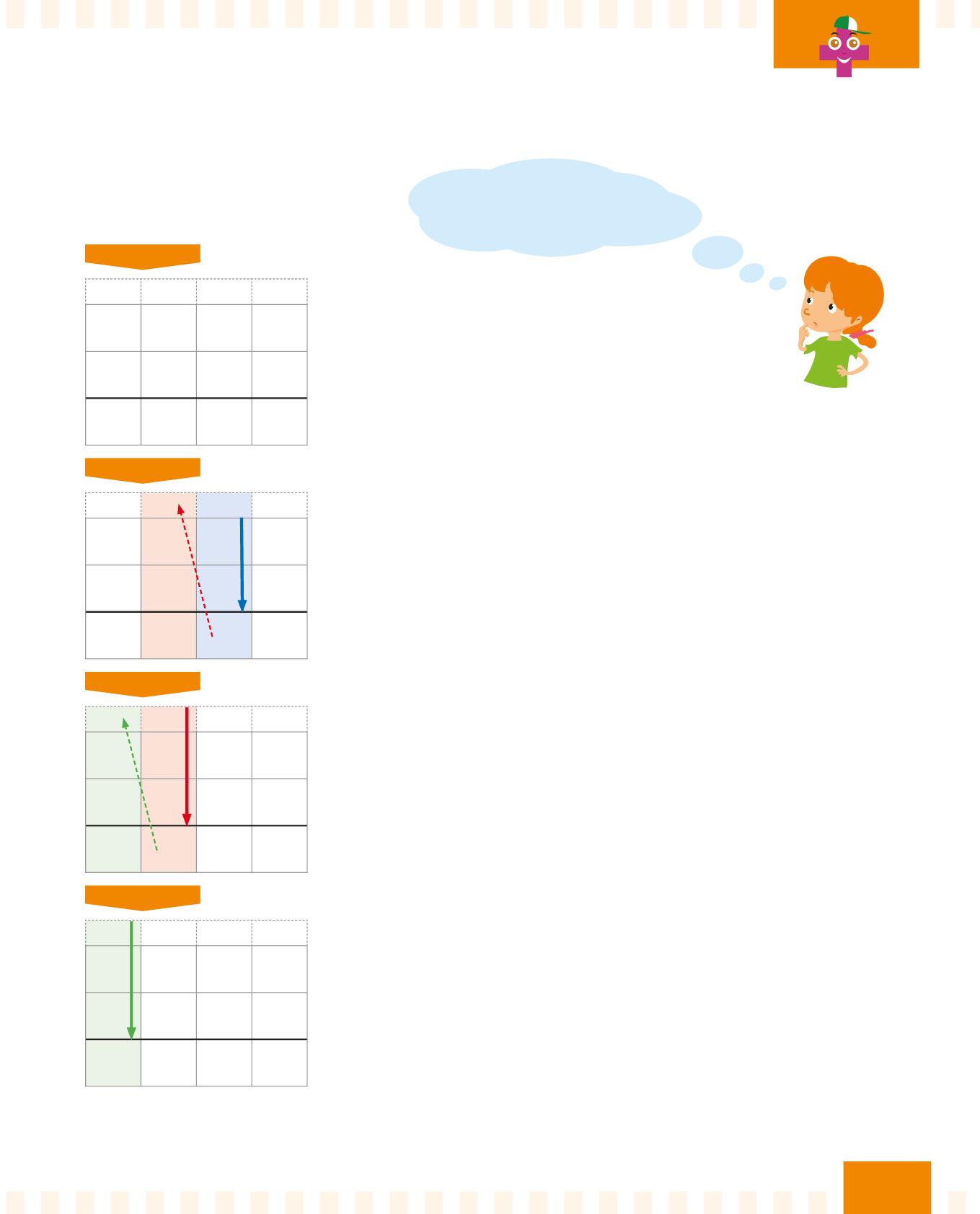
Segui la freccia blu e svolgi l’addizione: 5 + 7 = 12.
Scrivi 2 nella colonna blu e 1 in alto nella colonna rossa.
Adesso segui la freccia rossa
e svolgi l’addizione: 1 + 7 + 4 = 12.
Scrivi 2 nella colonna rossa e 1 in alto nella colonna verde. PASSO
Infine, segui la freccia verde
e svolgi l’addizione: 1 + 2 + 3 = 6.
L’addizione con il cambio è terminata. Il risultato è 622.
Svolgi le seguenti addizioni con il cambio.
Quanto fa 568 + 163?

PASSO 1
Incolonna bene i numeri.
PASSO 2
Segui la freccia blu e svolgi l’addizione.
Se serve, fai un cambio.
Quanto fa 488 + 261?
PASSO 3
Segui la freccia rossa e svolgi l’addizione.
Se serve, fai un cambio.
PASSO 4
Segui la freccia verde e svolgi l’addizione.
PASSO 1
Incolonna bene i numeri.
PASSO 2
Segui la freccia blu.
PASSO 3
Segui la freccia rossa.
PASSO 4
Segui la freccia verde.
Usa lo stesso procedimento e svolgi le seguenti addizioni con il cambio sul tuo quaderno.
PASSO 1
PARTE INTERA PARTE DECIMALE
33 , 541+ 13 , 7 =
PASSO 2
PARTE INTERA PARTE DECIMALE
33 , 54 1 + 13 , 70 0 =
PASSO 3
PARTE

Quanto fa
33,541 + 13,7?
Aiutati con la griglia e incolonna
bene i numeri: la virgola del primo addendo deve essere in colonna con la virgola del secondo addendo.
Se ci sono, completa i buchi
della parte decimale con degli 0.
Poi inizia dalle cifre più a destra.
Segui la freccia gialla e svolgi
l’addizione:
1 + 0 = 1.
Adesso segui la freccia rosa e svolgi l’addizione: 4 + 0 = 4.
PASSO 4
PARTE INTERA PARTE DECIMALE
Ora segui la freccia arancione
e svolgi l’addizione: 5 + 7 = 12.
Scrivi 2 nella colonna arancione
e 1 in alto nella colonna blu.
PROCEDIMENTI
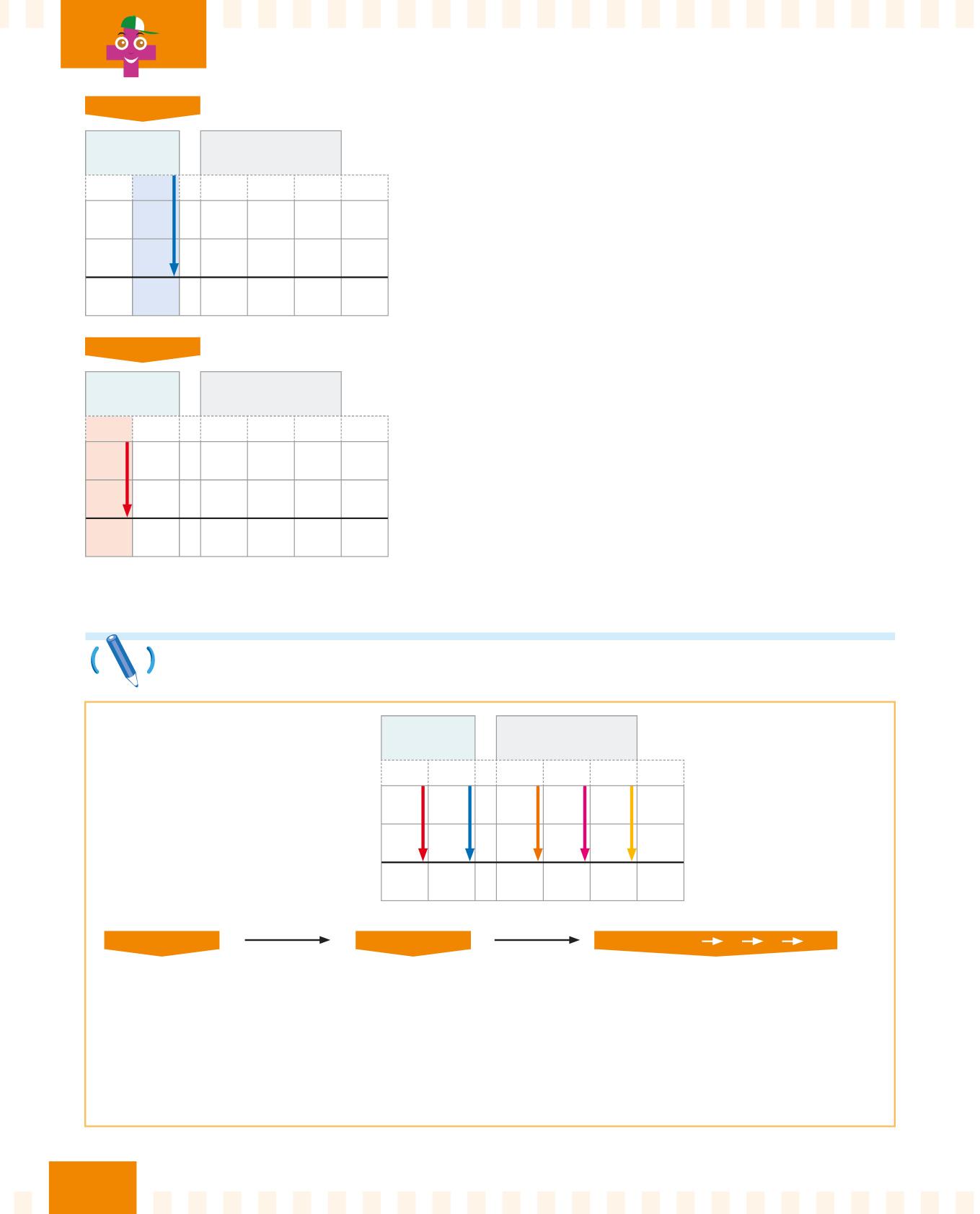
PASSO 5
PARTE INTERA PARTE DECIMALE 1
Segui la freccia blu e svolgi
l’addizione: 1 + 3 + 3 = 7.
PASSO 6 PARTE
Poi segui la freccia rossa e svolgi l’addizione: 3 + 1 = 4.
Scrivi 4 nella colonna rossa.
Infine, trascrivi la virgola.
L’addizione con i numeri decimali è terminata. Il risultato è 47,241.
Svolgi la seguente addizione con i numeri decimali.
Quanto fa 23,7 + 3,227?
PASSO 1
Incolonna bene i numeri e la virgola.
PARTE INTERA PARTE DECIMALE + =
PASSO 2
Se ci sono, completa i buchi della parte decimale con degli 0.
Poi segui la freccia
gialla.
PASSI 3 4 5 6
Segui prima la freccia rosa, poi la freccia arancione, la freccia blu e la freccia rossa.
Infine trascrivi la virgola.
Quanto fa 399 – 237?

Inizia dalle cifre più a destra. Segui la freccia blu e svolgi la sottrazione: 9 – 7 = 2.
Infine, segui la freccia verde e svolgi la sottrazione: 3 – 2 = 1.
La sottrazione senza il cambio è terminata. Il risultato è 162.
Svolgi le seguenti sottrazioni senza il cambio.
Quanto fa 827 – 102?
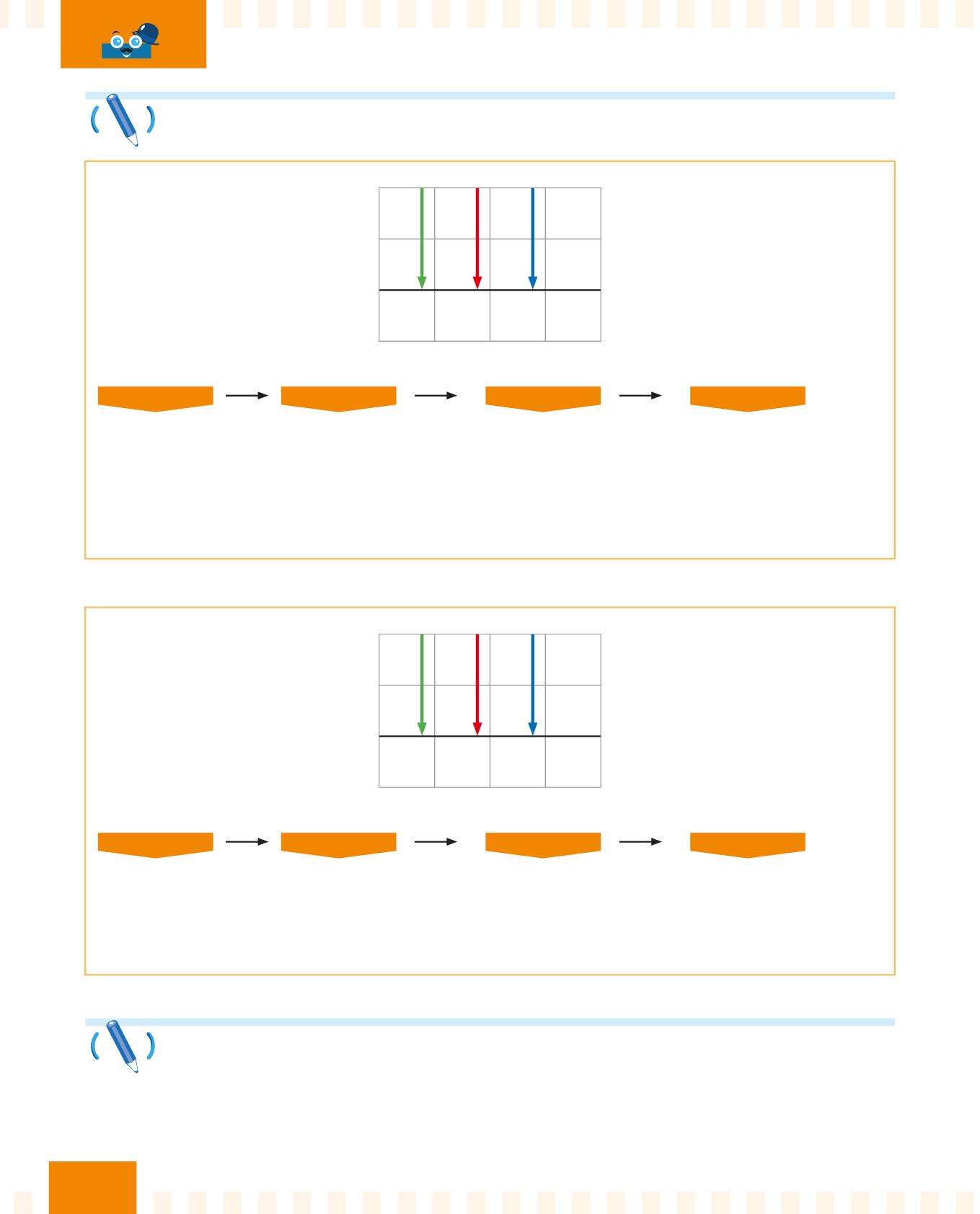
PASSO 1
Incolonna bene i numeri.
PASSO 2
Segui la freccia blu e svolgi la sottrazione.
Quanto fa 488 – 272?
PASSO 3
Segui la freccia rossa e svolgi la sottrazione.
PASSO 4
Segui la freccia verde e svolgi la sottrazione.
PASSO 1
Incolonna bene i numeri.
PASSO 2
Segui la freccia blu.
PASSO 3
Segui la freccia rossa.
PASSO 4
Segui la freccia verde.
Usa lo stesso procedimento e svolgi le seguenti sottrazioni senza il cambio sul tuo quaderno.
Quanto fa 223 – 156?
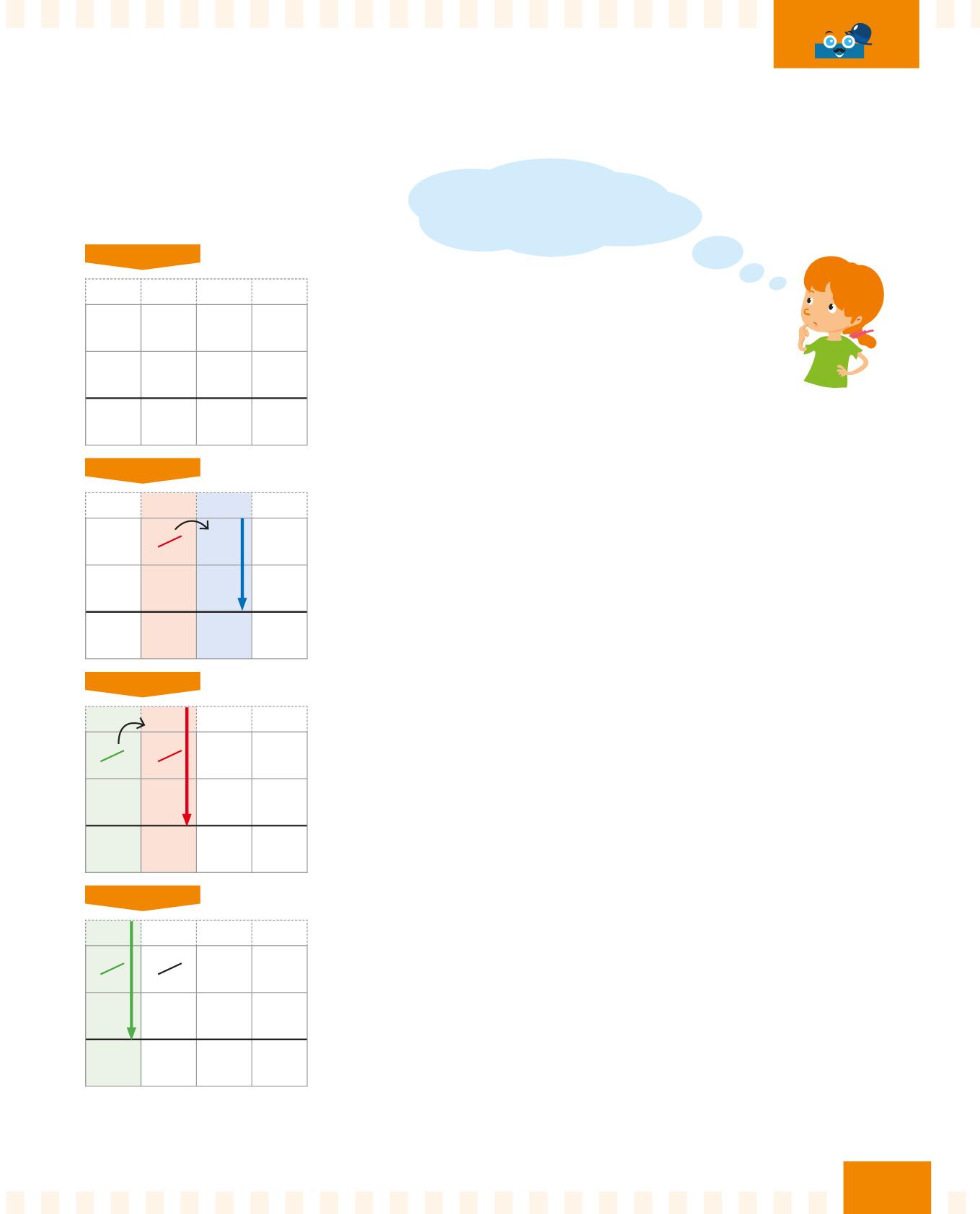
PASSO
Aiutati con la griglia e incolonna bene i numeri. Ricorda: svolgi sempre la sottrazione dall’alto verso il basso.
Inizia dalle cifre più a destra.
Segui la freccia blu. Se la cifra in basso è maggiore (più grande) di quella in alto, chiedi in prestito una decina:
2 diventa 1 e 3 diventa 13.
13 – 6 = 7.
Adesso segui la freccia rossa.
Se la cifra in basso è maggiore di quella in alto, chiedi in prestito una centinaia: 2 diventa 1
e 1 diventa 11.
11 – 5 = 6.
Infine, segui la freccia verde.
La sottrazione si può svolgere:
1 –
.
La sottrazione con il cambio è terminata. Il risultato è 67.
Svolgi le seguenti sottrazioni con il cambio.
Quanto fa 544 – 268?
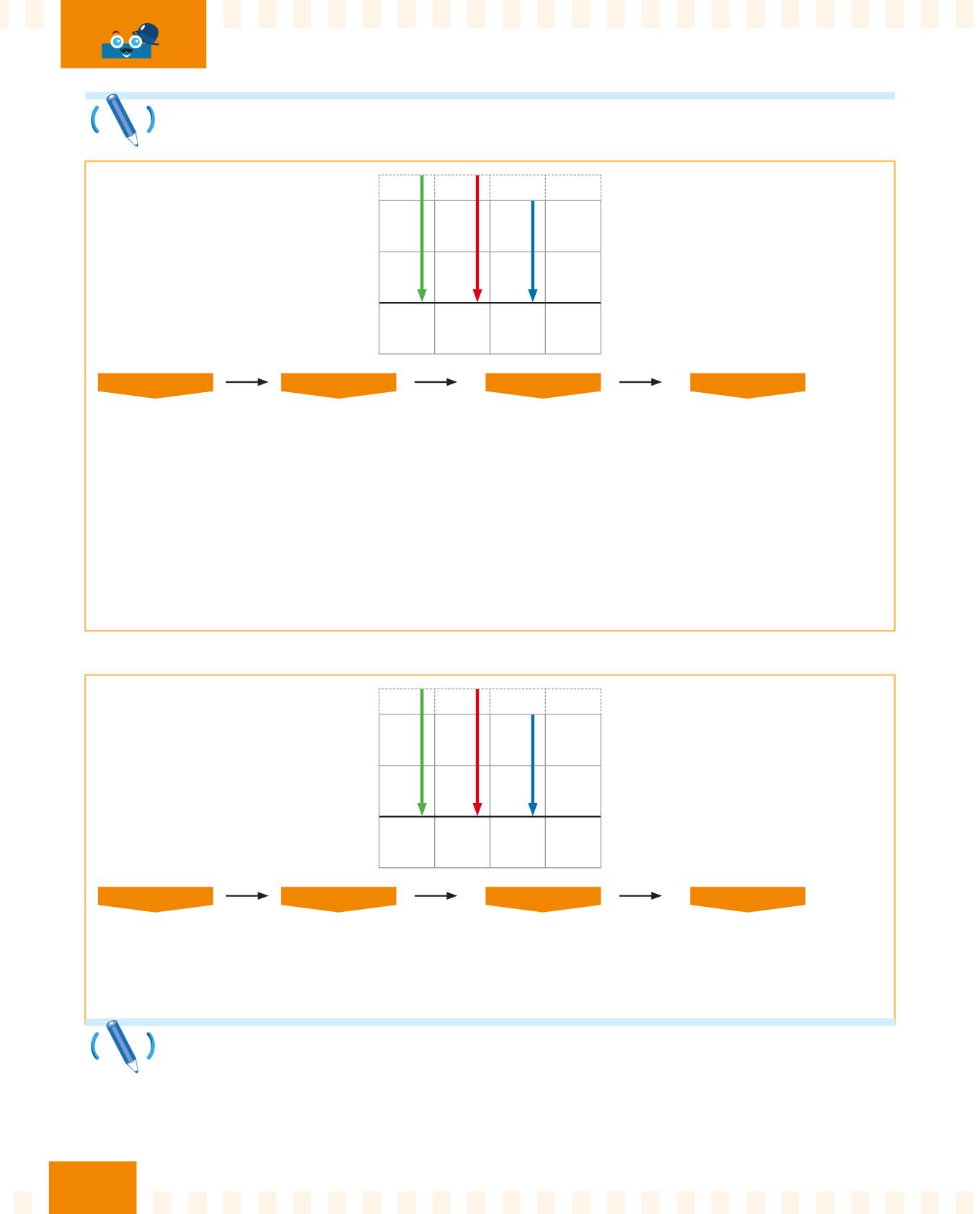
PASSO 1
Incolonna bene i numeri.
PASSO 2
Segui la freccia blu e svolgi la sottrazione.
Se la cifra in basso è maggiore di quella in alto, chiedi un prestito.
Quanto fa 923 – 185?
PASSO 3
Segui la freccia rossa e svolgi la sottrazione.
Se la cifra in basso è maggiore di quella in alto, chiedi un prestito.
PASSO 4
Segui la freccia verde e svolgi la sottrazione.
PASSO 1
Incolonna bene i numeri.
PASSO 2
Segui la freccia blu.
PASSO 3
Segui la freccia rossa.
PASSO 4
Segui la freccia verde.
Usa lo stesso procedimento e svolgi le seguenti sottrazioni con il cambio sul tuo quaderno.
PASSO 1
PARTE INTERA PARTE

PASSO 2 PARTE
Aiutati con la griglia e incolonna bene i numeri: la virgola del minuendo deve essere in colonna con la virgola del sottraendo.
Se ci sono, completa i buchi della parte decimale con degli 0. Inizia dalle cifre più a destra.
Segui la freccia gialla. Se la cifra in basso è maggiore della cifra in alto, chiedi in prestito una decina ai centesimi:
PROCEDIMENTI

PASSO 5
PASSO 6
Quanto fa 68,54 – 19,523? 1 1
La sottrazione con i numeri decimali è terminata. Il risultato è 28,208.
Svolgi la seguente sottrazione con i numeri decimali.
PARTE INTERA PARTE DECIMALE –=
PASSO 1
Incolonna bene
i numeri e la virgola.
PASSO 2
Se ci sono, completa i buchi della parte decimale con degli 0.
Poi segui la freccia gialla.
PASSI 3 4 5 6
Segui la freccia rosa, segui la freccia arancione, segui la freccia blu e segui la freccia rossa. Infine, trascrivi la virgola.
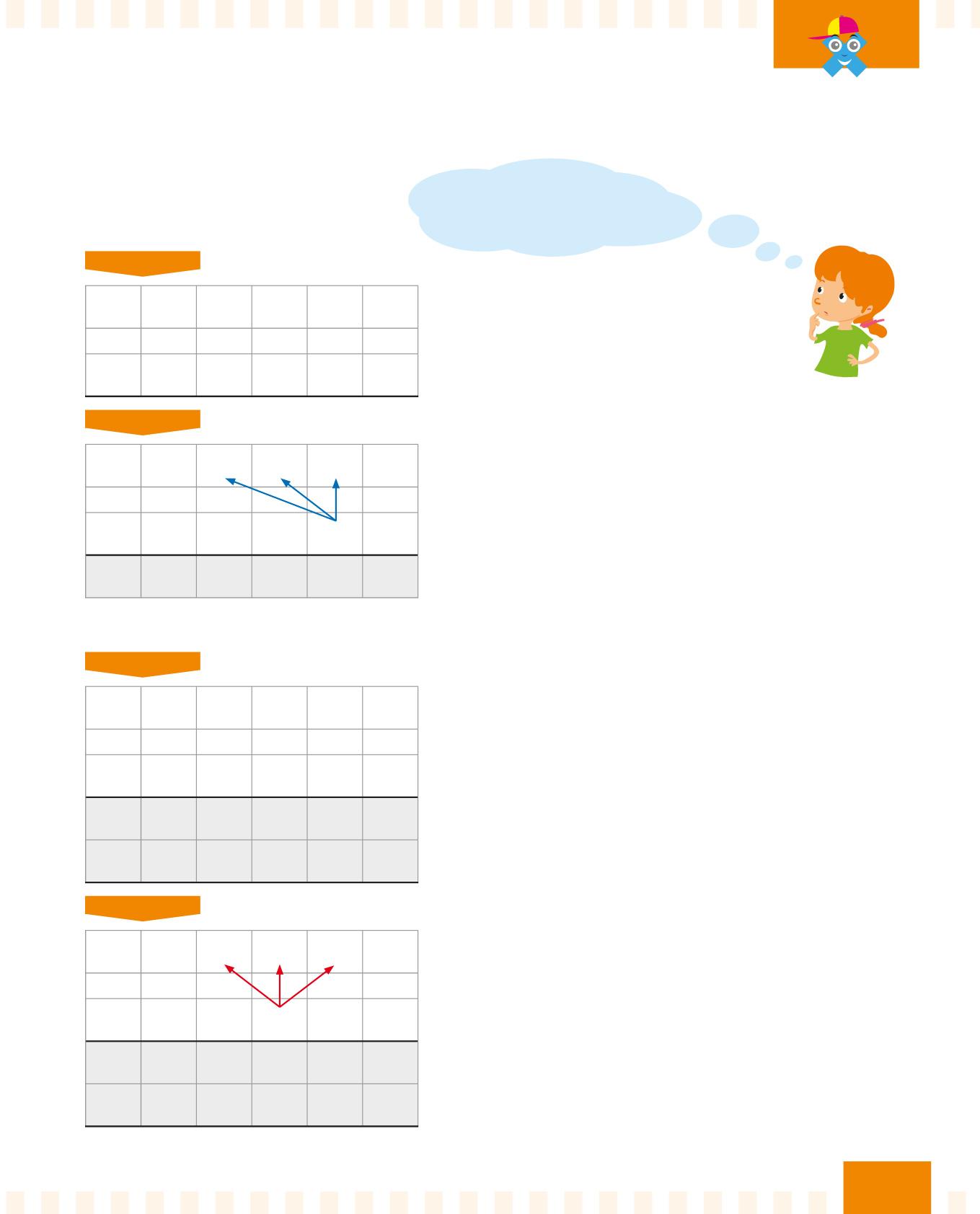
PASSO 1
PASSO
=
Quanto fa 221 × 14?
Aiutati con la griglia e incolonna bene i numeri.
Per proseguire con la moltiplicazione aggiungerai altri riquadri.
Segui le frecce blu e moltiplica la cifra blu 4 per ogni cifra del moltiplicando; vai in ordine e parti dalle unità:
4 × 1 = 4;
4 × 2 = 8;
4 × 2 = 8.
PASSO 3
Inserisci lo 0 sotto la prima cifra che hai scritto, cioè il 4.
PASSO 4
Adesso segui le frecce rosse e moltiplica la cifra rossa 1 per ogni cifra del moltiplicando; vai in ordine e parti dalle unità:
1 × 1 = 1;
1 × 2 = 2;
1 × 2 = 2.
PROCEDIMENTI
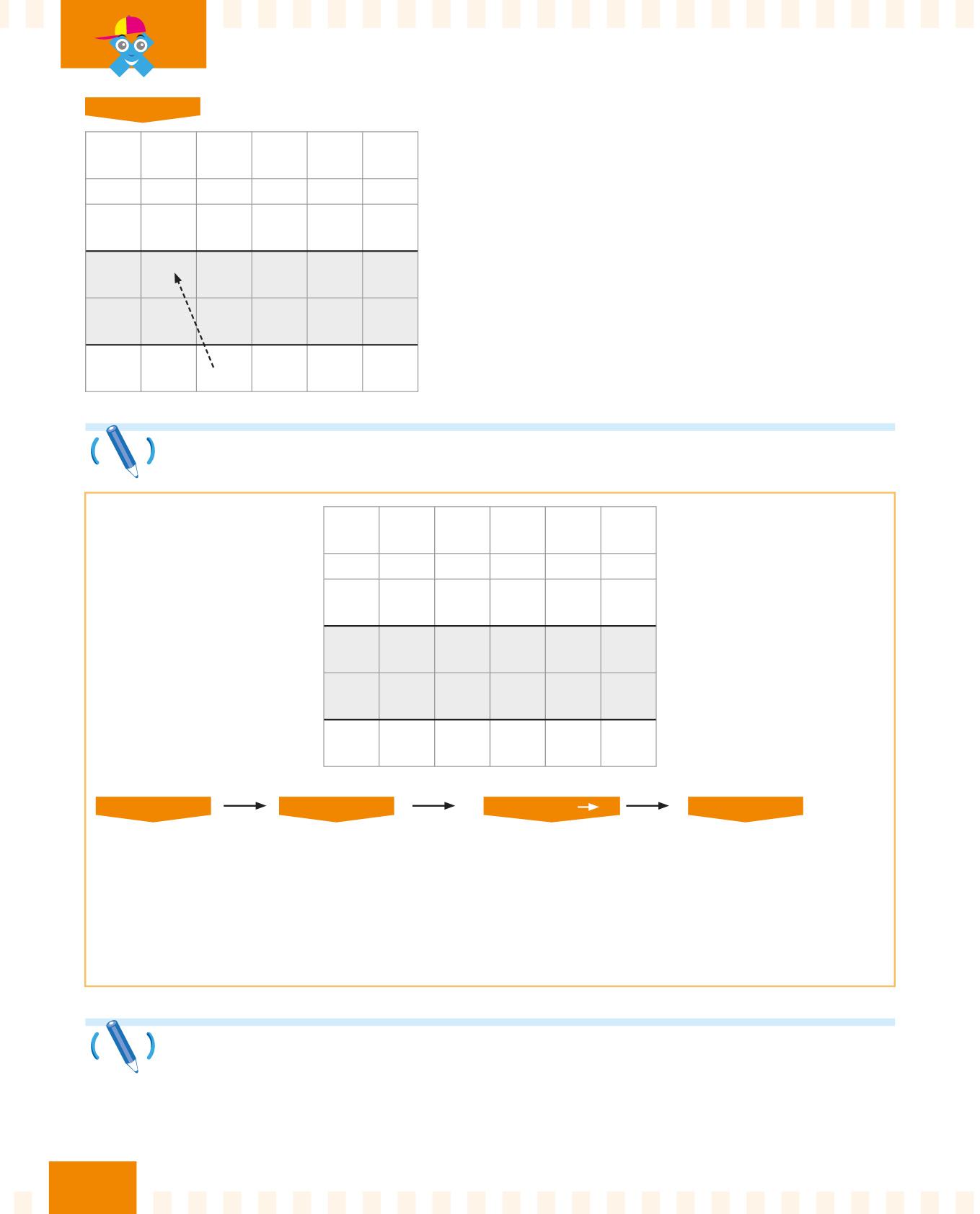
PASSO 5
Scrivi un + a fianco del primo prodotto e svolgi l’addizione
nella parte grigia.
La moltiplicazione senza il cambio è terminata.
Svolgi la seguente moltiplicazione senza il cambio.
Quanto fa 413 × 12?
Il risultato è 3094. × = =
PASSO 1
Incolonna bene i numeri.
PASSO 2
Moltiplica la cifra blu per ogni cifra del moltiplicando.
PASSI 3 4
Aggiungi lo 0. Moltiplica
la cifra rossa per ogni cifra del moltiplicando.
PASSO 5
Scrivi un + a fianco del primo prodotto e svolgi l’addizione
nella parte grigia.
Usa lo stesso procedimento e svolgi le seguenti moltiplicazioni senza il cambio sul tuo quaderno.
Quanto fa 121 × 56?

PASSO 1
×
=
PASSO 2
PASSO 3
×
=
Aiutati con la griglia e incolonna bene i numeri.
Segui le frecce blu e moltiplica la cifra blu 6 per ogni cifra del moltiplicando:
6 × 1 = 6; 6 × 2 = 12; 6 × 1 = 6.
Se ci sono, ricordati di aggiungere
ai risultati i cambi che hai scritto
nelle caselle blu.
Inserisci lo 0 sotto la prima cifra che hai scritto, cioè il 6.
Adesso segui le frecce rosse e moltiplica la cifra rossa 5 per ogni cifra del moltiplicando:
5 × 1 = 5; 5 × 2 = 10; 5 × 1 = 5.
Se ci sono, ricordati di aggiungere
ai risultati i cambi che hai scritto
nelle caselle rosse.
I cambi che hai scritto prima non valgono più.
PROCEDIMENTI
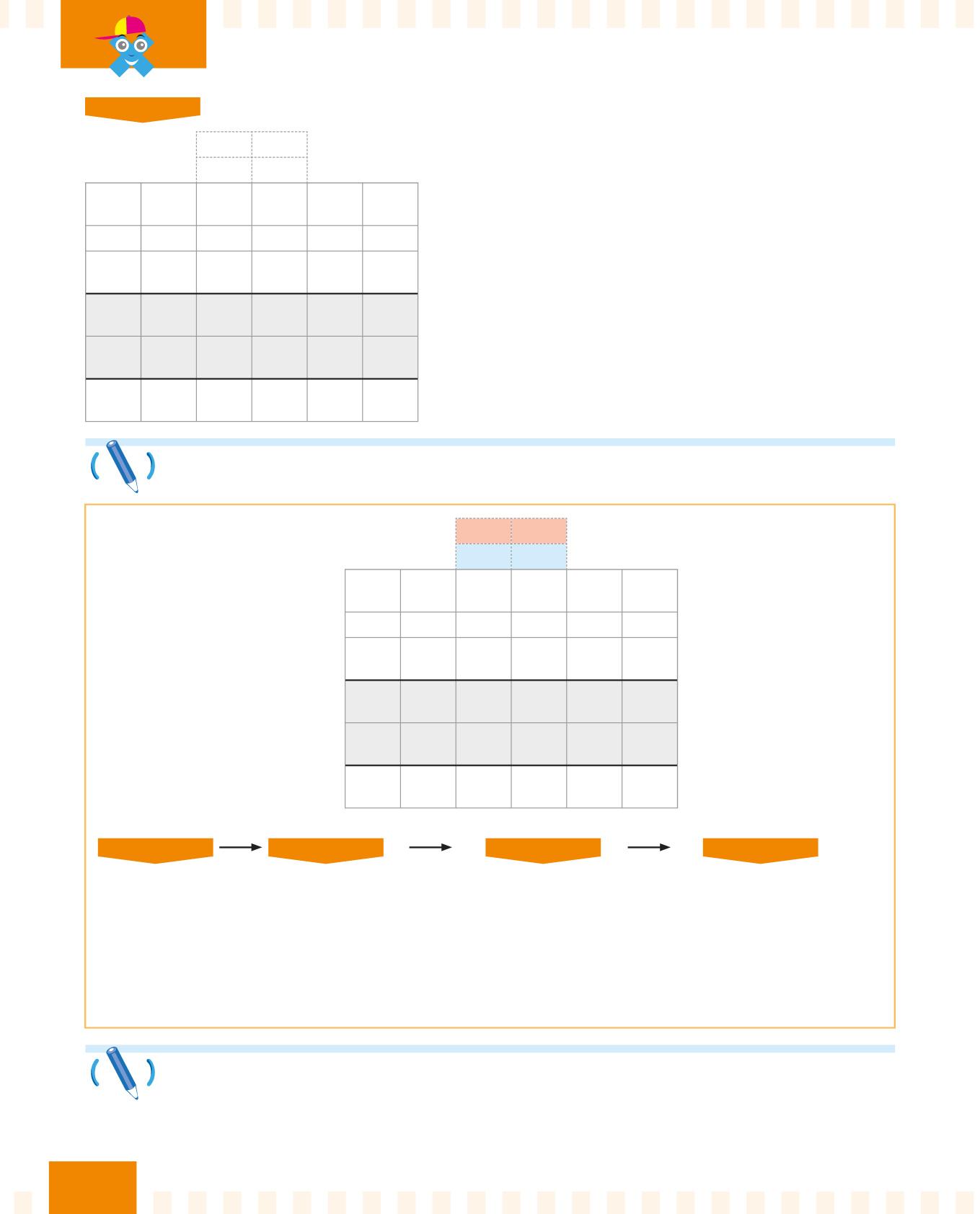
PASSO 4
Scrivi un + a fianco del primo prodotto e svolgi l’addizione nella parte grigia.
La moltiplicazione con il cambio è terminata. Il risultato è 6776.
Svolgi la seguente moltiplicazione con il cambio.
Quanto fa 322 × 65?
PASSO 1
Incolonna bene i numeri.
PASSO 2
Moltiplica la cifra blu per ogni cifra del moltiplicando. Se serve, fai un cambio.
PASSO 3
Moltiplica la cifra rossa per ogni cifra del moltiplicando. Se serve, fai un cambio.
PASSO 4
Svolgi l’addizione nella parte grigia.
Usa lo stesso procedimento e svolgi le seguenti moltiplicazioni con il cambio sul tuo quaderno.
99 × 52 = 19 × 23 =
789 × 12 =
Quanto fa 34 × 10? 34 × 100? 34 × 1000?
PASSO 1
dakukhdau 3 4

PASSO 2
dakukhdau 3 4 3 4
PASSO 3
dakukhdau 3 4 3 4 0
Inserisci il moltiplicando nella riga arancione della tabella: scrivi le unità sotto “u”, le decine sotto “da” e così via…
Adesso sposta le cifre verso sinistra di un posto, perché il 10 ha uno zero!
Scrivi le cifre nella riga azzurra.
Infine scrivi 0 nel posto vuoto.
La moltiplicazione × 10 è terminata: 34 × 10 = 340.
PASSO 1
dakukhdau 3 4
PASSO 2
dakukhdau 3 4 3 4
Inserisci il moltiplicando nella riga arancione della tabella: scrivi le unità sotto “u”, le decine sotto “da” e così via…
Adesso sposta le cifre verso sinistra di due posti, perché il 100 ha due zeri!
Scrivi le cifre nella riga azzurra.

Infine scrivi due 0 nei posti vuoti.
La moltiplicazione × 100 è
terminata: 34 × 100 = 3400. 34 × 1 000 PASSO
Inserisci il moltiplicando nella riga
arancione della tabella: scrivi le unità sotto “u”, le decine sotto “da” e così via…
Adesso sposta le cifre verso sinistra di tre posti, perché il 1000 ha tre zeri!
Scrivi le cifre nella riga azzurra.
Infine scrivi tre 0 nei posti vuoti.
La moltiplicazione × 1000
è terminata: 34 × 1 000 = 34 000.
Usa lo stesso procedimento e svolgi le seguenti moltiplicazioni × 10, × 100, × 1000.
Quanto fa 0,5 × 10? 0,5 × 100? 0,5 × 1000?
PASSO 1
dak ukhdau , dcm 0 , 5 ,
PASSO 2

Inserisci il moltiplicando nella riga arancione della tabella. Fai attenzione alla parte intera e alla parte decimale: scrivi i decimi sotto “d”, le unità sotto “u” e così via…
dak ukhdau , dcm 0 , 5 05 , Sposta le cifre verso sinistra di un posto, perché il 10 ha uno zero! Poi scrivi le cifre nella riga azzurra.
PASSO 3
dak ukhdau , dcm
0 , 5 05 ,
PASSO 1
dak ukhdau , dcm
0 , 5 ,
PASSO 2
dak ukhdau , dcm
La moltiplicazione × 10 è terminata. Il risultato è 5.
Inserisci il moltiplicando nella riga arancione della tabella. Fai attenzione alla parte intera e alla parte decimale: scrivi i decimi sotto “d”, le unità sotto “u” e così via…
0 , 5 05 , Sposta le cifre verso sinistra di due posti, perché il 100 ha due zeri! Scrivi le cifre nella riga azzurra.
PROCEDIMENTI

PASSO 3
dak ukhdau , dcm
0 , 5 05 0 ,
Se serve, scrivi tanti 0 quanti sono i posti vuoti prima della virgola.
La moltiplicazione × 100 è terminata.
Il risultato è 50.
0,5 × 1 000
PASSO 1
dak ukhdau , dcm 0 , 5 , Inserisci il moltiplicando nella riga arancione della tabella. Fai attenzione alla parte intera e alla parte decimale: scrivi i decimi sotto “d”, le unità sotto “u” e così via…
PASSO 2
dak ukhdau , dcm 0 , 5 05 , Sposta le cifre verso sinistra di tre posti, perché il 1000 ha tre zeri! Scrivi le cifre nella riga azzurra.
PASSO 3
dak ukhdau , dcm 0 , 5 05 00 ,
Se serve, scrivi tanti 0 quanti sono i posti vuoti prima della virgola.
La moltiplicazione × 1000 è terminata. Il risultato è 500.
Usa lo stesso procedimento e svolgi le seguenti moltiplicazioni × 10, × 100, × 1000 con i numeri decimali.
2,3 × 10 dak ukhdau , dcm , , 63,1 × 100 dak ukhdau , dcm , , 0,15 × 1000 dak ukhdau , dcm , , 0,08 × 10
ukhdau , dcm , ,
PASSO 1
Quanto fa 4,21 × 5,6?
4,2 1 × 5,6 = Aiutati con la griglia e incolonna i numeri.
Non considerare la virgola.

PASSO 2
Svolgi la moltiplicazione con i numeri decimali allo stesso modo di quella con i numeri interi. Una volta terminata, conta le cifre decimali del primo e del secondo fattore e metti la virgola al prodotto finale.
Segui le frecce arancioni e moltiplica
la cifra arancione 6 per ogni cifra del moltiplicando:
6 × 1 = 6; 6 × 2 = 12; 6 × 4 = 24.
Se ci sono, ricordati di aggiungere ai risultati i cambi che hai scritto nelle caselle arancioni.
PASSO 3
Inserisci lo 0 sotto la prima cifra che hai scritto, cioè il 6.
Adesso segui le frecce blu e moltiplica
la cifra blu 5 per ogni cifra del moltiplicando:
5 × 1 = 5; 5 × 2 = 10; 5 × 4 = 20.
Se ci sono, ricordati di aggiungere ai risultati i cambi che hai scritto nelle caselle blu.
Infine posiziona la virgola. Conta quante cifre del primo e del secondo fattore ci sono dopo la virgola: le cifre sono tre. Conta tre cifre a partire da destra e inserisci quindi la virgola.
La moltiplicazione con i numeri decimali è terminata. Il risultato è 23,576.
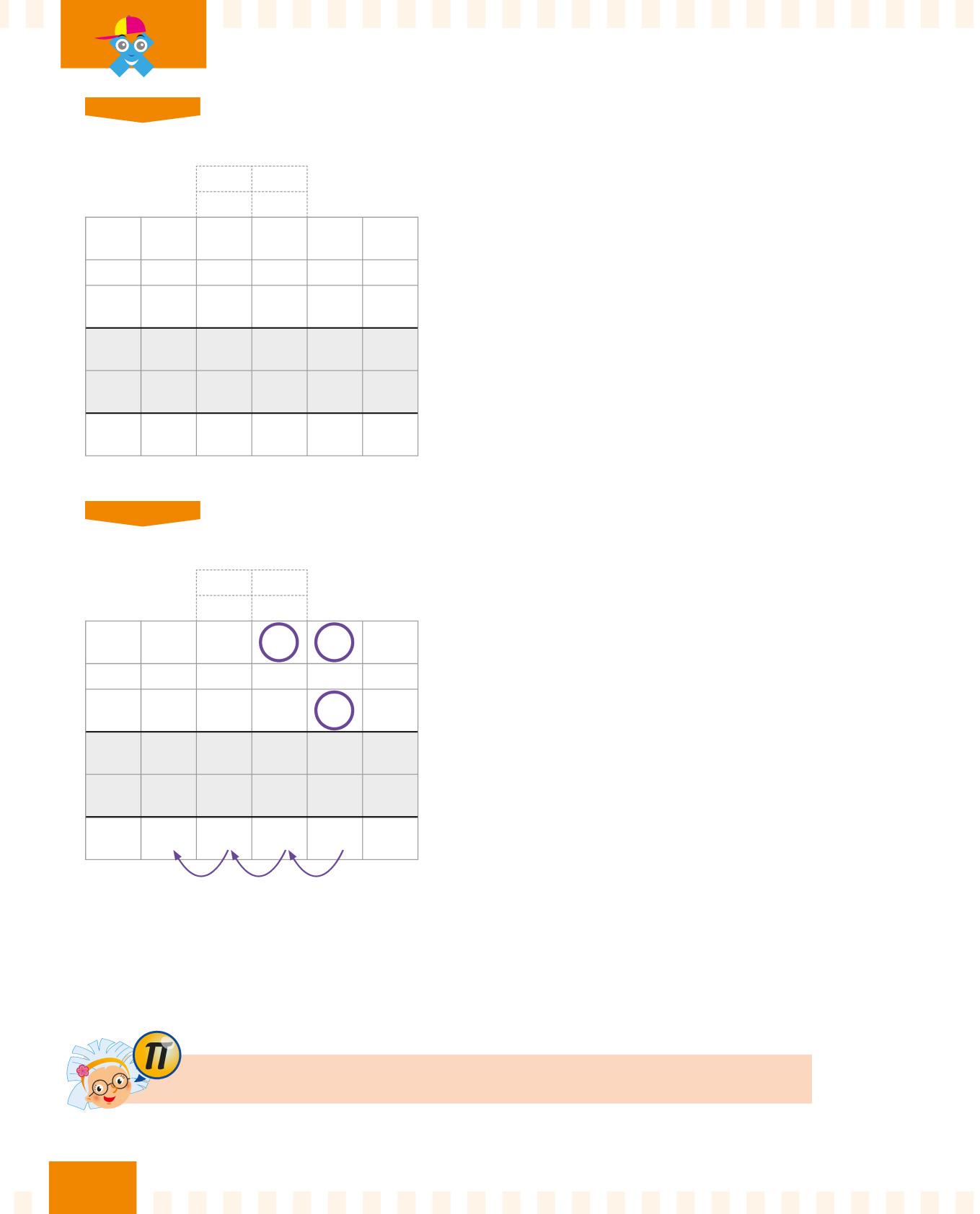
Al termine della moltiplicazione, ricordati di inserire la virgola!
Svolgi la seguente moltiplicazione con i numeri decimali.
Quanto fa 24,1 × 2,3?

PASSO 1
Incolonna i numeri senza considerare la virgola.
PASSI 2 3 4
Svolgi la moltiplicazione con i numeri decimali come una normale moltiplicazione con i numeri interi.
PASSO 5
Conta le cifre decimali del primo e del secondo fattore e metti la virgola al prodotto finale.
Usa lo stesso procedimento e svolgi sul tuo quaderno le seguenti moltiplicazioni con i numeri decimali.
Quanto fa 162 : 3?
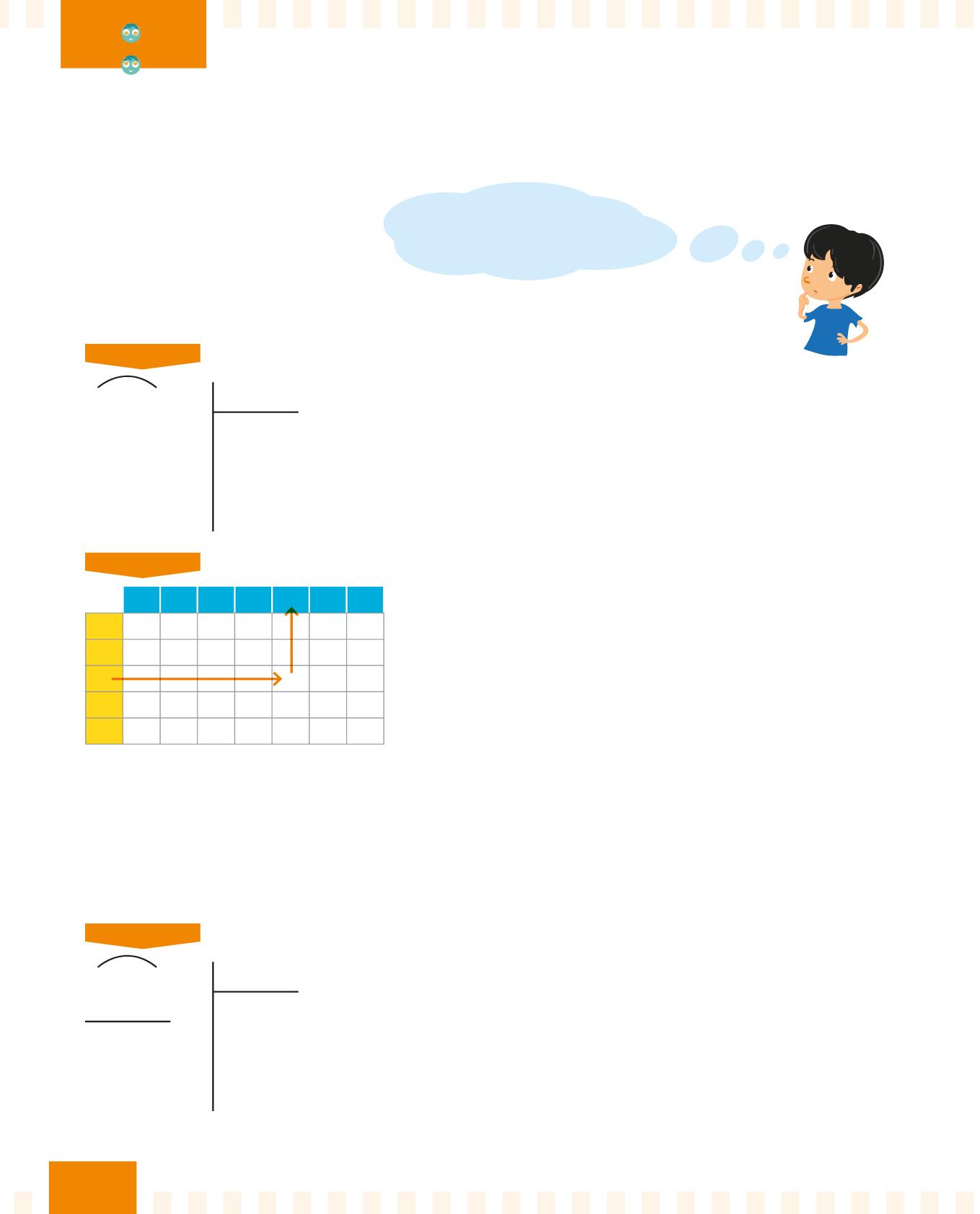
PASSO 1
16 2 3
Osserva il divisore e la prima cifra a sinistra del dividendo. Il divisore 3 è maggiore dell’1, quindi il 3 non sta nell’1.
Prendi quindi le prime due cifre del dividendo: 16.
PASSO 2
PASSO 3
16 2 3 15 5 01
Chiediti: quante volte il 3 sta nel 16?
Se non lo sai, puoi usare la tavola pitagorica a pagina 116:
• trova il 3 nella colonna gialla;
• scorri con il dito la riga del 3 e cerca il numero 16;
• se non trovi il 16, fermati sul primo numero minore di 16, in questo caso il 15;
• sali con il dito verso l’alto, fino alla riga azzurra, e trovi il 5.
Il 3 sta nel 16 cinque volte.
Scrivi 5 nel risultato.
Ora calcola il resto. Anche qui puoi aiutarti con la tavola pitagorica:
5 × 3 = 15.
Sottrai il risultato (15) dal numero iniziale (16):
16 – 15 = 1.
PASSO 4
16 2 3
15 5
012
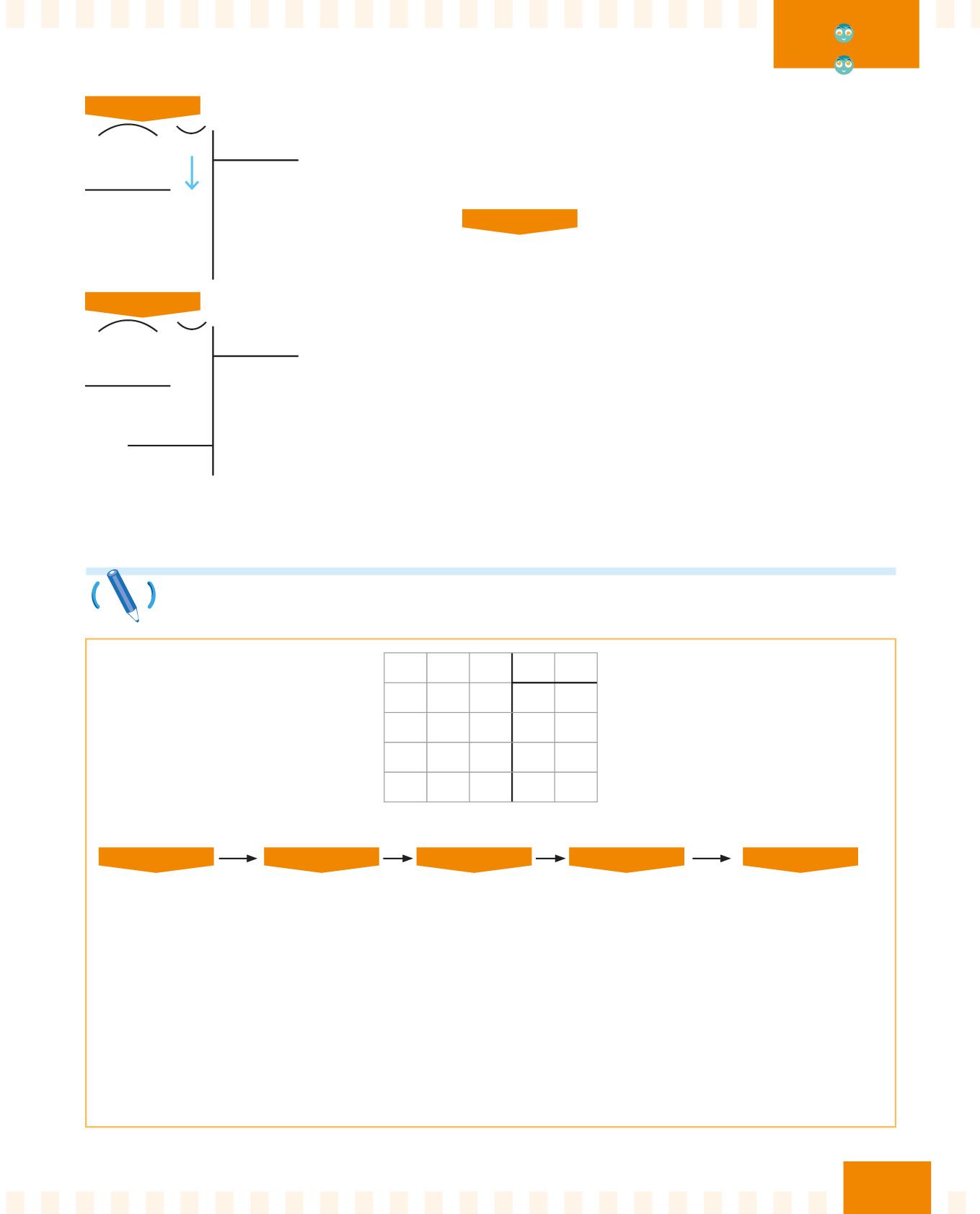
Trascrivi il 2. Quante volte il 3 sta nel 12?
Se hai difficoltà, usa la tavola pitagorica come nel PASSO 2 .
Il 3 sta nel 12 quattro volte.
PASSO 5
162 3
15 54
0 12 12 00
Scrivi 4 nel risultato.
Ora calcola il resto. Anche qui puoi aiutarti con la tavola pitagorica:
4 × 3 = 12.
Sottrai il risultato (12) dal numero iniziale (12): 12 – 12 = 0.
La divisione con una cifra e senza il resto è terminata. Il risultato è 54 resto 0.
Svolgi la seguente divisione con una cifra e senza il resto.
Quanto fa 174 : 2?
PASSO 1
Prendi le cifre del dividendo.
PASSO 2 Chiediti quante volte il divisore 2
sta nelle cifre che hai preso.
PASSO 3
Calcola il resto.
PASSO 4
Trascrivi l’ultima cifra del dividendo e chiediti quante volte il divisore 2 sta nel numero ottenuto.
PASSO 5
Calcola il resto.
Quanto fa 265 : 4?
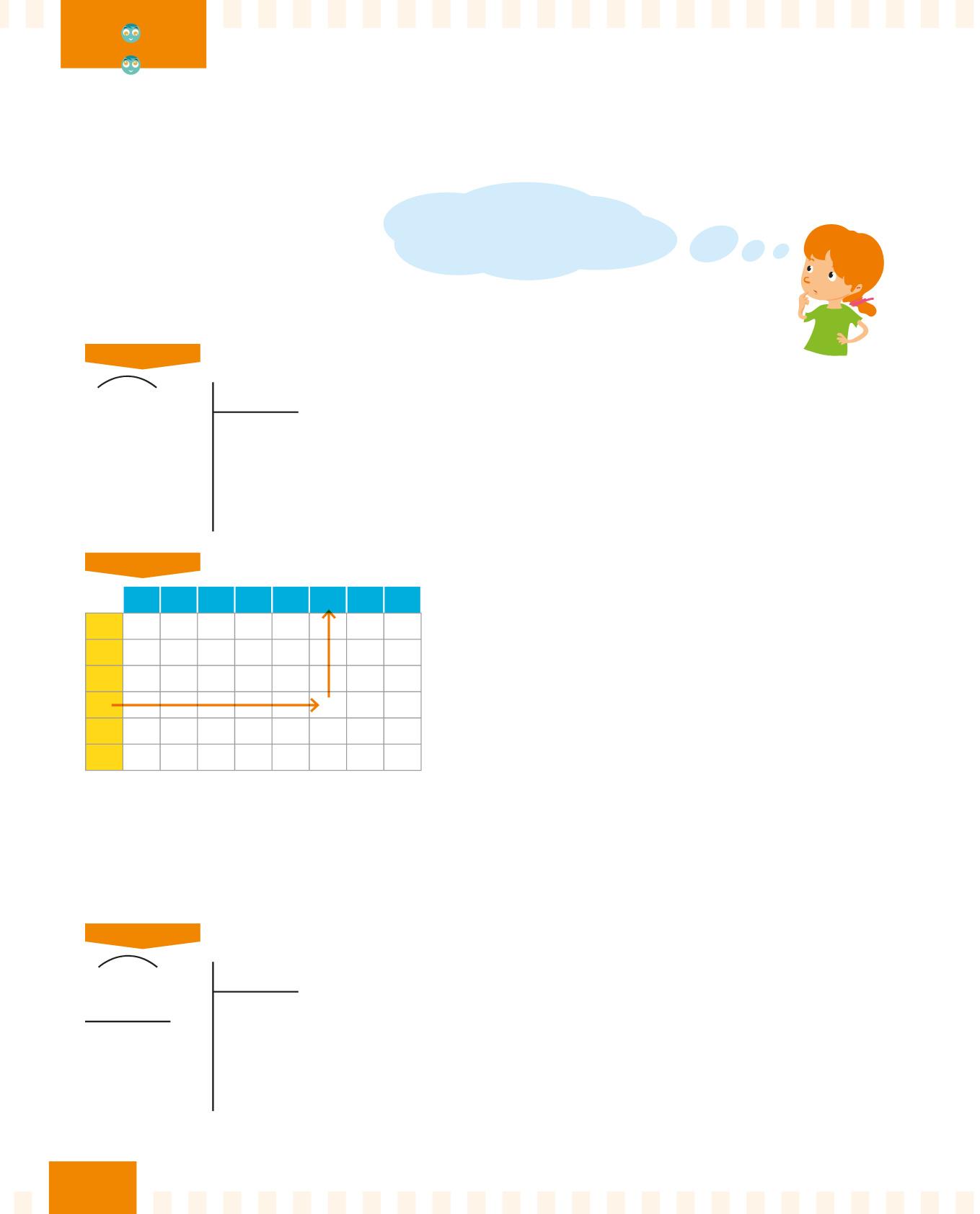
PASSO 1
26 5 4
Osserva il divisore e la prima cifra a sinistra del dividendo. Il divisore 4 è maggiore del 2, quindi il 4 non sta nel 2.
Prendi quindi le prime due cifre del dividendo:
26.
PASSO 2
PASSO 3
265 4
24 6 02
Chiediti: quante volte il 4 sta nel 26?
Se non lo sai, puoi usare la tavola pitagorica a pagina 116:
• trova il 4 nella colonna gialla;
• scorri con il dito la riga del 4 e cerca il numero 26;
• se non trovi il 26, fermati sul primo numero minore di 26, in questo caso il 24;
• sali con il dito verso l’alto, fino alla riga azzurra, e trovi il 6.
Il 4 sta nel 26 sei volte.
Scrivi 6 nel risultato.
Ora calcola il resto. Anche qui puoi aiutarti con la tavola pitagorica:
6 × 4 = 24.
Sottrai il risultato (24) dal numero iniziale (26):
26 – 24 = 2.
PROCEDIMENTI
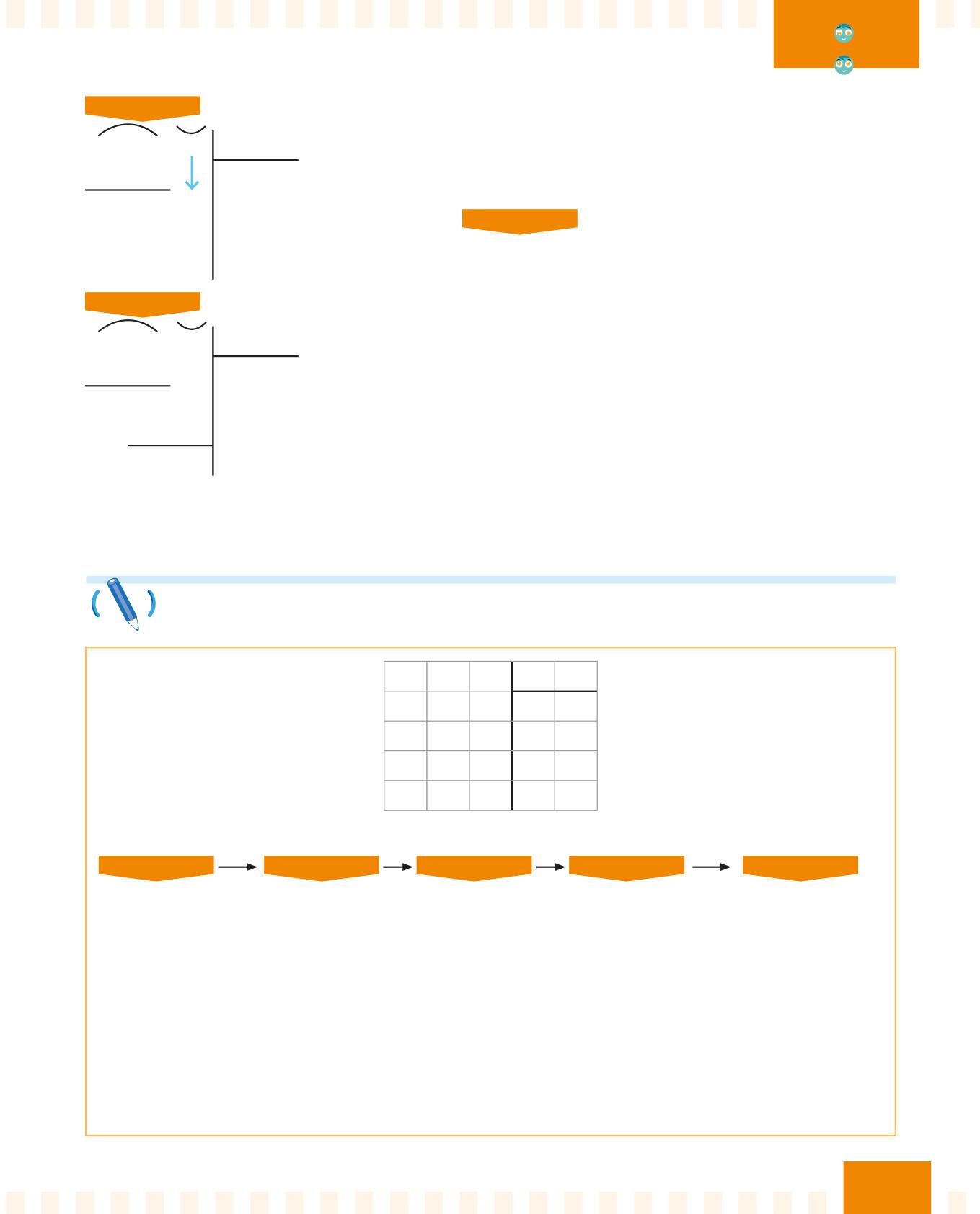
PASSO 4 26 5 4
6
25
PASSO 5
265 4 24 66 0 25 24 01
Trascrivi il 5. Quante volte il 4 sta nel 25?
Se hai difficoltà, usa la tavola pitagorica come nel PASSO 2 .
Il 4 sta nel 25 sei volte.
Scrivi 6 nel risultato.
Ora calcola il resto. Anche qui puoi aiutarti con la tavola pitagorica:
6 × 4 = 24.
Sottrai il risultato (24) dal numero iniziale (25)
25 – 24 = 1.
La divisione con una cifra e con il resto è terminata. Il risultato è 66 resto 1.
Svolgi la seguente divisione con una cifra e con il resto.
Quanto fa 169 : 3?
PASSO 1
Prendi le cifre del dividendo.
PASSO 2
Chiediti quante volte il divisore 3
sta nelle cifre che hai preso.
PASSO 3
Calcola il resto.
PASSO 4
Trascrivi l’ultima cifra del dividendo e chiediti quante volte il divisore 3
sta nel numero ottenuto.
PASSO 5
Calcola il resto.
Quanto fa 492 : 13?
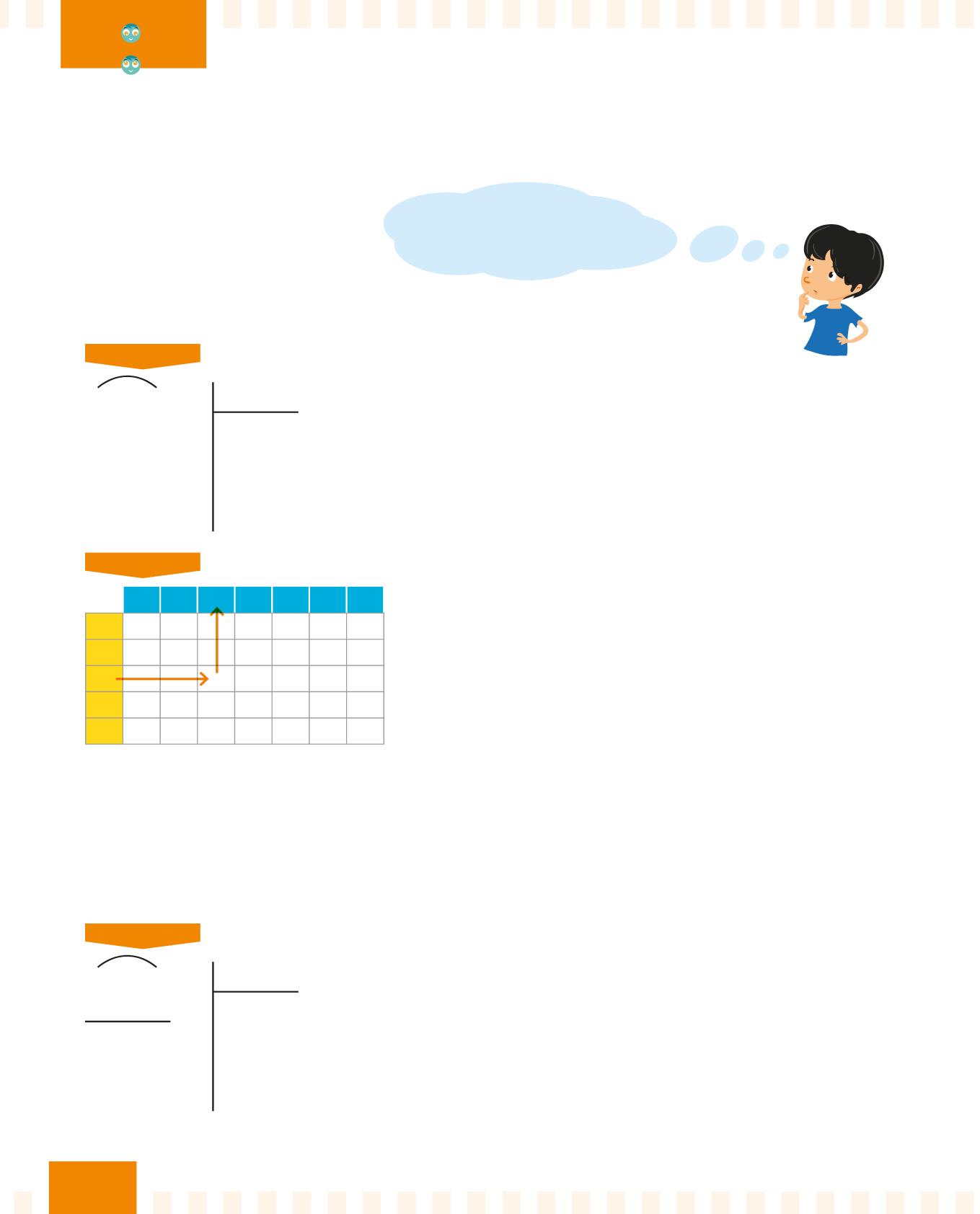
PASSO 1
49 2 13
Osserva il divisore e la prima cifra a sinistra del dividendo. Il divisore 13 è maggiore del 4, quindi il 13 non sta nel 4.
Prendi quindi le prime due cifre del dividendo: 49.
PASSO 2
PASSO 3
49 2 13 39 3 10
Chiediti: quante volte il 13 sta nel 49?
Se non lo sai, puoi usare la tavola pitagorica a pagina 117:
• trova il 13 nella colonna gialla;
• scorri con il dito la riga del 13 e cerca il numero 49;
• se non trovi il 49, fermati sul primo numero minore di 49, in questo caso 39;
• sali con il dito verso l’alto, fino alla riga azzurra, e trovi il 3.
Il 13 sta nel 49 tre volte.
Scrivi 3 nel risultato.
Ora calcola il resto. Anche qui puoi aiutarti con la tavola pitagorica:
3 × 13 = 39.
Sottrai il risultato (39) dal numero iniziale (49):
49 – 39 = 10.
PROCEDIMENTI
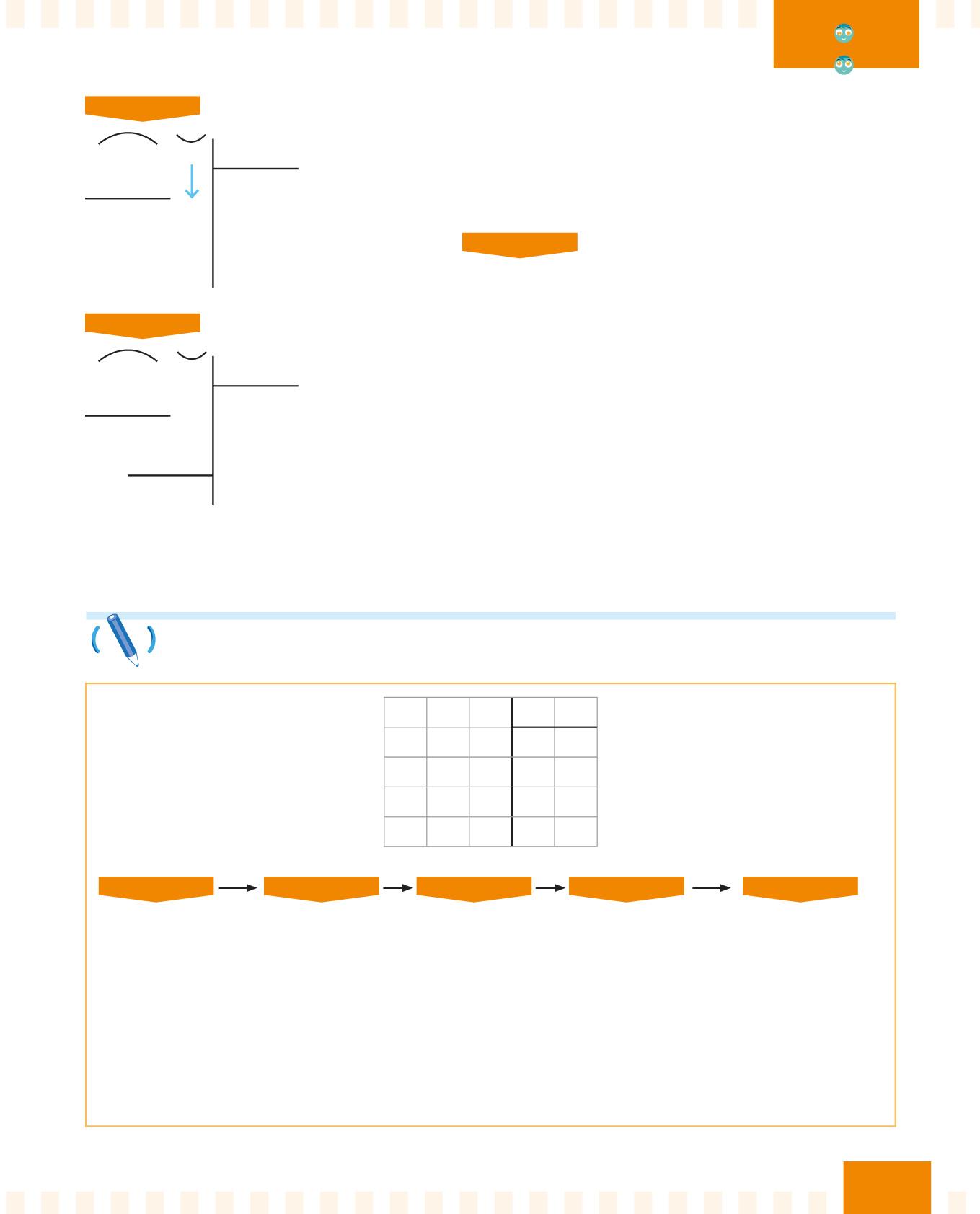
PASSO 4
49 2 13
39 3 102
Trascrivi il 2.
Quante volte il 13 sta nel 102?
Se hai difficoltà, usa la tavola pitagorica come nel PASSO 2 .
Il 13 sta nel 102 sette volte.
PASSO 5
492 13
39 37 102 91 11
Scrivi 7 nel risultato.
Ora calcola il resto. Anche qui puoi aiutarti con la tavola pitagorica:
7 × 13 = 91.
Sottrai il risultato (91) dal numero iniziale (102): 102 – 91 = 11.
La divisione con due cifre e con il resto è terminata. Il risultato è 37 resto 11.
Svolgi le seguenti divisioni con due cifre e con il resto.
Quanto fa 625 : 14?
PASSO 1
Prendi le cifre del dividendo.
PASSO 2
Chiediti quante volte il divisore 14
sta nelle cifre che hai preso.
PASSO 3
Calcola il resto.
PASSO 4
Trascrivi l’ultima cifra del dividendo e chiediti quante volte il divisore 14 sta nel numero.
PASSO 5
Calcola il resto.
Quanto fa 326 : 25?
PASSO 1
Prendi le cifre del dividendo.
PASSO 2
Chiediti quante volte il divisore 25 sta nelle cifre che hai preso.
PASSO 3
Calcola il resto.
PASSO 4
Trascrivi l’ultima cifra del dividendo e chiediti quante volte il divisore 25 sta nel numero ottenuto.
PASSO 5
Calcola il resto.
Usa lo stesso procedimento e svolgi le seguenti divisioni con due cifre e con il resto sul tuo quaderno.
428 : 12 = resto
589 : 55 = resto
194 : 15 = resto
128 : 13 = ..................................... resto ....................
392 : 13 = resto
642 : 42 = resto
355 : 22 = resto
287 : 23 = resto
il dividendo nella riga arancione della tabella: scrivi le unità sotto “u”, le decine sotto “da” e così via…
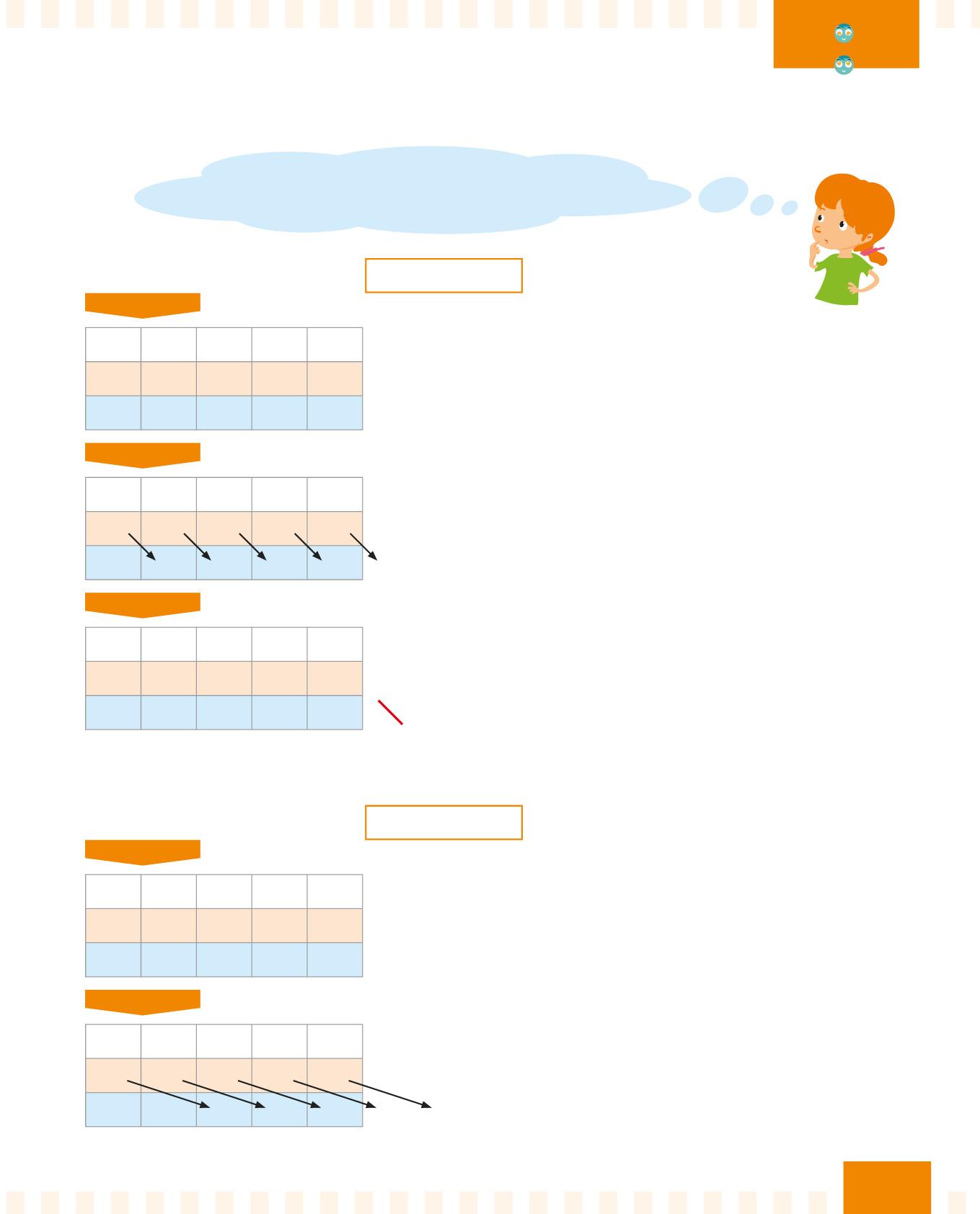
Sposta le cifre verso destra di un posto, perché il 10 ha uno zero!
Scrivi le cifre nella riga azzurra.
Uno zero rimane fuori dalla riga!
Lo elimini.
La divisione : 10 è terminata. Il risultato è 7000.
il dividendo nella riga
della tabella: scrivi le unità sotto “u”, le decine sotto “da” e così via…
Sposta le cifre verso destra di due posti, perché il 100 ha due zeri!
Scrivi le cifre nella riga azzurra.
Due zeri rimangono fuori dalla riga!
Li elimini.
La divisione : 100 è terminata.
Il risultato è 700.
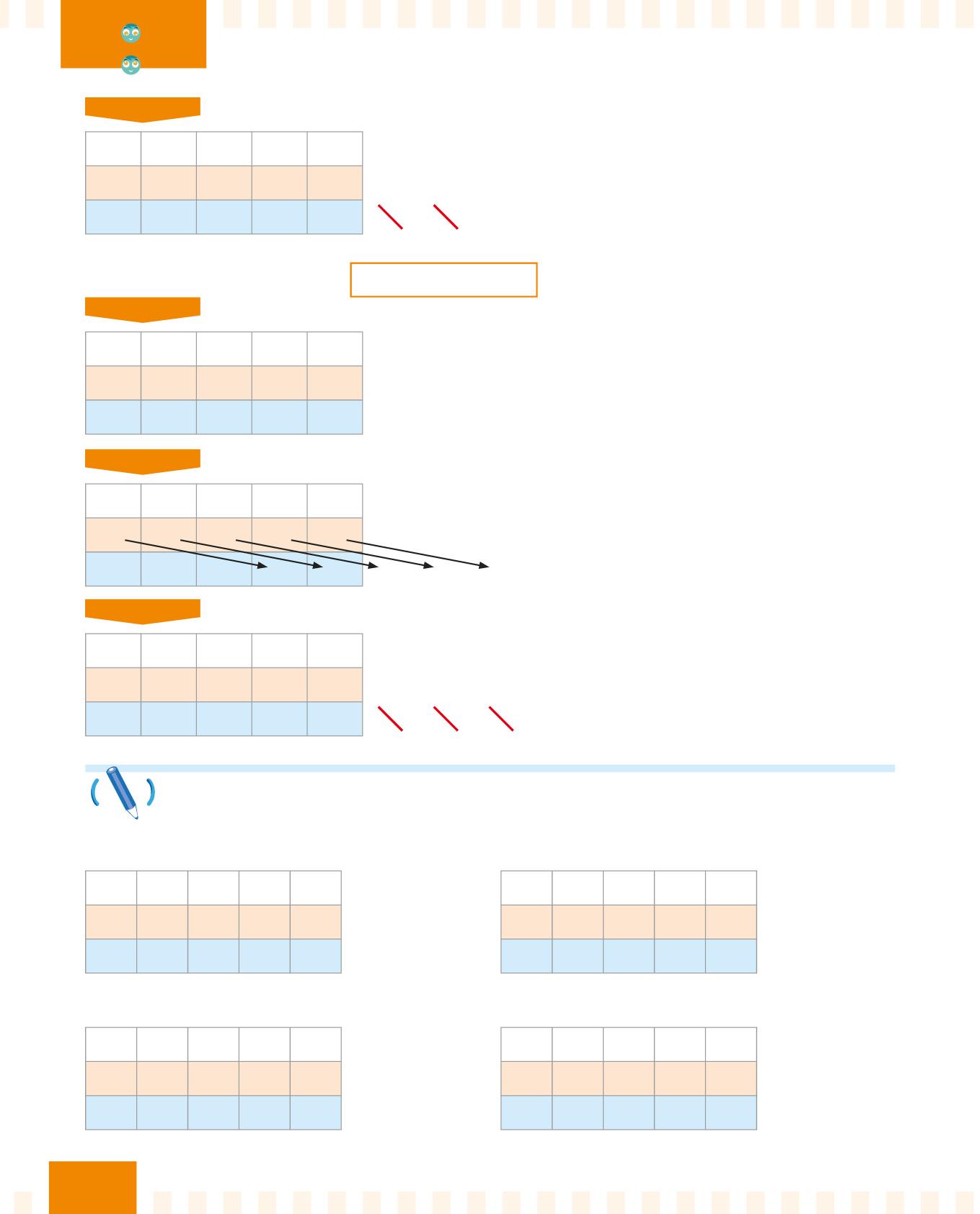
Inserisci il dividendo nella riga arancione della tabella: scrivi le unità sotto “u”, le decine sotto “da” e così via… PASSO
Sposta le cifre verso destra di tre posti, perché il 1000 ha tre zeri! Scrivi le cifre nella riga azzurra.
Tre zeri rimangono fuori
dalla riga! Li elimini.
La divisione : 1000 è terminata. Il risultato è 70.
Inserisci il dividendo nelle tabelle e svolgi le seguenti divisioni : 10, : 100, : 1000.

PASSO 1
dakukhdau , dcm 6 , 2 , Inserisci il dividendo nella riga arancione della tabella. Fai attenzione alla parte intera e alla parte decimale!
PASSO 2
dakukhdau , dcm 6 , 2 , 62
PASSO 3
dakukhdau , dcm 6 , 2 0 , 62
Sposta le cifre verso destra di un posto, perché il 10 ha uno zero!
Scrivi le cifre nella riga azzurra.
Se prima o dopo la virgola non c’è nessun numero, metti 0. La divisione : 10 è terminata. Il risultato è 0,62.
PASSO 1
dakukhdau , dcm 6 , 2 , Scrivi il dividendo nella riga arancione della tabella. Fai attenzione alla parte intera e alla parte decimale!
PASSO 2
dakukhdau , dcm 6 , 2 , 62
Sposta le cifre verso destra di due posti, perché il 100 ha due zeri!
Scrivi le cifre nella riga azzurra.
PROCEDIMENTI

PASSO 3
dakukhdau , dcm
6 , 2 0 , 0 62
Se prima o dopo la virgola non c’è
nessun numero, metti 0.
La divisione : 100 è terminata.
Il risultato è 0,062.
662 : 1 000
PASSO 1
dakukhdau , dcm
662 , , Scrivi il dividendo nella riga arancione della tabella. Fai attenzione alla parte intera e alla parte decimale!
PASSO 2
dakukhdau , dcm
6 6 2 , , 662
PASSO 3
dakukhdau , dcm
662 , 0 , 662
Sposta le cifre verso destra di tre posti, perché il 1000 ha tre zeri!
Scrivi le cifre nella riga azzurra.
Se prima o dopo la virgola non c’è
nessun numero, metti 0.
La divisione : 1000 è terminata.
Il risultato è 0,662.
Inserisci il dividendo nelle tabelle e svolgi le seguenti divisioni : 10, : 100, : 1000 con i numeri decimali.
2,3 : 100
dakukhdau , dcm , , 65,4 : 10 dakukhdau , dcm , , 7631 : 1000
dakukhdau , dcm , , 48 : 100 dakukhdau , dcm , ,
Quanto fa 98,4 : 12?
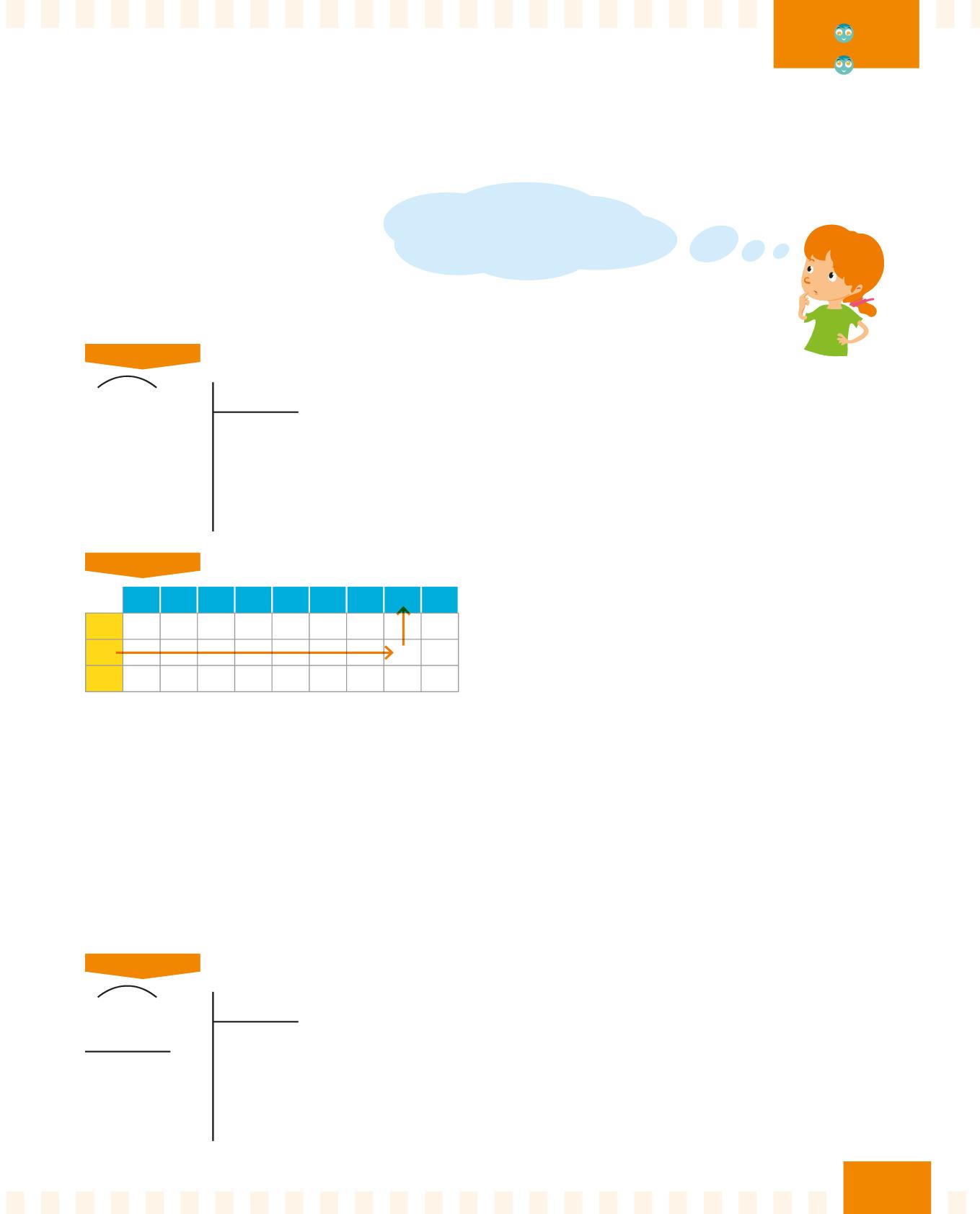
PASSO 1
98,4 12 Osserva il divisore e la prima cifra a sinistra del dividendo. Il divisore 12 è maggiore del 9, quindi il 12 non sta nel 9.
Prendi quindi le prime due cifre del dividendo: 98.
PASSO 2
Chiediti: quante volte il 12 sta nel 98?
Se non lo sai, puoi usare la tavola pitagorica a pagina 117:
• trova il 12 nella colonna gialla;
• scorri con il dito la riga del 12 e cerca il numero 98;
• se non trovi il 98, fermati sul primo numero minore di 98, in questo caso il 96;
• sali con il dito verso l’alto, fino alla riga azzurra, e trovi l’8.
Il 12 sta nel 96 otto volte.
PASSO 3
9 8,4 12 96 8 02
Scrivi 8 al risultato.
Ora calcola il resto. Anche qui puoi aiutarti con la tavola pitagorica:
8 × 12 = 96
98 – 96 = 2.
PROCEDIMENTI
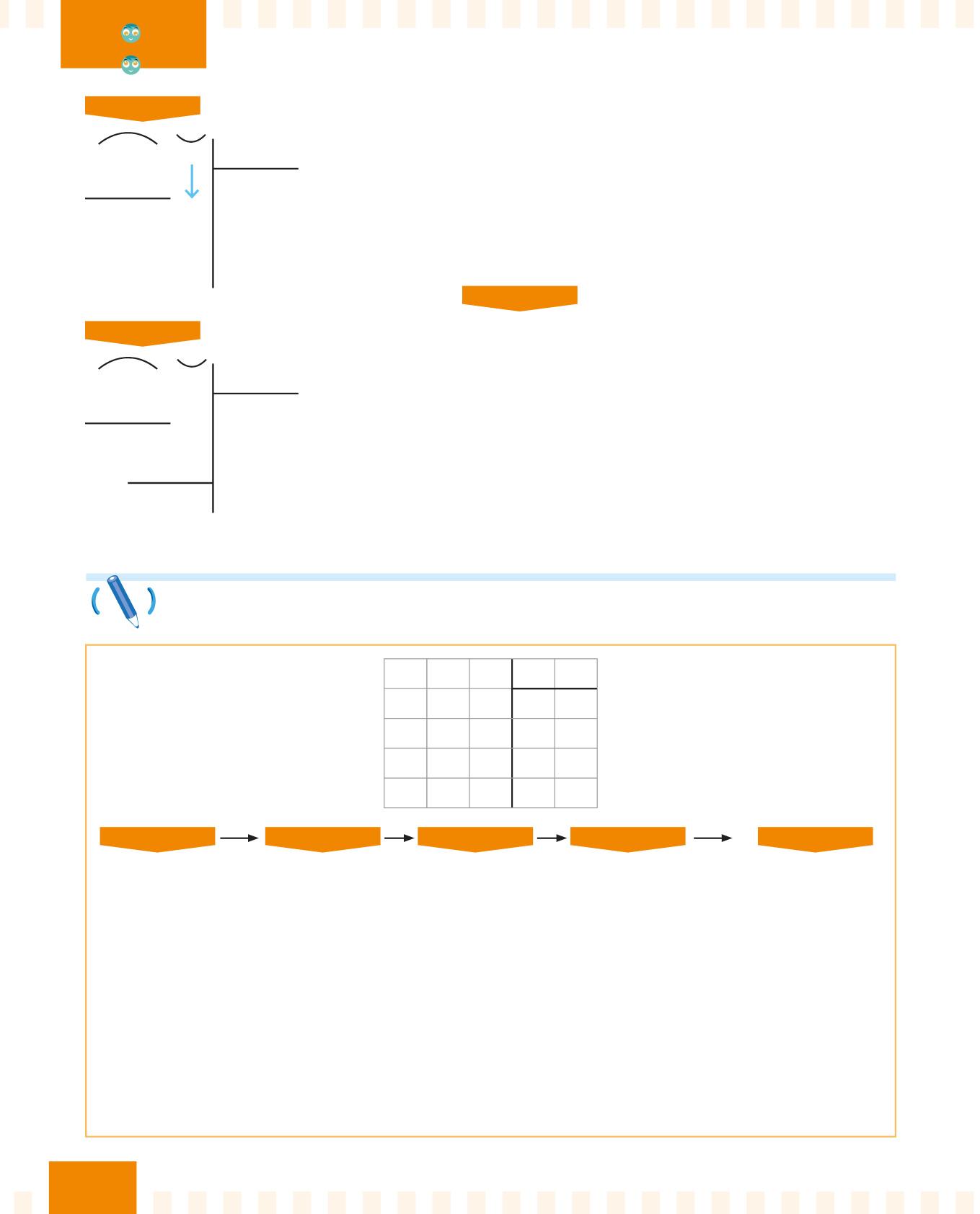
PASSO 4
98, 4 12
96 8, 024
Trascrivi il 4 e metti la virgola al risultato, perché hai appena trascritto il primo numero decimale.
Quante volte il 12 sta nel 24?
Se hai difficoltà, usa la tavola pitagorica come nel PASSO 2 . Il 12 sta nel 24 due volte.
PASSO 5
98,4 12
96 8,2 0 24 24 00
Scrivi il 2 al risultato.
Ora calcola il resto. Anche qui puoi aiutarti con la tavola pitagorica: 2 × 12 = 24.
Sottrai il risultato (24) dal numero iniziale (24): 24 – 24 = 0.
La divisione con il dividendo decimale è terminata. Il risultato è 8,2 resto 0.
Svolgi le seguenti divisioni con il dividendo decimale.
Quanto fa 86,4 : 12?
PASSO 1
Prendi le cifre del dividendo.
PASSO 2
Chiediti quante volte il divisore 12
sta nelle cifre che hai preso.
PASSO 3
Calcola il resto.
PASSO 4
Trascrivi l’ultima cifra del dividendo, quella decimale.
Metti la virgola al risultato. Poi chiediti quante volte il divisore 12 sta nel numero.
PASSO 5
Calcola il resto.
Quanto fa 75,4 : 26?
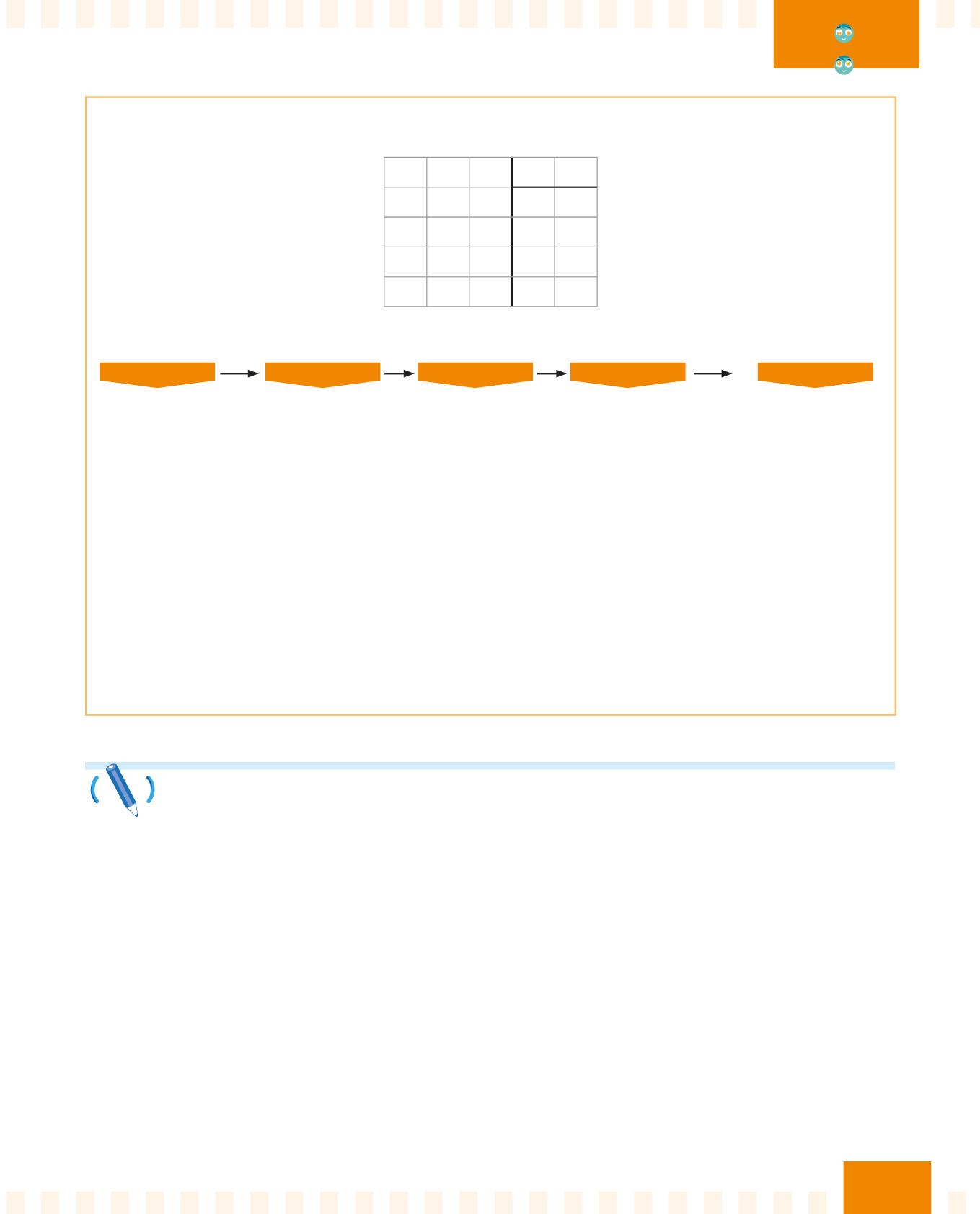
PASSO 1
Prendi le cifre del dividendo.
PASSO 2
Chiediti quante volte il divisore 26
sta nelle cifre che hai preso.
PASSO 3
Calcola il resto.
PASSO 4
Trascrivi l’ultima cifra del dividendo, quella decimale.
Metti la virgola al risultato.
Poi chiediti quante volte il divisore 26
sta nel numero.
PASSO 5
Calcola il resto.
Usa lo stesso procedimento e svolgi le seguenti divisioni con dividendo decimale sul tuo quaderno.
Quanto fa 5,12 : 3,2?
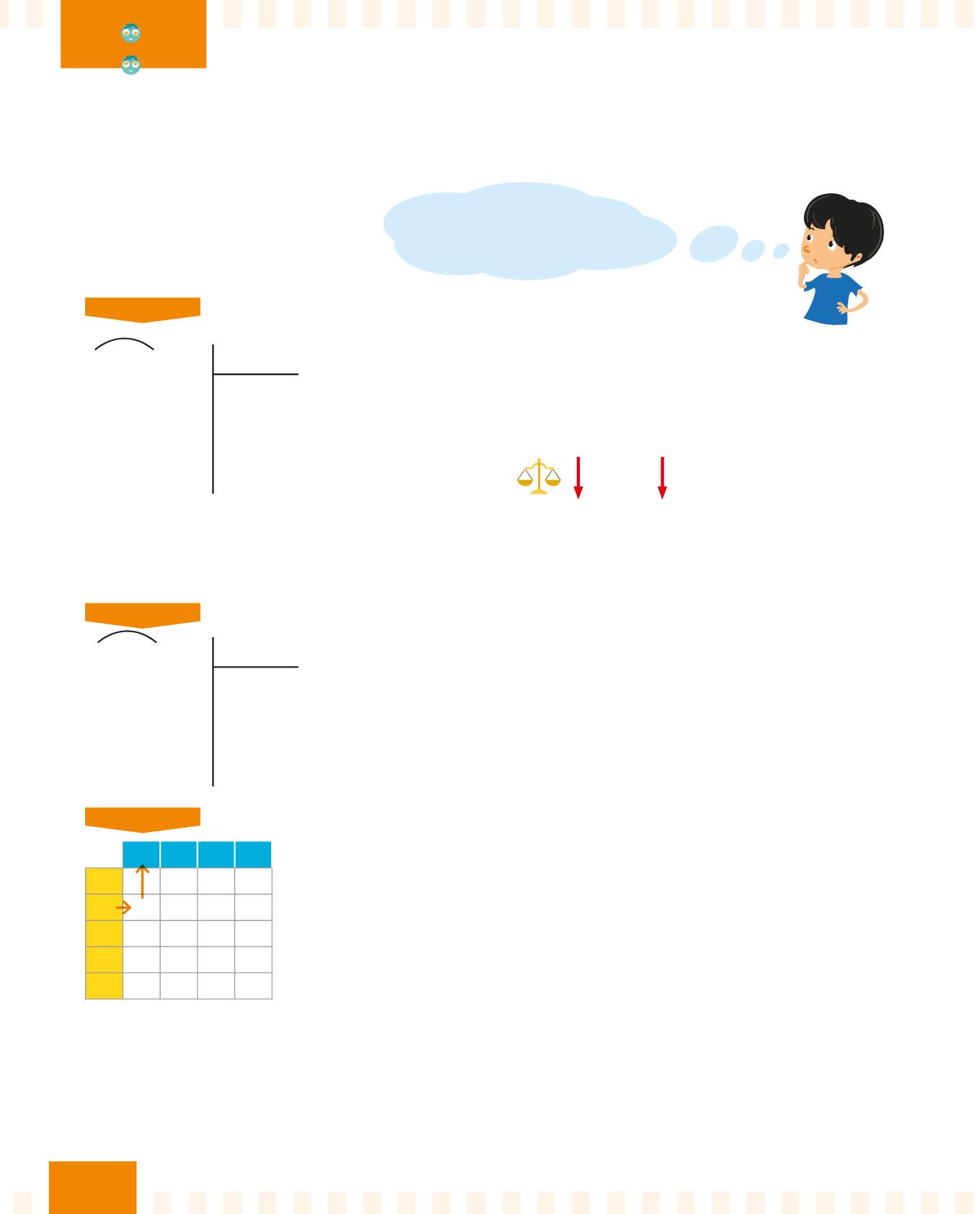
PASSO 1
5,123,2
Controlla il divisore 3,2. È un numero decimale, quindi applica la proprietà invariantiva per rendere il divisore 3,2 un numero intero:
5,12 : 3,2 =
× 10 × 10
51,2 : 32 =
Poi applica lo stesso procedimento della divisione con il dividendo decimale.
PASSO 2
51,2 32
Osserva il divisore e la prima cifra a sinistra del dividendo. Il divisore 32 è maggiore del 5, quindi il 32 non sta nel 5.
Prendi quindi le prime due cifre del dividendo: 51.
PASSO 3
Chiediti: quante volte il 32 sta nel 51?
Se non lo sai, puoi usare la tavola pitagorica a pagina 117:
• trova il 32 nella colonna gialla;
• scorri con il dito la riga del 32 e cerca il numero 51;
• se non trovi il 51, fermati sul primo numero minore di 51, in questo caso 32;
• sali con il dito verso l’alto, fino alla riga azzurra, e trovi l’1.
Il 32 sta nel 51 una volta.
PASSO 4
5 1,2 32 32 1 19

Scrivi 1 al risultato.
Ora calcola il resto: anche qui puoi aiutarti con la tavola pitagorica!
1 × 32 = 32
Sottrai il risultato (32) dal numero iniziale (51):
51 – 32 = 19.
PASSO 5
5 1, 2 32 32 1, 192
Trascrivi il 2 e metti la virgola nel risultato, perché hai trascritto il primo numero decimale.
Chiediti: quante volte il divisore 32 sta nel 192?
Se hai difficoltà, usa la tavola pitagorica come nel PASSO 3 .
Il 32 sta nel 192 sei volte.
PASSO 6
5 1,2 32 32 1,6 192 192 000
PASSO 7
Trascrivi il 6 al risultato.
Ora calcola il resto: anche qui puoi aiutarti con la tavola pitagorica!
6 × 32 = 192
Sottrai il risultato (192) dal numero iniziale (192): 192 – 192 = 0.
Nel PASSO 1 hai applicato la proprietà invariantiva.
Torna quindi alla divisione iniziale: 51,2 : 32 = 1,6 resto 0
: 10 : 10 5,12 : 3,2 = 1,6 resto 0
Il risultato di 51,2 : 32 corrisponde al risultato di 5,12 : 3,2.
La divisione con il divisore decimale è terminata.
Il risultato è 1,6 resto 0.
Svolgi la seguente divisione con il divisore decimale.
Quanto fa 8,64 : 1,2?
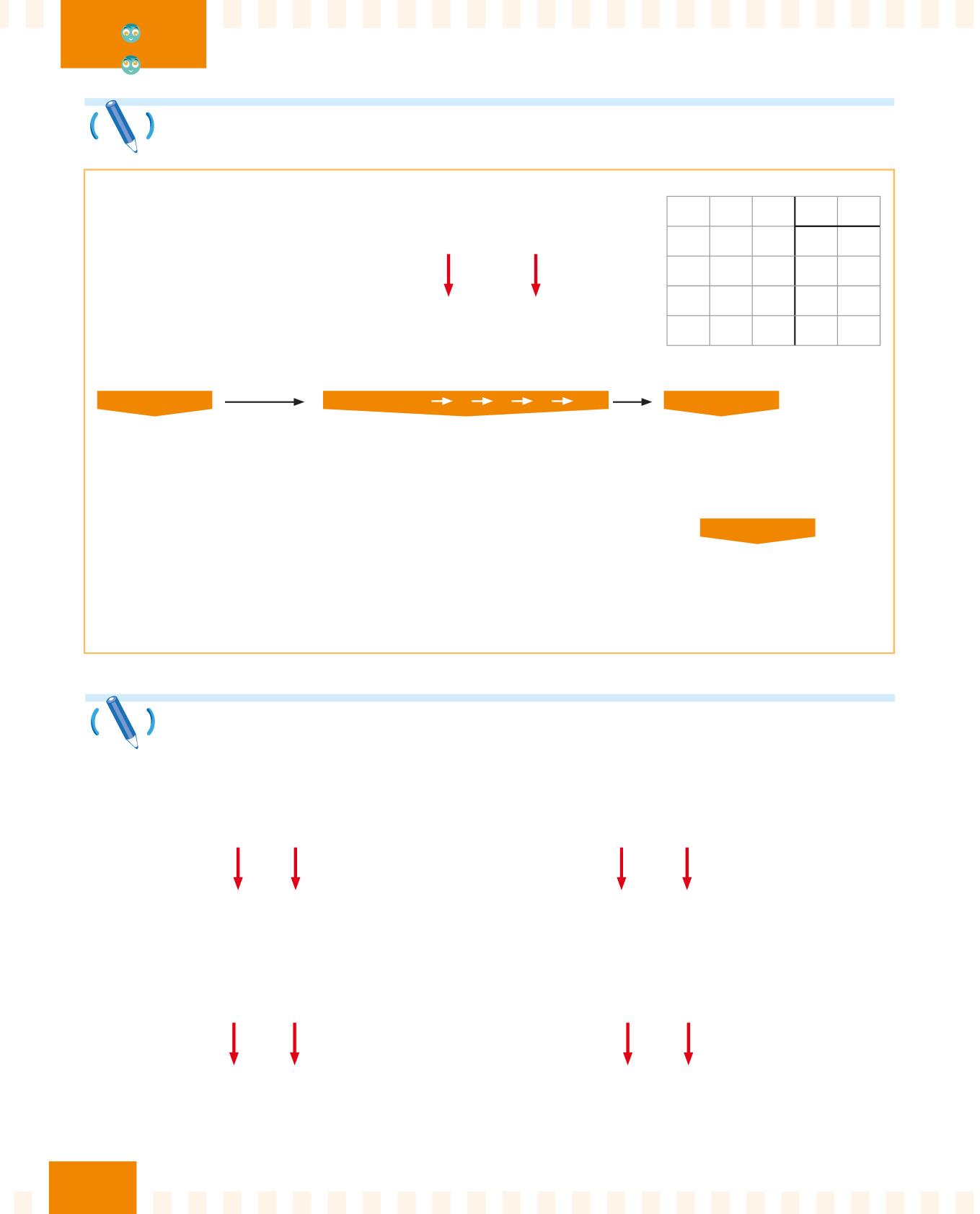
PASSO 1
Applica la proprietà invariantiva per rendere il divisore un numero intero.
Usa lo stesso procedimento: applica la proprietà invariantiva alle seguenti divisioni, poi risolvi le divisioni che hai ottenuto sul tuo quaderno. : = ............. ............. : =
PASSI 2 3 4 5 6
Svolgi la divisione con lo stesso procedimento della divisione con il dividendo decimale.
PASSO 7
Ricorda che hai applicato la proprietà invariantiva nel PASSO 1 . Torna quindi alla divisione di partenza.
Frazionare significa dividere un intero in parti uguali.
Osserva l’immagine:
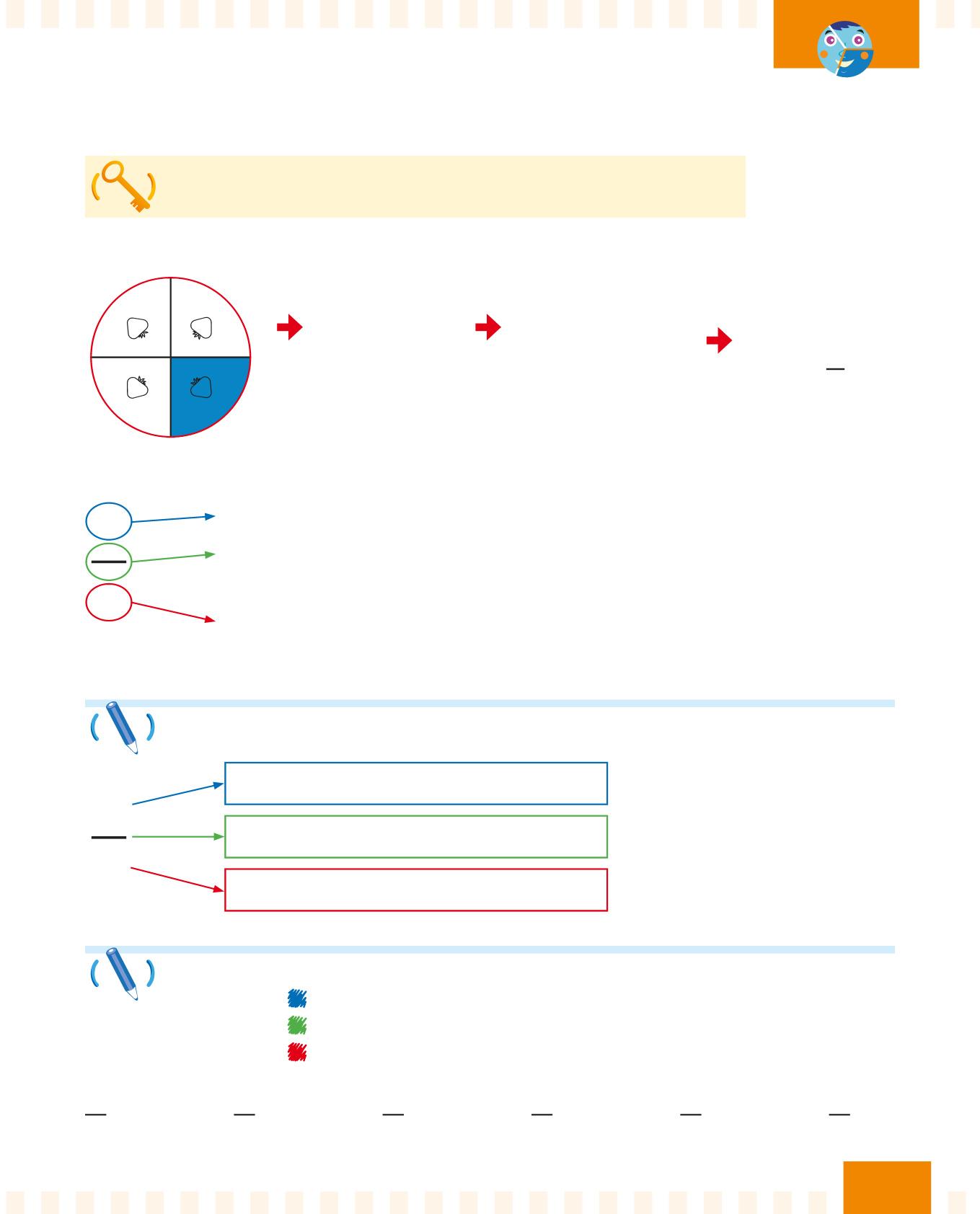
La torta
è un intero. È stata colorata una parte su quattro. Si dice: “un quarto” e si scrive: 1 4 .
Osserva ora i termini della frazione.
DENOMINATORE: indica in quante parti uguali è diviso l’intero. 1
NUMERATORE: indica quante parti dell’intero consideri.
LINEA DI FRAZIONE: indica una divisione dell’intero in parti uguali.
Ora scrivi tu i nomi dei termini della frazione. 4
Per ognuna delle seguenti frazioni:
• cerchia di il numeratore;
• cerchia di la linea di frazione;
• cerchia di il denominatore.
Una frazione propria rappresenta una quantità minore di un intero. Quindi in una frazione propria il numeratore è minore del denominatore.
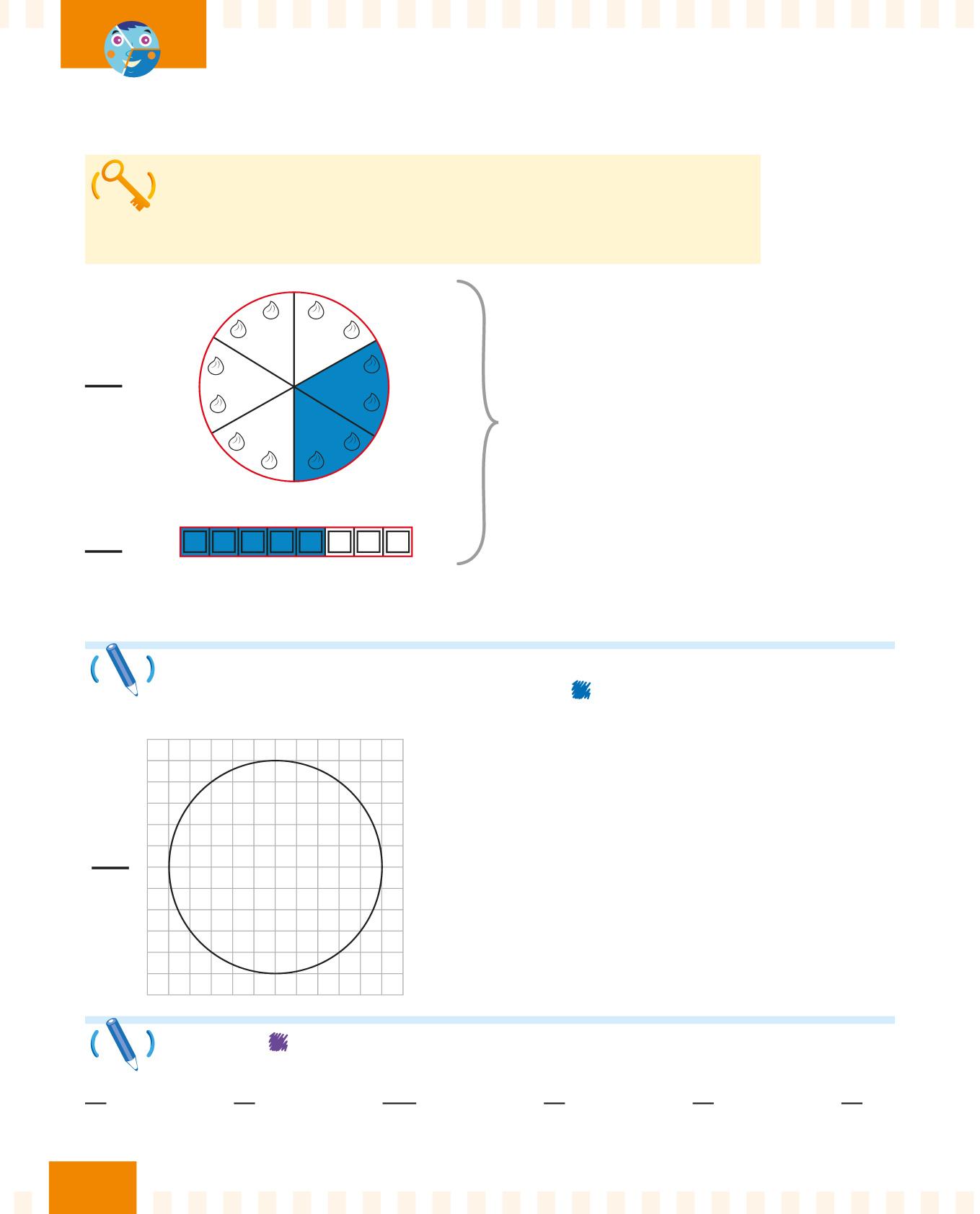
Il numeratore è minore del denominatore. Quindi è una frazione propria. 2
Osserva gli esempi sopra. Dividi la torta nel numero di parti uguali indicate dal denominatore. Poi colora di il numero di parti dell’intero indicate dal numeratore. Infine, completa la frase.
Cerchia di le frazioni proprie.
5 4
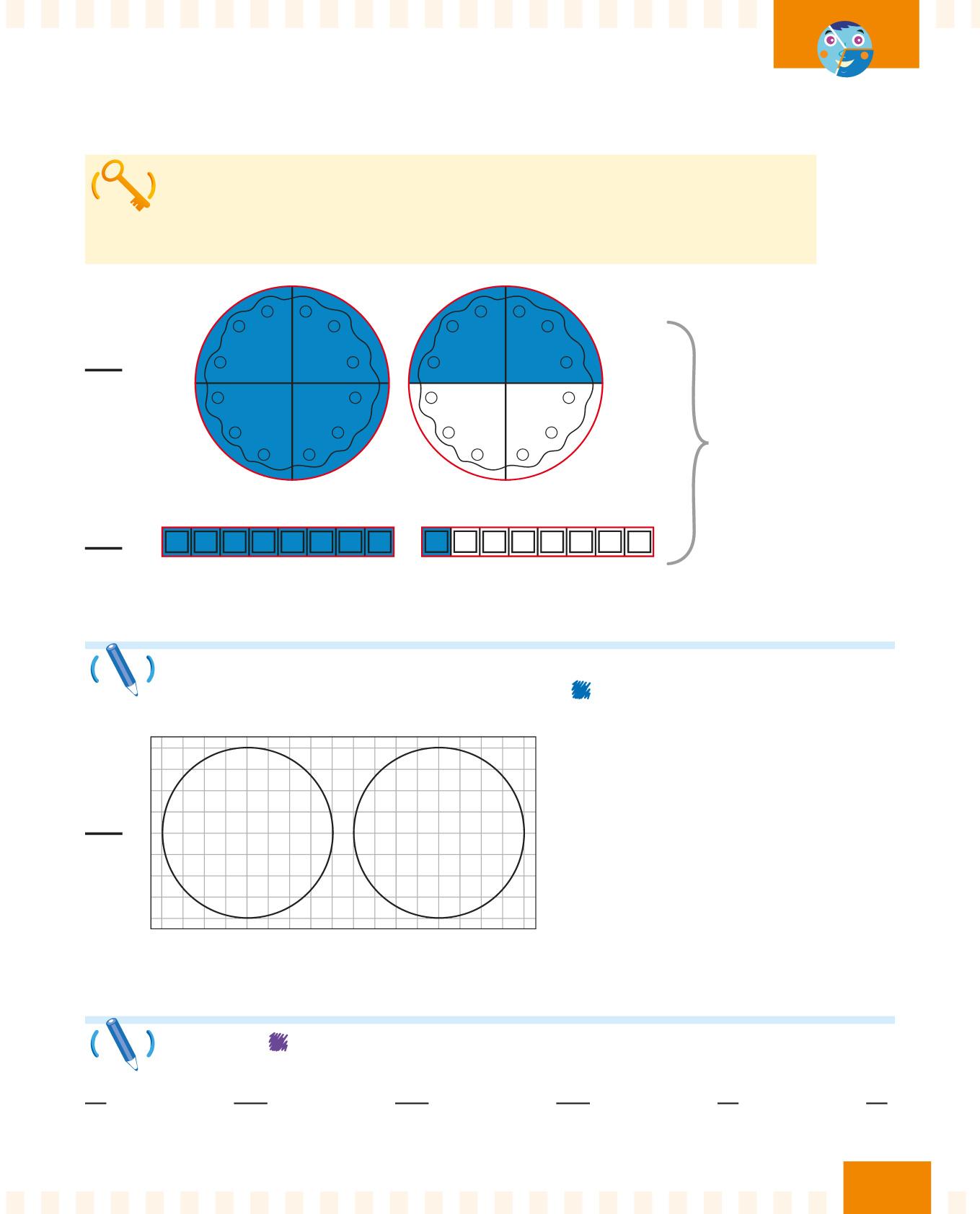
Una frazione impropria rappresenta una quantità maggiore di un intero. Quindi in una frazione impropria il numeratore è maggiore del denominatore.
Il numeratore è maggiore del denominatore. Quindi è una frazione impropria.
Osserva gli esempi sopra. Dividi la torta nel numero di parti uguali indicate dal denominatore. Poi colora di il numero di parti dell’intero indicate dal numeratore. Infine, completa la frase.
Ti bastano gli spicchi di una sola torta? ................................................................
Quanti altri spicchi hai bisogno di disegnare? .....................................................
Il numeratore è del denominatore. Quindi è una .......................................................................................................... .
Cerchia di le frazioni improprie.
4 4
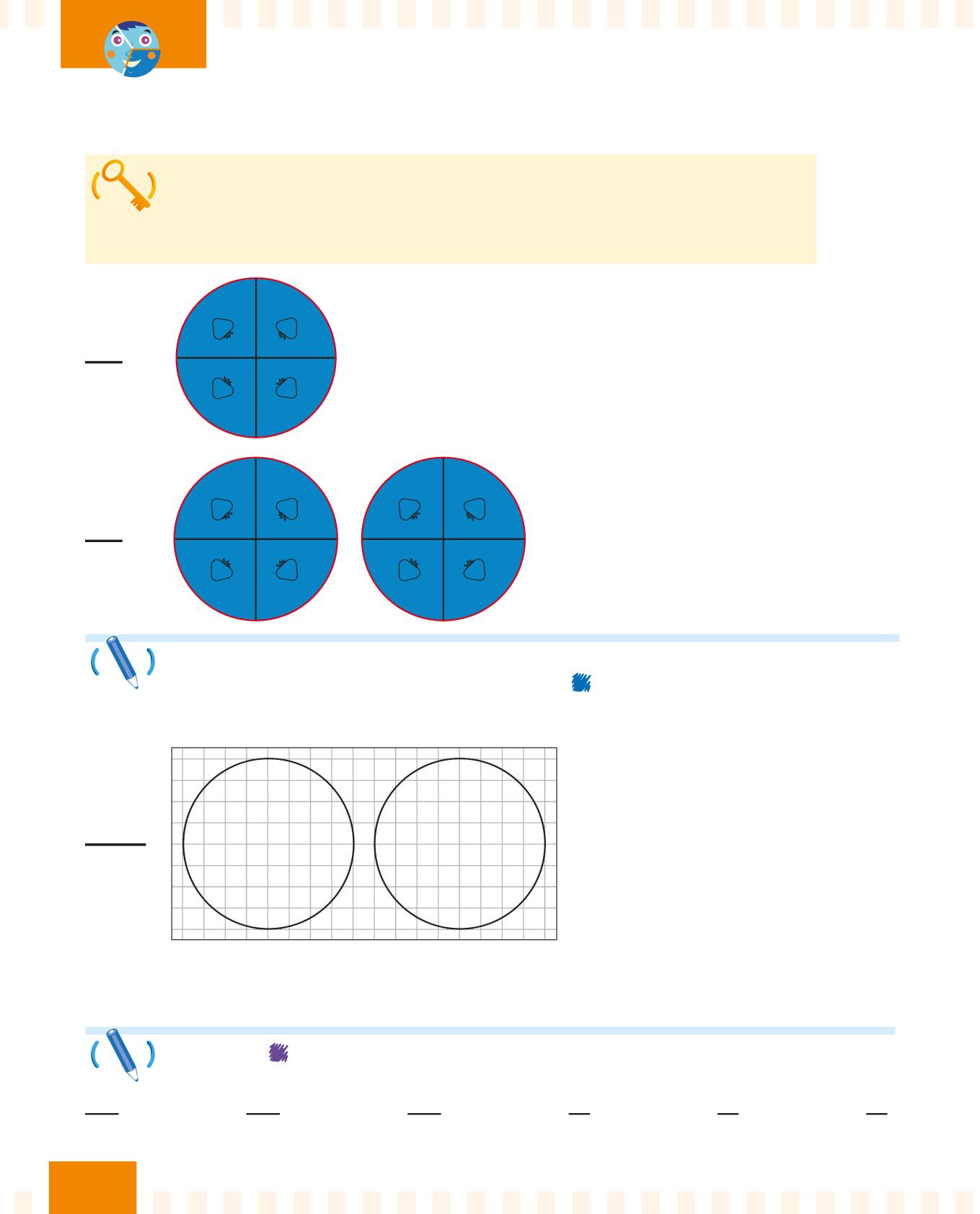
8
4
Una frazione apparente rappresenta uno o più interi completi. Quindi in una frazione apparente il numeratore è uguale al denominatore o è un multiplo del denominatore.
Il numeratore è uguale al denominatore. È una frazione apparente.
Il numeratore è un multiplo del denominatore. È una frazione apparente.
Osserva gli esempi sopra. Dividi le torte nel numero di parti uguali indicate dal denominatore. Poi colora di il numero di parti dell’intero indicate dal numeratore, rispondi alle domande e completa le frasi.
16 8
Ti bastano gli spicchi di una sola torta? ..................................................... Restano degli spicchi non colorati? .....................................................
Il numeratore è ..................................................... del denominatore. Quindi è una .......................................................................................................... .
Cerchia di le frazioni apparenti.
14
Due o più frazioni sono complementari quando insieme rappresentano un intero.
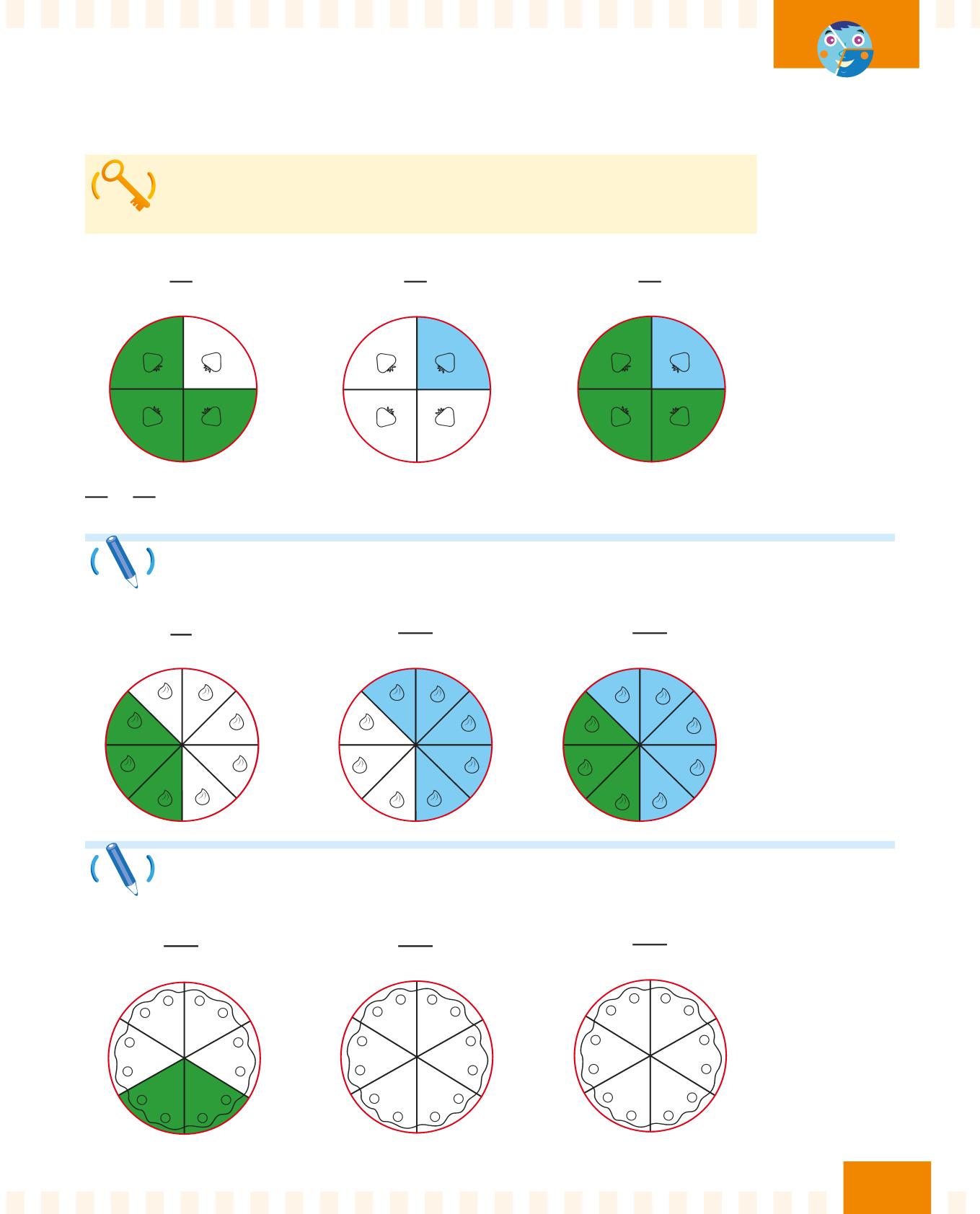
3
4 e 1 4
sono frazioni complementari perché insieme formano un intero.
Osserva la prima frazione, scrivi la sua frazione complementare e completa.
Scrivi i numeratori corretti per avere due frazioni complementari. Poi completa i disegni.
Due o più frazioni sono equivalenti quando rappresentano la stessa quantità.
Se vuoi ottenere una frazione equivalente a un’altra, applica la proprietà invariantiva: dividi o moltiplica per lo stesso numero il numeratore e il denominatore.
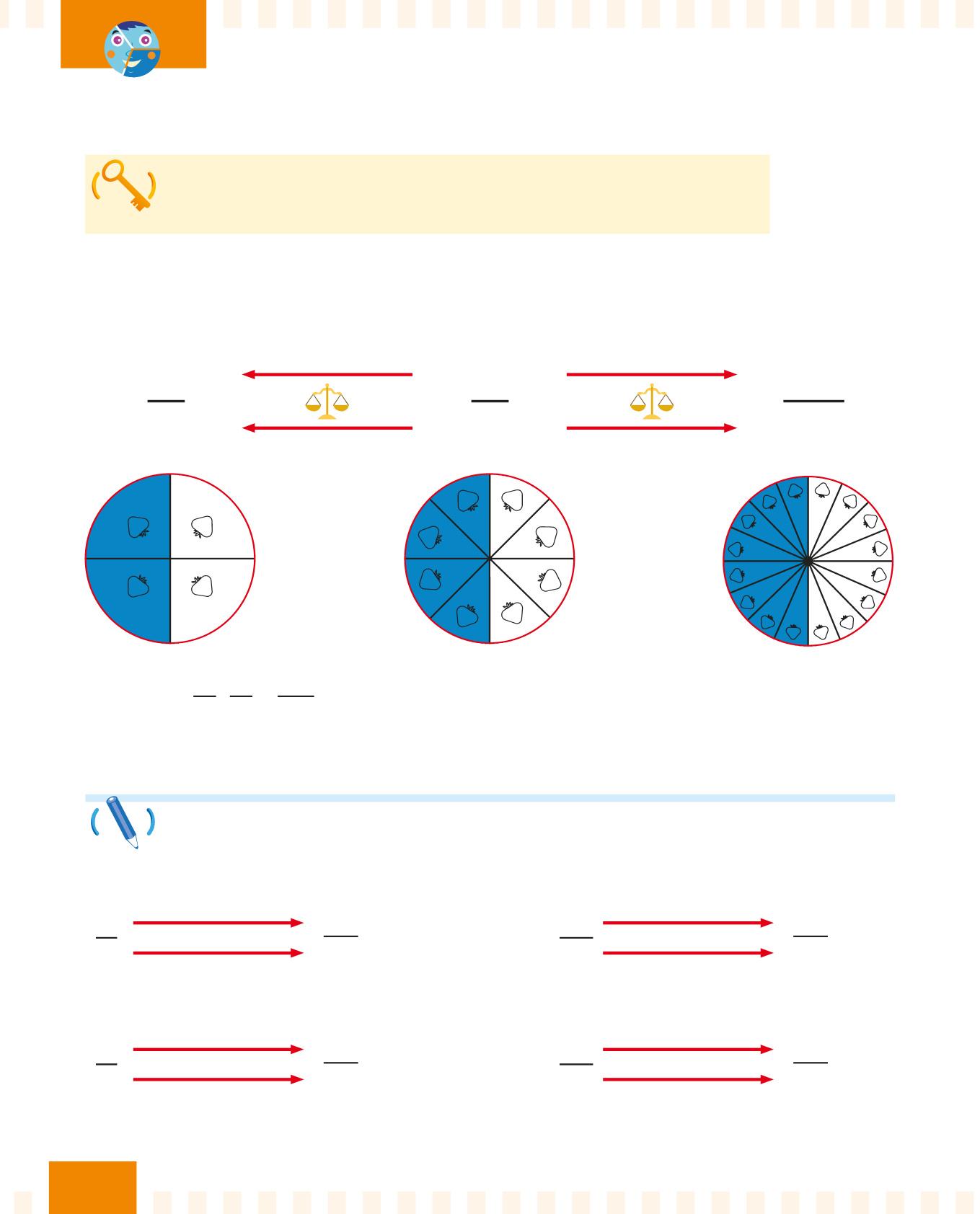
Le frazioni 2 4 , 4 8 e 8 16 sono frazioni equivalenti: tutte rappresentano la metà di un intero.
Applica la proprietà invariantiva alle seguenti frazioni: moltiplica o dividi per lo stesso numero il numeratore e il denominatore e trova le frazioni equivalenti.
Una frazione decimale ha 10, 100 o 1000 al denominatore.
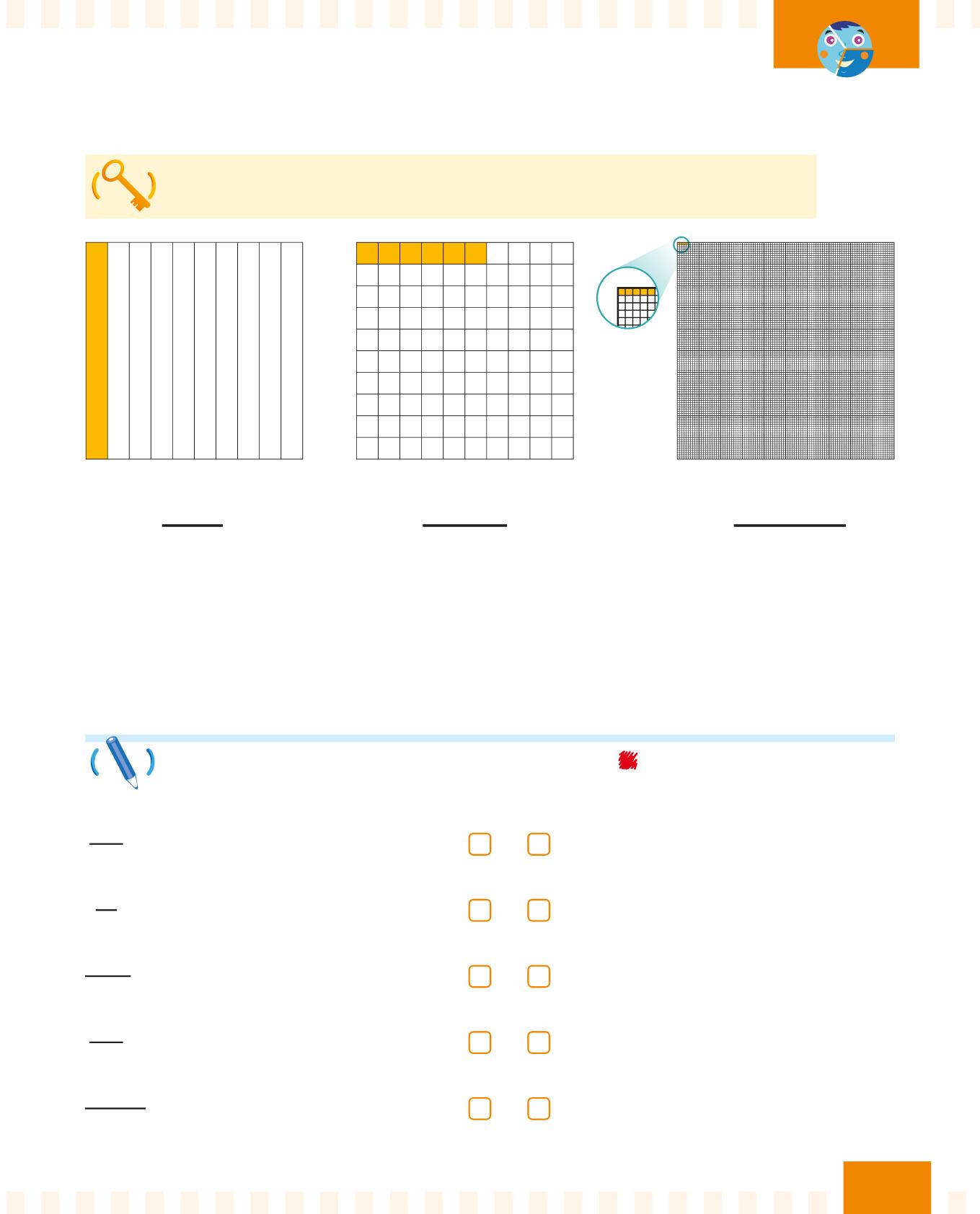
Il denominatore è 10. Quindi è una frazione decimale. 1 10
Il denominatore è 100. Quindi è una frazione decimale.
Il denominatore è 1000. Quindi è una frazione decimale.
Per ogni frazione, cerchia il denominatore di e poi indica con una X la risposta corretta alle domande.
Esistono tre tipi di frazioni:
LINEA DI FRAZIONE
DENOMINATORE
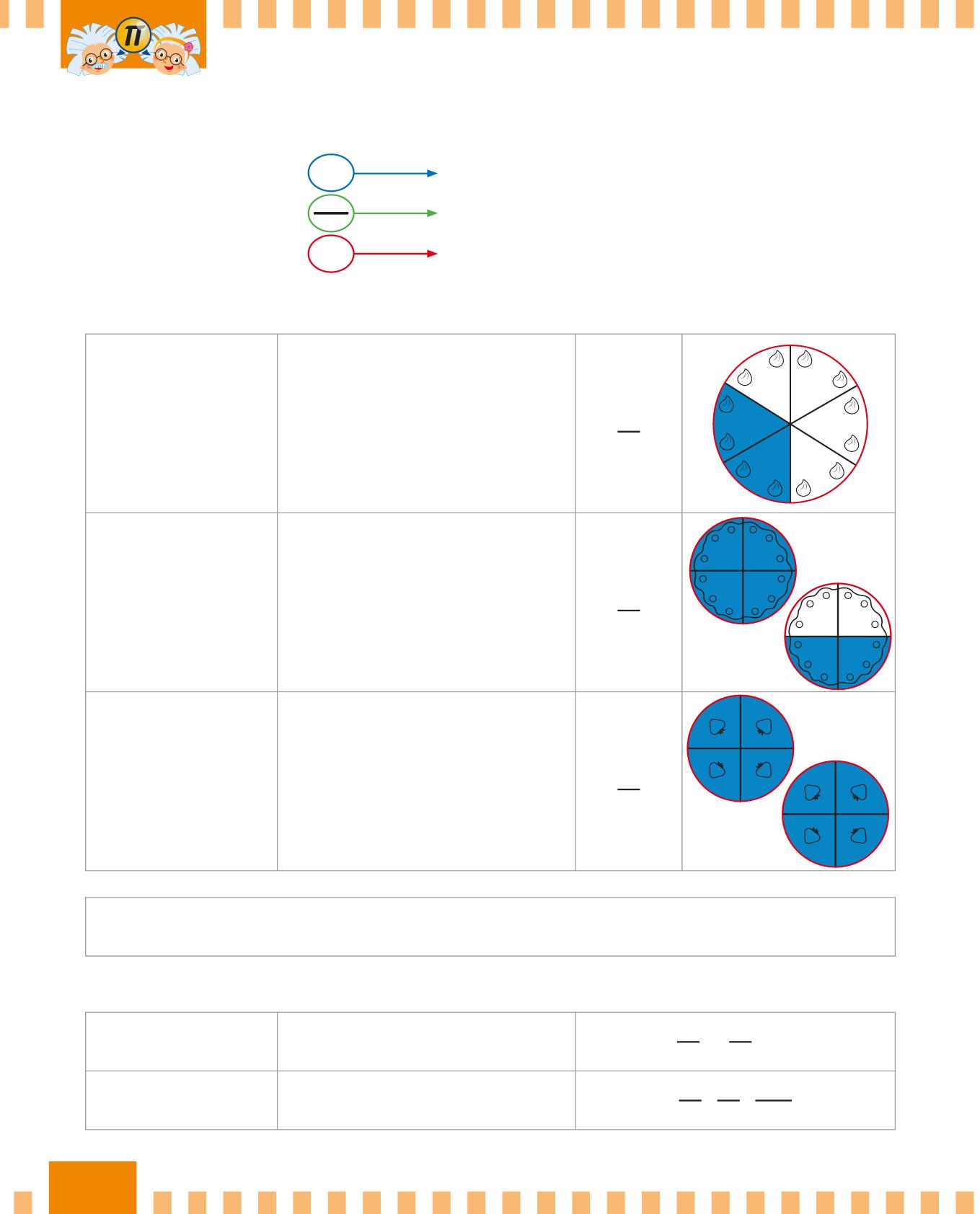
Se una frazione ha 10, 100 o 1000 al denominatore si chiama frazione decimale.
Due o più le frazioni possono essere:
Quant’è 4 5 di 10?
Calcolare i 4 5 di 10 vuol dire prendere l’intero, cioè 10, dividere l’intero per il numero di parti indicate dal denominatore, cioè 5, e infine considerare il numero di parti indicato dal numeratore, cioè 4.
PASSO 1
Prendi il numero 10.
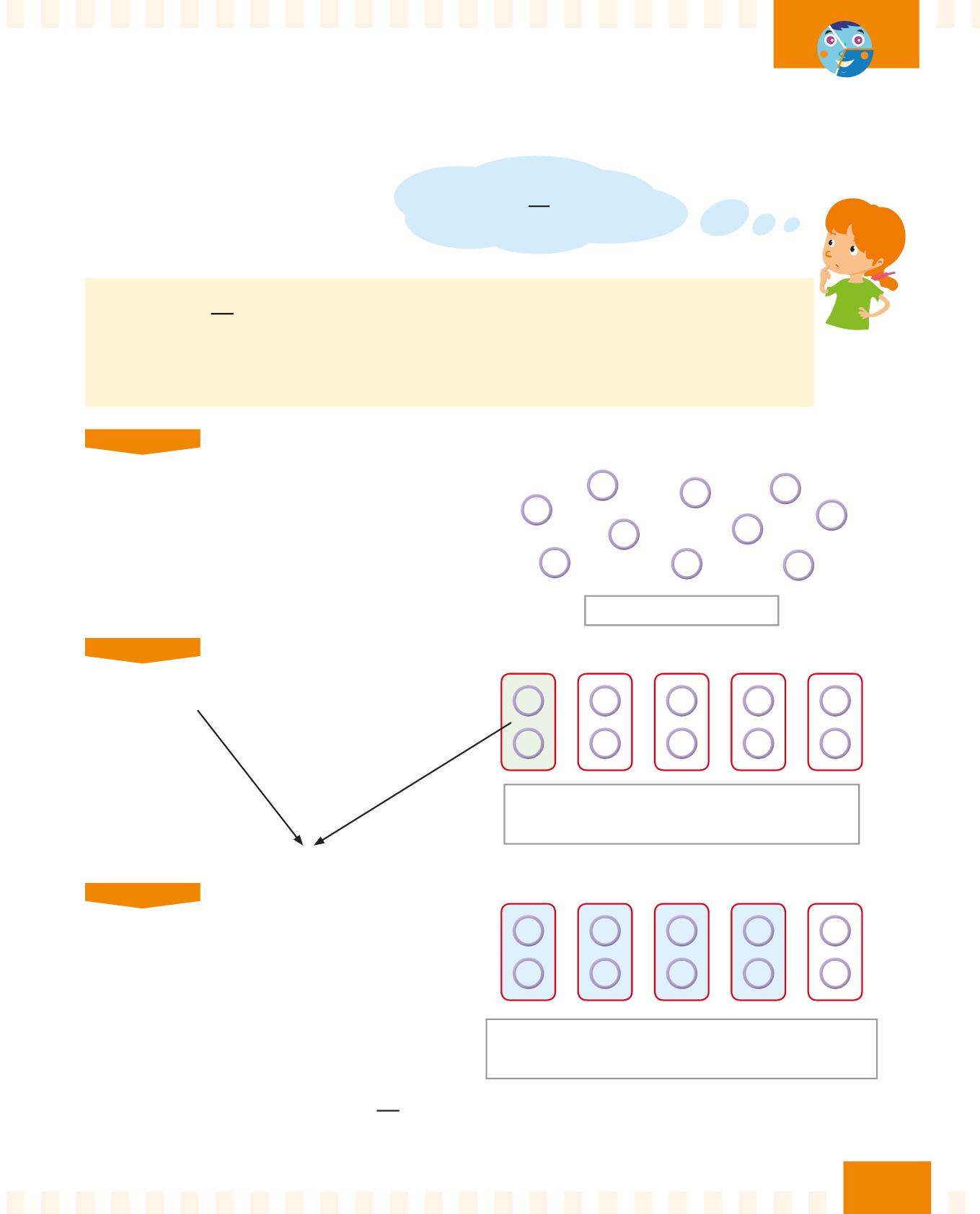
PASSO 2
Dividi il 10 per il denominatore 5. 10 : 5 = 2
Disegna 10 anelli.
Raggruppa gli anelli in 5 scatoline. In ogni scatolina ci sono 2 anelli.
Hai trovato l’unità frazionaria.
PASSO 3
Moltiplica l’unità frazionaria 2
per il numeratore 4.
2 × 4 = 8
Considera 4 scatoline e conta gli anelli al loro interno: gli anelli sono 8.
Il procedimento è terminato: 4 5 di 10 = 8.
Calcola la frazione del seguente numero. Aiutati con i disegni.
3 4 di 8
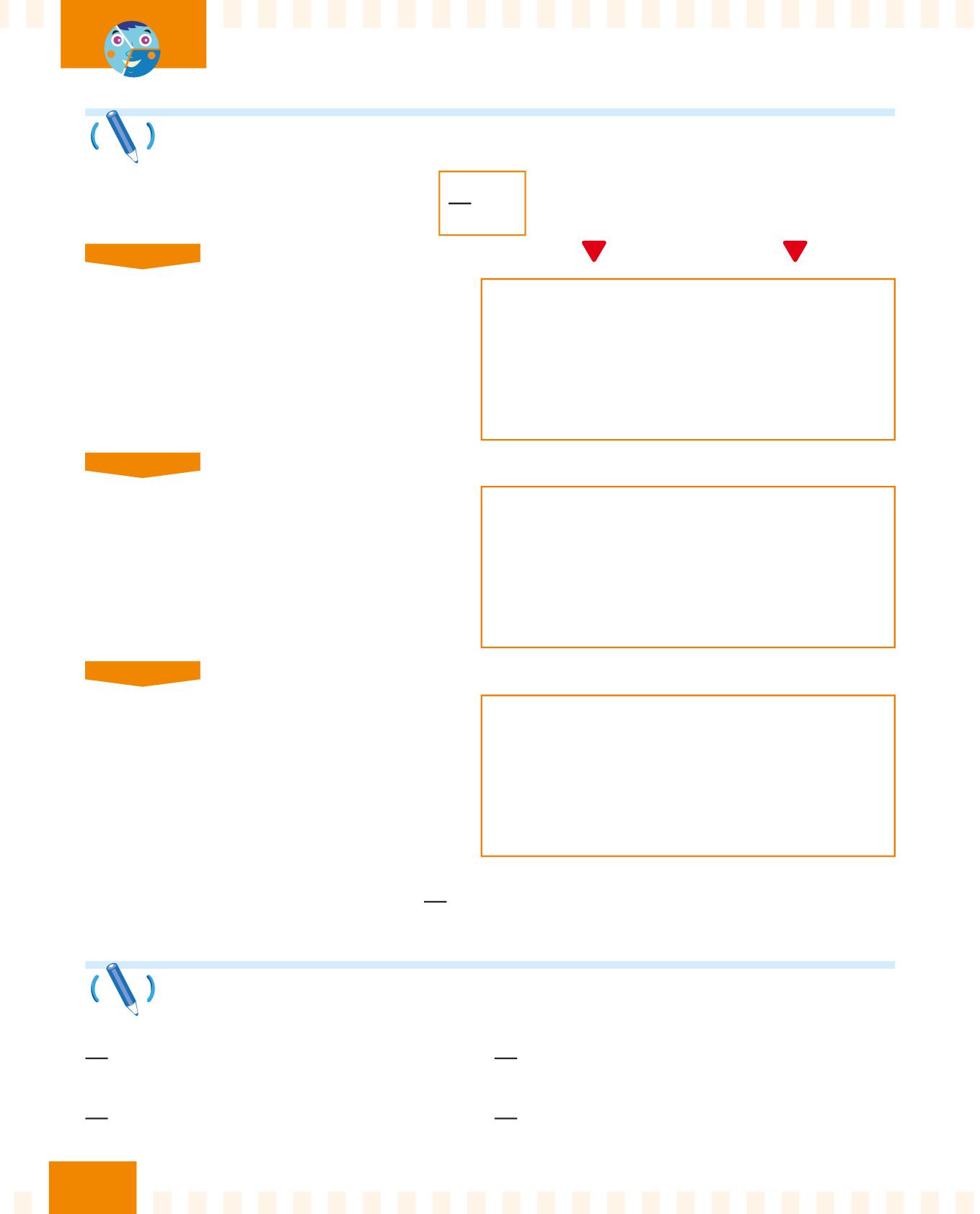
PASSO 1
Prendi il numero ........ .
PASSO 2
Dividi ........ per il denominatore ........ ........ : ........ = ........
Hai trovato l’unità frazionaria.
PASSO 3
Moltiplica l’unità frazionaria ........ per il numeratore ......... ........ × ........ = ........
DISEGNA QUI
3 4 di 8 = ........
Usa lo stesso procedimento e calcola la frazione dei seguenti numeri sul tuo quaderno.

L’unità di misura della lunghezza è il metro (m).
• I multipli del metro servono a misurare la lunghezza, l’altezza e la larghezza di oggetti o esseri viventi grandi, ma anche di distanze grandi.
• I sottomultipli del metro servono a misurare la lunghezza, l’altezza e la larghezza di oggetti o esseri viventi piccoli, ma anche di distanze piccole.
Osserva la tabella:

chilometroettometrodecametro metro decimetrocentimetromillimetro
Completa le seguenti frasi con l’aiuto della tabella.
• Chilometro (km), ettometro ( ) e decametro ( ) sono i del metro (m).
• Il metro (…...........) è l’unità di misura fondamentale per misurare la ………...........…….……. .
• Decimetro (…............), centimetro (cm) e millimetro (mm) sono i …….......…………………… del (m).
Osserva gli esempi a sinistra, poi collega i disegni a destra all’unità di misura più adatta.

chilometro
ettometro
decametro
decimetro
centimetro
millimetro
La capacità è la quantità di liquido che un recipiente può contenere. L’unità di misura della capacità è il litro (l).
• I multipli del litro servono a misurare la quantità di liquido contenuta in oggetti grandi.
• I sottomultipli del litro servono a misurare la quantità di liquido contenuta in oggetti piccoli.
Osserva la tabella:
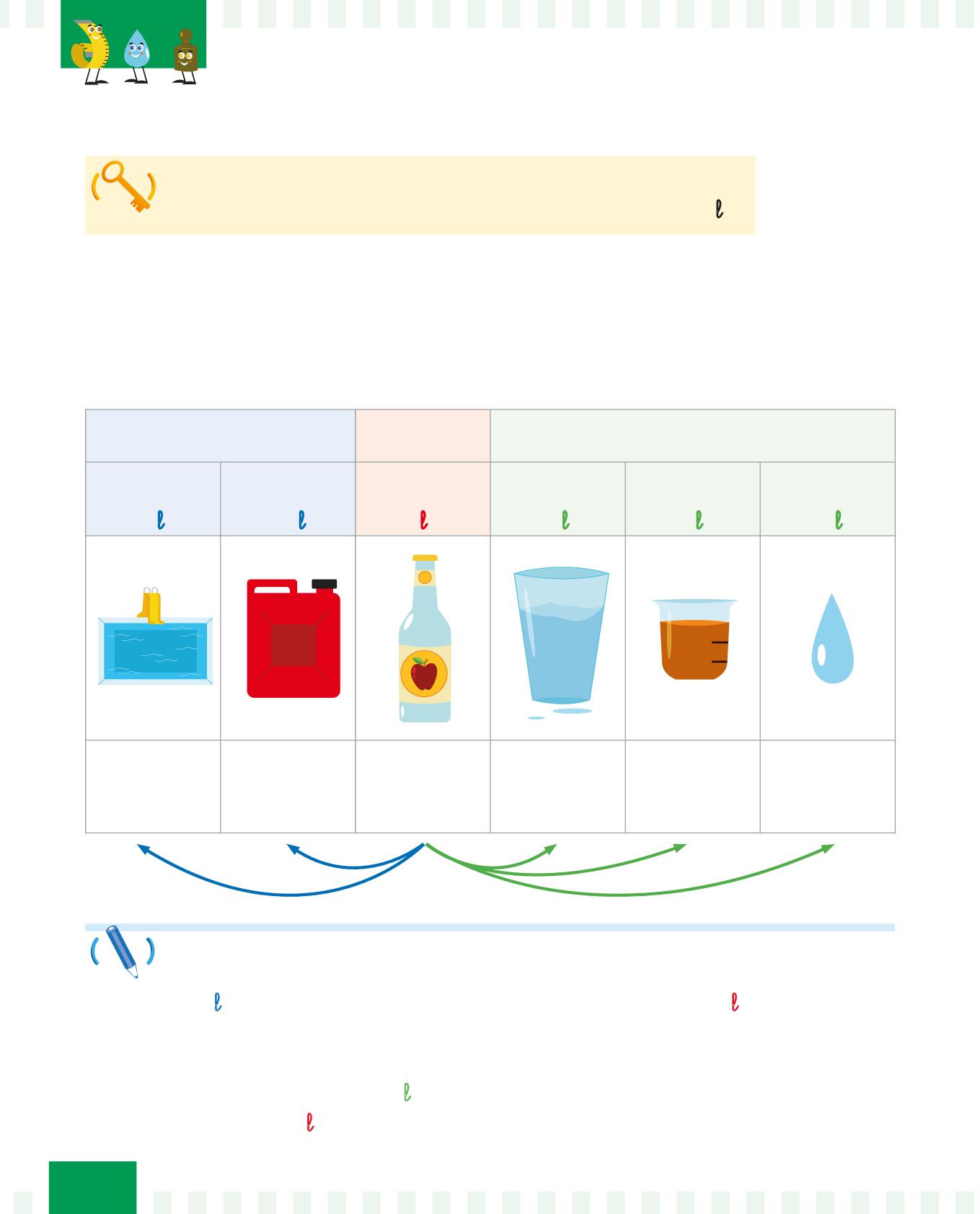
ettolitro decalitro litro decilitro centilitro millilitro
Completa le seguenti frasi con l’aiuto della tabella.
• Ettolitro (hl) e decalitro (…………...) sono i ………..........…………. del litro (l).
• Il litro (…...........) è l’unità di misura fondamentale per misurare la ….......…………..…………, cioè la quantità di liquido che un recipiente può contenere.
• Decilitro ( ), centilitro (cl) e millilitro ( ) sono i del …………...........………… (l).
Osserva gli esempi a sinistra, poi collega i disegni a destra all’unità di misura più adatta.

ettolitro
hl
decalitro
dal
litro l
decilitro dl
L’unità di misura del peso-massa è il chilogrammo (kg).
• I multipli del chilogrammo servono a misurare il peso di oggetti o esseri viventi pesanti.
• I sottomultipli del chilogrammo servono a misurare il peso di oggetti o esseri viventi leggeri.
Osserva la tabella:

megagrammo centinaia didecine di chilogrammo ettogrammodecagrammogrammo Mg
Completa le seguenti frasi con l’aiuto della tabella.
• Il megagrammo (…………...) è un ………..........…………. del chilogrammo (kg).
• Il chilogrammo (…...........) è l’unità di misura fondamentale per misurare il …….......…………………… .
• Ettogrammo (…............), decagrammo (dag) e grammo (…............) sono
i …….......…………...............………… del …….......…………...............………… (kg).
• I sottomultipli del grammo servono a misurare il peso-massa di oggetti o esseri viventi molto leggeri.
Osserva la tabella:
50 cent
Completa le seguenti frasi con l’aiuto della tabella.
Se dobbiamo misurare il peso-massa di oggetti o animali molto leggeri dobbiamo usare i …….......…………………… del grammo: decigrammo (…............), centigrammo (cg) e milligrammo (…............).
• 1 decigrammo (dg) vale ......……………… grammi (g).
Infatti, se dividi 1 grammo in dieci parti uguali, 1 decigrammo corrisponde a una parte ( 1 10 ).
• 1 centigrammo (cg) vale 0,01 ......……………… (g).
Infatti, se dividi 1 grammo in cento parti uguali, 1 …….......…………………… corrisponde a una parte ( 1 100 ).
• 1 milligrammo (…............) vale ......……………… grammi (g).
Infatti, se dividi 1 grammo in ......……………… parti uguali, 1 milligrammo corrisponde a una parte ( 1 1000 ).
Il peso lordo è il peso della merce e del suo contenitore.
Il peso netto è il peso della merce senza il contenitore.
La tara è il peso del contenitore senza la merce.
Osserva la tabella:
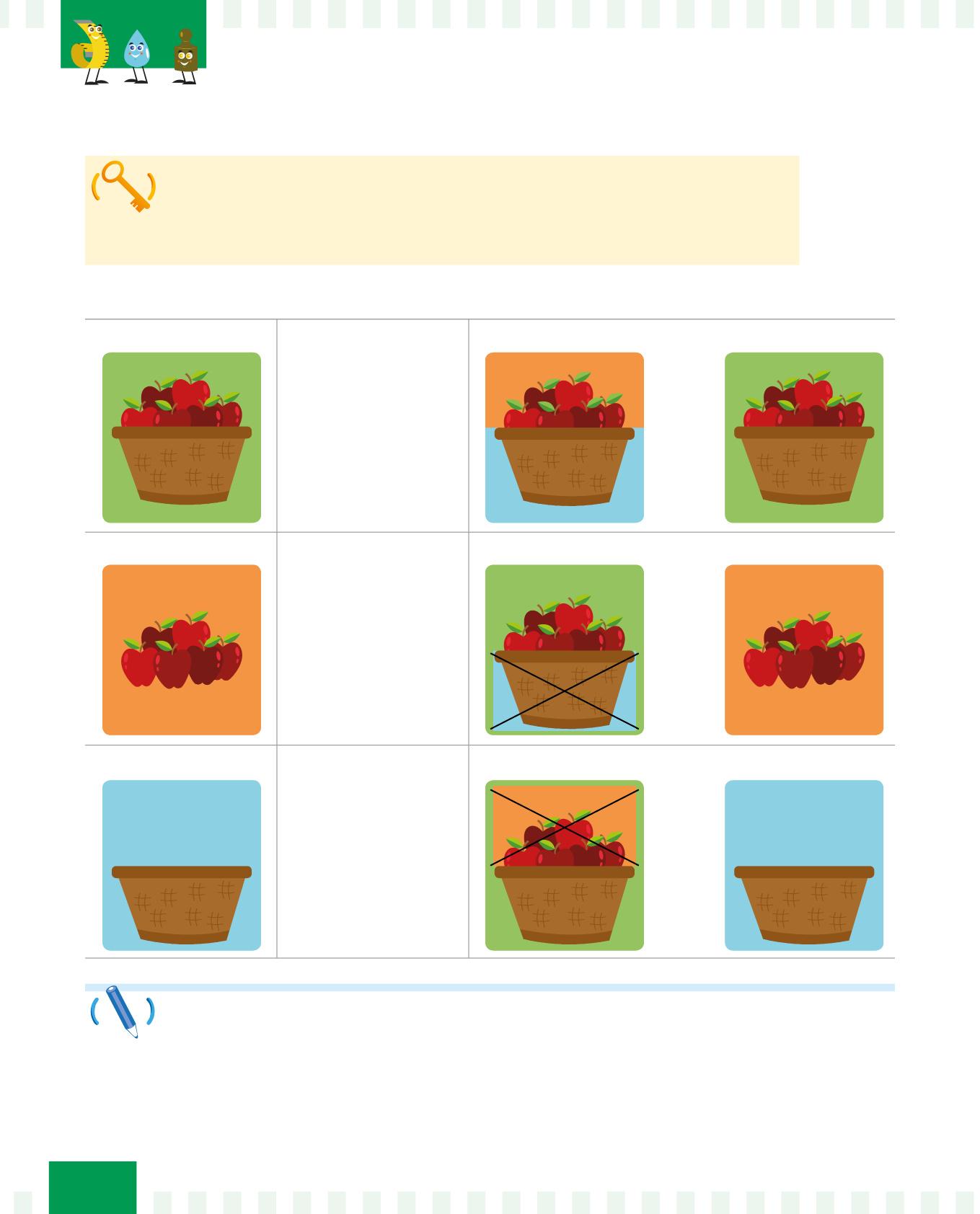
PESO LORDO: il peso delle mele e del cesto.
PESO NETTO + TARA = PESO LORDO
PESO NETTO: il peso delle mele.
PESO LORDO – TARA = PESO NETTO
TARA: il peso del cesto vuoto.
PESO LORDO – PESO NETTO = TARA
Completa con l’aiuto della tabella.
Peso netto + tara = …….......………………................……
Peso lordo – tara = …….......……………...................……
Peso lordo – peso netto = …….......……………………
Osserva i disegni. Poi indica con una X se si tratta di peso lordo, peso netto o tara.

peso lordo
peso netto
tara
peso lordo
peso netto tara
peso lordo
peso netto tara
peso lordo
peso netto
tara
peso lordo
peso netto tara
peso lordo
peso netto tara
peso lordo
peso netto
tara
peso lordo
peso netto tara
peso lordo
peso netto tara
peso lordo
peso netto
tara
peso lordo
peso netto tara
peso lordo
peso netto tara
L’unità di misura della superficie è il metro quadrato (m2).
• I multipli del metro quadrato servono a misurare superfici grandi.
• I sottomultipli del metro quadrato servono a misurare superfici piccole.
Osserva la tabella:

Il metro quadrato (m2) è un’unità di misura diversa dal metro lineare (m), che hai visto per le misure di lunghezza (pagine 70-71).
Il 2 dopo la “m” indica che il metro quadrato ha due dimensioni: la lunghezza e la larghezza.
Il metro quadrato (insieme ai suoi multipli e ai sottomultipli)
è l’unità di misura utilizzata per misurare la superficie, cioè l’area.
Studierai l’area nella sezione Spazio e figure.
Osserva gli esempi a sinistra, poi collega i disegni a destra all’unità di misura più adatta.

chilometro
quadrato
km2
ettometro
quadrato
hm2
decametro
quadrato
dam2 metro quadrato
m2
decimetro
quadrato
dm2
centimetro
quadrato
cm2
millimetro
quadrato
mm2
L’unità di misura del tempo è il secondo (s) ed è utile per misurare la durata di eventi.
Con quale unità di misura esprimi la durata dei seguenti eventi?
Indica con una X la misura di tempo più adatta.
Le vacanze estive secondo minuto ora giorno mese anno
Un battito di ciglia secondo minuto ora giorno mese anno
Una partita di calcio

secondo minuto ora giorno mese anno
Una gita al parco divertimenti secondo minuto ora giorno mese anno
Un film in TV
secondo minuto ora giorno mese anno
La ricreazione a scuola
secondo minuto ora giorno mese anno
Il denaro permette di conoscere il costo degli oggetti e dei servizi che si comprano e si vendono. In Italia e in altri Paesi dell’Unione Europea, l’unità di misura di valore è l’euro (€).
Osserva la tabella:

MULTIPLI
UNITÀ DI MISURA SOTTOMULTIPLI (in cent)
50 cent = € 0,50
20 cent = € 0,20
10 cent = € 0,10
5 cent = € 0,05
Completa le frasi seguenti con l’aiuto della tabella.
• L’unità di misura del valore in Italia e in altri Paesi dell’Unione Europea si chiama …….......…………………… (€).
• I 50 euro sono …….......……............……………… dell’euro (€).
• I 5 cent sono …….......……........……....………… dell’euro (€).
• 50 cent corrispondono a € …….......…………………… .
Quanto costano i seguenti oggetti?
Indica con una X il costo più adatto.
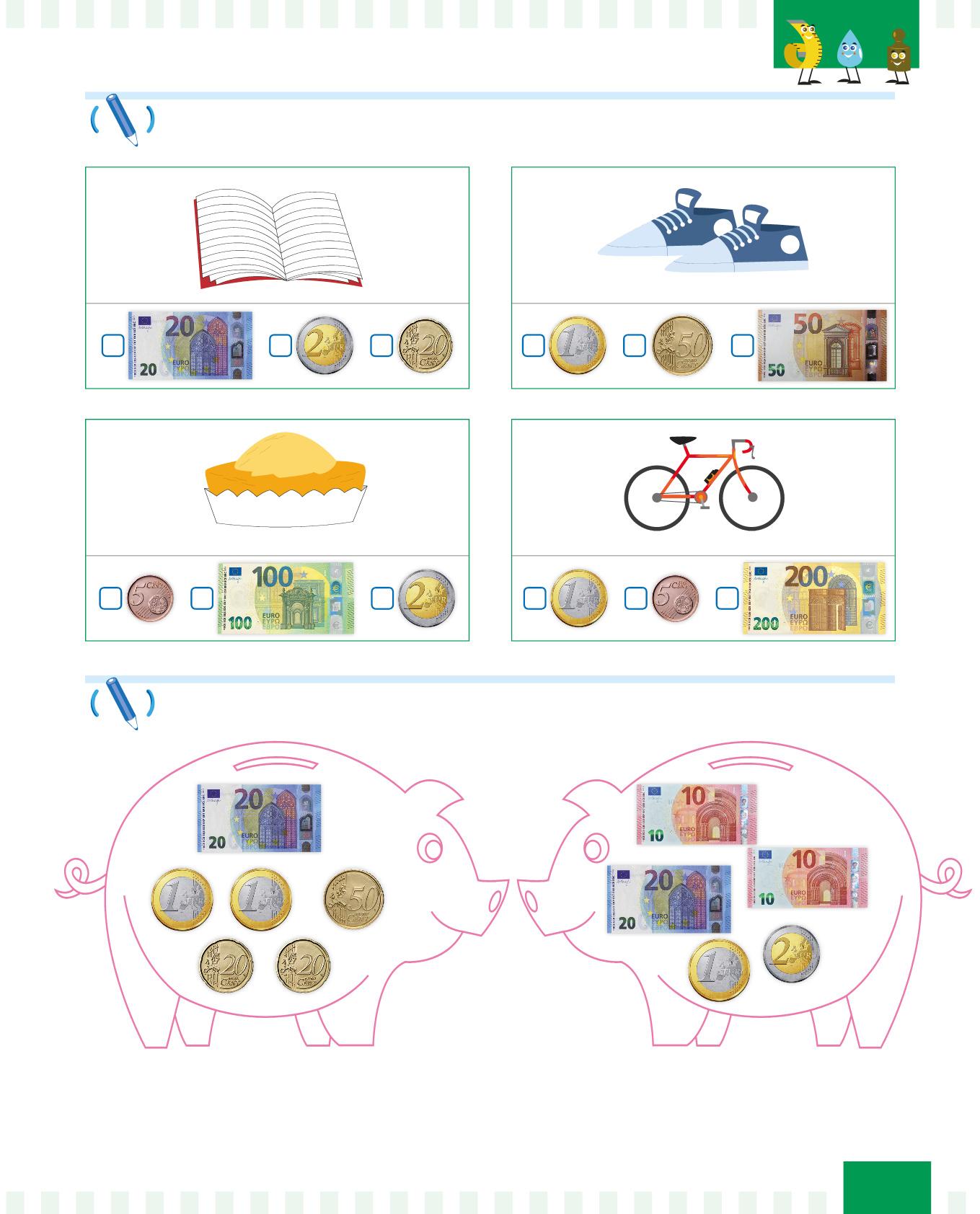
Aiuta Giorgio e Fatima a contare i risparmi nei propri salvadanai.
Giorgio: €
Chi ha più soldi nel proprio salvadanaio?
Fatima: €
La spesa è la quantità di denaro che il negoziante paga per acquistare la merce da rivendere.
Il ricavo è la quantità di denaro che il negoziante riceve quando vende la merce al cliente. Il ricavo corrisponde alla cifra che compare sugli scontrini.
Il guadagno è la quantità di denaro che rimane al negoziante dopo che ha tolto la spesa dal ricavo.
Osserva la tabella:

Il fruttivendolo ha acquistato all’ingrosso, cioè da un grande commerciante, frutta e verdura e ha speso 100 euro.
A fine giornata, il fruttivendolo ha venduto ai suoi clienti tutta la frutta e la verdura. Ha ricavato 140 euro.
Il fruttivendolo ha calcolato che ha guadagnato 40 euro.
Se conosci due valori, puoi calcolare il terzo valore!
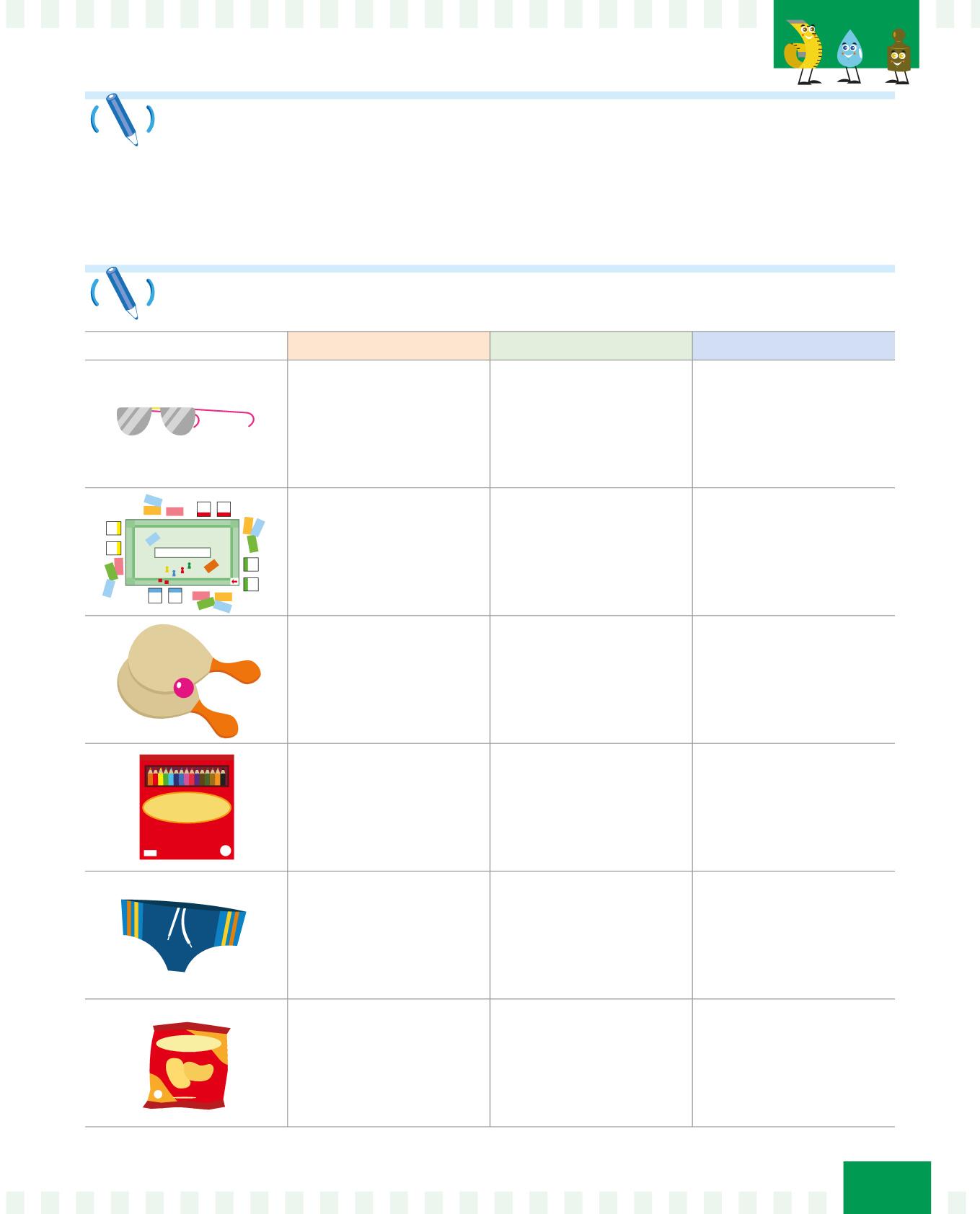
Completa con l’aiuto della tabella.
Ricavo – guadagno = …….......……………………
Guadagno + spesa = …….......………………….…
Ricavo – spesa = ………..........………...............….
Completa la tabella. Puoi aiutarti con la calcolatrice.
LE MISURE DI LUNGHEZZA: puoi misurare lunghezza, dimensioni e distanze.
chilometroettometrodecametro metro decimetrocentimetromillimetro
km hm dam m dm cm mm

LE MISURE DI CAPACITÀ: puoi misurare la quantità di liquido contenuta in oggetti.
ettolitro decalitro litro decilitro centilitro millilitro
hl dal l dl cl ml
LE MISURE DI PESO-MASSA: puoi misurare il peso-massa di oggetti o esseri viventi.
megagrammo centinaia di decine di chilogrammo ettogrammo decagrammo grammo
sottomultipli del grammo
decigrammo centigrammo milligrammo
Mg kg kg kg hg dag g dg cg mg
LE MISURE DI SUPERFICIE: puoi misurare le superfici.
chilometro quadrato ettometro quadrato decametro quadrato metro quadrato decimetro quadrato centimetro quadrato millimetro quadrato

Il testo di un problema può contenere dati utili e dati inutili.
I dati utili servono a rispondere alla domanda del problema.
I dati inutili non servono a rispondere alla domanda del problema.
1. Leggi il testo del problema e sottolinea la domanda. La domanda di solito si trova alla fine del problema e finisce con il punto interrogativo. La domanda ti dice che cosa devi trovare alla fine del problema.
Lo scoiattolo Gigi, che ha 5 anni, ha mangiato a pranzo
34 ghiande. Poi lo scoiattolo Gigi ha mangiato altre
27 ghiande a cena.
Quante ghiande ha mangiato in tutto lo scoiattolo Gigi?
2. Cerchia di i dati utili e cancella i dati inutili.
Lo scoiattolo Gigi, che ha 5 anni, ha mangiato a pranzo
34 ghiande. Poi lo scoiattolo Gigi ha mangiato
altre 27 ghiande a cena.
Quante ghiande ha mangiato in tutto lo scoiattolo Gigi?
Usa lo stesso procedimento: leggi i problemi, sottolinea la domanda, poi cerchia di i dati utili e cancella i dati inutili.
• Al rifugio per animali ci sono 15 cani a pelo marrone, 4 cani a pelo nero, 6 cani a pelo bianco e marrone, 7 gatti e 6 tartarughe.
Quanti cani ci sono in tutto nel ricovero per animali?
• Marco ha bisogno di 256 figurine per completare un album.
Marco compra 5 pacchetti di figurine; in ogni pacchetto ci sono 10 figurine.
Quante figurine ha in tutto Marco?
In un problema ci possono essere dei dati nascosti.
I dati nascosti servono a risolvere il problema e non sono numeri, ma parole che rappresentano una quantità.
1. Leggi il testo del problema e sottolinea la domanda.
Ogni giorno Lavinia legge 12 pagine di un libro di avventure.
In una settimana Lavinia finisce di leggere il libro.
Quante sono in tutto le pagine del libro?
2. Cerchia di i dati.
Ogni giorno Lavinia legge 12 pagine di un libro di avventure.
In una settimana Lavinia finisce di leggere il libro.
Quante sono in tutto le pagine del libro?
Hai tutti i dati necessari per rispondere alla domanda? No.
3. C’è qualche parola che puoi trasformare in numero? Sì. Quale? Settimana.
Ogni giorno Lavinia legge 12 pagine di un libro di avventure.
In una settimana (cioè in 7 giorni) Lavinia finisce di leggere il libro.
Quante sono in tutto le pagine del libro?
Usa lo stesso procedimento: leggi i problemi, sottolinea la domanda, poi individua e trasforma i dati nascosti in numeri.
• La maestra Angelica ha contato i partecipanti alla cena di fine anno: 16 bambini e una dozzina di bambine.
Quanti alunni parteciperanno in tutto alla cena di fine anno?
DATO NASCOSTO: =
• Una fabbrica di automobili produce 25 vetture elettriche al giorno.
Quante vetture elettriche produce in un anno?
DATO NASCOSTO: =
A volte non puoi risolvere un problema perché alcuni dati mancano nel testo, cioè sono mancanti.
1. Leggi il testo del problema e sottolinea la domanda.
Papà Gaetano ha portato al cinema suo figlio Andrea con i suoi amici. Ha pagato ogni biglietto 5 euro. Quanto ha speso per comprare tutti i biglietti?
2. Cerchia di i dati utili.
Papà Gaetano ha portato al cinema suo figlio Andrea con i suoi amici. Ha pagato ogni biglietto € 5 . Quanto ha speso per comprare tutti i biglietti?
Hai tutti i dati utili per risolvere il problema? No.
3. C’è qualche parola che puoi trasformare in numero, cioè un dato nascosto? No, quindi c’è un dato mancante, cioè il numero di amici di Andrea.
Usa lo stesso procedimento: leggi i problemi, poi cerchia di i dati utili e individua i problemi con i dati mancanti. Infine, inventa tu il dato mancante quando serve.
• In una sera il pizzaiolo Adriano inforna pizze alla boscaiola e pizze vegetariane per un totale di 50 pizze.
Quante pizze alla boscaiola inforna?
Hai tutti i dati utili per risolvere il problema? sì no
DATO MANCANTE: ………………………………......…………… = ………………………
• La fioraia Olena ha preparato un mazzo di 15 rose e violette. 10 sono rose.
Quante violette ci sono nel mazzo di fiori?
Hai tutti i dati utili per risolvere il problema? sì no
DATO MANCANTE: =
Per risolvere un problema è utile rappresentare i dati.
Puoi rappresentare i dati in diversi modi, per esempio con un disegno oppure con dei simboli.
1. Leggi il testo del problema e sottolinea la domanda.
Durante le vacanze estive Francesca svolge 8 pagine di esercizi al giorno.
Quante pagine completa in 7 giorni?
2. Cerchia di i dati utili.
Durante le vacanze estive Francesca svolge 8 pagine di esercizi al giorno.
Quante pagine completa in 7 giorni?
3. Rappresenta i dati: devi rappresentare 8 pagine che si ripetono per 7 giorni.
Puoi procedere in due modi:
Disegno Simboli
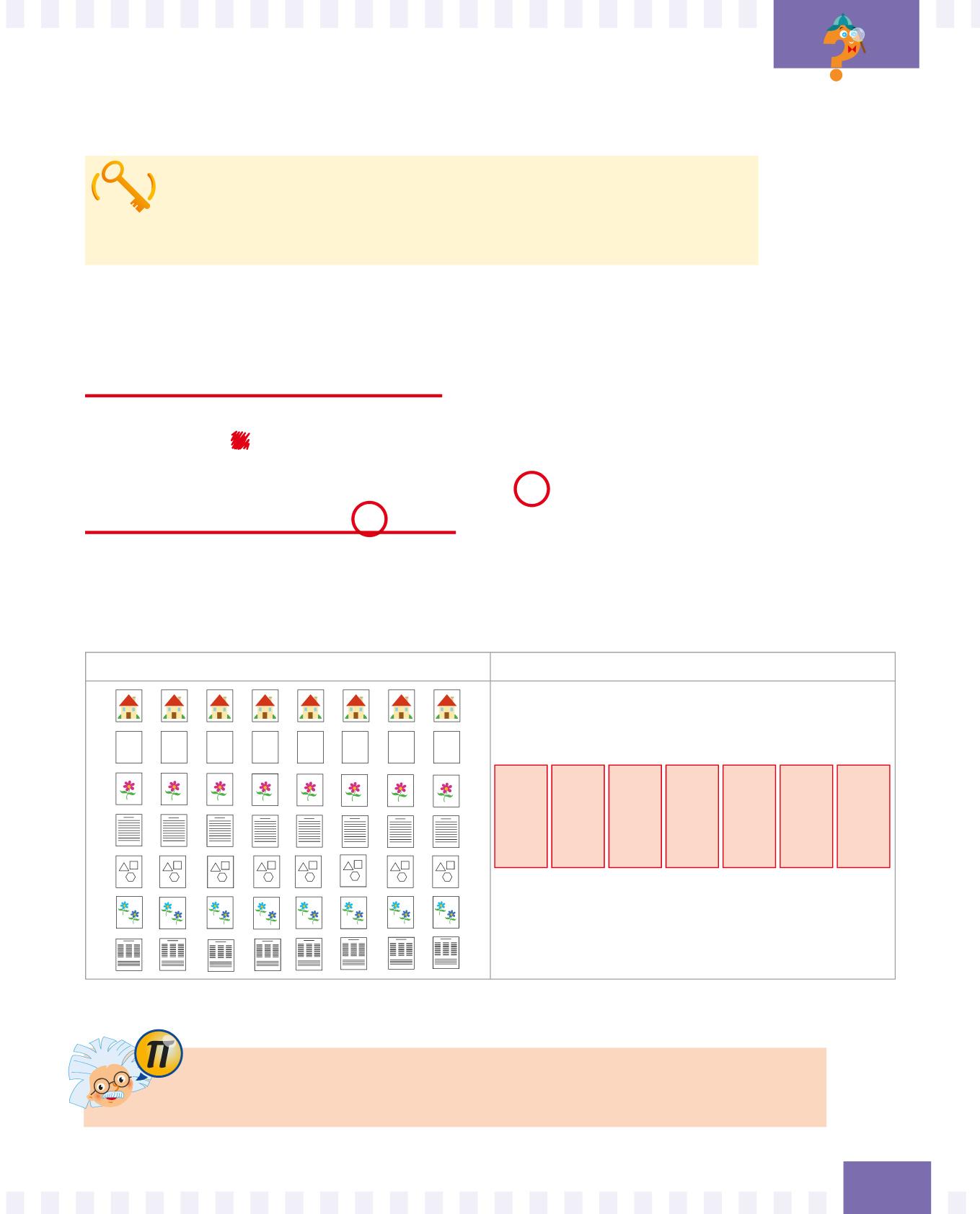
Spesso è più facile e più utile rappresentare i dati con simboli perché ci vuole molto tempo per disegnare dati grandi!
Leggi i problemi e osserva i simboli o i disegni. Poi cerchia il modo corretto per rappresentare i dati del problema.
• Sul suo balcone Nicole ha 4 vasi. Ogni vaso ha 12 fiori.
Quanti fiori ci sono in tutto sul balcone di Nicole?

• 10 ragazzi decidono di fare una gita e vogliono usare il numero minore possibile di automobili. Ogni automobile ha 5 posti.
Quante automobili occorrono ai ragazzi?
Usa il procedimento che hai imparato prima: leggi il problema, sottolinea la domanda e cerchia di i dati utili. Infine, rappresenta i dati.
Giacomo ha preparato 9 gelati. Su ogni gelato ha messo 3 palline: una al cioccolato, una alla crema e una alla fragola.
Quante palline ha messo in tutto sui gelati Giacomo?
Segui questi quattro passaggi per risolvere un problema:
1 COMPRENDI
• Leggi il testo del problema e sottolinea la domanda.
In una pasticceria dove ci sono più di 20 tipi di torte, il pasticciere Andrea prepara 15 torte al giorno.
Quante torte prepara Andrea in una settimana?
• Cerchia di i dati utili e cancella i dati inutili.
Cerca i dati nascosti: se ci sono parole che indicano un dato nascosto, riquadrale di . Poi trasforma i dati nascosti in numeri.
In una pasticceria dove ci sono più di 20 tipi di torte, il pasticciere Andrea prepara 15 torte al giorno.
Quante torte prepara Andrea in una settimana?
2 RAPPRESENTA
Inserisci in una tabella i dati, la rappresentazione e la domanda. Dati Rappresentazione
15 torte al giorno
7 giorni
Domanda Quante torte prepara Andrea in 7 giorni?
• Quali passaggi devi fare per risolvere il problema?
So che il pasticciere Andrea prepara 15 torte al giorno. Devo trovare quante torte prepara in 7 giorni. Moltiplico le 15 torte per 7 giorni.
• Svolgi le operazioni e rispondi alla domanda.
15 × 7 =
1 5 ×
7 =
RISPOSTA Il pasticciere Andrea prepara in una settimana 105 torte.
Usa i quattro passaggi e risolvi il problema.
Nella classe 4a C ci sono 22 alunni. Venerdì sono assenti 6 alunni:
3 femmine e 3 maschi.
Quanti alunni ci sono venerdì in aula?
1 COMPRENDI
• Leggi attentamente il problema e sottolinea la domanda.
• Cerchia di i dati utili; cancella i dati inutili; cerca i dati nascosti.
2 RAPPRESENTA
Dati
........................................................................... Domanda
Rappresentazione
• Quali passaggi devi fare per risolvere il problema?

Usa i quattro passaggi e risolvi i seguenti problemi sul tuo quaderno.
• Nella piccola biblioteca scolastica ci sono 15 libri di avventura, 18 libri di Storia, 16 libri fantasy e 14 libri di Geografia.
Quanti libri ci sono in tutto nella biblioteca?
• Nella mensa della scuola ci sono 200 posti a sedere.
Ogni tavolo ha 5 posti a sedere.
Quanti tavoli ci sono nella mensa?

• Leggi il testo del problema e sottolinea la domanda.
• Cerchia di i dati utili e cancella i dati inutili. Se trovi un dato nascosto, riquadralo di e trasforma il dato nascosto in numero.
• Anno: 12 mesi oppure 365 giorni
• Mese: 30 giorni circa
• Settimana: 7 giorni
• Giorno: 24 ore
• Ora: 60 minuti
• Minuto: 60 secondi
• Una coppia: 2
• Un paio: 2
• Doppio: si moltiplica per 2
• Triplo: si moltiplica per 3
• Dozzina: 12
• Metà: si divide per 2
Inserisci in una tabella i dati, la rappresentazione e la domanda.
Usa i simboli per rappresentare dati grandi, altrimenti impiegherai troppo tempo per la rappresentazione.
Dati Rappresentazione
Domanda
Pensa: quali passaggi devi fare per risolvere il problema?
Svolgi le operazioni e rispondi alla domanda.

La linea retta è una linea senza inizio e senza fine e ha sempre la stessa direzione. La linea retta si indica con una lettera minuscola dell’alfabeto (per esempio r).
Osserva: I trattini indicano che la retta r è senza inizio e senza fine e che continua all’infinito verso sinistra e verso destra.
Le rette parallele sono due o più rette che mantengono sempre la stessa distanza e non si incontrano mai.
Per ricordarti come sono fatte le rette parallele, pensa alle strisce pedonali che trovi per strada. Osserva:
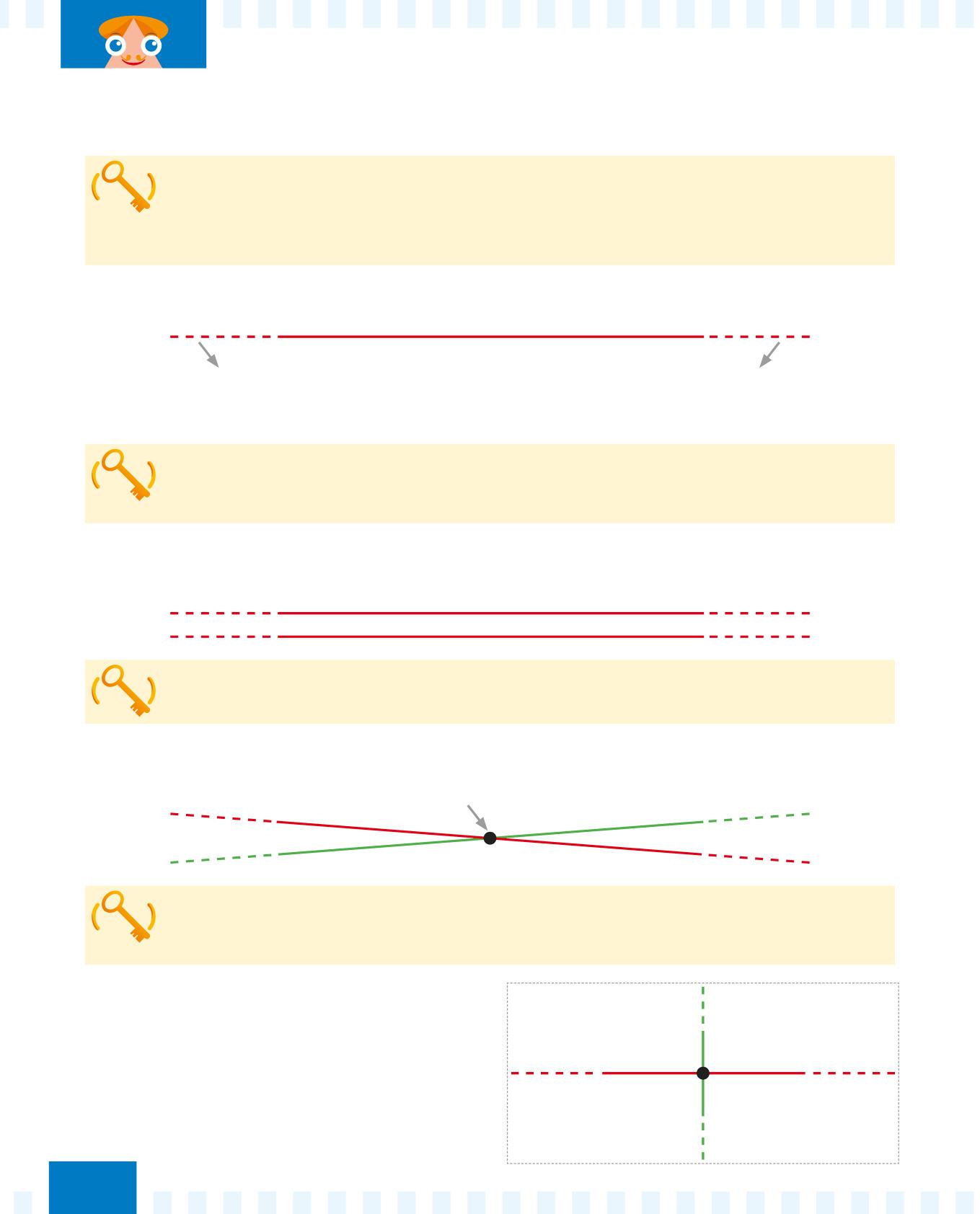
Le rette incidenti sono due o più rette che si incontrano in un punto.
Per ricordarti come sono fatte due rette incidenti, pensa a quando disegni una “x”. Osserva:
Le rette perpendicolari sono due rette incidenti che si incontrano in un punto e dividono il piano in quattro parti uguali. punto di incontro delle due rette
Per ricordarti come sono fatte due rette perpendicolari, pensa a quando disegni il segno più, +. Osserva:
La semiretta è una parte di retta che inizia da un punto, non ha una fine e ha sempre la stessa direzione. La semiretta si indica con una lettera minuscola dell’alfabeto (per esempio t).
Il punto di origine si indica con una lettera maiuscola (per esempio A).
Osserva:
È il punto di origine della semiretta. t A
I trattini indicano che la semiretta t è senza una fine e che prosegue all’infinito in una sola direzione.
Il segmento è una parte di retta compresa tra due punti.
Il segmento ha un inizio e una fine e ha sempre la stessa direzione.
Il punto di inizio e il punto di fine si indicano con le lettere maiuscole (per esempio C e D) e si chiamano estremi.
Il segmento si indica con le due lettere agli estremi e si può mettere una piccola linea sopra (per esempio CD) per indicare la misura del segmento.
Osserva: I punti indicati dalle lettere maiuscole si chiamano estremi. C D
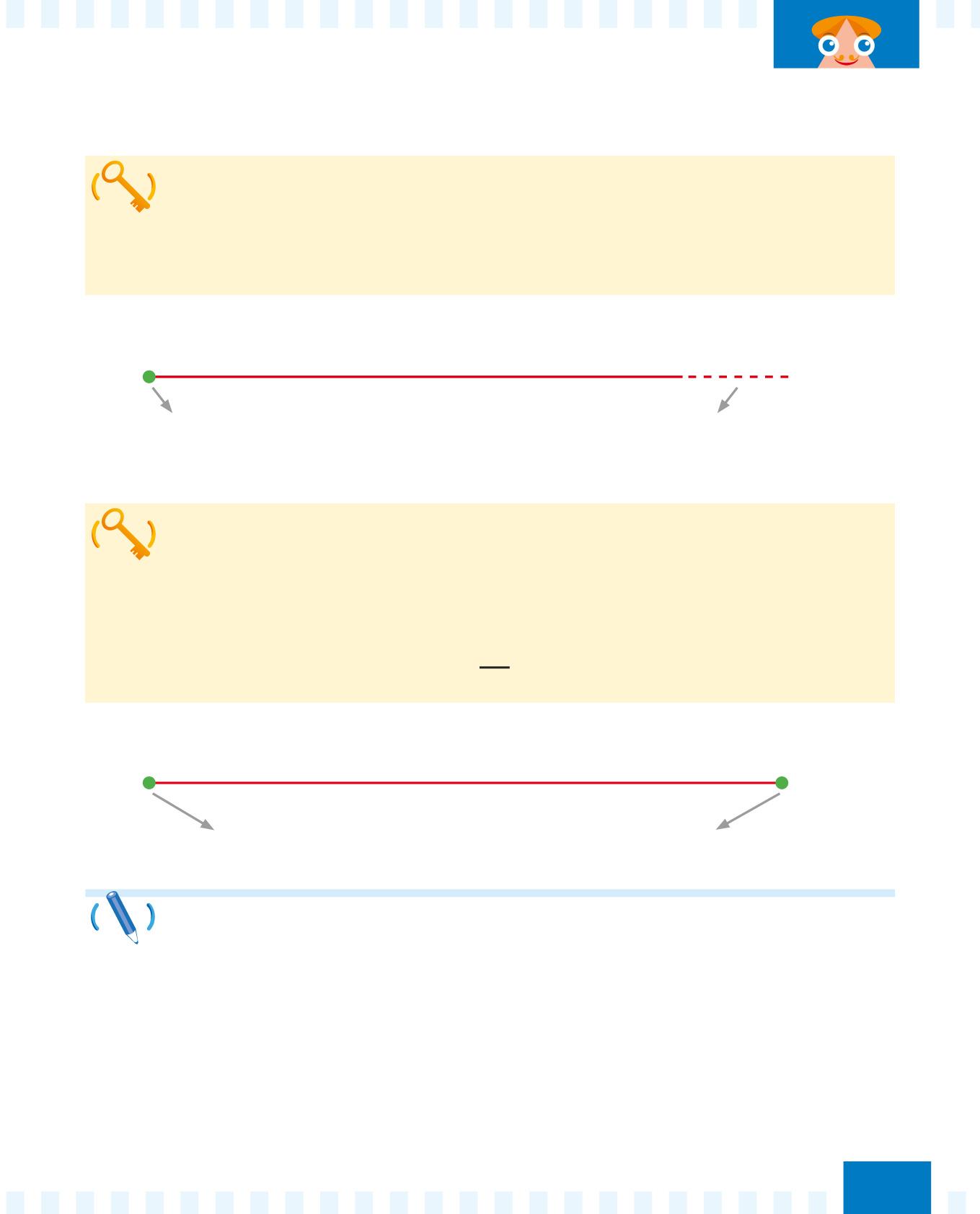
Completa le seguenti frasi.
• Una linea che ha un inizio ma non una fine e mantiene la stessa direzione si chiama .
• Il punto di origine di una semiretta si indica con una lettera .
• Una parte di retta compresa tra due punti che ha un inizio e una fine si chiama
• I punti di inizio e di fine di un segmento si chiamano .
L’angolo è una parte di piano compresa tra due semirette. Le due semirette hanno origine nel vertice e sono i lati dell’angolo.
L’ampiezza dell’angolo è la parte di piano compresa dalle semirette e si misura in gradi (°).
Osserva: vertice
lato lato ampiezza Il piano continua all’infinito in ogni direzione.
In base all’ampiezza, l’angolo può essere:
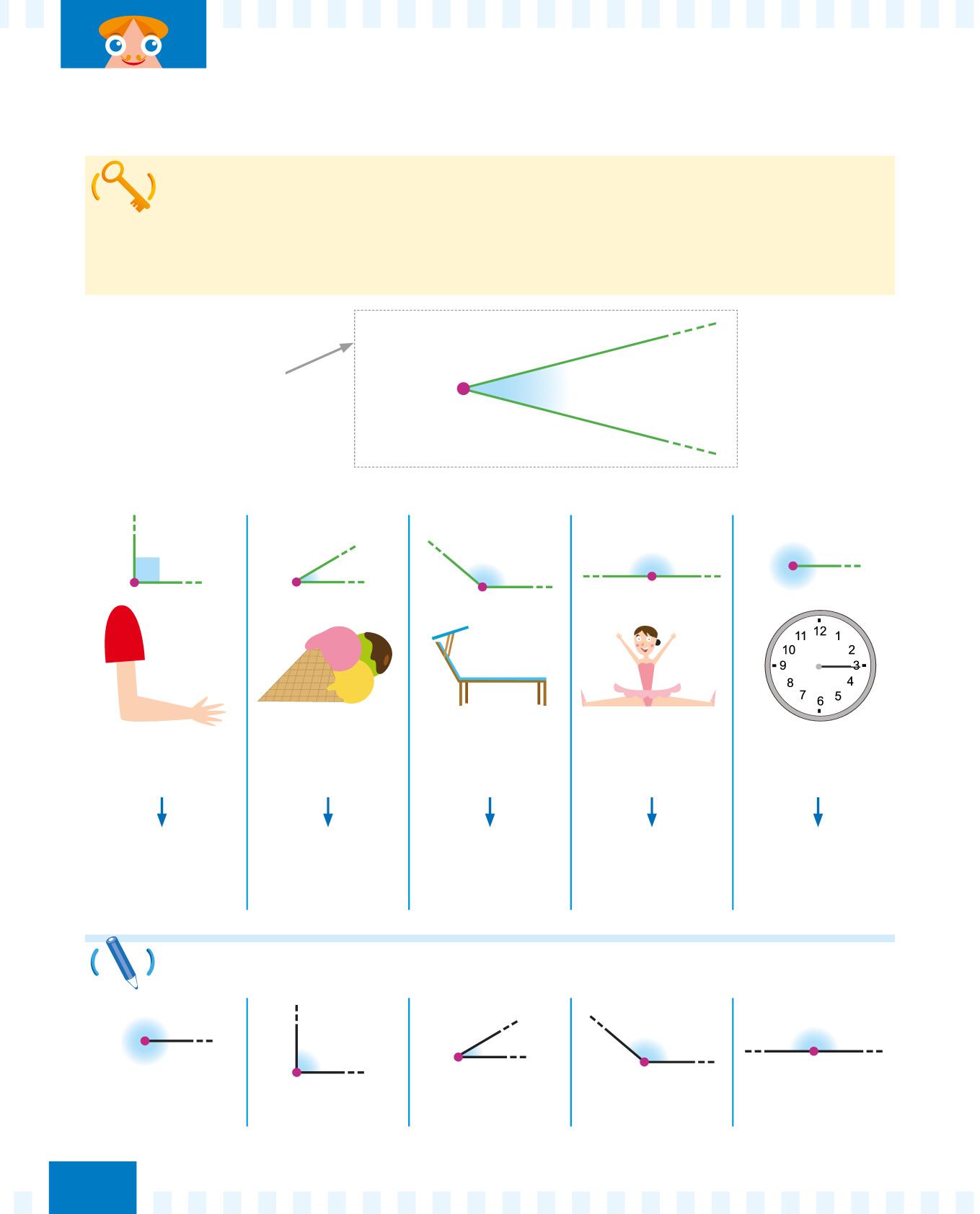
ANGOLO RETTO
I lati sono perpendicolari.
ANGOLO ACUTO È meno ampio di un angolo retto.
ANGOLO OTTUSO È più ampio di un angolo retto.
ANGOLO PIATTO È ampio come due angoli retti.
Osserva i seguenti angoli e completa con il nome corretto.
ANGOLO GIRO È ampio come quattro angoli retti.
Il poligono è una figura piana formata da una linea spezzata chiusa. In base al numero di lati, i poligoni hanno nomi diversi.
Ogni poligono ha lo stesso numero di lati, di angoli e di vertici.
Osserva:
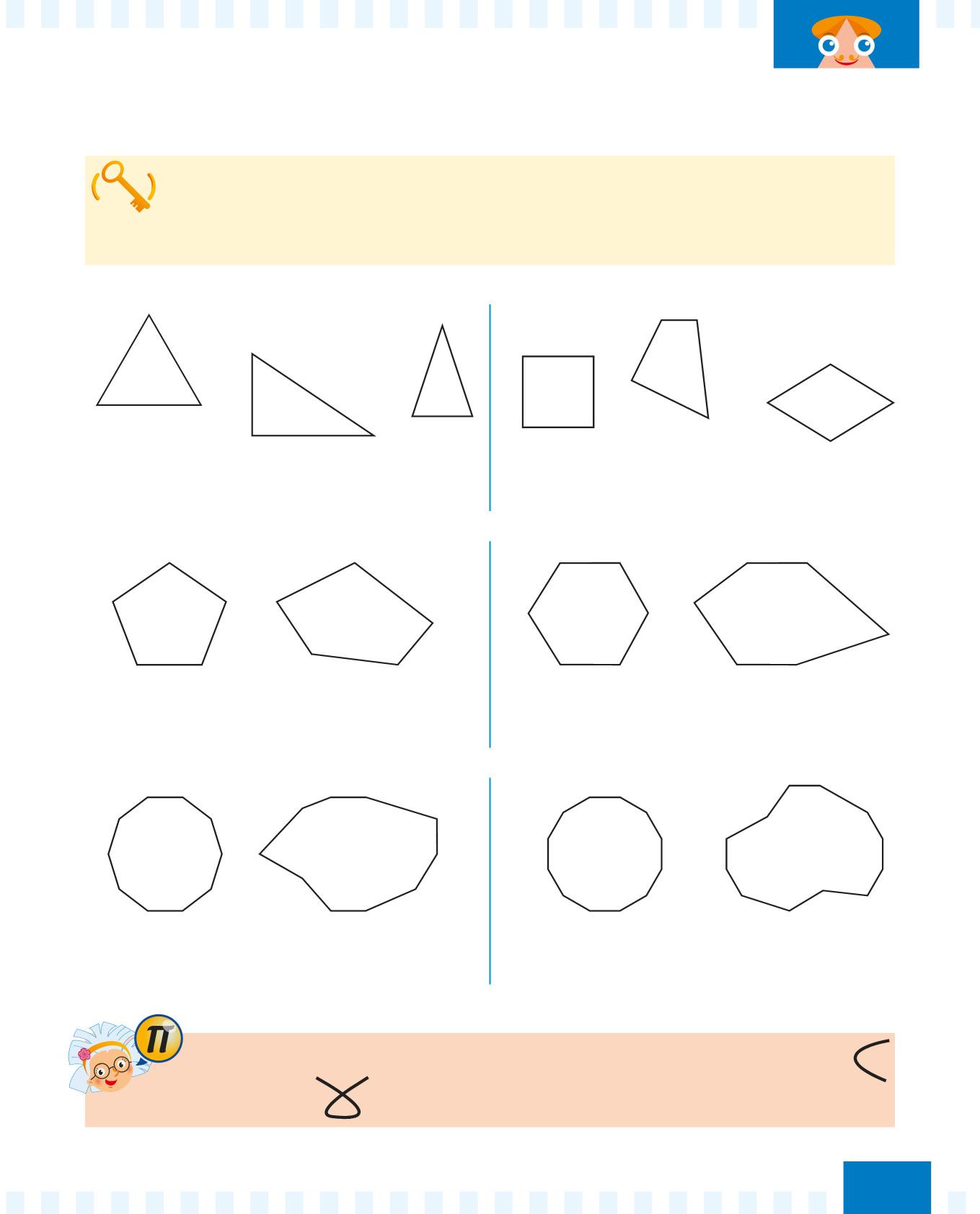
TRIANGOLI
Hanno 3 lati, 3 angoli, 3 vertici.
QUADRILATERI
Hanno 4 lati, 4 angoli, 4 vertici.
PENTAGONI
Hanno 5 lati, 5 angoli, 5 vertici.
ESAGONI
Hanno 6 lati, 6 angoli, 6 vertici.
DECAGONI
Hanno 10 lati, 10 angoli, 10 vertici.
DODECAGONI
Hanno 12 lati, 12 angoli, 12 vertici.
Se il contorno di una figura geometrica comprende una linea curva
o intrecciata , quella figura geometrica non è un poligono!
I triangoli sono poligoni con tre lati e tre angoli.
Puoi classificare i triangoli in base ai lati e in base agli angoli.
LATI ANGOLI
Triangolo equilatero: ha tutti i lati lunghi uguali.
Triangolo isoscele: ha due lati lunghi uguali.
Triangolo scaleno: ha tutti i lati di lunghezza diversa.
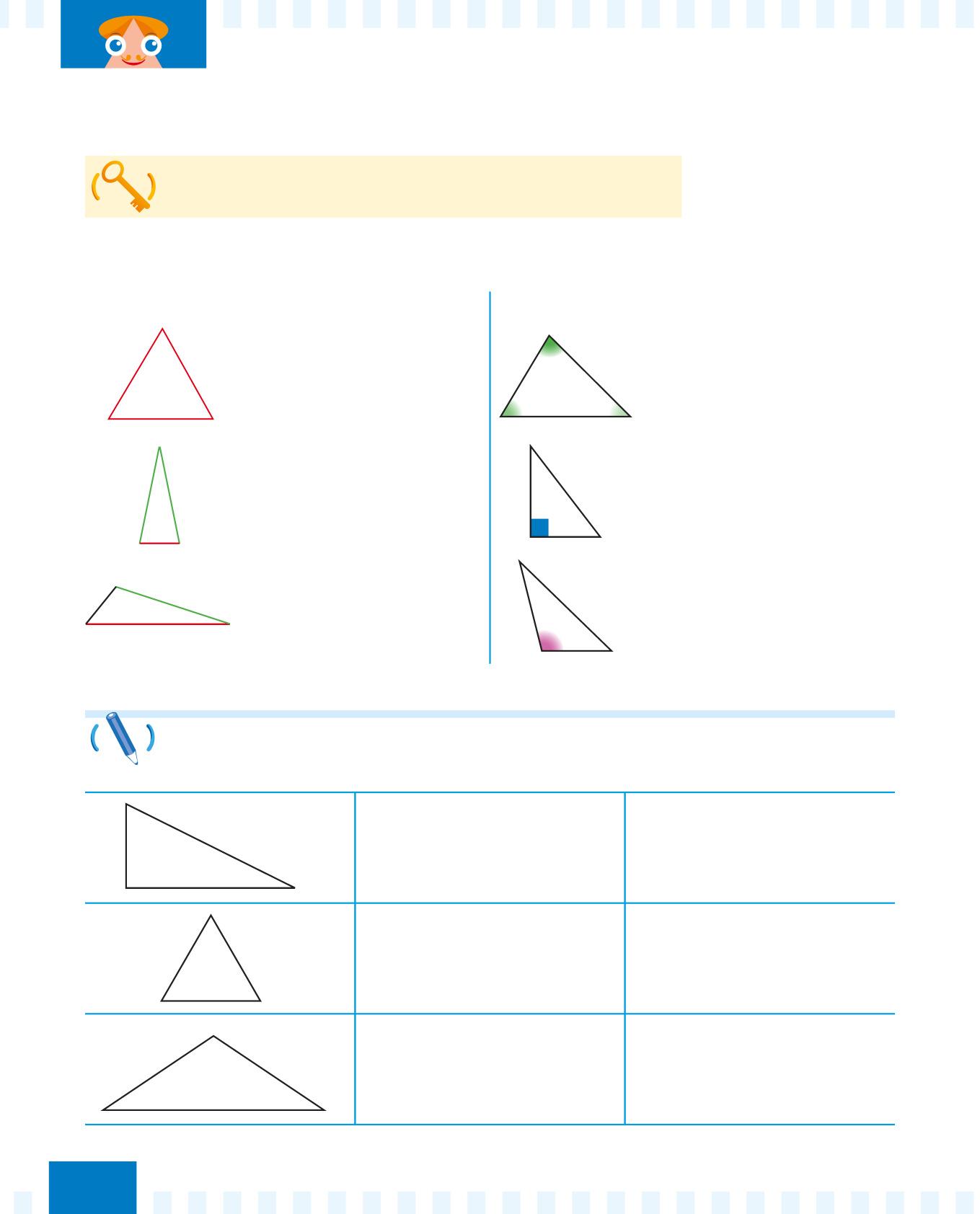
Triangolo acutangolo: ha tutti gli angoli acuti, cioè minori di 90°.
Triangolo rettangolo: ha un angolo retto, cioè uguale a 90°.
Triangolo ottusangolo: ha un angolo ottuso, cioè maggiore di 90°.
Classifica i triangoli in base ai lati e in base agli angoli. Usa il righello per misurare i lati e il goniometro per misurare gli angoli.
In base ai LATI è un triangolo
In base ai LATI è un triangolo
In base ai LATI è un triangolo
.
In base agli ANGOLI è un triangolo
.
. In base agli ANGOLI è un triangolo
.
In base agli ANGOLI è un triangolo .
.
I quadrilateri sono poligoni con quattro lati e quattro angoli.
Tutte le figure qui sotto sono quadrilateri: hanno quattro lati e quattro angoli.
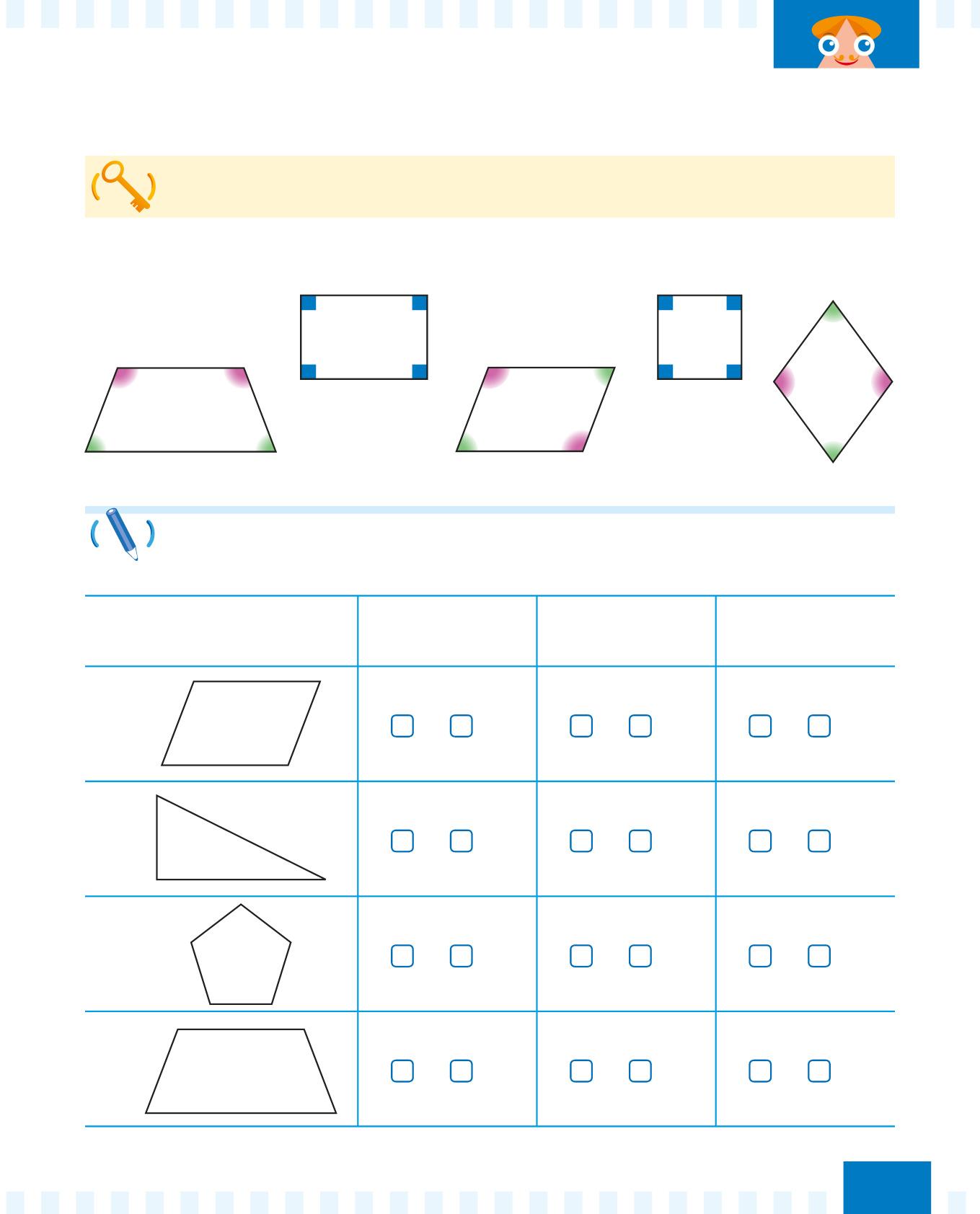
Conta i lati delle seguenti figure. Poi conta gli angoli.
Infine, indica con una X la risposta corretta alle domande.
Figura
Ha 4 lati?
Ha 4 angoli?
È un quadrilatero?
sì no sì no sì no
sì no sì no sì no
sì no sì no sì no
sì no sì no sì no
I parallelogrammi hanno tutti i lati opposti paralleli e lunghi uguali.
Puoi classificare i parallelogrammi in base ai lati e in base agli angoli. Osserva:
Parallelogramma
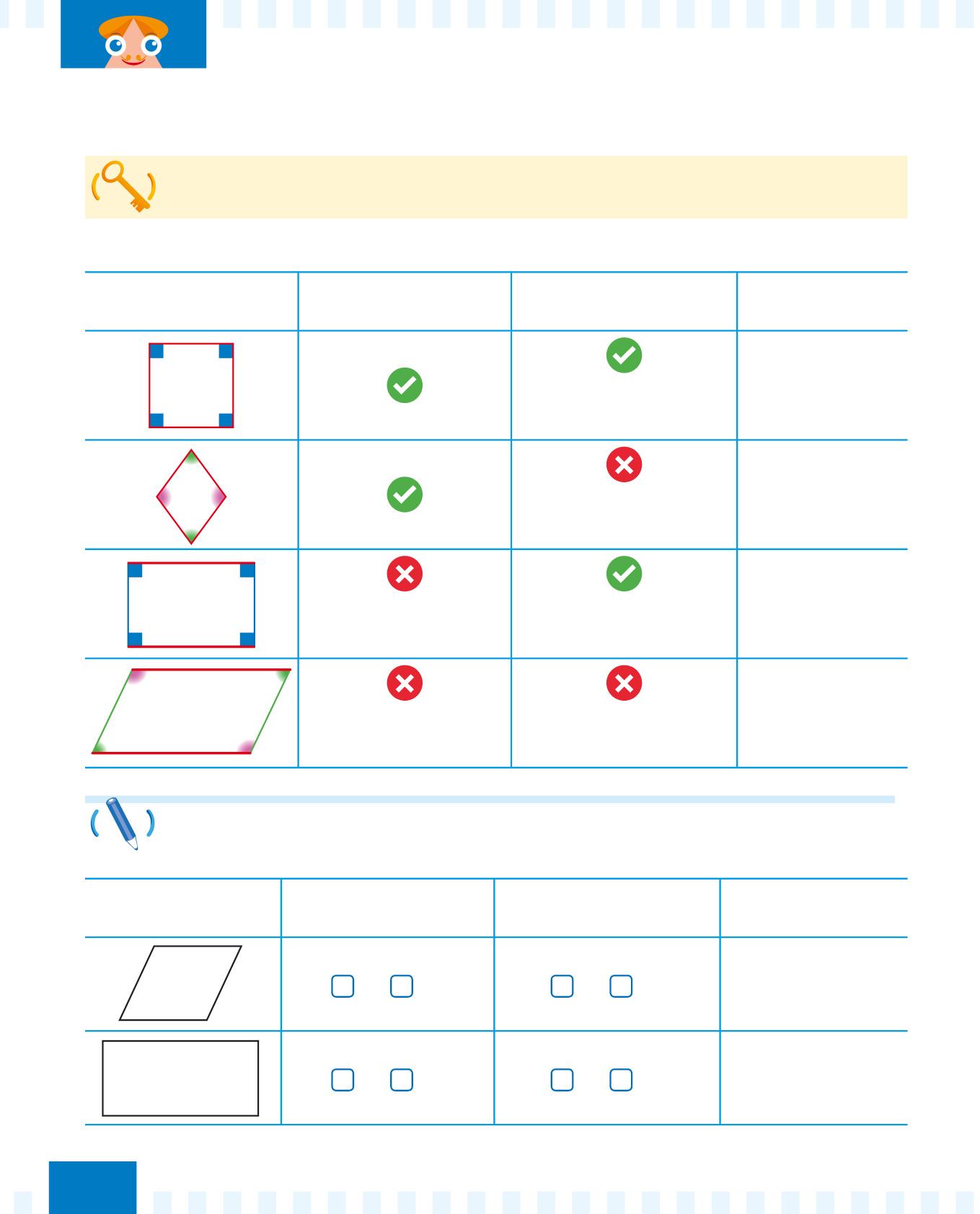
Ha TUTTI i lati lunghi uguali?
Ha TUTTI gli angoli ampi uguali? Nome
Sì, sono tutti angoli retti.
No, solo gli angoli opposti sono uguali.
No, solo i lati opposti sono uguali. Sì, sono tutti angoli retti.
QUADRATO
ROMBO
RETTANGOLO
ROMBOIDE
No, solo i lati opposti sono uguali.
No, solo gli angoli opposti sono uguali.
Usa il righello per misurare i lati e il goniometro per misurare gli angoli dei seguenti parallelogrammi. Poi completa la tabella.
Parallelogramma
Ha TUTTI i lati lunghi uguali?
sì no
sì no
Ha TUTTI gli angoli ampi uguali? Nome
sì no
sì no
I trapezi sono quadrilateri che hanno due lati opposti paralleli. I due lati opposti paralleli si chiamano base maggiore (B) e base minore (b).
L’altezza (h) è la distanza tra le due basi.
Osserva gli elementi del trapezio:
b
B lato obliquo lato obliquo
B = base maggiore
b = base minore
h = altezza
d = diagonale
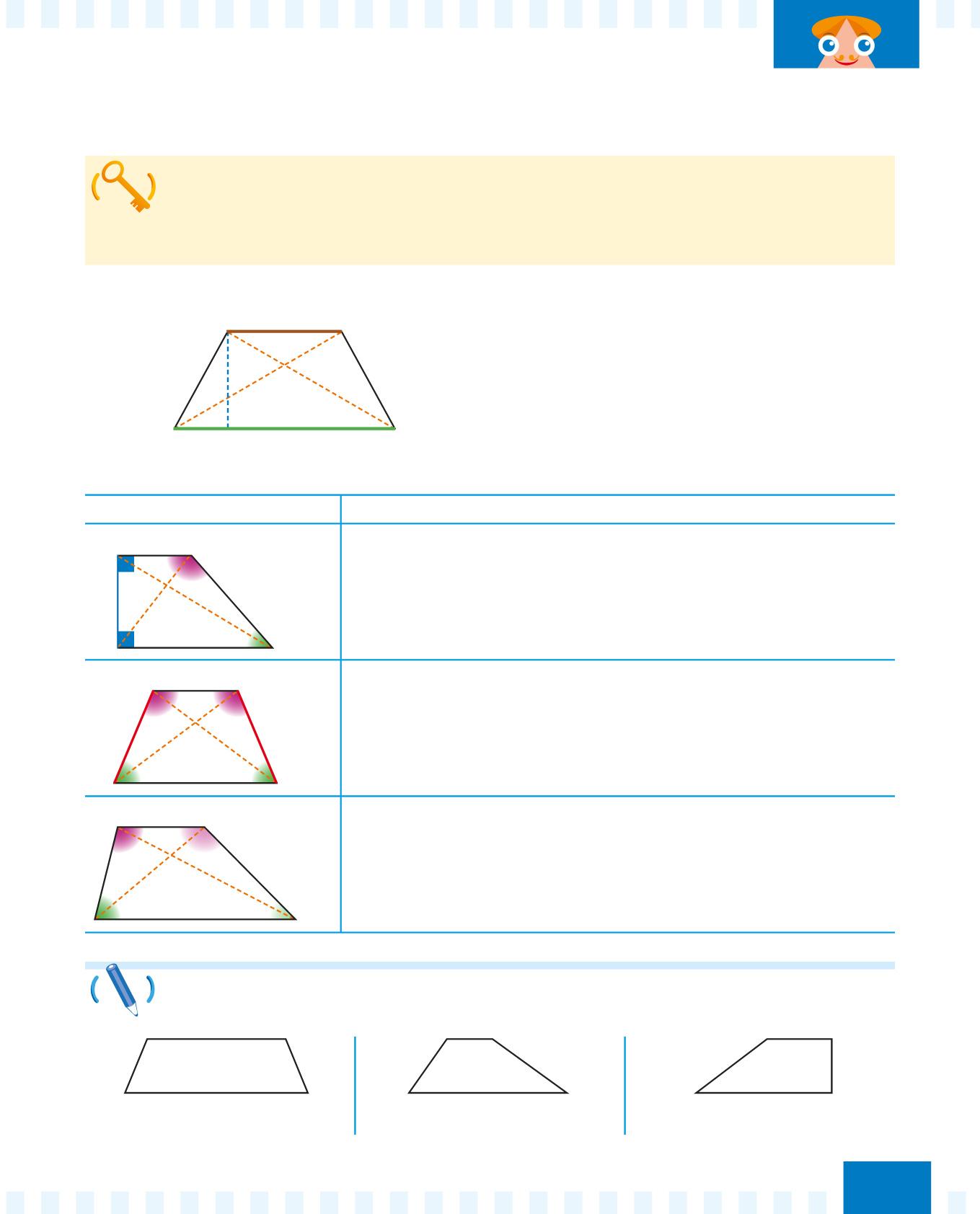
Puoi classificare i trapezi in base ai lati e in base agli angoli. Osserva:
Trapezio
RETTANGOLO
ISOSCELE
SCALENO
Usa il righello per misurare i lati e per tracciare le diagonali dei seguenti trapezi. Poi osserva gli angoli e le diagonali e completa con il nome corretto. h d d
Caratteristiche
• Il lato corto corrisponde all’altezza.
• Ha due angoli retti (90°), un angolo acuto e un angolo ottuso.
• Ha le due diagonali di lunghezza diversa.
• Ha i due lati obliqui lunghi uguali;
• Ha due angoli ottusi di ampiezza uguale e due angoli acuti di ampiezza uguale.
• Ha le due diagonali di lunghezza uguale.
• Ha tutti i lati di lunghezza diversa.
• Ha due angoli ottusi di ampiezza diversa e due angoli acuti di ampiezza diversa.
• Ha le due diagonali di lunghezza diversa.
Il perimetro (P) di un triangolo (cioè il suo contorno) è la somma della lunghezza dei suoi tre lati (l).
Triangolo Caratteristiche Perimetro
TRIANGOLO SCALENO: ha tutti i lati di lunghezza diversa. P = l + l + l
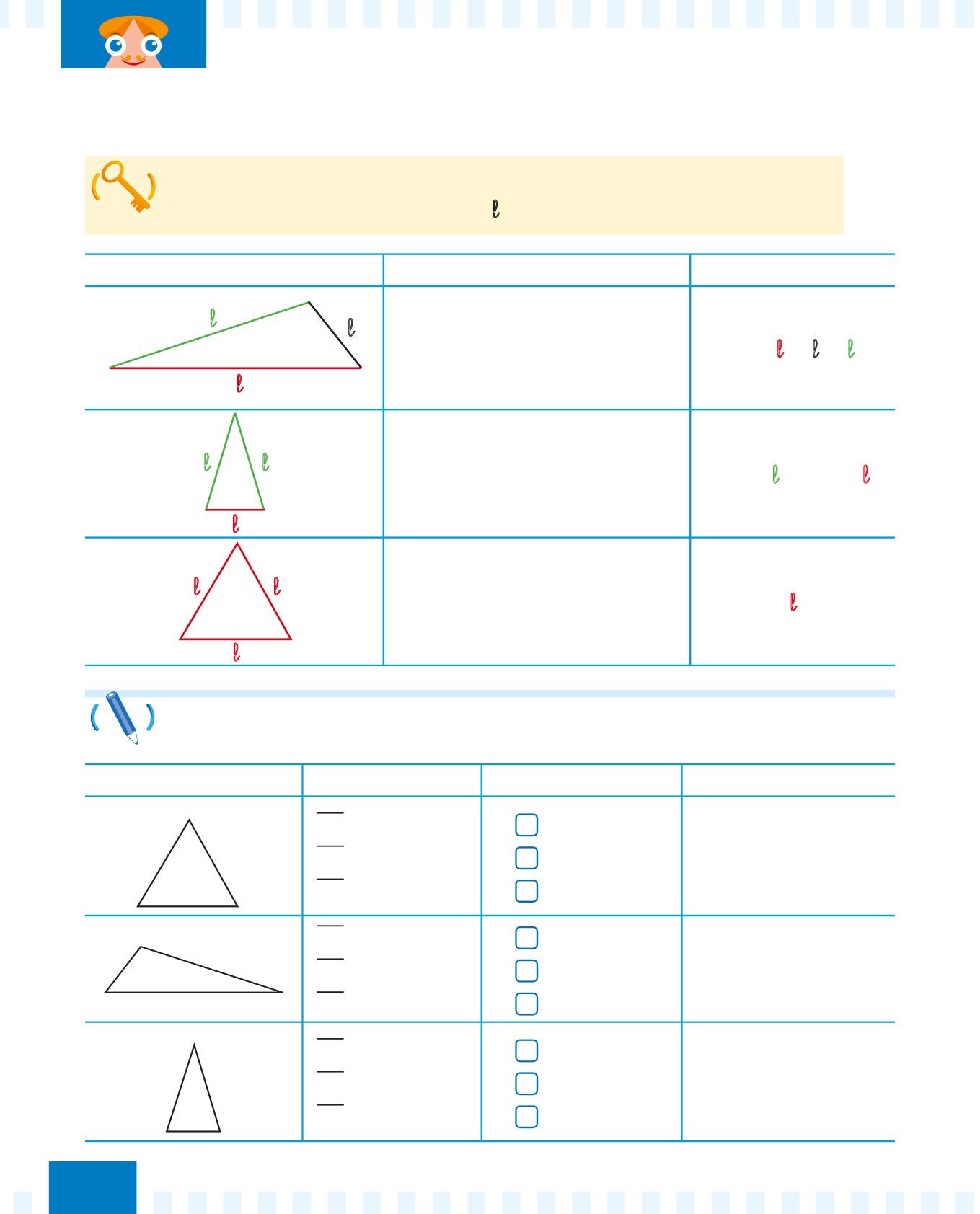
TRIANGOLO ISOSCELE: ha due lati lunghi uguali. P = (l × 2) + l
TRIANGOLO EQUILATERO: ha tutti i lati lunghi uguali. P = l × 3
Usa il righello per misurare i lati dei seguenti triangoli. Poi indica con una X la risposta corretta alla domanda e calcola il perimetro.
Triangolo Misura dei latiChe triangolo è? Perimetro
AB = cm
BC = cm
CA = cm scaleno isoscele equilatero P =
AB = cm
BC = cm
CA = cm scaleno isoscele equilatero P =
AB = cm
BC = cm
CA = cm scaleno isoscele equilatero P =
Il perimetro (P) di un parallelogramma (cioè il suo contorno)
è la somma della lunghezza dei suoi quattro lati (l).
Parallelogramma Ha TUTTI i lati lunghi uguali? Perimetro
QUADRATO
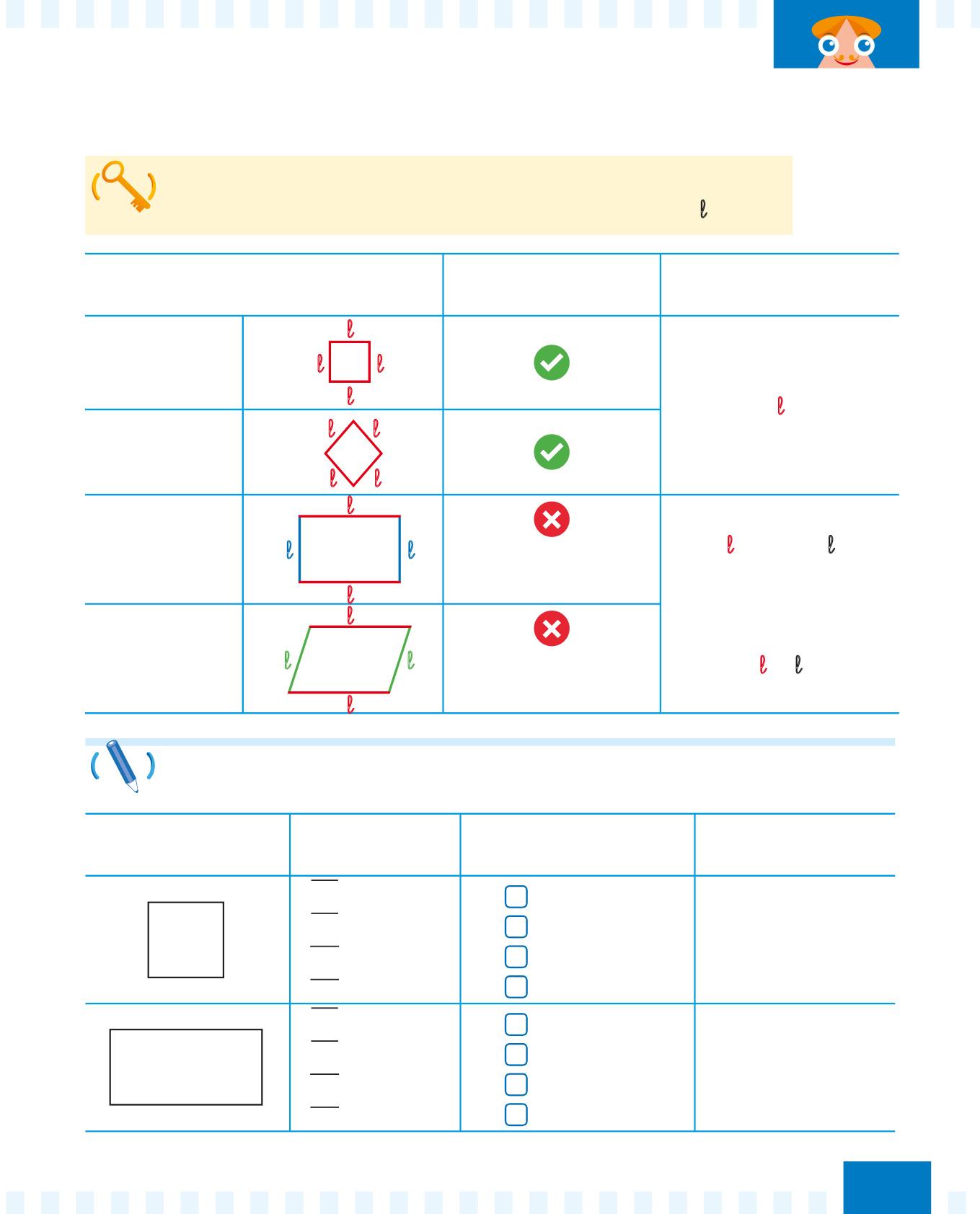
P = l × 4
ROMBO
RETTANGOLO
ROMBOIDE
No, solo i lati opposti sono uguali.
No, solo i lati opposti sono uguali.
P = (l × 2) + (l × 2) oppure
P = (l + l) × 2
Usa il righello per misurare i lati dei seguenti parallelogrammi. Poi indica con una X la risposta corretta alla domanda e calcola il perimetro.
Parallelogramma Misura dei lati Che parallelogramma è? Perimetro
AB = cm
BC = cm
CD = cm
DA = ........... cm quadrato rombo rettangolo romboide
AB = cm
BC = cm
CD = ........... cm
DA = cm quadrato rombo rettangolo romboide
P =
P =
Il perimetro (P) di un trapezio, è la somma della lunghezza dei suoi quattro lati, cioè la somma delle due basi e dei due lati obliqui.
Trapezio Caratteristiche Perimetro
TRAPEZIO SCALENO: ha tutti i lati di diversa lunghezza.
TRAPEZIO RETTANGOLO: ha tutti i lati di diversa lunghezza.
P = B + b + l1 + l2
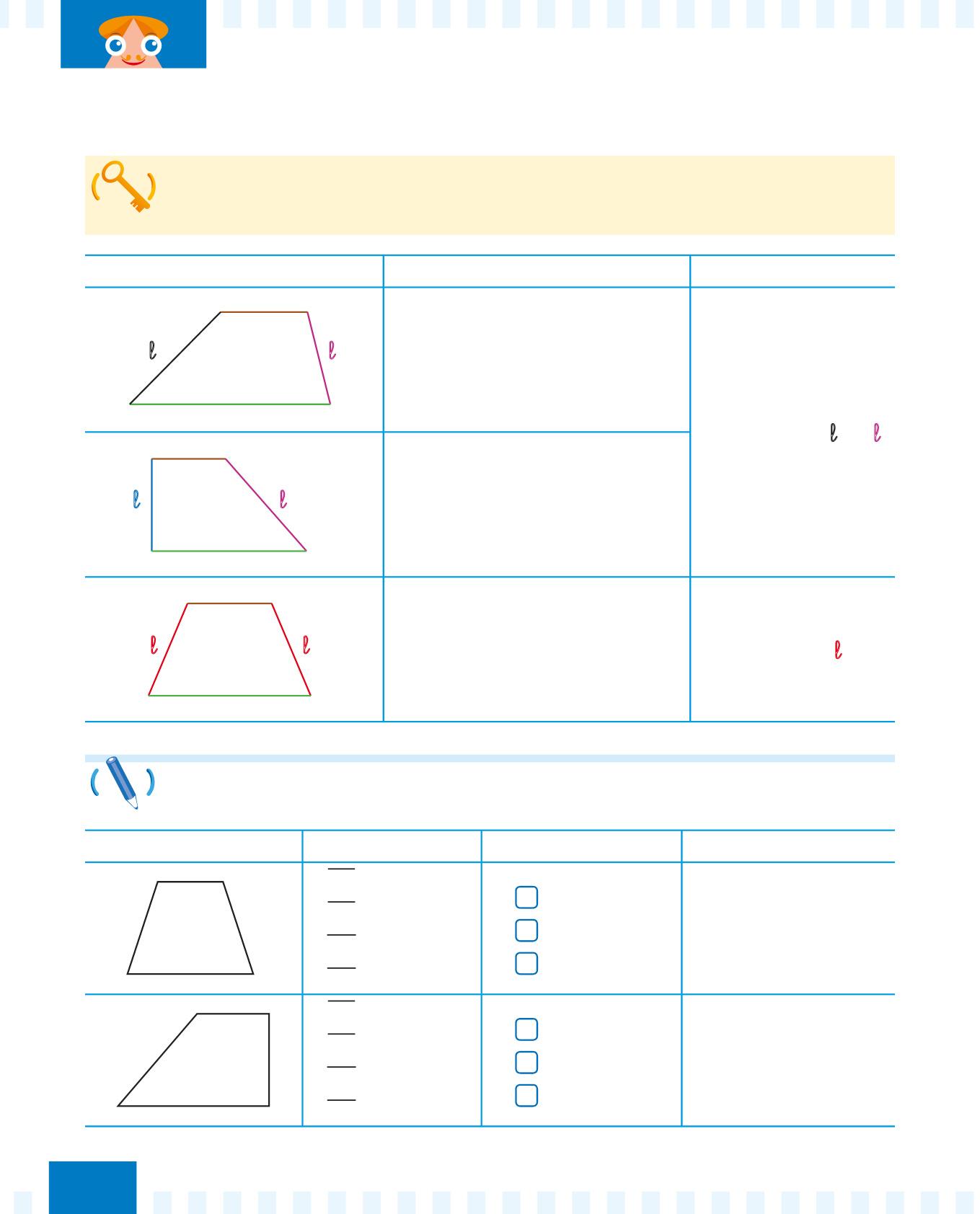
TRAPEZIO ISOSCELE: ha i due lati obliqui lunghi uguali.
P = B + b + (l × 2) A
Usa il righello per misurare i lati dei seguenti trapezi. Poi indica con una X la risposta corretta alla domanda e calcola il perimetro.
Trapezio Misura dei latiChe trapezio è? Perimetro
AB = ........... cm
BC = cm
CD = cm
DA = cm scaleno rettangolo isoscele P =
AB = cm
BC = ........... cm
CD = cm
DA = cm scaleno rettangolo isoscele P =
Per calcolare l’area (A) del rettangolo (cioè lo spazio che occupa)
moltiplica la lunghezza della base (b) per la lunghezza dell’altezza (h).
Quanto misura in quadretti l’area del bigliettino di auguri?
Ogni vale 1 quadretto.
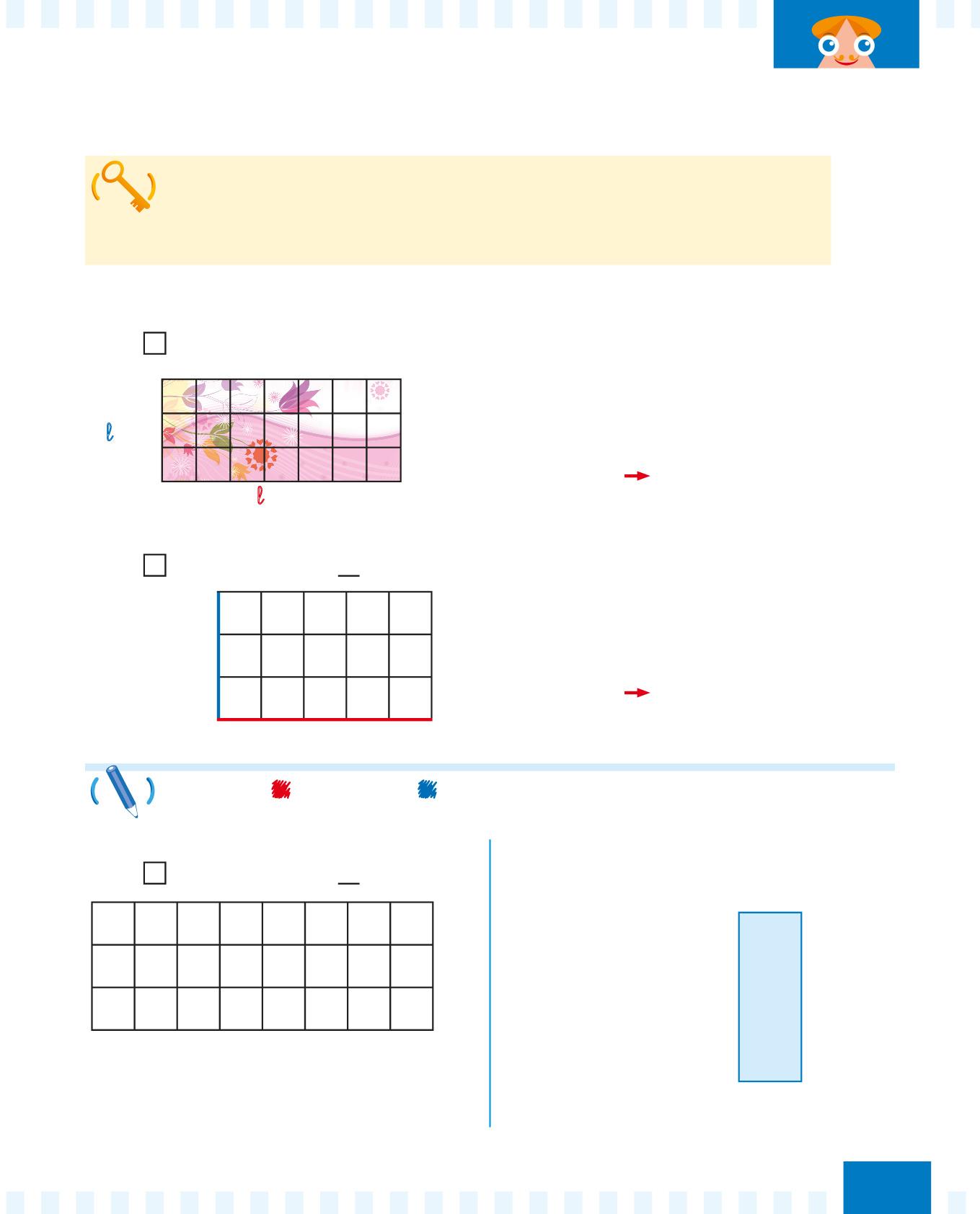
l = h
b = 7
h = 3
l = b
A = b × h 7 × 3 = 21 quadretti
Quanto misura in cm2 l’area del rettangolo?
Ogni vale 1 cm2, ogni vale 1 cm.
b = 5 cm
h = 3 cm
A = b × h 5 cm × 3 cm = 15 cm2
Ripassa di la base e di l’altezza dei seguenti rettangoli. Poi:
calcola l’area;
Ogni vale 1 cm2, ogni vale 1 cm
b = cm
h = cm
A = A = b h
misura la base e l’altezza con un righello e calcola l’area.
b = cm
h = cm
Per calcolare l’area (A) del quadrato (cioè lo spazio che occupa)
moltiplica la lunghezza del lato (l) per se stessa.
Quanto misura in quadretti l’area del bigliettino di auguri?
Ogni vale 1 quadretto.
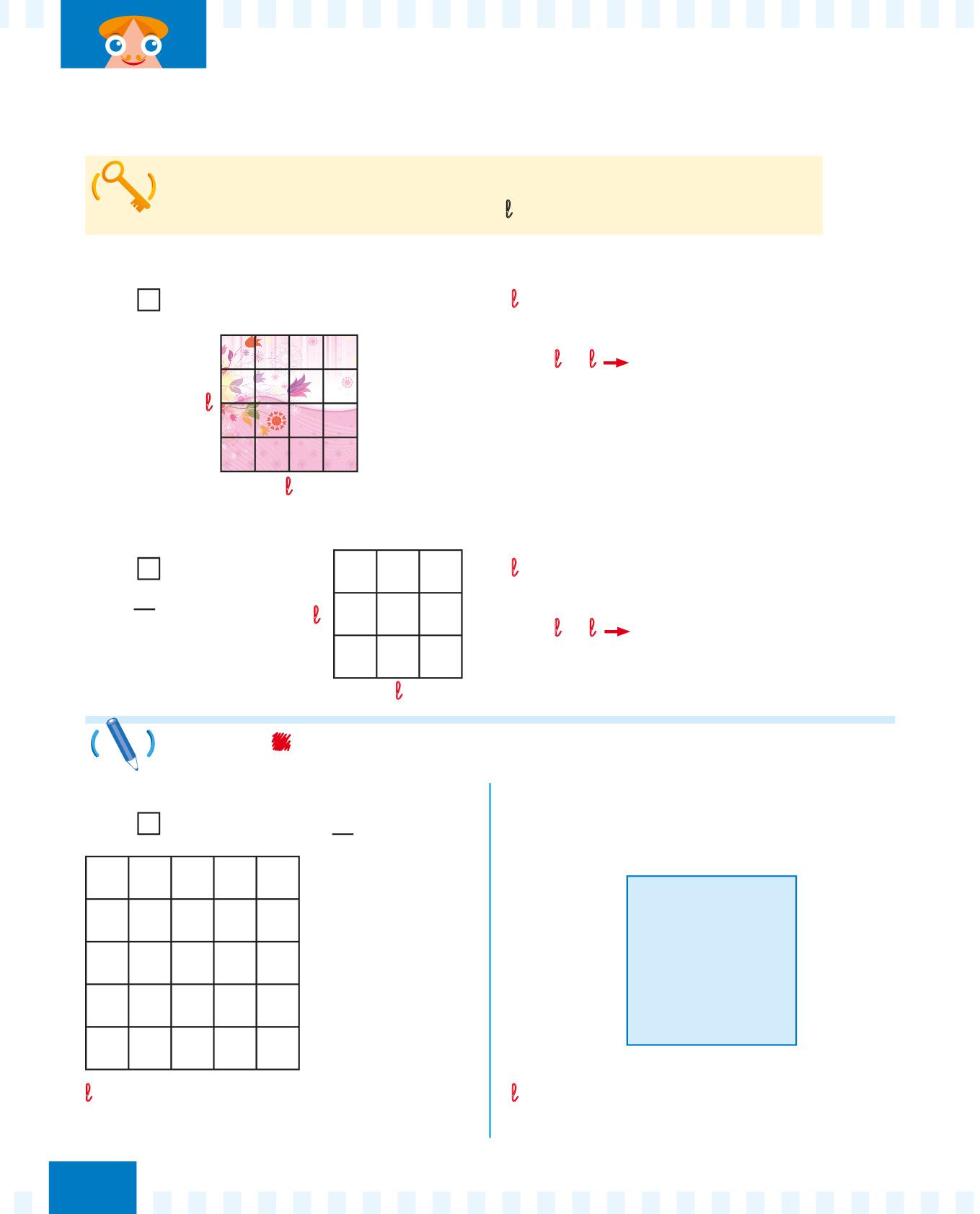
l = 4
A = l × l 4 × 4 = 16 quadretti
Quanto misura in cm2 l’area del quadrato?
Ogni vale 1 cm2 , ogni vale 1 cm.
l = 3 cm
A = l × l 3 cm × 3 cm = 9 cm2
Ripassa di un lato dei seguenti quadrati. Poi:
calcola l’area;
Ogni vale 1 cm2, ogni vale 1 cm
misura i lati con il righello e calcola l’area.
Per calcolare l’area (A) del romboide moltiplica la lunghezza della base (b) per la lunghezza dell’altezza (h), come in un rettangolo.
Quanto misura in quadretti l’area del pavimento?
Ogni vale 1 quadretto.
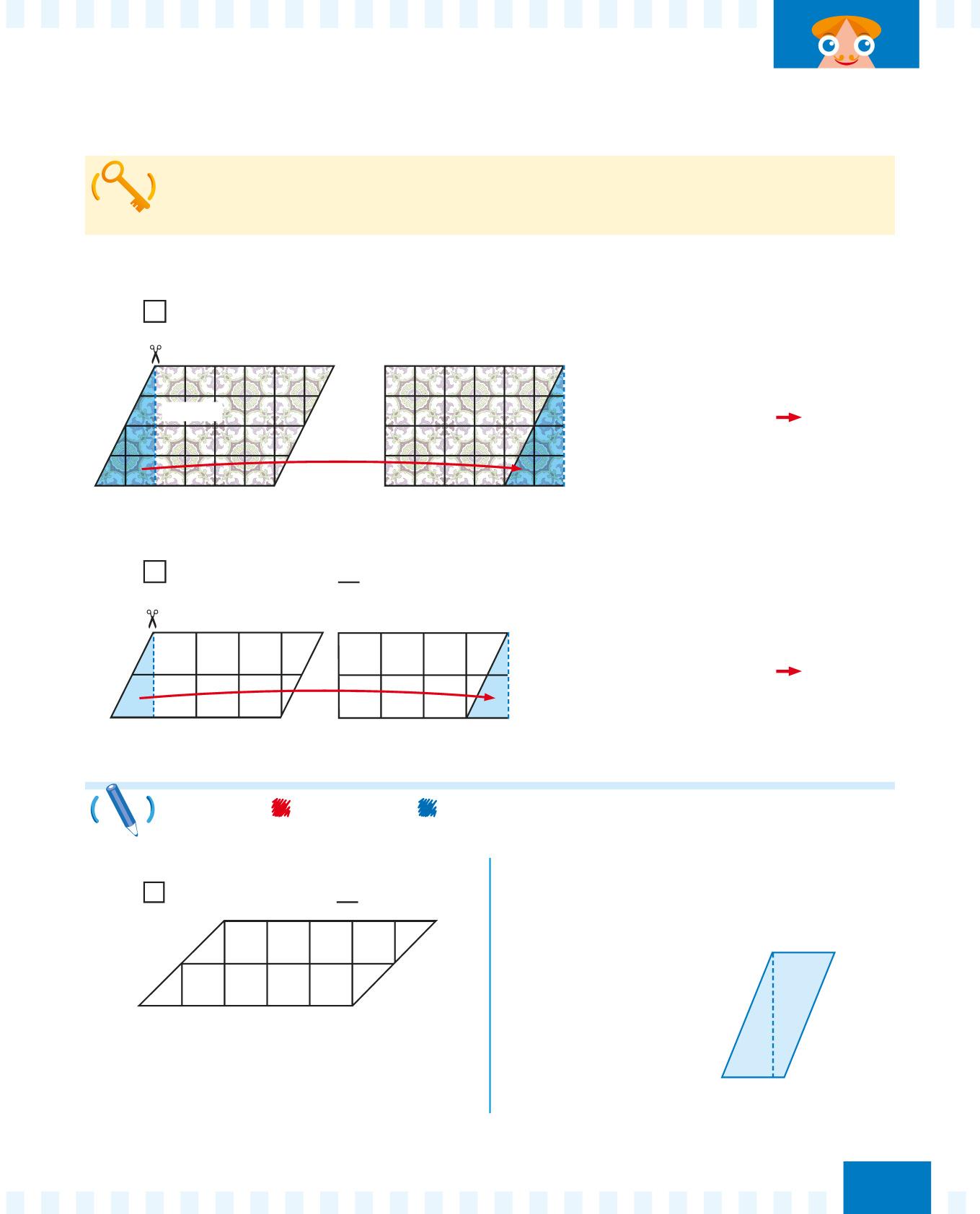
h = 4
b = 6 b = 6
Quanto misura in cm2 l’area del romboide?
Ogni vale 1 cm2, ogni vale 1 cm.
h = 2 cm
b = 4 cm
h = 4
b = 6
h = 4
A = b × h
6 × 4 = 24 quadretti
h = 2 cm
b = 4 cm
Ripassa di la base e di l’altezza. Poi:
calcola l’area;
Ogni vale 1 cm2, ogni vale 1 cm
b = 4 cm
h = 2 cm
A = b × h
4 cm × 2 cm = 8 cm2
misura la base e l’altezza con un righello e calcola l’area.
b = cm
h = cm
b = cm
h = .................. cm
A = A =
Per calcolare l’area (A) del rombo moltiplica la lunghezza della diagonale maggiore (D) per la lunghezza della diagonale minore (d) e dividi per 2 il risultato.
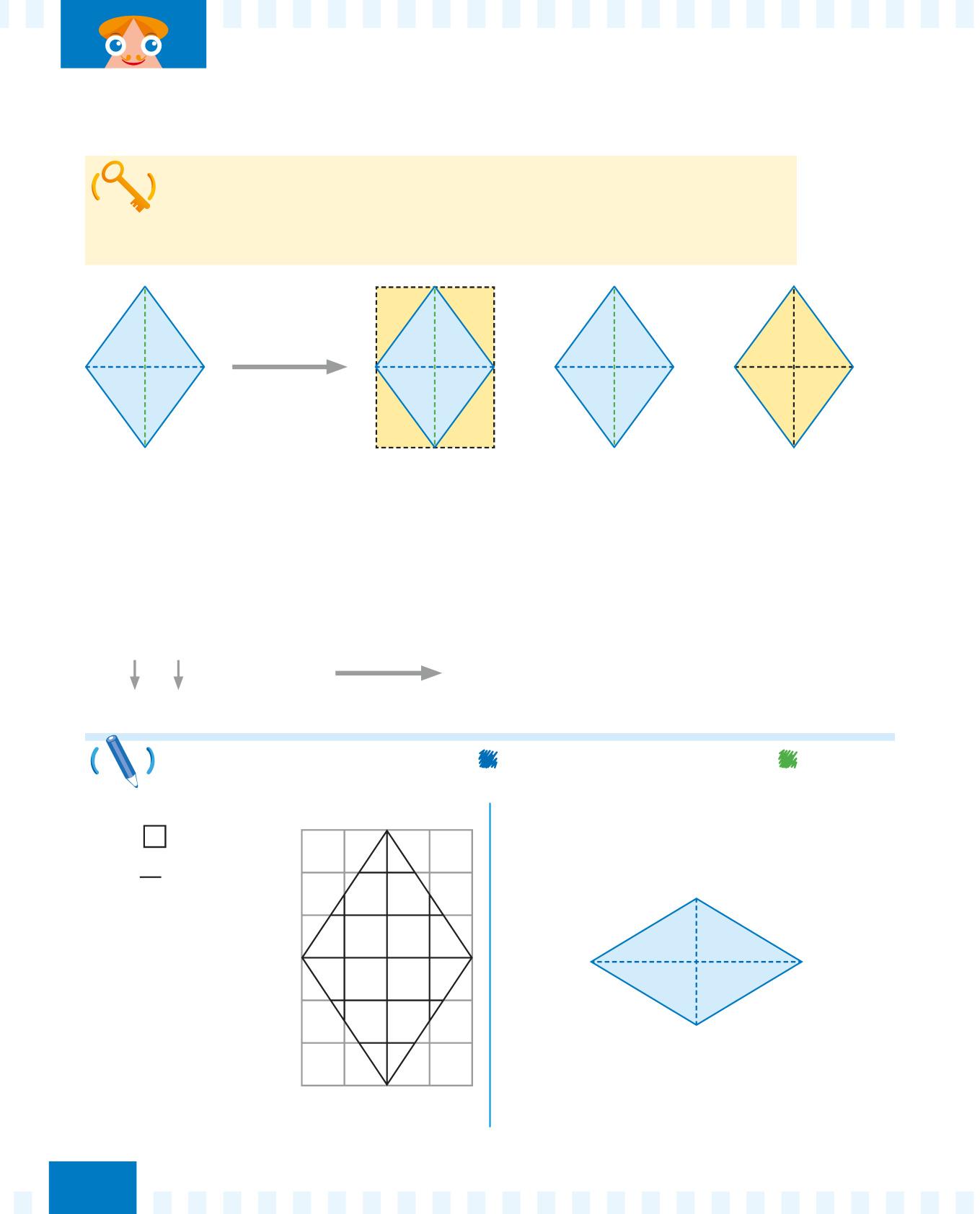
d = diagonale minore
D = diagonale maggiore
Ottieni la formula per calcolare l’area del rombo dalla formula dell’area del rettangolo diviso 2: il rombo è la metà del rettangolo!
Ripassa la diagonale minore di e la diagonale maggiore di . Poi:
calcola l’area; Ogni vale 1 cm2 , ogni vale 1 cm
misura la diagonale minore e la diagonale maggiore con un righello e calcola l’area.
d = cm D
Per calcolare l’area (A) di un triangolo, moltiplica la lunghezza della base (b) per la lunghezza dell’altezza (h) e dividi per 2 il risultato.
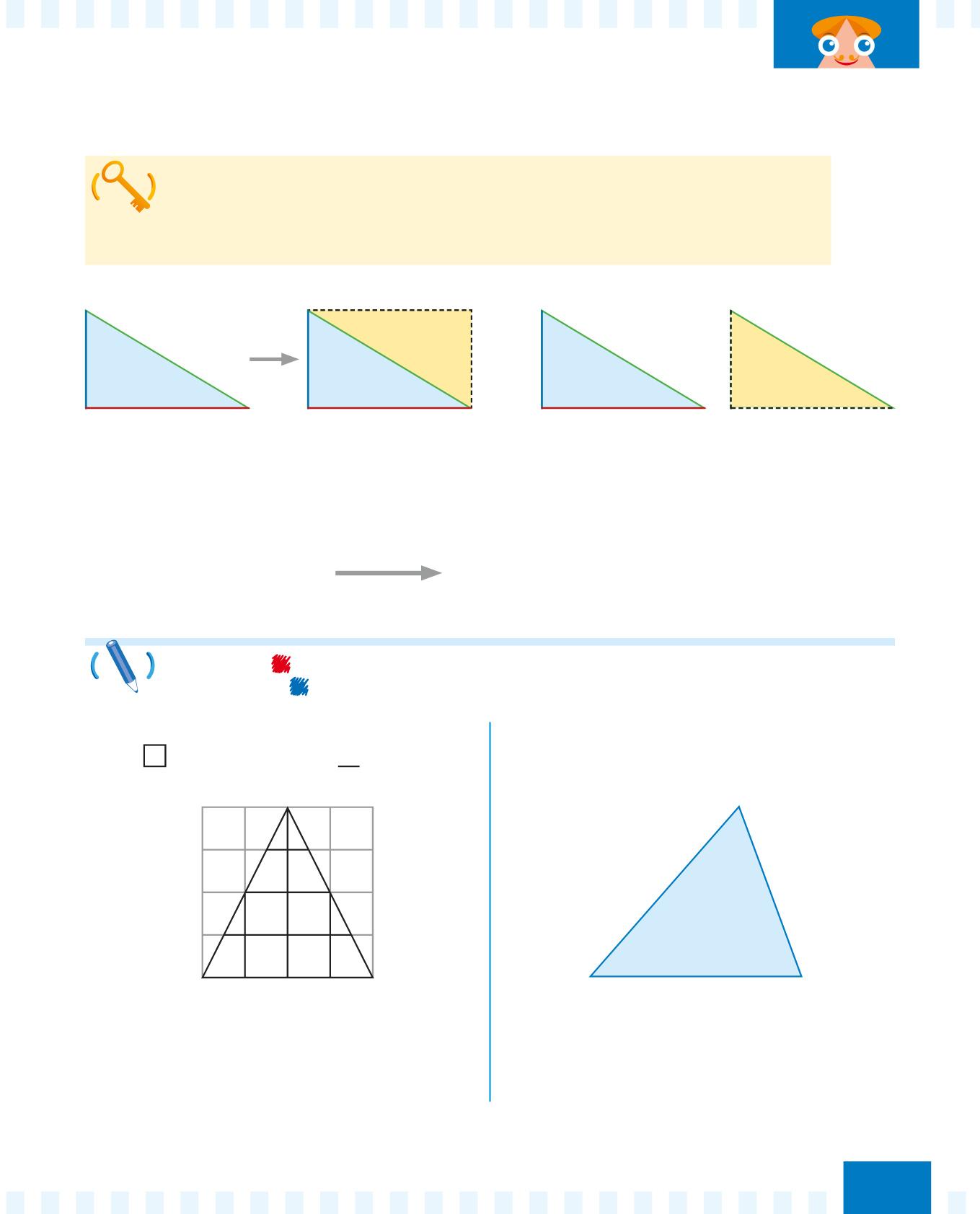
Ottieni la formula per calcolare l’area del triangolo dalla formula dell’area del rettangolo diviso 2: il triangolo è la metà del rettangolo!
A
Ripassa di la base e disegna l’altezza con una linea tratteggiata . Poi:
calcola l’area; Ogni vale 1 cm2, ogni vale 1 cm
misura la base e l’altezza con un righello e calcola l’area.
Per calcolare l’area (A) del trapezio somma le basi, poi moltiplica il risultato per la lunghezza dell’altezza e infine dividi per 2 il risultato.
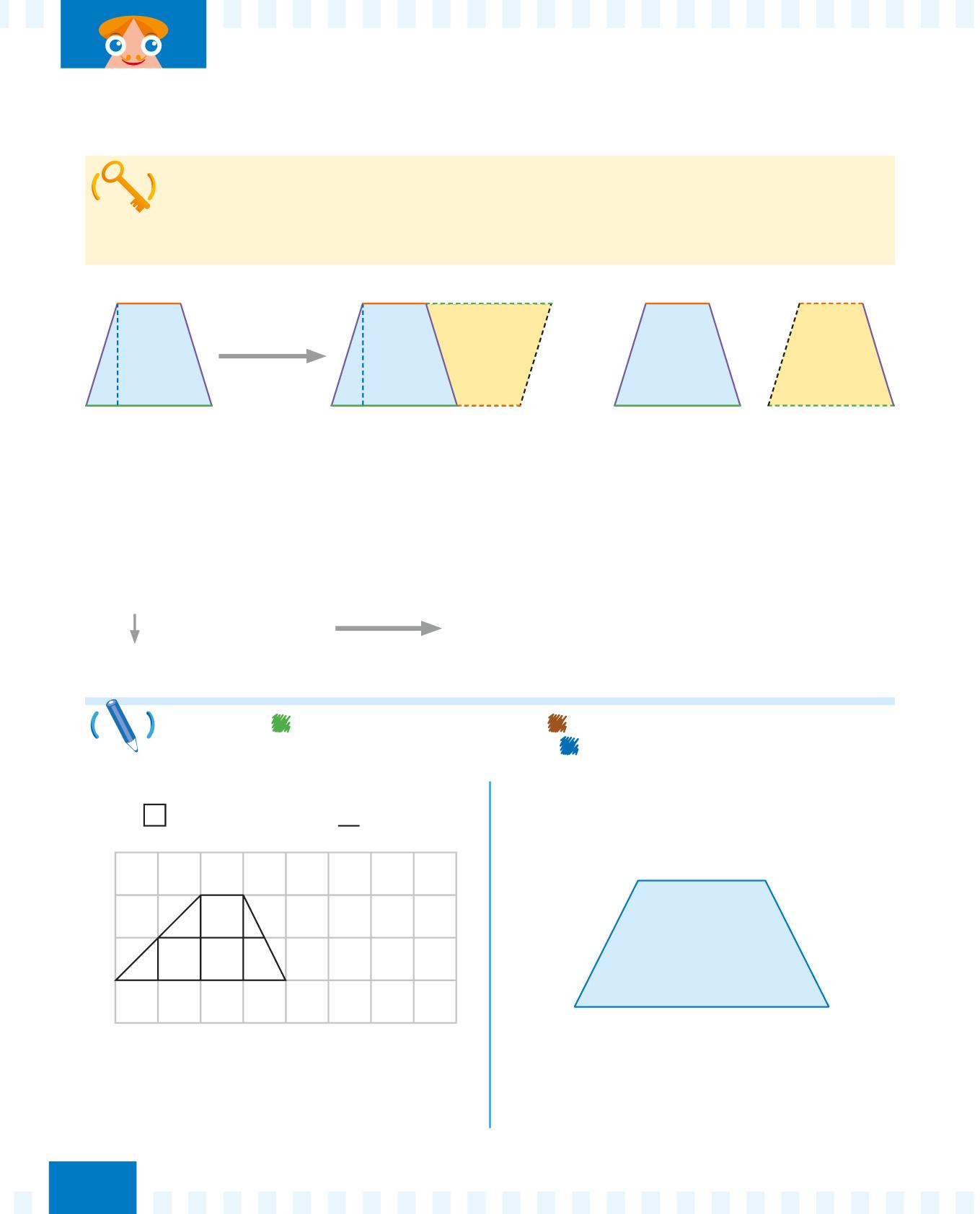
B = base maggiore b = base minore h = altezza
Ottieni la formula per calcolare l’area del trapezio dalla formula dell’area del romboide diviso 2: il trapezio è la metà del romboide! Area
Ripassa di la base maggiore (B), di la base minore (b) e disegna l’altezza (h) con una linea tratteggiata . Poi:
calcola l’area;
Ogni vale 1 cm2, ogni vale 1 cm
misura la base maggiore, la base minore e l’altezza con un righello, infine, calcola l’area.
QUADRATO RETTANGOLO
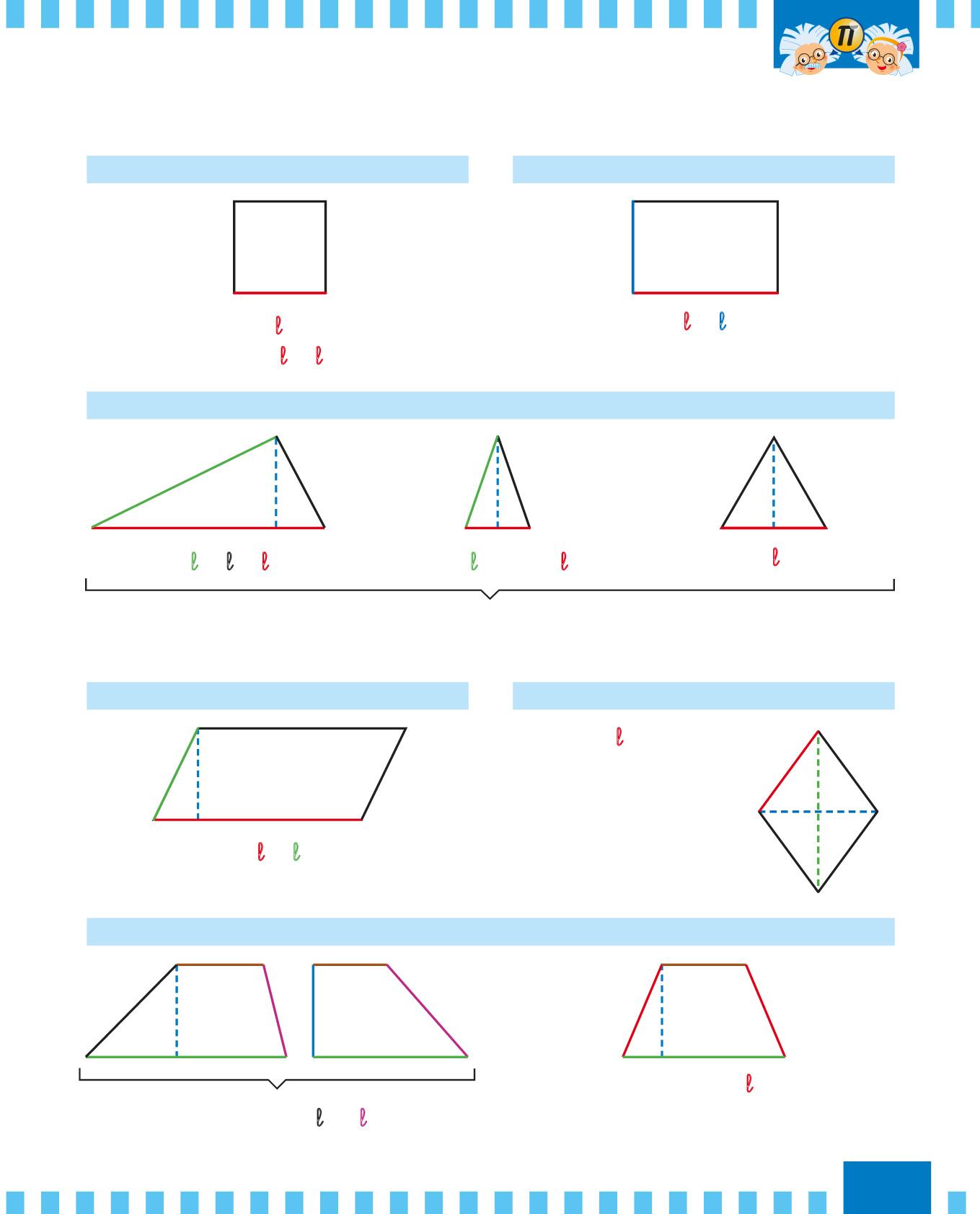
P
P = l × 4
A = l × l
P = (l + l) × 2
A = b × h
TRIANGOLO SCALENO, ISOSCELE, EQUILATERO
A = ( b × h ) : 2
ROMBOIDE ROMBO
P = l × 4
A = (d × D) : 2
P = (l + l) × 2
A = b × h
TRAPEZIO SCALENO, RETTANGOLO, ISOSCELE
P = B + b + l1 + l2
P = B + b + (l × 2)
A = [(B + b) × h] : 2
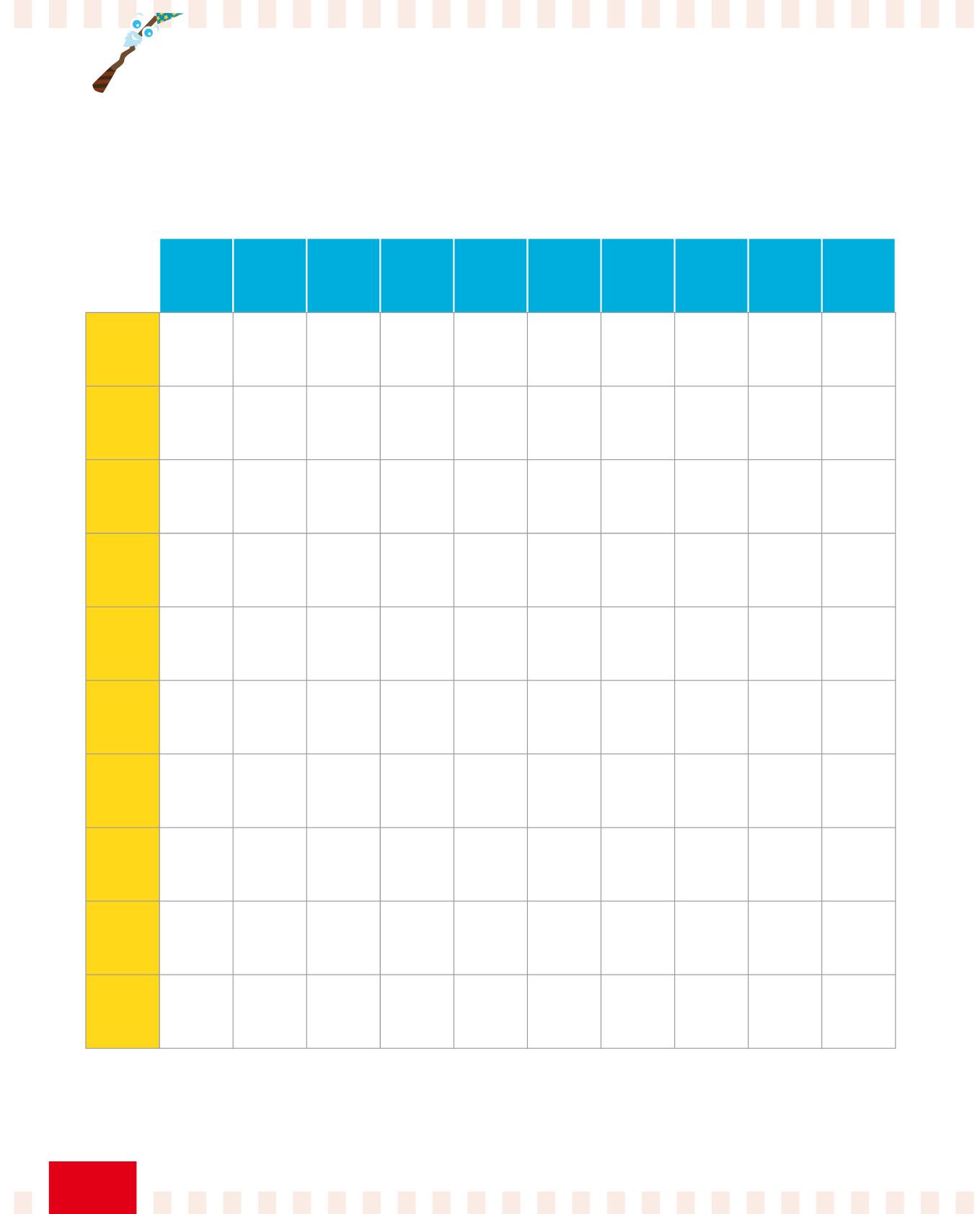



• Fotocopia e ritaglia le tabelle tratteggiate con le diverse unità di misura.
• Appoggia la tabella che ti serve per fare l’equivalenza nello spazio indicato qui sotto.
• Scrivi a matita il numero di partenza nel riquadro giallo corrispondente.
• Scrivi a matita il risultato dell’equivalenza nel riquadro arancione corrispondente.
Ricorda: per moltiplicare o dividere il numero della riga gialla segui le frecce.
Inserisci qui la tabella in base all’unità di misura che ti serve per fare l’equivalenza
chilometroettometrodecametro metro decimetrocentimetromillimetro km hm dam m dm cm mm
ettolitro decalitro litro decilitro centilitro millilitro hl dal l dl cl ml
megagrammo centinaia di kg decine di kg chilogrammo ettogrammodecagrammo grammo Mg kg hg dag g
chilogrammoettogrammodecagrammo grammo decigrammocentigrammomilligrammo kg hg dag g dg cg mg
Per le misure di lunghezza, capacità e peso:
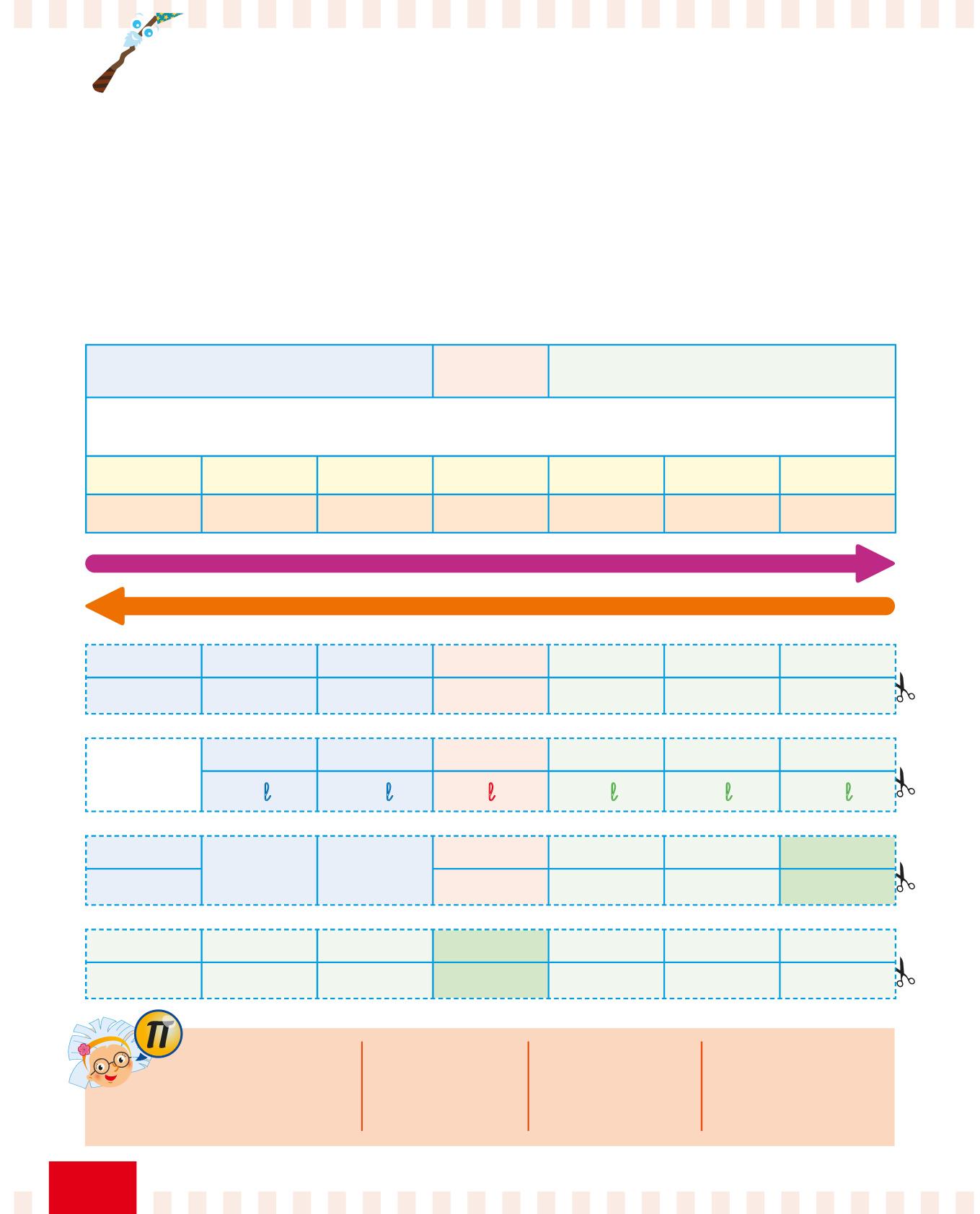
1 posizione = Moltiplica o dividi per 10 2 posizioni = Moltiplica o dividi per 100 3 posizioni = Moltiplica o dividi per 1000