Maths Plus NSW Student Book 6 Full Digital Sample

Harry O’Brien

NEW SOUTH WALES SYLLABUS

STUDENT BOOK

To the teacher

The Maths Plus NSW Syllabus/Australian Curriculum series, Year K to Year 6, is based on the NSW Education Standards Authority 2023 Mathematics K-6 Syllabus for the Australian Curriculum Mathematics (ACARA). Each book after Year K builds upon prior knowledge and works towards an understanding of the achievement standards for the relevant year level and beyond. Maths Plus provides students with opportunities to sequentially develop their skills and knowledge in the strands of the Australian Curriculum Mathematics: Number, Algebra, Measurement, Space, Statistics and Probability

Series components

Student Books

Work towards achieving the relevant outcomes by developing skills and competency in understanding mathematical structures, fluency, reasoning and problem solving.

Mentals and Homework Books

Provide concise, essential revision and consolidation activities that correspond with the concepts and units of work presented in the Student Books.

Assessment Books

Include short post-tests with a simple marking system to assess students’ skills and understanding of the concepts in the Student Books.

Student Book features

• All pages are colour coded.

Number and Algebra Measurement and Space Dictionary

Statistics and Probability

• Australian Curriculum Mathematics content descriptions, proficiency strand references and general capabilities appear on each page.

• The Dictionary (Years 2 to 6) features clear and simple explanations of mathematical terms and language.

DRAFT

Diagnostic term reviews

• Diagnostic term reviews (Years 1 to 6) assist in pinpointing students’ strengths and weaknesses, allowing intervention and re-teaching opportunities where required.

Find

Teacher Book and Teacher Dashboard

Provide access to a wealth of resources and support material:

• curricula and planning documents

• interactive teaching tools

• potential difficulties videos

• learning activities

• support and extension activities

• reflection

• blackline masters and investigation pages

• links to Advanced Primary Maths (Years 3 to 6)

• assessment tests

www.oxfordowl.com.au

MP_NSW_SB6_38350_TXT_4PP.indb 4 25-Aug-23 17:54:11

MEASUREMENT AND SPACE

NSW Syllabus Outcomes

MA3-RN-01

Applies an understanding of place value and the role of zero to represent the properties of numbers

MA3-RN-02

Compares and orders decimals up to 3 decimal places

MA3-RN-03

Determines percentages of quantities, and finds equivalent fractions and decimals for benchmark percentage values

MA3-AR-01

Selects and applies appropriate strategies to solve addition and subtraction problems

MA3-MR-01

Selects and applies appropriate strategies to solve multiplication and division problems

MA3-MR-02

Constructs and completes number sentences involving multiplicative relations, applying the order of operations to calculations

MA3-RQF-01

Compares and orders fractions with denominators of 2, 3, 4, 5, 6, 8 and 10

MA3-RQF-02

Determines

MA3-GM-01

of measures and quantities

Locates and describes points on a coordinate plane

MA3-GM-02

MEASUREMENT AND SPACE

Selects and uses the appropriate unit and device to measure lengths and distances including perimeters

MA3-GM-03

Measures and constructs angles, and identifies the relationships between angles on a straight line and angles at a point

MA3-2DS-01

Investigates and classifies two-dimensional shapes, including triangles and quadrilaterals based on their properties

MA3-2DS-02

Selects and uses the appropriate unit to calculate areas, including areas of rectangles

MA3-2DS-03

Combines, splits and rearranges shapes to determine the area of parallelograms and triangles

MA3-3DS-01

Visualises, sketches and constructs three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations

MA3-3DS-02

Selects and uses the appropriate unit to estimate, measure and calculate volumes and capacities

MA3-NSM-01

Selects and uses the appropriate unit and device to measure the masses of objects

MA3-NSM-02

Measures and compares duration, using 12- and 24-hour time and am and pm notation

MA3-DATA-01

Constructs graphs using many-to-one scales

MA3-DATA-02

Interprets data displays, including timelines and line graphs

MA3-CHAN-01

Conducts chance experiments and quantifies the probability

MAO-WM-01 Working mathematically

STATISTICS AND PROBABILITY

Develops understanding and fluency in mathematics through exploring and connecting mathematical concepts, choosing and applying mathematical techniques to solve problems, and communicating their thinking and reasoning coherently and clearly

STATISTICS AND PROBABILITY

MA3-DATA-01

MA3-DATA-02

MA3-CHAN-01

MAO-WM-01 Working mathematically

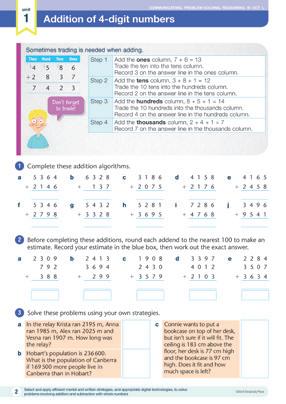
Addition of 4-digit numbers/estimation

Step 1 Add the ones column, 7 + 6 = 13

Trade the ten into the tens column. Record 3 on the answer line in the ones column.

Step 2 Add the tens column, 3 + 8 + 1 = 12

Trade the 10 tens into the hundreds column. Record 2 on the answer line in the tens column.

Step 3 Add the hundreds column, 8 + 5 + 1 = 14

Trade the 10 hundreds into the thousands column. Record 4 on the answer line in the hundreds column.

Step 4 Add the thousands column, 2 + 4 + 1 = 7

Record 7 on the answer line in the thousands column.

Complete these addition algorithms.

Before completing these additions, round each addend to the nearest 100 to make an estimate. Record your estimate in the blue box, then work out the exact answer.

Solve these problems using your own strategies.

a In the relay, Krista ran 2195 m, Anna ran 1985 m, Alex ran 2025 m and Vesna ran 1907 m. How long was the relay?

b Hobart’s population is 236 600. What is the population of Canberra if 169 500 more people live in Canberra than in Hobart?

c Connie wants to put a bookcase on top of her desk, but isn’t sure if it will fit. The ceiling is 183 cm above the floor, her desk is 77 cm high and the bookcase is 97 cm high. Does it fit and how much space is left?

Use your knowledge of number facts to answer these questions.

Multiply by 10, then halve to multiply by 5.

Use the ‘double, then double again’ strategy to multiply by 4. Or use the ‘double, double, double’ strategy to multiply by 8.

Round to the nearest 10 or 100 to make an estimate of these multiplications.

Measuring angles

An angle is the amount of turn between two arms around a common point (vertex). vertex arm arm amount of turn

There are 6 categories of angles measuring between 0° and a full rotation of 360°.

Acute angle Right angle Obtuse Straight Reflex angle Revolution angle (full turn) Between 90° Between 180° Between 360° 0° and 90° 90° and 180° 180° and 360°

Name each angle and then write its size in degrees. Remember that protractors can be read from both ends.

Use a protractor to measure and name each angle.

Longer distances are measured in kilometres. There are 1000 m in 1 kilometre.

DRAFT

km km km km

f Kedron km

g Coopers Plain km

h Hamilton km

i Mt Gravatt km

j Woolloongabba km

k Graceville km

Record these distances in kilometres using decimal notation. a 9154 metres = 9.154 km

Sheree keeps a log book of all her work trips. On the left is the odometer reading at the start of her day. Show the odometer reading at the end of the day if she made three trips.

Addition and subtraction strategies

Add these numbers mentally.

Give an estimate for each question by rounding each number. The first one has been done for you.

Subtract these numbers mentally.

7 Estimate first, then solve the problems mentally.

a Joseph had 155 sheep in one paddock and 38 sheep in another. How many sheep did he have altogether?

b Marina had 379 g of flour and 122 g of sugar. If she mixed them together, how much would the mixture weigh?

c Jessica had a collection of 156 hair clips but sold 39 of them. How many hair clips does she have left?

d Sai travelled 1106 km on Tuesday and 488 km on Wednesday. How far has he travelled altogether?

e Uncle Sam’s Car Sales had 173 vehicles in the lot. If 58 of them were damaged by hail, how many were not damaged?

Percentages, fractions and decimals

A percentage is another way of recording a fraction with a denominator of 100. Per cent means ‘out of 100’. A percentage sign % is used to display percentages. EXAMPLE 85 100 can be written as 85%.

Compares and order decimals up to 3 decimal places

Determine percentages of quantities, and find equivalent fractions and decimals for benchmark percentage values

Revising shapes 2

Name each shape, then record the number of sides and angles on each.

Which shapes above are parallelograms?

Draw an example of each shape. The 5 mm dot paper may help you.

What am I? I am not a square but I have 4 sides of equal length and my opposite angles are equal.

Investigate and classify two-dimensional shapes, including triangles and quadrilaterals based on their properties

Square centimetres and square metres 2

The formula used to calculate the area of a rectangle is Area = length × width. Width Length

Break these shapes into rectangles in order to work out their area. The first one has been done for you.

Selects and use the appropriate unit to calculate areas, including areas of rectangles

Subtracting 4-digit numbers/problems

Step 1 7 from 6 can’t do. Trade a 10 from the tens column. There are now 7 tens in the tens column and 16 ones in the ones column. 16 7 = 9

Record 9 on the answer line in the ones column.

Step 2 5 tens from 7 tens = 2 tens

Record 2 on the answer line in the tens column.

Step 3 9 hundreds from 4 hundreds can’t do. Trade 1000 from the thousands column.

There are now 5 thousands in the thousands column and 14 hundreds in the hundreds column. 14 9 = 5

Record 5 on the answer line in the hundreds column.

Step 4 2 thousands from 5 thousands = 3 thousands.

Record 3 on the answer line in the thousands column.

1 Complete each algorithm.

2 Fill in the empty boxes to complete these algorithms.

Trade the 2 hundreds left for 20 tens. Now share the 26 tens. Each school gets 5. 1 5 | 7 6 7 1 5 5 | 726 7 1 5 3r2 5 | 72617

Trade the 1 ten left over for 10 ones. Now share the 17 ones. Each school gets 3 and there is a remainder of 2.

a Which team won the game?

b What was the average score of each Wombat?

c What was the average score of each Galah?

d Which Wombats scored higher than the team average?

e Which Galahs scored less than the team average?

Create 4 different divisions that have a remainder of 2. 6 r2 r2 r2 r2 MP_NSW_SB6_38350_TXT_4PP.indb 11 25-Aug-23 17:54:22 DRAFT

Mr Cook did a survey to find out how children most commonly use technology, then recorded the data in the form of a picture graph.

KEY = 10 children

Technology use

Use the key to answer the questions.

a How many children answered Study?

b How many children answered Internet?

c How many children answered Messaging?

d How many more answered Internet than Study?

e What were the least common answers?

Games Study Messaging Internet Email

Ms Zhang’s class did a survey to find out the most common eye colour of senior students. They made a table of the data. Eye colours

Colour Tally

Blue

Green

Brown Hazel

7 8 9

Create a picture graph using the given key.

= 4 children

Answer the questions.

a Which eye colour was the most common?

b Which eye colour was the least common?

c How many more children had blue eyes than brown eyes?

Blue Green Brown Hazel

Explain how you could make this survey more reflective of the whole population of people in NSW.

Constructing angles

3

Use a protractor to construct the following acute, obtuse and right angles with the vertex on the left. •

acute angle 20°

acute angle 30°

right angle 90°

acute angle 25°

vertex

obtuse angle 160°

obtuse angle 120°

acute angle 60°

Use a protractor to construct the following angles with the vertex on the right. The first one has been done for you.

obtuse angle 170°

obtuse angle 110°

obtuse angle 130°

acute angle 80°

acute angle 20°

right angle 90°

Addition/distance by car 4

Use the chart below to calculate the distance between airports and the total distance of each journey. The first one has been done for you. Round numbers to 100 and check your answers by estimating the distances.

Mark 2 flights on the map. Colour one blue and the other red. Calculate the total distance of each flight. 3 Blue flight Red flight

6

Write the numbers represented on each abacus. Don’t forget ‘0’ as a place holder.

Draw beads on the abacuses to represent the numbers.

When we read numbers, we read them in groups of hundreds, tens and ones. The following chart best illustrates this concept.

Note: A space separates the millions, thousands and ones when the number is larger than 9999.

Write the numbers on the place value grid before adding the correct spaces to the number. The first one has been done for you.

b 32451

c 736041

d 5425006

e 7325400

f 76245236

Negative numbers

There are many instances in the real world where we need negative numbers. Negative numbers are numbers less than zero written with a minus sign (–) in front of them.

Estimate the distance between these points.

a The shipwreck and the octopus.

b The shipwreck and the hut.

Display how these problems can be calculated on a number line. The first one has been started for you.

=

Apply an understanding of place value and the role of zero to represent the properties of numbers

Classifying three-dimensional objects

Draw a line to match each net and three-dimensional object to its name.

Triangular pyramid

Hexagonal prism

Triangular prism

Rectangular prism

Square pyramid Cylinder

Classify the objects by stating the number of faces, edges and vertices on each.

Object Faces Edges Vertices

a Triangular pyramid

b Hexagonal prism

c Triangular prism

d Rectangular prism

e Square pyramid

What am I?

a I am made from 4 triangles, which are the same shape, and a square. I also have 5 vertices, 5 faces and 8 edges.

b I am made from 2 identical pentagons and 5 identical rectangles. I also have 15 edges, 10 vertices and 7 faces.

Vertex Edge Face

5 Revising multiplication/estimation

Doing multiplication

• 3 × 5 = 15 Write 5 in the ones column and trade the 10 ones for 1 ten. Put 1 in the tens column.

• 3 × 3 tens equals 9 tens, plus 1 ten equals 10 tens. Trade the 10 tens for 1 hundred. Write the 0 in the tens column and a 1 in the hundreds column.

• 3 × 6 hundreds equals 18 hundreds, plus 1 hundred equals 19 hundreds. Write the 9 in the hundreds column and the 1 in the thousands.

Complete these algorithms.

Round to the nearest 10 or 100 to estimate each question, then answer them.

Solve the problems.

a 807 people attended a tennis match. If they all paid $8 each, how much money was collected? $

b Maria bought a new phone. How much did it cost her if she paid a $100 deposit and made 8 monthly payments of $129? $

11:30

Decimals, percentages and fractions

Use your calculator to convert the fractions to decimals by dividing the numerator by the denominator. Once you have converted them to a decimal, write them as a percentage as well.

Write some fractions, then convert them to decimals then percentages with a calculator.

Courtney has 5 cards with 2D shapes drawn on them. She is going to put them in a bag and will get her friend to pick one out.

Predict the probability of each shape card being selected as her first pick. Record each probability as a fraction.

Experiment

a Make a set of cards like the ones above.

b Place your cards in a bag and make 20 draws using all 5 cards each time.

c Use tally marks ( IIII ) to record your results.

Explain how your experiment results compare with your predictions in Question 7.

Jimmy has bought 100 lollies for his party. They only came in 4 colours. He put his hand in his bag and pulled out the following sample of 10 lollies.

R Y B R B B R P B P

Use the sample above to estimate how many lollies of each colour could be in the bag of 100 lollies.

a red b blue c pink d yellow

If there were a bag of 500 lollies and Jimmy pulled out the same 10 lollies, how many of each colour do you estimate could be in the bag?

a red b blue c pink d yellow

Estimating mass

10 Estimate and then use calibrated scales or balance scales to measure the mass of each item. Estimate only one mass at a time.

h Did your estimates improve as you worked through the exercise?

11 Ten grams

Estimate first and then measure to see how many of each object are needed to balance 10 g.

How many of each item are needed to fill the boxes below?

2673

Division strategies/problems

Trade the 1 hundred left over for 10 tens. Now share the 17 tens. Each paddock gets 3 tens. 5 2673 5 3 5 26 1 73 5 3 4r3 5 261723

Trade the 2 tens left over for 20 ones. Now share the 23 ones. Each paddock gets 4 ones. There is a remainder of 3.

a 5 | 2 6 5 5 b 6 | 3 7 8 6 c 4 | 2 7 2 8 d 4 | 3 9 6 4 e 6 | 4 0 2 6 f 5 | 2 7 5 4 g 6 | 2 7 7 7 h 6 | 2 9 2 6 i 5 | 3 7 7 5 j 4 | 2 6 7 5

a 5 9 3 r 3 | 4 7 4 7 b 5 3 0 r 4 | 4 7 7 4 c 4 4 2 r 6 | 3 5 4 2 d 6 3 2 r 3 | 3 7 9 5 e 4 3 3 r 1 | 3 0 3 2 Music

Island Railway

e

Pop

Find a 4-digit number that can be divided by 2, 4 and 8, then complete the divisions. 4

MP_NSW_SB6_38350_TXT_4PP.indb 22 25-Aug-23 17:54:29 DRAFT

5 paddocks.

Number patterns

Follow the instructions to answer the questions. This machine makes 20 milk cartons every minute.

Minutes 1 2 3 4 5 6 7 Cartons 20

This bath fills at a rate of 15 litres every minute.

Minutes 1 2 3 4 5 6 7 Litres 15

This car travels 13 km on every litre of petrol.

Litres 1 2 3 4 5 6 7

Kilometres 13

Radio station Double Z plays 12 songs every hour.

Hours 1 2 3 4 5 6 7 Songs 12

a Complete the number pattern and record the rule.

b How many cartons would the machine make in 10 minutes?

c Complete the number pattern and record the rule.

d How many litres would be in the bath after 12 minutes?

e Complete the number pattern and record the rule.

f How far would the car travel on 15 L of petrol?

g Complete the number pattern and record the rule.

h How many songs would be played in 12 hours?

6 7

Number pattern

a Find the pattern in the table below, then complete it.

First number 1 2 3 4 5 6 7

Second number 18 45 63

b Describe the relationship between the first number and the second number.

c What would be the 10th term in the pattern?

Number pattern.

a Find the pattern in the table below, then complete it.

First number 11 12 13 14 15 16 17

Second number 24 26 29

b Describe the relationship between the first number and the second number.

c What would be the 10th term in the pattern?

Side-by-side column graphs

The Walters family is leaving soon on a world trip. They need to know what clothes to take, so they are looking very carefully at the temperatures of the cities they will visit.

Cities of the world: temperatures

Answer these questions.

a Which city has the highest maximum temperature?

b Which city has the lowest maximum temperature?

c Which city has the highest minimum temperature?

d Which city has the lowest minimum temperature?

DRAFT

e How many degrees hotter is Bangkok than Athens?

f How many degrees hotter is Athens than New York?

g Which city has the greatest difference in minimum and maximum temperatures?

h Which city has the smallest difference in minimum and maximum temperatures?

What is the difference between the minimum and maximum temperatures of these cities?

What is the average maximum temperature of Melbourne, Sydney and Darwin?

Which minimum temperature appears most often?

Which maximum temperature appears most often?

Constructs graphs using many-to-one scales

Melbourne Sydney Darwin Bangkok Athens

London New York

Tokyo Beijing

Complete the clockfaces for each digital time. The first one is done for you.

I think 30 days is equal to 720 hours.

Multiplication strategies/problems

Find the answers through multiplication.

a 1 2 of 18 pigs

b 1 4 of 20 marbles

c 1 5 of 35 pencils

d 1 10 of 100 cattle

e 1 10 of 70 children

f 1 4 of 32 dogs

g 1 8 of 32 lollies

1 10 of $20

1 8 of $40

1 5 of 25 ducks

1 6 of $42

1 7 of $63

1 8 of 72 cats

1 8 of 48 marbles

Use multiplication facts and your knowledge of place value to answer these questions. For example, 40 × 60 equals 4 tens × 6 tens, which equals 24 hundreds (2400). a

Mentally calculate the answers to these multiplications.

Use the skills you have learned above to solve these problems.

a One fifth of a group of 45 children were sick. How many children were sick?

b Muhammad saved $25 per week for 7 weeks. How much did he save?

c Sarah saved $50 per week for 70 weeks. How much did she save?

d Trent lost one seventh of his marbles. If he had 56 to start with, how many were lost?

e Oliver needed to construct some paddocks on a farm. He needed to make 40 fences with a length of 50 m each. How many metres of fencing would he need?

f Ruby collected an average of 76 shells every time she went to the beach. If Ruby visited the beach 6 times, how many shells would she collect?

Comparing fractions/equivalence

Shade the second fraction shape to be the same as the first shape.

What fraction of the octagon:

a is shaded yellow?

b is shaded green?

c is shaded blue?

Continue the equivalent fraction pattern.

Answer true or false.

9

This spinner is divided into 10 sections. Each section has a probability of 1 10 . Describe the probability of the spinner landing on the colour using fractions.

a blue 10

b green 10

c yellow 10

Frequency is the number of times an outcome occurs.

Joe made 100 spins on the spinner above and recorded the frequency of each colour occurring.

Blue Green Yellow Orange

Record the frequency of:

a blue

b green

Which colour matched its probability exactly?

Which colour exceeded its expected probability?

Did green exceed its expected probability?

DRAFT

c yellow

d orange

This spinner is divided into 20 sections. Each two sections add to make a probability of 1 10

Colour the spinner to reflect these probabilities.

a green 2 10

b blue 1 10

c red 3 10

d yellow 3 10

e orange 1 10

Colour the marbles in the bag.

a Two of the marbles are green.

b Red is twice as likely to be drawn out than green.

c Orange is only half as likely to be drawn out than green.

d Green and orange match the likelihood of pink.

Give the length in millimetres for each letter above.

a mm b mm c mm d mm e mm

Measure the length of each line to the nearest Nearest cm mm centimetre, then measure in millimetres.

19

Perimeter is the distance around the outside of a shape.

Draw the two sizes of photo that he is offering on the 5 mm dot paper. They may overlap.

Addition/checking using an inverse operation

Supply the missing numbers to complete the additions.

Complete these algorithms, then use the reverse operation to check your answers. The first one is done for you.

Solve the problems.

a Fiona went jewellery shopping and bought a bracelet for $1367, a pair of earrings for $800 and a necklace for $4500. What was the total amount of money she spent?

b Jack bought a new car for $19 990 but added air-conditioning for $1450, tinted windows for $499 and bluetooth for $450. What was the final cost of the new car?

Find the correct answer by substituting the given numbers into the number sentences.

Find the matching card to balance the scales.

Backyard cricket rules

Complete the equations to show how many runs each player scored in a game of backyard cricket.

Shortcuts can be used to find the perimeter of some polygons.

EXAMPLE The perimeter of a square with sides of 3 cm can be found by multiplying the sides by 4. (3 cm × 4 = 12 cm)

Rectangles with the same area do not always have the same perimeter. Draw 3 rectangles with an area of 24 cm2 to prove this.

Selects and uses the appropriate unit and device to measure lengths and distances including perimeters

Many to one scales/different data displays 8

Dot plots can show many-to-one correspondence. EXAMPLE = 10 students

High schools that 280 children will be attending

Key = 10 children

a Which school will have the most children attending?

b How many children will be attending Peechley High?

c How many children will be attending St Pat’s High?

d How many children will be attending Waratah College?

Use the supplied data to make the dot plot. Make sure you supply a scale for the key.

Division with fractional remainders/problems

Changing remainders into common fractions

A remainder can be written as a common fraction by dividing the remainder by the divisor. In this division the remainder of 1 is divided by 4 to become 1 4 .

Solve the problems.

a 748 centicubes were shared among 4 girls. How many centicubes did each girl receive?

b 975 leaflets were distributed to 5 selected streets. How many leaflets were delivered to each street?

c Sheree’s netball team scored 376 goals in 8 games. What was the average score for each game?

d Mark scored 630 runs in 10 innings. What was his average score?

Complete the number cross.

Improper fractions and mixed numerals

Improper fractions have numerators larger than their denominators.

EXAMPLE 5 4, 7 5, 9 4, 6 5, 10 9

A mixed numeral consists of a whole number and a fraction.

EXAMPLE 112, 214, 134, 245, 7 1 10

This diagram can be viewed as both 5 4 and 11 4

Write an improper fraction and a mixed number for each set of modelled shapes. Models

Use the number line to write an improper fraction for the mixed numerals.

Write a mixed numeral that has the same value as the improper fraction.

To convert an improper fraction to a mixed numeral, divide the numerator by the denominator.

Convert each improper fraction to a mixed numeral.

Grid references revision

Grid maps give the location of an area.

Give the grid references for the seat of each student.

a Tom

b Jim

Maria

Sally

Put a small tick on these seats. a A6

Solve these seating problems for the students.

a Is Jim the person closest to the front of the hall?

b Is Jane the person closest to the rear of the hall?

c Sally said her seat for the exam was 2A. Is this correct?

d Tom’s seat is marked by a diamond and his best friend is sitting 5 seats to his right. Put a cross on that seat.

e Maria’s seat is marked by a triangle. Her friend is sitting 3 rows behind her and 11 seats to her right. Put a cross on that seat.

f Harry’s seat is marked by a pentagon. He likes Susan who is sitting 7 rows behind him and 13 seats to his left. Put a cross on that seat.

g The school netball team booked seats F3 to N3. Shade these seats.

h Is it possible that Maria’s friend is in the netball team?

13 Testing conjectures

a Tom said that the most frequently occurring total when you roll 3 dice is 6. Do you agree?

b Predict the most likely score from rolling 3 dice.

c Roll 3 dice 60 times. Use tally marks to record the frequency of each score, then transfer this information onto a column graph.

d What was the most frequently occurring score?

e Explain why you would be more likely to throw a score of 11 than a score of 3.

f Write a fraction to describe the frequency of even numbers.

13

In Game of the Century you have to roll a double 6 before you start.

a Choose 6 teams to try to roll a double 6. Do a tally of the turns you take until you roll a double 6.

Team 1 Team 2 Team 3 Team 4 Team 5

b Is having to roll a double 6 a fair way to start a game?

Constructs graphs using many-to-one scales Conducts chance experiments and quantifies the probability

PART

Write the numbers represented on each abacus.

Draw beads on the abacuses to represent the numbers.

n If Tim’s average for 9 cricket games was 67 runs, what was his total score? runs

e 3580 people attended day one of the cricket match but only 2376 attended day two. How many more people attended on day one?

f John saved $234 in January, $437 in February and $567 in March. How much more does he need to save to buy a computer worth $1599?

PART

Complete the fraction, decimal and percentage table.

Complete the number patterns.

Complete the facts.

Draw a line to match each shape with its name.

Draw two rectangles with different dimensions that both have 16 cm perimeters.

a Which season was the most popular?

b Which season was least popular for children?

c How many people attended in spring?

d How many adults attended over the year?

e What was the total attendance over the year?

Geometric patterns

a Build the geometric pattern of triangles with matches, then sketch the next set of triangles in the sequence.

b Complete and extend the table to record the number of matches needed to make the pattern of triangles.

c In small groups discuss a rule to describe the number pattern formed by the triangles, then write it.

Matches 1 3 2 6 3 4 5 6 7

Triangles

a Build the pattern of pentagons with matches, then sketch the next set of pentagons. 2

b Complete and extend the table to record the number of sides needed to make the pattern of pentagons.

c Write a rule to describe the pattern.

d Use the rule to state how many matches would be needed for 15 triangles. Pentagons Sides

d How many sides would there be on 10 pentagons?

a Build the pattern of squares with matches, then sketch the next set of squares. 3

b Complete and extend the table to record the number of sides needed to make the pattern of squares.

c Write a rule to describe the pattern.

Squares Sides 1 4 2 3 4 5 6 7

d How many sides would there be on 12 squares?

10 Write a rule to describe the triangle pattern below.

Prime and composite numbers 10

Study the rules for divisibility to aid you in identifying factors.

÷ 2 The last digit is an even number.

÷ 3 The sum of the digits is a multiple of 3, for example 63: 6 + 3 = 9.

÷ 4 The last 2 digits are multiples of 4, for example 912.

÷ 5 The last digit is a 5 or a 0.

÷ 6 The last digit is an even number and the sum of the digits is a multiple of 3, for example 18: 1 + 8 = 9.

÷ 7 No rule.

÷ 8 The last 3 digits are multiples of 8, for example 5160

÷ 9 The sum of the digits is a multiple of 9, for example 54: 5 + 4 = 9.

÷ 10 The last digit is a 0.

Prime numbers are numbers that only have themselves and 1 as factors. Composite numbers are numbers with more than 2 factors.

Use these rules to identify the prime and composite numbers below.

Shade the numbers in the grid that are divisible by the given divisor.

297 is divisible by 9 because

+ 9 + 7 = 18, which is a multiple of 9.

Create 4 numbers of at least 3 digits that are divisible by 4. 8

Create 4 numbers of at least 3 digits that are divisible by 8. 9

Create 4 numbers of at least 3 digits that are divisible by 9. 10

Right-angle triangle Equilateral triangle Scalene triangle Isosceles triangle

Study the triangles above, then answer the questions.

a Which triangle above always has a right angle?

b Which triangle has 3 sides the same length and 3 angles the same size?

c Which triangle has two sides the same length and two angles the same size?

d Which triangle has no sides the same length, no angles the same size and does not contain a right angle?

Name each triangle then measure their angles. Remember that the total of all the angles in a triangle must add up to 180°.

Find the missing angle in each triangle.

and classify two-dimensional shapes, including triangles and quadrilaterals based on their properties

Area of triangles 10

Convert these triangles into rectangles that are double in area. Record the area of each shape in the grid. The first one has been done for you.

The area of a triangle is found by applying the formula:

Area = 1 2 base × perpendicular height

perpendicular height base DRAFT

Use the formula to calculate the area of the triangles.

Measures of quantities 11

A fraction strip from 0 to 1 is divided into fifths. Each strip is labelled 5 because there are 5 sections of 5 in 25. 1 5 of 25 = 5

Show how people voted if:

a 1 2 voted for the Elephant exhibit.

b 1 4 voted for the Giraffe exhibit.

c 1 6 voted for the Lion exhibit.

d 1 12 voted for another exhibit.

Solve the problems.

a Jack had a bag of 320 marbles but lost 1 8 of them through a hole in the bag.

How many did he lose?

b Tina had 240 trading cards but gave 1 6 of them away. How many did she give away?

c Soula had 420 trading cards. If she gave 1 4 to Alana how many would she have left?

d Tom had 100 toy soldiers but gave 1 4 of them away and sold 1 10 of them. How many did he have left?

ZOO

I scored 1 4 of our team’s 48 points. 48 ÷ 4 = 12

Chance from zero to one

Events that are certain to happen are given a probability of 1. Events that will never happen are given a probability of 0. Events that could happen are rated between 0 and 1.

Describe an event to match each likelihood.

Use the scale of 0 to 1 to rate the likelihood of green being the winning colour on these spinner wheels. The first one has been done for you.

Creating three-dimensional objects

Make skeletal models of these prisms and pyramids using toothpicks and modelling clay. a

When drawing three-dimensional objects we often use dotted lines to show the hidden edges. This allows us to view all the faces, edges and vertices of an object.

DRAFT

Visualise, sketch and construct three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations

Adding decimals/money problems

Decimal

Remember:

Solve the problems. (You will need some working paper.)

a Find the cost of the T-Shirt and a set of headphones. $

b Find the cost of a game, a skateboard and a calculator. $

c How much would 2 sets of headphones and a T-Shirt cost? $

d How much would 3 T-Shirts and a skateboard cost? $

e If Joseph had saved $151, would he have enough to buy a skateboard and a game?

f How much would 3 calculators and 2 sets of headphones cost? $

g How much would a calculator, a set of headphones and a game cost? $

h How much would one of each item cost altogether? $

Decimals, percentages and fractions

Colour the paper strips to represent the percentages. The dotted lines may help you.

Express these decimals as percentages.

Express these percentages as decimals.

Write decimals and then percentages for each fraction. You may need to use your calculator to divide the numerator by the denominator to find the decimal, which will then help you with the percentage (%). The first and last ones have been done for you.

Mr and Mrs Taylor and their children travel 400 km every year for their annual holidays.

a How long does the trip take them? hrs

b How far do they travel after 1 hour? km

c For how long do they stop on their way? hrs

d How far do they travel after 2 hours? km

e If they leave at 5 am, what time would they arrive at their destination?

f How far do they travel after 4 1 2 hours? km

g If they leave at 5 am, what would be the time after they have travelled 200 km?

h One year Mr and Mrs Wally and their children went on the same holiday. Plot, then draw their graph over the Taylors’ graph.

i Why was their trip much quicker?

Peta recorded the temperature every hour from noon to 7 pm.

Which graph represents Peta’s data?

The base unit for measuring small volumes is the cubic centimetre.

Select the unit

a How many large boxes can be packed neatly into the container?

b How many small boxes will fit into the container?

Operations with decimals/problems

Decimal point alignment

Remember: Always keep the decimal points in a vertical line.

2 10

9

12 3 4 8 5

1 11 2 10 6

a Find the cost of a set of headphones and a watch. $

b Find the cost of a game, a cricket bat and a baseball cap. $

c How much would 2 watches and a set of headphones cost? $

d How much would 3 sets of headphones and a cricket bat cost? $

e If Joseph had saved $151, would he have enough to buy a cricket bat and a game?

f How much would 3 baseball caps and 2 sets of headphones cost? $

g How much would headphones, a watch and a game cost? $

h How much would one of each item cost altogether? $

3 9

Phuong needs to cut some lengths of timber. She needs 4 pieces of timber measuring 1.2m each. Which length of timber should Phuong buy?

MP_NSW_SB6_38350_TXT_4PP.indb 52 25-Aug-23 17:54:56

Equivalent number sentences

Both sides of the equals sign have to give the same answer.

Create your own equivalent number sentences by placing numbers in the boxes and operation signs in the triangles. Test to see that your sentences work.

the number cross.

Constructing quadrilaterals 13

Construct a rectangle and a square from the given directions.

a Place a set square along line AB with the right angle on A.

b Draw a faint vertical line to form a 90° angle at A

c Repeat the procedure for B.

d Measure 6 cm up each vertical line and put in a dot.

Follow the directions and construct a square.

a Repeat the procedure above to create a 6 cm square.

b Draw in the diagonals.

c Are they the same length?

d How many lines of symmetry has a square?

e Join the dots and firm in the rectangle.

f Draw diagonals on your rectangle. (If both measure the same, you have constructed a true rectangle.)

g How many sets of parallel sides has a rectangle?

h How many lines of symmetry has a rectangle?

24-hour time/timetables/elapsed time

A security guard has to be at the destinations listed in the table at the given times. Write 24-hour times on his timetable to help him achieve his goal.

Answer the questions in 24-hour time.

a If he arrived at Petersham 9 minutes early, what time would it be?

b If he arrived at Brighton 12 minutes late, what time would it be?

c If he arrived at Penrith at the correct time and was there for 26 minutes, at what time would he be ready to leave?

8:06 pm Penrith

Many televisions use 24-hour time to record programs. TV guides are often written in 12-hour am/pm form.

Display the starting time and finishing time of each program in 24-hour time, as well as the duration of each program.

Complete the subtraction algorithms. In some cases you will have to fill in the empty boxes.

Solve the problems. Problems Working out

a A jar of jelly beans has a mass of 1.450 kg. If the jar’s mass is 245 g, what is the mass of the jelly beans?

b The distance between two towns was 10.95 km. The new road took 3.58 km off the trip. What is the distance between the towns now?

c 4800 L of water were stored in the tank. After irrigating the crop the level fell to 1358 L. How much water was used?

d Eight thousand, two hundred and forty-three people attended the concert. If 3950 were adults, how many children attended?

e The price of a television is $1056 and the price of a phone is $795. How much does Ms Kaur have to pay if she has already paid $185 as a deposit?

f On a full tank of petrol, our car travels an average of 440 km. The fuel gauge indicates I have used one quarter of a full tank. How many more kilometres can I travel before I need to refill?

g The total cost of Annabel’s holiday in Europe was $9376. How much did she spend on airfares if the total amount spent on other expenses was $5829?

Comparing and ordering fractions

Draw an arrow to match each fraction with its place on the number line.

Draw an arrow to match each fraction with its place on the number line.

Draw a line to show your estimate of where each fraction is located on the number line.

Order the fractions from smallest to largest.

Continue the counting sequences and write the rule in the box. The first rule is written for you.

Make up two counting sequences of your own that involve fractions.

Drawing objects from views

Sketch these common three-dimensional objects given their top, front and side views. Top view Front view Side view Sketch

DRAFT

Describe the similarities and differences between these two objects.

phoning a friend to find out!

Visualise, sketch and construct three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations

11 Find a suitable place in the playground and mark off a 10 m line. Count how many of your paces are needed to cover 10 m. paces Use this information to estimate these lengths before measuring them.

Length Estimate Metres

a The width of a netball court

b The length of a netball court

c The width of a school building

d The length of a school building

e The width of the playground

Measurement facts

10 millimetres = 1 centimetre 1000 millimetres = 1 metre

100 centimetres = 1 metre 1000 metres = 1 kilometre

DRAFT

Solve these comparison problems.

a What would be the perimeter of a square if its area was 25 cm2?

b A rectangle has a length of 9 cm and a perimeter of 27 cm. What would be its width?

c A rectangle is twice as long as it is wide. What is its perimeter if its area is 32 cm2?

15 4-digit × 1-digit multiplication/problems

Find the missing numbers in each multiplication.

The BMP office tower

• There are 8 floors.

• 1354 tiles were used on each floor.

• Each floor has 298 light fittings.

• Each floor has a carpeted area of 284 m2

• The average rent for each floor is $1769.

Use the information above to solve the problems.

a How many light fittings are there in the whole building?

b How many square metres of carpet are there in the whole building?

• The cost of carpet is $100 per m2 Write a problem to suit the multiplication, then solve it.

c How many tiles were used on floors 3, 4, 5 and 6?

d What is the rent for the whole building?

Use two different colours to add the fractions on the diagrams, then record your answers below as an improper fraction and a mixed numeral. The first one is done for you.

How many questions can you write that have an answer of 1 5 10 ? 8

Potentially misleading data

The following data may be misleading when you look at the source of the data (where it is collected).

(90 out of 100 children interviewed at a children's book shop said that they read every night.)

Study both graphs about the Australasian Mining Company

Weekly prices (July first week)

(AMC).

10 A B

Half-yearly prices

Mon Tues Wed Thurs Fri

Huge rise in the price of AMC shares!

Jan Feb Mar Apr May June

Market unsure on AMC shares!

a Which graph and statement could be viewed as misleading?

b Explain why.

Parallelograms can be rearranged to form rectangles (parallelograms). The formula for the area of a parallelogram is Area

base × height.

1 Find the area of the triangles a and b below by creating parallelograms around them. An example has been given. Calculate the area of the triangles by halving the area of the surrounding parallelograms with the same bases and heights.

234 x 23 is the same as 234 x 3 plus 234 x 20.

Calculate how much money each worker would save.

a How much would Spiro save in 12 weeks if he saved $272 each week?

c How much would Maria save in 46 weeks if she saved $354 each week?

b Billy saved $453 each week for 15 weeks. What were his total savings?

d Jean saved $368 each week for 27 weeks. What were her total savings?

Expanding numbers

Expand the numbers. The first one is done for you.

a 227 386 200 000 + 20 000 + 7000 + 300 + 80 + 6

b 576 491 + + + + +

c 963 237 + + + + +

d 425 310 + + + +

e 240 300 + +

f 780 407 + + +

g 6 029 256 + + + + +

Write the numbers in words.

a 356 257

b 479 807

c 906 007

d 4 274 300

e 27 360 027

Phone numbers. Grid A Grid B

a Look online to find the phone numbers of seven businesses in your area. Write them in Grid A.

b Order the phone numbers from smallest to largest in Grid B.

11:30

Write the number.

a I am a number that has a 6 in the tens of thousands place, a 7 in the hundreds of thousands and a 4 in the thousands. My last three digits are 319.

What am I?

b I am a number that has a 7 in the millions place, a 4 in the thousands place, a 6 in the tens, a 3 in the tens of thousands and a 9 in the ones. The other places have zeros.

What am I?

Mass experiments

Experiment 1 — What is the mass of 1 litre of water?

Materials

• Kitchen scales

• Jug

• Litre of water

Follow the instructions.

a Place the empty jug on the scales and measure its mass.

b Fill the jug with 1 litre of water and measure its mass.

c Subtract the mass of the jug.

d Result: One litre of water has a mass of kilogram.

Experiment 2 — What is the mass of 1 millilitre of water?

Materials

• Plastic bottle

• Water

• Balance scales

Follow the instructions.

a Measure the mass of the empty plastic bottle.

b Pour 50 mL of water into the bottle and record the mass.

c Calculate the mass of the water by subtracting the mass of the bottle.

d Repeat this for 100 mL, 250 mL, 500 mL. Record your results in the chart.

Quantity 50 mL 100 mL 250 mL 500 mL

Mass g g g g

Result: One millilitre of water has a mass of gram.

15

11

Research at home or at school to find the mass of containers holding these volumes of liquids.

Volume of liquid

a 2 L bottle of orange juice

b 1.25 L bottle of lemonade

Selects and uses the appropriate unit and device to measure the masses of objects

Mass

What is line symmetry?

A shape has line symmetry if both of its parts match when it is folded along a line.

DRAFT

What is rotational symmetry?

A shape has rotational symmetry if, after the shape is turned around its centre point, it matches the original shape more than once through a full rotation.

Colour all the shapes that have rotational symmetry. You may need to trace the shapes

Order of operations 17

Add and subtract fractions 17

Show how these fractions can be added or subtracted on the number lines supplied.

Add or subtract these fractions. The first one is done for you.

Common fractions have denominators that are the same.

Converting improper fractions to mixed numbers When adding fractions we often obtain an answer that is greater than 1. In such cases the answer is first given as an improper fraction and then converted to a mixed numeral by dividing its numerator by its denominator.

Add the fractions, then convert the improper fraction answers to a mixed number. The number line may help you. The first one is done for you.

Add the fractions to get an improper fraction, then convert it to a mixed number. The first one is done for you.

Describing chance 17

Draw a line to display the chance on the scale of 0 to 1 of each colour being drawn from the bag.

a Red

b Blue

c Yellow

d Green

Draw a line to display the chance on a scale of 0% to 100% of each of 100 ships leaving Australia for its destination.

Write simple statements to describe the chance of these things happening. You may use fractions, percentages, decimals or descriptive terms like those in the box below. even chance fifty-fifty unlikely likely impossible certain one in two 1 10 1 4 50% 0.7 less likely more likely one in four 100%

a A dice is rolled and lands on the number 4.

b Three dice are rolled and each lands on the number 6.

c A baby is born a male.

d A wheel of 100 numbers is spun and lands on 3.

e The Sydney Swans win the premiership.

f Your class never has to do homework.

g The next person entering the room has blue eyes.

h A dice lands on a multiple of 3.

Construct and draw 3D objects

Construct the objects from centicubes, then draw the top, front and side views of each.

Top view Front view Side view

Use construction cubes to construct the 3D objects from their given views.

Jack made a prism that used 36 cubes Create 2 more rectangular prisms using in its construction. 36 cubes and record their dimensions below.

Its dimensions were:

length 6 cubes

width 2 cubes

height 3 cubes

Visualise, sketch and construct three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations

Answer the questions on bank transactions.

Mr and Mrs Snake run a debit card account to pay their bills. The bank issues a monthly statement so the Snakes can check that their deposits and debits have been correctly recorded.

a How much was in the account at the start of the month?

b Where was the purchase made on 3/6?

c How much was deducted for Mr and Mrs Snake’s home loan?

d What was the balance on 10/6?

e What was the total amount of deposits for the month up to 15/6?

f What is Mr and Mrs Snake’s account number?

Complete more transactions.

Mr and Mrs Snake had four more transactions in June that will need to be added to the above statement in the spaces provided for you.

Don’t forget to write the purchase item, complete the debit column and deduct each transaction from the balance.

The Snakes paid the following bills: electricity $74.00 on 17/6, dance class $12 on 21/6, school camp $25 on 28/6 and gas $23.80 on 29/6.

Answer the questions.

a What was the final balance for the month? $

b Do you think this amount will be carried forward to next month’s statement?

c What other ways are there of paying for items other than by card?

Making a pattern of triangles.

Making a pattern of houses.

a Complete and extend the table to record the number of sides needed to make the pattern of triangles.

a Complete and extend the table to record the number of sides needed to make the pattern of houses.

b Write a rule to describe the pattern.

b Write a rule to describe the pattern.

Follow the rules to find the outputs of the function machines.

Write a rule for each function machine.

acute angle obtuse angle right angle straight angle reflex angle

8

What types of angles are used in:

a Tessellation A c Tessellation C

b Tessellation B

Angles on a straight line add up to 180˚. Angles that combine over a full rotation, such as intersecting lines, total 360˚.

Intersecting lines

When two or more lines cross each other we call them intersecting lines. Vertically opposite angles on sets of intersecting lines are equal to each other.

EXAMPLE Angle A = Angle C

Measure and construct angles, and identify the relationships between angles on a straight line and angles

Volume and capacity

Experiment 1

Todd made a model out of centicubes that had a volume of 50 cm3. His teacher asked him to find how many millilitres of water his model would displace. Conduct this experiment then colour the new liquid level on the beaker.

Complete the facts.

a 1 mL of water has a volume of cm3

b 1 cm3 displaces mL of water.

Experiment 2

How much water will a 10 cm × 10 cm cube displace?

Materials

• Tote tray

• Saucepan

• Base 10 cube

• Measuring jug

Follow the instructions.

a Place the saucepan in the tote tray and fill it carefully to the brim with water, without spilling any in the tote tray.

b Submerge the Base 10 cube in the water.

c Pour the overflow from the tote tray into the measuring jug.

d Colour the jug to show how much water you gathered.

e Result: A cube 10 cm × 10 cm × 10 cm (1000 cm3) displaces litre of water.

How many millilitres of water would be displaced by centicube models of these volumes?

Use decimal notation to record the following capacities in litres, e.g. 3758 mL = 3.758 L.

a Draw a line to estimate the place of each mixed numeral on the number line.

Write ‘prime’ or ‘composite’ next to each number.

If 0 is impossible and 1 is certain, what is the probability of this spinner landing on red? Put a cross on the scale to show your answer.

Add or subtract the fractions. b 3 8 + 2 8 = g 3 5 + 3 5 = = c

=

Colour the strips to match the labels.

75% 60%

Draw a line to name the triangles.

a Equilateral triangle

b Scalene triangle

c Isosceles triangle

d Tick the shapes that have rotational symmetry.

Calculate the volume of these cubes built from centicubes (1 cm cubes).

Use a protractor to measure the angles.

c Colour the shape with the larger volume.

Use your knowledge that parallelograms can be rearranged into rectangles to calculate the area of this parallelogram.

Convert these measurements to another unit, as marked.

a 7 cm = mm e 80 mm = cm

b 10 cm = mm f 3 m = cm

c 18 cm = mm g 800 cm = m

d 60 mm = cm h 3 1 2 km = m

a What was the temperature at 6 am?

b What was the temperature at 10 am?

c Approximately what was the temperature at 8 am?

Dividing 5-digit numbers/problems 19

Use your division skills to divide these. Record any remainders as a fraction.

Solve the problems.

a The team scored 564 runs in 6 innings. What is the average number of runs per innings?

b Divide 258 m2 of land into 6 equal paddocks.

c 3600 mL of water was poured into 8 jugs of equal size. How much water in each jug?

d How many scouts attended the camp if 1 4 of the 3000 scouts were there?

e Divide 5648 km into 8 equal sections.

Crack the secret code by substituting the division answers for the letters and writing them in the numbered grid below. You may use your calculator.

Percentages

Finding

10% of $20 can be looked upon as 1 10 of $20, which equals $2.

DRAFT

During the netball tournament the following data was recorded. Calculate the number of goals each player scored. The first one has been done for you.

Answer the questions.

a Who scored the most goals?

b Who scored the least goals?

c How many goals do you think Lara would score if she had 100 shots?

8

Use decimal notation to convert each measurement to a new unit, e.g. 75 mm = 7.5 cm.

a 55 mm = cm

b 87 mm

c 99 mm = cm

d 125 mm = cm

e 156 cm = m

1600 m = km

Write these kilometre measurements as metres.

a 1 km and 237 m = m b 2 km and 307 m = m

Write each of these measurements as centimetres e.g. 2 m = 200 cm.

a 40 mm = cm d 10 m = cm

b 120 mm = cm

c 1.5 m = cm

Rectangles with same perimeter

100 m = cm

1 km = cm

Many rectangles have the same perimeter. The orange rectangle below is just one rectangle that has a perimeter of 32 cm. Use the 1 cm grid paper below to draw at least 5 more, they may overlap. (A square is also a rectangle.)

Greg has a large delivery van but it has a 2-tonne limit on its load capacity.

How many of each item below would he be able to pack into his van?

Square numbers 20

Square numbers are numbers that can be arranged in the shape of a square array. They are equal to a number multiplied by itself.

Sally said I could predict the next square number because square numbers go up in a pattern of odd numbers.

a Use the pattern below to find the next square number after 16.

b Use the pattern to complete the square numbers to 100.

Use a calculator to square these numbers:

Dividing by tens and finding averages

Divide first by multiples of 10 using the mental strategy outlined by the boy below.

Finding averages

Averages are found by totalling the scores, then dividing by the number of scores.

The average of 20, 30 and 40 equals (20 + 30 + 40) divided by 3 = 30.

What was the average time spent on homework by each child if the 30 children in Mr Wilson’s class took a total of 750 minutes to complete their homework?

c Over 40 games the Lions had scored 960 points. What was their average score per game?

How many groups of numbers can you make that have an average of 20?

Reflect each shape. a b c

Translate = slide

Rotate = turn

Reflect = flip

Translate each shape as directed.

a To the right

b To the left

c Directly above

d Directly below

DRAFT

Rotate each shape clockwise around 360°. The first one has been started for you.

Explain the movements needed to construct this pattern.

Investigate and classify two-dimensional shapes, including triangles and quadrilaterals based on their properties

How sector graphs are used Sector graphs are circular graphs used to show how a total is divided.

around the circle with chalk, and then mark off and label the sectors according to hair colour.

b On the blank sector graph, record the graph you made in the playground, labelling all the sectors and fractional parts.

Population of states and territories

(For this exercise, Australia’s population has been rounded to 25 000 000.)

a Which two states have the largest populations?

b Which territory has the smallest population?

c Which state and territory are reasonably close in population?

d Do you think that NSW has a population of over 5 000 000?

e What would you estimate Queensland’s population to be?

21 Extended multiplication

1 Complete these extended multiplications. The first one has been done for you. Why does the 2nd line of each algorithm always have zero in the ones column?

Solve the problem.

Ms Hassan bought 7 digital television sets to sell in her shop. If she paid $789 each for them and sold them for $1000 each, how much profit did she make?

Solve the number cross. You may need a calculator.

Subtracting fractions from whole numbers

Fractions can be subtracted from whole numbers.

EXAMPLE Jad had a chocolate bar and gave away 1 3 of it.

Use the diagrams to help you subtract the fractions from one whole.

Fractions can be subtracted from more than one whole number.

EXAMPLE Alexis had 2 pizzas and gave away 1 4 of one.

Subtract the fractions.

Look at the diagram below to see how the mixed numerals were added.

Add or subtract these mixed numerals.

Computer graph making

Forty children in Year 6 were surveyed and their results tabled.

Create a side-by-side column graph of the hair colour data. It has been started for you.

Straight Curly

Computer software graphing

Create a graph using basic software, such as word processing software. The temperature data you will need is below.

City Lowest Highest Perth 14° 32° Melbourne 8° 16° Canberra 4° 14°

Sydney 13° 23° Brisbane 15° 28°

If you enter this data in the chart correctly, the graph you make should look like the one below.

You will need to enter your data on a table that could look like this.

B C D 1 Lowest Highest

14 32

8

Decimal time units/elapsed time 21

Use bridging to solve the problems. E.g. 4.15 pm plus 2 hours and 15 minutes – think 4.15 + 2 hours = 6.15 pm + 15 minutes = 6.30 pm.

a 7:15 am add 2 hours and 20 minutes

b 2:10 pm add 3 hours and 5 minutes

c 3:05 pm add 5 hours and 12 minutes

d 3:30 am add 10 hours and 30 minutes

e 11:30 am subtract 1 hour and 15 minutes

f 1330 add 3 hours and 22 minutes

g 1810 subtract 4 hours and 7 minutes

1.35 pm plus 2 hours and 15 minutes = 3.50 pm

15 minutes = 0.25 hr (1 4 hr) 30 minutes = 0.5 hr (1 2 hr) 45 minutes = 0.75 hr (3 4 hr)

Use the information in the green box above to write each time in decimals

a 2 hours and 15 minutes _____ hr

b 4 hours and 30 minutes _____ hr

DRAFT

c Five hours and 45 minutes _____ hr

d Twelve hours and 15 minutes _____ hr

Calculate the work time from start to finish for these occupations.

The armed forces often use 24-hour time when conducting their exercises. Calculate the amount of time each person spent on these activities.

a Private Smee went on manoeuvres at 2200 and finished them at 0830. How long did the manoeuvres take?

b Captain Zero started flying at 1600 and finished his journey at 0515. How long did the flight take?

c Captain Hook took the RAN Commander on a short cruise that started at 1105 and finished at 1345. How long did it take?

Captain! Take me back please, I’m seasick again.

Making a pattern of hexagons

Making a pattern of decagons

a Complete and extend the table to record the number of sides needed to make the pattern of hexagons.

Hexagons 1 2 3 4 5 6 7

Sides

b Write a rule to describe the pattern.

c How many sides would there be on 9 hexagons?

Making a pattern of octagons

a Complete and extend the table to record the number of sides needed to make the pattern of octagons.

Octagons 1 2 3 4 5 6 7

Sides

b Write a rule to describe the pattern.

a Complete and extend the table to record the number of sides needed to make the pattern of decagons.

Decagons 1 2 3 4 5 6 7

Sides

b Write a rule to describe the pattern.

c How many sides would there be on 15 decagons?

Making a pattern of dodecagons

a Complete and extend the table to record the number of sides needed to make the pattern of dodecagons.

Dodecagons 1 2 3 4 5 6 7

Sides

b Write a rule to describe the pattern.

c How many sides would there be on 11 octagons?

c How many sides would there be on 10 dodecagons?

Make up a table of your own based on any shape below.

Shapes 1 2 3 4 5 6 7

Sides

Comparing fractions/equivalent fractions

Equivalent fractions can be made using overlays of congruent shapes. The example below shows a clear plastic overlay and a model of the fraction 2 3 . When the overlay is put on top of the model 2 3 becomes 4 6 .

Overlay Model 2 3 Model of 2 3 with overlay on top

Draw and record the fraction formed when the overlay is placed over the model.

We can make equivalent fractions by multiplying the numerator and the denominator by the same number.

Make equivalent fractions for the ones given. The first one has been done for you.

Coordinates are used to locate position on a number plane.

The order of the numbers is very important.

The first number is the reading on the x-axis

The second number is the reading on the y-axis

The number plane shows 3 points:

Plot the coordinates, then connect them to form angles.

(6,1) (8,1) (8,3)

Draw two more angles on the number plane and list their coordinates below.

Data presented in graphs and charts can be misleading. It may be true but its appearance may give a false impression.

Compare the two graphs to see if the statements are true or false. True or false

a Graph A gives the impression that membership has increased considerably over 10 years.

b Graph B shows the same data but the increase appears less significant.

c Graph A indicates that gym membership is full.

Shannon noticed two articles about computers in the newspaper. Use all the information to answer the questions below.

The manager of Switched on Computers said he has never seen prices so low: ‘This graph shows that prices are falling rapidly’.

a By how much did the price actually fall in six months?

b Explain why this graph would not accurately represent the price of all computers.

c Explain why the word ‘tumble’ is misleading.

Yobisha Deletes XL5100

Ms Kim Kyoo of Yobisha

Computers recently announced that the XL5100 computer would no longer be produced, as it is being replaced by the XL6100.

Challenge: Search newspapers, magazines or other media sources to find examples of misleading data. Explain your reasons for describing it as misleading.

When multiplying a decimal by a whole number there will be the same number of digits after the decimal point in the answer as in the decimal being multiplied.

Decimals can be rounded to the nearest whole number to give fairly accurate estimates. The greater than > and less than < symbols can also be used to make estimates even more accurate.

EXAMPLE 2.704 × 8 I’ll round up to give 3 × 8 = 24. Because I rounded up, my estimate will be a bit too big. I’ll record my estimate as < 24

c 3 loaves of bread and 2 L of milk

d 5 Kolas, 3 packets of biscuits and a loaf of bread

e 1 jar of honey, 3 Kolas, 2 milks and 2 boxes of chocolates

f 7 loaves of bread, 7 L of milk and 3 packets of biscuits

4

Sarah spent between $26 and $29 on two of the grocery items above. If she bought 7 of one item and 9 of another item, what items could she have bought?

1L

Biscuits

Kola Bread

Comparing fractions/equivalent fractions

Equivalent fractions have the same value, for

Write an equivalent fraction for each.

Write true or false beside each set of fractions.

Making equivalent fractions

We can make equivalent fractions by multiplying the numerator and denominator by the same number. For example 2 3 × 3 3 = 6 9

9 10 11

Quadrilaterals are shapes that have 4 straight sides. There are many types of quadrilaterals and some have special names.

DRAFT

Place a tick on all quadrilaterals above that are also parallelograms.

Do all quadrilaterals have to have a set of parallel sides?

Sketch 3 parallelograms below.

Investigate and classify two-dimensional shapes, including triangles and quadrilaterals based on their properties

Give the coordinate points of the houses of the children marked on the map.

Put a cross for these coordinates on the map.

Use the scale to calculate the shortest distance by road from:

Use the scale, coordinates and compass directions to find the secret destination on the map.

a Start at coordinates (10,4) then head east for 100 m.

b Turn north and travel another 100 m before heading west for another 50 m.

c Follow Book Rd north until you find Main St then turn left and follow Main St until you find a bridge.

d Head north across the bridge and along Joker Rd until it meets Mall Rd.

e Head east 600 m, then turn left and proceed another 150 m.

f Turn east and travel 150 m to find the secret destination.

g What is the secret destination?

Dividing large numbers/problems

Use your division skills to divide these large numbers.

Mental strategies can be used to estimate the quotient when dividing by 9 and 5. Some strategies are:

÷ 9 Round the number up and then divide by 10.

÷ 5 Round the number, divide by 10, then double.

Use any mental strategy you wish to give the approximate answer to these divisions.

Using a calculator to divide Larger divisions with divisors larger than 10 can be done with

Use your calculator to answer these divisions.

Use your calculator or other methods to solve these problems.

a A train travels 636 km and stops at 12 stations. What is the average distance between stops?

b Redleaf Soccer Association received $1365 in fees from the 21 teams in the competition. How much did each team pay?

c Kylie paid $3690 for a TV and video. She is going to pay it off in 18 instalments. How much is each instalment?

d Kilcoy cricket team scored 296 runs and 199 runs. What was the average amount of runs scored by the 11 batsmen?

Add and subtract fractions with related denominators

To add and subtract fractions with related denominators you must make both fractions have the same denominator.

add

to

10 you would change the

to

Add the fractions with related denominators. Use the equivalence chart above if you need to. The first one is done for you.

Solve the problems.

a If Jack ate 1 4 of a pizza and Jim ate 3 8 of a pizza, how much pizza did they eat altogether?

b Samantha was given a cake. If she ate 1 4 of it and her friend ate 3 8 , how much cake was left?

Adjacent angles are two angles that share a common side and vertex. Angle BAC and angle CAD share a common vertex.

Vertically opposite angles are angles that are opposite each other when two straight lines intersect. Angles around a full rotation add to 360˚.

The base unit for measuring small volumes is the cubic centimetre, which is a cube measuring 1 cm on all sides. A centicube is a good example of a cubic centimetre.

Volume can be found by counting the volumes of each layer.

a How many centicubes are in each layer of Con’s model?

b How many layers are there? ___________

c What is the volume of Con’s model? ___________cm3

d How many centicubes are in each layer of Nanda’s model?

e How many layers are there? ___________

f What is the volume of Nanda’s model? ___________cm3

the dimensions and volume of each prism in cubic centimetres (cm ) in the table.

Did you notice any relationship between the length, width and height of the prism and its volume? What is the relationship?

Selects and uses the appropriate unit to calculate areas, including areas of rectangles.

Nanda’s model

Con’s model

Con’s model DRAFT

25 Addition of 4-, 5- and 6-digit numbers/problems

Use the information given to calculate the area of each state and territory. Record your information on the map.

Area

• The ACT’s area is 2000 km2.

• Tasmania is 66 000 km2 larger than the Australian Capital Territory.

• Victoria is 160 000 km2 larger than Tasmania.

• New South Wales is 574 000 km2 larger than Victoria.

• South Australia is 182 000 km2 larger than New South Wales.

• Northern Territory is 362 000 km2 larger than South Australia.

• Queensland is 381 000 km2 larger than the Northern Territory.

• Western Australia is 799 000 km2 larger than Queensland.

Use your calculator to decide whether these statements are true or false.

a The total area of Australia is 7 683 000 km2.

b Queensland is larger than the combined areas of New South Wales, Victoria, Tasmania and the Australian Capital Territory.

c New South Wales and South Australia, if combined, would be smaller than Queensland.

Record 0 because you are multiplying by a ten.

2: Multiply by 4 using the shortened method.

Estimate an answer to the problems by rounding each large number to the nearest 100 or 1000 before multiplying them.

a The jeweller bought 20 watches at $398 each. Approximately how much did he spend?

b On average there are 411 pupils at each of 30 schools. Approximately how many students are there altogether?

c The car yard bought 40 cars at an average price of $7993. What was the approximate amount of money spent?

Reflect each shape.

a b c d

Rotate each shape as directed.

a 90° clockwise

b 180° clockwise

c 270° clockwise

Rotated 360°

Translate each shape as directed.

a Directly below

b To the left

c Directly above

d To the right

e Does moving the shapes, as above, change their shape or size in any way?

10

Create a tessellating pattern through shape movements.

a Draw 4 arrows identical to the one displayed on four pieces of graph paper measuring 3 cm × 3 cm.

b Cut out the 4 squares and translate, rotate and reflect them to make the four patterns below.

1 cm graph paper

Surveys are used to gather information. A survey may involve the entire population or only a sample

Population: The whole group, such as every student in a school.

Sample: A random selection taken from the population, such as five students from every class in the school.

c Record your data as a percentage. % %

Calculator steps: numerator ÷ denominator %

If possible, and on a separate piece of paper, conduct a survey of your whole school population to find out how many are left-handed. This could be done quickly, with a raise of hands for left-handers in classes and the class teacher giving you the total number of children in the class.

a Total school population Left-handed children Fraction of left-handers

Percentage of left-handers

b What was wrong with Sophie’s conclusion from her survey of the netball team?

12 13

a If you increase the size of a data sample will it become more accurate?

b Recently a group of 20 children at a hamburger restaurant were surveyed by the owners of the restaurant. The owner found that their favourite food was hamburgers.

Is this a reasonable survey for the whole country?

Explain why.

Multiplication by 2 digits

Complete these multiplications. The first one is done for you.

Use the strategy of ‘guess and check’ to choose the correct multipliers.

Negative numbers

Negative numbers

There are many instances in the real world where we need negative numbers Negative numbers are numbers less than zero and are written with a minus sign ( ) in front of them. Positive numbers are greater than zero. The term integers refers to positive and negative whole numbers.

There are many places around the world and in Australia where temperatures below zero exist. Look carefully at the thermometers below and record the temperatures.

Look carefully at this diagram representing sea level, then estimate an answer to each question.

a How far above sea level is the top of the flag?

b How far below sea level is the fish?

c How far above sea level is the aerial on the house?

d How far below sea level is the swimmer’s foot?

e How far above sea level is the top of the roof of the house?

f Give the height above sea level of both birds.

g Give the height of the top of the wave.

Round these numbers to the nearest 100 and complete the operations.

Round these numbers to the nearest 1000 to complete the multiplications.

Round

decimals to the nearest whole number to complete the operations.

Many advertisements that deal in large numbers use a K to show thousands.

23K = 23 000.

The K is an abbreviation for the Greek word khilioi, which means thousand.

Write each of these numbers using K as an abbreviation.

Round each number in the number sentences below to the nearest 1000 and estimate an answer for each. Record your answer in an abbreviated form, using a K.

Design a survey to find the most popular form of electronic entertainment. Write some associated questions you could ask in your survey to gain extra information.

Conduct your survey and report on its findings.

How could you make your survey more representative of the whole of NSW?

Design a column graph to record your survey data.

You will have noticed that the calculator gives a different answer to questions where there is a remainder. This is because the calculator gives the remainder as a decimal. You can do this as well by dividing the numerator by the denominator to give a decimal remainder, or by adding a decimal point and zeros until you get a suitable answer.

6 1 4 becomes 6.25

4 2 5 because 1 4 = 0.25

6 . 2 5

4 2 5 . 0 0 Adding zeros

Solve these divisions by adding zeros until a suitable answer is found. The first one is done for you.

Use your calculator to answer these problems. Round any overflow displays on your calculator to 3 decimal places.

a Sarah divided a 49 m piece of rope into 4 sections. How long was each section?

b Janice shared 565 mL of liquid between 6 vessels. How much was in each vessel?

c $85 054 was shared between 8 people. How much did each person receive?

3

Find the fractions of the group, then use a calculator to record any remainder as a decimal. E.g. 3 4 = 0.75

a Find 1 4 of 25 apples.

b Find 1 8 of 25 apples.

c Find 1 5 of 25 apples.

d Find 1 2 of 25 apples.

4 DRAFT

Find the fractions of the group, writing the remainders as decimals.

a Find 1 8 of 66 oranges.

b Find 1 4 of 66 oranges.

c Find 1 5 of 66 oranges.

d Find 1 6 of 66 oranges.

Solve the problems using fractions.

a 7 cakes shared among 5 people.

b 12 litres shared among 10 children.

c 9 pizzas shared among 8 children.

d 15 cakes shared among 10 people.

e 13 plates of nachos shared among 5 people.

f 7 buckets of water shared among 5 cows.

The Cartesian plane

The Cartesian plane consists of two intersecting lines. These are called the x-axis and the y-axis The x and y axes intersect at point zero, which allows us to graph negative numbers. The first coordinate graphed is always the x-axis and the second is the y-axis. They are called ordered pairs.

Plot these coordinates on the Cartesian plane supplied. Remember that the first number in the coordinates is always graphed on the x-axis.

a A (6,3) E ( 4, 2)

B (2,1) F ( 2, 1)

C ( 6,4) G ( 6, 3)

D (4,2) H (7, 4)

b List all coordinates that are in a straight line. Hint: It takes at least 3 to be sure there is a straight line.

Jack has put 3 coordinates in each quadrant of the Cartesian plane.

Write the coordinates that represent the position of each letter on the Cartesian plane.

One hectare (ha) is 10 000 m2 Two soccer fields are about 1 hectare.

Last year we marked out a hectare around our school. Use this knowledge to find areas to suit each category.

Use suitable measuring instruments to calculate the area of your school to the nearest hectare. ha

1 Large areas, such as continents, countries and states, are measured in square kilometres (km2). Solve these problems comparing Australian areas to other countries.

Country Area km2

a What is the difference in size between Victoria and Italy?

b What is the difference in size between Victoria and Vietnam?

c Is the combined area of Turkey and Vietnam larger than the combined area of NSW and Victoria?

d Would the combined sizes of Turkey, Sweden, Norway and Greece be larger than Queensland?

PART

Circle the square numbers. Find these squares.

a 32 =

b 5² =

c 72 =

d 82 =

e 92 =

Calculate the answers. a

PART

3 2 × 4 5

f A farm of 68 865 hectares is divided into 5 equal sections. What is the size of each section? ha

g 2700 kilograms of iron is placed into 6 containers on a train. How many kilograms are in each container? kg

h If 72 224 litres of water is shared into 8 barrels, how many litres are in each barrel? L

Calculate the answers.

a 10% of $50 $

b 25% of $100 $

c 50% of $40 $

d 75% of $80 $

e 20% of $90 $

f Davina scored 75% in her spelling test. How many words did she spell correctly if there were 60 words in the test?

PART

Make more equivalent fractions.

a 1 3 = 2 6 = 9 = 12 = 15

b 1 5 = 10 = 15 = 20 = 25

Complete these operations.

PART

Solve the decimal multiplications.

Plot these coordinates on the Cartesian plane. Join them to make a shape.

Find the average for each set of scores.

c 5 8 1

+

=

=

= e 4 10 + 2 5 = d

Round the larger numbers to 1000 to make an estimate.

a 3796 + 5230 ≈

b 7987 + 9103 ≈

c 9987 3013 ≈

d 7987 × 3 ≈

e 6096 × 5 ≈

Record the remainders as decimals.

Convert each measurement to a different unit. a 7 t = kg e 3125 kg = t

b 5.5 t = kg f 9645 kg = t c 3.25 t = kg g 6005 kg = t d 2.4 t = kg h 4104 kg =

Calculate the elapsed time for each activity.

Draw the shape in its new position after it has been rotated 270° clockwise.

How many minutes in: f 1.5 hours

Estimate the size of each angle.

Colour of 800 cars

Measure and label the four angles on each set of intersecting lines.

Answer true or false.

a There were at least 400 white cars.

b There were about 100 red cars.

Use a calculator to help you answer the below purchases.

a 2 staplers and 5 glue sticks $

b 8 calculators, 3 staplers and 6 pens $

c 2 pairs of scissors, 5 staplers and 7 pens $

d 12 glue sticks, 12 staplers and 25 pens $

e 40 pens, 20 scissors, 9 glue sticks and 8 calculators $

Write and solve a question that uses the items above. 2

Solve these number sentences. (Do the work in brackets first. You may need a calculator.)

a (37 + 64) + (18 × 23) + (37 19) =

b (35 + 18) + (37 16) + (18 × 5) =

c (5 × 19) + (36 ÷ 9) + (40 × 7) =

d (100 57) (80 ÷ 16) =

e 87 + (195 89) (35 × 3) =

f (137 × 9) + (99 87) (36 × 3) =

Place brackets in the number sentences to make them correct.

Write equations using brackets and solve them. 5

Negative numbers

Display how these number sentences can be done on a number line. The first one has been done for you.

Solve the number sentences. The number line above will assist you.

Write a number sentence or story of your own and solve it on the number line.

Fractional quantities

Timelines

Draw a line to estimate a place on the timeline for each of these major inventions.

Calculate the difference in time between these inventions.

a The invention of the typewriter and the telephone.

b The invention of paper and the typewriter.

c The invention of paper and paper money.

d How many years between 800 BCE and 2000 CE?

Design a timeline starting at 2011 to record the events in Prani’s life. Draw a line to match the events to a place on the timeline.

On a separate piece of paper, design a timeline for events in your life. You will need to devise a scale first.

A large company is renewing its communications equipment. Use long multiplication to find the cost of the purchases.

Check the rent for each shop by rounding both the rent amount and the number of weeks to make an estimate. Put a tick if you think the rent is correct and a cross if you don’t.

A simple way of finding percentages of quantities is to convert the percentage to a fraction. EXAMPLE 20% of $20 becomes 1 5 of $20 = $4

Answer the questions.

a Which would be the cheapest skateboard?

b Which would be the most expensive?

c Which skateboard would cost $80?

d Which skateboard would cost $70?

29 Word problems/multiplication and division

Solve the problems.

a 100 m 400 m

? 9 m3

A builder needs 9 cubic metres of concrete to build a path that is 100 m long. How many cubic metres of concrete are needed for a path that is 400 m long?

b 1 hr ?

6 km

42 km

A boat travels 6 km each hour. How long would it take the boat to travel 42 km?

c $2.25 ?

20 cupcakes

200 cupcakes

20 cupcakes cost $2.25 to make. How much would 200 cupcakes cost?

d $7.00 ?

6 bananas

42 bananas

Jarrah bought 6 bananas for a cost of $7.00. How much would 42 bananas?

e Narooma Moruya Home ?

51.3 km

DRAFT

Alinta drove from Moruya to Narooma, which is 51.3 km. However, the distance to her home is still 3 times that distance. How much further does Alinta need to drive?

f 1 dozen 96 eggs ?

$6.50

A dozen eggs cost $6.50. How much would Prisha need to buy 96 eggs?

g 6 cakes of soap

4 dozen cakes of soap ? $4.50

Fatima bought 6 cakes of soap for $4.50. How much would Fatima spend to buy 4 dozen cakes of soap?

h Gravel Sand

3 gravel

4 sand

15 gravel ? sand

A builder mixes his cement in the ratio of four shovels of sand, three shovels of gravel, and two shovels of cement. If the builder has used 15 shovels of gravel, how many shovels of sand has he used?

Volume can be found by using the formula

Volume = length × width × height

3 cm × 2 cm × 2 cm = 12 cm3

1 Calculate the volumes of each object above using the formula Volume = Length × Width × Height.

1 Waru said that there was only one rectangular prism with a volume of 48 cm3. Prove that he is wrong by drawing another rectangular prism with a volume of 48 cm3.

30 Decimal number patterns

Complete

Use

Prime factors

Prime numbers are numbers that have only themselves and 1 as factors.

EXAMPLE 2, 3, 5 and 7 are prime numbers but 4, 8 and 9 are not.

Composite numbers are numbers with more than two factors.

EXAMPLE 24 has factors of 1, 2, 3, 4, 6, 8, 12 and 24.

Multiply the prime factors in questions a, b and c in question 6.

Choosing units and measuring devices

1 Tick the best unit with which to measure the items.

a The length of a ruler

b The mass of a pencil

c Your mass

d The length of a fingernail

e The mass of a submarine

f The area of a piece of paper

g The width of a pencil

h The distance between Brisbane and Cairns

i The area of your bedroom

j The mass of a matchbox

k The area of Bathurst

1 Draw a line to match each instrument to a measurement.

1 Show how the same quantity can be expressed using different units. You will have to use decimal notation in some cases.

Selects and uses the appropriate unit and device to measure the masses of objects

Finding the mean

The mean is the average of a collection of numbers or set of scores. It is found by finding the total of the scores then dividing it by the number of scores.

Find the mean of these scores.

a 4, 8, 12, 8, 16, 6

b 3, 39, 28, 14, 22, 20

39, 3, 26, 16, 21

70, 62, 50, 30, 38

The mode is the most frequent value. For example, in this set of scores, 6 is the mode. 3 4 7 8 3 6 9 2 6 7 9 6 The number 6 occurs more times than any other number.

Decimals × powers of ten 31

Use your calculator to answer these questions.

Predict the answers to these questions and then check with a classmate.

a 23.1 × 10 =

d What happened to the numbers when they were multiplied by 10?

e What happened when they were multiplied by 100?

f What happened when they were multiplied by 1000?

Use your calculator to answer these questions.

Predict the answers to these and then check with a classmate.

d What happened to the numbers when they were divided by 10?

e What happened when they were divided by 100?

f What happened when they were divided by 1000?

Multiply these numbers mentally.

Write a number with 3 decimal places, then multiply it by 10, 100 and 1000.

9

Rearranging shapes 31

Combine the designated shapes to make other shapes. Then sketch your results. You will need to copy some of these shapes on 1 cm grid paper.

a Use right-angle triangles to make a parallelogram.

b Use 4 isosceles triangles to make a square.

c Use 2 right-angle triangles to make a rectangle.

d Use 4 right-angle triangles to make a larger right-angle triangle.

DRAFT

e Use 2 scalene triangles to make a kite.

f Use 4 equilateral triangles to make a parallelogram.

Comparing distances in kilometres

Sydney–Adelaide 1412 1165

Sydney–Canberra 286 237

Sydney–Melbourne 872 706

Canberra–Melbourne 648 470

Melbourne–Adelaide 731 650

Melbourne–Broken Hill 853 702

Adelaide–Brisbane 2045 1616

Darwin–Alice Springs 1489 1307

Cairns–Brisbane 1716 1392

Brisbane–Sydney 1001 748

Brisbane–Melbourne 1674 1379

Calculate the difference between the distance by road and by air for each journey.

a Darwin to Alice Springs

DRAFT

e Brisbane to Cairns

b Sydney to Melbourne f Brisbane to Adelaide

c Sydney to Brisbane

g Brisbane to Melbourne

d Sydney to Adelaide h Adelaide to Melbourne

Solve the problems.

a Leon went on a bus tour around southern Australia. The bus travelled from Sydney to Canberra, from Canberra to Melbourne, from Melbourne to Adelaide and from Adelaide to Sydney. How many kilometres did he travel?

b Ms Diaz went on an adventure holiday. She flew from Melbourne to Sydney, from Sydney to Adelaide, from Adelaide to Brisbane and from Brisbane to Melbourne. How much did it cost her if her airfares averaged 60c per km?

c Adrian caught a plane from Sydney to Melbourne, then a bus from Melbourne to Broken Hill and back. He then flew to Adelaide and caught a bus back to Sydney. How many kilometres did Adrian travel?

Relative place value 32

Multiply each decimal by 10 or a multiple of 10.

×10 ×100 ×1000

×10 ×100 ×1000

a 0.5

b 0.3

c 0.4

d 0.6

e 1.3

f 1.5

Colour the circle to identify the relative size of the number.

a 2

⚬ ten times larger than 0.2

⚬ a hundred times larger than 0.2

⚬ a thousand times larger than 0.2

b 25 ⚬ ten times larger than 2.5

⚬ a hundred times larger than 2.5

⚬ a thousand times larger than 2.5

c 17 ⚬ ten times larger than 1.7

⚬ a hundred times larger than 1.7

⚬ a thousand times larger than 1.7

d 31 ⚬ ten times larger than 0.31

⚬ a hundred times larger than 0.31

⚬ a thousand times larger than 0.31

e 604 ⚬ ten times larger than 0.604

⚬ a hundred times larger than 0.604

⚬ a thousand times larger than 0.604

f 0.5 ⚬ ten times smaller than 5

⚬ a hundred times smaller than 5

⚬ a thousand times smaller than 5

Answer the questions.

a What number is ten times larger than 3.2?

b What number is 100 times larger than 4.43?

c What number is 1000 times larger than 5.62?

d What number is 10 times smaller than 2.8?

e What number is 100 times smaller than 1.6?

0.375 is 1000 times smaller than 375.

Ways of finding 3 5 of 20

Method 1: Find 1 5 of 20 = 4

3 5 of 20 = 4 + 4 + 4

Answer = 12

Find the fractions.

Method 2: Find 1 5 of 20 = 4

Multiply 4 by the numerator (3). 4 × 3

Answer = 12

a

b

c

d

e

Find the number of lollies for each fraction.

DRAFT

Method 3: Find 3 5 × 20 = 60 5

Divide 60 by 5

Answer = 12

Solve the problems.

a Phillip had a bag of 28 lollies. If he gave 1 4 of his lollies to his sister, how many did he give away?

b Sally had 40 plates but lent 3 8 of them to Mihi. How many did she have left?

c Issa saved $60 but spent 7 10 on new clothes. How much did she have left for other items?

d Peter saved $30 but gave 3 5 of it away to his friend. How much did he have left to spend on himself?

e A new bike costs $200. If the store owner gives the purchaser 3 10 off the price, how much would the bike cost?

f Mia borrowed 2 5 of Asher’s card collection. If Mia borrowed 20 cards, how many were in the collection?

What can be found at these ordered pairs? (Remember to always read the x-axis first.)

a (14,6) d ( 16,6)

b ( 6,6) e ( 16, 6)

c (14, 7)

Give the coordinate points for the following towns.

a Hopetown

b Laketown

c Sugarville

Join these sets of coordinates to make shapes on the Cartesian plane.

a (1,1) (5,1) (3,3)

b ( 2,3) ( 2,5) (2,3) (2,5)

c ( 7,0) ( 4,0) ( 5,7)

d ( 3, 2) ( 3,2) ( 1, 2) ( 1,2)

e (1,0) (4,0) (1, 3)

f (2, 3) (2, 5) (7, 3) (7, 5)

g ( 4, 4) ( 6, 5) ( 2, 5) ( 5, 7) ( 3, 7)

Mass units

32

Convert these measurements into tonnes using decimal notation, e.g. 2500 kg = 2.5 t a 3563 kg =

How many of each box could you pack onto a 1 tonne truck?

Some extremely small amounts of mass, like dosages of medicine, are measured in milligrams. 1000 mg = 1 g

Choose a measuring unit from the box to measure the mass of:

a yourself f a small tablet

b an elephant g a truck

c a ruler h a key

milligrams: mg grams: g tonnes: t kilograms: kg

d a bag of potatoes i a box of books

e a hair j a pen

Convert these mass units.

Solve the problems.

a A jar of jelly beans has a mass of 1 kg. If the jar’s mass is 210 g, what is the mass of the jelly beans?

b How many 65 kg sacks of potatoes can be made from a load with a mass of 1.040 tonnes?

c If 20 apples have a combined mass of 4 kg, what is the average mass of each apple?

d The maximum load permitted on a truck is 5 t. What is the mass of 35 containers if each has a mass of 145 kg? Would this load be permitted on the truck?

Decimal/fraction number patterns 33

Use the number line to help you continue these sequences.

Use the number line of decimals to help you continue these sequences.

Remember: Multiplication and division are done before addition and subtraction!

Solve these equations.

a 15 + 21 ÷ 3 = e 0.5 + 2.5 × 4 =

b 5 + 20 × 4 = f 36 ÷ 4 + 54 =

c 8 × 5 ÷ 4 = g 30 × 5 ÷ 10 =

d 3.5 × 2 4 =

Use your own strategies to find the missing numbers.

a 3 × 8 ÷ + 1 = 7 f 4 × ÷ 3 = 28

b 105 100 ÷ = 80 g 1 5 × ( + 3 ) + 6 = 9

c 45 ÷ × 6 = 30 h × 1 6 + 97 = 100

d (30 5) × 6 ÷ 3 = i 1 5 of × 7 3 = 53

e 30 5 × 6 ÷ 3 = j 3 4 × (15 7) × 7

The builder’s kit

Costs: timber strips $1.80, hammers $7.80, scissors $3.50, cuphooks 35c, ruler $1.20, mixed screws $2.50.

a Which number sentence is correct for the costs of the timber strips and cuphooks needed to hang the items in the diagram above? 10 × $1.80 + 2 × 35c

$1.20 × 2 + 10 × 35c

15 + 21 ÷ 3 = 21 divided by 3 has to be done first.

15 + 7 = 22

I estimate the answer, then I check to see if my estimate works.

b Which number sentence is correct for the cost of the hammers, mixed screws, hooks and timber strips used in the picture above?

5 × $3.50 + 2 × $2.50 + 10 × $0.35

5 × $7.80 + 3 × $1.20 + 2 × $1.80 + 10 × 35c

3 × $7.80 + 2 × $2.50 + 2 × $1.80 + 10 × 35c

When two sets of grouping symbols are used, ( ) and [ ], the innermost symbols must be completed first. EXAMPLE 8 + [40 ÷ (5 + 3) ] = 13

Range and median 33 Range

The range is the spread of distribution of scores. It is the difference between the highest score and the lowest score.

E.g. Scores 4, 5, 7, 9, 12, 20, 36, 41, 44, 50 The scores range from 4 to 50, so the range is 46.

8 Use

Calculate the range of these test scores.

Scores Lowest score Highest score Range

a 46, 50, 60, 65, 67, 70, 74, 76, 90

b 27, 33, 40, 46, 50, 56, 58, 59, 61, 79

c 37, 40, 41, 48, 51, 53, 60, 70, 72, 77

d 14, 30, 32, 38, 57, 60, 66, 70, 73, 79

e 60, 30, 40, 70, 50, 54, 62, 84, 72, 56

f 64, 60, 50, 70, 84, 90, 44, 56, 35, 75

g 28, 38, 50, 40, 39, 60, 60, 90, 77, 81

Median

The median is the middle score. It has as many scores below it as above it. When there is an even number of scores the median becomes the average of the two middle scores.

E.g. 10, 12, 14, 15, 16, 19, 19, 20, 22: The median is 16 (the middle score).

E.g. 10, 20, 40, 50, 60, 70, 80, 90: The median is 55 (average of 2 middle scores).

9

Find the median of these scores. (You will need to reorder the numbers in questions c–f.)

a 20, 25, 27, 30, 46, 77, 90, 91, 93

b 13, 15, 19, 21, 24, 30, 36, 40, 70

c 40, 12, 13, 19, 37, 80, 77, 15, 35

d 21, 3, 30, 7, 19, 40, 55, 27, 60

e 30, 45, 25, 60, 70, 50, 42, 37, 55

f 13, 19, 30, 55, 46, 77, 90, 7, 14

Find the median of these scores. You will have to average the 2 middle scores.

a 2, 4, 6, 8, 10, 11, 13

b 22, 23, 28, 30, 32, 44, 50, 60

c 37, 40, 45, 50, 70, 78, 98, 100

d 35, 40, 46, 50, 54, 60, 66, 80

e 76, 98, 99, 110, 120, 130, 133, 140

f 21, 15, 12, 20, 22, 30, 40, 50

Eleven children from class 6T listed the amount of time they spent travelling to school.

Toby 45 mins Jake 15 mins

Melissa 40 mins Sam 20 mins

Jasmine 35 mins Larissa 30 mins

Answer these questions.

a What is the range?

50 mins

35 mins

26 mins

b What is the mean?

35 mins

10 mins

Making a cubic metre

Cubic metres are needed to measure the volume of larger objects. A cube with edges that are all 1 metre long has a volume of 1 cubic metre (1 m3).

Make a cubic metre from timber strips, cardboard and tape.

Decide whether these objects are less than 1 m3, about equal to 1 m3 or greater than 1 m3

A large fridge is about 2 m3

to calculate the volume of each

How many 50 cm × 50 cm × 50 cm boxes would fit inside a cubic metre?

Calculate the volume of your classroom in cubic metres.

Apply the rule to complete the sequences.

Create number sequences using the operations, then write a rule for each. The first one has been done as an example for you.

10 20 30 40 50 60 70 80 90 A 1-metre ruler.

Use the ruler to find the fractions of the metre ruler.

a 1 2 of the ruler

b 3 10 of the ruler

c 3 4 of the ruler

d 7 10 of the ruler

Use the number line to help you find the lengths.

If 3 5 of a length is 15 cm, what is the whole length? b

If 3 4 of a length is 12 cm, what is the whole length?

e 9 10 of the ruler

f 1 5 of the ruler

If 3 6 of a length is 15 cm, what is the whole length?

If 3 8 of a length is 12 cm, what is the whole length? e

If 4 5 of a length is 32 cm, what is the whole length? f

If 3 4 of a length is 30 cm, what is the whole length? g

If 5 8 of a length is 35 cm, what is the whole length?

10

If 4 10 of a length is 28 cm, what is the whole length?

Intersection L

6

Intersection M

There are 3 sets of intersecting lines above labelled L, M and N.

Intersection N

a On set L firm in two arms to make a right angle using a colour pencil or highlighter.

b On set M firm in four arms to show adjacent angles that add to make 180˚.

c On set N firm in as many arms as needed to demonstrate a full rotation of 360˚.

Intersection O

Intersection P

d On set O firm in two arms to form an angle of 60˚.

e On set P firm in two arms to form an angle of 120˚.

f On set Q firm in two arms to form an angle of 240˚.

7

Use your knowledge of intersecting lines to state the degrees of each angle without using a protractor.

a Angle A =

b Angle B =

c Angle C =

d Angle D =

DRAFT

The two graphs show the average temperature for each city, for each month of the year.

The months are shown on the horizontal axis and the temperatures are shown on the vertical axis.

Estimate to the nearest whole number the average temperature for Darwin:

a in November

b in September

8 9

Answer true or false.

a The average temperature for Echuca in June was 14˚.

b The average temperature for Echuca in August was close to 10˚.

c The average temperature for Echuca in March was close to 24˚.

Explain why Echuca’s temperatures dip more in the winter months compared to Darwin.

The average monthly temperature for Waru’s cattle farm, well south of Hobart, is listed in the table below.

a What is the range of the temperatures?

b What is the median temperature?

c What is the mean temperature?

Equivalent number sentences 35

Given that the value of the = 5, calculate the value of all other shapes.

Complete the number sentences by supplying the missing decimal. The first one is done for you.

I work backwards to solve these problems!

Create your own number sentences to solve these problems. When you have your solution, substitute your missing number in the sentence to check that it works. The first one is done for you.

a If you multiply me by 3 and add 4 the answer is 19. 5 × 3 + 4 = 19

b If you divide me by 6 and add 7 the answer is 10.

c If you divide me by 8 and then multiply by 4 the answer is 12.

d Multiply me by 8, divide by 2 and the answer is 16.

e Divide me by 6 and multiply by 5 to get 30.

f Divide me by 4 and multiply by 3 to give 15.

g If you divide me by 25 and multiply by 20 the answer is 80.

h Divide me by 12, multiply by 4 and the answer is 32.

i Add 24 to me and divide by 6 to give an answer of 6.

j Subtract 2 from me and divide by 12 to give the answer of 4.

Nicole wants to buy a TV that costs $1800. She isn’t sure if she can afford it, but the salesman says she can take the TV today on no deposit and 12 easy payments of $198 per month.

a Do you think this is a fair deal?

b Explain why.

How many ways do you think a kindergarten child would be able to stack the 3 colour blocks opposite?

Exhaust every possible combination by drawing your solutions in the space below.

Speedy Gonzales wants to buy a new car. These are Speedy Gonzales’s choices. Colours: red, black or green

Wheels: mags or plain

Style: convertible or hard top

Gearing: manual or auto

a How many different combinations of car do you think he can have?

b Explain how you solved this problem.

c Compare your answer with others to discover if anybody solved it in a different way to you, then record what they did.

d Do you prefer their method or yours?

Red Blue Green

Red Blue Green

10

Negative numbers review

There are many instances in the real world where we need numbers less than zero, for example, temperatures. We call these numbers negative numbers and we use a minus sign in front of them (–).

Find the difference in temperature between:

Rules

Each out = 5 runs (you can get out more than once). Runs are scored similar to real cricket.

Peter 4 runs and 2 outs 6

Kai 5 runs and 3 outs

Hailey 10 runs and 1 out

Jessie 2 runs and 1 out

Marco 0 runs and 3 outs

Dimi 7 runs and 2 outs

Matt 4 runs and 0 outs

Total score

Answer the questions.

a Who won the game?

b Who was the best batsman for the Royals?

c Who was the worst batsman for the Giants?

d Who scored the most runs for the Giants?

Luke 8 runs and 0 outs

Tom 16 runs and 0 outs

Tama 0 runs and 3 outs

Sid 4 runs and 2 outs

Elisa 6 runs and 3 outs

Maxi 0 runs and 2 outs

Barney 25 runs and 0 outs

Total score

A diagonal is a line that joins two non-adjacent vertices (corners) of a polygon. A rectangle has two diagonals.

Draw the diagonals on the polygons. Make sure you end up with the number of diagonals given in the boxes. The heptagon has been done for you.

Complete the table to identify the shape, number of sides and diagonals.

Can you see any pattern in the growing number of diagonals on the shapes in the table?

What is it?

How many diagonals would be on an octagon?

Look at the shapes in Question 11. In which shapes are some of the diagonals different lengths?

Which shapes in Question 11 have diagonals that are also lines of symmetry?

Complete these sequences.

PART

Find the percentage of each quantity.

a 20% of $150 =

b 25% of $160 =

c 10% of 900 kg =

d 50% of 200 km =

e 20% of 500 mL =

Apply the rule to complete the sequence.

f 75% of 200 kg =

PART

Use the number line to answer the questions.

Find

Solve these problems.

25 m2 of carpet costs $50. How much would it cost for 125 m2?

b

A ferry boat travels about 20 km per hour. How long would it take to complete a 120 km trip?

Multiply the decimals.

a 5.25

b 6.09

c 1.01

d 2.323

e 24.071

f 63.007

g 395.5

Find the mean of these scores.

a 22, 21, 20, 29, 30, 28

b 40, 38, 48, 46, 54, 32

c 90, 65, 75, 73, 67, 50

d 114, 85, 86, 115, 103, 97

PART

Plot the coordinates, then join in order.

This is an equilateral triangle. On the shape below show how 4 equilateral triangles can be joined to create a parallelogram. Colour two of your equilateral triangles to form a rhombus and colour it blue.

Draw diagonals on the polygons.

Calculate the volume of these objects.

PART

Hexagon Pentagon Quadrilateral

Complete the table for the heptagon and octagon to show how many diagonals they would have.

Shape Sides Diagonals

Quadrilateral 4 2 Pentagon 5 2 + 3 = 5

Hexagon 6 2 + 3 + 4 = 9

Heptagon 7

Octagon 8

PART

Draw a line to estimate each event to a place on the timeline.

Dad was born 1980 Mum was born 1985 Sally was born 2009 Jack was born 2013

Estimate the size of the angles that have not been identified.

acute angle

An angle less than 90° .

acute angle

addend

Any number that is added to obtain the sum or total.

3 + 7 + 8 = 18

(addends) (sum)

average

The total of a series of numbers divided by the amount of numbers in the group.

Average of 3, 5, 7, 9:

• add 3 + 5 + 7 + 9 = 24

• divide 24 by the number of scores

24 ÷ 4 = 6

The average is 6.

adjacent

Next to; adjacent sides of a triangle have a common vertex.

X

Y Z

XY and YZ are adjacent because they have a common vertex, Y.

algebra

Where letters or symbols are substituted for numbers in a number sentence.

3 × b = 15 (b = 5)

axis

A line that divides a shape symmetrically in half.

axis of symmetry

Lines of reference for a graph.

axis

algorithm

The calculation procedure for setting out a mathematical problem in a certain way.

324 874 364 + 207 23 × 30

Celsius

A scale for measuring temperature.

begins to melt

boiling point of water 36.9

circumference

The distance around a circle.

am

Abbreviation from the Latin words ante meridiem (before noon). Any time from midnight to noon.

apex apex

The highest point of a solid (3D) object from its base.

associative property

When using addition and multiplication, it doesn’t matter how the numbers are grouped. The answers will always remain the same.

5 × 4 × 2 = 40 3 + 6 + 7 = 16 and and

5 × 2 × 4 = 40 7 + 3 + 6 = 16

column graph

A graph where vertical columns or horizontal bars are used to represent data.

CIRCUMFERENCE

commutative law

Numbers can be added or multiplied in any order. 5 + 6 is equal to 6 + 5

5 × 7 is equal to 7 × 5

complementary angles

Two angles whose sum is 90

composite number

A number that has more than two factors. Example: 10 has four factors – 1, 2, 5 and 10.

congruent

Two shapes or objects that are identical in all ways.

coordinate points

Coordinates locate points on a grid using ordered pairs. The horizontal position is given before the vertical position, e.g. the circle is located at (C,3).

dot plot

A graph that uses scale to represent data. Each value is recorded as a dot.

edge

The intersection of two faces.

elapsed time (duration)

The time taken to do something. For example, the time it takes to prepare a meal is elapsed time.

equilateral triangle

cross-section

The shape of the face made by slicing through a solid. Example:

cubic metre (m3)

A metre cube has a volume equal to one cubic metre.

denominator

The bottom number of a fraction that tells how many equal parts are in the whole.

1 ➔ numerator

4 ➔ denominator

diameter

A straight line touching both sides of a circle which passes through the centre point.

divided bar graph

diameter

A graph that shows how a total is divided into parts.

A triangle that has three equal sides and three equal angles.

equivalent fractions

Fractions that have the same value.

faces

70

100 = 7 10

The surfaces of a three-dimensional (solid) object.

face

face face

factor

Any whole number that can be multiplied with another to make a given number.

Factors of 12: 12, 6, 4, 3, 2 and 1

factor tree

A diagram that displays factors of a number. 36 6 × 6 3 ×

frequency

In a collection of data, the frequency of a category is the number of occurrences for that category.

Animal Frequency Sheep Horses Cows Dogs

The frequency of the horses in the table is 7.

greater than (>)

Symbol used to show that one number has a value greater than the other number.

27 > 15

isosceles triangle

A triangle that has two sides of equal length and two angles the same size.

kilogram (kg)

A mass unit.

1 kg = 1000 grams

kilolitre (kL)

A capacity unit.

1 kL = 1000 litres

kilometre (km)

A length unit.

1 km = 1000 metres

less than (<)

grid references

Grid references locate positions on a map or grid. The horizontal position is given before the vertical position, e.g. the circle is located at C3.

gross mass

The total mass of any item, including its packaging.

hectare (ha)

A unit of area.

1 ha = 10 000 m2

hexagon

A 2D shape with six straight sides. regular hexagon irregular hexagon

horizontal

A straight line at right angles to the vertical and parallel to the horizon.

vertical line

horizontal line

improper fraction

A fraction where the numerator is greater than the denominator. Improper fractions have a value greater than one whole.

5 ➔ numerator

3 ➔

Symbol used to show that one number has a value less than the other number.

line graph

Information represented on a graph by joining plotted points with a line.

mean

The mean is found by adding all the values in a data sample, then dividing the total by the number of values in the set. It is often called ‘the average’.

8 is the mean for the scores:

metre (m)

The basic SI unit of length.

1 metre = 1000 mm

1 metre = 100 cm

millilitre (mL)

A measurement of capacity.

1000 mL = 1 litre

millimetre (mm)

A measurement of length.

1 mm = 1 thousandth of a metre

10 mm = 1 centimetre

denominator

million 1 000 000 1000 × 1000 = 1 000 000 or 10 × 100 000 = 1 000 000

mixed numerals

A number that consists of a whole number and a fractional part.

For example: 4 1 2

order of rotational symmetry

The number of times a shape matches the original as it completes one full rotation.

multiple

The result of multiplying a given number by any other number is a multiple of that given number. Multiples of 3 are: 3, 6, 9, 12, 15, 18, etc.

negative numbers

Numbers that have a value less than zero. A minus sign is placed in front of a number to identify it as negative.

For example: The temperature was 5°C

net

A flat shape which can be folded to make a 3D object.

Net of a triangular prism

net mass

The mass of any item without its packaging.

numerator

The top number of a fraction, telling us how many parts there are out of the whole.

3 ➔ numerator

4 ➔ denominator

obtuse angle

An angle larger than 90° but less than 180° . 130°

4

Any shape that still looks the same when it is turned around a fixed point has rotational symmetry.

outcome

The result of a mathematical investigation. For example, when three coins are tossed there are 8 possible outcomes.

per cent (%)

A fraction of 100.

Example: 87% means 87 out of 100

87 100 = 87% = 0.87

perimeter

The distance around the outside of a shape.

m

m

Perimeter = 3 m + 4 m + 5 m

Perimeter = 12 m

perpendicular lines

Lines which meet at right angles.

pie sector graph

A circular graph whose parts look like portions of a pie. plan

Tennis Hockey

Softball

Netball

radius

A straight line extending from the centre of a circle to the circumference.

radius

Bowls

A diagram from above, showing the position of objects. Also known as the top view of a 3D object.

ray

A line that has a starting point but does not end.

rectangle

A four-sided figure with four right angles and two pairs of parallel sides.

rectangular prism

A 3D object which consists of six rectangular faces.

pm

Abbreviation for the Latin words post meridiem which means after midday.

polygon

A 2D shape with three or more angles and straight sides.

hexagon pentagon

prime number

A number that is divisible only by itself and 1.

Examples:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29

probability

The likelihood or chance of an event happening. The range of probability is from zero to one.

0 1

unlikely to happen likely to happen

Probability of zero Impossible

quadrilateral

Probability of 1 Certain

A 2D shape with four straight sides.

Examples: square oblong

reflective symmetry

A mirror image of a shape.

reflex angle

An angle between 180° and 360° .

Example: 330°

revolution

A full turn of 360°

rhombus

A four-sided shape with four equal sides. Opposite angles are equal and it has two sets of parallel lines.

Roman numerals

Number system devised by the ancient Romans.

Examples:

I = 1

V = 5

X = 10

D = 500

M = 1000

L = 50 XCV = 95

C = 100 MMX = 2010

rotation

The turning of an object through a fixed point.

scalene triangle

A triangle with sides of different lengths and angles of different sizes.

sequence

fixed point

supplementary angles

Two angles that have a total of 180

An order of numbers or objects arranged according to a rule or pattern:

Example: Number 1 2 3 4

$ $5 $10 $15 $20

square centimetre (cm2) A unit for measuring area.

surface area

The total area of all faces of a 3D object.

square number

The product of a number multiplied by itself.

Examples:

22 = 2 × 2 = 4

32 = 3 × 3 = 9

42 = 4 × 4 = 16

A rectangular prism has six faces.

tally marks

Groups of marks used to keep count. Every fifth mark usually crosses the four before it.

three-dimensional (3D)

Solid objects have three dimensions: height, length, width (breadth). height

width (breadth)

timeline

A line which represents a span of time.

2003 Born 2008 School 2013 2018 2023 Work High school

tonne

A mass unit.

1000 kilograms = 1 tonne

translate (slide)

The sliding of a shape into a new position.

slide

trapezium

A four-sided figure that has two parallel sides and two that are not parallel.

triangular numbers

Numbers that can be arranged as a triangular pattern.

triangular prism

A prism with two congruent triangles as bases, 3 rectangular faces, 9 edges and 6 vertices.

3 6

two-dimensional (2D)

triangular pyramid (tetrahedron)

3D object with 4 triangular faces, 6 edges and 4 vertices.

turn

To rotate a shape around a point.

twelve-hour time

Analog clocks break the day into two lots of 12 hours: am (midnight–midday) pm (midday–midnight)

twenty-four hour time

Time divided into 24-hour intervals, so as to distinguish between am and pm.

Plane shapes have only two dimensions: length and width (breadth). length

unit fraction

Fractions with a numerator of 1.

Examples:

1 2 , 1 3 , 1 4 , 1 5 , 1 10

vertex

The point where two or more lines meet to form an angle.

vertical

width (breadth)

vertex

DRAFT

Vertical lines are at right angles to the horizontal.

vertices

Plural of vertex. A triangle has 3 vertices.

vertical line

horizontal line

vertices

A rectangular prism has 8 vertices.

volume

The amount of space an object occupies.

Formula:

Volume = length × width × height

2 m

2 m 3 m

Volume = 3 m × 2 m × 2 m = 12 m3

whole numbers

The counting numbers from one to infinity. 1, 2, 3, 4, ➔ infinity

UNIT

11

12

DRAFT

a 150 b 200 c 100 d 50

12–13 Hands on. 14 a 5 e 20

4 f 16 c 6 g 24 d 20 h 80

1 a 531 f 550r4

b 631 g 462r5

c 682 h 487r4

d 991 i 755

e 671 j 668r3

2 a 8 d 6 b 9 e 7

c 8

3 a 943 m c 1139 m e 1073r4 m

b 1371r1m d 1502 m

4 Hands on.

5 a 20 40 60 80 100 120 140

b 200

c 15 30 45 60 75 90 105

d 180

e 13 26 39 52 65 78 91

f 195

g 12 24 36 48 60 72 84

h 144

6 a 9 18 27 36 45 54 63

b Multiply by 9 c 90

7 a 24 25 26 27 28 29 30

b Add 13 c 33

a Two marbles green.

Four marbles red.

One marble orange.

Three marbles pink.

8 8 a 12 m b 12 m c 12 m

The equilateral triangle could be

× 4 m = 12 m

1.25 m f 1.5 m b 1.36 m g 2.15 m c 1.75 m h 3.16 m d 1.4 m i 7.4 m e 1.13 m 11 Hands on. 12 a 20 b 12 c 16 d 28 e 8 f 0

13 a Burton High c 45

b 40 d 50

14 Hands on. (• = 5 children is an appropriate scale. A dot plot using this scale is represented below.)

DIAGNOSTIC REVIEW

4

Matches = triangles × 2 + 1

5 Hands on.

6 a 54 composite l 66 composite

b 80 composite m 76 composite

c 64 composite n 98 composite

d 81 composite o 63 composite e 71 prime p 65 composite f 83 prime q 67 prime g 99 composite r 69 composite h 77 composite s 73 prime i 93 composite t 75 composite j 97 prime u 79 prime

86 composite

8–10 Hands

11

8 Hands on.

9 Hands on and discussion.

DRAFT

a Not credible (the survey was conducted in a place where a bias towards Rocket Sports Drink is likely to exist)

b Not credible (the children surveyed in a bookstore are not likely to be representative of the general population)

c Credible. (Although the difference may only be slight, the Government census is a reliable, official source of data.)

10

b 576 491

80 + 6

500 000 + 70 000 + 6000 + 400 + 90 + 1

c 963 237

900 000 + 60 000 + 3000 + 200 + 30 + 7

d 425 310

400 000 + 20 000 + 5000 + 300 + 10

e 240 300

200 000 + 40 000 + 300

f 780 407

700 000 + 80 000 + 400 + 7

g 6 029 256

6 000 000 + 20 000 + 9000 + 200 + 50 +

6

6 a 356 257 Three hundred and fifty-six thousand, two hundred and fifty-seven

b 479 807 Four hundred and seventynine thousand, eight hundred and seven

c 906 007 Nine hundred and six thousand and seven

d 4 274 300 Four million, two hundred and seventy-four thousand, three hundred

e 27 360 027 Twenty-seven million, three hundred and sixty thousand and twenty-seven

7 Hands on.

8 a 764 319 b 7 034 069

9 a–c Hands on. d 1 kg 10 a–b Hands on. c 50 kg

d 100 g, 250 g, 500 g 1 mL has a mass of 1 gram.

11 Hands on. 12 a

If the parallelogram is rearranged to become a rectangle, the area becomes

on. (For example rectangle with dimensions of 13 cm and 3 cm, 12 cm and 4 cm, 14 cm and 2 cm, 10 cm and 6 cm etc.)

12 Hands on. (rotate 90°, translate, rotate 90°, translate, rotate 90°, translate, rotate 90°, translate.) 13

15

UNIT

12

b Hands on (the graph refers to a ‘discontinued model’ computer). c

on (the word ‘tumble’ indicates a rapid and steep decline whereas the fall is only $10 per month).

13 Hands on.

143.68 i $3600.54

$2051.84 2

a Kelly (3,18) e Mihi (10,8)

b Joe (16,2) f Angus (23,20)

c Sam (2,6) g Jim (25,12)

d Kim (18,10) h Tom (26,1)

14 a Kelly’s house to Kim’s 1450 m

b Sam’s house to Mihi’s 600 m

c Kelly’s house to Jim’s 1400 m

d Joe’s house to Mihi’s 900 m

15 g Angus’s house

DRAFT

e No

10–11 Hands on.

12 a Hands on.

b The sample size is not big enough to represent the whole population.

c Probably, yes

13

This survey is biased because the sample group is actually buying

2 Possible solutions:

a ≈ 120 (1200 ÷ 10)

b ≈ 300 (1500 ÷ 10 = 150 then double)

c ≈ 1200 (12 000 ÷ 10)

d ≈ 20 000 (100 000 ÷ 5)

e ≈ 70 (350 ÷ 5)

f ≈ 60 (600 ÷ 10)

g ≈ 60 (600 ÷ 10)

h ≈ 34 (176.8 ÷ 10 = 17.68 then double)

3 a 7.12 e 86.5 i 300

b 5.17 f 14.71 j 563

c 10.52 g 72.125

d 9.7 h 26.25

4 a 53 km c $205

b $65 d 45 runs

= 26 286 km

4 a 10°C c −5°C e 40°C g 35°C

b 25°C d −15°C f −20°C

5 a 2 m d −1 m g 1 m

b −4 m e 8 m

c 11 m f 8 m & 13 m

6 a 900 c 200 e 0 g 300

b 900 d 500 f 800 h 200

7 a 30 000 d 12 000 g 36 000

b 25 000 e 16 000 h 25 000

c 64 000 f 42 000

8 a 15 c 28 e 8 g 4

b 48 d 24 f 4 h 7

9 a 7K d 13K g 36K

b 3K e 27K h 74K

c 9K f 18K i 56K

10 a 3K d 15K g 41K i 43K

b 6K e 11K h 45K j 65K

c 10K f 33K

11–15 Hands on.

UNIT

27

DIAGNOSTIC REVIEW

3 a 6.25 apples

b 3.125 apples

c 5 apples d 12.5 apples

4 a 8.25 oranges d 11 oranges

b 16.5 oranges e 6.6 oranges

b 1 2 10 litres.

c 1 1 8 pizzas.

d 1 5 10 (1 1 2 ) cakes.

e 2 3 5 plates.

f 1 2 5 buckets.

b (–6,–3) (–4,–2) (–2,–1) (2,1) (4,2) (6,3) 8 a (−2, 6) e (5, 3) i (−3, −3)

b (6, 6) f (−4, 2) j (2, −4)

c (−3, 4) g (2, −2) k (−2, −5)

d (2, 4) h (−5, −3) l (5, −5)

9 Hands on. 10 Hands on. 11 a 73 400 km2 c Yes

b 105 400 km2 d No 12 a hectares b km2 c m2

DRAFT

5 No (square numbers have 2 factors other than 1).

right.

e Decimal point moved 2 places right.

f Decimal point moved 3 places right.

3 a 0.452 d 0.846

b 0.0452 e 0.0846

c 0.00452 f 0.00846

4 a 2.31 b 0.231 c 0.0231

d Decimal point moved 1 place left.

e Decimal point moved 2 places left.

f Decimal point moved 3 places left.

5 a 3.74

6 Hands on.

87.4

7 a 8 16 24 32 40 48 56

Multiply by 8

b 7 14 21 28 35 42 49

Multiply by 7

c 15 30 45 60 75 90 105

Multiply by 15

d 27 28 29 30 31 32 33

Add 16

e 4 5 6 7 8 9 10

Divide by 7

f 26 32 38 44 50 56 62

Multiply by 2

g 9 18 27 36 45 54 63

Multiply by 9

Multiply by 10, then add 2

i 1 4 9 16 25 36 49

Square each number

j 8 12 16 20 24 28 32

Multiply by 4

8 Hands on.

9 Hands on - some examples.

13 Hands on.

14 Hands on.

The polygons displayed have a pattern.

4 sides 2 diagonals

5 sides 5 diagonals—up by 3

6 sides 9 diagonals—up by 4

7 sides 14 diagonals—up by 5

8 sides 20 diagonals—up by 6

9 sides 27 diagonals—up by 7

10 sides 35 diagonals—up by 8

15 20

16

17